小学奥数-几何五大模型(蝴蝶模型)整理版
小学奥数几何篇 五大模型——蝴蝶定理(附答案)

五大模型——蝴蝶模型例1. 四边形ABCD的对角线AC与BD交于点O,如果三角形ABD1,且AO=2,DO=3,那么CO的长的面积等于三角形BCD的面积3度是DO的长度的倍例2. 如图,平行四边形ABCD的对角线交与点O点,△CEF、△OEF、△ODF、△BOE的面积依次是2、4、4和6 求:(1)△OCF 的面积;(2)求△GCE的面积例3.如图,边长为1的正方形ABCD中,BE=3EC,CF=FD,求三角形AEG的面积。
例4. 如图,边长为1的正方形ABCD的边长为10厘米,E为AD 中点,F为CE中点,G为BF中点,求三角形BDG的面积例5. 如下图,梯形ABCD的AB平行于CD,对角线AC,BD交于O,已知AOB于BOC的面积分别为25平方厘米于35平方厘米,那么梯形ABCD的面积是平方厘米例6.梯形ABCD的对角线AC与BD交与点O,已知梯形上底为2,2,求三角形AOD与且三角形ABO的面积等于三角形BOC面积的3三角形BOC的面积之比。
例7. 如下图,一个长方形一些直线分成了若干个小块,已知三角形ADG的面积是11,三角形BCH的面积是23,求四边形EGFH 的面积。
例8. 右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米例9. 如图,长方形ABCD被CE、DF分成四块,已知期中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为平方厘米例10. 如图,正六边形面积为6,那么阴影部分面积为多少?蝴蝶模型习题1、如图,长方形ABCD中,BE:EC=2:3,DF:FC=1:2,三角形DFC面积为2平方厘米,求长方形ABCD的面积.2、梯形的下底是上底的1.5倍,三角形OBC的面积是9cm2,问三角形AOD的面积是多少?3、如图,长方形中,若三角形1的面积与三角形3的面积比为4:5,四边形2的面积为36,则三角形1的面积为4、如图,长方形ABCD中,阴影部分是直角三角形且面积为54,OD的长是16,OB的长是9,那么四边形OECD的面积是多少?5、如图,△ABC是等腰三角形,DEFG是正方形,线段AB与CD相较于K点,已知正方形DEFG的面积48,AK:KB=1:3,则△BKD的面积是多少?答案【例1】因为AO : OC =S∆ABD : S∆BDC= 1: 3 ,所以OC = 2⨯3 = 6 ,所以OC : OD = 6: 3 = 2:1.解法二:作AH ⊥BD于H ,CG ⊥BD 于G .因为S所以S ∆ABD=1S3=1S∆BCD,所以AH =1 CG ,3,∆AOD 3 ∆DOCAO =1CO ,3OC = 2⨯3 = 6 ,OC : OD = 6: 3 = 2:1.C【例2】⑴⑴BCD 的面积为2 + 4 + 4 + 6 =16 ,⑴BCO 和∆CDO 的面积都是16 ÷ 2 = 8 ,所以⑴OCF 的面积为8 - 4 = 4 ;⑴由于⑴BCO 的面积为8,⑴BOE 的面积为6,所以⑴OCE 的面积为8 - 6 = 2 ,根据蝴蝶定理,EG : FG =S∆COE : S∆COF= 2 : 4 = 1: 2所以S∆GCE : S∆GCF=EG : FG = 1: 2 ,S∆GCE =11+ 2S∆CEF=1⨯ 2 =2 .33【例3】A DFB EC 连接EF .因为BE = 2EC ,CF =FD ,所以S∆DEF = (1⨯1⨯1)S2 3 2ABCD=1S12ABCD.因为S∆AED =1S2ABCD,由蝴蝶定理,AG : GF =1 : 12 12= 6 :1 ,所以S∆AGD = 6S∆GDF=6S7∆ADF=6⨯1S74ABCD=3S14ABCD.所以S∆AGE =S∆AED-S∆AGD=1S2ABCD-3 S14ABCD=2S7ABCD=2,7【例4】A E DB C设BD 与CE 的交点为O ,连接BE 、DF .由蝴蝶定理EO : OC =S BED : S BCD ,而SBED =1S4ABCD,SBCD=1S2ABCD,所以EO : OC =SBED : SBCD= 1: 2 ,故EO =1EC .3F 为CE 中点,所以EF =1 EC ,2故EO: EF = 2: 3,FO : EO =1: 2 .由蝴蝶定理SBFD : SBED=FO : EO = 1: 2 ,所以SBFD =1S2BED=1S8ABCD,SBGD =1S2BFD=1S16ABCD=1⨯10⨯10 = 6.2516AOB BOC AOB DOC 梯形蝴蝶定理B① S 1 : S 3 C= a 2 : b 2② S : S : S : S = a 2 : b 2 : ab : ab ; 1 3 2 4 ③ S 的对应份数为(a + b )2【例 5】由梯形蝴蝶定理, S : S = a 2 : ab = 25 : 35 , 可得 a : b = 5: 7 ,再根据梯形蝴蝶定理, S : S = a 2 :b 2 = 52 : 72 = 25 : 49 , 所以S DOC = 49梯形 ABCD 的面积为25 + 35 + 35 + 49 =144【例 6】由蝴蝶定理, S AOB : S BOC = ab : b 2 = 2 : 3得a : b = 2: 3,S AOD : S BOC = a 2 : b 2 = 22 : 32 = 4 : 9O∆OCD ∆OCD【例 7】AF BDE C如图,连结 EF ,显然 ADEF 和 BCEF 都是梯形, 于是 EFG 的面积等于三角形 ADG 的面积三角形 BCH 的面积等于三角形 EFH 的面积所以四边形 EGFH 的面积是11+ 23 = 34.【例 8】A DB C连接 AE .由于 AD 与 BC 平行,所以 AECD 也是梯形,那么S ∆OCD = S ∆OAE .据蝴蝶定理, S ∆OCD ⨯ S ∆OAE = S ∆OCE ⨯ S ∆OAD = 2 ⨯ 8 = 16 故 S 2 = 16 ,所以S = 4另解:在平行四边形 ABED 中, S ∆ADE =1 S2 ABED = 1 ⨯(16 + 8) = 12 2 所以S ∆AOE = S ∆ADE - S ∆AOD = 12 - 8 = 4根据蝴蝶定理,阴影部分的面积为8⨯ 2 ÷ 4 = 4【例 9】A EBD连接 DE 、CF . EDCF 为梯形,所以S ∆EOD = S FOC , 又根据蝴蝶定理, S ∆EOD ⋅ S ∆FOC = S ∆EOF ⋅ S ∆COD 所以S ∆EOD = 4 , S ∆ECD = 4 + 8 = 12ABCD 面积为12⨯2 = 24S ∆EOD ⋅ S ∆FOC = S ∆EOF ⋅ S ∆COD = 2 ⨯ 8 = 16 ,四边形OFBC 的面积为24 - 5 - 2 -8 = 9 (平方厘米).【例 10】连接阴影图形的长对角线,此时六边形被平分为两半根据六边形的特殊性质,和梯形蝴蝶定理把六边形分为 18 份 阴影部分占了其中 8 份,所以阴影部分的面积 8 ⨯ 6 = 8 .183∆ AOD ∆ AOD ∆BOC123作业题答案1.AD FBEC连接 AE , FE .因为 BE : EC = 2: 3 , DF : FC =1: 2 ,所以S = (3 ⨯ 1 ⨯ 1)S = 1S. DEF 5 3 2长方形ABCD10 长方形ABCD 因为S= 1 S , A G : GF = 1 : 1= 5 :1,所以S = 5S = 10 平方厘米,所AED2 长方形ABCD 2 10AGD GDF 以 S = 12 平方厘米.因为S = 1S ,所以长方形 ABCD 的面积是72 平方 AFD厘米.2.AFDA D6 长方形ABCDBC根据梯形蝴蝶定理, a : b =1:1.5 = 2: 3 , S : S = a 2:b 2 = 22 : 32 = 4 : 9 , 所以S = 4(cm 2 ) .3.O 做辅助线如下:利用梯形模型,这样发现四边形 2 分成左右两边,其面积正好等于三角形 1 和三角形 3,所以 1 的面积就是36 ⨯44 + 5= 16 ,3 的面积就是 36 ⨯54 + 5= 20 .4.ADBEC因为连接 ED 知道⑴ABO 和⑴EDO 的面积相等即为54 ,又因为OD ⑴OB =16⑴9 ,所以 ⑴AOD 的面积为54 ÷ 9⨯16 = 96 ,根据四边形的对角线性质知道:⑴BEO 的面积为:54⨯54 ÷ 96 = 30.375 ,所以四边形OECD 的面积为: 54 + 96 - 30.375 =119.625 (平方厘米).5.BM C由于 DEFG 是正方形,所以 DA 与 BC 平行,那么四边形 ADBC 是梯形.在梯形ADBC 中,∆BDK 和∆ACK 的面积是相等的.而 AK : KB =1: 3 ,所以∆ACK 的面积是∆ABC 面积的 1 = 1 ,那么∆BDK 的面积也是∆ABC 面积的 1.1+ 3 4 4由于∆ABC 是等腰直角三角形,如果过 A 作 BC 的垂线,M 为垂足,那么 M 是BC 的中点,而且 AM = DE ,可见∆ABM 和∆ACM 的面积都等于正方形 DEFG 面积的一半,所以∆ABC 的面积与正方形 DEFG 的面积相等,为 48. 那么∆BDK 的面积为48⨯ 1= 12 .4。
小学奥数-几何五大模型(蝴蝶模型)..

模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?任意四边形、梯形与相似模型B【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
AB C DOH GA BC D O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
小学奥数几何五大模型蝴蝶模型分解

模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?A BCDG321【解析】 ⑴根据蝴蝶定理,123BGCS ⨯=⨯,那么6BGCS=;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)任意四边形、梯形与相似模型【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
AB C DOH GA BC D O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
小学奥数-几何五大模型蝴蝶模型

任意四边形、梯形与相似模型模塑三期礫模型(任意模型)任sriasi形中的比例关系(“期燥定理”):(3)5, :52 =S4 :S3 (者Sj xS3 =S2 x S4②AO:OC=(S|+S2):(S J+SJ妁噪定理为我<]提供了解决不的面稅何题的一个^go通it构殖模型,一方面可以使不規覓四也形的面秋关系与0J1®的三角形相联系;另一方面.也可以得對与面釈对应的对角箜的比傍关系。
【例1】(小数报竞赛活动贰题)如图,某公园的外乾縻是四迪形ABCD.被对角»AC.加分成四个部分,△ 力防面稅为1平方千米,面稅为2平方千米,的面稅为3平方千米,公园由隋地面枳是6. 92平方干米和人工湖组成,求人工湖的面枳是多少平方干米?【分析】根据掛蝶定理求得S“o°=3xl*2 = l・5平方千米,公同呱边形ABCD的面枳是1 + 2 + 3 + 1.5 = 7.5平方千米,所以人工湖的面枳是7.5-6.92 = 0.58平方千米【贝固】如图,四边形被两条对角城分廉4个三角形.其中三个三角形的面稅巳知. 求:(1)三角形BGC的面枳;(2)AG:GC=?A D【解析】(1)根据州喋定理,S BCC xl = 2x3,那么5^c=6;(2)根据捌礫定理,AG:GC = (l + 2):(3 + 6) = l:3. (? ? ?)【例2】四边形A3CD的对角SAC与3Q交于点0(如图所示)。
如果三角HABD的面稅等于三角形3CD的面积的且AO = 29 DO = 3t那么CO的长度是DOff}长度的________________________ 倍。
【解析】在本题中,WH^ABCD为任恿呱边形,对干迪FT不良呱边形”,无外乎两种业理方法:(1)利用已知条件,向已有模型靠拢,)!而快速解决;(2)通过画来孜造不良四边形。
看到题目中给岀条件S“0B C D=\:3,逹可以向模里一脚蝶定理靠拢,干是得岀一种解法。
小学的奥数-几何五大模型(蝴蝶模型)

模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?任意四边形、梯形与相似模型B【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
AB C DOH GA BC D O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
小学六年级奥数 五大模型——蝴蝶模型、燕尾模型
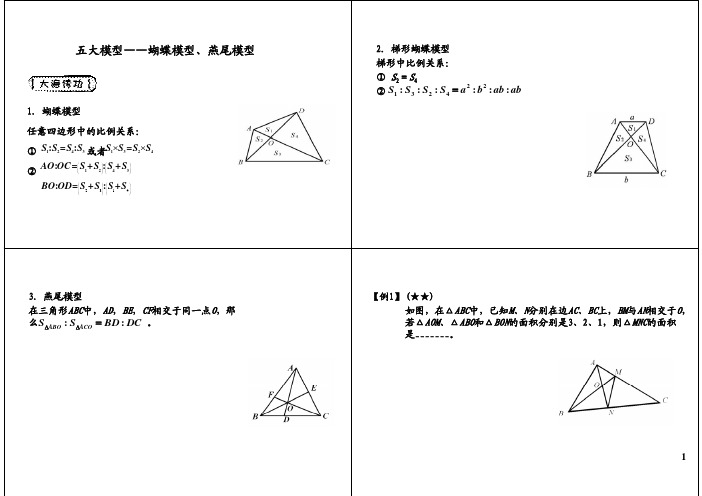
1
【例2】(★★★)
如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别 为2、5、8平方厘米,那么余下的四边形OFBC的面积为 ___________平方厘米。
【例3】 (★★★)
如图,ABCD长方形中,阴影部分是直角三角形且面积为54,OD 的长是16,OB的长是9。那么四边形OECD的面积是多少?
五大模型——蝴蝶模型、燕尾模型
1.蝴蝶模型
任意四边形中的比例关系:
①
S :S =S :S
12
43
或者S1
S 3
=
S 2
S 4
② AO:OC = S +S : S +S
1
2
4
3
BO:OD= S +S : S +S
ቤተ መጻሕፍቲ ባይዱ
2
3
Aa D S1
S2 O S4
S3
B
C
b
二、本讲经典例题 例1,例4,例6,例7,例8
3.燕尾模型 在三角形ABC中,AD,BE,CF相交于同一点O,那么 SABO : SACO BD : DC 。
4
1
4
3.燕尾模型
在三角形ABC中,AD,BE,CF相交于同一点O,那 么SABO : SACO BD : DC 。
2.梯形蝴蝶模型 梯形中比例关系: ① S2=S4 ② S1 : S3 : S2 : S4 a2 : b2 : ab : ab
小学奥数几何五大模型蝴蝶模型分解

模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ⨯=⨯ ②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
看到题目中给出条件:1:3ABD BCD S S =V V ,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。
小学奥数几何篇五大模型蝴蝶定理(附答案)

小学奥数几何篇五大模型蝴蝶定理(附答案)在小学奥数的几何部分,蝴蝶定理是一个非常有用的工具,它可以帮助我们解决一些复杂的几何问题。
蝴蝶定理主要描述了在四边形中,当两条对角线互相垂直时,四边形被分成四个小三角形,而这四个小三角形的面积之间存在一定的关系。
蝴蝶定理的内容如下:设四边形ABCD中,AC和BD是互相垂直的对角线,交于点O。
设四个小三角形的面积分别为S1、S2、S3、S4。
那么,蝴蝶定理可以表述为:S1 + S2 = S3 + S4。
这个定理听起来可能有些抽象,但实际上它的应用非常广泛。
我们可以通过蝴蝶定理来解决一些看似复杂的问题。
下面,我将通过一些例子来展示蝴蝶定理的应用。
例1:在四边形ABCD中,AC和BD是互相垂直的对角线,且AC =8cm,BD = 6cm。
如果三角形ABC的面积是24cm²,那么三角形ADC的面积是多少?解答:根据蝴蝶定理,我们有S1 + S2 = S3 + S4。
由于三角形ABC的面积是24cm²,所以S1 = 24cm²。
又因为AC = 8cm,BD = 6cm,我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 8cm6cm = 24cm²。
因此,三角形ADC的面积也是24cm²。
例2:在四边形ABCD中,AC和BD是互相垂直的对角线,且AC = 10cm,BD = 5cm。
如果三角形ABC的面积是20cm²,那么三角形ADC的面积是多少?解答:同样地,根据蝴蝶定理,我们有S1 + S2 = S3 + S4。
由于三角形ABC的面积是20cm²,所以S1 = 20cm²。
又因为AC = 10cm,BD = 5cm,我们可以计算出三角形ADC的面积S3 = 1/2 AC BD = 1/2 10cm 5cm = 25cm²。
因此,三角形ADC的面积是25cm²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
任意四边形、梯形与相似模型卜亠\模型三蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):DS1: S2 = S4: S3或者S S3 =S2 S4② AO : OC =[S S2 : S4 S3蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例1】(小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD被对角线AC BD分成四个部分,△ AOB面积为1平方千米,△ BOC面积为2平方千米,△ COD勺面积为3平方千米,公园由陆地面积是6. 92平方千米和人工湖组成,求人工湖的面积是多少平方千米?【分析】根据蝴蝶定理求得S^AOD=3 1-'2=1.5平方千米,公园四边形ABCD的面积是12 3 45 = 7.5平方千米,所以人工湖的面积是7.5-6.92=0.58平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积:⑵AG:GC= ?【解析】⑴根据蝴蝶定理,S BGC 1=2 3,那么S BGC=6 ;⑵根据蝴蝶定理,AG:G^ 1 2 : 3 6 =1:3 . (? ??)【例2】四边形ABCD的对角线AC与BD交于点0(如图所示)。
如果三角形ABD的面积等于三角形BCD的面积的1,且AO =2 , DO =3,那么CO的长度是DO的长度的_____________ 倍。
3【解析】在本题中,四边形ABCD为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
看到题目中给出条件S A BD : S BCD =1:3,这可以向模型一蝴蝶定理靠拢,于是得出一种解法。
又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH垂直BD于H , CG垂直BD于G,面积比转化为高之比。
再应用结论:三角形高相同,则面积之比等于底边之比,得出结果。
请老师注意比较两种解法,使学生体会到蝴蝶定理的优势,从而主观上愿意掌握并使用蝴蝶定理解决问题。
解法一:T AO :OC = S ABD: S BDC =1:3 ,二OC =2 3 =6 ,••• OC:OD =6:3 2:1 .解法二:作AH _BD 于H , CG_BD 于G .•- AH」CG ,31•- AO CO ,3•OC =2 3=6 ,•OC:OD =6:3 =2:1 •【例3】如图,平行四边形ABCD的对角线交于O点,A CEF、△OEF、△ODF、△BOE的面积依次是2、4、4和6。
求:⑴求A OCF的面积;⑵求A GCE的面积。
【解析】⑴根据题意可知,△BCD的面积为2 4 4 ^16,那么△BCO和:CDO的面积都是16亠2=8 , 所以A OCF 的面积为8—4=4;⑵由于△ BCO的面积为8, △BOE的面积为6,所以A OCE的面积为8-6=2 , 根据蝴蝶定理,EG:FG 二Sg E:S.COF =2:4 =1:2,所以S.GCE:S.GCF = EG : FG =1:2 ,1 1 2那么S GCE S CEF 2 ~~•1+2 3 3【例4】图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷。
那么最大的一个三角形的面积是多少公顷?S 'ABD S BCD3审S AOD =—S DOC3【解析】在L ABE , LCDE 中有.AEB =/CED ,所以L ABE , LCDE 的面积比为(AE EB) :(CE DE)。
同理有 L ADE , L BCE 的面积比为(AE DE): (BE EC)。
所以有 S ABE X S CDE =S ADE X S BCE ,也就是 说在所有凸四边形中,连接顶点得到2条对角线,有图形分成上、下、左、右4个部分,有:上、下部分的面积之积等于左右部分的面积之积。
即SI ABE 6 = S ADE 7,所以有L ABE 与L ADE 的面积比为 7:6,S ABE = — 39=21 公顷,S ADE = — 39=18 公顷。
6+7 6+7显然,最大的三角形的面积为 21公顷。
【例5】(2008年清华附中入学测试题)如图相邻两个格点间的距离是为 ________ 。
【解析】连接AD 、CD 、BC 。
则可根据格点面积公式,可以得到「ABC 的面积为:1,4-1=2, ACD 的面积为:3・总-1=3.5,2 24ABD 的面积为:21=3 .24412 所以 BO : 0D = S ABC : S ACD -2.3.5 =4.7,所以 S ABOS ABD 3 =.4十7 11 1155 10因为 BD.CE =2:5,且 BD // CE ,所以 DA:AC=2:5 , S ABC, S DB c =52 二10.2+57 7【例6】(2007年人大附中考题)如图,边长为1的正方形 ABCD 中,BE=2EC , CF =FD ,求三角形 AEG 的面积.1,则图中阴影三角形的面积1,求三角形 ABC 的面积。
【解析】C【巩【解析】连接AE , FE .3 11 1因为 BE: EC =2:3 , DF : FC = 1: 2,所以 S DEF 二(’:’:)S 长方形 ABCD S 长方形ABCD ・5 3 2 101 1 1因为 S A ED = — S 长方形 ABCD , AG : GF = — : —5:1 ,所以 S AGD =5§ GDF =10 平方厘米,所以 S AFD = 12 平2 2 10 _方厘米.因为 S AFD =^S 长方形ABCD ,所以长方形 ABCD 的面积是72平方厘米.6 形【解析】 连接因为BE =2EC , CF =FD 所以S DEFABCD・因为 S AED=尹ABCD,根据蝴蝶定理, AG : GF =丄:丄2 12= 6:1 ,所以 S.AGD =6S G DF 6 6 1SADF§ ABCD7' 7 4—S 14 -ABCD・所以 1 3S AGE =S AED -■ S AGD =? S|_ABCD -'14 S_ABCD 厶ABCD7 -即三角形AEG 的面积是-・7【例7】如图,长方形 ABCD 中, 方形ABCD 的面积.BE: EC =2:3 , DF:FC=1:2,三角形 DFG 的面积为 2平方厘米,求长【例8】如图,已知正方形 ABCD 的边长为10厘米, 形BDG 的面积. E 为AD 中点,F 为CE 中点,G 为BF 中点,求三角【解析】设BD与CE的交点为O ,连接BE、DF .1 1由蝴蝶定理可知EO:OC = S BED : SBCD,而S BED =—S ABCD , S BCD = 一S ABCD ,4 21 所以EO :OC =S BED : S BCD =1:2,故EO EC .一3由于F 为CE 中点,所以EF =-EC ,故EO:EF =2:3,2N 分别在边AC 、BC 上,BM 与AN 相交于O ,若.AOM 、厶ABO 和BON 的面积分别是 3、2、1「'MNC 的面积是 ___________ .【解析】这道题给出的条件较少,需要运用共边定理和蝴蝶定理来求解._ S AOMSBON_ 3 13S誉OB2 2设S MON =x ,根据共边定理我们可以得3虫―32,解得 x = 22.5.x13x2【例10】(2009年迎春杯初赛六年级)正六边形AAzAdAA e 的面积是2009平方厘米,B 1B 2B 3B 4B 5B 6分别是正六边形各边的中点;那么图中阴影六边形的面积是【解析】如图,设B 6A 2与的交点为O ,则图中空白部分由6个与;A 2OA B 一样大小的三角形组成, 只要求出了「A 2OA 3的面积,就可以求出空白部分面积,进而求出阴影部分面积. 连接人人、B 6^、B 6A 3 .设「AB 1B 6的面积为” 1 “,则BAB 6面积为” 1 “,UAA 2B 6面积为” 2 “,那么=A G A 3B 6面积为 A 1A 2B 6 的2倍,为” 4 “,梯形 AA 2A 3A 6的面积为2 2 4 2=12 , A 2B 6A 3的面积为” 面积为2 . 根据蝴蝶定理,BO ”3。
二S.B 1A 2B 6: S.A 3A 2B 6=1:6,故 S./A312所以S.A OA J S 弟形AA 2AA 二〒:12:1: 7,即卩A 2OA 3的面积 为梯形 AAAA 面积的 A 1A 2A 3A 4A 5A 3面积的—,那么空白部分的面积为正六边形面积的— 6=3,所以阴影部分面积为 14 14 72009: 11 ―? =1148(平方厘米)•I 7丿FO:EO =1:2 .由蝴蝶定理可知 S BFD :S_BED =FO :EO=1:2,所以S BFD1 S BED2 -1 S ABCD , 8 -那么 S| BGDSBFD S ABCDU2 - 16 -110 10=6.25 (平方厘米).16【例9】如图,在 ABC 中,已知M 、 根据蝴蝶定理得S.MON -,故为六边形 7CA 3平方厘米.3板块二梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):①S1:S3二a2:b22 2②S i: S3: S? : S4 = a : b : ab: ab ;③S的对应份数为 a b .梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果. (具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)【例11】如图,S =2 , S3 =4,求梯形的面积.【解析】设0为a2份,S3为b2份,根据梯形蝴蝶定理,&=4"2,所以b=2 ;又因为S2=2 = a b,所以a =1 ;那么S =a2=1, S4 =ab =2,所以梯形面积^S i S2 S3 ^1 ■ 2 4 ^9,或者根据梯形蝴蝶定理,S二aF2 = 1,22=9 .【巩固】(2006年南京智力数学冬令营)如下图,梯形ABCD的AB平行于CD,对角线AC , BD交于O,已知厶AOB与厶BOC的面积分别为25平方厘米与35平方厘米,那么梯形ABCD的面积是__________________________ 平方厘米.【解析】根据梯形蝴蝶定理,S AOB :S_BOC二a2:ab =25: 35 ,可得a:b=5:7 ,再根据梯形蝴蝶定理,2 2 2 2S AOB:S DOC =a : b =5:7 =25: 49 ,所以S DOC =49 (平方厘米).那么梯形ABCD的面积为25 35 35 49二14平方厘米).【例12】梯形ABCD的对角线AC与BD交于点O ,已知梯形上底为2,且三角形ABO的面积等于三角形BOC面积的-,求三角形AOD与三角形BOC的面积之比.3【解析】根据梯形蝴蝶定理,S AOB:S BOC=ab:b2=2:3,可以求出a:b=2:3 ,再根据梯形蝴蝶定理,S AO D : S BOC =a2:b 2 =22:32 =4:9 .通过利用已有几何模型,我们轻松解决了这个问题,而没有像以前一样,为了某个条件的缺乏而千辛万苦进行构造假设,所以,请同学们一定要牢记几何模型的结论.【例13】(第十届华杯赛)如下图,四边形ABCD中,对角线AC和BD交于0点,已知AO =1,并且三角形ABD的面积J,那么OC的长是多少?二角形CBD的面积5【例14】梯形的下底是上底的1.5倍,三角形OBC的面积是9cm2,问三角形AOD的面积是多少?【解析】根据梯形蝴蝶定理,a:b =1:1.5 =2:3 , S「AOD :S.BOC二a2 :b2 =22 :32 = 4:9 , 所以S「AOD=4 cm2.如图,梯形ABCD中,AOB、COD的面积分别为1.2和2.7,求梯形ABCD的面积.S弟形ABCD—1.2V.8 V.8 ■ 2.7 =7.5 .【例15】如下图,一个长方形被一些直线分成了若干个小块,已知三角形ADG的面积是11,三角形BCH 的面积是23,求四边形EGFH的面积.【解析】根据蝴蝶定理,三角形ABD的面积三角形CBD的面积=A0,所以COA0 3CO =55又AOJ,所以CO飞.【巩固】【解析】根据梯形蝴蝶定理,S AOB : S ACOD2S L AOD : S AOB =ab : a b:a= 3:=a2: b2=4:9,所以a :b = 2:3 ,3S AOD - S COB一2A D【解析】如图,连结EF,显然四边形ADEF和四边形BCEF都是梯形,于是我们可以得到三角形EFG的面积等于三角形ADG的面积;三角形BCH的面积等于三角形EFH的面积,所以四边形EGFH的面积是1123 =34.【巩固】(人大附中入学测试题)如图,长方形中,若三角形1的面积与三角形3的面积比为4比5,四边形2的面积为36,则三角形1的面积为_____________形3,所以1的面积就是36 —L =16 , 3的面积就是36 =20 .4+5 4 + 5【解析】因为M是AD边上的中点,所以AM :BC =1:2,根据梯形蝴蝶定理可以知道所以正方形的面积为1 2 2 4 ^12份,S阴影=2*2=4份,所以s阴影:s正方形=1: 3,所以s阴影二1平方厘米.【巩固】在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是___________________ 平方厘米.【解析】连接DE ,根据题意可知BE: AD =1:2 ,根据蝴蝶定理得S梯形(1 2)2 =9 (平方厘米),S A ECD = 3 (平方厘米),那么S ABCD-12(平方厘米).【例17】如图面积为12平方厘米的正方形ABCD中,E,F是DC边上的三等分点,求阴影部分的面积.【解析】做辅助线如下:利用梯形模型,这样发现四边形2分成左右两边,其面积正好等于三角形1和三角M是AD边上的中点•求图中阴影部分的面积.AMG : ABG : MCG : S^BCG=12 :(1 2):(1 2) :22 =1: 2:2:4,设S AGM-1 份,则S A MCD=1 • 2=3 份,【例16】【解析】因为E,F是DC边上的三等分点,所以EF : AB =1:3,设S^OEF =1份,根据梯形蝴蝶定理可以知道S A AOE 二S OFB =3份,S A AOB =9 份,S^ADE = B C F =(1 3)份,因此正方形的面积为4 • 4 • (1 •=24 份,s阴影6,所以s阴影:s正方形=6:241:4,所以s阴影=3平方厘米・AB=6厘米,AD =2厘米,AE二EF二FB,求阴影部分的面积.【解析】方法一:如图,连接DE , DE将阴影部分的面积分为两个部分,其中三角形AED的面积为2汇6十3十2=2平方厘米.由于EF:DC=1:3,根据梯形蝴蝶定理,S DEO :S EFO =3:1,所以S DE^-S DEF ,而S O F =S =2_ 4 _ _平方厘米,所以S DEO2=1.5平方厘米,阴影部分的面积为2,1.5=3.5平方厘米.4方法二:如图,连接DE , FC,由于EF :DC =1:3,设S A旺=1份,根据梯形蝴蝶定理,S A OED= 3份,S梯形EFCD =(1 3^ =16 份,S A ADE BCF二1 4份,因此S长方形ABCD =4 16 ' 4 = 24份,S阴影=4・3=7份,而s长方形ABCD =6 2=12平方厘米,所以s阴影二3.5平方厘米【例19】(2008年”奥数网杯”六年级试题)已知ABCD是平行四边形,BC:CE =3: 2,三角形ODE的面积为6平方厘米•则阴影部分的面积是 ___________ 平方厘米.【解析】连接AC .由于ABCD是平行四边形,BC:CE=3:2,所以CE:AD=2:3 ,根据梯形蝴蝶定理,S C OE : S_AOC : Sj DOE : S_AOD = 22:2X3: 2汉3:32 = 4:6:6:9 ,所以S AOC =6 (平方厘米),S AOD=9(平方厘米),又S ABC二S ACD=6 • 9 =15(平方厘米),阴影部分面积为6 75 = 21(平方厘米).【例18】如图,在长方形ABCD中,【巩固】右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是________ 平方厘米.【分析】连接AE.由于AD与BC是平行的,所以AECD也是梯形,那么S .O C^ S OAE. 根据蝴蝶疋理,S OCD S OAE = S OCE S OAD = 4 9 = 36,故S -QCD 36 ,所以S OCD =6(平方厘米).【巩固】(2008年三帆中学考题)右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是_________ 平方厘米.【解析】连接AE .由于AD与BC是平行的,所以AECD也是梯形,那么S -OC^S OAE.根据蝴蝶定理,S OCD S OA^S OCE S OAD=2 8 =16,故S ?CD^16,所以S^CD=4(平方厘米).1 1另解:在平仃四边形ABED中,S 'ADE S ABED 16 8 =12(平方厘米),2 2所以S AOE = S.ADE -S.AOD 12 -8 = 4 (平方厘米),根据蝴蝶定理,阴影部分的面积为8 2 “4 =4(平方厘米).【例20】如图所示,BD、CF将长方形ABCD分成4块,厶DEF的面积是5平方厘米,ACED的面积是10平方厘米•问:四边形ABEF的面积是多少平方厘米?【分析】连接BF ,根据梯形模型,可知三角形BEF的面积和三角形DEC的面积相等,即其面积也是10平方厘米,再根据蝴蝶定理,三角形BCE的面积为10"0十5 = 20(平方厘米),所以长方形的面积为20 10 2 =60(平方厘米).四边形ABEF的面积为60-5-10-20=25(平方厘米).【巩固】如图所示,BD、CF将长方形ABCD分成4块,6DEF的面积是4平方厘米,CED的面积是6平方厘米•问:四边形ABEF的面积是多少平方厘米?【解析】(法1)连接BF,根据面积比例模型或梯形蝴蝶定理,可知三角形BEF的面积和三角形DEC的面积相等,即其面积也是6平方厘米,再根据蝴蝶定理,三角形BCE的面积为6汉6十4 = 9(平方厘米),所以长方形的面积为9 6 2 =30(平方厘米).四边形ABEF的面积为30-4-6-9=11(平方厘米).(法2)由题意可知,,根据相似三角形性质,旦=取,所以三角形BCE的面积为:EC 6 3 EB EC 326-:-三=9(平方厘米)•则三角形CBD面积为15平方厘米,长方形面积为15 2 =30(平方厘米)•四3边形ABEF的面积为30 _4 _6—9=11(平方厘米)•【巩固】(98迎春杯初赛)如图,ABCD长方形中,阴影部分是直角三角形且面积为54 , OD的长是16 , OB 的长是9.那么四边形OECD的面积是多少?【解析】因为连接ED知道△ ABO和厶EDO的面积相等即为54,又因为OD:OB=16:9,所以△ AOD的面积为54一9x16=96,根据四边形的对角线性质知道:△ BEO的面积为:54x54-96 = 30.375,所以四边形OECD的面积为:54 96 -30.375 =119.625(平方厘米).【例21】(2007年”迎春杯”高年级初赛)如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC的面积为_________________ 平方厘米.【解析】连接DE、CF •四边形EDCF为梯形,所以S EOD二S FOC,又根据蝴蝶定理,SEODSFOC =S EOF 'S COD,所以S'EOD S.FOC =S*OF S. COD =1 2 3 8=16,所以S^OD = 4(平方厘米),S.ECD=4 *8=12(平方厘米)•那么长方形ABCD的面积为12 2 =24平方厘米,四边形OFBC的面积为24-5 -2 -8 =9(平方厘米)•【例22】(98迎春杯初赛)如图,长方形ABCD中,AOB是直角三角形且面积为54, OD的长是16, OB 的长是9 .那么四边形OECD的面积是_____________ •1 1【解析】解法一:连接DE ,依题意S AOB BO AO 9 AO =54,所以AO =12 ,2 2小 1 1则S AOD DO AO 16 12 =96 •2 21 3又因为S AOB =S DOE =54 16 OE,所以OE =6- ,_ 2 41 1 3 3得s BOE BO EO 9 6 30 ,2 2 4 8、 3 5所以S OE CD = S|_BDC —S_BOE = S_ ABD _ S BOE = 54 ' 96 - 30 ' 11^_•_ _ _ 8 816解法二:由于S AOD : S AOB=OD : OB 匸16 :9,所以S AOD =54 96,而S DOE=S AOB=54,根据_9 _DC3DDBBC CE FE FCB2 14 2 4212【例23】A GA GM F 【例26】如图,已知D 是BC 中点,E 是CD 的中点,F 是AC 的中点.三角形 ABC 由①〜⑥这6部分 组成,其中②比⑤多 6平方厘米•那么三角形 ABC 的面积是多少平方厘米?所以S OECD=S L BDC — S BOE =S _ABD — S BOE =[54 96 -30- ^119-." " " 8 8ABC 是等腰直角三角形,DEFG 是正方形,线段 AB 与CD 相交于K 点.已知正方形 BKD 的面积是多少?如图, DEFG 的面积 48, AK:KB =1:3,则1 1ACK 的面积是相等的.而AK :KB =1:3,所以 ACK 的面积是AABC 面积的亠=丄,那么.BDK 1+3 4的面积也是AABC 面积的-.4由于「ABC 是等腰直角三角形,如果过 A 作BC 的垂线,M 为垂足,那么 M 是BC 的中点,而且 AM 二DE ,可见JABM 和JACM 的面积都等于正方形 DEFG 面积的一半,所以 ABC 的面积与正 方形DEFG 的面积相等,为48.1那么 BDK 的面积为481=12 .4【例24】如图所示,ABCD 是梯形,「ADE 面积是1.8 , ABF 的面积是9, :BCF 的面积是27•那么阴影MEC 面积是多少?__ D ” E FC 二 AF : FC = 9:27 =1:3 ,S AEC=S AEF4".24=4.8 .S.BFC 27并且 S AEF - S ADF - S AED- 3 - 1.^ = 1.2,而 S AFB: S Bl 所以阴影AEC 的面积是: 【解析】根据梯形蝴蝶定理,可以得到S AFB S DFC 二S AFD S BFC ,而S AFB 二S DFC (等积变换),所以可得S» F 亠 *3 ,【例25】如图,正六边形面积为 6,那么阴影部分面积为多少?【解析】 连接阴影图形的长对角线,此时六边形被平分为两半,根据六边形的特殊性质,和梯形蝴蝶定理把六边形分为十八份,阴影部分占了其中八份,所以阴影部分的面积-6=8 . 183蝴蝶定理, S |_BOE【解析】由于DEFG 是正方形,所以DA 与BC 平行,那么四边形 ADBC 是梯形.在梯形ADBC 中,UBDK 和S ,正方形PCNG 的面积为S ,则S 1: S 2 =【解析】因为E 是DC 中点,F 为AC 中点,有AD=2FE 且平行于AD ,则四边形 ADEF 为梯形•在梯形 ADEF 中有③二④,②X ⑤二③^④,②:⑤=AD 2: FE 2=4.又已知②-⑤=6,所以⑤=6-:-(4_1)=2 , ②二⑤4=8,所以②X ⑤二④^④=16,而③迪,所以③二④=4,梯形ADEF 的面积为②、③、④、 ⑤四块图形的面积和,为 8 4 4^18 .有L CEF 与L ADC 的面积比为CE 平方与CD 平方的比, 即为1:4 .所以L ADC 面积为梯形 ADEF 面积的 —=4,即为18 - ^24 .因为D 是BC 中点,所4-1 3 3以L ABD 与L ADC 的面积相等,而|_ABC 的面积为ABD 、L ADC 的面积和,即为24*24=48平方 厘米.三角形 ABC 的面积为48平方厘米.【例27】如图,在一个边长为 6的正方形中,放入一个边长为 2的正方形,保持与原正方形的边平行,现在分别连接大正方形的一个顶点与小正方形的两个顶点,形成了图中的阴影图形,那么阴影部分 的面积为 .【解析】本题中小正方形的位置不确定,所以可以通过取特殊值的方法来快速求解,也可以采用梯形蝴蝶定 理来解决一般情况.解法一:取特殊值,使得两个正方形的中心相重合,如右图所示,图中四个空白三角形的高均为1.5 ,因此空白处的总面积为 6 1.5“2 4 2 2 =22,阴影部分的面积为 6 6-22=14 .解法二:连接两个正方形的对应顶点,可以得到四个梯形,这四个梯形的上底都为 2,下底都为6,上底、下底之比为 2: 6 =1:3,根据梯形蝴蝶定理,这四个梯形每个梯形中的四个小三角形的面积之2 29比为1 :1 3:1 3:3 =1:3:3:9 ,所以每个梯形中的空白三角形占该梯形面积的一,阴影部分的面16A①② ④ ⑥③F积占该梯形面积的—,所以阴影部分的总面积是四个梯形面积之和的-,那么阴影部分的面积为16 167(6 -2 ) =14 .16【例28】如图,在正方形ABCD中,E、F分别在BC与CD上,且CE = 2 BE,CF=2DF,连接BF、DE,相交于点G,过G作MN、PQ得到两个正方形MGQA和PCNG,设正方形MGQA的面积为S,正方形PCNG的面积为S,则S1: S2 =【解析】 连接BD 、EF •设正方形ABCD 边长为3,贝U CE =CF =2 , BE =DF =1 ,所以,EF^22 2^8 ,2 2 2 2 2 2BD =3 3 =18 •因为EF BD =8 18=144=12,所以EF ・BD=12 •由梯形蝴蝶定理,得2 2S^ GEF: S^ GBD:S^ DGF: Sn BGE = EF : BD : EF BD:E FBD=8:18:12:12=4:9:6:6 ,所以 AM : CN =DN :CN =3:2,贝U S :3 =AM 2:CN 2【例29】如下图,在梯形 ABCD 中,AB 与CD 平行,且CD =2AB ,点E 、F 分别是AD 和BC 的中点,已知阴影四边形 EMFN 的面积是54平方厘米,则梯形 ABCD 的面积是 _____________ 平方厘米.【解析】 连接EF ,可以把大梯形看成是两个小梯形叠放在一起,应用梯形蝴蝶定理,可以确定其中各个小 三角形之间的比例关系,应用比例即可求出梯形 ABCD 面积.13 设梯形ABCD 的上底为a ,总面积为S .则下底为2a , EF =丄a • 2a =- a •223 3所以 AB: EF =a : a =2:3 , EF : DC a:2a=3:4 •2 2由于梯形ABFE 和梯形EFCD 的高相等,所以f二 AB EF : EF DC 二 a 「2所以,S A BGE 所以S 梯形BDFES 梯形BDFES 梯形BDFE • 4 9 6 6 25=S A BCD - S A CEF =—,所以, S A BGE 2 25 9因为 S A BCD 二 3 3 亡 2 二,CEF 二2 2十 2 二2 ,6 5—X2由于△ BGE 底边BE 上的高即为正方形 PCNG 的边长, 所以CN 6, ND,555= 9:4 •3a 2a =5: 7 ,S 梯形 ABFE : S 梯形 EFCD 故S 梯形ABFES 12 根据梯形蝴蝶定理, 9同理可得S ENF—S • 12 ABFE 内各三角形的面积之比为9 5 3S S ; 25 1220 9 7 3 S 梯形 EFCD S S , S 梯形EFCD 梯形 A,,. 9S 梯形ABFE 9所以 所以 2 22 :2 3: 2 3:3 =4: 6: 6:9,所以 9 12 12 16 49 12 283 3 9 、S E MFN =S E MF ' S_ENF S ■ S S ,由于 S EMFN - 54平方厘米,_ 20 28 35 9SW°(平方厘米)•(2006年“迎春杯”高年级组决赛)下图中,四边形ABCD都是边长为1的正方形,E、F、G、【例30】H 分别是AB , BC , CD , DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简 分数m,那么,(m 5)的值等于n【解析】左、右两个图中的阴影部分都是不规则图形,不方便直接求面积,观察发现两个图中的空白部分面 积都比较好求,所以可以先求出空白部分的面积,再求阴影部分的面积. 如下图所示,在左图中连接 EG .设AG 与DE 的交点为M . 左图中AEGD 为长方形,可知 JAMD 的面积为长方形 AEGD 面积的1,所以三角形 AMD 的面积为4如上图所示,在右图中连接 AC 、EF .设AF 、EC 的交点为N .可知EF // AC 且AC=2EF .那么三角形BEF 的面积为三角形 ABC 面积的-,所以三角形BEF 的4111 113面积为1 ,梯形AEFC 的面积为2 4 8 2 8 8在梯形AEFC 中,由于EF: AC1 : 2根据梯形蝴蝶定理,其四部分的面积比为:3 1 1 12:12:12: 22=1:2: 2: 4,所以三角形 EFN 的面积为311,那么四边形BENF 的81+2+2+424111面积为1•丄 1 •而右图中四个空白四边形的面积是相等的,所以右图中阴影部分的面积为8 2461 1 1 4 =6 3那么左图中阴影部分面积与右图中阴影部分面积之比为丄丄2,即m二色,2 3n 2A HDB F C又左图中四个空白三角形的面积是相等的,所以左图中阴影部分的面积为21那么m n =3 2 =5。
