第四章 信息率失真函数-习题答案
ch04 信息率失真函数

P (Y X )
⎧0 xi = y j d ( xi , y j ) = ⎨ ⎩a xi ≠ y j
3
⎡ p ( y1 x1 ) p ( y2 x1 ) ... p ( ym x1 ) ⎤ ⎢ ⎥ ⎢ p ( y1 x2 ) p ( y2 x2 ) ... p ( ym x2 ) ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ p ( y1 xn ) p ( y2 xn ) ... p ( ym xn ) ⎦ ⎥ ⎣
⎡ d ( x1, y1 ) d ( x1, y2 ) ⎢d ( x , y ) d ( x , y ) 2 1 2 2 D= ⎢ ⎢ ⎢ ⎣d ( xn , y1 ) d ( xn , y2 )
d ( x1, ym ) ⎤ d ( x2 , ym )⎥ ⎥ ⎥ ⎥ d ( xn , ym )⎦
4
4.1 基本概念
i =1 j n
(
)
离散信源 连续信源
Dmin = ∑ p(xi )min d(xi , y j )
i=1 j
n
仅当失真矩阵每行均 有零元素时, Dmin= 0
R(Dmin ) = R(0) = H ( X )
R(Dmin ) = R(0) = H(x) =∞
12
4.1 基本概念
西华师范大学 物理与电子信息学院
失真函数d(αi,βj)
d(αi , β j ) = d(xi1 xi2
N k =1
xiN , yj1 yj2
= ∑d(xik , yjk )
D ≤ D ,D——允许失真的上界
7
平均失真度—— 单符号时的N倍
D( N ) = ND
8
4.1 基本概念
西华师范大学 物理与电子信息学院
《信号处理原理》 第4章 信息失真率

d(0,2)=d(1,2)=0.5
则得失真矩阵
d
0 1
1 0
0.5 0.5
4.1 平均失真和信息率失真函数
说明:失真函数d (xi, yj) 的数值是依据实际应 用情况,用 yj代替xi, 所导致的失真大小是人为决 定的。比如上例中,用y=2代替x=0和x=1所导致 的失真程度相同,用0.5表示;而用y=0代替x=1 所导致的失真程度要大,用1表示。失真函数d (xi, yj) 的函数形式可以根据需要任意选取,例如平方 代价函数、绝对代价函数、均匀代价函数等。
信源编码器的目的是使编码后所需的信 息传输率R尽量小,然而R越小,引起的平 均失真就越大。给出一个失真的限制值D,
在满足平均失真 D D的条件下,选择一种
编码方法使信息率R尽可能小。信息率R就 是所需输出的有关信源X的信息量。
16
4.1 平均失真和信息率失真函数
将此问题对应到信道,即为接收端Y需要 获得的有关X的信息量,也就是互信息 I(X;Y)。这样,选择信源编码方法的问题就 变成了选择假想信道的问题,符号转移概 率p(yj/xi)就对应信道转移概率。
输入符号集 X:{a1, a2, …, an}中有n种不同的符 号xi (i =1, 2, …, n) ;输出符号集Y:{b1, b2, …, bm}中有m种不同的符号yj (j =1, 2, …, m);对于 图所示的系统,对应于每一对(xi, yj)(i = 1, 2, …,n;j=1, 2, …, m),定义一个非负实值函数
平均失真D是对给定信源分布p(ai)经过某一种 转移概率分布为p(bj|ai)的有失真信源编码器后产 生失真的总体量度。
13
4.1 平均失真和信息率失真函数
第四章信道率失真函数后续习题课

2018/10/13
Department of Communication China Ji Liang University
2
第四章 信息 率失真函数
• 实际中允许一定程度的失真
2018/10/13
Department of Communication China Ji Liang University
3
第四章 信息 率失真函数
• 问题:在允许一定程度的失真条件下,信
4.1.1 失真函数
源信息能够压缩到何种程度?至少需要多 少比特的信息率才能描述信源?
•香农信息率失真理论指出:
• 这样就将选择信源编码方法的问题转化为选择假想信道的问题,
2018/10/13
Department of Communication China Ji Liang University
13
第四章 信息 率失真函数
• 试验信道
4.1.3 信息率失真函数R(D)
平均失真 是信源统计特性p(xi) 、信道统计特性p(yj/xi ) 和失真度d(xi,yj)的函数 。当p(xi)和d(xi,yj)给定后,则可以 求出满足保真度准则 下的所有转移概率分布 pij,构 成一个信道集合PD,
i=n i=n i=n 2n 2n 2n
a1 a2 an
a n+1
an
n 1 2n
a 2n
输出熵H(Y)为: 1 1 1+n n+1 H(Y)=H( ,... , ) log 2n log(n 1) 2n 2n 2n 2n
《信息论与编码》习题解答-第四章(新)

《信息论与编码》习题解答第四章 信息率失真函数-习题答案4.1解:依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=0110d ,转移概率⎥⎦⎤⎢⎣⎡--=εεεε11)|(i j a b p 平均失真:εεεεε=⨯-⨯+⨯⨯+⨯⨯+⨯-⨯==∑∑==0)1(2/112/112/10)1(2/1),()|()(2121j i i j i j i b a d a b p a p D4.2解:依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=0210d , 0min =D ,∑=⨯+⨯=⨯+⨯===ij i i j j y x d x p D D )102/122/1(2/112/102/1),()(min min max 舍去当0min =D ,bit X H R D R 12log )()0()(min ====因为没有失真,此时的转移概率为⎥⎦⎤⎢⎣⎡=1001P当2/1max =D ,0)(max =D R因为取的是第二列的max D 值,所以输出符号概率:,1)(,0)(21==b p b p ,,2221b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=1010P 4.3解:0min =D0041041041041),(min )(43041141141141),()(min min min max =⨯+⨯+⨯+⨯===⨯+⨯+⨯+⨯===∑∑i j i j i i j i i j j y x d x p D y x d x p D D 当0min =D ,bit X H R D R 24log )()0()(min ==== 因为没有失真,此时的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001P 当4/3max =D ,0)(max =D R因为任何一列的max D 值均为3/4,所以取输出符号概率:0)(,0)(,0)(,1)(4321====b p b p b p b p ,即14131211,,,b a b a b a b a →→→→因此编码器的转移概率为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001000100010001P 4.4解: 依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=4/1014/110d , 0min =D∑=⨯+⨯===ij i i j j y x d x p D D )2/12(4/1)4/12/14/12/1min(),()(min min max 个均为其它当0min =D ,bit X H R D R 12log )()0()(min ====因为没有失真,此时的转移概率为⎥⎦⎤⎢⎣⎡=010001P 当4/1max =D ,0)(max =D R因为取的是第三列的max D 值为1/4,所以取输出符号概率:1)(,0)(,0)(321===b p b p b p ,即3231,b a b a →→因此编码器的转移概率为⎥⎦⎤⎢⎣⎡=100100P 4.5解:(1)依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡=0110d ,转移概率为:⎥⎦⎤⎢⎣⎡-=q q P 101 )1(0)1()1(1)1(1001),()|()(11p q q p q p p p y x d x y p x p D n i mj j i i j i -⨯=⨯-⨯-+⨯⨯-+⨯⨯+⨯⨯==∑∑==(2) 0min =D因为)(D R 是D 的递减函数,所以)1log()1(log )()()())(m ax (min min p p p p D H p H D R D R ----=-==当0=q 时可达到))(max(D R ,此时0=D(3) ∑-=⨯+⨯===iji i j j ,p p p p y x d x p D D )1(10),()(min min max 舍去更大另一个 因为)(D R 是D 的递减函数,所以0)()()())(m in(max max =-==D H p H D R D R当1=q 时可达到))(min(D R ,此时p D -=1(图略,见课堂展示)4.6解:依题意可知:失真矩阵:⎥⎦⎤⎢⎣⎡∞∞=1010d ,信源⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡2/12/110)(u p u 0min =D ,∑⨯+⨯⨯+∞⨯∞⨯+⨯===iji i j j y x d x p D D )12/112/1,02/12/1,2/102/1min(),()(min min max )(1]1,,m in[舍去另二个,∞=∞∞=10≤≤D因为二元等概信源率失真函数:⎪⎭⎫ ⎝⎛-=a D H n D R ln )( 其中1,2==a n ,所以率失真函数为:D D R -=1)(4.7解:失真矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=011101110d ,按照P81页方法求解。
信息率失真函数 第4章— 1

② 均方失真: d(ai ,bj ) (ai bj )2
③ 绝对失真: d (ai ,bj ) | ai bj |
④ 相对失真: d (ai ,bj ) | ai bj | / | ai |
⑤
误码失真:
d
(ai
,bj
)
(ai
bj
)
0, 1,
ai bj 其他
9
4.1.2 平均失真
• xi和yj都是随机变量,所以失真函数d(xi,yj)也是随 机变量,限失真时的失真值只能用数学期望表示
11
4.1.3 信息率失真函数R(D)
• 若平均失真度 D 不大于我们所允许的失真,即
DD
• 则称此为保真度准则
• 当信源p(xi)给定,单个符号失真度d(xi,yj) 给定时, 选择不同的试验信道p(yj|xi),相当于不同的编码 方法,其所得的平均失真度不同。
• 试验信道
D D 满足保真度准则
D
>D
12
4.1.3 信息率失真函数R(D)
• 满足 D D 条件的所有转移概率分布pij ,构成 了一个信道集合
PD {p(bj | a)i :D D} • D失真允许的试验信道:
– 满足保真度准则的试验信道。
• PD:
– 所有D失真允许的试验信道组成的一个集合。
13
4.1.3 信息率失真函数R(D)
信道容量
• 信道容量:
– 假定信道固定的前提下,选择一种试验信源 使信息传输率最大。
– 它所反映的是信道传输信息的能力,是信道 可靠传送的最大信息传输率。
• 一旦找到了信道容量,它就与信源不再有关, 而是信道特性的参量,随信道特性的变化而变 化。
第4章1、失真函数

P∈PD1
R( D1 ) = min I ( P) = I ( P1 ) R( D2 ) = min I ( P) = I ( P2 )
P∈PD 2
D ≤ D1
使 I ( P ) 达到最小,且
D ≤ D2
25 26
R(D)性质
θ 1 因为 d ( Pθ ) = ∑∑ Q(u ) Pθ (v | u )d (u , v)
16
寻找平均 互 信息量 I(U;V) 的 最 小 值 。 BD 是 所有满足保真度准则的试验信道集合,可以在 D失真 许可的试验信道 集合BD 中寻找某 一个信 道 p(vj|ui), 使 I(U;V) 取 最 小 值 。由于 平均 互 信息量I(u;v)是p (vj|u i)的U型凸函数,所以在BD 集合中,极小值存在。这个最小值就是在 D ≤ D 条件下,信源必须传输的最小平均信息量。 即
称R(D) 为信息率失真函数(或率失真 函数),其 单位为 奈特/信源符号或比特/信源 符号。 N维信源符号序列的信息率失真函数 RN(D):
RN ( D ) =
p ( y|s ): D ( N ) ≤ ND
min
{I (U ;V )
(4― 28)
R( D ) =
式中 : x ——信源的一个输出 序列; y—— 信宿的一个接收序列 ;
{
}
P V |U ( v | u ) = p (v ) Dmax = min ∑ p(v)∑ p (u )d (u , v) Dmax = min ∑ p(u )d (u, v)
v∈V v u u n
n
当失真矩阵D中每行至少有一个零元素时 Dmin=0
最大允许失真度
信息论考试答案

第4章作业1. 设输入符号表与输出符号表为X =Y ={0,1,2,3},且输入信号的分布为p (X = i ) = 1/4,i =0,1,2,3,设失真矩阵为0111101111011110⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦d 求D min 、D max 和R (D min )、R (D max )以及相应的编码器转移概率矩阵,并求出信源的R(D)函数,画出其曲线(取4至5个点)。
解:10110 41011A A n A P n A A n -⎡⎤⎢⎥⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥=↔==⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥-⎣⎦d有114i p n ==得:()()111011i ji ij ijA AD p P d n n n A n n n-==-⨯⨯+⨯⨯=--∑∑所以1A D =-,进而:()()1111j i ji iA A q p P n n n n n-==+-⨯=-∑()()()()()()()()()1111 ,,,,,1111 ,,1,,,11 log 1log 11log11log ,1log 1 2,1log 3j ji R D H q H p AA H H A n n n n D D H H D n n n n D Dn D D n n n n H D D D n H D D D ==--⎛⎫⎛⎫=- ⎪ ⎪--⎝⎭⎝⎭⎛⎫⎛⎫=-- ⎪ ⎪--⎝⎭⎝⎭=+--+-⨯--=----=--- ()minmin 0,2D R D bit ==,此时1000010000100001⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦P()maxmax 3/4,0D R D ==,此时1000100010001000⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦P2. 设输入符号为X ={0,1},输出符号为Y ={0,1}。
输入信号的概率分布为P =(1/2,1/2),失真函数为d (0,0) = d (1,1) = 0,d (0,1) =d (1,0) =α。
陈运 信息论与编码 第四章 信息率失真函数

d (a1 , b1 ) d (a1 , b2 ) d (a , b ) d (a , b ) 2 1 2 2 [ D] ... ... d (an , b1 ) d (an , b2 )
... d (a1 , bm ) ... d (a2 , bm ) ... ... ... d (an , bm )
D p(ai ) p(b j / ai )d (ai , b j )
i 1 j 1 n m
D1 (1 ) D2 D (1 ) D D
' ''
满足保真 度准则
' ''
I ( X ; Y ) R( D) R[D (1 ) D ]
k 1 N
由信源和信道的无记忆性
p (ai ) p ( x jk )
k 1 N N
p (b j / ai ) p ( y jk / x jk )
k 1
D( N ) p(ai ) p(b j / ai )d (ai , b j )
i 1 j 1
nN mN
D1 D N
第1章:概述 第2章:信源熵 第3章:信道容量
第4章:信息率失真函数
第5章:信源编码 第6章:信道编码 第7章:密码体制的安全性测度
§4.1 信息率失真函数
§4.2 离散信源的信息率失真函数 §4.3 连续信息的率失真函数
§4.4 保真度准则下的信源编码定理
§4.1 信息率失真函数
§4.1.1 失真函数和平均失真度
n m
'
D 2 p(ai ) p 2 (b j / ai )d (ai , b j ) D
第四章信息率失真函数-习题答案

4.1 一个四元对称信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡4/14/1324/14/110)(X P X ,接收符号Y = {0, 1, 2, 3},其失真矩阵为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0111101111011110,求D max 和D min 及信源的R(D)函数,并画出其曲线(取4至5个点)。
解: 0041041041041),(min )(43041141141141),()(min min min max =⨯+⨯+⨯+⨯===⨯+⨯+⨯+⨯===∑∑ij i j i i j i i j j y x d x p D y x d x p D D 因为n 元等概信源率失真函数:⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+-+=a D a D n a Da D n D R 1ln 11ln ln )( 其中a = 1, n = 4, 所以率失真函数为:()()D D D D D R --++=1ln 13ln4ln )( 函数曲线:D 其中:sym bol nat D R D sym bol nat D R D sym bol nat D R D sym bolnat R D /0)(,43/12ln 214ln )(,21/316ln 214ln )(,41/4ln )0(,0==-==-==== 4.2 若某无记忆信源⎭⎬⎫⎩⎨⎧-=⎥⎦⎤⎢⎣⎡3/113/13/101)(X P X ,接收符号⎭⎬⎫⎩⎨⎧-=21,21Y ,其失真矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=112211D 求信源的最大失真度和最小失真度,并求选择何种信道可达到该D max 和D min 的失真度。
4.3 某二元信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡2/12/110)(X P X 其失真矩阵为⎥⎦⎤⎢⎣⎡=a a D 00求这信源的D max 和D min 和R(D)函数。
解:0021021),(min )(202121),()(min min min max =⨯+⨯===⨯+⨯===∑∑ij i j i i j i i j j y x d x p D a a y x d x p D D 因为二元等概信源率失真函数:⎪⎭⎫ ⎝⎛-=a D H n D R ln )( 其中n = 2, 所以率失真函数为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+-=a D a D a D a D D R 1ln 1ln 2ln )( 4.4 已知信源X = {0, 1},信宿Y = {0, 1, 2}。
第4章 信息率失真理论

R[D1 (1 )D2 ] R(D1 ) (1 )R(D2 )
③对D具有单调递减性
由R(D)对D具有的非负性、严格下凸性及R(Dmax) =0说明
信息率失真理论
当Dmin=0时,信息率失真函数R(D)的大致曲线 R(D) H(X)
Dmin
Dmax D
信息率失真理论
3、信息率失真函数的表达式
ˆ P( x j / x i ) i ˆ ln Sd( x i , x j ) 0 ˆ P( x j ) P( x i ) i 1,2,, n j 1,2,, n
i 令 ln i P( x i ) ˆ P( x j / x i ) ˆ Sd ( x i , x j ) ln ln i e ˆ P( x j )
信息率失真理论
第2个实验信道满足D2条件下R(D)的定义 ˆ ˆ P (X / X) {P(X / X) : D D }
D2 2
ˆ ˆ R (D 2 ) min I(X; X) I 2 (X; X) ˆ
PD2 ( X / X )
取一个新的实验信道
ˆ ˆ PD1 (X / X) (1 )PD2 (X / X) ˆ {P(X / X) : D D1 (1 )D 2 }
ˆ ... d( x1 , x n ) ˆ ... d( x 2 , x n ) ... ... ˆ ... d( x n , x n )
汉明失真矩阵
0 1 [ D] ... 1 1 0 ... 1 ... ... ... ... 1 1 ... 0
R[D1 (1 )D2 ] R(D1 ) (1 )R(D2 )
设第1个实验信道满足D1条件下R(D)的定义
信息论第四章失真率函数

(1) 根据式(4-14)和(4-18)可求出R(D)的定义域 Dmin = 0·δ+0·(1-δ) = 0 D max = min {1-δ, δ}=δ (2) 求R(D)的值域
ij
式中D是预先给定的失真度,上式称为保真度准则。
根据[定理2.2],当信源q (x)一定时,平均互信息量I (X ; Y) 是信道转移概率函数p(y∣x)的∪型凸函数,这意味着可以 关于p(y∣x)对平均互信息量I (X ; Y)求得极小值,定义这个
极小值为率失真函数R(D),即:
RD min I X ;Y : D D p(y x)
xi )
( xi
y j )( y j )
q(xi )
。
1-δ = D (y1)+(1-D) (y2)
由上面方程组解出,
(
y1
)
D
1 2D
(
y
2
)
1
1
D 2D
② 再算出
p( y1
x1 )
(x1 y1 ) ( y1 )
q(x1 )
(1
D)
D 1 2 D
(1 D)( D) (1 2D)
d d 21 d 22
d1J
d
2
J
(4-1)
d I 1 d I 2 d I J
【例4.1】 汉明(Hamming)失真测度
信源输出符号X = {x1, x2, …, xK},信道输出符号Y = {y1, y2, …,
第四章总结习题

U 0 1
P(u)
1 4
1 4
2 3
1 4
1 4
接收符号为V={0,1,2,3},其失真矩阵为 0 1 1 1
D 1 0 1 1 1 1 0 1 1 1 1 0
求Dmax,Dmin及信源的R(D)函数,并作出其曲线(取4到5 个点)
2024/7/16
13
习题1
第四章 信息率失真函数
解答:四元对称信源在汉明失真矩阵下,它的平均失真度
信息率失真函数也是一个界限。只要信息率大于这个界限, 译码失真就可限制在给定的范围内。即通信的过程中虽然有 失真,但仍能满足要求,否则就不能满足要求。
2024/7/16
11
第四章 信息率失真函数
研究信道编码和率失真函数的意义
研究信道容量的意义:在实际应用中,研究信道容量是为 了解决在已知信道中传送最大信息率问题。目的是充分利 用已给信道,使传输的信息量最大而发生错误的概率任意 小,以提高通信的可靠性。这就是信道编码问题。
第四步:求D(S),将上述结果代入式(4.2.14)有
nm
D(S)
p(xi ) p( y j )d (xi , y j )ieSd (xi ,y j )
i1 j1
D(S)
p(x1) p( y1)d (x1,
y ) eSd (x1, y1 ) 11
p(x2 ) p( y1)d (x2 ,
y ) eSd (x2 , y1 ) 11
(4.2.10)
p( y1 / x1) p( y1 / x2 ) p( y2 / x1)
p( y1)1eSd (x1, y1) p( y1)2eSd (x2 , y1) p( y2 )1eSd (x1, y2 )
第四章 信道失真率函数

n n
N p(ai ) k 1 p( xik ) N p(b j | ai ) k 1 p( y jk | xik )
nN m N
i1 1 m
i N 1 j1 1
6
常用的失真函数
失真函数是根据人们的实际需要和失真引起的损失、风险、 主观感觉上的差别等因素人为规定的,可以有多种形式 平方误差失真函数 d ( xi , y j ) ( y j xi )2 适用于 d ( x , y ) | y x | 绝对误差失真函数 i j j i 连续信源 相对误差失真函数 d ( xi , y j ) | y j xi | | xi |
率失真函数的定义域 (D 的下界)
允许失真度 D 是平均失真度的上限,而 D 是非负函数 d ( xi , y j ) 的数学期望,因此 D 的下界至多为 0,对应于无失真的情况, 此时信息传输率应等于信源输出的信息熵,即 Dmin 0 时: 离散信源:R( Dmin ) R(0) H ( X ) 连续信源:R( Dmin ) lim R( D )
N
由于 N 次扩展信源和 N 次扩展信道都是无记忆的,因此:
p(ai ) p( xi1 xi2
N xiN ) k 1 p( xik )
p(b j | ai ) p( y j1 y j2
y jN | xi1 xi2
N xiN ) k 1 p( y jk | xik )
9
符号序列的 平均失真度
i 1, 2, j 1, 2,
,n ,m
上述非负的失真函数共有 n m 个,可以整体表示成失真矩阵 d ( x1 , ym ) d ( x1 , y1 ) d ( x1 , y2 ) d ( x , y ) d ( x , y ) d ( x , y ) 2 1 2 2 2 m D d ( x n , ym ) d ( xn , y1 ) d ( xn , y2 ) 由于信源发出的符号 X 和信宿收到(再现)的符号 Y 均是随机 变量,因此单个符号的失真函数 d ( xi, yj ) 也是随机变量(的一 次实现)
第四章 信息率失真函数

失真在传输中是不可避免的。
连续信源输出的信息量为无穷大,不可能实现无失真信源编码. 接收者(信宿)无论是人还是机器设备,都有一定的分辨能力与 即使信宿能分辨、能判别,但对通信质量的影响不大,也可以
灵敏度,超过分辨能力与灵敏度的信息传送过程是毫无意义的。
因此 D 取决于以下几个因素:
) i=1,2, ,n) 1)信源的统计特性,即 p(ai(
2)信道的统计特性,即 p(b j / ai ) 3)失真函数,即 d (ai , b j ) 一般情况下,人们所允许的失真指的都是平均意义 上的失真。如果规定其平均失真度 D不能超过某一限 定的值D,即D就是允许失真的上界。
称它为允许范围内的失真。
如果R>C,就必须对信源压缩,使得压缩后的R*<C,但同时要 求引入的失真不能超过规定的限度。 对于给定的信源,在允许失真的条件下信源熵所能压缩的理论 极限值就是率失真函数R(D) 。
综上所述,一般可以对信源输出的信息进行限失真
处理,降低信息率,提高传输效率。
在允许一定程度的失真条件下,能够把信息压缩到 什么程度?需要多少比特的信息率才能描述信源? 本章主要讨论一定程度的失真情况下所需的最少的 信息率,即信息率失真函数R(D) 。 思路:从分析失真函数、平均失真出发求出信息率 失真函数R(D)。
失真函数的数值是依据实际应用情况,用bj代替ai所导致的失 真大小是人为决定的。上例中用b=2代替a=0和a=1所导致的失 真程度相同,均为0.5;而用b=0代替a=1所导致的失真程度要大 些,为1。
二、平均失真度
1. 离散随机变量平均失真度定义
失真函数的数学期望称为平均失真度。
n m n m
信息论与编码---第4章信息率失真函数

6
[D]称为信道 {X-P(Y/X)-Y} 的失真矩阵. 称为信道 失真矩阵.
长江大学电信学院
X
4.1 基本概念
常用的失真函数有 (1)
d ( xi , y j ) = a 0, i= j a > 0, i ≠ j
7
当i = j时,x和y的消息符号都是 i,说明收发 的消息符号都是x 时 和 的消息符号都是 之间没有失真,所以失真函数 之间没有失真,所以失真函数dij = 0;反之, ;反之, 当i ≠ j时,信宿收到的消息不是信源发出的符 时 而是y 出现了失真,所以失真函数d 号xi,而是 j,出现了失真,所以失真函数 ij 值的大小可以表示这种失真的程度. ≠0,而dij值的大小可以表示这种失真的程度. ,
长江大学电信学院
X
4.1 基本概念
d (a i , b j ) = d ( x i1 x i2 L x i N , y j1 y j2 L y j N ) = d ( x i1 , y j1 ) + d ( x i2 , y j2 ) + L + d ( x i N , y j N ) = ∑ d ( x i k , y jk )
长江大学电信学院
X
4.1 基本概念
2. 平均失真度的定义 若信源和信宿的消息集合分别为X:{x1, 若信源和信宿的消息集合分别为 x2, …, xn}和Y:{y1, y2, …, ym},其概率分别为 和 , p(xi)和p(yj) (i=1, 2, …, n ; j=1, 2, …, n ),信道 和 , 的转移概率为p(y ,失真函数为d 的转移概率为 j|xi),失真函数为 (xi,yj),则 , 称随机变量X和 的联合概率 的联合概率p(x 称随机变量 和Y的联合概率 i yj )对失真函数 对失真函数 的统计平均值为该通信系统的平均失真 d (xi, yj)的统计平均值为该通信系统的平均失真 的统计平均值为该通信系统的 度.
信号与系统课后答案第四章作业答案_第二次
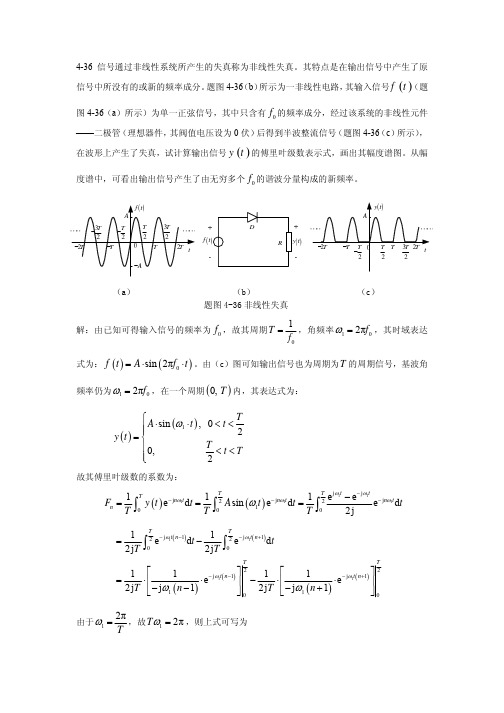
1ω
0
e−3
jω
e
jωt
dω
⎤ ⎥⎦
0
=
−1 2π
⎧⎪ ⎨ ⎪⎩
ω
j(t −
3)
e jω(t−3)
−
⎡⎣ j(t
1
− 3)⎤⎦2
e jω(t−3)
⎫⎪ ⎬ ⎪⎭
−1
+
1 2π
⎧⎪ ⎨ ⎪⎩
ω
j(t −
3)
e jω(t−3)
−
⎡⎣ j(t
1
− 3)⎤⎦2
e jω(t−3)
⎫⎪ 1 ⎬ ⎪⎭ 0
=
−1 2π
Fn
=
−2
4π (n −1)
−
−2
4π (n +1)
=
1 2
⎡ ⎢ ⎣
1
π (n +1)
−
1⎤
π
(n
−1)
⎥ ⎦
⎧0
, n is odd
( ) 所以,
Fn
=
⎪
⎨1
⎪ ⎩
2
⎡1
⎢ ⎣
π
(n
+
1)
−
1⎤
π
(
n
−1)
⎥ ⎦
=
−
1 n2 −1
, π
n is even
其频谱图如下图所示:
Fn 1 π
−6ω1 −4ω1 −2ω1
)
↔
2πSa
⎛ ⎜⎝
2πω 2
⎞ ⎟⎠
,cos(ω0t)
↔
π
[δ(ω
+
ω0
)
+
δ(ω
第四章总结习题.

信息率失真函数也是一个界限。只要信息率大于这个界限, 译码失真就可限制在给定的范围内。即通信的过程中虽然有 失真,但仍能满足要求,否则就不能满足要求。
2018/8/6
11
第四章 信息率失真函数
研究信道编码和率失真函数的意义
对偶问题:信道容量和信息率失真函数的问题,都是求平均 互信息极值问题。分三个方面说明:
求极值问题
平均互信息I(X;Y)是信源概率分布p(xi)(i=1,2,…,n) 的上凸函数, 信道容量就是在固定信道情况下,求平均互信息极大值的问题, 即 I(X;Y) 又是信道转移概率分布 p(yj /xi)(i=1,2,…,n;j=1,2,…,m) 的下 凸函数,信息率失真函数就是在试验信道(满足保真度准则的信 道)中寻找平均互信息极小值的问题,即
4
2018/8/6
第四章 信息率失真函数
允许平均失真度:率失真函数中的自变量 D,也就 是人们规定的平均失真度 D 的上限值。 率失真函数的定义域问题就是在信源和失真函数已 知的情况下,讨论允许平均失真度 D 的最小和最大 值问题。 D 的选取必须根据固定信源 X 的统计特性 P(X) 和选 定的失真函数 d(xi , yj),在平均失真度 D 的可能取 值范围内。
这个最小值 R(D) 称为信息率失真函数,简称率失真函数。
在信源给定以后,总希望在允许一定失真的情况下,传送信源所 必须的信息率越小越好。从接收端来看,就是在满足保真度准则 的条件下,寻找再现信源消息必须的最低平均信息量,即平均互 信息的最小值。
2018/8/6
7
第四章 信息率失真函数
求信息率失真函数的方法
信息率失真函数 R(D) 是假定信源给定的情况下,在用户 可以容忍的失真度内再现信源消息所必须获得的最小平 均信息量。它反映的是信源可压缩程度。率失真函数一 旦找到,就与求极值过程中选择的试验信道不再有关, 而只是信源特性的参量。不同的信源,其 R(D)是不同的。
信息论与编码(清华出版社)第4章信息率失真函数-Qtech

{
i = 1,2, L , n; j = 1,2, L , m
}
14
信息率失真函数R(D) 信息率失真函数
由于互信息取决于信源分布和信道转移概率分布, 根据2-2 由于互信息取决于信源分布和信道转移概率分布 , 根据 节所述, 一定时, 是关于p(y 型凸函数, 节所述,当p(xi)一定时,互信息 是关于 j/xi) 的U型凸函数, 一定时 互信息I是关于 型凸函数 存在极小值。因而在上述允许信道P 存在极小值。因而在上述允许信道 D中,可以寻找一种信道 pij,使给定的信源 i)经过此信道传输后,互信息 ;Y)达 使给定的信源p(x 经过此信道传输后 互信息I(X; 达 经过此信道传输后, 到最小。该最小的互信息就称为信息率失真函数R(D),即 到最小。该最小的互信息就称为信息率失真函数 ,
3
4.1 平均失真和信息率失真函数
4.1.1 4.1.2 4.1.3 4.1.4 失真函数 平均失真 信息率失真函数R(D) 信息率失真函数 信息率失真函数的性质
4
4.1 平均失真和信息率失真函数
在实际问题中, 在实际问题中,信号有一定的失真是可以容 忍的。但是当失真大于某一限度后, 忍的。但是当失真大于某一限度后,信息质量将 被严重损伤,甚至丧失其实用价值。要规定失真 被严重损伤,甚至丧失其实用价值。 限度,必须先有一个定量的失真测度。 限度,必须先有一个定量的失真测度。为此可引 入失真函数。 入失真函数。
如何减小失真,允许失真到什么程度; 如何减小失真,允许失真到什么程度; 在允许一定程度的失真条件下, 在允许一定程度的失真条件下,把信源信息压 缩到什么程度。 缩到什么程度。
2
第4章 在信源允许一定失真情况下 所需的最少信息率, 从分析失真函数、 所需的最少信息率 , 从分析失真函数 、 平 均失真出发,求出信息率失真函数R(D) 。 均失真出发,求出信息率失真函数 4.1 平均失真和信息率失真函数 4.2 离散信源的R(D)计算 离散信源的 ( )
信息论与纠错编码(电子工业出版社)第四章率失真编码 参考答案

4.1 当率失真函数R (D )取什么值的时候,表示不允许有任何失真。
解:当D=0时,表示不允许有任何失真,此时R (D )= H (X ), 即R max ((D )= H (X )4.2 说明信源在不允许失真时,其信息率所能压缩到的极限值是什么?当允许信源存在一定的失真时,其信息率所能压缩到的极限值又是什么?解:不允许失真时,信息率压缩极限值R (D )= H (X );不允许失真时,信息率压缩极限值 R (D )= 04.3 在例4.8中,当允许D= 0.5δ时,请问每个信源符号至少需要几个二进制符号来对其编码?解:因为二元信源率失真函数:⎪⎭⎫⎝⎛-=a D H p H D R )()(其中a = 1(汉明失真), 所以二元信源率失真函数为:)()()(D H p H D R -=当D= 2P 时[]symbol nat p p p p p p p p p H p H p R /21ln 212ln 2)1ln()1(ln 2)(2⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-++--+-=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛4.4 给定信源分布⎥⎦⎤⎢⎣⎡)(q X X = ⎥⎦⎤⎢⎣⎡25.025.05.0x 321x x ,失真测度矩阵[d]=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡011302120,求率失真函数R (D )。
解:定义域:D min =0×0.5+0×0.25+0×0.25=0D max =min{2×0.25+1×0.25,2×0.5+1×0.25,1×0.5+3×0.25}=0.75值域:R (D min )= -0.5log0.5-0.25log0.25-0.25log0.25=0.45 R (D max )= 04.5 给定二元信源⎥⎦⎤⎢⎣⎡)(q X X = ⎥⎦⎤⎢⎣⎡5.05.0x x 21, 失真测度矩阵为[d]=⎥⎦⎤⎢⎣⎡00αα,求率失真函数R(D)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.1 一个四元对称信源⎭
⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡4/14/1324/14/110)(X P X ,接收符号Y = {0, 1, 2, 3},其失真矩阵为⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡0111
101111011110,求D max 和D min 及信源的R(D)函数,并画出其曲线(取4至5个点)。
解: 0041041041041),(min )(43041141141141),()(min min min max =⨯+⨯+⨯+⨯===⨯+⨯+⨯+⨯===∑∑i
j i j i i j i i j j y x d x p D y x d x p D D 因为n 元等概信源率失真函数:
⎪⎭
⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+-+=a D a D n a D
a D n D R 1ln 11ln ln )( 其中a = 1, n = 4, 所以率失真函数为:
()()D D D D D R --++=1ln 13
ln
4ln )( 函数曲线:
D 其中:
symbol nat D R D symbol nat D R D symbol nat D R D symbol
nat R D /0)(,4
3/12ln 2
14ln )(,21/3
16ln 214ln )(,41/4ln )0(,0==-==-==== 4.2 若某无记忆信源⎭⎬⎫⎩⎨⎧-=⎥⎦⎤⎢⎣⎡3/113/13/101)(X P X ,接收符号⎭⎬⎫⎩⎨⎧-=21,21Y ,其失真矩阵⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡=112211D 求信源的最大失真度和最小失真度,并求选择何种信道可达到该D max 和D min 的失真度。
4.3 某二元信源⎭⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡2/12/110)(X P X 其失真矩阵为⎥⎦
⎤⎢⎣⎡=a a D 00求这信源的D max 和D min 和R(D)
函数。
解:
0021021),(min )(202121),()(min min min max =⨯+⨯===⨯+⨯===∑∑i
j i j i i j i i j j y x d x p D a a y x d x p D D 因为二元等概信源率失真函数:
⎪⎭
⎫ ⎝⎛-=a D H n D R ln )( 其中n = 2, 所以率失真函数为:
⎥⎦
⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+-=a D a D a D a D D R 1ln 1ln 2ln )( 4.4 已知信源X = {0, 1},信宿Y = {0, 1, 2}。
设信源输入符号为等概率分布,而且失真函数⎥⎦⎤⎢⎣⎡∞∞=1100D ,求信源的率失真函数R(D)。
4.5 设信源X = {0, 1, 2, 3},信宿Y = {0, 1, 2, 3, 4, 5, 6}。
且信源为无记忆、等概率分布。
失真函数定义为
⎪⎪⎩⎪⎪⎨⎧∞======其他
且且53,21
41,010),(j i j i j i y x d j i 证明率失真函数R(D)如图所示。
log2
2log2
D
4.6 设信源X = {0, 1, 2},相应的概率分布p (0) = p (1) = 0.4,p (2) = 0.2。
且失真函数为 )2,1,0,(10),(=⎩⎨⎧≠==j i j i j i y x d j i
(1) 求此信源的R(D);
(2) 若此信源用容量为C 的信道传递,请画出信道容量C 和其最小误码率P k 之间的曲线关系。
4.7 设0 < α, β < 1, α + β = 1。
试证明:αR(D ’) +βR(D ”) ≥ R(αD ’ +βD ”)
4.8 试证明对于离散无记忆N 次扩展信源,有R N (D) = NR(D)。
其中N 为任意正整数,D ≥ D min 。
4.9 设某地区的“晴天”概率p (晴) = 5/6,“雨天”概率p (雨) = 1/6,把“晴天”预报为“雨天”,把“雨天”预报为“晴天”造成的损失为a 元。
又设该地区的天气预报系统把“晴天”预报为“晴天”,“雨天”预报为“雨天”的概率均为0.9;把把“晴天”预报为“雨天”,把“雨天”预报为“晴天”的概率均为0.1。
试计算这种预报系统的信息价值率v (元/比特)。
4.10 设离散无记忆信源⎭
⎬⎫⎩⎨⎧=⎥⎦⎤⎢⎣⎡3/13/13/1)(321x x x X P X 其失真度为汉明失真度。
(1) 求D min 和R(D min ),并写出相应试验信道的信道矩阵;
(2) 求D max 和R(D max ),并写出相应试验信道的信道矩阵;
(3) 若允许平均失真度D = 1/3,试问信源的每一个信源符号平均最少有几个二进制符号表示?
解:
⎪⎪⎩⎪⎪⎨⎧≠-+=-+==⨯+⨯+⨯==∑j i e n e j i e n x y p y x d x p D sa sa sa i j i
j i j i ,)1(1,)1(11)/(0031031031),(min )(min
4.11 设信源⎭
⎬⎫⎩⎨⎧-=⎥⎦⎤⎢⎣⎡p p x x X P X 1)(21(p < 0.5),其失真度为汉明失真度,试问当允许平均失真度D = 0.5p 时,每一信源符号平均最少需要几个二进制符号表示?
解:
因为二元信源率失真函数:
⎪⎭
⎫ ⎝⎛-=a D H p H D R )()( 其中a = 1(汉明失真), 所以二元信源率失真函数为:
)()()(D H p H D R -= 当2
p D =时 []symbol nat p p p p p p p p p H p H p R /21ln 212ln 2)1ln()1(ln 2)(2⎥⎦
⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-++--+-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛。
