几种典型电场线分布示意图及场强电势特点表
几种典型电场线分布示意图及场强电势特点

匀强电场等量异种点电荷的电场等量同种点电荷的电场 - - - - 点电荷与带电平+孤立点电荷周围的电场 几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷 电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的负点电荷 电场线 直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量电场大部分是曲线,起于正电荷,终止于无穷远;有两条同种正点电荷线电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点

匀强电场等量异种点电荷的电场等量同种点电荷的电场点电荷与带电平孤立点电荷周围的电场 几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷 电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷电场线直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量电场大部分是曲线,起于正电荷,终止于无穷远;有两条同种正点电荷线电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点
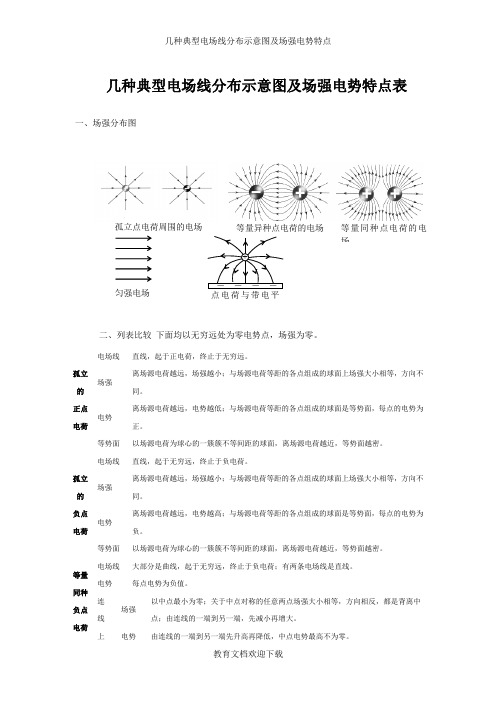
匀强电场 等量异种点电荷的电场 等量同种点电荷的电场- - - - 点电荷与带电平+孤立点电荷周围的电场几种典型电场线分布示意图及场强电势特点表一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷电场线直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点

匀强电场 等量异种点电荷的电场 等量同种点电荷的电场- - - - 点电荷与带电平+孤立点电荷周围的电场创作编号:GB8878185555334563BT9125XW创作者: 凤呜大王*几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线直线,起于正电荷,终止于无穷远。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的负点电荷电场线直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
几种典型电场线分布示意图及场强电势特点之欧阳术创编
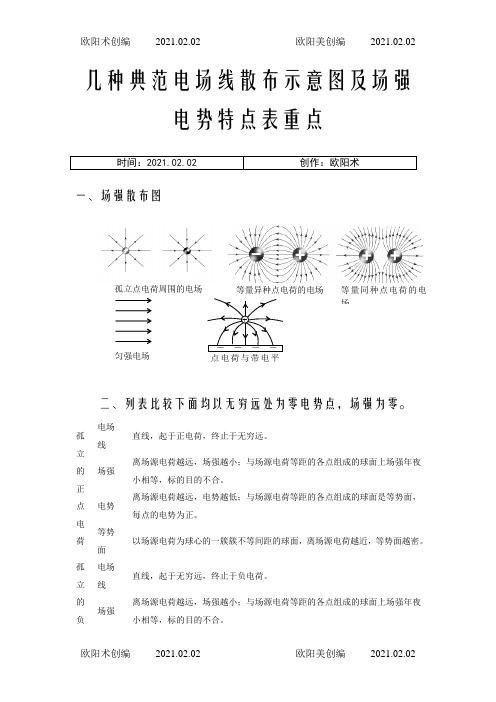
匀强电场等量异种点电荷的电场等量同种点电荷的电场- - - -点电荷与带电平+孤立点电荷周围的电场 几种典范电场线散布示意图及场强电势特点表重点时间:2021.02.02创作:欧阳术一、场强散布图二、列表比较下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷电场线 直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强年夜小相等,标的目的不合。
电势 离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的负电场线 直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强年夜小相等,标的目的不合。
点电荷电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线年夜部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强年夜小相等,标的目的相反,都是叛变中点;由连线的一端到另一端,先减小再增年夜。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强年夜小相等,标的目的相反,都沿着中垂线指向中点;由中点至无穷远处,先增年夜再减小至零,必有一个位置场强最年夜。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线年夜部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强年夜小相等,标的目的相反,都是指向中点;由连线的一端到另一端,先减小再增年夜。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
高中物理选修3-1几种典型电场线分布示意图及场强电势特点表
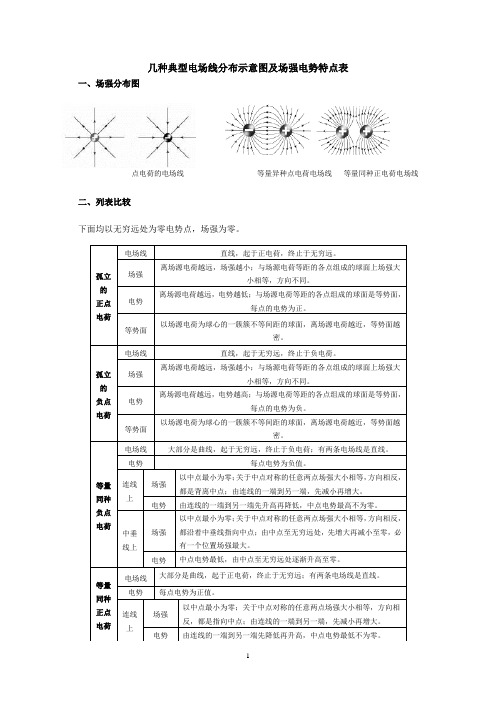
几种典型电场线分布示意图及场强电势特点表一、场强分布图点电荷的电场线等量异种点电荷电场线等量同种正电荷电场线二、列表比较下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷电场线直线,起于正电荷,终止于无穷远。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的负点电荷电场线直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点

匀强电场等量异种点电荷的电场等量同种点电荷的电场 - - - -点电荷与带电平+孤立点电荷周围的电场 几种典型电场线散布示意图及场强电势特点表重点之老阳三干创作时间:二O 二一年七月二十九日一、场强散布图二、列表比较下面均以无穷远处为零电势点,场强为零. 孤立的正点电荷电场线 直线,起于正电荷,终止于无穷远. 场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,标的目的不合. 电势 离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正. 等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密. 孤立的负点电电场线 直线,起于无穷远,终止于负电荷. 场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,标的目的不合. 电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负.荷等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密.等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线.电势每点电势为负值.连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,标的目的相反,都是叛变中点;由连线的一端到另一端,先减小再增大.电势由连线的一端到另一端先升高再降低,中点电势最高不为零.中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,标的目的相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大.电势中点电势最低,由中点至无穷远处逐渐升高至零.等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线.电势每点电势为正值.连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,标的目的相反,都是指向中点;由连线的一端到另一端,先减小再增大.电势由连线的一端到另一端先降低再升高,中点电势最低不为零.中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,标的目的相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大.电势中点电势最高,由中点至无穷远处逐渐降低至零.等量异种点电场线大部分是曲线,起于正电荷,终止于负电荷;有三条电场线是直线.电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负.连线场强以中点最小不等于零;关于中点对称的任意两点场强大小相等,标的目的相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大.电荷上电势由正电荷到负电荷逐渐降低,中点电势为零.中垂线上场强以中点最大;关于中点对称的任意两点场强大小相等,标的目的相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小.电势中垂面是一个等势面,电势为零例如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径成等差数列.A、B、C辨别是这三个等势面上的点,且这三点在同一条电场线上.A、C两点的电势依次为φA=10V和φC=2V,则B点的电势是A.一定等于6VB.一定低于6VC.一定高于6VD.无法确定解:由U=Ed,在d相同时,E越大,电压U也越大.因此UAB> UBC,选B要牢记以下6种罕见的电场的电场线和等势面:注意电场线、等势面的特点和电场线与等势面间的关系:①电场线的标的目的为该点的场强标的目的,电场线的疏密暗示场强的大小.②电场线互不相交,等势面也互不相交.③电场线和等势面在相交处互相垂直.④电场线的标的目的是电势降低的标的目的,并且是降低最快的标的目的.⑤电场线密的地方等差等势面密;等差等势面密的地方电场线也密.二、电荷引入电场1.将电荷引入电场将电荷引入电场后,它一定受电场力Eq,且一定具有电势能φq.2.在电场中移动电荷电场力做的功在电场中移动电荷电场力做的功W=qU,只与始末位置的电势差有关.在只有电场力做功的情况下,电场力做功的过程是电势能和动能相互转化的过程.W= -ΔE=ΔEK.⑴无论对正电荷还是负电荷,只要电场力做功,电势能就减小;克服电场力做功,电势能就增大.⑵正电荷在电势高处电势能大;负电荷在电势高处电势能小.⑶利用公式W=qU进行计算时,各量都取绝对值,功的正负由电荷的正负和移动的标的目的判定.⑷每道题都应该画出示意图,抓住电场线这个关头.(电场线能暗示电场强度的大小和标的目的,能暗示电势降低的标的目的.有了这个直不雅的示意图,可以很便利地判定点电荷在电场中受力、做功、电势能变更等情况.)例. 如图所示,在等量异种点电荷的电场中,将一个正的试探电荷由a 点沿直线移到o点,再沿直线由o点移到c点.在该过程中,检验电荷所受的电场力大小和标的目的如何改动?其电势能又如何改动?解:按照电场线和等势面的散布可知:电场力一直减小而标的目的不变;电势能先减小后不变.例. 如图所示,将一个电荷量为q = +3×10-10C 的点电荷从电场中的A 点移到B 点过程,克服电场力做功6×10-9J.已知A 点的电势为φA= - 4V,求B 点的电势.解:先由W=qU,得AB 间的电压为20V,再由已知阐发:向右移动正电荷做负功,说明电场力向左,因此电场线标的目的向左,得出B 点电势高.因此φB=16V.例.α粒子从无穷远处以等于光速十分之一的速度正对着静止的金核射去(没有撞到金核上).已知离点电荷Q 距离为r 处的电势的计算式为φ=r kQ,那么α粒子的最大电势能是多大?由此预算金原子核的半径是多大?解:α粒子向金核靠近过程克服电场力做功,动能向电势能转化.设初动能为E,到不克不及再接近(两者速度相等时),可认为两者间的距离就是金核的半径.按照动量守恒定律和能量守恒定律,动能的损失()22v M m mM E k +=∆,由于金核质量远大于α粒子质量,所以动能几乎全部转化为电势能.无穷远处的电势能为零,故最大电势能E=122100.321-⨯=mv J,再由E=φq=r kQq ,得r =1.2×10-14m,可见金核的半径不会大于1.2×10-14m.例.已知ΔABC 处于匀强电场中.将一个带电量q= -2×10-6C 的点电荷从A 移到B 的过程中,电场力做功W1= -1.2×10-5J ;再将该点电荷从B 移到C,电场力做功W2= 6×10-6J.已知A点的电势vφA=5V,则B、C两点的电势辨别为____V和____V.试在右图中画出通过A点的电场线.解:先由W=qU求出AB、BC间的电压辨别为6V和3V,再按照负电荷A→B电场力做负功,电势能增大,电势降低;B→C电场力做正功,电势能减小,电势升高,知φB= -1VφC=2V.沿匀强电场中任意一条直线电势都是均匀变更的,因此AB中点D的电势与C点电势相同,CD为等势面,过A做CD的垂线必为电场线,标的目的从高电势指向低电势,所以斜向左下方.例.如图所示,虚线a、b、c是电场中的三个等势面,相邻等势面间的电势差相同,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P、Q是轨迹上的两点.下列说法中正确的是A.三个等势面中,等势面a的电势最高B.带电质点一定是从P点向Q点运动C.带电质点通过P点时的加速度比通过Q点时小D.带电质点通过P点时的动能比通过Q点时小解:先画出电场线,再按照速度、合力和轨迹的关系,可以判定:质点在各点受的电场力标的目的是斜向左下方.由于是正电荷,所以电场线标的目的也沿电场线向左下方.答案仅有D四、带电粒子在电场中的运动1.带电粒子在匀强电场中的加速一般情况下带电粒子所受的电场力远大于重力,所以可以认为只有电场力做功.由动能定理W=qU=ΔEK,此式与电场是否匀强无关,与带电粒子的运动性质、轨迹形状也无关.例.如图所示,两平行金属板竖直放置,左极板接地,中间有小孔.右极板电势随时间变更的规律如图所示.电子原来静止在左极板小孔处.(不计重力作用)下列说法中正确的是A.从t=0时刻释放电子,电子将始终向右运动,直到打到右极板上B.从t=0时刻释放电子,电子可能在两板间振动C.从t=T/4时刻释放电子,电子可能在两板间振动,也可能打到右极板上D.从t=3T/8时刻释放电子,电子势必打到左极板上解:从t=0时刻释放电子,如果两板间距离足够大,电子将向右先匀加速T/2,接着匀减速T/2,速度减小到零后,又开始向右匀加速T/2,接着匀减速T/2……直到打在右极板上.电子不成能向左运动;如果两板间距离不敷大,电子也始终向右运动,直到打到右极板上.从t=T/4时刻释放电子,如果两板间距离足够大,电子将向右先匀加速T/4,接着匀减速T/4,速度减小到零后,改成向左先匀加速T/4,接着匀减速T/4.即在两板间振动;如果两板间距离不敷大,则电子在第一次向右运动过程中就有可能打在右极板上.从t=3T/8时刻释放电子,如果两板间距离不敷大,电子将在第一次向右运动过程中U就打在右极板上;如果第一次向右运动没有打在右极板上,那就一定会在第一次向左运动过程中打在左极板上.选AC2.带电粒子在匀强电场中的偏转质量为m 电荷量为q 的带电粒子以平行于极板的初速度v0射入长L 板间距离为d 的平行板电容器间,两板间电压为U,求射出时的侧移、偏转角和动能增量. ⑴侧移:d U UL v L dm Uq y '=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=42122千万不要死记公式,要清楚物理过程.按照不合的已知条件,结论改用不合的表达形式(已知初速度、初动能、初动量或加速电压等). ⑵偏角:d U UL dmv UqL v v y'===2tan 2θ,注意到θtan 2L y =,说明穿出时刻的末速度的反向延长线与初速度延长线交点恰好在水平位移的中点.这一点和平抛运动的结论相同.⑶穿越电场过程的动能增量:ΔEK=Eqy (注意,一般来说不等于qU )例如图所示,热电子由阴极飞出时的初速忽略不计,电子发射装置的加速电压为U0.电容器板长和板间距离均为L=10cm,下极板接地.电容器右端到荧光屏的距离也是L=10cm.在电容器两极板间接一交变电压,上极板的电势随时间变更的图象如左图.(每个电子穿过平3t m ,t行板的时间极短,可以认为电压是不变的)求:①在t=0.06s 时刻,电子打在荧光屏上的何处?②荧光屏上有电子打到的区间有多长?③屏上的亮点如何移动?解:①由图知t=0.06s 时刻偏转电压为1.8U0,可求得y = 0.45L=4.5cm,打在屏上的点距O 点13.5cm.②电子的最大侧移为0.5L (偏转电压超出2.0U0,电子就打到极板上了),所以荧光屏上电子能打到的区间长为3L=30cm.③屏上的亮点由下而上匀速上升,间歇一段时间后又重复出现.3.带电物体在电场力和重力配合作用下的运动.当带电体的重力和电场力大小可以相比时,不克不及再将重力忽略不计.这时研究对象经常被称为“带电微粒”、“带电尘埃”、“带电小球”等等.这时的问题实际上酿成一个力学问题,只是在考虑能量守恒的时候需要考虑到电势能的变更.例 已知如图,水平放置的平行金属板间有匀强电场.一根长l 的绝缘细绳一端固定在O 点,另一端系有质量为m 并带有一定电荷的小球.小球原来静止在C 点.当给小球一个水平冲量后,它可以在竖直面内绕O 点做匀速圆周运动.若将两板间的电压增大为原来的3倍,求:要使小球从C 点开始在竖直面内绕O 点做圆周运动,至少要给小球多大的水平冲量?在这种情况下,在小球运动过程中细绳所受的最大拉力是多大?解:由已知,原来小球受到的电场力和重力大小相等,增大电压后电+场力是重力的3倍.在C 点,最小速度对应最小的向心力,这时细绳的拉力为零,合力为2mg,可求得速度为v=gl 2,因此给小球的最小冲量为I= m gl 2.在最高点D 小球受到的拉力最大.从C 到D 对小球用动能定理:22212122C D mv mv l mg -=⋅,在D 点l mv mg F D 22=-,解得F=12mg.例已知如图,匀强电场标的目的水平向右,场强E=1.5×106V/m,丝线长l=40cm,上端系于O 点,下端系质量为m=1.0×10-4kg,带电量为q=+4.9×10-10C 的小球,将小球从最低点A 由静止释放,求:⑴小球摆到最高点时丝线与竖直标的目的的夹角多大?⑵摆动过程中小球的最大速度是多大? 解:⑴这是个“歪摆”.由已知电场力Fe=0.75G 摆动到平衡位置时丝线与竖直标的目的成37°角,因此最大摆角为74°.⑵小球通过平衡位置时速度最大.由动能定理:1.25mg 0.2l=mvB2/2,vB=1.4m/s.五、电容器1.电容器两个彼此绝缘又相隔很近的导体都可以看成一个电容器.2.电容器的电容电容UQ C =是暗示电容器容纳电荷本领的物理量,是由电容器自己的性质(导体大小、形状、相对位置及电介质)决定的.3.平行板电容器的电容平行板电容器的电容的决定式是:d s kd s C επε∝=4 4.两种不合变更θ θ电容器和电源连接如图,改动板间距离、改动正对面积或改动板间电解质资料,都会改动其电容,从而可能引起电容器两板间电场的变更.这里一定要分清两种罕见的变更:⑴电键K 坚持闭合,则电容器两端的电压恒定(等于电源电动势),这种情况下带d d U E d S kd S C C CU Q 14∝=∝=∝=,,而电量επε ⑵充电后断开K,坚持电容器带电量Q 恒定,这种情况下sE s d U d sC εεε1,,∝∝∝ 例如图所示,在平行板电容器正中有一个带电微粒.K 闭合时,该微粒恰好能坚持静止.在①坚持K 闭合;②充电后将K 断开;两种情况下,各用什么办法能使该带电微粒向上运动打到上极板?A.上移上极板MB.上移下极板NC.左移上极板MD.把下极板N 接地解:由上面的阐发可知①选B,②选C.例计算机键盘上的每一个按键下面都有一个电容传感器.电容的计算公式是d S C ε=,其中常量ε=9.0×10-12F m-1,S 暗示两金属片的正对面积,d 暗示两金属片间的距离.当某一键被按下时,d 产生改动,引起电容器的电容产生改动,从而给电子线路收回相应的信号.已知两金属片的正对面积为50mm2,键未被按下时,两金属片间的距离为0.60mm.只要电容变更达0.25pF,电子线路就能收回相应的信号.那么为使按键得到反响,至少需要按下多大距离?KN A解:先求得未按下时的电容C1=0.75pF,再由1221d d C C =得12d d C C ∆=∆和C2=1.00pF,得Δd=0.15mm.。
几种典型电场线分布示意图及场强电势特点
解:先由W=qU,得AB间的电压为20V,再由已知分析:向右移动正电荷做负功,说明电场力向左,因此电场线方向向左,得出B点电势高。因此φB=16V。
例.α粒子从无穷远处以等于光速十分之一的速度正对着静止的金核射去(没有撞到金核上)。已知离点电荷Q距离为r处的电势的计算式为φ= ,那么α粒子的最大电势能是多大?由此估算金原子核的半径是多大?
以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷
电场线
大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势
每点电势为负值。
连线上
场强
以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势
由连线的一端到另一端先升高再降低,中点电势最高不为零。
连线上
场强
以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势
由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上
场强
以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
2.带电粒子在匀强电场中的偏转
质量为m电荷量为q的带电粒子以平行于极板的初速度v0射入长L板间距离为d的平行板电容器间,两板间电压为U,求射出时的侧移、偏转角和动能增量。
几种典型电场线分布示意图及场强电势特点

匀强电等量异种点电荷的电等量同种点电荷- - - 点电荷与带电+孤立点电荷周围的几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线 直线,起于正电荷,终止于无穷远。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 电场线直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球负点电荷面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等电场大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是量同种正点电荷线直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点
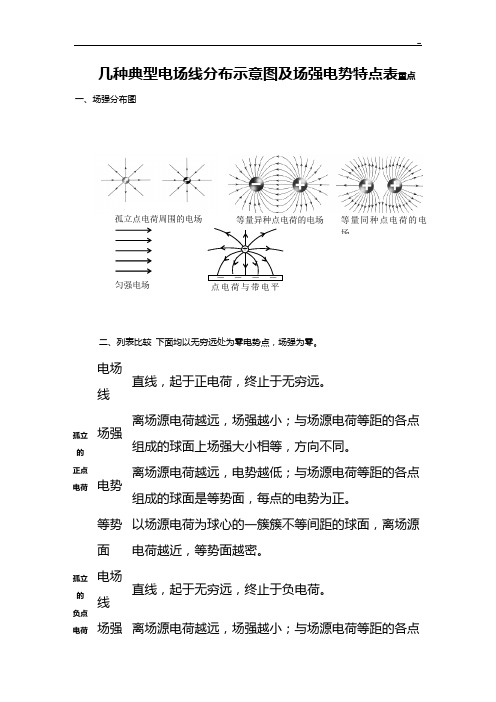
匀强电场 等量异种点电荷的电场 等量同种点电荷的电场- - - - 点电荷与带电平+孤立点电荷周围的电场几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线直线,起于正电荷,终止于无穷远。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷电场线直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点.

匀强电场 等量异种点电荷的电场 等量同种点电荷的电场- - - - 点电荷与带电平+孤立点电荷周围的电场几种典型电场线分布示意图及场强电势特点表一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷电场线直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强电势特点

匀强电场 等量异种点电荷的电场 等量同种点电荷的电场- - - - 点电荷与带电平+孤立点电荷四周的电场几种典范电场线散布示意图及场强电势特色表重点【2 】一.场强散布图二.列表比较下面均以无限远处为零电势点,场强为零. 孤立的 正点电荷电场线 直线,起于正电荷,终止于无限远.场强离场源电荷越远,场强越小;与场源电荷等距的各点构成的球面上场壮大小相等,偏向不同.电势 离场源电荷越远,电势越低;与场源电荷等距的各点构成的球面是等势面,每点的电势为正.等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密.孤立的 负点电荷电场线 直线,起于无限远,终止于负电荷.场强 离场源电荷越远,场强越小;与场源电荷等距的各点构成的球面上场壮大小相等,偏向不同.电势 离场源电荷越远,电势越高;与场源电荷等距的各点构成的球面是等势面,每点的电势为负.等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密.等量同种负点电荷电场线大部分曲直线,起于无限远,终止于负电荷;有两条电场线是直线.电势每点电势为负值.连线上场强以中点最小为零;关于中点对称的随意率性两点场壮大小相等,偏向相反,都是背离中点;由连线的一端到另一端,先减小再增大.电势由连线的一端到另一端先升高再下降,中点电势最高不为零.中垂线上场强以中点最小为零;关于中点对称的随意率性两点场壮大小相等,偏向相反,都沿着中垂线指向中点;由中点至无限远处,先增大再减小至零,必有一个地位场强最大.电势中点电势最低,由中点至无限远处逐渐升高至零.等量同种正点电荷电场线大部分曲直线,起于正电荷,终止于无限远;有两条电场线是直线.电势每点电势为正值.连线上场强以中点最小为零;关于中点对称的随意率性两点场壮大小相等,偏向相反,都是指向中点;由连线的一端到另一端,先减小再增大.电势由连线的一端到另一端先下降再升高,中点电势最低不为零.中垂线上场强以中点最小为零;关于中点对称的随意率性两点场壮大小相等,偏向相反,都沿着中垂线指向无限远处;由中点至无限远处,先增大再减小至零,必有一个地位场强最大.电势中点电势最高,由中点至无限远处逐渐下降至零.等量异种点电电场线大部分曲直线,起于正电荷,终止于负电荷;有三条电场线是直线.电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负.连线上场强以中点最小不等于零;关于中点对称的随意率性两点场壮大小相等,偏向雷同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增大.电势由正电荷到负电荷逐渐下降,中点电势为零.荷中垂线上场强以中点最大;关于中点对称的随意率性两点场壮大小相等,偏向雷同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无限远处,逐渐减小.电势中垂面是一个等势面,电势为零例如图所示,三个齐心圆是统一个点电荷四周的三个等势面,已知这三个圆的半径成等差数列.A.B.C分离是这三个等势面上的点,且这三点在统一条电场线上.A.C两点的电势依次为φA=10V和φC=2V,则B点的电势是A.必定等于6VB.必定低于6VC.必定高于6VD.无法肯定解:由U=Ed,在d雷同时,E越大,电压U也越大.是以UAB> UBC,选B要切记以下6种常见的电场的电场线和等势面:留意电场线.等势面的特色和电场线与等势面间的关系:①电场线的偏向为该点的场强偏向,电场线的疏密表示场强的大小.②电场线互不订交,等势面也互不订交.③电场线和等势面在订交处互相垂直.④电场线的偏向是电势下降的偏向,并且是下降最快的偏向.⑤电场线密的地方等差等势面密;等差等势面密的地方电场线也密.二.电荷引入电场1.将电荷引入电场将电荷引入电场后,它必定受电场力Eq,且必定具有电势能φq.2.在电场中移动电荷电场力做的功在电场中移动电荷电场力做的功W=qU,只与始末地位的电势差有关.在只有电场力做功的情形下,电场力做功的进程是电势能和动能互相转化的进程.W= -ΔE=ΔEK.⑴无论对正电荷照样负电荷,只要电场力做功,电势能就减小;战胜电场力做功,电势能就增大.⑵正电荷在电势高处电势能大;负电荷在电势高处电势能小.⑶应用公式W=qU 进行盘算时,各量都取绝对值,功的正负由电荷的正负和移动的偏向剖断.⑷每道题都应当画出示意图,抓住电场线这个症结.(电场线能表示电场强度的大小和偏向,能表示电势下降的偏向.有了这个直不雅的示意图,可以很便利地剖断点电荷在电场中受力.做功.电势能变化等情形.)例. 如图所示,在等量异种点电荷的电场中,将一个正的试探电荷由a 点沿直线移到o 点,再沿直线由o 点移到c 点.在该进程中,磨练电荷所受的电场力大小和偏向若何转变?其电势能又若何转变?解:依据电场线和等势面的散布可知:电场力一向减小而偏向不变; 电势能先减小后不变.例. 如图所示,将一个电荷量为q = +3×10-10C 的点电荷从电场中的A 点移到B 点进程,战胜电场力做功6×10-9J.已知A 点的电势为φA= - 4V ,求B 点的电势.解:先由W=qU,得AB 间的电压为20V ,再由已知剖析:向右移动正电荷做负功,解释电场力向左,是以电场线偏向向左,得出B 点电势高.是以φB=16V .例.α粒子从无限远处以等于光速十分之一的速度正对着静止的金核射去(没有撞到金核上).已知离点电荷Q 距离为r 处的电势的盘算式为φ=rkQ,那么α粒子的最大电势能是多大?由此估算金原子核的半径是多大?解:α粒子向金核接近进程战胜电场力做功,动能向电势能转化.设初动能为E,到不能再接近(两者速度相等时),可以为二者间的距离就是金核的半径.依据动量守恒定律和能量守恒定律,动能的损掉()22v M m mME k +=∆,因为金核质量弘远于α粒子质量,所以动能几乎全体转化为电势能.无限远处的电势能为零,故最大电势能E=122100.321-⨯=mv J,再由E=φq=r kQq,v例.已知ΔABC 处于匀强电场中.将一个带电量q= -2×10-6C 的点电荷从A 移到B 的进程中,电场力做功W1= -1.2×10-5J;再将该点电荷从B 移到C,电场力做功W2= 6×10-6J.已知A 点的电势φA=5V,则B.C 两点的电势分离为____V 和____V .试在右图中画出经由过程A 点的电场线.解:先由W=qU 求出AB.BC 间的电压分离为6V 和3V ,再依据负电荷A→B 电场力做负功,电势能增大,电势下降;B→C 电场力做正功,电势能减小,电势升高,知φB= -1VφC=2V .沿匀强电场中随意率性一条直线电势都是平均变化的,是以AB 中点D 的电势与C 点电势雷同,CD 为等势面,过A 做CD 的垂线必为电场线,偏向从高电势指向低电势,所以斜向左下方. 例.如图所示,虚线a.b.c 是电场中的三个等势面,相邻等势面间的电势差雷同,实线为一个带正电的质点仅在电场力感化下,经由过程该区域的活动轨迹,P.Q 是轨迹上的两点.下列说法中准确的是A.三个等势面中,等势面a 的电势最高B.带电质点必定是从P 点向Q 点活动C.带电质点经由过程P 点时的加快度比经由过程Q 点时小D.带电质点经由过程P 点时的动能比经由过程Q 点时小解:先画出电场线,再依据速度.合力和轨迹的关系,可以剖断:质点在各点受的电场力偏向是斜向左下方.因为是正电荷,所以电场线偏向也沿电场线向左下方.答案仅有D四.带电粒子在电场中的活动1.带电粒子在匀强电场中的加快一般情形下带电粒子所受的电场力弘远于重力,所以可以以为只有电场力做功.由动能定理W=qU=ΔEK,此式与电场是否匀强无关,与带电粒子的活动性质.轨迹外形也无关. 例.如图所示,两平行金属板竖直放置,左极板接地,中央有小孔.右极板电势随时光变化的纪律如图所示.电子本来静止在左极板小孔处.(不计重力感化)下列说法中准确的是UA.从t=0时刻释放电子,电子将始终向右活动,直到打到右极板上 B.从t=0时刻释放电子,电子可能在两板间振动C.从t=T/4时刻释放电子,电子可能在两板间振动,也可能打到右极板上D.从t=3T/8时刻释放电子,电子必将打到左极板上解:从t=0时刻释放电子,假如两板间距离足够大,电子将向右先匀加快T/2,接着匀减速T/2,速度减小到零后,又开端向右匀加快T/2,接着匀减速T/2……直到打在右极板上.电子不可能向左活动;假如两板间距离不够大,电子也始终向右活动,直到打到右极板上.从t=T/4时刻释放电子,假如两板间距离足够大,电子将向右先匀加快T/4,接着匀减速T/4,速度减小到零后,改为向左先匀加快T/4,接着匀减速T/4.即在两板间振动;假如两板间距离不够大,则电子在第一次向右活动进程中就有可能打在右极板上.从t=3T/8时刻释放电子,假如两板间距离不够大,电子将在第一次向右活动进程中就打在右极板上;假如第一次向右活动没有打在右极板上,那就必定会在第一次向左活动进程中打在左极板上.选AC 2.带电粒子在匀强电场中的偏转质量为m 电荷量为q 的带电粒子以平行于极板的初速度v0射入长L 板间距离为d 的平行板电容器间,两板间电压为U,求射出时的侧移.偏转角和动能增量.⑴侧移:dU UL v L dm Uq y '=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=42122万万不要逝世记公式,要清晰物理进程.依据不同的已知前提,结论改用不同的表达情势(已知初速度.初动能.初动量或加快电压等).⑵偏角:dU UL dmv UqL v v y '===2tan 2θ,留意到θtan 2L y =,解释穿出时刻的末速度的反向延伸线与初速度延伸线交点正好在程度位移的中点.这一点和平抛活动的结论雷同.⑶穿越电场进程的动能增量:ΔEK=Eqy (留意,一般来说不等于qU ) m ,t电压为U0.电容器板长和板间距离均为L=10cm,下极板接地.电容器右端到荧光屏的距离也是L=10cm.在电容器南北极板间接一交变电压,上极板的电势随时光变化的图象如左图.(每个电子穿过平行板的时光极短,可以以为电压是不变的)求:①在t=0.06s 时刻,电子打在荧光屏上的何处?②荧光屏上有电子打到的区间有多长?③屏上的亮点若何移动?解:①由图知t=0.06s 时刻偏转电压为1.8U0,可求得y = 0.45L= 4.5cm,打在屏上的点距O 点13.5cm.②电子的最大侧移为0.5L (偏转电压超过2.0U0,电子就打到极板上了),所以荧光屏上电子能打到的区间长为3L=30cm.③屏上的亮点由下而上匀速上升,间歇一段时光后又反复消失.3.带电物体在电场力和重力配合感化下的活动.当带电体的重力和电场力大小可以比拟时,不能再将重力疏忽不计.这时研讨对象经常被称为“带电微粒”.“带电尘埃”.“带电小球”等等.这时的问题现实上变成一个力学问题,只是在斟酌能量守恒的时刻须要斟酌到电势能的变化.例 已知如图,程度放置的平行金属板间有匀强电场.一根长l 的绝缘细绳一端固定在O 点,另一端系有质量为m 并带有必定电荷的小球.小球本来静止在C 点.当给小球一个程度冲量后,它可以在竖直面内绕O 点做匀速圆周活动.若将两板间的电压增大为本来的3倍,求:要使小球从C 点开端在竖直面内绕O 点做圆周活动,至少要给小球多大的程度冲量?在这种情形下,在小球活动进程中细绳所受的最大拉力是多大?解:由已知,本来小球受到的电场力和重力大小相等,增大电压后电场力是重力的3倍.在C 点,最小速度对应最小的向心力,这时细绳的拉力为零,合力为2mg,可求得速度为v=gl 2,是以给小球的最小冲量为I= m gl 2.在最高点D 小球受到的拉力最大.从C 到D 对小球用动能定理:22212122CD mv mv l mg -=⋅,在D 点l mv mg F D 22=-,解得F=12mg. +于O 点,下端系质量为m=1.0×10-4kg,带电量为q=+4.9×10-10C 的小球,将小球从最低点A 由静止释放,求:⑴小球摆到最高点时丝线与竖直偏向的夹角多大?⑵摆动进程中小球的最大速度是多大?解:⑴这是个“歪摆”.由已知电场力Fe=0.75G 摆动到均衡地位时丝线与竖直偏向成37°角,是以最大摆角为74°.⑵小球经由过程均衡地位时速度最大.由动能定理:1.25mg 0.2l=mvB2/2,vB=1.4m/s.五.电容器 1.电容器两个彼此绝缘又相隔很近的导体都可以算作一个电容器. 2.电容器的电容电容UQC =是表示电容器容纳电荷本领的物理量,是由电容器本身的性质(导体大小.外形.相对地位及电介质)决议的. 3.平行板电容器的电容平行板电容器的电容的决议式是:dskd s C επε∝=4 4.两种不同变化电容器和电源衔接如图,转变板间距离.转变正对面积或转变板间电解质材料,都邑转变其电容,从而可能引起电容器两板间电场的变化.这里必定要分清两种常见的变化:⑴电键K 保持闭合,则电容器两头的电压恒定(等于电源电动势),这种情形下带dd U E d S kd S C C CU Q 14∝=∝=∝=,,而电量επε⑵充电后断开K,保持电容器带电量Q 恒定,这种情形下sE s d U dsC εεε1,,∝∝∝例如图所示,在平行板电容器正中有一个带电微粒.K 闭应时,该微粒正好能保持静止.在①保持K 闭合;②充电后将K 断开;两种情形下,各用什么办法能使该带电微粒向上活动打到上极板?KNA.上移上极板MB.上移下极板NC.左移上极板MD.把下极板N 接地 解:由上面的剖析可知①选B,②选C.例盘算机键盘上的每一个按键下面都有一个电容传感器.电容的盘算公式是dSC ε=,个中常量ε=9.0×10-12F m-1,S 表示两金属片的正对面积,d 表示两金属片间的距离.当某一键被按下时,d 产生转变,引起电容器的电容产生转变,从而给电子线路发出响应的旌旗灯号.已知两金属片的正对面积为50mm2,键未被按下时,两金属片间的距离为0.60mm.只要电容变化达0.25pF,电子线路就能发出响应的旌旗灯号.那么为使按键得到反响,至少须要按下多大距离?解:先求得未按下时的电容C1=0.75pF,再由1221d d C C =得12d dC C ∆=∆和C2=1.00pF,得Δd= 0.15mm.A。
几种典型电场线分布示意图及场强电势特点
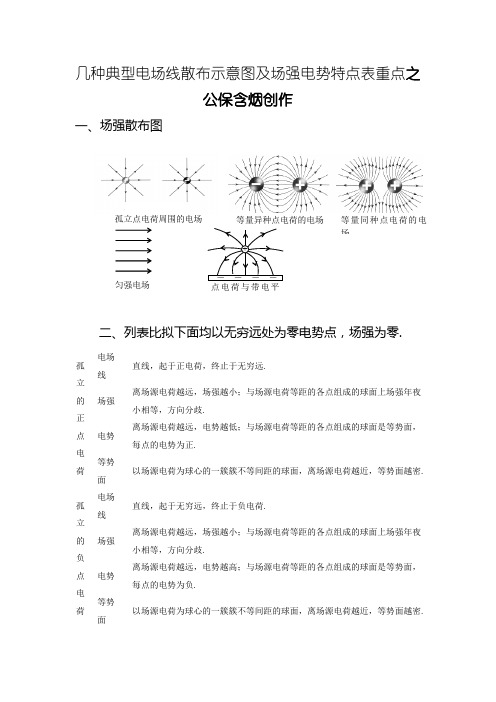
匀强电场等量异种点电荷的电场等量同种点电荷的电场- - - -点电荷与带电平+孤立点电荷周围的电场 几种典型电场线散布示意图及场强电势特点表重点之公保含烟创作一、场强散布图二、列表比拟下面均以无穷远处为零电势点,场强为零. 孤立的正点电荷 电场线 直线,起于正电荷,终止于无穷远. 场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强年夜小相等,方向分歧. 电势 离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正. 等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密. 孤立的负点电荷 电场线直线,起于无穷远,终止于负电荷. 场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强年夜小相等,方向分歧. 电势 离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负. 等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密.等量同种负点电荷电场线年夜局部是曲线,起于无穷远,终止于负电荷;有两条电场线是直线.电势每点电势为负值.连线上场强以中点最小为零;关于中点对称的任意两点场强年夜小相等,方向相反,都是叛变中点;由连线的一端到另一端,先减小再增年夜.电势由连线的一端到另一端先升高再降低,中点电势最高不为零.中垂线上场强以中点最小为零;关于中点对称的任意两点场强年夜小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增年夜再减小至零,必有一个位置场强最年夜.电势中点电势最低,由中点至无穷远处逐渐升高至零.等量同种正点电荷电场线年夜局部是曲线,起于正电荷,终止于无穷远;有两条电场线是直线.电势每点电势为正值.连线上场强以中点最小为零;关于中点对称的任意两点场强年夜小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增年夜.电势由连线的一端到另一端先降低再升高,中点电势最低不为零.中垂线上场强以中点最小为零;关于中点对称的任意两点场强年夜小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增年夜再减小至零,必有一个位置场强最年夜.电势中点电势最高,由中点至无穷远处逐渐降低至零.等量异种点电荷电场线年夜局部是曲线,起于正电荷,终止于负电荷;有三条电场线是直线.电势中垂面有正电荷的一边每一点电势为正,有负电荷的一边每一点电势为负.连线上场强以中点最小不等于零;关于中点对称的任意两点场强年夜小相等,方向相同,都是由正电荷指向负电荷;由连线的一端到另一端,先减小再增年夜.电势由正电荷到负电荷逐渐降低,中点电势为零.中垂线上场强以中点最年夜;关于中点对称的任意两点场强年夜小相等,方向相同,都是与中垂线垂直,由正电荷指向负电荷;由中点至无穷远处,逐渐减小.电势中垂面是一个等势面,电势为零例如图所示,三个同心圆是同一个点电荷周围的三个等势面,已知这三个圆的半径成等差数列.A、B、C辨别是这三个等势面上的点,且这三点在同一条电场线上.A、C两点的电势依次为φA=10V和φC=2V,则B点的电势是A.一定等于6VB.一定低于6V解:由U=Ed,在d相同时,E越年夜,电压U也越年夜.因此UAB> UBC,选B要牢记以下6种罕见的电场的电场线和等势面:注意电场线、等势面的特点和电场线与等势面间的关系:①电场线的方向为该点的场强方向,电场线的疏密暗示场强的年夜小.②电场线互不相交,等势面也互不相交.③电场线和等势面在相交处相互垂直.④电场线的方向是电势降低的方向,而且是降低最快的方向.⑤电场线密的中央等差等势面密;等差等势面密的中央电场线也密.二、电荷引入电场将电荷引入电场后,它一定受电场力Eq,且一定具有电势能φq.在电场中移动电荷电场力做的功W=qU,只与始末位置的电势差有关.在只有电场力做功的情况下,电场力做功的进程是电势能和动能相互转化的进程.W= -ΔE=ΔEK.⑴无论对正电荷还是负电荷,只要电场力做功,电势能就减小;克制电场力做功,电势能就增年夜.⑵正电荷在电势高处电势能年夜;负电荷在电势高处电势能小.⑶应用公式W=qU停止计算时,各量都取相对值,功的正负由电荷的正负和移动的方向判定.⑷每道题都应该画出示意图,抓住电场线这个关键.(电场线能暗示电场强度的年夜小和方向,能暗示电势降低的方向.有了这个直观的示意图,可以很方便地判定点电荷在电场中受力、做功、电势能变卦等情况.)例. 如图所示,在等量异种点电荷的电场中,将一个正的试探电荷由a 点沿直线移到o点,再沿直线由o点移到c点.在该进程中,检验电荷所受的电场力年夜小和方向如何改动?其电势能又如何改动?解:依据电场线和等势面的散布可知:电场力一直减小而方向不变;电势能先减小后不变.例. 如图所示,将一个电荷量为q = +3×10-10C的点电荷从电v场中的A 点移到B 点进程,克制电场力做功6×10-9J.已知A 点的电势为φA= - 4V ,求B 点的电势.解:先由W=qU ,得AB 间的电压为20V ,再由已知剖析:向右移动正电荷做负功,说明电场力向左,因此电场线方向向左,得出B 点电势高.因此φB=16V.例.α粒子从无穷远处以等于光速十分之一的速度正对着运动的金核射去(没有撞到金核上).已知离点电荷Q 间隔为r 处的电势的计算式为φ=r kQ,那么α粒子的最年夜电势能是多年夜?由此预算金原子核的半径是多年夜?解:α粒子向金核接近进程克制电场力做功,动能向电势能转化.设初动能为E ,到不能再接近(两者速度相等时),可认为二者间的间隔就是金核的半径.依据动量守恒定律和能量守恒定律,动能的损失()22v M m mM E k +=∆,由于金核质量远年夜于α粒子质量,所以动能简直全部转化为电势能.无穷远处的电势能为零,故最年夜电势能E=122100.321-⨯=mv J ,再由E=φq=r kQq,得r =1.2×10-14m ,可见金核的半径不会年夜于1.2×10-14m.例.已知ΔABC 处于匀强电场中.将一个带电量q= -2×10-6C 的点电荷从A 移到B 的进程中,电场力做功W1= -1.2×10-5J ;再将该点电荷从B 移到C ,电场力做功W2= 6×10-6J.已知A 点的电势φA=5V,则B 、C 两点的电势辨别为____V 和____V.试在右图中画出通过A 点的电场线.解:先由W=qU 求出AB 、BC 间的电压辨别为6V 和3V ,再依据负电荷A→B 电场力做负功,电势能增年夜,电势降低;B→C 电场力做正功,电势能减小,电势升高,知φB= -1VφC=2V.沿匀强电场中任意一条直线电势都是平均变卦的,因此AB 中点D 的电势与C 点电势相同,CD 为等势面,过A 做CD 的垂线必为电场线,方向从高电势指向低电势,所以斜向左下方.例.如图所示,虚线a 、b 、c 是电场中的三个等势面,相邻等势面间的电势差相同,实线为一个带正电的质点仅在电场力作用下,通过该区域的运动轨迹,P 、Q是轨迹上的两点.下列说法中正确的是A.三个等势面中,等势面a 的电势最高解:先画出电场线,再依据速度、合力和轨迹的关系,可以判定:质点在各点受的电场力方向是斜向左下方.由于是正电荷,所以电场线方向也沿电场线向左下方.谜底仅有D四、带电粒子在电场中的运动一般情况下带电粒子所受的电场力远年夜于重力,所以可以认为只有电场力做功.由动能定理W=qU=ΔEK,此式与电场是否匀强无关,与带电粒子的运动性质、轨迹形状也无关. 例.如图所示,两平行金属板竖直放置,左极板接地,中间有小孔.右极板电势随时间变卦的规律如图所U示.电子原来运动在左极板小孔处.(不计重力作用)下列说法中正确的是A.从t=0时刻释放电子,电子将始终向右运动,直到打到右极板上B.从t=0时刻释放电子,电子能够在两板间振动C.从t=T/4时刻释放电子,电子能够在两板间振动,也能够打到右极板上D.从t=3T/8时刻释放电子,电子势必打到左极板上解:从t=0时刻释放电子,如果两板间间隔足够年夜,电子将向右先匀减速T/2,接着匀减速T/2,速度减小到零后,又开端向右匀减速T/2,接着匀减速T/2……直到打在右极板上.电子不成能向左运动;如果两板间间隔不足年夜,电子也始终向右运动,直到打到右极板上.从t=T/4时刻释放电子,如果两板间间隔足够年夜,电子将向右先匀减速T/4,接着匀减速T/4,速度减小到零后,改为向左先匀减速T/4,接着匀减速T/4.即在两板间振动;如果两板间间隔不足年夜,则电子在第一次向右运动进程中就有能够打在右极板上.从t=3T/8时刻释放电子,如果两板间间隔不足年夜,电子将在第一次向右运动进程中就打在右极板上;如果第一次向右运动没有打在右极板上,那就一定会在第一次向左运动进程中打在左极板上.选AC质量为m 电荷量为q的带电粒子以平行于m t极板的初速度v0射入长L 板间间隔为d 的平行板电容器间,两板间电压为U ,求射出时的侧移、偏转角和动能增量. ⑴侧移:d U UL v L dm Uq y '=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=42122千万不要死记公式,要清楚物理进程.依据分歧的已知条件,结论改用分歧的表达形式(已知初速度、初动能、初动量或减速电压等). ⑵偏角:d U UL dmv UqL v v y'===2tan 2θ,注意到θtan 2L y =,说明穿出时刻的末速度的反向延长线与初速度延长线交点恰好在水平位移的中点.这一点战争抛运动的结论相同.⑶穿越电场进程的动能增量:ΔEK=Eqy (注意,一般来说不等于qU )例如图所示,热电子由阴极飞出时的初速疏忽不计,电子发射装置的减速电压为U0.电容器板长和板间间隔均为L=10cm ,下极板接地.电容器右端到荧光屏的间隔也是L=10cm.在电容器两极板直接一交变电压,上极板的电势随时间变卦的图象如左图.(每个电子穿过平行板的时间极短,可以认为电压是不变的)求:①在t=0.06s 时刻,电子打在荧光屏上的何处?②荧光屏上有电子打到的区间有多长?③屏上的亮点如何移动?解:①由图知t=0.06s 时刻偏转电压为1.8U0,可求得y =3t0.45L= 4.5cm ,打在屏上的点距O 点13.5cm.②电子的最年夜侧移为0.5L (偏转电压超越2.0U0,电子就打到极板上了),所以荧光屏上电子能打到的区间长为3L=30cm.③屏上的亮点由下而上匀速上升,间歇一段时间后又重复呈现.3.带电物体在电场力和重力共同作用下的运动.当带电体的重力和电场力年夜小可以相比时,不能再将重力疏忽不计.这时研究对象常常被称为“带电微粒”、“带电尘埃”、“带电小球”等等.这时的问题实际上酿成一个力学问题,只是在思索能量守恒的时候需要思索到电势能的变卦.例 已知如图,水平放置的平行金属板间有匀强电场.一根长l 的绝缘细绳一端固定在O 点,另一端系有质量为m 并带有一定电荷的小球.小球原来运动在C 点.当给小球一个水平冲量后,它可以在竖直面内绕O 点做匀速圆周运动.若将两板间的电压增年夜为原来的3倍,求:要使小球从C 点开端在竖直面内绕O 点做圆周运动,至少要给小球多年夜的水平冲量?在这种情况下,在小球运动进程中细绳所受的最年夜拉力是多年夜?解:由已知,原来小球受到的电场力和重力年夜小相等,增年夜电压后电场力是重力的3倍.在C 点,最小速度对应最小的向心力,这时细绳的拉力为零,合力为2mg ,可求得速度为v=gl 2,因此给小球的最小冲量为I= m gl 2.在最高点D 小球受到的拉力最年夜.从C 到D 对小球用动能定理:22212122C D mv mv l mg -=⋅,在D 点+l mv mg F D 22=-,解得F=12mg. 例已知如图,匀强电场方向水平向右,场强E=1.5×106V/m,丝线长l=40cm ,上端系于O 点,下端系质量为m=1.0×10-4kg ,带电量为q=+4.9×10-10C 的小球,将小球从最低点A 由运动释放,求:⑴小球摆到最高点时丝线与竖直方向的夹角多年夜?⑵摆动进程中小球的最年夜速度是多年夜?解:⑴这是个“歪摆”.由已知电场力Fe=0.75G 摆动到平衡位置时丝线与竖直方向成37°角,因此最年夜摆角为74°.⑵小球通过平衡位置时速度最年夜.由动能定理:1.25mg 0.2l=mvB2/2,vB=1.4m/s.五、电容器两个彼此绝缘又相隔很近的导体都可以看成一个电容器.电容UQ C =是暗示电容器容纳电荷身手的物理量,是由电容器自己的性质(导体年夜小、形状、相对位置及电介质)决议的. 平行板电容器的电容的决议式是:ds kd s C επε∝=4 电容器和电源衔接如图,改动板间间隔、改动正对面积或改动板间电解质资料,都会改动其电容,从而能够引起电容器两板间电场的变卦.这里一定要分清两种罕见的变卦:⑴电键K 坚持闭合,则电容器两端的电压恒定(等于电源电动势),这种情况下带d d U E d S kd S C C CU Q 14∝=∝=∝=,,而电量επε θ θ⑵充电后断开K ,坚持电容器带电量Q 恒定,这种情况下s E s d U d sC εεε1,,∝∝∝ 例如图所示,在平行板电容器正中有一个带电微粒.K 闭合时,该微粒恰好能坚持运动.在①坚持K 闭合;②充电后将K 断开;两种情况下,各用什么办法能使该带电微粒向上运动打到上极板?解:由上面的剖析可知①选B ,②选C.例计算机键盘上的每一个按键下面都有一个电容传感器.电容的计算公式是dS C ε=,其中常量ε=9.0×10-12F m-1,S 暗示两金属片的正对面积,d 暗示两金属片间的间隔.当某一键被按下时,d 发作改动,引起电容器的电容发作改动,从而给电子线路收回相应的信号.已知两金属片的正对面积为50mm2,键未被按下时,两金属片间的间隔为0.60mm.只要电容变卦达0.25pF ,电子线路就能收回相应的信号.那么为使按键失掉反响,至少需要按下多年夜间隔? 解:先求得未按下时的电容C1=0.75pF ,再由1221d d C C =得12d d C C ∆=∆和C2=1.00pF ,得Δd=0.15mm. KN A。
几种典型电场线分布示意图及场强电势特点表
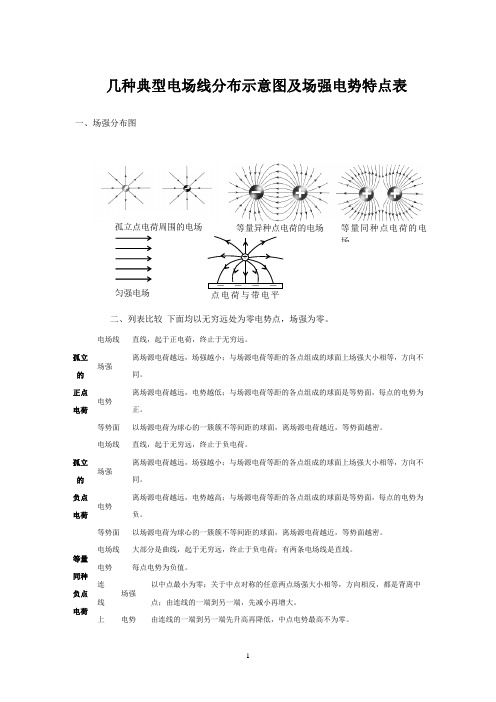
匀强电场 等量异种点电荷的电场 等量同种点电荷的电场- - - - 点电荷与带电平+孤立点电荷周围的电场几种典型电场线分布示意图及场强电势特点表一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的 正点电荷电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的 负点电荷电场线直线,起于无穷远,终止于负电荷。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面 以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量同种正点电荷电场线大部分是曲线,起于正电荷,终止于无穷远;有两条电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
几种典型电场线分布示意图及场强、电势的特点
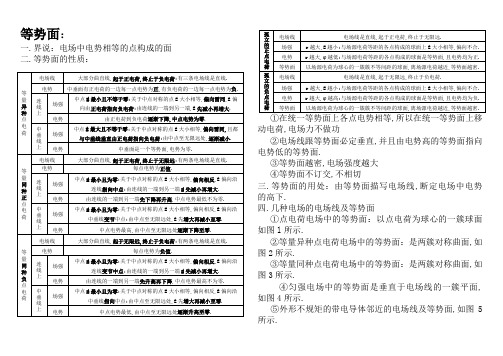
等势面:
一.界说:电场中电势相等的点构成的面
二.等势面的性质:
动电荷,电场力不做功
②电场线跟等势面必定垂直,并且由电势高的等势面指向电势低的等势面.
③等势面越密,电场强度越大
④等势面不订交,不相切
三.等势面的用处:由等势面描写电场线,断定电场中电势的高下.
四.几种电场的电场线及等势面
①点电荷电场中的等势面:以点电荷为球心的一簇球面如图l所示.
②等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示.
③等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示.
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示.
⑤外形不规矩的带电导体邻近的电场线及等势面,如图5所示.
中的等势“面”画成了线,即以“线”代“面”.
等势面:
一.界说:电场中电势相等的点构成的面
二.等势面的性质:
①在统一等势面上各点电势相等,所以在统一等势面上移动电荷,电场力不做功
②电场线跟等势面必定垂直,并且由电势高的等势面指向电势低的等势面.
③等势面越密,电场强度越大
④等势面不订交,不相切
三.等势面的用处:由等势面描写电场线,断定电场中电势的高下.
四.几种电场的电场线及等势面
①点电荷电场中的等势面:以点电荷为球心的一簇球面如图l所示.
②等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示.
③等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示.
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示.
⑤外形不规矩的带电导体邻近的电场线及等势面,如图5所示.
留意:带偏向的线暗示电场线,无偏向的线暗示等势面.图中的等势“面”画成了线,即以“线”代“面”.。
几种典型电场线分布示意图及场强电势特点

匀强电场等量异种点电荷的电场等量同种点电荷的电场 - - - -点电荷与带电平+孤立点电荷周围的电场 几种典型电场线分布示意图及场强电势特点表重点一、场强分布图二、列表比较 下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷 电场线直线,起于正电荷,终止于无穷远。
场强 离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是等势面,每点的电势为正。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
孤立的负点电荷 电场线 直线,起于无穷远,终止于负电荷。
场强离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上场强大小相等,方向不同。
电势离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是等势面,每点的电势为负。
等势面以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等势面越密。
等量同种负点电荷电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是背离中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先升高再降低,中点电势最高不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向中点;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
电势中点电势最低,由中点至无穷远处逐渐升高至零。
等量电场大部分是曲线,起于正电荷,终止于无穷远;有两条同种正点电荷线电场线是直线。
电势每点电势为正值。
连线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都是指向中点;由连线的一端到另一端,先减小再增大。
电势由连线的一端到另一端先降低再升高,中点电势最低不为零。
中垂线上场强以中点最小为零;关于中点对称的任意两点场强大小相等,方向相反,都沿着中垂线指向无穷远处;由中点至无穷远处,先增大再减小至零,必有一个位置场强最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几种典型电场线分布示意图及场强电势特点表一、场强分布图
二、列表比较
下面均以无穷远处为零电势点,场强为零。
孤立的正点电荷电场线直线,起于正电荷,终止于无穷远。
场强
离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上
场强大小相等,方向不同。
电势
离场源电荷越远,电势越低;与场源电荷等距的各点组成的球面是
等势面,每点的电势为正。
等势面
以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等
势面越密。
孤立的负点电荷电场线直线,起于无穷远,终止于负电荷。
场强
离场源电荷越远,场强越小;与场源电荷等距的各点组成的球面上
场强大小相等,方向不同。
电势
离场源电荷越远,电势越高;与场源电荷等距的各点组成的球面是
等势面,每点的电势为负。
等势面
以场源电荷为球心的一簇簇不等间距的球面,离场源电荷越近,等
势面越密。
等量同种负电场线大部分是曲线,起于无穷远,终止于负电荷;有两条电场线是直线。
电势每点电势为负值。
连线上场强
以中点最小为零;关于中点对称的任意两点场强大小相等,方
向相反,都是背离中点;由连线的一端到另一端,先减小再增
大。
等势面
(1)定义:电场中电势相等的点构成的面
(2)等势面的性质:
①在同一等势面上各点电势相等,所以在同一等势面上移动电荷,电场力不做功
②电场线跟等势面一定垂直,并且由电势高的等势面指向电势低的等势面。
③等势面越密,电场强度越大
④等势面不相交,不相切
(3)等势面的用途:由等势面描绘电场线,判断电场中电势的高低。
(4)几种电场的电场线及等势面
①点电荷电场中的等势面:以点电荷为球心的一簇球面如图l所示。
②等量异种点电荷电场中的等势面:是两簇对称曲面,如图2所示。
③等量同种点电荷电场中的等势面:是两簇对称曲面,如图3所示。
④匀强电场中的等势面是垂直于电场线的一簇平面,如图4所示。
⑤形状不规则的带电导体附近的电场线及等势面,如图5所示。
注意:带方向的线表示电场线,无方向的线表示等势面。
图中的等势“面”画成了线,即以“线”代“面”。
+
图1 图2 图3 图5
电场线等势面
图4。
