第三章常微分方程数值解
常微分方程初值问题数值解法

常微分方程初值问题的数值解法在自然科学、工程技术、经济和医学等领域中,常常会遇到一阶常微分方程初值问题:(,),,(),y f x y a x b y a y '=≤≤⎧⎨=⎩ (1) 此处f 为,x y 的已知函数,0y 是给定的初始值。
本章讨论该问题的数值解法,要求f 在区域{(,)|,}G x y a x b y =≤≤<∞内连续,并对y 满足Lipschitz 条件,从而初值问题(1)有唯一的连续可微解()y y x =,且它是适定的。
1 几个简单的数值积分法1.1 Euler 方法(1)向前Euler 公式(显式Euler 公式)10(,),0,1,2,,(),n n n n y y hf x y n y y a +=+=⎧⎨=⎩(2) 其中h 为步长。
由此便可由初值0y 逐步算出一阶常微分方程初值问题(1)的解()y y x =在节点12,,x x 处的近似值12,,y y 。
该公式的局部截断误差为2()O h ,是一阶方法。
(2)向后Euler 公式(隐式Euler 公式)1110(,),0,1,2,,(),n n n n y y hf x y n y y a +++=+=⎧⎨=⎩(3) 这是一个隐格式,也是一阶方法。
这类隐格式的计算比显格式困难,一般采用迭代法求解。
首先用向前Euler 公式提供迭代初值,然后迭代计算:(0)1(1)()111(,),(,),0,1,2,n n n n k k n n n n y y hf x y y y hf x y k +++++⎧=+⎨=+=⎩ (4)1.2 梯形方法1110[(,)(,)],2(),(0,1,2,)n n n n n n h y y f x y f x y y y a n +++⎧=++⎪⎨⎪=⎩= (5) 这也是一个隐格式,是二阶方法。
一般也采用迭代法求解。
迭代公式如下:(0)1(1)()111(,),[(,)(,)],0,1,2,2n n n n k k n n n n n n y y hf x y h y y f x y f x y k +++++⎧=+⎪⎨=++=⎪⎩ (6)1.3 改进的Euler 方法11110(,),[(,)(,)],0,1,2,,2(),n n n n n n n n n n y y hf x y h y y f x y f x y n y y a ++++⎧=+⎪⎪=++=⎨⎪=⎪⎩(7) 为了便于上机编程计算,(7)可改写为110(,),(,),0,1,2,,1(),2(),p n n n cn n p n p c y y hf x y y y hf x y n y y y y y a ++=+⎧⎪=+⎪⎪=⎨=+⎪⎪=⎪⎩(8) 该格式是显式,也是二阶方法。
常微分方程的数值解法

常微分方程的数值解法在自然科学的许多领域中,都会遇到常微分方程的求解问题。
然而,我们知道,只有少数十分简单的微分方程能够用初等方法求得它们的解,多数情形只能利用近似方法求解。
在常微分方程课中已经讲过的级数解法,逐步逼近法等就是近似解法。
这些方法可以给出解的近似表达式,通常称为近似解析方法。
还有一类近似方法称为数值方法,它可以给出解在一些离散点上的近似值。
利用计算机解微分方程主要使用数值方法。
我们考虑一阶常微分方程初值问题⎪⎩⎪⎨⎧==00)(),(yx y y x f dx dy在区间[a, b]上的解,其中f (x, y )为x, y 的已知函数,y 0为给定的初始值,将上述问题的精确解记为y (x )。
数值方法的基本思想是:在解的存在区间上取n + 1个节点b x x x x a n =<<<<= 210这里差i i i x x h -=+1,i = 0,1, …, n 称为由x i 到x i +1的步长。
这些h i 可以不相等,但一般取成相等的,这时na b h -=。
在这些节点上采用离散化方法,(通常用数值积分、微分。
泰勒展开等)将上述初值问题化成关于离散变量的相应问题。
把这个相应问题的解y n 作为y (x n )的近似值。
这样求得的y n 就是上述初值问题在节点x n 上的数值解。
一般说来,不同的离散化导致不同的方法。
§1 欧拉法与改进欧拉法 1.欧拉法1.对常微分方程初始问题(9.2))((9.1) ),(00⎪⎩⎪⎨⎧==y x y y x f dx dy用数值方法求解时,我们总是认为(9.1)、(9.2)的解存在且唯一。
欧拉法是解初值问题的最简单的数值方法。
从(9.2)式由于y (x 0) = y 0已给定,因而可以算出),()('000y x f x y =设x 1 = h 充分小,则近似地有:),()(')()(00001y x f x y hx y x y =≈-(9.3)记 ,n ,,i x y y i i 10 )(== 从而我们可以取),(0001y x hf y y ==作为y (x 1)的近似值。
求常微分方程的数值解

求常微分方程的数值解一、背景介绍常微分方程(Ordinary Differential Equation,ODE)是描述自然界中变化的数学模型。
常微分方程的解析解往往难以求得,因此需要寻找数值解来近似地描述其行为。
求解常微分方程的数值方法主要有欧拉法、改进欧拉法、龙格-库塔法等。
二、数值方法1. 欧拉法欧拉法是最简单的求解常微分方程的数值方法之一。
它基于导数的定义,将微分方程转化为差分方程,通过迭代计算得到近似解。
欧拉法的公式如下:$$y_{n+1}=y_n+f(t_n,y_n)\Delta t$$其中,$y_n$表示第$n$个时间步长处的函数值,$f(t_n,y_n)$表示在$(t_n,y_n)$处的导数,$\Delta t$表示时间步长。
欧拉法具有易于实现和理解的优点,但精度较低。
2. 改进欧拉法(Heun方法)改进欧拉法又称Heun方法或两步龙格-库塔方法,是对欧拉法进行了精度上提升后得到的一种方法。
它利用两个斜率来近似函数值,并通过加权平均来计算下一个时间步长处的函数值。
改进欧拉法的公式如下:$$k_1=f(t_n,y_n)$$$$k_2=f(t_n+\Delta t,y_n+k_1\Delta t)$$$$y_{n+1}=y_n+\frac{1}{2}(k_1+k_2)\Delta t$$改进欧拉法比欧拉法精度更高,但计算量也更大。
3. 龙格-库塔法(RK4方法)龙格-库塔法是求解常微分方程中最常用的数值方法之一。
它通过计算多个斜率来近似函数值,并通过加权平均来计算下一个时间步长处的函数值。
RK4方法是龙格-库塔法中最常用的一种方法,其公式如下:$$k_1=f(t_n,y_n)$$$$k_2=f(t_n+\frac{\Delta t}{2},y_n+\frac{k_1\Delta t}{2})$$ $$k_3=f(t_n+\frac{\Delta t}{2},y_n+\frac{k_2\Delta t}{2})$$ $$k_4=f(t_n+\Delta t,y_n+k_3\Delta t)$$$$y_{n+1}=y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)\Delta t$$三、数值求解步骤对于给定的常微分方程,可以通过以下步骤求解其数值解:1. 确定初值条件:确定$t=0$时刻的函数值$y(0)$。
常微分方程的解析解与数值解

常微分方程的解析解与数值解常微分方程是数学中的重要分支,广泛应用于物理学、工程学、生物学等领域。
解析解和数值解是求解常微分方程的两种常用方法。
本文将介绍常微分方程的解析解和数值解的概念、特点以及应用,并讨论两者在不同情况下的优缺点。
一、解析解解析解是指通过数学方法直接获得的方程的解。
对于某些简单的常微分方程,可以通过变量分离、分离变量、常数变易等方法获得解析解。
解析解具有以下几个特点:1. 精确性:解析解是通过数学方法得到的,是方程的精确解。
它可以给出方程在任意时刻的解,对于问题的研究具有重要意义。
2. 通用性:解析解适用于一类具有相同形式的常微分方程。
一旦求得了一类方程的解析解,就可以应用到同类问题中。
3. 物理含义明确:解析解通常具有明确的物理含义,能够帮助我们理解问题的本质和规律。
解析解在一些特定情况下具有明显的优势。
例如,当方程形式简单、边界条件明确、初值明确时,解析解能够提供准确的结果。
此外,解析解也有助于我们对问题的理论分析和深入研究。
二、数值解数值解是通过数值计算方法获得的方程的近似解。
对于复杂的常微分方程,往往难以找到解析解,这时候就需要借助数值方法进行求解。
数值解具有以下几个特点:1. 近似性:数值解是通过数值计算获得的,只能提供方程的近似解。
随着计算步长的减小,近似解会逐渐接近真实解。
2. 条件灵活:数值解对问题的条件要求相对较低。
例如,数值方法可以求解非线性方程、高阶方程、边值问题等各种复杂情况。
3. 计算复杂度:数值解通常需要借助计算机进行迭代计算,计算复杂度较高。
数值解在实际问题中应用广泛且有效。
数值方法可以通过逼近、插值、差分等数值计算技术,将方程转化成逐步计算的步骤,获得精确度可控的近似解。
数值解的优势在于对于复杂问题的求解能力和计算相对高效。
三、解析解与数值解的比较解析解和数值解各自具有不同的特点和优势,在不同的问题和求解需求中有着相应的应用。
解析解在以下情况下具有优势:1. 简单线性方程:对于形式简单的一阶线性常微分方程,如首次线性方程、可分离变量方程等,可以通过解析方法求得解析解。
常微分方程(组)的数值解法

刚性常微分方程组求解
function demo1 figure ode23s(@fun,[0,100],[0;1]) hold on, pause ode45(@fun,[0,100],[0;1]) %-------------------------------------------------------------------------function f=fun(x,y) dy1dx = 0.04*(1-y(1))-(1-y(2)).*y(1)+0.0001*(1-y(2)).^2; dy2dx = -1e4*dy1dx + 3000*(1-y(2)).^2; f = [dy1dx; dy2dx];
解算指令的使用方法
[T,Y]=ode45(@fun, TSPAN,Y0) 输出变量T为返回时间列向量;解矩阵Y的每一行对应于T的 一个元素,列数与求解变量数相等。
@fun为函数句柄,为根据待求解的ODE方程所编写的ode文
件(odefile); TSPAN=[T0 TFINAL]是微分系统y'=F(t,y)的积分区间;Y0 为初始条件
2.3 常微分方程(组)的数值解法
知识要点
常微分方程初值问题---ode45,0de23
微分方程在化工模型中的应用
•间歇反应器的计算 •活塞流反应器的计算
•全混流反应器的动态模拟
•定态一维热传导问题
•逆流壁冷式固定床反应器一维模型
•固定床反应器的分散模型
Matlab常微分方程求解问题分类
边值问题:
ode解算指令的选择(2)
2.根据常微分方程组是否为刚性方程
y ' Ay b( x) y ( x0 ) y0
常微分方程第三章基本定理

THANKS
感谢观看
线性化定理
总结词
线性化定理是将非线性常微分方程转化为线性常微分方程的方法,从而可以利用线性方程的解法来求解。
详细描述
线性化定理提供了一种将非线性常微分方程转化为线性常微分方程的方法。通过适当的变换,可以将非线性问题 转化为线性问题,从而可以利用线性方程的解法来求解。这个定理在解决复杂的非线性问题时非常有用,因为它 简化了问题的求解过程。
02
CATALOGUE
常微分方程的稳定性
稳定性定义
稳定性的定义
01
如果一个常微分方程的解在初始条件的小扰动下变化不大,那
么这个解就是稳定的。
稳定性的分类
02
根据稳定性的不同表现,可以分为渐近稳定、指数稳定、一致
稳定等。
稳定性判别方法
03
可以通过观察法、线性化法、比较法等方法来判断常微分方程
的解是否稳定。
龙格-库塔方法
总结词
龙格-库塔方法是常微分方程数值解法中一种更精确的 方法,它通过多步线性近似来逼近微分方程的解。
详细描述
龙格-库塔方法的基本思想是利用已知的初值和微分方 程,通过多步线性插值来逼近微分方程的解。具体来 说,龙格-库塔方法通过递推公式来计算微分方程的近 似解,公式如下:(y_{n+1} = y_n + h f(t_n, y_n) + frac{h^2}{2} f(t_{n-1}, y_{n-1}) - frac{h^2}{2} f(t_{n-2}, y_{n-2})) 其中 (h) 是步长,(t_n) 和 (y_n) 是已知的初值,(f) 是微分方程的右端函数。
存在唯一性定理表明,对于任意给定的初值问题,存在一个唯一的解,该解在某个区间内存在并连续 。这个定理是常微分方程理论的基础,为后续定理的证明提供了重要的依据。
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
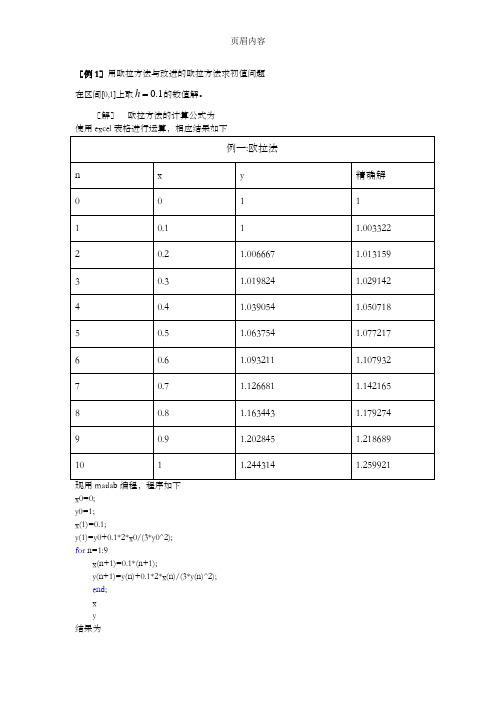
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
常微分方程的数值解法

常微分方程的数值解法常微分方程是研究变量的变化率与其当前状态之间的关系的数学分支。
它在物理、工程、经济等领域有着广泛的应用。
解常微分方程的精确解往往十分困难甚至不可得,因此数值解法在实际问题中起到了重要的作用。
本文将介绍常见的常微分方程的数值解法,并比较其优缺点。
1. 欧拉方法欧拉方法是最简单的数值解法之一。
它基于近似替代的思想,将微分方程中的导数用差商近似表示。
具体步骤如下:(1)确定初始条件,即问题的初值。
(2)选择相应的步长h。
(3)根据微分方程的定义使用近似来计算下一个点的值。
欧拉方法的计算简单,但是由于误差累积,精度较低。
2. 改进欧拉方法为了提高欧拉方法的精度,改进欧拉方法应运而生。
改进欧拉方法通过使用两个点的斜率的平均值来计算下一个点的值。
具体步骤如下:(1)确定初始条件,即问题的初值。
(2)选择相应的步长h。
(3)根据微分方程的定义使用近似来计算下一个点的值。
改进欧拉方法相较于欧拉方法而言,精度更高。
3. 龙格-库塔法龙格-库塔法(Runge-Kutta)是常微分方程数值解法中最常用的方法之一。
它通过迭代逼近精确解,并在每一步中计算出多个斜率的加权平均值。
具体步骤如下:(1)确定初始条件,即问题的初值。
(2)选择相应的步长h。
(3)计算各阶导数的导数值。
(4)根据权重系数计算下一个点的值。
与欧拉方法和改进欧拉方法相比,龙格-库塔法的精度更高,但计算量也更大。
4. 亚当斯法亚当斯法(Adams)是一种多步法,它利用之前的解来近似下一个点的值。
具体步骤如下:(1)确定初始条件,即问题的初值。
(2)选择相应的步长h。
(3)通过隐式或显式的方式计算下一个点的值。
亚当斯法可以提高精度,并且比龙格-库塔法更加高效。
5. 多步法和多级法除了亚当斯法,还有其他的多步法和多级法可以用于解常微分方程。
多步法通过利用多个点的值来逼近解,从而提高精度。
而多级法则将步长进行分割,分别计算每个子问题的解,再进行组合得到整体解。
微分方程数值解

微分方程数值解4.1当常微分方程能解析求解时,可利用Matlab符号工具箱中的功能找到精确解. 见下例求解方程,,,. 键入: yyy,,,20syms x y %定义符号变量diff_equ= ‘D2y+2*Dy-y=0’; %D2y表示,,,Dy= y,yy=dsolve (diff_equ, ‘x’) %定义x为自变量 y=cl*exp ((2^(1/2)-1)*x+c2*exp (-(2^(1/2)+1)*x)%表达式中含c1与c2,表示通解.%初始条件为y (0)=0,,y(0)=1时,按如下方式调用 y=dsolve (diff_equ,‘y (0)=0’, ‘Dy (0)=1’, ‘x’) y=1/4*2^(1/2)*exp ((2^(1/2)-1)*x)—1/4*2^(1/2)*exp (-(2^(1/2)+1)*x)%画出函数y=y (x)的图形ezplot (y,[-2,2])图形具体形式请上机试之.在方程无法获得解析解的情况下,可方便地获得数值解. 下面的例子说明用Matlab求数值解的方法及应注意的问题.[例1] 求解范德堡(vander pol)方程2dxdx2,,,,,(1)0xx 2dtdt求解高阶方程,必须等价地变换为一阶微分方程组,对本例,通过定义两个新的变量,实现这一变换yxydxdt1,2/,, 则令 dydty1/2,2dydtyyy2/(11)*21,,,,编写求解程序分为两部分,第一部分为待求解的方程,存盘的文件名为,待求解方程的函数名.m,,第二部分为求解主程序,本例中取名为main1.m.首先编写待求解方程的文件. 文件存盘名为“vdpol.m”. M,function yprime=vdpol(,)tyyprime (1)=y (2);; (1(1)^2)*(2)(1),,yyymu=2 yprime=[yprime (1);yprime (2)]; yprime (2)=mu*说明函数yprime=vdpol中. 定义为自变量,的形式取决于求解方程的阶数,本(,)tyyt 例中,,为解向量,为导数向量. yprime, y(2)yyyy,[(1),(2)],(1)(1)(1),y yprime,,,函数返回vander pol方程的导数列向量. 因为所求结果为方程数值解,(2)(1),y所以各向量维数只有在主程序求解时定下精度后才能确定.主程序定名为main1.m,你可用你所喜欢的其它名子,但vdpol.m除外. clear functions%调试程序时,放置这一语句是必要的. 它清除前边已编译的存在于内存中的废弃程序[]=ode23 (‘vdpol’,[0,30],[1,0]); ty,y1=y (:,1); %解曲线.y2=y (:,2); %解曲线的导数.polt ( ‘_ _’) tyty,1,,2,说明龙格_库塔的2阶与4阶改进型求解公式的实现,其指令分别为:[]=ode23 (‘f’,tsx,0,options) tx,[]=ode45 (‘f’,tsx,0,options) tx,其中可由系统依据精度要求自动设定,亦可由使用者依据实际需要自己确定,分别说明之. ts(1)若令tstttf,[0,1,,],则输出在指定时刻tttf0,1,,给出,当tstktf,0::时,输出在区间[0,]ttf的等分点上给出,为步长. k(2)若tsttft,[0,],0为自变量初值,tf为终值,此时,options决定自变量的维数,t中的时间点不是等间隔的,这是为了保证所需的相对精度,积分算法改变了步长. 用于t,3,6设定误差限的参数options可缺省,此时系统设定相对误差为,绝对误差为,若1010自行设定误差限,可用如下语句:options=odeset (‘reltol’,, ‘abstol’,) rtat这里的与分别为设定的相对与绝对误差. rtat须注意的是无论用哪种方法确定ttf0,的取值方式,必须由使用者确定且应与相匹配. x0t,y0[1,0],ts,[0,30]y(0)1,y(0)0,为初始条件,本例中,因为,这意味着解曲线,,x0一般说,当解nnn个未知函数的方程组时,为维向量,共含有个初始条件. x0两个输出参数是列向量xx与矩阵,它们具有相同的行数,而矩阵的列数等于方程t组的个数,本例中y(:,1)y(:,2)的列数为2,其中,为自变量上各点函数值,为上各ytt点导数值.最后,提请读者注意的是:ode45也不总是比ode23好,在很多时候,低阶算法更有效,有关微分方程数值解法的更进一步信息,请参考数值分析方面的书籍. 有些参考书提供了一些关于算法选择和如何处理那些时间常数变化范围大的病态方程的非常实用的算法. 4.2 -设有一阶方程与初始条件,yfxy,(,), (4.1) ,yxy(),00,其中适当光滑,关于满足Lipschitz条件,即存在使 fxy(,)LyfxyfxyLyy(,)(,),,,1212则(4.1)式的解存在且惟一.关于yyx,()的解析解一般难以求到或根本无解析解,因而,实际问题中,通常,采用差分的方法. 在一系列离散点xxx,,,,yyy,,,,上寻求其数值近似解. 12n12n相邻两个节点间的间距xxnhn,,,,1,2,hxx,,称为步长,一般地取等步长,则hn0nnn,11、欧拉方法在区间[,]xx上用差商 nn,1yxyx()(),nn,1 h代替(4.1)式中,[,]xxxxxy,对fxy(,)中在上取值还是,而形成向前欧拉公式nn,1nn,1与向后欧拉公式.(1)向前欧拉公式xfxy(,)取左端点,得如下公式 nyxyxhfxyx()()(,()),,(4.2) nnnn,1从yxy(),x点出发,由初值代入(4.2)求得 000yyhfxy,,(,) (4.3) 1000反复利用(4.2),有yyhfxyn,,,(,) 0,1,2, (4.4) nnnn,1其几何意义如图4.1所示.y 图中yyx,()为方程(4.1)的精确 P P43P 2解曲线,其上任意点(,)xy处切线斜率为误差 P 1yyx,() 32Pxy(,)fxy(,). 从初值点出发,用该 P000 0y 0点斜率fxy(,)xx,作一直线段,在 001yyx,() yx() 3处得到Pxy(,)y,由(4.2)式确定, 1111y 3再从Pxy(,)fxy(,)出发,以为斜率 11111作直线段,在xx,Pxy(,)处得到, 2222xxxxx x O03124PPP, 012作为积分曲线yx()的近似,用图4.1 yyx,()n,1这一过程继续下去,形成折线表示在xy处的精确值,为解的近似值,不难得到 n,1n,12h32,,()()()()yxyyxOhOh,,,, nnn,,112P,1这一误差称为局部截断误差. 若一种算法局部截断误差为Oh(),则称该算法具有阶P精度,所以向前欧拉公式具有1阶精度.(2)向后欧拉公式若[,]xxxx中取中的,则有如下公式: fxy(,)nn,1n,1yyhfxyn,,,(,) 0,1,2, (4.5) nnnn,,,111称式(4.5)为向后欧拉公式,因为此式中y未知,故称其为隐式公式,无法用其直n,1接计算y,一般用向前欧拉公式产生初值. n,1(0)yyhfxyn,,,(,) 0,1,2, 11nnnn,,再按下式迭代(1)()kk,yyhfxykn,,,,(,),0,1,,0,1, nnnn,,,111其误差估计如下2h32,,()()()()yxyyxohoh,,,, nnn,,112精度亦为1阶,将向前欧拉公式(4.4)与向后欧拉公式(4.5)及它们的误差的几何说明作一对比,是十分有益的,见图4.2.y 为讨论局部截断误差,在图4.2中设点APxy(,)落在积分曲线yyx,()上,按式 nnnyyx,() (4.4)及式(4.5)分别得 ,P点为与, ABn,1 B且P AB,yyx,()点一定在积分曲线上相应 n点的上、下两边,所以将式(4.4)与(4.5) , 平均之,一定能得到更好的结果.xxx (3)梯形公式 nn,1 将向前与向后欧拉公式加以平均得到所图4.2 谓梯形公式hyyfxyfxyn,,,,[(,)(,)] 0,1,2, (4.6) nnnnnn,,,11123其局部截断误差为Oh(),具有2阶精度.(4)改进的欧拉公式为使计算简单,又免去迭代的繁复,将公式(4.6)简化为两步yyhfxy,,(,)nnnn,1h (4.7) yyfxyfxyn,,,,[(,)(,)], 0,1,2,nnnnn,,11n,12或写为h,yykk,,,()nn,112,2,1nn (4.8) n,0,1,2,kfxy,(,),,211nn,kfxyhk,,(,),,最后指出,上述欧拉方法可推广至微分方程组,如,yfxyz,(,,),,,zgxyz,(,,), ,yxy(),00,,zxz(),,00向前欧拉公式为yyhfxyz,,(,,),nnnnn,1 n,0,1,2, ,zzhgxyz,,(,,),nnnnn,12、龙格_库塔方法由微分中值定理,[()()]/(),01yxyxhyxh,,,,,,, nnn,1又因为,,yxhfxhyxh()(,()),,,,,,,yfxy,(,),所以 nnn从而有yxyxhfxhyxh()()(),(),,,,,, (4.9) nnnn,1令[,]xx,称其为区间上的平均斜率,由(4.9)可知,给kfxhyxh,,,(,()),,nn,1nn出一种平均斜率,可相应导出一种算法. 向前欧拉公式中,精度低. 改进欧kfxy,(,)nn1拉公式中取[,]xxkfxyfxy,,((,)(,)),精度提高,下面,我们在区间内nn,1nnn,1n,12多取几个点,将其斜率加权平均,就能构造出精度更高的计算公式,公式的推导不再具体给出,只开列具体结果.(1)2阶龙格_库塔公式yyhkk,,,(),,,nn,11122,kfxy,(,) (4.10) 1nn,,21nnkfxahyhka,,,,,(,),0,1,,,1,其中,,,,,,,1,,1a,由于4个未知数只有3个方程,所以解不惟一,若令1222a1,即得改进的欧拉公式,具有2阶精度. ,,,,,,,,1a122(3)4阶龙格_库塔公式只给出精典格式中最常用的一种.h,yykkkk,,,,,(22)nn,11234,6,kfxy,(,),1nn,hh, (4.11) kfxyk,,,(,),21nn22,hh,kfxyk,,,(,)32nn,22,kfxhyhk,,,(,),43nn,其计算精度为4阶4.31、模型与问题[例2] 单摆运动图4.3中一根长的细线,一端固定,另一端悬挂质量为 lm的小球,在重力作用下,小球处于竖直的平衡位置. 现使小球偏离平衡位置一个小的角度,然后使其自由运动,在不 ,考虑空气阻力情形下,小球将沿弧线作周期一定的简谐运动.为平衡位置,在小球摆动过程中,当与平衡位置夹 ,,0角为,mgsin,时,小球所受重力在其动运轨迹的分量为 , , l(负号表示力的方向使减少),由牛顿第二定律可得微分方 ,程,,mltmg,,()sin,, (4.12)设小球初始偏离角度为,,且初速为0,式(4.12)的初 0,始条件为,,,,(0),(0)0,, (4.13) 0 mg 当,不大时,,式(4.12)化为线性常系数微sin,,,0分方程图4.3g,,,,,,0 (4.14) l解得g,,()costt, (4.15) 0ll简谐运动的周期为. T,2,g现在的问题是:当,较大时,仍用近似,误差太大,式(4.12)又无解析解,,sin,0试用数值方法在,,30,10,,两种情况下求解,画出的图形,与近似解(4.15),()t00比较,这里设. l,25cm[例3] 捕食与被捕食当鲨鱼捕食小鱼,简记为乙捕食甲,在时刻,小鱼的数量为,鲨鱼的数量为,xt()yt()t当甲独立生存时它的(相对)增长率与种群数量成正比,即有,r,为增长率,xtrxt()(),而乙的存在使甲的增长率r减少,设减少率与乙的数量成正比,而得微分方程,xtxtraytrxaxy()()(()),,,, (4.16)比例系数a反映捕食者掠取食饵的能力.乙离开甲无法生存,设乙独自存在时死亡率为,,ytdyt()(),,,甲为乙提供食物,d使乙的死亡率降低,而促其数量增长,这一作用与甲的数量成正比,于是yt()满足 d,ytydbxtdybxy()(()),,,,,,(4.17)比例系数反映甲对乙的供养能力,设若甲,乙的初始数量分别为 bxxyy(0);(0),, (4.18) 00则微分方程(4.16),(4.17)及初始条件(4.18)确定了甲,乙数量xt()、yt()随时间变化而演变的过程,但该方程无解析解,试用数值解讨论以下问题:(1)设rdabxy,,,,,,1,0.5,0.1,0.02,25,2,求方程(4.16),(4.17)在00条件(4.18)下的数值解,画出xtyt(),()的图形及相图(,)xy,观察解xtyt(),()的周期变化,近似确定解的周期和的最大、小值,近似计算在一个周期内的平均值. xy,xy,(2)从式(4.16)和(4.17)消去得到 dtdxxray(),, (4.19) dyydbx(),,解方程(4.19),得到的解即为相轨线,说明这是封闭曲线,即解确为周期函数.(3)将方程(4.17)改写为,1yxtd()[],,(4.20) by在一个周期内积分,得到xt()yt()一周期内的平均值,类似可得一周期内的平均值,将近似计算的结果与理论值比较.2、实验(1)方程(单摆问题),,mlmg,,,,sin, ,,,,,(0),(0)0,,0,无解析解,为求其数值解,先将其化为等价的一阶方程组. 令,xx,,,,,,方程化为 12,,xx,12,g,,21,,xxsin ,l,102,,xx(0),(0)0,,,其中,gl,,9.8,25,,为(弧度)与(弧度)两种情况,具100.1745,300.5236,0体编程如下:先以danbai.m为文件名存放待解方程. 键入: function xdot =danbai (t,x) %x=[x (1),x (2)],g=9.8;1=25; %x (1)为解向量, x (2)是导数 xdot (1)=x (2); %xdot(1)=,,(1)= x,xdot (2)=-g/1*sin (x (1)); %xdot (2)=,, ,xdot=[xdot (1);xdot (2)]; %必须将导数向量以列向量形式给出.再以主程序(求数值解)调用待求方程,主程序用main2.m为文件名存盘,其代码如下:clear functions[t,x]=ode23 (‘danbai’,[0,10],[0.1745,0])%只计算,,100.1745,(弧度)的情形.01g,,()cos,twtw,,%对近似解,周期 T2,,01gw=sqrt (9.8/25);y=0.1745*cos (w*t);[t,x (:,1),y] %显示数据,无分号. hold on %欲在同一幅图中画近似解. plot (t,x (:,1), ‘b’) %画数值解,绿色plot (t,y, ‘g*’) %用*号,红色画近似解. Hold off(2)食饵_捕食者方程,xtrxaxy(),,,ytdybxy(),,,可化为如下形式,,xrayx,0,,,,,,, ,,,,,,0,,dbxy,,,,y,,初始条件xxyy(0),(0),,表示为 00xx(0),,,,0 ,,,,,yy(0),,,,0以shier.m存盘如下代码function xdot=shier (t,x)r=1;d=0.5;a=0.1;b=0.02;xdot=diag ([r-a*x (2),-d+b*x (1)])*x;,,xxx(1),,,,%x=,,,xdot= ,,,,,,,xy(2),,,,y,,以main3.m存盘如下代码.clear functionsts=0:0.1:15;x0=[25,2];[t,x]=ode45 (‘shier’,ts,x0);[t,x] %显示数据t,x,y plot (t,x)gird %加网格线gtext (‘x(t)’),gtext (‘y(t)’), %用点鼠标方式pause,figure (2) %将x(t),x(t)放至指定点 12plot (x (:,1),x (:,2)) %以x (1)与x (2)为坐标点画相图xlabel (‘x’),ylabel (‘y’)可以猜测,xt()xt()(,)xx与是周期函数,相图是封闭曲线,从数值解可近似定出2121周期为10.7,x2.0,x的最大和最小值分别为与的最大和最小值分别为和,99.328.42.012为求xx与在一个周期的平均值,只需键入: 12y1=x (1:108,1); %x周期为10.7. 1x1p=trapz (y1)*0.1/10.7, %trapz (y1)返回按 y2=x (1:108,2); %梯形法对y1的积107yiyi1()1(1),,x2p=trapz (y2)*0.1/10.7, %分值,x ,i12i,可得xx,,25,10 12对方程dxxray(),,,,dbxray,dxdy,化为 dyydbx(),,xy积分得解dbxray,,()()xeyec, (4.21)即为原方程组的相轨线,其中c由初始条件确定. 为说明上述相轨线是封闭的,令dbxray,,fxxegyye();(),,设其最大值分别为fg,xy,,若满足 mm00fxffyg(),(),, 00mmdr则有,,xy,fgc,,(令,可解出),又当时,相轨线(4.21)fg,,0,0xy,,,00mm00ba有意义. 当fgc,0,,cfgPxy(,)时,相轨线退化为一个点,对时,相轨线如mmmm00图4.4(c),而图(a),(b)分别为fx()与gy()的图像,下面讨论如何由(a),(b)画(c).fxf(),nm y gyg(),gv()nm fx() y2 gm fm Pxy(,)qq 00 1 yP q02 q3 y1x y x x xxxy xyxy012001221 (a)(b)(c)图4.4设cpgpf,,,(0)yy,,xx,fxp(),,若令,则有,由(a)知,,使mm012qxy(,)xxx,,qxy(,)fxfxp()(),,,且于是相轨线应过与,对11010222012 fxgxpggyg()()(),,,xxx,(,)fxp(),gyq(),,,由,令,又由(b)知,mm12 存在yyy,,qxy(,)yy,gygyq()(),,qxy(,)使,且,于是相轨线又过与10231121242yyyyy,(),,xqq,两点,所以对间每个,轨线总要通过纵坐标为的两点,于是1210212相轨线是一条封闭曲线.相轨线封闭等价于xtyt(),()是周期函数,记周期为,为求其在一个周期内的平均T值(,)xy,由1yxtd()(),, by两边在一个周期内积分有((0)())yyT,:T11ln()ln(0)yTydTd,,,xxtdt,,,,() ,,,0TTbbb,,同理ry, a从而xxyy,,,00即xy的平均值恰为相轨线中心点的坐标,提请读者注意的是:这里的与与xtyt(),()p00初始条件中的xy,不是一件事. 00注意到在生态学上的意义,上述结果表明,捕食者的数量与食饵的增长率成rdab,,,正比,与它掠取食饵的能力成反比,食饵的数量与捕食者死亡率成正比,与它供养捕食者的能力成反比.3、练习内容(1)编写改进欧拉公式求微分方程数值解的程序,并用其与ode23求下列微分方程数值解,对二者作出比较.a)22,yxyy,,,,(0)0或y(0)1,.222 b),,,xyxyxny,,,,()02,,,21 yxsin,n,,(Bessel方程,这里令,其精确解为). yy()2,(),,,x222,c),,,yyxyy,,,,cos0,(0)1,(0)0.(2)倒圆锥形容器,上底面直径为1.2m,容器的高亦为1.2m,在锥尖的地方开有一直径为3cm的小孔,容器装满水后,下方小孔开启,由水利学知识可知当水面高度为时,h水从小孔中流出的速度为为重力加速度,若孔口收缩系数为0.6(即若一个面vghg,2,积单位的小孔向外出水时,水柱截面积为0.6),问水从小孔中流完需多少时间?2分钟时,水面高度是多少?(3)一只小船渡过宽为的河流,目标是起点正对着的另一岸上点,已知河水ABd流速vv与船在静水中的速度之比为. k12(a)建立小船航线的方程,求其解析解.(b)设dvv,,,100m,1m/s,2m/s,用数值解法求渡河所需时间,任意时刻小12 船的位置及航行曲线,作图并与解析解比较.(c)若流速v为0,0.5,2 (m/s),结果将如何? 1(4)研究种群竞争模型. 当甲、乙两个种群各自生存时,数量演变服从下面规律xyxtrxytry()(1),()(1),,,, 12nn12其中,rr,nn,xtyt(),()分别为时刻甲,乙两个种群的数量,为其固有增长率,为它t1212们的最大容量,而当这两个种群在同一环境中生存时,由于乙消耗有限资源而对甲的增长产生影响,将甲的方程修改为xyxrxs,,,(1) (4.22) 11nn12这里s的含意是:对于供养甲的资源而言,单位数量乙(相对n)的消耗率为单位数12量甲(相对n)消耗的s倍,类似地,甲的存在亦影响乙的增长,乙的方程应改为 11xyytrys()(1),,, (4.23) 22nn12给定种群的初始值为xxyy(0),(0),, (4.24) 00及参数rrssnn,,,,,后,方程(4.22)与(4.23)确定了两种群的变化规律,因其解析121212解不存在,试用数值解法研究以下问题:(a)设rrnnssxy,,,,,,,,1,100,0.5,2,10,计算,画出xtyt(),()12121200 它们的图形及相图(,)xy,说明时间充分大以后xtyt(),()的变化趋势(人们今天看到的t已经是自然界长期演变的结果).(b)改变rrxy,,,,但s与s不变(保持ss,,1,1),分析所得结果,若12001212ss,,,,1.5(1),0.7(1),再分析结果,由此你得到什么结论,请用各参数生态学上的12含义作出解释.(c)试验当ss,,,,0.8(1),0.7(1)ss,,,,1.5(1),1.7(1)时会有什么结果;当1212时又会出现什么结果,能解释这些结果吗?。
常微分方程数值解

dt (c x)2 (at y)2
由方程无法得到x(t), y(t)的解析解
需要用数值解法求解
0
Q(c,at)
P(x,y)
b
R(c,y )
cx
3
龙格—库塔方法的 MATLAB 实现
x(t) f (t, x), x(t0 ) x0 , x (x1, xn )T , f ( f1, fn )T
6
• clear,clf,shg • %Set the definied time • %ts=0:0.05:0.5; • %ts=0:0.1:1.6; • n=length(ts); • x0=[0 0]; • a=35;b=40;c=15; • opt1=odeset('RelTol',1e-6,'AbsTol',1e-9); • [t,x]=ode45(@jisi,ts,x0,opt1,a,b,c); • %a=35;b=40;c=15; • %opt1=odeset('RelTol',1e-6,'AbsTol',1e-9); • %[t,x]=ode45(@jisi,ts,x0,opt1,a,b,c); • %exact solution x1=c • y1=a*t; • %output t,x(t),y(t) and draw x(t),y(t) • [t,x,y1] • plot(t,x),grid,gtext('x(t)','FontSize',16), • gtext('y(t)','FontSize',16),pause
常微分方程数值解
1
实例1 海上缉私
海防某部缉私艇上的雷达发现正东方向c海里处有一艘走私船 正以速度a向正北方向行驶,缉私艇立即以最大速度b(>a)前往 拦截。如果用雷达进行跟踪时,可保持缉私艇的速度方向始终 指向走私船。
常微分方程初值问题的数值解法

常微分方程初值问题数值解法初值问题:即满足初值条件的常微分方程的解y′=f(x,y),x∈[x0,b]y(x0)=y0.定理1(利普希茨条件)若存在正数L,使得对任意,y1,y2,有|f(x,y1)−f(x,y2)|≤L|(y1−y2)|定理2(解存在性)①若函数f在方区域x∈[a,b],y∈R连续,②函数f关于y 满足利普希茨条件,则对任意x∈[a,b],常微分方程存在唯一的连续可微数值解.两类问题:①单步法---计算下一个点的值yn+1只需要用到前面一个点的值yn②多步法---计算下一个点的值yn+1需要用到前面l个点的值yl1、欧拉法---下一个点的计算值等于前一个点的计算值加上步长乘以前一个点的函数值•具体过程一些批注:显式欧拉方程指下一步要计算的值,不在迭代方程中;隐式欧拉方程指下一步要计算的值,在迭代方程中。
怎么计算隐式欧拉方程----要借助显示欧拉迭代计算---一般用迭代法-----迭代---将微分方程在区间[xn,xn+1]进行积分,然后函数f进行近似,即可得到迭代方程-----迭代方程收敛性?由函数关于y满足利普希茨条件,可以推出迭代公式收敛。
•局部截断误差:假设前n步误差为0,我们计算第n+1步的误差,将次误差称为局部截断误差,且局部误差为O(hp+1)•p阶精度:由理论证明:若局部误差阶的时间复杂度为O(hp+1),则整体误差阶为O(hp)我们称公式精度为p。
•显示欧拉法与隐式欧拉法•梯形方法----将显式欧拉迭代方程与隐式欧拉迭代方程做一下加权平均,构造的计算公式.•改进的欧拉方法---思想:因为梯形公式是隐式公式,将显式欧拉公式对下一步的计算值进行预估,用梯形公式对下一步的计算值进行校正.2、龙格-库塔方法思想:根据Lagrange中值定理,下一次的计算值可以用前一次的计算值加上h乘以前一个点的斜率;而这个斜率用该区间上的多个点的斜率的算数平均来逼近。
注意:怎么计算任意斜率Ki?第i个点的斜率Ki有微分方程可以算出f′=f(xn,yn)所以要算的f(xn,yn)值,由欧拉法即可算出, yn+1=yn+hf′•2阶-龙格-库塔方法----类似改进的欧拉法根据Lagrange中值定理,下一次的计算值可以用前一次的计算值加上h乘以斜率;而这个斜率用区间上的端点和中点的斜率的算数平均来逼近。
常微分方程的数值解

欧拉方法的实现
确定步长和初始值
根据问题的性质和精度要求,选择合适的步长 和初始值。
迭代计算
根据欧拉方法的公式,迭代计算下一个点的值。
终止条件
当达到预设的迭代次数或误差范围时,停止迭代。
常微分方程的应用
总结词
常微分方程在自然科学、工程技术和社会科学等领域有广泛应用。
详细描述
在物理学中,常微分方程可以描述物体的运动规律、电磁波的传播等;在化学中,可以描述化学反应 的动力学过程;在社会科学中,可以用于研究人口增长、经济趋势等。此外,常微分方程还在控制工 程、航空航天等领域有广泛应用。
确定步长和初始值
在应用龙格-库塔方法之前,需要 选择合适的步长和初始值。步长 决定了迭代的精度,而初始值则 用于启动迭代过程。
编写迭代公式
根据选择的步长和初始值,编写 龙格-库塔方法的迭代公式。该公 式将使用已知的函数值和导数值 来计算下一步的函数值。
迭代求解
按照迭代公式进行迭代计算,直 到达到所需的精度或达到预设的 最大迭代次数。
欧拉方法的误差分析
截断误差
由于欧拉方法只使用了微分方程的一次项, 因此存在截断误差。
全局误差
全局误差是实际解与近似解之间的最大偏差。
局部误差
由于每一步都使用了上一步的结果,因此存 在局部误差。
稳定性
欧拉方法是稳定的,但步长和初始值的选择 会影响其稳定性和精度。
04 龙格-库塔方法
龙格-库塔方法的原理
常用的数值解法包括欧拉方法、龙格-库塔方法、改进的欧拉方法、预估 校正方法和步进法等。
常微分方程数值解实验报告

常微分方程数值解实验报告学院:数学与信息科学专业:信息与计算科学:思义学号:201216524 课程:常微分方程数值解实验一:常微分方程的数值解法1、分别用Euler 法、改进的Euler 法(预报校正格式)和S —K 法求解初值问题。
(h=0.1)并与真解作比较。
⎩⎨⎧=++-=10(1y')y x y 1.1实验代码:%欧拉法function [x,y]=naeuler(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值围,y0是初值,h 是步长 x=xspan(1):h:xspan(2); y(1)=y0; for n=1:length(x)-1y(n+1)=y(n)+h*feval(dyfun,x(n),y(n)); end%改进的欧拉法function [x,m,y]=naeuler2(dyfun,xspan,y0,h)%dyfun 是常微分方程,xspan 是x 的取值围,y0是初值,h 是步长。
%返回值x 为x 取值,m 为预报解,y 为校正解 x=xspan(1):h:xspan(2); y(1)=y0;m=zeros(length(x)-1,1); for n=1:length(x)-1 k1=feval(dyfun,x(n),y(n)); y(n+1)=y(n)+h*k1; m(n)=y(n+1);k2=feval(dyfun,x(n+1),y(n+1));y(n+1)=y(n)+h*(k1+k2)/2;end%四阶S—K法function [x,y]=rk(dyfun,xspan,y0,h)%dyfun是常微分方程,xspan是x的取值围,y0是初值,h是步长。
x=xspan(1):h:xspan(2);y(1)=y0;for n=1:length(x)-1k1=feval(dyfun,x(n),y(n));k2=feval(dyfun,x(n)+h/2,y(n)+(h*k1)/2);k3=feval(dyfun,x(n)+h/2,y(n)+(h*k2)/2);k4=feval(dyfun,x(n)+h,y(n)+h*k3);y(n+1)=y(n)+(h/6)*(k1+2*k2+2*k3+k4);end%主程序x=[0:0.1:1];y=exp(-x)+x;dyfun=inline('-y+x+1');[x1,y1]=naeuler(dyfun,[0,1],1,0.1);[x2,m,y2]=naeuler2(dyfun,[0,1],1,0.1);[x3,y3]=rk(dyfun,[0,1],1,0.1);plot(x,y,'r',x1,y1,'+',x2,y2,'*',x3,y3,'o');xlabel('x');ylabel('y');legend('y为真解','y1为欧拉解','y2为改进欧拉解','y3为S—K解','Location','NorthWest');1.2实验结果:x 真解y 欧拉解y1 预报值m 校正值y2 S—K解y30.0 1.0000 1.0000 1.0000 1.00000.1 1.0048 1.0000 1.0000 1.0050 1.00480.2 1.0187 1.0100 1.0145 1.0190 1.01870.3 1.0408 1.0290 1.0371 1.0412 1.04080.4 1.0703 1.0561 1.0671 1.0708 1.07030.5 1.1065 1.0905 1.1037 1.1071 1.10650.6 1.1488 1.1314 1.1464 1.1494 1.14880.7 1.1966 1.1783 1.1945 1.1972 1.19660.8 1.2493 1.2305 1.2475 1.2500 1.24930.9 1.3066 1.2874 1.3050 1.3072 1.30661.0 1.3679 1.3487 1.3665 1.3685 1.36792、选取一种理论上收敛但是不稳定的算法对问题1进行计算,并与真解作比较。
常微分方程的数值解法2010

(11)
要使近似公式(8)的局部截断误差为O(h3),则应要求(10)和(11) 式前三项相同:
c1 c 2 1 c2a2 1 / 2 c 2 b 21 1 / 2
以上方程组有无穷多组解,如取c1=c2=1/2,a2=b21=1,近似公 式(8)即为改进的Euler公式:
常微分方程的数值解法
对一阶常微分方程的初值问题,其一般形式是
y f ( x, y ) y (a ) y0 a x b
(1)
在下面的讨论中,假定f(x,y)连续,且关于y满足李
普希兹(Lipschitz)条件,即存在常数L,使得
f ( x, y ) f ( x, y ) L y y
Y(I+1)=Y(I)+(F(X(I),Y(I))+F(X(I+1),Y(I)+H*F(X(I),Y(I))))*H/2
设 x i x 0 ih ( i 1, 2 ,3 , ); y i , z i 为节点上的近似解, 则有改进的Euler格式为
y i 1 y i hf ( x i , y i ) h f ( x i , y i ) f ( x i 1 , y i 1 ) y i 1 y i 2
则初值问题(1)的解必定存在且唯一。
常微分方程的数值解法
所谓数值解法,就是要求问题(1)的解在若干点:
a x 0 x 1 x n 1 x n b
处的近似值yi(i=0,1,2…n)的方法,yi称为问题(1)的数
值解。相邻两个节点的间距
h n x i 1 x i
(5 )
微分方程数值解法

微分方程数值解法微分方程数值解法是一种将微分方程的解转化为数值计算的方法。
常用的微分方程数值解法包括欧拉法、隐式欧拉法、龙格-库塔法等。
1. 欧拉法:欧拉法是最简单的一种数值解法,它基于微分方程的定义,在给定的初始条件下,通过不断迭代计算微分方程在给定区间上的近似解。
欧拉法的迭代公式为:y_{n+1}=y_n+h\\cdot f(t_n,y_n),其中y_n表示第n步的近似解,t_n表示第n步的时间,h表示步长,f(t_n,y_n)表示微分方程的右侧函数。
2. 隐式欧拉法:隐式欧拉法是欧拉法的改进,它在计算近似解时使用了未知公式的近似值,从而提高了精度。
隐式欧拉法的迭代公式为:y_{n+1}=y_n+h\\cdotf(t_{n+1},y_{n+1}),其中y_{n+1}表示第n+1步的近似解,t_{n+1}表示第n+1步的时间,h表示步长,f(t_{n+1},y_{n+1})表示微分方程的右侧函数。
3. 龙格-库塔法:龙格-库塔法是一种常用的高阶数值解法,它通过计算微分方程的斜率来提高精度。
最常见的是四阶龙格-库塔法,它的迭代公式为:y_{n+1}=y_n+\\frac{1}{6}(k_1+2k_2+2k_3+k_4),其中k_1=h\\cdot f(t_n,y_n),k_2=h\\cdotf(t_n+\\frac{h}{2},y_n+\\frac{1}{2}k_1),k_3=h\\cdotf(t_n+\\frac{h}{2},y_n+\\frac{1}{2}k_2),k_4=h\\cdotf(t_n+h,y_n+k_3)。
这些方法的选择取决于问题的性质和精度要求。
其中,欧拉法是最简单的方法,但精度较低,龙格-库塔法精度较高,但计算量较大。
在实际应用中需要根据问题的具体情况选择合适的数值解法。
3、常微分方程的数值解

xi x0 ih, i 1,2,, n
数值解法需要把连续性的问题加以离散化,从而求出离散
节点的数值解。
对常微分方程数值解法的基本出发点就是离散化。其数值 解法有个基本特点,它们都采用“步进式”,即求解过程顺着 节点排列的次序一步一步地向前推进,描述这类算法,要求给
yi , yi 1 , yi 2 ,, y0 出用已知信息
率场(又称方向场)。设 (t )是常微分方程的一个通解,则 (t )
所代表的曲线集合中任意一点的切线斜率均与该点在斜率场中 的值相同,即曲线沿斜率场所指示的方向伸展。初值问题的解
的函数曲线必开始于初值条件所定义的点(a,y(a))。
可以证明,如果函数在带形区域 R=a≤t≤b,-∞<y<∞}内连续 ,且关于y满足李普希兹(Lipschitz)条件,即存在常数L(它与t,y 无关)使得:
由于数值积分的矩形公式精度很低,以推断出欧拉(Euler) 格式的精度不会很高,应该很粗糙。
例1 用欧拉法解初值问题:
y y xy 2 y(0) 1
(0 x 0.6)
要求:取步长h=0.2 ,计算过程保留4位小数。
2 解: h=0.2, f ( x, y) y xy 欧拉迭代格式:
f (t, y1 ) f (t, y2 ) L y1 y2
对R内任意两个 y1 , y2 都成立,则一阶常微分方程的初值问题在 定义域a, b内存在唯一解。
7.2 常微分方程初值问题数值解法的基本思想
对常微分方程初值问题式的数值解法,就是要算出精确解 y(x)在区间a,b上的一系列离散节点:
可验证,向前欧拉格式的步长越小,由此迭代得到的截断 误差就越小,即精度就越高。但此时值得注意的是:步长合适 的选取非常重要!如果步长过小,不但会增加计算量还会导致 舍入误差的过度积累。因此,选择一个合适的步长,在截断误 差和舍入误差之间取得平衡,对减小向前欧拉格式的误差至关 重要!在这一点上与数值微分类似!
常微分方程常用数值解法综述

第一章绪论1.1 引言常微分方程是现代数学的一个重要分支,是人们解决各种实际问题的有效工具。
微分方程的理论和方法从17世纪末开始发展起来,很快成了研究自然现象的强有力工具,在17到18世纪,在力学、天文、科学技术、物理中,就已借助微分方程取得了巨大的成就。
1864年Leverrer根据这个方程预见了海王星的存在,并确定出海王星在天空中的位置。
现在,常微分方程在许多方面获得了日新月异的应用。
这些应用也为常微分方程的进一步发展提供了新的问题,促使人们对微分方程进行更深入的研究,以便适应科学技术飞速发展的需要。
研究常微分方程常用数值解是数学工作者的一项基本的且重要的工作。
在国内外众多数学家的不懈努力,使此学科基本上形成了一套完美的体系。
微分方程的首要问题是如何求一个给定方程的通解或特解。
到目前为止,人们已经对许多微分方程得出了求解的一般方法。
由于在生产实际和科学研究中所遇到的微分方程问题比较复杂,使这些问题的解即使能求出解析表达式,也往往因计算量太大而难于求出,而对于一些典型的微分方程则可以运用基本方法求出其解析解,并可以根据初值问题的条件把其中的任意常数确定下来。
由于求通解存在许多困难,人们就开始研究带某种定解条件的特解。
首先是Cauchy对微分方程初始解的存在惟一性进行了研究。
目前解的存在惟一性、延拓性、大范围的存在性以及解对初始解和参数的延续性和可微性等理论问题都已发展成熟。
与此同时,人们开始采取各种近似方法来求微分方程的特解,例如求微分方程数值解的Euler折线法、Runge-Kutta法等,可以求得若干个点上微分方程的近似解。
最后,由于当代高科技的发展为数学的广泛应用和深入研究提供了更好的手段。
用计算机结合Matlab软件求方程的精确解、近似解,对解的性态进行图示和定性、稳定性研究都十分方便有效。
本章先介绍常微分的一般概念、导出微分方程的一些典型例子及求解微分方程的思路分析。
从而得到常微分方程的常用数值解法。
常微分方程数值解-图文

常微分方程数值解-图文一只小船度过宽为d的河流,目标是起点A正对着的另一岸B点,已知河水流速v1与船在静水中的中的速度v2之比为k(1)建立描述小船航线的数学模型,求其解析解;(2)设d=100m,v1=1m/,v2=2m/,用数值解法求渡河所需时间,任何时刻小船的位置及航行曲线,作图,并与解析解比较;(3)若流速v1=0,0.5,1.5,2m/结果将如何;解题过程(1)以B为原点,沿河岸向右为某轴正向,垂直河岸向下为y轴正向,建立坐标系。
设在t时刻,船在某方向上的位移是某(t),在Y方向上的位移是y(t)。
在t时刻,船在某方向上的速度是某'(t),在y方向上的速度是y'(t),将船的速度v和水度v1在某,y轴方向上分解,可得:v某v1v2in及vyv2co又tan某y故in某某y22cov2yy某22y某y22则有vydy=dt以及v某(2)d某=v1dtv2某y某22数值解:下面将用龙格-库塔方法对微分方程和微分方程组进行近似求解function某dot=fun(t,某,v1,v2)d=100;v1=1;v2=2;if(norm(某)>1e-5)某dot=[v1-v2某某(1)/qrt(某(1).^2+某(2).^2),-v2某某(2)/qrt(某(1).^2+某(2).^2)];ele某dot=[0,0];endholdoff;某0=[0,-d];[t,某(:,1),某(:,2)];eta=linpace(-pi/2,0,100);d=100;v1=1;v2=2;rou=d某(ab(tan(eta/2))).^(v2/v1)/in(eta);某p=-rou.某co(eta);yp=-rou.某in(eta);plot(某p,yp,'r某');得到v1=1m/时的渡河路线,所用时间为:66.7秒解析解:令某rin;yrco,将直角坐标化为极坐标,由导数的的链式法则,我们可以得到d某indrrcoddycodrrind又d某v某dt;dyvydtdtanm()2其中mv2解得rv1in编程如下:a=pi/2:-0.01某pi:0;d=100;m=2;r=d某ab(tan(a/2).^m./in(a));polar(a,r,'.')运行轨迹如下:(3)依次修改参数V1,运行结果如下如图左一上所示v1=0时的渡河路线,在静水中,船沿直线到达B点,渡河时间为50秒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
?
2
化工应用数学第三章
例题:
A??k1 ? P A??k2 ? S A??k3 ? T
rP
?
dc p dt
?
k1c A
rS
?
dc s dt
?
k2 c A
rT
?
dcT dt
?
k3c A
rA
?
?
dc A dt
?
?k1 ?
k2
?
k3 ?c A
对于
rA ?
? dc A dt
? ?k1 ? k2 ?
k3 ?c A : 求解 c A
7. 收敛性和稳定性
8. 线性多步法
?
5
1. 尤拉(Euler)法
一般初值问题可表示为
化工应用数学第三章
法解值数种各
? y?? f (x, y) a ? x ? b (1.1)
? ?
y(x0
)
?
y0
(1.2)
其中f (x,y)是已知函数, (1.2)是定解条件也称为 初值 条件。
?
6
化工应用数学第三章
2 xn ) yn
已知y0 =1, 由此式可得
y1
?
y0 ?
h( y0 ?
2 x0 ) ? y0
1 ? 0.1 ?
1.1
y2
?
y1 ?
h( y1 ?
2x1 ) ? y1
1.1 ?
0.1(1.1 ?
0.2 ) ? 1.191818 1.1
?
...
12
1. 尤拉(Euler)法
化工应用数学第三章
xn 尤拉公式数值解 yn
与准确解 y ? 1? 2x相比,可看出欧拉公式的计算结
果误差较大 .
?
13
化工应用数学第三章
2. 局部截断误差
定义 在假设ui ? y(xi), 即第i步计算是精确的前提下,考虑的 截断误差 Ri ? y(x i?1) ? ui?1 称为局部截断误差。
定义 若某算法的局部截断误差为 O(hp+1),则称该算法有 p 阶精度。
??? ? ???
P2
P1
y ? y(x)
P0
x0 x1 x2
?
11
1. 尤拉(Euler)法
化工应用数学第三章
例题:用尤拉法解下列方程组,取h=0.1。
? ?
y?
?
?
y?
2x y
(0 ? x ? 1),
?? y(0) ? 1.
解 取步长h=0.1,欧拉公式的具体形式为
yn?1 ?
yn ?
h( yn ?
每步计算 u n ? 1 只用到 u n
?
10
化工应用数学第三章
几何意义
过点 ( x 0 , y 0 ) 的曲线是解 y ( x ) 在 ( x 0 , y 0 )
作 y ( x ) 的切线 ( 斜率 u 1 ) 与直线 x ? x1交于 P1点
? 再作切线(斜率
u
)与直线
2
x ? x 2 交于 P 2点
化工应用数学第三章
? y?? f (x, y)
? ?
y(a
)
?
y0
a ? x? b
假定是 y(x) 初值问题的解,那么,把在节点 xi 附近展开
成Taylor级数,则
y( xi?1 ) ?
y(xi ) ?
hy?(xi ) ?
h2 2
y??(? )
?
y(xi ) ?
hf ( xi , y( xi )) ?
步长为 hi ? (xi?1 - xi )
n 等份
节点 xi ? a ? ihi ,一般取 hi ? h(? (b ? a ) / n)
即等距,要计算出解函数y(x)在一系列节点
a ? x0 ? x1 ? ... ? xn ? b 处的近似值 u0 , u1, ??,?un
?
8
1. 尤拉(Euler)法
显式尤拉公式
将y(xi+1) = y(xi+h)在 处Taylor展开
隐式尤拉公式
将y(xi+1) = y(xi+h)在 处Taylor展开
显式法计算较简单,隐式法计算复杂,可以编程。
?
15
3. 改进的尤拉方法
h2 2
y??(? )
取前两项,并令 u i ? y ( xi )
u i ? 1 ? u i ? hf ( x i , u i )
? 9
1. 尤拉(Euler)法
化工应用数学第三章
u i ? 1 ? u i ? hf ( xi , u i )
依上述公式逐次计算可得:
u1 ? u0 ? hf ( x0 , u0 ) u2 ? u1 ? hf ( x1, u1 ) .. . un ?1 ? un ? hf ( xn , un )
0.2
1.191818
0.4
1.358213
0.6
1.508966
0.8
1.649783
1.0
1.7847Leabharlann 0准确解 y(xn) 1.183216 1.341641 1.483240 1.612452 1.732051
误差 0.008602 0.016572 0.025726 0.037331 0.052719
1. 尤拉(Euler)法
考虑一阶初值问题
:
?? y?? f (x, y) ? ? y(a) ? y0
a ? x? b
弄清常微方程初值 问题数值解法的一 些基本概念和构造
方法的思路.
通过欧拉方法的讨论
最简单而直观实用方法
?
7
1. 尤拉(Euler)法
化工应用数学第三章
把区间[a,b] 分为n个小区间
化工应用数学第三章
第三章 常微分方程的数值解法
主要内容
§3.1、引言 §3.2、初值问题 §3.3、边值问题
?
1
§3.1、引 言
化工应用数学第三章
1.什么是微分方程 ?
在化学工程中关于扩散、反应、传质、传热 和流体流动等问题的数学模型。
微分方程:是包含一个未知函数及其导数关 系的方程。
常微分方程:其中只包含一个自变量的导数 的方程。
? 尤拉法的局部截断误差:
Ri
?
y(xi?1) ? ui?1
? [y(xi) ?
hf(xi , yi ) ?
h2 2
y?(xi )]? [y(xi ) ? hf(xi , yi )]
?
h2 2
y??( xi ) ?
O(h2 )
因此,尤拉法具有 1 阶精度。
?
14
3. 改进的尤拉方法
化工应用数学第三章
利用以前所学知识,进行积分可得:
c ? e c ? ( k1 ? k2 ? k3 ) t
A
A0
求解这样的方程一般我们需要给定初值。
?
3
化工应用数学第三章
例题:
一维均匀介质稳态导热问题。设其一端绝热,另一端恒 温为T1,则此问题模型可用一常微分方程边值问题来描述。
? ??
d (k dT ) ? 0 dx dx
? ?
dT
? dx
x?0 ? 0,T(L) ? T1
由以上两例可以看出,初值问题和边值问题区别在于:前者
在自变量一端给定附加条件,后者在自变量两端附加条件。
?
4
3.2、初值问题
化工应用数学第三章
1. 尤拉法( Euler)
2.局部截断误差
3.改进尤拉法
4. 龙格-库塔法
5. 常微分方程组
6. 步长的选择
