矢量分析
合集下载
矢量分析
性质
∇ × ∇ϕ = 0
梯度
三、矢量场的通量、散度
1、通量
r 定义：若矢量场 A 分布于空间中，在空间中存在任意曲面 S
r 上。定义 A 在曲面上的积分为通量。
r r Ψ = ∫ A ⋅ dS
s
曲面 S 的方向 开表面： 作一封闭线圈，选定绕行方向后，沿绕行方向 按右手螺旋法则，拇指方向为开表面方向 闭合面：外法线方向
s l
无旋场 性质
r ∇× A = 0
r ∇ ⋅ (∇ × A) = 0
旋度
例题讲解（课本） 例题1-8 例题1-9 例题1-10
例题
五、亥姆霍兹定理
内容：位于空间有限区域内的矢量场，当它的散度，旋度 以及它在区域边界上的场分布给定之后，该矢量场就被唯 一确定；对于无限大空间，如果矢量在无限远处减少至零 则该矢量由其散度和旋度唯一确定。
基础
矢量表示式
r r r r A = er Ar + eϕ Aϕ + e z Az
微分长度
r r r r dl = er dr + eϕ rdϕ + e z dz
微分面积
r r dS r = er rdϕdz r r dS ϕ = eϕ drdz r r dS z = e z rdrdϕ
微分体积
dV = rdrd ϕdz
只改变大小，不改变方向 矢量与矢量点乘
s r r r A ⋅ B = A B cosθ AB = Ax Bx + Ay B y + Az Bz
r r r r A⋅B = B⋅A
基础
说明： 1、两个矢量的标量积或点积，是一个标量 。 2、Θ是A、B之间较小的夹角，小于Π弧度。 3、其结果表示一个矢量的模和另一个矢量在该矢量 上的投影和乘积。 矢量与矢量叉乘
∇ × ∇ϕ = 0
梯度
三、矢量场的通量、散度
1、通量
r 定义：若矢量场 A 分布于空间中，在空间中存在任意曲面 S
r 上。定义 A 在曲面上的积分为通量。
r r Ψ = ∫ A ⋅ dS
s
曲面 S 的方向 开表面： 作一封闭线圈，选定绕行方向后，沿绕行方向 按右手螺旋法则，拇指方向为开表面方向 闭合面：外法线方向
s l
无旋场 性质
r ∇× A = 0
r ∇ ⋅ (∇ × A) = 0
旋度
例题讲解（课本） 例题1-8 例题1-9 例题1-10
例题
五、亥姆霍兹定理
内容：位于空间有限区域内的矢量场，当它的散度，旋度 以及它在区域边界上的场分布给定之后，该矢量场就被唯 一确定；对于无限大空间，如果矢量在无限远处减少至零 则该矢量由其散度和旋度唯一确定。
基础
矢量表示式
r r r r A = er Ar + eϕ Aϕ + e z Az
微分长度
r r r r dl = er dr + eϕ rdϕ + e z dz
微分面积
r r dS r = er rdϕdz r r dS ϕ = eϕ drdz r r dS z = e z rdrdϕ
微分体积
dV = rdrd ϕdz
只改变大小，不改变方向 矢量与矢量点乘
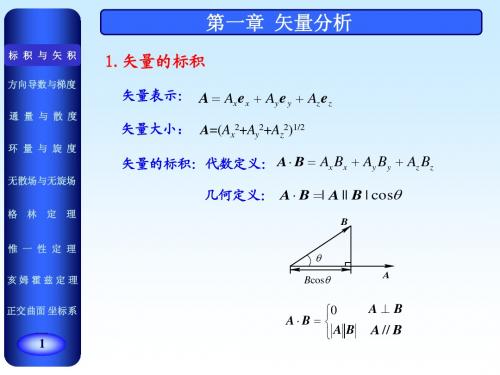
s r r r A ⋅ B = A B cosθ AB = Ax Bx + Ay B y + Az Bz
r r r r A⋅B = B⋅A
基础
说明： 1、两个矢量的标量积或点积，是一个标量 。 2、Θ是A、B之间较小的夹角，小于Π弧度。 3、其结果表示一个矢量的模和另一个矢量在该矢量 上的投影和乘积。 矢量与矢量叉乘
矢量分析
矢 量 分 析一：定义标量：只有大小，没有方向的物理量。
如质量，时间，温度等矢量：即有大小，又有方向的物理量。
如力，位移，速度等 二：矢量表示法线段的长度表示矢量的大小箭头的指向表示矢量的方向 记为：A或x o三：矢量的模和单位矢量模： 矢量的大小，记为A单位矢量：若矢量0A的模为1，且方向与 A 相同,则称0A 为A方向上的单位矢量。
有A =A0A----大小和方向分离表示四：矢量运算相等：两个大小相等且方向相同的矢量相等。
平移：矢量平移后，大小和方向均保持不变。
负矢量：大小相等，方向相反的矢量，记为-A加法：既矢量合成，服从平行四边形法则=A+ BA可演化成三角形法则多矢量合成服从多边形法则减法：既矢量的分解，是加法的逆运算)(BABAC-+=-=大小Am数乘：AmAm=⨯方向: m＞0 与A同向m＜0 与A反向五：矢量的坐标表示222ZY X Z Y X A A A A kA j A i A A ++=++= 令 两矢量kB j B i B B kA j A i A A Z Y X Z Y X++=++=则有kmA j mA i mA k A j A i A m A m k B A j B A i B A B A z y x z y x z z y y x x ++=++=±+±+±=±)()()()( B A = 当且仅当 z z y y x x B A B A B A===六：标积（点积）两矢量相乘得到一个标量A B Cos B A B A C⋅==⋅=θ c由定义可知当θ=0时 C οS θ=1 BA B A=⋅ B当θ=π/2时 C οS θ=00=⋅B A七：矢积（叉积）A两矢量相乘得到一个矢量B A C⨯= 大小: ),(B A Sin B A Sin B A =θ方向: 右手系由定义可知当θ=0时 Sin θ=0 0=⨯B A当θ=π/2时 Sin θ=1 B A B A=⨯)(A B B A⨯-=⨯ 不服从交换律八：矢量的求导令存在矢量 k t A j t A i t A t A z y x )()()()(++=则有:k dtt dA j dt t dA i dt t dA dt t A d z y x)()()()(++=例： 一人字原点出发，先向东走了30米，又向南走了10米，再向西北走了18米，求合位移的大小和方向。
01 第一章 矢量分析
t t0
⑴极限：设 F (t ) 在点 t 0 的某个邻域内有定义（但在 t 0 点
则称，当 t t0
⑵连续：若矢性函数 F (t )在点 t 0 的某个邻域内有定义，且 lim F t F t0 t t0 则称F (t ) 在 t t0 处连续。
(x)
ui
2
(
2 y 2 ) ( z ) ui ui
4、拉梅系数的几何意义
u i 线上的弧微分
x 2 y 2 z 2 dli ( ) ( ) ( ) dui hi dui ui ui ui
dli hi dui
表明：拉梅系数hi是M点处曲线坐标ui的微分dui与该坐标线ui 上弧微分的比例系数。
r(M )
hi
根据全微分运算法则
r r r dl d r du1 du 2 du3 u1 u2 u3
y 矢量线元
引入拉梅系数,矢量线元表示为
图1－7
dl h1du1e1 h2 du2 e2 h3 du3e3 dl1e1 dl2 e2 dl3 e3
2、拉梅系数
空间任意一点 M (u1 , u 2 , u 3 ) ，矢径
若M点在 u1 线上，则矢径 于是，单位矢量表示为
r e1 u1 r u1
r r (u1 , u 2 , u3 )
r (u1 , u 2 c2 , u3 c3 )
M
F (t )
说明：矢径函数对其矢端曲线弧长的导数为曲线上的单位矢量。
3、积分
⑴不定积分：若 A(t ) F (t ) ，则称 A(t )为 F (t )的一个原函数， F (t ) 的原函数的集合叫做的F (t ) 不定积分，记作 )d t A(t ) C F (t ⑵定积分：若矢性函数 F (t ) 在区间 [T1 , T2 ]上的极限
⑴极限：设 F (t ) 在点 t 0 的某个邻域内有定义（但在 t 0 点
则称，当 t t0
⑵连续：若矢性函数 F (t )在点 t 0 的某个邻域内有定义，且 lim F t F t0 t t0 则称F (t ) 在 t t0 处连续。
(x)
ui
2
(
2 y 2 ) ( z ) ui ui
4、拉梅系数的几何意义
u i 线上的弧微分
x 2 y 2 z 2 dli ( ) ( ) ( ) dui hi dui ui ui ui
dli hi dui
表明：拉梅系数hi是M点处曲线坐标ui的微分dui与该坐标线ui 上弧微分的比例系数。
r(M )
hi
根据全微分运算法则
r r r dl d r du1 du 2 du3 u1 u2 u3
y 矢量线元
引入拉梅系数,矢量线元表示为
图1－7
dl h1du1e1 h2 du2 e2 h3 du3e3 dl1e1 dl2 e2 dl3 e3
2、拉梅系数
空间任意一点 M (u1 , u 2 , u 3 ) ，矢径
若M点在 u1 线上，则矢径 于是，单位矢量表示为
r e1 u1 r u1
r r (u1 , u 2 , u3 )
r (u1 , u 2 c2 , u3 c3 )
M
F (t )
说明：矢径函数对其矢端曲线弧长的导数为曲线上的单位矢量。
3、积分
⑴不定积分：若 A(t ) F (t ) ，则称 A(t )为 F (t )的一个原函数， F (t ) 的原函数的集合叫做的F (t ) 不定积分，记作 )d t A(t ) C F (t ⑵定积分：若矢性函数 F (t ) 在区间 [T1 , T2 ]上的极限
第一章 矢量分析
格 林 定 理
立了面积分和线积分的关系。从物理角度可以理解为斯托克 立了面积分和线积分的关系。从物理角度可以理解为斯托克 斯定理建立了区域 S 中的场和包围区域 S 的闭合曲线 l 上的 场之间的关系。因此， 中的场， 场之间的关系。因此，如果已知区域 S 中的场，根据斯托克 上的场，反之亦然。 斯定理即可求出边界 l 上的场，反之亦然。
Ψ = ∫ A ⋅ dS
S
通量可为正、或为负、或为零 当矢量穿出某个闭合面时， 通量可为正、或为负、或为零。当矢量穿出某个闭合面时， 认为该闭合面中存在产生该矢量场的源 认为该闭合面中存在产生该矢量场的源；当矢量进入这个闭合 面时，认为该闭合面中存在汇聚该矢量场的洞 ）。闭合 面时，认为该闭合面中存在汇聚该矢量场的洞（或汇）。闭合
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
10
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度 通 量 与 散 度 环 量 与 旋 度 环 量 与 旋 度 无散场与无旋场 格 林 定 理
2. 旋度：旋度是一个矢量。若以符号 rot A 表示矢量 A 的旋 旋度：旋度是一个矢量。 具有最大环量强度的方向， 度, 则其方向是使矢量 A 具有最大环量强度的方向， 其大小等于对该矢量方向的最大环量强度， 其大小等于对该矢量方向的最大环量强度，即
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
1
0 A⋅ B = A B
A⊥B
A // B
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度
2.矢量的失积 2.矢量的失积
矢量的失积：代数定义： 矢量的失积：代数定义：
ex A × B = Ax Bx ey Ay By ez Az Bz
立了面积分和线积分的关系。从物理角度可以理解为斯托克 立了面积分和线积分的关系。从物理角度可以理解为斯托克 斯定理建立了区域 S 中的场和包围区域 S 的闭合曲线 l 上的 场之间的关系。因此， 中的场， 场之间的关系。因此，如果已知区域 S 中的场，根据斯托克 上的场，反之亦然。 斯定理即可求出边界 l 上的场，反之亦然。
Ψ = ∫ A ⋅ dS
S
通量可为正、或为负、或为零 当矢量穿出某个闭合面时， 通量可为正、或为负、或为零。当矢量穿出某个闭合面时， 认为该闭合面中存在产生该矢量场的源 认为该闭合面中存在产生该矢量场的源；当矢量进入这个闭合 面时，认为该闭合面中存在汇聚该矢量场的洞 ）。闭合 面时，认为该闭合面中存在汇聚该矢量场的洞（或汇）。闭合
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
10
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度 通 量 与 散 度 环 量 与 旋 度 环 量 与 旋 度 无散场与无旋场 格 林 定 理
2. 旋度：旋度是一个矢量。若以符号 rot A 表示矢量 A 的旋 旋度：旋度是一个矢量。 具有最大环量强度的方向， 度, 则其方向是使矢量 A 具有最大环量强度的方向， 其大小等于对该矢量方向的最大环量强度， 其大小等于对该矢量方向的最大环量强度，即
惟 一 性 定 理 亥姆霍兹定理 正交曲面 坐标系
1
0 A⋅ B = A B
A⊥B
A // B
第一章 矢量分析
标 积 与 矢 积 方向导数与梯度
2.矢量的失积 2.矢量的失积
矢量的失积：代数定义： 矢量的失积：代数定义：
ex A × B = Ax Bx ey Ay By ez Az Bz
矢量分析
二、方向导数 在实际应用中，不仅需要宏观上了解场在空间的数值，还要知道在不同 方向上场变化的情况。方向导数表征标量场空间中，某点处场沿各个方向变 化的规律。
取等位面 u 1、定义：
x, y , z
增加的方向，相互垂直且满足右手螺旋法则
v ˆ ˆ ˆ 矢量表示： A = e x Ax + e y Ay + e z Az
v 位置矢量： r = e x x + e y y + e z z ˆ ˆ ˆ
v ˆ ˆ ˆ dr = e x dx + e y dy + e z dz 微分长度元：
（2）球面坐标系下矢量运算
v ˆ ˆ ˆ A = er Ar + eθ Aθ + eϕ Aϕ v ˆ ˆ ˆ B = er Br + eθ Bθ + eϕ Bϕ
v v ˆ ˆ ˆ A ± B = er ( Ar ± Br ) + eθ ( Aθ ± Bθ ) + eϕ ( Aϕ ± Bϕ )
v v A• B = Ar Br + Aθ Bθ + Aϕ Bϕ
e 单位矢量：ˆ ρ
ρ
,φ
ˆ , eφ
,z
ˆ , ez
0 ≤ ρ < ∞ , 0 ≤ φ ≤ 2π , − ∞ < z < ∞
ˆ ˆ ˆ e z = e ρ × eφ ˆ ˆ ˆ e ρ = eφ × e z ˆ ˆ ˆ eφ = e z × e ρ
ˆ ˆ ˆ ↑ e ρ 、eφ 、e z
分别代表ρ、φ、z 增加的方向，相互垂直且满足右手螺旋法则
ˆ 由于 θ、ϕ 不是常矢量，与 er
ˆ ∂er ˆ =eθ ∂θ ˆ ∂ eθ ˆ = −er ∂θ ˆ ∂ eϕ = 0 ∂θ
矢量分析
对于矢量也存在相应的函数，称为矢性函数
例如：卫星的速度是时间 t 的矢性函数
V V t
第一章
矢量分析
场的定义：
如果在某一空间区域内的每一点，都对应着某 个物理量的一个确定的值，则称在此区域内确定了 该物理量的一个场。
若该物理量为标量，则称标量场,
可用标量函数表示f(x,y,z)；
x
证明：M点的坐标为M(x0+Δx, y0+Δy, z0+Δz)，由于函数φ在 M0处可微，故
( M ) ( M 0 ) x y z x y z
第一章
矢量分析
z
两边除以ρ，可得
x y z x y z cos cos cos x y z
x 2 y 2 c2 解之即得矢量方程 z c1 x
c1和c2是积分常数。
第一章
矢量分析
1.2 标量场的方向导数和梯度
1.2.1 标量场的方向导数
方向导数表征标量 场空间中，某点处场值沿
各个方向变化的规律。
方向导数的定义：
图 1-2 方向导数的定义
第一章
矢量分析
设M0是标量场φ=φ(M)中的一个已知点，从M0出发沿某一方
A B
矢量的加法运算
A B B A
A B
A B
A B A ( B)
矢量的减法运算
A B
第一章
矢量分析
两个矢量的乘积
两个矢量的乘积有两个定义： 点积
运算结果 运算结果
标量 矢量
标积 矢积
第1章-矢量分析
⎝
2⎠
⎝
2⎠
Ay
⎜⎛ x,y+Δy,z ⎟⎞ ⎝ 2⎠
=
Ay
(x,y,z)
+
∂Ay ∂y
(x,y,z)
Δy 2
+
1 2!
∂2 Ay ∂y2
( Δy )2 2
+ ...
得
ΔΨr
=
( Ay
+
∂Ay ∂y
Δy 2
+ .........) ΔxΔz
divA 直角坐标表示式的推导
11
§1.2通量、散度、散度定理
8
§1.2通量、散度、散度定理
作业：1.1-1,1.1-3,1.1-5
S为封闭面时： 若Ψ > 0， 有净通量流出，说明S内有源； 若Ψ < 0， 有净通量流入，说明S内有洞(负源); 若Ψ = 0， 则净通量为零，说明S内无源。
举例：
由《大学物理》知，电通量 Ψe = ∫sD ⋅ ds = Q（高斯定理） 水流的单位时间流量（米3/秒）＝ v ⋅ d s
A 矢量的模：
γ
β o
Ay
α Ax
y
A = A = Ax2 + Ay 2 + Az 2
x
A 的单位矢量：
Aˆ = A = xˆ Ax + yˆ A y + zˆ Az AA AA
= xˆ cosα + yˆ cos β + zˆ cosγ
2
§1.1矢量代数
二、标量积和矢量积
a) 标量积（点乘）
加减乘除
∂y 4π r 5
∂Dz = q r 2 − 3z 2
∂z 4π r 5
1第一章 矢量分析
∂u ∂n
∂u 可得 ∂x = grad u ⋅ e x ∂u ∂u = grad u ⋅ e l ⇒ = grad u ⋅ e y ∂l ∂y ∂u = grad u ⋅ e z ∂z
在直角坐标系中梯度的计算#43; ey + ez =∇ ϕ ∂x ∂y ∂z
d iv A = lim
计算公式
∆v→ 0
1 ∆v
∫
s
A ⋅ dS
divA=∇⋅ A=
∂A x ∂x
+
∂A y ∂y
+
∂A z ∂z
三、散度的物理意义 • 矢量的散度是一个标量，是空间坐标点的函数； 矢量的散度是一个标量，是空间坐标点的函数； • 散度代表矢量场的通量源的分布特性
∇• A = 0 (无源） 无源）
v 1 ∂ ( ρ Fρ ) 1 ∂Fϕ ∂Fz ∇⋅F = + + ρ ∂ρ ρ ∂ϕ ∂z
ˆ eρ 1 ∂ ∇× A = ρ ∂ρ Aρ ˆ ρ eϕ ˆ ez
∂ ∂ ∂ϕ ∂z ρ Aϕ Az
3、在球坐标系
ˆ ∇ = er ∂ 1 ∂ 1 ∂ ˆ ˆ + eθ + eϕ r ∂θ r sin θ ∂ϕ ∂r
2）在柱面坐标系中： ）
∂u 1 ∂u ∂u ˆ ˆ ˆ gradu = eρ + eϕ + ez ∂ρ ∂z r ∂ϕ
3）在球面坐标系中： ）在球面坐标系中：
∂u 1 ∂u 1 ∂u ˆ ˆ ˆ g ra d u = er + eθ + eϕ ∂r r ∂θ r sin θ ∂ ϕ
【例题】 例题】
斯托克斯定理
∫l A⋅dl = ∫
第1章矢量分析
F dS S
S1 F dS1
S2 F dS2
S3 F dS3
S4 F dS4
S5 F dS5
S6 F dS6
aˆx aˆz 0, aˆy aˆy 1,
aˆy aˆz 0 aˆz aˆz 1
A B (Axaˆx Ayaˆy Azaˆz ) (Bxaˆx Byaˆy Bzaˆz )
Ax Bx Ay By Az Bz
•结论: 两矢量点积等于对应分量的乘积之和。
电磁场与电磁波
第1章 矢量分析
其中：dl ,dS 和 dV 称为微分元。
dS
dl
1. 直角坐标系
在直角坐标系中，坐标变量为(x,y,z)，如图，做一微分体元。
线元：dlx dxaˆx
dly dyaˆy
面元： dSx dydzaˆx dSy dxdzaˆy
dlz dzaˆz dl dxaˆx dyaˆy dzaˆz
电磁场与电磁波
第1章 矢量分析
3.乘法：
（1）标量与矢量的乘积：
k 0 方向不变，大小为|k|倍
kA k | A | aˆ
k
0
k 0 方向相反，大小为|k|倍
（2）矢量与矢量乘积分两种定义
a. 标量积（点积）：
B
A B | A| | B | cos
A
两矢量的点积含义： 一矢量在另一矢量方向上的投影与另一矢量模的乘积，
定义： A BC | A|| B || C | sin cos
含义： 标量三重积结果为三矢量构成
的平行六面体的体积 。
h BC
A C
B
电磁场与电磁波
第1章 矢量分析
V A (BC) C (A B) B (C A)
第一章矢量分析
r u ( x, y , z , t ) 、 F ( x , y , z , t )
r u ( x, y, z )、 F ( x, y, z )
第一章 矢量分析
1.1.1 标量场的等值面
标量场空间中，由所有场值相等的点所构成的面，即为等值面。 即若标量函数为 u u( x, y, z) ，则等值面方程为：
第一章 矢量分析
第一章
主 要
矢量分析
内 容
梯度、散度、旋度、亥姆霍兹定理 1. 标量场的方向导数与梯度
2. 矢量场的通量与散度 3. 矢量场的环量与旋度 4. 无散场和无旋场 5. 格林定理
6. 矢量场的惟一性定理
7. 亥姆霍兹定理 8. 正交曲面坐标系
第一章 矢量分析
1.1 矢量代数
1.1.1 标量和矢量
空间中存在任意曲面S，则定义：
v v S A(r ) dS
为矢量 A(r ) 沿有向曲面 S 的通量。
矢量场的通量
第一章 矢量分析
若S 为闭合曲面
s
v v v Ñ A ( r ) dS
物理意义：表示穿入和穿出闭合面S的通量的代数和。 说明：1) 面元矢量 dS 定义：面积很小的有向曲面。
s
第一章 矢量分析
通过闭合面S的通量的物理意义：
0
0
若 0 ，通过闭合曲面有净的矢量线穿出，闭合面内有发 出矢量线的正源； 若 0 ，有净的矢量线进入，闭合面内有汇集矢量线的负源； 若 0 ，进入与穿出闭合曲面的矢量线相等，闭合面内无 源，或正源负源代数和为0。 局限：只能判断闭合曲面中源的正负特性，不能显示源的特 性。如果令包围某点的闭合面无限收缩，那么该点就可以通量 可以表示源的特性。
矢量分析的知识点总结
矢量分析的知识点总结一、矢量的定义和表示1.1 矢量的定义矢量是指在空间中具有大小和方向的量，它可以用来表示物理量的大小和方向，如力、速度等。
矢量通常用箭头表示，箭头的长度表示矢量的大小，箭头的方向表示矢量的方向。
1.2 矢量的表示矢量可以用不同的方式表示，常见的表示方法有坐标表示和分量表示。
坐标表示是指用矢量所在空间的坐标系来表示矢量，分量表示是指将矢量在坐标系中的投影表示为一组数值。
1.3 矢量的运算矢量的运算包括加法、减法、数量乘法和点乘等。
加法和减法的运算结果是一个新的矢量，数量乘法是指将矢量的长度进行缩放，点乘是指将两个矢量的长度和夹角进行运算得到一个标量。
二、矢量的微积分2.1 矢量的导数矢量的导数是指对矢量的每个分量分别求导，得到的是一个新的矢量。
矢量的导数在物理学中有着广泛的应用，如速度、加速度等物理量都可以用矢量的导数来表示。
2.2 矢量场矢量场是指在空间中的每个点都有一个矢量与之对应的场，它可以用来描述流体的速度场、电场、磁场等。
矢量场的微积分可以用来研究矢量场的性质和行为。
2.3 曲线积分曲线积分是指对沿着曲线的矢量场进行积分，得到的是一个标量。
曲线积分在物理学中有着重要的应用，如对力沿着曲线的功的计算等。
2.4 曲面积分曲面积分是指对矢量场在曲面上的投影进行积分，得到的是一个标量。
曲面积分在物理学中也有着广泛的应用，如对电场在闭合曲面上的通量计算等。
三、矢量分析的应用3.1 物理学中的应用矢量分析在物理学中有着广泛的应用，如在力学中用于描述力、速度、加速度等物理量；在电磁学中用于描述电场、磁场等物理量。
3.2 工程学中的应用矢量分析在工程学中也有很多应用，如在流体力学中用于描述流体的速度场、压力场等；在航空航天工程中用于描述飞行器的运动状态、姿态等。
3.3 计算机科学中的应用矢量分析在计算机科学中也有着重要的应用，如在图形学中用于描述图像的旋转、平移等运动；在机器学习中用于描述数据的特征、相似度等。
矢量分析
关于散度的一些计算
r r r r ∇ ⋅ ( A ± B) = ∇ ⋅ A ± ∇ ⋅ B r r r ∇ ⋅ (ϕ A) = ϕ∇ ⋅ A ± A ⋅∇ϕ
3)、散度定理（奥——高定理） 、散度定理（ 高定理） 高定理
∫
V
r r r ∇ ⋅ AdV = A ⋅ dS ∫
S
它将矢量散度的体积分变换成该矢量的面积分， 它将矢量散度的体积分变换成该矢量的面积分，或将矢量 的面积分转换为该矢量散度的体积分。 的面积分转换为该矢量散度的体积分。
第一章 矢量分析
场的几何描述 r 矢量场 A( x, y, z ) 的场线及场线方程
dx dy dz = = Ax Ay Az
标量场
ϕ (x, y, z) 的等值面方程为
ϕ ( x, y , z ) = const.
第一章 矢量分析
2 通过点M 的等值面方程。 例1、 求标量场 ϕ = ( x + y ) − z 通过点 (1, 0, 1)的等值面方程。 、 的等值面方程
第一章 矢量分析
4、 矢量场的环量和旋度
1）、环流（环量 ） 环流（
r r 沿曲线c关于 在矢量场 A 中，沿曲线 关于 的线积分称为该矢量场 A
的环流 。
∫
c
r r A ⋅ dl = A cos θ dl ∫
c
环流表示闭合曲线内存在另 一种源——涡旋源 一种源 涡旋源
第一章 矢量分析
2）、 矢量场的旋度 ）、
max
r ∂ϕ r ∂ϕ r ∂ϕ r = G =| ex + ey + ez | ∂x ∂y ∂z
第一章 矢量分析
中的一点M处有一矢量 处有一矢量， 定义：在标量场 ϕ ( x, y , z )中的一点 处有一矢量，其方向取函 r 点处变化率最大的方向， 数 ϕ 在M点处变化率最大的方向，其模等于 | G | ，该矢量称为标 点处变化率最大的方向 点处的梯度 表示。 量场 ϕ 在M点处的梯度，用grad ϕ 表示。 点处的梯度， 在直角坐标系中， 梯度的表达式为 直角坐标系中
第1章 矢量分析
体积元
dV dxdydz
z
z
z0
（ 平面） ez
P
ey
ex
o
点P(x0,y0,z0)
y
y y0（平面） x x x0 （平面）
直角坐标系
z dSz ezdxdy
dz
dSy eydxdz
o
dy
dx dSx exdydz
y
x
直角坐标系的长度元、面积元、体积元
第一章 矢量分析
A Axex Ayey Azez
sin cos
0
0 ex
0
e y
1 ez
ex cos
ey
sin
ez 0
sin cos
0
0 e
0
e
1 ez
第一章 矢量分析
2、直角坐标系与球坐标系的关系
er ex sin cos ey sin sin ez cos e cos cos ex cos sin ey sin ez e ex sin ey cos
坐标变量 坐标单位矢量 位置矢量 线元矢量 面元矢量
x, y, z,( x, y, z )
ex , ey , ez
r ex x ey y ez z
dl
exdx
ey
dy
ezdz
dSx exdlydlz exdydz
dSy eydlxdlz eydxdz
dSz ezdlxdly ezdxdy
A B AxBx Ay By Az Bz
ex ey ez
A B Ax Ay Az Bx By Bz
ex
Ay By
Az Bz
ey
Ax Bx
第一章 矢量分析
第一章 矢量分析§1 场的概念 一. 矢量与标量1.概念标量 实数域内只有大小的量。
如：电压、温度、时间、电荷等。
矢量 实数域内既有大小又有方向的量，且加法运算遵循平行四边形法则。
如：力F 、电场强度E 、磁场强度H、速度等。
常矢：矢量的模和方向都不变。
如：x e 、y e 、z e。
变矢：模和方向或两者之一变化的矢量(在实际问题中遇到的更多)。
如：r e 、θe 、ϕe 、ρe。
物理量 标量或矢量被赋予物理单位，成为有物理意义的量。
2.矢量的表示印刷 黑体 A ；A(白体)表示A的模。
手写 模和方向均表示出。
表示A 的方向(模为1)。
A 表示矢量A 的模。
▪ 零矢（空矢）：模为零的矢量。
0▪单位矢量：模为1的矢量。
如直角坐标系坐标轴方向x e 、y e 、z e （参考书）。
也有用x a、y a 、z a或i 、j 、k 或 x ˆ、y ˆ、z ˆ 等表示。
若三个相互垂直的坐标轴上的分量已知，一个矢量就确定了。
如直角坐标系中，矢量A的三个分量模值分别是A x , A y , A z ，则直角坐标系： A的模为 A的单位矢量为判断以下手写表示是否正确：（矢量≠标量） （标量≠矢量） ☹ 常见手写表示错误： Aa A 0=A A a=0zz y y x x A e A e A e A ++=222z y x A A A A ++=γβcos cos cos ˆ0z y x zz y y x x A e e a e A A e A A e A A e A A a A++=++===5=E 5x e E=5x e E =765zy x e e e E ++= 765z y x e e e E++=二. 矢量的代数运算1.矢量的加减法2.矢量的乘法a.标量积(点乘) 结果为标量！b.矢量积(叉乘) 结果为矢量！直角坐标系：∙ 点乘 垂直 平行点乘符合交换律： ∙ 叉乘平行 垂直注意：z x y e e e-=⨯ 叉乘不符合交换律： 三.矢量场与标量场1.场在某一空间区域内的每一点，都对应着某个物理量的一个确定的值，则称在此区域内确定了该物理量的一个场。
矢量分析
t → t0 → → → →
4°
lim
t → t0 →
[ A （t）× B （t）]=
→
lim A （t）× lim B （t）
t → t0 t → t0
5°若 A （t）= Ax（t）
→
i
+Ay（t）
j
→
+Az（t）
→
k ，则
→
lim A （t）= lim Ax（t） i + lim Ay（t）
t → t0 t → t0 t → t0
第一章 矢量分析
矢量分析，是矢量代数的继续，也是场论的基础知识，同时它还是研究其他许多学科的有用 工具。 本章主要介绍矢性函数及其微分，积分。
第一节 矢性函数
1 矢量函数的定义 常矢： 模和方向都保持不变的矢量。 局限性：不能刻划所有矢量 变矢：模和方向或其中之一会改变的矢量 例：质点 M 沿曲线 l 运动时，其速度矢量 V 在运动过程中就是一个变矢 V2
o
y
注： 矢径
→
r
= OM =x
i
+y
j
+z
k
， 因此， 若矢性函数 A（t） 的起点取在坐标原点， 则 A（t）
→
= OM ，而 A （t）={ Ax（t） ，Ay（t） ，Az（t）}， OM ={x，y，z}， 从而
⎧ x = Ax (t ) ⎪ ⎨ y = Ay(t) ……矢端曲线 L 的以 t 为参数的参数方程 ⎪ z = Az(t) ⎩
3 矢性函数的微分 ，称 △定义：设有矢性函数 A = A （t） 为矢性函数 A （t）在 t 处的微分
→ → → →
d A = A ˊ（t）dt
4°
lim
t → t0 →
[ A （t）× B （t）]=
→
lim A （t）× lim B （t）
t → t0 t → t0
5°若 A （t）= Ax（t）
→
i
+Ay（t）
j
→
+Az（t）
→
k ，则
→
lim A （t）= lim Ax（t） i + lim Ay（t）
t → t0 t → t0 t → t0
第一章 矢量分析
矢量分析，是矢量代数的继续，也是场论的基础知识，同时它还是研究其他许多学科的有用 工具。 本章主要介绍矢性函数及其微分，积分。
第一节 矢性函数
1 矢量函数的定义 常矢： 模和方向都保持不变的矢量。 局限性：不能刻划所有矢量 变矢：模和方向或其中之一会改变的矢量 例：质点 M 沿曲线 l 运动时，其速度矢量 V 在运动过程中就是一个变矢 V2
o
y
注： 矢径
→
r
= OM =x
i
+y
j
+z
k
， 因此， 若矢性函数 A（t） 的起点取在坐标原点， 则 A（t）
→
= OM ，而 A （t）={ Ax（t） ，Ay（t） ，Az（t）}， OM ={x，y，z}， 从而
⎧ x = Ax (t ) ⎪ ⎨ y = Ay(t) ……矢端曲线 L 的以 t 为参数的参数方程 ⎪ z = Az(t) ⎩
3 矢性函数的微分 ，称 △定义：设有矢性函数 A = A （t） 为矢性函数 A （t）在 t 处的微分
→ → → →
d A = A ˊ（t）dt
矢量分析
运 算 规律： A B B A （交换律）
A (B C) A B AC （分配律）
AB
AB 0
A// B
A B AB
ex ey ey ez ez ex 0
ex ex ey ey ez ez 1
第一章 矢量分析
（4）矢量的矢量积（叉积）
A B
A B en ABsin
C=A+B
A
AB
B
C2 C C (A B) (A B)
A A B B 2A B
A2 B2 2 ABcosAB A2 B2 2 ABcos
第一章 矢量分析
1.2 三种常用的正交曲线坐标系
三维空间任一点的位置可通过三条相互正交曲线的交点来确定。 三条正交曲线组成的确定三维空间任意点位置且满足右手螺旋 规则的体系，称为正交曲线坐标系；三条正交曲线称为坐标轴； 描述坐标轴的量称为坐标变量。 在电磁场与波理论中，三种常用的正交曲线坐标系为：直角坐 标系、圆柱坐标系和球坐标系。
B
推论：任意多个矢量首尾相连组成闭合多边
矢量的减法
形，矢量和必为零。
第一章 矢量分析
（2）标量乘矢量（数乘）
kA exkAx eykAy ezkAz
（3）矢 量 的标量积（点积）
A B AB cos AxBx Ay By Az Bz
两矢量点积含义：矢量在另一矢量方向上的投影与另一
矢量模的乘积，其结果是一标量。
0
坐标变量
,, z 0 2
坐标单位矢量
e , e , ez
z
位置矢量
r e ez z
线元矢量
dl ed e d ezdz
面元矢量
dS
e dldlz
第一章 矢量分析
(
)
( )
( )
(
)
(
)
16
导矢的物理意义 M0
z
s
M
dr dr ds 导矢： 导矢： = ⋅ l dt ds dt o y dr : 点M 处的单位切向矢量τ x ds ds 处质点的速度大小， : 点M 处质点的速度大小，用v 表示 dt dr 质点M 质点M 的速度矢量 = vτ = v dt dv d 2 r w= = 2 质点M 质点M 的加速度矢量 dt dt
d dA dB d A± B = ± C = 0, C为常矢 dt dt dt dt d dA d du dA kA = k , k为常数 uA = A+u dt dt dt dt dt d dB dA d 2 dA A⋅ B = A⋅ + ⋅B 特例： A = 2 A ⋅ dt dt dt dt dt d dB dA A× B = A× + ×B dt dt dt dA dA du = ⋅ 若有复合函数 A＝A ( u ) dt du dt
7
第一章
第二节 矢性函数的导数与微分
1. 矢性函数的导数 定义 设矢性函数 A ( t )在点 t的某一邻 的某一邻 域内有定义， 域内有定义，并设 t +△t 也在这邻域内。 △ 也在这邻域内。 若
M
A (t ) A′ ( t )
∆A
N l
其极限存在， 在 ∆t → 0 时，其极限存在，则称此极限 ∆A=A ( t +∆t ) -A ( t ) 为矢性函数 A ( t ) 在点 处的导数（简称 导数（ 在点t 处的导数 导矢）， ），记作 导矢），记作 dA/dt 或 A′ ( t ) 。
13
第1章 矢量分析
在直角坐标系中称之为哈米尔顿算子 哈米尔顿算子，是一个微分 哈米尔顿算子 符号，同时又要当作矢量看待。算子与矢性函数A 的点积 点积为一标量 标量函数。 点积 标量 散度的表达式可以写为: 散度 直角坐标系
∂ ∇ ⋅ A = ax + ay ∂x ∂Ax = ax + ay ∂x ∂ ∂ + a z ⋅ (a x Ax + a y Ay + a z Az ) ∂y ∂z ∂Ay ∂Az + az ∂y ∂z
Φ = ∫ A ⋅ dS = ∫ A cos θ dS
S S
1.2.2. 矢量场的散度 (1) 散度的定义 设有矢量场A，在其中任一点P处作一个包含P点在内 的闭合曲面S，设S所限定的体积为∆V，当体积∆V以任 意方式缩向P点时，取下列极限:
∆V ndS ∆V
如果上式的极限存在，则称此极限为矢量场A在点P处 的散度，记作
∫
l
∫
S
•斯托克斯定理的几何意义 矢量场A的旋度沿曲面S法向分量的面积分等于该矢 量沿围绕此面积曲线边界的线积分。
1.4 标量的方向导数和梯度 1.4.1标量的方向导数和梯度 等值面 一个标量场u可以用标量函数来表示。在直角坐标系中， 可将u表示为 u = u ( x, y , z ) u = u ( x, y , z ) = C 令 C为任意常数。该式在几何上一般表示一个曲面，在 这个曲面上的各点，虽然坐标(x, y, z)不同，但函数值 相等，称此曲面为标量场u的等值面 等值面。 等值面 等值线 对于由二维函数v=v(x,y)所给定 的平面标量场，可按v(x, y)=C得 到一系列不同值的等值线。
第一章 矢量分析
本章重点及知识点 标量场的方向导数和梯度 矢量场的通量和散度 矢量场的环量和旋度 亥姆霍兹定理
矢量分析-PPT
0
2 2 2 2
x2 y2 z2
1 .4 .2 格林定理
将散度定理中矢量A表示为某标量函数的梯度 ψ与另一标 量函数 φ的乘积, 则有
A ( ) 2
取上式在体积V内的积分, 并应用散度定理, 得
(2 )dv
V
s( ) nˆds
s
n
ds
(1 -49)
式中S是包围体积V的封闭面, nˆ 是封闭面S的外法线方向单位矢
量。此式对于在体积V内具有连续二阶偏导数的标量函数φ和ψ都 成立, 称为格林( G .Green)第一定理。
divA A
A
xˆ
x
yˆ
y
zˆ
z
(xˆAx
yˆAy
zˆAz
)
Ax Ay Az x y z
利用哈密顿算子, 读者可以证明, 散度运算符合下列规则:
(A B) A B
(A) A A
1 .2 .3 散度定理
既然矢量的散度代表的是其通量的体密度, 因此直观地可知, 矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总 通量, 即
ds nˆds
nˆ 是面元的法线方向单位矢量。nˆ 的取法(指向)有两种情形: 对
开曲面上的面元, 设这个开曲面是由封闭曲线l所围成的, 则当选
定绕行l的方向后, 沿绕行方向按右手螺旋的姆指方向就是 nˆ 的方 向, 如图1 -4所示; 对封闭曲面上的面元, nˆ 取为封闭面的外法线方
向。
图 1 -4 开曲面上的面元
为A , B崐所在平面的右手法向 n:ˆ
A B nˆAB sin aAB
它不符合交换律。 由定义知,
A B (B A)
并有
xˆ xˆ yˆ yˆ zˆ zˆ 0 xˆ yˆ zˆ, yˆ zˆ xˆ, zˆ xˆ yˆ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章 矢 量 分 析
例1 .1 点电荷q在离其r处产生的电通量密度为
D
q
4r 3
r,
r xˆx yˆy zˆz,
r (x2 y2 z2 )1/ 2
求任意点处电通量密度的散度▽·D，并求穿出r为半径的
球面的电通量 e
[解]
D
q
4
xˆx yˆy zˆz (x2 y2 z2 )3/2
yˆ Ax z
Az x
zˆ
Ay x
Ax y
第一章 矢 量 分 析 即
xˆ yˆ zˆ A
x y z Ax Ay Az
第一章 矢 量 分 析 旋度运算符合如下规则:
(A B) A B
(A) A A
第一章 矢 量 分 析
第一章 矢 量 分 析
§1.1 矢量表示法和代数运算 §1.2 通量与散度,散度定理 §1.3 环量与旋度,斯托克斯定理 §1.4 方向导数与梯度,格林定理 §1.5 曲面坐标系 §1.6 亥姆霍兹定理
第一章 矢 量 分 析
§1 .1 矢量表示法和代数运算
1 .1 .1 矢量表示法及其和差
A B B A
并有
xˆ yˆ yˆ zˆ zˆ xˆ 0
xˆ xˆ yˆ yˆ zˆ zˆ 1
第一章 矢 量 分 析
因而得
A B AxBx Ay By AzBz
A A Ax2 Ay2 Az2 A2
矢量积A×B是一个矢量, 其大小等于两个矢量的模值相乘, 再乘以它们夹角αAB(≤π)的正弦, 其方向与A , B成右手螺旋关系,
y r3
3 yz r5
可见, xˆ 向分量为零; 同样, yˆ 向和 zˆ 向分量也都为零。 故
E 0
这说明点电荷产生的电场是无旋场。
第一章 矢 量 分 析 例1 .4 证明下述矢量斯托克斯定理：
V ( A)dv s A ds
式中S为包围体积V的封闭面。 [证] 设C为一任意常矢，则
第一章 矢 量 分 析
1 .3 .2 旋度的定义和运算
为反映给定点附近的环量情况, 我们把封闭曲线收小, 使它包 围的面积ΔS趋近于零, 取极限
A dl
l lim S0 S
这个极限的意义就是环量的面密度, 或称环量强度。 由于面 元是有方向的, 它与封闭曲线l的绕行方向成右手螺旋关系, 因此 在给定点处, 上述极限值对于不同的面元是不同的。 为此, 引入 如下定义, 称为旋度(rotation):
sபைடு நூலகம்
q
4r 2
ds
s
q
4r 2
4r 2
q
这证明在此球面上所穿过的电通量 e 的源正是点电荷q。
第一章 矢 量 分 析
例1 .2 球面S上任意点的位置矢量为 r xˆx yˆy zˆz rˆr,
Sr ds
［解］
r x y z 3 x y z
第一章 矢 量 分 析 矢量A的旋度可表示为算子与A的矢量积, 即
rotA A
计算▽×A时, 先按矢量积规则展开, 然后再作微分运算, 得
A
xˆ
x
yˆ
y
zˆ
z
( xˆAx
yˆAy
zˆAz )
xˆ
Az y
Ay z
第一章 矢 量 分 析
1 .2 .2 散度, 哈密顿算子 ;
定义如下极限为矢量A在某点的散度(divergence), 记为divA:
divA lim SA ds
V 0 V
式中ΔV为封闭面S所包围的体积。 此式表明, 矢量A的散度 是标量, 它是A通过某点处单位体积的通量(即通量体密度)。 它 反映A在该点的通量源强度。 显然, 在无源区中, A在各点的散度 为零。 这个区域中的矢量场称为无散场或管形场。
第一章 矢 量 分 析
哈密顿( W .R .Hamilton )
(
del
(德尔)”
nabla (那勃拉)”)表示下述矢量形式的微分算子:
xˆ yˆ zˆ x y z
它兼有矢量和微分运算双重作用, 因而与普通矢量有所不同:
A A ; A A ;
(A B) B A A B
( A) 0
A ( A) 2 A
在直角坐标系中有
2 A xˆ2 Ax yˆ2 Ay zˆ2 Az
第一章 矢 量 分 析
1 .3 .3 斯托克斯定理 因为旋度代表单位面积的环量, 因此矢量场在闭曲线l上的环
（1-37）
(C A) A (C) C ( A) C ( A)
为A , B崐所在平面的右手法向 nˆ:
A B nˆAB sin aAB
它不符合交换律。 由定义知,
A B (B A)
第一章 矢 量 分 析 并有
xˆ xˆ yˆ yˆ zˆ zˆ 0 xˆ yˆ zˆ, yˆ zˆ xˆ, zˆ xˆ yˆ
(A) A A
第一章 矢 量 分 析
1 .2 .3 散度定理
既然矢量的散度代表的是其通量的体密度, 因此直观地可知, 矢量场散度的体积分等于该矢量穿过包围该体积的封闭面的总 通量, 即
V AdV SA dS
上式称为散度定理, 也称为高斯公式。 利用散度定理可将矢量 散度的体积分化为该矢量的封闭面积分, 或反之。
若三个相互垂直的坐标轴上的分量已知, 一个矢量就确定了。 例如在直角坐标系中, 矢量A的三个分量模值分别是Ax , Ay , Az, 则A可表示为
A xˆAx yˆAy zˆAz
该矢量的模为
A Ax2 Ay2 Az2
第一章 矢 量 分 析
A的单位矢量为
Aˆ A xˆ Ax yˆ Ay zˆ Az AA AA
第一章 矢 量 分 析 将曲面S各面元上的A·ds相加, 它表示A穿过整个曲面S的通量, 也称为A在曲面S上的面积分:
s A ds s A nˆds
如果S是一个封闭面, 则
SA ds
表示A穿过封闭面的通量。 若Φ＞0, 表示有净通量流出, 这说明S 内必定有矢量场的源; 若Φ ＜0, 表示有净通量流入, 说明S内有洞 (负的源)。 通过封闭面的电通量Φ等于该封闭面所包围的自由电荷 Q。 若Q为正电荷, Φ为正, 有电通量流出; 反之, 若Q为负电荷, 则Φ 为负, 有电通量流入。
Dz z
q
4
r2
3z2 r5
第一章 矢 量 分 析
D
Dx x
Dy y
Dz z
q
4
3r 2
3(x2 r5
y2
z2)
0
可见，除点电荷所在源点（r=0）外，空间各点的电通量密
度散度均为零。它是管形场。
e
q
D
s
ds
4r 3
r rˆds
A的散度可表示为算子与矢量A的标量积, 即
divA A
第一章 矢 量 分 析
A
xˆ
x
yˆ
y
zˆ
z
(xˆAx
yˆAy
zˆAz
)
Ax Ay Az x y z
利用哈密顿算子, 读者可以证明, 散度运算符合下列规则:
(A B) A B
量就等于l所包围的曲面S上的旋度之总和, 即
s( A) ds l A dl
此式称为斯托克斯(Stokes )定理或斯托克斯公式。 它可将矢量 旋度的面积分变换为该矢量的线积分, 或反之。
第一章 矢 量 分 析
例1 .3 自由空间中的点电荷q所产生的电场强度为
E
q
4 0r3
公式右边为“BAC-CAB”, 故称为“Back -Cab”法则, 以便记忆。
第一章 矢 量 分 析 图 1 -3 矢量乘积的说明
第一章 矢 量 分 析
§1 .2 通量与散度, 散度定理
在描绘矢量场的特性时, 矢量场穿过一个曲面的通量是一个 很有用的概念。 在矢量分析中, 将曲面的一个面元用矢量ds来表 示, 其方向取为面元的法线方向, 其大小为ds, 即
r
q
4 0
xˆx yˆy zˆz (x2 y2 z2 )3/2
求任意点处(r≠0)电场强度的旋度▽×E。
第一章 矢 量 分 析 [解]
xˆ yˆ zˆ
E q
4 0 x y z
xyz r3 r3 r3
q
4
0
xˆ y
其第二项下标则次序对调: z→y, 依次类推。并有
xˆ yˆ zˆ A B Ax Ay Az
Bx By Bz
第一章 矢 量 分 析 1 .1 .3 三重积 ;
矢量的三连乘也有两种。 标量三重积为
A (B C) B (C A) C ( A B)
矢量三重积为
A (B C) B( AC) C( A B)
ds nˆds
nˆ 是面元的法线方向单位矢量。nˆ 的取法(指向)有两种情形: 对
开曲面上的面元, 设这个开曲面是由封闭曲线l所围成的, 则当选