任意角度弯头加直管段外弧高度计算公式
弯头外弧长度计算公式

1.5倍弯头中心高=通径*1.524,其实就是通径*倍数,将得出的结果的小数点后面的数字四舍五入取整数,如219的通径是200,中心高即为200*1.524=304.8,取305;又如114的通径为100,中心高即为100*1.524=15
2.4,取152.(注:1倍弯头和2倍弯头的中心高,可用通径*倍数即可,必须是精确的倍数。
我就以前将1.5倍弯头的通径直接乘以1.5,结果闹出了笑话)
戳高=中心高+弯头的半径,如 1.5倍直径219的弯头的戳高=305+219/2=305+109.5=414.5
外弧长度=(中心高+半径)*3.14*2/360*度数,即(戳高)*3.14*2/360*度数,由此可以推算出90度弯头的外弧长度=戳高*3.14/2
内弧长度=(中心高-半径)*3.14*2/360*度数
注:中心高即R,也就是曲率半径。
90。弯头内外弧长速查表(理论值)

Hale Waihona Puke
弯头的制作计算公式

弯头的制作计算公式弯头的制作计算公式弯头尺寸标准执行:ASME/ANSI B16.9,内容包括公称尺寸:DN1/2"-DN48",45度弯头尺寸、90度弯头尺寸、180度弯头尺寸、长半径、短半径、中心高(曲率半径)、公制管与英制管口径等。
弯弯头曲率半径计算公式:英寸×25.4×1.5=1.5D弯头曲率半径(小数点后4舍5入)例如:DN80是3"弯头3×25.4×1.5=114.3(4舍5入)=114 这是1.5倍弯头曲率半径计算公式。
3×25.4×1=76.2(4舍5入)=76 这是1.0倍弯头曲率半径计算公式。
弯头外弧长度计算公式:R+(口径÷2)×1.57=90°弯头外弧长度。
例如:108*6 152+(108÷2)×1.57=323.42mm弯头重量计算公式:(口径-壁厚)×壁厚×0.0387×R÷1000=弯头理论重量例如:219*10 (219-10)×10×0.0387×305÷1000=24.664舍5入=24.7圆环体积=2X3.14X3.14(r^2)Rr--圆环圆半径R--圆环回转半径中空管圆环体积=2X3.14X3.14((r^2)-(r'^2))Rr'--圆环内圆半径90,60,45度的弯头(肘管)体积分别是对应中空管圆环体积的1/4、1/6、1/8。
钢的密度工程上计算重量时按7.85公斤/立方分米,密度X体积=重量(质量)。
1、180°弯头按表2倍计算,45°按1/2计算;2、R1.0DN弯头重量按表2/3计算;3、表中未列出壁厚的重量,可取与之相近的两个重量计算平均值;4、90°弯头计算公式;0.0387*S(D-S)R/1000 式中S=壁厚mm D=外径mm R=弯曲半径mm2 90°弯头重量计算公式:W=9.685*10-6R(D2-d2)式中:W 90°弯头重量,kg;R 弯头的曲率半径(结构尺寸),mm;D 弯头外径,mm;d 弯头内径,mm。
任意弯管的计算
任意弯管的计算
任意弯管就是指任意弯曲角度与任意弯曲半径的弯管。
这种弯管弯曲部分的展开长度可按下式进行计算:
R R
L απα01745.0180
==
式中L ——弯曲部分的展开长度(mm);
α——弯曲角度(°); π——圆周率; R ——弯曲半径(MM)。
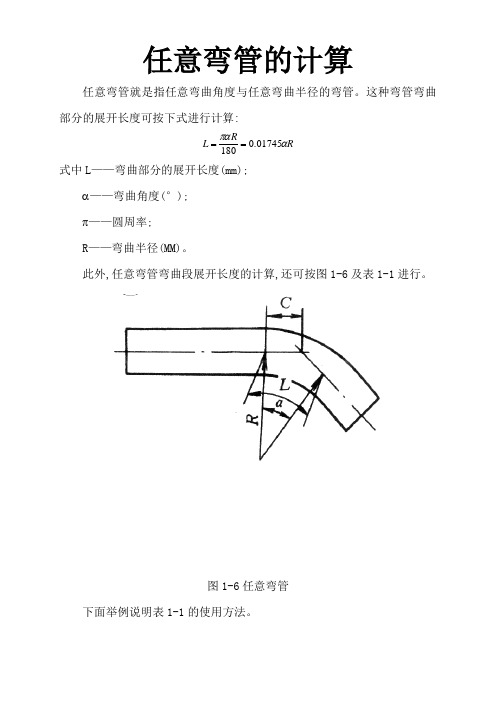
此外,任意弯管弯曲段展开长度的计算,还可按图1-6及表1-1进行。
图1-6任意弯管
下面举例说明表1-1的使用方法。
表1-1任意弯管计算
注:引用表中C、L值时,应乘以弯曲半径R。
例已知图1-7中弯头的弯曲角度α=25°,弯曲半径R=500mm,安装管段距转角点M 的距离为91lmm,取一根直管来煨制弯头,试问应如何划线?
解需加工的弯管端直管段长度
b=911-CR
查表1-1得,当α=25°时,C=0、2216,L=0、4363;故CR为:
0、2216R=0、2216×500=111mm
因此,得b=911-111=800 mm
弯曲部分实际展开长度
L=0、4363R=0、4363×500=218 mm
根据计算出来的直管段长度b及弯曲部分展开长度L,便可进行划线。
如图1-7b 所示。
图1—7弯管计算
由上面的例子可以瞧出,只要弯曲角度与弯曲半径一定,利用表1—1就能很方便地进行任意角度、任意弯曲半径的弯管计算。
而在热煨时,其加热管段长度一般应比弯曲长度稍长一些,以便保证弯曲部分加热均匀。
增加的长度一般规定为:对于弯曲角度大的管子,可增加二倍管外径长度;对弯曲角度小的则增加弯曲长度的20%。
弯弧管长度计算公式

弯弧管长度计算公式在工程设计中,弯弧管是一种常见的管道连接方式,它可以将管道在不同方向上连接起来,使得管道系统更加灵活和多样化。
在设计和安装弯弧管时,需要计算其长度,以确保管道连接的准确性和稳定性。
本文将介绍弯弧管长度的计算公式及其相关知识。
弯弧管长度的计算公式可以通过几何原理来推导。
一般来说,弯弧管的长度取决于其弯曲角度、弯曲半径和弯曲方式。
根据不同的弯曲方式,弯弧管可以分为弯头和弯管两种类型。
对于弯头来说,其长度计算公式可以表示为:L = π R α / 180。
其中,L表示弯头的长度,R表示弯曲半径,α表示弯曲角度。
这个公式的推导过程可以通过几何原理和圆弧长度的计算来得到。
而对于弯管来说,其长度计算公式可以表示为:L = π R (α / 180 + 2 n)。
其中,L表示弯管的长度,R表示弯曲半径,α表示弯曲角度,n表示弯管的数量。
这个公式的推导过程同样可以通过几何原理和圆弧长度的计算来得到。
在实际的工程设计中,弯弧管长度的计算公式可以帮助工程师们快速准确地计算出所需的管道长度,从而避免浪费和错误。
此外,弯弧管长度的计算公式还可以帮助工程师们优化管道系统的设计,提高其稳定性和效率。
除了弯弧管长度的计算公式外,工程师们在设计和安装弯弧管时还需要考虑一些其他因素。
例如,弯曲角度和弯曲半径的选择应该符合实际使用要求,并且需要考虑管道系统的整体布局和连接方式。
此外,工程师们还需要注意弯弧管的材质和制造工艺,以确保其质量和可靠性。
在实际的工程项目中,弯弧管长度的计算公式可以帮助工程师们更好地控制成本和提高效率。
通过合理计算弯弧管的长度,工程师们可以避免浪费材料和人力,并且可以减少工程周期和成本。
因此,弯弧管长度的计算公式在工程设计和施工中具有重要的意义。
总之,弯弧管长度的计算公式是工程设计中的重要知识点,它可以帮助工程师们快速准确地计算出所需的管道长度,从而提高工程效率和质量。
在实际工程项目中,工程师们需要根据实际情况选择合适的弯弧管长度计算公式,并结合其他因素进行综合考虑,以确保管道系统的稳定性和可靠性。
弯头的制作计算公式

弯头的制作计算公式
弯头是管道系统中常用的管件之一,用于改变管道方向。
弯头的制作
计算公式是通过计算来确定弯头的尺寸和形状,以便满足管道系统的要求。
下面将详细介绍弯头的制作计算公式。
1.弯头尺寸计算公式:
弯头的尺寸计算可以通过以下公式进行计算:
2.弯头发育长度计算公式:
弯头的发育长度可以通过以下公式进行计算:
h = R x tan(θ/2) x π/180 x n
其中,h表示弯头的发育长度,R表示弯头的半径,θ表示弯头的弯
曲角度,π/180是弧度和角度之间的转化系数,n表示弯头的转向次数。
3.弯头切角计算公式:
弯头的切角可以通过以下公式进行计算:
c = R x tan(α/2) x n
其中,c表示弯头的切角,R表示弯头的半径,α表示弯头的开孔角度,n表示弯头的转向次数。
4.弯头开孔长度计算公式:
弯头的开孔长度可以通过以下公式进行计算:
L1 = h - c x tan(θ/2)
其中,L1表示弯头的开孔长度,h表示弯头的发育长度,c表示弯头的切角,θ表示弯头的弯曲角度。
5.弯头开孔角度计算公式:
弯头的开孔角度可以通过以下公式进行计算:
α = 2 x arctan(L1 / (2 x R x n))
其中,α表示弯头的开孔角度,L1表示弯头的开孔长度,R表示弯头的半径,n表示弯头的转向次数。
以上就是弯头的制作计算公式的基本介绍。
在实际应用中,还需要考虑到一些特殊情况,如弯头的材质、壁厚、管道直径等因素,以确保弯头能够满足管道系统的要求。
因此,在具体计算时,还需要结合实际情况进行综合考量。
{JZ}弯头外弧长度计算公式231

倍弯头中心高通径*,其实就是通径*倍数,将得出的结果的小数点后面的数字四舍五入取整数,如的通径是,中心高即为*,取;又如的通径为,中心高即为*,
取.(注倍弯头和倍弯头的中心高,可用通径*倍数即可,必须是精确的倍数。
我就以前将倍弯头的通径直接乘以,结果闹出了笑话)
戳高中心高弯头的半径,如倍直径的弯头的戳高
外弧长度(中心高半径)***度数,即(戳高)***度数,由此可以推算出度弯头的外弧长度戳高*
内弧长度(中心高半径)***度数
注:中心高即,也就是曲率半径。
弯头长度的计算公式

弯头长度的计算公式一、90°弯头长度计算。
1. 对于焊接弯头(以管径为D的无缝钢管为例)- 当弯曲半径R = 1.5D时(这是常见的一种规格),90°弯头的长度L计算如下:- 根据弯头的几何形状,其弧长公式为L=(απ R)/(180),对于90°弯头,α = 90。
- 当R = 1.5D时,L=(90π×1.5D)/(180)=(π D)/(2)≈1.57D。
- 当弯曲半径R = 1D时,同样根据弧长公式L=(90π× D)/(180)=(π D)/(2)≈0.785D。
2. 对于成品弯头(如玛钢弯头)- 一般其中心至端面的距离A值是标准值。
对于等径90°弯头,长度可近似认为是A值的2倍。
例如,公称直径为DN50的玛钢弯头,查标准可知A = 38mm,那么弯头长度约为2×38 = 76mm。
- 如果是异径弯头(大小头弯管),计算较为复杂,要考虑大小头的锥度和弯头的弯曲角度等因素。
一般先分别计算出大小头的斜边长度,再根据弯头角度确定弧长部分,然后将各部分相加。
不过在实际工程中,更多是查阅相关标准手册获取其尺寸。
二、45°弯头长度计算。
1. 对于焊接弯头(以管径为D的无缝钢管为例)- 当弯曲半径R = 1.5D时,根据弧长公式L=(απ R)/(180),对于45°弯头,α = 45。
- 所以L=(45π×1.5D)/(180)=(3π D)/(8)≈1.178D。
- 当弯曲半径R = 1D时,L=(45π× D)/(180)=(π D)/(4)≈0.785D。
2. 对于成品45°弯头(如玛钢弯头)- 同样其中心至端面的距离A值是标准值,弯头长度近似为A×√(2)(根据45°直角三角形的斜边计算原理)。
例如,公称直径为DN50的玛钢45°弯头,查标准可知A = 38mm,那么弯头长度约为38×√(2)≈53.74mm。
弯头放样计算公式

弯头放样计算公式在弯头放样计算中,需要根据给定的参数来确定以下几个关键尺寸:曲率半径、弯头长度、支管长度、弯角和波纹增减。
下面将一一介绍这些尺寸的计算公式。
1.曲率半径(R)的计算公式:弯头的曲率半径是弯头外缘至弯中心的垂直距离。
可以通过下面的公式来计算曲率半径:R=1.5xD其中,R为曲率半径,D为弯头的直径。
2.弯头长度(L)的计算公式:弯头长度是指弯头外缘的长度。
可以通过以下公式计算弯头长度:L=πxDx(θ/360)其中,L为弯头长度,D为弯头的直径,θ为弯头的弯角。
3.支管长度(T)的计算公式:支管长度是指弯头两侧的直管段长度。
可以通过以下公式计算支管长度:T = Tan(θ/2) x R其中,T为支管长度,θ为弯头的弯角,R为曲率半径。
4.弯角(θ)的计算公式:弯角是指弯头的弯曲程度。
可以通过以下公式计算弯角:θ=360xL/(πxD)其中,θ为弯头的弯角,L为弯头长度,D为弯头的直径。
5.波纹增减的计算公式:波纹增减是根据管道流体的压力和温度来计算的。
具体的计算公式根据不同情况而异。
常用的波纹增减计算公式为:ΔP=ρxgxΔh其中,ΔP为波纹增减压力,ρ为流体密度,g为重力加速度,Δh为管道的高度差。
通过以上公式,可以计算出弯头的各个关键尺寸。
不同的情况可能需要采用不同的计算公式,具体应根据实际情况进行选择和计算。
同时,在进行弯头放样计算时,还需要考虑材料的切割和连接方式,以及对弯头进行弯曲和成形的工艺要求。
这些因素都需要在计算过程中综合考虑。
总结:弯头放样计算公式通过计算弯头的各个关键尺寸来确保弯头的顺利连接和流体的正常流动。
根据给定的参数,可以计算出曲率半径、弯头长度、支管长度、弯角和波纹增减等关键尺寸。
这些公式可以根据实际情况进行选择和使用,并且需要综合考虑材料和加工工艺等因素。
钢管弯头计算公式

钢管弯头计算公式
钢管弯头的计算公式取决于弯头的类型和设计要求。
以下是两种常见的弯头计算公式:
1. 弯头的弯曲半径(R)计算公式为:R=(D/2)/tan(θ/2)。
其中,D代表管道直径,θ代表弯头的弯曲角度。
2. 弯头的长度计算公式是R×。
另外,弯头的重量也可以通过特定的公式进行计算。
例如,对于90度弯头(外径-壁厚)壁厚系数(碳钢按)公称通径倍数/1000=90度弯头理论重
量(公斤)。
其中,公称通径是管路系统中所有管路附件用数字表示的尺寸,公称通径用字母“DN”后面紧跟一个数字标志。
弯头倍数是弯头中心弧的
半径(曲率半径)与弯头口径的比,R=就是曲率半径是直径的倍。
请注意,这些公式仅适用于特定类型的弯头,如90度弯头。
对于不同类型
的弯头,可能存在不同的计算公式。
因此,在实际应用中,应选择适合特定情况的计算公式,并确保所使用的数据准确无误,以免出现计算错误。
任意角度弯头高度计算方法图解文档

任意角度弯头高度计算方法图解在管道安装过程中,经常用到计算弯头中心高度,有时弯头弯曲半径也不数值固定。
下面我就对任意角度弯头高度计算方法进行图解,希望对广大管道安装人员提供方便资料,施工计算不再是个难题。
一、首先了解弯头尺寸数据。
这个问题的对象估计是钢制无缝管件。
各种工业和民用管道安装工程中,所需要的对焊无缝管件,应符合GB/T12459-1990《钢制对焊无缝管件》的要求。
选用的管件其材质应与管道材质相同、外径相同、壁厚相同或稍厚。
45度弯头的规格见下图表:二、45度弯头高度计算公式Axtan22.5°就是指弯头弯曲半径乘以tan22.5°例如:108*4的弯头45度弯头高度计算:152*tan22.5°=152*0.414=62.928mm45弯头高度总结简单公式就是弯头弯曲半径*0.414三、60度弯头高度计算公式Axtan30°就是指弯头弯曲半径乘以tan30°例如89*4的弯头60度弯头高度计算:114*tan30°=114*0.577=65.778mm60弯头高度总结简单公式就是弯头弯曲半径*0.577四、30度弯头高度计算公式Axtan15°就是指弯头弯曲半径乘以tan15°30弯头高度总结简单公式就是弯头弯曲半径*0.268五、1.5倍弯头中心高=通径*1.524,其实就是通径*倍数,将得出的结果的小数点后面的数字四舍五入取整数,如219的通径是200,中心高即为200*1.524=304.8,取305;又如114的通径为100,中心高即为100*1.524=152.4,取152。
(适用于DN100及以上弯头曲率半径的算法方便快捷计算)。
管道弯头计算公式

管道弯头计算公式
一、弯头的长度计算公式怎么算
以90°和45°的弯头为例,90°弯头的长度(㎜)=R*1.57 (弯曲半du径单位㎜)2);90°弯头所需料(M)=直径*2.5*所需个数+半径;45°弯头长度(㎜)弯曲半径乘*ta n22.5°(弯头度数的一半)。
大家在选购弯头的时候,应该根据弯头材质、外径尺寸、厚度而定,会更加合适。
二、管道弯头施工注意事项
1、在切割管道弯头前,要确定管道弯头有无吊好,还先看清两端的直管上有无安装吊筋,是否可靠。
如果无法吊筋的话,两侧直管先用葫芦吊好,方可使用。
这样才牢固,不会出现问题。
2、施工人员在施工前,要先检查看看管道弯头有无存在沙眼、气孔等情况,而且还要看看管道弯头的弯曲角度、外径、长度等等是否正确,如果没问题的话,方可开始施工。
3、为了不让管道弯头受到意外伤害,大家应将待安装的管道弯头放置在木板上,注意不要摆放在地面上。
任意角度弯头中间直管长度计算公式

一、引言在工程设计和建筑领域中,管道设计是一个非常重要的环节。
而在管道设计中,任意角度弯头中间直管长度的计算公式是一个至关重要的问题。
本文将就这一主题展开讨论,以帮助读者更好地理解和运用这一计算公式。
二、任意角度弯头中间直管长度计算公式的概念解析在管道设计中,任意角度弯头中间直管长度计算公式是用来计算弯头与直管之间的连接长度的公式。
它的作用在于在管道连接过程中,确保管道的合理布局和连接,避免资源的浪费和管道设计的不合理性。
这个公式的正确使用,对于管道的稳定运行和安全性具有非常重要的意义。
三、任意角度弯头中间直管长度计算公式的详细推导和应用在管道设计过程中,我们经常会遇到不同角度的弯头,为了计算任意角度弯头中间直管长度,我们首先需要了解弧长、弦长和夹角之间的关系,并结合三角函数的知识,推导出相应的计算公式。
一般来说,我们可以利用三角函数的正弦、余弦、正切等函数,结合弯头的夹角,来计算任意角度弯头中间直管的长度。
四、任意角度弯头中间直管长度计算公式的实际应用案例为了更好地理解和应用这一计算公式,我们举例说明其在实际管道设计中的应用。
在工业生产中,如果需要连接两根管道。
其中一根管道需要设置一个45度的弯头,为了计算这个弯头后中间直管的长度,我们可以通过具体的公式和计算方法,得到准确的长度数据,从而实现合理的管道连接和布局。
五、总结与展望通过本文的讨论,我们对任意角度弯头中间直管长度计算公式有了更深入的理解。
这一计算公式在工程设计中具有重要的应用价值,我们需要在实际工作中不断总结和应用,以更好地服务于工程建设。
在今后的工作中,我们还可以进一步结合实际案例,深化对该计算公式的理解和应用,从而提高工程设计的质量和效率。
个人观点:任意角度弯头中间直管长度计算公式是管道设计中的重要工具,正确的理解和应用对于工程设计和建筑具有重要的意义。
希望通过不断的学习和实践,我们能够更好地掌握这一计算公式,为工程建设贡献自己的力量。
弯头尺寸的计算公式

.
弯头尺寸的计算公式
对弯头尺寸的计算公式这个话题有着自己独道的见解,下面经验之谈,希望大家多多学习。
1、1.5倍弯头中心高=通径*1.524,其实就是通径*倍数,将得出的结果的小数点后面的数字四舍五入取整数,如219的通径是200,中心高即为200*1.524=304.8,取305;又如114的通径为100,中心高即为100*1.524=152.4,取152。
(适用于DN100 及以上弯头曲率半径的算法方便快捷计算)。
2、戳高=中心高+弯头的半径,如1.5倍直径219的弯头的戳高
=305+219/2=305+109.5=414.5
3、外弧长度=(中心高+半径)*3.14*2/360*度数,即(戳高)*3.14*2/360*度数,由此可以推算出90度弯头的外弧长度=戳高*3.14/2
4、内弧长度=(中心高-半径)*3.14*2/360*度数
5、弯头的下料长度=弯头中心高*3.14/2*弯头外径/管材直径+(管材壁厚*3)+加工余量,如用180*8的管子下料,推制273的弯头,用以上公式可以算出,下料长度
=381*1.57*273/180+24=931.22mm+加工余量。
;.。
管道对接弯头角度计算公式

管道对接弯头角度计算公式在工程设计和施工中,管道对接弯头是常见的管道连接方式,它可以改变管道的流向和流速,使得管道系统更加灵活和高效。
在实际工程中,对接弯头的角度计算是非常重要的,它直接影响着管道的连接和运行效果。
因此,掌握对接弯头角度计算公式是非常必要的。
对接弯头的角度计算公式主要涉及到管道的弯曲半径、弯头的曲率半径、管道直径等参数。
下面,我们将介绍一些常见的对接弯头角度计算公式,希望对工程师和施工人员有所帮助。
1. 弯头的曲率半径计算公式。
对接弯头的曲率半径是指弯头的外部曲线半径,它是影响弯头角度的重要参数。
通常情况下,弯头的曲率半径可以通过下面的公式进行计算:R = D / tan(A/2)。
其中,R为弯头的曲率半径,D为管道的直径,A为弯头的角度。
2. 弯头的角度计算公式。
在实际工程中,有时候我们需要根据弯头的曲率半径和管道直径来计算弯头的角度。
这时,可以使用下面的公式:A = 2 arctan(D / (2 R))。
其中,A为弯头的角度,D为管道的直径,R为弯头的曲率半径。
3. 弯头的内径计算公式。
对于一些特殊情况,我们需要计算弯头的内径。
通常情况下,可以使用下面的公式来计算:d = D 2 (R tan(A/2))。
其中,d为弯头的内径,D为管道的直径,R为弯头的曲率半径,A为弯头的角度。
4. 弯头的压降计算公式。
在管道系统中,弯头的存在会导致一定的压降。
为了准确计算管道系统的流体压降,可以使用下面的公式:ΔP = K ρ V^2 / 2。
其中,ΔP为弯头的压降,K为弯头的阻力系数,ρ为流体的密度,V为流体的流速。
综上所述,管道对接弯头角度计算公式涉及到许多参数,包括弯头的曲率半径、管道直径、弯头的角度等。
在实际工程中,根据具体情况选择合适的公式进行计算,可以帮助工程师和施工人员更好地设计和施工管道系统,提高工程质量和效率。
希望本文介绍的对接弯头角度计算公式对大家有所帮助。
管道定额弯头长度计算公式

管道定额弯头长度计算公式在工程设计中,管道的安装和布局是一个重要的环节。
在管道的布局中,弯头是常用的连接元件,用于改变管道的流向和方向。
为了保证管道系统的正常运行,需要合理计算和选择弯头的长度。
管道定额弯头长度计算公式是根据流体力学原理和经验公式推导而来的。
它可以用来计算不同直径和角度的弯头的长度,帮助工程师在实际设计中确定合适的弯头尺寸。
在计算弯头长度时,需要考虑到管道流体的流速、流量、密度等因素。
根据流体力学原理,流体在弯头中会产生一定的损失,因此需要根据流速和流量来选择合适的弯头长度,以减小流体的损失和能量消耗。
还需要考虑管道系统的实际情况,如管道的材质、管道的连接方式等。
这些因素也会对弯头长度的计算和选择产生影响。
根据经验公式和实际工程经验,我们可以得出以下管道定额弯头长度计算公式:L = K * D其中,L表示弯头的长度,K是经验系数,D是管道的直径。
经验系数K根据弯头的角度和弯头的类型而定。
一般来说,经验系数K会随着弯头的角度增大而增大,因为较大角度的弯头会导致流体损失增加。
同时,不同类型的弯头也会有不同的经验系数K。
在实际应用中,可以根据经验公式和实际工程情况来选择合适的经验系数K,并结合管道直径D来计算弯头的长度L。
通过合理选择弯头长度,可以减小流体的损失和能量消耗,提高管道系统的运行效率。
管道定额弯头长度计算公式是根据流体力学原理和经验公式推导而来的,可以用来计算不同直径和角度的弯头的长度。
合理选择弯头长度可以减小流体的损失和能量消耗,提高管道系统的运行效率。
在实际工程设计中,工程师需要根据实际情况选择合适的经验系数K,并结合管道直径D来计算弯头的长度L,以确保管道系统的正常运行。
任意弯管的计算

任意弯管的计算
任意弯管是指任意弯曲角度和任意弯曲半径的弯管。
这种弯管弯曲部分的展开长度可按下式进行计算:
R R
L απα01745.0180
==
式中L ——弯曲部分的展开长度(mm);
α——弯曲角度(°); π——圆周率; R ——弯曲半径(MM)。
此外,任意弯管弯曲段展开长度的计算,还可按图1-6及表1-1进行。
图1-6任意弯管
下面举例说明表1-1的使用方法。
表1-1任意弯管计算
注:引用表中C、L值时,应乘以弯曲半径R。
例已知图1-7中弯头的弯曲角度α=25°,弯曲半径R=500mm,安装管段距转角点M的距离为91lmm,取一根直管来煨制弯头,试问应如何划线?
解需加工的弯管端直管段长度
b=911-CR
查表1-1得,当α=25°时,C=0.2216,L=0.4363;故CR为:
0.2216R=0.2216×500=111mm
因此,得b=911-111=800 mm
弯曲部分实际展开长度
L=0.4363R=0.4363×500=218 mm
根据计算出来的直管段长度b及弯曲部分展开长度L,便可进行划线。
如图1-7b 所示。
图1—7弯管计算
由上面的例子可以看出,只要弯曲角度和弯曲半径一定,利用表1—1就能很方便地进行任意角度、任意弯曲半径的弯管计算。
而在热煨时,其加热管段长度一般应比弯曲长度稍长一些,以便保证弯曲部分加热均匀。
增加的长度一般规定为:对于弯曲角度大的管子,可增加二倍管外径长度;对弯曲角度小的则增加弯曲长度的20%。
