MATLAB--simulink-通信系统建模与仿真--第四章部分习题标准答案
matlab学习资料:Simulink学习中的100个问答

matlab学习资料:Simulink学习中的100个问答1.命令行如何运行simulink外部模式build和start用sim()函数该函数的调用格式为:[t,x,y]=sim(f1,tspan,options,ut)其中f1为SIMULINK的模型名,tspan为仿真时间控制变量;参数options为模型控制参数;ut为外部输入向量。
2.请问matlab中的仿真模块,可以看到起源程序吗?那些基本模块是看不了源代码的,有很多模块是用subsystem组成的,你可以用look under mask(鼠标右键)看到里面是怎样用子模块搭接的,还有很多是由s函数写成的simulink的模块,这些直接edit sfunname(s函数的名字)就可以看到源代码3.请问:在simulink参数中设置的步长是50e-6,在系统中有一个simout模块向MA TLAB 中传递数据,但是希望以1e-3的步长获取数据,因该如何设计?在simout模块中直接设定仿真步长是不能运行的。
需要插入一个"zero order hold"模块,将该模块的采样时间设置为1e-03就可以了4.simulink中IGBT等电力元件都有个m极,是什么作用的?用于测量流过IGBT电流及其电压5.用simlink画的图,在示波器中显示,如何复制到word中告诉你一个办法,在加上示波器的地方加上to workspace,改为array,在主窗口中plot,直接抓过去也行吧。
Edit下有copy model选项6.simulink中的mask问题,请问如何封装,prompt,varible填啥,如何初始化prompt中,填写变量的提示,如:直线斜率variable中填写变量名.如:k-------------------------------------------------------------------------有关神经网络工具箱1.为什么当训练和仿真时,命令窗口会出现一堆warning?如:*WARNING* TRAINBPX is an obsolete function.Use NNT2FF and TRAIN to update and train your network.Type NNTW ARN OFF to suppress NNT warning messages.2.trainbpx,simuff这些命令应该怎么用?你用的神经网络不太适合你的matlab版本,有点过时了,对于BP网络,像用newff训练就没问题,建议你可买一本较新的神经网络参考书。
matlab的simulink仿真建模举例 -回复

matlab的simulink仿真建模举例-回复Matlab的Simulink仿真建模举例Simulink是Matlab附带的一款强大的仿真建模工具,它能够帮助工程师们通过可视化的方式建立和调试动态系统模型。
Simulink通过简化传统的数学模型建立过程,使得工程师们能够更加直观地理解和分析复杂的系统。
在本文中,我们将介绍一个关于电机控制系统的Simulink仿真建模的例子。
一、了解电机控制系统在开始建模之前,我们首先需要了解电机控制系统的基本原理。
电机控制系统通常包括输入、电机和输出三个主要部分。
输入通常是来自于传感器或用户的命令信号,例如转速、位置或力矩。
电机是通过接受输入信号并根据特定的控制算法生成输出信号。
输出信号通常是电机的转速、位置或功率等。
控制算法通常采用比例-积分-微分(PID)控制或者其他控制算法。
二、建立Simulink模型1. 创建新的Simulink模型在Matlab主界面中,选择Simulink选项卡下的“New Model”创建一个新的Simulink模型。
2. 添加输入信号在Simulink模型中,我们首先需要添加输入信号模块。
在Simulink库浏览器中选择“Sources”类别,在右侧面板中找到“Step”模块,并将其拖放到模型中。
3. 添加电机模型接下来,我们需要将电机模型添加到Simulink模型中。
Simulink库浏览器中选择“Simscape”类别,在右侧面板中找到“Simscape Electrical”子类别,然后找到“Simscape模型”模块,并将其拖放到模型中。
4. 连接输入信号和电机模型将输入信号模块的输出端口与电机模型的输入端口相连,以建立输入信号与电机模型之间的连接。
5. 添加输出信号模块在Simulink模型中,我们还需要添加输出信号模块。
在Simulink库浏览器中选择“Sinks”类别,在右侧面板中找到“Scope”模块,并将其拖放到模型中。
详解MATLAB Simulink通信系统建模与仿真 刘学勇编著

MATLAB/Simulink/C++/Java等编程援助联系方式:QQ:1829074016邮箱:1829074016@QQ空间:更多学习资料,请加我为QQ好友,或者直接访问我的QQ空间有编程问题的朋友,请直接加我为QQ好友,提供在线答疑如果我QQ不在线,请给我QQ留言,上线后,及时给你答复专业提供以下方向的编程援助:1.MATLAB/Simulink/C++/Java等编程问题;2.数字图像处理、信号处理、通信仿真设计;3.机器人路径规划、轨迹规划、机器人控制;4.各类数值计算、小波分析算法、优化设计;5.自动控制、电机控制、智能控制、模糊控制;6.粒子群算法、神经网络、遗传算法等智能算法;7.其他编程和仿真问题。
编辑推荐117个案例+65个习题+超过22小时多媒体视频教学,赠送超值多媒体语音教学视频:提供《详解MATLAB/Simulink通信系统建模与仿真(配视频教程)》PP了课件和所有案例的源程序;提供MATLAB软件的多媒体教学视频,时长超过7小时;提供与《详解MATLAB/Simulink通信系统建模与仿真(配视频教程)》内容配套的多媒体教学视频,时长超过15小时。
内容简介本书着重讲述MATLAB/Simulink通信仿真的应用,通过理论与实例相结合的方式,详细介绍了MATLAB/Simulink通信系统建模与仿真设计的方法和技巧。
全书共分12章。
第1-2章为MATLAB/Simulink基础篇,简要介绍了MATLAB/Simulink的使用。
第3-8章介绍通信系统常用模块仿真,重点对信号与信道、调制与解调、信道编码/译码等模块的建模与仿真技术进行介绍。
第9-12章是通信系统综合仿真实例,深入浅出地剖析了OFDM通信系统、CDMA通信系统、多址接入协议,以及MIMO通信系统的建模与仿真设计,这几个案例典型实用,是当前通信系统的研究热点。
本书语言通俗易懂,内容丰富详实,突出了以实例为中心的特点。
电机与拖动基础及MATLAB仿真习题答案(第四章)

电机与拖动基础及MATLAB仿真习题答案(第四章)4-14 ⼀台直流电动机技术数据如下:额定功率PN=40kW ,额定电压UN=220V ,额定转速nN=1500r/min ,额定效率η=87.5%,求电动机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-15 ⼀台直流发电机技术数据如下:额定功率PN=82kW ,额定电压UN=230V ,额定转速nN=970r/min ,额定效率η=90%,求发电机的额定电流和额定负载时的输⼊功率?解:(1)额定电流(2)输⼊功率4-16 已知⼀台直流电机极对数p=2,槽数Z 和换向⽚数K 均等于22,采⽤单叠绕组。
试求:(1)绕组各节距;(2)并联⽀路数。
解:(1)第⼀节距5424222y 1=-=±=εp z ,为短距绕组。
单叠绕组的合成节距及换向器节距均为1,即1y ==k y第⼆节距415y 12=-=-=y y(2)并联⽀路数等于磁极数,为4。
4-17 已知直流电机极数2p=6,电枢绕组总导体数N=400,电枢电流Ia=10A ,⽓隙每极磁通Φ=2.1×10-2Wb ,试求:(1)采⽤单叠绕组时电枢所受电磁转矩;(2)绕组改为单波保持⽀路电流ia 不变时的电磁转矩。
解: 电枢绕组为单叠绕组时,并联⽀路对数a=p=3,电磁转矩 m N I a pN T a ?==Φ=38.1310021.0314.3240032π如果把电枢绕组改为单波绕组, 保持⽀路电流a i 的数值不变,则电磁转矩也不变,仍为 13.369m N ?,因为⽆论是叠绕组还是波绕组,所有导体产⽣的电磁转矩的⽅向是⼀致的, 保持⽀路电流a i 不变,就保持了导体电流不变,也就保持了电磁转矩不变。
也可以⽤计算的⽅法: 单叠绕组时并联⽀路数为6,⽀路电流 A I i a a 6106==改为单波绕组, 保持⽀路电流a i 的数值不变,仍为A 610,⽽并联⽀路数为2 (a=1), 电枢电流A i I a a 3102== 电磁转矩 m N T ?==38.13310021.0114.324003。
详解MATLAB/SIMULINK 通信系统建模与仿真资料

本章内容
1.1 MATLAB简介 1.2 MATLAB程序设计 1.3 通信系统仿真
1.1 MATLAB简介
● 数值计算和符号计算功能 ● 具有很好的图形功能 ● 可以直接处理声言和图像文件 ● 具有功能强大的工具箱 ● 使用方便,具有很好的扩展功能 ● Simulink
1.2.2 MATLAB的帮助系统
● 查看命令或函数帮助 ● 联机帮助系统 ● PDF文件帮助系统 ● MATLAB网络资源
1.2.3 MATLAB的基本操作
数据类型
• (1)变量与赋值 • (2)变量的删除与修改 • (3)局部变量和全局变量
矩阵
• (1) 一般矩阵的生成 • (2)特殊矩阵的生成
1.2.5.5 用户参数交互输入
input函数用于向计算机输入一个参数 pause函数暂停程序的执行 disp函数是向命令窗口输出提示信息
1.2.6 文件操作
文件的打开与关闭
• fopen函数 、fclose函数
文件的读写操作
• fread 、fwrite 、fscanf 、fprintf
矩阵运算
1.2.4 MATLAB图形处理和数据可视化
plot函数
subplot函数 多图形窗口 hold命令 对数坐标图形
1.2.5 M文件编程
M脚本文件 函数文件 函数调用和参数传递 matlab的程序结构 用户参数交互输入
1.2.5.1 M脚本文件
1.2.5.4 matlab的程序结构
顺序结构 — 依次顺序执行程序的各条语句 循环结构 — 被重复执行的一组语句,循环是 计算机解决问题的主要手段。 分支结构 — 根据一定条件来执行的各条语句。
matlab语言与控制系统仿真参考答案第4章

4.5 控制系统的数学模型MATLAB 实训1.练习并掌握TF 模型、ZPK 模型、SS 模型的建立方法。
2.练习并掌握TF 模型、ZPK 模型、SS 模型间的转换方法。
3.练习并掌握求取多个模块串联、并联、反馈后总的模型的方法。
4.练习并掌握模型数据的还原方法。
1.写出以下系统的多项式模型,并将其转换为零极点模型;(1)2153173261552115.35291)(23452341++++++-+-=s s s s s s s s s s G >> n1=[91,-52,3.5,-11,52];d1=[1,15,26,73,31,215];sys1=tf(n1,d1)[z1,p1,k1]=tf2zp(n1,d1)sys1zp=zpk(z1,p1,k1)运行结果如下:Transfer function:91 s^4 - 52 s^3 + 3.5 s^2 - 11 s + 52-------------------------------------------s^5 + 15 s^4 + 26 s^3 + 73 s^2 + 31 s + 215z1 =0.7705 + 0.5468i0.7705 - 0.5468i-0.4848 + 0.6364i-0.4848 - 0.6364ip1 =-13.4656-1.3473 + 1.9525i-1.3473 - 1.9525i0.5801 - 1.5814ik1 =91Zero/pole/gain:91 (s^2 - 1.541s + 0.8927) (s^2 + 0.9697s + 0.6401)--------------------------------------------------------------------------(s+13.47) (s^2 - 1.16s + 2.837) (s^2 + 2.695s + 5.627)(2)21.311395.2251315239.5621.635.711017.38)(23456723452++-+-++++-+-=s s s s s s s s s s s s s G >> n2=[1,-38.7,101,-71.5,63.1,562.39];d2=[1,2,5,-31,51,-22.5,39,311.21];sys2=tf(n2,d2)[z2,p2,k2]=tf2zp(n2,d2)sys2zpkmx=zpk(z2,p2,k2)Transfer function:s^5 - 38.7 s^4 + 101 s^3 - 71.5 s^2 + 63.1 s + 562.4---------------------------------------------------------------------------s^7 + 2 s^6 + 5 s^5 - 31 s^4 + 51 s^3 - 22.5 s^2 + 39 s + 311.2z2 =35.94372.95890.5590 + 1.9214i0.5590 - 1.9214i-1.3206p2 =-2.5015 + 3.1531i-2.5015 - 3.1531i1.9492 + 1.0027i1.9492 - 1.0027i0.2072 - 1.7349i-1.3097k2 =1Zero/pole/gain:(s-35.94) (s-2.959) (s+1.321) (s^2 - 1.118s + 4.004)--------------------------------------------------------------------------------------------------(s+1.31) (s^2 - 3.898s + 4.805) (s^2 - 0.4143s + 3.053) (s^2 + 5.003s + 16.2)2.写出以下系统的零极点模型,并将其转换为多项式模型,并将其展开成为部分分式形式;(1))11.5)(9.4)(5.3)(6.2)(3.1()02.6)(5.0(36)(1+++++++=s s s s s s s s s G >> z=[-0.5;-6.02];>> p=[0;-1.3;-2.6;-3.5;-4.9;-5.11];>> k=36;>> sys=zpk(z,p,k)Zero/pole/gain:36 (s+0.5) (s+6.02)--------------------------------------------------s (s+1.3) (s+2.6) (s+3.5) (s+4.9) (s+5.11)>> [n,d]=zp2tf(z,p,k)n =0 0 0 0 36.0000 234.7200 108.3600d =1.0000 17.4100 116.1430 367.5889 544.8325 296.2114 0>> systfxs=tf(n,d)Transfer function:36 s^2 + 234.7 s + 108.4-------------------------------------------------------------------------------s^6 + 17.41 s^5 + 116.1 s^4 + 367.6 s^3 + 544.8 s^2 + 296.2 s>> [r,p,k]=residue(n,d);>> [r';p']ans =9.1407 -14.8730 17.4236 -14.7227 2.6656 0.3658-5.1100 -4.9000 -3.5000 -2.6000 -1.3000 0即部分分式分解结果为 s s s s s s s G 3658.03.16656.26.27227.145.34236.179.4873.1411.51407.9)(++++-+++-+=(2))6)(5)(4)(2()5.3)(3)(1(15.9)(22+-++-++=s s s s s s s s s G >> z=[-1;-3;3.5];>> p=[0;0;-2;-4;5;6];>> k=9.15;>> sys=zpk(z,p,k)Zero/pole/gain:9.15 (s+1) (s+3) (s-3.5)-------------------------------s^2 (s+2) (s+4) (s-5) (s-6)>> [n,d]=zp2tf(z,p,k)n =0 0 0 9.1500 4.5750 -100.6500 -96.0750d =1 -5 -28 92 240 0 0>> systfxs=tf(n,d)Transfer function:9.15 s^3 + 4.575 s^2 - 100.7 s - 96.08---------------------------------------------------s^6 - 5 s^5 - 28 s^4 + 92 s^3 + 240 s^2>> [r,p,k]=residue(n,d);>> [r';p']ans =0.5004 -0.4183 0.0715 0.1123 -0.2659 -0.40036.0000 5.0000 -4.0000 -2.0000 0 0即部分分式分解结果为 24003.02659.021123.040715.054183.065004.0)(s s s s s s s G --++++---= 3.已知系统的状态空间表达式,写出其SS 模型,并求其传递函数矩阵(传递函数模型),若状态空间表达式为⎩⎨⎧+=+=DuCx y Bu Ax x ,则传递函数矩阵表达式为: D B A sI C s G +-=-1)()(。
matlab1-8章课后作业

MATLAB基础教程1~8章作业Matlab第一章1.阐述Matlab的功能Matlab作为一种高级计算软件,是进行算法开发、数据可视化、数据分析以及数值计算的交互式应用开发环境,已被广泛应用于不同领域。
Matlab的基本功能包括:数学计算功能、图形化显示功能、M语言编程功能、编译功能、图形用户界面开发功能、Simulink建模仿真功能、自动代码生成功能。
Matlab第二章1.创建double的变量,并进行计算。
(1)a=87,b=190,计算a+b、a-b、a*b。
(2)创建uint8 类型的变量,数值与(1)中相同,进行相同的计算。
>> a=87,b=190a =87b =190>> a+bans =277>> a-bans =-103>> a*bans =16530>> c=uint8(87), d=uint8(190)c =87d =190>> c+dans =255>> c-dans =>> c*dans =2552.计算(1)sin(60)(2)e^3(3)cos(3π/4)>> sind(60)ans =0.8660>> exp(3)ans =20.0855>> cos(3*pi/4)ans =-0.70713.设u=2,v=3,计算:(1)(2)(3)>> u=2;>> v=3;>> 4*u*v/log(v)ans =21.8457>> (exp(u)+v)^2/(v^2-u)ans =15.4189>> sqrt(u-3*v)/(u*v)ans =0 + 0.4410i4.计算如下表达式:(1)(2)>> (3-5*i)*(4+2*i)ans =22.0000 -14.0000i>> sin(2-8*i)ans =1.3553e+003 +6.2026e+002i5.判断下面语句的运算结果。
MATLAB-SIMULINK讲解完整版

点击图3-2中“树状结构目录窗口”中各模块库名前带 “+”的小方块可展开二级子模块库的目录。“模块窗口” 中显示的是用户在“树状结构目录窗口”中选中的模块库所 包含的模块图标。如果显示的模块图标前带“+”的小方块, 表明该图标下还有三级目录,直接点击该图标可在该窗口中 展现三级目录下的模块图标。
为了叙述方便,本书将模块库中以图标形式表示的典型 环节称为模块,将用典型环节模块组成的系统仿真模型简称 为模型。
在SIMULINK中创建子系统一般有两种方法。
1) 通过“子系统”模块的方法 该方法要求在用户的模型里添加一个称为Subsystem的 子系统模块,然后再往该模块里加入组成子系统的各种模块。 这种方法适合于采用自上而下设计方式的用户,具体实现步 骤如下: (1) 新建一个空白模型。 (2) 打开“端口和子系统”(Ports&Subsystems)模块库, 选取其中的“子系统”(Subsystem)模块并把它复制到新建的 仿真平台窗口中。
第3章 SIMULINK应用基础
3.1 SIMULINK仿真环境 3.2 SIMULINK的基本操作 3.3 SIMULINK系统建模 3.4 SIMULINK运行仿真 3.5 SIMULINK模块库 3.6 SIMULINK系统仿真应用 习题
3.1 SIMULINK仿真环境 SIMULINK是MATLAB的一个分支产品,主要用来实 现对工程问题的模型化及动态仿真。SIMULINK体现了模块 化设计和系统级仿真的思想,采用模块组合的方法使用户能 够快速、准确地创建动态系统的计算机模型,使得建模仿真 如同搭积木一样简单。SIMULINK现已成为仿真领域首选的 计算机环境。
单击模块,拖曳模块到合适的位置,松开鼠标按键
方法 1:选中模块,选择菜单命令[Format>Rotate Block], 模块顺时针旋转 90°;选择菜单命令[Format>Flip Block],
MatlabSimulink通信系统建模与仿真

电子信息课程设计题目:Matlab/Simulink通信系统建模与仿真班级:2008级电子(1)班学号:200895024026姓名:白阳电子信息课程设计Matlab/Simulink通信系统建模与仿真一、设计目的:学习Matlab/Simulink的功能及基本用法,对给定系统进行建模与仿真。
二、基本知识:Simulink是用来对动态系统进行建模、仿真和分析的软件包,依托于MATLAB丰富的仿真资源,可应用于任何使用数学方式进行描述的动态系统,其最大优点是易学、易用,只需用鼠标拖动模块框图就能迅速建立起系统的框图模型。
三、设计内容:1、基本练习:(1)启动SIMULINK:先启动MATLAB,在命令窗口中键入:simulink,回车;或点击窗口上的SIMULINK图标按钮。
图(1)建立simulink(2)点击File\new\Model或白纸图标,打开一个创建新模型的窗口。
(3)移动模块到新建的窗口,并按需要排布。
(4)连接模块:将光标指向起始模块的输出口,光标变为“+”,然后拖动鼠标到目标模块的输入口;或者,先单击起始模块,按下Ctrl键再单击目标模块。
(5)在连线中插入模块:只需将模块拖动到连线上。
(6)连线的分支与改变:用鼠标单击要分支的连线,光标变为“+”,然后拖动到目标模块;单击并拖动连线可改变连线的路径。
(7)信号的组合:用Mux模块可将多个标量信号组合成一个失量信号,送到另一模块(如示波器Scope)。
(8)生成标签信号:双击需要加入标签的信号线,会出现标签编辑框,键入标签文本即可。
或点击Edit\Signal Properties。
传递:选择信号线并双击,在标签编辑框中键入<>,并在该尖括号内键入信号标签即可。
四、建立模型1. 建立仿真模型(1)在simulink library browser中查找元器件,并放置在创建的新模型的窗口中,连接元器件,得到如下的仿真模型。
MatlabSimulink系统建模和仿真

图:电容的充电、放电过程的仿真结果。在充电仿真中,输出信号 为系统的零状态响应。在放电过程仿真中,输出信号为系统的零输 入响应。 如果要仿真系统输入信号为任意函数的情况,只需要修改仿 真程序中的输入信号设臵即可。
“实例2.3”单摆运动过程的建模和仿真。 (1)单摆的数学模型 设单摆摆线的固定长度为l ,摆线的质量忽略不计,摆锤质 量为m ,重力加速度为g ,设系统的初始时刻为t=0 ,在任 意 t 0 时刻摆锤的线速度为v(t) ,角速度为 w(t ) ,角位移 为 (t ) 。以单摆的固定位臵为坐标原点建立直角坐标系, 水平方向为x 轴方向。如下图所示。
图:电容的充电电路以及等价系统
(1)数学分析
首先根据网络拓扑和元件伏安特性建立该电路方程组
dy (t ) i (t ) C dt
dy (t ) 1 1 x(t ) y (t ) dt RC RC
y(t ) x(t ) Ri (t )
并化简得
该方程也称为系统的状态方程。在方程中,变量y 代表电 容两端的电压,是电容储能的函数。本例中它既是系统的 状态变量,又是系统的输出变量。
7.1 Matlab编程仿真的方法
7.1.1 概述 通过编程的形式建立计算机仿真模型是最基本的 计算机建模方法。Matlab编程仿真过程就是用编 写脚本文件或函数文件来描述数学模型,并实现 计算机数值求解的过程。 我们把外界对系统产生作用的物理量称为输入 信号或激励,把由于系统内部储存的能量称为系 统的状态,而将系统对外界的作用物理量称为系 统的输出信号或响应。
图:模拟真实示波器显示的调幅仿真波形,仿真中考虑了输 入信号与示波器扫描不同步,载波相位噪声以及加性信道噪 声的影响
7.1.3 连续动态系统的Matlab编程仿真 7.1.3.1 几个实例
MATLAB及Simulink应用实验指导书+答案

《MATLAB及应用》实验指导书班级:姓名:学号:总评成绩:汽车工程系电测与汽车数字应用中心目录实验04051001 MATLAB语言基础1实验04051002 MATLAB科学计算及绘图4实验04051003 MATLAB综合实例编程6实验04051001MATLAB 语言基础1实验目的1) 熟悉MATLAB 的运行环境 2) 掌握MATLAB 的矩阵和数组的运算 3) 掌握MATLAB 符号表达式的创建 4) 熟悉符号方程的求解2实验内容说明:从下面的题目、第1~4章课后习题中任选10题,学号为奇数的选择奇数号题,学号为偶数的选择偶数号题,并在答案之前标注题目来源,例如“课本第1章题2”、“指导书题3”等。
可以采用notebook 格式输出结果(关于notebook 请查阅其他参考资料,或上网搜索) 例如:课本第4章题1.一个半径为r 的求体积V 和表面积A 分别为:334r V π=、24r A π= a.给出以下程序的伪代码描述:计算当30≤≤r 米时的V 和A ,并同时绘制V 相对于A 的图形。
b.编写和运行部分a 中所描述的程序。
解:clc,clear; r=0:0.1:3; V=4/3*pi*r.^3; A=4*pi*r.^2; plot(A,V);grid on; xlabel('Surface Area'); ylabel('Volume');1.在一个已知的测量矩阵T(100×100)中,删除整行全为0的行,删除整列内容全为0的整列(判断某列元素是否为0方法:检查T(: ,i).*(T(: ,j))是否为0)。
2.假设汽车系在下列各年度的人口统计如表所示试用一个二维矩阵STU表示上述数据,并请计算出下列各数值:(1)汽车系在2002~2006年之间的每年平均新生、毕业生人数。
(2)5年来汽车系共有多少毕业生?(3)在哪几年,新生数目比毕业生多?(4)5年来每年的毕业生对新生的比例平均值为何?3.完成下列矩阵运算:(1) 使用randn 产生一个(10×10)的矩阵A(2) 计算B=(A+A ’)/2。
《Simulink建模与仿真》

《Simulink建模与仿真》§2.11、>> A=[1 2 3;4 5 6]A = 1 2 34 5 62、>> B=[1 2 3]B = 1 2 33、>> C=[4;5;6]C =4564、>> A(2,3)ans =6(说明:ans是answer的缩写,默认的输出符号)5、MATLAB中分号(;)的作用有两点:一是作为矩阵或向量的分行符,二是作为矩阵或向量的输出开关控制符。
即如果输入矩阵或向量后键入分号,则矩阵与向量不在MATLAB命令窗中显示,否别将在命令窗口中显示。
6、冒号操作符(:)的应用。
冒号操作符在建立矩阵的索引与引用时非常方便且直接。
如上述对多维矩阵F的建立中,冒号操作符表示对矩阵F第一维与第二维所有元素按照其顺序进行引用,从而对F进行快速赋值,无需一一赋值。
如>> B=2:5 %对向量进行赋值;B = 2 3 4 5>> B(1:3)=2 %向量B从第2个到第3个元素全部赋值为2B = 2 2 2 5>> C=6:-2:0 %将向量C放行递减赋值.初始值为6,终止位为0,步长为一2C = 6 4 2 07、冒号的使用很灵活:§2.2 矩阵单元的基本运算1、矩阵的加减法>>a=[1 2 3;4 5 6]a =1 2 34 5 6>> b=[0 2 1;2 5 3]b =0 2 12 5 3>> c=a+bc =1 4 46 10 9>> d=a-bd =1 0 22 0 3矩阵与标量的加法与减法是指标量本身与矩阵所有元素进行相应运算,如若B=1,则>> e=a+Be =2 3 45 6 72、矩阵的乘方与除法>>a =1 2 34 5 6>> b=[1 2;0 3;2 1]b =1 20 32 1>> c=a*bc =7 1116 29在Matlab中,矩阵除法有两种形式,即左除(\)和右除(/)。
matlab课后习题及答案

第一章5题已知a=4.96,b=8.11,计算)ln(b a e b a +-的值。
解:clearclca=4.96;b=8.11;exp(a-b)/log(a+b)ans =0.01676题已知三角形的三边a=9.6,b=13.7,c=19.4,求三角形的面积。
提示:利用海伦公式area =))()((c s b s a s s ---计算,其中S=(A+B+C)/2.解:clearclca=9.6;b=13.7;c=19.4;s=(a+b+c)/2area=sqrt(s*(s-a)*(s-b)*(s-c))s =21.3500第二章8题已知S=1+2+2^2+2^3+……+2^63,求S 的值解:clearclcS=0;for i=0:1:63S=S+2^i;endSS =1.8447e+0199题分别用for 和while 循环结构编写程序,计算∑=-1001n 1n 2)(的值。
解:clearclcs=0;for n=1:100s=s+(2*n-1);endss =10000clearclcn=1;s=0;while n<=100s=s+(2*n-1);n=n+1;endss =10000第三章2题在同一坐标下绘制函数x ,,2x -,2x xsin(x)在()∏∈,0x 的曲线。
解:clearclcx=0:0.2:pi;y1=x;y2=x.^2;y3=-(x.^2);y4=x.*sin(x);plot(x,y1,'-',x,y2,'-',x,y3,'-',x,y4,'-')00.51 1.52 2.53-10-8-6-4-22468109题用不同的线型和颜色在同一坐标内绘制曲线y1=2e x 5.0 、y2=sin(2∏x )的图形。
解:clearclcx=0:0.01:pi;y1=2*exp(-0.5*x);y2=sin(2*pi*x);plot(x,y1,'b:',x,y2,'r--')00.51 1.52 2.53 3.5-1-0.50.511.52第四章1题对表达式f=3238641+++x x x 进行化简。
MATlab 仿真部分习题答案
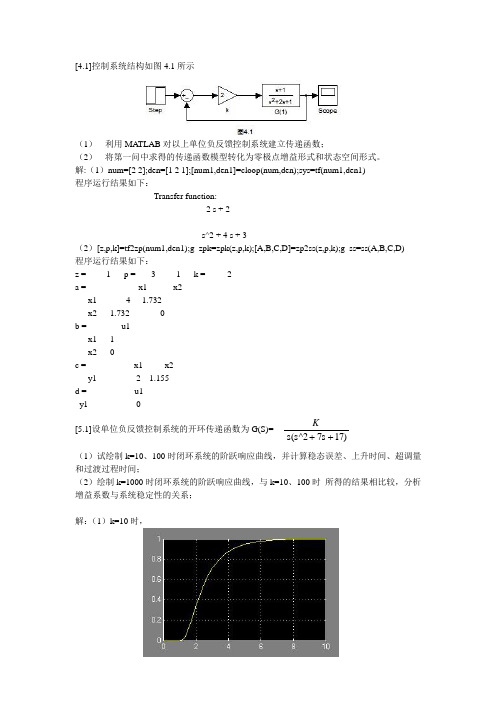
[4.1]控制系统结构如图4.1所示(1)利用MATLAB对以上单位负反馈控制系统建立传递函数;(2)将第一问中求得的传递函数模型转化为零极点增益形式和状态空间形式。
解:(1)num=[2 2];den=[1 2 1];[num1,den1]=cloop(num,den);sys=tf(num1,den1)程序运行结果如下:Transfer function:2 s + 2-------------s^2 + 4 s + 3(2)[z,p,k]=tf2zp(num1,den1);g_zpk=zpk(z,p,k);[A,B,C,D]=zp2ss(z,p,k);g_ss=ss(A,B,C,D)程序运行结果如下:z = -1 p = -3 -1 k = 2a = x1 x2x1 -4 -1.732x2 1.732 0b = u1x1 1x2 0c = x1 x2y1 2 1.155d = u1y1 0K[5.1]设单位负反馈控制系统的开环传递函数为G(S)=+s(s^2+7s17)(1)试绘制k=10、100时闭环系统的阶跃响应曲线,并计算稳态误差、上升时间、超调量和过渡过程时间;(2)绘制k=1000时闭环系统的阶跃响应曲线,与k=10、100时所得的结果相比较,分析增益系数与系统稳定性的关系;解:(1)k=10时,K=100时,K=10时,利用MA TLAB工作区输入程序:num=[10];den=[1,7,17,0];[z,p,k]=tf2zp( num,den);运行得z,p,k的值p= -3.5+2.1794*i -3.5-2.1794*i k=10G=zpk([ ],[-3.5+2.1794*i,-3.5-2.1794*i],10);c=dcgain(G);[y,t]=step(G);plot(t,y)[Y,K]=max(y);timetopeak=t(k);percentovershoot=100*(y-c)/cn=1;while y(n)<c n=n+1;end risetime=t(n) i=length(t);while(y(i)>0.98*c&y(i)<1.02*c) i=i-1;End setllingtime=t(i) 运行程序结果为:稳定值c=0.5882,响应时间setllingtime=1.0096s,上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555% 同理得k=100时,稳定值c=5.882,响应时间setllingtime=1.0096s, 上升时间risetime=1.1989s,最大峰值时间timetopeak=1.4356,超调量percentovershoot=0.555%(3)k=1000时,由其响应曲线可知,增益系数越大,其稳定性越差。
2020年智慧树知道网课《数学建模与系统仿真》课后章节测试满分答案》课后章》课后章

第一章测试1【判断题】(10分)数学模型是对于现实世界的一个特定对象,一个特定目的,根据特有的内在规律,做出一些必要的假设,运用适当的数学工具,得到一个数学结构.A.错B.对2【判断题】(10分)数学建模是利用数学方法解决实际问题的一种实践.即通过抽象、简化、假设、引进变量等处理过程后,将实际问题用数学方式表达,建立起数学模型,然后运用先进的数学方法及计算机技术进行求解,是对实际问题的完全解答和真实反映,结果真实可靠。
A.错B.对3【判断题】(10分)数学模型是用数学符号、数学公式、程序、图、表等刻画客观事物的本质属性与内在联系的理想化表述.数学建模就是建立数学模型的全过程(包括表述、求解、解释、检验).A.错B.对4【判断题】(10分)数学模型(MathematicalModel):重过程;数学建模(MathematicalModeling):重结果。
A.对B.错5【判断题】(10分)人口增长的Logistic模型,人口增长过程是先慢后快。
A.错B.对6【多选题】(10分)MATLAB的主要功能有A.符号计算B.绘图功能C.数值计算D.与其它程序语言交互的接口7【多选题】(10分) Mathematica的基本功能有A.数值运算(NumericComputation)B.符号运算(AlgebricComputation)C.图像处理(Graphics)D.语言功能(ProgramingLanguage)8【多选题】(10分)数值计算是下列哪些软件的一个主要功能A.MathematicaB.MATLABC.JavaD.Maple9【多选题】(10分)评阅数学建模论文的标准有:A.建模的创造性B.表述的清晰性C.完全一致的结果D.论文假设的合理性10【单选题】(10分)关于中国(全国)大学生数学建模竞赛(CUMCM)描述正确的是A.一年举办一次B.一年举办2次C.开始于70年代初D.2年举办一次第二章测试1【判断题】(10分)衡量一个模型的优劣在于它是否使用了高深的数学方法。
第4章电力系统的MATLABSIMULINK仿真与应用_

解:(1) 理论分析。由已知,得稳态运行时发电机的转
速n为
其中,f为系统频率,按我国标准取为50 Hz;p为隐极机的 极对数,此处为2。 电磁功率Pe = 0.8 p.u.,功率角δ为
60 f n = = 1500 r/min p
(4-1)
Pe X 0.8 0.9 arcsin arcsin 46.05 EV 1 1
第4章 电力系统主要元件等效模型
【例4.1】额定值为50 MVA、10.5 kV的两对极隐极同
步发电机与10.5 kV无穷大系统相连。隐极机的电阻R=0.005 p.u.,电感L = 0.9 p.u.,发电机供给的电磁功率为0.8 p.u.。 求稳态运行时的发电机的转速、功率角和电磁功率。
第4章 电力系统主要元件等效模型
第4章 电力系统主要元件等效模型
第4章 电力系统主要元件等效模型
4.1 同步发电机模型 4.2 电力变压器模型 4.3 输电线路模型
4.4 负荷模型
习题
第4章 电力系统主要元件等效模型
4.1 同步发电机模型
4.1.1 同步发电机等效电路 SimPowerSystems中同步发电机模型考虑了定子、励磁 和阻尼绕组的动态行为,经过Park变换后的等值电路如图41所示。
mq , m d
Vq,Vd Δθ ωm Pe Δω θ Te δ Peo,Qeo
第4章 电力系统主要元件等效模型
通过“电机测量信号分离器”(Machines Measurement
Demux)模块可以将输出端子m中的各路信号分离出来,典 型接线如图4-10所示。
图4-1 同步发电机等效电路图
(a) d轴等效电路;(b) q轴等效电路
第4章 电力系统主要元件等效模型
matlab第四章课后答案

%Exerc ise 1(1)r oots([1 11])%Exer cise1(2)roots([3 0 -4 0 2 -1])%Exerc ise 1(3)p=zero s(1,24);p([1 17 1822])=[5 -6 8 -5];ro ots(p)%E xerci se 1(4)p1=[2 3];p2=conv(p1,p1);p3=co nv(p1, p2);p3(end)=p3(en d)-4; %原p3最后一个分量-4r oots(p3)%Exer cise2fun=inli ne('x*log(sqrt(x^2-1)+x)-sqrt(x^2-1)-0.5*x');fzer o(fun,2)%Exer cise3fun=inli ne('x^4-2^x');fplot(fun,[-2 2]);gr id on;fze ro(fu n,-1),fzer o(fun,1),f minbn d(fun,0.5,1.5)%Exe rcise 4fu n=inl ine('x*sin(1/x)','x');fp lot(f un, [-0.10.1]);x=z eros(1,10);fori=1:10, x(i)=fz ero(f un,(i-0.5)*0.01);end;x=[x,-x]%Ex ercis e 5f un=in line('[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2]','x');[a,b,c]=fso lve(f un,[0 0 0])%E xerci se 6fun=@(x)[x(1)-0.7*si n(x(1))-0.2*cos(x(2)),x(2)-0.7*cos(x(1))+0.2*sin(x(2))]; [a,b,c]=fsolv e(fun,[0.5 0.5])%E xerci se 7clear; clo se; t=0:p i/100:2*pi;x1=2+sqr t(5)*cos(t); y1=3-2*x1+sq rt(5)*sin(t);x2=3+s qrt(2)*cos(t);y2=6*sin(t);pl ot(x1,y1,x2,y2); gri d on; %作图发现4个解的大致位置,然后分别求解y1=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.5,2])y2=fsolv e('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[1.8,-2])y3=fsol ve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[3.5,-5])y4=fso lve('[(x(1)-2)^2+(x(2)-3+2*x(1))^2-5,2*(x(1)-3)^2+(x(2)/3)^2-4]',[4,-4])%Exerc ise 8(1)c lear;fun=inlin e('x.^2.*(x.^2-x-2)');fp lot(f un,[-2 2]);grid on;%作图观察x(1)=-2;x(2)=fminb nd(fu n,-1,-0.5);x(4)=fmi nbnd(fun,1,2);fun2=inlin e('-x.^2.*(x.^2-x-2)');x(3)=f minbn d(fun2,-0.5,0.5);x(5)=2feval(fun,x)%答案: 以上x(2)(4)是局部极小,x(1)(3)(5)是局部极大,从最后一句知道x(1)全局最大, x(4)最小。
Matlab与通信仿真实验报告册答案

Matlab 与通信仿真34.0000 22.0000 62.00001. 在Command Window 里面计算_7 8 914 5 6,计算:C = AxB,D =A + B,A C,C/B ; 12 3>> a=[1 2 3;4 5 6;7 8 9]; >> b=[7 8 9;4 5 6;1 2 3]; >> c=a*b c =18 24 30 5469 84 90114138>> d=a+b d =8 10 12 8 10 12 81012>> e=a\cWarning: Matrix is close to singular or badly scaled.Results may be inaccurate. RCOND = 1.54 佃76e-018.(1) (3 5 8)- 5 10 ;>>(3+5+8)/5*10 ans=32>>sin(3*pi)/sqrt(9/5) ans=2.7384e-161 2 3(3)A= 4 5 6 ,B 78 9JMatlab 与通信仿真-50.0000-23.0000 -100.0000 28.0000 16.000056.0000>> f=c/bWarning: Matrix is singular to working precision.NaN NaN NaNNaN -Inf Inf NaNNaNNaN3 1.2 4(4) A= 7.5 6.6 3.1,求A :A, A ;(求矩阵的行列式)5.4 3.46.1 _>> a=[3 1.2 4;7.5 6.6 3.1;5.4 3.4 6.1]; >> a' ans =2.1555 0.4555 -1.6449 -2.1040-0.2393 1.5013 -0.7354-0.26980.7833>> det(a) ans =13.78803.0000 1.20004.0000>> inv (c )7.5000 6.6000 3.10005.4000 3.40006.1000Matlab 与通信仿真1 2 0 0 0(5) Z =『+2i 站如I 输入复数矩阵;§+6i 7 + 8i>> z=[1+2*i 3+4*i;5+6*i 7+8*i] 1.0000 + 2.0000i 3.0000 + 4.0000i 5.0000 + 6.0000i7.0000 + 8.0000i1 2川23 HI2.建立.m 文件,用for 循环语句生成5>5的矩阵A :* ..■fa ri H *RF弓 6 III>> a=zeros(5); for m=1:5for n=1:5 a(m,n)=m+n-1 end end1 0 0 0 0a = 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0直翻转得到矩阵 B 和C 。
matlab及在电子信息课程中的应用课后习题答案第四章

clc,clear,clf,close all;disp('题解4.5,4.6,4.7');pause;echo on;a=[3 4 7 2 9 12],roots(a),pause,b=[1 0 0 0 0 -1],roots(b),pause,c=[-3 -5 -8 -9],poly(c),echo off;disp('题解4.8');pause;echo on;a=[1 2 5 4 3],b=[1],[r,p,k]=residue(b,a)pause,t=0:0.2:10;ys=r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t)+r(3)*exp(p(3)*t)+r(4)*exp(p(4)*t); h=plot(t,ys);set(h,'linewidth',2),echo off;disp('题解4.9,4.10');pause;echo on;R1=randn(8,6),mean(R1),std(R1),pause,mean(R1(:)),std(R1(:)),pause,R=ceil(16*rand(4,6)),a=R(:,[1,2,3,4]),inv(a),echo off;disp('题解4.11');echo on;t=[0:0.05:10];x1=2.*cos(t)+3.*t;y1=2.*sin(t)+3;plot(x1,y1),shg,hold on;x2=3.*cos(t)+3.*t;y2=3.*sin(t)+3;plot(x2,y2),shgx3=4.*cos(t)+3.*t;y3=4.*sin(t)+3;plot(x3,y3),shghold off;pause;figure;plot(x1,y1,x2,y2,x3,y3)echo off;disp('题解4.12');echo on;t=[-2*pi:0.05:2*pi];a=0;x=sin(t);y1=sin(t+a);y2=sin(2.*t+a);y3=sin(3.*t+a);y4=sin(4.*t+a);subplot(2,2,1),plot(x,y1), subplot(2,2,2),plot(x,y2), subplot(2,2,3),plot(x,y3), subplot(2,2,4),plot(x,y4), pause;y11=sin(2.*t);y22=sin(2.*t+pi/3);y33=sin(2.*t+pi/2);y44=sin(2.*t+pi);figure;subplot(2,2,1),plot(x,y11), subplot(2,2,2),plot(x,y22), subplot(2,2,3),plot(x,y33), subplot(2,2,4),plot(x,y44), echo off;disp('题解4.13');pause; echo on;p=[1 -4 0 3 -2 6],x=linspace(-2,8,100);y=polyval(p,x);plot(x,y),pauseaxis([-2 8 -20 20])pause,roots(p),echo off;disp('题解4.14')echo on;z=[0:0.05:10];x=z.*sin(3.*z);y=z.*cos(3.*z);plot3(x,y,z);pause;figure,plot3(x,y,z,'r:')pause;xlabel('x'),ylabel('y'),zlabel('z'), echo off;disp('题解4.15 4.16');echo on;[x,y]=meshgrid(-2:0.1:2,-2:0.1:2); z=x.^2.*exp(-(x.^2+y.^2)); mesh(z);hold on;pause;z1=0.05.*x-0.05.*y+0.1;mesh(z1);echo off;for i=1:41for j=1:41if z(i,j)==z1(i,j)a=z(i,j);plot3(i,j,a,'r+');endendendhold off;disp('题解4.18');pause;type f1.mi=1;a(1)=fzero('f1',-2);for m=-2:1:8b=fzero('f1',m);if abs(a(i)-b)>0.00001i=i+1;a(i)=b;endendapause,echo on,fplot('f1',[-2 8]);shg;hold on,plot(a,0,'ro'),shg,pause,axis([-2 8 -20 20]),grid,hold off;echo off;disp('题解4.18第二问');pause; type f11.mi=1;a(1)=fzero('f11',-2);for m=-2:1:8b=fzero('f11',m);if abs(a(i)-b)>0.00001i=i+1;a(i)=b;endendapause,echo on,fplot('f11',[-2 8]);shg;hold on,plot(a,0,'ro'),shg,pause,axis([-2 8 -20 20]),grid,hold off;echo off;disp('题解4.19');echo on;x=[0:0.05:4];y=f31(x);plot(x,y)echo off;disp('题解420');pause;type f420.mi=1;a(1)=fzero('f420',0.1);for m=0.1:0.1:4b=fzero('f420',m);if abs(a(i)-b)>0.0001i=i+1;a(i)=b;endendapause,echo on,fplot('f420',[0 4]);shg;hold on,plot(a,f420(a),'ro'),shg,pause, axis([0 4 -20 20]),grid,hold off;pause,quad('f420',a(1),a(2)),echo off;disp('题解421');pause;type f421.mecho on[x,y]=ode23('f421',[0 5],1);plot(x,y),shg,pause,p=polyfit(x,y,9),xi=0:0.1:5;yi=polyval(p,xi);plot(x,y,'ro',xi,yi,'b')echo off,disp('题解422');pause;echo onpause,s='magic(3)',pause,eval(s);pause,y(3,:)='magic(3)';y(4,:)='magic(4)';y(5,:)='magic(5)';y,pausefor n=3:5eval(y(n,:));endecho offdisp('题解424');pause;echo one=exp(1);pause,st=sprintf('自然对数底数e=%21.20f',e);disp(st) echo offdisp('题解425');pause;echo on='Jone';student.birthplace='Shanghai';student(2).name='David';student(2).birthplace='Nanjing';student(3).name='Tom';student(3).birthplace='Hangzhou';student,pause,name={'Jone';'David';'Tom'};birthplace={'Shanghai';'Nanjing';'Hangzhou'}; studentt={name;birthplace};studentt,pause,student1=['Jone ';'Shanhai'],student2=['David ';'Nanjing'],student3=['Tom ';'Hongzhou'],echo off调用子程序f1.mfunction y=f1(x)y=x.^5-4*x.^4+3*x.^2-2*x+6;f11.mfunction y=f11(x)y=x.^5-4*x.^4+3*x.^2-2*x+6+x.*sin(x);f31.mfunction f1=f31(x)f1=1./((x-2).^2+0.1)+1./((x-3).^4+0.01);f420.mfunction y=f420(x)y=x.^3-2*(x.^2).*sin(x)+5*x.*cos(x)+1./(x); f421.mfunction yp=f421(x,y)yp=(x.^2)./y-x.*cos(y);。
