现代控制理论--1.状态空间模型
现代控制理论 第九章 现代控制理论-控制系统的数学模型

1 C
∫ i (t )dt
= u c (t )
i (t ) | t = t 0 = i (t 0 )
u c (t ) | t = t 0 = u c (t 0 )
若将 i (t ) 和 u c (t ) 视为一组信息量,则这样一 组信息量就称为状态。这组信息量中的每个变 量均是该电路的状态变量。 状态:表征系统运动的信息和行为 状态 表征系统运动的信息和行为。 表征系统运动的信息和行为 状态变量:系统的状态变量就是确定系 统状态的最小一组变量。(或完全表征 系统运动状态的最小一 组变量。)
di dt
=
R x1 L
1 L
x2+ 1 u( t )
L
x
2
1 x c 1
y = x2 = u c (t )
写成矩阵— 写成矩阵—向量的形式为:
x
1
=
R L
1 L
x1
x
2
1 c
0
x2
+
1 L u( t )
0
y=
x1
0 1
x2
为状态向量
x 1 x2 T 令x =
则:
x=
R L
1 L
1 c
1 x+ L
状态方程 输出方程
一 、状态、状态变量和状态空间
R + u(t)
输入
L
+ + y C uc(t) _ 输出 _
i(t)
_
解:以 i(t) 作为中间变量,列写该回路的微分方程
di (t ) L + Ri (t ) + u c (t ) = u (t ) dt
求解这个微分方程组, 出现两个积分常数。 它们由初始条件
现代控制系统的状态空间模型

状态空间模型--系统的内部描述。
第1章 控制系统的状态空间模型
一些特殊的模型
f ( x , u, t ) = A(t ) x + B (t )u
线性系统模型
& = A(t ) x + B (t )u x
g ( x , u, t ) = C (t ) x + D(t )u
y = C (t ) x + D(t )u
¾ 线性系统是实际非线性对象的线性化近似; ¾ 线性系统的处理方法可以为非线性系统问题的解决 提供思路
例子:倒立摆装置
用小车的位移和速度及摆杆 偏离垂线的角度和角速度来 描述系统的动态特性 小车的水平位移:y 小球中心位置:y + l sin θ
&& cos θ − mlθ & 2 sin θ = u & + mlθ y 水平方向: (M + m) &
u y l m mg
θ
M
&& = mg sin θ & cos θ + mlθ y 垂直方向: m&
g:重力加速度
非线性模型
例子:倒立摆装置
考虑在垂直位置附近的线性化模型
sin θ ≈ θ , cos θ ≈ 1
由
&& cos θ − mlθ & 2 sin θ = u & + mlθ ( M + m) & y && = mg sin θ & cos θ + mlθ m& y
是否可能? 如何得到?
传递函数到状态空间模型
传递函数的一般形式:
【武汉大学】控制系统的状态空间模型【现代控制理论】

的结构图如图2-5所示。
D(t)
+
u
+ B(t)
x& ∫
x C(t)
y
+
+
A(t)
图2-5 多输入多输出线性时变系统的结构图
现代控制理论
武汉大学 自动化系 丁李
2.1.3线性系统状态空间模型的结构图
若需要用结构图表示出各状态变量、各输入变量和各输出变 量间的信息传递关系,则必须根据实际的状态空间模型,画出各 变量间的结构图。
或观测的量; – 可以是物理的,也可以是非物理的、没有实际物理量与之
直接相对应的抽象数学变量。
现代控制理论
武汉大学 自动化系 丁李
2.1.1.1系统的状态和状态变量
状态变量与输出变量的关系: – 状态变量是能够完全描述系统内部动态特性行为的变
量。
– 而输出变量是仅仅描述在系统分析和综合(滤波、优化 与控制等)时所关心的系统外在表现的动态特性,并非 系统的全部动态特性。
RiL
L
diL dt
uC
ui
iL
C
duC dt
现代控制理论
武汉大学 自动化系 丁李
2.1.2系统的状态空间模型
2. 选择状态变量。 状态变量的个数应为独立一阶储能元件(如电感和电容) 的个数。 对本例
x1(t) iL , x2 (t) uC
3. 将状态变量代入各物理量所满足的方程,整理得一规范形式 的一阶矩阵微分方程组--状态方程。
武汉大学 自动化系 丁李
目录
2.1 状态和状态空间模型 2.2 根据系统机理建立状态空间模型 2.3 根据系统的输入输出关系建立状态空间模型 2.4 状态空间模型的线性变换和约旦规范形 2.5 传递函数阵 2.6 用MATLAB进行系统模型转换
现代控制理论状态空间法

根据系统微分方程建立状态空间表达式.
1.输入项中不含输入导数项的线性系统空间状态 表达式
• 系统描述为:
y (n ) a1 y (n1) an1 y an y u
(1)
讨论:状态如何选择
y(t) C (t)x(t) D(t)u(t)
2)线性时不变系统: x Ax Bu y Cx Du
在通常情况下,大多数还是研究线性时不变 系 统,即线性定常系统,因此本课程的主要研究对 象是线性定常系统。
4.状态空间描述的结构图(或称状态变量图)
• 例:根据上例画出结构图. • 解:先将例子写成下述形式
现代控制理论
第一章 状态空间法
控制系统的状态空间描述
一.问题的引出 1 --古典控制理论的局限性 1、仅适用于SISO的线性定常系统(外部描述,
时不变系统) 2、古典控制理论本质上是复频域的方法.(理论) 3、设计是建立在试探的基础上的.(应用) 4、系统在初始条件为零,或初始松驰条件下,才
能采用传递函数.
定义2.状态变量
状态变量是确定系统状态的最小一组变量,如果以最
少的n个变量 x1 (t ), x2 (t ), , xn (t ) 可以完全描述系
统的行为 (即当t≥ 时输入和
t0
在t= t0初始状态给定后,系统的状态完全可以确定),那 么
x1 (t ), x2 (t ), 是一, xn组(t )状态变量.
(2)状态变量选取不唯一,有时选取状态变量仅为数 学描述所需,而非明确的物理意义。
(3)状态变量是系统的内部变量,一般情况下输出是 状态的函数,但输出总是希望可量测的。
(4)仅讨论有限个状态变量的系统。 (5)有限个数的状态变量的集合,称为状态向量。 (6)状态向量的取值空间称为状态空间。
现代控制理论控制系统的状态空间模型

方程 x:小车的水平位移
x l sin : 摆心瞬时位置
m
x l
在水平方向,利用牛顿第二定律,得到
2024/6/22
9
1.1 状态空间模型 1.1.1 状态空间模型表达式
设: x1 i(t) x2 uC (t)
x
x1
x2
A -1RL
-
1 L
0
C
1
b
L 0
C 0 1
x Ax bu
则可以写成状态空间表达式:
y Cx
内部描述
2024/6/22
10
1.1 状态空间模型 1.1.1 状态空间模型表达式
uc
u
传函表示形式:
图 R-L-C网络
Uc (s)
1
U (s) LCS 2 RCS 1
外部描述
2024/6/22
7
1.1 状态空间模型 1.1.1 状态空间模型表达式
一阶微分方程表示形式:
C
d uc dt
i
L
di dt
Ri
uc
u
di(t) R i(t) uC (t) u(t)
dt L
x1 x2
ub
x
x
a
18
1.1 状态空间模型
1.1.1 状态空间模型表达式
线性定常多变量系统
状态变量图:
输入向量
r×1 维
u
+ B
Bu
输入矩阵 +
n ×r维
传递矩阵 m×r维
x Ax Bu
y
Cx
Du
D
状态向量
+
x
∫
nx×1
维
状态空间模型

状态空间模型状态空间模型是一种用于描述动态系统行为的数学模型。
在状态空间模型中,系统的行为由状态方程和观测方程确定。
状态方程描述系统状态如何随时间演变,而观测方程则描述系统状态如何被观测。
通过利用状态空间模型,我们可以对系统进行建模、预测和控制。
状态空间模型的基本概念状态空间模型通常由以下几个要素构成:1.状态变量(State Variables):描述系统状态的变量,通常用向量表示。
状态变量是系统内部的表示,不可直接观测。
2.观测变量(Observation Variables):直接观测到的系统状态的变量,通常用向量表示。
3.状态方程(State Equation):描述状态变量如何随时间演变的数学方程。
通常表示为状态向量的一阶微分方程。
4.观测方程(Observation Equation):描述观测变量与状态变量之间的关系的数学方程。
状态空间模型的应用状态空间模型在许多领域都有着广泛的应用,包括控制系统、信号处理、经济学和生态学等。
其中,最常见的应用之一是在控制系统中使用状态空间模型进行系统建模和控制设计。
在控制系统中,状态空间模型可以用于描述系统的动态行为,并设计控制器来实现系统性能的优化。
通过对状态方程和观测方程进行数学分析,可以确定系统的稳定性、可控性和可观测性,并设计出满足特定要求的控制器。
状态空间模型的特点状态空间模型具有以下几个特点:1.灵活性:可以灵活地描述各种复杂系统的动态行为,适用于各种不同的应用领域。
2.结构化:将系统分解为状态方程和观测方程的结构使得系统的分析更加清晰和系统化。
3.预测性:通过状态空间模型,可以进行系统状态的预测和仿真,帮助决策者做出正确的决策。
4.优化性:可以通过状态空间模型设计出有效的控制器,优化系统的性能指标。
在实际应用中,状态空间模型可以通过参数估计和参数辨识等方法进行模型的训练和调整,以适应实际系统的特性。
结语状态空间模型是一种强大的数学工具,可以帮助我们理解和分析动态系统的行为。
1.控制系统的状态空间模型

Chapter1控制系统的状态空间模型1.1 状态空间模型在经典控制理论中,采用n 阶微分方程作为对控制系统输入量)(t u 和输出量)(t y 之间的时域描述,或者在零初始条件下,对n 阶微分方程进行Laplace 变换,得到传递函数作为对控制系统的频域描述,“传递函数”建立了系统输入量)]([)(t u L s U =和输出量)]([)(t y L s Y =之间的关系。
传递函数只能描述系统的外部特性,不能完全反映系统内部的动态特征,并且由于只考虑零初始条件,难以反映系统非零初始条件对系统的影响。
现代控制理论是建立在“状态空间”基础上的控制系统分析和设计理论,它用“状态变量”来刻画系统的内部特征,用“一阶微分方程组”来描述系统的动态特性。
系统的状态空间模型描述了系统输入、输出与内部状态之间的关系,揭示了系统内部状态的运动规律,反映了控制系统动态特性的全部信息。
1.1.1 状态空间模型的表示法例1-1(6P 例1.1.1) 如下面RLC (电路)系统。
试以电压u 为输入,以电容上的电压C u 为输出变量,列写其状态空间表达式。
例1-1图 RLC 电路图解:由电路理论可知,他们满足如下关系⎪⎩⎪⎨⎧==++)(d )(d )()()(d )(d t i t t u C t u t u t Ri t t i L C C 经典控制理论:消去变量)(t i ,得到关于)(t u C 的2=n 阶微分方程:)(1)(1d )(d d )(d 22t u LCt u LC t t u L R t t u C C C =++ 对上述方程进行Laplace 变换:)()()2(20202s U s U s s C ωωζ=++得到传递函数:202202)(ωζω++=s s s G ,LC10=ω,L R 2=ζ 现代控制理论:选择⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛)()(21t u t i x x C 流过电容的电流)(t i 和电容上的电压)(t u C 作为2个状态变量,2=n (2个储能元件);1个输入为)(t u ,1=m ;1个输出C u y =,1=r 。
第一章状态空间模型

2.一般形式: 对于一般的n阶线性定常系统(n个状态,r个输 入,m个输出)
u1 u2 对象 ur
x1 x2 xn 多输入多输出系统
输出
y1 y2 ym
元件
X ( t ) A X ( t ) B u( t ) n n n1 n r r 1 n1 C D Y ( t ) mn X ( t ) mr u( t ) n1 r 1 m1
3.列写系统的状态方程和输出方程,即得状态 空间表达式。
2.一般形式: 对于一般的n阶线性定常系统(n个状态,r个输 入,m个输出)
u1 u2 对象 ur
x1 x2 xn 多输入多输出系统
输出
y1 y2 ym
元件
X ( t ) A X ( t ) B u( t ) n n n1 n r r 1 n1 C D Y ( t ) mn X ( t ) mr u( t ) n1 r 1 m1
三 .线性系统的结构图 根据线性系统的状态空间表达式的一般形式 :
X AX Bu Y CX Du
按单变量系统的结构图绘制原则,一般线性 系统可用这种图形象的表达出来。
结构图: D(t)
u(t)
B(t)
+ +
X ∫dt
X
C(t)
+ Y(t) +
A(t)
在采用模拟计算机对系统模拟时,必须根据实 际的状态空间表达式,画出各分量间的结构图 例:单输入-单输出系统
a11 b1
+ x1 + +
∫dt a12
x1
c1 + + y
a21
b2
x2
∫dt a22
现代控制理论-第1章

i,得到二阶微分方程为:
(5) 其相应的传递函数为:
(6) 回到式(5)或式(6)的二阶系统,若改选 和 作为两个状态变量,
即令
则一阶微分方程为:
(7)
关于状态变量的选取: 理论上,不要求物理上一定可测; 工程上,以选取易测的量为宜,因为有时需要反馈状态变量。
简记为:
设系统2为:
简记为:
1.并联连接
所谓并联连接,是指各子系统在相同输入下,组合系统的输出是各子系
统输出的代数和,结构简图如下图所示。
由式(72)和式(73),并考虑 间表达式:
得系统的状态空
从而系统的传递函数阵为:
故子系统并联时,系统传递函数阵等于子系统传递函数阵的代数和。
2.串联连接
串联连接下如图所示。读者可自己证明,其串联连接传递函数阵为:
其中各元素
都是标量函数,它表征第 个输入对第 个输出的传递关系。
当
时 ,意味着不同标号的插入与输出有相互关联,称为有耦合关系,
这正是多变量系统的特点。
式(69)还可以表示为:
可以看出,
的分母,就是系统矩阵A的特征多项式,
的分子是
一个多项式矩阵。
应当指出,同一系统,尽管其状态空间表达式可以作各种非奇异变换而
(66) 式中, 为r×1输入列矢量; 为m×1输出列矢量;B为n×r控制矩阵;
C为m×n输出矩阵;D为m×r直接传递阵;X,A为同单变量系统。
同前,对式(66)作拉氏变换并认为初始条件为零,得:
(67)
故
间的传递函数为
(68)
它是一个 n×r 矩阵函数。 故 间的传递函数为: (69) 它是一个m×r矩阵函数,即
现代控制理论知识点汇总

第一章控制系统的状态空间表达式1. 状态空间表达式n 阶 DuCx y Bu Ax x +=+= 1:⨯r u 1:⨯m y n n A ⨯: r n B ⨯: n m C ⨯:r m D ⨯:A 称为系统矩阵,描述系统内部状态之间的联系;B为输入(或控制)矩阵,表示输入对每个状态变量的作用情况;C 输出矩阵,表示输出与每个状态变量间的组成关系,D直接传递矩阵,表示输入对输出的直接传递关系。
2. 状态空间描述的特点①考虑了“输入-状态-输出”这一过程,它揭示了问题的本质,即输入引起了状态的变化,而状态决定了输出。
②状态方程和输出方程都是运动方程。
③状态变量个数等于系统包含的独立贮能元件的个数,n 阶系统有n 个状态变量可以选择。
④状态变量的选择不唯一。
⑤从便于控制系统的构成来说,把状态变量选为可测量或可观察的量更为合适。
⑥建立状态空间描述的步骤:a 选择状态变量;b 列写微分方程并化为状态变量的一阶微分方程组;c 将一阶微分方程组化为向量矩阵形式,即为状态空间描述。
⑦状态空间分析法是时域内的一种矩阵运算方法,特别适合于用计算机计算。
3. 模拟结构图(积分器 加法器 比例器)已知状态空间描述,绘制模拟结构图的步骤:积分器的数目应等于状态变量数,将他们画在适当的位置,每个积分器的输出表示相应的某个状态变量,然后根据状态空间表达式画出相应的加法器和比例器,最后用箭头将这些元件连接起来。
4. 状态空间表达式的建立① 由系统框图建立状态空间表达式:a 将各个环节(放大、积分、惯性等)变成相应的模拟结构图;b 每个积分器的输出选作i x ,输入则为i x;c 由模拟图写出状态方程和输出方程。
② 由系统的机理出发建立状态空间表达式:如电路系统。
通常选电容上的电压和电感上的电流作为状态变量。
利用KVL 和KCL 列微分方程,整理。
③由描述系统的输入输出动态方程式(微分方程)或传递函数,建立系统的状态空间表达式,即实现问题。
《现代控制理论》课后习题答案

=
3 2
, c2
=
2s + 5 lim s→−3 s + 1
=
1 2
。
从输入通道直接到输出通道上的放大系数 d = 1,由此可得:
⎡ x1
⎢ ⎣
x 2
⎤ ⎥ ⎦
=
⎡− 1
⎢ ⎣
0
0⎤ − 3⎥⎦
⎡ ⎢ ⎣
x1 x2
⎤ ⎥ ⎦
+
⎡1⎤ ⎢⎣1⎥⎦u
y
=
⎡ ⎢⎣
3 2
1 2
⎤ ⎥⎦
⎡ ⎢ ⎣
x1 x2
u
d
d
b2
dt
dt
d
b1
m
dt
b0
因此,两个环节调换后的系统状态变量图为
u
d
d
b2
dt
dt
d
b1
dt
b0
m
−∫
−∫
y −∫
a0
a1
a2
进一步简化,可得系统状态变量图为 u
b0
b1
b2
− ∫ x1
− ∫ x2
− ∫ x3 y
a0
a1
a2
3
取 y = x3 , y = x2 , y = x1 ,可以得到两个环节调换后的系统的状态空间模型为
a(s)
1 a(s)
=
s3
+
1 a2s2 +
a1s
+
a0
, b(s)
=
b2 s 2
+ b1s
+ b0
。
2
由于 s−3 y 相当于对 y 作 3 次积分,故 y = 1 可用如下的状态变量图表示: m a(s)
现代控制理论1控制系统的状态空间模型3

17
设 A有q个1的重根,其余互异,则变换阵
P111
P1'11
1 2!
P'' 111
L
(q
1
1)!
P ( q 1) 111
P( q 1)11
T
P112
P1'12
1 2!
P'' 112
L
(q
1
1)!
P ( q 1) 112
P( q 1)12
M M M M
M
M
P11n
P1'1n
1 2!
1
2 L
T
12
M
22 L
ML
1n1
n1 2
L
1
n
n2
M
nn1
1
则
T 1AT
2
O
n
20
A有重特征根情形
设 A有m个1的重根,其余互异,则变换阵
1
0
0
L
1
1
0
L
T
12
M
21
M
1
L
MO
M
M
ML
1n1
d
d 1
n1 1
1 2!
d2
d 12
n1 1
L
0
1L
0
m+1 L
0
2 m1
P'' 11n
L
(q
1
1)!
P ( q 1) 11n
P( q 1)1n
L
Pn11
L
Pn12
M M
L Pn1n
其中:P1'ij
现代控制理论第一章-控制系统数学模型

y b0
b1
bn1
xn
注:如果输入项的导数阶次和输出项导数阶次相同,则有d。
Y (s) R(s)
bn s n an s n
b1s b0 a1s a0
d
bn1sn1 b1s b0 ansn a1s a0
例1-4 已知描述系统的微分方程为 y18y 192y 640y 160u 640u
y bn1z(n1) b1z b0 z b0 x1 b1x2 bn1xn
写成矩阵形式
x1
x2
xn
0
0
0
a0
1 0 0 a1
0 1 0 a2
0 0 0 a3
0
0
0 1 an1
x1 x2
xn
0 u 0
1
x1
第1章 控制系统数学模型
本课程的任务是系统分析和系统设计。而不论是系统分析还是系 统设计,本课程所研究的内容是基于系统的数学模型来进行的。因 此,本章首先介绍控制系统的数学模型。
本章内容为: 1、状态空间表达式 2、由微分方程求出系统状态空间表达式 3、传递函数矩阵 4、离散系统的数学模型 5、线性变换(状态变量选取非唯一)
写成矩阵形式
x1 0 1 0 x1 0
x2
0
0
1
x2
0
u
x3 a0 a1 a2 x3 b0
x1
y 1
0
0
x2
x3
状态图如下:
一般情况下,n 阶微分方程为: y(n) an1 y(n1) a1 y a0 y b0u
选择状态变量如下:
x1 y x1 x2 y x2 x3 y
0
x2
1 M
现代控制理论_第1章

现代控制理论 机械工程硕士研究生学位课
状态空间表达式
ɺ = Ax + bu x y = cx
x1 0 x 0 2 x = ⋮ , A = ⋮ xn −1 0 xn −a0 1 0 ⋮ 0 −a1 0 1 ⋮ ⋯ ⋯ ⋱ 0 0 0 0 ⋮ , b = ⋮ , c = [1 0 ⋯ 0] 1 0 −an −1 b0
现代控制理论 机械工程硕士研究生学位课
实现问题
实现问题:由描述系统输入-输出动态关系 的运动方程式或传递函数,建立系统的状态 空间表达式。 揭示系统的内部关系 讨论单输入单输出线性定常系统
ɺ = Ax + bu x y = cx + du
现代控制理论 机械工程硕士研究生学位课
两类实现问题
di 1 Ri + L + ∫ idt = u dt C
本例子中 1. 输入和输出都已 明确; 2. 选择两个独立的 储能元件作为状 态变量; 3. 根据电路的基本 定律列出方程
现代控制理论 机械工程硕士研究生学位课
1 y = uc = ∫ idt C
系统状态方程的建立
设状态变量为电感器电流和电容器电压,即
现代控制理论 Modern Control Theory
现代控制理论 机械工程硕士研究生学位课
本课程主要内容
系统描述:状态空间表示法 系统分析:状态方程的解、线性系统的能 控和能观测性、稳定性分析 系统设计:状态反馈和状态观测器 最优控制:最优控制系统及其解法
现代控制理论习题之状态空间模型
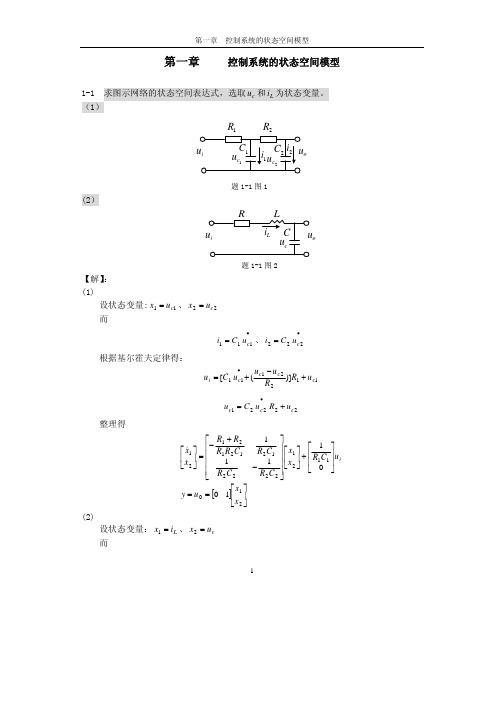
(1)
R1
ui
C1 uc1
R2
i1 u
C 2 i2 u o
c2
题 1-1 图 1
(2)
R
ui
iL
L
C uc
uo
题 1-1 图 2
【解】 : (1) 设状态变量: x1 = u c1 、 x 2 = u c 2 而
i1 = C1 u c1 、 i 2 = C 2 u c 2
• •
根据基尔霍夫定律得:
u i = [C1 u c1 + (
c s+a
1 s
Y1 ( s )
U 2 (s)
d s+b
f s+e
Y2 ( s )
g
题 1-3 图 2
【解】 : (1) 如题 1-3 图 3 设状态变量
3
U ( s)
K1 T1
6 x
x6
1 T1
K2 T2
4 x
1 T2
x4
K3
2 x
x2
1 T4
1 x 1 T4
x1
Y ( s)
x3
3 x
(4)传递函数为:
G(s) = −3s + 1 −3s + 1 = 4 2 2 3 s + 3s + 2 s + 0 s + 3s + 0 s + 2
4
状态空间表达式为:
⎡ 0 1 0 0⎤ ⎡0 ⎤ ⎢ 0 0 1 0⎥ ⎢ ⎥ ⎥ x + ⎢0 ⎥ u =⎢ x ⎢0 ⎥ ⎢ 0 0 0 1⎥ ⎢ ⎥ ⎢ ⎥ ⎣− 2 0 − 3 0⎦ ⎣1⎦ y = [1 − 3 0 0]x
(2) 设状态变量: x1 = i L 、 x 2 = u c 而
现代控制理论课后习题及答案
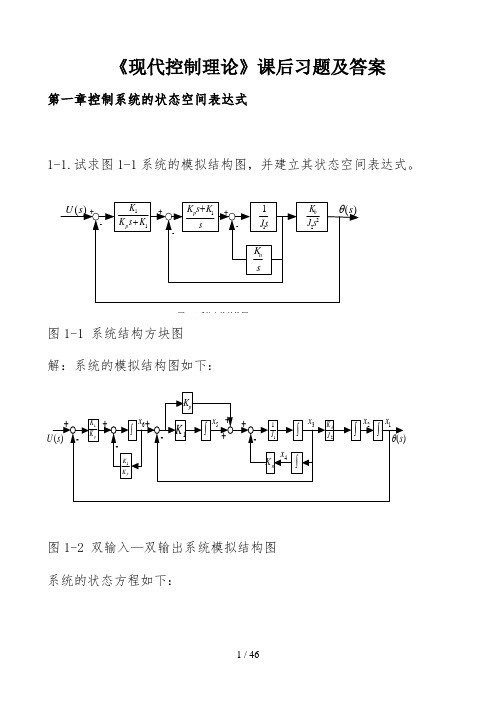
《现代控制理论》课后习题及答案第一章控制系统的状态空间表达式1-1.试求图1-1系统的模拟结构图,并建立其状态空间表达式。
图1-27系统方块结构图图1-1 系统结构方块图解:系统的模拟结构图如下:图1-30双输入--双输出系统模拟结构图图1-2 双输入—双输出系统模拟结构图系统的状态方程如下:u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ,则1x y =所以,系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••6543211654321111111126543210000010000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2.有电路如图1-3所示。
以电压)(t u 为输入量,求以电感中的电流和电容上的电压作为状态变量的状态方程,和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图图1-3 电路图解:由图,令32211,,x u x i x i c===,输出量22x R y =有电路原理可知:•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论控制系统的状态空间模型

线性时变系统的特点
线性时变系统的动态行为由线性时变微 分方程描述,其特点是系统参数随时间 变化。
线性时变系统的稳定性分析较为复杂,需要 考虑参数变化对系统稳定性的影响。
线性时变系统在航空航天、机器人、 化工等领域有广泛应用,其控制策 略需要根据具体应用场景进行设计。
05
非线性系统的状态空间 模型
状态空间模型的近似线性化
线性化方法
由于非线性系统的分析和设计通常比较复杂,因此常常采 用近似线性化的方法将非线性系统转化为线性系统进行分 析。
泰勒级数展开
一种常用的近似线性化方法是使用泰勒级数展开,将非线 性函数展开成多项式形式,并保留低阶项以获得近似的线 性模型。
局部线性化
另一种常用的近似线性化方法是局部线性化,即将非线性 系统在某个平衡点附近进行线性化处理,以获得该点附近 的线性模型。
线性微分方程具有叠加性和时不变性,即对于任意常数c,若x(t) 是方程的解,则cx(t)也是方程的解;同时,若在时间t=t0时, x(t0)=x0,则对于任意时间t>t0,x(t)都等于x0。
状态空间模型的建立
状态空间模型是一种描述控制系统动态行为的方法,它由状态方程和输出方程组成。状态方程描述了系统内部状态的变化规 律,输出方程描述了系统输出与内部状态和输入的关系。
状态空间模型的建立需要确定系统的状态变量、输入变量和输出变量,然后根据系统的物理特性和实际需求来选择合适的系 统矩阵A、B和C。
线性时不变系统的特点
01
线性时不变系统具有叠加性、 均匀性和时不变性,这些性质 使得线性时不变系统在分析和 设计上相对简单。
02
线性时不变系统的动态行为可 以通过系统的极点和零点来描 述,这些极点和零点决定了系 统的动态响应特性和稳定性。
第1章控制系统的状态空间表达式

u
X
y
●状态方程的一般形式为:
x Ax Bu
§1-1 状态空间变量及状态空间表达式
五. 输出方程
在指定系统输出y 的情况下,输出y 与状态变量x 及系统输入u 的
函数关系式,称为系统的输出方程 。
●系统的状态和输入决定了系统输出的变化 。
2.根据给定的数学模型,画出相应的加法器和比例器。
3.用箭头将这些元件连接起来。
§1-2 状态空间表达式的模拟结构图
二. 绘制状态空间模拟结构图的例子
例1 一阶标量微分方程x: ax bu
u
b+
x x
+
a
§1-2 状态空间表达式的模拟结构图
二. 绘制状态空间模拟结构图的例子
例2 三阶微分方程 : x a2 x a1x a0 x bu
值以及t≥t0时间的输入,就完全能够确定系统在任何t≥t0时间的动态行 为;
●状态变量的最小性,体现在减少变量个数就不能够完全表征系统的动态
行为,而增加变量数则是完全表征系统动态行为所不需要的。
●状态变量在数学上是线性无关的。
●状态变量的选取不是唯一的。
●对于一个实际的物理系统,状态变量个数等于系统独立储能元件的个数。
Kn
J2 x2
x1
Kb
x2
x1
§1-3 状态空间表达式的建立(一)
由以上方框图可知:x1 x2
x2
J2 Kb
x4
x3 K n x4
状态方程:
x4
1 J1
x3
Kp J1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
UC ( s) 1 U ( s ) LCs 2 RCs 1
只反映外部情况,无法获知内部联系
7
duc (t) 1 i(t) dt C 1 R 1 di(t) uc ( t ) i ( t ) u( t ) dt L L L
8
2
2018/6/1
1.2 状态空间模型的建立
x3
试写出其状态空间表达式。 解:选择状态变量:
u
, x3 x1 y, x2 y y
则状态空间表达式为:
3 x
5
x2
x1 y x1
1 x2 x 2 x3 x 3 6 x1 8 x2 5 x3 u x y x1
17
8 6
18
(t ) A(t ) x(t ) B(t )u(t ) x y(t ) C (t ) x(t ) D(t )u(t )
线性离散时间系统状态空间表达式
x (k 1) G (k ) x (k ) H (k )u(k ) y ( k ) C ( k ) x ( k ) D ( k ) u( k )
n r维 输入矩阵 , 表征输入对每个状态变 量的作用
状态空间表达式的系统框图
和经典控制理论相类似,可以用框图表示系统信号传递 的关系。对于上述系统,它们的框图分别如图a和b所示。
Hale Waihona Puke c1n c2 n , c mn
d 1r d 2r , d mr
Ap1
1
0
x1 x1 x Px 2 2
即
x 1 1 0 1 2 1 x1 R x2 y x u x2 LC L LC 1 0 0 1 u 1 x x R L LC LC
1.2 状态空间模型的建立
1 1 (t ) x2 (t ) x C 1 R 1 2 ( t ) x1 ( t ) x 2 ( t ) u( t ) x L L L y x1 ( t )
状态方程
•状态空间表达式:状态方程和输出方程合起来构成对 一个动态系统完整的描述,称为动态系统的状态空间 表达式。 图1所示电路,若 uc (t )为输出,取 x1 (t ) uc (t ), x2 (t ) i (t ) 作为状态变量,则其状态空间表达式为
输出方程
1 x1 (t ) 0 C 1 u (t ) R L x2 (t ) L
矩阵 相乘
(t ) 0 x 1 1 x2 (t ) L
x (t ) y 1 0 1 x2 ( t )
系统描述中常用的基本概念
• 系统的外部描述 • 系统的内部描述 传递函数 状态空间描述
3
4
1
2018/6/1
1.1状态空间模型基本概念 •(1)状态:是完全地描述动态系统运动状况的信 息,系统在某一时刻的运动状况可以用该时刻系统 运动的一组信息表征,定义系统运动信息的集合为 状态。 •(2)状态变量:是指足以完全描述系统运动状态 的最小个数的一组变量。 •(3)状态空间:以状态变量x1 (t ), , xn (t ) 为坐标轴所 构成的n维空间。在某一特定时刻t,状态向量 x (t ) 是 状态空间的一个点。
状态变量选择不同,状态方程也不同。 若按照如下所示的微分方程:
duc (t) 1 i(t) dt C di(t) 1 R 1 uc (t ) i (t ) u (t ) dt L L L x 0
1.2 状态空间模型的建立
两组状态变量之间 的关系
x1 uc x2 i
x( t ) [ x1 ( t ), x 2 ( t )]T
i(t)
图1
_
解:
c ( t ) RCu c ( t ) uc ( t ) u( t ) LCu
微分方程 传递函数
定义输出变量 y( t ) x1 ( t ) 整理得一阶微分方程组为
di(t) uc u ( t ) dt du i(t ) C c dt Ri ( t ) L
1.2 状态空间模型的建立
1 0 x 1 0 C x1 u 1 1 R x x 1.举例 2 2 L L L 例1-1:建立RCL电路的状态方程和输出方程。 x1 y 1 0 x 2. 建立状态空间表达式的步骤 2 1)选取 n个状态变量;确定输入、输出变量;
1.3 状态矢量的线性变换
P:非奇异线性变换矩阵 单输入 单输出 系统
Ax bu x y cx du
2)根据系统微分方程列出n个一阶微分方程; 状态变量、输入变量、参数 3)根据系统微分方程,列出m个代数方程。 输出变量、状态变量、输入变量、参数 结论: (1)状态变量选取具有非唯一性。状态变量个数系统的阶次; (2)状态变量具有独立性; (3)不同组状态变量之间可做等价变换线性变换。
2018/6/1
现代控制原理预览
建立
本部分主要教学内容
求解 转换 第二章 系统性能分析 状态反馈控制器设计 第一章 状态空间模型建立
建模
可控性 可观性 稳定性
状态空间 表达式
分析
状态反馈
第三章
设计
状态观测器 最优控制
1
2
第一章
状态空间模型建立
本章主要内容: • 1-1 状态空间模型基本概念 • 1-2 状态空间模型的建立 • 1-3 状态矢量的线性变换 • 1-4 状态空间表达式的解 • 1-5 从状态空间表达式求传递函数阵
Ap i i p i (i 1,2, , n)
1 2 1 1 x1 7 x x 2 0 1 0 x2 2 u 3 x 0 2 1 x3 3
19
x Px
Ax b u x y y cx d u
P变换
非奇异线性变换
A P 1AP, b P 1b, c cP, d d
用途: 通过线性非奇异变换,可以使 A P 1 AP 规范化 (对角化、约当化),且不改变系统的原有性质, 20 是等价变换。
m n维 输出矩阵
表征输出和每个状态变 量的关系
m r维前馈矩阵 , 又称为 直接传递矩阵 表征输入对输出的直接 传递关系 通常 D=0
d m2
4
2018/6/1
例1-2 考虑系统
6y u y 5 y 8y
标量系统结构图
1 x2 x 2 x3 x 3 6 x1 8 x2 5 x3 u x y x1
9
1 x 1 0 x1 0 C u 1 R 1 2 x x2 L L L x 1 y 1 0 x 2
10
x1 uc c x2 u 1 i C
1 C x1 u c ,则得到一阶微分方程组: 选 x1 uc , x2 u 1 R 1 2 x x2 1 x2 x L L L
6
1.2 状态空间模型的建立
1.举例 例1-1:建立如图1所示的RCL电路的 状态方程和输出方程。
R + u(t)
输入
L + uc(t) _
输出
1.2 状态空间模型的建立
+ y _
定义状态变量 x1 ( t ) uc ( t ) x 2 ( t ) i ( t ) 二阶微分方程,选择两个状态变量 状态向量
y y1
c11 c C 21 c m1
d 11 d D 21 d m1
状态方程
输出方程
…
c12 c 22 cm 2
d 12 d 22
(t ) A(t ) x(t ) B(t )u(t ) x y(t ) C (t ) x(t ) D(t )u(t )
y c1
c2 cn x
约当标准型
的解为特征根。
22
( I A)x
0 的解为特征向量。
3.利用线性变化化为对角标准型 (1)A为任意形式的方阵,有n个互异实特征值 1 , 2 , , n 对应的特征向量 p1 , p 2 , , p n ,满足:
[例1-3]
变换系统为对角标准型。
对角标准型
x Ax ( A)x 0
(I A)x 0
方阵 A 的 n 次多项式f ( ) I A 为A 的特征 多项式。 I A 0 为 A 的特征方程。
I A 0
21
1 1 0 0 1 1 x u x 1 1 1
5
2018/6/1
1.3 状态矢量的线性变换
1.3 状态矢量的线性变换
1.两种标准型
1 x
2
1 x 1 u n 1
y c1
c2 cn x
2. 方阵的特征值与特征向量 设 A 是 n 阶方阵,如果数 和 n 维非零向量 x 使 关系式 x Ax成立,那么数 称为方阵 A 的特征 值,非零向量 x 称为 A 的对应于 的特征向量。
a12 a1n a 22 a 2 n , a n 2 a nn
n n 维系统矩阵 , 表征各状态变量间的关 系
