计算方法实验截图
四年级数学上册树状算图与算法流程课件沪教版

引入:
根据题意,填写树状算图,并列式计算:
2.小亚每分钟能打50个字,打2000个字需要几分钟?
2000 50 ÷
2000 ÷50=40(分钟)
40 答:打2000个字需要40分钟。
探究一
小胖、小巧和小亚一起去游泳,小胖游了600米,比小巧多游200米,小亚游的距 离正好是小巧的2倍,小亚游了多少米?
练习二
本课小结
树状算图能帮助我们分析应用 题的数量关系。
本节课我们主要来学习树状算图和算 法流程,同学们要能够分析应用题的 题意准确的画出树状算图,并且能够 根据树状算图中的数量关系列式进行 计算。
引入:
根据题意,填写树状算图,并列式计算:
1.小胖每分钟能打40个字,半小时能打字多少个?
40 30
×
40×30=1200(个)
1200
答:半小时能打字1200个。
23
8
-
11 ÷
23减去8的差除以 11,商是多少?
练习一
练习二
练习二
先画出树状算图,再解答: 小亚:我游了800米。 小丁丁:小亚游的比
我少400米。
小胖:小丁丁游的距离是我的2倍,我游了多少米?
800 400
(800+400)÷2
+
=1200÷2
1200
2
÷
=600(米)
600
练习一
答:小胖游了600米。
小胖 600 要解2决00问题,分几个步骤去考虑?
600
200
--
(1)小巧游了多少米?
(600-200)×2 =400×2 =800(米)
小巧400 400
2
600-200=400(亚游了多少米?
计算方法实验报告

班级:地信11102班序号: 20姓名:任亮目录计算方法实验报告(一) (3)计算方法实验报告(二) (6)计算方法实验报告(三) (9)计算方法实验报告(四) (13)计算方法实验报告(五) (18)计算方法实验报告(六) (22)计算方法实验报告(七) (26)计算方法实验报告(八) (28)计算方法实验报告(一)一、实验题目:Gauss消去法解方程组二、实验学时: 2学时三、实验目的和要求1、掌握高斯消去法基础原理2、掌握高斯消去法法解方程组的步骤3、能用程序语言对Gauss消去法进行编程实现四、实验过程代码及结果1、实验算法及其代码模块设计(1)、建立工程,建立Gauss.h头文件,在头文件中建类,如下:class CGauss{public:CGauss();virtual ~CGauss();public:float **a; //二元数组float *x;int n;public:void OutPutX();void OutputA();void Init();void Input();void CalcuA();void CalcuX();void Calcu();};(2)、建立Gauss.cpp文件,在其中对个函数模块进行设计2-1:构造函数和析构函数设计CGauss::CGauss()//构造函数{a=NULL;x=NULL;cout<<"CGauss类的建立"<<endl;}CGauss::~CGauss()//析构函数{cout<<"CGauss类撤销"<<endl;if(a){for(int i=1;i<=n;i++)delete a[i];delete []a;}delete []x;}2-2:函数变量初始化模块void CGauss::Init()//变量的初始化{cout<<"请输入方程组的阶数n=";cin>>n;a=new float*[n+1];//二元数组初始化,表示行数for(int i=1;i<=n;i++){a[i]=new float[n+2];//表示列数}x=new float[n+1];}2-3:数据输入及输出验证函数模块void CGauss::Input()//数据的输入{cout<<"--------------start A--------------"<<endl;cout<<"A="<<endl;for(int i=1;i<=n;i++)//i表示行,j表示列{for(int j=1;j<=n+1;j++){cin>>a[i][j];}}cout<<"--------------- end --------------"<<endl;}void CGauss::OutputA()//对输入的输出验证{cout<<"-----------输出A的验证-----------"<<endl;for(int i=1;i<=n;i++){for(int j=1;j<=n+1;j++){cout<<a[i][j]<<" ";}cout<<endl;}cout<<"---------------END--------------"<<endl;}2-4:消元算法设计及实现void CGauss::CalcuA()//消元函数for(int k=1 ;k<n;k++){for(int i=k+1;i<=n;i++){double lik=a[i][k]/a[k][k];for(int j=k;j<=n+1;j++){a[i][j]-=lik*a[k][j];}a[i][k]=0; //显示消元的效果}}}2-5:回代计算算法设计及函数实现void CGauss::CalcuX()//回带函数{for(int i=n;i>=1;i--){double s=0;for(int j=i+1;j<=n;j++){s+=a[i][j]*x[j];}x[i]=(a[i][n+1]-s)/a[i][i];}}2-6:结果输出函数模块void CGauss::OutPutX()//结果输出函数{cout<<"----------------X---------------"<<endl;for(int i=1 ;i<=n;i++){cout<<"x["<<i<<"]="<<x[i]<<endl;}}(3)、“GAUSS消元法”主函数设计int main(int argc, char* argv[]){CGauss obj;obj.Init();obj.Input();obj.OutputA();obj.CalcuA();obj.OutputA();obj.CalcuX();obj.OutPutX();//obj.Calcu();return 0;2、实验运行结果计算方法实验报告(二)一、实验题目:Gauss列主元消去法解方程组二、实验学时: 2学时三、实验目的和要求1、掌握高斯列主元消去法基础原理(1)、主元素的选取(2)、代码对主元素的寻找及交换2、掌握高斯列主元消去法解方程组的步骤3、能用程序语言对Gauss列主元消去法进行编程实现四、实验过程代码及结果1、实验算法及其代码模块设计(1)、新建头文件CGuassCol.h,在实验一的基础上建立类CGauss的派生类CGuassCol公有继承类CGauss,如下:#include "Gauss.h"//包含类CGauss的头文件class CGaussCol:public CGauss{public:CGaussCol();//构造函数virtual ~CGaussCol();//析构函数public:void CalcuA();//列主元的消元函数int FindMaxIk(int k);//寻找列主元函数void Exchange(int k,int ik);//交换函数void Calcu();};(2)、建立CGaussCol.cpp文件,在其中对个函数模块进行设计2-1:头文件的声明#include "stdafx.h"#include "CGuassCol.h"#include "math.h"#include "iostream.h"2-2:派生类CGaussCol的构造函数和析构函数CGaussCol::CGaussCol()//CGaussCol类构造函数{cout<<"CGaussCol类被建立"<<endl;}CGaussCol::~CGaussCol()//CGaussCol类析构函数{cout<<"~CGaussCol类被撤销"<<endl;}2-3:高斯列主元消元函数设计及代码实现void CGaussCol::CalcuA()//{for(int k=1 ;k<n;k++){int ik=this->FindMaxIk(k);if(ik!=k)this->Exchange(k,ik);for(int i=k+1;i<=n;i++){float lik=a[i][k]/a[k][k];for(int j=k;j<=n+1;j++){a[i][j]-=lik*a[k][j];}}}}2-4:列主元寻找的代码实现int CGaussCol::FindMaxIk(int k)//寻找列主元{float max=fabs(a[k][k]);int ik=k;for(int i=k+1;i<=n;i++){if(max<fabs(a[i][k])){ik=i;max=fabs(a[i][k]);}}return ik;}2-5:主元交换的函数模块代码实现void CGaussCol::Exchange(int k,int ik)//做交换{for(int j=k;j<=n+1;j++){float t=a[k][j];a[k][j]=a[ik][j];a[ik][j]=t;}}(3)、建立主函数main.cpp文件,设计“Gauss列主元消去法”主函数模块3-1:所包含头文件声明#include "stdafx.h"#include "Gauss.h"#include "CGuassCol.h"3-2:主函数设计int main(int argc, char* argv[]){CGaussCol obj;obj.Init();//调用类Gauss的成员函数obj.Input();//调用类Gauss的成员函数obj.OutputA();//调用类Gauss的成员函数obj.CalcuA();obj.OutputA();obj.CalcuX();obj.OutPutX();return 0;}2、实验结果计算方法实验报告(三)一、实验题目:Gauss完全主元消去法解方程组二、实验学时: 2学时三、实验目的和要求1、掌握高斯完全主元消去法基础原理;2、掌握高斯完全主元消去法法解方程组的步骤;3、能用程序语言对Gauss完全主元消去法进行编程(C++)实现。
实验2截图及结果
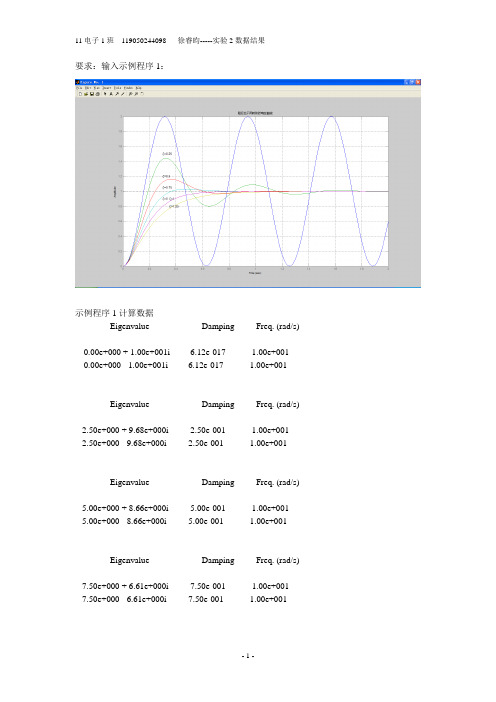
要求:输入示例程序1:示例程序1计算数据Eigenvalue Damping Freq. (rad/s)0.00e+000 + 1.00e+001i -6.12e-017 1.00e+001 0.00e+000 - 1.00e+001i -6.12e-017 1.00e+001Eigenvalue Damping Freq. (rad/s)-2.50e+000 + 9.68e+000i 2.50e-001 1.00e+001 -2.50e+000 - 9.68e+000i 2.50e-001 1.00e+001Eigenvalue Damping Freq. (rad/s)-5.00e+000 + 8.66e+000i 5.00e-001 1.00e+001 -5.00e+000 - 8.66e+000i 5.00e-001 1.00e+001Eigenvalue Damping Freq. (rad/s)-7.50e+000 + 6.61e+000i 7.50e-001 1.00e+001 -7.50e+000 - 6.61e+000i 7.50e-001 1.00e+001Eigenvalue Damping Freq. (rad/s)-1.00e+001 1.00e+000 1.00e+001 -1.00e+001 1.00e+000 1.00e+001Eigenvalue Damping Freq. (rad/s)-5.00e+000 1.00e+000 5.00e+000 -2.00e+001 1.00e+000 2.00e+001要求:输入示例程序2:要求:<2>求系统G(s)=10/(s2+2s+10)的特征根、闭环极点和单位阶跃响应。
分别改变系统阻尼比和自振角频率,观察系统单位阶跃响应的变化规律。
程序:num=10; i=0;for sigma=0: 0.25: 1.25den=[1 2*sigma*sqrt(10) 10];damp(den)sys=tf(num, den);i=i+1;step(sys,2)hold onendgridhold offtitle('阻尼比不同时阶跃响应曲线')lab1='ζ=0'; text(0.3,0.9,lab1),lab2='ζ=0.25'; text(0.3,1.5,lab2),lab3='ζ=0.5'; text(0.3,1.2,lab3),lab4='ζ=0.75'; text(0.3,1.05,lab4),lab5='ζ=1'; text(0.35,0.9,lab5),lab6='ζ=1.25'; text(0.35,0.8,lab6)程序图像:程序计算数据:Eigenvalue Damping Freq. (rad/s)0.00e+000 + 3.16e+000i -6.12e-017 3.16e+000 0.00e+000 - 3.16e+000i -6.12e-017 3.16e+000Eigenvalue Damping Freq. (rad/s)-7.91e-001 + 3.06e+000i 2.50e-001 3.16e+000-7.91e-001 - 3.06e+000i 2.50e-001 3.16e+000 Eigenvalue Damping Freq. (rad/s)-1.58e+000 + 2.74e+000i 5.00e-001 3.16e+000 -1.58e+000 - 2.74e+000i 5.00e-001 3.16e+000Eigenvalue Damping Freq. (rad/s)-2.37e+000 + 2.09e+000i 7.50e-001 3.16e+000 -2.37e+000 - 2.09e+000i 7.50e-001 3.16e+000Eigenvalue Damping Freq. (rad/s)-3.16e+000 1.00e+000 3.16e+000-3.16e+000 1.00e+000 3.16e+000Eigenvalue Damping Freq. (rad/s)-1.58e+000 1.00e+000 1.58e+000-6.32e+000 1.00e+000 6.32e+000要求:<3>已知系统结构如图,使用梅森公式和SIMULINK结构图模型求系统的闭环传递函数。
四年级数学 工作效率 树状算图和算法流程

周周练八工作效率树状算图和算法流程姓名班级学号得分一、直接写出得数16%100÷20= 15×7= 800÷20= 70-70÷70=88÷8= 6×400= 24×5= 100÷25×4=18×60= 9000÷20= 150÷75= 50÷50×20=500÷25= 38÷19= 250×6= 64÷4×2=二、竖式计算 6%4007×360= 18750÷25=三、求□里的数 6%□÷54=54 15×□=270四、递等式计算,能简便的要简便运算 16%125×42×8 37×99955-415÷5×7 67×76+76×33五、画出树状算图并计算 10%1、树状算图算式2、树状算图算式六、填空 10%1、填数量关系6%工作效率=工作量=工作时间=2、填表4%七、选择4%1、数球7930通过计算盒后变成了A、1536B、2006C、3400D、19962、小胖5小时运送225千克大米,小巧6小时运送252000克大米,两人相比A、小胖运送多B、小巧运送多C、一样多.D、不能比较八、判断2%1、小李1分钟能打125个字,1小时能打多少个字?数量关系是: 工作量÷工作时间=工作效率……………………………() 2、一辆客车3小时行180千米.照这样计算,12小时可行多少千米?正确的算式是: 180÷3÷12 …………………………………………( )九、先画出树状图,再计算30%1、数球105通过计算盒后变成了多少?2、一个电器厂原计划15天生产洗衣机4200台,实际提前3天完成任务,实际每天生产洗衣机多少台?3、小胖计划9天看完一本450页的故事书,实际每天看60页。
八年级数学下册7.7用计算器求平方根和立方根计算器的程序图素材青岛版(new)

计算器的“程序图”随着生活的不断改善,计算机或计算器越来越多地走进普通人的视野,而利用其设计一些程序就可以解决一些难题,因此读懂程序不仅是数学素养的表现,而且也是适应信息社会一种要求。
一、利用程序图,进行求值。
例1有一个数值转换器,原理如下:当输入的x 为64时,输出的y 是 。
分析:通入程序图,可知输入一个数时,要求进行求算术平方根运算,然后把所得结果进行判断,如果是无理数就输出结果,如果是有理数,就继续进行求算术平方根运算。
直到得到结果是无理数,就输出。
解:输入64,求得64的算术平方根是8,由于8是有理数,所以还要求8的算术平方根,8的算术平方根是8,由于8是无理数,所以应输出8,但考虑填空题的答案要求是最简的,因此需把8进行化简,结果为22点评:会读数学上的程序图,是解决这个问题的关键。
一般是按箭头所指的方向进行,如果出现两个箭头,就按箭头所给出的条件进行即可.二、由所给出的结果,判断按键顺序例2在计算器上按照下面的程序进行操作:下表中的x 与y 分别是输入的6个数及相应的计算结果:x 2- 1- 0 1 2 3 y 5- 2- 1 4 7 10xy 输入x 取算术平方根 是有理数 是无理数 输出y上面操作程序中所按的第三个键和第四个键应是.分析:由表格所给的数据可以发现:当x=0时,y=1;当x增大(或减小)1时,y就增大(或减小)3,如果输入x时,由于x比0大x,因此y就应该比1增大3x,所以有y=3x+1这样的话,按键顺序应该是乘以3再加上1。
解:+,1点评:由所给的数据发现输入数值和输出数值所隐藏的一般规律,进而就可以知道程序具体过程,具体做法就是看如果x均匀变化时,y是不是也变化规律。
尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
数值计算实验报告----LU分解、追赶法、迭代法(高斯-赛德尔Gauss_Seidel、雅。。。

数值计算实验报告----LU分解、追赶法、迭代法(⾼斯-赛德尔Gauss_Seidel、雅。
数值实验报告----------------------个⼈作业,如果有后辈的作业习题⼀致,可以参考学习,⼀起交流,请勿直接copy⼀、实验⽬的1. 了解并分析LU分解法的优点;2. 追赶法的应⽤与其与LU分解法的对⽐;3. 认识迭代法收敛的含义以及迭代法初值和⽅程组系数矩阵性质对收敛速度的影响。
⼆、实验题⽬三、实验原理l LU分解:·如果对A(0)x = b(0)施⾏第⼀次消元后化为A(1)x = b(1),则存在L1,使得L1A(0)=A(1),L1b(0)= b(1)⼀般地,进⾏k次消元化后为A(k)x = b(k), 则有L k A(k-1)=A(k),L k b(k-1)= b(k)重复这⼀过程,最后得到L n-1…L2L1A(0) = A(n-1)L n-1…L2L1b(0) = b(n-1)将上三⾓形矩阵A(n-1)记为U,则 A=LU ,其中为下三⾓矩阵。
利⽤⾼斯消元法实质上产⽣了⼀个将A分解为两个三⾓形矩阵相乘的因式分解,称为A的三⾓形分解或LU分解。
·矩阵分解不⼀定采⽤⾼斯消元法,以下为直接计算的计算公式:把增⼴矩阵A 采⽤LU 分解格式,即可得到与原⽅程同解的⽅l 追赶法:求解Ax = b 等价于解两个⼆对⾓线⽅程组Ly = bUx =y⾃上⽽下解⽅程组Ly = b 形象地被称为“追”。
y1 = b1/l11y i =b i-l ii-1y i-1/l ii, i = 2, 3, … ,n⾃下⽽上解⽅程组Ux = y 形象地被称为“赶”。
x n=y nx i =y i-u ii+1x i+1, i = n-1, … ,2,1习惯上,上述求解⽅法称为“追赶法”。
l 迭代法:·雅克⽐迭代雅克⽐迭代法基本思想与迭代法相同是⼀种逐次逼近的⽅法。
⾸先给定⼀个较粗糙的初值,然后采⽤迭代公式,进⾏多次迭代,直到满⾜所要求的精度为⽌。
1.14 用计算器进行计算课件(共17张PPT)

.
7
3
随 堂 小 测
B
1.下面科学计算器的按键顺序: 对应的计算任务是( ) A. B. C. D.
2.若用我们数学课本上采用的科学计算器进行计算,其按键顺序如下:则数出结果应为( ) A.-2 B. C.2 D.-
解:按键顺序为 .计算器显示运算式子345+21.3.再按 ,显示结果为 .若需得到小数形式的结果,可继续按 (小数) ,显示366.3,即345+21.3= =366.3.
例2 用计算器求31.2÷(-0.4)的值.
解:按键顺序为 .计算器显示结果为-78.
输入0.4时,也可以省去小数点前的0,按 即可.
.
4
例3 用计算器求62.2+4×7.8.
解:按键顺序为计算器显示结果为93.4.
对于加、减、乘、除和乘方的混合运算,按算式的书写顺序输入即可.
例4 用计算器求2.73.
解:按键顺序为计算器显示结果为19.683.
使用专用键 时,可以先输入底数,再按此键,最后输入指数;也可以先按 ,再输入底数,然后按 ,之后再输入指数,最后按 求解.
B
3.用计算器求下列各式的值: (1)(-15)3÷52=______; (2)-10+8÷22-(-4)×(-3)=______.
-135
-20
小结
用计算器进行计算
计算器的认识与使用
课后作业
1.从课后习题中选取;2.完成练习册本课时的习题。
同学们再见!
授课老师:
时间:2024年9月15日
1.14 用计算器进行计算
课时导入
知识讲解
随堂小测
小结
学习目标
1.让学生学会使用计算器进行有理数加、减、乘、除、乘方运算.2.让学生能运用计算器进行实际问题的有关运算.3.让学生体会解决问题的程序思想,探索使用规律和技巧.
计算机图形学实验代码及截图

目录实验一:OpenGL基础知识 0实验二 OpenGL中的建模与变换 (1)实验三 OpenGL中的光照 (4)实验四 OpenGL中的拾取 (7)实验五 OpenGL中的纹理映射 (10)实验一:OpenGL基础知识一、实验目的1、建立Windows系统下的OpenGL实验框架。
2、学习理解OpenGL工作流程。
二、实验环境⒈硬件:每个学生需配备计算机一台。
⒉软件:Visual C++;三、实验内容1、建立非控制台的Windows程序框架。
2、建立OpenGL框架。
3、建立OpenGL框架的类文件。
4、完善Windows框架。
5、理解程序间的相互关系。
四、实验要求1、学习教材第2章的内容。
2、理解教材中相关实例的代码,按要求添加到适当的地方,调试并通过运行。
3、运行结果应该与教材中的相关实例相符。
4、编译第2章的框架代码,修改背景色、窗口标题。
五、程序设计提示(略)六、报告要求1.认真书写实验报告,字迹清晰,格式规范。
报告中应写清姓名、学号、实验日期、实验题目、实验目的、实验原理。
2.报告中应书写主要源程序,且源程序中要有注释。
3.报告中应包含运行结果及结果分析。
如调试通过并得到预期的效果,请注明‘通过’并粘贴运行效果图;如未调试通过或结果不正确,试分析原因。
4.报告最后包含实验总结和体会。
实验二 OpenGL中的建模与变换一、实验目的1.学习配置OpenGL环境。
2.掌握在OpenGL中指定几何模型的方法。
3. 掌握OpenGL中的透视投影和正投影的设置方法,学会诊断投影问题导致的显示异常。
二、实验环境⒈ 硬件:每个学生需配备计算机一台。
⒉ 软件:Visual C++;三、实验内容1.建立OpenGL编程环境(注:Windows自带gl和glu,还需要安装glut库文件。
)(a)查看Windows自带的OpenGL文件。
在文件夹c:\windows\system32下查看是否存在文件opengl32.dll和glu32.dll;在Visual Studio的安装目录Vc7\PlatformSDK\Include\gl下查看是否存在gl.h和glu.h;在Vc7\PlatformSDK\Lib 下是否存在opengl32.lib和glu32.lib。
北师大版数学四年级上册 第三单元 第3课时 神奇的计算工具 课件(共18张PPT)

学以致用
2.括号内可以填几?先估计,再用计算器检验,找 到合适的答案。
35
56
36
55
37
57
38
学以致用
3.读一读,算一算。
学以致用
4.数学游戏。 用1,2,3,4,5这五个数字,任意组成一个两位数和一个 三位数,用计算器求出它们的积,积大者获胜。
04 课后作业
课后作业
完成《导学案》同步练习。
情景导学
Байду номын сангаас
02 探索与发现
探索与发现
关机 清除 开机
探索与发现
03 学以致用
学以致用
1.用计算器计算下面各题。
876+569= 1445
756+685-298= 1143
416000÷128= 3250 3363×21÷57= 1239
782×534= 417588 438×36-1734= 14034
四年级数学上册教学课件(北师版)
第三课时 神奇的计算工具
目录
1 情景导学 2 探索与发现 3 学以致用 4 课后作业
01 情景导学
情景导学 两千多年前,中国人用算筹计算。
情景导学
一千多年前,中国人开始广泛使用算盘,使计 算的速度快多了。
情景导学
1822年,第一台能按一定程序自动控制 的计算机诞生了。
感谢观看
MATLAB计算方法迭代法牛顿法二分法实验报告

完美WORD格式姓名实验报告成绩评语:指导教师(签名)年月日说明:指导教师评分后,实验报告交院(系)办公室保存。
实验一 方程求根一、 实验目的用各种方法求任意实函数方程0)(=x f 在自变量区间[a ,b]上,或某一点附近的实根。
并比较方法的优劣。
二、 实验原理 (1)、二分法对方程0)(=x f 在[a ,b]内求根。
将所给区间二分,在分点2a b x -=判断是否0)(=x f ;若是,则有根2a b x -=。
否则,继续判断是否0)()(<∙x f a f ,若是,则令x b =,否则令x a =。
否则令x a =。
重复此过程直至求出方程0)(=x f 在[a,b]中的近似根为止。
(2)、迭代法将方程0)(=x f 等价变换为x =ψ(x )形式,并建立相应的迭代公式=+1k x ψ(x )。
(3)、牛顿法若已知方程 的一个近似根0x ,则函数在点0x 附近可用一阶泰勒多项式))((')()(0001x x x f x f x p -+=来近似,因此方程0)(=x f 可近似表示为+)(0x f 0))(('0=-x x x f 设0)('0≠x f ,则=x -0x )(')(00x f x f 。
取x 作为原方程新的近似根1x ,然后将1x 作为0x 代入上式。
迭代公式为:=+1k x -0x )(')(k k x f x f 。
三、 实验设备:MATLAB 7.0软件四、 结果预测(1)11x =0.09033 (2)5x =0.09052 (3)2x =0,09052 五、 实验内容(1)、在区间[0,1]上用二分法求方程0210=-+x e x 的近似根,要求误差不超过3105.0-⨯。
(2)、取初值00=x ,用迭代公式=+1k x -0x )(')(k k x f x f ,求方程0210=-+x e x的近似根。
要求误差不超过3105.0-⨯。
《计算方法实验》课件

计算方法实验 PPT 课件
实验介绍
实验安排
详细介绍了实验进行的时间安排和实验室要求。
实验目的
阐述了学习计算方法实验的重要目标和价值。
实验内容概述
概括性地介绍了实验涉及的主要内容和操作。
计算方法基础知识回顾
数值计算方法概述
概括了数值计算方法的定义和应用领域。
插值法简介
解释了插值法在数值计算中的作用和原理。
1 实验步骤
具体描述了进行插值法实验的步骤和操作流程。
2 实验要求
列举了完成实验所需的前置条件和要求。
3 实验结果和分析
总结了实验结果并给出了相关数据的分析和解释。
实验三:数值微积分实验
1 实验步骤
具体说明了进行数值微 积分实验的步骤和具体 操作。
2 实验要求
概述了完成实验所需的 前提条件和技术要求。
其他资料
介绍了一些其他有关计算方法实验的相关资料和参考。
3 实验结果和分析
总结了实验的结果,并 进行了相应数据分析和 解读。
实验总结
实验心得
分享了在完成实验过程中 的感悟和收获。
实验成果展示
展示了实验中获得的数据 和图表等成果知识和技能。
参考资料
书籍
推荐了一些计算方法方面的经典教材和参考书籍。
网络资源
提供了一些在线学习计算方法实验的优质网站和资源。
矩阵运算基础
介绍了矩阵的基本运算规则和重要性。
数值微积分概述
回顾了数值微积分的基本概念和计算方法。
实验一:矩阵运算实验
1 实验步骤
详细说明了进行矩阵运 算实验的步骤和操作。
2 实验要求
列出了完成实验所需的 前提条件和要求。
实验报告截图要求
项目文件列表图(截图示例九)
实验报告截图要求
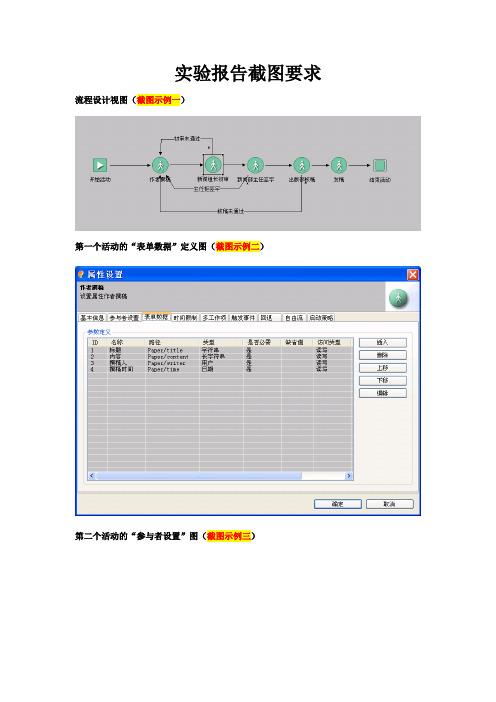
流程设计视图(截图示例一)
第一个活动的“表单数据”定义图(截图示例二)
第二个活动的“参与者设置”图(截图示例三)
某次审核活动中未通过连线的设计截图(截图示例四)
最后一个活动的“表单数据”定义图(截图示例个活动截图(截图示例七)
整个流程执行完毕的截图(截图示例八)
