最新二叉树的基本知识
二叉树基本知识

{
int capacity;
int size;
int *elements;
}*tryit;
struct priorityqueue *initialize ( int maxelements )
{
struct priorityqueue *h;
(6)给定N个节点,能构成h(N)种不同的二叉树。
h(N)为卡特兰数的第N项。h(n)=C(n,2*n)/(n+1)。
4.二叉树的存储结构
(1)顺序存储方式
type node=record
Байду номын сангаасata:datatype
l,r:integer;
end;
var tr:array[1..n] of node;
(1)前序遍历
访问根;按前序遍历左子树;按前序遍历右子树
(2)中序遍历
按中序遍历左子树;访问根;按中序遍历右子树
(3)后序遍历
按后序遍历左子树;按后序遍历右子树;访问根
(4)层次遍历
即按照层次访问,通常用队列来做。访问根,访问子女,再访问子女的子女(越往后的层次越低)(两个子女的级别相同)
(2)链表存储方式,如:
type btree=^node;
node=record
data:datatye;
lchild,rchild:btree;
end;
5.普通树转换成二叉树
二叉树很象一株倒悬着的树,从树根到大分枝、小分枝、直到叶子把数据联系起来,这种数据结构就叫做树结构,简称树。树中每个分叉点称为结点,起始结点称为树根,任意两个结点间的连接关系称为树枝,结点下面不再有分枝称为树叶。结点的前趋结点称为该结点的"双亲",结点的后趋结点称为该结点的"子女"或"孩子",同一结点的"子女"之间互称"兄弟"。
二叉树知识点总结

二叉树知识点总结1. 二叉树的性质1.1 二叉树的性质一:二叉树的深度二叉树的深度是指从根节点到叶子节点的最长路径长度。
对于一个空树而言,它的深度为0;对于只有一个根节点的树而言,它的深度为1。
根据定义可知,深度为k的二叉树中,叶子节点的深度值为k。
由此可知,二叉树的深度为所有叶子节点深度的最大值。
1.2 二叉树的性质二:二叉树的高度二叉树的高度是指从根节点到叶子节点的最短路径长度。
对于一个空树而言,它的高度为0;对于只有一个根节点的树而言,它的高度为1。
由此可知,二叉树的高度总是比深度大一。
1.3 二叉树的性质三:二叉树的节点数量对于一个深度为k的二叉树而言,它最多包含2^k - 1个节点。
而对于一个拥有n个节点的二叉树而言,它的深度最多为log2(n+1)。
1.4 二叉树的性质四:满二叉树满二叉树是一种特殊类型的二叉树,它的每个节点要么是叶子节点,要么拥有两个子节点。
满二叉树的性质是:对于深度为k的满二叉树而言,它的节点数量一定是2^k - 1。
1.5 二叉树的性质五:完全二叉树完全二叉树是一种特殊类型的二叉树,它的所有叶子节点都集中在树的最低两层,并且最后一层的叶子节点从左到右依次排列。
对于一个深度为k的完全二叉树而言,它的节点数量一定在2^(k-1)和2^k之间。
2. 二叉树的遍历二叉树的遍历是指按照一定的顺序访问二叉树的所有节点。
二叉树的遍历主要包括前序遍历、中序遍历和后序遍历三种。
2.1 前序遍历(Pre-order traversal)前序遍历的顺序是:根节点 -> 左子树 -> 右子树。
对于一个二叉树而言,前序遍历的结果就是按照“根-左-右”的顺序访问所有节点。
2.2 中序遍历(In-order traversal)中序遍历的顺序是:左子树 -> 根节点 -> 右子树。
对于一个二叉树而言,中序遍历的结果就是按照“左-根-右”的顺序访问所有节点。
2.3 后序遍历(Post-order traversal)后序遍历的顺序是:左子树 -> 右子树 -> 根节点。
二叉树基础知识讲解

二叉树基础知识讲解嘿,朋友们!今天咱来聊聊二叉树这个神奇的玩意儿。
二叉树啊,就像是一棵特别的大树,不过它可不像咱平常看到的大树那样枝繁叶茂、随心所欲地长。
你想啊,二叉树它有个特点,每个节点最多就俩孩子,就像咱人啊,最多也就俩胳膊。
这俩孩子还分左右呢,左边一个右边一个,多有意思!二叉树在计算机的世界里那可是大有用处啊!它就像一个超级整理大师,能把一堆乱七八糟的数据整理得井井有条。
比如说,咱要找个什么东西,在二叉树里找可比在一堆乱麻里找容易多了吧!它的结构也很巧妙呢!有的节点在上面,有的在下面,就像一个大家庭,有长辈有晚辈。
而且啊,通过那些连接的线,它们之间都有着特别的关系。
这是不是很像咱家里的亲戚关系网呀?二叉树的遍历也是很有讲究的哦!什么前序遍历、中序遍历、后序遍历,听起来是不是很玄乎?其实啊,就是从不同的角度去看看这棵树。
前序遍历就像是先看上面再看下面,中序遍历呢就有点像从中间开始看,后序遍历就是最后再看上面。
咱再想想,二叉树不就跟咱生活中的很多事情一样嘛!有时候咱得有条理地去做事,不能瞎搞一气。
就像二叉树,它的结构那么清晰,让我们能很容易地找到需要的东西。
而且二叉树还特别稳定呢!只要你一开始把它构建好了,它就乖乖地在那,不会随便出乱子。
这多让人放心啊!不像有些东西,一会儿变一个样,让人摸不着头脑。
那要是二叉树变得很大很大了呢?那可就更厉害了呀!它能处理超多的数据,就像一个超级大脑,什么都能记住。
你说,这二叉树是不是很神奇?它虽然看起来简单,但是里面蕴含的智慧可不少呢!它能帮我们解决好多问题,让我们的计算机世界变得更加精彩。
所以啊,可别小瞧了这二叉树哦!它真的是计算机领域里的一个宝贝呢!。
基本二叉树知识讲解

基本二叉树知识讲解一、有关二叉树的学习性质1:二叉树上叶子结点数等于度为2的结点数加1。
性质2:二叉树的第i层上至多有2的i次方减1个结点(i>=1)。
性质3:深度为h的二叉树至多有2的h次方减1个结点。
满二叉树:在一棵二叉树中,当第i层的结点树为2的i次方减1个时,称此层的结点数是满的。
当一棵二叉树中的每一层都满时,称此树为满二叉树。
特性:除叶子结点以外的其他的结点的度皆为2,且叶子结点在同一层上。
深度为h的满二叉树中的结点数为2的h次方减1。
性质4:设含有n个结点的完全二叉树的深度为k,则k=(int)(log2n)+1,即深度k等于log2n的整数部分再加1。
二叉树的存储结构1:顺序存储结构二叉树的顺序存储结构类型定义如下:#define TREEMINSIZE 10typedef struct{BTreeDT(数据类型) *base;int spacesize;BTreeDT nullvalue;}SeqTree;2:链式存储结构(一般的二叉树主要采用链式存储结构通常有二叉链表和三叉链表两种形式)1>二叉链表存储结构二叉链表中的每个结点由data,lchild和rchild三个域组成,定义如下:typedef struct bkbtnode{BTreeDT data;struct bkbtnode *lchild;struct bkbtnode *rchild;}BTNode,*BKBTree;在二叉链表中,查找某结点的孩子很容易实现,但查找某结点的双亲不方便。
一棵喊有n个结点的二叉树采用二叉链表存储时,将有2n-(n-1)=n+1个指针域是空的。
2>三叉链表存储结构typedef struct tkbtnode{BTreeDT data;struct tkbtnode *lchild;struct tkbtnode *rchild;struct tkbtnode *parent;}TKBTNode,*TKBTree;其中,parent域存放该结点双亲的指针。
数据结构二叉树先序中序后序考研题目

数据结构二叉树先序中序后序考研题目
摘要:
一、二叉树的基本概念和性质
二、二叉树的遍历方式
三、考研题目中关于二叉树的问题
正文:
一、二叉树的基本概念和性质
二叉树是一种非常重要的数据结构,在计算机科学中有着广泛的应用。
它由一个根节点和两个子节点组成,每个节点也可以有零个或多个子节点。
二叉树具有以下几个重要的性质:
1.每个节点最多只有两个子节点,即左子节点和右子节点。
2.所有节点的左子节点都比它小,所有节点的右子节点都比它大。
3.每个节点的左子树和右子树也是二叉树。
二、二叉树的遍历方式
二叉树的遍历方式有三种:先序遍历、中序遍历和后序遍历。
先序遍历:根节点- > 左子树- > 右子树
中序遍历:左子树- > 根节点- > 右子树
后序遍历:左子树- > 右子树- > 根节点
三、考研题目中关于二叉树的问题
在考研题目中,关于二叉树的问题通常涉及以下几个方面:
1.二叉树的遍历:要求根据二叉树的结构,写出其先序遍历、中序遍历或
后序遍历。
2.二叉树的应用:要求利用二叉树解决具体问题,例如求二叉树的高度、求两个二叉树的最近公共祖先等。
3.二叉树的结构:要求根据二叉树的遍历结果,画出其结构图或者判断其是否存在。
以上就是关于数据结构中二叉树的基本概念、遍历方式和在考研题目中的应用的介绍。
《二叉树的概念》课件

05
二叉树的应用
Chapter
在数据结构中的应用
二叉搜索树
二叉搜索树是一种特殊的二叉树,它的每个节点的左子树上的所有元素都小于 该节点,右子树上的所有元素都大于该节点。这种数据结构可以用于快速查找 、插入和删除操作。
AVL树和红黑树
这两种二叉树都是自平衡二叉搜索树,它们通过调整节点的左右子树的高度来 保持树的平衡,从而在插入、删除等操作时具有较好的性能。
VS
详细描述
平衡二叉树的特点是,它的左右子树的高 度差不会超过1,且左右子树都是平衡二 叉树。平衡二叉树的性质还包括,它的所 有叶节点的层数相等,且所有非叶节点的 左右子树的高度差不超过1。平衡二叉树 的查找、插入和删除操作的时间复杂度为 O(log n),其中n为节点数。
04
二叉树的遍历
Chapter
决策树
在机器学习和人工智能领域,决策树 是一种重要的分类和回归方法。其基 础结构就是二叉树,通过构建决策树 ,可以解决分类和回归问题。
THANKS
感谢观看
代码表示法
总结词:严谨规范
详细描述:使用编程语言的语法结构来表示二叉树,每个节点用对象或结构体表示,节点间的关系通 过指针或引用表示,严谨规范,易于编写和调试。
03
二叉树的性质
Chapter
深度最大的二叉树
总结词
深度最大的二叉树是指具有最大 可能深度的二叉树。
详细描述
在二叉树中,深度最大的二叉树 是满二叉树,即每个层级都完全 填满,没有空缺的节点。满二叉 树的深度等于其节点总数减一。
02
二叉树的表示方法
Chapter
图形表示法
总结词:直观明了
详细描述:通过图形的方式展示二叉树的结构,每个节点用圆圈或方框表示,节 点间的关系用线段表示,直观易懂,易于理解。
数据结构二叉树知识点总结

数据结构⼆叉树知识点总结术语1. 节点的度:⼀个节点含有的⼦树的个数称为该节点的度;2. 叶节点或终端节点:度为零的节点;3. ⾮终端节点或分⽀节点:度不为零的节点;4. ⽗亲节点或⽗节点:若⼀个节点含有⼦节点,则这个节点称为其⼦节点的⽗节点;5. 兄弟节点:具有相同⽗节点的节点互称为兄弟节点;6. 节点的层次:从根开始定义起,根为第1层,根的⼦节点为第2层,以此类推;7. 树的⾼度或深度:树中节点的最⼤层次;8. 堂兄弟节点:⽗节点在同⼀层的节点互为堂兄弟;9. 节点的祖先:从根到该节点所经分⽀上的所有节点;10. 孙:以某节点为根的⼦树中任⼀节点都称为该节点的⼦孙。
11. 森林:由m(m>=0)棵互不相交的树的集合称为森林;12. 满⼆叉树:⼀棵深度为k,且有2^k-1 (2的k次⽅减⼀)个节点称之为满⼆叉树13. 完全⼆叉树:完全⼆叉树是由满⼆叉树⽽引出来的。
对于深度为K的,有n个结点的⼆叉树,当且仅当其每⼀个结点都与深度为K的满⼆叉树中编号从1⾄n的结点⼀⼀对应时称之为完全⼆叉树。
叶节点只能出现在最下层和次下层,并且最下⾯⼀层的结点都集中在该层最左边的若⼲位置的⼆叉树⼆叉树的性质1.在⾮空⼆叉树中,第i层的结点总数不超过2^(i-1),i>=1;2.深度为h的⼆叉树最多有2^h-1个结点(h>=1),最少有h个结点;3.对于任意⼀棵⼆叉树,如果其叶结点数为N0,⽽度数为2的结点总数为N2,则N0=N2+1;4.具有n个结点的完全⼆叉树的深度为K =[log2n」+1(取下整数)5.有N个结点的完全⼆叉树各结点如果⽤顺序⽅式存储,则结点之间有如下关系:若I为结点编号则如果I>1,则其⽗结点的编号为I/2;6.完全⼆叉树,如果2*I<=N,则其左⼉⼦(即左⼦树的根结点)的编号为2*I;若2*I>N,则⽆左⼉⼦;如果2*I+1<=N,则其右⼉⼦的结点编号为2*I+1;若2*I+1>N,则⽆右⼉⼦。
二 叉 树
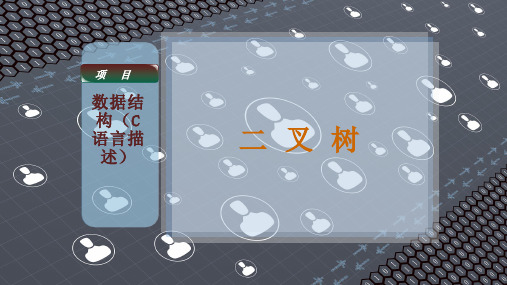
下图是1.2中所示的完全二叉树的顺序存储示意图。
例如,bt[3]
3=/12, 即在bt[1]中,其左
孩子在bt[2i]=bt[6]中,右孩子在bt[2i+1]=bt[7]中。
目录
二 叉 树
2)一般二叉树的顺序存储 一般的二叉树采取的办法是按完全二叉树的形式补齐 二叉树所缺少的结点,对补齐后的二叉树进行编号,将二 叉树的原有结点按编号存储到一维数组中。 下图给出了一棵一般二叉树改造后的完全二叉树形态 和其顺序存储状态示意图。
目录
二 叉 树
2021年1月30日星期六
性质3 对于一棵非空的二叉树,如果叶子结点数 为n0,度数为2的结点数为n2,则有n0=n2+1。
性质4 具有n个结点的完全二叉树的深度k log2n +1。
性质5 对于具有n个结点的完全二叉树,如果按照 」 从上到下和从左到右的顺序对二叉树中的所有结点从1
则ki无左孩子结点,即ki是叶子结点。因此完全二叉
树中编号i> n / 2 的结点必定是叶子结点。 (3)若2i+1≤n,则ki的右孩子结点编号是2i+1;
否则ki无右孩子结点。
目录
二 叉 树
2021年1月30日星期六
可用一维数组bt[]存放一棵完全二叉树,将标号 为i的结点的数据元素存放在分量bt[i]中,bt[0]不 用或用来存储结点数目。
typedef struct BiTNode { // 结点结构
ElemType data;
2021年1月30日星期六
目录
二 叉 树
二叉树、树及有序树是有区别的,二叉树不是树的特 例,主要差别在于二叉树的子树有左右之分。
在有序树中,虽然一个结点的孩子之间是有左右次序 的,但若该结点只有一个孩子时,就无须区分其左右次序。
二叉树实验知识点总结

二叉树实验知识点总结
一、二叉树的基本概念
二叉树是一种特殊的树形结构,其每个节点最多只有两个子节点。
二叉树分为满二叉树、完全二叉树和普通二叉树等类型。
二、遍历方式
1.前序遍历:先访问当前节点,再遍历左子树和右子树;
2.中序遍历:先遍历左子树,再访问当前节点,最后遍历右子树;
3.后序遍历:先遍历左子树和右子树,最后访问当前节点;
4.层次遍历:按照从上到下、从左到右的顺序依次访问每个节点。
三、常见操作
1.插入节点:在二叉搜索树中插入一个新的节点;
2.删除节点:在二叉搜索树中删除一个指定的节点;
3.查找节点:在二叉搜索树中查找一个指定的节点;
4.求深度:计算二叉搜索树的深度。
四、平衡二叉树
平衡二叉树是一种特殊的二叉搜索树,其左右子树高度差不能超过1。
常见的平衡二叉搜索包括红黑树、AVL 树等。
五、应用场景
1.数据库索引;
2.哈夫曼编码;
3.表达式求值;
4.图形处理等。
六、注意事项
1.二叉树的插入、删除和查找操作需要保证二叉树的结构不被破坏;
2.平衡二叉树的实现需要注意平衡因子的计算和旋转操作的实现;
3.在使用二叉树进行算法设计时,需要考虑遍历方式和时间复杂度等问题。
七、总结
二叉树是一种重要的数据结构,在算法设计中有广泛的应用。
掌握二叉树的基本概念、遍历方式、常见操作和应用场景,可以帮助我们更好地理解和使用这种数据结构。
同时,我们需要注意在实际应用中遵循相关规范,保证程序的正确性和效率。
数据结构树和二叉树知识点总结

数据结构树和二叉树知识点总结
1.树的概念:树是一种非线性的数据结构,由节点和边构成,每个节点只能有一个父节点,但可以有多个子节点。
2. 二叉树的概念:二叉树是一种特殊的树结构,每个节点最多只有两个子节点,一个是左子节点,一个是右子节点。
3. 二叉树的遍历:二叉树的遍历分为前序遍历、中序遍历和后序遍历三种方式。
前序遍历是先访问根节点,再访问左子树,最后访问右子树;中序遍历是先访问左子树,再访问根节点,最后访问右子树;后序遍历是先访问左子树,再访问右子树,最后访问根节点。
4. 二叉搜索树:二叉搜索树是一种特殊的二叉树,它满足左子树中所有节点的值均小于根节点的值,右子树中所有节点的值均大于根节点的值。
因此,二叉搜索树的中序遍历是一个有序序列。
5. 平衡二叉树:平衡二叉树是一种特殊的二叉搜索树,它的左子树和右子树的高度差不超过1。
平衡二叉树的插入和删除操作可以保证树的平衡性,从而提高树的查询效率。
6. 堆:堆是一种特殊的树结构,它分为最大堆和最小堆两种。
最大堆的每个节点的值都大于等于其子节点的值,最小堆的每个节点的值都小于等于其子节点的值。
堆常用于排序和优先队列。
7. Trie树:Trie树是一种特殊的树结构,它用于字符串的匹配和检索。
Trie树的每个节点代表一个字符串的前缀,从根节点到叶子节点的路径组成一个完整的字符串。
以上是数据结构树和二叉树的一些基本知识点总结,对于深入学
习数据结构和算法有很大的帮助。
计算机二级二叉树知识点

计算机二级二叉树知识点1.二叉树的定义:二叉树是一种常见的树形结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。
二叉树的节点结构通常包括一个数据元素和指向左右子节点的指针。
2.二叉树的性质:(1)二叉树的第i层最多有2^(i-1)个节点。
(2)高度为h的二叉树最多有2^h-1个节点。
(3)对于任意一棵二叉树,如果其叶子节点数为n0,度为2的节点数为n2,则n0=n2+1(4)一棵深度为k且节点总数为n的二叉树,当且仅当其满足2^(k-1)<=n<=2^k-1时,才称为完全二叉树。
3.二叉树的分类:(1)满二叉树:除了叶子节点之外,每个节点都有两个子节点,且所有叶子节点在同一层次上。
(2)完全二叉树:最后一层之前的层都是满的,并且最后一层的节点都靠左排列。
(3)平衡二叉树:左右子树的高度差不超过1的二叉树。
(4)线索二叉树:对于每个节点,除了指向其左右子节点的指针外,还包含指向其在其中一种序列下的前驱节点和后继节点的指针。
4.二叉树的遍历方法:(1)前序遍历:先访问根节点,然后递归地遍历左子树,最后递归地遍历右子树。
(2)中序遍历:先递归地遍历左子树,然后访问根节点,最后递归地遍历右子树。
(3)后序遍历:先递归地遍历左子树,然后递归地遍历右子树,最后访问根节点。
(4)层次遍历:按照从上到下、从左到右的顺序逐层访问每个节点。
5.二叉树:二叉树(Binary Search Tree,BST)是一种特殊的二叉树,它的每个节点的值都大于其左子树中的所有节点值,小于其右子树中的所有节点值。
因此,对于一个二叉树,可以采用中序遍历的方法得到一个有序序列。
二叉树的插入操作:按照二叉树的定义,从根节点开始,将要插入的值与当前节点的值比较,如果小于当前节点的值,则向左子树递归插入,如果大于当前节点的值,则向右子树递归插入,直至找到一个空节点,然后插入新节点。
二叉树的删除操作:删除一个节点需要考虑三种情况:删除节点没有子节点、只有一个子节点、有两个子节点。
二叉树知识点总结

二叉树知识点总结二叉树是一种常见的数据结构,它由节点和边组成,每个节点最多有两个子节点。
以下是关于二叉树的知识点总结。
1. 二叉树的基本概念二叉树是一种树形结构,它由节点和边组成。
每个节点最多有两个子节点,分别称为左子节点和右子节点。
如果一个节点没有子节点,则称其为叶子节点。
二叉树可以为空。
2. 二叉树的遍历方式遍历是指按照一定顺序访问二叉树中的所有节点。
常见的遍历方式有前序遍历、中序遍历和后序遍历。
前序遍历:先访问当前节点,然后递归访问左子树和右子树。
中序遍历:先递归访问左子树,然后访问当前节点,最后递归访问右子树。
后序遍历:先递归访问左子树和右子树,最后访问当前节点。
3. 二叉搜索树二叉搜索树(Binary Search Tree)也称为有序二叉树或排序二叉树。
它是一种特殊的二叉树,在满足以下条件的情况下被称为“搜索”:对于任意节点,其左子树中的所有节点的值都小于该节点的值。
对于任意节点,其右子树中的所有节点的值都大于该节点的值。
左右子树也分别为二叉搜索树。
二叉搜索树支持快速查找、插入和删除操作。
它还有一些变种,如平衡二叉搜索树(AVL Tree)和红黑树(Red-Black Tree)等。
4. 二叉堆二叉堆是一种特殊的完全二叉树,它分为最大堆和最小堆两种类型。
最大堆满足父节点的值大于等于其子节点的值,最小堆满足父节点的值小于等于其子节点的值。
在最大堆中,根节点是整个堆中最大的元素;在最小堆中,根节点是整个堆中最小的元素。
二叉堆常用来实现优先队列(Priority Queue),即按照一定优先级顺序处理元素。
5. 二叉树常见问题5.1 判断是否为平衡二叉树平衡二叉树(Balanced Binary Tree)是指任意节点左右子树高度差不超过1的二叉搜索树。
判断一个二叉搜索树是否为平衡二叉树可以通过递归遍历每个节点,计算其左右子树的高度差。
5.2 判断是否为完全二叉树完全二叉树(Complete Binary Tree)是指除了最后一层外,其他层都是满的,并且最后一层的节点都靠左排列的二叉树。
数据结构二叉树知识点总结

数据结构二叉树知识点总结二叉树是指每个节点最多有两个子节点的树结构。
它是一种重要的数据结构,在算法和程序设计中被广泛应用。
下面是对二叉树的主要知识点进行详细总结。
1.二叉树的基本概念:-树节点:树的基本单元,包含数据项(节点值)和指向其他节点的指针。
-根节点:树的第一个节点。
-叶节点(又称为终端节点):没有子节点的节点。
-子节点:一些节点的下一级节点。
-父节点:一些节点的上一级节点。
-兄弟节点:拥有同一父节点的节点。
-深度:从根节点到当前节点的路径长度。
-高度:从当前节点到最远叶节点的路径长度。
2.二叉树的分类:-严格二叉树:每个节点要么没有子节点,要么有两个子节点。
-完全二叉树:除了最后一层外,其他层的节点数都达到最大,并且最后一层的节点依次从左到右排列。
-满二叉树:每个节点要么没有子节点,要么有两个子节点,并且所有叶节点都在同一层上。
-平衡二叉树:任意节点的两棵子树的高度差不超过13.二叉树的遍历:-前序遍历:根节点->左子树->右子树。
递归实现时,先访问当前节点,然后递归遍历左子树和右子树。
-中序遍历:左子树->根节点->右子树。
递归实现时,先递归遍历左子树,然后访问当前节点,最后递归遍历右子树。
-后序遍历:左子树->右子树->根节点。
递归实现时,先递归遍历左子树,然后递归遍历右子树,最后访问当前节点。
-层序遍历:从上到下,从左到右依次访问每个节点。
使用队列实现。
4.二叉查找树(BST):-二叉查找树是一种有序的二叉树,对于树中的每个节点,其左子树的节点的值都小于当前节点的值,右子树的节点的值都大于当前节点的值。
-插入操作:从根节点开始,递归地比较要插入的值和当前节点的值,根据比较结果向左或向右移动,直到找到插入位置为止。
-查找操作:从根节点开始,递归地比较要查找的值和当前节点的值,根据比较结果向左或向右移动,直到找到目标节点或到叶节点。
-删除操作:有三种情况:-被删除节点是叶节点:直接将其删除。
数据结构与算法(3):二叉树
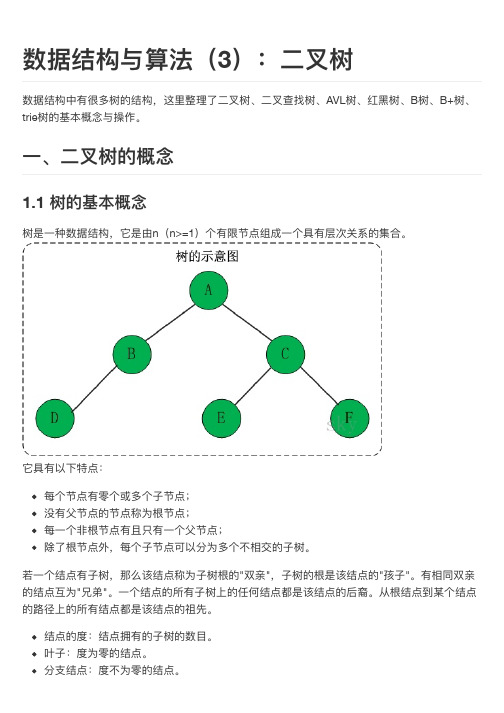
1.3.3 性质三
包含n个结点的二二叉树的高高度至至少为log2(n + 1);
证明:根据"性质2"可知,高高度为h的二二叉树最多有2{h}–1个结点。反之,对于包含n个节点的二二
叉树的高高度至至少为log2(n + 1)。
1.3.4 性质四
对任何一一颗二二叉树T,如果其终端结点数为n0 ,度为2的结点数为n2 ,则n0 = n2 + 1 证明:因为二二叉树中所有结点的度数均不不大大于2,所以结点总数(记为n)="0度结点数(n0)" + "1度 结点数(n1)" + "2度结点数(n2)"。由此,得到等式一一。(等式一一) n = n0 + n1 + n2
}
还有一一种方方式就是利利用用栈模拟递归过程实现循环先序遍历二二叉树。这种方方式具备扩展性,它模拟 了了递归的过程,将左子子树不不断的压入入栈,直到null,然后处理理栈顶节点的右子子树。
java
public void preOrder(Node root){ if(root==null)return;
2. 叶子子数为2h 3. 第k层的结点数是:2k−1; 4. 总结点数是2k − 1,且总节点数一一定是奇数。
1.4.2 完全二二叉树
定义:一一颗二二叉树中,只有最小小面面两层结点的度可以小小于2,并且最下一一层的叶结点集中在靠左 的若干干位置上。这样现在最下层和次下层,且最小小层的叶子子结点集中在树的左部。显然,一一颗 满二二叉树必定是一一颗完全二二叉树,而而完全二二叉树未必是满二二叉树。
} root = s.pop(); root = root.right;//如果是null,出栈并处理理右子子树 } }
二叉树知识点总结

二叉树知识点总结二叉树是数据结构中常见且重要的一种形式,它可以用于解决许多实际问题,并在算法和编程中扮演着重要的角色。
本文将对二叉树的基本概念、性质以及常见的应用进行总结。
一、基本概念和性质1. 二叉树的定义:二叉树是一种特殊的树形结构,每个节点最多有两个子节点,分别称为左子节点和右子节点。
左子节点小于等于父节点,右子节点大于等于父节点。
2. 二叉树的特点:二叉树具有递归性质,即每个子节点都可以视为一棵二叉树。
同时,二叉树的遍历方式有前序遍历、中序遍历、后序遍历和层次遍历等。
3. 二叉树的性质:a. 二叉树的第i层至多有2^(i-1)个节点;b. 深度为k的二叉树至多有2^k - 1个节点;c. 对于任意一棵二叉树,若其叶节点数为n0,度为2的节点数为n2,则n0 = n2 + 1;d. 具有n个节点的完全二叉树的深度为(log2 n) + 1。
二、二叉树的应用1. 二叉搜索树:二叉搜索树(BST)是一种特殊的二叉树,它满足左子节点小于父节点,右子节点大于父节点的条件。
BST的特性使得查找、插入和删除操作的时间复杂度为O(log n),因此在数据库、图形处理等领域经常被使用。
2. 平衡二叉树:由于BST的特性,如果数据插入的顺序不合理,可能导致树的高度过高,使得操作效率降低。
为了解决这个问题,人们提出了平衡二叉树(AVL)的概念。
AVL树通过旋转操作保持树的平衡,使得左右子树的高度差不超过1,从而保证了操作的效率。
3. 红黑树:红黑树是一种自平衡的二叉查找树,它在AVL树的基础上做了一些调整。
红黑树的特点是节点可以为红色或黑色,并且满足以下规则:根节点为黑色,叶节点为黑色且为空,红色节点的两个子节点都是黑色。
红黑树在C++标准库(STL)中的map和set等容器中得到了广泛应用。
4. 堆:堆是一种完全二叉树,它可以分为大顶堆和小顶堆。
大顶堆中,父节点的值大于或等于两个子节点的值,小顶堆则相反。
堆在排序算法中有广泛应用,如堆排序、优先队列等。
二叉树的基本概念

二叉树的基本概念一、引言二叉树是计算机科学中最基础的数据结构之一,它是由节点和边组成的树形结构,其中每个节点最多有两个子节点。
在计算机科学中,二叉树被广泛应用于搜索、排序、编译器等领域。
本文将详细介绍二叉树的基本概念。
二、定义二叉树是一种特殊的树形结构,其中每个节点最多有两个子节点。
通常将左子节点称为左子树,右子节点称为右子树。
三、基本术语1. 根节点:二叉树的顶层节点称为根节点。
2. 叶子节点:没有任何子节点的节点称为叶子节点。
3. 父节点和子节点:一个父亲可以有多个儿子,但是一个儿子只能有一个父亲。
4. 兄弟:具有相同父亲的两个或多个儿子称为兄弟。
5. 深度:从根到某个节点所经过的边数称为该节点的深度。
6. 高度:从某个节点到其所有后代中深度最大者加一(即包括该结点)称为该结点所在的二叉树的高度。
四、分类1. 满二叉树:一棵深度为k且有2^k-1个节点的二叉树称为满二叉树。
2. 完全二叉树:对于一棵深度为k的,有n个节点的二叉树,当且仅当其每一个节点都与深度为k的满二叉树中编号从1至n的节点一一对应时,称之为完全二叉树。
3. 平衡二叉树:平衡二叉树也称为AVL树,是一种自平衡的排序二叉搜索树。
它具有以下性质:左右子树高度差不超过1,并且左右子树也是平衡二叉树。
五、遍历遍历是指按照某种顺序访问每个节点。
常见的遍历方式有三种:1. 前序遍历(Pre-order):先访问当前节点,再依次遍历左子树和右子树。
2. 中序遍历(In-order):先依次遍历左子树,再访问当前节点,最后遍历右子树。
3. 后序遍历(Post-order):先依次遍历左子树和右子树,最后访问当前节点。
六、应用1. 搜索算法:在搜索算法中,二叉树被广泛应用于二分查找。
2. 排序算法:在排序算法中,二叉树被广泛应用于堆排序和快速排序。
3. 编译器:在编译器中,二叉树被广泛应用于语法分析和代码生成。
七、总结本文介绍了二叉树的基本概念、术语、分类、遍历以及应用。
理论基础 —— 二叉树
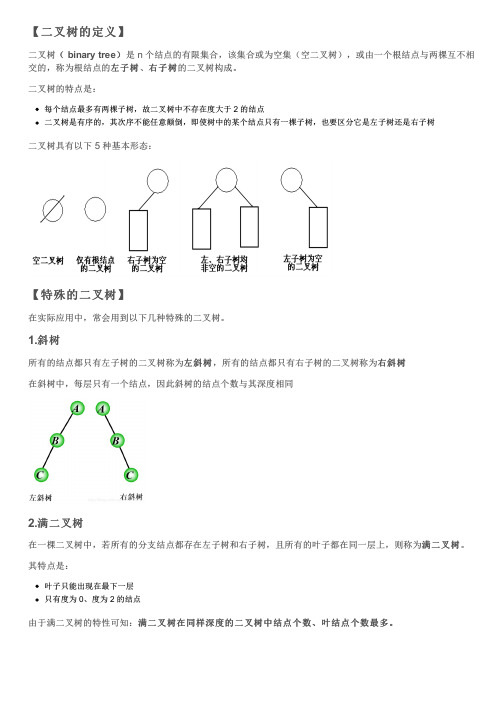
【二叉树的定义】( binary tree)是 n 个结点的有限集合,该集合或为空集(空二叉树),或由一个根结点与两棵互不相二叉树(右子树的二叉树构成。
交的,称为根结点的左子树左子树、右子树二叉树的特点是:每个结点最多有两棵子树,故二叉树中不存在度大于 2 的结点二叉树是有序的,其次序不能任意颠倒,即使树中的某个结点只有一棵子树,也要区分它是左子树还是右子树二叉树具有以下 5 种基本形态:【特殊的二叉树】在实际应用中,常会用到以下几种特殊的二叉树。
1.斜树右斜树左斜树,所有的结点都只有右子树的二叉树称为右斜树所有的结点都只有左子树的二叉树称为左斜树在斜树中,每层只有一个结点,因此斜树的结点个数与其深度相同2.满二叉树满二叉树。
在一棵二叉树中,若所有的分支结点都存在左子树和右子树,且所有的叶子都在同一层上,则称为满二叉树其特点是:叶子只能出现在最下一层只有度为 0、度为 2 的结点满二叉树在同样深度的二叉树中结点个数、叶结点个数最多。
由于满二叉树的特性可知:满二叉树在同样深度的二叉树中结点个数、叶结点个数最多。
3.完全二叉树对一棵具 n 个结点的二叉树按层序编号,若编号为 i 的结点与同样深度的满二叉树中编号 i 的结点在二叉树中的满二叉树是完全二叉树位置完全相同,则称为完全二叉树完全二叉树,那么显然有:满二叉树是完全二叉树其特点是:叶结点只能出现在最下两层,且最下层的叶结点都集中在二叉树左侧连续的位置若有度为 1 的结点,只可能有一个,且其只有左孩子深度为 k 的完全二叉树在 k -1 层上行一定是满二叉树简单来说,在满二叉树中,从最后一个结点开始,连续去掉任意个的结点,即是一棵完全二叉树【二叉树的性质】1.二叉树二叉树的第 i 层上行最多有个结点2.二叉树中,最多有个结点,最少有 k 个结点在一棵深度为 k 的二叉树推论:深度为 k 且具个结点的二叉树一定是满二叉树,但深度为 k 具有 k 个结点的二叉树不一定是斜树3.具有 n 个结点的二叉树二叉树,其分支数:B=n-1,对于任意一个结点,每度贡献一个分支,即:度为 0 的结点贡献 0 个分支,度为 1 的结点贡献 1 个分支,度为 2 的结点贡献 2 个分支。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
// 根结点的位置
} BPTree
Байду номын сангаас
树的三种存储结构
一、双亲表示法 二、孩子链表表示法
三、树的二叉链表(孩子-兄弟) 存储表示法
一、双亲表示法:
data parent
A BC D
0 A -1 r=0 1 B 0 n=6 2C 0
EF
3D 0 4E 2
G
5F 2 6G 5
C语言的类型描述:
#define MAX_TREE_SIZE 100
二叉树的基本知识
数据对象 D:
D是具有相同特性的数据元素的集合。
数据关系 R:
若D为空集,则称为空树; 否则: (1) 在D中存在唯一的称为根的数据元素root, (2) 当n>1时,其余结点可分为m (m>0)个互
不相交的有限集T1, T2, …, Tm, 其中每一 棵子集本身又是一棵符合本定义的树, 称为根root的子树。
ClearTree(&T) // 将树清空 DestroyTree(&T) // 销毁树的结构
DeleteChild(&T, &p, i) // 删除结点p的第i棵子树
二叉树 的重要特性
性质 1 : 在二叉树的第 i 层上至多有 2i-1 个结点。(i≥1)
性质 2 : 深度为 k 的二叉树上至多含 2k-1 个结点
二叉树的主要基本操作: 查找类 插入类 删除类
查找类:
Root(T) // 求树的根结点 Value(T, cur_e) // 求当前结点的元素值 Parent(T, cur_e) // 求当前结点的双亲结点 LeftChild(T, cur_e) // 求当前结点的最左孩子 RightSibling(T, cur_e) // 求当前结点的右兄弟 TreeEmpty(T) // 判定树是否为空树 TreeDepth(T) // 求树的深度 TraverseTree( T, Visit() ) // 遍历
} TriTNode, *TriTree;
结点结构: parent lchild data rchild
3.双亲链表
0B 4L 1D 4R
2C 0
3E 1R 根 4 A -1 R n=65 F 3 L
6
结点结构: data parent LRTag
A B
C
D E
F
typedef struct { // 结点结构
TElemType data;
int *parent; // 指向双亲的指针
char LRTag; // 左、右孩子标志域
} BPTNode
typedef struct { // 树结构
BPTNode nodes[MAX_NODE_SIZE];
int num_node; // 树中含结点数目
int root;
} BiTNode, *BiTree;
结点结构: lchild data rchild
2.三叉链表
结点结构:
root
parent lchild data rchild
A B
C
D E
F
C 语言的类型描述如下:
typedef struct { // 结点结构 TElemType data; struct TriTNode *lchild, *rchild; // 左右孩子指针 struct TriTNode *parent; //双亲指针
二、孩子链表表示法:
parent data firstchild
A
0 A -1 1 2 3
BC
D
1B0 2 C0
45
E F 3D0
G
4E2 6 5F2
r=0
6 G 44
n=6
C语言的类型描述:
孩子结点结构: child nextchild
typedef struct CTNode { int child; struct CTNode *nextchild;
#define MAX_TREE_SIZE 100 // 设二叉树的最大结点数
typedef struct { ElemType *data; // 初始化时分配存储空间
// 0号单元存储根结点 int nodeNum; // 二叉树中的结点数目
}SqBiTree ;
例如:
0
A
1
B
4
C
(k+1)2-1
结点结构: data parent
typedef struct PTNode { Elem data; int parent; // 双亲位置域
} PTNode;
树结构:
typedef struct { PTNode nodes [MAX_TREE_SIZE]; int r, n; // 根结点的位置和结点个数 } PTree;
插入类:
InitTree(&T) // 初始化置空树
CreateTree(&T, definition) // 按定义构造树
Assign(T, cur_e, value) // 给当前结点赋值
InsertChild(&T, &p, i, c) // 将以c为根的树插入为结点p的第i棵子树
删除类:
=2k+1
2
D
6
E
13
F
0 1 2 3 4 5 6 7 8 9 10 11 12 13
AB D C E
F
二、二叉树的链式存储表示
1. 二叉链表 2.三叉链表 3.双亲链表
1. 二叉链表
root
A
B C
结点结构: lchild data rchild
D E
F
C 语言的类型描述如下:
typedef struct { // 结点结构 TElemType data; struct BiTNode *lchild, *rchild; // 左右孩子指针
(k≥1)
性质 3 :
对任何一棵二叉树,若它含有n0 个叶子结 点、n2 个。度为 2 的结点,则必存在关系式:
n0 = n2+1。
性质 4 :
具有 n 个结点的完全二叉树的深度为 log2n +1
性质 5 若对含 n 个结点的完全二叉树从上到下且从左至右
进行 1 至 n 的编号,则对完全二叉树中任意一个 编号为 i 的结点: (1) 若 i=1,则该结点是二叉树的根,无双亲,
否则,编号为 i/2 的结点为其双亲结点;
(2) 若 2i>n,则该结点无左孩子, 否则,编号为 2i 的结点为其左孩子结点; (3) 若 2i+1>n,则该结点无右孩子结点, 否则,编号为2i+1 的结点为其右孩子结点
二叉树的存储结构
一、 二叉树的顺序 存储表示
二、二叉树的链式 存储表示
一、 二叉树的顺序存储表示
