天津市第一中学2015-2016学年高中数学期末复习1新人教A版必修4
《红对勾》2015-2016学年人教A版高中数学必修4课件1-5-1函数y=Asin(ωx+φ)的图象

(2)用“变换法”作图. 由函数 y=sinx 的图象通过变换得到 y=Asin(ωx+ φ)(ω>0)的图象,主要有两种途径:“先平移后伸缩”与“先 伸缩后平移”. 方法一:先平移后伸缩 y=sinx向左平φ移>―0|φ或―|个→向单右位φ<0 y=sin(x+φ)
2.由 y=sin2x 的图象如何平移得到 y=sin2x+π3的图 象?是向左平移π3个单位吗?
的图象向右平移
π 2
个单位后,与函数y=sin(2x+
π 3
)的图象重
合,则φ=________.
【分析】 通过诱导公式将函数化为“同名”函数,
在图象平移中,要注意“x”的系数对平移结果的影响.
【解析】
将y=cos(2x+φ)的图象向右平移
π 2
个单位后
得到y=cos[2(x-
π 2
)+φ]的图象,化简得y=-cos(2x+φ),
π 3
-
π 4
)=
sin(2x-
7π 12
),再将所得图象上所有点的横坐标缩短到原来
的
1 2
,则与其对应的函数的解析式为y=sin2(2x-
7π 12
)=
sin(4x-76π)=sin(4x+56π).
【错因分析】 以上两种解法都是错误的,错解产生 的根本原因是没有抓住变换的对象.错解1在进行平移变换 时,错误地把2x看成了变换对象,错解2在平移变换和伸缩 变换上都犯了错误.
第一章
三角函数
1.5 函数y=Asin ωx+φ 的图象
第1课时 函数y=Asin(ωx+φ)的图象
预习篇
提高篇
课堂篇
巩固篇
课时作业
学习目标
人教A版高中数学必修4课后习题 第一章 1.3 第2课时 诱导公式五、六

第一章三角函数1.3 三角函数的诱导公式第2课时诱导公式五、六课后篇巩固探究基础巩固1.若α∈(π,3π2),则√1-sin2(3π2-α)=( )A.sin αB.-sin αC.cos αD.-cos α(π,3π2),∴sinα<0.∴√1-sin2(3π2-α)=√1-cos2α=√sin2α=-sinα.2.已知P(sin 40°,-cos 140°)为锐角α终边上的点,则α=( )A.40°B.50°C.70°D.80°-cos140°)为角α终边上的点,因而tanα=-cos140°sin40°=-cos(90°+50°) sin(90°-50°)=sin50°cos50°=tan50°,又α为锐角,则α=50°,故选B.3.已知sin(π-α)=-2sin(π2+α),则sin αcos α=()A.25B.-25C.25或-25D.-15-α)=-2sin(π2+α),∴sinα=-2cosα.再由sin 2α+cos 2α=1可得sinα=2√55,cosα=-√55,或sinα=-2√55,cosα=√55,∴sinαcosα=-25.故选B.4.在△ABC 中,若sin A+B 2=45,则cos C2=( )A.-35B.-45C.35D.45解析∵A+B+C=π,∴A+B 2=π2−C2.∴sin A+B 2=sin (π2-C2)=cos C2=45.5.已知cos(60°+α)=13,且-180°<α<-90°,则cos(30°-α)的值为( ) A.-2√23B.2√23C.-√23D.√23-180°<α<-90°,得-120°<60°+α<-30°.又cos(60°+α)=13>0,所以-90°<60°+α<-30°,即-150°<α<-90°,所以120°<30°-α<180°,cos(30°-α)<0,所以cos(30°-α)=sin(60°+α)=-√1-cos 2(60°+α)=-√1-(13) 2=-2√23.6.若cos α=13,且α是第四象限的角,则cos (α+3π2)= .α是第四象限的角,所以sinα=-√1-cos 2α=-2√23. 于是cos (α+3π2)=-cos (α+π2)=sinα=-2√23. -2√237.若sin (π2+θ)=37,则cos 2(π2-θ)= .(π2+θ)=cosθ=37,则cos 2(π2-θ)=sin 2θ=1-cos 2θ=1-949=4049.8.求值:sin 2(π4-α)+sin 2(π4+α)= .解析∵π4-α+π4+α=π2,∴sin 2(π4+α)=sin 2[π2-(π4-α)]=cos 2(π4-α).∴sin 2(π4-α)+sin 2(π4+α)=sin 2(π4-α)+cos 2(π4-α)=1.9.化简:sin(-α-3π2)·sin(3π2-α)·tan 2(2π-α)cos(π2-α)·cos(π2+α)·cos 2(π-α).=sin(-α+π2)·[-sin(π2-α)]·tan 2(2π-α)cos(π2-α)·cos(π2+α)·cos 2(π-α)=cosα·(-cosα)·tan 2αsinα·(-sinα)·cos 2α=tan 2αsin 2α=1cos 2α.10.已知角α的终边经过点P (45,-35).(1)求sin α的值; (2)求sin(π2-α)tan (α-π)sin (α+π)cos (3π-α)的值.∵P (45,-35),|OP|=1,∴sinα=-35.(2)sin(π2-α)tan (α-π)sin (α+π)cos (3π-α)=cosαtanα-sinα(-cosα)=1cosα,由三角函数定义知cosα=45,故所求式子的值为54.能力提升1.已知π<α<2π,cos(α-9π)=-35,则cos (α-11π2)的值为( )A.35B.-35C.-45D.45cos(α-9π)=-cosα=-35,所以cosα=35.又因为α∈(π,2π),所以sinα=-√1-cos 2α=-45,cos (α-11π2)=-sinα=45.2.已知角α的终边上有一点P(1,3),则sin (π-α)-sin(π2+α)cos(3π2-α)+2cos (-π+α)的值为( )A.-25B.-45C.-47D.-4=sinα-cosα-sinα-2cosα=tanα-1-tanα-2.因为角α终边上有一点P(1,3), 所以tanα=3,所以原式=3-1-3-2=-25.故选A.3.已知α为第二象限角,则cos α√1+tan 2α+sin α√1+1tan 2α= .√sin 2α+cos 2αcos 2α+sinα√sin 2α+cos 2αsin 2α=cosα1|cosα|+sinα1|sinα|.因为α是第二象限角,所以sinα>0,cosα<0, 所以cosα1|cosα|+sinα1|sinα|=-1+1=0,即原式等于0.4.sin 21°+sin 22°+sin 23°+…+sin 289°= .sin 21°+sin 22°+sin 23°+…+sin 289°=sin 21°+sin 22°+sin 23°+…+sin 245°+cos 244°+…+cos 21°=(sin 21°+cos 21°)+(sin 22°+cos 22°)+…+(s in 244°+cos 244°)+sin 245°=44+12=892.5.已知函数f(x)=√2cos x-π12,x ∈R.若cos θ=35,θ∈3π2,2π,则fθ-5π12= .解析f θ-5π12=√2cos θ-5π12−π12=√2cos θ-π2=√2cosπ2-θ=√2sinθ,由已知可得θ为第四象限角,所以sinθ<0,故sinθ=-√1-cos 2θ=-45,f θ-5π12=√2sinθ=√2×-45=-4√25.-4√256.是否存在角α,β,α∈(-π2,π2),β∈(0,π),使等式sin(3π-α)=√2cos (π2-β),√3cos(-α)=-√2cos(π+β)同时成立?若存在,求出α,β的值;若不存在,请说明理由. ,得{sinα=√2sinβ,√3cosα=√2cosβ,①②①2+②2得sin 2α+3cos 2α=2,∴sin 2α=12.又α∈(-π2,π2),∴α=π4或α=-π4.将α=π4代入②,得cosβ=√32.又β∈(0,π),∴β=π6,代入①可知符合.将α=-π4代入②得cosβ=√32,又β∈(0,π),∴β=π6,代入①可知不符合.综上可知,存在α=π4,β=π6满足条件.。
《红对勾》2015-2016学年人教A版高中数学必修4课件1-4-1正弦函数、余弦函数的图象

关于三角函数的图象,有下列说法: ①y=sin|x|与y=sinx的图象关于y轴对称; ②y=cos(-x)与y=cos|x|的图象相同; ③y=|sinx|与y=sin(-x)的图象关于x轴对称; ④y=cosx与y=cos(-x)的图象关于y轴对称. 其中正确的序号是________.
解析:对②,y=cos(-x)=cosx,y=cos|x|=cosx, 故其图象相同;对④,y=cos(-x)=cosx, 故其图象关于y轴对称,由作图可知①③均不正确.
域为{x|x≠kπ+π2,k∈Z}.
而y=csoinsxx· cos2x
=csoinsxx|cosx|
=s-insxi,nxc,oscxo>s0x<0
即y=s-insxi,nxx,∈x∈-2π2π+ +22kkππ, ,π322π++22kπkπ
,k∈Z
其函数图象如图所示:
解决此类问题)
(2)用数形法结合判断k的取值范围.
f(x)=3-sisninx,x,0≤ π<xx≤≤π2,π. 图象如下图所示. 结合图象可知1<k<3.
答案:(1)x∈[2kπ+6π,2kπ+56π],k∈Z (2)1<k<3
提高篇03
自我超越
——易错警示系列—— 忽视函数定义域致使出错 【例】 作函数y=ta1nx·sinx的图象.
称;③正、余弦函数的图象不超过直线y=1和y=-1所
夹的范围.
A.0个
B.1个
C.2个
D.3个
(2)对于余弦函数y=cosx的图象,有以下三项描述: ①向左向右无限延伸; ②与x轴有无数多个交点; ③与y=sinx的图象形状一样,只是位置不同. 其中正确的有( ) A.0个 B.1个 C.2个 D.3个
天津一中2014--2015学年度第二学期高一数学期末试卷及答案

天津一中2021-2021 -2高一年级数学期末试卷一.选择题(每题3分,共30分)1.假设a<b<0,那么以下不等式不能成立的是A.1a>1bB.2a>2bC.|a|>|b|D.(12)a>(12)b2.不等式2x2+ax+b>0的解集是{x|x>3或x<-2},那么a、b的值分别是A.2,12B.2,-2C.2,-12D.-2,-123.如图,方程y=ax+1a表示的直线可能是B4.设x,y满足24,1,22,x yx yx y+≥⎧⎪-≥-⎨⎪-≤⎩那么z=x+yA.有最小值2,最大值3B.有最大值3,无最小值C.有最小值2,无最大值D.既无最小值,也无最大值5.等差数列的首项为125,且从第10项开场为比1大的项,那么公差d的取值范围是A.d>875B.d<325C.875<d<325D.875<d≤3256.从装有4个红球和3个黑球的口袋内任取3个球,那么互斥而不对立的事件是A.至少有一个红球与都是黑球B.至少有一个红球与恰有一个黑球C.至少有一个红球与至少有一个黑球D.恰有一个红球与恰有两个红球7.函数f(x)=⎩⎪⎨⎪⎧x+2,x≤0-x+2, x>0,那么不等式f(x)≥x2的解集为A.[-1,1]B.[-2,2]C.[-2,1]D.[-1,2]8.袋中共有6个除了颜色外完全一样的球,其中有1个红球,2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于A.15B.25C.35D.459.f(x)是定义在R 上的奇函数,当x ≤0时, f(x)=x 2,假设∀x ∈[t,t+1],不等式f(x)≤9f(x+t)恒成立,那么实数t 的最大值为A .25- B.32- C.23- D.210.如果执行下面的程序框图,那么输出的S=A.2450B.2500 C .2550 D.2652二.填空题(每题4分,共24分)11.假设直线x+my+2=0与2x+3y+1=0互相垂直,那么m=_____.-2/312.1,a 1,a 2,4成等差数列,1,b 1,b 2,b 3,4成等比数列,那么a 1+a 2b 2的值为_ .5/2 13. 某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的安康情况,用分层抽样的方法从中抽取样本 . 假设样本中的青年职工为7人,那么样本容量为 .1514.在区间[-1,2]上随机取一个数x,那么x∈[0,1]的概率为______.1/315.把J 、Q 、K 三张牌随机地排成一排,那么JK 两牌相邻而排的概率为_____.2/316.不等式y x a y x +≤+对一切x>0,y>0恒成立,那么实数a 的取值范围为 [√2,+∞)三.解答题(共46分)17.袋中有4个不同的红球,2个不同的白球,从中任取2个球.试求:(1)所取的2球都是红球的概率;(2)所取的2球不是同一颜色的概率.解:(1)将4红球编号为1,2,3,4;2个白球编号为5,6.任取2球,根本领件为:{1,2},{1,3},{1,4},{1,5},{1,6},{2,3},{2,4},{2,5},{2,6},{3,4},{3,5},{3,6},{4,5},{4,6},{5,6},共15个,而且这些根本领件的出现是等可能的.用A 表示“都是红球〞这一事件,那么A 包含的根本领件有{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},共6个,所以P(A)=615=25. (2)根本领件同(1),用B 表示“不同色〞这一事件,那么B 包含的根本领件有{1,5},{1,6},{2,5},{2,6},{3,5},{3,6},{4,5},{4,6},共8个,所以P(B)=815.(12分)18.在△ABC 中,a,b,c 分别为内角A,B,C 的对边,且2asinA=(2b+c)sinB+(2c+b)sinC 〔1〕求A 的大小;〔2〕求sinB+sinC 的最大值.解:〔1〕由,根据正弦定理得22(2)(2)a b c b c b c =+++即 222a b c bc =++ 由余弦定理得 2222cos a b c bc A =+-故 1cos 2A =-,A=120° 〔2〕由〔1〕得: sin sin sin sin(60)BC B B +=+︒-1sin 2sin(60)B B B =+=︒+ 故当B=30°时,sinB+sinC 取得最大值1。
高中化学(新人教版)必修第一册同步习题:第四章复习提升(同步习题)【含答案及解析】

本章复习提升易混易错练易错点1 对原子符号中各概念理解不清而导致出错1.(2020北京西城高一期末,)92235U常用于核裂变反应。
下列关于92235U的叙述正确的是( )A.质子数为235B.电子数为143C.核电荷数为235D.中子数为1432.(2019浙江温州十五校联合体高一上期中,)下列说法不正确的是( )A.质量数是将原子核内所有的质子和中子的相对质量取整数值之和B.Z A X表示X元素的一种原子,中子数为A-ZC.Z A X中A为该原子的相对原子质量的近似值D.原子都是由质子、中子和电子组成的,原子不带电易错点2 元素、核素、同位素、同素异形体的辨析3.(2020山东淄博高一期末,)13C-NMR(核磁共振)可用于含碳化合物的结构分析,15N-NMR可用于测定蛋白质、核酸等生物大分子的空间结构。
下列有关13C、15N 的叙述正确的是( )A.13C与15N具有相同的中子数B.13C与14C的核外电子排布不同C.15N与14N互为同位素D.15N的核外电子数与中子数相同4.(2019浙江嘉兴一中高一上期中,)下列表示正确的是( )A.S2-的结构示意图:B.H、D、T表示同一种核素C.H2O2中氧元素的化合价为-2价D.H2SO4的摩尔质量是98 g易错点3 对元素周期表的结构记忆不清而出错5.(2019安徽安庆白泽湖中学高一下月考,)下列关于元素周期表的叙述,错误的是( )A.元素周期表揭示了化学元素间的内在联系,是化学发展史上的重要里程碑之一B.在周期表中,把电子层数相同的元素按原子序数从左到右递增排成一横行,称为一周期C.元素周期表中,总共有18个纵列,18个族D.第ⅠA族(除了H)的元素又称为碱金属元素,第ⅦA族的元素又称为卤族元素6.(2020山东聊城高一期末,)下列有关原子结构和元素周期表的说法中正确的是( )A.ⅠA族的元素均为金属元素B.元素原子的最外层电子数等于该元素的最高化合价C.短周期元素X、Y形成的离子m X a+与n Y b-电子层结构相同,则m-a=n+bD.在元素周期表中金属与非金属的交界处可寻找制造催化剂和耐高温、耐腐蚀合金的元素易错点4 元素性质递变规律的应用有误7.(2020福建仙游第一中学、福州八中高三质检,)短周期主族元素X、Y、Z、W 原子序数依次增大,X、W同主族,Y的原子半径是所有短周期主族元素中最大的,Z 是地壳中含量最多的金属元素,四种元素原子的最外层电子数总和为16。
《红对勾》2015-2016学年人教A版高中数学必修4课件1-2-2同角三角函数的基本关系

【例】 已知 tanα=2,则 (1)24ssiinnαα- -39ccoossαα=________; (2)4sin2α-3sinαcosα-5cos2α=________.
【思维导图】
【解】 (1)24ssiinnαα- -39ccoossαα=24ttaannαα--39=24× ×22- -39=-1. (2)4sin2α-3sinαcosα-5cos2α =4sin2α-si3ns2iαn+αccoossα2-α 5cos2α, 因为 cos2α≠0,所以分子和分母同除以 cos2α, 则 4sin2α-3sinαcosα-5cos2α=4tan2tαa-n2α3+tan1α-5 =4×4-4+3×1 2-5=1.
(2)sin2α是(sinα)2的简写,不能写成sinα2.
(3)在使用同角三角函数关系式时要注意使式子有意 义,如式子tan90°=csoins9900°°不成立.
(4)注意公式变形的灵活应用. (5)在应用平方关系式求sinα或cosα时,其正负号是由角 α所在的象限决定的.当角所在象限不明确时,要进行分类 讨论.
cos2α sin2α
(2)原式=1-sincoαsα·
csoinsαα-sinα csoinsαα+sinα
=1-sincoαsα·
1-cosα 1+cosα
=1-sincoαsα·
1-cosα2 1-cos2α
=1-sincoαsα·1-|sincoαs| α
=±1.
通法提炼 同角三角函数关系化简常用方法有: ①化切为弦,减少函数名称;②对含根号的,应先把 被开方式化为完全平方,去掉根号;③对含有高次的三角 函数式,可借助于因式分解,或构造平方关系,以降幂化 简.
【评析】 形如(2)式的求解,应灵活利用“1”的代换, 将整式变为分式,即可利用分式的性质将式子变为关于 tanα 的代数式,从而代入求值.
《红对勾》2015-2016学年人教A版高中数学必修4课件1-1-2弧度制

3.角α=6这种表达方式正确吗? 答:正确.角α=6表示6弧度的角,这里将“弧度”省 去了.
角度与弧度的互化
4.在同一个式子中,角度制与弧度制能否混用?为什 么?
答:角度制和弧度制是表示角的两种不同的度量方 法,两者有着本质的不同,因此在同一个表达式中不能出 现两种度量方法的混用,如α=2kπ+30°,k∈Z是不正确的 写法,应写成α=2kπ+6π,k∈Z.
扇形的弧长和面积的计算
【例 3】 已知一扇形的周长为 8 cm,当它的半径 和圆心角取什么值时,扇形的面积最大?并求出最大面 积.
【分析】 (1)用哪些量表达扇形的周长?(半径和弧 长)
(2)扇形的面积公式是什么?能否用半径表示?(S= 12lr,能)
(3)如何求扇形面积的最大值?(利用二次函数)
答:随着半径的变化,弧长也在变化,但对于一定大 小的圆心角所对应的弧长与半径的比值是唯一确定的,与 半径的大小无关.
任意角的弧度数与实数的对应关系
(1)正角:正角的弧度数是一个 正数 (2)负角:负角的弧度数是一个 负数 (3)零角:零角的弧度数是 0 . (4)如果半径为r的圆的圆心角α所对弧的长为l,那
角度制与弧度制的互化
【例 2】 设 α1=510°,α2=-750°,β1=45π,β2= -161π.
(1)将 α1,α2 用弧度表示出来,并指出它们各自终边 所在的象限;
(2)将 β1,β2 用角度表示出来,并在[-360°,360°) 内找出与它们终边相同的所有的角.
【分析】 首先利用 1°=18π0rad 可将角度化成弧度,利 用 1rad=18π0°可将弧度化成角度,然后再根据要求指出 α1, α2 终边所在的象限,与 β1,β2 终边相同且在[-360°,360°) 内的角.
天津市第一中学2015-2016学年高中数学 期末复习2 新人教A版必修4
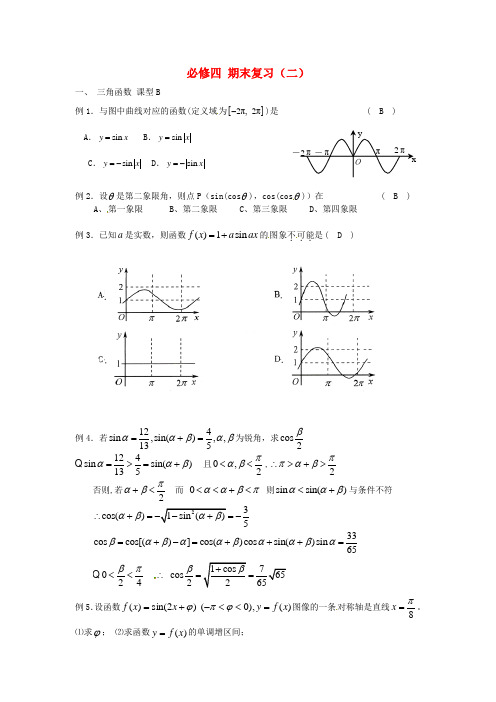
必修四 期末复习(二)一、 三角函数 课型B例1.与图中曲线对应的函数(定义域为[]2π,2π-)是 ( B ) A .sin y x = B .sin y x =C .sin y x =-D .sin y x =-例2.设θ是第二象限角,则点P (sin(cos θ),cos(cos θ))在 ( B )A 、第一象限B 、第二象限C 、第三象限D 、第四象限例3.已知a 是实数,则函数()1sin f x a ax =+的图象不.可能..是( D )例4.若124sin ,sin(),,135ααβαβ=+=为锐角,求cos 2β 124sin sin()135ααβ=>=+ 且0,2παβ<<,2ππαβ∴>+>否则,若2παβ+<而 0ααβπ<<+<则sin sin()ααβ<+与条件不符3cos() 5αβ∴+==-33cos cos[()]cos()cos sin()sin 65βαβααβααβα=+-=+++= 024βπ<<∴ cos2β==例5.设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x 。
⑴求ϕ; ⑵求函数)(x f y =的单调增区间;解:⑴)(8x f y x ==是函数π的图像的对称轴,,1)82sin(±=+⨯∴ϕπ.,24Z k k ∈+=+∴ππππ.43,0πϕϕπ-=<<- ⑵由(Ⅰ)知).432sin(,43ππϕ-=-=x y 因此 由题意得.,2243222Z k k x k ∈+≤-≤-πππππ所以函数.],85,8[)432sin(Z k k k x y ∈++-=πππππ的单调增区间为二、三角函数 课型C例6. 若1sin()63πα-=,则2cos(2)3πα+等于 ( A ) A .79- B.13- C.13 D.79例7.将函数sin y x x =的图像沿x 轴向右平移a 个单位(0)a >,所得图像关于y 轴对称,则a 的最小值为 ( C ) A.76π B.2π C .6π D.3π例8.若函数()(1)cos ,02f x x x x π=≤<,则()f x 的最大值为 ( B )A.1 B .21 D. -2 例9.计算3tan11°+3tan19°+tan11°·tan19°0000000000tan11tan1919)(1tan11tan19)tan11tan19+=+-+0000tan11tan19)tan11tan191-+=, 例10.已知函数)0(23cos 3cos sin )(2>++-⋅=a b a x a x x a x f . (Ⅰ)求函数)(x f 的单调递减区间;(Ⅱ)已知函数)(x f 在区间]20[π,上的最小值是2-,最大值是3,求实数b a ,的值.解:b a x a x a x f +++-=23)2cos 1(232sin 21)(b x a b x a x a +-=+-=)32sin(2cos 232sin 2π2323222πππππ+≤-≤+k x k ,1211125ππππ+≤≤+k x kZ k k k ∈++],1211,125[ππππ为所求 (II )1)32sin(23,32323,20≤-≤-≤-≤-≤≤πππππx x x , ,3)(,223)(max min =+=-=+-=b a x f b a x f ⎩⎨⎧+-==⇒⎪⎩⎪⎨⎧=+-=+-3223223b a b a b a例11.已知向量(cos(),sin())44a x x ππ=--,(cos(),sin())44b x x ππ=+-+, ()f x a b k a b =⋅-+, [0,].x π∈ (1)若712x π=,求⋅及+a b ; (2)若1k =,当x 为何值时,()f x 有最小值,最小值是多少? (3)若()f x 的最大值为3,求k 的值.解:(1)32a b ⋅=-62a b -+= (2)2()2cos 2cos 1f x x x =-- 当3x π=或23x π=时,()f x 有最小值 min 3()2f x =- (3)2()2cos 2cos 1f x x k x =--设:cos x t =,由[0,][0,1]x t π∈⇒∈ 则:2()()221[0,1]f x g t t kt t ==--∈当:1122kk≤⇒≤时,max()(1)22131f xg k k==--=⇒=-111kkk≤⎧⇒=-⎨=-⎩当:1122kk>⇒>时,max()(0)13f x g==-≠综上之:1k=-。
《红对勾》2015-2016学年人教A版高中数学必修4课件1-4-2正弦函数、余弦函数的性质-2

若函数 f(x)=sin(2x+φ)(|φ|<π2)与函数 g(x)=cos(ωx- π6)(ω>0)的图象具有相同的对称中心,则 φ=________.
解析:∵两函数图象具有相同的对称中心, ∴它们的周期相同, ∴ω=2.令 2x+φ=kπ(k∈Z),则 x=k2π-φ2(k∈Z),即 f(x) 的图象的对称中心为(k2π-φ2,0)(k∈Z).令 2x-π6=k′π+2π (k′∈Z),则 x=k′2 π+π3(k′∈Z),即 g(x)的图象的对称中 心为(k′2 π+3π,0)(k′∈Z).又 g(x),f(x)的图象的对称中心
解:(1)由 x∈(-4π,π)知,23x∈(-6π,23π). 当23x∈(-π6,2π],即 x∈(-π4,34π]时, 函数 y=-2sin23x 为减函数.
所以 2kπ<x+π4<2kπ+π,k∈Z, 即 2kπ-π4<x<2kπ+34π,k∈Z. 所以 u= 2sin(x+π4)的单调递减区间为[2kπ+π4,2kπ+34 π),k∈Z. 所以 y=log 1 [ 2sin(x+4π)]的单调递增区间为[2kπ+4π,
π
2kπ+34π),k∈Z.
求函数的单调区间:y=-2sin23x,x∈(-4π,π).
(4)要注意定义域对单调区间的制约.
2.求三角函数最值或值域的常用方法 (1)对于求形如y=asinx+b(或y=acosx+b)的函数的最 值或值域问题,常利用正、余弦函数的有界性(-1≤sinx, cosx≤1)求解.求三角函数取最值时相应自变量x的集合 时,要注意考虑三角函数的周期性.
(2)求解形如y=asin2x+bsinx+c(或y=acos2x+bcosx+ c),x∈D的函数的值域或最值时,一般先通过换元,令t= sinx(或cosx),将原函数转化为关于t的二次函数,然后利用 配方法求值域或最值即可.求解过程中要注意t=sinx(或 cosx)的取值范围.
天津市第一中学高中数学 期末复习3 新人教A版必修4

必修四 期末复习(三)一、 三角函数 课型A例1.若tan θ+1tan θ=4,则sin2θ= A .15 B. 14 C. 13 D . 12例2.若02πα<<,02πβ-<<,1cos()43πα+=,3cos()423πβ-=,则cos()2βα+= A .33 B .33- C .539 D .69-例3.α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为 .17250。
例4.函数ϕϕ,,(),sin()(w A wx A x f +=是常数,)0,0>>w A 的部分图象如图所示,则____)0(=f 26例5.已知向量(cos sin ,sin )x x x ωωω=-a ,(cos sin ,23cos )x x x ωωω=--b ,设函数()f x λ=⋅+a b ()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.(Ⅰ)求函数()f x 的最小正周期; (Ⅱ)若()y f x =的图象经过点π(,0)4,求函数()f x 在区间3π[0,]5上的取值范围.【答案】(Ⅰ)因为22()sin cos 23sin cos f x x x x x ωωωωλ=-+⋅+cos 23sin 2x x ωωλ=-++π2sin(2)6x ωλ=-+.由直线πx =是()y f x =图象的一条对称轴,可得πsin(2π)16ω-=±,所以ππ2ππ()62k k ω-=+∈Z ,即1()23k k ω=+∈Z .又1(,1)2ω∈,k ∈Z ,所以1k =,故56ω=.所以()f x 的最小正周期是6π5.(Ⅱ)由()y f x =的图象过点π(,0)4,得π()04f =,即5πππ2sin()2sin 26264λ=-⨯-=-=-,即2λ=-.故5π()2sin()236f x x =--,由3π05x ≤≤,有π5π5π6366x -≤-≤,所以15πsin()1236x -≤-≤,得5π122sin()22236x --≤--≤-,故函数()f x 在3π[0,]5上的取值范围为[12,22]---.二、三角函数 课型B例6.给定两个长度为1的平面向量OA u u u r 和OB uuu r ,它们的夹角为120o.如图所示,点C 在以O 为圆心的圆弧AB u u u v上变动. 若,OC xOA yOB =+u u u r u u u r u u u r其中,x y R ∈,则x y +的最大值是________. [解析]设AOC α∠=,,OC OA xOA OA yOB OA OC OB xOA OB yOB OB ⎧•=•+•⎪⎨•=•+•⎪⎩u u u r u u u r u u u r u u u r u u u r u u u v u u ur u u u r u u u r u u u r u u u r u u u v ,即01cos 21cos(120)2x y x y αα⎧=-⎪⎪⎨⎪-=-+⎪⎩ ∴02[cos cos(120)]cos 3sin 2sin()26x y πααααα+=+-=+=+≤例7.已知函数)2sin()(ϕ+=x x f ,其中ϕ为实数,若|)6(|)(πf x f ≤对R x ∈恒成立,且)()2(ππf f >,则)(x f 的单调递增区间是(A) )(6,3Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ(B) )(2,Z k k k ∈⎥⎦⎤⎢⎣⎡+πππ(C ) )(32,6Z k k k ∈⎥⎦⎤⎢⎣⎡++ππππ(D) )(,2Z k k k ∈⎥⎦⎤⎢⎣⎡-πππ 例8.已知函数f(x)=3sin(x-)(>0)6πωω和g(x)=2cos(2x+)+1ϕ的图象的对称轴完全相同。
高中数学 阶段质量检测(一)(含解析)新人教A版必修4-新人教A版高一必修4数学试题

阶段质量检测(一)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.若角α的终边经过点P (-1,3),则tan α的值为( ) A .-13 B .-3C .-1010 D.31010解析:选B 由定义,若角α的终边经过点P (-1,3),∴tan α=-3.故选B. 2.若sin α=33,π2<α<π,则sin ⎝⎛⎭⎪⎫α+π2=( )A .-63 B .-12C.12 D.63解析:选A ∵sin ⎝ ⎛⎭⎪⎫π2+α=cos α,又π2<α<π,sin α=33,∴cos α=-63. 3.已知扇形的半径为r ,周长为3r ,则扇形的圆心角等于( ) A.π3 B .1C.2π3D .3 解析:选B 弧长l =3r -2r =r ,则圆心角α=lr=1.4.函数f (x )=sin ⎝⎛⎭⎪⎫x -π4的图象的一条对称轴是( )A .x =π4B .x =π2C .x =-π4D .x =-π2解析:选C f (x )=sin ⎝ ⎛⎭⎪⎫x -π4的图象的对称轴为x -π4=k π+π2,k ∈Z ,得x =k π+3π4, 当k =-1时,则其中一条对称轴为x =-π4.5.下列函数中,周期为π,且在⎣⎢⎡⎦⎥⎤π4,π2上为减函数的是( )A .y =sin ⎝ ⎛⎭⎪⎫x +π2B .y =cos ⎝⎛⎭⎪⎫x +π2C .y =cos ⎝ ⎛⎭⎪⎫2x +π2D .y =sin ⎝⎛⎭⎪⎫2x +π2 解析:选D 周期为π,排除A ,B ;y =cos ⎝ ⎛⎭⎪⎫2x +π2=-sin 2x 在⎣⎢⎡⎦⎥⎤π4,π2上为增函数,y =sin ⎝ ⎛⎭⎪⎫2x +π2=cos 2x 在⎣⎢⎡⎦⎥⎤π4,π2上为减函数,所以选D.6.函数f (x )=tan ⎝⎛⎭⎪⎫x +π4的单调增区间为( )A.⎝⎛⎭⎪⎫k π-π2,k π+π2,k ∈ZB .(k π,(k +1)π),k ∈Z C.⎝⎛⎭⎪⎫k π-3π4,k π+π4,k ∈Z D.⎝⎛⎭⎪⎫k π-π4,k π+3π4,k ∈Z 解析:选C 令k π-π2<x +π4<k π+π2,k ∈Z ,解得k π-3π4<x <k π+π4,k ∈Z ,选C.7.已知sin ⎝ ⎛⎭⎪⎫π4+α=32,则sin ⎝ ⎛⎭⎪⎫3π4-α的值为( )A.12 B .-12C.32 D .-32 解析:选C ∵⎝ ⎛⎭⎪⎫π4+α+⎝ ⎛⎭⎪⎫3π4-α=π,∴3π4-α=π-⎝ ⎛⎭⎪⎫π4+α,∴sin ⎝⎛⎭⎪⎫3π4-α=sin ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π4+α=sin ⎝ ⎛⎭⎪⎫π4+α=32.8.为了得到函数y =sin ⎝ ⎛⎭⎪⎫2x -π6的图象,可以将函数y =cos 2x 的图象( )A .向右平移π6个单位长度B .向右平移π3个单位长度C .向左平移π6个单位长度D .向左平移π3个单位长度解析:选B 函数y =sin ⎝ ⎛⎭⎪⎫2x -π6=cos π2-2x -π6=cos ⎝ ⎛⎭⎪⎫2π3-2x =cos ⎝ ⎛⎭⎪⎫2x -2π3=cos2x -π3.故选B.9.函数y =cos 2x +sin x ⎝ ⎛⎭⎪⎫-π6≤x ≤π6的最大值与最小值之和为( )A.32 B .2C .0 D.34解析:选A f (x )=1-sin 2x +sin x =-⎝ ⎛⎭⎪⎫sin x -122+54,∵-π6≤x ≤π6,∴-12≤sin x ≤12.当sin x =-12时,f (x )min =14;当sin x =12时,f (x )max =54,∴f (x )min +f (x )max =14+54=32.10.同时具有下列性质的函数可以是( ) ①对任意x ∈R ,f (x +π)=f (x )恒成立; ②图象关于直线x =π3对称;③在⎣⎢⎡⎦⎥⎤-π6,π3上是增函数. A .f (x )=sin ⎝ ⎛⎭⎪⎫x 2+π6 B .f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6 C .f (x )=cos ⎝ ⎛⎭⎪⎫2x +π3 D .f (x )=cos ⎝⎛⎭⎪⎫2x -π6解析:选B 依题意知,满足条件的函数的周期是π,图象以直线x =π3为对称轴,且在⎣⎢⎡⎦⎥⎤-π6,π3上是增函数.对于A 选项,函数周期为4π,因此A 选项不符合;对于C 选项,f ⎝ ⎛⎭⎪⎫π3=-1,但该函数在⎣⎢⎡⎦⎥⎤-π6,π3上不是增函数,因此C 选项不符合;对于D 选项,f ⎝ ⎛⎭⎪⎫π3≠±1,即函数图象不以直线x =π3为对称轴,因此D 选项不符合.综上可知,应选B.11.已知函数y =A sin(ωx +φ)(A >0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )A .y =2sin ⎝⎛⎭⎪⎫2x -π4 B .y =2sin ⎝ ⎛⎭⎪⎫2x -π4或y =2sin ⎝ ⎛⎭⎪⎫2x +3π4 C .y =2sin ⎝ ⎛⎭⎪⎫2x +3π4 D .y =2sin ⎝⎛⎭⎪⎫2x -3π4 解析:选C 由图象可知A =2,因为π8-⎝ ⎛⎭⎪⎫-π8=π4,所以T =π,ω=2.当x =-π8时,2sin ⎝ ⎛⎭⎪⎫-π8·2+φ=2,即sin ⎝⎛⎭⎪⎫φ-π4=1,又|φ|<π,解得φ=3π4.故函数的解析式为y =2sin ⎝⎛⎭⎪⎫2x +3π4. 12.函数f (x )=A sin ωx (ω>0),对任意x 有f ⎝ ⎛⎭⎪⎫x -12=f ⎝ ⎛⎭⎪⎫x +12,且f ⎝ ⎛⎭⎪⎫-14=-a ,那么f ⎝ ⎛⎭⎪⎫94等于( )A .aB .2aC .3aD .4a解析:选A 由f ⎝ ⎛⎭⎪⎫x -12=f ⎝ ⎛⎭⎪⎫x +12,得f (x +1)=f ⎝ ⎛⎭⎪⎫⎝ ⎛⎭⎪⎫x +12+12=f ⎝ ⎛⎭⎪⎫x +12-12=f (x ),即1是f (x )的周期.而f (x )为奇函数,则f ⎝ ⎛⎭⎪⎫94=f ⎝ ⎛⎭⎪⎫14=-f ⎝ ⎛⎭⎪⎫-14=a .二、填空题(本大题共4小题,每小题5分,共20分) 13.已知tan α=-3,π2<α<π,那么cos α-sin α的值是________. 解析:因为π2<α<π,所以cos α<0,sin α>0,所以cos α=-cos 2α=-cos 2αcos 2α+sin 2α=-11+tan 2α=-11+3=-12.sin α=32,所以cos α-sin α=-1+32.答案:-1+3214.函数f (sin x )=cos 2x ,那么f ⎝ ⎛⎭⎪⎫12的值为________. 解析:令sin x =12,得x =2k π+π6或x =2k π+5π6,k ∈Z ,所以f ⎝ ⎛⎭⎪⎫12=cos π3=12. 答案:1215.定义运算a *b 为a *b =⎩⎪⎨⎪⎧aa ≤b ,b a >b ,例如1*2=1,则函数f (x )=sin x *cos x的值域为________.解析:由题意可知,这实际上是一个取小的自定义函数,结合函数的图象可得其值域为⎣⎢⎡⎦⎥⎤-1,22.答案:⎣⎢⎡⎦⎥⎤-1,22 16.给出下列4个命题:①函数y =⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x -π12的最小正周期是π2;②直线x =7π12是函数y =2sin ⎝ ⎛⎭⎪⎫3x -π4的一条对称轴;③若sin α+cos α=-15,且α为第二象限角,则tan α=-34;④函数y =cos(2-3x )在区间⎝ ⎛⎭⎪⎫23,3上单调递减.其中正确的是________.(写出所有正确命题的序号).解析:函数y =sin ⎝ ⎛⎭⎪⎫2x -π12的最小正周期是π,则y =⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫2x -π12的最小正周期为π2,故①正确. 对于②,当x =7π12时,2sin ⎝⎛⎭⎪⎫3×7π12-π4=2sin 3π2=-2,故②正确.对于③,由(sin α+cos α)2=125得2sin αcos α=-2425,α为第二象限角,所以sin α-cos α=1-2sin αcos α=75,所以sin α=35,cos α=-45,所以tan α=-34,故③正确. 对于④,函数y =cos(2-3x )的最小正周期为2π3,而区间⎝ ⎛⎭⎪⎫23,3长度73>2π3,显然④错误.答案:①②③三、解答题(本大题共6小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)已知tan α+1tan α=52,求2sin 2(3π-α)-3cos π2+αsin ⎝ ⎛⎭⎪⎫3π2-α+2的值.解:tan α+1tan α=52,即2tan 2α-5tan α+2=0,解得tan α=12或tan α=2.2sin 2(3π-α)-3cos ⎝ ⎛⎭⎪⎫π2+αsin ⎝ ⎛⎭⎪⎫3π2-α+2 =2sin 2α-3sin αcos α+2 =2sin 2α-3sin αcos αsin 2α+cos 2α+2 =2tan 2α-3tan αtan 2α+1+2. 当tan α=12时,原式=2×⎝ ⎛⎭⎪⎫122-3×12⎝ ⎛⎭⎪⎫122+1+2=-45+2=65;当tan α=2时,原式=2×22-3×222+1+2=25+2=125. 18.(12分)已知函数f (x )=2sin ⎝ ⎛⎭⎪⎫13x -π6,x ∈R .(1)求f ⎝⎛⎭⎪⎫5π4的值;(2)求函数f (x )的单调递增区间. 解:(1)f ⎝⎛⎭⎪⎫5π4=2sin ⎝⎛⎭⎪⎫13×5π4-π6=2sin π4= 2(2)令2k π-π2≤13x -π6≤π2+2k π,k ∈Z ,所以2k π-π3≤13x ≤2π3+2k π,k ∈Z ,解得6k π-π≤x ≤2π+6k π,k ∈Z ,所以函数f (x )=2sin ⎝ ⎛⎭⎪⎫13x -π6的单调递增区间为[6k π-π,2π+6k π],k ∈Z .19.(12分)已知函数f (x )=3sin ⎝⎛⎭⎪⎫x +π4.(1)用五点法画出它在一个周期内的闭区间上的图象; (2)写出f (x )的值域、最小正周期、对称轴,单调区间.解:(1)列表如下:x -π4 π4 3π4 5π4 7π4 x +π4π2 π3π2 2πsin ⎝ ⎛⎭⎪⎫x +π40 10 -13sin ⎝⎛⎭⎪⎫x +π4 0 3 0 -3 0描点画图如图所示.(2)由图可知,值域为[-3,3],最小正周期为2π, 对称轴为x =π4+k π,k ∈Z ,单调递增区间为⎣⎢⎡⎦⎥⎤-3π4+2k π,π4+2k π(k ∈Z ),单调递减区间为⎣⎢⎡⎦⎥⎤π4+2k π,5π4+2k π(k ∈Z ).20.(12分)如图,函数y =2sin(πx +φ),x ∈R ⎝ ⎛⎭⎪⎫其中0≤φ≤π2的图象与y 轴交于点(0,1).(1)求φ的值;(2)求函数y =2sin(πx +φ)的单调递增区间; (3)求使y ≥1的x 的集合. 解:(1)因为函数图象过点(0,1), 所以2sin φ=1,即sin φ=12.因为0≤φ≤π2,所以φ=π6.(2)由(1)得y =2sin ⎝⎛⎭⎪⎫πx +π6,所以当-π2+2k π≤πx +π6≤π2+2k π,k ∈Z ,即-23+2k ≤x ≤13+2k ,k ∈Z 时,y =2sin ⎝⎛⎭⎪⎫πx +π6是增函数,故y =2sin ⎝⎛⎭⎪⎫πx +π6的单调递增区间为⎣⎢⎡⎦⎥⎤-23+2k ,13+2k ,k ∈Z . (3)由y ≥1,得sin ⎝⎛⎭⎪⎫πx +π6≥12,所以π6+2k π≤πx +π6≤5π6+2k π,k ∈Z ,即2k ≤x ≤23+2k ,k ∈Z ,所以y ≥1时,x 的集合为⎩⎨⎧⎭⎬⎫x |2k ≤x ≤23+2k ,k ∈Z .21.(12分)已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π),在同一周期内,当x =π12时,f (x )取得最大值3;当x =7π12时,f (x )取得最小值-3. (1)求函数f (x )的解析式;(2)求函数f (x )的单调递减区间;(3)若x ∈⎣⎢⎡⎦⎥⎤-π3,π6时,函数h (x )=2f (x )+1-m 的图象与x 轴有两个交点,某某数m 的取值X 围.解:(1)由题意,A =3,T =2⎝⎛⎭⎪⎫7π12-π12=π,ω=2πT =2.由2×π12+φ=π2+2k π,k ∈Z ,得φ=π3+2k π,k ∈Z ,又因为-π<φ<π,所以φ=π3.所以f (x )=3sin ⎝ ⎛⎭⎪⎫2x +π3.(2)由π2+2k π≤2x +π3≤3π2+2k π,k ∈Z ,得π6+2k π≤2x ≤7π6+2k π,k ∈Z , 则π12+k π≤x ≤7π12+k π,k ∈Z , 所以函数f (x )的单调递减区间为⎣⎢⎡⎦⎥⎤π12+k π,7π12+k π(k ∈Z ).(3)由题意知,方程sin ⎝ ⎛⎭⎪⎫2x +π3=m -16在⎣⎢⎡⎦⎥⎤-π3,π6上有两个根.因为x ∈⎣⎢⎡⎦⎥⎤-π3,π6,所以2x +π3∈⎣⎢⎡⎦⎥⎤-π3,2π3.所以m -16∈⎣⎢⎡⎭⎪⎫32,1.所以m ∈[33+1,7).22.(12分)已知函数f (x )=sin(ωx +φ)-b (ω>0,0<φ<π)的图象两相邻对称轴之间的距离是π2.若将f (x )的图象先向右平移π6个单位长度,再向上平移3个单位长度,所得图象对应的函数g (x )为奇函数.(1)求f (x )的解析式;(2)求f (x )的对称轴及单调区间;(3)若对任意x ∈⎣⎢⎡⎦⎥⎤0,π3,f 2(x )-(2+m )f (x )+2+m ≤0恒成立,某某数m 的取值X 围.解:(1)因为2πω=2×π2,所以ω=2,所以f (x )=sin(2x +φ)-b .又因为函数g (x )=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x -π6+φ-b +3为奇函数,且0<φ<π,所以φ=π3,b =3,故f (x )=sin ⎝⎛⎭⎪⎫2x +π3- 3. (2)令2x +π3=π2+k π,k ∈Z ,得对称轴为直线x =π12+k π2,k ∈Z .令2x +π3∈⎣⎢⎡⎦⎥⎤-π2+2k π,π2+2k π,k ∈Z ,得单调递增区间为⎣⎢⎡⎦⎥⎤-5π12+k π,π12+k π,k ∈Z ,令2x +π3∈⎣⎢⎡⎦⎥⎤π2+2k π,3π2+2k π,k ∈Z ,得单调递减区间为⎣⎢⎡⎦⎥⎤π12+k π,7π12+k π,k ∈Z .(3)因为x ∈⎣⎢⎡⎦⎥⎤0,π3,所以-3≤f (x )≤1-3,所以-1-3≤f (x )-1≤- 3.因为f 2(x )-(2+m )f (x )+2+m ≤0恒成立, 整理可得m ≤1f x -1+f (x )-1.由-1-3≤f (x )-1≤-3,得-1-332≤1f x -1+f (x )-1≤-433, 故m ≤-1-332,即实数m 的取值X 围是⎝ ⎛⎦⎥⎤-∞,-1-332.。
(人教版)天津高中化学必修一第四章《物质结构元素周期律》知识点(1)
一、选择题1.下列说法错误的是( )A.侯德榜发明了联合制碱法B.诺贝尔提出了原子学说C.屠呦呦合成了双氢青蒿素D.门捷列夫制作了世界上第一张元素周期表2.短周期元素A和B,其中A元素的原子最外层电子数是a,次外层电子数是b; B元素的原子M层电子数是(a- b),L层电子数是(a+b),则A、B两种元素形成的化合物的化学式可能表示为A.B3A2B.AB2C.A3B2D.BA23.X、Y、Z、M、Q五种短周期元素,原子序数依次增大。
Q元素的最高正价为+7,Y元素的原子最外层电子数是次外层的两倍,YM2和YZ2的最外层电子总数相同,X元素的原子半径最小。
下列说法正确的是A.原子半径: M>Z> YB.最高价氧化物的水化物的酸性: M>Q> YC.等物质的量时,Q2的杀菌能力大于QZ2D.X2Z2与X2M反应生成淡黄色固体4.下列说法中正确的是A.某元素的阳离子与同种阴离子可形成多种化合物B.阳离子中肯定含有金属元素,但含有金属元素的离子不一定是阳离子C.某物质经科学测定只含有一种元素,则可断定该物质一定是纯净物D.1 molNa和1 molAl各自发生化学反应时钠失去的电子少,则钠单质的还原性弱于铝单质5.根据表中短周期元素的有关信息判断,下列说法错误的是()A.最高价氧化物对应水化物的酸性:H>IB.简单离子半径:K>FC.同温下,形状、大小相同的单质与等浓度、等体积的稀硫酸反应的速率:L>K>J D.J、K、L的单质可以通过电解法冶炼获得6.五种短周期元素X、Y、Z、W、Q原子序数依次增大,W元素在短周期元素中原子半径最大,X、W同族,Z、Q同族,X、Y两种元素的最高正价和最低负价代数和均为0,由上述五种元素中的某几种元素组成的两种化合物均可在一定条件下洗涤含硫的试管,以下说法正确的是A.酸性:H2YO3<H2QO3,所以非金属性Y<QB.X与W形成的化合物中各原子均满足最外层8电子稳定结构C.X与Y形成的化合物只含有共价键D.由Z、W、Q三种元素形成的盐只有两种7.下列对结构与性质的大小排序不正确的是A.键角:NH3>H2O>P4B.阴离子配位数:CsCl>NaCl>CaF2 C.第一电离能:Se>As>Ge D.酸性:H2SO4>H2SO3>HClO8.某种化合物的结构如图所示,其中 X、Y、Z、Q、W 为原子序数依次增大的五种短周期元素,Q 核外最外层电子数与 Y 核外电子总数相同,X 的原子半径是元素周期表中最小的。
天津市第一中学2020学年高中数学 期末复习1 新人教A版必修4

必修四 期末复习(一)一、 平面向量 课型A例1.设b a ,是夹角为︒60的单位向量,,1=c 则()()c b c a +⋅-的取值范围是( C ) A.[]1,1- B.[]3,3- C .⎥⎦⎤⎢⎣⎡-21,23 D. ⎥⎦⎤⎢⎣⎡---213,213 例2.在ABC ∆所在的平面上有一点P ,满足PA PB PC AB ++=u u u r u u u r u u u r u u u r ,则PBC ∆与ABC ∆的面积之比是 ( C )A .13B .12C .23D .34 【解析】由PA PB PC AB ++=u u u r u u u r u u u r u u u r ,得PA PB BA PC +++=0u u u r u u u r u u u r u u u r , 即2PC AP =u u u r u u u r ,所以点P 是CA 边上的第二个三等分点,如图所示.故23PBC ABC S BC PC S BC AC ∆∆⋅==⋅. 例3.已知2||2||0,||0,x x x =≠++⋅=a b a a b 且关于的方程有实根a b 则与的夹角的取值范围是 ( A )A .],3[ππB .]32,3[ππC .],6[ππD .]6,0[π例4.平面上三点A 、B 、C 满足,5,4,3===CA BC AB求AB CA CA BC BC AB ⋅+⋅+⋅的值 -25例5.在平面直角坐标系xOy 中,点A(-1,-2)、B(2,3)、C(-2,-1)(1)求以线段AB 、AC 为邻边的平行四边形两条对角线的长(2)设实数t 满足(OC t AB -)·OC =0,求t 的值(1)对角线长为40和42 ,(2)115t =- 二、平面向量 课型B例6. 如图,半圆的直径AB =6,O 为圆心,C 为半圆上不同于A 、B 的任意一点,若P 为半径OC 上的动点,则PC PB PA ⋅+)(的最小值为 ( C ) O PC BAA.92;B.9;C.92-;D.-9;例7.P 是△ABC 边BC 的中线AD 上异于A 、D 的动点,AD =4,求)(PC PB PA +⋅的取值范围【解析】设PA DA λ=u u u r u u u r ,所以(1)DP DA λ=-u u u r u u u r ,其中01λ<<因为AD 是ABC ∆边BC 上的中线,所以0DB DC +=u u u r u u u r r所以()()2PA PB PC PA PD DB PD DC PA PD ⋅+=⋅+++=⋅u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r22212()[(1)]2(1)||323232()82DA DA DA λλλλλλλ=⋅--=--=-=--u u u r u u u r u u u r 因为01λ<<所以21()32()8[8,0)2PA PB PC λ⋅+=--∈-u u u r u u u r u u u r 例8.如图,在ΔABC 中,AD AB ⊥,3BC =u u u r BD u u u r ,1AD =u u u r ,则AC AD ⋅u u u r u u u r =( D )A .23B .32C .33D .3例9.设11(,)a x y =r ,22(,)b x y =r ,若||2a =r ,||3b =r ,6a b ⋅=-r r ,则1122x y x y +=+( C ) A .23 B .32 C .23- D .32- 例9.如图在ABC ∆中,3,7,2AB BC AC ===,若O 为ABC ∆的外心,求AC AO ⋅u u u r u u u r ,BC AO ⋅u u u r u u u r 的值 AB P2AC AO ⋅=u u u r u u u r ,52BC AO ⋅=-u u u r u u u r 例11.已知平面上三个向量,,,a b c r r r 的模均为1,它们相互之间的夹角均为120o 。
天津市第一中学2015-2016学年高中数学 期末复习2 新人教A版必修4
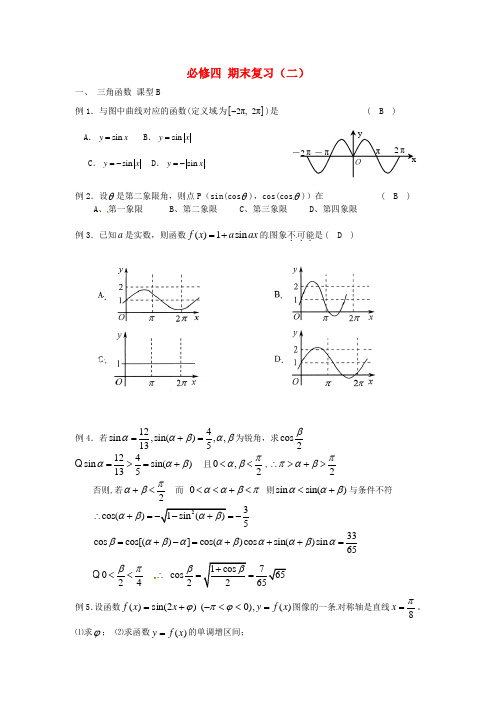
必修四 期末复习(二)一、 三角函数 课型B例1.与图中曲线对应的函数(定义域为[]2π,2π-)是 ( B ) A .sin y x = B .sin y x =C .sin y x =-D .sin y x =-例2.设θ是第二象限角,则点P (sin(cos θ),cos(cos θ))在 ( B )A 、第一象限B 、第二象限C 、第三象限D 、第四象限例3.已知a 是实数,则函数()1sin f x a ax =+的图象不.可能..是( D )例4.若124sin ,sin(),,135ααβαβ=+=为锐角,求cos 2β 124sin sin()135ααβ=>=+ 且0,2παβ<<,2ππαβ∴>+>否则,若2παβ+<而 0ααβπ<<+<则sin sin()ααβ<+与条件不符3cos() 5αβ∴+==-33cos cos[()]cos()cos sin()sin 65βαβααβααβα=+-=+++= 024βπ<<∴ cos2β==例5.设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x。
⑴求ϕ; ⑵求函数)(x f y =的单调增区间;解:⑴)(8x f y x ==是函数π的图像的对称轴,,1)82sin(±=+⨯∴ϕπ.,24Z k k ∈+=+∴ππππ.43,0πϕϕπ-=<<- ⑵由(Ⅰ)知).432sin(,43ππϕ-=-=x y 因此 由题意得.,2243222Z k k x k ∈+≤-≤-πππππ所以函数.],85,8[)432sin(Z k k k x y ∈++-=πππππ的单调增区间为二、三角函数 课型C例6. 若1sin()63πα-=,则2cos(2)3πα+等于 ( A ) A .79- B.13- C.13 D.79例7.将函数sin y x x =的图像沿x 轴向右平移a 个单位(0)a >,所得图像关于y 轴对称,则a 的最小值为 ( C ) A.76π B.2π C .6π D.3π例8.若函数()(1)cos ,02f x x x x π=≤<,则()f x 的最大值为 ( B )A.1 B .21 D. -2 例9.计算3tan11°+3tan19°+tan11°·tan19°0000000000tan11tan1919)(1tan11tan19)tan11tan19+=+-+0000tan11tan19)tan11tan191-+=, 例10.已知函数)0(23cos 3cos sin )(2>++-⋅=a b a x a x x a x f . (Ⅰ)求函数)(x f 的单调递减区间;(Ⅱ)已知函数)(x f 在区间]20[π,上的最小值是2-,最大值是3,求实数b a ,的值.解:b a x a x a x f +++-=23)2cos 1(232sin 21)(b x a b x a x a +-=+-=)32sin(2cos 232sin 2π2323222πππππ+≤-≤+k x k ,1211125ππππ+≤≤+k x kZ k k k ∈++],1211,125[ππππ为所求 (II )1)32sin(23,32323,20≤-≤-≤-≤-≤≤πππππx x x , ,3)(,223)(max min =+=-=+-=b a x f b a x f ⎩⎨⎧+-==⇒⎪⎩⎪⎨⎧=+-=+-3223223b a b a b a例11.已知向量(cos(),sin())44a x x ππ=--,(cos(),sin())44b x x ππ=+-+, ()f x a b k a b =⋅-+, [0,].x π∈ (1)若712x π=,求⋅及+a b ; (2)若1k =,当x 为何值时,()f x 有最小值,最小值是多少? (3)若()f x 的最大值为3,求k 的值.解:(1)32a b ⋅=-62a b -+= (2)2()2cos 2cos 1f x x x =-- 当3x π=或23x π=时,()f x 有最小值 min 3()2f x =- (3)2()2cos 2cos 1f x x k x =--设:cos x t =,由[0,][0,1]x t π∈⇒∈ 则:2()()221[0,1]f x g t t kt t ==--∈当:1122kk≤⇒≤时,max()(1)22131f xg k k==--=⇒=-111kkk≤⎧⇒=-⎨=-⎩当:1122kk>⇒>时,max()(0)13f x g==-≠综上之:1k=-。
天津市第一中学2020学年高中数学 期末复习2 新人教A版必修4
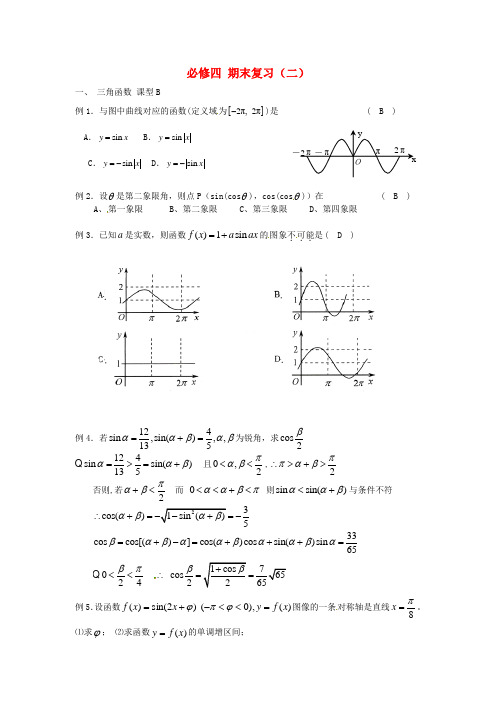
-πOxy-2π π2π必修四 期末复习(二)一、 三角函数课型B例1.与图中曲线对应的函数(定义域为[]2π,2π-)是 ( B ) A .sin y x = B .sin y x =C .sin y x =-D .sin y x =-例2.设θ是第二象限角,则点P (sin(cos θ),cos(cos θ))在 ( B )A 、第一象限B 、第二象限C 、第三象限D 、第四象限例3.已知a 是实数,则函数()1sin f x a ax =+的图象不.可能..是( D )例4.若124sin ,sin(),,135ααβαβ=+=为锐角,求cos 2β 124sin sin()135ααβ=>=+Q 且0,2παβ<<,2ππαβ∴>+>否则,若2παβ+<而 0ααβπ<<+< 则sin sin()ααβ<+与条件不符23cos()1sin () 5αβαβ∴+=--+=-33cos cos[()]cos()cos sin()sin 65βαβααβααβα=+-=+++=024βπ<<Q ∴ 1cos 7cos652265ββ+== 例5.设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x 。
⑴求ϕ; ⑵求函数)(x f y =的单调增区间;解:⑴)(8x f y x ==是函数πΘ的图像的对称轴,,1)82sin(±=+⨯∴ϕπ.,24Z k k ∈+=+∴ππππ.43,0πϕϕπ-=<<-Θ ⑵由(Ⅰ)知).432sin(,43ππϕ-=-=x y 因此 由题意得.,2243222Z k k x k ∈+≤-≤-πππππ所以函数.],85,8[)432sin(Z k k k x y ∈++-=πππππ的单调增区间为二、三角函数 课型C例6. 若1sin()63πα-=,则2cos(2)3πα+等于 ( A ) A .79- B.13- C.13 D.79例7.将函数sin 3cos y x x =-的图像沿x 轴向右平移a 个单位(0)a >,所得图像关于y 轴对称,则a 的最小值为 ( C ) A.76π B.2π C .6π D.3π 例8.若函数()(13)cos ,02f x x x x π=+≤<,则()f x 的最大值为 ( B )A.1 B .231 D. -2 例9.计算3tan11°+3tan19°+tan11°·tan19°000000000033tan11tan19319)(1tan11tan19)tan11tan19++=+-+000033tan11tan19)tan11tan191-+=, 例10.已知函数)0(23cos 3cos sin )(2>++-⋅=a b a x a x x a x f . (Ⅰ)求函数)(x f 的单调递减区间;(Ⅱ)已知函数)(x f 在区间]20[π,上的最小值是2-,最大值是3,求实数b a ,的值.解:b a x a x a x f +++-=23)2cos 1(232sin 21)(b x a b x a x a +-=+-=)32sin(2cos 232sin 2π2323222πππππ+≤-≤+k x k ,1211125ππππ+≤≤+k x kZ k k k ∈++],1211,125[ππππ为所求 (II )1)32sin(23,32323,20≤-≤-≤-≤-≤≤πππππx x x , ,3)(,223)(max min =+=-=+-=b a x f b a x f ⎩⎨⎧+-==⇒⎪⎩⎪⎨⎧=+-=+-3223223b a b a b a例11.已知向量(cos(),sin())44a x x ππ=--r ,(cos(),sin())44b x x ππ=+-+r ,()f x a b k a b =⋅-+r r r r, [0,].x π∈(1)若712x π=,求b a ⋅及+r r a b ;(2)若1k =,当x 为何值时,()f x 有最小值,最小值是多少? (3)若()f x 的最大值为3,求k 的值.解:(1)32a b ⋅=-r r 622a b -+=r r(2)2()2cos 2cos 1f x x x =-- 当3x π=或23x π=时,()f x 有最小值 min 3()2f x =- (3)2()2cos 2cos 1f x x k x =--设:cos x t =,由[0,][0,1]x t π∈⇒∈ 则:2()()221[0,1]f x g t t kt t ==--∈时,max ()(1)22131f x g k k ==--=⇒=- 111k k k ≤⎧⇒=-⎨=-⎩时,max ()(0)13f x g ==-≠。
高中数学(新课标人教A版)必修4 第一章三角函数精品课件 1.2任意角的三角函数(3课时)

tan 3
例5.求下列三角函数值
sin1480 10
'
9 s 4
11 tan( ) 6
小结:
1.任意角的三角函数是由角的终边与单 位圆交点的坐标来定义的. 2.三角函数值的符号是利用三角函数的 定义来推导的.要正确记忆三个三角函数 在各个象限内的符号; 3.诱导公式一的作用可以把大角的三角 函数化为小角的三角函数.
应用 1.利用同角三角函数的基 本关系求某个角的三角函数 值 例1.已知sinα=-3/5,且 α在第三象限,求cosα和 tanα的值.
例2.已知 cos m (m 0, m 1), 求的其他三角函数值
4 sin 2 cos 例3.已知 tanα=3,求值(1) 5 cos 3 sin
y
a的终边 P(x,y)
1
P(x,y)
a
O
M
A(1,.0)
x
(1)y叫做 的正弦,记作sin ,即 sin y (2)x叫做 的余弦,记作cos,即 cos x y y (3) 叫做 的正切,记作tan ,即 tan x x
阅读课本P12:三角函数的定义
例题:
5 1 求 的正弦、余弦和正切值. 3
作业:
课本P20习题1.2A组
1,2,6,7,9
1.2.1任意角的三角函数(2)
复习回顾
1、三角函数的定义; 2、三角函数在各象限角的符号; 3、三角函数在轴上角的值; 4、诱导公式(一):终边相同的角的 同一三角函数的值相等; 5、三角函数的定义域.
角是一个图形概念,也是一个数量概 念(弧度数). 作为角的函数——三角函数是一个 数量概念(比值),但它是否也是一个 图形概念呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修四期末复习(一)
平面向量 课型A
例1设a,b 是夹角为60的单位向量,旧=1,则a-c ・b ・c 的取值范围是(C )
面积之比是
PA P B P^.A B ,得存 PB BA K = 0,
即PC 二2AP ,所以点P 是CA 边上的第二个三等分点,如图所示•
S
PBC
_ BC PC _ 2
例3•已知|a |=2| b |=0,且关于
x 的方程x 2 |a |x • a b = 0有实根,则a 与b 的夹角的取 值范围是
・(A ) , 2 , , , A.[—,二] B. [ —, ] C .[—,二] D • [0,—] 3 3 3 6 6
例4•平面上三点 A B 、C 满足AB =3, BC =4, CA =5,
求 AB BC BC CA CA AB 的值-25
例5.在平面直角坐标系 xOy 中,点A( — 1, — 2)、B(2,3)、C( — 2, — 1) (1 )求以线段AB AC 为邻边的平行四边形两条对角线的长(
2)设实数t 满足(AB -tOC ) • OC =0,求t 的 值
(1)对角线长为,40 和 4'.. 2 , (2) t - -11
5
二、平面向量 课型B 例6.如图,半圆的直径 AB = 6, O 为圆心,C 为半圆上不同于 A B 的任意一点,
若P 为半径OC 上的动点,贝U (PA - PB) PC 的最小值为 (C )
A J-1,11 B. L ...3, ...3】 D.
例2.在ABC 所在的平面上有一点
p ,满足 PA PB PC 二蛊, 贝则:PBC 与:ABC 的
A.
B. 1 2 C . 2 3 D. 【解析】由 S ABC BC AC 3 A O
A. 2 ;
B.9;
C. —9;
D. —9;
例7. P是厶ABC边BC的中线AD上异于A、D的动点,AD- 4,
求PA (PB PC)的取值范围
【解析】设= ■ DA,所以=(^ )DA,其中0「::: 1
因为AD是. ABC边BC上的中线,所以DB • DC = 0
所以PA (PB PC)二
P A(PD DB PD DC^2PAPD
=2( ■ DA) [ 一(1 一■ )DA] - -2 (1 - ■ ) |DA |2=32'2-32怎=32( • - ;)2-8
PC) =32(,-丄)2-8 [-8,0)
2
例8如图,在厶ABC中, AD _ AB,
A. 2,3
B. D. 3
例9 .设a = (x「yj , b = (x2 , y2),右|a|= 2, |b|=3
a b _ -6,则
3 - 2 -
D
2 - 3
例9.如图在ABC中, AB =3,BC =、、7, AC =2,若 O 为ABC 的外心,
因为0 ::
所以
AD =1,贝U AC AD = ( D )求AC AO BC AO的值
以便进一步分析求证.
T T T 证明 充分性,由PC =m PA + n PB , m + n=1,
T T T T
PA + PC =m PA + n ( PA +
(n ) PA + n AB = PA + n AB ,
--AC =n AB .
••• A 、B 、C 三点共线.
必要性:由A 、B 、C 三点共线知,存在常数 入,使得AC =入AB , 即 AP^ + PC =入(A P+PB ). PC =(入—1) A P + 入 P B = (1—入)PA + 入 P B ,
m=1—入,n=入,m + n=1,
AC 話二2
TB T.A O 例ii .已知平面上三个向量
a,b,c,的模均为1,它们相互之间的夹角均为 120。
(I )求证:(a - b') _ e ; (||)若 (k • R ),求k 的取值范围。
(I)根据向量垂直的条件可证 °: (a • • b)・c 二a c • • b c /)即可
42
(II)不等式 ka +b +c >1 w Ika +b +c| >1 =k 2;2 2 2
b c 2ka ・b 2ka ・c 2b ・c1
7 a £」c =1,且a,b,c,的夹角均为120, a 二b
" 4"4-*心過,
k 2
-2k 0, k 2或k :: 0. 例12.已知A 、B C 、P 为平面内四点,求证: 在一对实数 m 、n ,使 PC =m PA +n PB ,且 m+n=1.
A 、
B 、
C 三点在一条直线上的充要条件是存 【解析】A BC 三点共线的一个充要条件是存在 实数入,使得云C =入AB •很显然,题 设条件中向量表达式并未涉及
AC 、 AB ,对此, 我们不妨利用 TC =PA +A C 来转化,
PC =m PA + n PB .。
