fft_原理详解
fft原理通俗易懂

fft原理通俗易懂
快速傅里叶变换(Fast Fourier Transform,FFT)是一种数字信
号处理技术,用于将时域信号转换为频域信号的高效算法。
这意味着
可以将一个连续变化的时域信号变换成一系列的不同频率的频域信号,进而用以检测特定频率所对应的信号分量,对特定频率的信号成分进
行测量以及统计分析。
fft原理非常简单,根据傅里叶变换的原理,任何时域信号都可以
表示为可见太阳的不同的 sin 和 cos 激励函数的正弦波之和组成的
复合函数,并且由于 sin 和 cos 的频率有所不同,所以时域信号会
被分解为不同的频率分量。
而快速傅立叶变换就是一种技术,可以把
这些 sin 和 cos 组合到一起,使其有效地结合在一起,从而及时得
到这些不同频率分量的信号分布,也就是所谓的频谱,根据不同的频
率分量从而获得信号的性质。
FFT 是一种精确、快速的数字信号处理方法,可以用来提取信号
和特征,fft 的本质就是一种直接的数值计算,将时域信号变换为频
域信号,这样能够实现从高频段到低频段的提取,从而更容易检测和
识别出信号中的特殊特征。
它的实施方式明显优于傅里叶变换,可以
减少实现时间和存储空间的占用,这使得 FFT 技术在各类社会应用中
得到了广泛应用。
FFT算法详解

FFT算法详解FFT (Fast Fourier Transform) 是一种高效的离散傅里叶变换算法,用于将时域信号转换为频域信号。
它在信号处理、图像处理、通信领域等具有广泛的应用。
本文将详细介绍FFT算法的原理和实现。
一、傅里叶变换的基本原理傅里叶变换是一种将信号从时域转换到频域的方法。
它将时域信号分解成多个不同频率的正弦和余弦函数的叠加。
傅里叶变换的基本公式为:F(k) = Σ_{n=0}^{N-1} f(n)e^{-2πikn/N}其中,F(k)是频域信号的复数表示,f(n)是时域信号的复数表示,N是信号长度,k是频率。
二、傅里叶变换的问题传统的傅里叶变换算法的时间复杂度为O(N^2),计算量较大,不适用于实时处理大型信号。
FFT算法通过分治的思想,将DFT(Digital Fourier Transform)问题转化为多个子问题,从而降低了计算复杂度。
三、蝶形运算蝶形运算的公式为:y_0=x_0+W_N^k*x_1y_1=x_0-W_N^k*x_1其中,x_0、x_1是输入,y_0、y_1是输出,W_N^k是旋转因子,N是信号长度,k是频率。
四、FFT算法的步骤1.将输入信号分成偶数下标和奇数下标的两个子序列。
2.对两个子序列分别进行FFT变换,得到两个子序列的频域表示。
3.将两个子序列的频域表示合并成完整的频域信号。
4.重复上述步骤,直到得到最终的频域信号。
五、FFT算法的实现1.初始化输入信号和旋转因子。
2.将输入信号按照偶数下标和奇数下标分成两个子序列。
3.对两个子序列分别进行FFT变换,递归调用FFT函数。
4.将两个子序列的频域表示合并成完整的频域信号。
5.返回最终的频域信号。
总结:FFT算法是一种高效的离散傅里叶变换算法,通过分治的思想将DFT问题分解为多个子问题,从而降低了计算复杂度。
它在信号处理、图像处理、通信领域等有着广泛的应用。
掌握FFT算法的原理和实现对于理解信号处理技术和提高算法效率具有重要意义。
简述fft变换的原理

简述fft变换的原理
FFT(快速傅里叶变换)是一种用于计算离散傅里叶变换(DFT)的高效算法。
它能够将离散序列从时域(时间域)转换到频域(频率域),在信号处理、图像处理、通信等领域具有广泛的应用。
FFT通过降低傅里叶变换的计算复杂度,大大提高了计算效率。
FFT的原理可以简述如下:
1.傅里叶变换:傅里叶变换是将时域信号转换为频域信号的方法,它将信号分解为不同频率的正弦和余弦成分。
傅里叶变换的公式表达复杂,计算复杂度较高。
2.分治策略: FFT的核心思想是分治法,将原始信号分成若干子信号,分别计算它们的DFT,然后通过合并这些DFT的结果得到原始信号的DFT。
这样,FFT将原本需要O(N^2)次乘法和加法运算的傅里叶变换降低到了O(N log N)次运算。
3.蝶形运算:在FFT的计算过程中,采用了一种称为“蝶形运算”的策略,将多项式的乘法和加法运算通过重新排列计算,从而减少计算量。
蝶形运算实际上是一个特定的运算单元,它将两个复数相乘并进行加法操作。
4.迭代计算: FFT算法是递归性质的,它将原始信号不断分解为规模更小的子信号,然后逐步合并计算出最终的DFT。
这个过程不断迭代,直至计算出所有频率成分。
总之,FFT通过巧妙的分治策略和蝶形运算,将原本计算复杂度较高的傅里叶变换转化为高效的计算过程,使得在信号处理和频谱分析等领域中,能够更快速、有效地进行频域转换。
1/ 1。
fft的计算原理

fft的计算原理FFT(Fast Fourier Transform)是一种高效地计算离散傅里叶变换(Discrete Fourier Transform, DFT)的算法。
FFT能够将一个时域上的离散信号转换到频域上,并可以用于信号分析、滤波、图像处理以及编码等领域。
FFT的计算原理可以从两个角度来讲解:一是从离散傅里叶变换(DFT)的定义出发,二是从FFT的具体计算过程中各个步骤的推导和实现。
首先,从DFT的定义出发,对一个离散信号x(n)进行DFT计算,可以得到其频域表示X(k),表示为:X(k) = Σ(x(n) * exp(-j2πkn/N))其中,N为信号的长度,k为频域采样点的索引,n为时域采样点的索引。
直接按照DFT的定义计算的复杂度是O(N^2),当信号长度很大时,计算量非常大。
FFT算法通过对DFT的变换矩阵进行分解,将复杂度降低到O(NlogN)。
然后,从FFT的具体计算过程中各个步骤的推导和实现来看。
以下是常见的快速傅里叶变换算法,即Cooley-Tukey算法的计算过程:1. 将信号x(n)分为两个部分:偶数索引部分x_e(n)和奇数索引部分x_o(n),分别由原信号的偶数索引和奇数索引采样得到。
2. 对x_e(n)和x_o(n)分别进行FFT计算,得到频域表示X_e(k)和X_o(k)。
3. 将得到的频域表示X_e(k)和X_o(k)按照以下公式合并得到最终的频域表示X(k):X(k) = X_e(k) + W_N^k * X_o(k)其中,W_N^k = exp(-j2πk/N)为旋转因子,可由欧拉公式得到。
4. 重复以上步骤,直到计算得到所有频域采样点的值。
以上就是FFT算法的基本原理和计算过程。
通过对信号进行分解和合并的方式,FFT算法能够大大减少计算量,快速地计算得到离散信号的频域表示。
后续还有一些对FFT算法进行改进和优化的方法,如快速傅里叶变换的再加工算法(Radix-2 FFT Algorithm)以及快速余弦和正弦变换(Fast Cosine and Sine Transform)等。
fft原理介绍

fft原理介绍《FFT原理介绍》1. 引言你有没有想过,当我们听音乐、看视频或者处理图像的时候,背后有一个超级厉害的数学工具在默默发挥作用呢?这个工具就是快速傅里叶变换(FFT)。
今天啊,咱们就来一起深入了解一下FFT的原理,从它最基础的概念,到它是怎么运行的,再到它在实际生活和高端技术中的应用,还有那些容易让人迷糊的地方,咱们都要搞个清清楚楚。
2. 核心原理2.1基本概念与理论背景FFT其实是一种算法,它是基于傅里叶变换来的。
傅里叶变换呢,是由法国的数学家傅里叶提出来的。
这老兄就像是一个魔法厨师,他发现任何复杂的信号啊,就好比是一道复杂的菜肴,都可以分解成不同频率的简单成分,就像菜肴可以分解成不同的食材一样。
一开始傅里叶变换的计算可复杂了,计算量超级大。
就好像你要从一堆沙子里一颗一颗挑出特定颜色的珠子,效率特别低。
后来呢,人们就发明了FFT算法,这个算法就像是一个超级筛子,能够快速地把那些珠子筛出来,大大提高了计算的速度。
2.2运行机制与过程分析咱们来简单说说FFT的运行过程。
假设我们有一个信号,这个信号就像是一群人在不同时间发出的声音,杂乱无章。
FFT首先把这个信号分成很多小段,就好像把这群人按照一定的规则分成了几个小组。
然后呢,FFT算法会对每个小段进行计算,这个计算过程有点像分析每个小组里人的声音特点。
比如说,是高音多还是低音多,声音是持续的还是断断续续的。
最后,把这些小段的计算结果组合起来,就得到了这个信号在不同频率下的组成情况。
说白了,就像是把一群人的声音按照高低音、长短音等特点进行了分类整理。
3. 理论与实际应用3.1日常生活中的实际应用在我们的日常生活中,FFT无处不在。
就拿音乐播放器来说吧,当你播放一首歌曲的时候,播放器里面的软件可能就用到了FFT。
因为音乐也是一种信号,里面有各种不同的音符,对应着不同的频率。
FFT可以把音乐信号分解,然后根据不同的频率进行调整,比如说增强低音或者高音,这样我们听到的音乐就更加符合我们的喜好了。
fft频谱原理

FFT(快速傅里叶变换)是一种用于将时域信号转换为频域表示的算法。
它是通过将信号分解为不同频率的正弦和余弦成分来实现的。
以下是FFT频谱原理的简要说明:
1.傅里叶分析:傅里叶分析是将一个周期性信号分解为许多不同频率的正弦和余弦波
的过程。
这些正弦和余弦波的幅度和相位表示了信号在不同频率上的贡献。
2.时域与频域:时域表示信号随时间变化的振幅。
频域表示信号在不同频率上的振幅
特性。
傅里叶变换将信号从时域转换为频域,以便更好地理解信号的频率分布。
3.快速傅里叶变换(FFT):FFT是一种高效计算傅里叶变换的算法。
它利用了信号的
对称性和周期性,通过减少计算量来加速傅里叶变换的过程。
4.频谱表示:FFT计算出信号在不同频率上的振幅,生成一个频谱图。
频谱图显示了
信号中各个频率成分的相对强度和相位关系。
频谱图通常以频率(横轴)和振幅或功率(纵轴)表示。
5.应用:FFT被广泛应用于信号处理、音频处理、图像处理等领域。
它可以用于频谱
分析、滤波、降噪、频率识别等任务。
通过FFT频谱分析,我们可以了解信号的频率成分和能量分布,从而对信号进行更深入的分析和处理。
fft 原理

fft 原理
FFT(快速傅里叶变换)是一种计算机算法,它可以将一个时域信号(如一段音频或图像)转换为其频域表示,并且在计算效率上相对于传统傅里叶变换算法有较大优势。
它是由James Cooley和John Tukey在1965年发明的,被广泛应用于信号处理、图像处理、音频处理、视频压缩、计算机图形学等领域。
FFT原理基于傅里叶变换,它将时域信号转换为频域信号,将一段时间内的信号分解成各个频率成分,这样就可以分析信号的频率、频谱等特征。
快速傅里叶变换通过将N点离散傅里叶变换(DFT)分解为多组较小的DFT进行计算,从而大大减少了计算量。
通常使用快速傅里叶变换算法对信号进行频谱分析。
FFT算法的核心思想是将一个N点序列分成两个N/2点序列,分别进行DFT变换,然后将结果合并,得到一个N点DFT的结果。
这个过程可以递归进行下去,直到变成两个1点序列的DFT变换。
将所有小的DFT结果合并起来就得到了最终的DFT结果。
这个过程的时间复杂度为O(NlogN),比传统的DFT算法的时间复杂度O(N^2)快得多。
FFT算法在分析音频、图像等信号时具有广泛的应用,如音频频率分析、图像噪声滤波、图像边缘检测等。
此外,FFT算法也是很多信号处理算法的核心组成部分,如数字滤波、信号压缩等。
快速傅里叶变换(FFT)的原理及公式
快速傅里叶变换(FFT)的原理及公式原理及公式非周期性连续时间信号x(t)的傅里叶变换可以表示为式中计算出来的是信号x(t)的连续频谱。
但是,在实际的控制系统中能够得到的是连续信号x(t)的离散采样值x(nT)。
因此需要利用离散信号x(nT)来计算信号x(t)的频谱。
有限长离散信号x(n),n=0,1,…,N-1的DFT定义为:可以看出,DFT需要计算大约N2次乘法和N2次加法。
当N较大时,这个计算量是很大的。
利用WN的对称性和周期性,将N点DFT分解为两个N/2点的DFT,这样两个N/2点DFT总的计算量只是原来的一半,即(N/2)2+(N/2)2=N2/2,这样可以继续分解下去,将N/2再分解为N/4点DFT等。
对于N=2m点的DFT都可以分解为2点的DFT,这样其计算量可以减少为(N/2)log2N 次乘法和Nlog2N次加法。
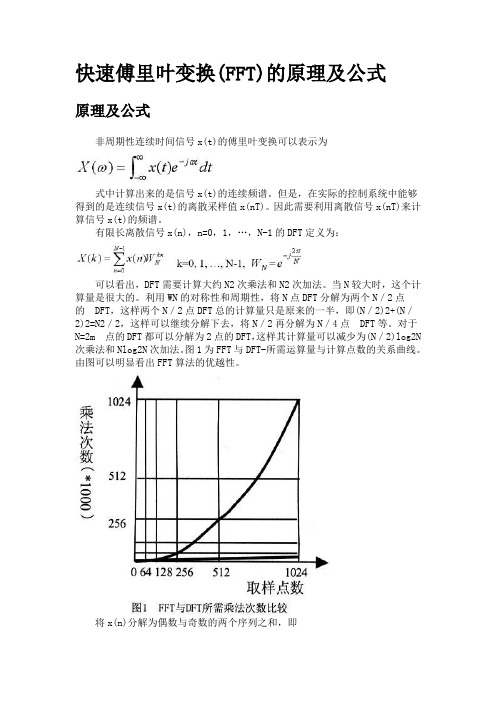
图1为FFT与DFT-所需运算量与计算点数的关系曲线。
由图可以明显看出FFT算法的优越性。
将x(n)分解为偶数与奇数的两个序列之和,即x1(n)和x2(n)的长度都是N/2,x1(n)是偶数序列,x2(n)是奇数序列,则其中X1(k)和X2(k)分别为x1(n)和x2(n)的N/2点DFT。
由于X1(k)和X2(k)均以N/2为周期,且WN k+N/2=-WN k,所以X(k)又可表示为:上式的运算可以用图2表示,根据其形状称之为蝶形运算。
依此类推,经过m-1次分解,最后将N点DFT分解为N/2个两点DFT。
图3为8点FFT的分解流程。
FFT算法的原理是通过许多小的更加容易进行的变换去实现大规模的变换,降低了运算要求,提高了与运算速度。
FFT不是DFT的近似运算,它们完全是等效的。
关于FFT精度的说明:因为这个变换采用了浮点运算,因此需要足够的精度,以使在出现舍入误差时,结果中的每个组成部分的准确整数值仍是可辨认的。
为了FFT的舍入误差,应该允许增加几倍log2(log2N)位的二进制。
傅里叶变换(FFT)详解

关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解,最近,我偶尔从网上看到一个关于数字信号处理的电子书籍,是一个叫Steven W. Smith, Ph.D.外国人写的,写得非常浅显,里面有七章由浅入深地专门讲述关于离散信号的傅立叶变换,虽然是英文文档,我还是硬着头皮看完了有关傅立叶变换的有关内容,看了有茅塞顿开的感觉,在此把我从中得到的理解拿出来跟大家分享,希望很多被傅立叶变换迷惑的朋友能够得到一点启发,这电子书籍是免费的,有兴趣的朋友也可以从网上下载下来看一下,URL地址是:/pdfbook.htm要理解傅立叶变换,确实需要一定的耐心,别一下子想着傅立叶变换是怎么变换的,当然,也需要一定的高等数学基础,最基本的是级数变换,其中傅立叶级数变换是傅立叶变换的基础公式。
二、傅立叶变换的提出让我们先看看为什么会有傅立叶变换?傅立叶是一位法国数学家和物理学家的名字,英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣,于1807年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号可以由一组适当的正弦曲线组合而成。
当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在近50年的时间里,拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。
法国科学学会屈服于拉格朗日的威望,拒绝了傅立叶的工作,幸运的是,傅立叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。
快速傅里叶变换(FFT)算法原理及代码解析

快速傅里叶变换(FFT)算法原理及代码解析•FFT与DFT关系:快速傅里叶变换(Fast Fourier Transform)是离散傅里叶(DFT)变换的一种快速算法,简称FFT,通过FFT可以将一个信号从时域变换到频域;FFT(快速傅里叶变换)其本质就是DFT,只不过可以快速的计算出DFT结果,它只是傅立叶变换算法实现过程的一种改进。
要弄懂FFT,必须先弄懂DFT,DFT(DiscreteFourier Transform) 离散傅里叶变换的缩写,咱们先来简单讨论一下DFT。
DFT(FFT)的作用:可以将信号从时域变换到频域,而且时域和频域都是离散的,通俗的说,可以求出一个信号由哪些正弦波叠加而成,求出的结果就是这些正弦波的幅度和相位。
•DFT的公式:其中X(k)表示DFT变换后的数据,x(n)为采样的模拟信号,公式中的x(n)可以为复信号,实际当中x(n)都是实信号,即虚部为0,此时公式可以展开为:那么,对于一个的序列进行不断分解,就可以得出如下所谓的蝶形图:•FFT处理蝶形运算蝶形运算的规律:同一级中所有蝶形的输入点在同一竖直线上,意味着我们可以按级来运算,对于M级的蝶形,编个M次循环就好了;所有数据点在运算后不会窜位,即计算后可以将结果存入原来的地址空间。
每级N/2个蝶都需要用到系数WN,这里称它为旋转因子。
我们来观察旋转因子WN的规律。
以8点的蝶形图为例:可见,第L级的旋转因子为:可以看到,每个蝶的两个输入点下标跨度是不一样的。
比如第一级中是相邻两个数据作蝶运算,第二级中是两个输入点隔开一个点,而第三级隔开三个点。
不难找到规律:第L级中,第二个输入点的坐标是第一个点的坐标+space,space=Math.Pow(2, L)=num。
FFT的算法是写一个三重循环:•第一重循环对每一级运算(每级含num=Math.Pow(2, L)个蝶形);•第二重对每一个旋转因子对应的蝶运算,那么有几个蝶呢?很简单,每级都应该有N/2个蝶,而每个因子对应N/2 / num个蝶;•第三重循环对每个蝶进行计算,需要注意的一是循环下标起始点的位置,二是每次计算需要申明临时变量来保存输入数据点。
FFT原理与实现

FFT原理与实现FFT(快速傅里叶变换)是一种高效的算法,用于计算数值序列的离散傅里叶变换(DFT)。
FFT广泛应用于信号处理,图像处理,数据压缩,声音分析等领域。
在本文中,我们将探讨FFT的原理、实现和应用。
一、FFT原理1.傅里叶变换傅里叶变换是一种将一个连续信号(或离散信号)分解成一系列由正弦和余弦函数组成的频谱的方法。
它将信号从时域转换到频域,可以揭示信号中包含的频率成分。
2.DFT离散傅立叶变换(DFT)是傅立叶变换的离散形式。
它将离散信号分解为一系列复数频域分量。
DFT的公式如下:其中,N是离散信号的长度,k是频率序号,x[n]是离散信号的值。
3.FFT快速傅里叶变换(FFT)是一种通过分治算法减少计算复杂度的DFT算法。
它的核心思想是将DFT分解为更小规模的计算,然后通过递归地执行这些计算来得到结果。
FFT算法的关键在于将DFT的计算复杂度从O(N^2)降低到O(NlogN)。
它通过将长度为N的信号分解为两个长度为N/2的信号,然后进一步分解为更小规模的信号。
具体而言,FFT算法包括以下步骤:1)将信号分为偶数项和奇数项,然后对分别对它们进行FFT变换。
2)将奇数项和偶数项的结果合并,得到完整的FFT结果。
二、FFT实现FFT的实现有多种方法,其中最常用的是基于蝶形算法的Cooley-Tukey算法。
该算法采用迭代的方式实现了FFT,思路如下:1.将输入信号分为偶数项和奇数项,得到两个较短的信号。
2.对这两个信号分别进行FFT变换。
3.将两个变换结果合并成一个结果。
关键的步骤是FFT的合并过程。
这一过程可以通过蝶形算法来实现。
蝶形算法是一种基于矩阵运算的方法,用于合并两个FFT变换的结果。
它通过乘以不同的旋转因子来实现信号的合并。
这样做可以大大减少计算量。
三、FFT应用FFT在很多领域都有广泛的应用。
1.信号处理:通过FFT,我们可以将信号从时域转换到频域,以便进行频谱分析、滤波、降噪等处理。
fft_原理详解

FFT原理FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在圈圈就根据实际经验来说说FFT结果的具体物理意义。
一个模拟信号,经过ADC采样之后,就变成了数字信号。
采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。
为了方便进行FFT 运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N倍。
而每个点的相位呢,就是在该频率下的信号的相位。
第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。
fft结果的物理意义

fft结果的物理意义摘要:一、引言二、傅里叶变换(FFT)的基本原理三、FFT结果的物理意义1.频域分析2.时域分析四、FFT在实际应用中的案例五、结论正文:一、引言傅里叶变换(FFT)是一种在信号处理、图像处理等领域具有重要应用的算法。
它是一种将时域信号转换为频域信号的数学方法,可以帮助我们更好地分析信号的频率特性。
本文将详细介绍FFT结果的物理意义,以及它在实际应用中的案例。
二、傅里叶变换(FFT)的基本原理傅里叶变换是一种将时域信号转换为频域信号的数学方法。
其基本原理是将复杂的信号分解为多个简单的正弦和余弦函数的叠加。
在频域中,这些正弦和余弦函数分别表示信号的不同频率分量。
傅里叶变换的核心思想是将时域信号分解成不同频率的成分,以便于分析和处理。
三、FFT结果的物理意义1.频域分析FFT结果中的频域表示信号的频率成分。
通过观察频域图,我们可以了解信号在不同频率下的能量分布情况。
这对于分析信号的稳定性、谐波失真等方面具有重要意义。
此外,通过对频域信号进行滤波等处理,我们还可以改善信号的性能。
2.时域分析FFT结果中的时域表示信号的脉冲响应。
通过观察时域图,我们可以了解信号在时间上的变化趋势。
这对于分析信号的传输、系统的稳定性等方面具有重要意义。
同时,时域分析还可以帮助我们识别信号中的周期性成分,从而进一步进行滤波和降噪等处理。
四、FFT在实际应用中的案例1.信号处理:在通信系统中,FFT被广泛应用于基带处理、频带压缩等领域。
通过FFT,我们可以将复杂的信号分解为简单的正弦和余弦函数,从而降低信号处理的复杂度。
2.图像处理:在图像处理中,FFT被用于频域滤波、图像增强、去噪等任务。
通过对图像进行FFT,我们可以更好地分析图像的频率特性,从而设计出更有效的滤波器。
3.音频处理:在音频处理领域,FFT被用于音频分析、均衡、降噪等任务。
通过对音频信号进行FFT,我们可以了解音频信号的频率成分,从而调整音频系统的性能。
FFT相关原理及使用注意事项

FFT相关原理及使用注意事项FFT(Fast Fourier Transform)是一种高效的离散傅里叶变换算法,用于将时域信号转换为频域表示。
FFT算法的发展与电子计算机的出现和发展有着密切关系。
FFT广泛应用于信号处理、图像处理、音频处理、通信等领域。
以下是FFT相关的原理及使用注意事项。
一、FFT原理:FFT基于快速傅里叶变换的思想,可以将原始时域信号快速转换为频域信号,通过对频域信号的分析,可以获取信号的频谱、频率分量等信息。
1.1傅里叶变换:傅里叶变换是一种将时域信号转换为频域信号的数学工具。
对于一个周期性信号或有限长的信号,可以用一系列正弦波的叠加来表示。
傅里叶变换可以将信号分解为不同频率的正弦波成分,输出的频谱表示了信号在各个频率上的强度。
1.2DFT(离散傅里叶变换):DFT是对连续信号进行离散化处理,将信号从连续的时域变换到离散的频域。
DFT将信号视为一系列离散的采样点,并计算每个采样点的频率成分。
DFT的计算复杂度为O(N^2),对于大规模信号处理效率较低。
1.3FFT(快速傅里叶变换):FFT是一种高效的计算DFT的算法,能够将复杂度从O(N^2)降低到O(NlogN)。
FFT算法的核心思想是将复杂的DFT计算分解为多个规模较小的DFT计算,然后通过递归计算来提高计算效率。
二、FFT使用注意事项:在使用FFT进行信号处理时,需要注意以下几个问题。
2.1信号预处理:在应用FFT之前,通常需要对原始信号进行一些预处理。
例如,去除信号中的直流分量、滤除噪声、对信号进行加窗等处理。
这样可以提高FFT的性能,并减小由于非理想因素引起的误差。
2.2信号采样率:FFT对输入信号的采样率有一定的要求。
根据采样定理,信号的采样率要大于信号频率的两倍才能正常重构信号。
如果信号采样率过低,则会引起谱漏;如果信号采样率过高,则会浪费计算资源。
2.3零填充:FFT算法对于长度为N的输入信号,计算得到长度为N的频域信号。
FFT原理

N M N log2 N
而直接进行DFT运算时则与N2 成正比。
算法的运算速度
N2 直接DFT运算次数 G N N 2 log 2 FFT运算次数
例: N=2048,N2=4194304 , N log 2 N 11264 ,
N
2
2
N 2
372.4 log 2 N
显然,FFT要比直接DFT运算快得多。
按时间抽取的蝶形运算流图:
(3) X1 k 和 X 2 k 可以继续分解下去,可将N/2点的 子序列再按奇、偶项分解,一直到最后分解成 两两点的DFT为止。
四 个
N 4
点 DFT
偶序列中的偶序列
x1 (2l ) x3 (l )
偶序列中的奇序列
奇序列中的偶序列 奇序列中的奇序列
(2)求:X ( k N )=?
2
k =0,1,...,
rk
N
N
1
2
X 1 (k )
N / 21 r 0
x1(r ) W
令 k= k
N 2
2
X 1 (k
N 2
)
N / 2 1
r 0
x1(r ) w
r k N / 2 2
N
N / 2 1
r 0
x1(r ) wrk
j 2 nk N
w w
nk N
n ( N k ) N
w
nk N
k ( N n ) N
N wN / 2 1
w
n ( k N / 2) N
w
nk 我们利用系数 w N 的周期性和对称性,考察它 是如何简化DFT运算的过程。
FFT原理讲解及实现指南

FFT原理讲解及实现指南FFT(快速傅里叶变换)是一种高效的算法,用于将一个离散的时间域信号转换为频域信号。
在信号处理、图像处理以及通信领域,FFT是一种非常重要的工具。
一、FFT原理讲解傅里叶变换是一种将一个连续时间域信号转换为频域信号的方法。
其数学表达式为:X(f) = ∫x(t)e^(-j2πft)dt其中,X(f)表示频域信号,x(t)表示时间域信号,f表示频率,j表示虚数单位。
然而,对于离散时间信号,我们可以使用离散傅里叶变换(DFT)来对其进行频域分析。
DFT的公式如下:X(k) = Σx(n)e^(-j2πnk/N)其中,X(k)表示离散频域信号,x(n)为离散时间信号,N为采样点数,k表示频率。
FFT是一种用于快速计算DFT的算法,其基本原理是将DFT的计算复杂度从O(N^2)降低到O(NlogN)。
FFT的算法思路是:将N个采样点分为偶数和奇数序列,然后对偶数和奇数序列分别进行DFT变换,得到两个较小的DFT结果。
然后再将这两个较小的DFT结果合并,得到最终的DFT结果。
二、FFT实现指南1.选择合适的FFT库:在实际应用中,我们可以选择一些已有的FFT库来实现FFT算法,例如FFTW、MKL等。
2.确定输入信号:首先,需要确定待处理的离散时间信号x(n)。
3.计算FFT:使用FFT库提供的函数,对输入信号进行FFT计算。
常见的FFT库一般提供了相应的API,通过输入参数,得到计算出的离散频域信号X(k)。
4.获取频域信息:根据需要,可以从计算出的离散频域信号X(k)中提取相应的频域信息,例如频率分量、频谱等。
5.可选步骤:根据实际需求,可以进行滤波、频率域增强等操作。
6.反变换:如果需要将频域信号转换为时间域信号,可以使用反变换。
需要注意的是,FFT算法主要适用于离散时间信号的频域分析。
在实际应用中,可能还需要考虑信号预处理、采样率等因素。
三、总结FFT是一种高效的算法,用于离散时间信号的频域分析。
fft的原理

fft的原理傅里叶变换(Fast Fourier Transform,简称FFT)是一种重要的信号处理方法,广泛应用于图像处理、音频处理、通信系统等多个领域。
它通过将信号从时域转换到频域,实现了信号的频谱分析和滤波等操作。
本文将以人类的视角,介绍FFT的原理和应用。
我们来了解一下FFT的基本原理。
FFT的核心思想是将一个时域信号转换为频域信号。
在时域中,信号是以时间为自变量的函数,而在频域中,信号是以频率为自变量的函数。
通过将信号从时域转换到频域,我们可以观察到信号中各个频率分量的强度和相位信息。
FFT的基本原理可以通过以下步骤进行说明:1. 首先,我们需要将时域信号进行采样。
采样是将连续时间信号离散化为离散时间信号的过程。
通过采样,我们可以得到一系列离散的信号样本。
2. 接下来,我们将采样到的时域信号进行加窗处理。
加窗是为了减小信号的边界效应,使得信号在频域中更加平滑。
常用的加窗函数有矩形窗、汉宁窗等。
3. 然后,我们将加窗后的信号进行快速傅里叶变换。
FFT算法通过分治法将傅里叶变换的计算复杂度从O(n^2)降低到O(nlogn),提高了计算效率。
在FFT算法中,信号被划分为多个子信号,分别进行频域计算,最后将结果合并得到完整的频域信号。
4. 最后,我们可以对得到的频域信号进行频谱分析、滤波、降噪等操作。
通过观察频域中各个频率分量的强度和相位信息,我们可以对信号进行分析和处理。
除了频谱分析和滤波,FFT还有许多其他应用。
在图像处理中,FFT 可以用于图像的频域滤波、图像的变换和压缩等。
在音频处理中,FFT可以用于音频的频谱分析、音频的合成和混响等。
在通信系统中,FFT可以用于OFDM(正交频分复用)技术,实现高速数据传输。
总结起来,FFT是一种重要的信号处理方法,通过将信号从时域转换到频域,实现了信号的频谱分析和滤波等操作。
它在图像处理、音频处理、通信系统等多个领域有着广泛的应用。
通过深入理解FFT的原理和应用,我们可以更好地利用它来处理和分析信号,提高系统性能和用户体验。
fft变换原理

fft变换原理
FFT(快速傅里叶变换)是一种高效的算法,用于计算离散傅里叶变换(DFT)。
它的原理是将DFT分解为多个较小的DFT,从而提高计算速度。
在DFT中,将一个信号分解成其频率成分的方法是将其与一组正弦和
余弦函数相乘,并对结果求和。
FFT算法通过使用一种称为蝴蝶算法的技术,将这个操作分解为多个较小的操作,从而加速计算。
具体来说,FFT将DFT分解为两个N/2点DFT,其中N是信号的长度。
这两个DFT
分别对信号的偶数点和奇数点进行计算。
这个过程被称为“蝴蝶操作”,因为它看起来像一只蝴蝶。
蝴蝶操作的效率非常高,因为它可以在O(NlogN)的时间内完成。
这比
直接计算DFT的O(N^2)时间要快得多。
此外,FFT还具有一些其他的
优点。
例如,它可以使用矩阵乘法来计算多项式乘法,这是计算机代
数中的一个重要问题。
FFT的应用非常广泛。
它被广泛用于数字信号处理、图像处理、声音处理、计算机图形学等领域。
例如,在图像处理中,FFT可以用于计算图像的频率成分,从而实现图像滤波、压缩和解压缩等操作。
在声音处
理中,FFT可以用于计算音频信号的频率成分,从而实现音频滤波、降噪和音高转换等操作。
总之,FFT是一种非常重要的算法,它可以大大提高计算效率,并广泛应用于各种领域。
对于那些需要处理数字信号的人来说,了解FFT的
原理和应用是非常重要的。
fft功率频谱

FFT功率频谱一、引言傅里叶变换(FFT)是一种在信号处理、图像处理、通信系统等领域广泛应用的重要工具。
其中,FFT功率频谱是描述信号在频率域上的能量分布情况,对于音频分析、图像处理、通信系统等领域具有重要的应用价值。
本文将就FFT功率频谱的基本原理、应用场景、性能评估以及性能提升策略等方面进行详细阐述。
二、FFT功率频谱基本原理1.FFT基本原理傅里叶变换(FFT)是一种将时域信号转换为频域信号的算法。
其基本思想是将一个信号分解为一系列正弦和余弦函数的线性组合,通过计算这些函数的系数,可以得到信号在频域上的表示。
FFT算法具有高效性、并行性等优点,因此在信号处理领域得到了广泛应用。
2.功率谱密度基本原理功率谱密度是描述信号在频率域上的能量分布情况。
对于一个时域信号,其功率谱密度可以通过FFT算法计算得到。
在计算功率谱密度时,需要对FFT 变换的结果进行归一化处理,即将每个频率分量的幅度除以总幅度,得到该频率分量的相对幅度。
3.FFT功率频谱计算过程FFT功率频谱的计算过程包括以下步骤:(1)对时域信号进行FFT变换;(2)对FFT变换的结果进行归一化处理;(3)计算每个频率分量的功率谱密度;(4)绘制功率谱密度曲线。
三、FFT功率频谱应用场景1.音频分析在音频分析中,FFT功率频谱可以用于分析音频信号的频率成分、能量分布等特征。
通过对音频信号的FFT功率频谱进行分析,可以提取出音频信号中的音调、节奏等信息,为音频处理、音乐分析等领域提供有力支持。
2.图像处理在图像处理中,FFT功率频谱可以用于分析图像的频率成分、纹理特征等。
通过对图像的FFT功率频谱进行分析,可以提取出图像中的边缘、纹理等特征信息,为图像增强、目标检测等领域提供有效手段。
3.通信系统在通信系统中,FFT功率频谱可以用于分析信号的频率分布、调制方式等特征。
通过对通信信号的FFT功率频谱进行分析,可以提取出信号中的调制信息、信道状态等参数,为通信系统的设计和优化提供重要依据。
fft的原理

fft的原理
快速傅里叶变换(FFT)是一种高效的算法,用于将时域信号转换为频域信号。
它可以高速计算出信号的频域特征,使许多应用程序(例如音频信号处理和图像处理)变得更加有效和可靠。
FFT的原理基于傅里叶变换(FT)。
傅里叶变换是将一个信号分解成其频率成分的一种方法。
它将时域信号转换为频域信号,表示该信号在不同频率下的振幅和相位。
FFT基于傅里叶变换的离散版本,通过递归地将信号分解成较小的子信号来进行计算。
该算法基于信号具有对称性,这使得它可以在计算过程中有效地减少计算量,从而提高计算速度。
在FFT算法中,信号通过进行分段来进行计算。
每个分段包含信号中的一定数量的点。
将这些点作为输入,FFT算法将计算出相应的频域特征。
FFT的应用非常广泛,从音频和视频处理到科学和工程中的数据分析都有涉及。
虽然FFT不是唯一的频域分析方法,但由于其高效性和广泛应用,它已成为了许多应用程序中的标准技术。
- 1 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FFT算法FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。
有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在圈圈就根据实际经验来说说FFT结果的具体物理意义。
一个模拟信号,经过ADC采样之后,就变成了数字信号。
采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此罗嗦了。
采样得到的数字信号,就可以做FFT变换了。
N个采样点,经过FFT之后,就可以得到N个点的FFT结果。
为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。
那么FFT之后结果就是一个为N点的复数。
每一个点就对应着一个频率点。
这个点的模值,就是该频率值下的幅度特性。
具体跟原始信号的幅度有什么关系呢假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。
而第一个点就是直流分量,它的模值就是直流分量的N倍。
而每个点的相位呢,就是在该频率下的信号的相位。
第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。
例如某点n所表示的频率为:Fn=(n-1)*Fs/N。
由上面的公式可以看出,Fn所能分辨到频率为为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。
1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到。
如果要提高频率分辨力,则必须增加采样点数,也即采样时间。
频率分辨率和采样时间是倒数关系。
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号a*a+b*b,相位就是Pn=atan2(b,a)。
根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即2*An/N*cos(2*pi*Fn*t+Pn)。
对于n=1点的信号,是直流分量,幅度即为A1/N。
由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
好了,说了半天,看着公式也晕,下面圈圈以一个实际的信号来做说明。
假设我们有一个信号,它含有2V的直流分量,频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率为75Hz、相位为90度、幅度为的交流信号。
用数学表达式就是如下:S=2+3*cos(2*pi*50*t-pi*30/180)+*cos(2*pi*75*t+pi*90/180)式中cos参数为弧度,所以-30度和90度要分别换算成弧度。
我们以256Hz的采样率对这个信号进行采样,总共采样256点。
按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。
我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。
实际情况如何呢我们来看看FFT的结果的模值如图所示。
图1 FFT结果从图中我们可以看到,在第1点、第51点、和第76点附近有比较大的值。
我们分别将这三个点附近的数据拿上来细看:1点: 512+0i2点: -3点: -50点: -51点: - 192i52点: -75点:76点: + 192i77点: +很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。
接着,我们来计算各点的幅度值。
分别计算这三个点的模值,结果如下:1点: 51251点:38476点:192按照公式,可以计算出直流分量为:512/N=512/256=2;50Hz信号的幅度为:384/(N/2)=384/(256/2)=3;75Hz信号的幅度为192/(N/2)=192/(256/2)=。
可见,从频谱分析出来的幅度是正确的。
然后再来计算相位信息。
直流信号没有相位可言,不用管它。
先计算50Hz信号的相位,atan2(-192, =,结果是弧度,换算为角度就是180*/pi=。
再计算75Hz信号的相位,atan2(192, =弧度,换算成角度就是180*pi=。
可见,相位也是对的。
根据FFT结果以及上面的分析计算,我们就可以写出信号的表达式了,它就是我们开始提供的信号。
总结:假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应该频率下的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。
相位的计算可用函数atan2(b,a)计算。
atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。
要精确到xHz,则需要采样长度为1/x 秒的信号,并做FFT。
要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。
解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。
具体的频率细分法可参考相关文献。
[附录:本测试数据使用的matlab程序]实例一:S=2+3cos(2pi*50t-pi/6)+(2pi*75t+pi/2)close all; %先关闭所有图片Adc=2; %直流分量幅度A1=3; %频率F1信号的幅度A2=; %频率F2信号的幅度F1=50; %信号1频率(Hz)F2=75; %信号2频率(Hz)Fs=256; %采样频率(Hz)P1=-30; %信号1相位(度)P2=90; %信号相位(度)N=256; %采样点数t=[0:1/Fs:N/Fs]; %采样时刻%信号S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180); %显示原始信号plot(S);title('原始信号');figure;Y = fft(S,N); %做FFT变换Ayy = (abs(Y)); %取模plot(Ayy(1:N)); %显示原始的FFT模值结果title('FFT 模值');figure;Ayy=Ayy/(N/2); %换算成实际的幅度Ayy(1)=Ayy(1)/2;F=([1:N]-1)*Fs/N; %换算成实际的频率值plot(F(1:N/2),Ayy(1:N/2)); %显示换算后的FFT模值结果title('幅度-频率曲线图');figure;Pyy=[1:N/2];for i=1:N/2Pyy(i)=phase(Y(i)); %计算相位Pyy(i)=Pyy(i)*180/pi; %换算为角度end;plot(F(1:N/2),Pyy(1:N/2)); %显示相位图title('相位-频率曲线图');实例一:S=1+(2pi*20t)+(2pi*60t)close all; %先关闭所有图片Adc=1; %直流分量幅度A1=; %频率F1信号的幅度A2=; %频率F2信号的幅度F1=20; %信号1频率(Hz)F2=60; %信号2频率(Hz)Fs=256; %采样频率(Hz)P1=0; %信号1相位(度)P2=0; %信号相位(度)N=256; %采样点数t=[0:1/Fs:N/Fs]; %采样时刻%信号S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180); %显示原始信号plot(S);title('原始信号');figure;Y = fft(S,N); %做FFT变换Ayy = (abs(Y)); %取模plot(Ayy(1:N)); %显示原始的FFT模值结果title('FFT 模值');figure;Ayy=Ayy/(N/2); %换算成实际的幅度Ayy(1)=Ayy(1)/2;F=([1:N]-1)*Fs/N; %换算成实际的频率值plot(F(1:N/2),Ayy(1:N/2)); %显示换算后的FFT模值结果title('幅度-频率曲线图');Pyy=[1:N/2];for i=1:N/2Pyy(i)=phase(Y(i)); %计算相位Pyy(i)=Pyy(i)*180/pi; %换算为角度end;plot(F(1:N/2),Pyy(1:N/2)); %显示相位图title('相位-频率曲线图');实例三close all; %先关闭所有图片Adc=2; %直流分量幅度A1=3; %频率F1信号的幅度F1=50; %信号1频率(Hz)P1=-30; %信号1相位(度)A2=; %频率F2信号的幅度F2=75; %信号2频率(Hz)P2=90; %信号相位(度)Fs=512; %采样频率(Hz)N=1024; %采样点数t=[0:1/Fs:(N-1)/Fs]; %采样时刻S=Adc+A1*cos(2*pi*F1*t+pi*P1/180)+A2*cos(2*pi*F2*t+pi*P2/180); %% 显示原始信号plot(S);title('原始信号');%% FFT变换后figure;Y = fft(S,N); %做FFT变换Ayy = (abs(Y)); %取模plot(Ayy(1:N)); %显示原始的FFT模值结果title('FFT 模值');%% 幅度频率曲线图figure;Ayy=Ayy/(N/2); %换算成实际的幅度Ayy(1)=Ayy(1)/2;F=([1:N]-1)*Fs/N; %换算成实际的频率值plot(F(1:N/2),Ayy(1:N/2)); %显示换算后的FFT模值结果title('幅度-频率曲线图');%% 相位频率曲线图figure;Pyy=[1:N/2];for i=1:N/2Pyy(i)=phase(Y(i)); %计算相位Pyy(i)=Pyy(i)*180/pi; %换算为角度end;plot(F(1:N/2),Pyy(1:N/2)); %显示相位图title('相位-频率曲线图');实例四关于FFT的相位谱(2011-07-13 11:41:56)转载▼分类:机械技术标签:相位谱正弦信号延拓进行it先看一下我收到的程序,作为研究对象的信号是这样产生的:T=128;N=128;dt=T/N;t=dt*(1:N);x=2*cos(2*t-pi/4);...(我觉得这个信号存在一点问题,因为t是从1开始的,所以它的初相应该和-pi/4有点差别吧。
