闭函数计算 2013年湖南长沙中考数学压轴题第一道
2013年湖南长沙中考数学试卷及答案(word解析版)

一、选择题:1.(2013湖南长沙 第 1题 3分)下列实数是无理数的是( )1 2A.-1B.0C. 【答案】D.【答案】C 。
3 .(2013湖南长沙 第 3题 3分)如果一个三角形的两边长分别是2和 4,则第三边可能是 ( ) A.2 B.4 C.6 D.8 【答案】B.1)B.外切C.相交D.内切)6338222221则该校篮球队 12名同学的身高的众数是(单位:cm))AAaa12 121 2 b1 bBBD CCABCD【答案】D8.(2013湖南长沙 第 8题 3分)下列多边形中,内角和与外角和相等的是()A.四边形B.五边形C.六边形D.八边形【答案】A.9.(2013湖南长沙第9题3分)在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是()【答案】C.)A.a>0B.c>0 D.a+b+c>0【答案】D.=8 2 2=(2-1)。
【答】根据完全平方公式得,x +2x+1=(x+1),故填(x+1)2 22度2 114.(2013湖南长沙第14题3分)方程【答案】x=1【答案】4.17.(2013湖南长沙第17题3分)在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒子中的求摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球实验后发现,摸到红球的频率稳定于0.2,那么可以推算出n19.(2013湖南长沙第19题6分)计算:3【解】原式=3+4-1=6。
+(-2)2-(+1)0520.(2013湖南长沙第20题6分)解不等式组来,(1)统计图共统计了天的空气质量情况。
4022.(2013湖南长沙第22题8分)如图,△A B C 中,以A B 为直径的⊙O 交A C 于点D, ∠D B C=∠B A C.O B=O D,∴△O B D 是等边三角形,∴S =S阴影扇形△23 .360 2 3(1)求证:△AB N≌△C D M;1 12 213股定理求的NE=232013是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;x21 1,12013,即1≤y≤2013,所以反比例函数y= 是闭区间[1,2013]上的“闭函x≤n,得k m+b≤kx+b≤kn+b,根据“闭函数”的规定有,方程相减得k(m-n)=m-n,15 5115475 5≤x ≤b 时, b 2- b - ≤y ≤ a 2- a - ,由规定可得,方程相减得5 5 5 5 5 5 1 54511b=-2 或 b=1,由于 a <b ,b=1,此时 a=-2.故.②当 a <2<b 时,函数的最小值为- ,5 11 1 4 7 11 14 7 555 55 5 5 5115, 解 得( 其 中1 4 71a 2b 25 55552 1 4 7 55 5222229 109 根,s= ,不合题意,应舍去.211 11a a 5 综上所述:a 、b 的值为.52(2)求证△A OF ∽△BE O ;1 2 1 22 0a2a 2 2 22 点 E 坐 标 为 ( a ,-a+2), 点 F 坐 标 为 ( , ), AF=a a a 2 2O A BE 22 O A AF BE O B a,∴2a2a 2b 2a 2ab 4 ,∴O A ·O B=AF ·BE ,∴2222222 2 2 22222222212 【,2 21 1=a+b-2;∴S +S = (a+b-2) +(a+b-2)= [(a+b-2)+ ] - ,对2 2 21 22 212称轴是 x=- ,抛物线的开口向上。
湖南省长沙市中考数学真题试题(解析版)

2013年湖南省长沙市中考数学试卷(数学)注意事项:1、答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2、必须在答题卡上答题,在草稿纸、试题卷上答题无效;3、答题时,请考生注意各大题题号后面的答题提示;4、请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁; 5.答题卡上不得使用涂改液、涂料胶和贴纸;6.本学科试卷共26个小题,考试时量120分钟,满分120分。
一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本题共10个小题,每小题3分,共30分) 1.下列实数是无理数的是( ) A.-1 B.0 C.21D.3 2.小星同学在“百度”搜索引擎中;输入“中国梦,我的梦”,能搜索到与之相关的结果的条数约为61 700 000,这个数用科学记数法表示为( )A.617×105B.6.17×106C.6.17×107D.0.617×1083.如果一个三角形的两边长分别为2和4,则第三边长可能是( ) A.2 B.4 C.6 D.84.已知⊙O 1的半径为1㎝、⊙O 2的半径为3㎝,两圆的圆心距O 1O 2为4㎝,则两圆的位置关系是( )A.外离B.外切C.相交D.内切 5.下列计算正确的是( )A.336a a a =÷B.()832a a = C.()222b a b a -=- D.422a a a =+6.某校篮球队12名同学的身高如下表:则该校篮球队12名同学身高的众数是(单位:㎝)( )A.192B.188C.186D.180 7.下列各图中,∠1大于∠2的是( )8.下列多边形中,内角和与外角和相等的是( )A.四边形B.五边形C.六边形D.八边形9.在下列某品牌T 恤的四个洗涤说明图案的设计中,没有..运用旋转或轴对称知识的是( )10.二次函数c bx axy ++=2的图象如图所示,则下列关系错误..的是( ) A. a >0 B. c >0 C. ac b 42->0 D. a +b +c >0 二、填空题(本题共8个小题,每小题3分,共24分) 11.计算:28-= .12.因式分解:122++x x = . 13.已知∠A=67°,则∠A 的余角等于 度.21(AB=AC )C B Aba21(a b )ba 21D21CBAAB C DAB C D14.方程xx 112=+的解为x = .15.如图,BD 是∠ABC 的平分线,P 是BD 上的一点,PE ⊥BA 于点E ,PE=4㎝,则点P 到边BC 的距离为 ㎝.16.如图,在⊿ABC 中,点D ,点E 分别是边AB ,AC 的中点,则⊿ADE 与⊿ABC 的周长之比等于 .17.在一个不透明的盒子中装有n 个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球实验后发现,摸到红的频率稳定于0.2,那么可以推算出n 大约是 .18.如图,在梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AE ∥CD 交BC 于点E ,若AD=2,BC=5,则CD 的长是 .三、解答题(本题共2个小题,每小题6分,共12分) 19.计算:()()021523+--+-20.解不等式组()⎩⎨⎧-+≤+xx x x 34312π并将其解集在数轴上表示出来.E PD CB A E D CBA E DCB A(第10题)(第15题) (第16题) (第18题)四、解答题(本题共2个小题,每小题8分,共16分)21.“宜居长沙”是我们的共同愿景,空气质量倍受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月至4月份若干天的空气质量情况,并绘制了如下不完整的统计图,请根据图中信息,解答下列问题:(1)统计图共统计了 天的空气质量情况.(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形的圆心角度数. (3)从小源所在班级的40名同学中,随机选取一名同学去该空气质量监测站点参观,则恰好选到小源的概率是多少?22.如图,⊿ABC 中,以AB 为直径的⊙O 交AC 于点D ,∠DBC=∠BAC. (1)求证:BC 是⊙O 的切线;(2)若⊙O 的半径为2,∠BAC=30°,求图中阴影部分的面积.-24各类空气质量天数条形统计图类别污染污染良各类空气质量天数扇形统计图(第21题)五、解答题(本题共2个小题,每小题9分,共18分)23.为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线..已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元. (1)求1号线,2号线每千米的平均造价分别是多少亿元?(2)除1,2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网,据预算,这91.8千米地铁线网每千米的平均造价是1号线的平均造价的1.2倍,则还需投资多少亿元?24.如图,在□ABCD 中,M ,N 分别是AD ,BC 的中点,∠AND=90°,连接CM 交DN 于点O. (1)求证:⊿ABN ≌⊿CDM ;(2)过点C 作CE ⊥MN 于点E ,交DN 于点P ,若PE=1,∠1=∠2,求AN 的长.六、解答题(本题共2个小题,每小题10分,共20分)25.设a ,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为[]a,b .对于一个函数,如果它的自变量x 与函数值y 满足:当m ≤x ≤n 时 ,有m ≤y ≤n ,我们就称此函数是闭区间[]m,n 上的“闭函数”. (1)反比例函数xy 2013=是闭区间[]20131,上的“闭函数”吗?请判断并说明理由; (2)若一次函数()0≠+=k b kx y 是闭区间[]m,n 上的“闭函数”,求此函数的解析P NMEO D21CBA(第22题)(第24题)式;(3)若二次函数5754512--=x x y 是闭区间[]a,b 上的“闭函数”,求实数a ,b 的值.26.如图,在平面直角坐标系中,直线2+-=x y 与x 轴,y 轴分别交于点A ,点B ,动点P (a ,b )在第一象限内,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点P (a ,b )运动时,矩形PMON 的面积为定值2. (1)求∠OAB 的度数; (2)求证:⊿AOF ∽⊿BEO ;(3)当点E ,F 都在线段AB 上时,由三条线段AE ,EF ,BF 组成一个三角形,记此三角形的+S 2是否存在最小值?若存在,请求出该最(第26题)2013年湖南省长沙市中考数学试卷答案及解析一、选择题、1、D 【详解】根据无理数的定义可知,只有D是无理数.2、C 【详解】根据科学记数法的原则可知选C.3、B 【详解】三角形任意两边之和大于第三边、任意两边之差小于第三边,只有B符合.4、B 【详解】因为1+3=4,即两圆半径之和等于圆心距,所以两圆外切.5、A 【详解】B、(a2)3=a2×3=a6C、(a-b)2=a2-2ab+b2D、a2+a2=2a26、B 【详解】众数就是出现次数最多的数,表格中188出现了5次,是最多的,所以12名同学身高的众数是188,选B.7、D 【详解】A、△ABC是等腰三角形,所以∠1=∠2;B、∠1与∠2是对顶角,所以∠1=∠2;C、对顶角相等与根据两直线平行、同位角相等性质可知∠1与∠2;D、由于∠1是△ABC的外角,且∠1=∠B+∠2,所以∠1>∠2;综上所述,选D8、A 【详解】所有多边形的外角和都是360°,而内角和公式为180°(n-2),其中n表示多边形的边数,所以当180°(n-2)=360°时,n=4,即四边形的内角和与外角和相等,选A。
2013年中考真题二次函数综合压轴题60题

1、(2013潍坊)如图,抛物线c bx ax y ++=2关于直线1=x 对称,与坐标轴交于C B A 、、三点,且4=AB ,点⎪⎭⎫ ⎝⎛232,D 在抛物线上,直线是一次函数()02≠-=k kx y 的图象,点O 是坐标原点.(1)求抛物线的解析式;(2)若直线平分四边形OBDC 的面积,求k 的值.(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线交于N M 、两点,问在y 轴正半轴上是否存在一定点P ,使得不论k 取何值,直线PM 与PN 总是关于y 轴对称?若存在,求出P 点坐标;若不存在,请说明理由.2、(2013绵阳)如图,二次函数y =ax 2+bx +c 的图象的顶点C 的坐标为(0,-2),交x 轴于A 、B 两点,其中A (-1,0),直线l :x =m (m >1)与x 轴交于D 。
(1)求二次函数的解析式和B 的坐标;(2)在直线l 上找点P (P 在第一象限),使得以P 、D 、B 为顶点的三角形与以B 、C 、O 为顶点的三角形相似,求点P 的坐标(用含m 的代数式表示);(3)在(2)成立的条件下,在抛物线上是否存在第一象限内的点Q ,使△BP Q 是以P 为直角顶点的等腰直角三角形?如果存在,请求出点Q 的坐标;如果不存在,请说明理由。
3、(2013昆明)如图,矩形OABC 在平面直角坐标系xOy 中,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC 边上,且抛物线经过O ,A 两点,直线AC 交抛物线于点D .(1)求抛物线的解析式;(2)求点D 的坐标;(3)若点M 在抛物线上,点N 在x 轴上,是否存在以A ,D ,M ,N 为顶点的四边形是平行四边形?若存在,求出点N 的坐标;若不存在,请说明理由.4(2013山西)综合与探究:如图,抛物线213442y x x =--与x 轴交于A,B 两点(点B 在点A 的右侧)与y 轴交于点C,连接BC,以BC 为一边,点O 为对称中心作菱形BDEC,点P 是x 轴上的一个动点,设点P 的坐标为(m ,0),过点P 作x 轴的垂线l 交抛物线于点Q(1)求点A,B,C 的坐标。
2013年长株潭衡中考压轴题

26.(8分)(2013•衡阳)如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.(1)试说明AE2+CF2的值是一个常数;(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.27.(10分)(2013•衡阳)如图,已知抛物线经过A(1,0),B(0,3)两点,对称轴是x=﹣1.(1)求抛物线对应的函数关系式;(2)动点Q从点O出发,以每秒1个单位长度的速度在线段OA上运动,同时动点M从M从O点出发以每秒3个单位长度的速度在线段OB上运动,过点Q作x轴的垂线交线段AB于点N,交抛物线于点P,设运动的时间为t秒.①当t为何值时,四边形OMPQ为矩形;②△AON能否为等腰三角形?若能,求出t的值;若不能,请说明理由.经过原点O及点A、B.(1)求⊙M的半径及圆心M的坐标;(2)过点B作⊙M的切线l,求直线l的解析式;(3)∠BOA的平分线交AB于点N,交⊙M于点E,求点N的坐标和线段OE的长.=,可解得OC=点坐标为(﹣ND,所以OD=ON=AN=﹣= =10=,即=,点坐标为(﹣,点(﹣,y=,,ON=ND=,,即AN=﹣,,即NE=,解得NE= OE=ON+NE=.24.(2013湖南长沙 第24题 9分)如图,在平行四边形ABCD 中,M,N 分别是AD,BC 的中点,∠AND=900,连接CM 交DN 于点O. (1)求证:△ABN ≌△CDM ;(2)过点C 作CE ⊥MN 于点E ,交DN 于点P ,若PE=1,∠1=∠2,求AN 的长。
25.(2013湖南长沙 第25题 10分)设a,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x 与函数值y 满足:当m ≤x ≤n 时,有m ≤y ≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.(1)反比例函数y=x2013是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由; (2)若一次函数y=kx+b(k ≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式; (3)若二次函数y=51x 2-54x-57是闭区间[a,b]上的“闭函数”,求实数a,b 的值。
长沙市中考数学试卷及答案

2013年湖南省长沙市中考数学试卷注意事项:1、答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2、必须在答题卡上答题,在草稿纸、试题卷上答题无效;3、答题时,请考生注意各大题题号后面的答题提示;4、请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁; 5.答题卡上不得使用涂改液、涂料胶和贴纸;6.本学科试卷共26个小题,考试时量120分钟,满分120分。
一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本题共10个小题,每小题3分,共30分) 1.下列实数是无理数的是() A.-.0 C 21.32.小星同学在“百度”搜索引擎中;输入“中国梦,我的梦”,能搜索到与之相关的结果的条数约为×105×106 C.×107×1083.如果一个三角形的两边长分别为2和4,则第三边长可能是().4 C 已知⊙O 1的半径为1㎝、⊙O 2的半径为3㎝,两圆的圆心距O 1O 2为4㎝,则两圆的位置关系是() A.外离B.外切C.相交D.内切 5.下列计算正确的是()336a a a =÷()832a a =()222b a b a -=-422a a a =+某校篮球队12名同学的身高如下表:则该校篮球队12名同学身高的众数是(单位:㎝)() .188 C 下列各图中,∠1大于∠2的是()8.下列多边形中,内角和与外角和相等的是()A.四边形B.五边形C.六边形D.八边形9.在下列某品牌T 恤的四个洗涤说明图案的设计中,没有..运用旋转或轴对称知识的是()10.二次函数ax y =2..的是() A.a >0B.c >0 C.ac b 42->0D.a +b +c >0 二、填空题(本题共8个小题,每小题3分,共2411.计算:28-=. 12.因式分解:122++x x =.13.已知∠A=67°,则∠A 的余角等于度. 14.方程xx 112=+的解为x =. 15.如图,BD 是∠ABC 的平分线,P 是BD 上的一点,PE ⊥BA 于点E ,PE=4㎝,则点P 到边BC 的距离 为㎝.16.如图,在⊿ABC 中,点D ,点E 分别是边AB ,AC 的中点,则⊿ADE 与⊿ABC 的周长之比等于.A B CDA C D (第10题)17.在一个不透明的盒子中装有n 个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球实验后发现,摸到红的频率稳定于,那么可以推算出n 大约是.18.如图,在梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AE ∥CD 交BC 于点E ,若AD=2,BC=5,则CD 的长是.三、解答题(本题共2个小题,每小题6分,共1219.计算:()()021523+--+-20.解不等式组()⎩⎨⎧-+≤+xx x x 34312 并将其解集在数轴上表示出来.四、解答题(本题共2个小题,每小题8分,共16分)21.“宜居长沙”是我们的共同愿景,空气质量倍受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月至4月份若干天的空气质量情况,并绘制了如下不完整的统计图,请根据图中信息,解答下列问题:(. (.( 22.如图,⊿ABC 中,以AB 为直径的⊙O 交AC 于点D ,∠DBC=∠BAC. (1)求证:BC 是⊙O 的切线;(2)若⊙O 的半径为2,∠BAC=30°,求图中阴影部分的面积.五、解答题(本题共2个小题,每小题9分,共18分)C各类空气质量天数条形统计图类别污染污染良各类空气质量天数扇形统计图(第15题)(第16题)(第21题) (第22题)23.为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线..已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多亿元. (1)求1号线,2号线每千米的平均造价分别是多少亿元?(2)除1,2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网,据预算,这91.8千米地铁线网每千米的平均造价是1号线的平均造价的倍,则还需投资多少亿元?24.如图,在□ABCD 中,M ,N 分别是AD ,BC 的中点,∠AND=90°,连接CM 交DN 于点O.(1)求证:⊿ABN ≌⊿CDM ;(2)过点C 作CE ⊥MN 于点E ,交DN 于点P ,若PE=1,∠1=∠2,求AN 的长.六、解答题(本题共2个小题,每小题10分,共20分)25.设a ,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为[]a,b .对于一个函数,如果它的自变量x 与函数值y 满足:当m ≤x ≤n 时,有m ≤y ≤n ,我们就称此函数是闭区间[]m,n 上的“闭函数”. (1)反比例函数xy 2013=是闭区间[]20131,上的“闭函数”吗?请判断并说明理由; (2)若一次函数()0≠+=k b kx y 是闭区间[]m,n 上的“闭函数”,求此函数的解析式;(3)若二次函数5754512--=x x y 是闭区间[]a,b 上的“闭函数”,求实数a ,b 的值. 26.如图,在平面直角坐标系中,直线2+-=x y 与x 轴,y 轴分别交于点A ,点B ,动点P (a ,b )在第一象限内,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,(第24题)N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.(1)求∠OAB的度数;(2)求证:⊿AOF∽⊿BEO;(3)当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,⊿OEF的面积为S2.试探究:S1+S2是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.(第26题)2013年湖南省长沙市中考数学试卷答案及解析一、选择题、1、D【详解】根据无理数的定义可知,只有D是无理数.2、C【详解】根据科学记数法的原则可知选C.3、B【详解】三角形任意两边之和大于第三边、任意两边之差小于第三边,只有B 符合.4、B【详解】因为1+3=4,即两圆半径之和等于圆心距,所以两圆外切.5、A【详解】B、(a2)3=a2×3=a6C、(a-b)2=a2-2ab+b2D、a2+a2=2a26、B【详解】众数就是出现次数最多的数,表格中188出现了5次,是最多的,所以12名同学身高的众数是188,选B.7、D【详解】A、△ABC是等腰三角形,所以∠1=∠2;B、∠1与∠2是对顶角,所以∠1=∠2;C、对顶角相等与根据两直线平行、同位角相等性质可知∠1与∠2;D、由于∠1是△ABC的外角,且∠1=∠B+∠2,所以∠1>∠2;综上所述,选D8、A【详解】所有多边形的外角和都是360°,而内角和公式为180°(n-2),其中n表示多边形的边数,所以当180°(n-2)=360°时,n=4,即四边形的内角和与外角和相等,选A。
长沙市近5年数学中考压轴题专题训练

长沙市近5年数学中考压轴题专题训练1.设a,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为{a,b},对于一个函数,如果它的自变量x 与函数值y 满足:当m ≤x ≤n 时,有m ≤y ≤n,我们就称此函数是闭区间{m,n}上的“闭函数”.(2013·长沙)(1)反比列函数2013y x=是闭区间{1,2013}上的“闭函数”吗?请判断并说明理由; (2)若一次函数y=kx+b(k ≠0)是闭区间{m,n}上的“闭函数”,求此函数的解析式:(3)若二次函数2147555y x x =--是闭区间{a,b}上的“闭函数”,求实数a,b 的值.2.如图,在平面直角坐标系中,直线y=-x+2与x 轴,y 轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P 向x 轴,y 轴所作的垂线PM,PN (垂足为M,N )分别于直线AB 相交于点E,点F ,当点P(A,B)运动时,矩形PMON 的面积为定值2.(2013·长沙)(1)求∠OAB 的度数; (2)求证△AOF ∽△BEO ;(3)当点E,F 都在线段AB 上时,由三条线段AE,EF,BF 组成一个三角形,记此三角形的外接圆面积为1S △OEF 的面积为2S 试探究: 12S S +是否存在最小值? 若存在,请求出该最小值:若不存在,请说明理由.3.在平面直角坐标系中,我们把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),(,),…都是“梦之点”,显然,这样的“梦之点”有无数个.(2014·长沙)(1)若点P(2,m)是反比例函数y=(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+,试求出t的取值范围.4.(2014•长沙)如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.5.在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
2013年湖南省长沙市中考数学试卷解析

2013年湖南省长沙市中考数学试卷参考答案与试题解析一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本题共10个小题,每小题3分,共30分)1.(3分)(2013•长沙)下列实数是无理数的是()A.﹣1 B.0 C.D.【考点】M116 无理数.【分析】无理数就是无限不循环小数.由此即可判定选择项.A、是整数,是有理数,选项错误;B、是整数,是有理数,选项错误;C、是分数,是有理数,选项错误;D、是无理数.【难度】容易题【解答】D.【点评】本题重点考查了无理数的概念,即无理数就是无限不循环小数,比较简单,是一道基础题.2.(3分)(2013•长沙)小星同学在“百度”搜索引擎中输入“中国梦,我的梦”,能搜索到与之相关的结果的条数约为61700000,这个数用科学记数法表示为()A.617×105 B.6.17×106C.6.17×107D.0.617×108【考点】M11D 科学记数法.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.所以61700000用科学记数法表示为6.17×107.【难度】容易题【解答】C.【点评】本题主要考查用科学记数法表示较大的数.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,解题关键是要正确确定a的值以及n的值.3.(3分)(2013•长沙)如果一个三角形的两边长分别为2和4,则第三边长可能是()A.2 B.4 C.6 D.8【考点】M322 三角形三边的关系.【分析】设第三边长为x,则由三角形三边关系定理得4﹣2<x<4+2,即2<x <6.因此,本题的第三边应满足2<x<6,把各项代入不等式符合的即为答案.2,6,8都不符合不等式2<x<6,只有4符合不等式.【难度】容易题【解答】B.【点评】本题重点考查了三角形三边关系,较为简单,解题关键是要根据三角形三边关系定理列出不等式.4.(3分)(2013•长沙)已知⊙O1的半径为1cm,⊙O2的半径为3cm,两圆的圆心距O1O2为4cm,则两圆的位置关系是()A.外离B.外切C.相交D.内切【考点】M34E 圆与圆的位置关系.【分析】∵⊙O1和⊙O2的半径分别为1cm和3cm,圆心距O1O2=4cm,∴O1O2=1+3=4,∴两圆外切.【难度】容易题【解答】B.【点评】本题重点考查了圆与圆的位置关系,较为简单,若d表示圆心距,R,r分别表示两圆的半径,当两圆外离时,则d>R+r;两圆外切时,则d=R+r;两圆相交时,则R﹣r<d<R+r;两圆内切时,则d=R﹣r;两圆内含时,则d<R ﹣r.5.(3分)(2013•长沙)下列计算正确的是()A.a6÷a3=a3 B.(a2)3=a8C.(a﹣b)2=a2﹣b2 D.a2+a2=a4【考点】M11T 同底数幂的除法;M11Q 幂的乘方;M11R 积的乘方;M11L 完全平方公式和平方差公式;M11U 合并同类项.【分析】A、根据同底数幂的除法,底数不变指数相减,a6÷a3=a3,故A选项正确;B、(a2)3=a6,根据幂的乘方,底数不变指数相乘,故B选项错误,C、(a ﹣b)2=a2﹣2ab+b2,故C选项错误;D、合并同类项,a2+a2=2a2,故D选项错误.【难度】容易题【解答】A.【点评】本题重点考查同底数幂的除法,幂的乘方和积的乘方、完全平方公式以及合并同类项等知识的运用,比较简单,记准运算法则是解题关键.A.192 B.188 C.186 D.180【考点】M214 中位数、众数.【分析】一组数据中出现次数最多的数据叫做众数,身高188的人数最多,故该校篮球队12名同学身高的众数是188cm.【难度】容易题【解答】B.【点评】本题主要考查了众数的概念,较为简单,熟记众数的定义是解题的关键.7.(3分)(2013•长沙)下列各图中,∠1大于∠2的是()A.B. C.D.【考点】M327 等腰三角形性质与判定;M31B 相交线(对顶角、邻补角、同位角、同旁内角、内错角、);M31C 平行线的判定及性质.【分析】A、∵AB=AC,∴∠1=∠2,故本选项错误;B、∠1=∠2(对顶角相等),故本选项错误;C、根据对顶角相等,∠1=∠3,∵a∥b,∴∠2=∠3,∴∠1=∠2,故本选项错误;D、根据三角形的外角性质,∠1>∠2,故本选项正确.【难度】容易题【解答】D.【点评】本题重点考查了等腰三角形的性质、对顶角相等以及平行线的性质,较为简单,灵活运用各性质是解题关键.8.(3分)(2013•长沙)下列多边形中,内角和与外角和相等的是()A.四边形B.五边形C.六边形D.八边形【考点】M331 多边形的内(外)角和.【分析】设多边形的边数是n,则(n﹣2)•180=360,解得n=4.【难度】容易题【解答】A.【点评】本题重点考查了多边形的内角和定理这一知识点,属于基础题型,熟记多边形的内角和公式是解题关键.9.(3分)(2013•长沙)在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是()A.B.C.D.【考点】M411 中心对称图形及轴对称图形.【分析】根据轴对称及旋转对称的定义,结合各选项进行判断即可.A、即运用了轴对称也利用了旋转对称,故本选项错误;B、利用了轴对称,故本选项错误;C、没有运用旋转,也没有运用轴对称,故本选项正确;D、即运用了轴对称也利用了旋转对称,故本选项错误;【难度】容易题【解答】C.【点评】本题重点考查了中心对称图形及轴对称图形的概念,比较简单,解答本题的关键是熟练掌握中心对称图形与轴对称图形的性质.10.(3分)(2013•长沙)二次函数y=ax2+bx+c的图象中如图所示,则下列关系式错误的是()A.a>0 B.c>0 C.b2﹣4ac>0 D.a+b+c>0【考点】M162 二次函数的的图象、性质M128 一元二次方程根的判别式.【分析】A、∵抛物线的开口向上,∴a>0,正确,故A选项不符合题意;B、∵抛物线与y轴的交点在y轴的正半轴上,∴c>0,正确,故B选项不符合题意;C、∵抛物线与x轴有两个交点,∴b2﹣4ac>0,正确,故C选项不符合题意;D、把x=1代入抛物线的解析式得:y=a+b+c<0,错误,故D选项符合题意;【难度】中等题【解答】D.【点评】本题重点考查了二次函数的的图象、性质以及一元二次方程根的判别式等知识,难度适中,解题关键是懂得灵活运用二次函数的相关知识.二、填空题(本题共8小题,每小题3分,共24分)11.(3分)(2015•衡阳)化简:﹣=.【考点】M11J 二次根式混合运算M11E 二次根式的化简.【分析】首先把各根式化为最简二次根式,再根据二次根式的减法进行计算即可.所以原式=2﹣=.【难度】容易题【解答】.【点评】本题重点考查的是二次根式的减法运算,较为简单,解题关键是掌握二次根式的化简.12.(3分)(2014•济南)分解因式:x2+2x+1=.【考点】M11K 因式分解M11L 完全平方公式和平方差公式【分析】直接运用完全平方公式进行因式分解.所以x2+2x+1=(x+1)2.【难度】容易题【解答】(x+1)2.【点评】本题主要考查了公式法分解因式,较为简单,解题关键是要熟记完全平方公式.13.(3分)(2013•长沙)已知∠A=67°,则∠A的余角等于度.【考点】M317 周角、平角、钝角、直角、锐角、余角、补角.【分析】∵∠A=67°,∴∠A的余角=90°﹣67°=23°.【难度】容易题【解答】23.【点评】本题重点考查了余角的定义,较为简单,掌握互余两角之和为90°是解题关键.14.(3分)(2013•长沙)方程的解为x=.【考点】M12B 解可化为一元一次方程的分式方程.【分析】方程两边都乘(x+1)x,得2x=x+1,解得x=1,检验:当x=1时,(x+1)x≠0.∴原方程的解是x=1.【难度】容易题【解答】1.【点评】本题主要考查了解分式方程的基本步骤,是一道基础题,掌握解分式方程的基本思想即“转化思想”是本题的解题关键.15.(3分)(2013•长沙)如图,BD是∠ABC的平分线,P为BD上的一点,PE⊥BA 于点E,PE=4cm,则点P到边BC的距离为cm.【考点】M318 角平分线的性质与判定M315 点到直线的距离.【分析】∵BD是∠ABC的平分线,PE⊥AB于点E,PE=4cm,∴点P到BC的距离=PE=4cm.【难度】容易题【解答】4.【点评】本题重点考查了点到直线的距离,同时也考查了角平分线的性质,较为简单,解题关键是能由已知注意到P到BC的距离即为PE长这一点.16.(3分)(2013•长沙)如图,在△ABC中,点D,点E分别是边AB,AC的中点,则△ADE和△ABC的周长之比等于.【考点】M32H 相似三角形性质与判定;M323 三角形的中位线;M325 三角形的面积、周长.【分析】∵点D,点E分别是边AB,AC的中点,∴DE是△ABC的中位线,∴DE∥BC,且DE:BC=1:2,∴△ADE∽△ABC,∴△ADE与△ABC的周长比为1:2.【难度】中等题【解答】1:2.【点评】本题重点考查了相似三角形的判定与性质以及三角形的中位线定理,难度适中,解题关键是要理解相似三角形的周长之比等于边长之比.17.(3分)(2014•朝阳)在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是.【考点】M224 概率的意义、应用M225 利用频率估计概率.【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,由题意可得,=0.2,解得,n=10.故估计n大约有10个.【难度】中等题【解答】10.【点评】本题重点考查了概率的意义、应用以及利用频率估计概率,难度中等,解题关键是根据红球的频率得到相应的等量关系.18.(3分)(2013•长沙)如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是.【考点】M336 梯形及其中位线;M327 等腰三角形性质与判定;M332 平行四边形的性质与判定;M321 三角形内(外)角和.【分析】∵AD∥BC,AE∥CD,∴四边形AECD是平行四边形,∴AD=EC=2,CD=AE,∵AD=2,BC=5,∴BE=BC﹣EC=5﹣2=3,∵AE∥CD,∠C=80°,∴∠AEB=∠C=80°,在△ABE中,∠BAE=180°﹣∠B﹣∠AEB=180°﹣50°﹣80°=50°,∴∠B=∠BAE,∴AE=BE=3,∴CD=3.【难度】中等题【解答】3.【点评】本题重点考查了梯形的性质,平行四边形的判定与性质,等腰三角形的性质以及三角形的内角和定理等知识点,综合性较强,难度适中,解答本题的关键在于将角的相等转换成边相等.三、解答题(本题共2小题,每小题6分,共12分)19.(6分)(2013•长沙)计算:.【考点】M11A 实数的混合运算;M11O 指数幂;M113 绝对值;M11P 乘方.【分析】先将每一项的值求出来,然后进行实数的运算即可得出答案.【难度】容易题【解答】解:原式=3+4﹣1=6.(6分)【点评】本题是一道计算题,考查了考生的计算功底,做计算类题型时一定要细心运算,防止粗心大意,解决本题的关键是熟练掌握指数幂、绝对值以及乘方等考点的运算.20.(6分)(2013•长沙)解不等式组并将其解集在数轴上表示出来.【考点】M12J 解一元一次不等式(组);M12M 在数轴上表示不等式(组)的解集.【分析】此题较为简单,首先分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.【难度】容易题【解答】解:由①得,x≤1;由②得,x>﹣2,故此不等式组的解集为:﹣2<x≤1.(4分)在数轴上表示为:(6分)【点评】本题重点考查的是解一元一次不等式组等知识,难度不大,充分掌握不等式解集在数轴上的表示方法是解答此题的关键.四、解答题(本大题共2小题,每小题8分,共16分)21.(8分)(2013•长沙)“宜居长沙”是我们的共同愿景,空气质量倍受人们的关注.我市某空气质量检测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:(1)统计图共统计了天空气质量情况.(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形圆心角度数.(3)从小源所在班级的40名同学中,随机选取一名同学去该空气质量监测点参观,则恰好选到小源的概率是多少?【考点】M216 统计图(扇形、条形、折线);M222 概率的计算;M344 圆心角与圆周角.【分析】(1)从统计图中可以看出,良的天数是70天,占70%,即可求得统计的总天数;(2)要求空气质量为“优”所在扇形圆心角度数,直接利用360度乘以对应的百分比即可求解;(3)直接利用概率公式即可求解.【难度】中等题【解答】解:(1)70÷70%=100(天),故答案是:100;(2分)(2)空气质量为“优”所在扇形圆心角度数是:360°×20%=72°;如图所示:(5分)(3)班级的40名同学中,随机选取一名同学去该空气质量监测点参观,则恰好选到小源的概率是.(8分)【点评】本题重点考查了条形统计图和扇形统计图的综合运用,同时也考查了概率的计算,难度适中,需要考生有一定的读图能力并能从图表中获取必要的解题信息.22.(8分)(2013•长沙)如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.【考点】M348 切线的性质与判定;M343 扇形、弓形M34D 直线与圆的位置关系M325 三角形的面积、周长M344 圆心角与圆周角M328 等边三角形性质与判定.【分析】(1)要证BC是⊙O的切线,首先求出∠ADB的度数,求出∠ABD+∠DBC=90°,根据切线判定推出即可;(2)已知⊙O的半径为2,∠BAC=30°,分别求出等边三角形DOB面积和扇形DOB面积,即可求出答案.【难度】中等题【解答】(1)证明:∵AB为⊙O直径,∴∠ADB=90°,∴∠BAC+∠ABD=90°,∵∠DBC=∠BAC,∴∠DBC+∠ABD=90°,∴AB⊥BC,(3分)∵AB为直径,∴BC是⊙O切线;(4分)(2)解:连接OD,过O作OM⊥BD于M,∵∠BAC=30°,∴∠BOD=2∠A=60°,∵OB=OD,∴△OBD是等边三角形,∴OB=BD=OD=2,∴BM=DM=1,(7分)由勾股定理得:OM=,﹣S△DOB=﹣×2×=π﹣.(8分)∴阴影部分的面积S=S扇形DOB【点评】本题重点考查了切线的性质与判定、扇形面积,直线与圆的位置关系、等边三角形的性质和判定等知识,难度适中,三角形与圆的综合题属于中考常考知识点,需要考生牢牢掌握相关性质来解题.本题的解题关键是分别求出扇形DOB和三角形DOB的面积.五、解答题(本题共2小题,每小题9分,共18分)23.(9分)(2013•长沙)为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.(1)求1号线,2号线每千米的平均造价分别是多少亿元?(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?【考点】M12F 解二元一次方程组M12G 二元一次方程组的应用.【分析】(1)要求的是1号线,2号线每千米的平均造价,直接设1号线,2号线每千米的平均造价分别是x亿元,y亿元,根据“修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线的平均造价多0.5亿元”分别得出等式求出即可;(2)由第(1)问中所求得出建91.8千米的地铁线网每千米的造价,进而求出即可.【难度】中等题【解答】解:(1)设1号线,2号线每千米的平均造价分别是x亿元,y亿元,由题意得出:,(2分)解得:,(4分)答:1号线,2号线每千米的平均造价分别是6亿元和5.5亿元;(5分)(2)由(1)得出:91.8×6×1.2=660.96(亿元),(8分)答:还需投资660.96亿元.(9分)【点评】本题是一道应用题,主要考查了二元一次方程组的应用,解答此类题型的关键是要学会在题目中找到合适的等量关系并列出方程解答,须注意的是应用题一定要作答.24.(9分)(2013•长沙)如图,在平行四边形ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.(1)求证:△ABN≌△CDM;(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.【考点】M332 平行四边形的性质与判定;M32A 全等三角形性质与判定;M329 直角三角形性质与判定M32D 特殊角三角函数的值M328 等边三角形性质与判定.【分析】(1)要证△ABN≌△CDM,首先由四边形ABCD是平行四边形,可得AB=CD,AD=BC,∠B=∠CDM,又由M、N分别是AD,BC的中点,即可利用SAS证得△ABN≌△CDM;(2)要求AN的长,由△ABN≌△CDM得AN=CM,转换成求CM的长,求出∠MND=∠CND=∠2=30°,证出△CNM是等边三角形,从而求出AN=CM=2.【难度】较难题【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠B=∠CDM,∵M、N分别是AD,BC的中点,∴BN=DM,(2分)∵在△ABN和△CDM中,,∴△ABN≌△CDM(SAS);(4分)(2)解:∵M是AD的中点,∠AND=90°,∴MN=MD=AD,∴∠1=∠MND,∵AD∥BC,∴∠1=∠CND,∵∠1=∠2,∴∠MND=∠CND=∠2,∴PN=PC,(5分)∵CE⊥MN,∴∠CEN=90°,∠END+∠CNP+∠2=180°﹣∠CEN=90°又∵∠END=∠CNP=∠2∴∠2=∠PNE=30°,∵PE=1,∴PN=2PE=2,∴CE=PC+PE=3,∴CN==2,(7分)∵∠MNC=60°,CN=MN=MD,∴△CNM是等边三角形,∵△ABN≌△CDM,∴AN=CM=2.(9分)【点评】本题重点考查了平行四边形的性质、全等三角形性质与判定、直角三角形的性质、等边三角形性质与判定以及特殊角三角函数的值等知识点,有一定难度,属于中考常考知识点,解题关键是要熟练掌握这些性质,同时也要注意数形结合思想的应用.六、解答题(本大题共2小题,每小题10分,共20分)25.(10分)(2013•长沙)设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.(1)反比例函数y=是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;(3)若二次函数y=x2﹣x﹣是闭区间[a,b]上的“闭函数”,求实数a,b的值.【考点】M162 二次函数的的图象、性质M165 二次函数的最值M142 一次函数的的图象、性质M152 反比例函数的的图象、性质M12G 二元一次方程组的应用M12F 解二元一次方程组.【分析】(1)根据题意,由反比例函数y=的单调区间进行判断;(2)此问不难,但需要分k>0或k<0两种情况讨论,根据新定义运算法则列出关于系数k、b的方程组或,通过解该方程组即可求得系数k、b的值;(3)此问比较复杂,已知y=x2﹣x﹣=(x﹣2)2﹣,所以该二次函数的图象开口方向向上,最小值是﹣,且当x<2时,y随x的增大而减小;当x >2时,y随x的增大而增大;根据新定义运算法则列出关于系数a、b的方程组或,通过解方程组即可求得a、b的值.【难度】较难题【解答】解:(1)反比例函数y=是闭区间[1,2013]上的“闭函数”.理由如下:反比例函数y=在第一象限,y随x的增大而减小,当x=1时,y=2013;当x=2013时,y=1,所以,当1≤x≤2013时,有1≤y≤2013,符合闭函数的定义,故反比例函数y=是闭区间[1,2013]上的“闭函数”;(3分0(2)分两种情况:k>0或k<0.①当k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=x;(5分)②当k<0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而减小,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=﹣x+m+n;(6分)(3)∵y=x2﹣x﹣=(x﹣2)2﹣,∴该二次函数的图象开口方向向上,最小值是﹣,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大;(7分)①当a≤2时,此二次函数y随x的增大而减小,则根据“闭函数”的定义知,,解得,(不合题意,舍去)或;②当a<2<b时,此时二次函数y=x2﹣x﹣的最小值是﹣=a,根据“闭函数”的定义知,b=a2﹣a﹣或b=b2﹣b﹣;a)当b=a2﹣a﹣时,由于b=(﹣)2﹣×(﹣)﹣=<2,不合题意,舍去;b)当b=b2﹣b﹣时,解得b=,由于b>2,所以b=;③当a≥2时,此二次函数y随x的增大而增大,则根据“闭函数”的定义知,,解得,,∵<0,∴舍去.综上所述,或.(10分)【点评】本题重点考查了二次函数的图象、性质,反比例函数图象的性质以及一次函数图象的性质,同时也考查了二次函数的最值以及二元一次方程组的应用,综合性较强,难度较大,解题关键是读懂题意,弄清楚“闭函数”的定义,同时也要注意“分类讨论”数学思想的应用.26.(10分)(2013•长沙)如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.(1)求∠OAB的度数;(2)求证:△AOF∽△BEO;(3)当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:S1+S2是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.【考点】M142 一次函数的的图象、性质M327 等腰三角形性质与判定M329 直角三角形性质与判定M32B 勾股定理M325 三角形的面积、周长M338 四边形的面积M34F 圆的相关计算M165 二次函数的最值M31C 平行线的判定及性质M333 矩形的性质与判定.【分析】(1)要求∠OAB的度数,首先得求OA与OB的长,当x=0或y=0时分别可以求出y的值和x的值就可以求出OA与OB的值,从而就可以得出结论;(2)已经求出∠OAB=45°,可知△AOB是等腰直角三角形,所以AB:OA=:1,根据平行线的性质可以得出,,就可以得出.再由∠OAF=∠EBO=45°就可以得出结论;(3)此问有一定难度,首先根据E、F的坐标表示出相应的线段,由勾股定理求出线段AE、EF、BF组成的三角形为直角三角形,且EF为斜边,则可以表示此三角形的外接圆的面积S1,再由梯形的面积公式和三角形的面积公式就可以表示出S2,就可以表示出和的解析式,再由如此函数的性质就可以求出最值.【难度】较难题【解答】解:(1)∵直线y=﹣x+2,∴当x=0时,y=2,B(0,2),当y=0时,x=2,A(2,0)∴OA=OB=2.∵∠AOB=90°∴∠OAB=45°;(3分)(2)∵四边形OMPN是矩形,∴PM∥ON,NP∥OM,∴,,∴BE=OM,AF=ON,∴BE•AF=OM•ON=2OM•ON.∵矩形PMON的面积为2,∴OM•ON=2∴BE•AF=4.∵OA=OB=2,∴OA•OB=4,∴BE•AF=OA•OB,即.(4分)∵∠OAF=∠EBO=45°,∴△AOF∽△BEO;(6分)(3)∵四边形OMPN是矩形,∠OAF=∠EBO=45°,∴△AME、△BNF、△PEF为等腰直角三角形.∵E点的横坐标为a,E(a,2﹣a),∴AM=EM=2﹣a,∴AE2=2(2﹣a)2=2a2﹣8a+8.∵F的纵坐标为b,F(2﹣b,b)∴BN=FN=2﹣b,∴BF2=2(2﹣b)2=2b2﹣8b+8.∴PF=PE=a+b﹣2,∴EF2=2(a+b﹣2)2=2a2+4ab+2b2﹣8a﹣8b+8.∵ab=2,∴EF2=2a2+2b2﹣8a﹣8b+16∴EF2=AE2+BF2.∴线段AE、EF、BF组成的三角形为直角三角形,且EF为斜边,则此三角形的外接圆的面积为S1=EF2=•2(a+b﹣2)2=(a+b﹣2)2.(8分)∵S=(PF+OM)•PM,S△PEF=PF•PE,S△OME=OM•EM,梯形OMPF∴S2=S梯形OMPF﹣S△PEF﹣S△OME,=(PF+OM)•PM﹣PF•PE﹣OM•EM,=[PF(PM﹣PE)+OM(PM﹣EM)],=(PF•EM+OM•PE),=PE(EM+OM),=(a+b﹣2)(2﹣a+a),=a+b﹣2.∴S1+S2=(a+b﹣2)2+a+b﹣2.设m=a+b﹣2,则S1+S2=m2+m=(m+)2﹣,∵面积不可能为负数,∴当m>﹣时,S1+S2随m的增大而增大.当m最小时,S1+S2最小.∵m=a+b﹣2=a+﹣2=(﹣)2+2﹣2,∴当=,即a=b=时,m最小,最小值为2﹣2∴S1+S2的最小值=(2﹣2)2+2﹣2,=2(3﹣2)π+2﹣2.(10分)【点评】本题考查了一次函数的的图象、性质、等腰直角三角形的性质、勾股定理、二次函数的最值、平行线的判定及性质、矩形的性质与判定、梯形的面积公式的运用、三角形的面积公式、圆的面积公式等众多知识点,综合性较强,难度较大,需要考生有扎实的数学基础,能够综合运用所学知识进行解题,同时要注意数形结合思想的运用.。
2013年湖南省中考数学压轴题解析汇编

【2013·湖南长沙·26题】如图,在平面直角坐标系中,直线y=-x+2与x轴、y轴交于点A、B,动点P(a,b)在第一象限内,由点P向x轴、y轴所作的垂线PM、PN(垂足为M、N)分别与直
AF的中点,连接MB、ME。
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
【2013·湖南衡阳·28题】如图,在平面直角坐标系中,已知A(8,0),B(0,6),⊙M经过原点O及点A、B。
(1)求⊙M的半径及圆心M的坐标;
(2)过点B作⊙M的切线l,求直线l的解析式;
(3)∠BOA的平分线交AB于点N,交⊙M于点E,求点N的坐标和线段OE的长
【2013·湖南湘潭·26题】如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,
2),抛物线
C点。
(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在直线l。
当l移动到何处时,恰好将△ABC的面积分为相等的两部分?
(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标,若不存在,说明理由。
【
,B三点为顶点的三角形与以、D
B
B
,请问
B
P
【。
◇2013年长沙中考数学试题和答案√

湖南省长沙市2013年中考数学试卷一、选择题(本题共10个小题,每小题3分,共30分)1.下列实数是无理数的是()A.﹣1 B.0C.D.2.小星同学在“百度”搜索引擎中输入“中国梦,我的梦”,能搜索到与之相关的结果的条数约为61700000,这个数用科学记数法表示为()A.617×105B.6.17×106C.6.17×107D.0.617×1083.如果一个三角形的两边长分别为2和4,则第三边长可能是()A.2 B.4C.6D.84.已知⊙O1的半径为1cm,⊙O2的半径为3cm,两圆的圆心距O1O2为4cm,则两圆的位置关系是()A.外离B.外切C.相交D.内切5.下列计算正确的是()A.a6÷a3=a3B.(a2)3=a8C.(a﹣b)2=a2﹣b2D.a2+a2=a4A.192 B.188 C.186 D.1807.下列各图中,∠1大于∠2的是()A.B.C.D.8.下列多边形中,内角和与外角和相等的是()A.四边形B.五边形C.六边形D.八边形9.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是()A.B.C.D.10.二次函数y=ax2+bx+c的图象中如图所示,则下列关系式错误的是()A.a>0 B.c>0 C.b2﹣4ac>0 D.a+b+c>0二、填空题(本题共8小题,每小题3分,共24分)11.计算:﹣=.12.分解因式:x2+2x+1=.13.已知∠A=67°,则∠A的余角等于度.14.方程的解为x=.15.如图,BD是∠ABC的平分线,P为BD上的一点,PE⊥BA于点E,PE=4cm,则点P到边BC 的距离为cm.16.如图,在△ABC中,点D,点E分别是边AB,AC的中点,则△ADE和△ABC的周长之比等于.17.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是.18.如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是.三、解答题本题共2小题,每小题6分,共12分)19.(6分)计算:.20.(6分)解不等式组并将其解集在数轴上表示出来.四、解答题(本大题共2小题,每小题8分,共16分)21.(8分)“宜居长沙”是我们的共同愿景,空气质量倍受人们的关注.我市某空气质量检测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:(1)统计图共统计了100天空气质量情况.(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形圆心角度数.(3)从小源所在班级的40名同学中,随机选取一名同学去该空气质量监测点参观,则恰好选到小源的概率是多少?22.(8分)如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.五、解答题(本题共2小题,每小题9分,共18分)23.(9分)为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.(1)求1号线,2号线每千米的平均造价分别是多少亿元?(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?解:(1)设1号线,2号线每千米的平均造价分别是x亿元,y亿元,24.(9分)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.(1)求证:△ABN≌△CDM;(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.六、解答题(本大题共2小题,每小题10分,共20分)25.(10分)设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.(1)反比例函数y=是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;(3)若二次函数y=x2﹣x﹣是闭区间[a,b]上的“闭函数”,求实数a,b的值.26.(10分)如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.(1)求∠OAB的度数;(2)求证:△AOF∽△BEO;(3)当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:S1+S2是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.湖南省长沙市2013年中考数学试卷一、选择题(本题共10个小题,每小题3分,共30分)1.下列实数是无理数的是(D)A.﹣1 B.0C.D.2.小星同学在“百度”搜索引擎中输入“中国梦,我的梦”,能搜索到与之相关的结果的条数约为61700000,这个数用科学记数法表示为(C)A.617×105B.6.17×106C.6.17×107D.0.617×1083.如果一个三角形的两边长分别为2和4,则第三边长可能是(B)A.2 B.4C.6D.84.已知⊙O1的半径为1cm,⊙O2的半径为3cm,两圆的圆心距O1O2为4cm,则两圆的位置关系是(B)A.外离B.外切C.相交D.内切5.下列计算正确的是(A)A.a6÷a3=a3B.(a2)3=a8C.(a﹣b)2=a2﹣b2D.a2+a2=a4A.192 B.188 C.186 D.1807.下列各图中,∠1大于∠2的是(D)A.B.C.D.8.下列多边形中,内角和与外角和相等的是(A)A.四边形B.五边形C.六边形D.八边形9.在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是(C)A.B.C.D.10.二次函数y=ax2+bx+c的图象中如图所示,则下列关系式错误的是(D)A.a>0 B.c>0 C.b2﹣4ac>0 D.a+b+c>011.计算:﹣=.12.分解因式:x2+2x+1=(x+1)2.13.已知∠A=67°,则∠A的余角等于23度.14.方程的解为x=1.15.如图,BD是∠ABC的平分线,P为BD上的一点,PE⊥BA于点E,PE=4cm,则点P到边BC 的距离为4cm.16.如图,在△ABC中,点D,点E分别是边AB,AC的中点,则△ADE和△ABC的周长之比等于1:2.17.在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是10.18.如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是3.三、解答题本题共2小题,每小题6分,共12分)19.(6分)计算:.解:原式=3+4﹣1=6.20.(6分)解不等式组并将其解集在数轴上表示出来.解:由①得,x≤1;由②得,x>﹣2,故此不等式组的解集为:﹣2<x≤1.在数轴上表示为:21.(8分)“宜居长沙”是我们的共同愿景,空气质量倍受人们的关注.我市某空气质量检测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:(1)统计图共统计了100天空气质量情况.(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形圆心角度数.(3)从小源所在班级的40名同学中,随机选取一名同学去该空气质量监测点参观,则恰好选到小源的概率是多少?解:(1)70÷70%=100(天),故答案是:100;(2)空气质量为“优”所在扇形圆心角度数是:360°×20%=72°;(3)班级的40名同学中,随机选取一名同学去该空气质量监测点参观,则恰好选到小源的概率是.22.(8分)如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.(1)证明:∵AB为⊙O直径,∴∠ADB=90°,∴∠BAC+∠ABD=90°,∵∠DBC=∠BAC,∴∠DBC+∠ABD=90°,∴AB⊥BC,∵AB为直径,∴BC是⊙O切线;(2)解:连接OD,过O作OM⊥BD于M,∵∠BAC=30°,∴∠BOD=2∠A=60°,∵OB=OD,∴OB=BD=OD=2,∴BM=DM=1,由勾股定理得:OM=,∴阴影部分的面积S=S扇形DOB﹣S△DOB=﹣×2×=π﹣.五、解答题(本题共2小题,每小题9分,共18分)23.(9分)为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.(1)求1号线,2号线每千米的平均造价分别是多少亿元?(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?解:(1)设1号线,2号线每千米的平均造价分别是x亿元,y亿元,由题意得出:,解得:,答:1号线,2号线每千米的平均造价分别是6亿元和5.5亿元;(2)由(1)得出:91.8×6×1.2=660.96(亿元),答:还需投资660.96亿元.24.(9分)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.(1)求证:△ABN≌△CDM;(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠B=∠CDM,∵M、N分别是AD,BC的中点,∴BN=DM,∵在△ABN和△CDM中,,∴△ABN≌△CDM(SAS);(2)解:∵M是AD的中点,∠AND=90°,∴MN=MD=AD,∴∠1=∠MND,∵AD∥BC,∴∠1=∠CND,∵∠1=∠2,∴∠MND=∠CND=∠2,∴PN=PC,∵CE⊥MN,∴∠CEN=90°,∴∠2=∠PNE=30°,∵PE=1,∴PN=2PE=2,∴CE=PC+PE=3,∴CN==2,∵∠MNC=60°,CN=MN=MD,∴△CNM是等边三角形,∵△ABN≌△CDM,∴AN=CM=2.六、解答题(本大题共2小题,每小题10分,共20分)25.(10分)设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.(1)反比例函数y=是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;(3)若二次函数y=x2﹣x﹣是闭区间[a,b]上的“闭函数”,求实数a,b的值.分析:(1)根据反比例函数y=的单调区间进行判断;(2)根据新定义运算法则列出关于系数k、b的方程组或,通过解该方程组即可求得系数k、b的值;(3)y=x2﹣x﹣=(x﹣2)2﹣,所以该二次函数的图象开口方向向上,最小值是﹣,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大;根据新定义运算法则列出关于系数a、b的方程组或,通过解方程组即可求得a、b的值.解答:解:(1)反比例函数y=是闭区间[1,2013]上的“闭函数”.理由如下:反比例函数y=在第一象限,y随x的增大而减小,当x=1时,y=2013;当x=2013时,y=1,所以,当1≤x≤2013时,有1≤y≤2013,符合闭函数的定义,故反比例函数y=是闭区间[1,2013]上的“闭函数”;(2)分两种情况:k>0或k<0.①当k>0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而增大,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=x;②当k<0时,一次函数y=kx+b(k≠0)的图象是y随x的增大而减小,故根据“闭函数”的定义知,,解得.∴此函数的解析式是y=﹣x+m+n;(3)∵y=x2﹣x﹣=(x﹣2)2﹣,∴该二次函数的图象开口方向向上,最小值是﹣,且当x<2时,y随x的增大而减小;当x>2时,y随x的增大而增大;①当b≤2时,此二次函数y随x的增大而减小,则根据“闭函数”的定义知,,解得,(不合题意,舍去)或;②当a<2<b时,此时二次函数y=x2﹣x﹣的最小值是﹣=a,根据“闭函数”的定义知,b=a2﹣a﹣、b=b2﹣b﹣;a)当b=a2﹣a﹣时,由于b=(﹣)2﹣×(﹣)﹣=<2,不合题意,舍去;b)当b=b2﹣b﹣时,解得b=,由于b>2,所以b=;③当a≥0时,此二次函数y随x的增大而增大,则根据“闭函数”的定义知,,解得,,∵<0,∴舍去.综上所述,或.26.(10分)如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.(1)求∠OAB的度数;(2)求证:△AOF∽△BEO;(3)当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:S1+S2是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.解:(1)∵直线y=﹣x+2,∴当x=0时,y=2,B(0,2),当y=0时,x=2,A(2,0)∴OA=OB=2.∵∠AOB=90°∴∠OAB=45°;(2)∵四边形OAPN是矩形,∴PM∥ON,NP∥OM,∴,,∴BE=OM,AF=ON,∴BE•AF=OM•ON=2OM•ON.∵矩形PMON的面积为2,∴OM•ON=2∴BE•AF=4.∵OA=OB=2,∴OA•OB=4,∴BE•AF=OA•OB,即.∵∠OAF=∠EBO=45°,∴△AOF∽△BEO;(3)∵四边形OAPN是矩形,∠OAF=∠EBO=45°,∴△AME、△BNF、△PEF为等腰直角三角形.∵E点的横坐标为a,E(a,2﹣a),∴AM=EM=2﹣a,∴AE2=2(2﹣a)2=2a2﹣8a+8.∵F的纵坐标为b,F(2﹣b,b)∴BN=FN=2﹣b,∴BF2=2(2﹣b)2=2b2﹣8b+8.∴PF=PE=a+b﹣2,∴EF2=2(a+b﹣2)2=2a2+4ab+2b2﹣8a﹣8b+8.∵ab=2,∴EF2=2a2+2b2﹣8a﹣8b+16∴EF2=AE2+BF2.∴线段AE、EF、BF组成的三角形为直角三角形,且EF为斜边,则此三角形的外接圆的面积为S1=EF2=•2(a+b﹣2)2=(a+b﹣2)2.∵S梯形OMPF=(PF+ON)•PM,S△PEF=PF•PE,S△OME=OM•EM,∴S2=S梯形OMPF﹣S△PEF﹣S△OME,=(PF+ON)•PM﹣PF•PE﹣OM•EM,=[PF(PM﹣PE)+OM(PM﹣EM)],=(PF•EM+OM•PE)=PE(EM+OM),=(a+b﹣2)(2﹣a+a)=a+b﹣2.∴S1+S2=(a+b﹣2)2+a+b﹣2.设m=a+b﹣2,则S1+S2=m2+m=(m+)2﹣,∵面积不可能为负数,∴当m>﹣时,S1+S2随m的增大而增大.当m最小时,S1+S2最小.∵m=a+b﹣2=a+﹣2=(﹣)2+2﹣2,∴当=,即a=b=时,m最小,最小值为2﹣2∴S1+S2的最小值=(2﹣2)2+2﹣2,=2(3﹣2)π+2﹣2.。
2013年湖南省长沙市中考数学试卷

2013年湖南省长沙市中考数学试卷(数学)注意事项:1.答题前,请考生先将自己的姓名、准考证号填写清楚,并认真核对条形码上的姓名、准考证号、考室和座位号;2.必须在答题卡上答题,在草稿纸、试题卷上答题无效; 3.答题时,请考生注意各大题题号后面的答题提示; 4.请勿折叠答题卡,保持字体工整、笔迹清晰、卡面清洁; 5.答题卡上不得使用涂改液、涂料胶和贴纸;6.本学科试卷共26个小题,考试时量120分钟,满分120分.一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本题共10个小题,每小题3分,共30分) 1.下列实数是无理数的是( ) A.-1 B.0 C.21D.3 2.小星同学在“百度”搜索引擎中;输入“中国梦,我的梦”,能搜索到与之相关的结果的条数约为61 700 000,这个数用科学记数法表示为( ) **×105 B.6.17×106 C.6.17×107 D.0.617×1083.如果一个三角形的两边长分别为2和4,则第三边长可能是( ) ** B.4 C.6 D.84.已知⊙O 1的半径为1㎝、⊙O 2的半径为3㎝,两圆的圆心距O 1O 2为4㎝,则两圆的位置关系是( )A.外离B.外切C.相交D.内切 5.下列计算正确的是( ) A.336a aa=÷ B.()832a a= C.()222b a b a -=- D.422a a a =+6.某校篮球队12名同学的身高如下表:身高(㎝) 180 186 188 192 195 人 数12531则该校篮球队12名同学身高的众数是(单位:㎝)( ) ** B.188 C.186 D.180 7.下列各图中,∠1大于∠2的是( )8.下列多边形中,内角和与外角和相等的是( ) A.四边形 B.五边形 C.六边形 D.八边形9.在下列某品牌T 恤的四个洗涤说明图案的设计中,没有..运用旋转或轴对称知识的是( )10.二次函数c bx axy ++=2的图象如图所示,则下列关系错误..的是( ) A. a >0 B. c >0 C. ac b 42->0 D. a +b +c >0 二、填空题(本题共8个小题,每小题3分,共24分) 11.计算:28-= .12.因式分解:122++x x = . 13.已知∠A=67°,则∠A 的余角等于 度. 14.方程xx 112=+的解为x = .15.如图,BD 是∠ABC 的平分线,P 是BD 上的一点,PE ⊥BA 于点E ,PE=4㎝,则点P 到边BC 的距离为 ㎝.16.如图,在⊿ABC 中,点D ,点E 分别是边AB ,AC 的中点,则⊿ADE 与⊿ABC 的周长之比等于 .17.在一个不透明的盒子中装有n 个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复摸球实验后发现,摸到红的频率稳定于0.2,那么可以推算出n 大约是 .21(AB=AC )CB Aba21(a b )ba 21D21C BAOxy-11ABCDAB C D(第10题)18.如图,在梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AE ∥CD 交BC 于点E ,若AD=2,BC=5,则CD 的长是 .三、解答题(本题共2个小题,每小题6分,共12分) 19.计算:()()021523+--+-20.解不等式组()⎩⎨⎧-+≤+xx x x 34312π并将其解集在数轴上表示出来.四、解答题(本题共2个小题,每小题8分,共16分)21.“宜居长沙”是我们的共同愿景,空气质量倍受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月至4月份若干天的空气质量情况,并绘制了如下不完整的统计图,请根据图中信息,解答下列问题:(1)统计图共统计了 天的空气质量情况.EPD CBA E D CBA E DCB A-4-3-2430-121各类空气质量天数条形统计图天数类别中度污染轻度污染良优287070503010各类空气质量天数扇形统计图中度污染轻度污染良70%优20%(第15题)(第16题) (第18题)(第21题)(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形的圆心角度数.(3)从小源所在班级的40名同学中,随机选取一名同学去该空气质量监测站点参观,则恰好选到小源的概率是多少?22.如图,△ABC 中,以AB 为直径的⊙O 交AC 于点D ,∠DBC=∠BAC. (1)求证:BC 是⊙O 的切线;(2)若⊙O 的半径为2,∠BAC=30°,求图中阴影部分的面积.五、解答题(本题共2个小题,每小题9分,共18分)23.为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线..已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.(1)求1号线,2号线每千米的平均造价分别是多少亿元?(2)除1,2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网,据预算,这91.8千米地铁线网每千米的平均造价是1号线的平均造价的1.2倍,则还需投资多少亿元?24.如图,在□ABCD 中,M ,N 分别是AD ,BC 的中点,∠AND=90°,连接CM 交DN 于OD CB A(第22题)点O.(1)求证:△ABN ≌△CDM ;(2)过点C 作CE ⊥MN 于点E ,交DN 于点P ,若PE=1,∠1=∠2,求AN 的长.六、解答题(本题共2个小题,每小题10分,共20分)25.设a ,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为[]a,b .对于一个函数,如果它的自变量x 与函数值y 满足:当m≤x ≤n 时 ,有m≤y ≤n ,我们就称此函数是闭区间[]m,n 上的“闭函数”. (1)反比例函数xy 2013=是闭区间[]20131,上的“闭函数”吗?请判断并说明理由; (2)若一次函数()0≠+=k b kx y 是闭区间[]m,n 上的“闭函数”,求此函数的解析式;(3)若二次函数5754512--=x x y 是闭区间[]a,b 上的“闭函数”,求实数a ,b 的值.26.如图,在平面直角坐标系中,直线2+-=x y 与x 轴,y 轴分别交于点A ,点B ,动P NMEO D21CBA(第24题)点P (a ,b )在第一象限内,由点P 向x 轴,y 轴所作的垂线PM ,PN (垂足为M ,N )分别与直线AB 相交于点E ,点F ,当点P (a ,b )运动时,矩形PMON 的面积为定值2. (1)求∠OAB 的度数; (2)求证:△AOF ∽△BEO ;(3)当点E ,F 都在线段AB 上时,由三条线段AE ,EF ,BF 组成一个三角形,记此三角形的外接圆面积为S 1,⊿OEF 的面积为S 2.试探究:S 1+S 2是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.FNMEP Oxy B A(第26题)2013年湖南省长沙市中考数学试卷答案及解析一、选择题1、D 【详解】根据无理数的定义可知,只有D是无理数.2、C 【详解】根据科学记数法的定义可知选C.3、B 【详解】三角形任意两边之和大于第三边、任意两边之差小于第三边,只有B符合.4、B 【详解】因为1+3=4,即两圆半径之和等于圆心距,所以两圆外切.5、A 【详解】B、(a2)3=a2×3=a6C、(a-b)2=a2-2ab+b2D、a2+a2=2a26、B 【详解】众数就是出现次数最多的数,表格中188出现了5次,是最多的,所以12名同学身高的众数是188,选B.7、D 【详解】A、△ABC是等腰三角形,所以∠1=∠2;B、∠1与∠2是对顶角,所以∠1=∠2;C、对顶角相等与根据两直线平行、同位角相等性质可知∠1与∠2;D、由于∠1是△ABC 的外角,且∠1=∠B+∠2,所以∠1>∠2;综上所述,选D.8、A 【详解】所有多边形的外角和都是360°,而内角和公式为180°(n-2),其中n表示多边形的边数,所以当180°(n-2)=360°时,n=4,即四边形的内角和与外角和相等,选A.9、C 【详解】A、D既是轴对称图形,也是中心对称图形,B是轴对称图形,所以只能选C.10、D 【详解】观察图像可知,该抛物线开口向上,所以a>0,即A对;抛物线与y轴的交点在x轴上方,所以c>0,即B对;抛物线与x轴有两个交点,所以b2-4ac>0,即C 对;当x=1时,最小值为a+b+c,抛物线顶点在x轴下方,所以a+b+c<0,所以D错.二、填空题13、23【详解】如果两角互余,那么这两个角的和为90°,所以∠A的余角等于90°-67°=23°.15、4【详解】根据角平分线的性质可知,角平分线上的点到角两边的距离相等,所以为4cm 16、1:2【详解】由于点D、E分别是AB、AC的中点,即DE是△AB C的中位线,所以DE∥BC、且DE=0.5BC,所以△ADE∽△ABC,两三角形的周长比等于相似比,即为0.5:1=1:2.18、3【详解】因为AE∥CD、AD∥BC,所以∠AEB=∠C=80°、CD=AE、AD=EC;在△ABE中,根据三角形内角和可知∠BAE=180°-80°-50°=50°,即AE=BE=BC-EC=5-2=3,所以CD=3.三、解答题19、6.【详解】原式=3+4-1=6.20、-2<x≤1【详解】因为2(x+1)≤x+3,化简得x≤1;因为x-4<3x,化简得2x>-4,即x>-2;所以该不等式组的解集为-2<x≤1(数轴表示略).四、解答题五、解答题六、解答题(2)过点F 作FH ⊥x 轴于点H ,过点E 作EG ⊥y 轴于点G. ∵P (a ,b ),又E ,F 均在y=-x+2上,∴点E (a ,2-a ),点F (2-b ,b ).∵∠OAB=45°,∴Rt △AFH 中,AF=2FH=2b. 同理,Rt △EGB 中,BE=2EG= 2a.∴在△AOF 和△BEO 中,∠FAO=∠OBE=45°. ① 又AF AO =b22=b 2,BO BE =22a . 又矩形PMON 的面积为定值2,∴ab=2,22a =2b 22 =b 2, ∴AF AO =BO BE .② 综合①②,可知△AOF ∽△BEO.。
精选2013年数学中考压轴题
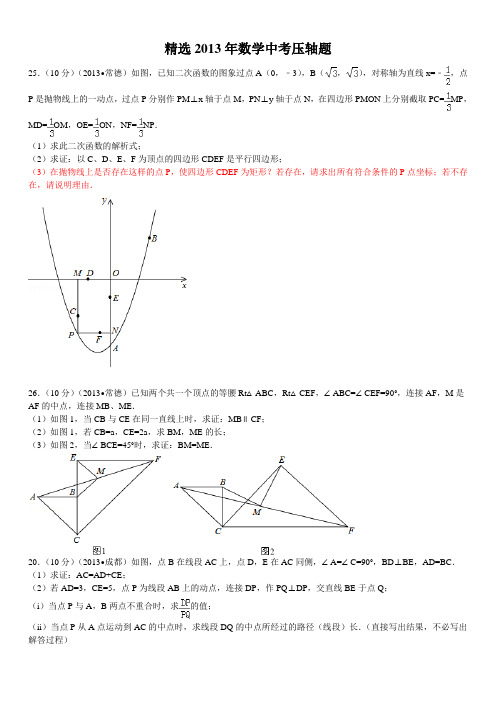
精选2013年数学中考压轴题25.(10分)(2013•常德)如图,已知二次函数的图象过点A(0,﹣3),B(,),对称轴为直线x=﹣,点P是抛物线上的一动点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,在四边形PMON上分别截取PC=MP,MD=OM,OE=ON,NF=NP.(1)求此二次函数的解析式;(2)求证:以C、D、E、F为顶点的四边形CDEF是平行四边形;(3)在抛物线上是否存在这样的点P,使四边形CDEF为矩形?若存在,请求出所有符合条件的P点坐标;若不存在,请说明理由.26.(10分)(2013•常德)已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;(2)如图1,若CB=a,CE=2a,求BM,ME的长;(3)如图2,当∠BCE=45°时,求证:BM=ME.20.(10分)(2013•成都)如图,点B在线段AC上,点D,E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.(1)求证:AC=AD+CE;(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q;(i)当点P与A,B两点不重合时,求的值;(ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长.(直接写出结果,不必写出27.(10分)(2013•成都)如图,⊙O的半径r=25,四边形ABCD内接圆⊙O,AC⊥BD于点H,P为CA延长线上的一点,且∠PDA=∠ABD.(1)试判断PD与⊙O的位置关系,并说明理由;(2)若tan∠ADB=,PA=AH,求BD的长;(3)在(2)的条件下,求四边形ABCD的面积.28.(12分)(2013•成都)在平面直角坐标系中,已知抛物线y=x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;(ii)取BC的中点N,连接NP,BQ.试探究是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.23.(10分)(2013•大连)如图,AB是⊙O的直径,CD与⊙O相切于点C,DA⊥AB,DO及DO的延长线与⊙O 分别相交于点E、F,EB与CF相交于点G.(1)求证:DA=DC;(2)⊙O的半径为3,DC=4,求CG的长.24.(11分)(2013•大连)如图,一次函数y=﹣x+4的图象与x轴、y轴分别相交于点A、B.P是射线BO上的一个动点(点P不与点B重合),过点P作PC⊥AB,垂足为C,在射线CA上截取CD=CP,连接PD.设BP=t.(1)t为何值时,点D恰好与点A重合?(2)设△PCD与△AOB重叠部分的面积为S,求S与t的函数关系式,并直接写出t的取值范围.25.(12分)(2013•大连)将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF.(1)如图1,若∠ABC=α=60°,BF=AF.①求证:DA∥BC;②猜想线段DF、AF的数量关系,并证明你的猜想;(2)如图2,若∠ABC<α,BF=mAF(m为常数),求的值(用含m、α的式子表示).26.(12分)(2013•大连)如图,抛物线y=﹣x2+x﹣4与x轴相交于点A、B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上).分别过点A、B作(2)△MDE能否为等腰直角三角形?若能,求此时点P的坐标;若不能,说明理由;(3)若将“P是抛物线在x轴上方的一个动点(点P、M、C不在同一条直线上)”改为“P是抛物线在x轴下方的一个动点”,其他条件不变,△MDE能否为等腰直角三角形?若能,求此时点P的坐标(直接写出结果);若不能,说明理由.25.(12分)(2013•南平)在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB.设=k.(1)证明:△BGF是等腰三角形;(2)当k为何值时,△BGF是等边三角形?(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.26.(14分)(2013•南平)如图,已知点A(0,4),B(2,0).(1)求直线AB的函数解析式;(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x﹣m)2+n与线段OA交于点C.①求线段AC的长;(用含m的式子表示)②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.24.(12分)(2013•莆田)如图,抛物线y=ax2+bx+c的开口向下,与x轴交于点A(﹣3,0)和点B(1,0).与y 轴交于点C,顶点为D.(1)求顶点D的坐标.(用含a的代数式表示);(2)若△ACD的面积为3.①求抛物线的解析式;②将抛物线向右平移,使得平移后的抛物线与原抛物线交于点P,且∠PAB=∠DAC,求平移后抛物线的解析式.25.(14分)(2013•莆田)在Rt△ABC,∠C=90°,D为AB边上一点,点M、N分别在BC、AC边上,且DM⊥DN.作MF⊥AB于点F,NE⊥AB于点E.(1)特殊验证:如图1,若AC=BC,且D为AB中点,求证:DM=DN,AE=DF;(2)拓展探究:若AC≠BC.①如图2,若D为AB中点,(1)中的两个结论有一个仍成立,请指出并加以证明;②如图3,若BD=kAD,条件中“点M在BC边上”改为“点M在线段CB的延长线上”,其它条件不变,请探究AE 与DF的数量关系并加以证明.25.(12分)(2013•泉州)如图,直线y=﹣x+2分别与x、y轴交于点B、C,点A(﹣2,0),P是直线BC 上的动点.(1)求∠ABC的大小;(2)求点P的坐标,使∠APO=30°;(3)在坐标平面内,平移直线BC,试探索:当BC在不同位置时,使∠APO=30°的点P的个数是否保持不变?若不变,指出点P的个数有几个?若改变,指出点P的个数情况,并简要说明理由.22.(12分)(2013•三明)如图①,AB是半圆O的直径,以OA为直径作半圆C,P是半圆C上的一个动点(P与点A,O不重合),AP的延长线交半圆O于点D,其中OA=4.(1)判断线段AP与PD的大小关系,并说明理由;(2)连接OD,当OD与半圆C相切时,求的长;(3)过点D作DE⊥AB,垂足为E(如图②),设AP=x,OE=y,求y与x之间的函数关系式,并写出x的取值范围.23.(14分)(2013•三明)如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.(1)证明四边形ABCD是菱形,并求点D的坐标;(2)求抛物线的对称轴和函数表达式;(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.25.(12分)(2013•天水)如图1,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点.(1)求抛物线的解析式;(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P 坐标(点P、O、D分别与点N、O、B对应).26.(12分)(2013•天水)如图1,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B 在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;(2)当点P运动到点(,0)时,求此时DP的长及点D的坐标;(3)是否存在点P,使△OPD的面积等于?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.4. 25(广东省)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=3将这副直角三角板按如题25图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如题25图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC=______度;(2)如题25图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围.23.(11分)(2013•梅州)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF 的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.26.(12分)(2013•百色)如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2.C2的图象与x轴交于A、B两点(点A在点B的左侧).(1)求抛物线C2的解析式;(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形?如果存在,请求出点G的坐标;如果不存在,请说明理由.25.(广西河池卷)如图(1),在Rt△ABC, ∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED,连结AD、CF,AD与CF交于点M。
2013年湖南省各地数学综合压轴题集

y
A
O
B
x
答案: (1) k 0 或
6 6 2 1 ; (2) k 0 , x ; (3) (0, )或(0, ) 。 4 4 3 k
第 6 页 共 26 页
【湖南省郴州市】 如图, △ ABC 中,AB BC ,AC 8 , 设 PC x , tan A k ,P 为 AC 边上一动点, 作 PE // AB 交 BC 于 E , PF // BC 交 AB 于 F 。 (1)证明:△ PCE 是等腰三角形; (2) EM 、 FN 、 BH 分别是△ PEC 、△ AFP 、△ ABC 的高,用含 x 和 k 的代数式表示 EM 、 FN 并探究 EM 、 FN 、 BH 之间的数量关系; (3)当 k 4 时,求四边形 PEBF 的面积 S 与 x 的函数关系式。 x 为何值时,S 有最大值?并求出 S 的 最大值?
3 都是 2
y 随 x 的增大而增大,求 k 应满足的条件以及 x 的取值范围;
(3)设抛物线 y kx2 2 x
3 2 2 与 x 轴交于 A( x1 ,0) ,B ( x 2 ,0)两点,且 x1 x2 ,x1 x 2 1 。 2
在 y 轴上,是否存在点 P ,使△ ABP 是直角三角形?若存在,求出点 P 及△ ABP 的面积;若不存在, 请说明理由。
2013 是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由; x
(2)若一次函数 y kx b ( k 0 )是闭区间[ m , n ]上的“闭函数” ,求此函数的解析式; (3)若二次函数 y
1 2 4 7 x x 是闭区间[ a , b ]上的“闭函数”,求实数 a , b 的值。 5 5 5
2013年湖南省长沙市中考数学试卷(含解析版)

2013年湖南省长沙市中考数学试卷一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
请在答题卡中填涂符合题意的选项。
本题共10个小题,每小题3分,共30分)1.(3分)(2013•长沙)下列实数是无理数的是()A.﹣1 B.0C.D.2.(3分)(2013•长沙)小星同学在“百度”搜索引擎中输入“中国梦,我的梦”,能搜索到与之相关的结果的条数约为61700000,这个数用科学记数法表示为()A.617×105B.6.17×106C.6.17×107D.0.617×1083.(3分)(2013•长沙)如果一个三角形的两边长分别为2和4,则第三边长可能是()A.2B.4C.6D.84.(3分)(2013•长沙)已知⊙O1的半径为1cm,⊙O2的半径为3cm,两圆的圆心距O1O2为4cm,则两圆的位置关系是()A.外离B.外切C.相交D.内切5.(3分)(2013•长沙)下列计算正确的是()A.a6÷a3=a3B.(a2)3=a8C.(a﹣b)2=a2﹣b2D.a2+a2=a46.(3分)(2013•长沙)某校篮球队12名同学的身高如下表:身高(cm)180 186 188 192 195人数 1 2 5 3 1则该校篮球队12名同学身高的众数是(单位:cm)()A.192 B.188 C.186 D.1807.(3分)(2013•长沙)下列各图中,∠1大于∠2的是()A.B.C.D.8.(3分)(2013•长沙)下列多边形中,内角和与外角和相等的是()A.四边形B.五边形C.六边形D.八边形9.(3分)(2013•长沙)在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是()A.B.C.D.10.(3分)(2013•长沙)二次函数y=ax2+bx+c的图象中如图所示,则下列关系式错误的是()A.a>0 B.c>0 C.b2﹣4ac>0 D.a+b+c>0二、填空题(本题共8小题,每小题3分,共24分)11.(3分)(2013•长沙)计算:﹣= .12.(3分)(2013•长沙)分解因式:x2+2x+1= .13.(3分)(2013•长沙)已知∠A=67°,则∠A的余角等于度.14.(3分)(2013•长沙)方程的解为x= .15.(3分)(2013•长沙)如图,BD是∠ABC的平分线,P为BD上的一点,PE⊥BA于点E,PE=4cm,则点P到边BC的距离为cm.16.(3分)(2013•长沙)如图,在△ABC中,点D,点E分别是边AB,AC的中点,则△ADE 和△ABC的周长之比等于.17.(3分)(2013•长沙)在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是.18.(3分)(2013•长沙)如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD 交BC于点E,若AD=2,BC=5,则边CD的长是.三、解答题本题共2小题,每小题6分,共12分)19.(6分)(2013•长沙)计算:.20.(6分)(2013•长沙)解不等式组并将其解集在数轴上表示出来.四、解答题(本大题共2小题,每小题8分,共16分)21.(8分)(2013•长沙)“宜居长沙”是我们的共同愿景,空气质量倍受人们的关注.我市某空气质量检测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图,请根据图中信息,解答下列问题:(1)统计图共统计了天空气质量情况.(2)请将条形统计图补充完整,并计算空气质量为“优”所在扇形圆心角度数.(3)从小源所在班级的40名同学中,随机选取一名同学去该空气质量监测点参观,则恰好选到小源的概率是多少?22.(8分)(2013•长沙)如图,△ABC中,以AB为直径的⊙O交AC于点D,∠DBC=∠BAC.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为2,∠BAC=30°,求图中阴影部分的面积.五、解答题(本题共2小题,每小题9分,共18分)23.(9分)(2013•长沙)为方便市民出行,减轻城市中心交通压力,长沙市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.(1)求1号线,2号线每千米的平均造价分别是多少亿元?(2)除1、2号线外,长沙市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?24.(9分)(2013•长沙)如图,在▱ABCD中,M、N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点O.(1)求证:△ABN≌△CDM;(2)过点C作CE⊥MN于点E,交DN于点P,若PE=1,∠1=∠2,求AN的长.六、解答题(本大题共2小题,每小题10分,共20分)25.(10分)(2013•长沙)设a、b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.(1)反比例函数y=是闭区间[1,2013]上的“闭函数”吗?请判断并说明理由;(2)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式;(3)若二次函数y=x2﹣x﹣是闭区间[a,b]上的“闭函数”,求实数a,b的值.26.(10分)(2013•长沙)如图,在平面坐标系中,直线y=﹣x+2与x轴,y轴分别交于点A,点B,动点P(a,b)在第一象限内,由点P向x轴,y轴所作的垂线PM,PN(垂足为M,N)分别与直线AB相交于点E,点F,当点P(a,b)运动时,矩形PMON的面积为定值2.(1)求∠OAB的度数;(2)求证:△AOF∽△BEO;(3)当点E,F都在线段AB上时,由三条线段AE,EF,BF组成一个三角形,记此三角形的外接圆面积为S1,△OEF的面积为S2.试探究:S1+S2是否存在最小值?若存在,请求出该最小值;若不存在,请说明理由.2013年湖南省长沙市中考数学试卷参考答案与试题解析一、选择题(在下列各题的四个选项中,只有一项是符合题意的。
数学中考压轴题

数学中考压轴题(函数)1.图1,已知抛物线211(1)444b y x b x =-++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C . (1)点B 的坐标为______,点C 的坐标为__________(用含b 的代数式表示); (2)请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;(3)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.图12.如图2,已知抛物线的方程C 1:1(2)()y x x m m =-+- (m >0)与x 轴交于点B 、C ,与y 轴交于点E ,且点B 在点C 的左侧.(1)若抛物线C 1过点M (2, 2),求实数m 的值;(2)在(1)的条件下,求△BCE 的面积;(3)在(1)的条件下,在抛物线的对称轴上找一点H ,使得BH +EH 最小,求出点H 的坐标; (4)在第四象限内,抛物线C 1上是否存在点F ,使得以点B 、C 、F 为顶点的三角形与△BCE 相似?若存在,求m的值;若不存在,请说明理由.图2 3.如图3,抛物线经过点A (4,0)、B (1,0)、C (0,-2)三点.(1)求此抛物线的解析式;(2)P 是抛物线上的一个动点,过P 作PM ⊥x 轴,垂足为M ,是否存在点P ,使得以A 、P 、M 为顶点的三角形与△OAC 相似?若存在,请求出符合条件的 点P 的坐标;若不存在,请说明理由;(3)在直线AC 上方的抛物线是有一点D ,使得△DCA 的面积最大,求出点D 的坐标.图3 Be lie vey o u r self,an d t h e n y o uwills u c c e e d !4.已知:如图4,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连结DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在成立,请说明理由.图45.如图5,已知抛物线y =x 2+bx +c 与x 轴交于A 、B 两点(点A 在点B 左侧),与y轴交于点C (0,-3),对称轴是直线x =1,直线BC 与抛物线的对称轴交于点D .(1)求抛物线的函数表达式;(2)求直线BC 的函数表达式; (3)点E 为y 轴上一动点,CE 的垂直平分线交CE 于点F ,交抛物线于P 、Q 两点,且点P 在第三象限.①当线段34PQ AB 时,求tan ∠CED 的值;②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答. 图56.在直角梯形OABC 中,CB //OA ,∠COA =90°,CB =3,OA =6,BA =35.分别以OA 、OC 边所在直线为x 轴、y 轴建立如图1所示的平面直角坐标系.(1)求点B 的坐标;(2)已知D 、E 分别为线段OC 、OB 上的点,OD =5,OE =2EB ,直线DE 交x 轴于点F .求直线DE 的解析式; (3)点M 是(2)中直线DE 上的一个动点,在x 轴上方的平面内是否存在另一点N ,使以O 、D 、M 、N 为顶点的四边形是菱形?若存在,请求出点N 的坐标;若不存在,请说明理由.B e li e v ey o urself,an d t he ny o uwills u c c e e d !图6(1) 图6(2)7.如图7,把两个全等的Rt △AOB 和Rt △COD 方别置于平面直角坐标系中,使直角边OB 、OD 在x 轴上.已知点A (1,2),过A 、C 两点的直线分别交x 轴、y 轴于点E 、F .抛物线y =ax 2+bx +c 经过O 、A 、C 三点.(1)求该抛物线的函数解析式;(2)点P 为线段OC 上的一个动点,过点P 作y 轴的平行线交抛物线于点M ,交x 轴于点N ,问是否存在这样的点P ,使得四边形ABPM 为等腰梯形?若存在,求出此时点P 的坐标;若不存在,请说明理由;(3)若△AOB 沿AC 方向平移(点A 始终在线段AC上,且不与点C 重合),△AOB 在平移的过程中与△COD重叠部分的面积记为S .试探究S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.图7 8.如图8,在平面直角坐标系中,直线112y x =+与抛物线y =ax 2+bx -3交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上的一动点(不与点A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a 、b 及sin ∠ACP 的值;(2)设点P 的横坐标为m . ①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连结PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 的值,使这两个三角形的面积比为9∶10?若存在,直接写出m 的值;若不存在,请说明理由.图8 9.如图9,在平面直角坐标系中,抛物线y =-x 2+2x +3与x 轴交于A 、B 两点,与y轴交于点C ,点D 是抛物线的顶点.(1)求直线AC 的解析式及B 、D 两点的坐标;(2)点P 是x 轴上的一个动点,过P 作直线l //AC 交抛物线于点Q .试探究:随着点P 的运动,在抛物线上是否存在点Q ,使以A 、P 、Q 、C 为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点Q 的坐标;若不存在,请说明理由;(3)请在直线AC 上找一点M ,使△BDM 的周长最小,求出点M 的坐标.图9B e li e v ey o urself,a n d t he n y o uw i l ls u c c eed!10.如图10,抛物线213922y x x =--与x 轴交于A 、B 两点,与y 轴交于点C ,联结BC 、AC . (1)求AB 和OC 的长; (2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合),过点E 作BC 的平行线交AC 于点D .设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变量m 的取值范围; (3)在(2)的条件下,联结CE ,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留π).图10 11.如图11,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D . (1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴; (2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m . ①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形? ②设△BCF 的面积为S ,求S 与m 的函数关系. 图11 12.如图12,在Rt △ABC 中,∠C =90°,AC =6,BC =8,动点P 从点A 开始沿边AC 向点C 以每秒1个单位长度的速度运动,动点Q 从点C 开始沿边CB 向点B 以每秒2个单位长度的速度运动,过点P 作PD //BC ,交AB 于点D ,联结PQ .点P 、Q 分别从点A 、C 同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t 秒(t ≥0). (1)直接用含t 的代数式分别表示:QB =_______,PD =_______; (2)是否存在t 的值,使四边形PDBQ 为菱形?若存在,求出t 的值;若不存在,说明理由,并探究如何改变点Q 的速度(匀速运动),使四边形PDBQ 在某一时刻为菱形,求点Q 的速度; (3)如图2,在整个运动过程中,求出线段PQ 的中点M 所经过的路径长.图12(1) 图12(2)B e l i e v e y o u r s e l f ,a n d t h e n y o u w i l l s u c c e e d !。
