2013年常州市中考数学试题及答案
2013年江苏省十三市中考数学试题(1)
第4题l O 2O 12013年南京中考数学试题一、选择题（本大题共有6小题，共12分，每小题2分．） 1.计算12-7×（-4）+8÷（-2）的结果是A ．-24B ．-20C ．6D ．362.计算23)1·a a （的结果是A ．aB ．5aC ．6aD ．9a3．设边长为3的正方形的对角线长为a.下列关于a 的四种说法：①a 是无理数；②a 可以用数轴上的一个点来表示；③3＜a ＜4；④a 是18的算术平方根。
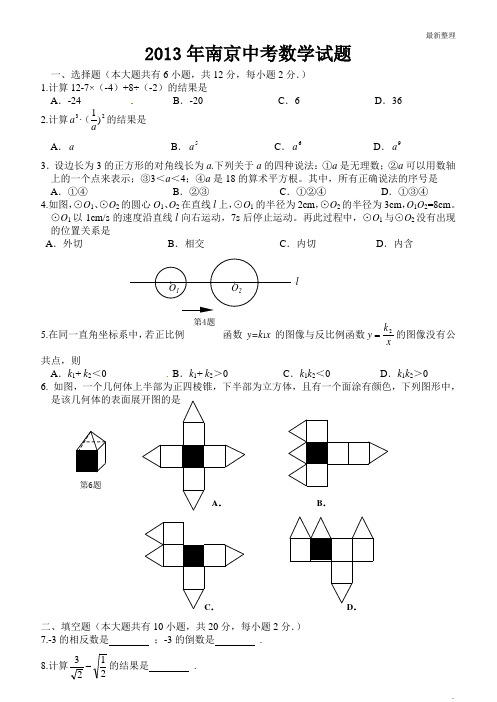
其中，所有正确说法的序号是 A ．①④ B ．②③ C ．①②④ D ．①③④ 4.如图，⊙O 1、⊙O 2的圆心O 1、O 2在直线l 上，⊙O 1的半径为2cm ，⊙O 2的半径为3cm ，O 1O 2=8cm 。
⊙O 1以1cm/s 的速度沿直线l 向右运动，7s 后停止运动。
再此过程中，⊙O 1与⊙O 2没有出现的位置关系是A ．外切B ．相交C ．内切D ．内含函数y=k 1x 的图像与反比例函数xk y 2=的图像没有公5.在同一直角坐标系中，若正比例共点，则A ．k 1+ k 2＜0B ．k 1+ k 2＞0C ．k 1k 2＜0D ．k 1k 2＞06. 如图，一个几何体上半部为正四棱锥，下半部为立方体，且有一个面涂有颜色，下列图形中，是该几何体的表面展开图的是二、填空题（本大题共有10小题，共20分，每小题2分．）7.-3的相反数是 ；-3的倒数是 . 8.计算2123-的结果是 . 第6题A ．B ．C ．D ．F E O D B A 1D'B'C'D CB A 第12题第11题N PMAB9.使式子111-+x 有意义的x 的取值范围是 . 10.第二节亚洲青年运动会将于2013年8月16日至24日在南京举办，在此期间约有13000名青少年志愿者提供服务，将13000用科学计数法表示为 .11.如图将矩形ABCD 绕点A 顺时针旋转到AB ’C ’D ’的位置，旋转角α（0°＜α＜90°）.若 ∠1=110°，则∠α= °.12. 如图，将菱形纸片ABCD 折叠，使点A 恰好落在菱形的对称中心O 处，折痕为EF .若菱形ABCD 的边长为2cm ，∠A =120°，则EF = cm .13.△OAB 是以正多边形相邻的两个顶点A 、B 与它的中心O 为顶点的三角形，若△OAB 的一个内角为70°，则该正多边形的边数为 .14. 已知如图所示的图形的面积为24，根据图中的条件，可列出方程 . 15. 如图，在梯形ABCD 中，AD ∥BC ，AB =DC ，AC 与BD 相交于点P ，已知A （2,3），B (1,1), D (4,3),则点P 的坐标为（ ， ）.16.计算⎪⎭⎫⎝⎛+++⎪⎭⎫ ⎝⎛------⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛----51413121615141312116151413121514131211的结果是.三、解答题（本大题共有11小题，共88分．）17.（6分）化简b a a b a b b a +÷⎪⎭⎫ ⎝⎛---221. 18.（6分）解方程x x x --=-2112219.（8分）如图，在四边形ABCD 中，AB =BC ，对角线BD 平分∠ABC ，P 是BD 上一点，过点P 作PM ⊥AD ，PN ⊥CD ，垂足分别为M 、N.（1）求证：∠ADB =∠CDB ；(2)若∠ADC =90°，求证：四边形MPND 是正方形.x第14题第15题20.（8分）(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各1个，这些球除颜色外都相同，求下列事件的概率：①搅匀后从中任意摸出1个球，恰好是红球；②搅匀后从中任意摸出1个球，记录下颜色后放回袋子中并搅匀，再从中任意摸出1个球，两次都是是红球；（2）某次考试共有6道选择题，每道题所给出的4个选项中，恰有一项是正确的.如果小明从每道题的4个选项中随机的选择一个，那么他6道选择题全部选正确的概率是（ ）A ．41B ．641⎪⎭⎫ ⎝⎛ C ．6411⎪⎭⎫ ⎝⎛- D ．6431⎪⎭⎫ ⎝⎛-21.（9分）某校有2000名学生，为了解全校学生的上学方式，该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查，整理样本数据，得到下列图表：问题：如果名学生全部在同一个年级抽取，这样的抽样是否合理？请说明理由；步行10%其它6%乘私家车 20%乘公共交通工具 30%骑车34% 某校150名学生上学方式 频数分布表 某校150名学生上学方式 扇形统计图（2）根据抽样调查的结果，将估计出的全校2000名学生上学方式的情况绘制成条形统计图：（3）该校数学兴趣小组结合调查获取的信息，向学校提出了一些建议，如：骑车上学的学生数约占全校的34%，建议学生合理安排自行车停车场地，请你结合上述统计的全过程，再提出一条合理化建议： .22.（8分）已知不等臂跷跷板AB 长4m ，如图①，当AB 的一端A 碰到地面时，AB 与地面的夹角为α；如图②，当AB 的另一端B 碰到地面时，AB 与地面的夹角为β.求跷跷板AB 的支撑点O 到地面的高度OH .（用含α、β的式子表示）23.（8分）某商场促销方案规定：商场内所有商品按标价的80%出售，同时，当顾客在商场内700~900某校2000名学生上学方式条形统计图 步行 骑车 乘公共 乘私 其它 上学方式 交通工具 家车 人数 H ① H ②注：300~400表示消费金额大于300元且小于或等于400元，其他类同.根据上述促销方案，顾客在该商场购物可以获得双重优惠，例如，若购买标价为400元的商品，则消费金额为320元，获得的优惠额为400×(1-80%)+30=110（元） （1）购买一件标价为1000元的商品，顾客获得的优惠额是多少？（2）如果顾客购买标价不超过800元的商品，要使获得的优惠额不少于226元，那么该商品的标价至少为多少元？24.（8分）小丽驾车从甲地到乙地，设她出发第x min 时的速度为y km/h ，图中折线表示她在整个驾车过程中第y 与 x 之间的函数关系.（1）小丽驾车的最高速度是 km/h;(2)当20≤x ≤30时，求y 与 x 之间的函数关系式，并求出小丽出发第22min 时的速度； （3）如果汽车每行驶100km 耗油10L ，那么小丽驾车从甲地到乙地共耗油多少升？25.（8分）如图，AD 是⊙O 的切线，切点为A ，AB 是⊙O 的弦，过点B 作BC ∥AD ，交⊙O 于点C ，连接AC ，过点C 作CD ∥AB ，交AD 于点D ，连接AO 并延长交BC 于点M ，交过点C 的直线于点P ，且∠BCP =∠ACD . （1）判断直线PC 与⊙O （2）若AB =9，BC =6，求PC 的长.O y 方法指导 如果物体的运动速度随着时间均匀增加（或减少），那么其在某个时间段内的平均速度为该时间段开始时刻的速度与结束时刻的速度的平均数。
2013常州数学中考模拟试题
2013常州数学中考模拟试题一、选择题（本大题共10小题，每题3分，共30分） 1．下列二次根式中属于最简二次根式的是（ ） A ．44 aB ．48C ．14D ．ba2．抛物线y=-(x-3)2+2的对称轴是（ ） A ．直线x=-3 B ．直线x=3C ．直线x=-2D ．直线x=23. 用数学的方式理解“两岸猿声啼不住，轻舟已过万重山”和“坐地日行八万里”（只考虑地球的自转），其中蕴含的图形运动是（ ）A ．平移和旋转B ．对称和旋转C ．对称和平移D ．旋转和平移 4. 某人沿坡度 i ＝1：3的坡面向上走50米，则此人离地面的高度为( ) A ．25米 B ．50米C ．253米D ．503米5.如图所示，小红要制作一个母线长为8cm ，底面圆周长是12πcm 的圆锥形小漏斗，若不计损耗，则她所需纸板的面积是（ ） A ．60πcm 2B ．96πcm 2C ．120πcm 2D ．48πcm 26.在△ABC 中，∠C=90°，BC=3，AB=5，则cos A 的值是（ ） A ．45 B ． 35 C ． 43D ． 437．如图是二次函数y 1＝ax 2＋bx ＋c 和一次函数y 2＝mx ＋n 的图象，观察图象写出y 2 ≥ y 1时，x 的取值范围 （ ） A ．x ≥0 B ．0≤x ≤1 C ．－2≤x ≤1 D ．x ≤-2或x ≥18.如图，在平面直角坐标系中，⊙A 与y 轴相切于原点O ，平行于x 轴的直线交⊙A 于M 、N 两点，若点M 的坐标是(－4，－2)，则点N 的坐标为 （ ）A ． (1，－2)B ．(－1，－2)C ．(－1.5，－2)D ．(1.5，－2) 9．如图所示，小华从一个圆形场地的A 点出发，沿着与半径OA 夹角为α的方向行走，走到场地边缘B 后，再沿着与半径OB 夹角为α的方向行走。
按照这种方式，小华第五次走到场地边缘时处于弧AB 上，此时∠AOE ＝56°，则α的度数是（ ） A ．52° B ．60° C ．72° D ．76°10．如图，Rt △ABC 中，AC ⊥BC ，AD 平分∠BAC 交BC 于点D ，DE ⊥AD 交AB 于点E ，M 为AE 的中点，BF ⊥BC 交CM 的延长线于点F ，BD ＝2，CD ＝1．下列结论：①∠AED ＝∠ADC ；②DEDA ＝21；③AC ·BE ＝2；④ BF ＝2AC ；⑤BE=DE其中结论正确的个数有 （ ）A ．1个B ．2个C ．3个D ．4个第5题图第7题图（第10题）二、填空题（本大题共8小题，每空3分，共24分）11. 若式子3x -有意义，则x 的取值范围是 。
数学：中考2013年各地数学试题解析(郴州、常州)
湖南省郴州市2013年中考数学试卷一、选择题（本大题共8小题，每小题3分，共24分）1．（3分）（2013•郴州）5的倒数是（）A．﹣5B．5C．D．﹣考点：倒数．分析：根据倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．解答：解：∵5×=1，∴5的倒数是．故选C．点评：本题主要考查倒数的定义，要求熟练掌握．需要注意的是：倒数的性质：负数的倒数还是负数，正数的倒数是正数，0没有倒数．倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．2．（3分）（2013•郴州）函数y=中自变量x的取值范围是（）A．x＞3B．x＜3C．x≠3D．x≠﹣3考点：函数自变量的取值范围．分析：根据分母不等于0列式计算即可得解．解答：解：根据题意得，3﹣x≠0，解得x≠3．故选C．点评：本题考查了函数自变量的范围，一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．3．（3分）（2013•郴州）下列图案中，不是中心对称图形的是（）A．B．C．D．考点：中心对称图形．分析：根据中心对称图形的概念求解．解答：解：A、是中心对称图形，故本选项错误；B、不是中心对称图形，故本选项正确；C、是中心对称图形，故本选项错误；D、是中心对称图形，故本选项错误；故选B．点评：本题考查了中心对称图形的知识，解题的关键是掌握中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180度后重合．4．（3分）（2013•郴州）下列运算正确的是（）A．x•x4=x5B．x6÷x3=x2C．3x2﹣x2=3D．（2x2）3=6x6考点：同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．分析：结合各选项分别进行同底数幂的乘法、同底数幂的除法、合并同类项、幂的乘方等运算，然后选出正确选项即可．解答：解：A、x•x4=x5，原式计算正确，故本选项正确；B、x6÷x3=x3，原式计算错误，故本选项错误；C、3x2﹣x2=2x2，原式计算错误，故本选项错误；D、（2x2）3=8x，原式计算错误，故本选项错误；故选A．点评：本题考查了同底数幂的除法、同底数幂的乘法、幂的乘方等运算，属于基础题，掌握各运算法则是解题的关键．5．（3分）（2013•郴州）化简的结果为（）A．﹣1B．1C．D．考点：分式的加减法．分析：先把分式进行通分，把异分母分式化为同分母分式，再把分子相加，即可求出答案．解答：解：=﹣==1；故选B．点评：此题考查了分式的加减，根据在分式的加减运算中，如果是同分母分式，那么分母不变，把分子直接相加减即可；如果是异分母分式，则必须先通分，把异分母分式化为同分母分式，然后再相加减即可．6．（3分）（2013•郴州）数据1，2，3，3，5，5，5的众数和中位数分别是（）A．5，4B．3，5C．5，5D．5，3考点：众数；中位数．分析：根据众数的定义即众数是一组数据中出现次数最多的数和中位数的定义即中位数是将一组数据从小到大重新排列后，最中间的那个数即可求出答案．解答：解：数据1，2，3，3，5，5，5中，5出现了3次，出现的次数最多，则众数是5；最中间的数是3，则中位数是3；故选D．点评：此题考查了众数和中位数，掌握众数和中位数的定义是解题的关键，众数是一组数据中出现次数最多的数，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数）．7．（3分）（2013•郴州）在一年一度的“安仁春分药王节”市场上，小明的妈妈用280元买了甲、乙两种药材．甲种药材每斤20元，乙种药材每斤60斤，且甲种药材比乙种药材多买了2斤．设买了甲种药材x斤，乙种药材y斤，你认为小明应该列出哪一个方程组求两种药材各买了多少斤？（）A．B．C．D．考点：由实际问题抽象出二元一次方程组．分析：设买了甲种药材x斤，乙种药材y斤，根据甲种药材比乙种药材多买了2斤，两种药材共花费280元，可列出方程．解答：解：设买了甲种药材x斤，乙种药材y斤，由题意得：．故选A．点评：本题考查了有实际问题抽象出二元一次方程组，难度一般，关键是读懂题意设出未知数找出等量关系．8．（3分）（2013•郴州）如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）A．25°B．30°C．35°D．40°考点：翻折变换（折叠问题）．分析：先根据三角形内角和定理求出∠B的度数，再由图形翻折变换的性质得出∠CB′D的度数，再由三角形外角的性质即可得出结论．解答：解：∵在Rt△ACB中，∠ACB=90°，∠A=25°，∴∠B=90°﹣25°=65°，∵△CDB′由△CDB反折而成，∴∠CB′D=∠B=65°，∵∠CB′D是△AB′D的外角，∴∠ADB′=∠CB′D﹣∠A=65°﹣25°=40°．故选D．点评：本题考查的是图形的翻折变换及三角形外角的性质，熟知图形反折不变性的性质是解答此题的关键．二、填空题（本大题共8小题，每小题3分，共24分）9．（3分）（2013•郴州）据统计，我国今年夏粮的播种面积大约为415000000亩，415000000用科学记数法表示为 4.15×108．考点：科学记数法—表示较大的数．分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解答：解：将415000000用科学记数法表示为4.15×108．故答案为4.15×108．点评：此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．10．（3分）（2013•郴州）已知a+b=4，a﹣b=3，则a2﹣b2=12．考点：平方差公式．分析：根据a2﹣b2=（a+b）（a﹣b），然后代入求解．解答：解：a2﹣b2=（a+b）（a﹣b）=4×3=12．故答案是：12．点评：本题重点考查了用平方差公式．平方差公式为（a+b）（a﹣b）=a2﹣b2．本题是一道较简单的题目．11．（3分）（2013•郴州）已知一个多边形的内角和是1080°，这个多边形的边数是8．考点：多边形内角与外角．分析：根据多边形内角和定理：（n﹣2）•180（n≥3）且n为整数）可得方程180（x﹣2）=1080，再解方程即可．解答：解：设多边形边数有x条，由题意得：180（x﹣2）=1080，解得：x=8，故答案为：8．点评：此题主要考查了多边形内角和定理，关键是熟练掌握计算公式：（n﹣2）•180（n≥3）且n为整数）．12．（3分）（2013•郴州）已知关于x的一元二次方程x2+bx+b﹣1=0有两个相等的实数根，则b的值是2．考点：根的判别式．专题：计算题．分析：根据方程有两个相等的实数根，得到根的判别式的值等于0，即可求出b的值．解答：解：根据题意得：△=b2﹣4（b﹣1）=（b﹣2）2=0，则b的值为2．故答案为：2点评：此题考查了根的判别式，根的判别式的值大于0，方程有两个不相等的实数根；根的判别式的值等于0，方程有两个相等的实数根；根的判别式的值小于0，方程没有实数根．13．（3分）（2013•郴州）如图，AB是⊙O的直径，点C是圆上一点，∠BAC=70°，则∠OCB= 20°．考点：圆周角定理．分析：根据圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半得：∠BOC=2∠BAC，在等腰三角形OBC中可求出∠OCB．解答：解：∵⊙O是△ABC的外接圆，∠BAC=70°，∴∠B0C=2∠BAC=2×70°=140°，∵OC=OB（都是半径），∴∠OCB=∠OBC=（180°﹣∠BOC）=20°．故答案为：20°．点评：此题考查了圆周角定理，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半．14．（3分）（2013•郴州）如图，点D、E分别在线段AB，AC上，AE=AD，不添加新的线段和字母，要使△ABE≌△ACD，需添加的一个条件是∠B=∠C（答案不唯一）（只写一个条件即可）．考点：全等三角形的判定．专题：开放型．分析：由题意得，AE=AD，∠A=∠A（公共角），可选择利用AAS、SAS进行全等的判定，答案不唯一．解答：解：添加∠B=∠C．在△ABE和△ACD中，∵，∴△ABE≌△ACD（AAS）．故答案可为：∠B=∠C．点评：本题考查了全等三角形的判定，属于开放型题目，解答本题需要同学们熟练掌握三角形全等的几种判定定理．15．（3分）（2013•郴州）掷一枚质地均匀的骰子，骰子的六个面上分别标有数字1～6，掷得朝上的一面的数字为奇数的概率是．考点：概率公式．分析：让向上一面的数字是奇数的情况数除以总情况数6即为所求的概率．解答：解：正方体骰子，六个面上分别刻有的1，2，3，4，5，6六个数字中，奇数为1，3，5，则向上一面的数字是奇数的概率为=．故答案为：．点评：此题主要考查了概率公式的应用，明确概率的意义是解答的关键，用到的知识点为：概率等于所求情况数与总情况数之比．16．（3分）（2013•郴州）圆锥的侧面积为6πcm2，底面圆的半径为2cm，则这个圆锥的母线长为3cm．考点：圆锥的计算．分析：圆锥的侧面积=底面周长×母线长÷2，把相应数值代入即可求解．解答：解：设母线长为R，底面半径是2cm，则底面周长=4π，侧面积=2πR=6π，∴R=3．故答案为：3．点评：本题利用了圆的周长公式和扇形面积公式求解．比较基础，重点是掌握公式．三、解答题（本大题共6小题，每小题6分，共36分）17．（6分）（2013•郴州）计算：|﹣|+（2013﹣）0﹣（）﹣1﹣2sin60°．考点：实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．专题：计算题．分析：先分别根据0指数幂及负整数指数幂的计算法则，特殊角的三角函数值计算出各数，再根据实数混合运算的法则进行计算即可．解答：解：原式=2+1﹣3﹣2×=2+1﹣3﹣=﹣2．点评：本题考查的是实数的运算，熟知0指数幂及负整数指数幂的计算法则，特殊角的三角函数值是解答此题的关键．18．（6分）（2013•郴州）解不等式4（x﹣1）+3≥3x，并把解集在数轴上表示出来．考点：解一元一次不等式；在数轴上表示不等式的解集．分析：首先去括号，然后移项、合并同类项，系数化成1，即可求得不等式的解集．解答：解：去括号得：4x﹣4+3≥3x，移项得：4x﹣3x≥4﹣3则x≥1．把解集在数轴上表示为：点评：本题考查了解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数或整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．19．（6分）（2013•郴州）在图示的方格纸中（1）作出△ABC关于MN对称的图形△A1B1C1；（2）说明△A2B2C2是由△A1B1C1经过怎样的平移得到的？考点：作图-轴对称变换；作图-平移变换．专题：作图题．分析：（1）根据网格结构找出点A、B、C关于MN的对称点A1、B1、C1的位置，然后顺次连接即可；（2）根据平移的性质结合图形解答．解答：解：（1）△A1B1C1如图所示；（2）向右平移6个单位，再向下平移2个单位（或向下平移2个单位，再向右平移6个单位）．点评：本题考查了利用轴对称变换作图，利用平移变换作图，熟练掌握网格结构准确找出对应点的位置以及变化情况是解题的关键．20．（6分）（2013•郴州）已知：如图，一次函数的图象与y轴交于C（0，3），且与反比例函数y=的图象在第一象限内交于A，B两点，其中A（1，a），求这个一次函数的解析式．考点：反比例函数与一次函数的交点问题．分析：把A点坐标代入反比例函数解析式，即可求出a，求得A点坐标，然后再把A、C点的坐标代入一次函数的解析式，利用待定系数法求出一次函数的解析式．解答：解：∵A（1，a）在y=的图象上，∴a=2，∴A（1，2）．又∵C（0，3）在一次函数的图象，设一次函数的解析式为y=kx+b，则解得：k=﹣1，b=3，故一次函数的解析式为y=﹣x+3．点评：考查了反比例函数与一次函数的交点问题，本类题目的解决需把点的坐标代入函数解析式，灵活利用方程组求出所需字母的值，从而求出函数解析式．21．（6分）（2013•郴州）游泳是一项深受青少年喜爱的体育活动，学校为了加强学生的安全意识，组织学生观看了纪实片“孩子，请不要私自下水”，并于观看后在本校的2000名学生中作了抽样调查．请根据下面两个不完整的统计图回答以下问题：（1）这次抽样调查中，共调查了400名学生；（2）补全两个统计图；（3）根据抽样调查的结果，估算该校2000名学生中大约有多少人“一定会下河游泳”？考点：条形统计图；用样本估计总体；扇形统计图．分析：（1）根据一定会的人数和所占的百分比即可求出总人数；（2）用总人数减去其它人数得出不会的人数，再根据家长陪同的人数除以总人数得出家长陪同时会的所占的百分比，从而补全统计图；（3）用2000乘以一定会下河游泳所占的百分百，即可求出该校一定会下河游泳的人数．解答：解：（1）总人数是：20÷5%=400（人）；（2）一定不会的人数是400﹣20﹣50﹣230=100（人），家长陪同的所占的百分百是×100%=57.5%，补图如下：（3）根据题意得：2000×5%=100（人）．答：该校2000名学生中大约有多少人“一定会下河游泳”有100人．点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小，用到的知识点是频率=．22．（6分）（2013•郴州）我国为了维护队钓鱼岛P的主权，决定对钓鱼岛进行常态化的立体巡航．在一次巡航中，轮船和飞机的航向相同（AP∥BD），当轮船航行到距钓鱼岛20km 的A处时，飞机在B处测得轮船的俯角是45°；当轮船航行到C处时，飞机在轮船正上方的E处，此时EC=5km．轮船到达钓鱼岛P时，测得D处的飞机的仰角为30°．试求飞机的飞行距离BD（结果保留根号）．考点：解直角三角形的应用-仰角俯角问题．分析：作AF⊥BD，PG⊥BD，在Rt△ABF和△PDG中分别求出BF、GD的值，继而可求得BD=BF+FG+DC的值．解答：解：作AF⊥BD，PG⊥BD，垂足分别为F、G，由题意得：AF=PG=CE=5km，FG=AP=20km，在Rt△AFB中，∠B=45°，则∠BAF=45°，∴BF=AF=5，∵AP∥BD，∴∠D=∠DPH=30°，在Rt△PGD中，tan∠D=，即tan30°=，∴GD=5，则BD=BF+FG+DC=5+20+5=25+5（km）．答：飞机的飞行距离BD为25+5km．点评：本题考查了解直角三角形的应用，解答本题的关键是根据仰角和俯角构造直角三角形，然后解直角三角形，难度一般．四、证明题（本题8分）23．（8分）（2013•郴州）如图，已知BE∥DF，∠ADF=∠CBE，AF=CE，求证：四边形DEBF是平行四边形．考点：平行四边形的判定；全等三角形的判定与性质．专题：证明题．分析：首先根据平行线的性质可得∠BEC=∠DFA，再加上条件∠ADF=∠CBE，AF=CE，可证明△ADF≌△CBE，再根据全等三角形的性质可得BE=DF，根据一组对边平行且相等的四边形是平行四边形进行判定即可．解答：证明：∵BE∥DF，∴∠BEC=∠DFA，在△ADF和△CBE中，∴△ADF≌△CBE（AAS），∴BE=DF，又∵BE∥DF，∴四边形DEBF是平行四边形．点评：此题主要考查了平行四边形的判定，关键是掌握一组对边平行且相等的四边形是平行四边形．五、应用题（本题8分）24．（8分）（2013•郴州）乌梅是郴州的特色时令水果．乌梅一上市，水果店的小李就用3000元购进了一批乌梅，前两天以高于进价40%的价格共卖出150kg，第三天她发现市场上乌梅数量陡增，而自己的乌梅卖相已不大好，于是果断地将剩余乌梅以低于进价20%的价格全部售出，前后一共获利750元，求小李所进乌梅的数量．考点：分式方程的应用．分析：先设小李所进乌梅的数量为xkg，根据前后一共获利750元，列出方程，求出x的值，再进行检验即可．解答：解：设小李所进乌梅的数量为xkg，根据题意得：•40%﹣150（x﹣150）••20%=750，解得：x=200，经检验x=200是原方程的解，答：小李所进乌梅的数量为200kg．点评：此题考查了分式方程的应用，解题的关键是读懂题意，找出之间的等量关系，列出方程，解分式方程时要注意检验．六、综合题（本大共2小题，每小题10分，共20分）25．（10分）（2013•郴州）如图，△ABC中，AB=BC，AC=8，tanA=k，P为AC边上一动点，设PC=x，作PE∥AB交BC于E，PF∥BC交AB于F．（1）证明：△PCE是等腰三角形；（2）EM、FN、BH分别是△PEC、△AFP、△ABC的高，用含x和k的代数式表示EM、FN，并探究EM、FN、BH之间的数量关系；（3）当k=4时，求四边形PEBF的面积S与x的函数关系式．x为何值时，S有最大值？并求出S的最大值．考点：等腰三角形的判定与性质；二次函数的最值；解直角三角形．分析：（1）根据等边对等角可得∠A=∠C ，然后根据两直线平行，同位角相等求出∠CPE=∠A ，从而得到∠CPE=∠C ，即可得证；（2）根据等腰三角形三线合一的性质求出CM=CP ，然后求出EM ，同理求出FN 、BH 的长，再根据结果整理可得EM+FN=BH ；（3）分别求出EM 、FN 、BH ，然后根据S △PCE ，S △APF ，S △ABC ，再根据S=S △ABC ﹣S △PCE ﹣S △APF ，整理即可得到S 与x 的关系式，然后利用二次函数的最值问题解答．解答：（1）证明：∵AB=BC ，∴∠A=∠C ，∵PE ∥AB ，∴∠CPE=∠A ，∴∠CPE=∠C ，∴△PCE 是等腰三角形；（2）解：∵△PCE 是等腰三角形，EM ⊥CP ，∴CM=CP=，tanC=tanA=k ，∴EM=CM •tanC=•k=，同理：FN=AN •tanA=•k=4k ﹣，由于BH=AH •tanA=×8•k=4k ，而EM+FN=+4k ﹣=4k ，∴EM+FN=BH ；（3）解：当k=4时，EM=2x ，FN=16﹣2x ，BH=16，所以，S △PCE =x •2x=x 2，S △APF =（8﹣x ）•（16﹣2x ）=（8﹣x ）2，S △ABC =×8×16=64，S=S △ABC ﹣S △PCE ﹣S △APF ，=64﹣x 2﹣（8﹣x ）2，=﹣2x 2+16x ，配方得，S=﹣2（x ﹣4）2+32，所以，当x=4时，S 有最大值32．点评：本题考查了等腰三角形的判定与性质，平行线的性质，锐角三角函数，二次函数的最值问题，表示出各三角形的高线是解题的关键，也是本题的难点．26．（10分）（2013•郴州）如图，在直角梯形AOCB中，AB∥OC，∠AOC=90°，AB=1，AO=2，OC=3，以O为原点，OC、OA所在直线为轴建立坐标系．抛物线顶点为A，且经过点C．点P在线段AO上由A向点O运动，点O在线段OC上由C向点O运动，QD⊥OC 交BC于点D，OD所在直线与抛物线在第一象限交于点E．（1）求抛物线的解析式；（2）点E′是E关于y轴的对称点，点Q运动到何处时，四边形OEAE′是菱形？（3）点P、Q分别以每秒2个单位和3个单位的速度同时出发，运动的时间为t秒，当t 为何值时，PB∥OD？考点：二次函数综合题．分析：（1）根据顶点式将A，C代入解析式求出a的值，进而得出二次函数解析式；（2）利用菱形的性质得出AO与EE′互相垂直平分，利用E点纵坐标得出x的值，进而得出BC，EO直线解析式，再利用两直线交点坐标求法得出Q点坐标，即可得出答案；（3）首先得出△APB∽△QDO，进而得出=，求出m的值，进而得出答案．解答：解：（1）∵A（0，2）为抛物线的顶点，∴设y=ax2+2，∵点C（3，0），在抛物线上，∴9a+2=0，解得：a=﹣，∴抛物线为；y=﹣x2+2；（2）如果四边形OEAE′是菱形，则AO与EE′互相垂直平分，∴EE′经过AO的中点，∴点E纵坐标为1，代入抛物线解析式得：1=﹣x2+2，解得：x=±，∵点E在第一象限，∴点E为（，1），设直线BC的解析式为y=kx+b，把B（1，2），C（3，0），代入得：，解得：，∴BC的解析式为：y=﹣x+3，将E点代入y=ax，可得出EO的解析式为：y=x，由，得：，∴Q点坐标为：（，0），∴当Q点坐标为（，0）时，四边形OEAE′是菱形；（3）法一：设t为m秒时，PB∥DO，又QD∥y轴，则有∠APB=∠AOE=∠ODQ，又∵∠BAP=∠DQO，则有△APB∽△QDO，∴=，由题意得：AB=1，AP=2m，QO=3﹣3m，又∵点D在直线y=﹣x+3上，∴DQ=3m，因此：=，解得：m=，经检验：m=是原分式方程的解，∴当t=秒时，PB∥OD．法二：作BH⊥OC于H，则BH=AO=2，OH=AB=1，HC=OC﹣OH=2，∴BH=HC，∴∠BCH=∠CBH=45°，易知DQ=CQ，设t为m秒时PB∥OE，则△ABP∽△QOD，∴=，易知AP=2m，DQ=CQ=3m，QO=3﹣3m，∴=，解得m=，经检验m=是方程的解，∴当t为秒时，PB∥OD．点评：此题主要考查了菱形的判定与性质以及顶点式求二次函数解析式以及相似三角形的判定与性质等知识，根据数形结合得出△APB∽△QDO是解题关键．江苏省常州市2013年中考数学试卷一．选择题（本大题共有8小题，每小题2分，共16分，在每小题所给的四个选项中，只有一项是正确的）1．（2分）（2013•常州）在下列实数中，无理数是（）A．2B．3.14C．D．考点：无理数．分析：根据无理数，有理数的定义对各选项分析判断后利用排除法求解．解答：解：A、2是有理数，故本选项错误；B、3.14是有理数，故本选项错误；C、﹣是有理数，故本选项错误；D、是无理数，故本选项正确．故选D．点评：主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．2．（2分）（2013•常州）如图所示圆柱的左视图是（）A．B．C．D．考点：简单几何体的三视图分析：找到从左面看所得到的图形即可．解答：解：此圆柱的左视图是一个矩形，故选C．点评：本题考查了三视图的知识，左视图是从物体的左面看得到的视图．3．（2分）（2013•常州）下列函数中，图象经过点（1，﹣1）的反比例函数关系式是（）A．B．C．D．考点：反比例函数图象上点的坐标特征分析：设将点（1，﹣1）代入所设的反比例函数关系式y=（k≠0）即可求得k的值．解答：解：设经过点（1，﹣1）的反比例函数关系式是y=（k≠0），则﹣1=，解得，k=﹣1，所以，所求的函数关系式是y=﹣或．故选A．点评：本题主要考查反比例函数图象上点的坐标特征．所有反比例函数图象上点的坐标都满足该函数解析式．4．（2分）（2013•常州）下列计算中，正确的是（）A．（a3b）2=a6b2B．a•a4=a4C．a6÷a2=a3D．3a+2b=5ab考点：同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．分析：根据积的乘方，等于把每一个因式分别乘方，再把所得的幂相乘；同底数幂相乘，底数不变指数相加；同底数幂相除，底数不变指数相减对各选项分析判断后利用排除法求解．解答：解：A、（a3b）2=a6b2，故本选项正确；B、a•a4=a5，故本选项错误；C、a6÷a2=a6﹣2=a4，故本选项错误；D、3a与2b不是同类项，不能合并，故本选项错误．故选A．点评：本题考查了同底数幂的除法，同底数幂的乘法，积的乘方的性质，理清指数的变化是解题的关键．5．（2分）（2013•常州）已知：甲乙两组数据的平均数都是5，甲组数据的方差，乙组数据的方差，下列结论中正确的是（）A．甲组数据比乙组数据的波动大B．乙组数据的比甲组数据的波动大C．甲组数据与乙组数据的波动一样大D．甲组数据与乙组数据的波动不能比较考点：方差．分析：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好，结合选项进行判断即可．解答：解：由题意得，方差＜，A、甲组数据没有乙组数据的波动大，故本选项错误；B、乙组数据的比甲组数据的波动大，说法正确，故本选项正确；C、甲组数据没有乙组数据的波动大，故本选项错误；D、甲组数据没有乙组数据的波动大，故本选项错误；故选B．点评：本题考查了方差的意义，解答本题的关键是理解方差的意义，方差表示的是数据波动性的大小，方差越大，波动性越大．6．（2分）（2013•常州）已知⊙O的半径是6，点O到直线l的距离为5，则直线l与⊙O的位置关系是（）A．相离B．相切C．相交D．无法判断考点：直线与圆的位置关系．分析：根据圆O的半径和圆心O到直线l的距离的大小，相交：d＜r；相切：d=r；相离：d ＞r；即可选出答案．解答：解：∵⊙O的半径为6，圆心O到直线l的距离为5，∵6＞5，即：d＜r，∴直线L与⊙O的位置关系是相交．故选；C．点评：本题主要考查对直线与圆的位置关系的性质的理解和掌握，能熟练地运用性质进行判断是解此题的关键．7．（2分）（2013•常州）二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：x﹣3﹣2﹣1012345y1250﹣3﹣4﹣30512给出了结论：（1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；（2）当时，y＜0；（3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（）A．3B．2C．1D．0考点：二次函数的最值；抛物线与x轴的交点．分析：根据表格数据求出二次函数的对称轴为直线x=1，然后根据二次函数的性质对各小题分析判断即可得解．解答：解；由表格数据可知，二次函数的对称轴为直线x=1，所以，当x=1时，二次函数y=ax2+bx+c有最小值，最小值为﹣4；故（1）小题错误；根据表格数据，当﹣1＜x＜3时，y＜0，所以，﹣＜x＜2时，y＜0正确，故（2）小题正确；二次函数y=ax2+bx+c的图象与x轴有两个交点，分别为（﹣1，0）（3，0），它们分别在y轴两侧，故（3）小题正确；综上所述，结论正确的是（2）（3）共2个．故选B．点评：本题考查了二次函数的最值，抛物线与x轴的交点，仔细分析表格数据，熟练掌握二次函数的性质是解题的关键．8．（2分）（2013•常州）有3张边长为a的正方形纸片，4张边长分别为a、b（b＞a）的矩形纸片，5张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（）A．a+b B．2a+b C．3a+b D．a+2b考点：完全平方公式的几何背景．分析：根据3张边长为a的正方形纸片的面积是3a2，4张边长分别为a、b（b＞a）的矩形纸片的面积是4ab，5张边长为b的正方形纸片的面积是5b2，得出a2+4ab+4b2=（a+2b）2，再根据正方形的面积公式即可得出答案．解答：解；3张边长为a的正方形纸片的面积是3a2，4张边长分别为a、b（b＞a）的矩形纸片的面积是4ab，5张边长为b的正方形纸片的面积是5b2，∵a2+4ab+4b2=（a+2b）2，∴拼成的正方形的边长最长可以为（a+2b），故选D．点评：此题考查了完全平方公式的几何背景，关键是根据题意得出a2+4ab+4b2=（a+2b）2，用到的知识点是完全平方公式．二．填空题（本大题共有9小题，第9小题4分，其余8小题每小题4分，共20分，）9．（4分）（2013•常州）计算﹣（﹣3）=3，|﹣3|=3，（﹣3）﹣1=﹣，（﹣3）2=9．考点：有理数的乘方；相反数；绝对值；有理数的减法．分析：根据相反数的定义，绝对值的性质，负整数指数幂，有理数的乘方的意义分别进行计算即可得解．解答：解：﹣（﹣3）=3，|﹣3|=3，（﹣3）﹣1=﹣，（﹣3）2=9．故答案为：3；3；﹣；9．点评：本题考查了相反数的定义，绝对值的性质，负整数指数幂，以及有理数的乘方的意义，是基础题．10．（2分）（2013•常州）已知点P（3，2），则点P关于y轴的对称点P1的坐标是（﹣3，2），点P关于原点O的对称点P2的坐标是（﹣3，﹣2）．考点：关于原点对称的点的坐标；关于x轴、y轴对称的点的坐标．分析：根据关于y轴对称的点的横坐标互为相反数，纵坐标相同；关于原点对称的点的横坐标与纵坐标都互为相反数解答．解答：解：点P（3，2）关于y轴的对称点P1的坐标是（﹣3，2），点P关于原点O的对称点P2的坐标是（﹣3，﹣2）．故答案为：（﹣3，2）；（﹣3，﹣2）．。
2013常州数学中考模拟试题
2013常州数学中考模拟试题一、选择题（本大题共10小题，每题3分，共30分）1．下列二次根式中属于最简二次根式的是（）A．44a B．48C．14D．ba2．抛物线y=-(x-3)2+2的对称轴是（）A．直线x=-3 B．直线x=3 C．直线x=-2 D．直线x=23. 用数学的方式理解“两岸猿声啼不住，轻舟已过万重山”和“坐地日行八万里”（只考虑地球的自转），其中蕴含的图形运动是（）A．平移和旋转 B．对称和旋转 C．对称和平移D．旋转和平移4. 某人沿坡度 i ＝1：3的坡面向上走50米，则此人离地面的高度为( )A．25米 B．50米 C．253米D．503米5.如图所示，小红要制作一个母线长为8cm，底面圆周长是12πcm的圆锥形小漏斗，若不计损耗，则她所需纸板的面积是（）A．60πcm2B．96πcm2 C．120πcm2 D．48πcm26.在△ABC中，∠C=90°，BC=3，AB=5，则cos A的值是（）A．45B．35C．43D．437．如图是二次函数y1＝ax2＋bx＋c和一次函数y2＝mx＋n的图象，观察图象写出y2 ≥ y1时，x的取值范围（）A．x≥0 B．0≤x≤1 C．－2≤x≤1 D．x≤-2或x≥18.如图，在平面直角坐标系中，⊙A与y轴相切于原点O，平行于x轴的直线交⊙A于M、N两点，若点M的坐标是(－4，－2)，则点N的坐标为（）A． (1，－2) B．(－1，－2)C．(－1.5，－2) D．(1.5，－2)9．如图所示，小华从一个圆形场地的A点出发，沿着与半径OA夹角为α的方向行走，走到场地边缘B后，再沿着与半径OB夹角为α的方向行走。
按照这种方式，小华第五次走到场地边缘时处于弧AB上，此时∠AOE＝56°，则α的度数是（）第5题图第7题图A ．52°B ．60°C ．72°D ．76°10．如图，Rt △ABC 中，AC ⊥BC ，AD 平分∠BAC 交BC 于点D ，DE ⊥AD 交AB 于点E ，M 为AE 的中点，BF ⊥BC 交CM 的延长线于点F ，BD ＝2，CD ＝1．下列结论：①∠AED ＝∠ADC ；②DEDA ＝21；③AC ·BE ＝2；④ BF ＝2AC ；⑤BE=DE其中结论正确的个数有 （ ）A ．1个B ．2个C ．3个D ．4个 二、填空题（本大题共8小题，每空3分，共24分）11. 若式子3x -有意义，则x 的取值范围是 。
2013年常州市中考试卷
常州市二O—三年初中毕业■升学统一文化考试英语试题注■事项：I *试直共*页•全卷満分为90分・才试时絢为100分钟.才生須将答案书写在答題卡上•写建试卷上的一律无效•2•答覇績•舟生务必将自己的堆名.#i*a号填耳在试卷上.并填写答題卡上的考生信息。
芳试结耒JB,请将本试卷和答是卡一并交回。
一、单念选择（共10小H;毎小• 1分•需分1U分）从A.B.C.DIW个选現中■迭出町以填人空白处的最佳选項•并在答题卡上将该项涂爬.1. — Have you got any books on English grammar? I want to borrow _________________ •—Yes t here you are. But you must return it by Friday・A. oneB.it C・ some D. that2・—I will buy you a new bike if you learn how to swim this summer・—!s that a ________ ? I'm sure I'll set the bike.A・ chance B・ promiflf C. trick D. treat3・ He spenks _______ English ______ French・丄d. he speaks German•A. either; or B・ not onl/; but alsoC both: and D. neither； nor4・—Shall 1 take my swimming si?：—No, you ________ • Wc will just go hiking in the mountain.A. mustn'tB.couldn e tC. n<edn*tD. can't5・ He offered _______ valuable advice th^t _________ p eople disagreed.A. such; a fewB.such; few C・so; A few D・so； few6・ This listening material, together with its CD ROMs. ______________ well.A. sellsB. sellC. is soldD. tre sold7. — Why are you worried?—I m expecting a call from my daughter・ She ___________ New York for three days.A. has gone to B・ has been to C・h・s been in D・ has come in8・ Many social workers went to Ya*an to help ___________ clean water and food to local people to reduce their pain from the earthquakeA. put outB. come out C・ work out D・ give out9. — How soon will you ・tart your journey?— Ftn not sure. I haven't decided •---------- 9A. when shall I ask the boss for leaveB. where I will go to spend the holidayC・ whether 1 would go by train or by planeD. who could invite me to go10. — How did you find the trip to the West Lake?常英第1页〈共8页）trainD・】l was not far from our hotelC・ Very fantastic indeed二、宪影填空（共12小H；e/hK 1分•満分12分）阅读下面短文•从短文后各题所给的A.B.C.D四个选厦中■选出量隹选頊•并亦答题卡上将谈项济黑.* You know t Ann. - my friend Nick said, "Lisa and Anita were just talking about you.w I immediately got 11・ *They said that you join the Students Union just because the teacher likes you. not because you're excellent・ *I 12 to keep myself from crying, getting down to my knees. After Nick told me everything my supposedbest friends said about me. 1 felt I was 13 <Lisa and Anita came in, acting as if(好偉〉14 had happened. Liso was still my deskmate and Anita was still my partner for our history project. I waft 15 that they were able to pretcnd(fR%) we had the perfect friendship, 16 since they*d said such hurtful things ・J felt like I didn't have a friend in the world9 all Lecause of a rumor(i£pf).The tongue(舌头)can be our worit _17 _・ Rumors do harm to friendship・ They arc like sharp knives, breaking one's dignity K尊严)in；o pieces・ When we say 18 things about others, we re hurting their heaxts.So how was 1 to act next? 1 thought of 19 th^m back. But instead* I told them directly they had hurt me.Lisa started 2J and Ani“ was spccchles9・ I knew they were both sorry for what they had said・ They said Jtorty to me, ^nd I forgave them 21 I was still unhappy. Sure, things were a little r nUrrassing(M) at first. but soon enough everything was back to the way it had l»ccn before・1 22 rumors from tim* to time・ ^^iking others is part of our life, but themore I learn about friendship・ the more T realise the importance of tolerating(%$) others.11 ・ A・ relaxed B・ nerve u C. scared D・ energetic12・ A・ struggled B. decided C・ continued D・ preferred13・ A. different B・ wrong C・ sick D. alone14 ・ A. everything B. something C. anything D. nothing15・ A. surprised B・ satisfied C・ frightened D・ worried16・ A.simply B・ especially C・o bviously D・ probably17・ A. criminal B. rictim C・ suspect D・ enemy18. A. unpopular R. unlucky C. unkind D・UTHI・UQ119・ A. attackinx B・ keepinx C・ bringing 0. pulling20. A. shouting B・ arguing C・ fighting L)・ crying21 • A・ because B・ althcxigh C. after D・ unless22. A. play with B・ agree with C. deal with D. help with常英第Z贝（共8贝）二、阀读理驚（共13彷題；毎小越2为分航分）厠读节列痰文■从姮文后蓉範斷蜡的A.BX.DH个送耳i中”透岀量隹选頊.井任再■卡上帚读現徐国.AWt were doing our best to control the file of the burning giiraget^ Outride. 1 keard the sound of c>tjt Frying.I cauldn'i step — I would hsve to look for the uts Atisr tht lire put out.Er took 詣Ic*% rim^ to finAlly brin^ the big fire utidpr conlrolNo one infddr was hurt. At that point I wa»fr€t to find out where lhe cal noises were from・ Thfre was still A lot o： smoke .Tid heat coming from the biiiidinj^- 1 followed ike meowing to Lhe sidewalk in iront o：the “riigtt* There, cry ing snd huddlciK挤作一團1 logether, were five irightcneii kimnM小描）.They must have been imide the buildingah their fur was badlyburned-I ^dtmd to find ihe mother, 11 was pbviuu^ ih?i i新hu had ^onc into the burning garfigf and carried out allher babies t one by one ‘一unbeLitvAble^Wc finally foicud bet L Her face and pavs wtre blftckrncrdu «nd her fur wa^ burned al. ever. You could tven see her reriden^d 取kin u^ider tht jrned fur， She could hardly move. 1 picked her up t and she rela KSC in my arms B-S mpch as her pa tn would aLScw. I wns <icterfnined（下宦决心的、to save th' . brave lit Jr cel - id her himily*The YcterinAtian（出医｝told me they wcuM watch the kittens and their mother for th* night T buE they weren't ronfidrnt abjut th*- mother chances.About i w«ek la!er d t fotinJ out 性WJIH gninp *•、|iv^. W P tiatrird her Scarlcit because of her r申ddened jikin.I wag happy tn sre Scarlrt get 1 with the kittens Again. She iosjehrii pnch otihcm. note to nose. She had risked ei life five limcrs. — ind ii hail paid off. AH of h^i Labie^ had snirviwed.Ah « hrelighier.】see heroic acts every day- But wliai Scarlet showed me （ha^ dnj was the kind of bravery [hat can only r* 山亡froir』mtnb护丁* love.23 Which oF thr folia榨15 TRUE accordin耳to fht story?A. The wtitrr went to look for the cats as s&on As he heard them crying.ti. The firefighters put our tkc firr quirkly nnd no ont kurt.C The writer didn t find the cam unul the ^wokc and htat were goneD. The mother eiT moved zill her babi^c Out of the fir# te a safe place*.24 Why wns the wnirr determined to save the cats?A E^«rausf tie wis ninzzed nt the mother cat's fnuragr.B. Because the cats anmered mfiny peopled aitcntion.C. Bceause he didn't want to sec any Living things dip,D. Hcriiuse it had taken him riiuch lime and effort id find them,25* The writer talks about tht cal's story mainly to show that ・A - animiiH shvuId be 1 >ikcn good «rc of L3. mothtrr F J love can bt greal and braveC it i各tn«aninxlul to help others D. a cat ^Iwtys has nine livea常英第日页（）来源:Z,xx,]来源学科网］Have you ever noticed that your fiiigcrtip5 arc wrinklcd（£^t） when you ve justfinished swimming or washing dishes? It seems as if your hinds have aged 30 years in ■second・ But is this an accdcnt? Or is it something that nature has built into our bodies?If your finger's wrinkling up had no use at all. *it wouldn*t need to. * Professor Tom Smuldcrs from Newcastle University. UK. told BBCNews. By studying wet fingers closely9 Smulders and hit partner・ found thut thewrinkles looked a bit like the patterns（花纹）on a car tire（轮胎）or on the bottom of a running shoe. So they made a guess that wrinkles on fingers might be able to help the hand hold thing・ more tightly・To test this, reseirchers asked 20 people to pick up marbles（玻璃珠）from water with their hands・But before the/ started. some of the people had to ke<*p their hands in water for half >n hour.The researchers found that the people with wrinkled fingers completed the task faster thiin those with dry h^nds. But when they were asked to move dry murbleR, all the people performed equally well, no matter whether they wrinkled fingers or not.Our anceslors（祖先）might not have played with -narblcs, but wrinkled fingers could • have made it easier for them to uimb aiound in wet forests and catch fish from rivers・ researchers say.Similarly, our toes also Ret wrinkled in water. This may have developed from our ancestors' need to run on wet ground・But the question ts. if wrinkled fingr rs nre so helpful• why don't our hands just stay that way all the time?Researchert < xphined thut wrinkling his its disadvantage: wet fingertips are far less scnsitive（t han smcx>th or<n, reducing our «ense of touch・26. What docs the underlined word in the third paragraph refer to（捋代）？A・ Whether fingers have wrink!u> after ・huy arc put in water.B・ Whether wrinkled fingers can hold things more tightly・C・ Why keeping fingers in water makes them wrinkled・D・ Why wrinkles help hands hold things more tightly.27. The test shows that _________ •A wrinkled hnndsi hold dry things more tightly than dry hands doB. dry hands hold dry things more tightly than wrinkled hands doC・ wrinkled hands hold wet thing・ more tightly than dry hxnds doD.dry hands hold wet things more tightly than wrinkled hands do28. Wlut might be a disadvantage of wrinkled fingers?A. They are loo sensitive to be touched・B・ They might be more likely to get hurt ・C. They cannot hold things tightly enough ・D. They arc not so sensitive as dry fingers・常英第4页（共8页）Dm* of my sweetest me mor its as a child is of Koine dovn to the fiver tnrf fitting ci?rnfurt»bly on the hwiik.There 1 would rnjoy the p<ii-e and q'jict, watch the water rusn dnwnstream And hsrpn tii songs □! birds, 1 uouEd A\AQ watch the banitiGD irecs bend undrr the prdnv frum ihr wiml And ^alth them rciurr. gractfully(优章地)lo thtir onginai(^.5L 的j ^IP nltpt th# wind had fiE?d drtwn\Vhun t ihink al>vuI ：li匕L^iiiboo :ir：e a ability lo bend and move back, the vord flijtilienrr' ccmesi ny MHTTI L When it is tis^d for a person. thu word TTluns the ability to Ttadily rroovrrt fruni ^hm：k.汕山irz Or arty othersmfitrmg. E lave you cwt fell lik= yon were IO ^niip? HAv** j<OU ev#r 1p|t hkp you were at your breakins point?Tlunkfu Lb * yvu have 3tirviY«I io i^'k ft bout ，l.ifr ir % mixture (^5£) nl 呂啦制竹me n nd bad TiEz, h^ppy mftmertK And unhappy rTiometHs. Tlir “rxt tim^ you art rxpciicncinK one uf :huac bid -1111=? ot unhdppy momt'nls t hat ta ke you c losf to y<j ur break JXJI nT. b«nd., but doti'T birii. fry ynur I M-S! roJ 1 rt \vi I he aiiu&tion fet die best oi yuu.An arnount of hope will yo‘ thrntii?- the ur^j^asATit AiiLfering. With hope for -* betttr tomorrow or 3 betier ^EiuauoEi* 〔hit电,may not Lt- HS> bad they srertb, The iirtpbDRjnt fluffeTing tnsy b** t JISUT *诫〜川、nh if thi rc^tilt k vtnrihIf things 百亡t Toufih und you arc al your b~<- A+J lg point, resilience. Like the bamboo tree<t, bend« but don '( bjea k r29. Whfli docs tht word *L snap" in the L md parA^r^ph HHIM |；T jkibly m^ ri?A, break B chanp^C. winD. complain3G, What C^TI help people gor throy^h snf(r 川沪urrc 1 ding Trt thr wtit*TA・ HokliDg peace snd quiet in mind・C. ExpefLerLcinj; more ba J tfltip 幅-B r Wciiun^ .1 HI il sufferings disappear.D. Hoping for a lielttr lomoFTtiw.31, Whai would be the best title of this pasuge?A . Memories of Ramhon R”JV 1 ik。
常州市中考数学试卷及答案(Word解析版)
江苏省常州市中考数学试卷一．选择题（本大题共有8小题，每小题2分，共16分，在每小题所给的四个选项中，只有一项是正确的）1．（2分）（•常州）在下列实数中，无理数是（）A．2B．3.14 C．D．考点：无理数．分析：根据无理数，有理数的定义对各选项分析判断后利用排除法求解．解答：解：A、2是有理数，故本选项错误；B、3.14是有理数，故本选项错误；C 、﹣是有理数，故本选项错误；D 、是无理数，故本选项正确．故选D．点评：主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．2．（2分）（•常州）如图所示圆柱的左视图是（）A．B．C．D．考点：简单几何体的三视图分析：找到从左面看所得到的图形即可．解答：解：此圆柱的左视图是一个矩形，故选C．点评：本题考查了三视图的知识，左视图是从物体的左面看得到的视图．3．（2分）（•常州）下列函数中，图象经过点（1，﹣1）的反比例函数关系式是（）A．B．C．D．考点：反比例函数图象上点的坐标特征分析：设将点（1，﹣1）代入所设的反比例函数关系式y=（k≠0）即可求得k的值．解答：解：设经过点（1，﹣1）的反比例函数关系式是y=（k≠0），则﹣1=，解得，k=﹣1，所以，所求的函数关系式是y=﹣或．故选A．点评：本题主要考查反比例函数图象上点的坐标特征．所有反比例函数图象上点的坐标都满足该函数解析式．4．（2分）（•常州）下列计算中，正确的是（）A．（a3b）2=a6b2B．a•a4=a4C．a6÷a2=a3D．3a+2b=5ab考点：同底数幂的除法；合并同类项；同底数幂的乘法；幂的乘方与积的乘方．分析：根据积的乘方，等于把每一个因式分别乘方，再把所得的幂相乘；同底数幂相乘，底数不变指数相加；同底数幂相除，底数不变指数相减对各选项分析判断后利用排除法求解．解答：解：A、（a3b）2=a6b2，故本选项正确；B、a•a4=a5，故本选项错误；C、a6÷a2=a6﹣2=a4，故本选项错误；D、3a与2b不是同类项，不能合并，故本选项错误．故选A．点评：本题考查了同底数幂的除法，同底数幂的乘法，积的乘方的性质，理清指数的变化是解题的关键．5．（2分）（•常州）已知：甲乙两组数据的平均数都是5，甲组数据的方差，乙组数据的方差，下列结论中正确的是（）A．甲组数据比乙组数据的波动大B．乙组数据的比甲组数据的波动大C．甲组数据与乙组数据的波动一样大D．甲组数据与乙组数据的波动不能比较考点：方差．分析：方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好，结合选项进行判断即可．解答：解：由题意得，方差＜，A、甲组数据没有乙组数据的波动大，故本选项错误；B、乙组数据的比甲组数据的波动大，说法正确，故本选项正确；C、甲组数据没有乙组数据的波动大，故本选项错误；D、甲组数据没有乙组数据的波动大，故本选项错误；故选B．点本题考查了方差的意义，解答本题的关键是理解方差的意义，方差表示的是数据波评：动性的大小，方差越大，波动性越大．6．（2分）（•常州）已知⊙O的半径是6，点O到直线l的距离为5，则直线l与⊙O的位置关系是（）A．相离B．相切C．相交D．无法判断考点：直线与圆的位置关系．分析：根据圆O的半径和圆心O到直线l的距离的大小，相交：d＜r；相切：d=r；相离：d＞r；即可选出答案．解答：解：∵⊙O的半径为6，圆心O到直线l的距离为5，∵6＞5，即：d＜r，∴直线L与⊙O的位置关系是相交．故选；C．点评：本题主要考查对直线与圆的位置关系的性质的理解和掌握，能熟练地运用性质进行判断是解此题的关键．7．（2分）（•常州）二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：x ﹣3 ﹣2 ﹣1 0 1 2 3 4 5y 12 5 0 ﹣3 ﹣4 ﹣3 0 5 12给出了结论：（1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；（2）当时，y＜0；（3）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（）A．3B．2C．1D．0考点：二次函数的最值；抛物线与x轴的交点．分析：根据表格数据求出二次函数的对称轴为直线x=1，然后根据二次函数的性质对各小题分析判断即可得解．解答：解；由表格数据可知，二次函数的对称轴为直线x=1，所以，当x=1时，二次函数y=ax2+bx+c有最小值，最小值为﹣4；故（1）小题错误；根据表格数据，当﹣1＜x＜3时，y＜0，所以，﹣＜x＜2时，y＜0正确，故（2）小题正确；二次函数y=ax2+bx+c的图象与x轴有两个交点，分别为（﹣1，0）（3，0），它们分别在y轴两侧，故（3）小题正确；综上所述，结论正确的是（2）（3）共2个．故选B．点评：本题考查了二次函数的最值，抛物线与x轴的交点，仔细分析表格数据，熟练掌握二次函数的性质是解题的关键．8．（2分）（•常州）有3张边长为a的正方形纸片，4张边长分别为a、b（b＞a）的矩形纸片，5张边长为b的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（）A．a+b B．2a+b C．3a+b D．a+2b考点：完全平方公式的几何背景．分析：根据3张边长为a的正方形纸片的面积是3a2，4张边长分别为a、b（b＞a）的矩形纸片的面积是4ab，5张边长为b的正方形纸片的面积是5b2，得出a2+4ab+4b2=（a+2b）2，再根据正方形的面积公式即可得出答案．解答：解；3张边长为a的正方形纸片的面积是3a2，4张边长分别为a、b（b＞a）的矩形纸片的面积是4ab，5张边长为b的正方形纸片的面积是5b2，∵a2+4ab+4b2=（a+2b）2，∴拼成的正方形的边长最长可以为（a+2b），故选D．点评：此题考查了完全平方公式的几何背景，关键是根据题意得出a2+4ab+4b2=（a+2b）2，用到的知识点是完全平方公式．二．填空题（本大题共有9小题，第9小题4分，其余8小题每小题4分，共20分，）9．（4分）（•常州）计算﹣（﹣3）=3，|﹣3|=3，（﹣3）﹣1=﹣，（﹣3）2=9．考点：有理数的乘方；相反数；绝对值；有理数的减法．分析：根据相反数的定义，绝对值的性质，负整数指数幂，有理数的乘方的意义分别进行计算即可得解．解答：解：﹣（﹣3）=3，|﹣3|=3，（﹣3）﹣1=﹣，（﹣3）2=9．故答案为：3；3；﹣；9．点评：本题考查了相反数的定义，绝对值的性质，负整数指数幂，以及有理数的乘方的意义，是基础题．10．（2分）（•常州）已知点P（3，2），则点P关于y轴的对称点P1的坐标是（﹣3，2），点P关于原点O的对称点P2的坐标是（﹣3，﹣2）．考点：关于原点对称的点的坐标；关于x轴、y轴对称的点的坐标．分析：根据关于y轴对称的点的横坐标互为相反数，纵坐标相同；关于原点对称的点的横坐标与纵坐标都互为相反数解答．解答：解：点P（3，2）关于y轴的对称点P1的坐标是（﹣3，2），点P关于原点O的对称点P2的坐标是（﹣3，﹣2）．故答案为：（﹣3，2）；（﹣3，﹣2）．点评：本题考查了关于原点对称点点的坐标，关于y轴对称的点的坐标，熟记对称点的坐标特征是解题的关键．11．（2分）（•常州）已知一次函数y=kx+b（k、b为常数且k≠0）的图象经过点A（0，﹣2）和点B（1，0），则k=2，b=﹣2．考点：待定系数法求一次函数解析式．分析：把点A、B的坐标代入函数解析式，利用待定系数法求一次函数解析式解答即可．解答：解：∵一次函数y=kx+b（k、b为常数且k≠0）的图象经过点A（0，﹣2）和点B （1，0），∴，解得．故答案为：2，﹣2．点评：本题主要考查了待定系数法求一次函数解析式，待定系数法是求函数解析式常用的方法之一，要熟练掌握并灵活运用．12．（2分）（•常州）已知扇形的半径为6cm，圆心角为150°，则此扇形的弧长是5πcm，扇形的面积是15πcm2（结果保留π）．考点：扇形面积的计算；弧长的计算．分析：根据扇形的弧长公式l=和扇形的面积=，分别进行计算即可．解答：解：∵扇形的半径为6cm，圆心角为150°，∴此扇形的弧长是：l==5π（cm），根据扇形的面积公式，得S扇==15π（cm2）．故答案为：5π，15π．点评：此题主要考查了扇形弧长公式以及扇形面积公式的应用，熟练记忆运算公式进行计算是解题关键．13．（2分）（•常州）函数y=中自变量x的取值范围是x≥3；若分式的值为0，则x=．考点：分式的值为零的条件；函数自变量的取值范围．分析：根据被开方数大于等于0列式计算即可得解；根据分式的值为0，分子等于0，分母不等于0列式计算即可得解．解答：解：根据题意得，x﹣3≥0，解得x≥3；2x﹣3=0且x+1≠0，解得x=且x≠﹣1，所以，x=．故答案为：x≥3；．点评：本题主要考查了分式的值为零，需同时具备两个条件：（1）分子为0；（2）分母不为0．这两个条件缺一不可．14．（2分）（•常州）我市某一周的每一天的最高气温统计如下表：最高气温（℃）25 26 27 28天数 1 1 2 3则这组数据的中位数是27，众数是28．考点：众数；中位数．分析：根据中位数、众数的定义，结合表格信息即可得出答案．解答：解：将表格数据从大到小排列为：25，26，27，27，28，28，28，中位数为：27；众数为：28．故答案为：27、28．点评：本题考查了众数、中位数的定义，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会出错．15．（2分）（•常州）已知x=﹣1是关于x的方程2x2+ax﹣a2=0的一个根，则a=﹣2或1．考点：一元二次方程的解．分析：方程的解就是能使方程左右两边相等的未知数的值，把x=﹣1代入方程，即可得到一个关于a的方程，即可求得a的值．解答：解：根据题意得：2﹣a﹣a2=0 解得a=﹣2或1点评：本题主要考查了方程的解得定义，是需要掌握的基本内容．16．（2分）（•常州）如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则DC=2．考点：圆周角定理；含30度角的直角三角形；勾股定理；圆心角、弧、弦的关系．分析：根据直径所对的圆周角是直角可得∠BAD=∠BCD=90°，然后求出∠CAD=30°，利用同弧所对的圆周角相等求出∠CBD=∠CAD=30°，根据圆内接四边形对角互补求出∠BDC=60°再根据等弦所对的圆周角相等求出∠ADB=∠ADC，从而求出∠ADB=30°，解直角三角形求出BD，再根据直角三角形30°角所对的直角边等于斜边的一半解答即可．解答：解：∵BD为⊙O的直径，∴∠BAD=∠BCD=90°，∵∠BAC=120°，∴∠CAD=120°﹣90°=30°，∴∠CBD=∠CAD=30°，又∵∠BAC=120°，∴∠BDC=180°﹣∠BAC=180°﹣120°=60°，∵AB=AC，∴∠ADB=∠ADC，∴∠ADB=∠BDC=×60°=30°，∵AD=6，∴在Rt△ABD中，BD=AD÷cos60°=6÷=4，在Rt△BCD中，DC=BD=×4=2．故答案为：2．点评：本题考查了圆周角定理，直角三角形30°角所对的直角边等于斜边的一半，以及圆的相关性质，熟记各性质是解题的关键．17．（2分）（•常州）在平面直角坐标系xOy中，已知第一象限内的点A在反比例函数的图象上，第二象限内的点B在反比例函数的图象上，连接OA、OB，若OA⊥OB，OB=OA，则k=﹣．考点：反比例函数综合题．分析：过点A作AE⊥x轴于点E，过点B作BF⊥x轴于点F，设点A的坐标为（a，），点B的坐标为（b，），判断出△OBF∽△AOE，利用对应边成比例可求出k的值．解答：解：过点A作AE⊥x轴于点E，过点B作BF⊥x轴于点F，设点A的坐标为（a，），点B的坐标为（b，），∵∠AOE+∠BOF=90°，∠OBF+∠BOF=90°，∴∠AOE=∠OBF，又∵∠BFO=∠OEA=90°，∴△OBF∽△AOE，∴==，即==，则=﹣b①，a=②，①×②可得：﹣2k=1，解得：k=﹣．故答案为：﹣．点评：本题考查了反比例函数的综合题，涉及了相似三角形的判定与性质，反比例函数图象上点的坐标的特点，解答本题要求同学们能将点的坐标转化为线段的长度．三、解答题（本大题共2小题，共18分）18．（8分）（•常州）化简（1）（2）．考点：分式的加减法；实数的运算；零指数幂；特殊角的三角函数值．专题：计算题．分析：（1）分别进行二次根式的化简、零指数幂的运算，代入特殊角的三角函数值即可得出答案．（2）先通分，然后再进行分子的加减运算，最后化简即可．解答：解：（1）原式=2﹣1+2×=2．（2）原式=﹣==．点评：本题考查了分式的加减运算、特殊角的三角函数值及零指数幂的运算，属于基础题，掌握各部分的运算法则是关键．19．（10分）（•常州）解方程组和分式方程：（1）（2）．考点：解分式方程；解二元一次方程组．分析：（1）利用代入消元法解方程组；（2）最简公分母为2（x﹣2），去分母，转化为整式方程求解，结果要检验．解答：解：（1），由①得x=﹣2y ③把③代入②，得3×（﹣2y）+4y=6，解得y=﹣3，把y=﹣3代入③，得x=6，所以，原方程组的解为；（2）去分母，得14=5（x﹣2），解得x=4.8，检验：当x=4.8时，2（x﹣2）≠0，所以，原方程的解为x=4.8．点评：本题考查了解分式方程，解二元一次方程组．（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．四、解答题（本大题共2小题，共15分请在答题卡指定区域内作答，解答或写出文字说明及演算步骤）20．（7分）（•常州）为保证中小学生每天锻炼一小时，某校开展了形式多样的体育活动项目，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的统计图（1）和图（2）．（1）请根据所给信息在图（1）中将表示“乒乓球”项目的图形补充完整；（2）扇形统计图（2）中表示”足球”项目扇形的圆心角度数为72°．考点：条形统计图；扇形统计图．分析：（1）首先根据打篮球的人数是20人，占40%，求出总人数，再用总人数减去篮球、足球和其它人数得出乒乓球的人数，用各个爱好的人数除以总人数，即可得出所占的百分百，从而补全统计图；（2）用360°乘以足球所占的百分百，即可得出扇形的圆心角的度数．解答：解：（1）总人数是：20÷40%=50（人），则打乒乓球的人数是：50﹣20﹣10﹣15=5（人）．足球的人数所占的比例是：×100%=20%，打乒乓球的人数所占的比例是：×100%=10%；其它的人数所占的比例是：×100%=30%．补图如下：（2）根据题意得：360°×=72°，则扇形统计图（2）中表示”足球”项目扇形的圆心角度数为72°；故答案为：72°．点评：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．21．（8分）（•常州）一只不透明的箱子里共有3个球，其中2个白球，1个红球，它们除颜色外均相同．（1）从箱子中随机摸出一个球是白球的概率是多少？（2）从箱子中随机摸出一个球，记录下颜色后不将它放回箱子，搅匀后再摸出一个球，求两次摸出的球都是白球的概率，并画出树状图．考点：列表法与树状图法．专题：图表型．分析：（1）根据概率的意义列式即可；（2）画出树状图，然后根据概率公式列式计算即可得解．解答：解：（1）∵共有3个球，2个白球，∴随机摸出一个球是白球的概率为；（2）根据题意画出树状图如下：一共有6种等可能的情况，两次摸出的球都是白球的情况有2种，所以，P（两次摸出的球都是白球）==．点评：本题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．五．解答题（本大题共2小时，共13分，请在答题卡指定区域内作答，解答应写出证明过程）22．（6分）（•常州）如图，C是AB的中点，AD=BE，CD=CE．求证：∠A=∠B．考点：全等三角形的判定与性质．专题：证明题．分析：根据中点定义求出AC=BC，然后利用“SSS”证明△ACD和△BCE全等，再根据全等三角形对应角相等证明即可．解答：证明：∵C是AB的中点，∴AC=BC，在△ACD和△BCE中，，∴△ACD≌△BCE（SSS），∴∠A=∠B．点评：本题考查了全等三角形的判定与性质，比较简单，主要利用了三边对应相等，两三角形全等，以及全等三角形对应角相等的性质．23．（7分）（•常州）如图，在△ABC中，AB=AC，∠B=60°，∠FAC、∠ECA是△ABC 的两个外角，AD平分∠FAC，CD平分∠ECA．求证：四边形ABCD是菱形．考点：菱形的判定．专题：证明题．分析：根据平行四边形的判定方法得出四边形ABCD是平行四边形，再利用菱形的判定得出．解答：证明：∵∠B=60°，AB=AC，∴△ABC为等边三角形，∴AB=BC，∴∠ACB=60°，∠FAC=∠ACE=120°，∴∠BAD=∠BCD=120°，∴∠B=∠D=60°，∴四边形ABCD是平行四边形，∵AB=BC，∴平行四边形ABCD是菱形．点评：此题主要考查了平行四边形的判定以及菱形的判定和角平分线的性质等内容，注意菱形与平行四边形的区别，得出AB=BC是解决问题的关键．六．解答题（本大题共2小题，请在答题卡指定区域内作答，共13分）24．（6分）（•常州）在Rt△ABC中，∠C=90°，AC=1，BC=，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：∠ABC=30°，∠A′BC=90°，OA+OB+OC=．考点：作图-旋转变换．专题：作图题．分析：解直角三角形求出∠ABC=30°，然后过点B作BC的垂线，在截取A′B=AB，再以点A′为圆心，以AO为半径画弧，以点B为圆心，以BO为半径画弧，两弧相交于点O′，连接A′O′、BO′，即可得到△A′O′B；根据旋转角与∠ABC的度数，相加即可得到∠A′BC；根据直角三角形30°角所对的直角边等于斜边的一半求出AB=2AC，即A′B的长，再根据旋转的性质求出△BOO′是等边三角形，根据等边三角形的三条边都相等可得BO=OO′，等边三角形三个角都是60°求出∠BOO′=∠BO′O=60°，然后求出C、O、A′、O′四点共线，再利用勾股定理列式求出A′C，从而得到OA+OB+OC=A′C．解答：解：∵∠C=90°，AC=1，BC=，∴tan∠ABC===，∴∠ABC=30°，∵△AOB绕点B顺时针方向旋转60°，∴△A′O′B如图所示；∠A′BC=∠ABC+60°=30°+60°=90°，∵∠C=90°，AC=1，∠ABC=30°，∴AB=2AC=2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B=AB=2，BO=BO′，A′O′=AO，∴△BOO′是等边三角形，∴BO=OO′，∠BOO′=∠BO′O=60°，∵∠AOC=∠COB=BOA=120°，∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C===，∴OA+OB+OC=A′O′+OO′+OC=A′C=．故答案为：30°；90°；．点评：本题考查了利用旋转变换作图，旋转变换的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，勾股定理，等边三角形的判定与性质，综合性较强，最后一问求出C、O、A′、O′四点共线是解题的关键．25．（7分）（•常州）某饮料厂以300千克的A种果汁和240千克的B种果汁为原料，配制生产甲、乙两种新型饮料，已知每千克甲种饮料含0.6千克A种果汁，含0.3千克B种果汁；每千克乙种饮料含0.2千克A种果汁，含0.4千克B种果汁．饮料厂计划生产甲、乙两种新型饮料共650千克，设该厂生产甲种饮料x（千克）．（1）列出满足题意的关于x的不等式组，并求出x的取值范围；（2）已知该饮料厂的甲种饮料销售价是每1千克3元，乙种饮料销售价是每1千克4元，那么该饮料厂生产甲、乙两种饮料各多少千克，才能使得这批饮料销售总金额最大？考点：一次函数的应用；一元一次不等式组的应用．分析：（1）表示出生产乙种饮料（650﹣x）千克，然后根据所需A种果汁和B种果汁的数量列出一元一次不等式组，求解即可得到x的取值范围；（2）根据销售总金额等于两种饮料的销售额的和列式整理，再根据一次函数的增减性求出最大销售额．解答：解：（1）设该厂生产甲种饮料x千克，则生产乙种饮料（650﹣x）千克，根据题意得，，由①得，x≤425，由②得，x≥200，所以，x的取值范围是200≤x≤425；（2）设这批饮料销售总金额为y元，根据题意得，y=3x+4（650﹣x）=3x+2600﹣4x=﹣x+2600，即y=﹣x+2600，∵k=﹣1＜0，∴当x=200时，这批饮料销售总金额最大，为﹣200+2600=2400元．点评：本题考查了一次函数的应用，列一元一次不等式组解实际问题，根据A、B果汁的数量列出不等式组是解题的关键，（2）主要利用了一次函数的增减性．七．解答题（本大题共2小题，共25分，解答应写出文字说明，证明过程或演算步骤）26．（6分）（•常州）用水平线和竖起线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形．设格点多边形的面积为S，该多边形各边上的格点个数和为a，内部的格点个数为b，则S=a+b﹣1（史称“皮克公式”）．小明认真研究了“皮克公式”，并受此启发对正三角开形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，下图是该正三角形格点中的两个多边形：根据图中提供的信息填表：格点多边形各边上格点边多边形内部格点多边形的面积的格点的个数的格点个数多边形1 8 1多边形2 7 3…………一般格点多边形 a b S则S与a、b之间的关系为S=a+2（b﹣1）（用含a、b的代数式表示）．考点：规律型：图形的变化类．分析：根据8=8+2（1﹣1），11=7+2（3﹣1）得到S=a+2（b﹣1）．解答：解：填表如下：格点多边形各边上的格点的个数格点边多边形内部的格点个数格点多边形的面积多边形1 8 1 8多边形2 7 3 11…………一般格点多边形 a b S则S与a、b之间的关系为S=a+2（b﹣1）（用含a、b的代数式表示）．点评：考查了作图﹣应用与设计作图．此题需要根据图中表格和自己所算得的数据，总结出规律．寻找规律是一件比较困难的活动，需要仔细观察和大量的验算．27．（9分）（•常州）在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．（1）当OC∥AB时，∠BOC的度数为45°或135°；（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．（3）连接AD，当OC∥AD时，①求出点C的坐标；②直线BC是否为⊙O的切线？请作出判断，并说明理由．考点：圆的综合题．专题：综合题．分析：（1）根据点A和点B坐标易得△OAB为等腰直角三角形，则∠OBA=45°，由于OC∥AB，所以当C点在y轴左侧时，有∠BOC=∠OBA=45°；当C点在y轴右侧时，有∠BOC=180°﹣∠OBA=135°；（2）由△OAB为等腰直角三角形得AB=OA=6，根据三角形面积公式得到当点C到AB的距离最大时，△ABC的面积最大，过O点作OE⊥AB于E，OE的反向延长线交⊙O于C，此时C点到AB的距离的最大值为CE的长然后利用等腰直角三角形的性质计算出OE，然后计算△ABC的面积；（3）①过C点作CF⊥x轴于F，易证Rt△OCF∽Rt△AOD，则=，即=，解得CF=，再利用勾股定理计算出OF=，则可得到C点坐标；②由于OC=3，OF=，所以∠COF=30°，则可得到∴BOC=60°，∠AOD=60°，然后根据“SAS”判断△BOC≌△AOD，所以∠BCO=∠ADC=90°，再根据切线的判定定理可确定直线BC为⊙O的切线．解答：解：（1）∵点A（6，0），点B（0，6），∴OA=OB=6，∴△OAB为等腰直角三角形，∴∠OBA=45°，∵OC∥AB，∴当C点在y轴左侧时，∠BOC=∠OBA=45°；当C点在y轴右侧时，∠BOC=180°﹣∠OBA=135°；（2）∵△OAB为等腰直角三角形，∴AB=OA=6，∴当点C到AB的距离最大时，△ABC的面积最大，过O点作OE⊥AB于E，OE的反向延长线交⊙O于C，如图，此时C点到AB的距离的最大值为CE的长，∵△OAB为等腰直角三角形，∴AB=OA=6，∴OE=AB=3，∴CE=OC+CE=3+3，△ABC的面积=CE•AB=×（3+3）×6=9+18．∴当点C在⊙O上运动到第三象限的角平分线与圆的交点位置时，△ABC的面积最大，最大值为9+18．（3）①如图，过C点作CF⊥x轴于F，∵OC∥AD，∴∠ADO=∠COD=90°，∴∠DOA+∠DAO=90°而∠DOA+∠COF=90°，∴∠COF=∠DAO，∴Rt△OCF∽Rt△AOD，∴=，即=，解得CF=，在Rt△OCF中，OF==，∴C点坐标为（﹣，）；②直线BC是⊙O的切线．理由如下：在Rt△OCF中，OC=3，OF=，∴∠COF=30°，∴∠OAD=30°，∴∠BOC=60°，∠AOD=60°，∵在△BOC和△AOD中，∴△BOC≌△AOD（SAS），∴∠BCO=∠ADC=90°，∴OC⊥BC，∴直线BC为⊙O的切线．点评：本题考查了圆的综合题：掌握切线的判定定理、平行线的性质和等腰直角三角形的判定与性质；熟练运用勾股定理和相似比进行几何计算．28．（10分）（•常州）在平面直角坐标系xOy中，一次函数y=2x+2的图象与x轴交于A，与y轴交于点C，点B的坐标为（a，0），（其中a＞0），直线l过动点M（0，m）（0＜m＜2），且与x轴平行，并与直线AC、BC分别相交于点D、E，P点在y轴上（P 点异于C点）满足PE=CE，直线PD与x轴交于点Q，连接PA．（1）写出A、C两点的坐标；（2）当0＜m＜1时，若△PAQ是以P为顶点的倍边三角形（注：若△HNK满足HN=2HK，则称△HNK为以H为顶点的倍边三角形），求出m的值；（3）当1＜m＜2时，是否存在实数m，使CD•AQ=PQ•DE？若能，求出m的值（用含a 的代数式表示）；若不能，请说明理由．考点：一次函数综合题分析：（1）利用一次函数图象上点的坐标特征求解；（2）如答图1所示，解题关键是求出点P、点Q的坐标，然后利用PA=2PQ，列方程求解；（3）如答图2所示，利用相似三角形，将已知的比例式转化为：，据此列方程求出m的值．解答：解：（1）在直线解析式y=2x+2中，令y=0，得x=﹣1；x=0，得y=2，∴A（﹣1，0），C（0，2）；（2）当0＜m＜1时，依题意画出图形，如答图1所示．∵PE=CE，∴直线l是线段PC的垂直平分线，∴MC=MP，又C（0，2），M（0，m），∴P（0，2m﹣2）；直线l与y=2x+2交于点D，令y=m，则x=，∴D（，m），设直线DP的解析式为y=kx+b，则有，解得：k=﹣2，b=2m﹣2，∴直线DP的解析式为：y=﹣2x+2m﹣2．令y=0，得x=m﹣1，∴Q（m﹣1，0）．已知△PAQ是以P为顶点的倍边三角形，由图可知，PA=2PQ，∴，即，整理得：（m﹣1）2=，解得：m=（＞1，不合题意，舍去）或m=，∴m=．（3）当1＜m＜2时，假设存在实数m，使CD•AQ=PQ•DE．依题意画出图形，如答图2所示．由（2）可知，OQ=m﹣1，OP=2m﹣2，由勾股定理得：PQ=（m﹣1）；∵A（﹣1，0），Q（m﹣1，0），B（a，0），∴AQ=m，AB=a+1；∵OA=1，OC=2，由勾股定理得：CA=．∵直线l∥x轴，∴△CDE∽△CAB，∴；又∵CD•AQ=PQ•DE，∴，∴，即，解得：m=．∵1＜m＜2，∴当0＜a≤1时，m≥2，m不存在；当a＞1时，m=．∴当1＜m＜2时，若a＞1，则存在实数m=，使CD•AQ=PQ•DE；若0＜a≤1，则m不存在．点评：本题是代数几何综合题，考查了坐标平面内一次函数的图象与性质、待定系数法、相似三角形、勾股定理、解方程等知识点．题目综合性较强，有一定的难度．第（3）问中，注意比例式的转化，这样可以简化计算．。
【2013中考真题】常州中考数学试题+答案
常州市二〇一三年初中毕业、升学统一文化考试数 学 试 题一．选择题（本大题共有8小题，每小题2分，共16分，在每小题所给的四个选项中，只有一项是正确的） 1. 在下列实数中，无理数是 （ D ） A ．2B ．3.14C ．21-D ．32.如图所示圆柱的左视图是 （ C ）（第2题） A ． B ． C ． D ． 下列函数中，图像经过点（1，-1)的反比例函数关系式是 （ A ）A.x y 1-=B.x y 1=C.xy 2=D.xy 2-= 4.下列计算中，正确的是 （ A ） A ．（a 3b ）2=a 6b 2 B ．a*a 4=a 4 C ．a 6÷a 2=a 3D ．3a+2b=5ab 5.已知：甲乙两组数据的平均数都是5，甲组数据的方差1212=甲S ，乙组数据的方差1012=乙S ，下列结论中正确的是 （ B ）A ．甲组数据比乙组数据的波动大B ．乙组数据的比甲组数据的波动大C ．甲组数据与乙组数据的波动一样大D ．甲组数据与乙组数据的波动不能比较6.已知⊙O 的半径是6，点O 到直线l 的距离为5，则直线l 与⊙O 的位置关系是（ C ） A ．相离B ．相切C ．相交D ．无法判断7.二次函数c bx ax y ++=2（a 、b 、c 为常数且a ≠0）中的x 与y 的部分对应值如下表：x -3 -2 -1 0 1 2 3 4 5 y12 5 0 -3 -4 -3 0 5 12给出了结论：(1)二次函数c bx ax y ++=2有最小值，最小值为-3；(2)当221<<-x 时，y<0; (3)二次函数c bx ax y ++=2的图象与x 轴有两个交点，且它们分别在y 轴两侧。
则其中正确结论的个数是 （ B ） A ．3 B ．2 C ．1 D ．08.有3张边长为a 的正方形纸片，4张边分别为a 、b(b>a)的矩形纸片，5张边长为b 的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸片进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（ D ） A ．a+b B ．2a+b C ．3a+b D ．a+2b二．填空题（本大题共有9小题，第9小题4分，其余8小题每小题2分，共20分） 9.计算-(-3)=__3_____,|-3|=___3____,(-3)－²=1-3,(-3)²=____9___. 10.已知点P （3，2），则点P 关于y 轴的对称点P 1的坐标是_(-3,2)_,点P 关于原点O 的对称点P 2的坐标是___(-3,-2)_____.11.已知一次函数y=kx+b(k 、b 为常数且k ≠0)的图象经过点A （0,-2）和点B （1,0），则k=__2____，b=_-2_____。
江苏省常州市2002-2013年中考数学试题【专题03】方程(组)和不等式(组)(含解析)
专题3：方程（组）和不等式（组） 江苏泰州锦元数学工作室 编辑一、选择题1.（江苏省常州市2002年2分）一元二次方程x 2－x ＋1=0的根的情况是【 】 A.有两个相等的实数根 B.无实数根C.两个实数根的和与积都等于1D.有两个不相等的实数根2. （江苏省常州市2002年2分）若x 1和x 2是方程2x 2＋3x －1=0的两个实数根，则1211x x +的值等于 【 】A. 31-B. 31 C. –3 D.33. （江苏省常州市2002年2分）已知:a<b<0，则下列不等式成立的是【 】 A. ab<0 B. –a －b<0 C. a+b >0 D. ab>14. （江苏省常州市2003年2分）一元二次方程0422=-+y y 的根的情况是【 】 （A ）有两个相等的实数根 （B ）有两个不相等的实数根，且两根同号 （C ）有两个不相等的实数根，且两根异号 （D ）没有实数根5. （江苏省常州市2003年2分）已知关于x 的不等式32->-m x 的解集如图所示，则m 的值为【 】（A ）2 （B ）1 （C ）0 （D ）－16. （江苏省常州市2004年2分）用换元法解方程433322=-+-xx x x 时，设x x y 32-=，则原方程可化为【 】（A ）043=-+y y （B ）043=+-y y （C ）0431=-+y y （D ）0431=++yy7. （江苏省常州市2004年2分）关于x 的一元二次方程2x (2k 1)x k 10+++-=根的情况是【 】（A ）有两个不相等实数根 （B ）有两个相等实数根 （C ）没有实数根 （D ）根的情况无法判定8. （江苏省常州市2006年2分）小刘同学用10元钱买两种不同的贺卡共8张，单价分别是1元与2元，设1元的贺卡为x 张，2元的贺卡为y 张，那么x 、y 所适合的一个方程组是【 】A ．⎪⎩⎪⎨⎧=+=+8102y x y x B ．⎪⎩⎪⎨⎧=+=+1028102y x y x C ．⎩⎨⎧=+=+8210y x y x D ．⎩⎨⎧=+=+1028y x y x9. （江苏省常州市2006年2分）如果0,0,0a <b >a b <+，那么下列关系式中正确的是【 】A ．a >b >b >a --B ．a >a >b >b --C ．b >a >b >a --D ．a >b >b >a --【答案】D。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2013年江苏省常州市中招考试数学试卷一．选择题（本大题共有8小题，每小题2分，共16分，在每小题所给的四个选项中，只有一项是正确的）1．在下列实数中，无理数是（ ）A ．2B ．3.14C ．12- D ．3 2．如图所示圆柱的左视图是（ ）A ．B ．C ．D ．3．下列函数中，图象经过点（1，﹣1）的反比例函数关系式是（ ） A ．1y x =-B ．1y x =C ．2y x =D ．2y x=- 4．下列计算中，正确的是（ ）A ．（a 3b ）2=a 6b 2B ．a•a 4=a 4C ．a 6÷a 2=a 3D ．3a+2b=5ab 5．已知：甲乙两组数据的平均数都是5，甲组数据的方差21S 12=甲，乙组数据的方差21S 10=乙，下列结论中正确的是（ ）A ．甲组数据比乙组数据的波动大B ．乙组数据的比甲组数据的波动大C ．甲组数据与乙组数据的波动一样大D ．甲组数据与乙组数据的波动不能比较 6．已知⊙O 的半径是6，点O 到直线l 的距离为5，则直线l 与⊙O 的位置关系是（ ） A ．相离 B ．相切 C ．相交 D ．无法判断7．二次函数2y ax bx c =++（a 、b 、c 为常数且a≠0）中的x 与y 的部分对应值如下表：x ﹣3 ﹣2 ﹣1 0 1 2 3 4 5 y125﹣3﹣4﹣3512给出了结论：（1）二次函数2y ax bx c =++有最小值，最小值为﹣3； （2）当1<x<22-时，y ＜0；（3）二次函数2y ax bx c =++的图象与x 轴有两个交点，且它们分别在y 轴两侧． 则其中正确结论的个数是（ ）A ．3B ．2C ．1D ．08．有3张边长为a 的正方形纸片，4张边长分别为a 、b （b ＞a ）的矩形纸片，5张边长为b 的正方形纸片，从其中取出若干张纸片，每种纸片至少取一张，把取出的这些纸片拼成一个正方形（按原纸张进行无空隙、无重叠拼接），则拼成的正方形的边长最长可以为（ ） A ．a+b B ．2a+b C ．3a+b D ．a+2b二．填空题（本大题共有9小题，第9小题4分，其余8小题每小题2分，共20分，） 9．（2013年江苏常州4分）计算()3--=__________，3-=__________，()13--=__________，()23-=__________．10．已知点P （3，2），则点P 关于y 轴的对称点P 1的坐标是__________，点P 关于原点O 的对称点P 2的坐标是__________．11．已知一次函数y=kx+b （k 、b 为常数且k≠0）的图象经过点A （0，﹣2）和点B （1，0），则k=__________，b=__________．12．已知扇形的半径为6cm ，圆心角为150°，则此扇形的弧长是__________cm ，扇形的面积是__________cm 2（结果保留π）．13．函数y x 3=-中自变量x 的取值范围是__________；若分式2x 3x 1-+的值为0，则x= __________．14．我市某一周的每一天的最高气温统计如下表：最高气温（℃）25 26 27 28 天数1123则这组数据的中位数是__________，众数是__________．15．已知x=－1是关于x 的方程222x ax a 0+-=的一个根，则a=__________．16．如图，△ABC 内接于⊙O ，∠BAC=120°，AB=AC ，BD 为⊙O 的直径，AD=6，则DC=__________．17．在平面直角坐标系xOy 中，已知第一象限内的点A 在反比例函数1y x=的图象上，第二象限内的点B在反比例函数ky x=的图象上，连接OA 、OB ，若OA ⊥OB ，OB=2OA ，则k=__________．三、解答题（本大题共2小题，共18分） 18．（ 8分）化简（1）（4()0020132cos60-+（2）（4分）22x 1x 4x 2--+．19．（10分）解方程组和分式方程：（1）解方程组（5分）x 2y 03x 4y 6+=⎧⎨+=⎩（2）（5分）解分式方程75x 22=-．四、解答题（本大题共2小题，共15分请在答题卡指定区域内作答，解答或写出文字说明及演算步骤）20．（7分）为保证中小学生每天锻炼一小时，某校开展了形式多样的体育活动项目，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的统计图（1）和图（2）．（1）请根据所给信息在图（1）中将表示“乒乓球”项目的图形补充完整；（2）扇形统计图（2）中表示”足球”项目扇形的圆心角度数为__________．21．（8分）一只不透明的箱子里共有3个球，其中2个白球，1个红球，它们除颜色外均相同．（1）从箱子中随机摸出一个球是白球的概率是多少？（2）从箱子中随机摸出一个球，记录下颜色后不将它放回箱子，搅匀后再摸出一个球，求两次摸出的球都是白球的概率，并画出树状图．五．解答题（本大题共2小时，共13分，请在答题卡指定区域内作答，解答应写出证明过程）22．（6分）如图，C是AB的中点，AD=BE，CD=CE．求证：∠A=∠B．23．（7分）如图，在△ABC中，AB=AC，∠B=60°，∠FAC、∠ECA是△ABC的两个外角，AD平分∠FAC，CD平分∠ECA．求证：四边形ABCD是菱形．六．解答题（本大题共2小题，请在答题卡指定区域内作答，共13分）24．（6分）在Rt△ABC中，∠C=90°，AC=1，BC=3，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：∠ABC=__________，∠A′BC=__________，OA+OB+OC=__________．25．（7分）某饮料厂以300千克的A种果汁和240千克的B种果汁为原料，配制生产甲、乙两种新型饮料，已知每千克甲种饮料含0.6千克A种果汁，含0.3千克B种果汁；每千克乙种饮料含0.2千克A种果汁，含0.4千克B种果汁．饮料厂计划生产甲、乙两种新型饮料共650千克，设该厂生产甲种饮料x（千克）．（1）列出满足题意的关于x的不等式组，并求出x的取值范围；（2）已知该饮料厂的甲种饮料销售价是每1千克3元，乙种饮料销售价是每1千克4元，那么该饮料厂生产甲、乙两种饮料各多少千克，才能使得这批饮料销售总金额最大？七．解答题（本大题共3小题，共25分，解答应写出文字说明，证明过程或演算步骤）26．（6分）用水平线和竖起线将平面分成若干个边长为1的小正方形格子，小正方形的顶点称为格点，以格点为顶点的多边形称为格点多边形．设格点多边形的面积为S，该多边形各边上的格点个数和为a，内部的格点个数为b，则1S a b12=+-（史称“皮克公式”）．小明认真研究了“皮克公式”，并受此启发对正三角开形网格中的类似问题进行探究：正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，下图是该正三角形格点中的两个多边形：根据图中提供的信息填表：格点多边形各边上的格点的个数格点边多边形内部的格点个数格点多边形的面积多边形1 8 1多边形2 7 3…………一般格点多边形 a b S则S与a、b之间的关系为S=__________（用含a、b的代数式表示）．27．（9分）在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D按逆时针方向排列），连接AB．（1）当OC∥AB时，∠BOC的度数为__________；（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC的面积的最大值．（3）连接AD，当OC∥AD时，①求出点C的坐标；②直线BC是否为⊙O的切线？请作出判断，并说明理由．28．（10分）在平面直角坐标系xOy中，一次函数y=2x+2的图象与x轴交于A，与y轴交于点C，点B 的坐标为（a，0），（其中a＞0），直线l过动点M（0，m）（0＜m＜2），且与x轴平行，并与直线AC、BC分别相交于点D、E，P点在y轴上（P点异于C点）满足PE=CE，直线PD与x轴交于点Q，连接PA．（1）写出A、C两点的坐标；（2）当0＜m＜1时，若△PAQ是以P为顶点的倍边三角形（注：若△HNK满足HN=2HK，则称△HNK 为以H为顶点的倍边三角形），求出m的值；（3）当1＜m＜2时，是否存在实数m，使CD•AQ=PQ•DE？若能，求出m的值（用含a的代数式表示）；若不能，请说明理由．2013年江苏省常州市中招考试数学试卷答案一、选择题二、填空题 9．3，3，13，9 10．（－3，2），（－3，－2） 11．2，﹣2 12．5π，15π 13．3x ≥，32x = 14．27，2815．﹣2或116．17．12-三、解答题18．（1）原式=121222-+⨯= （2）解：原式=()()()()()()2x x 2x 21x 2x 2x 2x 2x 2x 2x 2-+-==+-+-+--19．（1）解：x 2y 03x 4y 6+=⎧⎨+=⎩①②，由①得x=﹣2y ③把③代入②，得3×（﹣2y ）+4y=6，解得y=﹣3 把y=﹣3代入③，得x=6∴原方程组的解为x 6y 3=⎧⎨=-⎩（2）解：去分母，得14=5（x ﹣2）， 解得x=4.8，检验：当x=4.8时，2（x ﹣2）≠0， ∴原方程的解为x=4.820．解：（1）总人数是：20÷40%=50（人），则打乒乓球的人数是：50﹣20﹣10﹣15=5（人）。
补图如下：（2）72°21．解：（1）∵共有3个球，2个白球，∴随机摸出一个球是白球的概率为23。
（2）根据题意画出树状图如下：∵一共有6种等可能的情况，两次摸出的球都是白球的情况有2种，∴P（两次摸出的球都是白球）21 63 ==22．∵C是AB的中点，∴AC=BC。
在△ACD和△BCE中，∵AD=BE，CD=CE．AC=BC，∴△ACD≌△BCE（SSS）∴∠A=∠B23．∵∠B=60°，AB=AC，∴△ABC为等边三角形∴AB=BC，∠ACB=60°∴∠FAC=∠ACE=120°∴∠BAD=∠BCD=120°∴∠B=∠D=60°∴四边形ABCD是平行四边形∵AB=BC，∴平行四边形ABCD是菱形24．作图如下：30°，90°725．（1）设该厂生产甲种饮料x千克，则生产乙种饮料（650﹣x）千克，根据题意得，()()0.6x0.2650x3000.3x0.4650x240⎧+-≤⎪⎨+-≤⎪⎩①②，由①得，x≤425，由②得，x≥200，∴x的取值范围是200≤x≤425。