高等数学第五章_定积分总结
高等数学 第5章 第一节 定积分的概念
定积分存在的两个充分条件:
定理1 设 f ( x) 在区间 [a, b]上连续, 则 f ( x)在区间 [a, b] 上可积. 定理2 设 f ( x)在区间 [a, b] 上有界, 且只有有限个间断点,则
f ( x)在区间 [a, b]上可积.
6
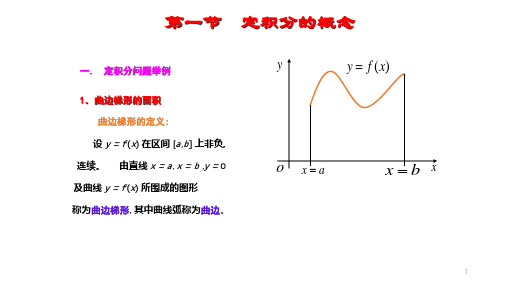
定积分的几何意义
y y f (x)
A
o xa xb x
lim
n
6n 2
3
10
1 i n
i
},
0,
n
A lim 0 i1
f ( i )xi
An
x xn1 nxn b
3
2. 变速直线运动的路程
设物体作直线运动,
已知速度 v v(t )是时间间隔 [T1 ,T2 ]上 的
连续函数, 且 v(t ) 0, 计算在这段时间内物体所经过的路程。
匀速直线运动:
路程=速度×时间.
(1) 分割
T1 t0 t1 ti1 ti tn T2 ,
v( i )
ti ti ti1
(i 1,2,, n)
(2) 近似代替
si v( i )t i
T1
i
T2
t t0 t1 t2 ti1 ti tn1 tn
(3) 求和 (4) 取极限
s
n i 1
s
i
n v(
i 1
i )t i
每 个小区间的长度 xi xi xi1 (i 1,2,n).
2
(2)近似代替
y Ai f (i )xi
(i 1,2,, n)
(3)求和
y f (x)
A1 A2
Ai
A
n i 1
Ai
n
高等数学第五章定积分及其应用

⾼等数学第五章定积分及其应⽤第五章定积分及其应⽤第⼀节定积分概念1、内容分布图⽰★曲边梯形★曲边梯形的⾯积★变速直线运动的路程★变⼒沿直线所作功★定积分的定义★定积分存在定理★定积分的⼏何意义★定积分的物理意义★例1 ★定积分的近似计算★例2★内容⼩结★课堂练习★习题5-1 ★返回2、讲解注意:3、重点难点:4、例题选讲:例1利⽤定积分的定义计算积分01dx x 2?.讲解注意:例2的近似值.⽤矩形法和梯形法计算积分-102dx ex讲解注意:第⼆节定积分的性质1、内容分布图⽰★性质1-4★性质5及其推论★例1★性质6★例2★例3★性质7★例4★函数的平均值★例5★内容⼩结★课堂练习★习题5-2★返回2、讲解注意:例1⽐较积分值dx e x ?-2和dx x ?-2的⼤⼩.讲解注意:例2估计积分dx xπ+03sin 31的值.讲解注意:例3估计积分dx xxππ/2/4sin 的值.讲解注意:例4设)(x f 可导1)(lim =+∞→x f x 求且,,dt t f tt x x x ?++∞→2)(3sin lim .讲解注意:例5计算纯电阻电路中正弦交流电t I i m ωsin =在⼀个周期上的()功率的平均值简称平均功率.讲解注意:第三节微积分基本公式1、内容分布图⽰★引例★积分上限函数★积分上限函数的导数★例1-2★例3★例4★例5★例6★例7-8 ★例9★例10★例11★例12★例13★例14★内容⼩结★课堂练习★习题5-3★返回2、讲解注意:3、重点难点:4、例题选讲:例1?x tdt dxd 02cos 求[].讲解注意:例2dt e dxdx t ?321求[].讲解注意:例3.)()((3);)()((2);)((1).,)(00sin cos )(?-===x x x x t f dt t x f x F dt t xf x F dt e x F x f 试求以下各函数的导数是连续函数设讲解注意:例4求.1cos 02x dte x t x ?-→讲解注意:设)(x f 在),(+∞-∞内连续0)(>x f .证明函数且,??=xxdtt f dtt t x F 00)()()(在),0(+∞内为单调增加函数.f 例5讲解注意:例6],1[)ln 21()(1上的最⼤值与最⼩在求函数e dt t t x I x ?+=.值讲解注意:例7求.dx x ?12讲解注意:例8求.1dxx ?--12讲解注意:例9设求??≤<≤≤=215102)(x x x x f ?2讲解注意:例10.|12|10-dx x 计算讲解注意:.cos 1/3/22?--ππdx x 计算例11讲解注意:例12求.},max{222?-dx x x讲解注意:例13计算由曲线x y sin =在,0π之间及x .轴所围成的图形的⾯积x =x =A讲解注意:例14?,./5.,362了多少距离问从开始刹车到停车刹车汽车以等加速度到某处需要减速停车速度⾏驶汽车以每⼩时s m a km -=汽车驶过设讲解注意:第四节换元法积分法和分部积分法1、内容分布图⽰★定积分换元积分法★例1★例2★例3★例4★定积分的分部积分法★内容⼩结★课堂练习★习题5-4★返回★例5★例6★例7★例16★例17★例182、讲解注意:3、重点难点:4、例题选讲:例1计算.sin cos /25?πxdx x讲解注意:例2?a0dx 计算.0a >)(-2x 2a讲解注意:例3计算.sin sin 053?π-dx x x讲解注意:例4计算定积分dx x x ++412.2?讲解注意:例5当)(x f 在],[a a -上连续,,,)(x f 为偶函数当当有(1)(2)则 ??-=aaadx x f dx x f 0)(2)()(x f 为奇函数有?-=aa dx x f 0)(.;讲解注意:例6.--+dx e x x x 计算讲解注意:例7计算.11cos 21122?--++dx x xx x讲解注意:例8若)(x f 在]1,0[上连续证明,(1)?=00)(cos )(sin dx x f dx x f ;(2)πππ=)(sin 2)(sin dx x f dx x xf ,由此计算?π+02cos 1sin dx x x x ./2π/2π讲解注意:例9计算.arcsin 0?xdx 1/2讲解注意:例10计算.2cos 10+x xdx/4π讲解注意:例11计算.sin 0?xdx /2π2x讲解注意:例12.1dx e x 计算1/2讲解注意:例13.1)1ln(102++dx x x 求定积分讲解注意:例14-22ln e e dx x x求.讲解注意:例15.,612ln 2x e dt xt 求已知?=-π讲解注意:例16).(,)(13)()(1022x f dx x f x x x f x f 求满⾜⽅程已知? --=讲解注意:例17证明定积分公式xdx I n n n 0--?-??--?-=n n n n n n n n n n ,3254231,22143231π为正偶数.为⼤于1的正奇数./2π/2π??讲解注意:例18?π05.2cos dx x 求讲解注意:第五节定积分的⼏何应⽤1、内容分布图⽰★平⾯图形的⾯积A ★例1 ★例2 ★平⾯图形的⾯积B ★例3 ★例4 ★平⾯图形的⾯积C ★例5 ★平⾯图形的⾯积D★例6 ★例7 ★例8 旋转体★圆锥★圆柱★旋转体★旋转体的体积★例9 ★例 10 ★例 11 ★平⾏截⾯⾯积为已知的⽴体的体积★例 12 ★例 13 ★内容⼩结★课堂练习★习题5-5 ★返回2、讲解注意:3、重点难点:4、例题选讲:例1]1,1[]1,0[2之间的⾯积.和轴上⽅在下⽅与分别求曲线-∈∈=x x x x y讲解注意:例2],1[ln 之间的⾯积.轴上⽅在下⽅与求e x x y =讲解注意:例3.1,1,03所围图形⾯积与直线求=-===x x y x y讲解注意:例44,0,042所围图形⾯积.和直线求由曲线===-=x x y x y讲解注意:例5.2所围成平⾯图形的⾯积与求由抛物线x y x y ==讲解注意:例642,2,所围成图形的⾯积.求由三条直线=-=+=y x y x x y422围成图形的⾯积与求+-==x y x y讲解注意:例8.0cos sin 之间所围图与在和求由曲线π====x x x y x y 形的⾯积讲解注意:例9r 圆锥体的直线、h x =及x 轴围直线连接坐标原点O 及点),(r h P 成⼀个直⾓三⾓形.x 轴旋转构成⼀个底半径为计算圆锥体的体积.h ,将它绕⾼为,的讲解注意:例10.12222y x V V y x by a x 和积轴旋转所得的旋转体体轴和分别绕求椭圆=+讲解注意:例112,22轴旋转⽽成的旋转体的体积.轴和所围成的图形分别绕求由曲线y x x y x y -==讲解注意:例12⼀平⾯经过半径为R 的圆柱体的底圆中⼼计算这平⾯截圆柱体所得⽴体的体积.并与底⾯交成,,⾓讲解注意:例13.的正劈锥体的体积的圆为底、求以半径为h R ⾼位平⾏且等于底圆直径的线段为顶、讲解注意:第六节积分在经济分析中的应⽤1、内容分布图⽰★由边际函数求原经济函数★需求函数★例1★总成本函数★例2★总收⼊函数★例3★利润函数★例4由边际函数求最优问题★例5★例6其它经济应⽤★例7⼴告策略★消费者剩余★例8★国民收⼊分配★例9★返回2、讲解注意:3、重点难点:4、例题选讲:例1),80,(80,4) (,==-='q pp qp格的函数关系.时即该商品的最⼤需求量为且边际需求的函数已知对某商品的需求量是价格求需求量与价讲解注意:例2, 90,2)(0.2 ==ceqCq 求总成本函数.固定成本的函数若⼀企业⽣产某产品的边际成本是产量讲解注意:例310,40),/(2100)(个单位时单位时的总收⼊及平均收⼊求⽣产单位元单位时的边际收⼊为已知⽣产某产品-='q q R q 并求再增加⽣产所增加的总收⼊.讲解注意:例45,10,413)(,225)(0==-='-='q c q q C q q R 时的⽑利和纯利.求当固定成本为边际成本已知某产品的边际收⼊讲解注意:例5吨产品时的边际成本为某企业⽣产q )/30501)(吨元q q C +='(?,900试求产量为多少时平均成本最低元且固定成本为讲解注意:例6q q q C q q R ,1(3)?(2);54(1)),/(/44)(),/(9)(+='-='求总成本函数和利润函数.万元已知固定成本为当产量为多少时利润最⼤万台时利润的变化量万台增加到试求当产量由其中产量万台万元成本函数为万台万元假设某产品的边际收⼊函数为以万台为单位.边际讲解注意:例70.02,10%,,100000,130000)(,.10%,1000000t e t 则决如果新增销售额产⽣的利润超过⼴告投资的美元的⼴告活动对于超过按惯例⾏⼀次类似的总成本为以⽉为单位下式的增长曲线⼴告宣传期间⽉销售额的变化率近似服从如根据公司以往的经验平均利润是销售额的美元某出⼝公司每⽉销售额是美元的⼴告活动.试问该公司按惯例是否应该做此⼴告.1000000公司现在需要决定是否举定做⼴告讲解注意:8例.2,318)(-=CS q q D 并已知需求量为如果需求曲线为个单位试求消费者剩余,表⽰某国某年国民收⼊在国民之间分配的劳伦茨曲线可近似地由讲解注意:第七节⼴义积分1、内容分布图⽰★⽆穷限的⼴义积分★⽆穷限的⼴义积分⼏何解释★例1★例2★例3★例4★例5★例6★⽆界函数的⼴义积分例7★例8★例9★例10★例11★例12★例13★内容⼩结★课堂练习★习题5-7★返回★2、讲解注意:3、重点难点:4、例题选讲:例1?∞+-0.dx e x 计算⽆穷积分讲解注意:例2.sin 0的收敛性判断⽆穷积分∞+xdx讲解注意:例312?∞+∞-+x dx计算⼴义积分讲解注意:例4计算⼴义积分.1sin 12∞+dx x x 2/π讲解注意:例5计算⼴义积分∞+-pt dt e 且0>p 时收敛p 是常数,(). t 0讲解注意:例6证明⼴义积分∞+11dxx p当1>p 时收敛当1≤p 时发散.,讲解注意:例7计算⼴义积分).0(022>-?a x a dxa讲解注意:例8证明⼴义积分11dx x q当1""讲解注意:例9计算⼴义积分.ln 21x dx讲解注意:例10计算⼴义积分.30dx1=x 瑕点)1(2/3-x .讲解注意:例11计算⼴义积分?∞+03+x x dx1().讲解注意:例12.)1(arcsin 10-dx x x x计算⼴义积分讲解注意:例13.11105?∞+++x x x dx 计算⼴义积分讲解注意:。
高等数学第五章_定积分总结

第五章 定积分创新生技102班 张梦菲2010015066一、主要内容Ⅰ. 定积分概念:1. 定积分定义:设()f x 在区间[,]a b 上有界,在[,]a b 中任意插入若干个分点 0121n n a x x x x x b -=<<<<<=.把[,]a b 分成n 个小区间1[,],(1,2,,)i i x x i n -=,小区间的长度记为1,(1,2,,)i i i x x x i n -∆=-=,在1[,]i i x x -上任意取一点i ξ,作1()ni i i f x ξ=∆∑,若01lim()niii f x λξ→=⋅∆∑ 1(max{})ii nx λ≤≤=∆存在. 就称该极限为()f x 在[,]a b 上的定积分.记为1()lim ()nbi i ai f x dx f x λξ→==⋅∆∑⎰当上述极限存在时,称()f x 在[,]a b 上可积. 2. 若()f x 在[,]a b 上连续,则()f x 在[,]a b 上可积。
3. 若()f x 在[,]a b 上有界,且只有有限个间断点,则()f x 在[,]a b 上可积. Ⅱ. 定积分的几何意义 定积分()baf x dx ⎰在几何上表示:由曲线()y f x =,直线x a =和x b =以及x 轴所围图形面积的代数和 (x 轴上方的面积取正,x 轴下方的面积取负) Ⅲ. 定积分的性质1. 补充规定:(1)当a b =时,()0baf x dx =⎰(2)当a b >时,()()baabf x dx f x dx =-⎰⎰2. 性质:(1) [()()]()()bbbaaaf xg x dx f x dx g x dx --+=+⎰⎰⎰(2) ()(),()bba akf x dx k f x dx k =⎰⎰为常数(3) ()()()bc baacf x dx f x dx f x dx =+⎰⎰⎰(4)b adx b a =-⎰(5) 若在[,]a b 上,()0f x ≥,则()0,()baf x dx a b ≥<⎰推论1:若在[,]a b 上,()()f x g x ≤,则()(),()bbaaf x dxg x dx a b ≤<⎰⎰.推论2:()(),()bbaaf x dx f x dx a b ≤<⎰⎰.(6 ) 若在[,]a b 上,()m f x M ≤≤,则()()(),()bam b a f x dx M b a a b -≤≤-<⎰(7) (定积分中值定理):若()f x 在[,]a b 上连续,则在[,]a b 上至少存在ξ,使()()(),()baf x dx f b a a b ξξ=-≤≤⎰. 3. 连续函数()f x 在[,]a b 上的平均值,1()ba y f x dxb a-=-⎰ Ⅳ. 积分上限函数及其导数 1. 若对任意[,]x a b ∈,()xaf t dt ⎰存在,则称()()xax f t dt Φ=⎰为积分上限的函数.2. 若()f x 在[,]a b 上可积,则()f x 在[,]a b 上有界. 且积分上限函数()()xax f t dt Φ=⎰在[,]a b 上连续.3. 设()f x 在[,]a b 上连续,则()()xax f t dt Φ=⎰在[,]a b 上可导,且'()()(),()xa d x f t dt f x a xb dxΦ==≤≤⎰. 4. 设()f x 连续,()x φ可导,则()''()()[()]()x ad x f t dt f x x dx φφφΦ==⎰. 5. 设()f x 连续,()x φ,()x ϕ可导,则 ()'''()()()[()]()[()]()x x d x f t dt f x x f x x dxφϕφφϕϕΦ==-⎰. Ⅴ. 牛顿——莱布尼兹公式.(微积分基本定理)设()f x 在[,]a b 上连续,()F x 为()f x 在[,]a b 上的一个原函数,则()()()baf x dx F b F a =-⎰.Ⅵ. 定积分的换元法设()f x 在[,]a b 上连续,()x t φ=满足: (1) (),()a b φαφβ==.(2)()t φ在[,]αβ(或[,]βα)上具有连续导数,且()x t φ=的值域不越出[,]a b 的范围,则有'()[()]()baf x dx f t t dt βαφφ=⎰⎰.注:当()t φ的值域[,]R A B φ=越出[,]a b 的范围,但满足其余条件时,只要()f x 在[,]A B 上连续,则换元法的结论仍然成立.Ⅶ. 定积分的分部积分法设()u x 与()v x 在[,]a b 上具有连续导数,则有()()()()()()bbbaaau x dv x u x v x v x du x =-⎰⎰ Ⅷ. 几类特殊的积分公式1. 设()f x 在[,]a a -上连续,则有0()[()()]aaaf x dx f x f x dx -=+-⎰⎰.2()()[,]()()[,]aaaf x dx f x a a f x dx f x a a -⎧-⎪=⎨⎪-⎩⎰⎰当为上连续的偶函数时0当为上连续的奇函数时2. 设()f x 是以l 为周期的连续函数,则对任意实数a ,有()()a llaf x dx f x dx +=⎰⎰.3. 设()f x 在[0,1]上连续,则220(sin )(cos )f x dx f x dx ππ=⎰⎰(sin )(sin )2xf x dx f x dx πππ=⎰⎰20(sin )2(sin )f x dx f x dx ππ=⎰⎰4. 2200123134221242sin cos 13531n n n n n n n n n xdx xdx n n n n πππ--⎧⎪-⎪--⎪==⎨-⎪=⎪⎪⎩⎰⎰为正偶数为大于1的正奇整数1 Ⅸ. 反常积分(广义积分) 1. 无穷限的反常积分(1) 设()f x 在[,)a +∞上连续, ()lim ()ba ab f x dx f x dx ∞→+∞=⎰⎰(2) 设()f x 在(,]b -∞上连续,()lim ()bbaa f x dx f x dx -∞→-∞=⎰⎰(3) 设()f x 在(,)-∞+∞上连续,000()()()lim ()lim ()baa b f x dx f x dx f x dx f x dx f x dx ∞∞-∞-∞→-∞→+∞=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散. 注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有()f x dx ∞-∞⎰收敛. 只要有一个极限不存在,()f x dx ∞-∞⎰就发散.2. 无界函数的反常积分(1) 设()f x 在(,]a b 上连续,点a 为()f x 的瑕点,()lim ()bba tt af x dx f x dx +→=⎰⎰(2) 设()f x 在[,)a b 上连续,点b 为()f x 的瑕点,()lim ()btaat bf x dx f x dx -→=⎰⎰(3) 设()f x 在[,]a b 上除点c ()a c b <<外连续,点c 为()f x 的瑕点,()()()lim ()lim ()bc b t baacatt ct cf x dx f x dx f x dx f x dx f x dx -+→→=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散. 注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有()baf x dx ⎰收敛. 只要有一个极限不存在,()baf x dx ⎰就发散.3. 反常积分的审敛法(1) (比较审敛法1) 设()f x 在[,)(0)a a +∞>上连续,且()0f x ≥. 若存在常数0M >及1p >,使得()p Mf x x≤ ()a x ≤<+∞,则反常积分()a f x dx +∞⎰收敛;若存在常数0N >,使得()Nf x x≥ ()a x ≤<+∞,则反常积分()a f x dx +∞⎰发散.(2) (极限审敛法1) 设()f x 在[,)a +∞上连续,且()0f x ≥. 若存在常数1p >,使得lim ()px x f x →∞存在,则反常积分()af x dx +∞⎰收敛;若lim ()0x xf x d →∞=>,(或lim ()x xf x →∞=+∞)则反常积分()af x dx +∞⎰发散.(3) (比较审敛法2)设()f x 在(,]a b 上连续,且()0f x ≥. x a =为()f x 的瑕点.若存在常数0M >及1q <,使得()()()q Mf x a x b x a ≤<≤-,则反常积分()b a f x dx ⎰收敛;若存在常数0N >,使得()Nf x x a≥- ()a x b <≤,则反常积分()b a f x dx ⎰发散.(4) (极限审敛法2) 设()f x 在(,]a b 上连续,且()0f x ≥. x a =为()f x 的瑕点. 若存在常数01q <<,使得l i m ()()qx ax a f x +→-存在,则反常积分()baf x dx ⎰收敛;若lim ()()0x ax a f x d +→-=>,(或lim ()()x ax a f x +→-=+∞)则反常积分()baf x dx ⎰发散.2'0'02)()()(a M dx x M dx x f dx x f dx x f aa aa=≤≤=⎰⎰⎰⎰ξξ.。
第5章定积分95525

第五章定积分一、基本内容(一)基本概念1.定积分的定义:设函数f (x)在[a, b]上有定义,任取分点a =Xo c Xj c X2 <••• < x n_^ < x^ b .把区间[a,b]分成n个小区间[x ij X i]称为子区间,其长度记为△X i =X i —X i」(i =1,2,…,n)在每个小区间[X i^X i]上任取一点q(X i」<X i),得相应的函数值f(E i),作乘f GM X i (i =1,2,…,n)把所有这些乘积加起来,得和式nZ f(©i)心X i,i =1如果不论区间[a,b]分成n个小区间[X i」,X i]的分法如何及点©怎样取法,当分点无限增多(记作n T K)而每个小区间长度无限缩小(h=max{A x i}T 0),此和n式的极限存在,即设I “im S f^JA X i,贝U称函数f(x)在[a,b]可积,并将此极b限值I称为函数f (X)在[a,b]上的定积分。
记作/ f (x)dx,即L aa f(x)dx=i f G)i X i.(二)定积分的计算1.变上限积分X定义如果函数f(x)在[a,b]上连续,则①(x) = J f(t)dt, xFa,b]是积分上限XaX的函数,称f f(t)dt为变上限的定积分.“a2.牛顿-莱布尼兹公式设函数f(x)在[a,b]上连续,F(x)是f(x)的一个原函数,则b baf(x)dx = F(b)-F(a)=F(x) .3. 定积分换元积分公式设函数f(x)在[a,b ]上连续,函数x =^t)在区间[a ,P ]上单值且连续可导,其 值在[a,b ]上变化,且护(a ) =a,申(P ) =b ,则有b Paf(x)dx =『 伴(t))®'(t)dt在使用定积分换元公式时,要注意还原同时换积分限 4. 定积分的分部积分公式设函数u =u(x),v =v(x)在[a,b ]上有连续导数uTx)V(x),则bbau(X)dv(X)=u(X)v(X)|a (三) 广义积分 无穷区间上的广义积分-be b 驭a f(x)dx. blim f f (x)dx .c a ^If g dx +J %! f (x)dx .2 .无界函数的广义积分(1) 设 f (x)在(a, b ]上连续,lim/(X)=处,贝 UX —j a十b baf(x)dx =绞^+[七f(x)dx .⑵设f(x)在[a,b)上连续,lim f(x)=处,贝UX —j b —bb一名[f(x)dx = linn a f (x)dx . (3)设 f (x)在[a,c)和(c,b ]上连续,lim f (x)=处,则 X TbCb[f(x)dx = [ f(x)dx+.C f(x)dxc Yb=lim.f f (x)dx + lim.f , f (x)dx .二、练习题5. 1计算下列定积分:丑 1 ⑴為一dx. 三1 + COSX⑴[f(x)dx=bb (2) J f(x)dx =a 二-be⑶ Lcf(x)dx =b- av(x)du(x).1dx上 2”e%x.所以原式=-In | e 」+ Je^x -1『2 +山—e 2x (4) 『|sinx - cosx| dx .JI解:原式 =『(cosx - sin X)dx + g(sin x - cosx) dx4=sinx]# +cosx|4-cosx|2—sinx|24=返+2^_1+返 _1+返=2(血-1).2a⑸ Lx[f(x) + f(—x)]dx.aa解:原式=L xf (x)dx + xf (-x)dx ,解:原式= "2COS 2|f\sec 2xd- 今 2 2解:原式=f 6 dx= .016J x + 9 詈 |(2|063x 2 16j xdx+[于 dx|?=12.16解 :原式上21 -e 2xJn 2J 1 - e 2x_ln 2 dx= 0= dx- 訴-e 2xJn 2e2x兀_x edx£上2 de 2xL 2xP 1 -e上2 de^J e ^x _1丄 1 /n2d(1-e 2x )2^由于dx=In | X + J x 2 -1 | + C .『2 —In(2+7l)+¥XCM_xL| —co I 00+ co u」X—L)Xpx+L +CML | CM+ co _cL | COIIL I oq oT —X-I CM+ -1 CM+CO _c-I 00II■ I00IIXCMXCM VX L I CJ_P¥3n-x —L3X—L。
定积分的知识点总结

定积分的知识点总结一、定积分的基本概念定积分是微积分学中的重要概念,可以用来计算曲线下的面积,曲线的弧长,质心等物理量。
定积分的基本思想是将曲线下的面积划分为无穷多个微小的矩形,然后求和得到整体的面积。
定积分的符号表示为∫。
对于一个函数f(x),在区间[a, b]上的定积分表示为:∫[a, b]f(x)dx其中,a和b为区间的端点,f(x)为函数在该区间上的取值。
定积分表示在区间[a, b]上的函数f(x)所确定的曲线下的面积。
二、定积分的计算方法1. 黎曼和定积分的计算基本思想是将曲线下的面积划分为很多个小矩形,然后对这些小矩形的面积求和。
这就是定积分的计算方法。
在实际计算中,根据黎曼和的定义,我们可以将区间[a, b]等分为n个小区间,每个小区间长度为Δx=(b-a)/n,然后在每个小区间上取一个样本点xi,计算f(xi)Δx的和:∑[i=1,n]f(xi)Δx当n趋近于无穷大时,这个和就可以逼近定积分的值。
这就是黎曼和的基本思想。
2. 定积分的几何意义定积分可以用来计算曲线下的面积,也可以用来计算曲线的弧长。
对于一个函数f(x),其在区间[a, b]上的定积分表示的是曲线y=f(x)和x轴之间的面积。
这个面积就是曲线下的面积。
如果函数f(x)在区间[a, b]上非负且连续,那么函数y=f(x)、直线x=a、x=b以及x轴所围成的区域的面积就是∫[a, b]f(x)dx。
3. 定积分的物理意义定积分还可以用来计算物理量,比如质量、质心等。
在物理学中,可以用定积分来计算物体的质量、质心等物理量。
对于一个连续的物体,将其质量密度函数表示为ρ(x),则物体的质量可以表示为定积分:M=∫[a, b]ρ(x)dx三、定积分的性质1. 线性性定积分具有线性性质,即∫[a, b](c1f1(x)+c2f2(x))dx=c1∫[a, b]f1(x)dx+c2∫[a, b]f2(x)dx。
其中c1、c2为常数,f1(x)、f2(x)为函数。
高数《定积分》章节重点--期末重点

1exdx 1ex2dx
0
0
高 3. 积分的导数
变限积分求导公式:
d ( (x) f (t)dt) f ( (x)) (x) f ((x))(x)
dx ( x)
帮
常见题型 1.计算下列各导数:
(1) d x2 1 t3 dt ;
dx 0
解: d x2 1 t3 dt 1 (x2 )3 d (x 2 ) 2x 1 x6 .
帮 (换元法)
解 令 1 e2x =u ,则 u2 1 e2x e2x 1 u2来自 x= 1 ln 1 u2 . 2
数 数 原式
3 2
ud
(
1
ln(1
u
2
))
0
2
0
3 2
u(
1 2
)
2 u 1 u2
du
3 2 0
1
u
2
u
2du
3 2 0
u
2
1
1 u2
1du
.
3
高 高
3 2
x
dx.
(凑微分)
解
原式
0
1
1 cos2
x
d
cos
x
arctan(cos
x)
0
arctan(cos ) arctan(cos 0) ( ) . 4 42
常考题型 3 1 xe2xdx. 0
(分部积分)
帮
数 解
原式 1 2
1 xde2x
0
1 2
xe2 x
1 0
1
帮
lim
x0
x sin t 2dt
0
x3
lim x0
高等数学-高等数学-第5章定积分

教学过程教学思路、主要环节、主要内容我们先来看一个实际问题———求曲边梯形的面积。
设曲边梯形是有连续曲线y=f(x)、x轴与直线x=a、x=b所围成。
现在计算它的面积A.我们知道矩形面积的求法,但是此图形有一边是一条曲线,该如何求呢?我们知道曲边梯形在底边上各点处的高f(x)在区间[a,b]上变动,而且它的高是连续变化的,因此在很小的一段区间的变化很小,近似于不变,并且当区间的长度无限缩小时,高的变化也无限减小。
因此,如果把区间[a,b]分成许多小区间,在每个小区间上,用其中某一点的高来近似代替同一个小区间上的窄曲变梯形的变高,我们再根据矩形的面积公式,即可求出相应窄曲边梯形面积的近似值,从而求出整个曲边梯形的近似值。
显然:把区间[a,b]分的越细,所求出的面积值越接近于精确值。
为此我们产生了定积分的概念。
定积分的概念:设函数f(x)在[a,b]上有界,在[a,b]中任意插入若干个分点a=x0<x1<...<x n-1<x n=b 把区间[a,b]分成n个小区间[x0,x1],...[x n-1,x n], 在每个小区间[x i-1,x i]上任取一点ξi(x i-1≤ξi≤x i),作函数值f(ξi)与小区间长度的乘积f(ξi)△x i并作出和,如果不论对[a,b]怎样分法,也不论在小区间上的点ξi怎样取法,只要当区间的长度趋于零时,和S总趋于确定的极限I,这时我们称这个极限I为函数f(x)在区间[a,b]上的定积分,记作。
即:定理(1):设f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上可积。
(2):设f(x)在区间[a,b]上有界,且只有有限个间断点,则f(x)在区间[a,b]上可积。
如果我们对面积赋以正负号,在x轴上方的图形面积赋以正号,在x轴下方的图形面积赋以负号,则在一般情形下,定积分的几何意义为:它是介于x轴、函数f(x)的图形及两条直线x = a、x = b之间的各部分面积的代数和。
定积分的计算知识点总结

定积分的计算知识点总结一、定积分的定义。
1. 概念。
- 设函数y = f(x)在区间[a,b]上连续,用分点a=x_0将区间[a,b]等分成n个小区间,每个小区间长度为Δ x=(b - a)/(n)。
在每个小区间[x_i - 1,x_i]上取一点ξ_i(i =1,2,·s,n),作和式S_n=∑_i = 1^nf(ξ_i)Δ x。
当nto∞时,如果S_n的极限存在,则称这个极限为函数y = f(x)在区间[a,b]上的定积分,记作∫_a^bf(x)dx,即∫_a^bf(x)dx=limlimits_n→∞∑_i = 1^nf(ξ_i)Δ x。
- 这里a与b分别叫做积分下限与积分上限,区间[a,b]叫做积分区间,函数f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积表达式。
2. 几何意义。
- 当f(x)≥slant0时,∫_a^bf(x)dx表示由曲线y = f(x),直线x = a,x = b以及x 轴所围成的曲边梯形的面积。
- 当f(x)≤slant0时,∫_a^bf(x)dx表示由曲线y = f(x),直线x = a,x = b以及x 轴所围成的曲边梯形面积的相反数。
- 当f(x)在[a,b]上有正有负时,∫_a^bf(x)dx表示位于x轴上方的曲边梯形面积减去位于x轴下方的曲边梯形面积。
二、定积分的基本性质。
1. 线性性质。
- ∫_a^b[k_1f(x)+k_2g(x)]dx = k_1∫_a^bf(x)dx + k_2∫_a^bg(x)dx,其中k_1,k_2为常数。
2. 区间可加性。
- ∫_a^bf(x)dx=∫_a^cf(x)dx+∫_c^bf(x)dx,其中a < c < b。
3. 比较性质。
- 如果在区间[a,b]上f(x)≥slant g(x),那么∫_a^bf(x)dx≥slant∫_a^bg(x)dx。
- 特别地,<=ft∫_a^bf(x)dxright≤slant∫_a^b<=ftf(x)rightdx。
高等数学第五章定积分总结

高等数学第五章定积分总结定积分作为微积分的重要概念,是无穷积分的一种形式,并在多个领域中有着广泛的应用。
本章主要介绍了定积分的定义和性质,以及定积分的计算方法和应用。
首先,本章介绍了定积分的概念和定义。
定积分是一个数值,表示在给定的区间上,函数曲线与x轴之间的面积。
定积分可以分为两个部分:积分号和被积函数。
积分号表示积分的区间,被积函数表示要求积分的函数。
定积分的计算可以通过数值方法或解析方法进行,具体方法和结论有不少。
其次,本章介绍了定积分的性质。
定积分具有线性性、区间可加性和保号性等性质。
线性性质表示定积分可以进行加减运算,并且可以乘以一个常数。
区间可加性是指定积分的区间可以分为多个子区间,进行分段积分。
保号性表示如果被积函数在一些区间上恒大于等于0,那么该区间上的定积分也大于等于0。
这些性质为定积分的计算和应用提供了更多的方便性。
然后,本章介绍了定积分的计算方法。
定积分的计算可以通过不定积分和定积分的关系来进行。
通过求解原函数,并利用牛顿-莱布尼茨公式,可以简化计算过程。
本章还介绍了定积分的几何意义,即定积分表示函数曲线与x轴围成的面积,也可以表示其中一种物理量在一定时间或一定空间内的累积变化量。
最后,本章介绍了定积分的应用。
定积分在几何学、物理学、经济学等多个领域中有着广泛的应用。
例如,通过定积分可以计算曲线的弧长、曲线围成的面积、质心的坐标等几何问题;通过定积分可以计算物体的质量、重心、转动惯量等物理问题;通过定积分可以计算收益、成本、利润等经济问题。
这些应用都是建立在定积分的几何意义和计算方法的基础之上,对于深入理解和运用定积分具有重要意义。
总之,定积分是微积分中的重要概念,不仅具有丰富的理论性质,还有着广泛的应用价值。
通过学习定积分的定义、性质、计算方法和应用,可以帮助学生更好地理解和掌握微积分的知识,为解决实际问题提供更有效的数学工具。
定积分知识点总结等价

定积分知识点总结等价在本文中,我们将对定积分的基本概念、性质和求解方法进行总结,希望能够帮助读者更好地理解和运用定积分。
一、定积分的基本概念定积分可以看作是一个区间上面积的度量,它描述了函数在一定区间上的总体变化情况。
在数学上,定积分可以理解为函数在指定区间内的面积或者是曲线的弧长,在物理上可以表示为质量、能量、熵等的总量。
1.1 定积分的定义设f(x)在区间[a, b]上有定义,且[a, b]是有限闭区间,将[a, b]上的分割记作Δ,记Δ的任一分点为x0, x1, ..., xn,对应的区间为[x0, x1], [x1, x2], ..., [xn-1, xn]。
则对应的分割Δ表示为:Δ = {x0, x1, ..., xn}Δ的长度记作δxi = xi - xi-1,假设Δ长度的最大值为δ = max{δxi}。
我们将区间[a, b]分成n个小区间,当n趋于无穷大时,(也就是每个小区间的长度趋于0),则这个过程称为区间[a, b]的分割,也称之为区间[a, b]的划分。
对于函数f(x)在区间[a, b]上的定积分,可以用如下的极限形式定义:∫(a->b)f(x)dx = lim(Δ->0)Σ(i=1->n)f(xi*)δxi其中,xi*是区间[xi-1, xi]上的任意一点。
1.2 定积分的几何意义定积分的几何意义是非常直观的,它表示了曲线与坐标轴以及两条直线之间的面积。
当函数f(x)在区间[a, b]上是非负的时候,定积分表示了曲线y=f(x)与x轴以及直线x=a, x=b之间的面积。
当函数f(x)在区间[a, b]上是有正有负的时候,定积分表示了曲线y=f(x)与x轴之间的面积,其中函数f(x)在区间[a, b]上的正值与负值部分面积互相抵消,最终得到曲线与x轴之间的面积。
1.3 定积分的物理意义在物理上,定积分可以用来描述某一物理量在一定的时间或空间范围内的总量。
例如,对于质量密度为ρ(x)的一根杆在区间[a, b]上的质量总量可以表示为:m = ∫(a->b)ρ(x)dx这里ρ(x)dx表示了杆上长度为dx的小段的质量。
高等数学(第五章)定积分

二、定积分的定义
定义 设 f ( x) 在[ a , b ]上有界
(1) 将[ a , b ] 任意分成 n 个小区间 [ x0 , x1 ],[ x1 , x2 ],, [ xi 1 , xi ] ,, [ xn 1 , xn ], x0 a , xn b . xi xi xi 1 (i 1, 2,, n), 为第 i 个小区间的长度 .
f ( )x . 在 x 与 x x 之间 . x 0 , x
定理 2 (变上限的积分求导定理) 设 f ( x) 在[ a , b ] 上连续 , x 则 f (t )dt f ( x) .
a
x a
f (t )dt
f (t)
b a
o a
c1
c2
b
f ( x) dx .
x
根据定积分的几何意义 我们可以计算一些简单的定积分 .
y
yx
例1
b a
1dx b a . ?
ab 1 2 2 x dx ? (b a) (b a ) . 2 2
o
a
b
x
例2
例3
b a
R 0
R x dx
2 2
0
i 1
n
并称极限值为 f ( x) 在[ a , b ]上的定积分.
记为
b a
f ( x)dx
上限
b a
f ( x)dx lim f (i )xi .
0
i 1
n
下限
a 叫积分下限 , b 叫积分上限 ,[ a , b ]叫积分区间. f ( x) 叫被积函数 , x 叫积分变量 . f ( x)dx叫被积表达式 .
高数定积分知识点总结

高数定积分知识点总结一、定积分的定义定积分是微积分中的一个重要概念,它是对一个函数在一个区间上的积分结果进行计算的过程。
在数学上,定积分是用来计算曲线下面的面积或者函数在某一区间上的平均值的方法。
定积分可以写成以下形式:\[ \int_{a}^{b} f(x)dx \]其中,\( f(x) \)是被积函数,\( a \)和\( b \)是积分区间的端点。
定积分的计算过程就是求解被积函数在给定区间上的曲线下面的面积。
定积分在物理学、工程学和经济学等领域都有着广泛的应用,是微积分中不可或缺的重要工具。
二、定积分的性质1. 定积分的可加性如果函数\( f(x) \)在区间\([a, b]\)上是可积的,那么对于任意的\( c \)满足\( a \leq c \leq b \),都有:\[ \int_{a}^{b} f(x)dx = \int_{a}^{c} f(x)dx + \int_{c}^{b} f(x)dx \]这个性质表明了定积分的可加性,即在一个区间上进行积分的结果可以根据任意划分点\( c \)进行分割。
2. 定积分的线性性对于任意的实数\( \alpha, \beta \)和函数\( f(x), g(x) \),如果\( f(x), g(x) \)在区间\([a, b]\)上是可积的,那么有:\[ \int_{a}^{b} (\alpha f(x) + \beta g(x))dx = \alpha \int_{a}^{b} f(x)dx + \beta \int_{a}^{b} g(x)dx \]这个性质表明了定积分的线性性,即在一个区间上进行线性组合的函数的积分等于线性组合的函数的积分的线性组合。
3. 定积分的保号性如果在区间\([a, b]\)上有\( f(x) \geq 0 \),那么有:\[ \int_{a}^{b} f(x)dx \geq 0 \]这个性质表明了定积分的保号性,即当被积函数在一个区间上非负时,其积分结果也是非负的。
同济大学数学系《高等数学》(第7版)(上册)-复习笔记-第五章 定积分【圣才出品】

上任取一点 的乘积
,作函数值 ,并作出和
,记
,如果当 λ→0 时,这和
的极限总存在,且与闭区间[a,b]的分法及点 的取法无关,则称这个极限为函数 f(x)在
区间[a,b]上的定积分,记作
,即
其中,f(x)称为被积函数,f(x)dx 称为被积表达式,x 称为积分变量,a 称为积分下限,b
1 / 21
十万种考研考证电子书、题库视频学习平 台
曲边梯形位于 x 轴的下方,定积分
表示上述曲边梯形面积的负值;
(3)在[a,b]上 f(x)既取得正值又取得负值时,函数 f(x)的图形某些部分在 x 轴的上
方,而其他部分在 x 轴下方(见图 5-1-1),此时定积分 面积减去 x 轴下方图形面积所得之差.
表示 x 轴上方图形
圣才电子书
十万种考研考证电子书、题库视频学习平
台
称为积分上限,[a,b]称为积分区间.
(2)“ε-δ”表达式
设有常数 I,对于任意正数 ε,总存在一个正数 δ,使得对于区间[a,b]的任何分法,
不论 在
中怎样选取,只要
δ,总有
成立,则称 I 是 f(x)在区间[a,b]上的定积分,记作
[a,b]上的一个原函数.
2.牛顿-莱布尼茨公式
就是
在
其中 F(x)是连续函数 f(x)在区间[a,b]上的一个原函数.
三、定积分的换元法和分部积分法 1.定积分的换元法 (1)定理
设函数 f(x)在区间[a,b]上连续,函数
① =a, =b ;
② 域
,则有
满足条件: 上具有连续导数,且其值
该公式称为换元公式.
和
合起来,用过
三
第五章-定积分总结

有效沟通,架起家校合作桥梁在家庭教育中,家长与学校之间的沟通是至关重要的。
有效的沟通可以帮助家长了解学校的教育理念和教学情况,帮助学校了解学生在家庭中的情况和需求,从而促进家校合作,共同促进学生的成长和发展。
架起家校合作的桥梁,加强家长与学校之间的沟通,是非常重要的。
有效的沟通需要双方都有一定的意识和技巧。
家长要重视和主动参与学校的家长会、家长学堂等活动,了解学校的教学管理、教师教学进程和教育理念,并与教师和学校管理者建立良好的关系。
学校也要重视家长的参与和意见,主动与家长沟通,了解家庭的情况,尊重家长的选择。
只有双方都重视起家校合作,才能够建立起有效的沟通桥梁。
家长应该了解学校的教学情况,主动了解学生的学习情况。
家长可以通过参加家长会、家长学堂等方式了解学校的教学理念和教学方式,同时关注学生的在校表现、学习习惯等方面的情况。
在了解学校的情况的基础上,家长可以有针对性地对学生进行家庭教育,帮助他们更好地适应学校的教学要求。
也可以对学校进行合理的建议,共同促进学校的发展和改进。
双方应该保持常态化的沟通,建立稳定的合作桥梁。
只有通过不断的沟通和交流,双方才能够建立起稳定的合作关系。
家长应该与学校保持密切的联系,了解学校的最新情况,及时反馈学生在家庭中的情况和需求。
学校也应该与家长保持密切的联系,了解学生的情况和家庭的需求,及时对家长提出的问题进行解决。
通过这种双向的沟通和反馈,才能够建立起稳定的、顺畅的合作桥梁。
有效的家校沟通是架起家校合作桥梁的重要基础。
只有双方都重视和主动参与家校沟通,才能够建立起稳定、顺畅的合作关系,共同促进学生的成长和发展。
希望家长和学校能够共同努力,为孩子们提供更好的教育服务。
高等数学-第5章 5.1 定积分的概念与性质

第5章 定积分及其应用定积分起源于求图形的面积和体积等实际问题,这类问题往往归结为计算“和式的极限”.定积分与不定积分是两个不同的概念,微积分基本定理揭示了这两个概念之间的关系,解决了定积分的计算问题.本章将从两个实例出发引出定积分的概念,然后讨论定积分的性质和计算方法,介绍定积分在几何上和物理学上的一些应用.§5.1 定积分的概念与性质一、引例 1. 曲边梯形的面积在中学,我们学过求三角形、矩形等以直线为边的图形的面积。
但在实际应用中,有时需要求以曲线为边的图形的面积(图5.1),这种图形可以分割为若干个一条边为曲线,而其余边为直线的图形(图5.2)。
现考虑求由连续曲线()(()0)y f x f x =≥以及直线0===y b x a x 、、所围成图形(图 5.3)的面积,这种图形称为曲边梯形,曲线()y f x =叫做曲边梯形的曲边。
怎样计算曲边梯形的面积呢?不妨回顾一下我们是怎样求函数在某点的瞬时变化率(切线的斜率、瞬时速度)的,都是先求某一区间内的平均变化率(割线的斜率、平均速度),得到某点变化率的近似值,再取极限由近似变化率过渡到精确变化率(切线的斜率、瞬时速度)。
简言之,就图5.3图5.1图5.2是先求近似值,再取极限由近似值过渡到精确值。
我们也采取这种方法来求曲边梯形的面积,先将曲边梯形分割成若干个小的曲边梯形,每个小曲边梯形都用一个小矩形近似代替,则所有小矩形面积之和就是曲边梯形面积的近似值,当把曲边梯形无限细分时,所有小矩形面积之和的极限就是曲边梯形的面积.为了便于表述,按下面四个步骤求曲边梯形的面积A : (1)分割 用1n +个分点01211i i n n a x x x x x x x b --=<<<<<<<<= ,把区间],[b a 分成n 个小区间011211[,],[,],,[,],,[,]i i n n x x x x x x x x -- ,它们的长度依次为11022111,,,,,i i i n n n x x x x x x x x x x x x --∆=-∆=-∆=-∆=- ,经过每一个分点作平行于y 轴的直线段, 把曲边梯形分成n 个小曲边梯形,第i 个小曲边梯形的面积记为(1,2,,)i A i n ∆= ,则所求曲边梯形的面积可表示为121nn i i A A A A A ==∆+∆+⋅⋅⋅+∆=∆∑。
定积分的应用公式总结

定积分的应用公式总结定积分是微积分中的重要概念,具有广泛的应用范围。
在实际问题中,定积分可以用于求解曲线下的面积、求解容积、质量、中心矩等问题。
接下来,我们将总结定积分的应用公式,包括面积、体积、质量、中心矩等几个重要应用。
1. 曲线下的面积定积分最常见的应用是求解曲线下的面积。
对于一个函数f(x),在区间[a, b]上,曲线y=f(x)与x轴所围成的面积可以通过定积分来计算。
公式为:S = ∫(a到b)f(x)dx其中S表示曲线下的面积,∫表示定积分,f(x)是函数曲线在x轴上的对应值。
2. 旋转体的体积定积分还可以用于计算旋转体的体积。
考虑一个曲线y=f(x),在[a, b]区间上绕x轴旋转一周,所形成的旋转体体积可以通过定积分来计算。
公式为:V = π∫(a到b)f(x)^2dx其中V表示旋转体的体积,π表示圆周率。
3. 弧长定积分可以用于计算曲线的弧长。
设有曲线y=f(x),在区间[a,b]上的弧长可以通过定积分来计算。
公式为:L = ∫(a到b)√(1+(f'(x))^2)dx其中L表示曲线的弧长,f'(x)表示f(x)的导数。
4. 质量和质心对于一条位于直角坐标系中的线密度分布曲线,其质量可以通过定积分来计算。
设密度函数为ρ(x),曲线上的质量可以表示为:m = ∫(a到b)ρ(x)dx其中m表示曲线上的质量,ρ(x)表示密度函数。
同时,还可以通过定积分来计算曲线的质心。
曲线的质心可以通过以下公式来计算:x_c = (1/m)∫(a到b)xρ(x)dxy_c = (1/m)∫(a到b)yρ(x)dx其中x_c和y_c表示曲线的质心的坐标。
以上的公式总结了定积分的一些重要应用,包括面积、体积、弧长、质量和质心等。
在实际问题中,我们可以根据具体的问题情况,选择适当的公式来计算所需的结果。
这些公式可以帮助我们更好地理解和应用定积分的概念,解决实际问题。
高数定积分知识点总结大一

高数定积分知识点总结大一高数定积分知识点总结定积分是高等数学中的重要概念,它在微积分学中具有极其重要的地位。
本文将对高数定积分的相关知识点进行总结,并帮助大一的学生更好地理解和掌握这一内容。
一、定积分的基本概念定积分是微积分中的一种重要工具,用于求解曲线下的面积以及曲线长度等问题。
定积分可以表示为∫f(x)dx,其中f(x)为被积函数,dx为微元。
定积分的计算可以通过曲线下的面积进行解释,也可以通过定积分的定义与性质进行推导。
二、定积分的计算方法1. 牛顿-莱布尼兹公式牛顿-莱布尼兹公式是定积分与不定积分之间的重要联系,它建立了被积函数与积分函数之间的关系,可以简化定积分的计算过程。
2. 基本积分公式基本积分公式是定积分计算中的基础知识,掌握了基本积分公式能够大大简化定积分的计算过程。
常见的基本积分公式包括幂函数的积分、三角函数的积分等。
3. 分部积分法分部积分法是定积分计算中常用的一种方法,它通过将被积函数进行分解,并利用积分的性质进行求解。
分部积分法适用于一些复杂函数的积分计算,能够简化计算过程。
4. 曲线下面积的计算曲线下面积是定积分的一个重要应用,通过定积分可以准确地计算曲线下的面积。
对于给定的曲线和积分区间,可以先求出曲线方程,再进行积分计算以得到准确的面积值。
三、定积分的应用1. 曲线长度的计算通过定积分可以准确计算曲线的长度,这在几何学中具有很大的意义。
计算曲线长度时需要先将曲线分割成无穷小的线段,再进行求和得到整体的长度。
2. 平面图形的质心通过定积分可以计算平面图形的质心位置。
平面图形的质心是图形内各个点的横纵坐标之和除以图形面积,这一计算可以通过定积分进行求解。
3. 物理中的应用定积分在物理学中有广泛的应用,如质点的位移、功、引力场中的重力势能等问题,都可以通过定积分进行计算。
四、定积分的性质1. 线性性质定积分具有线性性质,即对于定积分∫(af(x)+bg(x))dx,可以进行分解为a∫f(x)dx+b∫g(x)dx。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 定积分创新生技102班 张梦菲2010015066一、主要内容Ⅰ. 定积分概念:1. 定积分定义:设()f x 在区间[,]a b 上有界,在[,]a b 中任意插入若干个分点 0121n n a x x x x x b -=<<<<<=.把[,]a b 分成n 个小区间1[,],(1,2,,)i i x x i n -=,小区间的长度记为1,(1,2,,)i i i x x x i n -∆=-=,在1[,]i i x x -上任意取一点i ξ,作1()ni i i f x ξ=∆∑,若01lim()niii f x λξ→=⋅∆∑ 1(max{})ii nx λ≤≤=∆存在. 就称该极限为()f x 在[,]a b 上的定积分.记为1()lim ()nbi i ai f x dx f x λξ→==⋅∆∑⎰当上述极限存在时,称()f x 在[,]a b 上可积. 2. 若()f x 在[,]a b 上连续,则()f x 在[,]a b 上可积。
3. 若()f x 在[,]a b 上有界,且只有有限个间断点,则()f x 在[,]a b 上可积. Ⅱ. 定积分的几何意义 定积分()baf x dx ⎰在几何上表示:由曲线()y f x =,直线x a =和x b =以及x 轴所围图形面积的代数和 (x 轴上方的面积取正,x 轴下方的面积取负) Ⅲ. 定积分的性质1. 补充规定:(1)当a b =时,()0baf x dx =⎰(2)当a b >时,()()baabf x dx f x dx =-⎰⎰2. 性质:(1) [()()]()()bbba aaf xg x dx f x dx g x dx --+=+⎰⎰⎰(2) ()(),()bba akf x dx k f x dx k =⎰⎰为常数(3) ()()()bc baacf x dx f x dx f x dx =+⎰⎰⎰(4)badx b a =-⎰(5) 若在[,]a b 上,()0f x ≥,则()0,()baf x dx a b ≥<⎰推论1:若在[,]a b 上,()()f x g x ≤,则()(),()bbaaf x dxg x dx a b ≤<⎰⎰.推论2:()(),()bbaaf x dx f x dx a b ≤<⎰⎰.(6 ) 若在[,]a b 上,()m f x M ≤≤,则()()(),()bam b a f x dx M b a a b -≤≤-<⎰(7) (定积分中值定理):若()f x 在[,]a b 上连续,则在[,]a b 上至少存在ξ,使()()(),()baf x dx f b a a b ξξ=-≤≤⎰.3. 连续函数()f x 在[,]a b 上的平均值,1()ba y f x dxb a-=-⎰ Ⅳ. 积分上限函数及其导数 1. 若对任意[,]x a b ∈,()xaf t dt ⎰存在,则称()()xax f t dt Φ=⎰为积分上限的函数.2. 若()f x 在[,]a b 上可积,则()f x 在[,]a b 上有界. 且积分上限函数()()xax f t dt Φ=⎰在[,]a b 上连续.3. 设()f x 在[,]a b 上连续,则()()xax f t dt Φ=⎰在[,]a b 上可导,且'()()(),()xa d x f t dt f x a xb dxΦ==≤≤⎰. 4. 设()f x 连续,()x φ可导,则()''()()[()]()x a d x f t dt f x x dxφφφΦ==⎰. 5. 设()f x 连续,()x φ,()x ϕ可导,则 ()'''()()()[()]()[()]()x x d x f t dt f x x f x x dxφϕφφϕϕΦ==-⎰. Ⅴ. 牛顿——莱布尼兹公式.(微积分基本定理)设()f x 在[,]a b 上连续,()F x 为()f x 在[,]a b 上的一个原函数,则()()()baf x dx F b F a =-⎰.Ⅵ. 定积分的换元法设()f x 在[,]a b 上连续,()x t φ=满足: (1) (),()a b φαφβ==.(2)()t φ在[,]αβ(或[,]βα)上具有连续导数,且()x t φ=的值域不越出[,]a b 的范围,则有'()[()]()baf x dx f t t dt βαφφ=⎰⎰.注:当()t φ的值域[,]R A B φ=越出[,]a b 的范围,但满足其余条件时,只要()f x 在[,]A B 上连续,则换元法的结论仍然成立.Ⅶ. 定积分的分部积分法设()u x 与()v x 在[,]a b 上具有连续导数,则有()()()()()()bbba aau x dv x u x v x v x du x =-⎰⎰Ⅷ. 几类特殊的积分公式1. 设()f x 在[,]a a -上连续,则有0()[()()]aaaf x dx f x f x dx -=+-⎰⎰.2()()[,]()()[,]a aaf x dx f x a a f x dx f x a a -⎧-⎪=⎨⎪-⎩⎰⎰当为上连续的偶函数时0当为上连续的奇函数时2. 设()f x 是以l 为周期的连续函数,则对任意实数a ,有()()a llaf x dx f x dx +=⎰⎰.3. 设()f x 在[0,1]上连续,则220(sin )(cos )f x dx f x dx ππ=⎰⎰(sin )(sin )2xf x dx f x dx πππ=⎰⎰20(sin )2(sin )f x dx f x dx ππ=⎰⎰4. 2200123134221242sin cos 13531n n n n n n n n n xdx xdx n n n n πππ--⎧⎪-⎪--⎪==⎨-⎪=⎪⎪⎩⎰⎰为正偶数为大于1的正奇整数1 Ⅸ. 反常积分(广义积分) 1. 无穷限的反常积分(1) 设()f x 在[,)a +∞上连续, ()lim()ba ab f x dx f x dx ∞→+∞=⎰⎰(2) 设()f x 在(,]b -∞上连续,()lim()bbaa f x dx f x dx -∞→-∞=⎰⎰(3) 设()f x 在(,)-∞+∞上连续,()()()lim()lim()baa b f x dx f x dx f x dx f x dx f x dx ∞∞-∞-∞→-∞→+∞=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散. 注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有()f x dx ∞-∞⎰收敛. 只要有一个极限不存在,()f x dx ∞-∞⎰就发散.2. 无界函数的反常积分(1) 设()f x 在(,]a b 上连续,点a 为()f x 的瑕点,()lim ()bba tt af x dx f x dx +→=⎰⎰(2) 设()f x 在[,)a b 上连续,点b 为()f x 的瑕点,()lim ()btaat bf x dx f x dx -→=⎰⎰(3) 设()f x 在[,]a b 上除点c ()a c b <<外连续,点c 为()f x 的瑕点,()()()lim ()lim ()bc b t baacatt ct cf x dx f x dx f x dx f x dx f x dx -+→→=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在,则对应的反常积分收敛,否则称该反常积分发散. 注:(3)的右端是两个独立的极限,只有当两个极限都存在使,才有()baf x dx ⎰收敛. 只要有一个极限不存在,()baf x dx ⎰就发散.3. 反常积分的审敛法(1) (比较审敛法1) 设()f x 在[,)(0)a a +∞>上连续,且()0f x ≥. 若存在常数0M >及1p >,使得()p Mf x x≤ ()a x ≤<+∞,则反常积分()a f x dx +∞⎰收敛;若存在常数0N >,使得()Nf x x≥ ()a x ≤<+∞,则反常积分()a f x dx +∞⎰发散.(2) (极限审敛法1) 设()f x 在[,)a +∞上连续,且()0f x ≥. 若存在常数1p >,使得lim ()px x f x →∞存在,则反常积分()af x dx +∞⎰收敛;若lim ()0x xf x d →∞=>,(或lim ()x xf x →∞=+∞)则反常积分()af x dx +∞⎰发散.(3) (比较审敛法2)设()f x 在(,]a b 上连续,且()0f x ≥. x a =为()f x 的瑕点.若存在常数0M >及1q <,使得()()()q Mf x a x b x a ≤<≤-,则反常积分()b a f x dx ⎰收敛;若存在常数0N >,使得()Nf x x a≥- ()a x b <≤,则反常积分()b a f x dx ⎰发散.(4) (极限审敛法2) 设()f x 在(,]a b 上连续,且()0f x ≥. x a =为()f x 的瑕点. 若存在常数01q <<,使得lim()()qx ax a f x +→-存在,则反常积分()baf x dx ⎰收敛;若lim()()0x a x a f x d +→-=>,(或lim()()x ax a f x +→-=+∞)则反常积分()baf x dx ⎰发散.2'0'02)()()(a M dx x M dx x f dx x f dx x f aa aa=≤≤=⎰⎰⎰⎰ξξ.。
