材料科学基础课后习题谜底第二章
《材料科学基础》第二版 (张联盟 著)课后习题答案 武汉理工大学出版社

2-13 根据半径比关系,说明下列离子与O2—配位时的配位数各是多少?已 知rO2-=0.132nm,rSi4+=0.039nm,rK+=0.131nm,rAl3+=0.057nm,rMg2+=0.078nm。
2-14 为什么石英不同系列变体之间的转化温度比同系列变体之间的转化温度高得多?
2-15 有效离子半径可通过晶体结构测定算出。在下面NaCl型结构晶体中,测得MgS和MnS的晶胞参数均 为a=0.520nm(在这两种结构中,阴离子是相互接触的)。
为NaCl型结构时,体积变化的百分数是多少?已
知CN=6时,rMn
2+=0.08nm,rS2
-=0.184nm;CN
=4时,rMn
2+=0.073nm,r
2 S
-=0.167nm。
2-25 钛酸钡是一种重要的铁电陶瓷,其晶型是钙钛矿结构,试问:(1)属于什么点阵?(2)这个结构 中离子的配位数为若干?(3)这个结构遵守鲍林规则吗?请作充分讨论。
2-5 依据结合力的本质不同,晶体中的键合作用分为哪几类?其特点是什么?
2-6 等径球最紧密堆积的空隙有哪两种?一个球的周围有多少个四面体空隙、多少个八面体空 隙?
2-7 n个等径球作最紧密堆积时可形成多少个四面体空隙、多少个八面体空隙?不等径球是如何进行堆积 的?
2-8 写出面心立方格子的单位平行六面体上所有结点的坐标。
2-14 为什么石英不同系列变体之间的转化温度比同系列变体之间的转化温度高得多?
答: 石英同一系列之间的转变是位移性转变,不涉及晶体结构中键的破裂和重建,仅是键长、键角的调 整、需要能量较低,且转变迅速可逆;而不同系列之间的转变属于重建性转变,都涉及到旧键的破裂和新键 的重建,因而需要较的能量,且转变速度缓慢;所以石英不同系列之间的转化温度比同系列变体之间转化的 温度要高的多。
武汉理工大学材料科学基础(第2版)课后习题和答案

武汉理工大学材料科学基础(第2版)课后习题和答案第一章绪论1、仔细观察一下白炽灯泡,会发现有多少种不同的材料?每种材料需要何种热学、电学性质?2、为什么金属具有良好的导电性和导热性?3、为什么陶瓷、聚合物通常是绝缘体?4、铝原子的质量是多少?若铝的密度为2.7g/cm3,计算1mm3中有多少原子?5、为了防止碰撞造成纽折,汽车的挡板可有装甲制造,但实际应用中为何不如此设计?说出至少三种理由。
6、描述不同材料常用的加工方法。
7、叙述金属材料的类型及其分类依据。
8、试将下列材料按金属、陶瓷、聚合物或复合材料进行分类:黄铜钢筋混凝土橡胶氯化钠铅-锡焊料沥青环氧树脂镁合金碳化硅混凝土石墨玻璃钢9、Al2O3陶瓷既牢固又坚硬且耐磨,为什么不用Al2O3制造铁锤?第二章晶体结构1、解释下列概念晶系、晶胞、晶胞参数、空间点阵、米勒指数(晶面指数)、离子晶体的晶格能、原子半径与离子半径、配位数、离子极化、同质多晶与类质同晶、正尖晶石与反正尖晶石、反萤石结构、铁电效应、压电效应.2、(1)一晶面在x、y、z轴上的截距分别为2a、3b、6c,求出该晶面的米勒指数;(2)一晶面在x、y、z 轴上的截距分别为a/3、b/2、c,求出该晶面的米勒指数。
3、在立方晶系的晶胞中画出下列米勒指数的晶面和晶向:(001)与[210],(111)与[112],(110)与[111],(322)与[236],(257)与[111],(123)与[121],(102),(112),(213),[110],[111],[120],[321]4、写出面心立方格子的单位平行六面体上所有结点的坐标。
5、已知Mg2+半径为0.072nm,O2-半径为0.140nm,计算MgO晶体结构的堆积系数与密度。
6、计算体心立方、面心立方、密排六方晶胞中的原子数、配位数、堆积系数。
7、从理论计算公式计算NaC1与MgO的晶格能。
MgO的熔点为2800℃,NaC1为80l℃, 请说明这种差别的原因。
材料科学基础课后习题答案

《材料科学基础》课后习题答案第一章材料结构的基本知识4. 简述一次键和二次键区别答:根据结合力的强弱可把结合键分成一次键和二次键两大类。
其中一次键的结合力较强,包括离子键、共价键和金属键。
一次键的三种结合方式都是依靠外壳层电子转移或共享以形成稳定的电子壳层,从而使原子间相互结合起来。
二次键的结合力较弱,包括范德瓦耳斯键和氢键。
二次键是一种在原子和分子之间,由诱导或永久电偶相互作用而产生的一种副键。
6. 为什么金属键结合的固体材料的密度比离子键或共价键固体为高?答:材料的密度与结合键类型有关。
一般金属键结合的固体材料的高密度有两个原因:(1)金属元素有较高的相对原子质量;(2)金属键的结合方式没有方向性,因此金属原子总是趋于密集排列。
相反,对于离子键或共价键结合的材料,原子排列不可能很致密。
共价键结合时,相邻原子的个数要受到共价键数目的限制;离子键结合时,则要满足正、负离子间电荷平衡的要求,它们的相邻原子数都不如金属多,因此离子键或共价键结合的材料密度较低。
9. 什么是单相组织?什么是两相组织?以它们为例说明显微组织的含义以及显微组织对性能的影响。
答:单相组织,顾名思义是具有单一相的组织。
即所有晶粒的化学组成相同,晶体结构也相同。
两相组织是指具有两相的组织。
单相组织特征的主要有晶粒尺寸及形状。
晶粒尺寸对材料性能有重要的影响,细化晶粒可以明显地提高材料的强度,改善材料的塑性和韧性。
单相组织中,根据各方向生长条件的不同,会生成等轴晶和柱状晶。
等轴晶的材料各方向上性能接近,而柱状晶则在各个方向上表现出性能的差异。
对于两相组织,如果两个相的晶粒尺度相当,两者均匀地交替分布,此时合金的力学性能取决于两个相或者两种相或两种组织组成物的相对量及各自的性能。
如果两个相的晶粒尺度相差甚远,其中尺寸较细的相以球状、点状、片状或针状等形态弥散地分布于另一相晶粒的基体内。
如果弥散相的硬度明显高于基体相,则将显著提高材料的强度,同时降低材料的塑韧性。
复旦大学材料科学导论课后习题答案(搭配:石德珂《材料科学基础》教材)

资料科学导论课后习题谜底之巴公井开创作第二章资料科学概论1.氧化铝既牢固又坚硬且耐磨,但为什么不能用来制造榔头?答:氧化铝脆性较高,且抗震性欠安.2.将下列资料按金属、陶瓷、聚合物和复合资料进行分类:黄铜、环氧树脂、混泥土、镁合金、玻璃钢、沥青、碳化硅、铅锡焊料、橡胶、纸杯答:金属:黄铜、镁合金、铅锡焊料;陶瓷:碳化硅;聚合物:环氧树脂、沥青、橡胶、纸杯;复合资料:混泥土、玻璃钢3.下列用品选材时,哪些性能特别重要?答:汽车曲柄:强度,耐冲击韧度,耐磨性,抗疲劳强度;电灯胆灯丝:熔点高,耐高温,电阻年夜;剪刀:硬度和高耐磨性,足够的强度和冲击韧性;汽车挡风玻璃:透光性,硬度;电视机荧光屏:光学特性,足够的发光亮度.第三章资料结构的基础知识1.下列电子排列方式中,哪一个是惰性元素、卤族元素、碱族、碱土族元素及过渡金属?(1) 1s2 2s2 2p6 3s2 3p6 3d7 4s2(2) 1s2 2s2 2p6 3s2 3p6(3) 1s2 2s2 2p5(4) 1s2 2s2 2p6 3s2(5)1s2 2s2 2p6 3s2 3p6 3d2 4s2(6) 1s2 2s2 2p6 3s2 3p6 4s1答:惰性元素:(2);卤族元素:(3);碱族:(6);碱土族:(4);过渡金属:(1),(5)2.稀土族元素电子排列的特点是什么?为什么它们处于周期表的同一空格内?答:稀土族元素的电子在填满6s态后,先依次填入远离外壳层的4f、5d层,在此过程中,由于电子层最外层和次外层的电子分布没有变动,这些元素具有几乎相同的化学性质,故处于周期表的同一空格内.3.描述氢键的实质,什么情况下容易形成氢键?答:氢键实质上与范德华键一样,是靠分子间的偶极吸引力结合在一起.它是氢原子同时与两个电负性很强、原子半径较小的原子(或原子团)之间的结合所形成的物理键.当氢原子与一个电负性很强的原子(或原子团)X结合成份子时,氢原子的一个电子转移至该原子壳层上;分子的氢酿成一个裸露的质子,对另外一个电负性较年夜的原子Y暗示出较强的吸引力,与Y之间形成氢键.4.为什么金属键结合的固体资料的密度比离子键或共价键固体高?答:一是金属原子质量年夜;二是金属键的结合方式没有方向性,原子趋于紧密排列,获得简单的原子排列形态.离子键和共价键结合的原子,相邻原子的个数受到共价键数目的限制,离子键结合还要满足正、负离子间电荷的平衡,原子不成能紧密聚积,而且存在孔洞缺陷,故金属键结合的固体资料的密度比离子键或共价键固体高.5.应用公式计算Mg2+O2-离子对的结合键能,以及每摩尔MgO晶体的结合键能.假设离子半径为rMg2+=0.065nm;rO2-=0.140nm;n=7.答:在平衡时,F吸引=F排斥故,解得晶体的结合键能:转换为每摩尔MgO晶体的结合键能:6.原子序数为12的Mg有三种同位素:78.70%的Mg原子由12个中子,10.13%的Mg原子由13个中子,11.17%的Mg原子由14个中子,试计算Mg的原子量.答:7.试计算原子N壳层内的最年夜电子数.若K,L,M和N壳层中所有能级都被填满,试确定该原子的原子数.答:N壳层内最年夜电子数:1s22s22p63s23p63d104s24p64d104f145s25p66s2该原子的原子数是708.试写出Al原子13个电子的每个电子的全部量子数.答:n l m ms10020021021121-13003109.资料的三级和四级结构可以通过加工工艺来改变,那么资料的二级结构可以改变吗?为什么?答:原子的结合键是资料的二级结构.对单一的资料来说,其价键结构是不成以通过加工工艺来改变的.可是实际工程应用中,通过一定的加工工艺来改变资料的二级结构,比如金刚石具有共价键,石墨具有共价键和物理键,而石墨等碳质原料和某些金属在高温高压下可以反应生成金刚石,即一定水平上改变了资料的二级结构.第四章固体资料的晶体学基础1.回答下列问题:(1)在立方晶系的晶胞内画出具有下列密勒指数的晶面和晶向:(001)与[210],(111)与,与[111],与[123],与[236].(2)在立方晶系的一个晶胞中画出(111)和(112)晶面,并写出两晶面交线的晶向指数.(3)在立方晶系的一个晶胞中画出同时位于(101),(011),(112)晶面上的晶向.答:作图略.(2)两晶面交线的晶向指数为.2.有一正交点阵的a=b,c=a/2.某晶面在三个晶轴上的截距分别为6个,2个,4个原子间距,求该晶面的密勒指数.答:(263)3.写出六方晶系的晶面族中所有晶面的密勒指数,在六方晶胞中画出、晶向和晶面,并确定晶面与六方晶胞交线的晶向指数.答:晶面族中所有晶面的密勒指数为:作图略,()晶面与六方晶胞交线的晶向指数为:4.根据刚性球模型回答下列问题:(1)以点阵常数为单位,计算体心立方、面心立方和密排六方晶体中的原子半径及四面体和八面体的间隙半径.(2)计算体心立方、面心立方和密排六方晶胞中的原子数、致密度和配位数.答:体心立方面心立方密排六方原子半径 a a a四面体间隙 a a a八面体间隙 a a a原子数 2 4 6致密度0.68 0.74 0.74配位数8 12 125.用密勒指数暗示出体心立方、面心立方和密排六方结构中的原子密排面和原子密排方向,并分别计算这些晶面和晶向上的原子密度.答:体心立方面心立方密排六方原子密排面{110} {111} {0001}晶面的原子密度原子密排方向<111> <110> <>晶向的原子密度6.求下列晶面的晶面间距,并指出晶面间距最年夜的晶面.(1)已知室温下α-Fe的点阵常数为0.286nm,分别求出(100)、(110)、(123)的晶面间距.(2)已知916℃时γ-Fe的点阵常数为0.365nm,分别求出(100)、(111)、(112)的晶面间距.(3)已知室温下Mg的点阵常数为a=0.321nm,c=0.521nm,分别求出的晶面间距.答:(1)其中,晶面间距最年夜的晶面为(100)(2)其中,晶面间距最年夜的晶面为(110)(3)其中,晶面间距最年夜的晶面为7.已知Na+和Cl-的半径分别为0.097nm和0.181nm,请计算NaCl中钠离子中心到:(1)最近邻离子中心间的距离;(2)最近邻正离子中心间的距离;(3)第二个最近的氯离子中心间的距离;(4)第三个最近的氯离子中心间的距离;(5)它最近的同等位置间的距离.答:(1) r=r++r-=0.278nm (2) r=(3) r=(4) r= (5) r=8.根据NaCl的晶体结构及Na+和Cl-的原子量,计算氯化钠的密度.答:9.示意画出金刚石型结构的晶胞,说明其中包括有几个原子,并写出各个原子的坐标.答:作图略,其中包括原子数:极点坐标:(000),(100),(010),(001),(110),(101),(011),(111)(选填一个即可)面心坐标:(选填三个即可)晶胞内坐标:(),(),(),()10.何谓单体、聚合物和链节?它们相互之间有什么关系?请写出以下高分子链节的结构式:聚乙烯;聚氯乙烯;聚丙烯;聚苯乙烯;聚四氟乙烯.答:单体是合成聚合物的起始原料,是化合物自力存在的基本单位,是单个分子存在的稳定状态.聚合物是由一种或多种简单低分子化合物聚合而成的相对分子质量很年夜的化合物.链节是组成年夜分子链的特定结构单位.聚乙烯:[-CH2-CH2-]n; 聚氯乙烯:[-CHCl-CH2-]n; 聚丙烯:[-CHCH3-CH2-]n;聚苯乙烯:[-CHAr-CH2-]n; 聚四氟乙烯:[-CF2-CF2-]n第四章固体资料的晶体缺陷1.纯Cu的空位形成能为1.5aJ/atom,(1aJ=10-18J),将纯Cu加热至850℃后激冷至室温(20℃),若高温下的空位全部保管,试求过饱和空位浓度与室温平衡空位浓度的比值.答:2.空位对资料行为的主要影响是什么?答:首先,资料中原子(或分子)的扩散机制与空位的运动有关.其次,空位可以造成资料物理性能与力学性能的改变,如密度降低,体积膨胀,电阻增加,强度提高,脆性也更明显,晶体高温下发生蠕变等.3.某晶体中有一条柏氏矢量为a[001]的位错线,位错线的一端露头于晶体概况,另一端与两条位错线相连接,其中一条柏氏矢量为,求另一条位错线的柏氏矢量.答:a[001]=4.如附图a所示,试求某一晶格参数为2.5A0的立方金属刃型位错的burgers矢量的Miller指数及其长度.答:柏氏矢量垂直于(220),故其Miller指数为[110]5.如附图b所示,写出在FCC金属的滑移方向的晶向指数.答:第五章固体资料的凝固与结晶1.液体金属在凝固时必需过冷,而加热使其融化却毋需过热,即一旦加热到熔点就立即熔化,为什么?答:液体金属在凝固时必需克服概况能,形核时自由能变动年夜于零,故需要过冷.固态金属在熔化时,液相与气相接触,当有少量液体金属在固相概况形成时,就会很快覆盖在整个概况(因为液体金属总是润湿同一种固体金属).概况能变动决定过程能否自发进行.根据实验数据,在熔化过程中,概况自由能的变动小于零,即不存在概况能障碍,也就不用过热.2.金属凝固时的形核率常桉下式做简化计算,即试计算液体Cu在过冷度为180K、200K和220K时的均匀形核率.并将计算结果与书图6-4b比力.(已知)答:代入数据得,180K时N均=7.50;200K时N均=7.89;220K时N均=13.36与图6-4b相比,结果吻合,标明只有过冷度到达一定水平,使凝固温度接近有效成核温度时,形核率才会急剧增加.3.试解释凝固与结晶、晶胚与形核的相互关系.答:凝固是指物质从液态冷却成固态的一种转变过程,可以形成晶态或非晶态.若冷却后成为晶体,这种凝固成为结晶.根据热力学判断,在过冷液态金属中,短程规则排列的结构尺寸越年夜,就越稳定,只有尺寸较年夜的短程规则排列的结构,才华成为晶核.晶胚即是过冷液态金属中短程规则排列尺寸较年夜的原子有序排列部份.一定温度下,最年夜晶胚有一个极限值rmax;而液态金属的过冷度越年夜,实际可能呈现的最年夜晶胚尺寸也越年夜.当液态金属中形成的晶胚尺寸年夜于或即是一定临界尺寸时,成为晶核,其有两种形成方式:均匀成核(依靠液态金属自己能量的变动获得驱动力并由晶胚直接成核的过程)和非均匀成核(晶胚是依附在其他物质概况上形核的过程).4.金属结晶的热力学条件和结构条件是什么?答:过冷度是金属结晶的热力学条件;结构起伏和能量起伏是结构条件.5.哪些因素会影响金属结晶时的非均匀形核率?答:过冷度,固体杂质及其概况形貌,物理性能如液相宏观流动,外加电磁场,受机械作用等.第六章资料的扩散与迁移1. 把P原子扩散到单晶硅中的搀杂工艺是制备n型半导体的经常使用方法.若将原来的每107个Si原子中含有一个P原子的1mm厚的硅片,通过扩散搀杂处置后概况到达每107 Si原子中含有400个P原子,试分别按:(a) 原子百分数/cm, (b) 原子数/cm3.cm 的暗示方法计算浓度梯度.硅的晶格常数为5.4307A0.答:(a)(b) 硅的晶胞体积为:单位晶胞中有8个Si原子,则107Si所占体积为:2.试说明影响扩散的因素.答:温度,原子键力和晶体结构,固溶体类型和浓度,晶体缺陷,第三组元.3.试利用公式D=α2РГ,解释各因素对扩散的影响.答:D与α2,Р,Г成正比.其中,α为最邻近的间隙原子距离,与晶体结构有关;Р为跃迁几率,,跟温度,畸变能等有关;为跃迁频率,,与温度、晶体结构、畸变能、扩散机制等因素有关.4. 自扩散与空位扩散有何关系?为什么自扩散系数公式要比空位扩散系数Dv小很多?(Dv=D/nv,nv为空位的平衡浓度)答:对纯金属或间隙固溶体合金,原子都处于正常的晶格结点位置.若晶格结点某处的原子空缺时,相邻原子可能跃迁到此空缺位置,之后又留下新的空位,原子的这种扩散方式叫空位扩散.当晶体内完全是同类原子时,原子在纯资料中的扩散为自扩散.自扩散是空位扩散的一种特殊形式.对置换固溶体合金和纯金属,溶质原子与溶剂原子的尺寸和化学性质分歧,与空位交换位置的几率也分歧,D=D0exp(-Q/RT),自扩散的扩散激活能要比空位扩散的扩散激活能年夜.空位扩散系数Dv=D/nv,由于空位平衡浓度nv远小于1,Dv比D年夜很多.第七章热力学与相图1.分析共晶反应,包晶反应和共析反应的异同点.答:(1)分歧点:共晶反应是一定成份的液体合金,在一定温度下,同时结晶形成另外一种固相的反应过程;包晶反应是一定成份的固相与一定成份的液相作用,形成另外一种固相的反应过程;共析反应是由特定成份的单相固态合金,在恒定的温度下,分解成两个新的,具有一定晶体结构的固相的反应过程.(2)相同点:均是在恒温下发生,处于三相平衡的状态.2.试分析图7-6中合金IV的结晶过程(wsn=70%),计算室温下组元成份的含量及显微组织.答:结晶过程为匀晶反应+共晶反应+二次析出,冷却过程如下图所示,室温下组元成份:αII+ β+(α+β)共晶室温下组元成份的含量:3.铋(熔点为271.5℃)和锑(熔点为630.7℃)在液态和固态时均能彼此无限互溶,wBi=50%的合金在520时开始结晶处成份为wSb=87%的固相.wBi=80%的合金在400℃时开始结晶出成份为wSb=64%的固相.根据上述条件,(1)绘出Bi-Sb相图,并标出各线和各相区的名称.(2)从相图上确定含锑量为wSb=40%合金的开始结晶和结晶终了温度,并求出它在400℃时的平衡相成份及相对量.答:(1)(2)根据相图,含锑量为40%合金开始结晶温度年夜约为490℃,终了温度为350℃,液相含量54.5%,固相含量45.5%.4. (1)应用相律时需考虑哪些限制条件?(2)试指出图5-115中的毛病之处,并用相律说明理由,且加以改正.答:(1)A.相律只适用于热力学平衡状态.平衡状态下各相的温度应相等;各相的压力应相等;每一阻元在各相中的化学位必需相同.B.相律只能暗示体系中组元和相的数目,不能指明组元或相的类型和含量.C.相律不能预告反应动力学.D.自由度的值不得小于零.(2)A.二元体系两相平衡,自由度为1,故不成为直线.B.单一体系两相平衡,自由度为0,故应为一点.C.二元体系最多只能三相平衡,此处含四相.D.二元体系三相平衡,自由度为0,故应为水平线.5.分析wc=0.2%的铁-碳合金从液态平衡冷却至室温的转变过程,用冷却曲线和组织示意图,说明各阶段的组织,并分别计算室温下的相组织物及组织组成物的相对量.答:合金在t1~t2之间发生匀晶反应析出δ固溶体,冷却至t2(1495℃)时,液相L与δ固溶体发生包晶转变生成γ.包晶转变完成后,剩余的液相L在t2~t3之间不竭结晶出奥氏体,冷却至t3,合金全部为奥氏体.单相奥氏体在t4开始析出铁素体.当温度达t5(727℃)时,剩余的奥氏体发生共析反应转酿成珠光体,此时合金组织为铁素体加珠光体.727℃以下,铁素体中会析出少量三次渗碳体.该合金室温时的组织为铁素体与珠光体,相组成为α与Fe3C.冷却至室温的转变过程如图所示.相组成物的相对量:组织组成物的相对量:时间:二O二一年七月二十九日。
《材料科学与工程基础》-第二章-课后习题答案.pdf

材料科学与工程基础第二章课后习题答案1. 介绍材料科学和工程学的基本概念和发展历程材料科学和工程学是研究材料的组成、结构、性质以及应用的学科。
它涉及了从原子、分子层面到宏观的材料特性的研究和工程应用。
材料科学和工程学的发展历程可以追溯到古代人类使用石器和金属制造工具的时代。
随着时间的推移,人类不断发现并创造出新的材料,例如陶瓷、玻璃和合金等。
工业革命的到来加速了材料科学和工程学的发展,使得煤炭、钢铁和电子材料等新材料得以广泛应用。
2. 分析材料的结构和性能之间的关系材料的结构和性能之间存在着密切的关系。
材料的结构包括原子、晶体和晶界等方面的组成和排列方式。
而材料的性能则反映了材料在特定条件下的机械、热学、电学、光学等方面的性质。
材料的结构直接决定了材料的性能。
例如,金属的结晶结构决定了金属的塑性和导电性。
硬度和导电性等机械和电学性能取决于晶格中原子的排列方式和原子之间的相互作用。
因此,通过对材料的结构进行了解,可以预测和改变材料的性能。
3. 论述材料的性能与应用之间的关系材料的性能决定了材料的应用范围。
不同的材料具有不同的性能特点,在特定的应用领域中会有优势和局限。
例如,金属材料具有良好的导电性和导热性,适用于制造电子器件和散热器件。
聚合物材料具有良好的绝缘性和韧性,适用于制造电线和塑料制品等。
陶瓷材料具有良好的耐高温性和耐腐蚀性,适用于制造航空发动机和化学设备等。
因此,在材料科学和工程学中,对材料性能的研究是为了确定材料的应用和优化材料的性能。
4. 解释与定义材料的特性及其测量方法材料的特性是指材料所具有的特定性质或行为。
它包括了物理、化学、力学、热学、电学等方面的特性。
测量材料的特性需要使用特定的实验方法和设备。
例如,材料的硬度通常可以通过洛氏硬度试验仪或布氏硬度试验仪进行测量。
材料的强度可以通过拉伸试验或压缩试验来测量。
材料的导电性可以通过四探针法或霍尔效应进行测量。
通过测量材料的特性,可以对材料的性能进行评估和比较,并为材料的应用提供参考。
《材料科学与工程基础》-第二章-课后习题答案.pdf

材料科学与工程基础 - 第二章 - 课后习题答案2.1 选择题1.D2.B3.C4.A5.D2.2 填空题1.结构、性质、性能、制备、应用2.金属、陶瓷、聚合物3.晶体4.金属材料、陶瓷材料、聚合物材料、复合材料5.原子、分子2.3 简答题1.材料科学与工程的基础概念和特点有:–材料科学:研究材料的结构、性质、制备和性能等方面的科学。
–材料工程:研究通过控制材料的结构和制备方法,得到具有特定性能和使用寿命的材料并应用于工程中。
材料科学与工程的特点包括:–综合性:材料科学与工程是一门综合性的学科,涉及物理、化学、力学、热学等各个学科。
–实用性:材料科学与工程以实际应用为目的,研究如何通过控制材料的结构和性能,满足工程和产品的需求。
–发展性:随着科技的进步和社会的发展,材料科学与工程也在不断发展,涌现出各种新材料和新技术。
2.不同材料的结构特点及其对材料性能的影响–金属材料:金属材料具有密排列的晶体结构,其晶粒间有较好的连续性,导致金属材料具有良好的导电性、导热性和机械性能。
–陶瓷材料:陶瓷材料以离子键或共价键为主要结合方式,具有非常硬、脆和耐高温的特点,但导电性差。
–聚合物材料:聚合物材料由长链状分子构成,具有良好的绝缘性、柔韧性和可塑性,但强度和硬度较低。
–复合材料:复合材料由不同的两种或更多种材料组成,通过它们的相互作用产生优异的整体性能。
同时,复合材料的结构也决定其性能。
3.材料的制备方法包括:–金属材料的制备方法有铸造、锻造、挤压、焊接等。
–陶瓷材料的制备方法有干法制备和湿法制备等。
–聚合物材料的制备方法有合成聚合法、溶液聚合法、熔融聚合法等。
–复合材料的制备方法有增强相法、混合相法、层压法等。
4.材料性能的测试方法包括:–机械性能的测试方法有拉伸试验、压缩试验、弯曲试验等。
–热性能的测试方法有热膨胀试验、热导率测试等。
–电学性能的测试方法有导电性测试、介电常数测试等。
–光学性能的测试方法有透光率测试、折射率测试等。
材料科学基础课后习题答案

(3) cosφ
=
n3 ⋅ F | n3 || F
|
=
1 3
cosα
=
b⋅F |b || F
|
=
1 2
由 Schmid 定律,作用在新生位错滑移面上滑移方向的分切应力为:
τ 0 = σ cosϕ cos λ = 17.2 ×
1× 3
1 = 7.0 MPa 2
∴作用在单位长度位错线上的力为:
f = τb = aτ 0 = 10 − 3 N/m 2
滑移面上相向运动以后,在相遇处
。
(B
)
A、相互抵消
B、形成一排空位
C、形成一排间隙原子
7、位错受力运动方向处处垂直与位错线,在运动过程中是可变的,
晶体作相对滑动的方向
。
(C
)
A、亦随位错线运动方向而改变 B、始终是柏氏矢量方向 C、始
终是外力方向
8、两平行螺型位错,当柏氏矢量同向时,其相互作用力
。
(B
二、(15 分)有一单晶铝棒,棒轴为[123],今沿棒轴方向拉伸,请分析:
(1)初始滑移系统; (2)双滑移系统 (3)开始双滑移时的切变量 γ; (4)滑移过程中的转动规律和转轴; (5)试棒的最终取向(假定试棒在达到稳定取向前不断裂)。
三、(10
分)如图所示,某晶体滑移面上有一柏氏矢量为
v b
的圆环形位错环,并受到一均匀
14、固态金属原子的扩散可沿体扩散与晶体缺陷扩散,其中最慢的扩
散通道是:
。
(A)
A、体扩散
B、晶界扩散
C、表面扩散
15、高温回复阶段,金属中亚结构发生变化时,
。
(C)
A、位错密度增大 B、位错发生塞积 C、刃型位错通过攀移和滑移构
材料科学基础 课后习题

课后习题练习题1第一章绪论1.什么叫材料?2.材料科学与工程研究内容是什么?第二章物质结构基础原子结构1.材料结构的含义(层次)是什么?2.原子中一个电子的空间位置和能量可用哪4个量子数决定?3.在多电子的原子中,核外电子排布应遵循哪些原则(3个)?4.何谓同位素?为什么元素的相对原子质量不总为正整数?5.教材p102 题2-246.铬的原子序数为24,共有4种同位素:4.31%的Cr原子含有26个中子,83.76%含有28个中子,9.55%含有29个中子,2.38%含有30个中子,试求铬的相对原子质量。
7.铜原子序数29,相对原子质量63.54,共有两种同位素Cu63和Cu65,试求两同位素之含量百分数。
8.原子间的结合键共有几种?各自特点(饱和性和方向性)如何?练习题2原子有序:晶体结构1.纯铝的晶体为面心立方点阵。
已知铝的相对原子质量Ar(Al)=26.97,原子半径r=0.143nm,求铝晶体的密度。
2.按晶体刚性模型,若球直径不变,当Fe从fcc转变为bcc时,计算其体积膨胀率。
3.教材p102 题2-32 (共8题,每个晶胞中画2个晶向)4.教材p102 题2-335.教材p102 题2-34 (写出密勒指数推算过程)6.教材p102 题2-35 (题中的中括号应当改成小括号;共8题,每个晶胞中画2个晶面)练习题3原子无序:固溶体1.什么叫固溶体?2.根据溶质在点阵中的位置,固溶体有哪些类型?3.影响置换型固溶体形成的因素有哪些?4.Al和Ag都是面心立方结构,Al原子半径0.143 nm, Ag原子半径0.144 nm,试问:Al在Ag中能否形成无限固溶体?为什么?原子无序:晶体缺陷1.晶体缺陷有哪些类型?2.为何说点缺陷是热力学平衡缺陷?3.什么叫位错?位错的基本类型?4.位错能否终止于晶体内部?原子无序:材料中的扩散指出下列概念中的错误(判断和回答为什么)1.如果固溶体中不存在宏观扩散流,则说明原子没有发生迁移。
材料科学基础 第二章习题

1)计算fcc,bcc结构的(001)、(110)、(111)晶面的面密度,计算密排六方结构的(0001)、(101—0)晶面的面密度。
(面密度定义为一定面积上的原子数)。
2)从晶体结构的角度,间隙固溶体、间隙相、间隙化合物之间的区别?3)钛具有hcp结构,在20℃时六方晶胞体积为0.106nm3,c/a = 1.59,求a和c,并计算基面上的原子半径。
4)根据下表所给之值,确定哪一种金属可作为溶质与钛形成固溶度较大的固溶体:5)试计算金刚石结构的致密度。
6)In具有四方结构,其相对原子质量为114.82,原子半径为0.1625nm,晶格常数a=0.3252nm,c=0.4946nm,密度ρ= 7.286g/cm3,试问In的单位晶胞内有多少个原子?In的致密度为多少?7)按晶体的钢球模型,若球的直径不变,当Fe从fcc转变为bcc时,计算其体积膨胀多少?经X射线衍射测定,在912℃时,α-Fe(bcc)的a = 0.2892nm,γ-Fe(fcc)的a = 0.3633nm,计算从γ-Fe转变为α-Fe时,其体积膨胀为多少?试说明产生差别的原因。
8)渗碳体(Fe3C)是一种间隙化合物,它具有正交点阵结构,其点阵常数a =0.4514nm,b = 0.508nm,c = 0.6734nm,其密度为7.66g/cm3,试求Fe3C每单位晶胞中含Fe原子与C原子的数目。
9)铜的相对原子质量为63.55,密度为8.96g/cm3。
(i)计算铜的点阵常数和原子半径。
(ii)测得Au的摩尔分数为40%的Cu-Au固溶体点阵常数a = 0.3795nm,密度为14.213g/cm3,计算说明它是什么类型的固溶体。
10)Zn原子的摩尔分数为3%Zn的Cu-Zn合金固溶体,铜的原子半径为0.128nm,Zn的原子半径为0.133nm。
假设点阵常数随Zn原子增加呈线性变化,求这个合金的密度。
(Cu和Zn的原子量分别为63.55 和65.37,阿佛加得罗常数是6.0238×1023)。
材料科学基础课后习题解答

其它为混合位错。
(2)位错受力为 F = τ b ,方向为垂直位错线。
(3)位错线将扩展
(4)τ
=
Gb 2R
2.6
⇒
Rmin
=
Gb 2τ
F
=
−τ 1b2
=
−
Gb1b2 2r
∫ W
=
r1
−
Fdr
=
−
Gb1b2 2Π
ln
3 100
= 1.76 ×10−9 J
r0
2.7 (1)(100)面的螺型位错形成刃型扭折,(001)面的刃型位错 形成刃型割阶 (2)两个面内的位错都形成刃型割阶
材 料 科 学 基 础 部 分 课 后 习 题 参 考 答 案
中南大学 郑子樵
第一章、材料的结构
2.晶体结构=空间点阵+实际原子(原子团等)
3.
原子个数 致密度 配位数 r 与 a 的关系 密排方向 面
fcc
4
0.74
12
3a = 4r {111} <110>
bcc
2
0.68
8
2a = 4r
{,棒轴为[123],今沿棒轴方向拉伸,请分析:
(1)初始滑移系统; (2)双滑移系统 (3)开始双滑移时的切变量 γ; (4)滑移过程中的转动规律和转轴; (5)试棒的最终取向(假定试棒在达到稳定取向前不断裂)。
三、(10
分)如图所示,某晶体滑移面上有一柏氏矢量为
v b
的圆环形位错环,并受到一均匀
用时的反应方向:
(1)
1 2
[10
1]
⇔
1 6
[2
1
1] +
1 6
材料科学基础习题与答案

第二章思考题与例题1. 离子键、共价键、分子键和金属键的特点,并解释金属键结合的固体材料的密度比离子键或共价键固体高的原因?2. 从结构、性能等方面描述晶体与非晶体的区别。
3. 何谓理想晶体?何谓单晶、多晶、晶粒及亚晶?为什么单晶体成各向异性而多晶体一般情况下不显示各向异性?何谓空间点阵、晶体结构及晶胞?晶胞有哪些重要的特征参数?4. 比较三种典型晶体结构的特征。
(Al、α-Fe、Mg三种材料属何种晶体结构?描述它们的晶体结构特征并比较它们塑性的好坏并解释。
)何谓配位数?何谓致密度?金属中常见的三种晶体结构从原子排列紧密程度等方面比较有何异同?5. 固溶体和中间相的类型、特点和性能。
何谓间隙固溶体?它与间隙相、间隙化合物之间有何区别?(以金属为基的)固溶体与中间相的主要差异(如结构、键性、性能)是什么?6. 已知Cu的原子直径为2.56A,求Cu的晶格常数,并计算1mm3Cu的原子数。
7. 已知Al相对原子质量Ar(Al)=26.97,原子半径γ=0.143nm,求Al晶体的密度。
8 bcc铁的单位晶胞体积,在912℃时是0.02464nm3;fcc铁在相同温度时其单位晶胞体积是0.0486nm3。
当铁由bcc转变为fcc时,其密度改变的百分比为多少?9. 何谓金属化合物?常见金属化合物有几类?影响它们形成和结构的主要因素是什么?其性能如何?10. 在面心立方晶胞中画出[012]和[123]晶向。
在面心立方晶胞中画出(012)和(123)晶面。
11. 设晶面(152)和(034)属六方晶系的正交坐标表述,试给出其四轴坐标的表示。
反之,求(31)及(2112)的正交坐标的表示。
(练习),上题中均改为相应晶向指数,求相12互转换后结果。
12.在一个立方晶胞中确定6个表面面心位置的坐标,6个面心构成一个正八面体,指出这个八面体各个表面的晶面指数,各个棱边和对角线的晶向指数。
13. 写出立方晶系的{110}、{100}、{111}、{112}晶面族包括的等价晶面,请分别画出。
材料科学基础课后习题答案

材料科学基础课后习题答案材料科学基础课后习题答案第一章:晶体结构和晶体缺陷1. 什么是晶体?晶体的特点是什么?答:晶体是由有序排列的原子、离子或分子组成的固态材料。
晶体的特点包括有规则的、重复的、周期性的结构,具有明确的晶体面和晶面间角度。
2. 简述晶体中离子束缚以及普通共价键束缚的区别?答:晶体中离子束缚是指由电荷相反的离子通过电磁力相互吸引而形成的结合力,例如NaCl晶体。
普通共价键束缚是由共享电子对形成的,例如金刚石晶体。
离子束缚通常较为强烈,晶体具有高熔点和脆性;而共价键束缚相对较弱,晶体具有低熔点和韧性。
3. 什么是晶体缺陷?列举几种晶体缺陷并简要描述其影响。
答:晶体缺陷是指晶体中排列异常的原子、离子或分子。
常见的晶体缺陷包括点缺陷、线缺陷和面缺陷。
点缺陷指的是晶体中原子位置的缺失或替代,如空位、间隙原子和杂质原子;线缺陷是晶体中晶面上原子位置的错误,如位错和螺旋位错;面缺陷是指晶面之间的错配,如晶界和孪生界。
这些晶体缺陷会影响晶体的物理性质和力学性能。
4. 什么是晶体结构中的定义因素?它们的作用是什么?答:晶体结构中的定义因素包括晶胞和晶格参数。
晶胞是最小重复单元,由一定数量的晶体中的原子、离子或分子组成。
晶格参数描述晶胞的大小和形状。
晶胞和晶格参数共同定义了晶体的结构。
晶胞和晶格参数的作用是确定晶体的晶体面、晶面间角度以及晶体的物理性质。
5. 什么是晶格点?晶格点的种类有哪些?答:晶格点是位于晶体内部的原子、离子或分子的位置。
晶格点的种类包括普通晶格点、间隙晶格点和特殊晶格点。
普通晶格点是晶体中原子、离子或分子的晶格点,如AB型晶体中的A和B原子;间隙晶格点是晶体中没有原子、离子或分子的晶格点,如金刚石中的间隙晶格点;特殊晶格点是具有非普通晶格点性质的晶体中的晶格点,如晶体中的空位或杂质原子。
第二章:物质的结构与性能关系1. 简述晶体结构对物质性能的影响。
答:晶体结构直接影响物质的物理性质和化学性质。
材料科学基础课后习题答案2

Solutions for Chapter 21. Find: Number of valence electrons in Group IIIB and GroupVB elements.Data: Periodic Table in Appendix A.Solution: By definition and/or by examination of Appendix B, Group IIIB elements contain 3 valence electronswhile Group VB elements contain 5 valence electrons.2. Find: The electron configuration of the element that comesnext in the series Si, Ge, ?Data: Periodic Table in Appendix A.Solution: Examination of the Periodic Table shows that Si and Ge are both Group IVB elements. As shown inExample Problem 2.2-1, have a valence electronconfiguration of the form xs2xp2 when x=3 for Si andx=4 for Ge. The next group IVB element in the seriesis Sn with an electron configuration (from the PeriodicTable) of [1s22s22p63s23p63d104s24p64d10]5s25p2. Note thatthe valence electron configuration for Sn is also ofthe form xs2xp2 with x=5.Comments: The similarity of their valence electronconfigurations suggests that Sn should displayproperties similar to those of Si and Ge. This istrue over a limited temperature range but thereare other factors (to be discussed in the nextchapter) that explain why Sn also has someproperties that differ from those of the other twoelements.3. Find: Should Ca and Zn exhibit similar properties?Data: Periodic Table in Appendix A.Solution: Examination of the Periodic Table shows that Ca has the electron configuration [1s22s22p63s23p64s2]while Zn has configuration [1s22s22p63s23p63d10]4s2.Since both elements have two valence electrons (4s2)we should expect these elements to display somesimilar properties.Comments: Although Zn and Ca have similar valence electron configurations, they have other structuraldifferences that result in differences inproperties.4. Find: Suggest some consequences of electron energies notbeing quantized.Solution: Although there are many possible answers to this question, one of the more important results mightbe a breakdown in the periodic arrangement of theelements. The Periodic Table owes its existenceto the quantization of energy. If quantization ofenergy did not exist, we would lose the ability tounderstand and predict properties based on valenceelectron configuration.5. FIND: How many electrons, protons, and neutrons are in Cu?DATA: From Appendix A, the atomic number of Cu is 29 and the atomic mass is 63.54 g/mole.SOLUTION: Cu has 29 electrons and 29 protons, each proton weighing about 1 g/mole. The balance of the atomic mass is from neutrons.COMMENTS: Elements can have different masses, from having different numbers of neutrons. They are called isotopes.6. FIND: What is the electronic structure of C?DATA: From Appendix A, the atomic number of C isSOLUTION: Carbon is capable of 4 covalent bonds of equal strength. Just think of some hydrocarbons that you know, such as methane, CH4. Four H bond to a central C. The bonding of Cmight be expected to be 1s22s22p2, again from Appendix A. What occurs in practice is called hybridization. The four electronsin the 2s and 2p levels hybridize, giving four electrons of equal bond strength capability. The bonds are as far apart as possible in space (tetrahedral bond angles).7. FIND: Describe the desirable environmental stability of a "gold standard".ASSUMPTIONS: You want the standard's critical properties to be invariant with timeSOLUTION: Gold is one of the few metals whose pure metallic state is more thermodynamically table than its oxide. Hence,gold does not oxidize. If it did, then it might gain or lose weight with time of exposure to air.COMMENTS: This is why gold is found in nature as nuggets, whereas, for example, iron and aluminum are found as oxides or sulfides.8. Find: Can pure water exist at -1o C?Solution: Yes, if the pressure of the system is raisedabove one atmosphere, water can exist at -1o C.Comments: Since most of our daily experiences occur at (or near) atmospheric pressure, we tend to forgetabout pressure as an important system variable.There are, however, many important engineeringprocesses that occur at either substantiallyhigher or lower pressures.9. Find: Change in flow rate when molasses is heated from 10o Cto 25o C.Given: Activation energy, Q, for Arrhenius Process is50 kJ/mole.Data: R= 8.314 J/mol-K, K=o C+273Assumptions: Flow rate at temperature T is given byF(T)= F o exp(-Q/RT)Solution: The ratio of the flow rates at any twotemperatures is:F(T1) = F o exp(-Q/RT1) = exp(-Q/R(1/T1-1/T2))F(T2) F o exp(-Q/RT2)F(25︒C) = exp(-50,000J/mol/8.134J/mol-K)(1/298K- 1/283K)) = 2.91 F(10o C)A temperature increase of 15o C results in almost afactor of three increase in the flow rate ofmolasses.10.Find: Change in polymerization rate when temperatureincreases by 10o C.Given: Activation energy, Q, for Arrhenius Process is80 kJ/mole.Data: R= 8.314 J/mole-K, K= o C+273Assumption: Polymerization rate at temperature T is given by P(T)= P o exp(-Q/RT)Solution: The ratio of the polymerization rates at any two temperatures is:P(T1) = P o exp(-Q/RT1) = exp(-Q/R(1/T1 - 1/T2))P(T2) P o exp(-Q/RT2)P(T1) = exp[-Q/R((T2-T1)/T1T2))] = exp[-Q/R(∆T/T1T2)]P(T2)This form of the expression shows that the problemcan not be solved with the information given. Aknowledge of ∆T is not sufficient. We must alsoknow the two temperatures.Comments: When the temperature increases from 10o C to20o C, the rate increases by a factor of 3.19. Incontrast, a temperature increase from 40o C to 50o Cresults in a rate increase of 2.59. This exampleillustrates the general result that a fixed changein temperature has a greater influence on thereaction rate if the average temperature is low. 11.FIND: Why are high quality electronic cable ends or contact points gold-coated?SOLUTION: You do not want the resistance of theconnection to increase with time. Oxides are generally good electrical insulators. Steel points rust and the oxide prevents them from working. Car points, for example, need to be changed frequently.COMMENTS: In some electronic devices a slight impedance increase due to oxide formation can cause a circuit to fail catastrophically, destroying a number of components.12.Find: Explanation for man's ability to convert aluminum oxide to aluminum.Given: Oxide represents a lower energy state than pure Al. Solution: Thermodynamics describes the direction ofspontaneous change. That is, balls roll down hilland Al will transform to Al2O3 if the kinetics arefavorable and no other factors are acting on thesystem. We know, however, that a ball can be moveduphill if energy is supplied to the system (i.e.if it is carried uphill). Furthermore, it mayremain at a higher elevation if there are activa-tion barriers associated with its return to thelowest energy position. Similar logic applies tothe reduction of Al2O3 to 2Al+1.5O2. If mansupplies (thermal) energy, the metal can beextracted from its ore and will remain in ametastable state. However, the metal will returnto its more stable oxide at a later time ifconditions permit.13.Find: Characteristics of primary bonds.Solution: Provided in the form of a table.+----------------------------------------------------------+|primary | types of | bonding | if sharing || bond | atoms | electrons | occurs is it|| type | usually | shared or | localized or|| | involved | transferred | delocalized|+----------+-----------------+--------------+--------------|| ionic | electroneg. and | transferred | --------- || | electropositive | | |+----------+-----------------+--------------+--------------|| covalent | electronegative | shared | localized || |(usually w N VE>3)+----------+-----------------+--------------+--------------|| metallic | electropositive | shared | delocalized|| |(usually w N VE 3)+----------------------------------------------------------+14.Find: Primary bond type in each of a series of compounds. Data: Electronegativities and numbers of valence electronsfor each element can be obtained from thePeriodic Table in Appendix A.Element | Electronegativity | No. of valence electrons--------+-------------------+-------------------------O | 3.44 | 6Na | 0.93 | 1F | 3.98 | 7In | 1.78 | 3P | 2.19 | 5Ge | 2.01 | 4Mg | 1.31 | 2Ca | 1.00 | 2Si | 1.90 | 4C | 2.55 | 4H | 2.20 | 1| |Assumptions: Percent ionic character of a bond is afunction of the difference in the electro-negativities of the elements involved (SeeAppendix A for conversion table). In a metal,the average number of valence electrons isgenerally ≤ 3. In a covalent solid the averagenumber of valence electrons is generally > 3.Solution:• O2, ∆EN=0 so that the bond is not ionic. Since O is an electronegative element and the average number ofvalence electrons is 6, we predict a covalentbond.• NaF, ∆EN = EN(F)-EN(Na) = 3.98-0.93 = 3.05. This ∆ENcorresponds to a bond that is approximately90% ionic.• InP, ∆EN = EN(P)-EN(In) = 2.19-1.78 = 0.41. Since thisbond is only about 4% ionic, we must examine the average number of electrons, N VE. Since N VE =(3+5)/2 = 4, we predict that the bond will becovalent.• Ge, ∆EN=0 so the bond is not ionic. Ge is neitherstrongly electropositive or electronegative, but it does have N VE=4. Thus we predict covalentbonding.• Mg, ∆EN=0 so the bond is not ionic. Mg is an electro-positive element with N VE =2. It will havemetallic bonds.• CaF2, ∆EN = EN(F)-EN(Ca) = 3.98-1.0 = 2.98. This ∆ENcorresponds to a bond that is appproximately 89% ionic.• SiC, ∆EN = EN(C)-EN(Si) = 2.55-1.90 = 0.65. Since thiscorresponds to a bond that is only ≈10% ionic, we must consider N VE. The average number ofvalence electrons is (4+4)/2 = 4 so the bond ispredicted to be covalent.• (CH2), ∆EN = 2.55-2.20 = 0.35 so the bond is not ionic.Although the average N VE in this compound is(4+1)/2 = 2.5, the bond is predicted to becovalent because H is a recognized exception tothe trend and is known to favor the formation ofcovalent bonds.• MgO, ∆EN = EN9O)-EN(Mg) = 3.44-1.31 = 2.13 whichcorresponds to a bond that is ≈68% ionic.• CaO, ∆EN = EN(O)-EN(Ca) = 3.44-1.0 = 2.44 whichcorresponds to a bond that is 77% ionic.Comments: All of these predictions are in agreement with experimental observations.15.FIND: Show the octet rule in C.DATA: Carbon forms four equal bonds.SKETCH: Shown is methane, simply as an example:HHHCHSOLUTION: The 8 dots represent the electrons: 4 come from the central carbon and 1 from each of the 4 hydrogen. The electrons are localized between the atoms sharing the electrons.16.Find: Characteristics of the Coulombic Force.Data: F a(x) is given in Equation 2.4-1 and sketched inFigure 2.4-2(a).Solution: The Coulombic Force varies inversely with thesquare of the separation distance between the charge centers. Another familiar example of aninverse square law is the force of gravity. Afunction of this form has no local maxima orminima because the derivative of equation 2.4-1has a nontrivial values for which it is equal tozero and the maximum value occurs as x approachesinfinity (for the sign convention adopted inFigure 2.4-2(a)).17.Find: Definitions of ionization potential and electronaffinity.Solution: Ionization potential is the energy required toremove an electron from an isolated neutralatom. The energy released when an isolatedneutral electronegative atom gains an electron isits electron affinity.Comments: The significance of these variables is that thedifference between the ionization potentialand the electron affinity is the amount of workthat must be done to create a pair of isolatedmonovalent ions. This quantity is important inthe determination of the total bond energy in anionic bond.18.Find: Reason why covalent bonds are restricted to electro-negative elements.Assumptions: During bonding, atoms seek to obtain a filledvalence electron shell.Solution: Electronegative elements generally have nearlyfilled valence shells and are seeking a fewadditional electrons. If electropositive atomsare nearby, they can transfer electrons to theelectronegative atoms and an ionic bond is formed.If, however, only electronegative atoms arepresent then the only way they can all acquireextra electrons is to share them. This is thedefinition of a covalent bond.Comments: Hydrogen also forms covalent bonds.19.Find: Is the Si-O bond covalent?Given: O forms covalent bonds with itself and Si alsoforms covalent bonds with other Si atoms.Data: From Appendix B: EN(Si)=1.90 and EN(O)=3.44.Assumptions: The percent ionic character of a bond isgiven by the table in Appendix A.Solution: It is impossible to form ionic bonds in any pureelement since there will be no difference inEN values for identical atoms. In the case ofSi-O, however, the difference inelectronegativity is 1.54. This corresponds to abond that is approximately 45% ionic and 55%covalent.Comments: This type of primary bond is often described asa mixed ionic/covalent bond.20.Find: Can an ionic solid be a good electrical conductor?Assumptions: High electrical conductivity requires a highdensity of mobile charge carriers.Solution: In ionic solids there are usually few, if any,free electrons. Charge transport requiresthe motion of comparatively large ions which isgenerally a more difficult process than electronmotion. If, however, an ionic solid had either ahigh free electron density or extremely mobileions, then it would be a good electricalconductor.Comments: We will find some examples of materials withthese characteristics in Chapter 10.21.Find: Physical significance of p<q in Equation 2.4-7.Data: Equation 2.4-7 states: F A+F R=0=A'/x p-B'/x q.Solution: This equation describes the competing forces ofattraction and repulsion in a covalent bond.Since the repulsive force is known to dominate atsmall separation distances (x→0), we requireB'/x q >> A'/x p as x→0. This is equivalent to requiring that x q << x p (for x→0) which issatisfied if and only if q>p.22.Find: Types of information available from the bond-energycurve.Solution: The depth of the bond-energy curve describes thestrength of the bond (i.e. the bond energy)and also provides information about thevaporization temperature since it is anindication of the amount of energy that must besupplied to move atoms to an infinite separationdistance. The value of x for which the bondenergy is a minimum corresponds to theequilibrium separation distance. It is, however,not possible to gain information about theprimary bond type from the general shape of thebond energy curve.23.FIND: Identify which material shown in Fig.2.5-1 has a higher melting temperature.GIVEN: The slope of material A at zero force is greater than that of B.SOLUTION: The ease of separating atoms or molecules with heat is similar to the ease of separating atoms with force. Hence, A has a higher melting temperature than does B.24.Find: Relationship between x th and melting temperature.Data: x th(Al)=25x10-6︒C-1 and x th(SiC)=4.3x10-6︒C-1.Assumptions: Melting temperature is related to the depthof the bond energy curve and thermalexpansion coefficient is related to the asymmetryof the curve.Solution: Since "deep" energy wells tend to be moresymmetric, materials with high meltingtempera-tures tend to have low expansioncoefficients. Thus, we expect SiC to have ahigher T m than Al.Comments: This prediction is consistent with experiment -T m(SiC) = 2700︒C and T m(Al) = 660︒C.25.Find: Relationship between stiffness and thermal expansion. Assumptions: Stiffness is related to the curvature (secondderivative) of the bond energy curve at itsminimum and expansion coefficient is related toasymmetry of the curve.Solution: Bond energy curves that are sharply curved havelarge second derivatives and high stiffness.However, such curves will also be relativelysymmetric so they will exhibit low coefficientsof thermal expansion. In order to obtain a stiffmaterial with a high expansion coefficient itwould require a tightly curved but asymmetricshape. This combination is difficult to achieve.26.Find: Explanation for the similarity of the moduli ofoxide ceramics.Solution: Elastic modulus is one of the properties thatcan be determined from the bond energy curve.If several materials have similar bondcharacter-istics then we should expect thosematerials to display similar modulus values.This is the case with many oxide ceramics andother ionic solids.27.Find: Estimate relative deflections of oxide and polymerglasses.Given: E(oxide)=10 E(polymer)Data: Deflection is inversely proportional to modulus(stiffness).Solution: The material with the higher modulus willdeflect less under the same load. Therefore, the plastic will display 10 times as muchdeflection as the oxide.28.Find: Sketch bond curves for a material with x th <0.Solution: Sketch|||↑ ||E |+-----------------------| x|||| |||↑ ||F |+-----------------------| x||||Comments: The bond energy curve is steeper to the right ofx︒ than to the left. This means that themidpoints of the constant energy line segmentsshift to the left as energy (temperature)increases.29.FIND: Calculate the atomic separation of pure Ti and Cu at 625︒C.GIVEN: The atomic separation at room temperature (25︒C) for Ti is 2.94 A and the thermal expansion coefficient is 9 x 10-6 / ︒C.DATA: The atomic separation of Cu is 1.28 A x 2 = 2.56 A according to Appendix C. The thermal expansioncoefficient of Cu is 17 x 10-6 / ︒C, according to Table 2.5-1.SOLUTION: The atomic spacing of Ti at 625︒C is:2.94 A + 600︒C x (9 x 10-6 / ︒C) = 2.94 A + 0.0054 A = 2.9454 A. Similarly, the atomic spacing of Cu at 625︒C is:2.56 A + 600︒C x (17 x 10-6 / ︒C) = 2.94 A + 0.0102 A = 2.57 A.COMMENTS: There is a problem with significant digits in thisproblem. The atomic spacing at 25︒C was provided only to 2 decimal places. Better accuracy is required in the atomic spacings if better accuracy in the calculated results are required.30.Find: Methods for measuring Young's modulus and coefficient of thermal expansion in the lab.Sketch:Solution: Young's Modulus relates the stiffness ordeflection of a material to the magnitude of the force or load causing that deflection. Themodulus of a material could be measured usingeither of the methods sketched above, that is, bymeasuring the deflection of a cantilever beam orthe change in length of an axially loaded rod.Coefficient of thermal expansion is measuredby observing the change in length of asample resulting from a temperature change(see Equation 2.5-4).31.Find: CNs for ions in CaF2Given: r(Ca)=0.197nm, r(Ca2+)=0.106nm, r(F)=0.06nm,r(F-) = 0.133nmData: r/R ranges for various CNs given in Table 2.6-1.Solution: Since this is an ionic compound user(Ca2+)/R(F-) = 0.106nm/0.133nm = 0.797From Table 2.6-1, this corresponds to CN(Ca2+)=8.Since the anion:cation ratio is 2:1, theCN(F-) is given by:CN(F-)= 1/2[CN(Ca2+)] = 4.Comments: This prediction is consistent with experiment. 32.Find: CNs of cations in NiO, ZnS, and CsI.Data: Radii in Appendix B→r(Ni2+)=0.078, r(O2-)=0.132,r(Zn2+)=0.083, r(S2-)=0.174, r(Cs+)=0.165, r(I-)=0.220Assumptions: Ionic bonding in all three compounds. Thiscould be checked by investigating ∆EN values.Solution: For NiO: r(Ni2+)/R(O2-)=0.105/0.132=0.795, so thatfrom Table 2.6-1 we find CN(Ni2+)=6. For ZnS: r(Zn2+)/R(S2-)=0.083/0.174=0.477, so that fromTable 2.6-1 we find CN(Zn2+)=6. For CsI:r(Cs+)/R(I-)=0.165/0.220=0.750, so that from Table2.6-1 we find CN(Cs+)=8.33.FIND: Sketch the structure of methane andO as in Fig. 2.6-5. SKETCH: Methane is a covalently-bonded material.SOLUTION:COMMENTS: In methane the C is in the center ofthe cube and the H are centered on the appropriate cube corners. The bond angles are 109.5︒ and the bond lengths are all the same. In the ketone the C is located within an equilateral triangle. The O double bond and the other two single bonds are planar, essentially 120︒ apart. 34. Find: Relationship between bond type and density. Solution: Density depends on the mass and radius of the atoms in the solid and on the efficiency with which the atoms are packed together. The later factor is a function of bond type through its influence on coordination numbers. Metals tend to have high CNs, typically 8 or 12. Ionic solids typically have CNs ranging from 3 to 8. Covalent solids typically have CNs ranging from 2 to 4. Therefore, if all other factors are roughly equal, covalent solids will display the lowest densities and metals will have the highest densities.Comments: For covalent solids CN= 8-N VE and N VE ≥ 4. This combination implies that CN(covalent) ≤ 4. 35. Find: When do you use r/R to predict CN in a covalent compound? Solution: Since in covalent compounds CN is determined by the 8-N VE rule, the r/R rule is never used to predict CN in covalent compounds. 36. Find: Find CN in pure Ge. Given: Ge is a Group IV covalently bonded compound. Solution: In a covalent compound CN=8-N VE . For Group IV Ge N VE =4. Therefore, CN(Ge)=8-4=4. Comment: This prediction is consistent with experiment.37.Find: Radius range for CN=4.Assumption: Assume ionic bondingSketches:Solution: The appropriate figures are sketched above andin Table 2.6-1. The minimum r/R ratio isfound using the sketch on the left. For thisgeometry:r+R=a√3/2 [anions touch cations along 1/2 a body diagonal]and R+R=a√2 [anions touch each other alongface diagonals]Dividing the first equation by the second gives:(r+R)/2R = 3/2√2orr/R = (√3/√2)-1 = 0.225The maximum r/R for CN=4 in the minimum valuefor CN=6. Using the geometry on the right:(r+R) = a/2and(R+R) = a√2/2Dividing the first equation by the second gives:r/R = (2/√2) -1 = 0.414Therefore, the radius ratio range for CN=4 is0.225 ≤ (r/R) < 0.414.38.Find: Characteristics of an ionic bond.Given: A2B compound with r(A)=0.12nm, r(B)=0.15nm,r(B+)=0.14nmSolution:A. Anions are generally larger than their neutralcounterparts because the added electronsincrease electron-electron mutual repulsion anddecrease the relative magnitude of the nuclearcharge. Therefore, r(A-) > r(A). Using theinverse argument we predict r(B+) < r(B).B. If the compound is ionic we must use an r/R ratioto predict the CN of the smaller ion (in this case the anion).r(A-)/R(B+)=0.13/0.14=0.929From Table 2.6-1, this implies CN(A-)=8. Sincethe anion:cation ratio is 2:1, thecoordination number for the cation is predictedto be CN(B+)= 2[CN(A-)]= 16. A CN of 16, howeveris not possible. Therefore, the most likelyvalues are CN(B+)=12 and CN(A-)=6. Recall thatlower CN values are always possible but aregenerally not energetically favorable.39.Find: Relative size of atoms if CN(A)=CN(B)=12.Solution: A coordination number of 12 for all atoms/ionsin a compound suggests that all of theatoms/ions are the same size. That is r/R=1.40.Find: Bond characteristics of Si and C.Solution: Both Si and C are Group IV elements and incovalent compounds they will each have CN=4.Thus we should expect some similarity between C-based (organic) structures and Si-basedstructures.Comments: These similarities will be investigated inChapter 6.41.Find: Structure of C2H6Assumptions: This is a covalent compoundSolution/Sketch:H H| || |H ----- C ------ C ------ H| || |H HComments: CN(C)=4 and CN(H)=1.42.Find: Explanation for no solids with CN = 5, 7 or 9.Solution: It is geometrically impossible to fill threedimensional space with the polyhedrons (solid geometrical figures) that result from CNs of 5, 7,or 9.Comment: To get a "feeling" for this statement you mighttry to "fill" two dimensional space with aseries of equal sized (regular) pentagons orheptagons.43.Find: Location of tacks in a room to maximize separationdistance.Sketch/Solution:The "tacks" or atoms should be placedin four of the eight corners of thecube (room) such that no two adjacentcorners are occupied. The separationis a√2.44.Find: Bond angle H-N-H in NH3Assumptions: Covalent bonding with CN(N)=3 and CN(H)=1Sketch:Solution: The bond angle is close to the tetrahedral angleof 109.5︒ (see Figure 2.6-4(a) and associated text).Comments: See Example Problem 2.6-4.45.Find: Type of bond between (NH4)+ and Cl-.Solution: The bonding in (NH4)+ essentially results infour exposed protons. These H+ ions can form hydrogen bridges between the electronegative N and Cl ions resulting in comparatively strong secondary bonds.46.Find: Predict which material has the higher T m.Assumptions: For compounds with secondary bonds, theimportant factors are the relative strengthof the bonds and the size of the molecules (sincelarger molecules have a greater surface area overwhich secondary bonds can occur).Solutions:A. H F | || | ----- C ------ C ------ | | | | H F will have a higher T m thanF F| || |----- C ------ C ------| || |F Fbecause the former is a permanent dipole while thelatter is too symmetric to have strongsecondary bonds.B. H | | H ----- C ------ H | | Hwill have a lower T V thanH | | H ----- N ------ H |⋅|⋅← (nonbonding electron pair)because the latter is permanent dipole while theformer is too symmetric to have strongsecondary bonds.C. Although their structures are very similar, C14H30will have a higher T m than C5H12 because it isa larger molecule with more surface for secondarybond formation.47.FIND: Suggest whether natural polymers - amides and cellulose - are moisture sensitive.GIVEN: Amides contain the group Handcellulose contains - OH's.SOLUTION: N contains a lone pair of electrons. Hence,the N tends to be partially negative and the H partially positive. O has two lone pairs of electrons, so O is partially negativeand the H is partially positive. Hence, both groups are dipolar. Water is also a dipole. Hence, water and NH's and OH's are attracted to one another. Cellulose and amides are moisture sensitive. Their properties - volume, strength, mass, etc. - depend on relative humidity.COMMENTS: This is in part why cotton (cellulose) and wool (a polyamide) are such comfortable fibers.48.FIND: Describe what binds the molecules in a。
中南大学 材料科学基础 课后习题答案

第一章 原子排列与晶体结构1. [110], (111), ABCABC…, 0.74 , 12 , 4 ,a r 42=; [111], (110) , 0.68 , 8 , 2 , a r 43= ; ]0211[, (0001) , ABAB , 0.74 , 12 , 6 , 2a r =。
2.0.01659nm 3 , 4 , 8 。
3.FCC , BCC ,减少 ,降低 ,膨胀 ,收缩 。
4. 解答:见图1-1 5. 解答:设所决定的晶面为(hkl ),晶面指数与面上的直线[uvw]之间有hu+kv+lw=0,故有:h+k-l=0,2h-l=0。
可以求得(hkl )=(112)。
6 解答:Pb 为fcc 结构,原子半径R 与点阵常数a 的关系为a r 42=,故可求得a =0.4949×10-6mm 。
则(100)平面的面积S =a 2=0.244926011×0-12mm 2,每个(100)面上的原子个数为2。
所以1 mm 2上的原子个数s n 1==4.08×1012。
第二章 合金相结构一、 填空1) 提高,降低,变差,变大。
2) (1)晶体结构;(2)元素之间电负性差;(3)电子浓度 ;(4)元素之间尺寸差别3) 存在溶质原子偏聚 和短程有序 。
4) 置换固溶体 和间隙固溶体 。
5) 提高 ,降低 ,降低 。
6) 溶质原子溶入点阵原子溶入溶剂点阵间隙中形成的固溶体,非金属原子与金属原子半径的比值大于0.59时形成的复杂结构的化合物。
二、 问答1、 解答: α-Fe 为bcc 结构,致密度虽然较小,但是它的间隙数目多且分散,间隙半径很小,四面体间隙半径为0.291Ra ,即R =0.0361nm ,八面体间隙半径为0.154Ra ,即R =0.0191nm 。
氢,氮,碳,硼由于与α-Fe 的尺寸差别较大,在α-Fe 中形成间隙固溶体,固溶度很小。
材料科学基础课后习题答案第二章

第2章 习题2-1 a) 试证明均匀形核时,形成临界晶粒的△G K 与其临界晶核体积V K 之间的关系式为2K K V V G G ∆=-∆; b) 当非均匀形核形成球冠形晶核时,其△G K 与V K 之间的关系如何?a) 证明 因为临界晶核半径 2K Vr G σ=-∆ 临界晶核形成功 32163()K V G G πσ∆=∆ 故临界晶核的体积 3423K K K Vr G V G π∆==∆ 所以 2K K V V G G ∆=-∆ b) 当非均匀形核形成球冠形晶核时,SL 2K Vr G σ=-∆非 临界晶核形成功 3324(23cos cos )3()K SL V G G πσθθ∆=-+∆非故临界晶核的体积 331(23cos cos )3K K V r πθθ=-+非() 3333SL 3281(23cos cos )(23cos cos )33()SL K V V V V V G G G G σπσπθθθθ∆=--+∆=-+∆∆() 所以 2K K V V G G ∆=-∆非 2-2 如果临界晶核是边长为a 的正方体,试求出其△G K 与a 的关系。
为什么形成立方体晶核的△G K 比球形晶核要大?解:形核时的吉布斯自由能变化为326V V G V G A a G a σσ∆=∆+=∆+ 令()0d G da∆= 得临界晶核边长4K Va G σ=-∆ 临界形核功3333222244649632()6()()()()K tK V K V V V V V V G V G A G G G G G G σσσσσσσ∆=∆+=-∆+-=-+=∆∆∆∆∆ 2K Vr G σ=-∆,球形核胚的临界形核功 332242216()4()33()K bV V V V G G G G G σσπσππσ∆=-∆+=∆∆∆ 将两式相比较3232163()13262()K K b V t V G G G G πσπσ∆∆==≈∆∆ 可见形成球形晶核得临界形核功仅为形成立方形晶核的1/2。
材料科学基础(武汉理工大学,张联盟版)课后习题及答案第二章
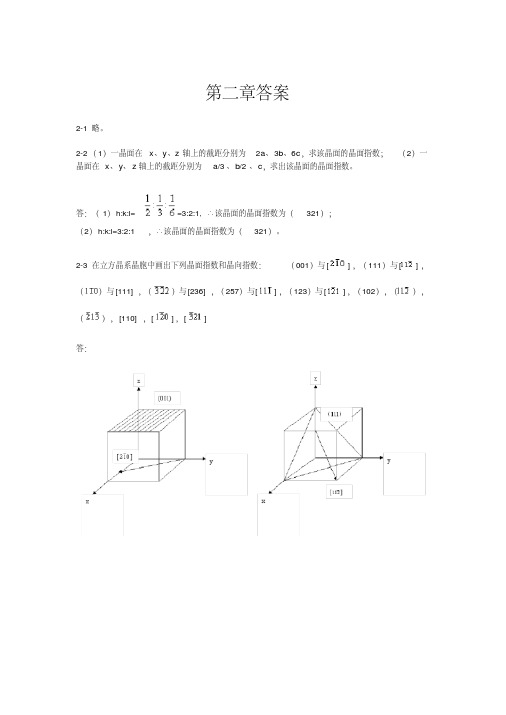
第二章答案2-1略。
2-2(1)一晶面在x、y、z轴上的截距分别为2a、3b、6c,求该晶面的晶面指数;(2)一晶面在x、y、z轴上的截距分别为a/3、b/2、c,求出该晶面的晶面指数。
答:(1)h:k:l==3:2:1,∴该晶面的晶面指数为(321);(2)h:k:l=3:2:1,∴该晶面的晶面指数为(321)。
2-3在立方晶系晶胞中画出下列晶面指数和晶向指数:(001)与[],(111)与[],()与[111],()与[236],(257)与[],(123)与[],(102),(),(),[110],[],[]答:2-4定性描述晶体结构的参量有哪些?定量描述晶体结构的参量又有哪些?答:定性:对称轴、对称中心、晶系、点阵。
定量:晶胞参数。
2-5依据结合力的本质不同,晶体中的键合作用分为哪几类?其特点是什么?答:晶体中的键合作用可分为离子键、共价键、金属键、范德华键和氢键。
离子键的特点是没有方向性和饱和性,结合力很大。
共价键的特点是具有方向性和饱和性,结合力也很大。
金属键是没有方向性和饱和性的的共价键,结合力是离子间的静电库仑力。
范德华键是通过分子力而产生的键合,分子力很弱。
氢键是两个电负性较大的原子相结合形成的键,具有饱和性。
2-6等径球最紧密堆积的空隙有哪两种?一个球的周围有多少个四面体空隙、多少个八面体空隙?答:等径球最紧密堆积有六方和面心立方紧密堆积两种,一个球的周围有8个四面体空隙、6个八面体空隙。
2-7n个等径球作最紧密堆积时可形成多少个四面体空隙、多少个八面体空隙?不等径球是如何进行堆积的?答:n个等径球作最紧密堆积时可形成n个八面体空隙、2n个四面体空隙。
不等径球体进行紧密堆积时,可以看成由大球按等径球体紧密堆积后,小球按其大小分别填充到其空隙中,稍大的小球填充八面体空隙,稍小的小球填充四面体空隙,形成不等径球体紧密堆积。
2-8写出面心立方格子的单位平行六面体上所有结点的坐标。
答:面心立方格子的单位平行六面体上所有结点为:(000)、(001)(100)(101)(110)(010)(011)(111)(0)(0)(0)(1)(1)(1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2章 习题2-1 a) 试证明均匀形核时,形成临界晶粒的△G K 与其临界晶核体积V K 之间的关系式为;2K K V V G G ∆=-
∆b) 当非均匀形核形成球冠形晶核时,其△G K 与V K 之间的关系如何?a) 证明 因为临界晶核半径 2K V r G σ=-∆临界晶核形成功 32163()K V G G πσ∆=∆故临界晶核的体积 3423K K K V r G V G π∆==∆所以 2K K V V G G ∆=-∆b) 当非均匀形核形成球冠形晶核时,SL 2K V
r G σ=-∆非临界晶核形成功 3324(23cos cos )3()K SL V G G πσθθ∆=-+∆非故临界晶核的体积 331(23cos cos )3K K V r πθθ=-+非()3333SL 3281(23cos cos )(23cos cos )33()SL K V V V V V G G G G σπσπθθθθ∆=--+∆=-+∆∆()所以 2K K V V G G ∆=-∆非2-2 如果临界晶核是边长为a 的正方体,试求出其△G K 与a 的关系。
为什么形成立方体晶
核的△G K 比球形晶核要大?解:形核时的吉布斯自由能变化为326V V G V G A a G a σσ∆=∆+=∆+令()0d G da ∆=得临界晶核边长4K V a G σ=-∆临界形核功
3333222244649632()6()()()()K t
K V K V V V V V V G V G A G G G G G G σσσσσσσ∆=∆+=-∆+-=-+=∆∆∆∆∆,球形核胚的临界形核功2K V
r G σ=-∆332242216(4()33()K b
V V V V G G G G G σσπσππσ∆=-∆+=∆∆∆将两式相比较
3232163()13262()K K b V t V G G G G πσπσ∆∆==≈∆∆可见形成球形晶核得临界形核功仅为形成立方形晶核的1/2。
2-3 为什么金属结晶时一定要有过冷度?影响过冷度的因素是什么?固态金属熔化时是否会出现过热?为什么?答:金属结晶时要有过冷度是相变热力学条件所需求的,只有△T>0时,才能造成固相的自由能低于液相的自由能的条件,液固相间的自由能差便是结晶的驱动力。
金属结晶需在一定的过冷度下进行,是因为结晶时表面能增加造成阻力。
固态金属熔
化时是否会出现过热现象,需要看熔化时表面能的变化。
如果熔化前后表面能是降低的,则不需要过热;反之,则可能出现过热。
如果熔化时,液相与气相接触,当有少量液体金属在固体表面形成时,就会很快覆盖在整个固体表面(因为液态金属总是润湿其同种固体金属)。
熔化时表面自由能的变化为:()
GL SL SG G G G A σσσ∆=-=+-表面终态始态式中G 始态表示金属熔化前的表面自由能;G 终态表示当在少量液体金属在固体金属表面形成时的表面自由能;A 表示液态金属润湿固态金属表面的面积;σGL 、σSL 、σSG 分别表示气液相比表面能、固液相比表面能、固气相比表面能。
因为液态金属总是润湿其同种固体金属,根据润湿时表面张力之间的关系式可写出:σSG ≥σGL +σSL 。
这说明在熔化时,表面自由能的变化△G 表≤0,即不存在表面能障碍,也就不必过热。
实际金属多属于这种情况。
如果固体金属熔化时液相不与气相接触,则有可能时固态金属过热。
液体覆盖在整个固体表面
2-4 试比较均匀形核与非均匀形核的异同点。
答:相同点
1)形核的驱动力和阻力相同;
2)临界晶核半径相等;
3)形成临界晶核需要形核功;
4)结构起伏和能量起伏是形核的基础;
5)形核需要一个临界过冷度;
6)形核率在达到极大值之前,随过冷度增大而增加。
与均匀形核相比,非均匀形核的特点:
1)非均匀形核与固体杂质接触,减少了表面自由能的增加;
2)非均匀形核的晶核体积小,形核功小,形核所需结构起伏和能量起伏就小;形核容易,临界过冷度小;
3)非均匀形核时晶核形状和体积由临界晶核半径和接触角共同决定;临界晶核半径相同时,接触角越小,晶核体积越小,形核越容易;
4)非均匀形核的形核率随过冷度增大而增加,当超过极大值后下降一段然后终止;此外,非均匀形核的形核率还与固体杂质的结构和表面形貌有关。
2-5 说明晶体成长形状与温度梯度的关系。
解:纯金属生长形态是指晶体长大时截面的形貌。
界面形貌取决于界面前沿液体中的温度
分布。
纯金属凝固时,液固相界面前沿的液体过冷区由金属的理论结晶温度和实际温度分
布曲线围成。
由于理论结晶温度为定值,因此过冷区的形状仅由实际温度分布所决定。
(1) 平面状界面。
当液体具有正温度梯度时,晶体以平界面方式推移长大。
此时,界面上任何偶然的、小的凸起深入液体时,都会使其过冷度减小,长大速率降低或停止长大,而被周围部分赶上,因而能保持平界面的推移。
长大中晶体沿平行温度梯度的方向生长,或沿散热的反方向生长,而其他方向的生长则受到抑制。
(2) 树枝状平面。
当液体具有负温度梯度时,在界面上若形成偶然的凸起伸入前沿液体时,由于前方液体有更大的过冷度,有利于晶体长大和凝固潜热的散失,从而形成枝晶的一次轴。
一个枝晶的形成,其潜热使邻近液体温度升高,过冷度降低,因此,类似的枝晶只在相邻一定间距的界面上形成,相互平行分布。
在一次枝晶处的温度比枝晶间温度要高,如图(a)中所示的bb断面上TA>TB,这种负温度梯度使一次轴上又长出二次轴分枝,如图(b)所示。
同样,还会产生多次分枝的枝晶生长的最后阶段,由于凝固潜热放出,使枝晶周围的液体温度升高至熔点以上,液体中出现正温度梯度,此时晶体长大依靠平界面方式推进,直至枝晶间隙全部被填满为止。
2-6 简述三晶区形成的原因及每个晶区的性能特点。
答:铸锭三晶区的形成原因:
最外层为细小等晶区。
其形成是由于模壁的温度较低,液体的过冷度较大,因而形核率较高所致。
中间为柱状晶区。
其形成主要是模壁的温度升高,晶核的成长率大于晶核的形成率,且沿垂直于模壁方向的散热较为有利。
在细晶区中取向有利的晶粒优先生长为柱状晶。
中心为等轴晶区。
其形成是由于模壁温度进一步升高,液体过冷度进一步降低,剩余液体的散热方向性已不明显,处于均匀冷却状态;同时,未熔杂质、破断枝晶等易集中于剩余液体中,这些都促使等轴晶的形成。
铸锭三晶区的性能特点:外表层的细晶区:晶粒细小、组织致密、力学性能良好;中间的柱状晶区:晶粒取向、组织致密、缺陷聚集、塑性较差;心部的等轴晶区:晶粒无方向性、树枝状晶体、组织不够致密、性能一般。
2-7 为了得到发达的柱状晶区应该采取什么措施?为了得到发达的等轴晶区应该采取什么措施?其基本原理如何?
答:铸锭组织控制,主要是对柱状晶区和等轴晶区的分布范围和晶粒大小的控制。
变更合金成分和浇铸条件可以改变各晶区分布范围的大小。
对给定合金而言,有利于柱状晶区发展的因素有:较快的冷却速度,高的熔化温度和浇注温度,定向散热等;有利于等轴晶区发展的因素有:较慢的冷却速度,低的熔化温度和浇注温度,均匀散热等。
为了获得细小的等轴晶粒,可采用变质处理、振动和搅拌等措施。
2-8 指出下列各题错误之处,并改正之。
1) 所谓临界晶核,就是体系自由能的减少完全补偿表面自由能增加时的晶胚大小。
改正:临界晶核是体积自由能的减少补偿2/3表面自由能增加时的晶胚大小。
2) 在液态金属中,凡是涌现小于临界晶核半径的晶胚都不能成核,但是只要有足够的能量起伏提供形核功,还是可以成核的。
改正:即使有足够的能量起伏供给,小于临界晶核半径的晶胚也不能成核。
3) 无论温度分布如何,纯金属都是以树枝状方式生长。
改正:在负的温度梯度下,纯金属以树枝状方式生长。
