离散数学教程与范例
(完整word版)《离散数学》教案详解

《离散数学》教案第一章集合与关系集合是数学中最基本的概念,又是数学各分支、自然科学及社会科学各领域的最普遍采用的描述工具。
集合论是离散数学的重要组成部分,是现代数学中占有独特地位的一个分支。
G. Cantor(康脱)是作为数学分支的集合论的奠基人。
1870年前后,他关于无穷序列的研究导致集合论的系统发展。
1874年他发表了关于实数集合不能与自然数集合建立一一对应的有名的证明。
1878年,他引进了两个集合具有相等的“势”的概念。
然而,朴素集合论中包含着悖论。
第一个悖论是布拉利-福尔蒂的最大序数悖论。
1901年罗素发现了有名的罗素悖论。
1932年康脱也发表了关于最大基数的悖论。
集合论的现代公理化开始于1908年策梅罗所发表的一组公理,经过弗兰克尔的加工,这个系统称为策梅罗-弗兰克尔集合论(ZF),其中包括1904年策梅罗引入的选择公理。
另外一种系统是冯·诺伊曼-伯奈斯-哥德尔集合论。
公理集合论中一个有名的猜想是连续统假设(CH)。
哥德尔证明了连续统假设与策梅罗-弗兰克尔集合论的相容性,科恩证明了连续统假设与策梅罗-弗兰克尔集合论的独立性。
现在把策梅罗-弗兰克尔集合论与选择公理一起称为ZFC系统。
一、学习目的与要求本章目的是介绍集合的基本概念,讲授集合运算的基本理论,关系的定义与运算。
通过本章的学习,使学生了解集合是数学的基本语言,掌握主要的集合运算方法和关系运算方法,为学习后续章节打下良好基础。
二、知识点1.集合的基本概念与表示方法;2.集合的运算;3.序偶与笛卡尔积;4.关系及其表示、关系矩阵、关系图;5.关系的性质,符合关系、逆关系;6.关系的闭包运算;7.集合的划分与覆盖、等价关系与等价类;相容关系;8.序关系、偏序集、哈斯图。
三、要求1.识记集合的层次关系、集合与其元素间的关系,自反关系、对称关系、传递关系的识别,复合关系、逆关系的识别。
2.领会领会下列概念:两个集合相等的概念几证明方法,关系的闭包运算,关系等价性证明。
《离散数学教案》课件

《离散数学教案》课件第一章:离散数学简介1.1 离散数学的定义与意义离散数学的定义离散数学在计算机科学中的应用1.2 离散数学的基本概念集合逻辑函数图论1.3 离散数学的研究方法形式化方法归纳法构造法第二章:集合与逻辑2.1 集合的基本概念与运算集合的定义与表示方法集合的运算(并、交、差、补)2.2 逻辑基本概念命题与联结词逻辑推理规则(蕴涵、逆否、德摩根定律)2.3 命题逻辑与谓词逻辑命题逻辑的形式化表示与推理谓词逻辑的形式化表示与推理第三章:函数与图论3.1 函数的基本概念与性质函数的定义与表示方法函数的单调性、连续性、奇偶性3.2 图的基本概念与运算图的定义与表示方法图的运算(节点、边、路径、连通性)3.3 树的基本概念与应用树与图的关系树的结构性质与应用(二叉树、堆、平衡树)第四章:组合数学4.1 组合数学的基本概念排列组合的定义与公式组合数学的应用(计数原理、图论)4.2 组合数学的计算方法直接法、间接法、递推法、函数法4.3 组合数学在计算机科学中的应用算法设计与分析(动态规划、贪心算法)程序语言中的组合类型(类型系统、类型检查)第五章:数理逻辑与计算复杂性5.1 数理逻辑的基本概念命题逻辑的数学模型(布尔代数、逻辑函数)谓词逻辑的数学模型(一阶逻辑、描述逻辑)5.2 计算复杂性的基本概念与分类计算复杂性的定义与度量(时间复杂性、空间复杂性)计算复杂性的分类(P与NP问题、整数分解问题)5.3 离散数学在算法设计与分析中的应用算法设计与分析的基本原则离散数学在算法优化与分析中的作用第六章:关系与映射6.1 关系的基本概念关系的定义与性质关系的类型(对称性、传递性、反身性)6.2 关系的闭包与简化关系的闭包概念关系的简化与规范化6.3 函数与二元关系函数与关系的联系与区别二元组与二元关系的应用第七章:代数结构7.1 代数结构的基本概念群、环、域的定义与性质代数结构在计算机科学中的应用7.2 群与群作用群的定义与运算群作用与群同态7.3 环与域环的定义与性质域的特殊性质与应用第八章:数理逻辑与计算理论8.1 数理逻辑的进一步应用命题逻辑与谓词逻辑的推理规则数理逻辑在计算机科学中的应用8.2 计算理论的基本概念计算模型的定义与分类计算复杂性的理论基础8.3 离散数学在计算理论中的应用计算理论中的逻辑与证明离散数学在算法设计与分析中的作用第九章:组合设计与计数原理9.1 组合设计的基本概念组合设计的定义与类型组合设计在编码理论中的应用9.2 计数原理的基本概念鸽巢原理、包含-排除原理函数的方法与应用9.3 图论与网络流图的遍历与路径问题网络流与最优化问题第十章:离散数学的综合应用10.1 离散数学在计算机科学中的应用算法设计与分析数据结构与程序语言设计10.2 离散数学在数学与应用数学中的作用组合数学在概率论与数论中的应用图论在网络科学与社会网络分析中的应用10.3 离散数学在未来科技发展中的展望量子计算与离散数学与逻辑推理重点和难点解析重点环节一:集合的基本概念与运算集合的表示方法(列举法、描述法)集合的运算(并、交、差、补)重点环节二:逻辑基本概念与推理命题与联结词(且、或、非)逻辑推理规则(蕴涵、逆否、德摩根定律)重点环节三:函数的基本概念与性质函数的定义与表示方法函数的单调性、连续性、奇偶性重点环节四:图的基本概念与运算图的定义与表示方法图的运算(节点、边、路径、连通性)重点环节五:组合数学的基本概念与计数原理排列组合的定义与公式组合数学的应用(计数原理、图论)重点环节六:关系与映射关系的定义与性质关系的类型(对称性、传递性、反身性)重点环节七:代数结构的基本概念群、环、域的定义与性质代数结构在计算机科学中的应用重点环节八:数理逻辑与计算理论数理逻辑的推理规则计算理论的基本概念(计算模型、计算复杂性)重点环节九:组合设计与计数原理组合设计的定义与类型计数原理的应用(鸽巢原理、包含-排除原理)重点环节十:离散数学的综合应用离散数学在计算机科学中的应用(算法设计与分析、数据结构与程序语言设计)离散数学在数学与应用数学中的作用(组合数学在概率论与数论中的应用、图论在网络科学与社会网络分析中的应用)全文总结和概括:本《离散数学教案》课件涵盖了离散数学的基本概念、逻辑推理、函数与图论、组合数学、数理逻辑与计算理论、组合设计与计数原理等多个重要环节。
离散数学教案范本

离散数学教案范本《离散数学》教案课⽬:第⼀章命题逻辑教师:熊建英学时: 12课时Ⅰ教学提要⼀、教学对象(⼈数)学⽣:信息安全专业本科⼆年级学⽣50⼈⼆、教学⽬标(任务)各⼩结中知识点掌握程度(* 理解;** 基本掌握;***熟练掌握)三、教学要求(⼀)学⽣:着重知识点的学习,积极思考,参与提问。
(⼆)教官:严格纪律,严密组织、保持良好教学秩序,确保教学效果。
四、教官分⼯主讲教师1名:负责教案编写,课堂的组织教学,教学总结编写。
五、本章重点1、利⽤联接词构造复合命题公式2、真值表的构建3、等值演算4、复合命题公式转化为主析取范式、主合取范式的⽅法5、推理证明六、本章难点1、利⽤命题公式演算、真值表进⾏等值判断和公式类型判断2、利⽤命题公式演算、真值表转化主析取范式、主合取范式3、将现实背景下的条件约束构造为命题公式七、教学⽅法采⽤课堂教授,主要使⽤多媒体课件,部分内容及例题⽤⿊板解释。
⼋、课时分配1.1 命题及联接词2课时;1.2 命题公式及其赋值2课时;1.3 等值式2课时;1.4 析取范式与合取范式2课时;1.5 推理理论与消解法2课时;1.6 命题逻辑应⽤案例2课时;九、场地器材多媒体教室⼗、参考书⽬1、杨圣洪、张英杰、陈义明:《离散数学》,科学出版社,2011年。
2、屈婉玲、耿素云、张⽴昂:《离散数学》,⾼等教育出版社,2008年。
3、屈婉玲、耿素云、张⽴昂:《离散数学学习指导与习题解析》,⾼等教育出版社,2008年。
Ⅱ教学进程1.1 命题及联接词(2课时)⼀、教学内容1、命题的概念表⽰与分类2、五种基本的联接词的逻辑关系3、复合命题的符号化4、复合命题的真值判断⼆、课程时间安排1、⾸先介绍本课程的性质,任务和教学安排,对学⽣明确提出教学上的要求(10分钟)2、介绍离散数学学科的发展历史(20分钟)3、命题与真值、命题的分类、简单命题符号化(15分钟)4、联结词与复合命题(35分钟)5、本次课⼩结(10分钟)三、教学实施(⼀)创设意境、导⼊课程(10分钟)⽬的体会离散数学理论在现实⽣活中的应⽤、是计算机专业多门核⼼课程的基础,让学⽣明⽩“离散数学”课程作⽤和意义。
(完整版)离散数学电子教材1(可编辑修改word版)

(完整版)离散数学电子教材1(可编辑修改word版)第1 章命题逻辑逻辑是研究人的思维的科学,包括辩证逻辑和形式逻辑。
辩证逻辑是研究反映客观世界辩证发展过程的人类思维的形态的。
形式逻辑是研究思维的形式结构和规律的科学,它撇开具体的、个别的思维内容,从形式结构方面研究概念、判断和推理及其正确联系的规律。
数理逻辑是用数学方法研究推理的形式结构和推理的规律的数学学科。
所谓的数学方法也就是用一套有严格定义的符号,即建立一套形式语言来研究。
因此数理逻辑也称为符号逻辑。
数理逻辑的基础部分是命题逻辑和谓词逻辑。
本章主要讲述命题逻辑,谓词逻辑将在第2 章进行讨论。
1.1命题及其表示1.1.1命题的基本概念数理逻辑研究的中心问题是推理(Inference),而推理就必然包含前提和结论,前提和结论都是表达判断的陈述句,因而表达判断的陈述句就成为推理的基本要素。
在数理逻辑中,将能够判断真假的陈述句称为命题。
因此命题就成为推理的基本单位。
在命题逻辑中,对命题的组成部分不再进一步细分。
定义1.1.1 能够判断真假的陈述句称为命题(Proposition)。
命题的判断结果称为命题的真值,常用T(True)(或1)表示真,F(False)(或0)表示假。
真值为真的命题称为真命题,真值为假的命题称为假命题。
从上述的定义可知,判定一个句子是否为命题要分为两步:一是判定是否为陈述句,二是能否判定真假,二者缺一不可。
例1.1.1 判断下列句子是否为命题(1)北京是中国的首都。
(2)请勿吸烟!(3)雪是黑的。
(4)明天开会吗?(5)x+y=5。
(6)我正在说谎。
(7)9+5≤12 。
(8)1+101=110 。
(9)今天天气多好啊!(10)别的星球上有生物。
解在上述的十个句子中,(2)、(9)为祈使句,(4)为疑问句,(5)、(6)虽然是陈述句,但(5)没有确定的真值,其真假随x、y 取值的不同而有改变,(6)是悖论(Paradox)(即由真能推出假,由假也能推出真),因而(2)、(4)、(5)、(6)、(9)均不是命题。
《离散数学》电子教案

第一章集合论一、教学内容及要求授课学时:2教学内容1.1 集合的基本概念集合的概念及其表示;集合与集合之间的包含、真包含和相等关系的定义,数学描述及判定和证明方法;空集、全集和幂集三个特殊集合的定义、性质以及幂集的计算算法。
1.2 集合的运算集合运算的定义、性质及证明1.3 无限集可数集合和不可数集合的概念。
1.4 与集合相关的应用与集合相关的简单应用实例。
基本要求1)能正确地用枚举法或叙述法表示一个集合,会画文氏图。
2)能判定元素与集合的属于关系。
3)能利用集合与集合关系的判定与证明方法证明两个集合之间的包含、相等、和真包含的关系。
4)能熟练计算集合之间的并、交、差、补运算,掌握集合运算的定律;5)能熟练地计算P(A)。
6)理解集合的归纳法表示。
7)理解集合的对称差运算。
8)了解集合的递归指定法表示。
9)了解无限集的基本概念。
10)了解集合的简单应用。
能力培养通过课堂讲解和课后实践作业,培养学生的抽象思维和问题解决能力。
二、教学重点、难点及解决办法教学重点:集合的概念及集合间关系的证明;集合的表示方法:列举法、描述法和文氏图;集合运算及定律和幂集P(A)的计算。
教学难点:从集合与元素两个角度去分析集合;集合与集合关系的证明和无限集基数的理解。
解决办法:1)在教学过程中,为了加强学生对一个集合“双重身份”的理解,可以通过实例教学法,让学生具体体会一个集合的“双重身份”带来的问题及解决办法;2)对于新概念—幂集,让学生编程实现求一个集合的幂集,从而加深对幂集的理解。
初步建立学生的发散思维能力以及实际动手编写程序的能力。
三、教学设计从集合伦论的创始人康托尔到集合论的最终完备,让学生明白科学研究的道路是坎坷的,但为全人类做出自己的贡献是有价值和意义的,从而要树立为科学献身的精神和爱国主义情怀。
从集合的定义入手,结合高中阶段对集合的认识,指出当时定义存在的不足,提出新的定义方法;重点介绍大学阶段学习集合的主要意义和内容,关注重点概念的理解;介绍属于关系与包含关系之间的区别与联系,特别是一个集合“双重身份”的理解;强调集合的基本运算,特别是幂集的计算;集合与集合包含、真包含和相等关系的数学描述及相应的证明方法。
离散数学完整版课件全套ppt教学教程最全整套电子讲义幻灯片(最新)

1.1 命题及联结词
定义1.5双条件:当p与q值相同时,pq为1,不同 为0。 称p当且仅当q
“普通老师赚了100万当且仅当他 中了100万的彩票”, 普通老师赚了100万 普通老师买彩票中了100万大奖
故pq为0
1.1 命题及联结词
定义1.4条件式当p是1 ,q是0时,pq为0,即 10为0,其他情况为1。 p称为前件,q称为后件
(1)当p为1即“我期终考了年级前10”
q为0即“我老妈没有奖励1000元” 这时老妈的话为假,即pq为0 (2)当p为1即“我期终考了年级前10” q为1即“我老妈奖励1000元” 这时妈妈的话就对了,即pq为1
由于所有内容(整数,实数,字符,汉字,图片,声 音,视频,网页,……)进入电脑后,全是01组成的字 符串,从而都可以用布尔运算即逻辑运算实现,命题逻 辑成为计算机的基础。
命题逻辑将数学由连续变到离散,由高数进入离散。
Google采用逻辑运算进行搜索:数字之美 吴军 杨圣洪 000100010001110000 两者对应位置与运算。 离散数学 100100000000100001
陈述句(6)的正确性,到2018年12月时能确定的,若届 时建成了则它是对的、为真命题,否为假命题。
1.1 命题及联结词
对错确定的陈述语句称为命题。如:
(7) x与y之和为100,其中x为整数,y为整数 (8)1加1等于10 (7)的对错不确定。当x为50、y为50时是对的,当x为 51、y为52时是错的。 (8)的对错是不确定的,为二进制时正确,当为八进制、 十进制时是错的,因此这两个陈述句不是命题。 (9)青枫峡的红叶真美呀! (10)动作快点! (11)你是杨老师吗? 这三个语句不是陈述语句,因此不是命题。
离散数学6(共15张PPT)
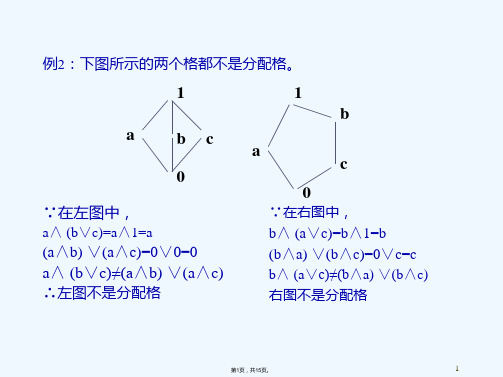
1
a
bc
0
∵在左图中,
a∧ (b∨c)=a∧1=a
(a∧b) ∨(a∧c)=0∨0=0 a∧ (b∨c)≠(a∧b) ∨(a∧c) ∴左图不是分配格
1 b
a c∧1=b (b∧a) ∨(b∧c)=0∨c=c
b∧ (a∨c)≠(b∧a) ∨(b∧c) 右图不是分配格
第1页,共15页。
1
注意:按照定义证明某个格是分配格不容易,但要证明一个格 不是分配格,只要找出一组元素不满足某一分配式即可。上例 中的两个五元格可用来判断某格是否是分配格。
定理1:一个格是分配格的充要条件是在该格中没有任何子格与这
两个五元格中的任一个同构。
例3:右图所示的两个格都不是分配格
第2页,共15页。
(1) 设 b≤a且c≤a,∴a∧b = b,a∧c = c ∴ (a∧b)∨(a∧c) = b∨c 又∵ b∨c≤a,∴ a∧(b∨c) = b∨c
∴ a∧(b∨c) = (a∧b)∨(a∧c)
(2) 设 a≤b或a≤c,不论b≤c还是c≤b ,都有a≤b∨c
∴ a ∧( b∨c) = a,(a∧b)∨(a∧c)=a
∴ a∧(b∨c) = (a∧b)∨(a∧c) 由定理1,有a∨ (b∧c) = (a ∨ b) ∧(a∨c)
因此<A, ≤>是分配格。
第4页,共15页。
4
定理4:设<A, ≤>是分配格,则对a,b,cA, 若有 a∧b = a∧c且a∨b = a∨c ,则必有b = c 。
证明:∵a∧b≤b b = b∨(a∧b) = b∨(a∧c) = (b∨a)∧(b∨c) = (a∨c)∧(b∨c)
《离散数学教案》课件2

《离散数学教案》PPT课件第一章:离散数学简介1.1 离散数学的定义介绍离散数学的概念和特点强调离散数学在计算机科学中的应用1.2 离散数学的重要性解释离散数学在算法设计、编程和计算机科学其他领域的应用强调离散数学对于解决问题和逻辑思维的重要性1.3 离散数学的基本概念介绍集合、图、逻辑、组合等基本概念解释这些概念在离散数学中的作用和相互关系第二章:集合论2.1 集合的基本概念定义集合、元素、集合之间的关系介绍集合的表示方法:列举法和描述法2.2 集合的运算介绍集合的并、交、差、补等基本运算解释集合运算的性质和规律2.3 集合的推理和公理化介绍集合论的基本公理和公理化体系解释集合论的公理化意义和作用第三章:逻辑与布尔代数3.1 逻辑的基本概念定义逻辑联结词、命题、真值表等基本概念介绍逻辑推理和论证的基本方法3.2 布尔代数的基本概念介绍布尔代数的基本元素和运算解释布尔代数在计算机科学中的应用3.3 逻辑与布尔代数的关系解释逻辑和布尔代数之间的联系和转化举例说明逻辑表达式和布尔代数表达式的相互转化第四章:图论4.1 图的基本概念定义图、顶点、边等基本概念介绍图的表示方法和图的类型4.2 图的运算和性质介绍图的连通性、路径、圈等基本概念解释图的运算和性质的应用和意义4.3 图的应用介绍图在计算机科学中的应用:算法设计、网络结构等举例说明图的应用实例和解决实际问题的方法第五章:组合数学5.1 组合数学的基本概念定义组合、排列、组合数等基本概念介绍组合数学的基本原理和方法5.2 组合计数原理介绍排列组合计数原理及其应用解释组合计数原理在离散数学中的重要性5.3 图着色和组合优化问题介绍图着色问题的定义和解决方案举例说明组合优化问题及其解决方法第六章:算法设计与分析6.1 算法的基本概念定义算法、输入、输出、有效性和可读性等基本概念解释算法在解决问题中的重要性6.2 算法设计技术介绍常用的算法设计技术:贪心法、分而治之、动态规划等解释每种技术的应用场景和特点6.3 算法分析与复杂性介绍算法分析和时间复杂度、空间复杂度的概念解释常用算法分析方法和评价标准第七章:数理逻辑与命题逻辑7.1 数理逻辑的基本概念介绍数理逻辑中的基本概念:命题、联结词、逻辑运算等解释数理逻辑在计算机科学中的应用7.2 命题逻辑的推理规则介绍命题逻辑中的推理规则:蕴含式、否定式、De Morgan定律等解释这些规则在逻辑推理中的应用和意义7.3 数理逻辑与计算机科学解释数理逻辑在计算机科学中的重要作用:编程语言、形式验证等举例说明数理逻辑在计算机科学中的应用实例第八章:集合论与数理逻辑的应用8.1 集合论在计算机科学中的应用介绍集合论在计算机科学中的应用:数据结构、数据库等解释集合论在计算机科学中的重要性和作用8.2 数理逻辑在计算机科学中的应用介绍数理逻辑在计算机科学中的应用:形式语言、编译原理等解释数理逻辑在计算机科学中的重要性和作用8.3 集合论和数理逻辑在其他领域的应用介绍集合论和数理逻辑在其他领域的应用:数学、哲学等解释集合论和数理逻辑在其他领域的重要性第九章:图论的应用9.1 社交网络与图论介绍社交网络中的图论应用:网络结构、关系分析等解释图论在社交网络分析中的作用和意义9.2 路径与圈的应用介绍路径和圈在图论中的应用:最短路径、环路检测等解释路径和圈在解决实际问题中的重要性9.3 网络流与匹配问题介绍网络流和匹配问题的定义和解决方案解释网络流和匹配问题在计算机科学中的应用第十章:组合数学的应用10.1 组合数学在计算机科学中的应用介绍组合数学在计算机科学中的应用:数据存储、编码理论等解释组合数学在计算机科学中的重要性和作用10.2 组合优化问题介绍组合优化问题的定义和解决方案解释组合优化问题在离散数学中的重要性和应用10.3 组合数学在其他领域的应用介绍组合数学在其他领域的应用:生物学、经济学等解释组合数学在其他领域的重要性第十一章:离散数学与计算机科学11.1 离散数学与算法强调离散数学在算法设计和分析中的作用解释如何使用离散数学工具解决算法问题11.2 离散数学与数据结构探讨离散数学在数据结构设计中的应用解释离散数学概念如何帮助优化数据结构11.3 离散数学与编程语言讨论离散数学在编程语言设计和实现中的角色举例说明离散数学在编程语言特性中的应用第十二章:离散数学与实际应用12.1 离散数学与网络科学介绍离散数学在网络科学中的应用解释图论和其他离散数学概念在网络结构和分析中的重要性12.2 离散数学与密码学探讨离散数学在密码学中的核心作用解释离散数学如何帮助设计和分析密码系统12.3 离散数学与讨论离散数学在领域的应用解释离散数学在知识表示、推理和问题解决中的作用第十三章:离散数学的实践项目13.1 离散数学项目的设计与实施介绍如何设计离散数学实践项目强调项目实施的重要性和方法13.2 离散数学项目的案例分析分析成功的离散数学项目案例从中提炼经验教训,为今后的项目提供参考13.3 离散数学项目的评价与反馈讨论离散数学项目评价的标准和方法强调项目反馈在持续改进和学习中的重要性第十四章:离散数学与数学逻辑14.1 离散数学与数理逻辑探讨离散数学与数理逻辑的紧密联系解释数理逻辑在离散数学问题求解中的作用14.2 离散数学与模型论介绍模型论及其在离散数学中的应用解释模型论在形式系统验证和解释中的重要性14.3 离散数学与计算理论讨论离散数学在计算理论中的应用强调计算理论在理解计算过程和设备中的价值第十五章:离散数学的未来发展15.1 离散数学的新兴研究领域介绍离散数学新兴研究领域和发展趋势强调跨学科合作在离散数学研究中的重要性15.2 离散数学在新技术中的应用探讨离散数学在云计算、大数据等新技术中的应用解释离散数学在未来信息技术发展中的关键作用15.3 离散数学教育的挑战与机遇讨论离散数学教育面临的挑战和机遇强调离散数学教育在培养创新人才中的重要性重点和难点解析重点:1. 离散数学的基本概念和特点2. 集合论、逻辑、图论和组合数学的核心理论和方法3. 离散数学在计算机科学中的应用,如算法设计、数据结构、网络科学、密码学等4. 离散数学实践项目的设计、实施和评价5. 离散数学教育的挑战与机遇难点:1. 集合论、逻辑、图论和组合数学的高级理论和复杂应用2. 算法设计和分析中的数学建模与优化3. 离散数学在跨学科领域中的应用,如生物学、经济学等4. 离散数学教育中的教学方法和策略设计5. 离散数学研究的前沿领域和未来发展趋势希望本文的重点和难点解析能对学习离散数学的教案有所帮助。
离散数学课件第六章第4讲

定理:在一个环中,加法的幺元必是对乘法的零元。
证明:对环<U,+, > ,a,b ,cU,有:
a(b +c)=a b +a c (b +c) a= b a+ c a ∵(U,+)是群,故必存在幺元,θU,使得 a (b+θ)=a b= a b +θ= a b + a θ 由于群满足消去律,故 θ=a θ (b+θ) a = b a =b a+θ= b a+θ a ∴θ=θ a ∴ a θ=θ a=θ 故加法幺元“θ”是乘法的零元,
注:两个代数系统是同构,他们之间的同构映射可以是不唯一的。
例: 设代数系统V1=<I,+>,V2=<2I,+>,其中I是整 数集合,+ 运算是一般的加运算,V1 和 V2 是否同构?
解:作映射 f:I2I,f(x) =2x, 则 f 是双射。 对任何a,bI, f(a+b)=2(a+b)=2a+2b=f(a)+f(b) 因此,V1 和 V2 同构
2、域的定义
对具有两个二元运算的代数系统(A,+,.>,如果 (1)<A, + >是交换群; (2)<A-{θ},.>是交换群;
(3)“ . ”对“+ ”满足分配律
则称<U, + , .>是域。
有理数、实数、复数集合对普通的加法及乘法运算 构成的代数系统是域。
<Q;+, . ><R;+, .>、 <C,+,.>都是域
大学离散数学教案模板范文

课程名称:离散数学授课班级:XX级XX班授课教师:XXX授课时间:第X周星期X 第X节教学目标:1. 知识目标:使学生掌握图的基本概念、图的表示方法、图的遍历算法以及最小生成树的概念。
2. 能力目标:培养学生运用图论解决实际问题的能力,提高逻辑思维和抽象思维能力。
3. 情感目标:激发学生对离散数学的兴趣,培养严谨的学术态度。
教学内容:1. 图的基本概念2. 图的表示方法3. 图的遍历算法4. 最小生成树教学重点:1. 图的基本概念和图的表示方法2. 图的遍历算法3. 最小生成树的概念和构造方法教学难点:1. 图的遍历算法的理解和应用2. 最小生成树的构造方法教学过程:一、导入新课1. 回顾上节课的内容,引导学生回顾图论的基本概念。
2. 引入本节课的主题:图论基础。
二、讲授新课1. 图的基本概念- 介绍图的定义、图的种类(无向图、有向图)、图的性质(连通性、度、路径、圈等)。
2. 图的表示方法- 介绍邻接矩阵、邻接表、边列表等图的表示方法,并举例说明。
3. 图的遍历算法- 介绍深度优先搜索(DFS)和广度优先搜索(BFS)算法,并给出算法的基本思想和步骤。
4. 最小生成树- 介绍最小生成树的概念和构造方法(普里姆算法、克鲁斯卡尔算法)。
三、课堂练习1. 让学生完成课后习题,巩固所学知识。
2. 教师挑选几道典型题目进行讲解,加深学生对知识的理解。
四、课堂小结1. 回顾本节课所学内容,强调重点和难点。
2. 布置课后作业,巩固所学知识。
五、课后作业1. 完成课后习题,包括选择题、填空题、计算题和证明题。
2. 查阅相关资料,了解图论在实际生活中的应用。
教学反思:本节课通过讲解图论基础,使学生掌握了图的基本概念、图的表示方法、图的遍历算法以及最小生成树的概念。
在教学过程中,教师应注重以下几点:1. 注重理论与实践相结合,引导学生运用所学知识解决实际问题。
2. 鼓励学生积极思考,培养学生的逻辑思维和抽象思维能力。
离散数学课件第一章

图的连通性
04
CHAPTER
逻辑基础
命题逻辑中的基本概念包括命题、真值和逻辑运算,通过这些基本概念可以表达和推理复杂的命题关系。
命题逻辑在计算机科学、人工智能、自动化等领域有广泛应用,是形式化方法的重要基础。
命题逻辑是研究命题之间关系的逻辑分支,主要涉及命题的否定、合取、析取、蕴含等基本运算。
命题逻辑
详细描述
集合的运算包括并集、交集、差集等。并集是指两个或多个集合合并为一个新的集合,包含所有元素;交集是指两个或多个集合中共有的元素组成的集合;差集是指从一个集合中去掉另一个集合中的元素后剩余的元素组成的集合。这些运算在离散数学中有着广泛的应用。
总结词
集合的运算
集合的基数是指集合中元素的个数,通常用大写字母表示。
鸽巢原理
THANKS
感谢您的观看。
集合论
图论是研究图(由节点和边构成的结构)的数学分支,它广泛应用于计算机科学和工程学科。
图论
逻辑是离散数学的另一个重要分支,它研究推理的形式和规则,是计算机科学和人工智能的基础。
逻辑
组合数学是研究计数、排列和组合问题的数学分支,它在计算机科学和统计学中有重要的应用。
组合数学
离散数学的研究内容
02
CHAPTER
离散数学课件第一章
目录
绪论 集合论基础 图论基础 逻辑基础 组合数学基础
01
CHAPTER
绪论
离散数学是研究离散对象(如集合、图、树等)的数学分支,它不涉及连续的量或函数。
离散数学的定义
离散数学的起源
离散数学的特点
离散数学的起源可以追溯到古代数学,如欧几里得几何和数论。
离散数学强调结构、关系和组合,而不是连续性和微积分。
最简单的离散数学教程

最简单的离散数学教程
以下是一份简单的离散数学教程大纲:
1. 集合和逻辑:
- 集合的基本概念和符号
- 集合的运算:并、交、差、补集
- 集合的属性:空集、全集、子集、幂集
- 逻辑运算:命题、联结词、真值表、逻辑等价、析取范式和合取范式
2. 图论:
- 图的基本概念:顶点、边、路径、环
- 图的表示:邻接矩阵、邻接链表
- 图的遍历:深度优先搜索、广度优先搜索
- 最小生成树:Prim算法、Kruskal算法
- 最短路径:Dijkstra算法、Floyd-Warshall算法
3. 组合数学:
- 排列与组合:基本计数原理、乘法原理、加法原理
- 二项式定理和多项式展开
- 递归关系和递归计数
- 基本图形计数:点、线、平面、多面体
4. 离散数学的应用:
- 布尔代数:逻辑电路、布尔函数化简
- 网络和通信:编码理论、错误检测和纠正、图的路由
- 计算机科学:算法分析和设计、数据结构、图算法
请注意,这只是一个简单的离散数学教程大纲,你可以根据自己的需要和学习水平来进一步扩展和深入学习相关的内容。
离散数学教案

离散数学教案主要是针对离散数学课程的教学内容和教学方法进行设计和安排。
以下是一个简单的离散数学教案示例:一、教学目标1. 理解离散数学的基本概念和基本原理,如集合、图论、数理逻辑等。
2. 掌握离散数学的基本运算和方法,如集合运算、图论分析、逻辑推理等。
3. 培养学生的逻辑思维和抽象思维能力,提高解决实际问题的能力。
二、教学内容1. 集合的基本概念和运算- 集合的定义和性质- 集合的运算:并、交、差、对称差等- 集合的运算规律和定理2. 图论的基本概念和分析方法- 图的定义和性质- 图的表示方法- 图的连通性、路径和距离等概念- 图的染色问题、最短路径算法等分析方法3. 数理逻辑的基本概念和推理方法- 命题和命题联结词- 推理和证明的基本方法- 谓词和量化词- 命题逻辑和谓词逻辑的基本定理和推论三、教学方法1. 讲授式教学:教师通过讲解、示范和示例等方式,向学生传授离散数学的基本概念和原理。
2. 案例教学:通过引入实际问题,引导学生运用离散数学的知识和方法进行分析和解决。
3. 练习和讨论:布置适量的练习题,让学生通过练习巩固所学知识,并组织课堂讨论,促进学生之间的交流和合作。
四、教学评价1. 课堂参与度:通过观察学生在课堂上的参与程度,了解他们对离散数学的兴趣和学习的积极性。
2. 练习题完成情况:通过批改学生的练习题,评估他们对离散数学知识的掌握程度。
3. 期末考试:组织期末考试,测试学生对离散数学知识的综合运用能力和解决问题的能力。
以上是一个简单的离散数学教案示例,具体的教学内容和教学方法可以根据实际情况进行调整和改进。
《离散数学教案》课件

《离散数学教案》课件一、引言1.1 离散数学的定义:研究离散结构及其相互关系的数学分支。
1.2 离散数学的应用领域:计算机科学、信息技术、运筹学、生物学等。
1.3 离散数学的重要性:为计算机科学提供数学基础,培养逻辑思维和抽象能力。
二、逻辑基础2.1 命题逻辑:概念、命题、逻辑运算符(与、或、非、蕴含、等价)、真值表。
2.2 谓词逻辑:个体、谓词、逻辑运算符(量词、连接词)、真值表。
2.3 推理规则:演绎推理、归纳推理、反证法。
三、集合与函数3.1 集合的概念:集合、元素、集合运算(并、交、补、幂集)。
3.2 集合的表示:列举法、描述法、图示法。
3.3 函数的定义:函数、域、值域、函数运算(复合函数、反函数)。
四、图论4.1 图的基本概念:图、顶点、边、无向图、有向图、图的表示(邻接矩阵、邻接表)。
4.2 图的性质:连通性、路径、圈、树、网络流。
4.3 图的应用:最短路径问题、最小树问题、网络流问题。
五、组合数学5.1 组合的概念:组合、排列、组合数、排列数。
5.2 组合数的计算:二项式定理、组合恒等式。
5.3 组合数学的应用:计数原理、概率计算、图的着色问题。
《离散数学教案》课件六、组合数学(续)6.4 排列组合问题的解决方法:插板法、捆绑法、倒置法。
6.5 鸽巢原理:鸽巢定理及其应用。
6.6 数论基础:整数、素数、最大公约数、最小公倍数。
七、数理逻辑7.1 命题逻辑的等值关系:等价、蕴涵、矛盾。
7.2 谓词逻辑的等值关系:量词、域、谓词、逻辑等值。
7.3 逻辑推理:演绎推理、归纳推理、反证法。
八、代数结构8.1 群的概念:封闭性、结合律、单位元、逆元。
8.2 环和域的概念:加法群、乘法群、环、域。
8.3 群的作用:对称性、编码理论、密码学。
九、关系与函数9.1 关系的定义:关系、有序对、自反性、对称性、传递性。
9.2 等价关系与序关系:等价类、序关系、偏序集。
9.3 函数的性质:单射、满射、双射、复合函数。
《离散数学教案》课件

《离散数学教案》课件一、引言1. 离散数学的定义和意义2. 离散数学与其他数学分支的区别3. 离散数学在计算机科学和信息技术领域的应用4. 学习离散数学的目标和要求二、逻辑与集合1. 逻辑基础命题与联结词逻辑推理与证明2. 集合的基本概念集合的表示方法集合的运算集合的性质3. 集合的运算律和集合恒等式4. 集合的分类和应用三、图论基础1. 图的基本概念图的定义和表示方法图的类型和例子2. 图的运算邻接矩阵和邻接表子图、补图和连通性3. 路径和圈路径和圈的概念最短路径问题环的性质和应用4. 树和森林树的概念和性质树的表示方法树的算法四、组合数学1. 组合的基本概念排列和组合的定义组合数的计算公式2. 组合计数原理包含-排除原理鸽巢原理和球和箱子问题3. 组合设计区块设计和平面设计拉丁方和Steiner系统4. 组合数学的应用组合数学在计算机科学中的应用组合数学在其他领域的应用五、离散数学的应用实例1. 布尔代数和逻辑电路布尔代数的基本概念逻辑电路的设计和分析2. 计算复杂性理论计算复杂性的基本概念时间和空间复杂性的分析方法3. 信息论和编码理论信息论的基本概念编码理论和错误纠正码4. 离散数学在其他领域的应用实例离散数学在生物学中的应用离散数学在经济学中的应用六、关系与函数1. 关系的基本概念关系的定义和表示关系的性质和分类2. 关系的运算关系的复合和逆关系关系的闭包和分解3. 函数的基本概念函数的定义和表示函数的性质和分类4. 函数的运算和性质函数的复合和反函数函数的连续性和differentiability七、组合设计与计数1. 组合设计的基本概念区块设计和平面设计-拉丁方和Steiner系统2. 组合计数原理包含-排除原理鸽巢原理和球和箱子问题3. 代数结构群、环和域的基本概念群的作用和群的分解八、图论进阶1. 欧拉图和哈密顿图欧拉图的定义和性质哈密顿图的定义和性质2. 网络流和匹配网络流的基本概念和定理最大流和最小费用流问题匹配的概念和算法3. 树的同构和唯一分解定理树的同构概念唯一分解定理的证明和应用九、离散数学在计算机科学中的应用1. 计算理论和算法计算模型的基本概念算法的描述和分析2. 数据结构和算法基本数据结构常见算法和分析方法3. 形式语言和编译原理形式语言的基本概念编译器的设计和实现1. 离散数学的主要概念和定理2. 离散数学在不同领域的应用3. 离散数学的发展趋势和未来展望重点和难点解析一、引言难点解析:离散数学与其他数学分支的区别,学习离散数学的目标和要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散数学是现代数学的一个重要
绪 言
分支,是计算机科学与技术的基 础理论的核心课程之一。离散数 学与计算机科学中的数据结构、 操作系统、编译理论、算法分析、 逻辑设计、系统结构、机器定理 证明等课程息息相关。 基本内容包括数理逻辑、集合论、 代数系统、图论等几大部分。
离散数学
离散数学(Discrete Mathematics):"研究离散
七桥问题
哥尼斯堡城位于普雷格尔河畔,河中有两个岛,七 座桥使两个河心岛及两岸彼此相连。十八世纪的城中居 民热衷于这样一个问题:游人从四块陆地中的任何一地 出发,能否找到一条路线,通过每桥一次且仅一次,最 后返回原地?
欧拉对七桥问题的解 1736年,著名数学家欧拉研究了七桥问题,他将这 个问题用结点和弧边组成的图来表示,问题归结为从 图中任一结点出发,经过每边一次且仅一次的回路是 否存在?他找到了存在这样一条回路的充分必要条件, 并由此判断七桥问题无解而结束了哥尼斯堡城民的烦 恼。例2 Nhomakorabea2.4 解
(1)根据乘法原理,可能的选法种数为 6×5×4= 120; (2)[法一] 根据题意,确定职位可分为3个 步骤:确定主席有2种选择;主席选定后, 秘书有5个人选;主席和秘书都选定后,出 纳有4个人选。根据乘法原理,可能的选法 种数为2×5×4 = 40;
2013-7-28
例2.2.4 解(续)
解(二)
用一一对应技术 一场比赛对应一个被淘汰者,反之也真,那 么比赛场数与被淘汰者人数是相等的。由于 优胜者只有一人,全部被淘汰者是100人, 因此要进行100场比赛方可决出优胜者。
土耳其商人和帽子的故事
这是著名物理学家爱因斯坦出过的一道题。
一个土耳其商人,想找一个十分聪明的助手协助他经商, 有两个人前来应聘,这个商人为了试一试哪一个聪明些,就 把两个人带进一间漆黑的屋子里,他打开电灯后:“这张桌 子上有五顶帽子,两顶是红色的,三顶是黑色的。现在,我 把灯关掉,而且把帽子摆的位置弄乱,然后我们三个人每人 摸一顶帽子戴在头上,在我开灯后,请你们尽快的说出自己 头上戴的帽子是什么颜色的。”说完之后,商人将电灯关掉, 然后三人都摸了一顶帽子戴在头上,同时商人将余下的两顶 帽子藏了起来,接着把电灯打开,这时,那两个有应试者看 到商人头上戴的是一顶红帽子,过了一会儿,其中一个人便 喊到:“我戴的是黑帽子。” 请问这个人猜得对吗?是怎么推导出来的?
2013-7-28
例2.2.4 解(续)
(4)将给Dolph、Francisco和另一个人指定职 位分为3步: 给Dolph指定职位,有3个职位可选; 给Francisco指定职位,有2个职位可选; 确定最后一个职位的人选,有4个人选。 根据乘法原理,共有3×2×4 = 24种选法。
2013-7-28
2.2.2 加法原理
假定X1, X2, „, Xt均为集合,第i个集合Xi 有ni个元素。如{X1, X2, „, Xt}为两两不相交 的集合,则可以从X1, X2, „, Xt中选出的元 素总数为: n1 + n2 + „ + nt。
即集合X1∪X2∪…∪Xt含有n1 + n2 + … + nt个元素。
2.2.1 乘法原理
如果一些工作需要t步完成,第一步有n1种 不同的选择,第二步有n2种不同的选择,„ , 第t步有nt种不同的选择,那么完成这项工作 所有可能的选择种数为:
n1 n2 nt
2013-7-28
例2.2.2 Melissa病毒
1990年,一种名叫Melissa的病毒利用侵吞系统 资源的方法来破坏计算机系统,通过以含恶意 宏的字处理文档为附件的电子邮件传播。当字 处理文档被打开时,宏从用户的地址本中找出 前50个地址,并将病毒转发给他们。用户接收 到这些被转发的附件并将字处理文档打开后, 解 根据Melissa病毒的扩散原理,经过四次转发, 病毒会自动继续转发,不断往复扩散。病毒非 共有 常快速地转发邮件,将被转发的邮件临时存储 50×50×50×50+50×50×50+50×50+ 50 +1 在某个磁盘上,当磁盘占满后,系统将会死锁 = 6377551个接收者。 甚至崩溃。问经过四次转发,共有多少个接收 者? 2013-7-28
聪明的囚徒
古希腊有个国王,对处死囚徒的方法作了两种规定:
一种是砍头,一种是绞刑。并他自恃聪明的做出一 种规定:囚徒可以说一句话,并且这句话是马上可 以验证其真假。如果囚徒说的是真话,那么处以绞 刑,如果囚徒说的是假话,那么处以砍头。许多囚 徒或者是因为说了假话而被砍头或者因为说了真话 而被处以绞刑。 有一位极其聪明的囚徒,当轮到他来选择处死方法 时,他说出一句巧妙的话,结果使这个国王按照哪 种方法处死他,都违背自己的决定,只得将他放了。 试问:这囚徒说的是句什么话?
@淘汰赛
有101个人参加乒乓球淘汰赛(每一轮比赛 在参加人数是奇数时,让一人轮空),共需 进行多少场比赛方可决出优胜者(一场比赛 指两人的一次对垒)
解(一)
第一轮 50场, 剩50名优胜者 1名轮空 第二轮 25场, 剩25名优胜者 1名轮空 第三轮 13场, 剩13名优胜者 第四轮 6场, 剩6名优胜者 1名轮空 第五轮 3场, 剩3名优胜者 1名轮空 第六轮 2场, 剩2名优胜者 第七轮 1场, 剩1名优胜者 共计 50+25+13+6+3+2+1=100场
方世昌主编 西安电子科大出版社
Discrete Mathematics Structures
Bemard Kolman Robert C. Busby Sharon Ross Prentice-Hall International,Inc. 1997.11 (英文原版影印)清华大学出版社
离散数学是培养抽象思维和逻辑推理的学科,
公開徵答 1878年,英國數學家Cayley 將上述問題曝光取名為「四 色猜想」(因為還不確定對不對,所以說是猜想),公開徵求解 答。 問題一傳出後,馬上就有了回應。1879年和1880年, Kempe 和Tait 分別發表論文證明了四色問題。轟動一時的熱 度終於平息。不料事隔11年後,一個名叫Heawood 的年輕人指 出了Kempe 證明中的錯誤,並利用Kempe 的方法證明出若用5 種顏色就保證一定能區分出地圖上相鄰的區域。雖然四色問題 未被破解,但是至此算是邁出了一大步。而另一方面,Tait 的論文亦被陸陸續續發現多處錯誤,甚至最後一個錯誤是一直 到1946年才被發現的。從這裡我們可看出這些人的研究精神是 多麼可敬,被發現錯誤的東西並未被棄之如敝屣般丟在一旁, 仍舊不斷有人去研究它,甚至是在事隔半個多世紀之後。 當然這兩篇錯誤的論文在數學上仍然有其貢獻,不可小覷。
[法二] 若Alice被选为主席,共有5×4 = 20种方法 确定其他职位;若Ben为主席,同样有20种 方法确定其他职位。由于两种选法得到的集 合不相交,所以根据加法原理,共有20+20 = 40种选法;
2013-7-28
例2.2.4 解(续)
(3)[法一] 将确定职位分为3步:确定 Egbert的职位,有3种方法;确定余下的较 高职位人选, 有5个人选;确定最后一个 职位的人选, 有4个人选。根据乘法原理, 共有3×5×4 = 60种选法;
学 习 方 法 建 议
因此要重视基本概念的学习,一定要认真研读 教材,特别要从实例和习题中搞清众多概念的 涵义。
适当多做习题,至少要按时完成作业,强迫自
己通过特定条件下运用所学的概念和理论,才 能真正掌握和理解它们,提高分析和解决问题 的能力。
与教材配套的习题解答是离散数学的初学者必
备的参考书,钻研习题解答,从中领会典型问 题的解题方法。不会求解的作业题,可以看习 题解答,但务求读懂,决不可一抄了事,养成 依赖习惯,白白浪费宝贵的时光!
解題花絮 一番風風雨雨下來,四色問題更加受到矚目了。由於 Heawood 的「五色定理」的證明並不難,因此就有許多人 也小看了「四色問題」的難度。最有趣的是以下這個例子。 1902年秋天,閔可夫斯基教授(Hermann Minkowsky, 1864 -1909,愛因斯坦的數學導師)在上拓樸學的課堂上 就當著學生面前說:「四色問題之所以尚未被解決是因為 世界上第一流的數學家都還沒空去研究它。」而且興之所 至,當場就證了起來;但是寫了好幾個黑板,卻依舊未能 得證。接下來幾個星期的課,他繼續證下去,課一堂一堂 地過去了,他如身陷泥沼,仍舊無法證明出來。他終於投 降,承認自己也無能為力了。就在這個時候,天空正好霹 靂一聲巨響,他感嘆地說:「上帝在責備我的狂妄!」然 後就繼續上他的拓樸課了。
同构
四色问题
任何一張平面地圖,如果相鄰的兩 個國家,必須塗上不同的顏色以便 劃清邊界,則至多只要四種顏色就 搞定了,不管這張地圖有多麼奇特 複雜。
發現者 這是在西元1852年,由畢業於英國倫敦大學的弗朗 西斯 (Francis Guthrie)發現的。當時他正在畫英國各 郡的地圖,而發現了這個有趣的現象。格里斯覺得這其 中一定有什麼奧妙,於是便寫信告訴他那數學很好的哥 哥佛德雷克(Frederick Guthrie)。佛德雷克百思不得 其解,又求教於他的老師----數學家摩根(Morgan)。摩 根也無法確定這個說法對不對,於是又寫信給他的好朋 友哈彌爾頓(Hamilton),希望他要嘛就證明出這個說法 是正確的,要不就舉一個反例,建構出一張需要5 種顏 色的地圖來。大師級的哈彌爾頓耗了13年心血,仍一籌 莫展,抱憾而逝。
表2.2.1
开胃食品 主食 种类 种类 价格 价 (元) 格 玉米片 2.15 汉堡(H) 3.2 (Co) 5 色拉(Sa) 1.90 三明治 3.6 (S) 5 鱼排(F) 3.1 5
2013-7-28
饮料 种类 价 格 茶水 0.7 (T) 0 牛奶 0.8 (M) 5 可乐 0.7 (C) 5 0.7
