第5次课(基于字典编码和算术编码)
精品课课件信息论与编码(全套讲义)

跨学科交叉融合
信息论将与更多学科进行交叉融合,如物理学、 化学、社会学等,共同推动信息科学的发展。
编码技术的发展趋势
高效编码算法
随着计算能力的提升,更高效的编码算法将不断涌现,以提高数据 传输和存储的效率。
智能化编码
借助人工智能和机器学习技术,编码将实现智能化,自适应地调整 编码参数以优化性能。
跨平台兼容性
未来的编码技术将更加注重跨平台兼容性,以适应不同设备和网络环 境的多样性。
信息论与编码的交叉融合
理论与应用相互促进
信息论为编码技术提供理论支持, 而编码技术的发展又反过来推动 信息论的深入研究。
共同应对挑战
精品课课件信息论与编码(全套 讲义)
目
CONTENCT
录
• 信息论基础 • 编码理论 • 信道编码 • 信源编码 • 信息论与编码的应用 • 信息论与编码的发展趋势
01
信息论基础
信息论概述
信息论的研究对象
研究信息的传输、存储、处理和变换规律的科学。
信息论的发展历程
从通信领域起源,逐渐渗透到计算机科学、控制论、 统计学等多个学科。
卷积编码器将输入的信息序列按位输入到一个移位寄存器中,同时根据生成函数将移位寄存 器中的信息与编码器中的冲激响应进行卷积运算,生成输出序列。
卷积码的译码方法
卷积码的译码方法主要有代数译码和概率译码两种。代数译码方法基于最大似然译码准则, 通过寻找与接收序列汉明距离最小的合法码字进行译码。概率译码方法则基于贝叶斯准则, 通过计算每个合法码字的后验概率进行译码。
04
视频压缩 基本算法与标准

视频压缩视频压缩又称视频编码,所谓视频编码方式就是指通过特定的压缩技术,将某个视频格式的文件转换成另一种视频格式文件的方式。
一般的通用数据压缩方案如下图:压缩就是一个传播的过程,所以在压缩与解压缩之间,没有信号的丢失则称这种压缩就是无损的,相反的就是有损的,都有各自的算法,下面介绍。
无损压缩算法一游长编码(Run-Length Coding, RLC)产生年代:未知。
主要人物:未知。
基本思想:如果我们压缩的信息源中的符号具有这样的连续的性质,即同一个符号常常形成连续的片段出现,那么我们可以对这个符号片段长度进行这样的的编码。
例子:输入:5555557777733322221111111游长编码为:(5,6)(7,5)(3,3)(2,4)(l,7)二变长编码:1 香农-凡诺算法产生年代:未知主要人物:Shannon 和Robert Fano基本思想:对于每个符号出现的频率对符号进行排序,递归的将这些符号分成两部分,每一部分有相近的频率,知道只有一个符号未止。
说明:过程用一颗二叉树完成,它是一种自顶向下的过程,对于此输入5个字符则自然的分成2,3左右两子树,接着就是递归的过程。
因为分法不唯一,所以下列输出是一种情况。
例子:输入:HELLO输出:10 110 0 0 111(左子树标0)2赫夫曼编码产生年代:1952年主演人物:David A.Huffman基本思想:与香农-凡诺算法的区别在于,赫夫曼编码采用的是一种自下而上的描述方式,先从符号的频率中选取最小的两个符号,合成一个新的结点,进行等效的代替,然后也是个递归过程。
说明:赫夫曼编码具有唯一的前缀性质和最优性。
例子:对于输入:HELLO 建立的一刻赫夫曼树 扩展:扩展的赫夫曼编码,这是相对于数据中某个符号的概率较大(接近1.0)时,将几个符号组成组,然后为整个组赋予一个码字。
自适应的赫夫曼编码,这是一个边接收边编码的过程,完全的体现了适应的过程,需要对二叉树进行改变,由接收到的数据去添加进二叉树中,自动生成新的“赫夫曼树”。
冀教版小学信息技术五年级上册《第5课 算法的特征》教学设计

冀教版小学信息技术五年级上册《第5课算法的特征》教学设计教材分析:冀教版小学信息技术第5课主要介绍了算法的基本概念和特征。
教材以生动的实例,如做家务、走迷宫等,引导学生理解算法是解决问题的一系列步骤,强调了算法的逻辑性和可执行性。
教材还通过简单的编程示例,让学生初步感知到算法在信息技术中的应用。
学情分析:学生在学习本课前,已经对计算机有了一定的了解,能够进行基本的计算机操作。
但他们对“算法”这个概念可能比较陌生,理解起来可能会有一定的难度。
此外,小学生的逻辑思维能力正在发展中,需要通过具体实例和活动来帮助他们理解和掌握。
教学目标:1. 知识与技能:理解算法的定义,掌握算法的四个基本特征(明确性、有限性、输入、输出)。
2. 过程与方法:通过实例分析和讨论,培养学生的逻辑思维能力和问题解决能力。
3. 情感态度与价值观:激发学生对信息技术的兴趣,认识到算法在日常生活和学习中的重要性。
教学重难点:教学重点:理解并能描述算法的四个基本特征。
教学难点:如何将生活中的问题抽象为算法,理解算法的逻辑性和可执行性。
教学过程:在教育的广阔领域中,引导学生理解和应用“算法”这一概念是现代科技教育的重要一环。
以下是一种有效的教学策略,旨在将抽象的理论知识转化为生动的实践体验。
1. 导入新课:教学活动始于一个日常生活中的常见问题,例如“如何煮一个完美的鸡蛋”。
教师可以引导学生详细描述煮鸡蛋的步骤,如加热水、设定时间、搅拌等。
这样的开场白不仅吸引学生的注意力,也自然地引出了“算法”这一主题——即一系列有序的步骤,用于解决特定问题或完成特定任务。
2. 讲解新知:接着,教师将深入介绍算法的四个关键特征:明确性、有限性、输入和输出。
每讲到一个特征,都要配以生动的实例。
例如,明确性可以通过描述每一步的具体操作来体现,有限性则可以通过说明煮鸡蛋的步骤是有限的,不会无休止地进行来解释。
这样的讲解方式使抽象的概念变得具体可感。
3. 实践操作:理论讲解后,是实践操作的时间。
压缩算法的分类

压缩算法的分类
压缩算法的分类可以根据不同的标准和角度进行。
以下是一些常见的分类方式:
1.有损压缩和无损压缩:根据压缩后数据是否可逆,可以分为有损和无
损压缩。
无损压缩能够完全还原原始数据,而有损压缩则无法完全还原,会丢失一些数据。
2.熵编码和非熵编码:根据是否利用数据本身存在的冗余和相关性,可
以分为熵编码和非熵编码。
熵编码是一种无损压缩方法,它利用数据本身存在的冗余和相关性进行压缩;而非熵编码则是一种有损压缩方法,它通过去除数据中的冗余和相关性来压缩数据。
3.字典编码和算术编码:根据使用数据的存储方式,可以分为字典编码
和算术编码。
字典编码将出现过的字符串存入字典中,并用位置来代替这些字符串;而算术编码则是将数据表示为一个范围在0到1之间的概率值。
4.单独压缩和联合压缩:根据是否针对单个文件进行压缩,可以分为单
独压缩和联合压缩。
单独压缩是对单个文件进行压缩,而联合压缩则是将多个文件组合在一起进行压缩。
5.基于预测的压缩和基于统计的压缩:根据使用数据的不同方法,可以
分为基于预测的压缩和基于统计的压缩。
基于预测的压缩利用前一个或多个数据点的值来预测当前数据点的值,并去除预测误差来压缩数据;而基于统计的压缩则是利用数据的概率分布来进行压缩。
这些分类方式只是其中的一部分,根据不同的标准还可以将压缩算法分为更多类别。
了解压缩算法的不同分类方式有助于更好地选择和应用适当的算法。
信源编码的方案实施

信源编码的方案实施引言信源编码是信息论中的一个重要概念,用于在信息传输中提高数据的传输效率。
信源编码方案的选择及实施对于信息传输的性能有很大的影响。
本文将介绍信源编码方案的实施过程,并讨论其在实际应用中的一些考虑因素。
信源编码方案的选择在实施信源编码方案之前,首先需要选择一个合适的编码方案。
常用的信源编码方案包括霍夫曼编码、算术编码和基于字典的编码等。
选择合适的编码方案需要考虑以下几个因素:数据特性不同的数据具有不同的特性,例如数据的统计特性、冗余程度等。
对于具有较高冗余程度的数据,应选择具有较好压缩效果的编码方案,如霍夫曼编码。
对于具有较低冗余程度的数据,应选择具有较高编码效率的方案,如算术编码。
处理能力选择的信源编码方案要考虑实际系统的处理能力。
某些编码方案可能需要较高的计算能力来进行编解码操作,这对于资源受限的系统来说可能不太适合。
因此,在选择编码方案时,需要权衡计算能力和编码效率之间的关系。
误码率对于一些对误码率要求较高的系统,例如无线通信系统,选择能够提供具有很好错误保护能力的编码方案是十分重要的。
这种编码方案需要具备较好的纠错能力,并能提供较低的误码率。
在选择编码方案时,需要考虑系统的误码率要求以及编码方案所能提供的错误保护能力。
信源编码方案的实施步骤信源编码方案的实施包括编码器和解码器的设计及实现两个步骤。
以下是信源编码方案的实施步骤:步骤一:设计编码器根据选择的编码方案,在设计编码器时需要确定编码的规则和算法。
根据数据特性和处理能力,可以选择合适的编码算法,并进行相应的优化。
编码器的设计需要根据具体的应用场景和系统要求来进行,例如可以考虑加入压缩算法来提高编码效率。
步骤二:实现编码器根据设计的编码规则和算法,进行编码器的实现。
实现编码器可以采用软件实现或硬件实现的方式,具体根据系统平台和资源情况来选择。
编码器的实现需要将设计的编码算法转化为具体的编码逻辑,同时要考虑性能和内存消耗等因素。
四种压缩算法原理介绍

四种压缩算法原理介绍压缩算法是将数据经过特定的编码或转换方式,以减少数据占用空间的方式进行压缩。
常见的压缩算法可以分为四种:无损压缩算法、有损压缩算法、字典压缩算法和算术编码压缩算法。
一、无损压缩算法是指在数据压缩的过程中不丢失任何信息,压缩前后的数据完全相同,通过对数据进行编码或转换,以减少数据的存储空间。
常见的无损压缩算法有:1. 霍夫曼编码(Huffman Coding):霍夫曼编码是一种可变长度编码方式,通过根据数据出现频率给予高频率数据较低的编码长度,低频率数据较高的编码长度,从而达到减少数据存储空间的目的。
2.雷霍尔曼编码(LZ77/LZ78):雷霍尔曼编码是一种字典压缩算法,它通过在数据中并替换相同的字节序列,从而实现数据的压缩。
LZ77算法是将数据划分为窗口和查找缓冲区,通过在查找缓冲区中查找与窗口中相匹配的字节序列来进行压缩。
LZ78算法主要通过建立一个字典,将数据中的字节序列与字典中的序列进行匹配并进行替换,实现数据的压缩。
3.哈夫曼-雷霍尔曼编码(LZW):哈夫曼-雷霍尔曼编码是一种常见的字典压缩算法,它综合了霍夫曼编码和雷霍尔曼编码的特点。
它通过维护一个字典,将数据中的字节序列与字典中的序列进行匹配并进行替换,实现数据的压缩。
二、有损压缩算法是指在数据压缩的过程中会丢失一部分信息,压缩后的数据无法完全还原为原始数据。
常见的有损压缩算法有:1. JPEG(Joint Photographic Experts Group):JPEG 是一种常用的图像压缩算法,它主要通过对图像的颜色和亮度的变化进行压缩。
JPEG算法将图像分成8x8的块,对每个块进行离散余弦变换(DCT),并通过量化系数来削减数据,进而实现压缩。
2. MP3(MPEG Audio Layer-3):MP3 是一种常用的音频压缩算法,它通过分析音频中的声音频率以及人耳对声音的敏感程度,对音频数据进行丢弃或砍切,以减少数据的占用空间。
信息论与编码教学大纲(2024)

LDPC码在无线通信中的应用研究。探讨LDPC码在无线通信系统中的 编译码算法及性能优化方法。
选题三
极化码原理及性能分析。研究极化码的编译码原理,分析其在不同信 道条件下的性能表现,并与传统信道编码方案进行比较。
选题四
5G/6G通信中的信道编码技术。调研5G/6G通信系统中采用的信道编 码技术,分析其优缺点,并提出改进方案。
Polar码应用
探讨Polar码在5G通信、物联网等领域的应用,并分 析其性能表现。
22
06 实验环节与课程 设计
2024/1/25
23
实验环节介绍
实验一
信道容量与编码定理验证。 通过搭建简单的通信系统, 验证不同信道条件下的信道 容量及编码定理的有效性。
实验二
线性分组码编译码实验。利 用计算机软件实现线性分组 码的编译码过程,并分析其 纠错性能。
LDPC码基本原理
介绍LDPC码的编码结构、译码原理以及性 能分析。
LDPC码应用
探讨LDPC码在光纤通信、数据存储等领域 的应用,并分析其性能表现。
21
Polar码原理及应用
2024/1/25
Polar码基本原理
介绍Polar码的编码结构、信道极化原理以及性能分 析。
Polar码编译码算法
详细阐述Polar码的编码算法、译码算法以及关键技 术的实现。
2024/1/25
预测编码
利用信源符号间的相关 性进行预测,并对预测 误差进行编码,如差分 脉冲编码调制(DPCM )。
变换编码
将信源信号通过某种变 换转换为另一域的信号 ,再对变换系数进行编 码,如离散余弦变换( DCT)编码。
14
04 信道编码
2024/1/25
词典编码课程设计

词典编码课程设计一、教学目标本课程旨在让学生掌握词典编码的基本知识和技巧,包括词条的编排规则、字母顺序、拼音标注等,使学生能够熟练运用词典进行自主学习和查阅资料。
通过本课程的学习,学生将能够:1.理解词典编码的基本原理和方法。
2.掌握词典编码的技巧和要点。
3.能够独立使用词典进行词汇学习和查阅。
4.培养学生的自主学习能力和信息检索能力。
二、教学内容本课程的教学内容主要包括以下几个部分:1.词典编码的基本原理:介绍词典编码的起源和发展,解释词典编码的基本概念和规则。
2.词典编码的技巧:讲解词典编码的方法和技巧,包括字母顺序、词条编排等。
3.词典的使用方法:教授学生如何正确使用词典,包括查阅词汇、理解词条等。
4.实践练习:提供相关的练习题目,让学生通过实际操作来巩固所学的知识。
三、教学方法为了提高学生的学习兴趣和主动性,本课程将采用多种教学方法相结合的方式进行教学:1.讲授法:通过讲解词典编码的基本原理和方法,使学生掌握编码的基本知识。
2.案例分析法:通过分析具体的词典编码案例,使学生理解编码的技巧和要点。
3.实验法:通过实际的编码练习,使学生熟练掌握词典编码的技巧和方法。
四、教学资源为了支持教学内容和教学方法的实施,丰富学生的学习体验,我们将准备以下教学资源:1.教材:选用权威、实用的词典编码教材,为学生提供系统、科学的学习材料。
2.参考书:提供相关的参考书籍,为学生提供更多的学习资源和拓展知识。
3.多媒体资料:制作相关的教学课件和视频,以图文并茂的形式展示词典编码的知识和方法。
4.实验设备:准备相关的实验设备,如计算机、词典等,为学生提供实际操作的机会。
五、教学评估为了全面反映学生的学习成果,本课程将采用多种评估方式相结合的方法进行评估:1.平时表现:通过观察学生在课堂上的参与程度、提问回答等情况,评估学生的学习态度和理解程度。
2.作业:布置适量的作业,通过学生的完成情况和质量,评估学生的掌握程度。
2024-2025学年人教版新教材信息技术五年级上册 第05课 数学运算讲方法 教案

第5课数学运算讲方法一、教学目标1.学生掌握数学解题时的算法。
2.理解算法是解决问题的方法描述。
3.学会用流程图表示算法的顺序结构。
二、教学重点与难点教学重点1.掌握数学解题的算法。
2.用流程图表示算法。
教学难点1.理解复杂数学问题中的算法。
2.准确绘制流程图表示算法。
三、教学准备1.多媒体课件,包含数学问题示例及流程图绘制方法。
2.练习纸和彩笔。
四、教学过程(一)导入新课师:同学们,在我们的学习和生活中,经常会遇到各种各样的数学问题。
那么,大家有没有想过,我们在解决这些数学问题的时候,其实也在运用一种方法呢?这种方法就是算法。
今天,我们就一起来学习数学运算讲方法,看看如何用算法来解决数学问题。
(二)新课讲解1.数学解题中的算法概念(1)引入数学问题师:我们先来看看一个简单的数学问题。
小明有5个苹果,小红有3个苹果,他们一共有多少个苹果?同学们很快就能回答出是8个苹果。
那么,我们是怎么得到这个答案的呢?其实,我们在心里进行了一个简单的计算过程,先把小明的5个苹果和小红的3个苹果数出来,然后把它们加在一起,就得到了8个苹果。
这个计算过程就是一种算法。
(2)算法的定义师:算法就是解决问题的方法和步骤。
在数学解题中,算法就是我们解决数学问题的具体方法和步骤。
比如,我们要计算两个数的和,就需要先确定这两个数,然后把它们相加,最后得到结果。
这个过程就是一个算法。
2.数学解题算法的示例(1)加法算法师:我们再来看看一个加法问题。
比如,12+15=?我们可以这样来解决这个问题。
首先,我们把12和15分别拆分成10+2和10+5。
然后,我们先把两个十相加,得到20。
接着,把2和5相加,得到7。
最后,把20和7相加,得到27。
这个过程就是一个加法算法。
(2)减法算法师:再来看一个减法问题。
比如,2513=?我们可以这样来解决这个问题。
首先,我们把25拆分成20+5,把13拆分成10+3。
然后,我们先从20里面减去10,得到10。
三种常用的统计编码法

三种常用的统计编码法统计编码法是一种将符号转化为二进制编码的方法,常用于数据的存储和传输。
在统计编码法中,最常用的有三种方法,分别为霍夫曼编码、算术编码和字典编码。
下面将对这三种编码法进行详细介绍。
首先是霍夫曼编码法。
霍夫曼编码法是一种无损压缩编码方法,适用于频率分布不均匀的数据。
该编码法利用数据出现的概率进行编码,出现频率高的符号用较短的码字表示,而出现频率低的符号则用较长的码字表示。
这样可以使编码后的数据占用的位数最少。
算术编码是另一种常用的统计编码法。
它将整个消息作为一个整体来编码,而不是将消息划分为固定长度的符号进行编码。
算术编码通过维护一个区间,根据符号的概率分布,逐渐缩小区间的范围,最后将落在最终区间内的小数编码输出。
这样可以实现更高的压缩比,但解码复杂度较高。
最后是字典编码法。
字典编码法通过建立符号和编码之间的一一对应关系来进行编码。
它根据数据中的重复模式,将重复出现的符号用较短的码字表示,而不重复的符号则用较长的码字表示。
字典编码法常用于无损压缩算法中,如LZW算法。
三种常用的统计编码法在具体的应用场景和数据特征上都有所不同。
在选择编码方法时,需要考虑数据的分布、数据的类型、压缩比要求和解码复杂度等因素。
霍夫曼编码法适用于频率分布不均匀的数据,并且对解码的要求不高。
它可以在一定程度上提高压缩比,但解码时需要使用相同的霍夫曼编码表进行解码,因此对于无法完全传输编码表的场景可能不适用。
算术编码在压缩比方面优于霍夫曼编码,但解码复杂度较高,需要使用相同的符号概率分布来进行解码。
算术编码适用于数据中存在较多冗余信息的情况,可以达到较高的压缩比。
字典编码法通过建立符号和编码的对应关系,适用于数据中存在较多重复模式的情况。
它可以实现较高的压缩比,但需要建立和传输字典表,在某些场景下不便于使用。
综上所述,霍夫曼编码、算术编码和字典编码是三种常用的统计编码法。
它们在不同的应用场景和数据特征下具有不同的优势和适用性。
算术编码(Arithmeticcoding)的实现
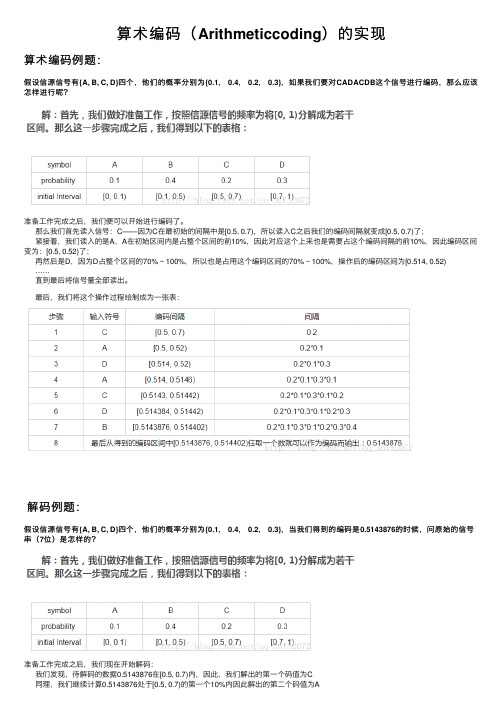
算术编码(Arithmeticcoding)的实现算术编码例题:假设信源信号有{A, B, C, D}四个,他们的概率分别为{0.1, 0.4, 0.2, 0.3},如果我们要对CADACDB这个信号进⾏编码,那么应该怎样进⾏呢?准备⼯作完成之后,我们便可以开始进⾏编码了。
那么我们⾸先读⼊信号:C——因为C在最初始的间隔中是[0.5, 0.7),所以读⼊C之后我们的编码间隔就变成[0.5, 0.7)了; 紧接着,我们读⼊的是A,A在初始区间内是占整个区间的前10%,因此对应这个上来也是需要占这个编码间隔的前10%,因此编码区间变为:[0.5, 0.52)了; 再然后是D,因为D占整个区间的70% ~ 100%,所以也是占⽤这个编码区间的70% ~ 100%,操作后的编码区间为[0.514, 0.52) …… 直到最后将信号量全部读出。
最后,我们将这个操作过程绘制成为⼀张表:解码例题:假设信源信号有{A, B, C, D}四个,他们的概率分别为{0.1, 0.4, 0.2, 0.3},当我们得到的编码是0.5143876的时候,问原始的信号串(7位)是怎样的?准备⼯作完成之后,我们现在开始解码: 我们发现,待解码的数据0.5143876在[0.5, 0.7)内,因此,我们解出的第⼀个码值为C 同理,我们继续计算0.5143876处于[0.5, 0.7)的第⼀个10%内因此解出的第⼆个码值为A …… 这个过程持续直到执⾏七次全部执⾏完为⽌。
那么以上的过程我们同样可以列表表⽰:作业:对任⼀概率序列,实现算术编码,码长不少于16位,不能固定概率,语⾔⾃选。
基于Python实现:from collections import Counter #统计列表出现次数最多的元素import numpy as npprint("Enter a Sequence\n")inputstr = input()print (inputstr + "\n")res = Counter(inputstr) #统计输⼊的每个字符的个数,res是⼀个字典类型print (str(res))# print(res)#sortlist = sorted(res.iteritems(), lambda x, y : cmp(x[1], y[1]), reverse = True)#print sortlistM = len(res)#print (M)N = 5A = np.zeros((M,5),dtype=object) #⽣成M⾏5列全0矩阵#A = [[0 for i in range(N)] for j in range(M)]reskeys = list(res.keys()) #取字典res的键,按输⼊符号的先后顺序排列# print(reskeys)resvalue = list(res.values()) #取字典res的值totalsum = sum(resvalue) #输⼊⼀共有⼏个字符# Creating TableA[M-1][3] = 0for i in range(M):A[i][0] = reskeys[i] #第⼀列是res的键A[i][1] = resvalue[i] #第⼆列是res的值A[i][2] = ((resvalue[i]*1.0)/totalsum) #第三列是每个字符出现的概率i=0A[M-1][4] = A[M-1][2]while i < M-1: #倒数两列是每个符号的区间范围,与输⼊符号的顺序相反A[M-i-2][4] = A[M-i-1][4] + A[M-i-2][2]A[M-i-2][3] = A[M-i-1][4]i+=1print (A)# Encodingprint("\n------- ENCODING -------\n" )strlist = list(inputstr)LEnco = []UEnco = []LEnco.append(0)UEnco.append(1)for i in range(len(strlist)):result = np.where(A == reskeys[reskeys.index(strlist[i])]) #满⾜条件返回数组下标(0,0),(1,0) addtollist = (LEnco[i] + (UEnco[i] - LEnco[i])*float(A[result[0],3]))addtoulist = (LEnco[i] + (UEnco[i] - LEnco[i])*float(A[result[0],4]))LEnco.append(addtollist)UEnco.append(addtoulist)tag = (LEnco[-1] + UEnco[-1])/2.0 #最后取区间的中点输出LEnco.insert(0, " Lower Range")UEnco.insert(0, "Upper Range")print(np.transpose(np.array(([LEnco],[UEnco]),dtype=object))) #np.transpose()矩阵转置print("\nThe Tag is \n ")print(tag)# Decodingprint("\n------- DECODING -------\n" )ltag = 0utag = 1decodedSeq = []for i in range(len(inputstr)):numDeco = ((tag - ltag)*1.0)/(utag - ltag) #计算tag所占整个区间的⽐例for i in range(M):if (float(A[i,3]) < numDeco < float(A[i,4])): #判断是否在某个符号区间范围内decodedSeq.append(str(A[i,0]))ltag = float(A[i,3])utag = float(A[i,4])tag = numDecoprint("The decoded Sequence is \n ")print("".join(decodedSeq))Arithmetic coding Code参考:。
第五讲 无损数据压缩

等长与不等长编码
• 例如:符号序列x=“aa bb cccc dddd eeeeeeee • 采用ASCII编码: 等长编码:24*8=192bit
– – – – – – a=01100001 b=01100010 c=01100011 d=01100100 e=01100101 空=00100000
技术准备:编码
通过模型,我们可以确定对某一个符号该用多少位二进制数进行编码。 现在的问题是,如何设计一种编码方案,使其尽量精确地用模型计算出 来的位数表示某个符号。
前缀编码规则:任何一个符号的编码都不是另一个符号编码的前缀。 最简单的前缀编码
字符 A B C D E 0 10 110 1110 11110 编码
字典编码时代:LZ77和LZ78压缩算法 字典编码时代:
LZW算法
Terry Welch
1984 年 发表论文:“高性能数据压缩技术” A Technique for High-Performance Data Compression Welch 实现了 LZ78 算法的一个变种 —— LZW算法 LZW算法 UNIX:使用 LZW 算法的 Compress 程序 MS-DOS:ARC 程序,以及PKWare、PKARC 等仿制品。
• 有损压缩
– 指使用压缩后的数据进行重构,重构后的数据与原来 的数据有所不同,但不影响人对原始资料表达的信息 造成误解。 – 图像和声音的压缩就可以采用有损压缩,因为其中包 含的数据往往多于我们的视觉系统和听觉系统所能接 收的信息,丢掉一些数据而不至于对声音或者图像所 表达的意思产生误解,但可大大提高压缩比。
Shannon-Fano编码例1
• 有一幅40个象素组成的灰度图像,灰度共有5级,分别用 符号A、B、C、D和E表示,40个象素中出现灰度A的象素 数有15个,出现灰度B的象素数有7个,出现灰度C的象素 数有7个等等。如果用3个位表示5个等级的灰度值,也就 是每个象素用3位表示,编码这幅图像总共需要120位。 符 号 A 出现的次数 15 H(S) = (15/40)* + (5/40) ∗ B 7 C 7 D 6 E 5
信息论与编码教学课件(全)

目录
• 课程介绍与背景 • 信息论基础 • 编码理论基础 • 信道编码技术 • 数据压缩技术 • 多媒体信息编码技术 • 课程总结与展望
01
课程介绍与背景
Chapter
信息论与编码概述
信息论的基本概念
01
信息、信息量、信息熵等
编码的基本概念
02
信源编码、信道编码、加密编码等
02
极化码(Polar Codes)
一种新型信道编码方式,通过信道极化现象实现高效可靠的信息传输。
03
深度学习在信道编码中的应用
利用深度学习技术优化传统信道编码算法,提高编码性能和效率。
05
数据压缩技术
Chapter
数据压缩概述与分类
数据压缩定义
通过去除冗余信息或使用更高效的编码方式,减小数据表示所需存储空间的过 程。
线性分组码原理:线性分组码是一 种将信息序列划分为等长的组,然 后对每组信息进行线性变换得到相 应监督位的编码方式。
具有严谨的代数结构,易于分析和 设计;
具有一定的检错和纠错能力,适用 于各种通信和存储系统。
循环码原理及特点
循环码原理:循环码是一种特殊的线 性分组码,其任意两个码字循环移位
后仍为该码的码字。
03
编码理论基础
Chapter
编码的基本概念与分类
编码的基本概念
编码是将信息从一种形式或格式转换为另一种形式的过程,以 满足传输、存储或处理的需要。
编码的分类
根据编码的目的和原理,可分为信源编码、信道编码、加密编 码等。
线性分组码原理及特点
线性分组码特点
监督位与信息位之间呈线性关系, 编码和解码电路简单;
无损压缩算法的比较和分析

无损压缩算法的比较和分析常见的无损压缩算法包括LZ77、LZ78、LZW、Huffman编码、算术编码等。
下面对这些算法进行比较和分析。
1.LZ77LZ77算法是一种字典编码方法,通过寻找重复出现的数据片段,并用指针和长度来表示这些片段,从而实现无损压缩。
与其他算法相比,LZ77算法在压缩速度方面较快,但压缩率相对较低。
2.LZ78LZ78算法是一种基于字典编码的压缩算法,它将重复出现的片段替换为对应的指针,并在字典中新增新的片段。
与LZ77相比,LZ78算法具有更好的压缩效果,但压缩和解压缩的速度较慢。
3.LZWLZW算法是LZ78的改进版本,也是一种字典编码方法。
LZW算法通过将重复出现的片段编码为对应的指针,并将这些片段以及对应的指针存储在字典中,来实现压缩。
与LZ78相比,LZW算法在压缩效果上更好,但对字典的管理较复杂,导致压缩和解压缩速度较慢。
4. Huffman编码Huffman编码是一种基于字符出现频率的编码算法。
它通过统计字符出现的频率来构建一个最优前缀编码的树结构,从而实现无损压缩。
Huffman编码的压缩率较高,但压缩和解压缩的速度相对较慢。
5.算术编码算术编码是一种基于字符出现概率的编码算法。
它通过使用一个区间来表示整个数据流,将出现频率较高的字符用较短的区间表示,从而实现无损压缩。
算术编码的压缩率通常比Huffman编码更高,但压缩和解压缩的速度更慢。
综合比较上述算法,可以得出以下结论:1.LZ77和LZ78算法适用于实时压缩,因为它们在压缩和解压缩的速度方面较快,但压缩率较低。
2.LZW算法在压缩效果上较好,但对字典的管理较复杂,导致压缩和解压缩的速度较慢。
3. Huffman编码和算术编码在压缩率上较高,但压缩和解压缩的速度相对较慢。
根据具体需求,可以选择适合的无损压缩算法。
如果需要更快的压缩和解压缩速度,可以选择LZ77或LZ78算法;如果需要更好的压缩效果,可以选择LZW算法、Huffman编码或算术编码。
数据编码说课稿

数据编码课程说课稿一、课程概述数据编码是信息科学和工程领域中非常重要的一个分支,主要研究如何将信息转换为适合数字系统传输和存储的格式。
本课程将介绍数据编码的基本原理、方法和应用,以及数据压缩、差错控制和加密等相关的主题。
通过学习本课程,学生将掌握数据编码的基本概念和技能,为进一步学习其他信息科学和工程领域的相关课程打下基础。
二、课程目标1.理解数据编码的基本原理和方法,包括无损编码和有损编码。
2.掌握常见的数据编码技术,如Huffman编码、算术编码、游程编码、LZ77和LZ78等。
3.了解数据压缩技术,包括基于统计的方法和基于字典的方法。
4.掌握差错控制编码,如奇偶校验码、CRC码和纠错码等。
5.了解数据加密的基本原理和方法,包括对称加密和公钥加密。
6.培养学生的实践能力和创新思维,能够运用所学知识解决实际问题和进行相关研究。
三、课程内容1.数据编码基础:介绍数据编码的基本概念、原理和方法,包括信源编码和信道编码。
2.数据压缩:介绍基于统计的方法和基于字典的方法进行数据压缩,如Huffman编码、算术编码、游程编码、LZ77和LZ78等。
3.差错控制:介绍奇偶校验码、CRC码和纠错码等差错控制编码方法。
4.数据加密:介绍对称加密和公钥加密等数据加密方法,如DES、AES和RSA等。
5.数据编码应用:介绍数据编码在通信、存储和安全等领域的应用,如JPEG图像压缩、MP3音频压缩、Zip文件压缩等。
6.数据编码实践:通过实验和实践环节,让学生亲自动手实现数据编码算法,加深对数据编码的理解和应用。
四、教学方法本课程将采用多种教学方法相结合的方式,包括理论授课、案例分析、实验和实践等。
通过理论授课,使学生掌握数据编码的基本概念和原理。
通过案例分析,使学生了解数据编码的实际应用和解决方法;通过实验和实践,提高学生的实践能力和创新思维。
还可以结合多媒体教学、在线学习平台和小组讨论等方式,提高教学效果和学习体验。
人工智能课件第五次课

Open
c=6
s=2 c=5 h=4
Open
Open
Open
c=6
s=1 c=6 h=5
s=1 c=6 h=5
Examining tile (5,5)
1 1 2 3 4 5 6 7 8 9 10
Open
s=1 h=3
2
3
4
5
6
7
8
9
10
Closed Closed
Closed
Open
c=5
s=1 c=4 h=3
初始化每一点的数值 Initial tile path scores
• The s value is the cost of getting there from the starting tile. s=从开始点到当前点的累计代价值 • The h value is the heuristic which is an estimate of the number of steps from the given tile to the destination tile. h=从当前点到目标点的步数值 • The c value is the sum of s and h. c=s+h
s=1 c=4 h=3
s=2 c=4 h=3
Open
s=1 h=4 s=1 h=5 c=5
Open
s=1 h=4
Open
c=6
s=2 c=5 h=4
Open
Open
Open
c=6
s=1 c=6 h=5
s=1 c=6 h=5
Examining tile (5,4)
1 1 2 3 4 5 6 7 8 9 10
信源编码的范畴

信源编码的范畴信源编码的范畴概述:信源编码是一种将信息转换为数字或二进制形式的技术,它可以用于压缩数据以减少存储空间或传输带宽。
信源编码的范畴包括熵编码、字典编码和算术编码。
一、熵编码1.1 概述熵编码是一种无损压缩技术,它利用信息的统计特性来减少数据的冗余。
熵编码可分为霍夫曼编码和算术编码两种。
1.2 霍夫曼编码霍夫曼编码是一种基于字符出现频率的无损数据压缩技术,它通过将频率较高的字符映射到较短的二进制字符串上来实现数据压缩。
霍夫曼树是构建霍夫曼编码的主要工具,它可以通过贪心算法得到。
1.3 算术编码算术编码是一种将符号序列映射到一个区间上的无损数据压缩技术,它利用了符号出现概率之间的关系来实现更高效的压缩。
算法步骤包括初始化、更新区间、规范化和输出。
二、字典编码2.1 概述字典编码是一种基于预定义字典的数据压缩技术,它通过将输入序列中的重复片段替换为短的符号来实现数据压缩。
字典编码可分为静态字典编码和动态字典编码两种。
2.2 静态字典编码静态字典编码是一种在压缩前已经构建好固定字典的数据压缩技术,它可以通过查找表来实现快速的解压。
LZ77和LZ78是两种经典的静态字典编码算法。
2.3 动态字典编码动态字典编码是一种在压缩时动态构建字典的数据压缩技术,它可以根据输入序列中出现的模式来不断更新和扩展字典。
LZW是一种经典的动态字典编码算法。
三、算术编码3.1 概述算术编码是一种将符号序列映射到一个区间上的无损数据压缩技术,它利用了符号出现概率之间的关系来实现更高效的压缩。
算法步骤包括初始化、更新区间、规范化和输出。
3.2 算法步骤(1)初始化:将区间初始化为[0,1),并根据符号出现概率计算每个符号对应的区间大小。
(2)更新区间:根据输入序列中的符号,将当前区间划分为多个子区间,并选择包含目标符号的子区间作为下一轮更新的区间。
(3)规范化:当区间长度小于一定阈值时,需要进行规范化操作以避免精度损失。
LZW 编码详解

为空 b
bb
d
bbd
此时已无 输入
输出结果 4H
0H 0H 1H 2H
7H 1H
BH 3H 5H
S1 NULL
a a
b
生成的新字符串及索引
S1+S2在字符表 中S1,+SS12=不S1在+S字2 符 表 S1a中+aS,2<S不61H=在>S2字=“符a” 表a中b ,<S71H=>S2=“b”
c
bc <8H>
生成新字符及索引
S2
1 NULL
NULL 2H
NULL
2a
a
a
3a
aa
0H
a
aa<4H>
4b
ab
0H
b
ab<5H>
5b
bb
1H
b
bb<6H>
6b
bb
bb
7a
bba
6H
a
bba<7H>
8a
aa
aa
9b
aab
4H
b
Aab<8H>
10 b
bb
bb
11
6H
解码步骤
1)读第一个编码code=2H,无输出 2)读code=0H,输出0H对应的 a,oldcode=code=0H 3)code=0H,输出0H对应的a,然后将 oldcode=0H所对应的字符串“a”加上 code=0H对应的字符串的第一个字 符”a”,即”aa”添加到字典中,其索引 为4H,同时oldcode=code=0H
1 NULL
NULL 2H
信息论课程设计报告(唯一可译码,lzw编码,算数编码)

1.判定唯一可译码2.LZw 编码3.算数编码一 判定唯一可译码1.任务说明输入:任意的一个码(即已知码字个数及每个具体的码字)输出:判决结果(是/不是)输入文件:in1.txt ,含至少2组码,每组的结尾为”$”符输出文件:out1.txt ,对每组码的判断结果说明:为了简化设计,可以假定码字为0,1串2.问题分析、实现原理、流程图参考算法伪代码:For all ,i j W W C ∈ doif i W 是j W 的前缀 then将相应的后缀作为一个尾随后缀放入集合0F 中End ifEnd forLoopFor all i W C ∈ doFor all j n W F ∈ doif i W 是j W 的前缀 then将相应的后缀作为一个尾随后缀放入集合1n F +中Else if j W 是i W 的前缀 then将相应的后缀作为一个尾随后缀放入集合1n F +中End ifEnd forEnd fori i F F ←If ,i i W F W C ∃∈∈ thenReturn falseElse if F 中未出现新的元素 thenReturn trueEnd if//能走到这里,说明F 中有新的元素出现,需继续End loop3.实现源码#include <iostream>#include <string>using namespace std;struct strings{char *string;struct strings *next;};struct strings Fstr, *Fh, *FP;//输出当前集合void outputstr(strings *str){do{cout<<str->string<<endl;str = str->next;}while(str);cout<<endl;}inline int MIN(int a, int b){ return a>b?b:a; }inline int MAX(int a, int b){ return a>b?a:b; }#define length_a (strlen(CP))#define length_b (strlen(tempPtr))//判断一个码是否在一个码集合中,在则返回0,不在返回1int comparing(strings *st_string,char *code){while(st_string->next){st_string=st_string->next;if(!strcmp(st_string->string,code))return 0;}return 1;}//判断两个码字是否一个是另一个的前缀,如果是则生成后缀码void houzhui(char *CP,char *tempPtr){if (!strcmp(CP,tempPtr)){cout<<"集合C和集合F中有相同码字:"<<endl<<CP<<endl<<"不是唯一可译码码组!"<<endl;exit(1);}if (!strncmp(CP, tempPtr, MIN(length_a,length_b))){struct strings *cp_temp;cp_temp=new (struct strings);cp_temp->next=NULL;cp_temp->string=new char[abs(length_a-length_b)+1];char *longstr;longstr=(length_a>length_b ? CP : tempPtr);//将长度长的码赋给longstr //取出后缀for (int k=MIN(length_a,length_b); k<MAX(length_a,length_b); k++) cp_temp->string[k - MIN(length_a,length_b)]=longstr[k];cp_temp->string[abs(length_a-length_b)]=NULL;//判断新生成的后缀码是否已在集合F里,不在则加入F集合if(comparing(Fh,cp_temp->string)){FP->next=cp_temp;FP=FP->next;}}}void main(){//功能提示和程序初始化准备cout<<"\t\t唯一可译码的判断!\n"<<endl;struct strings Cstr,*Ch, *CP,*tempPtr;Ch=&Cstr;CP=Ch;Fh=&Fstr;FP=Fh;char c[]="C :";Ch->string=new char[strlen(c)];strcpy(Ch->string, c);Ch->next=NULL;char f[]="F :";Fh->string=new char[strlen(f)];strcpy(Fh->string, f);Fh->next=NULL;//输入待检测码的个数int Cnum;cout<<"输入待检测码的个数:";cin>>Cnum;cout<<"输入待检测码"<<endl;for(int i=0; i<Cnum; i++){cout<<i+1<<" :";char tempstr[10];cin>>tempstr;CP->next=new (struct strings);CP=CP->next;CP->string=new char[strlen(tempstr)] ;strcpy(CP->string, tempstr);CP->next = NULL;}outputstr(Ch);CP=Ch;while(CP->next->next){CP=CP->next;tempPtr=CP;do{tempPtr=tempPtr->next;houzhui(CP->string,tempPtr->string);}while(tempPtr->next);}outputstr(Fh);struct strings *Fbegin,*Fend;Fend=Fh;while(1){if(Fend == FP){cout<<"是唯一可译码码组!"<<endl;exit(1);}Fbegin=Fend;Fend=FP;CP=Ch;while(CP->next){CP=CP->next;tempPtr=Fbegin;for(;;){tempPtr=tempPtr->next;houzhui(CP->string,tempPtr->string);if(tempPtr == Fend)break;}}outputstr(Fh);//输出F集合中全部元素}}4.运行结果:输入、输出及结果分析5.设计体会通过对判定唯一可译码算法的实现,我进一步了解判定唯一可译码缩的基本原理及过,体会到了其重要性,同时也锻炼了我独立分析问题以及解决问题的能力,这次课程设计让我深刻认识到了自己编程能力的不足,在以后的学习中要加强自己的编程能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8 9
10 11 12 13
107 042
109 105 10B FFF
041 107
042 109 105
AA B
BB ABC ABCA
107 108
109 10A 10B
AA AAB
BB BBA ABCA
P1=p(x1) P2=P1+p(x2)…
Pn-1=Pn-2+p(xn-1) Pn=1
算术编码具体过程
(3)如果文件中再没字符,输出当前单词W的序号, 编码过程完备.如果文件中还有字符, 把当前单 词W作为前缀 ,再从被压缩文件中读入一个字符 CH,把CH作为尾字符,得到一个单词W1. (4)在字典中查找 ,如果字典中已经有W1,则更新 当前单词,将 W1看作当前单词W,返回第 (3)步 ;如 果字典中没有W1, 先将原单词W的序号输出, 再将 新单词 W1增加到字典中 ,然后把刚刚读入的字符 CH作为当前单词W,返回第(3)步.
记忆码字 041 042 043 100 044 100 102
解码输出 A B C AB D AB CA A
字典位置 100 101 102 103 104 105 106
新单词 AB BC CA ABD DA ABC CAA
算术编码的思想
假设某离散独立信源有n个消息:x1 ,…,xn, 且对应的概率分别为:p(x1), …,p(xn). 如果将这 些概率用线段的长度来表示 ,则概率大的消息对 应长的线段, 概率小的消息对应短的线段.再将 这些线段顺序连接起来 ,其总长度必然等于1.
(1)字典初始化: 将被压缩文件中所有使用到的 单字节字符放入字典中 .为了压缩任何类型的文 件,可以将字典前 256个位置分配给计算机文件 中出现的所有256 个可能的单个字符.
(2)动态数据初始化:初始化新单词存放位置 指针P, 将它指向字典的第一个空位置; 读入被 压缩文件的第一个字符 cha, 作为待处理单词 W. 单词的前缀为空, 即Q=4095, 尾字符就是cha, 码字N 也是cha.
LZW 解码算法的例子
(5)如果在字典有码字对应的单词 ,则采用递归 算法, 输出该单词的内容.并将该单词的第一个 字符作为尾字符, 将已经记忆的前一个码字作 为前缀 ,组成一个新的单词, 写入字典, 然后记 下当前码字, 返回第(3) 步; 否则先在字典生成 新的单词,再输出这个单词, 将新单词的码字记 忆下, 再返回第(3)步.
码字 长度 1 1
3 4 4 5 7 7
码
字
1 2
3 4 5 6 7 8
1 1
0 1 1 1 0 1
0.01 0.0111
0.0111 0.01111001 0.0111111111 0.100001001101 0.100001001101
0.11 0.1001
0.001001 0.00011011 0.0001010001 0.000011110011 0.00000011110011
从而码字为1000011
4
2017/1/11
算术编码的译码原理
设码字为C, 起点为P,宽度为 A,译码过程如下 :
(1)初始化: 区间起点P =0, 区间宽度A =1; (2)计算分割点Q 的位置 ; (4)进入分割点右边的区间, 若该区间宽度小于 码字最低位的值, 则译码结束;否则译码输出码 元“1”,然后将分割点作为新的区间起点,使用 迭代公式A=A(1-p)进行计算后返回第二步;
用线段长度表示如下:
X0 (p0=0.20) P0=0 X1 (p1=0.30) P1=0.2 X2 (p2=0.35) X3 (p3=0.15) P4=1
算术具体编码
[编码] 由条件p3=0.15 ,P3=0.85得: I Log 2 0.15 2.737 取L=3, 将消息X3的起点 P3=0.85用二进制表示为
2017/1/11
Lz算法基本原理
信息论基础
The Basis of Information Theory
基于字典编码概论
哈夫曼编码和游程编码得到的结果是变长 码,而基于字典的编码方法得到的结果是定长 码,特别适合计算机文件的压缩和保存。此类 压缩编码方法是两位以色列研究人员在1977 年 提出来的,由于他们的名字分别为Abraham Lempel 和Jakob Ziv,所以基于字典的压缩编 码方法简称为LZ 算法。
x1 0 x2 … xn
算术编码的基本原理
由于每个消息的起点位置等于前面各个消 息的概率累积,故将它定义为累积概率Pk. 反过来, 也可以由累积概率来计算某个消 息的概率:pk =Pk-Pk-1 , 即两个相邻起点之间的 距离等于这个线段的长度. 每个消息所对应的 线段从起点开始, 到下一个线段的起点为此, 但 不包含下一个线段的起点, 即消息 Xk的对应区 间为[Pk-1,Pk). 任意选择一个小数 ,它必然落在某个消息 对应的线段上这说明, 可以用一个具有大小概 念的小数来表示某个消息, 这就是算术编码的 基本出发点.
无 无 无 100 无 无 100 无 102 无 无
A B C
041 042 043
100 101 102
AB BC CA
13 14 15 16
AA B
107 042
108 109
AAB BB
ABCABDABCAAAABBBABACBCA
用LZW 算法,具体编码过程如下表 .
3 4 5 6 7 8 9 10 11
接着上面例1 编码后的解码, 在实际解码过 程中, 每次读入三个字节,分解为两个码字. 假设有一个压缩文件,其内容为: 041 042 043 100 102 041 107 042 109 105 10B FFF
2
2017/1/11
步
骤 0 1 2 3 4 5 6 7
读入码字 041 042 043 100 044 100 102 041
通常序号的长度为 12比特,即 0到4095, 而 “单词”的平均长度远大于 12比特,从而达到压 缩的效果.从而达到压缩目的.
LZW 编码算法
LZW压缩编码算法如下:
由于字典的容量有限, 不可能包罗万象. 故 在LZ压缩算法中, 字典的内容直接由被压缩的 文件生成.一边编码,一边将新发现的“单词” 增加到字典中.在解码的过程中, 同样是一边解 码,一边生成字典 .故LZ 编码算法在储存压缩文 件时不需要保存字典, 是一种自适应算法. 1984年,Terry Welch对 LZ算法进行改进 , 使得所以的单词有同样的结构,推出LZW压缩编 码算法 .
二元独立信源的算术编码过程
设码元0 的概率为p,则码元1 的概率为1 -p, 编码过程如下: (1)初始化: 区间的起点 P=0,区间的宽度A= 1;
Pk Ck Pk 1
即码字 Ck必定落在消息 Xk的区间内 ,这样Ck就可 以唯一代表消息Xk . 解码过程是一个比较判断过程,只要将码字C k 和一系列的累积概率Pk 进行比较, 就可以确定 消息Xk. 因为C3 =(0.111)B=0.875,(p0 +p1+p2 )=P3 , 译码为消息X 3.
0.1 0.1
0.100 0.1000 0.1000 0.10001 0.1000011 0.1000011
(5)根据最终区间宽度A,通过2-L≤A<2-(L-1)求得 码字长度L, 然后将区间起点 P截取小数点后的L 位,剩余部分如果不为零,则进位到小数点后的 第L位, 便得到最终编码结果 .
0.1000010111000011 0.0000001011011001
读入 字符 A B B B A B C A B C A 无
查找 对象 AA AAB BB BB BBA AB ABC ABCA AB ABC ABCA
查找 结果 107 无 无 109 无 100 105 无 ቤተ መጻሕፍቲ ባይዱ00 105 10B
编码输出
内容 码字
字典扩充
位置 新单词
AB BC CA AB ABD DA AB ABC CA CAA AA
读入 字符 A B C A B D A B C A A A
查找 对象
查找 结果
编码输出 内容 码字
字典扩充 位置 新单词 步骤 前缀 12 FFF 041 FFF FFF 042 FFF 041 100 FFF 041 100 105
当 前 单 词
尾字符 A A B B B A B C A B C A 码字 041 107 042 042 109 041 100 105 041 100 105 10B
主题 No5 :基于字典编码和算术编码
计算机文件是以字节为单位组成的,每个 字节的取值从0到 255(2 8=256). 把每个字节都 看成一个“字符”,我们再把连续的若干个 “字符”看成一个“单词”将全部“单词”组 合起来就成为“字典” . 只要知道某个“单词”在字典中的位置 (即 序号), 就可以知道这个“单词”的内容,“单词” 的序号和“单词”的内容存在一一对应的关系. 我们将计算机文件按“单词”进行分割,然后用 “单词”在字典中的序号取代“单词”的内容, 就可以得到全部由序号组成的编码结果.
1
2017/1/11
LZW 编码算法的例子
例1 设有一文件内容为
当 前 单 词 步骤 前缀 0 1 2 FFF FFF FFF FFF 041 FFF FFF 041 FFF 043 FFF A B C A B D A B C A A 041 042 043 041 100 044 041 100 043 102 041 尾字符 码字
P3 0.85D 0.11011001B
故C 3 =(0.111)B
P2=0.5
P3=0.85
3
2017/1/11
