fluent 动网格
Fluent动网格的经典21个问题

Fluent动⽹格的经典21个问题Fluent动⽹格的经典21个问题弹簧近似光滑模型(spring-based smoothing)、动态分层模型(dynamiclayering)和局部重划模型(local remeshing)。
6.在Fluent中,弹簧近似光滑模型的使⽤范围是什么?原则上弹簧光顺模型可以⽤于任何⼀种⽹格体系,但是在⾮四⾯体⽹格区域(⼆维⾮三⾓形),最好在满⾜下列条件时使⽤弹簧光顺⽅法:(1)移动为单⽅向。
(2)移动⽅向垂直于边界。
如果两个条件不满⾜,可能使⽹格畸变率增⼤。
另外,在系统缺省设置中,只有四⾯体⽹格(三维)和三⾓形⽹格(⼆维)可以使⽤弹簧光顺法,如果想在其他⽹格类型中激活该模型,需要在dynamic-mesh-menu下使⽤⽂字命令spring-on-all-shapes?,然后激活该选项即可。
7.在Fluent中,动态分层模型的应⽤有什么限制?(1)与运动边界相邻的⽹格必须为楔形或者六⾯体(⼆维四边形)⽹格。
(2)在滑动⽹格交界⾯以外的区域,⽹格必须被单⾯⽹格区域包围。
(3)如果⽹格周围区域中有双侧壁⾯区域,则必须⾸先将壁⾯和阴影区分割开,再⽤滑动交界⾯将⼆者耦合起来。
(4)如果动态⽹格附近包含周期性区域,则只能⽤FLUENT的串⾏版求解,但是如果周期性区域被设置为周期性⾮正则交界⾯,则可以⽤FLUENT的并⾏版求解。
8.在Fluent中,应⽤局部⽹格重划模型应注意什么事项?局部⽹格重划模型仅能⽤于四⾯体⽹格和三⾓形⽹格。
在定义了动边界⾯以后,如果在动边界⾯附近同时定义了局部重划模型,则动边界上的表⾯⽹格必须满⾜下列条件:(1)需要进⾏局部调整的表⾯⽹格是三⾓形(三维)或直线(⼆维)。
(2)将被重新划分的⾯⽹格单元必须紧邻动⽹格节点。
(3)表⾯⽹格单元必须处于同⼀个⾯上并构成⼀个循环。
(4)被调整单元不能是对称⾯(线)或正则周期性边界的⼀部分。
9.在Fluent中,动⽹格更新⽅法应该根据什么来选择?通常来讲,在⼀个case中,我们使⽤的更新⽅法都是根据⽹格类型以及和要实现的运动来选择的,很多时候都是⼏种更新⽅法搭配起来使⽤的。
Fluent动网格系列篇

不一样那就要另外计算了。 3)这里首先,你已经会怎么会使用fluent计算颗粒在流场中 的运动轨迹了,然后,你跟踪某一个颗粒,观察这个颗粒是 否到达壁面,然后用plot看是否能输出这个颗粒的运动轨迹 ,最后可以根据运动轨迹,确定你需要的坐标位置的速度分
布。
4)关于碰撞角度,这个就困难了,再思考,能否借用fluent 里面现有的参数进行计算。 个人的看法,仅供交流,如有不妥,请多包涵。
7.Fluent软件知多少 Fluent软件经典问题汇总
8.FLUENT动网格专题讨论
9.FLUENT News—Dynamic Mesh.pdf
பைடு நூலகம்10.包含运动边界的多体非定常流场数值模拟方法研究
气温度么?希望大家帮忙解惑,这个问题困扰我好久了
A:这个是不是只设好壁面初始温度,选好壁面材料参数,模 型里都有默认的导热系数吧。如果考虑室外空气对流的影响 ,我觉得就把壁面做出来,把室外的壁面作为模型边界。输
入温度和传热系数属于传热学的第三类边界条件,这样应该
就清楚了不是,温度就是室外空气的温度,或者说是自由流 体的温度对流换热系数指的是壁面和外面的自由流体发生对 流换热时,那个对流换热系数,用这个条件的时候,要输入 壁面的厚度,其实就是间接地算了一次热传导。
A:不同初始化条件下,每次迭代的截断误差可能不同,致使
最终的结果存在不一致性,但一般的话,只要误差没有超过
5%,都还是可以接受的。迭代了多少次?如果迭代次数过少 会进入伪收敛。收敛的标准不仅仅是残差,还要看迭代次数 以及守恒量守恒等指标。
8.急求fluent第二类边界条件的UDF:边界条件如下 u为x方向速度分量,我用的是速度入口,和压力出口,上述 边界条件应该如何UDF?
Fluent_动网格总结

0.3
Maximum Length Scale
1.4
Maximum Cell Skewness
0.7
Size Remeshing Interval
5
结论:(2)(3)中 Minimum Length Scale 和 Maximum Length Scale 差距过大,导致新生成 网格的长细比大,看上去质量应不高。(4)(5)(6)中的网格同差,但比(2)(3)强一点。 由于尺度差距较大,很难设置的好,除非全局网格都画小。否则 Max/Min 大了后,网格质 量不会好的哪里去。sizing function 应该可以解决这个问题。以(4)的参数作为基本参数,进 行 sizing function 参数设置的分析。
Value 0.3 1.4 0.7 5 3 1 0.3
网格质量明显变好,但无关网格也发生了变化,物体周围的局部网格也令人满意。
江之上制作
7
(8)
Parameter Minimum Length Scale Maximum Length Scale Maximum Cell Skewness Size Remeshing Interval
Resolution Variation(a) Rate(beta)
Value 0.3 1.4 0.7 5 10 1 0.3
不知道怎么回事,远处的网格不变了。附近的网格(全局图中)密了一些。
(9)
Parameter
Value
Minimum Length Scale
0.3
Maximum Length Scale
江之上制作
8
Parameter Minimum Length Scale Maximum Length Scale Maximum Cell Skewness Size Remeshing Interval
Fluent 动网格实例具体操作步骤

目录实例:Profile定义运动 (2)I、参数说明 (2)II、操作步骤 (3)一、将计算域离散为网格 (3)二、Fluent操作步骤 (4)1.启动Fluent 14.5求解器 (4)2.初始设置 (4)3.选择湍流模型 (5)4.设置流体物性 (6)5.设置边界条件 (7)6.动网格设置 (8)7.设置其它选项 (12)在Fluent中,动网格模型可以用来模拟由于流域边界运动引起流域形状随时间变化的流动情况,动网格在求解过程中计算网格要重构,例如汽车发动机中的气缸运动、阀门的开启与关闭、机翼的运动、飞机投弹等等。
CFD中的动网格大体分为两类:(1)显式规定的网格节点速度。
配合瞬态时间,即可很方便的得出位移。
当然一些求解器(如FLUENT)也支持稳态动网格,这时候可以直接指定节点位移。
(2)网格节点速度是通过求解得到的。
如6DOF模型基本上都属于此类。
用户将力换算成加速度,然后将其积分成速度。
在Fluent中,动网格涉及的内容包括:(1)运动的定义。
主要是PROFILE文件与UDF中的动网格宏。
(2)网格更新。
FLUENT中关于网格更新方法有三种:网格光顺、动态层、网格重构。
需要详细了解这些网格更新方法的运作机理,每个参数所代表的具体含义及设置方法,每种方法的适用范围。
动网格的最在挑战来自于网格更新后的质量,避免负体积是动网格调试的主要目标。
在避免负网格的同时,努力提高运动更新后的网格质量。
拉格朗日网格(固体有限元计算)网格欧拉网格(流体计算)实例:Profile定义运动I、参数说明本次实例采用的场景来自于流体中高速飞行的物体。
如子弹、火箭、导弹等。
这里只是为了说明profile在动网格运动定义中的应用,因此为了计算方便不考虑高速问题。
问题描述如下图所示:图 1 (1为运动刚体,2为计算域)图2计算说明:由于不考虑也没办法考虑刚体的变形,因此在构建面域的时候,将1中的部分通过布尔运算去除。
计算域总长度300mm,其中固体运动最大位移为:300-40-30-6mm=224mm。
Fluent动网格系列篇

A:求解uds不,求解选specified flux就行了。一般来说速度
的第二类边界条件不用特别设置吧
Q:边界条件设置UDS菜单的中,编号为0的标量方程应该是自 定义的第一个标量方程还是动量方程?动量方程的flux在哪 里设置呢?如果需要求解一个自定义的标量方程,那么第二 类边界条件如何编写UDF?还有一个问题,flux给定的是对x 的偏导还是对y的偏导?
散,各位有木有碰到这种情况的?
A:VOF法比较容易发散,且引起发散的原因很多。 1.调小点时间步长、松弛因子。 2、检查求解格式 3、检查网格
4、检查边界条件
2.Fluent风扇用fan模型计算知道PQ曲线 :大家好,在fluent, 没有风扇的结构尺寸,但是厂家给了风扇的PQ曲线,想利用 fluent的Fan模型,设置了PQ曲线,但是计算的流量为0之类
到边界运动的流体力学的问题都可以解决。
咨讯: 1.FLUENT动网格系列:公转&自转
2.FLUENT动网格系列:System Coupling流固耦合
3.FLUENT动网格系列:区域运动
问答:
1.使用vof功能时,为什么经常会发散?无论是结构网格还是非
结构网格,使用vof功能时,基于压力的求解器下,很容易发
却。我在 Gambit中已经把网格划分完毕,先划十节圆柱形电
池,然后通过布尔操作把电池和风扇减去,最后划分剩下的 部分。由于电池在充放电时需要发热,所以需要 给电池加载 生热率,我以前用ANSYS可以直接添加生热率,但是不知道 Fluent该如何处理,网上有人说使用UDF,但是大约看了一下 UDF的介绍,也还不太清楚。有哪位.pdf 网格与CFD求解精度的关系,Fluent公司工程师崔凯的文章。 曾经想整理出版,但是他自己找不到原稿了,翻箱底我竟然 找到了,哈哈哈,分享给需要者。
【ANSYS Fluent培训】15-动网格分析

性 表面运动表现出CFD计算中的压力和反作用力 重力和其它力可以加入力的平衡
3.动网格更新方法
Smoothing (弹性光顺) Local Remeshing (几何重构) Layering (铺层法) 混合使用
3.动网格更新方法
Smoothing (弹性光顺)
网格的移动就像相连的弹簧,或者是海绵 连通性并没有改变 当使用独立网格形式时,受相关最小变形的限
Split Factor(分割因子)
Collapse Factor(合并因子)
式中 h min为单元的最小高度,h0 为理想单元高度, a s 为层的 分割因子,在满足上述条件的情况下,就可以对网格单元进行分 割。 式中 a c 为合并因子,在紧邻动边界的网格层高度满足这个条件 时,则将这一层网格与外面一层网格相合并。
弹性系数等于1 时
3.动网格更新方法
Boundary Node Relaxation(边界点松弛因子) 边界点松弛因子用于控制动边界上网格点的移动。当这个值为零时,边界节
点不发生移动;在这个值为1 时,则边界节点的移动计算中不采用松弛格式。在 大多数情况下,这个值应该取为0 到1 之间的一个值,以保证边界节点以合适的 移动量发生移动 Convergence Tolerance(收敛判据) 收敛判据就是网格节点移动计算中,迭代计算的判据 Number of Iterations(迭代次数) 迭代次数是指网格节点移动计算的最大迭代次数
fluent动网格

题记:在学习使用Fluent的时候,有不少朋友需要使用动网格模型(Dynamic Mesh Model),因此,本版推出这个专题,进行大讨论,使大家在使用动网格时尽量少走弯路,更快更好地掌握;也欢迎使用过的版友积极参与讨论指导,谢谢!该专题主要包括以下的主要内容:##1.动网格的相关知识介绍;##2.以NACA0012翼型俯仰振荡实例进行讲解动网格的应用过程;##3. 与动网格应用有关的参考文献;##4. 使用动网格进行计算的一些例子。
##1.动网格的相关知识介绍有关动网格基础方面的东西,请具体参考FLUENT User’s Guide或FLUENT全攻略的相关章节,这里只给出一些提要性的知识要点。
1、简介动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。
边界的运动形式可以是预先定义的运动,即可以在计算前指定其速度或角速度;也可以是预先未做定义的运动,即边界的运动要由前一步的计算结果决定。
网格的更新过程由FLUENT 根据每个迭代步中边界的变化情况自动完成。
在使用动网格模型时,必须首先定义初始网格、边界运动的方式并指定参予运动的区域。
可以用边界型函数或者UDF 定义边界的运动方式。
FLUENT 要求将运动的描述定义在网格面或网格区域上。
如果流场中包含运动与不运动两种区域,则需要将它们组合在初始网格中以对它们进行识别。
那些由于周围区域运动而发生变形的区域必须被组合到各自的初始网格区域中。
不同区域之间的网格不必是正则的,可以在模型设置中用FLUENT软件提供的非正则或者滑动界面功能将各区域连接起来。
注:一般来讲,在Fluent中使用动网格,基本上都要使用到UDF,所以你最好具备一定的C 语言编程基础。
2、动网格更新方法动网格计算中网格的动态变化过程可以用三种模型进行计算,即弹簧近似光滑模型(spring-based smoothing)、动态分层模型(dynamic layering)和局部重划模型(local remeshing)。
Fluent中的动网格

Fluent中的动网格动网格是目前求解计算域变化问题的常用方法。
参考Fluent帮助,可以知道动网格技术与一般流动计算设置的主要区别在于网格更新方法和更新域设置。
这里就这两方面问题的一点体会作一简单记录。
一、网格更新方法弹簧近似光滑法将任意两网格节点之间的连线理想地看成一条弹簧,并通过近似弹簧的压缩或拉伸实现网格和计算域的改变。
该方法网格拓扑不变,无需网格的插值处理,对结构化(四边形、六面体)和非结构化(三角形、四面体)网格同样适用。
但不适合于大变形情况,当计算区域变形较大时,变形后的网格质量变差,严重影响计算精度。
动态分层法在运动边界相邻处根据运动规律动态增加或减少网格层数,以此来更新变形区域的网格。
该方法适用于结构化网格,通过设置适当的分层和缩减系数,更新后的网格依然为较为均匀的结构化网格,对计算精度影响较小。
对于运动域具有多自由度和任意变形情况,该方法处理起来非常困难。
网格重生方法在整个网格更新区域内依据设定的最大和最小网格尺寸判断需要进行网格重生的网格,并依据设置的更新频率进行网格重生处理。
该方法适用于非结构化网格,能够较好的应用于任意变形的计算区域处理。
二、更新域设置更新域设置是动网格设置中的一项重要工作,最常用的设置是刚体运动域和变形域,这里针对这两种域的设置注意事项和技巧作一简单介绍。
1、域动网格一般来讲,设置为刚体运动域的区域一般为壁面类边界,通过设置固壁的运动,模拟计算域内物体的运动。
由于固壁边界有时形状较为复杂,壁面附近网格尺度与周围网格尺度存在较大差别,网格更新时变形较大。
在这种情况下,可以设置一个包含固壁运动边界的计算域,通过该计算域的整体运动模拟域内物体的运动,在有的地方将这种方法称为域动网格法。
在域动网格法中,需要设置包含运动物体的内部计算域、内部计算域界面均为刚体运动域。
如下图所示。
2、动态分层法中的分界面在应用动态分层网格更新方法时,当分层界面在计算域内部时,需要采用Split interface(这里称分界面)将运动域运动范围与固定计算域区分开来,以保证动态分层网格处理(如果运动域网格与固定域网格没有分界面,动态分层无法执行)。
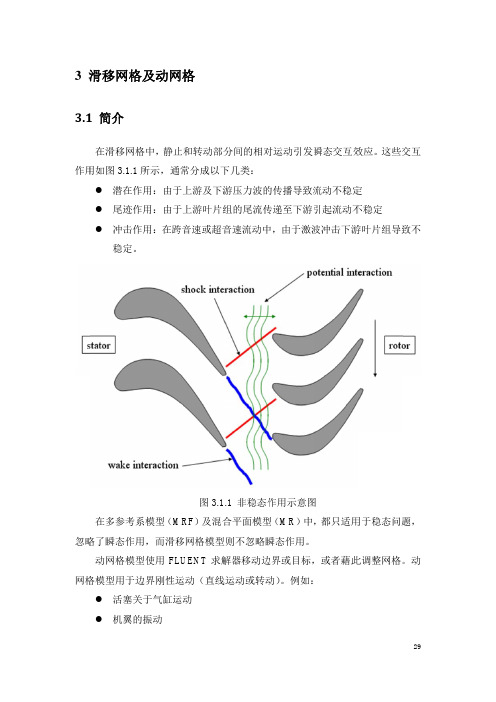
Fluent理论手册3—滑移网格及动网格理论
− 转捩模型
4.7:SST 转捩模型 4.8: − 模型
4.9:雷诺应力模型(RSM) 4.10:分离涡模型(DES) 4.11:大涡模拟模型(LES) 4.12:壁面边界湍流流动的近壁处理
更多关于 ANSYS FLUENT 中湍流模拟的资料, 可以查看用户手册第 12 章: 湍流模拟。
4.1 简介
例如仅有转子作用时如图态近似感兴时必须采动参考系问题也就是说周瞬态类型包子使用旋图322兴趣则可以31采用周期包括旋转323以使32要在位置要使32直线滑移网滑移网格在计算开始一个计算区成网格分在计算中图324分界面上使用瞬态分网格分网格交界线327图322转子网格技术格技术使用两始前将网格文域与其相邻分界的形式一个计算及325上网格并不需分析
湍流流动通过速度场波动进行表征。这些脉动混合诸于动量、能量及组分浓 度等标量方程, 引起传输量的脉动。 由于这些脉动存在于小尺度, 且频率非常高, 因此对其进行直接模拟非常消耗计算资源。
37
图 3.2. .8 3D 圆锥网格交界面 面 对于轴向转子/定子结构,转动 动及静止部 部分对齐于轴 轴线,分界 界面可能为平 平面 形。此面为 为垂直于沿着 着静子至转 转子的旋转轴 轴向的横截 截面。 扇形
33
图 3.2.9 9 3D 平面扇 扇形网格界面 面
3.2.3 滑移网 网格概念
如 3.2 节: :滑移网格 格理论中所讨 讨论,滑移 移网格模型允 允许相邻网 网格相对于其 其他 网格 格滑动。在这 这种情况下 下,网格面不 不需要在网 网格分界面上 上对齐。这 这种条件需要 要对 穿过 过两个非保 保角区域分界 界面的通量 量进行计算。 更多的关于 于 ANSYS FLUENT 中非 中 保角 角界面信息,查看用户 户手册 6.4 节 节:非保角 角网格。
FLUENT动网格技术简介

FLUENT动网格简介在固体有限元计算中,网格运动实非什么稀奇事儿。
而且在绝多数固体计算的基本物理量是网格的节点位移,所以,固体计算中,网格节点运动是对的,没有运动反而不正常了。
也可以这么说:正因为计算域内部节点间的相对运动,才导致了内应力的产生。
流体计算与固体完全不同。
其根源在于它们使用的网格类型不同。
当前固体有限元计算采用的是拉格朗日网格,而流体计算则大多数采用的欧拉网格。
如果说把拉格朗日网格中的节点点看作是真实世界的物质原子的话,那么欧拉网格的节点则好比是真实世界中的一个个传感器,它们总是呆在相同的位置,真实的记录着各自位置上的物理量。
正常情况下,欧拉网格系统是这样的:计算域和节点保持位置不变,发生变化的是物理量,网格节点就像一个个布置在计算域中的传感器,记录该位置上的物理量。
这其实是由流体力学研究方法所决定的。
宏观与微观的差异决定了固体力学计算采用拉格朗日网格,流体计算采用欧拉网格。
关于这部分的详细解说,可以参阅任何一本计算流体动力学书籍。
世界是公平的。
有利必有弊。
朗格朗日网格适合计算节点位移,然而对于过大的网格变形却难以处理。
欧拉网格生来可以处理大变形(因为节点不动),然而对于对于节点运动的处理,则是其直接软肋。
然而很不幸的是,现实生活中有太多网格边界运动的实例。
如汽车发动机中的气缸运动、阀门开启与关闭、机翼的运动、飞机投弹等等等等举不胜举。
计算流体动力学计算的基本物理量通常为:速度、温度、压力、组分。
并不计算网格节点位移。
因此要让网格产生运动,通常给节点施加的物理约束是速度。
CFD中的动网格大体分为两类:(1)显式规定的网格节点速度。
配合瞬态时间,即可很方便的得出位移。
当然一些求解器(如FLUENT)也支持稳态动网格,这时候可以直接指定节点位移。
(2)网格节点速度是通过求解得到的。
如6DOF模型基本上都属于此类。
用户将力换算成加速度,然后将其积分成速度。
对于第一类动网格问题,在fluent中通常可以使用profile与UDF进行网格设置,通过规定节点或区域的速度、角速度或位移等方式来显式确定网格的运动,通常大部分的动网格问题都归于此类。
Fluent学习资料教程集锦15-Fluent_动网格

– 当轴向流问题在出口处有旋转时,可以选择径向平衡选项( radial equilibrium
assumption option )
• 指定的压力为中心压力
• SRF问题的其它边界条件
p
V2
– 无反射边界条件
R outlet
R
– 目标质量流出口(Target mass flow outlet)
运动区域
Introductory FLUENT Training
大纲
• 介绍和模型建立方法概览 • 单参考系 (SRF)模型 • 多重域和多参考系(MRF)模型 • 混合面模型 (MPM) • 滑移网格模型 (SMM) • 动网格 (DM) 模型 • 概要 • 附录
介绍
• 许多工程问题中流体的流域都会移动或者旋转 – 平移运动的例子:
– 绝对速度公式 (AVF)
• 由相对速度方程得到
• 绝对速度和绝对总内
能为依赖变量
z
– 动量方程中的旋转源项
stationary frame
ro
z
r
R
rotating frame
x
CFD domain
x
axis of rotation
公式比较
• 相对速度方程:x方向上动量方程
wx t
运动坐标系和动网格对比
Domain
y
运动坐标系 --域随着坐标系 转动
x
动网格
-- 域的形状是 时间函数
建模方法概览
• 单参考系 (SRF)
– 整体计算域都置于运动坐标系下。
• 多参考系 (MRF)
– 选择域中的部分区域置于运动坐标系下。 – 忽略相互作用 稳态
FLUENT中被动型动网格问题求解方案:6DOF

CAE联盟论坛精品讲座系列FLUENT中被动型动网格问题求解方案:6DOF主讲人:流沙 CAE联盟论坛—总版主利用CFD软件解决动网格问题,通常可分为以下两类:(1)主动型动网格主动型动网格问题通常指的是边界运动规律及运动状态已知,通常可由软件使用者通过函数或程序进行描述。
在程序计算过程中,求解器调用边界运动轨迹描述程序实现边界运动。
这类动网格例子很多,如各类泵、风扇等。
(2)被动型动网格还有一类动网格问题,其边界运动规律往往是未知的,常常需要通过计算边界上的力或力矩,以此来求取边界的运动。
在这类动网格计算设置中,网格变化规律难以预料,导致网格参数经常需要进行多次调整才能达到目的。
这类例子在现实中其实也很多,比如风力发电机的叶轮、水轮机等。
解决主动型动网格问题比较容易,利用CFD软件提供的动网格模拟能力很容易解决。
需要关注的地方是边界运动后,网格节点如何重新布置和生成。
如在FLUENT软件中,其动网格主要包括三种网格功能:弹簧光顺、动态层及网格重构。
利用网格重构功能几乎可以解决所有主动型动网格问题。
那被动型动网格问题怎么处理呢?一般来说,这类边界的运动都是由于内部流体对其压力所造成的,那么就涉及到力和力矩计算的问题。
对于这类问题,在FLUENT软件中可以采用6DOF 模型进行计算。
需要注意的是,以上所有类型动网格计算均建立在边界为刚性的情况下。
即不会计算由于流动产生的力的作用导致的边界变形。
若要计算边界变形,则需要采用流固耦合方法,利用固体求解器计算。
被动型动网格中的力和力矩均是压力对面的积分计算而来。
1、6DOF UDF宏在FLUENT中利用6DOF是需要定义UDF宏的。
该宏的定义形式如下:DEFINE_SDOF_PROPERTIES(name, properties, dt ,time ,dtime)函数中:Name:宏名称Real *properties:存储6DOF属性的数组Dynamic_Thread *dt:存储制定的动网格属性Real time:当前时间Real dtime:时间步长该UDF宏没有返回值。
Fluent UDF计算动网格区域的形心、转动惯量

Fluent UDF计算动网格区域的形心、转动惯量在使用动网格和重叠网格计算刚体的运动时,可能需要用到刚体的形心和三个轴的转动惯量。
一般来说,三维建模软件如Creo、SW、Spacecliam都可以直接计算出上述变量,但如果你拿到的只有一个fluent的case,阁下又该如何应对呢?1、形心(重心)对于密度均匀的物体,质心就是重心。
我们来看看质心的计算公式:\bar{x}_i=\iiint x_i\rm{d} v\\ 在fluent里, x_i 是网格三个方向的坐标,dv是网格体积。
用该公式,通过遍历网格可以很轻松地求出流体域的形心,但动网格区域都是没有网格的,所以无法直接应用上式。
观察到,虽然动网格区域没有网格,但它的边界我们是可以得到的,根据三维有界闭区域的高斯公式:\iiint\nabla\cdot \vec{F} \text{dv}=\oint \vec{F}\cdot \text d\vec{\text {S}}\\ 通过构造合适的向量场函数,形心公式可以转化为:\iiint\frac{\partial 0.5x_i^2}{\partialx_i}\text{dv}=\sum0.5x_i^2\cdot\text{d}\vec{\text{S}}\\ 应用上述环路积分可以通过遍历动网格区域的壁面就可以得到形心。
2. 转动惯量与上述思路相同,将转动惯量的体积分转化为环路积分,以Ixx为例:Ixx=\rho\iiint(y^2+z^2)\text{dv}=\text{fabs}\left(\fra c{1}{3}\rho\sum (y^3A[1]+z^3A[2])\right)\\ 其中 \rho 为你固体的材料密度,A为网格面的面积向量,可由以下宏得到:最后得到值是负的,因此需要加个fabs()求绝对值。
扣1送源代码。
Fluent动网格

Fluent动网格----layering个一个简单实例我这几天看了点动网格技术方面的东西,在学习过程中发现这方面的例子很少,自己也走了一些弯路。
现在还好,弄明白了一些,能够应付现在我的工作。
为了让更多学习者快速了解动网格,我打算尽量把我学习心得在这里和大家分享,这里给出一个layering的一个简单例子。
1.Gambit画网格本例很简单,在Gambit里画一个10*10的矩形,网格间隔为1,也就是有100个网格,具体见下图。
都学动网格的人了,不至于这个不会做!这里需要注意一个问题:设置边界条件的时候,一定要把要移动的边单独设定,本例中一右边界作为移动的边,设成wall就可以,这里再后面需要制定。
2.编写UDF#include "udf.h"#include "unsteady.h"#include "stdio.h"#include "stdlib.h" /************************************************************/real current_time = 0.0 ;Domain * domain ;Thread * thread ;real NV_VEC( origin ),NV_VEC( force ),NV_VEC( moment ) ;/************************************************************/DEFINE_CG_MOTION(throttle,dt,vel,omega,time,dtime){current_time = CURRENT_TIME ;vel[0] = 30;Message("time=%f omega=%f\n",current_time) ; }上面这段代码就是设置x轴方向的速度为30米每秒(UDF默认是SI单位制)。
FLUENT动网格需要的常用宏

FLUENT动网格需要的常用宏虽然瞬态PROFILE文件可以在一定程度上定义网格运动,然而其存在着一些缺陷。
最主要的一些缺陷存在于以下一些方面:(1)PROFILE无法精确的定义连续的运动。
其使用离散的点值进行插值。
如果想获得较为精确的运动定义,势必要定义很多点。
(2)一些情况下无法使用profile。
比如稳态动网格。
在FLUENT中定义网格运动,更多的是采用UDF宏。
fluent中与动网格有关的UDF 宏一共有5个,其中四个用于常规的网格运动定义,一个用于6DOF模型。
这些宏分别为:DEFINE_CG_MOTION、DEFINE_DYNAMIC_ZONE_PROPERTY、DEFINE_GEOM、DEFINE_GRID_MOTION、DEFINE_SDOF_PROPERTIES注意:动网格宏只能为编译型UDF。
1、DEFINE_CG_MOTION最常用的运动网格宏。
用户可以使用该宏定义每一时间步上的线速度或角速度来指定fluent中某一特定区域的运动。
DEFINE_CG_MOTION(name,de,vel,omega,time,dtime)参数说明:name:UDF的名字。
体现在fluent中表现为可选择的函数列表。
Dynamic_Thread *dt:存储了用户所指定的动网格属性和结构指针。
real vel[]:线速度。
vel[0]为x方向速度,vel[1]为y方向速度,vel[2]为z 方向速度real omega[]:角速度。
与线速度定义相同。
real time:当前时间。
real dtime:时间步长。
函数返回值为:void从函数的参数类型,配合c语言的参数调用方式可知,vel,omega为数值类型,属于传入类型。
因此只需在函数体中显式定义vel与omega即可将速度传入fluent求解器。
time与dtime是用于定义速度的。
详细实例可参看fluent udf 文档p182。
2、DEFINE_DYNAMIC_ZONE_PROPERTY该宏能用于以下一些场合:(1)在in-cylinder应用中定义旋转中心。
Fluent动网格【3】:DEFINE_CG_MOTION宏

Fluent动⽹格【3】:DEFINE_CG_MOTION宏除了利⽤Profile进⾏运动指定之外,Fluent中还可以使⽤UDF宏来指定部件的运动。
其中⽤于运动指定的宏主要有三个:DEFINE_CG_MOTIONDEFINE_GEOMDEFINE_GRID_MOTION今天主要看第⼀个UDF宏DEFINE_CG_MOTION。
⽤途DEFINE_CG_MOTION宏主要⽤于描述刚体的运动。
所谓“刚体”,指的是在运动过程中部件⼏何形状不会发⽣任何改变,只是其质⼼位置发⽣改变。
在定义刚体的运动时,通常以速度⽅式进⾏显式定义。
形式DEFINE_CG_MOTION宏的结构很简单。
DEFINE_CG_MOTION(name,dt,vel,omega,time,dtime)其中:name:为宏的名称,可以随意定义dt:⼀个指针Dynamic_Thread *dt,存储动⽹格属性,通常不需要⽤户⼲预。
vel:平动速度,为⼀个数组,其中vel[0]为x⽅向速度,vel[1]为y⽅向速度,vel[2]为z⽅向速度。
omega:转动速度,omega[0]为x⽅向⾓速度,omega[1]为y⽅向⾓速度,omega[2]为z⽅向⾓速度。
time:当前时间。
dtime:时间步长。
实例实例1:利⽤DEFINE_CG_MOTION宏定义速度:u x=2sin(3t)可以写成:#include "udf.h"DEFINE_CG_MOTION(velocity,dt,vel,omega,time,dtime){vel[0] = 2* sin(3*time);}很简单,对不对?再来个复杂点的例⼦。
实例2:已知作⽤在部件上的⼒F,计算部件在⼒F作⽤下的运动。
可以采⽤⽜顿第⼆定律:∫t t0dv=∫t t(F/m)dt则速度可写为:v t=v t−Δt+(F/m)Δt 可写UDF宏为:/************************************************************* 1-degree of freedom equation of motion (x-direction)* compiled UDF************************************************************/#include "udf.h"static real v_prev = 0.0;static real time_prev = 0.0;DEFINE_CG_MOTION(piston,dt,vel,omega,time,dtime){Thread *t;face_t f;real NV_VEC(A);real force_x, dv;/* reset velocities */NV_S(vel, =, 0.0);NV_S(omega, =, 0.0);if (!Data_Valid_P())return;/* get the thread pointer for which this motion is defined */t = DT_THREAD(dt);/* compute pressure force on body by looping through all faces */force_x = 0.0;begin_f_loop(f,t){F_AREA(A,f,t);force_x += F_P(f,t) * A[0];}end_f_loop(f,t)/* compute change in velocity, dv = F*dt/mass */dv = dtime * force_x / 50.0;/* motion UDFs can be called multiple times and should not causefalse velocity updates */if (time > (time_prev + EPSILON)){v_prev += dv;time_prev = time;}Message("time = %f, x_vel = %f, x_force = %f\n", time, v_prev, force_x); /* set x-component of velocity */vel[0] = v_prev;}Processing math: 100%。
fluent 动网格

Remeshing方法中的一些参数设定:Remeshing中的参数Minimum length scale和Maximum Length Scale,这两个参数你可以参考mesh scale info中的值,仅是参考,因为mesh scale info中的值是整个网格的评价值,设置的时候看一下动网格附近的网格和整个网格区域的大小比较,然后确定这两个参数,一般来讲,动网格附近的网格较密,这些值都比整体的小,所以在设置时通常设置为比mesh scale info中的Minimum length scale大一点,比Maximum Length Scale小一点。
以上是一般来讲的设置思路。
下面是我在NACA0012翼型动网格例子中的设置:Remeshing中的参数设定:为了得到较好的网格更新,本例在使用局部网格重新划分方法时,使用尺寸函数,也就是Remeshing+Must Improve Skewness+Size Function的策略。
将Minimum Length Scale及Maximum Length Scale均设置为0,为了使所有的区域都被标记重新划分;Maximum Cell Skewness(最大单元畸变),参考Mesh Scale Info…中的参考值0.51,将其设定为0。
4,以保证更新后的单元质量;Size Remesh Interval(依照尺寸标准重新划分的间隔),将这个值设定为1,在FLUENT,不满足最大网格畸变的网格在每个时间步都会被标记,而后重新划分,而不满足最小,最大及尺寸函数的网格,只有在Current Time=(Size Remesh Interval)*delta t的时候,才根据这些尺寸的标准标记不合格的单元进行重新划分,为了保证每步的更新质量,将其修改为1,就是每个时间都根据尺寸的标准标记及更新网格.Size Function Resolution(尺寸函数分辨率),保持默认的3;Size Function Variation(尺寸函数变量):建议使用一个小值,在0.1到0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Remeshing方法中的一些参数设定:Remeshing中的参数Minimum length scale和Maximum Length Scale,这两个参数你可以参考mesh scale info中的值,仅是参考,因为mesh scale info中的值是整个网格的评价值,设置的时候看一下动网格附近的网格和整个网格区域的大小比较,然后确定这两个参数,一般来讲,动网格附近的网格较密,这些值都比整体的小,所以在设置时通常设置为比mesh scale info中的Minimum length scale大一点,比Maximum Length Scale小一点。
以上是一般来讲的设置思路。
下面是我在NACA0012翼型动网格例子中的设置:Remeshing中的参数设定:为了得到较好的网格更新,本例在使用局部网格重新划分方法时,使用尺寸函数,也就是Remeshing+Must Improve Skewness+Size Function的策略。
将Minimum Length Scale及Maximum Length Scale均设置为0,为了使所有的区域都被标记重新划分;Maximum Cell Skewness(最大单元畸变),参考Mesh Scale Info…中的参考值0.51,将其设定为0。
4,以保证更新后的单元质量;Size Remesh Interval(依照尺寸标准重新划分的间隔),将这个值设定为1,在FLUENT,不满足最大网格畸变的网格在每个时间步都会被标记,而后重新划分,而不满足最小,最大及尺寸函数的网格,只有在Current Time=(Size Remesh Interval)*delta t的时候,才根据这些尺寸的标准标记不合格的单元进行重新划分,为了保证每步的更新质量,将其修改为1,就是每个时间都根据尺寸的标准标记及更新网格.Size Function Resolution(尺寸函数分辨率),保持默认的3;Size Function Variation(尺寸函数变量):建议使用一个小值,在0.1到0。
5之间,本例将其设置为0.3;Size Function Rate(尺寸函数变化率),保持默认的0.3。
动网格(dynamic mesh)是CFD中专有的概念。
由于当前流体计算多采用欧拉坐标系,该坐标系区别于拉格朗日坐标系的一个最直观特点是:计算过程中网格保持静止.因此,在CFD计算中应用动网格,具有其特别的难处。
1、动网格控制方式最主要的困难在于边界运动后的网格质量控制。
由于边界的运动,不可避免的导致网格变形。
我们知道,求解器对于网格质量的容忍是有限度的。
当网格扭曲过大引起网格质量的急剧下降,可能导致计算发散、形成负网格,进而终止计算。
因此,在边界运动过程中,对网格质量进行控制尤为重要。
在fluent软件中动网格主要有三种控制方式:smoothing,layering,remeshing.其中layering主要应用与四边形网格及六面体网格,remeshing主要应用于三角形网格及四面体网格等费结构网格中,至于smoothing方法则在各类网格中均可应用。
layering方法应用于结构网格也是有条件限制的:边界运动最好是沿着某单一方向。
如若是旋转,最好还是采用非结构网格配合remeshing方式。
非结构网格是最适合应用动网格模型的,但是网格质量不好控制,通常需要仔细调节。
结构网格采用layering 方法,能够很好的控制网格质量,但是几何适应性差。
具体采用何种网格类型以及何种控制方式,还是要从实际的模拟模型来考虑。
2、运动控制方式边界的运动控制方式主要有两种:PROFILE文件与UDF.采用profile的方式是最简单的,存在的限制也比较多.首先profile主要是采用线性插值的方式,如果速度是关于时间的高阶幂函数,则难以采用此种方式。
另外,采用profile定义边界的运动方式,最主要的是指定边界的运动速度,对于其他的涉及到力的转换的,比如说6DOF模型中经常用到的将受力转换为加速度再换算成速度的话,基本上无能为力。
最常见的profile文件格式如下:((vel 2 point)(time 0 0。
1)(v_x 0 1))这里定义了一个两点格式,在0s时刻速度为0,0。
1s时刻速度为1,中间时刻速度采用线性插值获得。
注意profile中统一采用国际单位制.关于速度v_x,v_y,v_z分别表示x,y,z三方向平动速度,omega_x,omega_y,omega_z表示x,y,z三方向转动速度。
至于UDF方式定义运动,最主要的还是采用DEFINE_CG_MOTION宏,注意此UDF宏只能用于编译型.解释形式的虽然不会报错,但是在使用中是无效的。
应用于动网格的宏还包括DEFINE_DYNAMIC_ZONE_PROPERTY,DEFINE_GEOM,DEFINE_GRID_MOTION,DEFINE_SDOF_PROPERTIES,各宏的详细用法,可以参阅UDF手册第二章第六小节,里面包含了宏中的参数以及各类例子。
3、应用动网格的时机动网格其实是比较复杂的技术,想要用好不是一件容易的事情。
在使用过程中经常会出现计算发散、负网格的问题,更可能出现由于网格扭曲导致网格质量差,计算精度低的问题。
因此,对于运动问题,fluent中还是提供了很多的简化模型。
最接近动网格的是滑移网格。
滑移网格是唯一一种不改变网格而能计算瞬态的模型。
滑移网格的基本思想是将运动区域与静止区域通过滑移面进行分割,通过滑移面传递流动数据。
在运动区域中采用运动参考系的方式。
另外几类运动问题都可以归结为运动参考系的问题:SRF,MRF以及MP。
SRF与MRF的区别主要在参考系的数量上。
而MRF与MP的区别在与数据传递方式。
MRF通过交界面直接传递数据,主要是通过绝对速度的方式传递,而MP则是流量或压力平均的方式进行传递。
总之,若能够应用这些简化的模型,是不推荐采用动网格的方式的。
§一、动网格的相关知识介绍有关动网格基础方面的东西,请具体参考FLUENT User’s Guide或FLUENT全攻略的相关章节,这里只给出一些提要性的知识要点。
1、简介动网格模型可以用来模拟流场形状由于边界运动而随时间改变的问题。
边界的运动形式可以是预先定义的运动,即可以在计算前指定其速度或角速度;也可以是预先未做定义的运动,即边界的运动要由前一步的计算结果决定。
网格的更新过程由FLUENT 根据每个迭代步中边界的变化情况自动完成。
在使用动网格模型时,必须首先定义初始网格、边界运动的方式并指定参予运动的区域。
可以用边界型函数或者UDF 定义边界的运动方式.FLUENT 要求将运动的描述定义在网格面或网格区域上。
如果流场中包含运动与不运动两种区域,则需要将它们组合在初始网格中以对它们进行识别。
那些由于周围区域运动而发生变形的区域必须被组合到各自的初始网格区域中。
不同区域之间的网格不必是正则的,可以在模型设置中用FLUENT软件提供的非正则或者滑动界面功能将各区域连接起来。
注:一般来讲,在Fluent中使用动网格,基本上都要使用到UDF,所以你最好具备一定的C语言编程基础。
2、动网格更新方法动网格计算中网格的动态变化过程可以用三种模型进行计算,即弹簧近似光滑模型(spring—based smoothing)、动态分层模型(dynamic layering)和局部重划模型(local remeshing)。
弹簧近似光滑模型原则上弹簧光顺模型可以用于任何一种网格体系,但是在非四面体网格区域(二维非三角形),最好在满足下列条件时使用弹簧光顺方法:(1)移动为单方向。
(2)移动方向垂直于边界.如果两个条件不满足,可能使网格畸变率增大。
另外,在系统缺省设置中,只有四面体网格(三维)和三角形网格(二维)可以使用弹簧光顺法,如果想在其他网格类型中激活该模型,需要在dynamic—mesh—menu 下使用文字命令spring—on—all-shapes?,然后激活该选项即可。
动态分层模型动态分层模型的应用有如下限制:(1)与运动边界相邻的网格必须为楔形或者六面体(二维四边形)网格。
(2)在滑动网格交界面以外的区域,网格必须被单面网格区域包围.(3)如果网格周围区域中有双侧壁面区域,则必须首先将壁面和阴影区分割开,再用滑动交界面将二者耦合起来。
(4)如果动态网格附近包含周期性区域,则只能用FLUENT 的串行版求解,但是如果周期性区域被设置为周期性非正则交界面,则可以用FLUENT 的并行版求解。
如果移动边界为内部边界,则边界两侧的网格都将作为动态层参与计算。
如果在壁面上只有一部分是运动边界,其他部分保持静止,则只需在运动边界上应用动网格技术,但是动网格区与静止网格区之间应该用滑动网格交界面进行连接。
局部网格重划模型需要注意的是,局部网格重划模型仅能用于四面体网格和三角形网格。
在定义了动边界面以后,如果在动边界面附近同时定义了局部重划模型,则动边界上的表面网格必须满足下列条件:(1)需要进行局部调整的表面网格是三角形(三维)或直线(二维)。
(2)将被重新划分的面网格单元必须紧邻动网格节点。
(3)表面网格单元必须处于同一个面上并构成一个循环。
(4)被调整单元不能是对称面(线)或正则周期性边界的一部分.动网格的实现在FLUENT 中是由系统自动完成的。
如果在计算中设置了动边界,则FLUENT 会根据动边界附近的网格类型,自动选择动网格计算模型.如果动边界附近采用的是四面体网格(三维)或三角形网格(二维),则FLUENT 会自动选择弹簧光顺模型和局部重划模型对网格进行调整。
如果是棱柱型网格,则会自动选择动态层模型进行网格调整。
在静止网格区域则不进行网格调整.动网格问题中对于固体运动的描述,是以固体相对于重心的线速度和角速度为基本参数加以定义的。
既可以用型函数定义固体的线速度和角速度,也可以用UDF 来定义这两个参数.同时需要定义的是固体在初始时刻的位置。
注:这一小节主要讲述了动网格的更新方法,最好能掌握,尤其是各种方法的适用范围,通常来讲,在一个case中,我们使用的更新方法都是根据网格类型以及和要实现的运动来选择的,很多时候都是几种更新方法搭配起来使用的。
总结一下:使用弹簧近似光滑法网格拓扑始终不变,无需插值,保证了计算精度。
但弹簧近似光滑法不适用于大变形情况,当计算区域变形较大时,变形后的网格会产生较大的倾斜变形,从而使网格质量变差,严重影响计算精度。
动态分层法在生成网格方面具有快速的优势,同时它的应用也受到了一些限制。
它要求运动边界附近的网格为六面体或楔形,这对于复杂外形的流场区域是不适合的。
