高等数学-复旦大学出版社-课后习题答案(精品文档)
高等数学复旦大学出版社习题答案五
在总利润最大的基础上再多生产100台时,利润的增量为
ΔL(x)= .
即此时总利润减少1万元.
21.某企业投资800万元,年利率5%,按连续复利计算,求投资后20年中企业均匀收入率为200万元/年的收入总现值及该投资的投资回收期.
解:投资20年中总收入的现值为
在(3,0)处的切线是y=2x+6
两切线交点是( ,3).故所求面积为
(7)
(8)摆线x=a(tsint),y=a(1cost)的一拱(0t2)与x轴;
解:当t=0时,x=0,当t=2时,x=2a.
所以
(8)
(9)极坐标曲线ρ=asin3φ;
解:
.
(9)
(10)ρ=2acosφ;
解:
.
(10)
2.求下列各曲线所围成图形的公共部分的面积:
1.求下列各曲线所围图形的面积:
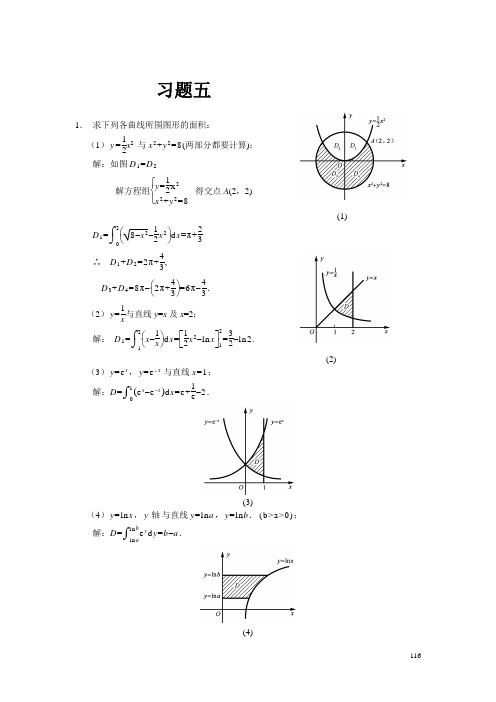
(1) 与x2+y2=8(两部分都要计算);
解:如图D1=D2
解方程组 得交点A(2,2)
(1)
∴ ,
.
(2) 与直线y=x及x=2;
解: .
(2)
(3)y=ex,y=ex与直线x=1;
解: .
(3)
(4)y=lnx,y轴与直线y=lna,y=lnb.(b>a>0);
≈0.385386万元=3853.86元.
yt′=3asin2tcost
xt′2+yt′2=9a2sin2tcos2t,利用曲线的对称性,
.
9.求对数螺线 相应θ=0到θ=φ的一段弧长.
解:
.
10.求半径为R,高为h的球冠的表面积.
高等数学上复旦第三版 课后习题答案

283高等数学上(修订版)(复旦出版社)习题六 无穷数级 答案详解1.写出下列级数的一般项: (1)1111357++++ ;(2)22242462468x x x x x ++++⋅⋅⋅⋅⋅⋅ ;(3)35793579a a a a -+-+ ;解:(1)121n U n =-; (2)()2!!2n n xU n =;(3)()211121n n n a U n ++=-+; 2.求下列级数的和: (1)()()()1111n x n x n x n ∞=+-+++∑;(2)()1221n n n n ∞=+-++∑;(3)23111555+++ ; 解:(1)()()()()()()()111111211n u x n x n x n x n x n x n x n =+-+++⎛⎫-=⎪+-++++⎝⎭284从而()()()()()()()()()()()()()()11111211212231111111211n S x x x x x x x x x n x n x n x n x x x n x n ⎛-+-= +++++++⎝⎫++-⎪+-++++⎭⎛⎫-=⎪++++⎝⎭因此()1lim 21n n S x x →∞=+,故级数的和为()121x x +(2)因为()()211n U n n n n =-+-++- 从而()()()()()()()()324332215443211211211221n S n n n n n n n n =-+-----+-++---+-++-=+-++-=+-+++所以lim 12n n S →∞=-,即级数的和为12-. (3)因为21115551115511511145n nn n S =+++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎣⎦=-⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎣⎦ 从而1lim 4n n S →∞=,即级数的和为14. 3.判定下列级数的敛散性: (1) ()11n n n ∞=+-∑;(2)()()11111661111165451n n +++++⋅⋅⋅-+ ; (3) ()23133222213333n n n --+-++- ;285(4)311115555n +++++ ; 解:(1) ()()()3212111n S n n n =+++-+--=+-从而lim n n S →∞=+∞,故级数发散. (2) 1111111115661111165451111551n S n n n ⎛⎫=-+-+-++-⎪-+⎝⎭⎛⎫=- ⎪+⎝⎭从而1lim 5n n S →∞=,故原级数收敛,其和为15. (3)此级数为23q =-的等比级数,且|q |<1,故级数收敛. (4)∵15n n U =,而lim 10n n U →∞=≠,故级数发散. 4.利用柯西审敛原理判别下列级数的敛散性:(1) ()111n n n +∞=-∑;(2)1cos 2nn nx∞=∑; (3)1111313233n n n n ∞=⎛⎫+- ⎪+++⎝⎭∑. 解:(1)当P 为偶数时,()()()()122341111112311111231111112112311n n n pn n n n p U U U n n n n pn n n n pn p n p n n p n n n +++++++++++----=++++++++-+--=++++⎛⎫⎛⎫-=----- ⎪ ⎪+-+-++++⎝⎭⎝⎭<+当P 为奇数时,286()()()()1223411111123111112311111112311n n n pn n n n p U U U n n n n pn n n n pn p n p n n n n +++++++++++----=++++++++-+-+=++++⎛⎫⎛⎫-=---- ⎪ ⎪+-++++⎝⎭⎝⎭<+因而,对于任何自然数P ,都有12111n n n p U U U n n++++++<<+ , ∀ε>0,取11N ε⎡⎤=+⎢⎥⎣⎦,则当n >N 时,对任何自然数P 恒有12n n n pU U U ε++++++< 成立,由柯西审敛原理知,级数()111n n n +∞=-∑收敛. (2)对于任意自然数P ,都有()()()1212121cos cos cos 12222111222111221121112212n n n p n n n p n n n p n p n p nU U U x n p x xn n ++++++++++++++++=+++≤+++⎛⎫- ⎪⎝⎭=-⎛⎫=- ⎪⎝⎭<于是, ∀ε>0(0<ε<1),∃N =21log ε⎡⎤⎢⎥⎣⎦,当n >N 时,对任意的自然数P都有12n n n p U U U ε++++++< 成立,由柯西审敛原理知,该级数收敛. (3)取P =n ,则287()()()()()121111113113123133213223231131132161112n n n pU U U n n n n n n n n n n ++++++⎛⎫=+-+++- ⎪++++++⋅+⋅+⋅+⎝⎭≥++++⋅+≥+> 从而取0112ε=,则对任意的n ∈N ,都存在P =n 所得120n n n p U U U ε++++++> ,由柯西审敛原理知,原级数发散.5.用比较审敛法判别下列级数的敛散性. (1)()()111465735n n ++++⋅⋅++ ;(2)22212131112131nn +++++++++++ (3)1πsin 3n n ∞=∑;(4) 3112n n∞=+∑;(5)()1101nn a a∞=>+∑;(6)()1121nn ∞=-∑.解:(1)∵ ()()21135n U nn n =<++而211n n ∞=∑收敛,由比较审敛法知1n n U ∞=∑收敛. (2)∵221111n n n U n n n n++=≥=++ 而11n n∞=∑发散,由比较审敛法知,原级数发散.(3)∵ππsinsin 33lim lim ππ1π33n nn n n n→∞→∞=⋅=288而1π3n n ∞=∑收敛,故1πsin 3n n ∞=∑也收敛.(4)∵33321112n U nnn=<=+ 而3121n n∞=∑收敛,故3112n n∞=+∑收敛.(5)当a >1时,111n n n U a a =<+,而11n n a ∞=∑收敛,故111nn a∞=+∑也收敛. 当a =1时,11lim lim 022n n n U →∞→∞==≠,级数发散. 当0<a <1时,1lim lim 101n n n n U a →∞→∞==≠+,级数发散. 综上所述,当a >1时,原级数收敛,当0<a ≤1时,原级数发散.(6)由021limln 2xx x →-=知121lim ln 211nx n→∞-=<而11n n∞=∑发散,由比较审敛法知()1121nn ∞=-∑发散.6.用比值判别法判别下列级数的敛散性:(1) 213n n n ∞=∑;(2)1!31nn n ∞=+∑; (3)232333*********nn n +++++⋅⋅⋅⋅ ; (1) 12!n n n n n ∞=⋅∑解:(1) 23n n n U =,()2112311lim lim 133n n n n n n U n U n ++→∞→∞+=⋅=<, 由比值审敛法知,级数收敛.289(2) ()()111!311lim lim 31!31lim 131n n n n n nn n n U n U n n ++→∞→∞+→∞++=⋅++=⋅++=+∞所以原级数发散.(3) ()()11132lim lim 2313lim 21312n nn n n n n nn U n U n n n +++→∞→∞→∞⋅=⋅⋅+=+=> 所以原级数发散.(4) ()()1112!1lim lim 2!1lim 21122lim 1e 11n nn n n n n nnn n n U n n U n n n n n +++→∞→∞→∞→∞⋅+=⋅⋅+⎛⎫= ⎪+⎝⎭==<⎛⎫+ ⎪⎝⎭故原级数收敛.7.用根值判别法判别下列级数的敛散性:(1) 1531nn n n ∞=⎛⎫⎪+⎝⎭∑;(2)()[]11ln 1nn n ∞=+∑;(3) 21131n n n n -∞=⎛⎫⎪-⎝⎭∑;(4) 1nn n b a ∞=⎛⎫⎪⎝⎭∑,其中a n →a (n →∞),a n ,b ,a 均为正数.解:(1)55lim lim 1313n n n n n U n →∞→∞==>+, 故原级数发散.(2) ()1lim lim 01ln 1n n n n U n →∞→∞==<+,290故原级数收敛.(3)121lim lim 1931nn nn n n U n -→∞→∞⎛⎫==< ⎪-⎝⎭, 故原级数收敛.(4) limlim nn n n n nb b b a a a →∞→∞⎛⎫== ⎪⎝⎭, 当b <a 时,ba <1,原级数收敛;当b >a 时,b a>1,原级数发散;当b =a 时,b a=1,无法判定其敛散性.8.判定下列级数是否收敛?若收敛,是绝对收敛还是条件收敛?(1)1111234-+-+ ;(2)()()1111ln 1n n n ∞-=-+∑;(3) 2341111111153535353⋅-⋅+⋅-⋅+ ;(4)()21121!n n n n ∞-=-∑; (5)()()1111n n R n αα∞-=∈-∑;(6) ()11111123nn n n ∞=⎛⎫-++++ ⎪⎝⎭∑ . 解:(1)()111n n U n -=-,级数1n n U ∞=∑是交错级数,且满足111n n >+,1lim 0n n →∞=,由莱布尼茨判别法级数收敛,又11121n n n U n∞∞===∑∑是P <1的P级数,所以1n n U ∞=∑发散,故原级数条件收敛.(2)()()111ln 1n n U n -=-+,()()1111ln 1n n n ∞---+∑为交错级数,且()()11ln ln 12n n >++,()1lim 0ln 1n n →∞=+,由莱布尼茨判别法知原级数收敛,但由于()11ln 11n U n n =≥++291所以,1n n U ∞=∑发散,所以原级数条件收敛.(3)()11153n n n U -=-⋅民,显然1111115353n n n n n n U ∞∞∞=====⋅∑∑∑,而113nn ∞=∑是收敛的等比级数,故1n n U ∞=∑收敛,所以原级数绝对收敛.(4)因为2112lim lim 1n n n n nU U n ++→∞→∞==+∞+. 故可得1n n U U +>,得lim0n n U →∞≠, ∴lim 0n n U →∞≠,原级数发散. (5)当α>1时,由级数11n nα∞=∑收敛得原级数绝对收敛. 当0<α≤1时,交错级数()1111n n n α∞-=-∑满足条件:()111n n αα>+;1lim 0n n α→∞=,由莱布尼茨判别法知级数收敛,但这时()111111n n n nn αα∞∞-===-∑∑发散,所以原级数条件收敛.当α≤0时,lim0n n U →∞≠,所以原级数发散. (6)由于11111123n nn ⎛⎫⋅>++++ ⎪⎝⎭而11n n∞=∑发散,由此较审敛法知级数()11111123nn n n ∞=⎛⎫-⋅++++ ⎪⎝⎭∑ 发散. 记1111123n U nn ⎛⎫=⋅++++ ⎪⎝⎭ ,则292()()()()()()1222111111123111111112311111111231110n n U U n n n n n n n n n n n n n n +⎛⎫⎛⎫-=-++++- ⎪⎪+⎝⎭⎝⎭+⎛⎫=-++++ ⎪⎝⎭++⎛⎫⎛⎫-=++++ ⎪ ⎪⎝⎭+++⎝⎭>即1n n U U +>又01111lim lim 12311d n n n n U n n x n x→∞→∞⎛⎫=++++ ⎪⎝⎭=⎰ 由0111lim d lim 01t t t t x t x→+∞→+∞==⎰ 知lim 0n n U →∞=,由莱布尼茨判别法,原级数()11111123nn n n ∞=⎛⎫-⋅++++ ⎪⎝⎭∑ 收敛,而且是条件收敛.9.判别下列函数项级数在所示区间上的一致收敛性.(1) ()1!1nn x n ∞=-∑,x ∈[-3,3]; (2) 21nn x n ∞=∑,x ∈[0,1];(3) 1sin 3n n nx∞=∑,x ∈(-∞,+∞); (4)1!nxn e n -∞=∑,|x |<5; (5)3521cos n nxn x∞=+∑,x ∈(-∞,+∞)解:(1)∵()()3!!11nnx n n ≤--,x ∈[-3,3],而由比值审敛法可知()13!1nn n ∞=-∑收敛,所以原级数在 [-3,3]上一致收敛.(2)∵221nx n n≤,x ∈[0,1],293而211n n∞=∑收敛,所以原级数在[0,1]上一致收敛. (3)∵1sin 33n n nx ≤,x ∈(-∞,+∞),而113nn ∞=∑是收敛的等比级数,所以原级数在(-∞,+∞)上一致收敛. (4)因为5!!nnx ee n n -≤,x ∈(-5,5), 由比值审敛法可知51!nn e n ∞=∑收敛,故原级数在(-5,5)上一致收敛.(5)∵53523cos 1nxn xn≤+,x ∈(-∞,+∞),而5131n n∞=∑是收敛的P -级数,所以原级数在(-∞,+∞)上一致收敛.10.若在区间Ⅰ上,对任何自然数n .都有|U n (x )|≤V n (x ),则当()1n n V x ∞=∑在Ⅰ上一致收敛时,级数()1n n U x ∞=∑在这区间Ⅰ上也一致收敛.证:由()1n n V x ∞=∑在Ⅰ上一致收敛知, ∀ε>0,∃N (ε)>0,使得当n >N 时,∀x ∈Ⅰ有|V n +1(x )+V n +2(x )+…+V n +p (x )|<ε,于是,∀ε>0,∃N (ε)>0,使得当n >N 时,∀x ∈Ⅰ有|U n +1(x )+U n +2(x )+…+U n +p (x )|≤V n +1(x )+V n +2(x )+…+V n +p (x ) ≤|V n +1(x )+V n +2(x )+…+V n +p (x )|<ε,因此,级数()1n n U x ∞=∑在区间Ⅰ上处处收敛,由x 的任意性和与x 的无关294性,可知()1n n U x ∞=∑在Ⅰ上一致收敛.11.求下列幂级数的收敛半径及收敛域:(1)x +2x 2+3x 3+…+nx n +…; (2)1!nn x n n ∞=⎛⎫⎪⎝⎭∑;(3)21121n n x n -∞=-∑; (4)()2112nn x n n∞=-⋅∑; 解:(1)因为11limlim 1n n n n a n a n ρ+→∞→∞+===,所以收敛半径11R ρ==收敛区间为(-1,1),而当x =±1时,级数变为()11n n n ∞=-∑,由lim(1)0n x nn →-≠知级数1(1)nn n ∞=-∑发散,所以级数的收敛域为(-1,1).(2)因为()()1111!11lim lim lim lim e 1!11nn n n n n n n n na n n n a n n n n ρ-+-+→∞→∞→∞→∞⎡⎤+⎛⎫⎛⎫==⋅===+ ⎪⎢⎥ ⎪+⎝⎭+⎝⎭⎣⎦ 所以收敛半径1e R ρ==,收敛区间为(-e,e).当x =e 时,级数变为1e nn n n n∞=∑;应用洛必达法则求得()10e e1lim 2xx x x →-+=-,故有111lim 12n n n a n a +→∞⎛⎫-=-<⎪⎝⎭由拉阿伯判别法知,级数发散;易知x =-e 时,级数也发散,故收敛域为(-e,e).(3)级数缺少偶次幂项.根据比值审敛法求收敛半径.211212221lim lim 2121lim21n n n n n nn U x n U n x n x n x ++-→∞→∞→∞-=⋅+-=⋅+= 所以当x 2<1即|x |<1时,级数收敛,x 2>1即|x |>1时,级数发散,故295收敛半径R =1.当x =1时,级数变为1121n n ∞=-∑,当x =-1时,级数变为1121n n ∞=--∑,由1121lim 012n n n→∞-=>知,1121n n ∞=-∑发散,从而1121n n ∞=--∑也发散,故原级数的收敛域为(-1,1). (4)令t =x -1,则级数变为212nn t n n∞=⋅∑,因为()()2122lim lim 1211n n n na n na n n ρ+→∞→∞⋅===⋅++ 所以收敛半径为R =1.收敛区间为 -1<x -1<1 即0<x <2.当t =1时,级数3112n n ∞=∑收敛,当t =-1时,级数()31112n n n ∞=-⋅∑为交错级数,由莱布尼茨判别法知其收敛.所以,原级数收敛域为 0≤x ≤2,即[0,2] 12.利用幂级数的性质,求下列级数的和函数: (1)21n n nx∞+=∑;(2) 22021n n x n +∞=+∑;解:(1)由()321lim n n n x n x nx++→∞+=知,当|x |=<1时,原级数收敛,而当|x |=1时,21n n nx ∞+=∑的通项不趋于0,从而发散,故级数的收敛域为(-1,1).记 ()23111n n n n S nxxnxx ∞∞+-====∑∑易知11n n nx∞-=∑的收敛域为(-1,1),记()111n n S n xx ∞-==∑296则()1011xn n x S x x x∞===-∑⎰ 于是()()12111x S x x x '⎛⎫== ⎪-⎝⎭-,所以()()()3211x S x x x =<-(2)由2422221lim 23n n n x n x n x++→∞+=⋅+知,原级数当|x |<1时收敛,而当|x |=1时,原级数发散,故原级数的收敛域为(-1,1),记()2221002121n n n n x x S x x n n ++∞∞====++∑∑,易知级数21021n n x n +∞=+∑收敛域为(-1,1),记()211021n n x S x n +∞==+∑,则()21211n n S x x x∞='==-∑, 故()1011d ln 21xx S x x x +'=-⎰ 即()()1111ln 021x S S x x +-=-,()100S =,所以()()()11ln 121x xS xS x x x x+==<-13.将下列函数展开成x 的幂级数,并求展开式成立的区间: (1)f (x )=ln(2+x ); (2)f (x )=cos 2x ; (3)f (x )=(1+x )ln(1+x ); (4)()221x f x x=+;(5)()23xf x x=+; (6)()()1e e 2x x f x -=-; (7)f (x )=e x cos x ;(8)()()212f x x =-.解:(1)()()ln ln 2ln 2ln 11222x x f x x ⎛⎫⎛⎫===++++ ⎪ ⎪⎝⎭⎝⎭由于()()0ln 111n nn x x n ∞==+-+∑,(-1<x ≤1)故()()110ln 11221n nn n x x n +∞+=⎛⎫=+- ⎪⎝⎭+∑,(-2≤x ≤2)297因此()()()11ln ln 22121n nn n x x n +∞+==++-+∑,(-2≤x ≤2) (2)()21cos 2cos 2x f x x +==由()()20cos 1!2nnn x x n ∞==-∑,(-∞<x <+∞)得()()()()()220042cos 211!!22n n n nn n n x x x n n ∞∞==⋅==--∑∑ 所以()()22011()cos cos 222114122!2n nn n f x x x x n ∞===+⋅=+-∑,(-∞<x <+∞) (3)f (x )=(1+x )ln(1+x ) 由()()()10ln 111n nn x x n +∞==+-+∑,(-1≤x ≤1)所以()()()()()()()()()()()()()1120111111111111111111111111111n nn n n nn n n n n nn n n n n n n n n n x f x x n x x n n x x x n n n n x xn n x xn n +∞=++∞∞==++∞∞+==+∞+=-∞+==+-+=+--++=++--+++--=+⋅+-=++∑∑∑∑∑∑∑ (-1≤x ≤1)(4)()2222111x f x x xx==⋅++由于()()()2211!!2111!!21n n n n x n x∞=-=+-+∑ (-1≤x ≤1)298故()()()()221!!2111!!2n n n n x f x x n ∞=⎛⎫-+=- ⎪⎝⎭∑()()()()2211!!211!!2n n n n x xn ∞+=-=+-∑ (-1≤x ≤1) (5)()()()()2202111313133133nn n n nn n xf x x x x x x ∞=+∞+==⋅+⎛⎫=⋅- ⎪⎝⎭=-<∑∑(6)由0e !nxn x n ∞==∑,x ∈(-∞,+∞)得()01e !n nxn x n ∞-=⋅-=∑,x ∈(-∞,+∞)所以()()()()()()0002101e e 2112!!1112!,!21x x n n n n n n n n n n f x x x n n x n x x n -∞∞==∞=+∞==-⎛⎫-=- ⎪⎝⎭=⋅⎡⎤--⎣⎦=∈-∞+∞+∑∑∑∑(7)因为e cos x x 为()()1e cos sin x x i e x i x +=+的实部, 而()()[]()10002011!1!ππ2cos sin !44ππ2cos sin !44nxi n nn n nn n n n n ex i n x i n x i n x n n i n ∞+=∞=∞=∞==+=+⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦⎛⎫=⋅+ ⎪⎝⎭∑∑∑∑299取上式的实部.得2π2cos4cos !n xn n n e x x n ∞==⋅∑(-∞<x <+∞)(8)由于()1211n n nx x ∞-==-∑ |x |<1而()211412f x x =⋅⎛⎫- ⎪⎝⎭,所以()111001422n n n n n n x x f n x --∞∞+==⋅⎛⎫=⋅= ⎪⎝⎭∑∑ (|x |<2) 14.将()2132f x x x =++展开成(x +4)的幂级数.解:21113212x x x x =-++++而()()()0101113411431314413334713nn nn n x x x x x x x ∞=∞+==+-++=-⋅+-+⎛+⎫⎛⎫=-< ⎪⎪⎝⎭⎝⎭+=--<<∑∑又()()()0101122411421214412224622nn nn n x x x x x x x ∞=∞+==+-++=-+-+⎛+⎫⎛⎫=-< ⎪⎪⎝⎭⎝⎭+=--<<-∑∑300所以()()()()()2110011013244321146223n nn n n n nn n n f x x x x x x x ∞∞++==∞++==++++=-+⎛⎫=-+-<<- ⎪⎝⎭∑∑∑15.将函数()3f x x =展开成(x -1)的幂级数. 解:因为()()()()()2111111!2!m nmm mm m m x xx x n---+=++++++-<<所以()()[]()()()33221133333331121222222211111!2!!n f x x x n x x x n ==+-⎛⎫⎛⎫⎛⎫⎛⎫----+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=+++++---(-1<x -1<1) 即()()()()()()()()()()()()()2323133131313251111111222!23!2!3152111022!n nnnn n f x x x x x n n x x n ∞=⋅⋅⋅⋅⋅⋅--+--=+++++----⋅⋅⋅⋅⋅⋅--=+-<<⋅∑ 16.利用函数的幂级数展开式,求下列各数的近似值: (1)ln3(误差不超过0.0001); (2)cos20(误差不超过0.0001)解:(1)35211ln 213521n x x x x x x n -+⎛⎫=+++++ ⎪--⎝⎭,x ∈(-1,1)令131x x +=-,可得()11,12x =∈-,301故()35211111112ln3ln 212325222112n n -+⎡⎤+++++==⎢⎥⋅⋅⋅-⎣⎦-又()()()()()()()()()()2123212121232521242122112222123222212112222123252111222212112211413221n n n n n n n n n n n r n n n n n n n n n n +++++++++-⎡⎤++=⎢⎥⋅⋅++⎣⎦⎡⎤⋅⋅++=+++⎢⎥⋅⋅+++⎣⎦⎛⎫<+++ ⎪⎝⎭+=⋅+-=+ 故5810.000123112r <≈⨯⨯61010.000033132r <≈⨯⨯. 因而取n =6则35111111ln32 1.098623252112⎛⎫=≈++++ ⎪⋅⋅⋅⎝⎭(2)()()2420ππππ909090cos 2cos 11902!4!!2nn n ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭==-+-++-∵24π906102!-⎛⎫ ⎪⎝⎭≈⨯;48π90104!-⎛⎫⎪⎝⎭≈ 故2π90cos2110.00060.99942!⎛⎫⎪⎝⎭≈-≈-≈17.利用被积函数的幂级数展开式,求定积分0.5arctan d xx x⎰(误差不超过0.001)的近似值.302解:由于()3521arctan 13521n n x x x x x n +=-+-++-+ ,(-1≤x ≤1) 故()2420.50.5000.5357357arctan d d 113521925491111111292252492nx x x x x x x n x x x x ⎡⎤=-+-++-⎢⎥+⎣⎦⎛⎫=-+-+ ⎪⎝⎭=-⋅+⋅-⋅+⎰⎰ 而3110.013992⋅≈,5110.0013252⋅≈,7110.0002492⋅≈. 因此0.535arctan 11111d 0.487292252x x x ≈-⋅+⋅≈⎰ 18.判别下列级数的敛散性:(1)111n nnn nn n +∞=⎛⎫+ ⎪⎝⎭∑;(2)21cos 32n n nx n ∞=⎛⎫ ⎪⎝⎭∑; (3)()1ln 213nn n n ∞=+⎛⎫+ ⎪⎝⎭∑.解:(1)∵122111n nnnnn nn n n n n n n +⎛⎫>= ⎪+⎝⎭⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭ 而()22211221lim lim 10111nnn n n n nn n --++→∞→∞⎡⎤⎛⎫-⎛⎫==≠+⎢⎥⎪ ⎪+⎝⎭+⎝⎭⎣⎦故级数2211nn n n ∞=⎛⎫⎪+⎝⎭∑发散,由比较审敛法知原级数发散. (2)∵2cos 3022n nnx n n ⎛⎫⎪⎝⎭<≤ 由比值审敛法知级数12n n n ∞=∑收敛,由比较审敛法知,原级数21cos 32nn nx n ∞=⎛⎫ ⎪⎝⎭∑303收敛. (3)∵()()ln ln 220313nnn n n ++<<⎛⎫+ ⎪⎝⎭ 由()()()()11ln 33lim lim 3ln 21ln 3lim3ln 2113nn n n n nn U n U n n n ++→∞→∞→∞+=⋅++=+=< 知级数()1ln 23nn n ∞=+∑收敛,由比较审敛法知,原级数()1ln 213n n n n ∞=+⎛⎫+ ⎪⎝⎭∑收敛. 19.若2lim n nn U →∞存在,证明:级数1n n U ∞=∑收敛. 证:∵2lim n n n U →∞存在,∴∃M >0,使|n 2U n |≤M , 即n 2|U n |≤M ,|U n |≤2M n而21n Mn ∞=∑收敛,故1n n U ∞=∑绝对收敛. 20.证明,若21n n U ∞=∑收敛,则1nn U n∞=∑绝对收敛. 证:∵222211111222n n n nU U n U U n n n+=⋅≤=+⋅而由21n n U ∞=∑收敛,211n n∞=∑收敛,知 22111122n n U n ∞=⎛⎫+⋅ ⎪⎝⎭∑收敛,故1n n U n∞=∑收敛, 因而1nn U n∞=∑绝对收敛.30421.若级数1n n a ∞=∑与1n n b ∞=∑都绝对收敛,则函数项级数()1cos sin n n n a nx b nx ∞=+∑在R 上一致收敛.证:U n (x )=a n cos nx +b n sin nx ,∀x ∈R 有()cos sin cos sin n n n n n n n U a nx b nx a nx b nx a b x =+≤+≤+由于1n n a ∞=∑与1n n b ∞=∑都绝对收敛,故级数()1n n n a b ∞=+∑收敛.由魏尔斯特拉斯判别法知,函数项级数()1cos sin n n n a nx b nx ∞=+∑在R 上一致收敛.22.计算下列级数的收敛半径及收敛域:(1) 1311nn n n x n ∞=⎛⎫+ ⎪+⎝⎭∑;(2)()1πsin12nnn x ∞=+∑; (3) ()2112nn n x n ∞=-⋅∑解:(1)()111lim 1331lim 3123311311lim lim lim 22313e e 3n n nn nn nnn n n a a n n n n n n n n n n ρ+→∞+→∞→∞→∞→∞-=+⎛⎫⎛⎫++=⋅ ⎪ ⎪+⎝⎭+⎝⎭⎛⎫++++⎛⎫+=⋅⋅ ⎪ ⎪++⎝⎭+⎝⎭=⋅⋅=∴133R ρ==, 又当33x =±时,级数变为()113133311333nnnn n n n n n n ∞∞==⎛⎫⎛⎫⎛⎫++=±± ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭∑∑, 因为33333lim 033nn n en -→∞⎛⎫+=≠ ⎪+⎝⎭305所以当33x =±,级数发散,故原级数的收敛半径33R =,收敛域(-33,33). (2) 111ππsin122lim lim lim ππ2sin 22n n n n n n nnna a ρ+++→∞→∞→∞==== 故12R ρ==,又∵πsinπ2limsin 2lim ππ0π22n n n n n n→∞→∞⋅==≠.所以当(x +1)=±2时,级数()1πsin12n n n x ∞=+∑发散, 从而原级数的收敛域为-2<x +1<2,即-3<x <1,即(-3,1)(3) ()212121lim lim 221n n n n n na n a n ρ++→∞→∞⋅===⋅+ ∴2R =,收敛区间-2<x -1<2,即-1<x <3. 当x =-1时,级数变为()2111nn n∞=-∑,其绝对收敛,当x =3时,级数变为211n n ∞=∑,收敛. 因此原级数的收敛域为[-1,3]. 23.将函数()0arctan d xtF t x t=⎰展开成x 的幂级数. 解:由于()21arctan 121n nn t t n +∞==-+∑306所以()()()()()20002212000arctan d d 121d 112121nxx n n n n xnnn n t t F t t x t n t x t n n ∞=+∞∞====-+==--++∑⎰⎰∑∑⎰(|x |≤1)24.判别下列级数在指定区间上的一致收敛性:(1)()113n nn x ∞=-+∑,x ∈[-3,+∞); (2)1n n n x ∞=∑,x ∈(2,+∞); (3)()()222211n nx x n n ∞=⎡⎤+++⎣⎦∑,x ∈(-∞,+∞);解:(1)考虑n ≥2时,当x ≥-3时,有()1111133333nn n n nx x --=<<+-+ 而1113n n ∞-=∑收敛,由魏尔斯特拉斯判别法知,级数()113nnn x ∞=-+∑在[-3,+∞)上一致收敛. (2)当x >2时,有2n nn nx=< 由1112lim 122n n nn n +→∞+=<知级数12n n n ∞=∑收敛,由魏尔斯特拉斯判别法知,级数1n n nx ∞=∑在(2,+∞)上一致收敛. (3)∀x ∈R 有()()()22224322111nn n x n n nx n n n ≤<=⎡⎤+⋅+++⎣⎦而311n n ∞=∑收敛,由魏尔斯特拉斯判别法知,级数()()222211n n x x n n ∞=⎡⎤+++⎣⎦∑在(-∞,+∞)上一致收敛. 25.求下列级数的和函数:307(1)()211121n n n x n ∞-=--∑; (2)2121n n x n +∞=+∑; (3)()11!1n n nxn ∞-=-∑; (4)()11n n x n n ∞=+∑.解:(1)可求得原级数的收敛半径R =1,且当|x |=1时,级数()111121n n n ∞-=--∑是收敛的交错级数,故收敛域为[-1,1] 记()()()()22111111112121n n n n n n x x S x xS x x n n -∞∞--=====----∑∑ 则S 1(0)=0,()()122121111n n n S x x x∞--='==-+∑ 所以()()1121d arctan 01xS S x x x x-==+⎰ 即S 1(x )=arctan x ,所以S (x )=x arctan x ,x ∈[-1,1].(2)可求得原级数的收敛半径R =1,且当|x |=1时,原级数发散.记()21021n n x S x n +∞==+∑则()22011n n S x x x ∞='==-∑ ()200111d d ln 121xxx S x x x x x +'==--⎰⎰,即()()11ln 021xS S x x+-=-,S (0)=0 所以()11ln 21xS x x+=-,(|x |<1)(3)由()11!lim lim 0!1n n n n n a n n a n +→∞→∞+==-知收敛域为(-∞,+∞).记()()11!1n n n S x x n ∞-==-∑则()()()1011d e !!11nn xx n n x x S x x x x n n -∞∞=====--∑∑⎰,所以()()()e 1e x x S x x x '==+,(-∞<x <+∞)(4)由()()()112lim111n n n n n →∞++=+知收敛半径R =1,当x =1时,级数变为308()111n n n ∞=+∑,由()2111n n n <+知级数收敛,当x =-1时,级数变为()()111n n n n ∞=-+∑是收敛的交错级数,故收敛域为[-1,1].记()()11nn x S x n n ∞==+∑则S (0)=0,()()111n n x xS x n n +∞==+∑,()[]1111n n x xS x x∞-=''==-∑ (x ≠1) 所以()[]()0d ln 1xxS x x x ''=--⎰ 即()[]()ln 1xS x x '=--()[]()()()00d ln 1d 1ln 1xxxS x x x x x x x '=--=--+⎰⎰ 即()()()1ln 1xS x x x x =--+当x ≠0时,()()111ln 1S x x x⎛⎫=+-- ⎪⎝⎭,又当x =1时,可求得S (1)=1(∵()1lim lim 111n n S x n →∞→∞⎛⎫=-= ⎪+⎝⎭) 综上所述()()[)()0,01,1111ln 1,1,00,1x S x x x x x =⎧⎪==⎪⎨⎛⎫⎪+--∈- ⎪⎪⎝⎭⎩ 26.设f (x )是周期为2π的周期函数,它在(-π,π]上的表达式为()32π0,0π.x f x x x -<≤⎧=⎨<≤⎩ 试问f (x )的傅里叶级数在x =-π处收敛于何值?解:所给函数满足狄利克雷定理的条件,x =-π是它的间断点,在x =-π处,f (x )的傅里叶级数收敛于()()[]()33ππ11π22π222f f -+-+-=+=+30927.写出函数()21π00πx f x x x --≤≤⎧=⎨<≤⎩的傅里叶级数的和函数. 解:f (x )满足狄利克雷定理的条件,根据狄利克雷定理,在连续点处级数收敛于f (x ),在间断点x =0,x =±π处,分别收敛于()()00122f f -++=-,()()2πππ122f f -++-=,()()2πππ122f f -+-+--=,综上所述和函数.()221π00π102π1π2x x x S x x x --<<⎧⎪<<⎪⎪=-=⎨⎪⎪-=±⎪⎩28.写出下列以2π为周期的周期函数的傅里叶级数,其中f (x )在[-π,π)上的表达式为:(1)()π0π,4ππ0;4x f x x ⎧≤<⎪⎪=⎨⎪--≤<⎪⎩(2)()()2πx π=-≤≤f x x ;(3)()ππ,π,22ππ,,22ππ,π;22⎧--≤<-⎪⎪⎪=-≤<⎨⎪⎪≤<⎪⎩x f x x x x (4)()()cosππ2=-≤≤x f x x .310解:(1)函数f (x )满足狄利克雷定理的条件,x =n π,n ∈z 是其间断点,在间断占处f (x )的傅里叶级数收敛于()()ππ0044022f f +-⎛⎫+- ⎪+⎝⎭==,在x ≠n π,有()π0π-ππ011π1πcos d cos d cos d 0ππ4π4n a f x nx x nx x nx x -⎛⎫==-+= ⎪⎝⎭⎰⎰⎰ ()π0π-ππ011π1πsin d sin d sin d ππ4π40,2,4,6,,1,1,3,5,.n b f x nx x nx x nx xn n n-⎛⎫==-+ ⎪⎝⎭=⎧⎪=⎨=⎪⎩⎰⎰⎰于是f (x )的傅里叶级数展开式为()()11sin 2121n f x n x n ∞==--∑(x ≠n π) (2)函数f (x )在(-∞,+∞)上连续,故其傅里叶级数在(-∞,+∞)上收敛于f (x ),注意到f (x )为偶函数,从而f (x )cos nx 为偶函数,f (x )sin nx 为奇函数,于是()π-π1sin d 0πn b f x nx x ==⎰,2π20-π12πd π3a x x ==⎰,()()ππ22-π0124cos d cos d 1ππnn a f x nx x x nx x n ===-⋅⎰⎰ (n =1,2,…) 所以,f (x )的傅里叶级数展开式为:()()221π41cos 3nn f x nx n∞==+-⋅∑ (-∞<x <∞)(3)函数在x =(2n +1)π (n ∈z )处间断,在间断点处,级数收敛于0,当x ≠(2n +1)π时,由f (x )为奇函数,有a n =0,(n =0,1,2,…)311()()()πππ2π002222πsin d sin d sin d ππ212π1sin 1,2,π2n nb f x nx x x nx x nx x n n n n ⎡⎤==+⎢⎥⎣⎦=--+=⎰⎰⎰ 所以()()12112π1sin sin π2n n n f x nx n n ∞+=⎡⎤=-⋅+⎢⎥⎣⎦∑ (x ≠(2n +1)π,n ∈z )(4)因为()cos 2xf x =作为以2π为周期的函数时,处处连续,故其傅里叶级数收敛于f (x ),注意到f (x )为偶函数,有b n =0(n =1,2,…),()()ππ-π0π0π1212cos cos d cos cos d π2π2111cos cos d π2211sin sin 12211π224110,1,2,π41n n x xa nx x nx xn x n x x n x n x n n n n +==⎡⎤⎛⎫⎛⎫=++- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫⎛⎫+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥=+⎢⎥+-⎢⎥⎣⎦⎛⎫=-= ⎪-⎝⎭⎰⎰⎰所以f (x )的傅里叶级数展开式为:()()12124cos 1ππ41n n nxf x n ∞+==+--∑ x ∈[-π,π]29.将下列函数f (x )展开为傅里叶级数: (1)()()πππ42x f x x =--<<(2)()()sin 02πf x x x =≤≤解:(1) ()ππ0-ππ11ππcos d d ππ422x a f x nx x x -⎛⎫==-= ⎪⎝⎭⎰⎰[]()ππππ-π-πππ1π11cos d cos d x cos d π4242π1sin 001,2,4n x a nx x nx x nx x nx n n--⎛⎫=-=- ⎪⎝⎭=-==⎰⎰⎰312()ππππ-π-π1π11sin d sin d xsin d π4242π11n n x b nx x nx x nx x n-⎛⎫=-=- ⎪⎝⎭=-⋅⎰⎰⎰故()()1πsin 14n n nxf x n∞==+-∑ (-π<x <π)(2)所给函数拓广为周期函数时处处连续, 因此其傅里叶级数在[0,2π]上收敛于f (x ),注意到f (x )为偶函数,有b n =0,()ππ0πππ011cos0d sin d ππ24sin d ππa f x x x x x x x --====⎰⎰⎰ ()()()()()()ππ0ππ02222cos d sin cos d ππ1sin 1sin 1d π211π10,1,3,5,4,2,4,6,π1n na f x nx x x nx x n x n x x n n n n -===+--⎡⎤⎣⎦-⎡⎤=+-⎣⎦-=⎧⎪-=⎨=⎪-⎩⎰⎰⎰所以()()2124cos2ππ41n nxf x n ∞=-=+-∑ (0≤x ≤2π) 30.设f (x )=x +1(0≤x ≤π),试分别将f (x )展开为正弦级数和余弦级数. 解:将f (x )作奇延拓,则有a n =0 (n =0,1,2,…)()()()()ππ0022sin d 1sin d ππ111π2πn nb f x nx x x nx x n==+--+=⋅⎰⎰从而()()()1111π2sin πnn f x nx n∞=--+=∑ (0<x <π)313若将f (x )作偶延拓,则有b n =0 (n =1,2,…)()()ππ00222cos d 1cos d ππ0,2,4,64,1,3,5,πn a f x nx x x nx x n n n ==+=⎧⎪=-⎨=⎪⎩⎰⎰ ()()ππ0π012d 1d π2ππa f x x x x -==+=+⎰⎰ 从而()()()21cos 21π242π21n n xf x n ∞=-+=--∑ (0≤x ≤π) 31.将f (x )=2+|x | (-1≤x ≤1)展开成以2为周期的傅里叶级数,并由此求级数211n n∞=∑的和. 解:f (x )在(-∞,+∞)内连续,其傅里叶级数处处收敛,由f (x )是偶函数,故b n =0,(n =1,2,…)()()11010d 22d 5a f x x x x -==+=⎰⎰()()()1112cos d 22cos d 0,2,4,64,1,3,5,πn a f x nx x x nx xn n n -==+=⎧⎪-=⎨=⎪⎩⎰⎰所以()()()221cos 21π542π21n n xf x n ∞=-=--∑,x ∈[-1,1]取x =0得,()2211π821n n ∞==-∑,故 ()()22222111111111π48212n n n n n n n n ∞∞∞∞=====+=+-∑∑∑∑ 所以211π6n n∞==∑31432.将函数f (x )=x -1(0≤x ≤2)展开成周期为4的余弦级数.解:将f (x )作偶延拓,作周期延拓后函数在(-∞,+∞)上连续,则有b n =0 (n =1,2,3,…)()()220201d 1d 02a f x x x x -==-=⎰⎰ ()()()222022221ππcos d 1cos d 2224[11]π0,2,4,6,8,1,3,5,πn nn x n xa f x x x x n n n n -==-=--=⎧⎪=⎨-=⎪⎩⎰⎰ 故()()()22121π81cos π221n n xf x n ∞=-=-⋅-∑(0≤x ≤2)33.设()()011,0,2cos π1222,1,2n n x x a f x s x a n x x x ∞=⎧≤≤⎪⎪==+⎨⎪-<<⎪⎩∑,-∞<x <+∞,其中()12cos πd n a f x n x x =⎰,求52s ⎛⎫- ⎪⎝⎭. 解:先对f (x )作偶延拓到[-1,1],再以2为周期延拓到(-∞,+∞)将f (x )展开成余弦级数而得到 s (x ),延拓后f (x )在52x =-处间断,所以515511122222221131224s f f f f +-+-⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-+-=-+-⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎛⎫=+= ⎪⎝⎭34.设函数f (x )=x 2(0≤x <1),而()1s i n πn n s x b nx ∞==∑,-∞<x <+∞,其中()12sin πd n b f x n x x =⎰ (n =1,2,3,…),求12s ⎛⎫- ⎪⎝⎭. 解:先对f (x )作奇延拓到,[-1,1],再以2为周期延拓到(-∞,+∞),并将315f (x )展开成正弦级数得到s (x ),延拓后f (x )在12x =-处连续,故.211112224s f ⎛⎫⎛⎫⎛⎫-=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 35.将下列各周期函数展开成为傅里叶级数,它们在一个周期内的表达式分别为:(1)f (x )=1-x 2 1122x ⎛⎫-≤< ⎪⎝⎭;(2)()21,30,1,0 3.x x f x x +-≤<⎧=⎨≤<⎩解:(1) f (x )在(-∞,+∞)上连续,故其傅里叶级数在每一点都收敛于f (x ),由于f (x )为偶函数,有b n =0 (n =1,2,3,…)()()112221002112d 41d 6a f x x x x -==-=⎰⎰, ()()()()112221021222cos2n πd 41cos2n πd 11,2,πn n a f x x x x x x n n -+==--==⎰⎰所以()()12211111cos 2π12πn n f x n x n +∞=-=+∑ (-∞<x <+∞)(2) ()()303033011d 21d d 133a f x x x x x --⎡⎤==++=-⎢⎥⎣⎦⎰⎰⎰, ()()()()330330221πcos d 331π1π21cos d cos d 3333611,1,2,3,πn nn xa f x x n x n x x x x n n --==++⎡⎤=--=⎣⎦⎰⎰⎰316()()()()33033011πsin d 331π1π21sin d sin d 333361,1,2,πn n n xb f x x n x n x x x x n n --+==++=-=⎰⎰⎰ 而函数f (x )在x =3(2k +1),k =0,±1,±2,…处间断,故()()()122116π6π11cos 1sin 2π3π3n n n n x n x f x n n ∞+=⎧⎫⎡⎤=-+--+-⎨⎬⎣⎦⎩⎭∑ (x ≠3(2k +1),k =0,±1,±2,…)36.把宽为τ,高为h ,周期为T 的矩形波(如图所示)展开成傅里叶级数的复数形式.解:根据图形写出函数关系式()0,22,220,22T t u t h t T t ττττ⎧-≤<-⎪⎪⎪=-≤<⎨⎪⎪≤≤⎪⎩()()22022111d d d 2T l T l h c u t t u t t h t l T T Tτττ---====⎰⎰⎰ ()()π2π222π2π22222π2211e d e d 212πe d e d 2ππsin e 2ππn T n i t l i t l T T n l n n i t i t T T n i t T c u t t u t tl T h T n h t i t T T n i T h h n n i n T τττττττ----------==-⎛⎫⎛⎫==⋅- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎡⎤=-= ⎪⎣⎦⎝⎭⎰⎰⎰⎰。
高等数学(经管类)下、林伟初 郭安学主编、复旦大学出版社、课后习题答案

1. 指出下列各点所在的坐标轴、坐标面或卦限: A (2,1,-6),B (0,2,0),C (-3,0,5),D (1,-1,-7).解:A 在V 卦限,B 在y 轴上,C 在xOz 平面上,D 在VIII 卦限。
2. 已知点M (-1,2,3),求点M 关于坐标原点、各坐标轴及各坐标面的对称点的坐标. 解:设所求对称点的坐标为(x ,y ,z ),则(1) 由x -1=0,y +2=0,z +3=0,得到点M 关于坐标原点的对称点的坐标为:(1,-2,-3). (2) 由x =-1,y +2=0,z +3=0,得到点M 关于x 轴的对称点的坐标为:(-1,-2,-3).同理可得:点M 关于y 轴的对称点的坐标为:(1, 2,-3);关于z 轴的对称点的坐标为:(1,-2,3).(3)由x =-1,y =2,z +3=0,得到点M 关于xOy 面的对称点的坐标为:(-1, 2,-3).同理,M 关于yOz 面的对称点的坐标为:(1, 2,3);M 关于zOx 面的对称点的坐标为:(-1,-2,3).3. 在z 轴上求与两点A (-4,1,7)和B (3,5,-2)等距离的点. 解: 设所求的点为M (0,0,z ),依题意有|MA |2=|MB |2,即(-4?0)2?(1?0)2?(7?z)2?(3?0)2?(5?0)2?(-2?z)2?解之得z =11,故所求的点为M (0,0,149). 4. 证明以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 解:由两点距离公式可得21214M M =,2213236,6M M M M ==所以以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 5. 设平面在坐标轴上的截距分别为a =2,b =-3,c =5,求这个平面的方程.解:所求平面方程为1235y x z++=-。
高等数学复旦大学出版第三版下册课后答案习题全之欧阳美创编

习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2)s==(3)s==(4)s==5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).故s==5s==.z6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点.解:设此点为M(0,0,z),则解得14z=9).即所求点为M(0,0,1497. 试证:以三点A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC为等腰直角三角形.8. 验证:()()a b c a b c.++=++证明:利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a, b, c 表示23.-u v 解:10. 把△ABC 的BC 边分成五等份,设分点依次为D1,D2,D3,D4,再把各分点与A 连接,试以AB =c,BC =a 表示向量1D A ,2D A ,3D A 和4D A .解:1115D A BA BD =-=--c a11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影.解:设M 的投影为M ',则12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标. 解:设此向量的起点A 的坐标A(x, y, z),则 解得x=-2, y=3, z=0故A 的坐标为A(-2, 3, 0).13. 一向量的起点是P1(4,0,5),终点是P2(7,1,3),试求:(1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量. 解:(1)12Pr j 3,x x a PP == (2)12(7PP ==(3) 12cos 14x a PP α==12cos 14z a PP γ==(4) 12012{14PP PP ===+e j . 14. 三个力F1=(1,2,3), F2=(-2,3,-4), F3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R=(1-2+3,2+3-4,3-4+5)=(2,1,4)15. 求出向量a= i+j+k, b=2i-3j+5k 和c=-2i-j+2k 的模,并分别用单位向量,,a b c e e e 来表达向量a, b, c. 解:||==a16. 设m=3i+5j+8k,n=2i-4j-7k, p=5i+j-4k,求向量a=4m+3n-p 在x 轴上的投影及在y 轴上的分向量.解:a=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k 在x 轴上的投影ax=13,在y 轴上分向量为7j. 17.解:设{,,}x y z a a a a =则有 求得12x a =.设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 4a ba bπ⋅=⇒=⋅ 则214y a = 求得12y a =±又1,a=则2221x y z a a a ++=从而求得11{,,22a =或11{,,22-18. 已知两点M1(2,5,-3),M2(3,-2,5),点M 在线段M1M2上,且123M M MM =,求向径OM 的坐标. 解:设向径OM ={x, y, z}因为,123M M MM =所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}.19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标.解:设P 的坐标为(x, y, z ),2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+又122190cos 2, 749x x α==⇒==故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a, b 的夹角2π3ϕ=,且3,4==b a ,计算: (1) a·b; (2) (3a -2b)·(a+ 2b). 解:(1)a·b=2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b 21. 已知a=(4,-2, 4), b=(6,-3, 2),计算:(1)a·b; (2) (2a -3b)·(a+ b); (3)2||-a b解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影. 解:AB ={3,-2,-6},CD ={6,2,3}23. 若向量a+3b 垂直于向量7a-5b,向量a-4b 垂直于向量7a-2b,求a 和b 的夹角.解: (a+3b)·(7a -5b)=227||1615||0+⋅-=a a b b ①(a-4b)·(7a -2b) = 227||308||0-⋅+=a a b b ②由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos 23θ==.24. 设a=(-2,7,6),b=(4,-3,-8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明:以a,b 为邻边的平行四边形的两条对角线分别为a+b,a -b,且a+b={2,4,-2} a-b={-6,10,14}又(a+b)·(a -b)= 2×(-6)+4×10+(-2)×14=0 故(a+b)⊥(a-b).25. 已知a=3i+2j-k, b=i-j+2k,求: (1) a×b;(2) 2a×7b;(3) 7b×2a; (4) a×a. 解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k (4) 0⨯=a a .26. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算: (1) |(a +b)×(a-b)|; (2) |(3a +b)×(a-2b)|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b a27. 求垂直于向量3i-4j-k 和2i-j+k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b 平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||θ⨯===⨯a b a b . 28. 一平行四边形以向量a=(2,1,-1)和b=(1,-2,1)为邻边,求其对角线夹角的正弦. 解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++=l l i j k 所以1212||sin 1||||θ⨯===l l l l .即为所求对角线间夹角的正弦.29. 已知三点A(2,-1,5), B(0,3,-2), C(-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为 故 1()4MN MP AC BC ⨯=⨯.30.(1)解: x y zxyzi j k a b a a a b b b ⨯=则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅()()()()若,,C a b 共面,则有 a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=() 反之亦成立. (2)C xyz x y z xyza a a ab b b b C C C ⨯⋅=() 由行列式性质可得: 故C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅()()()31. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积.解:设四顶点依次取为A, B, C, D. 则由A ,B ,D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i j k . 同理可求其他三个三角形的面积依次为12故四面体的表面积122S =32.解:设四面体的底为BCD ∆,从A 点到底面BCD ∆的高为h ,则13BCDV Sh =⋅⋅,而11948222BCDSBC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h == 故1942323V =⋅⋅=33. 已知三点A(2,4,1), B(3,7,5), C(4,10,9),证:此三点共线.证明:{1,3,4}AB =,{2,6,8}AC = 显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯= 故A ,B ,C 三点共线.34. 一动点与M0(1,1,1)连成的向量与向量n=(2,3,-4)垂直,求动点的轨迹方程.解:设动点为M(x, y, z) 因0M M n ⊥,故00M M n ⋅=. 即2(x-1)+3(y-1)-4(z-1)=0整理得:2x+3y-4z-1=0即为动点M 的轨迹方程.35.求通过下列两已知点的直线方程:(1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3).解:(1)两点所确立的一个向量为s={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解:所给直线的方向向量为另取x0=0代入直线一般方程可解得y0=7,z0=17 于是直线过点(0,7,17),因此直线的标准方程为: 且直线的参数方程为:37. 求过点(4,1,-2)且与平面3x-2y+6z=11平行的平面方程. 解:所求平面与平面3x-2y+6z=11平行 故n={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x-4)-2(y-1)+6(z+2)=0 即3x-2y+6z+2=0.38. 求过点M0(1,7,-3),且与连接坐标原点到点M0的线段OM0垂直的平面方程.解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x-1+7(y-7)-3(z +3)=0即x+7y-3z-59=039. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有得b=2. 故所求平面方程为1424x y z ++=40. 求过(1,1,-1), (-2,-2,2)和(1,-1,2)三点的平面方程. 解:由平面的三点式方程知 代入三已知点,有1112121210111121x y z --+----+=---+ 化简得x-3y-2z=0即为所求平面方程.41. 指出下列各平面的特殊位置,并画出其图形:(1) y =0; (2) 3x-1=0;(3) 2x-3y-6=0; (4) x –y=0;(5) 2x-3y+4z=0.解:(1) y=0表示xOz 坐标面(如图7-2)(2) 3x-1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x –y=0表示过z 轴的平面(如图7-5)(5) 2x-3y+4z=0表示过原点的平面(如图7-6).图7-4 图7-5 图7-642. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x+y-z=0的平面.解:设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0 0, .0A B C C A B A B C +-=⎧⇒==-⎨++=⎩ 所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.43. 决定参数k 的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6); (2) 与平面2x-3y+z=0成π4的角.解:(1) 因平面过点(5,-4,6)故有 5-4k-2×6=9得k=-4.(2)两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得2k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解:(1)n1={2,l,3}, n2={m,-6,-1}(2) n1={3, -5,l }, n2={1,3,2}45. 通过点(1,-1,1)作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解:设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}又(1,-1,1)在所求平面上,故A-B+C+D=0,得D=0故所求平面方程为即2x-y-3z=046. 求平行于平面3x-y+7z=5,且垂直于向量i-j+2k的单位向量.解:n1={3,-1,7}, n2={1,-1,2}. 故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k47. 求下列直线与平面的交点: (1) 11126x y z-+==-, 2x+3y+z-1=0; (2) 213232x y z +--==, x+2y-2z+6=0.解:(1)直线参数方程为1126x ty t z t=+⎧⎪=--⎨⎪=⎩代入平面方程得t=1故交点为(2,-3,6).(2) 直线参数方程为221332x ty t z t=-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t=0.故交点为(-2,1,3).48. 求下列直线的夹角:(1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z x y z +-+=⎧⎨++-=⎩;(2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩解:(1)两直线的方向向量分别为:s1={5,-3,3}×{3,-2,1}=533321i j k--={3,4,-1}s2={2,2,-1}×{3,8,1}=221381i j k-={10,-5,10}由s1·s2=3×10+4×(-5)+(-1) ×10=0知s1⊥s2 从而两直线垂直,夹角为π2.(2) 直线2314123x y z ---==-的方向向量为s1={4,-12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s2={0,2,-1}×{1,0,0}={0,-1,-2},于是49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x-y+2z-4=0垂直;(2)过点(0,2,4),且与两平面x+2z=1和y-3z=2平行;(3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为s={3,-1,2}故过点(2,-3,4)的直线方程为(2)所求直线平行两已知平面,且两平面的法向量n1与n2不平行,故所求直线平行于两平面的交线,于是直线方向向量 故过点(0,2,4)的直线方程为(3)所求直线与已知直线平行,故其方向向量可取为s={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z ++==--和4x-2y-2z=3; (2)327x y z ==-和3x-2y+7z=8; (3)223314x y z -+-==-和x+y+z=3. 解:平行而不包含. 因为直线的方向向量为s={-2,-7,3} 平面的法向量n={4,-2,-2},所以于是直线与平面平行.又因为直线上的点M0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上.51. 求过点(1,-2,1),且垂直于直线的平面方程. 解:直线的方向向量为12123111-=++-i jk i j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x+2y+3z=0.52. 求过点(1,-2,3)和两平面2x-3y+z=3, x+3y+2z+1=0的交线的平面方程.解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++=其中λ为待定常数,又因为所求平面过点(1,-2,3) 故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x+15y+7z+7=053. 求点(-1,2,0)在平面x+2y-z+1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s=n={1,2,-1}所以垂线的参数方程为122x ty t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t)+2(2+2t)-(-t)+1=0 得23t =- 于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333- 54. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量即11133211==-=---i jk n s j k故过已知点的平面方程为y+z=1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d == 55. 求点(1,2,1)到平面x+2y+2z-10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s=n={1,2,2}所以垂线的参数方程为12212x ty t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333,且与点(1,2,1)的距离为1d == 即为点到平面的距离.56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程.解:球的半径为R ==设(x,y,z)为球面上任一点,则(x-1)2+(y-3)2+(z+2)2=14 即x2+y2+z2-2x-6y+4z=0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.解:设该动点为M(x,y,z) 3.=化简得:8x2+8y2+8z2-68x+108y-114z+779=0即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=; (3)22194x z +=; (4)20y z -=; (5)220x y -=; (6)220x y +=.解:(1)母线平行于z 轴的抛物柱面,如图7-7.(2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8(3)母线平行于y 轴的椭圆柱面,如图7-9.(4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11.(6)z 轴,如图7-12.图7-11 图7-1259. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=; (3)222149y z x --=; (4)2221149y z x +-=;(5)22209z x y +-=. 解:(1)半轴分别为1,2,3的椭球面,如图7-13.(2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15.(4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-17.图7-1760. 作出下列曲面所围成的立体的图形:(1) x2+y2+z2=a2与z=0,z=2a(a>0); (2)x+y+z=4,x=0,x=1,y=0,y=2及z=0;(3) z=4-x2, x=0, y=0, z=0及2x+y=4; (4) z=6-(x2+y2),x=0, y=0, z=0及x+y=1.解:(1)(2)(3)(4)分别如图7-18,7-19,7-20,7-21所示.图7-18 图7-19图7-20 图7-2161. 求下列曲面和直线的交点: (1) 222181369x y z ++=与342364x y z --+==-;(2) 22211694x y z +-=与2434x y z +==-.解:(1)直线的参数方程为 代入曲面方程解得t=0,t=1.得交点坐标为(3,4,-2),(6,-2,2). (2) 直线的参数方程为 代入曲面方程可解得t=1, 得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程. 解:设(x ,y ,z )为圆上任一点,依题意有 即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程.(1) 平面x=2; (2) 平面y=0; (3) 平面y=5; (4) 平面z=2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x=2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ==⎩为平面y=5上的一个椭圆.(4) 截线方程为229252x y z ⎧-=⎪⎨⎪=⎩为平面z=2上的两条直线.64. 求曲线x2+y2+z2=a2, x2+y2=z2在xOy 面上的投影曲线. 解:以曲线为准线,母线平行于z 轴的柱面方程为 故曲线在xOy面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x2+y2=z, z=x+1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x2+y2=x+1即2215()24x y -+=.故曲线在xOy平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩ 习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界: (1) {(x, y)|x≠0};(2) {(x, y)|1≤x2+y2<4}; (3) {(x, y)|y<x2};(4) {(x, y)|(x-1)2+y2≤1}∪{(x, y)|(x+1)2+y2≤1}. 解:(1)开集、无界集,聚点集:R2,边界:{(x, y)|x=0}. (2)既非开集又非闭集,有界集, 聚点集:{(x, y)|1≤x2+y2≤4},边界:{(x, y)|x2+y2=1}∪{(x, y)| x2+y2=4}. (3)开集、区域、无界集, 聚点集:{(x, y)|y≤x2}, 边界:{(x, y)| y=x2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x, y)|(x-1)2+y2=1}∪{(x, y)|(x+1)2+y2=1}. 2. 已知f(x, y)=x2+y2-xytan x y,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u v f u v w u w +=+,试求(,,).f x y x y xy +-解:f( x + y, x-y, x y) =( x + y)xy+(x y)x+y+x-y =(x + y)xy+(x y)2x.4. 求下列各函数的定义域: 解:2(1){(,)|210}.D x y y x =-+>5. 求下列各极限: 解:(1)原式0ln 2.=(2)原式=+∞.(3)原式=01.4x y →→=-(4)原式=02.x y →→=(5)原式=0sin lim 100.x y xyy xy→→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O(0,0)处是否连续:(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y ++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O(0,0)处连续.(2)00sin lim lim 1(0,0)0x u y uz z u→→→==≠=故O(0,0)是z 的间断点.(3)若P(x,y) 沿直线y=x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P(x,y) 沿直线y=-x 趋于(0,0)点,则 故0lim x y z →→不存在.故函数z 在O(0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x,y)=233x y x y-+; (2) f (x,y)=2222y xy x+-; (3) f (x,y)=ln(1-x2-y2);(4)f (x,y)=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解:(1)因为当y=-x 时,函数无定义,所以函数在直线y=-x 上的所有点处间断,而在其余点处均连续.(2)因为当y2=2x 时,函数无定义,所以函数在抛物线y2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x2+y2=1时,函数无定义,所以函数在圆周x2+y2=1上所有点处间断.而在其余各点处均连续. (4)因为点P(x,y)沿直线y=x 趋于O(0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数: (1)z = x2y+2x y ;(2)s =22u v uv+;(4)z = lntan x y; (5)z = (1+xy)y; (6)u = zxy; (7)u = arctan(x-y)z; (8)yzu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂(2)u v s v u =+2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)222221ln 2ln(),2z x x x x y x x y ∂==++∂+ (4)21122sec csc ,tan z x xx x y y y yy∂=⋅⋅=∂ (5)两边取对数得ln ln(1)z y xy =+ 故 []221(1)(1)(1).ln(1)1y y y x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+ (6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+- (8)1.yz u y x x z-∂=∂9.已知22x y u x y=+,求证:3u u xy u x y∂∂+=∂∂. 证明: 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++.由对称性知 22322()u x y yx y x y ∂+=∂+.于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z z x y z x y∂∂+=∂∂. 证明: 11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x,y 的对称性得故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设fx(x,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角.解:(2,4,5)1,1,2z zx xx ∂∂==∂∂设切线与正向x 轴的倾角为α, 则tanα=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z = x4+ y4-4x2y2; (2)z = arctan y x; (3)z = yx;(4)z = 2e x y +.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x,y 的对称性知 (2)222211z y y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,(3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂(4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 14.设f (x, y, z) = xy2+yz2+zx2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解:2(,,)2x f x y z y zx=+15.设z = x ln ( x y),求32z x y ∂∂∂及32zx y ∂∂∂.解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22ex y z +=;(2)z =;(3)zy u x =; (4)yzu x =.解:(1)∵2222e 2,e 2x y x y z zx y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )x y xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;;(3)(1.97)1.05.解:(1)设f(x,y)=x3·y2,则223(,)3,(,)2,x y f x y x y f x y x y ==故df(x,y)=3x2y2dx+2x3ydy=xy(3xydx+2x2dy) 取x=1,y=1,dx=0.02,dy=-0.03,则 (1.02)3·(0.97)2=f(1.02,0.97)≈f(1,1)+df(1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d0.05d0.07(4.05,2.93)(4,3)d(4,3)0.053(0.07)]15(0.01)54.998xyf f f==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=xy,则df(x,y)=yxy-1dx+xylnxdy,取x=2,y=1,dx=-0.03,dy=0.05,则1.05d0.03d0.05(1.97)(1.97,1.05)(2,1)d(2,1)20.0393 2.0393.xyf f f=-==≈+=+=19.矩型一边长a=10cm,另一边长b=24cm, 当a边增加4mm,而b边缩小1mm时,求对角线长的变化.解:设矩形对角线长为l,则d d).l l x x y y==+当x=10,y=24,dx=0.4,dy=-0.1时,d0.4240.1)0.062l=⨯-⨯=(cm)故矩形的对角线长约增加0.062cm.20.解:因为圆锥体的体积为21.3V r hπ=⋅0030,0.1,60,0.5r r h h====-而221.33V VV dV r h yh r r hr hππ∂∂≈=⋅+⋅=⋅+⋅∂∂0030,0.1,60,0.5r r h h====-时,2213.1430600.130(0.5)33Vπ≈⨯⨯⨯⨯+⨯⨯-230()cm=-21.解:设水池的长宽深分别为,,x y z则有:V xyz=精确值为:50.242 2.850.22 3.6 2.80.2V=⨯⨯+⨯⨯⨯+⨯⨯⨯313.632()m=近似值为:V dV zx y xy z≈=+0.4,0.4,0.2x y z ===430.4530.4540.2V dV ≈=⨯⨯+⨯⨯+⨯⨯314.8()m =22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂; (2)z =arc tanx y ,x =u +v,y =u -v,求z u ∂∂,z v∂∂; (3)ln(e e )xyu =+,y =x3,求d d ux; (4)u =x2+y2+z2,x =e cos tt ,y =e sin tt ,z =e t,求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数:(1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+25. 设22()yz f x y =-,其中f(u)为可导函数,验证: 211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂ 由对称性知,22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,(2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂ ()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y zxf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y +++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证:利用变量替换1,3x y x y ξη=-=-,可将方程22222430u u ux x y y∂∂∂++=∂∂∂∂ 化简为20uξη∂=∂∂. 证明:设1(,),3u f f x y x y ξη⎛⎫==-- ⎪⎝⎭2222222222222222222222221411(1)(1)3333u u u u ux x x u u u u u u u ux x x x x u u u uuu u x y ξηξηξηξηξηξξηηξηξξηηξξηηξηξξη∂∂∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⋅+⋅+⋅+⋅=++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂⎛⎫⎛⎫=+⋅-+⋅+⋅-=----- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭22u η∂∂222222222222222222222222211(1)33111211(1)(1)33933343142433u u u u u y u u u uuu u u y u u u x x y yu u u u ξηξηξξηηξηξξηηξξηηξ∂∂∂∂∂⎛⎫=⋅+⋅-=--- ⎪∂∂∂∂∂⎝⎭∂∂∂∂∂∂∂∂⎛⎫⎛⎫=-⋅-⋅--⋅-⋅-=++-- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭∂∂∂++∂∂∂∂∂∂∂∂∂=+++--∂∂∂∂∂2222222221239340.3u u u u u u ξηηξξηηξη⎛⎫⎛⎫∂∂∂∂+-++ ⎪ ⎪∂∂∂∂∂∂∂⎝⎭⎝⎭∂=-=∂∂故20.uξη∂=∂∂ 29. 求下列隐函数的导数或偏导数:(1)2sin e 0xy xy +-=,求d d yx ;(2)arctan y x =,求d d y x;(3)20x y z ++-=,求,z zx y∂∂∂∂; (4)333z xyz a -=,求22,z z x y ∂∂∂∂. 解:(1)[解法1] 用隐函数求导公式,设F(x,y)=siny+ex-xy2, 则 2e ,cos 2,xx y F y F y xy =-=-故 22d e e d cos 2cos 2x xx y F y y y x F y xy y xy--=-=-=--. [解法2] 方程两边对x 求导,得()2cos e 02x y y y x yy '⋅+-='+⋅故 2e .cos 2xy y y xy-'=- (2)设()221(,)ln arctanln arctan ,2y y F x y x y x x==-+ ∵222222121,21x xx y y F x y x y x y x +⎛⎫=-⋅=- ⎪++⎝⎭⎛⎫+ ⎪⎝⎭222221211,21y yy x F x y x x y y x -=-⋅=++⎛⎫+ ⎪⎝⎭∴d .d x y F y x y x F x y+=-=- (3)方程两边求全微分,得d 2d d 0,x y z ++-=,z x y =则d ,z x y =+故z z x y ∂∂==∂∂ (4)设33(,,)3F x y z z xyz a =--,23,3,33,x y z F yz F xz F z xy =-=-=-则223,33x z F z yz yzx F z xy z xy∂-=-=-=∂-- 223,33y z F z xz xzy F z xy z xy∂-=-=-=∂--()()()()22222222322232222()zz z x x xz z xy xz y z y z xy y y z xy xzxzz x x xz z xy z xyx yzz xy xy z zxy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--30. 设F(x, y, z)=0可以确定函数x = x(y, z), y = y(x, z), z = z(x, y),证明:1x y zy z x∂∂∂⋅⋅=-∂∂∂. 证明:∵,,,y x z x y zF F F x y zy F z F x F ∂∂∂=-=-=-∂∂∂∴1.y z x y z x F F F x y z F F F y z x ⎛⎫⎛⎫∂∂∂⎛⎫---⋅⋅=⋅⋅=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z(x,y),其中F 可微,求,z z x y ∂∂∂∂.解:12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222011111z y x z y zF F F F F F F y F F F z x x F F x F F F F F y F zyy F F y F '''=⋅+⋅=⎛⎫''-=⋅+⋅ ⎪⎝⎭'-'∂=-=-=∂''''-''-∂=-=-=∂''32. 求由下列方程组所确定的函数的导数或偏导数:(1)22222,2320,z x y x y z ⎧=+⎪⎨++=⎪⎩ 求:d d ,;d d y z x x (2)1,0,xu yv yu xv +=⎧⎨-=⎩求:,,,;u v u v x x y y ∂∂∂∂∂∂∂∂ (3)2(,),(,),u f ux v y v g u x v y =+⎧⎨=-⎩ 其中f,g 具有连续偏导数函数,求,;u v x x∂∂∂∂(4)e sin ,e cos ,uux u v y u v ⎧=+⎪⎨=-⎪⎩ 求,,,.u u v v x y x y ∂∂∂∂∂∂∂∂ 解:(1)原方程组变为222222320y z xy z x⎧-=-⎪⎨+=-⎪⎩ 方程两边对x 求导,得d d 22d d d d 23d d y z y x x xy z y z x xx ⎧-=-⎪⎪⎨⎪-=-⎪⎩ 当 2162023y J yz y y z-==+≠21d 16(61),3d 622(31)22d 12.2d 6231x y xz x x z x z x J yz y y z y x z xy x y x x J yz y z ----+===--++-===-++(2)设(,,,)1,(,,,),F x y u v xu yv G x y u v yu xv =+-=-,,,,,,,,x y u v x y u v F u F v F x F y G v G u G y G x =====-===-22u v u v F F x yJ x y G G y x===---故 22xvx v F F u yG G v x uux yv x J J x y --∂-+=-=-=∂+ 222222,,.uxu x y v yvuy u y F F xuG G y v vvx uy x J J x y F F v yG G u x u vx uy yJ J x yF F x vG G y u vxu vy y J J x y-∂--=-=-=∂+-∂--=-=-=∂+∂-=-=-=∂+。
高等数学复旦大学出版第三版上册课后答案习题全 PDF 版本适合手机

x x x x ] = 时,邮资 y = × 0.80 = ; 20 20 20 25 x x ⎡ x ⎤ ]≠ 时, 由题意知邮资 y = + 1⎥ × 0.80 . ⎢ 20 20 ⎣ 20 ⎦
当 x 不能被 20 整除时,即 [
⎧x ⎡ x⎤ x , 0 < x ≤ 2000且 ⎢ ⎥ = ; ⎪ ⎪ 25 ⎣ 20 ⎦ 20 综上所述有 y = ⎨ ⎪ ⎡ x + 1⎤ × 0.80, 0 < x ≤ 2000且 ⎡ x ⎤ ≠ x . ⎢ ⎪ ⎣ 20 ⎥ ⎦ ⎣ 20 ⎥ ⎦ 20 ⎩⎢
1− x 1− y 解得 x = , 1+ x 1+ y
所以函数 y =
1− x 1− x 的反函数为 y = ( x ≠ −1) . 1+ x 1+ x
y−1
(2) 由 y = ln( x + 2) + 1 得 x = e
−2,
(x ∈R) .
所以, 函数 y = ln( x + 2) + 1 的反函数为 y = e x −1 − 2
习题一
1. 下列函数是否相等,为什么?
(1) f ( x ) = x 2 , g (x ) = x ; x 2 −1 (3) f ( x ) = , g ( x ) = x + 1. x −1
解: (1)相等.
(2)y = sin2 (3x + 1),u = sin2 (3t + 1);
因为两函数的定义域相同 ,都是实数集 R; 由
4
故
f ( x) − f (− x) 为奇函数.
12. 某厂生产某种产品 , 年销售量为 106 件, 每批生产需要准备费 103 元, 而每件的年库存费为 0.05 元, 如果销售是均匀的 , 求准备费与库存费之和的总费用与年销售批数之间的函数 ( 销售 均匀是指商品库存数为批量的一半). 解: 设年销售批数为 x, 则准备费为 103x; 又每批有产品
高等数学复旦大学出版第三版下册课后答案习题全(陈策提mai供huan)

习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2) s==(3) s==(4) s==5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).故2s=xs==ys==5zs==.6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点. 解:设此点为M(0,0,z),则222222(4)1(7)35(2)z z-++-=++--解得149z=173174即所求点为M (0,0,149). 7. 试证:以三点A (4,1,9),B (10,-1,6),C (2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB |=|AC |=7.且有|AC |2+|AB |2=49+49=98=|BC |2.故△ABC 为等腰直角三角形.8. 验证:()()++=++a b c a b c .证明:利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a , b , c 表示23.-u v解:232(2)3(3)2243935117-=-+--+-=-++-+=-+u v a b c a b c a b c a b c a b c10. 把△ABC 的BC 边分成五等份,设分点依次为D 1,D 2,D 3,D 4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解:1115D A BA BD =-=--c a 2225D A BA BD =-=--c a 3335D A BA BD =-=--c a 444.5D A BA BD =-=--c a 11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影.解:设M 的投影为M ',则1Pr j cos604 2.2u OM OM =︒=⨯= 12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标.解:设此向量的起点A 的坐标A (x , y , z ),则{4,4,7}{2,1,7}AB x y z =-=----175解得x =-2, y =3, z =0故A 的坐标为A (-2, 3, 0).13. 一向量的起点是P 1(4,0,5),终点是P 2(7,1,3),试求:(1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量.解:(1)12Pr j 3,x x a PP ==12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==-(2) 12(7PP ==(3) 12cos 14xa PP α== 12cos 14ya PP β==12cos 14za PP γ==(4) 12012{14PP PP ===+e j . 14. 三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点.求合力R 的大小和方向余弦. 解:R =(1-2+3,2+3-4,3-4+5)=(2,1,4)||==R cos cos cos αβγ=== 15. 求出向量a = i +j +k , b =2i -3j +5k 和c=-2i -j +2k 的模,并分别用单位向量,,a b c e e e 来表达向量a ,b ,c .解:||==a||==b ||3==c176, , 3. a b c ==a b c e16. 设m =3i +5j +8k , n =2i -4j -7k , p =5i +j -4k ,求向量a =4m +3n -p 在x 轴上的投影及在y 轴上的分向量.解:a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k在x 轴上的投影a x =13,在y 轴上分向量为7j .17.解:设{,,}x y z a a a a =则有c o s (1,1)3x a i a a i a iπ⋅====⋅ 求得12x a =. 设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 4a ba b π⋅=⇒=⋅ 则214y a = 求得12y a =± 又1,a =则2221x y z a a a ++=从而求得11{,,}222a =±或11{,,}222-± 18. 已知两点M 1(2,5,-3),M 2(3,-2,5),点M 在线段M 1M 2上,且123M M MM =,求向径OM 的坐标.解:设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为,123M M MM = 所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩177故OM ={111,,344-}. 19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标. 解:设P 的坐标为(x , y , z ), 2222||(12)49PA x y z =++-=得2229524x y z z ++=-+126570cos 6, 749z z γ==⇒==又122190cos 2, 749x x α==⇒==123285cos 3, 749y y β==⇒==故点P 的坐标为P (2,3,6)或P (190285570,,494949).20. 已知a , b 的夹角2π3ϕ=,且3,4==b a ,计算:(1) a ·b ; (2) (3a -2b )·(a + 2b ).解:(1)a ·b =2π1cos ||||cos 3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b(2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b21. 已知a =(4,-2, 4), b =(6,-3, 2),计算:(1)a ·b ; (2) (2a -3b )·(a + b ); (3)2||-a b解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b(2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b36238499=-⨯+=17822. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影.解:AB ={3,-2,-6},CD ={6,2,3}Pr j CD AB CD AB CD ⋅=4.7==- 23. 若向量a +3b 垂直于向量7a -5b ,向量a -4b 垂直于向量7a -2b ,求a 和b 的夹角.解: (a +3b )·(7a -5b ) =227||1615||0+⋅-=a a b b ①(a -4b )·(7a -2b ) = 227||308||0-⋅+=a a b b ② 由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos 23θ==. 24. 设a =(-2,7,6),b =(4, -3, -8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直. 证明:以a ,b 为邻边的平行四边形的两条对角线分别为a +b ,a -b ,且a +b ={2,4, -2}a -b ={-6,10,14}又(a +b )·(a -b )= 2×(-6)+4×10+(-2)×14=0故(a +b )⊥(a -b ).25. 已知a =3i +2j -k , b =i -j +2k ,求:(1) a ×b ; (2) 2a ×7b ;(3) 7b ×2a ; (4) a ×a . 解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k(4) 0⨯=a a .26. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算:(1) |(a +b )×(a -b )|;(2) |(3a +b )×(a -2b )|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b179π2||||sin 242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin 842=⨯⨯⨯= 27. 求垂直于向量3i -4j -k 和2i -j +k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a =(2,1,-1)和b =(1,-2,1)为邻边,求其对角线夹角的正弦. 解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++l l i j k12||||==l l 所以1212||sin 1||||θ⨯===l l l l . 即为所求对角线间夹角的正弦.29. 已知三点A (2,-1,5), B (0,3,-2), C (-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为31(1,1,), (1,3,), (0,1,3)22M N P -- {2,2,2}MN =--3{1,0,}2MP =- {4,4,4}AC =--{2,0,3}BC =-180 22222235233100122MN MP ----⨯=++=++--i j k i jk44444412208033220AC BC ---⨯=++=++--i j k i j k故 1()4MN MP AC BC ⨯=⨯.30.(1)解: x y zx y z i j ka b a a a b b b ⨯==-+-+-y z z y z x x z x y y x a b a b i a b a b j a b a b k ()()()则 C=-C +-+-y z z y x z x x z y x y y x ya b a b a b a b a b C a b a b C ⨯⋅()()()() x y zx y z x y za a ab b b C C C =若 ,,C a b 共面,则有 a b ⨯后与 C 是垂直的.从而 C 0a b ⨯⋅=() 反之亦成立.(2) C x y zx y z x y za a a ab b b b C C C ⨯⋅=()a x y zx y z x y zb b b b C C C C a a a ⨯⋅=()b x y z x y z x y zC C C C a a a a b b b ⨯⋅=()由行列式性质可得:x y z x y z x y zx y z x y z x y z x y z x y z x y za a ab b b C C C b b b C C C a a a C C C a a a b b b ==故 C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅()()()18131. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积.解:设四顶点依次取为A , B , C , D .{0,1,2}, {2,2,1}AB AD ==-则由A ,B ,D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i j k .同理可求其他三个三角形的面积依次为12故四面体的表面积122S =+.32.解:设四面体的底为BCD ∆,从A 点到底面BCD ∆的高为h ,则13BCD V S h =⋅⋅,而11948222BCD S BC BD i j k =⨯=--+=又BCD ∆所在的平面方程为:48150x y z +-+=则43h ==故1942323V =⋅⋅=33. 已知三点A (2,4,1), B (3,7,5), C (4,10,9),证:此三点共线.证明:{1,3,4}AB =,{2,6,8}AC =显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ,B ,C 三点共线.34. 一动点与M 0(1,1,1)连成的向量与向量n =(2,3,-4)垂直,求动点的轨迹方程.解:设动点为M (x , y , z )0{1,1,1}M M x y z =---因0M M n ⊥,故00M M n ⋅=.即2(x -1)+3(y -1)-4(z -1)=0整理得:2x +3y -4z -1=0即为动点M 的轨迹方程.35. 求通过下列两已知点的直线方程:(1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3).182 解:(1)两点所确立的一个向量为s ={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s ={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程. 解:所给直线的方向向量为 12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点(0,7,17),因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为:771719x t y t z t =⎧⎪=-⎨⎪=-⎩37. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程.解:所求平面与平面3x -2y +6z =11平行故n ={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x -4)-2(y -1)+6(z +2)=0即3x -2y +6z +2=0.38. 求过点M 0(1,7,-3),且与连接坐标原点到点M 0的线段OM 0垂直的平面方程.解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x -1+7(y -7)-3(z +3)=0即x +7y -3z -59=039. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有121122b b b-++=183得b =2. 故所求平面方程为1424x y z ++= 40. 求过(1,1,-1), (-2,-2,2)和(1,-1,2)三点的平面方程.解:由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点,有1112121*********x y z --+----+=---+ 化简得x -3y -2z =0即为所求平面方程.41. 指出下列各平面的特殊位置,并画出其图形:(1) y =0; (2) 3x -1=0;(3) 2x -3y -6=0; (4) x – y =0;(5) 2x -3y +4z =0.解:(1) y =0表示xOz 坐标面(如图7-2)(2) 3x -1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x -3y -6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x =3和y =-2的平面.(如图7-4)(4) x –y =0表示过z 轴的平面(如图7-5)(5) 2x -3y +4z =0表示过原点的平面(如图7-6).图7-4 图7-5 图7-642. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x +y -z =0的平面.解:设平面方程为Ax +By +Cz +D =0则其法向量为n ={A ,B ,C }已知平面法向量为n 1={1,1,-1}过已知两点的向量l ={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A B A B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.43. 决定参数k的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6);(2)与平面2x-3y+z=0成π4的角.解:(1)因平面过点(5,-4,6)故有5-4k-2×6=9得k=-4.(2)两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得2k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解:(1)n1={2,l,3}, n2={m,-6,-1}12232,18613lm lm⇒==⇒=-=--n n(2) n1={3, -5, l }, n2={1,3,2}12315320 6.l l⊥⇒⨯-⨯+⨯=⇒=n n45. 通过点(1,-1,1)作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解:设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}12203203A CA B CA B C CB⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n nn n又(1,-1,1)在所求平面上,故A-B+C+D=0,得D=0故所求平面方程为233CCx y Cz-++=即2x-y-3z=018418546. 求平行于平面3x -y +7z =5,且垂直于向量i -j +2k 的单位向量.解:n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n 故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k47. 求下列直线与平面的交点: (1) 11126x y z-+==-, 2x +3y +z -1=0; (2) 213232x y z +--==, x +2y -2z +6=0.解:(1)直线参数方程为1126x ty t z t=+⎧⎪=--⎨⎪=⎩代入平面方程得t =1故交点为(2,-3,6).(2) 直线参数方程为221332x ty t z t=-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0.故交点为(-2,1,3).48. 求下列直线的夹角:(1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z xy z +-+=⎧⎨++-=⎩;(2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩解:(1)两直线的方向向量分别为:s 1={5, -3,3}×{3, -2,1}=533321i j k--={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}186由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直,夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是1212cos 0.2064785θθ⋅==≈⋅'≈︒s s s s 49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x -y +2z -4=0垂直;(2)过点(0,2,4),且与两平面x +2z =1和y -3z =2平行;(3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为s ={3,-1,2}故过点(2,-3,4)的直线方程为 234312x y z -+-==- (2)所求直线平行两已知平面,且两平面的法向量n 1与n 2不平行,故所求直线平行于两平面的交线,于是直线方向向量12102{2,3,1}013=⨯==--i j ks n n 故过点(0,2,4)的直线方程为24231x y z --==- (3)所求直线与已知直线平行,故其方向向量可取为s ={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z ++==--和4x -2y -2z =3; (2)327x y z ==-和3x -2y +7z =8;187(3)223314x y z -+-==-和x +y +z =3. 解:平行而不包含. 因为直线的方向向量为s ={-2,-7,3}平面的法向量n ={4,-2,-2},所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上.51. 求过点(1,-2,1),且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩ 的平面方程. 解:直线的方向向量为12123111-=++-ij k i j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0.52. 求过点(1,-2,3)和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程.解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++=其中λ为待定常数,又因为所求平面过点(1,-2,3)故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x +15y +7z +7=053. 求点(-1,2,0)在平面x +2y -z +1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s =n ={1,2,-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t )+2(2+2t )-(-t )+1=0188 得23t =- 于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333-54. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离. 解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量 即11133211==-=---ij k n s j k故过已知点的平面方程为y +z =1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d == 55. 求点(1,2,1)到平面x +2y +2z -10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s =n ={1,2,2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333,且与点(1,2,1)的距离为1d == 即为点到平面的距离.56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程.解:球的半径为R ==设(x ,y ,z )为球面上任一点,则(x -1)2+(y -3)2+(z +2)2=14即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.189解:设该动点为M (x ,y ,z )3.=化简得:8x 2+8y 2+8z 2-68x +108y -114z +779=0即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22aax y -+=; (2)22149x y -+=;(3)22194x z +=; (4)20y z -=;(5)220x y -=; (6)220x y +=.解:(1)母线平行于z 轴的抛物柱面,如图7-7.(2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8(3)母线平行于y 轴的椭圆柱面,如图7-9.(4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11.(6)z 轴,如图7-12.图7-11 图7-1219059. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=;(3)222149y z x --=; (4)2221149y z x +-=;(5)22209z x y +-=.解:(1)半轴分别为1,2,3的椭球面,如图7-13.(2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15.(4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-17.图7-1760. 作出下列曲面所围成的立体的图形:(1) x 2+y 2+z 2=a 2与z =0,z =2a(a >0); (2) x +y +z =4,x =0,x =1,y =0,y =2及z =0;(3) z =4-x 2, x =0, y =0, z =0及2x +y =4; (4) z =6-(x 2+y 2),x =0, y =0, z =0及x +y =1.191解:(1)(2)(3)(4)分别如图7-18,7-19,7-20,7-21所示.图7-18 图7-19图7-20 图7-2161. 求下列曲面和直线的交点: (1) 222181369x y z ++=与342364x y z --+==-; (2) 22211694x y z +-=与2434x y z +==-. 解:(1)直线的参数方程为334624x t y t z t =+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t =0,t =1.得交点坐标为(3,4,-2),(6,-2,2).(2) 直线的参数方程为4324x t y tz t =⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t =1,得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程.192 解:设(x ,y ,z )为圆上任一点,依题意有2295x y z ⎧+=⎨=±⎩即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程.(1) 平面x =2; (2) 平面y =0;(3) 平面y =5; (4) 平面z =2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩其形状为x =2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ⎧==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.64. 求曲线x 2+y 2+z 2=a 2, x 2+y 2=z 2在xOy 面上的投影曲线. 解:以曲线为准线,母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x 2+y 2=z , z =x +1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=.193故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界: (1) {(x , y )|x ≠0};(2) {(x , y )|1≤x 2+y 2<4}; (3) {(x , y )|y <x 2};(4) {(x , y )|(x -1)2+y 2≤1}∪{(x , y )|(x +1)2+y 2≤1}.解:(1)开集、无界集,聚点集:R 2,边界:{(x , y )|x =0}. (2)既非开集又非闭集,有界集, 聚点集:{(x , y )|1≤x 2+y 2≤4},边界:{(x , y )|x 2+y 2=1}∪{(x , y )| x 2+y 2=4}. (3)开集、区域、无界集, 聚点集:{(x , y )|y ≤x 2}, 边界:{(x , y )| y =x 2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x , y )|(x -1)2+y 2=1}∪{(x , y )|(x +1)2+y 2=1}. 2. 已知f (x , y )=x 2+y 2-xy tanxy,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u vf u v w u w+=+,试求(,,).f x y x y xy +-解:f ( x + y , x -y , x y ) =( x + y )xy +(x y )x +y +x -y =(x + y )xy +(x y )2x . 4. 求下列各函数的定义域:2(1)ln(21);z y x =-+(2)z =(3)z =(4)u =+(5)z =(6)ln()z y x =-+194(7)u =解:2(1){(,)|210}.D x y y x =-+>(2){(,)|0,0}.D x y x y x y =+>->22222(3){(,)|40,10,0}.D x y x y x y x y =-≥-->+≠(4){(,,)|0,0,0}.D x y z x y z =>>> 2(5){(,)|0,0,}.D x y x y x y =≥≥≥ 22(6){(,)|0,0,1}.D x y y x x x y =->≥+< 22222(7){(,,)|0,0}.D x y z x y x y z =+≠+-≥5. 求下列各极限:10y x y →→ 22001(2)lim;x y x y →→+00x y →→x y →→00sin (5)lim ;x y xy x →→2222221cos()(6)lim.()ex y x y x y x y +→→-++解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=01.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+1956. 判断下列函数在原点O (0,0)处是否连续:33222222sin(),0,(1)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩33333333sin(),0,(2)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O (0,0)处连续. (2)000sin lim lim1(0,0)0x u y uz z u→→→==≠=故O (0,0)是z 的间断点.(3)若P (x ,y ) 沿直线y =x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0,0)点,则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x ,y )=233x y x y -+;(2) f (x ,y )=2222y xy x+-;(3) f (x ,y )=ln(1-x 2-y 2);(4)f (x ,y )=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩196解:(1)因为当y =-x 时,函数无定义,所以函数在直线y =-x 上的所有点处间断,而在其余点处均连续.(2)因为当y 2=2x 时,函数无定义,所以函数在抛物线y 2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x 2+y 2=1时,函数无定义,所以函数在圆周x 2+y 2=1上所有点处间断.而在其余各点处均连续.(4)因为点P (x ,y )沿直线y =x 趋于O (0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数:(1)z = x 2y +2xy;(2)s =22u v uv+;(3)z = x; (4)z = lntan x y; (5)z = (1+xy )y ; (6)u = z xy ;(7)u = arctan(x -y )z; (8)y zu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+ 2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+222.z xy x y y x y ∂==∂+ (4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂222122sec ()csc .tan z x x x x x y y y y yy∂=⋅⋅-=-∂ (5)两边取对数得ln ln(1)z y xy =+故[]221(1)(1)(1).ln(1)1y yy x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+197[]ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x z xy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z z u z x y z x y x x y x y --∂-=⋅-=∂+-+- 112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z z z zz z u z x y z x y y x y x y u x y x y x y x y z x y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yzu y x x z-∂=∂ 2211ln ln .ln ln .yyzz yy z zu x x x x y z zu y y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭9.已知22x y u x y =+,求证:3u uxy u x y∂∂+=∂∂. 证明: 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z z xy z x y∂∂+=∂∂. 证明: 11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x ,y 的对称性得1981121ex y z y y⎛⎫+- ⎪⎝⎭∂=∂ 故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设f (x ,y ) = x +(y,求f x (x ,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角.解:(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z = x 4+ y 4-4x 2y 2; (2)z = arctan y x; (3)z = y x ;(4)z = 2ex y+.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x ,y 的对称性知22222128.16.z z y x xy y y x∂∂=-=-∂∂∂ (2)222211zy y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,1992222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y x xyx x y x y z x y x x y y x z xyy x y z x y y y y x x y x y x y z x y x x y x y x x y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++ (3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ (4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 222222222e 22e 22e (21),e ,2e ,2e .x y x y x y x y x y x y z x x x xz z z x x y x y y x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂14.设f (x , y , z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f -解:2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===15315.设z = x ln ( x y ),求32z x y ∂∂∂及32zx y ∂∂∂.解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22ex y z +=;(2)z =;(3)zy u x =;(4)yzu x =.解:(1)∵2222e 2,e 2x y x y z z x y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )xy xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴ 223/2d (d d ).()x z y x x y x y =--+ (3)∵11,ln z z z y y z u uy x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂154ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;(3)(1.97)1.05.解:(1)设f (x ,y )=x 3·y 2,则223(,)3,(,)2,x y f x y x y f x y x y ==故d f (x ,y )=3x 2y 2d x +2x 3y d y =xy (3xy d x +2x 2d y ) 取x =1,y =1,d x =0.02,d y =-0.03,则(1.02)3·(0.97)2=f (1.02,0.97)≈f (1,1)+d f (1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设f (x ,y,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则155d 0.05d 0.07(4.05,2.93)(4,3)d (4,3)0.053(0.07)]15(0.01)54.998x y f f f ==-=≈+=⨯+⨯-=+⨯-=(3)设f (x ,y )=x y ,则d f (x ,y )=yx y -1d x +x y ln x d y , 取x =2,y =1,d x =-0.03,d y =0.05,则1.05d 0.03d 0.05(1.97)(1.97,1.05)(2,1)d (2,1)20.0393 2.0393.x y f f f =-==≈+=+=19.矩型一边长a =10cm ,另一边长b =24cm, 当a 边增加4mm ,而b 边缩小1mm 时,求对角线长的变化.解:设矩形对角线长为l ,则d d ).l l x x y y ==+当x =10,y =24,d x =0.4,d y =-0.1时,d 0.4240.1)0.062l =⨯-⨯=(cm)故矩形的对角线长约增加0.062cm. 20.解:因为圆锥体的体积为21.3V r h π=⋅ 0030,0.1,60,0.5r r h h ====- 而221.33V V V dV r h yh r r h r h ππ∂∂≈=⋅+⋅=⋅+⋅∂∂0030,0.1,60,0.5r r h h ====-时, 2213.1430600.130(0.5)33V π≈⨯⨯⨯⨯+⨯⨯- 230()cm =-21.解:设水池的长宽深分别为,,x y z 则有:V xyz =精确值为:50.242 2.850.22 3.6 2.V =⨯⨯+⨯⨯⨯+⨯⨯⨯ 313.632()m = 近似值为:156V dV zx y xy z ≈=+0.4,0.4,0.2x y z ===430.4530.454V d V ≈=⨯⨯+⨯⨯+⨯⨯ 314.8()m =22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,zv∂∂; (2)z =arc tanx y , x =u +v ,y =u -v , 求z u ∂∂,z v∂∂; (3)ln(e e )xyu =+, y =x 3, 求d d ux; (4) u =x 2+y 2+z 2, x =e cos tt , y =e sin tt , z =e t, 求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y xx x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.15723. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+15825. 设22()yz f x y =-,其中f (u )为可导函数,验证: 211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂ 由对称性知,22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂1592212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,(2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂ ()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y zxf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y +++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证:利用变量替换1,3x y x y ξη=-=-,可将方程。
高等数学上复旦大学出版习题1答案.pdf

x1
=
sin
x2
,即 A 中不同的元素
x1,
x2
有相同的
像,∴f 不是单射.
综上所述, f 为满射,但不是单射.
(3)∵∀x1, x2 ∈ A , 且 x1 ≠ x2 ,有 ex1 ≠ ex2 ,即 A 中不同的元素有不同的像,∴f 是单射.
又∵ 0 ∈ B,∀x ∈ A, ex ≠ 0 ,即 B 中的元素 0 没有原像,∴f 不是满射.
2. 设 X = {1, 2,3, 4,5, 6}, A = {1, 2,3}, B = {2, 4, 6},C = {1,3,5} ,求 A∪ B ∪ C, A ∩ B ∩C , CXA,CXA∪CXB,
CXA∩CXB.
解: A∪ B ∪ C = {1, 2,3}∪{2, 4, 6}∪{1,3,5} = X
⎨ ⎩
x
≠
0
所以函数的定义域是 (−∞, 0) ∪ (0, 4].
(2)要使函数有意义,必须
所以函数的定义域是[-3,0) ∪(0,1) . (3)要使函数有意义,必须
⎧ x+3≥0
⎧x ≥ −3
⎪⎨lg(1− x) ≠ 0
即
⎪ ⎨
x
≠
0
⎪⎩ 1− x > 0
⎪⎩ x < 1
x2 −1≠ 0 即 x ≠ ±1
(2)不正确. 例如: A={1,2},B={1},C={1,3}有 A∩B=A∩C={1},但 B≠C.
4. 判定下列映射哪些是满射,哪些是单射,哪些是一一映射?
(1) A=(-∞,+∞),B=(-∞,+∞), f : x ∈ A |→ y = x3 ∈ B ;
(2) A=(-∞,+∞),B=[-1,1], f : x ∈ A |→ y = sin x ∈ B ;
高等数学复旦大学出版第三版课后答案

206习题十1. 根据二重积分性质,比较ln()d D x y σ+⎰⎰与2[ln()]d D x y σ+⎰⎰的大小,其中:(1)D 表示以(0,1),(1,0),(1,1)为顶点的三角形; (2)D 表示矩形区域{(,)|35,02}x y x y ≤≤≤≤.解:(1)区域D 如图10-1所示,由于区域D 夹在直线x +y =1与x +y =2之间,显然有图10-112x y ≤+≤从而 0l n ()x y ≤+<故有2l n ()[l n ()]x y x y+≥+ 所以 2l n ()d [l n ()]dD Dx yx y σσ+≥+⎰⎰⎰⎰(2)区域D 如图10-2所示.显然,当(,)x y D ∈时,有3x y +≥.图10-2从而 ln(x +y )>1 故有2l n ()[l n ()]x y x y+<+207所以 2l n ()d [l n ()]dD Dx yx y σσ+<+⎰⎰⎰⎰2. 根据二重积分性质,估计下列积分的值: (1),{(,)|02,02}I D x y x y σ==≤≤≤≤⎰⎰;(2)22sin sin d ,{(,)|0π,0π}D I x y D x y x y σ==≤≤≤≤⎰⎰; (3)2222(49)d ,{(,)|4}D I x y D x y x y σ=++=+≤⎰⎰. 解:(1)因为当(,)x y D ∈时,有02x ≤≤, 02y ≤≤因而 04xy ≤≤.从而22≤故2d D D σσσ≤≤⎰⎰⎰⎰⎰⎰即2d d DDσσσ≤≤⎰⎰⎰⎰而 d D σσ=⎰⎰ (σ为区域D 的面积),由σ=4 得8σ≤≤⎰⎰(2) 因为220sin 1,0sin 1x y ≤≤≤≤,从而220sin sin 1x y ≤≤故 220d sin sin d 1d D D D x y σσσ≤≤⎰⎰⎰⎰⎰⎰ 即220sin sin d d D D x y σσσ≤≤=⎰⎰⎰⎰ 而2πσ=所以2220sin sin d πD x y σ≤≤⎰⎰(3)因为当(,)x y D ∈时,2204x y ≤+≤所以22229494()925x y x y ≤++≤++≤故 229d (49)d 25d D D D x y σσσ≤++≤⎰⎰⎰⎰⎰⎰ 即229(49)d 25Dx y σσσ≤++≤⎰⎰208而2π24πσ=⋅=所以2236π(49)d 100πDx y σ≤++≤⎰⎰3. 根据二重积分的几何意义,确定下列积分的值: (1)222(,{(,)|};D a D x y x y a σ=+≤⎰⎰(2)222,{(,)|}.D x y x y a σ=+≤⎰⎰解:(1)(,D a σ⎰⎰在几何上表示以D 为底,以z 轴为轴,以(0,0,a )为顶点的圆锥的体积,所以31(π3Da a σ=⎰⎰ (2)σ⎰⎰在几何上表示以原点(0,0,0)为圆心,以a为半径的上半球的体积,故32π.3a σ=⎰⎰ 4.设f (x ,y )为连续函数,求2220021lim(,)d ,{(,)|()()}πDr f x y D x y x x y y r r σ→=-+-≤⎰⎰.解:因为f (x ,y )为连续函数,由二重积分的中值定理得,(,),D ξη∃∈使得2(,)d (,)π(,)Df x y f r f σξησξη=⋅=⋅⎰⎰又由于D 是以(x 0,y 0)为圆心,r 为半径的圆盘,所以当0r →时,00(,)(,),x y ξη→ 于是:0022200000(,)(,)11lim(,)d limπ(,)lim (,)ππlim (,)(,)Dr r r x y f x y r f f r r f f x y ξησξηξηξη→→→→=⋅===⎰⎰5. 画出积分区域,把(,)d D f x y σ⎰⎰化为累次积分: (1) {(,)|1,1,0}D x y x y y x y =+≤-≤≥;(2)2{(,)|2,}D x y y x x y =≥-≥209(3)2{(,)|,2,2}D x y y y x x x=≥≤≤解:(1)区域D 如图10-3所示,D 亦可表示为11,01y x y y -≤≤-≤≤.所以1101(,)d d (,)d yD y f x y y f x y x σ--=⎰⎰⎰⎰(2) 区域D 如图10-4所示,直线y =x -2与抛物线x =y 2的交点为(1,-1),(4,2),区域D 可表示为22,12y x y y ≤≤+-≤≤.图10-3 图10-4所以2221(,)d d (,)d y D yf x y y f x y x σ+-=⎰⎰⎰⎰(3)区域D 如图10-5所示,直线y =2x 与曲线2y x=的交点(1,2),与x =2的交点为(2,4),曲线2y x=与x =2的交点为(2,1),区域D 可表示为22,1 2.y x x x≤≤≤≤图10-5210所以2221(,)d d (,)d xD xf x y x f x y y σ=⎰⎰⎰⎰.6. 画出积分区域,改变累次积分的积分次序: (1) 2220d (,)d yyy f x y x⎰⎰; (2)e ln 1d (,)d xx f x y y ⎰⎰;(3) 1320d (,)d yy f x y x-⎰; (4)πsin 0sin2d (,)d xx x f x y y -⎰⎰;(5) 1233001d (,)d d (,)d yyy f x y y y f x y x -+⎰⎰⎰⎰.解:(1)相应二重保健的积分区域为D :202,2.y y x y ≤≤≤≤如图10-6所示.图10-6D 亦可表示为:04,.2xx y ≤≤≤所以2224002d (,)d d (,)d .yx yy f x y x x f x y y =⎰⎰⎰⎰(2) 相应二重积分的积分区域D :1e,0ln .x y x ≤≤≤≤如图10-7所示.图10-7D 亦可表示为:01,e e,y y x ≤≤≤≤211所以e ln 1e10ed (,)d d (,)d y xx f x y y y f x y x =⎰⎰⎰⎰(3) 相应二重积分的积分区域D为:01,32,y x y ≤≤≤≤-如图10-8所示.图10-8D 亦可看成D 1与D 2的和,其中 D 1:201,0,x y x ≤≤≤≤D 2:113,0(3).2x y x ≤≤≤≤-所以2113213(3)2001d (,)d d (,)d d (,)d yx x y f x y x x f x y y x f x y y --=+⎰⎰⎰⎰⎰.(4) 相应二重积分的积分区域D 为:0π,sinsin .2xx y x ≤≤-≤≤如图10-9所示.图10-9D 亦可看成由D 1与D 2两部分之和,其中 D 1:10,2arcsin π;y y x -≤≤-≤≤ D 2:01,arcsin πarcsin .y y x y ≤≤≤≤-所以πsin 0π1πarcsin 0sin 12arcsin 0arcsin 2d (,)d d (,)d d (,)d xyx y yx f x y y y f x y x y f x y x ----=+⎰⎰⎰⎰⎰⎰(5) 相应二重积分的积分区域D 由D 1与D 2两部分组成,其212中 D 1:01,02,y x y ≤≤≤≤D 2:13,03.y x y ≤≤≤≤-如图10-10所示.图10-10D 亦可表示为:02,3;2xx y x ≤≤≤≤- 所以()1233230012d ,d d (,)d d (,)d yyxxy f x y x y f x y x x f x y y --+=⎰⎰⎰⎰⎰⎰7.解:因为(,)Df x y d σ⎰⎰为一常数,不妨设(,)Df x y C =⎰⎰则有(,)x y f xy C =+从而有(,)()x y Df xy f uv C dudv =++⎰⎰而{}2(,)0 1.0D x y x y x =≤≤≤≤21(,)00()u x y f xy uv C dv du ⎡⎤∴=+⎰⎰+⎣⎦2120012u xy uv cv du ⎡⎤=+⎰+⎢⎥⎣⎦ 152012xy u cu du ⎡⎤=+⎰+⎢⎥⎣⎦163011123xy u cu ⎡⎤=++⎢⎥⎣⎦11123xy C =++18C ∴=故(,)18x y f xy ∴=+8. 计算下列二重积分:213(1) 221d d ,:12,;Dx x y D x y x y x≤≤≤≤⎰⎰ (2) e d d ,x yD x y ⎰⎰D由抛物线y 2 = x ,直线x =0与y =1所围;(3) d ,x y ⎰⎰D 是以O (0,0),A (1,-1),B (1,1)为顶点的三角形; (4) cos()d d ,{(,)|0π,π}D x y x y D x y x x y +=≤≤≤≤⎰⎰.解:(1)()22222231221111d d d d d d xx D x x x x x x y x y x x x x y yy ==-=-⎰⎰⎰⎰⎰⎰2421119.424x x ⎡⎤=-=⎢⎥⎣⎦(2) 积分区域D 如图10-12所示.图10-12D 可表示为:201,0.y x y ≤≤≤≤所示22110000ed d de d d e d()xx x y y yyyD xx y y x y y y==⎰⎰⎰⎰⎰⎰ 2111100ed (e 1)d e d d y x y y yy y y y y y y y ==-=-⎰⎰⎰⎰1111120000011de d e e d .22yy yy y y y y y =-=--=⎰⎰⎰ (3) 积分区域D 如图10-13所示.214图10-13D 可表示为:01,.x x y x ≤≤-≤≤所以2110d d arcsin d 2xxxx y x y x y x x --⎡==+⎢⎣⎰⎰⎰⎰⎰ 112300ππ1πd .2236x x x ==⋅=⎰ ππππ0πππ0(4)cos()d d d cos()d [sin()]d [sin(π)sin 2]d (sin sin 2)d 11.cos cos 222x Dxx y x y x x y y x y xx x x x x x x x +=+=+=+-=--⎡⎤==+⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰⎰9. 计算下列二次积分:10112111224(1)d d ;(2)d e d d e d .yy y xxyxy x xy x y x +⎰⎰⎰⎰解:(1)因为sin d x x x⎰求不出来,故应改变积分次序。
高等数学习题08答案(复旦大学出版社)

习题八5. 求下列各极限:10(1)y x y →→00(3)x y →→00(4)l ;x y →→222222001cos()(6)lim .()e x y x y x y x y +→→-++ 解:(1)原式0ln 2.=(3)原式=01.4x y →→=-(4)原式=002.x y →→=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 讨论下列函数在原点O (0,0)处的连续性及偏导数:(3) 222222222,0,()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(3)若P (x ,y ) 沿直线y =x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0,0)点,则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0,0)处不连续.而…8. 求下列函数的偏导数: (1)z = x 2y +2xy; (6)u = z xy ;解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ 12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角.解:(2,4,5)1,1,2z zx x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4.13.求下列函数的二阶偏导数:(3)z = y x ;解:(3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ 14.设f (x ,y ,z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解:2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===22. 求下列复合函数的偏导数或全导数:(2)z =arc tanxy, x =u +v ,y =u -v , 求z u ∂∂,z v ∂∂;(3)ln(e e )xyu =+, y =x 3, 求d d u x;(4) u =x 2+y 2+z 2, x =e cos t t , y =e sin t t , z =e t, 求d d u t. 解:(2)222222211111x z z x z y y x v y u x u y uy x yu v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭ 2222222111(1)11.x z z x z yy v x v y vyx x y y y x ux y u v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x yx x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xy u f x y =-解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ 29. 求下列隐函数的导数或偏导数:(4)333z xyz a -=,求22,z zx y∂∂∂∂.解:(4)设33(,,)3F x y z z xyz a =--, 则23,3,33,x y z F yz F xz F z xy =-=-=-故223,33x z F z yz yz x F z xy z xy∂-=-=-=∂-- 223,33y z F z xz xz y F z xy z xy∂-=-=-=∂--()()()()22222222322232222()zz z x x xz z xy xz y z y z xy y y z xy xzxzz x x xz z xy z xyx yzz xy xy z z xy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z (x ,y ),其中F 可微,求,z z x y ∂∂∂∂.解:12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222110111y z x zy zF F F y F F F F F F F zx x F F x F F F F F y F zy y F F y F ⎛⎫''-=⋅+⋅ ⎪⎝⎭'''=⋅+⋅='-'∂∴=-=-=∂''''-''-∂=-=-=∂''。
高等数学复旦大学出版第三版下册课后答案习题全之欧阳语创编

习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2)s==(3)s=(4)s==5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).故s==5s==.z6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点.解:设此点为M(0,0,z),则解得14z=9).即所求点为M(0,0,1497. 试证:以三点A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC为等腰直角三角形.8. 验证:()()a b c a b c.++=++证明:利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a, b, c 表示23.-u v 解:10. 把△ABC 的BC 边分成五等份,设分点依次为D1,D2,D3,D4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解:1115D A BA BD =-=--c a 11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影.解:设M 的投影为M ',则12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标. 解:设此向量的起点A 的坐标A(x, y, z),则 解得x=-2, y=3, z=0 故A 的坐标为A(-2, 3, 0).13. 一向量的起点是P1(4,0,5),终点是P2(7,1,3),试求:(1) 12PP 在各坐标轴上的投影; (2) 12PP 的模; (3) 12PP 的方向余弦; (4) 12PP 方向的单位向量.解:(1)12Pr j 3,x x a PP == (2)12(7PP ==(3)12cos 14x a PP α==12cos 14z a PP γ==(4)12012{14PP PP ===+e j . 14. 三个力F1=(1,2,3), F2=(-2,3,-4), F3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R=(1-2+3,2+3-4,3-4+5)=(2,1,4)15. 求出向量a= i+j+k, b=2i-3j+5k 和c=-2i-j+2k 的模,并分别用单位向量,,a b c e e e 来表达向量a, b, c. 解:||=a16. 设m=3i+5j+8k, n=2i-4j-7k, p=5i+j-4k,求向量a=4m+3n-p 在x 轴上的投影及在y 轴上的分向量.解:a=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k在x 轴上的投影ax=13,在y 轴上分向量为7j. 17.解:设{,,}x y z a a a a =则有 求得12x a =.设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 42a ba b π⋅=⇒=⋅ 则214y a = 求得12y a =±又1,a=则2221x y z a a a ++=从而求得11{,,}222a =±或11{,,}222-± 18. 已知两点M1(2,5,-3),M2(3,-2,5),点M 在线段M1M2上,且123M M MM =,求向径OM 的坐标. 解:设向径OM ={x, y, z}因为,123M M MM =所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}. 19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标.解:设P 的坐标为(x, y, z ),2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+又122190cos 2, 749x x α==⇒==故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a, b 的夹角2π3ϕ=,且3,4==b a ,计算: (1) a·b; (2) (3a -2b)·(a+ 2b). 解:(1)a·b=2π1cos ||||cos 3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2)(32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b21. 已知a=(4,-2, 4), b=(6,-3, 2),计算:(1)a·b; (2) (2a -3b)·(a+ b); (3)2||-a b解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2)(23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影. 解:AB ={3,-2,-6},CD ={6,2,3}23. 若向量a+3b 垂直于向量7a-5b,向量a-4b 垂直于向量7a-2b,求a 和b 的夹角.解: (a+3b)·(7a -5b)=227||1615||0+⋅-=a a b b ①(a-4b)·(7a -2b) =227||308||0-⋅+=a a b b ②由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos23θ==. 24. 设a=(-2,7,6),b=(4,-3,-8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明:以a,b 为邻边的平行四边形的两条对角线分别为a+b,a -b,且a+b={2,4,-2} a-b={-6,10,14}又(a+b)·(a -b)= 2×(-6)+4×10+(-2)×14=0 故(a+b)⊥(a-b).25. 已知a=3i+2j-k, b=i-j+2k,求: (1) a×b;(2) 2a×7b;(3) 7b×2a; (4) a×a. 解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3)7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k(4) 0⨯=a a .26. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算: (1) |(a +b)×(a-b)|; (2) |(3a +b)×(a-2b)|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b a27. 求垂直于向量3i-4j-k 和2i-j+k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b 平行的单位向量)||⨯==--+⨯a b e i j k a b||sin||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a=(2,1,-1)和b=(1,-2,1)为邻边,求其对角线夹角的正弦. 解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++=l l i j k 所以1212||sin 1||||θ⨯===l l l l .即为所求对角线间夹角的正弦.29. 已知三点A(2,-1,5), B(0,3,-2), C(-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为 故1()4MN MP AC BC ⨯=⨯.30.(1)解: x y zxyzi j ka b a a a b b b ⨯=则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅()()()()若,,C a b 共面,则有 a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=() 反之亦成立. (2)C x y z x y z xyza a a ab b b b C C C ⨯⋅=()由行列式性质可得: 故C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅()()()31. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积.解:设四顶点依次取为A, B, C, D.则由A ,B ,D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i j k . 同理可求其他三个三角形的面积依次为12故四面体的表面积122S =+. 32.解:设四面体的底为BCD ∆,从A 点到底面BCD ∆的高为h ,则13BCDV Sh =⋅⋅,而11948222BCDSBC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h == 故1942323V =⋅⋅=33. 已知三点A(2,4,1), B(3,7,5), C(4,10,9),证:此三点共线. 证明:{1,3,4}AB =,{2,6,8}AC = 显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯= 故A ,B ,C 三点共线.34. 一动点与M0(1,1,1)连成的向量与向量n=(2,3,-4)垂直,求动点的轨迹方程. 解:设动点为M(x, y, z)因0M M n ⊥,故00M M n ⋅=. 即2(x-1)+3(y-1)-4(z-1)=0整理得:2x+3y-4z-1=0即为动点M 的轨迹方程. 35.求通过下列两已知点的直线方程:(1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3).解:(1)两点所确立的一个向量为s={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解:所给直线的方向向量为另取x0=0代入直线一般方程可解得y0=7,z0=17 于是直线过点(0,7,17),因此直线的标准方程为: 且直线的参数方程为:37. 求过点(4,1,-2)且与平面3x-2y+6z=11平行的平面方程.解:所求平面与平面3x-2y+6z=11平行故n={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x-4)-2(y-1)+6(z+2)=0即3x-2y+6z+2=0.38. 求过点M0(1,7,-3),且与连接坐标原点到点M0的线段OM0垂直的平面方程.解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x-1+7(y-7)-3(z +3)=0即x+7y-3z-59=039. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有得b=2. 故所求平面方程为1424x y z ++= 40. 求过(1,1,-1), (-2,-2,2)和(1,-1,2)三点的平面方程.解:由平面的三点式方程知 代入三已知点,有1112121210111121x y z --+----+=---+ 化简得x-3y-2z=0即为所求平面方程.41. 指出下列各平面的特殊位置,并画出其图形:(1) y =0; (2) 3x-1=0;(3) 2x-3y-6=0; (4) x –y=0;(5) 2x-3y+4z=0.解:(1) y=0表示xOz 坐标面(如图7-2)(2) 3x-1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x –y=0表示过z 轴的平面(如图7-5)(5) 2x-3y+4z=0表示过原点的平面(如图7-6).图7-4 图7-5 图7-642. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x+y-z=0的平面.解:设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0 0, .0A B C C A B A B C +-=⎧⇒==-⎨++=⎩ 所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.43. 决定参数k的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6);(2)与平面2x-3y+z=0成π4的角.解:(1)因平面过点(5,-4,6)故有5-4k-2×6=9得k=-4.(2)两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得k=44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解:(1)n1={2,l,3}, n2={m,-6,-1}(2) n1={3, -5,l }, n2={1,3,2}45. 通过点(1,-1,1)作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解:设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}又(1,-1,1)在所求平面上,故A -B+C+D=0,得D=0 故所求平面方程为即2x-y-3z=046. 求平行于平面3x-y+7z=5,且垂直于向量i-j+2k 的单位向量.解:n1={3,-1,7}, n2={1,-1,2}. 故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 47. 求下列直线与平面的交点: (1)11126x y z -+==-, 2x+3y+z-1=0; (2) 213232x y z +--==, x+2y-2z+6=0. 解:(1)直线参数方程为1126x t y t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t=1故交点为(2,-3,6).(2) 直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t=0.故交点为(-2,1,3).48. 求下列直线的夹角:(1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z x y z +-+=⎧⎨++-=⎩; (2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩ 解:(1)两直线的方向向量分别为:s1={5,-3,3}×{3,-2,1}=533321i j k--={3,4,-1}s2={2,2,-1}×{3,8,1}=221381i j k-={10,-5,10}由s1·s2=3×10+4×(-5)+(-1) ×10=0知s1⊥s2 从而两直线垂直,夹角为π2.(2) 直线2314123x y z ---==-的方向向量为s1={4,-12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s2={0,2,-1}×{1,0,0}={0,-1,-2},于是49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x-y+2z-4=0垂直;(2)过点(0,2,4),且与两平面x+2z=1和y-3z=2平行;(3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为s={3,-1,2}故过点(2,-3,4)的直线方程为(2)所求直线平行两已知平面,且两平面的法向量n1与n2不平行,故所求直线平行于两平面的交线,于是直线方向向量故过点(0,2,4)的直线方程为(3)所求直线与已知直线平行,故其方向向量可取为s={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z ++==--和4x-2y-2z=3; (2)327x y z ==-和3x-2y+7z=8; (3)223314x y z -+-==-和x+y+z=3. 解:平行而不包含. 因为直线的方向向量为s={-2,-7,3} 平面的法向量n={4,-2,-2},所以于是直线与平面平行.又因为直线上的点M0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上.51. 求过点(1,-2,1),且垂直于直线的平面方程. 解:直线的方向向量为12123111-=++-i j k i j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x+2y+3z=0.52. 求过点(1,-2,3)和两平面2x-3y+z=3, x+3y+2z+1=0的交线的平面方程.解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++=其中λ为待定常数,又因为所求平面过点(1,-2,3) 故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x+15y+7z+7=053. 求点(-1,2,0)在平面x+2y-z+1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s=n={1,2,-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t)+2(2+2t)-(-t)+1=0 得23t =- 于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333- 54. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离. 解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量 即11133211==-=---i jkn s j k故过已知点的平面方程为y+z=1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d == 55. 求点(1,2,1)到平面x+2y+2z-10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s=n={1,2,2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =.故垂足为485(,,)333,且与点(1,2,1)的距离为1d == 即为点到平面的距离.56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程. 解:球的半径为R ==设(x,y,z)为球面上任一点,则(x-1)2+(y-3)2+(z+2)2=14 即x2+y2+z2-2x-6y+4z=0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.解:设该动点为M(x,y,z), 3.=化简得:8x2+8y2+8z2-68x+108y-114z+779=0 即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=; (3)22194x z +=; (4)20y z -=; (5)220x y -=; (6)220x y +=.解:(1)母线平行于z 轴的抛物柱面,如图7-7.(2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8(3)母线平行于y 轴的椭圆柱面,如图7-9.(4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11.(6)z 轴,如图7-12.图7-11 图7-1259. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=; (3)222149y z x --=; (4)2221149y z x +-=; (5)22209z x y +-=. 解:(1)半轴分别为1,2,3的椭球面,如图7-13.(2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15.(4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-17.图7-1760. 作出下列曲面所围成的立体的图形:(1) x2+y2+z2=a2与z=0,z=2a (a>0); (2)x+y+z=4,x=0,x=1,y=0,y=2及z=0;(3) z=4-x2, x=0, y=0, z=0及2x+y=4; (4) z=6-(x2+y2),x=0, y=0, z=0及x+y=1.解:(1)(2)(3)(4)分别如图7-18,7-19,7-20,7-21所示.图7-18图7-19图7-20 图7-2161. 求下列曲面和直线的交点: (1) 222181369x y z ++=与342364x y z --+==-; (2)22211694x y z +-=与2434x y z +==-. 解:(1)直线的参数方程为 代入曲面方程解得t=0,t=1.得交点坐标为(3,4,-2),(6,-2,2). (2) 直线的参数方程为 代入曲面方程可解得t=1, 得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程. 解:设(x ,y ,z )为圆上任一点,依题意有即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程.(1) 平面x=2; (2) 平面y=0; (3) 平面y=5; (4) 平面z=2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x=2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ==⎩为平面y=5上的一个椭圆.(4) 截线方程为229252x y z ⎧-=⎪⎨⎪=⎩为平面z=2上的两条直线.64. 求曲线x2+y2+z2=a2, x2+y2=z2在xOy 面上的投影曲线.解:以曲线为准线,母线平行于z 轴的柱面方程为故曲线在xOy面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x2+y2=z, z=x+1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x2+y2=x+1即2215()24x y -+=. 故曲线在xOy平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩ 习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界: (1) {(x, y)|x≠0};(2) {(x, y)|1≤x2+y2<4}; (3) {(x, y)|y<x2};(4) {(x, y)|(x-1)2+y2≤1}∪{(x, y)|(x+1)2+y2≤1}.解:(1)开集、无界集,聚点集:R2,边界:{(x, y)|x=0}. (2)既非开集又非闭集,有界集, 聚点集:{(x, y)|1≤x2+y2≤4},边界:{(x, y)|x2+y2=1}∪{(x, y)| x2+y2=4}. (3)开集、区域、无界集, 聚点集:{(x, y)|y≤x2}, 边界:{(x, y)| y=x2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x, y)|(x-1)2+y2=1}∪{(x, y)|(x+1)2+y2=1}. 2. 已知f(x, y)=x2+y2-xytan x y,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u v f u v w u w +=+,试求(,,).f x y x y xy +-解:f( x + y, x-y, x y) =( x + y)xy+(x y)x+y+x-y =(x + y)xy+(x y)2x.4. 求下列各函数的定义域: 解:2(1){(,)|210}.D x y y x =-+>5. 求下列各极限: 解:(1)原式=0ln 2.=(2)原式=+∞. (3)原式=001.4x y →→=-(4)原式=02.x y →→=(5)原式=0sin lim 100.x y xyy xy→→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O(0,0)处是否连续:(3)222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O(0,0)处连续.(2)00sin lim lim 1(0,0)0x u y uz z u→→→==≠=故O(0,0)是z 的间断点.(3)若P(x,y) 沿直线y=x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P(x,y) 沿直线y=-x 趋于(0,0)点,则 故0lim x y z →→不存在.故函数z 在O(0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x,y)=233x y x y-+; (2) f (x,y)=2222y xy x+-; (3) f (x,y)=ln(1-x2-y2);(4)f (x,y)=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解:(1)因为当y=-x 时,函数无定义,所以函数在直线y=-x 上的所有点处间断,而在其余点处均连续.(2)因为当y2=2x 时,函数无定义,所以函数在抛物线y2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x2+y2=1时,函数无定义,所以函数在圆周x2+y2=1上所有点处间断.而在其余各点处均连续. (4)因为点P(x,y)沿直线y=x 趋于O(0,0)时.12lim (,)lime x x y x xf x y x -→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数: (1)z = x2y+2x y ;(2)s =22u v uv+;; (4)z = lntan x y; (5)z = (1+xy)y; (6)u = zxy; (7)u = arctan(x-y)z; (8)yzu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+ (4)21122sec csc ,tan z x xx x y y y yy∂=⋅⋅=∂ (5)两边取对数得ln ln(1)z y xy =+ 故[]221(1)(1)(1).ln(1)1y yy x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+- (8)1.yzu y x x z-∂=∂9.已知22x y u x y=+,求证:3u u xy u x y∂∂+=∂∂. 证明: 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z z x y z x y∂∂+=∂∂. 证明: 11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x,y 的对称性得 故11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y ⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂ 11.设,求fx(x,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角. 解:(2,4,5)1,1,2z zx xx ∂∂==∂∂设切线与正向x 轴的倾角为α, 则tanα=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z = x4+ y4-4x2y2; (2)z = arctan y x; (3)z = yx;(4)z =2ex y+.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x,y 的对称性知 (2)222211z y y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,(3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂(4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 14.设f (x, y, z) = xy2+yz2+zx2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解:2(,,)2x f x y z y zx=+15.设z = x ln ( x y),求32z x y ∂∂∂及32zx y∂∂∂. 解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y ∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22ex y z +=;(2)z =;(3)zy u x =; (4)yzu x =.解:(1)∵2222e 2,e 2x y x y z zx y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )x y xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()zx yx y ∂==∂+ ∴223/2d (d d ).()xz y x x y x y =--+ (3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1y zu y x x z-∂=∂1ln yz u x x y z∂=⋅⋅∂ ln y z u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz zz y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;(3)(1.97)1.05.解:(1)设f(x,y)=x3·y2,则223(,)3,(,)2,x y f x y x y f x y x y ==故df(x,y)=3x2y2dx+2x3ydy=xy(3xydx+2x2dy) 取x=1,y=1,dx=0.02,dy=-0.03,则 (1.02)3·(0.97)2=f(1.02,0.97)≈f(1,1)+df(1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d 0.05d 0.07(4.05,2.93)(4,3)d (4,3)0.053(0.07)]15(0.01)54.998x y f f f ==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=xy,则df(x,y)=yxy-1dx+xylnxdy , 取x=2,y=1,dx=-0.03,dy=0.05,则1.05d 0.03d 0.05(1.97)(1.97,1.05)(2,1)d (2,1)20.0393 2.0393.x y f f f =-==≈+=+=19.矩型一边长a=10cm ,另一边长b=24cm, 当a 边增加4mm ,而b 边缩小1mm 时,求对角线长的变化.解:设矩形对角线长为l ,则d d ).l l x x y y ==+当x=10,y=24,dx=0.4,dy=-0.1时,d 0.4240.1)0.062l =⨯-⨯=(cm)故矩形的对角线长约增加0.062cm. 20.解:因为圆锥体的体积为21.3V r h π=⋅0030,0.1,60,0.5r r h h ====-而221.33V V V dV r h yh r r h r h ππ∂∂≈=⋅+⋅=⋅+⋅∂∂ 0030,0.1,60,0.5r r h h ====-时,2213.1430600.130(0.5)33V π≈⨯⨯⨯⨯+⨯⨯-230()cm =-21.解:设水池的长宽深分别为,,x y z 则有:V xyz = 精确值为:50.242 2.850.22 3.6 2.80.2V =⨯⨯+⨯⨯⨯+⨯⨯⨯313.632()m =近似值为:V dV zx y xy z ≈=+ 0.4,0.4,0.2x y z ===430.4530.4540.2V dV ≈=⨯⨯+⨯⨯+⨯⨯314.8()m =22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂; (2)z =arc tanx y ,x =u +v,y =u -v,求z u ∂∂,z v∂∂; (3)ln(e e )xyu =+,y =x3,求d d ux; (4)u =x2+y2+z2,x =e cos tt ,y =e sin tt ,z =e t,求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx yu v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u zt x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+25. 设22()yz f x y =-,其中f(u)为可导函数,验证:211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f ''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y ∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂由对称性知,22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭, (2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,z y yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yz xf xy x f xy f x f xy f x y xf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂ ()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y z xf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y+++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证:利用变量替换1,3x y x y ξη=-=-,可将方程 22222430u u ux x y y∂∂∂++=∂∂∂∂ 化简为20uξη∂=∂∂. 证明:设1(,),3u f f x y x y ξη⎛⎫==-- ⎪⎝⎭2222222222222222222222221411(1)(1)3333u u u u ux x x u u u u u u u ux x x x x u u u uuu u x y ξηξηξηξηξηξξηηξηξξηηξξηηξηξξη∂∂∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⋅+⋅+⋅+⋅=++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂⎛⎫⎛⎫=+⋅-+⋅+⋅-=----- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭22u η∂∂222222222222222222222222211(1)33111211(1)(1)33933343142433u u u u u y u u u uuu u u y u u ux x y yu u u u ξηξηξξηηξηξξηηξξηηξ∂∂∂∂∂⎛⎫=⋅+⋅-=--- ⎪∂∂∂∂∂⎝⎭∂∂∂∂∂∂∂∂⎛⎫⎛⎫=-⋅-⋅--⋅-⋅-=++-- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭∂∂∂++∂∂∂∂∂∂∂∂∂=+++--∂∂∂∂∂2222222221239340.3u u u u u u ξηηξξηηξη⎛⎫⎛⎫∂∂∂∂+-++ ⎪ ⎪∂∂∂∂∂∂∂⎝⎭⎝⎭∂=-=∂∂故20.uξη∂=∂∂ 29. 求下列隐函数的导数或偏导数:(1)2sin e 0xy xy +-=,求d d yx ;(2)ln arctan y x =,求d d y x;(3)20x y z ++-=,求,z zx y∂∂∂∂; (4)333z xyz a -=,求22,z z x y ∂∂∂∂.解:(1)[解法1] 用隐函数求导公式,设F(x,y)=siny+ex-xy2, 则 2e ,cos 2,x x y F y F y xy =-=-故 22d e e d cos 2cos 2x xx y F y y y x F y xy y xy--=-=-=--. [解法2] 方程两边对x 求导,得()2cos e 02x y y y x yy '⋅+-='+⋅故 2e .cos 2xy y y xy-'=- (2)设()221(,)arctanln arctan ,2y y F x y x y x x==-+ ∵222222121,21x xx y y F x y x y x y x +⎛⎫=-⋅=- ⎪++⎝⎭⎛⎫+ ⎪⎝⎭222221211,21y yy x F x y x x y y x -=-⋅=++⎛⎫+ ⎪⎝⎭∴d .d x y F y x y x F x y+=-=- (3)方程两边求全微分,得d 2d d 0,x y z ++-=,z x y =则d ,z x y =+故z z x y ∂∂==∂∂ (4)设33(,,)3F x y z z xyz a =--,23,3,33,x y z F yz F xz F z xy =-=-=-则223,33x z F z yz yz x F z xy z xy∂-=-=-=∂-- 223,33y z F z xz xz y F z xy z xy∂-=-=-=∂-- ()()()()22222222322232222()z z z x xxz z xy xz y z y z xy y y z xy xz xz z x x xz z xy z xy x yzz xy xy z z xy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--30. 设F(x, y, z)=0可以确定函数x = x(y, z), y = y(x, z), z = z(x, y),证明:1x y zy z x∂∂∂⋅⋅=-∂∂∂. 证明:∵,,,y x z x y zF F F x y zy F z F x F ∂∂∂=-=-=-∂∂∂ ∴ 1.y z x y z x F F F x y z F F F y z x ⎛⎫⎛⎫∂∂∂⎛⎫---⋅⋅=⋅⋅=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z(x,y),其中F 可微,求,z z x y ∂∂∂∂.解:12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222011111z y x z y zF F F F F F F y F F F z x x F F x F F F F F y F z y y F F y F '''=⋅+⋅=⎛⎫''-=⋅+⋅ ⎪⎝⎭'-'∂=-=-=∂''''-''-∂=-=-=∂''32. 求由下列方程组所确定的函数的导数或偏导数:(1)22222,2320,z x y x y z ⎧=+⎪⎨++=⎪⎩ 求:d d ,;d d y z x x (2)1,0,xu yv yu xv +=⎧⎨-=⎩求:,,,;u v u v x x y y ∂∂∂∂∂∂∂∂ (3)2(,),(,),u f ux v y v g u x v y =+⎧⎨=-⎩ 其中f,g 具有连续偏导数函数,求,;u v x x∂∂∂∂ (4)e sin ,e cos ,uux u v y u v ⎧=+⎪⎨=-⎪⎩ 求,,,.u u v v x y x y ∂∂∂∂∂∂∂∂ 解:(1)原方程组变为222222320y z xy z x⎧-=-⎪⎨+=-⎪⎩ 方程两边对x 求导,得d d 22d d d d 23d d y z y x x xy z y z x xx ⎧-=-⎪⎪⎨⎪-=-⎪⎩ 当 2162023y J yz y y z-==+≠21d 16(61),3d 622(31)22d 12.2d 6231x y xz x x z x z x J yz y y z y x z xy x y x x J yz y z ----+===--++-===-++(2)设(,,,)1,(,,,),F x y u v xu yv G x y u v yu xv =+-=-,,,,,,,,x y u v x y u v F u F v F x F y G v G u G y G x =====-===-22u v u vF F x yJ x y G G y x===---故 22xvx v F F u yG G v x uux yv x J J x y --∂-+=-=-=∂+。
高等数学复旦大学出版第三版下册课后答案习题全

习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2) s==(3) s==(4) s==5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).故2s=xs==ys==5zs==.6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点. 解:设此点为M(0,0,z),则222222(4)1(7)35(2)z z-++-=++--解得149 z=即所求点为M(0,0,149).1731747. 试证:以三点A (4,1,9),B (10,-1,6),C (2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB |=|AC |=7.且有 |AC |2+|AB |2=49+49=98=|BC |2. 故△ABC 为等腰直角三角形. 8. 验证:()()++=++a b c a b c . 证明:利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a , b , c 表示23.-u v 解:232(2)3(3)2243935117-=-+--+-=-++-+=-+u v a b c a b c a b c a b c a b c10. 把△ABC 的BC 边分成五等份,设分点依次为D 1,D 2,D 3,D 4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解:1115D A BA BD =-=--c a 2225D A BA BD =-=--c a3335D A BA BD =-=--c a444.5D A BA BD =-=--c a11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影. 解:设M 的投影为M ',则1Pr j cos 604 2.2u OM OM =︒=⨯= 12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标.解:设此向量的起点A 的坐标A (x , y , z ),则{4,4,7}{2,1,7}AB x y z =-=----解得x =-2, y =3, z =0故A 的坐标为A (-2, 3, 0).17513. 一向量的起点是P 1(4,0,5),终点是P 2(7,1,3),试求: (1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量. 解:(1)12Pr j 3,x x a PP == 12Pr j 1,y y a PP == 12Pr j 2.z z a PP ==-(2) 12(7PP ==(3) 12cos 14x a PP α==12cos 14y a PP β==12cos 14z a PP γ==.(4) 12012{14PP PP ===+e j . 14. 三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R =(1-2+3,2+3-4,3-4+5)=(2,1,4)||==Rcos cos cos αβγ=== 15. 求出向量a = i +j +k , b =2i -3j +5k 和c=-2i -j +2k 的模,并分别用单位向量,,a b c e e e 来表达向量a, b , c .解:||==a ||==b||3==c, , 3. a b c ===a b c e17616. 设m =3i +5j +8k , n =2i -4j -7k , p =5i +j -4k ,求向量a =4m +3n -p 在x 轴上的投影及在y 轴上的分向量.解:a =4(3i +5j +8k )+3(2i -4j -7k )-(5i +j -4k )=13i +7j +15k 在x 轴上的投影a x =13,在y 轴上分向量为7j . 17.解:设{,,}x y z a a a a =则有 c o s (1,1)3x a i a a i a i π⋅====⋅ 求得12x a =. 设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 42a ba b π⋅=⇒=⋅ 则214y a =求得12y a =± 又1,a =则2221x y z a a a ++= 从而求得11{,,}222a =±或11{,,}222-± 18. 已知两点M 1(2,5,-3),M 2(3,-2,5),点M 在线段M 1M 2上,且123M M MM =,求向径OM 的坐标. 解:设向径OM ={x , y , z }12{2,5,3}{3,2,5}M M x y z MM x y z =--+=----因为,123M M MM =所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}.17719. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标.解:设P 的坐标为(x , y , z ), 2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+126570cos 6, 749z z γ=⇒==又122190cos 2, 749x x α==⇒==123285cos 3, 749y y β==⇒==故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a , b 的夹角2π3ϕ=,且3,4==b a ,计算: (1) a ·b ; (2) (3a -2b )·(a + 2b ). 解:(1)a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b21. 已知a =(4,-2, 4), b =(6,-3, 2),计算:(1)a ·b ; (2) (2a -3b )·(a + b ); (3)2||-a b 解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b (3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b36238499=-⨯+=22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在178向量CD 上的投影.解:AB ={3,-2,-6},CD ={6,2,3}Pr j CD AB CD AB CD⋅=4.7==-23. 若向量a +3b 垂直于向量7a -5b ,向量a -4b 垂直于向量7a -2b ,求a 和b 的夹角. 解: (a +3b )·(7a -5b ) =227||1615||0+⋅-=a a b b ① (a -4b )·(7a -2b ) = 227||308||0-⋅+=a a b b ②由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos23θ==. 24. 设a =(-2,7,6),b =(4, -3, -8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直. 证明:以a ,b 为邻边的平行四边形的两条对角线分别为a +b ,a -b ,且 a +b ={2,4, -2} a -b ={-6,10,14}又(a +b )·(a -b )= 2×(-6)+4×10+(-2)×14=0 故(a +b )⊥(a -b ).25. 已知a =3i +2j -k , b =i -j +2k ,求: (1) a ×b ; (2) 2a ×7b ; (3) 7b ×2a ; (4) a ×a . 解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k (4) 0⨯=a a .26. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算: (1) |(a +b )×(a -b )|;(2) |(3a +b )×(a -2b )|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b179π2||||sin242=⋅⋅=a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin842=⨯⨯⨯= 27. 求垂直于向量3i -4j -k 和2i -j +k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a =(2,1,-1)和b =(1,-2,1)为邻边,求其对角线夹角的正弦.解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++=l l i j k12||||l l 所以1212||sin 1||||θ⨯===l l l l .即为所求对角线间夹角的正弦.29. 已知三点A (2,-1,5), B (0,3,-2), C (-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为31(1,1,), (1,3,), (0,1,3)22M N P --{2,2,2}MN =--3{1,0,}2MP =-{4,4,4}AC =-- {2,0,3}BC =-18022222235233100122MN MP ----⨯=++=++--i j k i j k 44444412208033220AC BC ---⨯=++=++--i j k i j k故 1()4MN MP AC BC ⨯=⨯. 30.(1)解: xy z xyzij k a b a a a b b b ⨯==-+-+-y z z y z x x z x y y x a b a b i a b a b j a b a b k ()()()则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅()()()()xy z xy z xyza a ab b b C C C = 若 ,,C a b 共面,则有a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=() 反之亦成立. (2) C xy z xy z x y za a a ab b b b C C C ⨯⋅=() a xy z xy z x y z b b b b C C C C a a a ⨯⋅=() b xy z xy z xy z C C C C a a a a b b b ⨯⋅=() 由行列式性质可得:xy z x y z x y z xy z x y z xy z xyzxyzxyza a ab b b C C C b b b C C C a a a C C C a a a b b b == 故C a a b b C C a ⨯⋅=⨯⋅=⨯⋅()()()18131. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积. 解:设四顶点依次取为A , B , C , D .{0,1,2}, {2,2,1}AB AD ==-则由A ,B ,D 三点所确定三角形的面积为111|||542|22S AB AD =⨯=+-=i j k .同理可求其他三个三角形的面积依次为12故四面体的表面积12S =+32.解:设四面体的底为BCD ∆,从A 点到底面BCD ∆的高为h ,则 13BCDV S h =⋅⋅,而11948222BCDSBC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h ==故1942323V =⋅⋅= 33. 已知三点A (2,4,1), B (3,7,5), C (4,10,9),证:此三点共线. 证明:{1,3,4}AB =,{2,6,8}AC = 显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ,B ,C 三点共线.34. 一动点与M 0(1,1,1)连成的向量与向量n =(2,3,-4)垂直,求动点的轨迹方程. 解:设动点为M (x , y , z )0{1,1,1}M M x y z =---因0M M n ⊥,故00M M n ⋅=.即2(x -1)+3(y -1)-4(z -1)=0整理得:2x +3y -4z -1=0即为动点M 的轨迹方程. 35. 求通过下列两已知点的直线方程: (1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3).182解:(1)两点所确立的一个向量为s ={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s ={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解:所给直线的方向向量为 12311223719522335--=⨯=++=----s n n i j k i j k另取x 0=0代入直线一般方程可解得y 0=7,z 0=17于是直线过点(0,7,17),因此直线的标准方程为:7171719x y z --==-- 且直线的参数方程为:771719x t y t z t =⎧⎪=-⎨⎪=-⎩37. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程. 解:所求平面与平面3x -2y +6z =11平行 故n ={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x -4)-2(y -1)+6(z +2)=0 即3x -2y +6z +2=0.38. 求过点M 0(1,7,-3),且与连接坐标原点到点M 0的线段OM 0垂直的平面方程. 解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x -1+7(y -7)-3(z +3)=0 即x +7y -3z -59=039. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有121122b b b-++=183得b =2.故所求平面方程为1424x y z ++= 40. 求过(1,1,-1), (-2,-2,2)和(1,-1,2)三点的平面方程. 解:由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点,有1112121210111121x y z --+----+=---+化简得x -3y -2z =0即为所求平面方程.41. 指出下列各平面的特殊位置,并画出其图形: (1) y =0; (2) 3x -1=0; (3) 2x -3y -6=0; (4) x – y =0; (5) 2x -3y +4z =0.解:(1) y =0表示xOz 坐标面(如图7-2) (2) 3x -1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x -3y -6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x =3和y =-2的平面.(如图7-4) (4) x –y =0表示过z 轴的平面(如图7-5)(5) 2x -3y +4z =0表示过原点的平面(如图7-6).图7-4 图7-5 图7-6 42. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x +y -z =0的平面. 解:设平面方程为Ax +By +Cz +D =0 则其法向量为n ={A ,B ,C }已知平面法向量为n 1={1,1,-1} 过已知两点的向量l ={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A B A B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.43. 决定参数k的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6);(2)与平面2x-3y+z=0成π4的角.解:(1)因平面过点(5,-4,6)故有5-4k-2×6=9得k=-4.(2)两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得2k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解:(1)n1={2,l,3}, n2={m,-6,-1}12232,18613lm lm⇒==⇒=-=--n n(2) n1={3, -5, l }, n2={1,3,2}12315320 6.l l⊥⇒⨯-⨯+⨯=⇒=n n45. 通过点(1,-1,1)作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解:设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}12203203A CA B CA B C CB⎧=-⎪⊥⇒-+=⎪⇒⎨⊥⇒++=⎪=⎪⎩n nn n又(1,-1,1)在所求平面上,故A-B+C+D=0,得D=0故所求平面方程为233CCx y Cz-++=即2x-y-3z=018418546. 求平行于平面3x -y +7z =5,且垂直于向量i -j +2k 的单位向量. 解:n 1={3,-1,7}, n 2={1,-1,2}.12,⊥⊥n n n n故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 47. 求下列直线与平面的交点:(1)11126x y z-+==-, 2x +3y +z -1=0; (2) 213232x y z +--==, x +2y -2z +6=0. 解:(1)直线参数方程为1126x ty t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1 故交点为(2,-3,6).(2) 直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0. 故交点为(-2,1,3). 48. 求下列直线的夹角: (1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和2223038180x y z x y z +-+=⎧⎨++-=⎩; (2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩ 解:(1)两直线的方向向量分别为:s 1={5, -3,3}×{3, -2,1}=533321ij k--={3,4, -1}s 2={2,2, -1}×{3,8,1}=221381i j k-={10, -5,10}186由s 1·s 2=3×10+4×(-5)+( -1) ×10=0知s 1⊥s 2 从而两直线垂直,夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s 1={4, -12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s 2={0,2, -1}×{1,0,0}={0, -1, -2},于是1212cos 0.2064785θθ⋅==≈⋅'≈︒s s s s 49. 求满足下列各组条件的直线方程: (1)经过点(2,-3,4),且与平面3x -y +2z -4=0垂直; (2)过点(0,2,4),且与两平面x +2z =1和y -3z =2平行; (3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为 s ={3,-1,2}故过点(2,-3,4)的直线方程为234312x y z -+-==- (2)所求直线平行两已知平面,且两平面的法向量n 1与n 2不平行,故所求直线平行于两平面的交线,于是直线方向向量12102{2,3,1}013=⨯==--i j ks n n故过点(0,2,4)的直线方程为24231x y z --==- (3)所求直线与已知直线平行,故其方向向量可取为 s ={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z++==--和4x -2y -2z =3; (2)327x y z==-和3x -2y +7z =8;187(3)223314x y z -+-==-和x +y +z =3. 解:平行而不包含. 因为直线的方向向量为s ={-2,-7,3}平面的法向量n ={4,-2,-2},所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上. 51. 求过点(1,-2,1),且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩ 的平面方程.解:直线的方向向量为12123111-=++-ij ki j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0.52. 求过点(1,-2,3)和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程. 解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++= 其中λ为待定常数,又因为所求平面过点(1,-2,3) 故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x +15y +7z +7=053. 求点(-1,2,0)在平面x +2y -z +1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s =n ={1,2,-1}所以垂线的参数方程为122x t y t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t )+2(2+2t )-(-t )+1=0188得23t =-于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333-54. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量即11133211==-=---ij kn s j k故过已知点的平面方程为y +z =1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为d = 55. 求点(1,2,1)到平面x +2y +2z -10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s =n ={1,2,2}所以垂线的参数方程为12212x t y t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =. 故垂足为485(,,)333,且与点(1,2,1)的距离为1d ==即为点到平面的距离.56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程.解:球的半径为R =设(x ,y ,z )为球面上任一点,则(x -1)2+(y -3)2+(z +2)2=14 即x 2+y 2+z 2-2x -6y +4z =0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.189解:设该动点为M (x ,y ,z )3.=化简得:8x 2+8y 2+8z 2-68x +108y -114z +779=0 即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=; (3)22194x z +=; (4)20y z -=; (5)220x y -=; (6)220x y +=. 解:(1)母线平行于z 轴的抛物柱面,如图7-7. (2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8 (3)母线平行于y 轴的椭圆柱面,如图7-9. (4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11. (6)z 轴,如图7-12.图7-11 图7-1219059. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=; (3)222149y z x --=; (4)2221149y z x +-=; (5)22209z x y +-=. 解:(1)半轴分别为1,2,3的椭球面,如图7-13. (2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15. (4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-17.图7-1760. 作出下列曲面所围成的立体的图形: (1) x 2+y 2+z 2=a 2与z =0,z =2a(a >0); (2) x +y +z =4,x =0,x =1,y =0,y =2及z =0; (3) z =4-x 2, x =0, y =0, z =0及2x +y =4; (4) z =6-(x 2+y 2),x =0, y =0, z =0及x +y =1.191解:(1)(2)(3)(4)分别如图7-18,7-19,7-20,7-21所示.图7-18 图7-19图7-20 图7-21 61. 求下列曲面和直线的交点:(1) 222181369x y z ++=与342364x y z --+==-; (2) 22211694x y z +-=与2434x y z +==-.解:(1)直线的参数方程为334624x ty t z t =+⎧⎪=-⎨⎪=-+⎩代入曲面方程解得t =0,t =1. 得交点坐标为(3,4,-2),(6,-2,2). (2) 直线的参数方程为4324x t y tz t =⎧⎪=-⎨⎪=-+⎩代入曲面方程可解得t =1, 得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程.192解:设(x ,y ,z )为圆上任一点,依题意有2295x y z ⎧+=⎨=±⎩ 即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程. (1) 平面x =2; (2) 平面y =0; (3) 平面y =5; (4) 平面z =2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x =2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ==⎩为平面y =5上的一个椭圆.(4) 截线方程为2209252x y z ⎧-=⎪⎨⎪=⎩为平面z =2上的两条直线.64. 求曲线x 2+y 2+z 2=a 2, x 2+y 2=z 2在xOy 面上的投影曲线. 解:以曲线为准线,母线平行于z 轴的柱面方程为2222a x y +=故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x 2+y 2=z , z =x +1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x 2+y 2=x +1即2215()24x y -+=.193故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界: (1) {(x , y )|x ≠0};(2) {(x , y )|1≤x 2+y 2<4}; (3) {(x , y )|y <x 2};(4) {(x , y )|(x -1)2+y 2≤1}∪{(x , y )|(x +1)2+y 2≤1}.解:(1)开集、无界集,聚点集:R 2,边界:{(x , y )|x =0}. (2)既非开集又非闭集,有界集, 聚点集:{(x , y )|1≤x 2+y 2≤4},边界:{(x , y )|x 2+y 2=1}∪{(x , y )| x 2+y 2=4}. (3)开集、区域、无界集, 聚点集:{(x , y )|y ≤x 2}, 边界:{(x , y )| y =x 2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x , y )|(x -1)2+y 2=1}∪{(x , y )|(x +1)2+y 2=1}. 2. 已知f (x , y )=x 2+y 2-xy tanxy,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u v f u v w u w +=+,试求(,,).f x y x y xy +- 解:f ( x + y , x -y , x y ) =( x + y )xy +(x y )x +y +x -y =(x + y )xy +(x y )2x . 4. 求下列各函数的定义域:2(1)ln(21);z y x =-+(2)z =(3)z =(4)u =(5)z =(6)ln()z y x =-194(7)u =解:2(1){(,)|210}.D x y y x =-+>(2){(,)|0,0}.D x y x y x y =+>->22222(3){(,)|40,10,0}.D x y x y x y x y =-≥-->+≠(4){(,,)|0,0,0}.D x y z x y z =>>>2(5){(,)|0,0,}.D x y x y x y =≥≥≥ 22(6){(,)|0,0,1}.D x y y x x x y =->≥+< 22222(7){(,,)|0,0}.D x y z x y x y z =+≠+-≥5. 求下列各极限:10(1)y x y →→ 22001(2)lim;x y x y →→+00(3)x y →→x y →→00sin (5)lim ;x y xy x →→2222221cos()(6)lim.()ex y x y x y x y +→→-++解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=01.4x y →→=-(4)原式=002.x y →→=(5)原式=00sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+1956. 判断下列函数在原点O (0,0)处是否连续:33222222sin(),0,(1)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩33333333sin(),0,(2)0,0;x y x y z x y x y ⎧++≠⎪=+⎨⎪+=⎩(3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O (0,0)处连续. (2)000sin lim lim1(0,0)0x u y uz z u→→→==≠=故O (0,0)是z 的间断点.(3)若P (x ,y ) 沿直线y =x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0,0)点,则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x ,y )=233x y x y -+; (2) f (x ,y )=2222y xy x +-;(3) f (x ,y )=ln(1-x 2-y 2);(4)f (x ,y )=22e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩196解:(1)因为当y =-x 时,函数无定义,所以函数在直线y =-x 上的所有点处间断,而在其余点处均连续.(2)因为当y 2=2x 时,函数无定义,所以函数在抛物线y 2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x 2+y 2=1时,函数无定义,所以函数在圆周x 2+y 2=1上所有点处间断.而在其余各点处均连续.(4)因为点P (x ,y )沿直线y =x 趋于O (0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数:(1)z = x 2y +2xy;(2)s =22u v uv+;(3)z = x;(4)z = lntan x y; (5)z = (1+xy )y ; (6)u = z xy ;(7)u = arctan(x -y )z; (8)y zu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+ 2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+222.z xy x y y x y ∂==∂+ (4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂222122sec ()csc .tan z x x x x x y y y y yy∂=⋅⋅-=-∂ (5)两边取对数得ln ln(1)z y xy =+故[]221(1)(1)(1).ln(1)1y yy x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+197[]ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x z xy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+- 112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z z z zz zu z x y z x y y x y x y u x y x y x y x y z x y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yzu y x x z-∂=∂ 2211ln ln .ln ln .y yz z yy z zu x x x x y z zu y y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭9.已知22x y u x y=+,求证:3u u x y u x y ∂∂+=∂∂. 证明: 222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+.10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z z xy z x y∂∂+=∂∂. 证明: 11112211e e x y x y z x x x ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x ,y 的对称性得1981121e x y z y y ⎛⎫+- ⎪⎝⎭∂=∂ 故 11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂11.设f (x ,y ) = x +(y,求f x (x ,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角.解:(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z = x 4+ y 4-4x 2y 2; (2)z = arctan y x; (3)z = y x ;(4)z = 2ex y+.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,,由x ,y 的对称性知22222128.16.z z y x xy y y x∂∂=-=-∂∂∂ (2)222211zy y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,1992222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y x xyx x y x y z x y x x y y x z xyy x y z x y y y y x x y x y x y z x y x x y x y x x y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++ (3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ (4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 222222222e 22e 22e (21),e ,2e ,2e .x y x y x y x y x y x y z x x x xz z z x x y x y y x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂14.设f (x , y , z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解:2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===15315.设z = x ln ( x y ),求32z x y ∂∂∂及32zx y ∂∂∂.解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22e xy z +=;(2)z =(3)zyu x =;(4)yzu x =.解:(1)∵2222e 2,e 2x y x y z z x y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )xy x y x y z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴ 223/2d (d d ).()x z y x x y x y =--+ (3)∵11,ln z z z y y z u uy x x x zy x y --∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂154ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265e e e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;;(3)(1.97)1.05.解:(1)设f (x ,y )=x 3·y 2,则223(,)3,(,)2,x y f x y x y f x y x y ==故d f (x ,y )=3x 2y 2d x +2x 3y d y =xy (3xy d x +2x 2d y ) 取x =1,y =1,d x =0.02,d y =-0.03,则(1.02)3·(0.97)2=f (1.02,0.97)≈f (1,1)+d f (1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设f (x ,y,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则155d 0.05d 0.07(4.05,2.93)(4,3)d (4,3)0.053(0.07)]15(0.01)54.998x y f f f ==-=≈+=⨯+⨯-=+⨯-=(3)设f (x ,y )=x y ,则d f (x ,y )=yx y -1d x +x y ln x d y , 取x =2,y =1,d x =-0.03,d y =0.05,则1.05d 0.03d 0.05(1.97)(1.97,1.05)(2,1)d (2,1)20.0393 2.0393.x y f f f =-==≈+=+=19.矩型一边长a =10cm ,另一边长b =24cm, 当a 边增加4mm ,而b 边缩小1mm 时,求对角线长的变化.解:设矩形对角线长为l ,则d d ).l l x x y y ==+当x =10,y =24,d x =0.4,d y =-0.1时,d 0.4240.1)0.062l =⨯-⨯=(cm)故矩形的对角线长约增加0.062cm.20.解:因为圆锥体的体积为21.3V r h π=⋅0030,0.1,60,0.5r r h h ====- 而221.33V V V dV r h yh r r h r h ππ∂∂≈=⋅+⋅=⋅+⋅∂∂0030,0.1,60,0.5r r h h ====-时, 2213.1430600.130(0.5)33V π≈⨯⨯⨯⨯+⨯⨯- 230()cm =-21.解:设水池的长宽深分别为,,x y z 则有:V xyz =精确值为:50.242 2.850.22 3.62V =⨯⨯+⨯⨯⨯+⨯⨯⨯ 313.632()m = 近似值为:156V dV zx y xy z ≈=+0.4,0.4,0.2x y z ===430.4530.454V d V ≈=⨯⨯+⨯⨯+⨯⨯314.8()m =22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,zv∂∂; (2)z =arc tanxy, x =u +v ,y =u -v , 求z u ∂∂,z v ∂∂;(3)ln(e e )xyu =+, y =x 3, 求d d u x; (4) u =x 2+y 2+z 2, x =e cos tt , y =e sin tt , z =e t, 求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z yxy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uy x y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭ 2222222111(1)11.x z z x z yy v x v y vyx x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y xx x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.15723. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xy u f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z zxy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+15825. 设22()yz f x y =-,其中f (u )为可导函数,验证: 211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z z x x y y∂∂∂∂∂∂∂解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂ 由对称性知,22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂1592212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,(2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂ ()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y zxf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y +++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证:利用变量替换1,3x y x y ξη=-=-,可将方程。
复旦大学出版社,高等数学,第四版,教材习题答案详细解析

高等数学上(复旦大学出版社,第四版)教材习题答案第四章,一元函数积分学。
第三节 不定积分与原函数求法,习题4-3,答案5.0 用分部积分,求下列不定积分。
东风冷雪1.0=-=--=--=-+-=-+++⎰⎰⎰⎰⎰222222x sinxdxx dcosx (x cosx 2xcosxdx)(x cosx 2xdsinx)x cosx 2xsinx 2sinxdx x cosx 2xsinx 2cosx c2.0------=-=--=--+⎰⎰⎰x x x x x x xe dx xde (xe e dx)xe e c3.0==-=-+⎰⎰⎰22222111ln xdx (x ln x x *dx)22x11x ln x x c 24x ln xdx4.0==-++-=-+=--+=-+++⎰⎰⎰⎰23332232322322x arctanxdx111x arctanxdx x arctanx 3331x 11x(1x )x x arctanx dx 331x 1111x arctanx (x ln |1x |)3322111x arctanx x ln |1x |c 3665.0=+=-=-+⎰2arccosxdxx *arccosx x *arccosx x *arccosx c6.0=-=-=--=+-=+-+⎰⎰⎰⎰⎰222222x tan xdx1x(sec x 1)dx xdtanx x 21dcos x 1x tanx tanxdx x x tanx x 2cos x 21x tanx ln |cos x |x c 2 7.0------------==-=--=-=-+⎰⎰⎰⎰⎰⎰x x x x x x x x x x x x e cos xdxe dsinx e sinx e dcos xe sinx e cos x cos xe dx2e cos xdx e sinx e cos x1e cos xdx e (sinx cos x)c 28.0==-=--=-++⎰⎰⎰⎰xsinxcosxdx11xsin2xdx xdcos2x 24111(xcos2x cos2xdx)xcos2x sin2x c 4489.0=-=--=-+=--+=---=---+=-++++⎰⎰⎰⎰⎰⎰⎰323233223232232232(lnx)dxx 1ln x 3ln x ln x 1ln xd ()(3ln xd )x x x x xln x 3ln x 6lnx ln x 3ln x 1dx 6lnxd x x x x x xln x 3ln x 6lnx 6dx x x x x 1(ln x 3ln x 6lnx 6)c x10.0===-=--=++-=+++=+=++⎰⎰⎰⎰⎰222222222atant,a sec tdtant a sec t tant a tan tsec tdta (sec t tant (sec t 1)sec tdta (sec t tant ln |sec t tant |sec tdtant)1a (sec t tant ln |sec t tant |)21x x a (*ln ||2a a a 1ln |x 2+|c6.0 求下列不定积分;1.0++-+=+++-+-+-+-+++=+==-=+=-++-+-+=-+++⎰⎰⎰222222222222x 1dx(x 1)(x 1)x 1a b c x 1x 1(x 1)(x 1)(x 1)a(x 1)b(x 1)c(x 2x 1)x 111a ,b 1,c 2211x 1122dx ()dx x 1x 1(x 1)(x 1)(x 1)11ln |x 1|c 2x 12.0++=+++-+-+-++++===-=-==-++-+-+--=+--+=+--++-+=+⎰⎰⎰⎰⎰3222222223dx x 13a bx c x 1(x 1)(x x 1)x x 1a(x x 1)(bx c)(x 1)3a 1,b 1,c 23dx 1x 2dx ()dx x 1(x 1)(x x 1)x x 112x 13ln |x 1|2x x 1131ln |x 1|ln |x x 1|1322(x )24ln |+2c3.0 (这道题,有些坑人,没有意思)+--+-+-++-=----=++++---=+++-+-+-=++-+-+-=-+++-==-=-⎰⎰⎰⎰5423332332233323222x x 8x (x x)x(x x)x x x x 8dx dx x x x x 123x x 33(x x 1)dx x x x x 23x 1113x x x ln |x x |dx 323x(x 1)(x 1)23x a b c 3x(x 1)(x 1)x x 1x 123x a(x 1)b(x x)c(x x)323101a ,b ,c 33-=---+-+=---++++-+---+=---++--=+++--⎰⎰⎰543323323x 12310133dx ()x(x 1)(x 1)3x x 1x 1231013ln |x |ln |x 1|ln |x 1|3331(ln |x |ln |x 1|ln |x 1|23ln |x |10ln |x 1|13ln |x 1|31ln(24ln |x |9ln |x 1|12ln |x 1|)3x x 8dxx x 11x x x 8ln |x |3ln |x 1|32-++4ln |x 1|c 4.0+==++⎰⎰263332x dxx 11dx 1arctanx c 33(x )15.0+-==-=--=-++⎰⎰⎰⎰222sinx dx1sinx sinx(1sinx)dx (tanxsecx tan x)dx cos xsecx (sec x 1)dx secx tanx x c6.0++==+--+==+-++++++-==-=-=-+⎰⎰⎰⎰⎰222222222cot x dxsinx cos x 1x 2t tan ,dx dt 21t 1t 21t 1t 22t *dt **dt 2t 22t 2t 1t 1t 1t 11t 1t 11t 1111()dt (1)dt lnt t 2t 2t 221x 1x ln |tan |tan c 22227.0=====+=++⎰⎰⎰2sect 2sec t tant dt 2sectdt sect tant 2ln |sect tant |2ln ||c8.0==-===-=-+=-+++=-+++⎰⎰⎰(1t,2tdt12(1)2t2ln|1t|2ln|1t11tx4ln|1|c记住口诀,反,对,幂,指,三。
高等数学复旦大学出版第三版下册课后答案习题全之欧阳歌谷创编

习题七欧阳歌谷(2021.02.01)1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2)s==(3)s==(4)s==5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).故s==s==.5z6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点.解:设此点为M(0,0,z),则解得14z=9).即所求点为M(0,0,1497. 试证:以三点A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC为等腰直角三角形.8. 验证:()()a b c a b c.++=++证明:利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a, b, c 表示23.-u v 解:10. 把△ABC 的BC 边分成五等份,设分点依次为D1,D2,D3,D4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A .解:1115D A BA BD =-=--c a11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影.解:设M 的投影为M ',则12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标. 解:设此向量的起点A 的坐标A(x, y, z),则 解得x=-2, y=3, z=0 故A 的坐标为A(-2, 3, 0).13. 一向量的起点是P1(4,0,5),终点是P2(7,1,3),试求: (1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量. 解:(1)12Pr j 3,x x a PP ==(2) 12(7PP == (3) 12cos 14x a PP α==12cos 14z a PP γ==(4) 12012{14PP PP ===+e j . 14. 三个力F1=(1,2,3), F2=(-2,3,-4), F3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R=(1-2+3,2+3-4,3-4+5)=(2,1,4)15. 求出向量a= i+j+k, b=2i-3j+5k 和c=-2i-j+2k 的模,并分别用单位向量,,a b c e e e 来表达向量a, b, c. 解:||==a16. 设m=3i+5j+8k, n=2i-4j-7k, p=5i+j-4k,求向量a=4m+3n-p 在x 轴上的投影及在y 轴上的分向量.解:a=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k 在x 轴上的投影ax=13,在y 轴上分向量为7j. 17.解:设{,,}x y z a a a a =则有 求得12x a =.设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 42a ba b π⋅=⇒=⋅ 则214y a = 求得12y a =±又1,a =则2221x y z a a a ++=从而求得11{,,}222a =±或11{,,}222-± 18. 已知两点M1(2,5,-3),M2(3,-2,5),点M 在线段M1M2上,且123M M MM =,求向径OM 的坐标.解:设向径OM ={x, y, z}因为,123M M MM =所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}. 19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标.解:设P 的坐标为(x, y, z ),2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+又122190cos 2, 749x x α==⇒==故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a, b 的夹角2π3ϕ=,且3,4==b a ,计算: (1) a·b; (2) (3a-2b)·(a+ 2b). 解:(1)a·b=2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b 21. 已知a=(4,-2, 4), b=(6,-3, 2),计算:(1)a·b; (2) (2a-3b)·(a+ b); (3)2||-a b 解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影. 解:AB ={3,-2,-6},CD ={6,2,3}23. 若向量a+3b 垂直于向量7a-5b,向量a-4b 垂直于向量7a-2b,求a 和b 的夹角.解: (a+3b)·(7a-5b)=227||1615||0+⋅-=a a b b ①(a-4b)·(7a-2b) = 227||308||0-⋅+=a a b b ②由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b ,故1πarccos 23θ==.24. 设a=(-2,7,6),b=(4,-3,-8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明:以a,b 为邻边的平行四边形的两条对角线分别为a+b,a -b,且a+b={2,4,-2} a-b={-6,10,14}又(a+b)·(a-b)= 2×(-6)+4×10+(-2)×14=0 故(a+b)⊥(a-b).25. 已知a=3i+2j-k, b=i-j+2k,求: (1) a×b;(2) 2a×7b;(3) 7b×2a; (4) a×a.解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k (4) 0⨯=a a .26. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算: (1) |(a +b)×(a -b)|; (2) |(3a +b)×(a -2b)|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b a27. 求垂直于向量3i-4j-k 和2i-j+k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b 平行的单位向量()||3⨯==±--+⨯a b e i j k a b||sin||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a=(2,1,-1)和b=(1,-2,1)为邻边,求其对角线夹角的正弦. 解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++=l l i j k所以1212||sin 1||||θ⨯===l l l l .即为所求对角线间夹角的正弦.29. 已知三点A(2,-1,5), B(0,3,-2), C(-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为 故 1()4MN MP AC BC ⨯=⨯.30.(1)解: x y zxyzi j k a b a a a b b b ⨯=则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅()()()()若,,C a b 共面,则有 a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=() 反之亦成立. (2)C xyz x y z xyza a a ab b b b C C C ⨯⋅=() 由行列式性质可得: 故C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅()()()31. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积.解:设四顶点依次取为A, B, C, D.则由A ,B ,D 三点所确定三角形的面积为111|||542|222S AB AD =⨯=+-=i jk . 同理可求其他三个三角形的面积依次为12故四面体的表面积12S =+ 32.解:设四面体的底为BCD ∆,从A 点到底面BCD ∆的高为h ,则13BCDV Sh =⋅⋅,而11948222BCDSBC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h == 故1942323V =⋅⋅=33. 已知三点A(2,4,1), B(3,7,5), C(4,10,9),证:此三点共线. 证明:{1,3,4}AB =,{2,6,8}AC = 显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯= 故A ,B ,C 三点共线.34. 一动点与M0(1,1,1)连成的向量与向量n=(2,3,-4)垂直,求动点的轨迹方程.解:设动点为M(x, y, z) 因0M M n ⊥,故00M M n ⋅=. 即2(x-1)+3(y-1)-4(z-1)=0整理得:2x+3y-4z-1=0即为动点M 的轨迹方程. 35.求通过下列两已知点的直线方程:(1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3).解:(1)两点所确立的一个向量为s={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解:所给直线的方向向量为另取x0=0代入直线一般方程可解得y0=7,z0=17 于是直线过点(0,7,17),因此直线的标准方程为: 且直线的参数方程为:37. 求过点(4,1,-2)且与平面3x-2y+6z=11平行的平面方程. 解:所求平面与平面3x-2y+6z=11平行 故n={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x-4)-2(y-1)+6(z+2)=0 即3x-2y+6z+2=0.38. 求过点M0(1,7,-3),且与连接坐标原点到点M0的线段OM0垂直的平面方程.解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x-1+7(y-7)-3(z +3)=0 即x+7y-3z-59=039. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程. 解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有 得b=2.故所求平面方程为1424x y z ++=40. 求过(1,1,-1), (-2,-2,2)和(1,-1,2)三点的平面方程. 解:由平面的三点式方程知代入三已知点,有1112121210111121x y z --+----+=---+化简得x-3y-2z=0即为所求平面方程.41. 指出下列各平面的特殊位置,并画出其图形: (1) y =0; (2) 3x-1=0; (3) 2x-3y-6=0; (4) x –y=0; (5) 2x-3y+4z=0.解:(1) y=0表示xOz 坐标面(如图7-2) (2) 3x-1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x–y=0表示过z轴的平面(如图7-5)(5) 2x-3y+4z=0表示过原点的平面(如图7-6).图7-4 图7-5 图7-6 42. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x+y-z=0的平面.解:设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0,.A B CC A B A B C+-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.43. 决定参数k的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6);(2)与平面2x-3y+z=0成π4的角.解:(1)因平面过点(5,-4,6)故有5-4k-2×6=9得k=-4.(2)两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解:(1)n1={2,l,3}, n2={m,-6,-1}(2) n1={3, -5,l }, n2={1,3,2}45. 通过点(1,-1,1)作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解:设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}又(1,-1,1)在所求平面上,故A-B+C+D=0,得D=0故所求平面方程为即2x-y-3z=046. 求平行于平面3x-y+7z=5,且垂直于向量i-j+2k的单位向量.解:n1={3,-1,7}, n2={1,-1,2}.故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n =+-e i j k 47. 求下列直线与平面的交点: (1) 11126x y z-+==-, 2x+3y+z-1=0; (2)213232x y z +--==, x+2y-2z+6=0. 解:(1)直线参数方程为1126x t y t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t=1 故交点为(2,-3,6).(2) 直线参数方程为221332x ty t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t=0. 故交点为(-2,1,3). 48. 求下列直线的夹角: (1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和2223038180x y z x y z +-+=⎧⎨++-=⎩; (2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩ 解:(1)两直线的方向向量分别为:s1={5,-3,3}×{3,-2,1}=533321ijk--={3,4,-1}s2={2,2,-1}×{3,8,1}=221381i j k-={10,-5,10}由s1·s2=3×10+4×(-5)+(-1) ×10=0知s1⊥s2 从而两直线垂直,夹角为π2. (2) 直线2314123x y z ---==-的方向向量为s1={4,-12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s2={0,2,-1}×{1,0,0}={0,-1,-2},于是 49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x-y+2z-4=0垂直; (2)过点(0,2,4),且与两平面x+2z=1和y-3z=2平行; (3)过点(-1,2,1),且与直线31213xy z --==-平行. 解:(1)可取直线的方向向量为s={3,-1,2}故过点(2,-3,4)的直线方程为(2)所求直线平行两已知平面,且两平面的法向量n1与n2不平行,故所求直线平行于两平面的交线,于是直线方向向量 故过点(0,2,4)的直线方程为(3)所求直线与已知直线平行,故其方向向量可取为s={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系: (1)34273x y z++==--和4x-2y-2z=3;(2)327x y z==-和3x-2y+7z=8;(3)223314x y z -+-==-和x+y+z=3. 解:平行而不包含. 因为直线的方向向量为s={-2,-7,3} 平面的法向量n={4,-2,-2},所以 于是直线与平面平行.又因为直线上的点M0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面. (3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上.51. 求过点(1,-2,1),且垂直于直线 的平面方程.解:直线的方向向量为12123111-=++-i j k i j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-= 即x+2y+3z=0.52. 求过点(1,-2,3)和两平面2x-3y+z=3, x+3y+2z+1=0的交线的平面方程.解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++=其中λ为待定常数,又因为所求平面过点(1,-2,3)故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+= 解得λ=-4.故所求平面方程为2x+15y+7z+7=053. 求点(-1,2,0)在平面x+2y-z+1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s=n={1,2,-1}所以垂线的参数方程为122x ty t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t)+2(2+2t)-(-t)+1=0 得23t =-于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333- 54. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离.解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量即11133211==-=---ijk n s j k故过已知点的平面方程为y+z=1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-=即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d == 55. 求点(1,2,1)到平面x+2y+2z-10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s=n={1,2,2}所以垂线的参数方程为12212x ty t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =.故垂足为485(,,)333,且与点(1,2,1)的距离为1d ==即为点到平面的距离.56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程.解:球的半径为R ==设(x,y,z)为球面上任一点,则(x-1)2+(y-3)2+(z+2)2=14 即x2+y2+z2-2x-6y+4z=0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程. 解:设该动点为M(x,y,z)3.=化简得:8x2+8y2+8z2-68x+108y-114z+779=0 即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=;(3)22194x z +=; (4)20y z -=;(5)220x y -=; (6)220x y +=. 解:(1)母线平行于z 轴的抛物柱面,如图7-7. (2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8 (3)母线平行于y 轴的椭圆柱面,如图7-9. (4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11. (6)z 轴,如图7-12.图7-11 图7-12 59. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=;(3)222149y z x --=; (4)2221149y z x +-=;(5)22209z x y +-=.解:(1)半轴分别为1,2,3的椭球面,如图7-13. (2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15. (4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-17.图7-1760. 作出下列曲面所围成的立体的图形: (1) x2+y2+z2=a2与z=0,z=2a(a>0); (2)x+y+z=4,x=0,x=1,y=0,y=2及z=0;(3) z=4-x2, x=0, y=0, z=0及2x+y=4; (4) z=6-(x2+y2),x=0, y=0, z=0及x+y=1.解:(1)(2)(3)(4)分别如图7-18,7-19,7-20,7-21所示.图7-18 图7-19 图7-20 图7-2161. 求下列曲面和直线的交点: (1) 222181369x y z ++=与342364x y z --+==-; (2)22211694x y z +-=与2434x y z +==-. 解:(1)直线的参数方程为 代入曲面方程解得t=0,t=1.得交点坐标为(3,4,-2),(6,-2,2). (2) 直线的参数方程为 代入曲面方程可解得t=1, 得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程. 解:设(x ,y ,z )为圆上任一点,依题意有 即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程.(1) 平面x=2; (2) 平面y=0; (3) 平面y=5; (4) 平面z=2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x=2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y +==⎩为平面y=5上的一个椭圆.(4) 截线方程为229252x y z ⎧-=⎪⎨⎪=⎩为平面z=2上的两条直线.64. 求曲线x2+y2+z2=a2, x2+y2=z2在xOy 面上的投影曲线. 解:以曲线为准线,母线平行于z 轴的柱面方程为故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x2+y2=z, z=x+1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x2+y2=x+1即2215()24x y -+=.故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩ 习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界: (1) {(x, y)|x≠0};(2) {(x, y)|1≤x2+y2<4}; (3) {(x, y)|y<x2};(4) {(x, y)|(x-1)2+y2≤1}∪{(x, y)|(x+1)2+y2≤1}.解:(1)开集、无界集,聚点集:R2,边界:{(x, y)|x=0}. (2)既非开集又非闭集,有界集,聚点集:{(x, y)|1≤x2+y2≤4},边界:{(x, y)|x2+y2=1}∪{(x, y)| x2+y2=4}. (3)开集、区域、无界集, 聚点集:{(x, y)|y≤x2}, 边界:{(x, y)| y=x2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x, y)|(x-1)2+y2=1}∪{(x, y)|(x+1)2+y2=1}. 2. 已知f(x, y)=x2+y2-xytan x y,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u v f u v w u w +=+,试求(,,).f x y x y xy +-解:f( x + y, x-y, x y) =( x + y)xy+(x y)x+y+x-y =(x + y)xy+(x y)2x. 4. 求下列各函数的定义域: 解:2(1){(,)|210}.D x y y x =-+> 5. 求下列各极限: 解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=01.4x y →→=-(4)原式=02.x y →→=(5)原式=0sin lim100.x y xyy xy →→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O(0,0)处是否连续: (3)222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y ++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O(0,0)处连续. (2)00sin lim lim1(0,0)0x u y uz z u→→→==≠= 故O(0,0)是z 的间断点.(3)若P(x,y) 沿直线y=x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P(x,y) 沿直线y=-x 趋于(0,0)点,则 故0lim x y z →→不存在.故函数z 在O(0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x,y)=233x y x y-+; (2) f (x,y)=2222y xy x+-;(3) f (x,y)=ln(1-x2-y2); (4)f (x,y)=222e ,0,0,0.x y x y y y -⎧⎪≠⎨⎪=⎩解:(1)因为当y=-x 时,函数无定义,所以函数在直线y=-x 上的所有点处间断,而在其余点处均连续.(2)因为当y2=2x 时,函数无定义,所以函数在抛物线y2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x2+y2=1时,函数无定义,所以函数在圆周x2+y2=1上所有点处间断.而在其余各点处均连续. (4)因为点P(x,y)沿直线y=x 趋于O(0,0)时.12lim (,)lime x x y x xf x y x -→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数: (1)z = x2y+2x y ;(2)s =22u v uv+;(4)z = lntan x y; (5)z = (1+xy)y; (6)u = zxy; (7)u = arctan(x-y)z; (8)yzu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s vu =+2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+(4)21122sec csc ,tan z x x x x y y y yy∂=⋅⋅=∂ (5)两边取对数得ln ln(1)z y xy =+ 故 []221(1)(1)(1).ln(1)1y y y x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+ (6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+- (8)1.yzu y x x z-∂=∂9.已知22x y u x y=+,求证:3u u xy u x y∂∂+=∂∂. 证明:222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z zx y z x y∂∂+=∂∂. 证明:11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x,y 的对称性得 故11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y ⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂ 11.设fx(x,1) .解:1(,)1(x f x y y y =+-则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角. 解:(2,4,5)1,1,2z z x x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tanα=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z = x4+ y4-4x2y2; (2)z = arctan y x; (3)z = yx;(4)z = 2e x y +.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x,y 的对称性知 (2)222211z y y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭, (3)222ln ,ln ,xx z z y y y y x x ∂∂==∂∂(4)22e 2,e ,x y x y z z x x y++∂∂=⋅=∂∂14.设f (x, y, z) = xy2+yz2+zx2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解:2(,,)2x f x y z y zx=+15.设z = x ln ( x y),求32z x y ∂∂∂及32zx y ∂∂∂.解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22ex y z +=;(2)z =;(3)zy u x =;(4)yzu x =.解:(1)∵2222e 2,e 2x y x y z z x y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )xy xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂1ln yz u x x y z∂=⋅⋅∂ ln y z u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz zz y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;(3)(1.97)1.05.解:(1)设f(x,y)=x3·y2,则223(,)3,(,)2,x y f x y x y f x y x y ==故df(x,y)=3x2y2dx+2x3ydy=xy(3xydx+2x2dy) 取x=1,y=1,dx=0.02,dy=-0.03,则 (1.02)3·(0.97)2=f(1.02,0.97)≈f(1,1)+df(1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d 0.05d 0.07(4.05,2.93)(4,3)d (4,3)0.053(0.07)]15(0.01)54.998x y f f f ==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=xy,则df(x,y)=yxy-1dx+xylnxdy , 取x=2,y=1,dx=-0.03,dy=0.05,则1.05d 0.03d 0.05(1.97)(1.97,1.05)(2,1)d (2,1)20.0393 2.0393.x y f f f =-==≈+=+=19.矩型一边长a=10cm ,另一边长b=24cm, 当a 边增加4mm ,而b 边缩小1mm 时,求对角线长的变化.解:设矩形对角线长为l ,则d d ).l l x x y y ==+当x=10,y=24,dx=0.4,dy=-0.1时,d 0.4240.1)0.062l =⨯-⨯=(cm)故矩形的对角线长约增加0.062cm. 20.解:因为圆锥体的体积为21.3V r h π=⋅0030,0.1,60,0.5r r h h ====-而221.33V V V dV r h yh r r h r h ππ∂∂≈=⋅+⋅=⋅+⋅∂∂ 0030,0.1,60,0.5r r h h ====-时,2213.1430600.130(0.5)33V π≈⨯⨯⨯⨯+⨯⨯-230()cm =-21.解:设水池的长宽深分别为,,x y z 则有:V xyz = 精确值为:50.242 2.850.22 3.6 2.80.2V =⨯⨯+⨯⨯⨯+⨯⨯⨯313.632()m =近似值为:V dV zx y xy z ≈=+ 0.4,0.4,0.2x y z ===430.4530.4540.2V dV ≈=⨯⨯+⨯⨯+⨯⨯314.8()m =22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂; (2)z =arc tanx y ,x =u +v,y =u -v,求z u ∂∂,z v∂∂; (3)ln(e e )xyu =+,y =x3,求d d ux; (4)u =x2+y2+z2,x =e cos tt ,y =e sin tt ,z =e t,求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vy x x y y y x ux y u v -∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x yx x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y x y x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+ 25. 设22()yz f x y =-,其中f(u)为可导函数,验证: 211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂ 由对称性知,22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,(2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂ ()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y zxf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y +++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证:利用变量替换1,3x y x y ξη=-=-,可将方程22222430u u ux x y y∂∂∂++=∂∂∂∂ 化简为20uξη∂=∂∂. 证明:设1(,),3u f f x y x y ξη⎛⎫==-- ⎪⎝⎭2222222222222222222222221411(1)(1)3333u u u u ux x x u u u u u u u ux x x x x u u u uuu u x y ξηξηξηξηξηξξηηξηξξηηξξηηξηξξη∂∂∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⋅+⋅+⋅+⋅=++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂⎛⎫⎛⎫=+⋅-+⋅+⋅-=----- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭22u η∂∂222222222222222222222222211(1)33111211(1)(1)33933343142433u u u u u y u u u uuu u u y u u u x x y yu u u u ξηξηξξηηξηξξηηξξηηξ∂∂∂∂∂⎛⎫=⋅+⋅-=--- ⎪∂∂∂∂∂⎝⎭∂∂∂∂∂∂∂∂⎛⎫⎛⎫=-⋅-⋅--⋅-⋅-=++-- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭∂∂∂++∂∂∂∂∂∂∂∂∂=+++--∂∂∂∂∂2222222221239340.3u u u u u u ξηηξξηηξη⎛⎫⎛⎫∂∂∂∂+-++ ⎪ ⎪∂∂∂∂∂∂∂⎝⎭⎝⎭∂=-=∂∂故20.uξη∂=∂∂ 29. 求下列隐函数的导数或偏导数:(1)2sin e 0xy xy +-=,求d d yx ;(2)ln arctan y x =,求d d y x;(3)20x y z ++-=,求,z zx y∂∂∂∂; (4)333z xyz a -=,求22,z z x y ∂∂∂∂. 解:(1)[解法1] 用隐函数求导公式,设F(x,y)=siny+ex-xy2,则 2e ,cos 2,x x y F y F y xy =-=-故 22d e e d cos 2cos 2x xx y F y y y x F y xy y xy--=-=-=--. [解法2] 方程两边对x 求导,得()2cos e 02x y y y x yy '⋅+-='+⋅故 2e .cos 2xy y y xy-'=- (2)设()221(,)arctanln arctan ,2y y F x y x y x x==-+ ∵222222121,21x xx y y F x yx y x y x +⎛⎫=-⋅=- ⎪++⎝⎭⎛⎫+ ⎪⎝⎭222221211,21y yy x F x yx x yy x -=-⋅=++⎛⎫+ ⎪⎝⎭∴d .d x y F y x y x F x y+=-=- (3)方程两边求全微分,得d 2d d 0,x y z ++-=,z x y =则d ,z x y =+故z z x y ∂∂==∂∂ (4)设33(,,)3F x y z z xyz a =--,23,3,33,x y z F yz F xz F z xy =-=-=-则223,33x z F z yz yzx F z xy z xy∂-=-=-=∂--223,33y z F z xz xz y F z xy z xy∂-=-=-=∂-- ()()()()22222222322232222()zz z x x xz z xy xz y z y z xy y y z xy xz xz z x x xz z xy z xy x yzz xy xy z z xy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--30. 设F(x, y, z)=0可以确定函数x = x(y, z), y = y(x, z), z = z(x, y),证明:1x y zy z x∂∂∂⋅⋅=-∂∂∂. 证明:∵,,,y x z x y zF F F x y zy F z F x F ∂∂∂=-=-=-∂∂∂ ∴ 1.y z x y z x F F F x y z F F F y z x ⎛⎫⎛⎫∂∂∂⎛⎫---⋅⋅=⋅⋅=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z(x,y),其中F 可微,求,z z x y ∂∂∂∂.解:12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222011111z y x z y zF F F F F F F y F F F z x x F F x F F F F F y F z y y F F y F '''=⋅+⋅=⎛⎫''-=⋅+⋅ ⎪⎝⎭'-'∂=-=-=∂''''-''-∂=-=-=∂''32. 求由下列方程组所确定的函数的导数或偏导数:(1)22222,2320,z x y x y z ⎧=+⎪⎨++=⎪⎩ 求:d d ,;d d y z x x (2)1,0,xu yv yu xv +=⎧⎨-=⎩ 求:,,,;u v u v x x y y ∂∂∂∂∂∂∂∂(3)2(,),(,),u f ux v y v g u x v y =+⎧⎨=-⎩ 其中f,g 具有连续偏导数函数,求,;u v x x∂∂∂∂ (4)e sin ,e cos ,uux u v y u v ⎧=+⎪⎨=-⎪⎩ 求,,,.u u v v x y x y ∂∂∂∂∂∂∂∂ 解:(1)原方程组变为222222320y z xy z x⎧-=-⎪⎨+=-⎪⎩ 方程两边对x 求导,得d d 22d d d d 23d d y z y x x xy z y z x xx ⎧-=-⎪⎪⎨⎪-=-⎪⎩ 当 2162023y J yz y y z-==+≠21d 16(61),3d 622(31)22d 12.2d 6231x y xz x x z x z x J yz y y z y x z xy x y x x J yz y z ----+===--++-===-++(2)设(,,,)1,(,,,),F x y u v xu yv G x y u v yu xv =+-=-,,,,,,,,x y u v x y u v F u F v F x F y G v G u G y G x =====-===-22u v u v F F x yJ x y G G y x===---故 22xvx v F F u yG G v x uux yv x J J x y--∂-+=-=-=∂+。
高等数学复旦大学出版第三版课后答案习题十一

261习题十一1.设L 为xOy 面内直线x =a 上的一段,证明:(),d 0L P x y x =⎰其中P (x , y )在L 上连续.证:设L 是直线x =a 上由(a ,b 1)到(a ,b 2)这一段, 则 L :12x a b t b y t=⎧≤≤⎨=⎩,始点参数为t =b 1,终点参数为t =b 2故()()()221d ,d d 0d 0d b b Lb ba P x y x P a,t t P a,t t t ⎛⎫=⋅=⋅= ⎪⎝⎭⎰⎰⎰2.设L 为xOy 面内x 轴上从点(a ,0)到点(b ,0)的一段直线,证明:()(),d 0d b LaP x y x P x,x =⎰⎰,其中P (x , y )在L 上连续. 证:L :0x x a x b y =⎧≤≤⎨=⎩,起点参数为x =a ,终点参数为x =b .故()(),d ,0d b LaP x y x P x x =⎰⎰3.计算下列对坐标的曲线积分:(1)()22d -⎰Lx y x ,其中L 是抛物线y =x 2上从点(0,0)到点(2,4)的一段弧;(2)d Lxy x ⎰其中L 为圆周(x -a )2+y 2=a 2(a >0)及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行);(3)d d Ly x x y +⎰,其中L 为圆周x =R cos t ,y =R sin t 上对应t 从0到π2的一段弧;(4)()()22d d Lx y x x y yx y+--+⎰,其中L 为圆周x 2+y 2=a 2(按逆时针方向绕行);(5)2d d d x x z y y z Γ+-⎰,其中Γ为曲线x =kθ,y =a cos θ,z =a sin θ上对应θ从0到π的一段弧;(6)()322d 3d d x x zy y x y z Γ++-⎰,其中Γ是从点(3,2,1)到点(0,0,0)的一段直线;(7)d d d Lx y y z -+⎰ ,其中Γ为有向闭拆线ABCA ,这里A ,B ,C 依次为点(1,0,0),(0,1,0),(0,0,1);(8)()()222d 2d Lx xy x y xy y -+-⎰,其中L 是抛物线y =x 2上从点(-1,1)到点(1,1)的段弧.解:(1)L :y =x 2,x 从0变到2,262()()22222435001156d d 3515Lxyx x x x x x ⎡⎤-=-=-=-⎢⎥⎣⎦⎰⎰(2)如图11-1所示,L =L 1+L 2.其中L 1的参数方程为图11-1cos 0πsin x a a tt y a t=+⎧≤≤⎨=⎩L 2的方程为y =0(0≤x ≤2a ) 故()()()()()12π200π32ππ3223d d d 1+cost sin cos d 0d sin 1cos d sin d sin dsin π2LL L a xy x xy x xy xa a t a a t t xat t ta t t t ta=+'=⋅++=-+=-+=-⎰⎰⎰⎰⎰⎰⎰⎰(3)()π20π220π220d d sin sin cos cos d cos 2d 1sin 220Ly x x y R t R t R tR t tRt tR t +=-+⎡⎤⎣⎦=⎡⎤=⎢⎥⎣⎦=⎰⎰⎰(4)圆周的参数方程为:x =a cos t ,y =a sin t ,t :0→2π. 故()()()()()()222π202π22d d 1cos sin sin cos sin cos d 1d 2πLx y x x y yx ya t a t a t a t a t a t ta a ta+--+=+---⎡⎤⎣⎦=-=-⎰⎰⎰263(5)()()()2π220π322π3320332d d d sin sin cos cos d d 131ππ3x x z y y zkk a a a a kak a k a Γθθθθθθθθθθ+-=⋅+⋅--=-⎡⎤=-⎢⎥⎣⎦=-⎰⎰⎰(6)直线Γ的参数方程是32=⎧⎪=⎨⎪=⎩x ty t z t t 从1→0.故()()3223221031041d 3d d 27334292d 87d 1874874xx zy y x y zt t t t t t t t tΓ++-⎡⎤=⋅+⋅⋅+-⋅⎣⎦==⋅=-⎰⎰⎰(7)AB BC CA Γ=++(如图11-2所示)图11-21:0y xAB z =-⎧⎨=⎩,x 从0→1 ()01d d d 112ABx y y z dx -+=--=-⎡⎤⎣⎦⎰⎰.:1x BC y z =⎧⎨=-⎩,z 从0→1264()()()101120d d d 112d 12232B Cx y y z z dzz zz z -+=--+-⎡⎤⎣⎦=-⎡⎤=-⎢⎥⎣⎦=⎰⎰⎰:1y C A z x =⎧⎨=-⎩,x 从0→1 []1d d d 1001CAx y y z dx -+=-+=⎰⎰.故()()d d d d d d 312122LAB BC C Ax y y z x y y z-+=++-+=-++=⎰⎰⎰⎰(8)()()()()()221224211235412d 2d 222d 224d 1415Lxxy x y xy yx x xxx xx x xx x xx---+-⎡⎤=-⋅+-⋅⋅⎣⎦=-+-=-⎰⎰⎰4.计算()()d d L x y x y x y ++-⎰,其中L 是(1)抛物线y 2=x 上从点(1,1)到点(4,2)的一段弧;(2)从点(1,1)到点(4,2)的直线段;(3)先沿直线从(1,1)到点(1,2),然后再沿直线到点(4,2)的折线; (4)曲线x = 2t 2+t +1, y = t 2+1上从点(1,1)到点(4,2)的一段弧.解:(1)L :2x y y y⎧=⎨=⎩,y :1→2,故()()()()()2221232124321d d 21d 2d 111232343Lx y x y x yy y y y y y yy y yy y y ++-⎡⎤=+⋅+-⋅⎣⎦=++⎡⎤=++⎢⎥⎣⎦=⎰⎰⎰(2)从(1,1)到(4,2)的直线段方程为x =3y -2,y :1→2265故()()()()()2121221d d 32332d 104d 5411Lx y x y x yy y y y y y yy y ++-=-+⋅+-+⎡⎤⎣⎦=-⎡⎤=-⎣⎦=⎰⎰⎰(3)设从点(1,1) 到点(1,2)的线段为L 1,从点(1,2)到(4,2)的线段为L 2,则L =L 1+L 2.且 L 1:1x y y=⎧⎨=⎩,y :1→2;L 2:2x x y =⎧⎨=⎩,x :1→4;故()()()()()12122211d d 101d 1d 212L x y x y x yy y y y y y y ++-=+⋅+-⎡⎤⎣⎦⎡⎤=-=-⎢⎥⎣⎦=⎰⎰⎰()()()()()()24144211d d 220d 12d 22272L x y x y x yx x x x x x ++-=++-⋅⎡⎤⎣⎦⎡⎤=+=+⎢⎥⎣⎦=⎰⎰⎰从而()()()()()12d d d d 1271422LL L x y x y x yx y x y x y++-=+++-=+=⎰⎰⎰(4)易得起点(1,1)对应的参数t 1=0,终点(4,2)对应的参数t 2=1,故()()()()()()12213214320d d 32412d 10592d 10592432323Lx y x y x yt t t t t t ttt t tt t t t ++-⎡⎤=++++--⋅⎣⎦=+++⎡⎤=+++⎢⎥⎣⎦=⎰⎰⎰5.设质点受力作用,力的反方向指向原点,大小与质点离原点的距离成正比,若质点由(a ,0)沿椭圆移动到B (0,b ),求力所做的功.266解:依题意知 F =kxi +kyj ,且L :cos sin x a t y a t=⎧⎨=⎩,t :0→π2()()()()π2022π20π22222d d cos sin sin cos d sin 2d 2cos 2222LW kx x ky yka t t kb t b t tk b at tk b at k b a=+=-+⋅⎡⎤⎣⎦-=--⎡⎤=⎢⎥⎣⎦-=⎰⎰⎰(其中k 为比例系数)6.计算对坐标的曲线积分:(1)d Lxyz z ⎰,Γ为x 2+y 2+z 2=1与y =z 相交的圆,方向按曲线依次经过第Ⅰ、Ⅱ、Ⅶ、Ⅷ封限;(2)()()()222222d d d Ly z x z x y x y z -+-+-⎰,Γ为x 2+y 2+z 2=1在第Ⅰ封限部分的边界曲线,方向按曲线依次经过xOy 平面部分,yOz 平面部分和zOx 平面部分.解:(1)Γ:2221x y z y z ⎧++=⎨=⎩即2221x z y z ⎧+=⎨=⎩其参数方程为:cos 22x ty tz t =⎧⎪⎪⎪=⎨⎪⎪=⎪⎩ t :0→2π 故:2π02π2202π202π0d cos d 222sin cos d 4sin 2d 161cos 4d 16216xyz z t t t t tt t t t t ttΓ===-==⎰⎰(2)如图11-3所示.267图11-3Γ=Γ1+Γ2+Γ3.Γ1:cos sin 0x ty t z =⎧⎪=⎨⎪=⎩t :0→π2,故()()()()()1222222π2220π3320π320d d d sin sin cos cos d sin cos d 2sin d 24233yzx zxy xyz t t t t t t t tt tΓ-+-+-⎡⎤=--⋅⎣⎦=-+=-=-⋅=-⎰⎰⎰⎰又根据轮换对称性知()()()()()()1222222222222d d d 3d d d 4334yzx zxy xyzyzx zxy xyzΓΓ-+-+-=-+-+-⎛⎫=⨯- ⎪⎝⎭=-⎰⎰7.应用格林公式计算下列积分:(1)()()d d 24356+-++-⎰ x y x y x y Γ, 其中L 为三顶点分别为(0,0),(3,0)和(3,2)的三角形正向边界;(2)()()222d d cos 2sin e sin 2e x x L x y x y x xy x y x x y ++--⎰ ,其中L 为正向星形线()2223330x ya a +=>;(3)()()3222d d 2cos 12sin 3+--+⎰Lx y xy y x y x x y ,其中L 为抛物线2x =πy 2上由点(0,0)到(π2,1)的一段弧;(4)()()22d d sin Lx y x y x y --+⎰,L是圆周y =上由点(0,0)到(1,1)的一段弧;(5)()()d d e sin e cos x x L x y y my y m +--⎰,其中m 为常数,L 为由点(a ,0)到(0,0)经过圆x 2+y 2=ax上半部分的路线(a 为正数).268图11-4解:(1)L 所围区域D 如图11-4所示,P =2x -y +4, Q =3x +5y -6,3Q x∂=∂,1P y∂=-∂,由格林公式得()()d d 24356d d 4d d 4d d 1432212LD DDx yx y x y Q P x y x y x yx y +-++-∂∂⎛⎫-= ⎪∂∂⎝⎭===⨯⨯⨯=⎰⎰⎰⎰⎰⎰⎰(2)P =x 2y cos x +2xy sin x -y 2e x ,Q =x 2sin x -2y e x, 则2cos 2sin 2exP x x x x y y∂=+-∂,2cos 2sin 2e xQ x x x x y x∂=+-∂.从而P Q yx∂∂=∂∂,由格林公式得.()()222d d cos 2sin esin 2e d d 0++--∂∂⎛⎫-=⎪∂∂⎝⎭=⎰⎰⎰ xx LD x yxy x xy x y x x y Q Px y xy(3)如图11-5所示,记O A ,AB , BO 围成的区域为D .(其中 BO=-L )图11-5P =2xy 3-y 2cos x ,Q =1-2y sin x +3x 2y 2262cos P xy y xy∂=-∂,262cos Q xy y xx∂=-∂由格林公式有:269d d d d 0L OA ABD Q P P x Q y x y x y -++∂∂⎛⎫-+== ⎪∂∂⎝⎭⎰⎰⎰ 故π21220012202d d d d d d d d ππd d 12sin 3243d 12π4π4++=+=+++⎛⎫=+-+⋅⋅ ⎪⎝⎭⎛⎫=-+ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰LO A ABO A ABP x Q y P x Q yP x Q y P x Q yO x y y y y y y(4)L 、AB 、BO 及D 如图11-6所示.图11-6由格林公式有d d d d ++∂∂⎛⎫-+=- ⎪∂∂⎝⎭⎰⎰⎰L AB BOD Q P P x Q y x y x y而P =x 2-y ,Q =-(x +sin 2y ).1∂=-∂P y,1∂=-∂Q x,即,0∂∂-=∂∂Q P xy于是()d d d d 0+++++=+=⎰⎰⎰⎰LABBOL AB BOP x Q y P x Q y从而()()()()()()()2222221122011300d d d d sin d d d d sin sin d d 1sin 131sin 232471sin 264LL BA O BP x Q y x y xy x y x y x yx y x y xy x y y x xy x y y +=--+=-+--+-+=-++⎡⎤⎡⎤=+-+⎢⎥⎢⎥⎣⎦⎣⎦=-+⎰⎰⎰⎰⎰⎰(5)L ,OA 如图11-7所示.图11-7270P =e xsin y -my , Q =e xcos y -m ,e cos xP y my∂=-∂,e cos xQ yx∂=∂由格林公式得:22d d d d d d d d 1π22π8L O AD DDQ P P x Q y x y x y m x ym x y a m m a +∂∂⎛⎫-+=⎪∂∂⎝⎭==⎛⎫=⋅⋅ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰ 于是:()()[]220202πd d d d 8πd 0esin 00e cos 08π0d 8π8+=-+=-+⋅⋅-⋅⋅-=-=⎰⎰⎰⎰LO A axxa m a P x Q y P x Q ym a xm m m a xm a8.利用曲线积分,求下列曲线所围成的图形的面积: (1)星形线x = a cos 3t ,y = a sin 3t ; (2)双纽线r 2 = a 2cos2θ; (3)圆x 2+y 2 = 2ax . 解:(1)()()()()()2π322π2π2422222π202π22π202d sin 3cos d sin 33sin cos d sin 2sin d 43d 1cos 41cos 2163d 1cos 2cos 4cos 2cos 416312π+d cos 2cos 61623π8LA y x a t a t tt a t t t at t ta tt t a tt t t t at t t a=-=-⋅-==⋅=--=--+⎡⎤=+⎢⎥⎣⎦=⎰⎰⎰⎰⎰⎰⎰(2)利用极坐标与直角坐标的关系x =r cos θ,y =r sin θ得cos x a θ=sin y a θ=从而x d y -y d x =a 2cos2θd θ.于是面积为:271[]π24π4π24π4212d d 2cos 2d sin 22LA x y y x a aaθθθ--=⋅-===⎰⎰(3)圆x 2+y 2=2ax 的参数方程为cos 02πsin x a a y a θθθ=+⎧≤≤⎨=⎩故()()[]()2π22π021d d 21d a+acos sin 2d 1cos 2πcos sin LA x y y xa a aa a θθθθθθθ=-=-=+=⋅-⎰⎰⎰9.证明下列曲线积分与路径无关,并计算积分值: (1)()()()()1,10,0d d x y x y --⎰;(2)()()()()3,423221,2d d 663x y xy yx y xy +--⎰;(3)()()1,221,1d d xy x x y-⎰沿在右半平面的路径;(4)()()6,81,0⎰沿不通过原点的路径;证:(1)P =x -y ,Q =y -x .显然P ,Q 在xOy 面内有连续偏导数,且1P Q yx∂∂==-∂∂,故积分与路径无关.取L 为从(0,0)到(1,1)的直线段,则L 的方程为:y =x ,x :0→1.于是()()()()11,100,00d 0d d xx y x y ==--⎰⎰(2) P =6xy 2-y 3,Q =6x 2y -3xy 2.显然P ,Q 在xOy 面内有连续偏导数,且2123P xy yy∂=-∂,2123Q xy yx∂=-∂,有P Q yx∂∂=∂∂,所以积分与路径无关.取L 为从(1,2)→(1,4)→(3,4)的折线,则()()()()()()[]3,423221,2432214323212d d 663d d 63966434864236x y xy yx y xy y xy y x y y x x +--=+--=+⎡⎤--⎣⎦=⎰⎰⎰272(3)2y P x=,1Q x=-,P ,Q 在右半平面内有连续偏导数,且21P yx∂=∂,21Q xx∂=∂,在右半平面内恒有P Q yx∂∂=∂∂,故在右半平面内积分与路径无关.取L 为从(1,1)到(1,2)的直线段,则()()()21,2211,1d d d 11xy x x yy -==--⎰⎰(4) P =,Q =,且P Q yx∂∂==∂∂在除原点外恒成立,故曲线积分在不含原点的区域内与路径无关, 取L 为从(1,0)→(6,0)→(6,8)的折线,则()()686,811,081529x y=+⎡=+⎣=⎰⎰⎰10.验证下列P (x , y )d x +Q (x , y )d y 在整个xOy 面内是某一函数u (x , y )的全微分,并求这样的一个函数u (x , y ): (1)(x +2y )d x +(2x +y )d y ; (2)2xy d x +x 2d y ;(3)(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y)d y ; (4)(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y . 解:证:(1)P =x +2y ,Q =2x +y .2P Q yx∂∂==∂∂,所以(x +2y )d x +(2x +y )d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分.()()()()()(),0,0002222d d ,22d d 2222222x y xyyu x y x y x y x y x x yx y xy xy xyxy =+++=++⎡⎤=++⎢⎥⎣⎦=++⎰⎰⎰(2)P =2xy ,Q =x 2, 2P Q x yx∂∂==∂∂,故2xy d x +x 2d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分.()()(),20,020022d d ,0d d x y xy u xy x x y x y x x yx y=+=+=⎰⎰⎰(3)P =3x 2y +8xy 2,Q =x 3+8x 2y +12y e y,2316∂∂=+=∂∂P Q x xy yx,故(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y)d y273是某个定义在整个xOy 面内函数u (x ,y )的全微分,()()()()()(),22320,03200322d ,38812e 0d d 812e412e 12e 12x y y xyyyyu x x y x y x y x x y y x yxx y y x y x y y =++++=+++=++-+⎰⎰⎰(4)P =2x cos y +y 2cos x ,Q =2y sin x -x 2sin y ,2sin 2cos P x y y xy∂=-+∂,2cos 2sin Q y x x yx∂=-∂,有P Q yx∂∂=∂∂,故(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y 是某一个定义在整个xOy 面内的函数u (x ,y )的全微分,()()()()()(),220,020022d d ,2cos cos 2sin sin 2d d 2sin sin sin cos x y xy u x y x y x y y x y x x y x x yy x xy y x x y=++-=+-=+⎰⎰⎰11.证明:22d d x x y y x y++在整个xOy 平面内除y 轴的负半轴及原点外的开区域G 内是某个二元函数的全微分,并求出这样的一个二元函数. 证:22x P x y=+,22y Q x y=+,显然G 是单连通的,P 和Q 在G 内具有一阶连续偏导数,并且.()2222∂∂-==∂∂+P Q xyyxxy,(x ,y )∈G因此22d d x x y y x y++在开区域G 内是某个二元函数u (x ,y )的全微分.由()()22222222d d 11ln 22d x y x x y y dx y x yx y++⎡⎤==+⎢⎥++⎣⎦知()()221ln ,2u x y x y =+.12.设在半平面x >0中有力()3k F xi yj r=-+构成力场,其中k为常数,r =,证明:在此力场中场力所做的功与所取的路径无关.证:场力沿路径L 所作的功为.33d d Lk k W x x y yrr=--⎰其中3kx P r=-,3ky Q r=-,则P 、Q 在单连通区域x >0内具有一阶连续偏导数,并且53(0)P kxy Q x yrx∂∂==>∂∂因此以上积分与路径无关,即力场中场力所做的功与路径无关.13.当Σ为xOy 面内的一个闭区域时,曲面积分()d d ,,R x y x y z ∑⎰⎰与二重积分有什么关系?274解:因为Σ:z =0,在xOy 面上的投影区域就是Σ故()()d d d d ,,,,0R x y R x y x y z x y ∑∑=±⎰⎰⎰⎰当Σ取的是上侧时为正号,Σ取的是下侧时为负号. 14.计算下列对坐标的曲面积分:(1)22d d x y z x y ∑⎰⎰,其中Σ是球面x 2+y 2+z 2=R 2的下半部分的下侧;(2)d d d d d d z x y x y z y z x ∑++⎰⎰,其中Σ是柱面x 2+y 2=1被平面z =0及z =3所截得的在第Ⅰ封限内的部分的前侧;(3)()()()d d 2d d d d ,,,,,,f x y z f y z x f z x y x y z x y z x y z ∑+++++⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦⎰⎰,其中f (x , y , z )为连续函数,Σ是平面x -y +z =1在第Ⅳ封限部分的上侧;(4)d d d d d d xz x y xy y z yz z x ∑++⎰⎰ ,其中Σ是平面x =0, y =0, z =0, x +y +z =1所围成的空间区域的整个边界曲面的外侧;(5)()()()d d d d d d y z z x x y y z x y z x ∑++---⎰⎰ ,其中Σ为曲面z =z = h (h >0)所围成的立体的整个边界曲面,取外侧为正向;(6)()()22d d d d d d +++-⎰⎰ y y z x z x x y y xz x z ∑,其中Σ为x =y =z =0,x =y =z =a 所围成的正方体表面,取外侧为正向;解:(1)Σ:z =Σ在xOy 面上的投影区域D xy 为:x 2+y 2≤R 2.((()()()()()()22222π4222π222222202π2200354*******d d d d d cos sin d 1sin 2d 81d d 1cos421612422π1635xyD RRRxy z x y x yx yr r rR R r r R R RR r R R R r R r ∑θθθθθθθ=-=-=-⎡⎤+--⎣⎦⎡=----⎣=-⋅-+--⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰()72220772π105RR r R⎡⎤-⎢⎥⎣⎦=(2)Σ如图11-8所示,Σ在xOy 面的投影为一段弧,图11-8275故d d 0z x y ∑=⎰⎰,Σ在yOz 面上的投影D yz ={(y ,z )|0≤y ≤1,0≤z ≤3},此时Σ可表示为:x =(y ,z )∈D yz ,故30d d d d 3yzD x y z y z z yy∑===⎰⎰⎰⎰⎰⎰⎰Σ在xOz 面上的投影为D xz ={(x ,z )|0≤x ≤1,0≤z ≤3},此时Σ可表示为:y =(x ,z )∈D xz ,故30d d d d 3xzD y z x z xz xx∑===⎰⎰⎰⎰⎰⎰⎰因此:d d d d d d 236π643π2z x y x y z y z xx x∑++⎡⎤=⎢⎥⎣⎦==⋅=⎰⎰⎰⎰(3)Σ如图11-9所示,平面x -y +z =1上侧的法向量为n ={1,-1,1},n 的方向余弦为cos α=cos β=,cos γ=,图11-9由两类曲面积分之间的联系可得:276()()()()()()()()()d d 2d d d d ,,,,,,cos d (2)cos d ()d d cos cos d d (2)d d ()d d cos cos (2)()d d d d 1d d xyD f x y z f y z x fz x yx y z x y z x y z s f y s f z x yf x x y f y x y f z x yf x f y f z x y f x x yx y z x y x y x y ∑∑∑∑∑αβαβγγ+++++⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦=+++++=+++++=-+++⎡⎤+⎣⎦=-+=+-⎡⎤--⎣⎦⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰d d 111212xyD x y==⨯⨯=⎰⎰⎰⎰(4)如图11-10所示:图11-10Σ=Σ1+Σ2+Σ3+Σ4.其方程分别为Σ1:z =0,Σ2:x =0,Σ3:y =0,Σ4:x +y +z =1, 故()()12344110d d 000d d d d 11d d 124xyD x xz x yxz x yx x yx y x x y x y ∑∑∑∑∑∑-=+++=+++=--==--⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰由积分变元的轮换对称性可知.1d d dzd 24xy y z yz x ∑∑==⎰⎰⎰⎰因此.d d dyd d d 113248xz x y xy z yz z x∑++=⨯=⎰⎰(5)记Σ所围成的立体为Ω,由高斯公式有:277()()()()()()d d d d d d d d d 0d d d 0y z z x x yy z x y z x y z x y z x x y z x y z x y z ∑ΩΩ++---∂∂⎛⎫--∂-=++ ⎪∂∂∂⎝⎭==⎰⎰⎰⎰⎰⎰⎰⎰(6)记Σ所围的立方体为Ω,P =y (x -z ),Q =x 2,R =y 2+xz . 由高斯公式有()()()()()220000020204d d d d d d d d d d d d d d d d d d 2d 2a aa a a aa a y y z x z x x yy xz x z P Q Rx y z x y z x y z x y x y zx y x a yx y y a x xy a a x ax a∑ΩΩ+++-∂∂∂⎛⎫++=⎪∂∂∂⎝⎭=+=+=+⎡⎤=+⎢⎥⎣⎦⎡⎤=+⎢⎥⎣⎦=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰15.设某流体的流速V =(k ,y ,0),求单位时间内从球面x 2+y 2+z 2=4的内部流过球面的流量. 解:设球体为Ω,球面为Σ,则流量3d d d d d d d 432d d d π2π33k y z y z x P Qx y z x y x y z ∑ΩΩΦ=+∂∂⎛⎫+= ⎪∂∂⎝⎭==⋅=⎰⎰⎰⎰⎰⎰⎰⎰ (由高斯公式)16.利用高斯公式,计算下列曲面积分:(1)222d d d d d d x y z y z x z x y ∑++⎰⎰ ,其中Σ为平面x =0,y =0,z =0,x =a ,y =a ,z =a 所围成的立体的表面的外侧;(2)333d d d d d d x y z y z x z x y ∑++⎰⎰ ,其中Σ为球面x 2+y 2+z 2= a 2的外侧;(3)()()2232d d d d d d 2xz y z z x x y x y z xy y z ∑++-+⎰⎰ ,其中Σ为上半球体x 2+y 2≤a 2,0z ≤≤(4)d d d d d d x y z y z x z x y ∑++⎰⎰ ,其中Σ是界于z = 0和z = 3之间的圆柱体x 2+y 2 = 9的整个表面的外侧;278解:(1)由高斯公式()()2224d d d d d d d 2222d 6d 6d d d 3aaaxy z y z x z x yvx y z vx y z x vx x y za∑ΩΩΩ++=++=++==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ 对称性(2)由高斯公式:()3332222ππ45d d d d d d d 3d 3d d sin d 12π5axy z y z x z x yP QR v x y z vx y zr ra∑ΩΩθϕϕ++∂∂∂⎛⎫++=⎪∂∂∂⎝⎭=++==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(3)由高斯公式得()()()2232222π2π2220024π05d d d d d d 2d d d d sin d 2πsin d d 2π5aaxzy z z x x yx y z xy y z P QR v x y z vz x yr r rr ra∑ΩΩθϕϕϕϕ++-+∂∂∂⎛⎫++= ⎪∂∂∂⎝⎭=++=⋅==⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰(4)由高斯公式得:2d d d d d d d 3d 3π3381πx y z y z x z x yP Q R v x y z v∑ΩΩ++∂∂∂⎛⎫++=⎪∂∂∂⎝⎭==⋅⋅⋅=⎰⎰⎰⎰⎰⎰⎰⎰17.利用斯托克斯公式,计算下列曲线积分: (1)d d d y x z y x z Γ++⎰ ,其中Γ为圆周x 2+y 2+z 2 = a 2,x +y +z = 0,若从x 轴的正向看去,这圆周是取逆时针的方向; (2)()()()222222d d d x y z y z x y z x Γ++---⎰,其中Γ是用平面32x y z ++=截立方体:2790≤x ≤1,0≤y ≤1,0≤z ≤1的表面所得的截痕,若从Ox 轴的正向看去,取逆时针方向;(3)23d d d y x xz y yz z Γ++⎰,其中Γ是圆周x 2+y 2= 2z ,z =2,若从z 轴正向看去,这圆周是取逆时针方向;(4)22d 3d d +-⎰ y x x y z z Γ,其中Γ是圆周x 2+y 2+z 2 = 9,z =0,若从z 轴正向看去,这圆周是取逆时针方向.解:(1)取Σ为平面x +y +z =0被Γ所围成部分的上侧,Σ的面积为πa 2(大圆面积),Σ的单位法向量为{}111cos ,cos ,cos n αβγ==. 由斯托克斯公式22d d d cos cos cos d d 3y x z y x zR Q Q P P Rs y z x y z x ss aaΓ∑∑∑αβγ++⎡∂∂∂∂⎤⎛⎫⎛⎫∂∂⎛⎫--=++- ⎪⎢⎥ ⎪ ⎪∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎣⎦=-=-=-=⎰⎰⎰⎰⎰(2)记为Σ为平面32x y z ++=被Γ所围成部分的上侧,可求得Σ的面积为4长为2的正六边形);Σ的单位法向量为{}cos ,cos ,cos αβγ==n . 由斯托克斯公式()()()(()()()222222d d d2222d22d3d2432492x y zy z x yz xy z x y sz xsx y zsΓ∑∑∑++---⎡+----=--⎢⎣=-++=-=-⋅=-⎰⎰⎰⎰⎰⎰⎰(3)取Σ:z=2,D xy:x2+y2≤4的上侧,由斯托克斯公式得:()()()2223d d dd d0d d d d3d d35d d5π220π-+=++--+=-+=-=-⨯⨯=-⎰⎰⎰⎰⎰⎰⎰xyDy x xz y yz zy z z x x yzz xx yzx yΓ∑∑(4)圆周x2+y2+z2=9,z=0实际就是xOy面上的圆x2+y2=9,z=0,取Σ:z=0,D xy:x2+y2≤9由斯托克斯公式得:()()()222d3d dd d d d d d000032d dd dπ39π+-=++---===⋅=⎰⎰⎰⎰⎰⎰⎰xyDy x x y z zy z z x x yx yx yΓ∑∑18.把对坐标的曲线积分()()d d,,LP x Q yx y x y+⎰化成对弧长的曲线积分,其中L为:(1)在xOy面内沿直线从点(0,0)到点(1,1);(2)沿抛物线y = x2从点(0,0)到点(1,1);(3)沿上半圆周x2+y2 = 2x从点(0,0)到点(1,1).解:(1)L的方向余弦πcos cos cos42αβ===,280281故()()d d ,,d ,,LLP x Q y x y x y P x Q x y x y s++=⎰⎰(2)曲线y =x 2上点(x ,y )处的切向量T={1,2x }.其方向余弦为cosα=cos β=故()()d d ,,d 2,,LLP x Q y x y x y P x xQ x y x y s++=⎰⎰(3)上半圆周上任一点处的切向量为1x-⎧⎨⎩其方向余弦为cos α=cos 1x β=-故()()()()()d d ,,d ,,1LLP x Q yx y x y s Q x y x y x +⎤=+-⎦⎰⎰19.设Γ为曲线x = t ,y = t 2,z = t 3上相应于t 从0变到1的曲线弧,把对坐标的曲线积分d d d P x Q y R z Γ++⎰化成对弧长的曲线积分.解:由x =t ,y =t 2,z =t 3得d x =d t ,d y =2t d t =2x d t ,d z =3t 2dt =3y d t ,d s t =.故d 1cos d d cos d d cos d x s y s z sαβγ======因而d d d P x Q x R x s ΓΓ++=⎰⎰20.把对坐标的曲面积分()()()d d d d d d ,,,,,,P y z Q z x R x y x y z x y z x y z ∑++⎰⎰化成对面积的曲面积分,其中:282(1) Σ是平面326x y ++=在第Ⅰ封限的部分的上侧; (2) Σ是抛物面z = 8-(x 2+y 2)在xOy 面上方的部分的上侧.解:(1)平面Σ:326x y ++=上侧的法向量为n ={3,2,,单位向量为n 0={35,25,5},即方向余弦为3cos 5α=,2cos 5β=,cos 5γ=.因此:()()()()d d d d d d ,,,,,,d cos cos cos 32d 555P y z Q z x R x y x y z x y z x y z sP Q R s P Q R ∑∑∑αβγ++=++⎛⎫=++⎪⎝⎭⎰⎰⎰⎰⎰⎰(2)Σ:F (x ,y ,z )=z +x 2+y 2-8=0,Σ上侧的法向量n ={ F x ,F y ,F z }={ 2x ,2y ,1}其方向余弦:cos α=,cos β=,cos γ=故()()()()d d d d d d ,,,,,,d cos cos cos P y z Q z x R x y x y z x y z x y z sP Q R s∑∑∑αβγ++=++=⎰⎰⎰⎰⎰⎰。
高等数学复旦大学出版第三版下册课后答案习题全之欧阳术创编

习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s=(2)s==(3)s==(4)s==5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).故s==s==.5z6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点.解:设此点为M(0,0,z),则解得14z=9).即所求点为M(0,0,1497. 试证:以三点A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC为等腰直角三角形.8. 验证:()()a b c a b c.++=++证明:利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a, b, c 表示23.-u v解:10. 把△ABC 的BC 边分成五等份,设分点依次为D1,D2,D3,D4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解:1115D A BA BD =-=--c a11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影.解:设M 的投影为M ',则12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标.解:设此向量的起点A 的坐标A(x, y, z),则解得x=-2, y=3, z=0故A 的坐标为A(-2, 3, 0).13. 一向量的起点是P1(4,0,5),终点是P2(7,1,3),试求:(1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量. 解:(1)12Pr j 3,x x a PP ==(2) 12(7PP == (3) 12cos 14xa PP α==12cos 14za PP γ== (4) 12012{14PP PP ===+e j . 14. 三个力F1=(1,2,3), F2=(-2,3,-4), F3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R=(1-2+3,2+3-4,3-4+5)=(2,1,4)15. 求出向量a= i+j+k, b=2i-3j+5k 和c=-2i-j+2k 的模,并分别用单位向量,,a b c e e e 来表达向量a, b, c. 解:||==a 16. 设m=3i+5j+8k, n=2i-4j-7k, p=5i+j-4k,求向量a=4m+3n-p 在x 轴上的投影及在y 轴上的分向量.解:a=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k在x 轴上的投影ax=13,在y 轴上分向量为7j.17.解:设{,,}x y z a a a a =则有 求得12x a =. 设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 4a ba b π⋅=⇒=⋅ 则214y a = 求得12y a =± 又1,a =则2221x y z a a a ++=从而求得11{,,}222a =±或11{,,}222-± 18. 已知两点M1(2,5,-3),M2(3,-2,5),点M 在线段M1M2上,且123M M MM =,求向径OM 的坐标.解:设向径OM ={x, y, z}因为,123M M MM = 所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}.19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标.解:设P 的坐标为(x, y, z ),2222||(12)49PA x y z =++-=得2229524x y z z ++=-+又122190cos 2, 749x x α==⇒== 故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a, b 的夹角2π3ϕ=,且3,4==b a ,计算: (1) a·b; (2) (3a-2b)·(a+ 2b).解:(1)a·b=2π1cos ||||cos 3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b21. 已知a=(4,-2, 4), b=(6,-3, 2),计算:(1)a·b; (2) (2a-3b)·(a+ b); (3)2||-a b 解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b(2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影.解:AB ={3,-2,-6},CD ={6,2,3}23. 若向量a+3b 垂直于向量7a-5b,向量a-4b 垂直于向量7a-2b,求a 和b 的夹角.解: (a+3b)·(7a-5b)=227||1615||0+⋅-=a a b b ①(a-4b)·(7a-2b) = 227||308||0-⋅+=a a b b ②由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b 又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos 23θ==.24. 设a=(-2,7,6),b=(4,-3,-8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明:以a,b 为邻边的平行四边形的两条对角线分别为a+b,a -b,且a+b={2,4,-2}a-b={-6,10,14}又(a+b)·(a-b)= 2×(-6)+4×10+(-2)×14=0故(a+b)⊥(a-b).25. 已知a=3i+2j-k, b=i-j+2k,求:(1) a×b;(2) 2a×7b;(3) 7b×2a; (4) a×a.解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k(4) 0⨯=a a .26. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算:(1) |(a +b)×(a -b)|;(2) |(3a +b)×(a -2b)|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b(2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b a27. 求垂直于向量3i-4j-k 和2i-j+k 的单位向量,并求上述两向量夹角的正弦. 解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b 平行的单位向量()||3⨯==±--+⨯a b e i j k a b||sin||||26θ⨯===⨯a b a b . 28. 一平行四边形以向量a=(2,1,-1)和b=(1,-2,1)为邻边,求其对角线夹角的正弦.解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k 因为12|||2610|⨯=++=l l i j k所以1212||sin 1||||θ⨯===l l l l . 即为所求对角线间夹角的正弦.29. 已知三点A(2,-1,5), B(0,3,-2), C(-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯.证明:中点M ,N ,P 的坐标分别为故 1()4MN MP AC BC ⨯=⨯.30.(1)解: x y z x y z i j k a b a a a b b b ⨯=则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅()()()() 若,,C a b 共面,则有 a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=() 反之亦成立. (2)C xy z x y z x y z a a a a b b b b C C C ⨯⋅=() 由行列式性质可得:故 C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅()()()31. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积.解:设四顶点依次取为A, B, C, D.则由A ,B ,D 三点所确定三角形的面积为111|||542|22S AB AD =⨯=+-=ij k 同理可求其他三个三角形的面积依次为12故四面体的表面积122S = 32.解:设四面体的底为BCD ∆,从A 点到底面BCD ∆的高为h ,则13BCD V S h =⋅⋅,而11948222BCD S BC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+=则43h == 故1942323V =⋅⋅= 33. 已知三点A(2,4,1), B(3,7,5), C(4,10,9),证:此三点共线. 证明:{1,3,4}AB =,{2,6,8}AC =显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯=故A ,B ,C 三点共线.34. 一动点与M0(1,1,1)连成的向量与向量n=(2,3,-4)垂直,求动点的轨迹方程.解:设动点为M(x, y, z)因0M M n ⊥,故00M M n ⋅=.即2(x-1)+3(y-1)-4(z-1)=0整理得:2x+3y-4z-1=0即为动点M 的轨迹方程.35.求通过下列两已知点的直线方程:(1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3).解:(1)两点所确立的一个向量为s={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==-- 36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程.解:所给直线的方向向量为另取x0=0代入直线一般方程可解得y0=7,z0=17于是直线过点(0,7,17),因此直线的标准方程为:且直线的参数方程为:37. 求过点(4,1,-2)且与平面3x-2y+6z=11平行的平面方程. 解:所求平面与平面3x-2y+6z=11平行故n={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x-4)-2(y-1)+6(z+2)=0即3x-2y+6z+2=0.38. 求过点M0(1,7,-3),且与连接坐标原点到点M0的线段OM0垂直的平面方程.解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x-1+7(y-7)-3(z +3)=0即x+7y-3z-59=039. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有得b=2. 故所求平面方程为1424x y z ++=40. 求过(1,1,-1), (-2,-2,2)和(1,-1,2)三点的平面方程. 解:由平面的三点式方程知 代入三已知点,有1112121210111121x y z --+----+=---+ 化简得x-3y-2z=0即为所求平面方程.41. 指出下列各平面的特殊位置,并画出其图形:(1) y =0; (2) 3x-1=0;(3) 2x-3y-6=0; (4) x –y=0;(5) 2x-3y+4z=0.解:(1) y=0表示xOz 坐标面(如图7-2)(2) 3x-1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x –y=0表示过z 轴的平面(如图7-5)(5) 2x-3y+4z=0表示过原点的平面(如图7-6).图7-4 图7-5 图7-642. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x+y-z=0的平面.解:设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0 0, .0A B C C A B A B C +-=⎧⇒==-⎨++=⎩ 所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.43. 决定参数k 的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6); (2) 与平面2x-3y+z=0成π4的角.解:(1) 因平面过点(5,-4,6)故有 5-4k-2×6=9得k=-4.(2) 两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos||||42θ⋅====n nn n解得2k=±44. 确定下列方程中的l和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直.解:(1)n1={2,l,3}, n2={m,-6,-1}(2) n1={3, -5,l }, n2={1,3,2}45. 通过点(1,-1,1)作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解:设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}又(1,-1,1)在所求平面上,故A-B+C+D=0,得D=0故所求平面方程为即2x-y-3z=046. 求平行于平面3x-y+7z=5,且垂直于向量i-j+2k的单位向量.解:n1={3,-1,7}, n2={1,-1,2}.故1217733152122111--=⨯=++=+---n n n i j k i j k则2).n=+-e i j k47. 求下列直线与平面的交点:(1) 11126x y z-+==-, 2x+3y+z-1=0; (2) 213232x y z +--==, x+2y-2z+6=0.解:(1)直线参数方程为1126x ty t z t=+⎧⎪=--⎨⎪=⎩代入平面方程得t=1故交点为(2,-3,6).(2) 直线参数方程为221332x ty t z t=-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t=0.故交点为(-2,1,3).48. 求下列直线的夹角:(1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z x y z +-+=⎧⎨++-=⎩;(2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩解:(1)两直线的方向向量分别为:s1={5,-3,3}×{3,-2,1}=533321i j k--={3,4,-1}s2={2,2,-1}×{3,8,1}=221381i j k-={10,-5,10}由s1·s2=3×10+4×(-5)+(-1) ×10=0知s1⊥s2 从而两直线垂直,夹角为π2.(2) 直线2314123x y z ---==-的方向向量为s1={4,-12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s2={0,2,-1}×{1,0,0}={0,-1,-2},于是49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x-y+2z-4=0垂直;(2)过点(0,2,4),且与两平面x+2z=1和y-3z=2平行;(3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为s={3,-1,2}故过点(2,-3,4)的直线方程为(2)所求直线平行两已知平面,且两平面的法向量n1与n2不平行,故所求直线平行于两平面的交线,于是直线方向向量 故过点(0,2,4)的直线方程为(3)所求直线与已知直线平行,故其方向向量可取为s={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z ++==--和4x-2y-2z=3; (2)327x y z ==-和3x-2y+7z=8; (3)223314x y z -+-==-和x+y+z=3.解:平行而不包含. 因为直线的方向向量为s={-2,-7,3} 平面的法向量n={4,-2,-2},所以于是直线与平面平行.又因为直线上的点M0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上.51. 求过点(1,-2,1),且垂直于直线的平面方程. 解:直线的方向向量为12123111-=++-i jk i j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x+2y+3z=0.52. 求过点(1,-2,3)和两平面2x-3y+z=3, x+3y+2z+1=0的交线的平面方程.解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++=其中λ为待定常数,又因为所求平面过点(1,-2,3)故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x+15y+7z+7=053. 求点(-1,2,0)在平面x+2y-z+1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s=n={1,2,-1}所以垂线的参数方程为122x ty t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t)+2(2+2t)-(-t)+1=0 得23t =- 于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333- 54. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离. 解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量 即11133211==-=---i jk n s j k故过已知点的平面方程为y+z=1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-=即13(1,,)22-为平面与直线的垂足于是点到直线的距离为d==55. 求点(1,2,1)到平面x+2y+2z-10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s=n={1,2,2}所以垂线的参数方程为12212 x t y t z t=+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t=.故垂足为485(,,)333,且与点(1,2,1)的距离为1d==即为点到平面的距离.56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程.解:球的半径为R==设(x,y,z)为球面上任一点,则(x-1)2+(y-3)2+(z+2)2=14即x2+y2+z2-2x-6y+4z=0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.解:设该动点为M(x,y,z)3. =化简得:8x2+8y2+8z2-68x+108y-114z+779=0即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=; (3)22194x z +=; (4)20y z -=; (5)220x y -=; (6)220x y +=.解:(1)母线平行于z 轴的抛物柱面,如图7-7.(2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8(3)母线平行于y 轴的椭圆柱面,如图7-9.(4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11.(6)z 轴,如图7-12.图7-11 图7-1259. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=; (3)222149y z x --=; (4)2221149y z x +-=; (5)22209z x y +-=. 解:(1)半轴分别为1,2,3的椭球面,如图7-13.(2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15.(4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-17.图7-1760. 作出下列曲面所围成的立体的图形:(1) x2+y2+z2=a2与z=0,z=2a(a>0); (2)x+y+z=4,x=0,x=1,y=0,y=2及z=0;(3) z=4-x2, x=0, y=0, z=0及2x+y=4; (4) z=6-(x2+y2),x=0, y=0, z=0及x+y=1.解:(1)(2)(3)(4)分别如图7-18,7-19,7-20,7-21所示.图7-18 图7-19图7-20 图7-2161. 求下列曲面和直线的交点: (1)222181369x y z ++=与342364x y z --+==-; (2) 22211694x y z +-=与2434x y z +==-. 解:(1)直线的参数方程为代入曲面方程解得t=0,t=1.得交点坐标为(3,4,-2),(6,-2,2).(2) 直线的参数方程为代入曲面方程可解得t=1,得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程. 解:设(x ,y ,z )为圆上任一点,依题意有 即为所求圆的方程.63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程.(1) 平面x=2; (2) 平面y=0; (3) 平面y=5; (4) 平面z=2.解:(1)截线方程为2212x ⎧=⎪⎪⎨⎪⎪=⎩ 其形状为x=2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ==⎩为平面y=5上的一个椭圆.(4) 截线方程为229252x y z ⎧-=⎪⎨⎪=⎩为平面z=2上的两条直线.64. 求曲线x2+y2+z2=a2, x2+y2=z2在xOy 面上的投影曲线.解:以曲线为准线,母线平行于z 轴的柱面方程为 故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x2+y2=z, z=x+1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x2+y2=x+1即2215()24x y -+=.故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界: (1) {(x, y)|x≠0};(2) {(x, y)|1≤x2+y2<4}; (3) {(x, y)|y<x2};(4) {(x, y)|(x-1)2+y2≤1}∪{(x, y)|(x+1)2+y2≤1}.解:(1)开集、无界集,聚点集:R2,边界:{(x, y)|x=0}. (2)既非开集又非闭集,有界集, 聚点集:{(x, y)|1≤x2+y2≤4},边界:{(x, y)|x2+y2=1}∪{(x, y)| x2+y2=4}. (3)开集、区域、无界集, 聚点集:{(x, y)|y≤x2},边界:{(x, y)| y=x2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x, y)|(x-1)2+y2=1}∪{(x, y)|(x+1)2+y2=1}. 2. 已知f(x, y)=x2+y2-xytan x y,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u v f u v w u w +=+,试求(,,).f x y x y xy +-解:f( x + y, x-y, x y) =( x + y)xy+(x y)x+y+x-y =(x + y)xy+(x y)2x. 4. 求下列各函数的定义域: 解:2(1){(,)|210}.D x y y x =-+> 5. 求下列各极限: 解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=01.4x y →→=-(4)原式=02.x y →→=(5)原式=0sin lim 100.x y xyy xy→→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O(0,0)处是否连续:(3)222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y ++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+, 故0lim 0(0,0)x y z z →→==.故函数在O(0,0)处连续.(2)00sin lim lim 1(0,0)0x u y uz z u→→→==≠=故O(0,0)是z 的间断点.(3)若P(x,y) 沿直线y=x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P(x,y) 沿直线y=-x 趋于(0,0)点,则 故0lim x y z →→不存在.故函数z 在O(0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x,y)=233x y x y-+; (2) f (x,y)=2222y xy x+-;(3) f (x,y)=ln(1-x2-y2);(4)f (x,y)=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解:(1)因为当y=-x 时,函数无定义,所以函数在直线y=-x 上的所有点处间断,而在其余点处均连续.(2)因为当y2=2x 时,函数无定义,所以函数在抛物线y2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x2+y2=1时,函数无定义,所以函数在圆周x2+y2=1上所有点处间断.而在其余各点处均连续. (4)因为点P(x,y)沿直线y=x 趋于O(0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数: (1)z = x2y+2x y ;(2)s =22u v uv+;; (4)z = lntan x y; (5)z = (1+xy)y; (6)u = zxy; (7)u = arctan(x-y)z; (8)yzu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s vu =+2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+ (4)21122sec csc ,tan z x xx x y y y yy∂=⋅⋅=∂ (5)两边取对数得ln ln(1)z y xy =+ 故 []221(1)(1)(1).ln(1)1y y y x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+ (6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂(7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+- (8)1.yzu y x x z-∂=∂9.已知22x y u x y=+,求证:3u u xy u x y∂∂+=∂∂. 证明:222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z zx y z x y∂∂+=∂∂. 证明:11112211e e x y x y z x x x ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x,y 的对称性得 故11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y ⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂ 11.设fx(x,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x 轴所成的倾角.解:(2,4,5)1,1,2z zx xx ∂∂==∂∂设切线与正向x 轴的倾角为α, 则tanα=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z = x4+ y4-4x2y2; (2)z = arctan y x;(3)z = yx;(4)z = 2e x y +.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x,y 的对称性知 (2)222211z y y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,(3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂(4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 14.设f (x, y, z) = xy2+yz2+zx2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解:2(,,)2x f x y z y zx=+15.设z = x ln ( x y),求32z x y ∂∂∂及32zx y ∂∂∂.解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分: (1)22ex y z +=;(2)z =;(3)zy u x =; (4)yzu x =.解:(1)∵2222e 2,e 2x y x y z zx y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )x y xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z z zy y z y z u y x x x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂ 1ln yz u x x y z∂=⋅⋅∂ln yz u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz z z y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;;(3)(1.97)1.05.解:(1)设f(x,y)=x3·y2,则223(,)3,(,)2,x y f x y x y f x y x y ==故df(x,y)=3x2y2dx+2x3ydy=xy(3xydx+2x2dy) 取x=1,y=1,dx=0.02,dy=-0.03,则 (1.02)3·(0.97)2=f(1.02,0.97)≈f(1,1)+df(1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d0.05d0.07(4.05,2.93)(4,3)d(4,3)0.053(0.07)]15(0.01)54.998xyf f f==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=xy,则df(x,y)=yxy-1dx+xylnxdy,取x=2,y=1,dx=-0.03,dy=0.05,则1.05d0.03d0.05(1.97)(1.97,1.05)(2,1)d(2,1)20.0393 2.0393.xyf f f=-==≈+=+=19.矩型一边长a=10cm,另一边长b=24cm, 当a边增加4mm,而b边缩小1mm时,求对角线长的变化.解:设矩形对角线长为l,则d d).l l x x y y==+当x=10,y=24,dx=0.4,dy=-0.1时,d0.4240.1)0.062l=⨯-⨯=(cm)故矩形的对角线长约增加0.062cm.20.解:因为圆锥体的体积为21.3V r hπ=⋅0030,0.1,60,0.5r r h h====-而221.33V VV dV r h yh r r hr hππ∂∂≈=⋅+⋅=⋅+⋅∂∂0030,0.1,60,0.5r r h h====-时,2213.1430600.130(0.5)33Vπ≈⨯⨯⨯⨯+⨯⨯-230()cm=-21.解:设水池的长宽深分别为,,x y z则有:V xyz=精确值为:50.242 2.850.22 3.6 2.80.2V=⨯⨯+⨯⨯⨯+⨯⨯⨯313.632()m=近似值为:V dV zx y xy z≈=+0.4,0.4,0.2x y z ===430.4530.4540.2V dV ≈=⨯⨯+⨯⨯+⨯⨯314.8()m =22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂; (2)z =arc tanx y ,x =u +v,y =u -v,求z u ∂∂,z v∂∂; (3)ln(e e )xyu =+,y =x3,求d d ux; (4)u =x2+y2+z2,x =e cos tt ,y =e sin tt ,z =e t,求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数:(1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+25. 设22()yz f x y =-,其中f(u)为可导函数,验证: 211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,zf x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂ 由对称性知,22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭,(2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂ ()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y zxf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y +++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证:利用变量替换1,3x y x y ξη=-=-,可将方程22222430u u ux x y y∂∂∂++=∂∂∂∂ 化简为20uξη∂=∂∂. 证明:设1(,),3u f f x y x y ξη⎛⎫==-- ⎪⎝⎭2222222222222222222222221411(1)(1)3333u u u u ux x x u u u u u u u ux x x x x u u u uuu u x y ξηξηξηξηξηξξηηξηξξηηξξηηξηξξη∂∂∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⋅+⋅+⋅+⋅=++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂⎛⎫⎛⎫=+⋅-+⋅+⋅-=----- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭22u η∂∂222222222222222222222222211(1)33111211(1)(1)33933343142433u u u u u y u u u uuu u u y u u u x x y yu u u u ξηξηξξηηξηξξηηξξηηξ∂∂∂∂∂⎛⎫=⋅+⋅-=--- ⎪∂∂∂∂∂⎝⎭∂∂∂∂∂∂∂∂⎛⎫⎛⎫=-⋅-⋅--⋅-⋅-=++-- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭∂∂∂++∂∂∂∂∂∂∂∂∂=+++--∂∂∂∂∂2222222221239340.3u u u u u u ξηηξξηηξη⎛⎫⎛⎫∂∂∂∂+-++ ⎪ ⎪∂∂∂∂∂∂∂⎝⎭⎝⎭∂=-=∂∂故20.uξη∂=∂∂ 29. 求下列隐函数的导数或偏导数:(1)2sin e 0xy xy +-=,求d d yx ;(2)arctan y x =,求d d y x;(3)20x y z ++-=,求,z zx y∂∂∂∂; (4)333z xyz a -=,求22,z z x y ∂∂∂∂. 解:(1)[解法1] 用隐函数求导公式,设F(x,y)=siny+ex-xy2, 则 2e ,cos 2,xx y F y F y xy =-=-故 22d e e d cos 2cos 2x xx y F y y y x F y xy y xy--=-=-=--. [解法2] 方程两边对x 求导,得()2cos e 02x y y y x yy '⋅+-='+⋅故 2e .cos 2xy y y xy-'=- (2)设()221(,)ln arctanln arctan ,2y y F x y x y x x==-+ ∵222222121,21x xx y y F x y x y x y x +⎛⎫=-⋅=- ⎪++⎝⎭⎛⎫+ ⎪⎝⎭222221211,21y yy x F x y x x y y x -=-⋅=++⎛⎫+ ⎪⎝⎭∴d .d x y F y x y x F x y+=-=- (3)方程两边求全微分,得d 2d d 0,x y z ++-=,z x y =则d ,z x y =+故z z x y ∂∂==∂∂ (4)设33(,,)3F x y z z xyz a =--,23,3,33,x y z F yz F xz F z xy =-=-=-则223,33x z F z yz yzx F z xy z xy∂-=-=-=∂-- 223,33y z F z xz xzy F z xy z xy∂-=-=-=∂--()()()()22222222322232222()zz z x x xz z xy xz y z y z xy y y z xy xzxzz x x xz z xy z xyx yzz xy xy z zxy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--30. 设F(x, y, z)=0可以确定函数x = x(y, z), y = y(x, z), z = z(x, y),证明:1x y zy z x∂∂∂⋅⋅=-∂∂∂. 证明:∵,,,y x z x y zF F F x y zy F z F x F ∂∂∂=-=-=-∂∂∂∴1.y z x y z x F F F x y z F F F y z x ⎛⎫⎛⎫∂∂∂⎛⎫---⋅⋅=⋅⋅=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z(x,y),其中F 可微,求,z z x y ∂∂∂∂.解:12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222011111z y x z y zF F F F F F F y F F F z x x F F x F F F F F y F zyy F F y F '''=⋅+⋅=⎛⎫''-=⋅+⋅ ⎪⎝⎭'-'∂=-=-=∂''''-''-∂=-=-=∂''32. 求由下列方程组所确定的函数的导数或偏导数:(1)22222,2320,z x y x y z ⎧=+⎪⎨++=⎪⎩ 求:d d ,;d d y z x x (2)1,0,xu yv yu xv +=⎧⎨-=⎩求:,,,;u v u v x x y y ∂∂∂∂∂∂∂∂ (3)2(,),(,),u f ux v y v g u x v y =+⎧⎨=-⎩ 其中f,g 具有连续偏导数函数,求,;u v x x∂∂∂∂(4)e sin ,e cos ,uux u v y u v ⎧=+⎪⎨=-⎪⎩ 求,,,.u u v v x y x y ∂∂∂∂∂∂∂∂ 解:(1)原方程组变为222222320y z xy z x⎧-=-⎪⎨+=-⎪⎩ 方程两边对x 求导,得d d 22d d d d 23d d y z y x x xy z y z x xx ⎧-=-⎪⎪⎨⎪-=-⎪⎩ 当 2162023y J yz y y z-==+≠21d 16(61),3d 622(31)22d 12.2d 6231x y xz x x z x z x J yz y y z y x z xy x y x x J yz y z ----+===--++-===-++(2)设(,,,)1,(,,,),F x y u v xu yv G x y u v yu xv =+-=-,,,,,,,,x y u v x y u v F u F v F x F y G v G u G y G x =====-===-22u v u v F F x yJ x y G G y x===---故 22xvx v F F u yG G v x uux yv x J J x y --∂-+=-=-=∂+ 222222,,.uxu x y v yvuy u y F F xuG G y v vvx uy x J J x y F F v yG G u x u vx uy yJ J x yF F x vG G y u vxu vy y J J x y-∂--=-=-=∂+-∂--=-=-=∂+∂-=-=-=∂+。
最新版高等数学课后习题答案(复旦大学出版社)(李开复编)

高等数学(上)第一章 函数与极限1.设⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21= 224sin )4(==ππϕ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ;⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤ []ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由 ][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a ax a a x a x3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()xe x g =,求()[]x gf 和()[]x fg ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4. 设数列{}n x 有界, 又,0lim =∞→n n y 证明:.0lim =∞→n n n y x{}结论成立。
最新版高等数学课后习题标准答案(复旦大学出版社)(李开复编)

高等数学(上)第一章 函数与极限1. 设⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x ,求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21= 224sin )4(==ππϕ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ;⑵()x f s i n ; ⑶()()0>+a a x f ; ⑷()()a x f a x f -++()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤ []ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a a x a a x a x3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()xe x g =,求()[]x gf 和()[]x fg ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4.设数列{}nx 有界,又,0lim =∞→nn y证明:.0lim =∞→n n n y x{}结论成立。
从而时,有,当自然数即又有对有界,∴=<=-<>∃>∀=≤∀>∃∴∞→ ..0)(,0,0lim ,,0εεεεMM y x y x My N n N y Mx n M x n n n n n n n n n5. 根据函数的定义证明: ⑴()813lim 3=-→x x8)13(lim 813303,033,33813,03=-<--<-<>∀<-<-=-->∀→x x x x x x x 所以成立时,恒有,当=取故即可。
高等数学复旦大学出版第三版下册课后答案习题全之欧阳理创编

习题七1. 在空间直角坐标系中,定出下列各点的位置:A(1,2,3); B(-2,3,4); C(2,-3,-4);D(3,4,0); E(0,4,3); F(3,0,0).解:点A在第Ⅰ卦限;点B在第Ⅱ卦限;点C在第Ⅷ卦限;点D在xOy面上;点E在yOz面上;点F在x轴上.2. xOy坐标面上的点的坐标有什么特点?yOz面上的呢?zOx面上的呢?答: 在xOy面上的点,z=0;在yOz面上的点,x=0;在zOx面上的点,y=0.3. x轴上的点的坐标有什么特点?y轴上的点呢?z轴上的点呢?答:x轴上的点,y=z=0;y轴上的点,x=z=0;z轴上的点,x=y=0.4. 求下列各对点之间的距离:(1)(0,0,0),(2,3,4);(2)(0,0,0),(2,-3,-4);(3)(-2,3,-4),(1,0,3);(4)(4,-2,3),(-2,1,3).解:(1)s==(2)s==(3)s==(4)s==5. 求点(4,-3,5)到坐标原点和各坐标轴间的距离.解:点(4,-3,5)到x轴,y轴,z轴的垂足分别为(4,0,0),(0,-3,0),(0,0,5).故s==5s==.z6. 在z轴上,求与两点A(-4,1,7)和B(3,5,-2)等距离的点.解:设此点为M(0,0,z),则解得14z=9即所求点为M(0,0,14).97. 试证:以三点A(4,1,9),B(10,-1,6),C(2,4,3)为顶点的三角形是等腰直角三角形.证明:因为|AB|=|AC|=7.且有|AC|2+|AB|2=49+49=98=|BC|2.故△ABC 为等腰直角三角形. 8. 验证:()()++=++a b c a b c .证明:利用三角形法则得证.见图7-1图7-19. 设2, 3.=-+=-+-u a b c v a b c 试用a, b, c 表示23.-u v 解:10. 把△ABC 的BC 边分成五等份,设分点依次为D1,D2,D3,D4,再把各分点与A 连接,试以AB =c ,BC =a 表示向量1D A ,2D A ,3D A 和4D A . 解:1115D A BA BD =-=--c a 11. 设向量OM 的模是4,它与投影轴的夹角是60°,求这向量在该轴上的投影. 解:设M 的投影为M ',则12. 一向量的终点为点B (2,-1,7),它在三坐标轴上的投影依次是4,-4和7,求这向量的起点A 的坐标. 解:设此向量的起点A 的坐标A(x, y, z),则 解得x=-2, y=3, z=0 故A 的坐标为A(-2, 3, 0).13. 一向量的起点是P1(4,0,5),终点是P2(7,1,3),试求:(1) 12PP 在各坐标轴上的投影; (2) 12PP 的模;(3) 12PP 的方向余弦; (4) 12PP 方向的单位向量.解:(1)12Pr j 3,x x a PP ==(2)12(7PP ==(3) 12cos 14x a PP α==12cos 14z a PP γ==(4) 12012{14PP PP ===+e i j . 14. 三个力F1=(1,2,3), F2=(-2,3,-4), F3=(3,-4,5)同时作用于一点. 求合力R 的大小和方向余弦.解:R=(1-2+3,2+3-4,3-4+5)=(2,1,4)15. 求出向量a= i+j+k, b=2i-3j+5k 和c=-2i-j+2k 的模,并分别用单位向量,,a b c e e e 来表达向量a, b, c. 解:||=a 16. 设m=3i+5j+8k, n=2i-4j-7k, p=5i+j-4k,求向量a=4m+3n-p 在x 轴上的投影及在y 轴上的分向量. 解:a=4(3i+5j+8k)+3(2i-4j-7k)-(5i+j-4k)=13i+7j+15k 在x 轴上的投影ax=13,在y 轴上分向量为7j. 17.解:设{,,}x y z a a a a =则有 求得12x a =.设a 在xoy 面上的投影向量为b 则有{,,0}x y b a a =则222cos 42a ba b π⋅=⇒=⋅ 则214y a = 求得12y a =±又1,a=则2221x y z a a a ++=从而求得11{,,}222a =±或11{,,}222-± 18. 已知两点M1(2,5,-3),M2(3,-2,5),点M 在线段M1M2上,且123M M MM =,求向径OM 的坐标. 解:设向径OM ={x, y, z}因为,123M M MM =所以,11423(3)153(2) 433(5)3x x x y y y z z z ⎧=⎪-=-⎧⎪⎪⎪-=--⇒=-⎨⎨⎪⎪+=-⎩=⎪⎪⎩故OM ={111,,344-}. 19. 已知点P 到点A (0,0,12)的距离是7,OP 的方向余弦是236,,777,求点P 的坐标.解:设P 的坐标为(x, y, z ),2222||(12)49PA x y z =++-= 得2229524x y z z ++=-+ 又122190cos 2, 749x x α==⇒==故点P 的坐标为P (2,3,6)或P (190285570,,494949). 20. 已知a, b 的夹角2π3ϕ=,且3,4==b a ,计算:(1) a·b; (2) (3a-2b)·(a+ 2b). 解:(1)a·b=2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b (2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b 21. 已知a=(4,-2, 4), b=(6,-3, 2),计算:(1)a·b; (2) (2a-3b)·(a+ b); (3)2||-a b 解:(1)46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b(3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b22. 已知四点A (1,-2,3),B (4,-4,-3),C (2,4,3),D (8,6,6),求向量AB 在向量CD 上的投影. 解:AB ={3,-2,-6},CD ={6,2,3}23. 若向量a+3b 垂直于向量7a-5b,向量a-4b 垂直于向量7a-2b,求a 和b 的夹角.解: (a+3b)·(7a-5b)=227||1615||0+⋅-=a a b b ①(a-4b)·(7a-2b) = 227||308||0-⋅+=a a b b ②由①及②可得:222221()1||||2||||4⋅⋅⋅==⇒=a b a b a b a b a b又21||02⋅=>a b b ,所以1cos ||||2θ⋅==a b a b , 故1πarccos23θ==. 24. 设a=(-2,7,6),b=(4,-3,-8),证明:以a 与b 为邻边的平行四边形的两条对角线互相垂直.证明:以a,b 为邻边的平行四边形的两条对角线分别为a+b,a -b,且 a+b={2,4,-2} a-b={-6,10,14}又(a+b)·(a-b)= 2×(-6)+4×10+(-2)×14=0 故(a+b)⊥(a-b).25. 已知a=3i+2j-k, b=i-j+2k,求: (1) a×b;(2) 2a×7b;(3) 7b×2a; (4) a×a. 解:(1) 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k (4) 0⨯=a a .26. 已知向量a 和b 互相垂直,且||3, ||4==a b .计算: (1) |(a +b)×(a -b)|; (2) |(3a +b)×(a -2b)|.(1)|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a b (2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b a27. 求垂直于向量3i-4j-k 和2i-j+k 的单位向量,并求上述两向量夹角的正弦.解:411334555111221----⨯=++=--+--a b i j k i j k与⨯a b平行的单位向量)||⨯==--+⨯a b e i j k a b||sin ||||θ⨯===⨯a b a b . 28. 一平行四边形以向量a=(2,1,-1)和b=(1,-2,1)为邻边,求其对角线夹角的正弦. 解:两对角线向量为13=+=-l a b i j ,232=-=+-l a b i j k因为12|||2610|⨯=++=l l i j k 所以1212||sin 1||||θ⨯===l l l l .即为所求对角线间夹角的正弦.29. 已知三点A(2,-1,5), B(0,3,-2), C(-2,3,1),点M ,N ,P 分别是AB ,BC ,CA 的中点,证明:1()4MN MP AC BC ⨯=⨯. 证明:中点M ,N ,P 的坐标分别为 故 1()4MN MP AC BC ⨯=⨯. 30.(1)解: x y zxyzi j k a b a a a b b b ⨯=则 C=-C +-+-y z z y x z x x z y x y y x y a b a b a b a b a b C a b a b C ⨯⋅()()()()若,,C a b 共面,则有 a b ⨯后与 C 是垂直的. 从而C 0a b ⨯⋅=() 反之亦成立.(2)C xyz x y z xy za a a ab b b b C C C ⨯⋅=() 由行列式性质可得: 故C a ?b a b b C C a ⨯⋅=⨯⋅=⨯⋅()()()31. 四面体的顶点在(1,1,1),(1,2,3),(1,1,2)和(3,-1,2)求四面体的表面积.解:设四顶点依次取为A, B, C, D.则由A ,B ,D 三点所确定三角形的面积为111|||542|22S AB AD =⨯=+-=i jk .同理可求其他三个三角形的面积依次为12故四面体的表面积12S =+ 32.解:设四面体的底为BCD ∆,从A 点到底面BCD ∆的高为h ,则13BCDV Sh =⋅⋅,而11948222BCDSBC BD i j k =⨯=--+= 又BCD ∆所在的平面方程为:48150x y z +-+= 则43h == 故1942323V =⋅⋅=33. 已知三点A(2,4,1), B(3,7,5), C(4,10,9),证:此三点共线.证明:{1,3,4}AB =,{2,6,8}AC = 显然2AC AB =则22()0AB AC AB AB AB AB ⨯=⨯=⨯= 故A ,B ,C 三点共线.34. 一动点与M0(1,1,1)连成的向量与向量n=(2,3,-4)垂直,求动点的轨迹方程. 解:设动点为M(x, y, z) 因0M M n ⊥,故00M M n ⋅=. 即2(x-1)+3(y-1)-4(z-1)=0整理得:2x+3y-4z-1=0即为动点M 的轨迹方程. 35.求通过下列两已知点的直线方程:(1) (1,-2,1), (3,1,-1); (2) (3,-1,0),(1,0,-3).解:(1)两点所确立的一个向量为s={3-1,1+2,-1-1}={2,3,-2}故直线的标准方程为:121232x y z -+-==- 或 311232x y z --+==- (2)直线方向向量可取为s={1-3,0+1,-3-0}={-2,1,-3}故直线的标准方程为:31213x y z -+==-- 或 13213x y z -+==--36. 求直线234035210x y z x y z +--=⎧⎨-++=⎩的标准式方程和参数方程. 解:所给直线的方向向量为另取x0=0代入直线一般方程可解得y0=7,z0=17于是直线过点(0,7,17),因此直线的标准方程为:且直线的参数方程为:37. 求过点(4,1,-2)且与平面3x-2y+6z=11平行的平面方程.解:所求平面与平面3x-2y+6z=11平行故n={3,-2,6},又过点(4,1,-2)故所求平面方程为:3(x-4)-2(y-1)+6(z+2)=0即3x-2y+6z+2=0.38. 求过点M0(1,7,-3),且与连接坐标原点到点M0的线段OM0垂直的平面方程.解:所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为:x-1+7(y-7)-3(z +3)=0即x+7y-3z-59=039. 设平面过点(1,2,-1),而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍,求此平面方程.解:设平面在y 轴上的截距为b 则平面方程可定为122x y z b b b++= 又(1,2,-1)在平面上,则有得b=2.故所求平面方程为1424x y z ++= 40. 求过(1,1,-1), (-2,-2,2)和(1,-1,2)三点的平面方程.解:由平面的三点式方程知 代入三已知点,有1112121210111121x y z --+----+=---+ 化简得x-3y-2z=0即为所求平面方程.41. 指出下列各平面的特殊位置,并画出其图形:(1) y =0; (2) 3x-1=0;(3) 2x-3y-6=0; (4) x –y=0;(5) 2x-3y+4z=0.解:(1) y=0表示xOz 坐标面(如图7-2)(2) 3x-1=0表示垂直于x 轴的平面.(如图7-3)图7-2 图7-3(3) 2x-3y-6=0表示平行于z 轴且在x 轴及y 轴上的截距分别为x=3和y =-2的平面.(如图7-4)(4) x –y=0表示过z 轴的平面(如图7-5)(5) 2x-3y+4z=0表示过原点的平面(如图7-6).图7-4 图7-5 图7-642. 通过两点(1,1,1,)和(2,2,2)作垂直于平面x+y-z=0的平面.解:设平面方程为Ax+By+Cz+D=0则其法向量为n={A,B,C}已知平面法向量为n1={1,1,-1}过已知两点的向量l={1,1,1}由题知n·n1=0, n·l=0即0 0, .0A B C C A B A B C +-=⎧⇒==-⎨++=⎩所求平面方程变为Ax-Ay+D=0又点(1,1,1)在平面上,所以有D=0故平面方程为x-y=0.43. 决定参数k 的值,使平面x+ky-2z=9适合下列条件:(1)经过点(5,-4,6); (2) 与平面2x-3y+z=0成π4的角.解:(1) 因平面过点(5,-4,6)故有 5-4k-2×6=9得k=-4.(2) 两平面的法向量分别为n1={1,k,-2} n2={2,-3,1}且1212πcos cos ||||42θ⋅====n n n n解得k =44. 确定下列方程中的l 和m:(1) 平面2x+ly+3z-5=0和平面mx-6y-z+2=0平行;(2) 平面3x-5y+lz-3=0和平面x+3y+2z+5=0垂直. 解:(1)n1={2,l,3}, n2={m,-6,-1}(2) n1={3, -5,l }, n2={1,3,2}45. 通过点(1,-1,1)作垂直于两平面x-y+z-1=0和2x+y+z+1=0的平面.解:设所求平面方程为Ax+By+Cz+D=0其法向量n={A,B,C}n1={1,-1,1}, n2={2,1,1}又(1,-1,1)在所求平面上,故A -B+C+D=0,得D=0故所求平面方程为即2x-y-3z=046. 求平行于平面3x-y+7z=5,且垂直于向量i-j+2k 的单位向量.解:n1={3,-1,7}, n2={1,-1,2}. 故1217733152122111--=⨯=++=+---n n n i j k i j k 则2).n =+-e i j k 47. 求下列直线与平面的交点: (1) 11126x y z -+==-, 2x+3y+z-1=0;(2) 213232x y z +--==, x+2y-2z+6=0. 解:(1)直线参数方程为1126x ty t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t=1故交点为(2,-3,6).(2) 直线参数方程为221332x ty t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t=0.故交点为(-2,1,3).48. 求下列直线的夹角:(1)533903210x y z x y z -+-=⎧⎨-+-=⎩ 和 2223038180x y z x y z +-+=⎧⎨++-=⎩; (2)2314123x y z ---==- 和 38121y z x --⎧=⎪--⎨⎪=⎩ 解:(1)两直线的方向向量分别为:s1={5,-3,3}×{3,-2,1}=533321i j k--={3,4,-1}s2={2,2,-1}×{3,8,1}=221381i j k-={10,-5,10}由s1·s2=3×10+4×(-5)+(-1) ×10=0知s1⊥s2 从而两直线垂直,夹角为π2.(2) 直线2314123x y z ---==-的方向向量为s1={4,-12,3},直线38121y z x --⎧=⎪--⎨⎪=⎩的方程可变为22010y z x -+=⎧⎨-=⎩,可求得其方向向量s2={0,2,-1}×{1,0,0}={0,-1,-2},于是49. 求满足下列各组条件的直线方程:(1)经过点(2,-3,4),且与平面3x-y+2z-4=0垂直;(2)过点(0,2,4),且与两平面x+2z=1和y-3z=2平行;(3)过点(-1,2,1),且与直线31213x y z --==-平行. 解:(1)可取直线的方向向量为s={3,-1,2}故过点(2,-3,4)的直线方程为(2)所求直线平行两已知平面,且两平面的法向量n1与n2不平行,故所求直线平行于两平面的交线,于是直线方向向量故过点(0,2,4)的直线方程为(3)所求直线与已知直线平行,故其方向向量可取为s={2,-1,3}故过点(-1,2,1)的直线方程为121213x y z +--==-. 50. 试定出下列各题中直线与平面间的位置关系:(1)34273x y z ++==--和4x-2y-2z=3;(2)327x y z ==-和3x-2y+7z=8; (3)223314x y z -+-==-和x+y+z=3. 解:平行而不包含. 因为直线的方向向量为s={-2,-7,3} 平面的法向量n={4,-2,-2},所以于是直线与平面平行.又因为直线上的点M0(-3,-4,0)代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量,故直线垂直于平面.(3) 直线在平面上,因为3111(4)10⨯+⨯+-⨯=,而直线上的点(2,-2,3)在平面上.51. 求过点(1,-2,1),且垂直于直线的平面方程. 解:直线的方向向量为12123111-=++-i jk i j k , 取平面法向量为{1,2,3},故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x+2y+3z=0.52. 求过点(1,-2,3)和两平面2x-3y+z=3, x+3y+2z+1=0的交线的平面方程.解:设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++=其中λ为待定常数,又因为所求平面过点(1,-2,3) 故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+=解得λ=-4.故所求平面方程为2x+15y+7z+7=053. 求点(-1,2,0)在平面x+2y-z+1=0上的投影.解:过点(-1,2,0)作垂直于已知平面的直线,则该直线的方向向量即为已知平面的法向量,即s=n={1,2,-1}所以垂线的参数方程为122x ty t z t =-+⎧⎪=+⎨⎪=-⎩将其代入平面方程可得(-1+t)+2(2+2t)-(-t)+1=0 得23t =- 于是所求点(-1,2,0)到平面的投影就是此平面与垂线的交点522(,,)333- 54. 求点(3,-1,2)到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离. 解:过点(3,-1,2)作垂直于已知直线的平面,平面的法向量可取为直线的方向向量 即11133211==-=---i jk n s j k故过已知点的平面方程为y+z=1.联立方程组102401x y z x y z y z +-+=⎧⎪-+-=⎨⎪+=⎩解得131,,.22x y z ==-= 即13(1,,)22-为平面与直线的垂足于是点到直线的距离为2d == 55. 求点(1,2,1)到平面x+2y+2z-10=0距离.解:过点(1,2,1)作垂直于已知平面的直线,直线的方向向量为s=n={1,2,2}所以垂线的参数方程为12212x ty t z t =+⎧⎪=+⎨⎪=+⎩将其代入平面方程得13t =.故垂足为485(,,)333,且与点(1,2,1)的距离为1d == 即为点到平面的距离.56. 建立以点(1,3,-2)为中心,且通过坐标原点的球面方程.解:球的半径为R ==设(x,y,z)为球面上任一点,则(x-1)2+(y-3)2+(z+2)2=14 即x2+y2+z2-2x-6y+4z=0为所求球面方程.57. 一动点离点(2,0,-3)的距离与离点(4,-6,6)的距离之比为3,求此动点的轨迹方程.解:设该动点为M(x,y,z),由题意知3.=化简得:8x2+8y2+8z2-68x+108y-114z+779=0即为动点的轨迹方程.58. 指出下列方程所表示的是什么曲面,并画出其图形:(1)22()()22a a x y -+=; (2)22149x y -+=; (3)22194x z +=; (4)20y z -=; (5)220x y -=; (6)220x y +=.解:(1)母线平行于z 轴的抛物柱面,如图7-7.(2)母线平行于z 轴的双曲柱面,如图7-8.图7-7 图7-8(3)母线平行于y 轴的椭圆柱面,如图7-9.(4)母线平行于x 轴的抛物柱面,如图7-10.图7-9 图7-10(5)母线平行于z 轴的两平面,如图7-11.(6)z 轴,如图7-12.图7-11 图7-1259. 指出下列方程表示怎样的曲面,并作出图形:(1)222149y z x ++=; (2)22369436x y z +-=;(3)222149y z x --=; (4)2221149y z x +-=;(5)22209z x y +-=.解:(1)半轴分别为1,2,3的椭球面,如图7-13. (2) 顶点在(0,0,-9)的椭圆抛物面,如图7-14.图7-13 图7-14(3) 以x 轴为中心轴的双叶双曲面,如图7-15. (4) 单叶双曲面,如图7-16.图7-15 图7-16(5) 顶点在坐标原点的圆锥面,其中心轴是z 轴,如图7-17.图7-1760. 作出下列曲面所围成的立体的图形: (1) x2+y2+z2=a2与z=0,z=2a(a>0); (2)x+y+z=4,x=0,x=1,y=0,y=2及z=0;(3) z=4-x2, x=0, y=0, z=0及2x+y=4; (4) z=6-(x2+y2),x=0, y=0, z=0及x+y=1.解:(1)(2)(3)(4)分别如图7-18,7-19,7-20,7-21所示.图7-18 图7-19 图7-20 图7-2161. 求下列曲面和直线的交点: (1) 222181369x y z ++=与342364x y z --+==-; (2)22211694x y z +-=与2434x y z +==-. 解:(1)直线的参数方程为 代入曲面方程解得t=0,t=1.得交点坐标为(3,4,-2),(6,-2,2). (2) 直线的参数方程为 代入曲面方程可解得t=1, 得交点坐标为(4,-3,2).62. 设有一圆,它的中心在z 轴上,半径为3,且位于距离xOy 平面5个单位的平面上,试建立这个圆的方程. 解:设(x ,y ,z )为圆上任一点,依题意有 即为所求圆的方程. 63. 试考察曲面22219254x y z -+=在下列各平面上的截痕的形状,并写出其方程.(1) 平面x=2; (2) 平面y=0; (3) 平面y=5; (4) 平面z=2.解:(1)截线方程为221(()332x ⎧=⎪⎪⎨⎪⎪=⎩其形状为x=2平面上的双曲线.(2)截线方程为221940x z y ⎧+=⎪⎨⎪=⎩为xOz 面上的一个椭圆.(3)截线方程为2215y ==⎩为平面y=5上的一个椭圆.(4) 截线方程为229252x y z ⎧-=⎪⎨⎪=⎩为平面z=2上的两条直线.64. 求曲线x2+y2+z2=a2, x2+y2=z2在xOy 面上的投影曲线.解:以曲线为准线,母线平行于z 轴的柱面方程为 故曲线在xOy 面上的投影曲线方程为22220a x y z ⎧+=⎪⎨⎪=⎩65. 建立曲线x2+y2=z, z=x+1在xOy 平面上的投影方程. 解:以曲线为准线,母线平行于z 轴的柱面方程为x2+y2=x+1即2215()24x y -+=. 故曲线在xOy 平面上的投影方程为2215()240x y z ⎧-+=⎪⎨⎪=⎩习题八1. 判断下列平面点集哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点集和边界: (1) {(x, y)|x≠0};(2) {(x, y)|1≤x2+y2<4}; (3) {(x, y)|y<x2};(4) {(x, y)|(x-1)2+y2≤1}∪{(x, y)|(x+1)2+y2≤1}.解:(1)开集、无界集,聚点集:R2,边界:{(x, y)|x=0}. (2)既非开集又非闭集,有界集, 聚点集:{(x, y)|1≤x2+y2≤4},边界:{(x, y)|x2+y2=1}∪{(x, y)| x2+y2=4}. (3)开集、区域、无界集, 聚点集:{(x, y)|y≤x2}, 边界:{(x, y)| y=x2}.(4)闭集、有界集,聚点集即是其本身,边界:{(x, y)|(x-1)2+y2=1}∪{(x, y)|(x+1)2+y2=1}. 2. 已知f(x, y)=x2+y2-xytan x y,试求(,)f tx ty . 解:222(,)()()tan(,).tx f tx ty tx ty tx ty t f x y ty=+-⋅= 3. 已知(,,)w u v f u v w u w +=+,试求(,,).f x y x y xy +-解:f( x + y, x-y, x y) =( x + y)xy+(x y)x+y+x-y =(x + y)xy+(x y)2x.4. 求下列各函数的定义域: 解:2(1){(,)|210}.D x y y x =-+>5. 求下列各极限: 解:(1)原式0ln 2.=(2)原式=+∞. (3)原式=001.4x y →→=-(4)原式=02.x y →→=(5)原式=0sin lim 100.x y xyy xy→→⋅=⨯=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 判断下列函数在原点O(0,0)处是否连续: (3) 222222222,0,(2)()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解:(1)由于3333333322223333sin()sin()sin()0()x y x y x y x y y x x y x y x y x y++++≤=≤+⋅++++ 又00lim()0x y y x →→+=,且3333000sin()sin lim lim 1x u y x y ux y u →→→+==+,故0lim 0(0,0)x y z z →→==.故函数在O(0,0)处连续.(2)00sin lim lim 1(0,0)0x u y uz z u→→→==≠=故O(0,0)是z 的间断点.(3)若P(x,y) 沿直线y=x 趋于(0,0)点,则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P(x,y) 沿直线y=-x 趋于(0,0)点,则 故0lim x y z →→不存在.故函数z 在O(0,0)处不连续.7. 指出下列函数在向外间断:(1) f (x,y)=233x y x y-+; (2) f (x,y)=2222y xy x+-; (3) f (x,y)=ln(1-x2-y2);(4)f(x,y)=222e ,0,0,0.x y x y yy -⎧⎪≠⎨⎪=⎩解:(1)因为当y=-x 时,函数无定义,所以函数在直线y=-x 上的所有点处间断,而在其余点处均连续.(2)因为当y2=2x 时,函数无定义,所以函数在抛物线y2=2x 上的所有点处间断.而在其余各点处均连续.(3)因为当x2+y2=1时,函数无定义,所以函数在圆周x2+y2=1上所有点处间断.而在其余各点处均连续.(4)因为点P(x,y)沿直线y=x 趋于O(0,0)时.1200lim (,)lime x x y x xf x y x-→→=→==∞. 故(0,0)是函数的间断点,而在其余各点处均连续. 8. 求下列函数的偏导数: (1)z = x2y+2x y ;(2)s =22u v uv+;(4)z = lntan x y; (5)z = (1+xy)y; (6)u = zxy; (7)u = arctan(x-y)z; (8)yzu x =.解:(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (2)u v s v u =+2211,.s v s u u v u v v u∂∂=-=-+∂∂(3)2222212ln(),2z x x x x y x x y ∂==++∂+ (4)21122sec csc ,tan z x xx x y y y yy∂=⋅⋅=∂ (5)两边取对数得ln ln(1)z y xy =+ 故 []221(1)(1)(1).ln(1)1y y y x z y xy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+ (6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ (7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+-(8)1.y zu y x x z-∂=∂9.已知22x y u x y=+,求证:3u u xy u x y∂∂+=∂∂. 证明:222223222()2()()u xy x y x y x y xy x x y x y ∂+-+==∂++. 由对称性知 22322()u x y yx y x y ∂+=∂+. 于是 2223()3()u u x y x y x y u x y x y ∂∂++==∂∂+. 10.设11ex y z ⎛⎫+- ⎪⎝⎭=,求证:222z zx y z x y∂∂+=∂∂. 证明:11112211e e x y x y z x xx ⎛⎫⎛⎫++-- ⎪ ⎪⎝⎭⎝⎭∂⎡⎤⎛⎫=-=- ⎪⎢⎥∂⎝⎭⎣⎦, 由z 关于x,y 的对称性得 故11111122222211e e 2e 2.x y x y x y z z x y x y z x y x y ⎛⎫⎛⎫⎛⎫+++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∂∂+⋅=⋅+⋅==∂∂ 11.设,求fx(x,1) .解:1(,)1(x f x y y y =+- 则(,1)101x f x =+=.12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点(2,4,5)处的切线与正向x轴所成的倾角.解:(2,4,5)1,1,2z zx xx ∂∂==∂∂设切线与正向x 轴的倾角为α, 则tanα=1. 故α=π4. 13.求下列函数的二阶偏导数: (1)z = x4+ y4-4x2y2; (2)z = arctan y x;(3)z = yx;(4)z = 2e x y +.解:(1)2322224812816z z z x xy x y xy x x x y∂∂∂=-=-=-∂∂∂∂ ,, 由x,y 的对称性知 (2)222211z y y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭,(3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂(4)22e 2,e ,x y x y z zx x y++∂∂=⋅=∂∂ 14.设 f (x, y, z) = xy2+yz2+zx2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f -解:2(,,)2x f x y z y zx=+15.设z = x ln ( x y),求32z x y ∂∂∂及32zx y∂∂∂. 解:ln()1ln(),z yx xy xy x xy∂=⋅+=+∂ 232223221,0,11,.z y zx xy x x y z x z x y xy y x y y∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分:(1)22exy z +=;(2)z =;(3)zy u x =;(4)y zu x =.解:(1)∵2222e 2,e 2x y x y z z x y x y++∂∂=⋅=⋅∂∂ ∴222222d 2e d 2e d 2e (d d )x y xy xy z x x y y x x y y +++=+=+(2)∵22223/21()z xy y x y x x y ∂⎛⎫-=⋅=- ⎪+∂+⎝⎭2223/2()z x yx y ∂==∂+ ∴223/2d (d d ).()xz y x x y x y =--+(3)∵11,ln z z z y y z u u y x x x zy x y--∂∂==⋅⋅∂∂ 2ln ln y z ux x y y z∂=⋅⋅⋅∂ ∴211d d ln d ln ln d .z zzy y z y z u y xx x x zy y x x y y z --=+⋅+⋅⋅⋅(4)∵1yz u y x x z-∂=∂1ln yz u x x y z∂=⋅⋅∂ ln y z u y x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭∴121d d ln d ln d .y y yz zz y y u x x x x y x x z z z z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭17. 求下列函数在给定点和自变量增量的条件下的全增量和全微分: (1)222,2,1,0.2,0.1;z x xy y x y x y =-+==-∆=∆=- (2)e ,1,1,0.15,0.1.xy z x y x y ===∆=∆=解:(1)22()()()2()9.688 1.68z x x x x y y y y z ∆=+∆-+∆+∆++∆-=-=d (2)(4) 1.6z x y x x y y =-∆+-+∆=(2)()()0.265ee e(e 1)0.30e.x x y y xy z +∆+∆∆=-=-=d e e e ()0.25e xy xy xy z y x x y y x x y =∆+∆=∆+∆=18.利用全微分代替全增量,近似计算: (1) (1.02)3·(0.97)2;(3)(1.97)1.05.解:(1)设f(x,y)=x3·y2,则223(,)3,(,)2,x y f x y x y f x y x y ==故df(x,y)=3x2y2dx+2x3ydy=xy(3xydx+2x2dy) 取x=1,y=1,dx=0.02,dy=-0.03,则 (1.02)3·(0.97)2=f(1.02,0.97)≈f(1,1)+df(1,1)d 0.02d 0.03x y ==-=13×12+1×1[3×1×1×0.02+2×12×(-0.03)]=1.(2)设,则(,)(,)x y f x y f x y ===故d (,)d d )f x y x x y y =+取4,3,d 0.05,d 0.07x y x y ====-,则d 0.05d 0.07(4.05,2.93)(4,3)d (4,3)0.053(0.07)]15(0.01)54.998x y f f f ==-=≈+=⨯+⨯-=+⨯-=(3)设f(x,y)=xy,则df(x,y)=yxy-1dx+xylnxdy , 取x=2,y=1,dx=-0.03,dy=0.05,则1.05d 0.03d 0.05(1.97)(1.97,1.05)(2,1)d (2,1)20.0393 2.0393.x y f f f =-==≈+=+=19.矩型一边长a=10cm ,另一边长b=24cm, 当a 边增加4mm ,而b 边缩小1mm 时,求对角线长的变化.解:设矩形对角线长为l ,则d d ).l l x x y y ==+当x=10,y=24,dx=0.4,dy=-0.1时,d 0.4240.1)0.062l =⨯-⨯=(cm)故矩形的对角线长约增加0.062cm. 20.解:因为圆锥体的体积为21.3V r h π=⋅0030,0.1,60,0.5r r h h ====-而221.33V V V dV r h yh r r h r h ππ∂∂≈=⋅+⋅=⋅+⋅∂∂ 0030,0.1,60,0.5r r h h ====-时,2213.1430600.130(0.5)33V π≈⨯⨯⨯⨯+⨯⨯-230()cm =-21.解:设水池的长宽深分别为,,x y z 则有:V xyz =精确值为:50.242 2.850.22 3.6 2.80.2V =⨯⨯+⨯⨯⨯+⨯⨯⨯313.632()m =近似值为:V dV zx y xy z ≈=+ 0.4,0.4,0.2x y z ===430.4530.4540.2V dV ≈=⨯⨯+⨯⨯+⨯⨯314.8()m =22. 求下列复合函数的偏导数或全导数:(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v∂∂; (2)z =arc tanx y ,x =u +v,y =u -v,求z u ∂∂,z v∂∂; (3)ln(e e )xyu =+,y =x3,求d d ux; (4)u =x2+y2+z2,x =e cos tt ,y =e sin tt ,z =e t,求d d ut. 解:(1)222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v u x u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z yxy y u v x xy u v v x v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++ (2)222222211111x z z x z y y x v y u x u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y v x v y vyx x y y y x ux y u v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x y x x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u zt x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数,试求下列函数的一阶偏导数: (1)22(,e );xyu f x y =- (2),;x y u f y z ⎛⎫= ⎪⎝⎭(3)().,,u f x xy xyz = 解:(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ (2)1111u f f x y y∂''=⋅=∂ 121222222211..x u x f f f f y y z y z u y y f f z z z ∂⎛⎫''''-=⋅+⋅=-+ ⎪∂⎝⎭∂⎛⎫''=⋅=-- ⎪∂⎝⎭(3)1231231,uf f y f yz f yf yzf x∂''''''=⋅+⋅+⋅=++∂ 12323330,.uf f x f xz xf xzf yuf xy xyf z∂'''''=⋅+⋅+⋅=+∂∂''=⋅=∂24.设(),,()yz xy xF u u F u x=+=为可导函数,证明: .z z xy z xy x y∂∂+=+∂∂ 证明:2()()()()z y y y xF u F u F u y F u x x x ∂⎛⎫''=+⋅+=+-- ⎪∂⎝⎭1()().z x xF u x F u y x∂''=+⋅=+∂ 故[]()()()()()()().z z F u y xy x y x F u F u y x y x xF u xy yF u xy yF u xy xF u xy z xy '∂∂⎡⎤'+=+++-⎢⎥∂∂⎣⎦''=+-++=++=+25. 设22()yz f x y =-,其中f(u)为可导函数,验证:211z z zx x y y y∂∂+=∂∂. 证明:∵2222z yf x xyf x f f ''∂⋅=-=-∂, 222(2)2z f y f y f y f y f f ''∂-⋅⋅-+==∂, ∴22222112211z z yf f y f y zx x y y f yf yf f y y ''∂∂++=-+==⋅=∂∂⋅ 26. 22()z f x y =+,其中f 具有二阶导数,求22222,,.z z zx x y y ∂∂∂∂∂∂∂ 解:2,2,z zxf yf x y∂∂''==∂∂ 222222224,224,z f x xf f x f xzxf y xyf x y∂''''''=+⋅=+∂∂''''=⋅=∂∂由对称性知,22224.z f y f y∂'''=+∂27. 设f 具有二阶偏导函数,求下列函数的二阶偏导数: (1),;x x z f y ⎛⎫= ⎪⎝⎭(2)()22;,z f xy x y =(3)().sin ,cos ,e x y z f x y += 解:(1)1212111,z f f f f x y y∂''''=⋅+⋅=+∂ 2212211121112222221222122222222222222222223211121,1111,,2z f f f f f f f y x y y y yx x z x f f f f f f y y y x y y y y yx z x f f y y y z x x f f y y y ∂⎛⎫''''''''''''''+⋅=+⋅+=+⋅+ ⎪∂⎝⎭∂⎛⎫⎛⎫⎛⎫''''''''''--+=⋅-+⋅=-- ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭∂⎛⎫''-==- ⎪∂⎝⎭∂''=-∂22222342.x x x f f y yy ⎛⎫''''-⋅=+ ⎪⎝⎭, (2)22121222,zf y f xy y f xyf x∂''''=⋅+⋅=+∂ ()()22222211122122432221112222222244,zy yf xy f y f xy f y f xy x yf y f xy f x y f ∂'''''''''=++⋅+⋅⋅+⋅∂'''''''=+++()()()()222212111221223322121122122212122222121112212212222222225,22,22222zyf y xf xy f xy f x f xy f x x yyf xf xy f x yf x y f zf xy f x xyf x f yzxf xy x f xy f x f xy f x yxf ∂''''''''''=+++⋅+⋅⋅+⋅∂∂''''''''=++++∂''''=⋅+⋅=+∂∂'''''''''=++⋅+⋅⋅+⋅∂'=223411122244.x y f x yf x f ''''''+++(3)1313cos e cos e ,x y x y zf x f xf f x++∂''''=⋅+⋅=+∂()()1321113313322()311113332312133233sin cos e e cos e cos e e sin cos 2e cos e ,cos e e (sin )e (sin )x y x y x y x y x y x y x y x y x y x y zxf x f f x f f x f xf xf xf xf f z x f f y f f y f x y++++++++++∂''''''''''=-+++⋅+⋅+⋅∂''''''''=-+++∂'⎡⎤''''''=++⋅⋅-+⋅⋅-+⎣⎦∂∂2()3121332332323223222233233e e cos sin e cos e sin e ,(sin )e sin e ,cos sin e e (sin )e (sin )e x y x y x y x y x y x y x y x y x y x y x y f x yf xf yf f zf y f yf f yz yf y f f y f f y f y +++++++++++⎡⎤''⋅⎣⎦'''''''''=-+-+∂''''=-+=-+∂∂''⎡⎤⎡''''''''=--++-+⋅-+⋅⎣⎦∂22()32222333e cos sin 2e sin e .x y x y x y f yf yf yf f +++⎤⎣⎦''''''''=-+-+28. 试证:利用变量替换1,3x y x y ξη=-=-,可将方程 22222430u u ux x y y∂∂∂++=∂∂∂∂ 化简为20uξη∂=∂∂. 证明:设1(,),3u f f x y x y ξη⎛⎫==-- ⎪⎝⎭2222222222222222222222221411(1)(1)3333u u u u ux x x u u u u u u u ux x x x x u u u uuu u x y ξηξηξηξηξηξξηηξηξξηηξξηηξηξξη∂∂∂∂∂∂∂=⋅+⋅=+∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⋅+⋅+⋅+⋅=++∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂⎛⎫⎛⎫=+⋅-+⋅+⋅-=----- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭22u η∂∂222222222222222222222222211(1)33111211(1)(1)33933343142433u u u u u y u u u uuu u u y u u ux x y yu u u u ξηξηξξηηξηξξηηξξηηξ∂∂∂∂∂⎛⎫=⋅+⋅-=--- ⎪∂∂∂∂∂⎝⎭∂∂∂∂∂∂∂∂⎛⎫⎛⎫=-⋅-⋅--⋅-⋅-=++-- ⎪ ⎪∂∂∂∂∂∂∂∂∂∂∂⎝⎭⎝⎭∂∂∂++∂∂∂∂∂∂∂∂∂=+++--∂∂∂∂∂2222222221239340.3u u u u u u ξηηξξηηξη⎛⎫⎛⎫∂∂∂∂+-++ ⎪ ⎪∂∂∂∂∂∂∂⎝⎭⎝⎭∂=-=∂∂故20.uξη∂=∂∂ 29. 求下列隐函数的导数或偏导数:(1)2sin e 0xy xy +-=,求d d yx ;(2)ln arctan y x =,求d d y x;(3)20x y z ++-=,求,z zx y∂∂∂∂; (4)333z xyz a -=,求22,z z x y ∂∂∂∂. 解:(1)[解法1] 用隐函数求导公式,设F(x,y)=siny+ex-xy2, 则 2e ,cos 2,xx y F y F y xy =-=-故 22d e e d cos 2cos 2x xx y F y y y x F y xy y xy--=-=-=--. [解法2] 方程两边对x 求导,得()2cos e 02x y y y x yy '⋅+-='+⋅故 2e .cos 2xy y y xy-'=- (2)设()221(,)arctanln arctan ,2y y F x y x y x x==-+∵222222121,21x xx y y F x yx y x y x +⎛⎫=-⋅=- ⎪++⎝⎭⎛⎫+ ⎪⎝⎭222221211,21y yy x F x yx x yy x -=-⋅=++⎛⎫+ ⎪⎝⎭∴d .d x y F y x y x F x y+=-=- (3)方程两边求全微分,得d 2d d 0,x y z ++-=,z x y =则d ,z x y =+故z z x y ∂∂==∂∂ (4)设33(,,)3F x y z z xyz a =--,23,3,33,x y z F yz F xz F z xy =-=-=-则223,33x z F z yz yzx F z xy z xy∂-=-=-=∂-- 223,33y z F z xz xz y F z xy z xy∂-=-=-=∂-- ()()()()22222222322232222()z z z x xxz z xy xz y z y z xy y y z xy xzxzz x x xz z xy z xyx yzz xy xy z z xy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--30. 设F(x, y, z)=0可以确定函数x = x(y, z), y = y(x, z), z = z(x, y),证明:1x y zy z x∂∂∂⋅⋅=-∂∂∂. 证明:∵,,,y x z x y zF F F x y zy F z F x F ∂∂∂=-=-=-∂∂∂∴1.y z x y z x F F F x y z F F F y z x ⎛⎫⎛⎫∂∂∂⎛⎫---⋅⋅=⋅⋅=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ 31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z(x,y),其中F 可微,求,z z x y ∂∂∂∂.解:12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222011111z y x z y zF F F F F F F y F F F z x x F F x F F F F F y F zyy F F y F '''=⋅+⋅=⎛⎫''-=⋅+⋅ ⎪⎝⎭'-'∂=-=-=∂''''-''-∂=-=-=∂''32. 求由下列方程组所确定的函数的导数或偏导数:(1)22222,2320,z x y x y z ⎧=+⎪⎨++=⎪⎩ 求:d d ,;d d y z x x (2)1,0,xu yv yu xv +=⎧⎨-=⎩求:,,,;u v u v x x y y ∂∂∂∂∂∂∂∂ (3)2(,),(,),u f ux v y v g u x v y =+⎧⎨=-⎩ 其中f,g 具有连续偏导数函数,求,;u v x x∂∂∂∂ (4)e sin ,e cos ,uux u v y u v ⎧=+⎪⎨=-⎪⎩ 求,,,.u u v v x y x y ∂∂∂∂∂∂∂∂ 解:(1)原方程组变为222222320y z xy z x⎧-=-⎪⎨+=-⎪⎩方程两边对x 求导,得d d 22d d d d 23d d y z y x x xy z y z x xx ⎧-=-⎪⎪⎨⎪-=-⎪⎩ 当 2162023y J yz y y z-==+≠21d 16(61),3d 622(31)22d 12.2d 6231x y xz x x z x z x J yz y y z y x z xy x y x x J yz y z ----+===--++-===-++(2)设(,,,)1,(,,,),F x y u v xu yv G x y u v yu xv =+-=-,,,,,,,,x y u v x y u v F u F v F x F y G v G u G y G x =====-===-22u v uv F F x yJ x y G G y x===---故 22xvx v F F u yG G v x uux yv x J J x y --∂-+=-=-=∂+ 222222,,.uxu x y v yvuy u y F F xuG G y v vvx uy x J J x y F F v yG G u x u vx uy yJ J x yF F x vG G y u v xu vy y J J x y-∂--=-=-=∂+-∂--=-=-=∂+∂-=-=-=∂+ (3)设(,,,)(,),F u v x y f ux v y u =+-2(,,,)(,),G u v x y g u x v y v =--。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 解: (1)相等.因为两函数的定义域相同,都是实数集R ;x =知两函数的对应法则也相同;所以两函数相等.(2)相等.因为两函数的定义域相同,都是实数集R ,由已知函数关系式显然可得两函数的对应法则也相同,所以两函数相等.(3)不相等. 因为函数()f x 的定义域是{,1}x x x ∈≠R ,而函数()g x 的定义域是实数集R ,两函数的定义域不同,所以两函数不相等.2. 解: (1)要使函数有意义,必须400x x -≥⎧⎨≠⎩ 即40x x ≤⎧⎨≠⎩所以函数的定义域是(,0)(0,4]-∞.(2)要使函数有意义,必须30lg(1)010x x x +≥⎧⎪-≠⎨⎪->⎩ 即301x x x ≥-⎧⎪≠⎨⎪<⎩所以函数的定义域是[-3,0)∪(0,1).(3)要使函数有意义,必须210x -≠ 即 1x ≠±所以函数的定义域是(,1)(1,1)(1,)-∞--+∞.(4)要使函数有意义,必须12sin 1x -≤≤ 即 11sin 22x -≤≤即ππ2π2π66k x k -+≤≤+或5π7π2π2π66k x k +≤≤+,(k 为整数).也即ππππ66k x k -+≤≤+ (k 为整数).所以函数的定义域是ππ[π,π]66k k -++, k 为整数.3.解: 由已知显然有函数的定义域为(-∞,+∞),又当0x ≠时,1x 可以是不为零的任意实数,此时,1sinx 可以取遍[-1,1]上所有的值,所以函数的值域为[-1,1]. 4. 解: 10(0)110f -==+,1()1(),1()1x x f x x x --+-==+--1111().111x x f x x x --==++ 5.解: 1,1101,01(1).(1)1,012,13x x f x x x x x -≤-<≤<⎧⎧-==⎨⎨-+≤-≤≤≤⎩⎩6.解: ()ln (())22,g x x x f g x ==(())()ln ()2ln 2(ln 2)2,x x x g f x f x f x x ==⋅=⋅()2(())22,(())()ln ()ln ln(ln ).xf x f f xg g x g x g x x x x x ====7. 证:由321y x =-解得x =故函数3()21f x x =-的反函数是)y x =∈R ,这与()g x =数,所以3()21f x x =-和()g x =.8. 解: (1)由11x y x -=+解得11y x y -=+, 所以函数11x y x -=+的反函数为1(1)1x y x x -=≠-+.(2)由ln(2)1y x =++得1e 2y x -=-,所以,函数ln(2)1y x =++的反函数为1e 2()x y x -=-∈ R . (3)由253x y +=解得31(log 5)2x y =-所以,函数253x y +=的反函数为31(log 5)(0)2y x x =-> .(4)由31cos y x =+得cos x =又[0,π]x ∈,故x =又由1cos 1x -≤≤得301cos 2x ≤+≤,即02y ≤≤,故可得反函数的定义域为[0,2],所以,函数31cos ,[0,π]y x x =+∈的反函数为(02)y x =≤≤.9. 解: (1)()()f x f x -===()f x ∴=.(2)222222()e e sin()e e sin (e e sin )()x x x x x x f x x x x f x ----=-+-=-+=--+=-∴函数22e e sin x xy x -=-+是奇函数.10. 解: (1)函数的定义域为(-∞,+∞), 当0x ≤时,有201xx ≤+,当0x >时,有21122x x x x ≤=+,故(,),x ∀∈-∞+∞有12y ≤.即函数21x y x =+有上界. 又因为函数21x y x =+为奇函数,所以函数的图形关于原点对称,由对称性及函数有上界知,函数必有下界,因而函数21x y x =+有界.又由1212121222221212()(1)11(1)(1)x x x x x x y y x x x x ---=-=++++知,当12x x >且121x x <时,12y y >,而 当12x x >且121x x >时,12y y <.故函数21xy x =+在定义域内不单调.(2)函数的定义域为(0,+∞),10,0M x ∀>∃>且12;e 0M x M x >∃>>,使2ln x M >. 取012max{,}x x x =,则有0012ln ln 2x x x x M M +>+>>,所以函数ln y x x =+在定义域内是无界的. 又当120x x <<时,有12120,ln ln 0x x x x -<-<故1211221212(ln )(ln )()(ln ln )0y y x x x x x x x x -=+-+=-+-<. 即当120x x <<时,恒有12y y <,所以函数ln y x x =+在(0,)+∞内单调递增.11. 解: (1)124(1)y x =+是由124,1y u u x ==+复合而成. (2)2sin (12)y x =+是由2,sin ,12y u u v v x ===+复合而成.(3)512(110)x y -=+是由152,1,10,w y u u v v w x ==+==-复合而成.(4)11arcsin 2y x =+是由1,1,arcsin ,2y u u v v w w x -==+==复合而成. 12.证: (1)设()()()F x f x f x =+-,则(,)x ∀∈-∞+∞, 有()()()()F x f x f x F x -=-+= 故()()f x f x +-为偶函数.(2)设()()(),G x f x f x =--则(,)x ∀∈-∞+∞,有()()()[()()]()G x f x f x f x f x G x -=---=---=- 故()()f x f x --为奇函数.13.解: 设年销售批数为x , 则准备费为103x ;又每批有产品610x 件,库存数为6102x 件,库存费为6100.052x ⨯元.设总费用为,则63100.05102y x x ⨯=+. 14. 解: 当x 能被20整除,即[]2020x x =时,邮资0.802025x x y =⨯=; 当x 不能被20整除时,即[]2020x x ≠时,由题意知邮资0.80120x y ⎡⎤=⨯+⎢⎥⎣⎦.综上所述有,02000;2520200.80,02000.1202020x xx x y x x x x ⎧⎡⎤<≤=⎪⎢⎥⎪⎣⎦=⎨⎡⎤⎡⎤⎪⨯<≤≠+⎢⎥⎢⎥⎪⎣⎦⎣⎦⎩且且其中20x ⎡⎤⎢⎥⎣⎦,120x ⎡⎤+⎢⎥⎣⎦分别表示不超过20x ,120x +的最大整数.15. 证: (1)由e e sinh 2x xy x --==得2e 2e 10x xy --= 解方程2e 2e 10x xy --=得e x y =因为e 0x>,所以e x y =ln(x y = 所以sinh y x =的反函数是arcsin h ln(().y x x x ==+-∞<<+∞(2)由e e tanh e e x x x xy x ---==+得21e 1x y y +=-,得1112ln ,ln 121y yx x y y ++==--; 又由101yy +>-得11y -<<,所以函数tanh y x =的反函数为11arctan h ln (11).21xy x x x +==-<<-16. 解: 011()(2cot )(cot )22S h AD BC h h BC BC h BC h ϕϕ=+=++=+ 从而 0cot SBC h h ϕ=-.000()22cot sin sin 2cos 2cos 40sin sin 40L AB BC CD AB CD S h hBC h hS S h h h h ϕϕϕϕϕ=++==+=+---=+=+由00,cot 0S h BC h h ϕ>=->得定义域为. 17. 解:1(1),1n n x n -=+当n →∞时,1n x →. 1(2)cos π2n n x n -=,当n 无限增大时,有三种变化趋势:趋向于+∞,趋向于0,趋向于-∞.21(3)(1)21nn n x n +=--,当n 无限增大时,变化趁势有两种,分别趋于1,-1.18. 解: (1)lim 0n n a x →∞==,0ε∀>,要使11π0sin 2n n x n n ε-=<<,只须1n ε>.取1N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,必有0n x ε-<. 当0.001ε=时,110000.001N ⎡⎤==⎢⎥⎣⎦或大于1000的整数.(2)lim 0n n a x →∞==,0ε∀>,要使0n x ε-==<=<1ε>即21n ε>即可.取21N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,有0n x ε-<. 当0.0001ε=时, 821100.0001N ⎡⎤==⎢⎥⎣⎦或大于108的整数.19. 证: (1)0ε∀>,要使22110n n ε=<-,只要n >取N =,则当n>N 时,恒有210n ε<-.故21lim 0n n →∞=.(2) 0ε∀>,要使555313,2(21)4212n n n n n ε-=<<<-++只要5n ε>,取5N ε⎡⎤=⎢⎥⎣⎦,则当n>N 时,恒有313212n n ε-<-+.故313lim 212n n n →∞-=+. (3) 0ε∀>,要使2221a n ε=<<,只要n >,取n =,则当n>N 时,1ε<,从而lim 1n n →∞=.(4)因为对于所有的正整数n ,有10.99991n <-个,故0ε∀>,不防设1ε<,要使1,0.999110n n ε=<-个只要ln ,ln10n ε->取ln ,ln10N ε-⎡⎤=⎢⎥⎣⎦则当n N >时,恒有,0.9991n ε<-个故lim 0.9991n n →∞=个.20.证:lim 0n n x →∞=,由极限的定义知,0,0N ε∀>∃>,当n N >时,恒有nx a ε-<.而n n x x a a ε-<-<0,0N ε∴∀>∃>,当n N >时,恒有n x a ε-<,由极限的定义知lim .n n x a →∞=但这个结论的逆不成立.如(1),lim 1,n n n n x x →∞=-=但lim nn x →∞不存在.21. 解:1111(1)0(1)(1)1(1)1k k k kk k n n n n n n n -⎡⎤⎡⎤<+-=<=+-+-⎢⎥⎢⎥⎣⎦⎣⎦而lim 00n →∞=,当1k <时,11lim0k n n -→∞=lim[(1)]0k k n n n →∞∴+-=.(2)记12max{,,,}m a a a a =则有n <<即1na m a <⋅而 1lim , lim ,nn n a a m a a →∞→∞=⋅=故n a=即12lim max{,,,}m n a a a =.(3)111(3)(123)(33)n nn n nn n<++<⋅即 113(123)3n nn nn+<++< 而 1lim33,lim33n nn n +→∞→∞==故1lim(123)3nn nn →∞++=.(4)11111n n <+<+而 1lim10,lim(1)1n n n →∞→∞=+=故1n=.22. 证: (1)122x =<,不妨设2k x <,则12k x +<=.故对所有正整数n 有2n x <,即数列{}n x 有上界.又1n n nx xx +-=0>,又由2n x <从而10n n x x +->即1n nx x +>,即数列{}n x 是单调递增的.由极限的单调有界准则知,数列{}n x 有极限.设lim n n x a→∞=,则a =于是22a a =,2,0a a ==(不合题意,舍去),lim 2n n x →∞∴=.(2) 因为110x =>,且111nn n xx x +=++, 所以02n x <<, 即数列有界又111111111(1)(1)n n n n n n n n n n x x x x x x x x x x --+---⎛⎫⎛⎫++-=-=⎪ ⎪++++⎝⎭⎝⎭ 由110,10n n x x -+>+>知1n n x x +-与1n n x x --同号,从而可推得1n n x x +-与21x x -同号, 而1221131,1,022x x x x ==+=->故10n n x x +->, 即1n n x x +>所以数列{}n x 单调递增,由单调有界准则知,{}n x 的极限存在. 设lim n n x a→∞=, 则11a a a =++,解得a a ==(不合题意,舍去).所以1lim 2n n x →∞+=23. 证:(1)0ε∀>,要使1sin sin 0x xx x x ε=≤<-,只须1x ε>,取1X ε>,则当x X >时,必有sin 0xx ε<-,故sin limx xx →+∞=. (2)0ε∀>,要使 22221313313||44x x x x ε-=<<-++,只须x >取X =X x >时,必有223134x x ε-<-+,故2231lim 34x x x →∞-=+. (3) 0ε∀>,要使24(4)22x x x ε-=<--++,只要取δε=,则当02x δ<<+时,必有24(4)2x x ε-<--+,故224lim 42x x x →--=-+. (4) 0ε∀>,要使21142221221x x x x ε-==<+-++,只须122x ε<+,取2εδ=,则 当102x δ<<+时,必有214221x x ε-<-+ 故21214lim 221x x x →--=+.(5) 0ε∀>,要使11sin0sin x x x x x ε=≤<-,只要取δε=,则 当00x δ<<-时,必有1sin0x x ε<-,故 01lim sinx x x →=.24. 解:()()2232233lim 33933(1)lim 1lim 9151x x x x x x x →→→---===+++.2221424242112222333422424lim()11(2)lim 2.31lim(31)13111111(3)limlim .1121221111lim (4)lim lim 0.3131311lim 1(5x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x →→→→∞→∞→∞→∞→∞→∞+++===--+-+-⨯+--==----⎛⎫-- ⎪-⎝⎭===-+⎛⎫-+-+ ⎪⎝⎭222222121lim 21)lim lim 01111lim 1x x x x x x x x x x x x →∞→∞→∞→∞⎛⎫++ ⎪+⎝⎭===+⎛⎫++ ⎪⎝⎭由无穷大与无穷小的关系知, 21lim 21x x x →∞+=∞+.3(1)(2)(3)1123(6)limlim 1115511123lim lim lim .11155n n n n n n n n n n n n n n n →∞→∞→∞→∞→∞+++⎛⎫⎛⎫⎛⎫=+++ ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫=⋅⋅=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(7)因为221(1)()(1)11x a x a b x b ax b x x +--++---=++ 由已知211lim 21x x ax b x →∞⎛⎫+=-- ⎪+⎝⎭知,分式的分子与分母的次数相同,且x 项的系数之比为12,于是10a -= 且 ()112a b -+=解得31,2a b ==-. 25.解:22123(1)(1)111(1)limlim lim .1222n n n n n n n n n →∞→∞→∞++++--⎛⎫===- ⎪⎝⎭1221112244411112(2)lim lim 2.11221221(1)(3)limlim lim(1)0.1168(2)(4)22(4)lim lim lim .54(1)(4)13n n n n x x xx x x x xx x x x x xx x x x x xx x +→∞→∞→→→→→→⎛⎫- ⎪⎛⎫⎝⎭==+++ ⎪⎝⎭--+-==-=---+---===-+---322000(5)lim lim lim2.lim(1 2.x x x x x x x →+∞→→→=====-+=-5555x x x x →→→→=====3333ππ4422π422π41cot 1cot (8)lim lim 2cot cot (1cot )(1cot )(1cot )(1cot cot )lim (1cot )(11cot cot )1cot cot 3lim .2cot cot 4x x x x x xx x x x x x x x x x x x x x →→→→--=---+--++=-+++++==++122222(9)lim(1)(1)(1)(1)(1)(1)(1)(1)lim 111lim .11nnn x x x x x x x x x x x xx +→∞→∞→∞+++<-+++=--==-111211211(1)(1)(10)lim(1))(1))(1)11.234!n n x n n n n x n n n n x n x x x x x x x x n n -→--→-→--=++++=++++==⨯⨯⨯⨯ 22223111221113213(11)lim lim lim (1)(1)(1)(1)11(1)(2)(2)lim lim 1.(1)(1)1x x x x x x x x x x x x x x x x x x x x x x x x x →→→→→++-+-⎛⎫==- ⎪-++-++--⎝⎭-+-+===--++++2212211221lim(1)(1)(12)lim 01lim(1)1lim .(1)x x x x x x x x x x x x x →→→→--==-+-+-+∴=∞-1log (1)(13)log (1)a xa x x x +=+而10lim(1).xx x e →+= 而1limlog log ln a a u eu e a →==0log (1)1lim.ln a x x x a →+∴=(14)令1,xu a =-则log (1),a x u =+当0x →时,0u →. 所以00011lim lim ln log (1)log (1)limx x u a a u a u a u x u u →→→-===++(利用(13)题的结果).1122000336ln(12)ln(12)sin sin 2sin 0lim 6ln(12)6limlimln(12)sin sin 61ln e 6(15)lim(12)lim elim ee ee e .x xx x x xx x xxx xx x x xxx x xx x →→→++→→→⋅⋅+⋅⋅+⨯⨯+======(16)令sin x u x =, 则00sin lim lim 1x x xu x →→==而1limln 0u u →= 所以0sin limln 0.x x x →=26. 解:232200lim lim 022x x x x x x x x x →→--==--∴当0x →时,23x x -是比22x x -高阶的无穷小量.27.解:211111(1)lim lim 112x x x x x →→-==-+ ∴当1x →时,1x -是与21x -同阶的无穷小.2111(1)12(2)lim lim 112x x x xx →→-+==-∴当1x →时,1x -是与21(1)2x -等价的无穷小. 28. 解:(1)因为当0x →时,sin ~,sin ~,mx mx nx nx所以00sin limlim .sin x x mx mx mnx nx n →→== 000002000limcos cos (2)lim cot lim cos lim 1.sin sin sin lim 1cos 22sin sin (3)lim lim 2lim 2.sin sin x x x x x x x x x x x x x x x xx x xx x x x x x x x →→→→→→→→=⋅===-===(4)因为当0x →时,2221ln(1e sin)~e sin 1~2x x x x x+,所以22200002e sin sin lim lim 2e lim 2.12x x x x x x x x x x x →→→→⎛⎫==⋅= ⎪⎝⎭(5)因为当0x →时,arctan3~3,x x 所以00arctan 33limlim 3x x x xx x →→==. sin sin 22(6)lim 2sin lim lim .222n nn n n n n n n x x x x x x x x →∞→∞→∞=⋅==(7)因为当12x →时,arcsin(12)~12x x --,所以22111122224141(21)(21)lim lim lim lim(21) 2.arcsin(12)1212x x x x x x x x x x x x →→→→---+===-+=----(8)因为当0x →时,22arctan ~,sin~,arcsin ~,22x xx x x x 所以2200arctan lim lim 2sin arcsin 22x x x x xx x x →→==⋅.(9)因为当0x →时,2331sin ~,1cos ~,sin ~2x x x x x x -,所以233300001tan sin sin (1cos )2lim lim lim sin sin cos cos 11lim .2cos 2x x x x x x x x x x x x xx x x →→→→⋅--==⋅== (10)因为当0x →时,sin ~,sin ~2222x x x xαβαβαβαβ++--,所以220020222sin sin cos cos 22lim lim 222lim 1().2x x x x xx x x x x xxαβαβαβαβαββα→→→+---=+--⋅⋅==- (11)因为当0x →时,arcsin ~)~,x x --所以000 1.x x x →→→==-=-(12)因为当0x →时,sin ~,sin 2~2,x x x x 所以2222200222200201cos 42sin 2lim lim 2sin tan sin (2sec )2(2)8lim lim (2sec )2sec 84.lim(2sec )x x x x x x x x x x x x x x x x x x xx x →→→→→-=++⋅==++==+(13)因为ln cos ln[1(cos 1)],ln cos ln[1(cos 1)],ax ax bx bx =+-=+- 而当0x →时,cos 10,cos 10ax bx -→-→故 ln[1(cos 1)]~cos 1,ln[1(cos 1)]~cos 1,ax ax bx bx +--+--又当x →0进,2222111cos ~,1cos ~,22ax a x bx b x --所以22220000221ln cos cos 11cos 2lim lim lim lim .1ln cos cos 11cos 2x x x x a xax ax ax a bx bx bx b b x→→→→--====--(14)因为当0x →时,222sin 0,0e e x xx x→→故 222222sin sin ln ~,ln ~,11e e e e xx x x x x x x ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭ 所以22222222200022222000020sin ln 1ln(sin e )ln(sin e )ln e e lim lim lim ln(e )2ln(e )ln e ln 1e sin sin sin e lim lim e lim e lim e e 1 1.x x x x x x x x x x x x x xx x x x xx x x x x x x x xx x x x x →→→→→→→⎛⎫+ ⎪+-+-⎝⎭==+-+-⎛⎫+ ⎪⎝⎭⎛⎫⎛⎫==⋅=⋅ ⎪ ⎪⎝⎭⎝⎭=⋅=29.解:1112222111(1)lim lim e 1lim 11xxxx x x x x x →∞→∞→∞⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫====+++ ⎪⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦1022121553555(2)lim lim lim 1112222x x x x x x x x x x x -++→∞→∞→∞⎡⎤+⎛⎫⎛⎫⎛⎫⎛⎫==⋅++⎢⎥ ⎪ ⎪ ⎪+ ⎪---⎝⎭⎝⎭⎝⎭⎢⎥-⎝⎭⎣⎦102551051055lim e 1e .1lim 122x x x x x -→∞→∞⎡⎤⎡⎤⎛⎫⎛⎫=⋅=⋅=+⎢⎥ ⎪+⎢⎥ ⎪-⎝⎭⎣⎦⎢⎥-⎝⎭⎣⎦22233112cot323tan 23tan 000(3)lim(13tan )lim e .lim(13tan )(13tan )xx x x x x x x x →→→⎡⎤⎡⎤+===+⎢⎥+⎢⎥⎣⎦⎣⎦ [][][]cos 211cos 212221cos 2121cos 2120220333ln ln cos21(cos21)03(cos21)ln 1(cos21)0cos213limlim ln 1(cos21)2sin 3limln lim (4)lim(cos 2)lim elim elim ee e x x x x x x x x xx x x x x x x x x x x x x x x x x ----→→→→⎧⎫⎪⎪⎨⎬+-⎪⎪⎩⎭→→→-+-→-⋅+--⋅=====[]1cos 212201(cos21)sin 6ln e lim 6116ee e .x x x x x -→⎧⎫⎪⎪⎨⎬+-⎪⎪⎩⎭⎛⎫-⋅⋅ ⎪-⨯⨯-⎝⎭===22222(5)lim [ln(2)ln ]lim 2ln lim 2ln 12222lim ln 2ln 1lim 12ln e 2.x x x x xxx x x x x x x x x x x →∞→∞→∞→∞→∞+⎛⎫+-=⋅⋅=+ ⎪⎝⎭⎛⎫⎛⎫⎛⎫==⋅+ ⎪ ⎪+ ⎪ ⎪⎝⎭⎝⎭⎝⎭==(6)令1x t =+,则当1x →时,0t →.1110001111lim lim 1.ln ln(1)ln e ln lim ln(1)lim(1)x t tt t t x t x t t t →→→→-=-=-=-=-=-+⎡⎤++⎢⎥⎣⎦30. 解:(1)令1(e )x xy x =+,则1ln ln(e )x y x x =+于是:()0000ln e ln 111e lim ln lim ln lim ln e lim1e e x x x x x x x x x x x y x x x x →→→→⎛⎫++ ⎪⎛⎫⎝⎭===++ ⎪⎝⎭e 0001e 1lim 1lim lim ln 1ln 11e e e e 11ln e 2xx xx x x x x x x x x x →→→⎡⎤⎛⎫⎛⎫==+⋅+⋅++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=+⋅=即()lim ln 2x y →= 即2lim ex y →= 即()120lim e e xxx x →=+.(2)令13xxxxa b c y ⎛⎫++= ⎪⎝⎭,则1ln ln 3x x xa b c y x ++=于是00333303300001lim(ln )lim ln 313lim ln 1333lim lim ln 1331111lim ln lim 13x x x x x x xxx x x xx x a b c x x x a b c x xxxxxxa b c x x x x x x x x x x a b c y x a b c x a b c a b c x a b c a b c x x x →→++-++-→++-→→→→++=⎡⎤⎛⎫++-=⎢⎥+ ⎪⎢⎥⎝⎭⎣⎦++-⎛⎫++-=⋅+ ⎪⎝⎭⎛⎫---++=⋅++ ⎪+⎝⎭33331(ln ln ln )ln e ln 3x x x a b c a b c ++-⎡⎤⎛⎫-⎢⎥ ⎪⎢⎥⎝⎭⎣⎦=++⋅=即0lim(ln )x y →= 即()lim ln ln x y →=故0lim x y →=即1lim 3x x xxx a b c →⎛⎫++= ⎪⎝⎭.(3)令11sin cos xy x x ⎛⎫=+ ⎪⎝⎭,则11ln ln sin cos y x x x ⎛⎫=+ ⎪⎝⎭ 于是11sin cos 1111sin cos 1111sin cos 111lim ln lim ln 1sin cos 11111lim ln 1sin cos 1sin cos 111sin 1cos lim ln lim 11xx x x x x x xx x y x x x x x x x x x x x x ⎛⎫+- ⎪⎝⎭+-→∞→∞+-→∞→∞⎧⎫⎪⎪⎡⎤⎛⎫=⎨⎬++- ⎪⎢⎥⎝⎭⎪⎪⎣⎦⎩⎭⎡⎤⎛⎫⎛⎫=⋅++-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎛⎫- ⎪=-⋅ ⎪ ⎪⎝⎭111sin cos 1111sin cos 1x x x x x +-→∞⎧⎫⎪⎪⎡⎤⎛⎫⎨⎬++- ⎪⎢⎥⎝⎭⎪⎪⎣⎦⎩⎭2111sin 2ln e (10)ln e 1limlim 11x x x x x x →∞→∞⎛⎫⎛⎫ ⎪⎪⎝⎭=⋅=-⋅= ⎪- ⎪ ⎪⎝⎭即limln 1x y →∞= 从而()lim ln 1x y →∞= 故lim e x y →∞=即 11lim e sin cos xx x x →∞⎛⎫=+ ⎪⎝⎭.(4)令211xy x ⎛⎫=+ ⎪⎝⎭,则21ln ln 1y x x ⎛⎫=+ ⎪⎝⎭ 于是:22221222211lim(ln )lim ln lim ln 111111lim ln lim lim ln 110ln e 0x x x x x x x x x x y x x x x x x x x →∞→∞→∞→∞→∞→∞⎡⎤⎛⎫⎛⎫==+⎢⎥ ⎪+ ⎪⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫==⋅++ ⎪ ⎪⎝⎭⎝⎭=⋅=即()lim lim(ln )0,ln 0x x y y →∞→∞==lim 1x y →∞∴= 即21lim 11xx x →∞⎛⎫=+ ⎪⎝⎭.31.解:000(1)lim ()lim lim 1,x x x x x f x x x +++→→→=== 000lim ()lim lim 1x x x x xf x x x ---→→→-===-因为 0lim ()lim ()x x f x f x +-→→≠所以0lim ()x f x →不存在.(2)22221lim ()lim ,lim ()lim(2)42x x x x f x f x x x ++--→→→→==+∞=+=-因为2lim ()x f x +→不存在,所以2lim ()x f x →不存在.32. 解:(1)由初等函数的连续性知,()f x 在(0,1),(1,2)内连续, 又21111lim ()lim(2)1,lim ()lim 1x x x x f x x f x x ++--→→→→=-===1lim ()1,x f x →∴= 而(1)1f =,()f x ∴在1x =处连续,又,由2lim ()lim 0(0)x x f x x f ++→→===,知()f x 在0x =处右连续,综上所述,函数()f x 在[0,2)内连续. 函数图形如下:图1-2(2) 由初等函数的连续性知()f x 在(,1),(1,1),(1,)-∞--+∞内连续,又由1111lim ()lim 11,lim ()lim 1,x x x x f x f x x --++→-→-→-→-====-知1lim ()x f x -→-不存在,于是()f x 在1x =-处不连续.又由1111lim ()lim 1,lim ()lim11,x x x x f x x f x --++→→→→====及(1)1f =知1lim ()(1)x f x f →=,从而()f x 在x =1处连续,综上所述,函数()f x 在(,1)-∞-及(1,)-+∞内连续,在1x =-处间断.函数图形如下:图1-3(3)∵当x <0时,221()lim lim 1,1x x x x x x n n n n n f x n n n --→∞→∞--===-++ 当x =0时,0000()lim 0,n n n f x n n →∞-==+当x >0时,2222111()lim lim lim 1111xxxx x x x n n n xn n n n f x n n n n --→∞→∞→∞---====+++1,0,()lim 0,0,1,0.x xx xn x n n f x x n n x --→∞-<⎧-⎪∴===⎨+⎪>⎩由初等函数的连续性知()f x 在(,0),(0,)-∞+∞内连续,又由 00lim ()lim11,lim ()lim(1)1x x x x f x f x ++--→→→→===-=-知0lim ()x f x →不存在,从而()f x 在0x =处间断.综上所述,函数()f x 在(,0),(0,)-∞+∞内连续,在0x =处间断.图形如下:图1-4(4)当|x |=1时,221()lim 0,1nnn x f x x x →∞-==+当|x |<1时,221()lim ,1nnn x f x x x x →∞-==+当|x |>1时,2222111()limlim 111nnn nn n x x f x x x x x x →∞→∞⎛⎫- ⎪-⎝⎭==⋅=-+⎛⎫+ ⎪⎝⎭即,1,()0,1,,1.x x f x x x x <⎧⎪==⎨⎪->⎩ 由初等函数的连续性知()f x 在(-∞,-1),(-1,1),(1,+∞)内均连续,又由1111lim ()lim ()1,lim ()lim 1x x x x f x x f x x --++→-→-→-→-=-===-知1lim ()x f x →-不存在,从而()f x 在1x =-处不连续.又由 1111lim ()lim()1,lim ()lim 1x x x x f x x f x x ++--→→→→=-=-==知1lim ()x f x →不存在,从而()f x 在1x =处不连续.综上所述,()f x 在(-∞,-1),(-1,1),(1,+∞)内连续,在1x =±处间断.图形如下:图1-533. 解:22111(1)(1)(1)lim lim 232(1)(2)x x x x x x x x x →→--+==--+--2221lim 32x x x x →-=∞-+1x ∴=是函数的可去间断点.因为函数在x =1处无定义,若补充定义(1)2f =-,则函数在x =1处连续;x =2是无穷间断点.π0π2(2)lim1,lim 0tan tan x x k x x x x→→+==当0k ≠时,πlimtan x k xx →=∞. π0,π,0,1,2,2x x k k ∴==+=±±为可去间断点,分别补充定义f (0)=1,π(π)02f k +=,可使函数在x =0,及ππ2x k =+处连续.(0,1,2,k =±±);π,0,1,2,x k k k =≠=±±为无穷间断点(3)∵当0x →时,21cosx 呈振荡无极限,∴x =0是函数的振荡间断点.(第二类间断点). (4)11lim lim(3) 2.x x y x ++→→=-=11lim lim(1)0x x y x --→→=-=∴x =1是函数的跳跃间断点.(第一类间断点.)34.解:0003(1)lim ()2x x x f x →→→===∴补充定义3(0),2f =可使函数在x =0处连续. 000tan 22(2)lim ()lim lim 2.x x x x xf x x x →→→===∴补充定义(0)2,f =可使函数在x =0处连续.01(3)limsin sinx x x →=∴补充定义(0)0,f =可使函数在x =0处连续. 10(4)lim ()lim(1)exx x f x x →→=+=∴补充定义(0)e,f =可使函数在x =0处连续.35. 解:(1)()f x 在(,0),(0,)-∞+∞上显然连续,而00lim ()lim(),x x f x a x a ++→→=+=lim ()lim e 1,xx x f x --→→== 且(0)f a =,∴当(0)(0)(0)f f f -+==,即1a =时,()f x 在0x =处连续,所以,当1a =时,()f x 在(,)-∞+∞上连续.(2)()f x 在ππ(,),(,)22-∞+∞内显然连续.而ππ22ππ22lim ()lim (sin )1,πlim ()lim (1)1,2π()1,2x x x x f x x b b f x ax a f b ++--→→→→=+=+=+=+=+∴当π112b a +=+,即π2b a =时,()f x 在π2x =处连续,因而()f x 在(,)-∞+∞上连续. 36. 证:令()21xf x x =⋅-,则()f x 在[0,1]上连续,且(0)10,(1)10f f =-<=>,由零点定理,(0,1)ξ∃∈使()0f ξ=即210ξξ⋅-= 即方程21xx ⋅=有一个小于1的正根.37.证:令()sin f x x a x b =--,则()f x 在[0,]a b +上连续,且 (0)0,()(1sin )0f b f a b a x =-<+=-≥, 若()0f a b +=,则a b +就是方程sin x a x b =+的根. 若()0f a b +>,则由零点定理得.(0,)a b ξ∃∈+,使()0f ξ=即sin 0a b ξξ--=即sin a b ξξ=+,即ξ是方程sin x a x b =+的根,综上所述,方程sin x a x b =+至少有一个不超过a b +的正根.38. 证:令()()()F x f x f x a =-+,由()f x 在[0,2]a 上连续知,()F x 在[0,]a 上连续,且(0)(0)(),()()(2)()(0)F f f a F a f a f a f a f =-=-=-若(0)()(2),f f a f a ==则0,x x a ==都是方程()()f x f x a =+的根,若(0)()f f a ≠,则(0)()0F F a <,由零点定理知,至少(0,)a ξ∃∈,使()0F ξ=,即()()f f a ξξ=+,即ξ是方程()()f x f x a =+的根,综上所述,方程()()f x f x a =+在[0,]a 内至少有一根.39.证:令()()F x f x x =-,则()F x 在[0,1]上连续,且(0)(0)0,(1)(1)10,F f F f =≥=-≤ 若(0)0f =,则0,ξ=若(1)1f =,则1ξ=,若(0)0,(1)1f f ><,则(0)(1)0F F ⋅<,由零点定理,至少存在一点(0,1)ξ∈,使()0F ξ=即()f ξξ=.综上所述,至少存在一点[0,1]ξ∈,使()f ξξ=.. 12()()()()n f x f x f x f n ξ+++=.40证:已知()f x 在1[,]n x x 上连续,则()f x 在1[,]n x x 上有最大值M 和最小值m ,于是 12()()()n f x f x f x m Mn+++≤≤,由介值定理知,必有1[,]n x x ξ∈,使12()()()()n f x f x f x f nξ+++=.。
