八年级数学上册期末试卷培优测试卷

合集下载

八年级上册数学全册全套试卷(培优篇)(Word版含解析)

八年级上册数学全册全套试卷（培优篇）（Word 版含解析）一、八年级数学三角形填空题（难） 1．如图，C 在直线BE 上，∠=︒,∠A m ABC 与ACE ∠的角平分线交于点1A ，则1A =_____︒；若再作11A BE A CE ∠∠、的平分线，交于点2A ；再作22A BE A CE ∠∠、的平分线，交于点3A ；依此类推，10A ∠= _________︒．【答案】（2m ）（1024m ）【解析】【分析】根据“角平分线定义”和“三角形的外角等于与它不相邻的两个内角和”求出规律，直接利用规律解题．【详解】解：∵∠A 1=∠A 1CE-∠A 1BC=12∠ACE-12∠ABC=12（∠ACE-∠ABC ）=12∠A=2m °．依此类推∠A 2=224m m ︒︒=，∠A 3=328m m ︒︒=，…，∠A 10=1021024m m ︒︒=．故答案为：()2m ；()1024m ．【点睛】此题主要考查了三角形的内角和外角之间的关系以及角平分线的定义，三角形的外角等于与它不相邻的两个内角和．2．将等边三角形、正方形、正五边形按如图所示的位置摆放，如果∠1=40°，∠2=50°，那么∠ 3的度数等于______________．【答案】12°【解析】等边三角形的内角的度数是60°，正方形的内角度数是90°，正五边形的内角的度数是108°，则∠3=360°-60°-90°-108°-∠1-∠2=12°．点睛：本题考查的是多边形的内角，熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键．3．如图，在△ABC中，BD、BE分别是△ABC的高线和角平分线，点F在CA的延长线上，FH⊥BE交BD于点G，交BC于点H．下列结论：①∠DBE=∠F；②∠BEF=1 2（∠BAF+∠C）；③∠FGD=∠ABE+∠C；④∠F=12（∠BAC﹣∠C）；其中正确的是_____．【答案】①②③④【解析】【分析】①根据BD⊥FD，FH⊥BE和∠FGD=∠BGH，证明结论正确；②根据角平分线的定义和三角形外角的性质证明结论正确；③根据垂直的定义和同角的余角相等的性质证明结论正确；④证明∠DBE=∠BAC-∠C，根据①的结论，证明结论正确.【详解】解：①∵BD⊥FD，∴∠FGD+∠F=90°，∵FH⊥BE，∴∠BGH+∠DBE=90°，∵∠FGD=∠BGH，∴∠DBE=∠F，故①正确；②∵BE平分∠ABC，∴∠ABE=∠CBE，∠BEF=∠CBE+∠C，∴2∠BEF=∠ABC+2∠C，∠BAF=∠ABC+∠C，∴2∠BEF=∠BAF+∠C，∴∠BEF=12(∠BAF+∠C)，故②正确；③∵∠AEB=∠EBC+∠C，∵∠ABE=∠EBC，∴∠AEB=∠ABE+∠C，∵BD⊥FC，FH⊥BE，∴∠FGD=90︒-∠DFH，∠AEB=90︒-∠DFH，∴∠FGD=∠AEB∴∠FGD=∠ABE+∠C.故③正确；④∠ABD=90°-∠BAC，∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC=∠CBD-∠DBE-90°+∠BAC，∵∠CBD=90°-∠C，∴∠DBE=∠BAC-∠C-∠DBE，由①得，∠DBE=∠F，∴∠F=∠BAC-∠C-∠DBE，∴∠F=12(∠BAC-∠C)；故④正确，故答案为①②③④.【点睛】本题考查的是三角形内角和定理，正确运用三角形的高、中线和角平分线的概念以及三角形外角的性质是解题的关键4．如图，在△ABC中，∠B和∠C的平分线交于点O，若∠A＝50°，则∠BOC＝_____．【答案】115°．【解析】【分析】根据三角形的内角和定理得出∠ABC+∠ACB=130°，然后根据角平分线的概念得出∠OBC+∠OCB，再根据三角形的内角和定理即可得出∠BOC的度数．【详解】解；∵∠A＝50°，∴∠ABC+∠ACB＝180°﹣50°＝130°，∵∠B和∠C的平分线交于点O，∴∠OBC＝12∠ABC，∠OCB＝12∠ACB，∴∠OBC+∠OCB＝12×（∠ABC+∠ACB）＝12×130°＝65°，∴∠BOC＝180°﹣（∠OBC+∠OCB）＝115°，故答案为：115°．【点睛】本题考查了三角形的内角和定理和三角形的角平分线的概念，关键是求出∠OBC +∠OCB 的度数．5．已知ABC 中，90A ∠=，角平分线BE 、CF 交于点O ，则BOC ∠= ______ ．【答案】135【解析】解：∵∠A =90°，∴∠ABC +∠ACB =90°，∵角平分线BE 、CF 交于点O ，∴∠OBC +∠OCB =45°，∴∠BOC =180°﹣45°=135°．故答案为：135°．点睛：本题考查了角平分线的定义、三角形的内角和定理：三角形的内角和等于180°．6．如图，在△ABC 中，∠A ＝60°，若剪去∠A 得到四边形BCDE ，则∠1＋∠2＝______．【答案】240.【解析】【详解】试题分析：∠1+∠2=180°+60°=240°．考点：1.三角形的外角性质；2.三角形内角和定理．二、八年级数学三角形选择题（难）7．在多边形内角和公式的探究过程中，主要运用的数学思想是（）A ．化归思想B ．分类讨论C ．方程思想D ．数形结合思想【答案】A【解析】【分析】根据多边形内角和定理：（n-2）·180（n≥3）且n 为整数）的推导过程即可解答．【详解】解：多边形内角和定理：（n-2）·180（n≥3）且n 为整数），该公式推导的基本方法是从n 边形的一个顶点出发引出（n-3）条对角线，将n 边形分割为（n-2）个三角形，这（n-2）个三角形的所有内角之和正好是n 边形的内角和，体现了化归思想．故答案为A．【点睛】本题主要考查了在数学的学习过程应用的数学思想，弄清推导过程是解答此题的关键.8．已知非直角三角形ABC中，∠A=45°，高BD与CE所在直线交于点H，则∠BHC的度数是（）A．45°B．45° 或135°C．45°或125°D．135°【答案】B【解析】【分析】①△ABC是锐角三角形时，先根据高线的定义求出∠ADB=90°，∠BEC=90°，然后根据直角三角形两锐角互余求出∠ABD，再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解；②△ABC是钝角三角形时，根据直角三角形两锐角互余求出∠BHC=∠A，从而得解．【详解】①如图1，△ABC是锐角三角形时，∵BD、CE是△ABC的高线，∴∠ADB=90°，∠BEC=90°，在△ABD中，∵∠A=45°，∴∠ABD=90°-45°=45°，∴∠BHC=∠ABD+∠BEC=45°+90°=135°；②如图2，△ABC是钝角三角形时，∵BD、CE是△ABC的高线，∴∠A+∠ACE=90°，∠BHC+∠HCD=90°，∵∠ACE=∠HCD（对顶角相等），∴∠BHC=∠A=45°．综上所述，∠BHC的度数是135°或45°．故选B.【点睛】本题主要考查了三角形的内角和定理，三角形的高线，难点在于要分△ABC是锐角三角形与钝角三角形两种情况讨论，作出图形更形象直观．9．如图，七边形ABCDEFG中，AB，ED的延长线交于点O，若∠1，∠2，∠3，∠4的外角和等于215°，则∠BOD的度数为()A．20°B．35°C．40°D．45°【答案】B【解析】【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和，由五边形内角和可求得五边形OAGFE的内角和，则可求得∠BOD．【详解】解：∵∠1、∠2、∠3、∠4的外角的角度和为215°，∴∠1+∠2+∠3+∠4+215°=4×180°，∴∠1+∠2+∠3+∠4=505°，∵五边形OAGFE内角和=（5-2）×180°=540°，∴∠1+∠2+∠3+∠4+∠BOD=540°，∴∠BOD=540°-505°=35°，故选：B ．【点睛】本题主要考查多边形的内角和，利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键．10．在下列图形中，正确画出△ABC 的AC 边上的高的图形是（）A ．B ．C ．D ．【答案】C【解析】【分析】 △ABC 的AC 边上的高的就是通过顶点B 作的AC 所在直线的垂线段，根据定义即可作出判断．【详解】解：△ABC 的AC 边上的高的就是通过顶点B 作的AC 所在直线的垂线段．根据定义正确的只有C ．故选：C ．【点睛】本题考查了三角形的高线的定义，理解定义是关键．11．已知直线m n ，将一块含45︒角的直角三角板ABC 按如图方式放置，其中斜边BC 与直线n 交于点D .若125∠=︒，则2∠的度数为（）A ．60︒B ．65︒C ．70︒D ．75︒【答案】C【解析】【分析】先求出∠AED=∠1+∠B=25°+45°=70°，再根据平行线的性质可知∠2=∠AED=70°．【详解】设直线n 与AB 的交点为E 。

八年级数学上册期末试卷(培优篇)(Word版含解析)

八年级数学上册期末试卷（培优篇）（Word 版含解析）一、八年级数学全等三角形解答题压轴题（难）1．取一副三角板按图()1拼接，固定三角板60,()30ADC D ACD ∠=∠=，将三角板45()ABC BAC BCA ∠=∠=绕点A 依顺时针方向旋转一个大小为a 的角00)45(a ≤≤得到ABM ，图()2所示．试问：()1当a 为多少时，能使得图()2中//AB CD ？说出理由，()2连接BD ，假设AM 与CD 交于,E BM 与CD 交于F ，当00)45(a ≤≤时，探索DBM CAM BDC ∠+∠+∠值的大小变化情况，并给出你的证明．【答案】（1）15°；（2）DBM CAM BDC ∠+∠+∠的大小不变，是105，证明见解析．【解析】【分析】（1）由//AB CD 得到30BAC C ∠=∠=，即可求出a ；（2）DBM CAM BDC ∠+∠+∠的大小不变，是105︒,由FEM CAM C ∠=∠+∠，30C ∠=︒， EFM BDC DBM ∠=∠+∠， 45M ∠=︒，即可利用三角形内角和求出答案.【详解】()1当a 为15时，//AB CD ，理由：由图()2，若//AB CD ，则30BAC C ∠=∠=，453015a CAM BAM BAC ∴=∠=∠-∠=-︒=︒，所以，当a 为15时，//AB CD ．注意：学生可能会出现两种解法：第一种：把//AB CD 当做条件求出a 为15，第二种：把a 为15当做条件证出//AB CD ，这两种解法都是正确的．()2DBM CAM BDC ∠+∠+∠的大小不变，是105︒证明： ,30FEM CAM C C ∠=∠+∠∠=︒,30FEM CAM ∴∠=∠+︒,EFM BDC DBM ∠=∠+∠,DBM CAM BDC EFM CAM ∴∠+∠+∠=∠+∠,180,45EFM FEM M M ∠+∠+∠=∠=︒,3045180BDC DBM CAM ∴∠+∠+∠+︒+︒=︒,1803045105DBM CAM BDC ∴∠+∠+∠=︒--=︒,所以，DBM CAM BDC ∠+∠+∠的大小不变，是105.【点睛】此题考查旋转的性质，平行线的性质，三角形的外角定理，三角形的内角和，（2）中将角度和表示为三角形的外角是解题的关键.2．如图，∠BAD=∠CAE=90°，AB=AD ，AE=AC ，AF ⊥CB ，垂足为F ．（1）求证：△ABC ≌△ADE ；（2）求∠FAE 的度数；（3）求证：CD=2BF+DE ．【答案】（1）证明见解析；（2）∠FAE=135°；（3）证明见解析.【解析】【分析】（1）根据已知条件易证∠BAC=∠DAE ，再由AB=AD ，AE=AC ，根据SAS 即可证得△ABC ≌△ADE ；（2）已知∠CAE=90°，AC=AE ，根据等腰三角形的性质及三角形的内角和定理可得∠E=45°，由（1）知△BAC ≌△DAE ，根据全等三角形的性质可得∠BCA=∠E=45°，再求得∠CAF=45°，由∠FAE=∠FAC+∠CAE 即可得∠FAE 的度数；（3）延长BF 到G ，使得FG=FB ，易证△AFB ≌△AFG ，根据全等三角形的性质可得AB=AG ，∠ABF=∠G ，再由△BAC ≌△DAE ，可得AB=AD ，∠CBA=∠EDA ，CB=ED ，所以AG=AD ，∠ABF=∠CDA ，即可得∠G=∠CDA ，利用AAS 证得△CGA ≌△CDA ，由全等三角形的性质可得CG=CD ，所以CG=CB+BF+FG=CB+2BF=DE+2BF ．【详解】（1）∵∠BAD=∠CAE=90°，∴∠BAC+∠CAD=90°，∠CAD+∠DAE=90°，∴∠BAC=∠DAE ，在△BAC 和△DAE 中，AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩， ∴△BAC ≌△DAE （SAS ）；（2）∵∠CAE=90°，AC=AE ，∴∠E=45°，由（1）知△BAC ≌△DAE ，∴∠BCA=∠E=45°，∵AF ⊥BC ，∴∠CFA=90°，∴∠CAF=45°，∴∠FAE=∠FAC+∠CAE=45°+90°=135°；（3）延长BF 到G ，使得FG=FB ，∵AF ⊥BG ，∴∠AFG=∠AFB=90°，在△AFB 和△AFG 中，BF F AFB AFG AF AF G =⎧⎪∠=∠⎨⎪=⎩， ∴△AFB ≌△AFG （SAS ），∴AB=AG ，∠ABF=∠G ，∵△BAC ≌△DAE ，∴AB=AD ，∠CBA=∠EDA ，CB=ED ，∴AG=AD ，∠ABF=∠CDA ，∴∠G=∠CDA ，在△CGA和△CDA中，GCA DCACGA CDAAG AD∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△CGA≌△CDA，∴CG=CD，∵CG=CB+BF+FG=CB+2BF=DE+2BF，∴CD=2BF+DE．【点睛】本题考查全等三角形的判定与性质，解决第3问需作辅助线，延长BF到G，使得FG=FB，证得△CGA≌△CDA是解题的关键．3．综合实践如图①，90,,,ACB AC BC AD CE BE CE∠=︒=⊥⊥，垂足分别为点D E、，2.5, 1.7AD cm DE cm==．（1）求BE的长；（2）将CE所在直线旋转到ABC∆的外部，如图②，猜想AD DE BE、、之间的数量关系，直接写出结论，不需证明；（3）如图③，将图①中的条件改为：在ABC∆中，,AC BC D C E=、、三点在同一直线上，并且BEC ADC BCAα∠=∠=∠=，其中α为任意钝角．猜想AD DE BE、、之间的数量关系，并证明你的结论．【答案】(1)0.8cm;(2)DE=AD+BE;(3)DE=AD+BE，证明见解析．【解析】【分析】(1)本小题只要先证明ACD CBE ≅，得到AD CE =，CD BE =，再根据2.5, 1.7AD cm DE cm ==，CD CE DE =-，易求出BE 的值；(2)先证明ACD CBE ≅，得到AD CE =，CD BE =，由图②ED=EC+CD ，等量代换易得到AD DE BE 、、之间的关系；（３）本题先证明EBC DCA ∠=∠，然后运用“AAS”定理判定BEC CDA ≅，从而得到,BE CD EC AD ==，再结合图③中线段ED 的特点易找到AD DE BE 、、之间的数量关系．【详解】解：(1)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∵90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中，90ADC E ACD BCEAC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ 2.5, 1.7AD cm DE cm ==， 2.5 1.70.8()CD CE DE AD DE cm =-=-=-= ∴0.8BE cm =(2)∵,AD CD BE CE ⊥⊥∴90ADC E ︒∠=∠=∴90ACD DAC ︒∠+∠=∴90ACB ︒∠=∴90ACD BCE ︒∠+∠=∴ACD BCE ∠=∠在ACD 与CBE △中，90ADC E ACD BCE AC BC ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴ACD CBE ≅∴,AD CE CD BE ==又∵ED EC CD =+∴ED AD BE =+(3)∵BEC ADC BCAα∠=∠=∠=∴180BCE ACD a︒∠+∠=-180BCE BCE a︒∠+∠=-∴ACD BCE∠=∠在ACD与CBE△中，ADC E aACD BCEAC BC∠=∠=⎧⎪∠=∠⎨⎪=⎩∴ACD CBE≅∴,AD CE CD BE==又∵ED EC CD=+∴ED AD BE=+【点睛】本题考查的知识点是全等三角形的判定，确定一种判定定理，根据已知条件找到判定全等所需要的边相等或角相等的条件是解决这类题的关键．4．如图，ABC∆是等腰直角三角形，090BAC∠=，点D是直线BC上的一个动点（点D与点B C、不重合），以AD为腰作等腰直角ADE∆，连接CE.（1）如图①，当点D在线段BC上时，直接写出,BC CE的位置关系，线段,BC CD，CE之间的数量关系；（2）如图②，当点D在线段BC的延长线上时，试判断线段BC，CE的位置关系，线段,,BC CD CE之间的数量关系，并说明理由；（3）如图③，当点D在线段CB的延长线上时，试判断线段,BC CE的位置关系，线段,,BC CD CE之间的数量关系，并说明理由.【答案】（1）见解析；（2）BC CE⊥，CE BC CD=+，理由见解析；（3）,BC CE CD BC CE⊥=+，理由见解析【解析】【分析】（1）根据条件AB=AC，∠BAC=90°，AD=AE，∠DAE=90°，判定△ABD≌△ACE（SAS），利用两角的和即可得出BC CE⊥；利用线段的和差即可得出BC CE CD=+；（2）同（1）的方法根据SAS证明△ABD≌△ACE，得出BD=CE，∠ACE=∠ABD，从而得出结论；（3）先根据SAS证明△ABD≌△ACE，得出ADB AEC∠=∠，BD CE=，从而得出结论．【详解】（1）∵△ABC 、△ADE 是等腰直角三角形，∴AB＝AC ，AE ＝AD ，在△△ABD 和△ACE 中90AB AC BAC DAE AD AE ⎧⎪∠∠=︒⎨⎪⎩＝＝＝， ∴△ABD ≌△ACE （SAS ），∴∠B ＝∠ACE ，BD=CE,又∵△ABC 是等腰直角三角形，∴∠B+∠ACB=90︒,∴∠ACE +∠ACB=90︒,即BC CE ⊥，∵BC=BD+CD, BD=CE ，∴BC CE CD =+；（2）BC CE ⊥，CE BC CD =+，理由如下：∵ABC ∆、ADE ∆是等腰直角三角形，∴0,,90AB AC AD AE BAC DAE ==∠=∠=，∴BAC DAC DAE DAC ∠+∠=∠+∠即BAD CAE ∠=∠,在ABD ∆和ACE ∆中 AB AC BAD CAE AD AE ⎧⎪∠=∠⎨⎪⎩＝＝ ∴()ABD ACE SAS ∆≅∆∴BD CE =∵BD BC CD =+∴CE BC CD =+，∴ABD ACE ∠=∠，∵090ABD ACE ∠+∠=∴090ACE ACB ∠+∠=∴BC CE ⊥.（3）,BC CE CD BC CE ⊥=+，理由如下：∵ABC ADE ∆∆、是等腰直角三角形，∴0,,90AB AC AD AE BAC DAE ==∠=∠=，∴BAC BAE DAE BAE ∠-∠=∠-∠，即BAD CAE ∠=∠，在ABD ∆和ACE ∆中AB ACBAD CAEAD AE⎧⎪∠=∠⎨⎪⎩＝＝∴()ABD ACE SAS∆≅∆，∴ADB AEC∠=∠，BD CE=，∵CD BD BC=+，∴CD CE BC=+，∵090ADE AED∠+∠=，即090ADB CDE AED∠+∠+∠=∴090AEC CDE AED∠+∠+∠=，∴090DCE∠=，即BC CE⊥.【点睛】考查了全等三角形的判定与性质以及等腰直角三角形的性质的运用，解题关键是根据利用两边及其夹角分别对应相等的两个三角形全等判定三角形全等．5．已知：4590ABC A ACB∆∠=∠=，，，点D是AC延长线上一点，且22AD=+，，M是线段CD上一个动点，连接BM，延长MB到H，使得HB MB=，以点B为中心，将线段BH逆时针旋转45，得到线段BQ，连接AQ．（1）依题意补全图形；（2）求证：ABQ AMB∠=∠；（3）点N是射线AC上一点，且点N是点M关于点D的对称点，连接BN，如果QA BN=，求线段AB的长．【答案】（1）见解析；（2）证明见解析；（3）22AB=【解析】【分析】（1）根据题意可以补全图形；（2）根据三角形外角的性质即可证明；（3）作QE⊥AB，根据AAS证得QEB BCM≅，根据HL证得Rt QEA Rt BCN≅，设法证得2AB CD=，设AC BC x==，则2AB x=，22CD x=，结合已知22AD=，构建方程即可求解.【详解】（1）补全图形如下图所示：（2）解：∵∠ABH 是ABM 的一个外角，∴ ABH BAM AMB ∠=∠+∠∵ABH HBQ ABQ ∠=∠+∠ 又∵45HBQ BAM ∠=∠=︒∴ ABQ AMB ∠=∠（3）过Q 作QE ⊥AB，垂足为E ，如下图：∵⊥QE AB∴90QEB BCM ∠=∠=︒，在QEB 和BCM 中，QEB BCM QBE BMC QB BM ∠=∠⎧⎪∠=∠⎨⎪=⎩∴ QEB BCM ≅(AAS)∴EB CM =，QE BC =，在Rt QEA 和Rt BCN 中∵QE BC =，Q A BN = ∴Rt QEA Rt BCN ≅ (HL)∴AE CN CM MD DN ==++∵点N 是点M 关于点D 的对称点， ∴MD DN =∴22AE CM MD EB MD =+=+∴ ()2222AB AE EB EB MD EB MD CD =+=+=+=设AC BC x ==，则2AB x =，22CD x =，又∵22AD =+，2 AD AC CD x x =+=+ ∴2222x x +=+ 解得：2x =∴ 22AB =【点睛】本题主要考查了全等三角形的判定与性质、三角形外角定理、等腰直角三角形的判定与性质等知识点．熟悉全等三角形的判定方法以及正确作出辅助线、构建方程是解答的关键．二、八年级数学轴对称解答题压轴题（难）6．如图1，△ABC 中，AB ＝AC ，∠BAC ＝90º，D 、E 分别在 BC 、AC 边上，连接 AD 、BE 相交于点 F ，且∠CAD ＝12∠ABE ．(1)求证：BF ＝AC ；(2)如图2，连接 CF ，若 EF ＝EC ，求∠CFD 的度数；(3)如图3，在⑵的条件下，若 AE ＝3，求 BF 的长.【答案】（1）答案见详解；（2）45°，（3）4.【解析】【分析】（1）设∠CAD=x ，则∠ABE=2x ，∠BAF=90°-x ，∠AFB=180°-2x-(90°-x)= 90°-x ，进而得到∠BAF =∠AFB ，即可得到结论；(2)由∠AEB=90°-2x ，进而得到∠EFC=（90°-2x ）÷2=45°-x ，由BF ＝AB ，可得：∠EFD=∠BFA=90°-x ，根据∠CFD=∠EFD-∠EFC ，即可求解；(3)设EF ＝EC =x ，则AC=AE+EC=3+x ，可得BE=BF+EF=3+x+x=3+2x ，根据勾股定理列出方程，即可求解.【详解】（1）设∠CAD=x ，∵∠CAD ＝12∠ABE ，∠BAC ＝90º， ∴∠ABE=2x ，∠BAF=90°-x ，∵∠ABE+∠BAF+∠AFB=180°，∴∠AFB=180°-2x-(90°-x)= 90°-x ，∴∠BAF =∠AFB ，∴BF ＝AB ；∵AB ＝AC ，∴BF ＝AC ；（2）由（1）可知：∠CAD=x ，∠ABE=2x ，∠BAC ＝90º，∴∠AEB=90°-2x ，∵EF ＝EC ，∴∠EFC=∠ECF ，∵∠EFC+∠ECF=∠AEB=90°-2x ，∴∠EFC=（90°-2x ）÷2=45°-x ，∵BF ＝AB ,∴∠BFA=∠BAF=(180°-∠ABE)÷2=(180°-2x)÷2=90°-x ，∴∠EFD=∠BFA=90°-x ，∴∠CFD=∠EFD-∠EFC=(90°-x ）-(45°-x)=45°；（3）由（2）可知：EF ＝EC ，∴设EF ＝EC =x ，则AC=AE+EC=3+x ，∴AB=BF=AC=3+x ，∴BE=BF+EF=3+x+x=3+2x ，∵∠BAC ＝90º，∴222AB AE BE +=，∴222(3)3(32)x x ++=+，解得：11x =，23x =-（不合题意，舍去）∴BF=3+x=3+1=4.【点睛】本题主要考查等腰三角形的性质定理和勾股定理，用代数式表示角度和边长，把几何问题转化为代数和方程问题，是解题的关键.7．数学课上，同学们探究下面命题的正确性，顶角为36°的等腰三角形我们称之为黄金三角形，“黄金三角形“具有一种特性，即经过它某一顶点的一条直线可以把它分成两个小等腰三角形，为此，请你，解答问题：（1）已知如图1：黄金三角形△ABC 中，∠A=36°，直线BD 平分∠ABC 交AC 于点D ，求证：△ABD 和△DBC 都是等腰三角形；（2）如图，在△ABC中，AB=AC，∠A=36°，请你设计三种不同的方法，将△ABC分割成三个等腰三角形，不要求写出画法，不要求证明，但是要标出所分得的每个三角形的各内角的度数．（3）已知一个三角形可以被分成两个等腰三角形，若原三角形的一个内角为36°，求原三角形的最大内角的所有可能值．【答案】（1）见解析；（2）见解析；（3）最大角的可能值为72°，90°，108°，126°，132°【解析】【分析】（1）通过角度转换得到∠ABD=∠BAD，和∠BDC=72°=∠C，即可判断；（2）根据等腰三角形的两底角相等及三角形内角和定理进行解答即可；（3）设原△ABD中有一个角为36°，可分成两个等腰三角形，逐个讨论：①当分割的直线过顶点B时②当分割三角形的直线过点D时情况和过点B一样的，③当分割三角形的直线过点A时，在分别求出最大角的度数即可.【详解】解：（1）证明：∵∠ABC=（180-36）÷2=72；BD平分∠ABC，∠ABD=72÷2=36°，∴∠ABD=∠BAD，∴△ABD为等腰三角形，∴∠BDC=72°=∠C，∴△BCD为等腰三角形；（2）根据等腰三角形的两底角相等及三角形内角和定理作出，如图所示：（3）设原△ABD中有一个角为36°，可分成两个等腰三角形，逐个讨论：①当分割的直线过顶点B时，【1】：第一个等腰三角形ABC以A为顶点:则第二个等腰三角形BCD只可能以C为顶点此时∠A=36°,∠D=36°，∠B=72＋36=108°，最大角的值为108°；【2】：第一个等腰三角形ABC以B为顶点：第二个等腰三角形BCD只可能以C为顶点此时：∠A=36°,∠D=18°，∠B=108+18=126°，最大角的值为126°；【3】第一个等腰三角形ABC以C为顶点：第二个等腰三角形BCD有三种情况△BCD以B为顶点：∠A=36°，∠D=72°，∴∠ABD=72°，最大角的值为72°；△BCD以C为顶点：∠A=36°，∠D=54°，∴∠ABD=90°，最大角的值为90°；△BCD以D为顶点：∠A=36°，∠D=36°∴∠ABD=108°，最大角的值为108°；②当分割三角形的直线过点D时情况和过点B一样的；③当分割三角形的直线过点A时，此时∠A=36°，∠D=12°，∠B=132°，最大角的值为132°；综上所述：最大角的可能值为72°，90°，108°，126°，132°.【点睛】本题是对三角形知识的综合考查，熟练掌握等腰三角形的性质和角度转换是解决本题的关键，难度较大，分类讨论是解决本题的关键.8．定义：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的三分线．（1）如图1，在△ABC中，AB＝AC，点D在AC边上，且AD＝BD＝BC，求∠A的大小；（2）在图1中过点C作一条线段CE，使BD，CE是△ABC的三分线；在图2中画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（3）在△ABC中，∠B＝30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC 边上，且AD＝BD，DE＝CE，请直接写出∠C所有可能的值．【答案】（1）∠A＝36°；（2）如图所示：见解析；（3）如图所示：见解析；∠C为20°或40°的角．【解析】【分析】（1）利用等边对等角得到三对角相等，设∠A＝∠ABD＝x，表示出∠BDC与∠C，列出关于x的方程，求出方程的解得到x的值，即可确定出∠A的度数．（2）根据（1）的解题过程作出△ABC的三等分线；45°自然想到等腰直角三角形，过底角一顶点作对边的高，发现形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；第二种情形以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°作为等腰三角形的底角，易得此时所得的三个三角形恰都为等腰三角形；（3）用量角器，直尺标准作30°角，而后确定一边为BA，一边为BC，根据题意可以先固定BA的长，而后可确定D点，再分别考虑AD为等腰三角形的腰或者底边，兼顾A、E、C 在同一直线上，易得2种三角形ABC；根据图形易得∠C的值；【详解】（1）∵AB＝AC，∴∠ABC＝∠C，∵BD＝BC＝AD，∴∠A＝∠ABD，∠C＝∠BDC，设∠A＝∠ABD＝x，则∠BDC＝2x，∠C＝180?-x2，可得2x＝180?-x2，解得：x＝36°，则∠A＝36°；（2）根据（1）的解题过程作出△ABC的三等分线，如图1；由45°自然想到等腰直角三角形，有两种情况，①如图2，过底角一顶点作对边的高，形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；②如图3，以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°作为等腰三角形的底角，易得此时所得的三个三角形恰都为等腰三角形；（3）如图4所示：①当AD＝AE时，∵2x+x＝30°+30°，∴x＝20°；②当AD＝DE时，∵30°+30°+2x+x＝180°，∴x ＝40°；综上所述，∠C 为20°或40°的角．【点睛】本题主要考查了三角形内角、外角间的关系及等腰三角形知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．9．定义：如果两条线段将一个三角形分成3个等腰三角形，我们把这两条线段．．．．叫做这个三角形的三分线.（1）图①是顶角为36︒的等腰三角形，这个三角形的三分线已经画出，请你在图②中用不同于图①的方法画出顶角为36︒的等腰三角形的三分线，并标注每个等腰三角形顶角的度数（若两种方法分得的三角形成3对全等三角形，则视为同一种）；（2）图③是顶角为45︒的等腰三角形，请你在图③中画出顶角为45︒的等腰三角形的三分线，并标注每个等腰三角形顶角的度数.（3）ABC 中，30B ∠=︒，AD 和DE 是ABC 的三分线，点D 在BC 边上，点E 在AC 边上，且AD BD =，DE CE =，设c x ∠=︒，则x 所有可能的值为_________.【答案】（1）见详解；（2）见详解；（3）20或40.【解析】【分析】(1)作底角的平分线，再作底边的平行线，即可得到三分线；(2)过底角定点作对边的高，形成一个等腰直角三角形和一个直角三角形，然后再构造一个等腰直角三角形，即可.(3)根据题意，先确定30°角然后确定一边为BA ，一边为BC ，再固定BA 的长，进而确定D 点，分别考虑AD 为等腰三角形的腰和底边，画出示意图，列出关于x 的方程，即可得到答案.【详解】（1）如图所示：（2）如图所示：（3）①当AD=AE 时，如图4，∵DE CE =，c x ∠=︒，∴∠EDB=x °，∴∠ADE=∠AED=2x °，∵AD BD =，∴∠BAD=∠B=30°，∴30+30=2x+x ，解得：x=20；②当AD=DE 时，如图5，∵DE CE =，c x ∠=︒，∴∠EDB=x °，∴∠DAE=∠AED=2x °，∵AD BD =，∴∠BAD=∠B=30°，∴30+30+2x+x=180，解得：x=40.③当AE=DE 时，则∠EAD=∠EDA=1802(90)2x x -=-， ∴∠ADC=∠EDA+∠EDC=(90-x)+x=90°又∵∠ADC=30+30=60°，∴这种情况不存在.∴x 所有可能的值为20或40.故答案是：20或40图4 图5【点睛】本题主要考查等腰三角形的判定和性质定理的综合应用，分类讨论，画出图形，是解题的关键.10．如果一个三角形能被一条线段割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形．（1）如图1，ABC ∆是等腰锐角三角形，()AB AC AB BC =>，若ABC ∠的角平分线BD 交AC 于点D ，且BD 是ABC ∆的一条特异线，则BDC ∠= 度．（2）如图2，ABC ∆中，2B C ∠=∠，线段AC 的垂直平分线交AC 于点D ，交BC 于点E ，求证：AE 是ABC ∆的一条特异线；（3）如图3，若ABC ∆是特异三角形，30A ∠=，B 为钝角，不写过程，直接写出所有可能的B 的度数．【答案】（1）72；（2）证明见解析；（3）∠B 度数为：135°、112.5°或140°.【解析】【分析】（1）根据等腰三角形性质得出∠C=∠ABC=∠BDC=2∠A ，据此进一步利用三角形内角和定理列出方程求解即可；（2）通过证明△ABE 与△AEC 为等腰三角形求解即可；（3）根据题意分当BD 为特异线、AD 为特异线以及CD 为特异线三种情况分类讨论即可.【详解】（1）∵AB=AC ，∴∠ABC=∠C ，∵BD 平分∠ABC ，∴∠ABD=∠CBD=12∠ABC，∵BD是△ABC的一条特异线，∴△ABD与△BCD为等腰三角形，∴AD=BD=BC，∴∠A=∠ABD，∠C=∠BDC，∴∠ABC=∠C=∠BDC，∵∠BDC=∠A+∠ABD=2∠A，设∠A=x，则∠C=∠ABC=∠BDC=2x，在△ABC中，∠A+∠ABC+∠C=180°，即：x+2x+2x=180°，∴x=36°，∴∠BDC=72°，故答案为：72；（2）∵DE是线段AC的垂直平分线，∴EA=EC，∴△EAC为等腰三角形，∴∠EAC=∠C，∴∠AEB=∠EAC+∠C=2∠C，∵∠B=2∠C，∴∠AEB=∠B，∴△EAB为等腰三角形，∴AE是△ABC的一条特异线；（3）如图3，当BD是特异线时，如果AB=BD=DC，则∠ABC=∠ABD+∠DBC=120°+15°=135°；如果AD=AC，DB=DC，则∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°；如果AD=DB ，DC=DB ，则∠ABC=∠ABD+∠DBC=30°+60°=90°，不符合题意，舍去；如图4，当AD 是特异线时，AB=BD ，AD=DC ，则：∠ABC=180°−20°−20°=140°；当CD 为特异线时，不符合题意；综上所述，∠B 度数为：135°、112.5°或140°.【点睛】本题主要考查了等腰三角形性质的综合运用，熟练掌握相关概念是解题关键.三、八年级数学整式的乘法与因式分解解答题压轴题（难）11．阅读下列材料，然后解答问题：问题：分解因式：3245x x +-.解答：把1x =带入多项式3245x x +-，发现此多项式的值为0，由此确定多项式3245x x +-中有因式()1x -，于是可设()()322451x x x x mx n +-=-++，分别求出m ，n 的值.再代入()()322451x x x x mx n +-=-++，就容易分解多项式3245x x +-，这种分解因式的方法叫做“试根法”.（1）求上述式子中m ，n 的值；（2）请你用“试根法”分解因式：3299x x x +--.【答案】（1）5m =，5n =；（2）()()()133x x x ++-【解析】【分析】（1）先找出一个x 的值，进而找出一个因式，再将多项式设成分解因式的形式，即可得出结论；（2）先找出x=-1时，得出多项式的值，进而找出一个因式，再将多项式设成分解因式的形式，即可得出结论．【详解】解：（1）把1x =带入多项式3245x x +-，发现此多项式的值为0，∴多项式3245x x +-中有因式()1x -，于是可设322451xx x x mx n ，得出：3232451x x x m x n m x n ，∴14m ，0n m ，∴5m =，5n =，（2）把1x =-代入3299x x x +--，多项式的值为0，∴多项式3299x x x +--中有因式()1x +，于是可设322329911x x x x x mx n x m x n m x n ，∴11m +=，9n m，9n =- ∴0m =，9n =-，∴3229133991x x x x x x x x【点睛】此题是分解因式，主要考查了试根法分解因式的理解和掌握，解本题的关键是理解试根法分解因式．12．（1）填空：()()a b a b -+= ；22()()a b a ab b -++= ；3223()()a b a a b ab b -+++= ．（2）猜想：1221()(...)n n n n a b a a b ab b -----++++= （其中n 为正整数，且2n ≥）．（3）利用（2）猜想的结论计算：98732222...222-+-+-+．【答案】（1）22a b -，33a b -，44a b -；（2）n n a b -；（3）342．【解析】试题分析：（1）根据平方差公式与多项式乘以多项式的运算法则运算即可；（2）根据（1）的规律可得结果；（3）原式变形后，利用（2）得出的规律计算即可得到结果．试题解析：（1）()()a b a b -+=22a b -；3223()()a b a a b ab b -+++=33a b -；3223()()a b a a b ab b -+++=44a b -；故答案为22a b -，33a b -，44a b -；（2）由（1）的规律可得：原式=n n a b -，故答案为n n a b -；（3）令98732222...222S =-+-+-+，∴987321222...2221S -=-+-+-+-=98732[2(1)](222...2221)3---+-+-+-÷=10(21)3(10241)3341-÷=-÷=，∴S=342．考点：1．平方差公式；2．规律型．13．阅读理解：把两个相同的数连接在一起就得到一个新数，我们把它称为“连接数”，例如：234234，3939…等，都是连接数，其中，234234称为六位连接数，3939称为四位连接数．（1）请写出一个六位连接数，它（填“能”或“不能”）被13整除．（2）是否任意六位连接数，都能被13整除，请说明理由．（3）若一个四位连接数记为M ，它的各位数字之和的3倍记为N ，M ﹣N 的结果能被13整除，这样的四位连接数有几个？【答案】（1）证明见解析（2）abcabc 能被13整除（3）这样的四位连接数有1919，2525，3131，一共3个【解析】分析：（1）根据六位连接数的定义可知123123为六位连接数，再将123123进行因数分解，判断得出它能被13整除；（2）设abcabc 为六位连接数，将abcabc 进行因数分解，判断得出它能被13整除；（3）设xyxy 为四位连接数，用含x 、y 的代数式表示M 与N ，再计算M ﹣N ，然后将13M N -表示为77x +7y +3413x y +，根据M ﹣N 的结果能被13整除以及M 与N 都是1～9之间的整数，求得x 与y 的值，即可求解．详解：（1）123123为六位连接数；∵123123=123×1001=123×13×77，∴123123能被13整除；（2）任意六位连接数都能被13整除，理由如下：设abcabc 为六位连接数．∵abcabc =abc ×1001=abc ×13×77，∴abcabc 能被13整除；（3）设xyxy 为四位连接数，则M =1000x +100y +10x +y =1010x +101y ，N =3（x +y +x +y ）=6x +6y ，∴M ﹣N =（1010x +101y ）﹣（6x +6y ）=1004x +95y ，∴13M N -=10049513x y +=77x +7y +3413x y +．∵M ﹣N 的结果能被13整除，∴3413x y +是整数．∵3x +4y 取值范围大于3小于63，所以能被13整除的数有13，26，39，52，∴x =1，y =9；x =2，y =5；x =3，y =1；x =8，y =7；x =9，y =3；x =5，y =6；x =6，y =2；满足条件的四位连接数的3131，2525，6262，9393，8787，5656，1919共7个．点睛：本题考查了因式分解的应用，整式的运算，理解“连接数”的定义是解题的关键．14．阅读材料后解决问题：小明遇到下面一个问题：计算（2+1）（22+1）（24+1）（28+1）．经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：（2+1）（22+1）（24+1）（28+1）=（2+1）（2﹣1）（22+1）（24+1）（28+1）=（22﹣1）（22+1）（24+1）（28+1）=（24﹣1）（24+1）（28+1）=（28﹣1）（28+1）=216﹣1请你根据小明解决问题的方法，试着解决以下的问题：（1）（2+1）（22+1）（24+1）（28+1）（216+1）=_____．（2）（3+1）（32+1）（34+1）（38+1）（316+1）=_____．（3）化简：（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）．【答案】232﹣13231 2-；【解析】【分析】（1）原式变形后，利用题中的规律计算即可得到结果；（2）原式变形后，利用题中的规律计算即可得到结果；（3）分m=n与m≠n两种情况，化简得到结果即可．【详解】（1）原式=（2-1）（2+1）（22+1）（24+1）（28+1）（216+1）=232-1；（2）原式=12（3-1）（3+1）（32+1）（34+1）（38+1）（316+1）=32312-；（3）（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）．当m≠n时，原式=1m n-（m-n）（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）=3232m nm n--；当m=n时，原式=2m•2m2…2m16=32m31．【点睛】此题考查了平方差公式，弄清题中的规律是解本题的关键．15．由多项式的乘法：(x＋a)(x＋b)＝x2＋(a＋b)x＋ab，将该式从右到左使用，即可得到用“十字相乘法”进行因式分解的公式：x2＋(a＋b)x＋ab＝(x＋a)(x＋b)．实例分解因式：x2＋5x＋6＝x2＋(2＋3)x＋2×3＝(x＋2)(x＋3)．(1)尝试分解因式：x2＋6x＋8；(2)应用请用上述方法解方程：x2－3x－4＝0.【答案】(1) (x+2)(x＋4)；(2) x＝4或x＝－1.【解析】【分析】（1）类比题干因式分解方法求解可得；（2）利用十字相乘法将左边因式分解后求解可得．【详解】(1)原式=(x+2)(x＋4)；(2)x2－3x－4＝(x－4)(x＋1)＝0，所以x－4＝0或x＋1＝0，即x＝4或x＝－1.【点睛】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．四、八年级数学分式解答题压轴题（难）16．一件工程，甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的23；若由甲队先做 20 天，剩下的工程再由甲、乙两队合作 60天完成．(1)求甲、乙两队单独完成这项工程各需多少天？(2)已知甲队每天的施工费用为 8.6 万元，乙队每天的施工费用为 5.4 万元，工程预算的施工费用为 1000 万元，若在甲、乙工程队工作效率不变的情况下使施工时间最短，问安排预算的施工费用是否够用？若不够用，需追加预算多少万元？【答案】(1)甲、乙两队单独完成这项工程分别需120天、180天(2)工程预算的施工费用不够用，需追加预算8万元【解析】试题分析：（1）首先表示出甲、乙两队需要的天数，进而利用由甲队先做20天，剩下的工程再由甲、乙两队合作60天完成得出等式求出答案；（2）首先求出两队合作需要的天数，进而求出答案．试题解析：解：（1）设乙队单独完成这项工程需要x天，则甲队单独完成这项工程需要23x天．根据题意，得201160()12233x x x++=，解得：x=180．经检验，x=180是原方程的根，∴23x=23×180=120，答：甲、乙两队单独完成这项工程分别需120天和180天；（2）设甲、乙两队合作完成这项工程需要y天，则有11()1120180y+=，解得y=72．需要施工费用：72×（8.6+5.4）=1008（万元）．∵1008＞1000，∴工程预算的施工费用不够用，需追加预算8万元．点睛：此题主要考查了分式方程的应用以及一元一次方程的应用，正确得出等量关系是解题关键．17．探索：（1）如果32311x m x x -=+++，则m=_______；（2）如果53522x m x x -=+++，则m=_________；总结：如果ax b m a x c x c+=+++（其中a 、b 、c 为常数），则m=________；（3）利用上述结论解决：若代数式431x x --的值为整数，求满足条件的整数x 的值．【答案】（1）-5；（2）-13 ； b -ac ;（3）0或2【解析】试题解析： ()323(1)55133.1111x x m x x x x -+-==-=+++++ 5.m ∴=-()535(2)1313255.2222x x m x x x x -+-==-=+++++ 13.m ∴=- 总结：().ax b a x c b ac b ac m a a x c x c x c x c +++--==+=+++++ .m b ac ∴=-()434(1)1134.111x x x x x --+==+--- 又∵代数式431x x --的值为整数， 11x ∴-为整数， 11x ∴-=或11x -=-2x ∴=或 0.18．水蜜桃是无锡市阳山的特色水果，水蜜桃一上市，水果店的老板用2000元购进一批水密桃，很快售完；老板又用3300元购进第二批水蜜桃，所购件数是第一批的32倍，但进价比第一批每件多了5元．（1）第一批水蜜桃每件进价是多少元？（2）老板以每件65元的价格销售第二批水蜜桃，售出80％后，为了尽快售完，剩下的决定打折促销．要使得第二批水密桃的销售利润不少于288元，剩余的仙桃每件售价最多打几折？(利润=售价-进价)【答案】（1）50；（2）6折．【解析】【分析】（1）根据题意设第一批水蜜桃每件进价是x 元，利用第二批水密桃进价建立方程求解即可；（2）根据题意设剩余的仙桃每件售价最多打m 折，并建立不等式，求出其解集即可得出剩余的仙桃每件售价最多打几折.【详解】解：（1）设第一批水蜜桃每件进价是x 元，则有：20003(5)33002x x ⨯⨯+=，解得50x =，所以第一批水蜜桃每件进价是50元.（2）由（1）得出第二批水密桃的进价为：55元，数量为：33006055=件，设剩余的仙桃每件售价最多打m 折，则有： 6580606065(180)3300288m ⨯⨯+⨯⨯--≥％％，解得0.6m ≥，即最多打6折.【点睛】本题考查分式方程的实际应用以及不等式的实际应用，理解题意并根据题意建立方程和不等式是解题的关键.19．某商场计划购进一批甲、乙两种玩具，已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元，用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同．（1）求每件甲种、乙种玩具的进价分别是多少元？（2）商场计划购进甲、乙两种玩具共48件，其中甲种玩具的件数少于乙种玩具的件数，商场决定此次进货的总资金不超过1000元，求商场共有几种进货方案？【答案】（1）甲，乙两种玩具分别是15元/件，25元/件；（2）共有四种方案．【解析】【分析】（1）设甲种玩具进价x 元/件，则乙种玩具进价为（40﹣x ）元/件，根据已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元，用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同可列方程求解．（2）设购进甲种玩具y 件，则购进乙种玩具（48﹣y ）件，根据甲种玩具的件数少于乙种玩具的件数，商场决定此次进货的总资金不超过1000元，可列出不等式组求解．【详解】解：设甲种玩具进价x 元/件，则乙种玩具进价为（40﹣x ）元/件，x=15，经检验x=15是原方程的解．∴40﹣x=25．甲，乙两种玩具分别是15元/件，25元/件；（2）设购进甲种玩具y 件，则购进乙种玩具（48﹣y ）件，，解得20≤y ＜24．因为y 是整数，甲种玩具的件数少于乙种玩具的件数，∴y 取20，21，22，23，共有4种方案．考点：分式方程的应用；一元一次不等式组的应用．20．“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行，也给自行车商家带来商机．某自行车行经营的A 型自行车去年销售总额为8万元．今年该型自行车每辆售价预计比去年降低200元．若该型车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求：（1）A 型自行车去年每辆售价多少元；（2）该车行今年计划新进一批A 型车和新款B 型车共60辆，且B 型车的进货数量不超过A 型车数量的两倍．已知，A 型车和B 型车的进货价格分别为1500元和1800元，计划B 型车销售价格为2400元，应如何组织进货才能使这批自行车销售获利最多．【答案】(1) 2000元；（2） A 型车20辆，B 型车40辆．【解析】【分析】（1）设去年A 型车每辆售价x 元，则今年售价每辆为（x ﹣200）元，由卖出的数量相同列出方程求解即可；（2）设今年新进A 型车a 辆，则B 型车（60﹣a ）辆，获利y 元，由条件表示出y 与a 之间的关系式，由a 的取值范围就可以求出y 的最大值．【详解】解：（1）设去年A 型车每辆售价x 元，则今年售价每辆为（x ﹣200）元，由题意，得 8000080000(110%)200x x -=-，解得：x=2000．经检验，x=2000是原方程的根．答：去年A 型车每辆售价为2000元；（2）设今年新进A 型车a 辆，则B 型车（60﹣a ）辆，获利y 元，由题意，得y=a+（60﹣a ），y=﹣300a+36000．∵B 型车的进货数量不超过A 型车数量的两倍，∴60﹣a≤2a ，∴a≥20．∵y=﹣300a+36000．。

河南省信阳市息县2023_2024学年人教版八年级数学上学期期末培优卷(有答案)

河南省信阳市息县2023_2024学年人教版八年级数学上学期期末培优卷一、选择题（本题共10小题,共30分）1.以下四家银行的标志图中,不是轴对称图形的是( )A. B. C. D.2.若长度为,,的三条线段能组成一个三角形,则的值可能为( )x 23x A. B. C. D. 65133.下列计算正确的是( )A. B. C. D. (a −1)2=1a 2(−a 3)2=−a 6(a m )n =a m +n a 3÷2a =2a 24.如图,和中,,,添加下列哪一个条件无法证明≌△ABC △DEF AB =DE ∠B =∠DEF △ABC( )△DEF A. B. C. D. BE =CF ∠A =∠D AC =DF AC//DF5.等腰三角形的一个角是,它的底角的大小为( )70°A. B. C. 或 D. 或70°40°70°40°70°55°6.下列正确的是( )A. B. 2a 2b ⋅3a 2b 2=6a 6b 30.00076=7.6×104C. D. −2a(a +b)=−2a 2+2ab (2x +1)(x−2)=2x 2−3x−27.把代数式中的,同时扩大倍后,代数式的值( )x 2y x−y x y 2A. 扩大为原来的倍 B. 扩大为原来倍 C. 扩大为原来的倍D. 缩小为原来的一半1248.如图,在中,、分别是、边上的高,在上截取,在的延长线上截△ABC BE CF AC AB BE BD =AC CF取,连接、,则下列结论错误的是( )CG =AB AD AG A. B. AD =AG AD ⊥AGC. 为等腰直角三角形D. △ADG ∠G =∠ABD9.如图,在等边三角形中,是中线,点,分别在,上,且,ABC BD P Q AB AD BP =AQ =QD =1动点在上,则的最小值为( )E BD PE +QE A. B. C. D. 234510.如图,已知,点是的平分线上的一个定点,点,分别在射线和射线∠AOB =120°D ∠AOB E F OA 上,且下列结论：是等边三角形；四边形的面积是一个定值；OB ∠EDF =60°.①△DEF ②DEOF 当时,的周长最小；当时,也平行于其中正确的个数是( )③DE ⊥OA △DEF ④DE//OB DF OA.A. 个 B. 个 C. 个 D. 个1234二、填空题（本题共5小题,共15分）11.杜师傅在做完门框后,为防止门框变形常常需钉两根斜拉的木条,这样做的数学原理是______．12.如图,中,平分,于点,于点,,,,△ABC BD ∠ABC DE ⊥AB E DF ⊥BC F S △ABC =18AB =8BC =4则______．DE =13.若是完全平方式,则的值为______ ．x 2+2(m−1)x +16m 14.如图,的度数是______ ．∠A +∠B +∠C +∠D +∠E +∠F 15.已知关于的分式方程．x 3x x−1=m x−1+2若,分式方程的解为______ ；(1)m =4若分式方程无解,则的值为______ ．(2)m 三．解答题（本题共8小题,共75分）16.分计算：(8)；．(1)(−a )3⋅a 2+(2a 4)2÷a 3(2)(2x−1)2−(x +3)(x−3)17.分解分式方程：(8)；．(1)3x 2−3x −1x−3=2x (2)12x−1+34x−2=1218.分先化简,再求值：,从-2,0,1,2,3这5个数中选一个你(9)(1−1a−1)÷a 2−4a 2−2a +1喜欢的数代入求值.19.9分如图,三个顶点的坐标分别为,,．()△ABC A(1,1)B(4,2)C(3,4)请写出关于轴对称的的各顶点坐标；(1)△ABC x △A 1B 1C 1请画出关于轴对称的；(2)△ABC y △A 2B 2C 2在轴上求作一点,使点到、两点的距离和最小,(3)x P P A B 请标出点,并直接写出点的坐标______ ．P P 20.分认真观察下面这些等式,按其规律,完成下列各小题：(10)；①42−22=4×3；②62−42=4×5；③82−62=4×7______ ；④…将横线上的等式补充完整；(1)验证规律：设两个连续的正偶数为,为正整数,则它们的平方差是的倍数；(2)2n 2n +2(n )4拓展延伸：判断两个连续的正奇数的平方差是的倍数吗？并说明理由．(3)821.10分永州市万达广场筹建之初的一项挖土工程招标时,接到甲、乙两个工程队的投标书,()每施工一天,需付甲工程队工程款万元,付乙工程队工程款万元,工程领导小组根据甲、乙2.4 1.8两队的投标书测算,可有三种施工方案：方案一甲队单独完成这项工程,刚好按规定工期完成：()方案二乙队单独完成这项工程要比规定工期多用天；()6方案三若由甲、乙两队合作做天,剩下的工程由乙队单独做,也正好按规定工期完工．()5请你求出完成这项工程的规定时间；(1)(2)如果你是工程领导小组的组长,为了节省工程款,同时又能如期完工,你将选择哪一种方案？说明理由．()1 22.10分当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,例如,由图,(a+2b)(a+b)=a2+3ab+2b2可得等式：．(1)2由图,可得等式：______ ．(2)(1)a+b+c=12ab+bc+ac=28利用中所得到的结论,解决下面的问题已知,,求a2+b2+c2的值．()△ABC∠B=60°D BC AD=AC11分在中,,是上一点,且．(1)1BC E CE=BD AE.AB=AE如图,延长至,使,连接求证：；(2)2AB F DF=DB AF=BC如图,在边上取一点,使,求证：；(3)3(2)P BC PA PF PA=PF PC BD如图,在的条件下,为延长线上一点,连接,,若,猜想与的数量关系并证明．23.答案1.【正确答案】B2.【正确答案】D 解：由题意得：,即,3−2<x <3+21<x <5则的值可能是,x 33.【正确答案】A 解：,此选项计算正确,故符合题意；A.∵(a −1)2=a −2=1a 2∴B.,此选项计算错误,故不符合题意；∵(−a 3)2=a 6∴C.,此选项计算错误,故不符合题意；∵(a m )n =a mn ∴D.,此选项计算错误,故不符合题意；∵a 3÷2a =12a 2∴4.【正确答案】C 5.【正确答案】D 解：当这个角是顶角时,底角；①=(180°−70°)÷2=55°当这个角是底角时,另一个底角为,顶角为．②70°40°6.【正确答案】D 解：,原选项计算错误,不符合题意；A.2a 2b ⋅3a 2b 2=6a 4b 3B.,原科学记数法表示错误,故此选项不符合题意；0.00076=7.6×10−4C.,原选项计算错误,不符合题意；−2a(a +b)=−2a 2−2ab D. ,计算正确,符合题意,(2x +1)(x−2)=2x 2−3x−27.【正确答案】C 解：将,同时扩大倍,得：,x y 2(2x )2⋅2y 2x−2y =8x 2y 2(x−y)=4⋅x 2y x−y 即扩大为原来的倍；48.【正确答案】D 解：、分别是、两边上的高,∵BE CF AC AB 垂直定义,∴∠AFC =∠AEB =90°()同角的余角相等,∴∠ACG =∠DBA()在与中,∴△ABD △GCA ,{BD =AC ∠ACG =∠DBA AB =CG ≌,∴△ABD △GCA(SAS),,∴∠AGC =∠DAB AD =GA∵∠CGA+∠GAF=90°,∴∠GAF+∠BAD=90°AD⊥AG,即．∴△ADG是等腰直角三角形．B故选项A,,C正确,9.【正确答案】BBC P'BP'=BP=1PP'P'Q EP'解：如图,在上其一点,使,连接,,,∵△ABC BD⊥AC D是等边三角形,于点,∴BD△ABC P'P BD AC=2AD 直线是的对称轴,点与点关于对称,,∴PE=P'E,∴PE+QE=P'E+QE≥P'Q,∴PE+QE P'Q的最小值为线段的长,∵AQ=QD=1,∴AC=2(AQ+QD)=2×2=4,∵△ABC是等边三角形,∴AC=BC∠C=60°,,∵AQ=BP'=1,∴CP'=CQ,∴△CP'Q是等边三角形,∴P'Q=CQ,∵CQ=AC−AQ=4−1=3,∴PE+QE3的最小值为,10.【正确答案】CD DM⊥OB M DN⊥OA N解：过点作于点,于点,如图所示：∵D∠AOB点是的平分线上的一点,,∴DM =DN ,,∵∠AOB =120°∠DNO =∠DMO =90°,∴∠MDN =60°,∵∠EDF =60°,∴∠EDN =∠FDM ≌,∴△DEN △DFM(ASA),∴DE =DF 是等边三角形；故正确；∴△DEF ①,∵S △DEM =S △DFN ,∴S △DEM +S 四边形DEON =S 四边形DEON +S △DFN 即,S 四边形DEOF =S 四边形DMON 点是的平分线上的一个定点,∵D ∠AOB 四边形的面积是一个定值,∴DMON 四边形的面积是一个定值,故正确；∴DEOF ②,∵DE ⊥OA 点与重合,∴E N 垂线段最短,∵的值最小,∴DE 当最小时,的周长最小,DE △DEF 当时,最小,的周长最小,故正确,∴DE ⊥OA DE △DEF ③,,∵DE//OB ∠D =∠DFB =60°,∵∠AOB =120°,∴∠DFB ≠∠AOB 一定与不平行,故错误．∴DF OA ④11.【正确答案】三角形的稳定性12.【正确答案】3解：是的平分线,于点,于点,∵BD ∠ABC DE ⊥AB E DF ⊥BC F ,∴DE =DF ,∵S △ABC =S △ABD +S △BDC =12AB ⋅DE +12BC ⋅DF =18即,12×8⋅DE +12×4⋅DE =18解得：,DE =313.【正确答案】或5−3解：,∵x 2+2(m−1)x +16=(x ±4)2=x 2±8x +16,∴2(m−1)=±8或．∴m =5−314.【正确答案】360°解：如图：,,∵∠E +∠A =∠1∠B +∠F =∠2,∵∠1+∠2+∠C +D =360°,∴∠A +∠B +∠C +∠D +∠E +∠F =360°15.【正确答案】x =23解：当时,原方程即为：,(1)m =43x x−1=4x−1+2去分母得：,3x =4+2x−2解得：,x =2检验：当时,,x =2x−1≠0是原方程的根；∴x =2故；x =2方程去分母得：(2)3x =m +2x−2化简,得,x =m−2当时,分母为零,分式方程无解,x =1即,解得,m−2=1m =3时,方程无解．∴m =316.【正确答案】解：(1−1a−1)÷a 2−4a 2−2a +1=a−1−1a−1⋅(a−1)2(a +2)(a−2)=a−21⋅a−1(a +2)(a−2),=a−1a +2当时,原式．a =3=3−13+2=2517.【正确答案】解：解：(1)(−a )3⋅a 2+(2a 4)2÷a3=−a 3⋅a 2+4a 8÷a 3=−a 5+4a 5；=3a 5解：(2)(2x−1)2−(x +3)(x−3)=4x 2−4x +1−(x 2−9)=4x 2−4x +1−x 2+9．=3x 2−4x +1018.【正确答案】解：,(1)3x 2−3x −1x−3=2x ,3−x =2(x−3)解得：,x =3检验：当时,,x =3x(x−3)=0是原方程的增根,∴x =3原方程无解；∴,(2)12x−1+34x−2=12,2+3=2x−1解得：,x =3检验：当时,,x =34x−2≠0是原方程的根．∴x =319.【正确答案】(2,0)解：与关于轴对称,(1)∵△ABC △A 1B 1C 1x 点,,．∴A 1(1,−1)B 1(4,−2)C 1(3,−4)如图,即为所求．(2)△A 2B 2C 2如图,点即为所求,(3)P 点的坐标为．P (2,0)20.【正确答案】102−82=4×9解：由题意得：；(1)102−82=4×9故；102−82=4×9．(2)(2n +2)2−(2n )2=(2n +2+2n)(2n +2−2n)=4(2n +1)为正整数,∵n 为正整数,∴2n +1若两个连续的正偶数为,为正整数,则它们的平方差是的倍数；∴2n 2n +2(n )4是；理由：(3)设两个连续的正奇数为,为正数．2m−12m +1(m )(2m +1)2−(2m−1)2=[(2m +1)−(2m−1)][(2m +1)+(2m−1)]=2×4m．=8m 为正整数,∵m 两个连续的正奇数的平方差是的倍数．∴821.【正确答案】解：设完成这项工程的规定时间为天,则甲工程队需天完成这项工程,乙(1)x x 工程队需天完成这项工程,(x +6)根据题意得：,5×(1x +1x +6)+x−5x +6=1解得：,x =30经检验,是原方程的解,且符合题意．x =30答：完成这项工程的规定时间为天．30选择方案三,理由如下：(2)方案一需付工程款：万元；2.4×30=72()方案二不能如期完工,不符合题意；方案三需付工程款：万元．2.4×5+1.8×30=66(),∵72>66选择方案三．∴22.【正确答案】(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc解：,(1)(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc 故；(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc ,,(2)∵a +b +c =12ab +bc +ac =28∴a 2+b 2+c 2=(a +b +c )2−2(ab +ac +bc)=122−2×28．=8823.【正确答案】证明：,(1)∵AC =AD ,∴∠ADC =∠ACD ,∴180°−∠ADC =180°−∠ACD 即,∠ADB =∠ACE 在和中,△ABD △AEC ,{AD =AC ∠ADB =∠ACE BD =CE ≌,∴△ABD △AEC(SAS)；∴AB =AE 延长到,使,由知,,(2)CE E CE =BD (1)AB =AE ,∴∠E =∠B =60°,∴∠EAB =180°−∠E−∠B =60°是等边三角形,∴△ABE 同理,是等边三角形,△DBF ,∴AB =BE.BF =BD =CE ,∴AB−BF =BE−CE 即；AF =BC 猜想：,(3)PC =2BD 理由如下：在上取点,使,连接,CP E CE =BD AE 由可知：,(1)AB =AE,∴∠AEB =∠B =60°,∴∠AEP =180°−∠AEB =120°,,∵DF =DB ∠DFB =∠B =60°,∴∠PDF =∠DFB +∠B =120°,∴∠AEP =∠PDF 又,∵PA =PF ,∴∠PAF =∠PFA ,∵∠APE =180°−∠B−∠PAF =120°−∠PAF ,∠PFD =180°−∠DFB−∠PFA =120°−∠PFA ,∴∠APE =∠PFD 在和中,△APE △PFD ,{∠APE =∠PFD ∠AEP =∠PDF PA =PF ≌,∴△APE △PFD(AAS),∴PE =DF 又,∵DF =DB ,∴PE =DB 又,∵PC =PE +CE ．∴PC =2BD。

人教版八年级数学上册期末试卷培优测试卷

人教版八年级数学上册期末试卷培优测试卷一. 八年级数学全等三角形解答题压轴题(难)1. 如图，在ABC 中，ΛABC = ^5, AD 9BE 分别为BC t AC 边上的高，连接DE,过点 D 作DF 丄DE 与点F, G 为BE 中点,连接AF, DG ・(2)如图2,请写出AF 与DG 之间的关系并证明.【答案】⑴详见解析;(2)AF=2DG,且AF 丄DG,证明详见解析.【解析】【分析】(1) 利用条件先△ DAE 今ADBF,从而得出AFDE 是等腰直角三角形,再证明AAEF 是等腰直角三角形,即可•⑵延长DG 至点M,使GM=DG,交AF 于点H,连接BM,先证明△ BGM^∆EGD,再证明 ΔBDM^ΔDAF 即可推岀.【详解】解：(I)证明:设BE 与AD 交于点H ・・如图，VAD z BE 分别为BC Z AC 边上的髙,ΛZBEA=ZADB=90o.V ZABC=45°,ΛΔABD 是等腰宜角三角形. Λ AD=BD.∖∙ ZAHE=ZBHD zΛ ZDAC=ZDB H .∙.φZADB=ZFDE=90°, ∙∙∙ ZADE=ZBDRΛ∆DAE^∆DBF.ABF=AE z DF=DE.ΛΔFDE是等腰直角三角形.ΛZDFE=450.VG为BE中点，Λ BF=EF.Λ AE=ER.,.∆AEF是等腰直角三角形.∙∙∙ZAFE=45°・∙∙∙ ZAFD二90。

出卩 AFlDR（2）AF=2DG,且AF丄DG•理由涎长DG至点使GM=DG J交AF于点H,连接BM,VZBGMZEGD zΛ∆BGM^∆EGD ・∙∙∙ ZMBE=ZFED=45o,BM=DE.AZMBE=ZEFD Z BM=DRVZDAC=ZDBE Z∙∙∙ ZMBD=ZMBE+ZDBE=450+ZDBE.∖∙ ZEFD=45o=ZDBE+ZBDR∙∙∙ ZBDF二45°-ZDBE・∙/ ZADE=ZBDF,∙∙∙ ZADF=90o-ZBDF=45°+ZDBE=ZMBD.VBD=AD ZΛ∆BDM^ΔDARΛ DM=AF=2DG z Z FAD= ZBDM ・VZBDM+ZM DA=90o,AZMDA+ZFAD=90o.∙∙∙ZAHD=90°.∙∙∙AF 丄 DG ・∙∙∙AF=2DG,且 AFlDG【点睛】本题考查三角形全等的判左和性质,关键在于灵活运用性质.2.如图1,在平而直角坐标系中，点D(“，m+8)在第二彖限，点3 (0> n)在y轴正半轴上，作M丄X轴，垂足为儿已知QA比OB的值大2,四边形AOBD的而积为12.(1)求m和门的值・(2 )如图2, C为AO的中点，DC与AB相交于点F, AF±BD,垂足为F,求证：AF=DE.(3)如图3,点G在射线AD上，且GA = GB, H为GB延长线上一点，作ZHAN交y轴于点M且ZHAN=上HBO,求NB-HB的值.Irl = -4【答案】(1)< C (2)详见解析；(3) NB- FB=4 (是定值)，即当点H在GB的n = 2延长线上运动时，NB-HB的值不会发生变化.【解析】【分析】(1)由点D,点3的坐标和四边形AOBD的而积为12,可列方程组，解方程组即可：(2)由(2)可知，AD=OA = 4, 0B=2,并可求出AB=BD= 2卡,利用SAS可证△DAC也AAOB,并可得ZAEC= 90°,利用三角形而积公式即可求证：(3)取OC=OB,连接AC,根据对称性可得ZABC= ZACB, AB=AC,证明∆ABH^ΛCAN,即可得到结论.【详解】-m -/7 = 2解：(1)由题意Qi, OW、，-(n + m + 8)(-m) = 12W 2IrI = -4解得< ：H = 2由(1)可知,Λ ( -4t0) , β (0, 2) , D ( -4, 4), ：.AD=OA=4. OB=2,・•・由勾股泄理可得：AB = BD= 2炳,9： AC=OC=2,AC=OB99：ZDAC= ZAOB=90°, AD=OA9：.ADAC^AAOB (SAS),∙∙∙ ZADC=ZBAO.T ZADC^ZACD=90∖∙∙∙ZE4C+ZACE=90°,∙∙∙ZAEC= 90°,9：AF±BD. DE±AB.1 1•∙SχD8= —^AB^AE=—∙BD∙√4F,2 29： AB = BD,：.DE=AF ・(3)解：如图，取OC=OB,连接AC,根据对称性可得ZABC=ZACB. AB=AC.9：AG=BG./.ZGAB=ZGBA fTG为射线AD上的一点，•••AG〃y 轴，：.ZGAB=ZABC.：.ZACB=ZEBA.Λ180o - ZGBA = I80° - ZACB,即ZABG=Z ACN99： ZGAN=ZGBO,：.ZAGB=ZANC f∕±,∆ABG与"CN 中，ZABH=ZACN< ZAHB = ZANC ,AB = AC：.AABH^AACN (AAS) t：.BF= CN9：.NB - HB=NB ・ CN=BC=IOB9VOB=2:∙NB- FB=2χ2=4 (是定值)，即当点H在GB的延长线上运动时，NB - HB的值不会发生变化.【点睛］本题属于三角形综合题，全等三角形的判定和性质，解题的关键是相结合添加常用辅助线，构造图形解决问题，学会利用参数构建方程解决问题.3.在四边形ABCD中，F为BC边中点.(I )已知：如图，若处平分ZBAD. Z AED=90o f点F为AD上一点,AF=AB.求证：(1)Δ ABE^ AFE↑ (2) AD=AB+CD(∏)已知：如图，若处平分Z BAD. DE平分ΛADC. Z AED二120。

人教版八年级数学上册期末试卷(培优篇)(Word版含解析)

人教版八年级数学上册期末试卷（培优篇）（Word版含解析）一、八年级数学全等三角形解答题压轴题（难）1．(1)如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段EF，BE，FD之间的数量关系．小明同学探究的方法是：延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论是（直接写结论，不需证明）；(2)如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是BC，CD上的点，且∠EAF是∠BAD的二分之一，上述结论是否仍然成立，并说明理由．(3)如图3，四边形ABCD是边长为5的正方形，∠EBF=45°，直接写出三角形DEF的周长．【答案】（1）EF=BE+DF．（2）成立，理由见解析；（3）10.【解析】【分析】（1）如图1，延长FD到G，使得DG=DC,先证△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，进一步根据题意得∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.(2)如图2，延长FD到点G．使DG=BE．连结AG，证得△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，再结合题意得到∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.（3）如图3，延长DC到点G，截取CG=AE，连接BG，先证△AEB≌△CGB，得到BE=BG，∠ABE=∠CBG，结合已知条件得∴∠CBF+∠CBG=45°，再证明△EBF≌△GBF，得到EF=FG，最后求三角形的周长即可.【详解】解答：（1）解：如图1，延长FD到G，使得DG=DC在△ABE和△ADG中，∵DC DGB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵AE AGEAF GAFAF AF=⎧⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；故答案为：EF=BE+DF．（2）解：结论EF=BE+DF仍然成立；理由：如图2，延长FD到点G．使DG=BE．连结AG在△ABE和△ADG中，∵DG BEB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩，∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵AE AGEAF GAF AF AF=⎧⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；（3）解：如图3，延长DC到点G，截取CG=AE，连接BG，在△AEB与△CGB中，∵AE CGA BOG AF BF=⎧⎪∠=∠⎨⎪=⎩，∴△AEB≌△CGB（SAS），∴BE=BG，∠ABE=∠CBG．∵∠EBF=45°，∠ABC=90°，∴∠ABE+∠CBF=45°，∴∠CBF+∠CBG=45°．在△EBF与△GBF中，∵BE BGEBF GBF BF BF=⎧⎪∠=∠⎨⎪=⎩，∴△EBF≌△GBF（SAS），∴EF=GF，∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=10．【点睛】本题主要考查了三角形全等的判定和性质，灵活运用全等三角形的性质和判定是解答本题的关键.但本题分为三问，难度不断增加，对提升思维能力大有好处.2．如图1，在△ACB和△AED中，AC＝BC，AE＝DE，∠ACB＝∠AED＝90°，点E在AB上，F是线段BD的中点，连接CE、FE．（1）请你探究线段CE与FE之间的数量关系（直接写出结果，不需说明理由）；（2）将图1中的△AED绕点A顺时针旋转，使△AED的一边AE恰好与△ACB的边AC在同一条直线上（如图2），连接BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由；（3）将图1中的△AED绕点A顺时针旋转任意的角度（如图3），连接BD，取BD的中点F，问（1）中的结论是否仍然成立，并说明理由．【答案】（1）线段CE与FE之间的数量关系是CE2FE；（2）（1）中的结论仍然成立．理由见解析；（3）（1）中的结论仍然成立．理由见解析【解析】【分析】（1）连接CF，直角△DEB中，EF是斜边BD上的中线，因此EF=DF=BF，∠FEB=∠FBE，同理可得出CF=DF=BF，∠FCB=∠FBC，因此CF=EF，由于∠DFE=∠FEB+∠FBE=2∠FBE，同理∠DFC=2∠FBC，因此∠EFC=∠EFD+∠DFC=2（∠EBF+∠CBF）=90°，因此△EFC是等腰直角三角形，2EF；（2）思路同（1）也要通过证明△EFC是等腰直角三角形来求解．连接CF，延长EF交CB 于点G，先证△EFC是等腰三角形，可通过证明CF是斜边上的中线来得出此结论，那么就要证明EF=FG，就需要证明△DEF和△FGB全等．这两个三角形中，已知的条件有一组对顶角，DF=FB，只要再得出一组对应角相等即可，我们发现DE∥BC，因此∠EDB=∠CBD，由此构成了两三角形全等的条件．EF=FG，那么也就能得出△CFE是个等腰三角形了，下面证明△CFE是个直角三角形．由上面的全等三角形可得出ED=BG=AD，又由AC=BC，因此CE=CG，∠CEF=45°，在等腰△CFE中，∠CEF=45°，那么这个三角形就是个等腰直角三角形，因此就能得出（1）中的结论了；（3）思路同（2）通过证明△CFE来得出结论，通过全等三角形来证得CF=FE，取AD的中点M，连接EM，MF，取AB的中点N，连接FN、CN、CF．那么关键就是证明△MEF和△CFN全等，利用三角形的中位线和直角三角形斜边上的中线，我们不难得出EM=PN=12AD，EC=MF=12AB，我们只要再证得两对应边的夹角相等即可得出全等的结论．我们知道PN是△ABD的中位线，那么我们不难得出四边形AMPN为平行四边形，那么对角就相等，于是90°+∠CNF=90°+∠MEF，因此∠CNF=∠MEF，那么两三角形就全等了．证明∠CFE是直角的过程与（1）完全相同．那么就能得出△CEF是个等腰直角三角形，于是得出的结论与（1）也相同．【详解】（1）如图1，连接CF，线段CE与FE之间的数量关系是CE＝2FE；解法1：∵∠AED＝∠ACB＝90°∴B、C、D、E四点共圆且BD是该圆的直径，∵点F是BD的中点，∴点F是圆心，∴EF＝CF＝FD＝FB，∴∠FCB＝∠FBC，∠ECF＝∠CEF，由圆周角定理得：∠DCE＝∠DBE，∴∠FCB+∠DCE＝∠FBC+∠DBE＝45°∴∠ECF＝45°＝∠CEF，∴△CEF是等腰直角三角形，∴CE＝2EF．解法2：易证∠BED＝∠ACB＝90°，∵点F是BD的中点，∴CF＝EF＝FB＝FD，∵∠DFE＝∠ABD+∠BEF，∠ABD＝∠BEF，∴∠DFE＝2∠ABD，同理∠CFD＝2∠CBD，∴∠DFE+∠CFD＝2（∠ABD+∠CBD）＝90°，即∠CFE＝90°，∴CE＝2EF．（2）（1）中的结论仍然成立．解法1：如图2﹣1，连接CF，延长EF交CB于点G，∵∠ACB＝∠AED＝90°，∴DE∥BC，∴∠EDF＝∠GBF，又∵∠EFD＝∠GFB，DF＝BF，∴△EDF≌△GBF，∴EF＝GF，BG＝DE＝AE，∵AC＝BC，∴CE＝CG，∴∠EFC＝90°，CF＝EF，∴△CEF为等腰直角三角形，∴∠CEF＝45°，∴CE＝2FE；解法2：如图2﹣2，连结CF、AF，∵∠BAD＝∠BAC+∠DAE＝45°+45°＝90°，又点F是BD的中点，∴FA＝FB＝FD，而AC＝BC，CF＝CF，∴△ACF≌△BCF，∴∠ACF＝∠BCF＝12∠ACB＝45°，∵FA＝FB，CA＝CB，∴CF所在的直线垂直平分线段AB，同理，EF所在的直线垂直平分线段AD，又DA⊥BA，∴EF⊥CF，∴△CEF为等腰直角三角形，∴CE＝2EF．（3）（1）中的结论仍然成立．解法1：如图3﹣1，取AD的中点M，连接EM，MF，取AB的中点N，连接FN、CN、CF，∵DF＝BF，∴FM∥AB，且FM＝12 AB，∵AE＝DE，∠AED＝90°，∴AM＝EM，∠AME＝90°，∵CA＝CB，∠ACB＝90°∴CN=AN=12AB，∠ANC＝90°，∴MF∥AN，FM＝AN＝CN，∴四边形MFNA为平行四边形，∴FN＝AM＝EM，∠AMF＝∠FNA，∴∠EMF＝∠FNC，∴△EMF≌△FNC，∴FE＝CF，∠EFM＝∠FCN，由MF∥AN，∠ANC＝90°，可得∠CPF＝90°，∴∠FCN+∠PFC＝90°，∴∠EFM+∠PFC＝90°，∴∠EFC＝90°，∴△CEF为等腰直角三角形，∴∠CEF＝45°，∴CE＝2FE．【点睛】本题解题的关键是通过全等三角形来得出线段的相等，如果没有全等三角形的要根据已知条件通过辅助线来构建．3．已知△ABC中，AB=AC，点P是AB上一动点，点Q是AC的延长线上一动点，且点P从B运动向A、点Q从C运动向Q移动的时间和速度相同，PQ与BC相交于点D，若AB=82，BC=16．（1）如图1，当点P为AB的中点时，求CD的长；（2）如图②，过点P作直线BC的垂线，垂足为E，当点P、Q在移动的过程中，设BE+CD=λ，λ是否为常数？若是请求出λ的值，若不是请说明理由．【答案】（1）4；（2）8【解析】【分析】（1）过P点作PF∥AC交BC于F，由点P和点Q同时出发，且速度相同，得出BP=CQ ，根据PF ∥AQ ，可知∠PFB=∠ACB ，∠DPF=∠CQD ，则可得出∠B=∠PFB ，证出BP=PF ，得出PF=CQ ，由AAS 证明△PFD ≌△QCD ，得出，再证出F 是BC 的中点，即可得出结果；（2）过点P 作PF ∥AC 交BC 于F ，易知△PBF 为等腰三角形，可得BE=12BF ，由（1）证明方法可得△PFD ≌△QCD 则有CD=12CF ，即可得出BE +CD =8．【详解】解:（1）如图①，过P 点作PF ∥AC 交BC 于F ，∵点P 和点Q 同时出发，且速度相同，∴BP=CQ ，∵PF ∥AQ ，∴∠PFB=∠ACB ，∠DPF=∠CQD ，又∵AB=AC ，∴∠B=∠ACB ，∴∠B=∠PFB ，∴BP=PF ，∴PF=CQ ，又∠PDF=∠QDC ，∴△PFD ≌△QCD ，∴DF=CD=12CF ，又因P 是AB 的中点，PF ∥AQ ， ∴F 是BC 的中点，即FC=12BC=8， ∴CD=12CF=4；（2）8BE CD λ+==为定值．如图②，点P 在线段AB 上，过点P 作PF ∥AC 交BC 于F ，易知△PBF 为等腰三角形，∵PE ⊥BF∴BE=12BF ∵易得△PFD ≌△QCD ∴CD=12CF ∴()111182222BE CD BF CF BF CF BC λ+==+=+== 【点睛】此题考查了等腰三角形的性质，全等三角形的判断与性质，熟悉相关性质定理是解题的关键．4．如图（1），在ABC 中，90A ∠=︒，AB AC =，点D 是斜边BC 的中点，点E ，F 分别在线段AB ，AC 上，且90EDF ∠=︒．（1）求证：DEF 为等腰直角三角形；（2）若ABC 的面积为7，求四边形AEDF 的面积；（3）如图（2），如果点E 运动到AB 的延长线上时，点F 在射线CA 上且保持90EDF ∠=︒，DEF 还是等腰直角三角形吗．请说明理由．【答案】（1）证明见解析；（2）3.5；（3）是，理由见解析．【解析】【分析】（1）由题意连接AD ，并利用全等三角形的判定判定△BDE ≌△ADF(ASA)，进而分析证得DEF 为等腰直角三角形；（2）由题意分析可得S 四边形AEDF =S ∆ADF +S ∆ADE =S ∆BDE +S ∆CDF ，以此进行分析计算求出四边形AEDF的面积即可；（3）根据题意连接AD，运用全等三角形的判定判定△BDE≌△ADF(ASA)，进而分析证得DEF为等腰直角三角形.【详解】解：（1）证明：如图①，连接AD.∵∠BAC=90˚,AB=AC,点D是斜边BC的中点，∴AD⊥BC，AD=BD，∴∠1=∠B=45°，∵∠EDF=90°，∠2+∠3=90°，又∵∠3+∠4=90°，∴∠2=∠4，在△BDE 和△ADF中，∠1=∠B，AD=BD,∠2=∠4，∴△BDE≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°，∴ΔDEF为等腰直角三角形.（2）由（1）可知DE=DF，∠C=∠6=45°，又∵∠2+∠3=90°，∠2+∠5=90°，∴∠3=∠5，∴△ADE≌△CDF，∴S四边形AEDF=S∆ADF+S∆ADE=S∆BDE+S∆CDF，∴ S∆ABC=2 S四边形AEDF,∴S四边形AEDF=3.5 .（3）是.如图②，连接AD.∵∠BAC=90°，AB=AC，D是斜边BC的中点，∴AD⊥BC,AD=BD ，∴∠1=45°，∵∠DAF=180°-∠1=180°—45°=135°，∠DBE=180°-∠ABC=180°-45°=135°，∴∠DAF=∠DBE，∵∠EDF=90°，∴∠3+∠4=90°，又∵∠2+∠3=90°，∴∠2=∠4,在△BDE 和△ADF 中，∠DAF=∠DBE ，AD=BD,∠2=∠4,∴△BDE ≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°，∴△DEF 为等腰直角三角形.【点睛】本题考查等腰直角三角形的性质以及全等三角形的判定与性质，根据题意作辅助线构造出全等三角形是解题的关键．5．在ABC 中，AB AC =，点D 在BC 边上，且60,ADB E ∠=︒是射线DA 上一动点(不与点D 重合，且DA DB ≠)，在射线DB 上截取DF DE =，连接EF ．()1当点E 在线段AD 上时，①若点E 与点A 重合时，请说明线段BF DC =；②如图2，若点E 不与点A 重合，请说明BF DC AE =+；()2当点E 在线段DA 的延长线上()DE DB >时，用等式表示线段,,AE BF CD 之间的数量关系(直接写出结果，不需要证明)．【答案】（1）①证明见解析；②证明见解析；（2）BF ＝AE-CD【解析】【分析】（1）①根据等边对等角，求到B C ∠=∠，再由含有60°角的等腰三角形是等边三角形得到ADF ∆是等边三角形，之后根据等边三角形的性质以及邻补角的性质得到120AFB ADC ∠=∠=︒，推出ABF ACD ∆∆≌，根据全等三角形的性质即可得出结论；②过点A 做AG ∥EF 交BC 于点G ，由△DEF 为等边三角形得到DA ＝DG ，再推出AE ＝GF ，根据线段的和差即可整理出结论；（2）根据题意画出图形，作出AG，由（1）可知，AE=GF，DC=BG，再由线段的和差和等量代换即可得到结论．【详解】（1）①证明：AB AC=B C∴∠=∠,60DF DE ADB=∠=︒，且E与A重合，ADF∴∆是等边三角形60ADF AFD∴∠=∠=︒120AFB ADC∴∠=∠=︒在ABF∆和ACD∆中AFB ADCB CAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩ABF ACD∴∆∆≌BF DC∴=②如图2，过点A做AG∥EF交BC于点G，∵∠ADB＝60°DE＝DF∴△DEF为等边三角形∵AG∥EF∴∠DAG＝∠DEF＝60°，∠AGD＝∠EFD＝60°∴∠DAG＝∠AGD∴DA＝DG∴DA－DE＝DG－DF，即AE＝GF由①易证△AGB≌△ADC∴BG＝CD∴BF＝BG＋GF＝CD＋AE（2）如图3，和（1）中②相同，过点A做AG∥EF交BC于点G，由（1）可知，AE=GF ，DC=BG ，BF CD BF BG GF AE ∴+=+==故BF AE CD =-．【点睛】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的判定和性质，正确的作出辅助线是解题的关键．6．（1）问题发现：如图（1），已知：在三角形ABC ∆中，90BAC ︒∠=,AB AC =,直线l 经过点A ，BD ⊥直线l ，CE ⊥直线l ，垂足分别为点,D E ，试写出线段,BD DE 和CE 之间的数量关系为_________________．（2）思考探究：如图（2），将图（1）中的条件改为：在ABC ∆中, ,,,AB AC D A E =三点都在直线l 上，并且BDA AEC BAC α∠=∠=∠=，其中α为任意锐角或钝角．请问（1）中结论还是否成立？若成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图（3），,D E 是,,D A E 三点所在直线m 上的两动点，（,,D A E 三点互不重合），点F 为BAC ∠平分线上的一点，且ABF ∆与ACF ∆均为等边三角形，连接,BD CE ，若BDA AEC BAC ∠=∠=∠，试判断DEF ∆的形状并说明理由．【答案】（1）DE=CE+BD ；（2）成立，理由见解析；（3）△DEF 为等边三角形，理由见解析.【解析】【分析】（1）利用已知得出∠CAE=∠ABD ，进而根据AAS 证明△ABD 与△CAE 全等，然后进一步求解即可；（2）根据BDA AEC BAC α∠=∠=∠=，得出∠CAE=∠ABD ，在△ADB 与△CEA 中，根据AAS 证明二者全等从而得出AE=BD ，AD=CE ，然后进一步证明即可；（3）结合之前的结论可得△ADB 与△CEA 全等，从而得出BD=AE ，∠DBA=∠CAE ，再根据等边三角形性质得出∠ABF=∠CAF=60°，然后进一步证明△DBF 与△EAF 全等，在此基础上进一步证明求解即可.【详解】（1）∵BD⊥直线l，CE⊥直线l，∴∠BDA=∠AEC=90°，∴∠BAD+∠ABD=90°，∵∠BAC=90°，∴∠BAD+∠CAE=90°，∴∠CAE=∠ABD，在△ABD与△CAE中，∵∠ABD=∠CAE，∠BDA=∠AEC，AB=AC，∴△ABD≌△CAE(AAS)，∴BD=AE，AD=CE，∵DE=AD+AE，∴DE=CE+BD，故答案为：DE=CE+BD；（2）（1）中结论还仍然成立，理由如下：∠=∠=∠=，∵BDA AEC BACα∴∠DBA+∠BAD=∠BAD+∠CAE=180°−α，∴∠CAE=∠ABD，在△ADB与△CEA中，∵∠ABD=∠CAE，∠ADB=∠CEA，AB=AC，∴△ADB≌△CEA(AAS)，∴AE=BD，AD=CE，∴BD+CE=AE+AD=DE，即：DE=CE+BD，∆为等边三角形，理由如下：（3）DEF由（2）可知：△ADB≌△CEA，∴BD=EA，∠DBA=∠CAE，∵△ABF与△ACF均为等边三角形，∴∠ABF=∠CAF=60°，BF=AF，∴∠DBA+∠ABF=∠CAE+CAF，∴∠DBF=∠FAE，在△DBF与△EAF中，∵FB=FA，∠FDB=∠FAE，BD=AE，∴△DBF≌△EAF(SAS)，∴DF=EF，∠BFD=∠AFE，∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF为等边三角形.【点睛】本题主要考查了全等三角形性质与判定的综合运用，熟练掌握相关概念是解题关键.7．（1）如图（a ）所示点D 是等边ABC 边BA 上一动点（点D 与点B 不重合），连接DC ，以DC 为边在BC 上方作等边DCF ，连接AF ．你能发现线段AF 与BD 之间的数量关系吗？并证明．（2）如图（b ）所示当动点D 运动至等边ABC 边BA 的延长线上时，其他作法与（1）相同，猜想AF 与BD 在（1）中的结论是否仍然成立？（直接写出结论）（3）①如图（c ）所示，当动点D 在等边ABC 边BA 上运动时（点D 与点B 不重合），连接DC ，以DC 为边在BC 上方、下方分别作等边DCF 和等边DCF '，连接AF 、BF '，探究AF 、BF '与AB 有何数量关系？并证明．②如图（d ）所示，当动点D 在等边ABC 边BA 的延长线上运动时，其他作法与（3）①相同，①中的结论是否成立？若不成立，是否有新的结论？并证明．【答案】（1）AF=BD ，理由见解析；（2）AF=BD ，成立；（3）①AF BF AB '+=，证明见解析；②①中的结论不成立新的结论是AF AB BF '=+，理由见解析【解析】【分析】（1）根据等边三角形的三条边、三个内角都相等的性质，利用全等三角形的判定定理SAS 可证得BCD ACF △≌△，然后由全等三角形的对应边相等知AF BD = ．（2）通过证明BCD ACF △≌△，即可证明AF BD =．（3）①'AF BF AB += ，利用全等三角形BCD ACF △≌△的对应边BD AF = ，同理'BCF ACD △≌△ ，则'BF AD = ，所以'AF BF AB +=；②①中的结论不成立，新的结论是'AF AB BF =+ ，通过证明BCF ACD △≌△，则'BF AD =（全等三角形的对应边相等），再结合（2）中的结论即可证得'AF AB BF =+ ．【详解】（1）AF BD =证明如下：ABC 是等边三角形，BC AC ∴=，60BCA ︒∠=．同理可得：DC CF =，60DCF ︒∠=．BCA DCA DCF DCA ∴∠-∠=∠-∠．即BCD ACF ∠=∠．BCD ACF ∴△≌△．AF BD ∴=．（2）证明过程同（1），证得BCD ACF △≌△，则AF BD =（全等三角形的对应边相等），所以当动点D 运动至等边△ABC 边BA 的延长线上时，其他作法与（1）相同，AF BD =依然成立．（3）①AF BF AB '+=证明：由（1）知，BCD ACF △≌△．BD AF ∴=．同理BCF ACD '△≌△．BF AD '∴=．AF BF BD AD AB '∴+=+=．②①中的结论不成立新的结论是AF AB BF '=+；BC AC =，BCF ACD '∠=∠，F C DC '=，BCF ACD '∴△≌△．BF AD '∴=．又由（2）知，AF BD =．AF BD AB AD AB BF '∴==+=+．即AF AB BF '=+．【点睛】本题考查了三角形的综合问题，掌握等边三角形的三条边、三个内角都相等的性质、全等三角形的判定定理、全等三角形的对应边相等是解题的关键．8．操作发现：如图，已知△ABC 和△ADE 均为等腰三角形，AB ＝AC ，AD ＝AE ，将这两个三角形放置在一起，使点B ，D ，E 在同一直线上，连接CE ．（1）如图1，若∠ABC ＝∠ACB ＝∠ADE ＝∠AED ＝55°，求证：△BAD ≌△CAE ；（2）在（1）的条件下，求∠BEC 的度数；拓广探索：（3）如图2，若∠CAB ＝∠EAD ＝120°，BD ＝4，CF 为△BCE 中BE 边上的高，请直接写出EF 的长度．【答案】（1）见解析；（2）70°；（3）2【解析】【分析】（1）根据SAS 证明△BAD ≌△CAE 即可．（2）利用全等三角形的性质解决问题即可．（3）同法可证△BAD≌△CAE，推出EC=BD=4，由∠BEC=∠BAC=120°，推出∠FCE=30°即可解决问题．【详解】（1）证明：如图1中，∵∠ABC＝∠ACB＝∠ADE＝∠AED，∴∠EAD＝∠CAB，∴∠EAC＝∠DAB，∵AE＝AD，AC＝AB，∴△BAD≌△CAE（SAS）．（2）解：如图1中，设AC交BE于O．∵∠ABC＝∠ACB＝55°，∴∠BAC＝180°﹣110°＝70°，∵△BAD≌△CAE，∴∠ABO＝∠ECO，∵∠EOC＝∠AOB，∴∠CEO＝∠BAO＝70°，即∠BEC＝70°．（3）解：如图2中，∵∠CAB＝∠EAD＝120°，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴∠BAD＝∠ACE，BD＝EC＝4，同理可证∠BEC＝∠BAC＝120°，∴∠FEC＝60°，∵CF⊥EF，∴∠F＝90°，∴∠FCE＝30°，∴EF＝12EC＝2.【点睛】本题属于三角形综合题，考查了全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．9．在平面直角坐标系中，直线AB分别交x轴，y轴于A（a，0），B（0，b），且满足a2+b2+4a﹣8b+20＝0．（1）求a，b的值；（2）点P在直线AB的右侧；且∠APB＝45°，①若点P在x轴上（图1），则点P的坐标为；②若△ABP为直角三角形，求P点的坐标．【答案】（1）a＝﹣2，b＝4；（2）①（4，0）；②P点坐标为（4，2），（2，﹣2）．【解析】【分析】（1）利用非负数的性质解决问题即可．（2）①根据等腰直角三角形的性质即可解决问题．②分两种情形：如图2中，若∠ABP=90°，过点P作PC⊥OB，垂足为C．如图3中，若∠BAP=90°，过点P作PD⊥OA，垂足为D．分别利用全等三角形的性质解决问题即可．【详解】（1）∵a2+4a+4+b2﹣8b+16＝0∴（a+2）2+（b﹣4）2＝0∴a＝﹣2，b＝4．（2）①如图1中，∵∠APB＝45°，∠POB＝90°，∴OP＝OB＝4，∴P（4，0）．故答案为（4，0）．②∵a＝﹣2，b＝4∴OA＝2OB＝4又∵△ABP为直角三角形，∠APB＝45°∴只有两种情况，∠ABP＝90°或∠BAP＝90°①如图2中，若∠ABP＝90°，过点P作PC⊥OB，垂足为C．∴∠PCB＝∠BOA＝90°，又∵∠APB＝45°，∴∠BAP＝∠APB＝45°，∴BA＝BP，又∵∠ABO+∠OBP＝∠OBP+∠BPC＝90°，∴∠ABO＝∠BPC，∴△ABO≌△BPC（AAS），∴PC＝OB＝4，BC＝OA＝2，∴OC＝OB﹣BC＝4﹣2＝2，∴P（4，2）．②如图3中，若∠BAP＝90°，过点P作PD⊥OA，垂足为D．∴∠PDA＝∠AOB＝90°，又∵∠APB＝45°，∴∠ABP＝∠APB＝45°，∴AP＝AB，又∵∠BAD+∠DAP＝90°，∠DPA+∠DAP＝90°，∴∠BAD＝∠DPA，∴△BAO≌△APP（AAS），∴PD＝OA＝2，AD＝OB＝4，∴OD＝AD﹣0A＝4﹣2＝2，∴P（2，﹣2）．综上述，P点坐标为（4，2），（2，﹣2）．【点睛】本题属于三角形综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题．10．如图，∠BAD=∠CAE=90°，AB=AD，AE=AC，AF⊥CB，垂足为F．（1）求证：△ABC≌△ADE；（2）求∠FAE的度数；（3）求证：CD=2BF+DE．【答案】（1）证明见解析；（2）∠FAE=135°；（3）证明见解析.【解析】【分析】（1）根据已知条件易证∠BAC=∠DAE，再由AB=AD，AE=AC，根据SAS即可证得△ABC≌△ADE；（2）已知∠CAE=90°，AC=AE，根据等腰三角形的性质及三角形的内角和定理可得∠E=45°，由（1）知△BAC≌△DAE，根据全等三角形的性质可得∠BCA=∠E=45°，再求得∠CAF=45°，由∠FAE=∠FAC+∠CAE即可得∠FAE的度数；（3）延长BF到G，使得FG=FB，易证△AFB≌△AFG，根据全等三角形的性质可得AB=AG，∠ABF=∠G，再由△BAC≌△DAE，可得AB=AD，∠CBA=∠EDA，CB=ED，所以AG=AD，∠ABF=∠CDA，即可得∠G=∠CDA，利用AAS证得△CGA≌△CDA，由全等三角形的性质可得CG=CD，所以CG=CB+BF+FG=CB+2BF=DE+2BF．【详解】（1）∵∠BAD=∠CAE=90°，∴∠BAC+∠CAD=90°，∠CAD+∠DAE=90°，∴∠BAC=∠DAE，在△BAC和△DAE中，AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩， ∴△BAC ≌△DAE （SAS ）；（2）∵∠CAE=90°，AC=AE ，∴∠E=45°，由（1）知△BAC ≌△DAE ，∴∠BCA=∠E=45°，∵AF ⊥BC ，∴∠CFA=90°，∴∠CAF=45°，∴∠FAE=∠FAC+∠CAE=45°+90°=135°；（3）延长BF 到G ，使得FG=FB ，∵AF ⊥BG ，∴∠AFG=∠AFB=90°，在△AFB 和△AFG 中，BF F AFB AFG AF AF G =⎧⎪∠=∠⎨⎪=⎩， ∴△AFB ≌△AFG （SAS ），∴AB=AG ，∠ABF=∠G ，∵△BAC ≌△DAE ，∴AB=AD ，∠CBA=∠EDA ，CB=ED ，∴AG=AD ，∠ABF=∠CDA ，∴∠G=∠CDA ，在△CGA 和△CDA 中，GCA DCA CGA CDA AG AD ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△CGA ≌△CDA ，∴CG=CD ，∵CG=CB+BF+FG=CB+2BF=DE+2BF ，∴CD=2BF+DE ．【点睛】本题考查全等三角形的判定与性质，解决第3问需作辅助线，延长BF到G，使得FG=FB，证得△CGA≌△CDA是解题的关键．二、八年级数学轴对称解答题压轴题（难）11．如图，在平面直角坐标系中，已知点A（2，3），点B（﹣2，1）．（1）请运用所学数学知识构造图形求出AB的长；（2）若Rt△ABC中，点C在坐标轴上，请在备用图1中画出图形，找出所有的点C后不用计算写出你能写出的点C的坐标；（3）在x轴上是否存在点P，使PA=PB且PA+PB最小？若存在，就求出点P的坐标；若不存在，请简要说明理由（在备用图2中画出示意图）．【答案】（1）AB=52）C2（0,7），C4（0，-4），C5（-1,0）、C6（1,0）；（3）不存在这样的点P．【解析】【分析】（1）如图，连结AB，作B关于y轴的对称点D，利用勾股定理即可得出AB；（2）分别以A，B，C为直角顶点作图，然后直接得出符合条件的点的坐标即可；（3）作AB的垂直平分线l3，则l3上的点满足PA=PB，作B关于x轴的对称点B′，连结AB′，即x轴上使得PA+PB最小的点，观察作图即可得出答案．【详解】解：（1）如图，连结AB，作B关于y轴的对称点D，由已知可得，BD=4，AD=2．∴在Rt△ABD中，AB=25（2）如图，①以A为直角顶点，过A作l1⊥AB交x轴于C1，交y轴于C2．②以B为直角顶点，过B作l2⊥AB交x轴于C3，交y轴于C4．③以C为直角顶点，以AB为直径作圆交坐标轴于C5、C6、C7．（用三角板画找出也可）由图可知，C2（0,7），C4（0，-4），C5（-1,0）、C6（1,0）．（3）不存在这样的点P．作AB的垂直平分线l3，则l3上的点满足PA=PB，作B关于x轴的对称点B′，连结AB′，由图可以看出两线交于第一象限．∴不存在这样的点P．【点睛】本题考查了勾股定理，构造直角三角形，中垂线和轴对称--路径最短问题的综合作图分析，解题的关键是学会分类讨论，学会画好图形解决问题．12．如图，在△ABC中，AB＝AC，BD平分∠ABC交AC于点D，点E是BC延长线上的一点，且BD＝DE．点G是线段BC的中点，连结AG，交BD于点F，过点D作DH⊥BC，垂足为H．（1）求证：△DCE为等腰三角形；（2）若∠CDE＝22.5°，DC＝2，求GH的长；（3）探究线段CE，GH的数量关系并用等式表示，并说明理由．【答案】（1）证明见解析；（2）22；（3）CE＝2GH，理由见解析.【解析】【分析】（1）根据题意可得∠CBD＝12∠ABC＝12∠ACB，，由BD=DE，可得∠DBC＝∠E＝1 2∠ACB，根据三角形的外角性质可得∠CDE＝12∠ACB＝∠E，可证△DCE为等腰三角形；（2）根据题意可得CH=DH=1，△ABC是等腰直角三角形，由等腰三角形的性质可得BG=GC，2+1，即可求GH的值；（3）CE=2GH，根据等腰三角形的性可得BG=GC，BH=HE，可得GH＝GC﹣HC＝GC﹣（HE﹣CE）＝12BC﹣12BE+CE＝12CE，即CE=2GH【详解】证明：（1）∵AB＝AC，∴∠ABC＝∠ACB，∵BD平分∠ABC，∴∠CBD＝12∠ABC＝12∠ACB，∵BD＝DE，∴∠DBC＝∠E＝12∠ACB，∵∠ACB＝∠E+∠CDE，∴∠CDE＝12∠ACB＝∠E，∴CD＝CE，∴△DCE是等腰三角形（2）∵∠CDE＝22.5°，CD＝CE2，∴∠DCH＝45°，且DH⊥BC，∴∠HDC＝∠DCH＝45°∴DH＝CH，∵DH2+CH2＝DC2＝2，∴DH＝CH＝1，∵∠ABC＝∠DCH＝45°∴△ABC是等腰直角三角形，又∵点G是BC中点∴AG⊥BC，AG＝GC＝BG，∵BD＝DE，DH⊥BC∴BH＝HE2+1∵BH＝BG+GH＝CG+GH＝CH+GH+GH2+1∴1+2GH2+1∴GH＝2 2（3）CE＝2GH理由如下：∵AB＝CA，点G是BC的中点，∴BG＝GC，∵BD＝DE，DH⊥BC，∴BH＝HE，∵GH＝GC﹣HC＝GC﹣（HE﹣CE）＝12BC﹣12BE+CE＝12CE，∴CE＝2GH【点睛】本题是三角形综合题，考查了角平分线的性质，等腰三角形的性质，灵活运用相关的性质定理、综合运用知识是解题的关键.13．如图，将两个全等的直角三角形△ABD、△ACE拼在一起（图1）．△ABD不动，（1）若将△ACE绕点A逆时针旋转，连接DE，M是DE的中点，连接MB、MC（图2），证明：MB＝MC．（2）若将图1中的CE向上平移，∠CAE不变，连接DE，M是DE的中点，连接MB、MC （图3），判断并直接写出MB、MC的数量关系．（3）在（2）中，若∠CAE的大小改变（图4），其他条件不变，则（2）中的MB、MC的数量关系还成立吗？说明理由．【答案】（1）见解析；（2）MB=MC．理由见解析；（3）MB=MC还成立，见解析．【解析】【分析】（1）连接AM，根据全等三角形的对应边相等可得AD=AE，AB=AC，全等三角形对应角相等可得∠BAD=∠CAE，再根据等腰三角形三线合一的性质得到∠MAD=∠MAE，然后利用“边角边”证明△ABM和△ACM全等，根据全等三角形对应边相等即可得证；（2）延长DB、AE相交于E′，延长EC交AD于F，根据等腰三角形三线合一的性质得到BD=BE′，然后求出MB∥AE′，再根据两直线平行，内错角相等求出∠MBC=∠CAE，同理求出MC∥AD，根据两直线平行，同位角相等求出∠BCM=∠BAD，然后求出∠MBC=∠BCM，再根据等角对等边即可得证；（3）延长BM交CE于F，根据两直线平行，内错角相等可得∠MDB=∠MEF，∠MBD=∠MFE，然后利用“角角边”证明△MDB和△MEF全等，根据全等三角形对应边相等可得MB=MF，然后根据直角三角形斜边上的中线等于斜边的一半证明即可．【详解】（1）如图（2），连接AM，由已知得△ABD≌△ACE，∴AD=AE，AB=AC，∠BAD=∠CAE.∵MD=ME，∴∠MAD=∠MAE，∴∠MAD-∠BAD=∠MAE-∠CAE，即∠BAM=∠CAM.在△ABM和△ACM中，AB=AC，∠BAM=∠CAM，AM=AM，∴△ABM≌△ACM（SAS），∴MB=MC.（2）MB=MC．理由如下：如图（3），延长CM交DB于F，延长BM到G，使得MG=BM，连接CG.∵CE∥BD，∴∠MEC=∠MDF，∠MCE=∠MFD.∵M是ED的中点，∴MD=ME.在△MCE和△MFD中，∠MCE=∠MFD，∠MEC=∠MDF，MD=ME，∴△MCE≌△MFD（AAS）.∴MF=MC.∴在△MFB和△MCG中，MF=MC，∠FMB=∠CMG，BM=MG，∴△MFB≌△MCG（SAS）.∴FB=GC，∠MFB=∠MCG，∴CG∥BD，即G、C、E在同一条直线上.∴∠GCB=90°.在△FBC和△GCB中，FB=GC，∠FBC=∠GCB，BC=CB，∴△FBC≌△GCB（SAS）.∴FC=GB.∴MB=12GB=12FC=MC.（3）MB=MC还成立．如图（4），延长BM交CE于F，延长CM到G，使得MG=CM，连接BG.∵CE∥BD，∴∠MDB=∠MEF，∠MBD=∠MFE.又∵M是DE的中点，∴MD=ME.在△MDB和△MEF中，∠MDB=∠MEF，∠MBD=∠MFE，MD=ME，∴△MDB≌△MEF（AAS），∴MB=MF.∵CE∥BD，∴∠FCM=∠BGM.在△FCM和△BGM中，CM=MG，∠CMF=∠GMB，MF=MB，∴△FCM≌△BGM（SAS）.∴CF=BG，∠FCM=∠BGM.∴CF//BG，即D、B、G在同一条直线上.在△CFB和△BGC中，CF=BG，∠FCB=∠GBC，CB=BC，∴△CFB≌△BGC（SAS）.∴BF=CG.∴MC=12CG=12BF=MB．【点睛】本题考查了全等三角形的判定与性质，等腰三角形三线合一的性质，等角对等边的性质，直角三角形斜边上的中线等于斜边的一半的性质，以及三角形的中位线定理，综合性较强，但难度不大，作辅助线构造出等腰三角形或全等三角形是解题的关键．14．定义：如果一条线段将一个三角形分成2个小等腰三角形，我们把这条线段叫做这个三角形的“好线”：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的“好好线”.理解：（1）如图1，在ABC ∆中，AB AC =，点D 在AC 边上，且AD BD BC ==，求A ∠的大小；（2）在图1中过点C 作一条线段CE ，使BD ，CE 是ABC ∆的“好好线”；在图2中画出顶角为45的等腰三角形的“好好线”，并标注每个等腰三角形顶角的度数（画出一种即可）；应用：（3）在ABC ∆中，27B ∠=，AD 和DE 是ABC ∆的“好好线”，点D 在BC 边上，点E 在AC 边上，且AD BD =，DE CE =，请求出C ∠的度数.【答案】（1）36°；（2）见详解；（3）18°或42°【解析】【分析】（1）利用等边对等角得到三对角相等，设∠A=∠ABD=x ，表示出∠BDC 与∠C ，列出关于x 的方程，求出方程的解得到x 的值，即可确定出∠A 的度数．（2）根据（1）的解题过程作出△ABC 的“好好线”；45°自然想到等腰直角三角形，过底角一顶点作对边的高，发现形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；第二种情形以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°分别作为等腰三角形的底角或顶角，易得其中作为底角时所得的三个三角形恰都为等腰三角形；（3）用量角器，直尺标准作27°角，而后确定一边为BA ，一边为BC ，根据题意可以先固定BA 的长，而后可确定D 点，再分别考虑AD 为等腰三角形的腰或者底边，兼顾A 、E 、C 在同一直线上，易得2种三角形ABC ；根据图形易得∠C 的值；【详解】解：（1）∵AB=AC ，∴∠ABC=∠C ，∵BD=BC=AD ，∴∠A=∠ABD ，∠C=∠BDC ，设∠A=∠ABD=x，则∠BDC=2x，∠C=°180-2x可得°180-22x x∴x=36°则∠A=36°；（2）如图所示：（3）如图所示：①当AD=AE时，∵2x+x=27°+27°，∴x=18°；②当AD=DE时，∵27°+27°+2x+x=180°，∴x=42°；综上所述，∠C为18°或42°的角．【点睛】本题主要考查了三角形内角、外角间的关系及等腰三角形知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．15．（问题情境）学习《探索全等三角形条件》后，老师提出了如下问题：如图①，△ABC 中，若AB=12，AC=8，求BC边上的中线AD的取值范围．同学通过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，连接BE.根据SAS可证得到△ADC≌△EDB，从而根据“三角形的三边关系”可求得AD的取值范围是．解后反思：题目中出现“中点”“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中.（直接运用）如图②，AB⊥AC，AD⊥AE，AB=AC，AD=AE，AF是ACD的边CD上中线.求证：BE=2AF.（灵活运用）如图③，在△ABC中，∠C=90°，D为AB的中点，DE⊥DF，DE交AC于点E，DF交AB于点F，连接EF，试判断以线段AE、BF、EF为边的三角形形状，并证明你的结论.【答案】（1）2＜AD＜10；（2）见解析（3）为直角三角形，理由见解析.【解析】【分析】（1）根据△ADC≌△EDB，得到BE=AC=8，再根据三角形的构成三角形得到AE的取值，再根据D为AE中点得到AD的取值；（2）延长AF到H，使AF=HF，故△ADF≌△HCF，AH=2AF，由AB⊥AC，AD⊥AE，得到∠BAE+∠CAD=180°，又∠ACH+∠CAH+∠AHC=180°，根据∠D=∠FCH，∠DAF=∠CHF，得到∠ACH+∠CAD=180°，故∠BAE= ACH，再根据AB=AC，AD=AE即可利用SAS证明△BAE≌△ACH，故BE=AH,故可证明BE=2AF.（3）延长FD到点G，使DG=FD，连结GA，GE，证明△DBF≌△DAG，故得到FD=GD，BF=AG,由DE⊥DF，得到EF=EG,再求出∠EAG=90°，利用勾股定理即可求解.【详解】（1）∵△ADC≌△EDB，∴BE=AC=8，∵AB=12，∴12-8＜AE＜12+8，即4＜AE＜20，∵D为AE中点∴2＜AD＜10；（2）延长AF到H，使AF=HF，由题意得△ADF≌△HCF，故AH=2AF，∵AB⊥AC，AD⊥AE，。

八年级数学上册期末试卷(培优篇)(Word版含解析)

八年级数学上册期末试卷（培优篇）（Word 版含解析）一、八年级数学全等三角形解答题压轴题（难）1．如图1，在ABC ∆中，90ACB ∠=，AC BC =，直线MN 经过点C ，且AD MN ⊥于点D ，BE MN ⊥于点E ．易得DE AD BE =+（不需要证明）．（1）当直线MN 绕点C 旋转到图2的位置时，其余条件不变，你认为上述结论是否成立？若成立，写出证明过程；若不成立，请写出此时DE AD BE 、、之间的数量关系，并说明理由；（2）当直线MN 绕点C 旋转到图3的位置时，其余条件不变，请直接写出此时DE AD BE 、、之间的数量关系（不需要证明）．【答案】(1) 不成立，DE=AD-BE ，理由见解析；(2) DE=BE-AD【解析】【分析】(1)DE 、AD 、BE 之间的数量关系是DE=AD-BE ．由垂直的性质可得到∠CAD=∠BCE ，证得△ACD ≌△CBE ，得到AD=CE ，CD=BE ，即有DE=AD-BE ；(2)DE 、AD 、BE 之间的关系是DE=BE-AD ．证明的方法与(1)一样．【详解】(1)不成立．DE 、AD 、BE 之间的数量关系是DE=AD-BE ，理由如下：如图，∵∠ACB=90°，BE ⊥CE ，AD ⊥CE ，AC CB =，∴∠ACD+∠CAD=90°，又∠ACD+∠BCE=90°，∴∠CAD=∠BCE ，在△ACD 和△CBE 中，90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△CBE(AAS)，∴AD=CE，CD=BE，∴DE=CE-CD=AD-BE；(2)结论：DE=BE-AD．∵∠ACB=90°，BE⊥CE，AD⊥CE，AC CB=，∴∠ACD+∠CAD=90°，又∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ACD和△CBE中，90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△ADC≌△CEB(AAS)，∴AD=CE，DC=BE，∴DE=CD-CE=BE-AD．【点睛】本题考查了旋转的性质、直角三角形全等的判定与性质，旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角．2．（1）问题发现：如图（1），已知：在三角形ABC∆中，90BAC︒∠=,AB AC=,直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点,D E，试写出线段,BD DE和CE之间的数量关系为_________________．（2）思考探究：如图（2），将图（1）中的条件改为：在ABC∆中, ,,,AB AC D A E=三点都在直线l上，并且BDA AEC BACα∠=∠=∠=，其中α为任意锐角或钝角．请问（1）中结论还是否成立？若成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图（3），,D E是,,D A E三点所在直线m上的两动点，（,,D A E三点互不重合），点F为BAC∠平分线上的一点，且ABF∆与ACF∆均为等边三角形，连接,BD CE ，若BDA AEC BAC ∠=∠=∠，试判断DEF ∆的形状并说明理由．【答案】（1）DE=CE+BD ；（2）成立，理由见解析；（3）△DEF 为等边三角形，理由见解析.【解析】【分析】（1）利用已知得出∠CAE=∠ABD ，进而根据AAS 证明△ABD 与△CAE 全等，然后进一步求解即可；（2）根据BDA AEC BAC α∠=∠=∠=，得出∠CAE=∠ABD ，在△ADB 与△CEA 中，根据AAS 证明二者全等从而得出AE=BD ，AD=CE ，然后进一步证明即可；（3）结合之前的结论可得△ADB 与△CEA 全等，从而得出BD=AE ，∠DBA=∠CAE ，再根据等边三角形性质得出∠ABF=∠CAF=60°，然后进一步证明△DBF 与△EAF 全等，在此基础上进一步证明求解即可.【详解】（1）∵BD ⊥直线l ，CE ⊥直线l ，∴∠BDA=∠AEC=90°，∴∠BAD+∠ABD=90°，∵∠BAC=90°，∴∠BAD+∠CAE=90°，∴∠CAE=∠ABD ，在△ABD 与△CAE 中，∵∠ABD=∠CAE ，∠BDA=∠AEC ，AB=AC ，∴△ABD ≌△CAE(AAS)，∴BD=AE ，AD=CE ，∵DE=AD+AE ，∴DE=CE+BD ，故答案为：DE=CE+BD ；（2）（1）中结论还仍然成立，理由如下：∵BDA AEC BAC α∠=∠=∠=，∴∠DBA+∠BAD=∠BAD+∠CAE=180°−α，∴∠CAE=∠ABD ，在△ADB 与△CEA 中，∵∠ABD=∠CAE ，∠ADB=∠CEA ，AB=AC ，∴△ADB ≌△CEA(AAS)，∴AE=BD ，AD=CE ，∴BD+CE=AE+AD=DE，即：DE=CE+BD，为等边三角形，理由如下：（3）DEF由（2）可知：△ADB≌△CEA，∴BD=EA，∠DBA=∠CAE，∵△ABF与△ACF均为等边三角形，∴∠ABF=∠CAF=60°，BF=AF，∴∠DBA+∠ABF=∠CAE+CAF，∴∠DBF=∠FAE，在△DBF与△EAF中，∵FB=FA，∠FDB=∠FAE，BD=AE，∴△DBF≌△EAF(SAS)，∴DF=EF，∠BFD=∠AFE，∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF为等边三角形.【点睛】本题主要考查了全等三角形性质与判定的综合运用，熟练掌握相关概念是解题关键.3．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m 上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，求证:△DEF是等边三角形．【答案】(1)见解析；（2）成立，理由见解析；(3)见解析【解析】【分析】（1）因为DE=DA+AE ，故通过证BDA AEC ≅△△，得出DA=EC ，AE=BD ，从而证得DE=BD+CE.（2）成立，仍然通过证明BDA AEC ≅△△，得出BD=AE ，AD=CE ，所以DE=DA+AE=EC+BD.（3）由BDA AEC ≅△△得BD=AE ，=BDA AEC ∠∠，ABF 与ACF 均等边三角形，得==60BA AC ︒∠F ∠F ，FB=FA ，所以=BA BA AC AC ∠F ＋∠D ∠F ＋∠E ，即FBD FAB ≅∠∠，所以BDF AEF ≅△△，所以FD=FE ，BFD AFE ≅∠∠，再根据=60BFD FA BFA =︒∠＋∠D ∠，得=60AF FA =︒∠E ＋∠D ，即=60FE =︒∠D ，故DFE △是等边三角形.【详解】证明：(1)∵BD ⊥直线m ，CE ⊥直线m∴∠BDA ＝∠CEA=90°，∵∠BAC ＝90°∴∠BAD+∠CAE=90°，∵∠BAD+∠ABD=90°∴∠CAE=∠ABD ，又AB=AC ，∴△ADB ≌△CEA∴AE=BD ，AD=CE ，∴DE=AE+AD= BD+CE(2)∵∠BDA =∠BAC=α，∴∠DBA+∠BAD=∠BAD +∠CAE=180°—α∴∠DBA=∠CAE ，∵∠BDA=∠AEC=α，AB=AC∴△ADB≌△CEA，∴AE=BD，AD=CE∴DE=AE+AD=BD+CE（3）由（2）知，△ADB≌△CEA， BD=AE，∠DBA =∠CAE∵△ABF和△ACF均为等边三角形，∴∠ABF=∠CAF=60°∴∠DBA+∠ABF=∠CAE+∠CAF，∴∠DBF=∠FAE∵BF=AF，∴△DBF≌△EAF∴DF=EF，∠BFD=∠AFE∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°∴△DEF为等边三角形.【点睛】利用全等三角形的性质证线段相等是证两条线段相等的重要方法.4．如图1，已知CF是△ABC的外角∠ACE的角平分线，D为CF上一点，且DA＝DB．（1）求证：∠ACB＝∠ADB；（2）求证：AC+BC＜2BD；（3）如图2，若∠ECF＝60°，证明：AC＝BC+CD．【答案】（1）详见解析；（2）详见解析；（3）详见解析.【解析】【分析】（1）过点D分别作AC，CE的垂线，垂足分别为M，N，证明Rt△DAM≌Rt△DBN，得出∠DAM=∠DBN ，则结论得证；（2）证明Rt △DMC ≌Rt △DNC ，可得CM=CN ，得出AC+BC=2BN ，又BN ＜BD ，则结论得证；（3）在AC 上取一点P ，使CP=CD ，连接DP ，可证明△ADP ≌△BDC ，得出AP=BC ，则结论可得出．【详解】（1）证明：过点D 分别作AC ，CE 的垂线，垂足分别为M ，N ，∵CF 是△ABC 的外角∠ACE 的角平分线，∴DM ＝DN ，在Rt △DAM 和Rt △DBN 中，DA DB DM DN =⎧⎨=⎩， ∴Rt △DAM ≌Rt △DBN （HL ），∴∠DAM ＝∠DBN ，∴∠ACB ＝∠ADB ；（2）证明：由（1）知DM ＝DN ，在Rt △DMC 和Rt △DNC 中，DC DC DM DN =⎧⎨=⎩， ∴Rt △DMC ≌Rt △DNC （HL ），∴CM ＝CN ，∴AC +BC ＝AM +CM +BC ＝AM +CN +BC ＝AM +BN ，又∵AM ＝BN ，∴AC +BC ＝2BN ，∵BN ＜BD ，∴AC +BC ＜2BD ．（3）由（1）知∠CAD ＝∠CBD ，在AC 上取一点P ，使CP ＝CD ，连接DP ，∵∠ECF ＝60°，∠ACF ＝60°，∴△CDP 为等边三角形，∴DP ＝DC ，∠DPC ＝60°，∴∠APD ＝120°，∵∠ECF ＝60°，∴∠BCD ＝120°，在△ADP 和△BDC 中，APD BCD PAD CBD DA DB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△ADP ≌△BDC （AAS ），∴AP ＝BC ，∵AC ＝AP +CP ，∴AC ＝BC +CP ，∴AC ＝BC +CD ．【点睛】本题是三角形综合题，考查了等边三角形的判定与性质，全等三角形的判定与性质，角平分线的性质等知识，解题的关键是灵活运用所学知识解决问题．5．如图，ABC ∆是等边三角形，点D 在边AC 上（ “点D 不与,A C 重合），点E 是射线BC 上的一个动点（点E 不与点,B C 重合），连接DE ，以DE 为边作作等边三角形DEF ∆，连接CF .（1）如图1，当DE 的延长线与AB 的延长线相交，且,C F 在直线DE 的同侧时，过点D 作//DG AB ，DG 交BC 于点G ，求证：CF EG =；（2）如图2，当DE 反向延长线与AB 的反向延长线相交，且,C F 在直线DE 的同侧时，求证：CD CE CF =+；（3）如图3，当DE 反向延长线与线段AB 相交，且,C F 在直线DE 的异侧时，猜想CD 、CE 、CF 之间的等量关系，并说明理由.【答案】（1）证明见详解；（2）证明见详解；（3）CF =CD +CE ，理由见详解.【解析】【分析】(1)由ABC ∆是等边三角形，//DG AB ，得∠CDG=∠A=60°，∠ACB=60°，CDG ∆是等边三角形，易证∆ GDE ≅ ∆ CDF(SAS)，即可得到结论；(2)过点D 作DG ∥AB 交BC 于点G ，易证∆ GDE ≅ ∆ CDF(SAS)，即可得到结论；(3)过点D 作DG ∥AB 交BC 于点G ，易证∆ GDE ≅ ∆ CDF(SAS)，即可得到结论.【详解】（1）∵ABC ∆是等边三角形，//DG AB ，∴∠CDG=∠A=60°，∠ACB=60°，∴CDG ∆是等边三角形，∴DG=DC.∵DEF ∆是等边三角形，∴DE=DF ，∠EDF=60°，∴∠CDG-∠GDF=∠EDF-∠GDF ，即：∠GDE=∠CDF ，在∆ GDE 和∆ CDF 中，∵DE DF GDE CDF DG DC =⎧⎪∠=∠⎨⎪=⎩，∴∆ GDE ≅ ∆ CDF(SAS)，∴CF EG =；（2）过点D 作DG ∥AB 交BC 于点G ，如图2，∵ABC ∆是等边三角形，//DG AB ，∴∠CDG=∠A=60°，∠ACB=60°，∴CDG ∆是等边三角形，∴DG=DC.∵DEF ∆是等边三角形，∴DE=DF ，∠EDF=60°，∴∠CDG-∠CDE=∠EDF-∠CDE ，即：∠GDE=∠CDF ，在∆ GDE 和∆ CDF 中，∵DE DF GDE CDF DG DC =⎧⎪∠=∠⎨⎪=⎩，∴∆ GDE ≅ ∆ CDF(SAS)，∴CF GE=，∴CD CG CE GE CE CF==+=+（3）CF=CD+CE，理由如下：过点D作DG∥AB交BC于点G，如图3，∵ABC∆是等边三角形，//DG AB，∴∠CDG=∠A=60°，∠ACB=60°，∴CDG∆是等边三角形，∴DG=DC=GC.∵DEF∆是等边三角形，∴DE=DF，∠EDF=60°，∴∠CDG+∠CDE=∠EDF+∠CDE，即：∠GDE=∠CDF，在∆ GDE和∆ CDF中，∵DE DFGDE CDFDG DC=⎧⎪∠=∠⎨⎪=⎩，∴∆ GDE≅∆ CDF(SAS)，∴CF GE==GC+CE=CD+CE.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理，添加辅助线，构造全等三角形，是解题的关键.二、八年级数学轴对称解答题压轴题（难）6．如图，在ABC△中，已知AD是BC边上的中线，E是AD上一点，且BE AC=，延长BE交AC于点F，求证：AF EF=．【答案】证明见解析【解析】【分析】延长AD到点G，使得AD DG=，连接BG ，结合D是BC的中点，易证△ADC和△GDB全等，利用全等三角形性质以及等量代换，得到△AEF中的两个角相等，再根据等角对等边证得AE=EF.【详解】如图，延长AD到点G，延长AD到点G，使得AD DG=，连接BG．∵AD是BC边上的中线，∴DC DB=．在ADC和GDB△中，AD DGADC GDBDC DB=⎧⎪∠=∠⎨⎪=⎩（对顶角相等），∴ADC≌GDB△（SAS）．∴CAD G∠=∠，BG AC=．又BE AC=，∴BE BG=．∴BED G∠=∠．∵BED AEF∠=∠∴AEF CAD∠=∠，即AEF FAE∠=∠∴AF EF=．【点睛】本题考查的是全等三角形的判定与性质，根据题意构造全等三角形是解答本题的关键.7．定义：如果一条线段将一个三角形分成2个小等腰三角形，我们把这条线段叫做这个三角形的“好线”：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的“好好线”.理解：（1）如图1，在ABC ∆中，AB AC =，点D 在AC 边上，且AD BD BC ==，求A ∠的大小；（2）在图1中过点C 作一条线段CE ，使BD ，CE 是ABC ∆的“好好线”；在图2中画出顶角为45的等腰三角形的“好好线”，并标注每个等腰三角形顶角的度数（画出一种即可）；应用：（3）在ABC ∆中，27B ∠=，AD 和DE 是ABC ∆的“好好线”，点D 在BC 边上，点E 在AC 边上，且AD BD =，DE CE =，请求出C ∠的度数.【答案】（1）36°；（2）见详解；（3）18°或42°【解析】【分析】（1）利用等边对等角得到三对角相等，设∠A=∠ABD=x ，表示出∠BDC 与∠C ，列出关于x 的方程，求出方程的解得到x 的值，即可确定出∠A 的度数．（2）根据（1）的解题过程作出△ABC 的“好好线”；45°自然想到等腰直角三角形，过底角一顶点作对边的高，发现形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；第二种情形以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°分别作为等腰三角形的底角或顶角，易得其中作为底角时所得的三个三角形恰都为等腰三角形；（3）用量角器，直尺标准作27°角，而后确定一边为BA ，一边为BC ，根据题意可以先固定BA 的长，而后可确定D 点，再分别考虑AD 为等腰三角形的腰或者底边，兼顾A 、E 、C 在同一直线上，易得2种三角形ABC ；根据图形易得∠C 的值；【详解】解：（1）∵AB=AC ，∴∠ABC=∠C ，∵BD=BC=AD ，∴∠A=∠ABD ，∠C=∠BDC ，设∠A=∠ABD=x ，则∠BDC=2x ，∠C=°180-2x 可得°180-22x x = ∴x=36°则∠A=36°；（2）如图所示：（3）如图所示：①当AD=AE时，∵2x+x=27°+27°，∴x=18°；②当AD=DE时，∵27°+27°+2x+x=180°，∴x=42°；综上所述，∠C为18°或42°的角．【点睛】本题主要考查了三角形内角、外角间的关系及等腰三角形知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．8．如图，△ABC中，∠ABC=∠ACB，点D在BC所在的直线上，点E在射线AC上，且AD=AE，连接DE．⑴如图①，若∠B=∠C=35°，∠BAD=80°，求∠CDE的度数；⑵如图②，若∠ABC=∠ACB=75°，∠CDE=18°，求∠BAD的度数；⑶当点D在直线BC上（不与点B、C重合）运动时，试探究∠BAD与∠CDE的数量关系，并说明理由．【答案】(1)40°；（2）36°；（3）2∠CDE=∠BAD ，理由见解析．【解析】【分析】（1）根据等腰三角形的性质得到∠BAC=110°，根据等腰三角形的性质和三角形的外角的性质即可得到结论；（2）根据三角形的外角的性质得到∠E=75°-18°=57°，根据等腰三角形的性质和三角形的外角的性质即可得到结论；（3）设∠ABC=∠ACB=y°，∠ADE=∠AED=x°，∠CDE=α，∠BAD=β，分3种情况：①如图1，当点D 在点B 的左侧时，∠ADC=x°-α，②如图2，当点D 在线段BC 上时，∠ADC=y°+α，③如图3，当点D 在点C 右侧时，∠ADC=y°-α，根据这3种情况分别列方程组即，解方程组即可得到结论．【详解】解： (1)∵∠B=∠C=35°，∴∠BAC=110° ，∵∠BAD=80°,∴∠DAE=30°，∵AD=AE ，∴∠ADE=∠AED=75°，∴∠CDE=∠AED-∠C=75°−35°=40°；(2)∵∠ACB=75°,∠CDE=18° ，∴∠E=75°−18°=57°，∴∠ADE=∠AED=57°，∴∠ADC=39°,∵∠ABC=∠ADB+∠DAB=75° ，∴∠BAD=36°.（3）设∠ABC=∠ACB=y°，∠ADE=∠AED=x°，∠CDE=α，∠BAD=β①如图1，当点D 在点B 的左侧时，∠ADC=x°﹣α∴y x y x ααβ=+⎧⎨=-+⎩①②-②得，2α﹣β=0，∴2α=β；②如图2，当点D 在线段BC 上时，∠ADC=y°+α∴+y x y x ααβ=+⎧⎨=+⎩①② -①得，α=β﹣α，∴2α=β；③如图3，当点D 在点C 右侧时，∠ADC=y°﹣α∴180180y x y x αβα-++=⎧⎨++=⎩①②-①得，2α﹣β=0，∴2α=β．综上所述，∠BAD 与∠CDE 的数量关系是2∠CDE=∠BAD ．【点睛】本题考查了等腰三角形的性质，三角形外角的性质，三角形的内角和，熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键．9．已知如图1，在ABC ∆中，AC BC =，90ACB ∠=，点D 是AB 的中点，点E 是AB 边上一点，直线BF 垂直于直线CE 于点F ，交CD 于点G .（1）求证：AE CG =.（2）如图2，直线AH 垂直于直线CE ，垂足为点H ，交CD 的延长线于点M ，求证：BE CM =.【答案】（1）证明见解析；（2）证明见解析．【解析】【分析】（1）首先根据点D 是AB 中点，∠ACB =90°，可得出∠ACD =∠BCD =45°，判断出△AEC ≌△CGB ，即可得出AE =CG ；（2）根据垂直的定义得出∠CMA +∠MCH =90°，∠BEC +∠MCH =90°，再根据AC =BC ，∠ACM =∠CBE =45°，得出△BCE ≌△CAM ，进而证明出BE =CM ．【详解】（1）∵点D 是AB 中点，AC =BC ，∠ACB =90°，∴CD ⊥AB ，∠ACD =∠BCD =45°，∴∠CAD =∠CBD =45°，∴∠CAE =∠BCG ．又∵BF ⊥CE ，∴∠CBG +∠BCF =90°．又∵∠ACE+∠BCF=90°，∴∠ACE=∠CBG．在△AEC和△CGB中，∵CAE BCGAC BCACE CBG∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AEC≌△CGB（ASA），∴AE=CG；（2）∵CH⊥HM，CD⊥ED，∴∠CMA+∠MCH=90°，∠BEC+∠MCH=90°，∴∠CMA=∠BEC．在△BCE和△CAM中，BEC CMAACM CBEBC AC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCE≌△CAM（AAS），∴BE=CM．【点睛】本题考查了全等三角形的判定与性质，等腰直角三角形的性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．10．在等边ABC∆中，点O在BC边上，点D在AC的延长线上且OA OD=.（1）如图1，若点O为BC中点，求COD∠的度数；（2）如图2，若点O为BC上任意一点，求证AD AB BO=+.（3）如图3，若点O为BC上任意一点，点D关于直线BC的对称点为点P，连接,AP OP，请判断AOP∆的形状，并说明理由.【答案】（1）30；（2）见解析；（3）AOP∆是等边三角形，理由见解析.【解析】【分析】（1）根据三角形的等边三角形的性质可求1302CAO BAC∠=∠=︒且,90AO BC AOC⊥∠=︒，根据OA OD=，等腰三角形的性质得到D∠的度数，再通过内角和定理求AOD∠，即可求出COD∠的度数.（2）过O作//OE AB，OE交AD于E先证明COE∆为等边三角形，再根据等边三角形的性质求120AEO∠=︒，120DCO∠=︒，再证明()AOE DOC AAS∆≅∆，得到CD EA=，再通过证明得到EA BO=、AB AC=通过，又因为AD AC CD=+，通过等量代换即可得到答案.（3）通过作辅助线先证明()ODF OPF SAS ∆≅∆，得到OP OD =，又因为OA OD =，得到AO=OP ，证得AOP ∆为等腰三角形，如解析辅助线，由（2）可知得AOE DOC ∆≅∆得到AOE DOC ∠=∠,通过角的关系得到60AOP COE ∠=∠=°，即可证得AOP ∆是等边三角形.【详解】（1）∵ABC ∆为等边三角形∴60BAC ∠=︒∵O 为BC 中点∴1302CAO BAC ∠=∠=︒ 且,90AO BC AOC ⊥∠=︒∵OA OD =∴AOD ∆中，30D CAO ∠=∠=︒∴180120AOD D CAO ∠=︒-∠-∠=︒∴30COD AOD AOC ∠=∠-∠=︒（2）过O 作//OE AB ，OE 交AD 于E∵//OE AB∴60EOC ABC ∠=∠=︒60CEO CAB ∠=∠=︒∴COE ∆为等边三角形∴OE OC CE ==180120AEO CEO ∠=︒-∠=︒180120DCO ACB ∠=︒-∠=︒又∵OA OD =∴EAO CDO ∠=∠在AOE ∆和COD ∆中AOE DOCEAO CDOOA OD∠=∠⎧⎪∠=∠⎨⎪=⎩∴()AOE DOC AAS∆≅∆∴CD EA=∵EA AC CE=-BO BC CO=-∴EA BO=∴BO CD=，∵AB AC=，AD AC CD=+∴AD AB BO=+（3）AOP∆为等边三角形证明过程如下：连接,PC PD，延长OC交PD于F ∵P D、关于OC对称∴,90 PF DF PFO DFO=∠=∠=︒在ODF∆与OPF∆中，PF DFPFO DFOOF OF=⎧⎪∠=∠⎨⎪=⎩∴()ODF OPF SAS∆≅∆∴OP OD=,POC DOC∠=∠∵OA OD=∴AO=OP∴AOP∆为等腰三角形过O作//OE AB，OE交AD于E 由（2）得AOE DOC∆≅∆∴AOE DOC ∠=∠又∵POC DOC ∠=∠∴AOE POF ∠=∠∴AOE POE POF POE ∠+∠=∠+∠即AOP COE ∠=∠∵AB ∥OE ，∠B=60°∴60COE B ∠=∠=︒∴60AOP COE ∠=∠=°∴AOP ∆是等边三角形.【点睛】本题是考查了全等三角形和等边三角形的综合性问题，灵活应用全等三角形的性质得到边与角的关系，以及等边三角形的性质是解答此题的关键.三、八年级数学整式的乘法与因式分解解答题压轴题（难）11．图①是一个长为2m 、宽为2n 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形．（1）请用两种不同的方法求图②中阴影部分的面积：方法1：方法2：（2）观察图②请你写出下列三个代数式：（m+n ）2，（m ﹣n ）2，mn 之间的等量关系．；（3）根据（2）题中的等量关系，解决：已知：a ﹣b=5，ab=﹣6，求：（a+b ）2的值；【答案】（1）（m-n ）2；（m+n ）2-4mn ；（2）（m-n ）2=（m+n ）2-4mn ；（3）1.【解析】【分析】（1）方法1：表示出阴影部分的边长，然后利用正方形的面积公式列式；方法2：利用大正方形的面积减去四周四个矩形的面积列式；（2）根据不同方法表示的阴影部分的面积相同解答；（3）根据（2）的结论整体代入进行计算即可得解．【详解】解：（1）方法1：∵阴影部分的四条边长都是m-n,是正方形，∴阴影部分的面积=（m-n ）2方法2：∵阴影部分的面积=大正方形的面积减去四周四个矩形的面积∴阴影部分的面积=（m+n ）2-4mn ；（2）根据（1）中两种计算阴影部分的面积方法可知（m-n）2=（m+n）2-4mn；（3）由（2）可知（a+b）2=（a-b）2+4ab，∵a-b=5，ab=-6，∴（a+b）2=（a-b）2+4ab=52+4×（-6）=25-24=1.【点睛】本题考查几何图形与完全平方公式，应从整体和部分两方面来理解完全平方公式的几何意义；主要围绕图形面积展开分析．12．一个四位正整数m各个数位上的数字互不相同且都不为0，四位数m的前两位数字之和为5，后两位数字之和为11，称这样的四位数m为“半期数”；把四位数m的各位上的数字依次轮换后得到新的四位数m′，设m′＝abcd，在m′的所有可能的情况中，当|b+2c﹣a ﹣d|最小时，称此时的m′是m的“伴随数”，并规定F（m′）＝a2+c2﹣2bd；例如：m＝2365，则m′为：3652，6523，5236，因为|6+10﹣3﹣2|＝11，|5+4﹣6﹣3|＝0，|2+6﹣5﹣6|＝3，0最小，所以6523叫做2365的“伴随数”，F（5236）＝52+32﹣2×2×6＝10．（1）最大的四位“半期数”为；“半期数”3247的“伴随数”是．（2）已知四位数P＝abcd是“半期数”，三位数Q＝2ab，且441Q﹣4P＝88991，求F（P'）的最大值．【答案】（1）4192，7324；（2）42.【解析】【分析】（1）根据“半期数”的定义分析最大的四位“半期数”应该是千位最大，最大只能为4，所以百位是1，十位最大是9，个位是2，所以最大半期数为：4192，分析3247的所有可能为，2473，4732，7324．根据题意|b+2c﹣a﹣d|最小的数是7324，所以3247的“伴随数”是：7324．（2）根据定义可知a+b=5，c+d=11．再根据441Q﹣4P=88991，可以算出P的值，从而求出F（P'）的最大值．【详解】解；（1）根据题意可得最大的四位“半期数”应该是千位最大，最大只能为4，所以百位是1，十位最大是9，个位是2，所以最大半期数为：4192．∵3247的所有可能为，2473，4732，7324．∵|4+14﹣2﹣3|=13，|7+6﹣4﹣2|=7，|3+4﹣7﹣4|=4， 4最小，所以7324为3247的“伴随数”．故答案为4192；7324．（2）∵P为“半期数”∴a+b=5，c+d=11，∴b=5﹣a，d=11﹣c，∴P=1000a+100（5﹣a）+10c+11﹣c=900a+9c+511．∵Q=200+10a+c，∴441Q﹣4P=88991，∴441（200+10a+c）﹣4（900a+9c+511）=88991化简得：2a+c=7①当a=1时，c=5，此时这个四位数为1456符合题意；②当a=2时，c=3，此时这个四位数为2338不符合题意，舍去；③当a=3时，c=1，不符合题意，舍去；综上所述：这个四位数只能是1456，则P'可能为4561，5614，6145．∵|5+12﹣4﹣1|=12，|6+2﹣5﹣4|=1，|1+8﹣6﹣5|=2，1最小，所以5614为P的“伴随数”，∴F（5614）=a2+c2﹣2bd=25+1﹣2×6×4=﹣22；F（4561）=a2+c2﹣2bd=16+36﹣2×5×1=42；F（6145）=a2+c2﹣2bd=36+16﹣2×1×5=42；∴F（P'）的最大值为42．【点睛】解决本道题的关键是理解好半期数的定义：一个四位正整数m各个数位上的数字互不相同且都不为0，四位数m的前两位数字之和为5，后两位数字之和为11，称这样的四位数m 为“半期数”，然后根据当|b+2c﹣a﹣d|最小时，称此时的m'是m的“伴随数”来确定伴随数．13．阅读材料后解决问题：小明遇到下面一个问题：计算（2+1）（22+1）（24+1）（28+1）．经过观察，小明发现如果将原式进行适当的变形后可以出现特殊的结构，进而可以应用平方差公式解决问题，具体解法如下：（2+1）（22+1）（24+1）（28+1）=（2+1）（2﹣1）（22+1）（24+1）（28+1）=（22﹣1）（22+1）（24+1）（28+1）=（24﹣1）（24+1）（28+1）=（28﹣1）（28+1）=216﹣1请你根据小明解决问题的方法，试着解决以下的问题：（1）（2+1）（22+1）（24+1）（28+1）（216+1）=_____．（2）（3+1）（32+1）（34+1）（38+1）（316+1）=_____．（3）化简：（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）．【答案】232﹣13231 2-；【解析】【分析】（1）原式变形后，利用题中的规律计算即可得到结果；（2）原式变形后，利用题中的规律计算即可得到结果；（3）分m=n与m≠n两种情况，化简得到结果即可．【详解】（1）原式=（2-1）（2+1）（22+1）（24+1）（28+1）（216+1）=232-1；（2）原式=12（3-1）（3+1）（32+1）（34+1）（38+1）（316+1）=32312-；（3）（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）．当m≠n时，原式=1m n-（m-n）（m+n）（m2+n2）（m4+n4）（m8+n8）（m16+n16）=3232m nm n--；当m=n时，原式=2m•2m2…2m16=32m31．【点睛】此题考查了平方差公式，弄清题中的规律是解本题的关键．14．由多项式的乘法：(x＋a)(x＋b)＝x2＋(a＋b)x＋ab，将该式从右到左使用，即可得到用“十字相乘法”进行因式分解的公式：x2＋(a＋b)x＋ab＝(x＋a)(x＋b)．实例分解因式：x2＋5x＋6＝x2＋(2＋3)x＋2×3＝(x＋2)(x＋3)．(1)尝试分解因式：x2＋6x＋8；(2)应用请用上述方法解方程：x2－3x－4＝0.【答案】(1) (x+2)(x＋4)；(2) x＝4或x＝－1.【解析】【分析】（1）类比题干因式分解方法求解可得；（2）利用十字相乘法将左边因式分解后求解可得．【详解】(1)原式=(x+2)(x＋4)；(2)x2－3x－4＝(x－4)(x＋1)＝0，所以x－4＝0或x＋1＝0，即x＝4或x＝－1.【点睛】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．15．观察下列等式：12×231=132×21，13×341=143×31，23×352=253×32，34×473=374×43，62×286=682×26，…以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间具有相同规律，我们称这类等式为“数字对称等式”．（1）根据上述各式反映的规律填空，使式子称为“数字对称等式”：①52×=×25；② ×396=693× ．（2）设这类等式左边两位数的十位数字为a ，个位数字为b ，且2≤a+b≤9，写出表示“数字对称等式”一般规律的式子（含a 、b ），并证明．【答案】解：（1）①275；572.②63；36.（2）“数字对称等式”一般规律的式子为：（10a+b ）×[100b+10（a+b ）+a]=[100a+10（a+b ）+b]×（10b+a ），证明见解析.【解析】【分析】根据题意可得三位数中间的数等于两数的和，根据这一规律然后进行填空，从而得出答案；根据题意得出一般性的规律，然后根据多项式的计算法则进行说明理由．【详解】（1）①275,572; ②63,36；（2）“数字对称等式”一般规律的式子为：（10a+b ）×[100b+10（a+b ）+a]=[100a+10（a+b ）+b]×（10b+a ）.证明如下：∵左边两位数的十位数字为a ，个位数字为b ，∴左边的两位数是10a+b ，三位数是100b+10（a+b ）+a ，右边的两位数是10b+a ，三位数是100a+10（a+b ）+b ，∴左边=（10a+b ）×[100b+10（a+b ）+a]=（10a+b ）（100b+10a+10b+a ）=（10a+b ）（110b+11a ）=11（10a+b ）（10b+a ），右边=[100a+10（a+b ）+b]×（10b+a ）=（100a+10a+10b+b ）（10b+a ）=（110a+11b ）（10b+a ）=11（10a+b ）（10b+a ），∴左边=右边.∴“数字对称等式”一般规律的式子为：（10a+b ）×[100b+10（a+b ）+a]=[100a+10（a+b ）+b]×（10b+a ）.考点：规律题四、八年级数学分式解答题压轴题（难）16．阅读下面材料并解答问题材料：将分式322231x x x x --++-+拆分成一个整式与一个分式（分子为整数）的和的形式．解：由分母为21x -+，可设()322231()x x x x x a b --++=-+++，则323223x x x x ax x a b --++=--+++∵对任意x 上述等式均成立，∴2a =且3a b +=，∴2a =，1b =∴()2322221(2)12312111x x x x x x x x x -+++--++==++-+-+-+ 这样，分式322231x x x x --++-+被拆分成了一个整式2x +与一个分式211x -+的和解答：（1）将分式371x x +-拆分成一个整式与一个分式（分子为整数）的和的形式（2）求出422681x x x --+-+的最小值．【答案】（1）3+101x -；（2）8 【解析】【分析】（1）直接把分子变形为3(x-1)+10解答即可；（2）由分母为-x 2+1，可设-x 4-6x 2+8=(-x 2+1)(x 2+a)+b ，按照题意，求出a 和b 的值，即可把分式422681x x x --+-+拆分成一个整式与一个分式（分子为整数）的和的形式．【详解】解：（1）371x x +-=33101x x -+- =()31101x x -+- =3+101x -；（2）由分母为21x -+，可设4268x x --+()()221x x a b =-+++，则4268x x --+ ()()221x x a b =-+++422x ax x a b =--+++ 42(1)()x a x a b =---++．∵对于任意的x ，上述等式均成立，∴168a a b -=⎧⎨+=⎩解得71a b =⎧⎨=⎩∴422681x x x --+-+()()2221711x x x -+++=-+()()222217111x x x x -++=+-+-+ 22171x x =++-+． ∴当x=0时，22171x x ++-+取得最小值8，即 422681x x x --+-+的最小值是8．【点睛】本题主要考查分式的混合运算，解答本题的关键是理解阅读材料中的方法，并能加以正确应用．17．已知11x a b c ⎛⎫=+ ⎪⎝⎭，11y b a c ⎛⎫=+ ⎪⎝⎭，11z c a b ⎛⎫=+ ⎪⎝⎭．（1）当1a =，1b =，2c =时，求1111x y +--的值；（2）当0ab bc ac ++≠时,求111111x y z +++++的值．【答案】（1）4；（2）1【解析】【分析】（1）分别对x 、y 进行化简，然后求值即可；(2)分别求出1x ＋、1y ＋、和z 1＋值，然后代入化简即可.【详解】（1）,,ac ab bc ab bc ac x y z bc ac ab+++===，当1,1,2a b c ===时， 1211111=;122x ⨯+⨯∴-=-⨯ 1211111=122y ⨯+⨯∴-=-⨯ 1111=4111122x y ∴+=+-- （2）11ac ab ac ab bc x bc bc ++++=+=， 11bc ab bc ab ac y ac ac++++=+=，11bc ac bc ac ab z ab ab++++=+=， ∵+0ab bc ac +≠，∴111111;+++x y z bc ac ab ab bc ac ab bc ac ab bc ac+++++=+++++ ++ab bc ac ab bc ac+=+ =1.【点睛】本题考查了整式的化简求值问题，解题的关键是仔细认真的进行整式的化简.18．某商场计划销售A ，B 两种型号的商品，经调查，用1500元采购A 型商品的件数是用600元采购B 型商品的件数的2倍，一件A 型商品的进价比一件B 型商品的进价多30元．（1）求一件A ，B 型商品的进价分别为多少元？（2）若该商场购进A ，B 型商品共100件进行试销，其中A 型商品的件数不大于B 型的件数，已知A 型商品的售价为200元/件，B 型商品的售价为180元/件，且全部能售出，求该商品能获得的利润最小是多少？【答案】(1) B 型商品的进价为120元， A 型商品的进价为150元;(2) 5500元.【解析】分析：（1）设一件B 型商品的进价为x 元，则一件A 型商品的进价为（x+30）元，根据“用1500元采购A 型商品的件数是用600元采购B 型商品的件数的2倍”，这一等量关系列分式方程求解即可；（2）根据题意中的不等关系求出A 商品的范围，然后根据利润=单价利润×减数函数关系式，根据函数的性质求出最值即可.详解：（1）设一件B 型商品的进价为x 元，则一件A 型商品的进价为（x+30）元．由题意： =×2，解得x=120，经检验x=120是分式方程的解，答：一件B 型商品的进价为120元，则一件A 型商品的进价为150元．（2）因为客商购进A 型商品m 件，销售利润为w 元．m≤100﹣m ，m≤50，由题意：w=m （200﹣150）+（100﹣m ）（180﹣120）=﹣10m+6000，∵﹣10＜0，∴m=50时，w 有最小值=5500（元）点睛：此题主要考查了分式方程和一次函数的应用等知识，解题关键是理解题意，学会构建方程或一次函数解决问题，注意解方式方程时要检验.19．杨梅是漳州的特色时令水果.杨梅一上市，水果店的老板用1200元购进一批杨梅，很快售完；老板又用2500元购进第二批杨梅，所购件数是第一批的2倍，但进价每件比第一批多了5元.（1）第一批杨梅每件进价多少元？（2）老板以每件150元的价格销售第二批杨梅，售出80%后，为了尽快售完，决定打折促销.要使得第二批杨梅的销售利润不少于320元，剩余的杨梅每件售价至少打几折（利润-售价-进价）？【答案】（1）120元（2）至少打7折．【解析】【分析】（1）设第一批杨梅每件进价是x元，则第二批每件进价是（x+5）元，再根据等量关系：第二批杨梅所购件数是第一批的2倍；（2）设剩余的杨梅每件售价y元，由利润=售价-进价，根据第二批的销售利润不低于320元，可列不等式求解．【详解】解：(1)设第一批杨梅每件进价是x元，则120025002,5 x x⨯=+解得120.x=经检验，x=120是原方程的解且符合题意．答：第一批杨梅每件进价为120元．(2)设剩余的杨梅每件售价打y折．则2500250015080%150(180%)0.12?500320. 125125y⨯⨯+⨯⨯-⨯-≥解得y≥7.答：剩余的杨梅每件售价至少打7折．【点睛】考查分式方程的应用, 一元一次不等式的应用，读懂题目，从题目中找出等量关系以及不等关系是解题的关键.20．“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行，也给自行车商家带来商机．某自行车行经营的A型自行车去年销售总额为8万元．今年该型自行车每辆售价预计比去年降低200元．若该型车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求：（1）A型自行车去年每辆售价多少元；（2）该车行今年计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍．已知，A型车和B型车的进货价格分别为1500元和1800元，计划B 型车销售价格为2400元，应如何组织进货才能使这批自行车销售获利最多．【答案】(1) 2000元；（2） A型车20辆，B型车40辆．【解析】【分析】（1）设去年A 型车每辆售价x 元，则今年售价每辆为（x ﹣200）元，由卖出的数量相同列出方程求解即可；（2）设今年新进A 型车a 辆，则B 型车（60﹣a ）辆，获利y 元，由条件表示出y 与a 之间的关系式，由a 的取值范围就可以求出y 的最大值．【详解】解：（1）设去年A 型车每辆售价x 元，则今年售价每辆为（x ﹣200）元，由题意，得 8000080000(110%)200x x -=-，解得：x=2000．经检验，x=2000是原方程的根．答：去年A 型车每辆售价为2000元；（2）设今年新进A 型车a 辆，则B 型车（60﹣a ）辆，获利y 元，由题意，得y=a+（60﹣a ），y=﹣300a+36000．∵B 型车的进货数量不超过A 型车数量的两倍，∴60﹣a≤2a ，∴a≥20．∵y=﹣300a+36000．∴k=﹣300＜0，∴y 随a 的增大而减小．∴a=20时，y 最大=30000元．∴B 型车的数量为：60﹣20=40辆．∴当新进A 型车20辆，B 型车40辆时，这批车获利最大．【点睛】本题考查分式方程的应用；一元一次不等式的应用．五、八年级数学三角形解答题压轴题（难）21．（1）如图1，把△ABC 纸片沿DE 折叠，当点A 落在四边形BCDE 内部时，①写出图中一对全等的三角形，并写出它们的所有对应角；②设AED ∠的度数为x ，∠ADE 的度数为y ，那么∠1，∠2的度数分别是多少？（用含有x 或y 的代数式表示）③∠A 与∠1、∠2之间有一种数量关系始终保持不变，请找出这个规律．(2)如图2，把△ABC 纸片沿DE 折叠，当点A 落在四边形BCDE 外部时，∠A 与∠1、∠2的数量关系是否发生变化？如果发生变化，求出∠A 与∠1、∠2的数量关系；如果不发生变化，请说明理由.。

八年级上册数学期末试卷培优测试卷

八年级上册数学期末试卷培优测试卷一、八年级数学全等三角形解答题压轴题（难）1．取一副三角板按图()1拼接，固定三角板60,()30ADC D ACD ∠=∠=，将三角板45()ABC BAC BCA ∠=∠=绕点A 依顺时针方向旋转一个大小为a 的角00)45(a ≤≤得到ABM ，图()2所示．试问：()1当a 为多少时，能使得图()2中//AB CD ？说出理由，()2连接BD ，假设AM 与CD 交于,E BM 与CD 交于F ，当00)45(a ≤≤时，探索DBM CAM BDC ∠+∠+∠值的大小变化情况，并给出你的证明．【答案】（1）15°；（2）DBM CAM BDC ∠+∠+∠的大小不变，是105，证明见解析．【解析】【分析】（1）由//AB CD 得到30BAC C ∠=∠=，即可求出a ；（2）DBM CAM BDC ∠+∠+∠的大小不变，是105︒,由FEM CAM C ∠=∠+∠，30C ∠=︒， EFM BDC DBM ∠=∠+∠， 45M ∠=︒，即可利用三角形内角和求出答案.【详解】()1当a 为15时，//AB CD ，理由：由图()2，若//AB CD ，则30BAC C ∠=∠=， 453015a CAM BAM BAC ∴=∠=∠-∠=-︒=︒，所以，当a 为15时，//AB CD ．注意：学生可能会出现两种解法：第一种：把//AB CD 当做条件求出a 为15，第二种：把a 为15当做条件证出//AB CD ，这两种解法都是正确的．()2DBM CAM BDC ∠+∠+∠的大小不变，是105︒证明： ,30FEM CAM C C ∠=∠+∠∠=︒,30FEM CAM ∴∠=∠+︒,EFM BDC DBM ∠=∠+∠,DBM CAM BDC EFM CAM ∴∠+∠+∠=∠+∠,180,45EFM FEM M M ∠+∠+∠=∠=︒,3045180BDC DBM CAM ∴∠+∠+∠+︒+︒=︒,1803045105DBM CAM BDC ∴∠+∠+∠=︒--=︒,所以，DBM CAM BDC ∠+∠+∠的大小不变，是105.【点睛】此题考查旋转的性质，平行线的性质，三角形的外角定理，三角形的内角和，（2）中将角度和表示为三角形的外角是解题的关键.2．（1）如图（1），已知：在△ABC 中，∠BAC ＝90°，AB=AC ，直线m 经过点A ，BD ⊥直线m, CE ⊥直线m,垂足分别为点D 、E.证明:DE=BD+CE.（2）如图（2），将（1）中的条件改为：在△ABC 中，AB=AC ，D 、A 、E 三点都在直线m 上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.（3）拓展与应用：如图（3），D 、E 是D 、A 、E 三点所在直线m 上的两动点（D 、A 、E 三点互不重合）,点F 为∠BAC 平分线上的一点,且△ABF 和△ACF 均为等边三角形，连接BD 、CE,若∠BDA=∠AEC=∠BAC ，试判断△DEF 的形状.【答案】（1）见解析（2）成立（3）△DEF 为等边三角形【解析】解：（1）证明：∵BD ⊥直线m ，CE ⊥直线m ，∴∠BDA ＝∠CEA=900．∵∠BAC ＝900，∴∠BAD+∠CAE=900．∵∠BAD+∠ABD=900，∴∠CAE=∠ABD ．又AB="AC" ，∴△ADB ≌△CEA （AAS ）．∴AE=BD ，AD=CE ．∴DE="AE+AD=" BD+CE ．（2）成立．证明如下：∵∠BDA =∠BAC=α，∴∠DBA+∠BAD=∠BAD +∠CAE=1800—α．∴∠DBA=∠CAE ． ∵∠BDA=∠AEC=α，AB=AC ，∴△ADB ≌△CEA （AAS ）．∴AE=BD ，AD=CE ．∴DE=AE+AD=BD+CE ．（3）△DEF 为等边三角形．理由如下：由（2）知，△ADB ≌△CEA ，BD=AE ，∠DBA =∠CAE ，∵△ABF 和△ACF 均为等边三角形，∴∠ABF=∠CAF=600．∴∠DBA+∠ABF=∠CAE+∠CAF ．∴∠DBF=∠FAE ．∵BF=AF ，∴△DBF ≌△EAF （AAS ）．∴DF=EF ，∠BFD=∠AFE ．∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600．∴△DEF 为等边三角形．（1）因为DE=DA+AE ，故由AAS 证△ADB ≌△CEA ，得出DA=EC ，AE=BD ，从而证得DE=BD+CE ．（2）成立，仍然通过证明△ADB ≌△CEA ，得出BD=AE ，AD=CE ，所以DE=DA+AE=EC+BD ．（3）由△ADB ≌△CEA 得BD=AE ，∠DBA =∠CAE ，由△ABF 和△ACF 均等边三角形，得∠ABF=∠CAF=600，FB=FA ，所以∠DBA+∠ABF=∠CAE+∠CAF ，即∠DBF=∠FAE ，所以△DBF ≌△EAF ，所以FD=FE ，∠BFD=∠AFE ，再根据∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=600得到△DEF 是等边三角形．3．如图1，在ABC ∆中，ACB ∠是直角，60B ∠=︒，AD 、CE 分别是BAC ∠、BCA ∠的平分线，AD 、CE 相交于点F ．（1）求出AFC ∠的度数；（2）判断FE 与FD 之间的数量关系并说明理由．（提示：在AC 上截取CG CD =，连接FG ．）（3）如图2，在△ABC ∆中，如果ACB ∠不是直角，而（1）中的其它条件不变，试判断线段AE、CD与AC之间的数量关系并说明理由．【答案】（1）∠AFC＝120°；（2）FE与FD之间的数量关系为：DF＝EF．理由见解析；（3）AC＝AE+CD．理由见解析．【解析】【分析】（1）根据三角形的内角和性质只要求出∠FAC，∠ACF即可解决问题;（2）根据在图2的 AC上截取CG=CD，证得△CFG≌△CFD (SAS),得出DF= GF；再根据ASA 证明△AFG≌△AFE，得EF=FG，故得出EF=FD；（3）根据(2) 的证明方法，在图3的AC上截取AG=AE，证得△EAF≌△GAF (SAS)得出∠EFA=∠GFA；再根据ASA证明△FDC≌△FGC，得CD=CG即可解决问题．【详解】（1）解：∵∠ACB＝90°，∠B＝60°，∴∠BAC＝90°﹣60°＝30°，∵AD、CE分别是∠BAC、∠BCA的平分线，∴∠FAC＝15°，∠FCA＝45°，∴∠AFC＝180°﹣（∠FAC+∠ACF）＝120°（2）解：FE与FD之间的数量关系为：DF＝EF．理由：如图2，在AC上截取CG＝CD，∵CE是∠BCA的平分线，∴∠DCF＝∠GCF，在△CFG和△CFD中，CG CDDCF GCFCF CF=⎧⎪∠=∠⎨⎪=⎩，∴△CFG≌△CFD（SAS），∴DF＝GF．∠CFD＝∠CFG由（1）∠AFC＝120°得，∴∠CFD＝∠CFG＝∠AFE＝60°，∴∠AFG＝60°，又∵∠AFE＝∠CFD＝60°，∴∠AFE＝∠AFG，在△AFG和△AFE中，AFE AFGAF AFEAF GAF∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AFG≌△AFE（ASA），∴EF＝GF，∴DF＝EF；（3）结论：AC＝AE+CD．理由：如图3，在AC上截取AG＝AE，同（2）可得，△EAF≌△GAF（SAS），∴∠EFA＝∠GFA，AG＝AE∵∠BAC+∠BCA=180°-∠B=180°-60°=120°∴∠AFC＝180°﹣(∠FAC+∠FCA)＝180°-12(∠BAC+∠BCA)=180°-12×120°=120°，∴∠EFA＝∠GFA＝180°﹣120°＝60°＝∠DFC，∴∠CFG＝∠CFD＝60°，同（2）可得，△FDC≌△FGC（ASA），∴CD＝CG，∴AC＝AG+CG＝AE+CD．【点睛】本题考查了全等三角形的判定和性质的运用，全等三角形的判定和性质是证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造全等三角形．4．已知4AB cm=，3AC BD cm==.点P在AB上以1/cm s的速度由点A向点B运动，同时点Q在BD上由点B向点D运动，它们运动的时间为()t s．（1）如图①，AC AB⊥，BD AB⊥，若点Q的运动速度与点P的运动速度相等，当1t=时，ACP△与BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；（2）如图②，将图①中的“AC AB⊥，BD AB⊥”为改“60CAB DBA∠=∠=︒”，其他条件不变．设点Q的运动速度为/xcm s，是否存在实数x，使得ACP△与BPQ全等？若存在，求出相应的x 、t 的值；若不存在，请说明理由．【答案】（1）全等，PC 与PQ 垂直；（2）存在，11t x =⎧⎨=⎩或232t x =⎧⎪⎨=⎪⎩【解析】【分析】（1）利用SAS 证得△ACP ≌△BPQ ，得出∠ACP=∠BPQ ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；（2）由△ACP ≌△BPQ ，分两种情况：①AC=BP ，AP=BQ ，②AC=BQ ，AP=BP ，建立方程组求得答案即可．【详解】解：（1）当t=1时，AP=BQ=1，BP=AC=3，又∠A=∠B=90°，在△ACP 和△BPQ 中，AP BQ A B AC BP =⎧⎪∠=∠⎨⎪=⎩，∴△ACP ≌△BPQ （SAS ）．∴∠ACP=∠BPQ ，∴∠APC+∠BPQ=∠APC+∠ACP=90°．∴∠CPQ=90°，即线段PC 与线段PQ 垂直．（2）①若△ACP ≌△BPQ ，则AC=BP ，AP=BQ ，34t t xt =-⎧⎨=⎩，解得11t x =⎧⎨=⎩， ②若△ACP ≌△BQP ，则AC=BQ ，AP=BP ，34xtt t=⎧⎨=-⎩，解得232tx=⎧⎪⎨=⎪⎩，综上所述，存在11tx=⎧⎨=⎩或232tx=⎧⎪⎨=⎪⎩使得△ACP与△BPQ全等．【点睛】本题考查全等三角形的判定与性质，在解题时注意分类讨论思想的运用．5．如图，在平面直角坐标系中，A、B坐标为()6,0、()0,6，P为线段AB上的一点．（1）如图1，若P为AB的中点，点M、N分别是OA、OB边上的动点，且保持AM ON=，则在点M、N运动的过程中，探究线段PM、PN之间的位置关系与数量关系，并说明理由．（2）如图2，若P为线段AB上异于A、B的任意一点，过B点作BD OP⊥，交OP、OA分别于F、D两点，E为OA上一点，且PEA BDO=∠∠，试判断线段OD与AE的数量关系，并说明理由．【答案】（1）PM=PN，PM⊥PN，理由见解析；（2）OD=AE，理由见解析【解析】【分析】（1）连接OP．只要证明△PON≌△PAM即可解决问题；（2）作AG⊥x轴交OP的延长线于G．由△DBO≌△GOA，推出OD=AG，∠BDO=∠G，再证明△PAE≌△PAG即可解决问题；【详解】（1）结论：PM=PN，PM⊥PN．理由如下：如图1中，连接OP．∵A、B坐标为（6，0）、（0，6），∴OB=OA=6，∠AOB=90°，∵P为AB的中点，∴OP=12AB=PB=PA ，OP ⊥AB ，∠PON=∠PAM=45°， ∴∠OPA=90°，在△PON 和△PAM 中， ON AM PON PAM OP AP =⎧⎪∠=∠⎨⎪=⎩，∴△PON ≌△PAM （SAS ），∴PN=PM ，∠OPN=∠APM ，∴∠NPM=∠OPA=90°，∴PM ⊥PN ，PM=PN ．（2）结论：OD=AE ．理由如下：如图2中，作AG ⊥x 轴交OP 的延长线于G ．∵BD ⊥OP ，∴∠OAG=∠BOD=∠OFD=90°，∴∠ODF+∠AOG=90°，∠ODF+∠OBD=90°，∴∠AOG=∠DBO ，∵OB=OA ，∴△DBO ≌△GOA ，∴OD=AG ，∠BDO=∠G ，∵∠BDO=∠PEA ，∴∠G=∠AEP ，在△PAE 和△PAG 中，AEP G PAE PAG AP AP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PAE ≌△PAG （AAS ），∴AE=AG ，∴OD=AE ．【点睛】考查了等腰直角三角形的性质、全等三角形的判定和性质、坐标与图形性质、直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．6．如图①，在ABC中，90BAC∠=︒，AB AC=，AE是过A点的一条直线，且B、C在AE的异侧，BD AE⊥于D，CE AE⊥于E.（1）求证：BD DE CE=+.（2）若将直线AE绕点A旋转到图②的位置时（BD CE<），其余条件不变，问BD与DE、CE的关系如何？请予以证明.【答案】（1）见解析；（2）BD=DE-CE，理由见解析.【解析】【分析】（1）根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AE=AD+DE，所以BD=DE+CE；（2）根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AD+AE=BD+CE，所以BD=DE-CE．【详解】解：（1）∵∠BAC=90°，BD⊥AE，CE⊥AE，∴∠BDA=∠AEC=90°，∵∠ABD+∠BAE=90°，∠CAE+∠BAE=90°∴∠ABD=∠CAE，∵AB=AC，在△ABD和△CAE中，BDA AECABD CAEAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△CAE（AAS），∴BD=AE，AD=CE，∵AE=AD+DE，∴BD=DE+CE；（2）BD与DE、CE的数量关系是BD=DE-CE，理由如下：∵∠BAC=90°，BD⊥AE，CE⊥AE，∴∠BDA=∠AEC=90°，∴∠ABD+∠DAB=∠DAB+∠CAE，∴∠ABD=∠CAE，∵AB=AC，在△ABD 和△CAE 中，BDA AEC ABD CAE AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD ≌△CAE （AAS ），∴BD=AE ，AD=CE ，∴AD+AE=BD+CE ，∵DE=BD+CE ，∴BD=DE-CE ．【点睛】此题主要考查全等三角形的判定和性质，常用的判定方法有SSS ，SAS ，AAS ，HL 等．这种类型的题目经常考到，要注意掌握．7．如图1，Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D 是BC 边的中点连接AD ，则易证AD ＝BD ＝CD ，即AD ＝12BC ；如图2，若将题中AB ＝AC 这个条件删去，此时AD 仍然等于12BC ．理由如下：延长AD 到H ，使得AH ＝2AD ，连接CH ，先证得△ABD ≌△CHD ，此时若能证得△ABC ≌△CHA ，即可证得AH ＝BC ，此时AD ＝12BC ，由此可见倍长过中点的线段是我们三角形证明中常用的方法．（1）请你先证明△ABC ≌△CHA ，并用一句话总结题中的结论；（2）现将图1中△ABC 折叠（如图3），点A 与点D 重合，折痕为EF ，此时不难看出△BDE 和△CDF 都是等腰直角三角形．BE ＝DE ，CF ＝DF ．由勾股定理可知DE 2+DF 2＝EF 2，因此BE 2+CF 2＝EF 2，若图2中△ABC 也进行这样的折叠（如图4），此时线段BE 、CF 、EF 还有这样的关系式吗？若有，请证明；若没有，请举反例．（3）在（2）的条件下，将图3中的△DEF 绕着点D 旋转（如图5），射线DE 、DF 分别交AB 、AC 于点E 、F ，此时（2）中结论还成立吗？请说明理由．图4中的△DEF 也这样旋转（如图6），直接写出上面的关系式是否成立．【答案】（1）详见解析；（2）有这样分关系式；（3）EF2＝BE2+CF2.【解析】【分析】（1）想办法证明AB∥CH，推出∠BAC＝∠ACH，再利用SAS证明△ABC≌△CHA即可．（2）有这样分关系式．如图4中，延长ED到H山顶DH＝DE．证明△EDB≌△HD （SAS），推出∠B＝∠HCD，BE＝CH，∠FCH＝90°，利用勾股定理，线段的垂直平分线的性质即可解决问题．（3）图5，图6中，上面的关系式仍然成立．【详解】（1）证明：如图2中，∵BD＝DC，∠ADB＝∠HDC，AD＝HD，∴△ADB≌△HDC（SAS），∴∠B＝∠HCD，AB＝CH，∴AB∥CH，∴∠BAC+∠ACH＝180°，∵∠BAC＝90°，∴∠ACH＝∠BAC＝90°，∵AC＝CA，∴△BAC≌△HCA（SAS），∴AH＝BC，∴AD＝DH＝BD＝DC，∴AD＝12 BC．结论：直角三角形斜边上的中线等于斜边的一半．（2）解：有这样分关系式．理由：如图4中，延长ED到H山顶DH＝DE．∵ED＝DH，∠EDB＝∠HDC，DB＝DC，∴△EDB≌△HDC（SAS），∴∠B＝∠HCD，BE＝CH，∵∠B+∠ACB＝90°，∴∠ACB+∠HCD＝90°，∴∠FCH＝90°，∴FH2＝CF2+CH2，∵DF⊥EH，ED＝DH，∴EF＝FH，∴EF2＝BE2+CF2．（3）图5，图6中，上面的关系式仍然成立．结论：EF2＝BE2+CF2．证明方法类似（2）．【点睛】本题属于几何变换综合题，考查了旋转变换，翻折变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．8．操作发现：如图，已知△ABC和△ADE均为等腰三角形，AB＝AC，AD＝AE，将这两个三角形放置在一起，使点B，D，E在同一直线上，连接CE．（1）如图1，若∠ABC＝∠ACB＝∠ADE＝∠AED＝55°，求证：△BAD≌△CAE；（2）在（1）的条件下，求∠BEC的度数；拓广探索：（3）如图2，若∠CAB＝∠EAD＝120°，BD＝4，CF为△BCE中BE边上的高，请直接写出EF的长度．【答案】（1）见解析；（2）70°；（3）2【解析】【分析】（1）根据SAS证明△BAD≌△CAE即可．（2）利用全等三角形的性质解决问题即可．（3）同法可证△BAD≌△CAE，推出EC=BD=4，由∠BEC=∠BAC=120°，推出∠FCE=30°即可解决问题．【详解】（1）证明：如图1中，∵∠ABC＝∠ACB＝∠ADE＝∠AED，∴∠EAD＝∠CAB，∴∠EAC＝∠DAB，∵AE＝AD，AC＝AB，∴△BAD≌△CAE（SAS）．（2）解：如图1中，设AC交BE于O．∵∠ABC＝∠ACB＝55°，∴∠BAC＝180°﹣110°＝70°，∵△BAD≌△CAE，∴∠ABO＝∠ECO，∵∠EOC＝∠AOB，∴∠CEO＝∠BAO＝70°，即∠BEC＝70°．（3）解：如图2中，∵∠CAB＝∠EAD＝120°，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴∠BAD＝∠ACE，BD＝EC＝4，同理可证∠BEC＝∠BAC＝120°，∴∠FEC＝60°，∵CF⊥EF，∴∠F＝90°，∴∠FCE＝30°，∴EF＝12EC＝2.【点睛】本题属于三角形综合题，考查了全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．9．已知点P是线段MN上一动点，分别以PM，PN为一边，在MN的同侧作△APM，△BPN，并连接BM，AN．（Ⅰ）如图1，当PM＝AP，PN＝BP且∠APM＝∠BPN＝90°时，试猜想BM，AN之间的数量关系与位置关系，并证明你的猜想；（Ⅱ）如图2，当△APM，△BPN都是等边三角形时，（Ⅰ）中BM，AN之间的数量关系是否仍然成立？若成立，请证明你的结论；若不成立，试说明理由．（Ⅲ）在（Ⅱ）的条件下，连接AB得到图3，当PN＝2PM时，求∠PAB度数．【答案】（1）BM＝AN，BM⊥AN．（2）结论成立.（3）90°．【解析】【分析】(1)根据已知条件可证△MBP≌△ANP，得出MB＝AN，∠PAN＝∠PMB，再延长MB交AN于点C，得出MCN90∠=︒,因此有BM⊥AN；(2)根据所给条件可证△MPB≌△APN，得出结论BM＝AN；(3)取PB的中点C，连接AC，AB，通过已知条件推出△APC为等边三角形，∠PAC＝∠PCA＝60°，再由CA＝CB，进一步得出∠PAB的度数.【详解】解：（Ⅰ）结论：BM＝AN，BM⊥AN．理由：如图1中，∵MP＝AP，∠APM＝∠BPN＝90°，PB＝PN，∴△MBP≌△ANP（SAS），∴MB＝AN．延长MB交AN于点C．∵△MBP≌△ANP，∴∠PAN＝∠PMB，∵∠PAN+∠PNA＝90°，∴∠PMB+∠PNA＝90°，∴∠MCN＝180°﹣∠PMB﹣∠PNA＝90°，∴BM⊥AN．（Ⅱ）结论成立理由：如图2中，∵△APM，△BPN，都是等边三角形∴∠APM＝∠BPN＝60°∴∠MPB＝∠APN＝120°，又∵PM＝PA，PB＝PN，∴△MPB≌△APN（SAS）∴MB＝AN．（Ⅲ）如图3中，取PB的中点C，连接AC，AB．∵△APM，△PBN都是等边三角形∴∠APM＝∠BPN＝60°，PB＝PN∵点C是PB的中点，且PN＝2PM，∴2PC＝2PA＝2PM＝PB＝PN，∵∠APC＝60°，∴△APC为等边三角形，∴∠PAC＝∠PCA＝60°，又∵CA＝CB，∴∠CAB＝∠ABC＝30°，∴∠PAB＝∠PAC+∠CAB＝90°．【点睛】本题是一道关于全等三角形的综合性题目，充分考查了学生对全等三角形的判定定理及其性质的应用的能力，此类题目常常需要数形结合，借助辅助线才得以解决，因此，作出合理正确的辅助线是解题的关键.10．如图1，等腰△ABC中，AC=BC＝42, ∠ACB=45˚，AO是BC边上的高，D为线段AO 上一动点，以CD为一边在CD下方作等腰△CDE,使CD=CE且∠DCE=45˚，连结BE.(1) 求证：△ACD≌△BCE；(2) 如图2，在图1的基础上，延长BE至Q, P为BQ上一点，连结CP、CQ,若CP＝CQ＝5,求PQ的长.(3) 连接OE，直接写出线段OE的最小值．【答案】（1）证明见解析；（2）PQ=6；（3）OE=422【解析】试题分析：()1根据SAS即可证得ACD BCE≌；()2首先过点C作CH BQ⊥于H，由等腰三角形的性质，即可求得45DAC∠=︒，则根据等腰三角形与直角三角形中的勾股定理即可求得PQ的长．()3OE BQ⊥时，OE取得最小值.试题解析：()1证明：∵△ABC与△DCE是等腰三角形，∴AC=BC,DC=EC,45ACB DCE∠=∠=，45ACD DCB ECB DCB∴∠+∠=∠+∠=，∴∠ACD=∠BCE；在△ACD和△BCE中，,AC BCACD BCEDC EC=⎧⎪∠=∠⎨⎪=⎩(SAS)ACD BCE∴≌；()2首先过点C作CH BQ⊥于H，(2)过点C作CH⊥BQ于H，∵△ABC是等腰三角形，∠ACB=45˚，AO是BC边上的高，45DAC∴∠=，ACD BCE≌，45PBC DAC∴∠=∠=，∴在Rt BHC中,2242422CH BC=⨯==，54PC CQ CH===，，3PH QH∴==，6.PQ∴=()3OE BQ ⊥时，OE 取得最小值. 最小值为：42 2.OE =-二、八年级数学轴对称解答题压轴题（难）11．已知：在平面直角坐标系中，A 为x 轴负半轴上的点，B 为y 轴负半轴上的点.(1)如图1，以A 点为顶点、AB 为腰在第三象限作等腰Rt ABC ∆，若2OA =，4OB =，试求C 点的坐标；(2)如图2，若点A 的坐标为()23,0-，点B 的坐标为()0,m -，点D 的纵坐标为n ，以B 为顶点，BA 为腰作等腰Rt ABD ∆.试问：当B 点沿y 轴负半轴向下运动且其他条件都不变时，整式2253m n +-的值是否发生变化？若不发生变化，请求出其值；若发生变化，请说明理由；(3)如图3，E 为x 轴负半轴上的一点，且OB OE =，OF EB ⊥于点F ，以OB 为边作等边OBM ∆，连接EM 交OF 于点N ，试探索：在线段EF 、EN 和MN 中，哪条线段等于EM 与ON 的差的一半？请你写出这个等量关系，并加以证明.【答案】(1) C(-6,-2);(2)不发生变化，值为3-3）EN=12(EM-ON)，证明见详解. 【解析】【分析】（1）作CQ ⊥OA 于点Q,可以证明AQC BOA ≅，由QC=AD,AQ=BO,再由条件就可以求出点C 的坐标；（2）作DP ⊥OB 于点P ，可以证明AOB BPD ≅，则有BP=OB-PO=m-(-n)=m+n 为定值，从而可以求出结论2253m n +-3-（3）作BH ⊥EB 于点B ，由条件可以得出∠1=30°,∠2=∠3=∠EMO=15°,∠EOF=∠BMG=45°,EO=BM,可以证明ENO BGM ≅，则GM=ON,就有EM-ON=EM-GM=EG ,最后由平行线分线段成比例定理就可得出EN=12(EM-ON).【详解】（1）如图（1）作CQ⊥OA于Q,∴∠AQC=90°,△为等腰直角三角形，∵ABC∴AC=AB,∠CAB=90°,∴∠QAC+∠OAB=90°,∵∠QAC+∠ACQ=90°,∴∠ACQ=∠BAO,又∵AC=AB,∠AQC=∠AOB,≅(AAS),∴AQC BOA∴CQ=AO,AQ=BO,∵OA=2,OB=4,∴CQ=2,AQ=4,∴OQ=6,∴C(-6,-2).(2)如图（2）作DP⊥OB于点P,∴∠BPD=90°,△是等腰直角三角形，∵ABD∴AB=BD,∠ABD=∠ABO+∠OBD=90°,∵∠OBD+∠BDP=90°,∴∠ABO=∠BDP,又∵AB=BD,∠AOB=∠BPD=90°,≅∴AOB BPD∴AO=BP,∵BP=OB-PO=m-(-n)=m+n,∵A ()23,0-,∴OA=23,∴m+n=23,∴当点B 沿y 轴负半轴向下运动时，AO=BP=m+n=23,∴整式2253m n +-的值不变为3-.（3）()12EN EM ON =- 证明：如图（3）所示，在ME 上取一点G 使得MG=ON,连接BG 并延长，交x 轴于H.∵OBM 为等边三角形，∴BO=BM=MO,∠OBM=∠OMB=∠BOM=60°,∴EO=MO,∠EBM=105°,∠1=30°,∵OE=OB,∴OE=OM=BM,∴∠3=∠EMO=15°,∴∠BEM=30°,∠BME=45°,∵OF⊥EB,∴∠EOF=∠BME,∴ENO BGM ≅,∴BG=EN,∵ON=MG,∴∠2=∠3,∴∠2=15°,∴∠EBG=90°,∴BG=12EG, ∴EN=12EG, ∵EG=EM-GM,∴EN=12(EM-GM), ∴EN=12(EM-ON).【点睛】本题考查了等腰直角三角形的性质，等边三角形的性质，等腰三角形的性质，三角形的外角与内角的关系，全等三角形的判定与性质，平行线分线段成比例定理的运用.12．如图，在等腰直角ABC △中，AB AC =，90BAC ∠=︒，点D 是ABC △ 内一点，连接 AD ，AE AD ⊥ 且 AE AD =，连接 BD 、CE 交于点 F .（1）如图 1，求BFC ∠的度数；（2）如图 2，连接ED 交 BC 于点 G ，连接 AG ，若 AG 平分BAD ∠，求证：2EAC EDF ∠=∠；（3）如图 3，在（2）的条件下，BF 交 AG 、AC 分别于点M 、N ，DH AM ⊥，连接 HN ，若ADN ∆的面积与DHN 的面积差为 6，6DF =，求四边形 AMFE 的面积.【答案】（1）∠BFC =90°；（2）见解析；（3）20AMFE S =四边形.【解析】【分析】（1）根据SAS 证明ABD ACE ≌，所以ABD ACF ∠=∠，所以90BFC BAC ∠=∠=︒.（2）根据题意先求出180ABG ADG ∠+∠=︒，在AB 上截取AK AD =，连接KG ，由AKG ADG ≌，180BKG AKG ∠+∠=︒，可证得BKG KBG ∠=∠，GB GK DG ==，所以DBG BDG EDF α∠=∠=∠=，因为2CAE BAD α∠=∠=，所以2CAE EDF ∠=∠．（3）根据题意和（2）中结论先证明AD AN AE ==，过 A 作BF 、CE 垂线，垂足分别为R 、T ，连接AF ，证明ANR AET ≌，所以AR AT =，然后根据等腰三角形的性质可得出DM FN =，过点H 作HP FM ⊥，垂足为P ，所以HP PM DP ==，设DP x =，DR y =，所以ADN DHN S S ∆∆-= 1122DN AR DN HP ⋅⋅-⋅ ()6y x y =+=，226DF x y =+=，求出x ，y ，不难得到AEF ANF ADM S S S ∆∆∆===4，然后可得20AMFE S =四边形.【详解】（1）因为ABC 是等腰直角三角形，所以AB AC =，90BAC DAE ∠=︒=∠，所以BAD CAE ∠=∠，因为AD AE =，所以ABD ACE ≌，所以ABD ACF ∠=∠，所以90BFC BAC ∠=∠=︒.（2）因为AD AE =，90DAE ∠=︒，所以45AED ACG ∠=︒=∠，所以CAE CGE ∠=∠，由（1）知：BAD CAE ∠=∠，所以BAD CGD ∠=∠，设2BAD CGD α∠==∠，所以1802BGD α∠=︒-，所以180BAD BGD ∠+∠=︒，所以180ABG ADG ∠+∠=︒，因为AG 平分BAD ∠，所以BAG DAG α∠=∠=，在AB 上截取AK AD =，连接KG ，因为AG AG =，所以AKG ADG ≌，所以AKG ADG ∠=∠，DG KG =，因为180BKG AKG ∠+∠=︒，所以BKG KBG ∠=∠，所以GB GK DG ==，所以DBG BDG EDF α∠=∠=∠=，因为2CAE BAD α∠=∠=，所以2CAE EDF ∠=∠．（3）由（2）知：BAG DBG α∠=∠=，因为90BAC ∠=︒，45ABC ∠=︒，所以45ABN α∠=︒-，因为2BAD α∠=，所以45ADN α∠=︒+，因为902DAN α∠=︒-，所以45AND ADN α∠=︒+=∠，所以AD AN =，因为AD AE =，所以AE AN =，过 A 作BF 、CE 垂线，垂足分别为R 、T ，连接AF ，因为45ACE ABD α∠=∠=︒-，2CAE α∠=，所以45AET ANR α∠=︒+=∠，因为AE AN =，所以ANR AET ≌，所以AR AT =，所以FA 平分BFT ∠，所以45AFN AFE ∠=∠=︒，因为45AMN ∠=︒，所以AFM AMF ∠=∠，所以AF AM =，所以FR MR =，因为DR RN =，所以DM FN =，过点H 作HP FM ⊥，垂足为P ，因为45AMN ∠=︒，90DHM ∠=︒，所以45MHP DHP HDP ∠=∠=∠=︒，所以HP PM DP ==，设DP x =，所以2DM FN x ==，设DR y =，所以2DN y =，所以2MR x y =+，因为45MAR ∠=︒，所以2AR MR x y ==+，所以ADN DHN S S ∆∆-= 1122DN AR DN HP ⋅⋅-⋅ ()6y x y =+=，因为226DF x y =+=，所以3x y +=，所以2y =，1x =，因为AF AF =，ANF AEF ∠=∠，所以AEF ANF ≌，所以FN EF =，因为AR AT =，所以AEF ANF ADM S S S ∆∆∆==，因为142ADM S DM AR ∆=⋅⋅=，所以20ADM ADN ANF AEF AMFE S S S S S ∆∆∆∆=+++=四边形.【点睛】本题是三角形综合题，考查了等腰三角形的性质、三角形内角和定理、全等三角形的判定和性质等知识点，解题的难点在于学会添加常用辅助线，构造三角形全等解决问题，属于中考压轴题.13．如图，在等边ABC ∆中，线段AM 为BC 边上的中线．动点D 在直线AM 上时，以CD 为一边在CD 的下方作等边CDE ∆，连结BE ．（1）求CAM ∠的度数；（2）若点D 在线段AM 上时，求证：ADC BEC ∆≅∆；（3）当动点D 在直线AM 上时，设直线BE 与直线AM 的交点为O ，试判断AOB ∠是否为定值？并说明理由．【答案】（1）30°；（2）证明见解析；（3）AOB ∠是定值，60AOB ∠=︒.【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC AC =，DC EC =，，60ACB DCE ∠=∠=︒，由等式的性质就可以BCE ACD ∠=∠，根据SAS 就可以得出ADC BEC ∆≅∆；（3）分情况讨论：当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，就可以求出结论；当点D 在线段AM 的延长线上时，如图2，可以得出ACD BCE ≅∆∆而有30CBE CAD ∠=∠=︒而得出结论；当点D 在线段MA 的延长线上时，如图3，通过得出ACD BCE ≅∆∆同样可以得出结论．【详解】（1）ABC ∆是等边三角形，60BAC ∴∠=︒．线段AM 为BC 边上的中线，12CAM BAC ∴∠=∠， 30CAM ∴∠=︒．（2）ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACD DCB DCB BCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=．在ADC ∆和BEC ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆；（3）AOB ∠是定值，60AOB ∠=︒，理由如下：①当点D 在线段AM 上时，如图1，由（2）可知ACD BCE ≅∆∆，则30CBE CAD ∠=∠=︒，又60ABC ∠=︒，603090CBE ABC ∴∠+∠=︒+︒=︒，ABC ∆是等边三角形，线段AM 为BC 边上的中线AM ∴平分BAC ∠，即11603022BAM BAC ∠=∠=⨯︒=︒ 903060BOA ∴∠=︒-︒=︒．②当点D 在线段AM 的延长线上时，如图2，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，ACB DCB DCB DCE ∴∠+∠=∠+∠，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆，30CBE CAD ∴∠=∠=︒，同理可得：30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．③当点D 在线段MA 的延长线上时，ABC ∆与DEC ∆都是等边三角形，AC BC ∴=，CD CE =，60ACB DCE ∠=∠=︒，60ACD ACE BCE ACE ∴∠+∠=∠+∠=︒，ACD BCE ∠∠∴=，在ACD ∆和BCE ∆中AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，()ACD BCE SAS ∴∆≅∆，CBE CAD ∴∠=∠，同理可得：30CAM ∠=︒150CBE CAD ∴∠=∠=︒30CBO ∴∠=︒，∵30BAM ∠=︒，903060BOA ∴∠=︒-︒=︒．综上，当动点D 在直线AM 上时，AOB ∠是定值，60AOB ∠=︒．【点睛】此题考查等边三角形的性质，全等三角形的判定及性质，等边三角形三线合一的性质，解题中注意分类讨论的思想解题.14．定义：如果两条线段将一个三角形分成3个小等腰三角形，我们把这两条线段叫做这个三角形的三分线．（1）如图1，在△ABC中，AB＝AC，点D在AC边上，且AD＝BD＝BC，求∠A的大小；（2）在图1中过点C作一条线段CE，使BD，CE是△ABC的三分线；在图2中画出顶角为45°的等腰三角形的三分线，并标注每个等腰三角形顶角的度数；（3）在△ABC中，∠B＝30°，AD和DE是△ABC的三分线，点D在BC边上，点E在AC 边上，且AD＝BD，DE＝CE，请直接写出∠C所有可能的值．【答案】（1）∠A＝36°；（2）如图所示：见解析；（3）如图所示：见解析；∠C为20°或40°的角．【解析】【分析】（1）利用等边对等角得到三对角相等，设∠A＝∠ABD＝x，表示出∠BDC与∠C，列出关于x的方程，求出方程的解得到x的值，即可确定出∠A的度数．（2）根据（1）的解题过程作出△ABC的三等分线；45°自然想到等腰直角三角形，过底角一顶点作对边的高，发现形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；第二种情形以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°作为等腰三角形的底角，易得此时所得的三个三角形恰都为等腰三角形；（3）用量角器，直尺标准作30°角，而后确定一边为BA，一边为BC，根据题意可以先固定BA的长，而后可确定D点，再分别考虑AD为等腰三角形的腰或者底边，兼顾A、E、C 在同一直线上，易得2种三角形ABC；根据图形易得∠C的值；【详解】（1）∵AB＝AC，∴∠ABC＝∠C，∵BD＝BC＝AD，∴∠A＝∠ABD，∠C＝∠BDC，设∠A＝∠ABD＝x，则∠BDC＝2x，∠C＝180?-x2，可得2x＝180?-x2，解得：x＝36°，则∠A＝36°；（2）根据（1）的解题过程作出△ABC的三等分线，如图1；由45°自然想到等腰直角三角形，有两种情况，①如图2，过底角一顶点作对边的高，形成一个等腰直角三角形和直角三角形．直角三角形斜边的中线可形成两个等腰三角形；②如图3，以一底角作为新等腰三角形的底角，则另一底角被分为45°和22.5°，再以22.5°作为等腰三角形的底角，易得此时所得的三个三角形恰都为等腰三角形；（3）如图4所示：①当AD＝AE时，∵2x+x＝30°+30°，∴x＝20°；②当AD＝DE时，∵30°+30°+2x+x＝180°，∴x＝40°；综上所述，∠C为20°或40°的角．【点睛】本题主要考查了三角形内角、外角间的关系及等腰三角形知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．15．已知：等边ABC中．（1）如图1，点M 是BC 的中点，点N 在AB 边上，满足60AMN ∠=︒，求AN BN的值．（2）如图2，点M 在AB 边上（M 为非中点，不与A 、B 重合），点N 在CB 的延长线上且MNB MCB ∠=∠，求证：AM BN =．（3）如图3，点P 为AC 边的中点，点E 在AB 的延长线上，点F 在BC 的延长线上，满足AEP PFC ∠=∠，求BF BE BC-的值．【答案】（1）3；（2）见解析；（3）32．【解析】【分析】（1）先证明AMB ∆，MBN ∆与MAN ∆均为直角三角形，再根据直角三角形中30所对的直角边等于斜边的一半，证明BM=2BN ，AB=2BM ，最后转化结论可得出BN 与AN 之间的数量关系即得；（2）过点M 作ME ∥BC 交AC 于E ，先证明AM=ME ，再证明MEC ∆与NBM ∆全等，最后转化边即得；（3）过点P 作PM ∥BC 交AB 于M ，先证明M 是AB 的中点，再证明EMP ∆与FCP ∆全等，最后转化边即得．【详解】（1）∵ABC ∆为等边三角形，点M 是BC 的中点∴AM 平分∠BAC ，AM BC ⊥，60B BAC ∠=∠=︒∴30BAM ∠=︒，90AMB ∠=︒∵60AMN ∠=︒∴90AMN BAM ∠+=︒∠，30∠=︒BMN∴90ANM ∠=︒∴18090BNM ANM =︒-=︒∠∠∴在Rt BNM ∆中，2BM BN =在Rt ABM ∆中，2AB BM =∴24AB AN BN BM BN =+==∴3AN BN =即3AN BN=．（2）如下图：过点M 作ME ∥BC 交AC 于E∴∠CME=∠MCB ，∠AEM=∠ACB∵ABC ∆是等边三角形∴∠A=∠ABC=∠ACB=60︒∴60AEM ACB ∠=∠=︒，120MBN =︒∠∴120CEM MBN ∠==︒∠，60AEM A ∠=∠=︒∴AM=ME∵MNB MCB ∠=∠∴∠CME=∠MNB ，MN=MC∴在MEC ∆与NBM ∆中CME MNB CEM MBN MC MN ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()MEC NBM AAS ∆∆≌∴ME BN =∴AM BN=（3）如下图：过点P 作PM ∥BC 交AB 于M∴AMP ABC =∠∠∵ABC ∆是等边三角形∴∠A=∠ABC=∠ACB=60︒，AB AC BC ==∴60AMP A ==︒∠∠∴AP MP =，180120EMP AMP =︒-=︒∠∠，180120FCP ACB =︒-=︒∠∠ ∴AMP ∆是等边三角形，120EMP FCP ==︒∠∠∴AP MP AM ==∵P点是AC的中点∴111222AP PC MP AM AC AB BC======∴12AM MB AB==在EMP∆与FCP∆中EMP FCPAEP PFCMP PC∠=∠⎧⎪∠=∠⎨⎪=⎩∴()EMP FCP AAS∆∆≌∴ME FC=∴1322BF BE FC BC BE ME BC BE MB BC BC BC BC -=+-=+-=+=+=∴3322BCBF BEBC BC-==．【点睛】本题考查全等三角形的判定，等边三角形的性质及判定，通过作等边三角形第三边的平行线构造等边三角形和全等三角形是解题关键，将多个量转化为同一个量是求比值的常用方法．16．已知如图1，在ABC∆中，AC BC=，90ACB∠=，点D是AB的中点，点E是AB边上一点，直线BF垂直于直线CE于点F，交CD于点G.（1）求证：AE CG=.（2）如图2，直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M，求证：BE CM=.【答案】（1）证明见解析；（2）证明见解析．【解析】【分析】（1）首先根据点D是AB中点，∠ACB=90°，可得出∠ACD=∠BCD=45°，判断出△AEC≌△CGB，即可得出AE=CG；（2）根据垂直的定义得出∠CMA+∠MCH=90°，∠BEC+∠MCH=90°，再根据AC=BC，∠ACM=∠CBE=45°，得出△BCE≌△CAM，进而证明出BE=CM．【详解】（1）∵点D是AB中点，AC=BC，∠ACB=90°，∴CD⊥AB，∠ACD=∠BCD=45°，∴∠CAD=∠CBD=45°，∴∠CAE=∠BCG．又∵BF⊥CE，∴∠CBG+∠BCF=90°．又∵∠ACE+∠BCF=90°，∴∠ACE=∠CBG．在△AEC和△CGB中，∵CAE BCGAC BCACE CBG∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AEC≌△CGB（ASA），∴AE=CG；（2）∵CH⊥HM，CD⊥ED，∴∠CMA+∠MCH=90°，∠BEC+∠MCH=90°，∴∠CMA=∠BEC．在△BCE和△CAM中，BEC CMAACM CBEBC AC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BCE≌△CAM（AAS），∴BE=CM．【点睛】本题考查了全等三角形的判定与性质，等腰直角三角形的性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．17．如图，已知DCE∠与AOB∠，OC平分AOB∠．(1)如图1，DCE∠与AOB∠的两边分别相交于点D、E，90AOB DCE∠=∠=︒，试判断线段CD与CE的数量关系，并说明理由.以下是小宇同学给出如下正确的解法：解：CD CE=．理由如下：如图1，过点C作C F OC⊥，交O B于点F，则90OCF∠=︒，…请根据小宇同学的证明思路，写出该证明的剩余部分．(2)你有与小宇不同的思考方法吗？请写出你的证明过程．(3)若120AOB∠=︒，60DCE∠=︒．①如图3，DCE∠与AOB∠的两边分别相交于点D、E时，(1)中的结论成立吗？为什么？线段O D、OE、OC有什么数量关系？说明理由．②如图4，DCE∠的一边与AO的延长线相交时，请回答(1)中的结论是否成立，并请直接写出线段O D、OE、OC有什么数量关系；如图5，DCE∠的一边与BO的延长线相交时，请回答(1)中的结论是否成立，并请直接写出线段O D、OE、OC有什么数量关系．【答案】(1)见解析；(2)证明见解析；(3)①成立，理由见解析；②在图4中，(1)中的结论成立，OE OD OC-=.在图5中，(1)中的结论成立，OD OE OC-=【解析】【分析】（1）通过ASA证明CDO CEF∆∆≌即可得到CD=CE；（2）过点C作CM OA⊥，CN OB⊥，垂足分别为M，N，通过AAS证明CMD CNE∆∆≌同样可得到CD=CE；（3）①方法一：过点C作C M OA⊥，CN OB⊥垂足分别为M，N，通过AAS得到CMD CNE∆∆≌，进而得到,CD CE DM EN==，利用等量代换得到=OE OD ON OM++，在Rt CMO∆中，利用30°角所对的边是斜边的一半得12OM OC=，同理得到12ON OC=，所以OE OD OC+=；方法二：以CO为一边作60FCO∠=︒，交O B于点F，通过ASA证明CDO CEF∆∆≌，得到,CD CE OD EF==，所以OE OD OE EF OF OC+=+==；②图4：以OC为一边，作∠OCF=60°与OB交于F点，利用ASA证得△COD≌△CFE，即有CD=CE，OD=EF得到OE=OF+EF=OC+OD；图5:以OC为一边，作∠OCG=60°与OA交于G点，利用ASA证得△CGD≌△COE ，即有CD=CE，OD=EF，得到OE=OF+EF=OC+OD.【详解】解：(1)OC平分AOB∠，145∠=∠2=︒∴，390245,123︒︒∴∠=-∠=∴∠=∠=∠OC FC∴=又456590︒∠+∠=∠+∠=在CDO∆与CEF∆中，1346OC FC∠=∠⎧⎪=⎨⎪∠=∠⎩()CDO CEF ASA∴∆∆≌。

八年级数学上册期末试卷(培优篇)(Word版含解析)

八年级数学上册期末试卷（培优篇）（Word 版含解析）一、八年级数学全等三角形解答题压轴题（难）1．如图，在ABC 中，45ABC ∠=,AD ,BE 分别为BC ,AC 边上的高，连接DE ,过点D 作DF DE ⊥与点F ，G 为BE 中点，连接AF ，DG ．（1）如图1，若点F 与点G 重合，求证：AF DF ⊥；（2）如图2，请写出AF 与DG 之间的关系并证明．【答案】(1)详见解析;(2)AF=2DG,且AF ⊥DG,证明详见解析.【解析】【分析】(1) 利用条件先△DAE ≌△DBF,从而得出△FDE 是等腰直角三角形,再证明△AEF 是等腰直角三角形,即可.(2) 延长DG 至点M,使GM=DG,交AF 于点H,连接BM, 先证明△BGM ≌△EGD,再证明△BDM ≌△DAF 即可推出.【详解】解:（1）证明:设BE 与AD 交于点H..如图，∵AD,BE 分别为BC,AC 边上的高,∴∠BEA=∠ADB=90°.∵∠ABC=45°,∴△ABD 是等腰直角三角形.∴AD=BD.∵∠AHE=∠BHD,∴∠DAC=∠DBH.∵∠ADB=∠FDE=90°,∴∠ADE=∠BDF.∴△DAE ≌△DBF.∴BF=AE,DF=DE.∴△FDE是等腰直角三角形.∴∠DFE=45°.∵G为BE中点,∴BF=EF.∴AE=EF.∴△AEF是等腰直角三角形.∴∠AFE=45°.∴∠AFD=90°,即AF⊥DF.（2）AF=2DG,且AF⊥DG.理由:延长DG至点M,使GM=DG,交AF于点H,连接BM,∵点G为BE的中点,BG=GE.∵∠BGM∠EGD,∴△BGM≌△EGD.∴∠MBE=∠FED=45°,BM=DE.∴∠MBE=∠EFD,BM=DF.∵∠DAC=∠DBE,∴∠MBD=∠MBE+∠DBE=45°+∠DBE.∵∠EFD=45°=∠DBE+∠BDF,∴∠BDF=45°-∠DBE.∵∠ADE=∠BDF,∴∠ADF=90°-∠BDF=45°+∠DBE=∠MBD.∵BD=AD,∴△BDM≌△DAF.∴DM=AF=2DG,∠FAD=∠BDM.∵∠BDM+∠MDA=90°,∴∠MDA+∠FAD=90°.∴∠AHD=90°.∴AF⊥DG.∴AF=2DG,且AF⊥DG【点睛】本题考查三角形全等的判定和性质,关键在于灵活运用性质.2．如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．（1）求证：BG＝CF；（2）请你判断BE+CF与EF的大小关系，并说明理由．【答案】（1）详见解析；（2）BE+CF＞EF，证明详见解析【解析】【分析】（1）先利用ASA判定△BGD≅CFD，从而得出BG=CF；（2）利用全等的性质可得GD=FD，再有DE⊥GF，从而得到EG=EF，两边之和大于第三边从而得出BE+CF＞EF．【详解】解：（1）∵BG∥AC，∴∠DBG＝∠DCF．∵D为BC的中点，∴BD＝CD又∵∠BDG＝∠CDF，在△BGD与△CFD中，∵DBG DCFBD CDBDG CDF∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BGD≌△CFD（ASA）．∴BG＝CF．（2）BE+CF＞EF．∵△BGD≌△CFD，∴GD＝FD，BG＝CF．又∵DE⊥FG，∴EG＝EF（垂直平分线到线段端点的距离相等）．∴在△EBG中，BE+BG＞EG，即BE+CF＞EF．【点睛】本题考查了三角形全等的判定和性质，要注意判定三角形全等的一般方法有：SSS、SAS、AAS、ASA、HL．3．如图①，在ABC中，90BAC∠=︒，AB AC=，AE是过A点的一条直线，且B、C在AE的异侧，BD AE⊥于D，CE AE⊥于E.（1）求证：BD DE CE=+.（2）若将直线AE绕点A旋转到图②的位置时（BD CE<），其余条件不变，问BD与DE、CE的关系如何？请予以证明.【答案】（1）见解析；（2）BD=DE-CE，理由见解析.【解析】【分析】（1）根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AE=AD+DE，所以BD=DE+CE；（2）根据已知利用AAS判定△ABD≌△CAE从而得到BD=AE，AD=CE，因为AD+AE=BD+CE，所以BD=DE-CE．【详解】解：（1）∵∠BAC=90°，BD⊥AE，CE⊥AE，∴∠BDA=∠AEC=90°，∵∠ABD+∠BAE=90°，∠CAE+∠BAE=90°∴∠ABD=∠CAE，∵AB=AC，在△ABD和△CAE中，BDA AECABD CAEAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△CAE（AAS），∴BD=AE，AD=CE，∵AE=AD+DE，∴BD=DE+CE；（2）BD与DE、CE的数量关系是BD=DE-CE，理由如下：∵∠BAC=90°，BD⊥AE，CE⊥AE，∴∠BDA=∠AEC=90°，∴∠ABD+∠DAB=∠DAB+∠CAE，∴∠ABD=∠CAE，∵AB=AC，在△ABD和△CAE中，BDA AECABD CAEAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABD≌△CAE（AAS），∴BD=AE，AD=CE，∴AD+AE=BD+CE，∵DE=BD+CE，∴BD=DE-CE．【点睛】此题主要考查全等三角形的判定和性质，常用的判定方法有SSS，SAS，AAS，HL等．这种类型的题目经常考到，要注意掌握．4．（1）问题发现：如图（1），已知：在三角形ABC∆中，90BAC︒∠=,AB AC=,直线l经过点A，BD⊥直线l，CE⊥直线l，垂足分别为点,D E，试写出线段,BD DE和CE之间的数量关系为_________________．（2）思考探究：如图（2），将图（1）中的条件改为：在ABC∆中, ,,,AB AC D A E=三点都在直线l上，并且BDA AEC BACα∠=∠=∠=，其中α为任意锐角或钝角．请问（1）中结论还是否成立？若成立，请给出证明；若不成立，请说明理由．（3）拓展应用：如图（3），,D E是,,D A E三点所在直线m上的两动点，（,,D A E三点互不重合），点F为BAC∠平分线上的一点，且ABF∆与ACF∆均为等边三角形，连接,BD CE，若BDA AEC BAC∠=∠=∠，试判断DEF∆的形状并说明理由．【答案】（1）DE=CE+BD；（2）成立，理由见解析；（3）△DEF为等边三角形，理由见解析.【解析】【分析】（1）利用已知得出∠CAE=∠ABD，进而根据AAS证明△ABD与△CAE全等，然后进一步求解即可；（2）根据BDA AEC BACα∠=∠=∠=，得出∠CAE=∠ABD，在△ADB与△CEA中，根据AAS证明二者全等从而得出AE=BD，AD=CE，然后进一步证明即可；（3）结合之前的结论可得△ADB与△CEA全等，从而得出BD=AE，∠DBA=∠CAE，再根据等边三角形性质得出∠ABF=∠CAF=60°，然后进一步证明△DBF与△EAF全等，在此基础上进一步证明求解即可.【详解】（1）∵BD⊥直线l，CE⊥直线l，∴∠BDA=∠AEC=90°，∴∠BAD+∠ABD=90°，∵∠BAC=90°，∴∠BAD+∠CAE=90°，∴∠CAE=∠ABD，在△ABD与△CAE中，∵∠ABD=∠CAE，∠BDA=∠AEC，AB=AC，∴△ABD≌△CAE(AAS)，∴BD=AE，AD=CE，∵DE=AD+AE，∴DE=CE+BD，故答案为：DE=CE+BD；（2）（1）中结论还仍然成立，理由如下：∠=∠=∠=，∵BDA AEC BACα∴∠DBA+∠BAD=∠BAD+∠CAE=180°−α，∴∠CAE=∠ABD，在△ADB与△CEA中，∵∠ABD=∠CAE，∠ADB=∠CEA，AB=AC，∴△ADB≌△CEA(AAS)，∴AE=BD，AD=CE，∴BD+CE=AE+AD=DE，即：DE=CE+BD，∆为等边三角形，理由如下：（3）DEF由（2）可知：△ADB≌△CEA，∴BD=EA，∠DBA=∠CAE，∵△ABF与△ACF均为等边三角形，∴∠ABF=∠CAF=60°，BF=AF，∴∠DBA+∠ABF=∠CAE+CAF，∴∠DBF=∠FAE，在△DBF与△EAF中，∵FB=FA，∠FDB=∠FAE，BD=AE，∴△DBF≌△EAF(SAS)，∴DF=EF，∠BFD=∠AFE，∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，∴△DEF为等边三角形.【点睛】本题主要考查了全等三角形性质与判定的综合运用，熟练掌握相关概念是解题关键.5．如图，在边长为 4 的等边△ABC 中，点 D 从点A 开始在射线 AB 上运动，速度为 1 个单位/秒，点F 同时从 C 出发，以相同的速度沿射线 BC 方向运动，过点D 作 DE⊥AC，连结DF 交射线 AC 于点 G(1)当 DF⊥AB 时，求 t 的值；(2)当点 D 在线段 AB 上运动时，是否始终有 DG=GF?若成立，请说明理由。

部编数学八年级上册期末培优检测(一)(期末真题精选)(解析版)含答案

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！期末培优检测一学校:___________姓名：___________班级：___________考号：___________一．单项选择（共8小题，满分24分，每小题3分）1．（3分）化简（x+4）（x﹣1）+（x﹣4）（x+1）的结果是（）A．2x2﹣8B．2x2﹣x﹣4C．2x2+8D．2x2+6x试题分析：结果多项式乘法的法则进行计算，然后合并同类项即可．答案详解：解：（x+4）（x﹣1）+（x﹣4）（x+1）＝x2+3x﹣4+x2﹣3x﹣4＝2x2﹣8，所以选：A．2．（3分）已知长方形ABCD可以按图示方式分成九部分，在a，b变化的过程中，下面说法正确的有（）①图中存在三部分的周长之和恰好等于长方形ABCD的周长②长方形ABCD的长宽之比可能为2③当长方形ABCD为正方形时，九部分都为正方形④当长方形ABCD的周长为60时，它的面积可能为100．A．①②B．①③C．②③④D．①③④试题分析：根据正方形定义和长方形的周长公式判断①③，假设长方形的长宽比是2，推导出与已知的矛盾，排除②，根据长方形的周长为60，推导出该长方形的面积大于100，从而说明④错误．答案详解：解：①四边形AEFG、FHKM、SKWC的周长之和等于长方形ABCD的周长；②长方形的长为a+2b，宽为2a+b，若该长方形的长宽之比为2，则a+2b＝2（2a+b）解得a＝0．这与题意不符，故②的说法不正确；③当长方形ABCD为正方形时，2a+b＝a+2b所以a＝b，所以九部分都为正方形，故③的说法正确；④当长方形ABCD 的周长为60时，即2（2a +b +a +2b ）＝60整理，得a +b ＝10所以四边形GHWD 的面积为100．故当长方形ABCD 的周长为60时，它的面积不可能为100，故④的说法不正确．综上正确的是①③．所以选：B ．3．（3分）若分式2x−1x 23的值为正数，则x 需满足的条件是（）A ．x 为任意实数B ．x ＜12C ．x ＞12D ．x＞−12试题分析：易得分母恒为正数，因为整个分式的值为正数，那么分子应为正数．答案详解：解：∵分式2x−1x 23的值为正数，x 2+3恒为正数，∴2x ﹣1＞0，∴x ＞12．所以选：C ．4．（3分）下列运算中，错误的是（）A ．a b =ac bc B ．−a−ba b=−1C ．0.5a b 0.2a−0.3b =5a 10b2a−3b D ．y−x y x =−x−y x y试题分析：根据分式的基本性质，逐项判断即可．答案详解：解：∵c ＝0时，a b =acbc 不成立，∴选项A 符合题意；∵−a−b a b =−(a b)a b=−1，∴选项B 不符合题意；∵0.5a b 0.2a−0.3b =5a 10b2a−3b，∴选项C 不符合题意；∵y−x y x =−x−y x y ，∴选项D 不符合题意．所以选：A ．5．（3分）下列计算正确的是（）A ．a 3•a 4＝a 12B ．（﹣2ab 2）2＝4a 2b 4C ．（a 3）2＝a 5D ．3a 3b 2÷a 3b 2＝3ab试题分析：根据整式的除法、同底数幂的乘法、幂的乘方与积的乘方法则分别对每一项进行分析即可．答案详解：解：A 、a 3•a 4＝a 7，故本选项错误；B 、（﹣2ab 2）2＝4a 2b 4，故本选项正确；C 、（a 3）2＝a 6，故本选项错误；D 、3a 3b 2÷a 3b 2＝3，故本选项错误；所以选：B ．6．（3分）两个工程队共同参与一项筑路工程，甲队单独施工1个月完成总工程的13，这时增加了乙队，两队又共同工作了半个月，总工程全部完成，如果乙队单独完成总工程需多少个月？设乙队单独完成总工程共需x 个月，则下列方程正确的是（）A ．13+12+1x =1B ．13+16+1x =1C ．13+12+12x=1D ．13+12(13+1x)=1试题分析：设乙队单独施1个月能完成总工程的1x，甲1个月完成的工作量为13，根据甲队完成的任务量+乙队完成的任务量＝总工程量（单位1），即可得出关于x的分式方程，此题得解．答案详解：解：设乙队单独施1个月能完成总工程的1x，甲1个月完成的工作量为13，甲和乙半个月完成的工作量为12(13+1x)，根据题意得：13+12(13+1x)=1，所以选：D．7．（3分）如图，在△ABC中，AB边的中垂线DE，分别与AB边和AC边交于点D和点E，BC边的中垂线FG，分别与BC边和AC边交于点F和点G，又△BEG周长为16，且GE＝1，则AC 的长为（）A．13B．14C．15D．16试题分析：利用线段的垂直平分线的性质解决问题即可．答案详解：解：∵DE是线段AB的中垂线，GF是线段BC的中垂线，∴EB＝EA，GB＝GC，∵△BEG周长为16，∴EB+GB+EG＝16，∴EA+GC+EG＝16，∴GA+EG+EG+EG+EC＝16，∴AC+2EG＝16，∵EG＝1，∴AC＝14，所以选：B．8．（3分）如图，△ABC中，∠BAC＝60°，∠BAC的平分线AD与边BC的垂直平分线MD相交于D，DE⊥AB交AB的延长线于E，DF⊥AC于F，现有下列结论：①DE＝DF；②DE+DF＝AD；③DM平分∠ADF；④AB+AC＝2AE；其中正确的有（）A．1个B．2个C．3个D．4个试题分析：①由角平分线的性质可知①正确；②由题意可知∠EAD＝∠FAD＝30°，故此可知ED=12AD，DF=12DF，从而可证明②正确；③若DM平分∠ADF，则∠EDM＝90°，从而得到∠ABC为直角三角形，条件不足，不能确定，故③错误；④连接BD、DC，然后证明△EBD ≌△DFC，从而得到BE＝FC，从而可证明④．答案详解：解：如图所示：连接BD、DC．①∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴ED＝DF．∴①正确．②∵∠EAC＝60°，AD平分∠BAC，∴∠EAD＝∠FAD＝30°．∵DE⊥AB，∴∠AED＝90°．∵∠AED＝90°，∠EAD＝30°，∴ED=12 AD．同理：DF=12 AD．∴DE+DF＝AD．∴②正确．③由题意可知：∠EDA＝∠ADF＝60°．假设MD平分∠ADF，则∠ADM＝30°．则∠EDM＝90°，又∵∠E＝∠BMD＝90°，∴∠EBM＝90°．∴∠ABC＝90°．∵∠ABC是否等于90°不知道，∴不能判定MD平分∠ADF．故③错误．④∵DM是BC的垂直平分线，∴DB＝DC．在Rt△BED和Rt△CFD中DE=DF BD=DC，∴Rt△BED≌Rt△CFD．∴BE＝FC．∴AB+AC＝AE﹣BE+AF+FC又∵AE＝AF，BE＝FC，∴AB+AC＝2AE．故④正确．所以选：C．二．填空题（共8小题，满分24分，每小题3分）9．（3分）计算：a﹣5b﹣3•ab﹣2＝　1a4b5　（要求结果用正整数指数幂表示）．试题分析：根据单项式乘以单项式的法则计算即可．答案详解：解：a﹣5b﹣3•ab﹣2＝a﹣5+1b﹣3﹣2＝a﹣4b﹣5a4b5所以答案是：1a4b5．10．（3分）若a＝2019，b＝2020，则[a2（a﹣2b）﹣a（a﹣b）2]÷b2的值为　﹣2019　．试题分析：原式中括号中利用完全平方公式，单项式乘以多项式法则计算，合并后利用多项式除以单项式法则计算得到最简结果，把a与b的值代入计算即可求出值．答案详解：解：原式＝（a3﹣2a2b﹣a3+2a2b﹣ab2）]÷b2＝﹣a，当a＝2019时，原式＝﹣2019．所以答案是：﹣201911．（3分）分解因式：3x2+6x+3＝　3（x+1）2　．试题分析：先提取公因式3，再对余下的多项式利用完全平方公式继续分解．答案详解：解：3x2+6x+3，＝3（x2+2x+1），＝3（x+1）2．所以答案是：3（x+1）2．12．（3分）若m+n＝3，则2m2+4mn+2n2﹣4的值为　14　．试题分析：利用完全平方公式分解因式可得2m2+4mn+2n2﹣4＝2（m+n）2﹣4，代入可求解．答案详解：解：2m2+4mn+2n2﹣4＝2（m+n）2﹣4，∵m+n＝3，∴原式＝2×9﹣4＝14，所以答案是：14．13．（3分）已知a+b＝5，ab＝3，ba +ab=　193　．试题分析：将a+b＝5、ab＝3代入原式=b2a2ab=(a b)2−2abab，计算可得．答案详解：解：当a+b＝5、ab＝3时，原式=b2a2 ab=(a b)2−2abab=52−2×333所以答案是：193．14．（3分）北京大兴国际机场于2019年9月25日正式投入运营．小贝和小京分别从草桥和北京站出发赶往机场乘坐飞机，出行方式及所经过的站点与路程如下表所示：出行方式途径站点路程地铁草桥﹣大兴新城﹣大兴机场全程约43公里公交北京站﹣蒲黄榆﹣榴乡桥﹣大兴机场全程约54公里由于地面交通拥堵，地铁的平均速度约为公交平均速度的两倍，于是小贝比小京少用了半小时到达机场．若设公交的平均速度为x 公里/时，根据题意可列方程：　54x −432x =12　．试题分析：若设公交的平均速度为x 公里/时，则地铁的平均速度为2x 公里/时，根据“小贝比小京少用了半小时到达机场”列出方程即可．答案详解：解：若设公交的平均速度为x 公里/时，根据题意可列方程：54x −432x =12．所以答案是：54x −432x =12．15．（3分）如图，在△ABC 中，AD 、AE 分别是边BC 上的中线与高，AE ＝4，△ABC 的面积为12，则CD 的长为　3　．试题分析：利用三角形的面积公式求出BC 即可解决问题．答案详解：解：∵AE ⊥BC ，AE ＝4，△ABC 的面积为12，∴12×BC ×AE ＝12，∴12×BC ×4＝12，∴BC ＝6，∵AD 是△ABC 的中线，∴CD =12BC ＝3，所以答案是3．16．（3分）如图，在△ABC 中，AB ＝AC ＝5，BC ＝6，AD 是∠BAC 的平分线，AD ＝4．若P ，Q 分别是AD 和AC 上的动点，则PC +PQ 的最小值是　245　．试题分析：由等腰三角形的三线合一可得出AD 垂直平分BC ，过点B 作BQ ⊥AC 于点Q ，BQ 交AD 于点P ，则此时PC +PQ 取最小值，最小值为BQ 的长，在△ABC 中，利用面积法可求出BQ 的长度，此题得解．答案详解：解：∵AB ＝AC ，AD 是∠BAC 的平分线，∴AD 垂直平分BC ，∴BP ＝CP ．如图，过点B 作BQ ⊥AC 于点Q ，BQ 交AD 于点P ，则此时PC +PQ 取最小值，最小值为BQ 的长，如图所示．∵S △ABC =12BC •AD =12AC •BQ ，∴BQ =BC ×AD AC =245，即PC +PQ 的最小值是245．所以答案是：245．三．解答题（共11小题，满分92分）17．（4分）分解因式：x 2m +6xm +9m ．试题分析：先提取公因式，再用完全平方公式分解因式．答案详解：原式＝m （x 2+6x +9）＝m （x +3）2．18．（8分）计算：（1）3a 3b •（﹣2ab ）+（﹣3a 2b ）2（2）（2x +3）（2x ﹣3）﹣4x （x ﹣1）+（x ﹣2）2．试题分析：（1）首先计算乘方、乘法，然后计算加法，求出算式的值是多少即可．（2）首先计算乘方、乘法，然后从左向右依次计算，求出算式的值是多少即可．答案详解：解：（1）3a 3b •（﹣2ab ）+（﹣3a 2b ）2＝﹣6a 4b 2+9a 4b 2＝3a 4b 2（2）（2x +3）（2x ﹣3）﹣4x （x ﹣1）+（x ﹣2）2＝4x 2﹣9﹣4x 2+4x +x 2﹣4x +4＝x 2﹣519．（4分）化简：2a a 1−2a−4a 2−1÷a−2a 2−2a 1．试题分析：原式第二项利用除法法则变形，约分后两项通分并利用同分母分式的减法法则计算即可得到结果．答案详解：解：原式=2a a 1−2(a−2)(a 1)(a−1)•(a−1)2a−2=2a a 1−2(a−1)a 1=2a 1．20．（10分）已知，关于x 的分式方程a 2x 3−b−x x−5=1．（1）当a ＝1，b ＝0时，求分式方程的解；（2）当a ＝1时，求b 为何值时分式方程a 2x 3−b−x x−5=1无解；（3）若a ＝3b ，且a 、b 为正整数，当分式方程a 2x 3−b−x x−5=1的解为整数时，求b 的值．试题分析：（1）将a 和b 的值代入分式方程，解分式方程即可；（2）把a 的值代入分式方程，分式方程去分母后化为整式方程，分类讨论b 的值，使分式方程无解即可；（3）将a ＝3b 代入方程，分式方程去分母化为整式方程，表示出整式方程的解，由解为整数和b 为正整数确定b 的取值．答案详解：解：（1）把a ＝1，b ＝0代入分式方程a 2x 3−b−x x−5=1中，得12x 3−−x x−5=1方程两边同时乘以（2x +3）（x ﹣5），（x ﹣5）+x （2x +3）＝（2x +3）（x ﹣5）x ﹣5+2x 2+3x ＝2x 2﹣7x ﹣15x =−1011检验：把x =−1011代入（2x +3）（x ﹣5）≠0，所以原分式方程的解是x =−1011．答：分式方程的解是x =−1011．（2）把a ＝1代入分式方程a 2x 3−b−x x−5=1得12x 3−b−x x−5=1方程两边同时乘以（2x +3）（x ﹣5），（x ﹣5）﹣（b ﹣x ）（2x +3）＝（2x +3）（x ﹣5）x ﹣5+2x 2+3x ﹣2bx ﹣3b ＝2x 2﹣7x ﹣15（11﹣2b ）x ＝3b ﹣10①当11﹣2b ＝0时，即b =112，方程无解；②当11﹣2b ≠0时，x =3b−1011−2bx =−32时，分式方程无解，即3b−1011−2b=−32，b 不存在；x ＝5时，分式方程无解，即3b−1011−2b=5，b ＝5．综上所述，b =112或b ＝5时，分式方程a 2x 3−b−x x−5=1无解．（3）把a ＝3b 代入分式方程a 2x 3−b−x x−5=1，得：3b 2x3+x−bx−5=1方程两边同时乘以（2x+3）（x﹣5），3b（x﹣5）+（x﹣b）（2x+3）＝（2x+3）（x﹣5）整理得：（10+b）x＝18b﹣15∴x=18b−15 10b∵18b−1510b=18(b10)−19510b=18−19510b，且b为正整数，x为整数∴10+b必为195的因数，10+b≥11∵195＝3×5×13∴195的因数有1、3、5、13、15、39、65、195但1、3、5 小于11，不合题意，故10+b可以取13、15、39、65、195这五个数．对应地，方程的解x为3、5、13、15、17由于x＝5为分式方程的增根，故应舍去．对应地，b只可以取3、29、55、185所以满足条件的b可取3、29、55、185这四个数．21．（10分）某校“数学社团”活动中，小亮对多项式进行因式分解．m2﹣mn+2m﹣2n＝（m2﹣mn）+（2m﹣2n）＝m（m﹣n）+2（m﹣n）＝（m﹣n）（m+2）．以上分解因式的方法叫做“分组分解法”，请你在小亮解法的启发下，解决下面问题：（1）因式分解a3﹣3a2﹣9a+27；（2）因式分解x2﹣4xy+4y2﹣16；（3）已知a，b，c是△ABC的三边，且满足a2﹣ab+c2＝2ac﹣bc，判断△ABC的形状并说明理由．试题分析：（1）第一、二项一组，三、四项一组，分别提公因式，再分解．（2）前三项一组，用公式分解．（3）先因式分解找到a，b，c的关系，再判断三角形的形状．答案详解：解：（1）a3﹣3a2﹣9a+27＝a2（a﹣3）﹣9（a﹣3）＝（a2﹣9）（a﹣3）＝（a﹣3）（a+3）（a﹣3）＝（a+3）（a﹣3）2；（2）x2+4y2﹣4xy﹣16＝（x2﹣4xy+4y2）﹣16＝（x﹣2y）2﹣42＝（x﹣2y﹣4）（x﹣2y+4）；（3）△ABC是等腰三角形，理由如下：∵a2﹣ab+c2＝2ac﹣bc，∴a2﹣2ac+c2﹣ab+bc＝0，∴（a﹣c）2﹣b（a﹣c）＝0，∴（a﹣c）（a﹣c﹣b）＝0，∵a，b，c是△ABC的三边，∴a﹣c﹣b＜0．∴a﹣c＝0，∴a＝c，∴△ABC是等腰三角形．22．（8分）从贵阳到广州，乘特快列车的行程约为1800km，高铁开通后，高铁列车的行程约为900km，运行时间比特快列车所用的时间减少了16h．若高铁列车的平均速度是特快列车平均速度的2.5倍，求特快列车的平均速度．试题分析：设特快列车平均速度为xkm/h，则高铁列车平均速度为2.5xkm/h，根据高铁列车运行900km比特快列车运行1800km的时间减少了16h，列方程求解．答案详解：解：设特快列车的平均速度为x km/h，根据题意可列出方程为1800x=9002.5x+16，解得x＝90．检验：当x＝90时，2.5x≠0．所以x＝90是方程的解．答：特快列车的平均速度为90km/h．23．（8分）如图，在△ABC中，已知AC＝BC，E是AB边上一点，BE＝BC，BD平分∠CBE，分别交CE，AC于点D，F，连接EF．（1）若∠ACB＝100°，求∠BEC和∠FEC的度数．（2）若∠ACB＝90°，求证：AE＝CF．试题分析：（1）由等腰三角形的性质可求∠CAB＝∠CBA＝40°，∠BEC＝∠BCE＝70°，由“SAS”可证△EBF≌△CBF，可得∠BCF＝∠BEF＝100°，可求解；（2）由全等三角形的性质可得EF＝CF，∠BCF＝∠BEF＝90°，可得∠AFE＝∠CAB＝45°，可证AE＝EF＝CF．答案详解：解：（1）∵AC＝BC，∠ACB＝100°，∴∠CAB＝∠CBA＝40°，∵BE＝BC，∴∠BEC＝∠BCE＝70°，∵BD平分∠CBE，∴∠CBF＝∠EBF，又∵BE＝BC，BF＝BF，∴△EBF≌△CBF（SAS），∴∠BCF＝∠BEF＝100°，∴∠FEC＝∠BEF﹣∠BEC＝30°；（2）∵∠ACB＝90°，AC＝BC，∴∠CAB＝45°，∵△EBF≌△CBF，∴EF＝CF，∠BCF＝∠BEF＝90°，∴∠AFE＝90°﹣45°＝45°，∴∠AFE＝∠CAB＝45°，∴AE＝EF，∴AE＝CF．24．（8分）如图，△ABC三个顶点的坐标分别为A（1，1）、B．（4，2）、C（3，4）．（1）若△A1B1C1与△ABC关于y轴成轴对称，则△A1B1C1三个顶点坐标分别为：A1　（﹣1，1）　，B1　（﹣4，2）　，C1　（﹣3，4）　；（2）若P为x轴上一点，则PA+PB（3）计算△ABC的面积．试题分析：（1）分别作出点A ，B ，C 关于x 轴的对称点，再首尾顺次连接即可得；（2）作出点A 的对称点，连接A 'B ，则A 'B 与x 轴的交点即是点P 的位置，则PA +PB 的最小值＝A ′B ，根据勾股定理即可得到结论；（3）根据三角形的面积公式即可得到结论．答案详解：解：（1）如图所示，△A 1B 1C 1即为所求，由图知，A 1的坐标为（﹣1，1）、B 1的坐标为（﹣4，2）、C 1的坐标为（﹣3，4）；（2）如图所示：作出点A 的对称点，连接A 'B ，则A 'B 与x 轴的交点即是点P 的位置，则PA +PB 的最小值＝A ′B ，∵A ′B ==∴PA +PB 的最小值为（3）△ABC 的面积＝3×3−12×3×1−12×1×2−12×2×3=72，所以答案是：（﹣1，1），（﹣4，2），（﹣3，4），25．（10分）已知，在△ABC 中，∠ACB ＝90°，AC ＝BC ，AD ⊥CE ，BE ⊥CE ，垂足分别为D ，E．（1）如图1，求证：DE＝AD+BE；（2）如图2，点O为AB的中点，连接OD，OE．请判断△ODE的形状？并说明理由．试题分析：（1）根据条件可以得出∠E＝∠ADC＝90°，进而得出△CEB≌△ADC，就可以得出BE＝DC，AD＝CE；（2）如图2，连接OC，由等腰直角三角形的性质可得AO＝BO＝CO，∠CAB＝∠CBA＝45°，CO⊥AB，由“SAS”可证△DCO≌△EBO，△ADO≌△CEO，可得EO＝DO，∠EOB＝∠DOC，∠AOD＝∠COE，可证△DOE是等腰直角三角形．答案详解：（1）证明：如图1，∵BE⊥CE，AD⊥CE，∴∠E＝∠ADC＝90°，∴∠EBC+∠BCE＝90°．∵∠BCE+∠ACD＝90°，∴∠EBC＝∠DCA．在△CEB和△ADC中，∠E=∠D∠EBC=∠DCA，BC=AC∴△CEB≌△ADC（AAS），∴BE＝DC，AD＝CE．∴DE ＝DC +CE ＝AD +BE ，即DE ＝AD +BE ；（2）△DOE 等腰直角三角形，理由如下：如图2，连接OC ，∵AC ＝BC ，∠ACB ＝90°，点O 是AB 中点，∴AO ＝BO ＝CO ，∠CAB ＝∠CBA ＝45°，CO ⊥AB ，∴∠AOC ＝∠BOC ＝∠ADC ＝∠BEC ＝90°，∵∠BOC +∠BEC +∠ECO +∠EBO ＝360°，∴∠EBO +∠ECO ＝180°，且∠DCO +∠ECO ＝180°，∴∠DCO ＝∠EBO ，且DC ＝BE ，CO ＝BO ，∴△DCO ≌△EBO （SAS ），∴EO ＝DO ，∠EOB ＝∠DOC ，同理可证：△ADO ≌△CEO ，∴∠AOD ＝∠COE ，∵∠AOD +∠DOC ＝90°，∴∠DOC +∠COE ＝90°，∴∠DOE ＝90°，且DO ＝OE ，∴△DOE 是等腰直角三角形．26．（10分）尺规作图及探究：已知：线段AB ＝a ．（1）完成尺规作图：点P 在线段AB 所在直线上方，PA ＝PB ，且点P 到AB 的距离等于a 2，连接PA ，PB ．在线段AB上找到一点Q 使得QB ＝PB ，连接PQ ，并直接回答∠PQB 的度数；（2）若将（1）中的条件“点P 到AB 的距离等于a 2”替换为“PB 取得最大值”，其余所有条件都不变，此时点P的位置记为P′，点Q的位置记为Q′，连接P′Q′，并直接回答∠P′Q′B 的度数．试题分析：（1）作线段AB的垂直平分线DE，D为垂足，在射线DE上截取DP=12a，连接PA，PB即可解决问题．（2）作等边三角形P′AB即可解决问题．答案详解：解：（1）如图，点P即为所求．∵BP＝BQ，∠PBA＝45°，∴∠PQB＝∠BPQ＝67.5°．（2）如图，点P′即为所求．当P′B取得最大值时，△ABP′是等边三角形，△BQP′是等边三角形，∴∠P′QB＝60°．27．（12分）在△ABC中，AB＝AC，点D是直线BC上一点（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE．（1）如图1，当点D在线段BC上，如果∠BAC＝90°，则∠BCE＝　90　度；（2）如图2，如果∠BAC＝60°，则∠BCE＝　120　度；（3）设∠BAC＝α，∠BCE＝β．①如图3，当点D在线段BC上移动，则α，β之间有怎样的数量关系？请说明理由；②当点D在直线BC上移动，请直接写出α，β之间的数量关系，不用证明．试题分析：（1）由等腰直角三角形的性质可得∠ABC＝∠ACB＝45°，由“SAS”可证△BAD≌△CAE，可得∠ABC＝∠ACE＝45°，可求∠BCE的度数；（2）由条件可得△ABC为等边三角形，由“SAS”可证△ABD≌△ACE得出∠ABD＝∠ACE＝60°，则可得出结论；（3）①由“SAS”可证△ABD≌△ACE得出∠ABD＝∠ACE，再用三角形的内角和即可得出结论；②分两种情况画出图形，由“SAS”可证△ABD≌△ACE得出∠ABD＝∠ACE，再用三角形的内角和即可得出结论．答案详解：解：（1）∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∵∠DAE＝∠BAC，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS）∴∠ABC＝∠ACE＝45°，∴∠BCE＝∠ACB+∠ACE＝90°，所以答案是：90；（2）∵∠BAC＝60°，AB＝AC，∴△ABC为等边三角形，∴∠ABD＝∠ACB＝60°，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，在△ABD和△ACE中，∵∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ABD＝∠ACE＝60°，∴∠BCE＝∠ACE+∠ACB＝60°+60°＝120°，所以答案是：120．（3）①α+β＝180°，理由：∵∠BAC＝∠DAE，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC．即∠BAD＝∠CAE．在△ABD与△ACE中，AB=AC∠BAD=∠CAE AD=AE，∴△ABD≌△ACE（SAS），∴∠B＝∠ACE．∴∠B+∠ACB＝∠ACE+∠ACB．∵∠ACE+∠ACB＝β，∴∠B+∠ACB＝β，∵α+∠B+∠ACB＝180°，∴α+β＝180°．②如图1：当点D在射线BC上时，α+β＝180°，连接CE，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，在△ABD和△ACE中，AB=AC∠BAD=∠CAE，AD=AE∴△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，在△ABC中，∠BAC+∠B+∠ACB＝180°，∴∠BAC+∠ACE+∠ACB＝∠BAC+∠BCE＝180°，即：∠BCE+∠BAC＝180°，∴α+β＝180°，如图2：当点D在射线BC的反向延长线上时，α＝β．连接BE，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△ABD≌△ACE（SAS），∴∠ABD＝∠ACE，∴∠ABD＝∠ACE＝∠ACB+∠BCE，∴∠ABD+∠ABC＝∠ACE+∠ABC＝∠ACB+∠BCE+∠ABC＝180°，∵∠BAC＝180°﹣∠ABC﹣∠ACB，∴∠BAC＝∠BCE．∴α＝β；综上所述：点D在直线BC上移动，α+β＝180°或α＝β．。

初二数学培优试卷及答案

一、选择题（每题5分，共50分）1. 已知方程x^2 - 4x + 3 = 0，那么它的解是（）A. x1 = 1，x2 = 3B. x1 = 2，x2 = 2C. x1 = 3，x2 = 1D. x1 = -1，x2 = -32. 若a > 0，b < 0，那么下列不等式中正确的是（）A. a > bB. a < bC. -a > -bD. -a < -b3. 下列函数中，自变量x的取值范围是全体实数的是（）A. y = √(x - 1)B. y = √(x^2 - 1)C. y = √(x + 1)D. y = √(x^2 + 1)4. 已知一次函数y = kx + b，其中k ≠ 0，若函数图象经过点(2, 3)，则k和b 的值分别为（）A. k = 2，b = 1B. k = 1，b = 2C. k = -2，b = 1D. k = -1，b = 25. 已知等腰三角形ABC中，AB = AC，且∠BAC = 40°，则∠B和∠C的度数分别为（）A. ∠B = ∠C = 50°B. ∠B = ∠C = 70°C. ∠B = ∠C = 40°D. ∠B = ∠C = 30°6. 下列各数中，能被3整除的是（）A. 729B. 256C. 1234D. 9877. 已知直角三角形ABC中，∠C = 90°，AB = 5cm，BC = 12cm，那么AC的长度为（）A. 13cmB. 15cmC. 17cmD. 19cm8. 若一个数x满足不等式2x - 1 < 5，那么x的取值范围是（）A. x < 3B. x ≤ 3C. x > 3D. x ≥ 39. 已知二次函数y = ax^2 + bx + c（a ≠ 0），若函数图象开口向上，则a的取值范围是（）A. a > 0B. a < 0C. a ≥ 0D. a ≤ 010. 在平面直角坐标系中，点P(2, 3)关于x轴的对称点Q的坐标是（）A. (2, -3)B. (-2, 3)C. (2, 3)D. (-2, -3)二、填空题（每题5分，共50分）1. 若方程2x - 3 = 5的解为x = 3，则方程3x + 4 = 11的解为x = _______。

八年级上期末数学培优试卷

一、选择题（每题4分，共20分）1. 下列各数中，无理数是（）A. √2B. √4C. √9D. √162. 下列各式中，正确的是（）A. 2^3 = 8B. 2^4 = 16C. 2^5 = 32D. 2^6 = 643. 已知 a > b，则下列各式中正确的是（）A. a + 1 > b + 1B. a - 1 > b - 1C. a + 2 > b + 2D. a - 2 > b - 24. 下列各式中，能化简为最简二次根式的是（）A. √18B. √27C. √36D. √455. 下列各式中，能化简为有理数的是（）A. √2 - √3B. √5 + √7C. √8 - √9D. √10 + √12二、填空题（每题5分，共20分）6. 2^3 × 2^2 = _______；3^4 ÷ 3^2 = _______； (-2)^5 × (-2)^3 = _______； 5^0 = _______。

7. 若 a + b = 6，a - b = 2，则 a = _______，b = _______。

8. 已知 a = 3，b = 4，则 a^2 + b^2 = _______，ab = _______。

9. 若 a^2 + b^2 = 10，a - b = 2，则 ab 的值为 _______。

10. 若√a + √b = 6，√a - √b = 2，则 a + b 的值为 _______。

三、解答题（每题10分，共30分）11. （1）化简：2√3 - √3 + √3 - 2√3；（2）计算：√18 × √27 ÷ √36。

12. （1）已知a = √5 - 2，b = √5 + 2，求 a^2 + b^2 - ab 的值；（2）已知 a + b = 5，ab = 6，求 a^2 + b^2 的值。

13. （1）已知 a^2 + b^2 = 13，a - b = 3，求 ab 的值；（2）已知 a + b = 4，ab = 2，求 a^2 + b^2 - 2ab 的值。

(word完整版)初中数学八年级上册期末培优提高测试卷附参考答案

连结ED, EB ，则 BDE 周长的最小值为（)2014-1015学年八年级（上）期末培优提高测试卷（一）班级 ______ 姓名 ___________、选择题（每题 3分，共30 分）1、要使JFT 丄 <2x有意义，则x 应满足（ 1).A .1 —X 3 2r 1 B . x <3且 x M-C. 21丄 v X V 321D .丄 V x <322、已知 a 1 b ，且c 是非零实数，则可得（ )A .ac bc 2 2B. ac bcac bc2 2D. ac bc3、已知三角形相邻两边长分别为 20cm 和13cm .第三边上的高为12cm ,则第三边长（）A.19cmB.19cm 或 9 cmC.21cmD. 21cm 或 11cm4、在平面直角坐标系中，已知A （2,— 2）,在y 轴上确定点卩，使厶AOP 为等腰三角形，则符合条件的点P 共有（）个5、如图所示，在 △ ABC 中，AB=AC ,Z ABC 、/ ACB 的平分线 BD 、CE 相交于 O 点，且BD 交AC 于点D , CE 交AB 于点E .某同学分析图形后得出以下结论：①厶 BCD ◎△ CBE ;②、BAD ◎△ BCD :③厶 BDACEA :④厶 BOECOD :⑤厶 ACEBCE ，上述结论A. 2个B. 3个C. 4个D. 5B.②③④C.①③⑤6、如图，Rt A ABC中，AB=9, BC=6 , / B=90 °将厶ABC 折叠，使A 点与BC 的中点D 重合,折痕为MN ，则线段BN 的长为（定正确的是（ CD.①③④第7题7、如图，ABC 中，AB BC , ABBC 4 , D为BC的中点，在AC边上存在一点E , 连结ED, EB，则BDE周长的最小值为（)A 地驶往B 地，乙骑自行车从 B 地驶往A 地，两人同时出发，设行驶的时间为t(h),两车之间的距离为 s (km )，图中的折线表示s 与t 之间的函数关系，根据图像得出下列信息： ①A,B 两地相距90km ,②当乙行驶1.5h 时，甲和乙在点D 处相遇; ③ 骑摩托车的速度为乙骑自行车的速度的 3倍；④甲在相遇后2小时到达B 地。

八年级上册数学期末试卷(培优篇)(Word版含解析)

八年级上册数学期末试卷（培优篇）（Word版含解析）一、八年级数学全等三角形解答题压轴题（难）1．（1）已知△ABC是等腰三角形，其底边是BC,点D在线段AB上，E是直线BC上一点，且∠DEC=∠DCE,若∠A等于60°（如图①）.求证：EB=AD；（2）若将（1）中的“点D在线段AB上”改为“点D在线段AB的延长线上”，其他条件不变（如图②），（1）的结论是否成立，并说明理由．【答案】（1）证明见解析（2）证明见解析【解析】试题分析：（1）作DF∥BC交AC于F，由平行线的性质得出∠ADF=∠ABC，∠AFD=∠ACB，∠FDC=∠DCE，证明△ABC是等边三角形，得出∠ABC=∠ACB=60°，证出△ADF是等边三角形，∠DFC=120°，得出AD=DF，由已知条件得出∠FDC=∠DEC，ED=CD，由AAS证明△DBE≌△CFD，得出EB=DF，即可得出结论；（2）作DF∥BC交AC的延长线于F，同（1）证出△DBE≌△CFD，得出EB=DF，即可得出结论.试题解析：（1）证明：如图，作DF∥BC交AC于F，则△ADF为等边三角形∴AD=DF，又∵∠DEC=∠DCB，∠DEC+∠EDB=60°，∠DCB+∠DCF=60°，∴∠EDB=∠DCA ，DE=CD，在△DEB和△CDF中，120EBD DFCEDB DCFDE CD，，∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△DEB≌△CDF，∴BD=DF，∴BE=AD .(2).EB=AD成立；理由如下：作DF ∥BC 交AC 的延长线于F ，如图所示：同（1）得：AD=DF ，∠FDC=∠ECD ，∠FDC=∠DEC ，ED=CD ，又∵∠DBE=∠DFC=60°，∴△DBE ≌△CFD （AAS ），∴EB=DF ，∴EB=AD.点睛：此题主要考查了三角形的综合，考查等边三角形的判定与性质，全等三角形的判定与性质，等腰三角形的判定与性质，等腰直角三角形的判定与性质，平行线的性质等知识，综合性强，有一定的难度，证明三角形全等是解决问题的关键.2．如图，在ABC ∆中，90C ∠=︒，4cm AC BC ==，点D 是斜边AB 的中点．点E 从点B 出发以1cm/s 的速度向点C 运动，点F 同时从点C 出发以一定的速度沿射线CA 方向运动，规定当点E 到终点C 时停止运动．设运动的时间为x 秒，连接DE 、DF ．（1）填空：ABC S ∆=______2cm ；（2）当1x =且点F 运动的速度也是1cm/s 时，求证：DE DF =；（3）若动点F 以3cm /s 的速度沿射线CA 方向运动，在点E 、点F 运动过程中，如果存在某个时间x ，使得ADF ∆的面积是BDE ∆面积的两倍，请你求出时间x 的值．【答案】（1）8;(2)见解析；（3）45或4. 【解析】【分析】（1）直接可求△ABC 的面积；（2）连接CD ，根据等腰直角三角形的性质可求：∠A=∠B=∠ACD=∠DCB=45°，即BD=CD，且BE=CF ，即可证△CDF ≌△BDE ，可得DE=DF ；（3）分△ADF 的面积是△BDE 的面积的两倍和△BDE 与△ADF 的面积的2倍两种情况讨论，根据题意列出方程可求x 的值．【详解】解：（1）∵S △ABC =12⨯AC×BC ∴S △ABC =12×4×4=8（cm 2）故答案为：8（2）如图：连接CD∵AC=BC ，D 是AB 中点∴CD 平分∠ACB又∵∠ACB=90°∴∠A=∠B=∠ACD=∠DCB=45°∴CD=BD依题意得：BE=CF∴在△CDF 与△BDE 中BE CF B DCA BD CD =⎧⎪∠=∠⎨⎪=⎩∴△CDF ≌△BDE （SAS ）∴DE=DF（3）如图：过点D 作DM ⊥BC 于点M ，DN ⊥AC 于点N ，∵AD=BD ，∠A=∠B=45°，∠AND=∠DMB=90°∴△ADN ≌△BDM （AAS ）∴DN=DM当S △ADF =2S △BDE ．∴12×AF×DN=2×12×BE×DM ∴|4-3x|=2x ∴x 1=4，x 2=45综上所述：x=45或4 【点睛】本题考查了动点问题的函数图象，全等三角形的性质和判定，利用分类思想解决问题是本题的关键．3．在ABC 中，AB AC =，点D 在BC 边上，且60,ADB E ∠=︒是射线DA 上一动点(不与点D 重合，且DA DB ≠)，在射线DB 上截取DF DE =，连接EF ．()1当点E 在线段AD 上时，①若点E 与点A 重合时，请说明线段BF DC =；②如图2，若点E 不与点A 重合，请说明BF DC AE =+；()2当点E 在线段DA 的延长线上()DE DB >时，用等式表示线段,,AE BF CD 之间的数量关系(直接写出结果，不需要证明)．【答案】（1）①证明见解析；②证明见解析；（2）BF ＝AE-CD【解析】【分析】（1）①根据等边对等角，求到B C ∠=∠，再由含有60°角的等腰三角形是等边三角形得到ADF ∆是等边三角形，之后根据等边三角形的性质以及邻补角的性质得到120AFB ADC ∠=∠=︒，推出ABF ACD ∆∆≌，根据全等三角形的性质即可得出结论；②过点A 做AG ∥EF 交BC 于点G ，由△DEF 为等边三角形得到DA ＝DG ，再推出AE ＝GF ，根据线段的和差即可整理出结论；（2）根据题意画出图形，作出AG ，由（1）可知，AE=GF ，DC=BG ，再由线段的和差和等量代换即可得到结论．【详解】（1）①证明：AB AC=B C∴∠=∠,60DF DE ADB=∠=︒，且E与A重合，ADF∴∆是等边三角形60ADF AFD∴∠=∠=︒120AFB ADC∴∠=∠=︒在ABF∆和ACD∆中AFB ADCB CAB AC∠=∠⎧⎪∠=∠⎨⎪=⎩ABF ACD∴∆∆≌BF DC∴=②如图2，过点A做AG∥EF交BC于点G，∵∠ADB＝60°DE＝DF∴△DEF为等边三角形∵AG∥EF∴∠DAG＝∠DEF＝60°，∠AGD＝∠EFD＝60°∴∠DAG＝∠AGD∴DA＝DG∴DA－DE＝DG－DF，即AE＝GF由①易证△AGB≌△ADC∴BG＝CD∴BF＝BG＋GF＝CD＋AE（2）如图3，和（1）中②相同，过点A做AG∥EF交BC于点G，由（1）可知，AE=GF，DC=BG，BF CD BF BG GF AE∴+=+==故BF AE CD=-．【点睛】本题考查了全等三角形的判定和性质，等边三角形的判定和性质，等腰三角形的判定和性质，正确的作出辅助线是解题的关键．4．如图（1），AB=4cm，AC⊥AB，BD⊥AB，AC=BD=3cm，点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动，他们的运动时间为t(s).（1）若点Q的运动速度与点P的运动速度相等，当t=1时，△ACP与△BPQ是否全等，请说明理由（2）判断此时线段PC和线段PQ的关系，并说明理由。

培优测试卷八年级上册数学

一、选择题（每题3分，共30分）1. 下列各数中，属于有理数的是（）A. √2B. πC. 3.14D. 无理数2. 下列各式中，正确的是（）A. (a + b)^2 = a^2 + b^2B. (a - b)^2 = a^2 - b^2C. (a + b)^2 = a^2 + 2ab + b^2D. (a - b)^2 = a^2 - 2ab + b^23. 若a > 0，b < 0，则下列不等式中正确的是（）A. a + b > 0B. a - b > 0C. a - b < 0D. a + b < 04. 下列图形中，面积最小的是（）A. 正方形B. 长方形C. 等腰三角形D. 圆形5. 下列各式中，表示圆的周长的是（）A. 2πrB. πr^2C. πdD. 4r6. 若x^2 - 5x + 6 = 0，则x的值为（）A. 2B. 3C. 4D. 67. 下列各数中，绝对值最小的是（）A. -3B. -2C. 0D. 28. 下列各式中，表示圆柱体积的是（）A. πr^2hB. 2πrhC. πd^2hD. 4πrh9. 若一个三角形的两边长分别为3和4，则第三边的长度范围是（）A. 1 < 第三边 < 7B. 2 < 第三边 < 8C. 3 < 第三边 < 7D. 4 < 第三边 < 810. 下列各式中，正确的是（）A. √(a^2) = aB. √(a^2) = -aC. √(a^2) = |a|D. √(a^2) = a + b二、填空题（每题5分，共20分）11. 若a > 0，b < 0，则|a + b|的值为________。

12. 若x^2 - 5x + 6 = 0，则x的值为________。

13. 一个等边三角形的边长为6，其面积为________。

14. 若一个数的平方是25，则这个数是________。

八年级数学上期末培优训练(7份)

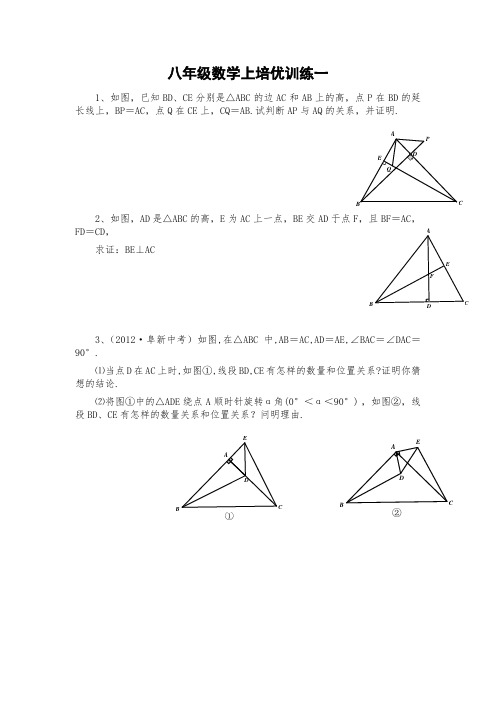
八年级数学上培优训练一1、如图，已知BD 、CE 分别是△ABC 的边AC 和AB 上的高，点P 在BD 的延长线上，BP ＝AC ，点Q 在CE 上，CQ ＝AB.试判断AP 与AQ 的关系，并证明.2、如图，AD 是△ABC 的高，E 为AC 上一点，BE 交AD 于点F ，且BF ＝AC ，FD ＝CD ，求证：BE ⊥AC3、（2012·阜新中考）如图,在△ABC 中,AB ＝AC,AD ＝AE,∠BAC ＝∠DAC ＝90°.⑴当点D 在AC 上时,如图①,线段BD,CE 有怎样的数量和位置关系?证明你猜想的结论.⑵将图①中的△ADE 绕点A 顺时针旋转α角(0°＜α＜90°) ，如图②，线段BD 、CE 有怎样的数量关系和位置关系？问明理由.B②B①B(1)D PE CBA (2)DPECBA4、在△ABC 中，AB ＝AC ，点D 是直线 BC 上一点（不与B 、C 重合），以AD 为一边在AD 的右侧作△ADE ，使AD ＝AE ，∠DAE ＝∠BAC ，连接CE.⑴如图①，当点D 在线段BC 上时，若∠BAC ＝90°，则∠BCE ＝_______度. ⑵设∠BAC ＝α，∠BCE ＝βa 、如图②，当点D 在线段BC 上移动时，α，β之间有怎样的数量关系？请说明理由.b 、当点D 在直线BC 上移动时，α，β之间有怎样的数量关系？请直接写出你的结论.5、在△ABC 中，AC ＝BC,∠C ＝90°，将一块三角板的直角顶点放在斜边AB 的中点P 处，将三角板绕P 点旋转，三角板的两直角边分别交AC 、CB 于D 、E 两点，如图（1）、（2）所示。

问PD 与PE 有何大小关系？在旋转过程中，还会存在与图⑴、⑵不同的情形吗？若存在，请在图⑶中画出，并选择图⑵或图⑶为例加以证明，若不存在请选择图⑵加以证明．①B②C八年级数学上培优训练二1．如图1，在△ABC中，△ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．如果AB=AC，△BAC=90°，①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD所在直线的位置关系为，线段CF、BD的数量关系为；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；2．（1）如图1，正方形ABCD中，点E，F分别在边BC，CD上，△EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：EF=FG．（2）如图，等腰直角三角形ABC中，△BAC=90°，AB=AC，点M，N在边BC上，且△MAN=45°，若BM=1，CN=3，求MN的长．3．如图，△ABC 中，∠BAC =90度，AB =AC ，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E ，直线CE 交BA 的延长线于F ．求证：BD =2CE ．4、在△ABC 中，D 是边BC 上的一点，且CD ＝AB ，∠BAD ＝∠BDA ，AE 是△ABD 的中线.求证∶AC ＝2AEFE DCB AB八年级数学上培优训练三1、如图,在△ABC 中,∠BAC ＝90°,AB ＝AC,BE 平分∠ABC,CE ⊥BE.求证:CE ＝12BD2、在四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于点E ，且AE ＝½（AB ＋AD ）.求证∶∠B ＋∠D ＝180°DB3、已知：如图，△ABC 中，∠C =90°，CM ⊥AB 于M ，AT 平分∠BAC 交CM 于D ，交BC 于T ，过D 作DE ∥AB 交BC 于E ，求证CT =BE ．4、如图所示，△ABC 是等边三角形，延长BC 至E ，延长BA 至F ，使AF =BE ，连结CF 、EF ，过点F 作直线FD ⊥CE 于D ，试发现∠FCE 与∠FEC 的数量关系，并说明理由．ACT EBM DBA CDEF八年级数学上培优训练四1．如图，AB=AC，AE=AF，△BAC=△EAF=90°，BE、CF交于M，连AM．（1）求证：BE=CF；（2）求证：BE△CF；2．如图，点D是△ABC的边BC上一动点，且AB=AC，DA=DE，△BAC=△ADE=120°，求△BCE 的度数．3．如图，△ABC中，AB=AC，△BAC=90°，D为BC上一点，过D作DE△AD，且DE=AD，连BE，求△DBE的度数．4．如图，△ABC中，AB=BC，AB△BC，B（0，2），C（2，﹣2），求点A的坐标．八年级数学上培优训练五1、如图，△ABC 为等边三角形，且BM=CN ，AM 与BN 相交于点P ，则∠APN=（） A 70 B 60 C 50 D 不确定2、如图，C 为线段AB 上一点，在AB 的同侧作等边△ACM 和等边△BCN ，连接AN 、BM ，若∠MBN=40°，则∠ANB 的大小是（）A 60B 65C 70D 803、如图2，在线段AE 同侧作两个等边三角形△ABC 和△CDE(∠ACE ＜120°)，点P 与点M 分别是线段BE 和AD 的中点，则△CPM 是( )A.钝角三角形B.直角三角形C.等边三角形D.非等腰三角形4、如图，在△ABC 中，AB=2，BC=3.6，∠B=60°，将△ABC 绕点A 按顺时针旋转一定角度得到△ADE ，当点B 的对应点D 恰好落在BC 边上时，则CD 的长为 _________．5、已知：2,3==n m x x ，求n m x 23+、n m x 23-的值。

八年级数学上册期末试卷(培优篇)(Word版含解析)

八年级数学上册期末试卷（培优篇）（Word版含解析）一、八年级数学全等三角形解答题压轴题（难）1．在平面直角坐标系中，直线AB分别交x轴，y轴于A（a，0），B（0，b），且满足a2+b2+4a﹣8b+20＝0．（1）求a，b的值；（2）点P在直线AB的右侧；且∠APB＝45°，①若点P在x轴上（图1），则点P的坐标为；②若△ABP为直角三角形，求P点的坐标．【答案】（1）a＝﹣2，b＝4；（2）①（4，0）；②P点坐标为（4，2），（2，﹣2）．【解析】【分析】（1）利用非负数的性质解决问题即可．（2）①根据等腰直角三角形的性质即可解决问题．②分两种情形：如图2中，若∠ABP=90°，过点P作PC⊥OB，垂足为C．如图3中，若∠BAP=90°，过点P作PD⊥OA，垂足为D．分别利用全等三角形的性质解决问题即可．【详解】（1）∵a2+4a+4+b2﹣8b+16＝0∴（a+2）2+（b﹣4）2＝0∴a＝﹣2，b＝4．（2）①如图1中，∵∠APB＝45°，∠POB＝90°，∴OP＝OB＝4，∴P（4，0）．故答案为（4，0）．②∵a＝﹣2，b＝4∴OA＝2OB＝4又∵△ABP为直角三角形，∠APB＝45°∴只有两种情况，∠ABP＝90°或∠BAP＝90°①如图2中，若∠ABP＝90°，过点P作PC⊥OB，垂足为C．∴∠PCB＝∠BOA＝90°，又∵∠APB＝45°，∴∠BAP＝∠APB＝45°，∴BA＝BP，又∵∠ABO+∠OBP＝∠OBP+∠BPC＝90°，∴∠ABO＝∠BPC，∴△ABO≌△BPC（AAS），∴PC＝OB＝4，BC＝OA＝2，∴OC＝OB﹣BC＝4﹣2＝2，∴P（4，2）．②如图3中，若∠BAP＝90°，过点P作PD⊥OA，垂足为D．∴∠PDA＝∠AOB＝90°，又∵∠APB＝45°，∴∠ABP＝∠APB＝45°，∴AP＝AB，又∵∠BAD+∠DAP＝90°，∠DPA+∠DAP＝90°，∴∠BAD＝∠DPA，∴△BAO≌△APP（AAS），∴PD＝OA＝2，AD＝OB＝4，∴OD＝AD﹣0A＝4﹣2＝2，∴P（2，﹣2）．综上述，P点坐标为（4，2），（2，﹣2）．【点睛】本题属于三角形综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题．2．已知OP平分∠AOB，∠DCE的顶点C在射线OP上，射线CD交射线OA于点F，射线CE交射线OB于点G．（1）如图1，若CD⊥OA，CE⊥OB，请直接写出线段CF与CG的数量关系；（2）如图2，若∠AOB=120º，∠DCE=∠AOC，试判断线段CF与CG的数量关系，并说明理由．【答案】（1）CF=CG；（2）CF=CG，见解析【解析】【分析】(1)结论CF=CG，由角平分线性质定理即可判断．(2)结论：CF=CG，作CM⊥OA于M，CN⊥OB于N，证明△CMF≌△CNG，利用全等三角形的性质即可解决问题．【详解】解：（1）结论：CF=CG；证明：∵OP平分∠AOB，CF⊥OA，CG⊥OB，∴CF=CG（角平分线上的点到角两边的距离相等）；（2）CF=CG.理由如下：如图，过点C作CM⊥OA，CN⊥OB，∵OP平分∠AOB，CM⊥OA，CN⊥OB，∠AOB=120º，∴CM=CN（角平分线上的点到角两边的距离相等），∴∠AOC=∠BOC=60º（角平分线的性质），∵∠DCE=∠AOC，∴∠AOC=∠BOC=∠DCE=60º，∴∠MCO=90º-60º =30º，∠NCO=90º-60º =30º，∴∠MCN=30º+30º=60º，∴∠MCN=∠DCE，∵∠MCF=∠MCN-∠DCN，∠NCG=∠DCE-∠DCN，∴∠MCF=∠NCG，在△MCF和△NCG中，CMF CNGCM CNMCF NCG∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MCF≌△NCG（ASA），∴CF=CG（全等三角形对应边相等）；【点睛】本题考查三角形综合题、角平分线的性质、全等三角形的判定和性质，解题的关键是掌握角平分线的性质的应用，熟练证明三角形全等．3．如图，AB=12cm，AC⊥AB，BD⊥AB ，AC=BD=9cm，点P在线段AB上以3 cm/s的速度，由A向B运动，同时点Q在线段BD上由B向D运动．（1）若点Q的运动速度与点P的运动速度相等，当运动时间t=1（s），△ACP与△BPQ 是否全等？说明理由，并直接判断此时线段PC和线段PQ的位置关系；（2）将“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA”，其他条件不变．若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能使△ACP与△BPQ全等.（3）在图2的基础上延长AC，BD交于点E，使C，D分别是AE，BE中点，若点Q以（2）中的运动速度从点B出发，点P以原来速度从点A同时出发，都逆时针沿△ABE三边运动，求出经过多长时间点P与点Q第一次相遇．【答案】（1）△ACP≌△BPQ，理由见解析；线段PC与线段PQ垂直（2）1或32（3）9s 【解析】【分析】（1）利用SAS证得△ACP≌△BPQ，得出∠ACP=∠BPQ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；（2）由△ACP ≌△BPQ ，分两种情况：①AC=BP ，AP=BQ ，②AC=BQ ，AP=BP ，建立方程组求得答案即可．（3）因为V Q ＜V P ，只能是点P 追上点Q ，即点P 比点Q 多走PB+BQ 的路程，据此列出方程，解这个方程即可求得．【详解】（1）当t=1时，AP=BQ=3，BP=AC=9，又∵∠A=∠B=90°，在△ACP 与△BPQ 中，AP BQ A B AC BP =⎧⎪∠=∠⎨⎪=⎩，∴△ACP ≌△BPQ （SAS ），∴∠ACP=∠BPQ ，∴∠APC+∠BPQ=∠APC+∠ACP=90°，∠CPQ=90°，则线段PC 与线段PQ 垂直.（2）设点Q 的运动速度x,①若△ACP ≌△BPQ ，则AC=BP ，AP=BQ ，912t t xt =-⎧⎨=⎩，解得31t x =⎧⎨=⎩， ②若△ACP ≌△BPQ ，则AC=BQ ，AP=BP ，912xt t t =⎧⎨=-⎩解得632t x =⎧⎪⎨=⎪⎩，综上所述，存在31t x =⎧⎨=⎩或632t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. （3）因为V Q ＜V P ，只能是点P 追上点Q ，即点P 比点Q 多走PB+BQ 的路程，设经过x 秒后P 与Q 第一次相遇，∵AC=BD=9cm ，C ，D 分别是AE ，BD 的中点；∴EB=EA=18cm.当V Q =1时，依题意得3x=x+2×9，解得x=9；当V Q=32时，依题意得3x=32x+2×9，解得x=12.故经过9秒或12秒时P与Q第一次相遇.【点睛】本题考查了一元一次方程的应用，解题的关键是熟练的掌握一元一次方程的性质与运算.4．如图，在△ABC中，∠ABC为锐角，点D为直线BC上一动点，以AD为直角边且在AD 的右侧作等腰直角三角形ADE，∠DAE＝90°，AD＝AE．（1）如果AB＝AC，∠BAC＝90°．①当点D在线段BC上时，如图1，线段CE、BD的位置关系为___________，数量关系为___________②当点D在线段BC的延长线上时，如图2，①中的结论是否仍然成立，请说明理由．（2）如图3，如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．探究：当∠ACB多少度时，CE⊥BC？请说明理由．【答案】（1）①垂直，相等．②都成立，理由见解析；（2）45°，理由见解析【解析】【分析】（1）①根据∠BAD=∠CAE，BA=CA，AD=AE，运用“SAS”证明△ABD≌△ACE，根据全等三角形性质得出对应边相等，对应角相等，即可得到线段CE、BD之间的关系；②先根据“SAS”证明△ABD≌△ACE，再根据全等三角形性质得出对应边相等，对应角相等，即可得到①中的结论仍然成立；（2）先过点A作AG⊥AC交BC于点G，画出符合要求的图形，再结合图形判定△GAD≌△CAE，得出对应角相等，即可得出结论．【详解】（1）：（1）CE与BD位置关系是CE⊥BD，数量关系是CE=BD．理由：如图1，∵∠BAD=90°-∠DAC，∠CAE=90°-∠DAC，∴∠BAD=∠CAE．又 BA=CA，AD=AE，∴△ABD≌△ACE （SAS）∴∠ACE=∠B=45°且 CE=BD．∵∠ACB=∠B=45°，∴∠ECB=45°+45°=90°，即 CE⊥BD．故答案为垂直，相等；②都成立，理由如下：∵∠BAC＝∠DAE＝90°，∴∠BAC＋∠DAC＝∠DAE＋∠DAC，∴∠BAD＝∠CAE，在△DAB与△EAC中，AD AEBAD CAEAB AC⎧⎪∠∠⎨⎪⎩＝＝＝∴△DAB≌△EAC，∴CE＝BD，∠B＝∠ACE，∴∠ACB＋∠ACE＝90°，即CE⊥BD；（2）当∠ACB＝45°时，CE⊥BD（如图）．理由：过点A作AG⊥AC交CB的延长线于点G，则∠GAC＝90°，∵∠ACB＝45°，∠AGC＝90°﹣∠ACB，∴∠AGC＝90°﹣45°＝45°，∴∠ACB＝∠AGC＝45°，∴AC＝AG，在△GAD与△CAE中，AC AGDAG EACAD AE⎧⎪∠∠⎨⎪⎩＝＝＝∴△GAD≌△CAE，∴∠ACE＝∠AGC＝45°，∠BCE＝∠ACB＋∠ACE＝45°＋45°＝90°，即CE⊥B C．5．在等边ABC中，点D是边BC上一点.作射线AD，点B关于射线AD的对称点为点E.连接CE并延长，交射线AD于点F.（1）如图，连接AE ，①AE 与AC 的数量关系是__________；②设BAF α∠=，用α表示BCF ∠的大小；（2）如图，用等式表示线段AF ，CF ，EF 之间的数量关系，并证明.【答案】(1) ①AB=AE ；②∠BCF=α；(2) AF-EF=CF ，理由见详解.【解析】【分析】（1）①根据轴对称性，即可得到答案；②由轴对称性，得：AE=AB ，∠BAF=∠EAF=α，由ABC 是等边三角形，得AB=AC ，∠BAC=∠ACB=60°，再根据等腰三角形的性质和三角形内角和等于180°，即可求解；（2）作∠FCG=60°交AD 于点G ，连接BF ，易证∆FCG 是等边三角形，得GF=FC ，再证∆ACG ≅∆BCF(SAS)，从而得AG=BF ，进而可得到结论.【详解】（1）①∵点B 关于射线AD 的对称点为点E ，∴AB 和AE 关于射线AD 的对称，∴AB=AE.故答案是：AB=AE ；②∵点B 关于射线AD 的对称点为点E ，∴AE=AB ，∠BAF=∠EAF=α，∵ABC 是等边三角形，∴AB=AC ，∠BAC=∠ACB=60°，∴∠EAC=60°-2α，AE=AC ，∴∠ACE=1180(602)602αα⎡⎤--=+⎣⎦， ∴∠BCF=∠ACE-∠ACB=60α+-60°=α. （2）AF-EF=CF ，理由如下：作∠FCG=60°交AD于点G，连接BF，∵∠BAF=∠BCF=α，∠ADB=∠CDF，∴∠ABC=∠AFC=60°，∴∆FCG是等边三角形，∴GF=FC，∵ABC是等边三角形，∴BC=AC，∠ACB=60°，∴∠ACG=∠BCF=α.在∆ACG和∆BCF中，∵CA CBACG BCFCG CF=⎧⎪∠=∠⎨⎪=⎩，∴∆ACG≅∆BCF(SAS)，∴AG=BF，∵点B关于射线AD的对称点为点E，∴AG=BF=EF，∵AF-AG=GF，∴AF-EF=CF.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理，添加辅助线，构造全等三角形，是解题的关键.二、八年级数学轴对称解答题压轴题（难）6．已知：AD是ABC∆的高，且BD CD=.（1）如图1，求证：BAD CAD∠=∠；（2）如图2，点E在AD上，连接BE，将ABE∆沿BE折叠得到'A BE∆，'A B与AC相交于点F，若BE=BC，求BFC∠的大小；（3）如图3，在（2）的条件下，连接EF，过点C作CG EF⊥，交EF的延长线于点G，若10BF=，6EG=，求线段CF的长.图1. 图2. 图3.【答案】（1）见解析，（2）BFC ∠=60（3）8=CF .【解析】【分析】（1）根据等腰三角形三线合一，易得AB=AC ，BAD CAD ∠=∠；（2）在图2中，连接CE ，可证得BCE ∆是等边三角形，60BEC ∠= ，30BED ∠=且由折叠性质可知1'2ABE A BE ABF ∠=∠=∠，可得BFC FAB ABF ∠=∠+∠ ()2BAD ABE =∠+∠ 260BED =∠=；（3）连接CE ，过点E 分别作EH AB ⊥于点H ，EM BF ⊥于点M ，EN AC ⊥于点N ，可证得Rt BEM Rt CEN ∆≅∆，BM CN =，BF FM CF CN -=+，可得线段CF 的长.【详解】解：（1）证明：如图1，AD BC ⊥，BD CD =AB AC ∴=BAD CAD ∴∠=∠；图1（2）解：在图2中，连接CEED BC ⊥，BD CD = BE CE ∴= 又BE BC = BE CE BC ∴== BCE ∴∆是等边三角形60BEC ∴∠= 30BED ∴∠=由折叠性质可知1'2ABE A BE ABF ∠=∠=∠ 2ABF ABE ∴∠=∠ 由（1）可知2FAB BAE ∠=∠BFC FAB ABF ∴∠=∠+∠ ()2BAD ABE =∠+∠ 223060BED =∠=⨯=图2（3）解：连接CE ，过点E 分别作EH AB ⊥于点H ，EM BF ⊥于点M ，EN AC ⊥于点N'ABE A BE ∠=∠，BAD CAD ∠=∠ EM EH EN ∴== AFE BFE ∴∠=∠ 又60BFC ∠= 60AFE BFE ∴∠=∠=在Rt EFM ∆中，906030FEM ∠=-= 2EF FM ∴=令FM m =，则2EF m = 62FG EG EF m ∴=-=- 同理12FN EF m ==，2124CF FG m ==-在Rt BEM ∆和Rt CEN ∆中，EM EN =，BE CE = Rt BEM Rt CEN ∴∆≅∆BM CN ∴=BF FM CF FN ∴-=+ 10124m m m ∴-=-+ 解得1m = 8CF ∴=图3故答案为（1）见解析，（2）BFC ∠= 60（3）8CF =. 【点睛】本题考查翻折的性质，涉及角平分线的性质、等腰三角形的性质和判定、等边三角形的判定和性质、含30度角的直角三角形、全等三角形的判定和性质等知识点，属于较难的题型.7．如图，在平面直角坐标系中，点B 坐标为()6,0-，点A 是y 轴正半轴上一点，且10AB =，点P 是x 轴上位于点B 右侧的一个动点，设点P 的坐标为()0m ,.（1）点A 的坐标为___________；（2）当ABP △是等腰三角形时，求P 点的坐标；（3）如图2，过点P 作PE AB ⊥交线段AB 于点E ，连接OE ，若点A 关于直线OE 的对称点为A '，当点A '恰好落在直线PE 上时，BE =_____________.（直接写出答案）【答案】（1）()0,8；（2）()4,0或()6,0或7,03⎛⎫ ⎪⎝⎭；（3）425【解析】【分析】（1）根据勾股定理可以求出AO 的长，则可得出A 的坐标；（2）分三种情况讨论等腰三角形的情况，得出点P 的坐标；（3）根据PE AB ⊥，点A '在直线PE 上，得到EAGOPG ，利用点A ，A '关于直线OE 对称点，根据对称性，可证'OPG EAO ，可得'8OP OA ，82AP，设BE x =，则有6AE x ，根据勾股定理，有：22222BP BE EP AP AE解之即可．【详解】解：（1）∵点B 坐标为6,0，点A 是y 轴正半轴上一点，且10AB =，∴ABO 是直角三角形，根据勾股定理有：22221068AOAB BO ，∴点A 的坐标为()0,8；（2）∵ABP △是等腰三角形，当BPAB 时，如图一所示：∴1064OP BP BO ，∴P 点的坐标是()4,0；当AP AB =时，如图二所示：∴6OP BO∴P 点的坐标是()6,0；当AP BP =时，如图三所示：设OP x =，则有6AP x∴根据勾股定理有：222OP AO AP += 即：22286x x解之得：73x =∴P 点的坐标是7,03；（3）当ABP △是钝角三角形时，点A '不存在；当ABP △是锐角三角形时，如图四示：连接'OA ， ∵PE AB ⊥，点A '在直线PE 上，∴AEG △和GOP 是直角三角形，EGAOGP∴EAGOPG ，∵点A ，A '关于直线OE 对称点，根据对称性，有'8OA OA ，'EAEA∴'FAO FAO，'FAE FAE∴'EAGEAO则有：'OPG EAO∴'AOP 是等腰三角形，则有'8OP OA ，∴22228882APAO OP ，设BE x =，则有6AE x ，根据勾股定理，有：22222BP BE EP AP AE即：2222688210x x解之得：425BE x【点睛】本题考查了三角形的综合问题，涉及的知识点有：解方程，等腰三角形的判定与性质，对称等知识点，能分类讨论，熟练运用各性质定理，是解题的关键．8．如图，在等边三角形ABC 的外侧作直线AP ，点C 关于直线AP 的对称点为点D ，连接AD ，BD ，其中BD 交直线AP 于点E ．（1）依题意补全图形；（2）若∠PAC ＝20°，求∠AEB 的度数；（3）连结CE ，写出AE ，BE ，CE 之间的数量关系，并证明你的结论．【答案】（1）补图见解析；（2）60°；（3）CE ＋AE ＝BE ．【解析】【分析】（1）根据题意补全图形即可；（2）根据轴对称的性质可得AC ＝AD ，∠PAC ＝∠PAD=20°，根据等边三角形的性质可得AC ＝AB ，∠BAC ＝60°，即可得AB ＝AD ，在△ABD 中，根据等腰三角形的性质和三角形的内角和定理求得∠D 的度数，再由三角形外角的性质即可求得∠AEB 的度数；（3）CE ＋AE ＝BE ，如图，在BE 上取点M 使ME ＝AE ，连接AM ，设∠EAC ＝∠DAE ＝x ，类比（2）的方法求得∠AEB ＝60°，从而得到△AME 为等边三角形，根据等边三角形的性质和SAS 即可判定△AEC ≌△AMB ，根据全等三角形的性质可得CE ＝BM ，由此即可证得CE ＋AE ＝BE ．【详解】 (1)如图：（2）在等边△ABC 中， AC ＝AB ，∠BAC ＝60°由对称可知：AC ＝AD ，∠PAC ＝∠PAD ， ∴AB ＝AD ∴∠ABD ＝∠D ∵∠PAC ＝20° ∴∠PAD ＝20°∴∠BAD ＝∠BAC+∠PAC +∠PAD =100°()1180402D BAD ︒︒∴∠=-∠=. ∴∠AEB ＝∠D +∠PAD ＝60° （3）CE ＋AE ＝BE ．在BE 上取点M 使ME ＝AE ，连接AM ，在等边△ABC中，AC＝AB，∠BAC＝60°由对称可知：AC＝AD，∠EAC＝∠EAD，设∠EAC＝∠DAE＝x．∵AD＝AC＝AB，∴()11802602D BAC x x︒︒∠=-∠-=-∴∠AEB＝60－x＋x＝60°．∴△AME为等边三角形．∴AM=AE，∠MAE=60°，∴∠BAC=∠MAE=60°，即可得∠BAM=∠CAE.在△AMB和△AEC中，AB ACBAM CAEAM AE=⎧⎪∠=∠⎨⎪=⎩，∴△AMB≌△AEC.∴CE＝BM.∴CE＋AE＝BE．【点睛】本题是三角形综合题，主要考查了轴对称的性质、三角形的内角和定理、等边三角形的性质及全等三角形的判定与性质等知识点，解决第三问时，通过做辅助线，把AE转化到BE 上，再证明CE＝BM即可得结论．9．如图，在等边三角形ABC右侧作射线CP，∠ACP=α（0°<α<60°），点A关于射线CP 的对称点为点D，BD交CP于点E，连接AD，AE.（1）求∠DBC的大小（用含α的代数式表示）；（2）在α（0°<α<60°）的变化过程中，∠AEB的大小是否发生变化？如果发生变化，请直接写出变化的范围；如果不发生变化，请直接写出∠AEB的大小；（3）用等式表示线段AE，BD，CE之间的数量关系，并证明.【答案】（1）∠DBC60α=︒-；（2）∠AEB的大小不会发生变化，且∠AEB=60°；（3）BD=2AE+CE，证明见解析.【解析】【分析】（1）如图1，连接CD，由轴对称的性质可得AC=DC，∠DCP=∠ACP=α，由△ABC是等边三角形可得AC=BC，∠ACB=60°，进一步即得∠BCD=602α︒+，BC=DC，然后利用三角形的内角和定理即可求出结果；（2）设AC、BD相交于点H，如图2，由轴对称的性质可证明△ACE≌△DCE，可得∠CAE=∠CDE，进而得∠DBC=∠CAE，然后根据三角形的内角和可得∠AEB=∠BCA，即可作出判断；（3）如图3，在BD上取一点M，使得CM=CE，先利用三角形的外角性质得出∠BEC60=︒，进而得△CME是等边三角形，可得∠MCE=60°，ME=CE，然后利用角的和差关系可得∠BCM=∠DCE，再根据SAS证明△BCM≌△DCE，于是BM=DE，进一步即可得出线段AE，BD，CE之间的数量关系.【详解】解：（1）如图1，连接CD，∵点A关于射线CP的对称点为点D，∴AC=DC，∠DCP=∠ACP=α，∵△ABC是等边三角形，∴AC=BC，∠ACB=60°，∴∠BCD=602α︒+，BC=DC，∴∠DBC=∠BDC()1806021806022BCDαα︒-︒+︒-∠===︒-；（2）∠AEB的大小不会发生变化，且∠AEB=60°.理由：设AC、BD相交于点H，如图2，∵点A关于射线CP的对称点为点D，∴AC=DC，AE=DE，又∵CE=CE，∴△ACE≌△DCE（SSS），∴∠CAE=∠CDE，∵∠DBC=∠BDC，∴∠DBC=∠CAE，又∵∠BHC=∠AHE，∴∠AEB=∠BCA=60°，即∠AEB的大小不会发生变化，且∠AEB=60°；（3）AE ，BD ，CE 之间的数量关系是：BD =2AE +CE . 证明：如图3，在BD 上取一点M ，使得CM=CE ， ∵∠BEC =∠BDC +∠DCE =6060αα︒-+=︒， ∴△CME 是等边三角形，∴∠MCE =60°，ME=CE ，∴60260BCM BCD MCE DCE ααα∠=∠-∠-∠=︒+-︒-=， ∴∠BCM =∠DCE ，又∵BC=DC ，CM=CE ， ∴△BCM ≌△DCE （SAS ），∴BM=DE ， ∵AE=DE ，∴BD=BM+ME+DE =2DE+ME =2AE+CE .【点睛】本题考查了等边三角形的判定和性质、全等三角形的判定和性质、三角形的内角和定理和轴对称的性质等知识，熟练掌握并运用上述知识解题的关键.10．（阅读理解）截长补短法，是初中数学儿何题中一种输助线的添加方法，截长就是在长边上载取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题.（1）如图1，△ABC 是等边三角形，点D 是边BC 下方一点，∠BDC ＝120°，探索线段DA 、DB 、DC 之间的数量关系.解题思路：延长DC 到点E ，使CE ＝B D ．连接AE ，根据∠BAC ＋∠BDC ＝180°，可证∠ABD ＝∠ACE ,易证得△ABD ≌△ACE ，得出△ADE 是等边三角形，所以AD ＝DE ，从而探寻线段DA 、DB 、DC 之间的数量关系.根据上述解题思路，请直接写出DA 、DB 、DC 之间的数量关系是___________（拓展延伸）（2）如图2，在Rt △ABC 中，∠BAC ＝90°，AB ＝A C ．若点D 是边BC 下方一点，∠BDC ＝90°，探索线段DA 、DB 、DC 之间的数量关系，并说明理由; （知识应用）（3）如图3,一副三角尺斜边长都为14cm ，把斜边重叠摆放在一起，则两块三角尺的直角项点之间的距离PQ 的长为________cm.【答案】（1）DA DB DC =+；（22DA DB DC =+，理由见详解；（3）7276+ 【解析】【分析】（1）由等边三角形知,60AB AC BAC ︒=∠=，结合120BDC ︒∠=知180ABD ACD ︒∠+∠=，则ABD ACE ∠=∠证得ABD ACE ≅得,AD AE BAD CAE =∠=∠,再证明三角形ADE 是等边三角形，等量代换可得结论；（2）同理可证ABD ACE ≅得,AD AE BAD CAE =∠=∠，由勾股定理得222DA AE DE +=，等量代换即得结论；（3）由直角三角形的性质可得QN 的长，由勾股定理可得MQ 的长，由（2）知2PQ QN QM =+，由此可求得PQ 长.【详解】解：（1）延长DC 到点E ，使CE ＝B D.连接AE ，ABC 是等边三角形,60AB AC BAC ︒∴=∠= 120BDC ︒∠=180ABD ACD ︒∴∠+∠=又180ACE ACD ︒∠+∠=ABD ACE ∴∠=∠ ()ABD ACE SAS ∴≅,AD AE BAD CAE ∴=∠=∠60BAC ︒∠= 60BAD DAC ︒∴∠+∠=60DAE DAC CAE ︒∴∠=∠+∠=ADE ∴是等边三角形DA DE DC CE DC DB ∴==+=+（2）2DA DB DC =+延长DC 到点E ，使CE ＝B D.连接AE ，90BAC ︒∠=，90BDC ︒∠=180ABD ACD ︒∴∠+∠=又180ACE ACD ︒∠+∠=ABD ACE ∴∠=∠,AB AC CE BD == ()ABD ACE SAS ∴≅,AD AE BAD CAE ∴=∠=∠90DAE BAC ︒∴∠=∠=222DA AE DE ∴+=222()DA DB DC ∴=+2DA DB DC ∴=+（3）连接PQ ，14,30MN QMN ︒=∠=172QN MN ∴== 根据勾股定理得222214714773MQ MN QN =-=-==由（22PQ QN QM =+773727622PQ ++∴=== 【点睛】此题是三角形的综合题，主要考查了全等三角形的判定和性质、直角三角形和等边三角形的性质，熟练掌握全等三角形的判定和性质是解题的关键.三、八年级数学整式的乘法与因式分解解答题压轴题（难）11．（1）你能求出（a ﹣1）（a 99+a 98+a 97+…+a 2+a +1）的值吗？遇到这样的问题，我们可以先从简单的情况入手，分别计算下列各式的值．（a ﹣1）（a +1）＝；（a ﹣1）（a 2+a +1）＝；（a ﹣1）（a 3+a 2+a +1）＝；…由此我们可以得到：（a ﹣1）（a 99+a 98+…+a +1）＝．（2）利用（1）的结论，完成下面的计算：2199+2198+2197+…+22+2+1．【答案】（1）21a -，31a -，41a -，1001a -（2）20021-【解析】【分析】根据简单的多项式运算推出同类复杂多项式运算结果的一般规律，然后根据找出的规律进行解决较难的运算问题．【详解】解：（1）21a - 31a - 41a - 1001a -（2）1991981972222221+++⋅⋅⋅++=()21- ⨯（1991981972222221+++⋅⋅⋅++）=20021-．【点睛】考查了学生的基础运算能力和对同一类运算问题计算结果的一般规律性洞察力．12．（1）阅读下列文字与例题：将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法例如：()()()()()()am an bm bn am bm an bn m a b n a b a b m n +++=+++=+++=++.22222221(21)(1)(1)(1)x y y x y y x y x y x y ---=-++=-+=++--.试用上述方法分解因式222a ab ac bc b ++++=（2）利用分解因式说明：22(5)(1)n n +--能被12整除.【答案】（1）()()a b a b c +++；（2）证明见解析.【解析】【分析】（1）a 2+2ab+ac+bc+b 2可以进行分组变成（a 2+2ab+b 2）+（ac+bc ），则前边括号内的三项可以利用完全平方公式分解，后边的三项可以提公因式，然后再利用提公因式法即可分解．（2）先利用平方差公式将22(5)(1)n n +--进行因式分解，之后即可得出答案.【详解】（1）原式=()()222a ab bac bc ++++=()()2a b c a b +++=()()a b a b c +++（2）22(5)(1)n n +--=[][](5)+(1)(5)(1)n n n n +-+--=()624n +=()122n +∴ 22(5)(1)n n +--能被12整除.【点睛】本题考查分组分解的因式分解方法，做题时先分析题中给的例子是解题关键.13．阅读下列材料：利用完全平方公式，可以将多项式2(0)ax bx c a ++≠变形为2()a x m n ++的形式, 我们把这样的变形方法叫做多项式2ax bx c ++的配方法．运用多项式的配方法及平方差公式能对一些多项式进行分解因式．例如：21124x x ++＝222111111()()2422x x ++-+ ＝21125()24x +- ＝115115()()2222x x +++-＝(8)(3)x x ++ 根据以上材料，解答下列问题：（1）用多项式的配方法将281x x +-化成2()x m n ++的形式；（2）下面是某位同学用配方法及平方差公式把多项式2340x x --进行分解因式的解答过程：老师说，这位同学的解答过程中有错误，请你找出该同学解答中开始出现错误的地方，并用“ ”标画出来，然后写出完整的、正确的解答过程：（3）求证：x ，y 取任何实数时，多项式222416x y x y +--+的值总为正数．【答案】（1）2(4)17x +- ；（2）(5)(8)x x +-；（3）见解析【解析】试题分析：（1）根据配方法，可得答案；（2）根据配方法，可得平方差公式，再根据平方差公式，可得答案；（3）根据交换律、结合率，可得完全平方公式，根据完全平方公式，可得答案．试题解析：解：（1）281x x +-=2228441x x ++--=2(4)17x +-（2）2340x x --=222333()()40222x x -+-- =23169()24x -- =313313()()2222x x -+-- =(5)(8)x x +- （3）证明：222416x y x y +--+=22214411x x y y -++-++=22(1)(2)11x y -+-+∵2(1)x -≥0，2(2)y -≥0，∴22(1)(2)110x y -+-+>．∴x ，y 取任何实数时，多项式222416x y x y +--+的值总是正数．点睛：本题考查了配方法，利用完全平方公式：a 2±2ab +b 2=（a ±b ）2配方是解题关键．14．阅读下列材料：在因式分解中，把多项式中某些部分看作一个整体，用一个新的字母代替（即换元），不仅可以简化要分解的多项式的结构，而且能使式子的特点更加明显，便于观察如何进行因式分解，我们把这种因式分解的方法称为“换元法”．下面是小涵同学用换元法对多项式（x2﹣4x+1）（x2﹣4x+7）+9进行因式分解的过程．解：设x2﹣4x＝y原式＝（y+1）（y+7）+9（第一步）＝y2+8y+16（第二步）＝（y+4）2（第三步）＝（x2﹣4x+4）2（第四步）请根据上述材料回答下列问题：（1）小涵同学的解法中，第二步到第三步运用了因式分解的；A．提取公因式法B．平方差公式法C．完全平方公式法（2）老师说，小涵同学因式分解的结果不彻底，请你写出该因式分解的最后结果：；（3）请你用换元法对多项式（x2+2x）（x2+2x+2）+1进行因式分解．【答案】（1）C；（2）（x﹣2）4；（3）（x+1）4．【解析】【分析】（1）根据完全平方公式进行分解因式；（2）最后再利用完全平方公式将结果分解到不能分解为止；（3）根据材料，用换元法进行分解因式．【详解】（1）故选C；（2）（x2﹣4x+1）（x2﹣4x+7）+9，设x2﹣4x=y，则：原式=（y+1）（y+7）+9=y2+8y+16=（y+4）2=（x2﹣4x+4）2=（x﹣2）4．故答案为：（x﹣2）4；（3）设x2+2x=y，原式=y（y+2）+1=y2+2y+1=（y+1）2=（x2+2x+1）2=（x+1）4．【点睛】本题考查了因式分解﹣换元法，公式法，也是阅读材料问题，熟练掌握利用公式法分解因式是解题的关键．15．材料阅读：若一个整数能表示成a2＋b2(a、b是正整数)的形式，则称这个数为“完美数”．例如：因为13＝32＋22，所以13是“完美数”；再如：因为a2＋2ab＋2b2＝(a＋b)2＋b2(a、b是正整数)，所以a2＋2ab＋2b2也是“完美数”．(1)请你写出一个大于20小于30的“完美数”，并判断53是否为“完美数”；(2)试判断(x2＋9y2)·(4y2＋x2)(x、y是正整数)是否为“完美数”，并说明理由．【答案】（1）25，53是完美数; (2)是，理由见解析.【解析】【分析】（1）根据“完美数”的定义判断即可；（2）根据多项式的乘法法则计算出结果后，根据“完美数”的定义判断即可．【详解】(1)25=4²+3²，∵53=49+4=7²+2²，∴53是“完美数”；(2)(x²+9y²)⋅(4y²+x²)是“完美数”，(x²+9y²)⋅(4y²+x²)=4x2y²+364y+4x+9x²y²=13x²y²+364y+4x=(6y²+x²) ²+x²y²，∴(x²+9y²)⋅(4y²+x²)是“完美数”.【点睛】本题考查了因式分解的应用，正确的理解新概念“完美数”是解题的关键．四、八年级数学分式解答题压轴题（难）16．某商场购进甲、乙两种空调共50台．已知购进一台甲种空调比购进一台乙种空调进价少0.3万元；用20万元购进甲种空调数量是用40万元购进乙种空调数量的2倍．请解答下列问题：（1）求甲、乙两种空调每台进价各是多少万元？（2）若商场预计投入资金不少于10万元，且购进甲种空调至少31台，商场有哪几种购进方案？（3）在（2）条件下，若甲种空调每台售价1100元，乙种空调每台售价4300元，甲、乙空调各有一台样机按八折出售，其余全部标价售出，商场从销售这50台空调获利中拿出2520元作为员工福利，其余利润恰好又可以购进以上空调共2台．请直接写出该商场购进这50台空调各几台．【答案】（1）0.1，0.4；（2）商场有3种购进方案：①购买甲种空调31台，购买乙种空调19台；②购买甲种空调32台，购买乙种空调18台；③购买甲种空调33台，购买乙种空调17台；（3）购买甲种空调32台，购买乙种空调18台【解析】【分析】（1）可设甲种空调每台进价是x万元，则乙种空调每台进价是（x+0.3）万元，根据等量关系用20万元购进甲种空调数量＝用40万元购进乙种空调数量×2，列出方程求解即可；（2）设购买甲种空调n台，则购买乙种空调（50﹣n）台，根据商场预计投入资金不少于10万元，且购进甲种空调至少31台，求出n的范围，即可确定出购买方案；（3）找到（2）中3种购进方案符合条件的即为所求．【详解】解：（1）设甲种空调每台进价是x万元，则乙种空调每台进价是（x+0.3）万元，依题意有20x ＝400.3x ×2，解得x ＝0.1，x+0.3＝0.1+0.3＝0.4．答：甲种空调每台进价是0.1万元，乙种空调每台进价是0.4万元；（2）设购买甲种空调n 台，则购买乙种空调（50﹣n ）台，依题意有0.10.4(50)1031sn n n +-⎧⎨⎩，解得31≤n≤3313， ∵n 为整数， ∴n 取31，32，33，∴商场有3种购进方案：①购买甲种空调31台，购买乙种空调19台；②购买甲种空调32台，购买乙种空调18台；③购买甲种空调33台，购买乙种空调17台；（3）①购买甲种空调31台，购买乙种空调19台，（31﹣1）×（1100﹣1000）+（1100×0.8﹣1000）+（19﹣1）×（4300﹣4000）+（4300×0.8﹣4000）﹣2520＝3000﹣120+5400﹣560﹣2520＝7720﹣2520＝5200（元），不符合题意，舍去；②购买甲种空调32台，购买乙种空调18台，（32﹣1）×（1100﹣1000）+（1100×0.8﹣1000）+（18﹣1）×（4300﹣4000）+（4300×0.8﹣4000）﹣2520＝3100﹣120+5100﹣560﹣2520＝7520﹣2520＝5000（元），符合题意；③购买甲种空调33台，购买乙种空调17台，（33﹣1）×（1100﹣1000）+（1100×0.8﹣1000）+（17﹣1）×（4300﹣4000）+（4300×0.8﹣4000）﹣2520＝3200﹣120+4800﹣560﹣2520＝7320﹣2520＝4800（元），不符合题意，舍去．综上所述，购买甲种空调32台，购买乙种空调18台．【点睛】此题考查了分式方程的应用，以及一元一次不等式组的应用，弄清题中的等量关系是解本题的关键．17．阅读下面的解题过程：已知2112x x =+，求241x x +的值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级数学上册期末试卷培优测试卷一、八年级数学全等三角形解答题压轴题（难）1．如图，在ABC 中，45ABC ∠=,AD ,BE 分别为BC ,AC 边上的高，连接DE ,过点D 作DF DE ⊥与点F ，G 为BE 中点，连接AF ，DG ．（1）如图1，若点F 与点G 重合，求证：AF DF ⊥；（2）如图2，请写出AF 与DG 之间的关系并证明．【答案】(1)详见解析;(2)AF=2DG,且AF ⊥DG,证明详见解析.【解析】【分析】(1) 利用条件先△DAE ≌△DBF,从而得出△FDE 是等腰直角三角形,再证明△AEF 是等腰直角三角形,即可.(2) 延长DG 至点M,使GM=DG,交AF 于点H,连接BM, 先证明△BGM ≌△EGD,再证明△BDM ≌△DAF 即可推出.【详解】解:（1）证明:设BE 与AD 交于点H..如图，∵AD,BE 分别为BC,AC 边上的高,∴∠BEA=∠ADB=90°.∵∠ABC=45°,∴△ABD 是等腰直角三角形.∴AD=BD.∵∠AHE=∠BHD,∴∠DAC=∠DBH.∵∠ADB=∠FDE=90°,∴∠ADE=∠BDF.∴△DAE ≌△DBF.∴BF=AE,DF=DE.∴△FDE是等腰直角三角形.∴∠DFE=45°.∵G为BE中点,∴BF=EF.∴AE=EF.∴△AEF是等腰直角三角形.∴∠AFE=45°.∴∠AFD=90°,即AF⊥DF.（2）AF=2DG,且AF⊥DG.理由:延长DG至点M,使GM=DG,交AF于点H,连接BM,∵点G为BE的中点,BG=GE.∵∠BGM∠EGD,∴△BGM≌△EGD.∴∠MBE=∠FED=45°,BM=DE.∴∠MBE=∠EFD,BM=DF.∵∠DAC=∠DBE,∴∠MBD=∠MBE+∠DBE=45°+∠DBE.∵∠EFD=45°=∠DBE+∠BDF,∴∠BDF=45°-∠DBE.∵∠ADE=∠BDF,∴∠ADF=90°-∠BDF=45°+∠DBE=∠MBD.∵BD=AD,∴△BDM≌△DAF.∴DM=AF=2DG,∠FAD=∠BDM.∵∠BDM+∠MDA=90°,∴∠MDA+∠FAD=90°.∴∠AHD=90°.∴AF⊥DG.∴AF=2DG,且AF⊥DG【点睛】本题考查三角形全等的判定和性质,关键在于灵活运用性质.2．已知：平面直角坐标系中，点A（a，b）的坐标满足|a﹣b|+b2﹣8b+16＝0．（1）如图1，求证：OA是第一象限的角平分线；（2）如图2，过A作OA的垂线，交x轴正半轴于点B，点M、N分别从O、A两点同时出发，在线段OA上以相同的速度相向运动（不包括点O和点A），过A作AE⊥BM交x轴于点E，连BM、NE，猜想∠ONE与∠NEA之间有何确定的数量关系，并证明你的猜想；（3）如图3，F是y轴正半轴上一个动点，连接FA，过点A作AE⊥AF交x轴正半轴于点E，连接EF，过点F点作∠OFE的角平分线交OA于点H，过点H作HK⊥x轴于点K，求2HK+EF的值．【答案】（1）证明见解析（2）答案见解析（3）8【解析】【分析】（1）过点A分别作x轴，y轴的垂线，垂足分别为M、N，则AN＝AM,根据非负数的性质求出a、b的值即可得结论；（2）如图2，过A作AH平分∠OAB，交BM于点H，则△AOE≌△BAH，可得AH＝OE，由已知条件可知ON=AM，∠MOE＝∠MAH，可得△ONE≌△AMH，∠ABH＝∠OAE，设BM 与NE交于K，则∠MKN＝180°﹣2∠ONE＝90°﹣∠NEA，即2∠ONE﹣∠NEA＝90°；（3）如图3，过H作HM⊥OF，HN⊥EF于M、N，可证△FMH≌△FNH，则FM＝FN，同理：NE＝EK，先得出OE+OF﹣EF＝2HK，再由△APF≌△AQE得PF＝EQ，即可得OE+OF＝2OP＝8，等量代换即可得2HK+EF的值．【详解】解：（1）∵|a﹣b|+b2﹣8b+16＝0∴|a﹣b|+（b﹣4）2＝0∵|a﹣b|≥0，（b﹣4）2≥0∴|a﹣b|＝0，（b﹣4）2＝0∴a＝b＝4过点A分别作x轴，y轴的垂线，垂足分别为M、N，则AN＝AM∴OA平分∠MON即OA是第一象限的角平分线（2）过A作AH平分∠OAB，交BM于点H∴∠OAH＝∠HAB＝45°∵BM⊥AE∴∠ABH＝∠OAE在△AOE 与△BAH 中OAE ABH OA ABAOE BAH ＝＝∠∠⎧⎪=⎨⎪∠∠⎩， ∴△AOE ≌△BAH （ASA ）∴AH ＝OE在△ONE 和△AMH 中OE AH NOE MAH ON AM =⎧⎪∠∠⎨⎪=⎩＝， ∴△ONE ≌△AMH （SAS ）∴∠AMH ＝∠ONE设BM 与NE 交于K∴∠MKN ＝180°﹣2∠ONE ＝90°﹣∠NEA∴2∠ONE ﹣∠NEA ＝90°（3）过H 作HM ⊥OF ，HN ⊥EF 于M 、N可证：△FMH ≌△FNH （SAS ）∴FM ＝FN同理：NE ＝EK∴OE+OF ﹣EF ＝2HK过A 作AP ⊥y 轴于P ，AQ ⊥x 轴于Q可证：△APF ≌△AQE （SAS ）∴PF ＝EQ∴OE+OF ＝2OP ＝8∴2HK+EF ＝OE+OF ＝8【点睛】本题考查非负数的性质，平面直角坐标系中点的坐标，等腰直角三角形，全等三角形的判定和性质.3．如图1，在ABC ∆中，90ACB ∠=，AC BC =，直线MN 经过点C ，且AD MN ⊥于点D，BE MN⊥于点E．易得DE AD BE=+（不需要证明）．（1）当直线MN绕点C旋转到图2的位置时，其余条件不变，你认为上述结论是否成立？若成立，写出证明过程；若不成立，请写出此时DE AD BE、、之间的数量关系，并说明理由；（2）当直线MN绕点C旋转到图3的位置时，其余条件不变，请直接写出此时DE AD BE、、之间的数量关系（不需要证明）．【答案】(1) 不成立，DE=AD-BE，理由见解析；(2) DE=BE-AD【解析】【分析】(1)DE、AD、BE之间的数量关系是DE=AD-BE．由垂直的性质可得到∠CAD=∠BCE，证得△ACD≌△CBE，得到AD=CE，CD=BE，即有DE=AD-BE；(2)DE、AD、BE之间的关系是DE=BE-AD．证明的方法与(1)一样．【详解】(1)不成立．DE、AD、BE之间的数量关系是DE=AD-BE，理由如下：如图，∵∠ACB=90°，BE⊥CE，AD⊥CE，AC CB=，∴∠ACD+∠CAD=90°，又∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ACD和△CBE中，90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△CBE(AAS)，∴AD=CE，CD=BE，∴DE=CE-CD=AD-BE；(2)结论：DE=BE-AD．∵∠ACB=90°，BE⊥CE，AD⊥CE，AC CB=，∴∠ACD+∠CAD=90°，又∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ACD和△CBE中，90ADC CEBCAD BCEAC CB∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，∴△ADC≌△CEB(AAS)，∴AD=CE ，DC=BE，∴DE=CD-CE=BE-AD．【点睛】本题考查了旋转的性质、直角三角形全等的判定与性质，旋转前后两图形全等，对应点到旋转中心的距离相等，对应点与旋转中心的连线段所夹的角等于旋转角．4．在等边ABC中，点D是边BC上一点.作射线AD，点B关于射线AD的对称点为点E.连接CE并延长，交射线AD于点F.（1）如图，连接AE，①AE与AC的数量关系是__________；②设BAFα∠=，用α表示BCF∠的大小；（2）如图，用等式表示线段AF，CF，EF之间的数量关系，并证明.【答案】(1)①AB=AE；②∠BCF=α；(2) AF-EF=CF，理由见详解.【解析】【分析】（1）①根据轴对称性，即可得到答案；②由轴对称性，得：AE=AB，∠BAF=∠EAF=α，由ABC是等边三角形，得AB=AC，∠BAC=∠ACB=60°，再根据等腰三角形的性质和三角形内角和等于180°，即可求解；（2）作∠FCG=60°交AD于点G，连接BF，易证∆FCG是等边三角形，得GF=FC，再证∆ACG≅∆BCF(SAS)，从而得AG=BF，进而可得到结论.【详解】（1）①∵点B关于射线AD的对称点为点E，∴AB和AE关于射线AD的对称，∴AB=AE.故答案是：AB=AE；②∵点B关于射线AD的对称点为点E，∴AE=AB，∠BAF=∠EAF=α，∵ABC是等边三角形，∴AB=AC，∠BAC=∠ACB=60°，∴∠EAC=60°-2α，AE=AC，∴∠ACE=1180(602)602αα⎡⎤--=+⎣⎦，∴∠BCF=∠ACE-∠ACB=60α+-60°=α.（2）AF-EF=CF，理由如下：作∠FCG=60°交AD于点G，连接BF，∵∠BAF=∠BCF=α，∠ADB=∠CDF，∴∠ABC=∠AFC=60°，∴∆FCG是等边三角形，∴GF=FC，∵ABC是等边三角形，∴BC=AC，∠ACB=60°，∴∠ACG=∠BCF=α.在∆ACG和∆BCF中，∵CA CBACG BCFCG CF=⎧⎪∠=∠⎨⎪=⎩，∴∆ACG≅∆BCF(SAS)，∴AG=BF，∵点B关于射线AD的对称点为点E，∴AG=BF=EF，∵AF-AG=GF，∴AF-EF=CF.【点睛】本题主要考查等边三角形的性质和三角形全等的判定和性质定理，添加辅助线，构造全等三角形，是解题的关键.5．如图，在边长为 4 的等边△ABC 中，点 D 从点A 开始在射线 AB 上运动，速度为 1 个单位/秒，点F 同时从 C 出发，以相同的速度沿射线 BC 方向运动，过点D 作 DE⊥AC，连结DF 交射线 AC 于点 G(1)当 DF⊥AB 时，求 t 的值；(2)当点 D 在线段 AB 上运动时，是否始终有 DG=GF?若成立，请说明理由。

(3)聪明的斯扬同学通过测量发现，当点 D 在线段 AB 上时，EG 的长始终等于 AC 的一半，他想当点D 运动到图 2 的情况时，EG 的长是否发生变化?若改变，说明理由；若不变，求出 EG 的长。

【答案】（1）43；（2）见详解；（3）不变.【解析】【分析】（1）设AD=x，则BD=4-x，BF=4+x．当DF⊥AB时，通过解直角△BDF求得x的值，易得t的值；（2）如图1，过点D作DH∥BC交AC于点H，构建全等三角形：△DHG≌△FCG，结合全等三角形的对应边相等的性质和图中相关线段间的和差关系求得DG=GF；（3）过F作FH⊥AC，可证△ADE≌△CFH，得DE=FH，AC=EH，再证△GDE≌△GFH，可得EG=GH，即可解题．【详解】解：（1）设AD=x，则BD=4-x，BF=4+x．当DF⊥AB时，∵∠B=60°，∴∠DFB=30°，∴BF=2BD，即4+x=2（4-x），解得x=43，故t=43；（2）如图1，过点D作DH∥BC交AC于点H，则∠DHG=∠FCG．∵△ABC是等边三角形，∴△ADH是等边三角形，∴AD=DH．又AD=CF，∴DH=FC．∵在△DHG与△FCG中，DGH FGCDHG FCGDH FC∠∠⎧⎪∠∠⎨⎪⎩＝＝＝，∴△DHG≌△FCG（AAS），∴DG=GF；（3）如图2，过F 作FH ⊥AC ，在△ADE 和△CFH 中，90AED FHC A FCH AD CF ∠∠︒⎧⎪∠∠⎨⎪⎩＝＝＝＝， ∴△ADE ≌△CFH （AAS ），∴DE=FH ，AE=CH ，∴AC=EH ，在△GDE 和△GFH 中，DEG FHG DGE FGH DE FH ∠∠⎧⎪∠∠⎨⎪⎩＝＝＝∴△GDE ≌△GFH （AAS ），∴EG=GH ，∴EG=12EH=12AC ．【点睛】本题考查了三角形综合题，需要掌握全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△GDE≌△GFH 是解题的关键．二、八年级数学轴对称解答题压轴题（难）6．（1）已知△ABC 中，∠A ＝90°，∠B ＝67.5°，请画一条直线，把这个三角形分割成两个等腰三角形．（请你选用下面给出的备用图，把所有不同的分割方法都画出来．只需画图，不必说明理由，但要在图中标出相等两角的度数）（2）已知△ABC 中，∠C 是其最小的内角，过顶点B 的一条直线把这个三角形分割成了两个等腰三角形，请探求∠ABC 与∠C 之间的关系．【答案】(1)图形见解析(2) ∠ABC 与∠C 之间的关系是∠ABC＝135°－34∠C 或∠ABC＝3∠C 或∠ABC＝180°－3∠C 或∠ABC＝90°，∠C 是小于45°的任意锐角．【解析】试题分析：（1）已知角度，要分割成两个等腰三角形，可以运用直角三角形、等腰三角形性质结合三角形内角和定理，先计算出可能的角度，或者先从草图中确认可能的情况，及角度，然后画上．（2）在（1）的基础上，由“特殊”到“一般”，需要把直角三角形分成两个等腰三角形的各种情形列方程，可得出角与角之间的关系．试题解析：(1)如图①②(共有2种不同的分割法)．(2)设∠ABC＝y，∠C＝x，过点B的直线交边AC于点D.在△DBC中，①若∠C是顶角，如图，则∠CBD＝∠CDB＝90°－12x，∠A＝180°－x－y.故∠ADB＝180°－∠CDB＝90°＋12x＞90°，此时只能有∠A＝∠ABD，即180°－x－y＝y－1902x⎛⎫-⎪⎝⎭，∴3x＋4y＝540°，∴∠ABC＝135°－34∠C.②若∠C是底角，第一种情况：如图，当DB＝DC时，∠DB C＝x.在△ABD中，∠ADB＝2x，∠ABD＝y－x.若AB＝AD，则2x＝y－x，此时有y＝3x，∴∠ABC＝3∠C.若AB＝BD，则180°－x－y＝2x，此时有3x＋y＝180°，∴∠ABC＝180°－3∠C.若AD＝BD，则180°－x－y＝y－x，此时有y＝90°，即∠ABC＝90°，∠C为小于45°的任意锐角．第二种情况：如图，当BD＝BC时，∠BDC＝x，∠ADB＝180°－x＞90°，此时只能有AD＝BD，∴∠A＝∠ABD＝12∠BDC＝12∠C＜∠C，这与题设∠C是最小角矛盾．∴当∠C是底角时，BD＝BC不成立．综上所述，∠ABC与∠C之间的关系是∠ABC＝135°－34∠C或∠ABC＝3∠C或∠ABC＝180°－3∠C或∠ABC＝90°，∠C是小于45°的任意锐角．点睛：本题考查了等腰三角形的性质；第（1）问是计算与作图相结合的探索．本问对学生运用作图工具的能力，以及运用直角三角形、等腰三角形性质等基础知识解决问题的能力都有较高的要求．第（2）问在第（1）问的基础上，由“特殊”到“一般”，“分类讨论”把直角三角形分成两个等腰三角形的各种情形并结合“方程思想”探究角与角之间的关系．本题不仅趣味性强，创造性强，而且渗透了由“特殊”到“一般”、“分类讨论”、“方程思想”、“转化思想”等数学思想，是一道不可多得的好题．7．已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图,E、F分别是AB、AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.(2)若E、F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么,△DEF是否仍为等腰直角三角形?画出图形,写出结论不证明.【答案】（1）见解析；（2）见解析【分析】(1)先连接AD，构造全等三角形：△BED和△AFD．AD是等腰直角三角形ABC底边上的中线，所以有∠CAD=∠BAD=45°，AD=BD=CD，而∠B=∠C=45°，所以∠B=∠DAF，再加上BE=AF，AD=BD，可证出：△BED≌△AFD，从而得出DE=DF，∠BDE=∠ADF，从而得出∠EDF=90°，即△DEF是等腰直角三角形；(2)根据题意画出图形,连接AD,构造△DAF≌△DBE.得出FD=ED ,∠FDA=∠EDB,再算出∠EDF=90°,即可得出△DEF是等腰直角三角形.【详解】解：（1）连结AD ,∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD⊥BC ,BD=AD ,∴∠B=∠BAD=∠DAC=45°,又∵BE=AF ,∴△BDE≌△ADF（SAS）,∴ED=FD ,∠BDE=∠ADF,∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°,∴△DEF为等腰直角三角形.（2）连结AD∵AB=AC ,∠BAC=90° ,D为BC中点 ,∴AD=BD ,AD⊥BC ,∴∠DAC=∠ABD=45° ,∴∠DAF=∠DBE=135°,又∵AF=BE ,∴△DAF≌△DBE（SAS）,∴FD=ED ,∠FDA=∠EDB,∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.∴△DEF为等腰直角三角形.本题利用了等腰直角三角形底边上的中线平分顶角，并且等于底边的一半，还利用了全等三角形的判定和性质，及等腰直角三角形的判定．8．如图，在ABC ∆中，CE 为三角形的角平分线，AD CE ⊥于点F 交BC 于点D （1）若9628BAC B ︒︒∠=∠=，，直接写出BAD ∠= 度（2）若2ACB B ∠=∠，①求证：2AB CF =②若 ,CF a EF b ==，直接写出BD CD= （用含 ,a b 的式子表示）【答案】（1）34；（2）①见详解；②2b a b- 【解析】【分析】（1）由三角形内角和定理和角平分线定义即可得出答案；（2）①证明B BCE ∠=∠，得出BE=CE ，过点A 作//AH BC 交CE 与点H ，则,H BCE ACE EAH B ∠=∠=∠∠=∠，得出AH=AC ，H EAH ∠=∠，得出AE=HE ，由等腰三角形的性质可得出HF=CF ，即可得出结论；②证明AHF DCF ≅，得出AH=DC ，求出HF=CF=a ，HE=HF-EF=a-b ，CE=a+b ，由 //AH BC 得出AH AE a b BC BE a b-==+，进而得出结论．【详解】解：（1）∵9628BAC B ︒︒∠=∠=，，∴180962856ACB ∠=︒-︒-︒=︒，∵CE 为三角形的角平分线，∴1282ACE ACB ∠=∠=︒， ∵AD CE ⊥，∴902862CAF ∠=︒-︒=︒，∴966234BAD ∠=︒-︒=︒．故答案为：34；（2）①证明：∵22ACB B BCE ∠=∠=∠∴B BCE ∠=∠∴BE CE=过点A作//AH BC交CE与点H，如图所示：则,H BCE ACE EAH B∠=∠=∠∠=∠∴AH=AC，H EAH∠=∠∴AE=HE∵AD CE⊥∴HF=CF∴AB=HC=2CF；②在AHF△和DCF中，H DCFHF CFAFH DFC∠=∠⎧⎪=⎨⎪∠=∠⎩∴AHF DCF≅∴AH=DC∵,CF a EF b==∴HF CF a==，由①得AE HE HF EF a b==-=-，BE CE a b==+∵//AH BC∴AH AE a bBC BE a b-==+∴CD a bBC a b-=+∴2BD bCD a b=-．故答案为：2ba b-．【点睛】本题考查的知识点是全等三角形的判定及其性质、等腰三角形的判定及其性质、三角形的内角和定理、三角形的角平分线定理等，掌握以上知识点是解此题的关键．9．如图，在等边△ABC中，线段AM为BC边上的中线．动点D在直线AM上时，以CD为一边在CD的下方作等边△CDE，连结BE．（1）求∠CAM的度数；（2）若点D在线段AM上时，求证：△ADC≌△BEC；（3）当动D在直线．．AM上时，设直线BE与直线AM的交点为O，试判断∠AOB是否为定值？并说明理由．【答案】（1）30°；（2）答案见解析；（3）∠AOB是定值，∠AOB＝60°．【解析】【分析】（1）根据等边三角形的性质可以直接得出结论；（2）根据等边三角形的性质就可以得出AC＝BC，DC＝EC，∠ACB＝∠DCE＝60°，由等式的性质就可以∠BCE＝∠ACD，根据SAS就可以得出△ADC≌△BEC；（3）分情况讨论：当点D在线段AM上时，如图1，由（2）可知△ACD≌△BCE，就可以求出结论；当点D在线段AM的延长线上时，如图2，可以得出△ACD≌△BCE而有∠CBE＝∠CAD＝30°而得出结论；当点D在线段MA的延长线上时，如图3，通过得出△ACD≌△BCE同样可以得出结论．【详解】（1）∵△ABC是等边三角形，∴∠BAC＝60°．∵线段AM为BC边上的中线，∴∠CAM12=∠BAC，∴∠CAM＝∠BAM＝30°．（2）∵△ABC与△DEC都是等边三角形，∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°，∴∠ACD+∠DCB＝∠DCB+∠BCE，∴∠ACD ＝∠BCE．在△ADC和△BEC中，∵AC BCACD BCECD CE=⎧⎪∠=∠⎨⎪=⎩，∴△ACD≌△BCE（SAS）；（3）∠AOB是定值，∠AOB＝60°．理由如下：①当点D在线段AM上时，如图1，由（2）可知△ACD≌△BCE，则∠CBE＝∠CAD＝30°，又∠ABC＝60°，∴∠CBE+∠ABC＝60°+30°＝90°．∵△ABC是等边三角形，线段AM为BC边上的中线，∴AM平分∠BAC，即11603022BAM BAC ∠∠==⨯︒=︒，∴∠BOA ＝90°﹣30°＝60°．②当点D 在线段AM 的延长线上时，如图2．∵△ABC 与△DEC 都是等边三角形，∴AC ＝BC ，CD ＝CE ，∠ACB ＝∠DCE ＝60°，∴∠ACB +∠DCB ＝∠DCB +∠DCE ，∴∠ACD ＝∠BCE ．在△ACD 和△BCE 中，∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△BCE （SAS ），∴∠CBE ＝∠CAD ＝30°．由（1）得：∠BAM ＝30°，∴∠BOA ＝90°﹣30°＝60°．③当点D 在线段MA 的延长线上时．∵△ABC 与△DEC 都是等边三角形，∴AC ＝BC ，CD ＝CE ，∠ACB ＝∠DCE ＝60°，∴∠ACD +∠ACE ＝∠BCE +∠ACE ＝60°，∴∠ACD ＝∠BCE ．在△ACD 和△BCE 中，∵AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACD ≌△BCE （SAS ），∴∠CBE ＝∠CAD ．由（1）得：∠CAM ＝30°，∴∠CBE ＝∠CAD ＝150°，∴∠CBO ＝30°，∠BAM ＝30°，∴∠BOA ＝90°﹣30°＝60°．综上所述：当动点D 在直线AM 上时，∠AOB 是定值，∠AOB ＝60°．【点睛】本题考查了等边三角形的性质的运用，直角三角形的性质的运用，等式的性质的运用，全等三角形的判定及性质的运用，解答时证明三角形全等是关键．10．如图1，△ABD ，△ACE 都是等边三角形，（1）求证：△ABE≌△ADC；（2）若∠ACD=15°，求∠AEB的度数；（3）如图2，当△ABD与△ACE的位置发生变化，使C、E、D三点在一条直线上，求证：AC∥BE．【答案】(1)见解析(2) ∠AEB=15°(3) 见解析【解析】试题分析：（1）由等边三角形的性质可得AB=AD，AE=AC，∠DAB=∠EAC=60°，即可得∠DAC=∠BAE，利用SAS即可判定△ABE≌△ADC；（2）根据全等三角形的性质即可求解；（3）由（1）的方法可证得△ABE≌△ADC，根据全等三角形的性质和等边三角形的性质可得∠AEB=∠ACD =60°，即可得∠AEB=∠EAC，从而得AC∥BE．试题解析：（1）证明：∵△ABD，△ACE都是等边三角形∴AB=AD，AE=AC，∠DAB=∠EAC=60°，∴∠DAC=∠BAE，在△ABE和△ADC中，∴，∴△ABE≌△ADC；（2）由（1）知△ABE≌△ADC，∴∠AEB=∠ACD，∵∠ACD=15°，∴∠AEB=15°；（3）同上可证：△ABE≌△ADC，∴∠AEB=∠ACD，又∵∠ACD=60°，∴∠AEB=60°，∵∠EAC=60°，∴∠AEB=∠EAC，∴AC∥BE．点睛：本题主要考查了等边三角形的性质、全等三角形的判定及性质，证得△ABE≌△ADC是解决本题的关键.三、八年级数学整式的乘法与因式分解解答题压轴题（难）11．在我国南宋数学家杨辉（约13世纪）所著的《详解九章算术》（1261年）一书中，用下图的三角形解释二项和的乘方规律．杨辉在注释中提到，在他之前北宋数学家贾宪（1050年左右）也用过上述方法，因此我们称这个三角形为“杨辉三角”或“贾宪三角”．杨辉三角两腰上的数都是1，其余每一个数为它上方（左右）两数的和．事实上，这个三角形给出了()n a b +(1,2,3,4,5,6)n =的展开式（按a 的次数由大到小的顺序）的系数规律．例如，此三角形中第三行的3个数1,2,1，恰好对应着222()2a b a ab b +=++展开式中的各项系数，第四行的4个数1,3,3,1，恰好对应着+=+++33223()33a b a a b ab b 展开式中的各项系数，等等．请依据上面介绍的数学知识，解决下列问题：（1）写出4()a b +的展开式；（2）利用整式的乘法验证你的结论．【答案】（1）++++432234a 4a b 6a b 4ab b ；（2）见解析【解析】【分析】(1)运用材料所提供的结论即可写出；（2）利用整式的乘法求解验证即可.【详解】（1）4322344()464a b a a b a b ab b +=++++，（2）方法一：()()()43a b a b a b +=+•+=()()322333a b a a b ab b ++++4322332234=33+33a a b a b ab a b a b ab b ++++++432234464a a b a b ab b =++++方法二：()()()422a b a b a b +=+•+=2222(2)(2)a ab b a ab b ++++=43223223223422422a a b a b a b a b ab a b ab b ++++++++= ++++432234a 4a b 6a b 4ab b .【点睛】解决阅读题的关键是读懂题目所给材料并理解，应用题目中给出的信息解决问题.12．把代数式通过配凑等手段，得到完全平方式，再运用完全平方式是非负性这一性质增加问题的条件，这种解题方法通常被称为配方法．配方法在代数式求值、解方程、最值问题等都有着广泛的应用．例如：若代数式M ＝a 2﹣2ab +2b 2﹣2b +2，利用配方法求M 的最小值：a 2﹣2ab +2b 2﹣2b +2＝a 2﹣2ab +b 2+b 2﹣2b +1+1＝（a ﹣b ）2+（b ﹣1）2+1．∵（a ﹣b ）2≥0，（b ﹣1）2≥0，∴当a ＝b ＝1时，代数式M 有最小值1．请根据上述材料解决下列问题：（1）在横线上添上一个常数项使之成为完全平方式：a 2+4a + ；（2）若代数式M ＝214a +2a +1，求M 的最小值；（3）已知a 2+2b 2+4c 2﹣2ab ﹣2b ﹣4c +2＝0，求代数式a +b +c 的值．【答案】（1）4；（2）M 的最小值为﹣3；（3）a +b +c=122. 【解析】【分析】（1）根据常数项等于一次项系数的一半进行配方即可；（2）先提取14，将二次项系数化为1，再配成完全平方，即可得答案；（3）将等式左边进行配方，利用偶次方的非负性可得a ，b ，c 的值，从而问题得解．【详解】（1）∵a 2+4a+4＝（a+2）2故答案为：4；（2）M ＝21a 4+2a+1 ＝14（a 2+8a+16）﹣3 ＝14（a+4）2﹣3 ∴M 的最小值为﹣3（3）∵a 2+2b 2+4c 2﹣2ab ﹣2b ﹣4c+2＝0，∴（a ﹣b ）2+（b ﹣1）2+（2c ﹣1）2＝0，∴a ﹣b ＝0，b ﹣1＝0，2c ﹣1＝0∴a ＝b ＝1，1c=2 ， ∴a+b+c=122.．【点睛】本题考查了配方法的应用，解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．13．你会对多项式(x 2+5x+2)(x 2+5x+3)﹣12分解因式吗？对结构较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替(即换元)，能使复杂的问题简单化、明朗化．从换元的个数看，有一元代换、二元代换等．对于(x 2+5x+2)(x 2+5x+3)﹣12．解法一：设x 2+5x ＝y ，则原式＝(y+2)(y+3)﹣12＝y 2+5y ﹣6＝(y+6)(y ﹣1) ＝(x 2+5x+6)(x 2+5x ﹣1)＝(x+2)(x+3)(x 2+5x ﹣1)．解法二：设x 2+5x+2＝y ，则原式＝y(y+1)﹣12＝y 2+y ﹣12＝(y+4)(y ﹣3) ＝(x 2+5x+6)(x 2+5x ﹣1)＝(x+2)(x+3)(x 2+5x ﹣1)．解法三：设x 2+2＝m ，5x ＝n ，则原式＝(m+n)(m+n+1)﹣12＝(m+n)2+(m+n)﹣12＝(m+n+4)(m+n ﹣3) ＝(x 2+5x+6)(x 2+5x ﹣1)＝(x+2)(x+3)(x 2+5x ﹣1)．按照上面介绍的方法对下列多项式分解因式： (1)(x 2+x ﹣4)(x 2+x+3)+10； (2)(x+1)(x+2)(x+3)(x+6)+x 2； (3)(x+y ﹣2xy)(x+y ﹣2)+(xy ﹣1)2．【答案】（1） (x+2)(x-1) (2 x x ++1) (2)(266x x ++)2 (3) (x+y-xy-1)2 【解析】【分析】（1）令m=2x x +,原式=()()4m 310m -++因式分解即可；（2）()()()()21236x x x x x +++++=(276x x ++)(256x x ++)+2x ,令n=256x x ++，再将原式=（n+2）n+x 2进行因式分解即可；（3）令a=x+y,b=xy ，代入原式即可因式分解. 【详解】（1）令m=2x x +, 原式=()()4m 310m -++ =m 2-m-2=(m-2)(m+1) = (2x x +-2)(2x x ++1) =(x+2)(x-1) (2x x ++1)(2)()()()()21236x x x x x +++++=(276x x ++)(256x x ++)+2x ,令n=256x x ++，原式=（n+2）n+x 2=n 2+2n+x 2=(n+x)2=(266x x ++)2(3) 令a=x+y,b=xy ，原式=()()()2221a b a b --+- =(a-b)2-2(a-b)+1 =(a-b-1)2 =(x+y-xy-1)2 【点睛】此题主要考查复杂的因式分解，解题的关键是读懂材料学会材料中因式分解的方法.14．已知一个三位自然数，若满足百位数字等于十位数字与个位数字的和，则称这个数为“和数”，若满足百位数字等于十位数字与个位数字的平方差，则称这个数为“谐数”．如果一个数即是“和数”，又是“谐数”，则称这个数为“和谐数”．例如321，321=+，∴321是“和数”，2232-1=，∴321是“谐数”，∴321是“和谐数”．（1）最小的和谐数是，最大的和谐数是；（2）证明：任意“谐数”的各个数位上的数字之和一定是偶数；（3）已知103817m b c =++（0714b c ≤≤≤≤，，且,b c 均为整数）是一个“和数”，请求出所有m ．【答案】（1）110；954；（2）见解析；（3）880m =或853或826. 【解析】【分析】（1）根据“和数”与“谐数”的概念求解可得；（2）设“谐数”的百位数字为x 、十位数字为y ，个位数字为z ，根据“谐数”的概念得x=y 2-z 2=（y+z ）（y-z ），由x+y+z=（y+z ）（y-z ）+y+z=（y+z ）（y-z+1）及y+z 、y-z+1必然一奇一偶可得答案；（3）先判断出2≤b+2≤9、10≤3c+7≤19，据此可得m=10b+3c+817=8×100+（b+2）×10+（3c-3），根据“和数”的概念知8=b+2+3c-3，即b+3c=9，从而进一步求解可得．【详解】（1）最小的和谐数是110，最大的和谐数是954.（2）设：“谐数”的百位数字为x ，十位数字为y ，个位数字为z （19,09,09x y z ≤≤≤≤≤≤且 y z >且 ,,x y z 均为正数），由题意知，()()22x y z y z y z =-=+-，∴()()()()1x y z y z y z y z y z y z ++=+-++=+-+， z∵y z +与y z -奇偶性相同， ∴y z +与1y z -+必一奇一偶， ∴()()1y z y z +-+必是偶数，∴任意“谐数”的各个数位上的数字之和一定是偶数；（3）∵07b ≤≤，∴229b ≤+≤， ∵14c ≤≤， ∴3312c ≤≤， ∴103719c ≤+≤， ∴817103m b c =++，()()810011037b c =⨯++⨯++ ()()81002103710b c =⨯++⨯++- ()()810021033b c =⨯++⨯+-，∵m 为和数， ∴8233b c =++-，即39b c +=， ∴61b c =⎧⎨=⎩或32b c =⎧⎨=⎩或03b c =⎧⎨=⎩， ∴880m =或853或826. 【点睛】本题考查因式分解的应用，解题的关键是理解题意、熟练掌握“和数”与“谐数”的概念及整式的运算、不等式的性质．15．由多项式的乘法：(x ＋a)(x ＋b)＝x 2＋(a ＋b)x ＋ab ，将该式从右到左使用，即可得到用“十字相乘法”进行因式分解的公式： x 2＋(a ＋b)x ＋ab ＝(x ＋a)(x ＋b)．实例分解因式：x 2＋5x ＋6＝x 2＋(2＋3)x ＋2×3＝(x ＋2)(x ＋3)． (1)尝试分解因式：x 2＋6x ＋8；(2)应用请用上述方法解方程：x 2－3x －4＝0. 【答案】(1) (x+2)(x ＋4)；(2) x ＝4或x ＝－1. 【解析】【分析】（1）类比题干因式分解方法求解可得；（2）利用十字相乘法将左边因式分解后求解可得．【详解】(1)原式=(x+2)(x ＋4)；(2)x 2－3x －4＝(x －4)(x ＋1)＝0，所以x －4＝0或x ＋1＝0，即x ＝4或x ＝－1. 【点睛】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．四、八年级数学分式解答题压轴题（难）16．我们知道，假分数可以化为整数与真分数的和的形式，例如：76112333+==+. 在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”.例如：像33x x -+，23x x -，…这样的分式是假分式；像23x -，23x x-，…这样的分式是真分式. 类似的，假分式也可以化为整式与真分式的和（差）的形式.例如：将分式2253x x x +-+拆分成一个整式与一个真分式的和（差）的形式.方法一：解：由分母为3x +，可设225(3)()x x x x a b +-=+++则由22225(3)()33(3)(3)x x x x a b x ax x a b x a x a b +-=+++=++++=++++ 对于任意x ，上述等式均成立， ∴3235a a b +=⎧⎨+=-⎩，解得12a b =-⎧⎨=-⎩∴225(3)(1)2(3)(1)22133333x x x x x x x x x x x x +-+--+-==-=--+++++ 这样，分式2253x x x +-+就被拆分成一个整式与一个真分式的和（差）的形式.方法二：解：2225332(3)(3)2(3)32213333333x x x x x x x x x x x x x x x x x x x +-+---+-+-++===--=--+++++++ 这样，分式2253x x x +-+就拆分成一个整式与一个真分式的和（差）的形式.（1）请仿照上面的方法，选择其中一种方法将分式2731x x x ---拆分成一个整式与一个真分式的和（差）的形式；（2）已知整数x 使分式225112x x x +-+的值为整数，求出满足条件的所有整数x 的值.【答案】（1）961x x ---；（2）x=-1或-3或11或-15. 【解析】【分析】（1）先变形2731x x x ---=26691x x x x --+--，由“真分式”的定义，仿照例题即可得出结论；（2）先把分式化为真分式，再根据分式的值为整数确定整数x 的值．【详解】解：（1）2731x x x ---=26691x x x x --+--=(1)6(1)91x x x x -----=961x x ---；（2）225112x x x +-+= 2242132x x x x +++-+=2(2)(2)132x x x x +++-+=13212x x +-+， ∵x 是整数，225112x x x +-+也是整数，∴x+2=1或x+2=-1或x+2=13或x+2=-13， ∴x=-1或-3或11或-15. 【点睛】本题考查了逆用整式和分式的加减法对分式进行变形．解决本题的关键是理解真分式的定义对分子进行拆分．17．阅读后解决问题：在“15.3分式方程”一课的学习中，老师提出这样的一个问题：如果关于x 的分式方程3111a x x+=--的解为正数，那么a 的取值范围是什么？经过交流后，形成下面两种不同的答案：小明说：解这个关于x 的分式方程，得到方程的解为x=a ﹣2．因为解是正数，可得a ﹣2＞0，所以a ＞2．小强说：本题还要必须a≠3，所以a 取值范围是a ＞2且a≠3．（1）小明与小强谁说的对，为什么？（2）关于x 的方程11222mx x x-+=--有整数解，求整数m 的值．【答案】（1）小强的说法对，理由见解析；（2）m=3，4，0．【解析】【分析】(1)先根据解分式方程的步骤和解法解分式方程可得x =a ﹣2,根据分式方程有解和解是正数可得:x ＞0且x ≠1, 即a ﹣2＞0, a ﹣2≠1,即可求解,(2) 先根据解分式方程的步骤和解法解分式方程可得（m﹣2）x=﹣2, 当m≠2时,解得:x=﹣22m-,根据分式方程有整数解可得: m﹣2=±1,m﹣2=±2,继而求m的值.【详解】解:（1）小强的说法对,理由如下:解这个关于x的分式方程,得到方程的解为x=a﹣2,因为解是正数,可得a﹣2＞0,即a＞2,同时a﹣2≠1,即a≠3,则a的范围是a＞2且a≠3,（2）去分母得：mx﹣1﹣1=2x﹣4,整理得:（m﹣2）x=﹣2,当m≠2时,解得: x=﹣22 m-,由方程有整数解,得到m﹣2=±1,m﹣2=±2,解得:m=3,4,0.【点睛】本题主要考查分式方程解是正数和解是整数问题,解决本题的关键是要熟练掌握解分式方程的解法.18．某快递公司有甲、乙、丙三个机器人分配快件，甲单独完成需要x小时，乙单独完成需要y小时，丙单独完成需要z小时．（1）求甲单独完成的时间是乙丙合作完成时间的几倍？（2）若甲单独完成的时间是乙丙合作完成时间的a倍，乙单独完成的时间是甲丙合作完成时间的b倍，丙单独完成的时间是甲乙合作完成时间的c倍，求111111 a b c+++++的值．【答案】（1）甲单独完成的时间是乙丙合作完成时间的xy xzyz+倍；（2）1【解析】分析：（1）先求出乙丙合作完成时间，再用甲单独完成的时间除以乙丙合作完成时间即可求解；（2）根据“甲单独作完成的天数为乙丙合作完成天数的a倍”，可得x=11ay z+，运用比例的基本性质、等式的性质及分式的基本性质可得11a+=yzxy yz xz++；同理，根据“乙单独作完成的天数为甲、丙合作完成天数的b倍”，可得11b+=xzxy yz xz++；根据“丙单独作完成的天数为甲、乙合作完成天数的c 倍”，可得11c +=xy xy yz xz ++，将它们分别代入所求代数式，即可得出结果．详解：（1）x ÷[1÷（1y +1z）]=x ÷[1÷y zyz+] =x ÷yzy z+ =xy xzyz+．答：甲单独完成的时间是乙丙合作完成时间的xy xzyz+倍；（2）由题意得x =11ayz +①，y =11bx z+②，z =11cx y +③．由①得a =x y +x z ，∴a +1=x y +x z +1，∴11a +=11x x y z++=yz xy yz xz ++；同理，由②得11b +=xz xy yz xz ++；由③得11c +=xy xy yz xz ++； ∴111111a b c +++++=yz xy yz xz +++xz xy yz xz +++xy xy yz xz ++=xy yz xz xy yz xz++++=1．点睛：本题主要考查分式方程在工程问题中的应用及代数式求值．工程问题的基本关系式为：工作总量=工作效率×工作时间．注意两人合作的工作效率等于两人单独作的工作效率之和．本题难点在于将列出的方程变形，用含有x 、y 、z 的代数式分别表示11a +、11b +、11c +的值．19．探索：（1）如果32311x mx x -=+++，则m=_______；（2）如果53522x m x x -=+++，则m=_________；总结：如果ax b ma x c x c+=+++（其中a 、b 、c 为常数），则m=________；（3）利用上述结论解决：若代数式431x x --的值为整数，求满足条件的整数x 的值．【答案】（1）-5；（2）-13 ； b -ac ;（3）0或2 【解析】试题解析：()323(1)55133.1111x x mx x x x -+-==-=+++++ 5.m ∴=-()535(2)1313255.2222x x mx x x x -+-==-=+++++ 13.m ∴=-总结：().ax b a x c b ac b ac ma a x c x c x c x c+++--==+=+++++ .m b ac ∴=-()434(1)1134.111x x x x x --+==+--- 又∵代数式431x x --的值为整数， 11x ∴-为整数， 11x ∴-=或11x -=- 2x ∴=或 0.20．某商店用1000元人民币购进水果销售，过了一段时间，又用2400元人民币购进这种水果，所购数量是第一次购进数量的2倍，但每千克的价格比第一次购进的贵了2元．（1）该商店第一次购进水果多少千克；（2）假设该商店两次购进的水果按相同的标价销售，最后剩下的20千克按标价的五折优惠销售．若两次购进水果全部售完，利润不低于950元，则每千克水果的标价至少是多少元？注：每千克水果的销售利润等于每千克水果的销售价格与每千克水果的购进价格的差，两批水果全部售完的利润等于两次购进水果的销售利润之和．【答案】（1）该商店第一次购进水果100千克；（2）每千克水果的标价至少是15元．【解析】【分析】（1）首先根据题意，设该商店第一次购进水果x 千克，则第二次购进水果2x 千克，然后根据：（1000÷第一次购进水果的重量 +2）×第二次购进的水果的重量=2400，列出方程，求出该商店第一次购进水果多少千克即可．（2）首先根据题意，设每千克水果的标价是x 元，然后根据：（两次购进的水果的重量﹣20）×x +20×0.5x ≥两次购进水果需要的钱数+950，列出不等式，求出每千克水果的标价是多。

八年级数学上册期末试卷培优测试卷

八年级上册数学 全册全套试卷(培优篇)(Word版 含解析)

八年级数学上册期末试卷(培优篇)(Word版 含解析)

河南省信阳市息县2023_2024学年人教版八年级数学上学期期末培优卷(有答案)

人教版八年级数学上册期末试卷培优测试卷

人教版八年级数学上册 期末试卷(培优篇)(Word版 含解析)

八年级数学上册期末试卷(培优篇)(Word版 含解析)

八年级上册数学 期末试卷培优测试卷

八年级数学上册期末试卷(培优篇)(Word版 含解析)

部编数学八年级上册期末培优检测(一)(期末真题精选)(解析版)含答案

初二数学培优试卷及答案

最新人教版八年级数学上册期末培优卷(附答案)

八年级上期末数学培优试卷

(word完整版)初中数学八年级上册期末培优提高测试卷附参考答案

八年级上册数学 期末试卷(培优篇)(Word版 含解析)

培优测试卷八年级上册数学

八年级数学上期末培优训练(7份)

八年级数学上册期末试卷(培优篇)(Word版 含解析)

八年级上册数学全册全套试卷(培优篇)(Word版含解析)

八年级数学上册期末试卷(培优篇)(Word版含解析)

人教版八年级数学上册期末试卷(培优篇)(Word版含解析)

八年级数学上册期末试卷(培优篇)(Word版含解析)

八年级上册数学期末试卷培优测试卷

八年级数学上册期末试卷(培优篇)(Word版含解析)

八年级上册数学期末试卷(培优篇)(Word版含解析)

八年级数学上册期末试卷(培优篇)(Word版含解析)