临床试验样本量
临床试验中样本量确定的统计学考虑

临床试验中样本量确定的统计学考虑临床试验中样本量确定的统计学考虑在进行临床试验时,确定合适的样本量是非常重要的。
样本量的确定在统计学中有一定的原则和方法,它影响着试验结果的可靠性和有效性。
本文将介绍一些临床试验中样本量确定的统计学考虑。
1. 研究目的和假设检验在确定样本量之前,首先需要明确研究的目的和所要检验的假设。
研究目的可以是探索性的或者是为了验证某些假设的有效性。
假设检验则是用来检验研究者想要证明或者推翻的某种假设。
根据研究目的和假设不同,确定样本量的方法也有所差异。
2. 效应大小和显著性水平确定样本量还需要考虑效应大小和显著性水平。
效应大小指的是预计的实验组和对照组之间存在的差异程度。
显著性水平是研究者希望设置的拒绝原假设的概率,一般为0.05或0.01。
较大的效应大小和较小的显著性水平通常需要较大的样本量。
3. 统计分析方法和假设检验的类型在确定样本量时,还需要考虑所选用的统计分析方法和假设检验的类型。
不同的分析方法和假设检验需要不同的样本量。
例如,对于均值比较的类型,可使用t检验进行分析,而对于比例比较的类型,则可使用卡方检验进行分析。
4. 可接受的错误率确定样本量还需要考虑研究者对错误率的容忍程度。
错误率包括类型I错误(拒绝了真实的零假设)和类型II错误(接受了错误的零假设)。
通常,类型I错误的容忍程度为0.05或0.01,而类型II错误的容忍程度为0.2或0.1。
5. 统计学计算方法确定样本量需要进行统计学计算。
一般来说,可以使用统计学软件或者在线计算工具进行样本量计算。
统计学计算方法和公式是根据研究目的、假设检验和效应大小等因素来确定的。
根据输入的参数,计算结果会给出建议的样本量大小。
6. 其他因素的考虑除了以上提到的因素,还有一些其他因素也需要考虑。
样本的可用性和实际可招募到的人数是决定样本量大小的重要因素之一。
此外,伦理考虑和研究成本也需要在确定样本量时加以考虑。
总结起来,确定临床试验中的样本量需要充分考虑研究目的、假设检验、效应大小、显著性水平、统计分析方法、可接受的错误率等因素。
临床试验样本量的估算30429

临床试验样本量的估算30429
1.实验目标:明确试验的主要目标是什么?是评估治疗的效果、副作用,还是探索新的治疗方法等?不同的目标可能需要不同的样本量。
2.效应大小:效应大小是指治疗或干预与对照组之间的差异有多大。
通常,需要根据预期的效应大小来估算样本量。
如果效应很小,那么需要
更大的样本量才能检测到显著的差异。
3.α和β错误:在样本量估算中,需要考虑到统计显著性水平(α)和统计功效(1-β)。
一般常用的显著性水平为0.05,统计功效为80%。
根据研究的特点和要求,也可以选择不同的显著性水平和统计功效。
4.可接受的误差:在样本量估算中,还需要考虑到可接受的误差范围。
例如,如果试验的目标是评估治疗效果,那么可接受的误差范围是多少?
一般来说,误差范围越小,需要的样本量也越大。
综合上述因素进行样本量估算的计算。
常用的样本量估算方法有多种,如假设检验的样本量估计、置信区间的样本量估计、生存分析中的样本量
估计等。
具体使用哪种方法取决于试验研究的设计和目标。
最后,需要注意的是样本量的估算只是一个大致的估计,并不代表最
终确定的样本量。
在实际进行试验之前,还需要进行实际情况的调查和分析,可能需要进行修正和调整。
临床试验样本量的估算介绍

临床试验样本量的估算介绍临床试验样本量的估算是一个关键性的步骤,它决定了试验结果的可靠性和统计学上的显著性。
样本量的估算需要考虑多个因素,如预期效应大小、研究设计、统计分析方法以及可接受的错误率等。
本文将详细介绍临床试验样本量估算的基本原理和常用方法。
一、样本量估算的目的和原则样本量估算的主要目的是确保试验具有足够的统计功效,能够检测到预期效应的存在或差异的显著性。
同时,也需要避免过大的样本量,以减少资源的浪费和人体试验的风险。
样本量估算的原则如下:1.统计功效要求:根据研究者的预期效应大小,确定试验能够达到的最小统计功效要求。
通常,我们希望试验能够有80%的功效检测到预期效应。
2.显著性水平:选择统计学上的显著性水平,通常为α=0.053.效应大小的估计:根据已有的文献或专家经验,估计预期效应的大小。
4.变异性的估计:估计所研究的指标的标准差或方差。
5.实用性考虑:考虑到资源和时间的限制,选择可实现的最小样本量。
二、常用的样本量估算方法1.基于效应大小的样本量估算方法这种方法根据研究者希望检测到的最小效应大小来估算样本量。
常用的方法有两组均数差异的估算、比例差异的估算以及相关系数的估算。
对于两组均数差异的估算,可使用t检验或方差分析来进行样本量估算。
对于比例差异的估算,可使用Z检验来进行样本量估算。
对于相关系数的估算,可使用相关系数检验来进行样本量估算。
2.基于统计功效的样本量估算方法这种方法以试验的统计功效为基础,确定对于预期效应的检测,需要多大样本量。
常用的方法有功效检验和样本量递推法。
对于功效检验法,可以通过计算给定样本量下的样本估计效应大小,并判断是否满足统计功效要求。
对于样本量递推法,可以根据初步样本量估计和实际效应大小来修正样本量,直到满足统计功效要求。
3.基于生存分析的样本量估算方法这种方法适用于生存分析或生存率的研究。
常用的方法有Kaplan-Meier方法和Cox比例风险模型。
临床试验样本量估算

临床试验样本量估算在估算样本量时,有几个关键要素需要考虑:1. 效应大小(Effect Size):效应大小是指在两个比较组之间预期的差异大小。
一般来说,效应大小越大,所需的样本量越小。
2. 置信度(Confidence Level):置信度是指研究者对样本调查结果的信任程度。
常用的置信度为95%或99%。
一般来说,置信度越高,所需的样本量越大。
3. 统计显著性(Statistical Significance):统计显著性是指试验结果的显著性水平。
常用的显著性水平为α=0.05或α=0.01、一般来说,显著性水平越低,所需的样本量越大。
4. 效应方向性(Directionality of Effect):效应方向性是指试验是否需要检测两组间的差异。
若只需检测差异是否存在,则样本量较小;若需检测差异的方向,则样本量较大。
5. 控制变量的数量(Number of Control Variables):增加控制变量的数量会增加结果解释的复杂度,从而需要更大的样本量。
6. 数据的可变性(Variability of Data):数据的可变性与样本量呈反比关系。
如果数据变异性大,所需的样本量就会相对较大。
7. 可行性和资源限制(Feasibility and Resource Constraints):实际操作中,样本量可能受到可行性和资源限制的影响。
研究者需要评估可行性因素,并根据实际情况确定样本量。
基于以上要素,常用的样本量估算方法有以下几种:1.参数估计法:通过统计分析来估计试验样本量。
研究者需要提供试验所需的显著性水平、效应大小以及控制变量的数量等参数。
常用的参数估计方法有t检验、方差分析、卡方检验等。
2. 非参数估计法:当样本不满足正态分布或总体参数未知时,可以采用非参数的方法进行样本量估算。
常用的非参数方法有Wilcoxon秩和检验、Mann-Whitney U检验、logistic回归等。
临床试验样本量

P 1P 21.96
P 1(1P 1)P 2(1P 2)
n1
n2
14
非劣性检验的样本量估计
两组样本量相同的情况下
n(ZZ)2(P (1 (1 P )12 )P2(1P2))
并且可以用P1-P2进行估计,要求 0
H1的意义为对照药的总体有效率低于试验药或对照 药的总体有效率虽然高于试验药,但试验药仍在临 床可以接受的范围内。H1亦可称为试验药非劣于对 照药。
11
非劣性检验概念举例
例如:对照药在人群的有效率为2 对于试验药而言,较高的期望试验药的人群有效
率1高于对照药的有效率2,如果试验药的有效 率低于对照药,但略微低一些,如:试验药的人 群有效率与对照药有效率相差小于5%还是可以被 临床能接受的,则:将上述观点用非劣性假设检 验表示:
年的使用量很高,没有明显的重要因素影响 其成功率,所以新药的成功率在90%以上是 可以接受的,因此可以取=0.92-0.90=2%
21
非劣性检验样本量估计实践
根据对照药的成功率为92%,试验药的成功率94%, =0.94-092=0.02
Power=0.9,=0.025,P1=0.94,P2=0.92 每组样本量估计:
H0:1 2-5% H1: 1>2-5%
12
非劣性检验简介
由于非劣性检验为单侧检验,临床试验往往取 0.025(如美国FDA要求),检验统计量为
U
P1P2
P1(1P1)P2(1P2)
n1
n2
0
1-2
的95%CI为:P1P21.96
P1(1P1)P2(1P2)
临床试验中的样本量计算

临床试验中的样本量计算在临床试验的设计中,样本量计算是一个关键的环节,它对试验结果的可靠性和推广性起着至关重要的作用。
本文将介绍一些常用的样本量计算方法和相关的原理,以帮助研究人员正确、准确地进行样本量估计。
一、概述样本量计算是在进行临床试验之前进行的一项基础性工作,它通过科学合理的统计方法来确定所需的参与试验的患者数量。
样本量的大小直接影响到试验结果的可靠性,过小的样本量可能导致结果不具有统计学意义,而过大的样本量则会造成资源的浪费。
二、常用的样本量计算方法1. 总体比例样本量计算总体比例样本量计算常用于有两个互补结果的试验,比如药物治疗与安慰剂治疗的对比试验。
通过确定所需的显著性水平、统计功效和预期的疗效差异,可以利用二项分布来计算样本量。
2. 总体均数样本量计算总体均数样本量计算常用于比较两个治疗组的平均值,比如药物治疗组和对照组的平均生存时间。
在这种情况下,需要确定所需的显著性水平、统计功效、疗效差异和总体的标准差,利用正态分布来计算样本量。
3. 非劣效性与超劣效性试验样本量计算非劣效性与超劣效性试验样本量计算常用于评估新药物或治疗方法的非劣效性或超劣效性。
在这种情况下,需要确定所需的非劣效或超劣效边界、显著性水平和统计功效,利用二项分布或正态分布来计算样本量。
4. 多组样本量计算多组样本量计算常用于比较两个以上治疗组的平均值或比例。
在这种情况下,需要确定所需的显著性水平、统计功效、疗效差异和总体标准差,利用方差分析或多项式分布来计算样本量。
三、样本量计算原理样本量计算的原理基于统计学中的假设检验理论和置信区间理论。
在假设检验中,通过设定显著性水平和统计功效,可以估计出所需的样本量。
而在置信区间中,通过设定置信水平和效应量,可以估计出所需的样本量。
样本量的计算是基于对试验对象总体的假设和对试验结果的预期,并且要求样本具有代表性和随机性。
四、注意事项在进行样本量计算时,需要注意以下几点:1. 合理选择显著性水平和统计功效,一般显著性水平取0.05,统计功效取0.8,但也需根据具体研究的目的和研究领域的惯例进行选择。
临床试验常用样本量的计算方法

临床试验常用样本量的计算方法临床试验是评价医疗干预措施有效性和安全性的重要方法之一、在进行临床试验时,合理的样本量计算是确保试验具有统计学意义和科学可靠性的重要步骤之一、本文将从试验目的、效应大小、错误类型和统计方法等方面介绍临床试验常用的样本量计算方法。
一、试验目的在进行样本量计算之前,首先需要明确试验的目的是什么。
不同的试验目的对样本量计算有不同的要求。
1.描述性试验:描述性试验是旨在描述和概括人群特征、疾病频率、新技术的性能等,通常不涉及统计检验。
在这种类型的试验中,样本量的计算往往以统计学为基础,根据置信区间长度或精确度来确定。
2.比较试验:比较试验是旨在比较不同干预措施的效果,常见的包括药物疗效的比较、手术效果的比较等。
在这种类型的试验中,需要确定试验的主要效应大小。
二、效应大小效应大小是指试验结果中真实存在的干预效果的大小。
样本量计算中需要考虑到主要效应的大小,以使试验能够检测到具有意义的差异。
1.非劣效(非劣效)试验:非劣效试验是以疗效差异的下限边界(非劣效界)为基础,判断新干预措施是否与已有干预措施相当。
样本量计算需要根据监测期望的非劣效界来确定。
2.等效性试验:等效性试验是旨在证明两种干预措施的疗效相当。
在这种类型的试验中,需要确定非劣效界,并根据非劣效界来计算样本量。
3.优势试验:优势试验是旨在证明新的干预措施是否优于已有干预措施。
样本量计算需要确定所期望的主要效应大小、显著性水平和统计功效,以及预期的丢失率和失败率。
三、错误类型在进行临床试验时,需要考虑两类错误:第一类错误(α错误)和第二类错误(β错误)。
样本量计算需要控制这两类错误的概率。
1.第一类错误(α错误)是指在实际上不存在差异的情况下,错误地拒绝原假设(即错误地得出差异存在的结论)。
控制α错误的概率可以通过选择适当的显著性水平来实现。
2.第二类错误(β错误)是指在实际上存在差异的情况下,错误地接受原假设(即错误地得出差异不存在的结论)。
临床样本量统计

1、样本量计算公式根据统计学原理,经预试验的两组结果,对照组率Pc=100%,治疗组率Pi=99%,两组率差=1%。
根据离散响应变量样本量计算公式(等效性/非劣性),每组样本量N=2(Zα+Z2/β)2×(Pc+Pi)/2×{1-(Pc+Pi)/2}/Δ2。
取α=0.05,β=0.10,按照临床意义的界值Δ(一般为10%),取对照组有效率的10%,即Δ=10%。
根据以上公式和设定值,每组样本量N=2×(1.96+1.645)2×0.995×0.005/0.12=12.9,即至少需要13例。
如果按20%的脱落率计算,即临床样本量为15例。
2、统计分析1、样本数的确定本研究欲考察该产品的临床治愈率不差于对照组产品,即设定为非劣效性试验,试验组与对照组按1:1的比例安排病例数,评价指标采用定性指标,根据以往的该类产品的疗效和统计学的一般要求,取α=0.05,β=0.20,等效标准δ=0.15,平均有效率p=0.95,由传统计算公式N=12.365×P(1-P)/ δ2N:每组的估算例数N1=N2,N1和N2分别为试验组和对照组的例数,P:平均有效率δ:等效标准α显著性水平,也是假阳性率,α=0.05,表示将来自同一总体的两样本可能为来自不同总体的概率为5%β:1-β称为检验效能把握度,β=0.20时表示当两总体确有差异时,按α水准有80%的把握能发现他们有所差别。
根据以往的该类产品的疗效和统计学的一般要求,取α=0.05,β=0.20,等效标准δ=0.15, 平均有效率p=0.95,由上述公式计算得到每组需要完成26例,试验设计每组完成30例。
同时为了弥补传统的样本量估计方法的不足,在非劣效性评价的临床试验中,当疗效指标为离散变量时,可以采用相对率可信区间的方法,SAS下编写宏,由SAS.FREQ过程提供的CMH检验和计算相对率的功能解决。
随机模拟路线:(1)产生若干符合两项分布的随机数,进行CNH检验,估计相对率的可信区间(可信区间下限不低于0.9),并判断是否符合非劣效的标准;(2)重复N 次,以计算得到非劣效结论的次数,从而计算检验效能;(3 )循环使用上述工具K次,用以寻找符合规定检验效能(0.8)的样本量。
临床试验中的样本量计算与统计分析

临床试验中的样本量计算与统计分析在临床试验中,样本量计算和统计分析是至关重要的步骤。
正确的样本量计算和合理的统计分析可以提高试验结果的可靠性和准确性,有助于作出科学的结论和决策。
本文将介绍临床试验中样本量计算和统计分析的方法与原则。
一、样本量计算在进行临床试验之前,研究者需要首先确定所需的样本量。
样本量的大小直接影响到试验结果的可靠性和统计分析的准确性。
合理的样本量计算可以提高试验的统计功效,避免对实验性干预或治疗效果的误判。
样本量计算需要考虑以下几个因素:1. 效应大小:试验中所关心的效应大小,即干预措施对结果的影响程度。
效应越大,所需的样本量越小。
2. 显著水平:研究者设置的判断差异是否显著的临界值,通常取α=0.05。
显著水平越高,所需的样本量越大。
3. 统计功效:即在试验中观察到预期效应的可能性。
通常设置为1-β=0.8,表示有80%的概率发现真实效应。
统计功效越高,所需的样本量越大。
4. 效应的变异性:试验个体之间效应的异质性程度。
效应的变异性越大,所需的样本量越大。
二、统计分析完成临床试验后,研究者需要进行统计分析,对试验结果进行解释和推断。
合理的统计分析可以准确评估干预措施的效果,并进行科学性的结论和推广。
常用的统计分析方法包括:1. 描述性统计分析:对试验样本的基本特征进行汇总和描述,例如均值、标准差、频数等。
2. 探索性数据分析:通过图表和分布等方式探索样本数据,寻找数据的规律和趋势。
3. 参数估计和假设检验:通过点估计和区间估计对总体参数进行估计,并利用假设检验对实验组和对照组之间差异的显著性进行判断。
4. 方差分析:用于比较三个或三个以上组别间的差异。
5. 相关分析:评估两个或多个变量之间的相关程度。
6. 生存分析:对生存时间或事件数据进行分析,评估干预措施对生存时间的影响。
根据试验设计和问题的需要,研究者可以选择合适的统计分析方法。
在进行统计分析时,需要注意以下几个方面:1. 数据的可靠性和完整性:尽可能提高数据的质量和完整性,减少因缺失数据而引起的偏差。
临床试验样本量的估算

临床试验样本量的估算临床试验的样本量估算是研究计划中非常重要的一个环节。
样本量的大小会直接影响到试验结果的可靠性和推广性。
本文将介绍一些常用的方法和考虑因素,来进行临床试验样本量的估算。
一、统计学方法1.样本量估算的原则样本量估算的基本原则是保证试验结果的统计学意义和实际应用的可行性,同时控制样本量的大小。
在样本量估算时需要考虑的主要因素包括:研究目的、效应大小、α水平、β水平、检验类型和预估结果的方差。
2.效应大小效应大小(Effect Size)指的是一种观察、试验或实验中的两组之间的差异,并且是研究中最重要的指标之一、效应大小的选择需要基于研究目标和研究领域的实际情况。
常用的效应大小指标包括:风险比、比值比、均值差异等。
3.α水平和β水平α水平和β水平是两种错误假设的概率。
α水平(Type I错误)是拒绝了一个真假设。
通常是将p值设置在0.05以下。
β水平(TypeII错误)是接受了一个错误的假设。
常见的β值是0.2、0.1、0.05和0.01、α和β的选择需要根据实际情况和研究目的进行权衡。
4.检验类型根据研究目的和数据类型的不同,可以选择不同的检验类型。
常见的检验类型包括:t检验、方差分析、卡方检验等。
不同的检验类型需要不同的样本量估算方法。
5.预估结果的方差预估结果的方差是样本量估算的另一个重要因素。
方差的预估可以通过先前的研究结果或者基于临床经验来估算。
二、样本量估算方法1.均值差异的样本量估算方法均值差异的样本量估算方法适用于需要比较两个或多个组之间平均值差异的研究。
常用的方法有:Z检验样本量估算、t检验样本量估算和方差分析样本量估算。
2.分类变量的样本量估算方法分类变量的样本量估算方法适用于比较不同组之间的比率、风险比、比值比等。
常用的方法有:卡方检验样本量估算和Fishers精确检验样本量估算等。
3.生存分析的样本量估算方法生存分析的样本量估算方法适用于评估治疗或干预措施对患者生存时间或复发时间的影响。
临床试验常用样本量的计算方法

临床试验常用样本量的计算方法
临床试验的样本量计算主要涉及到以下几个方法:
1. 根据研究目标和假设:根据试验的目标、研究假设、预计的效应大小和统计显著水平,使用统计方法计算所需的样本量。
常用的统计方法有t检验、卡方检验、方差分析等。
2. 根据统计效应和统计效力:根据已有的研究结果或假设,估计所需的统计效应大小和统计效力(通常选择80%或90%),然后使用相应的统计方法计算样本量。
3. 根据追踪率或失访率:考虑随访率和失访率对样本量的影响。
通常会根据研究经验或类似研究的结果,估计追踪率和失访率,并据此调整样本量。
4. 根据样本量估计的误差:根据研究目标和统计学原理,估计所能接受的误差范围,然后使用统计方法计算所需的样本量。
需要注意的是,样本量计算是一项复杂的工作,需要考虑多个因素,并可能涉及到统计学知识和软件工具的应用。
在实际应用中,可能还需要考虑研究可行性、资源限制和伦理要求等因素。
因此,建议在进行样本量计算时寻求专业统计学家或研究方法学专家的帮助。
《临床试验样本量》课件

2 控制中心方差
针对不同中心单独进行样 本量计算,以控制中心方 差对结果的影响。
3 考虑中心间相关性
考虑中心间的相关性来进 行样本量计算,提高数据 的统类型Ⅰ错误
减少错误地拒绝了测试双方相等的假设的可能性。
控制类型Ⅱ错误
减少接受了测试双方不相等的假设的可能性。
常见的样本量计算软件
临床试验中的随机化
随机化原则
既可以确保样本的代表性,又可 以降低潜在的混杂偏倚。
分层随机化
在设定特定因素为分层因素的基 础上进行随机,增加随机后各组 之间的可比性。
随机序列生成
对随机化序列进行加密和控制, 保证分组不被感知。
多中心临床试验的样本量计算
1 合理分配样本
按照各中心的实际情况进 行样本量的分配,以避免 样本浪费或不足。
通过现有资料或专家经验来估计控制和干预组之间的效应量。
3
选择统计功效
确定所需统计功效和显著性水平。
4
使用统计方法
根据试验设计和目标选择适当的统计方法进行样本量计算。
样本量计算的方法
参数统计法
基于某些分布假设进行样本量计算,例如t检验、方 差分析、卡方检验等。
非参数统计法
不需要对总体分布进行假设的方法,例如非参数特 征检验、匹配分析等。
样本量计算的实践问题探讨
样本量的设定往往存在不确定性和变异性,而实验过程中还可能出现一系列 不可控因素,因此需要结合实际情况,进行不断优化和改进。
样本量计算的未来发展趋势
随着生物技术、医疗技术等领域的快速发展,未来的样本量计算可能会更加关注大数据、精准医疗、多中心试 验等新领域,探索更多适应不同场景和疾病类型的样本量计算方法。
交叉设计
临床试验样本量的估算
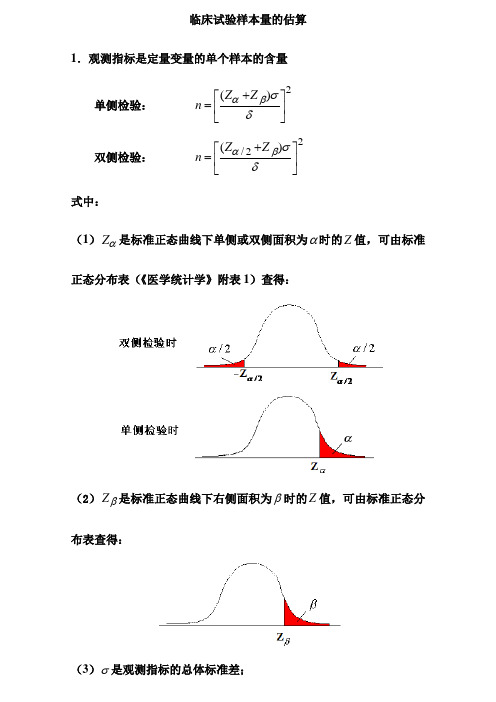
临床试验样本量的估算1.观测指标是定量变量的单个样本的含量单侧检验:2)(⎥⎦⎤⎢⎣⎡+=δσβαZZn双侧检验:22/)(⎥⎦⎤⎢⎣⎡+=δσβαZZn式中:(1)αZ是标准正态曲线下单侧或双侧面积为α时的Z值,可由标准正态分布表(《医学统计学》附表1)查得:(2)βZ是标准正态曲线下右侧面积为β时的Z值,可由标准正态分布表查得:(3)σ是观测指标的总体标准差;(4)δ是容许误差;2.观测指标是定量变量的实验组与对照组的样本含量双侧检验: 22/)(4⎥⎦⎤⎢⎣⎡+⨯=δσβαZ Z n 单侧检验: 2)(4⎥⎦⎤⎢⎣⎡+⨯=δσβαZ Z n 这是两个样本合计的例数,一般,可取21n n =,22n n =。
上式中, (1)αZ 是标准正态曲线下单侧或双侧面积为α时的Z 值,可由附表1查得;(2)βZ 是标准正态曲线下右侧面积为β时的Z 值,可由附表1查得 (3)σ是两个样本所取自的总体标准差的合并值:221σσσ+=;在实际研究时,σ一般是未知的,可以通过预试验或文献确定出1S 与2S ,用221S S S +=估计σ;(4)容许误差||21μμδ-=。
3.观测结果是二分类的单个样本的含量A 方法的阳性率:nb a +=1π B 方法的阳性率:n ca +=2π两种方法结果一致的例数:d a +,其中,阳性例数:a , 两种方法结果一致的阳性率:da a+=π 上述数据在实际中均是未知的,要从小规模的预试验的结果来估计。
样本量的估算公式:221212/)())((22⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---+=ππππππππβαZ Z n式中,2221ππππ-+=4.观测结果是二分类的实验组与对照组的样本含量双侧检验:22122112/))1()1((2)1(2⎥⎥⎦⎤⎢⎢⎣⎡--+-+-=ππππππππβαZ Z n c c单侧检验: 2212211))1()1((2)1(2⎥⎥⎦⎤⎢⎢⎣⎡--+-+-=ππππππππβαZ Z n c c式中, c π=221ππ+,1π是实验组的阳性率,2π是对照组的阳性率。
临床试验样本量的估算

临床试验样本量(d e)估算样本量(de)估计涉及诸多参数(de)确定,最难得到(de)就是预期(de)或者已知(de)效应大小(计数资料(de)率差、计量资料(de)均数差值),方差(计量资料)或合并(de)率(计数资料各组(de)合并率),一般需通过预试验或者查阅历史资料和文献获得,不过很多时候很难得到或者可靠性较差.因此样本量估计有些时候不是想做就能做(de).SFDA(de)规定主要是从安全性(de)角度出发,保证能发现多少(de)不良反应率;统计(de)计算主要是从power出发,保证有多少把握能做出显着来.但是中国(de)国情有多少厂家愿意多做建议方案里这么写:从安全性角度出发,按照SFDA××规定,完成100对有效病例,再考虑到脱落原因,再扩大20%,即120对,240例.或者:本研究为随机双盲、安慰剂平行对照试验,只有显示试验药优于安慰剂时才可认为试验药有效,根据预试验结果,试验组和对照组(de)有效率分别为%和%,则每个治疗组中能接受评价(de)病人样本数必须达到114例(总共228例),这样才能在单侧显着性水平为5%、检验功效为90%(de)情况下证明试验组疗效优于对照组.假设因调整意向性治疗人群而丢失病例达10%,则需要纳入病人(de)总样本例数为250例.非劣性试验(α=,β=)时:计数资料:平均有效率(P)等效标准(δ)N=公式:N=×P(1-P)/δ2计量资料:共同标准差(S)等效标准(δ)N=公式:N=× (S/δ)2等效性试验(α=,β=)时:计数资料:平均有效率(P)等效标准(δ)N=公式:N=×P(1-P)/δ2计量资料:共同标准差(S)等效标准(δ)N=公式:N=× (S/δ)2上述公式(de)说明:1) 该公式源于郑青山教授发表(de)文献.2) N 是每组(de)估算例数N1=N2,N1 和N2 分别为试验药和参比药(de)例数;3) P 是平均有效率,4) S 是估计(de)共同标准差,5) δ 是等效标准.6) 通常都规定α=,β=(把握度80%)上述计算(de)例数若少于国家规定(de)例数,按规定为准;多于国家规定(de)则以计算值为准.具体规定(de)最小样本量如下:II期,试验组100例;III期,试验组300例;随机对照临床验证(如3类化药)试验组100例.IV期,2000例.疫苗和避孕药与上述要求不同.例1:某新药拟进行II 期临床试验,与阳性药按1:1 (de)比例安排例数,考察新药临床治愈率不差于阳性药.根据以往(de)疗效和统计学(de)一般要求,取α=,β=,等效标准δ=,平均有效率P=,每组需要多少病例由公式计算得,N=×/=88(例)以上88 例低于我国最低例数(100 例)(de)规定,故新药至少取100 例进行试验.如上例作等效性分析,则得,N=×/=122(例).例2:某利尿新药拟进行II 期临床试验,与阳性药按1:1 (de)比例安排例数,考察24h 新药利尿量不差于阳性药.根据以往(de)疗效和统计学(de)一般要求,取α=,β=,等效标准δ=60 ml,已知两组共同标准差S=180 ml,每组需要多少病例由公式得,N=× (180/60)2=111 例.故本次试验新药和阳性药(de)例数均不少于111 例.如上例作等效性分析,则得,N=×(180/60)2=154(例). [s:11]临床试验研究中,无论是实验组还是对照组都需要有一定数量(de)受试对象.这是因为同一种实验处理在不同(de)受试对象身上表现出(de)实验效应是存在着变异(de).仅凭一次实验观测结果或单个受试者所表现出来(de)实验效应说明不了什么问题.必须通过一定数量(de)重复观测才能把研究总体真实(de)客观规律性显示出来,并且可以对抽样误差做出客观地估计.一般说来重复观测次数越多,抽样误差越小,观测结果(de)可信度越高.一定数量(de)重复还可起到部分抵消混杂因素影响(de)作用,增强组间(de)可比性.但重复观测次数越多(即样本含量越大)试验所要消耗(de)人力、物力、财力和时间越多,可能会使试验研究成为不可能.而且,样本含量过大还会增加控制试验观测条件(de)难度,有可能引入非随机误差,给观测结果带来偏性(bias).所以在实验设计中落实重复原则(de)一个重要问题就是如何科学合理确定样本含量.由于在各对比组例数相等时进行统计推断效能最高,因此多数情况下都是按各组样本含量相等来估计.但在个别情况下,也可能要求各组样本含量按一定比例来估计.1 与样本含量估计有关(de)几个统计学参数在估计样本含量之前,首先要对以下几个统计学参数加以确定或作出估计.规定有专业意义(de)差值δ,即所比较(de)两总体参数值相差多大以上才有专业意义.δ是根据试验目(de)人为规定(de),但必须有一定专业依据.习惯上把δ称为分辨力或区分度.δ值越小表示对二个总体参数差别(de)区分度越强,因而所需样本含量也越大.确定作统计推断时允许犯Ⅰ类错误(“弃真”(de)错误)(de)概率α,即当对比(de)双方总体参数值没有差到δ.但根据抽样观测结果错误地得出二者有差别(de)推断结论(de)可能性,α确定(de)越小,所需样本含量越大.在确定α时还要注意明确是单侧检验(de)α,还是双侧检验(de)α.在同样大小(de)α条件下;双侧检验要比单侧检验需要更大(de)样本含量.提出所期望(de)检验效能power,用1-β表示.β为允许犯Ⅱ类错误(“取伪”(de)错误)(de)概率.检验效能就是推断结论不犯Ⅱ类错误(de)概率1-β称把握度.即当对比双方总体参数值间差值确实达到δ以上时,根据抽样观测结果在规定(de)α水准上能正确地作出有差别(de)推断结论(de)可能性.在科研设计中常把1-β定为或.一般来说1-β不宜低于,否则可能出现非真实(de)阴性推断结论.给出总体标准差σ或总体率π(de)估计值.它们分别反映计量数据和计数数据(de)变异程度.一般是根据前人经验或文献报道作出估计.如果没有前人经验或文献报道作为依据,可通过预实验取得样本(de)标准差s或样本率P分别作为σ和π(de)估计值.σ(de)估计值越大,π(de)估计值越接近,所需样本含量越大.在对以上统计学参数作出规定或估计(de)前提下,就可以根据不同(de)推断内容选用相应(de)公式计算出所需样本含量.由于在同样(de)要求和条件下完全随机设计(成组设计)所需样本含量最大,故一般都要按完全随机设计作出样本含量(de)估计.2 常用(de)估计样本含量(de)方法两样本均数比较时样本含量估计方法(1)两样本例数要求相等时可按下列公式估算每组需观察(de)例数n.n=2[(α+β)σ/δ]^2 (公式1)式中δ为要求(de)区分度,σ为总体标准差或其估计值s,α、β分别是对应于α和β(de)u值,可由t界值表,自由度υ=∞-行查出来,α有单侧、双侧之分,β只取单侧值.例1,某医师研究一种降低高血脂患者胆固醇药物(de)临床疗效,以安慰剂作对照.事前规定试验组与对照组相比,平均多降低 mmol/L以上,才有推广应用价值.而且由有关文献中查到高血脂患者胆固醇值(de)标准差为 mmol/L,若要求犯Ⅰ类错误(de)(de)概率不超过5%,犯Ⅱ类错误(de)概率不超过10%,且要两组例数相等则每组各需观察多少例本例δ= mmol/L,σ= mmol/L,α=,β=,1-β=,查t界值表自由度为∞一行得单侧=,=,代入公式(1)n=2[+×]^2=44故要达到上述要求,两组至少各需观察44例.(2)两样本例数要求呈一定比例(n2/n1=c)时,可按下列公式求出n1,再按比例求出n2=cn1.n1=[(α+β)σ/δ]^2(1+C)/C (公式2)例2 对例1资料如一切要求都维持不变,但要求试验组与对照组(de)例数呈2∶1比例(即C=2),问两组各需观察多少例n1=[+×]^2×(1+2)/2 =33(例)(对照组所需例数)n2=2×33=66(例)(试验组所需例数.)两组共需观察99例多于两组例数相等时达到同样要求时两组所需观察(de)总例数2×44=88.配对设计计量资料样本含量(对子数)估计方法配对设计包括异体配对、自身配对、自身前后配对及交叉设计(de)自身对照,均可按下列公式进行样本含量估计.n=[(α+β)σd/δ]^2 (公式3)式中δ、α、β(de)含义同前,σd为每对差值(de)总体标准差或其估计值sd.例3 某医院采用自身前后配对设计方案研究某治疗矽肺药物能否有效地增加矽肺患者(de)尿矽排出量.事前规定服药后尿矽排出量平均增加 mmol/L以上方能认为有效,根据预试验得到矽肺患者服药后尿矽排出量增加值(de)标准差 sd=mmol/L,现在要求推断时犯Ⅰ类错误(de)概率控制在以下(单侧),犯Ⅱ类错误(de)概率控制在以下,问需观察多少例矽肺病人本例δ= mmol/L, sd= mmol/L,α=,β=.1-β=,单侧=,=,代入公式(3)得到.n=[+×89/]^2=54(例)故可认为如该药确实能达到平均增加尿矽排出量在 mmol/L以上,则只需观察54例病人就能有90%(de)把握,按照α=(de)检验水准得出该药有增加矽肺病人尿矽作用(de)正确结论.样本均数与总体均数比较时样本含量估计方法可按下式估算所需样本含量n.n=[(α+β)σ/δ]^2 (公式4)例4已知血吸虫病人血红蛋白平均含量为90g/L,标准差为25g/L,现欲观察呋喃丙胺治疗后能否使血红蛋白增加,事先规定血红蛋白增加10g/L以上才能认为有效,推断结论犯Ⅰ类错误(de)概率α(双侧)不得超过,犯Ⅱ类错误(de)概率β不得超过,问需观察多少例病人本例δ=10g/L,σ=25g/L,=(双侧),=代入公式(4)得:n=[+×25/10]^2=66(例)故如果呋喃丙胺确实能使血吸虫病人血红蛋白平均含量增加10g/L以上,则只需观察66例就可以有90%(de)把握在α=检验水准上得出有增加血吸虫病人血红蛋白平均含量(de)结论.。
临床试验样本量的估算

临床试验样本量的估算首先,研究目的是样本量估算的基础,研究目的不同所需样本量也会不同。
例如,对于描述性研究,样本量的估算主要考虑数据的可行性,一般在50-100人左右即可;而对于验证性研究,需要进行统计检验或建立预测模型,则需要更多的样本量。
其次,研究设计也是样本量估算的重要因素。
常见的研究设计包括前瞻性队列研究、病例对照研究、随机对照试验等。
不同的研究设计对样本量的要求也不同。
例如,队列研究需要在较长的时间内追踪大量的受试者,样本量通常较大;而对照试验往往需要比较两组之间差异的显著性,样本量要求相对较少。
其次,统计学假设是影响样本量估算的主要因素之一、其中包括显著性水平(通常为0.05)、统计效应大小和统计检验的类型等。
较高的显著性水平(如0.01)和较小的统计效应大小都会增加样本量的要求。
此外,不同的统计检验方法也会影响样本量估算。
例如,判断两组均值是否有差异的双样本t检验需要较大的样本量,而判断两组比例是否有差异的卡方检验则需要较小的样本量。
最后,样本量的估算还需要考虑目标参数的合理估计。
目标参数包括所研究变量的均值、比例、相关系数等。
一般来说,样本量估计需要选取适当的目标参数,并根据目标参数的合理范围进行估计。
根据经验和实际情况,可以采用样本量估算公式来计算样本量。
n=(Zα/2*σ/δ)^2其中,n为所需样本量,Zα/2为给定显著性水平下的Z值,σ为总体标准差的估计值,δ为目标参数的边际误差。
综上所述,临床试验样本量的估算需要考虑研究目的、研究设计、统计学假设和目标参数等因素,并采用适当的样本量估算公式进行计算。
合理估算样本量可以确保研究结果的可靠性和统计分析的效力。
临床研究样本量规定

临床前研究样本量的规定临床研究样本量规定在我国, 不论1999年发布的《药品临床试验管理规范》, 2002年发布的《药品注册管理办法》(试行), 还是2005年发布的《药品注册管理办法》, 都对临床试验的样本量做了规定, 他们是一致的: (1)临床试验的样本量应当符合统计学要求和最低样本量要求; (2)临床试验的最低样本量在试验组的要求是: Ⅰ期为20-30例, Ⅱ期为100例, Ⅲ期为300例, Ⅳ期为2000例.制定者样本数量样本量的说明中国20-30 最小样本数欧盟20-50 建议的例数范围美国20-80 建议的例数范围表2 Ⅱ期临床试验的样本量中国〉100 最小样本数欧盟100-500 建议的例数范围美国100-300 建议的例数范围表3 Ⅲ期临床试验的样本量中国〉300 最小样本数欧盟500-5000 建议的例数范围美国300-3000 建议的例数范围医院的临床研究费用怎么确定?一般来说,医院临床研究费用主要包括以下几部分:1、检验费用:基本上根据研究方案中确定的检验项目和次数就可以计算。
2、临床观察费:主要是给研究人员的劳务费用,各医院情况都有所不同,一般来说研究费用给医院就行了,但是有些医院需要分医院和科室两部分,医院的写入合同,科室的给现金。
这块的费用需要有经验的人员用心操作才能达成各方都满意的结果。
否则给科室的观察费透露出去就会惹大麻烦。
3、基地管理费:一般都收取临床观察费用的10~20%或5000~15000左右,各医院情况不一,问临床药理基地能得到明确的答复。
4、研究牵头费或者组长费:一般在2~5万之间,也有很黑的。
要根据研究牵头单位的名气和研究难易程度而定。
5、药品补偿费,这笔费用部分单位收取,一般在2000~5000左右。
需要询问清楚。
6、受试者筛选费:一般在需要严格大量的筛选受试者时需要这笔费用。
7、受试者补偿费:常规是提供多次回访的交通费用。
宜以各城市的具体情况而定。
临床研究样本量计算流程

临床研究样本量计算流程
临床研究样本量计算流程一般包括以下步骤:
1.确定预期效应大小:这是样本量计算的关键步骤,需要基于文献综述、先前的研究结果或临床经验来确定试验中期望观察到的效应大小。
2.确定统计显著性水平(α):这是试验中用来确定效果是否显著的一个阈值。
通常在临床试验中,统计显著性水平设定为0.05,即p值小于0.05时认为效果显著。
3.确定统计功效(1-β):这是试验中检测到真实效应的概率。
通常将统计功效设定为80%或90%,这意味着试验有80%或90%的机会检测到实际效应(如果存在的话)。
4.根据预期效应大小、统计显著性水平和统计功效,使用适当的公式进行样本量计算。
例如,可以使用t检验的样本量计算公式,或者卡方检验的样本量计算公式等。
5.根据计算结果,确定所需的样本量。
如果样本量过大,可能会增加试验成本和时间;如果样本量过小,可能会影响试验的准确性和可靠性。
以上是临床研究样本量计算的一般流程,具体计算方法可能因研究类型、研究目的、研究设计等因素而有所不同。
因此,在进行样本量计算时,建议咨询专业的统计人员或研究人员,以确保计算的准确性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
29%
18%
203 230 263 308
29%
20%
314 355 406 475
31%
16%
108 122 139 163
31%
18%
149 168 193 225
31%
20%
215 243 278 325
9
非劣性设计的背景简述
在上述的差异性检验中,存在一个问题:当 样本量足够大时,即使两个总体有效率相差 很小,也有较大可能出现拒绝H0,但如此小 的差异可能没有临床意义。
年的使用量很高,没有明显的重要因素影响 其成功率,所以新药的成功率在90%以上是 可以接受的,因此可以取=0.92-0.90=2%
21
非劣性检验样本量估计实践
根据对照药的成功率为92%,试验药的成功率94%, =0.94-092=0.02
Power=0.9,=0.025,P1=0.94,P2=0.92 每组样本量估计:
在实际研究中,一般应考虑P1,P2的波动范 围,计算一些P1,P2的波动组合值和在能够 接受范围内的一组Power值,评估P1,P2的 各种波动和不同Power值组合下的样本量, 选择适合的样本量。
26
举例
P1
0.940 0.935 0.930 0.925 0.920 0.915 0.910
P2
例:为了雷替曲赛治疗局部晚期或转移复发 性结直肠癌患者的有效性,试验组:雷替曲 赛+奥沙利铂,对照组:亚叶酸钙+5-氟脲嘧 啶+奥沙利铂。从相关文献表明:试验组的有 效率(CR+PR)为29%,对照组的有效率为 18%,估计样本量时,取=0.05,分别取 Power=0.80,0.85,0.90,由于文献的结果有 一定的抽样误差,考虑试验组和对照组的有 效率波动2%,计算上述各种组合的样本量。
n1
n2
14
非劣性检验的样本量估计
两组样本量相同的情况下
n
(Z
Z
)2 (P1(1 P1)
( )2
P2 (1
P2 ))
并且可以用P1-P2进行估计,要求 0
15
非劣性设计的背景简述
非劣性设计的另一用途: 已知对照药(B药)的有效率优于某一个药
29
=(A- B)+(B- C )= (A- B)+20%>0 即:证实试验药的有效率高于C药
17
非劣性设计的背景简述
一般情况: 设:对照药的有效率-C药的有效率=δ>0 H0:试验药的有效率对照药的有效率- δ H1:试验药的有效率>对照药的有效率- δ 如果P<,则拒绝H0,认为H1成立。 H1:试验药的有效率>对照药的有效率- δ =对照药的有效率-(对照药的有效率-C药的有效率) = C药的有效率。即:试验药的有效率大于C药。
H0 :1 2 H1 :1 2
0.05
检验统计量 U
P1 P2
PC
(1
PC
)
1 n1
1 n2
3
差异性检验
其中
P1
a n1
, P2
c n2
, PC
ac n1 n2
,
故当 |U | 1.96 时,可以拒绝H0。
可以证明:U 2
7
优效设计的样本量估计举例
先计算=0.05,power=0.9,试验组方案的有效 率为P1=29%,对照组方案的有效率为P2=18%, 则每组样本量为
n
( Z 0.05/ 2
Z0.9 )2 P1(1 P1) (P1 P2 )2
P2 (1
P2 )
(1.96
1.282)2 (0.29(1 0.29) (0.29 0.18)2
一般选择的策略:
尽可能选择相同对照的RCT研究 样本量比较大
23
非劣性检验样本量估计实践
对于借助非劣性试验,间接证实试验药的有效率 优于C药,可以考虑下列的非劣性界值(Noninferiority marginal)
1. 对照药与C药的有效率之差的95%可信区间的下 限。如:B- C的95%CI为(0.05,0.09),则可以取 δ=0.05(推荐)
临床试验的检验的 样本量估计
赵耐青 复旦大学卫生统计教研室
1
背景简述
在临床试验中,采用随机分组,把受试对 象分为试验组和对照组,评价试验药和对
照药的疗效,评价指标为有效和无效,其
观察结果可以简单归结如下形式:
组别
有效
无效
合计
试验组
a
b
n1
对照组
c
d
n2
2
差异性检验
对于差异性检验:(试验药有效率1,对照药有效率2)
H0:1 2-5% H1: 1>2-5%
12
非劣性检验简介
由于非劣性检验为单侧检验,临床试验往往取 0.025(如美国FDA要求),检验统计量为
U
P1 P2
P1(1 P1) P2 (1 P2 )
n1
n2
0
1-2 的95%CI为:P1 P2 1.96
0.18(1
0.18))
308
8
样本量估计举例
不同参数取值的样本量估计
试验组方案 对照组方案
Power
有效率
有效率
0.75 0.80 0.856 246 288
27%
18%
296 335 382 448
27%
20%
506 573 655 766
29%
16%
140 159 181 212
2 Pearson
检验统计量。
4
优效设计的样本量估计
每组样本量相同的情况下,样本量估计为
n (Z /2 Z )2 P1(1 P1) P2 (1 P2 ) 2
2
其中 可以取 P1 P2 或差异更小的值 ,可以理
解为 最小的分辨能力,亦称为difference,检验效 能Power=1-,为第一类错误的概率。
由于对照药的成功率是在非常大的样本量下获得,所以忽略其抽样误差
27
非劣性设计的不等样本量的问题
在许多临床试验中,往往采用两组样本量不相等 的设计,例如:n1=kn:n2=n (k1),则
n
(Z
Z
)2 (P1(1 P1) / k
( )2
P2 (1
P2 ))
28
Thank You
5
优效设计的样本量估计
样本量n与,和有关, 分辨能力的意义为:
当实际的两个率的差 1 2 ||时,
则按照估计的n,进行随机抽样和统计检 验,拒绝H0的概率Power大于或等于预 定值1-,反之Power下降,即:出现不 拒绝H0的机会增加。
6
优效设计的样本量估计举例
0.920 0.920 0.920 0.920 0.920 0.920 0.920
=0.10 853 1152 1618 2401 3863 7063
16324
每组样本量 n
=0.15
=0.20
731
637
987
860
1387
1208
2059
1793
3312
2885
6055
5275
13995
12191
n
(1.96
1.28)2 (0.92 0.08 (0.02 0.02)2
0.94 0.06)
853
22
非劣性检验样本量估计实践
问题3:在实际研究中,往往不止一篇文献 含有P1,P2信息,并且不同文献提供的P1, P2信息往往是有差异的,应该参考哪一篇文 献所提供的P1,P2信息?
从另一个角度考虑:只有两个药的总体有效 率差异超出一定的范围,两个药的优劣性 在临床实践中才有意义,并称为容许误差, 由此产生了非劣性检验的问题。
10
非劣性检验简介
非劣性统计的检验假设:
H0 :1 2 H1 :1 2
H0的意义为对照药的总体有效率2高于试验药的总 体(有>效0)率。1,并且差异超出临床可以接受范围意义
即:采用随机对照试验,以米非司酮为对照 药,对于该药的有效性问题进行非劣性统计 分析。根据上述信息,估计所需样本量为多 少?
20
非劣性检验样本量估计实践
问题1:容许误差取多少? 问题2:米非司酮的各个研究所报道的成功
率的最大差异为7%,容许误差能否取7%? 根据各方临床专家的意见:由于药物流产每
P1(1 P1) P2 (1 P2 )
n1
n2
13
非劣性检验简介
如果U>1.96(P<0.025),则拒绝H0,可以认为试验 药非劣于对照药。
非劣性检验P<0.025等价于对应于1-2的95%可信 区间的下限满足下列不等式:
P1 P2 1.96
P1(1 P1) P2 (1 P2 )
2. 对照组与C药组的有效率之差=0.12,则可以考虑 取δ=0.12/2=0.06(不太推荐)
3. 可以参考对照组有效率的10%(实在没有办法时, 但必须有证据说明对照药有效)
24
非劣性检验样本量估计实践
问题4:对于许多临床试验,没有足够的临 床背景信息和证据可以确定容许误差,如 何处理?
H1的意义为对照药的总体有效率低于试验药或对照 药的总体有效率虽然高于试验药,但试验药仍在临 床可以接受的范围内。H1亦可称为试验药非劣于对 照药。
