刚体大作业.doc
刚体力学习题答案.docx

连,m1和m2则挂在圆柱体的两侧,如3-8图所示.设R=0.20m,r=0.10m,m=4 kg,M=10
kg,m1=m2=2 kg,且开始时m1,m2离地均为h=2m.求:
(1)柱体转动时的角加速度;
(2)两侧细绳的张力.
2
1( J
2mr
2)
0
2
0
2
2
0
1
1
(5
2 4
0.22)
122
(5 2
4 0.82)
(2 )2
2
2
=183J
3-18如3-20图所示,质量为M,长为l的均匀直棒,可绕垂直于棒一端的水平轴O无摩擦地转动,它原来静止在平衡位置上. 现有一质量为m的弹性小球飞来,正好在棒的下端与棒垂
直地相撞.相撞后,使棒从平衡位置处摆动到最大角度30°处.
L2
m2
vr sin 30
1m1r2
2
2
v
1
2
故有
m2vr sin60 m22r sin30
2m1r
可解得:
(2 3 1)m2v
2m1r
3-16
一人站在一匀质圆板状水平转台的边缘
,转台的轴承处的摩擦可忽略不计
,人的质量
为m',转台的质量为
10m',半径为R.最初整个系统是静止的,这人把一质量为
m的石子
2
mv
6m'R
人的线速度为vR
mv
6m'
其中负号表示转台角速度转向和人的线速度方向与假设方向相反-
3-17一人站在转台上,两臂平举,两手各握一个m
刚体部分作业问题全解共33页

46、我们若已接受最坏的,就再没有什么损失。——卡耐基 47、书到用时方恨少、事非经过不知难。——陆游 48、书籍把我们引入最美好的社会,使我们认识各个时代的伟大智者。——史美尔斯 49、熟读唐诗三百首,不会作诗也会吟。——孙洙 50、谁和我一样用功,谁就会和我一样成功。——莫扎特
刚体部分作业问题全解
•
6、黄金时代是在我们的前面,而不在 我们的 后面。
•
Hale Waihona Puke 7、心急吃不了热汤圆。•
8、你可以很有个性,但某些时候请收 敛。
•
9、只为成功找方法,不为失败找借口 (蹩脚 的工人 总是说 工具不 好)。
•
10、只要下定决心克服恐惧,便几乎 能克服 任何恐 惧。因 为,请 记住, 除了在 脑海中 ,恐惧 无处藏 身。-- 戴尔. 卡耐基 。
大学物理刚体习题

大学物理刚体习题(总13页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习 题第三章 刚体的转动刚体的定轴转动47. 一定滑轮半径为R ,质量为M ,用一质量不计的绳绕在滑轮上,另一端系一质量为m 的物体并由静止释放,这时滑轮的角加速度为1β,若不系物体而用一力F = mg 拉绳子使滑轮转动,这时角加速度为2β,这时有()1β2β()1β2β (C )1β2β(D )无法判断 分析由转动定律M I β=本题中I 不变β的大小完全取决于M 的大小而 M TR =系物体m 时 : T mg <不系物体而用一力F = mg 时: TF mg ==因此力矩变大所以有12ββ<mF选49.一飞轮的转动惯量为J ,t = 0时角速度为0ω,轮子在转动过程中受到一力矩2ωk M-=,则当转动角速度为0/3ω时的角加速度β = 从0ω到0/3ω飞轮转动经过的时间t ∆= 解: (1) 求β当0/3ω时, 20()3M k ω=-由 M J β=, 可得此时 209k MJ J ωβ==-(2) d M J J dt ωβ== 2d k J dt ωω-=分离变量,两边积分32td kdt Jωωωω-=⎰⎰解得: 02J t k ω∆=50.长为l 的均匀直棒可绕其下端与棒垂直的水平光滑轴在竖直平面内转动。
抬起一端使与水平夹角为60=θ,棒对轴的转动惯量为231ml J =,由静止释放直棒,则t = 0时棒的β=?;水平位置时的β=?这时的ω=(1)求β 据转动定律M J β=, MJβ= 0t =时, cos 602lM mg =︒水平位置时, 2lM mg =代入MJβ=,可别解得034glβ= 和 32g l β= (2)求ωd d d d M J J J J dt d dt d ωωθωβωθθ====将cos 2l M mg θ=和213J ml =代入化简并积分得, 0033cos 2g d d l ωπθθωω=⎰⎰ 60可求得332g l ω=(本题还可用动能定律机械能守恒方便求解ω)2211sin 60223l mg ml ω︒=⋅ 332g lω⇒=51.一飞轮以min /600rev 的转速转动,其转动惯量为25.2m kg J ⋅=,以恒定力矩使飞轮在一分钟内停止转动,求该力矩M 。
大学物理刚体的运动及其习题答案共42页文档

35、不要以为自己成功一次就可以了 ,也不 要以为 过去的 光荣可 以被永 远肯定 。
大学物理刚体的运动及其习 题答案
31、别人笑我太疯癫,我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣,抱怨者 的牢骚 ,这是 羊群中 的瘟疫 ,我不 能被它 传染。 我要尽 量避免 绝望, 辛勤耕 耘,忍 受苦楚 。我一 试再试 ,争取 每天的 成功, 避免以 失败收 常在别 人停滞 不前时 ,我继 续拼搏 。
ห้องสมุดไป่ตู้
谢谢!
51、 天 下 之 事 常成 于困约 ,而败 于奢靡 。——陆 游 52、 生 命 不 等 于是呼 吸,生 命是活 动。——卢 梭
53、 伟 大 的 事 业,需 要决心 ,能力 ,组织 和责任 感。 ——易 卜 生 54、 唯 书 籍 不 朽。——乔 特
55、 为 中 华 之 崛起而 读书。 ——周 恩来
面向新世纪课程教材大学物理大作业答案——刚体力学作业
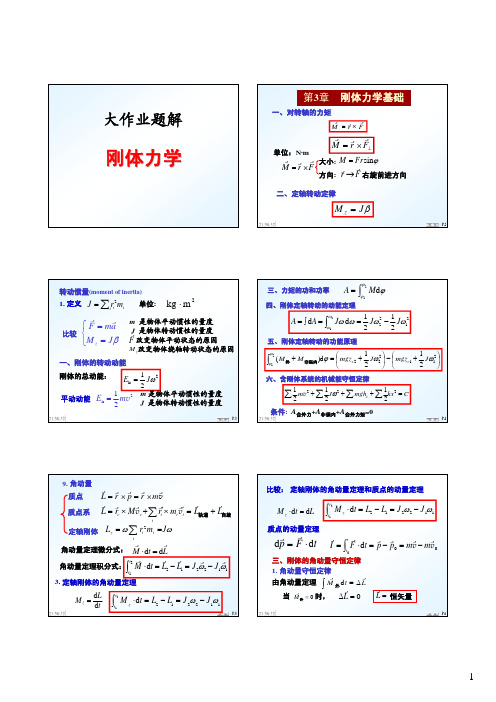
L2
−
L1
=
J 2ω2
−
J1ω1
质点的动量定理
dpr
=
r F
⋅
dt
∫ r
I
=
tr F ⋅ dt =
t0
pr − pr0 = mvr − mvr0
三、刚体的角动量守恒定律
1. 角动量守恒定律
∫ 由角动量定理
r M
当
r M外
=
0
时,
外
d
t r
ΔL
= =
Δ 0
r L
r L
=
恒矢量
P.6
1
区分两类冲击摆
(1)
大作业题解
刚体力学
第3章 刚体力学基础
一、对转轴的力矩
r M
=
rr
×
r F
单位:N·m
r M
=
rr
×
r F⊥
r M
=
rr
×
r F
大小: 方向:
M = Frsinϕ
rr
→
r F
右旋前进方向
二、定轴转动定律
M z = Jβ
P.2
转动惯量(moment of inertia)
∑ 1. 定义 J = iri2mi 单位: kg ⋅ m 2
l/4 O
[ A]
mg l = 1 Jω 2 J = 7 ml 2
22
48
⇒ ω = 4 3g 7l
P.11
9.如图所示,一人造卫星到地球中心C的最大距离和
最小距离分别为RA和RB。设人造卫星对应的角动量分
别为LA和LB,动能分别为EkA和EkB,则有
(A) LB > LA,EkB > EkA
多刚体大作业2(maple)

MAPLE理论力学学号:201431206024一、如图1,长0.40m l =、质量 1.00kg M =的匀质木棒,可绕水平轴O 在竖直平面内转动,开始时棒自然竖直悬垂,现有质量8g m =的子弹以200m/s v =的速率从A 点射入棒中,A 、O 点的距离为3/4l ,如图所示。
求:(1)棒开始运动时的角速度; (2)棒的最大偏转角。
解:(1)子弹射入前,子弹角动量为: l L 43mv 1⋅= 子弹射入后,木棒角动量为:ω22M 31l L =子弹射入后,子弹角动量为:ω23)43m(l L =应用角动量守恒定律:321L L L =+22313434mv l Ml m l ωω⎛⎫⋅=+ ⎪⎝⎭解得:3333810200448.9rad/s 191918100.4316310mv M m l ω--⨯⨯⨯===⎛⎫⎛⎫+⨯+⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭(2)子弹射入后,子弹角动能:221M 3121ωl E k ⋅=子弹射入后,木棍角动能:222)43m(21ωl E k =子弹摄入后,子弹重力势能:gl E M 211p -=子弹摄入后,木棍重力势能:gl E m 432p -=最大偏角时,子弹重力势能:θcos M 213p gl E -=最大偏角时,木棍重力势能:θcos m 434p gl E -=应用机械能守恒定律:432121p p p p k k E E E E E E +=+++2211333()cos cos 2342424l l l lMl m l Mg mg Mg mg ωθθ⎡⎤+--=--⎢⎥⎣⎦图1图2解得 2938cos 10.07923M ml M m gθω+=-⋅=-+, 94.5θ=︒答案:(1)8.9rad/s ;(2)94.5︒。
● Maple 程序:> restart: #清零> L[1]:=3/4*m*v*l: #射入前子弹的角动量L1 > L[2]:=1/3*M*omega*l^2: #射入后木棒的角动量L2 > L[3]:=m*(3/4*l)^2*omega: #射入后子弹的角动量L3 > eq1:= L[1]= L[2]+ L[3]: #角动量守恒> Ek[1]:=1/2*1/3*M*l^2*omega^2: #射入瞬间木棒角动能 > Ek[2]:=1/2*1/3*M*l^2*omega^2: #射入瞬间子弹角动能 > Ep[1]:=-1/2*M*g*l: #射入瞬间木棒重力势能 > Ep[2]:=-3/4*m*g*l: #射入瞬间子弹重力势能 > Ep[3]:=-1/2*M*g*l*cos(theta): #最大偏转时木棒重力势能 > Ep[4]:=-3/4*m*g*l*cos(theta): #最大偏转时子弹重力势能 > eq2:= Ek[1]+ Ek[2]+ Ep[1]+ Ep[2]= Ep[3]+ Ep[4]: #角动量守恒 > l:=0.4:M=1:m=0.008:v=200:g=9.8: #已知条件 > solve({eq1,eq2},{omega,theta}): #解方程二、如图3,一根长为l 、质量为M 的匀质棒自由悬挂于通过其上端的光滑水平轴上。
大学物理刚体习题

大学物理刚体习题在大学物理的学习中,刚体是一个重要的概念。
刚体是指物体内部各点之间没有相对位移,不发生形变,整体运动状态一致的理想化模型。
在解决物理问题时,刚体的性质为我们提供了极大的便利。
以下是一些常见的大学物理刚体习题。
一、基本概念题1、什么是刚体?列举一些常见的刚体实例。
2、刚体在什么情况下可以被视为刚体?其基本性质是什么?3、描述刚体的运动,并解释相关概念,如转动、角速度、角加速度等。
二、刚体的动力学问题4、一个刚体绕固定轴转动,在某时刻受到一个外力矩的作用,求该刚体接下来的运动状态。
41、一个刚体在平面上做纯滚动,如何计算其加速度和速度?411、一个刚体在重力场中处于平衡状态,求其重心的位置。
三、刚体的静力学问题7、一个刚体受到两个大小相等、方向相反的力作用,求该刚体的平衡状态。
71、一个刚体在平面上受到一个力矩的作用,求该刚体的转动效果。
711、一个刚体在三个不在同一直线上的力作用下处于平衡状态,求该刚体的重心位置。
四、刚体的运动学问题10、一个刚体绕固定轴转动,其角速度与时间成正比,求该刚体的角加速度和转速。
101、一个刚体在平面上做纯滚动,其速度与时间成正比,求该刚体的加速度和转速。
1011、一个刚体受到一个周期性外力矩的作用,求该刚体的运动状态。
以上就是一些常见的大学物理刚体习题。
解决这些问题需要我们深入理解刚体的性质和相关的物理概念,如力、力矩、重心等。
通过这些习题的练习,我们可以更好地掌握刚体的相关知识,提高我们的物理水平。
大学物理刚体力学标题:大学物理中的刚体力学在物理学的研究中,大学物理是引领我们探索自然界规律的重要途径。
而在大学物理中,刚体力学是一个相对独特的领域,它专注于研究物体在受到外力作用时的质点运动规律。
本文将探讨大学物理中的刚体力学。
一、刚体概念及特性刚体是指物体内部各质点之间没有相对位移,形状和体积不发生变化的理想化物体。
在刚体力学中,我们通常将刚体视为一个整体,研究其宏观运动规律。
刚体习题和答案

A
所示,滑块 A、重物 B 和滑轮 C
B
的质量分别为 mA、mB 和 mC,滑
轮的半径为
R
,滑 轮 对 轴 的 转 动 惯 量
J
=
1 2
mC
4
编号 ____________姓名 __________
《大学物理Ⅰ》答题纸
第五 章
R2.滑 块 A 与桌面间、滑轮与轴承之间均无摩
擦,绳的质量可不计,绳与滑轮之间无相对滑
碰前的角mv0动32 l 量为:
碰后的角动量为:
m
1 2
v0
2 3
l
[m( 2 3
l)2
2m(1 l)2 ] 3
所以 mv0
2 3
l
m
1 2
v0
2 3
l
[m( 2 3
l)2
2m(1 l)2 ] 3
得 3v0 2l
6、自测提高(17)如图 5-25 所示,
一质量均匀分布的圆盘,质量为 m0,
O
动.滑块 A 的加速度 a 2mB g 2(mA mB ) mC
【解答】
T
T
由转动定律得:
B
A
TB R TAR J GB TB mBa TA mAa a R
(1)
(2) (3) GB
(4)
4 个方程,共有 4 个未知量: TA 、TB 、 a 和 。可求:
a 2mB g 2mA mB mc
(1 2
mv0 m0 m)R
(2)圆盘的质量面密度 m0 在圆盘上取一 R2
半径为 r,宽为 dr 的小环带,
dM 2rdr 此 环 带 受 到 的 摩 擦 阻 力 矩
dM rgdm rg 2r 2dr
刚体力学习题解答.docx

第三章习题解答3.13 某发动机飞轮在时间间隔t内的角位移为。
求 t时刻的角速度和角加速度。
解:3.14桑塔纳汽车时速为 166km/h,车轮滚动半径为 0.26m,发动机转速与驱动轮转速比为 0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m,发动机转速为 n1, 驱动轮转速为 n2, 汽车速度为 v=166km/h 。
显然,汽车前进的速度就是驱动轮边缘的线速度,,所以:3.15 如题 3-15图所示,质量为 m的空心圆柱体,质量均匀分布,其内外半径为 r1和r2,求对通过其中心轴的转动惯量。
解:设圆柱体长为 h ,密度为,则半径为 r,厚为 dr的薄圆筒的质量 dm 为:对其轴线的转动惯量为3.17 如题 3-17图所示,一半圆形细杆,半径为,质量为,求对过细杆二端轴的转动惯量。
解:如图所示,圆形细杆对过 O轴且垂直于圆形细杆所在平面的轴的转动惯量为 mR2,根据垂直轴定理和问题的对称性知:圆形细杆对过轴的转动惯量为 mR2,由转动惯量的可加性可求得:半圆形细杆对过细杆二端轴的转动惯量为:3.18 在质量为 M ,半径为 R的匀质圆盘上挖出半径为 r的两个圆孔,圆孔中心在半径R的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
解:大圆盘对过圆盘中心 o且与盘面垂直的轴线(以下简称 o轴)的转动惯量为.由于对称放置,两个小圆盘对 o轴的转动惯量相等,设为 I ’,圆盘质量的面密度σ=M/πR2,根据平行轴定理,设挖去两个小圆盘后,剩余部分对o轴的转动惯量为 I ”3.19一转动系统的转动惯量为I=8.0kgm 2,转速为ω=41.9rad/s,两制动闸瓦对轮的压力都为 392N,闸瓦与轮缘间的摩擦系数为μ=0.4,轮半径为 r=0.4m,问从开始制动到静止需多长时间?解:由转动定理:制动过程可视为匀减速转动,3.20一轻绳绕于 r=0.2m的飞轮边缘,以恒力F=98N 拉绳,如题 3-20图(a)所示。
第三章 刚体力学基础 课后作业

第三章 刚体力学基础 课后作业班级 姓名 学号一、选择题1、一个质点作简谐振动,振幅为A ,在起始时刻质点的位移为2A , 且向x 轴正方向移动,代表此简谐振动的旋转矢量为( )1、有两个力作用在一个有固定转轴的刚体上:(1) 这两个力都平行于轴作用时,它们对轴的合力矩一定是零;(2) 这两个力都垂直于轴作用时,它们对轴的合力矩可能是零;(3) 当这两个力的合力为零时,它们对轴的合力矩也一定是零;(4) 当这两个力对轴的合力矩为零时,它们的合力也一定是零.对上述说法下述判断正确的是( )(A ) 只有(1)是正确的 (B )(1)、(2)正确,(3)、(4)错误(C ) (1)、(2)、(3)都正确,(4)错误 (D )(1)、(2)、(3)、(4)都正确2、关于力矩有以下几种说法:(1) 对某个定轴转动刚体而言,内力矩不会改变刚体的角加速度;(2) 一对作用力和反作用力对同一轴的力矩之和必为零;(3) 质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的运动状态一定相同.对上述说法下述判断正确的是( )(A ) 只有(2)是正确的 (B ) (1)、(2)是正确的(C )(2)、(3)是正确的 (D ) (1)、(2)、(3)都是正确的3、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动,如图所示,今使棒从水平位置由静止开始自由下落,在棒摆到竖直位置的过程中,下述说法正确的是( )(A ) 角速度从小到大,角加速度不变(B ) 角速度从小到大,角加速度从小到大(C ) 角速度从小到大,角加速度从大到小(D ) 角速度不变,角加速度为零4、 一圆盘绕通过盘心且垂直于盘面的水平轴转动,轴间摩擦不计.如图射来两个质量相同,速度大小相同,方向相反并在一条直线上的子弹,它们同时射入圆盘并且留在盘内,则子弹射入后的瞬间,圆盘和子弹系统的角动量L以及圆盘的角速度ω的变化情况为( ) (A) L 不变,ω增大 (B) 两者均不变(C) L不变,ω减小 (D) 两者均不确定5、假设卫星环绕地球中心作椭圆运动,则在运动过程中,卫星对地球中心的( )(A) 角动量守恒,动能守恒 (B) 角动量守恒,机械能守恒(C) 角动量不守恒,机械能守恒 (D) 角动量不守恒,动量也不守恒(E) 角动量守恒,动量也守恒二、填空题1、有甲、乙两个飞轮,甲是木制的,周围镶上铁制的轮缘。
刚体力学习题集库

第四章 刚体力学一、计算题1.如图所示,一个质量为m 的物体与绕在定滑轮上的绳子相联,绳子质量可以忽略,它与定滑轮之间无滑动.假设定滑轮质量为M 、半径为R ,其转动惯量为221MR ,滑轮轴光滑.试求该物体由静止开始下落的过程中,下落速度与时间的关系.解:根据牛顿运动定律和转动定律列方程对物体: mg -T =ma ① 2分 对滑轮: TR = J ② 2分 运动学关系: a =R③ 1分将①、②、③式联立得a =mg / (m +21M ) 1分 ∵ v 0=0,∴ v =at =mgt / (m +21M ) 2分2.如图所示,转轮A 、B 可分别独立地绕光滑的固定轴O 转动,它们的质量分别为m A =10 kg 和m B =20 kg ,半径分别为r A 和r B .现用力f A 和f B 分别向下拉绕在轮上的细绳且使绳与轮之间无滑动.为使A 、B 轮边缘处的切向加速度相同,相应的拉力f A 、f B 之比应为多少?(其中A 、B 轮绕O 轴转动时的转动惯量分别为221AA A r m J =和221B B B r m J =) 解:根据转动定律 f A r A = J A A① 1分其中221AA A r m J =,且 f B r B = J B B ② 1分 其中221B B B r m J =.要使A 、B 轮边上的切向加速度相同,应有a = r AA = r BB③ 1分由①、②式,有BB B AA AB A B A B A B A r m r m r J r J f f ββββ== ④ 由③式有 A /B = r B / r A将上式代入④式,得 f A / f B = m A / m B = 212分mM RMR βT mgaB A f Ar B r A3.一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r ,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t 内下降了一段距离S .试求整个轮轴的转动惯量(用m 、r 、t 和S 表示).解:设绳子对物体(或绳子对轮轴)的拉力为T ,则根据牛顿运动定律和转动定律得:mg T =ma ① 2分 T r =J ② 2分 由运动学关系有: a = r③ 2分由①、②、③式解得: J =m ( g -a ) r 2 / a ④又根据已知条件 v 0=0∴ S =221at , a =2S / t 2 ⑤ 2分将⑤式代入④式得:J =mr 2(Sgt22-1) 2分4.质量为5 kg 的一桶水悬于绕在辘轳上的轻绳的下端,辘轳可视为一质量为10 kg 的圆柱体.桶从井口由静止释放,求桶下落过程中绳中的张力.辘轳绕轴转动时的转动惯量为221MR ,其中M 和R 分别为辘轳的质量和半径,轴上摩擦忽略不计. 解:对水桶和圆柱形辘轳分别用牛顿运动定律和转动定律列方程mg -T =ma ① 1分 TR =J② 1分 a =R③ 1分由此可得 T =m (g -a )=m ()[]J TR g /∆-那么 mg J mR T =⎪⎪⎭⎫⎝⎛+21将 J =21MR 2代入上式,得mM mMgT 2+==24.5 N 2分5.一长为1 m 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动.抬起另一端使棒向上与水平面成60°,然后无初转速地将棒释放.已知棒对轴的转动惯量为21ml ,其中m 和l 分别为棒的质量和长度.求:(1) 放手时棒的角加速度; (2) 棒转到水平位置时的角加速度.解:设棒的质量为m ,当棒与水平面成60°角并开始下落时,根据转mOrT rβTmgTMRTmglO60°mg ϖ动定律M = J 1分其中 4/30sin 21mgl mgl M ==ο 1分 于是 2rad/s 35.743 ===lgJ M β 1分当棒转动到水平位置时, M =21mgl 1分那么 2rad/s 7.1423 ===lgJ M β 1分6.一轴承光滑的定滑轮,质量为M =2.00 kg ,半径为R =0.100 m ,一根不能伸长的轻绳,一端固定在定滑轮上,另一端系有一质量为m =5.00 kg 的物体,如图所示.已知定滑轮的转动惯量为J =221MR ,其初角速度0=10.0 rad/s ,方向垂直纸面向里.求:(1) 定滑轮的角加速度的大小和方向; (2) 定滑轮的角速度变化到=0时,物体上升的高度; (3) 当物体回到原来位置时,定滑轮的角速度的大小和方向.解:(1) ∵ mg -T =ma 1分TR =J 2分 a =R1分∴= mgR / (mR 2+J )()R M m mgMR mR mgR +=+=222122 =81.7 rad/s 2 1分 方向垂直纸面向外. 1分(2) ∵ βθωω2202-=当=0 时, rad 612.0220==βωθ 物体上升的高度h = R = 6.12×10-2 m 2分(3) ==βθω210.0 rad/s方向垂直纸面向外. 2分7.一质量为M =15 kg 、半径为R =0.30 m 的圆柱体,可绕与其几何轴重合的水平固定轴转动(转动惯量J =221MR ).现以一不能伸长的轻绳绕于柱面,而在绳的下端悬一质量m =8.0 kg 的物体.不计圆柱体与轴之间的摩擦,求:mMR ω0TTmga(1) 物体自静止下落, 5 s 内下降的距离; (2) 绳中的张力. 解: J =221MR =0.675 kg ·m 2 ∵ mg -T =ma1分 TR =J 2分 a =R1分∴ a =mgR 2 / (mR 2 + J )=5.06 m / s 2 1分因此(1)下落距离 h =221at =63.3 m 2分 (2) 张力 T =m (g -a )=37.9 N 1分8.一半径为25 cm 的圆柱体,可绕与其中心轴线重合的光滑固定轴转动.圆柱体上绕上绳子.圆柱体初角速度为零,现拉绳的端点,使其以1 m/s 2的加速度运动.绳与圆柱表面无相对滑动.试计算在t = 5 s 时(1) 圆柱体的角加速度, (2) 圆柱体的角速度,(3) 如果圆柱体对转轴的转动惯量为2 kg ·m 2,那么要保持上述角加速度不变,应加的拉力为多少?解:(1) 圆柱体的角加速度=a / r =4 rad / s 2 2分(2) 根据t t 0βωω+=,此题中0 = 0,则有t = t那么圆柱体的角速度 ====55 t t t βω20 rad/s 1分 (3) 根据转动定律fr = J则 f = J/ r = 32 N 2分9.一轴承光滑的定滑轮,质量为M =2.00 kg ,半径为R =0.100 m ,一根不能伸长的轻绳,一端固定在定滑轮上,另一端系有一质量为m =5.00kg 的物体,如图所示.已知定滑轮的转动惯量为J =221MR ,其初角速度0=10.0 rad/s ,方向垂直纸面向里.求:(1) 定滑轮的角加速度的大小和方向;(2) 定滑轮的角速度变化到=0时,物体上升的高度; (3) 当物体回到原来位置时,定滑轮的角速度的大小和方向.解:(1) ∵ mg -T =ma 1分 TR =J 2分 a =R1分mgTTMgaFβ RmMR ω0∴ = mgR / (mR 2+J )()R M m mgMRmR mgR +=+=222122 =81.7 rad/s 2 1分 方向垂直纸面向外. 1分(2) ∵ βθωω2202-=当=0 时, rad 612.0220==βωθ 物体上升的高度h = R = 6.12×10-2 m 2分(3) ==βθω210.0 rad/s方向垂直纸面向外. 2分10.一质量为M =15 kg 、半径为R =0.30 m 的圆柱体,可绕与其几何轴重合的水平固定轴转动(转动惯量J =221MR ).现以一不能伸长的轻绳绕于柱面,而在绳的下端悬一质量m =8.0 kg 的物体.不计圆柱体与轴之间的摩擦,求:(1) 物体自静止下落, 5 s 内下降的距离; (2) 绳中的张力.解: J =221MR =0.675 kg ·m 2 ∵ mg -T =ma1分 TR =J 2分 a =R1分∴ a =mgR 2 / (mR 2 + J )=5.06 m / s 2 1分因此(1)下落距离 h =221at =63.3 m 2分 (2) 张力 T =m (g -a )=37.9 N 1分11.一半径为25 cm 的圆柱体,可绕与其中心轴线重合的光滑固定轴转动.圆柱体上绕上绳子.圆柱体初角速度为零,现拉绳的端点,使其以1 m/s 2的加速度运动.绳与圆柱表面无相对滑动.试计算在t = 5 s 时(1) 圆柱体的角加速度, (2) 圆柱体的角速度,(3) 如果圆柱体对转轴的转动惯量为2 kg ·m 2,那么要保持上述角加速度不变,应加的拉力为多少?解:(1) 圆柱体的角加速度=a / r =4 rad / s 2 2分(2) 根据t t 0βωω+=,此题中0 = 0,则TTmgamgTTMgaFβ R有 t = t那么圆柱体的角速度 ====55 t t t βω20 rad/s 1分 (3) 根据转动定律fr = J则 f = J / r = 32 N 2分12.长为L 的梯子斜靠在光滑的墙上高为h 的地方,梯子和地面间的静摩擦系数为,若梯子的重量忽略,试问人爬到离地面多高的地方,梯子就会滑倒下来?解:当人爬到离地面x 高度处梯子刚要滑下,此时梯子与地面间为最大静摩擦,仍处于平衡状态 (不稳定的) .1分N 1-f =0, N 2-P =0 1分 N 1h -Px ·ctg =0 1分 f =N 21分解得 222/tg hL h h x -=⋅=μθμ1分13.一转动惯量为J 的圆盘绕一固定轴转动,起初角速度为0.设它所受阻力矩与转动角速度成正比,即M =-k (k 为正的常数),求圆盘的角速度从0变为021ω时所需的时间.解:根据转动定律:J d / d t = -k∴t Jkd d -=ωω2分 两边积分: ⎰⎰-=t t Jk 02/d d 100ωωωω得ln2 = kt / J∴ t =(J ln2) / k 3分LhN 1h N 2 PR θ R xR f14.一圆柱体截面半径为r ,重为P ,放置如图所示.它与墙面和地面之间的静摩擦系数均为31.若对圆柱体施以向下的力F =2P 可使它刚好要反时针转动,求(1) 作用于A 点的正压力和摩擦力,(2) 力F ϖ与P ϖ之间的垂直距离d .解:设正压力N A 、N B ,摩擦力f A ,f B 如图.根据力的平衡,有f A +N B = F+P = 3P ① 1分 N A =f B② 1分根据力矩平衡,有Fd = ( f A + f B ) r ③ 2分刚要转动有 A A N f 31=④ B B N f 31= ⑤ 1分(1) 把④及 ②、⑤代入①可求得 N A =0.9P , f A =0.3P 2分 (2) 由③可求得 d = 0.6 r 1分15.一轻绳跨过两个质量均为m 、半径均为r 的均匀圆盘状定滑轮,绳的两端分别挂着质量为m 和2m 的重物,如图所示.绳与滑轮间无相对滑动,滑轮轴光滑.两个定滑轮的转动惯量均为221mr .将由两个定滑轮以及质量为m 和2m 的重物组成的系统从静止释放,求两滑轮之间绳内的张力.解:受力分析如图所示. 2分 2mg -T 1=2ma 1分T 2-mg =ma 1分ϖϖT 1 r -T r =β221mr 1分 T r -T 2 r =β221mr 1分a =r2分解上述5个联立方程得: T =11mg / 82分16.质量分别为m 和2m 、半径分别为r 和2r 的两个均匀圆盘,同轴地粘在一起,可以绕通过盘心且垂直盘面的水平光滑固定轴转动,对转轴的转动惯量为9mr 2 / 2,大小圆盘边缘都绕有绳子,绳子下端都挂一质量为m 的重物,如图所示.求盘的角加速度的大小.解:受力分析如图. 2分mg -T 2 = ma 2 1分 T 1-mg = ma 1 1分 T 2 (2r )-T 1r = 9mr 2 / 2 2分 2r = a 2 1分r= a11分解上述5个联立方程,得: rg192=β 2分17.质量m =1.1 kg 的匀质圆盘,可以绕通过其中心且垂直盘面的水平光滑固定轴转动,对轴的转动惯量J =221mr (r 为盘的半径).圆盘边缘绕有绳子,绳子下端挂一质量m 1=1.0 kg 的物体,如图所示.起初在圆盘上加一恒力矩使物体以速率v 0=0.6 m/s 匀速上升,如撤去所加力矩,问经历多少时间圆盘开始作反方向转动.m2m βT 2 2P ϖ1P ϖTa T 1amrmm 2m2rT 2aT2P ϖ1P ϖβa 1m 1m ,r解:撤去外加力矩后受力分析如图所示. 2分 m 1g -T = m 1a 1分 Tr =J1分 a =r1分 a = m 1gr / ( m 1r + J / r )代入J =221mr , a =mm gm 2111+= 6.32 ms 2 2分∵ v 0-at =0 2分 ∴ t =v 0 / a =0.095 s 1分18.一轻绳绕过一定滑轮,滑轮轴光滑,滑轮的半径为R ,质量为M / 4,均匀分布在其边缘上.绳子的A 端有一质量为M 的人抓住了绳端,而在绳的另一端B 系了一质量为21M 的重物,如图.设人从静止开始相对于绳匀速向上爬时,绳与滑轮间无相对滑动,求B 端重物上升的加速度?(已知滑轮对通过滑轮中心且垂直于轮面的轴的转动惯量J =MR 2 / 4 )解:受力分析如图所示.设重物的对地加速度为a ,向上.则绳的A 端对地有加速度a 向下,人相对于绳虽为匀速向上,但相对于地其加速度仍为a 向下.2分根据牛顿第二定律可得:对人: Mg -T 2=Ma ① 2分对重物: T 1-21Mg =21Ma ② 2分根据转动定律,对滑轮有(T 2-T 1)R =J=MR 2/ 4 ③ 2分因绳与滑轮无相对滑动, a =R ④ 1分①、②、③、④四式联立解得 a =2g / 7 1分m 1 m , rβ0vPTaOBAOB MgT 2 T 1 Mg 21aa β19.如图所示,设两重物的质量分别为m 1和m 2,且m 1>m 2,定滑轮的半径为r ,对转轴的转动惯量为J ,轻绳与滑轮间无滑动,滑轮轴上摩擦不计.设开始时系统静止,试求t 时刻滑轮的角速度.解:作示力图.两重物加速度大小a 相同,方向如图.示力图 2分m 1g -T 1=m 1a 1分T 2-m 2g =m 2a 1分设滑轮的角加速度为,则 (T 1-T 2)r =J2分且有 a =r1分由以上四式消去T 1,T 2得:()()J r m m gr m m ++-=22121β2分开始时系统静止,故t 时刻滑轮的角速度.()()Jr m m grtm m t ++-==22121 βω 1分20.质量为M 1=24 kg 的圆轮,可绕水平光滑固定轴转动,一轻绳缠绕于轮上,另一端通过质量为M 2=5 kg 的圆盘形定滑轮悬有m =10 kg 的物体.求当重物由静止开始下降了h =0.5 m 时,(1) 物体的速度; (2) 绳中张力.(设绳与定滑轮间无相对滑动,圆轮、定滑轮绕通过轮心且垂直于横截面的水平光滑轴的转动惯量分别为21121R M J =,22221r M J =) 解:各物体的受力情况如图所示. 图2分 由转动定律、牛顿第二定律及运动学方程,可列出以下联立方程:m 2mrm 2gm 1g raaT 1T 2T 2T 1βR M 1M 2rmT 1R =J 11=12121βR M 方程各1分共5分 T 2r -T 1r =J 22=22121βr M mg -T 2=ma , a =R 1=r2 ,v 2=2ah 求解联立方程,得 ()42121=++=m M M mg a m/s 2ah 2=v =2 m/s 1分T 2=m (g -a )=58 N 1分T 1=a M 121=48 N 1分21.两个匀质圆盘,一大一小,同轴地粘结在一起,构成一个组合轮.小圆盘的半径为r ,质量为m ;大圆盘的半径r '=2r ,质量 m '=2m .组合轮可绕通过其中心且垂直于盘面的光滑水平固定轴O 转动,对O 轴的转动惯量J =9mr 2 / 2.两圆盘边缘上分别绕有轻质细绳,细绳下端各悬挂质量为m 的物体A 和B ,如图所示.这一系统从静止开始运动,绳与盘无相对滑动,绳的长度不变.已知r = 10 cm .求: (1) 组合轮的角加速度;(2) 当物体A 上升h =40 cm 时,组合轮的角速度.解:(1) 各物体受力情况如图. 图2分 T -mg =ma 1分 mg -T '=m a ' 1分 T ' (2r )-Tr =9mr 2 / 2 1分a =r1分a '=(2r ) 1分由上述方程组解得:=2g / (19r )=10.3 rad ·s -2 1分 (2) 设为组合轮转过的角度,则=h / r2=2所以,= (2h / r )1/2=9.08 rad ·s -1 2分22.物体A 和B 叠放在水平桌面上,由跨过定滑轮的轻质细绳相互连接,如图所示.今用大小为F 的水平力拉A .设A 、M 1M 2 mgM 2gM 1gN 1 N 2T 1 T 1T 2 maβ β2T 2r m '',m,rAOBmgAB N T T βaT 'T 'a 'BAϖRB 和滑轮的质量都为m ,滑轮的半径为R ,对轴的转动惯量J =221mR .AB 之间、A 与桌面之间、滑轮与其轴之间的摩擦都可以忽略不计,绳与滑轮之间无相对的滑动且绳不可伸长.已知F =10 N ,m =8.0 kg ,R =0.050 m .求:(1) 滑轮的角加速度; (2) 物体A 与滑轮之间的绳中的张力; (3) 物体B 与滑轮之间的绳中的张力.解:各物体受力情况如图. 图2分F -T =ma 1分 T '=ma 1分 (T T '-)R =β221mR 1分 a =R1分由上述方程组解得: =2F / (5mR )=10 rad ·s -2 2分 T =3F / 5=6.0 N 1分T '=2F / 5=4.0 N 1分23.两个大小不同、具有水平光滑轴的定滑轮,顶点在同一水平线上.小滑轮的质量为m ',半径为r ',对轴的转动惯量J =221mr .大滑轮的质量m =2m ,半径r =2r ,对轴的转动惯量221r m J ''='.一根不可伸长的轻质细绳跨过这两个定滑轮,绳的两端分别挂着物体A 和B .A 的质量为m ,B 的质量 m '=2m .这一系统由静止开始转动.已知m =6.0 kg ,r =5.0 cm .求两滑轮的角加速度和它们之间绳中的张力.解:各物体受力情况如图. 2分 T A -mg =ma 1分 (2m)g -T A =(2m )a 1分(T -T A )r =β221mr 1分 (T B -T )(2r )=21(2m )(2r )2β' 1分aBA FTa T β’ T’m,rABmm ' m ', r 'a =r =(2r )β' 1分 由上述方程组解得:=2g / (9r )=43.6 rad ·s -2 1分β'=β21=21.8 rad ·s -2 1分 T =(4/3)mg =78.4 N 1分24.一质量m = 6.00 kg 、长l = 1.00 m 的匀质棒,放在水平桌面上,可绕通过其中心的竖直固定轴转动,对轴的转动惯量J = ml 2 / 12.t = 0时棒的角速度0 = 10.0 rad ·s1.由于受到恒定的阻力矩的作用,t = 20 s 时,棒停止运动.求:(1) 棒的角加速度的大小; (2) 棒所受阻力矩的大小; (3) 从t = 0到t = 10 s 时间内棒转过的角度. 解:(1) 0=0+t=-0 / t =-0.50 rad ·s-22分(2) M r =ml 2/ 12=-0.25 N ·m 2分(3) 10=0t +21t 2=75 rad 1分25.如图所示的阿特伍德机装置中,滑轮和绳子间没有滑动且绳子不可以伸长,轴与轮间有阻力矩,求滑轮两边绳子中的张力.已知m 1=20 kg ,m 2=10 kg .滑轮质量为m 3=5 kg .滑轮半径为r =0.2 m .滑轮可视为均匀圆盘,阻力矩M f =6.6 N ·m ,已知圆盘对过其中心且与盘面垂直的轴的转动惯量为2321r m .解:对两物体分别应用牛顿第二定律(见图),则有m 1g -T 1 = m 1a ①T 2 – m 2g = m 2a ② 2分对滑轮应用转动定律,则有ββ⋅==-'-'232121r m J M r T r T f ③ 2分 对轮缘上任一点,有 a =r ④ 1分βT T A T BT T AT B gm 'mga ABaβ'm 3rm 1m 2又: 1T '= T 1, 2T '= T 2 ⑤ 则联立上面五个式子可以解出rm r m r m M gr m gr m a f3212121++--==2 m/s 2 2分T 1=m 1g -m 1a =156 NT 2=m 2g -m 2 a =118N 3分26.如图所示,一半径为R 的匀质小木球固结在一长度为l 的匀质细棒的下端,且可绕水平光滑固定轴O 转动.今有一质量为m ,速度为0v ϖ的子弹,沿着与水平面成角的方向射向球心,且嵌于球心.已知小木球、细棒对通过O 的水平轴的转动惯量的总和为J .求子弹嵌入球心后系统的共同角速度.解:选子弹、细棒、小木球为系统.子弹射入时,系统所受合外力矩为零,系统对转轴的角动量守恒. 2分mv 0(R + l )cos= [J + m (R + l )2 ] 2分()()20cos l R m J l R m +++=αωv 1分27.如图所示,一半径为R ,质量为m 的水平圆台,正以角速度绕通过其中心的竖直固定光滑轴转动,转动惯量J =221mR .台上原站有2人,质量各等于转台质量的一半,一人站于台边A 处,另一人站于距台中心R 21的B 处.今A 处的人相对于圆台以速率v 顺着圆台转向沿圆周走动,同时B 处的人相对于圆台以速率2v 逆圆台转向沿圆周走动.求圆台这时的角速度.m 1gm 2g m 1 m 21 T rβ2T 'T 'Ol Rαm0v ϖA RB O 2vω R /2解:以转台和二人为研究对象,所受外力只有重力及轴的支撑力,诸力对转轴的合力矩为零,所以系统角动量守恒.各转动惯量分别为2分 221mR J =,221mR J A=,()22/21R m J B=2分以地面为参照系,A 处的人走动的角速度为+(v / R ),B 处的人 1分 走动的角速度为-(2v /21R )=-(4v / R ).由角动量守恒定律 1分 ()02222/212121ω⎥⎦⎤⎢⎣⎡++R m mR mR = ()R mR mR /212122v ++=ωω()R R m /421212v -⎪⎭⎫ ⎝⎛+ω 2分解出=2分28.一质量均匀分布的圆盘,质量为M ,半径为R ,放在一粗糙水平面上(圆盘与水平面之间的摩擦系数为μ),圆盘可绕通过其中心O 的竖直固定光滑轴转动.开始时,圆盘静止,一质量为m 的子弹以水平速度v 0垂直于圆盘半径打入圆盘边缘并嵌在盘边上,求(1) 子弹击中圆盘后,盘所获得的角速度. (2) 经过多少时间后,圆盘停止转动.(圆盘绕通过O 的竖直轴的转动惯量为221MR ,忽略子弹重力造成的摩擦阻力矩)解:(1) 以子弹和圆盘为系统,在子弹击中圆盘过程中,对轴O 的角动量守恒.1分mv 0R =(21MR 2+mR 2) 2分 R m M m ⎪⎭⎫ ⎝⎛+=210v ω 1分(2) 设表示圆盘单位面积的质量,可求出圆盘所受水平面的摩擦力矩的大小m R O0v ϖ为 ⎰π⋅=Rf r rg r M 0d 2σμ=(2 / 3)σgR 3=(2 / 3)MgR 2分设经过t 时间圆盘停止转动,则按角动量定理有-M ft =0-J=-(21MR 2+mR 2)=- mv 0R 2分 ∴ ()Mg m MgR R m M R m t fμμ2v 33/2v v 000===∆ 2分29.有一质量为m 1、长为l 的均匀细棒,静止平放在滑动摩擦系数为的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动.另有一水平运动的质量为m 2的小滑块,从侧面垂直于棒与棒的另一端A 相碰撞,设碰撞时间极短.已知小滑块在碰撞前后的速度分别为1v ϖ和2v ϖ,如图所示.求碰撞后从细棒开始转动到停止转动的过程所需的时间.(已知棒绕O 点的转动惯量2131l m J =) 解:对棒和滑块系统,在碰撞过程中,由于碰撞时间极短,所以棒所受的摩擦力矩<<滑块的冲力矩.故可认为合外力矩为零,因而系统的角动量守恒,即 1分 m 2v 1l =-m 2v 2l +ω2131l m ① 3分碰后棒在转动过程中所受的摩擦力矩为gl m x x l m gM lf 10121d μμ-=⋅-=⎰ ② 2分 由角动量定理 ω210310l m dt M tf -=⎰ ③ 2分由①、②和③解得 gm m t 12122μv v += 2分OAm 1 ,l1v ϖ2ϖ俯视图。
-刚体力学-答案-推荐下载

t 时角速度为
d
2.解:设 绳 中 张 力 为 T 对于重物按牛顿第二定律有 m2g–T=m2a
0
t
kdt
0ekt
(1)
1
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
《刚体力学作业》word版

刚体力学作业班级:_____________ 姓名:_____________ 学号:_____________ 日期:__________年_______月_______日 成绩:_____________ 一、选择题 1.如图所示,A 、B 为两个相同的绕着轻绳的定滑轮.A 滑轮挂一质量为M 的物体,B 滑轮受拉力F ,而且F =Mg .设A 、B 两滑轮的角加速度分别为βA 和βB ,不计滑轮轴的摩擦,则有 (A) βA =βB . (B) βA >βB .(C) βA <βB . (D) 开始时βA =βB ,以后βA <βB . [ ]2.几个力同时作用在一个具有光滑固定转轴的刚体上,如果这几个力的矢量和为零,则此刚体(A) 必然不会转动. (B) 转速必然不变.(C) 转速必然改变. (D) 转速可能不变,也可能改变. [ ]3.关于刚体对轴的转动惯量,下列说法中正确的是 (A )只取决于刚体的质量,与质量的空间分布和轴的位置无关. (B )取决于刚体的质量和质量的空间分布,与轴的位置无关. (C )取决于刚体的质量、质量的空间分布和轴的位置. (D )只取决于转轴的位置,与刚体的质量和质量的空间分布无关. [ ]4.一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力(A) 处处相等. (B) 左边大于右边.(C) 右边大于左边. (D) 哪边大无法判断.[ ]5.花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为J 0,角速度为ω0.然后她将两臂收回,使转动惯量减少为31J 0.这时她转动的角速度变为 (A) 31ω0. (B) ()3/1 ω0.(C) 3 ω0. (D) 3 ω0. [ ]6.如图所示,一静止的均匀细棒,长为L 、质量为M ,可绕通过棒的端点且垂直于棒长的光滑固定轴O 在水平面内转动,转动惯量为231ML .一质量为m 、速率为v 的子弹在水平面内沿与棒垂直的方向射出并穿出棒的自由端,设穿过棒后子弹的速率为v 21,则此时棒的角速度应为(A) ML m v . (B) MLm 23v.(C) MLm 35v. (D) ML m 47v . [ ]7.一水平圆盘可绕通过其中心的固定竖直轴转动,盘上站着一个人.把人和圆盘取作系统,当此人在盘上随意走动时,若忽略轴的摩擦,此系统v21v俯视图(A) 动量守恒. (B) 机械能守恒. (C) 对转轴的角动量守恒. (D) 动量、机械能和角动量都守恒.(E) 动量、机械能和角动量都不守恒. [ ]8.质量为m 的小孩站在半径为R 的水平平台边缘上.平台可以绕通过其中心的竖直光滑固定轴自由转动,转动惯量为J .平台和小孩开始时均静止.当小孩突然以相对于地面为v 的速率在台边缘沿逆时针转向走动时,则此平台相对地面旋转的角速度和旋转方向分别为(A) ⎪⎭⎫⎝⎛=R JmR v 2ω,顺时针. (B) ⎪⎭⎫ ⎝⎛=R J mR v 2ω,逆时针. (C) ⎪⎭⎫ ⎝⎛+=R mR J mR v 22ω,顺时针. (D) ⎪⎭⎫⎝⎛+=R mR J mR v 22ω,逆时针. [ ]9.如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统(A) 只有机械能守恒. (B) 只有动量守恒. (C) 只有对转轴O 的角动量守恒.(D) 机械能、动量和角动量均守恒. [ ]10.关于力矩有以下几种说法:(1) 对某个定轴而言,内力矩不会改变刚体的角动量. (2) 作用力和反作用力对同一轴的力矩之和必为零.(3) 质量相等,形状和大小不同的两个刚体,在相同力矩的作用下,它们的角加速度一定相等. 在上述说法中, (A) 只有(2) 是正确的. (B) (1) 、(2) 是正确的. (C) (2) 、(3) 是正确的.(D) (1) 、(2) 、(3)都是正确的. [ ]二、填空题 11.半径为20 cm 的主动轮,通过皮带拖动半径为50 cm 的被动轮转动,皮带与轮之间无相对滑动.主动轮从静止开始作匀角加速转动.在4 s 内被动轮的角速度达到8πrad ·s -1,则主动轮在这段时间内转过了________圈.12.一飞轮以600 rev/min 的转速旋转,转动惯量为2.5 kg ·m 2,现加一恒定的制动力矩使飞轮在1 s 内停止转动,则该恒定制动力矩的大小M =_________.13.一个能绕固定轴转动的轮子,除受到轴承的恒定摩擦力矩M r 外,还受到恒定外力矩M 的作用.若M =20 N · m ,轮子对固定轴的转动惯量为J =15 kg · m 2.在t =10 s 内,轮子的角速度由ω =0增大到ω=10 rad/s ,则M r =_____________.14.一定滑轮质量为M 、半径为R ,对水平轴的转动惯量J =21MR 2.在滑轮的边缘绕一细绳,绳的下端挂一物体.绳的质量可以忽略且不能伸长,滑轮与轴承间无摩擦.物体下落的加速度为a ,则绳中的张力T =_________________.15.如图所示,一轻绳绕于半径为r 的飞轮边缘,并以质量为m 的物体挂在绳端,飞轮对过轮心且与轮面垂直的水平固定轴的转动惯量为J.若不计摩擦,飞轮的角加速度β =_______________.16.半径为R 具有光滑轴的定滑轮边缘绕一细绳,绳的下端挂一质量为m 的物体.绳的质量可以忽略,绳与定滑轮之间无相对滑动.若物体下落的加速度为a ,则定滑轮对轴的转动惯量J =______________________.17.一飞轮以角速度ω0绕光滑固定轴旋转,飞轮对轴的转动惯量为J 1;另一静止飞轮突然和上述转动的飞轮啮合,绕同一转轴转动,该飞轮对轴的转动惯量为前者的二倍.啮合后整个系统的角速度ω=__________________.18.质量为m 、长为l 的棒,可绕通过棒中心且与棒垂直的竖直光滑固定轴O 在水平面内自由转动(转动惯量J =m l 2 / 12).开始时棒静止,现有一子弹,质量也是m ,在水平面内以速度v 0垂直射入棒端并嵌在其中.则子弹嵌入后棒的角速度ω =_____________________.19.长为l 的杆如图悬挂.O 为水平光滑固定转轴,平衡时杆竖直下垂,一子弹水平地射入杆中.则在此过程中,_____________系统对转轴O的_______________守恒.20.质量分别为m 和2m 的两物体(都可视为质点),用一长为l 的轻质刚性细杆相连,系统绕通过杆且与杆垂直的竖直固定轴O 转动,已知O 轴离质量为2m 的质点的距离为31l ,质量为m 的质点的线速度为v 且与杆垂直,则该系统对转轴的角动量(动量矩)大小为___________________.三、计算题 21.一质量为m 的物体悬于一条轻绳的一端,绳另一端绕在一轮轴的轴上,如图所示.轴水平且垂直于轮轴面,其半径为r ,整个装置架在光滑的固定轴承之上.当物体从静止释放后,在时间t 内下降了一段距离S .试求整个轮轴的转动惯量(用m 、r 、t 和S 表示).22.m0v俯视图m2ml R俯视图盘开始作反方向转动.23.一轻绳绕过一定滑轮,滑轮轴光滑,滑轮的半径为R ,质量为M / 4,均匀分布在其边缘上.绳子的A 端有一质量为M 的人抓住了绳端,而在绳的另一端B 系了一质量为21M 的重物,如图.设人从静止开始相对于绳匀速向上爬时,绳与滑轮间无相对滑动,求B 端重物上升的加速度?(已知滑轮对通过滑轮中心且垂直于轮面的轴的转动惯量J =MR 2 / 4 )24.一轴承光滑的定滑轮,质量为M =2.00 kg ,半径为R =0.100 m ,一根不能伸长的轻绳,一端固定在定滑轮上,另一端系有一质量为m =5.00 kg 的物体,如图所示.已知定滑轮的转动惯量为J =221MR ,其初角速度 ω0=10.0 rad/s ,方向垂直纸面向里.求:(1) 定滑轮的角加速度的大小和方向; (2) 定滑轮的角速度变化到ω=0时,物体上升的高度; (3) 当物体回到原来位置时,定滑轮的角速度的大小和方向.参考答案1.C2.D3.C4.C5.D6.B7.C8.A9.C 10.B 11.20 3分参考解:r 1ω1=r 2ω2 , β1 = ω1 / t 1 ,θ1=21121t β 21211412ωθr r n π=π=4825411⨯π⨯⨯π=t =20 rev 12.157 N ·m 3分13.5.0 N ·m 3分14.Ma 213分 15.mr rJmg + 3分16.m (g -a )R 2 / a 3分17.031ω 3分18.3v 0 / (2l ) 3分19.杆和子弹 1分 角动量 2分20.m v l 3分21.解:设绳子对物体(或绳子对轮轴)的拉力为T ,则根据牛顿运动定律和转动定律得:mg T =ma ① 2分 T r =J β ② 2分 由运动学关系有: a = r β ③ 2分由①、②、③式解得: J =m ( g -a ) r 2 / a ④ 又根据已知条件 v 0=0∴ S =221at , a =2S / t 2 ⑤ 2分将⑤式代入④式得:J =mr 2(Sgt22-1) 2分22.解:撤去外加力矩后受力分析如图所示. 2分 m 1g -T = m 1a 1分 Tr =J β 1分a =r β 1分 a = m 1gr / ( m 1r + J / r )代入J =221mr , a =mm gm 2111+= 6.32 ms -2 2分 ∵ v 0-at =0 2分 ∴ t =v 0 / a =0.095 s 1分23.解:受力分析如图所示.设重物的对地加速度为a ,向上.则绳的A 端对地有加速度a 向下,人相对于绳虽为匀速向上,但相对于地其加速度仍为a 向下.2分根据牛顿第二定律可得:对人: Mg -T 2=Ma ① 2分对重物: T 1-21Mg =21Ma ② 2分 根据转动定律,对滑轮有(T 2-T 1)R =J β=MR 2β / 4 ③ 2分因绳与滑轮无相对滑动, a =βR ④ 1分 ①、②、③、④四式联立解得 a =2g / 7 1分24.解:(1) ∵ mg -T =ma 1分 TR =J β 2分 a =R β 1分∴ β = mgR / (mR 2+J )()R M m mgMR mR mgR +=+=222122 =81.7 rad/s 2 1分 方向垂直纸面向外. 1分(2) ∵ βθωω2202-=当ω=0 时, rad 612.0220==βωθ 物体上升的高度h = R θ = 6.12×10-2 m 2分 (3)==βθω210.0 rad/s方向垂直纸面向外.2分T a2a。
(完整word版)刚体的平面运动作业习题参考答案1
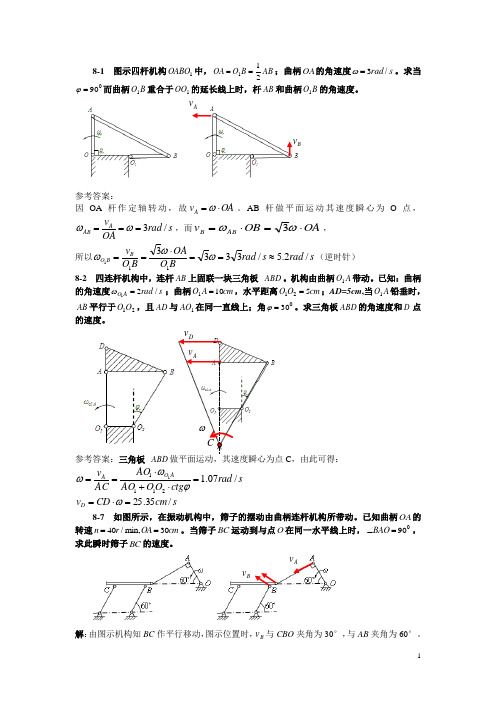
8-1 图示四杆机构1OABO 中,AB B O OA 211==;曲柄OA 的角速度s rad /3=ω。
求当090=ϕ而曲柄B O 1重合于1OO 的延长线上时,杆AB 和曲柄B O 1的角速度。
参考答案:因OA 杆作定轴转动,故OA v A ⋅=ω。
AB 杆做平面运动其速度瞬心为O 点,s rad OAv AAB /3===ωω,而OA OB v AB B ⋅=⋅=ωω3, 所以s rad s rad BO OAB O v B B O /2.5/3333111≈==⋅==ωωω(逆时针)8-2 四连杆机构中,连杆AB 上固联一块三角板 ABD 。
机构由曲柄A O 1带动。
已知:曲柄的角速度s rad A O /21=ω;曲柄cm A O 101=,水平距离cm O O 521=;AD=5cm ,当A O 1铅垂时,AB 平行于21O O ,且AD 与1AO 在同一直线上;角030=ϕ。
求三角板ABD 的角速度和D 点的速度。
参考答案:三角板 ABD C ,由此可得:s rad ctg O O AO AO AC v A O A/07.121111=⋅+⋅==ϕωωs cm CD v D /35.25=⋅=ω8-7 如图所示,在振动机构中,筛子的摆动由曲柄连杆机构所带动。
已知曲柄OA 的转速cm OA r n 30min,/40==。
当筛子BC 运动到与点O 在同一水平线上时,090=∠BAO ,求此瞬时筛子BC 的速度。
解:由图示机构知BC 作平行移动,图示位置时,B v 与CBO 夹角为30°,与AB 夹角为60°。
Av Bv Dv Av CωAv Bv由题意知 m/s π40.030.03040π=⨯⨯=⋅=OA v A ω 由速度投影定理 AB B AB A v v )()(= 得 ︒=60cos B A v vm/s 2.51π8.060cos ==︒==AB BC v v v8-6 图示机构中,已知cm EF cm DE cm BD cm OA 310,10,10,10==== OA ωs rad /4=,在图示位置,曲柄OA 与水平线OB 垂直,且B 、D 和F 在同一铅直线上。
作业5刚体力学答案2014版资料

♫刚体:在力的作用下不发生形变的物体⎰=-⇒=210t t dt dt d ωθθθω角速度⎰=-⇒=210t t dt dtd βωωωβ角加速度1、(基础8)绕定轴转动的飞轮均匀地减速,t =0时角速度为05rad s ω=,t =20s 时角速度为00.8ωω=,则飞轮的角加速度β= -0.05 rad/s 2 ,t =0到 t =100 s 时间内飞轮所转过的角度θ= 250rad . 【解答】飞轮作匀变速转动,据0t ωωβ=+,可得出:200.05rad tωωβ-==-据2012t t θωβ=+可得结果。
♫定轴转动的转动定律:定轴转动的角加速度与它所受的合外力矩成正比,与刚体的转动惯量成反比.J M =质点运动与刚体定轴转动对照[ C ] 1、(基础2)一轻绳跨过一具有水平光滑轴、质量为M 的定滑轮,绳的两端分别悬有质量为m 1和m 2的物体(m 1<m 2),如图5-7所示.绳与轮之间无相对滑动.若某时刻滑轮沿逆时针方向转动,则绳中的张力 (A) 处处相等. (B) 左边大于右边. (C) 右边大于左边. (D) 哪边大无法判断. 【解答】由于m 1<m 2,实际上滑轮在作减速转动,角加速度方向垂直纸面向内,设滑轮半径为R,受右端绳子向下拉力为T 2,左端绳子向下拉力为T 1,对滑轮由转动定律得:(T 2-T 1)R=J β [ D ] 2、(基础3)如图所示,一质量为m 的匀质细杆AB ,A 端靠在粗糙的竖直墙壁上,B 端置于粗糙水平地面上而静止,杆身与竖直方向成θ角,则A 端对墙壁的压力大小为θc o s 41(A )mg θtan 21(B)mg θs i n (C )mg(D)不能唯一确定【解答】因为细杆处于平衡状态,它所受的合外力为零,以B 为参考点,外力矩也是平衡的,则有:A B N f = A B f N mg +=θθθlcon N l f lmg A A +=sin sin 2三个独立方程有四个未知数,不能唯一确定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大学物理( A )大作业(三)刚体定轴转动教学班姓名学号成绩一、选择题【】1. 两个匀质圆盘 A 和 B 的密度分别为A 和B ,若 A > B ,但两圆盘的质量与厚度相同,如两盘对通过盘心垂直于盘面的轴的转动惯量各为J AB和 J ,则(A) J A > J B (B) J B >J A (C) J A = J B (D) 不能确定【】 2. 有一根水平杆子,一半是铁,一半是木头,长度、截面均相同,可分别绕 a , b , c 三根竖直轴转动,如图所示。
试问对哪根轴的转动惯量最大(A) a 轴(B) b 轴(C) c 轴(D) 都一样【 】 3. 如图所示,一摆由质量均为 m 的杆与圆盘构成,杆长等于圆盘直径 2 倍,则摆对通过 O 点并与圆盘平面垂直轴的转动惯量为D 的(A) 7 17mD 224(B)17mD 24(C) 5 17mD 224(D)17mD 26【】 4. 刚体绕定轴作匀变速转动时,刚体上距转轴为 r 的任一点的(A) 切向、法向加速度的大小均随时间变化(B) 切向、法向加速度的大小均保持恒定(C) 切向加速度的大小恒定,法向加速度的大小变化(D) 切向加速度的大小变化,法向加速度的大小恒定 【】 5. 在下列说法中错误的是(A) 刚体定轴转动时,各质点均绕该轴作圆周运动(B) 刚体绕定轴匀速转动时,其线速度不变(C) 力对轴的力矩 M 的方向与轴平行(D) 处理定轴转动问题时, 总要取一个转动平面 S ,只有 S 面上的分力对轴产生的力矩才对定轴转动有贡献【】 6. 下列说法中正确的是(A) 作用在定轴转动刚体上的力越大,刚体转动的角加速度越大(B) 作用在定轴转动刚体上的合力矩越大,刚体转动的角速度越大(C) 作用在定轴转动刚体上的合力矩越大,刚体转动的角加速度越大(D) 作用在定轴转动刚体上的合力矩为零,刚体转动的角速度为零【】 7. 均质细杆可绕过其一端且与杆垂直的水平光滑轴在竖直平面内转动。
今使细杆静止在竖直位置,并给杆一个初速度,使杆在竖直面内绕轴向上转动,在这个过程中(A) 杆的角速度减小,角加速度减小 (B) 杆的角速度减小,角加速度增大(C) 杆的角速度增大,角加速度增大(D) 杆的角速度增大,角加速度减小【 】 8. 如图所示, A 、 B 为两个相同的绕着轻绳的定滑轮. A 滑轮挂一质量为 M的物体, B 滑轮受拉力 F ,而且 F = Mg .设 A 、B 两滑轮的角加速度分别为 A 和 B ,不计滑轮轴的摩擦,则有(A)A =BAB(B)A > B(C)A <BMF(D)开始时 A = B ,以后A <B【 】9. 一转动惯量为J 的圆盘绕一固定轴转动,起初角速度为0 。
设它所受阻力矩与转动角速度成正比, 即 Mk ( k 为正的常数),则圆盘的角速度从变为2时所需的时间为(A) J lnkJ(B) ln 2(C) J ln k(D) J ln12k k【】10. 一质量为 m 、半径为 R 的均质圆盘, 绕过其中心的垂直于盘面的轴转动,由于阻力矩存在,角速度由0 减小到 0/ 2 ,则圆盘对该轴角动量的增量为(A) 1mR 20(B)1 mR2 0(C)1 mR2 0(D)1 mR2 02424【】 11. 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为 I,开始时转台以匀角速度0 转动,此时有一质量为m 的人站在转台中心.随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A)I ω(B)I ω(C)I ω(D) 0 I mR2 0 I m R2 0 mR2 0【】12. 人造地球卫星,绕地球作椭圆轨道运动,如果地球在椭圆的一个焦点上,则卫星的(A) 动量不守恒,动能守恒(B) 对地心的角动量守恒,动能不守恒(C) 动量守恒,动能不守恒(D) 对地心的角动量不守恒,动能守恒【】13. 一人站在旋转平台的中央,两臂侧平举,整个系统以 2 rad/s 的角速度旋转,转动惯量为kg·m2.如果将双臂收回则系统的转动惯量变为 2.0 kg·m2.此时系统的转动动能与原来的转动动能之比E k / E k0为(A) 2 (B)3 (C) 2 (D) 3【】 14. 一个圆盘在水平面内绕一竖直固定轴转动的转动惯量为J,初始角速度为0 ,后来变为10 .在上述过程中,阻力矩所作的功为2(A)1J42(B)1J82(C)1J42(D)3J82【】15. 有一质量为 m、长为 l 的均匀细棒,静止平放在滑动摩擦系数为的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动,在转动过程中,细棒受到的摩擦力矩为(A) mglmgl mgl 2 mgl(B) (C) (D)2 3 3【】16. 一质量为 m, 长为 l 的均质细杆可在水平桌面上绕杆的一端转动, 杆与桌面间的摩擦系数为, 求摩擦力矩 M . 先取微元细杆dr, 其质量 dm = dr = (m/ l)dr. 它受的摩擦力是df = (dm)g =( mg/l)dr, 再进行以下的计算(A) M = rdf l mg dmgl/ 2=l r r =mg(B) M =( df l)l/ 2=( dr )l/ 2= mgl/ 20 ll mg(C) M =( df )l/ 3=( dr )l/ 3= mgl/ 30 l(D) M =( df )l=( lmg dr )l= mgl0l【】 17. 质量为 m、长为 l 的均质细杆,可绕过其一端,与杆垂直的水平轴在竖直平面内转动。
开始杆静止于水平位置,释放后开始向下摆动,在杆摆过/ 2 的过程中,重力矩对杆的冲量矩为(A) 1 ml2 3g (B) 2 ml2 3g (C) ml23g(D) 4 ml2 3g3 l 3 l l 3 l 【】 18. 一根质量为m,长度为l 的细而均匀的棒,其下端绞接在水平面上,并且竖直的立起,如果让它自由落下,则棒将以角速度撞击地面,如图所示。
如果将棒截去一半,初始条件不变,则棒撞击地面的角速度为(A) 2 (B) 2(C) (D) O2【】19. 一根长为 l、质量为 m 的均匀细杆,可绕距离其一端l的水平轴 O 在竖4直平面内转动,当杆自由悬挂时,给它一个起始角速度,如杆恰能持续转动而不摆动,则3g(A) 4l/47lO 。
g(B)lg(C)l12g(D)l【】 20. 图 (a)为一绳长为l、质量为m 的单摆.图(b)为一长度为l、质量为m 能绕水平固定轴O 自由转动的匀质细棒.现将单摆和细棒同时从与竖直线成角度的位置由静止释放,如果运动到竖直位置时,单摆、细棒角速度分别以1、2 表示.则(A) (C) 11122322(B)(D)1 2 O1 2 / 3 2(a)(b)二、计算题1.计算如图所示系统中物体的加速度.设滑轮为质量均匀分布的圆柱体,其质量为M ,半径为r,在绳与轮缘的摩擦力作用下旋转,忽略桌面与物体间的摩擦,且m2m1.2. 质量为m,长为l的均匀细棒,可绕垂直于棒的一端的水平轴转动.如将此棒放在水平位置,然后任其落下,求:(1) 当棒转过 60°时的角加速度和角速度; (2) 下落到竖直位置时的动能;(3) 下落到竖直位置时的角速度.3.一质量为 kg,长为 m 的均匀细棒,支点在棒的上端点,开始时棒自由悬挂 .以 100 N 的力打击它的下端点,打击时间为s.(1) 若打击前棒是静止的,求打击时其角动量的变化;(2) 棒的最大偏转角.4.平板中央开一小孔,质量为 m 的小球用细线系住,细线穿过小孔后挂一质量为M 1的重物.小球作匀速圆周运动,当半径为r0时重物达到平衡.今在M 1的下方再挂一质量为M 2的物体,如图所示.试问这时小球作匀速圆周运动的角速度和半径 r 为多少5. 一匀质细棒长度为l ,质量为m ,可绕通过其一端的水平光滑固定轴O 转动,如m 图所示。
当棒自水平位置由静止摆下时,在竖直位置处与放在地面上的质量也是的物体作非弹性碰撞,碰后物体沿地面滑行距离S 而静止,设物体与地面间的摩擦系数为.求与物体相撞后瞬间棒的角速度.6. 如图所示,质量为M,长为l的均匀直棒,可绕垂直于棒一端的水平轴O 无摩擦地转动,它原来静止在平衡位置上.现有一质量为m 的弹性小球飞来,正好在棒的下端与棒垂直地相撞.相撞后,使棒从平衡位置处摆动到最大角度30°处.(1)设碰撞为弹性碰撞,计算小球初速v0的值;(2)相撞时小球受到多大的冲量。
