专题训练(四) 直角坐标系中的分类讨论

合集下载

高考直角坐标系知识点

高考直角坐标系知识点直角坐标系是高考数学中非常重要的知识点，它是解析几何的基础，也是理解和应用各种图形的关键。

在高考中，对直角坐标系的掌握不仅需要了解其定义和性质，还需要能够运用直角坐标系解决各类问题。

下面将从直角坐标系的基本概念、坐标变换、方程表示以及运动问题等几个方面进行探讨。

一、直角坐标系的基本概念直角坐标系由x轴和y轴组成，它们在原点O处相交，x轴和y 轴分别表示水平方向和垂直方向。

我们可以将平面上的任意一点P表示为有序数对(x, y)，其中x表示点P在x轴上的横坐标，y表示点P 在y轴上的纵坐标。

直角坐标系的单位长度可以根据具体问题进行选择，通常为1个单位长度表示1个单位，如1cm或1m。

二、坐标变换在直角坐标系中，我们常常需要进行坐标变换，即将一个点的坐标表示从一个直角坐标系变换到另一个直角坐标系中。

坐标变换有两种类型：平移和旋转。

平移是指将一个点沿着指定方向按照指定的距离进行移动，保持其在新的坐标系中的位置不变。

平移的规律可以用方程表示，对于点P(x, y)的平移，新的坐标为P'(x+a, y+b)，其中a表示在x轴上平移的距离，b表示在y轴上平移的距离。

旋转是指将一个点绕着某个中心按照指定的角度进行旋转，保持其在新的坐标系中的位置不变。

旋转的规律可以用方程表示，对于点P(x, y)的旋转，新的坐标为P'((x-c)cosθ-(y-d)sinθ+c, (x-c)sinθ+(y-d)cosθ+d)，其中c表示旋转中心的横坐标，d表示旋转中心的纵坐标，θ表示旋转的角度。

三、方程表示直角坐标系能够方便地表示各种图形的方程。

在直角坐标系中，我们可以将直线、圆、抛物线、椭圆、双曲线等形状用方程的形式表示出来，从而方便地进行计算和分析。

对于直线，方程一般表示为y = kx + b，其中k表示直线的斜率，b表示直线在y轴上的截距。

我们可以根据直线上的两个点P1(x1, y1)和P2(x2, y2)求出斜率k = (y2 - y1) / (x2 - x1)，然后可以根据斜率和一个点的坐标求出直线的方程。

初中平面直角坐标系经典题型

初中平面直角坐标系经典题型初中数学中，平面直角坐标系经典题型是一个非常重要的部分。

在这个主题下，我们将探讨平面直角坐标系的基本概念、相关的数学知识和一些典型的题型，希望能帮助大家更深入地理解这一概念。

1. 平面直角坐标系的基本概念在平面直角坐标系中，我们通常会用x轴和y轴来构建一个二维平面。

这两条轴的交点被称为原点，通常用O表示。

x轴和y轴将平面分成四个部分，分别为第一、第二、第三和第四象限。

2. 直角坐标系中的点表示在平面直角坐标系中，任意一个点都可以用一个有序的数对(x, y)来表示，其中x称为横坐标，y称为纵坐标。

这种表示方法被称为点的坐标表示法。

3. 直角坐标系中的距离计算利用平面直角坐标系，我们可以计算两个点之间的距离。

如果有两个点A(x1, y1)和B(x2, y2)，它们之间的距离可以通过勾股定理来计算。

4. 平面直角坐标系中的图形在平面直角坐标系中，我们可以绘制各种图形，如直线、圆、抛物线等。

这些图形在坐标系中有着规律的表示方法，通过这些表示方法，我们可以进行各种几何分析。

5. 典型题型的解题方法在初中数学中，常见的平面直角坐标系题型包括点的坐标计算、图形的方程和性质、距离和斜率的计算等。

解题时，通常会根据题目要求，利用坐标表示法、勾股定理、直线方程等知识来进行求解。

总结与回顾通过本文的介绍，我们对平面直角坐标系有了一个全面而深入的了解。

我们学习了坐标系的基本概念，了解了点的表示方法，掌握了距离计算的方法，思考了图形在坐标系中的性质，同时还了解了一些典型题型的解题方法。

通过这些学习和思考，我们对平面直角坐标系有了更深刻的认识，相信在今后的学习和工作中，这些知识都会派上用场。

个人观点与理解作为一个数学爱好者，我对平面直角坐标系有着浓厚的兴趣。

通过学习和实践，我深刻地认识到平面直角坐标系在数学中的重要性。

它不仅是一个基础概念，更是许多高等数学和工程技术中的重要工具。

我认为深入理解和熟练运用平面直角坐标系是非常重要的。

专题02 直角三角形中分类讨论问题(老师版)

专题2直角三角形中分类讨论问题【典型例题】1．（2022·江西九江·八年级期末）已知在平面直角坐标系中A（﹣0）、B（2，0）、C（0，2）．点P在x轴上运动，当点P与点A、B、C三点中任意两点构成直角三角形时，点P的坐标为________．【答案】（0，0），0），（﹣2，0）【解析】【分析】因为点P、A、B在x轴上，所以P、A、B三点不能构成三角形．再分Rt△PAC和Tt△PBC两种情况进行分析即可．【详解】解：∵点P、A、B在x轴上，∴P、A、B三点不能构成三角形．设点P的坐标为（m，0）．当△PAC为直角三角形时，①∠APC＝90°，易知点P在原点处坐标为（0，0）；②∠ACP＝90°时，如图，∵∠ACP＝90°∴AC2＋PC2＝AP2，22222∴+++=+，解得，m P0）；22(m m当△PBC为直角三角形时，①∠BPC＝90°，易知点P在原点处坐标为（0，0）；②∠BCP＝90°时，∵∠BCP＝90°，CO⊥PB，∴PO＝BO＝2，∴点P的坐标为（﹣2，0）．综上所述点P的坐标为（0，0），，0），（﹣2，0）．【点睛】本题考查了勾股定理及其逆定理，涉及到了数形结合和分类讨论思想．解题的关键是不重复不遗漏的进行分类．【专题训练】1．（2021·江苏兴化·八年级期中）在Rt △ABC 中，∠BAC =90°，点D 、E 在边BC 所在的直线上，且AB =DB ，AC =EC ，则∠DAE 的度数为________．【答案】45°或135°【解析】【分析】分四种情况：若点D 、E 在线段BC 上时；若点D 在线段BC 上，点E 在BC 的延长线上时；若点D 在CB 的延长线上点E 在BC 的延长线上时；若点D 在CB 的延长线上，点E 在线段BC 上时讨论，即可求解．【详解】解：如图，若点D 、E 在线段BC 上时，∵AB =DB ，AC =EC ，∴∠BAD =∠ADB ，∠CAE =∠AEC ，∴∠BAE +∠DAE =∠CAD +∠C ，∠CAD +∠DAE =∠BAE +∠B ，∴∠BAE +∠CAD +2∠DAE =∠CAD +∠BAE +∠B +∠C ，∴2∠DAE =∠B +∠C ，∵∠BAC =90°，∴∠B +∠C =90°，∴∠DAE =45°；如图，若点D 在线段BC 上，点E 在BC 的延长线上时，∵AC =EC ，∴可设∠E =∠CAE =x ，∴∠ACB =∠E +∠CAE =2x ，∵∠BAC =90°，∴∠B =90°-∠ACB =90°-2x ，∵AB =DB ，∴()1180452BAD ADB B x ∠=∠=︒-∠=︒+，∵∠ADB =∠DAE +∠E ，∴∠DAE =45°；如图，若点D 在CB 的延长线上，点E 在BC 的延长线上时，∵AC =EC ，∴∠E =∠CAE ，∴∠ACB =∠E +∠CAE =2∠CAE ，∵AB =DB ，∴∠D =∠BAD ，∴∠ABC =∠D +∠BAD =2∠BAD ，∵∠BAC =90°，∴∠ABC +∠ACB =90°，∴2∠CAE +2∠BAD =90°，∴∠CAE +∠BAD =45°，∴∠DAE =∠CAE +∠BAD +∠BAC =135°；如图，若点D 在CB 的延长线上，点E 在线段BC 上时，∵AB =DB ，∴可设∠D =∠BAD =y ，∴∠ABC =∠D +∠BAD =2y ，∴∠ABC =2y ，∵∠BAC =90°，∴∠C =90°-2y ，∵AC =EC ，∴∠AEC =∠CAE =()1180452C y ︒-∠=︒+，∵∠AEC =∠D +∠DAE ，∴∠DAE =45°综上所述，∠DAE 的度数为45°或135°．故答案为：45°或135°【点睛】本题主要考查了等腰三角形的性质，直角三角形两锐角互余，利用分类讨论思想解答是解题的关键．2．（2021·全国·八年级专题练习）如图，在ABC 中，AC BC =，CD AB ⊥，5CD =，24AB =．E 是AB 边上的一个动点，点F 与点A 关于直线CE 对称，当AEF 为直角三角形时，AE 的长为________．【答案】7或17【解析】【分析】分当E 在线段AD 上时，当E 在线段BD 上时分别求解即可．【详解】解：当E 在线段AD 上时，连接CE ，作A 关于CE 的对称点F ，连接AF ，EF ，CF ，∵∠AEF =90°，∴∠AEC =∠FEC =360902︒-︒=135°，∴∠CED =45°，∴CD =ED =5，∴AE =AD -ED =12-5=7；当E 在线段BD 上时，连接CE ，作A 关于CE 的对称点F ，连接EF ，CF ，AF ，∵∠AEF =90°，∴∠CEF =∠CEA =45°，∴ED =CD =5，∴AE =AD +DE =17，故答案为：7或17．【点睛】本题考查了等腰三角形三线合一的性质，等腰直角三角形的性质，轴对称的性质，解本题的关键是注意运用数形结合的思想解决问题．3．（2021·河南·郑州市第六十三中学三模）如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点P是边AC上一动点，把△ABP沿直线BP折叠，使得点A落在图中点A′处，当△AA′C是直角三角形时，则线段CP的长是_________．【答案】4或3【解析】【分析】分类讨论分别当∠AA′C=90°时，当∠ACA′=90°时，根据折叠的性质函数直角三角形的性质即可得到结论．【详解】解：如图1，当∠AA′C=90°时，∵以直线BP为轴把△ABP折叠，使得点A落在图中点A′处，∴AP=A′P，∴∠PAA′=∠AA′P，∵∠ACA′+∠PAA′=∠CA′P+∠AA′P=90°，∴∠PCA′=∠PA′C，∴PC=PA′，∴PC=12AC=4，如图2，当∠ACA′=90°时，∵在Rt△ABC中，∠ACB=90°，且AC=8，BC=6．∴AB=10，∵以直线BP为轴把△ABP折叠，使得点A落在图中点A′处，∴A′B=AB=10，PA=PA′，∴A′C=4，设PC=x，∴AP=8-x，∵A′C2+PC2=PA′2，∴42+x2=（8-x）2，解得：x=3，∴PC=3，综上所述：当△AA ′C 是直角三角形时，则线段CP 的长是4或3，故答案为：4或3．【点睛】本题考查了翻折变换（折叠问题）直角三角形的性质，正确的作出图形是解题的关键．4．（2021·全国·八年级专题练习）如图，60BOC ∠=︒，点A 是BO 延长线上的一点，10cm OA =，动点P 从点A 出发沿AB 以3cm/s 的速度移动，动点Q 从点O 出发沿OC 以1cm/s 的速度移动，如果点P Q ，同时出发，用(s)t 表示移动的时间，当t =_________s 时，POQ △是等腰三角形；当t =_________s 时，POQ △是直角三角形．【答案】52或54或10【解析】【分析】根据POQ ∆是等腰三角形，分两种情况进行讨论：点P 在AO 上，或点P 在BO 上；根据POQ ∆是直角三角形，分两种情况进行讨论：PQ AB ⊥，或PQ OC ⊥，据此进行计算即可．【详解】解：如图，当PO QO =时，POQ ∆是等腰三角形，103PO AO AP t =-=-，OQ t =，∴当PO QO =时，103t t -=，解得52t =；如图，当PO QO =时，POQ ∆是等腰三角形，310PO AP AO t =-=-，OQ t =，∴当PO QO =时，310t t -=，解得5t =；如图，当PQ AB ⊥时，POQ ∆是直角三角形，且2QO OP =，310PO AP AO t =-=-，OQ t =，∴当2QO OP =时，2(310)t t =⨯-，解得4t =；如图，当PQ OC ⊥时，POQ ∆是直角三角形，且2QO OP =，310PO AP AO t =-=-，OQ t =，∴当2QO OP =时，2310t t =-，解得：t =10．故答案为：52或5；4或10．【点睛】本题主要考查了等腰三角形的性质以及直角三角形的性质，解决问题的关键是进行分类讨论，分类时注意不能遗漏，也不能重复．5．（2021·广东广州·八年级阶段练习）在ABC 中，若过顶点B 的一条直线把这个三角形分割成两个三角形，其中一个为等腰三角形，另一个为直角三角形，则称这条直线为ABC 的关于点B 的二分割线．例如：如图1，在Rt ABC 中，90A ∠=︒，20C ∠=︒，若过顶点B 的一条直线BD 交AC 于点D ，且20DBC ∠=︒，则直线BD 是ABC的关于点B 的二分割线．如图2，已知18C ∠=︒，ABC 同时满足：①C ∠为最小角；②存在关于点B 的二分割线，则BAC ∠的度数为______．【答案】36︒或45︒或54︒【解析】【分析】根据关于点B 的二分割线的定义即可得到结论．【详解】解：如图2所示：36BAC ∠=︒，如图3所示：45BAC ∠=︒，如图所示：54BAC ∠=︒，故答案为：36︒或45︒或54︒．【点睛】本题考查了直角三角形，等腰三角形的性质，正确地理解“△ABC 的关于点B 的二分割线”是解题的关键．。

直角坐标系的应用和解题

直角坐标系的应用和解题直角坐标系是平面几何中常用的一种坐标系统，它以两条相互垂直的直线（通常称为x轴和y轴）为基准，将平面划分成四个象限。

直角坐标系广泛应用于解决各种几何和代数问题，本文将探讨直角坐标系的应用和解题方法。

一、直角坐标系的基本概念在直角坐标系中，每个点都可以用一对坐标（x，y）表示，其中x表示横坐标，y表示纵坐标。

x轴和y轴的交点称为原点，记作O，原点的坐标为(0,0)。

x轴上的点的纵坐标为0，y轴上的点的横坐标为0。

二、直角坐标系的象限直角坐标系将平面划分成四个象限。

第一象限为x大于0，y大于0的区域；第二象限为x小于0，y大于0的区域；第三象限为x小于0，y小于0的区域；第四象限为x大于0，y小于0的区域。

三、直角坐标系中点的距离公式在直角坐标系中，我们可以通过两点之间的距离公式来计算它们之间的距离。

设两点分别为A(x1, y1)和B(x2, y2)，则点A和点B之间的距离可以表示为：√((x2-x1)²+(y2-y1)²)。

四、直角坐标系中直线方程的表示方法直角坐标系中，我们可以用一般方程式y=mx+b来表示直线，其中m是斜率，b是y轴截距。

我们也可以用点斜式方程y-y1=m(x-x1)来表示直线，其中m是斜率，(x1, y1)是直线上的一点。

五、直角坐标系的应用举例例1：已知一个点A(2, 3)和一个点B(4, 5)，求线段AB的长度。

解：根据两点之间的距离公式，我们可以计算线段AB的长度为：√((4-2)²+(5-3)²)=√8。

例2：求直线y=3x+2在x轴和y轴上的截距。

解：直线与x轴的交点为(0, b)，代入y=3x+2得到0=3(0)+2，解得b=2。

直线与y轴的交点为(a, 0)，代入y=3x+2得到0=3a+2，解得a=-2/3。

例3：求过点C(1, 4)且与直线y=2x-1垂直的直线的方程。

解：直线y=2x-1的斜率为2，与其垂直的直线的斜率为-1/2。

2025年河北省中考数学提分专项训练++专项+分类讨论思想在圆中的课件

返回
类型5 动态问题引发的分类讨论
6.[2024石家庄校级月考] 如图，已知直线l的表达式是y = 4 x − 8，并且与x轴、y轴分别交
3
于A，B两点.一个半径为3的⊙ C，圆心C从点
(0,3)开始以每秒2个单位长度的速度沿着y轴向下运动，当
⊙ C与直线l相切时，⊙ C运动的时间为( A )
A.3 s或8 s
∴ 四边形QHCD是矩形.∴ HQ = CD = 12，
HQ//CD.
又∵
点O′是EF′的中点，∴
O′Q=Βιβλιοθήκη 1 2DE.∵ DE = DC − CE = 12 − 2 = 10，∴ O′Q = 5.
易知半圆O′的半径为6，
∴ MH = HQ − QO′ − O′M = 12 − 5 − 6 = 1，
返回
4.已知⊙ O的直径为6 cm，如果直线l上的一点C到圆心O的距离为3 cm，求直线l与⊙ O的位置关系. 【解】∵⊙ O的半径= 6 = 3(cm)，且直线l上存在一点到圆心
2
O的距离为3 cm， ∴ 直线l与⊙ O至少有一个交点. 当⊙ O与直线l有且只有一个交点时，直线l与⊙ O相切；当直线l与⊙ O有两个交点时，直线l与⊙ O相交. ∴ 直线l与⊙ O的位置关系是相切或相交.
∵ ∠AOP = 45∘ ,∴ 点P的横、纵坐标相等.可设P(a, a). ∵ ∠AOB = 90∘ ,∴ AB是直径. ∴ Rt △ AOB外接圆的圆心为AB的中点. 设AB的中点为C，则C( 3, 1).
过点P作PE ⊥ OA于点E，过点C作 CF//OA，交PE于点F，连接PC. 易得∠CFP = 90∘ ,PF = a − 1， CF = a − 3，PC = 2. ∴ 在Rt △ PCF中， (a − 3)2 + (a − 1)2 = 22，解得 a1 = 3 + 1，a2 = 0（舍去）.

【初中数学】人教版八年级上册专题训练（四）等腰三角形问题中的分类讨论思想(练习题)

人教版八年级上册专题训练（四）等腰三角形问题中的分类讨论思想(159)1.已知等腰三角形一腰上的中线把这个三角形的周长分成12和15两部分，求这个三角形的三边长．2.已知一个等腰三角形一边上的高等于这边的一半，求这个三角形顶角的度数．3.等腰三角形的一个外角是60∘，则它的顶角的度数是4.若等腰三角形的周长为16，其中一边长为6，则另两边长为．5.若等腰三角形的一个外角等于110∘，则这个三角形的三个角分别为6.若实数x，y满足|x−4|+√y−8=0,则以x，y的值为边长的等腰三角形的周长为．7.等腰三角形一腰上的高与另一腰的夹角为48∘，则该等腰三角形的底角的度数为．8.在等腰三角形中，马彪同学做了如下探究：已知一个角是60∘，则另两个角是唯一确定的(60∘，60∘)；已知一个角是90∘，则另两个角也是唯一确定的(45∘，45∘)；已知一个角是120∘，则另两个角也是唯一确定的(30∘，30∘)．由此马彪同学得出结论：在等腰三角形中，已知一个角的度数，则另两个角的度数是唯一确定的．马彪同学的结论是的(填“正确”或“错误”)．9.等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若三角形ABC的边长为1，AE=2，求线段CD的长．10.一个等腰三角形的一个内角比另一个内角的2倍少30∘，求这个三角形的三个内角的度数．11.若一个等腰三角形的两边长分别是2和5，则它的周长为（）A.12B.9C.12或9D.9或712.如图，在4×5的点阵图中，每两个横向和纵向相邻阵点的距离均为1，该点阵图中已有两个阵点分别标为A,B，请在此点阵图中找一个阵点C，使得以点A,B,C为顶点的三角形是等腰三角形，则符合条件的点C有（）A.3个B.4个C.5个D.6个13.在直角坐标系中，已知A(1，1)，在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P共有（）A.1个B.2个C.3个D.4个参考答案1.【答案】:如图，在△ABC中，AB=AC，且AD=BD，设AB=x，BC=y，(1)当AC+AD=15，BD+BC=12时，则{x2+x=15，x 2+y=12，解得{x=10，y=7.(2)当AC+AD=12，BC+BD=15时，有{x2+x=12，x2+y=15，解得{x=8，y=11.且这两种情况下三角形的三边都符合三角形的三边关系，故这个三角形的三边长为10，10，7或8，8，11【解析】:解决此题，注意进行分类讨论.2.【答案】:(1)若这一边为底边，如图①，AB=AC，AD⊥BC，AD=BD=CD，则△ABD和△ACD均为等腰直角三角形，所以∠BAC=45∘+45∘=90∘；(2)若这一边为腰，①当顶角为锐角时，如图②，AB=AC，CD⊥AB，CD=12AB=12AC，则顶角∠A=30∘；②当顶角为钝角时，如图③，AB=AC,CD⊥AB交BA的延长线于点D，因为CD=12AB=1AC，2所以∠DAC=30∘，所以∠BAC=150∘.综上所述，这个等腰三角形的顶角度数为90∘或30∘或150∘.【解析】:解决此题，注意进行分类讨论.3.【答案】:120∘【解析】:等腰三角形的一个外角为60∘，则与它相邻的内角为120∘.因为三角形内角和为180∘，如果这个内角为底角，内角和将超过180∘，所以120∘的角只可能是顶角．故答案为120∘4.【答案】:6，4或5，5【解析】:若6为腰长，则底边长为4,三边长6，6,4可以构成三角形；若6为底边长，则腰长为5，三边长5,5，6也可以构成三角形．故答案为6，4或5，55.【答案】:70∘，55∘，55∘或70∘，70∘，40∘【解析】:当顶角的外角是110∘时，这个三角形的三个角为70∘，55∘，55∘；当底角的外角是110∘时，这个三角形的三个角为70∘，70∘，40∘.所以这个三角形的三个角为70∘，55∘，55∘或70∘，70∘，40∘6.【答案】:20【解析】:由|x−4|+√y−8=0，x−4≥0，√y−8≥0，可得x−4=0，√y−8=0，求解可得x=4，y=8，于是此等腰三角形的三边长为4，4，8或8，8，4.由于4+4=8，利用三角形的三边关系，可得4，4，8不符合题意，同理可得8，8，4符合题意，故等腰三角形的周长为8+8+4=207.【答案】:69∘或21∘【解析】:分两种情况讨论：①若∠A<90∘，如图(a)所示：∵BD⊥AC，∴∠A+∠ABD=90∘.∵∠ABD=48∘，∴∠A=90∘−48∘=42∘.∵AB=AC，∴∠ABC=∠C=12×(180∘−42∘)=69∘.②若∠A>90∘，如图(b)所示：同①可得：∠DAB=90∘−48∘=42∘，∴∠BAC=180∘−42∘=138∘.∵AB=AC，∴∠ABC=∠C=12×(180∘−138∘)=21∘.综上所述，等腰三角形底角的度数为69∘或21∘8.【答案】:错误【解析】:举一个反例即可．如当等腰三角形一个角的度数是50∘时，若这个50∘的角为顶角，则另两个角是65∘，65∘；若这个50∘的角是底角，则另一个底角为50∘，顶角为80∘.综上所述，另两个角是65∘，65∘或50∘，80∘.因此另两个角的度数不是唯一确定的．故马彪同学的结论是错误的9.【答案】:当E在线段BA的延长线上，D在线段BC的延长线上时，如图①所示，过点E作EF⊥BD，垂足为F，可得∠EFB=90∘.∵EC=ED，∴F为CD的中点，即CF=DF=12CD．∵△ABC为等边三角形，∴∠ABC=60∘，∴∠BEF=30∘.∵BE=AB+AE=1+2=3，∴FB=12EB=32，∴CF=FB−BC=12，∴CD=2CF=1.当E在线段AB的延长线上，D在线段CB的延长线上时，如图②所示，过点E作EF⊥BD，垂足为F，可得∠EFC=90∘. ∵EC=ED，∴F为CD的中点，即CF=DF=12CD．∵△ABC为等边三角形，∴∠ABC=∠EBF=60∘，∴∠BEF=30∘.∵BE=AE−AB=2−1=1，∴FB=12BE=12，∴CF=BC+FB=32，∴CD=2CF=3.综上，CD的长为1或3【解析】:解决此题，注意进行分类讨论.10.【答案】:设其中一角的度数为x∘,则另一角的度数为(2x−30)∘,则x+x+2x−30=180或x+2(2x−30)=180或x=2x−30,解得x=52.5或x=48或x=30,所以这个三角形三个内角的度数为52.5∘，52.5∘，75∘或48∘，66∘，66∘或30∘，30∘，120∘.【解析】:设其中一角的度数为x∘,则另一角的度数为(2x−30)∘, 则x+x+2x−30=180或x+2(2x−30)=180或x=2x−30, 解得x=52.5或x=48或x=30, 所以这个三角形三个内角的度数为52.5∘，52.5∘，75∘或48∘，66∘，66∘或30∘，30∘，120∘.11.【答案】:A【解析】:∵一个等腰三角形的两边长分别是2和5，∴当腰长为2时，则2+2<5，此时不成立，当腰长为5时，能组成三角形，则这个等腰三角形的周长为5+5+2=12. 故选A12.【答案】:C13.【答案】:D【解析】:如图，以点O为圆心，OA长为半径画弧，交x轴于点B,C；以点A为圆心，AO长为半径画弧，交x轴于一点D(点O除外)，∴以OA为腰的等腰三角形有3个；当以OA为底时，作OA的垂直平分线，交x轴于一点，∴以OA为底的等腰三角形有1个．综上所述，符合条件的点P共有4个。

初二数学平面直角坐标系专题

初二数学平面直角坐标系专题1. 引言大家好，今天咱们来聊聊平面直角坐标系。

这可是数学里一个非常基础、又很重要的概念，绝对能帮助咱们在生活中找到方向，简直就像一把万能钥匙！有没有觉得，坐标系就像是数学的GPS，帮助我们在数字的海洋中畅游？那么，让我们一起“深入”这个神奇的世界吧！2. 坐标系的基本概念2.1 坐标系的组成首先，平面直角坐标系的“主角”就是那两条互相垂直的轴线：x轴和y轴。

简单来说，x轴是水平的，y轴是竖直的。

想象一下，咱们的生活中也有很多这样的交叉点，比如十字路口。

两条轴线的交点叫原点，记得哦，它的坐标是(0, 0)，就像家里的起点，无论你往哪儿去，都是从这儿出发的。

2.2 坐标的表示接下来，咱们来看看坐标是怎么表示的。

每一个点在坐标系里都用一个有序数对来表示，比如说点A的坐标是(3, 2)，这就意味着A在x轴上走了3步，在y轴上走了2步。

是不是特别形象？就像你和朋友约好在某个地方见面，事先定好地点，确保不迷路！3. 坐标的应用3.1 生活中的坐标系坐标系可不仅仅是数学课堂上的玩意儿哦，咱们生活中到处都能找到它的影子！想想咱们的城市地图，街道、商店、学校，都是用坐标来标记的。

如果你想找到一个新餐馆，首先要知道它的坐标，然后根据地图一步步前进，最后大功告成，美食就在眼前！这就像“千里之行，始于足下”，每一步都至关重要。

3.2 游戏中的坐标系而在游戏中，坐标系更是必不可少的。

无论是打怪升级，还是探索新世界，角色的每一步都是在坐标系里“舞动”。

如果你在一个游戏里迷路了，看看地图上的坐标，迅速调整方向，简直就是游戏小达人！这样不仅能节省时间，还能提高胜率，让你在游戏中如鱼得水，乐趣无穷。

4. 总结好啦，今天咱们围绕平面直角坐标系聊了很多，从基础概念到生活应用，希望大家对这个看似简单但又极其重要的知识点有了更深入的理解。

记住，数学不只是课本上的公式，它就在我们的日常生活中，时时刻刻影响着我们。

专题14 直角三角形中的分类讨论模型(解析版)

专题14直角三角形中的分类讨论模型模型1、直角三角形中的分类讨论模型【知识储备】凡是涉及直角三角形问题，优先考虑直角顶点（或斜边）分类讨论，再利用直角三角形的性质或勾股定理解题即可。

1）无图需分类讨论：①已知边长度无法确定是直角边还是斜边时要分类讨论；②已知无法确定是哪个角是直角时要分类讨论（常见与折叠、旋转中出现的直角三角形）。

2）“两定一动”直角三角形存在性问题：（常见于与坐标系综合出题，后续会专题进行讲解）即：如图：已知A ，B 两点是定点，找一点C 构成Rt ABC △方法：两线一圆具体图解：①当︒=∠90BAC 时，过点A 作AB 的垂线，点C 在该垂线上（A 除外）②当︒=∠90ABC 时，过点B 作AB 的垂线，点C 在该垂线上（B 除外）。

③当︒=∠90ACB 时，以AB 为直径作圆，点C 在该圆上（A ，B 除外）。

例1．（2023春·江苏·八年级假期作业）若三角形的三边长是6，8，x ，当2x 的值为时，该三角形是直角三角形.【答案】100或28【分析】三角形是直角三角形，这里给出三边的长，只要用两小边的平方和等于最长边的平方即可求解，所以要分情况讨论，当最长边为8时，和最长边不是8时，再根据勾股定理进行计算.【详解】①最长边为8时，82-62=2x ，则2x =28；②最长边不是8时，82+62=2x ，则2x =100.【点睛】本题考查勾股定理的逆定理，解题的关键是分情况讨论最长边.例2．（2023春·江苏宿迁·八年级统考期末）如图，在ABC 中，9040BAC C ∠=︒∠=︒，，AH 、BD 分别是ABC 的高和角平分线，点E 为BC 边上一点，当BDE 为直角三角形时，则CDE ∠=︒．【答案】50或25/25或50【分析】根据三角形内角和定理得ABC ∠形时，存在两种情况：分别根据三角形外角的性质即可得出结论．【详解】解：∵9040BAC C ∠=︒∠=︒，∵BD 平分ABC ∠∴1DBC ABC ∠=∠=∵40C ∠=︒，∴904050CDE ∠=︒-︒=︒②当90BDE ∠=︒时，如图2，∴902565BED ∠=︒-︒=︒，∵BED ∠=∠综上，CDE ∠的度数为50︒或25︒．故答案为：【点睛】本题考查的是直角三角形的两锐角互余，题的关键．A．1个【答案】C【分析】根据题意，结合图形，分两种情况讨论：其中的一条腰．【点睛】本题考查了等腰直角三角形的判定；解答本题关键是根据题意，画出符合实际条件的图形，数形结合的思想是数学解题中很重要的解题思想．例4．（2023·江苏·九年级假期作业）外部作等腰直角ABC，或(37)，【答案】(74)∵BAC AOB AEC ∠=∠=∠∵AB AC =，∴AOB △≌△同法可得，当AB BC ='，当AB 是等腰直角三角形的斜边时，综上所述，满足条件的点．【答案】2或5/5或2【分析】当90B ED ∠'=︒时，先求出时，作AH BC ⊥，证明出ADH 【详解】解：当90B ED ∠'=︒时，如图，AB AC = ，AE BC ⊥，BE ∴=由折叠得BD B D ='，AB AB '=在Rt B DE ' 中，224)8(x -+=当90B DE ∠'=︒时，如图，作AH 90B DE ∠'=︒ ，ADB ADB ∴∠=∠6DH AH ∴==，BD BH DH ∴=-【点睛】本题考查了轴对称的性质，勾股定理的应用及等腰直角三角形的性质，掌握勾股定理是解题关键．例8．（2023秋·广东·八年级专题练习）如图，5(1)如图1，若点F 恰好落在边BC 上，判断BDF V 的形状，并证明；(2)如图2，若点F 落在ABC 内，且DF 的延长线恰好经过点C ，CF EF =，求A ∠的度数；(3)若9AB =，当BDF V 是直角三角形时，直接．．写出AD 的长．【答案】(1)BDF V 是等边三角形；见解析(2)40A ∠=︒；(3)AD 的长是3或6【分析】（1）根据平行线的性质即可求出相等的角，再根据等边三角形的判定即可得到结论；（2）根据折叠的性质可知角相等，再根据三角形的内角和定理即可得到结果；（3）根据题意分两种情况，再根据图形以及折叠的性质得到AD 的长度．【详解】（1）解：BDF V 是等边三角形，理由如下：∵60B DE BC ∠=︒，∥，∴60ADE B ∠=∠=︒，由折叠可得60FDE ADE ∠=∠=︒，∴60BDF ∠=︒，∴60DFB B BDF ∠=∠=∠=︒，∴BDF V 是等边三角形；（2）解：由折叠可得A DFE ∠=∠，∵60FDE ADE ∠=∠=︒，∴120ADC ∠=︒，∵CF EF =，∴FEC FCE ∠=∠，设FEC FCE x ∠=∠=，则2A DFE FEC FCE x ∠=∠=∠+∠=，在ADC △中，180A ACD ADC ∠+∠+∠=︒，即2120180x x ++︒=︒，解得20x =︒，∴240A x ∠==︒；（3）解：AD 的长是3或6，理由如下：当90BFD ∠=︒时，点F 在ABC 内（如图所示）∵60BDF ∠=︒，∴30DBF ∠=︒，∴2BD DF=由折叠得DF AD =，∴2BD AD =，∴39AD =，∴3AD =；当90DBF ∠=︒时，点F 在ABC 外，同理可得2AD DF BD ==，∴6AD =．【点睛】本题考查了折叠的性质，等边三角形的性质，含30︒角的直角三角形的性质，平行线的性质，根据题意画出图形是解题的关键．例10．（2023秋·江苏盐城·八年级统考期末）如图，已知直线1l 经过点()5,6，交x 轴于点()30A -,，直线2:3l y x=交直线1l 于点B ．(1)求直线1l 的函数表达式和点B 的坐标；(2)求AOB 的面积；(3)在x 轴上是否存在点C ，使得ABC 是直角三角形？若存在，求出点C 的坐标：若不存在，请说明理由．39=+；()1,3(2)9(3)()1,0 y x②当90ABC ∠=︒时，点C 在图中C 的位置：设【答案】（1）见解析；（2）①721y x =--；②()4,2Q 或2022,33⎛⎫ ⎪⎝⎭．【分析】（1）：利用角的数量关系可求得D E ∠=∠，ACD EBC ∠=∠，然后根据（2）①：过点B 作BC AB ⊥交2l 于C ，过C 作CD y ⊥轴于D ，由（1三角形的性质求出C 的坐标，再利用待定系数法求2l 的解析式即可；②可得：(AAS)AMQ QNP ≌，利用全等三角形的性质建立关系式求解即可．∵45BAC ∠=︒，∴ABC ∵14:43l y x =+，令y =令0x =，则4y =，∴∴437OD =+=．∴C 将点(3,0)A -，(4,7C -当90AQP ∠=︒时，由（1）同理可证：∴QN AM =，即86(2m m -=--【点睛】本题主要考查了全等三角形的判定和性质、待定系数法求一次函数解析式等知识点，灵活运用全等三角形的性质是解题的关键．课后专项训练A．2【答案】D【分析】由条件可求得t<<两种情况，根据当610三角形的性质求解即可得．△【详解】解：在Rt ABC【答案】90︒或34︒【分析】分当90A ∠=︒时，当【详解】解：当90A ∠=︒时，满足【答案】2483-或【分析】由等边三角形的性质可得角三角形的性质可求【答案】125或247或325①当04t <≤时，3AP t =，BP 在Rt BPQ 中，2BP BQ =，即12②当46t <≤时，312BP t =-，①当04t <≤时，3AP t =，BP AB =在Rt BPQ 中，2BQ BP =，即2t =②当46t <≤时，312BP t =-，在【答案】3-【分析】分两种情况：即可求得EF；当EF．【答案】103或53【分析】分BMN ∠=【详解】解：由题意得，当90BMN ∠=︒时，【答案】30︒或45︒【分析】分两种情况：当点E在∆外时，由折叠可得：AE在ACB【详解】解：分两种情况：如图，由折叠可得：AE AC =，C ∠= AD 平分CAE ∠，45CAD ∴∠=︒，故答案为30︒或45︒．【点睛】本题考查折叠的性质，解本题要注意分类讨论．熟练掌握折叠的性质、直角三角形的性质和三角【答案】4，6或73【分析】由题意分AD =BD 【详解】解：如图，当AD ∵Rt △ABC 中，∠C =90°∵AB =BD ，∴CD BD BC =-如图，当AB =AD 时，∵AB =BD ，∠C =90°，∴综上可得CD 的长为4，【点睛】本题考查等腰三角形的性质以及勾股定理的应用，熟练掌握利用方程根据勾股定理建立方程求解以及进行全面思考、分类讨论是解题的关键12．（2023春·江苏·八年级期末）在为线段AB 上的动点，当【答案】69°或11°【分析】分情况讨论，当∠时，通过三角形内角和求出∠【详解】∵80C ∠=︒，∠∵BD平分∠ABC，∴∠DBE如图，当∠ADE=90°时，∵BD平分∠ABC，∴∠DBC∴∠ADB=∠DBC+∠C=21°+80°=101°【点睛】本题考查了三角形内角和定理、角平分线的定义和三角形外角的性质，解题的关键是根据题意画一共可作出6【点睛】本题考查了等腰直角三角形，作出图形，利用数形结合的思想求解更形象直观．14．（2023·江苏兴化·八年级期中）在Rt△ABC中，∠BAC=90°，点D、E在边BC所在的直线上，且AB=DB，AC=EC，则∠DAE的度数为________．【答案】45°或135°【分析】分四种情况：若点D 、E 在线段BC 上时；若点D 在线段BC 上，点E 在BC 的延长线上时；若点D 在CB 的延长线上点E 在BC 的延长线上时；若点D 在CB 的延长线上，点E 在线段BC 上时讨论，即可求解．【详解】解：如图，若点D 、E 在线段BC 上时，∵AB =DB ，AC =EC ，∴∠BAD =∠ADB ，∠CAE =∠AEC ，∴∠BAE +∠DAE =∠CAD +∠C ，∠CAD +∠DAE =∠BAE +∠B ，∴∠BAE +∠CAD +2∠DAE =∠CAD +∠BAE +∠B +∠C ，∴2∠DAE =∠B +∠C ，∵∠BAC =90°，∴∠B +∠C =90°，∴∠DAE =45°；如图，若点D 在线段BC 上，点E 在BC 的延长线上时，∵AC =EC ，∴可设∠E =∠CAE =x ，∴∠ACB =∠E +∠CAE =2x ，∵∠BAC =90°，∴∠B =90°-∠ACB =90°-2x ，∵AB =DB ，∴()1180452BAD ADB B x ∠=∠=︒-∠=︒+，∵∠ADB =∠DAE +∠E ，∴∠DAE =45°；如图，若点D 在CB 的延长线上，点E 在BC 的延长线上时，∵AC =EC ，∴∠E =∠CAE ，∴∠ACB =∠E +∠CAE =2∠CAE ，∵AB =DB ，∴∠D =∠BAD ，∴∠ABC =∠D +∠BAD =2∠BAD ，∵∠BAC =90°，∴∠ABC +∠ACB =90°，∴2∠CAE +2∠BAD =90°，∴∠CAE +∠BAD =45°，∴∠DAE =∠CAE +∠BAD +∠BAC =135°；如图，若点D 在CB 的延长线上，点E 在线段BC 上时，∵AB =DB ，∴可设∠D =∠BAD =y ，∴∠ABC =∠D +∠BAD =2y ，∴∠ABC =2y ，∵∠BAC =90°，∴∠C =90°-2y ，∵AC =EC ，∴∠AEC =∠CAE =()1180452C y ︒-∠=︒+，∵∠AEC =∠D +∠DAE ，∴∠DAE =45°综上所述，∠DAE 的度数为45°或135°．故答案为：45°或135°【点睛】本题主要考查等腰三角形的性质，直角三角形两锐角互余，利用分类讨论思想解答是解题的关键．15．（2022·广东·八年级课时练习）如图，60BOC ∠=︒，点A 是BO 延长线上的一点，10cm OA =，动点P 从点A 出发沿AB 以3cm/s 的速度移动，动点Q 从点O 出发沿OC 以1cm/s 的速度移动，如果点P Q ，同时出发，用(s)t 表示移动的时间，当t =_________s 时，POQ △是等腰三角形；当t =_________s 时，POQ △是直角三角形．5类时注意不能遗漏，也不能重复．16．（2022·浙江·义乌市八年级期中）如图，已知Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点P是BC 边上的一个动点，点B与B′是关于直线AP的对称点，当△CPB'是直角三角形时，BP的长＝_______．24＝5，PB′2，是矩形，2，1，17．（2022·河北承德·八年级期末）如图，60ABC ∠=︒，3AB =，动点P 从点B 出发，以每秒1个单位长度的速度沿射线BC 运动，嘉琪在研究过程中发现，随着点Р运动，ABP △形状在发生变化，设点P 的运动时间为t 秒．（1）当ABP △是直角三角形时，t 的值为______；（2）当ABP △是钝角三角形时，t 满足的条件是__________．19．（2022·江苏镇江·八年级期中）点P，Q分别是边长为4cm的等边△ABC的边AB，BC上的动点，点P 从顶点A，点Q从顶点B同时出发，且它们的速度都是1cm/s，设运动时间为t秒．（1）连接AQ，CP交于点M，则在P，Q运动的过程中，∠CMQ变化吗？若变化，则说明理由；若不变，则求出它的度数；（2）连接PQ．①当△BPQ为等边三角形时，t＝秒；②当△BPQ为直角三角形时，t＝秒．（直接写出结果）(1)点M，N运动几秒后，AMN如存在，请求出此时∆？到直角三角形AM N【答案】(1)12秒(2)存在，，AMN ANM ∴∠=∠，∴∠AB BC AC == ，ΔACB ∴AMC ANB Ð=ÐQ ，C ∠=CM BN ∴=，1236t ∴-=2BN t = ，AM t =，AN ∴如图，若90ANM ∠=︒，由2AN AM =，则2(12当点N 在AC 上运动时，点当点N 在BC 上运动时，如图，当点由ABC ∆时等边三角形知如图，当点M 位于BC 中点处时，由ABC ∆时等边三角形知AM 综上，当3t =或245或15或【点睛】本题考查了等边三角形的性质及判定，全等三角形的性质与判定，等腰三角形的性质，角三角形的性质，关键是根据题意设出未知数，理清线段之间的数量关系．(1)在图2的ABC 中，20C ∠=︒，110ABC ∠=︒．请在图2中画出ABCDBC ∠的度数；(2)已知20C ∠=︒，在图3中画出两种不同于图1、图2的ABC ，所画ABC 同时满足：①∠C 为最小角；②存在关于点B 的伴侣分割线，请画出其伴侣分割线，标出所画ABC 中各个角的度数．【答案】(1)见解析(2)见解析【分析】（1）首先了解伴侣分割线的定义，然后把∠ABC 分成90°角和20°角即可；（2）根据等腰三角形的性质，直角三角形的性质和三角形内角和求解即可．【详解】（1）如图所示：（2）如图所示：【点睛】本题考查了作图—应用与设计作图，直角三角形的性质，等腰三角形的性质及三角形内角和定理，涉及分类讨论，解题的关键是掌握等腰三角形的性质和直角三角形的性质．23．（2023秋·四川成都·八年级校考期末）如图，在平面直角坐标系内，点O 为坐标原点，经过A(-2，6)的直线交x 轴正半轴于点B ，交y 轴于点C ，OB=OC ，直线AD 交x 轴负半轴于点D ，若△ABD 的面积为27．（1）求直线AD 的解析式；（2）横坐标为m 的点P 在AB 上（不与点A ，B 重合），过点P 作x 轴的平行线交AD 于点E ，设PE 的长为y （y≠0），求y 与m 之间的函数关系式并直接写出相应的m 的取值范围；（3）在（2）的条件下，在x 轴上是否存在点F ，使△PEF 为等腰直角三角形？若存在求出点F 的坐标，若∴EF=-m+4，∴-m+4=3 2③当∠PFE=90°时，如图∵∠FPE+∠EFP+∠FEP=180°∴∠PFR=180°-∠FPE-∠∵点R与点E的纵坐标相同，∴∴PR=FR=-m+4=-107+4=18。

中考数学专题训练分类讨论及答案

第三节分类讨论【回顾与思考】数字间→确定分类的原则或标准→分类【例题经典】会根据字母的大小或取值范围分类例1 （天津市）已知│x │=4，│y │=，且xy<0，则=_______．【点评】由xy<0知x ，y 异与应分x>0，y<0，及x<0，y>0两类．会根据条件指待不明分类例2 （黑龙江省）为了美化环境，计划在某小区内用30m 2•的草皮铺设一块边长为10m 的等腰三角形绿地，请你求出等腰三角形绿地的另两边．【点评】因已知边为10指待不明，故应将已知边为10分底边或腰，当为腰时还要按三角形形状分类共三种．会根据图形的相对位置不同分类例3 ①（乌鲁木齐市）若半径为1cm 和2cm 的两圆相外切，•那么与这两个圆相切、且半径为3cm 的圆的个数为（）A ．5个B ．4个C ．3个D ．2个【点评】两圆相切，有内切，外切，故应分都外切，都内切，一内一外，一外一内共有五种．②⊙O 1与⊙O 2相交于AB ，且AB=24，两圆的半径分别为r 1=15，r 2=13，求两圆的圆心距．【点评】根据两圆圆心与公共弦的相对位置分O 1、O 2在AB 的同一侧和在AB•两侧进行分类．【考点精练】 1．（山西省）现有长度分别为2cm ，3cm ，4cm ，5cm 的木棒，从中任取三根，•能组成三角形的个数是（）A ．1B ．2C ．3D ．4 2．（哈尔滨市）直线y=x-1与坐标轴交于A 、B 两点，点C 在坐标轴上，•△ABC 为等腰三角形，则满足条件的点C 最多有（）A ．4个B ．5个C ．7个D ．8个 3．（山西省）已知⊙O 的半径为5，AB 是弦，P 是直线AB 上的一点，PB=3，AB=8，则tan ∠OPA 的值为（） A ．3 B ．C ．或D ．3或 4．（河南省）三角形两边的长分别是8和6，•第三边的长是一元二次方程x 2-16x+60=0的一个实数根，则该三角形的面积是（）⎧⎨⎩不重不漏12xy37133737A ．24B ．24或C ．48D ．5．（山西省）如图，AB ，AC 与⊙O 相切于B，C ，∠A=50°，点P 是圆上异于B 、•C 的一动点，则∠BPC 的度数是（）A ．65°B ．115°C ．65°和115°D ．130°和50° 6．（陕西省）要做甲、乙两个形状相同（相似）的三角形框架，•已有三角形框架甲，它的三边长分别为50cm ，60cm ，80cm ，三角形框架乙的一边长为20cm ，•那么符合条件的三角形框架乙共有（）A ．1种B ．2种C ．3种D ．4种 7．（甘肃省）若半径为3，5的两个圆相切，则它们的圆心距为（） A ．2 B ．8 C ．2或8 D ．1或48，则斜边上的高为________．9．已知⊙O 是△ABC 的外接圆，OD ⊥BC 于D ，∠BOD=42°，则∠BAC=______度． 10．在△ABC 中，AB=AC ，AB 的中垂线与直线AC 相交所得的锐角为50°，•则底角∠B 的大小为__________． 11．⊙O 1和⊙O 2交于A ，B ，且⊙O 1经过点O 2，∠AO 1B=90°，则∠AO 2B 的度数为____． 12．若一次函数当自变量x 的取值范围是-1≤x ≤3时，函数y 的范围为-2≤y ≤6，•则此函数的解析式为________． 13．（天津市）已知正方形ABCD 的边长是1，E•为CD•边的中点，•P•为正方形ABCD 边上的一个动点，动点P 从A 点出发，沿A →B →C →E 运动，到达点E ．若点P 经过的路程为自变量x ，△APE 的面积为函数y ，则当y=时，x 的值等于_______． 14．（日照市）在“五·一”黄金周期间，某超市推出如下购物优惠方案：（1）一次性购物在100元（不含100元）以内时，不享受优惠；（2）一次性购物在100元（含100元）以上，300元（不含300元）以内时，一律享受九折优惠；（3）一次性购物在300元（含300元）以上时，一律享受八折的优惠．王茜在本超市两次购物分别付款80元，•252元．如果王茜改成在本超市一次性购买与上两次完全相同的商品，则应付款（） A ．332元 B ．316元或332元 C ．288元 D ．288元或316元 15．（杭州市）在图所示的平面直角坐标系内，已知点A （2，1），O 为坐标原点．请你在坐标轴上确定点P ，使得△AOP 成为等腰三角形，•在给出的坐标系中把所有这样的点P 都找出来，画上实心点，并在旁边标上P 1，P 2，……，P k （有k 个就标到P k 为止，•不必写出画法）．1316．（河北省）如图，在直角梯形ABCD中，AD∥BC，∠C=90°，BC=16，DC=•12，AD=21．动点P从点D出发，沿射线DA的方向以每秒2两个单位长的速度运动，动点Q•从点C 出发，在线段CB上以每秒1个单位长的速度向点B运动，点P，Q分别从点D，C•同时出发，当点Q运动到点B时，点P随之停止运动．设运动的时间为t（秒）．（1）设△BPQ的面积为S，求S与t之间的函数关系式；（2）当t为何值时，以B，P，Q三点为顶点的三角形是等腰三角形？（3）当线段PQ与线段AB相交于点O，且2AO=OB时，求∠BQP的正切值；（4）是否存在时刻t，使得PO⊥BD？若存在，求出t的值；若不存在，请说明理由．17．（荆州市）已知：如图，在直角梯形COAB中，CB∥OA，以点O为原点建立平面直角坐标系，A，B，C的坐标分别为A（10，0），B（4，8），C（0，8），D为OA的中点，动点P•自A点出发沿A→B→C→O的路线移动，速度为每秒1个单位，移动时间记为t秒．（1）动点P在从A到B的移动过程中，设△APD的面积为S，试写出S与t的函数关系式，指出自变量的取值范围，并求出S的最大值；（2）动点P从A出发，几秒钟后线段PD将梯形COAB的面积分成1：3两部分？求出此时P点的坐标．18．（泉州市）如图，在△ABC 中，∠ACB=90°，AC=BC=6cm ，正方形DEFC•的边长为2cm ，其一边EF 在BC 所在的直线L 上，开始时点F 与点C 重合，让正方形DEFG•沿直线L 向右以每秒1cm 的速度作匀速运动，最后点E 与点B 重合．（1）请直接写出该正方形运动6秒时与△ABC 重叠部分面积的大小；（2）设运动时间为2）．①在该正方形运动6秒后至运动停止前这段时间内，求y 与x 之间的函数关系式；• ②在该正方形整个运动过程中，求当x 为何值时，y=．答案:12例题经典例1：-8例2：①当AB 为底边时，AD=DB=5，②当AB•为腰且三角形为锐角三角形时，AB=AC=10，=8，BD=2，③当AB为腰且三角形为钝角三角形时， AB=BC=10，BD=8，例3：①A ②14或4考点精练1．C 2．C3．D 4．B 5．C6．C 7．C 8 9．42°或138° 10．20°或70° 11．45°或135° 12．y=2x 或y=-2x+4 13．或 14．D15．P 1（4，0），P 2（0，2），P 30），P 4（0），P 5（0，，P 6（0，，P 7（，0），P 8（0，）16．（1）S=96-6t （2）•①若PQ=BQ ，t=②若BP=BQ 得3t 2-32t+144=0，△<0，无解，∴PB ≠BQ ③若PB=PQ 得t 2+122=（16-2t ）2+122，解得t 1=，t 2=16（舍去）， ∴当t=秒或秒时以B 、P 、Q•为顶点的△是等腰三角形（3）由△OAP ∽△OBQ 得（4）当t=9秒时，PQ ⊥BD ．17．（1）S=2t （0<t ≤10）当t=10时，S 最大值=20 （2）可得经过7秒或秒后，线段PD 将梯形COAB 的面积分成1：3两部分，此时符合题意的点坐标为（23535452721637216315830,,tan 2529AP AO t QPE BQ OB ==∴=∴∠=825292828,),(0,)55518．（1）重叠部分面积为×22=2（cm 2） •（2）①当正方形停止运动时，点E 与点B 重合，此时EB=90°，ME=EB=CB-CE=6-（x-2）=8-EB =（8-x ）2 • ②在正方形运动过程中分四种情况：Ⅰ．当0<x<2时，y=2x 且0<y<4令y=得x=． Ⅱ．•当2≤x ≤4时，重叠部分面积为4，此时y ≠．Ⅲ．当4<x ≤6时，y 随x 增大而减小，2≤y<4，此时y ≠． Ⅳ．当6<x<8时，由（2）①得y=（8-x ）2， ∵y 随x 增大而减小，当x=6时，y=2，当x=•8时，y=0，∴0<y<2，令（x-8）2=，且x 1=7，x 2=9（舍去）， ∴x=7，综上所述：x=或x=7时y=．1212121412121212121412。

八年级专题复习《坐标系中多解题——分类讨论思想》

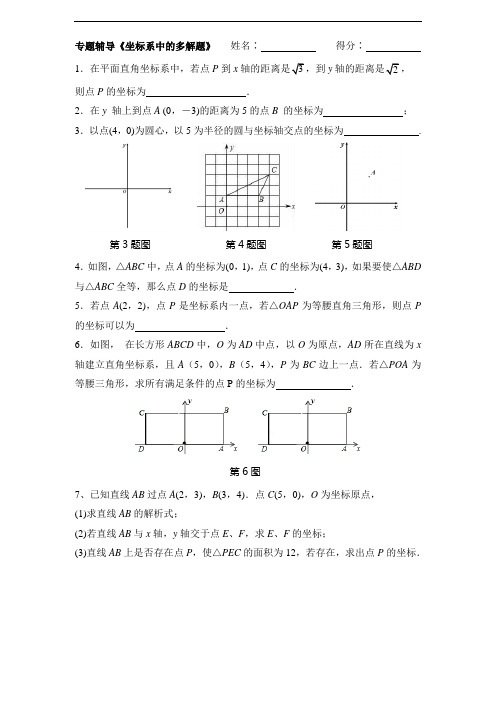
专题辅导《坐标系中的多解题》姓名∶得分∶
第3题图第5题图
4．如图，△ABC中，点A的坐标为(0，1)，点C的坐标为(4，3)，如果要使△ABD 与△ABC全等，那么点D的坐标是．
5．若点A(2，2)，点P是坐标系内一点，若△OAP为等腰直角三角形，则点P 的坐标可以为．
6．如图，在长方形ABCD中，O为AD中点，以O为原点，AD所在直线为x 轴建立直角坐标系，且A（5，0），B（5，4），P为BC边上一点．若△POA为等腰三角形，求所有满足条件的点P的坐标为．
第6图
7、已知直线AB过点A(2，3)，B(3，4)．点C(5，0)，O为坐标原点，
(1)求直线AB的解析式；
(2)若直线AB与x轴，y轴交于点E、F，求E、F的坐标；
(3)直线AB上是否存在点P，使△PEC的面积为12，若存在，求出点P的坐标．
8．在平面直角坐标系中，已知点A(－3，4)，为坐标原点．在坐标轴上是否存在点P，使得ΔAOP成为等腰三角形．若存在：
(1) 在图中标出所有这样的点P，画上实心点，并在旁边标上P1，P2，…，P k．
(2) 写出以OA为腰的等腰△AOP的P点坐标．
9．如图所示，已知直线y＝－x＋2与x轴、y轴分别交于点A和点B，另一直线y＝kx＋b经过C(1，0)，且把△AOB分成两部分．
(1)若△AOB被分成的面积相等，求k和b的值；
(2)若△AOB被分成的两部分的面积比为1∶5，求k和b的值．。

人教版八年级数学上册专题训练(四) 等腰三角形问题中的分类讨论思想

第十三章轴对称
专题训练(四) 等腰三角形问题中的分类讨论思想
专题训练(四) 等腰三角形问题中的分类讨论思想
类型一当顶角或底角不确定时，分类讨论
1．已知等腰三角形的一个内角为50°，则这个等腰三角形的顶角为
( )C
A．50°
B．80°
C．50°或80° D．40°或65°
2．一个等腰三角形的一个外角等于110°，则这个三角形的三个角应
∴∠B＝∠C＝21∠DAB＝25°
8．等腰三角形底边长为5 cm，一腰上的中线把其周长分为差为3 cm的两部分，求腰长．
解：设腰长为2x，一腰的中线为y，则(2x＋x)－(5＋x)＝3或(5＋x)－ (2x＋x)＝3，解得：x＝4或x＝1，∴2x＝8或2，①三角形ABC三边长为8， 8，5，符合三角形三边关系定理；②三角形ABC三边是2，2，5，2＋2 ＜5，不符合三角形三边关系定理；故腰长为8 cm
该为
70°，55°，5西州)一个等腰三角形一边长为 4 cm，另一边长为 5 cm，那么这个等腰三角形的周长是( C )
A．13 cm B．14 cm C．13 cm 或 14cm D．以上都不对
4．(2016·安顺)实数 x，y 满足|x－4|＋ y－8＝0，则以 x，y 的值为两边长的等腰三角形的周长是( B )
9．在直角坐标系中，O为坐标原点，已知A(2，2)，在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数共有( ) A
A．4个 B．3个 C．2个 D．1个 10．如图，在△ABC中，∠ACB＝90°，∠BAC＝30°，在直线BC或 AC上取一点P，使得△PAB为等腰三角形，这样的点P的个数为( )B A．5个 B．6个 C．4个 D．3个

平面直角坐标系与分类讨论

1、点P 到x 轴的距离是2，到y 轴的距离是3，则P 点的坐标是。

2、已知AB ∥x 轴，A 点的坐标为（3，2），并且AB ＝5，则B 的坐标为。

3、在Y 轴上且到点A （0，－3）的线段长度是4的点B 的坐标为___________________。

4、已知P 点坐标为（2－a ，3a ＋6），且点P 到两坐标轴的距离相等，则点P 的坐标是_________________________________________________。

5、已知点P 在第二象限，且横坐标与纵坐标的和为1，试写出一个符合条件的点P 。

点K 在第三象限，且横坐标与纵坐标的积为8，写出两个符合条件的点。

6、已知点A （a ，0）和点B （0，5）两点，且直线AB 与坐标轴围成的三角形的面积等于10，则a 的值是________________。

7．在x 轴上与点（0，-2）距离是4个单位长度的点有 __________ 。

8.以点（4，0）为圆心，以5为半径的圆与y 轴交点的坐标为______.9．在平面直角坐标系中，点A 的坐标为(11)，，点B 的坐标为(111)，，点C 到直线AB 的距离为4，且ABC △是直角三角形，则满足条件的点C 有个． 10． ABC ∆中，点A 的坐标为（0，1），点C 的坐标为（4，3），如果要使 ABD ∆与ABC ∆ 全等，那么点D 的坐标是 . 11．若x 轴上的点P 到y 轴的距离为3，则点P 的坐标为（） A ．（3，0） B ．（3，0）或（–3，0） C ．（0，3） D ．（0，3）或（0，–3） 12．在平面直角坐标系中，O 是坐标原点，已知A 点的坐标为（1，1），•请你在坐标轴上找出点B ，使△AOB 为等腰三角形，则符合条件的点B 共有（） A ．6个 B ．7个 C ．8个 D ．9个13、（2009温州）如图，在平面直角坐标系中，O 为坐标原点，四边形OABC 是矩形，点A 、C 的坐标分别为A （10，0）、C （0，4），点D 是OA 的中点，点P 在BC 边上运动，当△ODP 是腰长为5的等腰三角形时，点P 的坐标为。

新初中数学函数之平面直角坐标系分类汇编含解析

新初中数学函数之平面直角坐标系分类汇编含解析一、选择题1．已知在平面直角坐标系中，点A 的坐标为（﹣3，4），下列说法正确的有（）个 ①点A 与点B （-3，﹣4）关于x 轴对称②点A 与点C （3，﹣4）关于原点对称③点A 与点F （-4，3）关于第二象限的平分线对称④点A 与点C （4，-3）关于第一象限的平分线对称A ．1B ．2C ．3D ．4【答案】D【解析】【分析】根据关于x 轴对称点的坐标特点：横坐标不变，纵坐标互为相反数；关于y 轴对称点的坐标特点：横坐标互为相反数，纵坐标不变；关于第2象限角平分线对称的点的坐标特点：横纵坐标变换位置且变为相反数；关于第1象限角平分线对称的点的坐标特点：横纵坐标变换位置．综合以上即可得答案．【详解】∵点A 的坐标为(﹣3，4)，∴点A 关于x 轴对称的点的坐标为(﹣3，﹣4)，点A 关于原点对称的点的坐标为(3，-4)，点A 关于第二象限的角平分线对称的点的坐标为(-4，3)点A 关于第一象限的角平分线对称的点的坐标为(4，-3)∴①、②、③、④正确．故选：D ．【点睛】此题主要考查了关于x 轴、y 轴、第二象限的角平分线、第一象限的角平分线对称的点的坐标规律，关键是熟练掌握点的变化规律，不要混淆．2．在平面直角坐标系中，点(),P x y 经过某种变换后得到点()'1,2P y x -++，我们把点()'1,2P y x -++叫做点(),P x y 的终结点．已知点1P 的终结点为2P ，点2P 的终结点为3,P 点3P 的终结点为4P ，这样依次得到1234,,,,,n P P P P P ⋅⋅⋅.若点1P 的坐标为(50,)，则2017P 点的坐标为( )A ．()2,0B ．()3,0C ．()4,0D ．()5,0【答案】D【解析】【分析】根据题意先求出12345,,,,P P P P P L 的坐标，然后找到规律，利用规律即可求出答案．【详解】∵点1P 的坐标为(5)0，，根据题意有 ∴2345(1,7),(6,3),(2,4),(5,0)P P P P ---，由此可见，n P 点的坐标是四个一循环，201745041÷=Q L ，∴2017P 点的坐标为()5,0，故选：D ．【点睛】本题主要考查点的坐标的规律，找到规律是解题的关键．3．如果点P (),3m 在第二象限，那么点Q ()3,m -在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】【分析】根据第二象限的横坐标小于零可得m 的取值范围，进而判定Q 点象限.【详解】解：由点P (),3m 在第二象限可得m ＜0，再由-3＜0和m ＜0可知Q 点在第三象限，故选择C.【点睛】本题考查了各象限内坐标的符号特征.4．如图，在平面直角坐标系中，以O 为圆心，适当长为半径画弧，交x 轴于点M ，交y轴于点N ，再分别以点M 、N 为圆心，大于12MN 的长为半径画弧，两弧在第二象限交于点P ．若点P 的坐标为（2a ，b+1），则a 与b 的数量关系为（）A ．a=bB ．2a+b=﹣1C ．2a ﹣b=1D ．2a+b=1【答案】B【解析】试题分析：根据作图方法可得点P 在第二象限角平分线上，则P 点横纵坐标的和为0，即2a+b+1=0，∴2a+b=﹣1．故选B ．5．如图，ABCDEF 是中心为原点O ，顶点A ，D 在x 轴上，半径为4的正六边形，则顶点F 的坐标为（）A ．()2,23B ．()2,2-C ．()2,23-D ．()1,3- 【答案】C【解析】【分析】连接OF ，设EF 交y 轴于G ，那么∠GOF=30°；在Rt △GOF 中，根据30°角的性质求出GF ，根据勾股定理求出OG 即可．【详解】解：连接OF ，在Rt △OFG 中，∠GOF=13603026⨯=oo ，OF=4． ∴GF=2，3∴F （-2，3）．故选C ．【点睛】本题利用了正六边形的对称性，直角三角形30°的角所对的边等于斜边的一半，勾股定理等知识，熟练掌握正六边形的对称性是解答本题的关键．6．如图，在菱形ABCD 中，点,B C 在x 轴上，点A 的坐标为(0,23,分别以点,A B 为圆心、大于12AB 的长为半径作弧，两弧相交于点,E F ．直线EF 恰好经过点,D 则点B 的坐标为（）1,0B．)3,0C．()2,0D．()3,0 A．()【答案】C【解析】【分析】连接DB，如图，利用基本作图得到EF垂直平分AB，则DA＝DB，再根据菱形的性质得到AD∥BC，AD＝AB，则可判断△ADB为等边三角形，所以∠DAB＝∠ABO＝60°，然后计算出OB＝2，从而得到B点坐标．【详解】解：连接DB，如图，由作法得EF垂直平分AB，∴DA＝DB，∵四边形ABCD是菱形，∴AD∥BC，AD＝AB，∴AD＝AB＝DB，∴△ADB为等边三角形，∴∠DAB＝60°，∴∠ABO＝60°，∵A（0，23∴OA＝23∵∠ABO＝60°，∠AOB＝90°，∴∠BAO＝30°，∴在Rt△AOB中，AB＝2OB，∵OB2＋OA2＝AB2，∴OB2＋(232＝（2OB）2，∴OB＝2（舍负），∴B（2，0）．故选：C．【点睛】本题考查了作图基本作图：作已知线段的垂直平分线，也考查了线段垂直平分线的性质和菱形的性质以及30°的直角三角形的特殊性质．7．如图，在平面直角坐标系中，有若干个横坐标分别为整数的点，其顺序按图中“→”方向排列，如()()()()()()1,02,02,11,11,22,2，，，，，······根据这个规律，第2019个点的纵坐标为( )A ．5B ．6C ．7D ．8【答案】B【解析】【分析】观察图形可知，以最外边的矩形边长上的点为准，点的总个数等于x 轴上右下角的点的横坐标的平方，并且右下角的点的横坐标是奇数时最后以横坐标为该数，纵坐标为0结束，当右下角的点横坐标是偶数时，以横坐标为1，纵坐标为右下角横坐标的偶数减1的点结束，根据此规律解答即可．【详解】解：根据图形，以最外边的矩形边长上的点为准，点的总个数等于x 轴上右下角的点的横坐标的平方，例如：右下角的点的横坐标为1，共有1个，1＝12，右下角的点的横坐标为2时，共有4个，4＝22，右下角的点的横坐标为3时，共有9个，9＝32，右下角的点的横坐标为4时，共有16个，16＝42，…右下角的点的横坐标为n 时，共有n 2个，∵452＝2025，45是奇数，∴第2025个点是（45，0），第2019个点是（45，6），所以，第2019个点的纵坐标为6．故选：B．【点睛】本题考查了点的坐标，观察出点个数与横坐标的存在的平方关系是解题的关键．8．平面直角坐标系中，P(－2a－6，a－5)在第三象限，则a的取值范围是（）A．a＞5 B．a＜－3 C．－3≤a≤5D．－3＜a＜5【答案】D【解析】【分析】根据第三象限的点的坐标特点：x<0，y<0，列不等式组，求出a的取值范围即可.【详解】∵点P在第三象限，∴26050aa--<⎧⎨-<⎩，解得：-3<a<5，故选D.【点睛】本题考查了象限点的坐标的符号特征以及解不等式，该知识点是中考的常考点，常与不等式、方程结合起来求一些字母的取值范围，比如本题中求a的取值范围．9．如果点在第四象限，那么m的取值范围是（）．A．B．C．D．【答案】D【解析】【分析】横坐标为正，纵坐标为负，在第四象限．【详解】解：∵点p（m，1-2m）在第四象限，∴m＞0，1-2m＜0，解得：m＞，故选D．【点睛】坐标平面被两条坐标轴分成了四个象限，每个象限内的点的坐标符号各有特点，该知识点是中考的常考点，常与不等式、方程结合起来求一些字母的取值范围，比如本题中求m的取值范围．10．平面直角坐标系中，点A(-3，2)，()3,5B ，(),C x y ，若AC ∥x 轴，则线段BC 的最小值及此时点C 的坐标分别为( )A ．6，()3,4-B ．2，()3,2C ．2，()3,0D ．3，()3,2【答案】D【解析】【分析】由AC ∥x 轴，A （-3，2），根据坐标的定义可求得y 值，根据线段BC 最小，确定BC ⊥AC ，垂足为点C ，进一步求得BC 的最小值和点C 的坐标．【详解】∵AC ∥x 轴，A （-3，2），(),C x y ，()3,5B ，∴y=2，当BC ⊥AC 于点C 时，点B 到AC 的距离最短，即：BC 的最小值=5−2=3，∴此时点C 的坐标为(3，2)．故选D ．【点睛】本题主要考查平面直角坐标系中的点的坐标，根据题意，画出图形，掌握“直线外一点与直线上各个点的连线中，垂线段最短”，是解题的关键．11．在平面直角坐标系中，A ，B ，C 三点坐标分别是（0，0），（4，0），（3，2），以A ，B ，C 三点为顶点画平行四边形，则第四个顶点不可能在（）.A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】A 点在原点上，B 点在横轴上，C 点在第一象限，根据平行四边形的性质：两组对边分别平行，可知第四个顶点可能在第一、二、四象限，不可能在第三象限，故选C12．点 P（m + 3，m + 1）在x轴上，则P点坐标为（）A．（0，﹣2）B．（0，﹣4）C．（4，0）D．（2，0）【答案】D【解析】【分析】根据点在x轴上的特征,纵坐标为0,可得m+1=0,解得:m=-1,然后再代入m+3,可求出横坐标.【详解】解:因为点P（m + 3，m + 1）在x轴上,所以m+1=0,解得:m=-1,所以m+3=2,所以P点坐标为（2，0）.故选D.【点睛】本题主要考查点在坐标轴上的特征,解决本题的关键是要熟练掌握点在坐标轴上的特征.13．平面直角坐标系中，已知□ABCD的三个顶点坐标分别是A（m，n），B ( 2，－l )，C （－m，－n），则点D的坐标是（）A．（－2 ，l ) B．（－2，－l ) C．（－1，－2 ) D ．（－1，2 )【答案】A【解析】【分析】【详解】试题分析：∵平行四边形ABCD是中心对称图形，对称中心是对角线的交点，而A、C关于原点对称，故B、D也关于原点对称∴D（－2 ，l ）．故选A．考点：平行四边形的性质；坐标与图形性质．14．如图，若A、B两点的坐标分别为（﹣3，5）、（3，5），则点C坐标为（）A．（﹣2，6）B．（﹣1，6）C．（﹣2，7）D．（﹣1，7）【答案】D【解析】【分析】根据A、B的坐标判断出y轴在AB的垂直平分线上，结合图形可得点C的纵坐标比A、B 的纵坐标大2，然后解答即可．【详解】如图所示，∵A、B两点的坐标分别为（﹣3，5）、（3，5），∴则点C坐标为（﹣1，7），故选：D．【点睛】本题考查了坐标确定位置，准确识图，判断出y轴的位置以及点C的纵坐标与点A、B的纵坐标的关系是解题的关键．15．如图，直线m⊥n，在某平面直角坐标系中，x轴∥m，y轴∥n，点A的坐标为（－4，2），点B的坐标为（2，－4），则坐标原点为（）A．O1B．O2C．O3D．O4【答案】A【解析】试题分析：因为A点坐标为（－4，2），所以，原点在点A的右边，也在点A的下边2个单位处，从点B来看，B（2，－4），所以，原点在点B的左边，且在点B的上边4个单位处．如下图，O1符合．考点：平面直角坐标系．16．如图，在菱形OABC 中，30AOC ∠=︒，4OA =，以O 为坐标原点，以OA 所在的直线为x 轴建立平面直角坐标系，如图.按以下步骤作图：①分别以点A ，B 为圆心，以大于2AB 的长为半径作弧，两弧相交于点M ，N ；②作直线MN 交BC 于点P .则点P 的坐标为( )A ．(4,2)B ．438,2⎛⎫- ⎪ ⎪⎝⎭C ．234,2⎛⎫+ ⎪ ⎪⎝⎭D ．()33,2 【答案】C【解析】【分析】延长BC 交y 轴于点D 可求OD ，CD 的长，进一步求出BD 的长，再解直角三角形BPE ，求得BP 的长，从而可确定点P 的坐标.【详解】延长BC 交y 轴于点D ，MN 与AB 将于点E ，如图，∵四边形OABC 是菱形，∠AOC=30°,∴OA=OC=AB=BC=4，BC ∥OA ，∠ABC=30°,∴∠OCD=∠AOC=30°，∴OD=12OC=2，即点P 的纵坐标是2. ∴∴∵MN 是AB 的垂直平分线，∴BE=12AB=2， ∴BP=cos30BE ==︒ ∴. ∴点P的坐标为42⎛⎫ ⎪ ⎪⎝⎭故选C.【点睛】此题主要考查了坐标与图形的性质，也考查了菱形的性质和解直角三角形．17．在平面直角坐标系xOy 中，若点P 在第四象限，且点P 到x 轴的距离为1，到y 轴的距离为3，则点的坐标为( )A ．(3,-1)B ．(-3,1)C ．(1,-3)D ．(-1,3)【答案】A【解析】【分析】根据点到x 轴的距离是纵坐标的绝对值，到y 轴的距离是横坐标的绝对值，结合第四象限点（+，-），可得答案．【详解】解：若点P 在第四象限，且点P 到x 轴的距离为1，到y 轴的距离为3，则点的坐标为（3，-1），故选：A ．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．18．已知点P 位于y 轴右侧，距y 轴3个单位长度，位于x 轴上方，距离x 轴4个单位长度，则点P 坐标是( )A ．(3,4)B ．(-3,4)C ．(-4,3)D ．(4，3)【答案】A【解析】【分析】根据题意，P点应在第一象限，横、纵坐标为正，再根据P点到坐标轴的距离确定点的坐标．【详解】解：∵P点位于y轴右侧，x轴上方，∴P点在第一象限，又∵P点距y轴3个单位长度，距x轴4个单位长度，∴P点横坐标为3，纵坐标为4，即点P的坐标为（3，4）．故选A．【点睛】本题考查了点的位置判断方法及点的坐标几何意义．Y的顶点O，A，C的坐标分别为(0,0)，(4,0)，(1,3)，则顶点B 19．如图，若OABC的坐标为（）A．(4,1)B．(5,3)C．(4,3)D．(5,4)【答案】B【解析】【分析】根据平行四边形的性质，以及点的平移性质，即可求出点B的坐标.【详解】解：∵四边形OABC是平行四边形，∴OC∥AB，OA∥BC，∴点B的纵坐标为3，∵点O向右平移1个单位，向上平移3个单位得到点C，∴点A向右平移1个单位，向上平移3个单位得到点B，∴点B的坐标为：（5，3）；故选：B.【点睛】本题考查了平行四边形的性质，点坐标平移的性质，解题的关键是熟练掌握平行四边形的性质进行解题.20．下列说法中，正确的是（）A．点P（3，2）到x轴距离是3B．在平面直角坐标系中，点（2，﹣3）和点（﹣2，3）表示同一个点C．若y＝0，则点M（x，y）在y轴上D．在平面直角坐标系中，第三象限内点的横坐标与纵坐标同号【答案】D【解析】【分析】根据点的坐标到坐标轴的距离、坐标轴上点的坐标特点及第三象限内点的坐标符号特点逐一判断可得．【详解】A、点P（3，2）到x轴距离是2，此选项错误；B、在平面直角坐标系中，点（2，﹣3）和点（﹣2，3）表示不同的点，此选项错误；C、若y＝0，则点M（x，y）在x轴上，此选项错误；D、在平面直角坐标系中，第三象限内点的横坐标与纵坐标同为负号，此选项正确；故选D．【点睛】本题主要考查点的坐标，解题的关键是掌握点的坐标到坐标轴的距离、坐标轴上点的坐标特点及第三象限内点的坐标符号特点．。

淮安市初中数学函数之平面直角坐标系分类汇编含解析

淮安市初中数学函数之平面直角坐标系分类汇编含解析一、选择题1．在平面直角坐标系中，点P（0，﹣4）在（）A．x轴上B．y轴上C．原点D．与x轴平行的直线上【答案】B【解析】【分析】根据点P的坐标为（0，﹣4）即可判断点P（0，﹣4）在y轴上．【详解】在平面直角坐标系中，点P（0，﹣4）在y轴上，故选：B．【点睛】本题考查了坐标与图形性质，熟练掌握坐标轴上点的坐标特征是解题的关键．2．若点P(x，y)在第三象限，且点P到x轴的距离为3，到y轴的距离为2，则点P的坐标是( )A．(-2，3) B．(-2，-3) C．(2，-3) D．(2，3)【答案】B【解析】【分析】根据点P到x轴的距离为3，则这一点的纵坐标是3或-3，到y轴的距离为2，那么它的横坐标是2或-2，再根据点P所处的象限即可确定点P的坐标．【详解】∵点P到x轴的距离为3，∴点的纵坐标是3或-3，∵点P到y轴的距离为2，∴点的横坐标是2或-2，又∵点P在第三象限，∴点P的坐标为：（-2，-3），故选B.【点睛】本题考查了点的坐标的几何意义，横坐标的绝对值就是点到y轴的距离，纵坐标的绝对值就是到x轴的距离．3．在平面直角坐标系内，若点P（3﹣m，m﹣1）在第二象限，那么m的取值范围是（）A．m＞1 B．m＞3 C．m＜1 D．1＜m＜3【答案】B【解析】【分析】由第二象限点的横坐标为负数、纵坐标为正数得出关于m的不等式组，解之可得答案．【详解】∵点P （3﹣m ，m ﹣1）在第二象限，∴3-010m m ⎧⎨-⎩＜①＞② ，解不等式①，得：m ＞3，解不等式②，得：m ＞1，则m ＞3，故选：B ．【点睛】本题主要考查象限内点的坐标符号特点及解一元一次不等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．4．在平面直角坐标系中，点P(x ﹣3，x+3)是x 轴上一点，则点P 的坐标是（） A ．(0，6)B ．(0，﹣6)C ．(﹣6，0)D ．(6，0) 【答案】C【解析】【分析】根据x 轴上的点的纵坐标为0列式计算即可得解．【详解】∵点P （x ﹣3，x+3）是x 轴上一点，∴x+3＝0，∴x ＝﹣3，∴点P 的坐标是（﹣6，0），故选：C ．【点睛】本题考查了点的坐标，是基础题，熟记x 轴上的点的纵坐标为0是解题的关键．5．在平面直角坐标系中，若点P (m -3，m +1)在第二象限，则m 的取值范围（） A ．m <3B ．m >−1C ．−1<m <3D ．m ≥0【答案】C【解析】【分析】根据点P (m -3，m +1)在第二象限及第二象限内点的符号特点，可得一个关于m 的不等式组，解不等式组即可得m 的取值范围．【详解】解：∵点P (m -3，m +1)在第二象限， ∴可得到：3010m m -<⎧⎨+>⎩，解得：13m -<<，∴m 的取值范围为13m -<<，故选：C ．【点睛】本题考查了坐标在象限内的符号，以及不等式组的解法，属于基础题．6．已知平面内不同的两点A （a +2，4）和B （3，2a +2）到x 轴的距离相等，则a 的值为( )A ．﹣3B ．﹣5C ．1或﹣3D ．1或﹣5【答案】A【解析】分析：根据点A （a ＋2，4）和B （3，2a ＋2）到x 轴的距离相等，得到4＝|2a ＋2|，即可解答．详解：∵点A （a ＋2，4）和B （3，2a ＋2）到x 轴的距离相等，∴4＝|2a ＋2|，a ＋2≠3，解得：a ＝−3，故选A ．点睛：考查点的坐标的相关知识；用到的知识点为：到x 轴和y 轴的距离相等的点的横纵坐标相等或互为相反数．7．如图，若A 、B 两点的坐标分别为（﹣3，5）、（3，5），则点C 坐标为（）A ．（﹣2，6）B ．（﹣1，6）C ．（﹣2，7）D ．（﹣1，7）【答案】D【解析】【分析】根据A 、B 的坐标判断出y 轴在AB 的垂直平分线上，结合图形可得点C 的纵坐标比A 、B 的纵坐标大2，然后解答即可．【详解】如图所示，∵A 、B 两点的坐标分别为（﹣3，5）、（3，5），∴则点C 坐标为（﹣1，7），故选：D ．【点睛】本题考查了坐标确定位置，准确识图，判断出y 轴的位置以及点C 的纵坐标与点A 、B 的纵坐标的关系是解题的关键．8．如图，已知A ：(1，0)．A 2(1，-1)，A 3(-1,-l)．A 4 (-1, 1), A 5 (2, 1)，．．．则点A 2020的坐标是( )A ．(506，505)B ．(-505，-505)C ．(505，-505)D ．(-505，505)【答案】D【解析】【分析】经过观察可得在第一象限的在格点的正方形的对角线上的点的横坐标依次加1，纵坐标依次加1，在第二象限的点的横坐标依次加-1，纵坐标依次加1；在第三象限的点的横坐标依次加-1，纵坐标依次加-1，在第四象限的点的横坐标依次加1，纵坐标依次加-1，第二，三，四象限的点的横纵坐标的绝对值都相等，并且第三，四象限的横坐标等于相邻4的整数倍的各点除以4再加上1，由此即可求出点A 2020【详解】解：易得4的整数倍的各点如:4812,,A A A∵20204505÷=，∴点2020A 在第二象限，∴2020A 是第二象限的第505个点，∴2020A 的坐标为(-505,505)，故选：D【点睛】本题考查了点的坐标规律，属于规律型，考查点的坐标，首先确定象限，再找出点之间的规律．9．如图，在平面直角坐标系上有个点(1,0)P ，点P 第1次向上跳动1个单位至点1(1,1)P ，紧接着第2次向左跳动2个单位至点2(1,1)P -，第3次向上跳动1个单位到达3(1,2)P -，第4次向右跳动3个单位到达4(2,2)P ，第5次又向上跳动1个单位，第6次向左跳动4个单位，…，依此规律跳动下去，点2019P 的坐标为（）．A ．(505,1010)B ．(505,505)-C ．(505,1010)-D ．(505,505)-【答案】C【解析】【分析】设第n 次跳动至点Pn ，根据部分点An 坐标的变化找出变化规律“P 4n （n ＋1，2n ），P 4n ＋1（n ＋1，2n ＋1），P 4n ＋2（−n−1，2n ＋1），P 4n ＋3（−n−1，2n ＋2）”，依此规律结合2019＝504×4＋3即可得出点P 2019的坐标．【详解】设第n 次跳动至点Pn ，观察发现：P （1，0），P 1（1，1），P 2（−1，1），P 3（−1，2），P 4（2，2），P 5（2，3），P 6（−2，3），P 7（−2，4），P 8（3，4），P 9（3，5），…，∴P 4n （n ＋1，2n ），P 4n ＋1（n ＋1，2n ＋1），P 4n ＋2（−n−1，2n ＋1），P 4n ＋3（−n−1，2n ＋2）（n 为自然数）．∵2019＝504×4＋3，∴P 2019（-504-1，504×2＋2），即(505,1010)-．故选：C ．【点睛】本题考查了规律型中点的坐标，根据部分点An 坐标的变化找出变化规律“P 4n （n ＋1，2n ），P 4n ＋1（n ＋1，2n ＋1），P 4n ＋2（−n−1，2n ＋1），P 4n ＋3（−n−1，2n ＋2）（n 为自然数）”是解题的关键．10．如图，小手盖住的点的坐标可能为( )A．(-1，1) B．(-1，-1) C．(1，1) D．(1，-1)【答案】D【解析】【详解】解：根据第四象限的坐标特征，易得小手盖住的点的横坐标为正，纵坐标为负，选项D符合此特征，故选：D11．在平面直角坐标系中，A，B，C三点坐标分别是（0，0），（4，0），（3，2），以A，B，C三点为顶点画平行四边形，则第四个顶点不可能在（）.A．第一象限B．第二象限C．第三象限D．第四象限【答案】C【解析】A点在原点上，B点在横轴上，C点在第一象限，根据平行四边形的性质：两组对边分别平行，可知第四个顶点可能在第一、二、四象限，不可能在第三象限，故选C12．在平面直角坐标系中，点(－1, 3)在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【解析】【分析】根据各象限内点的坐标特征解答．【详解】解：点(－1, 3)在第二象限故选B.【点睛】本题考查了各象限内点的坐标的符号特征以，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．13．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如(1，0)，(2，0)，(2，1)，(3，2)，(3，1)，(3，0)，(4，0)．根据这个规律探索可得，第100个点的坐标为()A．(14，8)B．(13，0)C．(100，99)D．(15，14)【答案】A【解析】【详解】由图形可知：点的个数依次是1、2、3、4、5、…，且横坐标是偶数时，箭头朝上，∵1＋2＋3＋…＋13＝91，1＋2＋3＋…＋14＝105，∴第91个点的坐标为（13，0），第100个点横坐标为14．∵在第14行点的走向为向上，∴纵坐标为从第92个点向上数8个点，即为8；∴第100个点的坐标为（14，8）．故选A．【点睛】本题主要考查了根据图形的变化找规律的方法，首先要分析图形中每一列的点人个数的变化规律是，1，2，3，4，5，…，由此找出第100个点所在的列，再根据奇数列是从上往下依次增加1，偶数列是从下往上依次增加1，由此即可找到第100个点所对应的坐标.14．在平面直角坐标系xOy中，若点P在第四象限，且点P到x轴的距离为1，到y轴的距离为3，则点的坐标为( )A．(3,-1) B．(-3,1) C．(1,-3) D．(-1,3)【答案】A【解析】【分析】根据点到x轴的距离是纵坐标的绝对值，到y轴的距离是横坐标的绝对值，结合第四象限点（+，-），可得答案．【详解】解：若点P在第四象限，且点P到x轴的距离为1，到y轴的距离为3，则点的坐标为（3，-1），故选：A ．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．15．如图，在平面直角坐标系中．四边形OABC 是平行四边形，其中()()2,03,1,A B 、将ABCD Y 在x 轴上顺时针翻滚．如：第一次翻滚得到111,AB C O Y 第二次翻滚得到1122B AO C Y ，···则第五次翻滚后，C 点的对应点坐标为（）A ．(622,2+B ．2,622+ C ．2,622- D ．(622,2- 【答案】A【解析】【分析】ABCD Y 在x 轴上顺时针翻滚，四次一个循环，推出第五次翻滚后，点A 的坐标，再利用平移的性质求出C 的对应点坐标即可．【详解】连接AC ，过点C 作CH ⊥OA 于点H ，∵四边形OABC 是平行四边形，A(2，0)、B(3，1)，∴C(1，1)，∴∠COA=45°，2，∴2=1，∴AH=2-1=1，∴OA=AH ，∴OC=AC ，∴∆OAC 是等腰直角三角形，∴AC ⊥OC ，∵ABCD Y 在x 轴上顺时针翻滚，四次一个循环，∴第五次翻滚后点，A 的坐标为2，0)，把点A 2个单位得到点C ，∴第五次翻滚后，C 点的对应点坐标为()622,2+．故选：A ．【点睛】本题主要考查图形与坐标，涉及平行四边形的性质，等腰直角三角形的性质以及平移的性质，找到点的坐标的变化规律，是解的关键．16．如图，象棋盘上，若“将”位于点（1，﹣2），“象”位于点（5，0），则炮位于点（）A ．（﹣1，1）B ．（﹣1，2）C ．（﹣2，1）D ．（﹣2，2）【答案】C【解析】【分析】根据“将”的位置向左平移一个单位所得直线是y 轴，向上平移2个单位所得直线是x 轴，根据“炮”的位置，可得答案．【详解】解：根据题意可建立如图所示坐标系，由坐标系知炮位于点（﹣2，1），故选：C ．【点睛】本题考查了坐标确定位置，利用“将”的位置向左平移一个单位所得直线是y 轴，向上平移2个单位所得直线是x 轴是解题关键．17．如果代数式m mn -+有意义，那么直角坐标系中 P(m,n)的位置在（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】【分析】先根据二次根式与分式的性质求出m,n 的取值，即可判断P 点所在的象限.【详解】依题意的-m≥0，mn ＞0，解得m ＜0，n ＜0，故P(m,n)的位置在第三象限，故选C.【点睛】此题主要考查坐标所在象限，解题的关键是熟知二次根式与分式的性质.18．如图，在平面直角坐标系中，三角形AOB 的三个顶点的坐标分别是(1,3)A ，(0,0)O ，(2,0)B ，第一次将三角形AOB 变换成三角形11AOB ，1(2,3)A ，1(4,0)B ；第二次将三角形11AOB 变换成三角形22A OB ，2(4,3)A ，2(8,0)B ；第三次将三角形22A OB 变换成三角形33A OB …，则2020B 的横坐标是（）A ．20192B ．20202C ．20212D ．20222【答案】C【解析】【分析】对于A 1，A 2，A n 坐标找规律可将其写成竖列，比较从而发现A n 的横坐标为2n ，而纵坐标都是3，B n 的纵坐标总为0，横坐标为2n+1，即可得到2020B 的横坐标．【详解】解：因为B （2，0），B 1（4，0），B 2（8，0），B 3（16，0）…纵坐标不变，为0，同时横坐标都和2有关为2n+1，那么B 的坐标为2020B （20212，0）；故选：C ．【点睛】本题考查了学生观察图形及总结规律的能力，解题的关键是找到点B 横坐标都与2有关的规律．19．已知点P（1﹣a，2a+6）在第四象限，则a的取值范围是（）A．a＜﹣3 B．﹣3＜a＜1 C．a＞﹣3 D．a＞1【答案】A【解析】【分析】根据第四象限的点的横坐标是正数，纵坐标是负数列出不等式组求解即可．【详解】解：∵点P（1﹣a，2a+6）在第四象限，∴10 260aa->⎧⎨+<⎩解得a＜﹣3．故选A．【点睛】本题考查了点的坐标，一元一次不等式组的解法，求不等式组解集的口诀：同大取大，同小取小，大小小大中间找，大大小小找不到（无解）．20．为了保障艺术节表演的整体效果，某校在操场中标记了几个关键位置，如图是利用平面直角坐标系画出的关键位置分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示点A的坐标为，表示点B的坐标为，则表示其他位置的点的坐标正确的是（）A．B．C．D．【答案】B【解析】【分析】正确建立平面直角坐标系，根据平面直角坐标系，找出相应的位置，然后写出坐标即可．【详解】建立平面直角坐标系，如图：则 .表示正确的点的坐标是点D.故选B.【点睛】本题主要考查坐标确定位置，确定坐标原点和x，y轴的位置及方向，正确建立平面直角坐标系是解题关键.。

直角坐标系专题讲解

直角坐标系一：教学目标1：认识并能画出；能在方格纸上建立适当的直角坐标系，描述物体的位置；在给定的直角坐标系中，会根据坐标描出点的位置，由点的位置写出它的坐标。

2：经历画坐标系、描点、连线、看图以及由点找坐标等过程，发展学生的数形结合意识、合作交流意识。

二：教学重点能画出；会根据坐标描出点的位置，由点的位置写出它的坐标。

三：教学难点能能建立；求出点的坐标，由点的位置写出它的坐标。

四：教学时间三课时五：教学过程第一课时一）引入新课1：要在平面内确定一个地点的位置需要几个数据？2：练习如图你能确定各个景点的位置吗？“大成殿”在“中心广场”西、南各多少个格？“碑林”在“中心广场”东、北各多少个格？二）新课1：我们可以以“中心广场”为原点作两条互相垂直的数轴，分别取向右和向上的方向为数轴的正方向，一个方格的边长看做一个单位长度，你能表示出“碑林”的位置吗？“大成殿”的位置吗？（学生回答，老师小结）2：在平面内，两条互相垂直且有公共原点的数轴组成。

（通常两条数轴成水平位置与铅直位置，取向上或向右为正方向，水平位置的数轴叫横轴，铅直位置的数轴叫纵轴，它们的公共原点叫直角坐标系的原点。

）3：两条坐标轴把平面分成四部分：右上部分叫第一象限，其它三部分按逆时针方向依次叫第二象限、第三象限、第四象限。

4：怎样求平面内点的坐标？对于平面内任意一点，过该点分别向横轴、纵轴作垂线，垂足在横轴、纵轴上对应的数分别叫该点的横坐标、纵坐标。

例1 写出多边形ABCDEF各顶点的坐标yA BF O C xE D5：想一想（1）点A与B的纵坐标相同，线段AB的位置有什么特点？（2）线段DB的位置有什么特点？（3）坐标轴上点的坐标有什么特点？6：练习P131 做一做三：小结（1）怎样画？（2）怎样求平面内点的坐标？（4）知道点的坐标怎样描出点？四：作业P132第二课时一：复习1）怎样画？（学生练习画）（2）怎样求平面内点的坐标？yAB CO x已知等边三角形的边长为2cm，求出各顶点的坐标？（3）道点的坐标怎样描出点？二：新课例在直角坐标系中描出下列各点，并将各组内的点用线段依次连接起来。

函数之平面直角坐标系分类汇编及解析

函数之平面直角坐标系分类汇编及解析一、选择题1．我们知道：四边形具有不稳定性.如图，在平面直角坐标系中，边长为4的正方形ABCD 的边AB 在x 轴上，AB 的中点是坐标原点O ，固定点A ，B ，把正方形沿箭头方向推，使点D 落在y 轴正半轴上点D ¢处，则点C 的对应点C '的坐标为（）A ．()23,2B ．()4,2C ．(4,23D ．(2,23 【答案】C【解析】【分析】由已知条件得到AD′=AD=4，AO=12AB=2，根据勾股定理得到2223AD OA '-=于是得到结论．【详解】∵AD ′=AD=4， AO=12AB=2， ∴OD ′2223AD OA '-=∵C ′D ′=4，C′D′∥AB ，∴C ′（4，3），故选C ．【点睛】考查了正方形的性质，坐标与图形的性质，勾股定理，正确的识别图形是解题的关键．2．点P 的坐标为236()a a -+，，且到两坐标轴的距离相等，则点P 的坐标为( ) A ．(33)， B ．(33)，- C ． (66)，- D ．(33)，或(66)，-【答案】D【解析】【分析】根据点P 到两坐标轴的距离相等可得其点的横坐标与纵坐标的绝对值相等，据此进一步求解即可.【详解】∵点P 到两坐标轴的距离相等，∴236a a -=+，即：236a a -=+或()236a a -=-+，∴1a =-或4a =-，∴P 点坐标为：(33)，或(66)，-故选：D.【点睛】本题主要考查了坐标系中点的坐标的应用，熟练掌握相关概念是解题关键.3．在平面直角坐标系中，过点(3,2)A -画直线a x ⊥轴，过点(1,2)B -画直线b y ⊥轴，直线,a b 相交于点P ，则点P 的坐标是（）A ．()3,2B ．()2,3C ．()3,1-D ．()2,2- 【答案】A【解析】【分析】根据过点(3,2)A -画直线a x ⊥轴可以知道P 点的横坐标，根据过点(1,2)B -画直线b y ⊥轴可以知道p 点的纵坐标，由点P 的横纵坐标即可得到答案.【详解】解：∵点p 是通过点(3,2)A -画直线a x ⊥轴，过点(1,2)B -画直线b y ⊥轴得到的交点，∴点P 的横坐标与点A 的横坐标相同，即3，点P 的纵坐标与点B 的纵坐标相同，即2，因此，点p 的坐标为()3,2，故A 为答案.【点睛】本题主要考查了与直角坐标系有关的知识，掌握向x 轴画垂线得到的点横坐标相同，向y 轴作垂线得到的点纵坐标相同是解题的关键.4．如果点M （3a ﹣9，1+a ）是第二象限的点，则a 的取值范围在数轴上表示正确的是（）A ．B ．C ．D ．【答案】A【解析】试题分析：点在第二象限的条件是：横坐标是负数，纵坐标是正数．解：∵点M （3a ﹣9，1+a ）是第二象限的点， ∴，解得﹣1＜a ＜3．在数轴上表示为：．故选A ．考点：在数轴上表示不等式的解集；解一元一次不等式组；点的坐标．5．如图，动点P 从()0,3出发，沿箭头所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角.当点P 第2018次碰到矩形的边时，点P 的坐标为( )A ．()1,4B ．()5,0C ．()7,4D ．()8,3【答案】C【解析】【分析】理解题意，由反射角与入射角的定义作出图形，观察出反弹6次为一个循环的规律，解答即可.【详解】如图，经过6次反弹后动点回到出发点（0，3），∵2018÷6=336…2，∴当点P 第2018次碰到矩形的边时为第336个循环组的第2次反弹，点P 的坐标为（7，4）．故选C ．【点睛】本题考查了平面直角坐标系中点的坐标规律，首先作图，然后观察出每6次反弹为一个循环，据此解答即可.6．如图，ABCDEF 是中心为原点O ，顶点A ，D 在x 轴上，半径为4的正六边形，则顶点F 的坐标为（）A ．()2,23B ．()2,2-C ．()2,23-D ．()1,3- 【答案】C【解析】【分析】连接OF ，设EF 交y 轴于G ，那么∠GOF=30°；在Rt △GOF 中，根据30°角的性质求出GF ，根据勾股定理求出OG 即可．【详解】解：连接OF ，在Rt △OFG 中，∠GOF=13603026⨯=oo ，OF=4． ∴GF=2，3∴F （-2，3）．故选C ．【点睛】本题利用了正六边形的对称性，直角三角形30°的角所对的边等于斜边的一半，勾股定理等知识，熟练掌握正六边形的对称性是解答本题的关键．7．如图所示，正五边形ABCDE 放入某平面直角坐标系后，若顶点A ，B ，C ，D 的坐标分别是(0，a)，(－3，2)，(b ，m)，(c ，m)，则点E 的坐标是( )A ．(2，－3)B ．(2，3)C ．(3，2)D ．(3，－2) 【答案】C【解析】【分析】【详解】 ∵点A 坐标为（0，a ），∴点A 在该平面直角坐标系的y 轴上，∵点C 、D 的坐标为（b ，m ），（c ，m ），∴点C 、D 关于y 轴对称，∵正五边形ABCDE 是轴对称图形，∴该平面直角坐标系经过点A 的y 轴是正五边形ABCDE 的一条对称轴，∴点B 、E 也关于y 轴对称，∵点B 的坐标为（﹣3，2），∴点E 的坐标为（3，2），故选C..【点睛】本题考查了平面直角坐标系的点坐标特征及正五边形的轴对称性质，解题的关键是通过顶点坐标确认正五边形的一条对称轴即为平面直角坐标系的y 轴．8．已知点() ,3A a 、点()3, B b -关于y 轴对称，点(),P a b --在第( )象限A ．一B ．二C ．三D ．四【答案】C【解析】【分析】根据点A 、点B 关于y 轴对称，求出a ，b 的值，然后根据象限点的符号特点即可解答.【详解】∵点() ,3A a 、点()3, B b -关于y 轴对称，∴a=3，b=3，∴点P 的坐标为()3, 3 --，∴点P 在第三象限，故答案为：C.【点睛】本题考查了轴对称和象限内点的符号特点，解题的关键是熟练掌握其性质.9．如图，正方形ABCD 的顶点A （1，1），B （3，1），规定把正方形ABCD“先沿x 轴翻折，再向左平移1个单位”为一次变换，这样连续经过2019次变换后，正方形ABCD 的顶点C 的坐标为（）A ．（﹣2018，3）B ．（﹣2018，﹣3）C ．（﹣2016，3）D ．（﹣2016，﹣3）【答案】D【解析】【分析】首先由正方形ABCD ，顶点A （1，1）、B （3，1）、C （3，3），然后根据题意求得第1次、2次、3次变换后的点C 的对应点的坐标，即可得规律：第n 次变换后的点C 的对应点的为：当n 为奇数时为（3-n ，-3），当n 为偶数时为（3-n ，3），继而求得把正方形ABCD 连续经过2019次这样的变换得到正方形ABCD 的点C 的坐标．【详解】∵正方形ABCD ，顶点A （1，1）、B （3，1），∴C （3，3）．根据题意得：第1次变换后的点C 的对应点的坐标为（3﹣1，﹣3），即（2，﹣3），第2次变换后的点C 的对应点的坐标为：（3﹣2，3），即（1，3），第3次变换后的点C 的对应点的坐标为（3﹣3，﹣3），即（0，﹣3），第n 次变换后的点C 的对应点的为：当n 为奇数时为（3﹣n ，﹣3），当n 为偶数时为（3﹣n ，3），∴连续经过2019次变换后，正方形ABCD 的点C 的坐标变为（﹣2016，﹣3）．故选D ．【点睛】此题考查了对称与平移的性质．此题难度较大，属于规律性题目，注意得到规律：第n 次变换后的点C 的对应点的坐标为：当n 为奇数时为（3-n ，-3），当n 为偶数时为（3-n ，3）是解此题的关键．10．平面直角坐标系中，已知□ABCD 的三个顶点坐标分别是A （m ，n ），B ( 2，－l )，C（－m，－n），则点D的坐标是（）A．（－2 ，l ) B．（－2，－l ) C．（－1，－2 ) D ．（－1，2 )【答案】A【解析】【分析】【详解】试题分析：∵平行四边形ABCD是中心对称图形，对称中心是对角线的交点，而A、C关于原点对称，故B、D也关于原点对称∴D（－2 ，l ）．故选A．考点：平行四边形的性质；坐标与图形性质．11．在平面直角坐标中，点M(－2，3)在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【解析】∵−2<0，3>0，∴(−2,3)在第二象限，故选B.12．为了保障艺术节表演的整体效果，某校在操场中标记了几个关键位置，如图是利用平面直角坐标系画出的关键位置分布图，若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示点A的坐标为，表示点B的坐标为，则表示其他位置的点的坐标正确的是（）A．B．C．D．【答案】B【解析】【分析】正确建立平面直角坐标系，根据平面直角坐标系，找出相应的位置，然后写出坐标即可．【详解】建立平面直角坐标系，如图：则 .表示正确的点的坐标是点D.故选B.【点睛】本题主要考查坐标确定位置，确定坐标原点和x，y轴的位置及方向，正确建立平面直角坐标系是解题关键.13．在平面直角坐标系中，点A的坐标是（3a﹣5，a+1）．若点A到x轴的距离与到y轴的距离相等，且点A在y轴的右侧，则a的值为（）A．1 B．2 C．3 D．1 或 3【答案】C【解析】【分析】根据题意可知：点A的横、纵坐标相等或互为相反数，然后列出方程即可求出a的两个值，最后根据点A在y轴的右侧，即可得出结论．【详解】解：∵点A到x轴的距离与到y轴的距离相等，∴3a﹣5＝a+1或3a﹣5＝﹣（a+1），解得：a＝3或1，∵点A在y轴的右侧，∴点A的横坐标为正数，∴3a﹣5＞0，∴a＞53，∴a＝3，故选：C．【点睛】此题考查的是点的坐标特征，掌握点到x轴的距离与到y轴的距离相等则点的横、纵坐标相等或互为相反数是解决此题的关键．14．如果点P （m +3，m +1）在x 轴上，则点P 的坐标为（）A ．（0，2）B ．（2，0）C ．（4，0）D ．（0，﹣4）【答案】B【解析】【分析】根据点P 在x 轴上，即y =0，可得出m 的值，从而得出点P 的坐标．【详解】根据点P 在x 轴上，即y ＝0，可得出m 的值，从而得出点P 的坐标．解：∵点P （m +3，m +1）在x 轴上，∴y ＝0，∴m +1＝0，解得：m ＝﹣1，∴m +3＝﹣1+3＝2，∴点P 的坐标为（2，0）．故选：B ．【点睛】本题考查了点的坐标，注意平面直角坐标系中，点在x 轴上时纵坐标为0，得出m 的值是解题关键.15．在平面直角坐标系中，点(－1, 3)在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】B【解析】【分析】根据各象限内点的坐标特征解答．【详解】解：点(－1, 3)在第二象限故选B.【点睛】本题考查了各象限内点的坐标的符号特征以，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．16．若点(24,24)P m m -+在y 轴上，那么m 的值为（）A ．2B ．2-C ．2±D ．0【答案】A【解析】【分析】依据点P （2m-4，2m+4）在y 轴上，其横坐标为0，列式可得m 的值．【详解】∵P（2m-4，2m+4）在y轴上，∴2m-4=0，解得m=2，故选：A．【点睛】此题考查点的坐标，解题关键在于掌握y轴上点的横坐标为0．17．如图，将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变，横坐标变为原来的13，则点A的对应点A′的坐标是( )A．(2，3) B．(6，1) C．(2，1) D．(3，3)【答案】A【解析】【分析】先写出点A的坐标为（6，3），纵坐标保持不变，横坐标变为原来的13，即可判断出答案．【详解】点A变化前的坐标为(6,3)，将纵坐标保持不变,横坐标变为原来的13，则点A的对应点A′坐标是(2,3).故选A.【点睛】本题考查的是坐标，熟练掌握坐标是解题的关键.18．在平面直角坐标系中，对于平面内任一点（a，b），若规定以下三种变换：①f（a，b）=（-a，b），如f（1，2）=（-1，2）；②g（a，b）=（b，a），如g（1，2）=（2，1）；③h（a，b）=（-a，-b），如h（1，2）=（-1，-2）；按照以上变换有：g（h（f （1，2）））=g（h（-1，2））=g（1，-2）=（-2，1），那么h（f（g（3，-4）））等于（）A．（4，-3）B．（-4，3）C．（-4，-3）D．（4，3）【答案】C【解析】【分析】根据f（a，b）=（-a，b）．g（a，b）=（b，a）．h（a，b）=（-a，-b），可得答案．【详解】由已知条件可得h（f（g（3，-4）））= h（f（-4，3））= h（4，3）=（-4，-3）故选：C【点睛】本题考查了点的坐标，利用f（a，b）=（-a，b）．g（a，b）=（b，a）．h（a，b）=（-a，-b）是解题关键．19．在平面直角坐标系中．对于平面内任一点（m，n），规定以下两种变换：①f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；②g（m，n）=（﹣m，﹣n），如g（2，1）=（﹣2，﹣1）．按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（3，2）]等于（）A．（3，2） B．（3．﹣2） C．（﹣3，2） D．（﹣3，﹣2）【答案】C【解析】【分析】根据f、g的规定进行计算即可得解．【详解】g[f（3，2）]=g（3，﹣2）=（﹣3，2）．故选C．【点睛】本题考查了点的坐标，读懂题目信息，理解f、g的运算方法是解题的关键．20．若点M的坐标为b|+1),则下列说法中正确的是()A．点M在x轴正半轴上B．点M在x轴负半轴上C．点M在y轴正半轴上D．点M在y轴负半轴上【答案】C【解析】【分析】首先根据二次根式的定义及绝对值的性质分别判断出点M的横、纵坐标的符号；然后根据坐标轴上点的坐标特征进行分析即可作出判断.【详解】有意义，则－a2≥0，∴a＝0.∵|b|≥0，∴|b|＋1＞0，∴点M在y轴的正半轴上.故选C.【点睛】本题考查的是点的坐标的知识，解题关键是熟练掌握坐标轴上点的坐标特征.。

函数之平面直角坐标系分类汇编含解析

函数之平面直角坐标系分类汇编含解析一、选择题1．课间操时，小华、小军和小刚的位置如图所示，如果小华的位置用(0,0)表示，小军的位置用(2,1)表示，那么小刚的位置可以表示为()A．(5,4) B．(4,5) C．(3,4) D．(4,3)【答案】D【解析】【分析】根据已知两点的坐标确定平面直角坐标系，然后确定其它各点的坐标即可解答．【详解】如果小华的位置用（0，0）表示，小军的位置用（2，1）表示，如图所示就是以小华为原点的平面直角坐标系的第一象限，所以小刚的位置为（4，3）．故选D．【点睛】本题利用平面直角坐标系表示点的位置，关键是由已知条件正确确定坐标轴的位置．2．点P(1﹣2x，5x﹣1)在第四象限，则x的范围是（）A．15x<B．12x<C．1152x<<D．12x>【答案】A 【解析】【分析】根据点的位置得出不等式组，求出不等式组的解集即可．【详解】解：∵点P （1﹣2x ，5x ﹣1）在第四象限，120510x x ->⎧∴⎨-<⎩，解得：15x<，故选：A ．【点睛】本题考查了点的位置和解一元一次不等式组，能根据题意得出不等式组是解此题的关键．3．如果点P （3x+9，12x ﹣2）在平面直角坐标系的第四象限内，那么x 的取值范围在数轴上可表示为（）A ．B ．C ．D ．【答案】C【解析】解：由点P （3x +9，12x ﹣2）在平面直角坐标系的第四象限内，得：3901202x x +⎧⎪⎨-⎪⎩＞＜．解得：﹣3＜x ＜4，在数轴上表示为：故选C ．4．在平面直角坐标系中，若点P (m -3，m +1)在第二象限，则m 的取值范围（） A ．m <3B ．m >−1C ．−1<m <3D ．m ≥0【答案】C【解析】【分析】根据点P (m -3，m +1)在第二象限及第二象限内点的符号特点，可得一个关于m 的不等式组，解不等式组即可得m 的取值范围．【详解】解：∵点P (m -3，m +1)在第二象限， ∴可得到：3010m m -<⎧⎨+>⎩，解得：13m -<<，∴m 的取值范围为13m -<<，故选：C ．【点睛】本题考查了坐标在象限内的符号，以及不等式组的解法，属于基础题．5．已知点A 的坐标为（a +1，3﹣a ），下列说法正确的是（）A ．若点A 在y 轴上，则a ＝3B ．若点A 在一三象限角平分线上，则a ＝1C ．若点A 到x 轴的距离是3，则a ＝±6D ．若点A 在第四象限，则a 的值可以为﹣2【答案】B【解析】【分析】依据坐标轴上的点、一三象限角平分线上的点以及不同象限内点的坐标特征，即可得出结论.【详解】解：A ．若点A 在y 轴上，则a +1＝0，解得a ＝﹣1，故本选项错误；B ．若点A 在一三象限角平分线上，则a +1＝3﹣a ，解得a ＝1，故本选项正确；C ．若点A 到x 轴的距离是3，则|3﹣a |＝3，解得a ＝6或0，故本选项错误；D ．若点A 在第四象限，则a +1＞0，且3﹣a ＜0，解得a ＞3，故a 的值不可以为﹣2；故选：B ．【点睛】本题主要考查了坐标轴上的点、一三象限角平分线上的点以及不同象限内点的坐标特征，解题时注意：横轴上点的纵坐标为0，纵轴上点的横坐标为0.6．平面直角坐标系中，P (－2a －6，a －5)在第三象限，则a 的取值范围是（） A ．a ＞5B ．a ＜－3C ．－3≤a ≤5D ．－3＜a ＜5【答案】D【解析】【分析】根据第三象限的点的坐标特点：x<0，y<0，列不等式组，求出a 的取值范围即可.【详解】∵点P 在第三象限， ∴26050a a --<⎧⎨-<⎩，解得：-3<a<5，故选D.【点睛】本题考查了象限点的坐标的符号特征以及解不等式，该知识点是中考的常考点，常与不等式、方程结合起来求一些字母的取值范围，比如本题中求a 的取值范围．7．平面直角坐标系中，已知□ABCD 的三个顶点坐标分别是A （m ，n ），B ( 2，－l )，C （－m ，－n ），则点D 的坐标是（）A ．（－2 ，l )B ．（－2，－l )C ．（－1，－2 )D ．（－1，2 )【答案】A【解析】【分析】【详解】试题分析：∵平行四边形ABCD 是中心对称图形，对称中心是对角线的交点，而A 、C 关于原点对称，故B 、D 也关于原点对称∴D （－2 ，l ）．故选A ．考点：平行四边形的性质；坐标与图形性质．8．如图，已知A ：(1，0)．A 2(1，-1)，A 3(-1,-l)．A 4 (-1, 1), A 5 (2, 1)，．．．则点A 2020的坐标是( )A ．(506，505)B ．(-505，-505)C ．(505，-505)D ．(-505，505)【答案】D【解析】【分析】经过观察可得在第一象限的在格点的正方形的对角线上的点的横坐标依次加1，纵坐标依次加1，在第二象限的点的横坐标依次加-1，纵坐标依次加1；在第三象限的点的横坐标依次加-1，纵坐标依次加-1，在第四象限的点的横坐标依次加1，纵坐标依次加-1，第二，三，四象限的点的横纵坐标的绝对值都相等，并且第三，四象限的横坐标等于相邻4的整数倍的各点除以4再加上1，由此即可求出点A 2020【详解】解：易得4的整数倍的各点如:4812,,A A A∵20204505÷=，A在第二象限，∴点2020A是第二象限的第505个点，∴2020A的坐标为(-505,505)，∴2020故选：D【点睛】本题考查了点的坐标规律，属于规律型，考查点的坐标，首先确定象限，再找出点之间的规律．9．下列说法正确的是（）A．相等的角是对顶角B．在同一平面内，不平行的两条直线一定互相垂直C．点P(2，﹣3)在第四象限D．一个数的算术平方根一定是正数【答案】C【解析】【分析】直接利用对顶角的性质以及算术平方根和平行线的性质以及坐标与图形的性质分别分析得出答案．【详解】解：A、相等的角是对顶角，错误；B、在同一平面内，不平行的两条直线一定相交，故此选项错误；C、点P（2，﹣3）在第四象限，正确；D、一个数的算术平方根一定是正数或零，故此选项错误．故选：C．此题主要考查了坐标与图形的性质、对顶角的性质等知识，正确把握相关性质是解题关键．10．如图，直线m⊥n，在某平面直角坐标系中，x轴∥m，y轴∥n，点A的坐标为（－4，2），点B的坐标为（2，－4），则坐标原点为（）A．O1B．O2C．O3D．O4【答案】A试题分析：因为A点坐标为（－4，2），所以，原点在点A的右边，也在点A的下边2个单位处，从点B来看，B（2，－4），所以，原点在点B的左边，且在点B的上边4个单位处．如下图，O1符合．考点：平面直角坐标系．11．在平面直角坐标中，点M(－2，3)在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】B【解析】∵−2<0，3>0，∴(−2,3)在第二象限，故选B.12．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如(1，0)，(2，0)，(2，1)，(3，2)，(3，1)，(3，0)，(4，0)．根据这个规律探索可得，第100个点的坐标为()A．(14，8)B．(13，0)C．(100，99)【答案】A【解析】【详解】由图形可知：点的个数依次是1、2、3、4、5、…，且横坐标是偶数时，箭头朝上， ∵1＋2＋3＋…＋13＝91，1＋2＋3＋…＋14＝105，∴第91个点的坐标为（13，0），第100个点横坐标为14．∵在第14行点的走向为向上，∴纵坐标为从第92个点向上数8个点，即为8；∴第100个点的坐标为（14，8）．故选A ．【点睛】本题主要考查了根据图形的变化找规律的方法，首先要分析图形中每一列的点人个数的变化规律是，1，2，3，4，5，…，由此找出第100个点所在的列，再根据奇数列是从上往下依次增加1，偶数列是从下往上依次增加1，由此即可找到第100个点所对应的坐标.13．已知()0,2A 、()10B ,，点P 在x 轴上，且PAB ∆的面积为5，则点P 的坐标为（） A ．()6,0B ．()4,0-C ．()4,0-或()6,0D ．无法确定【答案】C【解析】【分析】根据A 点的坐标可知BP 边上的高为2，而△PAB 的面积为5，点P 在x 轴上，说明BP=5，已知点B 的坐标，可求P 点坐标．【详解】解：∵B （1，0），A （0，2），点P 在x 轴上，∴BP 边上的高为2，又△PAB 的面积为5，∴BP=5，而点P 可能在点B （1，0）的左边或者右边，∴P （-4，0）或（6，0）．故选：C ．【点睛】本题考查了直角坐标系中，利用三角形的面积公式来求出三角形的底边．14．如图，在平面直角坐标系中，四边形OABC 是菱形，点C 的坐标为()2,3，则菱形OABC 的面积是（）A ．6B ．13C ．3132D ．313【答案】D【解析】【分析】作CH ⊥x 轴于点H ，利用勾股定理求出OC 的长，根据菱形的性质可得OA ＝OC ，即可求解．【详解】如图所示，作CH ⊥x 轴于点H ，∵四边形OABC 是菱形，∴OA ＝OC ，∵点C 的坐标为()2,3，∴OH ＝2，CH ＝3，∴OC ＝22OH CH +＝2223+＝13∴菱形OABC 的面积＝OA·CH ＝313 故选：D【点睛】本题考查菱形的性质、勾股定理、坐标与图形的性质、菱形的面积公式，解题的关键是学会添加辅助线，构造直角三角形．15．在平面直角坐标系中，对于平面内任一点（a ，b ），若规定以下三种变换：①f （a ，b ）=（-a ，b ），如f （1，2）=（-1，2）；②g （a ，b ）=（b ，a ），如g （1，2）=（2，1）；③h （a ，b ）=（-a ，-b ），如h （1，2）=（-1，-2）；按照以上变换有：g （h （f （1，2）））=g （h （-1，2））=g （1，-2）=（-2，1），那么h （f （g （3，-4）））等于（）A．（4，-3）B．（-4，3）C．（-4，-3）D．（4，3）【答案】C【解析】【分析】根据f（a，b）=（-a，b）．g（a，b）=（b，a）．h（a，b）=（-a，-b），可得答案．【详解】由已知条件可得h（f（g（3，-4）））= h（f（-4，3））= h（4，3）=（-4，-3）故选：C【点睛】本题考查了点的坐标，利用f（a，b）=（-a，b）．g（a，b）=（b，a）．h（a，b）=（-a，-b）是解题关键．16．在平面直角坐标系中．对于平面内任一点（m，n），规定以下两种变换：①f（m，n）=（m，﹣n），如f（2，1）=（2，﹣1）；②g（m，n）=（﹣m，﹣n），如g（2，1）=（﹣2，﹣1）．按照以上变换有：f[g（3，4）]=f（﹣3，﹣4）=（﹣3，4），那么g[f（3，2）]等于（）A．（3，2） B．（3．﹣2） C．（﹣3，2） D．（﹣3，﹣2）【答案】C【解析】【分析】根据f、g的规定进行计算即可得解．【详解】g[f（3，2）]=g（3，﹣2）=（﹣3，2）．故选C．【点睛】本题考查了点的坐标，读懂题目信息，理解f、g的运算方法是解题的关键．17．在直角坐标系中，若点P(2x－6，x－5)在第四象限，则x的取值范围是( )A．3＜x＜5 B．－5＜x＜3 C．－3＜x＜5 D．－5＜x＜－3【答案】A【解析】【分析】点在第四象限的条件是：横坐标是正数，纵坐标是负数．【详解】解：∵点P（2x-6，x-5）在第四象限，∴260 {50xx－＞－＜，解得：3＜x＜5．故选：A．【点睛】主要考查了平面直角坐标系中第四象限的点的坐标的符号特点．18．如图所示在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，……，组成一条平滑的曲线，点P从原点O出发沿这条曲线向右运动，速度为每秒2个单位长度，则第2019秒时，点P的坐标是（）A．（2018，0）B．（2019，1）C．（2019，﹣1）D．（2020，0）【答案】C【解析】分析：计算点P走一个半圆的时间，确定第2019秒点P的位置．详解：点运动一个半圆用时为2ππ＝2秒∵2019=1009×2+1∴2019秒时，P在第1010个的半圆的中点处∴点P坐标为（2019，-1）故选C．点睛：本题是平面直角坐标系下的规律探究题，解答时既要研究动点的位置规律，又要考虑坐标的象限符号．19．如图，已知棋子“车”的坐标为（﹣2，﹣1），棋子“马”的坐标为（1，﹣1），则棋子“炮”的坐标为（）A．（3，2）B．（﹣3，2）C．（3，﹣2）D．（﹣3，﹣2）【答案】C【解析】【分析】先根据棋子“车”的坐标画出直角坐标系，然后写出棋子“炮”的坐标．【详解】解：如图，棋子“炮”的坐标为（3，﹣2）．故选C．20．点A（-4，3）和点B（-8，3），则A，B相距（）A．4个单位长度B．12个单位长度C．10个单位长度D．8个单位长度【答案】A【解析】【分析】先根据A，B两点的坐标确定AB平行于x轴，再根据同一直线上两点间的距离公式解答即可．【详解】解：∵点A和点B纵坐标相同，∴AB平行于x轴，AB=﹣4﹣（﹣8）=4．故选A．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题训练(四)直角坐标系中的分类讨论
►类型一由距离产生的分类讨论
1．若点P到x轴的距离为3，到y轴的距离为2，则点P的坐标为____________________________．
2．已知点A(2a＋1，a＋7)到x轴、y轴的距离相等，求a的值．
►类型二由面积产生的分类讨论
3．已知△ABC的三个顶点均在坐标轴上，A(2，0)，C(0，－4)，且△ABC的面积为6，求点B的坐标．
►类型三由直角三角形产生的分类讨论
4．已知Rt△ABC的顶点A(2，0)，B(2，3)，斜边BC的长为5，则顶点C的坐标为________________________________________________________________________．
►类型四由全等三角形产生的分类讨论
5．已知点A(2，3)，AB⊥x轴于点B，O为原点．已知点P，Q分别在x轴、y轴上，且以P，O，Q为顶点的三角形与△ABO全等．
(1)若P(3，0)，求点Q的坐标；
(2)若点P在x轴的正半轴上，求点Q的坐标．
►类型五由等腰三角形产生的分类讨论
6．在平面直角坐标系xOy中，已知点A(2，3)，在坐标轴上找一点P，使得△AOP是等腰三角形，则这样的点P共有________个．
7．如图4－ZT－1，在平面直角坐标系中，长方形OABC的顶点A，C的坐标分别为(10，0)，(0，4)，D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，求点P的坐标．
图4－ZT－1
详解详析
1．[答案] (2，3)或(2，－3)或(－2，3)或(－2，－3)
[解析] 由点P到x轴的距离为3，知点P的纵坐标为±3；由点P到y轴的距离为2，知点P的横坐标为±2.故点P的坐标为(2，3)或(2，－3)或(－2，3)或(－2，－3)．
2．解：由题意，得
2a ＋1＝a ＋7或2a ＋1＝－a －7，
解得a ＝6或a ＝－83
. 3．解：设O 为坐标原点．
①当点B 在x 轴上时，S △ABC ＝12
AB·OC ， ∴12
AB ×4＝6， ∴AB ＝3，即B(－1，0)或(5，0)；
②当点B 在y 轴上时，S △ABC ＝12
BC·OA ， ∴12
BC ×2＝6，∴BC ＝6，即B(0，－10)或(0，2)．综上可知，点B 的坐标为(－1，0)或(5，0)或(0，－10)或(0，2)．
4．[答案] (－2，0)或(6，0)
[解析] 由BC 是斜边知AB ⊥AC ，而AB ∥y 轴，∴点C 在x 轴上，且AC ＝BC 2－AB 2＝52－32＝4，∴C(－2，0)或(6，0)．
5．解：在△AOB 中，∠ABO ＝90°，AB ＝3，OB ＝2.在△POQ 中，∠POQ ＝90°.
(1)∵OP ＝3＝AB ，当OQ ＝OB ＝2时，△POQ ≌△ABO ，∴点Q 的坐标为(0，2)或(0，－2)．
(2)①当OP ＝AB ＝3，OQ ＝OB ＝2时，△POQ ≌△ABO ，∴Q(0，2)或(0，－2)； ②当OP ＝OB ＝2，OQ ＝AB ＝3时，△QOP ≌△ABO ，∴Q(0，3)或(0，－3)．综上可知，点Q 的坐标为(0，2)或(0，－2)或(0，3)或(0，－3)．
6．[答案] 8
[解析] 如图所示，使得△AOP 是等腰三角形的点P 共有8个．
7．解：由题意，当△ODP 是腰长为5的等腰三角形时，有三种情况：
(1)如图①所示，OP ＝OD ＝5.过点P 作PE ⊥x 轴于点E ，则PE ＝4.
在Rt△POE中，由勾股定理，得OE＝OP2－PE2＝52－42＝3，∴此时点P的坐标为(3，4)．
(2)如图②所示，PD＝OD＝5，点P在点D的左侧．
过点P作PE⊥x轴于点E，则PE＝4.
在Rt△PDE中，由勾股定理，得DE＝PD2－PE2＝52－42＝3，∴OE＝OD－DE＝5－3＝2，
∴此时点P的坐标为(2，4)．
(3)如图③所示，PD＝OD＝5，点P在点D的右侧．
过点P作PE⊥x轴于点E，则PE＝4.
在Rt△PDE中，由勾股定理，得DE＝PD2－PE2＝52－42＝3，∴OE＝OD＋DE＝5＋3＝8，
∴此时点P的坐标为(8，4)．
综上可知，点P的坐标为(2，4)或(3，4)或(8，4)．。