(完整)全等三角形的提高拓展经典题(教师版)
学而思初二数学秋季班第4讲.全等三角形的经典模型(二).提高班.教师版
1初二秋季·第4讲·提高班·教师版等等…腰漫画释义满分晋级阶梯4全等三角形的 经典模型(二)三角形11级特殊三角形之直角三角形 三角形10级 勾股定理与逆定理 三角形9级全等三角形的经典模型(二)2初二秋季·第4讲·提高班·教师版OFEC B A A F COBEDHABCDO EOGFE CBA“手拉手”数学模型:⑴ ⑵ ⑶【引例】 如图,等边三角形ABE 与等边三角形AFC 共点于A ,连接BF 、CE ,求证:BF =CE 并求出 EOB 的度数. 知识互联网思路导航例题精讲题型一:“手拉手”模型3初二秋季·第4讲·提高班·教师版NMCBABNC【解析】 ∵△ABE 、△AFC 是等边三角形∴AE =AB ,AC =AF ,60∠=∠=︒EAB FAC ∴∠+∠=∠+∠EAB BAC FAC BAC 即∠=∠EAC BAF ∴AEC ABF △≌△∴BF =EC ∠=∠AEC ABF 又∵AGE BGO ∠=∠ ∴60∠=∠=︒BOE EAB ∴60∠=︒EOB【例1】 如图,正方形BAFE 与正方形ACGD 共点于A ,连接BD 、CF ,求证:BD =CF 并求出∠DOH 的度数. 【解析】 同引例,先证明ABD AFC △≌△∴BD =FC ,∠=∠BDA FCA ∵∠=∠DHO CHA ∴90∠=∠=︒DOH CAD【例2】 如图,已知点C 为线段AB 上一点,ACM △、BCN △是等边三角形.⑴ 求证:AN BM =.⑵ 将ACM △绕点C 按逆时针方向旋转180°,使点A 落在CB 上,请你对照原题图在图中画出符合要求的图形;⑶ 在⑵得到的图形中,结论“AN BM =”是否还成立,若成立,请证明;若不成立,请说明理由;⑷ 在⑵所得的图形中,设MA 的延长线交BN 于D ,试判断ABD △的形状,并证明你的结论. 【分析】 这是一个固定后运动变化的探索题,且在一定的条件下,探究原结论的存在性(不变性); 需要画图分析、判断、猜想、推理论证.【解析】 ⑴ ∵ACM △、BCN △是等边三角形∴AC CM =,BC CN =60ACM BCN ∠=∠=°典题精练OHGDF ECBA4初二秋季·第4讲·提高班·教师版ABCMNDNM CBA∴∠=∠ACN MCB 在ACN △和MCB △中 =⎧⎪∠=∠⎨⎪=⎩AC MC ACN MCB CN CB ∴ACN MCB △≌△(SAS ) ∴AN BM =⑵ 将ACM △绕点C 旋转如图:⑶ 在⑵的情况,结论AN BM =仍然成立.证明:∵60BCM NCA ∠=∠=°,CA CM =,CN CB =. ∴CAN CMB △≌△(SAS ),∴AN MB =.⑷ 如图,延长MA 交BN 于D ,则ABD △为等边三角形. 证明:∵60CAM BAD ABD ∠=∠=∠=°. ∴ABD △是等边三角形.【例3】 在ABC △中,90∠=BAC °,⊥AD BC 于D ,BF 平分∠ABC 交AD 于E ,交AC 于F .求证:AE=AF .54321A BCDE F【解析】 90∠=BAC °,390∴∠+∠=DAC °90⊥∴∠=︒AD BC ADC 90∴∠+∠=︒C DAC 3∴∠=∠C43152∠=∠+∠∠=∠+∠C ,BF 是ABC ∠的角平分线 12∴∠=∠典题精练题型二:双垂+角平分线模型5初二秋季·第4讲·提高班·教师版EN MDCBA NMD CBA 45∴∠=∠∴=AE AF【例4】 如图,已知ABC △中,90ACB ∠=°,CD AB ⊥于D ,ABC ∠的角平分线BE 交CD 于G ,交AC 于E ,GF AB ∥交AC 于F . 求证:AF CG =. 【分析】 要证AF CG =,一般想到证明这两条线段所在的三角形全等,由图形可知,不存在直接全等三角形,因此要想到添加辅助线构造全等三角形.【解析】 作EH AB ⊥于H∵12∠=∠,90ACB ∠=° ∴EC EH =(角平分线定理) 又∵CD AB ⊥ ∴3A ∠=∠∵431∠=∠+∠,52A ∠=∠+∠ ∴45∠=∠ ∴CE CG = ∴CG EH =又∵GF AB ∥,90∠=∠=AHE FGC ° ∴A CFG ∠=∠∴CFG EAH △≌△(AAS ) ∴=CF EA ,∴-=-CF EF EA EF , ∴CE AF = ∴AF CG =【例5】 已知:正方形ABCD 中,45MAN ∠=︒,MAN ∠绕点A 顺时针旋转,它的两边分别交线段CB DC 、于点M N 、.求证BM DN MN +=.【解析】 延长ND 到E 使DE BM = 典题精练题型三:半角模型54321HG FEDC BA54321GFE DC BA6初二秋季·第4讲·提高班·教师版DHFECBA∵四边形ABCD 是正方形 ∴AD =AB在ADE △和ABM △ =⎧⎪∠=∠⎨⎪=⎩AD AB ADE B DE BM ∴ADE ABM △≌△∴AM =AE ∠=∠BAM DAE∵45MAN ∠=︒ ∴45∠+∠=︒BAM NAD ∴45∠=∠=︒MAN EAN在AMN △和AEN △中 =⎧⎪∠=∠⎨⎪=⎩MA EA MAN EAN AN AN ∴AMN AEN △≌△ ∴MN =EN∴DE +DN =BM +DN=MN【例6】 如图,在四边形ABCD 中,180∠+∠=︒=B D AB AD ,,E 、F 分别是线段BC 、CD 上的点,且BE +FD =EF . 求证:12∠=∠EAF BAD .ABCDEF【解析】 延长FD 到H ,使DH =BE ,易证ABE ADH △≌△, 再证AEF AHF △≌△1122∴∠=∠=∠=∠EAF FAH EAH BAD【例7】 在等边三角形ABC 的两边AB 、AC 所在直线上分别有两点M 、N ,D 为三角形ABC 外一点,且︒=∠60MDN ,︒=∠120BDC ,BD=DC . 探究:当M 、N 分别在直线AB 、AC 上移7初二秋季·第4讲·提高班·教师版动时,BM 、NC 、MN 之间的数量关系.AM N BCDDCBN M A图1 图2⑴如图1,当点M 、N 在边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; ⑵如图2,点M 、N 在边AB 、AC 上,且当DM ≠DN 时,猜想⑴问的结论还成立吗?写 出你的猜想并加以证明.【解析】 ⑴如图1, BM 、NC 、MN 之间的数量关系BM +NC=MN . ⑵猜想:结论仍然成立.证明:如图,延长AC 至E ,使CE=BM ,连接DE .BD=CD 且120BDC ∠=.∴ 30=∠=∠DCB DBC .又△ABC 是等边三角形,∴90MBD NCD ECD ∠=∠=∠=. 在MBD △与ECD △中:BM CEMBD ECD BD CD =⎧⎪∠=∠⎨⎪=⎩∴MBD △≌ECD △(SAS ) . ∴DM=DE , BDM CDE ∠=∠ ∴60EDN BDC MDN ∠=∠-∠=在△MDN 与△EDN 中:⎪⎩⎪⎨⎧=∠=∠=DN DN EDN MDN DE DM ENMDC BA8初二秋季·第4讲·提高班·教师版∴MDN EDN △≌△(SAS) ∴MN NE NC BM ==+第04讲精讲:典型的旋转全等构图:“手拉手”全等模型探究; 【探究一】“手拉手”模型基本构图;如图1,若ABC ∆与ADE ∆旋转全等,则必有ABD ∆与ACE ∆为两个顶角相等的等腰三角形(即相似的等腰三角形);反之,如图2,若有两个顶角相等的等腰三角形ABD ∆与ACE ∆共顶角顶点,则必有ABC ∆与ADE ∆旋转全等;而图2正是“手拉手”模型的基本构图;图1EDC BA图2EDC BA【探究二】将探究一中的普通等腰三角形换成特殊的图形,例如等边三角形、等腰直角三角形、正方形,然后再探究结论如何变化;图3DCB图4E D CB A FG 图5ED CB A如图3、图4、图5,当两个等边三角形、等腰直角三角形、正方形共顶点时,ABC ∆与ADE ∆仍然旋转全等,并且有两个共同的结论; 结论1:ABC ∆≌ADE ∆;DE BC =;结论2:BC 与DE 所夹锐角等于两个等腰三角形的顶角;(倒角方法如下图6、图7、图8的八字模型)9初二秋季·第4讲·提高班·教师版图6图7图8【探究三】将探究二中的特殊图形旋转后结论是否仍然成立; 如下图9、图10、图11易得探究二中的两个结论仍然成立;图9E图10图11【探究四】深化探究二中图3的结论; 如图12,可得结论1:ABC ∆≌ADE ∆;DE BC =;结论2:︒=∠=∠=∠=∠60CAE BAD COE BOD ; 结论3:如图12、图13、图14,可得三对三角形全等(ABC ∆≌ADE ∆;AHD ∆≌AGB ∆;AGC ∆≌AHE ∆)图12图13图14结论4:如图15,连接GH ,可得AGH ∆为等边三角形;(由结论3可得AH AG =)图15NM O 图16EDC BA10 初二秋季·第4讲·提高班·教师版结论5:BE GH ∥;(由结论4可得︒=∠=∠60BAD AGH ) 结论6:连接AO ,可得AO 平分BOE ∠;(如图16,分别作BC AM ⊥、DE AN ⊥,AM 与AN 分别是全等三角形ABC ∆与ADE ∆对应边BC 和DE 上的高,故相等)11初二秋季·第4讲·提高班·教师版SFEDCBA MPNMH GFEDCBANM DCBA题型一 手拉手模型 巩固练习【练习1】 如图,DA ⊥AB ,EA ⊥AC ,AD=AB ,AE=AC ,则下列正确 的是( )A. ABD ACE △≌△B. ADF AES △≌△C. BMF CMS △≌△D. ADC ABE △≌△【解析】 D【练习2】 如图,正五边形ABDEF 与正五边形ACMHG 共点于A ,连接BG 、CF ,则线段BG 、CF 具有什么样的数量关系并求出∠GNC 的度数. 【解析】 先证ABG AFC △≌△可得BG =CF ,∠=∠ACF AGB ∵∠=∠NPG APC∴108∠=∠=︒GNC GAC题型二 双垂+角平分线模型 巩固练习【练习3】 已知AD 平分∠BAC ,⊥DE AB ,垂足为E ,⊥DF AC , 垂足为F ,且DB =DC ,则EB 与FC 的关系( )A. 相等B. EB <FCC. EB >FCD.以上都不对 【解析】 A题型三 半角模型 巩固练习【练习4】 如图,△ABC 是边长为3的等边三角形,△BDC 是等腰三角形,且∠BDC =120°.以D 为顶点作一个60°角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,则△AMN 的周长为 . 【解析】 6【练习5】 如图,在四边形ABCD 中,180∠+∠=︒B ADC ,AB AD =,E 、F 分别是边BC 、CD 延长线上的点,且复习巩固F E DCBAFEDC BA12 初二秋季·第4讲·提高班·教师版EHGDCBAFDEGCBA12EAF BAD =∠∠,求证:EF BE FD =-【解析】 证明:在BE 上截取BG ,使BG DF =,连接AG .∵180B ADC +=︒∠∠,180ADF ADC +=︒∠∠,∴B ADF =∠∠. ∵AB AD =,∴ABG ADF △≌△.∴BAG DAF =∠∠,AG AF =.∴12BAG EAD DAF EAD EAF BAD +=+==∠∠∠∠∠∠.∴GAE EAF =∠∠. ∵AE AE =, ∴AEG AEF △≌△. ∴EG EF =∵EG BE BG =-,∴EF BE FD =-.训练1. 如图,C 为线段AB 上一点,分别以AC 、CB 为边在AB 同侧作等边ACD △和等边BCE △,AE 交DC 于G 点,DB 交CE 于H 点,求证:GH AB ∥. 思维拓展训练(选讲)13初二秋季·第4讲·提高班·教师版A B C DH QNM【分析】 本题中,ACD △与BCE △是等边三角形,因此AC CD =,BC CE =,60ACD ECB ∠=∠=°,因为A 、C 、B 在同一条直线上,故60DCE ∠=°.这样可以得到ACE DCB △≌△,AEC DBC ∠=∠,故可以得到CEG CBH △≌△,则GC HC =,60CGH CHG ∠=∠=°,所以60ACG CGH ∠=∠=°,故GH AB ∥.【解析】 ∵ACD △和BCE △是等边三角形(已知)∴AC CD =,BC CE =(等边三角形的各边都相等)60ACD BCE ∠=∠=°(等边三角形的每个角都等于60°)∵180ACD DCE BCE ∠+∠+∠=° ∴60DCE ∠=°,120ACE DCB ∠=∠=°. 在ACE △和DCB △中,=⎧⎪∠=∠⎨⎪=⎩AC DCACE DCB CE CB∴ACE DCB △≌△(SAS )∴AEC DBC ∠=∠(全等三角形的对应角相等) 在BCH △和ECG △中,60∠=∠=⎧⎪=⎨⎪∠=∠⎩BCH ECG BC CE CBH CEG °∴BCH ECG △≌△(ASA )∴CH CG =(全等三角形的对应边相等) ∴CGH CHG ∠=∠(等边对等角)∵180GCH GHC CGH ∠+∠+∠=°(三角形内角和定理) ∴60GHC CGH ∠=∠=°.∴60ACG CGH ∠=∠=°(等量代换) ∴GH AB ∥(内错角相等,两直线平行)训练2. 条件:正方形ABCD ,M 在CB 延长线上,N 在DC 延长线上,45MAN ∠=︒.结论:⑴ MN DN BM =-;⑵ AH AB =.A B M C H ND14 初二秋季·第4讲·提高班·教师版【解析】 ⑴在CD 上取一点Q ,使DQ =BM先证AMB AQD △≌△ 可得AM =AQ再证AMN AQN △≌△∴MN =NQ∴DN DQ DN BM NQ MN -=-==⑵可证△ANH ≌△AND ,∴AH=AD=AB训练3. 如图,在Rt ABC △中,锐角ACB ∠的平分线交对边于E ,又交斜边的高AD 于O ,过O引OF BC ∥,交AB 于F ,请问AE 与BF 相等吗?理由是什么?OO 12ABCD E F FEDCBA21543G O54321G FE DC BA【解析】 相等.理由如下:如图,过E 作EG BC ⊥于G ∵EC 平分ACB ∠,∴12∠=∠ ∵90EAC ∠=°,AD BC ⊥ ∴1490∠+∠=°,2390∠+∠=° ∴34∠=∠ ∵35∠=∠, ∴45∠=∠∴AE AO =∵EC 平分ACB ∠,EA AC ⊥,EG BC ⊥ ∴EA EG =,∴AO EG =,∵FO BC ∥∴AFO B ∠=∠,90BDA FOA ∠=∠=° ∴BEG FAO ∠=∠∴AFO EBG △≌△(AAS ) ∴AF BE =∴AF EF BE EF -=- ∴AE BF =.N M DBA15初二秋季·第4讲·提高班·教师版ABCDO E训练4. 如图,△ABD 为等腰直角三角形,45∠=︒MAN ,求证:以BM 、MN 、DN 为边的三角形是直角三角形. 【解析】 过B 作BD 的垂线并取BQ =ND ,连接AQ 、QM先证∴=AQB AND AQ AN △≌△, 再证∴=AQM ANM MN QM △≌△∴以BM 、MN 、DN 为边的三角形是直角三角形.测试1. 如图,等腰直角△ADB 与等腰直角△AEC 共点于A ,连接BE 、CD ,则线段BE 、CD具有什么样的数量关系和位置关系 【解析】 先证明ABE ADC △≌△∴BE =CD ,再类似例1倒角即可得到BE ⊥CD测试2. 如图,△ABD 为等腰直角三角形,45∠=︒MAN ,求证:以BM 、MN 、DN 为边的三角形是直角三角形. 【解析】 过B 作BD 的垂线并取BQ =ND ,连接AQ 、QM先证∴=AQB AND AQ AN △≌△, 再证∴=AQM ANM MN QM △≌△∴以BM 、MN 、DN 为边的三角形是直角三角形.课后测N M DA初二秋季·第4讲·提高班·教师版第十五种品格:创新学会变通,变则通一天早上,一位贫困的牧师,为了转移哭闹不止的儿子的注意力,将一幅色彩缤纷的世界地图,撕成许多细小的碎片,丢在地上,许诺说:“小约翰,你如果能拼起这些碎片,我就给你二角五分钱。
(完整)初二全等三角形提高习题精选

全等三角形提高练习1. 如图所示,△AB C ≌△ADE ,BC 的延长线过点E ,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF 的度数。
2. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB 交于点C (A ′不在OB 上),则∠A ′CO3. 如图所示,在△ABC 中,∠A=90°,D 、E 分别是AC、BC EDC ,则∠C 的度数是多少?4.如图所示,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C ,A′B ′交AC 于点D ,若∠A ′DC=90°,则∠A=5. 已知,如图所示,AB=AC ,A D ⊥BC 于D ,且AB+AC+BC=50cm,而AB+BD+AD=40cm ,则AD是多少?6. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE ,垂足分别为D 、E ,若BD=3,CE=2,则DE= 7. 如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,连接EF ,交AD于G ,AD 与EF 垂直吗?证明你的结论。
8. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,D E ⊥AB 于E ,DF ⊥AC 于F ,△ABC的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
A B'C A B9. 已知,如图:AB=AE ,∠B=∠E ,∠BAC=∠EAD ,∠CAF=∠DAF ,求证:AF10. 如图,AD=BD ,A D ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点H ,则BH 与AC 相等吗?为什么?11. 如图所示,已知,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于F,且有BF=AC ,FD=CD ,求证:B E ⊥AC12. △DAC 、△EBC 均是等边三角形,AF 、BD 分别与CD 、CE 交于点M 、N ,求证:(1)AE=BD(2)CM=CN (3)△CMN 为等边三角形 (4)MN13. 已知:如图1,点C 为线段AB 上一点,△ACM 、△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN 于点F (1) 求证:AN=BM(2) 求证:△CEF 为等边三角形14. 如图所示,已知△ABC 和△BDE 都是等边三角形,下列结论:①AE=CD ;②BF=BG ;③BH平分∠AHD ;④∠AHC=60°;⑤△BFG 是等边三角形;⑥FG ∥AD ,其中正确的有( ) A .3个 B. 4个 C. 5个 D. 6个15. 已知:BD 、CE 是△ABC 的高,点F 在BD 上,BF=AC ,点G 在CE 的延长线上,CG=AB ,求证:A G ⊥AFC B B A A B16. 如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG求证:(1)AD=AG (2)AD 与AG 的位置关系如何17.如图,已知E 是正方形ABCD 的边CD 的中点,点F 在BC 上,且∠DAE=∠FAE求证:AF=AD-CF18.如图所示,已知△ABC 中,AB=AC ,D 是CB 延长线上一点,∠ADB=60°,E 是AD 上一点,且DE=DB ,求证:AC=BE+BC19.如图所示,已知在△AEC 中,∠E=90°,AD 平分∠EAC ,DF ⊥AC ,垂足为F ,DB=DC ,求证:BE=CF20.已知如图:AB=DE ,直线AE 、BD 相交于C ,∠B+∠D=180°,AF ∥DE ,交BD 于F ,求证:CF=CD21.如图,OC 是∠AOB 的平分线,P 是OC 上一点,PD ⊥OA 于D ,PE ⊥OB 于E ,F 是OC 上一点,连接DF 和EF ,求证:DF=EF22.已知:如图,BF ⊥AC 于点F ,CE ⊥AB 于点E ,且BD=CD ,求证:(1)△BDE ≌△CDF (2) 点D 在∠A 的平分线上BDB23.如图,已知AB ∥CD ,O 是∠ACD 与∠BAC 的平分线的交点,OE ⊥AC 于E ,且OE=2,则AB 与CD 之间的距离是多少?24.如图,过线段AB 的两个端点作射线AM 、BN ,使AM ∥BN ,按下列要求画图并回答: 画∠MAB 、∠NBA 的平分线交于E (1)∠AEB 是什么角?(2)过点E 作一直线交AM 于D ,交BN 于C ,观察线段DE 、CE ,你有何发现?(3)无论DC 的两端点在AM 、BN 如何移动,只要DC 经过点E ,①AD+BC=AB ;②AD+BC=CD谁成立?并说明理由。
(完整)全等三角形证明之能力拔高(经典题目)

全等三角形能力拔高题姓名:一、角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4.如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l 的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.二、二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF.3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC.MF E CBA5、已知:如图,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC 于F ,DB=DC , 求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB ,AB ∥CD. 求证:△ADC 是等腰三角形。
2、如图:AB=AC ,ME ⊥AB ,MF ⊥AC ,垂足分别为E 、F ,ME=MF 。
求证:MB=MCG FEDC BA3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE= 。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。
《全等三角形》拓展50题(含解析)

第一种情况:当∠B 是直角时,如图 1,△ABC 和△DEF 中,AC=DF,BC=EF,∠B
=∠E=90°,根据“HL”定理,可以知道 Rt△ABC≌Rt△DEF.
第二种情况:当∠B 是锐角时,如图 2,BC=EF,∠B=∠E<90°,在射线 EM 上有点
28.如图,△ABC 和△EBD 中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接 AE,CD,
AE 与 CD 交于点 M,AE 与 BC 交于点 N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接 BM,有以下两个结论:①BM 平分∠CBE;②MB 平分∠AMD.其中正确的
学习了三角形全等的判定方法(即“SAS”“ASA”“AAS”“SSS”)和直角三角形全等的判
定方法(即“HL”)后,小聪继续对“两个三角形满足两边和其中一边的对角对应相等”
的情形进行研究
小聪将命题用符号语言表示为:在△ABC 和△DEF 中,AC=DF,BC=EF,∠B=∠E.
小聪的探究方法是对∠B 分为“直角、钝角、锐角”三种情况进行探究.
.(填写序号)
13.已知:如图,BD 为△ABC 的角平分线,且 BD=BC,E 为 BD 延长线上的一点,BE=
BA,过 E 作 EF⊥AB,F 为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;
③AD=EF=EC;④AE=EC,其中正确的是
(填序号)
14.如图,两个边长均为 2 的正方形重叠在一起,O 是正方形 ABCD 的中心,则阴影部分
P、Q(点 Q 是不同于点 F 的点),若以 O、P、Q 为顶点的三角形与△OFP 全等,则符
合条件的点 P 的坐标为
6 探索全等三角形的条件(1)-边角边(SAS)(拓展提高)(解析版)

专题1.6 探索全等三角形的条件(1)-边角边(SAS )(拓展提高)一、单选题1.如图所示,在△ABC 中,∠ACB =90°,CD 平分∠ACB ,在BC 边上取点E ,使EC =AC ,连接DE ,若∠A =50°,则∠BDE 的度数是( )A .10°B .20°C .30°D .40°【答案】A 【分析】先由直角三角形的性质得∠B =90°﹣∠A =40°,再证△CDE ≌△CDA (S A S ),得∠CED =∠A =50°,然后由三角形的外角性质即可得出答案.【详解】∵∠ACB =90°,∠A =50°,∴∠B =90°﹣∠A =40°,∵CD 平分∠ACB ,∴∠ECD =∠ACD ,在△CDE 和△CDA 中,EC AC ECD ACD CD CD =⎧⎪∠=∠⎨⎪=⎩,∴△CDE ≌△CDA (S A S ),∴∠CED =∠A =50°,又∵∠CED =∠B +∠BDE ,∴∠BDE =∠CED ﹣∠B =50°﹣40°=10°,故选:A .【点睛】本题考查了全等三角形的判定与性质.2.如图所示,AD 是ABC ∆的边BC 上的中线,5AB =cm ,4=AD cm ,则边AC 的长度可能是( )A .3cmB .5cmC .14cmD .13cm【答案】B 【分析】延长AD 至M 使DM =AD ,连接CM ,根据SAS 得出≅ADB MDC ,得出AB =CM =4cm ,再根据三角形的三边关系得出AC 的范围,从而得出结论;【详解】解:延长AD 至M 使DM =AD ,连接CM ,∵AD 是ABC ∆的边BC 上的中线,∴BD =CD ,∵∠ADB =∠CDM ,∴≅ADB MDC ,∴MC =AB =5cm ,AD =DM =4cm ,在AMC 中,3<AC <13,故选:B【点睛】本题考查了全等三角形的判定与性质以及三角形的三边关系,根据三角形的三边关系找出AC 长度的取值范围是解题的关键.3.如图,已知AB AD =,BC DE =,且10CAD ∠=︒,25B D ∠=∠=︒,120EAB ∠=︒,则EGF ∠的度数为( )A .120︒B .135︒C .115︒D .125︒【答案】C 【分析】由已知可得△ABC ≌△ADE ,故有∠BAC =∠DAE ,由∠EAB =120°及∠CAD =10°可求得∠AFB 的度数,进而得∠GFD 的度数,在△FGD 中,由三角形的外角等于不相邻的两个内角的和即可求得∠EGF 的度数.【详解】在△ABC 和△ADE 中AB AD B D BC DE =⎧⎪∠=∠⎨⎪=⎩∴ △ABC ≌△ADE (SAS )∴∠BAC =∠DAE∵∠EAB =∠BAC +∠DAE +∠CAD =120°∴∠BAC =∠DAE ()112010552=⨯︒-︒=︒ ∴∠BAF =∠BAC +∠CAD =65°∴在△AFB 中,∠AFB =180°-∠B -∠BAF =90°∴∠GFD =90°在△FGD 中,∠EGF =∠D +∠GFD =115°故选:C【点睛】本题考查了三角形全等的判定和性质、三角形内角和定理,关键求得∠BAC 的度数.4.如图,AD 是ABC 的中线,E ,F 分别是AD 和AD 延长线上的点,且DE DF =,连接BF ,CE ,下列说法:①ABD △和ACD △面积相等; ②BAD CAD ∠=∠; ③BDF ≌CDE △;④//BF CE ;⑤CE AE =.其中正确的是( )A.①②B.①③C.①③④D.①④⑤【答案】C【分析】根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE.【详解】解:∵AD是△ABC的中线,∴BD=CD,∴△ABD和△ACD面积相等,故①正确;∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;在△BDF和△CDE中,BD CDBDF CDE DF DE=⎧⎪∠=∠⎨⎪=⎩,∴△BDF≌△CDE(SAS),故③正确;∴∠F=∠DEC,∴BF∥CE,故④正确;∵△BDF≌△CDE,∴CE=BF,故⑤错误,正确的结论为:①③④,故选:C.【点睛】本题考查了全等三角形的判定与性质,等底等高的三角形的面积相等,熟练掌握三角形全等的判定方法并准确识图是解题的关键.5.如图已知ABC ∆中,12AB AC cm ==,B C ∠=∠,8BC cm =,点D 为AB 的中点.如果点P 在线段BC 上以2/cm s 的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.若点Q 的运动速度为v ,则当BPD ∆与CQP ∆全等时,v 的值为( )A .1B .3C .1或3D .2或3【答案】D 【分析】设运动时间为t 秒,由题目条件求出BD=12AB=6,由题意得BP=2t ,则CP=8-2t ,CQ=vt ,然后结合全等三角形的判定方法,分两种情况列方程求解.【详解】解:设运动时间为t 秒,∵12AB AC cm ==,点D 为AB 的中点.∴BD=12AB=6, 由题意得BP=2t ,则CP=8-2t ,CQ=vt ,又∵∠B=∠C∴①当BP=CQ ,BD=CP 时,BPD ∆≌CQP ∆∴2t=vt ,解得:v=2②当BP=CP ,BD=CQ 时,BPD ∆≌CPQ ∆∴8-2t=2t ,解得:t=2将t=2代入vt=6,解得:v=3综上,当v=2或3时,BPD ∆与CQP ∆全等故选:D【点睛】本题主要考查了全等三角形全等的判定、熟练掌握全等三角形的判定方法是解题的关键,学会用分类讨论的思想思考问题,属于中考常考题型.6.如图1,已知AB AC =,D 为BAC ∠的角平分线上面一点,连接BD ,CD ;如图2,已知AB AC =,D 、E 为BAC ∠的角平分线上面两点,连接BD ,CD ,BE ,CE ;如图3,已知AB AC =,D 、E 、F 为BAC ∠的角平分线上面三点,连接BD ,CD ,BE ,CE ,BF ,CF ;…,依次规律,第n 个图形中有全等三角形的对数是( ).A .nB .21n -C .(1)2n n +D .3(1)n +【答案】C 【分析】根据条件可得图1中△ABD ≌△ACD 有1对三角形全等;图2中可证出△ABD ≌△ACD ,△BDE ≌△CDE ,△ABE ≌△ACE 有3对三角形全等;图3中有6对三角形全等,根据数据可分析出第n 个图形中全等三角形的对数.【详解】解:∵AD 是∠BAC 的平分线,∴∠BAD=∠CAD .在△ABD 与△ACD 中,AB=AC ,∠BAD=∠CAD ,∴△ABD≌△ACD.∴图1中有1对三角形全等;同理图2中,△ABE≌△ACE,∴BE=EC,∵△ABD≌△ACD.∴BD=CD,又DE=DE,∴△BDE≌△CDE,∴图2中有3对三角形全等;同理:图3中有6对三角形全等;由此发现:第n个图形中全等三角形的对数是()12n n+.故选:C.【点睛】此题主要考查了三角形全等的判定以及规律的归纳,解题的关键是根据条件证出图形中有几对三角形全等,然后寻找规律.二、填空题7.如图所示,点O为AC的中点,也是BD的中点,那么AB与CD的关系是________.【答案】平行且相等【分析】只需要证明△AOB≌△COD,根据全等三角形的性质和平行线的判定定理即可得出结论.【详解】解:∵点O为AC的中点,也是BD的中点,∴AO=OC,BO=OD,又∵∠AOB=∠DOC,∴△AOB≌△COD(SAS)∴AB=CD,∠A=∠C,即AB 与CD 的关系是平行且相等,故答案为:平行且相等.【点睛】本题考查全等三角形的性质和判定,平行线的判定定理.掌握全等三角形的判定定理是解题关键.8.在ABC ∆中,AD 是BC 边上的中线,若7,5AB AC ==,则AD 长的取值范围是_________.【答案】16AD <<【分析】利用中线的性质,作辅助线AD=DE ,构造全等三角形()ADB EDC SAS ≅,再有全等三角形对应边相等的性质,解得7CE AB ==,最后由三角形三边关系解题即可.【详解】如图,AD 为BC 边上的中线,延长AD 至点E ,使得AD=DE在△ADB 和△EDC 中BD DC ADB CDE AD DE =⎧⎪∠=∠⎨⎪=⎩()ADB EDC SAS ∴≅7CE AB ∴==CE AC AE AC CE -<<+75275AD ∴-<<+16AD ∴<<故答案为:16AD <<.【点睛】本题考查三角形三边的关系,其中涉及全等三角形的判定与性质等知识,是重要考点,掌握相关知识、正确作出辅助线是解题的关键.9.如图,在ABC 中,,90AC BC ACB =∠=︒,点D 是BC 上的一点,过点B 作//BE AC ,使BE CD =,连接CE 与AD 相交于点G ,则AD 与CE 的关系是_______________.【答案】AD ⊥CE ,AD =CE【分析】证明△ACD ≌△CBE ,得到∠CAD =∠BCE ,AD =CE ,结合∠ACB =90°,可得∠CGD =90°,从而可得结果.【详解】解:由题意可知:∵∠ACB =90°,BE ∥AC ,∴∠ACB =∠EBC =90°,在Rt △ACD 和Rt △CBE 中,AC CB ACD CBE CD BE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△CBE (SAS ),∴∠CAD =∠BCE ,AD =CE ,∵∠CAD +∠CDA =90°,∴∠CDA +∠BCE =90°,∴∠CGD =180°-(∠CDA +∠BCE )=90°,∴AD ⊥CE ,综上:AD ⊥CE ,AD =CE ,故答案为:AD ⊥CE ,AD =CE .【点睛】本题考查了全等三角形的判定和性质,解题的关键是证明△ACD ≌△CBE ,得到角和线段之间的相等关系.10.如图,在ABC 中,90B ∠>︒,CD 为ACB ∠的角平分线,在AC 边上取点E ,使DE DB =,且90AED ∠>︒,若A x ∠=︒,ACB y ∠=︒,则AED =∠_______.(用x 、y 的代数式表示)【答案】180°-x°-y° 【分析】在AC 上截取CF =BC ,根据全等三角形的性质可得BD =DF =DE ,可得∠AED =∠ABC ,根据三角形的内角和可求解.【详解】解:如图,在AC 上截取CF =BC ,∵CD 为∠ACB 的角平分线,∴∠ACD =∠BCD ,∵CF =BC ,∠ACD =∠BCD ,CD =CD ,∴△BDC ≌△FDC (SAS ),∴∠ABC =∠CFD ,DF =BD ,∵BD =DE ,∴DE =DF ,∴∠DEF =∠DFE ,∴∠AED =∠CFD ,∵∠A =x°,∠ACB =y°,∴∠ABC =180°-∠A -∠ACB =180°-x°-y°,∴∠AED =∠DBC =180°-x°-y°,故答案为:180°-x°-y°.【点睛】本题考查了全等三角形的判定和性质,三角形内角和定理,添加恰当辅助线构造全等三角形是解本题的关键.11.如图,在ABC 中,90,,,ACB AC BC CE BE CE ∠=︒=⊥与AB 相交于点F ,且CD BE =,则ACD CBA DAF ∠∠∠、、之间的数量关系是_____________.【答案】=ACD CBA DAF ∠∠∠+【分析】先利用同角的余角相等得到ACD ∠=CBE ∠,再通过证ACD CBE ≌,得到==90ADC CEB ∠︒∠即==90ADF CEB ∠︒∠,再 利用三角形内角和得=AFD ADF EFB FEB ︒--︒-∠-180∠∠180∠可得=DAF EBF ∠∠,最后利用角的和差即可得到答案,ACD ∠==++CBE CBA EFB CBA DAF ∠∠∠=∠∠.【详解】证明:∵90ACB ∠=︒,CE BE ⊥∴+90ACD ECB ∠=︒∠,+90CBE ECB ∠=︒∠∴ACD ∠=CBE ∠又∵AC BC =,CD BE =∴ACD CBE ≌∴==90ADC CEB ∠︒∠即==90ADF CEB ∠︒∠∵=AFD EFB ∠∠∴=AFD ADF EFB FEB ︒--︒-∠-180∠∠180∠即=DAF EBF ∠∠∴ACD ∠==++CBE CBA EFB CBA DAF ∠∠∠=∠∠故答案为:=ACD CBA DAF ∠∠∠+.【点睛】本题考查了直角三角形的性质、内角和定理以及全等三角形的判定和性质,能通过性质找到角与角之间的关系是解答此题的关键.12.如图所示的是一张直角ABC 纸片(90C ∠=︒),其中30BAC ∠=︒,如果用两张完全相同的这种纸片恰好能拼成如图2所示的ABD △,若2BC =,则ABD △的周长为______.【答案】12【分析】根据题意证明三角形全等即可得解;【详解】如图所示,由题可知ABC ADC ≅△△,∴30BAC DAC ∠=∠=︒,90ACB ACD ∠=∠=︒,2BC BD ==,∴60BAD ∠=︒,180BCD ∠=︒,∴B ,C ,D 在一条直线上,∵60B D ∠=∠=︒,∴△ABD 是等边三角形,∴△ABD 的周长()3312BD BC CD==+=;故答案是12.【点睛】本题主要考查了全等三角形的判定与性质,结合等边三角形的性质计算是解题的关键. 13.已知:如图,在长方形ABCD 中,AB =4,AD =6.延长BC 到点E ,使CE =2,连接DE ,动点P 从点B 出发,以每秒2个单位的速度沿BC ﹣CD ﹣DA 向终点A 运动,设点P 的运动时间为t 秒,当t 的值为__秒时,△ABP 和△DCE 全等.【答案】1或7【分析】分两种情况进行讨论,根据题意得出BP=2t=2或AP=16-2t=2即可求得结果.【详解】因为AB=CD,若∠ABP=∠DCE=90°,BP=CE=2,根据SAS证得△ABP≌△DCE,由题意得:BP=2t=2,所以t=1,因为AB=CD,若∠BAP=∠DCE=90°,AP=CE=2,根据SAS证得△BAP≌△DCE,由题意得:AP=16﹣2t=2,解得t=7.所以,当t的值为1或7秒时.△ABP和△DCE全等.故答案为:1或7.【点睛】本题考查了全等三角形的判定,要注意分类讨论.14.如图,△P AB与△PCD均为等腰直角三角形,点C在PB上,若△ABC与△BCD的面积之和为10,则△P AB与△PCD的面积之差为_____.【答案】10【分析】由“SAS”可证△APC≌△BPD,可得S△APC=S△BPD,由面积和差关系可求解.【详解】解:∵△P AB与△PCD均为等腰直角三角形,∴PC=PD,∠APB=∠CPD=90°,AP=BP,∴△APC≌△BPD(SAS),∴S△APC=S△BPD,∵S△APB﹣S△PCD=S△APC+S△ABC﹣(S△BPD﹣S△BCD),∴S△APB﹣S△PCD=S△BCD+S△ABC=10,故答案为:10.【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,证明△APC≌△BPD是本题的关键.三、解答题15.如图所示,AC BC ⊥,DC EC ⊥,垂足均为点C ,且AC BC =,EC DC =.求证:AE BD =.【答案】见解析【分析】根据SAS 证明ACE BCD △≌△即可.【详解】证明:∵AC BC ⊥,DC EC ⊥,∴90ACB ECD ∠=∠=︒∴ACB BCE ECD BCE ∠+∠=∠+∠即ACE BCD ∠=∠在ACE 和BCD △中AC BC ACE BCD EC DC =⎧⎪∠=∠⎨⎪=⎩∴()SAS ACE BCD ≌△△ ∴AE BD =【点睛】此题主要考查了全等三角形的判定与性质,证明ACE BCD ∠=∠是解答此题的关键. 16.如图,点B ,E ,C ,F 在一条直线上,//,,AB DE AB DE BE CF ==.求证:A D ∠=∠.【答案】证明见解析【分析】根据平行得出B DEF ∠=∠,然后用“边角边”证明ABC DEF △≌△即可.【详解】证明:∵//AB DE ,∴B DEF ∠=∠.∵BE CF =,∴BE EC CF EC +=+.∴BC EF =.在ABC 和DEF 中,,,,AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩∴ABC DEF △≌△.∴A D ∠=∠.【点睛】本题考查了全等三角形的判定与性质,解题关键是熟练运用已知条件,推导证明出全等三角形判定所需条件,运用全等三角形判定定理证明.17.如图,四边形ABCD 的对角线交于点O ,点E 、F 在AC 上,//DF BE ,且DF BE =,AE CF =.求证:AB CD =,且//AB CD .【答案】见解析【分析】根据已知条件可证得ABE CDF △≌△,从而由全等三角形的性质可得要证的结论.【详解】//DF BEBEO DFO ∴∠=∠AEB CFD ∴∠=∠又DF BE =∵,AE CF =ABE CDF ∴△≌△AB CD ∴=,BAE DCF ∠=∠//AB CD ∴【点睛】本题考查了三角形全等的的判定的性质,关键是得出AEB CFD ∠=∠.18.如图,BD ,CE 分别是ABC 的边AC 和AB 边上的高,点P 在BD 的延长线上,点Q 在CE 上,BP AC =,CQ AB =,请说明AQ 与AP 的关系.【答案】AP =AQ 且AP ⊥AQ【分析】由于BD AC ⊥,CE AB ⊥,可得ABD ACE ∠=∠,又由对应边的关系,进而得出ABP QCA ∆≅∆,即可得出AQ=AP .在此基础上,可证明90PAQ ∠=︒.【详解】解:证明:BD AC ⊥,CE AB ⊥(已知),90BEC BDC ∴∠=∠=︒,90ABD BAC ∴∠+∠=︒,90ACE BAC ∠+∠=︒(直角三角形两个锐角互余),ABD ACE ∴∠=∠(等角的余角相等),在ABP ∆和QCA ∆中,BP AC ABD ACE CQ AB =⎧⎪∠=∠⎨⎪=⎩()ABP QCA SAS ∴∆≅∆,∴=AP AQ .ABP QCA ∆≅∆,CAQ P ∴∠=∠,BD AC ⊥,即90P CAP ∠+∠=︒,90CAQ CAP ∴∠+∠=︒,即90QAP ∠=︒,AP AQ ∴⊥.【点睛】本题主要考查了全等三角形的判定及性质问题,能够熟练掌握并运用.19.平面上有ACD △与,BCE AD 与BE 相交于点,P AC 与BE 相交于点,M AD 与CE 相交于点N ,若,,AC BC CD CE ECD ACB ==∠=∠.(1)求证:≌ACD BCE ;(2)55,145ACE BCD ∠=︒∠=︒,求BPD ∠的度数.【答案】(1)证明见解析;(2)∠BPD =140°.【分析】(1)利用SAS 证明△ACD ≌△BCE 即可;(2)由全等三角形的性质可知:∠A =∠B ,再根据已知条件和四边形的内角和为360°,即可求出∠BPD 的度数.【详解】解:(1)证明:∵∠ACB =∠ECD ,∠ACE =∠ACE ,∴∠BCE =∠ACD ,在△ACD 和△BCE 中,AC BC BCE ACD CD CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS );(2)∵△ACD ≌△BCE ,∴∠A =∠B ,∠BCE =∠ACD ,∴∠BCA =∠ECD ,∵∠ACE =55°,∠BCD =155°,∴∠BCA +∠ECD =100°,∴∠BCA =∠ECD =50°,∵∠ACE =55°,∴∠ACD =105°∴∠A +∠D =75°,∴∠B +∠D =75°,∵∠BCD =145°,∴∠BPD =360°-75°-145°=140°.【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理,解题的关键是利用整体的数学思想求出∠B+∠D=75°.20.(1)如图1,一扇窗户打开后,用窗钩AB将其固定,这里所运用的几何原理是:;(2)如图2,小河的旁边有一个甲村庄所示,现计划在河岸AB上建一个泵站,向甲村供水,使得所铺设的供水管道最短,请在上图中画出铺设的管道,这里所运用的几何原理是:(3)如图3,在新修的小区中,有一条“Z”字形长廊ABCD,其中AB∥CD,在AB,BC,CD三段长廊上各修一小凉亭E,M,F,且BE=CF,点M是BC的中点,在凉亭M与F之间有一池塘,不能直接到达,要想知道M与F之间的距离,只需要测出线段ME的长度(用两个字母表示线段).这样做合适吗?请说出理由.【答案】(1)三角形具有稳定性;(2)见解析,垂线段最短;(3)合理,见解析【分析】(1)根据三角形的稳定性解答;(2)根据垂线段最短解答;(3)首先证明△MEB≌△MFC,根据全等三角形的性质可得ME=MF.【详解】解:(1)一扇窗户打开后,用窗钩AB要将其固定,这里所运用的几何原理是三角形具有稳定性;故答案为:三角形具有稳定性;(2)过甲向AB作垂线,如图2所示;运用的原理是:垂线段最短;故答案为:垂线段最短;(3)合理,∵AB ∥CD ,∴∠B =∠C ,∵点M 是BC 的中点,∴MB =MC ,在△MCF 和△MBE 中BE CF B C BM CM =⎧⎪∠=∠⎨⎪=⎩,∴△MEB ≌△MFC (SAS ),∴ME =MF ,∴想知道M 与F 之间的距离,只需要测出线段ME 的长度.【点睛】此题主要考查了垂线段的性质,三角形的稳定性,以及全等三角形的应用,关键是掌握全等三角形判定定理,会用它证明对应边相等.。
全等三角形的提高拓展训练全等三角形经典题型50题(含答案)

全等三角形的提高拓展训练知识点睛全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等. 寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边常是对应边. (4)有公共角的,公共角常是对应角. (5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键. 全等三角形的判定方法:(1) 边角边定理(SAS ):两边和它们的夹角对应相等的两个三角形全等. (2) 角边角定理(ASA ):两角和它们的夹边对应相等的两个三角形全等. (3) 边边边定理(SSS ):三边对应相等的两个三角形全等.(4) 角角边定理(AAS ):两个角和其中一个角的对边对应相等的两个三角形全等. (5) 斜边、直角边定理(HL ):斜边和一条直角边对应相等的两个直角三角形全等. 全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.例题精讲板块一、截长补短【例1】 (06年北京中考题)已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.DOECB AD【例2】 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?【变式拓展训练】如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?【例3】 已知:如图,ABCD 是正方形,∠F AD =∠F AE . 求证:BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆,连结CD 、BE 相交于点O .求证:OA 平分DOE ∠.NC D EB M A F E DCB A O ED CA【例5】 (北京市、天津市数学竞赛试题)如图所示,ABC ∆是边长为1的正三角形,BDC∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.【例6】 五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°, 求证:AD 平分∠CDE板块二、全等与角度【例7】如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数.D CB ANM D CB AC EDBA【例8】在等腰ABC ∆中,AB AC =,顶角20A ∠=︒,在边AB 上取点D ,使AD BC =,求BDC ∠.【例9】(“勤奋杯”数学邀请赛试题) 如图所示,在ABC ∆中,AC BC =,20C ∠=︒,又M 在AC 上,N 在BC 上,且满足50BAN ∠=︒,60ABM ∠=︒,求NMB ∠.【例10】 在四边形ABCD 中,已知AB AC =,60ABD ︒∠=,76ADB ︒∠=,28BDC ︒∠=,求DBC ∠的度数.【例11】 (日本算术奥林匹克试题) 如图所示,在四边形ABCD 中,12DAC ︒∠=,36CAB ︒∠=,48ABD ︒∠=,24DBC ︒∠=,求ACD ∠的度数.CDBADCBAANMCBA【例12】 (河南省数学竞赛试题) 在正ABC ∆内取一点D ,使DA DB =,在ABC ∆外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.【例13】 (北京市数学竞赛试题) 如图所示,在ABC ∆中,44BAC BCA ︒∠=∠=,M 为ABC∆内一点,使得30MCA ︒∠=,16MAC ︒∠=,求BMC ∠的度数.M CA B全等三角形证明经典50题(含答案)1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知:D是AB中点,∠ACB=90°,求证:12 CD ABADB C3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF 。
人教版数学八年级上册《第十二章 全等三角形》期末高分突破卷附解析教师版

人教版数学八年级上册《第十二章全等三角形》期末高分突破卷附解析教师版一、单选题(每题3分,共30分)(共10题;共30分)1.(3分)如图,△ABC△△A'B'C',则△C的度数是()A.107°B.73°C.56°D.51°【答案】B【解析】【解答】解:∵△ABC△△A'B'C',∴△B'=△B=51°,∴△C=180°-△A-△B=180°-56°-51°=73°.故答案为:B.【分析】根据全等三角形的性质得出△B'=△B=51°,再根据三角形内角和定理得出△C=180°-△A-△B,即可得出答案.2.(3分)如图,在ΔABC中,∠C=90°,AD平分∠CAB,若AB=10,CD=3,则△ABD的面积是()A.9B.12C.15D.24【答案】C【解析】【解答】解:如图,过点D作DE⊥AB于E,∵∠C=90°,AD平分∠BAC,∴DE=CD=3,∴ΔABD的面积=12AB·DE=12×10×3=15.故答案为:C.【分析】过点D作DE△AB于E,由角平分线的性质可得DE=CD=3,然后根据三角形的面积公式进行计算.3.(3分)如图,用直尺和圆规作图,以点O为圆心,适当长为半径画弧,分别交OB,OA于点E、D,再分别以点E、D为圆心,大于12ED的长为半径画弧,两弧交于点C,连接OC,则△ODC△OEC的理由是()A.SSS B.SAS C.AAS D.ASA【答案】A【解析】【解答】解:连接EC,CD.在△ODC和△OEC中,{OE=OD OC=OC EC=DC,∴△ODC△△OEC(SSS).故答案为:A.【分析】由作图可知OE=OD,CE=CD,结合OC为公共边,根据SSS可证△ODC△△OEC.4.(3分)如图,要测量中心湖两岸相对两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再在BF的垂线DG上取点E,使点A,C,E在一条直线上,可得△ABC△△EDC.判定全等的依据是()A.SSS B.SAS C.ASA D.HL 【答案】C【解析】【解答】解:在△ABC和△EDC中{∠ABC=∠EDC=90°BC=CD∠BCA=∠DCE,∴△ABC△△EDC(ASA),依据是两角及这两角的夹边对应相等.故答案为:C.【分析】根据ASA证明△ABC△△EDC.5.(3分)如图,在△ABC和△DEF中,AB=DE,△A=△D,添加一个条件不能判定这两个三角形全等的是()A.AC=DF B.△B=△E C.BC=EF D.△C=△F【答案】C【解析】【解答】解:A、在△ABC与△DEF中,{AB=DE ∠A=∠D AC=DF,∴△ABC△△DEF(SAS),故A不符合题意;B、在△ABC与△DEF中,{∠B=∠E AB=DE ∠A=∠D,∴△ABC△△DEF(ASA),故B不符合题意;C、在△ABC与△DEF中,BC=EF,AB=DE,△A=△D ∴不能判断△ABC△△DEF,故C符合题意;D、在△ABC与△DEF中,{∠C=∠F ∠A=∠D AB=DE,∴△ABC△△DEF(AAS),故D不符合题意.故答案为:C.【分析】根据全等三角形的判定定理逐项进行判断,即可得出答案.6.(3分)如图,在△ABO和△CDO中,OA=OB=a,OC=OD=b,∠AOB与∠COD互补,连接AC、BD,E是BD的中点,下列结论正确的是()A.AD=BC B.AC=2OEC.∠BOD=2∠AOC D.|a−b|<OE<a+b【答案】B【解析】【解答】解:连接AD 、BC ,∵OA=OB,OC=OD,∴AD=BC需满足的条件是△AOD△ △BOC,∴∠AOB与∠COD不一定相等,∴∠AOD与∠BOC不一定相等,∴△AOD与△BOC不一定全等,∴AD与BC不一定相等,故A错误;作DF//OB交OE 的延长线于点F ,则∠F=∠BOE,∵E是BD 的中点,∴DE=BE,在△DFE和△BOE中,{∠F=∠BOE∠DEF=∠BEODE=BE,∴△DFE△ △BOE(AAS),∴DF=OB=OA,∵∠AOB+∠COD=180°,∴∠AOC+∠BOD=180°,∵∠FDO+∠BOD=180°,∴∠FDO=∠AOC,在△FDO和△AOC中,{DF=OA∠FDO=∠AOCDO=OC,∴△FDO△ △AOC(SAS),∴FO=AC,∴FO=2OE,∴AC=2OE,故B正确;∵∠AOC+∠BOD=180°,∴∠BOD=2∠AOC需满足的条件是∠AOC=60°,显然与已知条件不符,∴∠BOD不一定等于2∠AOC,故C错误;∵|DF−OD|<FO<DF+OD,且DF=OB=a,OD=b,∴|a−b|<2OE<a+b,∴12|a−b|<OE<12(a+b),故D错误,故答案为:B.【分析】连接AD、BC,AD=BC需满足的条件是△AOD△△BOC,由△AOB与△COD不一定相等,可推导出△AOD与△BOC不一定相等,则△AOD与△BOC不一定全等,可判断A错误;作DF△OB交OE的延长线于点F,则△F=△BOE,可证明△DFE△△BOE,则DF=OB=OA,再证明△FDO△△AOC,得FO=AC=2OE,可判断B正确;由△AOC+△BOD=180°,可知△BOD=2△AOC需满足的条件是△AOC=60°,与已知条件不符,可判断C错误;由|DF−OD|<FO<DF+OD,得|a−b|<2OE<a+b,则12|a−b|<OE<12(a+b),可判断D错误.7.(3分)如图,△ABC≌△ADE,∠BAC=80°,∠B=40°,则∠E的度数为()A.40°B.50°C.60°D.80°【答案】C【解析】【解答】解:∵△ABC≌△ADE,∴∠E=∠C,在△ABC中,∠BAC=80°,∠B=40°,∴∠E=∠C=180°−80°−40°=60°,故答案为:C.【分析】根据全等三角形的性质可得∠E=∠C,再利用三角形的内角和可得∠E=∠C=180°−80°−40°=60°。
专题02 全等三角形模型解题九年级数学中考复习专题训练模型解题高分攻略(教师版)

专题二全等三角形模型解题解题模型一平移模型针对训练1.(2018•桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.(1)求证:△ABC≌△DEF;(2)若∠A=55°,∠B=88°,求∠F的度数.解题模型二对称模型针对训练2.(2018•南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.3.(2018•广州)如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.图示:图示:4.(2018•乐山)如图,已知∠1=∠2,∠3=∠4,求证:BC=BD.5.(2018•武汉)如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.6.(2017•郴州)已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.7.(2018•泰州)如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.8.(2018•镇江)如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.(1)求证:△ABE≌△ACF;(2)若∠BAE=30°,则∠ADC=°.解题模型三旋转模型针对训练8.(2018•昆明)如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:BC=DE.10.(2018•柳州)如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.11.(2017•常州)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.图示:12.(2017•恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.解题模型四平移+旋转模型针对训练13.(2018•菏泽)如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.14.(2018•铜仁)已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.15.(2017•孝感)如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD.图示:16.(2018•怀化)已知:如图,点A,F,E,C在同一直线上,AB∥DC,AB=CD,∠B=∠D.(1)求证:△ABE≌△CDF;(2)若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.解题模型五角平分线模型针对训练17.(2016•咸宁)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.已知:如图,∠AOC=∠BOC,点P在OC上,.求证:.请你补全已知和求证,并写出证明过程.图示:解题模型六三垂直模型针对训练18.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.19.如图,将等腰直角三角形ABC的直角顶点置于直线l上,且过A,B两点分别作直线l的垂线,垂足分别为D,E,请你在图中找出一对全等三角形,并写出证明它们全等的过程.图示:解题模型一平移模型针对训练1.(2018•桂林)如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.(1)求证:△ABC≌△DEF;(2)若∠A=55°,∠B=88°,求∠F的度数.【分析】(1)求出AC=DF,根据SSS推出△ABC≌△DEF.(2)由(1)中全等三角形的性质得到:∠A=∠EDF,进而得出结论即可.【点睛】本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应角相等.解题模型二对称模型图示:针对训练2.(2018•南充)如图,已知AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.【分析】由∠BAE=∠DAC可得到∠BAC=∠DAE,再根据“SAS”可判断△BAC≌△DAE,根据全等的性质即可得到∠C=∠E.【点睛】本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应角相等,对应边相等.图示:3.(2018•广州)如图,AB与CD相交于点E,AE=CE,DE=BE.求证:∠A=∠C.【分析】根据AE=EC,DE=BE,∠AED和∠CEB是对顶角,利用S AS证明△ADE≌△CBE即可.【解答】证明:在△AED和△CEB中,,∴△AED≌△CEB(SAS).∴∠A=∠C(全等三角形对应角相等).【点睛】此题主要考查学生对全等三角形的判定与性质这一知识点的理解和掌握,此题难度不大,要求学生应熟练掌握.4.(2018•乐山)如图,已知∠1=∠2,∠3=∠4,求证:BC=BD.【分析】由∠3=∠4可以得出∠ABD=∠ABC,再利用ASA就可以得出△ADB≌△ACB,就可以得出结论.【点睛】本题考查了等角的补角相等的性质的运用,全等三角形的判定与性质的运用,解答时证明三角形全等是关键.5.(2017•郴州)已知△ABC中,∠ABC=∠ACB,点D,E分别为边AB、AC的中点,求证:BE=CD.【分析】由∠ABC=∠ACB可得AB=AC,又点D、E分别是AB、AC的中点.得到AD=AE,通过△ABE≌△ACD,即可得到结果.【点睛】本题考查了等腰三角形的性质,全等三角形的判定与性质,熟记定理是解题的关键.6.(2018•武汉)如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.【分析】求出BF=CE,根据SAS推出△ABF≌△DCE,得对应角相等,由等腰三角形的判定可得结论.【解答】证明:∵BE=CF,∴BE+EF=CF+EF.∴BF=CE.在△ABF和△DCE中,[来源:]∴△ABF≌△DCE(SAS).∴∠GEF=∠GFE.∴EG=FG.【点睛】本题考查了全等三角形的判定与性质,等腰三角形的判定,熟练掌握三角形全等的判定方法是解题的关键.7.(2018•泰州)如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.【分析】因为∠A=∠D=90°,AC=BD,BC=BC,知Rt△BAC≌Rt△CDB(HL),所以AB=CD,证明△ABO 与△CDO全等,所以有OB=OC.【点睛】此题主要考查了全等三角形的判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.8.(2018•镇江)如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.(1)求证:△ABE≌△ACF;(2)若∠BAE=30°,则∠ADC=75°.【分析】(1)要证明△ABE≌△ACF,由题意可得AB=AC,∠B=∠ACF,BE=CF,从而可以证明结论成立;(2)根据(1)中的结论和等腰三角形的性质可以求得∠ADC的度数.【点睛】本题考查全等三角形的判定与性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.¥解题模型三旋转模型针对训练9.(2018•柳州)如图,AE和BD相交于点C,∠A=∠E,AC=EC.求证:△ABC≌△EDC.【分析】依据两角及其夹边分别对应相等的两个三角形全等进行判断.【解答】证明:∵在△ABC和△EDC中,图示:,∴△ABC≌△EDC(ASA).【点睛】本题主要考查了全等三角形的判定,两角及其夹边分别对应相等的两个三角形全等.10.(2018•昆明)如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.求证:BC=DE.【点睛】本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.11.(2017•常州)如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.【分析】(1)根据同角的余角相等可得到∠3=∠5,结合条件可得到∠1=∠D,再加上BC=CE,可证得结论;(2)根据∠ACD=90°,AC=CD,得到∠2=∠D=45°,根据等腰三角形的性质得到∠4=∠6=67.5°,由平角的定义得到∠DEC=180°﹣∠6=112.5°.【点睛】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.12.(2017•恩施州)如图,△ABC、△CDE均为等边三角形,连接BD、AE交于点O,BC与AE交于点P.求证:∠AOB=60°.【分析】利用“边角边”证明△ACD和△BCE全等,可得可得∠CAE=∠CBD,根据“八字型”证明∠AOP=∠PCB=60°即可.【点睛】本题考查等边三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.解题模型四平移+旋转模型针对训练13.(2018•菏泽)如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.【分析】结论:DF=AE.只要证明△CDF≌△BAE即可;【解答】解:结论:DF=AE.理由:∵AB∥CD,∴∠C=∠B.∵CE=BF,图示:∴CF=BE.又∵CD=AB,∴△CDF≌△BAE(SAS).∴DF=AE.【点睛】本题考查全等三角形的判定和性质,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.14.(2017•孝感)如图,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE,求证:AB∥CD.[来源:Z|xx|]【分析】根据全等三角形的判定与性质,可得∠B=∠D,根据平行线的判定,可得答案.【点睛】本题考查了全等三角形的判定与性质,利用等式的性质得出BE=DF是解题关键,又利用了全等三角形的判定与性质.15.(2018•铜仁)已知:如图,点A、D、C、B在同一条直线上,AD=BC,AE=BF,CE=DF,求证:AE∥FB.【分析】可证明△ACE≌△BDF,得出∠A=∠B,即可得出AE∥BF;【点睛】本题考查了全等三角形的判定及性质以及平行线的判定问题,关键是SSS证明△ACE≌△BDF.16.(2018•怀化)已知:如图,点A,F,E,C在同一直线上,AB∥DC,AB=CD,∠B=∠D.(1)求证:△ABE≌△CDF;(2)若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.【分析】(1)根据平行线的性质得出∠A=∠C,进而利用全等三角形的判定证明即可;(2)利用全等三角形的性质和中点的性质解答即可.【解答】证明:(1)∵AB∥DC,∴∠A=∠C.在△ABE与△CDF中,,∴△ABE≌△CDF(ASA).(2)∵点E,G分别为线段FC,FD的中点,∴ED=CD.∵EG=5,∴CD=10.∵△ABE≌△CDF,∴AB=CD=10.【点睛】此题考查全等三角形的判定和性质,关键是根据平行线的性质得出∠A=∠C.解题模型五角平分线模型针对训练17.(2016•咸宁)证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程,下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.已知:如图,∠AOC=∠BOC,点P在OC上,.求证:.请你补全已知和求证,并写出证明过程.【分析】根据图形写出已知条件和求证,利用全等三角形的判定得出△PDO≌△PEO,由全等三角形的性质可得结论.【点睛】本题主要考查了角平分线的性质和全等三角形的性质及判定,利用图形写出已知条件和求证是解图示:答此题的关键.解题模型六三垂直模型针对训练18.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E,求证:DE=AD+BE.【分析】先证明∠BCE=∠CAD,再证明△ADC≌△CEB,可得到AD=CE,DC=EB,等量代换,可得出DE=AD+BE.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.证明两线段的和等于一条线段常常借助三角形全等来证明,要注意运用这种方法图示:19.如图,将等腰直角三角形ABC的直角顶点置于直线l上,且过A,B两点分别作直线l的垂线,垂足分别为D,E,请你在图中找出一对全等三角形,并写出证明它们全等的过程.【分析】分析图可知,全等三角形为:△ACD≌△CBE.根据这两个三角形中的数量关系选择ASA证明全等.【点睛】本题考查三角形全等的判定方法和全等三角形的性质,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.。
(完整版)全等三角形证明经典100题
1.已知: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求 AD AB CD12. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD AB2ADC B3.已知: BC=DE ,∠ B= ∠E,∠ C= ∠ D, F 是 CD 中点,求证:∠ 1=∠ 2A21B EC F D4.已知:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=ACA12FCDEB5.已知: AD 均分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CACB D6.已知: AC 均分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE7.已知: AB=4 ,AC=2 , D 是 BC 中点, AD 是整数,求 AD AB CD8. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB2ADC B9.已知: BC=DE ,∠ B= ∠E,∠ C= ∠ D, F 是 CD 中点,求证:∠ 1=∠ 2A21B EC F D10. 已知:∠ 1=∠ 2, CD=DE , EF//AB ,求证: EF=ACA12FCDEB11.已知: AD 均分∠ BAC , AC=AB+BD ,求证:∠ B=2 ∠ CACB D12. 已知: AC 均分∠ BAD , CE⊥ AB ,∠ B+ ∠D=180 °,求证: AE=AD+BE12.如图,四边形 ABCD 中, AB ∥ DC ,BE、 CE 分别均分∠ ABC 、∠ BCD ,且点 E 在 AD上。
求证: BC=AB+DC 。
13.已知: AB//ED ,∠ EAB= ∠ BDE , AF=CD , EF=BC ,求证:∠ F=∠ CE DCFA B14.已知: AB=CD ,∠ A= ∠ D,求证:∠ B= ∠ CADB C15.P 是∠ BAC 均分线 AD 上一点, AC>AB ,求证: PC-PB<AC-AB CAP DB16. 已知∠ ABC=3 ∠ C,∠ 1=∠2, BE⊥ AE ,求证: AC-AB=2BE17.已知, E 是 AB 中点, AF=BD , BD=5 , AC=7 ,求 DCDF A CE B18.( 5 分)如图,在△ABC 中, BD=DC ,∠ 1=∠ 2,求证: AD ⊥ BC.19.( 5 分)如图, OM 均分∠ POQ ,MA⊥ OP,MB ⊥OQ , A、B 为垂足, AB 交 OM 于点N.求证:∠ OAB=∠OBA(完满版)全等三角形证明经典100题20.( 5 分)如图,已知AD ∥BC,∠ PAB 的均分线与∠ CBA 的均分线订交于E, CE 的连线交 AP 于 D.求证: AD+BC=AB.PCEDA B21.( 6 分)如图,△ ABC 中, AD 是∠ CAB 的均分线,且AB=AC+CD,求证:∠ C=2∠ BACD B22.( 6 分)如图①, E、F 分别为线段AC 上的两个动点,且DE ⊥AC 于 E, BF⊥AC 于 F ,若 AB=CD , AF=CE, BD 交 AC 于点 M.(1)求证: MB=MD , ME =MF(2)当 E、F 两点搬动到如图②的地址时,其余条件不变,上述结论可否成立?若成立请恩赐证明;若不成立请说明原由.23.( 7 分)已知:如图,DC ∥AB,且 DC =AE, E 为 AB 的中点,( 1)求证:△ AED≌△ EBC.( 2)观看图前,在不添辅助线的情况下,除△EBC 外,请再写出两个与△AED 的面积相等的三角形.(直接写出结果,不要求证明):AE O DB C24.( 7 分)如图,△ABC 中,∠ BAC=90 度, AB=AC, BD 是∠ ABC 的均分线, BD 的延长线垂直于过 C 点的直线于 E,直线 CE 交 BA 的延长线于 F .求证: BD =2CE.F25、( 10 分)如图: DF=CE, AD=BC,∠ D=∠ C。
学而思初二数学秋季班第3讲.全等三角形的经典模型(一).提高班.教师版

作弊?三角形9级全等三角形的经典模型(二)三角形8级全等三角形的经典模型(一)三角形7级 倍长中线与截长补短 满分晋级漫画释义3全等三角形的 经典模型(一)DCBA45°45°CBA等腰直角三角形数学模型思路:⑴利用特殊边特殊角证题(AC=BC 或904545︒︒°,,).如图1; ⑵常见辅助线为作高,利用三线合一的性质解决问题.如图2; ⑶补全为正方形.如图3,4.图1 图2图3 图4思路导航知识互联网题型一:等腰直角三角形模型ABCOMN AB COMN【例1】 已知:如图所示,Rt △ABC 中,AB =AC ,90BAC ∠=°,O 为BC 的中点,⑴写出点O 到△ABC 的三个顶点A 、B 、C 的距离的关系(不要求证明)⑵如果点M 、N 分别在线段AC 、AB 上移动,且在移动中保持 AN =CM .试判断△OMN 的形状,并证明你的结论. ⑶如果点M 、N 分别在线段CA 、AB 的延长线上移动,且在移动中保持AN =CM ,试判断⑵中结论是否依然成立,如果是请给出证明. 【解析】 ⑴OA =OB =OC⑵连接OA ,∵OA =OC 45∠=∠=BAO C ° AN =CM∴△ANO ≌△CMO∴ON =OM∴∠=∠NOA MOC∴90∠+∠=∠+∠=︒NOA BON MOC BON ∴90∠=︒NOM∴△OMN 是等腰直角三角形 ⑶△ONM 依然为等腰直角三角形,证明:∵∠BAC =90°,AB =AC ,O 为BC 中点 ∴∠BAO =∠OAC =∠ABC =∠ACB =45°, ∴AO =BO =OC ,∵在△ANO 和△CMO 中,AN CM BAO C AO CO =⎧⎪∠=∠⎨⎪=⎩∴△ANO ≌△CMO (SAS ) ∴ON =OM ,∠AON =∠COM , 又∵∠COM -∠AOM =90°,典题精练A BCOMNFE DCB AN M 12A BCDEF3∴△OMN 为等腰直角三角形.【例2】 两个全等的含30,60角的三角板ADE 和三角板ABC ,如图所示放置,,,E A C 三点在一条直线上,连接BD ,取BD 的中点M ,连接ME ,MC .试判断EMC △的形状,并说明理由.【解析】EMC △是等腰直角三角形.证明:连接AM .由题意,得,90,90.DE AC DAE BAC DAB =∠+∠=∠=∴DAB △为等腰直角三角形. ∵DM MB =,∴,45MA MB DM MDA MAB ==∠=∠=. ∴105MDE MAC ∠=∠=, ∴EDM △≌CAM △.∴,EM MC DME AMC =∠=∠.又90EMC EMA AMC EMA DME ∠=∠+∠=∠+∠=. ∴CM EM ⊥,∴EMC △是等腰直角三角形.【例3】 已知:如图,ABC △中,AB AC =,90BAC ∠=°,D 是AC 的中点,AF BD ⊥于E ,交BC 于F ,连接DF . 求证:ADB CDF ∠=∠. 【解析】 证法一:如图,过点A 作AN BC ⊥于N ,交BD 于M .∵AB AC =,90BAC ∠=°, ∴345DAM ∠=∠=°. ∵45C ∠=°,∴3C ∠=∠. ∵AF BD ⊥,∴190BAE ∠+∠=° ∵90BAC ∠=°,∴290BAE ∠+∠=°. ∴12∠=∠.在ABM △和CAF △中, 123AB AC C ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ABM CAF △≌△.∴AM CF =. 在ADM △和CDF △中,M EDCBA MEDCBAM12A BCDEF 3P C B A PCBAD AD CD DAM C AM CF =⎧⎪∠=∠⎨⎪=⎩∴ADM CDF △≌△. ∴ADB CDF ∠=∠.证法二:如图,作CM AC ⊥交AF 的延长线于M . ∵AF BD ⊥,∴3290∠+∠=°, ∵90BAC ∠=°, ∴1290∠+∠=°, ∴13∠=∠.在ACM △和BAD △中, 1390AC ABACM BAD ∠=∠⎧⎪=⎨⎪∠=∠=⎩° ∴ACM BAD △≌△. ∴M ADB ∠=∠,AD CM = ∵AD DC =,∴CM CD =. 在CMF △和CDF △中, 45=⎧⎪∠=∠=⎨⎪=⎩CF CF MCF DCF CM CD ° ∴CMF CDF △≌△.∴M CDF ∠=∠ ∴ADB CDF ∠=∠.【例4】 如图,等腰直角ABC △中,90AC BC ACB =∠=,°,P 为ABC △内部一点,满足 PB PC AP AC ==,,求证:15BCP ∠=︒.【解析】 补全正方形ACBD ,连接DP ,易证ADP △是等边三角形,60DAP ∠=︒,45BAD ∠=︒, ∴15BAP ∠=︒,30PAC ∠=︒,∴75∠=︒ACP ,∴15BCP ∠=︒.【探究对象】等腰直角三角形添补成正方形的几种常见题型 在解有关等腰直角三角形中的一些问题,若遇到不易解决或解法比较复杂时,可将等腰直角三角形引辅助线转化成正方形,再利用正方形的一些性质来解,常常可以起到化难为易的效果,从而顺利地求解。
全等三角形的提高拓展训练典范题型50题(含答案解析)

全等三角形的提高拓展训练知识点睛全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等. 寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边常是对应边. (4)有公共角的,公共角常是对应角. (5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键. 全等三角形的判定方法:(1) 边角边定理(SAS ):两边和它们的夹角对应相等的两个三角形全等. (2) 角边角定理(ASA ):两角和它们的夹边对应相等的两个三角形全等. (3) 边边边定理(SSS ):三边对应相等的两个三角形全等.(4) 角角边定理(AAS ):两个角和其中一个角的对边对应相等的两个三角形全等. (5) 斜边、直角边定理(HL ):斜边和一条直角边对应相等的两个直角三角形全等. 全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.例题精讲板块一、截长补短【例1】 (06年北京中考题)已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.DOECB AND【例2】 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?【变式拓展训练】如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?【例3】 已知:如图,ABCD 是正方形,∠FAD =∠FAE . 求证:BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD∆、ACE ∆,连结CD 、BE 相交NCDE BMAFEDCBA OEDCBA于点O.求证:OA平分DOE∠.【例5】(北京市、天津市数学竞赛试题)如图所示,ABC∆是边长为1的正三角形,BDC∆是顶角为120︒的等腰三角形,以D为顶点作一个60︒的MDN∠,点M、N分别在AB、AC上,求AMN∆的周长.【例6】五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:AD平分∠CDEA NMD CBACE DBA板块二、全等与角度【例7】如图,在ABC∆中,60BAC∠=︒,AD是BAC∠的平分线,且AC AB BD=+,求ABC∠的度数.【例8】在等腰ABC∆中,AB AC=,顶角20A∠=︒,在边AB上取点D,使AD BC=,求BDC∠.【例9】(“勤奋杯”数学邀请赛试题) 如图所示,在ABC∆中,AC BC=,20C∠=︒,又M在AC上,N在BC上,且满足50BAN∠=︒,60ABM∠=︒,求NMB∠. NMCB A【例10】 在四边形ABCD 中,已知AB AC =,60ABD ︒∠=,76ADB ︒∠=,28BDC ︒∠=,求DBC ∠的度数.【例11】 (日本算术奥林匹克试题) 如图所示,在四边形ABCD 中,12DAC ︒∠=,36CAB ︒∠=,48ABD ︒∠=,24DBC ︒∠=,求ACD ∠的度数.【例12】 (河南省数学竞赛试题) 在正ABC ∆内取一点D ,使DA DB =,在ABC ∆外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.【例13】 (北京市数学竞赛试题) 如图所示,在ABC ∆中,44BAC BCA ︒∠=∠=,M 为ABC∆内一点,使得30MCA ︒∠=,16MAC ︒∠=,求BMC ∠的度数.全等三角形证明经典20题(含答案)1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求ADMCAB_延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC 证明:过E 点,作EG//AC ,交AD 延长线于G 则∠DEG=∠DCA ,∠DGE=∠2 又∵CD=DE∴⊿ADC ≌⊿GDE (AAS ) ∴EG=AC ∵EF//AB ∴∠DFE=∠1 ∵∠1=∠2 ∴∠DFE=∠DGE ∴EF=EG ∴EF=ACADBCBA CDF2 1 E3. 已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C证明:在AC 上截取AE=AB ,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ,AD=AD ∴⊿AED ≌⊿ABD (SAS ) ∴∠AED=∠B ,DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C4. 已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE 证明:在AE 上取F ,使EF =EB ,连接CF 因为CE ⊥ABCDB A所以∠CEB=∠CEF=90°因为EB=EF,CE=CE,所以△CEB≌△CEF所以∠B=∠CFE因为∠B+∠D=180°,∠CFE+∠CFA=180°所以∠D=∠CFA因为AC平分∠BAD所以∠DAC=∠FAC又因为AC=AC所以△ADC≌△AFC(SAS)所以AD=AF所以AE=AF+FE=AD+BE5. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
(完整)八年级上《全等三角形》单元检测卷(提高版)

O EA B D C八年级上《全等三角形》单元检测卷(提高)一、选择题1. 在下列条件中,能判断两个直角三角形全等的是 ( )A.一个锐角对应相等B.两锐角对应相等C.一条边对应相等D.两条边对应相等 2.如图1,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店 去配一块完全一样的玻璃,那么最省事的办法是( ) A. 带①去 B. 带②去 C. 带③去 D. 带①和②去3.如图2,将两根钢条AA ′、BB ′的中点 O 连在一起,使AA ′、BB ′ 能绕着点 O 自由转动,就做成了一个测量工具,则A ′B ′的长等于内槽 宽 AB ,那么判定△OAB ≌△OA ′B ′的理由是 ( ) A .SAS B .ASA C .SSS D .HL4.如图3,OA =OB ,OC =OD ,∠O =50°,∠D =35°,则∠AEC 等于 ( ) A .60° B .50° C .45° D .30°5.如图4,在CD 上求一点P ,使它到OA ,OB 的距离相等,则P 点是 ( ) A. 线段CD 的中点 B. OA 与OB 的中垂线的交点 C. OA 与CD 的中垂线的交点 D. CD 与∠AOB 的平分线的交点6.已知,如图5,△ABC 中,AB=AC ,AD 是角平分线,BE=CF ,则下列说法正确的有几个( )(1)AD 平分∠EDF ;(2)△EBD ≌△FCD ;(3)BD=CD ;(4)AD ⊥BC .(A )1个 (B )2个 (C )3个 (D )4个7.已知:如图6,AD 是ABC △的角平分线,且AB :AC=3:2,则ABD △与ACD △的面积之比为( )A.3:2 B.6:4C.2:3 D.不能确定图2 _ B _ D_ O _ C _ A 图4 图1 图3图58.直线L1、L2、L3表示三条相互交叉的公路,现要建立一个货物中转站,要求它到三条公路的距离相等,则可选择的地址有( )A 一处B 二处C 三处D 四处9.如图7,用直尺和圆规作一个角等于已知角的示意图如图所示,则说明A O B AOB '''∠=∠的依据是 .A 、SSSB 、SASC 、ASAD 、AAS 10.如图8,已知ABC △中,45ABC ∠=o,4AC =,H 是高AD 和BE 的交点,则线段BH 的长度为( )A .2B .4C .5D .不能确定二、填空题11. 如图9,若 △ABC ≌△DEF ,则∠E= °12.杜师傅在做完门框后,为防止门框变形常常需钉两根 斜拉的木条,这样做的数学原理是 13.如图10,如果△ABC ≌△DEF ,△DEF 周长是32cm ,DE=9cm, EF=13cm.∠E=∠B ,则AC=____ cm.14.如图11,AD ⊥BC ,D 为BC 的中点,则△ABD ≌_________.15.如图12,若AB =DE ,BE =CF ,要证△ABF ≌△DEC ,需补充条 件________或 。
10 探索全等三角形的条件(3)-角角边(AAS)(拓展提高)(解析版)

专题1.10探索全等三角形的条件(3)-角角边(AAS )(拓展提高)一、单选题1.如图,在四边形ABCD 中,点E 在边AD 上,BCE ACD ∠=∠,40BAC D ∠=∠=︒,AB DE =,则BCE ∠的度数为( )A .80︒B .90︒C .100︒D .110︒【答案】C 【分析】通过证明△ABC ≌△DEC ,可得AC =DC ,从而40CAD D ∠=∠=︒,然后求出∠ACD 的值,进而可求BCE ∠的度数.【详解】解:∵BCE ACD ∠=∠,∴BCE ACE ACD ACE ∠-∠=∠-∠,∴∠ACB =∠DCE .在△ABC 和△DEC 中ACB DCE BAC D AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEC ,∴AC =DC ,∴40CAD D ∠=∠=︒,∴∠ACD =180°-40°-40°=100°,∴∠BCE =∠BCA +∠ACE =∠DCE +∠ACE =∠ACD =100°,故选C .【点睛】本题主要考查了全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.也考查了等腰三角形的性质.2.如图,在四边形ABCD 中,AB //DC ,E 为BC 的中点,连接DE 、AE ,AE ⊥DE ,延长DE 交AB 的延长线于点F .若AB =5,CD =3,则AD 的长为( )A .2B .5C .8D .11【答案】C 【分析】由“AAS ”可证△BEF ≌△CED ,可得EF =DE ,BF =CD =3,由线段垂直平分线的性质可得AD =AF =8.【详解】解:∵E 为BC 的中点,∴BE =EC ,∵AB ∥CD ,在△BEF 与△CED 中,F CDE BEF CED BE EC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BEF ≌△CED (AAS )∴EF =DE ,BF =CD =3,∴AF =AB +BF =8,∵AE ⊥DE ,EF =DE ,∴AF =AD =8,故选:C .【点睛】本题考查全等三角形的判定与性质,以及垂直平分线的判定与性质,准确推导出全等三角形并理解线段垂直平分线的性质是解题关键.3.如图,在ABC 中,AB AC ⊥,AD BC ⊥,BE 平分ABC ∠,交AD 于点E ,//EF AC ,下列结论中一定成立的是( )A .ABE DFE ∠=∠B .AE ED =C .AD DC = D .AB BF =【答案】D 【分析】先利用等角的余角相等得到∠C=∠BAD ,再根据平行线的性质得∠C=∠BFE ,则∠BAD=∠BFE ,于是可根据“AAS”可判断△ABE ≌△FBE ,所以AB=BF .【详解】解:∵AB ⊥AC ,AD ⊥BC ,∴∠BAD+∠CAD=90°,∠CAD+∠C=90°,∴∠C=∠BAD ,∵EF ∥AC ,∴∠C=∠BFE ,∴∠BAD=∠BFE ,∵BE 平分∠ABC ,∴∠ABE=∠FBE ,在△ABE 和△FBE 中,BAD BFE ABE FBE BE BE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABE ≌△FBE ,∴AB=BF .故选:D .【点睛】本题考查了角平分线的性质:角的平分线上的点到角的两边的距离相等.也考查了平行线的性质和全等三角形的判定与性质.4.如图,在OAB 和△OCD 中,OA OB =,OC OD =,OA OC >,40AOB COD ∠=∠=︒,连接AC ,BD 交于点M ,连接OM .下列结论:①AC BD =;②40AMB ∠=︒;③OM 平分BOC ∠;④MO 平分BMC ∠.其中一定正确的为( )A.①②③B.①②④C.①③④D.②③④【答案】B【分析】由SAS证明△AOC≌△BOD得出∠OCA=∠ODB,AC=BD即可判断①;由全等三角形的性质得出∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,得出∠AMB=∠AOB=40°,即可判断②;作OG⊥MC于G,OH⊥MB于H,则∠OGC=∠OHD=90°,由AAS证明△OCG≌△ODH(AAS),得出OG=OH,由角平分线的判定方法得出MO平分∠BMC,即可判断④;由∠AOB=∠COD,得出当∠DOM=∠AOM时,OM平分∠BOC,假设∠DOM=∠AOM,由△AOC≌△BOD得出∠COM=∠BOM,由MO平分∠BMC得出∠CMO=∠BMO,推出△COM≌△BOM,得OB=OC,而OA=OB,所以OA=OC 即可判断③;【详解】∵∠AOB=∠COD=40°,∴∠AOB+∠AOD=∠COD+∠AOD,即∠AOC=∠BOD,在△AOC和△BOD中,OA OBOC ODAOC BOD=⎧⎪=⎨⎪∠=∠⎩,∴△AOC≌△BOD(SAS),∴∠OCA=∠ODB,AC=BD,故①正确;∴∠OAC=∠OBD,由三角形的外角性质得:∠AMB+∠OAC=∠AOB+∠OBD,∴∠AMB=∠AOB=40°,故②正确;作OG⊥MC于G,OH⊥MB于H,如图所示:则∠OGC=∠OHD=90°,在△OCG和△ODH中OCA ODBOGC OHD OC OD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△OCG≌△ODH(AAS),∴OG=OH,∴MO平分∠BMC,故④正确;∵∠AOB=∠COD,∴当∠DOM=∠AOM时,OM平分∠BOC,假设∠DOM=∠AOM,∵△AOC≌△BOD∴∠COM=∠BOM,∵MO平分∠BMC∴∠CMO=∠BMO,在△COM和△BOM中,COM BOMOM OMCMO BMO∠∠⎧⎪=⎨⎪∠=∠⎩,∴△COM≌△BOM(ASA)∴OB=OC,∵OA=OB,∴OA=OC与OA>OC矛盾,故③错误;故选:B.【点睛】本题考查了全等三角形的判定与性质,三角形的外角性质,角平分线的判定等知识,证明三角形全等是解题的关键;.5.如图,AP平分∠BAF,PD⊥AB于点D,PE⊥AF于点E,则△APD与△APE全等的理由是()A.SSS B.SAS C.SSA D.AAS【答案】D【分析】求出∠PDA=∠PEA=90°,∠DAP=∠EAP,根据AAS推出两三角形全等即可.【详解】解:∵PD ⊥AB ,PE ⊥AF ,∴∠PDA=∠PEA=90°,∵AP 平分∠BAF ,∴∠DAP=∠EAP ,在△APD 和△APE 中DAP EAP PDA PEA AP AP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△APD ≌△APE (AAS ),故选:D .【点睛】本题考查了全等三角形的判定的应用,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS .6.如图,在Rt △ABC 中,∠B =90°,BC =2,过A 点作AD ∥BC ;AE ⊥AC ,AC =AE ,AD =3,连接DE ,则△ADE 的面积为( )A .3B .6C .12D .18【答案】A 【分析】通过过E 作EF ⊥DA ,交DA 延长于F ,将三角形ABC 转移到三角形AFE 构造确定,求出三角形ADE 的高EF ,利用面积公式即可求出.【详解】过E 作EF ⊥DA ,交DA 延长于F ,∵AE ⊥AC ,∴∠EAF+∠FAC=90º,∵AD ∥BC ,∠B =90°,∴∠BAF+∠B=180º,∴∠BAF=90º,∴∠BAC+∠FAC=90º,∴∠EAF=∠BAC ,∠F=∠B ,∴△AEF ≌△ACB(AAS),∴EF=BC=2,∴S △ADE=11AD EF=3222⨯⨯=3, 故选择:A .【点睛】本题考查三角形的面积问题,利用辅助线构造三角形全等,解决三角形ADE 的高是解题关键.二、填空题7.如图,已知//AD BC ,AB BC ⊥,CD DE ⊥,CD ED =,3AD =,4BC =,则ADE 的面积为________.【答案】32【分析】知道AD 的长,只要求出AD 边上的高,就可以求出△ADE 的面积;过点D 作DG ⊥BC 于G ,过点E 作EF ⊥AD 交AD 的延长线于F ,构造出△EDF ≌△CDG ,求出GC 的长,即为EF 的长,利用三角形的面积公式解答即可.【详解】解:过点D 作DG ⊥BC 于G ,过点E 作EF ⊥AD 交AD 的延长线于F ,如图所示:则四边形ABGD 是矩形,∵∠EDF +∠FDC =90°,∠GDC +∠FDC =90°,∴∠EDF =∠GDC ,在△EDF 和△CDG 中,F DGC EDF GDC DE DC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EDF ≌△CDG (AAS ),∴EF =CG =BC -BG =BC -AD =4-3=1,∴S △ADE =12 AD •EF =12×3×1=32, 故答案为:32.【点睛】本题考查了全等三角形的判定与性质、矩形的判定与性质、三角形面积计算等知识,通过作辅助线构造△EDF ≌△CDG 是解题的关键.8.如图,在面积为36的四边形ABCD 中,∠ADC =∠ABC =90°,AD =CD ,DP ⊥AB 于点P ,则DP 的长是_____【答案】6【分析】作DE ⊥BC ,交BC 延长线于E ,如图,则四边形BEDP 为矩形,再利用等角的余角相等得到∠ADP =∠CDE ,则可利用“AAS ”证明△ADP ≌△CDE ,得到DP =DE ,S △ADP =S △CDE ,所以四边形BEDP 为正方形,S 四边形ABCD =S 正方形BEDP ,根据正方形的面积公式得到DP 2=36,易得DP =6.如图,作DE ⊥BC ,交BC 延长线于E ,∵DP ⊥AB ,ABC =90°,∴四边形BEDP 为矩形,∴∠PDE =90°,即∠CDE +∠PDC =90°,∵∠ADC =90°,即∠ADP +∠PDC =90°,∴∠ADP =∠CDE ,在△ADP 和△CDE 中APD CED ADP CDE AD DC ∠∠⎧⎪∠∠⎨⎪⎩===,∴△ADP ≌△CDE ,∴DP =DE ,S △ADP =S △CDE ,∴四边形BEDP 为正方形,S 四边形ABCD =S 正方形BEDP ,∴DP 2=36,∴DP =6.故答案为6.【点睛】本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了正方形和矩形的性质.本题的关键的作辅助线构造两个全等的三角形.9.如图,在△ABC 中,点D 为AB 延长线上一点,点E 为AC 中点,过C 作CF //AB 交射线DE 于F ,若BD =1,CF =5,则AB 的长度为_____.【答案】4【分析】根据CF ∥AB 就可以得出∠A =∠ECF ,∠ADE =∠F ,证明△ADE ≌△CFE 就可以求出答案.【详解】∵CF ∥AB ,∴∠ADE =∠F ,∠FCE =∠A .∵点E 为AC 的中点,∴AE =EC .∵在△ADE 和△CFE 中,ADE F FCE A AE EC ∠∠⎧⎪∠∠⎨⎪⎩===,∴△ADE ≌△CFE (AAS ).∴AD =CF =5,∵BD =1,∴AB =AD -BD =5-1=4.故答案为:4.【点睛】本题考查了全等三角形的判定及性质,平行线的性质,解答时证明三角形全等是关键. 10.如图,△ABC 中,AB =AC ,点E 在AB 的延长线上,点D 在边AC 上,且EB =CD =4,线段DE 交边BC 于点F ,过点F 作FG ⊥DE 交线段CE 于点G ,CE ⊥AC ,△GEF 的面积为5,则EG 的长_____.【答案】5【分析】过D 作//DH AB 交BC 于H ,求出EF DF =,延长GC 到M ,使EG GM =,连接DM ,DG ,根据三角形的面积公式求出即可.【详解】解:过D 作//DH AB 交BC 于H ,则,DHC ABC EBF DHF ∠=∠∠=∠,∵AB AC =,∴A ABC CB =∠∠,∴DHC ACB ∠=∠,∴DH CD =,∵BE CD =,∴DH BE =,在BEF 与HDF 中EBF DHF BFE HFD BE DH ∠=∠⎧⎪∠=∠⎨⎪=⎩∴BEF HDF ≌(AAS ),∴EF DF =,延长GC 到M ,使EG GM =,连接DM ,DG ,∵5,,S EFG EF DF EG MG ===,∴5S DFG S EFG ==,5510S DGM S DGE ==+=,∴101020S DEM =+=,∵4,DC AC CE =⊥, ∴12S DEM EM DC =⨯⨯, ∴12042EM =⨯⨯,解得:=10EM , ∴11052EG MG ==⨯=, 故答案为:5.【点睛】本题考查了全等三角形的性质和判定,等腰三角形的性质和判定,能综合运用定理进行推理是解此题的关键.11.如图,在△ABC 中,点D ,E 在AC 边上,且AE =ED =DC .点F ,M 在AB 边上,且////EF DM BC ,延长FD 交BC 的延长线于点N ,则EF BN的值=_____.【答案】14【分析】首先证明13EF BC =∶∶,再利用全等三角形的性质证明EF =CN 即可解决问题. 【详解】解:////EF DM BC AE DE CD ,==, ∴13EF AE BC AC ==, 在EFD △与CND △中,EDF CDN FED NCD ED DC ∠=∠⎧⎪∠=∠⎨⎪=⎩,EFD CND AAS ∴≌(),EF CN ∴=,13CN BC ∴∶=∶,1CN BN ∴=∶∶4,∴14EF BN =, 故答案为14. 【点睛】本题考查平行线分线段成比例定理,全等三角形的判定和性质,关键在于熟练掌握两个知识点的基本性质和定理,该类型题属常考题.12.如图,在等边ABC 中,12AC =,点O 在边AC 上,且4AO =,点P 是边AB 上的一动点.连结OP ,将线段OP 绕点O 逆时针旋转60︒得到线段OD .要使点D 恰好落在边BC 上,则AP 的长为______.【答案】8【分析】根据AC =12,AO =4,求出OC =8,再根据等边三角形的性质得∠A =∠C =60°,再根据旋转的性质得OD =OP ,∠POD =60°,根据三角形内角和和平角定义得∠AOP +∠APO +∠A =180°,∠AOP +∠COD +∠POD =180°,利用等量代换可得∠APO =∠COD ,然后证出△AOP ≌△CDO ,得出AP =CO =8.【详解】解:∵AC =12,AO =4,∴OC =8,∵△ABC 为等边三角形,∴∠A =∠C =60°,∵线段OP 绕点D 逆时针旋转60°得到线段OD ,要使点D 恰好落在BC 上,如图所示,∴OD =OP ,∠POD =60°,∵∠AOP +∠APO +∠A =180°,∠AOP +∠COD +∠POD =180°,∴∠AOP +∠APO =120°,∠AOP +∠COD =120°,∴∠APO =∠COD ,在△AOP 和△CDO 中,A C APO COD OP OD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AOP ≌△CDO (AAS ),∴AP =CO =8,故答案为8.【点睛】本题考查了旋转的性质、等边三角形的性质、全等三角形的判定与性质,熟练掌握对应点到旋转中心的距离相等、对应点与旋转中心所连线段的夹角等于旋转角,旋转前、后的图形全等是本题的关键. 13.如图,AE AB ⊥,且,AE AB BC CD =⊥,且BC CD =,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是___________.【答案】50【分析】求出∠F=∠AGB=∠EAB=90°,∠FEA=∠BAG ,根据AAS 证△FEA ≌△GAB ,推出AG=EF=6,AF=BG=2,同理CG=DH=4,BG=CH=2,求出FH=14,根据阴影部分的面积=S 梯形EFHD -S △EFA -S △ABC -S △DHC 和面积公式代入求出即可.【详解】解:∵AE ⊥AB ,EF ⊥AF ,BG ⊥AG ,∴∠F=∠AGB=∠EAB=90°,∴∠FEA+∠EAF=90°,∠EAF+∠BAG=90°,∴∠FEA=∠BAG ,在△FEA 和△GAB 中,∵F BGA FEA BAG AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△FEA ≌△GAB (AAS ),∴AG=EF=6,AF=BG=2,同理CG=DH=4,BG=CH=2,∴FH=2+6+4+2=14,∴梯形EFHD 的面积是12×(EF+DH )×FH=12×(6+4)×14=70, ∴阴影部分的面积是S 梯形EFHD -S △EFA -S △ABC -S △DHC =70-12×6×2-12×(6+4)×2-12×4×2 =50.故答案为50.【点睛】本题考查了三角形的面积,梯形的面积,全等三角形的性质和判定等知识点,关键是把不规则图形的面积转化成规则图形的面积.14.如图,△ABC中,AB=AC,BH⊥AC,垂足为点H,BD平分∠ABH,点E为BH上一点,连接DE,∠BDE=45°,DH:CH=3:2,BE=10,则CH=____.【答案】4【分析】延长DE交BC于F,根据等腰三角形的性质,三角形内角和定理和角平分线的性质,由AAS证明△BEF≌△DCF,再根据全等三角形的性质即可求解.【详解】解:延长DE交BC于F,∵AB=AC,设∠A=2α,则∠ABC=∠ACB=90°-α,∵BH⊥AC,∴∠HBC=90°-∠ACB=α,∠A+∠ABH=90°,∵BD平分∠ABH,∴∠DBH=12∠ABH=45°-α,∴∠DBF=45°-α+α=45°,∴∠BDF=∠DBF=45°,∠DFB=∠DFC=90°,∴DF=BF,∵∠DFB=∠DHB=90°,∴∠CDF=∠EBF ,在△BEF 和△DCF 中,CDF EBF BFE DFC BF DF ∠∠⎧⎪∠∠⎨⎪⎩===,∴△BEF ≌△DCF (AAS ),∴BE=CD=CH+DH=10,∵DH :CH=3:2,∴CH=4.故答案为:4.【点睛】考查了全等三角形的判定与性质,等腰三角形的性质,题目关键是得到∠DBF=45°,利用全等三角形的性质得到BE=CD .三、解答题15.如图AOB ∠是一个锐角.(1)用尺规作图法作出AOB ∠的平分线OC ;(2)若点P 是OC 上一点,过点P 作PD OA ⊥于点D ,PE OB ⊥于点E ,求证:OD OE =.【答案】(1)见解析;(2)见解析【分析】(1)根据要求作出图形即可.(2)利用全等三角形的性质证明即可.【详解】解:(1)如图,射线OC 即为所求作.(2)由作图可知,∠POD =∠POE ,∵PD ⊥OA ,PE ⊥OB ,∴∠PDO =∠PEO =90°,在△POD 和△POE 中,PDO PEO POD POE OP OP ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△POD ≌△POE (AAS ),∴OD =OE .【点睛】本题考查作图-基本作图,角平分线的定义,全等三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.16.如图,,,//AD BF EC AB DE ∠∠==.求证:AC DF =.【答案】证明见解析【分析】由已知//AB DE ,可得∠B =∠E ,由BF =EC ,可得BC =EF ,易证ABC DEF △≌△,即可得出AC =DF .【详解】证明:∵//AB DE ,,B E ∴∠∠=,BF CE =,BC EF ∴=在ABC 和DEF 中,,A D B E BC EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,ABC DEF AAS ∴≌(),AC DF ∴=.【点睛】本题主要考查了全等三角形的判定及性质,解题的关键是证出ABC DEF △≌△. 17.如图,在ABC 中,90ACB ∠=︒,AC BC =,点E 是ACB ∠内部一点,分别过A 、B 两点作,AD CE BE CE ⊥⊥,垂足分别为点D 、E ,求证:AD BE DE =+【答案】见解析【分析】由全等三角形的性质可得BE =DC ,AD =CE ,即可求解.【详解】解:证明:BE CE ⊥,AD CE ⊥,90E ADC ∴∠=∠=︒,90EBC BCE ∴∠+∠=︒.90BCE ACD ∠+∠=︒,EBC DCA ∴∠=∠,在BCE ∆和CAD ∆中,E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BCE CAD AAS ∴∆≅∆;BCE CAD ∆≅∆,BE DC ∴=,AD CE =,AD CE CD DE BE DE ∴==+=+.【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定是本题的关键.18.如图,四边形ABCD 中,//AD BC ,E 为CD 的中点,连结BE 并延长交AD 的延长线于点F .(1)求证:BCE FDE ≌;(2)连结AE ,当,2,1AE BF BC AD ⊥==时,求AB 的长.【答案】(1)见解析;(2)3【分析】(1)利用AAS 即可证明;(2)由BCE ≌FDE 可得BE FE =,2BC FD ==,从而证明AEB △≌AEF ,得到AB AF =,可得A B .【详解】解:(1)∵//AD BC ,∴CBE DFE ∠=∠,∵E 为CD 中点,∴CE DE =,在BCE 和FDE 中,CBE DFE BEC FED CE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴BCE ≌FDE (AAS ).(2)由(1)中BCE ≌FDE ,∴BE FE =,2BC FD ==,∵AE BF ⊥,∴90AEB AEF ∠=∠=︒,在AEB △和AEF 中,AE AE AEB AEF BE FE =⎧⎪∠=∠⎨⎪=⎩,∴AEB △≌AEF (SAS ),∴AB AF =,而123AF AD DF =+=+=,∴3AB =.【点睛】本题考查了全等三角形的判定和性质,关键是根据AAS 和SAS 证明三角形全等.19.已知:在矩形ABCD 中,点E 在BC 边上,连接DE ,且DE BC =,过点A 作AF DE ⊥于点F .求证:AB AF =;【答案】见解析【分析】由“AAS ”可证ADF DEC △≌△,可得AF CD AB ==.【详解】证明:∵四边形ABCD 是矩形,AF DE ⊥,∴//,,,90AD BC AD BC AB CD C AFD ==∠=∠=︒,∴ADE DEC ∠=∠,∵DE BC =,∴AD DE =,在ADF 和DEC 中,90AFD C ADE DEC AD DE ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴()ADF DEC AAS ≌,∴AF CD =,∴AF AB =.【点睛】本题考查了矩形的性质,全等三角形的判定和性质,灵活运用这些性质解决问题是本题的关键. 20.如图,点C 、F 、E 、B 在同一直线上,点A 、D 分别在BC 两侧,AB ∥CD ,BE =CF ,∠A =∠D . (1)求证:AB =DC ;(2)若AB =CE ,∠B =30°,求∠D 的度数.【答案】(1)见解析;(2)75°.【分析】(1)由两直线平行,内错角相等得到∠B =∠C ,继而证明△ABF ≌△CDE (AAS ),据此解题; (2)由(1)△ABF ≌△CDE 得,AB =CD ,BF =CE ,证明△ABF 是等腰三角形,再根据三角形内角和180°解题.【详解】证明:(1)∵//AB CD ,∴∠B =∠C ,∵BE =CF ,∴BF CE =,在△ABF 和△CDE 中,A DBC BF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABF ≌△CDE (AAS ),∴AB =CD ;(2)∵△ABF ≌△CDE ,∴AB =CD ,BF =CE ,∵AB =CE ,∠B =30°,∴AB =BF ,∴∠A =∠AFB ,∴△ABF 是等腰三角形,∴∠A =()1801180307522B ︒-∠=︒-︒=︒, ∴∠D =∠A =75°.【点睛】本题考查平行线的性质、全等三角形的判定与性质、等腰三角形的判定与性质、三角形内角和的应用等知识,是重要考点,难度较易,掌握相关知识是解题关键.。
全等三角形证明之能力提高(经典题目)
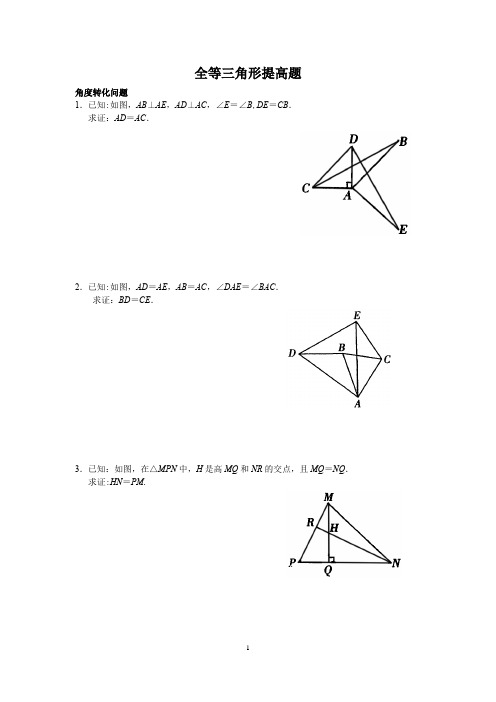
全等三角形提高题角度转化问题1.已知:如图,AB⊥AE,AD⊥AC,∠E=∠B,DE=CB.求证:AD=AC.2.已知:如图,AD=AE,AB=AC,∠DAE=∠BAC.求证:BD=CE.3.已知:如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ.求证:HN=PM.4。
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,求证:EF=AE+BF.5.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.求证:ED⊥AC.二次全等问题1.已知:如图,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.求证:BO=DO.2.已知:如图,AC与BD交于O点,AB∥DC,AB=DC.若过O点作直线l,分别交AB、DC于E、F两点,求证:OE=OF。
3.如图,E在AB上,∠1=∠2,∠3=∠4,那么AC等于AD吗?为什么?4.已知:如图,DE⊥AC,BF⊥AC,AD=BC,DE=BF.求证:AB∥DC。
5、已知:如图,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,DB=DC,求证:EB=FC【练习】1、已知∠B=∠E=90°,CE=CB,AB∥CD。
求证:△ADC是等腰三角形。
2、如图:AB=AC,ME⊥AB,MF⊥AC,垂足分别为E、F,ME=MF。
求证:MB=MCM FEC BA3、已知,△ABC 和△ECD 都是等边三角形,且点B ,C ,D 在一条直线上求证:BE=AD4、如图:在△ABC 中,∠C =90°,AD 平分∠ BAC ,DE ⊥AB 交AB 于E ,BC=30, BD :CD=3:2,则DE= 。
5、如图,已知,EG ∥AF ,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题.(只写出一种情况)①AB=AC ②DE=DF ③BE=CF 已知:EG ∥AF ,________,__________ 求证:_________6、如图,在Rt △ABC 中,∠ACB=45°,∠BAC=90°,AB=AC ,点D 是AB 的中点,AF ⊥CD 于H 交BC 于F ,BE ∥AC 交AF 的延长线于E , 求证:BC 垂直且平分DE.【思维拓展】EDCA BEDCBAG FEDC BA证明线段的和、差、倍、分问题时,常采用“割长”、“补短"等方法,构造全等三角形。
三角形全等几何模型(半角模型)(精选精练)(专项练习)(教师版)24-25学年八年级数学上册专项突破

专题12.16三角形全等几何模型(半角模型)(精选精练)(专项练习)1.如图,在正方形ABCD 中,点P 在直线BC 上,作射线AP ,将射线AP 绕点A 逆时针旋转45°,得到射线AQ ,交直线CD 于点Q ,过点B 作BE ⊥AP 于点E ,交AQ 于点F ,连接DF .(1)依题意补全图形;(2)用等式表示线段BE ,EF ,DF 之间的数量关系,并证明.2.如图,ABC 是边长为3的等边三角形,BDC 是等腰三角形,且120BDC ∠=︒,以D 为顶点作一个60︒角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,求AMN 的周长.3.(23-24八年级上·河南漯河·阶段练习)如图,在四边形ABCD 中,AB AD =,90B D ∠=∠=︒,E 、F分别是边BC 、CD 上的点,EAF ∠=12BAD .(1)求证:EF BE FD =+.(2)求证:AF 平分DFE ∠.4.问题背景:如图1:在四边形ABCD 中,AB AD =,120BAD ∠=︒,90B ADC ∠=∠=︒.E ,F 分别是BC ,CD 上的点,且60EAF ∠=︒.探究图中线段EF ,BE ,FD 之间的数量关系.(1)小王同学探究此问题的方法是:延长FD 到点G ,使DG BE =.连接AG ,先证明ABE ADG △≌△,再证明AEF AGF ≌,他的结论应是;(并写出证明过程)探索延伸:(2)如图2,若在四边形ABCD 中,AB AD =,180B D ∠∠=︒+,E ,F 分别是BC ,CD 上的点,且EAF ∠是BAD ∠的二分之一,上述结论是否仍然成立,并说明理由.5.(22-23九年级下·山东滨州·期中)(1)如图1,在四边形ABCD 中,120AB AD BAD =∠=︒,,90ABC ADC ∠=∠=︒,且60EAF ∠=︒,求证:EF BE FD =+.(2)如图2,若在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,E F 、分别是BC CD 、上的点,且12EAF BAD ∠=∠,上述结论是否仍然成立?请说明理由.6.【问题引领】问题1:如图1.在四边形ABCD 中,CB CD =,90B ADC ∠=∠=︒,120BCD ∠=︒.E ,F 分别是AB ,AD 上的点.且60ECF ∠=︒.探究图中线段BE ,EF ,FD 之间的数量关系.小王祠学探究此问题的方法是,延长FD 到点G .使DG BE =.连接CG .先证明CBE CDG △△≌,再证明CEF CGF ≌△△.他得出的正确结论是______.【探究思考】问题2:如图2,若将问题Ⅰ的条件改为:四边形ABCD 中,CB CD =,180ABC ADC ∠+∠=︒,12ECF BCD ∠=∠,问题1的结论是否仍然成立?请说明理由.【拓展延伸】问题3:如图3在问题2的条件下,若点E 在AB 的延长线上,点F 在DA 的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE ,EF ,FD 之间存在的等量关系是______.7.(1)如图1:在四边形ABCD 中,AB AD =,120BAD ∠=︒,90B ADC ∠=∠=︒.E ,F 分别是BC ,CD 上的点.且60EAF ∠=︒.探究图中线段EF ,BE ,FD 之间的数量关系.小明同学探究的方法是:延长FD 到点G .使DG BE =,连接AG ,先证明ABE ADG ≌△△,再证明AEF AGF △△≌,可得出结论,他的结论是________(直接写结论,不需证明);(2)如图2,若在四边形ABCD 中,AB AD =,180B D ∠+∠=︒,E 、F 分别是BC ,CD 上的点,且EAF ∠是BAD ∠的二分之一,上述结论是否仍然成立,并说明理由;(3)如图3,四边形ABCD 是边长为n 的正方形,45EBF ∠=︒,直接写出三角形DEF 的周长.8.(23-24八年级上·北京朝阳·阶段练习)在ABC 中,AB AC =,点D 是直线BC 上一点(不与B C 、重合),以AD 为一边在AD 的右侧作ADE V ,使,AE AD BD CE ==.设,BAC BCE αβ∠=∠=.(1)如图1,如果90,BAC BCE ∠=︒∠=___________度;(2)如图2,你认为αβ、之间有怎样的数量关系?并说明理由.(3)当点D 在直线BC 上移动时,αβ、之间又有怎样的数量关系?请在备用图上画出图形,并直接写出你的结论.(B 、C 、E 三点不共线)参考答案:1.(1)补全图形见解析;(2)BE+DF=EF,证明见解析.【分析】(1)根据题意补全图形即可.(2)延长FE到H,使EH=EF,根据题意证明△ABH≌△ADF,然后根据全等三角形的性质即可证明.【详解】(1)补全图形(2)BE+DF=EF.证明:延长FE到H,使EH=EF∵BE⊥AP,∴AH=AF,∴∠HAP=∠FAP=45°,∵四边形ABCD为正方形,∴AB=AD,∠BAD=90°∴∠BAP+∠2=45°,∵∠1+∠BAP=45°∴∠1=∠2,∴△ABH≌△ADF,∴DF=BH,∵BE+BH=EH=EF,∴BE+DF=EF.【点睛】此题考查了正方形的性质和全等三角形的性质,解题的关键是根据题意作出辅助线. 的周长为6.2.AMN【分析】要求△AMN的周长,根据题目已知条件无法求出三条边的长,只能把三条边长用其它已知边长来表示,所以需要作辅助线,延长AB至F,使BF=CN,连接DF,通过证明△BDF≌△CDN,及△DMN≌△DMF,从而得出MN=MF,△AMN的周长等于AB+AC的长.【详解】解:∵△BDC是等腰三角形,且∠BDC=120°∴∠BCD=∠DBC=30°∵△ABC是边长为3的等边三角形∴∠ABC=∠BAC=∠BCA=60°∴∠DBA=∠DCA=90°延长AB至F,使BF=CN,连接DF,在Rt△BDF和Rt△CND中,BF=CN,DB=DC∴△BDF≌△CDN,∴∠BDF=∠CDN,DF=DN∵∠MDN=60°∴∠BDM+∠CDN=60°∴∠BDM+∠BDF=60°,∠FDM=60°=∠MDN,DM为公共边∴△DMN≌△DMF,∴MN=MF∴△AMN的周长是:AM+AN+MN=AM+MB+BF+AN=AB+AC=6.【点睛】此题主要利用等边三角形和等腰三角形的性质来证明三角形全等,构造另一个三角形是解题的关键.3.(1)见解析(2)见解析【分析】本题考查了全等三角形的判定与性质;(1)延长EB 到G ,使BG DF =,连接AG .先说明ABG ADF ≌,然后利用全等三角形的性质和已知条件证得AEG AEF ≌,最后再运用全等三角形的性质和线段的和差即可解答;(2)根据(1)的结论可得G AFE ∠=∠,AFD G ∠=∠,即可得出AFD AFE ∠=∠,即可得证.【详解】(1)证明:延长EB 到G ,使BG DF =,连接AG .90ABG ABC D ∠=∠=∠=︒ ,AB AD =,ABG ADF ∴ ≌.AG AF ∴=,12∠=∠.1323EAF ∴∠+∠=∠+∠=∠=12BAD ∠.GAE EAF ∴∠=∠.又AE AE = ,AEG AEF ∴ ≌.EG EF ∴=.EG BE BG =+ .EF BE FD ∴=+;(2)证明:∵ABG ADF ≌,∴AFD G ∠=∠,∵AEG AEF ≌,∴G AFE ∠=∠,∴AFD AFE ∠=∠,即AF 平分DFE ∠.4.(1)EF BE DF =+,证明过程见解析(2)成立,理由见解析【分析】本题主要考查了全等三角形的判定与性质,正确作出辅助线构建全等三角形是解题的关键.(1)先利用“SAS ”判断ABE ADG △≌△得到AE AG =,BAE DAG ∠=∠,再证明EAF GAF ∠=∠,接着根据“SAS ”判断AEF AGF ≌,所以EF FG =,从而得到EF BE DF =+;(2)结论仍然成立,证明方法与(1)相同.【详解】解:(1)EF BE DF =+,证明如下:如下图,延长FD 到点G ,使得DG BE =,连接AG,∵90B ADC ∠=∠=︒,∴18090ADG ADC ∠=︒-∠=︒,在ABE 和ADG △中,90BE DG B ADG AB AD =⎧⎪∠=∠=︒⎨⎪=⎩,∴(SAS)ABE ADG ≌,∴AE AG =,BAE DAG ∠=∠,∵60EAF ∠=︒,120BAD ∠=︒,∴GAF DAG DAF BAE DAF EAF ∠=∠+∠=∠+∠=∠,在AEF △和AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)AEF AGF ≌△△,∴EF FG =,∵FG DG DF BE DF =+=+,∴EF BE DF =+;故答案为:EF BE DF =+;(2)结论EF BE DF =+仍然成立,理由如下:如下图,延长FD 到点G ,使得DG BE =,连接AG ,∵180B ADF ∠+∠=︒,180ADF ADG ∠+∠=︒,∴B ADG ∠=∠,在ABE 和ADG △中,BE DG B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)ABE ADG ≌,∴AE AG =,BAE DAG ∠=∠,∵12EAF BAD ∠=∠,∴GAF DAG DAF BAE DAF EAF ∠=∠+∠=∠+∠=∠,在AEF △和AGF 中,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩,∴(SAS)AEF AGF ≌△△,∴EF FG =,∵FG DG DF BE DF =+=+,∴EF BE DF =+.5.(1)见解析;(2)结论EF BE FD =+仍然成立;理由见解析【分析】本题主要考查的是三角形的综合题,主要涉及三角形全等的判定与性质,作辅助线构造全等三角形是解此题的关键.(1)延长FD 到G ,使DG BE =,连接AG ,根据SAS 证明ABE ADG △≌△可得AE AG =,再证明AEF AGF ≌,可得EF FG =,即可得出结论;(2)延长FD 到G ,使DG BE =,连接AG ,根据SAS 证明ABE ADG △≌△可得AE AG =,再证明AEF AGF ≌,可得EF FG =,即可得出结论.【详解】证明:如图,延长FD 到G ,使DG BE =,连接AG ,则18090ADG ADC ∠=︒-∠=︒,又90ABC ∠=︒,∴ABC ADG ∠=∠,在ABE 和ADG △中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,()SAS ABE ADG ∴ ≌,AE AG ∴=,BAE DAG ∠=∠,60EAF ∠=︒ ,120BAD ∠=︒,60GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=︒=∠,GAF EAF ∴∠=∠,在AEF △和AGF 中,AE AG GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩,()SAS AEF AGF ∴ ≌,EF FG ∴=,FG DG DF BE DF =+=+ ,EF BE DF ∴=+;(2)结论EF BE DF =+仍然成立,理由如下:如图,延长FD 到G ,使DG BE =,连接AG ,∵180,180B ADC ADC ADG ∠+∠=︒∠+∠=︒,∴B ADG ∠=∠,在ABE 和ADG △中,DG BE B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,()SAS ABE ADG ∴ ≌,AE AG ∴=,BAE DAG ∠=∠,12EAF BAD ∠=∠ ,GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠,GAF EAF ∴∠=∠,在AEF △和AGF 中,AE AG GAF EAF AF AF =⎧⎪∠=∠⎨⎪=⎩,()SAS AEF AGF ∴ ≌,EF FG ∴=,FG DG DF BE DF =+=+ ,EF BE DF ∴=+.6.问题1:BE FD EF +=;问题2:问题1中结论仍然成立,理由见解析;问题3:结论:DF EF BE =+.【分析】问题1,先证明CBE CDG ≌△△,得到CE CG =,BCE DCG ∠=∠,再证明CEF CGF ≌,得到EF GF =,即可得到EF DG DF BE DF =+=+;问题2,延长FD 到点G .使DG BE =.连接CG ,先判断出ABC GDC ∠=∠,进而判断出CBE CDG ≌△△,再证明CEF CGF ≌,最后用线段的和差即可得出结论;问题3,在DF 上取一点G .使DG BE =.连接CG ,然后同问题2的方法即可得出结论.【详解】解:问题1,如图1,延长FD 到点G .使DG BE =.连接CG,∵90ADC B ∠∠==︒,∴18090CDG ADC ∠-∠=︒=︒,∴90CBE CDG ∠∠==︒,在CBE △和CDG 中,===BE DG CBE CDG BC DC ⎧⎪∠∠⎨⎪⎩,∴()SAS CBE CDG △≌△,∴CE CG =,BCE DCG ∠=∠,∴BCE ECD DCG ECD ∠+∠=∠+∠,即120ECG BCD ∠∠==︒,∵60ECF ∠=︒,∴60GCF ECG ECF ∠∠-∠==︒,∴=ECF GCF ∠∠,在CEF △和CGF △中,===CE CG ECF GCF CF CF ⎧⎪∠∠⎨⎪⎩,∴()SAS CEF CGF ≌,∴EF GF =,∴EF DG DF BE DF =+=+;故他得到的正确结论是:=+EF BE DF ;问题2,问题1中结论仍然成立,如图2,理由:延长FD 到点G .使DG BE =.连接CG ,∵+=180ABC ADC ∠∠︒,+=180CDG ADC ∠∠︒,∴ABC GDC ∠=∠,在CBE △和CDG 中,BE DG CBE CDG BC DC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS CBE CDG △≌△,∴CE CG =,BCE DCG ∠=∠,∴BCE ECD DCG ECD ∠+∠=∠+∠,即ECG BCD ∠=∠,∵12ECF BCD ∠=∠,∴12ECF ECG ∠=∠,∴=ECF GCF ∠∠,在CEF △和CGF △中,CE CG ECF GCF CF CF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS CEF CGF ≌,∴EF GF =,∴EF DG DF BE DF =+=+;即=+EF BE DF ;问题3.结论:DF BE EF =+,理由如下:如图3,在DF 上取一点G .使DG BE =.连接CG ,∵180ABC ADC ∠+∠=︒,180ABC CBE ∠+∠=︒,∴ADC CBE ∠=∠,即CDG CBE ∠=∠,在CBE △和CDG 中,BE DG CBE CDG BC DC =⎧⎪∠=∠⎨⎪=⎩,∴()SAS CBE CDG △≌△,∴CE CG =,BCE DCG ∠=∠,∴BCE BCG DCG BCG ∠+∠=∠+∠,即ECG BCD ∠=∠,∵12ECF BCD ∠=∠,∴12ECF ECG ∠=∠,∴=ECF GCF ∠∠,在CEF △和CGF △中,CE CG ECF GCF CF CF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS CEF CGF ≌,∴EF GF =,∴EF GF DF DG DF BE ==-=-.即DF BE EF =+.【点睛】本题主要考查全等三角形的性质与判定,解题的关键在于能够正确作出辅助线构造全等三角形.7.(1)EF BE DF =+;(2)结论仍然成立,EF BE FD +=;(3)2n .【分析】(1)延长FD 到点G ,使DG BE =,连结AG ,由“SAS ”可证ABE ADG △≌△,可得AE AG =,BAE DAG ∠=∠,再由“SAS ”可证AEF AGF ≌,可得EF FG =,即可解题;(2)延长EB 到G ,使BG DF =,连接AG ,即可证明ABG ADF ≌,可得AF AG =,再证明AEF AEG △≌△,可得EF EG =,即可解题;(3)延长EA 到H ,使AH CF =,连接BH ,由“SAS ”可证ABH CBF ≌,可得BH BF =,ABH CBF ∠=∠,由“SAS ”可证EBH EBF ≌,可得EF EH =,可得EF EH AE CF ==+,即可求解.【详解】(1)延长FD 到点G ,使DG BE =,连结AG ,在ABE 和ADG △中,BE DG B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩,∴()SAS ABE ADG △△≌,∴AE AG =,BAE DAG ∠=∠,∵120BAD ∠=︒,60EAF ∠=︒,∴60BAE FAD DAG FAD ∠+∠=∠+∠=︒,∴60EAF FAG ∠=∠=︒,在EAF △和GAF 中,AG AE EAF FAG AF AF =⎧⎪∠=∠⎨⎪=⎩,∴()SAS EAF GAF ≌,∴EF FG DF DG ==+,∴EF BE DF =+,故答案为:EF BE DF =+;(2)结论仍然成立,理由如下:如图2,延长EB 到G ,使BG DF =,连接AG,∵180180ABC D ABG ABC ∠+∠︒∠+∠︒=,=,∴ABG D ∠∠=,同(1)理:()SAS ABG ADF △△≌,∴AG AF =,BAG DAF ∠=∠,∵12EAF BAD ∠=∠,∴12DAF BAE BAG BAE BAD EAF ∠+∠=∠+∠=∠=∠,∴GAE EAF ∠=∠,又AE AE =,∴()SAS AEG AEF △△≌,∴EG EF =,∵EG =BE +BG ,∴EF BE FD +=;(3)如图,延长EA 到H ,使AH CF =,连接BH ,∵四边形ABCD 是正方形,∴AB BC AD CD n ====,90BAD BCD ∠=∠=︒,∴90BAH BCF ∠=∠=︒,又∵AH CF =,AB BC =,∴()SAS ABH CBF ≌,∴BH BF =,ABH CBF ∠=∠,∵45EBF ∠=︒,∴45CBF ABE HBA ABE EBH ∠+∠=︒=∠+∠=∠,∴EBH EBF ∠=∠,又∵BH BF =,BE BE =,∴()SAS EBH EBF ≌,∴EF EH =,∴EF EH AE CF ==+,∴DEF 的周长2DE DF EF DE DF AE CF AD CD n =++=+++=+=.【点睛】此题主要考查了三角形全等的判定和性质,灵活运用全等三角形的性质和判定是解答本题的关键.8.(1)90;(2)=180αβ+︒;(3)图象见详解;=180αβ+︒;【分析】(1)先证明ABD ACE ≌(SSS ),则可得B ACE ∠∠=,根据90BAC ∠=︒,可知9090B ACB ACE ACB ∠∠∠∠+=︒+=︒,则;(2)已知ABD ACE ≌,则B ACE ∠∠=,则B ACB BCE ∠∠∠+=,根据180180B ACB BAC BCE BAC ∠∠∠++∠=︒+∠=︒,可得,则=180αβ+︒.(3)连接AD ,作AE 使得DAE BAC ∠∠=,AE AD =,连接DE 、CE :根据BAD BAC CAD ∠∠∠=+,CAE DAE CAD ∠∠∠=+,可得BAD CAE ∠∠=,证明ABD ACE ≌,进而可得B ACE ∠∠=,则B 180BCE AC ACE BCA B BAC ∠∠=+∠=∠+∠=︒-∠,由此可证明αβ、之间存在数量关系为=180αβ+︒;【详解】(1)解:在ABD 与ACE 中,AB AC AE AD BD CE =⎧⎪=⎨⎪=⎩,∴ABD ACE ≌(SSS ),∴B ACE ∠∠=,∵90BAC ∠=︒,∴90B ACB ∠∠+=︒,∴90ACE ACB ∠∠+=︒,故答案为:90;(2)解:已知ABD ACE ≌,∴B ACE ∠∠=,∴B ACB BCE ∠∠∠+=,∵180B ACB BAC ∠∠++∠=︒,∴180BCE BAC ∠+∠=︒,∴=180αβ+︒.(3)解:连接AD ,作AE 使得DAE BAC ∠∠=,AE AD =,连接DE 、CE,可得下图:∵BAD BAC CAD ∠∠∠=+,CAE DAE CAD ∠∠∠=+,∴BAD CAE ∠∠=;在ABD 和ACE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,∴ABD ACE ≌()SAS ;∴B ACE ∠∠=;∴B 180BCE AC ACE BCA B BAC ∠∠=+∠=∠+∠=︒-∠,∴αβ、之间存在数量关系为=180αβ+︒.【点睛】本题考查全等三角形的性质与判定,能够熟练掌握全等三角形的判定定理,找出相应的判定条件是解决本题的关键.。
(完整版)全等三角形经典例题(含答案)
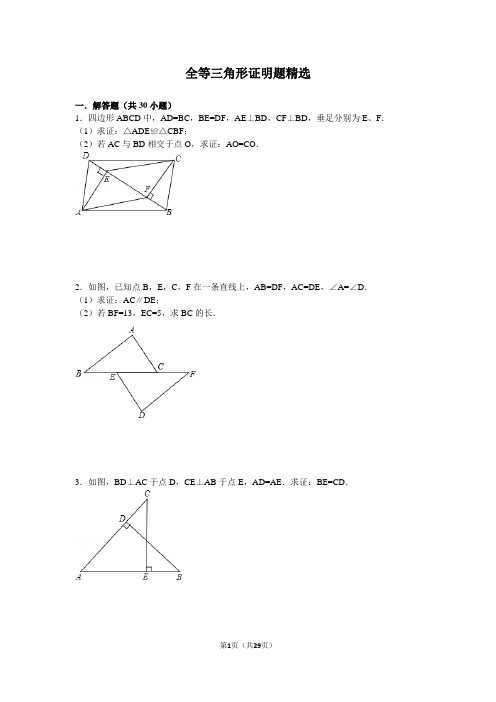
全等三角形证明题精选一.解答题(共30小题)1.四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.2.如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.3.如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.4.如图,点O是线段AB和线段CD的中点.(1)求证:△AOD≌△BOC;(2)求证:AD∥BC.5.如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.6.如图,已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC.求证:AE=BC.7.如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.8.如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.9.如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.10.如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.11.如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.12.已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)求证:BD=CE;(2)求证:∠M=∠N.13.如图,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC.14.如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.15.如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.(1)求证:AB=AC;(2)若AD=2,∠DAC=30°,求AC的长.16.如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.17.如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△ABC≌△BAD.18.已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:△ABC≌△DEF.19.已知:点A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.(1)你添加的条件是:;(2)证明:.20.如图,AB=AC,AD=AE.求证:∠B=∠C.21.如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.22.一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:∠BAC=∠DAC.23.在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:;结论:.(均填写序号)证明:24.如图,在△ABC和△DEF中,AB=DE,BE=CF,∠B=∠1.求证:AC=DF.(要求:写出证明过程中的重要依据)25.如图,已知AB=DC,AC=DB.求证:∠1=∠2.26.如图,D、E分别为△ABC的边AB、AC上的点,BE与CD相交于O点.现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD.(1)请你选出两个条件作为题设,余下的两个作为结论,写出一个正确的命题:命题的条件是和,命题的结论是和(均填序号);(2)证明你写出的命题.27.如图,已知AB∥DE,AB=DE,AF=DC,请问图中有哪几对全等三角形并任选其中一对给予证明.28.如图所示,在梯形ABCD中,AD∥BC,∠B=∠C,点E是BC边上的中点.求证:AE=DE.29.如图,给出下列论断:①DE=CE,②∠1=∠2,③∠3=∠4.请你将其中的两个作为条件,另一个作为结论,构成一个真命题,并加以证明.30.已知:如图,∠ACB=90°,AC=BC,CD是经过点C的一条直线,过点A、B分别作AE⊥CD、BF⊥CD,垂足为E、F,求证:CE=BF.全等三角形证明题精选参考答案与试题解析一.解答题(共30小题)1.(2016•连云港)四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)求证:△ADE≌△CBF;(2)若AC与BD相交于点O,求证:AO=CO.【分析】(1)根据已知条件得到BF=DE,由垂直的定义得到∠AED=∠CFB=90°,根据全等三角形的判定定理即可得到结论;(2)如图,连接AC交BD于O,根据全等三角形的性质得到∠ADE=∠CBF,由平行线的判定得到AD∥BC,根据平行四边形的性质即可得到结论.【解答】证明:(1)∵BE=DF,∴BE﹣EF=DF﹣EF,即BF=DE,∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB=90°,在Rt△ADE与Rt△CBF中,,∴Rt△ADE≌Rt△CBF;(2)如图,连接AC交BD于O,∵Rt△ADE≌Rt△CBF,∴∠ADE=∠CBF,∴AD∥BC,∴四边形ABCD是平行四边形,∴AO=CO.【点评】本题考查了全等三角形的判定和性质,平行四边形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.2.(2016•曲靖)如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.(1)求证:AC∥DE;(2)若BF=13,EC=5,求BC的长.【分析】(1)首先证明△ABC≌△DFE可得∠ACE=∠DEF,进而可得AC∥DE;(2)根据△ABC≌△DFE可得BC=EF,利用等式的性质可得EB=CF,再由BF=13,EC=5进而可得EB的长,然后可得答案.【解答】(1)证明:在△ABC和△DFE中,∴△ABC≌△DFE(SAS),∴∠ACE=∠DEF,∴AC∥DE;(2)解:∵△ABC≌△DFE,∴BC=EF,∴CB﹣EC=EF﹣EC,∴EB=CF,∵BF=13,EC=5,∴EB==4,∴CB=4+5=9.【点评】此题主要考查了全等三角形的判定和性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.3.(2016•孝感)如图,BD⊥AC于点D,CE⊥AB于点E,AD=AE.求证:BE=CD.【分析】要证明BE=CD,只要证明AB=AC即可,由条件可以求得△AEC和△ADB全等,从而可以证得结论.【解答】证明;∵BD⊥AC于点D,CE⊥AB于点E,∴∠ADB=∠AEC=90°,在△ADB和△AEC中,∴△ADB≌△AEC(ASA)∴AB=AC,又∵AD=AE,∴BE=CD.【点评】本题考查全等三角形的判定和性质,解题的关键是明确题意,找出所求问题需要的条件.4.(2016•湘西州)如图,点O是线段AB和线段CD的中点.(1)求证:△AOD≌△BOC;(2)求证:AD∥BC.【分析】(1)由点O是线段AB和线段CD的中点可得出AO=BO,CO=DO,结合对顶角相等,即可利用全等三角形的判定定理(SAS)证出△AOD≌△BOC;(2)结合全等三角形的性质可得出∠A=∠B,依据“内错角相等,两直线平行”即可证出结论.【解答】证明:(1)∵点O是线段AB和线段CD的中点,∴AO=BO,CO=DO.在△AOD和△BOC中,有,∴△AOD≌△BOC(SAS).(2)∵△AOD≌△BOC,∴∠A=∠B,∴AD∥BC.【点评】本题考查了全等三角形的判定与性质以及平行线的判定定理,解题的关键是:(1)利用SAS证出△AOD≌△BOC;(2)找出∠A=∠B.本题属于基础题,难度不大,解决该题型题目时,根据全等三角形的判定定理证出两三角形全等,结合全等三角形的性质找出相等的角,再依据平行线的判定定理证出两直线平行即可.5.(2016•云南)如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.【分析】根据全等三角形的判定方法SAS,即可证明△ABC≌△CDE,根据全等三角形的性质:得出结论.【解答】证明:∵点C是AE的中点,∴AC=CE,在△ABC和△CDE中,,∴△ABC≌△CDE,∴∠B=∠D.【点评】本题考查了全等三角形的判定和性质,全等三角形的判定方法:SSS,SAS,ASA,AAS,直角三角形还有HL.6.(2016•宁德)如图,已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC.求证:AE=BC.【分析】根据平行线的性质找出∠ADE=∠BAC,借助全等三角形的判定定理ASA证出△ADE≌△BAC,由此即可得出AE=BC.【解答】证明:∵DE∥AB,∴∠ADE=∠BAC.在△ADE和△BAC中,,∴△ADE≌△BAC(ASA),∴AE=BC.【点评】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理是解题的关键.7.(2016•十堰)如图,AB∥CD,E是CD上一点,BE交AD于点F,EF=BF.求证:AF=DF.【分析】欲证明AF=DF只要证明△ABF≌△DEF即可解决问题.【解答】证明:∵AB∥CD,∴∠B=∠FED,在△ABF和△DEF中,,∴△ABF≌△DEF,∴AF=DF.【点评】本题考查全等三角形的判定和性质,平行线的性质等知识,解题的关键是熟练掌握全等三角形的判断和性质,熟练掌握平行线的性质,属于基础题,中考常考题型.8.(2016•武汉)如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF,求证:AB∥DE.【分析】证明它们所在的三角形全等即可.根据等式的性质可得BC=EF.运用SSS证明△ABC与△DEF全等.【解答】证明:∵BE=CF,∴BC=EF,在△ABC与△DEF中,,∴△ABC≌△DEF(SSS),∴∠ABC=∠DEF,∴AB∥DE.【点评】本题考查了全等三角形的性质和判定.全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应角相等.9.(2016•昆明)如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB求证:AE=CE.【分析】根据平行线的性质得出∠A=∠ECF,∠ADE=∠CFE,再根据全等三角形的判定定理AAS得出△ADE≌△CFE,即可得出答案.【解答】证明:∵FC∥AB,∴∠A=∠ECF,∠ADE=∠CFE,在△ADE和△CFE中,,∴△ADE≌△CFE(AAS),∴AE=CE.【点评】本题考查了全等三角形的判定和性质,掌握全等三角形的判定定理SSS、SAS、ASA、AAS、HL是解题的关键.10.(2016•衡阳)如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.【分析】求出AD=BC,根据ASA推出△AED≌△BFC,根据全等三角形的性质得出即可.【解答】证明:∵AC=BD,∴AC+CD=BD+CD,∴AD=BC,在△AED和△BFC中,,∴△AED≌△BFC(ASA),∴DE=CF.【点评】本题考查了全等三角形的性质和判定的应用,能求出△AED≌△BFC是解此题的关键,注意:全等三角形的对应边相等.11.(2016•重庆)如图,点A,B,C,D在同一条直线上,CE∥DF,EC=BD,AC=FD.求证:AE=FB.【分析】根据CE∥DF,可得∠ACE=∠D,再利用SAS证明△ACE≌△FDB,得出对应边相等即可.【解答】证明:∵CE∥DF,∴∠ACE=∠D,在△ACE和△FDB中,,∴△ACE≌△FDB(SAS),∴AE=FB.【点评】此题主要考查全等三角形的判定与性质和平行线的性质;熟练掌握平行线的性质,证明三角形全等是解决问题的关键.12.(2016•南充)已知△ABN和△ACM位置如图所示,AB=AC,AD=AE,∠1=∠2.(1)求证:BD=CE;(2)求证:∠M=∠N.【分析】(1)由SAS证明△ABD≌△ACE,得出对应边相等即可(2)证出∠BAN=∠CAM,由全等三角形的性质得出∠B=∠C,由AAS证明△ACM≌△ABN,得出对应角相等即可.【解答】(1)证明:在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE;(2)证明:∵∠1=∠2,∴∠1+∠DAE=∠2+∠DAE,即∠BAN=∠CAM,由(1)得:△ABD≌△ACE,∴∠B=∠C,在△ACM和△ABN中,,∴△ACM≌△ABN(ASA),∴∠M=∠N.【点评】本题考查了全等三角形的判定与性质;证明三角形全等是解决问题的关键.13.(2016•恩施州)如图,BE⊥AC,CD⊥AB,垂足分别为E,D,BE=CD.求证:AB=AC.【分析】通过全等三角形(Rt△CBE≌Rt△BCD)的对应角相等得到∠ECB=∠DBC,则AB=AC.【解答】证明:∵BE⊥AC,CD⊥AB,∴∠CEB=∠BDC=90°.∵在Rt△CBE与Rt△BCD中,,∴Rt△CBE≌Rt△BCD(HL),∴∠ECB=∠DBC,∴AB=AC.【点评】本题考查了全等三角形的判定与性质,等腰三角形的判定.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.14.(2016•重庆)如图,在△ABC和△CED中,AB∥CD,AB=CE,AC=CD.求证:∠B=∠E.【分析】根据两直线平行,内错角相等可得∠BAC=∠ECD,再利用“边角边”证明△ABC和△CED全等,然后根据全等三角形对应角相等证明即可.【解答】证明:∵AB∥CD,∴∠BAC=∠ECD,在△ABC和△CED中,,∴△ABC≌△CED(SAS),∴∠B=∠E.【点评】本题考查了全等三角形的判定与性质,平行线的性质,熟练掌握三角形全等的判定方法并找出两边的夹角是解题的关键.15.(2016•湖北襄阳)如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.(1)求证:AB=AC;(2)若AD=2,∠DAC=30°,求AC的长.【分析】(1)先证明△DEB≌△DFC得∠B=∠C由此即可证明.(2)先证明AD⊥BC,再在RT△ADC中,利用30°角性质设CD=a,AC=2a,根据勾股定理列出方程即可解决问题.【解答】(1)证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,∴DE=DF,∠DEB=∠DFC=90°,在RT△DEB和RT△DFC中,,∴△DEB≌△DFC,∴∠B=∠C,∴AB=AC.(2)∵AB=AC,BD=DC,∴AD⊥BC,在RT△ADC中,∵∠ADC=90°,AD=2,∠DAC=30°,∴AC=2CD,设CD=a,则AC=2a,∵AC2=AD2+CD2,∴4a2=a2+(2)2,∵a>0,∴a=2,∴AC=2a=4.【点评】本题考查全等三角形的判定和性质、直角三角形30°性质、勾股定理等知识,解题的关键是正确寻找全等三角形,记住直角三角形30°角所对的直角边等于斜边的一半,属于中考常考题型.16.(2016•吉安校级一模)如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.【分析】根据全等三角形的性质得到CD=AF,证明∴△DGC≌△AGF,根据全等三角形的性质和角平分线的判定得到∠CBG=∠FBG,根据三角形内角和定理计算即可.【解答】解:∵Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∴BC=BF,BD=BA,∴CD=AF,在△DGC和△AGF中,,∴△DGC≌△AGF,∴GC=GF,又∠ACB=∠DFB=90°,∴∠CBG=∠FBG,∴∠GBF=(90°﹣28°)÷2=31°.【点评】本题考查的是全等三角形的性质角平分线的判定,掌握全等三角形的对应边相等、对应角相等是解题的关键.17.(2016•武汉校级四模)如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.求证:△ABC≌△BAD.【分析】由垂直的定义可得到∠C=∠D,结合条件和公共边,可证得结论.【解答】证明:∵AC⊥BC,BD⊥AD,∴∠C=∠D=90,在Rt△ACB和Rt△BDA中,,∴△ACB≌△BDA(HL).【点评】本题主要考查全等三角形的判定,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.18.(2016•济宁二模)已知:如图,点B、F、C、E在一条直线上,BF=CE,AC=DF,且AC∥DF.求证:△ABC≌△DEF.【分析】求出BC=FE,∠ACB=∠DFE,根据SAS推出全等即可.【解答】证明:∵BF=CE,∴BF+FC=CE+FC,∴BC=FE,∵AC∥DF,∴∠ACB=∠DFE,在△ABC和△DEF中,,∴△ABC≌△DEF(SAS).【点评】本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.19.(2016•诏安县校级模拟)已知:点A、C、B、D在同一条直线,∠M=∠N,AM=CN.请你添加一个条件,使△ABM≌△CDN,并给出证明.(1)你添加的条件是:∠MAB=∠NCD;(2)证明:在△ABM和△CDN中∵∠M=∠N,AM=CM,∠MAB=∠NCD∴△ABM≌△CDN(ASA)..【分析】判定两个三角形全等的一般方法有:ASA、SSS、SAS、AAS、HL,所以可添加条件为∠MAB=∠NCD,或BM=DN或∠ABM=∠CDN.【解答】解:(1)你添加的条件是:①∠MAB=∠NCD;(2)证明:在△ABM和△CDN中∵∠M=∠N,AM=CM,∠MAB=∠NCD∴△ABM≌△CDN(ASA),故答案为:∠MAB=∠NCD;在△ABM和△CDN中∵∠M=∠N,AM=CM,∠MAB=∠NCD∴△ABM≌△CDN(ASA).【点评】本题考查三角形全等的性质和判定方法,判定两个三角形全等的一般方法有:ASA、SSS、SAS、AAS、HL(在直角三角形中).判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.20.(2016•屏东县校级模拟)如图,AB=AC,AD=AE.求证:∠B=∠C.【分析】要证∠B=∠C,可利用判定两个三角形全等的方法“两边和它们的夹角对应相等的两个三角形全等”证△ABE≌△ACD,然后由全等三角形对应边相等得出.【解答】证明:在△ABE与△ACD中,,∴△ABE≌△ACD(SAS),∴∠B=∠C.【点评】本题主要考查了两个三角形全等的其中一种判定方法,即“边角边”判定方法.观察出公共角∠A是解决本题的关键.21.(2016•沛县校级一模)如图,在△ABC中,AD是△ABC的中线,分别过点B、C作AD及其延长线的垂线BE、CF,垂足分别为点E、F.求证:BE=CF.【分析】易证△BED≌△CFD,根据全等三角形对应边相等的性质即可解题.【解答】解:∵BE⊥AE,CF⊥AE,∴∠BED=∠CFD=90°,在△BED和△CFD中,,∴△BED≌△CFD(AAS),∴BE=CF.【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中找出全等三角形并证明是解题的关键.22.(2016•福州)一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:∠BAC=∠DAC.【分析】在△ABC和△ADC中,由三组对边分别相等可通过全等三角形的判定定理(SSS)证得△ABC≌△ADC,再由全等三角形的性质即可得出结论.【解答】证明:在△ABC和△ADC中,有,∴△ABC≌△ADC(SSS),∴∠BAC=∠DAC.【点评】本题考查了全等三角形的判定及性质,解题的关键是证出△ABC≌△ADC.本题属于基础题,难度不大,解决该题型题目时,根据全等三角形的判定定理证出两三角形全等是关键.23.(2012•漳州)在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E 在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:可以为①②③;结论:④.(均填写序号)证明:【分析】此题可以分成三种情况:情况一:题设:①②③;结论:④,可以利用SAS定理证明△ABC≌△DEF;情况二:题设:①③④;结论:②,可以利用AAS证明△ABC ≌△DEF;情况三:题设:②③④;结论:①,可以利用ASA证明△ABC≌△DEF,再根据全等三角形的性质可推出结论.【解答】情况一:题设:①②③;结论:④.证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF.在△ABC和△DEF中,,∴△ABC≌△DEF(SAS),∴∠1=∠2;情况二:题设:①③④;结论:②.证明:在△ABC和△DEF中,∵,∴△ABC≌△DEF(AAS),∴BC=EF,∴BC﹣FC=EF﹣FC,即BF=EC;情况三:题设:②③④;结论:①.证明:∵BF=EC,∴BF+CF=EC+CF,即BC=EF,在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),∴AB=DE.【点评】此题主要考查了全等三角形的判定与性质,此题为开放性题目,需要同学们有较强的综合能力,熟练应用全等三角形的全等判定才能正确解答.24.(2009•大连)如图,在△ABC和△DEF中,AB=DE,BE=CF,∠B=∠1.求证:AC=DF.(要求:写出证明过程中的重要依据)【分析】因为BE=CF,利用等量加等量和相等,可证出BC=EF,再证明△ABC≌△DEF,从而得出AC=DF.【解答】证明:∵BE=CF,∴BE+EC=CF+EC(等量加等量和相等).即BC=EF.在△ABC和△DEF中,AB=DE,∠B=∠1,BC=EF,∴△ABC≌△DEF(SAS).∴AC=DF(全等三角形对应边相等).【点评】解决本题要熟练运用三角形的判定和性质.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.25.(2006•平凉)如图,已知AB=DC,AC=DB.求证:∠1=∠2.【分析】探究思路:因为△ABO与△DCO有一对对顶角,要证∠1=∠2,只要证明∠A=∠D,把问题转化为证明△ABC≌△DCB,再围绕全等找条件.【解答】证明:在△ABC和△DCB中∵,∴△ABC≌△DCB.∴∠A=∠D.又∵∠AOB=∠DOC,∴∠1=∠2.【点评】本题是全等三角形的判定,性质的综合运用,可以由探究题目的结论出发,找全等三角形,再寻找判定全等的条件.26.(2006•佛山)如图,D、E分别为△ABC的边AB、AC上的点,BE与CD相交于O点.现有四个条件:①AB=AC;②OB=OC;③∠ABE=∠ACD;④BE=CD.(1)请你选出两个条件作为题设,余下的两个作为结论,写出一个正确的命题:命题的条件是①和③,命题的结论是②和④(均填序号);(2)证明你写出的命题.【分析】本题实际是考查全等三角形的判定,根据条件可看出主要是围绕三角形ABE和ACD 全等来求解的.已经有了一个公共角∠A,只要再知道一组对应角和一组对应边相等即可得出三角形全等的结论.可根据这个思路来进行选择和证明.【解答】解:(1)命题的条件是①和③,命题的结论是②和④.(2)已知:D,E分别为△ABC的边AB,AC上的点,且AB=AC,∠ABE=∠ACD.求证:OB=OC,BE=CD.证明如下:∵AB=AC,∠ABE=∠ACD,∠BAC=∠CAB,∴△ABE≌△ACD.∴BE=CD.又∠BCD=∠ACB﹣∠ACD=∠ABC﹣∠ABE=∠CBE,∴△BOC是等腰三角形.∴OB=OC.【点评】本题主要考查了全等三角形的判定,要注意的是AAA和SSA是不能判定三角形全等的.27.(2005•安徽)如图,已知AB∥DE,AB=DE,AF=DC,请问图中有哪几对全等三角形并任选其中一对给予证明.【分析】本题是开放题,应先确定选择哪对三角形,再对应三角形全等条件求解.做题时从已知结合全等的判定方法开始思考,做到由易到难,不重不漏.【解答】解:此图中有三对全等三角形.分别是:△ABF≌△DEC、△ABC≌△DEF、△BCF≌△EFC.证明:∵AB∥DE,∴∠A=∠D.又∵AB=DE、AF=DC,∴△ABF≌△DEC.【点评】三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.28.(2004•昆明)如图所示,在梯形ABCD中,AD∥BC,∠B=∠C,点E是BC边上的中点.求证:AE=DE.【分析】利用已知条件易证△AEB≌△DEC,从而得出AE=DE.【解答】证明:∵AD∥BC,∠B=∠C,∴梯形ABCD是等腰梯形,∴AB=DC,在△AEB与△DEC中,,∴△AEB≌△DEC(SAS),∴AE=DE.【点评】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.29.(2004•淮安)如图,给出下列论断:①DE=CE,②∠1=∠2,③∠3=∠4.请你将其中的两个作为条件,另一个作为结论,构成一个真命题,并加以证明.【分析】可以有三个真命题:(1)②③⇒①,可由ASA证得△ADE≌△BCE,所以DE=EC;(2)①③⇒②,可由SAS证得△ADE≌△BCE,所以∠1=∠2;(3)①②⇒⑧,可由ASA证得△ADE≌△BCE,所以AE=BF,∠3=∠4.【解答】解:②③⇒①证明如下:∵∠3=∠4,∴EA=EB.在△ADE和△BCE中,∴△ADE≌△BCE.∴DE=EC.①③⇒②证明如下:∵∠3=∠4,∴EA=EB,在△ADE和△BCE中,,∴△ADE≌△BCE,∴∠1=∠2.①②⇒⑧证明如下:在△ADE和△BCE中,∴△ADE≌△BCE.∴AE=BE,∠3=∠4.【点评】本题考查了全等三角形的判定和性质;题目是一道开放型的问题,选择有多种,可以采用多次尝试法,证明时要选择较为简单的进行证明.30.(2011•通州区一模)已知:如图,∠ACB=90°,AC=BC,CD是经过点C的一条直线,过点A、B分别作AE⊥CD、BF⊥CD,垂足为E、F,求证:CE=BF.【分析】根据AE⊥CD,BF⊥CD,求证∠BCF+∠B=90°,可得∠ACF=∠B,再利用(AAS)求证△BCF≌△CAE即可.【解答】证明:∵AE⊥CD,BF⊥CD∴∠AEC=∠BFC=90°∴∠BCF+∠B=90°∵∠ACB=90°,∴∠BCF+∠ACF=90°∴∠ACF=∠B在△BCF和△CAE中∴△BCF≌△CAE(AAS)∴CE=BF.【点评】此题主要考查全等三角形的判定与性质这一知识点,解答此题的关键是利用(AAS)求证△BCF≌△CAE,要求学生应熟练掌握.。
2024年中考数学复习 拓展 全等三角形提高证明题含辅助线(六种类型)(原卷+答案解析)

拓展全等三角形提高证明题含辅助线(六种类型)【类型一】利用角平分线构造全等1如图,在△ABC中,AD是角平分线,E,F分别为AC,AB上的点,且∠AED+∠AFD=180°.(1)求证:∠AFD=∠CED;(2)求证:DE=DF.2如图,在ΔABC中,∠C=90°,AD是∠BAC的角平分线交BC于D,过D作DE⊥BA于点E,点F 在AC上,且BD=DF.(1)求证:AC=AE;(2)求证:∠BAC+∠FDB=180°;(3)若AB=9.5,AF=1.5,求线段BE的长,3如图,AD是△ABC的角平分线,H,G分别在AC,AB上,且HD=BD.(1)求证:∠B与∠AHD互补;(2)若∠B+2∠DGA=180°,请探究线段AG与线段AH、HD之间满足的等量关系,并加以证明.4已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.求证:(1)AD=AE=EC.(2)BA+BC=2BF.【类型二】倍长中线5如图,AB=CD,E为BC的中点,∠BAC=∠BCA,求证:AD=2AE.6如图,已知ΔABC中,点M是BC边长的中点,过M作∠BAC的角平分线AD的平行线交AB于E,交CA的延长线于F,求证:(1)AE=AF.(2)BE=CF.7在△ABC中,∠ABC=45°,AM⊥MB,垂足为M,点C是BM延长线上一点,连接AC.(1)如图1,点D在线段AM上,且DM=CM.求证:△BDM≌△ACM;(2)如图2,在(1)的条件下,点E是△ABC外一点,且满足EC=AC,连接ED并延长交BC于点F,且F为线段BC的中点,求证:∠BDF=∠CEF.8规定:有两组边相等,且它们所夹的角互补的两个三角形叫兄弟三角形.如图,OA=OB,OC=OD,∠AOB=∠COD=90°,回答下列问题:(1)求证:△OAC和△OBD是兄弟三角形.(2)取BD的中点P,连接OP,请证明AC=2OP.【类型三】截长补短9如图,在△ABC中,AB=AC,∠A=108°,BD平分∠ABC交AC于D,试说明:BC=AB+CD.10如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,求证:AE+CD=AC.11在△ABC中,∠ABC=60°,点D、E分别在AC、BC上,连接BD、DE和AE;并且有AB=BE,∠AED=∠C.(1)求∠CDE的度数;(2)求证:AD+DE=BD.12(1)如图1,射线OP平分∠MON,在射线OM,ON上分别截取线段OA,OB,使OA=OB,在射线OP上任取一点D,连接AD,BD.求证:AD=BD.(2)如图2,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,求证:BC=AC+AD.(3)如图3,在四边形ABDE中,AB=9,DE=1,BD=6,C为BD边中点,若AC平分∠BAE,EC平分∠AED,∠ACE=120°,求AE的值.【类型四】直接连接13如图,在Rt△ABC中,AB=AC,∠A=90°,点D为BC中点,过点D作DM⊥DN,分别交BA,AC延长线于点M、N,求证:DM=DN.14△ABC中,∠A=90°,AB=AC,D为BC中点,E、F分别在AC、AB上,且DE⊥DF,试判断DE、DF的数量关系,并说明理由.15如图所示,在△ABC中,D为BC的中点,DE⊥BC,交∠BAC的平分线AE于点E,EF⊥AB于点F,EG⊥AC交AC延长线于点G.求证:BF=CG.16如图,在ΔABC中,∠ABC=90°,AB=BC,CD平分∠ACB交AB于D点,过A作AE⊥CD交CD延长线于E点,交CB延长线于F点,取FC中点G,连接DG,过C作CH⊥AC交DG延长线于H,(1)求证:AF=CD;(2)求证:AC=CH+2BD.【类型五】延长交于一点17如图,△ABC中,CD平分∠ACB,过点A作AD⊥CD于点D,点E是AB的中点,连接DE,若AC=20,BC=14,求DE的长.18已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=12 BE.19如图,在Rt△ABC中,∠ACB=90°,∠BAC的角平分线AD交BC于D,交∠ABC的角平分线于E,过点E作EF⊥AE,交AC于点F,求证:AF+BD=AB.20如图,在△ABC中,AB=AC,∠C=45°,点D为AC中点,AE⊥BD交BC于点E,交BD于点F.求证:(1)∠CAE=∠ABD;(2)BD=AE+ED.【类型六】半角模型21如图,△ABC中,AB=AC,∠BAC+∠BDC=180°.(1)求证:AD为∠BDC的平分线;∠BAC,且点E在BD上,直接写出BE、DE、DC三条线段之间的等量关系.(2)若∠DAE=1222(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF=12∠BAD,可求得EF、BE、FD之间的数量关系为.(只思考解题思路,完成填空即可,不必书写证明过程)(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF=12∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.23问题背景:如图1:在四边形ABCD中,AB=AD.∠BAD=120°.∠B=∠ADC=90°.E,F分别是BC.CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.(1)小王同学探究此问题的方法是:延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(直接写结论,不需证明)探索延伸:(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠ADF=180°.E,F分别是BC,CD上的点,且∠EAF=12∠BAD,(1)中结论是否仍然成立,并说明理由;(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=12∠BAD,(1)中的结论是否仍然成立?若成立,请证明:若不成立,请直接写出它们之间的数量关系.24【问题引领】问题1:如图1.在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.小王祠学探究此问题的方法是,延长FD到点G.使DG=BE.连接CG.先证明△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是.【探究思考】问题2:如图2,若将问题Ⅰ的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,∠ECF= 1∠BCD,问题1的结论是否仍然成立?请说明理由.2【拓展延伸】问题3:如图3在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE,EF,FD之间存在的等量关系是.拓展全等三角形提高证明题含辅助线(六种类型)【类型一】利用角平分线构造全等1如图,在△ABC 中,AD 是角平分线,E ,F 分别为AC ,AB 上的点,且∠AED +∠AFD =180°.(1)求证:∠AFD =∠CED ;(2)求证:DE =DF.【答案】(1)见解析;(2)见解析【分析】(1)根据同角的补角相等即可得解;(2)过D 作DM ⊥AB 于M ,DN ⊥AC 于N ,根据角平分线性质求出DM =DN ,由(1)知∠MFD =∠DEN ,证出△FMD ≌△END 即可.【详解】(1)证明:∵∠AED +∠AFD =180°,∠AED +∠CED =180°,∴∠AFD =∠CED ;(2)证明:过D 作DM ⊥AB 于M ,DN ⊥AC 于N ,∵AD 平分∠BAC ,∴DM =DN ,∠FMD =∠END =90°,∵∠AED +∠AFD =180°,∠AED +∠DEN =180°,∴∠MFD =∠DEN ,在△FMD 和△END 中,∠MFD =∠DEN∠FMD =∠END DM =DN,∴△FMD ≌△END (AAS ),∴DE =DF .【点睛】本题考查了全等三角形的性质和判定,角平分线性质的应用,解题关键是利用AAS 推出△FMD ≌△END .2如图,在ΔABC 中,∠C =90°,AD 是∠BAC 的角平分线交BC 于D ,过D 作DE ⊥BA 于点E ,点F 在AC 上,且BD =DF.(1)求证:AC =AE ;(2)求证:∠BAC +∠FDB =180°;(3)若AB =9.5,AF =1.5,求线段BE 的长,【答案】(1)证明见解析;(2)证明见解析;(3)BE 的长为4.【分析】(1)根据已知条件,利用AAS 证明△ACD ≌△AED 即可;(2)设∠1=∠2=α,在AB 上截取AM =AF ,连接MD ,证明△FAD ≌△MAD ,进而证明Rt ΔMDE ≌Rt ΔBDE ,再证明ΔCFD ≌ΔEBD ,根据∠FDB +∠BAC 即可求证;(3)由(2)可得EB =EM ,AF =AM ,根据BE =AB -AM -ME 即可求得BE 的长.【详解】证明:(1)∵AD 平分∠BAC ,∴∠1=∠2,∵DE ⊥BA ,∴∠DEA =∠DEB =90°,∵∠C =90°,∴∠C =∠DEA =90°,在ΔACD 和ΔAED 中,∠DCA =∠DEA∠1=∠2AD =AD,∴ΔACD ≌ΔAED (AAS ),∴AC =AE ,(2)设∠1=∠2=α,∵∠C =∠DEA =90°,在ΔADC 中,∠ADC =90°-α,在ΔADE 中,∠ADE =90°-α,∵∠FDB =∠FCD +∠CFD =90°+∠CFD ,在AB 上截取AM =AF ,连接MD ,在ΔFAD 和ΔMAD 中,FA =MA∠1=∠2AD =AD∴ΔFAD ≌ΔMAD (SAS ),∴FD =MD ,∠5=∠6,∵BD =DF ,∴BD =MD ,在Rt ΔMDE 和Rt ΔBDE 中,MD =BDDE =DE∴Rt ΔMDE ≌Rt ΔBDE (HL ),∴∠3=∠4,设∠5=∠6=β,∵∠1=∠2=α,∴∠1+∠5=∠2+∠6=α+β,在ΔFAD 中,∠1+∠5=∠DFC在ΔAMD 中,∠2+∠6=∠3,∴∠DFC =∠3,∴∠DFC =∠4,在ΔCFD 和ΔEBD 中,∠DCF =∠DEB ∠CFD =∠EBD FD =BD,∴ΔCFD ≌ΔEBD (AAS ),∴∠CFD =∠4,∵∠C =90°,在ΔABC 中,∠4=90°-2α,∴∠CFD =90°-2α,∴∠FDB =90°+90°-2α=180°-2α,∵∠BAC =∠1+∠2=2α,∴∠FDB +∠BAC =180°-2α+2α=180°,(3)∵AF =AM ,且AF =1.5,∴AM =1.5,∵AB =9.5,∴MB =AB -AM =9.5-1.5=8,∵MB =BE ,且ME +BE =BM ,∴BE =12BM =4【点睛】本题考查了三角形全等的性质与判定,角平分线的定义,掌握以上知识是解题的关键.3如图,AD 是△ABC 的角平分线,H ,G 分别在AC ,AB 上,且HD =BD .(1)求证:∠B 与∠AHD 互补;(2)若∠B +2∠DGA =180°,请探究线段AG 与线段AH 、HD 之间满足的等量关系,并加以证明.【答案】(1)见解析;(2)AG =AH +HD ,证明见解析【分析】(1)在AB 上取一点M ,使得AM =AH ,连接DM ,则利用SAS 可得出ΔAHD ≌ΔAMD ,从而得出HD =MD =DB ,即有∠DMB =∠B ,通过这样的转化可证明∠B 与∠AHD 互补.(2)由(1)的结论中得出的∠AHD =∠AMD ,结合三角形的外角可得∠DGM =∠GDM ,可将HD 转化为MG ,从而在线段AG 上可解决问题.【详解】证明:(1)在AB 上取一点M ,使得AM =AH ,连接DM∵AH =AM∠CAD =∠BADAD =AD∴ΔAHD ≌ΔAMD ∴HD =MD ,∠AHD =∠AMD∵HD =DB∴DB =MD∴∠DMB =∠B∵∠AMD +∠DMB =180°∴∠AHD +∠B =180°即∠B 与∠AHD 互补.(2)由(1)∠AHD=∠AMD,HD=MD,∠AHD+∠B=180°,∵∠B+2∠DGA=180°,∠AHD=2∠DGA∴∠AMD=2∠DGM又∵∠AMD=∠DGM+∠GDM∴2∠DGM=∠DGM+∠GDM即∠DGM=∠GDM∴MD=MG∴HD=MG∵AG=AM+MG∴AG=AH+HD.【点睛】本题考查角平分线的性质,应用角平分线构造全等是常用的构造全等的方法,遇到角平分线常有“翻折构造全等”“作角边的垂线段”两种辅助线方法.4已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.求证:(1)AD=AE=EC.(2)BA+BC=2BF.【答案】证明详见解析【详解】分析:(1)根据角平分线的性质,得到∠ABD=∠CBD,然后根据SAS证得△ABD≌△EBC,然后根据全等三角形的性质和三角形的外角得到等腰△ACE,由此可证;(2)过点E作EG⊥BC于点G,根据三角形全等的判定“HL”证得Rt△BEG≌Rt△BEF和Rt△CEG≌Rt△AFE,然后根据全等三角形的对应边相等,等量代换求解.详解:证明:(1)∵BD为△ABC的角平分线,∴∠ABD=∠CBD,∴在△ABD和△EBC中,BD=BC∠ABD=∠CBD BE=BA,∴△ABD≌△EBC(SAS),∴∠BCE=∠BDA,∵∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,∴∠DCE=∠DAE,∴△ACE为等腰三角形,∴AE=EC,∵△ABD≌△EBC,∴AD=EC,∴AD=EC=AE.(2)过点E作EG⊥BC于点G,∵E是BD上的点,EF⊥AB,EG⊥BC,∴EF=EG,∵在Rt△BEG和Rt△BEF中,BE=BE EF=EG,∴Rt△BEG≌Rt△BEF(HL),∴BG=BF,∵在Rt△CEG和Rt△AFE中,EF=EG AE=CE,Rt△CEG≌Rt△AFE,∴AF=CG,∴BA+BC=BF+FA+BG-CG,=BF+BG=∠BF,∴BA+BC=2BF.点睛:此题考查了角平分线定理,全等三角形的判定与性质,以及等腰三角形的性质,利用了转化及等量代换的数学思想,熟练掌握判定与性质是解本题的关键.【类型二】倍长中线5如图,AB=CD,E为BC的中点,∠BAC=∠BCA,求证:AD=2AE.【答案】见解析.【分析】延长AE至点F,使得EF=AE,连接BF,易证△AEC≌△FEB(SAS),得到BF=AC,∠FBE=∠ACE=∠BAC,可得∠ABF=∠DCA,然后通过SAS证明△ABF≌△△DCA即可.【详解】证明:延长AE至点F,使得EF=AE,连接BF,∵∠BEF=∠CEA,BE=CE,∴△AEC≌△FEB(SAS),∴BF=AC,∠FBE=∠ACE=∠BAC,∴∠ABF=∠FBE+∠ABE=∠BAC+∠ABC=∠DCA,在△ABF和△DCA中,AB=CD∠ABF=∠DCA BF=AC,∴△ABF≌△△DCA(SAS),∴AD=FA=2AE.【点睛】本题主要考查三角形全等的判定和性质,正确作出辅助线是解题关键,一般的中线辅助线都是用的倍长中线.6如图,已知ΔABC中,点M是BC边长的中点,过M作∠BAC的角平分线AD的平行线交AB于E,交CA的延长线于F,求证:(1)AE=AF.(2)BE=CF.【答案】见详解.【分析】(1)要证AE=AF,利用等角对等边只需证出∠AFE=∠AEF,利用平行不难发现这两个角和角平分线分成的两角是内错角和同位角;(2)利用倍长中线法构造出全等三角形即可.【详解】证明:(1)∵MF∥DA∴∠AFE=∠CAD,∠AEF=∠DAE又∵AD平分∠CAB∴∠CAD=∠DAE∴∠AFE=∠AEF∴AE=AF(2)将FM延长至N使FM=MN,连接BN.∵M 为CB 中点∴CM =MB在△FMC 和△NMB 中CM =MB∠FMC =∠NMBFM =MN∴△FMC ≌△NMB (SAS )∴CF =BN ,∠F =∠N又∵∠AFE =∠AEF ,∠AEF =∠BEN∴∠N =∠BEN∴BE =BN∴BE =CF【点睛】此题考查的(1)平行线的性质和等角对等边;(2)倍长中线法构造全等三角形.7在△ABC 中,∠ABC =45°,AM ⊥MB ,垂足为M ,点C 是BM 延长线上一点,连接AC .(1)如图1,点D 在线段AM 上,且DM =CM .求证:△BDM ≌△ACM ;(2)如图2,在(1)的条件下,点E 是△ABC 外一点,且满足EC =AC ,连接ED 并延长交BC 于点F ,且F 为线段BC 的中点,求证:∠BDF =∠CEF.【答案】(1)见解析;(2)见解析.【分析】(1)根据已知条件,利用(SAS )即可证明三角形全等;(2)延长EF 至点G ,使FG =EF ,由上题中△BDM ≌△ACM ,得出AC =BD ,再证△BFG ≌△CFE ,可得BG =CE ,∠G =∠CEF ,从而得BD =CE =BG ,即可得∠BDF =∠G =∠CEF .【详解】解:(1)如图,∵∠ABC =45°,AM ⊥MB∴BM =AM在△BMD 和△AMC 中∵DM =CM ∠BDM =∠AMC BM =AM∴△BDM ≌△ACM (SAS ).(2)如图,延长EF 至点G ,使FG =EF ,连接BG∵△BDM ≌△ACM∴BD =AC又∵CE =AC∴BD =CE在△BFG 和△CFE 中∵BF =FC ∠BFG =∠EFC FG =FE∴△BFG ≌△CFE (SAS )∴BG =CE ,∠G =∠CEF∴BD =CE =BG∴∠BDF =∠G =∠CEF .【点睛】本题主要考查全等三角形的判定与性质、等腰直角三角形的性质等知识点,熟练掌握全等三角形的判定和性质是解题的关键.8规定:有两组边相等,且它们所夹的角互补的两个三角形叫兄弟三角形.如图,OA =OB ,OC =OD ,∠AOB =∠COD =90°,回答下列问题:(1)求证:△OAC 和△OBD 是兄弟三角形.(2)取BD 的中点P ,连接OP ,请证明AC =2OP .【答案】(1)证明见解析(2)证明见解析【分析】(1)根据OA =OB ,OC =OD ,∠AOC +∠BOD =180°即可证明;(2)延长OP 至E ,使PE =OP ,先证△BPE ≌△DPO ,推出BE =OD ,∠E =∠DOP ,进而推出BE ∥OD ,再证△EBO ≌△COA ,即可推出OE =AC ,由此可证AC =2OP .【详解】(1)证明:∵∠AOB =∠COD =90°,∴∠AOC +∠BOD =360°-∠AOB -∠COD =360°-90°-90°=180°,又∵AO =OB ,OC =OD ,∴△OAC 和△OBD 是兄弟三角形.(2)证明:延长OP 至E ,使PE =OP,∵P 为BD 的中点,∴BP =PD ,∵在△BPE 和△DPO 中,PE =PO∠BPE =∠DPO BP =DP,∴△BPE ≌△DPO SAS ,∴BE =OD ,∠E =∠DOP ,∴BE ∥OD ,∴∠EBO +∠BOD =180°,又∵∠BOD +∠AOC =180°,∴∠EBO =∠AOC ,∵BE =OD ,OD =OC ,∴BE =OC ,在△EBO 和△COA 中,OB =AO∠EBO =∠AOCBE =OC∴△EBO ≌△COA SAS ,∴OE =AC ,又∵OE =2OP ,∴AC =2OP .【点睛】本题考查全等三角形的判定与性质、平行线的判定与性质,解题的关键是正确作出辅助线,构造全等三角形.【类型三】截长补短9如图,在△ABC 中,AB =AC ,∠A =108°,BD 平分∠ABC 交AC 于D ,试说明:BC =AB +CD.【答案】见解析【分析】在线段BC 上截取BE =BA ,连接DE .则只需证明CD =CE 即可.结合角度证明∠CDE =∠CED .【详解】解:证明:在线段BC 上截取BE =BA ,连接DE .∵BD 平分∠ABC ,∴∠ABD =∠EBD =12∠ABC .在△ABD 和△EBD 中,BE =BA∠ABD =∠EBD BD =BD,∴△ABD ≌△EBD .(SAS )∴∠BED =∠A =108°,∠ADB =∠EDB .又∵AB=AC,∠A=108°,∠ACB=∠ABC=12×(180°-108°)=36°,∴∠ABD=∠EBD=18°.∴∠ADB=∠EDB=180°-18°-108°=54°.∴∠CDE=180°-∠ADB-∠EDB=180°-54°-54°=72°.∴∠DEC=180°-∠DEB=180°-108°=72°.∴∠CDE=∠DEC.∴CD=CE.∴BC=BE+EC=AB+CD.【点睛】此题考查全等三角形的判定和性质及等腰三角形的判定,综合性较强.10如图,在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O,求证:AE+CD=AC.【答案】证明见解析【分析】根据三角形内角和定理和角平分线的定义,得到∠AOC=120°,∠AOE=∠COD=60°,在AC上截取AF=AE,连接OF,分别证明△AOE≌△AOF SAS,△COD≌△COF ASA,得到CD=CF,即可证明结论.【详解】证明:∵∠B=60°,∴∠BAC+∠ACB=180°-∠B=120°,∵AD、CE分别平分∠BAC、∠ACB,∴∠OAC=∠OAB=12∠BAC,∠OCA=∠OCB=12∠ACB,∴∠OAC+∠OCA=12∠BAC+12∠ACB=12∠BAC+∠ACB=60°,∴∠AOC=120°,∴∠AOE=∠COD=180°-∠AOC=60°,如图,在AC上截取AF=AE,连接OF,在△AOE和△AOF中,AE=AF∠OAE=∠OAF AO=AO,∴△AOE≌△AOF SAS,∴∠AOE=∠AOF=60°,∴∠COF=∠AOC-∠AOF=120°-60°=60°,∵∠COD=60°,∴∠COD=∠COF,在△COD和△COF中,∠OCD=∠OCF CO=CO∠COD=∠COF,∴△COD≌△COF ASA,∴CD=CF,∵AF=AE,∴AF+CF=AE+CD=AC.【点睛】本题考查了全等三角形的判定和性质,三角形内角和定理,角平分线的定义,做辅助线构造全等三角形是解题关键.11在△ABC中,∠ABC=60°,点D、E分别在AC、BC上,连接BD、DE和AE;并且有AB=BE,∠AED=∠C.(1)求∠CDE的度数;(2)求证:AD+DE=BD.【答案】(1)60°;(2)见解析【分析】(1)由AB=BE,∠ABC=60°,可得△ABE为等边三角形,由∠AEB=∠EAC+∠C,∠CDE=∠EAC+∠AED,∠AED=∠C,可证∠CDE=∠AEB=60°(2)延长DA至F,使AF=DE,连接FB,由∠BED=60°+∠AED,∠BAF=60°+∠C,且∠C=∠AED,可证△FBA≌△DBE(SAS)由DB=FB,可证△FBD为等边三角形,可得BD=FD,可推出结论,【详解】解:(1)∵AB=BE,∠ABC=60°,∴△ABE为等边三角形,∴∠BAE=∠AEB=60°,∵∠AEB=∠EAC+∠C,∠CDE=∠EAC+∠AED,∵∠AED=∠C,∴∠CDE=∠AEB=60°(2)如图,延长DA至F,使AF=DE,连接FB,由(1)得△ABE为等边三角形,∴∠AEB=∠ABE=60°,∵∠BED=∠AEB+∠AED=60°+∠AED,又∵∠BAF=∠ABE+∠C=60°+∠C,且∠C=∠AED,∴∠BED=∠BAF,在△FBA与△DBE中,AB=BE∠BAF=∠BED AF=DE∴△FBA≌△DBE(SAS)∴DB=FB,∠DBE=∠FBA∴∠DBE+∠ABD=∠FBA+∠ABD,∴∠ABE=∠FBD=60°又∵DB=FB,∴△FBD为等边三角形∴BD=FD,又∵FD=AF+AD,且AF=DE,∴FD=DE+AD=BD,【点睛】本题考查等边三角形的判定与性质,三角形全等判定与性质,线段和差,三角形外角性质,关键是引辅助线构造三角形全等证明等边三角形.12(1)如图1,射线OP平分∠MON,在射线OM,ON上分别截取线段OA,OB,使OA=OB,在射线OP上任取一点D,连接AD,BD.求证:AD=BD.(2)如图2,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,求证:BC=AC+AD.(3)如图3,在四边形ABDE中,AB=9,DE=1,BD=6,C为BD边中点,若AC平分∠BAE,EC平分∠AED,∠ACE=120°,求AE的值.【答案】(1)见详解;(2)见详解;(3)AE=13【分析】(1)由题意易得∠AOD=∠BOD,然后易证△AOD≌△BOD,进而问题可求证;(2)在BC上截取CE=CA,连接DE,由题意易得∠ACD=∠ECD,∠B=30°,则有△ACD≌△ECD,然后可得∠A=∠CED=60°,则根据三角形外角的性质可得∠EDB=∠B=30°,然后可得DE=BE,进而问题可求证;(3)在AE上分别截取AF=AB,EG=ED,连接CF、CG,同理(2)可证△ABC≌△AFC,△CDE≌△CGE,则有∠ACB=∠ACF,∠DCE=∠GCE,然后可得∠ACF+∠GCE=60°,进而可得△CFG是等边三角形,最后问题可求解.【详解】证明:(1)∵射线OP平分∠MON,∴∠AOD=∠BOD,∵OD=OD,OA=OB,∴△AOD≌△BOD(SAS),∴AD=BD.(2)在BC上截取CE=CA,连接DE,如图所示:∵∠ACB=90°,∠A=60°,CD平分∠ACB,∴∠ACD=∠ECD,∠B=30°,∵CD=CD,∴△ACD≌△ECD(SAS),∴∠A=∠CED=60°,AD=DE,∵∠B+∠EDB=∠CED,∴∠EDB=∠B=30°,∴DE=BE,∴AD=BE,∵BC=CE+BE,∴BC=AC+AD.(3)在AE 上分别截取AF =AB =9,EG =ED =1,连接CF 、CG ,如图所示:同理(1)(2)可得:△ABC ≌△AFC ,△CDE ≌△CGE ,∴∠ACB =∠ACF ,∠DCE =∠GCE ,BC =CF ,CD =CG ,DE =GE =1,∵C 为BD 边中点,∴BC =CD =CF =CG =3,∵∠ACE =120°,∴∠ACB +∠DCE =60°,∴∠ACF +∠GCE =60°,∴∠FCG =60°,∴△CFG 是等边三角形,∴FG =CF =CG =3,∴AE =AF +FG +GE =9+3+1=13.【点睛】本题主要考查三角形全等的性质与判定、角平分线的定义、等腰三角形的性质与判定及等边三角形的性质与判定,解题的关键是构造辅助线证明三角形全等.【类型四】直接连接13如图,在Rt △ABC 中,AB =AC ,∠A =90°,点D 为BC 中点,过点D 作DM ⊥DN ,分别交BA ,AC 延长线于点M 、N ,求证:DM =DN.【答案】见解析【分析】连接AD ,可得∠ADM =∠CDN ,可证△AMD ≌△CND ,可得DM =DN .【详解】解:连接AD ,∵D 为BC 中点,∴AD =BD ,∠BAD =∠C ,∵∠ADM +∠MDC =90°,∠MDC +∠CDN =90°,∴∠ADM =∠CDN ,∵∠MAD =MAC +DAC =135°,∠NCD =180°-∠ACD =135°在ΔAMD 和ΔCND 中,∠ADM =∠CDNAD =CD ∠MAD =∠NCD,∴ΔAMD ≅ΔCND (ASA ),∴DM =DN .【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AMD ≌△CND 是解题的关键.14△ABC 中,∠A =90°,AB =AC ,D 为BC 中点,E 、F 分别在AC 、AB 上,且DE ⊥DF ,试判断DE 、DF 的数量关系,并说明理由.【答案】DE =DF ,理由见解析【分析】连接AD ,则有AD =CD ,∠DAF =∠C =45°,且AD ⊥CD ,可得∠CDE +∠EDA =∠ADF +∠EDA =90°,所以∠CDE =∠ADF ,可证△CDE ≌△ADF ,可得结论.【详解】DE =DF ,理由如下:连接AD ,因为∠A =90°,AB =AC ,D 为BC 中点,∴CD =AD ,∠C =∠DAF =45°,AD ⊥CD ,∴∠CDE +∠EDA =∠ADF +∠EDA =90°,∴∠CDE =∠ADF ,在△CDE 和△ADF 中,∠C =∠DAFCD =AD ∠CDE =∠ADF,∴△CDE ≌△ADF (ASA ),∴DE =DF .【点睛】本题主要考查了三角形全等的判定和性质,正确掌握全等三角形的判定方法是解题的关键.15如图所示,在△ABC 中,D 为BC 的中点,DE ⊥BC ,交∠BAC 的平分线AE 于点E ,EF ⊥AB 于点F ,EG ⊥AC 交AC 延长线于点G .求证:BF =CG.【答案】见解析.【分析】连接EB 、EC ,利用已知条件证明Rt △BEF ≌Rt △CEG ,即可得到BF =CG .【详解】证明:连接BE 、EC ,∵ED ⊥BC ,D 为BC 中点,∴BE =EC ,∵EF ⊥AB ,EG ⊥AG ,且AE 平分∠FAG ,∴FE =EG,在Rt △BEF 和Rt △CEG 中,BE =CE EF =EG ,∴Rt △BEF ≌Rt △CEG (HL ),∴BF =CG .【点评】本题考查了全等三角形的判定:解题的关键是全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.16如图,在ΔABC 中,∠ABC =90°,AB =BC ,CD 平分∠ACB 交AB 于D 点,过A 作AE ⊥CD 交CD 延长线于E 点,交CB 延长线于F 点,取FC 中点G ,连接DG ,过C 作CH ⊥AC 交DG 延长线于H ,(1)求证:AF =CD ;(2)求证:AC =CH +2BD.【答案】(1)见解析;(2)见解析【分析】(1)根据垂直推出∠ABF =∠ABC =90°与∠FAB =∠BCD ,则可证明ΔABF ≌ΔCBD ,即可有AF =CD ;(2)连接FD 根据CE ⊥AF ,AB ⊥CF ,推出FD ⊥AC ,即可证明CH ⎳FD ,可有∠HCG =∠DFG ,然后证明ΔFGD ≌ΔCGH 推出CH =FD ,根据已知条件即可有AD =DF ,由(1)知FB =BD ,即可证明AC =CH +2BD .【详解】证:(1)∵∠ABC =90°,CE ⊥AF∴∠ABF =∠ABC =90°∴∠AFB +∠FAB =90°,∠EFC +∠BCD =90°∴∠FAB =∠BCD在ΔABF 与ΔCBD 中,∠ABF =∠CBDAB =CB∠FAB =∠DCB∴ΔABF ≌ΔCBD∴AF =CD (2)连接FD∵CE ⊥AF ,AB ⊥CF∴FD ⊥AC∵CH ⊥AC∴CH ⎳FD∴∠HCG =∠DFG∵G 是FC 中点∴FG =CG在ΔFGD 与ΔCGH 中,∠DFG =∠HCGFG =CG∠FGD =∠CGH∴ΔFGD ≌ΔCGH∴CH =FD ∵CE ⊥AF ,CE 平分∠FCA∴AC =CF∴AD =DF由(1)可知ΔABF ≌ΔCBD∴FB =BD∴CF =CB +BF =AB +BF =AD +DB +BF =CH +2DB即AC =CH +2BD【点睛】本题主要考查了三角形全等的性质与判定,角平分线的性质,在(1)中找出条件证明ΔABF ≌ΔCBD 是关键,在(2)中作出辅助线是解题的关键.【类型五】延长交于一点17如图,△ABC 中,CD 平分∠ACB ,过点A 作AD ⊥CD 于点D ,点E 是AB 的中点,连接DE ,若AC =20,BC =14,求DE的长.【答案】DE 的长为3.【分析】先添加辅助线,构造全等三角形,利用性质求出AD =DF ,最后用中位线定理即可求解.【详解】解:如图,延长AD ,CB 交于点F ,∵CD 平分∠ACB ,∴∠ACD =∠FCD ,∵AD ⊥CD ,∴∠ADC =∠FDC =90°,在△ACD 和△FCD 中,∠ACD =∠FCDCD =CD ∠ADC =∠FDC,∴△ACD ≌△FCD ASA ,∴AD =DF ,AC =CF =20,∴BF =CF -BC =20-14=6,∵点D 为AF 中点,点E 为AB 中点,∴DE 为△ABF 的中位线,∴DF =12BF =3,答:DE 的长为3.【点睛】此题考查了等腰三角形和全等三角形的判定和性质,三角形中位线定理,解题的关键是延长CB 交AD 延长线于F ,证明DE 是△ABF 的中位线.18已知,Rt△ABC 中,∠ACB =90°,AC =BC ,∠ABC 的角平分线交AC 于E ,AD ⊥BE 于D ,求证:AD =12BE .【答案】见解析【详解】试题分析:延长AD 和BC 交于F ,求出∠CBE =∠CAF ,AC =BC ,证△EBC ≌△FAC ,△ABD ≌△FBD ,推出BE =AF ,AD =DF ,即可得出答案.解:如图延长AD 和BC 交于F ,∵Rt △ABC 中,∠ACB =90°,∠BAC =45°,∴∠ABC =45°=∠BAC ,∴AC =BC ,∵∠ACB =90°,∴∠BCE =∠ACF =90°,∵BE 平分∠ABC ,∴∠ABD =∠EBC ,∵BD ⊥AD ,∴∠BCE =∠ADE =90°,∵∠BEC =∠AED ,∴根据三角形内角和定理得:∠DAE =∠CBE ,在△BCE 和△ACF 中,∠FAC =∠CBE AC =BC ∠ACF =∠BCE,∴△BCE ≌△ACF (SAS ),∴BE =AF ,在△ABD 和△FBD 中,∠ABD =∠FDN BD =BD ∠ADB =∠FDB,∴△ABD≌△FBD (ASA ),∴AD =DF ,即AF =2AD ,∴AD =12AF ,∴AD =12BE .考点:全等三角形的判定与性质.19如图,在Rt △ABC 中,∠ACB =90°,∠BAC 的角平分线AD 交BC 于D ,交∠ABC 的角平分线于E ,过点E 作EF ⊥AE ,交AC 于点F ,求证:AF +BD =AB.【答案】见解析【分析】延长EF ,BC 相交于点M ,分别证明△AEB ≌△MEB 和△AEF ≌△MED 即可得解.【详解】证明:延长EF ,BC 相交于点M ,∵∠ACB =90°,∴∠CAB +∠CBA =90°,∵AE 平分∠BAC ,BE 平分∠ABC ,∴∠EAB +∠EBA =45°,∴∠AEB =180°-45°=135°,∴∠DEB =180°-135°=45°,∵AE ⊥EF ,∴∠MEB =∠MED +∠DEB =90°+45°=135°=∠AEB ,在△AEB 和△MEB 中,∠AEB =∠MEBEB =EB ∠ABE =∠MBE,∴△AEB ≌△MEB ASA ,∴∠EAB =∠M ,AE =ME ,AB =MB ,∵AE 平分∠BAC ,∴∠FAE =∠EAB ,∴∠FAE =∠M ,在△AEF 和△MED 中,∠FAE =∠MAE =ME ∠AEF =∠MED =90°,∴△AEF ≌△MED ASA ,∴AF =MD ,∴AF +BD =MD +BD =MB =AB .【点睛】本题考查角平分线的定义和全等三角形的判定和性质.熟练掌握角平分线的定义,通过添加辅助线证明三角形全等是解题的关键.20如图,在△ABC 中,AB =AC ,∠C =45°,点D 为AC 中点,AE ⊥BD 交BC 于点E ,交BD 于点F.求证:(1)∠CAE=∠ABD;(2)BD=AE+ED.【答案】(1)见解析(2)见解析【分析】(1)根据三角形的内角和定理得出∠BAC=90°,再根据直角三角形两锐角互余得出∠CAE+∠BAF=∠ABD+∠BAF=90°,即可求证;(2)过点C作CA的垂线交AE延长线于点M,先证明△ACM≌△BAD ASA,得出AD=CM,BD= AM,则CM=CD,再证明△MCE≌△DCE SAS,得出EM=ED,即可求证.【详解】(1)证明:∵AB=AC,∠C=45°,∴∠CBA=45°,∴∠BAC=90°,∵AE⊥BD,∴∠AFB=90°∴∠CAE+∠BAF=∠ABD+∠BAF=90°,∴∠CAE=∠ABD.(2)证明:过点C作CA的垂线交AE延长线于点M∵CM⊥CA,∴∠MCA=90°即∠MCA=∠CAB,在△ACM和△BAD中,∠CAE=∠ABD AB=AC∠MCA=∠CAB∴△ACM≌△BAD ASA,∴AD=CM,∵D为AC中点,∴AD=CD,∴CM=CD∵∠MCA=90°,∠ACB=45°,∴∠ACB=∠MCB,在△MCE和△DCE中,CM=CD∠ACB=∠MCB CE=CE,∴△MCE≌△DCE SAS∴EM=ED,∴AM=AE+EM=AE+ED,∴BD=AE+ED.【点睛】本题主要考查了三角形的内角和定理,全等三角形的判定和性质,解题的关键是掌握三角形的内角和为180°,直角三角形两锐角互余,以及正确画出辅助线,构造全等三角形,根据全等三角形的性质进行证明.【类型六】半角模型21如图,△ABC中,AB=AC,∠BAC+∠BDC=180°.(1)求证:AD为∠BDC的平分线;(2)若∠DAE=12∠BAC,且点E在BD上,直接写出BE、DE、DC三条线段之间的等量关系.【答案】(1)见解析;(2)DE=B E+DC.【分析】(1)过A作AG⊥BD于G,AF⊥DC于F,先证明∠BAG=∠CAF,然后证明△BAG≌△CAF得到AG=AF,最后由角平分线的判定定理即可得到结论;(2)过A作∠CAH=∠BAE,证明△EAD≌△HAD,得到AE=AH,再证明△EAB≌△HAC中,即可得出BE、DE、DC三条线段之间的等量关系.【详解】证明:(1)如图1,过A作AG⊥BD于G,AF⊥DC于F,∵AG⊥BD,AF⊥DC,∴∠AGD=∠F=90°,∴∠GAF+∠BDC=180°,∵∠BAC+∠BDC=180°,∴∠GAF=∠BAC,∴∠GAF-∠GAC=∠BAC-∠GAC,∴∠BAG=∠CAF,在△BAG和△CAF中,∠AGB=∠F=90°∠BAG=∠CAF AB=AC∴△BAG≌△CAF(AAS),∴AG=AF,∴∠BDA=∠CDA,(2)BE、DE、DC三条线段之间的等量关系是DE=B E+DC,理由如下:如图2,过A作∠CAH=∠BAE交DC的延长线于H,∵∠DAE=12∠BAC,∴∠DAE=∠BAE+∠CAD,∵∠CAH=∠BAE,∴∠DAE=∠CAH+∠CAD=∠DAH,在△EAD和△HAD中,∠EAD=∠HAD AD=AD∠ADE=∠ADH ,∴△EAD≌△HAD(ASA),∴DE=DH,AE=AH,在△EAB和△HAC中,AB=AC∠BAE=∠CAH AE=AH,∴△EAB≌△HAC(SAS),∴BE=CH,∴DE=DH=DC+CH=DC+BE,∴DE=DC+BE.故答案是:DE=DC+BE.【点睛】本题考查了全等三角形的性质和判定,角平分线的判定定理,线段和差的证明,掌握截长法和补短法是解答此题的突破口.22(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,若∠EAF=12∠BAD,可求得EF、BE、FD之间的数量关系为.(只思考解题思路,完成填空即可,不必书写证明过程)(2)如图2,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,若∠EAF=12∠BAD,判断EF、BE、FD之间的数量关系还成立吗,若成立,请完成证明,若不成立,请说明理由.【答案】(1)BE+DF=EF;(2)EF+DF=BE.理由见解析.【分析】(1)线段EF、BE、FD之间的数量关系是BE+DF=EF.如图,延长CB至M,使BM=DF,连接AM,利用全等三角形的性质解决问题即可.(2)结论:EF+DF=BE.如图中,在BE上截取BM=DF,连接AM,证明△ABM≌△ADF SAS,推出AM=AF,∠BAM=∠DAF,再证明△AEM≌△AEF SAS,可得结论.【详解】(1)解:线段EF、BE、FD之间的数量关系是BE+DF=EF.如图,延长CB至M,使BM=DF,连接AM,∵∠ABC=∠D=90°,∠ABC+∠1=180°,即:∠ABC+∠D=180°,∴∠1=∠D,在△ABM 和△ADF 中,AB =AD∠1=∠D BM =DF,∴△ABM ≌△ADF SAS ,∴AM =AF ,∠3=∠2,∵∠EAF =12∠BAD ,∠EAF +∠2+∠4=∠BAD ,∴∠2+∠4=∠EAF ,∴∠EAM =∠3+∠4=∠2+∠4=∠EAF ,在△MAE 和△FAE 中,AM =AF∠MAE =∠FAE AE =AE,∴△MAE ≌△FAE SAS ,∴EF =EM ,∵EM =BM +BE =BE +DF ,∴EF =BE +FD ;故答案为:BE +DF =EF .(2)结论:EF +DF =BE .理由:在BE 上截取BM =DF ,连接AM ,∵∠B +∠ADC =180°,∠ADC +∠ADE =180°,∴∠B =∠ADF ,在△ABM 与△ADF 中,BM =DF∠ABM =∠ADF AB =AD,∴△ABM ≌△ADF SAS ,∴AM =AF ,∠BAM =∠DAF ,则∠BAM +∠MAD =∠DAF +∠MAD ,∴∠BAD =∠MAF∵∠EAF =12∠BAD ,∠EAF +∠EAM =∠MAF ,∴∠EAF =∠EAM ,在△AEM 与△AEF 中,AM =AF∠EAF =∠EAM AE =AE,∴△AEM ≌△AEF SAS ,∴EM =EF ,即BE -BM =EF ,即BE -DF =EF ,∴EF +DF =BE .【点睛】本题考查全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.23问题背景:如图1:在四边形ABCD 中,AB =AD .∠BAD =120°.∠B =∠ADC =90°.E ,F 分别是BC .CD 上的点,且∠EAF =60°,探究图中线段BE ,EF ,FD 之间的数量关系.(1)小王同学探究此问题的方法是:延长FD到点G.使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;(直接写结论,不需证明)探索延伸:(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠ADF=180°.E,F分别是BC,CD上的点,且∠EAF=12∠BAD,(1)中结论是否仍然成立,并说明理由;(3)如图3,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=12∠BAD,(1)中的结论是否仍然成立?若成立,请证明:若不成立,请直接写出它们之间的数量关系.【答案】(1)EF=BE+FD(2)(1)中的结论EF=BE+FD仍然成立.证明见解析;(3)结论EF=BE+FD不成立,结论是:EF=BE-FD.证明见解析.【分析】(1)延长FD到点G.使DG=BE.连接AG,利用全等三角形的性质解决问题即可;(2)延长CB至M,使BM=DF,连接AM.证明△ABM≌△ADF(SAS),由全等三角形的性质得出AF= AM,∠2=∠3.△AME≌△AFE(SAS),由全等三角形的性质得出EF=ME,即EF=BE+BM,则可得出结论;(3)在BE上截取BG,使BG=DF,连接AG.证明△ABG≌△ADF(SAS).由全等三角形的性质得出∠BAG=∠DAF,AG=AF.证明△AEG≌△AEF(SAS),由全等三角形的性质得出结论.【详解】(1)解:EF=BE+FD.延长FD到点G.使DG=BE.连接AG,∵∠ABE=∠ADG=∠ADC=90°,AB=AD,∴△ABE≌△ADG(SAS).∴AE=AG,∠BAE=∠DAG.∴∠BAE+∠DAF=∠DAG+∠DAF=∠EAF=60°.∴∠GAF=∠EAF=60°.又∵AF=AF,∴△AGF≌△AEF(SAS).∴FG=EF.∵FG=DF+DG.∴EF=BE+FD.故答案为:EF=BE+FD;(2)解:(1)中的结论EF=BE+FD仍然成立.证明:如图②中,延长CB至M,使BM=DF,连接AM.∵∠ABC +∠D =180°,∠1+∠ABC =180°,∴∠1=∠D ,在△ABM 与△ADF 中,AB =AD∠1=∠D BM =DF,∴△ABM ≌△ADF (SAS ).∴AF =AM ,∠2=∠3.∵∠EAF =12∠BAD ,∴∠2+∠4=12∠BAD =∠EAF .∴∠3+∠4=∠EAF ,即∠MAE =∠EAF .在△AME 与△AFE 中,AM =AF∠MAE =∠EAF AE =AE,∴△AME ≌△AFE (SAS ).∴EF =ME ,即EF =BE +BM ,∴EF =BE +DF ;(3)解:结论EF =BE +FD 不成立,结论:EF =BE -FD .证明:如图③中,在BE 上截取BG ,使BG =DF ,连接AG .∵∠B +∠ADC =180°,∠ADF +∠ADC =180°,∴∠B =∠ADF .在△ABG 与△ADF 中,AB =AD∠ABG =∠ADF BG =DF,∴△ABG ≌△ADF (SAS ).∴∠BAG =∠DAF ,AG =AF .∴∠BAG +∠EAD =∠DAF +∠EAD =∠EAF =12∠BAD .∴∠GAE =∠EAF .∵AE =AE ,∴△AEG ≌△AEF (SAS ),∴EG =EF ,∵EG =BE -BG ,∴EF =BE -FD .【点睛】本题是三角形综合题,考查了三角形全等的判定和性质等知识,解题的关键是添加辅助线,构造全等三角形解决问题.24【问题引领】问题1:如图1.在四边形ABCD 中,CB =CD ,∠B =∠ADC =90°,∠BCD =120°.E ,F 分别是AB ,AD 上的点.且∠ECF =60°.探究图中线段BE ,EF ,FD 之间的数量关系.小王祠学探究此问题的方法是,延长FD 到点G .使DG =BE .连接CG .先证明△CBE ≌△CDG ,再证明△CEF ≌△CGF .他得出的正确结论是.【探究思考】问题2:如图2,若将问题Ⅰ的条件改为:四边形ABCD 中,CB =CD ,∠ABC +∠ADC =180°,∠ECF =。
(完整版)全等三角形证明经典50题(含答案)
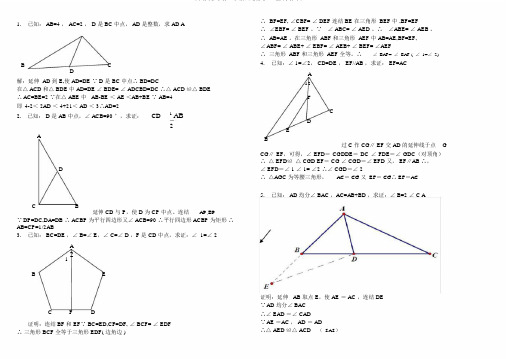
1.已知: AB=4 , AC=2 , D 是 BC 中点, AD 是整数,求 AD AB CD解:延伸 AD 到 E,使 AD=DE ∵ D 是 BC 中点∴ BD=DC在△ ACD 和△ BDE 中 AD=DE ∠ BDE= ∠ ADCBD=DC ∴△ ACD ≌△ BDE∴AC=BE=2 ∵在△ ABE 中 AB-BE < AE <AB+BE ∵ AB=4即4-2< 2AD < 4+21< AD < 3∴AD=22. 已知: D 是 AB 中点,∠ ACB=90 °,求证:CD 1 AB2ADC B延伸 CD 与 P,使 D 为 CP 中点。
连结AP,BP∵DP=DC,DA=DB ∴ ACBP 为平行四边形又∠ ACB=90 ∴平行四边形 ACBP 为矩形∴AB=CP=1/2AB3.已知: BC=DE ,∠ B=∠ E,∠ C=∠ D ,F 是 CD 中点,求证:∠ 1=∠ 2A12B EC F D证明:连结 BF 和 EF∵ BC=ED,CF=DF, ∠ BCF= ∠ EDF∴三角形 BCF 全等于三角形 EDF( 边角边 )∴BF=EF, ∠CBF= ∠ DEF 连结 BE 在三角形 BEF 中 ,BF=EF∴∠EBF= ∠ BEF 。
∵ ∠ ABC= ∠ AED 。
∴ ∠ABE= ∠ AEB 。
∴AB=AE 。
在三角形 ABF 和三角形 AEF 中 AB=AE,BF=EF,∠ABF= ∠ ABE+ ∠ EBF= ∠ AEB+ ∠ BEF= ∠AEF∴三角形 ABF 和三角形 AEF 全等。
∴∠ BAF=∠ EAF (∠ 1=∠ 2) 4.已知:∠ 1=∠2, CD=DE , EF//AB ,求证: EF=ACA12FCDEB过 C 作 CG∥ EF 交 AD 的延伸线于点G CG∥ EF,可得,∠ EFD= CGDDE= DC ∠ FDE=∠ GDC(对顶角)∴ △ EFD≌ △ CGD EF= CG ∠ CGD=∠ EFD 又, EF∥AB ∴,∠ EFD=∠ 1 ∠ 1= ∠2 ∴∠ CGD=∠ 2∴ △AGC 为等腰三角形,AC= CG 又 EF= CG∴ EF=AC5.已知: AD 均分∠ BAC ,AC=AB+BD ,求证:∠ B=2 ∠ C A证明:延伸AB 取点 E,使 AE = AC ,连结 DE∵AD 均分∠ BAC∴∠ EAD =∠ CAD∵AE =AC , AD = AD∴△ AED ≌△ ACD(SAS)∴∠ E=∠ C∵AC =AB+BD∴AE = AB+BD∵AE = AB+BE∴ BD =BE∴∠ BDE =∠ E∵∠ ABC =∠ E+ ∠ BDE∴∠ ABC = 2∠E∴∠ ABC = 2∠C6.已知: AC 均分∠ BAD ,CE⊥AB ,∠ B+ ∠ D=180 °,求证: AE=AD+BE证明:在AE 上取 F,使 EF=EB ,连结 CF∵ CE⊥ AB∴∠ CEB =∠ CEF= 90°∵ EB= EF, CE= CE,∴△ CEB ≌△ CEF∴∠ B =∠ CFE∵∠ B +∠ D= 180°,∠ CFE+∠ CFA = 180°∴∠ D =∠ CFA∵AC 均分∠ BAD∴∠ DAC =∠ FAC∵AC =AC∴△ ADC ≌△ AFC ( SAS)∴AD =AF ∴AE =AF + FE=AD + BE12.如图,四边形 ABCD 中, AB ∥ DC ,BE、CE 分别均分∠ ABC 、∠ BCD ,且点 E在AD 上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形的提高拓展训练知识点睛全等三角形的性质:对应角相等,对应边相等,对应边上的中线相等,对应边上的高相等,对应角的角平分线相等,面积相等.寻找对应边和对应角,常用到以下方法:(1)全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边. (2)全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角. (3)有公共边的,公共边常是对应边. (4)有公共角的,公共角常是对应角. (5)有对顶角的,对顶角常是对应角.(6)两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).要想正确地表示两个三角形全等,找出对应的元素是关键. 全等三角形的判定方法:(1) 边角边定理(SAS ):两边和它们的夹角对应相等的两个三角形全等. (2) 角边角定理(ASA ):两角和它们的夹边对应相等的两个三角形全等. (3) 边边边定理(SSS ):三边对应相等的两个三角形全等.(4) 角角边定理(AAS ):两个角和其中一个角的对边对应相等的两个三角形全等. (5) 斜边、直角边定理(HL ):斜边和一条直角边对应相等的两个直角三角形全等.全等三角形的应用:运用三角形全等可以证明线段相等、角相等、两直线垂直等问题,在证明的过程中,注意有时会添加辅助线.拓展关键点:能通过判定两个三角形全等进而证明两条线段间的位置关系和大小关系.而证明两条线段或两个角的和、差、倍、分相等是几何证明的基础.例题精讲板块一、截长补短【例1】 已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.D OECBA【例2】 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?【变式拓展训练】如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?【例3】 已知:如图,ABCD 是正方形,∠F AD =∠F AE . 求证:BE +DF =AE .【例4】 以ABC ∆的AB 、AC 为边向三角形外作等边ABD ∆、ACE ∆,连结CD 、BE 相交于点O .求证:OA 平分DOE ∠.NEB M A DF AB C D EO O E D C B A _ F _ E_ D_ C _ B _ A _ N _ C _ D _ E _ B _ M _ A【例5】 如图所示,ABC ∆是边长为1的正三角形,BDC ∆是顶角为120︒的等腰三角形,以D 为顶点作一个60︒的MDN ∠,点M 、N 分别在AB 、AC 上,求AMN ∆的周长.【例6】 五边形ABCDE 中,AB =AE ,BC +DE =CD ,∠ABC +∠AED =180°,求证:AD 平分∠CDE板块二、全等与角度【例7】如图,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC∠的度数.【例8】在等腰ABC ∆中,AB AC =,顶角20A ∠=︒,在边AB 上取点D ,使AD BC =,求BDC ∠.D CB A N MDCB AC ED BA DC BA【例9】 如图所示,在ABC ∆中,AC BC =,20C ∠=︒,又M 在AC 上,N 在BC 上,且满足50BAN ∠=︒,60ABM ∠=︒,求NMB ∠.【例10】 在四边形ABCD 中,已知AB AC =,60ABD ︒∠=,76ADB ︒∠=,28BDC ︒∠=,求DBC∠的度数.【例11】 如图所示,在四边形ABCD 中,12DAC ︒∠=,36CAB ︒∠=,48ABD ︒∠=,24DBC ︒∠=,求ACD ∠的度数.【例12】 在正ABC ∆内取一点D ,使DA DB =,在ABC ∆外取一点E ,使DBE DBC ∠=∠,且BE BA =,求BED ∠.CDB ADCBAD E C B A NMCBA【例13】 如图所示,在ABC ∆中,44BAC BCA ︒∠=∠=,M 为ABC ∆内一点,使得30MCA ︒∠=,16MAC ︒∠=,求BMC ∠的度数.M C A B全等三角形证明经典50题(含答案)1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD延长AD到E,使DE=AD,则三角形ADC全等于三角形EBD即BE=AC=2 在三角形ABE中,AB-BE<AE<AB+BE即:10-2<2AD<10+2 4<AD<6又AD是整数,则AD=52.已知:D是AB中点,∠ACB=90°,求证:12 CD AB3.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2 证明:连接BF和EF。
因为BC=ED,CF=DF,∠BCF=∠EDF。
所以三角形BCF全等于三角形EDF(边角边)。
所以BF=EF,∠CBF=∠DEF。
连接BE。
在三角形BEF中,BF=EF。
所以∠EBF=∠BEF。
又因为∠ABC=∠AED。
所以∠ABE=∠AEB。
所以AB=AE。
在三角形ABF和三角形AEF中,AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF。
所以三角形ABF和三角形AEF全等。
所以∠BAF=∠EAF (∠1=∠2)。
ADB C4.已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC 证明:过E点,作EG//AC,交AD延长线于G则∠DEG=∠DCA,∠DGE=∠2又∵CD=DE∴⊿ADC≌⊿GDE(AAS)∴EG=AC∵EF//AB∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE∴EF=EG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠C证明:在AC上截取AE=AB,连接ED∵AD平分∠BAC∴∠EAD=∠BAD又∵AE=AB,AD=AD∴⊿AED≌⊿ABD(SAS)∴∠AED=∠B,DE=DB∵AC=AB+BDAC=AE+CE∴CE=DE∴∠C=∠EDC∵∠AED=∠C+∠EDC=2∠C∴∠B=2∠C12. 如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。
求证:BC=AB+DC。
证明:在BC上截取BF=BA,连接EF.∠ABE=∠FBE,BE=BE,则⊿ABE≌ΔFBE(SAS),∠EFB=∠A;AB平行于CD,则:∠A+∠D=180°;又∠EFB+∠EFC=180°,则∠EFC=∠D;又∠FCE=∠DCE,CE=CE,故⊿FCE≌ΔDCE(AAS),FC=CD.所以,BC=BF+FC=AB+CD.ABACDF21ECDB13.已知:AB//ED,∠EAB=∠BDE,AF=CD,EF=BC,求证:∠F=∠CAB//ED,AE//BD推出AE=BD,又有AF=CD,EF=BC所以三角形AEF 全等于三角形DCB,所以:∠C=∠F14.已知:AB=CD,∠A=∠D,求证:∠B=∠C证明:设线段AB,CD所在的直线交于E,(当AD<BC时,E点是射线BA,CD 的交点,当AD>BC时,E点是射线AB,DC的交点)。
则:△AED是等腰三角形。
所以:AE=DE而AB=CD所以:BE=CE (等量加等量,或等量减等量)所以:△BEC是等腰三角形所以:角B=角C.15.P是∠BAC平分线AD上一点,AC>AB,求证:PC-PB<AC-AB作B关于AD的对称点B‘,因为AD是角BAC的平分线,B'在线段AC 上(在AC中间,因为AB较短)因为PC<PB’+B‘C,PC-PB’<B‘C,而B'C=AC-AB'=AC-AB,所以PC-PB<AC-AB16.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:AC-AB=2BE∠BAC=180-(∠ABC+∠C=180-4∠C∠1=∠BAC/2=90-2∠C∠ABE=90-∠1=2∠C延长BE交AC于F因为,∠1 =∠2,BE⊥AE所以,△ABF是等腰三角形AB=AF,BF=2BE∠FBC=∠ABC-∠ABE=3∠C-2∠C=∠CBF=CFAC-AB=AC-AF=CF=BF=2BEDCBAFEAB CDP D ACB17.已知,E是AB中点,AF=BD,BD=5,AC=7,求DC 作AG∥BD交DE延长线于GAGE全等BDEAG=BD=5AGF∽CDFAF=AG=5所以DC=CF=218.(5分)如图,在△ABC中,BD=DC,∠1=∠2,求证:AD⊥BC.延长AD至H交BC于H;BD=DC;所以:∠DBC=∠角DCB;∠1=∠2;∠DBC+∠1=∠角DCB+∠2;∠ABC=∠ACB;所以:AB=AC;三角形ABD全等于三角形ACD;∠BAD=∠CAD;AD是等腰三角形的顶角平分线所以:AD垂直BC19.(5分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A、B为垂足,AB交OM于点N.求证:∠OAB=∠OBA因为AOM与MOB都为直角三角形、共用OM,且∠MOA=∠MOB所以MA=MB所以∠MAB=∠MBA因为∠OAM=∠OBM=90度所以∠OAB=90-∠MAB ∠OBA=90-∠MBA所以∠OAB=∠OBA20.(5分)如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.证明:做BE的延长线,与AP相交于F点,∵PA//BC∴∠PAB+∠CBA=180°,又∵,AE,BE均为∠PAB和∠CBA的角平分线∴∠EAB+∠EBA=90°∴∠AEB=90°,EAB为直角三角形在三角形ABF中,AE⊥BF,且AE为∠FAB的角平分线FAE DCBPEDCBA∴三角形FAB 为等腰三角形,AB=AF,BE=EF 在三角形DEF 与三角形BEC 中,∠EBC=∠DFE,且BE=EF ,∠DEF=∠CEB ,∴三角形DEF 与三角形BEC 为全等三角形,∴DF=BC ∴AB=AF=AD+DF=AD+BC 21.(6分)如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B证明:在AB 上找点E ,使AE=AC ∵AE=AC ,∠EAD=∠CAD ,AD=AD∴△ADE ≌△ADC 。
DE=CD ,∠AED=∠C ∵AB=AC+CD ,∴DE=CD=AB-AC=AB-AE=BE ∠B=∠EDB∠C=∠B+∠EDB=2∠B 22.(6分)如图①,E 、F 分别为线段AC 上的两个动点,且DE ⊥AC 于E ,BF ⊥AC 于F ,若AB =CD ,AF =CE ,BD 交AC 于点M . (1)求证:MB =MD ,ME =MF(2)当E 、F 两点移动到如图②的位置时,其余条件不变,上述结论能否成立?若成立请给予证明;若不成立请说明理由.分析:通过证明两个直角三角形全等,即Rt △DEC ≌Rt △BFA 以及垂线的性质得出四边形BEDF 是平行四边形.再根据平行四边形的性质得出结论. 解答:解:(1)连接BE ,DF . ∵DE ⊥AC 于E ,BF ⊥AC 于F ,, ∴∠DEC=∠BFA=90°,DE ∥BF , 在Rt △DEC 和Rt △BFA 中, ∵AF=CE ,AB=CD , ∴Rt △DEC ≌Rt △BFA , ∴DE=BF .∴四边形BEDF 是平行四边形. ∴MB=MD ,ME=MF ; (2)连接BE ,DF .∵DE ⊥AC 于E ,BF ⊥AC 于F ,, ∴∠DEC=∠BFA=90°,DE ∥BF , 在Rt △DEC 和Rt △BFA 中, ∵AF=CE ,AB=CD ,D CB A∴Rt△DEC≌Rt△BFA,∴DE=BF.∴四边形BEDF是平行四边形.∴MB=MD,ME=MF.23.(7分)已知:如图,DC∥AB,且DC=AE,E为AB的中点,(1)求证:△AED≌△EBC.(2)观看图前,在不添辅助线的情况下,除△EBC外,请再写出两个与△AED的面积相等的三角形.(直接写出结果,不要求证明):(1)DC∥AE,且DC=AE,所以四边形AECD是平行四边形。
