语音倒谱分析汇编
7-语音信号的同态滤波和倒谱分析NEW10n

复倒谱的计算方法
计算中需考虑的几个具体问题:(有多种计算方法) (1)离散傅立叶变换及逆变换可以用快速傅立叶变换方 法实现,以提高运算速度; (2)相位展开,一般是在主值相位上加上一个校正相位 以得到瞬时相位; (3)复倒谱中对数计算是对绝对值进行的,符号的校正 及符号的见判定公式7.19; (4)线性相位计算可以简化;得到实用计算公式如下:
HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan,430074, P.R. China 中华人民共和国 湖北 武汉
数字语音处理
第7章
语音信号的同态滤波和倒谱分析
HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan,430074, P.R. China 中华人民共和国 湖北 武汉
HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan,430074, P.R. China 中华人民共和国 湖北 武汉
第四节 复倒谱的性质和计算方法
• 复倒谱的几个重要性质:证明过程略
ˆ (1)即使序列x(n)是有限长的,其复倒谱 x(n) 总是无
• 式中 z −1{ln[ z ( x ( n ))]} 称为复倒谱; • 卷积特征系统D*[ ]的作用是将两个信号的卷积运算变成了 它们的复倒谱的求和运算。 ˆ ˆ • 第二个线性系统L[ ]要根据问题的要求和复倒谱 x1 (n)和 x2 (n) 的性质来设计,目的是能将它们分开进行处理;提取其一
∗
D∗−1 [
]
• D*[ ]将两时间序列的卷积运算变为两时间序列的加法运算; • 具体而言, D*[ ]包括三步:①z变换将两时间序列的卷积变成 相应z变换之乘积;②采用对数运算将相乘的两个z变换变成它 们各自的对数的和;③逆z变换将z域转换回到时域; • 卷积特征系统D*[ ]如下图:
基于MATLAB的语音倒谱分析

基于MATLAB的语音倒谱分析语音倒谱分析是一种通过对语音信号进行倒谱变换来提取语音特征的方法。
MATLAB作为一种常用的科学计算软件,具有丰富的信号处理工具箱,可以用于实现语音倒谱分析。
语音倒谱分析的基本原理是将语音信号分解为一系列频率低通滤波器的输出,然后对滤波器输出进行离散傅立叶变换(DFT),得到倒谱系数。
倒谱系数反映了语音信号的频谱特征,可用于语音识别、语音合成、语音增强等应用。
在MATLAB中进行语音倒谱分析的步骤如下:1. 读取语音信号:使用`audioread`函数读取语音文件,得到语音信号的波形数据和采样率。
例如:```matlab[x, fs] = audioread('speech.wav');```2. 预处理语音信号:通常需要对语音信号进行预处理,例如去除噪声、端点检测等。
这可以使用MATLAB的信号处理工具箱实现。
例如,使用`medfilt1`函数对语音信号进行中值滤波去噪:```matlabx = medfilt1(x, 3); % 使用中值滤波去噪```3. 分帧:将语音信号分为若干帧,每帧包含N个采样点。
通常选择帧长为20-40毫秒左右,帧移为10-20毫秒。
可以使用`buffer`函数实现:```matlabframeLength = round(fs * 0.025); % 帧长为25msframeShift = round(fs * 0.01); % 帧移为10msframes = buffer(x, frameLength, frameLength-frameShift,'nodelay');```4. 加窗:对每一帧的数据应用窗函数,以减小频谱泄漏效应。
常用的窗函数有汉明窗(hamming window)和黑曼窗(hanning window)。
可以使用`hamming`或`hanning`函数实现:```matlabwindow = hamming(frameLength); % 汉明窗```5. 计算功率谱:对窗函数加权的每一帧信号进行离散傅立叶变换(DFT),得到每帧的功率谱。
7-语音信号的同态滤波和倒谱分析NEW10n

• 如果设语音信号为 x(n) ,则通过第一个卷积特征系统 ˆ ˆ D*[ ]变换为系统 x1 (n) + x 2 (n) ; ˆ ˆ • 设 x1 (n) 为声门激励信号, x2 (n) 为声道冲击响应,则 如果两者处于不同的位置,并且互不交替,那么,适当的 设计线性系统,便可将两者分开处理; • 或者是提取其中之一,而同时抑制另一个;
∗
D∗−1 [
]
• D*[ ]将两时间序列的卷积运算变为两时间序列的加法运算; • 具体而言, D*[ ]包括三步:①z变换将两时间序列的卷积变成 相应z变换之乘积;②采用对数运算将相乘的两个z变换变成它 们各自的对数的和;③逆z变换将z域转换回到时域; • 卷积特征系统D*[ ]如下图:
x1 (n) ∗ x2 (n) Ζ[
HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan,430074, P.R. China 中华人民共和国 湖北 武汉
第四节 复倒谱的性质和计算方法
• 复倒谱的几个重要性质:证明过程略
ˆ (1)即使序列x(n)是有限长的,其复倒谱 x(n) 总是无
1 arg[ X ( N )] ⎧ 2 π N为奇数 r=⎨ 1 N −1 N +1 ⎩ 2π {arg[ X ( 2 )] + arg[ X ( 2 )]} N为偶数
HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan,430074, P.R. China 中华人民共和国 湖北 武汉
浊音的倒谱分析实例
• 浊音倒谱分析如下图; 原信号
对数谱:DFT 后求对数,包 含慢变化包络 和快变化周期 性细致结构;
语音信号实验3

p
z
−k
e( n ) * h ( n ) = s ( n )
逆滤波
逆滤波器 A( z ) = p a z −k ∑ k
k =0
s ( n ) * a ( n ) = e( n )
LPC倒谱分析
60
实验报告要求
• 要求实验原理叙述清楚 • 实验步骤 实验数据的采集 实验流程分析 采用自己的录音数据,记录实验结果(包括实验中 间结果),并对结果进行必要的分析. 比较各种实验方法关于基音周期检测的性能.
实验三
语音信号进行倒谱 分析
实验内容 倒谱分析、LPC倒谱分析 短时相关分析、短时幅度差分析
一、倒谱分析
• • 1. 2. 3. 4. 5. 作用 把声门激励信号与声道冲击信号分开 倒谱计算公式 去直流 sp=sp-qq s1=abs(fft(sp(1:300).*hanning’)) s2=logm(s1) mm=real(ifft(s2)) 坐标调整
汉明窗
加窗前
加窗后
坐标调整前倒谱
60
坐标调整后倒谱
二、LPC倒谱分析
原始语音分帧、加窗
LPC分析 逆滤波 DFT 倒谱分析 Ln|. | 高频分量置零 IDFT 基音检出
LPC分析
Durbin 算法
(1)
( 2)
E 0 = R n (1) n
i k i = [ Rn (i ) − ∑ a ij−1 Rn (i − j )] / E n−1 j =1 i −1
(3) E n = (1 − k i2 ) E n−1
(5)
if
(6)
− a ij = a ij−1 − k i aii−1j
1 ≤ j < i −1
语音信号的倒谱分析

因为
ˆ X ' (Z ) X ' (Z ) X (Z )
求复倒谱的一种有效的递推算法
ˆ Z[nx(n)] Z (nx(n))Z[ x(n)]
ˆ n( x(n)) {nx(n)} x(n)
n 1
l ˆ ˆ x(n) ( ) x(l ) x(n l ) x(n) x(0) l 0 n 可推导出: ˆ x ( n)
i 1
P
ˆ e(n) s(n) s(n) s(n) ai s(n i) ai s(n i)
i 1 i 0
P
P
线性预测原理
线性预测是目前分析语音信号的最有效的方法之一,分 析的结果是得到一组信号的全极点模型参数,所以又称 为信号参数模型法。 这个方法的基本思想是将被分析信号模型化,即用有限 数目的模型参数来描述信号中的信息,具体来说,将被 分析信号s(n)视为某系统(即模型)的输出,而系统的 输入,在s(n)为确定性信号是采用单位取样序列。在s(n) 为随机信号是采用白噪声序列。
Linear
Prediction
1947年维纳提出; 1967年板仓等人应用于语音分析与合成;
语音信号处理与分析的核心技术
提供了预测功能;
提供了声道模型和声道模型的参数估计方法;
基本思想:
语音样本之间存在相关性,一个语音信号的样本可 以用过去若干个样本的线性组合来逼近;
ˆ s ( n) a i s ( n i )
g jZ
j 0
Q
j
, A( Z ) ai Z i
i 0
P
g j 和ai都是实数,且a0 1。如果能有一种算法,可能根据已知的s (n) 正确的估计出这些参数,那么未知的系统V(Z)便可求得。由于 E ( Z )V ( Z ) S ( Z ),根据V ( Z )和S ( Z )便可以求得E(Z),从而全部解决 解卷的的问题。
实验四 语音信号的LPC倒谱参数

实验四 语音信号的LPC 倒谱参数的提取1 实验目的通过Matlab 编程掌握语音信号的LPC 倒谱参数的求解方法。
2 实验原理线性预测分析的基本思想是:用过去P 个样点的值来预测现在或未来的样点值:预测误差为:理论上通常采用预测系数{a k }的取值使均方误差E[e 2(n)](是{a k }的函数)最小的准则。
]))()([()]([122∑=--=pk k k n x a n x E n e E 0)]([2=∂∂k a n e E p k ≤≤1)]()([0)]()([2)]([2=-=--=∂∂j n x n e E k n x n e E a n e E k 预测误差与过去的样点不相关[]0)()()()()]()([)(])()([0)()(111=--=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡-⋅---=⎭⎬⎫⎩⎨⎧-⋅--⇒=-∑∑∑===p k k p k k pk kk j R a j R j n x k n x a j n x n x E j n x k n x a n x E j n x n e E j=1…P求解以上P 个方程组则可得到预测系数a k 。
方程组的求解方法有自相关的算法,有协方差的方法,本实验采用Durbin 算法来求解,完整的递推过程如下:(1) )0(0n n R E =(2) 1111)()(--=-∑--=i n i k i k n n i E a k i Ri R k∑=--='-=pk k k n x a n x n x n x n e 1)()()()()((3) i i i k a =(4) ii k i i k i k k a a a 11----= 11-=i k (5) 12)1(--=i n i i n E k E if i<p go to (2)(6) pp p p p p p p a a a a a a a a ====--,,......,112211 3 实验过程[x,fs,bits]=wavread('c:\WINDOWS\Media\chimes.wav'); x=x(:,1);%[x,fs,bits]=wavread('E:\3_1.wav');x=x';len=length(x);N=256;M=128;Fn=fix((len-N)/M+1);y=[];for i=1:Fndown=1+(i-1)*M;up=down+N-1;temp=x(down:up);temp=temp.*hamming(N)';y=[y;temp];endP=12;a=[];k=[];lpc=[];for q=1:Fntemp2=y(q,:);R=corr(temp2,P);for i=1:Pif i==1E(1)=R(1);k(1)=R(2)/R(1);a(1,1)=k(1);E(2)=(1-k(i).^2)*E(1);elsetemp4=0;for s=1:i-1temp4=temp4+a(s,i-1)*R(i-s+1);%×¢ÒâR¼Ó1endk(i)=(R(i+1)-temp4)/E(i);%×¢ÒâÓ¦¸ÃÊÇR(i+1)a(i,i)=k(i);for s=1:i-1a(s,i)=a(s,i-1)-k(i)*a(i-s,i-1);endE(i+1)=(1-k(i).^2)*E(i);endendfor n=1:P;b(n)=a(n,P);endlpc=[lpc;b];end。
倒谱计算与分析

《视频语音处理技术》倒谱计算与分析学院名称:计算机与信息工程学院专业名称:计算机科学与技术年级班级:姓名:学号:计算机与信息技术学院综合性、设计性实验报告一、 实验目的:对语音信号进行同态分析可得到语音信号的倒谱参数。
语音的倒谱是将语音的短时谱取对数后再进行IDFT 得到的,所以浊音信号的激励反映在倒谱上是同样周期的冲激,借此,可从倒谱波形中估计出基音周期。
对倒谱进行低时窗选,通过语音倒谱分析的最后一级,进行DFT 后的输出即为平滑后的对数模函数,这个平滑的对数谱显示了特定输入语音段的谐振结构,即谱的峰值基本上对应于共振峰频率,对于平滑过的对数谱中的峰值进行定位,即可估计共振峰。
对于倒谱计算与分析的设计实验可作如下训练: 1、复倒谱的几种计算方法: 2、最小相位信号法和递归法; 3、基音检测; 4、共振峰检测。
二、实验仪器或设备:windowsXP 下的Matlab 编程环境 三、总体设计(设计原理、设计方案及流程等)1.复倒谱的几种计算方法:在复倒谱分析中,z 变换后得到的是复数,所以取对数时要进行复对数运算。
这时存在相位的多值性问题,称为“相位卷绕”。
设信号为则其傅里叶变换为对上式取复对数为 则其幅度和相位分别为:)()()(21n x n x n x *=)()()(21ωωωj j j e X e X e X ⋅=)(ln )(ln )(ln 21ωωωj j j e X e X e X +=)(ln )(ln )(ln 21ωωωj j j e X e X e X +=)()()(21ωϕωϕωϕ+=)()()(21ωϕωϕωϕ+=上式中,虽然 , 的范围均在 内,但 的值可能超过范围。
计算机处理时总相位值只能用其主值 表示,然后把这个相位主值“展开”,得到连续相位。
所以存在下面的情况:(K 为整数) 此时即产生了相位卷绕。
下面介绍几种避免相位卷绕求复倒谱的方法。
最小相位信号法这是解决相位卷绕的一种较好的方法。
语音信号数字处理-倒频谱和线谱对

4
卷积同态系统框图
H(·)
* D (·)
L(·)
-1 Z (·)
D
*-1
(·)
Z (·)
Log(·)
Z (·)
Exp(·)
-1 Z (·)
图2
5
“卷积同态系统”的输入输出信号都是 卷性信号,即具有相互卷积的关系。
同态系统的一个最主要理论结果就是同 态系统的分解,分解的目的是用两个特 征系统和一个线性系统来代替非线性的 同态系统。图2给出了同态系统H(z)的组 成。
1
Z Z log X Z X Z Z
1
1 Z Z X Z X Z X Z Z 1 Z Z X Z Z n x n 4.8
先对语音序列 xn 做DFT得到 X e j ,取对数之后 ˆ e j 做IDFT得到偶函数 x ˆe n ,再用 g n 将实部 X R ˆn 。 取出 x
xn
DFT
X e j
log
ˆ e j X R
ˆ e j X I
IDFT
ˆe n x
ˆ 0 log x0 ; x
x1 ˆ 1 x ; x0 x2 1 x1 ˆ 2 ˆ 1 x x ; x0 2 x0 x3 1 x2 2 x1 ˆ 3 ˆ 1 ˆ 2 x x x ; x0 3 x0 3 x0
1
k ˆ k xn k , xn x k n
n0
(4.9)
23
利用最小相位信号序列性质
ˆn 0, xn 0, x
第5章语音的同态滤波及倒谱分析
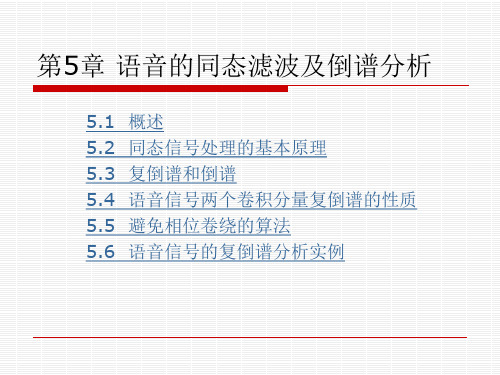
ln X z ln X1z ln X 2 z
argX z argX1z argX 2z
5.3 复倒谱和倒谱
但两个角度之和的主值通常不等于它 们各自相应的主值之和。
argX z argX1z argX2z ARGX z ARGX1z ARGX2z
5.3 复倒谱和倒谱
5.3 复倒谱和倒谱
倒谱(倒频谱/对数倒频谱) :
c(n) 1[ln x(e j ) ]
若c1(n)和c2 (n)分别为x1(n)和x2 (n)的倒谱, 则x(n) x1(n) x2 (n)的倒谱为
c(n) c1(n) c2 (n)
与复倒谱不同的是,在倒谱情况下一个序列经过正逆 两个特征系统变换后,不能还原成自身,因为c(n)中 只有幅值信息而无相位信息。尽管如此,但仍可用于 语音信号分析中,因为人们的听觉对语音的感知特征
输入矢量或输出矢量与标量之间的运算可以为: 乘法、幂或开方等运算
5.1 概述
广义叠加原理数学表达:
同态系统的规范形式:
5.1 概述
对语音信号进行同态分析后将得到其倒谱参数,所以 同态分析也称为倒谱分析。由于对语音信号分析是以 帧为单位进行的,所以得到的是短时倒谱参数。
无论是对于语音通信、语音合成还是语音识别 倒谱参数优点:所含的信息比其他参数多,也就是 说语音质量好、识别正确率高; 倒谱参数缺点:是运算量较大。 尽管如此,倒谱分析仍是一种有效的语音信号分析
n k 1 n1
n k 1 n1
则 xˆ(n) ln A (n) mi ak n u(n 1) mo bk n u(n 1)
k 1 n
k 1 n
pi ck n u(n 1) po dk n u(n 1)
(完整word版)语音信号进行倒谱分析

实验三 语音信号进行倒谱分析一、 实验目的、要求1. 理解倒谱分析的作用2. 掌握倒谱分析求基音周期的方法3. 了解LPC 倒谱分析方法二、实验原理1.倒谱分析原理同态信号处理也称为同态滤波,实现将卷积关系变换为求和关系的分离处理,即解卷。
如 进行如下3步处理对于语音信号进行解卷,可将语音信号的声门激励信息及声道响应信息分离开来,从而求得声道共振特征和基音周期,用于语音编码、合成和识别。
同态信号处理的基本原理(1)第一个子系统D*[](特征系统)完成将卷积信号转化为加性信号的运算。
)(ˆ1n x 和 )(ˆ2n x信号也均是时域序列,但它们所处的离散时域显然不同于x(n)所处的离散时域,故把它称之为复倒频谱域。
)(ˆn x是x(n)的复倒频谱,简称为复倒谱,有时也称为对数复倒谱。
复倒谱具体计算公式其中倒谱计算公式为:2 线性预测原理线性预测分析的基本思想由于语音样点之间存在相关性,所以可以用过去的样点值来预测现在或未来的样点值。
通过使实际语音抽样和线性预测抽样之间的误差在某个准则下达到最小值来决定唯一的一组预测系数,而这组系数就能反映语音信号的特性,可以作为语音信号特征参数来用于语音编码、语音合成和语音识别等应用中去。
线性预测分析的基本原理每个采样值由前面的p 个采样值线性组合所构成。
记为x '(n),有:)(ˆ)(ˆ)(ˆ)](ˆ)(ˆ[)](ˆ[)3()(ˆ)(ˆ)(ˆ)(ln )(ln )(ln )2()()()()]([)1(212111212121n x n x n x z X z X Z z X Z z X z X z Xz X z X z X z X z X z X n x Z =+=+==+=+=⋅==--12()()()x n x n x n =*1ˆ()[ln (())]x n Z Z x n -=[()]()ˆ()ln ()ˆˆ()[()]jw jw jw jw DFT x n X e Xe X e xn IDFT X e ===要提高预测精度,就是要预测系数{k a }的取值使e(n)最小。
语音信号的同态滤波和倒谱分析课件

同态滤波的原理
同态滤波的基本原理是通过非线性变换将原始信号转换为对数幅度谱,然后对其进行傅立叶逆变换得 到包络信号。接着,将包络信号通过一个低通滤波器得到最终的包络信号。最后,将原始信号通过一 个同态逆系统得到处理后的信号。
倒谱分析
在实践应用中,倒谱分析需要进行倒 谱变换和特征提取等操作,计算量相 对较小,且对噪声具有一定的鲁棒性 。
应用比较
同态滤波
主要用于语音信号的分离和增强,常用于语音降噪、语音识别等领域。
倒谱分析
主要用于语音信号的特征提取和识别,常用于语音合成、语音识别等领域。
04
CATALOGUE
语音信号处理的其他方法
理论比较
同态滤波
基于语音信号的频域处理,通过 将语音信号分解为激励信号和冲 激响应信号,实现对语音信号的 分离和增强。
倒谱分析
基于语音信号的倒谱变换,通过 将语音信号从时域变换到倒谱域 ,实现语音信号的特征提取和识 别。
实践比较
同态滤波
在实践应用中,同态滤波需要对语音 信号进行预加重、分帧、加窗等预处 理操作,计算量较大,且对噪声较为 敏感。
同态滤波还可以应用于其他领域,如雷达信号处理、图像处 理、生物医学工程等,以实现更灵活和有效的信号处理和分 析。
02
CATALOGUE
语音信号的倒谱分析
倒谱分析的定义
01
倒谱分析是一种语音信号处理技 术,通过对语音信号的倒谱变换 ,提取出语音信号的特征信息。
02
倒谱分析通过将语音信号的频谱 转换为倒谱形式,使得语音信号 中的各个组成部分更加清晰可辨 ,便于后续的分析和处理。
第03讲 语音信号变换域(频域+倒谱)分析

际上是Xn e j
在频域的取样,如下所示
j2k
N 1
j 2 km
Xn e N X n k xn m e N , 0 k N 1
m0
在语音信号数字处理中,都是采用 xn m 的离散傅立叶
变换 Xn k 代替 Xn e
变换(FFT)算法完成由
j , 并且可以用高效的快速傅立叶 xn m 至 Xn k 的转换。当然,
W e j 必须是一个冲激函数。窗长越长W,e j 的主瓣越狭
窄尖锐,则Xn e j
越接近X e j
。 但窗长太大时
,窗选信号已经不满足语音的短时平稳特性,此X时n e j
已不能正确反映短时语音的频谱了。为此,必须要折中选
择窗长。
▪ 令角频率 2 k n 则得到离散的短时傅立叶变换,它实
150
200
250
300
讨论:窗口形状对短时谱的影响
下面给出采样率8kHz,窗长400点(50ms)情况下 ,分别用矩形窗与汉明窗选取同一段浊音信号, 求得其对数幅度谱。简单分析一下不同的窗函数 对语音信号短时谱的影响。
矩形窗加窗的浊音波形及其短时频谱 汉明窗加窗的浊音波形及其短时频谱
由上图可看出:
(第二讲)
1 语音信号的频域分析
2 语音信号的倒谱分析
§3.4 语音信号的频域分析
▪ 语音信号的频域分析就是分析语音信号的频域特征。 从广义上讲,语音信号的频域分析包括语音信号的频 谱、功率谱、倒频谱、频谱包络分析等。
▪ 常用的频域分析方法有带通滤波器组法、傅里叶变换 法、线性预测法等几种。
▪ 本节介绍的是语音信号的傅里叶分析法。
“短时谱”
▪ 短时分析将语音流分为一段一段来处理,每一段称为一“帧” ;
(完整版)语音信号进行倒谱分析

实验三 语音信号进行倒谱分析一、 实验目的、要求1.理解倒谱分析的作用 2. 掌握倒谱分析求基音周期的方法3. 了解LPC 倒谱分析方法二、实验原理1.倒谱分析原理同态信号处理也称为同态滤波,实现将卷积关系变换为求和关系的分离处理,即解卷。
如 进行如下3步处理)(ˆ)(ˆ)(ˆ)](ˆ)(ˆ[)](ˆ[)3()(ˆ)(ˆ)(ˆ)(ln )(ln )(ln )2()()()()]([)1(212111212121n x n x n x z X z X Z z X Z z X z X z Xz X z X z X z X z X z X n x Z =+=+==+=+=⋅==--对于语音信号进行解卷,可将语音信号的声门激励信息及声道响应信息分离开来,从而求得声道共振特征和基音周期,用于语音编码、合成和识别.同态信号处理的基本原理(1)第一个子系统D *[](特征系统)完成将卷积信号转化为加性信号的运算。
)(ˆ1n x 和 )(ˆ2n x信号也均是时域序列,但它们所处的离散时域显然不同于x(n )所处的离散时域,故把它称之为复倒频谱域。
)(ˆn x是x(n)的复倒频谱,简称为复倒谱,有时也称为对数复倒谱.复倒谱具体计算公式其中倒谱计算公式为:2 线性预测原理12()()()x n x n x n 1ˆ()[ln (())]x n Z Z x n [()]()ˆ()ln ()ˆˆ()[()]jw jw jw jw DFT x n X e X e X e x n IDFT X e线性预测分析的基本思想由于语音样点之间存在相关性,所以可以用过去的样点值来预测现在或未来的样点值。
通过使实际语音抽样和线性预测抽样之间的误差在某个准则下达到最小值来决定唯一的一组预测系数,而这组系数就能反映语音信号的特性,可以作为语音信号特征参数来用于语音编码、语音合成和语音识别等应用中去。
线性预测分析的基本原理每个采样值由前面的p 个采样值线性组合所构成。
第03讲 语音信号变换域(频域+倒谱)分析

由图可见:
由于窗长很短,所选出的语音段甚至不到一个基音周期长度, 因此语音段丢失了关于基音周期的信息,表现在短时谱上 就是反映基音频率和谐波的快速变化特点消失了,短时谱 中只保留着慢速变化的特点,也就是还保持着声道滤波器
的共振峰。由于矩形窗具有更高的频谱分辨率,因此其短
时频谱不如汉明窗平滑。
从以上对窗函数和短时频谱的讨论可以得出以下结论: • 1)矩形窗和汉明窗的主瓣狭窄且旁瓣衰减较大,具有低 通的性质。窗越长,主瓣越窄,加窗后的频谱能更好地逼 近短时语音的频谱。 • 2)窗长越长,频谱分辨率越高,但由于长窗的时间平均 作用导致时间分辨率相应下降,如共振峰在不同的基音周 期是要发生变化,但如果使用较长的窗则会模糊这种变化。 • 3)窗长越短,时间分辨率越高,但频率分辨率相应降低。 如采用短窗可以清楚地观察到共振峰在不同基音周期的变 化情况,但是基频以及谐波的精细结构在短时频谱图上消 失了。 • 4)由于时间分辨率和频谱分辨率的相互矛盾关系,在进 行短时傅里叶变换时,应根据分析的目的来折中选择窗长。
X n (e j ) xn (m)e jm
m 0 N 1
m
x m w n m e jm
m
x m e jm w n m
当w固定不变时, X n (e j ) 可视为信号 x m e jm 与窗函数 w n 的卷积,此时,短时傅立叶变换可看作线性滤波.
• 在语音信号数字处理中,功率谱具有重要意义,在一些语音 应用系统中,往往都是利用语音信号的功率谱。根据功率谱 定义,可以写出短时功率谱与短时傅里叶变换之间的关系:
S n (e ) X n (e ) X (e ) X n (e )
第4章 语音信号短时频域及倒谱分析

对 数 幅 度 /dB
对 数 幅 度 /dB
浊 音
0 -20 -40 -60 -80
0
1000
2000 3000 f/Hz 加 Hamming窗 时 语 音 谱
4000
0 -20 -40 -60 -80
清 音
0
1000
2000 3000 f/Hz 加 Hamming窗 时 语 音 谱
4000
对 数 幅 度 /dB
wn m xm
(-∞≤m≤+∞)
的傅里叶变换或离散傅里叶变换。 (2) 当 或k 固定时,它们是一个卷积,这相当于滤波 器的运算。因此,语音信号的短时频域分析可以解释为傅 里叶变换或滤波器。
5
第四章语音信号短时频域及倒谱分析
“十二五”普通高等教育本科国家级规划教材
4.1 傅里叶变换 的解释
第四章语音信号短时频域及倒谱分析
“十二五”普通高等教育本科国家级规划教材
第四章 语音信号短时频域及倒谱分析
1
第四章语音信号短时频域及倒谱分析
“十二五”普通高等教育本科国家级规划教材
目
1
1 2
录
傅里叶变换的解释 2 滤波器的解释 短时综合的滤波器组相加法 4 语音信号的复倒谱和倒谱分析及应用
3
5
2
“十二五”普通高等教育本科国家级规划教材
i
hi (n) wi (n)e jin
X n (e ji ) e jin
x(n m)h (m)
m
(4.22)
26
4.3 短时综合的滤波器组相加法
“十二五”普通高等教育本科国家级规划教材
式(4.25)的图形解释
x(n)
语音信号的同态滤波和倒谱分析.

M
u(n) ar (n rN p ) r0 a r 为幅度因子
M,r均为正整数
N p 为用样点数表示的基音周期
u(n) u(n)的幅度呈衰减趋势
0 Np 2Np
MNp n
M
求u(n)的复倒谱 u(n) ar (n rN p ) r0
(1)对u(n)进行Z变换
(2)逆特征系统D*-1[] ,恢复为卷积性信号。
xˆ(n) xˆ1(n) xˆ2 (n) 进行如下处理:
(1)Z[xˆ(n)] Xˆ (z) Xˆ 1(z) Xˆ 2 (z) (2) exp(Xˆ (z)) X (z) X1(z) X 2 (z) (3)x(n) Z 1[ X1(z) X 2 (z)] x1(n) x2 (n)
声门激励信号的复倒谱mr均为正整数anmrprrnna为幅度因子nu0rp为用样点数表示的基音周期nun0np2npmnpun的幅度呈衰减趋势1对un进行z变换0r11rr002020100111maaazazaazapazmaazaaazaznuzurnrrnmnmnnmrrnrnnppppp求un的复倒谱mrprrnnanu02对uz取对数并进行泰勒级数展开krpalnamrkknkrmrnrppzkazaazuzu1z1010ln1lnlnln?rnknkrnazzkapp1113对进行逆z变换求得un的复倒谱001101101ln1kln1kln??0aknnaknnnaknmnanazuznukpkrkrkkpkkmrpkr?zu结论一个有限长的周期冲激序列其复倒谱也是一个周期冲激序列其周期不变只是序列变为无限长
N 1
X (k) DFT(x(n)) x(n)WNnk n0
x(n)
倒谱计算与分析综述

《视频语音处理技术》倒谱计算与分析学院名称:计算机与信息工程学院____________ 专业名称:计算机科学与技术________________ 年级班级:_________________姓名:________________________学号:______________________计算机与信息技术学院综合性、设计性实验报告专业:计算机科学技术年级/班级:2011级2012 —2013学年第一学期一、实验目的:对语音信号进行同态分析可得到语音信号的倒谱参数。
语音的倒谱是将语音的短时谱取对数后再进行IDFT得到的,所以浊音信号的激励反映在倒谱上是同样周期的冲激,借此,可从倒谱波形中估计出基音周期。
对倒谱进行低时窗选,通过语音倒谱分析的最后一级,进行DFT后的输出即为平滑后的对数模函数,这个平滑的对数谱显示了特定输入语音段的谐振结构,即谱的峰值基本上对应于共振峰频率,对于平滑过的对数谱中的峰值进行定位,即可估计共振峰。
对于倒谱计算与分析的设计实验可作如下训练:1、复倒谱的几种计算方法:2、最小相位信号法和递归法;3、基音检测;4、共振峰检测。
二、实验仪器或设备:windowsXP下的Matlab编程环境三、总体设计(设计原理、设计方案及流程等)1 .复倒谱的几种计算方法:在复倒谱分析中,z变换后得到的是复数,所以取对数时要进行复对数运算。
这时存在相位的多值性问题,称为“相位卷绕”。
设信号为x(n)=为(n) X2( n)则其傅里叶变换为X(e')二Xje八)/(e八)对上式取复对数为ln X(e')=lnX1(e「)7nX2(e「)则其幅度和相位分别为:ln X(e鬥=ln X'e鬥+ln X2(e今「)「(•) *)(■) = - i( ■)2()上式中,虽然 iCO ,2()的范围均在—二,二 内,但 (.)的值可能超过(―.兀)范围。
计算机处理时总相位值只能用其主值 ①(国)表示,然后把这个相位主值“展开”,得到连续相位。
语音信号的倒谱分析54页PPT

1Байду номын сангаас、机会是不守纪律的。——雨果
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
语音信号的倒谱分析
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Keywords: speech signal; cepstrum; MATLAB; pitch detection; resonance peak
海南大学 毕 业 论 文(设计)
题 目:基于 MATLAB 的语音倒谱分析 学 号: 姓名 年级 学 院: 专 业: 指导教师: 完成日期:2012 年
基于 MATLAB 的语音倒谱分析
摘要
语言是人类最重要的交流工具,它自然方便、准确高效。随着社会的不断发 展,各种各样的机器参与了人类的生产活动和社会活动,因此改善人与机器之间 的关系,使人对机器的操纵更加便利就显得越来越重要。随着电子计算机和人工 智能机器的广泛应用,人们发现,人和机器之间最好的通信方式是语言通信,而 语音是语言的声学表现形式。要使机器听的懂人话,就要对语音信号进行处理。 随着信息技术的不断发展,尤其是网络技术的日益普及和完善,语音信号处理技 术正发挥着越来越重要的作用。为了寻找具有良好性能的特征及提取重要参数以 提高识别系统性能,各种科学的算法应运而生,倒谱法作为信号处理的重要的方 法之一,能够得到比较好的识别性能。
I
基于 MATLAB 的语音倒谱分析
Abstract
Language is one of the most important communication tools, it is convenient and efficient. With the continuous development of the society, a variety of machines are used in the human’s production and social activities, thus improving the relationship between man and machine makes the machine more convenient what becomes more and more important. With the wide application of electronic computers and artificial intelligence machine, it was discovered that language communication is the best means of communication between man and machine, while the voice is the acoustic manifestations of the language.To make the machine understands people, it is necessary to process the speech signal. With the continuous development of IT, especially the growing popularity of network technology and improvement of the voice signal processing technology is playing an increasingly important role, in order to find a good performance characteristics and extract important parameters to improve the performance of the recognition system, a variety of scientific algorithms have emerged, the cepstrum, as the signal processing one of the important methods, can get better recognition performance.
本文以 MATLAB 为平台,通过编程实现对语音信号的倒谱分析。首先,本 文简要说明了倒谱与语音的相关理论原理,包括倒谱原理和语音的组成元素,为 之后的进一步研究奠定理论基础。然后,对语音倒谱各个方面的应用进行了 MATLAB 编程,得到了语音基音检测和共振峰检测的实验仿真结果。
关键词:语音信号;倒谱;MATLAB;基音检测;共振峰检测;
detection;
II
基于 MATLAB 的语音倒谱分析
目录
1 绪论.............................................................................................................................1 1.1 目的及意义......................................................................................................1 1.2 语音信号研究现状.........................................................................................1 1.3 主要研究内容..................................................................................................3
MATLAB as a platform, can achieve cepstrum analysis of the speech signal by programming. First, the article briefly described the itheoretical principles of cepstrum and voice, including the the cepstrum principles and elements of voice,which laied the theoretical foundation for the further research . Then the speech cepstrum application in all aspects was programmed in MATLAB, thus we got voice
