汽车理论第五版_余志生 主编 课后习题答案剖析
汽车理论第五版课后习题答案解析

2第一章汽车的动力性1.1试说明轮胎滚动阻力的定义,产生机理和作用形式。
定义:汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚 动祖力。
2)产生机理:由于轮胎内部摩擦产生弹性轮胎在硬支律路面上行驶时加载 变形曲线和卸载变形曲线不重合会有能全损失, 即弹性物质的迟滞损失。
这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对丰轮的法向反作用力的分布是前后对称的;当 车 轮滚动时,由于弹性阻滞现象,处于压缩过程的前部点的地面法向反作用力就会 大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分 布前后不对称,而使他们的合力F Z 相对于法线前移一个距离a ,它随弹性迟滞损 失的增大变大。
即滚动时有滚动阻力偶 T f = F z.?a 阻碍车轮滚动。
3]作用形式:T f = Wf ,T f = T f /r1.2滚动阻力系数与哪些因素有关? 答:滚动阻力系数与路面的种类、 行驶车速以及轮胎的构造、材料和气压有关。
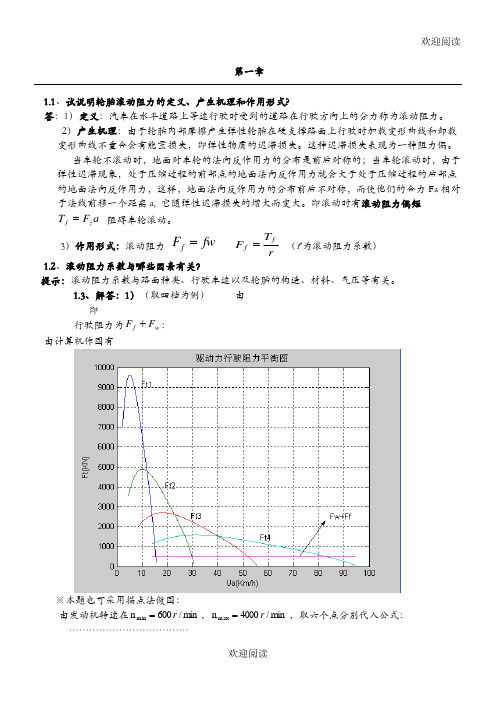
1.3①=T5 +氓环侖一 244倍护十40 一沁金F TX44宣命13.解苦:1)(取四裆为銅)由眞—TqTq —^n >=> 巧一u —> nO.3 77rn行我阻力为幵■!■凡:=494.312+0.13U2由计算机作图有:幾本毬也可采用滞点法做圏:由发动就韓速雇口丽=fSOO/mim =4000/min ,职六个点分別我.人公式:2)⑴駅舟车速:有耳二丹+吒^>7; =494,312 + 0.13 1TJ? 分别代入S 和百公孔:T. *6.9*5^3*0.850377*03691h ,*=494312+013 K ———-——『弓 5,83*6.09⑵載大爬坡度:挂T 档时速度慢,Fw 吁怂略:100009000rac700060005D *4003000200010000367把耳的拟和公或也代入可得: n>4000 而 n max = 400()r/mm二 % =山377 ^0367*4^00 = 04.93 Km/hL0*5.^可I10 2D 30 JO 50 Ua(Km^h)喊廿打行帥羽卄平誓图=>耳=Emk(Ff +凡) nG心耳唤-0 n= 1 440-0.0 1=0.366L _ dr白 du gQT> — 于、U 时,= 1 + —瓦[» + —m r tnI 〕 l 1.798+3占98 卜 I 0.218*二0竽 *5^3^ *0启5 _ +IS(H)__t!36f + 38OO-1.12R耳 _ TJ3咕我IZ 存侖皿钟侖尸十和胸侖7阿孟由以上关系可由计算机作出图为;②用计算机求汽车用用档起步加速至70km/h 的加速时间*(3)克服策坡度时相应的附着辜评=」忽唯空气醜力樹滚动阻力得:Fi9 ・ ----- N___耳 all a19473)⑴缕制汽车行驶加速倒数曲戢(巴装货):40.0626U 0,366*3,2—— ---------------- —t J.o036/{注:栽雳时汽羣制U档起步加速不能至^Okm/h)由适动学可知:dt = — dua—t —[ -L/u —Aa]即加建时间可用计算机进行机分计算农出,且二一叫曲銭下两速皮间的画<1 欷就足通it此速度去件的加速时间。
汽车理论课后习题答案(余志生版)(完全免费版)

D 第一章1.1、试说明轮胎滚动阻力的定义、产生机理和作用形式?答:1)定义:汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚动阻力。
2)产生机理:由于轮胎内部摩擦产生弹性轮胎在硬支撑路面上行驶时加载变形曲线和卸载变形曲线不重合会有能量损失,即弹性物质的迟滞损失。
这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对车轮的法向反作用力的分布是前后对称的;当车轮滚动时,由于弹性迟滞现象,处于压缩过程的前部点的地面法向反作用力就会大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分布前后不对称,而使他们的合力Fa 相对于法线前移一个距离a, 它随弹性迟滞损失的增大而变大。
即滚动时有滚动阻力偶矩 a F T z f = 阻碍车轮滚动。
3)作用形式:滚动阻力fw F f = rT F ff = (f 为滚动阻力系数)1.2、滚动阻力系数与哪些因素有关?提示:滚动阻力系数与路面种类、行驶车速以及轮胎的构造、材料、气压等有关。
1.3、解答:1)(取四档为例) 由u F n u n Tq Tq F t t →⇒⎪⎭⎪⎬⎫→→→ 即 ri i T F To g q t η=432)1000(8445.3)1000(874.40)1000(44.165)1000(27.25913.19n n n n Tq -+-+-=og i i rnu 377.0=行驶阻力为w f F F +: 215.21a D w f U A C Gf F F +=+ 2131.0312.494aU +=由计算机作图有※本题也可采用描点法做图:由发动机转速在m in /600n min r =,m in /4000n max r =,取六个点分别代入公式:……………………………… 2)⑴最高车速:有w f t F F F +=⇒2131.0312.494a t U F += 分别代入a U 和t F 公式:2)09.6*83.53697.0*377.0(131.0312.494367.085.0*83.5*9.6*n T q += 把q T 的拟和公式也代入可得: n>4000而4000m ax =n r/min∴93.9483.5*0.14000*367.0*377.0max ==U Km/h ⑵最大爬坡度:挂Ⅰ档时速度慢,Fw 可忽略: ⇒)(max w f t i F F F F +-=⇒GfF Git -=max⇒013.08.9*388014400max max -=-=f G F i t =0.366(3)克服该坡度时相应的附着率 zxF F =ϕ 忽略空气阻力和滚动阻力得:6.0947.12.3*366.0/=====a il l a i F Fi zϕ 3)①绘制汽车行驶加速倒数曲线(已装货):40.0626)(1f D g du dt a -==δ (G FwFt D -=为动力因素) Ⅱ时,22022111r i i I m r I m Tg f wηδ++=∑2222367.085.0*83.5*09.3*218.038001367.0598.3798.1380011+++= =1.128ri i T F To g q t η=432)1000(8445.3)1000(874.40)1000(44.165)1000(27.25913.19n n n n Tq -+-+-=215.21a D w U A C F =由以上关系可由计算机作出图为:②用计算机求汽车用Ⅳ档起步加速至70km/h 的加速时间。
汽车理论第五版课后习题答案

第一章【1 】汽车的动力性1.1 试解释轮胎滚动阻力的界说,产活力理和感化情势.界说:汽车在程度道路上等速行驶时受到的道路在行驶偏向上的分力称为滚动祖力.2)产活力理:因为轮胎内部摩擦产生弹性轮胎在硬支律路面上行驶时加载变形曲线和卸载变形曲线不重合会有能全损掉,即弹性物资的迟滞损掉.这种迟滞损掉表示为一种阻力偶.当车轮不滚动时,地面临丰轮的法向反感化力的散布是前后对称的;当车轮滚动时,因为弹性阻滞现象,处于紧缩进程的前部点的地面法向反感化力就会大于处于紧缩进程的后部点的地面法向反感化力,如许,地面法向反感化力的散布前后不合错误称,而使他们的合力F Z相对于法线前移一个距离a,它随弹性迟滞损掉的增大变大.即滚动时有滚动阻力偶T f=F Z.•a阻碍车轮滚动.3]感化情势:T f =Wf,T f =T f/r1.2 滚动阻力系数与哪些身分有关?答:滚动阻力系数与路面的种类.行驶车速以及轮胎的构造.材料和蔼压有关.1.3a2由盘算机作图有:1.4 空车.满载时汽车动力性有无变更?为什么?答:动力性会产生变更.因为满载时汽车的质量会增大,重心的地位也会产生转变.质量增大,滚动阻力.坡度阻力和加快阻力都邑增大,加快时光会增长,最高车速下降.重心地位的转变会影响车轮附着率,从而影响最大爬坡度.1.5 若何选择汽车发念头功率?答:发念头功率的选择常先从包管汽车预期的最高车速来初步肯定.若给出了期望的最高车速,选择的发念头功率应大体等于,但不小于以最高车速行驶时的行驶阻力功率之和.发念头的最大功率但也不宜过大,不然会因发念头负荷率偏低影响汽车的燃油经济性.在现实工作中,还应用现有汽车统计数据初步估量汽车比功率来肯定发念头应有功率.许多国度还对车辆应有的最小比功率作出划定,以包管路上行驶车辆的动力性不低于必定程度,防止某些机能差的车辆阻碍车流.1.6 超车时该不该换入低一挡的排挡?答:超车时排挡的选择,应当使车辆在最短的时光内加快到较高的车速,所所以否应当换入低一挡的排挡应当由汽车的加快度倒数曲线决议.假如在该车速时,汽车在此排档的加快度倒数大于低排挡时的加快度倒数,则应当换入低一档,不然不该换入低一挡.1.7可得.最大爬坡度为:第二章汽车的燃油经济性2.1“车开得慢,油门踩得小,就必定省油” ,或者“只要发念头省油,汽车就必定省油”这两种说法对不合错误?答:不合错误.由汽车百公里等速耗油量图,汽车一般在接近低速的中等车速时燃油消费量最低,其实不是在车速越低越省油.由汽车等速百公里油耗算式(2-1)知,汽车油耗量不但与发念头燃油消费率有关,并且还与车速.档位选择.汽车的状态.汽车的质量应用系数等应用身分有关,还与汽车的质量和总体尺寸.传动系.轮胎的选择有关,发念头省油时汽车不必定就省油.2.2 试述无级变速器与汽车动力性.燃油经济性的关系.答:①采取无级变速后,理论上战胜了发念头特点曲线的缺点,使汽车具有与等功率发念头一样的驱动功率,充分施展了内燃机的功率,大大地改良了汽车动力性.②同时,发念头的负荷率高,用无级变速后,使发念头在最经济工况机遇增多,进步了然油经济性.2.3 用发念头的“最小燃油消费特点”和战胜行驶阻力应供给的功率曲线,肯定包管发念头在最经济状态下工作的“无级变速器调节特点” .答:由发念头在各类转速下的负荷特点曲线的包络线即为发念头供给必定功率时的最低燃油消费率曲线,如教材图2-9a.应用此图可以找动身念头供给必定功率时的最经济状态(转速与负荷) .把各功率下最经济状态运转的转速与负荷率标明在外特点曲线上,便得到“最小燃油消费特点” .无级变速器的传动比 i'与发念头转速n及汽车行驶速度u a之间关系2.4 若何从改良汽车底盘设计方面来进步燃油经济性?答:汽车底盘设计应当从合理匹配传动系传动比.缩减尺寸和减轻质量.合理选择轮胎来进步燃油经济性.2.5 为什么汽车发念头与传动体系匹配不好会影响汽车燃油经济性与动力性?试举例解释. 答:在必定道路前提下和车速下,固然发念头发出的功率雷同,但传动比大时,后备功率越大,加快和爬坡才能越强,但发念头负荷率越低,燃油消费率越高,百公里燃油消费量就越大,传动比小时则相反.所以传动体系的设计应当分解斟酌动力性和经济性身分.如最小传动比的选择,根据汽车功率均衡图可得到最高车速u max(驱动力曲线与行驶阻力曲线的交点处车速),发念头达到最大功率时的车速为u p.当主传动比较小时,u p>u max,汽车后备功率小,动力性差,燃油经济性好.当主传动比较大时,则相反.最小传动比的选择则应使 u p与 u max邻近,不成为寻求单纯的的动力性或经济性而下降另一方面的机能.2.6 试剖析超速档对汽车动力性和燃油经济性的影响.答:汽车在超速档行驶时,发念头负荷率高,燃油经济性好.但此时,汽车后备功率小,所以须要设计适合的次一挡传动比包管汽车的动力性须要.2.8 轮胎对汽车动力性.燃油经济性有些什么影响?答:1)轮胎对汽车动力性的影响重要有三个方面:①轮胎的构造.帘线和橡胶的品种,对滚动阻力都有影响, 轮胎的滚动阻力系数还会随车速与充气压力变更.滚动阻力系数的大小直接影响汽车的最高车速.极限最大加快度和爬坡度. ②汽车车速达到某一临界值时,滚动阻力敏捷增长,轮胎会产生很安全的驻波现象,所以汽车的最高车速应当低于该临界车速.③轮胎与地面之间的附着系数直接影响汽车的极限最大加快度和爬坡度. 2)轮胎对燃油经济性的影响轮胎的滚动阻力系数直接影响汽车的燃油经济性.滚动阻力大燃油消费量显著升高. 2.9 为什么公共汽车起步后,驾驶员很快换入高级?答:因为汽车在低档时发念头负荷率低,燃油消费量好,高级时则相反,所认为了进步燃油经济性应当在起步后很快换入高级. 2.10 达到动力性最佳换档机会是什么?达到燃油经济性的最佳换档机会是什么?二者是否雷同?答:达到动力性最佳应当使汽车加快到必定车速的时光最短,换档机会应根据加快度倒数曲线肯定,包管其笼罩面积最小.达到燃油经济性的换档机会应当根据由“最小燃油消费特点”肯定的无级变速器幻想变速特点,斟酌道路的Ψ值,在最接近幻想变速特点曲线的点进行换档.二者一般是不雷同的.第四章汽车的制动性4.1 一轿车驶经有积水层的一优越路面公路,当车速为100km/h 时要进行制动.为此时有无可能消失划水现象而损掉制动才能?轿车轮胎的胎压为 179.27kPa.解:4.3作出这种划定的目标是为了包管束动时汽车的偏向稳固性和有足够的制动效力.4.56)两种回路的优缺点比较双回路体系 a)制动系增益最大,一个回路掉效时的最大制动减速度也比b),c)大,所以其机能较优. 双回路体系b).c)制动系增益雷同,假如不斟酌轴距的影响,两者在一个回路掉效时的制动效力雷同.但是,c) 在一个回路掉效时,制动力感化在一侧车轮上,车身阁下受力轻微不均衡,会产生跑偏等问题.第五章汽车的把持稳固性5.1 一轿车(每个)前轮的侧偏刚度为-50176N/rad.外倾刚度为-7665N/rad.若轿车向左转弯,将使前轮均产生正的外倾角,其大小为 4 度.设侧偏刚度与外倾刚度均不受左.右轮负载转移的影响,试求由外倾角引起的前轮侧偏角.解:(°5.2 6450N 轻型客车在实验中发明过多转向和中性转向现象,工程师们在悬架上加装横向稳固杆以进步前悬架的侧倾角刚度,成果汽车的转向特点变成缺少转向.试剖析其理论根据(请求有须要的公式和曲线) .5.3 汽车的稳态响应有哪几种类型?表征稳态响应的具体参数有哪些?它们彼此之间的关系若何?答:汽车的稳态响应有三种类型,即中性转向.缺少转向和过多转向. 表征稳态响应的参数有稳固性因数K,前.后轮的侧偏角角绝对值之差(α1–α21) ,转向半径的比R/R0,静态储备系数S.M.等. 它们之间的彼此关系为:5.4 举出三种暗示汽车稳态转向特点的办法,并解释汽车重心前后地位和内.外轮负荷转移若何影响稳态转向特点?5.5 汽车转弯时车轮行驶阻力是否与直线行驶时一样?答:不一样.汽车转弯时因为侧倾力矩的感化,左.右车轮的垂直载荷不再相等,所受阻力亦不相等.别的,车轮还将受到地面侧向反感化力.5.6 主销内倾角和后倾角功效有何不合?答:主销内倾角的感化,是使车轮在偏向盘收到渺小干扰时,前轮会在回正力矩感化下主动回正.别的,主销内倾还可削减前轮传至转向机构上的冲击,并使转向简便. 主销后倾的感化是当汽车直线行驶有时受外力感化而稍有偏转时, 主销后倾将产生车轮转向反偏向的力矩使车轮主动回正,可包管汽车支线行驶的稳固性. 汽车转向轮的回正力矩起源于两个方面,一个是主销内倾角,依附前轴轴荷,和车速无关;一个是主销后倾角, 依附侧倾力,和车速有关;速度越高,回正力矩就越大.5.7 横向稳固杆起什么感化?为什么有的车装在前悬架,有的装在后悬架,有的前后都装?答:横向稳固杆的主要感化是增长汽车的侧倾刚度,防止汽车在转向时产生过多的侧倾.别的,横向稳固杆还有转变汽车稳态转向特点的感化,其机理在题5.2 中有述.横向稳固装配的地位也是因为前.后侧倾刚度的请求,以及若何调节稳态转向特点的身分决议的.5.8 某种汽车的质心地位.轴距和前后轮胎的型号已定.按照二自由度把持稳固性模子,其稳态转向特点为过多转向,试找出五种改良其特点的办法.答:①增长主销内倾角;②增大主销后倾角;③在汽车前悬架加装横向稳固杆;④使汽车前束具有在紧缩行程减小,回复复兴行程增大的特点;⑤使后悬架的侧倾转向具有趋于缺少转向的特点.5.9 汽车空载和满载是否具有雷同的把持稳固性?答:不具有雷同的把持稳固.因为汽车空载和满载时汽车的总质量.质心地位会产生变更,这些将会影响汽车的稳固性因数.轮胎侧偏刚度.汽车侧倾刚度等把持稳固性参数.5.10 试用有关公式解释汽车质心地位对重要描写和评价汽车把持稳固性.稳态响应指标的影响.答:以静态储备系数为例解释汽车质心地位对稳态响应指标的影响:当中性转向点与质心地位重应时,S.M.=0,汽车为中性转向特点;当质心在中性转向点之前时, S.M.为正值,汽车具出缺少转向特点;当质心在中性转向点之后时, S.M.为负值,汽车具有过多转向特点.5.115.12 稳态响应中横摆角速度增益达到最大值时的车速称为特点车速uch .证实:特点车速uch ? 1/ K ,且在特征车速时的横摆角速度增益,为具有相等轴距 L 中性转向汽车横摆角速度增益的一半. 答:特点车速指汽车稳态横摆角速度增益达到最大值时的车速,汽车稳态横摆角速度增益为:5.136答:进步把持稳固性5.17 习题图5 为三种前自力悬架对车轮相对车身垂直高低位移时前束变更的影响.试问图中哪一条曲线具有侧倾过多转向后果?答:曲线1 对应的前自力悬架,转弯时车厢侧倾,内侧前轮处于反弹行程,前束增长,车轮向汽车纵向中间线转动,外侧前轮处于紧缩行程,前束减小,车轮向外迁移转变.采取这种悬架导致汽车的侧倾转向增长了缺少转向量,具有侧倾缺少转向后果. 曲线 2 对应的前自力悬架,曲线较其他两种更切近纵坐标轴,解释这种悬架的侧倾转向量很小,几乎等于零. 曲线 3 对应的前自力悬架,转弯时车厢侧倾,内侧前轮处于反弹行程,前束减小,车轮向汽车纵向中间线相反方向迁移转变,外侧前轮处于紧缩行程,前束增大,车轮向内迁移转变.采取这种悬架导致汽车的侧倾转向增长了过多转向量, 具有侧倾过多转向后果.5.18 转向盘力特点与哪些身分有关,试剖析之.答:转向盘力随汽车活动状态而变更的纪律称为转向盘力特点,与下列身分有关:转向器传动等到其变更纪律. 转向器效力.动力转向器的转向盘操纵力特点.转向杆系传动比.转向杆系效力.由悬架导向杆系决议的主销地位. 轮胎上的载荷.轮胎气压.轮胎力学特点.地面附着前提.转向盘迁移转变惯量.转向柱摩擦阻力以及汽车整体动力学特性等.5.19 地面感化于轮胎的切向反感化力是若何掌握转向特点的?答:参考教材第六节.第六章汽车的平顺性6.1查表得,人的主不雅感触感染为很不舒畅.6.26.36.5。
汽车理论课后习题答案余志生版版

第一章1.1、试说明轮胎滚动阻力的定义、产生机理和作用形式?答:1)定义:汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚动阻力。
2)产生机理:由于轮胎内部摩擦产生弹性轮胎在硬支撑路面上行驶时加载变形曲线和卸载变形曲线不重合会有能量损失,即弹性物质的迟滞损失。
这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对车轮的法向反作用力的分布是前后对称的;当车轮滚动时,由于弹性迟滞现象,处于压缩过程的前部点的地面法向反作用力就会大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分布前后不对称,而使他们的合力Fa 相对于法线前移一个距离a, 它随弹性迟滞损失的增大而变大。
即滚动时有滚动阻力偶矩 a F T z f = 阻碍车轮滚动。
3)作用形式:滚动阻力fw F f =rT F f f =(f 为滚动阻力系数)1.2、滚动阻力系数与哪些因素有关?提示:滚动阻力系数与路面种类、行驶车速以及轮胎的构造、材料、气压等有关。
1.3、解答:1)(取四档为例) 由u F n u n Tq Tq F t t →⇒⎪⎭⎪⎬⎫→→→ 即432)1000(8445.3)1000(874.40)1000(44.165)1000(27.25913.19nn n n Tq -+-+-= ri i T F To g q t η=og i i rnu 377.0=行驶阻力为w f F F +: 215.21a D w f U A C Gf F F +=+ 2131.0312.494aU +=由计算机作图有※本题也可采用描点法做图:由发动机转速在min /600n min r =,min /4000n max r =,取六个点分别代入公式:……………………………… 2)⑴最高车速:有w f t F F F +=⇒2131.0312.494a t U F +=分别代入a U 和t F 公式:2)09.6*83.53697.0*377.0(131.0312.494367.085.0*83.5*9.6*n T q += 把q T 的拟和公式也代入可得: n>4000而4000max =n r/min∴93.9483.5*0.14000*367.0*377.0max ==U Km/h ⑵最大爬坡度:挂Ⅰ档时速度慢,Fw 可忽略: ⇒)(max w f t i F F F F +-=⇒GfF Git -=max⇒013.08.9*388014400max max -=-=f G F i t =0.366(3)克服该坡度时相应的附着率 zxF F =ϕ 忽略空气阻力和滚动阻力得: 6.0947.12.3*366.0/=====a il l a i F Fi zϕ 3)①绘制汽车行驶加速倒数曲线(已装货):40.0626)(1f D g du dt a -==δ (G Fw Ft D -=为动力因素) Ⅱ时,22022111r i i I m r I m Tg f w ηδ++=∑ 2222367.085.0*83.5*09.3*218.038001367.0598.3798.1380011+++= =1.128ri i T F To g q t η=432)1000(8445.3)1000(874.40)1000(44.165)1000(27.25913.19n n n n Tq -+-+-=215.21a D w U A C F =由以上关系可由计算机作出图为:②用计算机求汽车用Ⅳ档起步加速至70km/h 的加速时间。
汽车理论第五版_课后习题答案(正确)(完整资料).doc

【最新整理,下载后即可编辑】第一章 汽车的动力性1.1试说明轮胎滚动阻力的定义,产生机理和作用形式。
答:车轮滚动时,由于车轮的弹性变形、路面变形和车辙摩擦等原因所产生的阻碍汽车行驶的力称为轮胎滚动阻力。
产生机理和作用形式:(1)弹性轮胎在硬路面上滚动时,轮胎的变形是主要的,由于轮胎有内部摩擦,产生弹性迟滞损失,使轮胎变形时对它做的功不能全部回收。
由于弹性迟滞,地面对车轮的法向作用力并不是前后对称的,这样形成的合力z F 并不沿车轮中心(向车轮前进方向偏移a )。
如果将法向反作用力平移至与通过车轮中心的垂线重合,则有一附加的滚动阻力偶矩f z T F a =⋅。
为克服该滚动阻力偶矩,需要在车轮中心加一推力P F 与地面切向反作用力构成一力偶矩。
(2)轮胎在松软路面上滚动时,由于车轮使地面变形下陷,在车轮前方实际形成了具有一定坡度的斜面,对车轮前进产生阻力。
(3)轮胎在松软地面滚动时,轮辙摩擦会引起附加阻力。
(4)车轮行驶在不平路面上时,引起车身振荡、减振器压缩和伸长时做功,也是滚动阻力的作用形式。
1.2滚动阻力系数与哪些因素有关?答:滚动阻力系数与路面的种类、行驶车速以及轮胎的构造、材料和气压有关。
这些因素对滚动阻力系数的具体影响参考课本P9。
1.3 确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h 的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h 的加速时间。
轻型货车的有关数据:汽油发动机使用外特性的Tq-n 曲线的拟合公式为23419.313295.27()165.44()40.874() 3.8445()1000100010001000q n n n n T =-+-+- 式中,Tq 为发动机转矩(N •m );n 为发动机转速(r/min )。
清华大学汽车理论余志生第五版课后答案

dU
g
.
. . .
可得,最大爬坡度为:
. D . f max max i
. 0.28255 max i .
. 16.41. max . .
课后答案网,用心为你服务!
大学答案 --- 中学答案 --- 考研答案 --- 考试答案
最全最多的课后习题参考答案,尽在课后答案网()!
答:可参看不同 0 i 时的汽车功率平衡图:
. . f w
t
e P . P . P
.
1
..
.
..
. . . 3
3600 max 76140 max
1
a
D
a
t
e P Gf u C A u
.
6
显而可见,当总的转动比较大时,发动机后备功率大,加速容易,更易
2
2
0
2
2
1 1 1
r
I i i
r m
I
m
w f g T .
. . . . .
代入数据有:. =1.4168
若地面不发生打滑,此时,地面最大驱动力
8
r
T i i
F tq g t
t
. 0
xb1max F . .
. F 6597.36N xb1max .
1
第一章
1.1、试说明轮胎滚动阻力的定义、产生机理和作用形式?
答:1)定义:汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力
称为滚动阻力。
2)产生机理:由于轮胎内部摩擦产生弹性轮胎在硬支撑路面上行驶时加载
汽车理论课后习题答案及MATLAB编程

汽车理论课后习题答案—附MATLAB编程教材:汽车理论(第5版)清华大学余志生主编机械工业出版社出版本文档包含第三章 4.3 5.11 6.2 6.4 6.5所要求的MATLAB编程其它习题答案:第一章:1.1 1.2 1.7 1.8第二章:2.2 2.3 2.4第三章第四章:4.1 4.2 4.3 4.5第五章:5.1 5.8 5.10 5.11 5.12 5.14 5.17第六章:6.1~6.5见本作者另一百度文库文档。
获取方法:点击左上角本作者的昵称,进入本作者的文库,《汽车理论课后习题答案(含MATLAB编程)》第三章:m=3880;%总质量g=9.8;%重力加速度r=0.367;%车轮半径eta_t=0.85;%传动系机械效率f=0.013;%滚动阻力系数CDA=2.77;%空气阻力系数*迎风面积i0=[5.175.435.836.176.33];%主减速器传动比If=0.218;%飞轮转动惯量Iw1=1.798;Iw2=3.598;%两前轮/四后轮转动惯量Iw=Iw1+Iw2;ig4=[6.09 3.091.711];%4挡变速器传动比ig5=[5.56 2.7691.64410.793];%5挡变速器传动比n=600:1:4000;%发动机转速Tq=-19.313+295.27*n/1000-165.44*(n/1000).^2+40.874*(n/1000).^3-3.8445*(n/1000).^4;%4挡发动机for i=1:5Ft1=Tq*ig4(1)*i0(i)/r;%各档对应转速下的驱动力Ft2=Tq*ig4(2)*i0(i)/r;Ft3=Tq*ig4(3)*i0(i)/r;Ft4=Tq*ig4(4)*i0(i)/r;u1=0.377*r*n/(i0(i)*ig4(1));%各档对应转速下的车速u2=0.377*r*n/(i0(i)*ig4(2));u3=0.377*r*n/(i0(i)*ig4(3));u4=0.377*r*n/(i0(i)*ig4(4));F1=m*g*f+CDA*u1.^2/21.15;%各档对应转速下的行驶阻力F2=m*g*f+CDA*u2.^2/21.15;F3=m*g*f+CDA*u3.^2/21.15;F4=m*g*f+CDA*u4.^2/21.15;delta1=1+(Iw+If.*ig4(1).^2.*i0(i).^2.*eta_t)./(m.*r.^2);%汽车旋转质量换算系数delta2=1+(Iw+If.*ig4(2).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta3=1+(Iw+If.*ig4(3).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta4=1+(Iw+If.*ig4(4).^2.*i0(i).^2.*eta_t)./(m.*r.^2);a1=(Ft1-F1)/(delta1*m);%加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);b1=1./a1;%加速度倒数b2=1./a2;b3=1./a3;b4=1./a4;figure(1)subplot(2,3,i)plot(u1,b1,u2,b2,u3,b3,u4,b4);title('加速度倒数-速度曲线');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')gtext(['i0='num2str(i0(i))]);%计算采用2挡起步加速至96.6km/h的原地起步加速时间u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=96.6;x1=[];x2=[];x3=[];x4=[];y=3401;for j=1:3401if u3(j)<=u3minx1=[j];endendq1=max(x1);ua3=u3(q1:y);a3=b3(q1:y);for k=1:3401if u4(k)<=u4minx2=[k];elseif u4(k)<=u4maxx3=[k];endendq2=max(x2);q3=max(x3);ua4=u4(q2:q3);a4=b4(q2:q3);s2=trapz(b2,u2);%二挡运行时间s3=trapz(ua3,a3);%三挡运行时间s4=trapz(ua4,a4);%四挡运行时间s=[s2s3s4];t=sum(s)*1000/3600;%总时间disp('t=');disp(t);gtext(['t='num2str(t)'s']);Pe1=Ft1.*u1./3600;%各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;endPemax=max([max(Pe1)max(Pe2)max(Pe3)max(Pe4)]);%发动机最大功率disp('90%负荷');Pe=0.9*Pemax%90%负荷rou=0.7;Ua=0.377*r*3401./(i0.*ig4(4));B=[1233.9-84.4782.9788-0.0474490.00028230];%负荷特性曲线拟合公式系数,对应n=3403r/min for i=1:5b=B*[1Pe Pe^2Pe^3Pe^4]';%根据拟合公式计算比油耗Qs4(i)=Pe.*b./(1.02.*Ua(i).*rou.*g);%百公里油耗量enddisp('Qs4=');disp(Qs4);tt=[48.423546.351141.555733.379630.5564];figure(2)plot(Qs4,tt,'*')hold onxi=25:0.001:31;pp=interp1(Qs4,tt,xi,'cubic');plot(xi,pp)title('燃油经济性-加速时间曲线');xlabel('燃油经济性--等速百公里油耗(L/100km)');ylabel('动力性--原地起步加速时间(s)');gtext('5.17')gtext('5.43')gtext('5.83')gtext('6.17')gtext('6.33')%5挡发动机for i=1:5Ft1=Tq*ig5(1)*i0(i)/r;%各档对应转速下的驱动力Ft2=Tq*ig5(2)*i0(i)/r;Ft3=Tq*ig5(3)*i0(i)/r;Ft4=Tq*ig5(4)*i0(i)/r;Ft5=Tq*ig5(5)*i0(i)/r;u1=0.377*r*n/(i0(i)*ig5(1));%各档对应转速下的车速u2=0.377*r*n/(i0(i)*ig5(2));u3=0.377*r*n/(i0(i)*ig5(3));u4=0.377*r*n/(i0(i)*ig5(4));u5=0.377*r*n/(i0(i)*ig5(5));F1=m*g*f+CDA*u1.^2/21.15;%各档对应转速下的行驶阻力F2=m*g*f+CDA*u2.^2/21.15;F3=m*g*f+CDA*u3.^2/21.15;F4=m*g*f+CDA*u4.^2/21.15;F5=m*g*f+CDA*u5.^2/21.15;delta1=1+(Iw+If.*ig5(1).^2.*i0(i).^2.*eta_t)./(m.*r.^2);%汽车旋转质量换算系数delta2=1+(Iw+If.*ig5(2).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta3=1+(Iw+If.*ig5(3).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta4=1+(Iw+If.*ig5(4).^2.*i0(i).^2.*eta_t)./(m.*r.^2);delta5=1+(Iw+If.*ig5(5).^2.*i0(i).^2.*eta_t)./(m.*r.^2);a1=(Ft1-F1)/(delta1*m);%加速度a2=(Ft2-F2)/(delta2*m);a3=(Ft3-F3)/(delta3*m);a4=(Ft4-F4)/(delta4*m);a5=(Ft5-F5)/(delta5*m);b1=1./a1;%加速度倒数b2=1./a2;b3=1./a3;b4=1./a4;b5=1./a5;figure(3)subplot(2,3,i)plot(u1,b1,u2,b2,u3,b3,u4,b4,u5,b5);title('加速度倒数-速度曲线');xlabel('u')ylabel('1/a')gtext('1/a1')gtext('1/a2')gtext('1/a3')gtext('1/a4')gtext('1/a5')gtext(['i0='num2str(i0(i))]);%计算采用2挡起步加速至96.6km/h的原地起步加速时间u1min=min(u1);u1max=max(u1);u2min=u1max;u2min=min(u2);u2max=max(u2);u3min=u2max;u3max=max(u3);u4min=u3max;u4max=max(u4);u5min=u4max;u5max=96.6;x1=[];x2=[];x3=[];x4=[];x5=[];y=3401;for j=1:3401if u3(j)<=u3minx1=[j];endendq1=max(x1);ua3=u3(q1:y);a3=b3(q1:y);for k=1:3401if u4(k)<=u4minx2=[k];endendq2=max(x2);ua4=u4(q2:y);a4=b4(q2:y);for l=1:3401if u5(l)<=u5minx3=[l];elseif u5(l)<=u5maxx4=[l];endendq2=max(x2);q3=max(x3);q4=max(x4);ua5=u5(q3:q4);a5=b5(q3:q4);s2=trapz(b2,u2);%二挡运行时间s3=trapz(ua3,a3);%三挡运行时间s4=trapz(ua4,a4);%四挡运行时间s5=trapz(ua5,a5);%五挡运行时间s=[s2s3s4s5];t=sum(s)*1000/3600;%总时间disp('t=');disp(t);gtext(['t='num2str(t)'s']);Pe1=Ft1.*u1./3600;%各档对应转速下的功率Pe2=Ft2.*u2./3600;Pe3=Ft3.*u3./3600;Pe4=Ft4.*u4./3600;Pe5=Ft5.*u5./3600;endPemax=max([max(Pe1)max(Pe2)max(Pe3)max(Pe4)max(Pe4)]);%发动机最大功率disp('90%负荷');Pe=0.9*Pemax%90%负荷rou=0.7;Ua=0.377*r*3401./(i0.*ig4(4));B=[1233.9-84.4782.9788-0.0474490.00028230];%负荷特性曲线拟合公式系数,对应n=3403r/min for i=1:5b=B*[1Pe Pe^2Pe^3Pe^4]';%根据拟合公式计算比油耗Qs5(i)=Pe.*b./(1.02.*Ua(i).*rou.*g);%百公里油耗量enddisp('Qs5=');disp(Qs5);tt=[93.973058.283444.678445.366744.9793];figure(2)plot(Qs5,tt,'*')hold onxi=30:0.001:100;pp=interp1(Qs5,tt,xi,'cubic');plot(xi,pp)%title('燃油经济性-加速时间曲线');%xlabel('燃油经济性--等速百公里油耗(L/100km)');%ylabel('动力性--原地起步加速时间(s)');gtext('5.17')gtext('5.43')gtext('5.83')gtext('6.17')gtext('6.33')运行结果:t=48.4235t=46.3511t=41.5557t=33.3796t=30.556490%负荷Pe=55.5647Qs4=25.103126.365628.307829.958730.7356图1加速度倒数-速度曲线图2燃油经济性-加速时间曲线4.3%空载(no load)—1;满载(full load)—2m1=4080;m2=9290;hg1=0.845;hg2=1.170;L=3.950;a1=2.100;a2=2.950;b1=L-a1;b2=L-a2;beta=0.38;%利用附着系数与制动强度的关系曲线z=0:0.01:1;phi_f1=L*beta.*z./(b1+z*hg1);%前轮利用附着系数(空载)phi_r1=L*(1-beta).*z./(a1-z*hg1);%空载时后轮利用附着系数(空载)phi_f2=L*beta.*z./(b2+z*hg2);%前轮利用附着系数(满载)phi_r2=L*(1-beta).*z./(a2-z*hg2);%后轮利用附着系数(满载)phi=z;%最理想情况figure(1);plot(z,phi_f1,'g--',z,phi_f2,'g-',z,phi_r1,'b--',z,phi_r2,'b-',z,phi,'k-'); axis([0,1,0,1]);grid on;box off;axis square;title('利用附着系数与制动强度的关系曲线');xlabel('制动强度z/g');ylabel('利用附着系数{\phi}');%ECE法规要求界限hold on;z1=0.2:0.01:0.8;z2=0.15:0.01:0.3;z3=0.3:0.01:1;phi1=(z1+0.07)/0.85;phi2=z2-0.08;phi3=z2+0.08;phi4=(z3-0.02)/0.74;plot(z1,phi1,'r-.',z2,phi2,'r-.',z2,phi3,'r-.',z3,phi4,'r-.'); legend('{\phi}_{f}(空载)','{\phi}_{f}(满载)','{\phi}_{r}(空载)',...'{\phi}_{r}(满载)','{\phi}=z','ECE法规要求界限');legend('Location','northwest');%制动效率曲线Ef1=z./phi_f1*100;Er1=z./phi_r1*100;Ef2=z./phi_f2*100;Er2=z./phi_r2*100;figure(2);plot(phi_f1,Ef1,'k',phi_r1,Er1,'k',phi_f2,Ef2,'b',phi_r2,Er2,'b'); axis([0,1,0,100]);grid on;box off;axis square;title('制动效率曲线');xlabel('附着系数{\phi}');ylabel('制动效率(%)');text(0.25,90,'E_f');text(0.6,88,'满载');text(0.8,90,'E_r');text(0.7,65,'空载');text(0.72,72,'E_r');程序运行结果如下:图1图2 5.11L=3.048;K=0.0024;i=20;ua=0:0.01:120;f=1/L.*(1./(3.6./ua+K.*ua./3.6));syms uF(u)=(1/L.*(1./(1./u+K.*u)))./i;plot(ua,f,'b-');xlabel('u_a(km/h)');ylabel('\omega_r/\delta)_s');F(22.35)运行结果:ans=0.1667386094155036.2f=0.1:0.1:100;Gq1=5.12*10^(-5)./f.^2;Gq2=2.02*10^(-3).*f./f;Gq3=7.98*10^(-2).*f.^2;figure(1);loglog(f,Gq1,'b-');box off;axis square;title('位移功率谱密度'); xlabel('f/Hz');ylabel('G_q(f)/(m^2s)');figure(2);loglog(f,Gq2,'b-');box off;axis square;title('速度功率谱密度'); xlabel('f/Hz');ylabel('G_q_''(f)/(m^2/s)');figure(3);loglog(f,Gq3,'b-');box off;axis square;title('加速度功率谱密度'); xlabel('f/Hz');ylabel('G_q_''_''(f)/(m^2/s^3)');运行结果如下:6.4f1=0.1:0.01:1;f2=1:0.01:10;G1=0.010106.*f1.^2;G2=0.010106.*f2./f2;loglog(f1,G1,'b-');hold onloglog(f2,G2,'b-');title('车身加速度的功率谱密度'); xlabel('f/Hz');ylabel('G_z_''_''(f)/m^-^1'); axis([0.1,10,0.0001,0.1]);运行结果如下:6.51.计算说明1)①幅频特性()122222114z q λζλγ⎡⎤-+⎢=⎢⎥∆⎣⎦,其中0ωλω=,()2222222111141λλγζλγλμμ⎡⎤⎡⎤⎛⎫⎛⎫∆=-+--+-⎢⎥⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦⎣⎦;()12222222211414z z ζλλζλ⎡⎤+⎢=⎢⎥-+⎣⎦;()1222222221414s s s s s p z ζλλζλ⎡⎤+⎢=⎢⎥-+⎣⎦,其中s s ωλω=;②均方根谱()()221~j 2z q H f f ωππ=;()()222~j 2z qH f f ωππ== ;()()2221~1j 2p qz z H f f z qωππ== ;③其他值()0.5360q q G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.536110z z G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.536220z z G f df σ⎡⎤=⎢⎥⎣⎦⎰ ,()0.5360a a G f df σ⎡⎤=⎢⎥⎣⎦⎰()()()()()()13622w 012222412.5362202412.5d 12.5 0.5d d 1d d 4a a a a a a W f G f f f G f f G f f G f f G f f f ⎡⎤=⎢⎥⎣⎦⎡⎤⎛⎫⎛⎫=+++⎢⎥ ⎪ ⎪⎝⎭⎢⎥⎝⎭⎣⎦⎰⎰⎰⎰⎰其中,()()()()()0.5 0.52 2441 412.512.512.536f f f W f f f f <<⎧⎪⎪<<⎪=⎨<<⎪⎪<<⎪⎩()aw w 020lg L a =2)见1)中计算式3)()()()22004q q q G f G G n n uωπ== ()()()1122363622d ~00d d dd f q q f q f H f G f f G f f q σ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎰⎰ ,其中122d 12f q f γλπ⎡⎤=⎢⎥∆⎣⎦ ()()()1122363622d //~00d d dd F Gq q F G q F H f G f f G f f Gq σ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦⎰⎰ ,其中122222d 1412F f Gq g λζλμπγ⎡⎤⎛⎫-+⎢⎥⎪+⎢⎥⎝⎭=⎢⎥∆⎢⎥⎢⎥⎣⎦其余见1)中计算式2.程序清单1)f0=1.5;zeta=0.25;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;omega_s=2*pi*fs;lambda=omega./omega0;lambda_s=omega./omega_s;%计算并绘制幅频特性delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;figure(1)loglog(f,z1_q,'b-',0:0.1:100,(0:0.1:100)./(0:0.1:100),'g-');axis([0.1,100,0.1,10]);grid on ;title('z_1~q 的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{z_1}{q}|$$','Interpreter','latex');gtext('0:1');figure(2)loglog(f,z2_z1,'b-',0:0.1:1,(0:0.1:1)./(0:0.1:1),'g-',1:0.1:100,1./...(1:0.1:100),'g-');axis([0.1,100,0.01,10]);grid on;title('z_2~z_1的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{z_2}{z_1}|$$','Interpreter','latex'); gtext('0:1');gtext('-1:1');figure(3)loglog(f,p_z2,'b-');axis([0.1,100,0.01,10]);grid on;title('p~z_2的幅频特性');xlabel('激振频率f/Hz');ylabel('$$|\frac{p}{z_2}|$$','Interpreter','latex');%计算并绘制均方根谱sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q; figure(4)loglog(f,sqrt_Gz1,'b-');grid on;title('车轮位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_{z''''1}(f)}$','Interpreter','latex'); figure(5)loglog(f,sqrt_Gz2,'b-');grid on;title('车身位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_{z''''2}(f)}$','Interpreter','latex'); figure(6)loglog(f,sqrt_Ga,'b-');grid on;title('传至人体的位移均方根谱');xlabel('激振频率f/Hz');ylabel('$\sqrt{G_a(f)}$','Interpreter','latex');%计算其它值sigma_q=sqrt(trapz(f,sqrt_Gq.^2));%路面不平度加速度均方根值sigma_z1=sqrt(trapz(f,sqrt_Gz1.^2));%车轮加速度均方根值sigma_z2=sqrt(trapz(f,sqrt_Gz2.^2));%车身加速度均方根值sigma_a=sqrt(trapz(f,sqrt_Ga.^2));%传至人体的加速度均方根值for i=1:Nif f(i)<=2W(i)=0.5;elseif f(i)<=4W(i)=f(i)/4;elseif f(i)<=12.5W(i)=1;elseW(i)=12.5/f(i);endendaw=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));%加权加速度均方根值a0=10^(-6);Law=20*log10(aw/a0);%加权振级format shortdisp('路面不平度加速度均方根值=');disp(sigma_q);disp('车轮加速度均方根值=');disp(sigma_z1);disp('车身加速度均方根值=');disp(sigma_z2);disp('传至人体的加速度均方根值=');disp(sigma_a);disp('加权加速度均方根值=');disp(aw);disp('加权振级=');disp(Law);2)%随fs变化f0=1.5;zeta=0.25;gamma=9;mu=10;fs=1.5:0.01:6;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;lambda=omega./omega0;for i=1:length(fs)omega_s=2*pi.*fs(i);lambda_s=omega./omega_s;delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q;for j=1:Nif f(j)<=2W(j)=0.5;elseif f(j)<=4W(j)=f(j)/4;elseif f(j)<=12.5W(j)=1;elseW(j)=12.5/f(j);endendaw(i)=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));enda0=10^(-6);Law=20*log10(aw/a0);figure(1)plot(fs,aw);grid ontitle('a_w随f_s的变化曲线');xlabel('f_s/Hz');ylabel('a_w/m·s^-^2');figure(2)plot(fs,Law);grid ontitle('L_aw随f_s的变化曲线');xlabel('f_s/Hz');ylabel('L_a_w/dB');%随zeta_s变化f0=1.5;zeta=0.25;gamma=9;mu=10;fs=3;zeta_ss=0.125:0.001:0.5;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega0=2*pi*f0;omega_s=2*pi.*fs;lambda=omega./omega0;lambda_s=omega./omega_s;for i=1:length(zeta_ss)zeta_s=zeta_ss(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;p_z2=((1+(2*zeta_s.*lambda_s).^2)./((1-lambda_s.^2).^2+(2*zeta_s.*...lambda_s).^2)).^0.5;sqrt_Gq=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u);sqrt_Gz1=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z1_q;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sqrt_Ga=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*p_z2.*z2_z1.*z1_q;for j=1:Nif f(j)<=2W(j)=0.5;elseif f(j)<=4W(j)=f(j)/4;elseif f(j)<=12.5W(j)=1;elseW(j)=12.5/f(j);endendaw(i)=sqrt(trapz(f,W.^2.*sqrt_Ga.^2));enda0=10^(-6);Law=20*log10(aw/a0);figure(1)plot(zeta_ss,aw);grid ontitle('a_w随\zeta_s的变化曲线');xlabel('\zeta_s');ylabel('a_w/m·s^-^2');figure(2)plot(zeta_ss,Law);grid ontitle('L_aw随\zeta_s的变化曲线');xlabel('\zeta_s');ylabel('L_a_w/dB');3)%随f0变化f0=0.25:0.01:3;zeta=0.25;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;lambda_s=omega./omega_s;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(f0)omega0=2*pi*f0(i);lambda=omega./omega0;delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(f0==1.5);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(f0,sm_z2,f0,sm_fd,f0,sm_FdG);axis([0.25,3,-25,10]);grid on;title('各响应量均方根值随f_0变化的曲线');xlabel('f_0/Hz');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');legend('Location','southeast');%随zeta变化f0=1.5;zeta0=0.125:0.001:0.5;gamma=9;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(zeta0)zeta=zeta0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(zeta0==0.25);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(zeta0,sm_z2,zeta0,sm_fd,zeta0,sm_FdG);axis([0.125,0.5,-4,4]);grid on;title('各响应量均方根值随\zeta变化的曲线');xlabel('\zeta');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');%随gamma变化f0=1.5;zeta=0.25;gamma0=4.5:0.1:18;mu=10;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(gamma0)gamma=gamma0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(gamma0==9);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(gamma0,sm_z2,gamma0,sm_fd,gamma0,sm_FdG);axis([4.5,18,-6,6]);grid on;title('各响应量均方根值随\gamma变化的曲线');xlabel('\gamma');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB'); legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');legend('Location','southeast');%随mu变化f0=1.5;zeta=0.25;gamma=9;mu0=5:0.1:20;fs=3;zeta_s=0.25;u=20;Gq_n0=2.56*10^(-8);n0=0.1;delta_f=0.2;N=180;f=delta_f*[1:N];omega=2*pi*f;omega_s=2*pi*fs;omega0=2*pi*f0;lambda_s=omega./omega_s;lambda=omega./omega0;Gq_f=4*pi^2*Gq_n0*n0^2*u;g=9.8;for i=1:length(mu0)mu=mu0(i);delta=((1-lambda.^2).*(1+gamma-1./mu.*lambda.^2)-1).^2+4*zeta^2.*lambda.^...2.*(gamma-(1./mu+1).*lambda.^2).^2;z1_q=gamma.*(((1-lambda.^2).^2+4*zeta.^2.*lambda.^2)./delta).^0.5;z2_z1=((1+4*zeta.^2.*lambda.^2)./((1-lambda.^2).^2+4*zeta.^2.*lambda.^2))....^0.5;sqrt_Gz2=4*pi^2.*f.*sqrt(Gq_n0*n0^2*u).*z2_z1.*z1_q;sigma_z2(i)=sqrt(trapz(f,sqrt_Gz2.^2));fd_q=gamma*lambda.^2./(2*pi.*f).*(1./delta).^0.5;sigma_fd(i)=sqrt(trapz(f,Gq_f.*fd_q.^2));Fd_Gq=2*pi.*f.*gamma./g.*(((lambda.^2./(1+mu)-1).^2+4*zeta.^2*lambda.^2)..../delta).^0.5;sigma_FdG(i)=sqrt(trapz(f,Gq_f.*Fd_Gq.^2));endm=find(mu0==10);sgm_z2=sigma_z2(m);sgm_fd=sigma_fd(m);sgm_FdG=sigma_FdG(m);sm_z2=20*log10(sigma_z2/sgm_z2);sm_fd=20*log10(sigma_fd/sgm_fd);sm_FdG=20*log10(sigma_FdG/sgm_FdG);plot(mu0,sm_z2,mu0,sm_fd,mu0,sm_FdG);axis([5,20,-2,2]);grid on;title('各响应量均方根值随\mu变化的曲线');xlabel('\mu');ylabel('\sigma_z_''_''_2,\sigma_f_d,\sigma_F_d_/_G/dB');legend('\sigma_z_''_''_2','\sigma_f_d','\sigma_F_d_/_G');3.结果分析1)路面不平度加速度均方根值=0.3523车轮加速度均方根值=0.2391车身加速度均方根值=0.0168传至人体的加速度均方根值=0.0161加权加速度均方根值=0.0100加权振级=80.0287分析:根据课本中表6-2,a w=0.0100<0.315,L aw=80.0287<110,故乘客没有不舒适。
余志生第五版汽车理论课后答案

第 五 章5.1一轿车(每个)前轮胎的侧偏刚度为-50176N /rad 、外倾刚度为-7665N /rad 。
若轿车向左转弯,将使两前轮均产生正的外倾角,其大小为40。
设侧偏刚度与外倾刚度均不受左、右轮载荷转移的影响.试求由外倾角引起的前轮侧偏角。
答: 由题意:F Y =k α+k γγ=0故由外倾角引起的前轮侧偏角: α=- k γγ/k=-7665⨯4/-50176=0.61105.2 6450轻型客车在试验中发现过多转向和中性转向现象,工程师们在前悬架上加装前横向稳定杆以提高前悬架的侧倾角刚度,结果汽车的转向特性变为不足转向。
试分析其理论根据(要求有必要的公式和曲线)。
答: 稳定性系数:⎪⎪⎭⎫ ⎝⎛-=122k b k a L m K 1k 、2k 变化,原来K ≤0,现在K>0,即变为不足转向。
5.3汽车的稳态响应有哪几种类型?表征稳态响应的具体参数有哪些?它们彼此之间的关系如何(要求有必要的公式和曲线)?答: 汽车稳态响应有三种类型 :中性转向、不足转向、过多转向。
几个表征稳态转向的参数:1.前后轮侧偏角绝对值之差(α1-α2);2. 转向半径的比R/R 0;3.静态储备系数S.M.彼此之间的关系见参考书公式(5-13)(5-16)(5-17)。
5.4举出三种表示汽车稳态转向特性的方法,并说明汽车重心前后位置和内、外轮负荷转移如何影响稳态转向特性? 答:方法:1.α1-α2 >0时为不足转向,α1-α2 =0时 为中性转向,α1-α2 <0时为过多转向;2. R/R0>1时为不足转向,R/R0=1时为中性转向,R/R0<1时为过多转向;3 .S.M.>0时为不足转向,S.M.=0时为中性转向,S.M.<0时为过多转向。
汽车重心前后位置和内、外轮负荷转移使得 汽车质心至前后轴距离a 、b 发生变化,K 也发生变化。
5.5汽车转弯时车轮行驶阻力是否与直线行驶时一样?答:否,因转弯时车轮受到的侧偏力,轮胎产生侧偏现象,行驶阻力不一样。
汽车理论第五版_课后习题答案(正确) (1)..

第一章 汽车的动力性1.3 确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h 的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h 的加速时间。
轻型货车的有关数据:汽油发动机使用外特性的Tq-n 曲线的拟合公式为23419.313295.27()165.44()40.874() 3.8445()1000100010001000q n n n n T =-+-+-式中,Tq 为发动机转矩(N •m );n 为发动机转速(r/min )。
发动机的最低转速n min =600r/min,最高转速n max =4000r/min 。
装载质量 2000kg 整车整备质量 1800kg 总质量 3880kg 车轮半径 0.367m 传动系机械效率 ηt =0.85 滚动阻力系数 f =0.013 空气阻力系数×迎风面积 C D A =2.77m 2 主减速器传动比 i 0=5.83飞轮转动惯量 I f =0.218kg •m 2 二前轮转动惯量 I w1=1.798kg •m 2 四后轮转动惯量 I w2=3.598kg •m 2 变速器传动比 ig(数据如下表)轴距 L=3.2m 质心至前轴距离(满载) a=1.974m 质心高(满载) hg=0.9m分析:本题主要考察知识点为汽车驱动力-行使阻力平衡图的应用和附着率的计算、等效坡度的概念。
只要对汽车行使方程理解正确,本题的编程和求解都不会有太大困难。
常见错误是未将车速的单位进行换算。
2)首先应明确道路的坡度的定义tan i α=。
求最大爬坡度时可以对行使方程进行适当简化,可以简化的内容包括两项cos 1α≈和sin tan αα≈,简化的前提是道路坡度角不大,当坡度角较大时简化带来的误差会增大。
汽车理论课后习题答案余志生版版-16页精选文档

第一章1.1、试说明轮胎滚动阻力的定义、产生机理和作用形式?答:1)定义:汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚动阻力。
2)产生机理:由于轮胎内部摩擦产生弹性轮胎在硬支撑路面上行驶时加载变形曲线和卸载变形曲线不重合会有能量损失,即弹性物质的迟滞损失。
这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对车轮的法向反作用力的分布是前后对称的;当车轮滚动时,由于弹性迟滞现象,处于压缩过程的前部点的地面法向反作用力就会大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分布前后不对称,而使他们的合力Fa 相对于法线前移一个距离a, 它随弹性迟滞损失的增大而变大。
即滚动时有滚动阻力偶矩 a F T z f = 阻碍车轮滚动。
3)作用形式:滚动阻力 fw F f = r T F ff = (f 为滚动阻力系数)1.2、滚动阻力系数与哪些因素有关?提示:滚动阻力系数与路面种类、行驶车速以及轮胎的构造、材料、气压等有关。
1.3、解答:1)(取四档为例) 由即行驶阻力为w f F F +:由计算机作图有※本题也可采用描点法做图:由发动机转速在min /600n min r =,m in /4000n max r =,取六个点分别代入公式:2)⑴最高车速:有w f t F F F +=分别代入a U 和t F 公式:把q T 的拟和公式也代入可得:n>4000而4000m ax =n r/min∴93.9483.5*0.14000*367.0*377.0max ==U Km/h ⑵最大爬坡度:挂Ⅰ档时速度慢,Fw 可忽略:=0.366(3)克服该坡度时相应的附着率 zx F F =ϕ 忽略空气阻力和滚动阻力得:3)①绘制汽车行驶加速倒数曲线(已装货):40.0626 )(1f D g du dt a -==δ (G Fw Ft D -=为动力因素) Ⅱ时,22022111r i i I m r I m T g f w ηδ++=∑=1.128由以上关系可由计算机作出图为:②用计算机求汽车用Ⅳ档起步加速至70km/h 的加速时间。
汽车理论课后习习题答案(余志生版)(免费版)
欢迎阅读第一章1.1、试说明轮胎滚动阻力的定义、产生机理和作用形式?答:1)定义:汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚动阻力。
2)产生机理:由于轮胎内部摩擦产生弹性轮胎在硬支撑路面上行驶时加载变形曲线和卸载变形曲线不重合会有能量损失,即弹性物质的迟滞损失。
这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对车轮的法向反作用力的分布是前后对称的;当车轮滚动时,由于弹性迟滞现象,处于压缩过程的前部点的地面法向反作用力就会大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分布前后不对称,而使他们的合力Fa 相对于法线前移一个距离a, 它随弹性迟滞损失的增大而变大。
即滚动时有滚动阻力偶矩a F T z f = 阻碍车轮滚动。
3)作用形式:滚动阻力 fw F f = r T F ff = (f 为滚动阻力系数)1.2、滚动阻力系数与哪些因素有关?提示:滚动阻力系数与路面种类、行驶车速以及轮胎的构造、材料、气压等有关。
1.3、解答:1)(取四档为例) 由即行驶阻力为w f F F +:由计算机作图有※本题也可采用描点法做图:由发动机转速在m in /600n min r =,m in /4000n max r =,取六个点分别代入公式:………………………………2)⑴最高车速:有w f t F F F +=分别代入a U 和t F 公式:把q T 的拟和公式也代入可得:n>4000而4000m ax =n r/min∴93.9483.5*0.14000*367.0*377.0max ==U Km/h ⑵最大爬坡度: 挂Ⅰ档时速度慢,Fw 可忽略:=0.366(3)克服该坡度时相应的附着率 zx F F =ϕ 忽略空气阻力和滚动阻力得:3)①绘制汽车行驶加速倒数曲线(已装货):40.0626)(1f D g du dt a -==δ (G Fw Ft D -=为动力因素) Ⅱ时,22022111r i i I m r I m T g f w ηδ++=∑ =1.128由以上关系可由计算机作出图为:②用计算机求汽车用Ⅳ档起步加速至70km/h 的加速时间。
汽车理论第五版_课后习题答案(正确)

qq第一章汽车的动力性2789731041.1试说明轮胎滚动阻力的定义,产生机理和作用形式。
答:车轮滚动时,由于车轮的弹性变形、路面变形和车辙摩擦等原因所产生的阻碍汽车行驶的力称为轮胎滚动阻力。
产生机理和作用形式:(1)弹性轮胎在硬路而上滚动时,轮胎的变形是主要的,由于轮胎有内部摩擦,产生弹性迟滞损失,使轮胎变形时对它做的功不能全部回收。
由于弹性迟滞,地面对车轮的法向作用力并不是前后对称的,这样形成的合力学不沿车轮中心(向车轮前进方向偏移a) o如果将法向反作用力平移至与通过车轮中心的垂线重合,则有一附加的滚动阻力偶矩T酱为克服该滚动阻力偶矩,需要在车轮中心加一推力F与地面切向反作用力构成一力偶(2)轮胎在松软路面上滚动时,由于车轮使地面变形下陷,在车轮前方实际形成了具有一定坡度的斜面,对车轮前进产生阻力。
(3)轮胎在松软地而滚动时,轮辙摩擦会引起附加阻力。
(4)车轮行驶在不平路面上时,引起车身振荡、减振器压缩和伸长时做功,也是滚动阻力的作用形式。
1. 2滚动阻力系数与哪些因素有关?答:滚动阻力系数与路面的种类、行驶车速以及轮胎的构造、材料和气压有关。
这些因素对滚动阻力系数的具体影响参考课本P9。
1・3确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h的车速一时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h的加速时间。
轻型货车的有关数据: 汽油发动机使甩外特性的Tq-n曲线的拟合公式为丄=— + --------------------- — -------------nnnn23419. 313295. 27 () 165. 44 () 40. 874 () 3. 8445 () 1000100010001000式中,Tq为发动机转矩(N?m) ;n为发动机转速(r/min)□ 发动机的最低转速min二600i7min,最高转速n aa>:=4000r/mino 装载质量2000kg 整车整备质量1800kg总质量3880kg 车轮半径0. 367m传动系机械效率n t=0. 85滚动阻力系数f=0. 0132 空气阻力系数X迎风面积C D A二2. 77m主减速器传动比i o=5. 832 飞轮转动惯量1尸0・218kg?m2二前轮转动惯量「二1・798kg?m四档变速器6. 093. 091. 711. 00-五档变速器5. 562. 7691. 6441. 000. 793轴距L=3. 2m质心至前轴距离(满载)&二1.974m 质心高(满载)hg=0. 9m分析:本题主要考察知识点为汽车驱动力一行使阻力平衡图的应用和附着率的计算、等效坡度的概念。
《汽车理论》第五版余志生版 课后答案(整理版)

第一章1.1、试说明轮胎滚动阻力的定义、产生机理和作用形式?答:1)定义:汽车在水平道路上等速行驶时受到的道路在行驶方向上的分力称为滚动阻力。
2)产生机理:由于轮胎内部摩擦产生弹性轮胎在硬支撑路面上行驶时加载变形曲线和卸载变形曲线不重合会有能量损失,即弹性物质的迟滞损失。
这种迟滞损失表现为一种阻力偶。
当车轮不滚动时,地面对车轮的法向反作用力的分布是前后对称的;当车轮滚动时,由于弹性迟滞现象,处于压缩过程的前部点的地面法向反作用力就会大于处于压缩过程的后部点的地面法向反作用力,这样,地面法向反作用力的分布前后不对称,而使他们的合力Fa 相对于法线前移一个距离a, 它随弹性迟滞损失的增大而变大。
即滚动时有滚动阻力偶矩 a F T z f = 阻碍车轮滚动。
3)作用形式:滚动阻力fw F f = rT F ff = (f 为滚动阻力系数)1.2、滚动阻力系数与哪些因素有关?提示:滚动阻力系数与路面种类、行驶车速以及轮胎的构造、材料、气压等有关。
1.3、解答:1)(取四档为例) 由u F n u n Tq Tq F t t →⇒⎪⎭⎪⎬⎫→→→r i i T F To g q t η=即432)1000(8445.3)1000(874.40)1000(44.165)1000(27.25913.19nn n n Tq −+−+−=o g i i rn u 377.0=行驶阻力为wf F F +:215.21a D w f U A C Gf F F +=+2131.0312.494a U +=由计算机作图有※本题也可采用描点法做图:由发动机转速在min /600n min r =,min /4000n max r =,取六个点分别代入公式:……………………………… 2)⑴最高车速: 有w f t F F F +=⇒2131.0312.494at U F +=分别代入a U 和t F 公式:2)09.6*83.53697.0*377.0(131.0312.494367.085.0*83.5*9.6*n T q +=把q T 的拟和公式也代入可得:n>4000而4000max =n r/min∴93.9483.5*0.14000*367.0*377.0max ==U Km/h⑵最大爬坡度:挂Ⅰ档时速度慢,Fw 可忽略: ⇒)(max w f t i F F F F +−=⇒GfF Git −=max⇒013.08.9*388014400max max −=−=f G F i t =0.366 (3)克服该坡度时相应的附着率 zxF F =ϕ 忽略空气阻力和滚动阻力得: 6.0947.12.3*366.0/=====a il l a i F Fi z ϕ3)①绘制汽车行驶加速倒数曲线(已装货):40.0626)(1f D g du dt a −==δ (G Fw Ft D −=为动力因素) Ⅱ时,22022111ri i I m r I mT g f wηδ++=∑2222367.085.0*83.5*09.3*218.038001367.0598.3798.1380011+++= =1.128ri i T F To g q t η=432)1000(8445.3)1000(874.40)1000(44.165)1000(27.25913.19n n n n Tq −+−+−=215.21a D w U A C F =由以上关系可由计算机作出图为:②用计算机求汽车用Ⅳ档起步加速至70km/h 的加速时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 汽车的动力性1.1试说明轮胎滚动阻力的定义,产生机理和作用形式。
答:车轮滚动时,由于车轮的弹性变形、路面变形和车辙摩擦等原因所产生的阻碍汽车行驶的力称为轮胎滚动阻力。
产生机理和作用形式:(1)弹性轮胎在硬路面上滚动时,轮胎的变形是主要的,由于轮胎有内部摩擦,产生弹性迟滞损失,使轮胎变形时对它做的功不能全部回收。
由于弹性迟滞,地面对车轮的法向作用力并不是前后对称的,这样形成的合力z F 并不沿车轮中心(向车轮前进方向偏移a )。
如果将法向反作用力平移至与通过车轮中心的垂线重合,则有一附加的滚动阻力偶矩f z T F a =⋅。
为克服该滚动阻力偶矩,需要在车轮中心加一推力P F 与地面切向反作用力构成一力偶矩。
(2)轮胎在松软路面上滚动时,由于车轮使地面变形下陷,在车轮前方实际形成了具有一定坡度的斜面,对车轮前进产生阻力。
(3)轮胎在松软地面滚动时,轮辙摩擦会引起附加阻力。
(4)车轮行驶在不平路面上时,引起车身振荡、减振器压缩和伸长时做功,也是滚动阻力的作用形式。
1.2滚动阻力系数与哪些因素有关?答:滚动阻力系数与路面的种类、行驶车速以及轮胎的构造、材料和气压有关。
这些因素对滚动阻力系数的具体影响参考课本P9。
1.3 确定一轻型货车的动力性能(货车可装用4挡或5挡变速器,任选其中的一种进行整车性能计算):1)绘制汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率。
3)绘制汽车行驶加速度倒数曲线,用图解积分法求汽车用2档起步加速行驶至70km/h 的车速-时间曲线,或者用计算机求汽车用2档起步加速行驶至70km/h 的加速时间。
轻型货车的有关数据:汽油发动机使用外特性的Tq-n 曲线的拟合公式为23419.313295.27()165.44()40.874() 3.8445()1000100010001000q n n n n T =-+-+-式中,Tq 为发动机转矩(N •m );n 为发动机转速(r/min )。
发动机的最低转速n min =600r/min,最高转速n max =4000r/min 。
装载质量 2000kg 整车整备质量 1800kg 总质量 3880kg 车轮半径 0.367m 传动系机械效率 ηt =0.85 滚动阻力系数 f =0.013 空气阻力系数×迎风面积 C D A =2.77m 2 主减速器传动比 i 0=5.83飞轮转动惯量 I f =0.218kg •m 2 二前轮转动惯量 I w1=1.798kg •m 2 四后轮转动惯量 I w2=3.598kg •m 2质心至前轴距离(满载) a=1.974m 质心高(满载) hg=0.9m分析:本题主要考察知识点为汽车驱动力-行使阻力平衡图的应用和附着率的计算、等效坡度的概念。
只要对汽车行使方程理解正确,本题的编程和求解都不会有太大困难。
常见错误是未将车速的单位进行换算。
2)首先应明确道路的坡度的定义tani α=。
求最大爬坡度时可以对行使方程进行适当简化,可以简化的内容包括两项cos 1α≈和sin tan αα≈,简化的前提是道路坡度角不大,当坡度角较大时简化带来的误差会增大。
计算时,要说明做了怎样的简化并对简化的合理性进行评估。
3)已知条件没有说明汽车的驱动情况,可以分开讨论然后判断,也可以根据常识判断轻型货车的驱动情况。
解:1)绘制汽车驱动力与行驶阻力平衡图汽车驱动力Ft=ri i T to g tq η行驶阻力F f +F w +F i +F j =G •f +2D 21.12A C a u +G •i+dtdum δ 发动机转速与汽车行驶速度之间的关系式为:0g i nr 0.377ua i ⋅= 由本题的已知条件,即可求得汽车驱动力和行驶阻力与车速的关系,编程即可得到汽车驱动力与行驶阻力平衡图。
2)求汽车最高车速,最大爬坡度及克服该坡度时相应的附着率①由1)得驱动力与行驶阻力平衡图,汽车的最高车速出现在5档时汽车的驱动力曲线与行驶阻力曲线的交点处,Ua max =99.08m/s 2。
②汽车的爬坡能力,指汽车在良好路面上克服w f F F +后的余力全部用来(等速)克服坡度阻力时能爬上的坡度,此时0=dt du,因此有()w f t i F F F F +-=,可得到汽车爬坡度与车速的关系式:()⎪⎪⎭⎫ ⎝⎛+-=G F F F i w f t arcsin tan ;而汽车最大爬坡度m ax i 为Ⅰ档时的最大爬坡度。
利用MATLAB 计算可得,352.0max =i 。
③如是前轮驱动,1ϕC =qb hg q L L -;相应的附着率1ϕC 为1.20,不合理,舍去。
如是后轮驱动,2ϕC =qa hg q L L+;相应的附着率2ϕC 为0.50。
3)绘制汽车行驶加速度倒数曲线,求加速时间 汽车旋转质量换算系数Ⅰ档Ⅱ档Ⅲ档Ⅳ档Ⅴ档220221mri i I mrITg f w ηδ++=∑1.3829 1.1027 1.0429 1.0224 1.0179利用MATLAB 画出汽车的行驶加速度图和汽车的加速度倒数曲线图:忽略原地起步时的离合器打滑过程,假设在初时刻时,汽车已具有Ⅱ档的最低车速。
由于各档加速度曲线不相交(如图三所示),即各低档位加速行驶至发动机转速达到最到转速时换入高档位;并且忽略换档过程所经历的时间。
结果用MATLAB 画出汽车加速时间曲线如图五所示。
如图所示,汽车用Ⅱ档起步加速行驶至70km/h 的加速时间约为26.0s 。
1.4空车、满载时汽车动力性有无变化?为什么?答:动力性会发生变化。
因为满载时汽车的质量会增大,重心的位置也会发生改变。
质量增大,滚动阻力、坡度阻力和加速阻力都会增大,加速时间会增加,最高车速降低。
重心位置的改变会影响车轮附着率,从而影响最大爬坡度。
1.5如何选择汽车发动机功率?答:发动机功率的选择常先从保证汽车预期的最高车速来初步确定。
若给出了期望的最高车速,选择的发动机功率应大体等于,但不小于以最高车速行驶时的行驶阻力功率之和,即)761403600(1max 3max a D a tu A C u GfPe +=η。
在实际工作中,还利用现有汽车统计数据初步估计汽车比功率来确定发动机应有功率。
不少国家还对车辆应有的最小比功率作出规定,以保证路上行驶车辆的动力性不低于一定水平,防止某些性能差的车辆阻碍车流。
1.6超车时该不该换入低一挡的排挡?答:超车时排挡的选择,应该使车辆在最短的时间内加速到较高的车速,所以是否应该换入低一挡的排挡应该由汽车的加速度倒数曲线决定。
如果在该车速时,汽车在此排档的加速度倒数大于低排挡时的加速度倒数,则应该换入低一档,否则不应换入低一挡。
1.7 统计数据表明,装有0.5~2L 排量发动机的轿车,若是前置发动机前轮驱动(F.F.)轿车,其平均的前轴负荷为汽车总重力的61.5%;若是前置发动机后轮驱动(F.R.)轿车,其平均的前轴负荷为汽车总重力的55.7%。
设一轿车的轴距L=2.6m ,质心高度h=0.57m 。
试比较采用F.F 及F.R.形式时的附着力利用情况,分析时其前轴负荷率取相应形式的平均值。
确定上述F.F 轿车在φ=0.2及0.7路面上的附着力,并求由附着力所决定的极限最高车速与极限最大爬坡度及极限最大加速度(在求最大爬坡度和最大加速度时可设Fw=0)。
其它有关参数为:m =1600kg,C D =0.45,A =2.00m 2,f =0.02,δ≈1.00。
分析:分析本题的核心在于考察汽车的附着力、地面法向反作用力和作用在驱动轮上的地面切向反作用力的理解和应用。
应熟知公式(1-13)~(1-16)的意义和推导过程。
分析1)比较附着力利用情况,即比较汽车前(F.F )、后轮(F.R.)地面切向反作用力与地面作用于前(F.F )、后轮(F.R.)的法向反作用力的比值。
解题时应注意,地面法向发作用力包括静态轴荷、动态分量、空气升力和滚动阻力偶矩产生的部分,如若进行简化要对简化的合理性给予说明。
地面作用于车轮的地面切向反作用力则包括滚动阻力和空气阻力的反作用力。
2)求极限最高车速的解题思路有两个。
一是根据地面作用于驱动轮的地面切向反作用力的表达式(1-15),由附着系数得到最大附着力,滚动阻力已知,即可求得最高车速时的空气阻力和最高车速。
二是利用高速行驶时驱动轮附着率的表达式,令附着率为附着系数,带入已知项,即可求得最高车速。
常见错误:地面切向反作用力的计算中滚动阻力的计算错误,把后轮的滚动阻力错计为前轮或整个的滚动阻力。
3)最极限最大爬坡度时依然要明确道路坡度的定义和计算中的简化问题,具体见1.3题的分析。
但经过公式推导本题可以不经简化而方便得求得准确最大爬坡度。
解:1. 比较采用F.F 及F.R.形式时的附着力利用情况i> 对于前置发动机前轮驱动(F.F.)式轿车,空气升力W12Z 1F 2Lf r C A u ρ=, 由m =1600kg ,平均的前轴负荷为汽车总重力的61.5%,静态轴荷的法向反作用力Fz s1 = 0.615X1600X9.8 = 9643.2N , ∴汽车前轮法向反作用力的简化形式为: Fz 1= Fz s1-Fz w1=9643.2--221r Lf u A C ρ 地面作用于前轮的切向反作用力为: Fx 1 = F f2+Fw = Gf 385.0+215.21a D u A C =120.7+215.21a D u A C附着力利用情况:1122120.721.1519643.22D aX Z Lf r C A u F F C A u ρ+=+ ii> 对于前置发动机后轮驱动(F.R.)式轿车同理可得:2222174.721.1516946.22D aX Z Lr rC A u F F C A u ρ+=+ 一般地,C Lr 与 C Lf 相差不大,且空气升力的值远小于静态轴荷的法向反作用力,以此可得1212X X Z Z F F F F <,前置发动机前轮驱动有着更多的储备驱动力。
结论: 本例中,前置发动机前轮驱动(F.F )式的轿车附着力利用率高。
2.对F.F.式轿车进行动力性分析1) 附着系数0.2ϕ=时i> 求极限最高车速:忽略空气升力对前轮法向反作用力的影响,Fz 1=9643.2 N 。
最大附着力1z1F =F =1928.6 N ϕϕ。
令加速度和坡度均为零,则由书中式(1-15)有:1X1W f2F =F =F +F ϕ , 则W 1f2F F F ϕ=-= 1928.6-0.02X0.385X1600X9.8= 1807.9 N , 又2W max F 21.15D a C A u =由此可推出其极限最高车速:max a u = 206.1 km/h 。
