初中数学典型例题100道

合集下载

初中数学最值问题专题

中考数学最值问题【例题1】(经典题)二次函数y二2 (x-3) 2-4的最小值为.【例题2】(2018江西)如图，AB是。

的弦，AB=5,点C是。

上的一个动点，且NACB=45°,若点M、N分别是AB、AC的中点，则MN长的最大值是___ .C【例题3】(2019湖南张家界)已知抛物线y=ax2+bx+c (a不0)过点A(1, 0), B(3, 0)两点，与y 轴交于点C, OC=3.(1)求抛物线的解析式及顶点D的坐标；(2)过点A作AM^BC,垂足为M,求证：四边形ADBM为正方形；(3)点P为抛物线在直线BC下方图形上的一动点，当^PBC面积最大时，求P点坐标及最大面积的值;(4)若点Q为线段OC上的一动点，问AQ+ 2 QC是否存在最小值若存在，求出这个最小值；若不存在，请说明理由.1.(2018河南)要使代数式V-2^37有意义，则乂的( )A.最大值为2B.最小值为2C.最大值为-D.最大值为°3 3 2 22.(2018四川绵阳)不等边三角形AABC的两边上的高分别为4和12且第三边上的高为整数，那么此高的最大值可能为。

3.（2018齐齐哈尔）设a、b为实数，那么“2+“〃 +从一” 的最小值为04.（2018云南）如图，MN是。

的直径，MN=4, NAMN=40° ,点B为弧AN的中点，点P是直径MN上的一个动点，则PA+PB的最小值为.C5.（2018海南）某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为元/斤，并且两次降价的百分率相同.（1）求该种水果每次降价的百分率；（2）从第一次降价的第1天算起，第x天（x为正数）的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为元/斤，设销售该水果第x（天）的利润为y（元），求y与x（1WxV15）之间的函数关系式，并求出第几天时销售利润最大（3）在（2）的条件下，若要使第15天的利润比（2）中最大利润最多少元，则第15天在第14天的价格基础上最多可降多少元6.（2018湖北荆州）某玩具厂计划生产一种玩具熊猫，每日最高产量为40只，且每日产出的产品全部售出，已知生产x只玩具熊猫的成本为R （元），售价每只为P （元），且R、P与x的关系式分别为R = 500 + 30x , P = 170 —2x。

初中数学100道最值问题经典

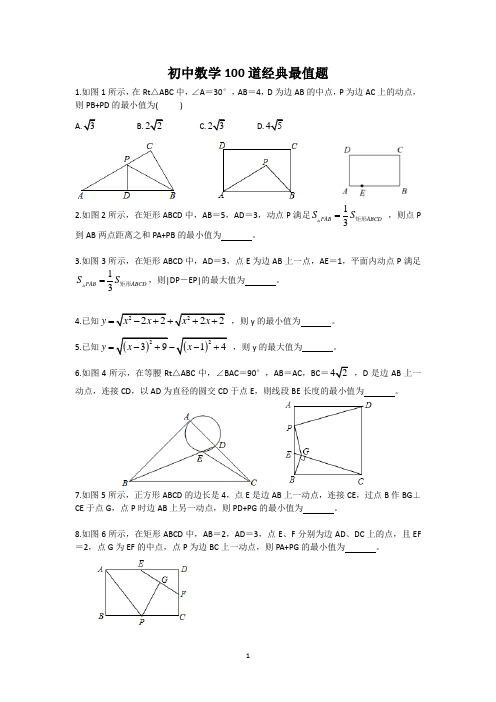
初中数学100道经典最值题1.如图1所示，在Rt △ABC 中，∠A ＝30°，AB ＝4，D 为边AB 的中点，P 为边AC 上的动点，则PB+PD 的最小值为( )B. C. D.2.如图2所示，在矩形ABCD 中，AB ＝5，AD ＝3，动点P 满足13PAB ABCD S S =矩形，则点P 到AB 两点距离之和PA+PB 的最小值为。

3.如图3所示，在矩形ABCD 中，AD ＝3，点E 为边AB 上一点，AE ＝1，平面内动点P 满足13PAB ABCD SS =矩形，则|DP －EP|的最大值为。

4.已知y ，则y 的最小值为。

5.已知y =，则y 的最大值为。

6.如图4所示，在等腰Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，BC ＝，D 是边AB 上一动点，连接CD ，以AD 为直径的圆交CD 于点E ，则线段BE 长度的最小值为。

7.如图5所示，正方形ABCD 的边长是4，点E 是边AB 上一动点，连接CE ，过点B 作BG ⊥CE 于点G ，点P 时边AB 上另一动点，则PD+PG 的最小值为。

8.如图6所示，在矩形ABCD 中，AB ＝2，AD ＝3，点E 、F 分别为边AD 、DC 上的点，且EF ＝2，点G 为EF 的中点，点P 为边BC 上一动点，则PA+PG 的最小值为。

9.在平面直角坐标系中，A(3，0)，B(a，2)，C(0，m)，D(n，0)，且m2+n2＝4，若点E为CD 的中点，则AB+BE的最小值为。

A.3B.4C.5D.2510.如图7所示，AB＝3，AC＝2，以BC为边向上构造等边三角形BCD，则AD的取值范围为。

11.如图8所示，AB＝3，AC＝2，以BC为腰(点B为直角顶点)向上构造等腰直角三角形BCD，则AD的取值范围为。

12.如图9所示，AB＝4，AC＝2，以BC为底边向上构造等腰直角三角形BCD，则AD的取值范围为。

初中数学典型例题100道

初中数学典型例题100道(二）选择填空题150道一．选择题：7,如图,直线，点A1坐标为（1，0),过点A1作x的垂线交直线于点B1，以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2x的垂线交直线于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3，…，按此做法进行下去,点A5的坐标为（，）．8，在Rt△ABC中，∠C=90°，∠A=30°，BC=2．若将此直角三角形的一条直角边BC或AC与x轴重合，使点A或点B刚好在反比例函数（x＞0)的图象上时，设△ABC在第一象限部分的面积分别记做S1、S2（如图1、图2所示）D是斜边与y轴的交点,通过计算比较S1、S2的大小．9，若不论k为何值，直线y=k（x﹣1)﹣与抛物线y=ax2+bx+c有且只有一个公共点，求a、b、c 的值.10，如图是二次函数y=ax2+bx+c的图象的一部分，对称轴是直线x=1．①b2＞4ac；②4a﹣2b+c＜0；③不等式ax2+bx+c＞0的解集是x≥3.5；④若（﹣2，y1）,（5，y2）是抛物线上的两点，则y1＜y2．上述4个判断中，正确的是(）A．①②B．①④C．①③④ D．②③④二，解答题4，如图，在平面直角坐标系中，将直线y=kx沿y轴向下平移3个单位长度后恰好经过B(﹣3,0）及y轴上的C点．若抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B的右侧）,且经过点C，其对称轴与直线BC交于点E，与x轴交于点F．（1）求直线BC及抛物线的解析式;（2）设抛物线的顶点为D，点P在抛物线的对称轴上，若∠APD=∠ACB，求点P的坐标；（3）在抛物线上是否存在点M,使得直线CM把四边形EFOC分成面积相等的两部分？若存在,请求出直线CM的解析式；若不存在，请说明理由．5，如图，在平面直角坐标系中，抛物线y=ax2﹣3ax﹣4a的图象经过点C（0，2），交x轴于点A、B（A点在B点左侧），顶点为D．（1)求抛物线的解析式及点A、B的坐标；（2)将△ABC沿直线BC对折,点A的对称点为A′，试求A′的坐标；（3）抛物线的对称轴上是否存在点P，使∠BPC=∠BAC？若存在,求出点P的坐标；若不存在，请说明理由．6,平面直角坐标系中，抛物线y=ax2+bx+c交x轴于点A、B（点A在点B左侧），与y轴交于点C，点A、C的坐标分别为（﹣3，0），(0，3），对称轴直线x=﹣1交x轴于点E，点D为顶点．（1）求抛物线的解析式；(2）点P是直线AC下方的抛物线上一点，且S△PAC=2S△DAC，求点P的坐标；（3)点M是第一象限内抛物线上一点,且∠MAC=∠ADE，求点M的坐标．。

初中数学100题

初中数学100题1. 简答题1. 两个数的和是30，差是10，求这两个数分别是多少？2. 在一组数据中，50%的数小于等于50，25%的数大于等于80，求这组数据的中位数和最大值。

3. 一个长方形的长是12米，宽是8米，求它的面积和周长。

4. 判断以下哪些数是素数：23，35，42，55，61。

5. 已知一个脸6个面、12个棱、8个顶点的立方体，求其体积和表面积。

2. 计算题1. 一个长方形的长是5米，宽是3米，求它的面积和周长。

2. 设直角三角形的斜边长为5，一条直角边长为3，求另外一条直角边长。

3. 一张纸的尺寸是20cm×25cm，现在要把这张纸等分成相等的小正方形，每个小正方形的边长是2cm，请问能等分出多少个小正方形？4. 现在有一组数：12，19，7，23，9，17，15，8，5。

请你将这些数从小到大排序。

5. 某书店打五折促销，一本原价80元的书现在卖多少钱？3. 应用题1. 一辆车以每小时60公里的速度行驶，行驶10小时后，行驶了多少公里？2. 一张纸的长度是30cm，宽度是20cm，现在要用这张纸制作一个长方体的盒子，求这个盒子的体积。

3. 如图所示，矩形ABCD的长是10cm，宽是8cm。

其中一条对角线AC的长度为12cm。

求另一条对角线BD的长度。

4. 甲、乙、丙三个人在一起走了一段路，甲走了3小时，乙走了4小时，丙走了5小时，他们一共走了30公里。

求甲、乙、丙三人每小时的平均行走速度。

5. 如图所示，ABCD是一个矩形，AD是一条直线，P是ABCD的内部一点，PC的长度为5cm，PB的长度为2cm。

求角CPD的度数。

4. 解答题1. 一辆汽车以10m/s的速度行驶了15秒后突然刹车停下来，求汽车刹车过程中的减速度。

2. 如图所示，正方形ABCD的边长为10cm，M是AB的中点，N是BC的中点。

求过M、N两点的直线与BC的交点P的坐标。

3. 一张纸从剪下一个等腰直角三角形，切去其中的1/4部分，剩下的部分的面积是多少？4. 如图所示，矩形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，连接EG，FH，求证：EH=FG。

初中数学典型例题集锦(无答案)

中考数学典型例题集锦例题1（考查分解因式）先化简再求值:,121232---++x x x x x 其中.23-=x练习①._________________96223=-+-y x xy y 练习②._______________3=-ab b a练习③()().________________24222=+-+b a b a练习④.______________________1164=-x练习③先化简再求值:,41221122-++÷⎪⎭⎫ ⎝⎛+-x x x x 其中.12-=x例题2（考查二次根式）使式子x211-有意义的x 的范围._______ 解析:考虑全面※二次根式的被开方数021≥-x※x 21-在分母上不能为.0 练习①计算._______2154=⋅练习②下列二次根式中,最简二次根式是（）x A 12. 9.-x B bba C +. y x D 25.练习③在二次根式03.0,3.04331，，，中,属于同类二次根式的是.___________________ 练习④若,2<a 则().________22=-a例题3（考查科学计数法）数据._____________14000000=练习①数据._____________4100000= 练习②数据.___________9600000= 练习③数据.___________00063.0= 练习④02.455亿元____________=元练习⑤3553万._______________= 练习⑥.____________000000017.0= 例题4（计算）计算:2212145sin 1-⎪⎭⎫⎝⎛-+--︒解:原式()221121221⎪⎭⎫⎝⎛-+-+=542122=+-+=练习①13221081252-⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛--- 练习②()︒----+⎪⎭⎫ ⎝⎛--30cos 22320192102π练习③()27160sin 1312121+-︒-++⎪⎭⎫⎝⎛-例题5（考查解分式方程）解方程:131332=-+-xx x练习①解方程:26513123-=--x x练习②解方程:131332=---x x x练习③()()21311+-=--x x x x例题5（一次与反比例综合中的分类讨论思想）如图,反比例函数xmy =的图象与一次函数b kx y +=的图象交于()()1,,6,2n B A 两点.(1) 求反比例函数和一次函数的表达式;(2) E 为y 轴上的一个动点,若,5=∆AEB S 求E 点; (3) 在y 轴上是否存在点,T 使ABT ∆为等腰三角形?若存在,请直接写出所有点T的坐标.练习①在平面直角坐标系xOy 中,一次函数b ax y +=的图象过点(),0,2-A 且与反比例函数()0>=x xky 的图象交于点().3,1B (1) 求反比例和一次函数的解析式;(2) 设P 是反比例函数()0>=x x ky 图象上一点,过点P 作y PD ⊥轴交直线AB 于点,D 若D P O A ,,,为顶点的四边形为平行四边形,求点D 的坐标.练习②在平面直角坐标系xOy 中,直线()0≠+=k b kx y 与双曲线x y 8=的一个交点为(),,2m P 与x 轴,y 轴分别交于点.,B A(3) 求m 的值;(4) 若,2AB PA =求k 的值.例题7（一场与师傅或徒弟的较量）如图,海中有一灯塔,P 它的周围8海里有暗礁.海轮以18海里/小时的速度由西向东航行,在A 处测得灯塔P 在北偏东︒58方向上;航行40分钟到达B 处,测得灯塔P 在北偏东︒26方向上.(1) 求灯塔P 到点B 的距离;(2) 如果海轮不改变航线由B 继续向东航行,你认为海轮是否存在触礁的危险?例题8（飞机滑行问题）飞机着陆后滑行的距离y （单位:m ）关于滑行时间t （单位:s ）的函数解析式是.23602t t y -=(1) 飞机滑行时间是;_______s (2) 飞机最远滑行;________m(3) 飞机最后4s 滑行的距离是.________m练习①汽车刹车后行驶的距离s （单位:m ）关于行驶的时间t （单位:s ）的函数解析式是.6152t t s -= (1) 汽车刹车后到停下来前进了;________m (2) 汽车最后s 5.0滑行的距离是.________m例题9（考查反比例函数k 的几何意义）如图,点,A B 分别是反比例函数()110ky x x=>和()220ky x x =>图象上的两点,AB x ⊥轴于点C ,已知OAB ∆的面积是3,则21______.k k -=练习❶如图,在平面直角坐标系中,O 为坐标原点,面积为3的等边三角形ABO 的顶点A 位于反比例函数ky x=的图象上,则_____.k =练习❷如图,点A 为反比例函数()80y x x =>图象上一点,连接OA ,交反比例函数()20y x x=>的图象于一点,B 点C 是x 轴上一点,且,AO AC =则_______.ABC S ∆=练习❸如图,点()2,0,A -点()0,1,B 以线段AB 为边在第二象限作矩形,ABCD 双曲线ky x=过点,D 连接,BD 若四边形OADB 的面积为6,则______.k =练习❹如图,直线y mx =与双曲线ky x=交于,A B 两点,过点A 作AM x ⊥轴于点,M 连接,BM 若2,ABM S ∆=则______.k =例题10（条件概率）动物学家通过大量的调查估计:某种动物活到20岁的概率为，8.0活到25岁的概率为5.0,活到30岁的概率为.3.0(1) 现年20岁的这种动物活到25岁的概率为___; (2) 现年25岁的这种动物活到30岁的概率为.___例题11（考查扇形弧长与面积及圆锥侧面积）如图,以点A 为圆心的两个同心圆中,大圆的弦AB 与小圆相切于点,P 若123, 6.AB OP == (1) 劣弧AB 的长为________; (2) 阴影部分的面积为________.练习❶如图,AC 是O 的直径,点B 在圆周上(不与,A C 重合),点D 在AC 的延长线上,连接BD 交O 于点,E 若367.5,AOB ADB ∠=∠=︒2,AC =则阴影部分的面积为_______.练习❷如图,半圆O 的直径4,AB =弦//,CD AB 且OC ⊥,OD 则阴影部分的面积为_________. 练习❸如图,四边形OABC 为菱形,点,A B 在以点O 为圆心的弧DE 上,若3,12,AO =∠=∠则扇形ODE 的面积为________.练习④一个底面直径是,cm 80母线长为cm 90的圆锥的侧面展开图的角的度数为._______练习⑤一个圆锥的侧面积为，π8母线长为，4则这个圆锥的全面积为.________练习⑥如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为.________例题12（考查利润及利润率计算公式）00==100⨯利润利润售价-进价，利润率进价某超市销售一种进价为21元的商品,按标价的九折出售,可获利0020,则该商品标价为______元. 练习❶某商品的标价为220元,按九折出售,获利0010,则这种商品的进价为______元.例题13（设计运算之整体思想）若关于,x y 的二元一次方程组22324x y mx y +=-⎧⎨+=⎩的解满足3,2x y +>-求满足条件的m 的所有正整数值.练习❶已知2230,x x --=则236x x -的值为____. 练习❷若实数,a b 满足()()444428a b a b ++--的值为0,则_______.a b +=练习③已知,41=+x x 则.______122=+x x 练习④已知,61=-x x 则.________122=+xx练习④已知()().9,2522=-=+y x y x(1)________;=xy (2).________22=+y x例题14（利用函数图象的性质比大小）已知点()()()112233,,,,,A x y B x y C x y 是函数3y x=-图象上的三点,且1230x x x <<<,则123,,y y y 的大小关系是__________（用“<”连接）练习❶已知一元二次方程230x bx +-=的一根是3,-在二次函数23y x bx =+-的图象上有三点14,,5y ⎛⎫- ⎪⎝⎭25,,4y ⎛⎫- ⎪⎝⎭31,,6y ⎛⎫⎪⎝⎭则123,,y y y 的大小关系是__________（用“<”连接）练习②若点()()()321,3,,3,5y y y --，都在反比例函数xy 3=的图象上,则123,,y y y 的大小关系是__________（用“<”连接）练习③在反比例函数xmy 21-=的图象上有两点()(),,,,2211y x B y x A 当210x x <<时,,21y y <则m 的取值范围是.________例题15（不等式中的分类讨论思想）关于x 的不等式1x a -≤<有三个整数解,则a 的取值范围是_____________.练习❶关于x 的不等式1x a -<≤有3个正整数解,则a 的取值范围是_____________.练习❷已知关于x 的不等式组()5231138222x x x x a +>-⎧⎪⎨≤-+⎪⎩有四个整数解,求a 的范围.练习③若不等式组⎪⎩⎪⎨⎧->>+412102a x a x 的解集中的任意,x 都能使不等式02019>-x 成立,则a 的取值范围是.__________练习④已知实数a 是一个不等于2的常数,解不等式组⎪⎩⎪⎨⎧>+--≥+-03332312x a x x ,并根据a 的取值情况写出其解集.练习⑤已知关于x 的不等式.1333->-xm mx (1) 当5=m 时,求该不等式的解集;(2) m 取何值时,该不等式有解,并求出解集.例题16（折叠问题中渗透方程思想）如图,在一张矩形纸片ABCD 中,,3=AB 点N M ,分别是CD AB ,的中点,现将这张纸片折叠,使点D 落到MN 上的点G 处,折痕为,CH 若HG 的延长线恰好过点,B 则._______=AD练习①在矩形ABCD 中,点F E ,分别是边DC BC ,上的动点,以直线EF 为对称轴折叠CEF ∆,使点C 的对称点P 落在AD 上,若,5,3==BC AB 则CF 的取值范围是._____________例题17（考查一元二次方程根与系数的关系的同时注意挖掘隐含条件）若关于x 的一元二次方程()22210x a a x a +-+-=的两个实数根互为相反数,则a 的值为______. 练习❶使关于x 的方程()081822=+++x a ax 有两个不相等的实数根的a 的取值范围是._________练习②已知关于x 的方程()02142=+--m x m x 有实数根,求实数m 的取值范围,并在数轴上表示出来.练习③当b a ,为方程012=--x x 的两根时,代数式()2211b a b a ++⎪⎭⎫ ⎝⎛+的值为._______ 练习④试证方程()0122=++-x k kx 必有实数根.练习⑤已知b a ,是关于x 的一元二次方程()03222=+++m x m x 的两个不相等的实数根,且满足,111-=+ba 则m 的值是._________ 练习⑥已知21,x x 是方程0522=-+x x 的两个实数根,则._______32=++-n m mn m练习⑦一元二次方程0242=+-x x 的两根为,,21x x 则2112124x x x x +-的值为._______例题18（考查增长率问题）现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某市某家小型快递公司,今年四月份与六月份完成投递的快递总件数分别为10万件与1.12万件,假定该公司765、、每月投递的快递总件数的增长率相同.请你预测7月份投递的快递件数?例题19（全等证明与平行四边形的性质与判定）如图,在Rt ABC ∆中,90,ABC ∠=︒点M 是AC 的中点,以AB 为直径作O 分别交,AC BM 于点,.D E (1) 求证:AEM ∆≌;BDM ∆(2) 连接,,OD OE 请直接写出使四边形ODME 为菱形时DME ∠的度数.练习❶如图,O 是ABC ∆内一点,O 与BC 相交于G F ,两点,且与AC AB ,分别相切于点.//,,BC DE E D 连接.,EG DF(1) 求证:;CE BD =(2) 已知,12,10==BC AB 请直接写出使四边形DFGE 为矩形时O 的半径.练习②如图,已知D C F A ,,,四点在同一条直线上,,//,DE AB CD AF =且.DE AB = (1) 求证:ABC ∆≌;DEF ∆(2) 若,90,4,3︒=∠==DEF DE EF 请直接写出使四边形EFBC 为菱形时AF 的长度.例题20（频率估计概率）表中记录了某种幼树在一定条件下移植成活情况.由此估计这种幼树在此条件下移植成活的概率是__________（精确到1.0）例题21（考查函数图象的平移法则）+左右平移:左右-(相对于自变量x 而言)上下平移:上+下-(给函数整体加减)将抛物线244y x x =--向左平移3个单位,再向上平移5个单位,得到抛物线的表达式____________练习❶把函数xky =的图象向右平移3个单位,再向下平移5个单位,所得函数的解析式为.__________ 例题22（外接圆与全覆盖）已知正ABC ∆的边长为2,那么能够完全覆盖这个正ABC ∆的最小圆面的半径是_______.练习❶已知直角三角形的两条边长分别为3和4,那么能够完全覆盖这个直角三角形的最小圆面的面积是_________.例题23（在三角函数中渗透方程思想）如图,一座山的一段斜坡BD 的长度为600米,且这段斜坡的坡度1:3.i =已知在地面B 处测得山顶A 的仰角为33,︒在斜坡D 处测得山顶A 的仰角为45,︒求山顶A 到地面BC 的高度AC 是多少米.(结果用非特殊角的三角函数与根式表示)解:过点D 作BC DH ⊥于点.H 斜坡BD 的坡度,3:1=i ∴,3:1:=BH DH ∴(),6003222=+DH DH∴.10180,1060==BH DH 设.x AE =在ADE Rt ∆中,,45︒=∠ADE ∴.x AE DE == 又,,DH EC DE HC ==∴,1060,==EC x HC 在ABC Rt ∆中, ,10180106033tan xx ++=︒∴,33tan 1106033tan 10180︒--︒=x∴106033tan 1106033tan 10180+︒--︒=+=EC AE AC︒-︒=33tan 133tan 10120∴山顶A 到地面BC 的高度为︒-︒33tan 133tan 10120米.练习❶如图,某数学活动小组选定测量古树BC 的高度,他们在斜坡上D 处测得古树顶端B 的仰角是30,︒朝古树方向下坡走6米到达坡底A 处,在A 处测得古树顶端B 的仰角是48,︒若斜坡AD 的坡比为1:3,i =求古树的高度.(结果用非特殊角的三角函数与根式表示)练习❷如图,建筑物AB 高为6,m 在其正东方向有一个通信塔,CD 在它们之间的地面点M 处测得建筑物顶端A 、塔顶C 的仰角分别为33︒和60,︒在A 处测得塔顶C 的仰角为30,︒求通信塔CD 的高度.（结果用非特殊角的三角函数和根式表示）例题24（在坐标系中考查对称）关于x 轴对称,x 不变,y 互为相反数关于y 轴对称,y 不变,x 互为相反数关于坐标原点中心对称,均互为相反数例题25（数据的波动程度、方差2s 的计算）()()()nx x x x x x s n222212-++-+-=越大越大,越小越小.例题26（考查正多边形与圆）半径为r 的圆内接正三角形的面积是._________ 练习①已知⊙O 的周长为，π2其内接正方形的面积为________.练习②同一个圆的内接正方形和正三角形的边心距的比为.__________练习③正三角形的外接圆与内切圆的面积比为___________.练习④正六边形的内切圆与外接圆的半径之比为___________.解题思维:构造基本图形例题27（考查位似）外位似内位似如图,正方形OEFG 和正方形ABCD 是位似图形, 点()1,1,F 点()4,2,C 则这两个正方形的位似中心的坐标为__________________.练习①如图,直线113y x =+与x 轴交于点,A 与y 轴交于点,B 四边形BOCD 与四边形''''B O C D 是以点A 为位似中心的位似图形,且相似比为1:3,则点B 的对应点'B 的坐标为_____________.练习②在平面直角坐标系中,点()n m P ,是ABC ∆的边AB 上的一点,以原点O 为位似中心把ABC ∆放大到原来的两倍,则点P 的对应点的坐标为._____________例题28（无图题中考查分类讨论思想）在ABC ∆中,,5,34==AC AB 若BC 边上的高等于，3则.___________=BC 练习①等腰三角形一腰上的高与另一腰的夹角为，︒36则该等腰三角形的底角的度数为.__________ 练习②如果等腰三角形两边长是cm 6和,3cm 那么它的面积为.__________练习③在正方形ABCD 中,以AD 为边作正三角形,ADE 则AEB ∠的度数为._________练习④矩形ABCD 中,,8,6==BC AB 点P 在矩形ABCD 的内部,点E 在边BC 上,满足P B E ∆∽DBC ∆,若APD ∆是等腰三角形,则.________=PE 例题29（由三视图还原几何体）下面是几个一样的小正方体摆出的立体图形的左视图和俯视图:(1) 小正方体的个数至少为_______个;(2) 小正方体的个数至多为_______个.练习①下面是几个一样的小正方体摆出的立体图形的主视图和左视图:(1) 小正方体的个数至少为_______个;(2) 小正方体的个数至多为_______个.例题30（圆与相似）如图,AB 为⊙O 的直径,点E 在⊙O 上,EAB ∠的平分线交⊙O 于点,C 过点C 作AE 的垂线,垂足为,D 直线DC 与AB 的延长线交于点.P(1) 求证:PC 是⊙O 的切线;(2) 若,6,43tan ==∠AD P 求线段AE 的长.练习①如图,PA 与⊙O 相切于点,A 过点A 作,OP AB ⊥垂足为,C 交⊙O 于点.B 连接,,AO PB 并延长,AO 交⊙O 于点,D 与PB 的延长线交于点.E (1) 求证:PB 是⊙O 的切线;(2) 若⊙O 的半径为，5,3=OC 求E cos 的值.练习②如图,已知,AC BC ⊥圆心O 在AC 上,点M 与点C 分别是AC 与⊙O 的交点,点D 是MB 与⊙O 的交点,点P 是AD 的延长线与BC 的交点,且.AOAMAP AD = (1) 求证:PD 是⊙O 的切线;(2) 若,12,==AD MC AM 求⊙O 的半径; (3) 在(2)的条件下,求MDBP的值.例题31（数与式同概率的结合）在2,1,2,4--四个数中,随机抽取两个数作为函数12++=bx ax y 中b a ,的值,则该二次函数图象恰好经过第一、二、四象限的概率为._________练习①从3,1,21,1,3---这五个数中,随机抽取一个数,记为，a 则数a 使关于x 的不等式组()⎪⎩⎪⎨⎧<-≥+037231a x x 无解,且使分式方程1323-=----x a x x 有整数解的概率为._________练习②从2,1,0,1,2--这五个数中,随机抽取一个数记为,a 则数a 使关于x 的不等式组⎪⎩⎪⎨⎧<--≥-a x x 21221612有解,且使关于x 的一元一次方程32123ax a x +=+-的解为负数的概率为.__________例题32（动态问题中的多解※难）如图,正方形A B CD 的边长是，16点E 在边AB 上,,3=AE 点F 是边BC 上不与点C B 、重合的一个动点,把EBF ∆沿EF 折叠,点B 落在'B 处.若'CDB ∆恰为等腰三角形,则'DB 的长为._________练习①如图,在矩形ABCD 中,,4,3==BC AB 点E 是BC 边上的一点,连接,AE 把B ∠沿AE 折叠,使点B 落在'B 处,当'CEB ∆为直角三角形时.BE 的长为.____________ 例题33（选择题中的代入法,体现“小题小做”）已知二次函数()12+-=h x y ,在自变量x 满足31≤≤x 的情况下,与其对应的函数值y 的最小值为，5则h 的值为（）51.-或A 51.或-B 31.-或C 31.或D 练习①已知二次函数(),2h x y --=当自变量x 的值满足52≤≤x 时,与其对应的函数值y 的最大值为,1-则h 的值为（）63.或A 61.或B 31.或C 64.或D 练习②当1+≤≤a x a 时,函数122+-=x x y 的最小值为，1则a 的值为（）1.-A2.B 20.或C 21.或-D练习③方程x xx 41102-=+-的正数根的取值范围是（）10.<<x A 21.<<x B 32.<<x C 43.<<x D 练习④估计方程0123=-+x x 的实根所在的范围.410.<<x A 3141.<<x B 2131.<<x C 121.<<x D例题34（单循环与双循环）要组织一次拔河比赛,参赛的每两个班都要比赛一场,共比赛了28场,设参赛的班级数为,x 根据题意可列方程为.________________练习①参加足球联赛的每两队之间都进行两场比赛,共要比赛90场,则有_____个球队参赛. 练习②正十边形的对角线条数为._______例题35（函数、方程、不等式）直线1:+=kx y l 与抛物线x x y 42-=的交点个数为._________练习①直线4+-=x y 与双曲线()04>=x xy 的交点个数为.__________练习②已知二次函数1412-+-=m x x y 的图象与x轴有交点,则m 的取值范围是.___________练习③如图,反比例函数()0ky x x=<与一次函数4y x =+的图象交于A B 、两点,且A B 、两点的横坐标分别为31--、，则关于x 的不等式()400kx x x--<<的解集为________________.练习④如图,正比例函数11y k x =的图象与反比例函数22k y x=的图象相交于,A B 两点,其中点B 的横坐标为5,当12y y <时,自变量x 的取值范围是_________________.练习⑤给出函数xy x y x y 1,,2===的图象:(1) 若,12a a a>>则a 的范围为._______________ (2) 若,12a a a >>则a 的范围为._______________(3) 若,12a aa >>则a 的范围为._______________例题36（不等式中渗透分类讨论思想）已知关于x 的不等式组⎩⎨⎧-≤-≥a x a x 5153无解,化简:._________31=--+a a练习①已知关于y 的不等式组()⎪⎩⎪⎨⎧≤->-+021232a y yy 的解集为,2-<y 则a 的取值范围为.___________ 练习②若数a 使关于x 的不等式组()()⎪⎩⎪⎨⎧-≤--≤-x a x x x 132121131有且仅有三个整数解,且使关于y 方程121223=-++-ya y y 有整数解,则满足条件的a 的取值范围是.___________________练习③已知,2≠m 解不等式组⎪⎩⎪⎨⎧>+-->+-0323312x m x ,并根据m 的取值情况写出其解集.例题37（︒45与正方形）如图,正方形ABCD 中,F E ,分别是边CD BC ,上的动点,,45︒=∠EAF 给出下列结论:(1) ;AE AD =(2) ();222DF BE CF CE +=+(3) .ADF ABE AEF S S S ∆∆∆+=练习①如图,点E 是正方形ABCD 的边DC 上一点,把ADE ∆绕点A 顺时针旋转︒90到ABF ∆的位置,若四边形AECF 的面积为,2,25=DE 则.______=AE 练习②边长为4的正方形ABCD 中,P 是BC 边上的一动点（不与C B ,重合）.将ABP ∆沿直线AP 翻折,点B 落在点E 处;在CD 上有一点,M 使得将CMP ∆沿直线MP 翻折后,点C 落在直线PE 上的点F 处,直线PE 交CD 于点,N 连接.,NA MA 则下列结论中正确的有___________（填序号） ①;45︒=∠NAP ②ABP ∆≌ADN ∆时,;424-=BP ③四边形AMCB 的面积的最大值为;10④当P 为BC 的中点时,AE 垂直平分.NP例题38（动中有静取特值）如图,已知点E 是矩形ABCD 的对角线AC 上的一动点,正方形EFGH 的顶点H G ,都在边AD 上,若,4,3==BC AB 则AFE ∠tan 的值为._______例题39（能用函数性质解决一些问题）若,9=ab 13-≤≤-b ,则a 的范围是.___________ 练习①若,2-=+b a 且,2b a ≥则ba的最大值为._________练习②已知,022,22=+-≥am m a ,0222=+-an n 则()()2211-+-n m 的最小值为._______例题40（考查配方法）将二次函数142+-=x x y 化为()k h x a y +-=2的形式为.________________练习①将二次函数322-+-=x x y 化成顶点式为.________________练习②用配方法和公式法两种方法解下列方程.0462=++x x x x 3122=+例题41（三角函数助你破解压轴）如图,抛物线432322--=x x y 与x 轴交于B A ,两点,与y 轴交于点.C (1) 求点C B A ,,的坐标;(2) 点P 从点A 出发,在线段AB 上以每秒2个单位长度的速度向B 点运动,同时,点Q 从B 点出发,在线段BC 上以每秒1个单位长度的速度向C 点运动,当其中一个点到达终点时,另一个点也停止运动.设运动时间为t 秒,求运动时间t 为多少秒时,PBQ ∆的面积S 最大,并求出其最大面积; (3) 在BC 下方的抛物线上是否存在点,M 使BMC ∆得面积是25?若存在,求点M 的坐标;若不存在,请说明理由.练习①如图,抛物线c bx ax y ++=2的图象经过点()()(),4,2,0,4,0,2D B A -与y 轴交于点,C 作直线,BC 连接.,CD AC(1) 求抛物线的函数表达式;(2) E 是抛物线上的点,求满足ACO ECD ∠=∠的点E 的坐标.(3) 若点P 为第一象限内抛物线上一点,求出使得PBC ∆的面积达到最大时的P 点坐标.。

完整版初一100道数学计算题及答案

完整版初一100道数学计算题及答案第1题：计算2.5+3.8的和。

答案：6.3。

第2题：计算6.3-2.9的差。

答案：3.4。

第3题：计算4.2x0.5的积。

答案：2.1。

第4题：计算9.3÷3的商。

答案：3.1。

第5题：计算2/5+1/4的和。

答案：0.65。

第6题：计算3/4-1/3的差。

答案：0.083。

第7题：计算5/8x3/5的积。

答案：0.375。

第8题：计算1/2÷1/4的商。

答案：2。

第9题：计算12÷4+6x2的值。

答案：30。

第10题：计算8-2x3÷6的值。

答案：7。

第11题：计算9+ (7-2)x4的值。

答案：33。

第12题：计算(5+4)x3-4的值。

答案：23。

第13题：计算3/8÷1/3的值。

答案：0.875。

第14题：计算2 3/4-1 2/3的值。

答案：1 1/12。

第15题：计算2 1/2x3 1/4的值。

答案：7 7/8。

第16题：计算0.75x12x4的值。

答案：9。

第17题：计算2.7+4.8的和。

答案：7.5。

第18题：计算8.3-6.2的差。

答案：2.1。

第19题：计算5x1.2的积。

答案：6。

第20题：计算9.6÷4的商。

答案：2.4。

第21题：计算1/4+2/5的和。

答案：0.65。

第22题：计算3/5-1/3的差。

答案：0.133。

第23题：计算4/7x5/6的积。

答案：0.476。

第24题：计算3/4÷1/3的商。

答案：2.25。

第25题：计算36÷6+8x2的值。

答案：52。

第26题：计算17-5x2+12÷3的值。

答案：10。

第27题：计算(5+6)x3-6的值。

答案：33。

第28题：计算3/4÷1/2的值。

答案：1.5。

第29题：计算3 1/2-2 2/5的值。

答案：1 3/10。

第30题：计算4 1/2x2 1/4的值。

答案：10 1/8。

初一数学基础题100道

1.一个数除以3的余数是2，那么这个数可能是哪些？答案：可能是3n+2的形式，其中n是任意整数。

2.一个长方形的长是10厘米，宽是4厘米，求它的周长和面积。

答案：周长是28厘米，面积是40平方厘米。

3.解方程：2x + 3 = 7。

答案：x = 2。

4.一个三角形的三个角的度数比是2:3:4，求每个角的度数。

答案：最小的角是30度，第二个角是45度，最大的角是60度。

5.一个班级有40名学生，其中有20名女生，求男生的人数。

答案：男生有20名。

6.一个数的2倍加上5等于17，求这个数。

答案：这个数是6。

7.一个圆的直径是14厘米，求它的半径和周长。

答案：半径是7厘米，周长是44厘米（使用π≈3.14）。

8.一个数乘以自己等于81，求这个数。

答案：这个数是9或-9。

9.一个数的1/3减去4等于-2，求这个数。

答案：这个数是6。

10.一个数的5倍减去10等于30，求这个数。

答案：这个数是8。

11.一个数的3倍加上2等于17，求这个数。

答案：这个数是5。

12.一个数的4倍减去3等于19，求这个数。

答案：这个数是5。

13.一个数的2倍加上1等于11，求这个数。

答案：这个数是5。

14.一个数的3倍减去5等于10，求这个数。

答案：这个数是5。

15.一个数的4倍加上2等于18，求这个数。

答案：这个数是4。

16.一个数的5倍减去1等于14，求这个数。

答案：这个数是3。

17.一个数的6倍加上3等于39，求这个数。

答案：这个数是6。

18.一个数的7倍减去4等于45，求这个数。

答案：这个数是7。

19.一个数的8倍加上5等于69，求这个数。

答案：这个数是9。

20.一个数的9倍减去6等于78，求这个数。

答案：这个数是9。

21.一个数的10倍加上7等于107，求这个数。

答案：这个数是10。

22.一个数的11倍减去8等于119，求这个数。

11答案：这个数是12。

24.一个数的13倍减去10等于153，求这个数。

答案：这个数是12。

七年级数学题100道

七年级数学题100道一、有理数运算相关题目。

1. 计算：(-2)+3-(-5)- 解析：- 去括号法则为：括号前是“+”，把括号和它前面的“+”去掉后，原括号里各项的符号都不改变；括号前是“ - ”，把括号和它前面的“ - ”去掉后，原括号里各项的符号都要改变。

- 所以(-2)+3 - (-5)= - 2+3 + 5。

- 接着按照从左到右的顺序计算：-2 + 3=1，1+5 = 6。

2. 计算：-3×(-4)÷(-2)- 解析：- 根据有理数的乘除法运算法则，先计算乘法-3×(-4) = 12。

- 再计算除法12÷(-2)= - 6。

3. 计算：((1)/(2)-(2)/(3))×(-6)- 解析：- 先计算括号内的式子(1)/(2)-(2)/(3)=(3)/(6)-(4)/(6)=-(1)/(6)。

- 再计算乘法-(1)/(6)×(-6)=1。

二、整式相关题目。

4. 化简：3a + 2b - 5a - b- 解析：- 合并同类项，同类项是指所含字母相同，并且相同字母的指数也相同的项。

- 对于3a和-5a是同类项，2b和-b是同类项。

- 合并得(3a - 5a)+(2b - b)= - 2a + b。

5. 先化简，再求值：(2x^2-3xy + 4y^2)-3(x^2-xy+(5)/(3)y^2)，其中x = - 1,y = 2- 解析：- 先去括号：- 2x^2-3xy + 4y^2-3x^2+3xy - 5y^2。

- 再合并同类项：(2x^2-3x^2)+(-3xy + 3xy)+(4y^2-5y^2)=-x^2-y^2。

- 当x=-1,y = 2时，代入式子得-(-1)^2-2^2=-1 - 4=-5。

三、一元一次方程相关题目。

6. 解方程：2x+3 = 5x - 6- 解析：- 移项，把含有x的项移到等号一边，常数项移到等号另一边，移项要变号。

(完整)100道初一数学计算题(11页)

100道初一数学计算题（11页）一、整数的运算1. 计算：3 + 7 5 + 42. 计算：(2³) × (4)3. 计算：(5)² 3²4. 计算：24 ÷ (3) × 25. 计算：(8) ÷ 2 (3) ÷ 2二、分数的运算6. 计算：1/2 + 1/3 1/67. 计算：2/5 × 3/48. 计算：5/8 ÷ 2/39. 计算：1 3/4 + 1/210. 计算：3/5 + 2/3 1/6三、小数的运算11. 计算：0.3 × 0.412. 计算：0.8 ÷ 0.213. 计算：0.5 + 0.7 0.314. 计算：1.2 × 0.515. 计算：2.4 ÷ 0.6四、混合运算16. 计算：2/3 + 0.4 × 517. 计算：3² ÷ 2/518. 计算：1/4 × (0.8 0.5)19. 计算：2/3 + 3/4 × 220. 计算：1.2 ÷ (0.3 + 0.2)五、简便计算21. 计算：99 + 98 + 97 + 9622. 计算：1001 × 1002 × 100323. 计算：1.25 × 824. 计算：0.125 × 825. 计算：4.5 × 2/3六、平方与立方运算26. 计算：7²27. 计算：(4)³28. 计算：10² 5²29. 计算：2³ + 3³30. 计算：(1/2)²七、根式运算31. 计算：√3632. 计算：√(49/81)33. 计算：3√2734. 计算：√(2/3) × √(3/2)35. 计算：√(16 + 9)八、百分数运算36. 计算：50% × 8037. 计算：120 ÷ 40%38. 计算：75% 25%39. 计算：150% + 50%40. 计算：20% of 500九、比例运算41. 如果 a : b = 3 : 4，且 a = 9，求 b 的值。

(完整)100道初一数学计算题(11页)

100道初一数学计算题（11页）一、整数的运算1. 计算：3 + 7 5 + 42. 计算：5 (2) + 6 33. 计算：4 × (3) ÷ 24. 计算：8 ÷ (2) × (4)5. 计算：15 ÷ (3) 5 × 26. 计算：3^2 + 4^27. 计算：(5)^2 (3)^28. 计算：4^3 ÷ 2^29. 计算：(2)^3 × (1)^210. 计算：7 × 8 + 9 ÷ 3 5二、分数的运算11. 计算：1/2 + 1/3 1/612. 计算：2/5 × 3/4 ÷ 2/313. 计算：3/8 1/4 + 1/214. 计算：5/6 ÷ 2/3 + 1/215. 计算：7/9 × 3/4 2/316. 计算：1/2 + 2/3 1/417. 计算：3/4 × 4/5 ÷ 2/318. 计算：5/8 3/8 + 1/419. 计算：2/3 ÷ 3/4 + 1/220. 计算：4/5 × 5/6 2/3三、小数的运算21. 计算：2.5 + 3.7 4.222. 计算：6.8 2.3 + 4.523. 计算：3.6 × 2.4 ÷ 1.224. 计算：7.2 ÷ 1.8 × 2.525. 计算：9.6 ÷ 3.2 4.8 × 1.526. 计算：4.5^2 3.2^227. 计算：(6.3)^2 (2.8)^228. 计算：1.5^3 ÷ 0.6^229. 计算：(0.8)^3 × (0.5)^230. 计算：8.4 × 5.6 + 7.2 ÷ 2.4 3.6四、混合运算31. 计算：(3/4 + 2/3) × 632. 计算：(7 1/2) ÷ 2/333. 计算：2/5 × (4 3/5)34. 计算：(8 + 1/2) ÷ (2/3 1/4)35. 计算：3^2 ÷ (2/3 + 1/4)36. 计算：(4/5 1/3) × 1537. 计算：2/3 ÷ (5/6 1/2)38. 计算：(9 3/4) × 2/539. 计算：(2/3 + 4/9) ÷ 2/540. 计算：5 × (2/3 1/4) + 3/8五、简便计算41. 计算：1001 × 99942. 计算：× 567843. 计算：1111 × 111144. 计算：9999 × 999945. 计算：1005 × 100646. 计算：5050 ÷ 2547. 计算：4545 ÷ 5548. 计算：8181 ÷ 949. 计算：12121 ÷ 1150. 计算：98765 ÷ 321六、方程与不等式的计算51. 解方程：3x 7 = 1152. 解方程：5 2x = 3x + 153. 解不等式：2(x 3) > 854. 解不等式：4 3x ≤ 2x + 155. 解方程：4(x + 3) = 2(x 1)56. 解方程：7 3(x 2) = 2(x + 4)57. 解不等式：5 2(x + 1) > 3x 258. 解不等式：3(x 2) ≤ 6 2x59. 解方程：1/2(x + 4) = 3/4(x 2)60. 解方程：2/3(x 3) = 4/5(x + 1)七、几何计算61. 计算长方形面积：长为15cm，宽为8cm62. 计算正方形面积：边长为12cm63. 计算三角形面积：底为10cm，高为6cm64. 计算圆的面积：半径为7cm65. 计算圆柱体积：底面半径为5cm，高为10cm66. 计算圆锥体积：底面半径为6cm，高为8cm67. 计算梯形面积：上底为6cm，下底为10cm，高为8cm68. 计算平行四边形面积：底为8cm，高为5cm69. 计算扇形面积：半径为10cm，圆心角为60°70. 计算环形面积：外圆半径为10cm，内圆半径为6cm八、比例与百分比71. 计算比例：若a:b=3:4，且a=9，求b的值72. 计算比例：若x:y=5:8，且y=40，求x的值73. 计算百分比：若80是200的百分之几74. 计算百分比：若15是30的多少百分比75. 计算增加的百分比：若原数为50，增加后为60，求增加的百分比76. 计算减少的百分比：若原数为120，减少后为90，求减少的百分比77. 计算比例分配：若总金额为120元，按2:3:5的比例分配给甲、乙、丙三人，求甲、乙、丙各得多少元78. 计算比例分配：若总重量为90kg，按1:2:3的比例分配给A、B、C三物体，求A、B、C各重多少kg79. 计算百分比转换：将50%转换为小数80. 计算百分比转换：将0.75转换为百分比（文档内容持续更新，敬请期待下一页的精彩题目。

初中数学经典试题100题

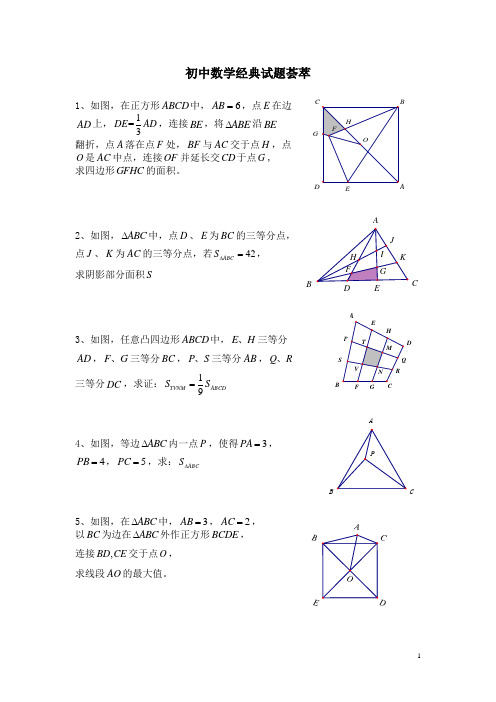
FG BDCBAGECDABCA初中数学经典试题荟萃1、如图，在正方形ABCD 中，6AB =，点E 在边AD 上，1=3DE AD ，连接BE ，将ABE ∆沿BE翻折，点A 落在点F 处，BF 与AC 交于点H ，点 O 是AC 中点，连接OF 并延长交CD 于点G , 求四边形GFHC 的面积。

2、如图，ABC ∆中，点D 、E 为BC 的三等分点，点J 、K 为AC 的三等分点，若42ABC S ∆=，求阴影部分面积S3、如图，任意凸四边形ABCD 中，E H 、三等分AD ，F G 、三等分BC ，P S 、三等分AB ，Q R 、三等分DC ，求证：19TVNMABCD S S =4、如图，等边ABC ∆内一点P ，使得3PA =，4PB =，5PC =，求：ABC S ∆5、如图，在ABC ∆中，3AB =，2AC =，以BC 为边在ABC ∆外作正方形BCDE ，连接,BD CE 交于点O ，求线段AO 的最大值。

D EFADEFABAB CDBAC6、如图，等边ABC ∆中，120BDC ∠=︒， DC GD =，AG 交CD 延长线于点E 。

求证：AE EG =7、如图，分别以锐角ABC ∆的三边为斜边向外作等腰Rt DAB ∆、等腰Rt EBC ∆、等腰Rt FAC ∆。

求证：①AE DF = ②AE DF ⊥8、如图，四边形ABCD 中，E F 、分别是AB CD 、的中点，P 为对角线AC 延长线上任意一点，PF 交AD 于M ，PE 交BC 于N ，EF 交MN 于K ，求证：K 点平分线段MN9、如图，ABCD 中，E F 、分别是AB BC 、上的点，DE 交AC 于M ，AF 交BD 于N ，若AF 平分BAC ∠，DE AF ⊥，DE 与AF 交于P ，记BE x OM =，BN y ON =，CF z BF =，试比较x y z 、、的大小关系。

初一年级数学题100道

初一年级数学题100道1. 45 + 27 = 。

2. 82 - 39 = 。

3. 56 × 8 = 。

4. 144 ÷ 12 = 。

5. 75 + 48 - 23 = 。

6. 1/2 + 1/3 = 。

7. 3/4 - 1/2 = 。

8. 2/5 × 3/4 = 。

9. 5/6 ÷ 2/3 = 。

10. 1/8 + 3/8 = 。

11. 0.75 + 0.25 = 。

12. 1.2 - 0.7 = 。

13. 3.6 × 2 = 。

14. 4.5 ÷ 1.5 = 。

15. 0.9 + 0.1 - 0.3 = 。

16. 20% 的300是多少。

17. 50% 的80是多少。

18. 如果一件商品原价是200元，打9折后价格是多少。

19. 60% 的150是多少。

20. 一项测试中，80%的学生及格，如果有200个学生，及格的学生有多少。

21. x + 5 = 12, x = 。

22. 3y = 24, y = 。

23. 2a - 4 = 10, a = 。

24. 5b + 2 = 17, b = 。

25. c/4 = 3, c = 。

26. (3 + 5) × 2 = 。

27. 10 - (6 ÷ 2) = 。

28. 8 + 2 × 5 = 。

29. (15 - 3) × (2 + 1) = 。

30. 12 ÷ (4 - 2) + 6 = 。

31. 如果一本书的价格是45元，买3本需要多少钱。

32. 小明有20元，他买了3个苹果，每个苹果3元，他还剩多少钱。

33. 一辆车每小时行驶60公里，行驶2.5小时后行驶了多少公里。

34. 如果一瓶水500毫升，5瓶水有多少升。

35. 一件商品的售价是120元，成本是80元，利润是多少。

36. 如果一个数字加上7等于15，这个数字是什么。

37. 一周有多少天。

完整版初一100道数学计算题及答案

完整版初一100道数学计算题及答案标题：初一数学100道计算题及答案解析引言：数学是一门让人们思维敏捷、逻辑清晰的学科，对于初一学生来说，通过大量的练习题可以更好地理解和掌握各种数学概念和计算方法。

本文将为大家提供100道初一数学计算题，并附上详细的解析和答案，相信这些题目能够对学生们的数学学习和提高有所帮助。

一、四则运算：1. 15 + 35 = ?答案：502. 76 - 32 = ?答案：443. 63 × 4 = ?答案：2524. 138 ÷ 6 = ?答案：23二、分数运算：5. 3/5 + 1/5 = ?答案：4/56. 7/8 - 1/3 = ?答案：37/247. 2/3 × 4/5 = ?答案：8/158. 5/6 ÷ 2/3 = ?答案：5/4三、整数运算：9. (6 × 3) - (4 × 5) = ?答案：210. 8² + 3² = ?答案：7311. 7³ - 5³ = ?答案：19212. 15 ÷ (20 - 18) = ?答案：7.5四、小数运算：13. 0.5 + 0.3 = ?答案：0.814. 2.6 - 1.8 = ?答案：0.815. 0.5 × 1.2 = ?答案：0.616. 0.8 ÷ 0.2 = ?答案：4五、单位换算：17. 1 km = ? m答案：1000 m18. 1 m = ? cm答案：100 cm19. 1 kg = ? g答案：1000 g20. 1 L = ? mL答案：1000 mL六、面积计算：21. 长为5m，宽为3m的矩形的面积是多少？答案：15平方米22. 半径为3cm的圆的面积是多少？答案：28.27平方厘米（取π=3.14）23. 半径为5cm的圆的周长是多少？答案：31.4厘米（取π=3.14）24. 一个直角边长分别为4cm和3cm的直角三角形的面积是多少？答案：6平方厘米七、百分数计算：25. 32的30%是多少？答案：9.626. 120增加15%，结果是多少？答案：13827. 一件原价80元的商品，打7折后的价格是多少？答案：56元28. 一个数的80%等于120，这个数是多少？答案：150八、代数计算：29. 2x + 3 = 9，求x的值。

初一年级100道数学计算题和答案解析

初一年级100道数学计算题和答案解析1. 计算：3 + 5 × 2 4 ÷ 2答案：13解析：根据运算法则，先乘除后加减，所以先计算5 × 2 = 10，再计算4 ÷ 2 = 2，进行加减运算，得出结果为13。

2. 计算：(4 + 6) × (5 3)答案：18解析：先计算括号内的加法和减法，4 + 6 = 10，5 3 = 2，然后将两个结果相乘，得出18。

3. 计算：8 ÷ 2(2 + 3)答案：1解析：先计算括号内的加法，2 + 3 = 5，然后将8除以2，得4，用4除以5，得出结果为1。

4. 计算：7 × 7 7 ÷ 7答案：48解析：先计算乘法，7 × 7 = 49，再计算除法，7 ÷ 7 = 1，进行减法运算，得出结果为48。

5. 计算：9 + 6 ÷ 3 2 × 4答案：1解析：根据运算法则，先乘除后加减。

先计算6 ÷ 3 = 2，再计算2 × 4 = 8，进行加减运算，得出结果为1。

6. 计算：15 3 × 2 + 4 ÷ 2答案：10解析：处理乘法，3 × 2 = 6，然后进行除法，4 ÷ 2 = 2。

接着，将15减去6，再加上2，得到最终答案10。

7. 计算：4² 6²答案：20解析：这里涉及到平方的计算，4² = 16，6² = 36。

将16减去36，得到的结果是20。

8. 计算：(8 5) × (3 + 2)答案：18解析：先解决括号内的运算，8 5 = 3，3 + 2 = 5。

然后将两个结果相乘，3 × 5 = 18。

9. 计算：12 ÷ (2 + 1)答案：4解析：计算括号内的加法，2 + 1 = 3。

接着，用12除以3，得到的结果是4。

数学计算题100道初中

数学计算题100道初中数学一直是学生们学习中不可或缺的一门学科，通过大量练习和计算题目的训练，可以帮助学生提高解决问题的能力和逻辑思维。

下面将给出100道初中数学计算题，供学生们进行练习。

1.45 + 32 =2.98 - 63 =3. 6 x 7 =4.84 ÷ 4 =5. 3.5 + 2.7 =6.9.8 - 4.3 =7. 5.6 x 4.2 =8.16.8 ÷ 2.4 =9.1/4 + 2/3 =10.3/5 - 1/10 =11.(5 + 3) x 2 =12.(20 - 6) ÷ 4 =13.2^3 =14.√49 =15.2/5 of 40 =16.30% of 150 =17.3/4 + 1/2 =18.0.6 x 0.7 =19.4^2 + 3^2 =20.√81 + √16 =21.(12 - 5) x 3 =22.54 ÷ (6 + 2) =23.3/8 of 64 =24.25% of 200 =25.5/6 - 1/3 =26.0.45 x 2.5 =27.7^2 - 4^2 =28.√144 - √25 =29.(9 + 7) x (5 - 3) =30.3/4 ÷ 1/2 =31. 2 x (4 x 2) =32.36 ÷ (4 x 2) =33.1/5 of 200 =34.40% of 120 =35.1/3 + 1/6 =36.0.75 x 2.8 =37.8^2 ÷ 4 =38.√256 + √36 =39.(15 - 7) x 2 =40.3/5 ÷ 2/3 =41. 5 x (9 + 3) =42.72 ÷ (8 + 4) =43.3/10 of 80 =44.60% of 180 =45.2/3 - 1/4 =46.0.85 x 3.5 =47.9^2 - 5^2 =48.√225 - √49 =49.(20 + 10) x (8 - 5) =50.5/8 ÷ 1/4 =51. 3 x (5 x 4) =52.48 ÷ (6 x 2) =53.1/6 of 300 =54.50% of 160 =55.1/2 + 1/3 =56.0.4 x 3.2 =57.6^2 ÷ 2 =58.√400 + √64 =59.(18 - 9) x 3 =60.4/7 ÷ 2/5 =61.7 x (8 + 2) =62.80 ÷ (10 + 2) =63.1/8 of 128 =64.70% of 140 =65.3/4 - 2/5 =66.0.6 x 1.9 =67.10^2 ÷ 5 =68.√625 - √81 =69.(14 + 6) x (7 - 4) =70.6/9 ÷ 1/3 =71. 4 x (6 x 3) =72.96 ÷ (8 x 3) =73.1/7 of 210 =74.45% of 240 =75.4/5 + 1/4 =76.0.25 x 4.6 =77.5^2 - 3^2 =78.√324 + √49 =79.(24 - 12) x 4 =80.7/9 ÷ 3/5 =81.8 x (3 + 5) =82.72 ÷ (9 + 3) =83.1/9 of 180 =84.80% of 220 =85.5/6 - 1/2 =86.0.35 x 3.6 =87.11^2 ÷ 3 =88.√729 - √121 =89.(22 + 8) x (6 - 2) =90.7/10 ÷ 2/5 =91. 6 x (7 x 2) =92.54 ÷ (6 x 3) =93.1/3 of 240 =94.70% of 180 =95.2/5 + 1/3 =96.0.8 x 3.2 =97.6^2 - 2^2 =98.√361 + √25 =99.(18 - 6) x 5 =100.8/11 ÷ 4/11 =这些计算题目涵盖了加减乘除、分数、百分比、幂次方、平方根等各种类型的题目，希會对学生们的数学能力有所提升。

(完整版)中考经典计算题100道

一、解不等式1. 8223-<+x x 2。

x x 4923+≥-3。

2x-19＜7x+31． 4．-2x+1＞0；5．x+8≥4x-1； 6. )1(5)32(2+<+x x7。

0)7(319≤+-x 8. 3(2x+5）＜2(4x+3）；9 10-4（x —3）≤2（x-1） 10. )1(281)2(3--≥-+y y11．2(x －4)－3＜1－3（x －2） 12。

1213<--m m13.31222+≥+x x 14。

223125+<-+x x15.0≤523x -≤1. 16．－1＜213-x ≤4二、解下列关于x 的不等式组 17。

1+2x >3+x 5x £4x -1ìíî , 18314,2 2.x x x ->⎧⎨<+⎩19。

512,324.x xx x->+⎧⎨+<⎩2021,24 1.x xx x>-⎧⎨+<-⎩21.3(1)5412123x xx x+>+⎧⎪⎨--⎪⎩ ①≤ ②22⎪⎩⎪⎨⎧-≥-->+356634)1(513xxxx23251,3311.48x xx x⎧+>-⎪⎪⎨⎪-<-⎪⎩24.()324,121.3x xxx--≥⎧⎪⎨+>-⎪⎩25。

253(2)123x xx x+≤+⎧⎪-⎨<⎪⎩26．⎪⎪⎩⎪⎪⎨⎧-<-+<-.3212112)2(31xxxx27。

． 28。

．三、解二元一次方程组29.30.31.32.．3334．35； 36．37。

38.39.40。

41。

42。

43.; 44.．45.46.；47。

． 48.四、先化简,再求值：49、先化简，再求值：（x －1x－错误!)÷错误!，其中x 满足x 2－x －1＝0．50、先化简,再求值:211(1)(2)11x x x -÷+-+-,其中6x =。

初中数学数列典型10类例题

初中数学数列典型10类例题1、有一个农妇，拿着一篮鸡蛋来到市场上，第一位顾客买了全部鸡蛋的一半再加半个;第二位顾客买了第一次剩下部分的一半再加半个;第三位顾客买了第二次剩下的一半再加半个，如此继续，当第六位顾客买了第五次剩下的一半再加半个时，他发现自己和其他顾客所买的鸡蛋都是整个的，而且农妇也刚好卖完所有鸡蛋，那么农妇一共拿了多少个鸡蛋到市场?你能算出来吗?(63个) 2、小明和小刚是好朋友，他们一个月里两次同时到一家超市买鸡蛋，两次鸡蛋的单价有变化，其中第一次鸡蛋的单价为x元/千克，第二次鸡蛋的单价为y元/千克。

现知道两人的购买方式不一样，小明每次总是买相同质量的鸡蛋，小刚则每次只拿出相同数量的钱买鸡蛋。

两种买鸡蛋的方式哪种合算?3、一小船由A港到B港顺流需行6小时，由B港到A港逆流需行8小时.一天，小船从早晨6点由A港出发顺流到达B 港时，发现一救生圈在途中落入水中，立刻返回，一小时后找到救生圈。

问:(1)若小船按水流速度由A漂流到B港需要多少小时?(2〉救生圈是在何时落入水中的?4、已知: b7+2ab-c2+2ac则三角形ABC是什么三角形(直角或等腰)5、已知: a+b2+c2-2ab+2ac+2bc,则三角形ABC是什么三角形（等边三角形)6、己知:(a-b)-是三角形的三边，则(a-b)-c?___(大于0或小于0）7、关于x的分式方程."_-1，下列说法正确的是（)A、方程的解是x=m+5.B、m>-5时，方程的解是正数.c、m<-5时，方程的解是负数. D、无法确定.8、某电脑公司经销甲种型号电脑,受经济危机影响，电脑价格不断下降.今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元.(1〉今年三月份甲种型号电脑每台售价多少元?(2)为了增加收入，该公司决定再经销乙种型号电脑，已知甲种型号电脑每台进价为3500元，乙种型号电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种型号的电脑共15台，有几种进货方案?(3）如果乙种型号电脑每台售价为3800元，为打开乙种型号电脑的销路，公司决定每售出一台乙种型号电脑，返还顾客现金a元，要使(2〉中所有方案获利相同，a的值应是多少?此时，哪种方案对公司更有利?9、甲志愿者计划用若干个工作日完成社区的某项工作，从第三个工作日起，乙志愿者加盟此项工作，且甲、乙两人工作效率相同，结果提前3天完成任务，则甲志愿者计划完成此项工作的天数是（A>A、8B、7c、6D、510、若x=2008/2009,y=2009/2010,则x,y的大小关系是_。

初一数学解方程计算题及答案(100道)

初一数学解方程计算题及答案(100道)一、一元一次方程1. 2x + 3 = 5x - 7，x = 102. 6a - 8 = 10 + 2a，a = 33. 3b - 5 = 7 - 2b，b = 24. 4x + 9 = 25，x = 45. 5a - 7 = 23，a = 66. 7 - 3b = 22，b = -57. 2x - 8 = 14，x = 118. 4a + 12 = 36，a = 69. 5b - 3 = 22，b = 510. 3x - 4 = 17，x = 7二、一元二次方程11. x^2 + 4x + 3 = 0，x = -1 or -312. 3x^2 - 10x + 3 = 0，x = 1/3 or 313. 2x^2 + 7x + 3 = 0，x = -1/2 or -314. x^2 - 6x + 8 = 0，x = 2 or 415. 2x^2 - 11x + 5 = 0，x = 1/2 or 5/216. 3x^2 - 14x + 5 = 0，x = 1 or 5/317. x^2 + 5x + 4 = 0，x = -1 or -418. 2x^2 + 5x - 3 = 0，x = -1/2 or 3/219. x^2 - 2x + 1 = 0，x = 120. 4x^2 - 4x - 3 = 0，x = (2 + √7)/2 or (2 - √7)/2三、分式方程21. (x + 3)/5 - 3/4 = (x - 1)/10，x = -3/222. (2x + 3)/(x - 1) + 1/(x + 1) = 2，x = 223. (x + 2)/(x - 1) - (x - 1)/(x + 2) = (2x - 3)/(x^2 - 4)，x = 1/2 or 7/324. 1/(x - 3) - 3/(2x + 1) = 1/(2x - 1)，x = -5 or 7/425. (5x + 3)/(9x - 5) - (3x - 4)/(3 - x) = (4x^2 - 40)/(x^2 - 9x + 15)，x = -2 or 2/3四、绝对值方程26. |x + 5| = 8，x = -13 or 327. |2x - 1| = 7，x = -3 or 428. |x - 2| = 1，x = 1 or 329. |3x + 4| = 13，x = -17/3 or 330. |x - 3| - 2 = 3x – 2，x = -1 or 13/7五、分段函数方程31. -3x + 2，x < 2；x + 1，x ≥ 2；x = 232. x + 2，x ≤ -2；-x + 7，-2 < x ≤ 3；-x + 4，x > 3；x = -2 or 333. 2x + 1，x < -2；x^2 + 2，-2 ≤ x < 1；-5x + 9，x ≥ 1；x = -2, -1/2, 134. -3，x ≤ -3；x + 2，-3 < x ≤ 0；-x^2 + 6x - 7，x > 0；x = -3 or 1, 535. -1，x ≤ -4；4 - x，-4 < x ≤ -1；-x^2 + 10x - 21，x > -1；x = -4 or 3, 7六、组合方程36. 3x - 5 = x + 7，x = 6；2x + 1 = 5，x = 2；x = 637. 4x - 7y = 10，y = (-4x + 10)/7；x + y = 4，x = 4 - y； y = (-4(4 - y) + 10)/7 = (18 - 4y)/7；y = 2，x = 238. x + y = 3，y = 3 - x；x^2 + y^2 = 13，x^2 + (3 - x)^2 = 13；2x^2 - 6x + 4 = 0；x = 1 or 2，y = 2 or 139. 3x - y = 7，y = 3x - 7；x^2 + y^2 = 50，x^2 + (3x - 7)^2 = 50；10x^2- 42x + 24 = 0；x = 1, 4，y = -4 or 540. 2x + 3y = 5，y = (5 - 2x)/3；x^2 + y^2 = 26，x^2 + (5 - 2x)^2/9 = 26；5x^2 - 30x + 32 = 0；x = 8/5 or 2，y = -1 or 3七、面积和周长方程41. 矩形的周长为20，面积为24，长和宽分别为6和4。

中考数学经典试题100例答案)

中考数学经典试题100例参考答案1．D设AB＝x，则AE＝EB＝x，由折叠，FE＝EB＝x，则∠AFB＝90°，由tan∠BCE＝，∴BC＝x，EC＝x，∵F、B关于EC对称，∴∠FBA＝∠BCE，∴△AFB∽△EBC，∴，∴y＝，∵圆锥的主视图是边长为4cm的正三角形，∴圆锥的母线长为4cm，底面圆的半径为2cm，故圆锥底面圆的周长为4πcm，故圆锥侧面展开图的面积为S＝×4×4π＝8π(cm2).故选C.3．C设这个多边形的边数为n，由多边形的内角和是720°，根据多边形的内角和定理得（n－2）180°=720°。

解得n=6.故选C.4．B由被开方数越大算术平方根越大，得2<<3,由不等式的性质得：-1<2-<0.故选B.5．B解：∵直径CD⊥弦AB，∴弧AD =弧BD，∴∠C=∠BOD．6．Cy=-2（x-3）2-4是抛物线的顶点式，根据顶点式的坐标特点可知，顶点坐标为（3，-4）．7．C解：将数据从小到大排序为：173，176，178，180，181，所以中位数为178.8．A 由题意得：=，解得：a=6，9．A∵点A（2，3）与点B关于y轴对称，∴点B的坐标为（-2，3），10．C解：如图，∵DE//BC，∴∠2+∠B=180°，∵∠2=∠1=70°，∴∠B=180°-70°=110°，故选C.【点睛】11．D解：A. 是轴对称图形，但不是中心对称图形，故不符合题意；B. 不是轴对称图形，是中心对称图形，故不符合题意；C. 是轴对称图形，但不是中心对称图形，故不符合题意；D. 既是轴对称图形又是中心对称图形，故符合题意．故选D.12．C科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．解：4 400 000 000=4.4×109，故选B．13．B 解：∵()×()=1，∴的倒数是，14．D由图知A(4,4),B(6,2)根据旋转中心P点,旋转方向顺时针,旋转角度90°，画图如下，从而得A′点坐标为(5，-1).15．B解：AB＝AC，,16．D连接OB，∵点B是弧AC的中点，∴∠AOB=∠AOC=70°，由圆周角定理得，∠D=∠AOB=35°17．C【详解】（a2）3-5a3•a3=a6-5a6=-4a6．18．A作CH⊥AB于H交⊙O于E、F．连接BC．∵A（4，0），B（0，3），∴OA=4，OB=3，AB=5．∵S△ABC= AB•CH=AC•OB，∴AB•CH=AC•OB，∴5CH=(4+1)×3，解得：CH=3，∴EH=3﹣1=2．当点P与E重合时，△PAB的面积最小，最小值5×2=5．19．C【详解】∵∠AOD=130°，∴∠BOD=50°，∴∠C=25°．故选C．20．C∵抛物线开口向上，∴a＞0，①是真命题；对称轴为直线x=1，②是真命题；当x＞1时，y随x的增大而增大，∴抛物线经过（2，y1），（4，y2）两点，则y1＜y2，③是假命题；顶点坐标是（1，﹣3），④是真命题；∴真命题的概率．21．B【详解】∵AB∥CD，∴∠EHD=∠EGB=25°．又∵∠PHD=60°，∴∠PHG=60°﹣25°=35°．22．D该空心圆柱体的俯视图是：23．C16.2亿=162000 0000=1.62×109．24．CA．x2+x2=2x2，故本选项不符合题意；B．x2•x3=x5，故本选项不符合题意；C．（x2）3=x6，故本选项符合题意；D．（2x2）3=8x6，故本选项不符合题意．25．A根据三角形数阵可知，第n行奇数的个数为n个，则前n-1行奇数的总个数为1+2+3+…+（n-1）=个，则第25行（n≥3）从左向右的第20个数为为第=320个奇数，所以此数是：320×2-1=639．26．D如图设AB交CD于O，连接BD，作OM⊥DE于M，ON⊥BD于N．,,，在Rt△ADB中，，∴AC=BC=2，，∵OD平分∠ADB，OM⊥DE于M，ON⊥BD于N，∴OM=ON，∵,.27．B解之即可得出答案.【详解】根据题意画出图如图所示：作BD⊥AC，取BE=CE，∵AC=30，∠CAB=30°∠ACB=15°，∴∠ABC=135°，又∵BE=CE，∴∠ACB=∠EBC=15°，∴∠ABE=120°，又∵∠CAB=30°∴BA=BE，AD=DE，设BD=x，在Rt△ABD中，∴AD=DE= x，AB=BE=CE=2x，∴AC=AD+DE+EC=2x+2x=30，∴x== ≈5.49，28．A设底面圆的半径为R，则，解得R=5，圆锥的母线长，所以圆锥的侧面积；圆柱的侧面积，所以需要毛毡的面积=(30+5) πm2．29．B如图，分别过A、B作x轴的垂线，垂足分别为C、D，∵A（3，4），∴OC=3，AC=4，∵把点A（3，4）逆时针旋转90°得到点B，∴OA=OB，且∠AOB=90°，∴∠BOD+∠AOC=∠AOC+∠CAO=90°，∴∠BOD=∠CAO，在△AOC和△OBD中，∴△AOC≌△OBD（AAS），∴OD=AC=4，BD=OC=3，∴B（-4，3），【点睛】30．D、不是中心对称图形，故此选项错误；、不是中心对称图形，故此选项错误；、不是中心对称图形，故此选项错误；、是中心对称图形，故此选项正确；31．CA、a2•a3=a5，故原题计算错误；B、a3和a2不是同类项，不能合并，故原题计算错误；C、（a2）4=a8，故原题计算正确；D、a3和a2不是同类项，不能合并，故原题计算错误；32．C∵∠ABC=60°，∠2=44°，∴∠EBC=16°，∵BE∥CD，∴∠1=∠EBC=16°，33．D（﹣2018）0=1，故选D.34．C ∵抛物线开口向上，∴a＞0，∵抛物线的对称轴在直线x=1的右侧，∴x=-＞1，∴b＜0，b＜-2a，即b+2a＜0，∵抛物线与y轴交点在x轴下方，∴c＜0，∴abc＞0，∵抛物线与x轴有2个交点，∴△=b2-4ac＞0，∵x=1时，y＜0，∴a+b+c＜0．35．B解：∵半径OC垂直于弦AB，∴AD=DB=AB=在Rt△AOD中，OA2=(OC-CD)2+AD2,即OA2=(OA-1)2+()2，解得，OA=4 ∴OD=OC-CD=3，∵AO=OE,AD=DB, ∴BE=2OD=636．A解：当1<x<3时，y1>y2．37．C解：该扇形的面积．故选：C．38．B解：A、有两条边和一个角对应相等的两个三角形全等，错误，必须是两边及其夹角分别对应相等的两个三角形全等；B、正方形既是轴对称图形又是中心对称图形，正确；C、矩形的对角线相等且互相平分，故此选项错误；D、六边形的内角和是720°，故此选项错误．故选：B．39．B，①+②得：3x=6，即x=2，把x=2代入①得：y=0，则方程组的解为，40．C解：A、x2+3x2=4x2，故此选项错误；B、0.00028=2.8×10-4，故此选项错误；C、（a3b2）3=a9b6，正确；D、(－a+b)(－a-b)=a2-b2，故此选项错误；41．B设EF=a，BC=b，AB=c，则PQ=a-c，RQ=b-a，PQ=RQ∴a=，∵▱ALMN的面积为50，∴bc+a2+(a-c)2=50,把a=代入化简求值得b+c=10, ∴a=5, ∴正方形EFGH的边长为5，∴正方形EFGH的面积为25，42．A解：∵▱ABCD的周长为36，∴2（BC+CD）=36，则BC+CD=18．∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，∴OD=OB=BD=6．又∵点E是CD的中点，DE=CD，∴OE是△BCD的中位线，∴OE=BC，∴△DOE的周长=OD+OE+DE=BD+（BC+CD）=6+9=15，即△DOE的周长为15．43．C解：∵△ABC绕点A逆时针旋转60°得到△AB1C1，∴∠BAC1=∠BAC+∠CAC1=30°+60°=90°，AC1=AC=6，在RtBAC1中，∠BAC=90°，AB=8，AC1=6,∴，44．由题意可知：△＝4m2−2（1−4m）＝4m2＋8m−2＝0，∴m2＋2m＝，∴（m−2）2−2m（m−1）＝−m2−2m＋4＝−＋=，45．②解：当BA=BC时，四边形ADCE是菱形．理由：∵AE∥CD，CE∥AD，∴四边形ADCE是平行四边形，∵BA=BC，∴∠BAC=∠BCA，∵AD，CD分别平分∠BAC和∠ACB，∴∠DAC=∠DCA，∴DA=DC，∴四边形ADCE是菱形．46．130∵∠AOB＝40°，OP平分∠AOB，∴∠AOC＝∠BOC＝20°，又∵CD⊥OA于点D，CE∥OB，∴∠DCP＝90°＋20°＝110°，∠PCE＝∠POB＝20°，∴∠DCE＝∠DCP＋∠PCE＝110°＋20°＝130°.47．【详解】连接OD，AD，∵BC=CD，BO=DO，∴∠1=∠2，∠3=∠DBO，∴∠1+∠3=∠2+∠DBO，∴∠CDO=∠CBO，∵OC=OB=OD，∴∠BCO=∠DCO，∴CO为等腰△BCD的角平分线，∴CO⊥BD，∵AB为直径，∴∠ADB=90°，∴∠3+∠5=∠3+∠4=90°，∴∠4=∠5，∴AD//CO，∵AE=AO=2，∴AD=CO=1，在Rt△ABD中，BD=.【点睛】48．解：∵点A，B的坐标分别为（3，5），（6，1），∴C的坐标为（4，2.5），则直线l经过点C．设直线l的函数解析式为y=kx，依题意有 2.5=4k，解得k=．故直线l的函数解析式为y=x．故答案为：y=x．49．2或2.5解：如图∵AB=2，AD=7，∴BD=BC+CD=AD-AB=5，∵AB，BC，CD可构成以BC为腰的等腰三角形，∴BC=AB或BC=CD，∴BC=2或BC=2.5，50．3解：原式=，∵m+n=3mn，∴原式==3.51．∵四边形ABCD为菱形，∴AC⊥BD，OB=OD=BD=3，OA=OC=AC=4，在Rt△OAD中，∵OD=3，OA=4，∴AD==5，∵OE⊥AD，∴OE•AD=OA•OD，∴OE==．∴EF=2OE=.52．k＜0解：∵一次函数y=kx-2的函数值y随自变量x的增大而减小，∴k＜0，故答案为：k＜0．53．π∵∠B=90°，∠C=30°，∴∠A=60°，∵OA=OF，∴△AOF是等边三角形，∴∠COF=120°，∵OA=2，∴扇形OGF的面积为：=∵OA为半径的圆与CB相切于点E，∴∠OEC=90°，∴OC=2OE=4，∴AC=OC+OA=6，∴AB=AC=3，∴由勾股定理可知：BC=3∴△ABC的面积为：×3×3=∵△OAF的面积为：×2×=，∴阴影部分面积为：﹣﹣π=﹣π54．甲工厂5月份用水量为x吨，乙工厂5月份用水量为y吨，根据题意得：，故答案为：．55．22﹣1×+2cos30°==+=2，56．∵第一个图形有2+1×2=4个，第二个图形有2+2×3=8个，第三个图形有2+3×4=14个，第四个图形有2+4×5=22个，…∴第n个图形共有：2+n×（n+1）=n2+n+2．故答案为：n2+n+2．57．2∵▱ABCD的面积为16cm2，∴S△PBC S▱ABCD=8．∵E、F分别是PB、PC的中点，∴EF∥BC，且EF BC，∴△PEF∽△PBC，∴）2，即，∴S△PEF=2．58．,由图象，得：y=﹣x+b与反比例函数y（k≠0）的图象相交于点P（1，2），把P点坐标带入函数解析式，得：﹣1+b=2，k=1×2=2，解得：b=3，k=2．关于x的方程﹣x+b，即﹣x+3，解得：x1=1，x2=2．59．设底面圆的半径为r．∵半径为10cm的半圆围成一个圆锥，∴圆锥的母线l=10cm，∴，解得：r=5（cm），∴圆锥的高h（cm）．故答案为：5．60．3∵一组数据：﹣1，3，2，x，5，它有唯一的众数是3，∴x=3，∴此组数据为﹣1，2，3，3，5，∴这组数据的中位数为3．故答案为：3．61．解：∵AD、BE为AC，BC边上的中线，∴BD=BC=2，AE=AC=，点O为△ABC的重心，∴AO=2OD，OB=2OE，∵BE⊥AD，∴BO2+OD2=BD2=4，OE2+AO2=AE2=，∴BO2+AO2=4，BO2+AO2=，∴BO2+AO2=，∴BO2+AO2=5，∴AB==．62．y（x++2y）（x-2y）原式．故答案是：y（x+2y）（x-2y）．63．(，0)解：作点A关于x轴的对称点A＇，连接A＇B，则A＇B与x轴的交点即为所求，∵抛物线y=ax2-4x+c(a0)与反比例函数y=的图象相交于点B，且B点的横坐标为3，抛物线与y轴交于点C （0,6），∴点B（3,3），∴解得，∴y=x2-4x+6=（x-2）2+2 ∴点A的坐标为（2,2），∴点A＇的坐标为（2，-2），设过点A＇（2，-2）和点B（3,3）的直线解析式为y=mx+n∴∴直线A＇B的函数解析式为y=5x-12,令y=0,则0=5x-12得x=,64．（2，6）∵四边形OCDB是平行四边形,点B的坐标为(16,0)，CD∥OA，CD=OB=16，过点M作MF⊥CD于F,则过C作CE⊥OA于E，∵A(20,0)，∴OA=20，OM=10，∴OE=OM−ME=OM−CF=10−8=2，连接MC,∴在Rt△CMF中，∴点C的坐标为(2,6).65．﹣4≤m≤4解：∵点M在直线y=﹣x上，∴M（m，﹣m），∵MN⊥x轴，且点N在直线y=x上，∴N（m，m），∴MN=|﹣m﹣m|=|2m|，∵MN≤8，∴|2m|≤8，∴﹣4≤m≤4，66．（1）证明见解析；（2）；（3）【详解】（1）证明：如图1，由旋转得：，，四边形是正方形，，，，即，，在和中，，，；（2）解：如图2，过作的垂线，交的延长线于，是的中点，且，，，三点共线，，由勾股定理得：，，，由（1）知：，，，，，，，，，设，则，由勾股定理得：，或（舍，，，由勾股定理得：，（3）解：如图3，由于，所以点可以看作是以为圆心，2为半径的半圆上运动，延长到点，使得，连接，，，，，当最小时，为、、三点共线，，，的最小值是．【点睛】67．(1);(2)k>1；（3）1或3.解：（1）把点代入抛物线，得解得（2）把点代入抛物线，得把点代入抛物线，得解得（3）抛物线解析式配方得将抛物线向右平移1个单位长度得到新解析式为当时，对应的抛物线部分位于对称轴右侧，随的增大而增大，时，，，解得，都不合题意，舍去；当时，，解得；当时，对应的抛物线部分位于对称轴左侧，随的增大而减小，时，，解得，（舍去）综上，或3．68．（1）A种商品的单价为20元，B种商品的单价为15元；(2) 当a=8时所花钱数最少，即购买A商品8件，B商品4件．解：（1）设种商品的单价为元，种商品的单价为元，根据题意可得：，解得：，答：种商品的单价为20元，种商品的单价为15元；（2）设第三次购买商品种件，则购买种商品件，根据题意可得：，得：，当时所花钱数最少，即购买商品8件，商品4件．69．(1)证明见解析；（2）10.（1）证明：，，，，，，；（2）为的直径，，，四边形是矩形，，，，，，，设的为，，，即，解得，，，70．(1)-8；（2）解：（1）原式；（2）原式．71．（1）；（2）△BCD为直角三角形，理由见解析；（3）当△AMN为直角三角形时，t的值为1或4．（1）将、代入，得：，解得：，二次函数解析式为．（2）为直角三角形，理由如下：，顶点的坐标为．当时，，点的坐标为．点的坐标为，，，．，，为直角三角形．（3）设直线的解析式为，将，代入，得：，解得：，直线的解析式为，将直线向上平移个单位得到的直线的解析式为．联立新直线与抛物线的解析式成方程组，得：，解得：，，点的坐标为，，点的坐标为，．点的坐标为，，，．为直角三角形，分三种情况考虑：①当时，有，即，整理，得：，解得：，（不合题意，舍去）；②当时，有，即，整理，得：，解得：，（不合题意，舍去）；③当时，有，即，整理，得：．，该方程无解（或解均为增解）．综上所述：当为直角三角形时，的值为1或4．72．（1）证明见解析；（2证明见解析；（3）BD=1.（1）证明：如图1中，，，，，，，，．（2）解：结论：．理由：如图2中，在上取一点，使得，连接．．，．，，，，，，，，．（3）如图3中，过点作交于点．，，，设，则，，，．，在中，，解得或（舍弃）73．（1）见解析；（2）AC=2.（1）是的直径；，，，，，点在上，是的切线（2），，，，，，，，，．74．（1）y=x+2；（2）6.（1）反比例函数y=，x=2，则y=4，∴点A的坐标为（2，4）；反比例函数y=中y=-2，则-2=，解得：x=-4，∴点B的坐标为（-4，-2）．∵一次函数过A、B两点，∴解得：．∴一次函数的解析式为y=x+2．（2））令y=x+2中x=0，则y=2∴点C的坐标为（0，2），∴S△AOB=OC•（x A-x B）=×2×[2-（-4）]=6．75．（1）50，18；（2）选择的市民均来自甲区的概率为．（1）解：（1）∵满意的有20人，占40%，∴此次调查中接受调查的人数为：20÷40%=50（人）；此次调查中结果为非常满意的人数为：50×36%=18（人）；（2）画树状图得：共有12种等可能的结果，选择的市民均来自甲区的有2种情况，选择的市民均来自甲区的概率为：=．76．m＜1.解：∵方程x2-2x+m=0有两个不相等的实数根，∴△=(-2)2-4×1×m=4-4m＞0，解得：m＜1．77．（1）AP= 10﹣2t；（2）S=t2﹣12t+78；（3）当t=s时，PQ⊥BD；（4）存在．当t=s时，点E在∠ABD的平分线．理由见解析.【详解】（1）如图作DH⊥AB于H，则四边形DHBC是矩形，∴CD=BH=8，DH=BC=6，∴AH=AB﹣BH=8，AD==10，BD==10，由题意AP=AD﹣DP=10﹣2t．（2）作PN⊥AB于N．连接PB．在Rt△APN中，PA=10﹣2t，∴PN=PA•sin∠DAH=（10﹣2t），AN=PA•cos∠DAH=（10﹣2t），∴BN=16﹣AN=16﹣（10﹣2t），S=S△PQB+S△BCP=•（16﹣2t）•（10﹣2t）+×6×[16﹣（10﹣2t）]=t2﹣12t+78（3）当PQ⊥BD时，∠PQN+∠DBA=90°，∵∠QPN+∠PQN=90∴∠QPN=∠DBA，∴tan∠QPN==，∴=，解得t=，经检验：t=是分式方程的解，∴当t=s时，PQ⊥BD．（4）存在．理由：连接BE交DH于K，作KM⊥BD于M．当BE平分∠ABD时，△KBH≌△KBM，∴KH=KM，BH=BM=8，设KH=KM=x，在Rt△DKM中，（6﹣x）2=22+x2，解得x=，作EF⊥AB于F，则△AEF≌△QPN，∴EF=PN=（10﹣2t），AF=QN=（10﹣2t）﹣2t，∴BF=16﹣[（10﹣2t）﹣2t]，∵KH∥EF，∴=，∴=，解得：t=，经检验：t=是分式方程的解，∴当t=s时，点E在∠ABD的平分线．本78．（1）W1=﹣x2+32x﹣236；（2）该产品第一年的售价是16元；（3）该公司第二年的利润W2至少为18万元．（1）W1=（x﹣6）（﹣x+26）﹣80=﹣x2+32x﹣236．（2）由题意：20=﹣x2+32x﹣236．解得：x=16，答：该产品第一年的售价是16元．（3）由题意：7≤x≤16，W2=（x﹣5）（﹣x+26）﹣20=﹣x2+31x﹣150，∵7≤x≤16，∴x=7时，W2有最小值，最小值=18（万元），答：该公司第二年的利润W2至少为18万元．79．（1）证明见解析；（2）结论：四边形ACDF是矩形．理由见解析.（1）证明：∵四边形ABCD是平行四边形，∴BE∥CD，AB=CD，∴∠AFC=∠DCG，∵GA=GD，∠AGF=∠CGD，∴△AGF≌△DGC，∴AF=CD，∴AB=CF．（2）解：结论：四边形ACDF是矩形．理由：∵AF=CD，AF∥CD，∴四边形ACDF是平行四边形，∵四边形ABCD是平行四边形，∴∠BAD=∠BCD=120°，∴∠FAG=60°，∵AB=AG=AF，∴△AFG是等边三角形，∴AG=GF，∵△AGF≌△DGC，∴FG=CG，∵AG=GD，∴AD=CF，∴四边形ACDF是矩形．80．（1）m=1；（2）点P坐标为（﹣2m，0）或（6m，0）．（1）设反比例函数的解析式为y=，∵反比例函数的图象经过点A（﹣4，﹣3），∴k=﹣4×（﹣3）=12，∴反比例函数的解析式为y=，∵反比例函数的图象经过点B（2m，y1），C（6m，y2），∴y1==，y2==，∵y1﹣y2=4，∴﹣=4，∴m=1；（2）设BD与x轴交于点E．∵点B（2m，），C（6m，），过点B、C分别作x轴、y轴的垂线，两垂线相交于点D，∴D（2m，），BD=﹣=．∵三角形PBD的面积是8，∴BD•PE=8，∴••PE=8，∴PE=4m，∵E（2m，0），点P在x轴上，∴点P坐标为（﹣2m，0）或（6m，0）．81．（1）参与问卷调查的学生人数为100人；（2）补全图形见解析；（3）估计该校学生一个月阅读2本课外书的人数约为570人．（1）参与问卷调查的学生人数为（8+2）÷10%=100人，（2）读4本的女生人数为100×15%﹣10=5人，读2本人数所占百分比为×100%=38%，补全图形如下：（3）估计该校学生一个月阅读2本课外书的人数约为1500×38%=570人．82．（1）﹣1＜x＜5；（2）．（1）解不等式＜1，得：x＜5，解不等式2x+16＞14，得：x＞﹣1，则不等式组的解集为﹣1＜x＜5；（2）原式=（﹣）•=•=．83．（1）2；（2）DM=DN；（3）（1）如图1．在Rt△ABC中，∵BC=2，∠B=60°，∴AC=BC•tan60°=6，AB=2BC=4．∵DF是线段AB的垂直平分线，∴AD=BD=2．在Rt△ADG中，AG4，∴CG=AC=AG=6﹣4=2．（2）如图2中，结论：DM=DN．理由：∵△ABC为直角三角形，D为斜边AB的中点，∴CD=BD=AD．又∠B=60°，∴△BDC为等边三角形，∴∠CDB=60°．又∠EDF=90°，∴∠HDA=30°．∵∠A=90°﹣∠B=30°，∴AH=HD，又HM⊥AD，∴MD=AM．在等边三角形BCD中，CN⊥BD，∴ND=NB．又AD=BD，∴MD=ND．（3）如图3中，作GK∥DE交AB由K．在△AGK中，AG=GK=4，∠A=∠GKD=30°，作GH⊥AB于H．则AH=AG•cos30°=2，可得AK=2AH=4，此时K与B重合，∴DD′=DB=2．84．（1）；（2）△ABC是直角三角形；（3）存在，、、．（1）将该抛物线向上平移2个单位，得：y x2x+2．故答案为：y x2x+2；（2）当y=0时，x2x+2=0，解得：x1=﹣4，x2=1，即B（﹣4，0），A（1，0）．当x=0时，y=2，即C（0，2）．AB=1﹣（﹣4）=5，AB2=25，AC2=（1﹣0）2+（0﹣2）2=5，BC2=（﹣4﹣0）2+（0﹣2）2=20．∵AC2+BC2=AB2，∴△ABC是直角三角形；（3）y x2x+2的对称轴是x，设P（，n），AP2=（1）2+n2n2，CP2（2﹣n）2，AC2=12+22=5.分三种情况讨论：①当AP=AC时，AP2=AC2，n2=5，方程无解；②当AP=CP时，AP2=CP2，n2（2﹣n）2，解得：n=0，即P1（，0）；③当AC=CP时，AC2=CP2，（2﹣n）2=5，解得：n1=2，n2=2，P2（，2），P3（，2）．综上所述：在抛物线对称轴上存在一点P，使得以A、C、P为顶点的三角形是等腰三角形，点P的坐标（，0），（，2），（，2）．85．（1）证明见解析（2）（1）连接OD．∵OA=OD，∴∠OAD=∠ODA．∵∠OAD=∠DAC，∴∠ODA=∠DAC，∴OD∥AC，∴∠ODB=∠C=90°，∴OD⊥BC，∴BC是⊙O的切线．（2）连接OE，OE交AD于K．∵，∴OE⊥AD．∵∠OAK=∠EAK，AK=AK，∠AKO=∠AKE=90°，∴△AKO≌△AKE，∴AO=AE=OE，∴△AOE是等边三角形，∴∠AOE=60°，∴S阴=S扇形OAE﹣S△AOE22．86．（1）三（2）A：30元/件，B：40元/件（3）6 （4）7件（1）观察表格数据，可知：第三次购买的A、B两种商品均比头两次多，总价反而少，∴第三次购买有折扣．故答案为：三．（2）设A商品的原价为x元/件，B商品的原价为y元/件，根据题意得：解得：．答：A商品的原价为30元/件，B商品的原价为40元/件．（3）设折扣数为z，根据题意得：5×307×40258 解得：z=6．（4）设购买A商品m件，则购买B商品（10﹣m）件，根据题意得：30m+40（10﹣m）≤200 解得：m．∵m为整数，∴m的最小值为7．87．（1）答案见解析（2）95% （3）（1）∵被调查的总户数为60÷60%=100，∴C类别户数为100﹣（60+20+5）=15，补全图形如下：（2）贫困户对扶贫工作的满意度（A、B、C类视为满意）是100%=95%．故答案为：95%；（3）画树状图如下：由树状图知共有20种等可能结果，其中这两户贫困户恰好都是同一乡镇的有8种结果，所以这两户贫困户恰好都是同一乡镇的概率为．88．（1）；（2）P点坐标为（4,6）或（,- ）；（3）Q点坐标（3，0）或（-2，15）（1）把，和点，代入抛物线得：，解得：，，则抛物线解析式为；（2）当在直线上方时，设坐标为，则有，，当时，，即，整理得：，即，解得：，即或（舍去），此时，；当时，，即，整理得：，即，解得：，即或（舍去），此时，；当点时，也满足；当在直线下方时，同理可得：的坐标为，，综上，的坐标为，或，或，或；（3）在中，，，根据勾股定理得：，，，，边上的高为，过作，截取，过作，交轴于点，如图所示：在中，，即，过作轴，在中，，，即，，设直线解析式为，把坐标代入得：，即，即，联立得：，解得：或，即，或，，则抛物线上存在点，使得，此时点的坐标为，或，．89．（1）证明见解析；（2）sin∠ACO=.（1）证明：连接，如图，、为的切线，，，，，，，，，，；（2）解：作于，如图，设的半径为，，，四边形为矩形，而，四边形为正方形，，易得和都为等腰直角三角形，，，在中，，在中，，即的值为．【90．（1）y=；（2）最小值即为，P（0，）.（1）反比例函数的图象过点，过点作轴的垂线，垂足为，面积为1，，，，故反比例函数的解析式为：；（2）作点关于轴的对称点，连接，交轴于点，则最小．由，解得，或，，，，最小值．设直线的解析式为，则，解得，直线的解析式为，时，，点坐标为．91．（1），点A的坐标为(-2，0)，点B的坐标为(8，0)；（2）存在点P，使△PBC的面积最大，最大面积是16，理由见解析；（3）点M的坐标为(4-2，)、(2，6)、(6，4)或(4+2，-)．（1）抛物线的对称轴是直线，，解得：，抛物线的解析式为．当时，，解得：，，点的坐标为，点的坐标为．（2）当时，，点的坐标为．设直线的解析式为．将、代入，，解得：，直线的解析式为．假设存在，设点的坐标为，过点作轴，交直线于点，则点的坐标为，如图所示．，．，当时，的面积最大，最大面积是 16 ．，存在点，使的面积最大，最大面积是 16 ．（3）设点的坐标为，则点的坐标为，．又，．当时，有，解得：，，点的坐标为或；当或时，有，解得：，，点的坐标为，或，．综上所述：点的坐标为，、、或，．92．（1）全班学生总人数为40人；（2）补全图形见解析；（3）全是B类学生的概率为．（1）全班学生总人数为（人；（2）类人数为，类所占百分比为，类百分比为，补全图形如下：（3）列表如下：A B B CA AB AB ACB BA BB BCB BA BB BCC CA CB CB由表可知，共有12种等可能结果，其中全是类的有2种情况，所以全是类学生的概率为．93．（1）见解析；（2）CM=2.（1）中，点是半圆的中点，，，又，，，即；（2）连接、，是的切线，，又，设的半径为，，，解得：，又是直径，，，是等腰直角三角形，在中，由勾股定理得，即，则，．94．（1）；（2）当点E(0,8)或(0,5)或(0,-5)或(0,)时，△AOE是等腰三角形．（1）一次函数与反比例函数图象交于与，且轴，，在中，，，，即，根据勾股定理得：，，代入反比例解析式得：，即，把坐标代入得：，即，代入一次函数解析式得：，解得：，即；（2）当，即，；当时，得到，即；当时，由，，得到直线解析式为，中点坐标为，垂直平分线方程为，令，得到，即，综上，当点或或或时，是等腰三角形．95．该一元二次方程有两个实数根，△，解得：，由韦达定理可得，，，，解得：，．96．证明：四边形是平行四边形，，，，，，四边形是平行四边形，，四边形是菱形．97．-3.当，时，原式98．（1）y=﹣x2+2x+3；（2）①S四边形ACFD= 4；②Q点坐标为（1，4）或（，）或（，）．（1）由题意可得，解得，∴抛物线解析式为y=﹣x2+2x+3；（2）①∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴F（1，4），∵C（0，3），D（2，3），∴CD=2，且CD∥x轴，∵A（﹣1，0），∴S四边形ACFD=S△ACD+S△FCD=×2×3+×2×（4﹣3）=4；②∵点P在线段AB上，∴∠DAQ不可能为直角，∴当△AQD为直角三角形时，有∠ADQ=90°或∠AQD=90°，i．当∠ADQ=90°时，则DQ⊥AD，∵A（﹣1，0），D（2，3），∴直线AD解析式为y=x+1，∴可设直线DQ解析式为y=﹣x+b′，把D（2，3）代入可求得b′=5，∴直线DQ解析式为y=﹣x+5，联立直线DQ和抛物线解析式可得，解得或，∴Q（1，4）；ii．当∠AQD=90°时，设Q（t，﹣t2+2t+3），设直线AQ的解析式为y=k1x+b1，把A、Q坐标代入可得，解得k1=﹣（t﹣3），设直线DQ解析式为y=k2x+b2，同理可求得k2=﹣t，∵AQ⊥DQ，∴k1k2=﹣1，即t（t﹣3）=﹣1，解得t=，当t=时，﹣t2+2t+3=，当t=时，﹣t2+2t+3=，∴Q点坐标为（，）或（，）；综上可知Q点坐标为（1，4）或（，）或（，）．99．（1）证明见解析；（2）证明见解析；（3）n=4．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADE=∠BFE，∠A=∠FBE，在△ADE和△BFE中，，∴△ADE≌△BFE；（2）如图2，作BN∥HC交EF于N，∵△ADE≌△BFE，∴BF=AD=BC，∴BN=HC，由（1）的方法可知，△AEK≌△BEN，∴AK=BN，∴HC=2AK；（3）如图3，作GM∥DF交HC于M，∵点G是边BC中点，∴CG=CF，∵GM∥DF，∴△CMG∽△CHF，∴==，∵AD∥FC，∴△AHD∽△GHF，∴===，∴=，∵AK∥HC，GM∥DF，∴△AHK∽△HGM，∴==，∴=，即HD=4HK，100．（1）地（市）属项目投资额为830亿元；补全图形见解析；（2）m=18，对应的圆心角为65°. （1）地（市）属项目投资额为3730﹣（200+530+670+1500）=830（亿元），补全图形如下：（2）县（市）属项目部分所占百分比为m%=×100%≈18%，即m=18，对应的圆心角为β=360°×≈65°.答案第41页，总41页。