三角函数与三角恒等变换-经典测试题-附答案

合集下载

高二数学三角函数三角恒等变换解三角形试题

高二数学三角函数三角恒等变换解三角形试题1.若，则．【答案】【解析】【考点】1．二倍角公式；2．同角三角函数2.将函数的图象向右平移个单位，得到函数的图象，若在上为增函数，则的最大值为．【答案】2【解析】由题意得：，因为在上为增函数，所以，即的最大值为2【考点】三角函数图像变换与性质3.函数（其中）的图象如图所示，为了得到的图象，只需把的图象上所有点（）A．向左平移个单位长度B．向右平移个单位长度C．向右平移个单位长度D．向左平移个单位长度【答案】C【解析】由图可知则，又，结合可知，即，为了得到的图象，只需把的图象上所有点向右平移个单位长度．【考点】函数图象、图象的平移．4.在中，角所对的边分别为，满足，且．（1）求角的大小；（2）求的最大值，并求取得最大值时角的值．【答案】（1）；（2）当时，取到最大值．【解析】本题主要考查余弦定理、正弦定理、两角和的正弦公式、基本不等式等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力．第一问，利用三角形的内角和定理转化为A的三角函数，利用两角和的正弦公式求解，结合正弦定理把边转化为角，求出表达式，求出结果即可；第二问，由余弦定理以及基本不等式求出的最值，注意等号成立的条件即可．试题解析：（1）由，可得，即，又，所以，由正弦定理得，因为，所以0，从而，即．（2）由余弦定理，得，又，所以，于是，--10当时，取到最大值．【考点】余弦定理、正弦定理、两角和的正弦公式、基本不等式．5.下列各式中，值为的是（）A．B．C．D．【答案】C【解析】A，B、，C、， D、，故选择C【考点】三角恒等变换6.在△ABC中，a，b，c分别是角A，B，C所对的边，已知则c＝．【答案】【解析】由余弦定理可得【考点】余弦定理解三角形7.已知面积为，，则BC长为．【答案】【解析】由三角形面积公式可知【考点】三角形面积公式8.在锐角△ABC中，a，b，c分别为角A，B，C所对的边，又c＝，b＝4，且BC边上的高h＝2．（1）求角C；（2）求边a的长【答案】（1）；（2）5；【解析】（1）角C在直角三角形ADC中，根据定义求解即可；（2）由（1）知的值，利用余弦定理即可．本题注意活用余弦定理．试题解析：（1）由于△ABC为锐角三角形，过A作AD⊥BC于D点，，则．（2）由余弦定理，可知则，即所以或（舍）因此边长为5．【考点】1．正弦的定义；2．余弦定理；9.△ABC中，，则△ABC一定是（）A．等腰三角形B．直角三角形C．等腰直角三角形D．等边三角形【答案】A【解析】由正弦定理可知，，整理得，所以，则△ABC为等腰三角形．【考点】正弦定理的应用．10.在中，，则边的长为（）A．B．3C．D．7【答案】A【解析】由三角形的面积公式，得，解得；由余弦定理，得，即；故选A．【考点】1．三角形的面积公式；2．余弦定理．11.（2011•安徽）已知△ABC的一个内角为120°，并且三边长构成公差为4的等差数列，则△ABC的面积为．【答案】15【解析】因为三角形三边构成公差为4的等差数列，设中间的一条边为x，则最大的边为x+4，最小的边为x﹣4，根据余弦定理表示出cos120°的式子，将各自设出的值代入即可得到关于x的方程，求出方程的解即可得到三角形的边长，然后利用三角形的面积公式即可求出三角形ABC 的面积．解：设三角形的三边分别为x﹣4，x，x+4，则cos120°==﹣，化简得：x﹣16=4﹣x，解得x=10，所以三角形的三边分别为：6，10，14则△ABC的面积S=×6×10sin120°=15．故答案为：15【考点】余弦定理；数列的应用；正弦定理．12.（2015秋•醴陵市校级期末）正弦函数y=sinx在x=处的切线方程为．【答案】【解析】先求导函数，利用导函数在x=处可知切线的斜率，进而求出切点的坐标，即可求得切线方程．解：由题意，设f（x）=sinx，∴f′（x）=cosx当x=时，∵x=时，y=∴正弦函数y=sinx在x=处的切线方程为即故答案为：【考点】利用导数研究曲线上某点切线方程．13.如图所示，甲船以每小时30海里的速度向正北方向航行，乙船按固定方向匀速直线航行．当甲船位于A1处时，乙船位于甲船的南偏西75°方向的B1处，此时两船相距20海里．当甲船航行20分钟到达A2处时，乙船航行到甲船的南偏西60°方向的B2处，此时两船相距10海里．问:乙船每小时航行多少海里？【答案】【解析】连接，则∴△是等边三角形，求出，在△中使用余弦定理求出的长，除以航行时间得出速度试题解析：如图，连接A1B2，由题意知，A1B1＝20，A2B2＝10，A1A2＝×30＝10（海里）又∵∠B2A2A1＝180°－120°＝60°，∴△A1A2B2是等边三角形，∠B1A1B2＝105-60°＝45°．在△A1B2B1中，由余弦定理得＝202＋（10）2－2×20×10×＝200，∴B1B2＝10（海里）．因此乙船的速度大小为×60＝30（海里/小时）．【考点】解三角形的实际应用；余弦定理14.（2015春•东城区期末）下列三句话按“三段论”模式排列顺序正确的是（）①y=cosx（x∈R）是三角函数；②三角函数是周期函数；③y=cosx（x∈R）是周期函数．A．①②③B．②①③C．②③①D．③②①【答案】B【解析】根据三段论”的排列模式：“大前提”→“小前提”⇒“结论”，分析即可得到正确的次序．解：根据“三段论”：“大前提”→“小前提”⇒“结论”可知：①y=cosx（（x∈R ）是三角函数是“小前提”；②三角函数是周期函数是“大前提”；③y=cosx（（x∈R ）是周期函数是“结论”；故“三段论”模式排列顺序为②①③故选B【考点】演绎推理的基本方法．15.在△ABC内部有任意三点不共线的2017个点，加上A、B、C三个顶点，共有2020个点，把这2020个点连线，将△ABC分割成以这些点为顶点，且互不重叠的小三角形，则小三角形的个数为（）A．4037 B．4035 C．4033 D．4032【答案】B【解析】三个点时，有1个三角形，4个点时有3个三角形，5个点时有5个三角形，每加一个点，三角形的个数加2，因此2020个点时三角形的个数为1＋（2020－3）×2＝4035．【考点】归纳推理．16.在锐角中，内角的对边分别为，且.（1）求角的大小；（2）若，求的面积.【答案】（1）；（2）.【解析】（1）由正弦定理得的值，再由题意可得的大小；（2）由已知条件代入余弦定理可求得的值，代入面积公式可得三角形的面积.试题解析：（1）∵中，，∴根据正弦定理，得∵锐角中，，∴等式两边约去，得∵是锐角的内角，∴；（2）∵，，∴由余弦定理，得，化简得，∵，平方得，∴两式相减，得，可得.因此，的面积.【考点】正弦定理、余弦定理.17.设函数，若为奇函数，则= ；【答案】【解析】，函数为奇函数，所以【考点】三角函数性质18.已知的三内角所对的边分别为，且，则．【答案】【解析】由正弦定理及得，所以，所以．【考点】正弦定理与余弦定理．19.函数的部分图像如图所示，则A．B．C．D．【答案】A【解析】由图象可知，，所以，当时，，故选A．【考点】函数的图象．20.在锐角中，分别为角所对的边，且．（1）确定角的大小；（2）若，且的面积为，求的值．【答案】（1）；（2）．【解析】（1）根据正弦定理化简已知的式子求出，在由锐角三角形的特征求出角的大小；（2）根据余弦定理和条件，可得，利用三角形的面积公式和条件求出和的值，由完全平方公式即可求出的值．试题解析：（1）由及正弦定理得，，∵，∴．∵是锐角三角形，∴．（2）∵，由面积公式得，即．．．．①由余弦定理得，即，∴．．．．②，由①②得，故．【考点】正弦定理与余弦定理．21.已知：f（x）=2cos2x+sin2x﹣+1（x∈R）．求：（Ⅰ）f（x）的最小正周期；（Ⅱ）f（x）的单调增区间；（Ⅲ）若x∈[﹣，]时，求f（x）的值域．【答案】见解析【解析】解：f（x）=sin2x+（2cos2x﹣1）+1=sin2x+cos2x+1=2sin（2x+）+1（Ⅰ）函数f（x）的最小正周期为T==π（Ⅱ）由2kπ﹣≤2x+≤2kπ+得2kπ﹣≤2x≤2kπ+∴kπ﹣≤x≤kπ+，k∈Z函数f（x）的单调增区间为[kπ﹣，kπ+]，k∈Z（Ⅲ）因为x∈[﹣，]，∴2x+∈[﹣，]，∴sin（2x+）∈[，1]，∴f（x）∈[0，3]．【点评】本题考查三角函数的最值，三角函数的周期性及其求法，正弦函数的单调性，考查计算能力，此类题目的解答，关键是基本的三角函数的性质的掌握熟练程度，是基础题．22.在中，三内角的对边分别为，面积为，若，则等于（）A．B．C．D．【答案】A【解析】因为，所以，所以，化为，又因为，解得或（舍去），所以．【考点】余弦定理．23.已知函数，（1）求函数的单调递减区间；（2）求函数的极小值和最大值，并写明取到极小值和最大值时分别对应的值．【答案】（1）;（2）详见解析．【解析】（1）先求函数的导数，并且根据辅助角公式化简函数，并求导数在的零点，同时讨论零点两侧的单调性，确定函数的单调递减区间；（2）根据（1）的讨论，可求得极值点和极值以及端点值的大小，经比较可得函数的最大值以及极小值．试题解析：（1）f′（x）＝cosx＋sinx＋1＝sin（x＋）＋1 （）令f′（x）＝0，即sin（x＋）＝－，解之得x＝π或x＝π．x，f′（x）以及f（x）变化情况如下表：（π，π）π（π，2π）－0＋∴f（x）的单调减区间为（π，π）．＝f（）＝．（2）由（1）知f （x）极小而f（π）＝π＋2，，所以．【考点】导数的简单应用24.在一个港口，相邻两次高潮发生的时间相距，低潮时水深为，高潮时水深为．每天潮涨潮落时，该港口水的深度（）关于时间（）的函数图象可以近似地看成函数的图象，其中，且时涨潮到一次高潮，则该函数的解析式可以是（）A．B．C．D．【答案】A【解析】由题意分析可知函数的最大值为15，最小值为9，周期T=12，所以，又当t=3时，函数取得最大值，所以答案为A。

三角恒等变换(测试题及答案)

三角恒等变换(测试题及答案)三角恒等变换测试题第I卷一、选择题（本大题共12个小题，每小题5分，共60分）1.求cos24cos36-cos66cos54的值。

A。

0.B。

1/2.C。

1/4.D。

1/82.已知tan(α+β)=3，tan(α-β)=5，则tan(2α)的值为：A。

1/2.B。

2/3.C。

3/4.D。

4/53.函数y=sin(x)+cos(x)的最小正周期为：A。

π。

B。

2π。

C。

4π。

D。

π/24.已知等腰三角形顶角的余弦值等于4/5，则这个三角形底角的正弦值为：A。

3/5.B。

4/5.C。

5/6.D。

5/45.α,β都是锐角，且sin(α)=1/3，cos(α+β)=-1/2，则sin(β)的值是：A。

-2/3.B。

-1/3.C。

1/3.D。

2/36.已知-x<π/3且cos(-x)=-√3/2，则cos(2x)的值是：A。

-7/24.B。

-1/8.C。

1/8.D。

7/247.函数y=sin(x)+cos(x)的值域是：A。

[0,1]。

B。

[-1,1]。

C。

[-1/2,1/2]。

D。

[1/2,√2]8.将y=2sin(2x)的图像向左平移π/4个单位，得到y=3sin(2x)-cos(2x)的图像，只需将y=2sin(2x)的图像：A。

向右平移π/4个单位。

B。

向左平移π/4个单位C。

向右平移π/2个单位。

D。

向左平移π/2个单位9.已知等腰三角形顶角的正弦值等于4/5，则这个三角形底角的余弦值为：A。

3/5.B。

4/5.C。

5/6.D。

5/410.函数y=sin(x)+3cos(2x)的图像的一条对称轴方程是：A。

x=π/4.B。

x=π/6.C。

x=π/2.D。

x=π/3二、填空题（本大题共4小题，每小题5分，共20分．请把答案填在题中的横线上）11.已知α,β为锐角，cosα=1/10，cosβ=1/5，则α+β的值为__ π/6 __。

12.在△ABC中，已知tanA,tanB是方程3x^2-7x+2=0的两个实根，则tanC=__ 1/2 __。

高三数学三角函数三角恒等变换解三角形试题答案及解析

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知函数的图象上关于轴对称的点至少有3对，则实数的取值范围是（）A．B．C．D．【答案】A【解析】原函数在轴左侧是一段正弦型函数图象，在轴右侧是一条对数函数的图象，要使得图象上关于轴对称的点至少有对，可将左侧的图象对称到轴右侧，即，应该与原来轴右侧的图象至少有个公共点如图，不能满足条件，只有此时，只需在时，的纵坐标大于，即，得．【考点】分段函数，函数图象，正弦型函数，对数函数2.若，则函数的最大值是___________．【答案】【解析】由题意因为，所以，所以函数的最大值是．【考点】求最大值．3.已知，，则下列不等式一定成立的是A．B．C．D．【答案】D【解析】,【考点】三角函数的性质4.若，且为第二象限角，则（）A．B．C．D．【答案】B【解析】由得又为第二象限角，所以，选B．【考点】两角差余弦公式5.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．-2D．【答案】C【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选C．【考点】三角函数的性质．6.设的最小值为，则．【答案】【解析】，根据题意，结合二次函数在某个区间上的最值问题，对参数进行讨论，当时，其最小值为，所以不合题意，当时，其最小值为，解得，当时，其最小值为，无解，所以．【考点】倍角公式，二次函数在给定区间上的最值问题．7.设函数对任意的，都有，若函数，则的值是（）A．1B．-5或3C．D．-2【答案】D【解析】根据题意有是函数图像的对称轴，从而有，所以有，故选D．【考点】三角函数的性质．8.下列函数中，以为最小正周期的偶函数是（）A．y=sin2x+cos2xB．y=sin2xcos2xC．y=cos（4x+）D．y=sin22x﹣cos22x【答案】D【解析】因为A项为非奇非偶函数，B项是奇函数，C项是奇函数，只有D项是符合题意的，故选D．【考点】诱导公式，倍角公式，三角函数的奇偶性和周期．9.函数的最大值为．【答案】【解析】解析式表示过的直线的斜率，由几何意义，即过定点（4，3）与单位圆相切时的切线斜率为最值．所以设切线得斜率为k，则直线方程为，即 ,【考点】三角函数最值【方法点睛】本题主要考查三角函数最值问题及转化的思想，解决问题的根据是根据所给函数式子转化为直线与圆的位置关系问题，即将所给式子看做定点与单位圆上点的连线的斜率的范围问题，通过模型转化使问题定点巧妙解决，属于经典试题．10.（本题满分12分）如图，在中，边上的中线长为3，且，．（1）求的值；（2）求边的长．【答案】（1）（2）4【解析】（1）利用角的关系，再结合两角差正弦公式展开就可求解（2）先在三角形ABD中，由正弦定理解出BD长，即CD长：由正弦定理，得，即，解得…故；再在三角形ADC中由余弦定理解出AC：；AC= 4试题解析：（1）（2）在中，由正弦定理，得，即，解得…故，从而在中，由余弦定理，得；AC= 4 ；【考点】正余弦定理11.中，，则的最大值为．【答案】【解析】设，由余弦定理的推论，所以，设，代入上式得，，故，当时，此时，符合题意，因此最大值为，故答案为：．【考点】解三角形．【思路点睛】首先假设，然后再根据余弦定理的推论，可得，找到与的关系，再设，代入上式得，利用根的判别式，进而求出结果．本题的关键是利用余弦定理的推论．12.已知函数的部分图象如图所示．（1）求函数的解析式；（2）若，求函数在区间上的单调减区间．【答案】（1）；（2），．【解析】（1）由图象中的最高点和最低点的纵坐标得到关于的方程组求得，再利用图象得到函数的周期，进而得到值，最后代入最低点坐标或最高点坐标结合的范围求出，即得到函数的解析式；（2）先求出，利用两角和差的正弦公式将其化为的形式，再利用整体思想求其单调递减区间．试题解析：（1）由图知，解得，又，所以，所以，将点代入，得，再由，得，所以；（2）因为由，解得；又，故所求的单调减区间为，．【考点】1.三角函数的图象与性质；2.三角恒等变形．13.已知角的终边经过点（-4，3），则= ，= ；【答案】;【解析】由题意可得.【考点】任意角三角函数的定义.14.在△ABC中，a、b、c分别是角A、B、C的对边，且．（Ⅰ）求角B的大小；（Ⅱ）若，求△ABC的面积．【答案】（Ⅰ）；（Ⅱ）．【解析】（Ⅰ）在解三角形的背景下，考查正弦定理，余弦定理，知值求值．（Ⅱ）综合余弦定理，求三角形的面积公式，需要把作为整体求之．试题解析：（Ⅰ）由正弦定理得将上式代入已知即，即．∵∵∵B为三角形的内角，∴．（Ⅱ）由余弦定理得，结合，可得，所以△ABC的面积．【考点】正弦定理，余弦定理，三角形的面积公式．15.在△中，角，，所对的边分别为，，，表示△的面积，若，，则．【答案】【解析】∵，∴，∴，∴，．∵，∴，∴，∴，∴．【考点】解三角形．【思路点睛】先利用余弦定理和三角形的面积公式可得，可得，再用正弦定理把中的边换成角的正弦，利用两角和公式化简整理可求得，最后根据三角形内角和，进而求得．16.中，角A，B，C的对边分别为a，b，c，若的面积，则 .【答案】【解析】由余弦定理，，又，，，即，，．【考点】1、余弦定理；2、同角三角函数的基本关系；3、三角形面积公式.【思路点睛】本题主要考查的是余弦定理、同角三角函数基本关系、三角形的面积公式，属于容易题.因为题目求，且的面积，边的平方的形式一般想到余弦定理，面积展开后利用余弦定理即可求得与的关系，从而利用同角三角函数的基本关系求得.17.（2012•安徽）设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC．（Ⅰ）求角A的大小；（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．【答案】（Ⅰ）；（Ⅱ）【解析】（Ⅰ）根据2sinBcosA=sinAcosC+cosAsinC，可得2sinBcosA=sin（A+C），从而可得2sinBcosA=sinB，由此可求求角A的大小；（Ⅱ）利用b=2，c=1，A=，可求a的值，进而可求B=，利用D为BC的中点，可求AD的长．解：（Ⅰ）∵2sinBcosA=sinAcosC+cosAsinC∴2sinBcosA=sin（A+C）∵A+C=π﹣B∴sin（A+C）=sinB＞0∴2sinBcosA=sinB∴cosA=∵A∈（0，π）∴A=；（Ⅱ）∵b=2，c=1，A=∴a2=b2+c2﹣2bccosA=3∴b2=a2+c2∴B=∵D为BC的中点，∴AD=．【考点】余弦定理；三角函数的恒等变换及化简求值．18.在中，已知．（Ⅰ）求sinA与角B的值；（Ⅱ）若角A,B,C的对边分别为的值．【答案】（Ⅰ）；（Ⅱ），．【解析】（I）给出了关于角的两个三角函数值，利用诱导公式和同角三角函数的基本关系式可求得其正弦、余弦，再根据三角形的性质可求得的值；（II）在第一问的基础上，利用正弦定理可求得边，再由余弦定理求边，注意利用三角形基本性质舍解．试题解析：（Ⅰ）∵，，又∵，．∵，且，．（Ⅱ）由正弦定理得，，另由得，解得或（舍去），，．【考点】三角函数的诱导公式，同角三角函数的基本关系式及利用正、余弦定理在解三角形．19.已知，则的值为．【答案】．【解析】，故填：．【考点】三角恒等变形．20.在中，角A，B，C的对边分别为，，，若，则角的值为（）A．或B．或C．D．【答案】A．【解析】，，∴或，故选A．【考点】余弦定理．【思路点睛】由已知条件，可先将切化弦，再结合正弦定理，将该恒等式的边都化为角，然后进行三角函数式的恒等变形，找出角之间的关系；或将角都化成边，然后进行代数恒等变形，可一题多解，多角度思考问题，从而达到对知识的熟练掌握．21.为了得到函数的图象，只需把函数图象上的所有点（）A．横坐标缩短到原来的倍，纵坐标不变B．横坐标伸长到原来的2倍，纵坐标不变C．纵坐标缩短到原来的倍，横坐标不变D．纵坐标缩短到原来的2倍，横坐标不变【答案】A【解析】这是一个三角函数的图象变换问题，一般的为了得到函数的图象，只需把函数的图象上所有点的横坐标伸长（）或缩短（）到原来的倍（纵坐标不变）即可，因此为了得到函数的图象，只需把函数图象上的所有点横坐标缩短到原来的倍，纵坐标不变，故选A.【考点】三角函数的图象变换．【方法点睛】本题是一个三角函数的图象变换问题，属于容易题.一般的要得到函数（其中）的图像可按以下步骤进行：先把的图象向左（）或向右（）平移个单位，再将所得函数的图象上各点的横坐标扩大（）或缩小（）为原来的（纵坐标不变），再把所得函数图象上各点的纵坐标扩大（）或缩小（）为原来的倍（横坐标不变），最后再将所得图像向上（）或向下（）平移个单位，即可得到函数的图象.22.如图，在中，，，点在边上，且，.（I）求；（II）求的长.【答案】（Ⅰ）；（Ⅱ），.【解析】（Ⅰ）由图可知，所以，又，所以，再由两角差的正弦公式可求得；（Ⅱ）由题意可用正弦定理、余弦定理即可求出、的长，在中，有，又从而可求得；在中，由余弦定理得，，从而可求出.试题解析：（Ⅰ）在中，因为，所以，所以（Ⅱ）在中，由正弦定理得，在中，由余弦定理得，所以【考点】1.解三角形；2.两角差的正弦公式.23.设的内角对边分别为，已知，且.（1）求角的大小；（2）若向量与共线，求的值.【答案】(1);(2)。

高二数学三角函数三角恒等变换解三角形试题

高二数学三角函数三角恒等变换解三角形试题1.已知⊿ABC和⊿BCD均为边长等于的等边三角形，且，则二面角的大小为（）A．30°B．45°C．60°D．90°【答案】C【解析】略2.锐角中，已知，则的取值范围是（）A．B．C．D．【答案】C【解析】由正弦定理可得，所以．因为为锐角三角形，所以．即．故C正确．【考点】1正弦定理；2三角函数化简求值．3.在中，三内角、、的对边分别是、、．（1）若求；（2）若，，试判断的形状．【答案】（1）或；（2）等边三角形【解析】（1）由题根据正弦定理得到，因为，所以，可得或；（2）根据正弦定理化简可得，结合条件，得到，判断三角形为等边三角形．试题解析：（1）由正弦定理得：又∴∴或（2）由得又是等边三角形．【考点】正弦定理；余弦定理4.圆锥的表面积是底面积的3倍，则该圆锥的侧面展开图扇形的圆心角的弧度数为．【答案】【解析】设母线长为R，底面半径为r，∴底面周长=，底面面积=，侧面面积，∵侧面积是底面积的3倍，∴，【考点】扇形和圆锥的相关计算5.在中，内角A 、B、C对的边长分别是a、b、c．（1）若c=2,C=,且的面积是，求a,b的值；（2）若,试判断的形状．【答案】（1）a=2, b=2（2）等腰三角形【解析】（Ⅰ）根据余弦定理，得，再由面积正弦定理得，两式联解可得到a，b的值；（Ⅱ）根据三角形内角和定理，得到sinC=sin（A+B），代入已知等式，展开化简合并，得sinBcosA=sinAcosA，最后讨论当cosA=0时与当cosA≠0时，分别对△ABC 的形状的形状加以判断，可以得到结论试题解析：（1）由余弦定理得又的面积为，得ab=4 解得 a=2, b=2（2）得得,为直角三角形；当时，A="B," 为等腰三角形【考点】1．正余弦定理解三角形；2．三角函数基本公式6.在中，，则边的长为（）A．B．3C．D．7【答案】A【解析】由三角形的面积公式，得，解得；由余弦定理，得，即；故选A．【考点】1．三角形的面积公式；2．余弦定理．7.在△ABC中，A=60°，，，则B=（）A．45°B．135°C．45°或135°D．以上答案都不对【答案】A【解析】由正弦定理，得，即，因为，所以，所以；故选A．【考点】正弦定理．【易错点睛】本题考查正弦定理的应用，属于基础题；在三角形中，若已知两边及其中一边的对角，则选用正弦定理求另一边的对角，但满足该条件的三角形并非唯一，可能一解、两解或无解，要根据题目中的条件合理取舍，如本题中由正弦定理得到后，部分学生会出现选C的错误答案，要注意利用“大边对大角”进行取舍．8.已知的三边长分别为，则的面积为__________．【答案】【解析】的边长由余弦定理得，，所以三角形的面积为．【考点】1、余弦定理的运用；2、三角形的面积公式．9.△ABC的内角A、B、C的对边分别为a、b、c，若a、b、c成等比数列，且c=2a，则cosB=（）A． B． C． D．【解析】根据等比数列的性质，可得b=a，将c、b与a的关系结合余弦定理分析可得答案．解：△ABC中，a、b、c成等比数列，则b2=ac，由c=2a，则b=a，=，故选B．【考点】余弦定理；等比数列．10.（2015秋•河南期末）已知△ABC的三内角A，B，C成等差数列，且AB=1，BC=4，则该三角形面积为（）A．B．2C．2D．4【答案】A【解析】由A，B，C成等差数列A+B+C=π可求B，利用三角形的面积公式S=bcsinA可求．解：∵△ABC三内角A，B，C成等差数列，∴B=60°又AB=1，BC=4，∴；故选A．【考点】三角形的面积公式．11.边长为5、7、8的三角形的最大角与最小角之和为（）A．90°B．120°C．135°D．150°【答案】B【解析】长为7的边对应的角满足，，所以最大角与最小角之和为120°【考点】余弦定理解三角形12.（2015秋•珠海期末）△ABC内角A，B，C的对边分别为a，b，c．已知，则B= ．【答案】45°．【解析】由已知及正弦定理可得sinB==，根据大边对大角由b＜a可得B∈（0，60°），即可求B的值．解：△ABC中，∵，∴由正弦定理可得：sinB===，∵b＜a，∴B∈（0，60°），∴B=45°．故答案为：45°．【考点】正弦定理．13.在锐角△ABC中，内角A，B，C的对边分别为a，b，c，且2asinB=b．（1）求角A的大小；（2）若a=4，b+c=8，求△ABC的面积．【答案】（1）（2）4【解析】（1）由正弦定理将已知等式化成角的正弦的形式，化简解出sinA=，再由△ABC是锐角三角形，即可算出角A的大小；（2）由余弦定理a2=b2+c2﹣2bccosA的式子，结合题意化简得b2+c2﹣bc=16，与联解b+c=8得到bc的值，再根据三角形的面积公式加以计算，可得△ABC的面积．解：（1）∵△ABC中，，∴根据正弦定理，得，∵锐角△ABC中，sinB＞0，∴等式两边约去sinB，得sinA=∵A是锐角△ABC的内角，∴A=；（2）∵a=4，A=，∴由余弦定理a2=b2+c2﹣2bccosA，得16=b2+c2﹣2bccos，化简得b2+c2﹣bc=16，∵b+c=8，平方得b2+c2+2bc=64，∴两式相减，得3bc=48，可得bc=16．因此，△ABC的面积S=bcsinA=×16×sin=4．【考点】余弦定理；正弦定理．14.在中，角对边分别是，且满足.（1）求角的大小；（2）若，且的面积为，求.【答案】（1）；（2）.【解析】（1）利用正弦定理，化边为角，利用两角差的正弦公式，可得进而得，即可求解角的大小；（2）利用三角形的面积公式得，再利用余弦定理得，联立方程组即可求解的值.试题解析：（1）；（2）①，利用余弦定理得：即②，联立①②，解得：.【考点】正弦定理、余弦定理及三角形的面积公式.15.在中，内角所对的边分别为，且.（1）求角的大小；（2）如果，求面积的最大值，并判断此时的形状。

高中数学三角函数及三角恒等变换精选题目(附解析)

高中数学三角函数及三角恒等变换精选题目（附解析）一、三角函数的定义若角α的终边上任意一点P (x ，y )(原点除外)，r ＝|OP |＝x 2＋y 2，则sin α＝y r ，cos α＝x r ，tan α＝y x (x ≠0)．1.已知角α的终边过点P (－3cos θ，4cos θ)，其中θ∈⎝ ⎛⎭⎪⎫π2，π，则sin α＝________，tan α＝________.[解析] ∵θ∈⎝ ⎛⎭⎪⎫π2，π，∴cos θ＜0，∴r ＝x 2＋y 2＝9cos 2θ＋16cos 2θ＝－5cosθ，故sin α＝y r ＝－45，tan α＝y x ＝－43.[答案] －45 －43 注：利用三角函数定义求函数值的方法当已知角的终边所经过的点或角的终边所在的直线时，一般先根据三角函数的定义求这个角的三角函数值，再求其他．但当角经过的点不固定时，需要进行分类讨论．求与正切函数有关问题时，不要忽略正切函数自身的定义域．2．已知点M ⎝ ⎛⎭⎪⎫13，a 在函数y ＝log 3x 的图象上，且角θ的终边所在的直线过点M ，则tan θ＝( )A ．－13 B ．±13 C ．－3D ．±3解析：选C 因为点M ⎝ ⎛⎭⎪⎫13，a 在函数y ＝log 3x 的图象上，所以a ＝log 313＝－1，即M ⎝ ⎛⎭⎪⎫13，－1，所以tan θ＝－113＝－3，故选C.3．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线y ＝2x 上，则cos 2θ＝( )A ．－45B ．－35 C.35D.45解析：选B 在角θ的终边上任取一点P (a,2a )(a ≠0)．则r 2＝|OP |2＝a 2＋(2a )2＝5a 2. 所以cos 2θ＝a 25a 2＝15，cos 2θ＝2cos 2 θ－1＝25－1＝－35.4．若θ是第四象限角，则点P (sin θ，tan θ)在第________象限．解析：∵θ是第四象限角，则sin θ＜0，tan θ＜0， ∴点P (sin θ，tan θ )在第三象限．答案：三二、同角三角函数的基本关系及诱导公式①牢记两个基本关系式sin 2α＋cos 2α＝1及sin αcos α＝tan α，并能应用两个关系式进行三角函数的求值、化简、证明．②诱导公式可概括为k ·π2±α(k ∈Z)的各三角函数值的化简公式．记忆规律是：奇变偶不变，符号看象限．其中的奇、偶是指π2的奇数倍或偶数倍，变与不变是指函数名称的变化．5.已知2＋tan (θ－π)1＋tan (2π－θ)＝－4，求(sin θ－3cos θ)(cos θ－sin θ)的值．[解] 法一：由已知得2＋tan θ1－tan θ＝－4，∴2＋tan θ＝－4(1－tan θ)，解得tan θ＝2.∴(sin θ－3cos θ)(cos θ－sin θ ) ＝4sin θcos θ－sin 2θ－3cos 2θ ＝4sin θcos θ－sin 2θ－3cos 2θsin 2θ＋cos 2θ＝4tan θ－tan2θ－3tan2θ＋1＝8－4－34＋1＝15.法二：由已知得2＋tan θ1－tan θ＝－4，解得tan θ＝2.即sin θcos θ＝2，∴sin θ＝2cos θ.∴(sin θ－3cos θ)(cos θ－sin θ)＝(2cos θ－3cos θ)(cos θ－2cos θ)＝cos2θ＝cos2θsin2θ＋cos2θ＝1tan2θ＋1＝15.注：三角函数式的求值、化简、证明的常用技巧(1)化弦：当三角函数式中三角函数名称较多时，往往把三角函数化为弦，再化简变形．(2)化切：当三角函数式中含有正切及其他三角函数时，有时可将三角函数名称都化为正切，再变形化简．(3)“1”的代换：在三角函数式中，有些会含有常数1，常数1虽然非常简单，但有些三角函数式的化简却需要利用三角函数公式将“1”代换为三角函数式．6．若sin(π＋α)＝35，且α是第三象限角，则sin⎝⎛⎭⎪⎫π2＋α－cos⎝⎛⎭⎪⎫π2＋αsin⎝⎛⎭⎪⎫π2－α－cos⎝⎛⎭⎪⎫π2－α＝()A．1B．7 C．－7 D．－1解析：选B由sin(π＋α)＝35，得sin α＝－35.又α是第三象限角，所以cos α＝－4 5，所以sin⎝⎛⎭⎪⎫π2＋α－cos⎝⎛⎭⎪⎫π2＋αsin⎝⎛⎭⎪⎫π2－α－cos⎝⎛⎭⎪⎫π2－α＝cos α＋sin αcos α－sin α＝－45＋⎝ ⎛⎭⎪⎫－35－45－⎝ ⎛⎭⎪⎫－35＝7.7．已知sin θ＋cos θ＝43，且0＜θ＜π4，则sin θ－cos θ的值为( )A.23 B ．－23 C.13D ．－13解析：选B ∵sin θ＋cos θ＝43，∴1＋2sin θcos θ＝169，则2sin θcos θ＝79.又0＜θ＜π4，所以sin θ－cos θ＜0，故sin θ－cos θ＝－(sin θ－cos θ)2＝－1－2sin θcos θ＝－23，故选B.8．已知α为第三象限角，且sin α＋cos α＝2m,2sin αcos α＝m 2，则m 的值为________．解析：由(sin α＋cos α)2＝1＋2sin αcos α，得4m 2＝1＋m 2，即m 2＝13.又α为第三象限角，所以sin α<0，cos α<0，则m <0，所以m ＝－33.答案：－339．已知sin(3π－α)＝2cos ⎝ ⎛⎭⎪⎫3π2＋β，cos(π－α)＝63cos(π＋β)，且0＜α＜π，0＜β＜π，求sin α和cos β的值．解：由已知，得sin α＝2sin β，① 3cos α＝2cos β，②由①2＋②2，得sin 2α＋3cos 2α＝2，即sin 2α＋3(1－sin 2α)＝2，所以sin 2α＝12. 又0＜α＜π，则sin α＝22. 将sin α＝22代入①，得sin β＝12.又0＜β＜π，故cos β＝±32.三、简单的三角恒等变换两角和与差的正弦、余弦、正切公式 ①sin(α±β)＝sin αcos β±cos αsin β； ②cos(α±β)＝cos αcos β∓sin αsin β； ③tan(α±β)＝tan α±tan β1∓tan αtan β.二倍角的正弦、余弦、正切公式 ①sin 2α＝2sin αcos α；②cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α； ③tan 2α＝2tan α1－tan 2α.10.已知tan α＝2. (1)求tan ⎝ ⎛⎭⎪⎫α＋π4的值；(2)求sin 2αsin 2α＋sin αcos α－cos 2α－1的值．[解] (1)tan ⎝ ⎛⎭⎪⎫α＋π4＝tan α＋tan π41－tan αtan π4＝2＋11－2×1＝－3.(2)sin 2αsin 2α＋sin αcos α－cos 2α－1＝2sin αcos αsin 2α＋sin αcos α－2cos 2α＝2tan αtan 2α＋tan α－2＝2×24＋2－2＝1.注：条件求值的解题策略(1)分析已知角和未知角之间的关系，正确地用已知角来表示未知角． (2)正确地运用有关公式将所求角的三角函数值用已知角的三角函数值来表示．(3)求解三角函数中给值求角的问题时，要根据已知求这个角的某种三角函数值，然后结合角的取值范围，求出角的大小．11．若θ∈⎣⎢⎡⎦⎥⎤π4，π2，sin 2θ＝378，则sin θ＝( )A.35 B.45 C.74D.34解析：选D 因为θ∈⎣⎢⎡⎦⎥⎤π4，π2，所以2θ∈⎣⎢⎡⎦⎥⎤π2，π，所以cos 2θ<0，所以cos 2θ＝－1－sin 22θ＝－18.又cos 2θ＝1－2sin 2θ＝－18，所以sin 2θ＝916，所以sin θ＝34.12．已知sin ⎝ ⎛⎭⎪⎫α＋π3＋sin α＝－435，－π2＜α＜0，则cos ⎝ ⎛⎭⎪⎫α＋8π3等于( )A ．－45 B ．－35 C.35D.45解析：选D 因为sin ⎝ ⎛⎭⎪⎫α＋π3＋sin α＝－435，所以sin ⎝ ⎛⎭⎪⎫α＋π3＋sin ⎝ ⎛⎭⎪⎫α＋π3－π3＝－435，所以sin ⎝ ⎛⎭⎪⎫α＋π3＋sin ⎝ ⎛⎭⎪⎫α＋π3cos π3－cos ⎝ ⎛⎭⎪⎫α＋π3sin π3＝－435，所以32sin ⎝ ⎛⎭⎪⎫α＋π3－32cos ⎝ ⎛⎭⎪⎫α＋π3＝－435，所以－3⎣⎢⎡⎦⎥⎤12cos ⎝ ⎛⎭⎪⎫α＋π3－32sin ⎝ ⎛⎭⎪⎫α＋π3＝－435，即－3cos ⎝ ⎛⎭⎪⎫α＋π3＋π3＝－435，cos ⎝ ⎛⎭⎪⎫α＋2π3＝45，所以cos ⎝ ⎛⎭⎪⎫α＋8π3＝cos ⎝ ⎛⎭⎪⎫α＋2π3＝45，故选D.13．(2017·全国卷Ⅲ)已知sin α－cos α＝43，则sin 2α＝( )A ．－79B ．－29 C.29D.79解析：选A 将sin α－cos α＝43的两边进行平方，得sin 2 α－2sin αcos α＋cos 2α＝169，即sin 2α＝－79.14．已知向量a ＝(1，－3)，b ＝⎝ ⎛⎭⎪⎫sin x ，2cos 2x 2－1，函数f (x )＝a ·b .(1)若f (θ)＝0，求2cos 2θ2－sin θ－12sin ⎝ ⎛⎭⎪⎫θ＋π4的值；(2)当x ∈[0，π]时，求函数f (x )的值域．解：(1)∵a ＝(1，－3)，b ＝⎝ ⎛⎭⎪⎫sin x ，2cos 2x 2－1，∴f (x )＝a ·b ＝sin x －3⎝ ⎛⎭⎪⎫2cos 2x 2－1＝sin x －3cos x .∵f (θ)＝0，即sin θ－3cos θ＝0，∴tan θ＝3，∴2cos 2θ2－sin θ－12sin ⎝ ⎛⎭⎪⎫θ＋π4＝cos θ－sin θsin θ＋cos θ＝1－tan θtan θ＋1＝1－33＋1＝－2＋ 3.(2)由(1)知f (x )＝sin x －3cos x ＝2sin ⎝ ⎛⎭⎪⎫x －π3，∵x ∈[0，π]，∴x －π3∈⎣⎢⎡⎦⎥⎤－π3，2π3，当x －π3＝－π3，即x ＝0时，f (x )min ＝－3；当x －π3＝π2，即x ＝5π6时，f (x )max ＝2，∴当x ∈[0，π]时，函数f (x )的值域为[－3，2]．。

高三数学三角函数三角恒等变换解三角形试题答案及解析

高三数学三角函数三角恒等变换解三角形试题答案及解析1.已知中，那么角=【答案】π/4【解析】略2.已知f(α)＝(1)化简f(α)；(2)若α是第三象限角，且cos(α－)＝，求f(α)的值．【答案】(1)f(α)＝＝－cosα.(2)∵α是第三象限角，且cos(α－)＝－sinα＝，∴sinα＝－，∴cosα＝－＝－，∴f(α)＝－cosα＝.【解析】略3.已知函数为奇函数，且，其中（1）求的值;（2）若，求的值．【答案】（1） , ；（2）【解析】（1）由为奇函数，可得，函数化为，又根据可求；（2）由（1）可得，由得又因为，所以，再根据两角和的正弦可求试题解析：因为为奇函数，所以，，则（2），因为，即又因为，所以，【考点】函数的奇偶性，三角函数的性质4.设命题函数是奇函数；命题函数的图象关于直线对称．则下列判断正确的是（）A．为真B．为假C．为假D．为真【答案】C【解析】因为是偶函数，所以命题是假命题，由余弦函数的性质可知命题是假命题，选项C正确.【考点】1.三角函数性质；2.逻辑联结词与命题.5.（本小题满分12分）某同学用五点法画函数在某一个周期内的图像时，列表并填入了部分数据，如下表：5-5（1）请将上表数据补充完整，并直接写出函数的解析式；（2）若函数的图像向左平移个单位后对应的函数为，求的图像离原点最近的对称中心．【答案】（1）；（2）．【解析】第一问结合三角函数的性质，确定出对应的值，完善表格，从而确定出函数解析式，第二问利用图形的平移变换，将函数的解析式求出来，利用函数的性质，找出函数图像的对称中心，给赋值，比较从而确定出离原点最近的对称中心．试题解析：（1）根据表中已知数据，解得数据补全如下表：050-50函数表达式为（2）函数图像向左平移个单位后对应的函数是，其对称中心的横坐标满足，所以离原点最近的对称中心是．【考点】三角函数的性质，图像的变换．6.（本小题满分10分）已知函数．（1）求的最小正周期；（2）设，求的值域和单调递减区间．【答案】（1）；（2）【解析】（1）先根据二倍角公式和两角和与差的公式进行化简，再求出周期即可；（2）先根据x的范围求得，再结合正弦函数的性质可得到函数f（x）的值域，求得单调递减区间．试题解析：（1）（2）∵，，的值域为．的递减区间为．【考点】三角函数的周期性及其求法；正弦函数的定义域和值域；正弦函数的单调性7.（本小题满分12分）在中，角的对边分别为，已知，向量，且∥．（1）求角的大小；（2）若成等差数列，求边的大小．【答案】（1）；（2）【解析】（1）利用数量积运算、正弦定理即可得出；（2）由成等差数列，可得，或，即2a=b．再利用直角三角形的边角关系、余弦定理即可得出．试题解析：（1）∥，得，由正弦定理可得，（2）成等差，所以化简整理得：即或得或若若【考点】正弦定理；平面向量数量积运算8.在中，角所对的边为．已知，且．（1）求的值；（2）当时，求的面积．【答案】（1）；（2）．【解析】（1）根据已知条件中的式子，结合正弦定理，将其化为的方程，即可求解；（2）利用已知条件，结合余弦定理，可求得，的值，再利用三角形面积计算公式即可求得的值．试题解析：（1）∵，∴①，又∵，∴②，联立①②，即可求得，；（2）由（1）结合余弦定理可知，或，由已知易得，∴，∴，．【考点】1．正余弦定理解三角形；2．三角恒等变形．9.（本题满分12分）已知，,函数．（1）求的最小正周期，并求其图像对称中心的坐标；（2）当时，求函数的值域．【答案】（1）的最小正周期为，其对称中心的坐标为（）（）；（2）的值域为．【解析】（1）先用降幂公式和辅助角公式，将进行化简整理得到，然后根据正弦函数的周期公式可得函数的最小正周期，进而求出函数的零点，即为函数的图像对称中心的坐标；（2）根据可得到，最后结合正弦函数的图像与性质可得函数的值域．试题解析：（1）因为=，所以的最小正周期为，令，得，∴故所求对称中心的坐标为（）（）．（2）∵，∴，∴，即的值域为．【考点】1、三角函数中的恒等变换；2、三角函数的周期性及其求法；3、正弦函数的图像及其性质．【方法点晴】本题考查了三角函数中的恒等变换、三角函数的周期性及其求法和正弦函数的图像及其性质，重点考查学生对三角函数的基本概念、基本性质和基本原理，属中档题．解决这类问题最关键的一步是运用降幂公式、倍角公式及三角函数的和差公式等将函数的表达式化简为同角的正弦或余弦形式．因此需要大家应熟练掌握相关公式并结合三角函数的图像及其性质进行求解．10.若函数在上单调递减，且在上的最大值为，则的值为（）A．B．C．D．【答案】A【解析】由题意得：，解得，选A．【考点】正切函数性质11.（本小题满分12分）已知向量，．（1）当时，求的值；（2）设函数，已知在中，内角、、的对边分别为、、，若，，，求当时，的取值范围．【答案】（1）；（2）．【解析】（1）平方关系和商数关系式中的角都是同一个角，且商数关系式中，利用，得出，把转化为的式子，从而求解；（2）熟悉三角公式的整体结构，灵活变换，要熟悉三角公式的代数结构，更要掌握公式中角和函数名称的特征，要体会公式间的联系，掌握常见的公式变形，倍角公式应用是重点，涉及倍角或半角的都可以利用倍角公式及其变形，把形如化为，研究函数的性质由的取值范围确定的取值范围，再确定的取值范围．试题解析：（1），，，（2）由正弦定理得，得或，，因此，，即．【考点】1、同角三角函数的基本关系；2、三角函数的化简；3、求三角函数的值域．12.（2012秋•泰安期中）已知函数f（x）=2sinωxcosωx﹣2sin2ωx+（ω＞0），直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2|的最小值为．（Ⅰ）求ω的值；（Ⅱ）求函数f（x）的单调增区间；（Ⅲ）若f（α）=，求sin（π﹣4α）的值．【答案】（Ⅰ）1；（Ⅱ）见解析；（Ⅲ）﹣．【解析】（I）利用二倍角公式即辅助角公式，化简函数，利用直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2|的最小值为，可得函数的最小正周期为π，根据周期公式，可求ω的值；（II）利用正弦函数的单调性，可得函数f（x）的单调增区间；（III）由f（a）=，可得sin（2a+）=，根据sin（π﹣4a）=sin[﹣2（2a+）]=﹣cos[2（2a+）]=2sin2（2a+）﹣1，即可求得结论．解：（I）∵f（x）=2sinωxcosωx﹣2sin2ωx+=sin2ωx+cos2ωx=2sin（2ωx+）∵直线x=x1，x=x2是函数y=f（x）的图象的任意两条对称轴，且|x1﹣x2|的最小值为，∴函数的最小正周期为π∴=π∴ω=1；（II）由（I）知，f（x）=2sin（2x+）∴﹣+2kπ≤2x+≤+2kπ，k∈Z∴﹣+kπ≤x≤+kπ，k∈Z∴函数f（x）的单调增区间为[﹣+kπ，+kπ]，k∈Z；（III）∵f（a）=，∴sin（2a+）=∴sin（π﹣4a）=sin[﹣2（2a+）]=﹣cos[2（2a+）]=2sin2（2a+）﹣1=﹣．【考点】三角函数中的恒等变换应用；由y=Asin（ωx+φ）的部分图象确定其解析式；复合三角函数的单调性．13.已知向量，且函数在时取得最小值．（Ⅰ）求的值；（Ⅱ）在中，分别是内角的对边，若，，，求的值．【答案】（Ⅰ）；（Ⅱ）【解析】（Ⅰ）利用向量的数量积公式，结合辅助角公式，求的值；（Ⅱ）先求出，再利用正弦定理，即可求的值．试题解析：（Ⅰ）由于（Ⅱ）由上知,于是由正弦定理得:【考点】正弦定理，余弦定理，两角和与差的三角函数，向量的数量积14.已知，函数在单调递减，则的取值范围是．【答案】【解析】，，由题意，所以，由于，所以只有，．【考点】三角函数的单调性．【名师】求形如y＝Asin（ωx＋φ）或y＝Acos（ωx＋φ）（其中A≠0，ω＞0）的函数的单调区间，可以通过解不等式的方法去解答，列不等式的原则是：①把“ωx＋φ（ω＞0）”视为一个“整体”；②A＞0（A＜0）时，所列不等式的方向与y＝sin x（x∈R），y＝cos x（x∈R）的单调区间对应的不等式方向相同（反）．15.（2015秋•南京校级期中）将函数f（x）=2sin（2x﹣）的图象向左平移m个单位（m＞0），若所得的图象关于直线x=对称，则m的最小值为．【答案】【解析】由条件利用函数y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，求得m的最小值．解：将函数f（x）=2sin（2x﹣）的图象向左平移m个单位（m＞0），可得y=2sin[2（x+m）﹣]=2sin（2x+2m﹣）的图象．∵所得的图象关于直线x=对称，∴2•+2m﹣=kπ+，k∈Z，即 m=+，k∈Z，则m的最小值为，故答案为：．【考点】函数y=Asin（ωx+φ）的图象变换．16.（2015秋•昌平区期末）已知函数．（Ⅰ）求函数f（x）的最小正周期；（Ⅱ）求函数f（x）的单调递减区间．【答案】（Ⅰ）；（Ⅱ）函数f（x）的单调递减区间是．）【解析】（Ⅰ）利用三角函数的倍角公式以及辅助角公式进行化简，即可求函数f（x）的最小正周期；（Ⅱ）利用三角函数的单调性即可求函数f（x）的单调递减区间．解：（Ⅰ）==所以最小正周期．（Ⅱ）由，得．所以函数f（x）的单调递减区间是．）【考点】三角函数中的恒等变换应用；正弦函数的图象．17.已知函数．（1）求的最小正周期和在上的单调递减区间；（2）若为第四象限角，且，求的值．【答案】（1）；（2）．【解析】（1）对的表达式进行三角恒等变形，利用三角函数的性质即可求解；（2）利用同角三角函数的基本关系求得的值后即可求解．试题解析：（1）由已知，所以最小正周期，由，得，故函数在上的单调递减区间；（2）因为为第四象限角，且，所以，所以．【考点】三角函数综合．18.已知是第二象限角，且，则（）A．B．C．D．【答案】C【解析】由,得，又∵是第二象限角,∴，∴原式=；故选C．【考点】1.诱导公式；2.同角三角函数基本关系式．19.在中，角所对的边分别为，且，则的最大值为_____.【答案】【解析】由及正弦定理得，又因为，于是可得，所以，所以，则的最大值为，故答案填.【考点】1、正弦定理；2、两角和与差的三角函数；3、基本不等式.20.将函数图象上各点的横坐标伸长到原来的倍，再向左平移个单位，纵坐标不变，所得函数图象的一条对称轴的方程是（）A．B．C．D．【答案】D【解析】将函数图象上各点的横坐标伸长到原来的倍，得，再向左平移个单位，得，令，解得，令，得，即所得函数图象的一条对称轴的方程是，故选D．【考点】三角函数的图象变换与三角函数的性质．21.设平面向量.（1）若，求的值；（2）若，求的取值范围.【答案】（1）；（2）.【解析】（1）先利用向量数量积的坐标表示求出，利用商数关系求出得值，再利用二倍角公式求出的值，最后代入到的展开式即可求得；（2）欲求，先求出，再根据求的范围，从而可得的取值范围.试题解析：（1）因为，所以，∴，∴.（2），，.【考点】1、向量数量积的坐标表示；2、二倍角公式；3、三角函数；4、商数关系；5、向量的模．22.设中的内角所对的边长分别为，且.（1）当时，求角的度数；（2）求面积的最大值.【答案】（1）；（2）.【解析】（1）求出,再由正弦定理求出,求出角；（2）求三角形面积的最大值,即求的最大值,由,,求出,就可以求出面积的最大值.试题解析：解：（1）因为，所以.因为，由正弦定理可得.因为，所以是锐角，所以.（2）因为的面积，所以当最大时，的面积最大.因为，所以.因为，所以，所以（当时等号成立）.所以面积的最大值为.【考点】1.正弦定理；2.余弦定理；3.重要不等式.23.在中，内角的对边为，已知.（1）求角的值；（2）若，且的面积为，求.【答案】（1）；（2）.【解析】根据正弦定理可得，根据内角和定理和两角和的正弦公式整理可得，即得角的值；（2）由的面积为，求得的值，根据余弦定理表示构造的另一个方程，解方程组即可求得.试题解析：（1）∵，∴，∴，即，∴，∴，又∵是三角形的内角，∴（2）∵，∴，∴，又∵，∴，∴，∴【考点】正余弦定理解三角形.24.的三个内角满足：，则（）A．B．C．D．或【答案】B【解析】由已知条件以及正弦定理可得：，即，再由余弦定理可得，所以，故选B.【考点】正弦定理、余弦定理.25.在中，角，，的对边分别是，，，已知，．（I）求的值；（II）若角为锐角，求的值及的面积．【答案】（I）；（II）【解析】（I）根据题意和正弦定理求出a的值；（II）由二倍角的余弦公式变形求出sin2A，由A 的范围和平方关系求出cosA，由余弦定理列出方程求出b的值，代入三角形的面积公式求出△ABC的面积．试题解析：（I）因为，且，所以．因为，由正弦定理，得．（II）由得．由余弦定理，得．解得或（舍负）．所以．【考点】正弦定理；余弦定理26.如图所示的是函数和函数的部分图象，则函数的解析式是（）A．B．C．D．【答案】C.【解析】由题意得，，故排除B，D；又∵，故排除A，故选C.【考点】三角函数的图象和性质．27.已知，则=（）A．B．C．D．【答案】A【解析】，故选A．【考点】和差倍半的三角函数．28.在中，角所对的边分别为,．（Ⅰ）求的值；（Ⅱ）若，，求的面积．【答案】（Ⅰ）（Ⅱ）【解析】（Ⅰ）先根据正弦定理将边统一成角：，再利用三角形内角关系、诱导公式、两角和正弦公式将三角统一成两角：，最后根据同角三角函数关系将弦化切：（Ⅱ）由（Ⅰ）易得，已知两角一对边，根据正弦定理求另一边：，利用三角形内角关系求第三角的正弦值：，最后根据面积公式求面积：试题解析：解：（Ⅰ）由及正弦定理得.所以,所以.（Ⅱ）,所以, ,,所以的面积为.【考点】正弦定理，弦化切【方法点睛】解三角形问题，多为边和角的求值问题，这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系，从而达到解决问题的目的.其基本步骤是：第一步：定条件即确定三角形中的已知和所求，在图形中标出来，然后确定转化的方向.第二步：定工具即根据条件和所求合理选择转化的工具，实施边角之间的互化.第三步：求结果.29.同时具有性质“①最小正周期是，②图象关于直线对称；③在上是增函数”的一个函数是（）A．B．C．D．【答案】C【解析】由题意得，函数的最小周期为，则，又函数图象关于直线对称，则函数为函数的最小值，则只有B、C满足，由当时，，则函数是单调递增函数，故选C．【考点】三角函数的性质．30.若函数的最大值为5，则常数______.【答案】【解析】，其中，故函数的最大值为，由已知得，，解得.【考点】三角函数的图象和性质.【名师】解决三角函数性质问题的基本思路是通过化简得到，结合角的范围求解.. 本题难度不大，能较好地考查考生的逻辑推理能力、基本计算能力等.31.定义在区间[0，]上的函数的图象与的图象的交点个数是 .【答案】7【解析】由，因为，所以故两函数图象的交点个数是7.【考点】三角函数图象【名师】求函数图象的交点个数，有两种方法：一是直接求解，如本题，解一个简单的三角方程，此方法立足于易于求解；二是数形结合，分别画出函数图象，数出交点个数，此法直观，但对画图要求较高，必须准确，尤其是要明确函数的增长幅度.32.△ABC的内角A、B、C的对边分别为a、b、c.已知，，，则b=（A）（B）（C）2 （D）3【答案】D【解析】由余弦定理得，解得（舍去），选D.【考点】余弦定理【名师】本题属于基础题,考查内容单一,根据余弦定理整理出关于b的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因,请考生切记！33.将函数y=2sin（2x+）的图像向右平移个周期后，所得图像对应的函数为A．y=2sin（2x+）B．y=2sin（2x+）C．y=2sin（2x–）D．y=2sin（2x–）【答案】D【解析】函数的周期为，将函数的图像向右平移个周期即个单位，所得图像对应的函数为，故选D.【考点】三角函数图像的平移【名师】函数图像的平移问题易错点有两个,一是平移方向,注意“左加右减”；二是平移多少个单位是对x而言的,不要忘记乘以系数.34.如图，在Rt△ABC中，AC⊥BC，D在边AC上，已知BC＝2，CD＝1，∠ABD＝45°，则AD＝．【答案】5【解析】，，所以，．【考点】解三角形．【名师】在解直角三角形时，直角三角形中的三角函数定义是解题的桥梁，利用它可以很方便地建立边与角之间的关系．35.设函数的部分图象如图所示，直线是它的一条对称轴，则函数的解析式为（）A．B．C．D．【答案】C【解析】因为直线是它的一条对称轴，排除B，D，因为图象过点，排除选项A,选C.【考点】三角函数图象与性质.36.在中，角，，的对边分别为，，，且满足，则角等于（）A．B．C．D．【答案】A【解析】由正弦定理可得，即，由余弦定理可得，所以，故应选A。

专题04：三角函数与三角恒等变换(解析版)

专题04：三角函数与三角恒等变换一、单选题1．（2021·山西晋中市·高三二模（文））已知函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭的部分图象如图所示，则使()()0f a x f a x +--=成立的a 的最小正值为（）A ．6πB ．5π C ．4π D ．3π 【答案】A【分析】利用五点作图法求出2422,11k k ω+=∈Z ，结合21112T ππω=>求出ω，将()()0f a x f a x +--=转化为函数()f x 关于直线x a =对称，根据正弦函数的图象的对称轴得到,26n a n ππ=+∈Z ，则可得到a 的最小正值. 【解答】由图象可知11012f π⎛⎫= ⎪⎝⎭，即11sin 0126ππω⎛⎫⋅+= ⎪⎝⎭，由五点作图法可知1122,126k k ππωππ⋅+=+∈Z ，解得2422,11k k ω+=∈Z ，又由图象可知21112T ππω=>，所以2411ω<，又0>ω，所以0,2k ω==．所以()2sin 26f x x π⎛⎫=+ ⎪⎝⎭．因为()()0f a x f a x +--=，所以函数()f x 关于直线x a =对称，即有2,62a n n πππ+=+∈Z ，解得,26n a n ππ=+∈Z ，所以a 的最小正值为6π. 故选：A ．【点评】关键点点睛：利用五点作图法以及周期求出ω是本题解题关键.2．（2021·江西高三其他模拟（理））若等差数列{}n a 满足22132a a +=，且11a ≥，求2312a a a a ++的取值范围（） A ．(1,1)- B ．[1,1]- C ．(,1)(1,)-∞-+∞ D ．(,1][1,)-∞-+∞【答案】B【分析】设132cos 2sin a a θθ⎧=⎪⎨=⎪⎩，[,)θππ∈-，根据11a ≥求出θ的范围，利用等差中项的性质得到2a ，再利用同角公式可求得结果.【解答】设132cos 2sin a a θθ⎧=⎪⎨=⎪⎩，[,)θππ∈-，又∵11a ≥，∴2cos 1θ≥，即2cos [,1]2θ∈，∴,44ππθ⎡⎤∈-⎢⎥⎣⎦，∴13222cos sin 222a a a θθ+==+， ∴231222cos sin 2sin 3sin cos 3tan 18223sin 3cos tan 3tan 3222cos cos sin 22a a a a θθθθθθθθθθθθθ+++++====-++++++，又∵,44ππθ⎡⎤∈-⎢⎥⎣⎦，所以tan [1,1]θ∈-，所以83[1,1]tan 3θ-∈-+， ∴2312[1,1]a a a a +∈-+．故选：B【点评】关键点点睛：利用三角换元化为三角函数求解是解题关键. 3．（2021·江苏高三一模）函数sin |21|xy x π=-的图象大致为（）A ．B ．C ．D ．【答案】D【分析】确定函数图象关于直线12x=对称，排除AC，再结合特殊的函数值的正负或函数零点个数排除B，得出正确结论．【解答】函数定义域是1|2x x⎧⎫≠⎨⎬⎩⎭，由于21y x=-的图象关于直线12x=对称，siny x=π的图象也关于直线12x=对称，因此()f x的图象关于直线12x=对称，排除AC，siny x=π有无数个零点，因此()f x也有无数个零点，且当x→+∞时，()0f x→，排除B．故选：D．【点评】思路点睛：函数图象的辨识可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势；(3)从函数的奇偶性，判断图象的对称性；(4)从函数的特征点，排除不合要求的图象.4．（2021·黑龙江哈尔滨市·哈尔滨三中高三一模（文））若1sin cos5αα+=，()0,απ∈，则1tan21tan2αα+=-（）A．3-B．13-C．13D．3【答案】A【分析】先求出43sin,cos55αα==-，1tan201tan2αα+<-，再求出21tan2()91tan2αα+=-，即得解.【解答】由已知得1sin cos5αα+=，()0,απ∈，联立22sin cos1αα+=，得4333sin ,cos ,,tan 155244282ππαααααππ==->∴<<∴<<∴>.所以1tan 201tan2αα+<-.sin21+1tan cos cos sin 22221tansin cossin22221cos2αααααααααα++==---,所以221tan cos sin1sin 222()()91sin 1tan cos sin 222αααααααα+++===---, 所以1tan 231tan 2αα+=--.故选：A【点评】关键点睛：解答本题的关键是通过已知分析出324παπ<<，得到1tan201tan 2αα+<-. 解答三角函数求值时，如果出现多解，经常要挖掘题目中的隐含范围解答.5．（2021·安徽淮南市·高三一模（文））已知函数()0()cos f x x x =≥，方程()f x kx =恰有两个根，记较大的根为θ，则sin 2θ=（） A ．21θθ+ B ．21θθ-+ C ．221θθ- D ．221θθ-+ 【答案】D【分析】将方程的根转化为两个函数图像的交点问题，结合导数知识求取切线方程，再结合三角计算可得. 【解答】如图所示：函数()0()cos f x x x =≥的图像与()f x kx =恰有两个交点，且最大的根为θ，则函数()f x 在x θ=处的切线为y kx =，显然,2x ππ⎛⎫∈ ⎪⎝⎭，当,2x ππ⎛⎫∈ ⎪⎝⎭时()cos cos f x x x =-=，则()sin f x x '=，切点坐标为(),cos θθ-所以由点斜式得切线方程为()cos sin y x θθθ+=-即sin sin cos y x kx θθθθ=--= 所以sin cos 0θθθ--=得1tan θθ=-， 22222122sin cos 2tan 2sin 22sin cos sin cos 1tan 111θθθθθθθθθθθθθ⎛⎫- ⎪-⎝⎭=====+++⎛⎫-+ ⎪⎝⎭ 故选：D6．（2021·江西高三其他模拟（文））已知函数()sin 232f x x x =-，则下列说法正确的是（）A ．()f x 的最大值是13+B ．()f x 在0,2π⎛⎫⎪⎝⎭上是递增的C ．551212f x f x ππ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭D ．()f x 向右平移6π后为奇函数【答案】C【分析】由两角差正弦公式化函数为一个角的一个三角函数形式，然后结合正弦函数性质判断各选项．【解答】由题意13()2sin 222sin 2223f x x x x π⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭， ∴函数最大值为2，A 错；0,2x π⎛⎫∈ ⎪⎝⎭时，22,333x πππ⎛⎫-∈- ⎪⎝⎭，232x ππ-=，即512x π=时，()f x 取得最大值2，()f x在0,2π⎛⎫ ⎪⎝⎭上不可能是递增的，B 错，实际上在50,12π⎛⎫⎪⎝⎭上递增，在5,122ππ⎛⎫ ⎪⎝⎭上递减；由上面解析知()f x 的图象关于直线512x π=对称，C 正确； ()f x 向右平移6π得2()2sin 2()2sin 2633g x x x πππ⎡⎤⎛⎫=--=- ⎪⎢⎥⎣⎦⎝⎭不是奇函数，D 错．故选：C ．【点评】方法点睛：本题考查两角差的正弦公式，二倍角公式，考查正弦函数的性质．此类问题的解题方法是：利用二倍角公式降幂，利用诱导公式、两角和与差的正弦（余弦）公式展开与合并，最终把函数化为()sin()f x A x m ωϕ=++形式，然后结合正弦函数性质求解．7．（2021·安徽黄山市·高三一模（理））已知2tan 4tan 10θθ-+=，则2cos 4πθ⎛⎫+=⎪⎝⎭（） A ．12B ．13C ．14 D ．15【答案】C【分析】由所给等式利用同角三角函数的关系可求得1cos sin 4θθ⋅=，再利用降幂公式及二倍角公式将2cos 4πθ⎛⎫+ ⎪⎝⎭整理为12sin cos 2θθ-，代入相应值即可得解. 【解答】由2tan 4tan 10θθ-+=可得1tan 4tan θθ+= 所以sin cos 4cos sin θθθθ+=，即22sin cos 4cos sin θθθθ+=⋅，即1cos sin 4θθ⋅= 211cos 2121sin 212sin cos 124cos 422224πθπθθθθ⎛⎫++-⨯⎪--⎛⎫⎝⎭+===== ⎪⎝⎭ 故选：C【点评】关键点睛：本题考查同角三角函数的关系、降幂公式、二倍角公式，解答本题的关键是由条件有1tan 4tan θθ+=，从而可得1cos sin 4θθ⋅=，由21cos 21sin 212sin cos 2cos 4222πθπθθθθ⎛⎫++ ⎪--⎛⎫⎝⎭+=== ⎪⎝⎭可解，属于中档题.8．（2021·湖南长沙市·长郡中学高三二模）已知函数()sin()f x x πϕ=+某个周期的图象如图所示，A ，B 分别是()f x 图象的最高点与最低点，C 是()f x 图象与x 轴的交点，则tan ∠BAC ＝（）A ．12B ．47C 255D 76565【答案】B【分析】过A 作AD 垂直于x 轴于点D ，AB 与x 轴交于E ，设C （a ，0），可得32CD =，11,2AD DE ==，3tan 2CD CAD AD ∠==，1tan 2ED EAD AD ∠==，再利用tan tan()BAC CAD EAD ∠=∠-∠计算即可.【解答】过A 作AD 垂直于x 轴于点D ，AB 与x 轴交于E ，由题可得周期为2，设(,0)C a ，则1(,1)2B a +-，3(,1)2A a +，所以32CD =，11,2AD DE ==，3tan 2CD CAD AD ∠==，1tan 2ED EAD AD ∠== 所以tan tan tan tan()1tan tan CAD EADBAC CAD EAD CAD EAD∠-∠∠=∠-∠=+∠⋅∠31422317122-==+⨯.故选：B【点评】本题主要考查两角差的正切公式，涉及到正弦型函数图象等知识，考查学生数学运算能力，是一道中档题.9．（2021·云南曲靖市·高三一模（理））若1cos 36πα⎛⎫+=- ⎪⎝⎭，且263ππα<<，则7sin 12πα⎛⎫+= ⎪⎝⎭（） A ．70212-B ．70212C ．27012D ．70212【答案】B【分析】利用同角三角函数的基本关系,结合题中α的范围求出sin 3πα⎛⎫+ ⎪⎝⎭,由两角和的正弦公式即可求解.【解答】因为263a ππ<<，所以23ππαπ<+<，sin 03πα⎛⎫+> ⎪⎝⎭，所以sin 3πα⎛⎫+= ⎪⎝⎭2135166⎛⎫--= ⎪⎝⎭，∴7sin sin sin cos cos sin12343434πππππππαααα⎛⎫⎛⎫⎛⎫⎛⎫+=++=+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭35212262=-⨯=702-故选：B【点评】本题考查同角三角函数的基本关系和两角和的正弦公式;考查运算求解能力;熟练掌握象限角的三角函数符号和两角和的正弦公式是求解本题的关键;属于中档题、常考题型.10．（2021·山西晋中市·高三二模（理））设()sin 2cos 2f x a x b x =+，其中0,0a b >>，若()6f x f π⎛⎫⎪⎝⎭对任意的x ∈R 恒成立，则下列说法正确的是（） A ．7105f f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭B ．对任意的x ∈R 有5()06f x f x π⎛⎫+-=⎪⎝⎭成立 C ．()f x 的单调递增区间是2,(k )63k k ππππ⎡⎤++∈⎢⎥⎣⎦Z D ．存在经过点(,)a b 的直线与函数()f x 的图象不相交【答案】B【分析】首先把函数解析式变形为正弦型函数，进一步利用函数的性质：函数的对称性/函数最值/函数的单调性的应用判定各选项正确与否.【解答】22()sin 2cos2)tan b f x a x b x x a b a ϕϕ⎫=+=++=⎪⎭，又1sin cos 6332f a b b πππ⎛⎫=+=+ ⎪⎝⎭，由题意()6f x f π⎛⎫⎪⎝⎭对任意的x ∈R 恒成立，且0,0a b >>，312a b +对任意的x ∈R 恒成立，即22223144a b a b +++22323a b ab ⇒+恒成立，由基本不等式可知22323a b ab +，此时0a =>，所以()sin 2cos 22sin 26f x x b x b x π⎛⎫=+=+ ⎪⎝⎭．对于A 选项，747132sin 2sin 103030f b b πππ⎛⎫== ⎪⎝⎭，17132sin 2sin 53030f b b πππ⎛⎫== ⎪⎝⎭，所以7105f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，故A 错误；对于B 选顼，因为()2sin 26f x b x π⎛⎫=+ ⎪⎝⎭，所以不妨令2,6x k k ππ+=∈Z ，解得,122k x k ππ=-+∈Z ，当1k =时，512x π=，所以5,012π⎛⎫⎪⎝⎭是()f x 的对称中心，故B 正确；对于C 选项，由222,262k x k k πππππ-++∈Z ，知,36k x k k ππππ-+∈Z ，故C 不正确；对于D 选项，由题知0a =>，要使经过点(,)a b 的直线与函数()f x 的图象不相交，则此直线与横轴平行，又()f x 的振幅为2b b >，所以直线必与()f x 的图象有交点，故D 不正确．故选：B.【点评】关键点点睛：该题考查的是有关三角函数的性质的问题，正确解题的关键是利用题中条件求得函数解析式.11．（2021·福建高三其他模拟）提鞋公式也叫李善兰辅助角公式，其正弦型如下：22sin cos sin()a x b xa b x，πϕπ-<<，下列判断错误的是（）A ．当0a >，0b >时，辅助角arctan baϕ= B ．当0a >，0b <时，辅助角arctan b aϕπ=+ C ．当0a <，0b >时，辅助角arctan b a ϕπ=+ D ．当0a <，0b <时，辅助角arctan b a ϕπ=- 【答案】B【分析】分别判断出a ，b 的值，对辅助角ϕ的影响． ①0a >，0b >，则辅助角ϕ在第一象限； ②0a >，0b <，则辅助角ϕ在第四象限； ③0a <，0b <，则辅助角ϕ在第三象限； ④0a <，0b >，则辅助角ϕ在第二象限．【解答】解：因为cos ϕ=sin ϕ=tan baϕ=，(,]ϕππ∈- 对于A ，因为0a >，0b >，则辅助角ϕ在第一象限02πϕ∴<<，0b a>，arctan (0,)2b a π∴∈，故A 选项正确；对于B ，因为0a >，0b <，则辅助角ϕ在第四象限02πϕ∴-<<；0b a <， arctan (,)2b a πππ∴+∈，故B 选项错误；对于C ，因为0a <，0b >，则辅助角ϕ在第二象限2πϕπ∴<<；0b a <， arctan (,)2b a πππ∴+∈，故C 选项正确；对于D ，因为0a <，0b <，则辅助角ϕ在第三象限2ππϕ∴-<<-，0b a <， arctan (,)2b a πππ∴-∈--，故D 选项正确；故选：B ．【点评】本题考查了三角函数的性质，考查学生的分析能力，属于中档题．12．（2021·江西上饶市·高三其他模拟（理））已知函数()3cos f x x a x =+，0,3x π⎡⎤∈⎢⎥⎣⎦的最小值为3a ，则实数a 的取值范围是（） A ．[]0,2 B ．[]22-, C ．(],1-∞ D ．(],3-∞【答案】C【分析】由()()min 30f x a f ==可得出不等式()3cos 3f x x a x a =+≥对任意的0,3x π⎡⎤∈⎢⎥⎣⎦恒成立，化简得出tan 12x ≤，分0a ≤、0a >两种情况讨论，结合max tan 12x ⎫≤⎪⎭可求得实数a 的取值范围.【解答】()03f a =且()()min 30f x a f ==，由题意可知，对任意的0,3x π⎡⎤∈⎢⎥⎣⎦，()3cos 3f x x a x a +≥，()31cos x a x ≥-，即222sin cos 112sinsin 2222x x x x ⎡⎤⎛⎫≥--= ⎪⎢⎥⎝⎭⎣⎦，0,3π⎡⎤∈⎢⎥⎣⎦x ，则0,26x π⎡⎤∈⎢⎥⎣⎦，cos 02x ∴>，0tan 2x ≤≤tan 12x ≤.当0a ≤tan012x≤≤成立；当0a >时，函数3tan 2x y a =在区间0,3π⎡⎤⎢⎥⎣⎦上单调递增，则max 1y a =≤，此时01a <≤.综上所述，实数a 的取值范围是(],1-∞. 故选：C.【点评】结论点睛：利用参变量分离法求解函数不等式恒（能）成立，可根据以下原则进行求解：（1）x D ∀∈，()()min m f x m f x ≤⇔≤；（2）x D ∀∈，()()max m f x m f x ≥⇔≥；（3）x D ∃∈，()()max m f x m f x ≤⇔≤；（4）x D ∃∈，()()min m f x m f x ≥⇔≥. 13．（2021·山西吕梁市·高三一模（文））函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭部分图象如图所示，则3f π⎛⎫= ⎪⎝⎭（）A 3B ．12C ．3D 3【答案】D【分析】由函数()sin()f x A x ωϕ=+的部分图象知，2A =，2411333T ππ=-，结合2T πω=，求出12ω=，又根据2122sin 2323f ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭，求得6π=ϕ，即可求得()f x 解析式，代入计算3f π⎛⎫⎪⎝⎭即可. 【解答】由函数()sin()f x A x ωϕ=+的部分图象知，2A =，11233334T πππ=-=，解得24T ππω==，∴12ω=，又2122sin 2323f ππϕ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭，可得122232k ππϕπ⨯+=+，Z k ∈，解得26k πϕπ=+，Z k ∈，∵||2ϕπ<，∴可得6π=ϕ， ∴1()2sin 26f x x π⎛⎫=+ ⎪⎝⎭，∴12sin 2sin 32363f ππππ⎛⎫⎛⎫=⨯+== ⎪ ⎪⎝⎭⎝⎭故选：D.【点评】思路点睛：利用三角函数的图象求三角函数的解析式，通常先结合图象看振幅、周期，求得A ，ω，再利用特殊点（最高点、最低点、零点）求初相ϕ，即得解析式.14．（2021·安徽淮南市·高三一模（理））在平面直角坐标系xOy 中，α为第四象限角，角α的终边与单位圆O 交于点()00,P x y ，若cos 6πα⎛⎫+= ⎪⎝⎭35，则0x =（）A ．310- B C ．410D ．310【答案】C【分析】根据α为第四象限角，再结合cos 6πα⎛⎫+= ⎪⎝⎭35，确定6πα+的范围，进而确定sin 6πα⎛⎫+ ⎪⎝⎭，然后由0cos cos 66x ππαα⎡⎤⎛⎫==+- ⎪⎢⎥⎝⎭⎣⎦求解．【解答】∵,02πα⎛⎫∈- ⎪⎝⎭，∴,636πππα⎛⎫+∈- ⎪⎝⎭，又3cos 652πα⎛⎫+=< ⎪⎝⎭，所以,063ππα⎛⎫+∈- ⎪⎝⎭，所以4sin 65πα⎛⎫+=- ⎪⎝⎭， ∴0cos cos cos cos sin sin 666666x ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫==+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦．341552=-⨯=故选：C【点评】易错点点睛：本题容易忽视6πα+的范围，而导致sin 6πα⎛⎫+ ⎪⎝⎭出错.二、填空题15．（2021·陕西榆林市·高三二模（文））关于函数()4sin 6f x x ππ⎛⎫=- ⎪⎝⎭有如下四个命题：①()f x 的最小正周期为2； ②()f x 的图象关于点7,06⎛⎫⎪⎝⎭对称； ③若()()f a x f a x -=+，则a 的最小值为23；④()f x 的图象与曲线12506y x x ⎛⎫=<< ⎪⎝⎭共有4个交点．其中所有真命题的序号是__________．【答案】①②④【分析】结合正弦函数的性质判断各命题的真假．【解答】由图可得：22ππ=，()f x 的最小正周期为2，①正确；7()4sin 0666f ππ7⎛⎫=-= ⎪⎝⎭，()f x 的图象关于点7,06⎛⎫⎪⎝⎭对称，②正确；离y 轴最近的对称轴为13x =-，所以若()()f a x f a x -=+，则a 的最小值为13，③错误；在y 轴右边离y 最近的对称为23x =，2()43f =，而134223=<，1y x =在(0,)+∞上是减函数，因此()f x 的图象在第一象限每个周期内与1y x=的图象都有两个交点，在区间113(,)66上有两个交点，在区间1325(,)66上有两个交点，从而在25(0,)6上有4个交点，④正确；故答案为：①②④．【点评】思路点睛：本题考查正弦型三角函数的性质，解题方法是利用正弦函数性质求得()f x 的最小正周期，对称中心，对称轴，利用周期性确定函数图象交点个数，最终得出结论．16．（2021·辽宁高三一模（理））关于函数()2sin sin 2f x x x =+有如下四个命题： ①()f x 的最小正周期为2π； ②()f x 在[0,2]π内有3个极值点； ③()f x 在[0,2]π内有3个零点； ④()f x 的图象关于直线3x π=对称.其中所有真命题的序号为___________. 【答案】①③【分析】根据函数周期的求法，可判定①正确；利用导数和极值的定义，可判定②不正确；根据函数零点的定义和求法，可判定③正确；根据函数的对称性的判定方法，可判定④不正确.【解答】由函数sin y x =的最小正周期为2π，函数sin 2y x =的最小正周期为π，所以函数()2sin sin 2f x x x =+的最小正周期为两个函数周期的最小公倍数，所以函数()f x 的最小正周期为2π，所以①正确；由()22cos 2cos22cos 4cos 22(2cos 1)(cos 1),[0,2]f x x x x x x x x π'=+=+-=-+∈，因为cos [1,1]x ∈-，可得cos 10x +≥，当[0,)3x π∈时，()0f x '>，()f x 单调递增；当5(,)33x ππ∈时，()0f x '<，()f x 单调递减；当5(,2]3x ππ∈时，()0f x '>，()f x 单调递增；所以当3x π=时，函数()f x 取得极大值，当53x π=时，函数()f x 取得极小值，即()f x 在[0,2]π内有2个极值点，所以②不正确；令()0f x =，即2sin sin 22sin (1cos )0x x x x +=+=，解得sin 0x =或cos 1x =-，因为[0,2]x π，所以0,,2x ππ=，即()f x 在[0,2]π内有3个零点，所以③正确；由2()2sin()sin[2()]4sin()cos ()()3333623x f x x x x f x ππππππ-=-+-=--≠+，所以④不正确. 故答案为：①③【点评】解答三角函数的图象与性质的基本方法：1、根据已知条件化简得出三角函数的解析式为sin()y A wx ϕ=+的形式；2、熟练应用三角函数的图象与性质，结合数形结合法的思想研究函数的性质（如：单调性、奇偶性、对称性、周期性与最值等），进而加深理解函数的极值点、最值点、零点及有界性等概念与性质，但解答中主要角的范围的判定，防止错解.17．（2021·湖南长沙市·长郡中学高三二模）如图，某湖有一半径为100m 的半圆形岸边，现决定在圆心O 处设立一个水文监测中心(大小忽略不计)，在其正东方向相距200m 的点A 处安装一套监测设备.为了监测数据更加准确，在半圆弧上的点B 以及湖中的点C 处，再分别安装一套监测设备，且满足AB AC =，90BAC ∠=︒.定义：四边形OACB 及其内部区域为“直接监测覆盖区域”；设AOB θ∠=.则“直接监测覆盖区域”面积的最大值为___________.【答案】()210000525000m【分析】先用θ表示54cos AB θ=-⋅θ表示出25100sin 2cos 2OACB S θθ⎛⎫=--+ ⎪⎝⎭，最后运用两角和差的正余弦公式求最值即可.【解答】在OAB 中，AOB θ∠=，100OB =，200OA =，2222cos AB OB OA OB OA AOB ∴=+-⋅⋅∠，即AB = 211sin 22OACB OAB ABC S S S OA OB AB θ∴=+=⋅⋅⋅+⋅△△，25100sin 2cos 2OACB S θθ⎛⎫∴=--+ ⎪⎝⎭令tan 2ϕ=，则()251002OACB S θϕ⎤=-+⎥⎦∴直接监测覆盖区域”面积的最大值为()225000m .故答案为：()225000m【点评】思路点睛：本题利用余弦定理、三角形面积公式、求sin cos a b θθ+的最值. 18．（2021·江西高三其他模拟（文））若将函数()cos sin cos sin 0,||662f x x x πππϕωωϕωϕ⎛⎫⎛⎫⎛⎫=+++>≤ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭的图象向右平移6πω个单位得到()g x 图象，且()g x 图象过点10,2⎛⎫ ⎪⎝⎭，若关于x 的方程()1g x =-在,6ππ⎡⎤⎢⎥⎣⎦上恰有一个实数解，则ω的取值范围是___________.【答案】410[,)33【分析】化简函数()sin()6f x x πωϕ=++，结合函数图象变换，得到()sin()g x x ωϕ=+，进而得到sin()6()g x x πω=+，根据题意，转化为in()61s x πω+=-在,6ππ⎡⎤⎢⎥⎣⎦上恰有一个实数解，得到不等式1241284102233k k k k ωω-<≤+⎧⎪⎨+≤<+⎪⎩，分类讨论，即可求解.【解答】由题意，函数()cos()sin cos sin()sin()666f x x x x πππϕωωϕωϕ=+++=++，函数()f x 的图像向右平移6πω个单位得到()sin[()]sin()66g x x x ππωϕωϕω=-++=+，因为()g x 图像过点10,2⎛⎫⎪⎝⎭，可得1(0)sin 2g ϕ==，又因为||2πϕ≤，可得6π=ϕ，所以sin()6()g x x πω=+，又由关于x 的方程()1g x =-在,6ππ⎡⎤⎢⎥⎣⎦上恰有一个实数解，即in()61s x πω+=-在,6ππ⎡⎤⎢⎥⎣⎦上恰有一个实数解，因为6[],x ππ∈，可得6666x ππππωωπω+≤+≤+，则满足37222,266262k k k k Z πππππππωππωπ-<+≤+≤+<+∈，可得1241284102233k k k k ωω-<≤+⎧⎪⎨+≤<+⎪⎩，若ω不存在时，则满足412823k k +<+或1012423k k -≥+，解得23k <-或3430k ≥；若ω存在时，则234330k -≤<，当0k =时，可得4841033ωω-<≤⎧⎪⎨≤<⎪⎩，解得41033≤<ω，当1k =时，可得820101633ωω<≤⎧⎪⎨≤<⎪⎩，此时ω不存在，综上可得，ω的取值范围是410[,)33. 【点评】解答三角函数的图象与性质的基本方法：1、根据已知条件化简得出三角函数的解析式为sin()y A wx ϕ=+的形式；2、熟练应用三角函数的图象与性质，结合数形结合法的思想研究函数的性质（如：单调性、奇偶性、对称性、周期性与最值等），进而加深理解函数的极值点、最值点、零点及有界性等概念与性质，但解答中主要角的范围的判定，防止错解.19．（2021·陕西咸阳市·高三一模（理））已知函数()sin(cos )cos(cos )f x x x =+，现有以下命题：①()f x 是偶函数； ②()f x 是以2π为周期的周期函数； ③()f x 的图像关于2x π=对称； ④()f x．其中真命题有________．【答案】①②④【分析】根据三角函数图象性质逐一进行判断：①根据()f x 写出()f x -，并判断与()f x 关系即可；②写出(2)f x π+，判断与()f x 是否相等；③判断()f x π-与()f x 的关系；④设cos ,[1,1]t x t =∈-，所以sin cos )4y t t t π=+=+，根据t 的取值范围确定最值并判断．【解答】①函数()sin(cos )cos(cos )f x x x =+定义域为R ，关于原点对称，()sin[cos()]cos[cos()]sin(cos )cos(cos )()f x x x x x f x -=-+-=+=，所以函数()f x 是偶函数；所以①正确；②(2)sin[cos(2)]cos[cos(2)]sin(cos )cos(cos )()f x x x x x f x πππ+=+++=+=，所以()f x 是以2π为周期的周期函数；所以②正确；③()sin[cos()]cos[cos()]sin(cos )cos(cos )()f x x x x x f x πππ-=-+-=-+≠，所以()f x 的图像不关于2x π=对称；所以③错误；④令cos ,[1,1]t x t =∈-，所以sin cos )4y t t t π=+=+，因为[1,1]444t πππ+∈-++，所以42t ππ+=，即4t π=时，max y =()f x；所以 ④正确；所以真命题为①②④，故答案为：①②④.【点评】正确理解奇函数和偶函数的定义，必须把握好两个问题：(1)定义域关于原点对称是函数f (x )为奇函数或偶函数的必要非充分条件；(2)f (－x )＝－f (x )或f (－x )＝f (x )是定义域上的恒等式．奇函数的图象关于原点对称，偶函数的图象关于y 轴对称，反之也成立．利用这一性质可简化一些函数图象的画法，也可以利用它去判断函数的奇偶性．20．（2021·河南高三其他模拟（文））已知点O 是ABC 内一点，3,4,AB AC BAO CAO OBC OCA ==∠=∠=∠=∠，则BC =_______________________．【答案】【分析】设BAC α∠=，ABC β∠=，ACB γ∠=，在ABO 和BCO ，由正弦定理得11sin sin 22OA BO αβα=⎛⎫- ⎪⎝⎭，11sin sin 22CO BOαγα=⎛⎫- ⎪⎝⎭，两式相比得：2111sin sin sin 222αβαγα⎛⎫⎛⎫=-⋅- ⎪ ⎪⎝⎭⎝⎭，化简后可得2BC AB AC =⋅，即可得解.【解答】12BAO CAO CBO ACO BAC ∠=∠=∠=∠=∠，AO OC∴=设BACα∠=，ABCβ∠=，ACBγ∠=在ABO和BCO，由正弦定理得11sinsin22OA BOαβα=⎛⎫-⎪⎝⎭，11sin sin22CO BOαγα=⎛⎫-⎪⎝⎭两式相比得：2111sin sin sin222αβαγα⎛⎫⎛⎫=-⋅-⎪ ⎪⎝⎭⎝⎭即()()111cos2sin sin cos cos22αβαγαβγβγα⎛⎫⎛⎫-=-⋅-=--+-⎪ ⎪⎝⎭⎝⎭()()1cos cos cosβγαβγα∴++-=-+又2βγαπα+-=-，()απβγ=-+()()21cos2cos cos2sin2sin sinαβγβγαβγ∴-=--+⇒∴=利用正弦定理得：2BC AB AC=⋅又3,4AB AC==，212BC∴=，23BC∴=故答案为：23【点评】关键点点睛：本题考查三角形求边长，正确运用正弦定理，三角形内角和及三角恒等变换公式是解题的关键，考查学生的数形结合及运算能力，属于一般题. 21．（2021·山东潍坊市·高三一模）某市为表彰在脱贫攻坚工作中做出突出贡献的先进单位，制作了一批奖杯，奖杯的剖面图形如图所示，其中扇形OAB的半径为10，60,PBA QAB AQ QP PB∠=∠===，若按此方案设计，工艺制造厂发现，当OP最长时，该奖杯比较美观，此时AOB∠=_______________________．【答案】2π【分析】作OM QP⊥交QP于M，交AB于C，且OC AB⊥，设AOCθ∠=，求出AB、OC，设AQ QP BP x===，作⊥QE AB交AB于E，PF AB⊥交AB于F，可得出10sin x θ=，10cos 53sin OM OC CM θθ=+=+，由勾股定理可得()()2222210cos 53sin 5sin OP OM MP θθθ=+=++然后求最值可得答案.【解答】作OM QP ⊥交QP 于M ，交AB 于C ，且OC AB ⊥，设AOC θ∠=，则20sin θ=AB ，10cos OC θ=，设AQ QP BP x ===，作⊥QE AB 交AB 于E ，PF AB ⊥交AB 于F ，因为60PBA QAB ∠=∠=，所以12AE BF x ==，32CM PF x ==， EF QP x ==，所以2AB x =，所以20sin 2AB x θ==，即10sin x θ=，310cos 10cos 53OM OC CM x θθθ=+==+，所以()()2222210cos 35sin OP OM MP θθθ=+=++222100cos 75sin 1003cos 25sin 1005032θθθθθθ=+++=+，因为[]sin 21,1θ∈-，所以当sin 21θ=即4πθ=时2OP 最大，也就是OP 最长时2AOB π∠=.故答案为：2π. 【点评】本题考查了用三角函数解决几何问题，关键点是作出辅助线利用勾股定理求出2OP ，考查了学生分析问题、解决问题的能力.三、解答题22．（2021·山东潍坊市·高三一模）在①函数()y f x =的图象关于直线3x π=对称，②函数()y f x =的图象关于点,06P π⎛⎫ ⎪⎝⎭对称，③函数()y f x =的图象经过点2,13Q π⎛⎫- ⎪⎝⎭这三个条件中任选一个，补充在下面问题中并解答．问题：已知函数()sin cos cos sin 0,||2f x x x πωϕωϕωϕ⎛⎫=+>< ⎪⎝⎭最小正周期为π，且，判断函数()f x 在,62ππ⎛⎫⎪⎝⎭上是否存在最大值？若存在，求出最大值及此时的x 值；若不存在，说明理由．注：如果选择多个条件分别解答，按第一个解答计分．【答案】答案不唯一，具体见解析【分析】先对函数化简得()sin()f x x ωϕ=+，由函数的最小正周期为π，可得2ω=，则()sin(2)f x x ϕ=+，若选①，则有2()32k k ππϕπ⨯+=+∈Z ，从而可求出ϕ的值，进而可求出函数的解析式，再利用换元法可求得最值；若选②，则有2()6k k πϕπ⨯+=∈Z ，从而可求出ϕ的值，然后利用换元法可求得最值；若选③，则有222()32k k ππϕπ⨯+=-∈Z ，从而可求出ϕ的值，再利用换元法可求最值即可【解答】解：()sin cos cos sin sin()f x x x x ωϕωϕωϕ=+=+，由已知函数()f x 的周期2T ππω==，求得2ω=，所以()sin(2)f x x ϕ=+，若选①，则有2()32k k ππϕπ⨯+=+∈Z ，解得()6k k πϕπ=-∈Z ，又因为2πϕ<，所以，0,6k πϕ==-，所以()sin 26f x x π⎛⎫=- ⎪⎝⎭，当,62x ππ⎛⎫∈ ⎪⎝⎭时，52,666t x πππ⎛⎫=-∈ ⎪⎝⎭，所以当2t π=，即3x π=时，函数()f x 取得最大值，最大值为1．若选②，则有2()6k k πϕπ⨯+=∈Z ，解得()3k k πϕπ=-∈Z ，又因为2πϕ<，所以0,3k πϕ==-，所以()sin 23f x x π⎛⎫=- ⎪⎝⎭，当,62x ππ⎛⎫∈ ⎪⎝⎭时，220,33t x ππ⎛⎫=-∈ ⎪⎝⎭，所以当2t π=，即512x π=时，函数()f x 取得最大值，最大值为1．若选③，则有222()32k k ππϕπ⨯+=-∈Z ，解得112()6k k πϕπ=-∈Z ，又因为2πϕ<，所以1,6k πϕ==，所以()sin 26f x x π⎛⎫=+ ⎪⎝⎭，当,62x ππ⎛⎫∈ ⎪⎝⎭时，72,626t x πππ⎛⎫=+∈ ⎪⎝⎭，显然，函数()f x 在该区间上没有最大值．【点评】关键点点睛：此题考查利用三角函数的性质求函数解析式，考查求三角函数的最值，考查计算能力，解题的关键是根据题意正确的求出函数的解析式，再利用换元法求函数的最值，属于中档题23．（2021·江西上饶市·高三一模（文））已知()22cos sin sin cos 3f x x x x x x π⎛⎫=++ ⎪⎝⎭.（1）求函数()f x 的单调递增区间；（2）若,46⎛⎫∈- ⎪⎝⎭x ππ，求()y f x =的值域.【答案】（1）5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦，k Z ∈；（2）(]1,2-. 【分析】（1）利用三角恒等变换思想化简函数()f x 的解析式为()2sin 23f x x π⎛⎫=+ ⎪⎝⎭，解不等式()222232k x k k Z πππππ-≤+≤+∈，可求得函数()f x 的单调递增区间；（2）由,46⎛⎫∈- ⎪⎝⎭x ππ可求出23x π+的取值范围，利用正弦型函数的基本性质可求得函数()y f x =的值域.【解答】（1）()()12cos sin 1cos 2sin 2322f x x x x x π⎛⎫=+--+ ⎪⎝⎭112cos sin 2sin 222x x x x x ⎛⎫=++ ⎪ ⎪⎝⎭()211sin 22cos 12sin 22222x x x x =+-++sin 222sin 23x x x π⎛⎫=+=+ ⎪⎝⎭，令222232k x k πππππ-≤+≤+，k Z ∈，解得51212k x k ππππ-≤≤+，k Z ∈，因此，函数()f x 的单调递增区间为5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦，k Z ∈；（2）,46x ππ⎛⎫∈- ⎪⎝⎭，22633x πππ-<+<，则1sin 2123x π⎛⎫-<+≤ ⎪⎝⎭，所以，()12f x -<≤，因此，当,46⎛⎫∈- ⎪⎝⎭x ππ时，()y f x =的值域为(]1,2-.【点评】方法点睛：求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤：第一步：三角函数式的化简，一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式；第二步：由x 的取值范围确定x ωϕ+的取值范围，再确定()sin x ωϕ+（或()cos x ωϕ+)的取值范围；第三步：求出所求函数的值域（或最值）.24．（2021·山西吕梁市·高三一模（文））在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知22cos a b c B -=⋅．（1）求角C ；（2）若2a =，D 是AC 的中点，BD =c ．【答案】（1）π3C =；（2）2c =.【分析】（1）先利用正弦定理将边转化到角的正弦，结合()sin sin sin cos cos sin A B C B C B C =+=+进行化简1cos 2C =，即求得角C ；（2）CBD 中利用余弦定理求得2b =，判断ABC 是等边三角形，即得到边c . 【解答】解：（1）因为22cos a b c B -=⋅，由正弦定理得：2sin sin 2sin cos A B C B -=⋅，因为()sin sin sin cos cos sin A B C B C B C =+=+，代入上式得，2sin cos 2cos sin sin 2sin cos B C B C B C B +-=，即2sin cos sin 0B C B -=，即()sin 2cos 10B C -= 因为ABC 中，sin 0B ≠，所以2cos 1C =，即1cos 2C =，又因为ABC 中，0C π<<，所以π3C =；（2）依题意，CBD 中，12,,2CB CD b BD ===π3C =，利用余弦定理可得，21114322422b b +-=⨯⨯⨯，即2440b b -+=，解得2b =，ABC 中，2b a ==，π3C =，故ABC 是等边三角形，故2c =. 【点评】思路点睛：一般地，解有关三角形的题目时，通常利用正弦定理或余弦定理对边角关系进行转化，要有意识地已知条件判断用哪个定理更合适. 如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理.25．（2021·安徽六安市·高三一模（文））已知函数()2sin 2sin12xf x x =+-．（1）求函数()f x 的单调递增区间；（2）将函数()f x 图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），再把图象向右平移24π个单位长度，得到函数()y g x =的图象，当0,2x π⎡⎤∈⎢⎥⎣⎦时，求函数()g x 的值域．【答案】（1）()32,244k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦；（2）⎡⎢⎣.【分析】（1）利用三角恒等变换思想化简函数()f x 的解析式为()4f x x π⎛⎫=- ⎪⎝⎭，然后解不等式()22242k x k k Z πππππ-+≤-≤+∈，即可求得函数()f x 的单调递增区间；（2）利用三角函数图象变换得出()23g x x π⎛⎫=- ⎪⎝⎭，由0,2x π⎡⎤∈⎢⎥⎣⎦求得23x π-的取值范围，然后利用正弦型函数的基本性质可求得函数()g x 在0,2π⎡⎤⎢⎥⎣⎦上的值域.【解答】（1）()sin cos 4f x x x x π⎛⎫=-=- ⎪⎝⎭，由()22242k x k k Z πππππ-+≤-≤+∈，解得()32244k x k k Z ππππ-+≤≤+∈． ∴函数()f x 的单调增区间为()32,244k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦；（2）将函数()f x 图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到函数24y x π⎛⎫=- ⎪⎝⎭的图象，再把所得函数图象向右平移24π个单位长度，得到函数()222443g x x x πππ⎡⎤⎛⎫⎛⎫=--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦由0,2x π⎡⎤∈⎢⎥⎣⎦时，可得22,333x πππ⎡⎤-∈-⎢⎥⎣⎦，所以，sin 213x π⎛⎫≤-≤ ⎪⎝⎭，可得函数()g x 在0,2π⎡⎤⎢⎥⎣⎦上的值域为⎡⎢⎣.【点评】方法点睛：求函数()()sin f x A x =+ωϕ在区间[],a b 上值域的一般步骤：第一步：三角函数式的化简，一般化成形如()sin y A x k ωϕ=++的形式或()cos y A x k ωϕ=++的形式；第二步：由x 的取值范围确定x ωϕ+的取值范围，再确定()sin x ωϕ+（或()cos x ωϕ+)的取值范围；第三步：求出所求函数的值域（或最值）.26．（2021·辽宁高三一模（理））已知函数()2cos 3cos 1f x x x x -+.（1）求函数()f x 的单调递减区间；（2）在锐角ABC 中，角,,A B C 所对的边分别,,a b c .若()1,f C c ==D 为AB 的中点，求CD 的最大值. 【答案】（1）递减区间511[,]1212k k k Z ππππ++∈；（2）32.【分析】（1）利用二倍角公式和辅助角公式得到函数()1232x f x π⎛⎫=-- ⎪⎝⎭，再利用正弦函数的性质求解.（2）()1f C =由，得到sin(2)3C π-=，再由ABC 为锐角三角形，求得3C π=，利用余弦定理得到2222cos a CD BDC =+-⋅∠，222(2cos 22b CD ADC =+-⋅⋅∠，两式相加得到22213)24CD a b =+-（，再利用基本不等式求解.【解答】（1）3()2(1cos 2)12f x x x =-++， 1232x π⎛⎫=-- ⎪⎝⎭，由3222,232k x k k Z πππππ+≤-≤+∈，解得：511,1212k x k k Z ππππ+≤≤+∈，所以()f x 递减区间511[,],1212k k k Z ππππ++∈.（2）1())132f C C π=--=由，得sin(2)32C π-=，ABC 为锐角三角形，(0,)2C π∈∴，22(,)333C πππ∴-∈-， 233C ππ∴-=，3C π∴=，由余弦定理得：2222cos a CD BDC =+-⋅∠，2222cos b CD ADC =+-⋅∠，且cos cos BDC ADC ∠=-∠，两式相加得：22213)24CD a b =+-（，由222232cos a b ab C a b ab =+-=+-，2222221()22a b a b a b +≥+-=+，当a b =时，等号成立，即22a b +的最大值为6，所以CD 的最大值为32. 【点评】关键点点睛：本题第二问关键是由CD 为中线，由∠+∠=BDC ADC π，在BDC ，ADC 中，分别利用余弦定理，进而得到22213)24CD a b =+-（求解.27．（2021·湖南永州市·高三二模）已知函数2()2cos122x f x x π⎛⎫=-+- ⎪⎝⎭. （1）求函数()f x 的最小正周期；（2）在ABC 中，角A ､B ､C 所对边分别为a ､b ､c ，若()2f A =，2b =，ABC的面积为ABC 外接圆的面积. 【答案】（1）2π；（2）283π. 【分析】（1）先化简()()sin f x A x ωϕ=+再结合最小正周期公式2T ωπ=即可；（2）由()2f A =得3A π=，结合余弦定理和正弦定理可求得圆半径，故面积可求得.【解答】解：（1）2()2cos1cos 22x f x x x x π⎛⎫=+-=+ ⎪⎝⎭2sin 6x π⎛⎫=+ ⎪⎝⎭，所以函数()f x 的最小正周期为2π.（2）因为()22sin 26f A A π⎛⎫=⇒+= ⎪⎝⎭，所以3A π=，由1sin 2ABCSbc A ==12bc =，因为2b =，所以6c =，由余弦定理得222222cos 28a c b bc A c b bc =+-=+-=，得a =设ABC 外接圆半径为R ，则2sin a R A ==，∴R = 所以ABC 外接圆的面积为2283S R ππ==. 【点评】本题准确应用正余弦定理和面积公式是解题的关键.28．（2021·河北张家口市·高三一模）在ABC 中，cos sin )sin cos B b C b B C -=．（1）求B ；（2）若2c a =，ABC ，求ABC 的周长．【答案】（1）3B π=；（2）2+.【分析】（1cos sin B b A =，根据正弦定理、三角形内角的性质，即可求B ；（2）由三角形面积公式求出a 、c ，再根据余弦定理求b ，即可求ABC 的周长．【解答】（1）由cos sin )sin cos B b C b B C -=，得cos cos sin sin cos B b B C b B C -=，cos sin cos cos sin B b B C b B C =+cos sin()B b B C =+，cos sin B b A =．cos sin sin A B B A =，又sin 0A ≠，sin B B =，即tan B =0B π<<， ∴3B π=．（2）由2,c a ABC =11sin 22223ABCSac B a a ==⨯⨯⨯=，解得3a =，即23c a ==由余弦定理2222cos b a c ac B =+-，可得2221242b =+-=⎝⎭⎝⎭，解得2b =．∴ABC 的周长为2233a b c ++=++=+ 【点评】关键点点睛：（1）利用三角恒等变换及正弦定理，将已知条件化简为一个内角的函数值，根据函数值确定角的大小.（2）综合应用正余弦定理求三角形的边，进而求其周长.29．（2021·广东韶关市·高三一模）在①()cos cos cos 0C A A B +=，②()cos23cos 1B A C -+=，③cos sin 3b C B a +=这三个条件中任选一个，补充在下面问题中.问题：在ABC 中，角A 、B 、C 对应的边分别为a 、b 、c ，若1a c +=，___________，求角B 的值和b 的最小值. 【答案】条件选择见解析；3B π=，b 最小值为12. 【分析】选①，利用三角形的内角和定理、诱导公式以及两角和的余弦公式化简得出tan B =结合()0,B π∈可求得B ，再利用余弦定理结合二次函数的基本性质可求得b 的最小值；选②，利用三角形的内角和定理、诱导公式以及二倍角的余弦公式求出cos B 的值，结合()0,B π∈可求得B ，再利用余弦定理结合二次函数的基本性质可求得b 的最小值；选③，利用正弦定理边角互化、三角形的内角和定理以及两角和的正弦公式化简可求得tan B =结合()0,B π∈可求得B ，再利用余弦定理结合二次函数的基本性质可求得b 的最小值.【解答】解：若选择①：在ABC 中，有A B C π++=，则由题可得：()()cos cos cos 0A B A A B π-++=⎡⎤⎣⎦，()cos cos cos cos 0A B A B A B -++=，sin sin cos cos cos cos cos 0A B A B A B A B -+-=，sin sin cos A B A B =，又sin 0A ≠，所以sin B B =，则tan B =又()0,B π∈，所以3B π=，因为1a c +=，所以1c a =-，()0,1a ∈. 由余弦定理可得：2222cos b a c ac B =+-22a c ac =+-()()2211a a a a =+---2331a a =-+，()0,1a ∈，又2211324b a ⎛⎫=-+ ⎪⎝⎭，所以，当12a =时，()2min14b =，即b 的最小值为12；若选择②：在ABC 中，有A B C π++=，则由题可得()222cos 13cos 2cos 3cos 11B B B B π---=+-=，解得1cos 2B =或cos 2B =-（舍去），又()0,πB ∈，所以3B π=.（剩下同①）若选择③：由正弦定理可将已知条件转化为sin cos sin sin 3B C C B A +=， ()()sin cos s s in cos in sin sin B C C B A B C B C π=+=-+=+⎡⎤⎣⎦，sin sin cos C B C B =，又sin 0C ≠，所以sin B B =，tan B =又()0,B π∈，所以3B π=.（剩下同①）【点评】方法点睛：在解三角形的问题中，若已知条件同时含有边和角，但不能直接使用正弦定理或余弦定理得到答案，要选择“边化角”或“角化边”，变换原则如下：（1）若式子中含有正弦的齐次式，优先考虑正弦定理“角化边”；（2）若式子中含有a 、b 、c 的齐次式，优先考虑正弦定理“边化角”；（3）若式子中含有余弦的齐次式，优先考虑余弦定理“角化边”；（4）代数式变形或者三角恒等变换前置；。

高二数学三角函数三角恒等变换解三角形试题答案及解析

高二数学三角函数三角恒等变换解三角形试题答案及解析1.．【答案】【解析】故答案为：．【考点】两角和与差的三角公式．2.若函数在区间上单调递增，则的最小值是（）A．B．C．D．【答案】D【解析】依题意，，令，在区间上，，单调递增，，所以；【考点】1．导数与单调性；2．化归的思想；3.函数在内是（）A．增函数B．减函数C．有增有减D．不能确定【答案】A【解析】函数，可得，所以函数在内是增函数．故选：A．【考点】利用导数研究函数的单调性．4.（12分）．已知在△ABC中，内角A，B，C所对的边长分别为a，b，c，且tan A＋tan B＝．（1）求角B的大小；（2）若，求sinA·sinC的值．【答案】（1）；（2）【解析】（Ⅰ）已知等式左边利用同角三角函数间的基本关系化简，整理后根据sinC不为0求出cosB的值，即可确定出B的度数；（Ⅱ）已知等式去分母整理后得到关系式，利用余弦定理列出关系式，把得出关系式及cosB的值代入，并利用正弦定理化简，即可求出sinAsinC的值试题解析：（Ⅰ）已知等式变形得：sinAcosA+sinBcosB=2sinCcosA，去分母得：sinAcosB+sinBcosA=2sinCcosB，即sin（A+B）=2sinCcosB=sinC，∵sinC≠0，∴cosB=12，则B=60°；（Ⅱ）由，整理得：，∵cosB=12，∴，由正弦定理得：sin2B=2sinA·sinC=，则sinA·sinC=【考点】1．同角间三角函数关系；2．正弦定理5.将函数的图象上所有点的横坐标伸长到原来的倍（纵坐标不变），再将所得图象向左平移个单位，则所得函数图象对应的解析式为（）A．B．C．D．【答案】D【解析】将函数的图象上所有点的横坐标伸长到原来的倍（纵坐标不变），得到函数的图像，再将所得图象向左平移个单位，则所得函数图象对应的解析式为．故选D．【考点】三角函数图像变换：周期变换、左右平移．6.已知在△ABC中,三个内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且,则tanC等于（）A．B．C．D．【答案】C【解析】【考点】1．余弦定理解三角形；2．同角间三角函数关系7.已知在△ABC中，内角A，B，C所对的边长分别为a，b，c，且tan A＋tan B＝．（1）求角B的大小；（2）若＋＝3，求sin Asin C的值．【答案】（1）；（2）【解析】（1）由题意切化弦，同分可得，整理可得，即可求得；（2）根据已知式子同分可得，由余弦定理得到，再结合正弦定理即可得到试题解析：（1）由题意可得：因为，所以，又因为，所以（2）有题意可得：即由余弦定理可得：，得到有正弦定理：【考点】1．正余弦定理；2．化简求值8.（本题满分11分）若的内角所对的边分别为，且满足（1）求；（2）当时，求的面积．【答案】（1）；（2）．【解析】（1）因为正弦定理，所以化为，因为三角形内角有，所以即，所以；（2）由余弦定理，得，而，，得，即，因为三角形的边，所以，则．试题解析：（1）因为由正弦定理，得，又，从而，由于所以（2）解法一：由余弦定理，得，而，，得，即因为，所以，故面积为．解法二：由正弦定理，得从而又由知，所以故，所以面积为．【考点】1．正弦定理与余弦定理；2．三角形的面积公式．9.在中，已知，,则的长为____________________．【答案】【解析】由正弦定理可得【考点】正弦定理解三角形10.（本小题满分10分）在△ABC中，是方程的一个根，（1）求；（2）当时，求△ABC周长的最小值．【答案】（1）（2）【解析】（1）解一元二次方程得到方程的根，结合三角函数有界性得到的值，从而求得大小；（2）由三角形余弦定理结合，可将转化为的表达式，从而求得其最小值，得到周长的最小值试题解析：（1）又是方程的一个根（2）由余弦定理可得：则：当时，c最小且，此时△ABC周长的最小值为．【考点】1．余弦定理解三角形；2．一元二次方程的根11.在△ABC中，角A，B，C所对的边分别为a，b，c，若（b－c）cosA＝acosC，则cosA＝_____【答案】【解析】由正弦定理可将已知条件转化为【考点】正弦定理与三角函数基本公式12.在△ABC中，cosA＝，sinB＝，则cosC的值为．【答案】【解析】由cosA＝，sinB＝得【考点】三角函数基本公式13.在△ABC中，如果，且为锐角，试判断此三角形的形状．【答案】等腰直角三角形．【解析】判定三角形的形状由三角形的三边长或三个角来确定．由可确定．根据正弦定理，可确定角，从而确定三角形的形状．试题解析：因为，所以,又为锐角，所以．，．由正弦定理得：，即展开得：，即，则，所以△ABC是等腰直角三角形．【考点】1．三角形形状；2．正弦定理；14.在△中，分别为角所对的边，若，则此三角形一定是（）A．正三角形B．直角三角形C．等腰三角形D．等腰或直角三角形【答案】C【解析】,三角形为等腰三角形【考点】1．正弦定理解三角形；2．三角函数基本公式15.在中，、、分别是三内角A、B、C的对应的三边，已知（1）求角C的大小；（2）满足的是否存在？若存在，求角A的大小．【答案】（1）；（2）不存在【解析】（1）由正弦定理将变形可得到关于角C的关系式，进而求得角C的大小；（2）结合角C的大小将变形求解A角，若A角存在则三角形存在试题解析：（1）由正弦定理，得因为由则（2）由（1）知，于是=这样的三角形不存在。

高二数学三角函数三角恒等变换解三角形试题

高二数学三角函数三角恒等变换解三角形试题1.已知，三个数，，中（）A．都小于B．至少一个大于或等于C．都大于或等于D．至多一个大于【答案】B【解析】因为，令，，，又因为，由函数的性质可知，，所以，所三个数，，中至少有一个大于，故选B.【考点】1.的性质与基本不等式；2.逻辑联结词与命题.2.锐角中，已知，则的取值范围是（）A．B．C．D．【答案】C【解析】由正弦定理可得，所以．因为为锐角三角形，所以．即．故C正确．【考点】1正弦定理；2三角函数化简求值．3.角的终边上有一点，则（）A．B．C．D．【答案】B【解析】【考点】三角函数定义4.在△ABC中，若，则与的大小关系为（）A．B．C．≥D．、的大小关系不能确定【答案】A【解析】在三角形中由正弦定理可知时有【考点】正弦定理解三角形5.下列函数中，周期为且为奇函数的是（）A．B．C．D．【答案】B【解析】函数为偶函数，故A错误；函数，周期为1且为奇函数，故选B；函数是周期为2的奇函数，故C错误；函数是周期为的偶函数，故D错误．【考点】函数的奇偶性、周期性．6.在中，角所对的边长为，则“”是“”的（）条件A．充分不必要B．必要不充分C．充要D．既不充分又不必要【答案】A【解析】因为时，所以，而时，由正弦定理知，即，得或，即不一定成立，故选A．【考点】1、充要条件；2、正弦定理．7.（2015秋•宁城县期末）在△ABC中，两直角边和斜边分别为a，b，c，若a+b=cx，试确定实数x的取值范围（）A．B．C．D．【答案】A【解析】由a+b=cx得，x=，由正弦定理得=sin（A+45°），由此能确定实数x的取值范围．解：由a+b=cx得，x=，由题意得在△ABC中，∠C=90°，则∠A+∠B=90°，由正弦定理得：===sinA+cosA=sin（A+45°），由A∈（0，90°）得，A+45°∈（45°，135°），所以sin（A+45°）∈（，1]，即sin（A+45°）∈（1，]，∴∈（1，]，∴x=∈（1，]．故选：A．【考点】三角形中的几何计算．8.（2015秋•宁德校级期中）在△ABC中，角A，B，C所对的边分别为a，b，c．（Ⅰ）若b2+c2=a2+bc，求角A的大小；（Ⅱ）若acosA=bcosB，试判断△ABC的形状．【答案】（Ⅰ）A=；（Ⅱ）△ABC是等腰三角形或直角三角形．【解析】（Ⅰ）由已知利用余弦定理可得cosA=，又结合∠A是△ABC的内角，即可求A的值．（Ⅱ）由正弦定理得sinAcosA=sinBcosB，可得sin2A=sin2B．利用正弦函数的图象和性质可得2A=2B或2A+2B=π，即可得解．解：（Ⅰ）∵由已知得cosA===，又∵∠A是△ABC的内角，∴A=．（Ⅱ）在△ABC中，由acosA=bcosB，得sinAcosA=sinBcosB，∴sin2A=sin2B．∴2A=2B或2A+2B=π．∴A=B或∴△ABC是等腰三角形或直角三角形．【考点】正弦定理．9.已知、、分别为的三边、、所对的角，的面积为，且．（1）求角的大小；（2）若，求周长的最大值．【答案】（1）；（2）【解析】（1）利用面积公式及，建立等式关系求出角C；（2）方法1：由（1）确定角C，用角表示角，由正弦定理，求出关于角的关系，这样周长就是表示成了关于角的函数，求出该函数的最大值；方法2：利用余弦定理，配方，利用基本不等式，，解出的范围，即可求出周长最大值．试题解析：（1）∵△ABC的面积为S，∴，又∵C为三角形内角，∴．（2）解法1：由正弦定理得：，∵，，，从而．综上：．解法2：由余弦定理即，（当且仅当时取到等号）综上：．【考点】 1．面积公式；2．正弦定理；3．余弦定理．10.已知的三边长分别为，则的面积为__________．【答案】【解析】的边长由余弦定理得，，所以三角形的面积为．【考点】1、余弦定理的运用；2、三角形的面积公式．11.海上有A、B两个小岛相距10海里，从A岛望C岛和B岛成600的视角，从B岛望C岛和A岛成300的视角，则B、C间的距离是___________________海里．【答案】【解析】依题意，作图如下：∵∠CAB=60°，∠ABC=30°，∴△ABC为直角三角形，∠C为直角，又|AB|=10海里，∴|BC|=|AB|sin60°=10×=海里，【考点】正弦定理的应用12.在中，分别是角A、B、C的对边，且（1）求角B的大小；（2）若，求的面积．【答案】（1）（2）【解析】（1）变形已知式子代入结合角的范围可得；（2）由余弦定理可得，代入数据配方整体可得ac，代入面积公式可得试题解析：（1）由已知得（2）将代入中，得，【考点】余弦定理；正弦定理13.已知函数．设时取得最大值．（1）求的最大值及的值；（2）在中，内角的对边分别为，且，求的值．【答案】（1）；（2）【解析】（1）根据三角函数的恒等变换公式，可得，又，则，可知当时，即可求出结果；（2）由（1）知，由正弦定理，可得，再根据余弦定理，可得由此可求出．试题解析：解：（1）由题意，．又，则．故当，即时，．（2）由（1）知．由，即．又．则，即．故．【考点】1．三角恒等变换；2．正弦定理；3．余弦定理．14.在△中，，，，则A．B．C．D．【答案】C【解析】由得【考点】正弦定理解三角形15.已知函数(其中)，其部分图像如图所示．（I）求的解析式；（II）求函数在区间上的最大值及相应的x值．【答案】（I）；(II) 当时，取得最大值.【解析】（I）根据图象可求出的值，再根据图象可求出周期，进而可求得的值，再结合函数在处有最大值以及，就可以求出的值，由此可求出函数的表达式；(II)根据（I）的结论先求出函数的表达式，再结合，就可求出在区间上的的最大值及相应的值．试题解析：（I）由图可知，，所以.又，且，所以.所以（II）由（I），所以因为，所以，.故：，当时，取得最大值【考点】1、三角函数的“由图求式”；2、形如的函数的最值问题.16.在△ABC中，如果lga﹣lgc=lgsinB=﹣lg，并且B为锐角，则△ABC的形状是（）A．等边三角形B．直角三角形C．等腰三角形D．等腰直角三角形【答案】D【解析】在中，如果，并且为锐角，∴，∴，，∴，∴，故的形状为等腰直角三角形，故选D．【考点】三角形的形状判断；对数的运算性质．17.已知中,角的对边分别为,,向量,,且.(Ⅰ)求的大小；(Ⅱ)当取得最大值时,求角的大小和的面积.【答案】（Ⅰ）；（Ⅱ）.【解析】（Ⅰ）通过向量的垂直，两角和与差的三角函数化简表达之，利用三角形的内角和，转化为的三角函数值，然后求的大小；（Ⅱ）通过的大小，推出的关系，化简为的三角函数的形式，通过的范围求出不等式取得最大值时，求角的大小，利用正弦定理求出的值，即可利用三角形的面积公式求解三角形的面积.试题解析：（Ⅰ）因为,所以即,因为,所以所以（Ⅱ）由,故由,故最大值时,由正弦定理,,得故【考点】正弦定理；平面向量数量积的运算；三角函数中的恒等变换应用.18.在中，角、、所对的边分别是、、，若（Ⅰ）求角；（Ⅱ）若，，求的面积。

数学课程三角恒等变换练习题及答案

数学课程三角恒等变换练习题及答案1. 练习题1.1 简单练习题1. 计算下列三角函数值，并化简为有理数：(1) sin 30°(2) cos 45°(3) tan 60°2. 利用三角恒等变换证明以下等式：(1) sin^2 x + cos^2 x = 1(2) 1 + tan^2 x = sec^2 x3. 使用三角恒等变换求解以下方程：(1) sin 2x = 0.5(2) cos 2x - sin 2x = 01.2 提高练习题1. 利用三角恒等变换化简下列表达式：(1) cos x + sin x + 1 - cos x(2) cot^2 x + 1 - csc^2 x2. 解下列方程：(1) 2 sin^2 x - 3 cos x - 1 = 0(2) tan^2 x + sec x = 22. 答案2.1 简单练习题答案1.(1) sin 30° = 1/2(2) cos 45° = 1/√2(3) tan 60° = √32. 证明以下等式：(1) 三角恒等变换：sin^2 x + cos^2 x = 1证明：根据三角恒等变换公式 sin^2 x + cos^2 x = 1代入 sin x = cos (90° - x)，可得：cos^2 (90° - x) + cos^2 x = 1sin^2 x + cos^2 x = 1(2) 三角恒等变换：1 + tan^2 x = sec^2 x证明：根据三角恒等变换公式 1 + tan^2 x = sec^2 x代入 tan x = sin x / cos x，可得：1 + (sin x / cos x)^2 = (1 / cos x)^21 + sin^2 x / cos^2 x = 1 / cos^2 x(cos^2 x + sin^2 x) / cos^2 x = 1 / cos^2 x1 / cos^2 x = 1 / cos^2 x2.2 提高练习题答案1. 化简以下表达式：(1) cos x + sin x + 1 - cos x= sin x + 1(2) cot^2 x + 1 - csc^2 x= (cos^2 x / sin^2 x) + 1 - (1 / sin^2 x)= (cos^2 x + sin^2 x) / sin^2 x= 1 / sin^2 x2. 解以下方程：(1) 2 sin^2 x - 3 cos x - 1 = 0首先，利用三角恒等变换将方程中的 cos x 表示为 sin x：2 (1 - cos^2 x) - 3 cos x - 1 = 02 - 2 cos^2 x -3 cos x - 1 = 0-2 cos^2 x - 3 cos x + 1 = 0然后，令 t = cos x，将方程转化为关于 t 的二次方程：-2 t^2 - 3 t + 1 = 0解这个二次方程可得 t = -1 或 t = 1/2。

高三数学三角函数三角恒等变换解三角形试题

高三数学三角函数三角恒等变换解三角形试题1.某航模兴趣小组的同学，为了测定在湖面上航模航行的速度，采用如下办法：在岸边设置两个观察点A、B ，且 AB长为80米，当航模在C处时，测得∠ABC=105°和∠BAC=30°，经过20秒后，航模直线航行到 D 处，测得∠BAD=90°和∠ABD=45°.请你根据以上条件求出航模的速度.（答案保留根号）【答案】法一：在△ABC中,∵∠BAD=90°,∠ABD=45°,∴∠ADB="45°"在中，在中，DC2=DB2+BC2-2DB·BC cos60°=(80)2+(40)2-2×80×40×=9600,航模的速度（米/秒）答：航模的速度为2（米/秒））法二:（略解）、在中，中在中，DC2=AD2+AC2-2AD·AC cos60°="9600"航模的速度（米/秒）答：航模的速度为2（米/秒）【解析】略2.函数的一部分图象如图所示，其中，，，则（）A．B．C．D．【答案】D【解析】由得：又，故选D3.函数的部分图象如图所示，设是图象的最高点，是图象与轴的交点，则A．B．C．D．【答案】B【解析】从向x轴作垂线，垂足为，由，可得，，，所以，故选B.【考点】1.三角函数的图像与性质；2.三角函数求值.4.中，角所对的边分别为，若（）．A．B．C．D．【答案】C【解析】由余弦定理，又由，得，故选C．【考点】余弦定理.5.（12分）已知向量，，设函数．（1）求函数的单调递减区间；（2）在△ABC中，角A，B，C的对边分别为a，b，c，且满足，，求的值．【答案】（1）；（2）．【解析】本题主要考查向量的数量积、倍角公式、两角差的正弦公式、三角函数的单调性、正弦定理、余弦定理等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力．第一问，先利用向量的数量积得到的解析式，再利用倍角公式和两角差的正弦公式化简表达式，使之成为的形式，再数形结合求函数的递减区间；第二问，先利用正弦定理将转化为，再将已知条件代入余弦定理中得出，从而得到特殊角，最后代入中．试题解析：（1）令，所以的递减区间为（2）由，⇒，∴，即，又∵，，∴．【考点】向量的数量积、倍角公式、两角差的正弦公式、三角函数的单调性、正弦定理、余弦定理．6.（本小题满分12分）在△ABC中，a, b, c分别为内角A, B, C的对边，且，（Ⅰ）求A的大小；（Ⅱ）求的最大值．【答案】（Ⅰ）120°；（Ⅱ）1【解析】（Ⅰ）求角的大小，从已知可看出，把已知条件用正弦定理化为边的关系，然后用余弦定理可得；（Ⅱ）由（Ⅰ），因此可把化为一个角的三角函数，再由两角和与差的正弦公式化为一个三角函数，可得最大值．试题解析：（Ⅰ）由已知，根据正弦定理得即由余弦定理得故，A=120°（Ⅱ）由（Ⅰ）得：故当B=30°时，sinB+sinC取得最大值1。

三角函数及三角恒等变换测试题及答案

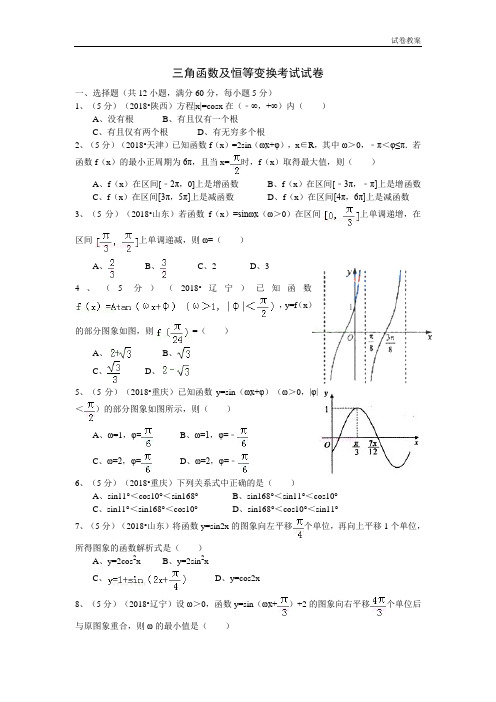
三角函数及恒等变换考试试卷一、选择题（共12小题，满分60分，每小题5分）1、（5分）（2018•陕西）方程|x|=cosx在（﹣∞，+∞）内（）A、没有根B、有且仅有一个根C、有且仅有两个根D、有无穷多个根2、（5分）（2018•天津）已知函数f（x）=2sin（ωx+φ），x∈R，其中ω＞0，﹣π＜φ≤π．若函数f（x）的最小正周期为6π，且当x=时，f（x）取得最大值，则（）A、f（x）在区间[﹣2π，0]上是增函数B、f（x）在区间[﹣3π，﹣π]上是增函数C、f（x）在区间[3π，5π]上是减函数D、f（x）在区间[4π，6π]上是减函数3、（5分）（2018•山东）若函数f（x）=sinωx（ω＞0）在区间上单调递增，在区间上单调递减，则ω=（）A、B、C、2 D、34、（5分）（2018•辽宁）已知函数，y=f（x）的部分图象如图，则=（）A、B、C、D、5、（5分）（2018•重庆）已知函数y=sin（ωx+φ）（ω＞0，|φ|＜）的部分图象如图所示，则（）A、ω=1，φ=B、ω=1，φ=﹣C、ω=2，φ=D、ω=2，φ=﹣6、（5分）（2018•重庆）下列关系式中正确的是（）A、sin11°＜cos10°＜sin168°B、sin168°＜sin11°＜cos10°C、sin11°＜sin168°＜cos10°D、sin168°＜cos10°＜sin11°7、（5分）（2018•山东）将函数y=sin2x的图象向左平移个单位，再向上平移1个单位，所得图象的函数解析式是（）A、y=2cos2xB、y=2sin2xC、D、y=cos2x8、（5分）（2018•辽宁）设ω＞0，函数y=sin（ωx+）+2的图象向右平移个单位后与原图象重合，则ω的最小值是（）A、B、C、D、39、（5分）（2018•江西）已知函数f（x）=Acos（ωx+φ）的图象如图所示，f（）=﹣，则f（0）=（）A、﹣B、﹣C、D、10、（5分）（2018•广东）函数y=2cos2（x﹣）﹣1是（）A、最小正周期为π的奇函数B、最小正周期为π的偶函数C、最小正周期为的奇函数D、最小正周期为的偶函数11、（5分）（2018•天津）设，，，则（）A、a＜b＜cB、a＜c＜bC、b＜c＜aD、b＜a＜c12、（5分）已知函数f（x）=sin（2x﹣），若存在a∈（0，π），使得f（x+a）=f（x+3a）恒成立，则a=（）A、B、C、D、二、填空题（共4小题，满分16分，每小题4分）13、（4分）（2018•辽宁）已知f（x）=sin（ω＞0），f（）=f（），且f（x）在区间上有最小值，无最大值，则ω=_________．14、（4分）（2018•四川）已知函数（ω＞0）在单调增加，在单调减少，则ω=_________．15、（4分）（2007•四川）下面有5个命题：①函数y=sin4x﹣cos4x的最小正周期是π；②终边在y轴上的角的集合是；③在同一坐标系中，函数y=sinx的图象和函数y=x的图象有3个公共点；④把函数的图象向右平移得到y=3sin2x的图象；⑤角θ为第一象限角的充要条件是sinθ＞0其中，真命题的编号是_________（写出所有真命题的编号）16、（4分）若=_________．三、解答题（共7小题，满分74分）17、（10分）（2018•四川）求函数y=7﹣4sinxcosx+4cos2x﹣4cos4x的最大值与最小值．18、（10分）（2018•北京）已知函数．（Ⅰ）求f（x）的最小正周期：（Ⅱ）求f（x）在区间上的最大值和最小值．19、（10分）（2018•陕西）如图，A，B是海面上位于东西方向相距5（3+）海里的两个观测点，现位于A点北偏东45°，B点北偏西60°的D点有一艘轮船发出求救信号，位于B点南偏西60°且与B点相距20海里的C点的救援船立即即前往营救，其航行速度为30海里/小时，该救援船到达D点需要多长时间？20、（10分）（2018•浙江）已知函数，x∈R，A＞0，．y=f（x）的部分图象，如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为（1，A）．（Ⅰ）求f（x）的最小正周期及φ的值；（Ⅱ）若点R的坐标为（1，0），，求A的值．21、（10分）（2018•江苏）某兴趣小组测量电视塔AE的高度H（单位：m），如示意图，垂直放置的标杆BC的高度h=4m，仰角∠ABE=α，∠ADE=β．（1）该小组已经测得一组α、β的值，tanα=1.24，tanβ=1.20，请据此算出H的值；（2）该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d（单位：m），使α与β之差较大，可以提高测量精确度．若电视塔的实际高度为125m，试问d为多少时，α﹣β最大？22、（10分）（2018•广东）已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），x∈R的最大值是1，其图象经过点．（1）求f（x）的解析式；（2）已知，且，，求f（α﹣β）的值．23、（14分）已知函数，（1）求函数f（x）的最小正周期；（2）求函数f（x）的单调减区间；（3）画出函数的图象，由图象研究并写出g（x）的对称轴和对称中心．答案与评分标准一、选择题（共12小题，满分60分，每小题5分）1、（5分）（2018•陕西）方程|x|=cosx在（﹣∞，+∞）内（）A、没有根B、有且仅有一个根C、有且仅有两个根D、有无穷多个根考点：余弦函数的图象。

高中数学三角恒等变换精选题目(附答案)

高中数学三角恒等变换精选题目（附答案）一、两角和与差的正弦、余弦和正切公式： ⑴()cos cos cos sin sin αβαβαβ-=+； ⑵()cos cos cos sin sin αβαβαβ+=-； ⑶()sinsin cos cos sin αβαβαβ-=-；⑷()sin sin cos cos sin αβαβαβ+=+； ⑸()tan tan tan 1tan tan αβαβαβ--=+⇒()()tan tan tan 1tan tan αβαβαβ-=-+⑹()tan tan tan 1tan tan αβαβαβ++=- ⇒()()tan tan tan 1tan tan αβαβαβ+=+-二、二倍角的正弦、余弦和正切公式：sin 22sin cos ααα=222)cos (sin cos sin 2cos sin 2sin 1ααααααα±=±+=±⇒⑵2222cos2cos sin 2cos 112sin ααααα=-=-=-⇒221cos 2cos1cos 2sin 22αααα+=-=，⇒2cos 21cos 2αα+=，21cos 2sin 2αα-=． ⑶22tan tan 21tan ααα=-．三、辅助角公式：()sin cos α+=+a x b x x ，cos sin ϕϕϕ==其中由决定四、三角变换方法：（1）角的变换：在三角化简，求值，证明中，表达式中往往出现较多的相异角，可根据角与角之间的和差，倍半，互补，互余的关系，运用角的变换，沟通条件与结论中角的差异，使问题获解，对角的变形如：①α2是α的二倍；α4是α2的二倍；α是2α的二倍；2α是4α的二倍；②2304560304515oooooo=-=-=；③()ααββ=+-；④()424πππαα+=--； ⑤2()()()()44ππααβαβαα=++-=+--；等等（2）函数名称变换：三角变形中，常常需要变函数名称为同名函数。

高一数学三角函数三角恒等变换解三角形试题答案及解析

高一数学三角函数三角恒等变换解三角形试题答案及解析1.(本小题满分12分)已知函数．(1)化简；(2)已知常数，若函数在区间上是增函数，求的取值范围；(3)若方程有解，求实数a的取值范围．【答案】（1）f(x)（2）（3）【解析】(1)························· 4分(2) ∵由∴的递增区间为∵在上是增函数∴当k = 0时，有∴解得∴的取值范围是····················· 8分(3) 解一：方程即为从而问题转化为方程有解，只需a在函数的值域范围内∵当；当∴实数a的取值范围为················ 12分解二：原方程可化为令，则问题转化为方程在［– 1，1］内有一解或两解，设，若方程在［– 1，1］内有一个解，则解得若方程在［– 1，1］内有两个解，则解得∴实数a的取值范围是［– 2，］2.已知函数（1）求函数f（x）的最小正周期及单调递增区间；（2）在中，A、B、C分别为三边所对的角，若a=f（A）=1，求的最大值．【答案】（1），单调增区间；（2）【解析】（1）首先借助于基本三角函数公式将函数式化简为的最简形式，周期由的系数求解，求增区间需令，解得的范围得到单调区间；（2）中由的值求得角，借助于三角形余弦定理可得到关于两边的关系式，进而结合不等式性质得到关于的不等式，求得范围试题解析：（1），所以函数的最小正周期为．由得所以函数的单调递增区间为．（2）由可得，又，所以。

简单的三角恒等变换专题及答案

简单的三角恒等变换专题及答案简单的三角恒等变换专题一、选择题1.已知sinα＝5115，则cos(π－2α)＝()。

答案：B。

通过sinα和cos(π－2α)的关系，可以得到cos(π－2α)＝－sinα＝－(1/5115)。

2.sin70°/(2cos10°－sin20°)的值是()。

答案：C。

通过三角函数的恒等变换，可以将sin70°/(2cos10°－sin20°)化简为sin70°/cos80°，再使用tan的定义式，得到tan70°=sin70°/cos70°=sin70°/sin10°cos80°=sin70°/sin10°sin10°=1/sin10°=3.3.若sin76°＝m，用含m的式子表示cos7°为()。

答案：B。

通过三角函数的恒等变换，可以得到cos(π/2－76°)＝sin76°＝m，即cos14°＝m，再通过三角函数的恒等变换，可以得到cos7°＝2cos2(7°)－1＝2cos2(14°)cos(π/2－14°)－1＝2(1－sin2(14°))－1＝1－2sin2(14°)＝1－2(cos14°)2＝1－2m2.4.若cos2α＝－2，则sinα＋cosα的值为sin(7π/4)()。

答案：B。

通过cos2α的值可以得到sin2α＝1－cos2α＝3，再通过三角函数的恒等变换，可以得到sinα＋cosα＝√2sin(π/4＋α)＝√2sin(π/4＋α－2π)＝√2sin(7π/4－α)。

5.已知f(x)＝2tanx－2/(x＋π/12)，则f(π/6)的值为()。

答案：D。

高三数学-三角函数的图象与性质、三角恒等变换-专题练习及答案

高三数学专题练习三角函数的图象与性质、三角恒等变换【重点把关】1．(2016·榆林一模)已知π,π2a æöÎç÷èø，且()3sin π5a +=-，则tan a =等于( )A ．34-B ．43 C ．34D ．43-2．(2016·湖南衡阳一模)已知角j 的终边经过点()4,3P -，函数()()()sin 0f x x w j w =+>的图象的相邻两条对称轴之间的距离等于π2，则π4f æöç÷èø的值为( )A ．35 B ．45C ．35-D ．45-3．(2016·四川卷，文4)为了得到函数πsin 3y x æö=+ç÷èø的图象，只需把函数sin y x =的图象上所有的点( )A ．向左平行移动π3个单位长度B ．向右平行移动π3个单位长度C ．向上平行移动π3个单位长度D ．向下平行移动π3个单位长度4．(2016·河南郑州一模)函数()11πsin 2tan cos 2223f x x x =+的最小正周期为( )A ．π2 B ．πC ．2πD ．4π 5．(教材拓展)函数πsin 23y x æö=-ç÷èø的单调递减区间是( )A ．π2ππ,π,63k k k éù-+-+ÎêúëûZ B ．π5π2π-,2π,1212k k k éù+ÎêúëûZ C ．πππ-,π,63k k k éù-+ÎêúëûZ D ．π5ππ,π,1212k k k éù++ÎêúëûZ 6．(2016·河南开封一模)已知函数()()π2sin πsin 3f x x x j æö=+++ç÷èø的图象关于原点对称，其中()0,πj Î，则j =________．7．(2016·吉林白山一模)已知1sin cos 3a a =+，且π0,2a æöÎç÷èø)，则cos 2πsin 4a a æö+ç÷èø的值为________．8．(2016·湖南常德模拟)已知函数()()2cos 2cos 0f x x x x w w w w =+>，且()f x 的最小正周期为π．(1)求w 的值及()f x 的单调递减区间；(2)将函数()f x 的图象向右平移π6个单位长度后得到函数()g x 的图象，求当π0,2x éùÎêúëû时()g x 的最大值．【能力提升】9．(2016·湖北八校联考)若()()()2cos 20f x x j j =+>的图象关于直线π3x =对称，且当j 取最小值时，0π0,2x æö$Îç÷èø，使得()0f x a =，则a 的取值范围是( )A ．(]1,2-B ．[)2,1--C ．()1,1--D ．[)2,1-10．(2016·山东青岛一模)已知函数()()()sin 000πf x A x A w j w j =+>><<,,是偶函数，它的部分图象如图所示．M 是函数()f x 图象上的点，K ，L 是函数()f x 的图象与x 轴的交点，且KML D 为等腰直角三角形，则()f x =________．11．(2016·北京卷，文16)已知函数()()2sin cos cos 20f x x x x w w w w =+>的最小正周期为π．（1）求w 的值；（2）求()f x 的单调递增区间．12．(2016·河北石家庄二模)已知函数()()π4cos sin 06f x x x a w w w æö=++>ç÷èø图象上最高点的纵坐标为2，且图象上相邻两个最高点的距离为π．（1）求a 和w 的值；（2）求函数()f x 在[]0,π上的单调递减区间．【创新选做】13．(2016·江西南昌模拟)已知函数()π1sin ,62f x x x w æö=-+Îç÷èøR ，且()12f a =-，()12f b =，若a b -的最小值为3π4，则函数的单调递增区间为( )A ．π2π,π2π,2k k k éù-++ÎêúëûZB ．π3π,π3π,2k k k éù-++ÎêúëûZC ．5ππ2π,2π,2k k k éù++ÎêúëûZ D ．5ππ3π,3π,2k k k éù++ÎêúëûZ高三数学专题练习三角函数的图象与性质、三角恒等变换答案【重点把关】1~5．ADABD6．π67．8．解：(1)()21cos 2f x x xw w ++π=2sin 216x w æö++ç÷èø．因为2πππ2T w =Þ=，所以1w =．从而()π=2sin 216f x x æö++ç÷èø，令()ππ3π2π22π262k x k k +£+£+ÎZ ，得()π3πππ62k x k k +££+ÎZ ，所以()f x 的单调递减区间为π2ππ,π,63k k k éù++ÎêúëûZ ．(2)()πππ2sin 212sin 21666g x x x éùæöæö=-++=-+ç÷ç÷êúèøèøëû，因为π0,2x éùÎêúëû，所以ππ5π2666x -£-£，所以当ππ262x -=，即π3x =时，()max 2113g x =´+=．【能力提升】9．D10．1cos π2x 11．解：(1)因为()2sin cos cos 2f x x x xw w w =+sin 2cos 2x xw w =+π24x w æö=+ç÷èø，所以()f x 的最小正周期2ππ2T w w ==．依题意，π=πw ，解得1w =．(2)由(1)知()π24f x x æö=+ç÷èø．函数sin y x =的单调递增区间为()ππ2π,2π+22k k k éù-ÎêúëûZ ．由πππ2π22π,242k x k k -£+£+ÎZ ，得3ππππ,88k x k k -££+ÎZ ．所以()f x 的单调递增区间为()3πππ,π88k k k éù-+ÎêúëûZ ．12．解：(1)()π4cos sin 6f x x x a w w æö=++ç÷èø14cos cos 2x x x a w w w ö=++÷÷ø2cos 2cos 11x x x aw w w =+-++22cos 21x x aw w =+++π2sin 216x A w æö=+++ç÷èø．当πsin 216x w æö+=ç÷èø时，()f x 取得最大值213a a ++=+，又()f x 图象上最高点的纵坐标为2，所以32a +=，即1a =-．又()f x 图象上相邻两个最高点的距离为π，所以()f x 的最小正周期为πT =，故2π22Tw ==，1w =．(2)由(1)得()π2sin 26f x x æö=+ç÷èø，由ππ3π2π22π,262k x k k +£+£+ÎZ ，得π3πππ,62k x k k +££+ÎZ ．令0k =，得π2π63x ££．故函数()f x 在[]0,π上的单调递减区间为π2π,63éùêúëû．【创新选做】13．B高三数学专题练习三角函数的图象与性质、三角恒等变换解析【重点把关】1．解析：因为α∈(，π)，sin(π+α)=-sin α=-，即sin α=，所以cos α=-=-，则tan α==-，故选A．2．解析：由题意得ω=2，cos j=-，所以f()=sin(2×+j)=cos j=-，选D．3．解析：由y=sin x图象上所有的点向左移动个单位长度就得到函数y=sin(x+)的图象，故选A．4．解析：函数f(x)=sin 2x+tan cos 2x=sin 2x+cos 2x=sin(2x+)的最小正周期为=π．故选B．5．解析：函数y=sin(-2x)=-sin(2x-)的单调递减区间，即函数y=sin(2x-)的单调递增区间．令2kπ-≤2x-≤2kπ+，k∈Z，求得kπ-≤x≤kπ+，k∈Z，故函数y=sin(2x-)的单调递增区间，即函数y=sin(-2x)的单调递减区间为[kπ-，kπ+]，k∈Z．故选D．6．解析：化简可得f(x)=-2sin xsin(x++j)，因为函数图象关于原点对称，故f(-)=-f()，代值计算可得-2×(-)sin j=-(-2)×sin(+j)，化简可得sin j=sin(+j)，又j∈(0，π)，所以j++j=π，解得j=．答案：7．解析：因为sin α=+cos α，即sin α-cos α=，所以===-．答案：-8．【能力提升】9．解析：因为函数f(x)=2cos(2x+j)(j>0)的图象关于直线x=对称，所以+j=kπ，k∈Z，所以j=kπ-，k∈Z，当j(j>0)取最小值时j=，所以f(x)=2cos(2x+)，因为x0∈(0，)，所以2x0+∈(，)，所以-1≤cos(2x0+)<，所以-2≤f(x0)<1，因为f(x0)=a，所以-2≤a<1．故选D．10．解析：由图象可知，A=，又f(x)=Asin(ωx+j)是偶函数，所以j=+2kπ，k∈Z，又因为0<j<π，所以j=．如图，过点M作MN⊥KL于N，因为△KLM为等腰直角三角形，所以MN=KN=NL=，KL=1，所以函数f(x)的周期T=2，即=2，ω=π．综上知，函数f(x)=cos πx．答案：cos πx11．12．【创新选做】13．解析：因为f(x)=sin(ωx-)+，且f(α)=-，所以sin(ωα-)+=-，解得sin(ωα-)=-1，同理可得sin(ωβ-)=0，由|α-β|的最小值为和三角函数图象可得·=，解得ω=，所以f(x)=sin(x-)+，由2kπ-≤x-≤2kπ+，k∈Z，可得3kπ-≤x≤3kπ+π，k∈Z，所以函数的单调递增区间为[3kπ-，3kπ+π]k∈Z．故选B．。

三角恒等变形测试题及答案解析

第三章恒等变换一、选择题(此题共12小题,每题5分,总分值60分) 1.277sin 16812π-的值为〔〕 2.假设sin()cos cos()sin m αβααβα---=，且β为第三象限角，则cos β的值为〔〕 3．在△ABC 中，2sinAcosB ＝sinC ，则△ABC 一定是 ( ) A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．正三角形4．2cos10°－sin20°sin70°的值是 ( )A ．12B ．32 C ．3 D ． 25．*∈(－π2,0)，cos*＝45，则tan2*等于 ( )A ．724B ．－724C ．247D ．－2476.假设ABC ∆的角A 满足2sin 23A =，则sin cos A A += ( )B． C ．53 D ．53-7．等式sin α＋3cos α＝4m －64－m 有意义，则m 的取值围是 ()A ．(－1,73)B ．[－1,73]C ．[－1,73]D ．[―73,―1]8．在△ABC 中，tan A ＋B2＝sinC ，则以下四个命题中正确的选项是 ()(1)tanA ·cotB ＝1．(2)1＜sinA ＋sinB ≤2．(3)sin 2A ＋cos 2B ＝1．(4)cos 2A ＋cos 2B ＝sin 2C ．A ．①③B ．②④C ．①④D ．②③ 9．α∈(0,π)，且sin α＋cos α＝15，则tan α的值为 ()A ．－43B ．－43 或－34C ．－34D ．43 或－3410．函数)cos (sin sin 2x x x y +=的最大值为( )A.21+B.12-C.2D.211.将函数212sin 22y x x =+-的图象进展以下哪一种变换就变为一个奇函数的图象 ( 〔〕 A ．向左平移12π个单位 B ．向左平移6π个单位 C ．向右平移12π个单位 D ．向右平移6π个单位cos 23x x a +=-中，a 的取值围是〔〕二．填空题(此题共5小题,每题6分,总分值30分)把答案填在第二卷的横线上13.sin cos ,x x m -=求sin cos x x ────── 14．函数x x x f 32sin)232sin()(++=π的图象相邻的两条对称轴之间的距离是 15.假设*＝π3是方程2cos(*＋α)＝1的解，α∈(0,2π)，则α＝．16.给出下面的3个命题：〔1〕函数|)32sin(|π+=x y 的最小正周期是2π；〔2〕函数)23sin(π-=x y 在区间)23,[ππ上单调递增；〔3〕45π=x 是函数)252sin(π+=x y 的图象的一条对称轴.其中正确命题的序号是．17．在△ABC 中，sinA ＋cosA ＝22，AC ＝2，AB ＝3，则tanA=，△ABC 的面积为第二卷二、填空题(本大题共6小题,每题5分,共30分.把答案填在题中横线上)11.________________________ 12._______________________ 13._________________________ 14.______________________ 15._________________________ 16._______________________三．解答题此题共小题〔,每题12分,总分值60分，解容许写出文字说明，证明过程或演算步骤)18.12cos ,13α=求sin α和tan α 19．设cos(α－β2)＝－19，sin(α2－β)＝23，且π2＜α＜π，0＜β＜π2，求cos 〔α＋β〕．20．6sin 2α＋sin αcos α－2cos 2α＝0，α∈[π2,π]，求sin(2α＋π3)的值．21．在矩形ABCD 中，AB ＝a ，BC ＝2a ，在BC 上取一点P ，使得AB ＋BP ＝PD ，求tan ∠APD 的值．22.函数2()2cos 2sin 4cos f x x x x =+- (1)求()3f π值的；(2)求()f x 的最大值和最小值。