使用SPSS进行两组独立样本的t检验、F检验、显著性差异、计算p值
显著性分析用SPSS进行统计检验

显著性分析用SPSS进行统计检验显著性分析用SPSS进行统计检验,这是我们今天要聊的话题。
你知道吗?在我们的日常生活中,我们经常会遇到各种各样的问题,需要我们去分析和解决。
而数据分析就是帮助我们解决这些问题的一种方法。
那么,什么是显著性分析呢?简单来说,就是通过统计学的方法来判断一个样本是否具有某种特定的性质。
如果具有这种性质,我们就可以说这个样本是显著的;如果不具有这种性质,我们就不能说这个样本是显著的。
那么,如何用SPSS来进行显著性分析呢?接下来,就让我来给大家详细介绍一下吧!我们需要了解一下SPSS的基本操作。
SPSS是一款非常强大的统计软件,它可以帮助我们完成各种复杂的数据分析任务。
在进行显著性分析之前,我们需要先准备好数据。
这些数据可以来自于各种各样的来源,比如问卷调查、实验数据等等。
接下来,我们就可以开始进行显著性分析了。
在SPSS中,我们可以使用多种方法来进行显著性分析。
其中最常用的方法就是t检验和方差分析。
t检验是用来比较两个样本均值是否有显著差异的一种方法;而方差分析则是用来比较三个或三个以上样本均值是否有显著差异的一种方法。
除了这两种方法之外,SPSS还提供了很多其他的方法,比如卡方检验、相关系数分析等等。
这些方法都可以用来进行显著性分析,具体使用哪一种方法,需要根据我们的实际需求来决定。
在进行显著性分析的过程中,我们需要注意一些细节问题。
比如,我们需要确保样本量足够大;我们需要确保各个变量之间的关系是独立的;我们需要确保我们所使用的假设是正确的等等。
只有注意到这些问题,我们才能得到准确的结果。
显著性分析用SPSS进行统计检验是一种非常实用的方法。
通过这种方法,我们可以帮助我们更好地理解数据背后的信息,从而做出更加科学的决策。
要想熟练掌握这种方法,我们需要不断地学习和实践。
希望这篇文章能对大家有所帮助!。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的?一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t 分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢?会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同?为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<0.05(少xx5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,xx,总体应该存在著差异。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的?一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢?会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同?为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<0.05(少xx5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,xx,总体应该存在著差异。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<(少於5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,简言之,总体应该存在著差异。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的?一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢?会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同?为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<0.05(少xx5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,xx,总体应该存在著差异。
用SPSS进行T检验

用SPSS进行T检验什么是T检验?T检验是统计学中的常用方法之一,用于检验两组样本的均值是否有显著差异。
它是通过计算样本的t值来确定两组样本均值差异是否显著。
因此,如果两组样本的t值越大,则它们之间的差异就越明显。
在进行T检验之前,我们首先需要明确两组样本是否满足正态分布的要求。
如果样本呈正态分布,则我们可以使用独立样本T检验或配对样本T检验进行检验。
如果不符合正态分布条件,我们需要使用非参数检验方法,例如Wilcoxon符号秩检验或Mann-Whitney U检验。
如何用SPSS进行T检验?下面我们将演示如何使用SPSS进行独立样本T检验和配对样本T检验。
独立样本T检验独立样本T检验用于检验两个独立样本的均值是否有差异。
例如,我们想知道男性和女性在身高上是否有显著差异,则可以使用独立样本T检验来验证。
我们使用一个示例数据集来展示如何进行独立样本T检验。
该数据集包含两组样本:一组是男子的身高,另一组是女子的身高。
在SPSS中,我们可以按照以下步骤进行独立样本T检验:1.打开SPSS软件并载入数据集。
2.单击菜单栏中的“分析”(Analyze),然后选择“比较均值”(CompareMeans),再选“独立样本T检验”(Independent-Samples T Test)。
3.在“独立样本T检验”对话框中,将男性身高和女性身高变量分别放到“变量1”和“变量2”框中。
4.点击“OK”按钮,SPSS将自动计算并输出T检验的结果和描述性统计数据。
下面是一个示例的SPSS的输出:执行男子控制女子均值174.609 161.164标准差 6.971 6.098标准误差均值 1.760 1.53595% CI(下限)171.023 158.126T 17.915df 38Sig。
(双尾).000T检验结果显示,在本例中,男性和女性的身高之间存在显著差异。
T值为17.915,df值为38,Sig值小于0.05,表明这两组数据的差异不是由于随机因素导致的,而是由于不同的性别所导致的。
用SPSS进行统计差异显著性分析检验的基本原理和方法

【例6-5】某项教育技术实验,对实验组和控制组的前测和后测的数据分别如表6-14所示,
比较两组前测和后测是否存在差异。
由于n>30,属于大样本,应采用Z检验。由于这是检验来自两个不同总体的两个样本平均数,
看它们各自代表的总体的差异是否显著,所以采用双总体的Z检验方法。
计算前测Z的值
它是用t分布理论来推断差异发生的概率,从而判定两个平均数的差异是否显著。其一般步骤如下:
第一步,建立虚无假设,即先假定两个总体平均数之间没有显著差异。
第二步,计算统计量t值,对于不同类型的问题选用不同的统计量计算方法。
(1)如果要评断一个总体中的小样本平均数与总体平均值之间的差异程度,其统计量t值的计算公式为:
(2)如果要评断两组样本平均数之间的差异程度,其统计量t值的计算公式为:
第三步,根据自由度df= n-1,查t值表,找出规定的t理论值(见附录)并进行比较。
理论值差异的显著水平为0.01级或0.05级。不同自由度的显著水平理论值记为t (df)0.01和t (df)0.05
第四步,比较计算得到的t值和理论t值,推断发生的概率,
依据表6-15给出的t值与差异显著性关系表作出判断。
第五步,根据是以上分析,结合具体情况,作出结论
用SPSS进行统计差异显著性分析检验的基本原理和方法
发布时间:2012-09-07 点击数: 462
用SPSS进行统计差异显著性分析检验的基本原理和方法
一、统计检验的基本原理
统计检验是先对总体的分布规律作出某种假说,然后根据样本提供的数据,通过统计运算,根据运算结果,
对假说作出肯定或否定的决策。如果现要检验实验组和对照组的平均数(μ1和μ2)有没有差异,其步骤为:
SPSS软件单个样本样品、两个独立样本样品和两个配对样本样品T检验的应用

表3
单个样本统计量 N 太空种子直径 10 均值 9.4640 标准差 .71787 均值的标准误 .22701
表3 表4太空种子直径T检验结果
单个样本检验 检验值 = 8.86 差分的 95% 置信区间 t 太空种子直径 2.661 df 9 Sig.(双侧) .026 均值差值 .60400 下限 .0905 上限 1.1175
2 S12 S 2 )2 n n2 f 21 S S2 ( 1 )2 ( 2 ) n1 n 2 n1 n2
(
⑶计算检验统计量观测值和概率 P-值。 该步的目的是计算 F 统计量和 t 统计量的观测值以及相应的概率 P-值。SPSS 将自动依 据单因素方差分析的方法计算 F 统计量和概率 P-值,并自动将两组样本的均值、样本数、 抽样分布方差等代入式③中,计算出 t 统计量的观测值和对应的概率 P-值。 ⑷给定显著性水平 ,并作出决策。 第一步,利用 F 检验判断两总体的方差是否相等,并据此决定抽样分布方差和自语度 的计算方法和计算结果。如果 F 检验统计量的概率 P-值小于显著想水平 ,则应拒绝原假 设,认为两总体方差没有显著差异,应选择式②和式③计算出的结果:反之,若果概率 P值大于显著性水平 则不应拒绝原假设,认为两总体方差无显著差异。 第二步,体用 t 检验判断两总体均值是否存在显著差异。如果 t 检验统计量的概率 P-值 小于显著性水平 ,则应拒绝原假设,认为两总体均值有显著性差异;反之,如果概率 P值大于显著性水平 ,则不应拒绝原假设,认为两总体均值无显著差异。 3.两独立样本 T 检验的应用举例:某种物料施加保润剂木糖醇 1%,对照为加等量的水,问 木糖醇是否能提高物料含水率?样品数量不相等
推断某种植物种子平均直径是 8.87mm。由于该问题设计的是单个总体,且要进行总体 均值比较,同时植物种子平均直径总体可近似认为服从正态分布,因此,可采用单样本 T 检验来进行分析。 SPSS 单样本 T 检验的基本操作步骤是: ⑴spss 输入数据和参数名称:
使用SPSS 进行两组独立样本的t检验、F检验、显著性差异、计算p值.
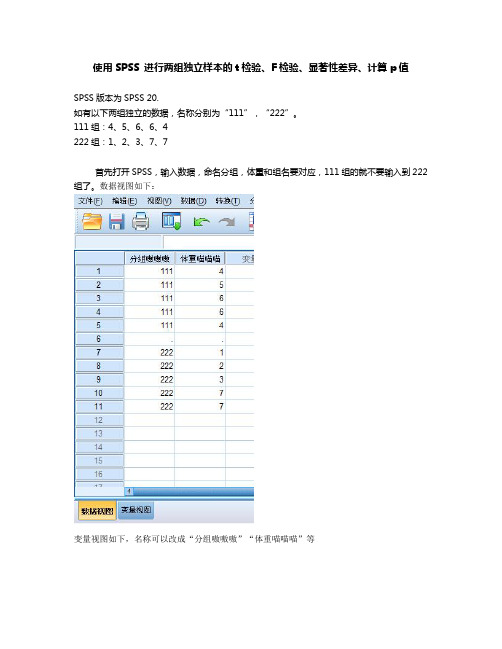
使用SPSS 进行两组独立样本的t检验、F检验、显著性差异、计算p值SPSS版本为SPSS 20.如有以下两组独立的数据,名称分别为“111”,“222”。
111组:4、5、6、6、4222组:1、2、3、7、7首先打开SPSS,输入数据,命名分组,体重和组名要对应,111组的就不要输入到222组了。
数据视图如下:变量视图如下,名称可以改成“分组嗷嗷嗷”“体重喵喵喵”等点击“分析”-“比较均值”-“独立样本T检验”来到这里,分组变量为“分组嗷嗷嗷”,检验变量为“体重喵喵喵”。
【关键的一步】点击分组嗷嗷嗷,进行“定义组”【关键的一步】输入对应的两组数据的组名:“111”和“222”点击确定,可见数据与组名对应上了。
点击“确定”,生成T检验的报告,即将大功告成!第一个表都知道什么回事就不缩了,excel都能实现的。
第二个表才是重点,不然用SPSS干嘛。
F检验:在两样本t检验中要用到F检验,F检验又叫方差齐性检验,用于判断两总体方差是否相等,即方差齐性。
如图:F旁边的Sig的值为.007 即0.007,<0.01, 即两组数据的方差显著性差异!看到“假设方差相等”和“假设方差不相等”了么?此时由于F检验得出Sig <0.01,即认为假设方差不相等!因此只关注红框中的数据即可。
如图,红框内,Sig(双侧),为.490即0.490,也就是你们要求的P值啦,Sig ( 也就是P值) >0.05,所以两组数据无显著性差异。
PS:同理,如果F检验的Sig >.05(即>0.05),则认为两个样本的假设方差相等。
所以相应的t检验的结果就看上面那行。
by 20150120 深大医学院FG。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<(少於5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,简言之,总体应该存在著差异。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的?一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢?会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同?为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<0.05(少xx5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,xx,总体应该存在著差异。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性的解释spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t 检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<(少於5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,简言之,总体应该存在著差异。
t检验使用条件及在SPSS中的应用

t 检验使用条件及在SPSS 中的应用t 检验是对均值的检验,有三种用途,分别对应不同的应用场景:1) 单样本t 检验(One Sample T Test ):对一组样本,检验相应总体均值是否等于某个值;2) 相互独立样本t 检验(Independent-Sample T Test ):利用来自某两个总体的独立样本,推断两个总体的均值是否存在显著性差异;3) 配对样本t 检验:是采用配对设计方法观察以下几种情形,1,两个同质受试对象分别接受两种不同的处理;2,同一受试对象接受两种不同的处理;3,同一受试对象处理前后。
下文将分别介绍三种t 检验的使用条件以及在SPSS 中的实现。
一、 单样本t 检验1.1简介1) 单样本t 检验的目的利用来自某总体的样本数据,推断该总体的均值是否与指定的检验值之间存在显著性差异,它是对总体均值的检验。
2) 单样本t 检验的前提样本来自的总体应服从和近似服从正态分布,且只涉及一个总体。
如果样本不符合正态分布或不清楚总体分布的形状,就不能用单样本t 检验,而要改用单样本的非参数检验。
3) 单样本t 检验的步骤a) 提出假设单样本t 检验需要检验总体的均值是否与指定的检验值之间存在显著性差异,为此,给定检验值μ0,提出假设:H 0:μ = μ0 (原假设,null hypothesis )H 1:μ ≠ μ0(备择假设,alternative hypothesis ,)b) 选择检验统计量属于总体均值和方差都未知的检验采用t 统计量:t =X ̅−μ0S ̂√n ⁄,其中,X ̅和S ̂分别为样本均值和方差,t 的自由度为n-1SPSS 中还将显示均值标准误差,计算公式为S ̂√n⁄,即t 统计量的分母部分。
c) 计算统计量的观测值和概率将样本均值、样本方差、μ0带入t 统计量,得到t 统计量的观测值,查t 分布界值表计算出概率P 值。
d) 给出显著性水平α,作出统计判断给出显著性水平α,与检验统计量的概率P 值作比较。
spss结果中,F值,t值及其显著性的解释

spss结果中,F值,t值及其显著性(sig)的解释用spss处理完数据的显示结果中,F值,t值及其显著性(sig)都分别是解释什么的?一般而言,为了确定从样本(sample)统计结果推论至总体时所犯错的概率,我们会利用统计学家所开发的一些统计方法,进行统计检定。
通过把所得到的统计检定值,与统计学家建立了一些随机变量的概率分布(probability distribution)进行比较,我们可以知道在多少%的机会下会得到目前的结果。
倘若经比较后发现,出现这结果的机率很少,亦即是说,是在机会很少、很罕有的情况下才出现;那我们便可以有信心的说,这不是巧合,是具有统计学上的意义的(用统计学的话讲,就是能够拒绝虚无假设null hypothesis,Ho)。
相反,若比较后发现,出现的机率很高,并不罕见;那我们便不能很有信心的直指这不是巧合,也许是巧合,也许不是,但我们没能确定。
F值和t值就是这些统计检定值,与它们相对应的概率分布,就是F分布和t分布。
统计显著性(sig)就是出现目前样本这结果的机率。
至於具体要检定的内容,须看你是在做哪一个统计程序。
举一个例子,比如,你要检验两独立样本均数差异是否能推论至总体,而行的t检验。
两样本(如某班男生和女生)某变量(如身高)的均数并不相同,但这差别是否能推论至总体,代表总体的情况也是存在著差异呢?会不会总体中男女生根本没有差别,只不过是你那麼巧抽到这2样本的数值不同?为此,我们进行t检定,算出一个t检定值,与统计学家建立的以「总体中没差别」作基础的随机变量t分布进行比较,看看在多少%的机会(亦即显著性sig值)下会得到目前的结果。
若显著性sig值很少,比如<0.05(少xx5%机率),亦即是说,「如果」总体「真的」没有差别,那麼就只有在机会很少(5%)、很罕有的情况下,才会出现目前这样本的情况。
虽然还是有5%机会出错,但我们还是可以「比较有信心」的说:目前样本中这情况(男女生出现差异的情况)不是巧合,是具统计学意义的,「总体中男女生不存差异」的虚无假设应予拒绝,xx,总体应该存在著差异。
显著性分析用SPSS进行统计检验

显著性分析用SPSS进行统计检验显著性分析用SPSS进行统计检验,这是我们今天要聊的话题。
你知道吗?在我们的日常生活中,我们经常会遇到各种各样的问题,需要我们去分析和解决。
而数据分析就是帮助我们解决这些问题的一种方法。
那么,什么是显著性分析呢?简单来说,就是通过统计学的方法来判断一个样本是否具有某种特定的性质。
如果具有这种性质,我们就可以说这个样本是显著的;如果不具有这种性质,我们就不能说这个样本是显著的。
那么,如何用SPSS来进行显著性分析呢?接下来,就让我来给大家详细介绍一下吧!我们需要了解一下SPSS的基本操作。
SPSS是一款非常强大的统计软件,它可以帮助我们完成各种复杂的数据分析任务。
在进行显著性分析之前,我们需要先准备好数据。
这些数据可以来自于各种各样的来源,比如问卷调查、实验数据等等。
接下来,我们就可以开始进行显著性分析了。
在SPSS中,我们可以使用多种方法来进行显著性分析。
其中最常用的方法就是t检验和方差分析。
t检验是用来比较两个样本均值是否有显著差异的一种方法;而方差分析则是用来比较三个或三个以上样本均值是否有显著差异的一种方法。
除了这两种方法之外,SPSS还提供了很多其他的方法,比如卡方检验、相关系数分析等等。
这些方法都可以用来进行显著性分析,具体使用哪一种方法,需要根据我们的实际需求来决定。
在进行显著性分析的过程中,我们需要注意一些细节问题。
比如,我们需要确保样本量足够大;我们需要确保各个变量之间的关系是独立的;我们需要确保我们所使用的假设是正确的等等。
只有注意到这些问题,我们才能得到准确的结果。
显著性分析用SPSS进行统计检验是一种非常实用的方法。
通过这种方法,我们可以帮助我们更好地理解数据背后的信息,从而做出更加科学的决策。
要想熟练掌握这种方法,我们需要不断地学习和实践。
希望这篇文章能对大家有所帮助!。
显著性分析用SPSS进行统计检验

显著性分析用SPSS进行统计检验显著性分析用SPSS进行统计检验,这是我们今天要聊的话题。
你知道吗?在我们的日常生活中,我们经常会遇到各种各样的问题,需要我们去分析和解决。
而数据分析就是帮助我们解决这些问题的一种方法。
那么,什么是显著性分析呢?简单来说,就是通过统计学的方法来判断一个样本是否具有某种特定的性质。
如果具有这种性质,我们就可以说这个样本是显著的;如果不具有这种性质,我们就不能说这个样本是显著的。
那么,如何用SPSS来进行显著性分析呢?接下来,就让我来给大家详细介绍一下吧!我们需要了解一下SPSS的基本操作。
SPSS是一款非常强大的统计软件,它可以帮助我们完成各种复杂的数据分析任务。
在进行显著性分析之前,我们需要先准备好数据。
这些数据可以来自于各种各样的来源,比如问卷调查、实验数据等等。
接下来,我们就可以开始进行显著性分析了。
在SPSS中,我们可以使用多种方法来进行显著性分析。
其中最常用的方法就是t检验和方差分析。
t检验是用来比较两个样本均值是否有显著差异的一种方法;而方差分析则是用来比较三个或三个以上样本均值是否有显著差异的一种方法。
除了这两种方法之外,SPSS还提供了很多其他的方法,比如卡方检验、相关系数分析等等。
这些方法都可以用来进行显著性分析,具体使用哪一种方法,需要根据我们的实际需求来决定。
在进行显著性分析的过程中,我们需要注意一些细节问题。
比如,我们需要确保样本量足够大;我们需要确保各个变量之间的关系是独立的;我们需要确保我们所使用的假设是正确的等等。
只有注意到这些问题,我们才能得到准确的结果。
显著性分析用SPSS进行统计检验是一种非常实用的方法。
通过这种方法,我们可以帮助我们更好地理解数据背后的信息,从而做出更加科学的决策。
要想熟练掌握这种方法,我们需要不断地学习和实践。
希望这篇文章能对大家有所帮助!。
显著性分析用SPSS进行统计检验

显著性分析用SPSS进行统计检验显著性分析用SPSS进行统计检验,这是我们今天要聊的话题。
你知道吗?在我们的日常生活中,我们经常会遇到各种各样的问题,需要我们去分析和解决。
而数据分析就是帮助我们解决这些问题的一种方法。
那么,什么是显著性分析呢?简单来说,就是通过统计学的方法来判断一个样本是否具有某种特定的性质。
如果具有这种性质,我们就可以说这个样本是显著的;如果不具有这种性质,我们就不能说这个样本是显著的。
那么,如何用SPSS来进行显著性分析呢?接下来,就让我来给大家详细介绍一下吧!我们需要了解一下SPSS的基本操作。
SPSS是一款非常强大的统计软件,它可以帮助我们完成各种复杂的数据分析任务。
在进行显著性分析之前,我们需要先准备好数据。
这些数据可以来自于各种各样的来源,比如问卷调查、实验数据等等。
接下来,我们就可以开始进行显著性分析了。
在SPSS中,我们可以使用多种方法来进行显著性分析。
其中最常用的方法就是t检验和方差分析。
t检验是用来比较两个样本均值是否有显著差异的一种方法;而方差分析则是用来比较三个或三个以上样本均值是否有显著差异的一种方法。
除了这两种方法之外,SPSS还提供了很多其他的方法,比如卡方检验、相关系数分析等等。
这些方法都可以用来进行显著性分析,具体使用哪一种方法,需要根据我们的实际需求来决定。
在进行显著性分析的过程中,我们需要注意一些细节问题。
比如,我们需要确保样本量足够大;我们需要确保各个变量之间的关系是独立的;我们需要确保我们所使用的假设是正确的等等。
只有注意到这些问题,我们才能得到准确的结果。
显著性分析用SPSS进行统计检验是一种非常实用的方法。
通过这种方法,我们可以帮助我们更好地理解数据背后的信息,从而做出更加科学的决策。
要想熟练掌握这种方法,我们需要不断地学习和实践。
希望这篇文章能对大家有所帮助!。
(完整版)SPSS两个独立样本秩和检验操作步骤.doc
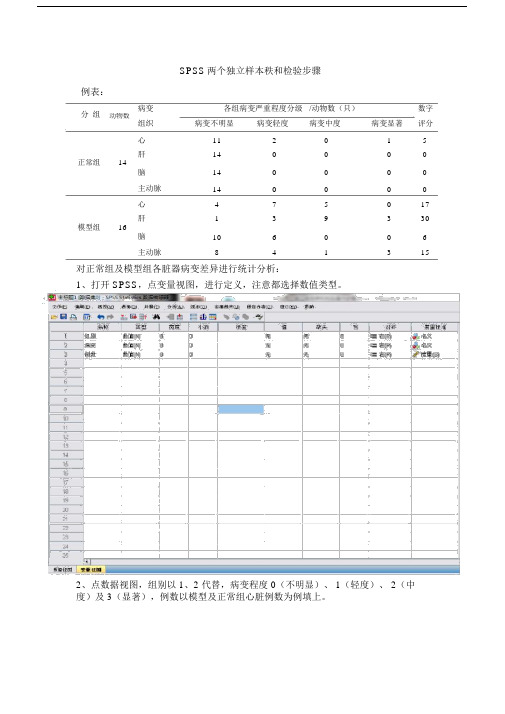
SPSS两个独立样本秩和检验步骤例表:
分组
病变各组病变严重程度分级/动物数(只)数字动物数
组织病变不明显病变轻度病变中度病变显著评分心11 2 0 1 5
肝14 0 0 0 0
正常组14
14 0 0 0 0
脑
主动脉14 0 0 0 0
心 4 7 5 0 17
肝 1 3 9 3 30 模型组16
10 6 0 0 6
脑
主动脉8 4 1 3 15 对正常组及模型组各脏器病变差异进行统计分析:
1、打开 SPSS,点变量视图,进行定义,注意都选择数值类型。
2、点数据视图,组别以 1、2 代替,病变程度 0(不明显)、 1(轻度)、 2(中度)及 3(显著),例数以模型及正常组心脏例数为例填上。
3、点数据→加权个案,频率变量选择例数,点确定,弹出输出数据对话框,可以选择不保存。
4、点击分析→非参数检验→2 个独立样本,检测变量列表选择病变,分组变量选择组别,点定义组,写上 1 和 2,再选择 Mann-Whitney U 检验,点确定。
5、分析结果看双侧P 值,示例结果为 0.008, P<0.01,具有显著性差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用SPSS 进行两组独立样本的t检验、F检验、显著性差异、计算p值
SPSS版本为SPSS 20.
如有以下两组独立的数据,名称分别为“111”,“222”。
111组:4、5、6、6、4
222组:1、2、3、7、7
首先打开SPSS,输入数据,命名分组,体重和组名要对应,111组的就不要输入到222组了。
数据视图如下:
变量视图如下,名称可以改成“分组嗷嗷嗷”“体重喵喵喵”等
点击“分析”-“比较均值”-“独立样本T检验”
来到这里,分组变量为“分组嗷嗷嗷”,检验变量为“体重喵喵喵”。
【关键的一步】点击分组嗷嗷嗷,进行“定义组”
【关键的一步】输入对应的两组数据的组名:“ 111”和“222”点击确定,可见数据与组名对应上了。
点击“确定”,生成T检验的报告,即将大功告成!
第一个表都知道什么回事就不缩了,excel都能实现的。
第二个表才是重点,不然用SPSS干嘛。
F检验:在两样本t检验中要用到F检验,F检验又叫方差齐性检验,用于判断两总体方差是否相等,即方差齐性。
如图:F旁边的 Sig的值为.007 即0.007, <0.01, 即两组数据的方差显著性差异!
看到“假设方差相等”和“假设方差不相等”了么?
此时由于F检验得出Sig <0.01,即认为假设方差不相等!因此只关注红框中的数据即可。
如图,红框内,Sig(双侧),为.490即0.490,也就是你们要求的P值啦,
Sig ( 也就是P值 ) >0.05,所以两组数据无显著性差异。
PS:同理,如果F检验的Sig >.05(即>0.05),则认为两个样本的假设方差相等。
所以相应的t检验的结果就看上面那行。
by 20150120 深大医学院 FG。
