您的位置：360文档中心› 高三数学期中测试试卷 文

高三数学期中测试试卷 文

合集下载

山东省青岛第五十八中学2024-2025学年高三上学期期中考试数学试题(含答案)

山东省青岛第五十八中学2024-2025学年高三上学期期中考试数学试题(含答案)

2022级高三调研测试4（期中）数学试题 2024.10注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置。

2．回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需要改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

第Ⅰ卷一、单项选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合，，则A ．{1，2，3} B ．{0，1，2}C ．{1，2，5}D ．{0，1，2，5}2．已知，则|z |＝A ．2B ．1CD3．已知，．若，则A ．B ． CD4．已知等比数列的前n 项和为，且，则“”是“的公比为2”的A ．必要不充分条件 B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件5，则此正四棱锥的体积为A．B ．C ．D ．6．已知函数则f （x ）图象上关于原点对称的点有A．1对B ．2对C ．3对D ．4对7．已知函数，函数f （x ）的图象各点的横坐标缩小为原来的6|,1P x y y x ⎧⎫=∈=∈⎨⎬+⎩⎭N N {}|15Q x x =-<≤P Q = i22iz =-||a = ||1b =()2a b a +⊥ cos ,a b ={}n a n S 31S ma =7m ={}n a ()21,0,2|2|,0,xx f x x x x ⎧⎛⎫⎪ ⎪=⎨⎝⎭⎪-+<⎩≥()2211cos sin cos 222222x x x x f x =-12（纵坐标不变），再向左平移个单位长度，得到函数的图象．若方程在上有两个不同的解，，则的值为A ．B ．C ．D ．π8．若关于x 不等式恒成立，则当时，的最小值为A ．B ．C ．eD ．1二．多项选择题（本大题共3小题，每小题6分，共18分。

在每小题给出的四个选项中，有多项符合题目要求。

北京市第十五中学2024-2025学年高三上学期期中考试数学试卷(含答案)

北京市第十五中学2024-2025学年高三上学期期中考试数学试卷(含答案)

北京十五中高三年级数学期中考试试卷2024.11本试卷共5页，150分.考试时长120分钟.考生务必将答案答在答题纸上，在试卷上作答无效.第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1．已知集合{}23A x x =-≤≤，{1B x x =<-或}4x >，那么集合A B = （A ）A ．{}21x x -≤<-B ．{3x x ≤或≥4C ．{}24x x -≤<D ．{}13x x -≤≤2．在复平面内，复数z 满足(1)2i z -=，则z =（D ）A ．1i--B ．1i-+C ．1i-D ．1i +3．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的是（A）A ．3()f x x =B ．2()f x x =C ．3()f x x=D ．()sin f x x=4．若0m n <<，则下列结论正确的是（B ）A ．22log log m n >B ．0.50.5log log m n>C ．1122m n⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D ．22m n>5．若α是第二象限角，且1tan 2α=-，则πcos 2α⎛⎫+= ⎪⎝⎭（D ）A ．2B ．2-C ．5D ．5-6．设等差数列{}n a 的前n 项和为n S ，且2822a a +=-，11110S =-，则n S 取最小值时，n 的值为（C ）A ．14B ．15C ．15或16D ．167．已知单位向量,a b ，则“a b ⊥”是“任意R λ∈都有a b a b -λ=λ+r r r r ”的（C ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件8．设函数()21cos cos 2f x x x x =--，则下列结论错误的是（D ）A ．()f x 的一个周期为πB ．()y f x =的图象关于直线4π3x =对称C ．将函数cos 2y x =的图象向左平移π6个单位可以得到函数()f x 的图象D ．()f x 在(π2,π)上单调递减9．在ABC V 中，2π3A =，D 为边BC 上一点，若AD AB ⊥，且1AD =，则ABC V 面积的最小值为（B ）AB C D 10．如图，曲线C 为函数5sin (0)2y x x π=≤≤的图象，甲粒子沿曲线C 从A 点向目的地B 点运动，乙粒子沿曲线C 从B 点向目的地A 点运动.两个粒子同时出发，且乙的水平速率为甲的2倍，当其中一个粒子先到达目的地时，另一个粒子随之停止运动.在运动过程中，设甲粒子的坐标为(,)m n ，乙粒子的坐标为(,)u v ，若记()n v f m -=，则下列说法中正确的是（B ）A ．()f m 在区间(,)2ππ上是增函数B ．()f m 恰有2个零点C ．()f m 的最小值为2-D ．()f m 的图象关于点5(,0)6π中心对称第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11．函数()f x =的定义域为________．[2，﹢∞)12．612x x ⎛⎫- ⎪⎝⎭的展开式中常数项为．(用数字作答)－16013．已知向量(,1),(1,2)a m b == ，且222||||||a b a b +=+，则m 的值为．－214．对于函数()ln21xf x x =-和()()ln ln 21g x x x =--，给出下列三个结论：①设()f x 的定义域为M ，()g x 的定义域为N ，则N 是M 的真子集.②函数()g x 的图像在1x =处的切线斜率为0.③函数()f x 的图像关于点1,ln24⎛⎫- ⎪⎝⎭对称.其中所有正确结论的序号是.①③解析：对于①，由题意得，函数()f x 的定义域()10,0,212x M xx ∞∞⎧⎫⎛⎫==-⋃+⎨⎬ ⎪-⎝⎭⎩⎭，函数()g x 的定义域12N x x ⎧⎫=⎨⎬⎩⎭.所以N 是M 的真子集，则①正确.对于②，()1221g x x x =--'，则在1x =处的切线斜率()1211121k g ='=-=--，则②错误.对于③只需验证：当1212x x +=时，()()()121212121212lnln ln 2ln22121421x x x x f x f x x x x x x x +=+==----++，则④正确.故答案为：①③.15．中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的民间艺术，剪纸具有广泛的群众基础，交融于各族人民的社会生活，是各种民俗活动的重要组成部分，其传承赓续的视觉形象和造型格式，蕴涵了丰富的文化历史信息，是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下：取一张半径为1的圆形纸片，记为O ，在O 内作内接正方形，接着在该正方形内作内切圆，记为1O ，并裁剪去该正方形与内切圆之间的部分(如图所示阴影部分)，记为一次裁剪操作，L ，重复上述裁剪操作n 次，最终得到该剪纸，则第2024次操作后，所有被裁剪部分的面积之和.()202414π12⎛⎫--⎪⎝⎭解析：设n O 的半径为n R ，则122R =，1n O + 的半径为22n R ，即122n n R R +=，故121221222nn nn R R -⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，n O 的面积为1ππ22nn S ⎛⎫== ⎪⎝⎭，又第n 次裁剪操作的正方形边长为12122n n R -⎛⎫= ⎪⎝⎭，故第n 次裁剪操作裁剪掉的面积为1222221111ππ2222n n n n⎛⎫-⨯⨯- ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫-⨯=-⨯ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21π4π222n n n --=-=，所以第n 次裁剪操作后，裁剪掉的面积之和为()()211114π...4π12222n n ⎛⎫⎛⎫-+++=--⎪⎝⎭⎝⎭，所以第2024次操作后，所有被裁剪部分的面积之和为()202414π12⎛⎫-- ⎪⎝⎭.故答案为：()202414π12⎛⎫-- ⎝⎭.三、解答题共5小题，共85分.解答应写出文字说明，演算步骤或证明过程.16．已知函数()sin si πn 3f x x x ⎛⎫=++ ⎪⎝⎭.（Ⅰ）求()f x 的最小正周期和单调增区间；（Ⅱ）若π6x =是函数()(0)y f x ϕϕ=+>的一个零点，求ϕ的最小值.解：（Ⅰ）由函数π1()sin sin sin sin cos 322f x x x x x x ⎛⎫=++=++ ⎪⎝⎭3πsin226x x x ⎛⎫=+=+ ⎪⎝⎭，……………3分所以函数()f x 的最小正周期为2πT =.……………5分由πππ2π2π262k x k -+≤+≤，k Z ∈，得2ππ2π2π33k x k -+≤≤+，k Z ∈，所以函数()f x 的单调增区间为2ππ[2,2π]33k k -++，k Z ∈.……………8分（Ⅱ）因为π6x =是函数()(0)f x ϕϕ+>的一个零点，ππ066ϕ⎛⎫++= ⎪⎝⎭，即πsin 03ϕ⎛⎫+= ⎪⎝⎭，……………10分所以ππ3k ϕ+=，Z k ∈，即ππ3k ϕ=-+，Z k ∈，……………12分又因为0ϕ>，所以ϕ的最小值为2π3.……………13分17．在ABC △中，6a =,1cos 3C =-，三角形面积为（Ⅰ）b 和c 的值；（Ⅱ）sin()A B -的值．解：（Ⅰ）在ABC △中，因为1cos 3C =-，所以(,)2C π∈π，22sin 3C =.……………2分因为1sin 2S ab C ==6a =，所以2b =.……………4分由余弦定理，2222cos 48c a b ab C =+-=，……………5分所以c =……………6分（Ⅱ）由正弦定理sin sin sin a b cA B C ==，可得62sin sin 223A B ==.…………7分所以sin 3A =，sin 9B =.……………9分因为,(0,2A B π∈，所以3cos 3A =，53cos 9B =.……………11分所以sin()sin cos cos sin A B A B A B-=-39399=⨯-⨯=.……………13分18．已知函数2()ln ,()e e x x f x x x g x ==-．（Ⅰ）求函数()f x 在区间[1,3]上的最小值；（Ⅱ）证明：对任意,(0,)m n ∈+∞，都有()()f m g n ≥成立．解：（Ⅰ）由()ln f x x x =，可得()ln 1f x x =+'．……………2分所以()0f x '>在区间[1,3]恒成立，……………4分所以()f x 在区间[1,3]上单调递增，……………5分所以()f x 在区间[1,3]上的最小值为(1)0f =．……………7分（Ⅱ）因为()ln 1f x x =+'．所以当1(0,),'()0e x f x ∈<，()f x 单调递减；1(,),'()0ex f x ∈+∞>，()f x 单调递增……………9分所以，()f x 在1e x =时取得最小值11()e ef =-，可知1()ef m ≥-．……………10分由2()e e x x g x =-，可得1'()e x x g x -=．……………11分所以当(0,1),'()0,()x g x g x ∈>单调递增，当(1,),'()0,()x g x g x ∈+∞<单调递减．……………12分所以函数()(0)g x x >在1x =时取得最大值，又1(1)e g =-，可知1()eg n ≤-，……………13分所以对任意,(0,)m n ∈+∞，都有()()f m g n ≥成立．……………14分19．某学校组织全体高一学生开展了知识竞赛活动．从参加该活动的学生中随机抽取了12名学生的竞赛成绩，数据如下表：男生818486868891女生728084889297（Ⅰ）从抽出的男生和女生中，各随机选取一人，求男生成绩高于女生成绩的概率；（Ⅱ）从该校的高一学生中，随机抽取3人，用样本频率估计概率，记成绩为优秀(90>分)的学生人数为X ，求X 的分布列和数学期望；（Ⅲ）表中男生和女生成绩的方差分别记为21s ，22s ，现在再从参加活动的男生中抽取一名学生，成绩为86分，组成新的男生样本，方差计为23s ，试比较21s 、22s 、23s 的大小．(只需写出结论)解：（Ⅰ）设“从抽出的男生和女生中，男生成绩高于女生成绩”为事件A ，由表格得：从抽出的12名学生中男女生各随机选取一人，共有1166C C 36=种组合，其中男生成绩高于女生()()()()()()()81,72,81,80,84,72,84,80,86,72,86,80,86,84，()()()86,72,86,80,86,84，()()()()()88,72,88,80,88,84,91,72,91,80，()91,84，()91,88.所以事件A 有17种组合，因此()1736P A =；……………3分（Ⅱ）由数据知，在抽取的12名学生中，成绩为优秀（90>分）的有3人，即从该校参加活动的高一学生中随机抽取1人，该学生成绩优秀的概率为14.……………4分X 可取0,1,2,3，……………5分()3327Χ0464P ⎛⎫=== ⎪⎝⎭，()2131327Χ1C 4464P ⎛⎫==⨯= ⎪⎝⎭，()223319Χ2C 4464P ⎛⎫==⨯=⎪⎝⎭，()311Χ3464P ⎛⎫=== ⎪⎝⎭所以随机变量X 的分布列……………10分数学期望2791483()0123646464644E X =+⨯+⨯+⨯.……………11分（Ⅲ）222312s s s <<.……………14分20．已知函数()()2e x f x x a x =--．（Ⅰ）当a =0时，求()f x 在x =0处的切线方程；（Ⅱ）当a =1时，求()f x 的单调区间；（Ⅲ）当()f x 有且仅有一个零点时，请直接写出a 的取值范围．解：（Ⅰ）当a =0时，()2e x f x x x =-，()00f =，……………1分因为()()1e 2x f x x x '=+-，……………2分所以()10f '=，……………3分所以()f x 在x =0处的切线方程为：y x=……………4分X0123P27642764964164（Ⅱ）当a =1时，()()21e x f x x x =--，所以()()()e 1e 2e 2e 2x x x x f x x x x x x =+--=-=-'，……………6分由()0f x '>，得0x <或ln 2x >，……………8分由()0f x '<，得0ln 2x <<，……………10分所以，()f x 的单调增区间为(),0∞-和(ln 2,)+∞，()f x 的单调减区间为(0,ln 2)．……………12分（Ⅲ）a R ∈．……………15分21.（本小题15分）已知项数为*(,2)N m m m ∈≥的数列{}n a 满足如下条件：①*(1,2,,)n a N n m ∈= ；②12m a a a <<< .若数列{}n b 满足*12()1m nn a a a a b N m +++-=∈- ，其中1,2,,n m = ，则称{}n b 为{}n a 的“伴随数列”.（Ⅰ）数列1,3,5,7,9是否存在“伴随数列”，若存在，写出其“伴随数列”；若不存在，请说明理由；（Ⅱ）若{}n b 为{}n a 的“伴随数列”，证明：12m b b b >>> ；（Ⅲ）已知数列{}n a 存在“伴随数列”{}n b ，且11a =，2049m a =，求m 的最大值.解：（Ⅰ）解：数列1,3,5,7,9不存在“伴随数列”.……………1分因为*41357979512b N ++++-==∉-，所以数列1,3,5,7,9不存在“伴随数列”.……………3分（Ⅱ）证明：因为111n n n n a a b b m ++--=-，*11,n m n N≤≤-∈……………4分又因为12m a a a <<< ，所以有10n n a a +-<所以1101n n n n a a b b m ++--=<-……………6分所以12m b b b >>> 成立……………7分（Ⅲ）∀1≤i <j ≤m ，都有1j i i j a a b b m --=-，……………8分因为*i b N ∈，12m b b b >>> .所以*i j b b N -∈，所以*1j i i j a a b b N m --=∈-……………9分所以*11204811m m a a b b N m m --==∈--因为*111n n n n a a b b N m ----=∈-，所以11n n a a m --≥-……………11分又112211()()()m m m m m a a a a a a a ----=-+-++- (1)(1)(1)m m m ≥-+-++- =2(1)m -……………13分所以2(1)2048m -≤，所以46m ≤……………14分又*20481N m ∈-，所以33m ≤例如：6463n a n =-（133n ≤≤），满足题意，所以，m 的最大值是33.……………15分北京十五中高三年级数学期中考试试卷2024.11本试卷共5页，150分.考试时长120分钟.考生务必将答案答在答题纸上，在试卷上作答无效.第一部分（选择题共40分）一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1．已知集合{}23A x x =-≤≤，{1B x x =<-或}4x >，那么集合A B = （A ）A ．{}21x x -≤<-B ．{3x x ≤或≥4C ．{}24x x -≤<D ．{}13x x -≤≤2．在复平面内，复数z 满足(1)2i z -=，则z =（D ）A ．1i--B ．1i-+C ．1i-D ．1i +3．下列函数中，既是奇函数又在区间（0，+∞）上单调递增的是（A）A ．3()f x x =B ．2()f x x =C ．3()f x x=D ．()sin f x x=4．若0m n <<，则下列结论正确的是（B ）A ．22log log m n >B ．0.50.5log log m n>C ．1122m n⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D ．22m n>5．若α是第二象限角，且1tan 2α=-，则πcos 2α⎛⎫+= ⎪⎝⎭（D ）A ．2B ．2-C ．5D ．5-6．设等差数列{}n a 的前n 项和为n S ，且2822a a +=-，11110S =-，则n S 取最小值时，n 的值为（C ）A ．14B ．15C ．15或16D ．167．已知单位向量,a b ，则“a b ⊥”是“任意R λ∈都有a b a b -λ=λ+r r r r ”的（C ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件8．设函数()21cos cos 2f x x x x =--，则下列结论错误的是（D ）A ．()f x 的一个周期为πB ．()y f x =的图象关于直线4π3x =对称C ．将函数cos 2y x =的图象向左平移π6个单位可以得到函数()f x 的图象D ．()f x 在(π2,π)上单调递减9．在ABC V 中，2π3A =，D 为边BC 上一点，若AD AB ⊥，且1AD =，则ABC V 面积的最小值为（B ）AB C D 10．如图，曲线C 为函数5sin (0)2y x x π=≤≤的图象，甲粒子沿曲线C 从A 点向目的地B 点运动，乙粒子沿曲线C 从B 点向目的地A 点运动.两个粒子同时出发，且乙的水平速率为甲的2倍，当其中一个粒子先到达目的地时，另一个粒子随之停止运动.在运动过程中，设甲粒子的坐标为(,)m n ，乙粒子的坐标为(,)u v ，若记()n v f m -=，则下列说法中正确的是（B ）A ．()f m 在区间(,)2ππ上是增函数B ．()f m 恰有2个零点C ．()f m 的最小值为2-D ．()f m 的图象关于点5(,0)6π中心对称第二部分（非选择题共110分）二、填空题共5小题，每小题5分，共25分.11．函数()f x =的定义域为________．[2，﹢∞)12．612x x ⎛⎫- ⎪⎝⎭的展开式中常数项为．(用数字作答)－16013．已知向量(,1),(1,2)a m b == ，且222||||||a b a b +=+，则m 的值为．－214．对于函数()ln21xf x x =-和()()ln ln 21g x x x =--，给出下列三个结论：①设()f x 的定义域为M ，()g x 的定义域为N ，则N 是M 的真子集.②函数()g x 的图像在1x =处的切线斜率为0.③函数()f x 的图像关于点1,ln24⎛⎫- ⎪⎝⎭对称.其中所有正确结论的序号是.①③解析：对于①，由题意得，函数()f x 的定义域()10,0,212x M xx ∞∞⎧⎫⎛⎫==-⋃+⎨⎬ ⎪-⎝⎭⎩⎭，函数()g x 的定义域12N x x ⎧⎫=⎨⎬⎩⎭.所以N 是M 的真子集，则①正确.对于②，()1221g x x x =--'，则在1x =处的切线斜率()1211121k g ='=-=--，则②错误.对于③只需验证：当1212x x +=时，()()()121212121212lnln ln 2ln22121421x x x x f x f x x x x x x x +=+==----++，则④正确.故答案为：①③.15．中国剪纸是一种用剪刀或刻刀在纸上剪刻花纹，用于装点生活或配合其他民俗活动的民间艺术，剪纸具有广泛的群众基础，交融于各族人民的社会生活，是各种民俗活动的重要组成部分，其传承赓续的视觉形象和造型格式，蕴涵了丰富的文化历史信息，是中国古老的民间艺术之一.已知某剪纸的裁剪工艺如下：取一张半径为1的圆形纸片，记为O ，在O 内作内接正方形，接着在该正方形内作内切圆，记为1O ，并裁剪去该正方形与内切圆之间的部分(如图所示阴影部分)，记为一次裁剪操作，L ，重复上述裁剪操作n 次，最终得到该剪纸，则第2024次操作后，所有被裁剪部分的面积之和.()202414π12⎛⎫--⎪⎝⎭解析：设n O 的半径为n R ，则122R =，1n O + 的半径为22n R ，即122n n R R +=，故121221222nn nn R R -⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，n O 的面积为1ππ22nn S ⎛⎫== ⎪⎝⎭，又第n 次裁剪操作的正方形边长为12122n n R -⎛⎫= ⎪⎝⎭，故第n 次裁剪操作裁剪掉的面积为1222221111ππ2222n n n n⎛⎫-⨯⨯- ⎪⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫-⨯=-⨯ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭21π4π222n n n --=-=，所以第n 次裁剪操作后，裁剪掉的面积之和为()()211114π...4π12222n n ⎛⎫⎛⎫-+++=--⎪⎝⎭⎝⎭，所以第2024次操作后，所有被裁剪部分的面积之和为()202414π12⎛⎫-- ⎪⎝⎭.故答案为：()202414π12⎛⎫-- ⎝⎭.三、解答题共5小题，共85分.解答应写出文字说明，演算步骤或证明过程.16．已知函数()sin si πn 3f x x x ⎛⎫=++ ⎪⎝⎭.（Ⅰ）求()f x 的最小正周期和单调增区间；（Ⅱ）若π6x =是函数()(0)y f x ϕϕ=+>的一个零点，求ϕ的最小值.解：（Ⅰ）由函数π1()sin sin sin sin cos 322f x x x x x x ⎛⎫=++=++ ⎪⎝⎭3πsin226x x x ⎛⎫=+=+ ⎪⎝⎭，……………3分所以函数()f x 的最小正周期为2πT =.……………5分由πππ2π2π262k x k -+≤+≤，k Z ∈，得2ππ2π2π33k x k -+≤≤+，k Z ∈，所以函数()f x 的单调增区间为2ππ[2,2π]33k k -++，k Z ∈.……………8分（Ⅱ）因为π6x =是函数()(0)f x ϕϕ+>的一个零点，ππ066ϕ⎛⎫++= ⎪⎝⎭，即πsin 03ϕ⎛⎫+= ⎪⎝⎭，……………10分所以ππ3k ϕ+=，Z k ∈，即ππ3k ϕ=-+，Z k ∈，……………12分又因为0ϕ>，所以ϕ的最小值为2π3.……………13分17．在ABC △中，6a =,1cos 3C =-，三角形面积为（Ⅰ）b 和c 的值；（Ⅱ）sin()A B -的值．解：（Ⅰ）在ABC △中，因为1cos 3C =-，所以(,)2C π∈π，22sin 3C =.……………2分因为1sin 2S ab C ==6a =，所以2b =.……………4分由余弦定理，2222cos 48c a b ab C =+-=，……………5分所以c =……………6分（Ⅱ）由正弦定理sin sin sin a b cA B C ==，可得62sin sin 223A B ==.…………7分所以sin 3A =，sin 9B =.……………9分因为,(0,2A B π∈，所以3cos 3A =，53cos 9B =.……………11分所以sin()sin cos cos sin A B A B A B-=-39399=⨯-⨯=.……………13分18．已知函数2()ln ,()e e x x f x x x g x ==-．（Ⅰ）求函数()f x 在区间[1,3]上的最小值；（Ⅱ）证明：对任意,(0,)m n ∈+∞，都有()()f m g n ≥成立．解：（Ⅰ）由()ln f x x x =，可得()ln 1f x x =+'．……………2分所以()0f x '>在区间[1,3]恒成立，……………4分所以()f x 在区间[1,3]上单调递增，……………5分所以()f x 在区间[1,3]上的最小值为(1)0f =．……………7分（Ⅱ）因为()ln 1f x x =+'．所以当1(0,),'()0e x f x ∈<，()f x 单调递减；1(,),'()0ex f x ∈+∞>，()f x 单调递增……………9分所以，()f x 在1e x =时取得最小值11()e ef =-，可知1()ef m ≥-．……………10分由2()e e x x g x =-，可得1'()e x x g x -=．……………11分所以当(0,1),'()0,()x g x g x ∈>单调递增，当(1,),'()0,()x g x g x ∈+∞<单调递减．……………12分所以函数()(0)g x x >在1x =时取得最大值，又1(1)e g =-，可知1()eg n ≤-，……………13分所以对任意,(0,)m n ∈+∞，都有()()f m g n ≥成立．……………14分19．某学校组织全体高一学生开展了知识竞赛活动．从参加该活动的学生中随机抽取了12名学生的竞赛成绩，数据如下表：男生818486868891女生728084889297（Ⅰ）从抽出的男生和女生中，各随机选取一人，求男生成绩高于女生成绩的概率；（Ⅱ）从该校的高一学生中，随机抽取3人，用样本频率估计概率，记成绩为优秀(90>分)的学生人数为X ，求X 的分布列和数学期望；（Ⅲ）表中男生和女生成绩的方差分别记为21s ，22s ，现在再从参加活动的男生中抽取一名学生，成绩为86分，组成新的男生样本，方差计为23s ，试比较21s 、22s 、23s 的大小．(只需写出结论)解：（Ⅰ）设“从抽出的男生和女生中，男生成绩高于女生成绩”为事件A ，由表格得：从抽出的12名学生中男女生各随机选取一人，共有1166C C 36=种组合，其中男生成绩高于女生()()()()()()()81,72,81,80,84,72,84,80,86,72,86,80,86,84，()()()86,72,86,80,86,84，()()()()()88,72,88,80,88,84,91,72,91,80，()91,84，()91,88.所以事件A 有17种组合，因此()1736P A =；……………3分（Ⅱ）由数据知，在抽取的12名学生中，成绩为优秀（90>分）的有3人，即从该校参加活动的高一学生中随机抽取1人，该学生成绩优秀的概率为14.……………4分X 可取0,1,2,3，……………5分()3327Χ0464P ⎛⎫=== ⎪⎝⎭，()2131327Χ1C 4464P ⎛⎫==⨯= ⎪⎝⎭，()223319Χ2C 4464P ⎛⎫==⨯=⎪⎝⎭，()311Χ3464P ⎛⎫=== ⎪⎝⎭所以随机变量X 的分布列……………10分数学期望2791483()0123646464644E X =+⨯+⨯+⨯.……………11分（Ⅲ）222312s s s <<.……………14分20．已知函数()()2e x f x x a x =--．（Ⅰ）当a =0时，求()f x 在x =0处的切线方程；（Ⅱ）当a =1时，求()f x 的单调区间；（Ⅲ）当()f x 有且仅有一个零点时，请直接写出a 的取值范围．解：（Ⅰ）当a =0时，()2e x f x x x =-，()00f =，……………1分因为()()1e 2x f x x x '=+-，……………2分所以()10f '=，……………3分所以()f x 在x =0处的切线方程为：y x=……………4分X0123P27642764964164（Ⅱ）当a =1时，()()21e x f x x x =--，所以()()()e 1e 2e 2e 2x x x x f x x x x x x =+--=-=-'，……………6分由()0f x '>，得0x <或ln 2x >，……………8分由()0f x '<，得0ln 2x <<，……………10分所以，()f x 的单调增区间为(),0∞-和(ln 2,)+∞，()f x 的单调减区间为(0,ln 2)．……………12分（Ⅲ）a R ∈．……………15分21.（本小题15分）已知项数为*(,2)N m m m ∈≥的数列{}n a 满足如下条件：①*(1,2,,)n a N n m ∈= ；②12m a a a <<< .若数列{}n b 满足*12()1m nn a a a a b N m +++-=∈- ，其中1,2,,n m = ，则称{}n b 为{}n a 的“伴随数列”.（Ⅰ）数列1,3,5,7,9是否存在“伴随数列”，若存在，写出其“伴随数列”；若不存在，请说明理由；（Ⅱ）若{}n b 为{}n a 的“伴随数列”，证明：12m b b b >>> ；（Ⅲ）已知数列{}n a 存在“伴随数列”{}n b ，且11a =，2049m a =，求m 的最大值.解：（Ⅰ）解：数列1,3,5,7,9不存在“伴随数列”.……………1分因为*41357979512b N ++++-==∉-，所以数列1,3,5,7,9不存在“伴随数列”.……………3分（Ⅱ）证明：因为111n n n n a a b b m ++--=-，*11,n m n N≤≤-∈……………4分又因为12m a a a <<< ，所以有10n n a a +-<所以1101n n n n a a b b m ++--=<-……………6分所以12m b b b >>> 成立……………7分（Ⅲ）∀1≤i <j ≤m ，都有1j i i j a a b b m --=-，……………8分因为*i b N ∈，12m b b b >>> .所以*i j b b N -∈，所以*1j i i j a a b b N m --=∈-……………9分所以*11204811m m a a b b N m m --==∈--因为*111n n n n a a b b N m ----=∈-，所以11n n a a m --≥-……………11分又112211()()()m m m m m a a a a a a a ----=-+-++- (1)(1)(1)m m m ≥-+-++- =2(1)m -……………13分所以2(1)2048m -≤，所以46m ≤……………14分又*20481N m ∈-，所以33m ≤例如：6463n a n =-（133n ≤≤），满足题意，所以，m 的最大值是33.……………15分。

2021-2022学年高三上学期数学(文)期中试题及答案

2021-2022学年高三上学期数学(文)期中试题及答案

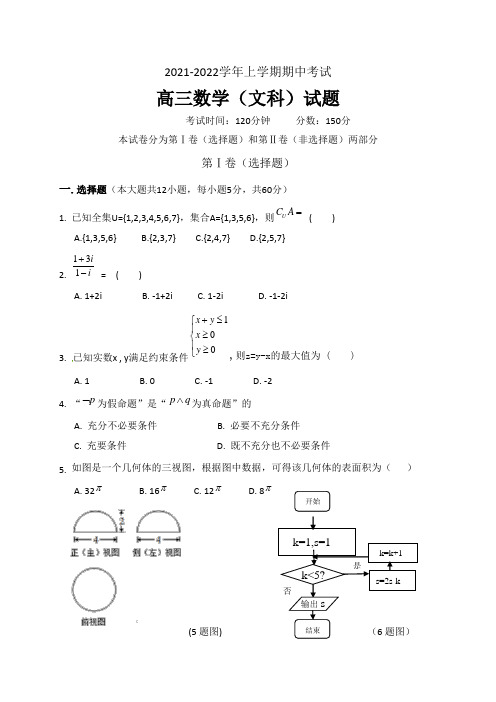
2021-2022学年上学期期中考试高三数学（文科）试题考试时间：120分钟 分数：150分本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷（选择题）一.选择题（本大题共12小题，每小题5分，共60分）1. 已知全集U={1,2,3,4,5,6,7}，集合A={1,3,5,6}，则U C A =( )A.{1,3,5,6}B.{2,3,7}C.{2,4,7}D.{2,5,7}2. 131ii +- = ( )A. 1+2iB. -1+2iC. 1-2iD. -1-2i3. 已知实数x , y 满足约束条件100x y x y +≤⎧⎪≥⎨⎪≥⎩,则z=y-x 的最大值为 ( )A. 1B. 0C. -1D. -2 4. “p ⌝为假命题”是“p q ∧为真命题”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积为（ ） A. 32π B. 16π C. 12π D. 8π(5题图) （6题图）是否开始k=1,s=1k<5?输出s结束 k=k+1s=2s-k6. 执行如图所示的程序框图，输出的s 值为 （ ） A. -10 B. -3 C. 4 D. 57. 已知x 与y 之间的几组数据如表：x 0 1 2 3 y267则y 与x 的线性回归方程y b x a ∧∧∧=+必过点 ( )A. (1,2)B. (2,6)C. (315,24) D. (3,7)8. 下列函数中，在定义域内与函数3y x =的单调性与奇偶性都相同的是 （ ）A. sin y x =B. 3y x x =-C. 2x y =D.2lg(1)y x x =++9. 对于使()f x N ≥成立的所有常数N 中，我们把N 的最大值叫作()f x 的下确界．若,a b ∈(0, +∞),且2a b +=，则133a b +的下确界为 （ ） A. 163 B. 83 C. 43 D. 2310.如图所示的数阵中，每行、每列的三个数均成等差数列．如果数阵中111213212223313233a a a a a a aa a ⎛⎫ ⎪ ⎪ ⎪⎝⎭所有数的和等于36，那么22a = （ ）A. 8B. 4C. 2D. 111.三棱锥P-ABC 的侧棱PA 、PB 、PC 两两垂直，侧面面积分别是6，4，3，则三棱锥的体积是 （ ）A. 4B. 6C. 8D.1012.函数()f x 的定义域为R ，f(0)=2,对x R ∀∈，有()()1f x f x '+>，则不等式()1x xe f x e >+ 的解集为 （ ） A. {}|0x x > B. {}|0x x < C. {}|11x x x <->或 D. {}|10x x x <->>或1第Ⅱ卷（非选择题）二．填空题（本大题共4小题，每小题5分，共计20分）13.已知-向量a 与b 的夹角为60°，且a =（-2，-6），10b =，则ab =14.已知数列{}n a 是等比数列，且1344,8a a a ==，则5a 的值为15.抛物线2(0)y ax a =<的焦点坐标为 16.将边长为2的等边∆ABC 沿x 轴正方向滚动，某时刻A 与坐标原点重合（如图），设顶点(,)A x y 的轨迹方程是y=f(x)，关于函数y=f(x)有下列说法：①f(x)的值域为[0，2]； ②f(x)是周期函数且周期为6 ; ③()(4)(2015)f f f π<<;④滚动后，当顶点A 第一次落在x 轴上时，f(x)的图象与x 轴所围成的面积为833π+．其中正确命题的序号为三．解答题(本大题共6道题,共70分,解答应写出文字说明，证明过程或演算步骤) 17.(本小题12分）在∆ABC 中，内角A,B,C 的对边分别为,,a b c .已知3cos 3cos c b C c B =+（I ）求sin sin C A 的值 (II)若1cos ,233B b =-=，求∆ABC 的面积。

高三文科数学上期中试卷及答案

高三文科数学上期中试卷及答案

高三文科数学上期中试卷及答案Last revised by LE LE in 2021高三第一学期期中数学考试卷（文科）(3)一、填空题：（5×14=70）1．已知全集U=R ，集合)(},021|{},1|{N M C x x x N x x M U 则≥-+=≥= 2. 等差数列{}n a 中，12010=S ，那么29a a +的值是3．直线2(1)(3)750m x m y m ++-+-=与直线(3)250m x y -+-=垂直的充要条件是4． 复数21i -的值为5．下列函数中，在其定义域内既是奇函数，又是减函数的是 ①0.5log y x =()0≠x ② x xy +=1 ()0≠x ③ x x y --=3 ④ x y 9.0=6．与直线2x －y －4＝0平行且与曲线x y 5=相切的直线方程是 ．7．函数y 的定义域和值域分别是 和8.在ABC ∆中， 60=∠C ，则=+++ac bc b a9.圆064422=++-+y x y x 截直线x-y-5＝0所得弦长等于 10. P 是椭圆221169x y +=上的动点, 作PD⊥y 轴, D 为垂足, 则PD 中点的轨迹方程为 .11.已知双曲线22x －my 2＝1的一条准线与抛物线y 2＝4x 的准线重合,则双曲线的离心率为12．若,a b 是正常数，a b ≠，,(0,)x y ∈+∞，则222()a b a b x y x y ++≥+，当且仅当a bx y=时上式取等号. 利用以上结论，可以得到函数29()12f x x x =+-（1(0,)2x ∈）的最小值为 ，取最小值时x 的值为 ．13．一水池有两个进水口，一个出水口，每水口的进出水速度如图甲、乙所示．某天0点到6点，该水池的蓄水量如图丙所示．（至少打开一个水口）给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水，则一定能确定正确的诊断是 ． 14. 如图，一个粒子在第一象限运动，在第一秒末，它从原点运动到（0，1），接着它按如图所示的x 轴、y 轴的平行方向来回运动，（即（0，0）→（0，1）→（1，1）→（1，0）→（2，0）→…），且每秒移动一个单位，那么第2008秒末这个粒子所处的位置的坐标为______。

福建省师范大学附属中学高三数学上学期期中试卷文(含解析)(最新整理)

福建省师范大学附属中学高三数学上学期期中试卷文(含解析)(最新整理)

12019届福建师范大学附属中学高三上学期期中考试数学（文）试题数学注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.2．选择题的作答：每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效.3．非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

一、单选题1．设集合则=A ．B ．C ．D ．2．命题“，”的否定是A ．，B ．，C ．, D ．，3．已知是虚数单位，复数在复平面上所对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．已知双曲线的离心率为，则双曲线的渐近线方程为A ．B ．C ．D ．只装订不密封准考证号 考场号 座位号5．已知函数,为图象的对称轴，将图象向左平移个单位长度后得到的图象，则的解析式为A ．B ．C ．D ．6．已知抛物线的焦点为，准线与轴的交点为，抛物线上一点，若，则的面积为A ．B ．C ．D ．7．函数的部分图象大致为A ．B ．C ．D ．8．直线与圆相交于、两点。

若，则的取值范围是A ．B ．C ．D ．9．某几何体的三视图如图所示，图中正方形的边长为2，四条用虚线表示的线段长度均相等,则该几何体的表面积为A ．B ．C ．D ．210．若四边形是边长为2的菱形，,分别为的中点，则A ．B ．C ．D ．11．在中，,，点在边上，且，则A ．B ．C ．D ．12．已知椭圆的左右焦点分别为、，过点的直线与椭圆交于两点，若是以为直角顶点的等腰直角三角形,则椭圆的离心率为A ．B ．C ．D ．二、填空题13．已知直线1:260l ax y++=和直线()22:110l x a y a+-+-=垂直，则实数a的值为__________．14．已知向量，，若,则向量与向量的夹角为_____．15．设函数，则函数的零点个数是_______.16．半径为4的球的球面上有四点A，B，C，D，已知为等边三角形且其面积为，则三棱锥体积的最大值为_____________________．三、解答题17．已知等差数列的公差为1，且成等比数列.3（1）求数列的通项公式；(2)设数列,求数列的前项和。

四川省成都市第七中学2022-2023学年高三上学期期中考试文科数学试题(解析版)

四川省成都市第七中学2022-2023学年高三上学期期中考试文科数学试题(解析版)

成都七中2022～2023学年度（上）高三年级半期考试数学试卷（文科）（试卷总分：150分，考试时间：120分钟）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 设全集{}0,1,2,3,4,5,6U =，集合{}1,2,4A =，{}1,3,5B =，则()U A B = ð（ ）A. {}0,6 B. {}1,4 C. {}2,4 D. {}3,5【答案】C【解析】【分析】根据交集、补集的定义，即得解【详解】由题意，全集{}0,1,2,3,4,5,6U =，集合{}1,2,4A =，{}1,3,5B =，故{0,2,4,6}U B =ð则(){2,4}U A B =∩ð故选：C2. 复数43i 2i z -=+（其中i 为虚数单位）的虚部为（ ）A. 2- B. 1- C. 1 D. 2【答案】A【解析】【分析】根据复数除法的运算法则，求出复数z ，然后由虚部的定义即可求解.【详解】解：因为复数()()()()2243i 2i 43i 510i 12i 2i 2i 2i 21z ----====-++-+，所以复数z 的虚部为2-，故选：A .3. 青少年视力被社会普遍关注，为了解他们的视力状况，经统计得到图中右下角12名青少年的视力测量值()1,2,3,,12i a i =⋅⋅⋅（五分记录法）的茎叶图，其中茎表示个位数，叶表示十分位数．如果执行如图所示的算法程序，那么输出的结果是（ ）A. 4B. 5C. 6D. 7【答案】B【解析】【分析】依题意该程序框图是统计这12名青少年视力小于等于4.3人数，结合茎叶图判断可得；【详解】解：根据程序框图可知，该程序框图是统计这12名青少年视力小于等于4.3的人数，由茎叶图可知视力小于等于4.3的有5人，故选：B4. 抛物线()220y px p =≠上的一点()9,12P -到其焦点F 的距离PF 等于（ ）A. 17B. 15C. 13D. 11【答案】C【解析】【分析】由点的坐标求得参数p ，再由焦半径公式得结论．【详解】由题意2122(9)p =⨯-，解得8p =-，所以4(9)132P p PF x =--=--=，故选：C ．5. 奥运会跳水比赛中共有7名评委给出某选手原始评分，在评定该选手的成绩时，去掉其中一个最高分和一个最低分，得到5个有效评分，则与7个原始评分（不全相同）相比，一定会变小的数字特征是（ ）A. 众数B. 方差C. 中位数D. 平均数【答案】B【解析】的【分析】根据题意，由数据的中位数、平均数、方差、众数的定义，分析可得答案．【详解】对于A：众数可能不变，如8,7,7,7,4,4,1，故A错误；对于B：方差体现数据的偏离程度，因为数据不完全相同，当去掉一个最高分、一个最低分，一定使得数据偏离程度变小，即方差变小，故B正确；对于C：7个数据从小到大排列，第4个数为中位数，当首、末两端的数字去掉，中间的数字依然不变，故5个有效评分与7个原始评分相比，不变的中位数，故C错误；对于C：平均数可能变大、变小或不变，故D错误；故选：B6. 已知一个几何体的三视图如图，则它的表面积为（）A. 3πB. 4πC. 5πD. 6π【答案】B【解析】【分析】由三视图可知，该几何体是圆锥和半球拼接成的组合体，且圆锥的底面圆和半球的大圆面半径相同，根据题干三视图的数据，以及圆锥的侧面积和球的表面积公式，即得解【详解】由三视图可知，该几何体是圆锥和半球拼接成的组合体，且圆锥的底面圆和半球的大圆面半径相同底面圆的半径1r =，圆锥的母线长2l ==记该几何体的表面积为S 故211(2)4422S r l r πππ=+⨯=故选：B7. 设平面向量a ，b 的夹角为120︒，且1a = ，2b = ，则()2a a b ⋅+= （ ）A. 1B. 2C. 3D. 4【答案】A【解析】【分析】利用向量数量积的运算律以及数量积的定义，计算即得解【详解】由题意，()22222112cos120211a ab a a b ⋅+=+⋅=⨯+⨯⨯=-= 则()21a a b ⋅+= 故选：A8. 设x ，y 满足240220330x y x y x y +-≤⎧⎪-+≤⎨⎪++≥⎩，则2z x y =+的最大值是（ ）A. 2- B. 1- C. 1 D. 2【答案】D【解析】【分析】画出不等式组表示的平面区域，如图中阴影部分所示, 转化2z x y =+为2y x z =-+,要使得2z x y =+取得最大值，即直线2y x z =-+与阴影部分相交且截距最大，数形结合即得解【详解】画出不等式组表示的平面区域，如图中阴影部分所示转化2z x y =+为2y x z=-+要使得2z x y =+取得最大值，即直线2y x z =-+与阴影部分相交且截距最大由图像可知，当经过图中B 点时，直线的截距最大240220x y x y +-=⎧⎨-+=⎩，解得(0,2)B 故2022z =⨯+=故2z x y =+的最大值是2故选：D9. “α为第二象限角”是“sin 1αα>”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】【分析】根据条件sin 1αα->求出α的范围，从而可判断出选项.【详解】因为1sin 2sin 2sin 23πααααα⎛⎫⎛⎫-==- ⎪ ⎪ ⎪⎝⎭⎝⎭，所以由sin 1αα>，得2sin 13πα⎛⎫-> ⎪⎝⎭，即1sin 32πα⎛⎫-> ⎪⎝⎭，所以522,636k k k Z ππππαπ+<-<+∈，即722,26k k k Z πππαπ+<<+∈，所以当α为第二象限角时，sin 1αα>；但当sin 1αα>时，α不一定为第二象限角，故“α为第二象限角”是“sin 1αα>”的充分不必要条件.故选：A .10. 已知直线()100,0ax by a b +-=>>与圆224x y +=相切，则22log log a b +的最大值为（ ）A. 3B. 2C. 2-D. 3-【答案】D【解析】【分析】由直线与圆相切可得2214a b +=，然后利用均值不等式可得18ab ≤，从而可求22log log a b +的最大值.【详解】解：因为直线()100,0ax by a b +-=>>与圆224x y +=相切，2=，即2214a b +=，因为222a b ab +≥，所以18ab ≤，所以22221log log log log 38a b ab +=≤=-，所以22log log a b +的最大值为3-，故选：D .11. 关于函数()sin cos 6x x f x π⎛⎫=-⎪⎝⎭的叙述中，正确的有（ ）①()f x 的最小正周期为2π；②()f x 在区间,63ππ⎡⎤-⎢⎥⎣⎦内单调递增；③3f x π⎛⎫+ ⎪⎝⎭是偶函数；④()f x 的图象关于点,012π⎛⎫⎪⎝⎭对称.A. ①③B. ①④C. ②③D. ②④【答案】C【解析】【分析】应用差角余弦公式、二倍角正余弦公式及辅助角公式可得()11sin(2)264f x x π=-+，再根据正弦型函数的性质，结合各项描述判断正误即可.【详解】()211sin cos sin sin )cos sin 622x f x x x x x x x x π⎛⎫=-=+=+= ⎪⎝⎭11112cos 2sin(2)44264x x x π-+=-+，∴最小正周期22T ππ==，①错误；令222262k x k πππππ-≤-≤+，则()f x 在[,63k k ππππ-+上递增，显然当0k =时,63ππ⎡⎤-⎢⎥⎣⎦，②正确；1111sin(2)cos 2322424f x x x ππ⎛⎫+=++=+ ⎪⎝⎭，易知3f x π⎛⎫+ ⎪⎝⎭为偶函数，③正确；令26x k ππ-=，则212k x ππ=+，Z k ∈，易知()f x 的图象关于1,124π⎛⎫ ⎪⎝⎭对称，④错误；故选：C12. 攒尖在中国古建筑（如宫殿、坛庙、园林等）中大量存在，攒尖式建筑的屋面在顶部交汇成宝顶，使整个屋顶呈棱锥或圆锥形状．始建于1752年的廓如亭（位于北京颐和园内，如图）是全国最大的攒尖亭宇，八角重檐，蔚为壮观．其檐平面呈正八边形，上檐边长为a ，宝顶到上檐平面的距离为h ，则攒尖的体积为（ ）A.B.C.D. 【答案】D【解析】【分析】攒尖是一个正八棱锥，由棱锥体积公式计算可得．【详解】如图底面正八边形ABCDEFGH 的外接圆圆心是O （正八边形对角线交点），设外接圆半径为R ，在OAB 中，4AOB π∠=，AB a =，由余弦定理得222222cos (24a R R R R π=+-=-，22R ==，正八边形的面积为218sin 24S R π=⨯22(1a =，所以攒尖体积13V Sh ==．故选：D ．二、填空题：本大题共4小题，每小题5分，共20分．13. 命题“x N ∃∈，22x x <”的否定是_______________________．【答案】2,2x x N x ∀∈≥【解析】【分析】根据命题的否定的定义求解．【详解】特称命题的否定是全称命题．命题“x N ∃∈，22x x <”的否定是：2,2x x N x ∀∈≥．故答案为：2,2x x N x ∀∈≥．14. 函数()ln f x x =-在1x =处的切线方程为_______________________．（要求写一般式方程）【答案】230x y +-=【解析】【分析】利用导函数求出斜率，即可写出切线方程.【详解】()ln f x x =-的导函数是()1f x x'=，所以()111122f '=-=-.又()11f =，所以函数()ln f x x =-在1x =处的切线方程为()1112y x -=--，即230x y +-=.故答案为：230x y +-=.15. 已知双曲线()2222:10,0x y C a b a b-=>>的两个焦点分别为1F 、2F ，且两条渐近线互相垂直，若C 上一点P 满足213PF PF =，则12F PF ∠的余弦值为_______________________．【答案】13【解析】【分析】由题意可得b a =，进而得到c =，再结合双曲线的定义可得123,PF a PF a ==，进而结合余弦定理即可求出结果.【详解】因为双曲线()2222:10,0x y C a b a b -=>>，所以渐近线方程为b y x a =±，又因为两条渐近线互相垂直，所以21b a ⎛⎫-=- ⎪⎝⎭，所以1b a =，即b a =，因此c =，因此213PF PF =，又由双曲线的定义可知122PF PF a -=，则123,PF a PF a ==，所以在12F PF △中由余弦定理可得222122112121cos 23PF PF F F F PF PF PF +-∠===⋅，故答案为：13.16. 已知向量(),a x m = ，()32,2b x x =-+ ．（1）若当2x =时，a b ⊥ ，则实数m 的值为_______________________；（2）若存在正数x ，使得//a b r r，则实数m 取值范围是__________________．【答案】①. 2- ②. (),0[2,)-∞⋃+∞【解析】【分析】（1）由2x =时，得到()2,a m = ，()4,4b = ，然后根据a b ⊥ 求解；（2）根据存在正数x ，使得//a b r r，则()22320x m x m +-+=，()0,x ∈+∞有解，利用二次函数的根的分布求解.【详解】（1）当2x =时，()2,a m = ，()4,4b = ，因为a b ⊥ ，所以2440m ⨯+=，解得2m =-，所以实数m 的值为-2；（2）因为存在正数x ，使得//a b r r，所以()()232x x m x +=-，()0,x ∈+∞有解，即()22320x m x m +-+=，()0,x ∈+∞有解，所以()223022380m m m -⎧->⎪⎨⎪∆=--≥⎩或230220m m -⎧-≤⎪⎨⎪<⎩，解得2m ≥或0m <，所以实数m 的取值范围是(),0[2,)-∞⋃+∞.故答案为：-2，(),0[2,)-∞⋃+∞三、解答题：解答应写出文字说明、证明过程或演算步骤．第17～21题为必考题，每个题目考生都必须作答．第22，23题为选考题，考生根据要求作答．（一）必考题：共60分．17. 某企业有甲、乙两条生产线，其产量之比为4:1．现从两条生产线上按分层抽样的方法得到一个样本，其部分统计数据如表（单位：件），且每件产品都有各自生产线的标记．的产品件数一等品二等品总计甲生产线2乙生产线7总计50（1）请将22⨯列联表补充完整，并根据独立性检验估计；大约有多大把握认为产品的等级差异与生产线有关？()20P K k ≥0.150.100.050.0250.0100.0050.0010k 2.0722.7063.8415.0246.6357.87910.828参考公式：()()()()()22n ad bc K a b c d a c b d -=++++（2）从样本的所有二等品中随机抽取2件，求至少有1件为甲生产线产品的概率．【答案】（1）列联表见解析，有97.5%的把握认为产品的等级差异与生产线有关； （2）710【解析】【分析】（1）完善列联表，计算出卡方，再与观测值比较即可判断；（2）记甲生产线的2个二等品为A ，B ，乙生产线的3个二等品为a ，b ，c ，用列举法列出所有可能结果，再根据古典概型的概率公式计算可得；小问1详解】解：依题意可得22⨯列联表如下：产品件数一等品二等品总计甲生产线38240乙生产线7310总计45550所以()225038327 5.5561040545K ⨯-⨯=≈⨯⨯⨯，因为5.024 5.556 6.635<<，所以有97.5%的把握认为产品的等【级差异与生产线有关；【小问2详解】解：依题意，记甲生产线的2个二等品为A ，B ，乙生产线的3个二等品为a ，b ，c ；则从中随机抽取2件，所有可能结果有AB ，Aa ，Ab ，Ac ，Ba ，Bb ，Bc ，ab ，ac ，bc 共10个，至少有1件为甲生产线产品的有AB ，Aa ，Ab ，Ac ，Ba ，Bb ，Bc 共7个，所以至少有1件为甲生产线产品的概率710P =；18. 如图，在正三棱柱111ABC A B C -中，D 是BC 的中点．（1）求证：平面1ADC ⊥平面11BCC B ；（2）已知1AA =，求异面直线1A B 与1DC 所成角的大小．【答案】（1）证明见解析； （2）6π【解析】【分析】（1）证得AD ⊥平面11BCC B ，结合面面垂直的判定定理即可证出结论；（2）建立空间直角坐标系，利用空间向量的夹角坐标公式即可求出结果.【小问1详解】因为正三棱柱111ABC A B C -，所以AB AC =，又因为D 是BC 的中点，所以AD BC ⊥，又因为平面ABC ⊥平面11BCC B ，且平面ABC ⋂平面11BCC B BC =，所以AD ⊥平面11BCC B ，又因为AD ⊂平面1ADC ，所以平面1ADC ⊥平面11BCC B ；【小问2详解】取11B C 的中点E ，连接DE ，由正三棱柱的几何特征可知,,DB DA DE 两两垂直，故以D 为坐标原点，分以,,DA DB DE 所在直线为x 轴，y 轴，z 轴建立如图所示空间直角坐标系，设2AB =，则1AA =，所以()()(11,0,1,0,0,0,0,0,1,A B D C -,则((11,0,1,A B DC =-=-u u u r u u u r，所以111111cos ,A B DC A B DC A B DC ⋅===⋅u u u r u u u ru u u r u u u r u u u r u u u r 由于异面直线成角的范围是0,2π⎛⎤⎥⎝⎦，所以异面直线1A B 与1DC ，因此异面直线1A B 与1DC 所成角为6π.19. 已知n N *∈，数列{}n a 的首项11a =，且满足下列条件之一：①1122n n n a a +=+；②()121n n na n a +=+．（只能从①②中选择一个作为已知）（1）求{}n a 的通项公式；（2）若{}n a 的前n 项和n S m <，求正整数m 的最小值．【答案】（1）22n nn a = （2）4【解析】【分析】（1）若选①，则可得11222n n n n a a ++⋅-⋅=，从而可得数列{}2nn a ⋅是以2为公差，2为首项的等差数列，则可求出2nn a ⋅，进而可求出n a ，若选②，则1112n n a a n n +=⋅+，从而可得数列n a n ⎧⎫⎨⎬⎩⎭是以12为公比，1为首项的等比数列，则可求出na n，进而可求出n a ，（2）利用错位相减法求出n S ，从而可求出正整数m 的最小值【小问1详解】若选①，则由1122n n n a a +=+可得11222n n n n a a ++⋅-⋅=，所以数列{}2n n a ⋅是以2为公差，1122a ⋅=为首项的等差数列，所以222(1)2nn a n n ⋅=+-=，所以22n nn a =，若选②，则由()121n n na n a +=+，得1112n n a a n n +=⋅+，所以数列n a n ⎧⎫⎨⎬⎩⎭是以12为公比，1111a a ==为首项的等比数列，所以1112n n a n -⎛⎫=⨯ ⎪⎝⎭，所以1222n n nnn a -==【小问2详解】因为12312462(1)222222n n n n n S --=+++⋅⋅⋅++，所以234112462(1)2222222n n n n nS +-=+++⋅⋅⋅++，所以23112222122222n n n n S +=+++⋅⋅⋅+-2311112()2222n nn=+++⋅⋅⋅+-111[1]42121212n nn -⎛⎫- ⎪⎝⎭=+⨯--222n n +=-，所以2442n nn S +=-，所以4n S <，所以正整数m 的最小值为4，20. 已知椭圆()2222:10x y C a b a b+=>>的短轴长为，左顶点A 到右焦点F 的距离为3．（1）求椭圆C 的方程（2）设直线l 与椭圆C 交于不同两点M ，N （不同于A ），且直线AM 和AN 的斜率之积与椭圆的离心率互为相反数，求证：l 经过定点．【答案】（1）22143x y +=（2）证明见解析【解析】【分析】（1）依题意可得b =、3a c +=，再根据222c a b =-，即可求出a 、c ，从而求出椭圆方程、离心率；（2）设直线l 为y kx m =+，()11,M x y ，()22,N x y ，联立直线与椭圆方程，消元列出韦达定理，依题意可得12AM AN k k ⋅=-，即可得到方程，整理得到225480m k km --=，即可得到m 、k 的关系，从而求出直线过定点；【小问1详解】解：依题意b =、3a c +=，又222c a b =-，解得2a =，1c =，所以椭圆方程为22143x y +=，离心率12c e a ==；【小问2详解】解：由（1）可知()2,0A -，当直线斜率存在时，设直线l 为y kx m =+，联立方程得22143y kx mx y =+⎧⎪⎨+=⎪⎩，消去y 整理得()2223484120k xkmx m +++-=，设()11,M x y ，()22,N x y ，所以122834km x x k +=-+，212241234m x x k-=+；因为直线AM 和AN 的斜率之积与椭圆的离心率互为相反数，所以12AM AN k k ⋅=-；即()()22121212121212121212222242AM ANk x x km x x m y y kx m kx m k k x x x x x x x x +++++⋅=⋅=⋅==-+++++++所以2222222241281343441282243434m km k km m k k m km k k -⎛⎫+-+ ⎪++⎝⎭=--⎛⎫+-+ ⎪++⎝⎭，即22221231164162k m k m km -+=-+-，所以225480m k km --=，即()()2520m k m k -+=，所以2m k =或25m k =-，当2m k =时，直线l ：2y kx k =+，恒过定点()2,0-，因为直线不过A 点，所以舍去；当25m k =-时，直线l ：25y kx k =-，恒过定点2,05⎛⎫ ⎪⎝⎭；当直线斜率不存在时，设直线0:l x x =，()00,M x y ，()00,N x y -，则00001222AM AN y y k k x x -⋅=⋅=-++，且2200143x y +=，解得025x =或02x =-（舍去）；综上可得直线l 恒过定点2,05⎛⎫⎪⎝⎭.21. 已知函数()sin xf x e k x =-，其中k 为常数．（1）当1k =时，判断()f x 在区间()0,∞+内的单调性；（2）若对任意()0,x π∈，都有()1f x >，求k 的取值范围．【答案】（1）判断见解析 （2）(,1]k ∈-∞【解析】【分析】小问1：当1k =时，求出导数，判断导数在()0,∞+上的正负，即可确定()f x 在()0,∞+上的单调性；小问2：由()1f x >得sin 10x e k x -->，令()sin 1x g x e k x =--，将参数k 区分为0k ≤，01k <≤，1k >三种情况，分别讨论()g x 的单调性，求出最值，即可得到k 的取值范围.【小问1详解】当1k =时，得()sin xf x e x =-，故()cos xf x e x '=-，当()0,∞+时，()0f x '>恒成立，故()f x 在区间()0,∞+为单调递增函数.【小问2详解】当()0,x π∈时，sin (0,1]x ∈，故()1f x >，即sin 1x e k x ->，即sin 10x e k x -->.令()sin 1x g x e k x =--①当0k ≤时，因为()0,x π∈，故sin (0,1]x ∈，即sin 0k x -≥，又10x e ->，故()0f x >在()0,x π∈上恒成立，故0k ≤；②当01k <≤时，()cos x g x e k x '=-，()sin x g x e k x ''=+，故()0g x ''>在()0,x π∈上恒成立，()g x '在()0,x π∈上单调递增，故0()(0)0g x g e k ''>=->，即()g x 在()0,x π∈上单调递增，故0()(0)10g x g e >=-=，故01k <≤；③当1k >时，由②可知()g x '在()0,x π∈上单调递增，设()0g x '=时的根为0x ，则()g x 在0(0,)x x ∈时为单调递减；在0(,)x x π∈时为单调递增又0(0)10g e =-=，故0()0g x <，舍去；综上：(,1]k ∈-∞【点睛】本题考查了利用导数判断函数单调性，及利用恒成立问题，求参数的取值范围的问题，对参数做到不重不漏的讨论，是解题的关键.（二）选考题：共10分．请考生在第22，23题中任选一题作答．如果多做，那么按所做的第一题计分．［选修4—4：坐标系与参数方程]（10分）22. 在平面直角坐标系xOy 中，伯努利双纽线1C （如图）的普通方程为()()222222x y x y +=-，曲线2C 的参数方程为cos sin x r y r θθ=⎧⎨=⎩（其中r ∈（，θ为参数）．的（1）以O 为极点，x 轴的非负半轴为极轴建立极坐标系，求1C 和2C 的极坐标方程；（2）设1C 与2C 的交于A ，B ，C ，D 四点，当r 变化时，求凸四边形ABCD 的最大面积．【答案】（1）1:C 2222cos 2sin ρθθ=-；2:C r ρ=（2）2【解析】【分析】（1）根据直角坐标方程，极坐标方程，参数方程之间的公式进行转化即可；（2）设点A 在第一象限，并且设点A 的极坐标，根据题意列出点A 的直角坐标，表示出四边形ABCD 的面积进行计算即可.小问1详解】1:C ()()222222x y x y +=-，由cos ,sin x y ρθρθ==，故222222()2(cos sin )ρρθρθ=-，即2222cos 2sin ρθθ=-2:C cos sin x r y r θθ=⎧⎨=⎩，即222x y r +=，即22r ρ=，rρ=【小问2详解】由1C 和2C 图象的对称性可知，四边形ABCD 为中心在原点处，且边与坐标轴平行的矩形，设点A 在第一象限，且坐标为(,)ρα(02πα<<，又r ρ=，则点A 的直角坐标为(cos ,sin )r r αα，又2222cos 2sin ραα=-，即2222cos 2sin 2cos 2r ααα=-=故S 四边形ABCD =22cos 2sin 2sin 2r r r ααα⋅==22cos 2sin 22sin 4ααα⋅⋅=又02πα<<，故042απ<<，因此当42πα=，即8πα=时，四边形ABCD 的面积最大为2.［选修4—5：不等式选讲]（10分）【23. 设M 为不等式1431x x ++≥-的解集．（1）求集合M 的最大元素m ；（2）若a ，b M ∈且a b m +=，求1123a b +++的最小值．【答案】（1）3m = （2）12【解析】【分析】（1）分类讨论13x ≥，1x ≤-，113x -<<，打开绝对值求解，即得解；（2）由题意1,3,3a b a b -≤≤+=，构造11(2)(3)132([11]2328113823a b b a a b a b a b ++++++=+⨯=+++++++++，利用均值不等式即得解【小问1详解】由题意，1431x x ++≥-（1）当13x ≥时，1431x x ++≥-，解得3x ≤，即133x ≤≤；（2）当1x ≤-时，1413x x --+≥-，解得1x ≥-，即=1x -；（3）当113x -<<时，1413x x ++≥-，解得1x ≥-，即113x -<<综上：13x -≤≤故集合{|13}M x x =-££，3m =【小问2详解】由题意，1,3,3a b a b -≤≤+=，故(2)(3)8a b +++=故11(2)(3)132()[112328113823a b b a a b a b a b ++++++=+⨯=+++++++++由于1,3a b -≤≤，故20,30a b +>+>由均值不等式，113211[11[1123823821b a a b a b +++=+++≥++=++++当且仅当3223b a a b ++=++，即2,1a b ==时等号成立故求1123a b +++的最小值为12。

高三数学(文科)期中考试试卷

高三数学(文科)期中考试试卷

2011--2012高三数学（文科）期中考试试题命题人：曹丽丽 考试时间：120分一、 选择题（5分×12=60分）1、 已知集合{}{}{}()()=⋃===B C A C B A U U U 则,5,4,3,7,5,4,2,7,6,5,4,3,2,1 （ ） A ．{}6,1 B ．{}5,4 C ．{}7,5,4,3,2 D ． {}7,6,3,2,12、若b a R c b a >∈,、、，则下列不等式成立的是 ( )A.ba 11<. B.1122+>+cbca C. 22ba >. D. ||||cbc a >3、 {}{}项和为的前则中，等比数列4,32,452n n a a a a ==（ ）A ．8B ．16C ．30D ．32 4、 函数2log2-=x y 的定义域是（ ）A ．),3(+∞B ．),4(+∞C ．),3[+∞D ．),4[+∞5、 函数⎪⎭⎫⎝⎛+=4tan )(πx x f 的单调增区间是( )A ．Z k k k ∈⎪⎭⎫ ⎝⎛+-,2,2ππππ B ．()Z k k k ∈+,,πππC ．Z k k k ∈⎪⎭⎫⎝⎛+-,4,43ππππ D ．Z k k k ∈⎪⎭⎫ ⎝⎛+-,43,4ππππ 6、在平行四边形ABCD 中，下列结论错误的是 ( )A ．0=+CB ADB ．AC AB AD =+C ．DC AB =D ． BD AD AB =-7、a ),3,(b )2,4(a 且，向量已知向量x ==∥等于则x b ,（ ） A ．6 B ．5 C ．9 D ．38、如果等差数列{}n a 中，,12543=++a a a 则7S =（ ） A.14 B.21 C.28 D. 359、在极坐标系中，直线2＝ 4π＋ sin )(θρ，被圆 ρ＝3截得的弦长为( )． A ．22B ．2C ．52D ．3210、为了得到函数R x x y ∈⎪⎭⎫⎝⎛+=,32sin π的图像，只需把R x x y ∈=,2sin 的图像上所有的点 A ．向左平移6π个单位长度 B ．向左平移3π个单位长度 C ．向右平移6π个单位长度 D ．向右平移3π个单位长度11 、 一个正整数数表如下(表中下一行中的数的个数是上一行中数的个数的2倍):则第8行中的第5个数是( )A.68B.132C.133D.260 12、若y x ,满足表达式1)2(22=+-yx ，则4-x y 的取值范围是（ ）A.]3,3[-B. )3,3(-C. ]33,33[- D. )33,33(-二、 填空题（5分×4=20分）13、 的值是0930sin __________14、已知23)(23++=xax x f ，若4)1(=-'f ，则a 的值为_______________15、正数b a ,满足121=+ba，则b a +的最小值为_______________16、若x 、y 满足约束条件⎪⎩⎪⎨⎧-≥≤+≤.1,1,y y x x y 则y x z +=2的最大值为_______________三、解答题（17题10分，18-22题每题12分）17、设锐角三角形ABC 的内角A ，B ，C 的对边分别为c b a ,,，2sin a b A =．（1）求B 的大小；（2）若a =5c =，求b ．18、有三个数成等差数列，它们的和是18，如果这三个数分别加上1，2，7，则成等比数列， （1）求这三个数的值：（2）在（1）的条件下，这三个数构成等差数列}{a n 若1001=a ，（)0<d ，求nS n 取何值时，当取最大值：19、已知向量),cos ,1(b ),1,(sin a θθ==向量22πθπ<<-（1）若b a ⊥，求θ； （2）求|b a |+的最大值．20、已知：in ,c o s ),(c o s ,c o s )a x xb x x ==，122)(-+⋅=m b a x f（R m x ∈,）．（1）求()f x 关于x 的表达式，并求()f x 的最小正周期； （2） 若]2,0[π∈x 时，()f x 的最小值为5，求m 的值．21. 已知关于x 的二次方程0112=+-+x a x a n n ，)(+∈N n 的两根α、β满足326=-+αββα）（，（1）试用n a 表示1+n a （其中0≠n a ）； （2）若11=a ，求证：⎭⎬⎫⎩⎨⎧-32n a 是等比数列； （3）当671=a 时，求数列}{a n 的通项公式。

河南省南阳市2021-2022学年高三上学期期中考试 数学文科试卷

河南省南阳市2021-2022学年高三上学期期中考试 数学文科试卷

2021年秋期高中三年级期中质量评估数学试题(文)注意事项：1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号写在答题卡上。

2.回答第I卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号框。

写在本试卷上无效。

3.回答第II卷时，将答案写在答题卡上。

写在本试卷和草稿纸上无效。

4.考试结束，只交答题卡。

第I卷选择题(共60分)一、选择题(本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知集合A＝{x∈N*|x2－3x－4<0}，则集合A的真子集有A.7个B.8个C.15个D.16个2.设iz＝4＋3i，则z＝A.－3－4iB.－3＋4iC.3－4iD.3＋4i3.意大利数学家列昂那多·斐波那契以兔子繁殖为例，引入“兔子数列”：1，1，2，3，5，8，13，21，34，55，…，即F(1)＝F(2)＝1，F(n)＝F(n－l)＋F(n－2)(n≥3，n∈N*)，此数列在现代物理“准晶体结构”、化学等领域都有着广泛的应用。

若此数列的各项除以2的余数构成一个新数列{a n}，则数列{a n}的前2021项的和为A.2020B.1348C.1347D.6724.已知命题p：“∃x0∈R，0x e－x0－1≤0”，则¬p为A.∀x∈R，e x－x－1≥0B.∀x∈R，e x－x－1>0C.∃x0∈R，0x e－x0－1≥0D.∃x0∈R，0x e－x0－1>05.已知f(x)＝14x2＋sin(2＋x)，f'(x)为f(x)的导函数，则y＝f'(x)的图象大致是6.设a＝log32，b＝log52，c＝log23，则A.a>c>bB.b>c>aC.c>b>aD.c>a>b7.设变量x ，y 满足约束条件x 1x 2y 30x y 0≥⎧⎪-+≥⎨⎪-≥⎩，则目标函数z ＝2x －y 的最小值为A.－1B.0C.1D.38.若实数a ，b 满足a>0，b>0，则“a>b ”是“a ＋lna>b ＋lnb ”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9.已知x>1，y>0，且1211x y+=-，则x ＋2y －1的最小值为 A.9 B.10 C.11 D.2＋26 10.已知OA 、OB 是两个夹角为120°的单位向量，如图示，点C 在以O 为圆心的AB 上运动。

2025届重庆市高三数学上学期期中调研联考测试卷及答案解析

2025届重庆市高三数学上学期期中调研联考测试卷及答案解析

2025年普通高等学校招生全国统一考试11月调研测试卷数学数学测试卷共4页，满分150分.考试时间120分钟.注意事项：1.答题前，考生务必将自己的准考证号、姓名、班级填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2.回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，用0.5毫米的黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答，答案无效.3.考试结束，考生必须将试题卷和答题卡一并交回.一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知i 为虚数单位，112i z =+，则z =（ ）A.15 B.13C.D.【答案】C 【解析】【分析】由复数的除法运算以及模的运算公式即可得解【详解】由()()112i 12i 12i 12i 12i 12i 555z --====-++-，=，故选：C2. 已知集合{}0,1,2,3,4,5M =，()(){}130N x x x =+-£，则M N =I （ ）A. {}3 B. {}2,3 C. {}1,2,3 D. {}0,1,2,3【答案】D 【解析】【分析】化简集合N ，然后根据交集的定义求解即可【详解】()(){}{}13013N x x x x x =+-£=-££，又{}0,1,2,3,4,5M =，所以{}0,1,2,3M N =I ，故选：D3. 已知a b >，0c d <<，则（ ）A. a c b d +>+ B. 22a cb d +>+ C. ac bd> D. 22ac bd >【答案】B 【解析】【分析】由不等式的性质可得B ；举出反例可得A 、C 、D.【详解】对A ：取1a =，0b =，2c =-，1d =-，此时1a c b d +=+=-，故A 错误；对B ：由0c d <<，则22c d >，又a b >，故22a c b d +>+，故B 正确；对C ：取1a =，0b =，2c =-，1d =-，此时20ac bd =-<=，故C 错误；对D ：取1a =-，2b =-，2c =-，1d =-，此时2242ac bd =-<=-，故D 错误；故选：B.4. 已知数列{}n a 满足：13a =，1111n n a a ++=，则6a =（ ）A32B.23C. 2D. 3【答案】A 【解析】【分析】由1111n n a a ++=可得2n n a a +=，再借助1a 求出2a 即可得解.【详解】由1111n n a a ++=，则12111n n a a +++=，故211n n a a +=，即2n n a a +=，则642a a a ==，又2111121133a a =-=-=，故6232a a ==.故选：A.5. 已知平面上的两个非零向量a r ，b r满足()()22a b a b a b b -×+=×=r r r r r r r ，则,a b =r r （ ）A.π6B.π4C.π3D.π2【答案】B 【解析】.【分析】借助向量数量积公式计算可得a =r .【详解】由()()2222a b a b a a b b a b -×+=+×-=×r r r r r r r r r，故a =r则cos ,a r ，又[],0,πa b Îr r ，故π,4a b =r r .故选：B6. 已知实数0a >，且1a ¹，若函数()log xa f x a x =+在()1,2上存在零点，则（ ）A. 2log 20a a +< B. 22log 0a a -< C. 4log 20a a +> D. log 20a a -<【答案】A 【解析】【分析】分1a >、01a <<进行讨论，结合()f x 的单调性与零点的存在性定理可判断A ，亦可得01a <<，由01a <<结合对数函数性质进行分析可判断B 、C 、D.【详解】当1a >时，易得()log xa f x a x =+在(0,+∞)上单调递增，则需()1log 10a f a a =+=<，与1a >矛盾，故舍去，当01a <<时，易得()log xa f x a x =+在(0,+∞)上单调递减，则需()1log 10a f a a =+=>，()22log 20a f a =+<，故A 正确；由01a <<，则222log 00a a a ->->，故B 错误；42log 2log 20a a a a +<+<，故C 错误；log 200a a a ->->，故D 错误.故选：A.7. 设ABC V 的三个内角A ，B ，C 的对边分别为a ，b ，c ，若sin2B =，且2222690a ac c c -+-+=，则b =（ ）A. B. 4C.D.【答案】C 【解析】.【分析】把题设条件变形可得3a c ==，然后根据等腰三角形的性质，在直角BDC V 中即可求出【详解】由2222690a ac c c -+-+=变形得()()2222690a ac ccc -++-+=，所以()()2230a c c -+-=，得3a c ==，所以ABC V 是以B 为顶角的等腰三角形，如图，取AC 中点D ，所以BD AC ^，且12CBD B Ð=Ð在直角BDC V 中，sin2B =，所以22sin 2sin 232B b CD BC CBD a ==Ð==´=故选：C8. 已知实数a ，b ，c 满足：2229a b +=，223448b c +=，225651c a +=，则32a b c -+的最大值为（ ）A. 6 B. 9C. 10D. 15【答案】C 【解析】【分析】由题意可计算出2a 、2b 、2c ，即可得32a b c -+的最大值.【详解】由2229a b +=，则2261254a b +=，又225651c a +=，则223512b c -=，由223448b c +=，则221216192b c +=，故221189c =，即29c =，则224844836433c b --===，则22921a b =-=，则1a =±，2b =±，3c =±，故()()max 323122310a b c -+=´-´-+=.故选：C.二、选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对得部分分，有选错的得0分.9. 已知p ：“x "ÎN ，21x +是奇数”，q ：“x $ÎN ，31x +是偶数”，则（ ）A. p Ø：x "ÎN ，21x +是偶数” B. p Ø：“x $ÎN ，21x +是偶数”C. q Ø：“x $ÎN ，31x +是奇数” D. q Ø：“x "ÎN ，31x +是奇数”【答案】BD 【解析】【分析】由全称命题与特称命题否定的定义判断即可得.【详解】由p ：“x "ÎN ，21x +是奇数”，q ：“x $ÎN ，31x +是偶数”，则p Ø：x $ÎN ，21x +是偶数”， q Ø：“x "ÎN ，31x +是奇数”，故B 、D 正确；A 、C 错误.故选：BD .10. 已知等比数列{}n a 的公比12q =-，其前n 项和记为n S ，且621S =，则（ ）A. 481a a = B. 2n a a ≥ C. 21n S ≤ D. 16n S ³【答案】ABD 【解析】【分析】借助等比数列求和公式可计算出数列{a n }的通项公式，借助通项公式即可得A ；借助作差法后对n 分奇偶进行讨论可得B ；求出n S 后对n 分奇偶讨论可得C 、D.【详解】由题意可得61116111212216421133212a a a S éùæöæö--êúç÷-ç÷èøêúëûèø====æö--ç÷èø，即132a =，故16113222n n n a --æöæö=×-=--ç÷ç÷èøèø，对A ：46864811141224a a --éùæöæö=--´--=´=êúç÷ç÷èøèøêúëû，故A 正确；对B ：646211116222n n n a a ---æöæöæö-=--+-=--ç÷ç÷ç÷èøèøèø，若n 为奇数，则626111616022n n n a a --æö-=--=+>ç÷èø，若n 为偶数，则62611161622n n n a a --æö-=--=-ç÷èø，随n 的增大而增大，故2220n a a a a -³-=，故B 正确；对C ：1132164122646411333212n n nnS éùéùæöæö----êúêúç÷ç÷èøèøêúêúæöëûëû===-×-ç÷æöèø--ç÷èø，当n 为奇数时，6464643323n n S =+>×，且随n 的增大而减小，当n 为偶数时，6464643323n nS =-<×，随n 的增大而增大，则当1n =时，n S 有最大值，即132n S S £=，当2n =时，n S 有最小值，即116n S S ³=，故C 错误，D 正确.故选：ABD.11. 设a ÎR ，函数()32f x x x a =-+-，则（ ）A. 当0a <时，函数()f x 为单调递增函数B. 点()0,2-为函数()y f x =图象的对称中心C. 存在,a b ，使得函数()y f x =图象关于直线x b =对称D. 函数()f x 有三个零点的充要条件是3a >【答案】BCD 【解析】【分析】求导可得()23f x x a ¢=-+，可判断A 错误；利用对称中心定义可知满足()()4f x f x +-=-，可知B 正确；利用轴对称函数定义可知存在,a b 满足23a b £时使得函数()y f x =图象关于直线x b =对称，即C 正确；由三次函数性质利用导函数求得()f x 的单调性，再根据极值的符号即可判断D 正确.【详解】易知()23f x x a ¢=-+，对于A ，当0a <时，可知()230x a f x =-+<¢恒成立，因此函数()f x 为单调递减函数，即A 错误；对于B ，由()32f x x x a =-+-可得()()()33224f x ax x ax x f x =-+-+-----=-，即可得对于x "ÎR 都满足()()4f x f x +-=-，所以点()0,2-为()y f x =图象的对称中心，可得B 正确；对于C ，若函数()y f x =图象关于直线x b =对称，则满足()()2f x f b x =-，又()()()32222f b x b x a b x -=--+--，可得()()3322x ax b x a b x -+=--+-，‘整理()()222240b x x bx b a --+-=，当224b a b -³时，即23a b £时，只有满足x b =时()()2f x f b x =-成立，因此存在,a b 满足23a b £时使得函数()y f x =图象关于直线x b =对称，即C 正确；对于D ，由A 选项可知当0a £时，()230x a f x =-+<¢恒成立，函数()f x 为单调递减函数，不合题意；所以0a >，令()230f x x a ¢=-+=，解得x =x =易知,x æÎ-¥ççè或x öÎ+¥÷÷时，()0f x ¢<，当x æÎçç时，()0f x ¢>；因此可得()f x在,æ-¥ççè和ö+¥÷÷ø上单调递减，在æççè上单调递增；即()f x 在x =x =若函数()f x有三个零点，可得2020ff ì=<ïïíï+->ïî，解得3a >；因此充分性成立；当3a >时，可知()f x在,æ-¥çç和ö+¥÷÷ø上单调递减，在æçç上单调递增；且极小值20f æ=-<ççè，极大值20f =->，由三次函数性质可知此时()f x 有三个零点，即必要性成立，所以函数()f x 有三个零点的充要条件是3a >，即D 正确.故选：BCD【点睛】关键点点睛：在求解三次函数零点个数时，关键是根据单调性限定出极值的符号，解不等式即可得出参数取值范围.三、填空题：本题共3小题，每小题5分，共15分.12. 已知平面直角坐标系中，向量()1,2a =-r ，单位向量(),b x y =r 满足a b a b +=-r r r r，则x 的值可以是__________.（写出一个正确结果即可）.【解析】【分析】借助模长与数量积的关系计算可得0a b ×=r r，再利用向量数量积的坐标公式与单位向量定义计算即可得解.【详解】由a b a b +=-r r r r，则()()22a ba b +=-r r r r ，即222222a a b b a a b b +×+=-×+r r r r r r r r ，即0a b ×=r r ，即有20a b x y ×=-+=r r ，又1b ===r ，则y =2x y ==.）.13. 已知()f x 为定义在R 上的奇函数，且当0x <时，()1e 2xf x x +=+，则()1f =__________.【答案】1【解析】【分析】由奇函数性质可得()()11f f =--.【详解】由奇函数性质可得()()()11e 2112111f f -+-´-=--=-+==-.故答案为：1.14. 已知函数()sin f x a x =，a ÎZ .若()()y f f x =的零点恰为()y f x =的零点，则a 的最大值是__________.【答案】3【解析】【分析】设(){}0A x f x ==，()(){}0B x f f x ==，根据三角函数的性质及集合间的基本关系计算即可.【详解】设(){}0A x f x ==，()(){}0B x f f x ==显然，集合A 非空.当0a =时，显然A B =，以下设0a ¹，此时{}sin 0A x a x ==，(){}{}sin sin 0sin π,Z B x a a x x a x k k ====Î.易知，B A Í当且仅当对任意的R x Î，有()sin πZ,0a x k k k ¹Î¹，即πa <，故整数a 的最大值为3.故答案为：3【点睛】思路点睛：利用函数的迭代及集合的基本关系结合三角函数的有界性计算即可.四、解答题：本题共5小题，共77分.解答应写出文字说明，证明过程或演算步骤.15. 已知非零等差数列{}n a 满足：10982a a a =-，1670a a a +=.（1）求数列{}n a 的通项公式；（2）记{}n a 的前n 项和为n S ，求n S 的最小值.【答案】（1）217n a n =- （2）64-【解析】【分析】（1）设出等差数列{}n a 的公差后，借助所给等式即可计算出公差与首项，即可得解；（2）求出n S 后由二次函数性质即可得【小问1详解】设等差数列{}n a 的公差为d ，由10982a a a =-可得()1118792a d a d a d =-+++，即1215a d =-，由1670a a a +=可得()()111560a a d a d +++=，即2211111300a a d d a +++=，即有22215151511300222d d d d æö--´+-=ç÷èø，化简得()20d d -=，故0d =或2=d ，则10a =或115a =-，由数列{}n a 为非零数列，故2=d ，115a =-，.故()1521217n a n n =-+-=-；【小问2详解】()()2215217168642n n n S n n n -+-==-=--，故当8n =时，n S 有最小值864S =-.16. 已知函数()22f x x x a =++.（1）讨论()f x 的奇偶性；（2）若()f x 在()1,1-上具有单调性，求实数a 的取值范围.【答案】（1）答案见解析 （2）(][),11,-¥-+¥U 【解析】【分析】（1）结合函数奇偶性定义，计算是否存在实数a ，使得对任意的x ÎR ，()()0f x f x +-=或()()0f x f x --=恒成立；（2）由函数单调性定义结合绝对值性质，分1a ³、1a £-及11a -<<判断即可得.【小问1详解】()f x 定义域为R ，()22f x x x a -=+-+，则()()()2222222f x x x a x x a a x x a x f x ++=+++-++-+-++=，则当0x ¹时，()()()2220f x x a f x x a x =++-+++->恒成立，故()f x 不可能为奇函数，()()()22222f x x x a x x a x a x f x a =++--++----=+-，若0x a x a -+-+=恒成立，则有()()22x a x a +=-+，即0a =，此时()f x 为偶函数，综上所述，当0a =时，()f x 为偶函数，当0a ¹时，()f x 为非奇非偶函数；【小问2详解】令1211x x -<<<，则1220x x ++>，1220x x +-<，当1a ³时，则()()()()2111222222f x x x a f x x x a =++--+-()()()2112122221220x x x x x x x x =+--++-=<，此时()f x 在()1,1-上单调递增，符合要求；当1a £-时，则()()()()2111222222f x x x a f x x x a =-+-++-()()()2222111212220x x x x x x x x =---+--=>，此时()f x 在()1,1-上单调递减，符合要求；当11a -<<时，则()22222,1222,1x x a a x f x x x a x x a x a ì++-£<=++=í---<<-î，由二次函数性质可知，()f x 在()1,a --上单调递增，在(),1a -上单调递减，故此时不符合要求；综上所述，(][),11,a Î-¥-È+¥.17. 在ABC V 中，已知π3A B +>，2sin 2cos cos tan 2sin 2cos sin A B A B B A A-+=-+.（1）证明：1sin 1cos 2C C =+；（2）若2AB =，求ABC V 面积的最大值.【答案】（1）证明见解析（2）1【解析】【分析】（1）借助三角恒等变换公式与三角形内角即可得证；（2）由（1）中所得结合同角三角函数基本关系与π3A B +>可得C ，再借助面积公式结合余弦定理与基本不等式即可得解.【小问1详解】由2sin 2cos cos sin tan 2sin 2cos sin cos A B A B B B A A B-+==-+,则有222sin cos 2cos cos cos 2sin 2sin cos sin sin A B B A B B B A A B -+=-+，即222sin cos 2sin cos cos cos sin sin 2sin 2cos A B B A A B A B B B++-=+即()()2sin cos 2A B A B +++=，即2sin cos 2C C -=，故1sin 1cos 2C C =+；【小问2详解】由1sin 1cos 2C C =+，则2221sin 1cos cos 1co 4s C C C C =++=-，化简得4cos cos 05C C æö+=ç÷èø，即cos 0C =或4cos 5C =-，由π3A B +>，则2π3C <，则2π1cos cos 32C >=-，故cos 0C =，即π2C =，则由余弦定理2222cos AB AC BC AC BC C =+-××可得224AC BC =+，则2242AC BC AC BC =+³×，即2AC BC ×£，当且仅当AC BC ==故1sin 122ABC AC BC S AC BC C V ×=××=£，即ABC V 面积的最大值为1.18. 已知函数()()ln f x x a x x =+-（a ÎR ）.（1）当1a =时，求曲线()y f x =在点()()1,1f 处的切线方程；（2）若函数()f x 有两个极值点，求a 的取值范围；（3）在（2）的条件下，确定函数()f x 零点的个数.【答案】（1）20x y --=（2）10e a <<（3）一个【解析】【分析】（1）利用导数几何意义，对()f x 求导即可得解；（2）利用二次求导，分类讨论0a £，1ea ³与10e a <<三种情况，结合导数与函数极值的关系即可得解；（3）利用（2）中结论，分析得()f x 的极大值的正负情况，结合零点存在定理即可得解.的【小问1详解】因为()()ln f x x a x x =+-，0x >，所以()ln af x x x ¢=+，当1a =时，()()1ln f x x x x =+-，()1ln f x x x¢=+，所以()()111ln111f =+´-=-，()11ln111f ¢=+=，则曲线()y f x =在点()()1,1f 处的切线方程为()111y x +=´-，即20x y --=.【小问2详解】函数()f x 有两个极值点，则()ln 0a f x x x ¢=+=有两个不等正根，令221()ln ,()a a x a g x x x x x x g x-===¢+-，当0a £时，()0,()g x g x ¢³单调递增，即()f x ¢单调递增，则()f x 至多只有一个极值点，不满足题意；当0a >时，令()0g x ¢<，得0x a <<；令()0g x ¢>，得x a >；则()g x 在(0,)a 上单调递减，在(,)a +¥上单调递增，()min ()ln 1g x g a a ==+，当1ea ³，即ln 10a +³时，()0g x ³，即()0f x ¢³，则()f x 在()0,¥+上单调递增，无极值点，不满足题意；当10ea <<时，()ln 10g a a =+<，令()ln 1m x x x =-+，则()111x m x x x -¢=-=，令()0m x ¢>，得01x <<；令()0m x ¢<，得1x >；所以()m x 在()0,1上单调递增，在()1,+¥上单调递减，所以()()1ln1110m x m ³=-+=，所以ln 1£-x x ，则ln 1x x x £-<，故11ln <a a ，即1e a a -<，则111211e e e a a a g a a a a -æöæö=-+=-ç÷ç÷èøèø，令2()e ,e x h x x x =->，则()e 2x h x x ¢=-，令()e 2,e x n x x x =->，则()e 20x n x ¢=->，则()n x 在()e,+¥上单调递增，所以()e()e e 2e 0n x n >=->，所以()h x 单调递增，从而e 2()(e)e e 0h x h >=->，即2e x x >，所以1e 0a g -æö>ç÷èø，从而存1(0,)x a Î，使得()10g x =，又1111e e 0,e a a a g a a a-æö=+>>ç÷èø，所以存在2(,)x a Î+¥，使得()20g x =，此时()f x 有两个极值点，满足题意综上，所以10e a <<.【小问3详解】在（2）的条件下，设()f x 的两个极值点为12,x x ，且12x a x 0<<<，则由（2）知，当10x x <<或2x x >时，()0g x >，即()0f x ¢>；当12x x x <<时，()0g x <，即()0f x ¢>；所以()f x 在()()120,,,x x +¥上单调递增，在()12,x x 上单调递减，又11ln 0a x x +=，即11ln a x x =-，所以()()()()()2111111111111ln ln ln ln ln 10f x x a x x x x x x x x x x =+-=--=--+<，则()()210f x f x <<，又111111e e e 1e 1a a a a f a aa æöæöæö=+-=-+ç÷ç÷ç÷èøèøèø，令()(1)e ,e x t x x x =->，由（2）知ln 1£-x x ，所以ln e e 1x x £-，即e 1x x ³+，所以2(1)e 1(1)(1)10x x x x x -+>-+=>+，则111e 10a a æö-+>ç÷èø，所以1e 0a f æö>ç÷èø，所以()f x 在()20,x 上没有零点，在()2,x +¥上有一个零点，即()f x 仅有一个零点.【点睛】方法点睛：利用导数解决函数零点问题的方法：在（1）直接法：先对函数求导，根据导数的方法求出函数的单调区间与极值，根据函数的基本性质作出图象，然后将问题转化为函数图象与x 轴的交点问题，突出导数的工具作用，体现了转化与化归思想、数形结合思想和分类讨论思想的应用；（2）构造新函数法：将问题转化为研究两函数图象的交点问题；（3）参变量分离法：由()0f x =分离变量得出()a g x =，将问题等价转化为直线y a =与函数()y g x =的图象的交点问题.19. 已知x ÎR ，[]x 表示不超过x 的最大整数，如[]33=，1=，[]1.52-=-.（1）若10a >，[]11n n a a +=，n +ÎN ，且{}n a 是无穷数列，求1a 的取值范围；（2）记[]x x x =-.①若11a =，22a =，21n n n a a a ++=+，求505014422log log k k k a a a a +=éù+êúëûå；②设1a =m +ÎN ，[]1n n n a a a +=×，证明：k +$ÎN ，使得n k ³时，0n a =.【答案】（1）1[1,2)a Î（2）①12-；②证明见解析.【解析】【分析】（1）分1(0,1)a Î，1[1,2)a Î和12a ³讨论即可；（2）①分析得2112n n a a ++<<，则221111n n n n n n a a a a a a +++++=-=，再计算出505022a a a éù=êúëû，最后代入计算即可；②分0k a =和0k a ¹讨论得[]2221k k k a a a +<<，则证明原命题.【小问1详解】若1(0,1)a Î，则[]120,a a =不存在，不符合题意，若1[1,2)a Î，则[][]12111,1a a a ===，从而1n a =，符合题意，若12a ³，设11,2, N k a k k k +£<+³Î，则[][]223111,0,a a a a k===不存在，不符合题意，综上，1[1,2)a Î.【小问2详解】①由题意知n a +ÎN ，且123n a a a a <<<<<L L ，从而2112n n n n a a a a +++=+<，即2112n n a a ++<<，则221111n n n n n n a a a a a a +++++=-=，所以5035150495041222350235050122a a a a a a a a a a a a a a a a a éùéùéù××=××=×êúêúêúëûëûëûL L ，由123451,2,3,5,8,a a a a a =====L 知50a 为偶数，所以505022a a a éù=êëû，则505015035144442222350log log log k k k a a a a a a a a a a a a +=éùéù+=××êúêúëûëûåL 504450111log log 222a a éù=×==-êúëû.②若0k a =，则1,0n n k a "³+=，若0k a ¹，则[][]222221k k n k k a a a a a +=×<<，又21,a m m +=ÎN ，从而0k +$ÎN ，且0k m <，使得020k a =，此时，对0,0n n k a "³=，得证.【点睛】关键点点睛：本题第二问第一小问的关键是利用根据数列单调性得到2112n n a a ++<<，进而分析出505022a a a éù=êúëû.。

河北省沧州市沧县中学2024-2025学年高三上学期11月期中考试数学试题(含答案)

河北省沧州市沧县中学2024-2025学年高三上学期11月期中考试数学试题(含答案)

2024—2025学年第一学期11月高三期中考试数学考试说明：1．本试卷共150分．考试时间120分钟．2．请将各题答案填在答题卡上．一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的．1．函数的定义域为（ ）A ．B ．C ．D ．2．已知平面向量，且∥，则（ ）A ．B ．C．D ．13．已知，若，则（ ）A ．B ．C ．D ．4．已知，则（ ）A ．B ．C ．D ．5．已知函数（其中，，）的部分图象如图所示，有以下结论：①②函数为偶函数③④在上单调递增所有正确结论的序号是（ ）A ．①②④B ．①②③C ．②③④D ．①③④6．若函数在（1，3）上不单调，则实数的取值范围是（ ）A ．B ．C ．D ．1()ln(22)1f x x x =++-(1,)+∞(0,1)(1,)-+∞ (,1)-∞(1,1)(1,)-+∞ (1,2),(1,1)a b λ=+()a b +a λ=12-1-123()2sin 2f x x x =-+()f m a -=()f m =4a-2a -2a +a-tan 3α=3cos 2sin 2cos 3sin αααα-=+511511-311311-()cos()f x A x B ωϕ=++0A >0ω>πϕ<23π()(6f x f ≤π(3f x +()()26f x f x π+-=()f x 4π13π[,]363()2ln f x x t x x=--7)(7,)+∞[7,)+∞7]7．将函数的图象向右平移个单位长度后得到函数的图象，且函数是奇函数，则的最小值是（ ）A ．B ．C ．D ．18．在锐角△中，、、分别是角、、所对的边，已知且，则的取值范围为（ ）A ．B ．C ．D ．二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，部分选对的得部分分，有选错的得0分．9．已知下列函数中，最小正周期为的是（）A ．B ． C ．D ．10．在△中，，为线段上一点，且有，则下列命题正确的是（ ）A ．B ．C ．的最大值为D ．的最小值为911．过点（2，）可以作两条直线与曲线相切，则实数的可能取值为（ ）A ．B ．C ．D ．三、填空题：本题共3小题，每小题5分，共15分．12．已知复数（为虚数单位），若是纯虚数，则实数________．13．已知平面向量，，则在上的投影向量为________（结果用坐标表示）14．在等边三角形的三边上各取一点，满足，，°，则三角形的面积的最大值是________．π()sin()(0)6f x x ωω=+>π3()g x ()g x ω132312ABC a b c A B C 23cos cos b c C A-=3a =b c +(3,6)(3,6]6]6)πcos 2y x=π2sin(213y x =++sin 2y x =tan()4y x π=-ABC 14CD CA = P BD ,,(0,)CP CA CB λμλμ=+∈+∞41λμ+=41λμ+=λμ1911λμ+a xy xe =a e 26e -21e -2e 122,3z a i z i =+=-12z z a =(2,1)a = (1,3)b =-b a ABC ,,M N P MN =4MP =30PMN ∠=ABC四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（本题满分13分）已知向量，满足．（1）求向量与夹角的余弦值；（2）求的值．16．（本题满分15分）（1）已知都是锐角，若，求的值；（2）已知，求的值．17．（本题满分15分）设函数．（1）当时，求函数的单调区间；（2）若函数有两个极值点，且，求的最小值．18．（本题满分17分）△的内角的对边分别为，已知．（1）求角的大小；（2）若是△边上的中线，且，求△面积的最大值．19．（本题满分17分）已知为坐标原点，对于函数，称向量为函数的相伴特征向量，同时称函数为向量的相伴函数．（1）记向量的相伴函数为，若当且时，求的值；（2）设，试求函数的相伴特征向量，并求出与同向的单位向量；（3）已知为函数的相伴特征向量，若在△中，，，若点为该△的外心，求的最大值．2024-2025学年第一学期11月高三期中考试数学答案1．D 2．D 3．A4．D5．B6．A7．C8．C9．ABD10．AD11．ABDa b 2,3,(2)a b a b b ==-⊥a b2a b -,αβ38sin ,cos()517ααβ=+=sin β1sin cos ,(0,π)3ααα-=∈πsin(26α-21()ln 1()2f x x x ax a R =+-+∈52a =()f x ()f x 12,x x 11(0,]2x ∈12()()f x f x -ABC ,,A B C ,,a b c cos sin 2A Cc b C +=B BE ABC AC 3BE =ABC O ()sin cos f x a x b x =+(,)OM a b =()f x ()f x OM(3,ON =()f x ()3f x =ππ(,33x ∈-x ππ())cos()()36g x x x x R =++-∈()g x OM OM(0,1)OA = ()h x ABC 2AB =πcos ()6C h =G ABC GC AB CA CB ⋅+⋅12． 13． 1415．【解析】（1）设与的夹角为，因为，所以，又，所以，所以所以向量与夹角的余弦值为；（2）由，所以．16．【解析】（1）∵已知、都是锐角，且，∴．∵，∴，∴．（2）因为，所以，即，所以，又，所以，故，故，故，所以，所以，，故17．【解析】（1），则定义域为（0，），23-21,55⎛⎫⎪⎝⎭a b θ(2)a b b -⊥2(2)20a b b a b b -⋅=⋅-=2,3a b == 223cos 90θ⨯⨯⨯-=3cos 4θ=a b 342223244442349224a b a a b b -=-⋅+=-⨯⨯⨯+⨯= 2a b -=αβ3sin 5α=4cos ,0π5ααβ==<+<8cos()17αβ+=15sin()17αβ+==1548336sin sin[()]sin()cos cos()sin 17517585βαβααβααβα=+-=+-+=⨯-⨯=1sin cos 3αα-=21(sin cos )9αα-=112sin cos 9αα-=4sin cos 9αα=(0,π)α∈sin 0α>cos 0α>π0,2α⎛⎫∈ ⎪⎝⎭22217(sin cos )sin cos 2sin cos 9αααααα+=++=sin cos αα+=8sin 22sin cos 9ααα==22cos 2cos sin (sin cos )(sin cos )ααααααα=-=-+-=81sin(2sin 2cos cos 2sin 66692πππααα-=-=+⨯=21()ln 12f x x x ax =+-+()f x +∞211()x ax f x x a x x-+'=+-=当时，，令，解得或，令，解得，所以的单调递增区间为，单调递减区间为（2）∵定义域为，由（1）可知当时有两个极值点等价于在上有两个不等实根，∴，∴ ∴设，则，∴在上单调递减，∴，即，∴的最小值为18．【解析】（1）在△中，由，根据正弦定理可得因为为△的内角可知，，且，所以，即因为为△的内角，，故；所以，即（2）由题知是边的中线，所以．两边平方得：52a =2511(2)(21)22()x x x x f x x x -+--'==()0f x '>2x >102x <<()0f x '<122x <<()0f x '>1(0,),(2,)2+∞1(,2)2()f x 211(0,),()x ax f x x a x x-+'+∞=+-=2a >()f x 12,x x 210x ax -+=(0,)+∞12,x x 1212,1x x a x x +==211x x =221211122211()()ln 1ln 122f x f x x x ax x x ax -=+-+--+-22211211112221111111111ln ln ()2ln 2222x x a x x x x x x x x x ==--+-=+-+-21121112ln 22x x x =-+22111()2ln 0222g x x x x x ⎛⎫=-+<≤ ⎪⎝⎭24223332121(1)()0x x x g x x x x x x---'=--==-≤()g x 1(0,]21115()2ln 222ln 2288g x g ⎛⎫≥=--+=-+ ⎪⎝⎭1215()()2ln 28f x f x -≥-+12()()f x f x -152ln 28-+ABC cos sin 2A Cc b C +=sin cos sin sin 2A CC B C+=C ABC sin 0C ≠A B C π++=πsin coscos sin 2222A C B B B +⎛⎫==-= ⎪⎝⎭2sin cos sin222B B B =B ABC sin02B ≠1cos 22B =π23B =2π3B =BE AC 2BE BA BC =+222(2)2cos BE c a ac B =++ 2236c a ac=+-又，故，当且仅当时等号成立．所以面积的最大值为19．【解析】（1）根据题意知，向量的相伴函数为当时，，又，则，所以，故（2）因为，故函数的相伴特征向量，则与同向的单位向量为（3）由题意得，，在△中，，，因此，设△外接圆半径为，根据正弦定理，，故所以，代入可得，所以当时，取得最大值14．222c a ac +≥2236c a ac ac =+-≥6a c ==11sin 3622ABC S ac B =≤⨯=V ABC (3,ON =π()3sin 6f x x x x =+=+π()36f x x ⎛⎫=+= ⎪⎝⎭πsin 6x ⎛⎫+= ⎪⎝⎭ππ,33x ⎛⎫∈-⎪⎝⎭πππ,662x ⎛⎫+∈- ⎪⎝⎭ππ63x +=π6x =ππππππ()cos cos cos sin sin cos cos sin sin363366g x x x x x x x ⎛⎫⎛⎫⎫=++-=-++ ⎪ ⎪⎪⎝⎭⎝⎭⎭sin x x =-+()g x (1,OM =-(1,OM =- 11(1,,22OM OM ⎛=-=- ⎝()cos h x x =ABC 2AB =ππcos (cos 66C h ===π6C =ABC R 24sin ABR C==2R =2GA GB GC ===()()()GC AB CA CB GC GB GA GA GC GB GC ⋅+⋅=⋅-+-⋅- =2GC GB GC GA GA GB GA GC GC GB GC⋅-⋅+⋅-⋅-⋅+ 228cos 4cos 4GC GA GA GB GC AGC AGB =-⋅+⋅+=-∠+∠+ πππ1,2,cos cos 6332C AGB C AGB =∠==∠==68cos GC AB CA CB AGC ⋅+⋅=-∠ πAGC ∠=GC AB CA CB ⋅+⋅。

四川省成都市2024-2025学年高三上学期11月期中数学试题(含答案)

四川省成都市2024-2025学年高三上学期11月期中数学试题(含答案)

成都2022级半期考试数学试卷注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分；2.本堂考试时间120分钟，满分150分；3.答题前考生务必先将自己的姓名、学号填写在答题卡上，并用2B 铅笔填涂；4.考试结束后将答题卡交回.第Ⅰ卷（选择题部分，共58分）一、单项选择题：本题共8个小题，每小题5分，共40分，在每小题给出的四个选项中只有一项是符合题目要求的.1.已知集合，，则（ ）A. B. C. D.2.若函数是周期为4的奇函数，且，则（ ）A.2B. C.3D.3.已知，，则为第几象限角（ ）A.第一象限角B.第二象限角C.第三象限角D.第四象限角4.若向量，，且，，三点共线，则（ ）A. B. C. D.5.若，则（ ）A.3 B. C. D.66.为了得到函数的图象，只需将函数的图象（ ）A.向左平移个单位，再将所有点的横坐标伸长到原来的2倍（纵坐标不变）B.向左平移个单位，再将所有点的横坐标缩短到原来的（纵坐标不变）C.所有点的横坐标缩短到原来的（纵坐标不变），再将图象向左平移个单位D.所有点的横坐标伸长到原来的2倍（纵坐标不变），再将图象向左平移个单位7.已知关于的不等式在上有解，则实数的取值范围是（ ）{}2log 1A x x =≤{}04B x x =<≤A B = {}04x x <≤{}4x x ≤{}2x x ≤{}02x x <≤()f x ()13f =()3f =2-3-()sin π0θ-<()cos π0θ+>θ()2,5AB = (),1AC m m =+A B C m =23-2332-32tan 3θ=-sin cos sin cos 2θθθθ+=103-56-()sin 2cos 2f x x x =+()g x x =π4π41212π4π8x 2230ax x a -+<(]0,2aA. B. C. D.8.设，，且，则下列结论正确的个数为（ ）① ② ③ ④A.1B.2C.3D.4二、多项选择题：本题共3个小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求；全部选对的得6分，部分选对得部分分，有选错的得0分.9.下列说法不正确的是（ ）A.钝角三角形的内角是第一象限角或第二象限角B.若向量，满足且，同向，则C.若，，三点满足，则，，三点共线D.将钟表的分针拨快10分钟，则分针转过的角的弧度数为10.函数（，）的部分图象如图所示，则（ ）A. B.C.的图象关于点对称 D.在区间上单调递增11.已知函数的定义域为，为奇函数，为偶函数，且时，单调递增，则下列结论正确的为（ ）A.是偶函数 B.的图象关于点中心对称C. D.第Ⅱ卷（非选择题部分，共92分）三、填空题：本题共3个小题，每小题5分，共15分.12.已知角的终边经过点，则______.4,7⎛⎫-∞ ⎪⎝⎭⎛-∞ ⎝(],0-∞(),0-∞0a >0b >1a b +=22log log 2a b +≥-22a b +≥ln 0a b +<1sin sin 4a b <a b a b > a b a b>P A B 3OP OA OB =+P A B π3()()sin f x x ωϕ=+0ω>π2ϕ<2ω=π6ϕ=()f x π,012⎛⎫⎪⎝⎭()f x 5ππ,4⎛⎫⎪⎝⎭()f x R ()1f x +()2f x +[]0,1x ∈()f x ()f x ()f x ()1,0-()20240f =51044f f ⎛⎫⎛⎫+-<⎪ ⎪⎝⎭⎝⎭α()3,4P -sin α=13.设函数，则满足的的取值范围是______.14.若，则的最大值为______.四、解答题：本题共5个小题，共70分，其中15题13分，16、17题每题15分，18、19题每题17分，解答应写出文字说明、证明过程或演算步骤.15.（本小题13分）已知数列为等差数列，，前项和为，数列为等比数列，，公比为2，且，.（1）求数列与的通项公式；（2）设数列满足，求数列的前项和.16.（本小题15分）在学校食堂就餐成为了很多学生的就餐选择.学校为了解学生食堂就餐情况，在校内随机抽取了100名学生，其中男生和女生人数之比为1:1，现将一周内在食堂就餐超过8次的学生认定为“喜欢食堂就餐”，不超过8次的学生认定为“不喜欢食堂就餐”.“喜欢食堂就餐”的人数比“不喜欢食堂就餐”人数多20人，“不喜欢食堂就餐”的男生只有10人.男生女生合计喜欢食堂就餐不喜欢食堂就餐10合计100（1）将上面的列联表补充完整，并依据小概率值的独立性检验，分析学生喜欢食堂就餐是否与性别有关；（2）用频率估计概率，从该校学生中随机抽取3名，记其中“喜欢食堂就餐”的人数为.事件“”的概率为，求随机变量的期望和方差.参考公式：，其中.0.10.050.010.0050.0012.7063.8416.6357.87910.82817.（本小题15分）已知锐角，内角，，所对的边分别为，，，面积为，.（1）求角；（2）若，求的取值范围.18.（本小题17分）已知抛物线：（）经过点，直线：与的交()11,02,0x x x f x x -+≤⎧=⎨>⎩112f x ⎛⎫-> ⎪⎝⎭x ()()sin cos 2sin αβααβ+=-()tan αβ+{}n a 11a =n n S {}n b 11b >2354b S =3216b S +={}n a {}n b {}n c n n n c a b =+{}n c n n T 0.001α=X X k =()P X k =X ()()()()()22n ad bc a b c d a c b d χ-=++++n a b c d =+++αx αABC △A B C a b c S πsin cos 6b A a B ⎛⎫=- ⎪⎝⎭B 2a =S E 22y px =0p >()1,2P l y kx m =+E点为，，且直线与倾斜角互补.（1）求抛物线在点处的切线方程；（2）求的值；（3）若，求面积的最大值.19.（本小题17分）设函数（），.（1）当时，判断在上的单调性；（2）当时，证明：；（3）设函数，若函数在上存在唯一极值点，求实数的取值范围.A B PA PB ()1,2P k 3m <PAB △()()cos sin f x a x x x =-a ∈R ()e x g x =1a =()f x ()0,2π0x >()2112g x x x >++()()()2112h x g x f x x x =----()h x ()0,πa成都2022级半期考试数学参考答案及评分标准一、单选题：1. A2. D3. C4. B5. C6. B7. B8.C二、多选题：9. BCD 10. ACD 11. ABD三、填空题：12.13.四、解答题15.（1）设等差数列的公差为，由题知，解得，，∴，.（2）∵，∴.16.（1）列联表见图，男生女生合计喜欢食堂就餐402060不喜欢食堂就餐103040合计5050100零假设：假设食堂就餐与性别无关，由列联表可得：，根据小概率的独立性检验推断不成立，即可以得到学生喜欢食堂就餐与性别有关，此推断犯错误的概率不超过0.001（2）由题意可知，抽取的3名学生，喜欢饭堂就餐的学生人数服从二项分布，453,2⎛⎫+∞ ⎪⎝⎭{}n a d ()11233544216b d b d ⎧+=⎨++=⎩13b =2d =()11221n a n n =+-⨯=-132n n b -=⋅()12132n n n n c a b n -=+=-+⋅()()2112132131222n n n T c c c n -⎡⎤=++⋅⋅⋅+=++⋅⋅⋅+-++++⋅⋅⋅+⎣⎦()()()21121213321212nn n n n ⨯-⎡⎤+-⎣⎦=+⨯=+--0H 0H ()221004030102016.66710.82850506040χ⨯-⨯=≈>⨯⨯⨯0.001α=0H X且喜欢饭堂就餐的频率为，则，故其期望，方差.17.（1）因为，由正弦定理可得，，且，且故，所以，.（2）由正弦定理可得，，且，则，由（1）知，则，且是锐角三角形，即，，所以，即，，..18.（1）由题意可知，，所以，所以抛物线的方程为；（），，则，则切线方程为.（2）如图：设，，将直线的方程代入，得，所以，，因为直线与倾斜角互补，所以600.6100=()3,0.6X B~() 1.8E X np ==()()10.72D X np p =-=πsin cos 6b A a B ⎛⎫=-⎪⎝⎭1sin sin sin sin 2B A A B B ⎫=+⎪⎪⎭1sin 0sin 2A B B ≠=cos 0B ≠tan B =π02B <<π3B =sin sin sin a b c A B C ==2a =2sin sin Cc A=π3B =2π3A C +=ABC △π02C <<2ππ032A <-<π2π63A <<ππ62A <<π113sin 22S ac B ⎫⎛⎫⎪⎪====⎪ ⎪⎝⎭ππ62A <<S <<42p =2p =E 24y x =y =0x >y '=11x k y ='==1y x =+()11,A x y ()22,B x y l 24y x =()222240k x km x m +-+=12242km x x k -+=2122m x x k=PA PB，即，所以，即，所以.（3）由（1）可知，所以，，则因为，所以，即，又点到直线的距离为所以因为，所以，即时，等号成立，所以19.（1）当时，，则，当时，；当时，，所以在上单调递减，在上单调递增.（2）证明：令（），则，令，则，21212121222201111PA PB y y kx m kx m k k x x x x --+-+-+=+=+=----()()()()122121211222201111x x k k m k k m x x x x ⎛⎫+-++-+=++-=⎪----⎝⎭()()()242222022km k k k m k m k m --++-=+-++2422442022km k k k k m k m --++==++++1k =-()22240x m x m -++=1242x x m +=+212x x m =AB ==()222440m m ∆=+->1m >-13m -<<P AB d 12S =⨯()()()()()213133222m m m m m -+=--+3133222562327m m m -+-++⎛⎫≤= ⎪⎝⎭S ≤322m m -=+13m =PAB △1a =()cos sin f x x x x =-()cos sin cos sin f x x x x x x x =--=-'()0,πx ∈()0f x '<()π,2πx ∈()0f x '>()f x ()0,π()π,2π()()22111e 122x G x g x x x x x ⎛⎫=-++=---⎪⎝⎭0x >()e 1x G x x =--'()e 1x k x x =--()e 1x k x '=-当时，，所以在上单调递增，即在上单调递增；所以，所以在上单调递增，所以，所以不等式成立.（3）由题可知：，则，令且，所以函数在上存在唯一极值点等价于在上存在唯一变号零点，又因为且，令，则且①当时，，（ⅰ）当时，在上单调递减，所以在上单调递增.又因为，，由零点存在性定理知：存在唯一，使得，所以当时，；当时，，（ⅱ）当时，，所以，所以由（ⅰ）（ⅱ）知：在上单调递减，在上单调递增，即在上单调递减，在上单调递增，所以当时，，又因为，0x >()0k x '>()k x ()0,+∞()G x '()0,+∞()()00G x G '>='()G x ()0,+∞()()00G x G >=()2112g x x x >++()()21e 1cos sin 2xh x x x a x x x =-----()e 1sin x h x x ax x =--+'()e 1sin x m x x ax x =--+()00m =()h x ()0,π()m x ()0,π()()e 1sin cos x m x a x x x =-++'()00m '=()()()e 1sin cos x n x m x a x x x =-+'=+()()e 2cos sin x n x a x x x =+-'()012n a '=+12a <-()0120n a =+<'π0,2x ⎛⎫∈ ⎪⎝⎭2cos sin y x x x =-π0,2⎛⎫⎪⎝⎭()()e 2cos sin x n x a x x x =+-'π0,2⎛⎫⎪⎝⎭π2ππe 022n a ⎛⎫=-> ⎪⎝⎭'()0120n a =+<'0π0,2x ⎛⎫∈ ⎪⎝⎭()00n x '=()00,x x ∈()0n x '<0π,2x x ⎛⎫∈ ⎪⎝⎭()0n x '>π,π2x ⎛⎫∈⎪⎝⎭2cos sin 0y x x x =-<()()e 2cos sin 0x n x a x x x '=+->()n x ()00,x ()0,πx ()m x '()00,x ()0,πx ()00,x x ∈()()00m x m '<='()ππe 1π0m a =-->'所以由零点存在性定理知：存在唯一，使得，所以当时，；当时，所以在上单调递减，上单调递增，所以当时，，又因为，由（2）知：，所以由零点存在性定理知：存在唯一，使得，当时，；当时，，即为在上唯一变号零点，所以符合题意；②当时，由时，得：，令且，则且，令，又因为，则在上单调递增，即在上单调递增，所以，所以在上单调递增，所以，所以当时，，即在上无零点，所以不符合题意.综上：，即实数的取值范围为.()10,πx x ∈()10m x '=()10,x x ∈()0m x '<()1,πx x ∈()0m x '>()m x ()10,x ()1,πx ()10,x x ∈()()00m x m <=()ππe π1m =--()π0m >()21,πx x ∈()20m x =()20,x x ∈()0m x <()2,πx x ∈()0m x >2x ()m x ()0,π12a <-12a ≥-()0,πx ∈sin 0y x x =>()1e 1sin e 1sin 2x x m x x ax x x x x =--+≥---()1e 1sin 2xM x x x x =---()00M =()()1e 1sin cos 2xM x x x x =--+'()00M '=()()()1e 1sin cos 2xx M x x x x ϕ=--+'=()01e cos sin e cos 0002x x x x x ϕ'=-+>-+=()x ϕ()0,π()M x '()0,π()()00M x M '>='()M x ()0,π()()00M x M >=()0,πx ∈()0m x >()m x ()0,π12a ≥-12a <-a 1,2⎛⎫-∞- ⎪⎝⎭。

辽宁省滨城高中联盟2024-2025学年高三上学期期中考试数学试题(含答案)

辽宁省滨城高中联盟2024-2025学年高三上学期期中考试数学试题(含答案)

滨城高中联盟2024-2025学年度上学期高三期中Ⅰ考试数学试卷命题人：大连市第二十高级中学卢永娜校对人：大连市第二十高级中学苑清治第Ⅰ卷（选择题共58分）一、选择题：本题共8小题，每题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合，，则（ ）A ．B ．C ．D ．2．“”是“函数在上单调递减”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．在中，点D 在边AB 上，．记，，则（ ）A ．B ．C ．D ．4．函数的值域为（ ）A ．B ．C ．D ．5．函数的单调递增区间为（ ）A ．B ．C ．D ．6．已知，，则（ ）A ．B ．C ．D ．7，设是定义域为R 的偶函数，且在单调递增，则（）A ．B ．C ．D ．8．已知向量，，函数．若对于任意的，，且(){}lg 3M x y x ==-{}2N y y =>M N = ∅()2,3()3,+∞()2,+∞π2ϕ=-()sin 2y x ϕ=+π,02x ⎡⎤∈-⎢⎥⎣⎦ABC △2AD DB =CB a = CD b = CA =32a b-32a b+23a b +23a b-+()cos 2cos f x x x =+[]0,3[]1,3-[]1,2-[]0,2()()23log 4f x x =-()0,+∞(),0-∞()2,+∞(),2-∞-()1os 4c αβ+=tan tan 2αβ=()cos αβ-=34-112-11234()f x ()0,+∞233221log 223f f f --⎛⎫⎛⎫⎛⎫>> ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭233221log 223f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭23322122log 3f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭23322122log 3f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(),1a x = ()sin ,sin cos b x x x =+ ()f x a b =⋅ 1x 2π0,2x ⎡⎫∈⎪⎢⎣⎭，均有成立，则实数t 的取值范围为（ ）A ．B ．C ．D ．二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9）A ．B ．C ．D．10．已知向量，，则（ ）A ．B ．与向量共线的单位向量是C ．D ．向量在向量上的投影向量是11．已知函数，且对，都有，把图象上所有的点，纵坐标不变，横坐标变为原来的，再把所得函数的图象向右平移个单位，得到函数的图像，则下列说法正确的是（ ）A ．B ．C ．为偶函数D ．在上有1个零点第Ⅱ卷（非选择题 共92分）三、填空题：本题共3小题，每小题5分，共15分．12．已知向量，，若，则实数______．13．已知函数，若，，且，则的最小值是______．14．已知函数，则的最大值是______．四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（本小题满分13分）12x x ≠()()1212x x f x f x t e e ->-[)0,+∞[)1,+∞(],1-∞(],0-∞1tan151tan15+︒-︒tan 20tan 4020tan 40︒+︒︒︒)sin 503tan10︒+︒22tan151tan 15︒-︒()4,2a = ()6,2b =-20a b +=a ()a b a+⊥ a b 12b-()()π2cos 033f x x ωω⎛⎫=+<< ⎪⎝⎭x ∀∈R ()π3f x f x ⎛⎫''=- ⎪⎝⎭()f x 12π4()g x 1ω=()2π3g x g x ⎛⎫-=-⎪⎝⎭π6g x ⎛⎫+⎪⎝⎭()g x π0,2⎛⎫⎪⎝⎭()4,3a =- (),9b m =-a b ∥m =()323f x x x =+0m >0n >()()()230f m f n f +-=29m n+()2211222024sin log sin 2024cos log cos f x x x x x =+()f x已知．（1）求的值；（2）若，是方程的两个根，求的值．16．（本小题满分15分）已知函数在时取得极大值1．（1）求曲线在点处的切线方程；（2）求过点与曲线相切的直线方程．17．（本小题满分15分）已知函数为奇函数．（1）求实数a 的值；（2）设函数，若对任意的，总存在，使得成立，求实数m 的取值范围．18．（本小题满分17分）已知函数，．（1）求函数的极值；（2）若函数在区间上单调递增，求a 的最小值；（3）如果存在实数m 、n ，其中，使得，求的取值范围．19．（本小题满分17分）已知函数的图象如图所示．()()π2sin πsin 323π135cos 3cos 2π2x x x x ⎛⎫-+ ⎪⎝⎭=⎛⎫++- ⎪⎝⎭tan x sin x cos x 20x mx n -+=23m n +()323f x x x bx c =-++0x =()y f x =()()3,3f ()0,2()y f x =()221x x af x +=+()22log log 24x xg x m =⋅+(]20,1x ∈[]12,8x ∈()()12g x f x =()ln f x x x =()()1,011,02f x x xg x x x +⎧>⎪⎪+=⎨⎪+≤⎪⎩()f x ()xf x y ae x=-()1,2m n <()()g m g n =n m -()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>≤⎪⎝⎭（1）求函数的单调递增区间；（2）求函数在上的最大值和最小值；（3）若函数在内恰有781个零点，求实数m 、n 的值．()f x ()π226x x f f h x =⎛⎫⎛⎫-⎪ ⎪⎝⎭⎝⎭π0,2⎡⎤⎢⎥⎣⎦()2π26π1x x g x f mf ⎛⎫- ⎪⎛⎫=+- ⎪⎝⎭⎭⎝()()*0,πn n ∈N滨城高中联盟2024-2025学年度上学期高三期中Ⅰ考试数学参考答案题号1234567891011答案CAD BCA BDABCCDABD12．1213．14．101215．（1）∵，∴，解得；（2）由题意可得，∴，，∴．16．（1），则，由题意可得，解得，即，，令，解得或，故在，上单调递增，在上单调递减，则在处取得极大值1，即，符合题意．（写经检验，当，时，在处取得极大值也给分）∵，，则切点坐标为，切线斜率，∴曲线在点处的切线方程为，即（2）由（1）可得：，，设切点坐标为，切线斜率，323()()π2sin πsin 2sin cos 323π5sin 3cos 135cos 3cos 2π2x x x x x x x x ⎛⎫--+ ⎪-⎝⎭==+⎛⎫++- ⎪⎝⎭2tan 135tan 313x x -=+tan 2x =sin cos sin cos x x mx x n +=⎧⎨=⎩()223sin cos 3sin cos 15sin cos m n x x x x x x +=++=+222sin cos tan 2sin cos sin cos tan 15x x x x x x x x ===++2231535m n +=+⨯=()323f x x x bx c =-++()236f x x x b '=-+()()0001f b f c '==⎧⎪⎨==⎪⎩01b c =⎧⎨=⎩()3231f x x x =-+()236f x x x '=-()0f x '>2x >0x <()f x (),0-∞()2,+∞()0,2()f x 0x =0b =1c =0b =1c =()f x 0x =()31f =()39f '=()3,19k =()y f x =()()3,3f ()193y x -=-9260x y --=()3231f x x x =-+()236f x x x '=-()32000,31x x x -+20036k x x =-则切线方程为，∵切线过点，则，整理得，即或，∴切线方程为或，即或．17．（1）由题意可得，函数的定义域为R ，因为是奇函数，所以，可得，经检验，对于，成立，所以．（2）由（1）可得因为，所以，，，，，所以当时的值域，（其他方法求值域酌情给分）又，，设，，则，当时，取最小值为，当时，取最大值为，即在上的值域，又对任意的，总存在，使得成立，即，所以，解得，即实数m 的取值范围是．18．（1）∵定义域为，，∴当时，；当时，；()()()32200003136y x x x x x x --+=--()0,2()()()322000023136x x x x x --+=--()()2001210x x -+=01x =12-()131y x +=--1151842y x ⎛⎫-=+ ⎪⎝⎭320x y +-=15480x y -+=()f x ()10011af +==+1a =-x ∀∈R ()()f x f x -=-1a =-()21212121x xx f x -==-++(]0,1x ∈(]21,2x∈(]212,3x+∈111,2132x ⎡⎫∈⎪⎢+⎣⎭221,213x ⎛⎤-∈-- ⎥+⎝⎦2110,213x ⎛⎤-∈ ⎥+⎝⎦(]0,1x ∈()f x 10,3A ⎛=⎤ ⎥⎝⎦()f x ()()()2222log log log 1log 224x xg x m x x m =⋅+=--+[]2,8x ∈2log t x =[]1,3t ∈()()21232y t t m t t m =--+=-++32t =14m -+3x =2m +()g x []2,8x ∈1,24B m m ⎡⎤=-++⎢⎥⎣⎦(]20,1x ∈[]12,8x ∈()()12g x f x =A B ⊆104123m m ⎧-+≤⎪⎪⎨⎪+≥⎪⎩5134m -≤≤51,34⎡⎤-⎢⎥⎣⎦()f x ()0,+∞()1ln f x x '=+()10,x e -∈()0f x '<()1,x e -∈+∞()0f x '>∴在上单调递减，在上单调递增，∴的极小值为，无极大值．（2）依题可知，，在上恒成立，显然，所以，设，，，所以在上单调递增，，故，即，即a 的最小值为．（3）方法1：由已知，则函数在、上为增函数，若存在实数m 、n ，其中，使得，则，，由可得，则，故，令，，，可得当时，，此时函数单调递减，当时，，此时函数单调递增，故，，又因为，，且，所以，，因此，的取值范围是．方法2：由已知，则函数在、上为增函数，若存在实数m 、n ，其中，使得，则，，令，则，可得，由可得，令，其中，令可得，()f x ()10,e -()1,e -+∞()f x ()11f e e-=-ln xy ae x =-10x y ae x '=-≥()1,20a >1x xe a≥()xg x xe =()1,2x ∈()()10xg x x e '=+>()g x ()1,2()()1g x g e >=1e a ≥1a e ≥1e()()ln 1,01,02x x g x x x ⎧+>⎪=⎨+≤⎪⎩()g x (],0-∞()0,+∞m n <()()g m g n =20m -<≤01n e <≤-()()g m g n =()1ln 12mn +=+()2ln 12m n =+-()2ln 12n m n n -=-++()()2ln 12x x x ϕ=-++(]0,1x e ∈-()211011x x x x ϕ-'=-==++1x =01x <<()0x ϕ'<()x ϕ11x e <<-()0x ϕ'>()x ϕ()()min 132ln 2x ϕϕ==-()02ϕ=()11e e ϕ-=-12e -<()32ln 22h t -≤<n m -[)32ln 2,2-()()ln 1,01,02x x g x x x ⎧+>⎪=⎨+≤⎪⎩()g x (],0-∞()0,+∞m n <()()g m g n =20m -<≤01n e <≤-()()g m g n t ==()ln 112t n mt ⎧=+⎪⎨=+⎪⎩122t n e m t ⎧=-⎨=-⎩20m -<≤01t <≤()21th t n m e t =-=-+01t <≤()20th t e '=-=ln 2t =当时，，此时函数单调递减，当时，，此时函数单调递增，故当时，，又因为，，且，所以，，因此，的取值范围是．（其他方法酌情给分）19．（1）由图象可得，最小正周期，则，由，所以，，又，则易求得，所以，由，，得，，所以单调递增区间为，．（2）由题意得，因为，所以，①从而可知，即因此，0ln 2t <<()0h t '<()h t ln 21t <≤()0h t '>()h t 01t <≤()()min ln 232ln 2h t h ==-()02h =()11h e =-12e -<()32ln 22h t -≤<n m -[)32ln 2,2-1A =7ππ2π1212T ⎛⎫=⨯-=⎪⎝⎭2π2Tω==77πsin 2π11212f ϕ⎛⎫⎛⎫=⨯+=- ⎪ ⎪⎝⎭⎝⎭5π2π3k ϕ=-+k ∈Z π2ϕ≤π3ϕ=()πsin 23x x f ⎛⎫=+ ⎪⎝⎭πππ2π22π232k x k -+≤+≤+k ∈Z 5ππππ1212k x k -+≤≤+k ∈Z 5πππ,π1212k k ⎡⎤-++⎢⎥⎣⎦k ∈Z ()ππsin sin 2263x x h x f f x x⎛⎫⎛⎫⎛⎫=-=+⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭111sin sin 2cos 2244x x x x x ⎛⎫==-+ ⎪ ⎪⎝⎭1π1sin 2264x ⎛⎫=-+ ⎪⎝⎭π02x ≤≤ππ5π2666x -≤-≤πππsin sin 2sin 662x ⎛⎫⎛⎫-≤-≤ ⎪ ⎪⎝⎭⎝⎭1πsin 2126x ⎛⎫-≤-≤ ⎪⎝⎭1π130sin 22644x ⎛⎫≤-+≤ ⎪⎝⎭故在上的最大值为，最小值为0．（3），令，可得，令，得，易知，方程必有两个不同的实数根、，由，则、异号，①当且或者且时，则方程和在区间均有偶数个根，不合题意，舍去；②当且时，则方程和在区间均有偶数个根，不合题意，舍去；③当，时，当时，只有一根，有两根，所以关于x 的方程在上有三个根，由于，则方程在上有780个根，由于方程在区间上有两个根，方程在区间上有一个根，因此，不合题意，舍去；④当，时，当时，只有一根，有两根，所以关于x 的方程在上有三个根，由于，则方程在上有780个根，由于方程在区间上只有一个根，方程在区间上两个根，此时，满足题意；因此，，，得，综上，，．（其他方法酌情给分）()h x π0,2⎡⎤⎢⎥⎣⎦34()ππcos 2sin 1226x g x f x mf x m x ⎛⎫⎛⎫=-+-=+⎪ ⎪⎝⎭⎝⎭()0g x =22sin sin 10x m x --=[]sin 1,1t x =∈-2210t mt --=0∆>1t 2t 1212t t =-1t 2t 11t >210t -<<101t <<21t <-1sin x t =2sin x t =()0,πn 101t <<201t <<1sin x t =2sin x t =()0,πn 11t =-212t =()0,2πx ∈sin 1x =-1sin 2x =22sin sin 10x m x --=()0,2πx ∈78132601=⨯+22sin sin 10x m x --=()0,520π1sin 2x =()520π,521πsin 1x =-()521π,522π11t =212t =-()0,2πx ∈sin 1x =1sin 2x =-22sin sin 1x m x --()0,2πx ∈78132601=⨯+22sin sin 10x m x --=()0,520πsin 1x =()520π,521π1sin 2x =-()521π,522π521n =1122m ⎛⎫⎪⎝=+⎭-1m =1m =521n =。

【高三】福建省师大附中届高三上学期期中考试数学(文)试题

【高三】福建省师大附中届高三上学期期中考试数学(文)试题

【高三】福建省师大附中届高三上学期期中考试数学（文）试题试卷说明：福建师大附中20-学年第学期考试卷高数学满足，则= ( *** ) A. B. C . D. 2. 命题“存在实数，使> 1”的否定是（ *** ）A. 对任意实数, 都有 > 1 B. 不存在实数，使 1 C. 对任意实数, 都有 1 D. 存在实数，使 13. 设，则（ *** ）A. B. C. D. 4. 若，且，则下列不等式中，恒成立的是（ *** ） A. B. C. D. 5. 若不等式的解集为，则的值为（ *** ）A.-10 B.10 C. -14 D. 146. 已知为等差数列，且则=( *** )A. B. C.D. 7. 已知的三个内角所对的边为，满足，则的形状是（ *** ）A.正三角形 B.等腰三角形 C. 等腰直角三角形 D. 等腰三角形或直角三角形8.已知数列的通项公式为，设为数列的前项和公式，则（ *** ） A. -100 B.100 C. -150 D. 1509.平面内有三个向量，其中与夹角为，与的夹角为，且，若，（）则（ ***）A. B. C. D. 10.函数的图象先向下移一个单位，再把纵坐标伸长到原来的2倍（横坐标不动）得到新函数，则( *** )A． B. C. D. 11.某家公司每月生产两种布料A和B，所有原料是两种不同颜色的羊毛，下表给出了生产每匹每种布料所需的羊毛量，以及可供使用的每种颜色的羊毛的总量.羊毛颜色每匹需要 ( kg)供应量(kg)布料A布料B红441400绿631800已知生产每匹布料A、B的利润分别为120元、80元. 那么公司每月应怎么安排生产两种布料A和B的匹数，才能够产生最大的利润，最大利润为（ *** ）元.A. 38000 B. 32000 C. 28000 D. 4800012.设为平面向量组成的集合，若对任意正实数和向量，都有，则称为“正则量域”.据此可以得出，下列平面向量的集合为“正则量域”的是（ *** ）A. B. C . D. 二、填空题（每小题4分，共16分）13.已知向量满足，且，则向量与的夹角为___***___；14.已知正实数满足，则的最小值是___***_____15.已知的一个内角为，并且三边长构成公差为4的等差数列，则的面积为_____***___16. 某种平面分形如下图所示，一级分形图是由一点出发的三条线段，长度均为1，两两夹角为；二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来的线段，且这两条线段与原线段两两夹角为；……;依此规律得到级分形图，则级分形图中所有线段的长度之和为_____***_____.三、解答题：（本大题共6题，满分74分）17.（本小题满分1分）的公比，前3项和.（Ⅰ）求数列的通项公式；（Ⅱ）若函数在处取得最大值，且最大值为，求函数解析式.18．（本小题满分1分）（Ⅰ）求函数的最小正周期和单调递增区间；（Ⅱ）若函数在内有零点，求实数k的取值范围.19．（本小题满分1分）已知定义在上的函数，其中为常数.,恒成立，求实数的取值范围；（Ⅱ）若，在处取得最大值，求正数的取值范围.本小题满分1分），宽设计为多少米时，才能使围成的网箱中筛网总长度最小；（Ⅱ）若大网箱的面积为160平方米，网衣的造价为112元/米，筛网的造价为96元/米，且大网箱的长与宽都不超15米，则小网箱的长、宽分别为多少米时，可使网衣和筛网的合计造价最低？21.（本小题满分1分）作曲线的切线，切点为，设点在轴上的投影是点，又过点作曲线的切线，切点为，设点在轴上的投影是点，…依此下去，得到点列记它们的横坐标构成数列.（Ⅰ）求与的关系式；（Ⅱ）令求数列的前项和.22.（本小题满分1分），（Ⅰ）求函数的最小值.（Ⅱ）当时,求证:福建师大附中20-学年第学期考试卷高数学，6，，（2）由（1）可知函数的最大值为3，时，取得最大值，，又，函数18.解：（1）单调区间为，最小正周期为，（2）19.解：（1），，恒成立令，当或，得（2）若时，对，恒成立，故在区间上为增函数，在处取到最大值.若时，在上为减函数，上为增函数，则综上所述：若，在处取得最大值，正数的取值范围20.解：（Ⅰ）由已知得，，网箱中筛网的总长度。

河北省保定市2024-2025学年高三上学期10月期中考试数学试题(含答案)

河北省保定市2024-2025学年高三上学期10月期中考试数学试题(含答案)

2024年高三摸底考数学试题本试卷共4页，19小题，满分150分.考试用时120分钟.注意事项：1.答题前，请务必将自己的姓名､准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题卡上.将条形码横贴在答题卡“条形码粘贴处”.2.作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.3.非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.考试结束后，将试卷和容题卡一并交回.一､选择题：本题共8小题，每小题5分，共40分.每小题给出的四个选项中，只有一个选项是正确的.1.已知，则（）A.B. C. D.2.已知是的共轭复数，则（）A.0 B. C.2D.3.已知向量，且，则（）A.1B.2C.D.04.若一个球的体积和表面积数值相等，则该球的半径的数值为（）A.2B.3C.45.设函数为偶函数.当满足时，|有最小值2，则和的值分别是（）A. B.C. D.6.若中，角所对的边分别为平分交于，且，则（）{}1,{5,}A xx B x x x ==<∈N ∣∣…A B ⋂={}0,1{}1[]0,1(]0,1()21i ,1i z z -=+z z =2i 2-()()1,1,2,a b λ==- ()0b λ=> a b ⋅= 1-r ()()πcos 0,2f x x ωϕωϕ⎛⎫=+><⎪⎝⎭12,x x ()()122f x f x -=12x x -∣ωϕπ,0ωϕ==ππ,2ωϕ==ππ,22ωϕ==π,02ωϕ==ABC ,,A B C ,,,4,16,a b c a b CD ==ACB ∠AB D 4CD =BD =B.3C.D.7.已知且，则的最小值是（）A.12 B.16 C.15 D.148.已知函数若关于的方程至少有5个不等的实数解，则的取值范围是（）A. B. C. D.二､多选题：本题共3小题，每小题6分，共18分.每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，选对但不全的得部分分，有选错的得0分.9.函数的图象经过（）A.第一象限 B.第二象限C.第三象限D.第四象限10.若是平面的一条斜线，，直线平面且直线，记直线与平面所成的角为，则下列说法正确的是（）A.与是一对异面直线B.若点和分别为直线上和平面内异于点的点，则C.若和分别是直线与上的动点，则满足且的直线不唯一D.过直线有且只有唯一平面与直线平行11.若函数存在两个极值点，下列说法正确的是（）A.时满足条件B.不存在实数使得均为正整数C.当时，D.对任意正整数，均存在对应的，使得三､填空题：本题共3小题，每小题5分，共计15分.12.已知曲线在处的切线斜率为4，则实数的值为__________.13.函数的最小正周期是__________，在上的单调递减区间是__________.0ab >21a b +=221a b ab++()()1,11,22,17,x x f x f x x ⎧--<⎪=⎨-⎪⎩………x ()f x a =a []1,0-[]2,0-[]4,0-[]8,0-()11x y a a a=->αl O α⋂=a ⊂αO ∉a αθa A B αO AOB ∠θ…M N a MN l ⊥MN a ⊥a ()21ln 2f x x x mx x =--()1221,x x x x >1m =m 12,x x 321x x …m n 12,x x ()222112ln x x n x x -=13e 1x y ax -=++1x =a ()2cos sin cos 1f x x x x =++()f x ()0,π14.已知递增数列共有项（为定值）且各项均不为零，末项.若从数列中任取两项和，当时，仍是数列中的项，则数列的通项公式__________（用含和的式子表示.）四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）已知向量.（1）若，且，求的值；（2）设函数，求函数的值域.16.（15分）已知直三棱柱中，，且，点分别为线段和的中点.（1）证明：平面；（2）求平面与平面的夹角.17.（15分）在中，角的对边分别为.（1）求角；（2）若，求的值；（3）在（2）的条件下，若边，点为线段上的动点，点为线段上的动点，且线段平分的面积，求线段长度的最小值.18.（17分）已知函数.{}n a m *,m m ∈N 1m a ={}n a i a j a i j <j i a a -{}n a {}n a n a =m n ()3cos ,1,sin ,2a x b x ⎛⎫==- ⎪⎝⎭ a ∥b ()0,πx ∈sin cos x x -()()π2,0,4f x a b a x ⎡⎤=+⋅∈⎢⎥⎣⎦ ()f x 111ABC A B C -12AB BC BB ===AB BC ⊥,E F AC 1CC 1A E ⊥BEF 1ABC BEF ABC ,,A B C 2,,,cos cos b a c a b c B C-=B 2222b c ac =+cos C 2c =D AB E BC DE ABC DE ()()e sin 2,2cos x f x x x g x x =+-=-（1）已知直线是曲线的切线，求实数a 的值；（2）求函数的单调区间；（3）求证：恒成立.19.（17分）已知数列，其前项和为，对任意正整数恒成立，且.（1）证明：数列为等比数列，并求实数的值；（2）若，数列前项和为，求证：；（3）当时，设集合，集合中元素的个数记为，求数列的通项公式.0x y a -+=()[],0,πy g x x =∈()f x ()()f x g x …{}n a n n S ,2n n n S a μ=-1212a a +={}n a μ21log n n b a =()n b n n T 2ln 2n n T +>1n …{}123232,1n n n i j i j B a a a a i j ++=+⋅<+<⋅<∣…*,i j ∈N n B n c {}n c2024年高三数学摸底试题参考答案一､选择题：（每小题5分，共40分）1.A2.B3.C4.B5.D6.C7.D8.B8.解析：由题意的图象如图所示，问题转化为函数的图象与直线的至少有5个公共点，故的范围是B 正确.二､多选题：（每小题6分，共18分）9.ABC11.解析：当时在上单调递增.此时至多有一个极值点，不符合题意.当时，若；若.在上单调递增，在上单调递减.又当时.当时，故只需A 错误.此时且由于是的两个零点且.则若为正整数则.此时.()f x ()f x y a =a []2,0.-()()()()1ln 0;0mx f x x mx x f x x x'-=->='>'0m ≤()()0f x f x ≥∴'''()0,∞+()f x 0m >()10,,0x f x m ⎛⎫⎪⎭''∈> ⎝()1,,0x f x m ∞⎛⎫∈+⎭''< ⎪⎝()f x ∴'10,m ⎛⎫ ⎪⎝⎭1,m ∞⎛⎫+ ⎪⎝⎭0x +→()f x ∞'→-x ∞→+()f x ∞'→-1110ln 100.e f m m m '⎛⎫>⇒->⇒<< ⎪⎝⎭1e m>()()e 1e 0,10f m f m '=->-'=<12,x x ()f x '12x x <121e 1e x x m <<⎧⎪⎨>>⎪⎩1x 12x =()()2ln22ln2242ln242ln22ln2042f m m f m x '=-⇒=⇒='-=-=⇒=所以存在使得均为正整数，B 错误.由于和是函数与直线交点的横坐标.当时恰有.所以当时，必有当（注：由图象与直线交点变化情况可知m 越小，越小，越大.m 越大，越大，越小）所以当时，m正确..由于当时此时，当时此时故的取值范围是，即对任意正整数均存在使得.D 正确综上可知：CD 正确.三､填空题：（每个小题5分，共15分）12.113.；（开闭区间均给分）14.14.解析：由题意：，若则.而是递增数列中的项，这与是ln22m =12x x 111212212ln ln ln ln x mx x x m x x mx x x =⎧⇒==⇒⎨=⎩2x ()ln x g x x =y m ===m =12x x ==321x x =0m <≤321x x ≥m >321x x <ln x y x=y m =1x 2x 1x 2x 321x x ≥()()()()()22212121212121121212ln ln ln x x x x x x x x x x x x x x x x mx mx m+-+---===++0m +→21x x ∞-→+21x x m∞-→+1e m →210x x +-→210x x m-→()222112ln x x x x -()0,∞+n 12,x x ()222112ln x x n x x -=ππ5π,88⎡⎤⎢⎥⎣⎦n m 10a ≠10a <11m m a a a ->=1m a a -{}n a 1m a =数列的最大项矛盾.故必有.因为数列是单调递增数列，所以有.从而有且它们均为数列中的项.因此由上可知所以数列是以为首项，以为公差的等差数列.所以四､解答题：（本题共5小题，共77分）15.（13分）解：（1），，又，，；（2）由题意：10a >{}n a 12301m a a a a <<<<<=2131411m m a a a a a a a a a -<-<-<<-< {}n a 121212a a a a a =-⇒=23131213a a a a a a a =-⇒=+=34143114a a a a a a a =-⇒=+=.⋯⋯⋯11111m m m m a a a a a a ma --=-⇒=+=11a m ={}n a 11a m=1m n n a m=a ∥3,cos sin 2b x x ∴-= 3tan 2x ∴=-()0,πx ∈ sin x x ∴==sin cos x x ∴-=1cos sin ,2a b x x ⎛⎫+=+- ⎪⎝⎭ ()()()2122cos sin ,cos ,12cos 2sin cos 12f x a b a x x x x x x ⎛⎫∴=+⋅=+-⋅=+- ⎪⎝⎭ πsin2cos224x x x ⎛⎫=+=+ ⎪⎝⎭，的值域是16.（15分）（1）证明平面平面，又，又平面又平面.又即.又平面.（2）解：如图所示，以点为原点，为轴，为轴建立空间直角坐标系，易得设平面的法向量，则，取，则法向量.由（1）可知平面的法向量.平面与平面的夹角为.πππ3π0,,2,4444x x ⎡⎤⎡⎤∈∴+∈⎢⎥⎢⎥⎣⎦⎣⎦ ()∴f x ⎡⎣1A A ⊥ ,ABC BE ⊂1,ABC A A BE ∴⊥,.AB BC AE EC BE AC ==∴⊥ 1A A AC A BE ⋂=∴⊥ 11ACC A 1A E ⊂ 111,A ACC A E BE ∴⊥1tan tan A EA EFC ∠∠== 11ππ22A EA EFC EFC FEC A EA FEC ∠∠∠∠∠∠∴=+=∴+= 1A E EF ⊥1.EF BE E A E ⋂=∴⊥BEFB BA x BC y 11(2,0,0),(0,0,0),(0,2,2),(2,0,2),(1,1,0)A B C A E ()()12,0,0,0,2,2,BA BC == 1ABC (),,n x y z = 120,220n BA x n BC y z ⋅==⋅=+= 1y =()0,1,1n =-()11,1,2A E =-- BEF 111cos ,||A E n A E n A E n ⋅∴<>===⋅ 1ABC BEF π617.（15分）解：（1），，，（2），又，（3）若边由（1）（2）可知，，令，则，又由余弦定理得：（当时等号成立）.18.（17分）解：（1），，解得切点为，2,sin cos 2sin cos cos sin cos cos b a c B C A B B C B C -=∴=- sin cos cos sin 2sin cos B C B C A B∴+=1sin 2sin cos ,cos 2A A B B ∴=∴=()π0,π,3B B ∈∴=222π1,232B b a c ac =∴=+-⋅ 2222b c ac =+ 233,,22ac a a c b ∴=∴=∴=222cos 2a b c C ab +-∴===2c =π3,3a b B ===1sin 2ABC BDE S ac B S ∴==∴= ,BD m BE n ==132BDE S mn ==∴= 2221232DE m n mn mn =+-≥=m n ==DE ∴()[]sin ,0,πg x x x =∈' ()sin 1g x x ='∴=π,2x =∴π,22⎛⎫ ⎪⎝⎭ππ20,222a a ∴-+=∴=-（2），当时，单调递减当时，，单调递增，单调递递增.综上所述，在上单调递减，在上单调递增.（3）证明：恒成立恒成立恒成立.令，则令则单调递增，又，当时，，即单调递减；当时，，即单调递增；恒成立.19.（17分）解：（1）令可得，即.令可得，即，所以又.，两式相减可得，数列为首项为4，公比为2得等比数列.（2）证明：由（1）可知，所以.()e cos 2xf x x =+'- (],0x ∞∈-()()e 1,cos 1,0,xx f x f x ≤'≤≤∴[)0,x ∞∈+()e sin ,e 1,sin 1x xf x x x =-≥'≤'()()0,f x f x ≥'∴''∴()()()00,f x f f x ='≥'∴()f x (],0∞-[)0,∞+()()f xg x ≥e sin 2cos 20x x x x ⇔+-+-≥sin cos 2210e xx x x +--⇔+≥()sin cos 221e x x x x h x +--=+()()()()cos sin 2sin cos 222sin e e x x x x x x x x x h x ---+'---==()sin m x x x =-()()1cos 0,m x x m x =-≥∴'()00m = ∴(],0x ∞∈-()0m x ≤()()0,h x h x '≤[)0,x ∞∈+()0m x ≥()()0,h x h x '≥()()()()00,h x h f x g x ∴≥=∴≥1n =112S a μ=-1a μ=2n =222S a μ=-1222a a a μ+=-22a μ=1212,4a a μ+=∴= 112424n n n n S a S a --=-⎧⎨=-⎩ 1122,2n n n n n a a a a a --=-∴=∴{}n a 12n n a +=211log 1n n b a n ==+要证成立，只需证，即令，当时，单调递增，（3）时，集合，即3中元素个数，等价于满足的不同解，如果.则.盾!如果j ，则，矛盾!，又，，即，共个不同解，所以.11122,ln ln .121n n n i i n i T i i ==++==++∑∑ ∴2ln 2n n T +>12ln 11n n n +>++11ln 111n n ⎛⎫>+ ⎪++⎝⎭()()()()1ln 1,10,0,11x f x x x f x x x x ∞=-+==>'-∈+++∴()0,x ∞∈+()f x ()()()1ln 100,01f x x x f f n ⎛⎫=-+>=∴> ⎪+⎝⎭112ln 1,ln 112n n T n n +⎛⎫∴>+∴> ⎪++⎝⎭1n ≥{}123232n n n i j i j B a a a a ++=+⋅<+<⋅∣1*22232,1,,,n i j n n i j i j B +⋅<+<⋅≤<∈N 1322232n i j n +⋅<+<⋅(),i j 2j n <+1122222232i j i n n n n +++++=⋅……2n >+31222232i j i n n +++≥+>⋅2j n ∴=+()12223224232220n n n n n ++-⋅=+⋅-⋅=+> 1222212322222222232n n n n n n n n ++++++∴⋅<+<+<<+<+=⋅ 1,2,3,,i n = n (),i j ()1n c n n =≥。

2024-2025学年山东省菏泽市高三上学期期中数学试题及答案

2024-2025学年山东省菏泽市高三上学期期中数学试题及答案

菏泽市2024—2025学年度第一学期期中考试高三数学试题本试卷共4页，19题.全卷满分150分.考试用时120分钟.注意事项：1．答题前，先将自己的姓名、准考证号填写在答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试题卷、草稿纸和答题卡上的非答题区域均无效.3．非选择题的作答：用签字笔直接写在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区域均无效.4．考试结束后，请将本试题卷和答题卡一并上交.一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合{}{}202,0M x x N x x x =∈<<=-≤Z ∣∣，则M N = （ ）A. {}0,1 B. {}1 C. {}1,1- D. ∅2. 已知函数()21f x +的定义域为[]1,2，则函数()1f x -的定义域为（ ）A. []1,2 B. []4,6 C. []5,9 D. []3,73. 已知2025π1sin sin 22αα⎛⎫-+=⎪⎝⎭，则cos2sin cos ααα=+（ ）A. 12-B.12C. 0D. 14. “函数()32f x x ax =-在[]2,3-上单调递增”是“3a ≤”的（ ）A. 充分不必要条件 B. 必要不充分条件C 充要条件D. 既不充分又不必要条件5. 过曲线9log =y x 上一点A 作平行于两坐标轴的直线，分别交曲线3log y x =于点,B C ，若直线BC 过原点，则其斜率为（ ）A. 1B.3log 22C.ln33D.2log 36.6. 函数()11ln sin 21x f x x x+=--的零点个数为（ ）A. 1B. 0C. 3D. 27. 自然界中许多流体是牛顿流体，其中水、酒精等大多数纯液体、轻质油、低分子化合物溶液以及低速流动的气体等均为牛顿流体；高分子聚合物的浓溶液和悬浮液等一般为非牛顿流体，非牛顿流体在实际生活和生产中有很多广泛的应用，如工业制造业常利用某些高分子聚合物做成“液体防弹衣”，已知牛顿流体符合牛顿黏性定律，即在一定温度和剪切速率范围内黏度值是保持恒定的：τηγ=，其中τ为剪切应力，η为黏度，γ为剪切速率；而当液体的剪切应力和剪切速率存在非线性关系时液体就称为非牛顿流体．其中宾汉流体（也叫塑性流体），是一种粘塑性材料，是非牛顿流体中比较特殊的一种，其在低应力下表现为刚体，但在高应力下表现为粘性流体（即粘度恒定），以牙膏为例，当我们挤压它的力较小时，它就表现为固体，而当力达到一个临界值，它就会变成流体，从开口流出．如图是测得的某几种液体的流变τγ-曲线，则其中属于牙膏和液体防弹衣所用液体的曲线分别是（ ）A. ①和④B. ③和④C. ③和②D. ①和②8. 已知函数()()1e xf x x =-，点(),m n 在曲线()y f x =上，则()()f m f n -（ ）A. 有最大值为1e -，最小值为1 B. 有最大值为0，最小值为1e-C. 有最大值为0，无最小值D. 无最大值，有最小值为1e-二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9 已知0c b a <<<，则（ ）A. ac bc <B. 333b c a +< C.a c ab c b+>+D.<10. 已知函数()21,2,5,2xx f x a b c d x x ⎧-≤⎪=<<<⎨->⎪⎩，且()()()()f a f b f d f c ==<，则（ ）A. 1a ≤- B. []1,4c ∈ C. ()20,5ad ∈ D. 222a b +=.11. 把一个三阶魔方看成是棱长为1的正方体，若顶层旋转x 弧度π02x ⎛⎫<<⎪⎝⎭，记表面积增加量为()S f x =，则（ ）A. π6f ⎛⎫=⎪⎝⎭B. ()f x 的图象关于直线π3x =对称C. S 呈周期变化D. 6S ≤-三、填空题：本题共3小题，每小题5分，共15分．12. 命题：“所有能被4整除的正整数能被2整除”的否定是______．13. 已知函数()sin2cos2f x x a x =+，将()f x 的图象向左平移π6个单位长度，所得图象与曲线()y f x =关于原点对称，则()0f =______．14. 已知22,e x ⎡⎤∈⎣⎦时，2log 2axx x ax ≥⋅，则正数a 的最大值为______．四、解答题：本题共5小题，共77分．解答应写出必要的文字说明，证明过程或演算步骤．15. 记ABC V 内角,,A B C 的对边分别为,,a b c ，已知πsin sin ,63C C b ⎛⎫+== ⎪⎝⎭，ABC V的面积为（1）求C ；（2）求ABC V 的周长．16. 已知函数()π2sin 43⎛⎫=- ⎪⎝⎭f x x ．（1）求()f x 的单调递减区间；（2）若ππ,68x ⎡⎤∈-⎢⎥⎣⎦，求()()23-=+f x y f x 的最大值．17. 记锐角ABC V 的内角,,A B C 的对边分别为,,a b c ，已知cos 2cos cos c CA b B-=．（1）求B ；的（2）延长AC 到D ，使2,15AC CD CBD =∠= ，求tan A ．18. 已知函数()()2e xf x x a =-．（1）求()f x 单调区间；（2）设12,x x 分别为()f x 的极大值点和极小值点，记()()()()1122,,,A x f x B x f x ．证明：直线AB 与曲线()y f x =交于另一点C ．19. 已知函数()()sin tan sin 2f x x x x =+-，其中01x <<，（1）证明：21cos 12x x >-；（2）探究()f x 否有最小值，如果有，请求出来；如果没有，请说明理由．的是菏泽市2024—2025学年度第一学期期中考试高三数学试题本试卷共4页，19题.全卷满分150分.考试用时120分钟.注意事项：1．答题前，先将自己的姓名、准考证号填写在答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试题卷、草稿纸和答题卡上的非答题区域均无效.3．非选择题的作答：用签字笔直接写在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区域均无效.4．考试结束后，请将本试题卷和答题卡一并上交.一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．【1题答案】【答案】B【2题答案】【答案】B【3题答案】【答案】A【4题答案】【答案】A【5题答案】【答案】B【6题答案】【答案】A【7题答案】【答案】D【8题答案】【答案】B二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．【9题答案】【答案】ABD 【10题答案】【答案】BCD 【11题答案】【答案】AD三、填空题：本题共3小题，每小题5分，共15分．【12题答案】【答案】存在能被4整除的正整数不能被2整除【13题答案】【答案】【14题答案】四、解答题：本题共5小题，共77分．解答应写出必要的文字说明，证明过程或演算步骤．【15题答案】【答案】（1）π3C =（2）10+【16题答案】【答案】（1）π5ππ11π,224224k k ⎡⎤++⎢⎥⎣⎦，()k ∈Z （2）0【17题答案】【答案】（1）45B =（2）2+【18题答案】【答案】（1）单调增区间为()(),2,,a a ∞∞--+，单调减区间为(2,)a a - （2）证明见解析【19题答案】【答案】（1）证明见解析（2）没有，理由见解析。

海淀区高三数学(文)期中试卷及答案

海淀区高三数学(文)期中试卷及答案

海淀区高三年级第一学期期中练习数学（文科）2015.11本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1．已知集合P{｜-≤0}，M{0,1,3,4}，则集合P M中元素的个数为A．1 B．2 C．3 D．42．下列函数中为偶函数的是A．B．|| C．D．3．在中，∠A60°，||2，||1，则的值为-1 A．B．-C．1 D．4．数列{}的前项和，若－2－1(≥2)，且3，则1的值为A．0 B．1 C．3 D．55．已知函数，下列结论中错误．．的是A．B．的最小正周期为C．的图象关于直线对称D．的值域为[,]6．“”是“”的A．充分不必要条件B．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．如图，点O 为坐标原点，点A （1,1）.若函数（>0，且≠1）及（，且≠1）的图象与线段OA 分别交于点M ，N ，且M ，N 恰好是线段OA 的两个三等分点，则，满 足 A ．<<1 B ．<<1 C ．>>1 D ．>>18.已知函数()1,1,,11,1,1,x f x x x x -≤-⎧⎪=-<<-⎨⎪≥⎩，函数21()4g x ax =+.若函数()()y f x g x =-恰好有2个不同的零点，则实数a 的取值范围是 A.(0,)+∞ B.(,0)(2,)-∞+∞C.1(,)(1,)2-∞-+∞ D.(,0)(0,1)-∞s二、填空题共6小题，每小题5分，共30分。

9.函数()22x f x =-的定义域为_____. 10.若角α的终边过点（1，-2），则cos()2πα+=_____.11. 若等差数列{}n a 满足14a =-，39108a a a a +=-，则n a = ______.12.已知向量(1,0)a =，点()4,4A ，点B 为直线2y x =上一个动点.若AB //，则点B 的坐标为____.13.已知函数()sin()(0)f x x ωϕω=+>.若()f x 的图像向左平移3π个单位所得的图像与()f x 的图像重合，则ω的最小值为____.14.对于数列{}n a ，若m ∀，()n N m n *∈≠，均有()为常数m na a t t m n-≥-，则称数列{}n a 具有性质()P t .（i ）若数列{}n a 的通项公式为2n a n =，且具有性质()P t ，则t 的最大值为____；（ii ）若数列{}n a 的通项公式为2n aa n n=-，且具有性质(7)P ，则实数a 的取值范围是____.三、解答题共6小题，共80分。

2024年高三数学期中试卷及答案

2024年高三数学期中试卷及答案

2024年高三数学期中试卷及答案一、选择题（每题5分，共30分）1. 设函数f(x) = 2x + 1，若f(a) = 3，求a的值。

A. -1B. 1C. 2D. -2{答案：B}2. 已知等差数列{an}的首项为3，公差为2，求第10项的值。

A. 21B. 19C. 23D. 17{答案：A}3. 若平面直角坐标系中，点P(2, 3)关于直线y = x的对称点为Q，求点Q的坐标。

A. (3, 2)B. (2, 3)C. (-2, -3)D. (-3, -2){答案：A}4. 已知函数f(x) = x^2 - 2x + 1，求f(f(-1))的值。

A. 4B. 2C. 0D. -2{答案：A}5. 设函数g(x) = |x - 1| - |x + 1|，求g(2)的值。

A. 1B. -1C. 2D. -2{答案：B}6. 若直线y = 2x + 3与圆(x - 1)^2 + (y - 2)^2 = 5相切，求圆心到直线的距离。

A. 1B. √5C. 2D. 3{答案：B}7. 设向量a = (2, 3)，向量b = (-1, 2)，求向量a与向量b的点积。

A. 4B. -4C. 5D. -5{答案：B}8. 已知复数z = 3 + 4i，求复数z的模。

A. 5B. 7C. 9D. 25{答案：A}9. 设矩阵A = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\)，求矩阵A的特征值。

A. 2B. 3C. 4D. 5{答案：A}10. 若f(x) = x^3 - 3x + 1，求f'(x)。

A. 3x^2 - 3B. x^2 - 3x + 1C. 3x^2 + 3D. x^2 + 3x - 1{答案：A}二、填空题（每题5分，共30分）1. 已知等比数列{bn}的首项为2，公比为3，求第5项的值。

{答案：2 * 3^4}2. 若平面直角坐标系中，点P(2, 3)关于原点的对称点为Q，求点Q的坐标。

高三数学文科期中考试试卷及答案

高三数学文科期中考试试卷及答案

俯视图福州三中2010—2011学年度高三上学期期中考试数学（文）试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）．本试卷共4页．满分150分．考试时间120分钟．第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{11}A =-，，{|124}x B x =≤<，则A B I 等于（ ）A ．{101}-，，B ．{1}C ．{11}-，D ．{01}， 2．函数⎪⎭⎫⎝⎛-=x y 22sin π是（ ） A ．周期为π的奇函数 B ．周期为π的偶函数C ．周期为π2的奇函数D ．周期为π2的偶函数3．在ABC ∆中，a b c ，，分别为角A B C ，，所对边，若2cos a b C =，则此三角形一定是（ ） A ．等腰直角三角形 B ．直角三角形C ．等腰三角形D ．等腰或直角三角形4．已知点n A （n ，n a ）（∈n N *）都在函数x y a =（01a a >≠，）的图象上，则37a a +与52a 的大小关系是（ ）A ．37a a +＞52aB ．37a a +＜52aC ．37a a +＝52aD ．37a a +与52a 的大小与a 有关5．如图，一个简单空间几何体的三视图其主视图 与侧视图都是边长为2的正三角形，俯视图 轮廓为正方形，则此几何体的表面积是（ ）A ．4+B ．12C ．D ．86．已知平面向量(21,3),(2,),a m b m a b r r r r且与=+=夹角为锐角，则实数m 的范围（ ）A ．2(,)7-+? B ．233(,)(,)722U -+?C ．2(,)7-? D ．22(2,)(,)77U ---+? 7．函数()10<<=a xxa y x的图象的大致形状是（ ）A B C D8．设函数1)6()(23++++=x a ax x x f ，既有极大值又有极小值，则实数a 的取值范围是（ ）A ．36-<>a a或B ． 63<<-aC ．36-≤≥a a 或D ．63≤≤-a9．下列说法错误．．的是（ ）A ．如果命题“p ”与命题“p 或q ”都是真命题，那么命题q 一定是真命题；B ．命题“若a =0，则ab =0”的否命题是：“若a ≠0，则ab ≠0”；C ．若命题p ：∃x ∈R ，x 2-x +1<0，则p ：∀x ∈R ，x 2-x +1≥0；D ． “21sin =θ”是“ο30=θ”的充分不必要条件 10．设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤≤22y x x y x ，则目标函数y x z +=2的最小值为（ ）A ．3B ．4C ．6D ．2 11．设25abm ==，且112a b+=，则m = （ ）A ．10B ．10C ）．20D ．10012．给出定义：若2121+≤<-m x m （其中m 为整数），则m 叫做离实数x 最近的整数，记作{}x = m ．在此基础上给出下列关于函数{}x x x f -=)(的四个命题：①函数y=)(x f 的定义域为R ，值域为⎥⎦⎤⎢⎣⎡21,0；②函数y=)(x f 的图像关于直线2kx =（Z k ∈）对称； ③函数y=)(x f 是周期函数，最小正周期为1；④函数y=)(x f 在⎥⎦⎤⎢⎣⎡-21,21上是增函数。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2016下学期 浏阳一中高三年级期中测试卷文 科 数 学时量： 120分钟 分值：150分一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.若集合{|0}1xA x x =≤-,2{|2}B x x x =<,则A B = （ ）A.{|01}x x <<B.{|01}x x ≤<C.{|01}x x <≤D.{|01}x x ≤≤ 2.已知复数12312z bi z i =-=-，,若12z z 是实数，则实数b 的值为 （ ）A ．0B ．32-C ．6-D ．63. 在平面直角坐标系中，不等式组0401x y x y x +≥⎧⎪-+≥⎨⎪≤⎩表示的平面区域面积是（ ）．A ．9B ．6C ．92D ．3 4. 执行如图所示的程序框图，若输入如下四个函数：①()sin f x x =，②()cos f x x =， ③1()f x x =， ④1()lg 1x f x x-=+，则输出的函数是 ( ) A.()sin f x x = B.()cos f x x = C.1()f x x =D.1()lg 1x f x x-=+ 5.以下判断正确的是 ( )A.函数()y f x =为R 上可导函数，则()0f x '=是0x 为函数()f x 极值点的充要条件B.命题“存在2,10x R x x ∈+-<”的否定是“任意2,10x R x x ∈+->” C.“()2k k Z πϕπ=+∈”是“函数()sin()f x x ωϕ=+是偶函数”的充要条C M NOBA件D.命题“在ABC ∆中，若,sin sin A B A B >>则”的逆命题为假命题6.一个长方体被一个平面截去一部分后，所剩几何体的三视图如图所示(单位：cm)， 则该几何体的体积为A.120 cm 3B.100 cm 3C.80 cm 3D.60 cm 37.若数列na 的通项公式为221n na n ，则数列n a 的前n 项和为（ ） A.221nn B.1221n n C.1222n n D.22n n8.已知m ，n 是两条不同直线，α，β是两个不同平面，则下列命题正确的是（ ） A ．若α，β垂直于同一平面，则α与β平行 B ．若m ，n 平行于同一平面，则m 与n 平行C ．若α，β不平行，则在α内不存在与β平行的直线D ．若m ，n 不平行，则m 与n 不可能垂直于同一平面 9.函数sin(2),()y x ϕπϕπ=+-≤<的图象向右平移4π个单位后，与函数sin(2)3y x π=+ 的图象重合，则ϕ的值为 ( ) A. 56π-B. 56πC. 6π D. 6π- 10.如图所示,两个不共线向量,OA OB 的夹角为，,M N 分别为,OA OB 的中点,点C 在直线MN 上,且(,)OC xOA yOB x y R =+∈,则22x y +的最小值为（ ）A.2B.18C.2D.1211.在ABC ∆中，三个内角,,A B C 所对的边为,,a b c ，若23ABC S ∆=6a b +=，cos cos 2cos a B b AC c+=，则c =（ ）A ． 23．7．3312.已知函数f (x )＝x (ln x －ax )有两个极值点，则实数a 的取值范围是 ( ) A ．(,0)-∞B ．1(0,)2C ．(0,1)D ．(0,)+∞ 二、填空题：本大题共4小题，每小题5分，共20分.13. 在等差数列{}n a 中，35710133()2()24a a a a a ++++=，则此数列前13项的和是 。

14.已知向量()()()()1,1,2,2,,==+=++⊥-m n m n m n λλλ若则 .15正四棱锥S ABCD -2,,,,S A B C D 都在同一球面上，则该球的体积为 ．16.设函数[],0()(1),0x x x f x f x x -≥⎧=⎨+<⎩，其中[]x 表示不超过x 的最大整数，如[ 1.2]2-=-，[1.2]1=，[1]1=.若直线(0)y kx k k =+>与函数()y f x =的图象恰有三个不同的交点，则k 的取值范围是_____________三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.17.（本小题10分） 已知函数2()2sin 23cos 1f x x x x =-++.（Ⅰ）求()f x 的最小正周期及对称中心； （Ⅱ）若[,]63x ππ∈-，求()f x 的最大值和最小值.18.（本小题12分）某班一次数学考试成绩频率分布直方图如图所示，数据分组依次为]150,130[),130,110[),110,90[),90,70[，已知成绩大于等于90分的人数为36人，现采用分层抽样的方式抽取一个容量为10的样本. （1）求每个分组所抽取的学生人数；（2）从数学成绩在)150,110[的样本中任取2人，求恰有1人成绩在)130,110[的概率.19.（本小题12分）如图，四棱锥P －ABCD 的底面是正方形，PA ⊥底面ABCD ，PA ＝2，∠PDA=45°，点E 、F 分别为棱AB 、PD 的中点．a（1）求证：AF ∥平面PCE ；（2）求证：平面PCE ⊥平面PCD ；20（本小题12分）已知美国苹果公司生产某款iphone 手机的年固定成本为40万美元，每生产1只还需另投入16美元．设苹果公司一年内共生产该款iphone 手机x 万只并全部销售完，每万只的销售收入为R （x ）万美元，且R （x ）=（1）写出年利润W （万元）关于年产量x （万只）的函数解析式；（2）当年产量为多少万只时，苹果公司在该款手机的生产中所获得的利润最大？并求出最大利润．21（本小题12分）设同时满足条件：①212n n n b b b +++≥；②n b M ≤（*,n N M ∈是常数）的无穷数列{}n b 叫做P 数列，已知数列{}n a 的前n 项和n S 满足(1)1n n aS a a =--（a 为常数，且0,1a a ≠≠）. （1）求数列{}n a 的通项公式； （2）设21n n nS b a =+，若数列{}n b 为等比数列，求a 的值；并证明数列1{}n b 为P 数列.22（本小题12分）设函数2()ln f x a x bx =-. （1）若函数)(x f 在1x =处与直线21-=y 相切， ①求实数a ，b 的值；②求函数()f x 在1[,]e e上的最大值；（2）当0b =时，若不等式x m x f +≥)(对所有的3[0,]2a ∈，(21,x e ⎤∈⎦都成立，求实数m 的取值范围.EFACDPπ34高三文科数学答案A D A D C,BCD B B, A B11[,)4326, -3,17 已知函数2()2sin 23sin cos 1f x x x x =-++.（Ⅰ）求()f x 的最小正周期及对称中心； （Ⅱ）若[,]63x ππ∈-，求()f x 的最大值和最小值. 解：（Ⅰ）()3sin 2cos 22sin(2)6f x x x x π=+=+ …4分∴()f x 的最小正周期为22T ππ==， ……5分 令ππk x =+62，则()212k x k Z ππ=-∈， ∴()f x 的对称中心为(,0),()212k k Z ππ-∈ ……6分 （Ⅱ）∵[,]63x ππ∈- ∴52666x πππ-≤+≤ ......8分∴1sin(2)126x π-≤+≤ ∴1()2f x -≤≤ .......10分∴当6x π=-时，()f x 的最小值为1-；当6x π=时，()f x 的最大值为218.（1）2,3,4,1；（2）35.19（1）取PC 的中点G ，连结FG 、EG ， ∴FG 为△CDP 的中位线 ∴FG 21//CD …………1分 ∵四边形ABCD 为矩形，E 为AB 的中点 ∴AB 21//CD ∴FG //AE ∴四边形AEGF 是平行四边形 ∴AF ∥EG ………3分 又EG ⊂平面PCE ，AF ⊄平面PCE ∴AF ∥平面PCE …………6分（2）∵ PA ⊥底面ABCD∴PA ⊥AD ，PA ⊥CD ，又AD ⊥CD ，PA AD=A∴CD ⊥平面ADP ，又AF ⊂平面ADP ∴CD ⊥AF …………8分 直角三角形PAD 中，∠PDA=45°∴△PAD 为等腰直角三角形 ∴PA ＝AD=2 ∵F 是PD 的中点，∴AF ⊥PD ，又CD PD=D∴AF ⊥平面PCD …………11分∵AF ∥EG ∴EG ⊥平面PCD …………12分又EG ⊂平面PCE ∴平面PCE ⊥平面PCD ……… 20解：（1）利用利润等于收入减去成本，可得 当0＜x ≤40时，W=xR （x ）﹣（16x+40）=﹣6x 2+384x ﹣40；当x ＞40时，W=xR （x ）﹣（16x+40）=∴W=；（2）当0＜x ≤40时，W=﹣6x 2+384x ﹣40=﹣6（x ﹣32）2+6104，∴x=32时，W max =W （32）=6104； 当x ＞40时，W=≤﹣2+7360，当且仅当，即x=50时，W max =W （50）=5760∵6104＞5760∴x=32时，W 的最大值为6104万美元． 21.(1)当1n =时，()11111aa S a a ==--，所以1a a =。

当2n ≥时，()111n n n n n aa S S a a a --=-=--，整理得1n n a a a -=，即数列{}n a 是以a 为首项、a 为公比的等比数列，所以1n n n a a aa -==。

(2)由(1)知，()()()()21312111n n n n naa a a a ab a a a ⨯----=+=*- 由数列{}n b 是等比数列，则2213b b b =⋅，故222323223a a a a a +++⎛⎫=⋅ ⎪⎝⎭，解得13a =， 再将13a =代入()*式得3nn b =。

由于222111111112113333223n n n n n n n n b b b ++++++⋅+=>==，满足条件①；又由于11133n n b =≤，故存在13M ≥满足条件②。

故数列1n b ⎧⎫⎨⎬⎩⎭为P 数列.22.解：（1）①'()2af x bxx=-∵函数()f x在1x=处与直线12y=-相切'(1)20,1(1)2f a bf b=-=⎧⎪∴⎨=-=-⎪⎩解得112ab=⎧⎪⎨=⎪⎩ (3)分②22111 ()ln,'()2x f x x x f x xx x-=-=-=当1x ee≤≤时，令'()0f x>得11<≤xe；令'()0f x<，得ex≤<1⎥⎦⎤⎢⎣⎡∴1,1)(exf在上单调递增，在[1，e]上单调递减，max1()(1)2f x f∴==-…………8分。

相关文档
最新文档