X射线衍射分析原理-
X射线衍射分析

X射线衍射分析X射线衍射分析是一种重要的材料表征方法,它能够帮助科学家研究物质的结构和性质。
X射线衍射分析技术被广泛应用于材料科学、化学、生物学等领域。
本文将介绍X射线衍射分析的原理、仪器设备,以及在实际应用中的一些案例。
X射线衍射分析的原理基于X射线与物质相互作用的规律。
当X射线照射到物质上时,X射线与物质中的原子发生散射,形成衍射图样。
这些衍射图样包含了物质的晶体结构信息。
通过分析这些衍射图样,我们可以了解物质的晶体结构、晶格参数以及晶体中的原子位置。
X射线衍射实验通常使用X射线衍射仪进行。
X射线衍射仪由X射线源、试样台和衍射检测器组成。
X射线源产生高能量的X射线束,试样台用于放置待测样品,而衍射检测器则用于检测经过试样台衍射的X射线。
在实验中,我们需要调整X射线源和试样台的相对位置,使得试样台上的样品能够受到均匀的X射线照射,并且衍射信号能够被检测器准确地记录下来。
X射线衍射实验的结果通常以X射线衍射图样的形式呈现出来。
X射线衍射图样是一系列强度和角度的关系曲线。
通过对衍射图样的分析,我们可以确定材料的晶体结构。
根据布拉格方程,我们可以计算出晶面的间距,从而推导出晶体中原子的位置和晶格参数。
X射线衍射分析可以应用于各种各样的材料。
例如,材料科学家可以通过X射线衍射分析来研究金属的晶体结构和晶格缺陷。
化学家可以使用X射线衍射分析来确定化合物的晶体结构,从而帮助他们理解化学反应的机理。
生物学家可以利用X射线衍射分析来研究蛋白质的三维结构,从而揭示生物分子的功能和活动机制。
除了单晶衍射分析,还有一种称为粉末衍射分析的技术。
粉末衍射分析可以用于不规则形状的晶体或非晶体材料的结构分析。
在粉末衍射分析中,试样通常是细粉末状的物质。
通过对粉末衍射图样的分析,我们可以推导出材料的平均晶体结构。
总之,X射线衍射分析是一种重要而强大的材料表征技术。
它可以帮助科学家研究物质的结构和性质,并为材料科学、化学、生物学等领域的研究提供有效的工具和方法。
x-ray衍射仪工作原理

x-ray衍射仪工作原理
X射线衍射仪是一种利用X射线与晶体相互作用产生衍射现象,从而得到物质的结晶结构信息的仪器。
其工作原理如下:
1. X射线产生:X射线衍射仪中有一个X射线发生器,通常采用高压电极发射电子来轰击阳极材料,产生高速电子流。
这些高速电子与阳极材料的原子相互作用,产生X射线。
2. X射线入射:X射线由发射器产生后,通过准直装置使其成为平行光束,然后射向待测物质。
这些入射的X射线束可以通过调整入射角度控制和调节。
3. 晶体衍射:当X射线束与晶体相互作用时,其中的光子会与晶体的原子发生相互散射。
这种散射现象称为衍射。
晶体的晶格结构决定了衍射的结果。
不同晶体结构的物质会产生不同的衍射模式。
4. 衍射图样记录:晶体衍射的结果会通过检测器接收并记录下来。
检测器可以是铟镓锗等材料制成的能够测量光强度的闪烁晶体。
根据衍射的角度和强度,可以绘制出衍射图样。
5. 结晶结构分析:根据衍射图样,可以使用衍射方程和晶体学原理来计算和推断物质的晶体结构信息。
包括晶胞参数、晶体对称性、原子排列等。
通过上述步骤,X射线衍射仪可以用来研究和分析固体物质的
晶体结构,对于材料科学、化学、生物科学等领域都具有重要的应用价值。
x-射线衍射原理

x-射线衍射原理
射线衍射原理是一种通过将电磁波(一般为X射线)通过晶
体或物体的结构进行衍射,从而获得物体结构信息的方法。
射线衍射原理是基于波动理论的一个重要应用,它利用射线的相交和衍射现象来研究物体内部的晶格结构、原子间距等参数。
射线衍射实验通常使用单晶体作为衍射物,因为单晶体具有长程的周期性结构。
在实验中,将单晶体置于射线束的路径上,当射线通过单晶体时,会根据晶体结构的周期性,经历衍射现象。
根据布拉格定律,当入射射线的波长与晶格间距等条件满足时,会出现相干衍射峰。
在射线衍射实验中,探测器会检测到一系列的衍射峰,这些峰代表了不同衍射角度的衍射波。
通过测量衍射峰的位置以及强度,可以得到一些重要的信息。
首先,由布拉格定律可得,衍射峰的位置与晶胞的尺寸及结构有关。
这种方法可以用于确定晶体的晶胞参数,如晶格常数、晶胞体积等。
其次,衍射峰的强度与晶体内部的原子排列、晶格缺陷等因素密切相关。
通过分析衍射峰的强度分布,可以研究晶体的有序性、晶格缺陷的性质等。
射线衍射原理广泛应用于材料科学、晶体学、结构生物学等领域。
利用射线衍射原理,人们可以研究材料的内部结构,揭示物质的微观性质,为新材料的设计与合成提供理论指导。
同时,射线衍射还在药物研发、蛋白质结构解析等领域发挥着重要作用。
总之,射线衍射原理是一种通过射线的相交和衍射现象来研究物体结构的方法。
通过测量衍射峰的位置和强度,可以获得物体的晶格参数、结构信息等。
射线衍射原理在材料科学和生物科学等领域有着广泛的应用。
简述x射线衍射法的基本原理和主要应用

简述X射线衍射法的基本原理和主要应用1. 基本原理X射线衍射法是一种研究晶体结构的重要方法,它利用X射线的特性进行衍射分析。
其基本原理包括以下几个方面:•布儒斯特定律:X射线在晶体中发生衍射时,入射角、出射角和入射光波长之间满足布儒斯特定律,即$n\\lambda = 2d\\sin\\theta$,其中n为整数,$\\lambda$为X射线的波长,d为晶面间的间距,$\\theta$为入射角或出射角。
•薛定谔方程:晶体中的原子排列形成周期性结构,电子在晶格中运动的波动性质可以用薛定谔方程描述。
X射线被晶体衍射时,其波长与晶体中电子的波动性相互作用,形成了衍射波。
•动态散射理论:根据动态散射理论,晶体中的原子或离子吸收入射的X射线能量,并以球面波的形式发出,与其他原子或离子产生相互干涉,从而形成衍射图样。
2. 主要应用X射线衍射法广泛应用于材料科学、化学、地质学等领域,具有以下主要应用:•晶体结构分析:X射线衍射法可以确定晶体的晶格常数、晶胞角度和晶体中原子的位置,通过分析衍射图样的强度和位置,获得晶体结构的信息。
•材料表征:X射线衍射法可用于分析材料的相变、晶体有序度、晶格缺陷和晶体生长方向等特征。
例如,在合金研究中,可以通过X射线衍射技术鉴定合金中出现的新相和晶格畸变。
•晶体品质评估:通过分析衍射峰的尺寸和宽度,可以评估晶体的品质,包括晶格结构的完整性、晶体中的位错和晶格缺陷等。
•结晶体制备与成分分析:利用X射线衍射法可以研究物质的结晶过程,了解晶体生长的动力学和晶体取向的控制方法。
此外,还可以使用X射线衍射方法对材料中的成分进行分析。
•衍射仪器的研发与改进:X射线衍射法的应用也推动了衍射仪器的研发与改进,包括X射线源、X射线衍射仪和探测器等,提高了测量精度和分辨率。
3. 总结X射线衍射法作为一种非破坏性的分析技术,通过衍射图样的分析,可以获得晶体结构和材料特性的信息。
其基本原理包括布儒斯特定律、薛定谔方程和动态散射理论。
x射线衍射仪的工作原理

x射线衍射仪的工作原理X射线衍射仪的工作原理是基于X射线的散射现象。
当X射线通过物质时,会与物质的原子产生相互作用,通过散射来改变其传播方向和能量。
具体工作原理如下:1. 产生X射线:X射线衍射仪使用X射线管产生X射线。
X射线管中有一个阴极和阳极,当高压施加在两个电极之间时,阴极上的电子会被加速,击中阳极,从而产生X射线。
2. 照射样品:产生的X射线通过选择性选择性照射到待测样品上。
样品中的原子核和电子会与X射线发生相互作用。
3. 散射现象:当X射线与样品中的原子相互作用时,会发生散射现象。
主要有两种类型的散射,即弹性散射和无弹性散射。
- 弹性散射(Rayleigh散射):在弹性散射中,X射线与样品中的原子表面相互作用,改变传播方向,但不改变能量。
这种散射通常被忽略,因为它对X射线衍射仪的结果没有贡献。
- 无弹性散射(Compton散射):在无弹性散射中,X射线与样品中的原子内部相互作用,改变了X射线的能量。
这种散射是X射线衍射仪中非常重要的现象,因为它提供了有关样品内部结构和晶体学信息的重要数据。
4. 衍射现象:当经过样品后的X射线进入到探测器时,会发生衍射现象。
衍射是由于入射X射线在样品中被散射后,不同方向上的散射波相互叠加形成的相干波的干涉现象。
5. 探测与记录:探测器将衍射产生的干涉图案转化为电信号,并通过信号处理和记录设备将其转化为可见图像或X射线衍射图谱。
这些图像或图谱可以用于分析样品的晶体结构、晶胞参数、晶体定向和有序结构等信息。
总的来说,X射线衍射仪的工作原理是通过利用X射线与样品中原子的相互作用和散射现象,来获取样品的晶体学信息和结构参数。
衍射图案的形状和强度可以提供关于样品原子排列和晶格结构的重要信息。
X射线衍射分析原理

X射线衍射分析原理X射线衍射分析是一种重要的材料表征技术,其原理基于X射线与晶体相互作用时发生的衍射现象。
这种技术可以用来确定物质的结晶结构、晶体畸变、晶粒尺寸、相对结晶取向以及晶体缺陷等信息。
下面我将详细介绍X射线衍射分析的原理。
1.X射线衍射的基本原理X射线是一种电磁波,其波长比可见光短得多,因此它能够穿透晶体射出到另一侧。
当X射线穿过晶体时,会与晶体内的原子相互作用,发生散射。
如果晶体具有周期性排列的原子结构,那么经过散射后的X射线将会发生衍射现象。
2.布拉格衍射原理布拉格衍射原理是X射线衍射分析的基础。
根据布拉格方程,当入射光束与平行晶面之间的入射角等于出射角时,X射线会以构成等边三角形的一系列角度散射出来。
这些出射角对应的散射光将相干地叠加在一起,形成衍射图样。
布拉格方程可以表示为:n·λ = 2d sinθ其中,n为衍射级别,λ为入射X射线的波长,d为晶体面间的距离,θ为入射角。
根据布拉格方程,通过测量入射角和衍射角的大小,可以计算出晶格的间距d。
3.X射线衍射仪器为了进行X射线衍射分析,需要使用特殊的仪器。
其中最常见的是X射线粉末衍射仪(X-ray powder diffraction, XRD)。
它通过将样品制成粉末并均匀散布在载体上,然后用X射线照射样品,测量出射的衍射波,进而得到衍射图案。
X射线衍射仪由X射线管、样品支架、光学系统、检测器和计算机等组成。
X射线管产生X射线,经过光学系统聚焦后通过样品。
样品中的晶体结构会散射入射的X射线,散射波经过光学系统再次聚焦到检测器上,通过检测器的信号可以得到衍射图案。
根据衍射图案,可以通过相关数据分析获得样品的结晶结构和特征。
4.衍射图案分析衍射图案是X射线衍射分析的核心结果。
通过衍射图案的分析,可以获取材料的晶格常数、晶体结构、晶格取向和晶体畸变等信息。
衍射图样的主要特征是峰(peak),峰对应于衍射波的散射角度。
每个峰的位置、强度和形状都包含了样品的结构信息。
X射线衍射分析原理及应用

X射线衍射分析原理及应用一、X射线衍射分析的原理X射线衍射的基本原理是当X射线入射到晶体表面时,由于晶体具有定向排列的原子或离子,X射线与晶体中的电子发生相互作用并散射,形成不同方向上的干涉条纹,通过测量和分析这些干涉条纹的位置和强度可以推断出晶体的结构特征。
具体来说,X射线衍射分析的原理可以归纳为以下几个方面:1. 布拉格法则:当入射角θ和出射角θ'满足布拉格方程nλ = 2d·sinθ,即入射的X射线与晶体晶面的倾角和衍射角满足特定的关系时,会发生衍射。
2.动态散射:在晶体中,入射的X射线会与晶格中的电子发生相互作用,散射成各个方向上的次级波,波的振动方向垂直于入射方向。
3.干涉:次级波在不同晶面的散射电子之间发生干涉,产生特定的干涉条纹。
4.衍射图样:干涉条纹的位置和形状与晶体的晶胞结构、晶面间距以及晶体取向有关,通过测量和分析衍射图样可以确定这些信息。
二、X射线衍射分析的应用1.晶体结构分析:通过在不同角度下测量样品的X射线衍射图样,可以推断出材料的晶体结构,包括晶胞参数、晶面间距、原子位置等信息。
这对于理解材料的物理、化学以及电子结构等性质非常重要。
2.晶体取向分析:X射线衍射分析可以用来确定晶体中不同晶向的取向分布,即晶体中晶面的取向。
这对于材料工艺和性能的控制具有重要意义,例如金属的冷轧、挤压等过程中,晶体的取向对材料的力学性能有很大影响。
3.晶体缺陷分析:晶体中存在着各种缺陷,如位错、晶界、析出相等。
通过观察和分析X射线衍射图样中的峰形和峰宽等信息,可以确定晶体的缺陷类型和含量,进而了解材料的机械、电学以及热学性质。
4.应力分析:在材料的变形过程中,晶体中会引入应力场。
应力会引起晶格的畸变,从而导致X射线衍射图样的形状和位置发生变化。
通过分析这些变化可以得到材料中的应力分布和大小,对于材料的力学性能的评估和优化具有重要意义。
总之,X射线衍射分析是一种非常重要的材料表征方法,可以提供丰富的关于晶体结构、晶胞参数、晶体取向以及晶体缺陷等信息。
X射线衍射分析

X射线衍射分析X射线衍射分析是一种广泛应用于材料科学和固态物理领域的实验技术。
通过照射物质样品,利用X射线在晶体中的衍射现象,可以获得有关物质结构和晶体学信息的重要数据。
本文将介绍X射线衍射分析的原理、应用和发展。
一、X射线衍射分析原理X射线衍射分析的基本原理是X射线的衍射现象。
当X射线照射到晶体上时,晶体中的原子会对X射线产生散射,形成一种有规律的衍射图样。
这个衍射图样会显示出晶体的结构信息,包括晶体的晶格常数、晶胞形状和晶体的定向等。
X射线衍射实验一般使用Laue方法或布拉格方法。
Laue方法是在一束平行的X射线照射下,观察其经过晶体后的衍射图样,通过分析该图样可以得到晶体的结构信息。
布拉格方法则是通过将一束X射线通过晶体,利用布拉格方程进行衍射角度的计算,从而确定晶体的晶格常数和定向。
二、X射线衍射分析应用X射线衍射分析被广泛应用于材料科学和固态物理领域。
它可以用来研究晶体的结构和晶体学性质,例如晶格参数、晶胞参数和晶体定向。
此外,X射线衍射还可以用于材料的质量控制和表征、相变研究、晶体缺陷分析等。
在材料科学领域,X射线衍射分析常用于矿物学、金属学和半导体学的研究。
例如,在矿物学中,通过X射线衍射分析可以确定矿石中的不同晶型矿物的比例和结构信息。
在半导体学中,X射线衍射分析可以帮助研究晶体管的晶格结构和界面形态。
三、X射线衍射分析的发展X射线衍射分析作为一种实验技术,随着科学研究的深入不断发展。
在仪器设备方面,X射线源的进步使得可以获得更高分辨率的衍射图样;探测器的改进使得观测和数据分析更加准确和高效。
同时,随着计算机技术的发展,数据处理和分析的速度大大提高,使得研究人员可以更直观、更准确地分析X射线衍射图样。
此外,X射线衍射分析的理论研究也在不断深入,衍射峰的定性和定量分析方法得到了大量改进,使得X射线衍射分析在材料科学研究中的应用更加广泛。
总结:X射线衍射分析是一种重要的实验技术,在材料科学和固态物理领域具有广泛的应用价值。
x射线衍射 原理

x射线衍射原理x射线衍射是一种重要的物理现象,它在材料科学、结构分析和晶体学等领域具有广泛的应用。
本文将介绍x射线衍射的原理及其在科学研究和工程应用中的重要性。
一、x射线衍射的原理x射线衍射是指当x射线通过物质时,由于物质中的原子或分子对x 射线的散射作用,使得x射线在特定角度下发生衍射现象。
这种衍射现象是由于x射线与物质中的电子发生相互作用而产生的。
具体来说,当x射线通过物质时,它会与物质中的电子发生相互作用。
这种相互作用导致x射线的波长发生改变,从而使得x射线在特定角度下发生衍射。
根据衍射的特点,我们可以通过测量衍射角度和衍射强度来研究物质的结构和性质。
二、x射线衍射的应用1. 材料科学:x射线衍射在材料科学中具有重要的应用。
通过测量材料的衍射图样,可以确定材料的晶体结构、晶格常数和晶体缺陷等信息。
这对于材料的设计和性能优化非常关键。
2. 结构分析:x射线衍射在结构分析中也起着重要的作用。
通过测量物质的衍射图样,可以确定物质的分子结构、晶体结构和晶体取向等信息。
这对于研究分子和晶体的性质以及化学反应机理具有重要意义。
3. 晶体学:x射线衍射是研究晶体学的重要工具。
通过测量晶体的衍射图样,可以确定晶体的空间群、晶胞参数和晶体结构等信息。
这对于研究晶体的对称性和性质具有重要意义。
4. 工程应用:x射线衍射在工程领域也有广泛的应用。
例如,在材料加工过程中,通过测量材料的衍射图样,可以评估材料的晶粒尺寸和应力状态,从而指导工艺优化和质量控制。
三、x射线衍射的发展和挑战随着科学技术的不断发展,x射线衍射技术也在不断进步。
例如,近年来,高分辨率x射线衍射技术的发展使得我们能够更加准确地研究物质的微观结构和性质。
此外,结合计算模拟和数据处理技术,可以进一步提高衍射数据的分析和解释能力。
然而,x射线衍射技术也面临一些挑战。
例如,对于非晶态材料和纳米材料等复杂体系,衍射图样的解析和解释更加困难。
此外,x 射线衍射技术在实际应用中还存在成本高、设备复杂等问题,限制了其在一些领域的推广和应用。
x射线衍射工作原理

X射线衍射是一种利用物质对X射线的散射和干涉现象来研究晶体结构的技术。
其工作原理可以描述如下:
1.X射线源:首先需要一个产生高能X射线的源,通常使用X射线管或放射性同位素。
这
些X射线源会产生一束高能X射线。
2.射线入射:产生的X射线束被定向照射到待测物质(通常是晶体)上。
X射线的波长与
晶格间距的数量级相当,所以它们可以与晶体中的原子发生散射现象。
3.散射过程:当X射线束穿过晶体时,它们会与晶体中的原子发生散射。
根据布拉格法则,
当入射X射线的波长与晶格间距匹配时,会发生构造性干涉,形成衍射图样。
4.衍射图样:被散射的X射线会以不同的角度和强度散射出去,形成特定的衍射图样,可
以通过探测器捕捉到。
5.分析和解读:通过分析衍射图样,可以确定晶体中的原子排列和晶格结构。
根据衍射图
样中出现的衍射点的位置和强度,使用数学方法进行解析,推断晶体的结构和晶胞参数。
总之,X射线衍射利用X射线与晶体中原子的相互作用,通过测量和分析产生的衍射图样来研究晶体的结构。
这种技术在材料科学、固态物理、化学等领域有广泛应用,并为了解晶体的性质和结构提供了重要手段。
第五章 X射线衍射原理

生的相互平行的反射线间的干涉作用导致了“选择反 射”的结果.
据此,导出布拉格方程
如图5-2所示,设一束平行的X射线(波长λ)以θ角照射到
晶体中晶面指数为(hkl)的各原子面上,各原子面产生反射.
任选两相邻面(A1与A2),反射线光程差 δ=ML+LN=2dsinθ;
有机化学家豪普物曼和卡尔勒在50年代后建立了应用X射线 分析的以直接法测定晶体结构的纯数学理论,特别对研究大分 子生物物质结构方面起了重要推进作用,他们因此获1985年诺 贝尔化学奖
第一节 衍射方向
一.Braag方程
1.布拉格实验(现代X射线衍射仪的原型) •在满足反射定律的方向设置反射线接收(记录)装 置 •记录装置与样品台以2∶1的角速度同步转动 得到了“选择反射”的结果.即当X射线以某些角度入射时,记录到 反射线(以CuKα射线照射NaCl表面,当θ=15°和θ=32°时记录到反 射线);其它角度入射,则无反射
每一个可能产生反射的(HKL)晶面均有各自的衍射矢量三
角形.各衍射矢量三角形的关系如图5-6所示.
s0为各三角形之公共边;若以s0矢量起点(O)为圆心,|s0|为半 径作球面(此球称为反射球或厄瓦尔德球),则各三角形之另一
腰即s的终点在此球面上;因s的终点为R*HKL之终点,即反射晶 面(HKL)之倒易点也落在此球面上
. X射线发展史:
•1895年德国物理学家伦琴在研究阴极射线时发现了X射线 (1901年获得首届诺贝尔奖)
•1912年,德国的Laue第一次成功地进行X射线通过晶体发生衍 射的实验,验证了晶体的点阵结构理论。并确定了著名的晶体 衍射劳埃方程式。从而形成了一门新的学科—X射线衍射晶体 学。 (1914年获得诺贝尔奖)
05-X射线衍射分析原理
布拉格方程是X射线在晶体中衍射必须满
足的基本条件。它反映了衍射线的方向(用θ表 示)与晶体结构(用d代表)之间的关系。可通 过θ的测定,在λ已知的情况下,解出d。或者d已 )选择反射 X射线从原子面的反射与可见光的镜面反射 不同,前者是有选择的反射,其选择条件为布拉格 定律;而一束可见光以任意角度投射到镜面上时都 可以产生反射,即反射不受条件限制。 因此,X射线的晶面反射称为选择反射。
衍射方向决定于:
晶胞大小、形状及位向等因素。 衍射强度决定于: 晶胞中的原子种类、数量及其具体分布排列。 X射线的衍射方向描述方法:
劳埃方程、布拉格方程和衍射矢量方程。
二、布拉格方程式(Bragg) 晶体对X射线的衍射在形式上可看成是在 特定条件下晶体的面网对X射线的“反射”。 将衍射成反射,是导出布拉格方程的基 础。1912年,由英国物理学家布拉格提出。
C
O
1/λ
O*
可将上述描述拓宽至三维空间,假设存在 一个半径为1/λ的球面,令X射线沿球面的直径 方向入射,则球面上所有点均满足布拉格条件, 该球被命名为反射球。
该法由厄瓦尔德提出,故称为厄瓦尔德球, 该作图方法被称为厄瓦尔德图解。
四、劳埃方程式(Laue)
1、一维原子列对X射线的衍射 一维原子列的衍射线可看成一个行列对 X射线的衍射。如下图,点阵周期为a0
满足劳埃第一方程式,即可产生衍射, 衍射线与行列成αh角,即与行列夹角为αh的 方向都可产生衍射,因此衍射线的分布是 以原子列为轴、以αh为半径角的圆锥母线。
h每等于一个整数值(0,1, 2……),即形成一 个圆锥状衍射面。 因此一维原子列对X射线的的衍射为一套 圆锥。
如果用单色X射线垂直照射原子列 (α0=90)时: a0 cosα h = h, cosα h = h / a0
x射线衍射法的原理

x射线衍射法的原理
x射线衍射法是一种分析材料的方法,它利用x射线穿过样品时发生的衍射现象来分析样品的结构。
x射线是一种高能电磁辐射,它可以穿透大多数物质,包括晶体。
当x射线穿过晶体时,它们会被晶体中的原子散射。
这些散射的x射线在某些方向上相互干涉,形成衍射图案。
这些图案可以用来确定晶体中原子的排列方式和相对位置。
x射线衍射法的原理是利用布拉格定律。
布拉格定律指出,当x
射线的波长和晶格常数之间满足一定的关系时,衍射峰的位置和强度可以被预测。
利用x射线衍射仪和探测器可以测量到这些衍射峰的位置和强度,从而得到晶体的结构信息。
在x射线衍射实验中,样品需要被制备成单晶或多晶。
单晶样品需要通过生长技术获得,而多晶样品则可以通过粉末衍射来进行分析。
在实验中,需要控制x射线的波长和角度,以获得清晰的衍射图案。
同时,也需要进行数据处理和结构分析,以确定晶体的结构和性质。
x射线衍射法是一种重要的分析方法,广泛用于材料科学、物理化学、生物学等领域。
它可以提供准确的结构信息,帮助研究人员理解材料的性质和反应机理。
- 1 -。
x射线衍射法基本原理

x射线衍射法基本原理X射线衍射法是一种常用的材料结构研究方法,它通过分析X射线在晶体上的散射模式,来确定晶体的结构和性质。
这种方法的基本原理是利用X射线的波动性和晶体的周期性结构之间的相互作用,从而产生衍射现象。
X射线是一种高能电磁波,具有较短的波长和较高的穿透能力。
当X射线照射到晶体上时,它们会与晶体中的原子相互作用,造成X 射线的散射。
根据散射的特点,可以推断出晶体中原子的排列方式和间距。
这样,通过分析X射线的衍射图样,就可以得到晶体的结构信息。
X射线衍射实验通常使用的装置是X射线衍射仪。
它由X射线源、样品台和衍射仪组成。
X射线源产生高能的X射线,经过准直器和滤波器后,射向样品台上的晶体。
样品台可以旋转,使得晶体可以在不同的角度下接受X射线的照射。
当X射线照射到晶体上时,会发生散射,形成衍射波。
衍射波经过衍射仪的光学系统后,最终形成衍射图样。
X射线的衍射图样是由许多亮暗相间的圆环或线条组成的。
这些衍射图样的形状和位置与晶体的结构有关。
根据布拉格方程,可以计算出不同晶面的衍射角,并通过测量衍射角的数值,推断出晶体的晶格常数和晶面的间距。
同时,根据衍射图样的强度分布,还可以得到晶体中原子的位置和排列方式。
X射线衍射法在材料科学、固体物理、化学等领域中具有广泛的应用。
它可以用来研究各种晶体材料的结构和性质,例如金属、陶瓷、聚合物等。
通过X射线衍射法,可以确定晶体的晶格常数、晶胞结构、晶面间距、晶体的对称性等重要参数,为材料的设计和制备提供了重要的依据。
除了研究晶体结构外,X射线衍射法还可以用于分析非晶态材料、薄膜、纳米材料等。
对于非晶态材料,由于其无长程有序结构,衍射图样呈现为连续的强度分布,通过分析衍射图样的形状和强度分布,可以推断出非晶态材料的局域有序性。
对于薄膜和纳米材料,由于其尺寸较小,可以通过调节X射线的入射角度和波长,来研究其表面形貌和结构特征。
X射线衍射法是一种非常重要的材料结构研究方法,它通过分析X 射线的衍射图样,可以确定晶体的结构和性质。
x射线衍射分析的原理及应用

X射线衍射分析的原理及应用1. 前言X射线衍射是一种用于研究物质晶体结构的强大技术。
本文将介绍X射线衍射分析的原理和一些常见的应用领域。
2. 原理X射线衍射是基于X射线和晶体的相互作用原理来进行分析的。
当X射线通过晶体时,会发生衍射现象。
根据布拉格定律,当入射X射线束的波长和晶格间距相等时,发生的衍射尖冲将具有最强的干涉响应。
3. X射线的产生X射线的产生可以通过两种方式实现,即X射线管和同步辐射。
3.1 X射线管X射线管通过在真空中加热金属阴极电子来产生X射线。
这些高速电子轰击阴极时会产生X射线。
X射线束可以通过调节电压和阴极材料来选择出不同的波长。
3.2 同步辐射同步辐射是通过将电子束加速到几近光速并使其通过磁场曲线运动来产生的,这样产生的高能量粒子会产生强烈的辐射,其中包括X射线。
4. X射线衍射仪X射线衍射仪是用于测量和分析X射线衍射模式的仪器。
它由X射线源、样品台、衍射次级仪和X射线检测器组成。
4.1 X射线源X射线源是一个用于产生X射线束的装置。
常见的X射线源有X射线管和同步辐射装置。
4.2 样品台样品台用于支撑待测样品。
它通常可以旋转以不同的角度来调整测量条件。
4.3 衍射次级仪衍射次级仪用于调整和聚焦X射线束,以便能够更好地与样品相互作用。
4.4 X射线检测器X射线检测器用于测量和记录经过样品衍射后的X射线强度。
常见的检测器包括点状检测器和区域检测器。
5. 应用领域X射线衍射分析在许多领域中都有广泛的应用。
以下是一些常见的应用领域:5.1 材料科学X射线衍射在材料科学中被广泛用于研究晶体结构、材料相变、晶体畸变等。
通过分析X射线衍射图谱,可以推断出材料的晶体结构、晶格参数和晶体缺陷等信息。
5.2 药物研发X射线衍射在药物研发领域中被用于确定分子和晶体的三维结构。
通过分析X 射线衍射图谱,可以确定药物分子的空间排列方式,从而帮助科学家设计出更有效的药物。
5.3 矿物学X射线衍射在矿物学领域中常用于矿石的鉴定和矿石含量的测量。
X射线衍射分析

X射线衍射分析X射线衍射是一种广泛应用于材料科学、生物学、化学等领域的分析技术,它通过衍射现象来研究晶体结构和晶体取向。
本文将介绍X 射线衍射分析的原理、方法以及在不同领域中的应用。
一、X射线衍射原理X射线衍射是指X射线入射到晶体上,由于晶体的周期性结构,X 射线在晶胞中遇到原子核或电子时会发生衍射。
根据布拉格定律,衍射角度与晶格常数、入射波长之间存在特定的关系,通过观察衍射角度和强度可以推断出晶体结构的信息。
二、X射线衍射方法1. 粉末衍射:将样品粉碎成粉末状,通过X射线衍射仪器进行衍射分析,可以获得材料的晶体结构信息。
2. 单晶衍射:用单一晶体进行X射线衍射分析,可以得到更为详细的结构信息,包括原子间的位置和取向。
三、X射线衍射在材料科学中的应用1. 晶体学研究:通过X射线衍射可以确定晶体结构和晶体学参数,揭示材料的性质和相态变化。
2. 晶体生长:X射线衍射可以监测晶体的生长过程,帮助调控晶体的形貌和性能。
四、X射线衍射在生物学中的应用1. 蛋白质结构:X射线衍射被广泛用于解析蛋白质的晶体结构,揭示蛋白质的功能和作用机制。
2. 细胞成像:通过X射线衍射可以对细胞结构进行高分辨率成像,为细胞生物学研究提供重要依据。
五、X射线衍射在化学分析中的应用1. 晶体化学:X射线衍射可以确定晶体中元素的位置和化学键的性质,为化学合成提供参考。
2. 晶体衍射敏感性分析:X射线衍射可以用于检测材料中微观结构的变化,分析化学反应的过程和机制。
总结:X射线衍射作为一种强大的分析技术,不仅在材料科学、生物学和化学领域有着重要的应用,还在许多其他领域有着广泛的应用前景。
随着仪器技术的不断进步,X射线衍射分析将在更多研究领域展现其重要作用。
X射线衍射分析法

X射线衍射分析法X射线衍射分析法是一种广泛应用于材料科学领域的非破坏性分析方法,它通过对材料中X射线的衍射模式进行研究,可以得到材料的结晶结构信息、晶体学参数以及晶体缺陷等重要信息。
X射线衍射技术已经成为材料科学研究中不可或缺的重要手段,被广泛应用于金属材料、半导体材料、无机晶体、有机晶体等材料的研究和分析中。
X射线衍射的原理是利用入射X射线借助晶体的晶格结构,发生衍射现象,通过测量样品中出射X射线的衍射角度和衍射强度,可以确定晶体的晶格常数、晶体结构、晶体取向和晶体缺陷等信息。
X射线衍射仪是一种专门用于进行X射线衍射分析的仪器,根据不同的应用需求,可以选择适合的X射线衍射仪进行实验。
X射线衍射分析法主要包括粉末衍射分析法和单晶衍射分析法两种常用的方法。
粉末衍射分析法适用于多晶材料或粉末材料的结构研究,可以获得晶体的空间点群、晶胞参数、结晶度等信息;单晶衍射分析法则适用于单晶材料的结构研究,可以获得晶体的真实结构信息,包括晶体的空间对称性、原子位置等详细信息。
X射线衍射分析法具有许多优点,如非破坏性、高灵敏度、高分辨率、快速测量和可定量分析等特点,因此在材料科学研究领域得到广泛应用。
在金属材料研究中,X射线衍射分析可以用于评估金属的晶体结构和相变行为;在半导体材料研究中,X射线衍射分析可以用于研究半导体晶体的缺陷结构和掺杂效应;在生物晶体学研究中,X射线衍射分析可以用于解决生物大分子的三维结构等问题。
在进行X射线衍射分析时,需要注意一些实验参数的选择和控制,以确保实验结果的准确性和可靠性。
在进行粉末衍射实验时,需要选择合适的X射线波长、样品旋转角度、测量范围和样品制备条件等参数;在进行单晶衍射实验时,需要控制晶体的取向和衍射仪的校准等条件。
总的来说,X射线衍射分析法是一种非常有价值的材料结构分析方法,可以为材料科学研究提供重要的结晶学信息。
随着仪器技术的进步和应用领域的拓展,X射线衍射分析方法将在材料科学研究中发挥愈发重要的作用,为解决材料科学领域的难题提供宝贵的帮助。
简述x射线衍射分析的原理及应用

简述X射线衍射分析的原理及应用1. 原理介绍1.1 X射线衍射的基本原理X射线衍射是一种通过射线与晶体相互作用来研究晶体结构的方法。
当X射线通过晶体时,射线会被晶体的原子散射,形成衍射现象。
根据衍射现象可以得到晶体的衍射图样,进而推断晶体的结构和参数。
1.2 劳厄方程X射线衍射的重要基本原理是劳厄方程,其数学表达式为:n λ = 2 d sin θ其中,n表示衍射级别,λ表示入射X射线波长,d表示晶体的晶面间距,θ表示衍射角。
2. 应用领域2.1 结晶学X射线衍射分析在结晶学领域中得到广泛应用。
通过衍射图样的解析,可以得到晶体结构的详细信息,如晶胞参数、晶胞对称性等。
这对于研究晶体的物理、化学性质以及材料的合成和制备具有重要意义。
2.2 材料科学X射线衍射分析在材料科学领域中也有着重要的应用。
利用衍射技术,可以研究材料的晶体结构和晶体取向关系,进而推测材料的内部缺陷、晶格畸变等信息。
这对于材料的改进和性能优化具有重要意义。
2.3 矿物学在矿物学领域,X射线衍射分析被广泛用于鉴定矿物样品的组成和结构。
通过衍射图样的解析,可以判断矿物中存在的晶系、晶胞参数等信息,从而对矿物进行鉴定和分类。
2.4 生物科学X射线衍射在生物科学领域中也扮演着重要的角色。
通过衍射探测技术,可以研究生物大分子(如蛋白质、核酸等)的结构和构象,揭示其功能和相互作用机理。
这对于理解生命的基本原理以及药物研发具有重要意义。
2.5 化学分析X射线衍射分析也可以用于化学分析领域。
通过衍射技术,可以定量分析样品中不同晶相的含量,判断样品中的氧化物、硫化物、氮化物等化合物的结构信息,同时还可以检测样品的晶格畸变和应力情况。
3. 总结X射线衍射分析是一种通过射线与晶体相互作用来研究晶体结构的重要方法。
其基本原理主要建立在劳厄方程的基础上。
X射线衍射分析广泛应用于结晶学、材料科学、矿物学、生物科学和化学分析等领域,为相关领域的研究和应用提供了重要的支持和帮助。
x射线衍射分析的原理应用

X射线衍射分析的原理应用引言X射线衍射是一种非常常用的材料分析技术,通过衍射现象来研究材料晶体结构。
本文将介绍X射线衍射分析的原理及其在各个领域的应用。
1. X射线衍射的原理X射线衍射是基于X射线与材料晶体相互作用产生的衍射现象。
当X射线经过晶体时,射线与晶体的晶格结构相互作用,并通过散射形成衍射图案。
这些衍射图案可以通过仪器进行捕捉和分析,从而得到材料的晶体结构信息。
1.1 X射线的性质X射线是一种具有高能量和强穿透力的电磁辐射。
它具有波粒二象性,既可以被看作是一种电磁波,也可以被看作是由高能量的光子组成的粒子流。
1.2 晶体结构与衍射晶体是由具有规则排列的原子、离子或分子组成的物质。
晶体的结构可以通过X射线衍射来研究。
当入射X射线与晶体结构相互作用时,根据布拉格法则,会出现衍射现象。
衍射是X射线通过晶体后,由于晶体的周期性结构而产生的干涉效应。
1.3 衍射图案的分析通过收集并分析衍射图案,可以推断出晶体的晶格常数、原子位置、结构类型等信息。
常用的分析方法包括粉末衍射法、单晶衍射法等。
2. X射线衍射分析的应用2.1 材料科学X射线衍射在材料科学领域有着广泛的应用。
它可以用于研究材料的晶体结构,探究材料的性质与结构之间的关系。
同时可以用于材料的相分析、缺陷检测、材料的晶体纯度等。
2.2 生物科学X射线衍射在生物科学中也有着重要的应用。
它可以用于研究蛋白质晶体结构,解析生物大分子的三维结构,从而揭示生物分子的功能和机制。
这对药物设计、疾病治疗等方面具有重要意义。
2.3 化学领域X射线衍射技术在化学领域也有着广泛的应用。
它可以用于鉴定化合物的晶体结构,分析化合物的物理性质,研究化学反应的机理等。
2.4 地质学地质学中的矿物分析也经常使用X射线衍射技术。
通过分析岩石中的矿物组成和结构,可以了解地球内部的构造和演化历史,研究地壳运动、地震活动等。
2.5 材料工业材料工业中的材料质量检测、工艺优化等也可以借助X射线衍射技术。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
32
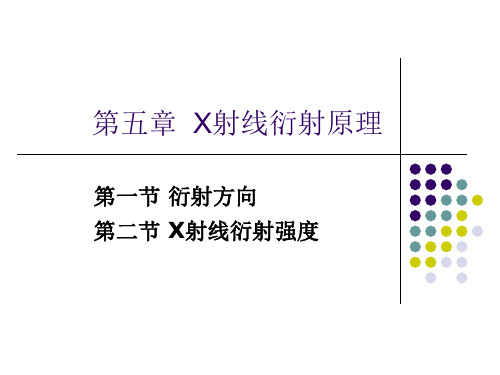
Smaller Crystals Produce Broader XRD Peaks
33
Formula
Crystallite size <1000 Å Peak broadening by other factors
Causes of broadening Size Strain Instrument If breadth consistent for each peak then assured
28
散射线干涉一致加强的条件为=H,即 a(cos-cos0)=H
式中:H——任意整数。 此式表达了单一原子列衍射线方向()与入射 线波长()及方向(0)和点阵常数的相互关系, 称为一维劳埃方程。 亦可写为
a· (s-s0)=H
29
2. 二维劳埃方程
a(cos-cos0)=H b(cos-cos0)=K 或 a· (s-s0)=H b· (s-s0)=K
P22课后习题3某原子的一个光谱项为45FJ
n=4,L=3,S=2,则J=5,4,3,2,1。 J=5时,MJ=0,1,2,3,4,5; J=4时,MJ=0,1, 2,3,4 ; J=3时,MJ=0 ,1, 2,3 ; J=2时,MJ=0,1, 2; J=1时,MJ=0 ,1;
OA= xja+yjb+zjc
O原子与A原子散射波位相差为
2
* HKL
2 ( Hx j Ky j Lz j )
讨论衍射矢量方程的几何图解形式。
s-s0=R*HKL
衍射矢量三角形——衍射矢量方程的几何图解
21
三、厄瓦尔德图解
晶体中有各种不同方位、不同晶面间距
的(HKL)晶面。当一束波长为的X 射线以一定方向照射晶体时,哪些晶面 可能产生反射?反射方向如何? 解决此问题的几何图解即为厄瓦尔德 (Ewald)图解。
d HKL
由倒易矢量性质可知, 则上式可写为
(s-s0)/=r*HKL (r*HKL=1/dHKL)
即称为衍射矢量方程。 若设R*HKL=r*HKL(为入射线波长,可视为比例系数),则上 式可写为 此式亦为衍射矢量方程。
s-s0=R*HKL
(R*HKL=/dHKL)
20
三、厄瓦尔德图解
15
(6)衍射产生的必要条件:
“选择反射” 即反射定律+布拉格方程是衍射产生的必要条 件。即当满足此条件时有可能产生衍射;若 不满足此条件,则不可能产生衍射。
16
Bragg衍射方程及其作用
n = 2d sin | sin | ≤1; n / 2d = | sin | ≤1, 当n = 1 时, 即: ≤ 2d ; d ≥ / 2
n2S+1LJ
1
第二章 衍射分析
(之一)、X射线衍射分析原理
第一节 衍射方向
布拉格方程**、衍射矢量方程、厄瓦尔德 图解*#、劳埃方程
第二节 X射线衍射强度
一个电子的散射强度、原子散射强度、晶胞 散射强度(结构因子**# )、影响衍射强度的 其它因素
2
参考文献
梁栋材著,
X射线晶体学基础,北京-科学出 版社,2006年 祁景玉主编,X射线结构分析,上海-同济大 学出版社,2003年 王培铭,许乾慰,材料研究方法,科学出版 社,北京,2005年
Ea Ia 1 f ( )2 Ee Ie
它表示一个原子在某一方向上散射波的振幅是一个电 子在相同条件下散射波振幅的f倍。 原子散射因子的大小与2θ、λ和原子序数有关,可直 38 接查附录得到。
原子对X射线的衍射
f的大小受Z,λ ,θ 影响 (见右图)
f
Aa 一个原子中所有电子相干散射波的合成振幅 Ae 一个电子相干散射波的振幅
39
(三)一个晶胞对X射线的散射
1、晶胞散射波的合成与晶胞衍射强度
A (xj,yj,zj)
考虑O原子与A原子在(HKL)面 反射线方向上的散射线,则其干 涉相长条件应满足衍射矢量方程:
面反 则O原子与A原子在(HKL) 射方向上散射线位相差为
r
* HKL
s s0
2OA r
34
第二节 X射线衍射强度
表现在底片上衍射线(点)的黑度或衍射图
中衍射峰的面积或高度来度量。
主要取决于晶体中原子的种类和它们在晶胞
中的相对位置。
35
X射线衍射强度问题的处理过程
36
(一) 一个电子的散射强度
公式(5-17)
e 1 (cos 2 ) Ie I0 2 2 4 [ ] Rmc 2
25
26
四、劳埃方程
由于晶体中原子呈周期性排列,劳埃设想
晶体为光栅(点阵常数为光栅常数),晶 体中原子受X射线照射产生球面散射波并 在一定方向上相互干涉,形成衍射光束。
27
1. 一维劳埃方程
衍射线
a cos
P
A
S
Q
s
入射线
B
0
0
a
0
a cos
设s0及s分别为入射线及任意方向上原子散射线单位矢量, a为点阵基矢,则原子列中任意两相邻原子散射线间光程差 ()为 =AP-BQ=acos-acos0
水波的干涉现象
5
干涉加强和相消
可见光波的杨氏干涉实验
6
7
8
多晶衍射原理示意图
9
第一节 衍射方向
一、布拉格方程** 二、衍射矢量方程 三、厄瓦尔德图解* 四、劳埃方程
10
一、布拉格方程
1.布拉格实验
布拉格实验装置 设入射线与反射面之夹角为,称掠射角或布拉格角,则按 反射定律,反射线与反射面之夹角也应为。 布拉格实验得到了“选择反射”的结果,以Cu K射线照射 NaCl表面,当=15和=32时记录到反射线;其它角度入射, 则无反射。
22
按衍射矢量方程,晶体中每一个可能产生反射的
(HKL)晶面均有各自的衍射矢量三角形。
同一晶体各晶面衍射矢量三角形关系
脚标1、2、3分别代表晶面指数H1K1L1、H2K2L2和H3K3L3
23
由上述分析可知,可能产生反射的晶面,其倒易点必落 在反射球上。据此,厄瓦尔德做出了表达晶体各晶面衍 射产生必要条件的几何图解,如图所示。
30
衍射方向 小结
衍射矢量方程、布拉格方程+反射定律、厄瓦
尔德图解、劳埃方程+协调方程作为衍射必要 条件都是等效的。 衍射矢量方程更具有普遍性。
31
思考题:
α-Fe属立方晶系,点阵参数a=0.2866nm。如
用CrKα X射线(λ=0.2291nm)照射,试求 (110)、(200)及(211)可发生衍射的掠 射角。
3. 三维劳埃方程
a(cos-cos0)=H b(cos-cos0)=K c(cos-cos0)=L 或 a· (s-s0)=H b· (s-s0)=K c· (s-s0)=L 劳埃方程的约束性或协调性 方程 cos20+cos20+cos20=1 cos2+cos2+cos2=1
只有当入射X射线的波长 ≤2倍晶面间距时, 才能产生衍射,当波长λ大于(或等于)晶面间距 的两倍时,将没有衍射产生。 这也就是为什么不能用可见光(波长约为 200―700纳米)来研究晶体结构的原因。
17
Bragg衍射方程重要作用:
(1)已知 ,测角,计算d;
(2)已知d 的晶体,测角,得到特征辐射波长 ,
入射的平行光照射到晶体中各平行原子面上,各
原子面各自产生的相互平行的反射线间的干涉作 用导致了“选择反射”的结果。
12
(hkl)
设一束平行的X射线(波长)以 角照射到晶体中晶面指数为 (hkl)的各原子面上,各原子面产生反射。 任选两相邻面(A1与A2),反射线光程差 干涉一致加强的条件为=n,即
broadening due to crystallite size
K depends on definition of t and B Within 20%-30% accuracy at best
Sherrer’s Formula References Corman, D. Scherrer’s Formula: Using XRD to Determine Average Diameter of Nanocrystals.
确定元素,X射线荧光分析的基础。
18
二、衍射矢量方程
设s0与s分别为入射线与反射线方向单位矢量,s-
s0称为衍射矢量,则反射定律可表达为:s-s0//N
s-s0=2sinθ
s-s0=/d
19
综上所述,“反射定律+布拉格方程”可用衍射矢量(s-s0)表示 为
s-s0//N
s s0
4 2
偏振因子或极化因子
Ie 一个电子散射的X射线的强度 I0 入射X射线的强度 R 电场中任一点P到发生散射电子的距离 2θ 散射线方向与入射X射线方向的夹角
37
(二) 原子散射强度
和电子引起的X射线散射相比,原子核引起的散射强 度要弱得多,可以忽略不计,只需考虑核外电子对X 射线的散射。 为了评价一个原子对X射线的散射本领,引入一个参 量f, 称原子散射因子。
厄瓦尔德图解
24
厄瓦尔德图解步骤为:
1.作OO*=s0,长度为1/ ; 2.作反射球(以O为圆心、OO*为半径作球); 3.以O*为倒易原点,做晶体的倒易点阵; 4. 若倒易点阵与反射球(面)相交,即倒易点落在反 射球(面)上(例如图中之 P 点),则该倒易点相应 之(HKL)面满足衍射矢量方程; 反 射 球 心 O 与 倒 易 点 的 连 接 矢 量 ( 如 OP) 即 为 该 ( HKL)面之反射线单位矢量 s,而 s 与 s0 之夹角( 2 ) 表达了该(HKL)面可能产生的反射线方位。
