吊车梁求最大弯矩
吊车梁设计计算表(带公式程序)

吊车梁的截面选择一.截面尺寸的确定:(1).梁的高度:①.经济要求:梁的平面内最大弯矩设计值:M xmax=464700000N·MM,支座处的最大剪力V max=梁选用钢材材质Q235,f=215N/mm2fv=Q345,f=315N/mm2fv=f=315N/mm2fv=梁需要的截面抵抗矩:W= 1.2*M xmax/f=1770286梁的经济截面高度:H=7*(W)^(1/3)-300=547②.刚度要求:对中级且Q<500KN,[l/w]=600,梁的跨度l=6000mm超过此限[l/w]=750取[l/w]=600,[w/l]=0.001667梁刚度要求的最小高度:Hmin=0.56*f*l/([w/l]*106)=③.建筑净空要求:H≤建筑净空要求根据以上三条要求确定吊车梁的高度,H=700mm二.腹板厚度Tw的确定:①.经验公式:T w=7+3h=10mm②.根据抗剪要求:T w≥ 1.2V max/h w fv= 2.9630843mm③.局部挤压应力的要求:数据准备:考虑动力系数的一个车轮的最大轮压a P max=136集中荷载增大系数,对轻、中级工作制吊车梁Y=1.0,对重级工作制吊车梁Y=1.35Y=1g Q= 1.4钢轨高度:140mm,吊车梁翼缘厚度t(暂估):轨顶至腹板计算高度上边缘的距离:h y=钢轨高度+吊车梁翼缘厚度t=车轮对腹板边缘挤压应力的分布长度,取L z=2h y+50=358T w≥aYg Q P max/(l w*f)=2mm根据以上三条要求暂估T w=8mm三.翼缘尺寸:翼缘所需的面积:A1=W x/H w-1/6HwTw=1696.6947根据翼缘的局部稳定判断翼缘不考虑局部稳定的最大宽度:b=336根据上面的翼缘最大宽度取b=330mm下翼缘厚度取10mm,下翼缘宽度Bb=300mm本吊车梁尺寸取如下值:吊车梁高度H=700mm上翼缘宽度Bt=330mm上翼缘厚度Tt=14mm下翼缘宽度Bb=300mm下翼缘厚度Tb=10mm腹板厚度Tw=8mm腹板高度Hw=676mm 根据上值转入《吊车梁截面计算》工作簿.支座处的最大剪力V max=310.63KN125N/mm2185N/mm2185N/mm2(板厚≤16mm) mm3mm636mm腹板高度暂定H w=680mmKN工作制吊车梁Y=1.3514mm车梁翼缘厚度t=154mmmmmm。
十四、吊车梁的设计与验算

十四、吊车梁的设计与验算吊车梁跨度L=6m ,无制动结构,钢材采用Q235,焊条采用E43系列,吊车梁资料如下:吊车采用LH 型的15t 中级电动葫芦桥式吊车,查《实用建筑结构荷载手册》知:桥架宽度B=4.716m ,轨道中心至吊车外端距离b=165㎜,主梁底面至轨面距离为H 2=720㎜,轨道至起重机顶距离为H=1.43m ,大车轮距K=4.0m ,小车Q 1=3t ,大车Q=18.8t ,最大轮压P max =141KN 。
1、吊车荷载计算吊车竖向荷载动力系数05.1=α,可近似轮压乘荷载增大系数β=1.03吊车荷载分项系数4.1=Q γ,软钩吊车取10.0=η则:竖向计算轮压:KN P P mzx Q 49.2131414.103.105.1=⨯⨯⨯==αβγm KN L M ⋅===65.28462maxKN L a LP V c 33.1426)13(49.2132)2(2=-⨯⨯=-∑=(2) 吊车梁的最大剪力:KN L a L P P V c 65.2846)46(49.21349.213)(1max =-⨯+=-+= (3) 计算强度时吊车梁的最大水平弯矩:m KN M P T M c T ⋅=⨯==80.1665.28449.2136.12max(4) 吊车梁竖向荷载标准值作用于下最大弯矩(求竖向挠度用):m KN Y M M Q X ⋅=⨯=⋅=64.1934.105.165.284max α 3、截面选择(1)按经济要求确定梁高2/215mm N f = 36max 15802151065.2842.12.1cm f M W =⨯⨯==所需经济梁高度:cm W h 553015803.7303.733=-=-=(2)按刚度要求确定梁高:容许相对挠度取,故750=⎥⎦⎤⎢⎣⎡υl 。
[min6.0⨯=f h 采用h w 700=(3) h t w w 37=+=(4f h v t v w w 2.1max ==采用h 700=截面特征:14300A +⨯=mm y 6.30813028)514676(10300)142/676(86767143300=++⨯⨯++⨯⨯+⨯⨯=12103006.3011433012143304.43867612676832323⨯+⨯⨯+⨯+⨯⨯+⨯=x I4621039.10844.38610300mm ⨯=⨯⨯+366105139.36.308/1039.1084mm W a x ⨯=⨯= 366107705.24.391/1039.1084mm W b x ⨯=⨯=上翼缘对Y 轴惯性矩:463109265.411233014mm I y ⨯=⨯=366102541.0165/109265.41mm W c y ⨯=⨯= 4、强度验算 (1)、正应力: 上翼缘226666max ./215/1.147102541.01080.16105139.31065.284mm N mm N W M W M c y t a x c <=⨯⨯+⨯⨯=+=σ 可以。
吊车梁计算程式(制动梁结构)
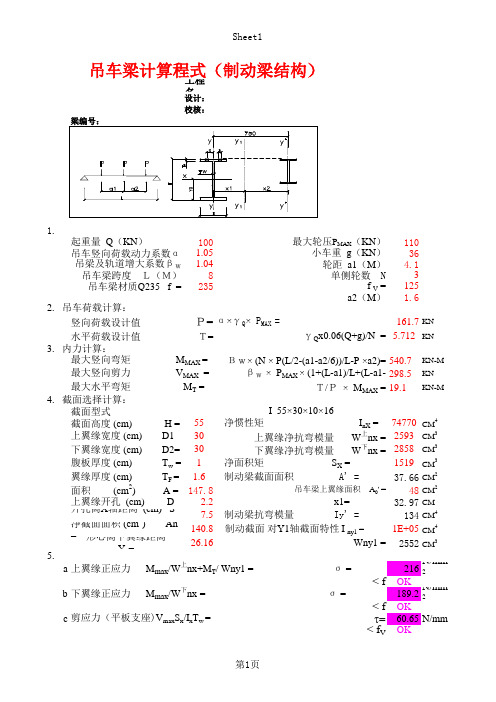
工程名称:设计:校核:1. 输入吊车设计资料: 起重量 Q (KN )100最大轮压P MAX (KN )110吊车竖向荷载动力系数α 1.05小车重 g (KN )36吊梁及轨道增大系数βW 1.04轮距 a1(M ) 4.1 吊车梁跨度 L(M)8单侧轮数 N3吊车梁材质Q235 f =235f V =125a2(M )1.6竖向荷载设计值P=α×γQ × P MAX =161.7水平荷载设计值T=γQ x0.06(Q+g)/N = 5.712Βw× (N × P(L/2-(a1-a2/6))/L-P ×a2)=540.7βW × P MAX × (1+(L-a1)/L+(L-a1-a2)/L)=298.5T/P × M MAX =19.1 截面型式I 55×30×10×16 截面高度 (cm) H =55 净惯性矩 I nX =74770上翼缘宽度 (cm) D1 =30上翼缘净抗弯模量 W 上nx =2593下翼缘宽度 (cm) D2=30下翼缘净抗弯模量 W 下nx =2858腹板厚度 (cm) T w =1 净面积矩 S X =1519翼缘厚度 (cm) T F = 1.6 制动梁截面面积 A' =37.66面积 (cm 2) A =147.8吊车梁上翼缘面积 A 0' =48上翼缘开孔 (cm) D =2.2 x1=32.97开孔离X 轴距离 (cm) S =7.5 制动梁抗弯模量 Iy' =134净截面面积 (cm 2) An =140.8 制动截面 对Y1轴截面特性 I ny1 =1E+05形心离下翼缘距离 Y 0=26.16Wny1 =25525. 强度验算: a 216 < f OKb 189.2< f OKc t=60.65< f VOK最大水平弯矩 M T =上翼缘正应力 M max /W 上nx+M T / Wny1 = σ =下翼缘正应力 M max /W 下nx = σ =剪应力(平板支座)V max S x /I x T w =吊车梁计算程式(制动梁结构)2. 吊车荷载计算:3. 内力计算:4. 截面选择计算:最大竖向弯矩 M MAX =最大竖向剪力 V MAX =d局部压应力L Z=a+2hy=5+2(15+1.6) =38.2ψP/T W L Z = σc =42.33ψ=1< f OK 7. 挠度验算:M KX = M X /1.4α =367.8V/L = M KX L/10EI X = V =0.002<[V/L]=[1/500]=0.002OKKNKNKN-M KNKN-MCM4 CM3 CM3 CM3 CM2 CM2 CM CM4 CM4 CM3N/mm2N/mm2N/mm2N/mm2 N/mm2。
吊车梁计算书
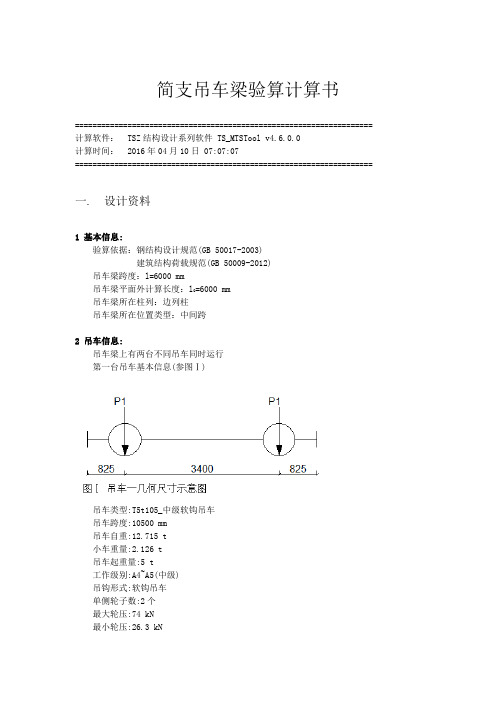
简支吊车梁验算计算书==================================================================== 计算软件:TSZ结构设计系列软件 TS_MTSTool v4.6.0.0计算时间:2016年04月10日 07:07:07====================================================================一. 设计资料1 基本信息:验算依据:钢结构设计规范(GB 50017-2003)建筑结构荷载规范(GB 50009-2012)吊车梁跨度:l=6000 mm吊车梁平面外计算长度:l0=6000 mm吊车梁所在柱列:边列柱吊车梁所在位置类型:中间跨2 吊车信息:吊车梁上有两台不同吊车同时运行第一台吊车基本信息(参图Ⅰ)吊车类型:T5t105_中级软钩吊车吊车跨度:10500 mm吊车自重:12.715 t小车重量:2.126 t吊车起重量:5 t工作级别:A4~A5(中级)吊钩形式:软钩吊车单侧轮子数:2个最大轮压:74 kN最小轮压:26.3 kN制动轮子数:1个轨道类型:43Kg/m吊车宽度:5050 mm吊车额定速度:90 m/min小车额定速度:40.1 m/min吊车轮距C1:3400 mm第二台吊车基本信息(参图Ⅱ)吊车类型:T5t105_重级软钩吊车吊车跨度:10500 mm吊车自重:13.9 t小车重量:2.762 t吊车起重量:5 t工作级别:A6(重级)吊钩形式:软钩吊车单侧轮子数:2个最大轮压:63.7 kN最小轮压:29 kN制动轮子数:1个轨道类型:38Kg/m吊车宽度:5622 mm吊车额定速度:90 m/min小车额定速度:40.1 m/min吊车轮距C1:3850 mm3 荷载信息:吊车竖向荷载增大系数:ηv=1.03吊车荷载分项系数:γc=1.4当地重力加速度值:g=9.8附加竖向均布活载标准值:0 kN/m附加水平均布活载标准值:0 kN/m吊车一动力系数:μ1=1.05吊车一横向水平刹车力系数:β1=0.12吊车一摆动力系数:α1=0吊车二动力系数:μ2=1.1吊车二横向水平刹车力系数:β2=0.12吊车二摆动力系数:α2=0.14 验算控制信息:吊车梁竖向挠度允许值:l/1000吊车梁水平挠度允许值:l/22005 吊车梁截面信息:截面型号:H-750*300*10*12用户自定义截面截面材料类型:Q235截面每米质量:113.51 kg/m截面几何参数如下:截面高度 H=750 mm上翼缘宽度 B1 =300 mm下翼缘宽度 B2 =300 mm腹板厚度 T w =10 mm上翼缘厚度 T f1=12 mm下翼缘厚度 T f2=12 mm截面力学参数如下:x轴毛截面惯性矩 I x =129932.658 cm^4 x轴净截面惯性矩 I nx =122646.136 cm^4 x轴上翼毛截面抵抗矩 W x =3464.871 cm^3 x轴上翼净截面抵抗矩 W nx =3155.656 cm^3 x轴下翼净截面抵抗矩 W nx1 =3394.155 cm^3 y轴上翼毛截面抵抗矩 W y =360.403 cm^3y轴上翼净截面抵抗矩 W ny =152.003 cm^3上翼缘有效净面积 A ne =30.84 cm^2净截面中和轴高度 C ny =361.345 mm吊车梁截面为梯形渐变式变腹板高度截面:截面端部高度 h d =400mm端部x轴毛截面惯性矩 I d =31536.341 cm^4端部x轴毛截面静矩 S d =875.12 cm^3端部x轴上翼缘静矩 S du =698.4 cm^3端部x轴下翼缘静矩 S dd =698.4 cm^36 吊车梁制动结构信息:吊车梁采用制动板结构制动结构宽度:B=1000 mm制动板搭在吊车梁上间距:70 mm制动板厚度:T=6 mm制动板宽度:B b=924.9 mm边梁截面选用:C-160*63*6.5*10制动板搭在边梁上间距:=50mm边梁面积:A e=21.95 cm^2边梁Y向惯性矩:I ye=73.4 cm^4边梁X向惯性矩:I xe=866.2 cm^4边梁形心到右下点X向距离:C xe=1.79 cm边梁形心到右下点Y向距离:C ye=8 cm制动结构绕y轴净截面惯性矩:I ny=174485 cm^4制动结构对梁上翼缘边净抵抗矩:W ny1=2769.05 cm^3制动结构对边梁翼缘边净抵抗矩:W ny2=3242.49 cm^3制动结构绕y轴毛截面惯性矩:I y=186286 cm^4吊车梁上翼缘对y轴的毛截面静矩:S y=1651.83 cm^37 吊车梁截面焊缝信息:吊车梁腹板与上翼缘采用焊透的T形组合焊缝吊车梁腹板与下翼缘采用部分焊透的T形组合焊缝下翼缘坡口深度:s d=5 mm吊车梁腹板与翼缘焊缝采用:自动焊8 腹板加劲肋信息:横向加劲肋布置方式:两侧成对布置横向加劲肋端部焊接方式:连续回焊,不断弧横向加劲肋选用:SB6_Q235横向加劲肋间距:a=1200 mm变截面区段横向加劲肋间距:a'=1200 mm横向加劲肋宽度:65 mm横向加劲肋端部到下翼缘距离:50 mm吊车梁不配纵向加劲肋和横向短加劲肋9 支座信息:吊车梁采用的支座类型:全部平板式支座,吊车梁下翼缘直接与牛腿栓接平板支座加劲肋选用:SB6_Q235平板支座加劲肋宽度:65 mm加劲肋焊缝焊脚高度:7 mm平板支座选用:SB20_Q235平板支座宽度:90 mm平板支座长度:540 mm10 计算参数:梁截面材料屈服强度:f y=235 N/mm^2梁截面材料转换系数:C F=(235/235)^0.5=1上翼缘截面抗拉强度:f t=215 N/mm^2下翼缘截面抗拉强度:f b=215 N/mm^2梁腹板截面抗剪强度:f v=125 N/mm^2梁腹板端面承压强度:f ce=325 N/mm^2吊车梁焊缝抗剪强度:f w=160 N/mm^2二. 验算结果一览受压(上)翼缘宽厚比 12.08 最大15.0 满足腹板高厚比 72.60 最大250.0 满足上翼缘受压强度比 0.37 最大1.0 满足下翼缘受拉强度比 0.33 最大1.0 满足端部腹板剪应力强度比 0.53 最大1.0 满足腹板局部承压强度比 0.16 最大1.0 满足腹板折算应力强度比 0.28 最大1.0 满足整体稳定强度比设制动结构不需验算满足竖向挠度计算值(mm) 1.72 最大6.0 满足水平挠度计算值(mm) 0 不需验算满足上翼缘焊缝强度比 T形组合焊缝不验算满足下翼缘焊缝强度比 0.76 最大1.0 满足下翼处金属应力幅(N/mm2) 19.53 最大118.0 满足下翼角焊缝剪应力幅(N/mm2) 6.51 最大59.0 满足肋端金属应力幅(N/mm2) 16.84 最大103.0 满足区格Ⅰ局稳强度比 0.27 最大1.0 满足区格Ⅱ局稳强度比 0.25 最大1.0 满足区格Ⅲ局稳强度比 0.22 最大1.0 满足区格Ⅳ局稳强度比 0.20 最大1.0 满足加劲肋布置方式双侧成对重级满足横向加劲肋间距(mm) 1200.00 最大1452.0 满足横向加劲肋间距(mm) 1200.00 最小363.0 满足横向加劲肋间距1(mm) 1200.00 最大1452.0 满足横向加劲肋间距1(mm) 1200.00 最小363.0 满足横向加劲肋外伸宽度(mm) 65.00 最小64.2 满足横向加劲肋厚度(mm) 6.00 最小4.3 满足无纵向加劲肋时ho/Tw 72.60 最大170.0 满足平板加劲肋稳定强度比 0.34 最大1.0 满足平板加劲肋焊缝强度比 0.22 最大1.0 满足平板加劲肋外伸宽度(mm) 65.00 最小64.2 满足横向加劲肋厚度(mm) 6.00 最小4.3 满足平板加劲肋焊脚高度(mm) 7.00 最小6.0 满足平板加劲肋焊脚高度(mm) 7.00 最大7.0 满足上翼柱侧板件正应力(MPa) 25.6 最大215 满足上翼柱侧角焊缝应力(MPa) 21.0 最大160 满足上翼柱侧角焊缝焊脚高度(mm) 4.00 最小4.00 满足上翼柱侧角焊缝焊脚高度(mm) 4.00 最大6.00 满足上翼梁柱连接板正应力(MPa) 31.0 最大215 满足上翼梁柱螺栓承担剪力(kN) 8.92 最大62.8 满足上翼梁柱螺栓轴向边距(mm) 35.0 最小33.0 满足上翼梁柱螺栓轴向边距(mm) 35.0 最大88.0 满足上翼梁柱螺栓垂向边距(mm) 45.0 最小44.0 满足上翼梁柱螺栓垂向边距(mm) 45.0 最大88.0 满足牛腿最大正应力(Mpa) 74.3 最大215 满足牛腿最大剪应力(Mpa) 110 最大125 满足牛腿最大折算应力(Mpa) 176 最大237 满足牛腿翼缘宽厚比 10.1 最大15.0 满足牛腿集中力截面剪应力(Mpa) 124 最大125 满足牛腿局部承压应力(Mpa) 83.4 最大325 满足牛腿综合应力(MPa) 149 最大160 满足牛腿焊脚高度(mm) 8.00 最大9.60 满足牛腿焊脚高度(mm) 8.00 最小4.74 满足支座螺栓承担剪力(kN) 49.5 最大62.8 满足支座螺栓轴向边距(mm) 55.0 最小44.0 满足支座螺栓轴向边距(mm) 55.0 最大96.0 满足支座螺栓垂向边距(mm) 55.0 最小33.0 满足支座螺栓垂向边距(mm) 55.0 最大96.0 满足支座螺栓垫板正应力(MPa) 206 最大215 满足支座螺栓垫板角焊缝应力(MPa) 58.7 最大160 满足支座螺栓垫板焊脚高度(mm) 8.00 最小7.00 满足支座螺栓垫板焊脚高度(mm) 8.00 最大9.00 满足上翼柱加劲肋板件宽厚比 14.0 最大14.9 满足上翼柱加劲肋板件剪应力(MPa) 1.69 最大180 满足上翼柱加劲肋焊缝剪应力(MPa) 2.95 最大200 满足牛腿处柱加劲肋板件宽厚比 14.5 最大14.9 满足牛腿处柱加劲肋板件剪应力(MPa) 23.2 最大180 满足牛腿处柱加劲肋焊缝剪应力(MPa) 40.5 最大200 满足纵向连接螺栓承担剪力(kN) 9.64 最大126 满足纵向连接螺栓轴向边距(mm) 45.0 最小44.0 满足纵向连接螺栓轴向边距(mm) 45.0 最大88.0 满足纵向连接螺栓竖向边距(mm) 35.0 最小33.0 满足纵向连接螺栓竖向边距(mm) 35.0 最大88.0 满足纵向连接螺栓间距(mm) 70.0 最小66.0 满足纵向连接螺栓间距(mm) 70.0 最大96.0 满足车挡截面自由外伸宽厚比 8.00 最大15.0 满足车挡截面腹板宽厚比 53.3 最大80.0 满足车挡截面最大剪应力(MPa) 40.9 最大125 满足车挡截面最大正应力(MPa) 131 最大215 满足车挡截面折算应力(MPa) 140 最大237 满足车挡集中力处板件宽厚比 10.0 最大14.9 满足车挡集中力处板件剪应力(MPa) 21.2 最大180 满足车挡集中力处焊缝剪应力(MPa) 15.8 最大200 满足车挡截面最大拉应力(MPa) 141 最大215 满足车挡截面最大压应力(MPa) -141 最小-215 满足车挡截面综合应力(MPa) 141 最大160 满足车挡截面腹板焊脚高(mm) 6.00 最大7.20 满足车挡截面腹板焊脚高(mm) 6.00 最小3.67 满足三. 吊车梁截面内力计算:1 吊车梁支座处最大剪力Vd计算(参图Ⅲ):竖向附加活载作用下端部剪力V da=0 kN吊车考虑动力系数后最大轮压标准值:P=1.05×74=77.7 kN吊车竖向荷载作用下端部剪力:V dc=1.4×1.03×77.7×(2×6000-1711)/6000=197.7 kN端部最大剪力计算值:V d=197.7 kN2 跨中最大竖向弯矩Mvm计算(参图Ⅳ):竖向附加活载作用下跨中弯矩M va=0 kN·m吊车考虑动力系数后单轮竖向作用力标准值:P=1.05×74=77.7 kN吊车荷载合力:F=77.7×2=147.8 kN左支座反力:R=147.8×2594/6000=63.89 kN吊车梁跨中弯矩M vc计算:M vc=1.4×1.03×63.89×2594×10^-3=239 kN·m跨中最大弯矩计算值:M vm=239 kN·m3 跨中最大竖向弯矩对应剪力Vm计算(参图Ⅳ):自重和竖向附加活载作用下端部剪力:V ma=(1.4*g v+1.2*q s)*S/l0=(1.4×0+1.2×1.135)×2594/6000×10^-3=0 kN 吊车考虑动力系数后单轮竖向作用力标准值:P=1.05×74=77.7 kN吊车荷载合力:F=77.7×2=147.8 kN左支座反力:R=147.8×2594/6000=63.89 kN最大弯矩点左侧剪力计算:V ml=1.4×1.03×63.89=92.14 kN最大弯矩点右侧剪力计算:V mr=V ml-1.4×1.03×77.7=(-19.91) kN跨中最大弯矩对应的剪力计算值:V m=92.14 kN4 吊车梁跨中最大水平弯矩Mhm计算(参图Ⅴ):水平附加活载作用下跨中弯矩M ha=0 kN·m吊车考虑卡轨力系数后单轮横向作用力标准值:Q=0.1×63.7=6.37 kN吊车荷载合力:F=6.37×1=6.37 kN左支座反力:R=6.37×3000/6000=3.185 kN吊车梁跨中弯矩M hc计算:M hc=1.4×3.185×3000×10^-3=13.38 kN·m跨中最大水平弯矩计算值:M hm=13.38 kN·m5 跨中最大竖向弯矩标准值Mvk计算(参图Ⅵ):竖向附加活载作用下跨中弯矩M vka=0 kN·m吊车单轮最大轮压标准值:P=1.0×74=74 kN吊车荷载合力:F=74×2=148 kN左支座反力:R=148×3850/6000=94.97 kN吊车梁跨中弯矩M vkc计算:M vkc=1×1.03×(94.97×3850-74×3400)×10^-3=117.4 kN·m 跨中最大弯矩计算值:M vk=117.4 kN·m6 跨中最大水平弯矩标准值Mhk计算(参图Ⅵ):水平附加活载作用下跨中弯矩M hka=0 kN·m吊车考虑刹车力系数及其放大后单轮横向作用力标准值:P=0.12×(5+2.126)/2×g/2=2.095 kN吊车荷载合力:F=2.095×2=4.19 kN左支座反力:R=4.19×3850/6000=2.689 kN吊车梁跨中弯矩M hkc计算:M hkc=1×(2.689×3850-2.095×3400)×10^-3=3.228 kN·m 跨中最大水平弯矩计算值:M hk=3.228 kN·m7 跨中最大竖向弯矩标准值Mvp计算(参图Ⅶ):竖向附加活载作用下跨中弯矩M vpa=0 kN·m吊车单轮最大轮压标准值:Q=1.0×63.7=101.9 kN吊车荷载合力:F=63.7×1=63.7 kN左支座反力:R=63.7×3000/6000=31.85 kN吊车梁跨中弯矩M vpc计算:M vpc=1×31.85×3000×10^-3=95.55 kN·m跨中最大弯矩计算值:M vp=95.55 kN·m8 支座最大竖向剪力标准值Vp计算(参图Ⅷ):竖向附加活载作用下端部剪力V pa=0 kN吊车最大轮压标准值:Q=1.0×63.7=101.9 kN吊车竖向荷载作用下端部剪力:V pc=1×1.03×101.9×(2×6000-3850)/6000=55.7 kN 端部最大剪力计算值:V p=55.7 kN四. 吊车梁板件宽厚比验算:1 受压(上)翼缘宽厚比验算:受压翼缘宽厚比限值:[b0/t]=15*(235/f y)^0.5=15翼缘自由外伸宽度:b0=145 mm翼缘宽厚比:b0/T f1=145/12=12.082 腹板高厚比验算:腹板高厚比限值:[h0/t]=250腹板计算高度:h0=726 mm腹板高厚比:h0/T w=726/10=72.6五. 吊车梁截面强度验算:1 上翼缘受压强度验算:吊车梁采用制动板吊车梁须验算疲劳强度或b0/T f1=12.08>13,取γx=1.0吊车梁须验算疲劳强度,取γy=1.0ξ=(M vm/W nx/γx+M hm/W ny1/γy)/f t=(239/3156/1+13.38/2769/1)×10^3/215=0.37482 下翼缘受拉强度验算:ξ=M vm/W nx1/f b=239×10^3/3394/215=0.32763 端部腹板剪应力强度验算:考虑截面削弱系数1.2τ=V d*S dx/(I dx*T w/1.2)/f v=197.7×875.1/(3.154e+004×10/1.2)/125×10^2=0.52684 最大轮压下腹板局部承压强度验算:考虑集中荷载增大系数后的最大轮压设计值按第二台吊车计算:吊车最大轮压:P max=63.7 kN轻、中级工作制吊车梁,依《钢规》4.1.3取增大系数:ψ=1.0 F=γc*ψ*μ*P max=1.4×1.35×1.1×63.7=132.4 kN 梁顶到腹板计算高度上边缘距离:h y=T f1=12 mm轨道高度:h R=140 mm集中荷载沿跨度方向支承长度取为:50 mm集中荷载在腹板计算高度上边缘的假定分布长度:l z=50+5*h y+2*h R=50+5×12+2×140=390 mmσc=F/T w l z=132.4×10^3/10/390=33.96 N/mm^2腹板抗压强度设计值:f=215 N/mm^2局部承压强度比ξ=σc/f=33.96/215=0.15795 腹板与上翼缘交接处折算应力强度验算:按跨中最大弯矩及其对应的剪力和最大轮压计算计算点局部压应力:σc=33.96 N/mm^2(参见腹板局部承压验算) 计算点正应力计算计算点到中和轴的距离:y1=H-C ny-T f1=376.7 mmσ=M vm/I n*y1=239/1.226e+005×376.7×10^2=73.41 N/mm^2计算点剪应力计算上翼缘对中和轴静矩:S1=(y1+0.5*T f1)*B1*T f1×10^-3=1378 cm^3τ=V m*S1/I x/T w=92.14×1378/1.299e+005/10×10^2=9.768 N/mm^2σ与σc同号,强度设计值增大系数:β1=1.1折算应力强度比ξ=(σ^2+σc^2-σ*σc+3*τ^2)^0.5/(β1*f)=(73.41^2+33.96^2-73.41×33.96+3×9.768^2)^0.5/(1.1×215) =0.27846 吊车梁整体稳定性验算吊车梁设置了制动结构,整体稳定不需验算。
吊车梁最大弯矩点计算

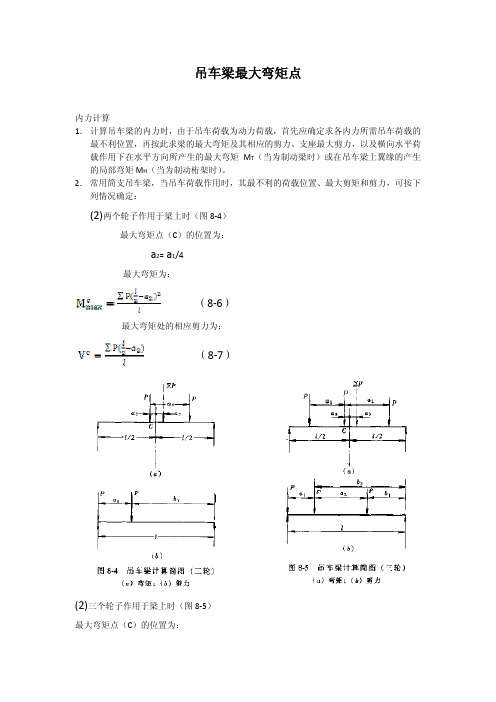
吊车梁最大弯矩点内力计算1.计算吊车梁的内力时,由于吊车荷载为动力荷载,首先应确定求各内力所需吊车荷载的最不利位置,再按此求梁的最大弯矩及其相应的剪力、支座最大剪力,以及横向水平荷载作用下在水平方向所产生的最大弯矩M T(当为制动梁时)或在吊车梁上翼缘的产生的局部弯矩M H(当为制动桁架时)。
2.常用简支吊车梁,当吊车荷载作用时,其最不利的荷载位置、最大剪矩和剪力,可按下列情况确定:(2)两个轮子作用于梁上时(图8-4)最大弯矩点(C)的位置为:a2= a1/4最大弯矩为:(8-6)最大弯矩处的相应剪力为:(8-7)(2)三个轮子作用于梁上时(图8-5)最大弯矩点(C)的位置为:最大弯矩为:(8-8)最大弯矩处的相应剪力为:(8-9)(3)四个轮子作用于梁上时(图8-6)最大弯矩点(C)的位置为:最大弯矩为:(8-10)最大弯矩处的相应剪力为:(8-11)当时最大弯矩及其相应剪力均与公式(8-10)及公式(8-11)相同,但公式中的应用代入(4)六个轮子作用于梁上时(图8-7):最大弯矩点(C)的位置为:最大弯矩为:(8-12)最大弯矩处的相应剪力为:(8-13)当及时,最大弯矩点(C点)的位置为:其最大弯矩及相应剪力均与公式(8-12)及公式(8-13)相同,但公式中的应用代入(5)最大剪力应在梁端支座处。
因此,吊车竖向荷载应尽可能靠近该支座布置(图8-4b)至图8-7b),并按下式计算支座最大剪力:(8-14)式中n—作用于梁上的吊车竖向荷载数。
选择吊车梁截面时所用的最大弯矩和支座最大剪力,可用吊车竖向荷载作用下所产生的最大弯矩和支座最大剪力乘以表8-2的(为考虑吊车梁等自重的影响系数)值,即(8-15)(8-16)3.吊车横向水平荷载作用下,在水平方向所产生的最大弯矩,可根据图8-4(a)至图8-7(a)所示荷载位置采用下列公式计算:当为轻、中工作制(A1-A5)吊车梁的制动梁时,(8-17)当为重级或特重级工作制(A6-A8)吊车梁的制动梁时,(8-18)(2)吊车横向水平荷载作用下制动桁架在吊车梁翼缘所产生的局部弯矩可近似地按下列公式计算(图8-8):当为起重量Q≥75t的轻、中级工作制吊车的制动桁架时(8-19)当为起重量Q≥75t的重级工作制(特重级不受起重量限制)吊车的制动桁架时(8-20)当为起重量Q≤50t的轻、中级工作制吊车的制动桁架时(8-21)当为起重量Q≤50t的重级工作制(特重级不受起重量限制)吊车的制动桁架时(8-22)。
混凝土吊车梁计算书
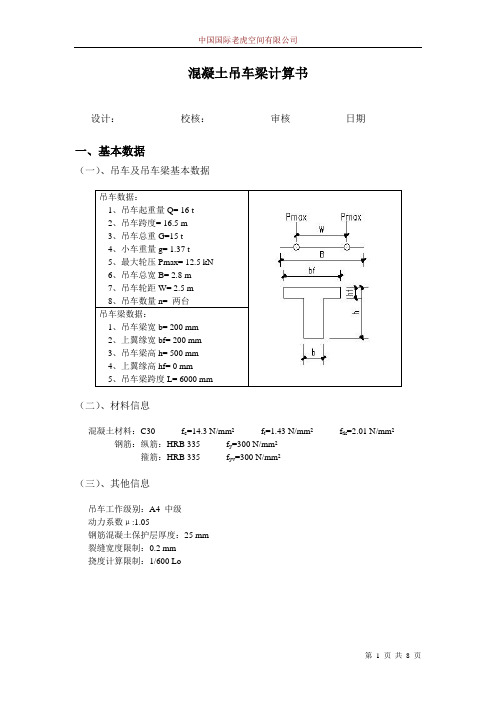
混凝土吊车梁计算书设计:____________校核:____________审核___________日期________一、基本数据(一)、吊车及吊车梁基本数据吊车数据:1、吊车起重量Q= 16 t2、吊车跨度= 16.5 m3、吊车总重G=15 t4、小车重量g= 1.37 t5、最大轮压Pmax= 12.5 kN6、吊车总宽B= 2.8 m7、吊车轮距W= 2.5 m8、吊车数量n= 两台吊车梁数据:1、吊车梁宽b= 200 mm2、上翼缘宽bf= 200 mm3、吊车梁高h= 500 mm4、上翼缘高hf= 0 mm5、吊车梁跨度L= 6000 mm(二)、材料信息混凝土材料:C30 f c=14.3 N/mm2f t=1.43 N/mm2f tk=2.01 N/mm2钢筋:纵筋:HRB 335 f y=300 N/mm2箍筋:HRB 335 f yv=300 N/mm2(三)、其他信息吊车工作级别:A4 中级动力系数μ:1.05钢筋混凝土保护层厚度:25 mm裂缝宽度限制:0.2 mm挠度计算限制:1/600 Lo二、正截面设计(一)计算吊车梁的绝对最大弯矩位置计算长度取为:L0= 5.8 m由结构力学可判断,吊车轮按上述作用时才能产生绝对最大弯矩计算可得:合力R = 3×μ×Pmax = 52.5 kNa0 = B-W2= 0.15 m(二)正截面配筋计算1、内力计算吊车梁自重:q1 = 25×[b×h+(b f-b)×h f] = 2.5 kN/m轨道联结重:q2 = 1.5 kN/m自重总和:q = q1 + q2 = 4 kN/m由自重在k点产生的弯矩:Mqk = qx2(Lo-x) = 16.81 kN・m由吊车荷载在k点产生的弯矩:Mpk = R(L0-a0)24L0= 39.43 kN・m总弯矩:M maxk = M qk + M pk= 56.24 kN・m2、按T型梁计算配筋按照混凝土规范7.2.2条a s = 35 mmh0 = h-2a s = 430 mmM = f c b f h f(h0-h f/2) = 0 < M maxk = 56.24 属于II类T型截面3验算垂直截面的双向受弯强度每个轮子产生的刹车力:T = 0.25×α(Q+g)×9.8 = 4.26 kN为简化计算,假设每个轮子都作用在吊车梁跨中,由水平力产生的弯矩为:M H =nT4Lo = 24.708 kN ・m 可见,水平方向产生的弯矩很小,双向受弯强度验算可以忽略 三、斜截面设计(一)复核截面条件吊车梁自重荷载作用下产生的剪力: V 1 = 0.5×q×Lo = 11.6 kN 吊车荷载按下图作用时产生最大剪力:由结构力学可知:V 2 = μP max (4-2B+WLo ) = 28.51 kN 最大总剪力:V = V 1 + V 2 = 40.11 kN 由混凝土规范7.5.1条:0.25βc f c bh 0 = 307.45 kN > V 截面满足要求 (二)计算所需箍筋1、确定计算方法y a = ΣI y y iΣI y = 112 h f b f 3×12 h f +112 (h-h f )b 3×(h/2+h f /2)112 h f b f 3+112 (h-h f )b 3= 250 mm 每个吊车轮产生的扭矩: m t = 0.7[μP max ×0.02+T(y a +0.2)] = 1.53 kN ・m则支座截面产生的最大扭矩为:T = 1.4×m t ×(4-2B+2WLo ) = 4.65 kN ・m 构件截面信息腹板: W tw = b 2(3h-b)/6 = 8666666.66666667mm 3 翼缘: W tf = h f 2(b f '-b)/2 = 0mm 3W t = W tw + W tf = 8666666.66666667 mm 3 由混凝土规范7.6.1V bh 0 + T0.8W t= 1.1371 < 0.25βc f c = 3.575截面尺寸满足按弯剪扭共同作用的构件计算腹板受扭矩: T w = W twW t ×T = 4.650 kN ・m翼缘受扭矩: T f ' = W tfW t×T = 0.000 kN ・m2、腹板配筋计算A cor = b cor h cor = 67500 mm 2 u cor = 2×(b cor + h cor ) = 1200 mma.腹板受扭箍筋计算,按混凝土规范7.6.8:T = 0.35f t βt W t + 1.2ζ f yv A st1A cor sβt =1.51+0.5 VW tTbh 0= 0.93 A st1s = T w -0.35βt f t W tw1.2ζ f yv A cor= 0.032136 mm 2/mm b.腹板受剪箍筋计算,按混凝土规范7.6.8:A sv1s = V -0.7(1.5-βt )f t bh 01.25f yv h 0= 0.045301 mm 2/mm腹板所需单肢箍筋总面积为:A st1s + A sv1s= 0.0547865 mm 2/mm实际配置:8@100 满足c.腹板抗扭纵筋计算,按混凝土规范7.6.4-2:A stl = ζf yv A st1u corf y s= 23.14 mm 2 构造配置钢筋3、翼缘配筋计算b 'cor = b f - b - 50 = -50 mm h 'cor = h f - 50 = -50 mmA 'cor = b 'cor ×h 'cor = 2500 mm 2 U 'cor = 2(b 'cor + h 'cor ) = -200 mm a.翼缘抗扭箍筋计算,按混凝土规范7.6.8:A st1s = T f -0.35βt f t W tf1.2ζ f yv A cor= 0.000 mm 2/mm 实际配置:8@100 满足b.翼缘抗扭纵筋计算,按混凝土规范7.6.4-2:A stl = ζf yv A st1u corf y s= 0.00 mm 2 构造配置钢筋四、验算吊车梁疲劳强度(一)验算正截面疲劳强度1、验算受压区混凝土边缘纤维的应力 一台吊车产生的最大弯矩:由结构力学可判断,吊车轮按上述作用时才能产生绝对最大弯矩计算可得:合力R = 2×μ×Pmax = 26.25 kNa0 = B-W2= 0.15 m由自重在k点产生的弯矩:Mqk = qx2(Lo-x) = 16.82 kN・m由吊车荷载在k点产生的弯矩:Mpk = μP max(L0-a0)22L0= 38.06 kN・m总弯矩:M maxk = M qk + M pk= 54.88 kN・mαf E= E sE f c= 13.33先假定中和轴通过翼缘,换算截面的受压区高度:b2x02 - αfE A s(h0 - x0) = 0 公式见《钢筋混凝土结构计算手册》P624简化:Ax02 + Bx0 + C = 0 其中:A = 100B = 20593.2504C = -9266962.68解方程得:x0 = 218.39mm >h f = 0 mm 所以须按下列公式重新计算:b f2x02 - αfE A s(h0 - x0)-(b f - b)(x0 - h f)22= 0简化:Ax02 + Bx0 + C = 0 其中:A = 100B = 20593.2504C = -9266962.68 解方程得:x0 = 218.39mmI fo=h f x033-(b f - b)(x0 - h f)33+αfE A s(h0 - x0)2 = 1799083328.02ρfc=ρfcminρfcmax=MqkMqk+Mpk= 0.317589268845645查混凝土规范表4.1.6得: γρ = 0.86σf cmax = M f max x 0I fo = 6.662 < f fc = γρf c = 12.298满足要求 2、验算受拉钢筋的应力σf simin = αf E M f min (h 0-x 0)I f o = 30.342 N/mm 2σf simax = αf E M fmax (h 0-x 0)I f o = 65.196 N/mm 2Δσf si = σf simax - σfsimin = 34.854 N/mm 2 ρf s= σfsiminσfsimax = 0.465根据混凝土规范表4.2.5-1,可查得:Δf f y = 135 > Δσfsi = 34.854 满足要求(二)验算斜截面疲劳强度 1、验算中和轴处的主应力 计算从略2、验算弯起钢筋所需面积 计算从略五、验算吊车梁裂缝宽度σρsk = M maxk0.87h 0A s= 92.9862630983486 N/mm 2A te = 0.5bh = 50000 mm 2 ρte = A s /A te = 0.0308976d eq = Σn i d i 2Σn i νd i= 18.2222222222222 mmψ=1.1-0.65f tkρte σρsk= 0.645257156827881由混凝土规范8.1.2得: αcr = 2.1 c=20 ψ=1.0ωmax = αcr ψσρsk E s 1.9c+0.08d eqρte= 0.0536640377934194 < 0.2 满足规范要求六、验算吊车梁挠度由混凝土规范8.2.3:B s = E s A s h 021.15ψ+0.2+6αE ρ1+3.5γf'其中: ψ=1.0 αE = 13.33 E s = 200000 A s = 1544.88 h 0 = 430 γf ' = 0ρ= A sbh 0= 0.0171653333333333代入公式可得:B s = 27027886193474.9 由混凝土规范8.2.2:B = M kM q (θ-1)+M k B s其中: θ=1.6 M k = 38.06 M q = 16.82 代入公式可得:B = 21128148926726.3f=5qlo 4384B= 2.78964728702648f/Lo=1/1981 < 1/600 满足要求七、验算吊车梁配筋率计算从略。
吊车梁最大弯矩

吊车梁最大弯矩引言吊车梁是用于起吊和搬运重物的工程机械设备,在工地和港口等场所被广泛使用。
在设计吊车梁时,需要考虑到各种力的作用,其中最大弯矩是一个重要的参数。
本文将介绍吊车梁最大弯矩的概念、计算方法和影响因素。
概念吊车梁最大弯矩是指吊车梁在使用过程中所能承受的最大弯曲力矩。
当吊车梁承受的力矩超过其所能承受的最大弯矩时,就会发生弯曲变形或破坏。
计算方法吊车梁最大弯矩的计算需要考虑各种加载情况,包括静态加载和动态加载。
以下是一些常见的计算方法:1.静态加载:当吊车梁处于静止状态时,可以使用静力学方法进行计算。
根据支持条件和施加载荷,可以通过应力和变形分析确定吊车梁的最大弯矩。
常用的方法包括叠加法、力矩法和三力共点法。
2.动态加载:当吊车梁处于运动状态时,需要考虑动力学效应。
除了考虑物体的重力外,还需要考虑各种运动和惯性力。
常见的方法包括动力学分析和有限元分析。
无论是静态加载还是动态加载,吊车梁的材料属性和几何形状都会对最大弯矩产生影响。
因此,在计算吊车梁最大弯矩时,需要准确地了解吊车梁的材料特性和结构参数。
影响因素吊车梁最大弯矩的大小受到许多因素的影响,包括但不限于以下几点:1.载荷重量:吊车梁所承受的物体重量是影响最大弯矩大小的关键因素。
当物体重量增加时,吊车梁所受弯矩也随之增加。
2.吊车梁的长度和截面形状:吊车梁的长度和截面形状会直接影响吊车梁的刚度和强度。
通常情况下,吊车梁越长,其最大弯矩也会越大。
而且,吊车梁的截面形状也会影响其抗弯能力,如梁的高度、宽度和厚度等。
3.材料特性:吊车梁所使用的材料的特性也会对最大弯矩产生影响。
材料的弹性模量、屈服强度和断裂韧性等都会影响吊车梁的强度和刚度。
4.支持条件:吊车梁的支持条件会对其最大弯矩和变形产生影响。
不同的支持方式,如简支、固定支承或悬臂支承等,会导致不同的弯矩分布和变形形态。
除了以上因素,环境条件如温度、湿度和风荷载等也会对吊车梁的最大弯矩产生一定影响。
吊车梁的设计

截面选择一.截面尺寸的确定:(1).梁的高度:①.经济要求:梁的平面内最大弯矩设计值:M xmax=464700000N·MM,支座处的最大剪力V max=梁选用钢材材质Q235,f=215N/mm2fv=Q345,f=315N/mm2fv=f=315N/mm2fv=梁需要的截面抵抗矩:W= 1.2*M xmax/f=1770286梁的经济截面高度:H=7*(W)^(1/3)-300=547②.刚度要求:对中级且Q<500K N,[l/w]=600,梁的跨度l=6000mm超过此限[l/w]=750取[l/w]=600,[w/l]=0.001667梁刚度要求的最小高度:Hmin=0.56*f*l/([w/l]*106)=③.净空要求:H≤净空要求根据以上三条要求确定吊车梁的高度,H=700mm厚度Tw的确定:①.经验公式:T w=7+3h=10mm ②.根据抗剪要求:T w≥1.2V max/hwfv=2.9630843mm③.局部挤压应力的要求:数据准备:考虑动力系数的一个车轮的最大轮压a P max=136集中荷载增大系数,对轻、中级工作制吊车梁Y=1.0,对重级工作制吊车梁Y=1.35 Y=1g Q= 1.4钢轨高度:140mm,吊车梁翼缘厚度t(暂估):轨顶至腹板计算高度上边缘的距离:h y=钢轨高度+吊车梁翼缘厚度t=车轮对腹板边缘挤压应力的分布长度,取L z=2h y+50=358T w≥aYg Q P max/(l w*f)=2mm根据以上三条要求暂估T w=8mm三.翼缘尺寸:翼缘所需的面积:A1=W x/Hw-1/6HwTw=1696.6947根据翼缘的局部稳定判断翼缘不考虑局部稳定的最大宽度:b=336根据上面的翼缘最大宽度取b=330mm下翼缘厚度取10mm,下翼缘宽度Bb=300mm本吊车梁尺寸取如下值:吊车梁高度H=700mm上翼缘宽度Bt=330mm上翼缘厚度Tt=14mm下翼缘宽度Bb=300mm下翼缘厚度Tb=10mm腹板厚度Tw=8mm腹板高度mmHw=676根据上值转入《吊车梁截面计算》工作簿.310.63KN125N/mm2185N/mm2185N/mm2(板厚≤16mm)mm3mm636mm腹板高度暂定H w=680mmKN14mm154mm mmmm。
某重级工作制吊车梁设计与计算

某重级工作制吊车梁设计与计算【摘要】本文通过某重级工作制硬钩吊车吊车梁设计实例,介绍钢吊车梁设计与计算的一般方法和内容,就如何通过影响线确定吊车梁最大弯矩进行了探讨和分析,并总结了重级工作制吊车梁设计的注意事项。
【关键词】重级工作制;吊车梁;硬钩;强度;疲劳一、概况某钢铁冶金厂房为多跨单层排架结构,柱距24m,由于工艺需要布置多台大吨位重级工作制硬钩桥式吊车。
下面就以其中一跨为例,介绍该跨吊车梁的一般设计方法,吊车资料如下表:二、吊车梁形式钢结构吊车梁系统通常由吊车(支承)梁、制动结构、辅助桁架以及支撑等构件组成。
吊车(支承)梁一般以吊车桁架、焊接工字型吊车梁或箱型吊车梁形式为多见,又以焊接工字型吊车梁最为常见。
由于其制作简单,结构受力性好,因此本工程采用焊接工字型吊车梁形式。
三、吊车梁设计与计算1、吊车荷载计算吊车竖向荷载: Pk=480kN; P=μrQPk=1.1*1.4*480=739.2kN吊车横向水平荷载:按荷载规范计算荷载:Hk=(94+120)*9.85*0.2/12=35.1kN; H=rQHk=1.4*35.1=49.2kN按卡轨力计算荷载:Hk=αPk=0.2*480=96kN; H=rQHk=1.4*96=134.4kN其中μ为动力系数;rQ 为荷载分项系数;α为卡轨力系数。
2、跨中最大竖向弯矩点的确定和最大竖向弯矩计算根据经验知道,简支型吊车梁在吊车轮压作用下,跨中最大弯矩位置(C点)位于吊车车轮荷载作用点,同时该位置左右侧剪力变号。
如下图所示,RA=∑P(L-X-a)/L, 跨中最大弯矩位置Mc= RAX-Mkc=∑P(L-X-a)X/L- Mkc;Mkc 为C点左侧梁上荷载P相对与C点的力矩和,为一与X无关常数。
当Mc为极大值时,根据极值条件=∑P(L-X-a)/L=0,解得X= (L-a)/2。
这表明,跨中最大弯矩位置C点与合力∑P对称于梁中心线。
根据以上结论,可以按以下方式找到一组集中荷载作用下的跨中最大弯矩C点位置:先求得该组集中荷载合力点位置,并将合力点和其紧邻的集中荷载对称布置在梁中心线两侧(如图1.1),求出支座反力;复核紧邻的集中荷载位置左右侧剪力是否变号,若变号,即可确认该集中荷载位置为跨中最大弯矩C点位置;否则需要将合力中心和下一个邻近的集中荷载对称布置在梁中心线两侧(如图1.2),继续复核直至找到最终找出符合条件的集中荷载位置,最后根据弯矩影响线求出最大弯矩。
吊车梁计算

一份详细的焊接工字钢吊车梁计算书!跨度6米,10吨单梁吊车!希望能给大家带来帮助!*****吊车梁计算书*****[设计资料]吊车数:1台吊车工作级别:A1-A3吊车的轮数2吊车轮子间间距a1=0.25m, a2=2m, a3=0m最大轮压标准值40KN横向荷载标准值5KN竖向轮压动力系数1.05钢材类型:Q235支座形式:平板式吊车梁长度6m轨道高度107mm建筑允许高度10m控制挠度值1/600欠载系数0受拉翼缘与腹板连接处焊缝及附近的主体金属疲劳应力幅0N/mm^2横向加劲肋端点处手工焊缝附近的主体金属疲劳应力幅0N/mm^2无制动结构支撑数:0(1)截面特征计算吊车梁高度h=450 mm腹板厚度tw=10 mm上翼缘宽度bs=330 mm上翼缘厚度ts=14 mm下翼缘宽度bx=200 mm下翼缘厚度tx=14 mm吊车梁截面面积A=11640 mm^2吊车梁X轴惯性矩Ix=4.01852e+008 mm^4吊车梁X轴抵抗矩Wx1=2.10488e+006 mm^3吊车梁X轴抵抗矩Wx2=1.55104e+006 mm^3吊车梁Y轴抵抗矩Wy=310879 mm^3吊车梁上翼缘截面对Y轴抵抗矩Wy1=254100 mm^3吊车梁最大面积矩Sx=1.22977e+006 mm^3(2)内力计算吊车竖向荷载标准值P=40KN吊车竖向荷载设计值P=1.4x1.05x40=58.8KN吊车横向荷载标准值T=5KN吊车横向荷载设计值T=1.4x5=7KN吊车梁的最大设计弯矩Mmax=122.5 kN*m吊车梁的最大设计弯矩处相应的设计剪力Vc=49 kN梁端支座处的最大设计剪力Vcmax=98 kN吊车梁在水平荷载作用下的最大设计弯矩MTmax=14.583 kN*m局部承压验算的集中荷载设计值F=58.8 kN(3)承载力验算1)强度验算上翼缘:最大正应力σ=Mmax/Wx1 + MTmax/Wy1=115.59N/mm2<f=215N/mm^2,满足下翼缘:最大正应力σ=Mmax/Wx2 =78.98 N/mm^2<f=215N/mm^2,满足腹板:最大剪应力τ=VcmaxSx/Ix/tw =29.99 N/mm^2<fv=125N/mm^2,满足ψ=1,lz=50+2x107+5x14=334 mm局部压应力σc=ψF/tw/lz =17.6 N/mm^2<f=215N/mm^2,满足2)整体稳定验算因6000/330=18.1818>13 ,所以需要验算吊车梁的整体稳定梁的整体稳定系数Фb = 0.918整体稳定应力σ=Mmax/Фb/Wx1 + MTmax/Wy=110.3N/mm^2<f=215N/mm^2,满足3)刚度验算吊车梁的竖向挠度验算按一台吊车荷载标准值作用下产生的最大弯矩Mkx=83.333 kN*m挠度v=Mkx*l*l/10/E/Ix=3.62mm < [v]=10mm,满足4)疲劳验算本吊车为A1-A3工作级别吊车,不必进行疲劳验算。
吊车梁最大弯矩 (2)

吊车梁最大弯矩引言吊车梁是一种常见的工业设备,用于吊装和搬运重物。
在使用吊车梁时,了解吊车梁的最大弯矩是非常重要的,它可以帮助我们评估吊车梁的承载能力和使用限制。
本文将介绍什么是吊车梁的最大弯矩,以及如何计算和应用这个参数。
什么是吊车梁最大弯矩吊车梁最大弯矩是指吊车梁在承受重物吊装过程中,材料受到曲线形变的最大程度。
在吊车梁的设计过程中,工程师需要考虑到最大弯矩,以确保吊车梁具备足够的强度和刚度来承受所需的载荷。
如何计算吊车梁的最大弯矩计算吊车梁的最大弯矩通常需要考虑以下几个因素:1. 负载吊车梁的最大弯矩与所搬运的负载有直接的关系。
负载的重量和形状将影响吊车梁的受力情况。
需要确定负载的重量、尺寸和形状,并考虑重心位置。
2. 吊杆长度和支撑方式吊车梁的长度和支撑方式也会影响最大弯矩的计算。
通常来说,吊车梁越长,承载能力越低。
吊车梁的支撑方式(如悬臂或固定支撑)也会对最大弯矩产生影响。
3. 材料的性能吊车梁所使用的材料也是计算最大弯矩的重要因素之一。
不同材料具有不同的力学性能,包括弹性模量、屈服强度和弯曲强度等。
材料的性能参数将用于计算吊车梁的最大弯矩。
4. 弯曲分布吊车梁在受到负载作用时,会发生弯曲。
弯曲分布是指吊车梁上不同位置的弯曲程度。
通常,最大弯矩发生在负载的重心位置。
在实际计算中,可以利用以下公式来计算吊车梁的最大弯矩:M = (W * L^2) / (8 * S)其中,M表示最大弯矩,W表示负载的重量,L表示吊杆的长度,S表示材料的抗弯承载力。
吊车梁最大弯矩的应用了解吊车梁的最大弯矩对于工程师和操作人员来说都是非常重要的。
它可以帮助我们评估吊车梁的承载能力,确定最大负载能力和操作限制。
如果超过了吊车梁的最大弯矩,可能会导致吊车梁的破坏或事故发生。
因此,在吊装作业中,必须根据吊车梁的最大弯矩选择适当的吊装设备和工艺。
此外,吊车梁的最大弯矩还可以用于吊装过程中的安全措施。
通过合理计算和设定最大弯矩的警戒线,在操作过程中及时监测和预警吊车梁的受力情况。
吊车梁最大弯矩

吊车梁最大弯矩引言在建筑和工程行业中,吊车梁被广泛应用于货物的运输和搬运。
吊车梁在承载重物的过程中承受着巨大的力和压力。
了解吊车梁的最大弯矩是设计和使用吊车梁的关键因素之一。
本文将介绍吊车梁最大弯矩的概念、计算方法以及影响吊车梁最大弯矩的因素。
吊车梁最大弯矩的概念吊车梁最大弯矩是指吊车梁在受力作用下所承受的最大弯曲力矩。
弯矩是指物体在受力作用下发生弯曲时两个端点或受力点之间产生的力矩。
对于吊车梁来说,最大弯矩通常发生在吊梁两端点之间。
吊车梁最大弯矩的计算方法吊车梁最大弯矩的计算涉及到结构力学的知识。
一般来说,可以使用以下公式来计算吊车梁最大弯矩:M = W * L / 4其中,M是吊车梁的最大弯矩,W是吊车梁所承受的重力或外力的大小,L是吊车梁的长度。
这个公式适用于简单的悬挑梁和梁的均布载荷情况。
如果吊车梁存在复杂的载荷分布或结构形状,可以使用更复杂的计算方法来确定吊车梁的最大弯矩。
影响吊车梁最大弯矩的因素吊车梁的最大弯矩不仅与承受的载荷有关,还受到以下几个因素的影响:1. 材料强度吊车梁的材料强度是指其在受力作用下能够承受的最大力。
材料的强度越高,吊车梁的最大弯矩也就越大。
2. 吊车梁的截面形状吊车梁的截面形状对其最大弯矩有影响。
一般来说,截面形状越大,吊车梁的最大弯矩也就越大。
3. 吊车梁的长度吊车梁的长度越长,其最大弯矩也会相应增大。
4. 载荷分布吊车梁所承受的载荷分布也会对其最大弯矩产生影响。
如果载荷不均匀分布在吊车梁上,可能会导致某些部分承受更大的力,从而使最大弯矩增大。
结论吊车梁最大弯矩是设计和使用吊车梁时需要考虑的重要参数之一。
了解吊车梁最大弯矩的计算方法和影响因素有助于确保吊车梁的安全和稳定性。
应根据实际情况选择合适的材料和结构形状,并合理考虑载荷分布,以确保吊车梁能够承受所需的最大负载。
吊车梁最大弯矩点计算

吊车梁最大弯矩点计算标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]吊车梁最大弯矩点内力计算1. 计算吊车梁的内力时,由于吊车荷载为动力荷载,首先应确定求各内力所需吊车荷载的最不利位置,再按此求梁的最大弯矩及其相应的剪力、支座最大剪力,以及横向水平荷载作用下在水平方向所产生的最大弯矩MT (当为制动梁时)或在吊车梁上翼缘的产生的局部弯矩MH (当为制动桁架时)。
2. 常用简支吊车梁,当吊车荷载作用时,其最不利的荷载位置、最大剪矩和剪力,可按下列情况确定:(2)两个轮子作用于梁上时(图8-4)最大弯矩点(C )的位置为:a2= a1/4最大弯矩为:M max c =∑P (l 2−l 2)2l (8-6)最大弯矩处的相应剪力为:V c =∑P (l 2−l 2)l (8-7)(2)三个轮子作用于梁上时(图8-5)最大弯矩点(C )的位置为:a 3=a 2−a 16最大弯矩为:M max c =∑P (l 2−l 3)2l −P l 1 (8-8)最大弯矩处的相应剪力为:V c =∑P (l 2−l 3)l −l (8-9)(3)四个轮子作用于梁上时(图8-6)最大弯矩点(C )的位置为:a 4=2a 2+a 3−a 18最大弯矩为:M max c =∑P (l 2−l 4)2l −P l 1 (8-10)最大弯矩处的相应剪力为:V c =∑P (l 2−l 4)l −l (8-11)当l 3=l 1时 l 4=l 24最大弯矩M max c 及其相应剪力V c 均与公式(8-10)及公式(8-11)相同,但公式中的l 4应用l 24代入(4)六个轮子作用于梁上时(图8-7):最大弯矩点(C )的位置为:a 6=3a 3+2a 4+a 5−a 1−2a 212最大弯矩为:M max c =∑P (l2−l 6)2l −P(l 1+2l 2) (8-12)最大弯矩处的相应剪力为:V c =∑P (l2−l 6)l −2l (8-13)当l 3=l 5=l 1及 l 4=l 2时,最大弯矩点(C 点)的位置为:l 6=l 14其最大弯矩M max c 及相应剪力V c 均与公式(8-12)及公式(8-13)相同,但公式中的l 6应用l 14代入 (5)最大剪力应在梁端支座处。
吊车梁计算书

吊吊车车梁梁计计算算书书一. 设计资料吊车情况:1台吊车;编号:3 工作制:轻级, 吊钩形式: 硬钩;起重量:Q=20吨,小车重:g=1吨;最大轮压:P max =100千牛最小轮压:P min =20千牛吊车一侧的轮数:n=2个吊车轮子间间距:a 1=3m钢材类型:Q235B支座类型:平板式;吊车梁跨度:L=6m吊车梁计算长度:L y =6m轨道高度:0.14允许挠度比:1/600=0.001667二. 设计荷载和内力考虑轨道重量及吊车梁自重的增大系数:1.02动力系数:1.05;max 1P P Q γα=竖向荷载标准值:P=1.02×1.05×100=107.1千牛竖向荷载设计值:P=1.4×107.1=149.94千牛 10201⨯+=n Q Q T η 横向荷载标准值:T=0.1×(200+10)/2=10.5千牛横向荷载设计值:T=1.4×10.5=14.7千牛吊车梁的最大竖向设计弯矩: ()L a L P M 420-∑= M max =253.024千牛·米吊车梁的最大竖向设计弯矩处相应的设计剪力:V=112.455千牛 吊车梁端支座处的最大设计剪力: ⎪⎭⎫ ⎝⎛-+=L a P P V 1211 V max =224.91千牛吊车梁的最大水平设计弯矩:M t =24.806千牛·米三. 截面特性吊车梁高度h=56cm腹板厚度t=1.2cm上翼缘宽度b f =32cm上翼缘厚度t f =1.4cm下翼缘宽度b f1=32cm下翼缘厚度t f1=1.4cm吊车梁面积A=153.44cm 2;吊车梁X 轴惯性矩I x =81849.495cm 4;吊车梁Y 轴惯性矩I y =7653.527cm 4;吊车梁X 轴抵抗矩W x =2923.196cm 3;吊车梁Y 轴抵抗矩W y =478.345cm 3;吊车梁X 轴转动惯量r x =23.096cm;吊车梁Y 轴转动惯量r y =7.063cm;吊车梁最大面积矩S max =1647.576cm 3;四. 验算1 强度验算: f W M W M nyy nx x ≤+=max σ 上翼缘正应力σ=253.024×106/2923196.251+24.806×106/238933.329=190.378N/mm2≤215N/mm 2,合格。
吊车梁计算
1E+12 有解
65 梁高h0=
585
65 mm
0
370.989 398.9872941
0.54
xb =
0.61 0.54
双筋
承受弯
受拉As
矩
As1=
0 受压As2= 0 总=
0 m㎡ Mu1=
剪力
370.99 V=
193
3、斜 截面配 筋:
箍钢
fg=
弯钢
fg=
210 N/m㎡ 310 N/m㎡
配弯起 筋直径
一、荷 载计算
bf
hf h
b
1、吊车 梁自重及 埋件重
bf=
吊车G1=
双轮 距吊 车梁 的计 算
h=
0.65 hf=
0.15
b=
0.25 m
轨道及埋
0.50 m 件每米重=
0.71 KN/m 轻级动力系数=
1.10
5.29 小车G2= 2.00 重物G3= 10.00 T
吊车跨度Lk= 8.74 m
3 实配As=
2280.8 满足
压配筋d1=
20 mm
根数n=
2 受拉筋d2=
22 根数n=
0 实配As=
628.32 满足
(一 )配 箍筋
安全系数
K=
截面应满足
1.55 的条件为
1.43 满足 混凝土 的轴心 抗压强
1.54 满足 度fc=
混凝土 的抗拉
强度ft=
按计 1.1 N/mm2 算配筋
箍筋保 护层
as=
10
N/mm2
配单筋 双层
0.025
m
箍 筋直径 d=
混凝土吊车梁计算书

混凝土吊车梁计算书设计:____________校核:____________审核___________日期________一、基本数据(一)、吊车及吊车梁基本数据吊车数据:1、吊车起重量Q= 16 t2、吊车跨度= 16.5 m3、吊车总重G=15 t4、小车重量g= 1.37 t5、最大轮压Pmax= 12.5 kN6、吊车总宽B= 2.8 m7、吊车轮距W= 2.5 m8、吊车数量n= 两台吊车梁数据:1、吊车梁宽b= 200 mm2、上翼缘宽bf= 200 mm3、吊车梁高h= 500 mm4、上翼缘高hf= 0 mm5、吊车梁跨度L= 6000 mm(二)、材料信息混凝土材料:C30 f c=14.3 N/mm2f t=1.43 N/mm2f tk=2.01 N/mm2钢筋:纵筋:HRB 335 f y=300 N/mm2箍筋:HRB 335 f yv=300 N/mm2(三)、其他信息吊车工作级别:A4 中级动力系数μ:1.05钢筋混凝土保护层厚度:25 mm裂缝宽度限制:0.2 mm挠度计算限制:1/600 Lo二、正截面设计(一)计算吊车梁的绝对最大弯矩位置计算长度取为:L0= 5.8 m由结构力学可判断,吊车轮按上述作用时才能产生绝对最大弯矩计算可得:合力R = 3×μ×Pmax = 52.5 kNa0 = B-W2= 0.15 m(二)正截面配筋计算1、内力计算吊车梁自重:q1 = 25×[b×h+(b f-b)×h f] = 2.5 kN/m轨道联结重:q2 = 1.5 kN/m自重总和:q = q1 + q2 = 4 kN/m由自重在k点产生的弯矩:Mqk = qx2(Lo-x) = 16.81 kN・m由吊车荷载在k点产生的弯矩:Mpk = R(L0-a0)24L0= 39.43 kN・m总弯矩:M maxk = M qk + M pk= 56.24 kN・m2、按T型梁计算配筋按照混凝土规范7.2.2条a s = 35 mmh0 = h-2a s = 430 mmM = f c b f h f(h0-h f/2) = 0 < M maxk = 56.24 属于II类T型截面3验算垂直截面的双向受弯强度每个轮子产生的刹车力:T = 0.25×α(Q+g)×9.8 = 4.26 kN为简化计算,假设每个轮子都作用在吊车梁跨中,由水平力产生的弯矩为:M H =nT4Lo = 24.708 kN ・m 可见,水平方向产生的弯矩很小,双向受弯强度验算可以忽略 三、斜截面设计(一)复核截面条件吊车梁自重荷载作用下产生的剪力: V 1 = 0.5×q×Lo = 11.6 kN 吊车荷载按下图作用时产生最大剪力:由结构力学可知:V 2 = μP max (4-2B+WLo ) = 28.51 kN 最大总剪力:V = V 1 + V 2 = 40.11 kN 由混凝土规范7.5.1条:0.25βc f c bh 0 = 307.45 kN > V 截面满足要求 (二)计算所需箍筋1、确定计算方法y a = ΣI y y iΣI y = 112 h f b f 3×12 h f +112 (h-h f )b 3×(h/2+h f /2)112 h f b f 3+112 (h-h f )b 3= 250 mm 每个吊车轮产生的扭矩: m t = 0.7[μP max ×0.02+T(y a +0.2)] = 1.53 kN ・m则支座截面产生的最大扭矩为:T = 1.4×m t ×(4-2B+2WLo ) = 4.65 kN ・m 构件截面信息腹板: W tw = b 2(3h-b)/6 = 8666666.66666667mm 3 翼缘: W tf = h f 2(b f '-b)/2 = 0mm 3W t = W tw + W tf = 8666666.66666667 mm 3 由混凝土规范7.6.1V bh 0 + T0.8W t= 1.1371 < 0.25βc f c = 3.575截面尺寸满足按弯剪扭共同作用的构件计算腹板受扭矩: T w = W twW t ×T = 4.650 kN ・m翼缘受扭矩: T f ' = W tfW t×T = 0.000 kN ・m2、腹板配筋计算A cor = b cor h cor = 67500 mm 2 u cor = 2×(b cor + h cor ) = 1200 mma.腹板受扭箍筋计算,按混凝土规范7.6.8:T = 0.35f t βt W t + 1.2ζ f yv A st1A cor sβt =1.51+0.5 VW tTbh 0= 0.93 A st1s = T w -0.35βt f t W tw1.2ζ f yv A cor= 0.032136 mm 2/mm b.腹板受剪箍筋计算,按混凝土规范7.6.8:A sv1s = V -0.7(1.5-βt )f t bh 01.25f yv h 0= 0.045301 mm 2/mm腹板所需单肢箍筋总面积为:A st1s + A sv1s= 0.0547865 mm 2/mm实际配置:8@100 满足c.腹板抗扭纵筋计算,按混凝土规范7.6.4-2:A stl = ζf yv A st1u corf y s= 23.14 mm 2 构造配置钢筋3、翼缘配筋计算b 'cor = b f - b - 50 = -50 mm h 'cor = h f - 50 = -50 mmA 'cor = b 'cor ×h 'cor = 2500 mm 2 U 'cor = 2(b 'cor + h 'cor ) = -200 mm a.翼缘抗扭箍筋计算,按混凝土规范7.6.8:A st1s = T f -0.35βt f t W tf1.2ζ f yv A cor= 0.000 mm 2/mm 实际配置:8@100 满足b.翼缘抗扭纵筋计算,按混凝土规范7.6.4-2:A stl = ζf yv A st1u corf y s= 0.00 mm 2 构造配置钢筋四、验算吊车梁疲劳强度(一)验算正截面疲劳强度1、验算受压区混凝土边缘纤维的应力 一台吊车产生的最大弯矩:由结构力学可判断,吊车轮按上述作用时才能产生绝对最大弯矩计算可得:合力R = 2×μ×Pmax = 26.25 kNa0 = B-W2= 0.15 m由自重在k点产生的弯矩:Mqk = qx2(Lo-x) = 16.82 kN・m由吊车荷载在k点产生的弯矩:Mpk = μP max(L0-a0)22L0= 38.06 kN・m总弯矩:M maxk = M qk + M pk= 54.88 kN・mαf E= E sE f c= 13.33先假定中和轴通过翼缘,换算截面的受压区高度:b2x02 - αfE A s(h0 - x0) = 0 公式见《钢筋混凝土结构计算手册》P624简化:Ax02 + Bx0 + C = 0 其中:A = 100B = 20593.2504C = -9266962.68解方程得:x0 = 218.39mm >h f = 0 mm 所以须按下列公式重新计算:b f2x02 - αfE A s(h0 - x0)-(b f - b)(x0 - h f)22= 0简化:Ax02 + Bx0 + C = 0 其中:A = 100B = 20593.2504C = -9266962.68 解方程得:x0 = 218.39mmI fo=h f x033-(b f - b)(x0 - h f)33+αfE A s(h0 - x0)2 = 1799083328.02ρfc=ρfcminρfcmax=MqkMqk+Mpk= 0.317589268845645查混凝土规范表4.1.6得: γρ = 0.86σf cmax = M f max x 0I fo = 6.662 < f fc = γρf c = 12.298满足要求 2、验算受拉钢筋的应力σf simin = αf E M f min (h 0-x 0)I f o = 30.342 N/mm 2σf simax = αf E M fmax (h 0-x 0)I f o = 65.196 N/mm 2Δσf si = σf simax - σfsimin = 34.854 N/mm 2 ρf s= σfsiminσfsimax = 0.465根据混凝土规范表4.2.5-1,可查得:Δf f y = 135 > Δσfsi = 34.854 满足要求(二)验算斜截面疲劳强度 1、验算中和轴处的主应力 计算从略2、验算弯起钢筋所需面积 计算从略五、验算吊车梁裂缝宽度σρsk = M maxk0.87h 0A s= 92.9862630983486 N/mm 2A te = 0.5bh = 50000 mm 2 ρte = A s /A te = 0.0308976d eq = Σn i d i 2Σn i νd i= 18.2222222222222 mmψ=1.1-0.65f tkρte σρsk= 0.645257156827881由混凝土规范8.1.2得: αcr = 2.1 c=20 ψ=1.0ωmax = αcr ψσρsk E s 1.9c+0.08d eqρte= 0.0536640377934194 < 0.2 满足规范要求六、验算吊车梁挠度由混凝土规范8.2.3:B s = E s A s h 021.15ψ+0.2+6αE ρ1+3.5γf'其中: ψ=1.0 αE = 13.33 E s = 200000 A s = 1544.88 h 0 = 430 γf ' = 0ρ= A sbh 0= 0.0171653333333333代入公式可得:B s = 27027886193474.9 由混凝土规范8.2.2:B = M kM q (θ-1)+M k B s其中: θ=1.6 M k = 38.06 M q = 16.82 代入公式可得:B = 21128148926726.3f=5qlo 4384B= 2.78964728702648f/Lo=1/1981 < 1/600 满足要求七、验算吊车梁配筋率计算从略。
10020t吊车梁计算探讨

10020t吊车梁计算探讨摘要:本文以抓斗起重机数据为基础,通过吊车梁内力计算,得出其参数设置,并基于此,从吊车刹车力、吊车梁剪力、吊车梁最大弯矩等不同角度,全面验算100/20t吊车承力数据,具有很实际的操作意义关键词:100/20t吊车梁参数设置承力数据1.吊车荷载资料抓斗起重机数据:吊车台数两台,中级工作制,小车重32.4t,大车轨距,大车轮距L=6100m,大车轮数4,吊车总重G=90.2t,最大轮压=389KN,最小轮压=78.5KN,选用轨道型号QU120,轨道自重1.2kN/m,轨道高度170mm。
2.吊车梁内力计算一、11m跨吊车梁计算1、支座处最大剪力计算:当吊车处于上图所示位置时支座A处剪力取得最大值:= + =1192KN考虑吊车梁自重:轨道自重1.2,梁自重(0.3×0.7+0.4×1.7)×25=22.25KN/m=23.45KN/m在支座处产生剪力: =L=129KN=1321KN考虑动力系数1.05,分项系数1.4则梁端最大剪力为:V=1321×1.05×1.4=1942KN2、吊车梁最大弯矩计算:当一台吊车在梁跨中时弯矩取得最大值,简图如下:则吊车荷载作用下最大弯矩为:=2567.4自重作用下产生的弯矩:=355考虑动力系数1.05,分项系数1.4=4296故吊车梁最大弯矩为: =4296综上所述吊车梁内力参数为:支座最大剪力: =1942KN绝对最大弯矩: =42963、截面配筋计算:初步估算,吊车梁截面采用T型截面:如下图,用C40混凝土,HRB335钢筋,考虑到受力钢筋会放两层或三层, 有效计算高度取2000-100=1900mm=4296×106/(700×19002)=1.7查表: =0.594%中和轴位置: ==177.3mm752.7KN,故需配置箍筋。
求得,实际配筋φ10@100。
吊车梁最大弯矩剪力计算
吊车梁最大弯矩点内力计算1.计算吊车梁的内力时,由于吊车荷载为动力荷载,首先应确定求各内力所需吊车荷载的最不利位置,再按此求梁的最大弯矩及其相应的剪力、支座最大剪力,以及横向水平荷载作用下在水平方向所产生的最大弯矩M T(当为制动梁时)或在吊车梁上翼缘的产生的局部弯矩M H(当为制动桁架时)。
2.常用简支吊车梁,当吊车荷载作用时,其最不利的荷载位置、最大剪矩和剪力,可按下列情况确定:(2)两个轮子作用于梁上时(图8‐4)最大弯矩点(C)的位置为:a2= a1/4最大弯矩为:(8‐6)最大弯矩处的相应剪力为:(8‐7)(2)三个轮子作用于梁上时(图8‐5)最大弯矩点(C)的位置为:最大弯矩为:(8‐8)最大弯矩处的相应剪力为:(8‐9)(3)四个轮子作用于梁上时(图8‐6)最大弯矩点(C)的位置为:最大弯矩为:(8‐10)最大弯矩处的相应剪力为:(8‐11)当时最大弯矩及其相应剪力均与公式(8‐10)及公式(8‐11)相同,但公式中的应用代入(4)六个轮子作用于梁上时(图8‐7):最大弯矩点(C)的位置为:最大弯矩为:(8‐12)最大弯矩处的相应剪力为:(8‐13)当及 时,最大弯矩点(C点)的位置为:其最大弯矩及相应剪力均与公式(8‐12)及公式(8‐13)相同,但公式中的应用代入(5)最大剪力应在梁端支座处。
因此,吊车竖向荷载应尽可能靠近该支座布置(图8‐4b)至图8‐7b),并按下式计算支座最大剪力:(8‐14)式中n—作用于梁上的吊车竖向荷载数。
选择吊车梁截面时所用的最大弯矩和支座最大剪力,可用吊车竖向荷载作用下所产生的最大弯矩和支座最大剪力乘以表8‐2的(为考虑吊车梁等自重的影响系数)值,即(8‐15)(8‐16)3.吊车横向水平荷载作用下,在水平方向所产生的最大弯矩,可根据图8‐4(a)至图8‐7(a)所示荷载位置采用下列公式计算:当为轻、中工作制(A1‐A5)吊车梁的制动梁时,(8‐17)当为重级或特重级工作制(A6‐A8)吊车梁的制动梁时,(8‐18)(2)吊车横向水平荷载作用下制动桁架在吊车梁翼缘所产生的局部弯矩可近似地按下列公式计算(图8‐8):当为起重量Q≥75t的轻、中级工作制吊车的制动桁架时(8‐19)当为起重量Q≥75t的重级工作制(特重级不受起重量限制)吊车的制动桁架时(8‐20)当为起重量Q≤50t的轻、中级工作制吊车的制动桁架时(8‐21)当为起重量Q≤50t的重级工作制(特重级不受起重量限制)吊车的制动桁架时 (8‐22)。
