RBF神经网络教程

合集下载

RBF神经网络：原理详解和MATLAB实现

RBF神经⽹络：原理详解和MATLAB实现RBF神经⽹络：原理详解和MATLAB实现——2020年2⽉2⽇⽬录RBF神经⽹络：原理详解和MATLAB实现 (1)⼀、径向基函数RBF (2)定义（Radial basis function——⼀种距离） (2)如何理解径向基函数与神经⽹络？ (2)应⽤ (3)⼆、RBF神经⽹络的基本思想（从函数到函数的映射） (3)三、RBF神经⽹络模型 (3)（⼀）RBF神经⽹络神经元结构 (3)（⼆）⾼斯核函数 (6)四、基于⾼斯核的RBF神经⽹络拓扑结构 (7)五、RBF⽹络的学习算法 (9)(⼀)算法需要求解的参数 (9)0.确定输⼊向量 (9)1.径向基函数的中⼼（隐含层中⼼点） (9)2.⽅差（sigma) (10)3.初始化隐含层⾄输出层的连接权值 (10)4.初始化宽度向量 (12)（⼆）计算隐含层第j 个神经元的输出值zj (12)（三）计算输出层神经元的输出 (13)（四）权重参数的迭代计算 (13)六、RBF神经⽹络算法的MATLAB实现 (14)七、RBF神经⽹络学习算法的范例 (15)（⼀）简例 (15)（⼆）预测汽油⾟烷值 (15)⼋、参考资料 (19)⼀、径向基函数RBF定义（Radial basis function——⼀种距离）径向基函数是⼀个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意⼀点c的距离，c点称为中⼼点，也就是Φ（x，c）=Φ(‖x-c‖)。

任意⼀个满⾜Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数。

标准的⼀般使⽤欧⽒距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。

在神经⽹络结构中，可以作为全连接层和ReLU层的主要函数。

⼀些径向函数代表性的⽤到近似给定的函数，这种近似可以被解释成⼀个简单的神经⽹络。

径向基函数在⽀持向量机中也被⽤做核函数。

常见的径向基函数有：⾼斯函数，⼆次函数，逆⼆次函数等。

径向基函数（RBF）神经网络

径向基函数（RBF）神经⽹络RBF⽹络能够逼近任意的⾮线性函数，可以处理系统内的难以解析的规律性，具有良好的泛化能⼒，并有很快的学习收敛速度，已成功应⽤于⾮线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。

简单说明⼀下为什么RBF⽹络学习收敛得⽐较快。

当⽹络的⼀个或多个可调参数（权值或阈值）对任何⼀个输出都有影响时，这样的⽹络称为全局逼近⽹络。

由于对于每次输⼊，⽹络上的每⼀个权值都要调整，从⽽导致全局逼近⽹络的学习速度很慢。

BP⽹络就是⼀个典型的例⼦。

如果对于输⼊空间的某个局部区域只有少数⼏个连接权值影响输出，则该⽹络称为局部逼近⽹络。

常见的局部逼近⽹络有RBF⽹络、⼩脑模型（CMAC）⽹络、B样条⽹络等。

径向基函数解决插值问题完全内插法要求插值函数经过每个样本点，即。

样本点总共有P个。

RBF的⽅法是要选择P个基函数，每个基函数对应⼀个训练数据，各基函数形式为，由于距离是径向同性的，因此称为径向基函数。

||X-X p||表⽰差向量的模，或者叫2范数。

基于为径向基函数的插值函数为：输⼊X是个m维的向量，样本容量为P，P>m。

可以看到输⼊数据点X p是径向基函数φp的中⼼。

隐藏层的作⽤是把向量从低维m映射到⾼维P，低维线性不可分的情况到⾼维就线性可分了。

将插值条件代⼊：写成向量的形式为，显然Φ是个规模这P对称矩阵，且与X的维度⽆关，当Φ可逆时，有。

对于⼀⼤类函数，当输⼊的X各不相同时，Φ就是可逆的。

下⾯的⼏个函数就属于这“⼀⼤类”函数：1）Gauss（⾼斯）函数2）Reflected Sigmoidal（反常S型）函数3）Inverse multiquadrics（拟多⼆次）函数σ称为径向基函数的扩展常数，它反应了函数图像的宽度，σ越⼩，宽度越窄，函数越具有选择性。

完全内插存在⼀些问题：1）插值曲⾯必须经过所有样本点，当样本中包含噪声时，神经⽹络将拟合出⼀个错误的曲⾯，从⽽使泛化能⼒下降。

RBF神经网络

的权向量为：W = [w , w
1
b j为节点的基宽度参数，且为大于零的数。网络为节点的基宽度参数，且为大于零的数。
2
⋯wj ⋯wm ]
k时刻网络的输出为：时刻网络的输出为：
y m ( k )=wh = w1h1+w 2 h2+ ⋯⋯ +w m hm
设理想输出为y(k)，设理想输出为y(k)，则性能指标函数为：
∂y (k ) ∂ym (k ) ≈ = ∂u (k ) ∂u (k )
m
∑w h
j =1
c1 j − x1 b2 j
j j
其中取 x1 = u(k) 。
6 RBF网络逼近仿真实例 RBF网络逼近仿真实例
使用RBF网络逼近下列对象：
y (k ) = u (k ) +
3
y ( k − 1) 1 + y ( k − 1)
Ii
wij
I
j
I1
. . .
R1
. . .
. .u .
u ..
R
j
. . .
1
1
.
V1
C1
. . .
j
j
.
Vj
.
u ..
Cj
i
i
.V
i
Ri
.
Ci
Hopfield网络模型 Hopfield网络模型
RBF神经网络 RBF神经网络
信息工程学院 Alen Fielding
1 RBF神经网络 RBF神经网络
径向基函数(RBF径向基函数(RBF-Radial Basis Function)神经网络 Function)神经网络是由J Moody和 Darken在80年代末提出的一种神经是由J.Moody和C.Darken在80年代末提出的一种神经网络,它是具有单隐层的三层前馈网络。网络,它是具有单隐层的三层前馈网络。由于它模拟了人脑中局部调整、相互覆盖接收域（或称感受野了人脑中局部调整、相互覆盖接收域（或称感受野Receptive Field）的神经网络结构，因此，RBF网络 Field）的神经网络结构，因此，RBF网络是一种局部逼近网络，是一种局部逼近网络，它能够以任意精度逼近任意连续函数，特别适合于解决分类问题。连续函数，特别适合于解决分类问题。

绝对经典RBF神经网络ppt课件

exp
1
2 i 2
X k ti
2
k 1,2,N;i 1,2,, I
该网络为局部逼近网络
RBF网络的工作原理
函数逼近：以任意精度逼近任一连续函数。一般函数都可表示成一组基函数的线性组合，RBF网络相当于用隐层单元的输出构成一组基函数，然后用输出层来进行线性组合，以完成逼近功能。
分类：解决非线性可分问题。RBF网络用隐层单元先将非线性可分的输入空间设法变换到线性可分的特征空间（通常是高维空间），然后用输出层来进行线性划分，完成分类功能。
j1
举1.问例题：的提R出：B假F设网如下络的输实入现输出函样本数，输逼入向近量为[-1 1] 区间上等间隔的数组成的向量P,相应的期望值向量为T。
P=-1:0.1:1; T=[-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609 0.1336 -
则扩展常数可取为
3.学权习值权的学值习可以用LMS学习算法
注意：①LMS算法的输入为RBF网络隐含层的输出
②RBF网络输出层的神经元只是对隐含层
神经元的输出加权和。
因此RBF网奇络异的矩实阵际或输非出方为阵Y的n矩阵不GnW n
其中 Y nXAXy=k存Aj ,在AnX逆,Ak矩=X阵1，,2则若, X称, N为; j 1,2, J
用用L伪M逆S方方法法A求求的解解伪pWi逆Wnv阵（n。AG）在1 D求ma伪Wtl逆aDnb中用d1X,n
e
dk
n
,
d
N
T
D为期望响应 G 是矩阵 G的伪逆
伪逆的求法 G G T G 1 G T

RBF（径向基）神经网络

RBF（径向基）神经⽹络只要模型是⼀层⼀层的，并使⽤AD/BP算法，就能称作 BP神经⽹络。

RBF 神经⽹络是其中⼀个特例。

本⽂主要包括以下内容：什么是径向基函数RBF神经⽹络RBF神经⽹络的学习问题RBF神经⽹络与BP神经⽹络的区别RBF神经⽹络与SVM的区别为什么⾼斯核函数就是映射到⾼维区间前馈⽹络、递归⽹络和反馈⽹络完全内插法⼀、什么是径向基函数 1985年，Powell提出了多变量插值的径向基函数（RBF）⽅法。

径向基函数是⼀个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意⼀点c的距离，c点称为中⼼点，也就是Φ（x，c）=Φ(‖x-c‖)。

任意⼀个满⾜Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数，标准的⼀般使⽤欧⽒距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。

最常⽤的径向基函数是⾼斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)^2) } 其中x_c为核函数中⼼,σ为函数的宽度参数 , 控制了函数的径向作⽤范围。

⼆、RBF神经⽹络 RBF神将⽹络是⼀种三层神经⽹络，其包括输⼊层、隐层、输出层。

从输⼊空间到隐层空间的变换是⾮线性的，⽽从隐层空间到输出层空间变换是线性的。

流图如下： RBF⽹络的基本思想是：⽤RBF作为隐单元的“基”构成隐含层空间，这样就可以将输⼊⽮量直接映射到隐空间，⽽不需要通过权连接。

当RBF的中⼼点确定以后，这种映射关系也就确定了。

⽽隐含层空间到输出空间的映射是线性的，即⽹络的输出是隐单元输出的线性加权和，此处的权即为⽹络可调参数。

其中，隐含层的作⽤是把向量从低维度的p映射到⾼维度的h，这样低维度线性不可分的情况到⾼维度就可以变得线性可分了，主要就是核函数的思想。

这样，⽹络由输⼊到输出的映射是⾮线性的，⽽⽹络输出对可调参数⽽⾔却⼜是线性的。

⽹络的权就可由线性⽅程组直接解出，从⽽⼤⼤加快学习速度并避免局部极⼩问题。

径向基神经网络学习算法(RBF)

径向基神经网络及其算法
Mezer chen 2018.5.9
RBF简介
1989年，Moody和Darken提出了一种由两个阶段组成的混合学习过程的思路。
①无监督的自组织学习阶段 ②有监督学习阶段
其任务是用自组织聚类方法为隐层节点的径向基函数确定合适的数据中心，并根据各中心之间的距离确定隐节点的扩展常数。一般采用Duda和Hart1973年提出的k-means聚类算法。
其任务是用有监督学习算法训练输出层权值，一般采用梯度法进行训练。
RBF网络的工作原理
RBF网络特点
只有一个隐含层，且隐层神经元与输出层神经元的模型不同。隐层节点激活函数为径向基函数，输出层节点激活函数为线性函数。隐层节点激活函数的净输入是输入向量与节点中心的距离（范数）而非向量内积，且节点中心不可调。隐层节点参数确定后，输出权值可通过解线性方程组得到。隐层节点的非线性变换把线性不可分问题转化为线性可分问题。局部逼近网络（MLP是全局逼近网络)，这意味着逼近一个输入输出映射时，在相同逼近精度要求下，RBF所需的时间要比MLP少。具有唯一最佳逼近的特性，无局部极小。合适的隐层节点数、节点中心和宽度不易确定。
RBF神经网络中心选取
① 从样本输入中选取中心
一般来说，样本密集的地方中心点可以适当多些，样本稀疏的地方中心点可以少些；若数据本身是均匀分布的，
中心点也可以均匀分布。总之，选出的数据中心应具有代
表性。径向基函数的扩展常数是根据数据中心的散布而确定的，为了避免每个径向基函数太尖或太平，一种选择方法是将所有径向基函数的扩展常数设为
d max 2I
② 自组织选取中心法
常采用各种动态聚类算法对数据中心进行自组织选择，在

神经网络配套ppt RBF(2)

6
5
RBF网络实现内插问题
• 内插问题（数值逼近）
– 给定样本数据：{p 1, t1} , { p 2, t 2} , …, {p Q, tQ } – 寻找函数，使之满足：ti = F (Pi ) ，1 ≤ i ≤ Q
• RBF网络解决内插问题
– – – – 网络隐层使用Ｑ个隐节点把所有Ｑ个样本输入分别作为Ｑ个隐节点的数据中心各基函数取相同的扩展常数确定权值可解线性方程组：
∑ w radbas( P − P
j =1 j i

j
) = ti
1≤ i ≤ Q
设第j 个隐节点在第i个样本的输出为： = radbas( Pi − Pj ) , rij Rw 可矩阵表示： = t，若R可求逆，则解为：w = R −1t 。根据Micchelli定理可得，如果隐节点激活函数采用径向基函数，且P , P2 ,..., PQ 各不相同，则线性方程组有唯一解。 1
RBF网络是个三层结构（Ｒ-S1-S2）的前馈网，其中，Ｒ代表输入层并指出输入维数； S1代表由径向基神经元构成的隐层并指出神经元数目； S2是线性输出层。
4
5
RBF网络结构
• RBF网络层间的连接
– 输入层到隐层之间的权值（数据中心）固定。 – 隐层到输出层之间的权值可调。
5
5
RBF网络工作原理
9
5
正则化方法（改进泛化性能）
– 设有样本数据:{p 1, t1} , { p 2, t 2} , … , {p Q, tQ }, F(P)是逼近函数。 – 传统方法是最小化标准误差项来实现 1 Q E S ( F ) = ∑ (t i − F (Pi )) 2 2 i =1 – 由于从有限样本导出一个函数的解有无穷多个，该问题是不适定的(ill-posed)。Tikhonov提出了正则化方法来解决这类问题。就是在标准误差项的基础上，增加一个限制逼近函数复杂性的项（称为正则化项），即 1 2 E C ( F ) = DF 2 其中，D是线性微分算子，关于解F(p)的形式的先验知识就包含在其中，即D的选取与所解的问题有关。 D也称为稳定因子，它使正则化问题的解稳定光滑，从而连续。

径向基神经网络学习算法

径向基神经网络学习算法径向基神经网络（Radial Basis Function Neural Network, RBF）是一种人工神经网络，常用于模式识别、函数逼近和分类问题等。

它的核心思想是利用径向基函数对输入数据进行映射，并通过训练来优化网络参数。

本文将介绍径向基神经网络的学习算法，并解释其算法步骤。

以下是径向基神经网络学习算法的步骤：1.数据预处理：将原始数据划分为训练集和测试集。

通常，训练集用于训练网络参数，而测试集用于评估网络性能。

2. 参数初始化：初始化径向基函数的中心和宽度，通常可以使用聚类算法（如K-means）对训练集进行聚类，其中每个聚类中心作为一个径向基函数的中心。

宽度可以根据聚类结果设置为聚类中心之间的最大距离。

3.训练隐含层权重：对于每个训练样本，计算其到每个径向基函数中心的距离，并将距离作为隐含层神经元的输入。

可以选择不同的径向基函数，常用的包括高斯函数和多项式函数。

然后，通过解线性回归问题，以最小化误差来调整隐含层的权重。

5.网络评估：使用测试集评估网络性能。

可以使用各种指标（如精确度、召回率和均方根误差）来评估网络的准确性和鲁棒性。

径向基神经网络的优点是可以处理非线性问题，并且在训练过程中可以进行参数的在线调整。

此外，它还避免了梯度消失问题。

然而，径向基神经网络也有一些缺点，如需要选择合适的径向基函数和确定合适的隐含层神经元数量。

在实际应用中，径向基神经网络在模式识别、函数逼近和分类问题等方面取得了很多成功。

它可以用于人脸识别、语音识别、股票预测和异常检测等领域。

总之，径向基神经网络是一种有效的学习算法，可以用于解决非线性问题。

通过合适的参数初始化和训练过程，它可以准确地拟合数据，并在实际应用中获得良好的性能。

神经网络控制RBF

神经网络控制RBF神经网络是一种模拟人脑处理信息的计算模型，可以通过学习数据来预测和控制各种系统。

在控制领域，神经网络已经被广泛应用，很多控制问题可以通过神经网络来实现优化控制。

而基于类RBF（径向基函数）神经网络的控制方法也得到广泛的研究和应用，该方法是一种自适应控制方法，可以处理非线性系统，具有一定的理论和实际应用价值。

1. RBF神经网络控制方法RBF神经网络是一种前馈神经网络，由输入层、隐层和输出层组成。

其中，输入层接受外界输入，隐层包含一组RBF神经元，其作用是将输入空间划分为若干子空间，并将每个子空间映射到一个神经元上。

输出层是线性层，负责将隐层输出进行线性组合，输出控制信号。

在控制系统中，RBF神经元用于计算控制信号，从而实现控制目标。

RBF神经网络的训练包括两个阶段：聚类和权重调整。

聚类过程将输入空间划分成若干个类别，并计算出每个类别的中心和半径。

聚类算法的目标是使得同一类别内的样本距离聚类中心最小，不同类别之间距离最大。

常用的聚类算法包括k-means算法和LVQ算法。

权重调整过程将隐层神经元的权重调整到最优状态，以便将隐层输出映射到目标输出。

在实际控制中，RBF神经网络控制方法应用较为广泛，可以替代PID控制器等传统控制方法，具有良好的鲁棒性、自适应能力和较好的控制性能。

2. 基于RBF神经网络的控制方法RBF神经网络控制方法广泛应用于各种领域的控制任务，特别是在非线性系统控制中具有重要的应用价值。

基于RBF神经网络的控制方法主要包括以下两种：（1）虚拟控制策略：将系统建模为线性结构和非线性结构两部分，其中线性结构可以采用传统的控制方法进行控制，而非线性结构则采用基于RBF神经网络的控制方法进行控制。

虚拟控制策略的优点是可以将传统控制和RBF神经网络控制各自的优势融合起来，减小系统的复杂度和计算量。

（2）基于反馈线性化的控制策略：利用反馈线性化的方法将非线性系统变为一个可控的线性系统，从而可以采用传统线性控制方法进行控制。

RBF、GRNN和PNN神经网络

课程目录⏹第一课MATLAB入门基础⏹第二课MATLAB进阶与提高⏹第三课BP神经网络⏹第四课RBF、GRNN和PNN神经网络⏹第五课竞争神经网络与SOM神经网络⏹第六课支持向量机（Support Vector Machine, SVM）⏹第七课极限学习机（Extreme Learning Machine, ELM）⏹第八课决策树与随机森林⏹第九课遗传算法（Genetic Algorithm, GA）⏹第十课粒子群优化（Particle Swarm Optimization, PSO）算法⏹第十一课蚁群算法（Ant Colony Algorithm, ACA）⏹第十二课模拟退火算法（Simulated Annealing, SA）⏹第十三课降维与特征选择RBF 神经网络概述• A radial basis function network is an artificial neural network that uses radial basis functions as activation functions.•It is a linear combination of radial basis functions.输入层隐含层输出层1,1IW 1b 2,1LW 2b p 1n 1a 2n 2a y =1R ⨯1S R⨯11S ⨯21S S ⨯21S ⨯2S 1S R 11,11()a radbas IW p b =-212,12()a purelin LW ab =+dist ∙*11S ⨯11S ⨯11S ⨯21S ⨯21S ⨯Problem•Assume that each case in the training set has two predictor variables, x and y.•Also assume that the target variable has two categories, positive which is denoted by a square and negative which is denoted by a dash.•suppose we are trying to predict the value of a new case represented by the triangle withpredictor values x=6, y=5.1.•Should we predict the target as positive or negative?• A generalized regression neural network (GRNN) is often used for function approximation. •It has a radial basis layer and a special linear layer.•It is similar to the radial basis network, but has a slightly different second layer.•The first layer is just like that for newrbe networks. It has as many neurons as there are input/ target vectors in P. The first-layer weights are set to P'. The bias b1 is set to a column vector of 0.8326/SPREAD.•The second layer also has as many neurons as input/target vectors, but here LW{2,1} is set to T.•Suppose you have an input vector p close to p i, one of the input vectors among the input vector/target pairs. This input p produces a layer 1 a i output close to 1. This leads to a layer 2 output close to t i.•Here the nprod box shown below (code function normprod) produces S2 elements in vector n2. Each element is the dot product of a row of LW2,1 and the input vector a1, all normalized by the sum of the elements of a1.• A larger spread leads to a large area around the input vector where layer 1 neurons will respond with significant outputs.•If spread is small, the radial basis function is very steep, so that the neuron with the weight vector closest to the input will have a much larger output than other neurons.•If spread becomes larger, the radial basis function's slope becomes smoother and several neurons can respond to an input vector. The network then acts as if it is taking a weighted average between target vectors whose design input vectors are closest to the new input vector.•The first-layer input weights, IW1,1 (net.IW{1,1}), are set to the transpose of the matrix formed from the Q training pairs, P'.•The second-layer weights, LW1,2 (net.LW{2,1}), are set to the matrix T of target vectors. Each vector has a1 only in the row associated with that particular class of input, and 0's elsewhere. (Use function ind2vecto create the proper vectors.)•newrbe–Design exact radial basis network–net = newrbe(P,T,spread)•newgrnn–Design generalized regression neural network–net = newgrnn(P,T,spread)•newpnn–Design probabilistic neural network–net = newpnn(P,T,spread)•cputime–Elapsed CPU time•round(ceil、fix、floor)–Round to nearest integer–Y = round(X)•length(size)– Length of vector– n = length(X)•find–Find indices and values of nonzero elements–[row,col] = find(X, ...)•.* ./ .\ .^ …… vs * / \ ^ ……– Multiplication (.*) right division (./) left division (.\) power (.^)–matrix multiplication (*) matrix right division (/) matrix left division (\) matrix power (^)案例分析RBF——近红外光谱汽油辛烷值预测GRNN、PNN——鸢尾花种类识别炼数成金逆向收费式网络课程⏹Dataguru（炼数成金）是专业数据分析网站，提供教育，媒体，内容，社区，出版，数据分析业务等服务。

RBF神经网络

RBF神经网络科学计算与数据处理实验报告S312060007 毛施平学姓名号实验RBF神经网络的非线性映射名称1、深入研究MATLAB在神经网络方面的应用实2、熟悉MATLAB中专业级Toolbox或Simulink的功能和用法验3、学会综合运用MATLAB解决神经网络方面的问题。

目的一、背景知识: 实神经网络本质上是一个大规模非线性连续时间自适应的信息处理系统, 通过大量验简单关系连接实现复杂的函数关系。

系统具有很强的鲁棒性和容错性, 善于联想、概括、类比和推广, 有很强的自学习能力, 可在学习过程中不断完善自己, 不断创新。

神方经网络模式识别理论的研究一直是非常活跃的学科, 其发展与神经网络理论可以说是案同步。

RBF(Radial basis function)网络是最早可能是Krige ,他在1951 年把矿藏的沉积看成是一个各向同性的稳定的随机函数的实现. 从而导出了广泛应用于矿藏分析的Kriging 方法。

1971 年Hardy 用径向基函数Multi-Quadric来处理飞机外形设计曲面拟合问题, 取得了非常好的效果。

1975 年Duchon 从样条弯曲能最小的理论出发导出了多元问题的薄板样条. 这些从不同领域导出的方法, 事实上都是径向基函数的插值方法,二、BP学习过程1、首先确定基函数的中心点和宽度2、其次是权值的学习本示例程序采用2层网络，隐层为径向基神经元,输出层为线性神经元，应用newrb()函数构建径向基网络，预先设定均方差精度eg以及散布常数sc，本例中eg为0.02，sc为1,。

应用grnn进行函数逼近，应用pnn进行变量的分类，使用离散的数据点，通过更改输入变量进行网络测试，就可以模拟具有很好的非线性映射能力的RBF神经网络。

三、实验步骤:1、通过工具箱Toolbox函数newrb()函数构建径向基网络2、通过改变输入值来获得不同的神经映射网络，来体会RBF神经网络的非线性映射能力。

RBF、GRNN、PNN神经网络学习笔记

RBF、GRNN、PNN神经⽹络学习笔记RBF神经⽹络：径向基函数神经⽹络（Radical Basis Function）GRNN神经⽹络：⼴义回归神经⽹络（General Regression Neural Network）PNN神经⽹络:概率神经⽹络（Probabilistic Neural Network）径向基函数神经⽹络的优点：逼近能⼒，分类能⼒和学习速度等⽅⾯都优于BP神经⽹络，结构简单、训练简洁、学习收敛速度快、能够逼近任意⾮线性函数，克服局部极⼩值问题。

原因在于其参数初始化具有⼀定的⽅法，并⾮随机初始化（见习下⾯的代码）。

⾸先我们来看RBF神经⽹络隐藏层中神经元的变换函数即径向基函数是对中⼼点径向对称且衰减的⾮负线性函数，该函数是局部响应函数，具体的局部响应体现在其可见层到隐藏层的变换，跟其它的⽹络不同。

RBF神经⽹络的基本思想：⽤RBF（径向基函数）作为隐单元的“基”构成隐藏层空间，隐藏层对输⼊⽮量进⾏变换，将低维的模式输⼊数据变换到⾼维空间内，使得在低维空间内的线性不可分问题在⾼维空间内线性可分。

详细⼀点就是⽤RBF的隐单元的“基”构成隐藏层空间，这样就可以将输⼊⽮量直接(不通过权连接)映射到隐空间。

当RBF的中⼼点确定以后，这种映射关系也就确定了。

⽽隐含层空间到输出空间的映射是线性的(注意这个地⽅区分⼀下线性映射和⾮线性映射的关系)，即⽹络输出是因单元输出的线性加权和，此处的权即为⽹络可调参数。

《模式识别与只能计算》中介绍：径向基⽹络传递函数是以输⼊向量与阈值向量之间的距离|| X-Cj ||作为⾃变量的，其中|| X -Cj ||是通过输⼊向量和加权矩阵C的⾏向量的乘积得到。

此处的C就是隐藏层各神经元的中⼼参数，⼤⼩为(隐层神经元数⽬*可见层单元数)。

再者，每⼀个隐神经元中⼼参数C都对应⼀个宽度向量D，使得不同的输⼊信息能被不同的隐层神经元最⼤程度地反映出来。

得到的这个R就是隐藏层神经元的值。

神经网络控制(RBF)

生物神经元的信息传递与处理1720生物神经元的基本特征神经元具有感知外界信息或其它神经元信息的输入端神经元具有向外界或其它神经元输出信息的输出端神经元之间的连接强度连接权决定信号传递的强弱而且联接强度是可以随训练改变的信号可以是起刺激作用的也可以是起抑制作用的每个神经元有一个阀值神经元可以对接受的信号进行累积加权神经元的兴奋程度输出值的大小取决于其传输函数及其输入输入信号的加权与阈值之和13基本概念1820人工神经元的一般模型13基本概念1920神经网络的结构人工神经网络是以工程技术手段来模拟人脑神经元网络的结构与特性的系统
17/20
1.3 基本概念生物神经元的基本特征
神经元具有感知外界信息或其它神经元信息的输入端神经元具有向外界或其它神经元输出信息的输出端神经元之间的连接强度（连接权）决定信号传递的强弱，而且联接强度是可以随训练改变的信号可以是起刺激作用的，也可以是起抑制作用的，即连接权的值（权值）可正、可负每个神经元有一个阀值神经元可以对接受的信号进行累积（加权）神经元的兴奋程度（输出值的大小），取决于其传输函数及其输入（输入信号的加权与阈值之和）
4/20
1.1 概述
神经细胞利用电-化学过程交换信号。输入信号来自另一些神经细胞。这些神经细胞的轴突末梢（也就是终端）和本神经细胞的树突相遇形成突触（synapse），信号就从树突上的突触进入本细胞。信号在大脑中实际怎样传输是一个相当复杂的过程，但就我们而言，重要的是把它看成和现代的计算机一样，利用一系列的0和1来进行操作。就是说，大脑的神经细胞也只有两种状态：兴奋（fire）和不兴奋（即抑制）。发射信号的强度不变，变化的仅仅是频率。神经细胞利用一种我们还不知道的方法,把所有从树突上突触进来的信号进行相加，如果全部信号的总和超过某个阀值，就会激发神经细胞进入兴奋（fire）状态，这时就会有一个电信号通过轴突发送出去给其他神经细胞。如果信号总和没有达到阀值，神经细胞就不会兴奋起来。这样的解释有点过分简单化，但已能满足我们的目的。。

6.4基于RBF网络辨识的自校正控制

RBF网络自校正控制程序为chap6_5.m
本方法的局限性
• 由于采用梯度下降法调节网络的权值，无法保证控制系统的稳定性和收敛性。
yk 1 gyk ykuk
其中 u ，y 分别为对象的输入、输出，• 为非
零函数。
若 g• ，• 已知，根据“确定性等价原
则”，控制器的控制算法为：
u(k)
g• •
rk 1
•
若 g• ，• 未知，则通过在线训练神经网
络辨识器，由辨识器结果Ng• 、N•代替 g•、• ，控制器的控制算法为：
u(k
网络的径向基向量为 H h1, , hm T ，h j 为高斯
基函数：
hj
exp(-
yk- C j
2b
2 j
2
)
其中 j 1,, m 。 b j 为节点 j 的基宽度参数，bj 0
，C j 为网络第 j 个结点的中心矢量，
，。 C j c11,, c1m
B b1, , bm T
神经间接自校正控制结构如下图所示，它由两个回路组成：
（1）自校正控制器与被控对象构成的反馈回路。
（2）神经网络辩识器与控制器设计，以得到控制器的参数。
辩识器的在线设计是自校正控制实现的关键。
控制器设计
自校正控制器
神经网络辩识器
被控对象
图1 神经网络间接自校正控制框图
自校正控制算法考虑被控对象：
)
Ng• N•
rk 1
N•
用于辨识的神经网络采用RBF网络实现，网络的权值采用梯度下降法来调节。
RBF网络自校正控制算法
采用两个RBF网络分别实现未知项g• 、•的辨识。RBF网络辨识器的结构如图2所示， W和 V 分别为两个神经网络的权值向量。

绝对经典RBF神经网络

1
RBF学习算法
RBF学习的三个参数：①基函数的中心 t i ②方差（扩展常数） i ③隐含层与输出层间的权值 wij 当采用正归化RBF网络结构时，隐节点数即样本数，基函数的数据中心即为样本本身，参数设计只需考虑扩展常数和输出节点的权值。
当采用广义RBF网络结构时，RBF网络的学习算法应该解决的问题包括：如何确定网络隐节点数，如何确定各径向基函数的数据中心及扩展常数，以及如何修正输出权值。
2I
2.中心自组织选取
常采用各种动态聚类算法对数据中心进行自组织选择，在学习过程中需对数据中心的位置进行动态调节。常用的方法是K-means聚类，其优点是能根据各聚类中心之间的距离确定各隐节点的扩展常数。由于RBF网的隐节点数对其泛化能力有极大的影响，所以寻找能确定聚类数目的合理方法，是聚类方法设计RBF网时需首先解决的问题。除聚类算法外，还有梯度训练方法、资源分配网络(RAN)等
i i
G ( P C1
p1 p2
pQ
G( P C2
w2
w1

F P
wQ
G( P CQ )
1.网络隐层使用Ｑ个隐节点。 2.把所有Ｑ个样本输入分别作为Ｑ个隐节点的中心。 3.各基函数取相同的扩展常数。 4.确定权值可解线性方程组：
w G(
j j 1
Q
pi p j ) t i 1 i Q
径向基函数（RBF）
1.
2 r Gauss（高斯）函数： r exp 2 2

2. 反演S型函数： r
1 r2 1 exp 2
1
3. 拟多二次函数：
r

RBF神经网络：原理详解和MATLAB实现

RBF神经网络：原理详解和MATLAB实现——2020年2月2日目录RBF神经网络：原理详解和MATLAB实现 (1)一、径向基函数RBF (2)定义（Radial basis function——一种距离） (2)如何理解径向基函数与神经网络？ (2)应用 (3)二、RBF神经网络的基本思想（从函数到函数的映射） (3)三、RBF神经网络模型 (3)（一）RBF神经网络神经元结构 (3)（二）高斯核函数 (6)四、基于高斯核的RBF神经网络拓扑结构 (7)五、RBF网络的学习算法 (9)(一)算法需要求解的参数 (9)0.确定输入向量 (9)1.径向基函数的中心（隐含层中心点） (9)2.方差（sigma) (10)3.初始化隐含层至输出层的连接权值 (10)4.初始化宽度向量 (12)（二）计算隐含层第j 个神经元的输出值zj (12)（三）计算输出层神经元的输出 (13)（四）权重参数的迭代计算 (13)六、RBF神经网络算法的MATLAB实现 (14)七、RBF神经网络学习算法的范例 (15)（一）简例 (15)（二）预测汽油辛烷值 (15)八、参考资料 (19)一、径向基函数RBF定义（Radial basis function——一种距离）径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。

任意一个满足Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数。

标准的一般使用欧氏距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。

在神经网络结构中，可以作为全连接层和ReLU层的主要函数。

如何理解径向基函数与神经网络？一些径向函数代表性的用到近似给定的函数，这种近似可以被解释成一个简单的神经网络。

径向基函数在支持向量机中也被用做核函数。

常见的径向基函数有：高斯函数，二次函数，逆二次函数等。

RBF神经网络学习算法

RBF神经网络学习算法RBF（径向基函数）神经网络是一种常用的神经网络模型，其学习算法主要分为两个步骤：网络初始化和参数优化。

本篇文章将详细介绍RBF 神经网络学习算法的原理和步骤。

1.网络初始化（1）选择隐藏层神经元的个数隐藏层神经元的个数决定了网络的复杂度。

一般情况下，隐藏层神经元的个数越多，网络的拟合能力越强。

但是隐藏层神经元个数的选择也受限于样本的数量和特征维度。

（2）选择径向基函数径向基函数用于将输入样本映射到隐藏层，常用的径向基函数有高斯函数、多项式函数等。

高斯函数是最常用的径向基函数，其具有良好的非线性映射性质。

选择合适的径向基函数如高斯函数可以提高网络的拟合能力。

（3）确定径向基函数的参数高斯函数有一个重要参数σ，控制了函数的宽度。

确定适当的σ值可以使得网络在训练过程中收敛更快，提高网络的学习效率。

2.参数优化（1）梯度下降法梯度下降法是一种常用的优化方法，通过不断迭代网络参数来最小化误差函数。

具体步骤如下：a.随机初始化网络的权值和偏置。

b.使用前向传播计算网络的输出。

d.根据误差计算参数的梯度。

e.根据梯度和学习率更新参数。

f.重复b-e直到满足停止准则。

（2）最小二乘法最小二乘法是一种基于最小化误差平方和的优化方法。

具体步骤如下：a.设置误差函数为平方和。

b.对误差函数求偏导，并令导数为0，得到参数的闭式解。

c.使用闭式解更新参数。

3.网络训练与预测（1）网络训练（2）网络预测网络预测是指使用训练好的网络来进行新样本的预测。

给定新样本的特征向量，通过前向传播计算网络的输出，即为网络对该样本的预测结果。

总结：本文首先介绍了RBF神经网络的基本原理和结构，然后详细描述了RBF神经网络的学习算法。

网络初始化包括选择隐藏层神经元个数、径向基函数和参数的确定。

参数优化主要通过梯度下降法和最小二乘法来优化网络的参数。

最后，本文介绍了网络训练和预测的过程。

通过合理选择网络结构和参数，RBF神经网络可以有效地处理非线性问题，具有很好的拟合能力和预测能力。

RBF网络

RBF 网络的学习过程与BP 网络的学习过程类似,两者的主要区别在于各使用不同的作用函数.BP 网络中隐层使用的是Sigmoid 函数,其值在输入空间中无限大的范围内为非零值，因而是一种全局逼近的神经网络；而RBF 网络中的作用函数是高斯基函数，其值在输入空间中有限范围内为非零值，因而RBF 网络是局部逼近的神经网络。

理论上，3层以上的BP 网络能够逼近任何一个非线性函数，但由于BP 网络是全局逼近网络，每一次样本学习都要重新调整网络的所有权值，收敛速度慢，易于陷入局部极小，很难满足控制系统的高度实时性要求.RBF 网络是一种3层前向网络，由输入到输出的映射是非线性的，而隐层空间到输出空间的映射是线性的，而且RBF 网络是局部逼近的神经网络,因而采用RBF 网络可大大加快学习速度并避免局部极小问题,适合于实时控制的要求。

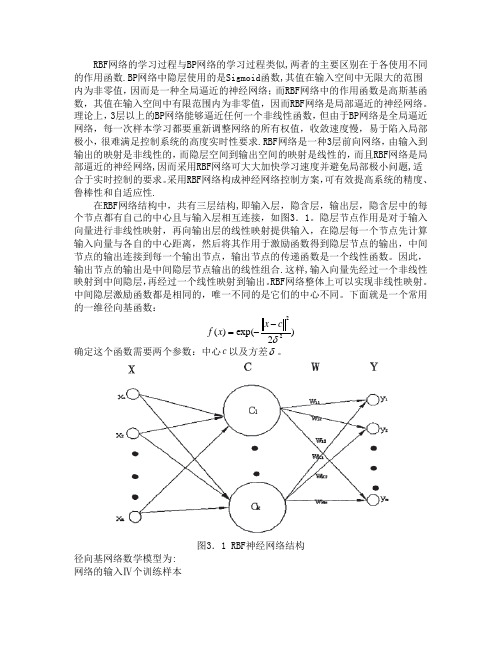
采用RBF 网络构成神经网络控制方案，可有效提高系统的精度、鲁棒性和自适应性.在RBF 网络结构中，共有三层结构,即输入层，隐含层，输出层，隐含层中的每个节点都有自己的中心且与输入层相互连接，如图3．1。

隐层节点作用是对于输入向量进行非线性映射，再向输出层的线性映射提供输入，在隐层每一个节点先计算输入向量与各自的中心距离，然后将其作用于激励函数得到隐层节点的输出，中间节点的输出连接到每一个输出节点，输出节点的传递函数是一个线性函数。

因此，输出节点的输出是中间隐层节点输出的线性组合.这样,输入向量先经过一个非线性映射到中间隐层，再经过一个线性映射到输出。

RBF 网络整体上可以实现非线性映射。

中间隐层激励函数都是相同的，唯一不同的是它们的中心不同。

下面就是一个常用的一维径向基函数：)2exp()(22δc x x f --=确定这个函数需要两个参数：中心c 以及方差δ。

图3．1 RBF 神经网络结构径向基网络数学模型为:网络的输入Ⅳ个训练样本{}km k k k x x x X ,....,21=(N k ,...2,1=）网络对应的输出：{}km k k k y y y Y ,...,21= （N k ,...2,1=）网络输出连接权系数构成连接矩阵：}{,,..2,1,,...2,1,,J j I i j i W ===隐层节点个数I,中心点:{i C } I i ,...2,1= 方差i δ网络输入输出之间的关系：221)21exp()(i k i I i ij k kj C X w X y --=∑=δRBF 网络逼近的性能指标函数为：)(k E =2)]([21k kj k X y Y - 3．2 RBF 神经网络的性能改进3．2．1 RBF 神经网络训练数据的预处理1．进行数据预处理的原因对于使用有教师训练算法的前向神经网络，训练样本的质量对网络的性能非常重要.RBF 神经网络是一种局部网络，只有在隐含层节点中心的一定范围内的点才会使网络产生一定的输出。

Python实现的径向基（RBF）神经网络示例

Python实现的径向基（RBF）神经⽹络⽰例本⽂实例讲述了Python实现的径向基（RBF）神经⽹络。

分享给⼤家供⼤家参考，具体如下：from numpy import array, append, vstack, transpose, reshape, \dot, true_divide, mean, exp, sqrt, log, \loadtxt, savetxt, zeros, frombufferfrom numpy.linalg import norm, lstsqfrom multiprocessing import Process, Arrayfrom random import samplefrom time import timefrom sys import stdoutfrom ctypes import c_doublefrom h5py import Filedef metrics(a, b):return norm(a - b)def gaussian (x, mu, sigma):return exp(- metrics(mu, x)**2 / (2 * sigma**2))def multiQuadric (x, mu, sigma):return pow(metrics(mu,x)**2 + sigma**2, 0.5)def invMultiQuadric (x, mu, sigma):return pow(metrics(mu,x)**2 + sigma**2, -0.5)def plateSpine (x,mu):r = metrics(mu,x)return (r**2) * log(r)class Rbf:def __init__(self, prefix = 'rbf', workers = 4, extra_neurons = 0, from_files = None):self.prefix = prefixself.workers = workersself.extra_neurons = extra_neurons# Import partial modelif from_files is not None:w_handle = self.w_handle = File(from_files['w'], 'r')mu_handle = self.mu_handle = File(from_files['mu'], 'r')sigma_handle = self.sigma_handle = File(from_files['sigma'], 'r')self.w = w_handle['w']self.mu = mu_handle['mu']self.sigmas = sigma_handle['sigmas']self.neurons = self.sigmas.shape[0]def _calculate_error(self, y):self.error = mean(abs(self.os - y))self.relative_error = true_divide(self.error, mean(y))def _generate_mu(self, x):n = self.nextra_neurons = self.extra_neurons# TODO: Make reusablemu_clusters = loadtxt('clusters100.txt', delimiter='\t')mu_indices = sample(range(n), extra_neurons)mu_new = x[mu_indices, :]mu = vstack((mu_clusters, mu_new))return mudef _calculate_sigmas(self):neurons = self.neuronsmu = self.musigmas = zeros((neurons, ))for i in xrange(neurons):dists = [0 for _ in xrange(neurons)]for j in xrange(neurons):if i != j:dists[j] = metrics(mu[i], mu[j])sigmas[i] = mean(dists)* 2# max(dists) / sqrt(neurons * 2))return sigmasdef _calculate_phi(self, x):C = self.workersneurons = self.neuronsmu = self.musigmas = self.sigmasphi = self.phi = Nonen = self.ndef heavy_lifting(c, phi):s = jobs[c][1] - jobs[c][0]for k, i in enumerate(xrange(jobs[c][0], jobs[c][1])):for j in xrange(neurons):# phi[i, j] = metrics(x[i,:], mu[j])**3)# phi[i, j] = plateSpine(x[i,:], mu[j]))# phi[i, j] = invMultiQuadric(x[i,:], mu[j], sigmas[j]))phi[i, j] = multiQuadric(x[i,:], mu[j], sigmas[j])# phi[i, j] = gaussian(x[i,:], mu[j], sigmas[j]))if k % 1000 == 0:percent = true_divide(k, s)*100print(c, ': {:2.2f}%'.format(percent))print(c, ': Done')# distributing the work between 4 workersshared_array = Array(c_double, n * neurons)phi = frombuffer(shared_array.get_obj())phi = phi.reshape((n, neurons))jobs = []workers = []p = n / Cm = n % Cfor c in range(C):jobs.append((c*p, (c+1)*p + (m if c == C-1 else 0)))worker = Process(target = heavy_lifting, args = (c, phi))workers.append(worker)worker.start()for worker in workers:worker.join()return phidef _do_algebra(self, y):phi = self.phiw = lstsq(phi, y)[0]os = dot(w, transpose(phi))return w, os# Saving to HDF5os_h5 = os_handle.create_dataset('os', data = os)def train(self, x, y):self.n = x.shape[0]## Initialize HDF5 cachesprefix = self.prefixpostfix = str(self.n) + '-' + str(self.extra_neurons) + '.hdf5'name_template = prefix + '-{}-' + postfixphi_handle = self.phi_handle = File(name_template.format('phi'), 'w')os_handle = self.w_handle = File(name_template.format('os'), 'w')w_handle = self.w_handle = File(name_template.format('w'), 'w')mu_handle = self.mu_handle = File(name_template.format('mu'), 'w')sigma_handle = self.sigma_handle = File(name_template.format('sigma'), 'w') ## Mu generationmu = self.mu = self._generate_mu(x)self.neurons = mu.shape[0]print('({} neurons)'.format(self.neurons))# Save to HDF5mu_h5 = mu_handle.create_dataset('mu', data = mu)## Sigma calculationprint('Calculating Sigma...')sigmas = self.sigmas = self._calculate_sigmas()# Save to HDF5sigmas_h5 = sigma_handle.create_dataset('sigmas', data = sigmas)print('Done')## Phi calculationprint('Calculating Phi...')phi = self.phi = self._calculate_phi(x)print('Done')# Saving to HDF5print('Serializing...')phi_h5 = phi_handle.create_dataset('phi', data = phi)del phiself.phi = phi_h5print('Done')## Algebraprint('Doing final algebra...')w, os = self.w, _ = self._do_algebra(y)# Saving to HDF5w_h5 = w_handle.create_dataset('w', data = w)os_h5 = os_handle.create_dataset('os', data = os)## Calculate errorself._calculate_error(y)print('Done')def predict(self, test_data):mu = self.mu = self.mu.valuesigmas = self.sigmas = self.sigmas.valuew = self.w = self.w.valueprint('Calculating phi for test data...')phi = self._calculate_phi(test_data)os = dot(w, transpose(phi))savetxt('iok3834.txt', os, delimiter='\n')return os@propertydef summary(self):return '\n'.join( \['-----------------','Training set size: {}'.format(self.n),'Hidden layer size: {}'.format(self.neurons),'-----------------','Absolute error : {:02.2f}'.format(self.error),'Relative error : {:02.2f}%'.format(self.relative_error * 100)])def predict(test_data):mu = File('rbf-mu-212243-2400.hdf5', 'r')['mu'].valuesigmas = File('rbf-sigma-212243-2400.hdf5', 'r')['sigmas'].valuew = File('rbf-w-212243-2400.hdf5', 'r')['w'].valuen = test_data.shape[0]neur = mu.shape[0]mu = transpose(mu)mu.reshape((n, neur))phi = zeros((n, neur))for i in range(n):for j in range(neur):phi[i, j] = multiQuadric(test_data[i,:], mu[j], sigmas[j])os = dot(w, transpose(phi))savetxt('iok3834.txt', os, delimiter='\n')return os更多关于Python相关内容感兴趣的读者可查看本站专题：《》、《》、《》、《》及《》希望本⽂所述对⼤家Python程序设计有所帮助。

RBF神经网络 教程

RBF神经网络：原理详解和MATLAB实现

径向基函数（RBF）神经网络

RBF神经网络

绝对经典RBF神经网络ppt课件

RBF（径向基）神经网络

径向基神经网络学习算法(RBF)

神经网络 配套ppt RBF(2)

径向基神经网络学习算法

神经网络控制RBF

RBF、GRNN和PNN神经网络

RBF神经网络

RBF、GRNN、PNN神经网络学习笔记

神经网络控制(RBF)

6.4基于RBF网络辨识的自校正控制

绝对经典RBF神经网络

RBF神经网络：原理详解和MATLAB实现

RBF神经网络学习算法

RBF网络

Python实现的径向基（RBF）神经网络示例

RBF神经网络教程

神经网络配套ppt RBF(2)