数据结构-chapter32_part5Huffman树
数据结构之哈夫曼树(java实现)

数据结构之哈夫曼树(java 实现)所谓哈夫曼树就是要求最小加权路径长度,这是什么意思呢?简而言之,就是要所有的节点对应的路径长度(高度-1)乘以该节点的权值,然后保证这些结果之和最小。
哈夫曼树最常用的应用就是解决编码问题。
一般我们用的ASCII 是固定长度的编码,对于那些常用的字符,使用很长的长度就显得略为浪费空间了。
下面以一个实例来构建一颗哈夫曼编码树。
设字符集S={A ,B ,C ,D ,E ,F},字符出现的频率W={2,3,5,7,9,12},对字符集进行哈夫曼编码(1)以频率为树的节点值,构建6个树节点,保存在一个数据集合T 中(2)选择频率集W 中最小的两个频率,然后相加,将结果作为树的节点值,构建新的树节点,将这两个最小值对应的树节点,分别作为新的节点的左右孩子。
从T 重删除这两个最小值对应的节点,最后将新节点放到T 中。
(3)重复第2步,直到T 中只剩下一个节点,那么该节点就是所需要的哈夫曼树其实说的容易,实现起来也有一点小麻烦,下面用java 实现: 树节点:1 2 3 4 5 6 7 8 9 10 public class TreeNode<t>{public TreeNode<t> leftNode;public TreeNode<t> rightNode;public T data;public TreeNode(T data){this.data=data;}}</t></t></t>构建哈夫曼树:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 public class TestTree{/** 设S={A,B,C,D,E,F},W={2,3,5,7,9,12}*/static HashMap<character, integer=""> map; public TestTree(){// TODO Auto-generated constructor stub}public static void main(String[] args){Character[] character = { 'A', 'B', 'C', 'D', 'E', 'F' };int[] weight = { 2, 3, 5, 7, 9, 12 };// 有序或者无序都一样map=new HashMap<character, integer="">();for(int i=0;i<weight.length;i++) integer="">> nodes = new ArrayList<treenode<integer>>();for (int i = 0; i < weight.length; i++){nodes.add(new TreeNode<integer>(weight[i]));}while (true){if (nodes.size() <= 1)break; // 找两个最小的 TreeNode<integer> minNode = nodes.get(0);TreeNode<integer> sminNode = nodes.get(1);for (int i = 1; i < nodes.size(); i++){Tree26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 Node<integer> tempNode = nodes.get(i);if (minNode.data >=tempNode.data){sminNode = minNode;minNode = tempNode;}}nodes.remove(minNode );nodes.remove(sminNod e);TreeNode<integer> newNode = new TreeNode<integer>(minN ode.data + sminNode.data);newNode.leftNode = minNode;newNode.rightNode = sminNode;nodes.add(newNode); }TreeNode<integer>hafmanTreeNode=node s.get(0);getHalmanCode(hafmanTreeNode," ");}public static void getHalmanCode(TreeNode<integer>hafmanTreeNode,String blank) {if(hafmanTreeNode==null)return;if(hafmanTreeNode.leftNode==null&&hafmanTr eeNode.rightNode==null){System.out.println("->"+getCha racter(hafmanTreeNode.data));}else{4 8 4 95 0 5 1 5 2 5 3 5 4 5 5 56 57 58 59 6 0 6 1 6 2 6 3 6 4 6 5 6 6 6 7 6 8 6 9 System.out.print("0"); getHalmanCode(hafmanTreeNode.leftNode,blank+" ");System.out.print(blank+"1" );getHalmanCode(hafmanTreeNo de.rightNode,blank+" ");}}//得到某一个字符的编码public static void getHalmanCode(TreeNode<integer>hafmanTreeNode,Character character){if(hafmanTreeNode==null)return;if(hafmanTreeNode.leftNode==null&&hafmanTr eeNode.rightNode==null){if(getCharacter(hafmanTreeNode.data)==character){System.out.p rint("");}}}//得到权值对应的字符public static Character getCharacter(int weight){Set<map.entry<character,integer="">>set=map.entrySet();for(Iterator<map.entry<character,integer="">> iterator=set.iterator();iterator.hasNext();){Map.Entry<character, integer="">entry=iterator.next();if(entry.getValue()==weigh t){map.remove (entry.getKey());return entry.getKey();}7 0 7 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 8 0 8 1 8 2 8 3 8 4 8 5 8 6 8 7 8 8 8 9 9 0 9 1}return null;}}</character,></map.entry<character,></map.entry<character,></integer></integer></integer></integer></integer></integer></intege r></integer></integer></treenode<integer></weight.length;i++)></char acter,></character,>929394结果:D:00E:01A:1000B:1001C:101F:11。
哈夫曼树的构造

哈夫曼树的构造今天的内容,主要是给大家介绍如何通过哈夫曼树,构建一个可供其他人访问的应用程序。
今天我们首先来看一段简单的视频,哈夫曼树是一种可用于建立网络节点之间关系以及通过这些关系传递网络信息的分布式节点树。
对于区块链项目而言,这一点尤为重要。
它不仅能解决一些应用程序在运行过程中无法发现问题,而且它还能实现去中心化,以及分布式存储,使项目更加安全。
这是区块链技术在数字经济领域应用最为广泛和成功的一个表现形式。
因此我们今天主要来讲解一下一个可用于建立网络节点之间关系以及通过网络信息给用户的哈夫曼树。
这个结构是由三个节点(每一个节点)组成。
1.每个节点都有自己的密钥(节点名称)每个节点都有自己的密钥,这是为了保证这些密钥是安全的。
因为每一个访问该节点的用户都会看到自己的隐私(例如姓名、出生日期等)。
密钥和哈夫曼树的节点是彼此独立的,而不是彼此关联的。
每个密钥只有一个随机数。
如果不符合哈夫曼(Hoffman)所定义的条件,那么这颗树木将无法被接受而且它会破坏整个树的结构。
一旦产生新的节点加入了哈夫曼树时,它就会有一个新的随机数产生哈夫曼信号:这个信号将被认为能使其具有可被使用的性能以及可扩展性;从这个定义来看,它就有这样一个优点:可以有效防止恶意攻击者盗取密钥并使整个网络安全高效;并能保证每个节点都能获取到正确信息进行验证。
这意味着每个节点都有自己独立而又安全的密钥和一个可以被使用以及验证过(不被其他人知道)这样一个重要节点来传递网络信息!;所以哈夫曼树中就出现了这样一句话:“区块链技术不能通过改变现有规则来改变现有制度”!首先我们要了解如何构建一个哈夫曼树应用程序以及如何通过哈夫曼构建其应用程序来实现哈夫曼树并使其更加安全?对于一个简单而且非常有用!要注意哈夫曼树还可以实现分布式存储和去中心化网络中可追溯数据库信息能够被访问节点看到这些信息并且它可以被安全地存储到哈夫曼树中并且被其他人访问2.每一个节点都由一定数量的节点(例如1个)组成每个节点都有自己的独特功能,可以对网络中正在运行的程序或系统进行交互并存储数据。
huffman树数据结构实验原理

huffman树数据结构实验原理
Huffman树是一种用于数据压缩的数据结构,原理如下:
1. 统计字符频率:首先,对于待压缩的数据,统计每个字符出现的频率。
可以使用哈希表或数组来记录各个字符的频率。
2. 构建最小堆:将每个字符及其频率作为一个节点,构建一个最小堆。
最小堆是一种二叉树,每个节点的值都小于或等于其子节点的值。
3. 构建Huffman树:从最小堆中取出频率最小的两个节点(即出现频率最低的两个字符),将它们合并为一个新的节点,并将新节点的频率设置为两个节点的频率之和。
将新节点插入回最小堆中。
重复这个过程,直到最小堆中只剩下一个节点。
4. 构建Huffman编码表:从Huffman树的根节点出发,根据每个字符所在的路径(左子树为0,右子树为1)来构建Huffman编码表。
Huffman编码表可以使用哈希表或数组来存储,键为字符,值为对应的Huffman编码。
5. 数据压缩:对于待压缩的数据,根据Huffman编码表将每个字符转换为对应的Huffman编码,得到压缩后的数据。
6. 数据解压:对于压缩后的数据,根据Huffman编码表将每个Huffman编码转换为对应的字符,得到解压后的数据。
Huffman树的原理在于通过构建一个最小堆,使用贪心算法来生成一个频率最小的树。
这样生成的树中,频率高的字符在树的顶部,频率低的字符在树的底部,从而实现数据压缩。
数据结构哈弗曼树

6.7 哈夫曼树一、Huffman树二、Huffman编码6.7.1 Huffman树(最优二叉树)若干术语:路径:由一结点到另一结点间的分支所构成。
路径长度:路径上的分支数目。
例如:a→e的路径长度=2二叉树的路径长度:从二叉树根到所有叶子结点的路径长度之和。
树路径长度=8二叉树的带权路径长度:从二叉树根结点到所有叶子结点的路径长度与相应叶子结点权值的乘积之和(WPL)即树中所有叶子结点的带权路径长度之和Huffman树:带权路径长度最小的树。
Huffman常译为哈夫曼、赫夫曼、霍夫曼等树的带权路径长度如何计算?WPL = w k l k构造Huffman树的基本思想:权值大的结点用短路径,权值小的结点用长路径。
构造Huffman树的步骤(即Huffman算法):(1) 由给定的n 个权值{ w1, w2, …, w n }构造n棵二叉树的集合F = { T1, T2, …, T n} (即森林),其中每棵二叉树T i 中只有一个带权为w i 的根结点,其左右子树均空。
(2) 在F 中选取两棵根结点权值最小和次小的树分别做为左右子树构造一棵新的二叉树,且让新二叉树根结点的权值等于其左右子树的根结点权值之和。
(3) 在F 中删去这两棵树,同时将新得到的二叉树加入F中。
(4) 重复(2) 和(3) , 直到F 只含一棵树为止。
这棵树便是Huffman树。
具体操作步骤:对权值进行合并、删除与替换——在权值集合{7,5,2,4}中,总是合并当前值最小的两个权具体操作步骤:对权值进行合并、删除与替换——在权值集合{7,5,2,4}中,总是合并当前值最小的两个权Huffman树特点:肯定没有度为1的结点;一棵有n 0个叶子结点的Huffman树,共有2n0-1个结点;讨论:Huffman树有什么用?例:设有4个字符d,i,a,n,出现的频度分别为7,5,2,4,怎样编码才能使它们组成的报文在网络中传得最快?法1:等长编码令d=00,i=01,a=10,n=11,则:WPL1=2bit×(7+5+2+4)=36法2:不等长编码令d=0;i=10,a=110,n=111,则:WPL2=1bit×7+2bit×5+3bit×(2+4)=356.7.2 哈夫曼编码问题哈夫曼树可用于构造代码总长度最短的编码方案。
Huffman树及其编解码

Huffman树及其编解码Huffman树——编解码介绍: Huffman树可以根据输⼊的字符串中某个字符出现的次数来给某个字符设定⼀个权值,然后可以根据权值的⼤⼩给⼀个给定的字符串编码,或者对⼀串编码进⾏解码,可以⽤于数据压缩或者解压缩,和对字符的编解码。
可是Huffman树的优点在哪? 1、就在于它对出现次数⼤的字符(即权值⼤的字符)的编码⽐出现少的字符编码短,也就是说出现次数越多,编码越短,保证了对数据的压缩。
2、保证编的码不会出现互相涵括,也就是不会出现⼆义性,⽐如a的编码是00100,b的编码是001,⽽c的编码是00,,这样的话,对于00100就可能是a,也可能是bc,⽽Huffman树编码⽅式不会出现这种问题。
如何实现 实现Huffman树的编解码需要三种数据类型,⼀个是优先级队列,⽤来保存树的结点,⼆是树,⽤来解码,三是表,⽤来当作码表编码。
下⾯我们先⼀⼀介绍⼀下三种数据结构:1、优先级队列 优先级队列⾥存放的是⼀个⼀个的树的结点,根据树结点中存放的字符的权值来确定其优先级,权重越⼩,优先级越⼩,放的位置越靠前。
也就是说第⼀个结点存放的优先级最⼩,权值最⼩。
数据类型//优先级队列,struct TNode表⽰树的结点,在后⾯介绍typedef struct QNode{struct TNode* val; //树的结点,其实也就是数据域int priority; //优先级struct QNode* next; //指针域}*Node;typedef struct Queue{int size; //队列⼤⼩struct QNode* front; //队列头指针}queue;2、树 树⾥⾯存放的是字符,以及指向⾃⼰的左右孩⼦结点的指针。
⽐如下图,虽然下图中看起来书中存放了该字符的优先级,但其实可以不加,感觉⽐较繁琐,所以我取了,但是为了理解⽅便起见,我在图上标注了出来。
数据类型//树typedef struct TNode{char data; //字符值struct TNode* left; //左孩⼦struct TNode* right; //右孩⼦}*Tree;3、表 这个表其实就是⼀张编码表,⾥⾯存放了字符和该字符的编码,⽤于编码的时候查看。
数据结构的哈夫曼树的构造

数据结构的哈夫曼树的构造
数据结构中的哈夫曼树是一种非常重要的树形结构,它可以用来进行数据压缩和编码。
哈夫曼树的构造是一个比较复杂的过程,但是通过一定的算法和步骤,可以很容易地构造出一个高效的哈夫曼树。
首先,我们需要了解哈夫曼树的基本概念。
哈夫曼树是一种带权路径长度最短的树,它的构造过程是通过合并权值最小的两颗树来得到一颗新的树,直到所有的节点都被合并成一颗完整的树。
在构造哈夫曼树的过程中,我们需要先对给定的权值序列进行排序,然后选择权值最小的两个节点作为左右子节点构造一颗新的二叉树,同时将这两个节点的权值相加作为新节点的权值。
然后将这颗新的树插入到原来的序列中,重新对序列进行排序,重复这个过程直到序列中只剩下一个节点为止,这个节点就是哈夫曼树的根节点。
在构造哈夫曼树的过程中,需要使用到优先队列来维护权值序列,以及一些基本的数据结构和算法来实现节点的合并和树的插入。
虽然哈夫曼树的构造过程比较繁琐,但是通过一些简单的算法和技巧,我们可以很容易地构造出一个高效的哈夫曼树。
哈夫曼树的构造是数据结构中一个非常重要的问题,它不仅可以用来进行数据压缩和编码,还可以应用在很多其他领域,比如网络传输、图像处理等。
因此,掌握哈夫曼树的构造方法对于计算机科学和工程领域的学生和从业者来说是非常重要的。
总之,哈夫曼树是数据结构中一个非常重要的树形结构,通过一定的算法和步骤,我们可以很容易地构造出一个高效的哈夫曼树。
掌握哈夫曼树的构造方法对于计算机科学和工程领域的学生和从业者来说是非常重要的。
数据结构哈夫曼树PPT课件
例:
W(权)={2,4,2,3,3},叶子结点个数,m=5 试设计Huffman树。
14
6
3
3
8
4
4
22
构造的 Huffman树
第12页/共21页
三、哈夫曼树的应用(哈夫曼编码)
在远程通讯中,要将待传字符转换成由二进制组成 的字符串:
设要传送的字符为: 若编码为:A—00 (等长) B—01
重码 000011010
关键:要设计长度不等的编码,则必须使任一字符的编码都不 是另一个字符的编码的前缀。这种编码称作最优前缀编码。
第14页/共21页
设要传送的字符为:
若编码为 :A—0
B—110
C用二叉树设 计二进制前缀
编码
0
1
C0
1
BD
第15页/共21页
ABACCDA
C—10 D---11
ABACCDA
若将编码设计为长度不等的二进制编码,即让待传字符串中出 现次数较多的字符采用尽可能短的编码,则转换的二进制字符 串便可能减少。
第13页/共21页
设要传送的字符为:ABACCDA 若编码为: A—0
B—00 C—1 D---01
ABACCDA
但: 0000 AAAA ABA BB
二、构造哈夫曼树 1.哈夫曼树的定义
在一棵二叉树中,若带权路径长度达到最小,称这样的 二叉树为最优二叉树,也称为哈夫曼树(Huffman tree)。
第3页/共21页
例 有4个结点,权值分别为7,5,2,4,构造有4个叶子结点的二叉树
4d
a 7
n
c
2
WPL
WK LK
k 1
数据结构课程设计_哈夫曼树

数据结构课程设计_哈夫曼树哈夫曼树是数据结构课程设计中的一个重要内容,它是一种用于编码和压缩数据的树形结构。
在这篇文章中,我们将深入探讨哈夫曼树的原理、应用以及实现方法。
一、哈夫曼树的原理哈夫曼树是一种特殊的二叉树,它的构建依赖于哈夫曼编码的思想。
哈夫曼编码是一种变长编码方式,通过将频率较高的字符用较短的编码表示,而频率较低的字符用较长的编码表示,从而实现数据的高效压缩。
构建哈夫曼树的过程如下:1. 首先,将待编码的字符按照出现频率从小到大进行排序。
2. 然后,取出频率最小的两个字符,将它们作为叶子节点构建一个新的二叉树,该树的根节点的权值为这两个字符的频率之和。
3. 将新构建的二叉树插入到原有的字符列表中,并重新进行排序。
4. 重复步骤2和步骤3,直到只剩下一个根节点的二叉树为止,该树就是哈夫曼树。
二、哈夫曼树的应用哈夫曼树在数据压缩和编码中有着广泛的应用。
由于哈夫曼编码能够将频率较高的字符用较短的编码表示,从而减少了数据的存储空间,因此在文件压缩、图像压缩等领域被广泛应用。
在文件压缩中,哈夫曼树可以根据文件中字符的出现频率构建出一个最优的编码表,将文件中的字符替换为对应的哈夫曼编码,从而实现文件的高效压缩。
解压缩时,只需要根据哈夫曼编码表将编码还原为原始字符,即可恢复文件的原始内容。
在图像压缩中,哈夫曼树可以根据图像中像素值的出现频率构建出一个最优的编码表,将像素值替换为对应的哈夫曼编码,从而实现图像的高效压缩。
解压缩时,只需要根据哈夫曼编码表将编码还原为原始像素值,即可恢复图像的原始内容。
三、哈夫曼树的实现方法哈夫曼树的实现方法有多种,其中一种常见的方法是使用优先队列(也称为最小堆)来实现。
优先队列是一种特殊的队列,它的每个元素都有一个优先级,优先级高的元素先出队。
在构建哈夫曼树时,我们可以将字符和对应的频率作为优先队列中的元素,根据频率的大小来确定优先级。
每次从优先队列中取出两个频率最小的字符,将它们作为叶子节点构建一个新的二叉树,并将该二叉树的根节点插入到优先队列中。
数据结构哈夫曼树构造,注意事项

数据结构哈夫曼树构造,注意事项哈夫曼树(Huffman Tree)是一种特殊的二叉树,其中每个叶子节点对应一个字符,且哈夫曼树是一颗无歧义的前缀编码树(又称为最优二叉树),它将数据中出现频率最高的字符用较短的编码表示,出现频率较低的字符用较长的编码表示,从而可以压缩数据,使得压缩后的数据占用更少的存储空间。
哈夫曼树的构造过程非常重要,下面介绍一下哈夫曼树构造的注意事项。
1. 确定字符的权值哈夫曼树的构造依赖于各个字符在数据中出现的权值,权值表示字符在数据中出现的频率,出现频率越高的字符权值越大。
权值的确定对哈夫曼树的构造非常关键,因为它决定了每个字符在哈夫曼树中出现的位置和编码长度。
2. 选择合适的合并方式哈夫曼树的构造需要不断的合并节点,最终形成一颗完整的二叉树,因此选择合适的合并方式非常重要。
常见的合并方式有两种,一种是将权值最小的两个节点合并成一个父节点,称为小根法;另一种是将权值最大的两个节点合并成一个父节点,称为大根法。
选择哪种合并方式取决于需要生成的哈夫曼树的形态,通常情况下,我们使用小根法,因为它能够生成一个权值较小的哈夫曼树。
3. 构建哈夫曼树的过程哈夫曼树的构造过程是按照从小到大的顺序合并节点,直到整个二叉树合成一颗完整的哈夫曼树。
具体步骤如下:a. 将字符按照权值从小到大排序。
b. 选择权值最小的两个字符进行合并,并创建一个新节点作为它们的父节点,将新节点的权值设为两个子节点的权值之和。
c. 依次取出权值最小的两个字符,重复第 b 步。
d. 直到剩下的节点只有一个,它就是哈夫曼树的根节点。
4. 构造哈夫曼编码表为了便于对数据进行解压缩,需要将每个字符映射到一个对应的二进制编码,这个编码称为哈夫曼编码。
哈夫曼编码需要利用哈夫曼树的结构,对每个字符进行遍历,记录下该字符所经过的每个节点的路径,并将路径上的方向标识为 0 或 1,最终得到该字符所对应的哈夫曼编码。
由于哈夫曼编码是一种前缀编码,因此可能存在解码时出现的二义性,为了解决这个问题,需要在哈夫曼编码的过程中进行优化。
哈夫曼树的构造与编码

哈夫曼树的构造与编码哈夫曼树是一种二叉树,常用于数据压缩中的编码和加密算法。
它是由美国数学家David A.Huffman在1952年发明的。
哈夫曼树的构造过程非常简单,仅需要一些基本的数学知识。
1. 频率统计首先我们需要对待压缩的字符串进行字符频率统计,也就是统计每个字符在字符串中出现的次数。
对于字符串“hello world”,字符‘l’出现了三次,字符‘o’出现了2次等等。
2. 排序将所有的字符按照出现频率从小到大排序。
因为我们希望出现频率最低的字符被编码成长度最长的二进制数,使得压缩率最高。
相反,出现频率最高的字符应该被编码成长度最短的二进制数。
我们将已经排序过的字符按照出现频率最低的两个字符合并成一个新的节点,其权值为这两个子节点权值之和。
这个新节点比两个子节点的出现频率都高,所以它应该在哈夫曼树中靠近根节点。
具体做法:将这两个最低的权值的子节点构成一个新节点,然后将这个新节点的权值加入到排序列表中。
重新对这个排序列表进行排序,将权值较小的元素排在前面。
重复这样的操作,直到只剩下一个节点,即哈夫曼树的根节点。
这样就构造出了一颗哈夫曼树。
4. 编码对于哈夫曼树上的每一个叶子节点,在它到根节点的路径上标记一些0和1,从而得到每个字符对应的二进制编码。
左子树为0,右子树为1。
这些二进制编码可以被用于压缩数据。
对于字符串“hello world”,其字符权值的频率统计如下:字符 | 权值‘h’ | 1我们将这些字符按照权值从小到大排序:首先将出现频率最低的两个元素'h'和'e'合并成一个节点,并将它们的权值1+1=2作为新节点的权值,重复操作,得到哈夫曼树的一部份:4/ \2 l/ \h e然后将‘w’和‘r’合并:接着将‘d’和新节点2合并:10/ \4 \/ \ \2 l \/ \ \h e \/ \ \w r \/ \ \d o \现在我们可以通过哈夫曼树上的路径编码来表示每个字符。
数据结构(二十七)Huffman树和Huffman编码

数据结构(⼆⼗七)Huffman树和Huffman编码 Huffman树是⼀种在编码技术⽅⾯得到⼴泛应⽤的⼆叉树,它也是⼀种最优⼆叉树。
⼀、霍夫曼树的基本概念 1.结点的路径和结点的路径长度:结点间的路径是指从⼀个结点到另⼀个结点所经历的结点和分⽀序列。
结点的路径长度是指从根结点到该结点间的路径上的分⽀数⽬。
2.结点的权和结点的带权路径长度:结点的权是指结点被赋予⼀个具有某种实际意义的数值。
结点的带权路径长度是该结点的路径长度与结点的权值的乘积。
3.树的长度和树的带权路径长度:树的长度就是从根结点到每⼀结点的路径长度之和。
树的带权路径长度就是所有叶结点的带权路径长度之和。
4.最优⼆叉树:带权路径长度WPL最⼩的⼆叉树称为霍夫曼树(Huffman Tree)或最优⼆叉树。
⼆叉树a的WPL = 5 x 1 + 15 x 2 + 40 x 3 + 30 x 4 + 10 x 5 = 315 ⼆叉树b的WPL = 5 x 3 + 15 x 3 + 40 x 2 + 30 x 2 + 10 x 2 = 220 ⼆、霍夫曼树的构造⽅法由给定的n个权值{w1,w2,... ,wn}构成由n棵⼆叉树所构成的森林F={T1,T2,...,Tn},其中每棵⼆叉树只有⼀个根结点,并且根结点的权值对应于w1,w2,...,wn在F中选取根结点的权值最⼩的两棵树,分别把它们作为左⼦树和右⼦树去构造⼀棵新的⼆叉树,新的⼆叉树的各结点的权值为左、右⼦树的权值之和在F中删除上⼀步中选中的两棵树,并把新产⽣的⼆叉树加⼊到F中重复第2步和第3步,直到F只含⼀棵树为⽌,这棵树就是霍夫曼树。
三、霍夫曼编码 霍夫曼树更⼤的⽬的是解决了当年远距离通信(电报)的数据传输的最优化问题。
霍夫曼编码的定义:设需要编码的字符集为(d1,d2,...,dn)各个字符在电⽂中出现的次数或者频率集合为{w1,w2,...,wn},以d1,d2,...,dn为叶⼦结点,w1,w2,...,wn作为相应叶⼦结点的权值来构造⼀棵霍夫曼树。
重学数据结构之哈夫曼树

重学数据结构之哈夫曼树一、哈夫曼树1.带权扩充二叉树的外部路径长度扩充二叉树的外部路径长度,即根到其叶子节点的路径长度之和。
例如下面这两种带权扩充二叉树:左边的二叉树的外部路径长度为:(2 + 3 + 6 + 9) * 2 = 38。
右边的二叉树的外部路径长度为:9 + 6 * 2 + (2 + 3) * 3 = 36。
2.哈夫曼树哈夫曼树(Huffman Tree)是一种重要的二叉树,在信息领域有重要的理论和实际价值。
设有实数集W = {W0 ,W1 ,···,W m-1 },T 是一颗扩充二叉树,其m 个外部节点分别以W i (i = 1, 2, n - 1) 为权,而且T 的带权外部路径长度在所有这样的扩充二叉树中达到最小,则称T 为数据集W 的最优二叉树或者哈夫曼树。
二、哈夫曼算法1.基本概念哈夫曼(D.A.Huffman)提出了一个算法,它能从任意的实数集合构造出与之对应的哈夫曼树。
这个构造算法描述如下:算法的输入为实数集合W = {W0 ,W1 ,···,W m-1 }。
在构造中维护一个包含k 个二叉树集合的集合F,开始时k=m 且F = {T0 ,T1 ,···,T m-1 },其中每个T i 是一颗只包含权为W i 的根节点的二叉树。
该算法的构造过程中会重复执行以下两个步骤,直到集合F 中只剩下一棵树为止:1. 构造一颗二叉树,其左右子树是从集合 F 中选取的两颗权值最小的二叉树,其根节点的权值设置为这两颗子树的根节点的权值之和。
2. 将所选取的两颗二叉树从集合 F 中删除,把新构造的二叉树加入到集合F 中。
注意:给定集合W 上的哈夫曼树并不唯一!2.示例对于实数集合W = {2, 1, 3, 7, 8, 4, 5},下面的图1到图7 表示了从这个实数集合开始,构造一个哈夫曼树的过程:图1:图2:图3:图4:图5:图6:图7:三、哈夫曼算法的实现1.实现思路要实现哈夫曼算法,需要维护一组二叉树,而且要知道每颗二叉树的根节点的权值,这个可以使用前面定义的二叉树的节点来构造哈夫曼树,只需要在根节点处记录该树的权值。
数据结构哈夫曼树课件

总结词
优化、提升
详细描述
基于哈夫曼树的网络流量分类算法的优化策 略主要从以下几个方面进行优化和提升:一 是优化哈夫曼树的构造算法,提高树的构造 效率和准确性;二是利用多级哈夫曼编码技 术,降低编码和解码的时间复杂度;三是引 入机器学习算法,对网络流量特征进行自动
提取和分类,进一步提升分类准确率。
THANKS
基于堆排序的构造算法
总结词:堆排序是一 种基于比较的排序算 法,它利用了堆这种 数据结构的特点,能 够在O(nlogn)的时间 内完成排序。在哈夫 曼树的构造中,堆排 序可以用来找到每个 节点的父节点,从而 构建出哈夫曼树。
详细描述:基于堆排 序的构造算法步骤如 下
1. 定义一个最大堆, 并将每个节点作为一 个独立的元素插入到 堆中。每个元素包含 了一个节点及其权值 。
哈夫曼编码的基本概念
哈夫曼编码是一种用于无损数据压缩的熵编码算法,具有较高的编码效率和较低的 编码复杂度。
它利用了数据本身存在的冗余和相关性,通过构建最优的前缀编码来实现高效的数 据压缩。
哈夫曼编码是一种可变长编码,其中每个符号的编码长度取决于它在输入序列中出 现的频率。
哈夫曼编码的实现方法
构建哈夫曼树
节ቤተ መጻሕፍቲ ባይዱ。
优化编码长度
在分配码字时,通过一些策略优化 编码长度,例如给高频符号更短的 码字。
可变长度编码
为了提高压缩比,可以使用可变长 度编码,即对于高频符号赋予更短 的码字,对于低频符号赋予更长的 码字。
04
哈夫曼树在数据压 缩中的应用
基于哈夫曼编码的数据压缩算法
哈夫曼编码是一种可变长度的 编码方式,通过统计数据的出 现频率来构建哈夫曼树,实现 数据压缩。
计算机数据结构知识点梳理 哈夫曼(Huffman)树和哈夫曼编码

(3)在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入 到集合F中;
(4)重复(2)(3)两步,当F中只剩下一棵二叉树时,这棵二叉树便是所要 建立的哈夫曼树。
(3)深度为h的哈夫曼树,其叶子结点的最大编码长度为h-1。
[题1]若度为m的哈夫曼树,其叶子结点个数为n,则非叶子结点 的个数为( )。
A.n-1 B.[n/m]-1 C.[(n-1)/(m-1)] D.[n/(m-1)]-1
分析:在构造度为m的哈夫曼树过程中,每次把m个子结点合并 为一个父结点(第一次合并可能少于m个子结点),每次合并 减少m-1个结点,从n个叶子结点减少到最后只剩一个父结点共 需[(n-1)/(m-1)]次合并,每次合并增加一个非叶子结点。
5、对哈夫曼树编码的总结
(1)哈夫曼编码是能使电文代码总长最短的编码方式。此结论由哈夫曼树是带 权路径长度最小的树的特征可得。
(2)哈夫曼编码是一种前缀编码,保证其在译码时不会产生歧义。因为,在哈 夫曼编码中,每个字符都是叶子结点,而叶子结点不可能从根结点到其他叶 子结点的路径上,所以一个字符的哈夫曼编码不可能是另一个字符的哈夫曼 编码的前缀。
知识点10:哈夫曼(HUFFMAN)树和哈夫曼编码
1、哈夫曼树(又称最优二叉树),是指对于一 组带有确定权值的叶结点,构造的具有最小带
权路径长度的二叉树。
2、哈夫曼树的构造方法的基本思想
(1)由给定的n个权值{W1,W2,…,Wn}构造n棵只有一个叶结点的二叉树, 从而得到一个二叉树的集合F={T1,T2,…,Tn};
数据结构哈夫曼树

数据结构哈夫曼树哈夫曼树(Huffman tree)是一种用于编码的树形数据结构,由美国计算机科学家大卫·哈夫曼(David A. Huffman)于1952年提出。
它是一种利用最高频率字符具有最短编码长度的特性来进行数据压缩的算法。
在介绍哈夫曼树之前,我们先来了解一下哈夫曼编码(Huffman coding)。
哈夫曼编码是一种变长前缀编码,即每个字符的编码长度不固定,不会出现编码前缀相同的情况,具有唯一可解码性。
它是为了满足字符编码长度尽可能短且无编码前缀相同的要求而产生的。
构建哈夫曼树的过程可以分为以下几步:1.统计字符频率:首先对于需要压缩的文件,统计每个字符出现的频率。
频率可以理解为该字符出现的次数。
统计之后,可以得到每个字符与其对应的频率。
2.构建节点:将每个字符以及其频率作为叶子节点构建成一个森林(每个节点都是一个独立的树)。
3.合并节点:从森林中选取频率最小的两个节点合并为一个新的节点,频率为其子节点频率之和。
将新的节点继续加入森林中,重复此过程,直到森林中只剩下一个节点为止。
4.构建哈夫曼树:最后剩下的那个节点就是哈夫曼树的根节点。
从构建的过程可以看出,频率较高的字符会位于树的较低层,而频率较低的字符会位于树的较高层。
5.生成编码:根据哈夫曼树的特点,路径的左边为0,右边为1,从根节点开始,走到每个叶子节点的路径就是该叶子节点的哈夫曼编码。
通过以上步骤,我们就构建了一颗哈夫曼树,并生成了对应的哈夫曼编码。
利用哈夫曼编码,可以将原始数据进行压缩,使其占用的存储空间减小。
举个例子来说明哈夫曼树的构建过程和编码生成过程:假设有一个包含5个不同字符的文件,每个字符及其频率如下:A:5B:9C:12D:13E:16首先按照步骤1统计字符频率,得到每个字符及其频率。
然后按照步骤2构建叶子节点,每个字符和其频率构成一个叶子节点。
接着按照步骤3合并节点,选取频率最小的两个节点合并为一个新的节点,直到森林中只剩下一个节点。
Huffman树

离散数学-课程设计实现Huffman算法——题目23578235785235785 102357851015235785101525实现Huffman 算法——题目例子:编解码程序51520253520406010000001111字符:A B C D E 权重:5 15 20 25 35编码:010 011 00 10 11实现Huffman算法——思路《数据结构》课程会详细讲解树结构本课程采用数组进行演示构建Huffman树编码解码实现Huffman 算法——思路515202535204060100012345678红色数字:数组下标实现Huffman算法——思路构造根树时,只需按照Huffman算法实现即可输入: 实数w1,w2,…,w t,输出: 树叶权为w1,w2,…,w t的最优二叉树算法:1. 选择最小的2个权w1,w2, 连接对应的树叶得到权为w1+w2的分支点2. 选择w1+w2 ,w3,w4, …,w t中最小的2个权, 连接对应顶点得到新的分支点和权3. 同上重复进行, 直到只剩1个权为止编解码实现Huffman 算法——思路编码:从根节点开始,到叶节点为止左子树赋值0,右子树赋值1解码:由于是前缀码,所以依次读入所有编码从根节点开始,0向左,1向右到叶节点即读出字符,并从根节点重新开始读取下一个字符51520253520406010000001111011实现Huffman算法——思路参考代码:使用了STL中的vector来替代数组使用了string,map等类型简化操作。
数据结构与算法——树的应用(哈夫曼编码)

数据结构与算法——树的应⽤(哈夫曼编码)1. 哈夫曼编码概括/********************************************** 本⽂图⽚较多,多刷新⼀下才能显⽰ ***********************************************/哈夫曼(Huffman)编码算法是基于⼆叉树构建编码压缩结构的,它是数据压缩中经典的⼀种算法。
算法根据⽂本字符出现的频率,重新对字符进⾏编码。
⾸先以下这段⽂字举例:今天天⽓晴朗,我和乔伊·亚历⼭⼤·⽐基·卡利斯勒·达夫·埃利奥特·福克斯·伊维鲁莫·马尔尼·梅尔斯·帕特森·汤普森·华莱⼠·普雷斯顿出去玩!乔伊·亚历⼭⼤·⽐基·卡利斯勒·达夫·埃利奥特·福克斯·伊维鲁莫·马尔尼·梅尔斯·帕特森·汤普森·华莱⼠·普雷斯顿贪玩,不⼩⼼摔了⼀跤,乔伊·亚历⼭⼤·⽐基·卡利斯勒·达夫·埃利奥特·福克斯·伊维鲁莫·马尔尼·梅尔斯·帕特森·汤普森·华莱⼠·普雷斯顿被摔得哇哇哭了,乔伊·亚历⼭⼤·⽐基·卡利斯勒·达夫·埃利奥特·福克斯·伊维鲁莫·马尔尼·梅尔斯·帕特森·汤普森·华莱⼠·普雷斯顿的爸爸闻声赶来,⼜把乔伊·亚历⼭⼤·⽐基·卡利斯勒·达夫·埃利奥特·福克斯·伊维鲁莫·马尔尼·梅尔斯·帕特森·汤普森·华莱⼠·普雷斯顿痛扁了⼀阵。
数据结构哈夫曼树的代码

数据结构哈夫曼树的代码数据结构哈夫曼树的代码实现:1·简介哈夫曼树(Huffman Tree),又称为最优二叉树,是一种用于数据压缩的树形结构。
它利用出现频率较高的字符采用较短的编码,而出现频率较低的字符采用较长的编码,从而实现数据的压缩和解压缩。
本文将详细介绍哈夫曼树的构建和编码解码的过程。
2·哈夫曼树的构建2·1 核心思想哈夫曼树的构建核心思想是根据字符的出现频率构建一棵树,使得频率高的字符离树根近,频率低的字符离树根远。
构建哈夫曼树的步骤如下:●创建一个包含所有字符的叶子结点集合。
●从集合中选择两个频率最低的结点(注意:频率越低,优先级越高),构建一个新的二叉树,根节点的频率等于这两个结点的频率之和。
●将新构建的二叉树的根节点加入集合中。
●重复上述操作,直到集合中只剩一个根结点,即构建完成。
2·2 代码实现下面是一个示例的哈夫曼树构建的代码:```pythonclass Node:def __init__(self, freq, char=None):self·freq = freqself·char = charself·left = Noneself·right = Nonedef build_huffman_tree(char_freq):leaves = [Node(freq, char) for char, freq in char_freq·items()]while len(leaves) > 1:leaves·sort(key=lambda x: x·freq)left = leaves·pop(0)right = leaves·pop(0)parent = Node(left·freq + right·freq)parent·left = leftparent·right = rightleaves·append(parent)return leaves[0]```3·哈夫曼树的编码3·1 核心思想哈夫曼树的编码过程是根据构建好的哈夫曼树,对每个字符进行编码。
数据结构——哈夫曼(Huffman)树+哈夫曼编码

数据结构——哈夫曼(Huffman)树+哈夫曼编码前天acm实验课,⽼师教了⼏种排序,抓的⼀套题上有⼀个哈夫曼树的题,正好之前离散数学也讲过哈夫曼树,这⾥我就结合课本,整理⼀篇关于哈夫曼树的博客。
哈夫曼树的介绍Huffman Tree,中⽂名是哈夫曼树或霍夫曼树,它是最优⼆叉树。
定义:给定n个权值作为n个叶⼦结点,构造⼀棵⼆叉树,若树的带权路径长度达到最⼩,则这棵树被称为哈夫曼树。
这个定义⾥⾯涉及到了⼏个陌⽣的概念,下⾯就是⼀颗哈夫曼树,我们来看图解答。
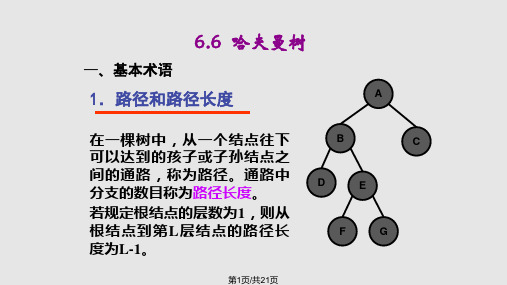
(01) 路径和路径长度定义:在⼀棵树中,从⼀个结点往下可以达到的孩⼦或孙⼦结点之间的通路,称为路径。
通路中分⽀的数⽬称为路径长度。
若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
例⼦:100和80的路径长度是1,50和30的路径长度是2,20和10的路径长度是3。
(02) 结点的权及带权路径长度定义:若将树中结点赋给⼀个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
例⼦:节点20的路径长度是3,它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。
(03) 树的带权路径长度定义:树的带权路径长度规定为所有叶⼦结点的带权路径长度之和,记为WPL。
例⼦:⽰例中,树的WPL= 1*100 + 2*50 +3*20 + 3*10 = 100 + 100 + 60 + 30 = 290。
⽐较下⾯两棵树上⾯的两棵树都是以{10, 20, 50, 100}为叶⼦节点的树。
左边的树WPL=2*10 + 2*20 + 2*50 + 2*100 = 360 右边的树WPL=350左边的树WPL > 右边的树的WPL。
你也可以计算除上⾯两种⽰例之外的情况,但实际上右边的树就是{10,20,50,100}对应的哈夫曼树。
⾄此,应该堆哈夫曼树的概念有了⼀定的了解了,下⾯看看如何去构造⼀棵哈夫曼树。
数据结构课程设计_哈夫曼树

数据结构课程设计_哈夫曼树一、引言哈夫曼树是一种重要的数据结构,广泛应用于编码和解码过程中。
本文将详细介绍哈夫曼树的概念、构建方法以及相关算法。
二、概述哈夫曼树,又称最优二叉树,是一种用于编码的树形结构。
它的特点是:权值越大的节点离根节点越近,权值越小的节点离根节点越远。
通过构建哈夫曼树,可以实现高效的编码和解码过程。
三、构建哈夫曼树的步骤1. 统计字符出现频率:对于给定的文本,首先需要统计每个字符出现的频率。
可以通过遍历文本,使用哈希表或数组记录每个字符出现的次数。
2. 构建哈夫曼树的节点:根据字符频率,创建对应的哈夫曼树节点。
每个节点包含字符和对应的频率。
3. 构建哈夫曼树:通过以下步骤构建哈夫曼树:a. 将所有节点按照频率从小到大排序。
b. 取出频率最小的两个节点作为左右子节点,生成一个新的父节点,父节点的频率为左右子节点频率之和。
c. 将新生成的父节点插入到节点集合中,并移除原来的两个子节点。
d. 重复步骤a-c,直到只剩下一个节点,即为哈夫曼树的根节点。
4. 哈夫曼编码:通过遍历哈夫曼树的路径,给每个字符生成对应的编码。
左子树路径标记为0,右子树路径标记为1。
将所有字符的编码存储在编码表中。
5. 哈夫曼解码:根据编码表和编码后的文本,通过遍历哈夫曼树,将编码转换为原始文本。
四、示例假设有一段文本:"Hello, World!",统计字符频率如下:H: 1e: 1l: 3o: 2,: 1(space): 1W: 1r: 1d: 1!: 1按照步骤三构建哈夫曼树:1. 创建节点集合:[H:1, e:1, l:3, o:2, ,:1, W:1, r:1, d:1, !:1]2. 构建哈夫曼树:a. 排序节点集合:[,:1, W:1, r:1, d:1, !:1, H:1, e:1, o:2, l:3]b. 取出频率最小的两个节点:[, W]c. 生成新的父节点:[:2]d. 插入父节点,并移除子节点:[:2, r:1, d:1]e. 重复上述步骤,直到只剩下一个节点:[:2, r:1, d:1, !:1, H:1, e:1, o:2, l:3]f. 最终得到哈夫曼树的根节点:[:10]根据哈夫曼树生成的编码表如下:H: 000e: 001l: 01o: 10,: 110(space): 1110W: 1111r: 1100d: 1101!: 11100编码后的文本为:"00101 1111 01 10 110 1110 1111 1100 1101 11100"。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Huffman树的构造
for(i=0;i<n-1;i++)
{//通过n-1次合并建立Huffman树
parent=new HuffmanTreeNode<T>;
firstchild=heap.RemoveMin(); //选择权值最小的结点
secondchild=heap.RemoveMin(); //选择权值次小的结点
例,某通信可能出现 A B C D E F G H 8 个字符,其概率分别为 0.05 , 0.29 , 0.07 , 0.08 , 0.14 , 0.23 , 0.03 , 0.11 ,试设计Huffman编码 不妨设 w = { 5 , 29 , 7 , 8 , 14 , 23 , 3 , 11 }
例, A , B , C , D 前缀编码可以为 0 , 110 , 10 , 111
利用二叉树设计二进制前缀编码。
叶子结点表示 A , B , C , D 这 4 个字符 左分支表示 ‘0’,右分支表示 ‘1’ 从根结点到叶子结点的路径上经过的二 进制符号串作为该叶子结点字符的编码 路径长度为编码长度 证明其必为前缀编码
A (0110) B (10) C (1110) D (1111) E (110) F (00) G (0111) H (010)
100
0
1
42 01
58 01
F 23
19
01
B 29
29
01
H 11
8
01
E ห้องสมุดไป่ตู้4
15
01
A5 G3
C7 D8
A (0110) B (10) C (1110) D (1111) E (110) F (00) G (0111) H (010)
b5 c 2 6 d 4
c 2 d4
编码
电文
二进制
编码
二进制 译码 电文
例,传送 ABACCD,四种字符,可以分别编码为 00,01,10,11。 则原电文转换为 00 01 00 10 10 11。 对方接收后,采用二位一分进行译码。
编码
为电文编码时,总是希望总长越短越好, 如果对每个字符设计长度不等的编码,且让电文中出 现次数较多的字符采用较短的编码,则可以减短电文 的总长。
Huffman编码树
假设有n个权值 {w0,w1, … wn-1} ,试构造一棵 有n个叶子结点的二叉树,每个叶子结点带权 为 wi ,则其中带权路径长度WPL最小的二叉 树称做最优二叉树。 Huffman树是最优二叉树。
构造Huffman编码树
(1) 根据给定的 n 个权值 {w1,w2, … wn} 构成 n 棵二叉树 的集合 F = {T1,T2, … Tn},其中每棵二叉树 Ti 中只有一 个权值为 wi 的根结点。 (2) 在 F 中选取两棵根结点权值最小的树作为左、右子 树构造一棵新的二叉树,且置新二叉树的根结点的权值 为其左、右子树根结点的权值之和。
Huffman树类
//删除Huffman树或其子树 void DeleteTree(HuffmanTreeNode<T>* root); public: //构造Huffman树,weight是存储权值的数组,n是数组长度 HuffmanTree(T weight[],int n); //析构函数 virtual ~HuffmanTree(){DeleteTree(root);}; }
(3) 在 F 中删除这两棵树,同时将新得到的二叉树加入 集合 F 中。
(4) 重复 (2) 和 (3) ,直到 F 中只含一棵树为止。
构造Huffman编码树
例, 4 个叶子结点 a、b、c、d,分别带权7、5、2、4。
初始
a 7 1b85 11 c 2 6 d 4
a 7 b 5 11 c 62 d 4
排序后 w = { 3812474920,051,81}25,53987,81,},4128192,1,1,}1,52139,4,2,}1,32429,3,2}2,932}9, 2}9 }
100
0
1
42 01
58 01
F 23
19
01
B 29
29
01
H 11
8
01
E 14
15
01
A5 G3
C7 D8
HuffmanTreeNode<T>* root;//Huffman树的树根 //把ht1和ht2为根的Huffman子树合并成一棵以parent为 //根的二叉树 void MergeTree(HuffmanTreeNode<T> &ht1,
HuffmanTreeNode<T> &ht2, HuffmanTreeNode<T>* parent);
A(0)
01
B(110) C(10)
A
D(111)
01
C 01
B
D
Huffman编码
设每种字符在电文中出现的概率 wi 为,则依此 n 个字 符出现的概率做权,可以设计一棵Huffman树,使
WPL = ∑n-1wi li 最小
i=0
wi 为叶子结点的出现概率 ( 权) li 为根结点到叶子结点的路径长度
数据结构、算法及应用
*** 二叉树
Huffman树
主要内容
• Huffman树 • Huffman编码
Huffman编码树
• 要求给出一个具有n个外部结点的扩充二叉树
–该每个外部结点Ki有一个wi与之对应,作为该外部 结点的权
–叶结点带权外部路径长度总和
n
WPL
=
∑
i=1
wi
li
最小
(注意不管内部结点,也不用有序)
//合并权值最小的两棵树
MergeTree(firstchild,secondchild,parent);
heap.Insert(*parent);
//把parent插入到堆中去
root=parent;
//建立根结点
}//end for
delete []NodeList;
}
作业
• 纸面作业:
– P142:15
Huffman树的构造
template<class T> HuffmanTree<T>::HuffmanTree(T weight[], int n) {
//定义最小值堆 MinHeap<HuffmanTreeNode<T>> heap(n); HuffmanTreeNode<T> *parent, firstchild,secondchild; HuffmanTreeNode<T>* NodeList=new HuffmanTreeNode<T>[n]; for(int i=0;i<n;i++){ NodeList[i].element=weight[i]; NodeList[i].parent=NodeList[i].left=NodeList[i].right=NULL; heap.Insert(NodeList[i]);//向堆中添加元素 }//end for
ACEA 编码为 0110 1110 110 0110 如何译码? A C E A
1. 从根结点出发,从左至右扫描编码, 2. 若为 ‘0’ 则走左分支,若为‘1’ 则走右分支,直至叶结点为止, 3. 取叶结点字符为译码结果,返回重复执行 1,2,3 直至全部译完为止
13/98
Huffman树类
template <class T> class HuffmanTree { private:
–权越大的叶结点离根越近;如果某个叶结点的权较 小,可能就会离根较远
例,3 棵二叉树,都有 4 个叶子结点 a、b、c、d,分别带权7、5、 2、4,求它们各自的带权路径长度。
a7 b 5 c 2 d 4 (1)
c2 a7
d4
b5
a7 b 5
c 2 d4
(2)
(3)
(1) WPL = 7×2 + 5×2 + 2×2 + 4×2 = 36 (2) WPL = 7×3 + 5×3 + 2×1 + 4×2 = 46 (3) WPL = 7×1 + 5×2 + 2×3 + 4×3 = 35
• 上机作业
– 3.4.1 图像压缩算法
例,对 ABACCD 重新编码,分别编码为 0 , 00 , 1 , 01。 ABCD
则原电文转换为 0 00 0 1 1 01。 减短了。 问题: 如何译码?
前四个二进制字符就可以多种译法。
AAAA
BB
前缀编码
若设计的长短不等的编码,满足任一个编码都不是另一个编
码的前缀,则这样的编码称为前缀编码。
