随机信号分析常建平,李林海课后习题答案第二章习题讲解
随机信号分析(常建平李海林)习题答案解析

完美 WORD 格式1-9 已知随机变量X的分布函数为0 , x 02F (x) kx , 0 x 1X1 , x 1求:①系数 k;②X落在区间(0.3,0.7) 内的概率;③随机变量X的概率密度。
解:第①问利用F X (x) 右连续的性质k =1P 0.3 X 0.7 P 0.3 X 0.7 P X 0.7 第②问F 0.7 F 0.3第③问f (x)Xd F(x)Xdx2x 0 x 10 else专业知识分享完美 WORD 格式x1-10 已知随机变量X 的概率密度为( ) ( )f x ke xX(拉普拉斯分布),求:①系数k ②X落在区间 (0,1)内的概率③随机变量 X的分布函数解:第①问f x dx 1 k12第②问x2P x X x F x F x f x dx1 2 2 1x1随机变量 X落在区间( x1 , x2 ] 的概率 P{ x1 X x2} 就是曲线y f x 下的曲边梯形的面积。
1P 0 X 1 P 0 X 1 f x dx1 2 1 e1第③问12 f x12xe xxe xxF x f ( x)dx1 1x x xe dx x 0 e x 02 20 1 1 1xx x xe dx e dx x 0 1 e x 02 0 2 2专业知识分享完美 WORD 格式1-11 某繁忙的汽车站,每天有大量的汽车进出。
设每辆汽车在一天内出事故的概率为0.0001,若每天有1000 辆汽车进出汽车站,问汽车站出事故的次数不小于 2 的概率是多少?n=1- 分布 (0 1)n ,p 0,np=二项分布泊松分布n 成立,0不成立, p q高斯分布实际计算中,只需满足,二项分布就趋近于泊松分布n 10 p 0.1P X kk e==np k!汽车站出事故的次数不小于 2 的概率P(k 2) 1 P k 0 P k 10.1P(k 2) 1 1.1e 答案专业知识分享完美 WORD 格式1-12 已知随机变量 (X,Y)的概率密度为f (x, y) XY(3 x 4 y),ke x 0, y 0, 其它0求:①系数k?②( X ,Y)的分布函数?③P{0 X 1,0 X 2} ?第③问方法一:联合分布函数F XY (x, y) 性质:若任意四个实数 a ab b ,满足1, 2, 1, 2a a bb ,满足a1 a2,b1 b2 ,则P{a X a ,b Y b}F XY(a ,b ) F XY(a ,b) F XY(a ,b ) F XY(a ,b)1 2 1 2 2 2 1 1 1 2 2 1P{0X 1,0 Y 2} F XY(1,2) F XY(0,0) F XY(1,0) F XY(0,2)方法二:利用P{( x, y) D } f XY u,v dudvD2 1P{0X 1,0 Y 2} f XY x,y dxdy0 0专业知识分享完美 WORD 格式1-13 已知随机变量(X,Y) 的概率密度为f (x, y)1, 0 x 1, y x0 , 其它①求条件概率密度 f X (x| y)和f Y ( y | x) ?②判断X 和Y 是否独立?给出理由。
随机信号分析(常建平李海林)习题答案解析

完美 WORD 格式1-9 已知随机变量X的分布函数为0 , x 02F (x) kx , 0 x 1X1 , x 1求:①系数 k;②X落在区间(0.3,0.7) 内的概率;③随机变量X的概率密度。
解:第①问利用F X (x) 右连续的性质k =1P 0.3 X 0.7 P 0.3 X 0.7 P X 0.7 第②问F 0.7 F 0.3第③问f (x)Xd F(x)Xdx2x 0 x 10 else专业知识分享完美 WORD 格式x1-10 已知随机变量X 的概率密度为( ) ( )f x ke xX(拉普拉斯分布),求:①系数k ②X落在区间 (0,1)内的概率③随机变量 X的分布函数解:第①问f x dx 1 k12第②问x2P x X x F x F x f x dx1 2 2 1x1随机变量 X落在区间( x1 , x2 ] 的概率 P{ x1 X x2} 就是曲线y f x 下的曲边梯形的面积。
1P 0 X 1 P 0 X 1 f x dx1 2 1 e1第③问12 f x12xe xxe xxF x f ( x)dx1 1x x xe dx x 0 e x 02 20 1 1 1xx x xe dx e dx x 0 1 e x 02 0 2 2专业知识分享完美 WORD 格式1-11 某繁忙的汽车站,每天有大量的汽车进出。
设每辆汽车在一天内出事故的概率为0.0001,若每天有1000 辆汽车进出汽车站,问汽车站出事故的次数不小于 2 的概率是多少?n=1- 分布 (0 1)n ,p 0,np=二项分布泊松分布n 成立,0不成立, p q高斯分布实际计算中,只需满足,二项分布就趋近于泊松分布n 10 p 0.1P X kk e==np k!汽车站出事故的次数不小于 2 的概率P(k 2) 1 P k 0 P k 10.1P(k 2) 1 1.1e 答案专业知识分享完美 WORD 格式1-12 已知随机变量 (X,Y)的概率密度为f (x, y) XY(3 x 4 y),ke x 0, y 0, 其它0求:①系数k?②( X ,Y)的分布函数?③P{0 X 1,0 X 2} ?第③问方法一:联合分布函数F XY (x, y) 性质:若任意四个实数 a ab b ,满足1, 2, 1, 2a a bb ,满足a1 a2,b1 b2 ,则P{a X a ,b Y b}F XY(a ,b ) F XY(a ,b) F XY(a ,b ) F XY(a ,b)1 2 1 2 2 2 1 1 1 2 2 1P{0X 1,0 Y 2} F XY(1,2) F XY(0,0) F XY(1,0) F XY(0,2)方法二:利用P{( x, y) D } f XY u,v dudvD2 1P{0X 1,0 Y 2} f XY x,y dxdy0 0专业知识分享完美 WORD 格式1-13 已知随机变量(X,Y) 的概率密度为f (x, y)1, 0 x 1, y x0 , 其它①求条件概率密度 f X (x| y)和f Y ( y | x) ?②判断X 和Y 是否独立?给出理由。
随机信号分析基础第二章习题 ppt课件

可得:
0, x 3
P(X
x, 2)
1
3
2
3
, ,
3 4
x x
4 6
1, x 6
2021/3/30
9
同理可得:
0, x 2
问题
FX
(x;
6)
P(
X
x,
6)
13 23
, ,
2 5
x x
5 7
1, x 7
F X(x;2)P X (2)x
3;
2021/3/30
CX (t1,t2)
15
2.9 解:(1)直接由定义可得:
E [X (t)] E [A c o s (0 t) B s in (0 t)] E [A ]c o s (0 t) E [B ]s in (0 t)
0
(2)由自相关函数的定义:
R X (t1 ,t2 ) E [X (t1 )X (t2 )]
用表格来表示所求的联合分布:
x2
x1
x1 3 3 x1 4 4 x1 6 x1 6
x2 2
0
0
0
0
ห้องสมุดไป่ตู้
2 x2 5 0
0
0
1/3
5 x2 7
0
1/3 1/3 2/3
x2 7
0
1/3 2/3 1
2021/3/30
11
问题
x2
x1
x2 2
x1 3 3 x1 4 4 x1 6 x1 6
所以:
E[X(2)]1(346)13;
3
3
E[X(6)]1(572)14;
3
第2章课后习题参考答案

第2章课后习题参考答案第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答:假设1、解释变量X 是确定性变量,Y 是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假设3、随机误差项ε与解释变量X 之间不相关: Cov(X i , εi )=0 i=1,2, …,n 假设4、ε服从零均值、同方差、零协方差的正态分布εi ~N(0, σ2 ) i=1,2, …,n2.2 考虑过原点的线性回归模型Y i =β1X i +εi i=1,2, …,n误差εi (i=1,2, …,n )仍满足基本假定。
求β1的最小二乘估计解:得:2.3 证明(2.27式),∑e i =0 ,∑e i X i =0 。
证明:其中:∑∑+-=-=nii i ni X Y Y Y Q 121021))??(()?(ββ2112)?()?(i ni i n i ii e X Y Y Y Q β∑∑==-=-=01i i i i iY X e Y Y ββ=+=-即:∑e i =0 ,∑e i X i =02.4回归方程E (Y )=β0+β1X 的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N (β0+β1X i , σ2 ) 最大似然函数:使得Ln (L )最大的0β,1?β就是β0,β1的最大似然估计值。
同时发现使得Ln (L )最大就是使得下式最小,上式恰好就是最小二乘估计的目标函数相同。
值得注意的是:最大似然估计是在εi ~N (0, σ2 )的假设下求得,最小二乘估计则不要求分布假设。
所以在εi ~N(0, σ2 ) 的条件下,参数β0,β1的最小二乘估计与最大似然估计等价。
随机信号分析(常建平李海林)习题答案解析

y
y
0
1
1
e
e
y
3
2
1
0
else
1-17 已知随机变量 X,Y 的联合分布律为
P X m,Y n
m ne 5
32
, m,n 0,1,2,
m! n!
***
求: ① 边缘分布律
***
P X m (m 0,1,2, ) 和
②条 件分布律 P X m |Y
和 n
PY
n|X
m?
专业 知识分享
P Y n (n 0,1,2,
0.0001 ,若每天有 1000 辆汽车进
出汽车站,问汽车站出事故的次数不小于
2 的概率是多少?
二项分布
n=1
- 分布 (0 1)
n
,p 0,np=
泊松分布
n
成立 , 0 不成立
,p q
高斯分布
实际计算中,只需满足
,二项分布就趋近于泊松分布 n 10 p 0.1
ke PX k =
k!
= np
汽车站出事故的次数不小于
X
3
6
7
求: ①X 的分布函数
P 0.2 0.1 0.7 ② 随机变量 Y 3X 1 的分布律
1-15 已知随机变量 X 服从标准高斯分布。 求:①随机变量 Z X 的概率密度? 的概率密度? ② 随机变量
分析 : ① f Y (y)
h '(y)
f X h( y)
② f Y ( y) | h' 1 (y) | f X [h 1 ( y)]
第③问
fx Fx
1x 2e
0 x
1x
e 2
0 x
随机信号分析课后习题答案

1第一次作业:练习一之1、2、3题1.1 离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=ii ix X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F 求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他201)](2π[cos 2)()(x x A dx x dF x f由 1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P 1.3 试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x2(2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x xx x F (3)0)]()([)(>--=a a x u x u ax x F (4)0)()()(>---=a a x u ax a x u a x x F解:(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数;1)(0≤≤x F 成立; )()(x F x F =+也成立。
随机信号分析(常建平,李林海)课后习题答案第二章习题讲解
A与 B独立 , f AB (a, b) f A (a) fB (b)
X (t) A Bt Y(t) A
A Y(t) X (t) Y (t)
B t
01 J1 1 1
t tt
1
xy 1
xy
f XY (x, y; t ) J f AB (a,b) t f AB ( y, t ) t f A ( y) f B ( t )
E X (t) E A cost XH cost EA XH
D X (t) E X 2 (t ) E2 X (t )
方法 2:
D X (t)
D Acost XH D Acost cos2 t DA cos2 t
12
D XH
公式: D aX+ bY a2 D X b2 D Y 2abC XY
RX (t1, t2 )=E Acost1 XH A cost2 XH
f X (x1;0)
1
x12 e 2,
2Байду номын сангаас
A
1
X (t)
~ N (0, )
t 30
2
4
f X ( x2; 3
)=
0
2 2
e
2
x2
2
,
X (t) t
=0,
f ( x3;2
)
0
20
( x3)
(离散型随机变量分布律 )
2-2 如图 2.23 所示,已知随机过程 X (t) 仅由四条样本函数组
成,出现的概率为
数 RX (t1, t2 ) ?②若已知随机变量相 A, B 互独立,
它们的概率密度分别为 f A (a) 和 f B (b) ,求 X (t) 的一
随机信号分析(常建平,李林海)课后习题答案第三章 习题讲解

、随机过程 X(t)=A+cos(t+B),其中A 是均值为2,方差为1的高斯变量,B 是(0,2π)上均匀分布的随机变量,且A 和B 独立。
求(1)证明X(t)是平稳过程。
(2)X(t)是各态历经过程吗?给出理由。
(3)画出该随机过程的一个样本函数。
(1)(2)3-1 已知平稳过程()X t 的功率谱密度为232()(16)X G ωω=+,求:①该过程的平均功率? ②ω取值在(4,4)-范围内的平均功率?解[][]()[]2()cos 211,cos 5cos 22X E X t E A E t B A B R t t EA τττ=++=⎡⎤⎣⎦+=+=+与相互独立()()()21521()lim2TT T E X t X t X t X t dt AT-→∞⎡⎤=<∞⇒⎣⎦==⎰是平稳过程()()[]()()4112211222222242'4(1)24()()444(0)41132(1)224414414(2)121tan 13224X X XE X t G d RFG F e R G d d d arc x x ττωωωωωππωωπωωπωπωω∞----∞∞-∞-∞∞--∞∞⎡⎤⨯⎡⎤==⋅=⋅⎢⎥+⎣⎦====+==⎛⎫+ ⎪==⎣⎦=++⎝⎭=⎰⎰⎰⎰⎰P P P P 方法一()方:时域法取值范围为法二-4,4内(频域的平均率法功)2d ω=3-7如图3.10所示,系统的输入()X t 为平稳过程,系统的输出为()()()Y t X t X t T =--。
证明:输出()Y t 的功率谱密度为()2()(1cos )Y X G G T ωωω=-[][]:()[()()]{()()}{()(}2()()()()()()()()2(()[)()(()()]()())Y X X X Y X X Y Y Y X X X Y Y j T j T R E Y t Y t E X t X t T X t X t T R R R R E Y t Y t G F R T T e e G R G R G G G G ωωτττττωτωττωττττωωωω-⇒⇒=+=--+-+-=--=+=-⇔⇔∴=-+-=已知平稳过程的表达式利用定义求利用傅解系统输入输出立叶平变稳换的延时特性2()2()22()(1cos )j T j T X X X e e G G G T ωωωωωω-⎡⎤+-⎢⎥⎣⎦=-3-9 已知平稳过程()X t 和()Y t 相互独立,它们的均值至少有一个为零,功率谱密度分别为216()16X G ωω=+22()16Y G ωωω=+令新的随机过程()()()()()()Z t X t Y t V t X t Y t =+⎧⎨=-⎩ ①证明()X t 和()Y t 联合平稳; ②求()Z t 的功率谱密度()Z G ω? ③求()X t 和()Y t 的互谱密度()XY G ω? ④求()X t 和()Z t 的互相关函数()XZ R τ? ⑤求()V t 和()Z t 的互相关函数()VZ R τ 解:()()4124(1)()()()2[()]()0[()]0()2[()]0()()(,)[()][()]0()()(2)()()()()[()()][()()][()X X X Y XY Z X t Y t R F G e E X t R E X t R eE Y t X t Y t R t t E X t E Y t X t Y t Z t X t Y t R E Z t Z t E X t Y t X t τττωτδττττττ---==∞=⇒=⎡⎤⎣⎦=-⇒=∴+=⋅+=⇒=+=+=++、都平稳=与与联合独平立稳[][]{}2214||()]()()()()()0()()()16()()()116(3)()0()0(4)()[()()]()()()()()()[()]2(5)(X YX XY Y XY Z X Y Z X Y XY XY XZ X XY X X VZ Y t R R R R R R R R G G G R G R E X t Z t E X t X t Y t R R R F G e R ττττττττττωωωωωτωτττττττωτ--++=+++=∴=++∴=+==+=→==+=+++=+==={}4||)[()()][()()][()()]()()()4X Y E V t Z t E X t Y t X t Y t R R e ττττττδτ-=+=-+++=-=+-3-11 已知可微平稳过程()X t 的自相关函数为2()2exp[]X R ττ=-,其导数为()()Y t X t '=。
随机信号分析中文版答案

1≤ y ≤ 6
1 b−a
+∞ −∞
X 1 ⋅⋅⋅ X n 相互独立
φ X (ω ) = ∫
i
f X ( xi )e jω xi dxi
=∫
b
a
1 jω xi 1 1 jωb e dxi = (e − e jω a ) b−a b − a jω
(b+ a ) ⎛ (b − a )ω ⎞ jω 2 = Sa ⎜ ⎟e 2 ⎝ ⎠
π
2
−2+
π2
8
2 2 2 ∴ D [ x] = σ X =E⎡ ⎣x ⎤ ⎦ − E [ x] 2 =σy =
π
2
−2+
π2
8
−
π2
16
=
π2
16
+
π
2
−2
(4)
Rxy = E [ xy ]
π 1 π 2 2 xy sin ( x + y ) dxdy 2 ∫0 ∫0 π π ⎤ 1 π ⎡ = ∫ 2 x ⎢ − y cos ( x + y ) 02 + sin ( x + y ) 02 ⎥ dx 2 0 ⎣ ⎦
5
《随机信号分析》 课后习题答案
武汉理工大学信息工程学院
cx1x 2 = rx1x 2 − mx1mx 2 cx1x 2 ⎞ ⎛10 2 ⎞ ⎛c cx ( x1, x 2) = ⎜ x1x1 ⎟=⎜ ⎟ ⎝ cx 2 x1 cx 2 x 2 ⎠ ⎝ 2 10 ⎠
1 − f x ( x1 , x2 ) = e 192π
1.8 解: C XY = E[( x − mx )( y − m y )] = E[ XY ] − mx m y = m11 − mx m y
随机信号分析(常建平,李林海)课后习题答案第三章 习题讲解可编辑】

、随机过程 X(t)=A+cos(t+B),其中A 是均值为2,方差为1的高斯变量,B 是(0,2π)上均匀分布的随机变量,且A 和B独立。
求(1)证明X(t)是平稳过程。
(2)X(t)是各态历经过程吗?给出理由。
(3)画出该随机过程的一个样本函数。
(1)(2) 3-1 已知平稳过程()X t 的功率谱密度为232()(16)X G ωω=+,求:①该过程的平均功率? ②ω取值在(4,4)-范围内的平均功率?解[][]()[]2()cos 211,cos 5cos 22X E X t E A E t B A B R t t EA τττ=++=⎡⎤⎣⎦+=+=+与相互独立()()()21521()lim 2TT T E X t X t X t X t dt A T -→∞⎡⎤=<∞⇒⎣⎦==⎰是平稳过程()()[]()()4112211222222242'4(1)24()()444(0)41132(1)224414414(2)121tan 13224X X X E X t G d R F G F e R G d d d arc x x ττωωωωωππωωπωωπωπωω∞----∞∞-∞-∞∞--∞∞⎡⎤⨯⎡⎤==⋅=⋅⎢⎥+⎣⎦====+==⎛⎫+ ⎪==⎣⎦=++⎝⎭=⎰⎰⎰⎰⎰P P P P 方法一()方:时域法取值范围为法二-4,4内(频域的平均率法功)2d ω=3-7如图3.10所示,系统的输入()X t 为平稳过程,系统的输出为()()()Y t X t X t T =--。
证明:输出()Y t 的功率谱密度为()2()(1cos )Y X G G T ωωω=-[][]:()[()()]{()()}{()(}2()()()()()()()()2(()[)()(()()]()())Y X X X Y X X Y Y Y X X X Y Y j T j TR E Y t Y t E X t X t T X t X t T R R R R E Y t Y t G F R T T e e G R G R G G G G ωωτττττωτωττωττττωωωω-⇒⇒=+=--+-+-=--=+=-⇔⇔∴=-+-=已知平稳过程的表达式利用定义求利用傅解系统输入输出立叶平变稳换的延时特性2()2()22()(1cos )j T j T X X X e e G G G T ωωωωωω-⎡⎤+-⎢⎥⎣⎦=-3-9 已知平稳过程()X t 和()Y t 相互独立,它们的均值至少有一个为零,功率谱密度分别为216()16X G ωω=+ 22()16Y G ωωω=+令新的随机过程()()()()()()Z t X t Y t V t X t Y t =+⎧⎨=-⎩ ①证明()X t 和()Y t 联合平稳;②求()Z t 的功率谱密度()Z G ω?③求()X t 和()Y t 的互谱密度()XY G ω?④求()X t 和()Z t 的互相关函数()XZ R τ?⑤求()V t 和()Z t 的互相关函数()VZ R τ解:()()4124(1)()()()2[()]()0[()]0()2[()]0()()(,)[()][()]0()()(2)()()()()[()()][()()][()X X X Y XY Z X t Y t R F G eE X t R E X t R e E Y t X t Y t R t t E X t E Y t X t Y t Z t X t Y t R E Z t Z t E X t Y t X t τττωτδττττττ---==∞=⇒=⎡⎤⎣⎦=-⇒=∴+=⋅+=⇒=+=+=++、都平稳=与与联合独平立稳[][]{}2214||()]()()()()()0()()()16()()()116(3)()0()0(4)()[()()]()()()()()()[()]2(5)(X YX XY Y XY Z X Y Z X Y XY XY XZ X XY X X VZ Y t R R R R R R R R G G G R G R E X t Z t E X t X t Y t R R R F G e R ττττττττττωωωωωτωτττττττωτ--++=+++=∴=++∴=+==+=→==+=+++=+==={}4||)[()()][()()][()()]()()()4X Y E V t Z t E X t Y t X t Y t R R e ττττττδτ-=+=-+++=-=+-3-11 已知可微平稳过程()X t 的自相关函数为2()2exp[]X R ττ=-,其导数为()()Y t X t '=。
随机信号分析常建平 李海林习题答案第三章 习题讲解.doc

J、随机过程X(t)=A+cos(t+B),其中A是均值为2,方差为1的高斯变量,B是(0, 2兀)上均匀分布的随机变量,且A和B 独立。
求(1)证明X(t)是平稳过程。
(2)X(t)是各态历经过程吗?给出理由。
(3)画出该随机过程的一个样本函数。
(1) E[X(t)] = E[A\ + E[cos(r + 8)] = 2A与与相互独立7?x + 丁] = EA~ H—cos T = 5 —cos T1 1r(2) E[x2(r)] = 5-<oo nX(r)是平稳过程--- 1 C T / \X(0= lim ——\ X (t)dt = AT Too 2T「T ''3-1己知平稳过程x(f)的功率谱密度为G、(〃)=y刀,求:①该过程的平均功率?0+16)②口取值在(-4,4)范围内的平均功率?2x4 42 + ®=4七州 R =R(0)=4 方法二(频域法) f] — ——J Gx(cd)dco =lr_71 J-8 1+ .oo 3? - r” =4CD \ '4JV 1arc tan x) = ---- r7 1 + x 2 (2) 口取值范围为(-4, 4)内的平均功率 •4 32,,da) =2P 2 2〃 7?(r) = F-1[G x (®)] = 4-F-1 (1): P = E [X 2 (?)] = —方法一(时域法)3-7如图3.10所示,系统的输入X。
)为平稳过程, 系统的输出为W) = x(。
-x(—『)。
证明:输出W) 的功率谱密度为Gy (口) = 2Gx㈣(1 - cos或)期) +--------------------------------------- ------------------- *—延时T ----解:已知平稳过程的表达式n 利用定义求R Y(r) = E[Y(t)Y(t + T)]^G y(®) = F[7?y(r)]7?r(r)= E[y(z)y(r + r)]= E[{X(t)-X(t-T)}{X(t + r)-X(t + T-T}]= 2Rx(f)-Rx(—T)-Rx("T)系统输入输出平稳GxO)0Rx(J)Gy®)。
随机信号分析第3版第二章 习题答案.pdf

k =0
k =0
如果将 4bit 串看作是一个随机向量,则随机向量的均值和方差为:
串平均: Ε ⎡⎣{B (n) , B (n +1) , B (n + 2) , B (n + 3)}⎤⎦ = {0.8, 0.8, 0.8, 0.8}
串方差:
Var ⎡⎣{B (n), B (n +1), B (n + 2) , B (n + 3)}⎤⎦ = {0.16, 0.16, 0.16, 0.16}
3
∑ 串(4bit 数据)为: X (n) = 2k B(n + k) ,其矩特性为: k =0
因为随机变量 B(n) 的矩为:
均值: E[B(n)] = 0× 0.2 +1× 0.8 = 0.8
{ } 方差:
Var
[
B(n)
]
=
Ε
⎡ ⎣
B
(
n
)2
⎤ ⎦
−
Ε ⎡⎣B (n)⎤⎦
2 = 02 × 0.2 +12 × 0.8 − 0.82
= E{[ X (s + a) − X (s)][X (t + a) − X (t)]} = E[ X (s + a) X (t + a)] − E[ X (s + a) X (t)] − E[ X (s) X (t + a)] + E[ X (s) X (t)] = RX (s + a, t + a) − RX (s + a, t) − RX ( s, t + a) + RX ( s, t)
P ⎡⎣{1011}⎤⎦ = P ⎡⎣B (n) = 1⎤⎦ × P ⎡⎣B (n) = 0⎤⎦ × P ⎡⎣B (n) = 1⎤⎦ × P ⎡⎣B (n) = 1⎤⎦
(仅供参考)随机信号分析与处理简明教程--第二章习题答案
⎧ 0,
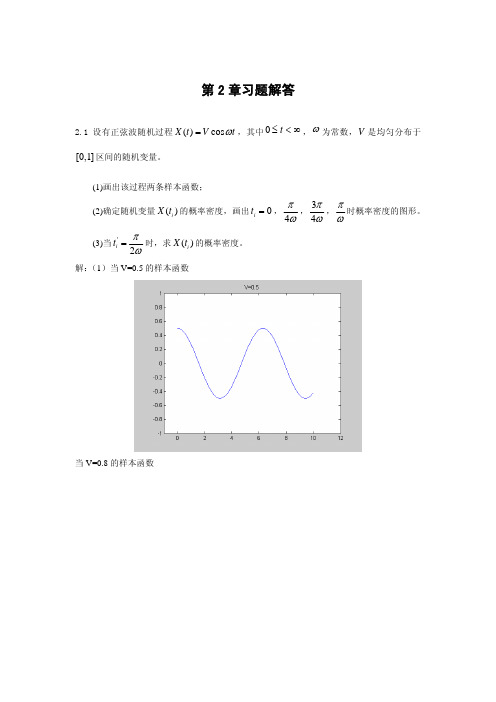
(2)
FX
⎜⎛ ⎝
x1
,
x2
;
1 2
,1⎟⎞ ⎠
=
⎪⎩⎪⎨ 121,,
x1 < 0,−∞ < x2 < ∞; 0 ≤ x1 < 1, x2 ≥ −1;
x1 ≥ 1,
x1 ≥ 0, x2 < −1 x1 ≥ 1,−1 ≤ x2 < 2
x2 ≥ 2
2.3 设某信号源,每 T 秒产生一个幅度为 A 的方波脉冲,其脉冲宽度 X 为均匀分布于[0,T ]
当 ti
=
0 时,
fX
( x, t )
=
⎧1 ⎨⎩ 0
0< x <1 else
当 ti
=
π 4ω
时,
fX (x,t)
=
⎧⎪ ⎨ ⎪⎩
2 0
0<x< π 4ω
时,
fX (x,t)
=
⎧⎪ ⎨ ⎪⎩
2 0
− 2 2<x<0 else
当 ti
=
π ω
时,
fX
( x, t )
=
⎧1 ⎨⎩ 0
当kl时有rtsx2????????????eakutkt0utkt01uskt0uskt01ea2eut?k?t?ut?k?t?1us?k?t?us?k?t?1k0000eut?k?t0?ut?k?t0?1us?k?t0?us?k?t0?1kt00faa?2??0a0是在02中均匀分布的随机变量且与a统计独立为常量
D[ X (t)] = D[ Acosωt + B sin ωt] = D[ A]cos2 ωt + D[B]sin2 ωt = σ 2
随机信号分析课后习题答案

第一次作业:练习一之1、2、3题1.1离散随机变量X 由0,1,2,3四个样本组成,相当于四元通信中的四个电平,四个样本的取值概率顺序为1/2,1/4,1/8,和1/8。
求随机变量的数学期望和方差。
解:875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=ii ix X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F 求(1)系数A ;(2)X 取值在(0.5,1)内的概率)15.0(<<x P 。
解:⎪⎩⎪⎨⎧<≤-π==其他201)](2π[cos 2)()(x x A dx x dF x f由 1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P 1.3试确定下列各式是否为连续随机变量的概率分布函数,如果是概率分布函数,求其概率密度。
(1)⎪⎩⎪⎨⎧<≥-=-000e1)(2x x x F x (2)⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x xx x F(3)0)]()([)(>--=a a x u x u ax x F (4)0)()()(>---=a a x u ax a x u a x x F解:(1)⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x当0≥x 时,对于12x x ≥,有)()(12x F x F ≥,)(x F 是单调非减函数;1)(0≤≤x F 成立; )()(x F x F =+也成立。
随机信号分析(常建平-李林海)课后习题答案第二章习题讲解

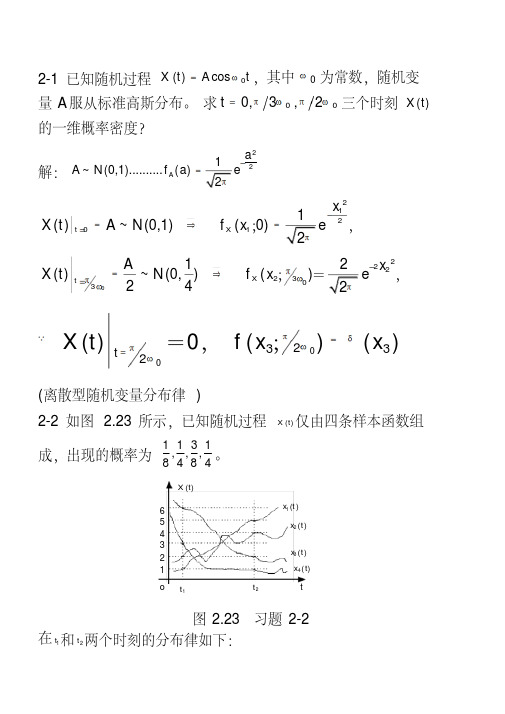
2-1 已知随机过程0()cos X t A t ω=,其中0ω为常数,随机变量A 服从标准高斯分布。
求000,3,2t πωπω=三个时刻()X t 的一维概率密度?解:221~(0,1)..........()A a A N f a -=21211()~(0,1)(0)t X x X t A N f x e-==⇒=;,2223203A 12()~(0,)()24X t x X t N f x e πωπω-==⇒;, 002323()0()()t X t f x x πωπωδ===,;(离散型随机变量分布律)2-2 如图2.23所示,已知随机过程()X t 仅由四条样本函数组成,出现的概率为1131,,,8484。
t()X t 1234561t 2t 1()x t 2()x t 3()x t 4(x t o图2.23 习题2-2在1t 和2t 两个时刻的分布律如下:求? 1212[()],[()],[()()]E X t E X t E X t X t ()41129[()]8k k k E X t x p t ===∑221[()]8E X t =()()(){}121212121122[()()],,X k k E X t X t R t t k k p X t k X t k ====∑∑2-23[][]12()cos (0,1)(;),()()(,)X X X t A t XH A U f x t E X t D X t R t t =+~随机过程,其中(均匀分布)。
求,,?[][][][][][][][][][][]()()()22221212221121222()cos cos ()()()()cos cos cos cos 12(,)cos cos cos cos cos cos 1cos c 232o X XYD aE X t E A t XH t EA XHD X tE X t E X t D X t D A t XH D A t D XH tt DA R t t E A t XH X a D X b D Y abC EA EA A t XH t t XH t t XH t =+=⋅+⎡⎤=-⎣⎦=+=+=⋅=++⎡⎤⎣⎦+==+=+++公式:+b =Y方法:()2212s cos cos 2XH t t t XH +++()()()()22cos 022~,322cos 022~,cos 0()2122,cos 2cos cos cos c 21322,(;)cos o 2s 2X k t k t tX t U XH XH k t k t t X t U XH XH t k t X t XHk t k XH x XH t k t k XH x XH f x t t x X t t t t ππππππππππππππππππδ-+<<+>+<<+<=+==-+<<+<<-++<<+<+++<=-对某一固定时刻对某一固定时刻概率密度用冲激函数表示(),20H t k x XH else ππ⎧⎪⎪⎪⎪⎨⎪=+=⎪⎪⎪⎩2-4 已知随机过程()X t A Bt =+,其中,A B 皆为随机变量。
随机习题课

总结
相关函数之间的关系
RX (τ ) ˆ
RM (τ )
谱之间的关系
RX (τ )
RXXˆ (τ ), RXX (τ ) ˆ
RX (τ ) %
% RX (τ )
ˆ RX (τ )
GXˆ (ω )
GM (ω )
GX (ω )
GXXˆ (ω ), GXX (ω ) ˆ
GX (ω ) %
AC (t ), AS (t )的统计特性总结
南京航空航天大学 信息科学与技术学院 常建平 李海林
第四章 随机信号通过线性系统
线性系统的基本理论 时域法 频域法 色噪声和白噪声的产生 白噪声通过线性系统
X (t )
L [⋅]
Y (t )
时域法
X(t)的期望、自相关函数 系统单位冲激响应h(t) Y(t)的期望E [Y (t ) ]
互相关函数 RXY (τ ) 平稳 互谱密度 GXY (ω )
宽带噪声 高频窄带系统 平方律检波器
A2 (t)
A2 (t)
加法器
χ2分布
独立取样m次
1 (归一化) 2
σ
习题课三
☆ 做在作业本上 ☆
试着不要看课本,独立完成
一、填空题 1、等效噪声带宽定义中应用了两个等效原则: (1)、 (1) (2)、 (2) (3) 。 。
2
2、希尔伯特变换的传递函数H(ω)=
H I (ω ) = K = H (ω ) MAX
系统的等效噪声带宽是系统固有的参数,与输入信号无关。 系统的等效噪声带宽是系统固有的参数,与输入信号无关。
线性系统输出端随机信号的概率分布
结论1: 结论 : 高斯 分布 线性系统 高斯 分布
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1 已知随机过程0()cos X t A t ω=,其中0ω为常数,随机变量A 服从标准高斯分布。
求000,3,2t πωπω=三个时刻()X t 的一维概率密度?解:221~(0,1)..........()A a A N f a -=(离散型随机变量分布律)2-2 如图2.23所示,已知随机过程()X t 仅由四条样本函数组成,出现的概率为1131,,,8484。
图2.23 习题2-2在1t 和2t求 1212[()],[E X t E X ()()(){}121212121122[()()],,X k k E X t X t R t t k k p X t k X t k ====∑∑2-23 [][]12()cos (0,1)(;),()()(,)X X X t A t XH A U f x t E X t D X t R t t =+~随机过程,其中(均匀分布)。
求,,?()()()()22cos 022~,322cos 022~,cos 0()2122,cos 2cos cos cos c 21322,(;)cos o 2s 2X k t k t tX t U XH XH k t k t t X t U XH XH t k t X t XHk t k XH x XH t k t k XH x XH f x t t x X t t t t ππππππππππππππππππδ-+<<+>+<<+<=+==-+<<+<<-++<<+<+++<=-对某一固定时刻对某一固定时刻概率密度用冲激函数表示(),20H t k x XH else ππ⎧⎪⎪⎪⎪⎨⎪=+=⎪⎪⎪⎩2-4 已知随机过程()X t A Bt =+,其中,A B 皆为随机变量。
①求随机过程的期望[()]E X t 和自相关函数12(,)X R t t ?②若已知随机变量相互独立,它们的概率密度分别为()A f a 和()B f b ,求()X t 的一维概率密度(;)X f x t第②问方法一:用雅克比做(求随机变量函数的分布) 步骤:t 时刻,()X t A Bt =+为两个随机变量的函数 ①设二维的随机矢量12X A Bt X A=+⎧⎨=⎩(题目要求的)(自己设的量,可以是其它量)②求反函数③求雅克比行列式J ,得到|J| ④利用公式12X X 12(,)(,)AB x x f b J f a =⋅⑤由联合概率密度求边缘概率密度()1X f x ⑥t 为变量,则得到(;)X f x t方法二: 用特征函数定义和性质(独立变量和的特征函数等于各特征函数的乘积)做(特征函数和概率密度一一对应),A B()()()()()()()()()()()()()()()()()(),;;;;;ju juX t ju A Bt ju a btX AB ju a b A B xX X ju A B j A B uxX t B X x A f a f b Q u t E eE e e f a b dadbedadbx Q u t e d dbedxf bt f Q u b f x t t f x t e dxf x bt f b d f x b f b x x bt b d ++∞+∞++-∞-∞+∞+∞+-∞-∞+∞+∞-∞-∞+∞-∞-∞+∞+-∞∞∞∞-⎡⎤⎡⎤===⎣⎦⎣⎦====--=-⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰取a=-bt2-5 已知()X t 为平稳过程,随机变量0()Y X t =。
判断随机过程()()Z t X t Y =+的平稳性? 随机过程()()Z t X t Y =+非平稳2-6 已知随机过程0()()cos()Y t X t t ω=+Φ,其中随机过程()X t 宽平稳,表示幅度;角频率0ω为常数;随机相位Φ服从(,)ππ-的均匀分布,且与过程()X t 相互独立。
①求随机过程()Y t 的期望和自相关函数?②判断随机过程()Y t 是否宽平稳? ①Φ与过程()X t 相互独立2-8 已知平稳过程()X t 的自相关函数为 ()4cos cos3X R eττπτπτ-=+,求过程的均方值和方差?()X t2-10 已知过程()cos sin X t A t B t=-和()cos sin Y t B t A t =+,其中随机变量,A B 独立,均值都为0,方差都为5。
①证明()X t 和()Y t 各自平稳且联合平稳;②求两个过程的互相关函数?① []()[]2()0,5cos ()5X E X t R t t E X t X t ττ⎡⎤=+==<∞⎣⎦⇒平稳2-11 已知过程()X t 和()Y t 各自平稳且联合平稳,且()()()Z t X t Y t =+。
①求()Z t 的自相关函数()Z R τ?②若()X t 和()Y t 独立,求()Z R τ?③若()X t 和()Y t 独立且均值均为0,求()Z R τ 第①问两个联合平稳的过程的互相关函数 第②问 两平稳过程独立第③问 ()X t 和()Y t 独立且均值均为02-12 已知两个相互独立的平稳过程()X t 和()Y t 的自相关函数为令随机过程,其中A 是均值为2,方差为9的随机变量,且与()X t 和()Y t 相互独立。
求过程()Z t 的均值、方差和()()()Z t AX t Y t 自相关函数?随机变量A ,与()X t 和()Y t 相互独立可以证明过程()Z t 平稳2-14 已知复随机过程式中(1,,)i A i n =为n 个实随机变量,(1,,)i i n ω=为n个实数。
求当i A 满足什么条件时,()Z t 复平稳?复过程()Z t 复平稳条件()()()+j ,Z zZ Z m t m m m R t t R ττ=⎧⎪⎨+=⎪⎩X Y 复常数, ①()()[]()11exp exp z i i i i i i m t E A j t j A t E ωω∞∞==⎡⎤==⎢⎥⎣⎦∑∑ ②2-16 已知平稳过程()X t 的均方可导,()()Y t X t '=。
证明(),()X t Y t 的互相关函数和()Y t 的自相关函数分别为若()X t 为宽平稳(实)过程,则'()X t 也是宽平稳(实)过程,且()X t 与'()X t 联合宽平稳。
2-17 已知随机过程()X t 的数学期望2[()]4E X t t =+,求随机过程2()()Y t tX t t '=+的期望?2-18 已知平稳过程()X t 的自相关函数21()2exp 2X R ττ⎛⎫=- ⎪⎝⎭。
求:①其导数()()Y t X t '=的自相关函数和方差?②()X t 和()Y t 的方差比? 不含周期分量补充题:若某个噪声电压()X t 是一个各态历经过程,它的一个样本函数为()2cos 4X t t π⎛⎫=+ ⎪⎝⎭,求该噪声的直流分量、交流平均功率解:直流分量()E X t ⎡⎤⎣⎦、交流平均功率()D X t ⎡⎤⎣⎦各态历经过程 可以用它的任一个样本函数的时间平均来代替整个过程的统计平均 再利用平稳过程自相关函数的性质 方法二:()()()222222()()()2cos ()011()limli 24m 22TTT T T T X t X t D X t E X t E X t X t X t dt dt TX t Tt π--→∞→∞⎛⎫+ ⎪⎡⎤=-=-⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦=⎡⎤==⎢⎥⎣⎭⎦⎝⎰⎰=01()()tY t X d tλλ=⎰2-19 已知随机过程()cos3X t V t =,其中V 是均值和方 差皆为1的随机变量。
令随机过程求()Y t 的均值、自相关函数、协方差函数和方差? 解:1. 求均值,利用[()][()]bba a E X t dt E X t dt=⎰⎰随机过程的积分运算与数学期望运算的次序可以互换2.求自相关函数3. 求互协方差函数4. 求方差 ()[],t Y C t t D Y t =⎡⎤⎣⎦是关于的方差一元函数()[]2222sin sin 3sin 39933t t V D Y ttV t D t D t ⎡⎤===⎡⎤⎣⎦⎢⎥⎣⎦方法二:2-20 已知平稳高斯过程()X t 的自相关函数为①()6exp 2X R ττ⎛⎫=- ⎪⎝⎭②sin ()6X R πττπτ=求当t 固定时,过程()X t 的四个状态(),(1),(2),(3)X t X t X t X t +++的协方差矩阵?分析:高斯过程四个状态的1112131421222324313233344142434444C C C C C C C C C C C C C C C C ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦C 解:①()τX t 平稳高斯,协方差阵只与时间差值有关 ②6000060000600006C ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦2-21 已知平稳高斯过程()X t 的均值为0,令随机过程2()[()]Y t X t =。
证明 [][]22()(0)2()Y X X R R R ττ=+2-22 已知随机过程0()cos()X t A t ω=+Φ,其中随机相位Φ服从(0,2)π上的均匀分布;A 可能为常数,也可能为随机变量,且若A 为随机变量时,和随机变量Φ相互独立。
当A 具备什么条件时,过程各态历经?分析:随机过程各态历经要求为平稳过程且()[()]X t E X t = 解:① A 为常数时()()2220(,)cos 22A A E X t R t t E X t ττ⎡⎤=+==⎡⎤⎣⎦⎣⎦()X t 为平稳过程A 为随机变量时和随机变量Φ相互独立()X t 为平稳过程② 01()lim cos()02TTT X t A t d Tt ω-→∞=+Φ=⎰③。
