图像型计算题

合集下载

专题二十初中物理图像问题

专题二十初中物理图像问题利用图像分析处理物理问题是一种科学方法，各个版本物理教材在研究物理规律时，通过实验数据可以得到图像，这个图像能直观形象的给出两个物理量之间的关系，结合物理公式就能知道其它量的数值。

物理学科的力电热光知识体系的问题都离不开图像法。

每年全国各地每年中考试题里都含有图像题，重视图像法解决物理问题是毕业班学生提高成绩的不可忽视的创新举措。

一、物理图像题1．图像内容对于图像类问题，主要考察温度——时间图像；路程——时间图像、速度——时间图像；质量——体积图像；电流——电压图像、电阻——温度图象、电阻——压力图象；压强——深度图像；像距——物距图像；力——时间图像；浮力——深度图像；大气压——高度图像等的认识和理解。

从而让学生在深层次上掌握图像和物理规律间的内在联系。

利用物理图象比较物理量、根据规律选择图象、利用图象获取信息、利用图象进行计算、绘制图象等。

利用图像处理物理问题是课程标准所要求的一种研究物理规律的方法。

是考试说明强调的每年必考的知识点。

2．图像题考法图像问题涵盖面广，在选择题、填空题、分析简答题、实验与探究题、综合题中都能经常遇到图像问题，要高度重视。

解答图象题的总纲领是：先搞清楚图象中横坐标、纵坐标所表示的物理量；弄清坐标上的分度值；明确图象所表达的物理意义，利用图象的交点坐标、斜率和截距及图象与坐标轴所包围的面积等，进行分析、推理、判断和计算；根据图象对题目中的问题进行数据计算或做出判断性结论。

河北省在中考试卷中，每年都在最后两道大题其中的一道题里出现一个涉及利用图象提供信息的计算题。

分值可观，加强训练。

二、用图像法解决物理问题基本思路解答图象题的总纲领是：先搞清楚图象中横坐标、纵坐标所表示的物理量；弄清坐标上的分度值；明确图象所表达的物理意义，利用图象的交点坐标、斜率和截距及图象与坐标轴所包围的面积等，进行分析、推理、判断和计算；根据图象对题目中的问题进行数据计算或做出判断性结论。

化学计算

1. 文字叙述型化学计算
解决综合计算的关键在于通过阅读、理解和分析，寻找其中某一个纯净物质量 (纯量)，根据化学方程式的计算分别求解相关纯净物的质量。
例1 为确定氨的组成，在一定温度、压强下进行如下实验:取20 mL 氨，设法使它完全分解为N2 和H2，体积为40 mL。加入20 mL O2 ，当H2 和O2 完全化合成水，剩余气体体积为15 mL(已知一定温度、压强下一定体积各种气体中的分子数相同)。请根据以上数据确定氨的分子式。
五、综合分析类计算题
★例：（2012•上海）常温下，称取不同氢氧化钠样品溶于水，加盐酸中和至pH=7，然后将溶液蒸干得氯化钠晶体，蒸干过程中产品无损失．
氢氧化钠质量（g） ① ② ③ 2.40 2.32 3.48 氯化钠质量（g） 3.51 2.34 3.51
上述实验①②③所用氢氧化钠均不含杂质，且实验数据可靠．通过计算，分析和比较上表3组数据，给出结论．

解析：因为是三种不同的氢氧化钠样品，只能分别求出每一组实验中样品的成分。可以根据每组实验中氢氧化钠中的钠和氯化钠中的钠守恒计算， NaOH + HCl = NaCl +H2O x 58.5 2.40 3.51 样品1的相对分子质量：x1=2.40÷（3.51÷58.5）=40、样品2的相对分子质量：x2=2.32÷（2.34÷58.5）=58、样品3的相对分子质量：x3=3.48÷（3.51÷58.5）=58. 根据氢氧化钠易潮解的性质，我们可以推测出②和③的样品中是含有水
加入稀盐酸的次数
烧杯及反应后混合物的总质量 /g 第一次第二次第三次第四次第五次
122.2
146.1

有关溶液的相关计算题及答案

初中化学有关溶液的溶质质量分数计算题拟卷人：辛丽丽班级：姓名：一、利用溶质质量分数的定义式及变形式的相关计算题1.在农业上，有时用10％～20％的食盐溶液来选种。

现配制15％的食盐溶液200kg需要食盐和水各多少千克?2. 将60g20％的食盐溶液和30g5％的食盐溶液相混合，求所得混合溶液的溶质的质量分数。

3. 向100ｇ溶质的质量分数为10%的KNO溶液中加入10ｇ水后，所得溶液的溶质质量3后，溶质的质量分数为分数为；若加入10ｇKNO34.200C时，将一溶质质量分数为20%的氯化钠溶液蒸干，得到20g固体，求该溶液质量。

5.实验室要配制50g溶质质量分数为20%的硝酸钾溶液。

现有25g溶质的质量分数为40%的硝酸钾溶液、20g溶质的质量分数为15%的硝酸钾溶液及足够多的硝酸钾晶体和蒸馏二、饱和溶液中溶质质量分数的相关计算1.已知T 0C时，硝酸钠的溶解度为80g，求这温度时硝酸钠饱和溶液的溶质的质量分数。

2.某种物质的水溶液，加热蒸发掉10g水，冷却到20℃，有晶体析出。

此时溶液中溶质的质量分数为26％，求20℃时该物质的溶解度。

3. 在60℃时， 50g水中最多能溶解55g硝酸钾把60℃时210g水中的硝酸钾饱和溶液蒸发掉50g水，再降到60℃，求析出晶体后溶液的溶质的质量分数。

三、溶液的稀释浓缩相关计算：（一）不涉及体积的计算：1.将200g含水99%的NaOH溶液的含水量变为98%，应蒸发掉多少克水？2.欲配制50g3%的氯化钠溶液，需6%的氯化钠溶液和水各多少克？，（二）涉及体积的计算1.用98％的浓硫酸（密度为1.84g/cm3）配制成25％的稀硫酸500g，需浓硫酸和水多少毫升？2.把5mL溶质的质量分数为62％的浓硝酸（密度为 l.38g/cm3）和20mL水混合，计算稀释后硝酸的溶质的质量分数。

3.用98％（密度为l.84g/cm3）的浓硫酸配制成1∶4的稀硫酸，求稀硫酸的溶质的质量分数。

初中化学经典溶液的计算题

①涉及沉淀的叙述型计算题：1、家里蒸馒头用的纯碱中含有少量的氯化钠，课外探究小组的同学欲测定纯碱中碳酸钠的含量。

他们取该纯碱样品11.0g，全部溶解在100.0g水中，再加入氯化钙溶液141.0g，恰好完全反应。

过滤干燥后，称得沉淀质量为10.0g。

请计算：（1）纯碱样品中碳酸钠的质量；（2）反应后所得滤液中溶质的质量分数。

2、50g Ca(NO3)2溶液与50g K2CO3溶液混合后，恰好完全反应。

经过滤、干燥、称量，得到5g 沉淀。

反应的化学方程式是：K2CO3+Ca(NO3)2==CaCO3↓+2KNO3。

请计算：(1) 参加反应的K2CO3的质量。

(2) 过滤后所得溶液的溶质质量分数。

②涉及气体的叙述型计算题：1、（2006天津市）将10g不纯的锌粒（杂质不容与水也不与酸反应）投入到100g稀硫酸中，恰好完全反应，得到0.2气体，试计算：（1）锌粒中纯锌的质量；（2）稀硫酸中溶质的质量分数。

2、我国化工专家侯得榜的“侯是制碱法”为世界制碱工业做出了杰出贡献。

工业上用侯氏制碱法制得的纯碱中含有一定量的氯化钠杂质。

现称取只含氯化钠的纯碱样品11g,全部溶解在50g 水中，当加入稀盐酸64.4g时，恰好完全反应，所得溶液质量为121g，试求：（1）该纯碱样品的纯度（计算结果精确到0.1%）（2）所的溶液中溶质的质量分数。

③由溶液质量和质量分数进行计算：1、现有Na2CO3和Na2SO4的固体混合物共12g，将它放入98g20%的H2SO4溶液中，充分反应后溶液呈酸性；在此酸性溶液中再加入80g10%的NaOH溶液，恰好完全中和。

计算:(1)恰好完全中和后，所得溶液中溶质的质量分数。

（计算结果精确到0.1%）（2）样品中碳酸钙的质量分数是。

（3）求盐酸中溶质的质量分数。

2、南充市名优特产阆中保宁醋，是中国四大名醋之一，其主要成分是醋酸，化学式为：CH3COOH。

测定保宁醋醋酸含量的原理是：CH3COOH + NaOH = CH3COONa + H2O。

2021届中考物理复习必考计算题专题精解精炼：02质量与密度专题计算【含答案】

2021届中考物理复习必考计算题专题精解精炼02 质量与密度专题计算考点解读（1）应用vmρ=计算时，单位要统一。

ρ表示密度、m 表示质量、V 表示体积。

在国际单位中，质量单位是kg ，体积单位就是m 3，密度单位是kg/m 3。

（2）在常用单位中，质量单位经常取g ，体积单位经常取cm 3（即mL ），因此常用密度单位是g/cm 3。

它与国际单位的换算关系是：。

（3）灵活运用速度公式及其变形公式ρv =m ，ρm v =。

（4）vmρ=公式的三个物理量必须对应同一对象。

重点考向考点一：图像问题1．（2019•扬州）在测量液体密度的实验中，小明利用天平和量杯测量出液体和量杯的总质量m 及液体的体积V ，得到几组数据并绘出如图所示的m ﹣V 图象，下列说法正确的是（）A ．量杯质量为40gB ．40cm 3的该液体质量为40g C ．该液体密度为1.25g/cm 3D．该液体密度为2g/cm3【解析】（1）设量杯的质量为m 杯，液体的密度为ρ，读图可知，当液体体积为V1＝20cm3时，液体和杯的总质量m总1＝m1+m杯＝40g，则由m＝ρV可得：ρ×20cm3+m杯＝40g，﹣﹣﹣﹣﹣﹣﹣﹣﹣①当液体体积为V2＝80cm3时，液体和杯的总质量m总2＝m2+m杯＝100g，可得：ρ×80cm3+m杯＝100g，﹣﹣﹣﹣﹣﹣﹣﹣②联立①②解得液体的密度：ρ＝1g/cm3，故CD错误；将ρ＝1g/cm3代入①解得m杯＝20g，故A错误；（2）当液体的体积V3＝40cm3，则液体的质量：m3＝ρ×V3＝1g/cm3×40cm3＝40g，故B正确。

故选：B。

2．（2019•青岛）如图为甲、乙两种物质的m﹣V图象。

下列说法正确的是（）A．体积为20cm3的甲物质的质量为10gB．乙物质的密度与质量成正比C．甲物质的密度比乙的密度小D．甲、乙质量相同时，乙的体积是甲的2倍【解析】A、由图象可知，体积为20cm3的甲物质的质量为20g，故A错误；B、密度是物质的一种特性，状态相同的同种物质的密度是相同的，与质量和体积无关，故B错误。

2020高考物理二轮专题复习专题17 电学图像问题(解析版)

专题17 电学图像问题在物理中，常常用图像来反映物理量之间的关系或描述某个物理过程，通过图像可以直观、简洁的反映物理量之间的关系或物理过程，所以在中考中常常会出现电学物理图像问题。

电学图像以信息为载体，主要考查学生识别图像、从中提取信息的能力。

图像类考题在中考中一直占有重要的地位，由于不会分析、处理，造成失分很多。

1、U -I 图像与I—U 图像：电阻两端的电压与流过电阻中的电流关系的图像：图像类型U—I 图像I —U 图像坐标意义图像的纵坐标表示电阻两端的电压，横坐标表示通过该电阻的电流。

图像的纵坐标表示通过该电阻的电流，横坐标表示电阻两端的电压。

图像图像意义及阻值计算当图像是一条过坐标原点直线时，表示定值电阻。

电阻大小等于图像上除原点以外的点的纵坐标和横坐标的比值。

R 1的阻值可以通过任意对应的U 、I 坐标计算：1111V =50.2AU R I ==Ω，或2222V=50.4AU R I ==Ω，或3333V =50.6AU R I ==Ω。

电阻大小等于图像上除原点以外的点的横坐标和纵坐标的比值。

R 1的阻值可以通过任意对应的U 、I 坐标计算：1111V =100.1A U R I ==Ω，或2122V=100.2AU R I ==Ω，或3133V =100.3AU R I ==Ω，或4144V =100.4AU R I ==Ω。

当图像为一条曲线时，表示可变电阻，电阻随电压的增大而增大。

电阻值大小只能通过图像上点的纵坐电阻值大小只能通过图像上点的横坐标与2、I—R图像：根据欧姆定律IR=可知：当电压一定的时候，电流与电阻成反比。

所以I-R图为反比例函数图像。

图像上每一点横纵坐标的乘积是个定值，即该电阻两端的电压值。

3、电学图像还有电压——电阻图像、电阻——温度图像、电阻——力图像、功率——电压图像、功率——时间图像等等，无论哪种图像，只要把握住坐标轴上的两个物理量，结合图像形状和相关物理知识就能从容的解决。

初中化学反应计算题

初中化学反应计算题计算题型一：文字叙述型1.黄铜是铜和锌的合金，在20g黄铜样品中加入足量稀盐酸使其完全反应，生成氢气0.2g，求样品中铜的质量分数？2．把7g含杂质的锌片（杂质不与硫酸反应）放在盛有100g足量的稀硫酸的烧杯里，反应停止后称得烧杯里物质的总质量为106.8g。

（1）计算反应后生成的氢气的质量；（2）计算不纯的锌片中单质锌的质量分数。

3、用氯酸钾和二氧化锰的混合物16g，加热制取氧气，待完全反应，冷却后称量，得到11.2g固体物质，计算原混合物中二氧化锰的质量？4、取34克过氧化氢溶液再加入0.5克二氧化锰后至质量不减小时，所得剩余物的质量33.7克。

求：（1）根据质量守恒定律，反应生成氧气的质量为。

（2）计算该过氧化氢溶液中溶质的质量分数。

5．某化学活动小组需要用溶质质量分数为19.6％的稀硫酸和锌粒反应来制取氢气，但实验室现有的是溶质质量分数为98％的浓硫酸。

试计算：（1）硫酸中氢、硫、氧元素的质量比为：_______________（2）将10g浓硫酸配制成所需的稀硫酸，需要水的质量为多少？（3）取上述配制好的稀硫酸20g与足量锌粒充分反应，能制得氢气质量为多少？计算题型二：图像呈上升趋势型1．在一烧杯中盛有22.3 g Na2CO3和NaCl组成的固体混合物，加足量水溶解，配成溶液。

向其中逐渐滴加溶质质量分数为10%的稀盐酸，放出气体的总质量与所滴入稀盐酸的质量关系曲线如图所示。

请根据题意回答问题：（1）当滴加了73 g稀盐酸时，放出气体的总质量为___________g。

（2）当滴加稀盐酸至图中B点时，烧杯中溶液里的溶质是___________。

（3）当滴加了73 g稀盐酸时（即A点时），烧杯中为不饱和溶液，试通过计算求出其中含溶质的质量。

2．现取13.4g含氯化钙的氯化钠固体样品，全部溶于96.6g水中，向所得的混合溶液中滴加溶质质量分数为10.6%的碳酸钠溶液，记录了如图所示的曲线关系。

初中化学计算题大全

初中化学计算专题（一）有关化学式计算题类型：第一种类型：标签型化学式计算题：1、在现代生活中，人们越来越注重微量元素的摄取。

碘元素对人体健康有至关重要的作用。

下表是某地市场销售的一种“加碘食盐”包装袋上的部分说明。

请回答下列问题：（1）由食用方法和贮藏指南可推测碘酸钾（KIO3）的化学性质之一是；（2）计算碘酸钾（KIO3）中，钾元素、碘元素、氧元素的质量比；（3）计算碘酸钾（KIO3）中，碘元素的质量分数是多少；（计算结果精确到，下同）（4）计算1kg这样的食盐中，应加入 g碘酸钾（用最高含碘量计算）第二种类型：叙述型化学式计算题：1、蛋白质是由多种氨基酸[丙氨酸：CH3CH(NH2)COOH等]构成的极为复杂的化合物，人体通过食物获得蛋白质，在胃肠道里与水发生反应，生成氨基酸，试计算：（1）丙氨酸分子中氮原子与氧原子的个数比。

（2）丙氨酸的相对分子质量。

（3）丙氨酸中碳、氢、氧、氮元素的质量比。

2、抗震救灾，众志成城。

用于汶川震后防疫的众多消毒剂中，有一种高效消毒剂的主要成分为三氯异氰尿酸(C3O3N3Cl3)，又称高氯精。

下列有关高氯精的说法不正确的是（）A．高氯精由4种元素组成 B．高氰精中C、O、N、Cl的原子个数比为1∶1∶1∶1 C．高氯精中C、N两种元索的质量比为12∶14 D．高氯精中氯元素的质量分数为25％第三种类型：综合型化学式计算题：1、青少年正处于生长发育时期，每天需要摄取足量的蛋白质，蛋白质的代谢产物主要是尿素[CO(NH2)2]。

若从食物中摄取的蛋白质经体内新陈代谢后完全转化为尿素排出体外，每人每天相当于排出尿素30g。

(1)30g尿素中含氮元素多少克(2)已知蛋白质中氮元素的平均质量分数为16％，则每人每天至少应从食物里摄取的蛋白质为多少克(3)请你根据下表中几种常见食物的蛋白质含量，计算出每天至少应摄人多少克下列食物才能满足你对蛋白质的需求(可以只摄取一种食物，也可同时摄取几种食物)。

化学计算专题

初中化学专题训练——计算题一、有关化学式计算题类型：1.1计算物质的相对分子质量1.2计算化合物中各元素原子的个数比 1.3计算化合物中各元素的质量比 1.4计算化合物中某元素的质量分数1.茶是我国的特产;种类很多..其中;绿茶是将新鲜的茶叶炒熬;破坏其中酵素;再经搓揉、烘焙而成..茶叶的化学成分主要是茶碱C 8H 10N 4O 2·H 2O;还有鞣酸及芳香油等..阅读以上信息后回答：①茶碱C 8H 10N 4O 2·H 2O 分子中原子的个数最多； ②茶碱C 8H 10N 4O 2·H 2O 中元素的质量分数最大..2.2011.烟台市4分低钠盐适合患有高血压、肾病、心脏病的患者服用;苹果酸钠盐C 4H 5O 5Na 是低钠盐的一种..请回答：1苹果酸钠盐的相对分子质量是 ..2苹果酸钠盐中各元素的质量比为C :H :O :Na ＝ ..3若某病人每天食用5．85g 苹果酸钠盐;比食用相同质量的食盐NaCl 少摄入钠元素多少克计算结果保留一位小数2.右图是某品牌补铁剂的标签..请回答：1富马酸亚铁颗粒中的铁属于元素填“常量”或“微量”；2富马酸亚铁中C 、H 元素的质量比为；3已知富马酸亚铁C 4H 2FeO 4中铁元素的质量分数为33%;若每次服用1包该补铁剂;摄入铁元素的质量为 mg.. 二、有关化合价的计算：3.据报道：“染色”馒头中添加柠檬黄铬酸铅PbCrO 4会使人体致癌;已被明文禁用..已知铬元素Cr 化合价为+6;则铅元素Pb 的化合价为A ．+1B ．+2C ．+3D ． +4 三、有关化学方程式的计算题： 1有关反应物和生成物的计算A 根据题意设未知量B 写出正确的化学方程式C 写出相关物质的相对分子质量和已知量、未知量D 列出比例式;求出未知量E 作答4.发射通信卫星的火箭用联氨N 2H 4做燃料;用四氧化二氮N 2O 4助燃;生成物不会对大气造成污染..1反应的化学方程式为2N 2H 4＋N 2O 4＝3 ＋4H 2O;请在横线上填写化学式以完成该化学方程式..2请计算9.6gN 2H 4完全燃烧需要助燃物N 2O 4的质量.. 2含有杂质的反应物和生成物的计算5.硅酸钠Na 2SiO 3是我国优先发展的精细化工产品;工业制备的反应为： 2NaOH+ SiO 2 == Na 2SiO 3 + H 2O ..现以125t 石英砂SiO 2质量分数为96％为原料;与足量的NaOH 溶液反应..试计算：1125t 石英砂中SiO 2的质量..2理论上得到硅酸钠的质量.. 3有关混合原料参加反应的化学方程式的计算6.将一定质量的NaCl 和Na 2SO 4 固体混合物完全溶于水后;加入一定质量分数的BaCl 2溶液208g;恰好完全反应;过滤;得到23.3g 沉淀;经测定滤液中含氯元素的质量为21.3g 不考虑过滤过程中物质质量的损失..计算：1所加BaCl 2溶液的溶质质量分数.. 2原固体混合物中Na 2SO 4的质量.. 3原固体混合物中NaCl 的质量.. 四、有关溶液的计算题： 1直接使用公式计算：7.1用NaCl 配制100ml 0.9％医用的生理盐水密度约为1g/ cm 3;需要NaCl 的质量为 g..2由右图可知;t 1℃时;硝酸钾溶解度＜氯化钠的溶解度填“＞”;“＜”或“＝”；从氯化钠和硝酸钾饱和溶液中提取硝酸钾;应采用下列方法中的填写编号.. a ．冷却结晶 b ．蒸发溶剂 c ．过滤 2溶质、溶剂的变化对质量分数的影响：8.现有200g 溶质质量分数为10%的硝酸钾溶液;若使溶液的溶质质量分数增加一倍;因向溶液加入硝酸钾 g;或蒸发掉 g.. 3有关溶液和化学方程式的简单综合计算：叙述型计算题：9.26g 锌样品含杂质与100g 稀硫酸在烧杯中恰好完全反应;反应后测得烧杯中剩余物的总质量为125.8克..假设杂质不与酸反应;也不溶于水求：⑴样品中杂质的质量分数；⑵反应后所得溶液中溶质质量分数..计算结果精确到0.1%10.小明同学想测量某赤铁矿样品中氧化铁的纯度假设其他成分不和酸反应;也不溶于水;进行如下实验:称取10g赤铁矿样品;加入到烧杯中;再加入92.5g的稀硫酸;恰好完全反应..过滤得滤渣2.5g..试计算：1赤铁矿样品中氧化铁的质量分数2上述反应所得滤液中溶质的质量分数2标签型计算题：11.右图是则配制好的硫酸钠溶液的标签;请根据标签上的文字信息;进行计算：1该硫酸钠溶液中溶剂质量为 g；2取氯化钡固体样品26g;放入烧杯中加水完全溶解并过滤;往滤液中滴加上述配制的硫酸钠溶液至完全反应;然后过滤、烘干..称得沉淀23.3g..计算：①该样品中氯化钡的质量分数是多少②用去硫酸钠溶液的质量是多少g3图像型计算题：12.为测定某未知浓度的氢氧化钡溶液的溶质质量分数;取某稀硫酸溶液20 g;逐滴加入氢氧化钡溶液30 g;同时用pH计测定并记录反应过程中混合溶液pH变化情况如图所示..过滤后得滤液47.67 g..请你通过计算;求出氢氧化钡溶液的溶质质量分数..4表格型计算题：13.为了测定某粉末状黄铜铜、锌合金样品中铜的质量分数;洋洋同学取一定质量的黄铜样品放入烧杯中;再取40g稀盐酸分四次加入烧杯中;均充分反应;实验数据如下：第一次第二次第三次第四次名称：硫酸钠溶液化学式：Na2SO4溶质质量分数：加入氢氧化溶液的PH2311上述反应的化学方程式为；2所用稀盐酸中溶质的质量分数为；3用36.5％的浓盐酸配制40g上述稀盐酸;需要浓盐酸的质量为；4黄铜样品中铜的质量分数为多少。

压轴题10 计算题(解析版)-2023中考化学压轴题专项训练(南通专用)

压轴题10计算题考向一：简单化学式和化学方程式的计算考向二：涉及溶液的综合计算考向三：图像图表型计算南通中考试题中，计算题一般不是单纯考查计算，而是具有一定的综合性，通常选择生活场景或工业生产等一定的情境。

可以为测定某个数据或达到某个目的而设计实验，依据实验结果进行计算；也可以是根据某个反应直接进行计算。

考查内容有：化学式计算、化学方程式的计算、溶液的稀释，质量守恒定律，化学方程式和溶液结合的综合计算。

○热○点○题○型○一简单化学式和化学方程式的计算1.正确书写化学式或化学反应方程式，找准相关物质及其质量。

2.化学方程式计算，格式规范、步骤完整、单位统一；3.不纯物质的质量应该先转化为纯净物的质量后才能代入化学方程式进行计算。

○热○点○题○型○二涉及溶液的综合计算1.在溶液中进行的反应，应用溶质的质量代入化学方程式进行计算2.反应后所得溶液的质量=反应前所有物质的总质量-生成气体的质量-生成沉淀的质量-反应前不溶性杂质的质量3.反应后所得溶液中溶质的质量=生成的溶质+原混合物中与生成的溶质相同的可溶性杂质○热○点○题○型○三图像图表型计算1.图像题关注转折点对应的横坐标和纵坐标，以及起点和转折点的坐标差，从中找到已知量。

（1）纵坐标多为产生气体或沉淀的质量，可以直接代入化学方程式计算；（2）若横坐标为溶液质量，注意需要换算成溶质质量代入化学方程式计算2.图表题解题的关键：是根据反应原理认真分析实验数据，选择适当的实验数据进行计算。

依据质量守恒定律，溶液中质量减小的一般是生成气体或沉淀的质量。

1．（2023·江苏海安·统考一模）某优良供氧剂过氧化钙晶体（CaO2·x H2O）中常混有CaO，已知CaO2·x H2O受热分解有CaO、O2和H2O生成。

①称取3.248g该产品，充分加热，在标准状况（0℃，101.3kPa）下生成268.8mL气体（标准状况下，22.4L氧气的质量为32g）。

初中化学计算题(带答案)

初中化学计算题一、根据化学式的计算1、计算相对分子质量相对分子质量＝化学式中各原子的相对原子质量的总和。

点拨：①计算物质的相对分子质量时，同种元素的相对原子质量与其原子个数是相乘的关系，不同种元素相对质量是相加的关系。

②计算结晶水合物的相对分子质量时，化学式中的“·”表示相加，而不表示相乘。

③化学式中原子团(或根)右下角的数字表示的是原子团(或根)的个数。

计算时先求一个原子团或根的总相对原子质量，再乘以原子团(或根)的个数，即得出几个原子团的总相对原子质量。

2、计算物质中各元素的质量比组成化合物的各元素的质量比＝化合物中各元素的相对原子质量总和(即相对原子质量与原子个数乘积)之比。

点拨：①计算时一定要写清楚各元素质量比顺序，因顺序不同，比值也不同。

②计算时的结果约成最简整数比。

3、计算物质中某元素的质量分数化合物中某元素的质量×100%4、已知某化合物的质量，求某元素的质量化合物里某元素的质量=化合物的质量×化合物中某元素的质量分数化合物的质量=化合物中已知元素的质量÷化合物中已知元素的质量分数5、求化学式点拨：求物质化学式的主要类型：①由元素的相对原子质量和化合物的相对分子质量，确定化学式。

②根据化合物中某元素质量分数确定化合物的化学式。

③已知化合物中元素的质量比和相对原子质量，确定化学式。

原子个数比＝元素的质量比：相对原子质量比④根据质量守恒定律确定化学式。

6、计算不纯物中某元素(或某纯净物)的质量分数计算公式：①某纯净物的质量分数= ×100%②不纯物中某元素的质量分数=不纯物中纯净物的质量分数×该纯净物中某元素的质量分数。

③某纯净物的质量分数=实际上某元素的质量分数÷化学式中该元素的质量分数×100%二、根据化学方程式的计算根据化学方程式的计算就是从量的方面来研究物质变化的一种重要的方法，其计算步骤和方法，一般分为以下几步： ①设未知量，未知量不带单位，常用X 表示．②根据题意确定反应物与生成物，写出并配平反应的化学方程式． ③在有关物质化学式下面写出相对分子质量并代入已知量和所设未知量． ④列比例式求解，写出答案．在初中阶段，根据化学方程式的计算，主要有以下几种基本类型．（1）根据化学方程式计算反应物、生成物间的质量比反应物、生成物间的质量比，就是各反应物、生成物相对分子质量×计量数之比．（2）根据化学方程式计算反应物或生成物的质量反应物或生成物质量的计算，一般是根据化学方程式中各反应物、生成物间的质量比来求算的，对某些反应，可直接依据质量守恒定律进行计算．（3）根据化学方程式进行含有一定且杂质的反应物或生成物的计算根据化学方程式的计算，其反应物或生成物的质量必须是纯物质的质量．含有一定量杂质的反应物或生成物的质量，必须换算成纯物质的质量，才能按根据化学方程式的计算步骤和方法进行计算．纯物质质量=含有一定量杂质的物质质量×该物质质量分数三、有要溶液组成的计算1．用溶质所占溶液的质量分数表示溶液的组成，其关系如下：溶质的质量分数= 溶质质量溶质+溶剂 × 100%＝溶液质量溶质质量 × 100%在饱和溶液中：溶质的质量分数=＋溶解度溶解度g 100 × 100%2、有关溶液加水稀释的计算在溶液加水稀释过程中，溶质的质量分数将随溶液的稀释而改变，溶质质量分数一定的溶液加水稀释，稀释前后溶质的总质量不会发生改变．溶液加水稀释的计算，根据的就是这个道理．M 浓溶液×浓溶液的溶质质量分数＝M 稀溶液×稀溶液的溶质质量分数＝（M 浓溶液＋M 水）×稀溶液的溶质质量分数 3、溶质的质量分数在化学方程式的应用反应后溶液的质量＝反应物的总质量（包含溶液的质量）－生成气体或沉淀的质量四、综合计算题分类解析从近几年全国各地的中考化学试题来看，化学计算已经走出了“为计算而计算”的考查误区，考题所涉及的内容更加注重与日常生活、工农业生产的联系；更加注重对同学们图表、数据、信息、实验综合分析能力的考查。

高三数学三角函数图象变换试题

高三数学三角函数图象变换试题1.将函数的图象向左平移个单位长度，所得图象对应的函数（）A．在区间上单调递减B．在区间上单调递增C．在区间上单调递减D．在区间上单调递增【答案】A【解析】将函数的图象向左平移个单位长度，所得图象对应的函数为，由得，故选A.【考点】1、三角函数图象的变换；2、三角函数的单调性.2.若把函数的图象向右平移m个单位（m＞0）后，所得到的图象关于轴对称，则m的最小值是（）A．B．C．D．【答案】D【解析】，图象向右平移m个单位（m＞0）后，得到，其图象关于轴对称，即是偶函数，所以，解得m的最小值是，选D.【考点】三角函数辅助角公式，三角函数图象的变换.3.若将函数的图像向右平移个单位，所得图像关于轴对称，则的最小正值是________.【答案】【解析】由题意，将其图象向右平移个单位，得，要使图象关于轴对称，则，解得，当时，取最小正值.【考点】1.三角函数的平移；2.三角函数恒等变换与图象性质.4.要得到函数y＝sin的图象，只需将函数y＝sin 2x的图象()A．向左平移个单位B．向右平移个单位C．向左平移个单位D．向右平移个单位【答案】D【解析】要得到函数y＝sin，只需将函数y＝sin 2x中的x减去，即得到y＝sin 2＝sin．5.将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数f(x)的图象,则f(－π)等于( )A．B．C．D．－【答案】D【解析】因为将函数的图像上所有的点向右平行移动个单位长度，得到的函数解析式为.再把函数各点的横坐标伸长到原来的2倍(纵坐标不变)得到.所以.【考点】1.三角函数的左右平移.2.三角函数的伸缩变换.6.将函数y＝sin的图像上各点向右平移个单位，则得到新函数的解析式为()A．y＝sin B．y＝sin C．y＝sin D．y＝sin【答案】A【解析】y＝sin的图像向右平移个单位后变为y＝sin＝sin7.已知函数（，c是实数常数）的图像上的一个最高点，与该最高点最近的一个最低点是，(1)求函数的解析式及其单调增区间；(2)在△ABC中，角A、B、C所对的边分别为，且，角A的取值范围是区间M，当时，试求函数的取值范围.【答案】（1），单调递增区间是；（2）.【解析】（1）三角函数问题一般都要化为的一个三角函数的形式，然后才可利用正弦函数的性质解题，这个函数图象上相邻有最高点与最低点的横坐标之差的绝对值为半个周期，而周期，再加上最高（低）点在函数图象上，我们就可出这个函数的解析式了（）；（2）由，根据向量数量积定义我们可求出，那么三角形的另一内角的范围应该是，即函数中的范围是，然后我们把一个整体，得出，而正弦函数在时取值范围是，因此可求出的值域．试题解析：(1)∵，∴.∵和分别是函数图像上相邻的最高点和最低点，∴解得∴.由，解得.∴函数的单调递增区间是.(2)∵在中，，∴.∴，即.∴.当时，，考察正弦函数的图像，可知，.∴，即函数的取值范围是.【考点】（1）五点法与函数的图象；（2）三角函数在给定区间的值域．8.函数的部分图象如图所示，则函数对应的解析式为（）A．B．C．D．【答案】A【解析】由图象知，，，，，因为，所以，所以，因此，故选A.【考点】1.三角函数的图象；2.三角函数的解析式9.为了得到函数的图像，只需将函数的图像（）A．向右平移个单位B．向右平移个单位C．向左平移个单位D．向左平移个单位【答案】D【解析】由于，所以，为了得到函数的图像，只需将函数的图像，向左平移个单位，选D.【考点】三角函数图像的平移10.将函数的图像向右平移个单位，再将图像上每一点横坐标缩短到原来的倍，所得图像关于直线对称，则的最小正值为（）A．B．C．D．【答案】D【解析】函数的图像向右平移个单位得的图象，将图像上每一点横坐标缩短到原来的倍得，将点代入得，故，所以的最小正值为.【考点】1，三角函数图象的变换；2、型函数的对称中心.11.已知函数，则下列结论正确的是（）A．函数的图象关于直线对称B．函数的最大值为D．函数在区间上是增函数D．函数的最小正周期为【答案】C【解析】令得错误；函数的最大值为，故错误；函数的最小正周期为，故错误；当时，，故函数在区间上是增函数，所以选．【考点】考查三角函数的图像及其性质．12.把函数的图像上的每一点的横坐标伸长为原来的2倍，纵坐标不变，然后再向左平移个单位后得到一个最小正周期为的奇函数。

二次函数图像和性质习题精选(含答案)

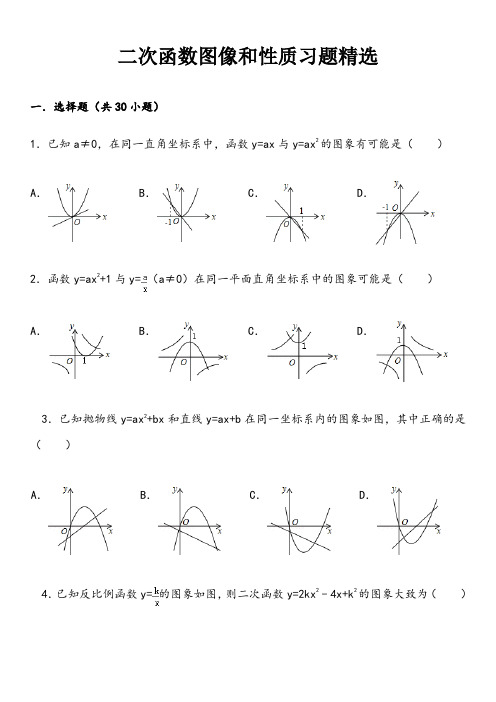
二次函数图像和性质习题精选一．选择题（共30小题）1．已知a≠0，在同一直角坐标系中，函数y=ax与y=ax2的图象有可能是（）A．B．C．D．2．函数y=ax2+1与y=（a≠0）在同一平面直角坐标系中的图象可能是（）A．B．C．D．3．已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图，其中正确的是（）A．B．C．D．4．已知反比例函数y=的图象如图，则二次函数y=2kx2﹣4x+k2的图象大致为（）A．B．C．D．5．二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：X﹣1013y﹣1353下列结论：（1）ac＜0；（2）当x＞1时，y的值随x值的增大而减小．（3）3是方程ax2+（b﹣1）x+c=0的一个根；（4）当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．其中正确的个数为（）A．4个B．3个C．2个D．1个6．二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（）A．函数有最小值B．对称轴是直线x=C．当x＜，y随x的增大而减小D．当﹣1＜x＜2时，y＞07．如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M是抛物线y=x2+bx+c的顶点，则方程x2+bx+c=1的解的个数是（）A．0或2B．0或1C．1或2D．0，1或28．已知二次函数y=a（x﹣h）2+k（a＞0），其图象过点A（0，2），B（8，3），则h 的值可以是（）A．6B．5C．4D．39．二次函数y=ax2+bx+c图象上部分点的坐标满足下表：x…﹣3﹣2﹣101…y…﹣3﹣2﹣3﹣6﹣11…则该函数图象的顶点坐标为（）A．（﹣3，﹣3）B．（﹣2，﹣2）C．（﹣1，﹣3）D．（0，﹣6）10．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（）A．图象关于直线x=1对称B．函数y=ax2+bx+c（a≠0）的最小值是﹣4C．﹣1和3是方程ax2+bx+c=0（a≠0）的两个根D．当x＜1时，y随x的增大而增大11．如图，二次函数的图象经过（﹣2，﹣1），（1，1）两点，则下列关于此二次函数的说法正确的是（）A．y的最大值小于0B．当x=0时，y的值大于1C．当x=﹣1时，y的值大于1D．当x=﹣3时，y的值小于012．设二次函数y=x2+bx+c，当x≤1时，总有y≥0，当1≤x≤3时，总有y≤0，那么c的取值范围是（）A．c=3B．c≥3C．1≤c≤3D．c≤313．如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系不正确的是（）A．h=m B．k=n C．k＞n D．h＞0，k＞014．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a＞0；②该函数的图象关于直线x=1对称；③当x=﹣1或x=3时，函数y的值都等于0．其中正确结论的个数是（）A．3B．2C．1D．015．二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论正确的是（）A．a c＜0B．当x=1时，y＞0C．方程ax2+bx+c=0（a≠0）有两个大于1的实数根D．存在一个大于1的实数x0，使得当x＜x0时，y随x的增大而减小；当x＞x0时，y 随x的增大而增大16．如图，抛物线y=ax2+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a ﹣b+c的值为（）A．0B．﹣1C．1D．217．下列图中阴影部分的面积相等的是（）A．①②B．②③C．③④D．①④18．已知抛物线y=ax2+bx+c（a＜0）的部分图象如图所示，当y＞0时，x的取值范围是（）A．﹣2＜x＜2B．﹣4＜x＜2C．x＜﹣2或x＞2D．x＜﹣4或x＞219．已知：二次函数y=x2﹣4x﹣a，下列说法错误的是（）A．当x＜1时，y随x的增大而减小B．若图象与x轴有交点，则a≤4C．当a=3时，不等式x2﹣4x+a＜0的解集是1＜x＜3D．若将图象向上平移1个单位，再向左平移3个单位后过点（1，﹣2），则a=320．下列表格给出的是二次函数y=ax2+bx+c（a≠0）的几组对应值，那么方程ax2+bx+c=0的一个近似解可以是（）xy﹣﹣A．B．C．D．21．已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（）A．抛物线开口向上B．抛物线与y轴交于负半轴C．当x=3时，y＜0D．方程ax2+bx+c=0有两个相等实数根22．已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A （﹣2，4），B（8，2）（如图所示），则能使y1＜y2成立的x的取值范围是（）A．x＞2B．x＜﹣2C．x＞0D．﹣2＜x＜823．在﹣3≤x≤0范围内，二次函数（a≠0）的图象如图所示．在这个范围内，有结论：①y1有最大值1、没有最小值；②y1有最大值1、最小值﹣3；③函数值y1随x的增大而增大；④方程ax2+bx+c=2无解；⑤若y2=2x+4，则y1≤y2．其中正确的个数是（）A．2B．3C．4D．524．抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：﹣1 134…x …﹣2y …04 640…根据上表判断下列四种说法：①抛物线的对称轴是x=1；②x＞1时，y的值随着x的增大而减小：③抛物线有最高点：④抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为36．其中正确说法的个数有（）A．1B．2C．3D．425．如图，已知抛物线y=x2+bx+c的对称轴为x=2，点A，B均在抛物线上，且AB与x 轴平行，其中点A的坐标为（0，3），则点B的坐标为（）A．（2，3）B．（3，2）C．（3，3）D．（4，3）26．如图为二次函数y=ax2+bx+c的图象，给出下列说法：①ab＜0；②方程ax2+bx+c=0的根为x1=﹣1，x2=3；③a+b+c＞0；④当x＜1时，y随x值的增大而增大；⑤当y＞0时，x＜﹣1或x＞3．其中，正确的说法有（）A．①②④B．①②⑤C．①③⑤D．②④⑤27．已知二次函数y=x2+2（a﹣1）x+2．如果x≤4时，y随x增大而减小，则常数a的取值范围是（）A．a≥﹣5B．a≤﹣5C．a≥﹣3D．a≤﹣328．如图，平行于y轴的直线l被抛物线y=+1，y=﹣1所截，当直线l向右平移3个单位时，直线l被两条抛物线所截得的线段扫过的图形面积为（）平方单位．A．3B．4C．6D．无法可求29．已知直线经过点A（0，2），B（2，0），点C在抛物线y=x2的图象上，则使得S△ABC=2的点有（）个．A．4B．3C．2D．130．如图，已知抛物线，直线y2=3x+3，当x任取一值时，x对应的函数值分别为y1，y2．若y1≠y2，取y1，y2中的较小值记为M；若y1=y2，记M=y1=y2．下列判断：①当x＞0时，y1＞y2；②使得M大于3的x值不存在；③当x＜0时，x值越大，M值越小；④使得M=1的x值是或．其中正确的是（）A．①③B．②④C．①④D．②③二次函数图像和性质习题精选（含答案）参考答案与试题解析一．选择题（共30小题）1．（2014•宁夏）已知a≠0，在同一直角坐标系中，函数y=ax与y=ax2的图象有可能是（）A．B．C．D．考点：二次函数的图象；正比例函数的图象．专题：数形结合．分析：本题可先由一次函数y=ax图象得到字母系数的正负，再与二次函数y=ax2的图象相比较看是否一致．（也可以先固定二次函数y=ax2图象中a的正负，再与一次函数比较．）解解：A、函数y=ax中，a＞0，y=ax2中，a＞0，但当x=1时，两函数图象有交点答：（1，a），故A错误；B、函数y=ax中，a＜0，y=ax2中，a＞0，故B错误；C、函数y=ax中，a＜0，y=ax2中，a＜0，但当x=1时，两函数图象有交点（1，a），故C正确；D、函数y=ax中，a＞0，y=ax2中，a＜0，故D错误．故选：C．点评：函数中数形结合思想就是：由函数图象确定函数解析式各项系数的性质符号，由函数解析式各项系数的性质符号画出函数图象的大致形状．2．（2014•北海）函数y=ax2+1与y=（a≠0）在同一平面直角坐标系中的图象可能是（）A．B．C．D．考点：二次函数的图象；反比例函数的图象．分析：分a＞0和a＜0两种情况讨论二次函数和反比例函数图象所在的象限，然后选择答案即可．解答：解：a＞0时，y=ax2+1开口向上，顶点坐标为（0，1），y=位于第一、三象限，没有选项图象符合，a＜0时，y=ax2+1开口向下，顶点坐标为（0，1），y=位于第二、四象限，B选项图象符合．故选：B．点评：本题考查了二次函数图象与反比例函数图象，熟练掌握系数与函数图象的关系是解题的关键．3．（2014•遵义）已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象如图，其中正确的是（）A．B．C．D．考点：二次函数的图象；一次函数的图象．分析：本题可先由二次函数图象得到字母系数的正负，再与一次函数和反比例函数的图象相比较看是否一致．逐一排除．解答：解：A、由二次函数的图象可知a＜0，此时直线y=ax+b经过二、四象限，故A 可排除；B、二次函数的图象可知a＜0，对称轴在y轴的右侧，可知a、b异号，b＞0，此时直线y=ax+b经过一、二、四象限，故B可排除；C、二次函数的图象可知a＞0，此时直线y=ax+b经过一、三，故C可排除；正确的只有D．故选：D．点评：此题主要考查了一次函数图象与二次函数图象，应该识记一次函数y=kx+b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质：开口方向、对称轴、顶点坐标等．4．（2014•南昌）已知反比例函数y=的图象如图，则二次函数y=2kx2﹣4x+k2的图象大致为（）A．B．C．D．考点：二次函数的图象；反比例函数的图象．分析：本题可先由反比例函数的图象得到字母系数k＜﹣1，再与二次函数的图象的开口方向和对称轴的位置相比较看是否一致，最终得到答案．解答：解：∵函数y=的图象经过二、四象限，∴k＜0，由图知当x=﹣1时，y=﹣k＞1，∴k＜﹣1，∴抛物线y=2kx2﹣4x+k2开口向下，对称为x=﹣=，﹣1＜＜0，∴对称轴在﹣1与0之间，故选：D．点评：此题主要考查了二次函数与反比例函数的图象与系数的综合应用，正确判断抛物线开口方向和对称轴位置是解题关键．属于基础题．5．（2014•泰安）二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：X﹣1013y﹣1353下列结论：（1）ac＜0；（2）当x＞1时，y的值随x值的增大而减小．（3）3是方程ax2+（b﹣1）x+c=0的一个根；（4）当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．其中正确的个数为（）A．4个B．3个C．2个D．1个考点：二次函数的性质；二次函数图象与系数的关系；抛物线与x轴的交点；二次函数与不等式（组）．专题：图表型．分析：根据表格数据求出二次函数的对称轴为直线x=，然后根据二次函数的性质对各小题分析判断即可得解．解解：（1）由图表中数据可得出：x=1时，y=5，所以二次函数y=ax2+bx+c开口向答：下，a＜0；又x=0时，y=3，所以c=3＞0，所以ac＜0，故（1）正确；（2）∵二次函数y=ax2+bx+c开口向下，且对称轴为x==，∴当x＞时，y的值随x值的增大而减小，故（2）错误；（3）∵x=3时，y=3，∴9a+3b+c=3，∵c=3，∴9a+3b+3=3，∴9a+3b=0，∴3是方程ax2+（b﹣1）x+c=0的一个根，故（3）正确；（4）∵x=﹣1时，ax2+bx+c=﹣1，∴x=﹣1时，ax2+（b﹣1）x+c=0，∵x=3时，ax2+（b﹣1）x+c=0，且函数有最大值，∴当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0，故（4）正确．故选：B．点评：本题考查了二次函数的性质，二次函数图象与系数的关系，抛物线与x轴的交点，二次函数与不等式，有一定难度．熟练掌握二次函数图象的性质是解题的关键．6．（2014•广东）二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（）A．函数有最小值B．对称轴是直线x=C．当x ＜，y随x的增大而减小D．当﹣1＜x＜2时，y＞0考点：二次函数的性质．专题：数形结合．分析：根据抛物线的开口方向，利用二次函数的性质判断A；根据图形直接判断B；根据对称轴结合开口方向得出函数的增减性，进而判断C；根据图象，当﹣1＜x＜2时，抛物线落在x轴的下方，则y＜0，从而判断D．解答：解：A、由抛物线的开口向上，可知a＞0，函数有最小值，正确，故A选项不符合题意；B、由图象可知，对称轴为x=，正确，故B选项不符合题意；C、因为a＞0，所以，当x ＜时，y随x的增大而减小，正确，故C选项不符合题意；D、由图象可知，当﹣1＜x＜2时，y＜0，错误，故D选项符合题意．故选：D．点评：本题考查了二次函数的图象和性质，解题的关键是利用数形结合思想解题．7．（2014•盘锦）如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M是抛物线y=x2+bx+c 的顶点，则方程x2+bx+c=1的解的个数是（）A．0或2B．0或1C．1或2D．0，1或2考点：二次函数的性质．专题：数形结合；分类讨论；方程思想．分析：分三种情况：点M的纵坐标小于1；点M的纵坐标等于1；点M的纵坐标大于1；进行讨论即可得到方程x2+bx+c=1的解的个数．解解：分三种情况：答：点M的纵坐标小于1，方程x2+bx+c=1的解是2个不相等的实数根；点M的纵坐标等于1，方程x2+bx+c=1的解是2个相等的实数根；点M的纵坐标大于1，方程x2+bx+c=1的解的个数是0．故方程x2+bx+c=1的解的个数是0或1或2．故选：D．点评：考查了二次函数的性质，本题涉及分类思想和方程思想的应用．8．（2014•淄博）已知二次函数y=a（x﹣h）2+k（a＞0），其图象过点A（0，2），B（8，3），则h的值可以是（）A．6B．5C．4D．3考点：二次函数的性质．专题：计算题．分析：根据抛物线的顶点式得到抛物线的对称轴为直线x=h，由于所给数据都是正数，所以当对称轴在y轴的右侧时，比较点A和点B到对称轴的距离可得到h＜4．解答：解：∵抛物线的对称轴为直线x=h，∴当对称轴在y轴的右侧时，A（0，2）到对称轴的距离比B（8，3）到对称轴的距离小，∴x=h＜4．故选：D．点评：本题考查了二次函数的性质：二次函数y=ax2+bx+c（a≠0）的顶点坐标为（﹣，），对称轴直线x=﹣，二次函数y=ax2+bx+c（a≠0）的图象具有如下性质：①当a＞0时，抛物线y=ax2+bx+c（a≠0）的开口向上，x ＜﹣时，y随x的增大而减小；x ＞﹣时，y随x的增大而增大；x=﹣时，y 取得最小值，即顶点是抛物线的最低点．②当a＜0时，抛物线y=ax2+bx+c（a≠0）的开口向下，x ＜﹣时，y随x的增大而增大；x ＞﹣时，y随x的增大而减小；x=﹣时，y 取得最大值，即顶点是抛物线的最高点．9．（2013•徐州）二次函数y=ax2+bx+c图象上部分点的坐标满足下表：x…﹣3﹣2﹣101…y…﹣3﹣2﹣3﹣6﹣11…则该函数图象的顶点坐标为（）A．（﹣3，﹣3）B．（﹣2，﹣2）C．（﹣1，﹣3）D．（0，﹣6）考点：二次函数的性质．专题：压轴题．分析：根据二次函数的对称性确定出二次函数的对称轴，然后解答即可．解答：解：∵x=﹣3和﹣1时的函数值都是﹣3相等，∴二次函数的对称轴为直线x=﹣2，∴顶点坐标为（﹣2，﹣2）．故选B．点评：本题考查了二次函数的性质，主要利用了二次函数的对称性，仔细观察表格数据确定出对称轴是解题的关键．10．（2013•南宁）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列说法错误的是（）A．图象关于直线x=1对称B．函数y=ax2+bx+c（a≠0）的最小值是﹣4 C．﹣1和3是方程ax2+bx+c=0（a≠0）的两个根D．当x＜1时，y随x的增大而增大考点：二次函数的性质．分析：根据对称轴及抛物线与x轴交点情况，结合二次函数的性质，即可对所得结论进行判断．解答：解：A、观察图象，可知抛物线的对称轴为直线x=1，则图象关于直线x=1对称，正确，故本选项不符合题意；B、观察图象，可知抛物线的顶点坐标为（1，﹣4），又抛物线开口向上，所以函数y=ax2+bx+c（a≠0）的最小值是﹣4，正确，故本选项不符合题意；C、由图象可知抛物线与x轴的一个交点为（﹣1，0），而对称轴为直线x=1，所以抛物线与x轴的另外一个交点为（3，0），则﹣1和3是方程ax2+bx+c=0（a≠0）的两个根，正确，故本选项不符合题意；D、由抛物线的对称轴为x=1，所以当x＜1时，y随x的增大而减小，错误，故本选项符合题意．故选D．此题考查了二次函数的性质和图象，解题的关键是利用数形结合思想解题．点评：11．（2012•济南）如图，二次函数的图象经过（﹣2，﹣1），（1，1）两点，则下列关于此二次函数的说法正确的是（）A．y的最大值小于0B．当x=0时，y的值大于1C．当x=﹣1时，y的值大于1D．当x=﹣3时，y的值小于0二次函数的图象；二次函数的性质．考点：专题：压轴题．分析：根据图象的对称轴的位置、增减性及开口方向直接回答．解答：解：A、由图象知，点（1，1）在图象的对称轴的左边，所以y的最大值大于1，不小于0；故本选项错误；B、由图象知，当x=0时，y的值就是函数图象与y轴的交点，而图象与y轴的交点在（1，1）点的左边，故y＜1；故本选项错误；C、对称轴在（1，1）的右边，在对称轴的左边y随x的增大而增大，∵﹣1＜1，∴x=﹣1时，y的值小于x=1时，y的值1，即当x=﹣1时，y的值小于1；故本选项错误；D、当x=﹣3时，函数图象上的点在点（﹣2，﹣1）的左边，所以y的值小于0；故本选项正确．故选D．点评：本题主要考查了二次函数图象上点的坐标特征．解答此题时，需熟悉二次函数图象的开口方向、对称轴、与x轴的交点等知识．12．（2012•德阳）设二次函数y=x2+bx+c，当x≤1时，总有y≥0，当1≤x≤3时，总有y≤0，那么c的取值范围是（）A．c=3B．c≥3C．1≤c≤3D．c≤3考点：二次函数的性质．专题：压轴题．分析：因为当x≤1时，总有y≥0，当1≤x≤3时，总有y≤0，所以函数图象过（1，0）点，即1+b+c=0①，由题意可知当x=3时，y=9+3b+c≤0②，所以①②联立即可求出c的取值范围．解答：解：∵当x≤1时，总有y≥0，当1≤x≤3时，总有y≤0，∴函数图象过（1，0）点，即1+b+c=0①，∵当1≤x≤3时，总有y≤0，∴当x=3时，y=9+3b+c≤0②，①②联立解得：c≥3，故选B．点评：本题考查了二次函数的增减性，解题的关键是由给出的条件得到抛物线过（1，0），再代入函数的解析式得到一次项系数和常数项的关系．13．（2009•新疆）如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系不正确的是（）A．h=m B．k=n C．k＞n D．h＞0，k＞0考点：二次函数的图象．专题：压轴题．分析：借助图象找出顶点的位置，判断顶点横坐标、纵坐标大小关系．解答：解：根据二次函数解析式确定抛物线的顶点坐标分别为（h，k），（m，n），因为点（h，k）在点（m，n）的上方，所以k=n不正确．故选：B．点本题是抛物线的顶点式定义在图形中的应用．评：14．（2009•丽水）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a＞0；②该函数的图象关于直线x=1对称；③当x=﹣1或x=3时，函数y的值都等于0．其中正确结论的个数是（）A．3B．2C．1D．0二次函数的性质．考点：根据抛物线的性质解题．分析：解：①抛物线开口向下，a＜0，所以①错误；解答：②抛物线是关于对称轴对称的轴对称图形，所以②该函数的图象关于直线x=1对称，正确；③当x=﹣1或x=3时，函数y的值都等于0，也正确．故选B．点本题考查了抛物线的开口方向，轴对称性和与x轴的交点等知识．评：15．（2009•南昌）二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列结论正确的是（）A．a c＜0B．当x=1时，y＞0C．方程ax2+bx+c=0（a≠0）有两个大于1的实数根D．存在一个大于1的实数x0，使得当x＜x0时，y随x的增大而减小；当x＞x0时，y 随x的增大而增大考二次函数的性质．点：专题：压轴题．分析：根据抛物线的形状与抛物线表达式系数的关系，逐一判断．解答：解：A、抛物线开口向上，a＞0，抛物线与y轴交于正半轴，c＞0，所以ac＞0，错误；B、由图象可知，当x=1时，y＜0，错误；C、方程ax2+bx+c=0（a≠0）有一个根小于1，一个根大于1，错误；D、存在一个大于1的实数x0，使得当x＜x0时，y随x的增大而减小；当x＞x0时，y随x的增大而增大，正确．故选D．点评：本题考查抛物线的形状与抛物线表达式系数的关系，涉及的知识面比较广．16．（2008•仙桃）如图，抛物线y=ax2+bx+c（a＞0）的对称轴是直线x=1，且经过点P（3，0），则a﹣b+c的值为（）A．0B．﹣1C．1D．2考点：二次函数的图象．专题：压轴题．分析：由“对称轴是直线x=1，且经过点P（3，0）”可知抛物线与x轴的另一个交点是（﹣1，0），代入抛物线方程即可解得．解答：解：因为对称轴x=1且经过点P（3，0）所以抛物线与x轴的另一个交点是（﹣1，0）代入抛物线解析式y=ax2+bx+c中，得a﹣b+c=0．故选A．点评：巧妙利用了抛物线的对称性．17．（2007•烟台）下列图中阴影部分的面积相等的是（）A．①②B．②③C．③④D．①④考点：二次函数的图象；一次函数的图象；反比例函数的图象．专题：压轴题．分析：根据坐标系的点的坐标特点，分别求出三角形的底和高，计算面积，再比较．解答：解：①与坐标轴的两个交点为（0，2）（2，0），阴影部分的面积为2×2÷2=2；②当x=1时，y=3，阴影部分的面积为1×3÷2=；③与x轴的两个交点的横坐标为﹣1，1，两点间的距离为：1﹣（﹣1）=2，与y 轴的交点为（0，﹣1）．阴影部分的面积为2×1÷2=1；④当x=1时，y=4，阴影部分的面积为1×4÷2=2．①④面积相等．故选D．点评：解决本题的关键是根据各函数的特点得到相应的三角形的边以及边上的高．18．（2007•达州）已知抛物线y=ax2+bx+c（a＜0）的部分图象如图所示，当y＞0时，x的取值范围是（）A．﹣2＜x＜2B．﹣4＜x＜2C．x＜﹣2或x＞2D．x＜﹣4或x＞2考点：二次函数的图象．专题：压轴题．分析：先根据对称轴和抛物线与x轴的交点求出另一交点；再根据开口方向，结合图形，求出y＞0时，x的取值范围．解答：解：因为抛物线过点（2，0），对称轴是x=﹣1，根据抛物线的对称性可知，抛物线必过另一点（﹣4，0），因为抛物线开口向下，y＞0时，图象在x轴的上方，此时，﹣4＜x＜2．故选B．点评：解答本题，利用二次函数的对称性，关键是判断图象与x轴的交点，根据开口方向，形数结合，得出结论．19．（2007•泰州）已知：二次函数y=x2﹣4x﹣a，下列说法错误的是（）A．当x＜1时，y随x的增大而减小B．若图象与x轴有交点，则a≤4C．当a=3时，不等式x2﹣4x+a＜0的解集是1＜x＜3D．若将图象向上平移1个单位，再向左平移3个单位后过点（1，﹣2），则a=3考点：二次函数的性质；二次函数图象与几何变换；抛物线与x轴的交点；二次函数与不等式（组）．专题：压轴题．分析：A、当x＜1时，在对称轴右侧，由此可以确定函数的单调性；B、若图象与x轴有交点，即△=16+4a≥0，利用此即可判断是否正确；C、当a=3时，不等式x2﹣4x+a＜0的解集可以求出，然后就可以判断是否正确；D、根据平移规律可以求出a的值，然后判断是否正确．解答：解：二次函数为y=x2﹣4x﹣a，对称轴为x=2，图象开口向上．则：A、当x＜1时，y随x的增大而减小，故选项正确；B、若图象与x轴有交点，即△=16+4a≥0则a≥﹣4，故选项错误；C、当a=3时，不等式x2﹣4x+a＜0的解集是1＜x＜3，故选项正确；D、原式可化为y=（x﹣2）2﹣4﹣a，将图象向上平移1个单位，再向左平移3个单位后所得函数解析式是y=（x+1）2﹣3﹣a．函数过点（1，﹣2），代入解析式得到：a=3．故选项正确．故选B．点评：此题主要考查了二次函数的性质与一元二次方程之间的关系，以及图象的平移规律．这些性质和规律要求掌握．20．（2009•塘沽区一模）下列表格给出的是二次函数y=ax2+bx+c（a≠0）的几组对应值，那么方程ax2+bx+c=0的一个近似解可以是（）xy﹣﹣A．B．C．D．考图象法求一元二次方程的近似根．点：把三点代入解方程式，则代入y等于0时，x的值是多少即可．分析：解：代入各点坐标解答：解得y=﹣+解得x=左右则C最符合，故选C．点评：本题考查了一元二次方程的近似根，代入求近似值，再进行对比则最接近的即可．21．（2010•徐汇区一模）已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（）A．抛物线开口向上B．抛物线与y轴交于负半轴C．当x=3时，y＜0D．方程ax2+bx+c=0有两个相等实数根考点：图象法求一元二次方程的近似根．专题：计算题．分析：结合图表可以得出当x=0或2时，y=1，可以求出此函数的对称轴是x=1，顶点坐标为（1，3），借助（0，1）两点可求出二次函数解析式，从而得出抛物线的性质．解解：∵由图表可以得出当x=0或2时，y=1，可以求出此函数的对称轴是x=1，顶答：点坐标为（1，3），∴二次函数解析式为：y=a（x﹣1）2+3，再将（0，1）点代入得：1=a（﹣1）2+3，解得：a=﹣2，∴y=﹣2（x﹣1）2+3，∵a＜0∴A，抛物线开口向上错误，故：A错误；∵y=﹣2（x﹣1）2+3=﹣2x2+4x+1，与y轴交点坐标为（0，1），故与y轴交于正半轴，故：B错误；∵x=3时，y=﹣5＜0，故：C正确；∵方程ax2+bx+c=0，△=16+4×2×1=22＞0，此方程有两个不相等的实数根，故：D．方程有两个相等实数根错误；故选：C．点此题主要考查了二次函数解析式的求法，以及由解析式求函数与坐标轴的交点评：以及一元二次方程根的判别式的应用．22．（2013•沙湾区模拟）已知二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A（﹣2，4），B（8，2）（如图所示），则能使y1＜y2成立的x的取值范围是（）A．x＞2B．x＜﹣2C．x＞0D．﹣2＜x＜8考点：二次函数的性质．分析：根据两函数交点坐标得出，能使y1＜y2成立的x的取值范围即是图象y2在图象y1上面是x的取值范围，即可得出答案．解答：解：∵二次函数y1=ax2+bx+c（a≠0）与一次函数y2=kx+m（k≠0）的图象相交于点A（﹣2，4），B（8，2），∵结合图象，∴能使y1＜y2成立的x的取值范围是：﹣2＜x＜8，故选：D．点评：此题主要考查了利用函数图象判定两函数的大小关系，此题型是中考中考查重点也是难点，同学们应熟练掌握．23．（2012•北辰区一模）在﹣3≤x≤0范围内，二次函数（a≠0）的图象如图所示．在这个范围内，有结论：①y1有最大值1、没有最小值；②y1有最大值1、最小值﹣3；③函数值y1随x的增大而增大；④方程ax2+bx+c=2无解；⑤若y2=2x+4，则y1≤y2．其中正确的个数是（）A．2B．3C．4D．5考点：二次函数的性质；二次函数的图象．专题：数形结合．分析：根据二次函数的性质，结合图象可判断①②③；根据二次函数与一元二次方程的关系可判断④；求出y2=2x+4与两坐标轴的交点画出直线y=2x+4，求出抛物线的解析式，根据y2﹣y1的符号即可判断出⑤．解答：解：由图象可知，在﹣3≤x≤0范围内，y1有最大值1、最小值﹣3，故①错误，②正确；由图象可知，当﹣3≤x＜﹣1时，y1随x的增大而增大，当﹣1＜x＜0时，y1随x 的增大而减小，故③错误；由于y1的最大值是1，所以y1=ax2+bx+c与y=2没有交点，即方程ax2+bx+c=2无解，故④正确；如图所示，由于y2=2x+4经过点（0，4），（﹣2，0），由图可知，二次函数（a≠0）中，当x=1时，y=﹣1；x=﹣2时，y=0，所以，解得，故此二次函数的解析式为y1=﹣x2﹣2x，所以y2﹣y1=2x+4+x2+2x=（x+2）2，因为=（x+2）2≥0，所以y1≤y2，故⑤正确．故选B．点评：本题考查的是二次函数的性质，能利用数形结合求出不等式的解集是解答此题的关键．24．（2011•苏州模拟）抛物线y=﹣x2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：x …﹣2﹣1 134…y …0 4 640…根据上表判断下列四种说法：①抛物线的对称轴是x=1；②x＞1时，y的值随着x的增大而减小：③抛物线有最高点：④抛物线的顶点、与x轴的两个交点三点为顶点的三角形的面积为36．其中正确说法的个数有（）A．1B．2C．3D．4考点：二次函数的性质．专题：计算题．分析：根据抛物线的对称性，抛物线的顶点坐标为（1，6），且函数值6为最大值，由此判断．解答：解：观察表格可知，抛物线的顶点坐标为（1，6），且抛物线开口向下，故①②③正确；∵抛物线与x轴的两个交点为（﹣2，0），（4，0），顶点坐标为（1，6），∴抛物线的顶点、与x 轴的两个交点三点为顶点的三角形的面积为×（4+2）×6=18，故④错误．其中正确说法是①②③．故选C．点评：本题考查了二次函数的性质．关键是由表格观察出抛物线的顶点坐标，开口方向及与x轴交点坐标．25．（2010•河北）如图，已知抛物线y=x2+bx+c的对称轴为x=2，点A，B均在抛物线上，且AB与x轴平行，其中点A的坐标为（0，3），则点B的坐标为（）A．（2，3）B．（3，2）C．（3，3）D．（4，3）考点：二次函数的性质．专题：综合题；压轴题．分析：已知抛物线的对称轴为x=2，知道A的坐标为（0，3），由函数的对称性知B点坐标．解答：解：由题意可知抛物线的y=x2+bx+c的对称轴为x=2，∵点A的坐标为（0，3），且AB与x轴平行，可知A、B两点为对称点，∴B点坐标为（4，3）故选D．本题主要考查二次函数的对称性．点评：26．如图为二次函数y=ax2+bx+c的图象，给出下列说法：①ab＜0；②方程ax2+bx+c=0的根为x1=﹣1，x2=3；③a+b+c＞0；④当x＜1时，y随x值的增大而增大；⑤当y＞0时，x＜﹣1或x＞3．其中，正确的说法有（）A．①②④B．①②⑤C．①③⑤D．②④⑤二次函数的性质．考点：压轴题．专题：根据二次函数图象反映出的数量关系，逐一判断正确性．分析：解答：解：根据图象可知：①对称轴﹣＞0，故ab＜0，正确；②方程ax2+bx+c=0的根为x1=﹣1，x2=3，正确；③x=1时，y=a+b+c＜0，错误；④当x＜1时，y随x值的增大而减小，错误；⑤当y＞0时，x＜﹣1或x＞3，正确．正确的有①②⑤．故选B．点评：主要考查了二次函数的性质，会根据图象获取所需要的信息．掌握函数性质灵活运用．27．已知二次函数y=x2+2（a﹣1）x+2．如果x≤4时，y随x增大而减小，则常数a的取值范围是（）A．a≥﹣5B．a≤﹣5C．a≥﹣3D．a≤﹣3考点：二次函数的性质．分抛物线开口向上，由x≤4时，y随x增大而减小，可知对称轴x=1﹣a≥4，解不。

数字图像处理计算题复习精华版

实用标准文档30452 计算题复习一、直方图均衡化（P68）对已知图像进行直方图均衡化修正。

例：表 1 为已知一幅总像素为 n=64×64 的 8bit 数字图像（即灰度级数为 8），各灰度级（出现的频率）分布列于表中。

要求将此幅图像进行均衡化修正（变换），并画出修正（变换）前后的直方图。

表1原图像灰原各灰度级原分布概率度级 rk 像素个数 nkpr(rk)r0=07900.19r1=110230.25r2=28500.21r3=36560.16r4=43290.08r5=52450.06r6=61220.03r7=7810.02解：对已知图像均衡化过程见下表：原图像灰度级 rk原各灰度级原分布概率累积分布函像素个数 nkpr(rk)数 sk 计取整扩展sk 并r0=07900.190.191r1=110230.250.443r2=28500.210.655r3=36560.160.816r4=43290.080.896r5=52450.060.957r6=61220.030.987r7=7810.021.007画出直方图如下：确定映射对应关系rk→sk0→1 1→3 2→5 3→6 4→6 5→7 6→7 7→7新图像灰度级 sk1 3 5新图像各灰度级像素个数 nsk7901023850新图像分布概率ps(sk)0.190.250.2169850.2474480.11（a）原始图像直方图 **以下部分不用写在答题中。

其中： ① rk、nk 中 k = 0，1，…，7文案大全（b）均衡化后直方图实用标准文档k ② p（r rk）= nk／n，即计算各灰度级像素个数占所有像素个数的百分比，其中 n  n j ，在此题中 n=64×64。

j0 k ③ sk计  pr (rj ) ，即计算在本灰度级之前（包含本灰度级）所有百分比之和。

j0④ sk并  int[( L 1)sk计  0.5]，其中 L 为图像的灰度级数（本题中 L = 8），int[ ]表示对方括号中的数字取整。

初中化学计算题知识点总结

初中化学计算题专题一根据化学式的计算（一）有关化学式的计算1、求相对分子质量，相对分子质量是指化学式中各原子的相对原子质量的总和。

在计算的过程中应留意化学式前面的数字(系数)与相对分子质量及元素符号右下角的数字与相对原子质量之间的关系是“相乘”不是“相加”；若计算结晶水合物的相对分子质量时，化学式中间的“·”与结晶水的相对分子质量之间是“相加”不是“相乘”。

例计算5CuSO4·5H2O 的相对分子质量总和。

5CuSO4·5H2O=5×[64+32+16×4+5×(1×2+16)] =5×[160+5×18] =12502、求化合物中各元素的质量比：以合物A m B n 为例。

A 、B 元素的质量比nm⨯⨯的相对原子质量的相对原子质量B A 。

例，计算氧化铁中铁元素和氧元素的质量比。

氧化物的化学式：Fe2O3，则 Fe ∶O=56×2∶16×3=112∶48=7∶33、求化合物中某元素的质量分数：化合物中任一元素的质量分数可以用下式计算：某元素的质量分数=%100⨯化合物的总质量该元素的质量。

另：混合物中某物质的质量分数=%100⨯混合物的质量某物质的质量（二）确定化学式的计算1、根据化合物中各元素的质量比求化学式将各元素的质量分别除以其相对原子质量，得到的商之比即为相应的原子个数之比，继而确定其化学式。

例，某硫的氧化物中S 、O 元素的质量比为2:3，该硫的氧化物的化学式为解析：S 、O 原子个数比为=163322：1:3，所以化学式为SO 3 2、根据化合物中某元素的质量分数求化学式已知某化合物中某元素的质量分数和相对分子质量，可确定该化合物中各原子个数之比，进而确定其化学式。

例，某铁的氧化物中ω（Fe ）=70%，则设其化学式为解析：可设该氧化物化学式为FexOy 。

则ω（Fe ）=%100y 16x 56x56⨯⨯=70%，解得x:y=2:3则其化学式为Fe2O3根据化合价确定化学式例，曾用作麻醉剂的“笑气”，是一种氮的氧化物，其中氮元素的化合价为+1，则“笑气”的化学式是（）A ．N2O5B ． NO2C ． NO Ｄ．Ｎ2Ｏ根据质量守恒定律确定化学式，反响前后元素的种类，原子数目不变。

初中化学七类计算题典型例题

初中化学七类计算题典型例题初中化学计算题的类型有多种，其中包括化学式计算、化合价计算、化学方程式计算、溶液计算、化学方程式和溶液简单综合计算、应用质量守恒定律计算等，下面简单进行一下归类：（一）有关化学式计算题类型：第一种类型：标签型化学式计算题：1、锌是人体健康必需的元素，锌缺乏容易造成发育障碍，易患异食癖等病症，使人体免疫功能低下。

市售的葡萄糖酸锌口服液对治疗锌缺乏病具有较好的疗效。

下图是某品牌葡萄糖酸锌口服液的标签，请根据标签信息回答：（1）葡萄糖酸锌中各元素的质量比；（2）葡萄糖酸锌中锌元素的质量分数。

（精确到0.01%）（3）某患者除正常饮食吸锌元素外，还需服用该品牌葡萄糖酸锌口服液。

若治疗一个疗程需补充104mg 锌元素，而这些锌有75%来自该口服液，则患者共需服用支葡萄糖酸锌口服液？（简写出解题过程）2、在现代生活中，人们越来越注重微量元素的摄取。

碘元素对人体健康有至关重要的作用。

下表是某地市场销售的一种“加碘食盐”包装袋上的部分说明。

请回答下列问题：（1）由食用方法和贮藏指南可推测碘酸钾（KIO 3）的化学性质之一是；（2）计算碘酸钾（KIO 3）中，钾元素、碘元素、氧元素的质量比；（3）计算碘酸钾（KIO 3）中，碘元素的质量分数是多少？；（计算结果精确到0.01，下同）（4）计算1kg 这样的食盐中，应加入 g 碘酸钾（用最高含碘量计算）第二种类型：叙述型化学式计算题：1、蛋白质是由多种氨基酸[丙氨酸：CH 3CH(NH 2)COOH 等]构成的极为复杂的化合物，人体通过食物获得蛋白质，在胃肠道里与水发生反应，生成氨基酸，试计算：（1）丙氨酸分子中氮原子与氧原子的个数比。

（2）丙氨酸的相对分子质量。

（3）丙氨酸中碳、氢、氧、氮元素的质量比。

2、抗震救灾，众志成城。

用于汶川震后防疫的众多消毒剂中，有一种高效消毒剂的主要成分为三氯异氰尿酸(C 3O 3N 3Cl 3)，又称高氯精。

浙教版九上科学化学计算题专题精讲附习题

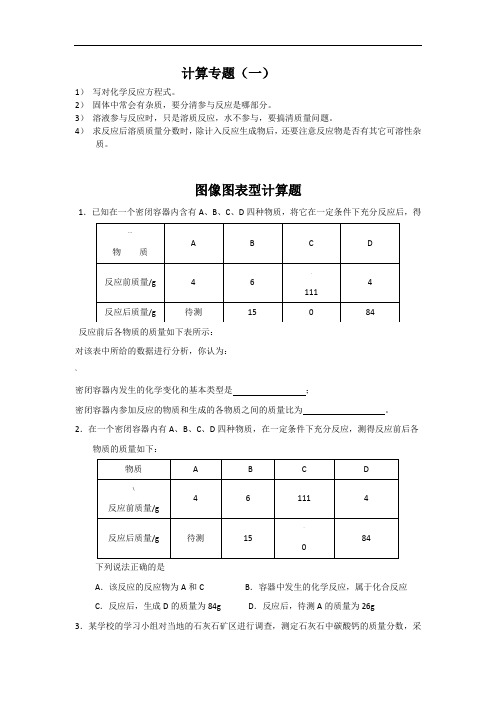
计算专题（一）1）写对化学反应方程式。

2）固体中常会有杂质，要分清参与反应是哪部分。

3）溶液参与反应时，只是溶质反应，水不参与，要搞清质量问题。

4）求反应后溶质质量分数时，除计入反应生成物后，还要注意反应物是否有其它可溶性杂质。

图像图表型计算题1．已知在一个密闭容器内含有A、B、C、D四种物质，将它在一定条件下充分反应后，得反应前后各物质的质量如下表所示：对该表中所给的数据进行分析，你认为：~密闭容器内发生的化学变化的基本类型是；密闭容器内参加反应的物质和生成的各物质之间的质量比为。

2．在一个密闭容器内有A、B、C、D四种物质，在一定条件下充分反应，测得反应前后各物质的质量如下：下列说法正确的是A．该反应的反应物为A和C B．容器中发生的化学反应，属于化合反应C．反应后，生成D的质量为84g D．反应后，待测A的质量为26g3．某学校的学习小组对当地的石灰石矿区进行调查，测定石灰石中碳酸钙的质量分数，采用的方法如下：取该石灰石样品16g，把80g稀盐酸分四次加入，测量过程所得数据见下表(已知石灰石样品中含有的二氧化硅等杂质不溶于水也不与稀盐酸反应)。

请计算：(1)上表中n的数值为___________。

（2）石灰石中碳酸钙的质量分数为。

(3)求盐酸中溶质的质量分数（写出计算过程）。

&4．为测定石灰石中碳酸钙的含量，某学校课外小组同学做了如下实验：首先称取50 g该地区的石灰石样品，然后将150 mL的稀盐酸分5次加入（假设其余杂质均不与盐酸反应）进行充分反应。

实验过程中的数据记录如下：（1）X = g；（2）计算该石灰石样品中碳酸钙的质量分数是多少%（3）若把该反应产生的二氧化碳全部收集起来，共有多少L（注意：①二氧化碳气体的密度为1.977g/L，②要求写出全部计算过程）5．某校九年级综合实践活动小组用一定量的溶质质量分数为10%的过氧化氢溶液和二氧化锰来制取氧气，最后所得气体质量】与时间的关系如右图所示。