机械原理-速度瞬心习题
机械原理-简单机构速度分析的速度瞬心法

三心定理
作平面运动的三个构件共有三个瞬ቤተ መጻሕፍቲ ባይዱ,
它们位于同一直线上.
Vk1 K 2 1 Vk2
瞬心的应用
瞬心的应用
1 与3 的关系 已知四杆机构的尺寸及 1求全部瞬心、
P24 1 2 2
v p13 1 p14 p13 l
p23
3
p12 1 P13 p14
4
3
v p13 3 p34 p13 l
∞
v2 v p1 2 1 p13 p12 l
p13
1
p12
已知下列机构的尺寸及
求全部瞬心、 与
的关系
3
∞ P23
2
p13
p12
1
v2 v p1 2 1 p13 p12 l
速度瞬心
VA A B VB
v p1 v p2 0
绝对瞬心
P12
VA1 A2
2 A B
v p1 v p2 0
VB1B 2
相对瞬心
1
P12
P12
瞬心的数目
n ( n 1) N 2
•N-瞬心数
•n-构件数
瞬心的求法
观察法
P12
P12在无穷远
P12 P12在公法线上
三心定理
4 p34
p34 p13 1 3 p14 p13
已知下列机构的尺寸及
求全部瞬心、 与
的关系
p13 P12 1
v p12 1 p13 p12 l 2 p23 p12 l
p23 p12 1 2 p13 p12
2
p23
3
已知下列机构的尺寸及
求全部瞬心、 与
的关系
机械原理习题及答案
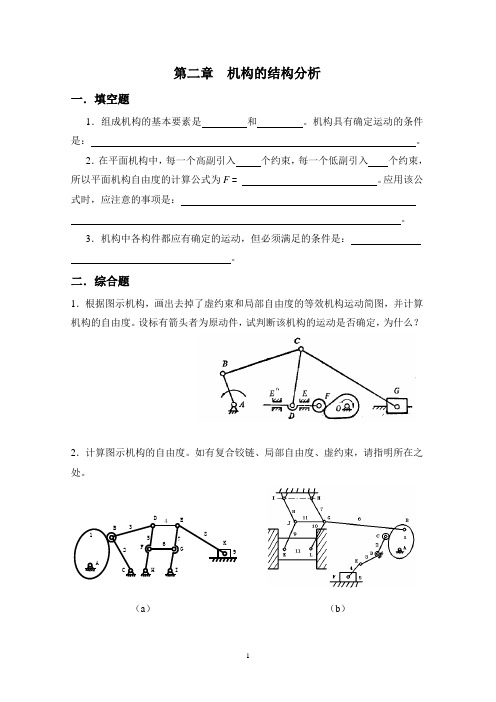
第二章 机构的结构分析一.填空题1.组成机构的基本要素是 和 。
机构具有确定运动的条件是: 。
2.在平面机构中,每一个高副引入 个约束,每一个低副引入 个约束,所以平面机构自由度的计算公式为F = 。
应用该公式时,应注意的事项是: 。
3.机构中各构件都应有确定的运动,但必须满足的条件是: 。
二.综合题1.根据图示机构,画出去掉了虚约束和局部自由度的等效机构运动简图,并计算机构的自由度。
设标有箭头者为原动件,试判断该机构的运动是否确定,为什么?2.计算图示机构的自由度。
如有复合铰链、局部自由度、虚约束,请指明所在之处。
(a ) (b )ADECHGF IBK1234567893.计算图示各机构的自由度。
(a)(b)(c)(d)(e)(f)4.计算机构的自由度,并进行机构的结构分析,将其基本杆组拆分出来,指出各个基本杆组的级别以及机构的级别。
(a)(b)(c)(d)5.计算机构的自由度,并分析组成此机构的基本杆组。
如果在该机构中改选FG 为原动件,试问组成此机构的基本杆组是否发生变化。
6.试验算图示机构的运动是否确定。
如机构运动不确定请提出其具有确定运动的修改方案。
(a)(b)第三章平面机构的运动分析一、综合题1、试求图示各机构在图示位置时全部瞬心的位置(用符号P直接在图上标出)。
ij2、已知图示机构的输入角速度ω1,试用瞬心法求机构的输出速度ω3。
要求画出相应的瞬心,写出ω3的表达式,并标明方向。
3、在图示的齿轮--连杆组合机构中,试用瞬心法求齿轮1与3的传动比ω1/ω2。
4、在图示的四杆机构中,AB l =60mm, CD l =90mm, AD l =BC l =120mm, 2ω=10rad/s ,试用瞬心法求:(1)当ϕ=165°时,点C 的速度c v ;(2)当ϕ=165°时,构件3的BC 线上速度最小的一点E 的位置及其速度的大小; (3)当0c v =u u u v时,ϕ角之值(有两个解)。
第4章 速度瞬心及其应用

直接以运动副相连的两构件的速度瞬心的确定
3
(P1m或P2n为瞬心但不是铰链时仍然正确) 为瞬心但不是铰链时仍然正确)
4
作平面运动三个构件之间的三个速度瞬心 必在同一条直线上。 (证明作习题 )
5
4.2 速度瞬心在机构速度分析中的应用 速度瞬心在机构速度分析中的应用 机构
已知各杆长和ω2,求ω4和ω3。(须标注转向或方向)
高副低代——采用低副代替高副进行变通处理的方法 采用低副代替高副进行变通处理的方法 高副低代
要点——找出两高副元素的接触点处的公法线和曲率中心 找出两高副元素的接触点处的公法线和曲率中心 要点
在机构运动分析仅考虑 机构的位置、速度和加速度的 情况下以及分析机构的级别时, 可以采用高副低代。
曲线与曲线形成的高副
VP23=ω3μl(P13P23)=ω2μl(P12P23) ω3=ω2(P12P23)/(P13P23)
6
(动画) V4=ω2μl(P12P24) VP23=ω3μl(P13P23)=ω2μl(P12P23) ω3=ω2(P12P23)/(P13P23)
7
ω1 ⋅ P01P12 µ l = v P12 = v2 (↑)
(动画)
(动画)
8
4.3 瞬心线和瞬心线机构 瞬心线和瞬心线机构
A、B轨迹为直线;AB中点轨迹为
圆;AB及其延长线上其它点轨迹为 椭圆。
(矩形对角线相等:OP≡AB。∠APB恒为直角)
为定瞬心线, 圆S4为定瞬心线,而圆 为定瞬心线 而圆S2 为动瞬心线 ,动瞬心线将沿定瞬 动瞬心线将沿定瞬 心线作无滑动的滚动 利用瞬心线设计而成的机构 利用瞬心线设计而成的机构 叫做瞬心线机构
11
曲线与点形成的高副
机械原理习题卡答案

4 试计算图 4 所示机构的自由度。不要求 解 该机构为空间机构,且公共约束 m=0,n=3,p5=2(A 处为转动副,C 处为移动副),p3=2 (B,D 处为球面副);又由图可知,连杆 2 及 3 绕自身转动为局部自由度 F’=1。由式(1.3) 求得
F=6n – 5p5 – 3p3 – F’=6×3 – 5×2 – 3×2 – 1=1 故该机构的自由度为 1。
图8
8
第二章 机构的结构分析
9 试计算图 9 所示运动链的自由度,如有复合铰链、局部自由度、虚约束需明确指出,并判 断是否为机构。 解 齿轮 2’及 4’引入虚约束,A 处为复合铰链,得
F=3n –(2pl + ph – p’)– F’= 3×7 – (2×7+8 – 2) –0=1
图9
9
第二章 机构的结构分析
F=3n –(2pl + ph – p’)– F’= 3×8 – (2×12+0 – 1) –0=1
图7
7
第二章 机构的结构分析
8 试计算图 8 所示机构的自由度。 解 n=5,pl=7(B 处为复合铰链),ph=0,则
F=3n –(2pl + ph – p’)– F’= 3×5– (2×7+0 – 0) –0=1
三简答题1何谓凸轮机构的压力角它在凸轮机构的设计中有何重要意义2直动从动件盘形凸轮机构压力角的大小与该机构的哪些因素有关3在直动从动件盘形凸轮机构中若凸轮作顺时针方向转动从动件向上移动为工作行程则凸轮的轴心应相对从动件导路向左偏置还是向右偏置为好为什么若偏置得太多会有什么问题产生4在直动从动件盘形凸轮机构中试问同一凸轮采用不同端部形状的从动件时其从动件运动规律是否相同为什么5图示为一凸轮机构从动件推程位移曲线oabcab平行横坐标轴
机械原理第一章速度瞬心介绍.ppt

• 例1-8 求图1-21所示铰链四杆机构的瞬心。 • P12,P13,P14-----绝对瞬心,P23,P34,P24------相对瞬心
• 例1—9 求图1—22所示曲柄滑块
机械原理第一章速度瞬心介绍
(1)在图1—18中,构件1和构件2的瞬心P12; (2) 当两构件组成转动副时,转动副的中心便是它们的瞬心;
(3) 当两构件组成移动副时、所以其瞬心位于导路垂线的无穷远处;
(4)当两构件组成纯滚动高副时,接触点就是其瞬心,
(3)当两构件组成滑动兼滚动的高副时,其瞬心应位于过接触点的公法线上
机械原理概念题

机械原理概念题一、正误推断题:(在括号内正确的画“√”,错误的画“×”)1.在平面机构中一个高副引入二个约束。
(×)2.任何具有确定运动的机构都是由机架加原动件再加自由度为零的杆组构成的。
(√)3.运动链要成为机构,务必使运动链中原动件数目大于或者等于自由度。
(×)4.平面机构高副低代的条件是代替机构与原机构的自由度、瞬时速度与瞬时加速度必需完全相同。
(√)5.当机构自由度F>0,且等于原动件数时,该机构具有确定运动。
(√)6.若两个构件之间构成了两个导路平行的移动副,在计算自由度时应算作两个移动副。
(×)7.在平面机构中一个高副有两个自由度,引入一个约束。
(√)8.在杆组并接时,可将同一杆组上的各个外接运动副连接在同一构件上。
(×)9.任何机构都是由机架加原动件再加自由度为零的基本杆组构成。
因此基本杆组是自由度为零的运动链。
(√)10.平面低副具有2个自由度,1个约束。
(×)二、填空题1.机器中每一个制造单元体称之零件。
2.机器是在外力作用下运转的,当外力作功表现为盈功时,机器处在增速阶段,当外力作功表现为亏功时,机器处在减速阶段。
3.局部自由度虽不影响机构的运动,却减小了高副元素的磨损,因此机构中常出现局部自由度。
4.机器中每一个独立的运动单元体称之构件。
5.两构件通过面接触而构成的运动副称之低副;通过点、线接触而构成的运动副称之高副。
6.平面运动副的最大约束数为 2 ,最小约束数为1。
7.两构件之间以线接触所构成的平面运动副,称之低副,它产生2 个约束。
三、选择题1.机构中的构件是由一个或者多个零件所构成,这些零件间 B 产生任何相对运动。
A.能够B.不能C.变速转动或者变速移动2.基本杆组的自由度应为 C 。
A.-1B. +1C. 03.有两个平面机构的自由度都等于1,现用一个带有两铰链的运动构件将它们串成一个平面机构,则其自由度等于 B 。
机械原理选择填空题(已整理)

一、填空题1.机构中的速度瞬心是两构件上()为零的重合点,它用于平面机构()分析。
2.下列机构中,若给定各杆长度,以最长杆为连架杆时,第一组为()机构;第二组为()机构。
(1) a = 250 b = 200 c = 80 d = 100;(2) a = 90 b = 200 c = 210 d = 100 。
3.机构和零件不同,构件是(),而零件是()。
4.凸轮的基圆半径越小,则机构尺寸()但过于小的基圆半径会导致压力角()。
5.用齿条型刀具范成法切制渐开线齿轮时,为使标准齿轮不发生根切,应使刀具的()。
6.当要求凸轮机构从动件的运动没有冲击时,应选用()规律。
7.间歇凸轮机构是将()转化为()的运动。
8.刚性转子的平衡中,当转子的质量分布不在一个平面内时,应采用()方法平衡。
其平衡条件为()。
9.机械的等效动力学模型的建立,其等效原则是:等效构件所具有的动能应()。
等效力、等效力矩所作的功或瞬时功率应()。
10.平面机构结构分析中,基本杆组的结构公式是()。
而动态静力分析中,静定条件是()。
一、选择题1.渐开线齿轮齿条啮合时,若齿条相对齿轮作远离圆心的平移,其啮合角()。
A)增大; B)不变; C)减少。
2.为保证一对渐开线齿轮可靠地连续传动,应便实际啮合线长度()基圆齿距。
A)等于; B)小于; C)大于。
3.高副低代中的虚拟构件的自由度为()。
A) -1 ; B) +1 ; C) 0 ;4.压力角是在不考虑摩擦情况下,作用力与作用点的()方向的夹角。
A)法线; B)速度; C)加速度; D)切线;5.理论廓线相同而实际廓线不同的两个对心直动滚子从动件盘形凸轮,其推杆的运动规律是()。
A)相同的; B)不相同的; C)不一定的。
6.飞轮调速是因为它能()能量,装飞轮后以后,机器的速度波动可以()。
① A)生产; B)消耗; C)储存和放出。
② A)消除; B)减小; C)增大。
7.作平面运动的三个构件有被此相关的三个瞬心。
机械原理习题附答案

第二章4.在平面机构中,具有两个约束的运动副是移动副或转动副;具有一个约束的运动副是高副。
5.组成机构的要素是构件和转动副;构件是机构中的_运动_单元体。
6.在平面机构中,一个运动副引入的约束数的变化范围是1-2。
7.机构具有确定运动的条件是_(机构的原动件数目等于机构的自由度)。
8.零件与构件的区别在于构件是运动的单元体,而零件是制造的单元体。
9.由M个构件组成的复合铰链应包括m-1个转动副。
10.机构中的运动副是指两构件直接接触所组成的可动联接。
1.三个彼此作平面平行运动的构件共有3个速度瞬心,这几个瞬心必定位于同一直线上。
2.含有六个构件的平面机构,其速度瞬心共有15个,其中有5个是绝对瞬心,有10个是相对瞬心。
3.相对瞬心和绝对瞬心的相同点是两构件相对速度为零的点,即绝对速度相等的点,不同点是绝对瞬心点两构件的绝对速度为零,相对瞬心点两构件的绝对速度不为零。
4.在由N个构件所组成的机构中,有(N-1)(N/2-1)个相对瞬心,有N-1个绝对瞬心。
5.速度影像的相似原理只能应用于同一构件上_的各点,而不能应用于机构的不同构件上的各点。
6.当两构件组成转动副时,其瞬心在转动副中心处;组成移动副时,其瞬心在移动方向的垂直无穷远处处;组成纯滚动的高副时,其瞬心在高副接触点处。
7.一个运动矢量方程只能求解____2____个未知量。
8.平面四杆机构的瞬心总数为_6__。
9.当两构件不直接组成运动副时,瞬心位置用三心定理确定。
10.当两构件的相对运动为移动,牵连运动为转动动时,两构件的重合点之间将有哥氏加速度。
哥氏加速度的大小为a*kc2c3,方向与将vc2c3沿ω2转90度的方向一致。
1.从受力观点分析,移动副的自锁条件是驱动力位于摩擦锥之内,转动副的自锁条件是驱动力位于摩擦圆之内。
2.从效率的观点来看,机械的自锁条件是η<0。
3.三角形螺纹的摩擦力矩在同样条件下大于矩形螺纹的摩擦力矩,因此它多用于联接。
机械原理复习题第3章

习题1.判断题(1)瞬心即彼此作一般平面运动的两构件上的瞬时等速重合点或瞬时相对速度为零的重合点。
(√)(2)以转动副相连的两构件的瞬心在转动副的中心处。
(√)(3)以平面高副相连接的两构件的瞬心,当高副两元素作纯滚动时位于接触点的切线上。
(×)(4)矢量方程图解法依据的基本原理是运动合成原理。
(√)(5)加速度影像原理适用于整个机构。
(×)2.单选题(1)以移动副相连的两构件间的瞬心位于( B )A.导路上B.垂直于导路方向的无穷远处C.过构件中心的垂直于导路方向的无穷远处 D.构件中心(2)速度影像原理适用于( C )A.整个机构B.通过运动副相连的机构C.单个构件D.形状简单机构(3)确定不通过运动副直接相连的两构件的瞬心,除了运用概念法外,还需要借助( A )A.三心定理B.相对运动原理C.速度影像原理D.加速度影像原理3.简答题(1)何谓速度瞬心?相对瞬心与绝对瞬心有何异同点。
答:当两构件作平面相对运动时,在任一瞬时,都可以认为它们是绕某一重合点做相对转动,该重合点就称为瞬时速度中心,简称为瞬心。
瞬心是两构件上绝对速度相等,相对速度为零的一对重合点。
若瞬心的绝对速度为零,就称为绝对瞬心;若瞬心的绝对速度不为零,就称为相对瞬心。
(2)何谓三心定理?何种情况下的瞬心需用三心定理来确定?答:三心定理是指三个彼此互作平面相对运动的构件的三个瞬心必位于同一个直线上。
利用三心定理来确定不直接以运动副联接的两构件的瞬心。
(3)当用速度瞬心法和用速度影像法求同一构件,如四杆机构连杆上任一点的速度时,它们的求解条件有何不同?各有何特点?答:用速度瞬心法求机构的速度是利用相对瞬心为两构件的瞬时绝对速度相等的重合点的概念,建立待求运动构件与已知运动构件的速度关系来求解的。
其优点是对于构件比较少的机构,简洁和直观;局限性是对于构件多的机构,求取瞬心的过程比较麻烦,且此方法只能用来进行机构的速度分析,不能用于机构的位移和加速度分析中。
机械原理典型例题(第三章运动分析)12-9-23

P14+∞
4
(P24 ) P12
P34
C 1
3
P13
4 C 3
M
P23 +∞ P13
2 3 B
P24+∞ P34
B P23
P14
νm
4 C
P12
A 1
2 P12
P24
1
P34+∞
P24
P14+∞
A
3-6:所示四杆机构中,LAB=60mm,LCD=90mm,LAD=LBC=120mm, ω2=10rad/S。试用瞬心法求:1)当φ =165°时,点C的速度VC; 2)当 VC=0时,φ 角之值; 3)当φ =165 °时,构件3的BC线上(或其延长线上)的 速度最小的一点E的位置及其速度。
例6:所示机构中,已知各构件的尺寸及点B的速度 ν B,试作出其在图示位置时的速度多变形。
VB D B C G F E A
F A B E VB D C
b f b d e
P(a,f)
d c
P (a,e )
c
g
3-8:所示机构中,已知各构件的尺寸及点B的速度 ν B,试作出其在图示位置时的速度多变形。
C
3
VE
4
E
VC= VC3= VC4
ω3=VB /LP23P13
P23B
ω2
2
VC
φ
P34
= ω3×LP34P13=ω4×LP34P14
D
=ω2×LP23P12 /LP23P13
P14
VB
P12
A
1
VC =ω2×LP23P12×LP34P13/LP2
机械原理第四章速度瞬心及其应用一类教资
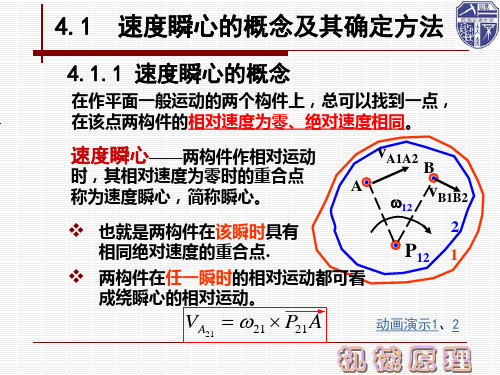
4.4 共轭曲线与共轭曲线机构(自学)
构件1曲线K1和构件2曲线K2 在点Q高副接触。
构件1、2之间的速度瞬心在点P
瞬心线S1是速度瞬心P 相对于构件1的轨迹线。
瞬心线S2是速度瞬心P 相对于构件2的轨迹线。
曲线K2包络了曲线K1的各个位置, 称K2为包络曲线, K1为被包络曲线
(大小、方向相等)
确定瞬心小结
4.2 速度瞬心在机构速度分析中的应用
P23
∞
P13
P12
情形1:求线速度
已知凸轮转速ω1,求推杆的速度。
求解过程: ①直接观察求瞬心P13、 P23 。
③求瞬心P12的速度 。
V2=V P12=μl(P13P12)·ω1
长度P13P12直接从图上量取。
ω1
1
2
3
P12
2
3
4
ω2
v2
P14→∞
P34
例题:如图所示的带有一移动副的平面四杆机构中, 已知原动件2以角速度w2等速度转动, 现需确定机构在图示位置时从动件4的速度v4。
求解过程:确定机构瞬心如图所示
P24 在P23、P34 连线和P12、P14 连线上。
P24
P13
ω2
情形2:求角速度
求解过程:①瞬心数为
高副低代的含义: 根据一定条件对平面高副机构的中高副虚拟地用低副来代替的方法。
高副低代的条件: ①代替前后机构的自由度不变; ②代替前后机构的瞬时速度和瞬时加速度不变。
高副低代的方法1
高副两元素均为圆弧
高副元素为非圆曲线
用一个含有两个低副的虚拟构件来代替高副,且两低副位置分别在两高副两元素接触点处的曲率中心。
机械原理第四章 速度瞬心及其应用概要

如图所示凸轮机构,设已知各构件尺寸和凸 轮的角速度w2,求从动件3的速度v3。
求解过程: 3 ω2 n K 2 确定构件2和3的相对瞬心P23
V3=V P23=μ l(P12P23)· ω2
P12 P23 1
n
动画演示1、2
例题:如图所示的带有一移动副的平面四杆机构中,
已知原动件2以角速度w2等速度转动, 现需确定机构 在图示位置时从动件4的速度v4。 求解过程:确定机构瞬心如图所示
vP 23 21 P21P23 vP 32 31 P31P32
∵ ∴ 2 A P21 1
Vk 31 K 21 31 3 B P31
21 // 31
P21 P23 // P31 P32
P21 、 P 31 、 P 32 位于同一条直线上。
确定瞬心小结
4.2
速度瞬心在机构速度分析中的应用
∴ω 3 =ω 2 · (P13P23/P12P23)
方向: ω 3与ω 2相反。
VP23
相对瞬心位于两绝对瞬心之间,两构件转向相反。
3.用瞬心法解题步骤:
①绘制机构运动简图; ②求瞬心的位置; ③求出相对瞬心的速度; ④求构件绝对速度V或角速度ω。
4.瞬心法的优缺点:
①适合于求简单机构的速度,机构复杂时因 瞬心数急剧增加而求解过程复杂。 ②有时瞬心点落在纸面外。 ③仅适机构(自学)
动画链接
定瞬心线:速度瞬心点相对于机架上的轨迹
动瞬心线:速度瞬心点相对于活动构件上的轨迹
由速度瞬心的概念可知:在机构的运动过程 中,动瞬心线上的每一点都有一个在定瞬心 线上相对应的点与之作无滑动的接触。
结论:动瞬心线沿定瞬心线作无滑动的滚动。
4.4 共轭曲线与共轭曲线机构(自学)
机械原理课后习题答案(部分)

第二章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答:参考教材5~7页。
2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答:机构运动简图可以表示机构的组成和运动传递情况,可进行运动分析,也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时,机构的运动将发生什么情况?答:参考教材12~13页。
2-5 在计算平面机构的自由度时,应注意哪些事项?答:参考教材15~17页。
2-6 在图2-22所示的机构中,在铰链C、B、D处,被连接的两构件上连接点的轨迹都是重合的,那么能说该机构有三个虚约束吗?为什么?答:不能,因为在铰链C、B、D中任何一处,被连接的两构件上连接点的轨迹重合是由于其他两处的作用,所以只能算一处。
2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答:参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答:参考教材20~21页。
2-11 如图所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构将使冲头上下运动以达到冲压目的。
试绘出其机构运动简图,分析其是否能实现设计意图?并提出修改方案。
解:1)取比例尺绘制机构运动简图。
2)分析其是否可实现设计意图。
F=3n-( 2P l +P h –p’)-F’=3×3-(2×4+1-0)-0=0此简易冲床不能运动,无法实现设计意图。
3)修改方案。
为了使此机构运动,应增加一个自由度。
办法是:增加一个活动构件,一个低副。
修改方案很多,现提供两种。
※2-13图示为一新型偏心轮滑阎式真空泵。
其偏心轮1绕固定轴心A转动,与外环2固连在一起的滑阀3在可绕固定轴心C转动的圆柱4中滑动。
当偏心轮按图示方向连续回转时可将设备中的空气吸入,并将空气从阀5中排出,从而形成真空。
机械原理--速度瞬心习题

习题 > 答案一.概念1.当两构件组成转动副时,其相对速度瞬心在转动副的圆心处;组成移动副时,其瞬心在垂直于移动导路的无穷远处;组成滑动兼滚动的高副时,其瞬心在接触点两轮廓线的公法线上.2.相对瞬心与绝对瞬心相同点是都是两构件上相对速度为零,绝对速度相等的点 ,而不同点是相对瞬心的绝对速度不为零,而绝对瞬心的绝对速度为零 .3.速度影像的相似原理只能用于同一构件上的两点,而不能用于机构不同构件上的各点.4.速度瞬心可以定义为互相作平面相对运动的两构件上,相对速度为零,绝对速度相等的点.5.3个彼此作平面平行运动的构件共有 3 个速度瞬心,这几个瞬心必位于同一条直线上 .含有6个构件的平面机构,其速度瞬心共有 15 个,其中 5 个是绝对瞬心,有 9 个相对瞬心.二.计算题1、2.关键:找到瞬心P36 6 Solution:The coordinates of joint B are y B =ABsin φ=0.20sin45°=0.141m x B =ABsin φ=0.20sin45°=0.141mThe vector diagram of the right Fig is drawn by representing the RTR (BBD) dyad. The vector equation, corresponding to this loop, is written asrB+r -rD=0 orr =rD-rBWherer=BD andr=γ.When the above vectorial equation is projected on the x and y axes, two scalar equations are obtained: r*cos(φ3+π)=x D-xB=-0.141mr*sin(φ3+π)=y D -y B =-0.541mAngle φ3is obtained by solving the system of the two previous scalar equations:tg φ3=141.0541.0φ3=75.36° The distance r isr=)cos(3BDx x =0.56mThe coordinates of joint C arex C=CDcosφ3=0.17m y C=CDsinφ3-AD=0.27mFor the next dyad RRT (CEE), the right Fig, one can write- φ4)= y E- y CCecos(π- φ4)=x E- x C Cesin(πVector diagram represent the RRT (CEE) dyad.When the system of equations is solved, the unknowns φ4 and x E are obtained: φ4=165.9° x E=-0.114m7. Solution:The origin of the system is at A, A≡0; that is,x A=y A=0.The coordinates of the R joints at B arex B =l 1cos φ yB = l 1sin φFor the dyad DBB (RTR), the following equations can be written with respect to thesliding line CD: mxB- yB+n=0 yD=mxD+nWith x D =d 1, y D=0 from the above system, slope m of link CD and intercept n canbe calculated:m=111cos sind l l n=cossin1111l d l d The coordinates x Cand y Cof the center of the R joint C result from the system oftwo equations:y C =mx C+n=cossin cossin1111111l d l d x d l l C,(x C - xD )2+(y C- yD)2=l23Because of the quadratic equation, two solutions are abstained for x Cand y C .For continuous motion of the mechanism, there are constraint relations for the Choice ofthe correct solution; that is xC< xB< xDand yC>0For the last dyad CEE (RRT), a position function can be written for joint E: (xC-xE)2+(yC-h)2=l24The equation produces values for x1E and x 2E , and the solution xE>xCis selectedfor continuous motion of the mechanism.。
机械原理模拟题8套-2(带答案)

模拟试题1一、填空题:(30分)1.机构中的速度瞬心是两构件上(相对速度)为零的重合点,它用于平面机构(速度)分析。
2.两构件之间可运动的连接接触称为(运动副)。
3.凸轮的基圆半径越小,则机构尺寸(越大)但过于小的基圆半径会导致压力角(增大)。
4.用齿条型刀具范成法切制渐开线齿轮时,为使标准齿轮不发生根切,应使刀具的(齿顶线不超过极限啮合点)。
5.间歇凸轮机构是将(主动轮的连续转动)转化为(从动转盘的间歇)的运动。
6.刚性转子的平衡中,当转子的质量分布不在一个平面内时,应采用(动平衡)方法平衡。
其平衡条件为(∑M = O ;∑F = 0 )。
7.机械的等效动力学模型的建立,其等效原则是:等效构件所具有的动能应(等于整个系统的总动能)。
等效力、等效力矩所作的功或瞬时功率应(等于整个系统的所有力,所有力矩所作的功或所产生的功率之和)。
8.平面机构结构分析中,基本杆组的结构公式是(3n = 2PL )。
而动态静力分析中,静定条件是(3n = 2PL )。
9.含有两个整转副的将铰链四杆机构,以最短杆为( 连杆)得到双摇杆机构。
10.渐开线齿轮的加工方法分为( 范成法)和(仿形法)两类。
二、选择题:(20分)1.渐开线齿轮齿条啮合时,若齿条相对齿轮作远离圆心的平移,其啮合角(B )。
A) 增大;B)不变;C)减少。
2.为保证一对渐开线齿轮可靠地连续传动,实际啮合线长度(C )基圆齿距。
A)等于;B)小于;C)大于。
3.高副低代中的虚拟构件的自由度为( A )。
A) -1;B) +1 ;C) 0 ;4.以滑块为主动件的曲柄滑块机构,死点位置出现在( A )。
A)曲柄与连杆共线时B)曲柄与连杆垂直时C)曲柄与滑块运动方向平行时D)曲柄与滑块运动方向垂直时5.渐开线齿轮发生根切的根本原因是啮合点跨越了( A )。
A)理论啮合线的端点B)实际啮合线的端点C)节点D)齿根圆6.飞轮调速是因为它能(C①)能量,装飞轮后以后,机器的速度波动可以(B②)。
机械原理复习题9

心,有10个是相对瞬心。
3. 相对瞬心与绝对瞬心的相同点是两构件上的同速点,不同点是;绝对速度为
零及不为零。
4. 速度比例尺的定义图上是单位长度(mm)所代表的实际速度值(m/s),在比例
尺单位相同的条件下,它的绝对值愈大,绘制出的速度多边形图形愈小。
5.
图示为六杆机构的机构运动简图及速度多边形,图中矢量cb
3.在同一构件上,任意两点的绝对加速度间的关系式中不包含哥氏加速度。( Y ) 4.在平面机构中,不与机架直接相连的构件上任一点的绝对速度均不为零。(N ) 三、选择题 1.图示连杆机构中滑块2上 E 点的轨迹应是 B 。
(A)直线;(B)圆弧;(C)椭圆;(D)复杂平面曲线。
2. 在两构件的相对速度瞬心处,瞬时重合点间的速度应有 A 。 (A)两点间相对速度为零,但两点绝对速度不等于零; (B)两点间相对速度不等于零,但其中一点的绝对速度等于零; (C)两点间相对速度不等于零且两点的绝对速度也不等于零; (D)两点间的相对速度和绝对速度都等于零。
速度瞬心在在接触点处的公法线上。
9. 速度瞬心是两刚体上瞬时相对速度_为零的重合点。
10.铰链四杆机构共有6个速度瞬心,其中3个是绝对瞬心, 3 个是相对瞬心。
11.作相对运动的3个构件的3个瞬心必位于一直线上。
12.在摆动导杆机构中,当导杆和滑块的相对运动为移动,牵连运动为转动时,
两构件的重合点之间将有哥氏加速度。哥氏加速度的大小为2vr ;方向与将vr 沿
转向转90的方向一致。
二、判断题
1.在图示机构中,已知1及机构尺寸,为求解C2 点的加速度,只要列出一个矢
量方程 aC 2
aB2
aCn 2B2
机械原理课后习题解答(最新)
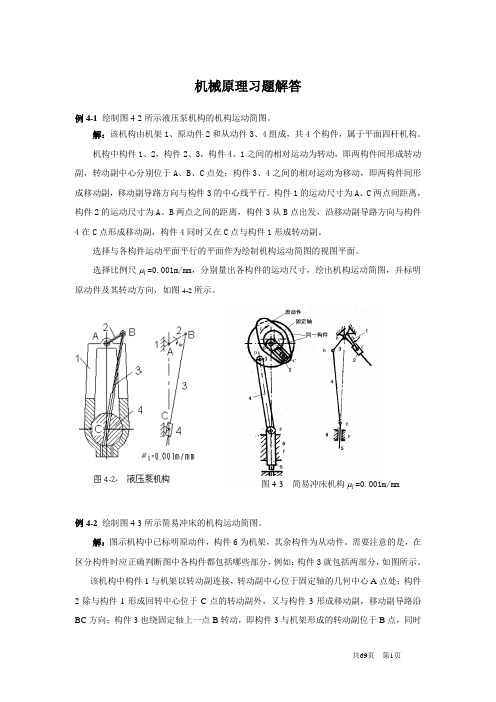
式中 和 可直接从所作的图中量取。由上式可解出
由绝对速度 方向,得出ω2方向为顺时针方向。
同理,在速度瞬心点P13有
由绝对速度 的方向,可知其为逆时针方向。
例5-2在图5-4所示的凸轮机构,已知该机构的结构尺寸和凸轮1的角速度 。利用瞬心法,求机构在图示位置时从动件2的线速度 。机构运动简图的比例尺为 。
按照以上分析,自由度分别为1、2和3的Ⅲ级机构最简单的结构分别如图中(a)、(b)和(c)所示。
4-12确定图4-19a所示机构当构件8为原动件时机构的级别。
解:确定机构的级别关键是要拆出机构中所含的基本杆组。当构件8为原动件时,拆基本杆组首先应当从最远离原动件的构件1拆起,可以拆出Ⅱ级基本杆组ABC,然后,又依次可以拆出Ⅱ级基本杆组DEF和GHI。如下图示。所以该机构为Ⅱ级机构。
(e)、 ,机构没有确定的运动。没有局部自由度、复合铰链、虚约束。
4-7计算题4-7图所示齿轮-连杆机构的自由度。
解:(a)、 ,铰链点A为复合铰链,齿轮副为高副。
(b)、 ,铰链点B、C、D均为复合铰链。
4-8题4-8图所示为缝纫机中的送料机构。计算该机构的自由度,该机构在什么条件下具有确定的运动?
则机构自由度为:
4-6在题4-6图所示所有机构中,原动件数目均为1时,判断图示机构是否有确定的运动。如有局部自由度、复合铰链和虚约束请予以指出。
解:(a)、 ,机构有确定的运动。其中:F、D、B、C四处均为复合铰链,没有局部自由度、虚约束;
(b)、 ,机构没有确定的运动。其中:A处为复合铰链,K处为局部自由度,没有虚约束;
去掉机构中的虚约束,则机构中活动构件数为 ,机构中低副数 ,得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题 > 答案
一.概念
1.当两构件组成转动副时,其相对速度瞬心在转动副的圆心处;组成移动副时,其瞬心在垂直于移动导路的无穷远处;组成滑动兼滚动的高副时,其瞬心在接触点两轮廓线的公法线上.
2.相对瞬心与绝对瞬心相同点是都是两构件上相对速度为零,绝对速度相等的点 ,而不同点是相对瞬心的绝对速度不为零,而绝对瞬心的绝对速度为零 .
3.速度影像的相似原理只能用于同一构件上的两点,而不能用于机构不同构件上的各点.
4.速度瞬心可以定义为互相作平面相对运动的两构件上,相对速度为零,绝对速度相等的点.
5.3个彼此作平面平行运动的构件共有 3 个速度瞬心,这几个瞬心必位于同一条直线上 .含有6个构件的平面机构,其速度瞬心共有 15 个,其中 5 个是绝对瞬心,有 9 个相对瞬心.
二.计算题
1、
2.关键:找到瞬心P36
6 Solution:
The coordinates of joint B are
y B=ABsinφ=0.20sin45°=0.141m
x B=ABsinφ=0.20sin45°=0.141m
The vector diagram of the right Fig is drawn by representing the RTR (BBD) dyad. The vector equation, corresponding to this loop, is written as
r B + r -r D =0 or r =r D -r B
Where r =BD and r =γ.
When the above vectorial equation is projected on the x and y axes, two scalar equations are obtained:
r*cos(φ3+π)=x D -x B =-0.141m
r*sin(φ3+π)=y D -y B =-0.541m
Angle φ3 is obtained by solving the system of the two previous scalar equations:
tgφ3=141.0541
.0 ⇒φ3=75.36°
The distance r is
r=)cos(3πϕ+-B D x x =0.56m
The coordinates of joint C are
x C =CDcosφ3=0.17m y C =CDsinφ3-AD=0.27m
For the next dyad RRT (CEE), the right Fig, one can write
Cecos(π- φ4)=x E - x C Cesin(π- φ4)= y E - y C
Vector diagram represent the RRT (CEE) dyad.
When the system of equations is solved, the unknowns φ4 and x E are obtained:
φ4=165.9° x E =-0.114m
7. Solution: The origin of the system is at A, A≡0; that is,
x A =y A =0.
The coordinates of the R joints at B are
x B =l 1cosφ y B = l 1sinφ For the dyad DBB (RTR), the following equations can be written with respect to the sliding line CD:
mx B - y B +n=0 y D =mx D +n
With x D =d 1
, y D =0 from the above system, slope m of link CD and intercept n can be calculated: m=111cos sin d l l -ϕϕ n=ϕϕcos sin 1111l d l d -
The coordinates x C and y C of the center of the R joint C result from the system of two equations:
y C =mx C +n=ϕϕϕϕcos sin cos sin 111
1111l d l d x d l l C -+-,
(x C- x D)2+(y C- y D)2=l 2 3
Because of the quadratic equation, two solutions are abstained for x C and y C.For continuous motion of the mechanism, there are constraint relations for the Choice of the correct solution; that is x C< x B< x D and y C>0
For the last dyad CEE (RRT), a position function can be written for joint E:
(x C-x E)2+(y C-h)2=l 2 4
The equation produces values for x1E and x2E, and the solution x E >x C is selected for continuous motion of the mechanism.
(注:文档可能无法思考全面,请浏览后下载,供参考。
)。
