第7章动态规划.

合集下载

第07章动态规划《运筹学》PPT课件

最优路径问题资源分配问题排序问题投资问题装载问题生产计划与库存问题生产过程的最优控制等
动态规划
模型分类
离散确定型离散随机型连续确定型连续随机型
§1 多阶段决策过程的最优
化
多阶段决策问题
(Multi-Stage decision process)
决策u1 决策u2
决策uk
32
维护费
8 8 9 9 10 6 6 8 8 10 5 6 8 9 5 5 6 4 54Βιβλιοθήκη 新设备购置费 5050
52 52 55 60
旧设备折价
20 15 10 5 2 30 25 20 15 10 31 26 21 15 33 28 20 35 30
40
§1 多阶段决策过程的最优
化
3)连续生产过程的控制问题：一般化工生产过程中，
本章内容
多阶段决策过程的最优化动态规划的基本概念和基本原理动态规划模型的建立与求解动态规划在经济管理中的应用马氏决策规划简介
创始时间创始人
上个世纪50年代
美国数学家贝尔曼（Richard. Bellman)
是运筹学的一个主要分支是解决多阶段决策过程的最优化的一
种方法多阶段决策过程：多阶段决策过程的最优化的目标：达到整个活动过程的总体效果最优 •主要用于解决：
不过，实际中尚有许多不包含时间因素的一类“静态”决策问题，就其本质而言是一次决策问题，是非动态决策问题，但是也可以人为地引入阶段的概念当作多阶段决策问题，应用动态规划方法加以解决。
§1 多阶段决策过程的最优
化
4）资源分配问题：便属于这类静态问题。如：某工业部门或公司，拟对其所属企业进行稀缺资源分配，为此需要制定出收益最大的资源分配方案。这种问题原本要求一次确定出对各企业的资源分配量，它与时间因素无关，不属动态决策，但是，我们可以人为地规定一个资源分配的阶段和顺序，从而使其变成一个多阶段决策问题(后面我们将详细讨论这个问题)。

运筹学概念整理

运筹学概念整理名解5、简答4、建模与模型转换2、计算5~6第1章线性规划与单纯形法(计算、建模:图解法)线性规划涉及的两个方面：使利润最大化或成本最小化线性规划问题的数学模型包含的三要素：一组决策变量：是模型中需要首确定的未知量。

一个目标函数：是关于决策变量的最优函数，max或min。

一组约束条件：是模型中决策变量受到的约束限制，包括两个部分：不等式或等式；非负取值（实际问题）。

线性规划问题(数学模型)的特点：目标函数和约束条件都是线性的。

1.解决的问题是规划问题；2解决问题的目标函数是多个决策变量的线性函数，通常是求最大值或最小值；3解决问题的约束条件是多个决策变量的线性不等式或等式。

图解法利用几何图形求解两个变量线性规划问题的方法。

求解步骤：第一步：建立平面直角坐标系；第二步：根据约束条件画出可行域；第三步：在可行域内平移目标函数等值线，确定最优解及最优目标函数值。

LP问题的解：（原因）唯一最优解、无穷多最优解（有2个最优解，则一定是有无穷多最优解）无界解（缺少必要的约束条件）、无可行解（约束条件互相矛盾，可行域为空集）标准形式的LP模型特点：目标函数为求最大值、约束条件全部为等式、约束条件右端常数项bi全部为非负值，决策变量xj的取值为非负●线性规划模型标准化（模型转化）(1) “决策变量非负”。

若某决策变量x k为“取值无约束”(无符号限制)，令：x k= x’k–x”k，(x’k≥0, x”k≥0) 。

(2) “目标函数求最大值”。

如果极小化原问题minZ = CX，则令Z’ = – Z，转为求maxZ’ = –CX 。

注意：求解后还原。

(3) “约束条件为等式”。

对于“≤”型约束，则在“≤”左端加上一个非负松弛变量，使其为等式。

对于“≥”型约束，则在“≥”左端减去一个非负剩余变量，使其为等式。

(4) “资源限量非负”。

若某个bi < 0，则将该约束两端同乘“–1” ，以满足非负性的要求。

算法设计技巧与分析答案

算法设计技巧与分析参考答案第1章算法分析基本概念(a)6 (b)5 (c)6 (d)6算法执行了7+6+5+4+3+2+1=28次比较(a)算法MODSELECTIONSORT执行的元素赋值的最少次数是0,元素已按非降序排列的时候达到最小值。

(b) 算法MODSELECTIONSORT执行的元素赋值的最多次数是3(1)2n n ,元素已按非升序排列的时候达到最小值。

由上图可以看到执行的比较次数为1+1+2+2+2+6+2=16次。

由上图可以得出比较次数为5+6+6+9=26次。

FTF,TTT,FTF,TFF,FTF(a) 执行该算法，元素比较的最少次数是n-1。

元素已按非降序排列时候达到最小值。

(b) 执行该算法，元素比较的最多次数是(1)2n n -。

元素已按非升序排列时候达到最大值。

元素已按非降序排列时候达到最小值。

(d) 执行该算法，元素赋值的最多次数是3(1)2n n -。

元素已按非升序排列时候达到最大值。

(e)n 用O 符号和Ω符号表示算法BUBBLESORT 的运行时间：2()t O n =，()t n =Ω(f)不可以用Θ符号来表示算法的运行时间：Θ是用来表示算法的精确阶的，而本算法运行时间由线性到平方排列，因此不能用这一符号表示。

不能用p 关系来比较2n 和2100n 增长的阶。

∵221lim0100100n n n →∞=≠ 2n ∴不是2(100)o n 的，即不能用p 关系来比较2n 和2100n 增长的阶。

(a)当n 为2的幂时，第六步执行的最大次数是：12,2k k n j -==时，11[log ]log n ni i k n n n ====∑∑(b)由(a)可以得到：当每一次循环j 都为2的幂时，第六步执行的次数最大，则当33,22k kmn j ===（其中32k 取整）时，11[log(31)]log(1)n nkii i m n n ===-=-∑∑(c)用O 符号表示的算法的时间复杂性是(log )O n n 已证明n=2k 的情况，下面证明n=2k +1的情况：因为有⎥⎦⎥⎢⎣⎢+=⎥⎦⎥⎢⎣⎢21222k k所以n=2k +1时，第六步执行的最大次数仍是n log n 。

运筹学习题答案(第七章)

page 19 9 July 2013
School of Management
运筹学教程
第七章习题解答
7.10 用顺序解法计算7.1题，7.4题。解：略。
page 20 9 July 2013
School of Management
运筹学教程
第七章习题解答
7.11 某工厂生产三种产品，各种产品重量与利润关系如表7-22所示，现将此三种产品运往市场出售，运输能力总重量不超过6t，问应运输每种产品各多少件可使总利润最大。解：只运产品2两件，最大总利润260（千元）。
运筹学教程
同样适合第三版黄皮版
page 1 9 July 2013
School of Management
运筹学教程（第二版）习题解答
安徽大学管理学院
洪文
电话：5108157(H)，5107443(O) E-mail: Hongwen9509_cn@
运筹学教程
第七章习题解答
7.1 现有天然气站A，需铺设管道到用气单位E，可以选择的设计路线如下图所示，Bl，…，D2各点是中间加压站，各线路的费用已标在线段旁(单位：万元)，试设计费用低的路线。
max F x 1 2 x 2 x 3 x 3 4 x 2 2 x 3
2 2
(2)
x1 x 2 x 3 3 x i 0 , ( i 1, 2 , 3 )
解： x 1 1, x 2 1, x 3 1, F 4
page 18 9 July 2013
page 23 9 July 2013
概率 0.4 0.3 0.3
School of Management
运筹学教程

《算法设计与分析》(全)

巢湖学院计算机科学与技术系
1.1、算法与程序
程序：是算法用某种程序设计语言的具体实现。程序可以不满足算法的性质(4)。例如操作系统，是一个在无限循环中执行的程序，因而不是一个算法。操作系统的各种任务可看成是单独的问题，每一个问题由操作系统中的一个子程序通过特定的算法来实现。该子程序得到输出结果后便终止。
渐近分析记号的若干性质
（1）传递性： ➢ f(n)= (g(n))， g(n)= (h(n)) f(n)= (h(n))； ➢ f(n)= O(g(n))， g(n)= O (h(n)) f(n)= O (h(n))； ➢ f(n)= (g(n))， g(n)= (h(n)) f(n)= (h(n))； ➢ f(n)= o(g(n))， g(n)= o(h(n)) f(n)= o(h(n))； ➢ f(n)= (g(n))， g(n)= (h(n)) f(n)= (h(n))；（2）反身性： ➢ f(n)= (f(n))；f(n)= O(f(n))；f(n)= (f(n)). （3）对称性： ➢ f(n)= (g(n)) g(n)= (f(n)) . （4）互对称性： ➢ f(n)= O(g(n)) g(n)= (f(n)) ； ➢ f(n)= o(g(n)) g(n)= (f(n)) ；
巢湖学院计算机科学与技术系
渐近分析记号的若干性质
规则O(f(n))+O(g(n)) = O(max{f(n),g(n)}) 的证明： ➢ 对于任意f1(n) O(f(n)) ，存在正常数c1和自然数n1，使得对
所有n n1，有f1(n) c1f(n) 。 ➢ 类似地，对于任意g1(n) O(g(n)) ，存在正常数c2和自然数
巢湖学院计算机科学与技术系
第1章算法引论

运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案第一章：引论1.1 课后习题习题1a)运筹学是一门应用数学的学科，旨在解决实际问题中的决策和优化问题。

它包括数学模型的建立、问题求解方法的设计等方面。

b)运筹学可以应用于各个领域，如物流管理、生产计划、流程优化等。

它可以帮助组织提高效率、降低成本、优化资源分配等。

c)运筹学主要包括线性规划、整数规划、指派问题等方法。

习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。

它可以帮助制定最佳的生产计划，优化供应链管理，提高运输效率等。

运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题，优化医疗资源分配等。

1.2 课后习题习题1运筹学方法可以应用于各个领域，如物流管理、生产计划、供应链管理、流程优化等。

在物流管理中，可以使用运筹学方法优化仓储和运输的布局，提高货物的运输效率。

在生产计划中，可以使用运筹学方法优化产品的生产数量和生产周期，降低生产成本。

在供应链管理中，可以使用运筹学方法优化订单配送和库存管理，提高供应链的效率。

在流程优化中，可以使用运筹学方法优化业务流程，提高整体效率。

习题2在物流管理中，可以使用运筹学方法优化车辆的调度和路线规划，以提高运输效率和降低成本。

在生产计划中，可以使用运筹学方法优化生产线的安排和产品的生产量，以降低生产成本和提高产能利用率。

在供应链管理中，可以使用运筹学方法优化供应链各个环节的协调和调度，以提高整体效率和减少库存成本。

在流程优化中，可以使用运筹学方法优化业务流程的排布和资源的分配，以提高流程效率和客户满意度。

第二章：线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法，用于解决包含线性约束和线性目标函数的优化问题。

其一般形式为：max c^T*xs.t. Ax <= bx >= 0其中，c是目标函数的系数向量，x是决策变量向量，A是约束矩阵，b是约束向量。

习题2使用线性规划方法可以解决许多实际问题，如生产计划、供应链管理、资源分配等。

《算法分析与设计》(李春葆版)课后选择题答案与解析

《算法及其分析》课后选择题答案及详解第1 章——概论1.下列关于算法的说法中正确的有（）。

Ⅰ.求解某一类问题的算法是唯一的Ⅱ.算法必须在有限步操作之后停止Ⅲ.算法的每一步操作必须是明确的，不能有歧义或含义模糊Ⅳ.算法执行后一定产生确定的结果A.1个B.2个C.3个D.4个2.T(n)表示当输入规模为n时的算法效率，以下算法效率最优的是（）。

A.T(n)=T(n-1)+1，T(1)=1B.T(n)=2nC.T(n)= T(n/2)+1，T(1)=1D.T(n)=3nlog2n答案解析：1.答：由于算法具有有穷性、确定性和输出性，因而Ⅱ、Ⅲ、Ⅳ正确，而解决某一类问题的算法不一定是唯一的。

答案为C。

2.答：选项A的时间复杂度为O(n)。

选项B的时间复杂度为O(n)。

选项C 的时间复杂度为O(log2n)。

选项D的时间复杂度为O(nlog2n)。

答案为C。

第3 章─分治法1.分治法的设计思想是将一个难以直接解决的大问题分割成规模较小的子问题，分别解决子问题，最后将子问题的解组合起来形成原问题的解。

这要求原问题和子问题（）。

A.问题规模相同，问题性质相同B.问题规模相同，问题性质不同C.问题规模不同，问题性质相同D.问题规模不同，问题性质不同2.在寻找n个元素中第k小元素问题中，如快速排序算法思想，运用分治算法对n个元素进行划分，如何选择划分基准？下面（）答案解释最合理。

A.随机选择一个元素作为划分基准B.取子序列的第一个元素作为划分基准C.用中位数的中位数方法寻找划分基准D.以上皆可行。

但不同方法，算法复杂度上界可能不同3.对于下列二分查找算法，以下正确的是（）。

A.intbinarySearch(inta[],intn,int x){intlow=0,high=n-1;while(low<=high){intmid=(low+high)/2;if(x==a[mid])returnmid;if(x>a[mid])low=mid;elsehigh=mid;}return –1;}B.intbinarySearch(inta[],intn,int x) { intlow=0,high=n-1;while(low+1!=high){intmid=(low+high)/2;if(x>=a[mid])low=mid;elsehigh=mid;}if(x==a[low])returnlow;elsereturn –1;}C.intbinarySearch(inta[],intn,intx) { intlow=0,high=n-1;while(low<high-1){intmid=(low+high)/2;if(x<a[mid])high=mid;elselow=mid;}if(x==a[low])returnlow;elsereturn –1;}D.intbinarySearch(inta[],intn,int x) {if(n>0&&x>=a[0]){intlow= 0,high=n-1;while(low<high){intmid=(low+high+1)/2;if(x<a[mid])high=mid-1;elselow=mid;}if(x==a[low])returnlow;}return –1;}答案解析：1.答：C。

运筹学

第一章：建模合理下料问题例1-2：假定现有一批某种型号的圆钢长8m ，需要截取长的毛坯100根、长的毛坯200根，问应怎样选择下料方式，才能既满足需要，又使总的用料最少根据经验，可先将各种可能的搭配方案列出来，如表1-3所示。

例1-2′某一机床需要用甲、乙、丙三种规格的轴各一根，这些轴的规格分别是，,（m ），这些轴需要用同一种圆钢来做，圆钢长度为。

现在要制造100台机床，最少要用多少圆钢来生产这些轴方案规格12345678需求量y 1 2 1 1 1 0 0 0 0 100 y 2 0 2 1 0 3 2 1 0 100 y 31 0 1 3 0234 100方案件数毛坯I Ⅱ Ⅲ Ⅳ需要根数3 2 1 01000 2 4 6200目标函数 minf ＝C1x1+C2x2+…+Cnxn. a11x1+ a12x2+…+a1nxn ≥ b1 a21x1+ a22x2+…+a2nxn ≥ b2 ┇ ┇ ┇ ┇ am1x1+ am2x2+…+amnxn ≥ bmxj ≥0 (j ＝1，2，…，n)运输问题(物资调运问题)例1-3：设某种物资(例如煤炭)共有m 个产地A1、A2 、…、Am ，其产量分别为a1、a2、…、am ；另有n 个销地B1、B2、…、Bn 其销量分别为b1、b2、…、bn 。

已知由产地Ai(i ＝1，2，…，m)运往销地Bj(j ＝1，2，…，n)的单位运价为Cij ，如表1—6所示。

当产销平衡 m n(即∑ai=∑bj 时，问如何调运，才能使总运费最省方式个数毛坯B 1 B 2 … B n需要毛坯数A1A2┇Ama 11 a 12 a 1n a 21 a 22 a 2n ┇ ┇ ┇ a m1 a m2 a mnb 1 b 2 ┇ b mi=1 j=1目标函数 min f=∑∑CijXij 最小i=1 j=1n∑Xij=ai （i＝1，2，…，m）j=1满足 m∑Xij=bj （ j＝1，2，…，n)i=1xij≥0 i＝1，2，…，m；j＝1，2，…，n)第二章：图解法整数规划步骤：写出模型，假设X1,X2…Xn是…1）作可行线2）作等值线3）平移等值线与可行线相交或相切于一点或直线4）例1：见笔记例2例1 某工厂在计划期内要安排工、Ⅱ两种产品的生产，已知生产单位产品所需的设备台时及A，B两种原材料的消耗，以及资源的限制，如下表所示。

运筹学习题答案(1)

第一章线性规划及单纯形法（作业）1.4 分别用图解法和单纯型法求解下列线性规划问题，并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。

（1）Max z=2x 1+x 2St.⎪⎩⎪⎨⎧≥≤+≤+0,24261553212121x x x x x x 解：①图解法：由作图知，目标函数等值线越往右上移动，目标函数越大，故c 点为对应的最优解，最优解为直线⎩⎨⎧=+=+242615532121x x x x 的交点，解之得X=(15/4,3/4)T 。

Max z =33/4. ② 单纯形法：将上述问题化成标准形式有： Max z=2x 1+x 2+0x 3+0x 4St. ⎪⎩⎪⎨⎧≥≤++≤++0,,,242615535421421321x x x x x x x x x x其约束条件系数矩阵增广矩阵为：P 1 P 2 P 3 P 4⎥⎦⎤⎢⎣⎡241026150153 P 3,P 4为单位矩阵，构成一个基，对应变量向，x 3,x 4为基变量，令非基变量x 1,x 2为零，找到T 优解，代入目标函数得Max z=33/4.1.7 分别用单纯形法中的大M 法和两阶段法求解下列线性规划问题，并指出属哪一类。

（3）Min z=4x 1+x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 解：这种情况化为标准形式： Max z ＇=-4x 1-x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 添加人工变量y1,y2Max z ＇=-4x 1-x 2+0x 3+0x 4-My 1-My 2⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x(2) 两阶段法： Min ω=y 1+y 2St.⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x第二阶段，将表中y 1,y 2去掉，目标函数回归到Max z ＇=-4x 1-x 2+0x 3+0x 4第二章线性规划的对偶理论与灵敏度分析（作业）2.7给出线性规划问题：Max z=2x 1+4x 2+x 3+x 4⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤+≤++)4,3,2,1(096628332143221421j x x x x x x x x x x x x j要求：（1）写出其对偶问题；（2）已知原问题最优解为X *=(2,2,4,0),试根据对偶理论，直接求出对偶问题的最优解。

运筹学教程第五版课后答案

运筹学教程第五版课后答案第一章课后答案1.1 选择题答案1.B2.D3.A4.C5.A1.2 填空题答案1.优化2.最优解3.最大化4.变量5.限制条件1.3 解答题答案1.运筹学是指运用数学方法来研究决策问题和优化问题的学科。

它包括数学规划、排队论、图论、线性规划等多个分支领域，并广泛应用于各个领域的管理和决策中。

2.线性规划是数学规划中的一种重要方法，用于解决特定形式的最优化问题。

线性规划的基本模型包括目标函数、决策变量、约束条件等要素。

线性规划的求解过程包括建立数学模型、确定最优解的条件和方法、利用线性规划软件进行求解等步骤。

第二章课后答案2.1 选择题答案1.B2.A3.C4.D5.B2.2 填空题答案1.线性不等式2.解空间3.最优解4.可行解5.凸集2.3 解答题答案1.线性规划模型由目标函数、决策变量和约束条件三部分组成。

其中，目标函数是优化的目标，决策变量是待确定的变量，约束条件是对决策变量的限制。

线性规划模型可以表示为：maximize Z = c1x1 + c2x2 + … + cnxn subject to: a11x1 + a12x2 + … + a1nxn <= b1 a21x1 + a22x2 + … + a2nxn <= b2 … am1x1 + am2x2 + … + amnxn <= bm x1, x2, …, xn >= 0 其中，Z表示要优化的目标函数，ci表示目标函数中的系数，aij表示约束条件中的系数，bi表示约束条件右侧的常数。

2.线性规划应用广泛，包括生产调度、资源分配、运输问题等。

例如，一个工厂生产两种产品，需要确定每种产品的产量使得总利润最大化，可以使用线性规划模型进行建模和求解。

又如，在物流领域中，需要确定货物的最优运输方案，可以使用线性规划模型来解决。

第三章课后答案3.1 选择题答案1.C2.A3.B4.D5.B3.2 填空题答案1.线性规划2.整数规划3.混合整数规划4.松弛问题5.整数线性规划3.3 解答题答案1.整数规划是指在线性规划的基础上，决策变量取整数值的最优化问题。

管理运筹学判断题背诵讲义

管理运筹学判断题背诵讲义第一章线性规划与单纯形表a)图解法同单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的； b) 线性规划模型中增加一个约束条件,可行域的范围般将缩小,减少一个约束条件,可行域的范围一般将扩大；c) 线性规划问题的每一个基解对应可行域的一个顶点； d)如线性规划问题存在可行域，则可行域定包含坐标的原点；e)对取值无约束的变量j x ，通常令'''j j j x x x =-其中'j x ≥0,''j x ≥0,在用单纯形法求得的最优解中有可能同时出现'j x >0，''j x >0；f)用单纯形法求解标准型的线性规划问题时，与j σ>0对应的变量都可以被选作换人变量；g)单纯形法计算中，如不按最小比值原则选取换出变量，则在下一个解中至少有一个基变量的值为负；h) 单纯形法计算中,选取最大正检验数k σ对应的变量k x 作为换入变量，将使目标函数值得到最快的增长；i)一旦一个人工变量在迭代中变为非基变量后，则该变量及相应列的数字可以从单纯形表中删除,而不影响计算结果；j)线性规划问题的任-可行解都可以用全部基可行解的线性组合表示；k)若X 1,X 2分别是某一线性规划问题的最优解则X=1λX 1 +2λX 2也是该线性规划问题的最优解，其中1λ，2λ可以为任意正的实数；1)线性规划用两阶段法求解时，第一阶段的目标函数通常写为 minz=ai ix ∑(ai x 为人工变量)，但也可写为minz=i ai ik x ,只要所有k i ,均为大于零的常数； m)对一个有n 个变量、m 个约束的标准型的线性规划问题,其可行域的顶点恰好为m n c 个；n) 单纯形法的迭代计算过程是从一个可行解转换到目标函数值更大的另一个可行解；o)线性规划问题的可行解如为最优解，则该可行解定是基可行解；p)若线性规划问题具有可行解，且其可行域有界，则该线性规划问题最多具有有限个数的最优解；q)线性规划可行域的某一顶点若其目标函数值优于相邻的所有顶点的目标函数值,则该顶点处的目标函数值达到最优；r) 将线性规划约束条件的“≤”号及“≥”号变换成“一”号,将使问题的最优目标函数值得到改善；s)线性规划目标函数中系数最大的变量在最优解中总是取正的值:t)一个企业利用3种资源生产4种产品建立线性规划模型求解得到的最优解中最多只含有3种产品的组合；u)若线性规划问题的可行域可以伸展到无限，则该问题一定具有无界解； v)一个线性规划问题求解时的选代工作量主要取决于变量数的多少，与约束条件的数量关系相对较小。

运筹学课程动态规划课件

5 A
3
1 B1 3
6
8 B2 7
6
C1 6 8
3 C2 5
3 C3 3
84 C4
2 D1
2
D2 1 2
3 D3
3
E1 3
5 5 E2 2
6 6
E3
F1 4
G 3 F2
1
2
3 4 运筹学课程动态规划
5
6
7
示例5（生产与存储问题）：
某工厂生产并销售某种产品。已知今后四个月市场需求预测及每月生产j个单位产品的费用如下：
上一个阶段的决策直接影响下一个阶段的决策
运筹学课程动态规划
8
示例6（航天飞机飞行控制问题）：
由于航天飞机的运动的环境是不断变化的，因此就要根据航天飞机飞行在不同环境中的情况，不断地决定航天飞机的飞行方向和速度（状态），使之能最省燃料和实现目的（如软着落问题）。
运筹学课程动态规划
9
所谓多阶段决策问题是指一类活动过程，它可以分为若干个相互联系的阶段，在每个阶段都需要作出决策。这个决策不仅决定这一阶段的效益，而且决定下一阶段的初
1 6
C3
D1
10
E
D2
6
运筹学课程动态规划
12
以上求从A到E的最短路径问题，可以转化为四个性质完
全相同，但规模较小的子问题，即分别从 Di 、 Ci 、Bi、
A到E的最短路径问题。
第四阶段：两个始点 D 1 和 D 2 ，终点只有一个；
本阶段始点（状态）
D1 D2
本阶段各终点（决策） E 10 6
cj30j
j0 j1,2,6
月1 2 3
4
需求 2 3 2

动态规划(完整)

(3) 决策、决策变量
所谓决策就是确定系统过程发展的方案，
决策的实质是关于状态的选择，是决策者
从给定阶段状态出发对下一阶段状态作出
的选择。
用以描述决策变化的量称之决策变量，和状态变量一样，决策变量可以用一个数，一组数或一向量来描述．也可以是状态变量
的函数，记以 xk xk (sk ) ，表示于 k 阶段状
动态规划的分类:
• 离散确定型 • 离散随机型 • 连续确定型 • 连续随机型
动态规划的特点:
• 动态规划没有准确的数学表达式和定义精确的算法, 它强调具体问题具体分析,
依赖分析者的经验和技巧。
• 与运筹学其他方法有很好的互补关系, 尤其在处理非线性、离散性问题时有其独到的特点。
通常多阶段决策过程的发展是通过状态的一系列变换来实现的。一般情况下，系统在某个阶段的状态转移除与本阶段的状态和决策有关外，还可能与系统过去经历的状态和决策有关。因此，问题的求解就比较困难复杂。而适合于用动态规划方法求解的只是一类特殊的多阶段决策问题，即具有 “无后效性”的多阶段决策过程。
4 6
C1
3
B2 3
4T
3 3
C2
阶段指标函数：
vk sk , xk cskxk
5
A3
B3
过程指标（阶段递推）函数:
fk(sk ) min
vk (sk , xk )
fk
1
(sk
1 )
k= 4
f4 (C1) = 3, f4 (C2) = 4
2
k=3
f3(B1)=min{1+f4(C1)=4*, 4+f4(C2)=8}=4
(6) 指标函数
用来衡量策略或子策略或决策的效果的某种数量指标，就称为指标函数。它是定义在全过程或各子过程或各阶段上的确定数量函数。对不同问题，指标函数可以是诸如费用、成本、产值、利润、产量、耗量、距离、时间、效用，等等。

运筹学第三版课后习题答案第7章网络计划——第十三章博弈论

第7章网络计划7.1(1)分别用节点法和箭线法绘制表7-16的项目网络图，并填写表中的紧前工序。

(2) 用箭线法绘制表7-17的项目网络图，并填写表中的紧后工序表7-16工序 A B C D E F G紧前工序－－－ A A、C －B、D、E、F紧后工序D,E G E G G G －表7-17工序 A B C D E F G H I J K L M 紧前工序- - - B B A,B B D,G C,E,F,H D,G C,E I J,K,L 紧后工序F E,D,F,G I,K H,J I,K I H,J I L M M M－【解】（1）节点图：箭线图：（2）节点图：箭线图：7.2根据项目工序明细表7-18：（1）画出网络图。

（2）计算工序的最早开始、最迟开始时间和总时差。

（3）找出关键路线和关键工序。

表7-18工序 A B C D E F G 紧前工序- A A B,C C D,E D,E 工序时间（周）9 6 12 19 6 7 8【解】(1)网络图(2)网络参数工序 A B C D E F G最早开始0 9 9 21 21 40 40最迟开始0 15 9 21 34 41 40总时差0 6 0 0 13 1 0(3)关键路线：①→②→③→④→⑤→⑥→⑦；关键工序：A、C、D、G；完工期：48周。

7.3表7-19给出了项目的工序明细表。

表7-19工序 A B C D E F G H I J K L M N 紧前工序- - - A,B B B,C E D,G E E H F,J I,K,L F,J,L 工序时间(天) 8 5 7 12 8 17 16 8 14 5 10 23 15 12 （1）绘制项目网络图。

（2）在网络图上求工序的最早开始、最迟开始时间。

（3）用表格表示工序的最早最迟开始和完成时间、总时差和自由时差。

（4）找出所有关键路线及对应的关键工序。

（5）求项目的完工期。

【解】(1)网络图（2）工序最早开始、最迟开始时间（3）用表格表示工序的最早最迟开始和完成时间、总时差和自由时差工序 tT EST EFT LST LF 总时差S 自由时差F A 8 0 8 9 17 9 0 B 5 0 5 0 5 00 C 7 0 7 7 7 0 0 D 12 8 20 17 29 9 9 E 8 5 13 5 13 0 0 F 17 7 24 7 24 0 0 G 16 13 29 13 29 0 0 H 8 29 37 29 37 0 0 I 14 13 27 33 47 20 20 J 5 13 18 19 24 6 6 K 10 37 47 37 47 0 0 L 23 24 47 24 47 0 0 M154762 47 62 0 0 N 12 47 59506233(4)关键路线及对应的关键工序关键路线有两条，第一条：①→②→⑤→⑥→⑦→○11→○12；关键工序：B,E,G ,H,K,M 第二条：①→④→⑧→⑨→○11→○12；关键工序：C,F,L,M （5）项目的完工期为62天。

运筹学第3版熊伟编著习题答案

最优解X=<30000,0,66000,0,109200,0>；Z＝84720
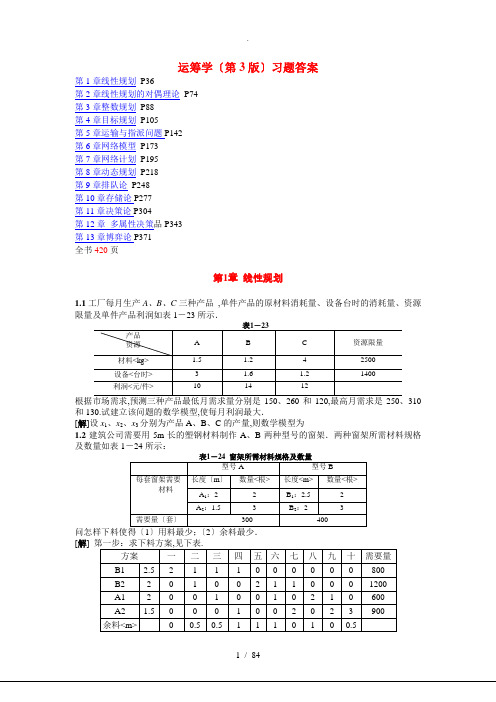
1.5炼油厂计划生产三种成品油,不同的成品油由半成品油混合而成,例如高级汽油可以由中石脑油、重整汽油和裂化汽油混合,辛烷值不低于94,每桶利润5元,见表1－26.
表1－26
成品油
高级汽油
一般汽油
航空煤油
一般煤油
半成品油
中石脑油
基本最优解 ,最优解的通解可表示为即
〔4〕
[解]单纯形表：
C<j>
3
2
1
0
0
R. H. S.
Ratio
Basis
C<i>
X1
X2
X3
X4
X5
X4
0
5
4
6
1
0
25
5
X5
0
[8]
6
3
0
1
24
3
C<j>-Z<j>
3
2
1
0
0
0
X4
0
0
1/4
33/8
1
-5/8
10
X1
3
1
3/4
3/8
0
1/8
3
C<j>-Z<j>
方案四：在三年内投资人应在第三年年初投资,一年结算一次,年收益率是30％,这种投资最多不超过1万元．
投资人应采用怎样的投资决策使三年的总收益最大,建立数学模型.
[解]是设xij为第i年投入第j项目的资金数,变量表如下
项目一
项目二
项目三
项目四
第1年
第2年