北京邮电大学 自动机 课后习题答案
第5章 北邮信号与系统课后习题解答

1 s2
e s 1
(4)
2
(t)
3e 2 t u (t )
2
s
3
2
(5)L
[
1 2a
3
(sin
at
at
cos at)]
1 2a3
(s2
a
a2
a
d ds
( s2
s
a2
))
1 2a2
( s2
1 a2
s2 a2 (s2 a2)2
)
1 (s2 a2)2
1)]
e(s2) s2
其波形题 5-3 解图所示。
f1 (t ) 1
f2 (t) 1
t
1
t
f3 (t) e2
t
f4 (t)
e-2
1
t
5-4 解:
题 5-3 解图
(a)L [ f1(t)] L [E[u(t t1) u(t t1 )] E[u(t t2) u(t t2 )]]
1[ (s2
s 1)2
]
1 2
t
sin
t
由拉氏变换的积分性质
L
1[
(
s
2
2
1)2
]
t
sin d
sin t
t cos t
,t
0
0
或:
s
1 2
1
sin
t
,
(s2
2 1)2
sin t *sin t
sin t t cos t
北邮通信原理 课后习题答案 第4章

(2) s ( t ) 可化为
s (t ) =
于是
Ac ( cos10π f mt − cos14π f mt ) 2
S( f ) =
Ac ⎡δ ( f − 5 f m ) + δ ( f + 5 f m ) − δ ( f − 7 f m ) − δ ( f + 7 f m ) ⎤ ⎦ 4 ⎣
(3)
4.2 已知 s (t ) = cos
( 2π ×10 t ) + 4 cos ( 2.2π ×10 t ) + cos ( 2.4π ×10 t ) 是某个 AM 已调
4 4 4
信号的展开式 (1)写出该信号的傅式频谱,画出它的振幅频谱图; (2)写出 s ( t ) 的复包络 sL ( t ) ; (3)求出调幅系数和调制信号频率; (4)画出该信号的解调框图。 解:(1) s ( t ) 的频谱为
(2)当 A 点输入是下单边带信号时,各点信号如下: A:
ˆ (t ) sin 2π f c t s (t ) = m(t ) cos 2π f c t + m
ˆ (t )sin ( 91× 104 π t ) = m(t ) cos ( 91× 104 π t ) + m
B:
sB (t ) = s ( t ) cos ( 91× 104 π t ) ˆ (t ) sin ( 91× 104 π t ) cos ( 91× 104 π t ) = m(t ) cos 2 ( 91× 104 π t ) + m = m (t ) ˆ (t ) m ⎡1 + cos (182 × 104 π t ) ⎤ + sin (182 × 104 π t ) ⎣ ⎦ 2 2
北京邮电大学《数字信号处理》习题及答案

习 题1. 给定 f(t) = rect(t+2) + rect(t-2), 画出下列函数的图形。
(a) f(t)(b) g(t) = f(t-1) (c) h(t) = f(t)u(t) (d) f(t/2)2. 设 f(t) 是某一函数,a, t 0, T 为实常数,证明:(a))()()()(000t t t t f a at t f -=-δδ(b))()(1)()(000a t a f a at t f t t t -=-δδ(c))()()()(00nT t nT f TTt comb t f t tt n --+=-∑∞-∞=δ3.(a) 如 f(t) F(Ω),证明:eeetjty j tj t f dy y F F Ω-∞∞--Ω-Ω-==*Ω⎰)(2)()()(π(b) 用 (a ) 的结果,证明频域卷积定理)()(21)()(2121Ω*Ω↔F Ffft t π4. 求下图中 f(t) 脉冲的傅氏变换。
5. (a) )()()(a H H -Ω=Ω*Ωδ(b) )()()(0Ω+Ω=Ω+Ω*Ω∑∑∞-∞=∞-∞=n H n H n n δ6. 设eta t f -=)(,证明脉冲序列)()(nT t nT f n -∑∞-∞=δ的傅氏变换等于aTaT aT e T e e 22cos 211---+Ω--7.(a) 证明T n n n jnT eπδ2),(1000=ΩΩ+Ω=Ω∑∑∞-∞=∞-∞=Ω-(b) 若f(t) F(Ω),证明)()(0Ω+Ω=∑∑∞-∞=∞-∞=Ω-n F nT f Tn n jnT e习 题1. 下列系统中,y(n) 表示输出,x(n) 表示输入,试确定输入输出关系是否线性?是否非移变?(a) y(n) = 2x(n) +3(b) y(n) = x 2(n)(c) ∑-∞==nm m x n y )()(2. 确定下列系统是否因果的?是否稳定的? (a) y(n) = g(n) x(n), g(n) 有界(b) ∑-==nk n k x n y 0)()( n>n 0 (c) y(n) = x(n-n 0)(d) x(n) = a nu(n), h(n) = u(n)(e) x(n) = a n u(n), h(n) = (1/2) nu(n)3. x(n) 为输入序列, h(n) 为系统的单位取样响应序列,确定输出序列 y(n), (a) 如图 p 2.1 (a) 所示 (b) 如图 p 2.1 (b) 所示 (c) 如图 p 2.1 (c) 所示⎪⎩⎪⎨⎧=0)(a n n h⎪⎩⎪⎨⎧=-0)(0βn n x n 的卷积 y(n) = x(n) * h(n)5. 讨论具有下列单位取样响应的线性时域离散非移变系统。
北邮数字电路与逻辑设计(第一版)刘培植习题答案第06章习题解答
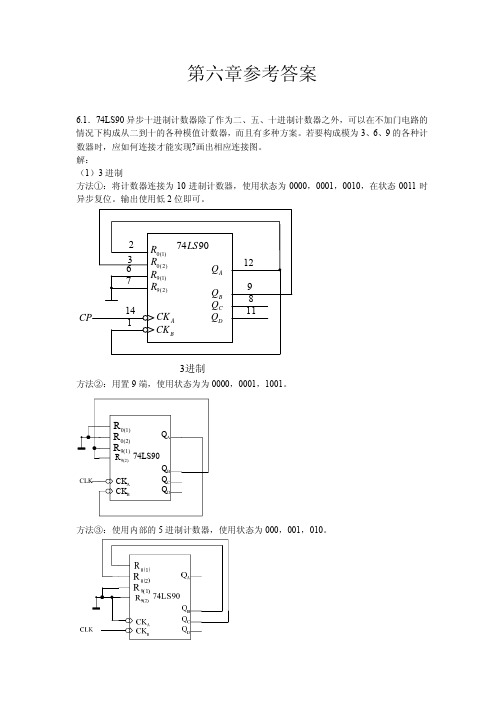
2 R0(1) 74LS90
3 6
7
R0(2) R9(1) R9(2)
CP
14 1
CK A
QA
12
QB QC
QD
9 8 11
CK B
9进制
方法②:用置 9 端,使用状态为 0000,0001,0010,0011,0100,1001。
CLK
R 0(1)
R 0(2)
QA
R9(1)
R9(2) 74LS90
解:74160 为 10 进制异步复位、同步预置计数器。在输出 Q3Q2Q1Q0 = 0101时产生复位。
因此使用的状态为:0000,0001,0010,0011,0100。
Qn+1 = Q1n f0 = Qn ⋅ Q1n = Qn + Q1n
注意:Q 的状态变换时刻比 74161 的状态变换时刻延迟半个时钟周期。
当预置 CBA=010 时,M=14;(初始预置值为 0010,0011,0100,0101,0110,0111,1000, 预置到 1010,1011,1100,1101,1110,1111,0000,再次预置为 0010……)
当预置 CBA=011 时,M=12;(初始预置值为 0011,0100,0101,0110,0111,1000,预置 到 1011,1100,1101,1110,1111,0000,再次预置为 0011……)
当 A=0 时,当 Q3Q2Q1Q0 = 1001时, Y = 1。因此使用的状态为:
0000,0001……1001。计数周期为 10。 状态转移表为:
Q3nQ2nQ1nQ0n
Q Q Q Q n+1 n+1 n+1 n+1 3 21 0
北邮随机信 分析与处理 习题解答

明:Z(t) X (t) Y (t) 是广义平稳随机过程。
证明:mZ (t) E[X (t) Y(t)] E[A(t)cost B(t)sint] E[A(t)]cost E[B(t)]sin t 0cost 0sint 0
解:(1)
mX2
lim
RX
(
)
lim 2e
0
2 X
RX (0) mX2
2
因此有 rX ( )
r0 0 rX ( )d
RX
( ) mX2
2 X
e d
e 1
0
(2)
mX2
lim
(1)计算均值 mX (t)和自相关函数 RX (t1,t2);
(2)该过程是否为平稳随机过程?
解:
mX
(t)
1 3
X (t, e1)
1 3
X (t, e2)
1 3
X (t, e3)
1 (1 sin t 3
cos t)
RX (t1,t2) E[X (t1)X (t2)] 1
3 (11 sin t1 sin t2 cos t1 cos t2 ) 1
0.9
2
解:由自相关函数的性质
由广义平稳的性质
RY (t1,t2) RY (t2,t1)
RY (0) E[Y 2(t)]为常数
2 1.3 0.4 0.9
RY
1.3 0.4
2 1.2
1.2
北京邮电大学电子电路基础课后答案

第一章 思考题与习题1.1. 半导体材料都有哪些特性?为什么电子有源器件都是由半导体材料制成的?1.2. 为什么二极管具有单向导电特性?如何用万用表判断二极管的好坏? 1.3. 为什么不能将两个二极管背靠背地连接起来构成一个三极管? 1.4. 二极管的交、直流等效电阻有何区别?它们与通常电阻有什么不同? 1.5. 三极管的放大原理是什么?三极管为什么存在不同的工作状态? 1.6. 如图P1-1(a)所示的三极管电路,它与图P1-1(b)所示的二极管有何异同?1.7.稳压二极管为何能够稳定电压?1.8.三极管的交、直流放大倍数有何区别?共射和共基电流放大倍数的关系是什么?1.9.三极管的输入特性和输出特性各是什么?1.10. 如图P1-2所示,设I S =10-11A ,U T =26mV ,试计算u i =0,0.3V ,0.5V ,0.7V 时电流I 的值,以及u i =0.7V 时二极管的直流和交流等效电阻。
解:由I= I S *(exp(U i / U T )-1) 当U i =0时,I=0;当U i =0.3V 时,I=1.026×10-6A ; 当U i =0.5V 时,I=2.248×10-3A ; 当U i =0.7V 时,I=4.927A ; 直流等效电阻R= U i /I = 0.7V/4.927A = 0.142 Ω∵exp(U i / U T )>>1∴交流等效电阻R d = 26/I = 26/4927 = 5.277×10-3 Ω(a)(b)图P1-1图P1-2u i Di1.11. 电路如图P1-3所示,二极管导通电压U D =0.7V ,U T =26mV ,电源U =3.3V ,电阻R =1k Ω,电容C 对交流信号可视为短路;输入电压u i 为正弦波,有效值为10mV 。
试问二极管中流过的交流电流有效值为多少?解:U =3.3V>>100mV ,I =(U -U D )/R = (3.3-0. 7)/1k = 2.6 mA 交流等效电阻:R d = 26/I = 10 Ω 交流电流有效值:Id = Ui/Rd = 1 mA1.12. 图P1-4(a)是由二极管D 1、D 2组成的电路,二极管的导通电压U D =0.3V 、反向击穿电压足够大,设电路的输入电压u 1和u 1如图P1-4(b)所示,试画出输出u o 的波形。
自动机理论、语言和计算导论课后习题答案(中文版)

Solutions for Section 2.2Exercise 2.2.1(a)States correspond to the eight combinations of switch positions, and also must indicate whether the previous roll came out at D, i.e., whether the previous input was accepted. Let 0 represent a position to the left (as in the diagram) and 1 a position to the right. Each state can be represented by a sequence of three 0's or 1's, representing the directions of the three switches, in order from left to right. We follow these three bits by either a indicating it is an accepting state or r, indicating rejection. Of the 16 possible states, it turns out that only 13 are accessible from the initial state, 000r. Here is the transition table:杠杆可能出现8种情况,影响着最终状态。
并且也要说明,前面一个大理石球是否从D滚出,也就是说,前一个输入是否被接受。
令0 代表向左方的状态(如图表),1 代表向右方。
这三个杠杆的每一个状态都可以用三个数(0或1)组成的序列表示。
这个序列后面跟着字母a或者r。
自动机习题中文解答全
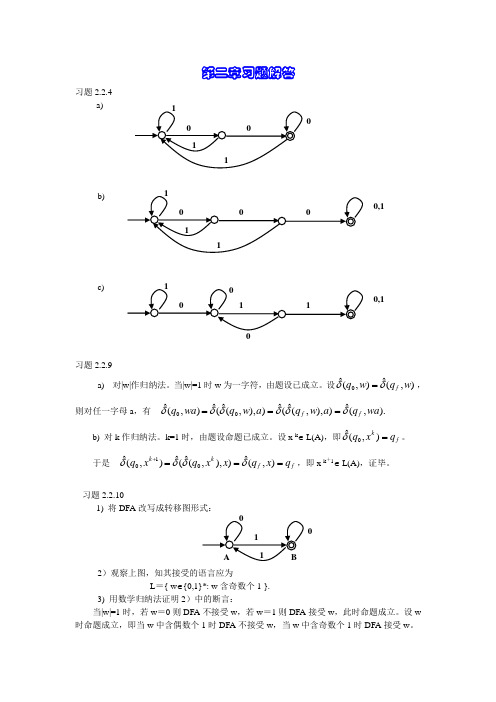
第二章习题解答习题2.2.4a) b) c) 习题2.2.9a) 对|w|作归纳法。
当|w|=1时w 为一字符,由题设已成立。
设),(ˆ),(ˆ0w q w q fδδ=, 则对任一字母a ,有 ).,(ˆ)),,(ˆ(ˆ)),,(ˆ(ˆ ),(ˆ00wa q a w q a w q wa q ff δδδδδδ=== b) 对k 作归纳法。
k=1时,由题设命题已成立。
设x k ∈ L(A),即f k q x q =),(ˆ0δ。
于是 ff k k q x q x x q x q ===+),(ˆ)),,(ˆ(ˆ ),(ˆ010δδδδ,即x k +1∈ L(A),证毕。
习题2.2.101) 将DFA 改写成转移图形式:2)观察上图,知其接受的语言应为L ={ w ∈{0,1}*: w 含奇数个1 }. 3) 用数学归纳法证明2)中的断言:当|w|=1时,若w =0则DFA 不接受w ,若w =1则DFA 接受w ,此时命题成立。
设w 时命题成立,即当w 中含偶数个1时DFA 不接受w ,当w 中含奇数个1时DFA 接受w 。
0,10,1对于任一字符c :若c=0,则当w 中含偶数个1时由于DFA 不接受w ,故A w q =),(ˆ0δ,从而A wc q =),(ˆ0δ;当w 中含奇数个1时由于DFA 接受w ,故B w q =),(ˆ0δ,从而B wc q =),(ˆ0δ。
若c=1,则当w 中含偶数个1时由于DFA 不接受w ,故A w q =),(ˆ0δ,从而B wc q =),(ˆ0δ;当w 中含奇数个1时由于DFA 接受w ,故B w q =),(ˆ0δ,从而A wc q =),(ˆ0δ。
总之,当wc 中含偶数个1时DFA 不接受wc ,当wc 中含奇数个1时DFA 接受wc 。
命题得证。
习题2.2.111) 将DFA 改写成转移图形式:2)观察上图,知其接受的语言应为L ={ w ∈{0,1}*: w 不含子串00 }.3) 用数学归纳法证明2)中的断言,过程与前题类似。
第4章 北邮信号与系统课后习题解答
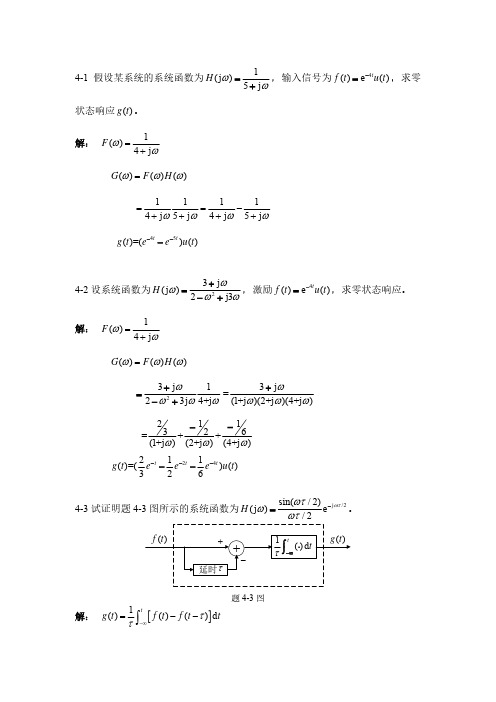
(1)抽样后在什么频率上会出现干扰信号?试画出抽样后信号的频谱示意 图。
(2)为了抗干扰,信号在抽样前通过一个抗混淆系统,将干扰信号滤除。 试在题 4-5 图所示的两图中选出合适的抗混淆系统,并画出幅频特性曲线。
(3)为了使有用信号的衰减低于 1dB,混淆信号的衰减高于 15dB,试求所 需的时间参数 RC 的范围。
c
R( j)
H
( j)
E( j)
c 0,
e jt0 ,
c c 其他
设
e2
(t)
sin(ct) ct
,则
F E2 ( j)
e2
(t )
c 0,
,
c c 其他
R2 ( j)
H ( j)
Y j X j
1 e j
2
cos
2
e
j2
可见,虽然该系统具有线性的相频特性,但幅频特性不是常数,因此,该系统不 是无失真传输系统。
4-9 题 4-9 图所示系统中, H1( j) 为理想低通滤波器,其频率特性为
H1
(
j
)
H
i
对
信号
Sa
t 2
是无失真传输的,因此当
Sa
1 2
(t
T
)
Sa(
1 2
t
)
作用时,输出
v2
(t)
Sa
1 2
t
第6章 北邮信号与系统课后习题解答

a
,
z a
H (z) [h(n)] [ (n 2)] z2, z 0
Y (z)
X
(z)
H (z)
z
z a
z2 ,
z a
由于 z a ,可知 y(n) 是右边序列,因此由位移特性知
y(n) an2u(n 2)
(3)
X
(z)
[ x(n)]
[anu(n)]zz 源自a,H (z)
[h(n)]
1
2
所以
X (z)
z
z
1 2
z
z
2
(1)当
z
2 时为右边序列,
x(n)
1 n 2
2n
u(n)
(2)当
z
0.5 为左边序列,
x(n) 2n
1 2
n
u
(n
1)
(3)当 0.5
z
2 时为双边序列,
x(n)
1 2
n
u
(n)
2n
u(n
1)
6-10 解:
(1)
X
(z)
[ x(n)]
z
z
1 2
z
1 3
z
3
1 2
z
2
1 3
7
得:
X (z)
3z
z
1 2
2z
z
1 3
,收敛域为: 1 3
z
1 2
所以:
x(n)
2
1 3
n
u(n)
3
1 2
n
u
(
n
1)
(6)由题:
X (z) z
北邮信号与系统课后答案第3章部分1
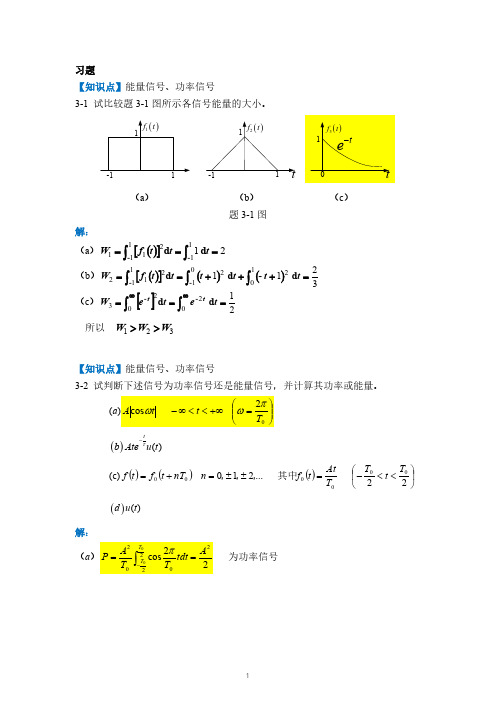
为功率信号
(d) P lim 1 T0 u t 2 dt lim 1 T0 1dt 1
T0
2T0 T0
T0 2T0 0
2
为功率信号。
【知识点】能量信号、功率信号 3-3 对信号 f (t) 在数值和时间两方面进行运算变成 af (bt)
(1)如果在全部时间
t
内, f (t) 是具有能量为 W 的能量信号,
f1 t 1
f2 t 1
0
1
2
3t
0
1
2
3t
锯齿形脉冲
正弦脉冲
题 3-6 图
解:
3
0 f1 t f2 t d t
31 t sin
tdt
- t cos
t - 3 sin
3
t
03 3
3
2 30
3
3
sin
2
tdt
31 1 - cos 2 t d t 3
03
02
3
2
C12 2
t2
fe t
- sin t
3
3
3 t - 2 sin t sin tdt
sin 2
1t
4
3 cos 2 1 t 4
15 cos 4 1 t 4
...
2
A 1 T A
sin 2
1t
2
2A 3 cos 2 1t
2A 15 cos 4 1t 2 ...
AA
2A
2A
cos 2
1t
3 cos 2 1t
15 cos 4 1t
...
9
随着T , C12 ,当T
时使得 C12 0 。
电路分析基础 北京邮电大学版 作业习题解汇总

第一,二讲作业题解1.10计算7.5×10-4N的力在14s内使物体移动2m所做的功和发出的功率。
解:447.51021510 1.5/ 1.5/140.107W mJ P W t mW--=⨯⨯=⨯====1.12 诺基亚手机锂电池容量为650mAh,额定工作电压为6V,最长通话时间为240min,求通话时电池提供功率是多少?解:65060162.52406162.5975I mAP UI mW⨯====⨯=1.13北京地区用电按每千瓦时(Kwh)收费0.45元计算。
某教室照明用电平均电流为10A,供电电压额定值为220V,每天开灯6小时,每月按30天计算,求出每月用电量和费用是多少?解:用电量Kwh39630622010=⨯⨯⨯=费用2.17839645.0=⨯=元。
1.16汽车启动电动机由12V蓄电池供电,发动时电流为250A,工作效率为90%,问能产生多少马力(hp)?解:122500.90 3.67735.5P⨯=⨯=hp。
3.9 求图3.18所示电路中电压源V及其极性,如果(a)I=2.0A;(b)I=-2.0A5Ω图3.18解:(a )U =20-2.0(10+5)=-10V ⨯ab b 点为正极(b) ab U 20 2.0(105)50V =+⨯+= a 点为正极 如何确定极性3.10 求图3.19所示电路,当(a) I 2 =1.0A,(b) I 2 =100mA,(c) I 2 =10mA 时,R 3 的值。
32.0Ω图3.19解: (a ) R 3 =∞;(b ) 32123230.10.11.00.10.110011.110.110.1R I I R R R R ===+⨯⨯===Ω--(c )32123230.010.011.00.010.011001.0110.0110.01R I I R R R R ===+⨯⨯===Ω--3.14 求图3.23所示电路中各电阻所消耗的功率P R1 ,P R2 ,P R3 ,P R4 。
北邮随机信号答案ch5

怎样的条件才能使
Z (t ) =
∑A e ω
j k =1 k
n
kt
是一个复平稳随机过程。 5.7 设有复随机过程
Z (t ) = ∑ (α i cos ω i t + jβ sin ω i t )
i =1
n
其中 α i 与 β k 是相互独立的随机变量, α i 与 α k 、 β i 与 β k (i ≠ k ) 是相互正交的,数学期 望和方差分别为 E[α i ] = E[ β i ] =0, 解:
πτ
= R0 (τ ) cos ω0τ
ˆ (τ ) = R (τ ) sin ω τ 是一个低频信号,所以 R n 0 0 πτ ˆ (τ ) sin ω τ = R (τ ) 所以 Rn (τ ) = Rn (τ ) = Rn (τ ) cos ω0τ + R n 0 0
由于 R0 (τ ) =
c s
=
1 2π
∫
∞
−∞
[2 X (ω − ω ′)U (ω − ω ′)][2 X (ω ′)U (ω ′)]d ω ′
Ω Ω ⎧ ω0 − ≤ ω ′ ≤ ω0 + ⎪ Ω Ω ⎪ 2 2 时亦不 由于有 ω0 − ≤ ω ≤ ω0 + 时 X (ω ) 不为零,因此有 ⎨ 2 2 ⎪ω − Ω ≤ ω − ω ′ ≤ ω + Ω 0 0 ⎪ 2 2 ⎩
5.2 设 A(t ) 与 ϕ(t ) 为低频信号,证明 (1) H [ A(t ) cos[ω 0 t + ϕ (t )] = A(t ) sin[ω 0 t + ϕ (t )] (2) H [ A(t ) sin[ω 0 t + ϕ (t )] = − A(t ) cos[ω 0 t + ϕ (t )]
北京邮电大学《计算机网络》2 课后题

increasing the payload before error correction from 260 ´ 50 = 13 kbps to 260 ´ 75 = 19.5 kbps. Thus, the quality loss was an intentional trade-off to put more users per cell and thus get away with bigger cells.
计算机网络 第2章课后习题详解
举一反三
北邮计算机学院 王小茹
2-2 学习应用 奈奎斯特定理和香农定理
• 一条无噪声4kHz信道,按照每1ms一次进行采样,请问 最大数据传输率是多少?
• 解题原理:
✓ 理解奈奎斯特原理,计算出信道的最高码元传输速率 ✓ 理解码元传输速率与信息传输速率的关系和区别 ✓ 学会排除无关的已知条件,如采样速率。
计算机学院:王小茹
分组总的数量为 x/p个,传送信息总量为 (p+h)x/p;
t=(p+h)x/pb 最后一个bit 发完
t=(p+h)x/pb+(k-1)(p+h)/b最后一个bit 到达接收 端
总时间T=(p+h)x/pb+(k-1)(p+h)/b;对T求 导:
T’=-hx/bp2+(k-1)/b p=(hx/(k-1))1/2
• 解答:
✓ 利用奈奎斯特计算码元传输速率=2×6=12Baut ✓ 利用4级数字信号,可知,每个码元代表2比特,则总的
信息传输速率=2×12=24bps
计算机学院:王小茹
2-3 香农和奈奎斯特的适用条件
• 如果在一条3kHz的信道上发送一个二进制信号,该信道的 信噪比为20dB,则最大的数据传输速率是多少?
信号与系统_北京邮电大学中国大学mooc课后章节答案期末考试题库2023年

信号与系统_北京邮电大学中国大学mooc课后章节答案期末考试题库2023年1.关于信号【图片】描述正确的是()。
参考答案:该信号的基波角频率是1 rad/s。
2.以频谱分割的方式进行频道划分,多路信号混合在一起传输,但每一信号占据着有限的不同频率区间,此区间不被其他信号占用。
这种复用方式称为频分复用。
参考答案:正确3.【图片】上图所示的周期矩形脉冲信号,其直流分量为【图片】。
参考答案:错误4.【图片】的能量是()。
参考答案:55.对于具有矩形幅度特性和线性相位特性的理性低通滤波器,【图片】是其截止频率,其阶跃响应【图片】波形如下图所示。
下面说法中不正确的是()【图片】参考答案:阶跃响应的上升时间为。
6.【图片】的收敛域是全s平面。
参考答案:正确7.因果信号【图片】的拉普拉斯变换为【图片】,则【图片】。
参考答案:正确8.【图片】的z变换为【图片】,收敛域为【图片】。
参考答案:正确9.线性时不变因果系统的单位阶跃响应【图片】与其单位冲激响应【图片】之间关系是【图片】。
参考答案:错误10.周期为T的冲激序列信号【图片】,有关该信号描述不正确的是()。
参考答案:该信号的频谱满足离散性、谐波性和收敛性。
11.在区间【图片】余弦信号【图片】与正弦信号【图片】相互正交。
参考答案:正确12.已知某离散时间线性时不变系统的单位样值响应为【图片】,则当输入信号为【图片】时,系统的零状态响应为【图片】。
参考答案:正确13.某系统的信号流图如下图所示。
则该系统的系统函数可表示为【图片】。
【图片】参考答案:正确14.某连续系统的系统函数为【图片】,该系统可以既是因果的,又是稳定的。
参考答案:正确15.因果系统的系统函数为【图片】,R>0,C>0,则该系统属于( )网络。
参考答案:高通滤波网络16.下图所示反馈系统,已知子系统的系统函数【图片】,关于系统函数及稳定性说法正确的是()。
【图片】参考答案:系统函数为,当时,系统稳定。
北邮随机信号分析与处理第1章习题解答

记
Y1 Y Y 2 YN
线性变换 Y LX
L 为 N N 矩阵
15
1.12
假定 L 为满秩,得 x L-1y 由多维随机变量的函数的求解表达式
f Y (y ) f X (L-1y ) J f X (L-1y )
1
条件均值为
f XY ( x, y ) 2(ax by) fY | X ( y | x ) (0 x, y 1) f X ( x) 2ax b 将 X 1/ 2 代入,得 a 2by fY | X ( y | x 1/ 2) (0 y 1) ab
E (Y | X 1/ 2)
因此的概率分布函数可写为其中为常数假定随机变量的概率分布函数已知其中为常数假定随机变量的概率分布函数已知设随机变量的联合概率密度为根据条件概率密度可得到条件均值为10已知随机变量由条件均值得到边缘均值为的边缘概率密度为因此11由条件均值得到边缘均值的详细推导过程
ftp服务器地址
ftp://10.108.142.57
n odd
3
1.3 (2/2)
fY ( y )
n
f X ( xn )
dxn dy d (arcsin y n ) d ( arcsin y n ) f X ( arcsin y n ) dy dy n odd
n even
f X (arcsin y n )
n even
f X (arcsin y n )
1 1 y2
f X ( arcsin y n )
北京邮电大学 自动机 课后习题答案
形式语言与自动机第二章4.找出右线性文法,能构成长度为1至5个字符且以字母为首的字符串。
答:G={N,T,P,S}其中N={S,A,B,C,D} T={x,y} 其中x∈{所有字母} y∈{所有的字符} P如下: S→x S→xA A→y A→yBB→y B→yC C→y C→yD D→y6.构造上下文无关文法能够产生L={ω/ω∈{a,b}*且ω中a的个数是b的两倍}答:G={N,T,P,S}其中N={S} T={a,b} P如下:S→aab S→aba S→baaS→aabS S→aaSb S→aSab S→SaabS→abaS S→abSa S→aSba S→SabaS→baaS S→baSa S→bSaa S→Sbaa7.找出由下列各组生成式产生的语言(起始符为S)(1)S→SaS S→b(2)S→aSb S→c(3)S→a S→aE E→aS答:(1)b(ab)n /n≥0}或者L={(ba)n b/n≥0}(2) L={a n cb n /n≥0}(3)L={a2n+1 /n≥0}第三章1.下列集合是否为正则集,若是正则集写出其正则式。
(1)含有偶数个a和奇数个b的{a,b}*上的字符串集合(2)含有相同个数a和b的字符串集合(3)不含子串aba的{a,b}*上的字符串集合答:(1)是正则集,自动机如下(2) 不是正则集,用泵浦引理可以证明,具体见17题(2)。
(3) 是正则集先看L’为包含子串aba的{a,b}*上的字符串集合显然这是正则集,可以写出表达式和画出自动机。
(略)则不包含子串aba的{a,b}*上的字符串集合L是L’的非。
根据正则集的性质,L也是正则集。
4.对下列文法的生成式,找出其正则式(1)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→abS A→bBB→b B→cCC→D D→bBD→d(2)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→cC A→bBB→bB B→aC→D C→abBD→d答:(1) 由生成式得:S=aA+B ①A=abS+bB ②B=b+cC ③C=D ④D=d+bB ⑤③④⑤式化简消去CD,得到B=b+c(d+bB)即B=cbB+cd+b =>B=(cb)*(cd+b) ⑥将②⑥代入①S=aabS+ab(cb)*(cd+b)+(cb)*(cd+b) =>S=(aab)*(ab+ε)(cb)*(cd+b) (2) 由生成式得:S=aA+B ①A=bB+cC ②B=a+bB ③C=D+abB ④D=dB ⑤由③得 B=b*a ⑥将⑤⑥代入④ C=d+abb*a=d+ab+a ⑦将⑥⑦代入② A=b+a+c(d+b+a) ⑧将⑥⑧代入① S=a(b+a+c(d+ab+a))+b*a=ab+a+acd+acab+a+b*a5.为下列正则集,构造右线性文法:(1){a,b}*(2)以abb结尾的由a和b组成的所有字符串的集合(3)以b为首后跟若干个a的字符串的集合(4)含有两个相继a和两个相继b的由a和b组成的所有字符串集合答:(1)右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→ε(2) 右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→abb(3) 此正则集为{ba*}右线性文法G=({S,A},{a,b},P,S)P: S→bA A→aA A→ε(4) 此正则集为{{a,b}*aa{a,b}*bb{a,b}*, {a,b}*bb{a,b}*aa{a,b}*}右线性文法G=({S,A,B,C},{a,b},P,S)P: S→aS/bS/aaA/bbBA→aA/bA/bbCB→aB/bB/aaCC→aC/bC/ε7.设正则集为a(b a)*(1)构造右线性文法(2)找出(1)中文法的有限自动机答:(1)右线性文法G=({S,A},{a,b},P,S)P: S→aA A→bS A→ε(2)自动机如下:9.对应图(a)(b)的状态转换图写出正则式。
自动机习题答案(0)

1.给出接受下列在字母表{0,1}上的语言的确定型有限自动机(DFA)图书P36(1)所有倒过来解释成二进制整数时是3的倍数的串的集合。
q0——对应倒过来除以3余数为0的x组成的等价类;q1——对应倒过来除以3余数为1的x组成的等价类;q2——对应倒过来除以3余数为2的x组成的等价类;q s——A的开始状态。
(1) q s——在此状态下有δ(q s,0)= q0;δ(q s,1)= q1。
(2) q0——满足此状态的x有:x=3*n+0,通过q0倒过来可以推导状态。
倒过来计算,当读入0的时候,x=2*(3n+0),所以,δ(q0,0)= q0当读入1的时候,x=2*(3n+0)+1,所以,δ(q0,1)= q1(3) q1——满足此状态的x有:x=3*n+1,通过q1倒过来可以推导状态。
倒过来计算,当读入0的时候,x=2*(3n+1),所以,δ(q1,0)= q2当读入1的时候,x=2*(3n+1)+1,所以,δ(q1,1)= q0(4) q2——满足此状态的x有:x=3*n+2,通过q2倒过来可以推导状态。
倒过来计算,当读入0的时候,x=2*(3n+2),所以,δ(q2,0)= q1当读入1的时候,x=2*(3n+2)+1,所以,δ(q2,1)= q2(2)、0的个数被5整除,1的个数被4整除的二进制整数串的集合。
2.把下列正则表达式转化成带ε转移的NFA ,并把该自动机转化成等价的状态最小的DFA 。
图书P72 (1)(0+1)01 (2)00(0+1)*带空串的非确定型自动机:1)2)确定型自动机:1====================================================================== 3.证明:(1)语言{0n|n是2的幂}不是正则语言;图书P88证明:记此语言为L。
反设L是正则的,则泵引理成立。
对于泵引理中相应于L 的正整数N, 取w = 0M, 其中M=2N,则w=xyz, |xy|<= N, y≠ε且xy i z在L中,i=0,1,2,….设xz = 0 p, y = 0 q, 则xy i z = 0 p+iq∈L, i= 0,1,2,…所以p+iq = 2Ni, i=1,2,….于是(p+(i+1)q)/(p+iq)≥2,令i趋于无穷大,则由以上不等式可得1≥2,矛盾。
【免费下载】北京邮电大学数字信号处理习题答案第5章

幅度函数:H()
d (n) 2h N n 2
O
H
| n | N -1 2
其它
π
N
2
n1
d(n) sin(n
n=1, 2, …, N/2
2π
-
1)
2
WR
(e j
)
三角窗(或巴特利特 Bartlett 窗)
w(n)
W (e j )
2N-2-nN12, n
0.23WR
0.23WR
布莱克曼(Blackman)窗——又称二阶升余弦窗
w(n) 0.42 0.5cos 2n 0.08cos 2 2n
N 1
j
N2n1
(
N 1) 2
汉宁(Hanning)窗 —— 升余弦窗
W(e
j N 1
e2
2 N
2 N
ห้องสมุดไป่ตู้
e
n , 1
1
j(
w(n) sin2 n 0.5 0.5cos 2n
j
)
0.5WR
0.5WR
N 1
()
()
(5.7) 汉明(Hamming)窗 —— 改进的升余弦窗
a(n) h( N 1) 2
a(n) 2h( N 1 n) n 0 2
O
H
π
θ(ω)
表 5.1 线性相位 FIR 滤波器特性
N-1
2
n0
n 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
形式语言与自动机课后练习答案第二章4.找出右线性文法,能构成长度为1至5个字符且以字母为首的字符串。
答:G={N,T,P,S}其中N={S,A,B,C,D} T={x,y} 其中x∈{所有字母} y∈{所有的字符} P如下: S→x S→xA A→y A→yBB→y B→yC C→y C→yD D→y6.构造上下文无关文法能够产生L={ω/ω∈{a,b}*且ω中a的个数是b的两倍}答:G={N,T,P,S}其中N={S} T={a,b} P如下:S→aab S→aba S→baaS→aabS S→aaSb S→aSab S→SaabS→abaS S→abSa S→aSba S→SabaS→baaS S→baSa S→bSaa S→Sbaa7.找出由下列各组生成式产生的语言(起始符为S)(1)S→SaS S→b(2)S→aSb S→c(3)S→a S→aE E→aS答:(1)b(ab)n /n≥0}或者L={(ba)n b/n≥0}(2) L={a n cb n /n≥0}(3)L={a2n+1 /n≥0}第三章1.下列集合是否为正则集,若是正则集写出其正则式。
(1)含有偶数个a和奇数个b的{a,b}*上的字符串集合(2)含有相同个数a和b的字符串集合(3)不含子串aba的{a,b}*上的字符串集合答:(1)是正则集,自动机如下(2) 不是正则集,用泵浦引理可以证明,具体见17题(2)。
(3) 是正则集先看L’为包含子串aba的{a,b}*上的字符串集合显然这是正则集,可以写出表达式和画出自动机。
(略)则不包含子串aba的{a,b}*上的字符串集合L是L’的非。
根据正则集的性质,L也是正则集。
4.对下列文法的生成式,找出其正则式(1)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→abS A→bBB→b B→cCC→D D→bBD→d(2)G=({S,A,B,C,D},{a,b,c,d},P,S),生成式P如下:S→aA S→BA→cC A→bBB→bB B→aC→D C→abBD→d答:(1) 由生成式得:S=aA+B ①A=abS+bB ②B=b+cC ③C=D ④D=d+bB ⑤③④⑤式化简消去CD,得到B=b+c(d+bB)即B=cbB+cd+b =>B=(cb)*(cd+b) ⑥将②⑥代入①S=aabS+ab(cb)*(cd+b)+(cb)*(cd+b) =>S=(aab)*(ab+ε)(cb)*(cd+b) (2) 由生成式得:S=aA+B ①A=bB+cC ②B=a+bB ③C=D+abB ④D=dB ⑤由③得 B=b*a ⑥将⑤⑥代入④ C=d+abb*a=d+ab+a ⑦将⑥⑦代入② A=b+a+c(d+b+a) ⑧将⑥⑧代入① S=a(b+a+c(d+ab+a))+b*a=ab+a+acd+acab+a+b*a5.为下列正则集,构造右线性文法:(1){a,b}*(2)以abb结尾的由a和b组成的所有字符串的集合(3)以b为首后跟若干个a的字符串的集合(4)含有两个相继a和两个相继b的由a和b组成的所有字符串集合答:(1)右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→ε(2) 右线性文法G=({S},{a,b},P,S)P: S→aS S→bS S→abb(3) 此正则集为{ba*}右线性文法G=({S,A},{a,b},P,S)P: S→bA A→aA A→ε(4) 此正则集为{{a,b}*aa{a,b}*bb{a,b}*, {a,b}*bb{a,b}*aa{a,b}*}右线性文法G=({S,A,B,C},{a,b},P,S)P: S→aS/bS/aaA/bbBA→aA/bA/bbCB→aB/bB/aaCC→aC/bC/ε7.设正则集为a(b a)*(1)构造右线性文法(2)找出(1)中文法的有限自动机答:(1)右线性文法G=({S,A},{a,b},P,S)P: S→aA A→bS A→ε(2)自动机如下:9.对应图(a)(b)的状态转换图写出正则式。
(图略)(1)由图可知q0=aq0+bq1+a+εq1=aq2+bq1q0=aq0+bq1+a=>q1=abq1+bq1+aaq0+aa=(b+ab) q1+aaq0+aa=(b+ab) *( aaq0+aa)=>q0=aq0+b(b+ab) *( aaq0+aa ) +a+ε= q0(a+b (b+ab) *aa)+ b(b+ab) *aa+a+ε=(a+b (b+ab) *aa) *((b+ab) *aa+a+ε)=(a+b (b+ab) *aa) *(3)q0=aq1+bq2+a+bq1=aq0+bq2+bq0=aq1+bq0+a=>q1=aq0+baq1+bbq0+ba+b=(ba)*(aq0 +bbq0+ba+b)=>q2=aaq0+abq2+bq0+ab+a=(ab)*(aaq0 +bq0+ ab+a)=>q0=a(ba)*(a+bb) q0 + a(ba)*(ba+b)+b(ab)*(aa+b)q0+ b(ab)*(ab+a)+a+b =[a(ba)*(a+bb) +b(ab)*(aa+b)]* (a(ba)*(ba+b)+ b(ab)*(ab+a)+a+b)10.设字母表T={a,b},找出接受下列语言的DFA:(1)含有3个连续b的所有字符串集合(2)以aa为首的所有字符串集合(3)以aa结尾的所有字符串集合14构造DFA M1等价于NFA M,NFA M如下:(1)M=({q0,q1 q2,q3},{a,b},ζ,q0,{q3}),其中ζ如下:ζ(q0,a)={q0,q1} ζ(q0,b)={q0}ζ(q1,a)={q2} ζ(q1,b)= {q2 }ζ(q2,a)={q3} ζ(q2,b)=Φζ(q3,a)={q3} ζ(q3,b)= {q3 }(2)M=({q0,q1 q2,q3},{a,b},ζ,q0,{ q1,q2}),其中ζ如下:ζ(q0,a)={q1,q2} ζ(q0,b)={q1}ζ(q1,a)={q2} ζ(q1,b)= {q1,q2 }ζ(q2,a)={q3} ζ(q2,b)= {q0}ζ(q3,a)=Φζ(q3,b)= {q0}答:(1)DFA M1={Q1, {a,b},ζ1, [q0],{ [q0,q1,q3],[q0,q2,q3],[q0, q1,q2,q3]}其中Q1 ={[q0],[q0,q1], [q0,q1,q2],[ q0,q2],[ q0,q1, q2,q3],[ q0,q1, q3],[ q0,q2, q3],[ q0,q3]}(2)DFA M1={Q1, {a,b},ζ1, [q0],{ [q1],[q3], [q1,q3],[q0,q1,q2],[q1,q2] ,[q1,q2,q3],[q2,q3]} 其中Q1 ={[q0],[q1,q3], [q1],[q2],[ q0,q1,q2],[q1,q2],[q3], [q1,q2,q3],[q2,q3]}(2)将此ε-NFA转换为没有ε的NFA答:(1)可被接受的的串共23个,分别为aac, abc, acc, bac, bbc, bcc, cac, cbc, ccc, caa, cab, cba, cbb, cca, ccb, bba, aca, acb, bca, bcb, bab, bbb, abb(2)ε-NFA:M=({p,q,r},{a,b,c},ζ,p,r) 其中ζ如表格所示。
因为ε-closure(p)= Φ则设不含ε的NFA M1=({p,q,r},{a,b,c},ζ1,p,r)ζ1(p,a)=ζ’(p,a)=ε-closure(ζ(ζ’(p,ε),a))={p}ζ1(p,b)=ζ’(p,b)=ε-closure(ζ(ζ’(p,ε),b))={p,q}ζ1(p,c)=ζ’(p,c)=ε-closure(ζ(ζ’(p,ε),c))={p,q,r}ζ1(q,a)=ζ’(q,a)=ε-closure(ζ(ζ’(q,ε),a))={p,q}ζ1(q,b)=ζ’(q,b)=ε-closure(ζ(ζ’(q,ε),b))={p,q,r}ζ1(q,c)=ζ’(q,c)=ε-closure(ζ(ζ’(q,ε),c))={p,q,r}ζ1(r,a)=ζ’(r,a)=ε-closure(ζ(ζ’(r,ε),a))={p,q,r}ζ1(r,b)=ζ’(r,b)=ε-closure(ζ(ζ’(r,ε),b))={p,q,r}ζ1(r,c)=ζ’(r,c)=ε-closure(ζ(ζ’(r,ε),c))={p,q,r}图示如下:(r为终止状态)a,b,c16.设NFA M=({q 0,q 1},{a,b},ζ,q 0,{q 1}),其中ζ如下: ζ(q 0,a)={q 0,q 1} ζ(q 0,b)={q 1} ζ(q 1,a)= Φ ζ(q 1,b)= {q 0, q 1} 构造相应的DFA M 1,并进行化简答:构造一个相应的DFA M 1={Q 1, {a,b},ζ1, [q 0],{ [q 1],[q 0,q 1]} 其中Q 1 ={[q 0],[q 1],[q 0,q 1]} 由于该DFA 已是最简,故不用化简17.使用泵浦引理,证明下列集合不是正则集:(1) 由文法G 的生成式S →aSbS/c 产生的语言L(G) (2) {ω/ω∈{a,b}*且ω有相同个数的a 和b} (3) {a k ca k /k ≥1}(4) {ωω/ω∈{a,b}*}证明:(1)在L(G)中,a 的个数与b 的个数相等假设L(G)是正则集,对于足够大的k 取ω= a k (cb)k c 令ω=ω1ω0ω2因为|ω0|>0 |ω1ω0|≤k 存在ω0使ω1ω0i ω2∈L 所以对于任意ω0只能取ω0=a n n ∈(0,k)则ω1ω0i ω2= a k –n (a n )i (cb)k c 在i 不等于0时不属于L 与假设矛盾。
则L(G)不是正则集(2)假设该集合是正则集,对于足够大的k 取ω= a k b k令ω=ω1ω0ω2因为|ω0|>0 |ω1ω0|≤k 存在ω0使ω1ω0iω2∈L 所以对于任意ω0只能取ω0=a n n ∈(0,k)则ω1ω0i ω2= a k –n (a n )i b k 在i 不等于0时a 与b 的个数不同,不属于该集合 与假设矛盾。
则该集合不是正则集(3)假设该集合是正则集,对于足够大的k 取ω= a k ca k 令ω=ω1ω0ω2因为|ω0|>0 |ω1ω0|≤k 存在ω0使ω1ω0i ω2∈L 所以对于任意ω0只能取ω0=a n n ∈(0,k)则ω1ω0i ω2= a k –n (a n )i ca k 在i 不等于0时c 前后a 的个数不同,不属于该集合 与假设矛盾。
