第二讲系统辨识的最优信号与PRBS
兰交课件系统辨识 第2章(输入信号的设计与选择)

(2.3.9)
系统辨识模拟方块图如图2.5所示。由于x(t)和 不相关,故 和 不相关,积分器输出 为 。(相关法)
相关法的优缺点:
优点: 不要求系统严格地处于稳定状态 输入的白噪声对系统的正常工作影响不大 对系统模型不要求验前知识 缺点: 噪声的非平稳会影响辨识精度 用白噪声作为输 入 信号时要求较长的观测时 间
( i 6)
i 1 12
(2.2.21)
(2)变换抽样法:设 均匀分布随机变量,则
是2个互相独立的(0,1)
1 2 1 ( 2 ln 1 ) cos 22 1 2 (2 ln 1 ) 2 sin 22
是相互独立、服从N(0,1)分布的随机变量。
交换律
分配律
0
1 1
1
0 1
1
1 0
2.3.2 M序列的产生
设有一无限长的二元序列x1 x2 … xp xp+1 …
x i a1 x i 1 a 2 x i 2 a p x i p
i=p+1,p+2,…
a1,a2,…ap-1取值为0或1;系数ap为1
)
采用极大似然法辨识时,如果辨识方法使得 模型参数的估计值是渐近有效的,最优输入信号 就是使Fisher信息矩阵的逆达到最小的一个标量函 数。这个标量函数可以作为评价模型精度的度量 函数,记作
J (M
1
)
(2.1.1)
T
Mθ是Fisher信息矩阵,且
ln L ln L M E y| (2.1.2)
2.2.2 白噪声序列
一种用于辨识MIMO系统的PRBS信号设计方法

文 中针对 辨识 MI MO 系 统 的 F R 模 型 , 用 I 采
经 过延迟 的 P B R S信 号作 为输入信 号 ]在 保证各 , 输 入信号 不 相关 与各 通 道 可 以被持 续 激 励 的前 提
P B R S信号 是一 种 长 周期 信 号 , 观 察 时 间 大 若 于一个 周期 , 是确 定 性 周 期 信 号 ., ZHAO u QI Ii J n, AN ixn J— i
(n tt t fS se En ie r g h j n iest ,Ha g h u3 0 2 I siueo y tm gn ei ,Z ei g Unv riy n a n z o 1 0 7,C ia hn)
法, 充分 利用 了信 号的 不相关 区间 , 优化 设计 的 P B R S信号 周期长度 远 小于常规设 计 方法.
关 键 词 :P B R S信 号 ; MO 系 统 ; 统 辨 识 MI 系 中图分 类号 : P2 3 T 7 文献标 识码 : A
An Optm i e sg pr a h o u t- i z d De i n Ap o c f M liPRBS Si n l g as f r M O y t m d ntfc to o I M S se I e iia in
( 浙江大 学 系统工程研 究所 , 浙江 杭州 3 0 2 ) 1 0 7 摘 要 : 对 多输入 多输 出( MO) 针 MI 系统的有 限脉 冲响应 ( I ) F R 函数 模型 , 究 了输入伪 随机二进 研
制 序 列 ( R S 信 号 的 优 化 设 计 问 题 , 出 了一 种 通 过 延 迟 方 法 产 生 多 个 P B P B) 提 R S信 号 的 优 化 设 计 方
《系统辨识》课件

23
第二章
过渡响应法和频率响应法
§21 过渡响应法(时域法) 采用非周期试验信号,通过系统的动态响应研究系 统的模型。 一、非参数模型的辨识 在时域中建立线性系统非参数模型时,用很简便的 方法就可得到脉冲响应曲线,阶跃响应曲线、方波响应 曲线或它们的离散采样数据表。 脉冲响应:可以采用幅值相当大,宽度很窄的方波 来近似δ 函数 。 对于线性系统,脉冲响应,阶跃响应和方波响应之 24 间是可以相互转换的。
过程的非线性与时变性(有助于模型类的选择)
噪声水平(以便用多大的输入,使得观测量有多
大的信噪比)
变量之间的延迟(滞后环节参数) 2)输入信号的选择(阶跃、方波、脉冲、PRBS)。
16
第一章
概
述
3)采样速度的选择(要采集数据就有采样速度选择 问题)。实际上先采用较短的采样间隔,在数据分析时, 可根据需要隔几个取一个数据。 4)试验长度的确定(试验时间问题)。辨识精度与 试验时间的长短有关。 2、模型结构确定 根据辨识的目的及对被辨识系统的先验知识,确定
系统辨识
电气工程与自动化学院 陈 冲
1
课程主要内容
第一章
第二章 第三章 第四章 第五章
概
述
过渡响应法和频率响应法 辨识线性系统脉冲响应函数的相关分析法 线性系统参数估计的最小二乘法 线性系统的状态估计法
结束
2
第一章
一、建模的必要性 二、模型 三、建模方法
概
述
四、系统辨识的内容(或步骤)
系统辨识的经典方法

⎧T
⎨⎩τ
= 2(t2 − t1) = 2t1 − t2
对于以上结果,也可在
⎧⎪⎨tt34
≤τ,
= 0.8T
+τ
,
⎪⎩t5 = 2T +τ ,
y(t3 ) = 0 y(t4 ) = 0.55 y(t5 ) = 0.87
这几点上对实际曲线的拟合精度进行检验。
系统辨识的经典方法
频率响应法
频率响应法-1
; 阶跃响应法辨识原理
¾ 在系统上施加一个阶跃扰动信号,并测定出对象的响应随时间 而变化的曲线,然后根据该响应曲线,通过图解法而不是通过 寻求其解析公式的方法来求出系统的传递函数,这就是阶跃响 应法系统辨识。
¾ 如果系统不含积分环节,则在阶跃输入下,系统的输出将渐进 于一新的稳定状态,称系统具有自平衡特性,或自衡对象。
+ b1s + a1s
+ +
b0 a0
,
n>m
¾ 对应的频率特性可写成:
G(
jω)
=
bm ( an (
jω)m +" + b2 ( jω)2 + b1( jω)n +" + a2 ( jω)2 + a1(
jω) + b0 jω) + a0
=
(b0 − b2ω 2 (a0 − a2ω 2
+ b4ω 4 + a4ω 4
系统辨识的经典方法
肖志云
内蒙古工业大学信息工程学院自动化系
系统辨识的经典方法
1
引言
2
阶跃响应法
3
频率响应法
4
相关分析法
系统辨识 相关分析法

1
σ
2 U
RUZ (τ )
M序列是最常用的一种伪随机二进制序列.由于 其易于 序列是最常用的一种伪随机二进制序列. 产生,易于处理并具有类似于白噪声的 性质,在系统 辨识中,M 辨识中,M序列常作为试验输入 信号,并已有成熟的 理论与应用结果, 理论与应用结果,提高系统脉冲响应函数精度的方法主 要有:减小M 要有:减小M序列 的时钟周期和增大其长度;用高精 度的方法求 解Wiener-Hopf方程;提高互相关函数的 Wiener-Hopf方程;提高互相关函数的 计算精度等. 计算精度等. 对于一个n级移位寄存器,所产生的序列长度若为
r Ru ≠ 0
谢谢观赏
�
Np 1 j =0
∑ g ( j ) RU (m j )
m = 0,1, L , N p 1
r RUZ = [ RUZ (0), RUZ (1),L , RUZ ( Np 1)]T
r g = [ g (0), g (1),L, g ( Np 1)]T
r r r Ruz = Ru g
2 1 r 1 Np Ru = ( Np + 1)a 2 M 1 r r 1 r g = Ru Ruz 1 2 M 1
RUZ (m) =
N p 1 j =0
∑ g ( j)R
U
(m j ) ∑+1g ( j ) j =m
N p 1 j =0 N p 1
a 2 m 1 2 = a g ( m) ∑ g ( j ) + N p j =0 a2 a2 = a 2 g ( m) + g ( m) Np Np = N p +1 Np
y(t) = ∫
∞
∞
g(τ )u(t τ )dτ
系统辨识实验报告
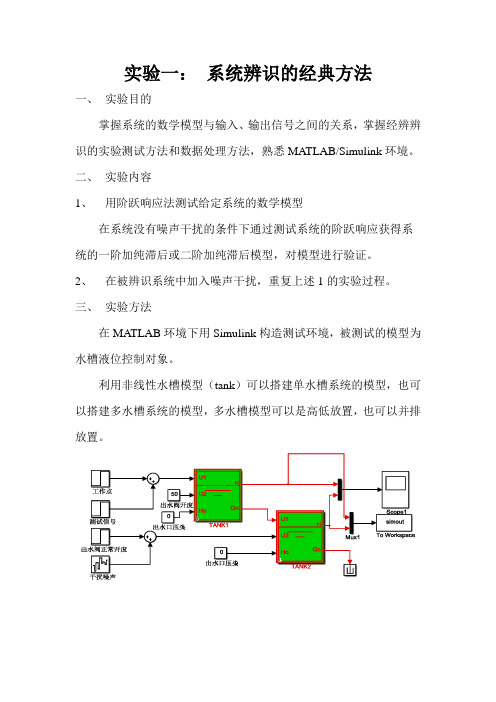
实验一:系统辨识的经典方法一、实验目的掌握系统的数学模型与输入、输出信号之间的关系,掌握经辨辨识的实验测试方法和数据处理方法,熟悉MATLAB/Simulink环境。
二、实验内容1、用阶跃响应法测试给定系统的数学模型在系统没有噪声干扰的条件下通过测试系统的阶跃响应获得系统的一阶加纯滞后或二阶加纯滞后模型,对模型进行验证。
2、在被辨识系统中加入噪声干扰,重复上述1的实验过程。
三、实验方法在MATLAB环境下用Simulink构造测试环境,被测试的模型为水槽液位控制对象。
利用非线性水槽模型(tank)可以搭建单水槽系统的模型,也可以搭建多水槽系统的模型,多水槽模型可以是高低放置,也可以并排放置。
1.噪声强度0.5,在t = 20的时候加入阶跃测试信号相应曲线2.乘同余法产生白噪声A=19;N=200;x0=37;f=2;M=512; %初始化;for k=1: N %乘同余法递推100次;x2=A*x0; %分别用x2和x0表示xi+1和xi-1;x1=mod(x2,M); %取x2存储器的数除以M的余数放x1(xi)中;v1=x1/M; %将x1存储器中的数除以256得到小于1的随v(:,k)=(v1-0.5 )*f;x0=x1; % xi-1= xi;v0=v1;end %递推100次结束;v2=v;k1=k;h=k1;%以下是绘图程序;k=1:1:k1;plot(k,v,'r');grid onset(gca,'GridLineStyle','*');grid(gca,'minor')3.白噪声序列图像020406080100120140160180200-1-0.8-0.6-0.4-0.20.20.40.60.81四、 思考题(1) 阶跃响应法测试系统数学模型的局限性。
答:只适用于某些特殊对象或者低阶简单系统;参数估计的精度有限,估计方法缺乏一般性。
系统辨识课件-经典的辨识方法

ˆ (t ) Ru (t )dt Ruz ( ) g
0
此为辨识过程脉冲响应的理论依据
2 Ru ( ) u ( ) 白噪声输入时 ˆ 1 g ( ) Ruz ( ) 2 u
4.5.2 用M序列作输入信号的离散算法
第4章 经典的辨识方法
4.1 引言 ● 辨识方法的分类 ▲ 经典的辨识方法 (Classical Identification) :首先获得系统的非参数模型(频 率响应,脉冲响应,阶跃响应),通过特定方法,将非参数模型转化成参数 模型 (传递函数)。 ① 阶跃响应辨识方法 (Step Response Identification) ② 脉冲响应辨识方法 (Impulse Response Identification) ③ 频率响应辨识方法 (Frequency Response Identification) ④ 相关分析辨识方法 (Correlation Analysis Identification) ⑤ 谱分析辨识方法 (Spectral Analysis Identification) ▲ 现代的辨识方法 (Modern Identification):假定一种模型结构,通过模型与过 程之间的误差准则来确定模型的结构参数)。 ① 最小二乘类辨识方法 (Least Square Identification) ② 梯度校正辨识方法 (Gradient Correction Identification) ③概率逼近辨识方法(Probability Approximation Identification) 经典的辨识方法 1)首先得到系统的非参数模型; 2)由非参数模型转换成参数模型。
K 1 lim h1 (t )
hr (t ) [ K r 1 hr 1 ( )]d
系统辨识原理及其应用(第二章)

韩 华 中南大学信息院
第2章 传递函数的辨识
经典的传递函数辨识方法可以分为时域法和频率域法 两种。
2.1传递函数辨识的时域法
2.1.1一阶惯性滞后环节的辨识 2.1.2二阶自衡对象的辨识 2.1.3二阶欠阻尼自衡对象的辨识 2.1.4高阶自衡对象的辨识 2.1.5自衡等容对象的辨识 2.1.6无自衡对象的辨识 2.1.7面积法
2.1传递函数辨识的时域法
传递函数辨识的时域法包括阶跃响应法、脉冲响 应法和矩形脉冲响应法等,其中以阶跃响应法最 为常用。阶跃响应法利用阶跃响应曲线对系统传 递函数进行辨识,阶跃响应曲线即输入量作阶跃 变化时,系统输出的变化曲线。在工业工程控制 系统的辨识中,阶跃响应曲线又常被称为飞升曲 线或系统的飞升特性。如果系统不含有积分环节 ,那么阶跃输入下,系统的输出将渐进于一新的 稳定状态,称系统具有自平衡特性,或称为自衡 对象。否则,系统 称为无自衡对象,输出无限地 扩大或减小,说明系统至少有一个纯积分环节。
用阶跃响应辨识的传递函数有以下几种形式:
Ke −τ s G(s) = Ts + 1 Ke −τ s G(s) = (T1s + 1)(T2 s + 1) Ke −τ s G(s) = (T1s + 1)(T2 s + 1)(T3s + 1) Ke −τ s G(s) = (Ts + 1) n Ke −τ s G(s) = s(T1s + 1) n (1) (2) (3) (4)
ln y (t ) − 1 − Ae
− t T1
= ln B − t T2
− t T1
(26)
采用同样的方法可得到 B 和 T2 。y (t ) − 1 − Ae 同理可得 C 和 T3 。 最后:
系统辨识方法

0.1
0.2
0.3
0.4
关节系统的李萨育图形
新疆大学电气工程学院
3/13/2010
0.4 0.3 0.2
25 20 15
0.1 幅幅/v 0 -0.1 -0.2
10 5 0
-0.3 -0.4 0 50 100 采采采 150 200 250
-5 0
100
200
300
400
500
600
700
800
900
新疆大学电气工程学院
3/13/2010
实例介绍
新疆大学电气工程学院
3/13/2010
新疆大学电气工程学院
3/13/2010
15 10 5 角角/ 0
10 8 6
角角 / 0
初初输输1.25/正正 初初输输1.25/反正 初初输输1.75/正正 初初输输1.75/反正
0 -5 -10
4 2 0 预预输输1V 预预输输1.25V 预预输输1.5V 预预输输1.75V
0
-45 -90 -135 -180 -1 10 10
0
频频 (rad/sec)
10
1
10
2
阻尼比为1.067,肌肉关节的截止频率1.6HZ,自然角频率为3.26。
新疆大学电气工程学院
3/13/2010
10
8
50阶阶阶阶 实实实实
50阶阶阶阶 仿仿实实
6 角角/ 0 / 4 2
30阶阶阶阶 仿பைடு நூலகம்实实
系统辨识
张宏立
新疆大学电气工程学院
3/13/2010
自衡对象:阶跃输入下,系统的输出能渐进于一 个新的稳定状态
自衡对象:
南京理工系统辨识第二章2讲义(NJUST)

————(315)
辨识系统脉冲响应的相关分析法(2)
若{u(t)}和{z(t)}是弱各态历经的,由相关函数定
义,输入的自相关函数和输入输出的互相关函数为:
∫ Ruu
(τ
−
λ)
=
lim
T →∞
1 T
T u(t − λ)u(t −τ )dt —————————(4)
0
∫ Ruz
(τ
)
=
lim
T →∞
1 T
U0——系统达到稳态时的输入值
Y0——系统达到稳态时的输出值
注意:在计算互相关函数Ruy(τ)时,
需在实际测量的输出y(k)中减去Y0。
24
4
∑ ∑ RuY (n) =
1 NP
N P −1
Y (k)u(k − n) =
k =0
1 NP
N P −1
[Y0
k =0
+
y(k)]u(k − n)
∑ ∑ =
u(t)关函数
在生产现场试验和测试,不可能对系统单纯地输入
一个伪随机二位式序列,只能在系统处于稳定状态时,
在原来正常的输入上面附加一个PRBS序列。
23
U0
线性系统
g(τ)
Y0
τ PRBS发生器 时延
Y(k) = Y0 + y(k)
× y(k)
∫
Ruy (τ ) = Kgˆ(τ ) 用PBRS作为实验信号辨识系统
1 NP
N P −1
Y0u(k − n) +
k =0
1 NP
N P −1
y(k )u(k − n)
k =0
∵PRBS在一个周期内,逻辑1状态比逻辑0状态多1个
系统辨识方法

新疆大学电气工程学院
3/13/2010
白噪声
白噪声是一种均值为零、谱密度为非零常数 的平稳随机过程。
自相关函数
Rw
(
)
2
(
)
0
0 0
谱密度 Sw (w) 2
以白噪声为输入,最小二乘辨识是无偏的
有色噪声可利用白噪声通过一个成形滤波器获 得白噪声序列的产生方法
新疆大学电气工程学院
3/13/2010
n(t)
U(t)
y(t) g(t)
z(t)
Ruz ( ) g(t)Ruu ( t)dt
0
新疆大学电气工程学院
3/13/2010
Wiener-Hopf方程表明:当系统的输入是原输入信号的自相 关函数时,系统的输出是原输入信号和它对应的输出信号的互相 关函数。
Wiener-Hopf方程是一个积分方程,要想解出脉冲响应的是很 困难的,但是当Ruu等于冲激函数时, Wiener-Hopf化简为:
C1
CP
C2
C3
4级M序列
C4
M序列
新疆大学电气工程学院
3/13/2010
最小二乘批处理方法
差分方程:
z(k)+a1z(k-1)+...+anz(k-n) b1u(k 1) b2u(k 2) ... bnu(k n) e(k)
z(k)=-a1z(k-1)-...-a n z(k-n) +b1u(k 1) b2u(k 2) ... bnu(k n) e(k)
0t t
归一化:
y(t)
0
t
(1 e T )
y(t)
1.0
0 t 0.632
t
系统辨识方法

第四章 系统辨识中的实际问题§4 —1 辨识的实验设计一、系统辨识的实验信号实验数据是辨识的基础,只有高质量的数据才能得出良好的数学模型,而且实验数据如果不能满足起码的要求,辨识根本得不出解。
系统辨识学科是在数理统计的时间序列分析的基础上发展起来的,两者的区别在于系统辨识的对象存在着人为的激励(控制)作用,而时序分析则没有。
因此,前者能通过施加激励信号u(k)达到获得较好辩识结果的目的(即实验信号的设计),而后者不能。
(一)系统辨识对实验信号的最起码的要求 为了辨识动态系统,激励信号u 必须在观测的周期内对系统的动态持续地激励。
满足辨识对激励信号最起码的要求的持续激励信号应具备的条件称“持续激励条件”,分以下四种情况讨论: 1. 连续的非参数模型辨识(辩识频率特性)如果系统通频带的上下限为 ωmin ≤ ω ≤ ωmax ,要求输入信号的功率密度谱在此范围内不等于零。
)()()}({)}({)(ωωωj U j Y t u F t y F j G ==2. 连续的参数模型辨识 被辩识的连续传函为,共包含(m+n+1)个参数对于u(t)的每一个频率成分ωi 的谐波,对应的频率响应有一个实部R(ωi )和一个虚部Im(ωi ),由此对应两个关系式(方程),能解出两个未知参数。
因此,为辩识(m+n+1)个参数,持续激励信号至少应包含:j ≥( m+n+1 )/2 个不同的频率成分。
3. 离散的脉冲响应 g(τ)的辨识g(τ) ;τ = 0,1,..m ,假设过程稳定,当 τ > m 时 g(τ)= 0 。
由维纳—何甫方程有:R uy (τ )=∑ g(σ)R uu (τ - σ) 式(4-1-1)由上式得出(m+1)个方程的方程组:上式表达成矩阵形式φuy = φuu G 式(4-1-2) 可解出 G = φuu -1 φuy 式(4-1-3)G s b b s b s a s a s m mn n ()=++++++0111R R R m R R R m R R R m R m R m R g g g m uy uy uy uu uu uu uu uu uu uuuu uu ()()()()()()()()()()()()()()()010******** ⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=----⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥⋅⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥G = [ g(0),…,g(m) ]T 有解的条件是:如果所有的输出自相关函数式(4-1-4)都存在,且方阵φuu 非奇异, 即det φuu ≠ 0 。
第二讲_系统辨识与滤波_辨识三要素

1
ξ 0 = 11
2 35
。
2 正态分布白噪声 N ( µ , σ 2 ) : {η ( k ) = µ + σ ( 1)均匀分布的白噪声(教材 51 页)。 例题:
∑ξ
E{W (t )} = 0 Cov{W (t ),W (t + τ )} = E{W (t )W (t + τ )} = Qδ (τ )
其中 Q 为正定常数矩阵,则称 W (t ) 为 n 维白噪声过程。
白噪声特点: 白噪声特点: 如果一个零均值、平稳随机过程的谱密度为常数,我们称之为白噪声(由白色光联想而 得)。一个平稳随机序列{w(k)}具有恒定功率谱密度,若这个过程是离散的,称白噪声 白噪声序列 白噪声序列。 序列。 白噪声有以下特点: 1 E (w)=w = 0 。
=
∞ ∞
− ∞− ∞
∫ ∫[x − µ
x
(t1 )][ y −
Cxy (τ = t2 − t1) = Rxy (τ ) − µx µ y
µ y (t 2 )] p 2 ( x, y; t1 , t 2 )dxdy
= R xy (t1 , t 2 ) − µ x (t1 ) µ y (t 2 )
R xy (τ ) = R yx (−τ )
∫
∞
−∞
x 2 (t )dt =
1 2π
∫
∞
−∞
|| X ( jω ) || 2 dω
1 T →∞ 2T lim
∫
T
−T
x 2 (t )dt =
1 2π
∫
∞
−∞ T →∞
lim
1 || X T ( jω ) ||2 d ω 2T
确定性信号 x(t)的平均谱密度:
(完整)系统辨识的常用方法

系统辨识的常用方法系统辨识是根据系统的输入输出时间函数来确定描述系统行为的数学模型,是现代控制理论中的一个分支。
对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。
传统的系统辨识方法(1)脉冲响应脉冲响应一般是指系统在输入为单位冲激函数时的输出(响应)。
对于连续时间系统来说,冲激响应一般用函数h(t)来表示.对于无随机噪声的确定性线性系统,当输入信号为一脉冲函数δ(t)时,系统的输出响应 h(t)称为脉冲响应函数。
辨识脉冲响应函数的方法分为直接法、相关法和间接法。
①直接法:将波形较理想的脉冲信号输入系统,按时域的响应方式记录下系统的输出响应,可以是响应曲线或离散值。
②相关法:由著名的维纳—霍夫方程得知:如果输入信号u(t)的自相关函数R(t)是一个脉冲函数kδ(t), 则脉冲响应函数在忽略一个常数因子意义下等于输入输出的互相关函数,即 h(t)=(1/k)Ruy(t)。
实际使用相关法辨识系统的脉冲响应时,常用伪随机信号作为输入信号,由相关仪或数字计算机可获得输入输出的互相关函数Ruy(t),因为伪随机信号的自相关函数 R(t)近似为一个脉冲函数,于是h(t)=(1/k)Ruy(t).这是比较通用的方法。
也可以输入一个带宽足够宽的近似白噪声信号,得到h (t)的近似表示。
③间接法:可以利用功率谱分析方法,先估计出频率响应函数H(ω),然后利用傅里叶逆变换将它变换到时域上,于是便得到脉冲响应h(t)。
(2)最小二乘法最小二乘法(LS)是一种经典的数据处理方法, 但由于最小二乘估计是非一致的、有偏差的, 因而为了克服它的不足, 形成了一些以最小二乘法为基础的辨识方法:广义最小二乘法(GLS)、辅助变量法(IVA)和增广矩阵法(EM),以及将一般的最小二乘法与其它方法相结合的方法,有相关分析——-最小二乘两步法(COR —LS)和随机逼近算法.(3)极大似然法极大似然法(ML)对特殊的噪声模型有很好的性能,具有很好的理论保证;但计算耗费大, 可能得到的是损失函数的局部极小值。
最优状态估计和系统辨识

最优状态估计和系统辨识最优状态估计和系统辨识是现代控制理论中的两个重要概念。
最优状态估计是指利用系统的输入和输出数据,通过数学模型对系统状态进行估计的过程。
系统辨识则是指通过对系统的输入和输出数据进行分析,建立系统的数学模型的过程。
这两个概念在现代控制理论中具有重要的应用价值。
最优状态估计的目的是通过对系统状态的估计,实现对系统的控制。
最优状态估计的方法有很多种,其中最常用的是卡尔曼滤波器。
卡尔曼滤波器是一种基于贝叶斯定理的滤波器,它可以通过对系统的输入和输出数据进行分析,对系统状态进行估计。
卡尔曼滤波器的优点是可以对系统的状态进行实时估计,并且可以适应系统的非线性和非高斯性。
系统辨识的目的是建立系统的数学模型,以便对系统进行控制。
系统辨识的方法有很多种,其中最常用的是参数辨识方法。
参数辨识方法是通过对系统的输入和输出数据进行分析,建立系统的数学模型。
参数辨识方法的优点是可以建立系统的精确数学模型,并且可以适应系统的非线性和非高斯性。
最优状态估计和系统辨识在现代控制理论中具有广泛的应用。
它们可以应用于机器人控制、航空航天控制、自动驾驶汽车控制等领域。
在机器人控制中,最优状态估计和系统辨识可以用于对机器人的位置和姿态进行估计和控制。
在航空航天控制中,最优状态估计和系统辨识可以用于对飞行器的位置和速度进行估计和控制。
在自动驾驶汽车控制中,最优状态估计和系统辨识可以用于对汽车的位置和速度进行估计和控制。
总之,最优状态估计和系统辨识是现代控制理论中的两个重要概念。
它们可以应用于机器人控制、航空航天控制、自动驾驶汽车控制等领域。
通过对系统的输入和输出数据进行分析,可以实现对系统状态的估计和建立系统的数学模型,从而实现对系统的控制。
《系统辨识》第二章

(1) 乘同余法
首先,用递推同余式产生正整数序列{xi},即
x i A x i 1 (m o d M ) , i 1, 2 , 3
M为2的方幂,即M=2k,k为大于2的整数; A≡3或A≡5(mod8),且A不能太小; 初值x0取正奇数。 再令
i
xi M
, i 1, 2 , 3,
18
19
2
1 0
( i ) p ( i ) d i
2
如 果 ~ N ( , )是 要 产 生 的 正 态 分 布 随 机 变 量 , 经标准化处理,则
2
~ N ( 0 ,1)
9
则有
+
i 1
N
i
N 12
N 2
其 中 i 为 ( 0, 均 与 分 布 随 机 数 ; 1)
15
二电平M序列的产生
由于M序列对时间是离散的,而输入需要对时间连续, 所以在实际应用中,总是把状态为“0”和 “1”的M序列变换 成幅度为+a和-a的二电平序列,其中“0”对应高电平+a, “1”对应低电平-a。这种对时间连续的序列称为二电平M序 列 111100010011010
+a
0 2△ -a
(2)输入信号对系统的“净扰动”要小,即应使正负向 扰动机会几乎均等; (3)工程上要便于实现,成本低。
2
2.1白噪声序列及其产生方法
白噪声过程是一种最简单的随机过程。它是一种均值为0、谱密度 为非0常数的平稳的随机过程。 白噪声过程没有“记忆性”。
定义:如果随机过程ω(t)的均值为0,自相关函数为: Rω(t)=σ2δ(t)
系统辨识基础教学大纲

主要内容: 1. 阶跃响应法 2. 脉冲响应法 3. 频率响应法 4. 相关分析法
基本要求: 掌握阶跃响应法、脉冲响应法、频率响应法 了解相关分析法基本原理
学时分配: 8 学时 第三章 最小二乘法
主要内容: 1. 最小二乘法问题的解 2. 最小二乘法问题的递推算法 3. 偏差补偿最小二乘法 4. 增广最小二乘法
基本要求: 掌握最小二乘法的基本概念、最小二乘法问题的解 掌握最小二乘法问题的递推算法 掌握偏差补偿最小二乘法 了解增广最小二乘法的基本原理
了解最小二乘法问题的统计性质 学时分配:8 学时
数辨识程序 六、教学参考书 1.方崇智主编,《过程辨识》(第一版),清华大学出版社,1998 年 2.刘 豹主编,《系统辨识》(第二版),机械工业出版社,1996 年 3.王秀峰主编,《系统建模与辨识》(第一版),电子工业出版社,2004 年
《系统辨识基础》教学大纲
课程名称:系统辨识基础(Basic of System Discrimination) 课程编码:152050 学 分:2 分 总 学 时:32 学时,理论学时:22 学时;上机学时:10 学时 适用专业:自动化专业 先修课程:自动控制理论、现代控制理论 一、课程的性质、目的与任务
第四章 梯度校正参数辨识方法 主要内容:
1. 确定性问题的梯度校正参数辨识方法 2. 随机问题的梯度校正参数辨识方法 基本要求: 掌握确定性问题的梯度校正参数辨识方法 了解随机问题的梯度校正参数辨识方法的基本原理 学时分配:4 学时 三、上机内容与学时分配 上机内容: 给定一个模拟或数字对象,编写计算机程序对其参数进行辨识 学时分配:10 学时 四、大纲说明 1. 本课程是自动化专业的一门专业选修课程。 2. 本课程的先修课程为自动控制理论、现代控制理论。 3. 本课程安排上机大作业,要求学生结合课程学习,编写调试数字、模拟对象的参
信号与系统分析PPT全套课件可修改全文

1.系统的初始状态
根据各电容及电感的状态值能够确定在 t 0
时刻系统的响应及其响应的各阶导数
( y(0 ) k 1, 2 , , n 1)
称这一组数据为该系统的初始状态。
2.系统的初始值
一般情况下,由于外加激励的作用或系统内 部结构和参数发生变化,使得系统的初始值与 初始状态不等,即:
y(0 ) y(0 )
自由响应又称固有响应,它反映了系统本身 的特性,取决于系统的特征根; 强迫响应又称强制响应,是与激励相关的响 应。 利用经典法可以直接求得自由响应与强迫响 应,强迫响应即特解
先求得系统的零输入响应和零状态响应,并 获得系统的全响应;
然后利用系统特性与自由响应、激励与强迫 响应的关系可以间接得到自由响应和强迫响应。
t
f (t) (t)dt f (0) (t)dt
f (0) (t)dt f (0)
(1)
0
t
ห้องสมุดไป่ตู้(3)偶函数
(4)
(at)
1 a
(t)
f (t) (t) ( f (0))
(5) (t)与U (t)的关系
0
t
1.2 基本信号及其时域特性
单位冲激偶信号 '(t)
f (t) 1/
f ' (t) (1/ )
第2章 连续系统的时域分析
2.1 LTI连续系统的模型 2.2 LTI连续系统的响应 2.3 冲激响应与阶跃响应 2.4 卷积与零状态响应
2.1 LTI连续系统的模型
2.1.1 LTI连续系统的数学模型 2.1.2 LTI连续系统的框图
返回首页
2.1.1 LTI连续系统的数学模型
对于任意一个线性时不变电路,当电路结构 和组成电路的元件参数确定以后, 根据元件的伏安关系和基尔霍夫定律,可以 建立起与该电路对应的动态方程。
OptiX OSN2500设备故障定位之PRBS功能测试法

OptiX OSN2500设备故障定位之PRBS功能测试法PRBS功能测试法是判断和定位故障的方法之一。
1.概述伪随机码测试(PRBS)模块相当于一个简单的自发自收的非成帧业务的仪表。
在开局或问题定位时,可以做到无仪表测试,一般用于网络的自检和维护。
实现了PRBS(Pseudo Random Bit Sequence)功能的网元,可以作为一个简单的仪表,分析业务通道是否有故障。
既可以分析本网元,也可以分析整个网络的情况。
2.PRBS功能测试法应用PRBS测试法分为低阶业务PRBS功能测试和高阶业务PRBS功能测试。
启用低阶或者高阶PRBS功能后,在相应位置进行环回,就可以进行交叉方向、支路方向、线路方向测试。
根据是否检测到误码判断相应测试通道的工作状态。
低阶业务PRBS功能测试:PRBS模块集成在支路板实现,如图1所示。
图1低阶业务PRBS测试信号流由支路板发起的PRBS功能测试,可以向两个方向发送。
向电口侧发送:经电缆或别的网元环回,可检测支路板发送方向的端口是否工作正常。
单板向该支路的发射(Tx)端口方向发送固定的伪随机码,在该支路端口的接收(Rx)端口接收伪随机码,如图2所示。
图2低阶业务支路方向PRBS测试向交叉方向发送:经高阶交叉芯片,从低阶交叉芯片返回,也可经低阶交叉芯片调度到其他单板(可以是支路板或线路板),从其他单板环回。
返回到交叉板后,再回到发起PRBS测试的支路板校验结果。
可检测高、低阶交叉芯片以及其他业务单板(支路板或线路板)通道是否正常。
如图3所示,单板在该通道向交叉方向发送固定的伪随机码,在该通道的下行方向接收伪随机码。
图3低阶业务交叉方向PRBS测试高阶业务PRBS功能测试:PRBS功能模块集成在线路板实现。
由线路板实现:由线路板发起的线路方向高阶PRBS测试用于检测线路板的某一高阶通道是否工作正常,可以向光口侧发送,经光纤或别的网元环回,可检测线路板发送方向的通道是否可用,如图4所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(周期)、各不同游程所占比例。
所有M序列都具有“移位相加”的性质。
M序列的相关函数在原点处为最大,相关函 数及功率谱密度分析略(可参见课本)。
3,7,10
注 意:
得到M序列的反馈形式不是唯一的。 书中第55页给出了确定反馈的具体产生 过程。 请看书中第55页的例2.6 一个周期为:111100010011010
(5)M序列的性质
n-----周期 Np 2n 1
逻辑1状态
Np
1,逻辑0状态
Np 1 2
2
“游程”-----若干个状态连在一起:总数
第二讲 系统辨识的最优信号与PRBS
1. 最优信号 “充分激励问题” 对辨识一般线性系统,最优输入信号的 设计问题将变成一个标准的非线性最优 化问题,但获得解析解是困难的。
2. 白噪声
白噪声是一种均值为零、谱密度为非零常 数的平稳随机过程。
自相关函数 Rw
(
)
2
()0源自0 0谱密度 Sw (w) 2
n 级 ------- Np 2n 1,M序列
n 4------- N p 15
(4)不同级数移位寄存器产生M序列的反馈列表如下:
移位寄存器
2 3 4 5 6 8 10
周期 反馈到第一级的各级输出的模2和
3
1,2
7
1,2,3
15
1,3,4
31
2,3,5
63
1,5,8
255
2,3,4,8
1023
以白噪声为输入,最小二乘辨识是无偏的
有色噪声可利用白噪声通过一个成形滤波器 获得
白噪声序列的产生方法
3. PRBS
Pseudo—random—binary series 伪随机二进制序列
最大长度PRBS-------M序列 (1)PRBS可由移位寄存器产生 (2)模2加法规则 (3)一个移位寄存器的输出序列的最大周期
