青岛版2020八年级数学下册期末模拟测试题(附答案)
2020-2021年度青岛版八年级数学下册《第6章平行四边形》综合培优训练(附答案)
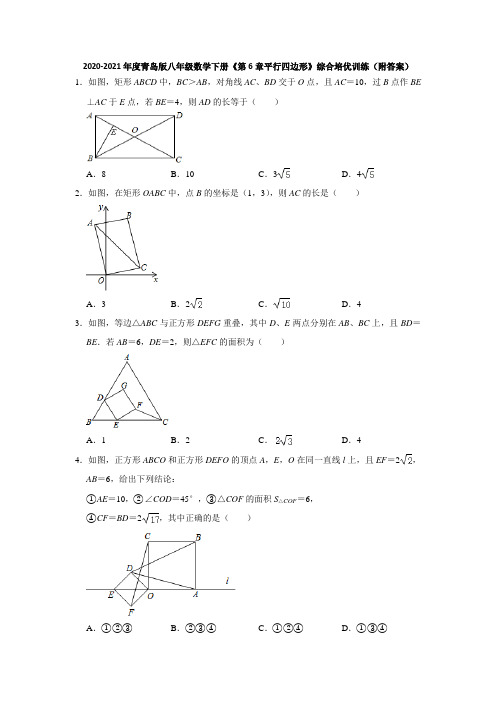
2020-2021年度青岛版八年级数学下册《第6章平行四边形》综合培优训练(附答案)1.如图,矩形ABCD中,BC>AB,对角线AC、BD交于O点,且AC=10,过B点作BE ⊥AC于E点,若BE=4,则AD的长等于()A.8B.10C.3D.42.如图,在矩形OABC中,点B的坐标是(1,3),则AC的长是()A.3B.2C.D.43.如图,等边△ABC与正方形DEFG重叠,其中D、E两点分别在AB、BC上,且BD=BE.若AB=6,DE=2,则△EFC的面积为()A.1B.2C.D.44.如图,正方形ABCO和正方形DEFO的顶点A,E,O在同一直线l上,且EF=2,AB=6,给出下列结论:①AE=10,②∠COD=45°,③△COF的面积S△COF=6,④CF=BD=2,其中正确的是()A.①②③B.②③④C.①②④D.①③④5.如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且AC=10,则OE的长度是()A.B.5C.3D.6.如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=2,若CE•DE=5,则正方形的面积为()A.5B.6C.7D.87.如图,矩形ABCD中,AB=6,AD=8,点E在边AD上,且AE:ED=1:3.动点P 从点A出发,沿AB运动到点B停止,过点E作EF⊥PE交射线BC于点F,联结PF,设M是线段PF的中点,则点P运动的整个过程中,线段DM长的最小值为()A.B.C.3D.8.如图,在矩形ABCD中,AB=2,AD=1,E为AB的中点,F为EC上一动点,P为DF 中点,连接PB,则PB的最小值是()A.2B.4C.D.29.如图,▱ABCD中,∠B=60°,AB=4,BC=5,P是对角线AC上任一点(点P不与点A,C重合),且PE∥BC交AB于E,PF∥CD交AD于F,则阴影部分的面积是.10.矩形ABCD的对角线交于O点,一条边的长为1,△AOB是正三角形,则这个矩形的周长为.11.如图,在四边形ABCO中,AB∥OC,AO⊥OC,AB=1,OC=4,P为AO边上一个动点,连接PB并延长至点E,使得点E落在直线x=3上,以PE,PC为边作▱PEFC,连接PF,则PF长的最小值为.12.如图,正方形ABCD的边长为4,E为BC上任意一点,EF⊥AC于F,EG⊥BD于G,则EF+EG的值为.13.如图,▱ABCD中,AB=10cm,AD=15cm,点P在AD边上以每秒1cm的速度从点A 向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,点P到达点D时停止(同时点Q也停止运动),在运动以后,当以点P、D、Q、B为顶点组成平行四边形时,运动时间t为秒.14.菱形ABCD的对角线AC=6cm,BD=4cm,以AC为边作正方形ACEF,则BF长为.15.矩形ABCD的周长是34cm,对角线相交于O,△AOD与△AOB的周长相差1cm,则AB的长是.16.如图,在四边形ABCD中,AB⊥BC,对角线AC、BD相交于点E,E为BD中点,且AD=BD,AB=2,∠BAC=30°,则DC=.17.如图,以正方形ABCD的边AD为一边作等边三角形ADE,F是DE的中点,BE、AF 相交于点G,连接DG,若正方形ABCD的面积为36,则BG=.18.如图,正方形ABCD的边长为15,AG=CH=12,BG=DH=9,连接GH,则线段GH 的长为.19.如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C 作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为.20.如图,在平行四边形ABCD中,AC是对角线,且AB=AC,CF是∠ACB的角平分线交AB于点F,在AD上取一点E,使AB=AE,连接BE交CF于点P.(1)求证:BP=CP;(2)若BC=4,∠ABC=45°,求平行四边形ABCD的面积.21.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.(1)求证:BD=DE;(2)求DM的长.22.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接CE、OE,连接AE交OD于点F.(1)求证:OE=CD;(2)若菱形ABCD的边长为2,∠ABC=60°.求AE的长.23.如图,在正方形ABCD中,M为AB上的一点,N为BC上的一点,且BM=BN,BP⊥MC于点P,求证:DP⊥NP.24.如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC;(2)求∠BEF大小.25.(1)如图1,在四边形ABCD中,AB=CD,E,F分别是AD,BC的中点,连接FE并延长,分别与BA,CD的延长线交于点M,N.求证:∠BME=∠CNE;(提示:取BD的中点H,连接FH,HE作辅助线)(2)如图2,在△ABC中,F是BC边的中点,D是AC边上一点,E是AD的中点,直线FE交BA的延长线于点G,若AB=DC=2,∠FEC=45°,求FE的长度.26.已知正方形ABCD中,点E、F分别为BC、CD上的点,连接AE,BF相交于点H,且AE⊥BF.(1)如图1,连接AC交BF于点G,求证:∠AGF=∠AEB+45°;(2)如图2,延长BF到点M,连接MC,若∠BMC=45°,求证:AH+BH=BM;(3)如图3,在(2)的条件下,若点H为BM的三等分点,连接BD,DM,若HE=1,求△BDM的面积.27.(1)如图1,在正方形ABCD中,点O是对角线AC的中点,点E是边BC上一点,连接OE,过点O作OE的垂线交AB于点F.求证:OE=OF.(2)若将(1)中,“正方形ABCD”改为“矩形ABCD”,其他条件不变,如图2,连接EF.ⅰ)求证:∠OEF=∠BAC.ⅱ)试探究线段AF,EF,CE之间数量上满足的关系,并说明理由.参考答案1.解:∵四边形ABCD是矩形,∴∠BAD=90°,设AD=BC=a,AB=DC=b,∵AC=10,BE⊥AC,BE=4,∴a2+b2=102,又∵S矩形ABCD=2S△ABC∴ab=2××10×4=40,∵BC>AB,解得:a=4,b=2,即AD=4,故选:D.2.解:连接OB,过B作BM⊥x轴于M,∵点B的坐标是(1,3),∴OM=1,BM=3,由勾股定理得:OB==,∵四边形OABC是矩形,∴AC=OB,∴AC=,故选:C.3.解:过F作FQ⊥BC于Q,则∠FQE=90°,∵△ABC是等边三角形,AB=6,∴BC=AB=6,∠B=60°,∵BD=BE,DE=2,∴△BED是等边三角形,且边长为2,∴BE=DE=2,∠BED=60°,∴CE=BC﹣BE=4,∵四边形DEFG是正方形,DE=2,∴EF=DE=2,∠DEF=90°,∴∠FEC=180°﹣60°﹣90°=30°,∴QF=EF=1,∴△EFC的面积为==2,故选:B.4.解:①∵EF=2,∴OE=4,∵AO=AB=6,∴AE=AO+OE=6+4=10,故正确;②∵∠AOC=90°,∠DOE=45°,∴∠COD=180°﹣∠AOC﹣∠DOE=45°,故正确;③作FG⊥CO交CO的延长线于G,则FG=2,∴△COF的面积S△COF=×6×2=6,故正确;④作DH⊥AB于H,CF==2,BH=6﹣2=4,DH=6+2=8,BD==4,故错误.故选:A.5.解:∵四边形ABCD是矩形,∴∠ADC=90°,AC=BD=10,OA=OC=AC=5,OB=OD=BD=5,∴OC=OD,∴∠ODC=∠OCD,∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,∴∠EDC=22.5°,∠EDA=67.5°,∵DE⊥AC,∴∠DEC=90°,∴∠DCE=90°﹣∠EDC=67.5°,∴∠ODC=∠OCD=67.5°,∴∠ODC+∠OCD+∠DOC=180°,∴∠COD=45°,∴OE=DE,∵OE2+DE2=OD2,∴(2DE)2=OD2=25,∴DE=,故选:D.6.解:如图,过点O作OM⊥CE于M,作ON⊥DE交ED的延长线于N,∵∠CED=90°,∴四边形OMEN是矩形,∴∠MON=90°,∵∠COM+∠DOM=∠DON+∠DOM,∴∠COM=∠DON,∵四边形ABCD是正方形,∴OC=OD,在△COM和△DON中,,∴△COM≌△DON(AAS),∴OM=ON,CM=DN,∴四边形OMEN是正方形,∵OE=2,∴2NE2=OE2=(2)2=8,∴NE=ON=2,∵DE+CE=DE+EM+MC=DE+EM+DN=EN+EM=2EN=4,设DE=a,CE=b,∴a+b=4,∵CE•DE=5,∴CD2=a2+b2=(a+b)2﹣2ab=42﹣2×5=6.∴S正方形ABCD=6.故选:B.7.解:连接BE、EM、BM,作BE的垂直平分线GH分别与DA的延长线、BC的延长线交于点G、H,过D作DN⊥GH于点N,连接EH,过H作HK⊥AD,与AD的延长线交于点K,∵∠ABC=∠PEF=90°,M是PF的中点,∴BM=EM,∴无论P点运动到什么位置时,M点始终在BE的垂直平分线上,∴M点在GH上,当M与N点重合时,DM=DN的值最小,设EH=x,∵GH是BE的垂直平分线,∴BH=EH=x,∴∠EHG=∠BHG,∵GD∥BH,∴∠EHG=∠BHG=∠G,∴EG=EH=x,∵∠ABH=∠BAK=∠K=90°,∴四边形ABHK为矩形,∴AK=BH=x,AB=KH=6,∵AD=8,点E在边AD上,且AE:ED=1:3,∴AE=2,ED=6,∴EK=AK﹣AE=x﹣2,∵EH2﹣EK2=KH2,∴x2﹣(x﹣2)2=62,解得,x=10,∴GE=x=10,GD=EG+DE=x+6=10+6=16,∵OE∥DN,∴△GEO∽△GDN,∴,∴DN=EO,∵,∴EO=BE=,∴,即线段DM长的最小值为,解法二:建立如图坐标系,过点F作FJ⊥AD于J.则D(8,6),E(2,6),设P(0,a),由△P AE∽△EJF,可得EM=18﹣3a,∴F(20﹣3a,0),∵PM=MF,∴M(10﹣0.5a,0.5a),∴DM==,∴当a=﹣=时,DM的值最小,此时DM=.故选:A.8.解:如图:当点F与点C重合时,点P在P1处,CP1=DP1,当点F与点E重合时,点P在P2处,EP2=DP2,∴P1P2∥CE且P1P2=CE.当点F在EC上除点C、E的位置处时,有DP=FP.由中位线定理可知:P1P∥CE且P1P=CF.∴点P的运动轨迹是线段P1P2,∴当BP⊥P1P2时,PB取得最小值.∵矩形ABCD中,AB=2,AD=1,E为AB的中点,∴△CBE、△ADE、△BCP1为等腰直角三角形,CP1=1.∴∠ADE=∠CDE=∠CP1B=45°,∠DEC=90°.∴∠DP2P1=90°.∴∠DP1P2=45°.∴∠P2P1B=90°,即BP1⊥P1P2,∴BP的最小值为BP1的长.在等腰直角BCP1中,CP1=BC=1.∴BP1=.∴PB的最小值是.故选:C.9.解:∵▱ABCD,∴AB∥CD,AD∥BC∵PE∥BC,∴PE∥AD∵PF∥CD,∴PF∥AB,∴四边形AEPF为▱.设▱AEPF的对角线AP、EF相交于O,则AO=PO,EO=FO,∠AOE=∠POF ∴△POF≌△AOE,∴图中阴影部分的面积等于△ABC的面积,过A作AM⊥BC交BC于M,∵∠B=60°,AB=4,∴AM=2,S△ABC=×5×2=5,即阴影部分的面积等于5.故填5.10.解:在矩形ABCD中,AC=2OB,∵△AOB是正三角形,∴OB=AB,∴AC=2AB,①AB=1时,AC=2,根据勾股定理,BC===,所以,矩形的周长=2(AB+BC)=2(1+)=2+2;②BC=1时,根据勾股定理,AB2+BC2=AC2,所以,AB2+12=(2AB)2,解得AB=,所以,矩形的周长=2(AB+BC)=2(+1)=+2;综上所述,矩形的周长为2+2或+2.故答案为:2+2或+2.11.解:作FN⊥x轴于N,EM⊥y轴于M,连接PF.∵四边形PEFC是平行四边形,∴PE=CF,PE∥CF,∴∠FCN=∠ETC,∵EM⊥y轴,FN⊥x轴,∴∠EMP=∠FNC=90°,∵EM∥TC,∴∠MEP=∠ETC,∴∠MEP=∠FCN,∴△EMC≌△CNF(AAS),∴EM=CN=3,∴ON=OC+CN=4+3=7,当PF⊥FN时,PF的值最小,此时PF=ON=7,∴PF的最小值为7.故答案为7.12.解:∵四边形ABCD是正方形,边长为4,∴AD=CD=4 AC⊥BD∠DAO=45°;∴AC2=AD2+CD2=42+42=32,则AC=4,∵EF⊥AC,GE⊥BD,∴∠OGE=∠OFE=90°;又∵AC⊥BD,∴四边形OGEF是矩形;∴EG=OF,又∵∠DAO=∠FCE=45°,∴EF=CF;∵OF+CF=OC=×4=2,∴GE+EF=2.故答案为213.解:设经过t秒,以点P、D、Q、B为顶点组成平行四边形,∵P在AD上运动,∴t≤,即t≤15,∵以点P、D、Q、B为顶点组成平行四边形,∴DP=BQ,分为以下情况:①点Q的运动路线是C﹣B﹣C,方程为4t﹣15=15﹣t,解得:t=6;②点Q的运动路线是C﹣B﹣C﹣B,方程为15﹣(4t﹣30)=15﹣t,③点Q的运动路线是C﹣B﹣C﹣B﹣C,方程为4t﹣45=15﹣t,解得:t=12;故答案为:6或10或12.14.解:∵AC=6cm,BD=4cm,∴AO=AC=×6=3cm,BO=BD=×4=2m,如图1,正方形ACEF在AC的上方时,过点B作BG⊥AF交F A的延长线于G,BG=AO=3cm,FG=AF+AG=6+2=8cm,在Rt△BFG中,BF===cm,如图2,正方形ACEF在AC的下方时,过点B作BG⊥AF于G,BG=AO=3cm,FG=AF﹣AG=6﹣2=4cm,在Rt△BFG中,BF===5cm,综上所述,BF长为5cm或cm.故答案为:5cm或cm.15.解:由图易得:OB=OD,那么△AOD与△AOB的周长相差1cm其实就是AD与AB相差1cm 当AD比AB长1cm时,AD+AB=AB+1+AB=17,AB=8;当AD比AB短1cm时,AD+AB=AB﹣1+AB=17,AB=9.因此AB的长为8或9cm.故AB的长为8或9cm.16.解:如图,在EA上取一点K,使得EK=CE,连接DK,BK,延长DK交AB于H.∵DE=EB,CE=EK,∴四边形BCDK是平行四边形,∴CD=BK,DK∥BC,∵BC⊥AB,∴DH⊥AB,∵DA=DB,∴AH=HB=1,∴KA=KB=CD,在Rt△AKH中,AK=AH÷cos30°=,∴CD=,故答案为.17.解:如图所示,连接BD,∵S正方形ABCD=36,∴AD=6,BD=6,在正方形ABCD和等边△ADE中,∠BAE=∠BAD+∠DAE=90°+60°=150°,AB=AD=AE,∴∠AEB=(180°﹣∠BAE)=(180°﹣150°)=15°,∴∠DEG=∠AED﹣∠AEB=60°﹣15°=45°,∵F为DE的中点,∴AF垂直平分DE,DF=DE=×6=3,∴DG=EG,∴∠GDE=45°=∠DEG,∴△DEG是等腰直角三角形,∴DG=DF=3,∠DGE=90°,∴Rt△BDG中,BG===3.故答案为:3.18.解:如图,延长BG交CH于点E,在△ABG和△CDH中,,∴△ABG≌△CDH(SSS),AG2+BG2=AB2,∴∠1=∠5,∠2=∠6,∠AGB=∠CHD=90°,∴∠1+∠2=90°,∠5+∠6=90°,又∵∠2+∠3=90°,∠4+∠5=90°,∴∠1=∠3=∠5,∠2=∠4=∠6,在△ABG和△BCE中,,∴△ABG≌△BCE(ASA),∴BE=AG=12,CE=BG=9,∠BEC=∠AGB=90°,∴GE=BE﹣BG=12﹣9=3,同理可得HE=3,在Rt△GHE中,GH=,故答案为:3.19.解:∵AD平分∠BAC,∴∠GAF=∠CAF,∵CG⊥AD,∴∠AFG=∠AFC,在△AGF和△ACF中,,∴△AGF≌△ACF(ASA),∴AG=AC=7,GF=CF,则BG=AB﹣AG=10﹣7=3.又∵BE=CE,∴EF是△BCG的中位线,∴EF=BG=1.5.故答案是:1.5.20.解:(1)设AP与BC交于H,∵在平行四边形ABCD中,AD∥BC,∴∠AEB=∠CBE,∵AB=AE,∴∠ABE=∠AEB,∴∠ABE=∠CBE,∴BE平分∠ABC,∵CF是∠ACB的角平分线,BE交CF于点P,∴AP平分∠BAC,∵AB=AC,∴AH垂直平分BC,∴PB=PC;(2)∵AH垂直平分BC,∴AH⊥BC,BH=CH=BC=2,∵∠ABH=45°,∴AH=BH=2,∴平行四边形ABCD的面积=4×2=8.21.(1)证明:∵AD平分∠BAC,∴∠BAD=∠DAE.∵AD⊥BD,∴∠ADB=∠ADE=90°.在△ADB与△ADE中,∴△ADB≌△ADE,∴BD=DE.(2)∵△ADB≌△ADE,∴AE=AB=12,∴EC=AC﹣AE=8.∵M是BC的中点,BD=DE,∴DM=EC=4.22.(1)证明:在菱形ABCD中,OC=AC.∴DE=OC.∵DE∥AC,∴四边形OCED是平行四边形.∴平行四边形OCED是矩形.∴OE=CD.(2)在菱形ABCD中,∠ABC=60°,∴AC=AB=2.∴在矩形OCED中,CE=OD=.在Rt△ACE中,AE=.23.解:如图,∵四边形ABCD为正方形,∴BC=CD,AB∥CD,∠ABC=∠BCD,∴∠PCD=∠BMC,∵BP⊥MC,∴∠PBC+∠BCM=90°,而∠PBC+∠PBM=90°,∴∠PBC=∠BMC,∠MCB=∠BCP,∴△BPC∽△MBC;∴CP:BC=BP:BM=BC:MC,∵BM=BN,BC=CD,∴CP:CD=BP:BN,而∠PCD=∠BMC=∠PBC,∴△BPN∽△CPD,∴∠BPN=∠CPD,∠CPD+∠NPC=90°,∴DP⊥PN.24.(1)证明:∵四边形ABCD是正方形,∴AD∥BF,∴四边形ACFE是平行四边形,∴EF∥AC,(2)解:连接BG,如图所示:∵EF∥AC,∴∠F=∠ACB=45°,∵∠GCF=90°,∴∠CGF=∠F=45°,∴CG=CF,∵AE=CF,∴AE=CG,在△BAE与△BCG中,,∴△BAE≌△BCG(SAS)∴BE=BG,∵BE=EG,∴△BEG是等边三角形,∴∠BEF=60°.25.(1)证明:连接BD,取DB的中点H,连接EH,FH,∵E,H分别是AD,BD的中点,∴EH∥AB,EH=AB,∴∠BME=∠HEF,∵F,H分别是BC,BD的中点,∴FH∥CD,FH=CD,∵AB=CD∴HE=FH,∴∠HEF=∠HFE∴∠BME=∠CNE;(2)连接BD,取DB的中点H,连接EH,FH,∵E,F分别是AD,BC的中点,∴EH=AB,FH=CD,FH∥AC,∴∠HFE=∠FEC=45°,∵AB=CD=2,∴HF=HE=1,∴∠HEF=∠HFE=45°,∴∠EHF=180°﹣∠HFE﹣HEF=90°,∴.26.(1)证明:∵四边形ABCD是正方形,∴∠ABC=∠BCD=90°,∴∠ACB=∠ACD=45°,∵AE⊥BF,∴∠AEB+∠FBC=90°,∵∠FBC+∠BFC=90°∴∠AEB=∠BFC,∵∠AGF=∠BFC+∠ACF,∴∠AGF=∠AEB+45°;(2)解:过C作CK⊥BM于K,∵∠BMC=45°,∴CK=MK,∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠BCD=90°,∴∠ABH=∠BCK,在△ABH与△BCK中,,∴△ABH≌△BCK,∴BH=CK=MK,AH=BK,∴BM=BK+MK=AH+BH;(3)解:由(2)得,BH=CK=BH,∵H为BM的三等分点,∴BH=HK=KM,过E作EN⊥CK于N,∴四边形HENK是矩形,∴HK=EN=BH,∠BHE=∠NEC,在△BHE与△ENC中,,∴△BHE≌△ENC,∴HE=CN=NK=1,∴CK=BH=2,∴BM=6,连接CH,∵HK=MK,CK⊥MH,∠BMC=45°,∴CH=CM,∠MCH=90°,∴∠BCH=∠DCM,在△BHC与△DMC中,,∴△BHC≌△DMC,∴BH=DM=2,∠BHC=∠DMC=135°∴∠DMB=90°,∴△BDM的面积=6.27.证明:(1)连接OB,∵在正方形ABCD中,O是AC的中点,∴OB=OA,∠OAB=∠OBA=∠OBC=45°,∴∠AOB=90°,又∵OE⊥OF,∴∠AOF=∠BOE,在△AOF和△BOE中,,∴△AOF≌△BOE,∴OE=OF;(2)①∵∠EOF=∠FBE=90°,∴O,E,F,B四点共圆,∴∠OBA=∠OEF,∵在矩形ABCD中,O是AC的中点,∴OA=OB,∠OAB=∠OBA,∴∠OEF=∠BAC;②如图,连接BD,延长EO交AD于G,∵BD与AC交于O,则△OGD≌△DEB,∴OG=OE,∴AG=CE,∵OF⊥GE,∴FG=EF,在Rt△AGF中,GF2=AG2+AF2,即EF2=CE2+AF2.。
青岛版八年级数学下册期末检测题试卷四及答案

青岛版八年级数学下册期末检测题四一选择题1.下列根式中是最简二次根式的是 ( )A 12+x B 22y x C 18 D 5.02.已知21aa -=a a-1,则a 的取值范围是 ( ) A a ≤0 B a <0 C 0<a ≤1 D a >03.如图所示,已知△ABC 中,∠ABC =450,AC =4,H 是高AD 和BE 的交点,则线段BH 的长度为 ( ) A 6 B 4 C 23 D 54. 如图,AC 是矩形ABCD 的对角线,E 是边BC 延长线上的一点,AE 与CD 相交于点F , 则图中的相似三角形共有 ( ) A 2对 B 3对 C 4对 D 5对。
(3题图) (4题图) (6题图) (8题图) 5.在Rt △ABC 中,如果每个边都缩小为原来的41,则锐角A 的余弦值 ( )A 缩小41B 扩大4倍C 没有变化D 不能确定 6.正方形网格中,∠AOB 如图放置,则cos ∠AOB 的值为 ( ) A55 B 552 C 21 D 27.下列命题中是真命题的是 ( )A 若︱a ︱=︱b ︱,则a =bB 若a 2=b 2,则a =bC 相等的两个角一定是对顶角D 两组角对应相等的两个三角形相似8.将一直角三角形与两边平行的纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=900;(4)∠4+∠5=1800,其中正确的个数是 ( ) A 1 B 2 C 3 D 49. 若一组数据2,4,x ,6, 8的平均数是6,则这组数据的方差是 ( ) A 22 B 8 C 210 D 40 二填空题10.化简:(1)22()-= ;(2)︱1-2︱= ;(3) (32)2=D C A BH E ┑ E B D C FA A OB 1 2 34511.计算 8+31-221=12.体育老师对甲、乙两名同学分别进行了8次调高测试,经计算,这两名同学成绩的平均数相同,,甲同学 的方差是s 2甲=6.4,乙同学的方差是s 2乙=8.2,那么这两名同学跳高成绩比较稳定的是 同学。
青岛版2024年八年级数学下册期末检测题+答案2

八年级下学期期末检测题一、选择题1、若()2x 24,x 2+=+则的平方根为( )A.16B.±16C.2D.±22、一直角三角形的斜边长比一直角边长大1,另一直角边长为4,则斜边长为( )A.4B.8C.10D.123、下列命题正确的是( )A.矩形不是平行四边形B.相似三角形不一定是全等三角形C.等腰梯形的对角线未必相等D.两直线平行,同位角不一定相等4、如图,在菱形ABCD 中,∠ADC=120°,则OD :OC 等于( )A.3:2B.3:3C.1:2D.3:15、119的估算结果应在( )之间.A 、9到10B 、10到11C 、11到12D 、12到136、如图中字母M 所代表的正方形的面积为( )A.4B.8C.16D.647、甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都是9.2环,方差分别为20.52S =甲,20.61S =乙,20.49S =丙,45.02=丁S ,则成绩最稳定的是( )A 、甲B 、乙C 、丙D 、丁8、如图,点O 王明家的位置,他家门前有一条东西走向的公路,水塔A 位于他家北偏东60°的300米处,那么水塔所在的位置到公路的距离是( )A.150米B.1503C.1003D.15029、如图△ABC 中,AD 垂直BC 于点D,BE 垂直AC 于点E ,AD 与BE 相交于点F ,若BF=AC ,那么∠ABC 的大小是( )AB C DEFA.40°B.45°C.50°D.60° 10、如图所示,在□ABCD 中,E 为AD 中点,已知△DEF 的面积为S ,则△ABE 的面积为( )A.SB.2SC.3SD.4S11、一组数据的方差为S 2,将这组数据的每个数据都加上2,所得到的一组新数据的方差为( )A.S 2B.2+S 2C.2S 2D.4S 212、在Rt △ABC 中,各边长度都扩大10倍,则锐角B 的正弦值( )A.扩大4倍B.扩大2倍C.不变D.缩小2倍二、填空题13、已知最简二次根式a +1与a 24-是同类二次根式,则a=____________.A B C DEF14、如图,已知AB=BE ,BC=BD ,∠1=∠2,那么图中 ≌ ,AC= ,∠ABC= .15、如图E 、F 、G 、H 分别是矩形ABCD 四边上的点,EF 垂直于GH ,若AB=2,BC=3,则EF :GH=____.A B C DEFG H 16、已知正方形的面积为3,点E 为DC 边上一点,DE=1,将线段AE 绕点A 旋转,使点E 落在直线BC 上,落点记为F ,则FC 的长为___________.17、如图:直角三角形纸片ABC 中,∠ABC=90o ,AC=8,BC=6,折叠该纸片使点B 与点C 重合,折痕与AB 、BC 的交点分别为D 、E ,(1)DE 的长为_________;(2)将折叠后的图形沿直线AE 剪开,原纸片被剪成3快,其中最小一块的面积为________________.AB C DE三、解答题18、计算:222sin30tan 60cos 45︒+︒-︒19、如图所示,已知点A 、E 、F 、D 在同一条直线上,AE=DF ,BF ⊥AD ,CE ⊥AD ,垂足分别为F 、E ,BF=CE ,求证:AB ∥CD.A 2 1 DC B14EAFC EB D20、在△ABC 中,∠C=90o ,∠CAB=60°,AD 是∠BAC 的平分线,已知AB=23.求AD 的长.AB CD21、如图所示,在□ABCD 中,对角线AC 、BD 交于点O ,过点O 作直线EF ⊥BD ,分别交AD 、BC 于点E 和点F ,求证:BEDF 是菱形.A BC DE F O参考答案:1-5BCBBB 6-12DDABAAC13.1 14.略 15.3:217.4 4 18.41219.略 21.略。
青岛版八年级下册数学期末测试卷(基础题)

青岛版八年级下册数学期末测试卷一、单选题(共15题,共计45分)1、如图,一棵树在一次强台风中于离地面4米处折断倒下,倒下部分与地面成30°夹角,这棵树在折断前的高度为()米.A.4B.8C.12D.2、在中,,两直角边,,在三角形内有一点到各边的距离相等,则这个距离是()A.1B.2C.3D.43、下列函数是一次函数的是()A.y=﹣8xB.y=﹣C.y=D.y=﹣+24、下列函数图象中,当x>0时,y随x的增大而减小的是()A.y=﹣B.y=xC.y=x 2D.y=﹣(x+1)25、如图,有a、b、c三户家用电路接入电表,相邻电路的电线等距排列,则三户所用电线()A.a户最长B.b户最长C.c户最长D.三户一样6、如图所示的车标,可以看作由“基本图案”经过平移得到的是()A. B. C. D.7、下列说法中不正确的是()A.-1的平方是1B.-1的立方是-1C.-1的平方根是-1D.-1的立方根是-18、点A , B , C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A , B , C , D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有()A.1个B.2个C.3个D.4个9、如图,在平行四边形中,,,,则的长是()A. B. C.3 D.510、某市为了鼓励节约用水,按以下规定收水费:每户每月用水量不超过,则每立方米水费为元,每户用水量超过,则超过的部分每立方米水费2元,设某户一个月所交水费为元,用水量为,则y与x的函数关系用图象表示为()A. B. C.D.11、下列实数中,是无理数的是()A.﹣0.101001B.C.D.﹣12、正比例函数图象y=(1-m)x的图像经过第一,三象限,则m的取值范围是()A.m=1B.m>1 C.m<1D.m≥113、如图,已知点A(﹣8,0),B(2,0),点C在直线y=﹣上,则使△ABC是直角三角形的点C的个数为()A.1B.2C.3D.414、如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是()A.2B.C.D.15、估计的结果在().A.6至7之间B.7至8之间C.8至9之间D.9至10之间二、填空题(共10题,共计30分)16、如图,在▱ABCD中,对角线AC,BD交于点O,AB⊥AC,AH⊥BD于点H,若AB=2,BC=2 ,则AH的长为________.17、计算6 -15 的结果是________.18、计算________.19、比较大小:________ .20、如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=________°21、一辆汽车由A地开往B地,它距离B地的路程s(km)与行驶时间t(h)之间的关系如图所示,如果汽车一直快速行驶,那么可以提前________小时到达B 地.22、如图,,,,,,,垂足分别为D,E,则的长为________.23、不等式组的解集是________ .24、已知,矩形ABCO的对角线AC、BO相交于点D,△ADO是等边三角形,且A 点的坐标为(0,2),则点D的坐标为________.25、)如图,Rt△ABC中,C= 90o,以斜边AB为边向外作正方形 ABDE,且正方形对角线交于点D,连接OC,已知AC=5,OC=6 ,则另一直角边BC的长为________.三、解答题(共5题,共计25分)26、先化简,再求值:,其中X的值从不等式组的整数解中选取.27、如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.28、某超市店庆期间开展了促销活动,出售A,B两种商品,A种商品的标价为60元/件,B种商品的标价为40元/件,活动方案有如下两种,顾客购买商品时只能选择其中的一种方案:A B方案一按标价的“七折”优惠按标价的“八折”优惠方案二若所购商品达到或超过35件(不同商品可累计),均按标价的“七五折”优惠若某单位购买A种商品x件(x>15),购买B种商品的件数比A种商品件数多10件,求该单位选择哪种方案才能获得更多优惠?29、判断下列各式哪些是等式,哪些是不等式,哪些既不是等式也不是不等式.① x+y;② 3x>7;③ 5=2x+3;④ x2>0;⑤ 2x-3y=1;⑥ 52;⑦ 2>3.30、计算:()﹣2+(π﹣3.14)0﹣| |﹣2cos30°.参考答案一、单选题(共15题,共计45分)1、C2、B3、A4、D5、D6、B7、C9、B10、C11、B12、C13、C14、D15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)29、30、。
青岛版2020八年级数学下册平行四边形单元基础达标练习题1(附答案)

青岛版2020八年级数学下册平行四边形单元基础达标练习题1(附答案)1.下列说法正确的是()A.有一组对边平行,另一组对边相等的四边形是平行四边形B.平行四边形的对角线相等C.平行四边形的对角互补,邻角相等D.平行四边形的两组对边分别平行且相等2.在下列条件中,不能够判定一个四边形是平行四边形的是()A.一组对边平行,另一组对边相等B.一组对边平行且相等C.两组对边分别平行D.对角线互相平分3.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.104.如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为()A BC.2 D5.给出下列四个命题⑴一组对边平行的四边形是平行四边形⑵一条对角线平分一个内角的平行四边形是菱形⑶两条对角线互相垂直的矩形是正方形⑷顺次连接四边形四边中点所得的四边形是平行四边形.其中正确命题的个数为()6.下列四边形中不一定为菱形的是( )A .对角线相等的平行四边形B .对角线平分一组对角的平行四边形C .对角线互相垂直的平行四边形D .用两个全等的等边三角形拼成的四边形8.如图,在矩形ABCD 中,E 、F 、G 、H 分别为边AB 、BC 、CD 、DA 的中点.若2AB =,4=AD ,则图中阴影部分的面积为( )A .8B .6C .4D .39.如图,在Rt △ABC 中,∠B =90°,AB =4,BC >AB ,点D 在BC 上,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是( ).A .2B .4C .6D .810.如图,在矩形ABCD 中,AB =4,BC =6,E 为BC 的中点.将△ABE 沿AE 折叠,使点B 落在矩形内点F 处,连接CF ,则△CDF 的面积为( )A .3.6B .4.32C .5.4D .5.7611.已知平行四边形的周长是100cm ,AB :BC=4:1,则AB 的长是______cm .12.如图,在菱形ABCD 中,P 是对角线AC 上的一点,PE AB ⊥于点E ,若5PE =,则点P 到AD 的距离为________.13.如图,,两点被池塘隔开,不能直接测量其距离.于是,小明在岸边选一点,连接,,分别延长到点,,使,,测得,则,间的距离为.14.如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为_______°.15.如图,菱形的一边在轴的负半轴上,是坐标原点,,反比例函数的图像经过点,与交于点,若的面积为20,则的值等于.16.矩形ABCD的两条对角线交于点O,AOD=60o,AD=2,则AB的长为____. 17.如图,矩形ABCD中,AD=3,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是_____.18.如图,把一张矩形的纸沿对角线BD折叠,若AD=8,AB=6,则BE=__.19.如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于_________.20.正方形ABCD的边长为8,点E为正方形边上一点,连接BE,且BE=10,则AE的长为____.21.已知,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H 分别在正方形ABCD边AB、CD、DA上,AH=2.(1)如图1,当DG=2,且点F在边BC上时.求证:①△AHE≌△DGH;②菱形EFGH是正方形;(2)如图2,当点F在正方形ABCD的外部时,连接CF.①探究:点F到直线CD的距离是否发生变化?并说明理由;②设DG=x,△FCG的面积为S,是否存在x的值,使得S=1,若存在,求出x的值;若不存在,请说明理由.22.如图,已知AE是正方形ABCD中∠BAC的平分线,AE交BD、BC于点E、F,AC、BD相交于点O.求证:OF=12 CE.23.已知:如图,∠C=90°,内切圆O分别与BC、AC相切于点D、E,判断四边形ODCE的形状,并说明理由。
青岛版2020八年级数学下册第六章平行四边形自主学习能力达标测试题4(附答案详解)

青岛版2020八年级数学下册第六章平行四边形自主学习能力达标测试题4(附答案详解)1.如图,平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果AC=12,BD=10,AB=m ,那么m 的取值范围是( )A .1<m <11B .2<m <22C .10<m <12D .2<m <62.如图,点P (3,4),⊙P 半径为2,A (2.8,0),B (5.6,0),点M 是⊙P 上的动点,点C 是MB 的中点,则AC 的最小值是( )A .1.4B .32C .52D .2.63.如图,在△ABC 中,点D 、E 分别是边AB 、AC 的中点,已知DE=6cm ,则BC 的长是( )A .3cmB .12cmC .18cmD .9cm 4.如图所示,DE 为△ABC 的中位线,点F 在DE 上,且∠AFB=90°,若AB=6,BC=10,则EF 的长为( )A .1B .2C .3D .55.如图,矩形ABCD 的对角线AC 与BD 相交于点O ,304ADB AB ∠︒=,=,则OC 等于()A.5 B.4 C.3.5 D.36.如图,在▱ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中共有平行四边形()A.6个B.7个C.8个D.9个7.下列命题中,假命题是()A.两组对角分别相等的四边形是平行四边形B.有一条对角线与一组邻边构成等腰三角形的平行四边形是菱形C.一组邻边互相垂直,两组对边分别平行的四边形是矩形D.有一组邻边相等且互相垂直的平行四边形是正方形8.在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长为()A.6 B.5 C.4 D.39.能够判别一个四边形是菱形的条件是()A.一组对角相等且一条对角线平分这组对角B.对角线互相平分C.对角线互相垂直且相等D.对角线相等且互相平分10.平行四边形的对角线分别为,一边长为12,则的值可能是下列各组数中的()A.8与14 B.10与14 C.18与20 D.10与28 11.在□ABCD中,∠A:∠B=2:3,则∠B=____,∠C=_____,∠D=____.12.如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1,则正方形A1B1C1D1的面积为______;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;……以此下去,则正方形A n B n C n D n的面积为______.13.如图,已知矩形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC 上.若BE =3,EC =5,则AB 的长为_____.14.如图,正方形ABCD 中,AB=2,对角线AC ,BD 相交于点O ,将△OBC 绕点B 逆时针旋转得到△O′BC′,当射线O′C′经过点D 时,线段DC′的长为_____.15.在面积为15的平行四边形ABCD 中,过点A 作AE ⊥直线BC 于点E ,作AF ⊥直线CD 于点F .若5AB =,6BC =,则CE CF +的值为__________.16.如图,在Y ABCD 中,AM=13AD ,BD 与MC 相交于点O ,则S △MOD ∶S △BOC =_____.17.用边长为10 cm 的正方形,做了一套七巧板.拼成如图所示的一座“桥”,则“桥”中涂色部分的面积为______cm.18.如图,正方形ABCD 的顶点D 在正方形ECGF 的边EC 上,顶点B 在GC 的延长线上,连接EG 、BE ,EGC ∠的平分线GH 过点D 交BE 于H ,连接HF 交EG 于M ,则MG ME的值为________.19.如图,正方形ABCD 的边长为12,点E 在边AB 上,BE=8,过点E 作EF ∥BC ,分别交BD 、CD 于G 、F 两点.若点P 、Q 分别为DG 、CE 的中点,则PQ 的长为_____.20.正方形ABCD 中,F 是AB 上一点,H 是BC 延长线上一点,连接FH ,将△FBH 沿FH 翻折,使点B 的对应点E 落在AD 上,EH 与CD 交于点G ,连接BG 交FH 于点M ,当GB 平分∠CGE 时,BM=226,AE=8,则ED=_____.21.如图,在□ABCD 中,点E ,F 分别在边AB ,DC 上,且AE =CF ,连接DE ,BF . 求证:DE =BF .22.已知,如图,在Rt ABC V 中,E 是两锐角平分线的交点,ED BC ⊥,EF AC ⊥,垂足分别为D ,F ,求证:四边形CDEF 是正方形.23.在一个平行四边形中若一个角的平分线把一条边分成长是2cm 和3cm•的两条线段,求该平行四边形的周长是多少?24.如图1,若四边形ABCD 、四边形GFED 都是正方形,显然图中有AG CE =,AG CE ⊥;()1当正方形GFED 绕D 旋转到如图2的位置时,AG CE =是否成立?若成立,请给出证明;若不成立,请说明理由;()2当正方形GFED 绕D 旋转到如图3的位置时,延长CE 交AG 于H ,交AD 于M . ①求证:AG CH ⊥;②当4AD =,2DG =时,求CH 的长.25.如图所示,O 为矩形ABCD 的对角线的交点,//DE AC ,//CE BD .()1试判断四边形OCED 的形状,并说明理由;()2若10AB =,12BC =,求四边形OCED 的面积.26.如图:在矩形ABCD 中,E 、F 分别是AB 、AD 边上的点,且BE=AF ,∠1=∠2. (1)Rt △AEF 与Rt △BCE 全等吗?说明理由; (2)△CEF 是不是直角三角形?说明理由.27.如图,在△ABC 中,∠C =2∠B ,D 是BC 上的一点,且AD ⊥AB ,点E 是BD 的中点,连结AE.(1)求证:∠AEC =∠C ;(2)若AE =6.5,AD =5,则△ABE 的周长是多少?28.如图,矩形OABC 的边OA ,OC 分别与坐标轴重合,并且点B 的坐标为OBE ∆.将该矩形沿OB 折叠,使得点A 落在点E 处,OE 与BC 的交点为D .(1)求证:△OBD 为等腰三角形;(2)求点E 的坐标;(3)坐标平面内是否存在一点F ,使得以点B ,E ,F ,O 为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.参考答案1.A【解析】∵四边形ABCD是平行四边形,AC=12,BD=10,∴OA=OC=6,OD=OB=5,在△OAB中,OA﹣OB<m<OA+OB,∴6﹣5<m<6+5,∴1<m<11.故选A.2.B【解析】【分析】如图,连接OP交⊙P于M′,连接OM.因为OA=AB,CM=CB,所以AC=12OM,所以当OM最小时,AC最小,可知当M运动到M′时,OM最小,由此即可解决问题.【详解】如图,连接OP交⊙P于M′,连接OM,由勾股定理得:,∵OA=AB,CM=CB,∴AC=12 OM,∴当OM最小时,AC最小,∴当M运动到M′时,OM最小,此时AC的最小值=12OM′=12(OP﹣PM′)=12×(5-2)=32,故选B.【点睛】本题考查了点与圆的位置关系、坐标与图形的性质、三角形中位线定理、最小值问题等知识,解题的关键是理解圆外一点到圆的最小距离以及最大距离,学会用转化的思想思考问题.3.B【解析】∵点D、E分别是边AB、AC的中点,∴BC=2DE=2×6=12cm,故选B.4.B【解析】∵DE为△ABC的中位线,∴DE=12BC=5,∵∠AFB=90°,D是AB 的中点,∴DF=12AB=3,∴EF=DE﹣DF=2,故选B.5.B【解析】试题解析:∵四边形ABCD是矩形,,,90 AC BD OA OC BAD∴==∠=o,30ADB∠=oQ,∴AC=BD=2AB=8,142OC AC ∴==; 故选B. 点睛:平行四边形的对角线互相平分.6.D【解析】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC .∵AD ∥EF ,CD ∥GH ,∴AB ∥GH ∥CD ,AD ∥EF ∥BC ,∴平行四边形有:▱ABCD ,▱ABHG ,▱CDGH ,▱BCFE ,▱ADFE ,▱AGOE ,▱BEOH ,▱OFCH ,▱OGDF 共9个.即共有9个平行四边形.故选D .7.B【解析】选项A , 两组对角分别相等的四边形是平行四边形,命题正确;选项B ,有一条对角线与一组邻边构成等腰三角形的平行四边形是菱形,命题错误;选项C ,一组邻边互相垂直,两组对边分别平行的四边形是矩形,命题正确;选项D ,有一组邻边相等且互相垂直的平行四边形是正方形,命题正确.故选A.8.C【解析】解:∵∠ACB =90°,D 是AB 的中点,∴CD =12AB =12×8=4.故选C . 9.A【解析】【分析】求出四边形是平行四边形和一组邻边相等,再根据菱形的判定推出,即可判断A ;对角线垂直的平行四边形是菱形,根据以上内容即可判断B 、C 、D .【详解】A 、∵AC 平分∠BAD 和∠BCD , ∴∠BAC=∠DAC=12∠BAD ,∠BCA=∠DCA=12∠BCD , ∵∠BAD=∠BCD , ∴∠BAC=∠DAC=∠BCA=∠DCA , ∴AB=BC ,AB ∥CD ,AD ∥BC , ∴四边形ABCD 是平行四边形, ∵AB=BC , ∴平行四边形ABCD 是菱形,故本选项正确; B 、对角线互相平分的四边形是平行四边形,不一定是菱形,故本选项错误;C 、只有在平行四边形的基础上,添加条件对角线互相垂直的四边形才是菱形,故本选项错误;D、对角线相等且平分的四边形是矩形,不是菱形,故本选项错误;【点睛】本题主要考查了对菱形、平行四边形、矩形的判定的应用,属于基础题型.注意:有一组邻边相等的平行四边形是菱形,对角线互相垂直的平行四边形是菱形.10.C【解析】根据三角形的两边之和大于第三边,两边之差小于第三边,若x y>,则12221222x yx y⎧+>⎪⎪⎨⎪-<⎪⎩,所以符合条件的,x y可能是18与20;所以选C.11.108º,72º,108º【解析】解:∵平行四边形ABCD中,∠A+∠B=180°,又∵∠A:∠B=2:3,∴∠A=72°,∠B=108°,∴∠D=∠B=108°,∠C=∠A=72°.故答案为108º,72º,108º.12.5 5n【解析】已知小正方形ABCD的面积为1,则把它的各边延长一倍后,三角形AA1D1的面积=×2AB×AB=AB2=1,新正方形A1B1C1D1的面积是4×1+1=5,从而正方形A2B2C2D2的面积为5×5=25,以此进行下去…,则正方形A n B n C n D n的面积为5n,故答案为:5, 5n.13.6.【解析】分析:根据折叠的性质得出AF=AB,EF=BE=3,在Rt△EFC中根据勾股定理求出CF=4,设AF=AB=x,则AC=x+4,在Rt△ABC中根据勾股定理列方程即可求出AB的长.详解:由△ABE沿着AE折叠至△AEF的位置可得:AF=AB,EF=BE=3,∠AFE=∠B=90°,在Rt△EFC中根据勾股定理得CF=4,设AF=AB=x,则AC=x+4,在Rt△ABC中根据勾股定理得:AB2+BC2=AC2,即x2+(3+5)2=(x+4)2,解得:x=6,即AB=6.点睛:本题主要考查了矩形中的折叠问题,根据勾股定理列出方程是解决此题的关键.14【解析】【分析】根据正方形与旋转的性质可得,设DC′=x,然后在Rt△BDO′中,根据勾股定理即可求得答案.【详解】∵四边形ABCD是正方形,∴AB=BC=CD=AD=2,∴∵△OBC绕点B逆时针旋转得到△O′BC′,∴,设DC′=x,在Rt△BDO′中,∵BD2=BO′2+O′D2,∴()2=2+)2,∴..【点睛】本题主要考查正方形的性质,旋转的性质,勾股定理.解此题的关键在于熟练掌握其知识点. 15.31+ 【解析】如下图,过A 作AE BC ⊥,AF CD ⊥,∴615AE ⋅=,解得:52AE =, 在Rt AEB V 中,∵90AEB =︒∠,12AE AB =, ∴30ABE ∠=︒,∴532BE =, ∴536CE =-, ∵平行四边形ABCD ,∴30ABE D ∠=∠=︒,∴132AF AD ==, 33DF =,∴335CF =-,∴536335CE CF +=-+-, 31=+. 故答案为:312+.16.4:9【解析】∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∵AM =13AD , ∴==23, ∵AD ∥BC ,∴△DOM ∽△BOC ,∴=()2=,故答案为4:9.17.50【解析】【分析】读图分析阴影部分与整体的位置关系;易得阴影部分的面积即为△ABC 的面积,是原正方形的面积的一半.【详解】观察得到阴影部分为正方形的一半,即为2110=502⨯. 故答案为50.【点睛】本题目考查了七巧板;正方形的性质.主要考查正方形对角线相互垂直平分相等的性质,读图也很关键.根据图形之间的关系得出面积关系是解题关键. 1821【解析】【分析】取EG 中点O, 连接OH, 先证明ΔBCE ≌ΔDCG 推出HG ⊥BE, 再证明ΔBGH ≌ΔEGH, 推出OH 是三角形中位线, 设HN=a, 则BC=2a, 设正方形ECGF 的边长是2b, 则NC=b, CD=2a, 利用ΔDHN ∽ΔDGC, 得到DN HN DC CG=, 求出a 、b 之间的关系,最后由ΔEFM ∽ΔOMH,得2b a+b EM EF OM OH ==,可得EM MG的值可得答案. 【详解】解:取EG 中点O,连接OHQ 四边形ABCD 是正方形,∴BC=DC,∠BCE=o 90,同理可得CE=CG, ∠DCG=o 90,在ΔBCE 和ΔDCG 中,BC=DC ,∠BCE=∠DCG=o 90,CE=CG∴ΔBCE ≌ΔDCG,∴∠BEC=∠DGC ,Q ∠EDH=∠CDG, ∠DGC+∠CDG=o 90,∴∠EDH+∠BEC=o 90,∴∠EHD=o 90,∴HG ⊥BE,在ΔBGH 和ΔEGH 中, ∠EHG=∠BHG ,HG=HG ,∠EGH=∠BGH∴ΔBGH ≌ΔEGH,∴BH=EH,Q EH=HB , EO=OG ,∴HO //BG,HO=12BG=12EF, 设EC 和OH 相交于点N.设HN=a,则BC=2a,设正方形ECGF 的边长是2b,则NC=b, CD=2a,Q OH//BC,∴ΔDHN ∽ΔDGC,∴DN HN DC CG =,即:b-2a a =2a 2b, 即:22a +2ab-b =0解得2或2) b (舍去),则a b-1, Q EF//OH,∴ΔEFM~ΔOMH, ∴2b a+bEM EF OM OH == ∴2b a+3b EM OE =,b a+3bEM EG =,∴b 1a a+2b +2bEM MG ==,∴1MG ME =1.【点睛】本题主要考查正方形的性质及三角形相似.19.【解析】【分析】根据题意作出合适的辅助线,利用三角形中位线定理、三角形的相似可以求得PH 和QH 的长,然后根据勾股定理即可求得PQ 的长.【详解】作QM ⊥EF 于点M ,作PN ⊥EF 于点N ,作QH ⊥PN 交PN 的延长线于点H ,如图所示,∵正方形ABCD 的边长为12,BE=8,EF ∥BC ,点P 、Q 分别为DG 、CE 的中点, ∴DF=4,CF=8,EF=12,∴MQ=4,PN=2,MF=6,∵QM ⊥EF ,PN ⊥EF ,BE=8,DF=4,∴△EGB ∽△FGD , ∴EG BE FG DF=, 即1284FG FG -=, 解得,FG=4,∴FN=2,∴MN=6﹣2=4,∴QH=4,∵PH=PN+QM,∴PH=6,∴PQ=22PH QH+=213,故答案为:213.【点睛】本题考查了三角形中位线定理、正方形的性质、勾股定理、相似三角形的判定与性质,正确添加辅助线、结合图形熟练应用相关性质和定理进行解题是关键. 20.4【解析】解:如图,过B作BP⊥EH于P,连接BE,交FH于N,则∠BPG=90°.∵四边形ABCD 是正方形,∴∠BCD=∠ABC=∠BAD=90°,AB=BC,∴∠BCD=∠BPG=90°.∵GB平分∠CGE,∴∠EGB=∠CGB.又∵BG=BG,∴△BPG≌△BCG,∴∠PBG=∠CBG,BP=BC,∴AB=BP.∵∠BAE=∠BPE=90°,BE=BE,∴Rt△ABE≌Rt△PBE(HL),∴∠ABE=∠PBE,∴∠EBG=∠EBP+∠GBP=12∠ABC=45°,由折叠得:BF=EF,BH=EH,∴FH垂直平分BE,∴△BNM是等腰直角三角形.∵BM=226,∴BN=NM=213,∴BE=413.∵AE=8,∴Rt△ABE中,AB=22BE AE-=12,∴AD=12,∴DE=12﹣8=4.故答案为4.点睛:本题考查了翻折变换、正方形的性质、全等三角形的判定和性质、角平分线的定义、勾股定理、线段垂直平分线的性质等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题.21.详见解析【解析】【分析】欲证明DE BF=,只要证明DAEV≌BCFV即可.由四边形ABCD是平行四边形,可证A C∠=∠,AD CB=,从而根据“SAS”可证明DAEV≌BCFV.【详解】证明:Q四边形ABCD是平行四边形,A C∴∠=∠,AD CB=,在DAEV和BCFV中,AD CBA CAE CF=⎧⎪∠=∠⎨⎪=⎩,DAEV∴≌()SASBCFV,DE BF∴=.【点睛】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.22.见解析【解析】【分析】过E作EM⊥AB,根据角平分线的性质可得EF=ED=EM.再证明四边形EFDC是矩形,可根据邻边相等的矩形是正方形得到四边形CDEF是正方形.【详解】证明:过E作EM AB⊥,∵AE平分CAB∠,∴EF EM=,∵EB平分CBA∠,∴EM ED=,∴EF ED=,∵ED BC ⊥,EF AC ⊥,ABC V 是直角三角形,∴90CFE CDE C ∠=∠=∠=o ,∴四边形EFDC 是矩形,∵EF ED =,∴四边形CDEF 是正方形.【点睛】考查角平分线的性质,正方形的判定,作出辅助线,熟练掌握角平分线上的点到角两边的距离相等是解题的关键.23.14cm 或16cm【解析】如图,因为AE 平分∠DAB ,所以∠DAE=∠BAE ;因为CD ∥AB ,所以∠DEA=∠BAE ,所以∠DAE=∠DEA ,则△ADE 是等腰三角形,DA=DE.①当DE=2时,AD=DE=2,EC=3,所以CD=5,则平行四边形的周长为5+5+2+2=14; ②当DE=3时,AD=DE=3,EC=2,所以CD=5,则平行四边形的周长为5+5+3+3=16. 答:该平行四边形的周长是14cm 或16cm.24.()1AG CE =成立.证明见解析;(2)①证明见解析,②810CH =. 【解析】【分析】(1)利用SAS 证△ADG ≌△CDE 即可; (2)①同样先证明△ADG ≌△CDE ,得出∠DAG=∠DCE ,而∠DCM+∠DMC=90°,从而∠DAG+∠AMH=90°,结论显然;②连接AC 、CG ,注意到DG ∥AC ,△GAC 与△DAC 的面积相等,于是考虑用等积变换,求出AG 即可求出CH .【详解】()1AG CE =成立.证明:∵四边形ABCD 、四边形DEFG 是正方形,∴GD DE =,AD DC =,90GDE ADC ∠=∠=o . ∴90GDA ADE EDC ∠=-∠=∠o .∴AGD CED ≅V V .∴AG CE =.()2①类似()1可得AGD CED ≅V V ,∴12∠=∠.又∵HMA DMC ∠=∠,∴90AHM ADC ∠=∠=o ,即AG CH ⊥.②连接GE ,交AD 于P ,连接CG ,由题意有2sin451GP PD ==︒=,∴3AP =,10AG =∵EG AD ⊥,CD AD ⊥,∴//EG CD ,∴以CD 为底边的CDG V 的高为1PD =,(延长CD 画高) AGD ACD ACG CGD ACDG S S S S S +==+V V V V 四边形∴41441041CH ⨯+⨯=+⨯∴810CH = 【点睛】本题考查了的四边形的相关知识点,解题的关键是熟练的掌握四边形的性质与应用.25.()1四边形OCED 是菱形,理由见解析;(2)60.【解析】【分析】(1)由条件可先证得四边形OCED 为平行四边形,结合矩形的性质可得OC OD =,可证得结论;(2)连接OE ,可证明四边形BCEO 为平行四边形,可求得OE 的长,结合条件可求得菱形OCED 的面积.【详解】()1四边形OCED 是菱形,理由如下:∵//DE AC ,//CE BD ,∴四边形OCED 是平行四边形,又∵在矩形ABCD 中,OC OD =,∴四边形OCED 是菱形;()2连接OE ,由菱形OCED 得CD OE ⊥,又∵BC CD ⊥,∴//OE BC ,又∵//CE BD ,∴四边形BCEO 是平行四边形,∴12OE BC ==,∴1110126022OCED S OE CD =⋅=⨯⨯=菱形. 【点睛】本题主要考查菱形、矩形的判定和性质,掌握菱形的判定和性质、矩形的对角线相等且平分是解题的关键,即①有一组邻边相等的平行四边形是菱形,②对角线互相垂直的平行四边形是菱形,③四边形都相等的四边形是菱形.26.(1)结论:Rt △AEF 与Rt △BCE 全等(2)结论:△CEF 是直角三角形.【解析】试题分析:(1)根据HL,由BE=AF、EC=EF,即可证明;(2)只要证明∠4+∠5=90°,即可解决问题;试题解析:(1)结论:Rt△AEF与Rt△BCE全等.理由:在矩形ABCD中,∠A=∠B=90°∵BE=AF,∵∠1=∠2,∴CE=EF∴Rt△AEF≌Rt△BCE.(2)结论:△CEF是直角三角形.理由:∵Rt△AEF≌Rt△BCE.∴∠3=∠5,∵∠3+∠4=90°,∠5+∠4=90°,∴∠CEF=180°﹣(∠4+∠5)=180°﹣90°=90°,所以△CEF是直角三角形.27.(1)见解析;(2)25【解析】试题分析:(1)在Rt△ADB中,点E是BD的中点,根据直角三角形的性质,可得BE=AE,故∠AEC=2∠B=∠C;(2)根据直角三角形的性质可得BD=2AE,根据勾股定理可得AB的长,可得答案.试题解析:(1)∵AD⊥AB,∴△ABD为直角三角形,又∵点E是BD的中点,∴AE =12BD =BE , ∴∠B =∠BAE ,∠AEC =∠B +∠BAE =2∠B ,又∵∠C =2∠B ,∴∠AEC =∠C ;(2)在Rt △ABD 中,AD =5,BD =2AE =2×6.5=13,∴AB 2=BD 2-AD 2=132-52=122,∴AB =12,∴△ABE 的周长为AB +BE +AE =12+6.5+6.5=25.28.(1)证明见解析;(2)点E 的坐标为2432(,)55;(3)F 点坐标为1612(,)55-,1612(,)55-,6452(,)55. 【解析】【分析】(1)根据折叠的性质,得到△OBE ≌△OBA ,由此得到∠EOB=∠AOB ,然后根据矩形的性质和平行线的性质得到OD=BD ,即△OBD 是等腰三角形;(2)过点E 作EF x ⊥轴于F 交BC 于G ,设CD 的长为x ,则8BD BC CD x =-=-,由(1)值OD=8-x ,然后根据勾股定理求出CD 、OB 、BD 的长,再根据AAS 证得△OCD ≌△BED ,得到3,4DE CD BE OC ====,最后根据三角形的面积求出EG 的长,进而利用矩形的性质和勾股定理求出E 点的坐标;(3)根据平行四边形的判定与性质,分类讨论F 点的坐标即可.【详解】(1)∵OBE ∆是由OBA ∆折叠所得∴OBE ∆≌OBA ∆.,∴12∠=∠,又∵四边形OABC 是矩形∴//OA BC .,∴13∠=∠∴OD BD =,∴OBD ∆为等腰三角形;(2)过点E 作EF x ⊥轴于F 交BC 于G设CD 的长为x ,则8BD BC CD x =-=-由(1)知8OD BD x ==-∵四边形OABC 是矩形∴90,OCD OAB OC AB ∠=∠=︒=∴在Rt OCD ∆中222OC CD OD +=即()22238x x +=-解得3x =即3,8835CD OD BD x ===-=-=由(1)知OBE ∆≌OBA ∆∴90OEB OAB ∠=∠=︒∴90OCD BED ∠=∠=︒∴ 在△OCD 和△BED 中 OCD BED ODC BDE OD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△OCD ≌△BED∴3,4DE CD BE OC ====∵EF x ⊥轴∴90OFB ∠=︒∵//OA BC∴90CGE OFB ∠=∠=︒∴CG BD ⊥∴1122BDE S DE BE BD EG ∆=⋅=⋅ 即1134522BDE S EG ∆=⨯⨯=⨯ ∴125EG =.∴在Rt DGE ∆中95DG === ∵90OCG OFE CGF ∠=∠=∠=︒∴四边形OFGC 是矩形 ∴924355OF CG CD DG ==+=+= 1232455EF EG GF =+=+=. ∴点E 的坐标为2432,55⎛⎫ ⎪⎝⎭; (3)11612,55F ⎛⎫-⎪⎝⎭ 21612,55F ⎛⎫- ⎪⎝⎭ 36452,55F ⎛⎫ ⎪⎝⎭. 【点睛】 此题主要考查了坐标系与四边形的综合,主要用到全等三角形的判定与性质,矩形的性质,平行四边形的判定与性质,勾股定理等知识,综合性比较强,难度较大.。
青岛版2020八年级数学下册期末综合复习基础过关测试题C(附答案)

青岛版2020八年级数学下册期末综合复习基础过关测试题C (附答案)1.下列计算正确的是( )A .2+3=5B .(-a 2)2=-a 4C .(a -2)2=a 2-4D .2÷12=2 2.-3的相反数是( )A .3B .-3C .3D .-3 3.将如图所示的图案通过平移后可以得到的图案是( )A .B .C .D .4.121的平方根是( )A .11±B .11C .11D 115.下列说法中错误的是( )A .平行四边形的对角线互相平分B .两组对角分別相等的四边形为平行四边形C .对角线互相平分的四边形是平行四边形D .一组对边平行,另一组对边相等的四边形是平行四边形6.在平面直角坐标系中,若直线2y x k =+经过第一、二、三象限,则k 的取值范围是( )A .0k > B .k 0< C .0k ≥ D .0k ≤7.在平行四边形ABCD 中,下列结论一定成立的是( )A .AC BD ⊥B .AB AD =C .A C ∠≠∠D .180A B ∠+∠=o8.有下面的判断:①若△ABC 中,a 2+b 2≠c 2,则△ABC 不是直角三角形;②△ABC 是直角三角形,∠C=90°,则a 2+b 2=c 2;③若△ABC 中,a 2-b 2=c 2,则△ABC 是直角三角形;④若△ABC 是直角三角形,则(a +b)(a -b)=c 2.其中判断正确的有( )A .4个B .3个C .2个D .1个 9.下列不是中心对称图形的是( )A .等边三角形B .正方形C .圆D .平行四边形10.如图,在△ABC 中,D ,E 分别是AB ,AC 的中点,若BC =10,则DE =____.11.如图,在Rt ABC △中,90︒∠=C ,2BC =,30A ︒∠=,点D 是AB 的中点,P 是AC 边上一动点,连接DP ,将DPA V 沿着DP 折叠,A 点落到F 处,DF 与AC交于点E ,当DPF V 的一边与BC 平行时,线段DE 的长为_____.12.如图所示,在平行四边形ABCD 中,∠ABC 的平分线交AD 于E ,且AE =2,DE =1,则平行四边形ABCD 的周长等于_____.13.如图所示,在平面内将△ABC 绕点B 旋转至△A 'BC '的位置时,有AC ∥BC ',∠C =40°,则旋转的角度是______.14.已知直线1:3l y x =-+与直线2:1l y x =+相交于点A .并且1l 交x 轴于点B ,2l 交x 轴于点C .若平面上有一点D ,构成平行四边形ABDC ,请写出D 点坐标________.15.如果点(3,)M m 在直线523y x =-+上,则m 的值是__________. 16.若|x 3(y+33)2=0,则(x•y )2013=________. 17.当a=2,b=32时,a 2﹣b 3= .18.不等式组54257263x x x x -≤+⎧⎨+<+⎩的整数解的和是_______.19.如图,△ABC 是等边三角形,高AD 、BE 相交于点H ,BC=43,在BE 上截取BG=2,以GE 为边作等边三角形GEF ,则△ABH 与△GEF 重叠(阴影)部分的面积为_____.20.一辆轿车从甲地出发开往乙地,同时,一辆客车从乙地开往甲地,一开始两车的速度相同,出发半小时后,客车因出现故障维修了一段时间,修好后为了不耽误乘客的时间,客车加快速度前进,结果与轿车同时到达各自的目的地.设轿车出发th 后,与客车的距离为Skm ,图中的折线(A→B→C→D→E )表示S 与t 之间的函数关系.(1)甲、乙两地相距 km ,轿车的速度为 km/h ;(2)求m 与n 的值;(3)求客车修好后行驶的速度;(4)求线段DE 所对应的函数关系式,并注明自变量的取值范围.21.已知:关于x ,y 的方程组52,25 4.x y a x y a +=-⎧⎨-=+⎩的解满足0x y >>. (1)求a 的取值范围;(2)化简8232a a +--.22.计算与解方程()1计算:023(1)8(2)--()2解方程:3(4)27x +=-.23.某物流公司引进A ,B 两种机器人用来搬运某种货物,这两种机器人充满电后可以连续搬运5小时,A 种机器人于某日0时开始搬运,过了1小时,B 种机器人也开始搬运,如图,线段OG 表示A 种机器人的搬运量A y (千克)与时间x (时)的函数图像,线段EF表示B种机器人的搬运量B y(千克)与时间x(时)的函数图像,根据图像提供的信息,解答下列问题:(1)求B y关于x的函数解析式;(2)如果A、B两种机器人连续搬运5个小时,那么B种机器人比A种机器人多搬运了多少千克?24.如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.(1)求证:△BDF是等腰三角形;(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.①判断四边形BFDG的形状,并说明理由;②若AB=6,AD=8,求FG的长.25.直线y=kx+b经过(-1,0)和(1,4),(1)求这条直线的解析式;(2)求关于x的不等式kx+b≤ 0的解集.26.已知,矩形中,,,的垂直平分线分别交、于点、,垂足为.(1)如图,连接、.求证四边形为菱形,并求的长;(2)如图,动点、分别从、两点同时出发,沿和各边匀速运动一周.即点自→→→停止,点自→→→停止.在运动过程中,①已知点的速度为每秒5,点的速度为每秒4,运动时间为秒,当、、、四点为顶点的四边形是平行四边形时,求的值. ②若点、的运动路程分别为、(单位:,),已知、、、四点为顶点的四边形是平行四边形,写出与满足的数量关系式.(直接写出答案,不要求证明)27.如图,在ABC V 中,D 是边AB 的中点,E 是边AC 上一动点,连接DE ,过点D 作DF ⊥DE 交边BC 于点F (点F 与点B 、C 不重合),延长FD 到点G ,使DG DF =,连接EF 、AG ,已知10AB =,6BC =,8AC =.(1)试说明GAB B ∠=∠;(2)请你连接EG ,设AE x =,CF y =,求y 关于x 的函数关系式;(3)当BDF V 是以BF 为腰的等腰三角形时,直接写出AE 的长,不必说明理由. 28.计算:112(tan 30)(31)13--︒+-+-.29.如图,在梯形ABCD 中,AD //BC ,E 是AD 的中点,BC =5,AD =12,梯形高为4,∠A =45°,P 为AD 边上的动点.(1)当P A 的值为____________时,以点P 、B 、C 、E 为顶点的四边形为直角梯形;(2)当P A 的值为____________时,以点P 、B 、C 、E 为顶点的四边形为平行四边形;(3)点P 在AD 边上运动的过程中,以P 、B 、C 、E 为顶点的四边形能否构成菱形?如果能,求出P A 长.如果不能,也请说明理由.参考答案1.D【解析】【分析】分别利用二次根式混合运算法则以及积的乘方运算法则以及幂的乘方运算法则、完全平方公式计算得出答案.【详解】解:A.B. (-a2)2=a4,故错误;C. (a-2)2=a2-4a+4,故错误;,故正确.故选D.【点睛】此题主要考查了二次根式混合运算以及积的乘方运算以及幂的乘方运算、完全平方公式等知识,正确掌握相关运算法则是解题关键.2.C【解析】【分析】根据一个数的相反数就是在这个数前面添上“-”号,求解即可.【详解】解:=故选C.【点睛】本题考查的知识点是相反数的意义,解题关键是熟记一个数的相反数就是在这个数前面添上“-”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.3.B【解析】【分析】根据平移只改变图形的位置,不改变图形的形状与大小进行分析.【详解】∵图形的平移只改变图形的位置,而不改变图形的形状和大小,∴只有选项B和原图一样.故选:B.【点睛】考查了生活中的平移现象,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转.4.A【解析】【分析】利用平方根的定义求解即可.【详解】()2±,故121的平方根±11,故选A.11=121【点睛】本题考查平方根的定义,要注意一个正数的平方根有两个.5.D【解析】【分析】由平行四边形的性质和判定得出选项A、B、C正确;由一组对边平行,另一组对边相等的四边形是平行边形或梯形,得出选项D错误;即可得出结论.【详解】解:A.平行四边形的对角线互相平分;正确;B.两组对角分別相等的四边形为平行四边形;正确;C.对角线互相平分的四边形是平行四边形;正确;D.一组对边平行,另一组对边相等的四边形是平行边形;错误;故选D.【点睛】本题考查了平行四边形的判定与性质、梯形的定义;熟练掌握平行四边形的判定与性质是解题的关键.6.A【解析】【分析】根据一次函数的图像性质进行求解即可.【详解】∵一次函数y=2x+k的图象经过第一、二、三象限,∴k>0,故选A.【点睛】本题考查一次函数图象与系数的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b 的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b >0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.7.D【解析】【分析】根据平行四边形的性质即可解决问题【详解】解:∵四边形ABCD是平行四边形,∠=∠,AD∥BC,∴A C∴180∠+∠=oA B故选:D【点睛】本题考查学生对平行四边形概念的掌握情况,平行四边形对边平行且相等,对角相等,邻角互补,对角线互相平分.解题的关键是熟练掌握平行四边形的性质,属于中考常考题型.8.B【解析】【分析】根据勾股定理及其逆定理依次判断即可解答.【详解】①c不一定是斜边,①错误;②根据勾股定理可得②正确;③根据勾股定理的逆定理可得③正确;④若△ABC是直角三角形,a是斜边,则(a+b)(a-b)=c2,④正确.共2个正确.故选B.【点睛】本题考查了勾股定理及其逆定理,熟练运用勾股定理及其逆定理是解决问题的关键.9.A【解析】【分析】根据中心对称图形的概念结合选项所给的图形即可得出答案.【详解】A、等边三角形不是中心对称图形,故本选项正确;B、正方形是中心对称图形,故本选项错误;C、圆是中心对称图形,故本选项错误;D、平行四边形是中心对称图形,故本选项错误;故选:A.【点睛】本题考查中心对称图形的概念:在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.10.5【解析】试题分析:∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线,∴BC=2DE,∵BC=10,∴DE=5.故答案为5.考点:三角形中位线定理.11.1或2或233【解析】【分析】 当DPF V 的一边与BC 平行时,会有三种情况,需分别讨论,①://DF BC ,②//DP BC ,③://PF BC ,分别计算出每种情况时线段DE 的长即可.【详解】当DPF V 的一边与BC 平行时,有三种情况,分别讨论:①://DF BC如下图所示,当//DF BC 时,90AED C ︒∠=∠=,则在Rt AED △中,30A ︒∠=,2AD =,则 12AD DE ==; ②: 如下图所示,当//DP BC 时,点A 的对应点F 与点C 、E 重合,由折叠的性质可知2AD DE ==;③: 当//PF BC 时,如下图所示,90CPF APF C ︒∠=∠=∠=,因为折叠,30A F ︒∠=∠=,过点D 作AC 边上的垂线,垂足为H ,则60DEH ︒∠=,根据中位线定理可知12BC DH ==,继而可23DE =【点睛】本题考查折叠的性质,中位线定理,熟知折叠的性质和中位线定理的应用是解题关键,本题属于三角形综合题 .12.10【解析】【分析】根据平行四边形性质AD=BC ,AB=CD ,AD ∥BC ,推出∠AEB=∠EBC ,根据角平分线定义得出∠ABE=∠EBC ,推出∠AEB=∠ABE ,求出AB=CD=AE=2,代入AB+BC+CD+AD 求出即可.【详解】解:∵平行四边形ABCD ,∴AD =BC ,AB =CD ,AD ∥BC ,∴∠AEB =∠EBC ,∵BE 平分∠ABC ,∴∠ABE =∠EBC ,∴∠AEB =∠ABE ,∴AB =AE =DC =2,∵AD =AE+DE =1+2=3,∴平行四边形ABCD 的周长是AB+BC+CD+AD =2+3+2+3=10,故答案为:10.【点睛】本题考查了角平分线定义,平行线性质,平行四边形性质等知识点的应用,关键是求出AE=AB ,难度也不大.13.40°.【解析】【分析】根据旋转角的定义:对应点与旋转中心所连线段的夹角等于旋转角可知∠CBC'为旋转角,由平行线的性质知∠CBC′=∠C ,问题得解.【详解】∵在平面内将△ABC 绕点B 旋转至△A'BC'的位置,∴BC=BC′,∴∠CBC'为旋转角,∵AC ∥BC',∴∠CBC′=∠C=40°,故答案为40°.【点睛】本题主要考查旋转的性质,解题的关键是熟练掌握旋转性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等. 14.(1,-2)【解析】分析:将y=0分别代入直线l 1、l 2中求出x 轴,由此即可得出点B 、C 的坐标,联立两直线解析式成方程组,通过解方程组即可得出交点C 的坐标,再根据平行四边形的性质即可得出线段AD 、BC 的中点重合,结合点A 、B 、C 的坐标即可求出点D 的坐标.详解:当y=-x+3=0时,x=3,∴点B 的坐标为(3,0);当y=x+1时,x=-1,∴点C 的坐标为(-1,0).联立两直线解析式成方程组:31y x y x -+⎧⎨+⎩== ,解得12x y ⎧⎨⎩==∴点A 的坐标为(1,2).∵四边形ABDC 为平行四边形,∴线段AD 、BC 的中点重合,∴点D 的坐标为(3-1-1,0+0-2),即(1,-2).故答案是:(1,-2).点睛:考查了一次函数图象上点的坐标特征、两条直线相交或平行问题、解二元一次方程组以及平行四边形的性质,根据平行四边形的性质结合点A 、B 、C 的坐标求出点D 的坐标是解题的关键.15.-3【解析】∵点()3,M m 在直线523y x =-+上, ∴5323m -⨯+=,解得3m =-.故答案为:-3.16.-1【解析】试题解析:∵|x |+(2=0∴x =0,解得:y=-3∴(x∙y)20132013=(-1)2013=-1. 17.0.【解析】试题分析:将a 与b 的值代入所求的式子,根据平方根以及立方根的性质可得,原式=(2)2﹣(32)3=2﹣2=0.考点:平方根以及立方根的性质.18.5【解析】【分析】求出不等式组的解集,找出解集中的所有整数解,求出它们的和.【详解】54257263x x x x -≤+⎧⎨+<+⎩①②,由①得:x≤3, 由②得:x >1,故不等式组的解集为1<x≤3,即整数解为:2,3,则原不等式的所有整数解的和为2+3=5.故答案为5.考点:一元一次不等式组的整数解.19【解析】试题分析:如图所示,由△ABC 是等边三角形,BC=AD=BE=2BC=6,∠ABG=∠HBD=30°,由直角三角的性质,得∠BHD=90°﹣∠HBD=60°,由对顶角相等,得∠MHE=∠BHD=60°,由BG=2,得EG=BE ﹣BG=6﹣2=4.由GE 为边作等边三角形GEF ,得FG=EG=4,∠EGF=∠GEF=60°,△MHE 是等边三角形;S △ABC =12AC•BE=12AC×EH×3EH=13BE=13×6=2.由三角形外角的性质,得∠BIF=∠FGE ﹣∠IBG=60°﹣30°=30°,由∠IBG=∠BIG=30°,得IG=BG=2,由线段的和差,得IF=FG ﹣IG=4﹣2=2,由对顶角相等,得∠FIN=∠BIG=30°,由∠FIN+∠F=90°,得∠FNI=90°,由锐角三角函数,得FN=1,.S 五边形NIGHM =S △EFG ﹣S △EMH ﹣S △FIN=221421442--.考点:1.等边三角形的判定与性质;2.三角形的重心;3.三角形中位线定理;4.综合题;5.压轴题.20.(1)120,60;(2)m=60,n=0.8;(3)客车修好后行驶的速度为75(千米/时).(4)线段DE所对应的函数关系式为S=135t﹣150(109≤t≤2).【解析】试题分析:(1)结合函数图象,可知当t=0时,S的值即为甲、乙两地之间的距离,再由“速度=路程÷时间”即可得出轿车的速度;(2)根据B点的横坐标结合“两车间减少的距离=两车速度和×行驶时间”即可得出m的值,再由B、C两点间的纵坐标,利用“时间=纵坐标之差÷轿车的速度”可得出点B、C横坐标之差,再加上0.5即可得出n的值;(3)由(2)可知客车修车耽误的时间,根据客车原来的速度可算出该时间段应该行驶的路程,将这段距离平摊到剩下的1.2小时中再加上原来的速度,即可得出客车修好后的速度;(4)利用“时间=路程÷两车速度和”得出点C、D横坐标之差,结合点C的横坐标即可得出点D的坐标,设线段DE所对应的函数关系式为S=kt+b,根据点D、E的坐标利用待定系数法即可得出结论.试题解析:(1)当t=0时,S=120,故甲、乙两地相距为120千米;轿车的速度为:120÷2=60(千米/时).故答案为120;60.(2)当t=0.5时,m=120﹣(60+60)×0.5=60.在BC段只有轿车在行驶,∴n=0.5+(60﹣42)÷60=0.8.故m=60,n=0.8.(3)客车维修的时间为:0.8﹣0.5=0.3(小时),客车修好后行驶的速度为:0.3×60÷(2﹣0.8)+60=75(千米/时).(4)∵42÷(60+75)=1445, ∴点D 的横坐标为:0.8+1445=109, 即点D 的坐标为(109,0). 设线段DE 所对应的函数关系式为S=kt+b ,将点D (109,0)、点E (2,120)代入函数解析式得: 100{91202k b k b=+=+,解得135{150k b ==-. ∴线段DE 所对应的函数关系式为S=135t ﹣150(109≤t≤2). 考点:一次函数的应用;待定系数法21.(1)-14<a<23;(2)11a 【解析】试题分析: (1)将a 看作常数解方程组,根据x >y>0得关于a 的不等式组,解不等式组可得a 的取值范围;(2)根据(1)中a 的范围结合绝对值性质去绝对值符号化简即可;试题解析: 52,25 4.x y a x y a +=-⎧⎨-=+⎩ 解方程组得323x a y a =+⎧⎨=-⎩∵0x y >>,∴a+3>2-3a>0,∴-14<a<23, (2)∵-14<a<23, ∴8a+2>0,3a-2<0 ∴8232a a +--=8a+2+3a-2=11a22.(1)5;(2)-7【解析】【分析】()1直接利用零指数幂的性质和二次根式的性质分别化简得出答案; ()2直接利用立方根的性质化简得出答案.【详解】() 1原式122=++5=;()32(4)27x +=-,则43x +=-,解得:7x =-.【点睛】此题主要考查了实数运算,正确化简立方根是解题关键. 23.(1)9090B y x =-(16x ≤≤);(2)B 种机器人比A 种机器人多搬运了150千克.【解析】【分析】(1)设B y 关于x 的函数解析式为1B y k x b =+,把E 、P 的坐标代入即可得到结论; (2)设A y 关于x 的函数解析式为2A y k x =,把P 的坐标代入即可得到A y 的表达式,令x=6,代入B y ,令x=5,代入A y ,两者相减即可得到结论.【详解】(1)设B y 关于x 的函数解析式为1B y k x b =+(10k ≠), 由线段EF 过点(1,0)E 和点(3,180)P ,得110{3180k b k b +=+=,解得190{90k b ==-, 所以B y 关于x 的函数解析式为9090B y x =-(16x ≤≤);(2)设A y 关于x 的函数解析式为2A y k x =(20k ≠),由题意,得21803k =,即260k =,∴60A y x =;当5x =时,560300A y =⨯=(千克),当6x =时,90690450B y =⨯-=(千克),450300150-=(千克). 答:如果A 、B 两种机器人各连续搬运5小时,那么B 种机器人比A 种机器人多搬运了150千克.24.(1)见解析;(2)①菱形,见解析;②152. 【解析】【分析】(1)根据两直线平行内错角相等及折叠特性判断;(2)①根据已知矩形性质及第一问证得邻边相等判断; ②根据折叠特性设未知边,构造勾股定理列方程求解.【详解】(1)证明:如图1,根据折叠,∠DBC=∠DBE ,又AD ∥BC ,∴∠DBC=∠ADB ,∴∠DBE=∠ADB ,∴DF=BF ,∴△BDF 是等腰三角形;(2)①∵四边形ABCD 是矩形,∴AD ∥BC ,∴FD ∥BG ,又∵DG ∥BE∴四边形BFDG 是平行四边形,∵DF=BF ,∴四边形BFDG 是菱形;②∵AB=6,AD=8,∴BD=10.∴OB=12BD=5. 假设DF=BF=x ,∴AF=AD−DF=8−x. ∴在直角△ABF 中,AB 2+AF 2=BF 2,即62+(8−x) 2=x 2,解得x=254, 即BF=254, ∴22222515=-5=44BF OB ⎛⎫ ⎪⎝⎭-, ∴FG=2FO=152【点睛】 此题考查四边形综合题,解题关键在于利用勾股定理进行计算. 25.(1)y=2x+2;(2)x≤ - 1【解析】分析:(1)把点(-1,0)、(1,4)代入y=kx+b得到关于k、b的二元一次方程组,解出方程组即可;(2)直接解不等式即可.详解:(1)∵直线y=kx+b经过点(-1,0)、(1,4),∴4k bk b-+=⎧⎨+=⎩,解得:k=2,b=2,∴直线的解析式为y=2x+2;(2)∵2x+2≤0,∴x≤ - 1.点睛:本题主要考查了待定系数法求一次函数的解析式和一次函数与不等式的关系,将已知两点的坐标代入解析式得到关于k、b的方程组是解决此题的关键.26.(1)证明略,(2)①秒. ②与满足的函数关系式是【解析】试题分析:(1)先证明四边形AFCE为平行四边形,再根据对角线互相垂直平分的平行四边形是菱形作出判定;根据勾股定理即可求得AF的长;(2)分情况讨论可知,当P点在BF上、Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可.试题解析:(1)证明:①∵四边形是矩形∴∥∴,∵垂直平分,垂足为∴∴≌∴∴四边形为平行四边形又∵∴四边形为菱形②设菱形的边长,则在中,解得∴(2)①显然当点在上时,点在上,此时、、、四点不可能构成平行四边形;同理点在上时,点在或上,也不能构成平行四边形.因此只有当点在上、点在上时,才能构成平行四边形∴以、、、四点为顶点的四边形是平行四边形时,∵点的速度为每秒10cm,点的速度为每秒6cm,运动时间为秒∴,∴,解得∴以、、、四点为顶点的四边形是平行四边形时,秒.②由题意得,以、、、四点为顶点的四边形是平行四边形时,点、在互相平行的对应边上.分三种情况:i)如图1,当点在上、点在上时,,,即ii)如图2,当点在上、点在上时,,,即iii)如图3,当点在上、点在上时,,,即综上所述,与满足的函数关系式是考点:平行四边形,菱形,一次函数27.(1)见解析;(2)473x y -=;(3)AE 的长度为52或258 【解析】 【分析】(1)由D 是AB 中点知AD=DB ,结合DG=DF ,∠ADG=∠BDF 即可证得ADG BDF ≅V V ,从而可得结论;(2)连接EG .根据垂直平分线的判定定理即可证明EF=EG,由△ADG ≌△BDF ,推出∠GAB=∠B ,推出∠EAG=90°,可得EF 2=(8-x )2+y 2,EG 2=x 2+(6-y )2,根据EF=EG ,可得(8-x )2+y 2=x 2+(6-y )2,由此即可解决问题;(3)如图2中,分两种情况讨论即可.①当BF=DB 时.②当DF=FB 时,连接DC ,过点D 作DH ⊥BC 于H ,想办法求出y 的值,再利用(2)的结论即可解决问题. 【详解】(1)∵D 是AB 中点, ∴AD DB =,∵DG DF =,ADG BDF ∠=∠ ∴ADG BDF ≅V V , ∴GAB B ∠=∠. (2)如图,连接EG .∵DG=FD ,DF ⊥DE , ∴EF=EG .∵6BC =,8AC =,∴223664100BC AC +=+=, 又∵2100AB =,∴222BC AC AB +=,∴ABC V 是直角三角形,且90ACB ︒∠=, ∴90CAB B ︒∠+∠=, 由(1)知GAB B ∠=∠ ∴90CAB GAB ︒∠+∠=, ∴90EAG ︒∠=, ∵AE x =,8AC =, ∴8EC x =-, ∵90ACB ︒∠=, ∴222(8)EF x y =-+, ∵ADG BDF ≅V V , ∴AG BF =, ∵CF y =,BC 6=, ∴6AG BF y ==-, ∵90EAG ︒∠=, ∴222(6)EG x y =+-, ∴2222(8)(6)x y x y -+=+-, ∴473x y -=. (3)如图2中,①当BF=DB时,6-y=5,∴y=1,1=473x-,∴x=52,即AE=52.②当DF=FB时,连接DC,过点D作DH⊥BC于H,则DF=FB=6-y,∵∠ACB=90°,D是AB中点,∴DC=DB=5,∵DH⊥BC,BC=6,∴CH=BH=3,∴FH=3-y,∵DH⊥BC,由勾股定理可得DH=4,在Rt△DHF中,(6-y)2=42+(3-y)2,解得y=11 6,∴116=473x-,解得x=258,即AE=258.综上所述,AE的长度为52或258.【点睛】本题考查三角形综合题、勾股定理以及逆定理、全等三角形的判定和性质等知识,解题的关键学会添加常用辅助线,构造直角三角形解决问题,学会用方程的思想思考问题.28.【解析】试题分析:根据零指数幂、负整数指数幂和特殊角的三角函数值进行化简,然后合并即可.试题解析:原式111-=++⎝⎭11=+=.29.(1)4或者9(2)1或11(3)见解析【解析】试题分析:解:25.(1)4或者9 …………2分(2)1或11 …………4分(对1个得1分全对2分)(3)①由(2)可知当PA=1时,四边形PBCE是平行四边形过点B作BF垂直AD,垂足为F,过点C作BG垂直AD,垂足为G∵∠A =45°梯形高为4∴可得AF=4,则EF=2,又∵FG=5∴EG=3,由勾股定理可=∴ CE=BC∴四边形PBCE是菱形…………6分5②由(2)可知当PA=11时,四边形PEBC是平行四边形≠不合题意舍去………8分由上题可知EF=2,BF=4,由勾股定理可得5考点:平行四边形的判定,菱形的性质点评:本题属于灵活变换类试题,其中,菱形的基本性质和判定要熟练把握,勾股定理和其逆定理也是考察的重点。
青岛版八年级数学下册期末检测题试卷七及答案

青岛版八年级数学下册期末检测题七一 选择题 36分每个3分1.下列式子一定是二次根式的是 ( ) A.2--x B.x C.22+x D.22-x2.若b b -=-3)3(2,则 ( )A.b>3B.b<3C.b ≥3D.b ≤33.若13-m 有意义,则m 能取的最小整数值是 ( )A.m=0B.m=1C.m=2D.m=34.化简)22(28+-得 ( )A.—2B.22-C.2D.224-5.下列根式中,最简二次根式是 ( ) A.a 25 B.22b a + C.2a D.5.0 6.如果)6(6-=-⋅x x x x ,那么 ( )A.x ≥0B.x ≥6C.0≤x ≤6D.x 为一切实数7、在Rt △ABC 中,∠C =90°,a =1,c =4,则sinA 的值是( ) A. 1515 B. 13 C. 14 D. 1548、已知△ABC 中,∠C=90°,tanA ·tan 50°=1,那么∠A 的度数是( )A. 50°B. 40°C. (150 )°D. (140)° 9、在直角三角形中,若各边的长度都缩小5倍,那么锐角∠A 的正弦值 ( )A. 扩大5倍B. 缩小5倍C. 没有变化D. 不能确定10、在Rt△ABC 中,∠C=90°,已知a 和A ,则下列关系式中正确的是( )A. c =α·sinAB. c =α sinAC. c =α·cosBD. c =α cosA11、根据下列已知条件,只能画出唯一一个△ABC 的是( )(A )AB =3,BC =4,CA =8 (B )AB =4,BC =3,∠A =30°(C )∠A =60°,∠B =45°,AB =4 (D )∠C =90°,AB =612.下列说法错误的是( )A 、全等三角形的角平分线相等;B 、 周长相等的等腰直角三角形都全等;C 、三角函数值是一个比值;D 、锐角A 的三角函数与角的大小有关,与角A 所在的三角形的大小无关二 填空题30分 每个空3分13.当x___________时,52+x 有意义,若xx -2有意义,则x________. 14.化简=⨯04.0225_________,=-22108117_____________.=⋅y xy 82 ,=⋅2712 .15.比较大小:.(填“>”、“=”、“<”)16.在实数范围内分解因式=-94x ___________ .17、如图:P 是∠α的边OA 上一点,且P 点的坐标为(3,4),则sin α=_____________. 19、当x = 时,xx x x cos sin cos sin -+无意义.(00<x <900 ) 20、已知:tanx=2 ,则sinx+2cosx 2sinx -cosx=____________. 三 解答与证明 54分21. 计算:8分① tan60°-tan45°1+tan60°·tan45° +2sin60°22如图,在△ABC 中,AB=AC ,它的一个外角为80°,底角平分线CD的长为3, 求腰上的高CE 的长.8分23、某型号飞机的机翼形状如图所示,AB ∥CD ,根据数据计算AC 、BD 和CD 的长度(精确到0.1米, 2 ≈1.414, 3 ≈1.732). (10分)24站在水平高度为h 米的地方看到可见的水平距离为d 米,它们近似地符号公式为C58h d 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
青岛版2020八年级数学下册期末模拟测试题(附答案)1.下列图形是中心对称图形的是( )A .B .C .D .2.在△ABC 中,∠A,∠B,∠C 的对边分别是a,b,c ,则满足下列条件但不是直角三角形的是( )A .a 2-c 2=b 2B .a=n 2-1, b=2n, c=n 2+1 ( n >1)C .∠A :∠B :∠C = 3:4:5D .∠A =∠B =12 ∠C 3.甲、乙两车从A 城出发匀速行驶至B 城.在整个行驶过程中,甲、乙两车离开A 城的距离y (千米)与甲车行驶的时间t (小时)之间的函数关系如图所示.则下列结论:①A ,B 两城相距300千米;②乙车比甲车晚出发1小时,却早到1.5小时;③乙车出发后2.5小时追上甲车;④当甲、乙两车相距40千米时,t =32或t =72,其中正确的结论有( )A .1个B .2个C .3个D .4个4.如图,在△ABC 中,高AD 和BE 交于点H ,∠ABC=45°,BE 平分∠ABC,下列结论:①∠DAC= 22.5°;②BH= 2CE ; ③若连结CH,则CH ⊥AB ;④若CD=1,则AH=2;其中正确的有( )A .1个B .2个C .3个D .4个5.直线PQ 上两点的坐标分别是()20,5P -,()10,20Q ,则这条直线所对应的一次函数的解析式为( )A .1152y x =+ B .2y x = C .1152y x =- D .310y x =-6.下列基本图形中,经过平移、旋转或轴对称变换后,不能得到如图的是( )A .B .C .D .7.将直线向下平移个单位后所得直线的解析式为( ) A .B .C .D . 8.已知是整数,则满足条件的最小的正整数n 的值是( ) A .0 B .1 C .2 D .59.下列式子不是二次根式的是( )A .5B .21a +C . 1.2D .1x -- 10.下列不等式中是一元一次不等式的是( )A .2x 2-5>0B .1x +x<5C .-5y+8>0D .2x+2=2(1+x) 11.如图,在ABC ∆中,已知3AC =,4BC =,点D 为边AB 的中点,连结CD ,过点A 作AE CD ⊥于点E ,将ACE ∆沿直线AC 翻折到ACE '∆的位置.若//CE AB ',则CE '=_______.12.菱形ABCD 中,∠A :∠B =1:5,若周长为8,则此菱形的高等于_____.13.如图,在平面直角坐标系中,直线l :y =x +1与y 轴交于点A 1,如图所示依次作正方形A 1B 1C 1O ,正方形A 2B 2C 2C 1……正方形A n B n ∁n C n ﹣1(n 为大于1的整数)使得点A 1,A 2,A 3…A n 在直线上,点C 1,C 2,C 3,…∁n 在x 轴正半轴上,请解决下列问题:(1)点A 6的坐标是 ;点B 6的坐标是 ;(2)点A n 的坐标是 ,正方形A n B n ∁n C n ﹣1的面积是 .14.在Rt △ABC 中,∠ACB=90°,D 为AB 上的中点,若CD=5cm ,则AB=_____________cm.15.已知:如图,在Rt ∆ABC 中,90︒∠=C ,AB=5cm, AC=3cm, 动点P从点B 出发沿射线BC 以2cm/s 的速度移动,设运动的时间为t 秒.t=__________ 时三角形ABP 为直角三角形.16.如果函数y kx b =+的图像平行于直线31y x =-且在y 轴上的截距为2,那么函数y kx b =+的解析式是__________.17.如图,Rt △ABC 中,∠ACB =90°,AB =4,分别以AC 和BC 为边,向外作等腰直角三角形△ACD 和△BCE ,则图中的阴影部分的面积是_____.18.如图,△ABC 中,AB=BC=a(a 为常数),∠B=90°,D 是AC 的中点,E 是BC 延长线上一点,F 是BC 边上一点,DE ⊥DF ,过点C 作CG ⊥BE 交DE 于点G ,则四边形DFCG 的面积为____(用含a 的代数式表示)19.点A (2,﹣1)关于原点对称的点B 的坐标为_____.20.在平行四边形ABCD 中,若260B D ∠+∠=o ,则A ∠的大小为__________(度). 21.如图,在Rt △ABC 中,∠ABC=90° ,∠ACB=30° ,AD 平分∠BAC , BD= 3,点P 为线段AC 上的一个动点(1)求AC 的长(2)作△ABC 中∠ACB 的角平分线CH ,求BH 的长(3)若点E 在直线1上,且在C 点的左侧,PE=PC , AP 为多少时,△ACE 为等腰三角22.某乡村在开展“美丽乡村”建设中,决定购买A ,B 两种树苗对村里的主干道进行绿化改造,已知购买A 种树苗2棵,B 种树苗3棵,共需要260元;购买A 种树苗4棵,B 种树苗5棵,共需要480元.(1)求购买A ,B 两种树苗每棵各需多少元?(2)该乡村现打算用不超过5000元的资金购买这两种树苗,问购买60棵B 种树苗后,至多还能购买多少棵A 种树苗?23.(1)计算11(24)6168-⨯+ (2)解不等式,并把解集在数轴上表示出来.21162x x -+≤-24.上海到北京的G 102次列车平均每小时行驶200公里,每天6:30发车,从北京到上海的G 5次列车平均每小时行驶280公里,每天7:00发车,已知北京到上海高铁线路长约1180公里,问两车几点相遇?25.完成下列各题.(1)计算:())03118212-(2)计算:(()0201412π2121-+--.(3)(0112441238-. (4)计算:()()302125323-⎛⎫-+--+ ⎪⎝⎭. (5)计算:12228323--+-. (6)13128233+-. (7)计算:2318192-⎛⎫- ⎪⎝⎭. 26.甲乙两家商场以同样价格销售相同的商品,在同一促销期间两家商场都让利酬宾.甲商场所有商品都按原价的八折出售,乙商场只对一次购物中超过100元后的价格部分按原价的七折出售.某顾客打算在促销期间到这两家商场中的一家去购物,设该顾客在一(2)该顾客应如何选择这两家商场去购物会更省钱?并说明理由.27.若x=3+22,y=3-22,求2x y xyx y x y+--+-的值.28.求下列各数的算术平方根.(1)169;(2);(3);(4);(5)6.参考答案1.B【解析】【分析】根据轴对称图形与中心对称图形的概念求解即可.【详解】解:A 、不是中心对称图形,不符合题意,故选项A 错误;B 、是中心对称图形,符合题意,故选项B 正确;C 、不是中心对称图形,不符合题意,故选项C 错误;D 、不是中心对称图形,符合题意,故选项D 错误;故选:B .【点睛】本题主要考查了中心对称图形的概念,掌握中心对称图形的概念是解题的关键.2.C【解析】【分析】根据直角三角形的判定方法,利用角,边的关系从而来判定是否是直角三角形.【详解】选项A ,222a c b -=,变形为222a b c =+,90A ∠=o ,即△ABC 是直角三角形; 选项B ,222+=a c b ,90B =o ∠,即△ABC 是直角三角形;选项C ,∵∠A :∠B :∠C =3:4:5,∠A+∠B+∠C =180°,∴∠A =45°,∠B =60°,∠C =75°,即△ABC 不是直角三角形,故本选项错误;选项D ,∠A =∠B =12∠C ,∠A+∠B+∠C=180°,即2∠C =180°,解得∠C =90°,即△ABC 是直角三角形.故选C.【点睛】本题考查直角三角形,解本题需要考生掌握直角三角形的判定方法,利用角,边的关系从而来判定是否是直角三角形.3.A【解析】【分析】由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,进而判断,再令两函数解析式的差为40,可求得t,可得出答案.【详解】由图象可知A、B两城市之间的距离为300km,故①正确;甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,故②错误;设甲车离开A城的距离y与t的关系式为y甲=kt,把(5,300)代入可求得k=60,∴y甲=60t,把y=150代入y甲=60t,可得:t=2.5,设乙车离开A城的距离y与t的关系式为y乙=mt+n,把(1,0)和(2.5,150)代入可得2.5150m nm n+=⎧⎨+=⎩,解得100100mn=⎧⎨=-⎩,∴y乙=100t﹣100,令y甲=y乙可得:60t=100t﹣100,解得t=2.5,即甲、乙两直线的交点横坐标为t=2.5,此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,故③错误;令|y甲﹣y乙|=40,可得|60t﹣100t+100|=40,即|100﹣40t|=40,当100﹣40t=40时,可解得t=32,当100﹣40t=﹣40时,可解得t=72,又当t=23时,y甲=40,此时乙还没出发,当t=133时,乙到达B城,y甲=260;综上可知当t的值为32或72或23或t=133时,两车相距40千米,故④不正确;故选A.【点睛】本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,学会构建一次函数,利用方程组求两个函数的交点坐标,属于中考常考题型.4.C【解析】【分析】①由同角的余角相等易得∠DAC=∠DBH;②由等腰三角形三线合一可得E为AC中点,再证明△ACD≌△BHD,可得BH=AC,即可判断;③由三角形ABC的三条高交于一点,可知连接CH,则CH⊥AB;④由△ACD≌△BHD得DH=CD=1,,易证,即可判断.【详解】①∵∠ABC=45°,BE平分∠ABC,∴∠CBE=22.5°,∵∠DAC+∠ACB=90°,∠CBE+∠ACB=90°,∴∠DAC=∠CBE=22.5°,故①正确;②∵BE平分∠ABC,BE⊥AC,∴AC=2CE∵AD⊥BC,∠ABC=45°,∴∠BAD=∠ABC=45°,∴AD=BD在△ACD和△BHD中,∵∠DAC=∠DBH,AD=BD,∠ADC=∠BDH=90°,∴△ACD≌△BHD(ASA)∴AC=BH∴BH=2CE故②正确;③∵H为△ABC两条高的交点,根据三角形ABC的三条高交于一点,可知连接CH,则CH⊥AB,故③正确;④如图,连接CH,∵△ACD≌△BHD∴DH=CD=1,∵HD⊥DC,∴△CDH为等腰直角三角形,∴2,∠HCD=45°,又∵∠ECB=90°-∠CBE=67.5°,∴∠HCA=22.5°=∠HAC∴2故④错误.①②③正确,故选C.【点睛】本题考查等腰三角形的综合问题,熟练掌握等腰直角三角形的性质以及勾股定理的运用是解决此题的关键.5.A【解析】【分析】利用待定系数法求函数解析式.【详解】解:∵直线y=kx+b经过点P(-20,5),Q(10,20),∴205 1020k bk b-+=⎧⎨+=⎩,解得1215 kb⎧=⎪⎨⎪=⎩,所以,直线解析式为1152y x=+.故选:A.【点睛】本题主要考查待定系数法求函数解析式,是中考的热点之一,需要熟练掌握.解题的关键是掌握待定系数法.6.C【解析】【分析】根据平移、旋转和轴对称的性质即可得出正确结论.【详解】A.经过平移可得到上图,错误;B.经过旋转可得到上图,错误;C.经过平移、旋转或轴对称变换后,都不能得到上图,正确;D.经过旋转可得到上图,错误.故选C.【点睛】本题考查了平移、旋转和轴对称的性质.掌握平移、旋转和轴对称的性质是解题的关键.7.D【解析】【分析】只向下平移,让比例系数不变,常数项减去平移的单位即可.【详解】直线向下平移个单位后所得直线的解析式为故选:D【点睛】本题考查了一次函数图象与几何变换,解题的关键是熟记函数平移的规则“上加下减”.本题属于基础题,难度不大,解决该题型题目时,根据平移的规则求出平移后的函数解析式是关键.8.D【分析】首先化简二次根式进而得出n的最小值.【详解】∵2是整数,∴最小正整数n的值是5.故选D.【点睛】本题考查了二次根式的定义,正确化简二次根式得出是解题的关键.9.D【解析】【分析】a a≥0)是二次根式,可得答案.【详解】A.是二次根式,故A不符合题意;B.是二次根式,故B不符合题意;C.是二次根式,故C不符合题意;D.被开方数小于零,故D符合题意.故选D.【点睛】本题考查了二次根式的定义,二次根式的被开方数是非负数.10.C【解析】【分析】主要依据一元一次不等式的定义进行辨别.含有一个未知数并且未知数的次数是一次的不等式叫一元一次不等式.【详解】A是一元二次不等式;B分母中含有未知数,所以不是一元一次不等式;C是一元一次不等式,D不是不等式,所以只有C正确,【点睛】本题考查一元一次不等式的定义中的未知数的最高次数为1次,本题还要注意一元一次不等式是在整式范围内考虑的.11.95. 【解析】【分析】如图,作CH AB ⊥于H .首先证明90ACB ︒∠=,解直角三角形求出AH ,再证明CE AH '=即可.【详解】解:如图,作CH AB ⊥于H .由翻折可知:90AE C AEC ︒'∠=∠=,ACE ACE '∠=∠,∵//CE AB ',∴ACE CAD '∠=∠,∴ACD CAD ∠=∠,∴DC DA =,∵AD DB =,∴DC DA DB ==, ∴90ACB ︒∠=,∴225AB AC BC +=,∵1122AB CH AC BC =g gg g , ∴125CH =, ∴2295AH AC CH =-=, ∵//CE AB ,∴180E CH AHC ︒'∠+∠=,∵90AHC ︒∠=,∴90E CH ︒'∠=,∴四边形AHCE '是矩形,∴95CE AH '==, 【点睛】本题考查翻折变换,平行线的性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.12.1【解析】【分析】如图作BH ⊥AD ,首先求出∠A=30°,在Rt △ABH 中,可得12BH AB =,由此即可解决问题. 【详解】解:如图,作BH ⊥AD ,∵菱形的周长为8,∴AB=2,BC ∥AD ,∴∠A+∠ABC=180°,∵∠A :∠ABC =1:5,∴∠A=30°,在Rt △ABH 中,112BH AB ==. 故答案是:1.【点睛】本题考查菱形的性质、直角三角形的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.13.(1)(25﹣1,25);(26﹣1,25);(2)(2 n ﹣1﹣1,2n ﹣1),2 2n ﹣2 .【解析】【分析】(1)由题意可得A1,A2,A3,A4的坐标,可得点A坐标规律,由题意可得B1,B2,B3的坐标,可求点B的坐标规律,即可求解.(2)由(1)可得正方形边长,即可求解.【详解】(1)由题意可得正方形OA1B1C1边长为1,正方形A2B2C2C1的边长为2,正方形A3B3C3C2的边长为4,…正方形A n B n∁n C n﹣1的边长为2 n﹣1,∴A1(0,1),A2(1,2),A3(3,4),A4(7,8)…A n(2 n﹣1﹣1,2n﹣1),B1(1,1),B2(3,2),B3(7,4),B4(15,8)…B n(2 n﹣1,2n﹣1),∴A6坐标为(25﹣1,25),B6坐标为(26﹣1,25)故答案为(25﹣1,25),(26﹣1,25)(2)由(1)可知A n(2 n﹣1﹣1,2n﹣1),正方形A n B n∁n C n﹣1的边长为2 n﹣1,∴正方形A n B n∁n C n﹣1的面积=(2 n﹣1)2=2 2n﹣2.故答案为(2 n﹣1﹣1,2n﹣1),2 2n﹣2【点睛】本题考查一次函数图象上点的坐标特征、规律型,解答本题的关键是明确题意,发现题目中点的横纵坐标的变化规律,利用数形结合的思想解答.14.10【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半解答.【详解】∵在Rt△ABC中,∠ACB=90°,D是AB的中点,∴线段CD是斜边AB上的中线;又∵CD=5cm,∴AB=2CD=10cm.故答案是:10.【点睛】本题考查了直角三角形斜边上的中线.直角三角形斜边上的中线等于斜边的一半.15.2s 或258s 【解析】【分析】 根据勾股定理求出BC 的长度,再分两种情况:①当∠APB 为直角时,②当∠BAP 为直角时,分别求出此时的t 值即可.【详解】解:∵∠C=90°,AB=5cm ,AC=3cm ,∴BC=4 cm .①当∠APB 为直角时,点P 与点C 重合,BP=BC=4 cm ,∴t=4÷2=2s .②当∠BAP 为直角时,BP=2tcm ,CP=(2t-4)cm ,AC=3 cm ,在Rt △ACP 中,AP 2=32+(2t-4)2,在Rt △BAP 中,AB 2+AP 2=BP 2,∴52+[32+(2t-4)2]=(2t )2,解得t=258s . 综上,当t=2s 或258s 时,△ABP 为直角三角形. 故答案为:2s 或258s . 【点睛】本题考查了勾股定理以及勾股定理的逆定理的知识,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.16.32y x =+【解析】【分析】利用两直线平行得到k 的值,利用在y 轴上的截距的意义得到b 的值,从而可确定函数y=kx+b 的解析式.∵函数y=kx+b的图象平行于直线y=3x-1且在y轴上的截距为2,∴k=3,b=2,∴函数y=kx+b的解析式为y=3x+2.故答案为y=3x+2.【点睛】本题考查了两条直线的交点或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.17.8【解析】【分析】由勾股定理求出BC2+AC2=AB2=16,由等腰直角三角形的性质和三角形面积公式,即可得出结果.【详解】∵Rt△ABC中,∠ACB=90°,AB=4,∴BC2+AC2=AB2=16,∵△ACD和△BCE是等腰直角三角形,∴图中的阴影部分的面积是:12BC2+12AC2=12×16=8.故答案为:8.【点睛】本题主要考查勾股定理和等腰直角三角形的性质,根据勾股定理求出BC2+AC2的值,是解题的关键.18.1 4 a2【解析】【分析】连结BD,根据等腰直角三角形的性质得到BD=CD,∠FBD=∠GCD=45°,根据等角的余角相等可得∠BDF=∠CDG,根据ASA证明△BDF≌△CDG,再根据三角形面积公式即可求解.连结BD ,∵△ABC 中,AB=BC=a(a 为常数),∠B=90︒,D 是AC 的中点,∴BD=CD,∠FBD=∠FCD=45︒,∵CG ⊥BE ,∴∠FBD=∠GCD=45︒,∵DE ⊥DF ,∴∠BDF=∠CDG ,在△BDF 与△CDG 中,BDF CDG BD CD FBD GCD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△BDF ≌△CDG , ∴四边形DFCG 的面积=2CDF?CDG CDF BDF BCD ABC 1124S S S S S S a +=+===V V V V V V . 故答案为:214a . 【点睛】本题考查全等三角形的判定与性质, 等腰直角三角形的性质.19.(-2,1)【解析】【分析】由关于原点对称的点,横坐标与纵坐标都互为相反数可得出答案.【详解】解:∵关于原点对称的点,横坐标与纵坐标都互为相反数,∴点A (2,-1)关于原点的对称点的坐标为(-2,1).故答案为:(-2,1).本题考查了对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.20.50【解析】【分析】由四边形ABCD是平行四边形,可得∠B=∠D,AD∥BC,又由∠B+∠D=260°,即可求得∠B的度数,继而求得答案.【详解】解:∵四边形ABCD是平行四边形,∴∠A=∠C,AD∥BC,∠B=∠D,∴∠A+∠B=180°,∵∠B+∠D=260°,∴∠B=130°,∴∠A=180°-∠B=50°.故答案为:50.【点睛】本题考查平行四边形的性质.注意掌握平行四边形的对角相等、邻角互补的知识.21.(1)6;(2)639;(3)623-或0或4.【解析】【分析】(1)易得∠BAD=30°,∴AD=2BD,再由勾股定理求出AB,最后再由30°的直角边是斜边的一半可得AC=2AB.(2)过H点作HG⊥AC于点G,设BH=x,在Rt△AHG中用勾股定理建立方程求解;(3)分三种情况讨论:①AC=EC ,②AC=AE ,③AE=EC ,分别根据题意找出P 点的位置,采用(2)的方法建立方程求解.【详解】解:(1)∵∠ABC=90°,∠ACB=30° ∴∠BAC=60°,又∵AD 平分∠BAC∴∠BAD=30°,在Rt △ABD 中,BD=3∴AD=2BD=23 22AB=AD BD =3-在Rt △ABC 中,∠ACB=30°,∴AC=2AB=6(2)如图所示,过H 点作HG ⊥AC 于点G ,在Rt △ABC 中,22BC=AC AB =33-∵CH 平分∠BCA ,∴∠HCB=∠HCG在△HCB 和△HCG 中HGC=HBC HCB=HCG CH=CH ∠∠⎧⎪∠∠⎨⎪⎩∴△HCB ≌△HCG (AAS )∴BH=HG ,CG=BC设BH=x ,则HG=x ,AH=3-x ,AG=633-在Rt △AHG 中,AG ²+HG ²=AH ²,即(()222633+3-=-x x解得639=-x∴BH 的长为639-(3)△ACE 为等腰三角形,①若AC=EC ,如图所示,由PE=PC 可知P 点在EC 的中垂线上,则作EC 的中垂线与AC 的交点即为P 点,∵PF 为EC 的中垂线,∴FC=11EC=AC=322, 在Rt △PCF 中,∵∠C=30°,∴PC=2PF设PF=a ,则PC=2a ,有勾股定理得()222a +3=2a ,解得a=3∴PC=23,∴623=-=-AP AC PC②若AC=AE ,如图所示,此时P 点与A 重合,∴AP=0③若AE=EC ,如图所示,由PE=PC 可知P 点在CE 的中垂线上,所以作EC 的中垂线与AC 的交点即为P 点,设AE=EC=x ,则BE=BC EC=33x -在Rt △ABE 中,由勾股定理得,()222x +3=x -,解得∴EC=又∵PM 垂直平分EC ,∴在Rt △PMC 中,∠C=30°,设PM=y ,则PC=2y ,由勾股定理得()22y =2y ,解得y=1∴PC=2,此时AP=6-2=4综上,当AP 为6-或0或4时,△ACE 为等腰三角形【点睛】本题考查角平分线,中垂线以及勾股定理,(3)问进行分类讨论,根据勾股定理建立方程是关键.22.(1)购买A ,B 两种树苗每棵分别需70元,40元;(2)至多还能购买37棵A 种树苗.【解析】【分析】(1)设购进A 种树苗的单价为x 元/棵,购进B 种树苗的单价为y 元/棵,根据“若购买A 种树苗2棵,B 种树苗3棵,共需要260元;购买A 种树苗4棵,B 种树苗5棵,共需要480元”,即可得出关于x 、y 的二元一次方程组,解之即可得出结论;(2) 设还能购买A 种树苗a 棵,根据用不超过5000元的资金购买这两种树苗,问购买60棵B 种树苗后,即可得出关于a 的一元一次不等式,解之取其中的最大正整数即可得出结论【详解】解:(1)设购买A ,B 两种树苗每棵分别需x 元,y 元由题意得:2326045480x y x y +=⎧⎨+=⎩, 解得7040x y =⎧⎨=⎩. 答:购买A ,B 两种树苗每棵分别需70元,40元.(2)设还能购买A 种树苗a 棵,由题意得:704060a +⨯≤5000解得:a≤1 377.∵树苗的数量为正整数,∴a的最大值为37.∴至多还能购买37棵A种树苗【点睛】此题考查二元一次方程组的应用,一元一次不等式的应用,解题关键在于根据题意列出方程.23.(1)32114+;(2)54x≥,见解析【解析】【分析】(1)首先化简二次根式进而合并求出即可.(2)先把不等式中分母去掉,再来解不等式,然后根据不等式的解集在数轴上表示方法画出图示即可求得.【详解】解:(1)原式=(26﹣6)×6+32=12﹣1+32 4=11+324;(2)去分母得2﹣x≤3(x+1)﹣6,去括号得2﹣x≤3x+3﹣6,移项得﹣x﹣3x≤3﹣6﹣2,合并得﹣4x≤﹣5,系数化为1得x≥54,用数轴表示为:【点睛】此题考查二次根式的加减法,在数轴上表示不等式的解集,解题关键在于掌握运算法则. 24.9时15分【解析】【分析】设从北京到上海的G5次列车行驶x 小时与G102次列车相遇,根据相遇时,两车行驶的路程和等于1180公里列出方程,求解即可.【详解】 7:00-6:30=12小时 设G 5次列车出发x 小时后与G 102次列车相遇,由题意知:1200(200280)11802x ⨯++= 解得:x =2.257+2.25=9.25=9时15分.答:两车于9时15分相遇.【点睛】此题考查一次函数的应用,解题关键在于根据题意列出方程.25.(1)(2)12+;(4)27;(5)1;(7)4. 【解析】【分析】(1)利用有理数的乘方,二次根式以及零次幂的意义化简求出式子的值;(2)利用负整数指数幂,零次幂,二次根式以及有理数的乘方的意义化简,并求出式子的值;(3)先计算零次幂,再进行二次根式的乘法运算即可得解;(4)利用有理数的乘方,负整数指数幂,绝对值以及零次幂的意义进行化简求值即可; (5)先计算绝对值,负整数指数幂和有理数的乘方,再进行二次根式的乘法运算,最后算加减法即可得解;(6)先进行二次根式,立方根和绝对值运算,最后进行加减运算即可;(7)先进行负整数指数幂,立方根和绝对值运算,最后进行加减运算即可;【详解】(1)原式11=-+=(2)原式111122=++=+(3)原式41===(4)原式4275127=+-+=.(5)原式2144133=++-=.(6)原式22=+=(7)原式42134224=+--=+-=.【点睛】此题主要考查了实数的混合运算,在计算过程中要准确运用运算法则,求出准确值. 26.(1)y 1=0.8x ,y 2=x (0≤x ≤100);(2)x >300时,到乙商场购物会更省钱,x =300时,到两家商场去购物花费一样,当x <300时,到甲商场购物会更省钱.理由见解析.【解析】【分析】(1)根据单价乘以数量,可得函数解析式;(2)分类讨论,根据消费的多少,可得不等式,根据解不等式,可得答案.【详解】(1)甲商场写出y 关于x 的函数解析式y 1=0.8x ,乙商场写出y 关于x 的函数解析式y 2=100+(x ﹣100)×0.7=0.7x +30 (x >100),y 2=x (0≤x ≤100);(2)由y 1>y 2,得0.8x >0.7x +30,x >300,当x >300时,到乙商场购物会更省钱;由y 1=y 2得0.8x =0.7x +30,x =300时,到两家商场去购物花费一样;由y 1<y 2,得0.8x <0.7x +30,x <300,当x <300时,到甲商场购物会更省钱;综上所述:x >300时,到乙商场购物会更省钱,x =300时,到两家商场去购物花费一样,当x <300时,到甲商场购物会更省钱.【点睛】本题考查了一次函数的应用,分类讨论是解题关键.27.0【解析】【分析】 先运用平方差及完全平方公式进行因式分解,再约分,将分式化到最简即可.【详解】y x xy y x yx yx --+-+-2 =()()2x y x y x y xy x yx y +-+--+- =2()()()x y x y x y x y x y+---+- =x y x y --+=0. 故当x =3+22,y =3−22时,原式=0.【点睛】本题考查了二次根式的化简求值.运用公式将分子因式分解可使运算简便.由于所求代数式化简之后是一个常数0,与字母取值无关.因而无论x 、y 取何值,原式都等于0. 28.(1);(2);(3);(4);(5)6的算术平方根是. 【解析】【分析】根据算术平方根的定义计算即可.【详解】(1)因为,所以169的算术平方根是13,即.(2)因为,所以的算术平方根是1.即.(3),因为,所以的算术平方根是,即.(4)因为,所以的算术平方根是,即.(5)因为,所以6的算术平方极是.【点睛】此题主要考查了算术平方根的定义,解题时注意:若一个正数x的平方等于a,即x2=a,则这个正数x为a的算术平方根.。
