结构力学几何组成分析例题
结构工程师结构力学几何组成分析例题
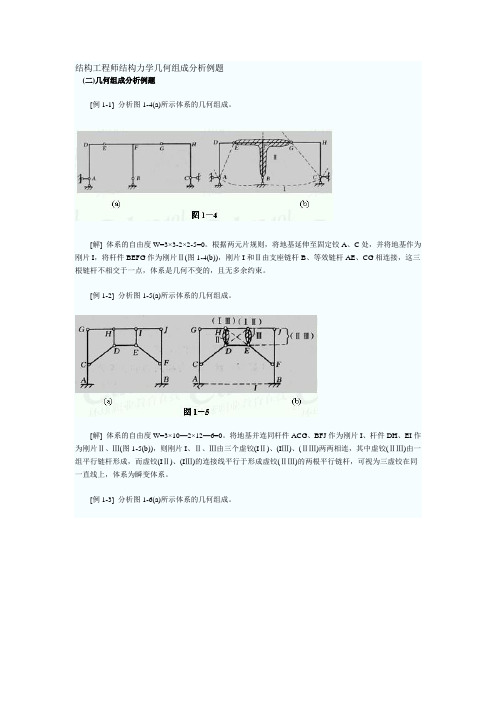
结构工程师结构力学几何组成分析例题(二)几何组成分析例题[例1-1] 分析图1-4(a)所示体系的几何组成。
[解] 体系的自由度W=3×3-2×2-5=0。
根据两元片规则,将地基延伸至固定铰A、C处,并将地基作为刚片I,将杆件BEFG作为刚片Ⅱ(图1-4(b)),刚片I和Ⅱ由支座链杆B、等效链杆AE、CG相连接,这三根链杆不相交于一点,体系是几何不变的,且无多余约束。
[例1-2] 分析图1-5(a)所示体系的几何组成。
[解] 体系的自由度W=3×10—2×12—6=0。
将地基并连同杆件ACG、BFJ作为刚片I、杆件DH、EI作为刚片Ⅱ、Ⅲ(图1-5(b)),则刚片I、Ⅱ、Ⅲ由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,其中虚铰(ⅡⅢ)由一组平行链杆形成,而虚铰(IⅡ)、(IⅢ)的连接线平行于形成虚铰(ⅡⅢ)的两根平行链杆,可视为三虚铰在同一直线上,体系为瞬变体系。
[例1-3] 分析图1-6(a)所示体系的几何组成。
[解] 体系的自由度W=3×8—2×10-4=0。
根据两元片规则,将地基延伸至固定铰A处,并将地基作为刚片I,将CEF作为等效刚片Ⅱ,DB杆作为刚片Ⅲ,这三个刚片由三个虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,如图1-6(b)所示。
因形成无穷远处的两个虚铰(IⅢ)、(ⅡⅢ)的两组平行链杆不相互平行,故体系是无多余约束的几何不变体。
[例1-4] 分析图1-7(a)所示体系的几何组成。
[解] 体系的自由度W=3×9—2×12—3=0。
根据一元片规则,去除图1-7(a)所示体系的一元片,得图1-7(b)所示体系。
再将杆件AB、CE、DF分别作为刚片I、Ⅱ、ⅡⅢ,这三个刚片由三组平行链杆形成的三个无穷远处的虚铰(IⅡ)、(IⅢ)、(ⅡⅢ)两两相连,根据三刚片连接规则,体系为无多余约束的几何可变体系(无穷远处的三个点在一广义直线上)。
结构力学几何组成分析例题讲课文档

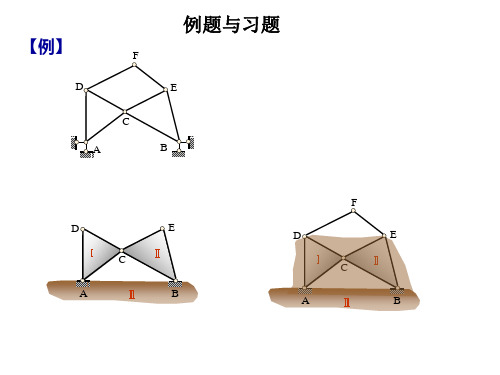
【例】
从基础开始增加杆件。几何不变体系,有4个多余约束
【例】
第二十页,共32页。
去掉与地基相连的约束,
几何不变体系, 没有多余约束。
【例】
【例】
第二十一页,共32页。
将折杆画成直杆,去掉二元体。
几何不变体系,且没有多余约束
瞬变体系, 无多余约束。
【例】
【例】
几何不变体系,且有一 个多余约束。
结构力学几何组成分析例题
第一页,共32页。
【例】
A
B
C
D
E
F
1,3
A
2,3
A
2,3
B 1,2 C
D
E
F
1,2
1,3
B
D
F
C
E
几何不变体系
几何瞬变体系
第二页,共32页。
【例】
【例】
A
第三页,共32页。
去掉二元体
可变体系,少一个约束
从A点开始,依次去掉二元体。 几何不变体系且无多余约束。
【例】
C B A
将ቤተ መጻሕፍቲ ባይዱ
画成
第十七页,共32页。
几何不变体系,没有多余约束。
【例】
BCD
A
EF G
从G点开始依次增加二元体,最后判断平行支链杆只需一 根,几何不变体系, 有一个多余约束。
【例】
从两边去掉二元 体,
几何不变体系, 没 有多余约束。
第十八页,共32页。
【例】 【例】
几何可变体系, 少1个约束
去掉二元体。 几何可变体系,少一个约束。
Ⅲ
Ⅱ
Ⅰ
几何不变体系且没 有多余约束。
对图示体系进行几何组成分析(10分)

一、对图示体系进行几何组成分析。
(10分)解:折杆ABC 、CDE 与BD 形成刚片I ,为几何不变体系且无多余约束。
(5分)刚片I 与地面由4链杆相连,整个结构为几何不变且有1个多余约束。
(5分)二、计算图示静定桁架的支座反力及1、2杆的轴力。
(14分)解:求支座反力)(2),(6),(2↑=↑=←=kN R kN Y kN X B A A (6分)求1、2杆的轴力截面法: )(52025111拉kN N N Y ==+⨯-=∑ (4分) 取E 结点: )(240214022压kN N N Y -==⨯--=∑(4分)三、P = 1在图示静定多跨梁ABCD 上移动。
(1)作截面E 的剪力影响线;(2)画出使Q E 达最大值和最小值时可动均布荷载的最不利布置;(3)当可动均布荷载q = 20 kN/m 时,求Q Emax 值。
(16分)(1) Q E 影响线见图(5分)(2)Q Emax 的最不利位置 (3分)Q Emin 的最不利位置 (3分)(3)kN q Q E 38)5332152521(20max =⨯⨯+⨯⨯⨯=∑=+ω(5分) 四、用力法计算图示刚架,画M 图。
EI 为常数(20分)解:1、一次超静定结构,基本体系和基本未知量,如图 (2分)A B C D E0.40.6 +-+0.4 C C D2、列力法方程 01111=∆+P X δ (1分)3、作图和P M M ___1 (6分)4、计算系数、自由项 EI 14411=δ (3分) EIP 8101-=∆ (3分) 5、解方程 kN X 625.51= (1分)6、作M 图 (4分)五、用位移法计算图示刚架,并作M 图。
各杆EI 为常数。
(20分)解:1、以刚结点角位移为基本未知量,得基本体系 (2分);2、绘1M P M 图(图略) (6分)3、列位移法典型方程: 01111=+P F z k (2分)(4分)图(kNm )33.75六、用力矩分配法绘制图示连续梁的弯矩图。
结构力学第二章 平面体系的几何组成分析

不完全铰节点 1个单铰
13/73
2-1 几何构造分析的几个概念
四、约束 两个互不相连的刚片,若用刚结点连接, 则两者被连为一体成为一个刚片,自由 度由6减少为3。 一个单刚结点相当于3个约束。 单刚结点
三个互不相连的刚片,若用刚结点连接, 自由度由9减少为3。
由此类推:
复刚节点
连接 n 个刚片的复刚结点,它相当于n-1 个单刚结点或3(n- 1)个约束。
A A
1 B
2 C B
1
3
2 C
B 1
A 2
C
几何可变 几何不变 有多余约束
几何不变 无多余约束
规律1 一个刚片与一个点用两根链杆相连,且三个铰不在同一 直线上,则组成几何不变的整体,并且没有多余约束。
23/73
2-2 平面几何不变体系的组成规律
二、两个刚片之间的联结方式
A 2 B I 3 C
A II B I 3 C
16/73
2-1 几何构造分析的几个概念
六、瞬变体系
B 1
I II A
2
I
C
A
II
1 B
2 C
两根链杆彼此共线 1、从微小运动的角度看,这是一个可变体系。 左图两圆弧相切,A点可作微小运动; 右图两圆弧相交,A点被完全固定。
17/73
2-1 几何构造分析的几个概念
六、瞬变体系
B 1
I II A
2
I A 1 B C 2 D
在体系运动的过程中,瞬铰的位臵随之变 化。 用瞬铰替换对应的两个链杆约束,这种约 束的等效变换只适用于瞬时微小运动。
20/73
2-1 几何构造分析的几个概念
八、无穷远处的瞬铰
结构力学习题及答案

构造力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系,那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕,kN F RQB 60=,kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕,m kN M B ⋅=40〔上侧受拉〕,kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c)4Fl M C =〔下侧受拉〕,θcos 2F F L QC =3-2 (a)0=E M ,m kN M F ⋅-=40〔上侧受拉〕,m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕,m kN M DF ⋅=8〔上侧受拉〕,m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕,m kN M DC ⋅=160〔上侧受拉〕,m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕,m kN M BD ⋅=45〔上侧受拉〕,kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕,m kN M DE ⋅=150〔上侧受拉〕,m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕,m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕,m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学几何组成分析例题

[例5] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
J
6
[例6] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
7
[例7] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
8
[例8] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
9
[例9] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
10
结构力学几何组成分析例题
1
结构力学几何组成分析例题
2
[例2] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
3
[例3] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
4
[例4] 试对图示体系进行几何组成分析,如是具有多余约 束的几何不变体系,则须指出多余约束的数目。
结构力学习题

第一部分平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O可视为虚铰。
二、分析题:对下列平面体系进行几何组成分析。
第二部分静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构。
(a) (b)5、图(b)所示结构支座A转动角,= 0, = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB是基本部分,BC是附属部分。
(c)8、图(d)所示结构B支座反力等于P/2。
(d)9、图(e)所示结构中,当改变B点链杆的方向(不通过A铰)时,对该梁的影响是轴力有变化。
(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图(f)所示桁架有7根零杆。
(f) (g)12、图(g)所示桁架有:=== 0。
13、图(h)所示桁架DE杆的内力为零。
(h) (i)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
二、作图题:作出下列结构的弯矩图(组合结构要计算链杆轴力)三、计算题:(求指定杆件的内力)第三部分静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C左侧截面的转角时,其虚拟状态应取:5、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知、图,用图乘法求位移的结果为:。
7、图a、b两种状态中,粱的转角与竖向位移间的关系为:=。
平面杆件体系的几何组成分析典型例题(附详细解题过程)

平面杆件体系的几何组成分析典型例题【例1】对如图1(a)示体系作几何组成分析。
图1【解】(1)对如图1(a)所示体系依次拆除二元体后如图1(b)所示。
(2)选取三个刚片Ⅰ、Ⅱ、Ⅲ,它们由三个虚铰O1、O2、O3两两相连,其中虚铰O1、O3的连线与形成无穷远虚铰O2的两平行链杆不平行。
(3)结论:无多余约束的几何不变体系。
【例2】对如图2(a)所示体系作几何组成分析。
图2【解】(1)根据二元体规则先将结点G固定在基础上,选扩大的基础作为刚片Ⅰ,如图2-(b)所示。
(2)选折杆AF为刚片Ⅱ,两刚片由三根链杆(DE、FG及A处支座链杆)相连,且不交于一点也不互相平行,满足两刚片规则。
(3)结论:无多余约束的几何不变体系。
【例3】对如图3(a)所示体系作几何组成分析。
图3【解】(1)对如图3(a)所示体系依次拆除二元体后如图3(b)所示。
(2)选取三个刚片Ⅰ、Ⅱ、Ⅲ,它们由三个铰O1、O2、O3两两相连,其中铰O1、O2的连线与形成无穷远虚铰O3的两平行链杆不平行。
(3)结论:无多余约束的几何不变体系。
【例4】对如图4所示体系作几何组成分析。
图4【解】对如图4(a)体系进行几何组成分析如下:(1)选取如图4(a)所示的两个刚片Ⅰ、Ⅱ,它们由三根链杆AC、EF及BD相连,且这三根链杆不交于一点也不互相平行,满足两刚片规则,因此上部体系是没有多余约束的几何不变部分。
(2)上部体系与基础间由四根支座链杆相连接。
(3)结论:有一个多余约束的几何不变体系(四根支座链杆中任一根均可看作多余约束)。
对如图4(b)体系进行几何组成分析如下:(1)先根据两刚片规则将杆123及结点7固定在基础上,再根据二元体规则依次固定结点4、5,扩大的基础刚片即刚片Ⅰ。
(2)固定结点6时,由于结点5、6、7共线,结论:几何瞬变体系。
【例5】对如图5(a)所示体系作几何组成分析。
图5【解】选取三个刚片Ⅰ、Ⅱ、Ⅲ,如图5(b)所示,它们由三个铰O1、O2、O3两两相连,其中铰O1、O2的连线与形成无穷远虚铰O3的两平行杆不平行。
02-2结构力学第二章 平面体系的几何组成分析-作业答案汇总

38 3 2 29 3 3
3个单铰结点, 3个折算为2个单铰结点的复铰结点
支杆
b3
11/73
(II III) 刚片II
(I II)
刚片III
几何不变且无多余约束
j9 单链杆:12根 复链杆:2根 折算为6根单链杆
W 2 j b 29 12 6 0
5/73
【作业1】分析图示体系的几何构造
图3
【作业1】分析图示体系的几何构造
图4
先考察如图所示结构
∞(II III)
9/73
【作业2】求图示系统的计算自由度
刚片 m 1 单刚结点 g 4 铰结点 h 0 支杆 b 3
内部无多余约束刚片
W 3m 3g 2h b
31 3 4 3 12
10/73
【作业2】求图示系统的计算自由度
刚片 m 8
单刚结点 g 2
W 3m 3g 2h b
铰结点 h 9
刚片 m 14 单铰链结点 h 18
刚片II
刚片III
(I II)
(I III) 刚片I
瞬变体系
其中折算为2个单铰结点的 复铰结点有6个
∞(II III)
其中折算为3个单铰结点的 复铰结点有2个 单刚结点 2个 g 2 和基础相连的支杆 0个 b 0
W 3m 3g 2h b
314 3 2 218 0
∞(II III)
刚片II (I II) (I III) 刚片III
刚片I
几何不变且无多余约束
(I II) 刚片II (I III) 刚片III
刚片I
几何不变且无多余约束
7/73
【作业2】求图示系统的计算自由度
图1 并进行几何构造分析
结构力学几何组成分析-例题
C B A
D E F
几何不变体系,AB 为一个多余约束。
按增加二元体顺序的不同,多余约束可以是AB、 BC、CD、DE、EF中的任意一个。
【例】
去掉一个多余约束。
去掉一个多余约束。
去掉一个必要约束。
#多余约束的个数是一定的,位 置不一定,但也不是任意的。
【例】
1.去掉与地基的几何 不变体系约束。 2.去掉二元体。
24
24
去掉与地基的连接, 几何不变体系, 无多余约束。 只考虑上部结构
【例】
Ⅰ
Ⅱ
去掉与地基的连接, 只考虑上部结构
几何不变体系, 有一个多余约束。
【例】
12
Ⅰ
Ⅱ
3
【例】
去掉与地基的连接, 只考虑上部结构
用三个链杆相连。几何不变 体系,且没有多余约束。
2
3
4
A
1
5
B
去掉与地基的连接, 只考虑上部结构
二元体。
几何不变体系, 没有 多余约束。
【例】
C B
去掉A、C两个二 元体。几何可变, 少二个约束。
A
【例】
D
E
AC
F
B
D E
F
■AB 、 AC 看 成 加 到 地 基上的二元体。 ■刚片DEF与地基用三 根支链杆相连。
几何不变体系, 且没有多余约束。
【例】
8
7
9
8
7
9
6
10
6
10
1
3
5
1
3
5
【例】
从基础开始增加杆件。几何不变体系,有4个多余约束 【例】
去掉与地基相连的约束, 几何不变体系, 没有多余约束。
《结构力学习题集》
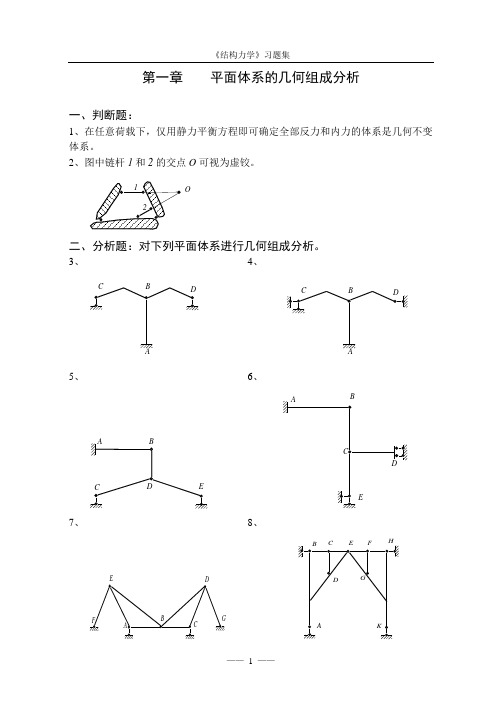
第一章 平面体系的几何组成分析一、判断题:1、在任意荷载下,仅用静力平衡方程即可确定全部反力和内力的体系是几何不变体系。
2、图中链杆1和2的交点O 可视为虚铰。
O二、分析题:对下列平面体系进行几何组成分析。
3、 4、CDBCDB5、 6、A CDBEABCDE7、 8、ABCD GE FA BCDEFGHK11、 12、1234513、 14、15、 16、17、 18、1245321、 22、123456781234523、 24、12345625、 26、27、 28、31、32、33、BA CFDE三、在下列体系中添加支承链杆,使之成为无多余约束的几何不变体系。
34、35、第二章 静定结构内力计算一、判断题:1、静定结构的全部内力及反力,只根据平衡条件求得,且解答是唯一的。
2、静定结构受外界因素影响均产生内力,内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图(a)所示结构||M C =0。
aa(a)BCa aAϕ2a2 (b)5、图(b)所示结构支座A 转动ϕ角,M AB = 0, R C = 0。
6、荷载作用在静定多跨梁的附属部分时,基本部分一般内力不为零。
7、图(c)所示静定结构,在竖向荷载作用下,AB 是基本部分,BC 是附属部分。
ABC(c)8、图(d)所示结构B 支座反力等于P /2()↑。
(d)9、图(e)所示结构中,当改变B 点链杆的方向(不通过A 铰)时,对该梁的影响是轴力有变化。
AB(e)10、在相同跨度及竖向荷载下,拱脚等高的三铰拱,水平推力随矢高减小而减小。
11、图(f)所示桁架有9根零杆。
(f)a a a a(g)12、图(g)所示桁架有:N1=N2=N3= 0。
13、图(h)所示桁架DE杆的内力为零。
a a(h)(i)14、图(i)所示对称桁架在对称荷载作用下,其零杆共有三根。
15、图(j)所示桁架共有三根零杆。
(j)3m3m3m(k)16、图(k)所示结构的零杆有7根。
15级结构力学试题库

第一部分:几何组成分析第二部分:静定梁、刚架内力计算1、作图示结构的M 、N 、Q 图。
a/2a1.5/22、作图示结构的M 、Q 、N 图。
2m 2m4m3、作图示结构的M 、Q 、N 图。
4、作图示结构的M 、Q 、N 图。
q5、作图示结构的M、Q、N图。
2ql6、作图示结构的M、Q、N图。
P7、作图示结构的M图。
3m1m8、作图示结构的弯矩图。
d=2m。
d2d d9、作图示结构的弯矩图。
第三部分:三铰拱、桁架、组合结构内力计算1、求图示桁架杆1的内力。
E2、求图示桁架杆1、2的内力。
a a a3、求图示桁架中a 、b 杆的内力a N 、b N 。
5×4m=20m4、求图示桁架杆1、2、3的内力。
5、作图示结构的内力图。
4m6、求图示桁架杆1、2、3、4的内力。
7、求图示桁架结构杆1和杆2的轴力。
8、求图示桁架结构杆1和杆2的轴力。
a a /2/29、作图示结构的内力图。
kN20第四部分:影响线1、试利用影响线求图示荷载作用下的ME 值。
CD2m1m3m1m10kN2、利用影响线求图示结构在固定荷载作用下的QB 左值。
q2m3m2m第五部分:静定结构位移计算1、图示两跨连续梁在荷载作用下的弯矩图已作出如图所示,试求B 与C 两截面的相对角位移。
EI =常数。
ql图M l2252ql 22ql 52ql2、图示连续梁EI =常数,已知其弯矩图(注意图中弯矩值均须乘以21000ql ),据此计算截面C 的转角。
()图 Mlllql 210003、已知图示结构M 图,求A 点水平位移。
h /4M 图4、试求当图示结构发生所示支座位移时铰A 两侧截面的相对转角A ϕ。
2∆ϕ5、已知荷载作用下结构的M 图如图所示,求横梁的水平位移。
横梁的抗弯刚度为EI 3,竖柱的抗弯刚度均为2EI ,6=l m 。
lM 图 (kN ·m )6、试求图示结构发生所示支座位移时D 点的竖向位移DV ∆和K 两侧截面的相对转角K ϕ。
《结构力学》习题解答(内含解答图)

习题2-13试对图示体系进行几何组成分析。
习题2-13图习题2-13解答图
解:将原图结点进行编号,并将支座6换为单铰,如图(b)。取基础为刚片Ⅰ,△134为刚片Ⅱ,△235为刚片Ⅲ,由规则一知,三刚片用三个不共线的铰联结组成几何不变体。在此基础上增加二元体674、785,而杆38看作多余约束。杆910由铰联结着链杆10,可看作二元体,则整个体系为有一个多余约束的几何不变体系。
习题2-7试对图示体系进行几何组成分析。
习题2-7图习题2-7解答图
解:将题中的折杆用直杆代替,如图(b)所示。杆CD和链杆1由铰D联结构成二元体可以去掉;同理,去掉二元体杆CE和链杆2,去掉二元体ACB,则只剩下基础,故整个体系为几何不变体系,且无多余约束。
另外也可用基础与杆AC、杆BC是由不共线的三个铰联结,组成几何不变体,在此几何不变体上增加二元体杆CD和链杆1、杆CE和链杆2的方法分析。,
习题2-8试对图示体系进行几何组成分析。
习题2-8图习题2-8解答图
解:为了便于分析,对图中的链杆和刚片进行编号,分析过程见图2-21(b)。首先去掉二元体NMI、JNI,然后分析剩余部分。杆AD由固定支撑与基础联结形成一体,构成几何不变体,在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ(注意固定铰支座与铰相同);铰结△GIJ为刚片Ⅱ;刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连,组成几何不变体。
习题2-18试对图示体系进行几何组成分析。
解:将原图结点进行编号,并将固定铰支座换为单铰,如图(b)。折杆AD上联结杆EF,从几何组成来说是多余约束;同理,折杆CD上联结杆EF也是多余约束。取基础为刚片Ⅰ,折杆AD为刚片Ⅱ,折杆CD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由链杆A和杆BD相连,刚片Ⅰ与刚片Ⅲ是由链杆C相连,注意,杆BD只能使用一次。由规则二知,体系为几何可变体系。
结构力学习题及答案

结构力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系,则需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1W=2-1 9-W=2-3 3-W=2-4 2-=W2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
(a)(b)(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
(a)(b)(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。
(a)(b)(c)(d)部分习题答案3-1 (a )m kN M B ⋅=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ⋅=20(上侧受拉),m kN M B ⋅=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ⋅-=40(上侧受拉),m kN M B ⋅-=120(上侧受拉)(b )m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11(下侧受拉)(c )m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10(左侧受拉),m kN M DF ⋅=8(上侧受拉),m kN M DE ⋅=20(右侧受拉) 3-4 m kN M BA ⋅=120(左侧受拉)3-5 m kN M F ⋅=40(左侧受拉),m kN M DC ⋅=160(上侧受拉),m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60(右侧受拉),m kN M BD ⋅=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ⋅=70下(左侧受拉),m kN M DE ⋅=150(上侧受拉),m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0(上侧受拉),m kN M BA ⋅=36.0(右侧受拉) 3-9 m kN M AB ⋅=10(左侧受拉),m kN M BC ⋅=10(上侧受拉) 3-10 (a )错误 (b )错误 (c )错误 (d )正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学典型例题_武汉理工大学范文

第2章平面体系的几何构造分析典型例题1. 对图2.1a体系作几何组成分析。
图2.1分析:图2.1a等效图2.1b(去掉二元体)。
对象:刚片Ⅰ、Ⅱ和Ⅲ;联系:刚片Ⅰ、Ⅲ有虚铰A(杆、2);刚片Ⅱ、Ⅲ有虚铰C(无穷远)(杆3、4);刚片Ⅰ、Ⅱ有虚铰B(杆5、6);结论:三铰共线,几何瞬变体系。
2. 对图2.2a体系作几何组成分析。
图2.1分析:去掉二元体(杆12、杆34和杆56图2.1b),等效图2.1c。
对象:刚片Ⅰ和Ⅱ;联系:三杆:7、8和9;结论:三铰不共线,无多余约束的几何不变体系。
3. 对图2.3a体系作几何组成分析。
图2.3 分析:图2.3a对象:刚片Ⅰ(三角形原则)和大地Ⅱ;联系:铰A和杆1;结论:无多余约束的几何不变体系。
对象:刚片Ⅲ(三角形原则)和大地Ⅱ;联系:杆2、3和4;结论:无多余约束的几何不变体系。
第3章静定结构的受力分析典型题1. 求图3.1结构的内力图。
图3.1解(1)支座反力(单位:kN)由整体平衡,得=100.= 66.67,=-66.67.(2)内力(单位:kN.m制)取AD为脱离体:,,;,,。
取结点D为脱离体:,,取BE为脱离体:3,,。
取结点E为脱离体:,,(3)内力图见图3.1b~d。
2. 判断图3.2a和b桁架中的零杆。
图3.2分析:判断桁架零杆的常用方法是找出桁架中的L型结点和T型结点。
如果这两种结点上无荷载作用.那么L型纪点的两杆及T型结点的非共线杆均为零杆。
解:图3.2a:考察结点C、D、E、I、K、L,这些结点均为T型结点,且没有荷载作用,故杆件CG、DJ、EH、IJ、KH、LF 均为零杆。
考察结点G和H,这两个结点上的两竖向链杆均已判断为零杆,故这两个结点的受力也已成为T型结点的情形.由于没有荷载作用,故杆件AG、BH也为零杆。
整个结构共有8根零杆.如图3.2c虚线所示。
图3.2b:考察结点D,为“K”型结点且无荷载作用,故;对称结构对称荷载(A支座处的水平反力为零),有,故杆件DE和DF必为零杆。
结构工程师结构力学几何组成分析例题

培养孩子的独立性非常重要转眼儿子都已经是大班的小朋友了,在园里已经算得上是大哥哥级别的人物了,很多同龄的小朋友表现出完全的独立性,可是看看宝贝,他却还很欠缺,经常连饭还得追着喂,造成这一事实的,很大的原因在于我们父母和我们的长辈无限的宠爱,无限的过份限制,造成孩子过渡的依赖,也许他在园里可以独立完成很多事,会自己吃饭,会自已收拾玩具,会叠自己的小被子,可是回了家,完全两样,饭来张口衣来伸手,完全地依赖着父母,过度地依赖,造成孩子自信能力的缺失,变得不自信,变得沉默,变得不主动。
所以希望其他父母能引以为鉴,还孩子一个独立的空间,重塑孩子的自信,找回一个自信的独立的孩子。
首先,我认为孩子能自己做的事情,一定要让他自己做。
说起来容易,做起来还真是有点困难,儿子早上有的时候,起迟了,吃饭洗脸刷牙那个慢,我看在眼里,急在心里,恨不得一下子上去帮他解决掉,可是你解决了一次,还得解决N多次,所以最好的办法,就是提早把孩子叫醒,别心疼孩子没睡醒,定时让他起床,不赖床,给他宽裕的时间,解决这些问题就更容易。
第二,孩子自己的事情尽量让他自己拿主意,不要过多的干涉他,孩子和孩子在一起争吵是难免的,千万不要立刻上去干涉他们,他们有他们的处理方式,请淡定,即使孩子在哭着寻求你的帮助时,请你告诉他,妈妈相信你能处理好的.第三,多和孩子沟通,现在我们都很忙,好像和孩子在一起的时间越来越少了,有时就是有时间也会因为累或是其它的原因放弃这个机会。
所以我感觉现在的父母和孩子好像很陌生,是一种心理的陌生,相互的不了解。
如果你不了解你的孩子,你就不可能知道他在想什么,生活中的他做了些什么,那么当遇到问题的时候你就给不了建议,即使你给了,也很可能是不合理的建议,这样会更增加你们之间的矛盾。
如果想避免这种情况你只能和他沟通,我和孩子就什么都说,是自然的闲谈,不是我问他答,在这个过程中我发现孩子有许多问题,千奇百怪,随着他的年龄增长,问题也会涉及不同的方面,有些还是特别需要我们正确引导的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例】
结构力学几何组成分析例题
从两边去掉二元 体, 几何不变体系, 没有多余约束。
【例】 【例】
几何可变体系, 少1个约束
去掉二元体。 几何可变体系,少一个约束。
结构力学几何组成分析例题
【例】
从基础开始增加杆件。几何不变体系,有4个多余约束 【例】
去掉与地基相连的约束, 几何不结变构力体学系几何,组没成分有析多例题余约束。
【例】
()
将折杆画成直杆;
将
画成
瞬变体系
结构力学几何组成分析例题
【例】
去掉二元体;
将
画成
瞬变体系:三杆延长 线交于一点。
结构力学几何组成分析例题
【例】
【例】
三杆平行且等长, 几何可变体系
将折杆用直杆 代替,
将
画成
结构力学几何组成分析例题
几何不变体系,且 没有多余约束。
三铰连三个刚片 【例】
() ()
多 缺
1.去掉与地基的几何不变体系 约束。 2.去掉二元体。
几何可变体系。缺一个必要约束; 多一个多余约束。
去掉二元体。
结构力学几何组可成分变析例体题系。少一个约束。
【例】
A
1去掉二元体。 2从A点开始增加二元体。
【例】
C
D
几何不变体系,没 有多余约束。
1去掉两个二元体。 2 从C、D两点开始增加 二元体CBD,CAD。
结构力学几何组成分析例题
【例】 【例】
() ()
()
几何不变体系, 且,没有多余约束
() ()
()
三铰共线。几何结瞬构力变学几体何组系成,分没析例有题多余约束。
去掉一个多余约束。
去掉一个必要约束。
#多余约束的个数是一定的,位 置不一定,但也不是任意的。
结构力学几何组成分析例题
【例】
1.去掉与地基的几何 不变体系约束。 2.去掉二元体。
几何可变体系,缺二 个约束。
#缺约束的个数是一定的,位置不一定, 但也不是任意的。
结构力学几何组成分析例题
【例】 【例】
AB
结构力学几何组成分析例题
几何不变, 有一个多 余约束。
【例】 【例】 A
折杆可以看成连接 两个端点的支链杆。
从上面去掉两个二 元体。
几何不变体系, 有一 个多余约束。
B
折杆可以看成连接两
个端点的支链杆。
C
A、B、C依次去掉
二元体。
几何不变体系, 没有 多余约束。
结构力学几何组成分析例题
【例】
结构力学几何组成分析例题
【例】 C
B A
D E F
从地基开始,依次依 次增加二元体AEF、 ADE、FCD、CBF。
C B A
D E F
几何不变体系,AB 为一个多余约束。
按增加二元体顺序的不同,多余约束可以是AB、 BC、CD、DE、EF中的任意一个。
结构力学几何组成分析例题
【例】
去掉一个多余约束。
C B
去掉A、C两个二 元体。几何可变, 少二个约束。
A
结构力学几何组成分析例题
【例】
D
E
AC
F
B
■AB 、 AC 看 成 加 到 地 基上的二元体。 ■刚片DEF与地基用三 根支链杆相连。
D E
F
几何不变体系, 且没有多余约束。
结构力学几何组成分析例题
【例】
8
7
9பைடு நூலகம்
8
7
9
6
10
6
10
1
3
5
1
3
5
几何不变体系,且 没有多余约束。
【例】
【例】
去掉与地基的连接, 只考虑上部结构 增加二元体
几何不变, 有4个多余 约束。
将折杆用直结杆构代力学替几何。组成分析几地例题基何相不连变的, 有约多束一。个与
【例】
1 将折杆用直杆代替, 2 去掉二元体。 几何不变体系, 且有一个多余约束。
结构力学几何组成分析例题
【例】
将折杆画成直杆;
将
画成
上部结构为一个刚片, 用四根杆与地基相连。 几何不变有一个多余 约束。
结构力学几何组成分析例题
【例】
将刚片画成直杆;
将
画成
几何不变体系,没有多余约束。
结构力学几何组成分析例题
【例】
BCD
A
EF G
从G点开始依次增加二元体,最后判断平行支链杆只 需一根,几何不变体系, 有一个多余约束。
Ⅰ Ⅱ Ⅲ
()
去掉与地基之间的连接。 上部结构为9根杆, 3根为刚片,6根为约束。几何不变体系, 没有 多余约束。
结构力学几何组成分析例题
【例】
()
()
去掉与地基之间连接的约束, 上部结构可看成 9个刚片,几何不变体系, 没有多余约束。
【例】
()
()
()
去掉与地基之间连接的约束, 上部结构可看成 9个刚片,结几构力何学几不何组变成体分析系例题, 没有多余约束。
【例】
【例】
将折杆画成直杆,去掉二元体。 几何不变体系,且没有多余约束
瞬变体系, 无多余约束。
结构力学几何组成分析例题
【例】
【例】
几何不变体系,且有一 个多余约束。
Ⅲ
Ⅱ
Ⅰ
几何不变体系且没 有多余约束。
【例】
【例】
(1.2)
Ⅲ
(2.3)
Ⅰ
Ⅱ (1.3)
几何不变体系,且没
几何不变体系且没有多
有多余约束。 结构力学几何组成分析例余题约束。
【例】
D
例题与习题
F E
C
A
B
D C
A
F
E
D
E
C
B
A
B
结构力学几何组成分析例题
【例】
A
B
C
D
E
F
1,3
A
2,3
A
2,3
B 1,2 C
D
E
F
1,3 1,2
B
D
F
C
E
几何不变体系
几何瞬变体系
结构力学几何组成分析例题
【例】
【例】 A
去掉二元体 可变体系,少一个约束
从A点开始,依次去掉二元体。 几何不变体系且无多余约束。
24
24
去掉与地基的连接, 几何不变体系, 无多余约束。 只考虑上部结构
【例】
Ⅰ
Ⅱ
去掉与地基的连接, 只考虑上结构部力学结几构何组成分析例题
几何不变体系, 有一个多余约束。
【例】
12
Ⅰ
Ⅱ
3
【例】
去掉与地基的连接, 只考虑上部结构
用三个链杆相连。几何不变 体系,且没有多余约束。
2
3
4
A
1
5
B
去掉与地基的连接, 只考虑上部结结构构力学几何组成分析例题
【例】
Ⅲ Ⅱ
Ⅰ
加上地基共有9个刚片, 瞬变体系。
结构力学几何组成分析例题
【例】
多余
Ⅲ Ⅱ
Ⅰ
将
画成
几何瞬变体系,有1个多余约束 有一个多余约束的结刚构力片学几。何组成分析例题
【例】
【例】
三根支链杆的延长线相交于一点。瞬变体系。
瞬变体系。
结构力学几何组成分析例题
【例】
()
() ()
选两个三角形为刚片,则整个体系可认为 是由9个刚片组成。 瞬变体系,没有多余约束。
