单位根检验、协整检验和格兰杰因果关系检验三者之间的关系_百度解读
ex7Granger

ex7Granger格兰杰(Granger)因果检验【实验⽬的】掌握格兰杰(Granger)因果检验的基本原理及操作。
【实验内容】⼀、Granger因果检验原理;⼆、数据的输⼊;三、单位根检验;四、协整检验;五、格兰杰检验【实验步骤】⼀、理解Granger因果检验原理在经济学上确定⼀个变量的变化是否是另⼀个变量变化的原因,⼀般⽤格兰杰因果关系(Granger Test of Causality)检验。
⽽进⾏格兰杰因果检验⾸先必须证明随机变量是平稳序列,因此,⼀个完整的格兰杰因果检验过程可描述为时间序列的单位根检验、变量之间的协整和格兰杰因果关系检验。
时间序列分析的⼀个难点是变量的平稳性考察,因为⼤部分整体经济时间序列都有⼀个随机趋势,这些时间序列被称为“⾮平稳性”时间序列,当⽤于平稳时间序列的统计⽅法运⽤于⾮平稳的数据分析时,⼈们很容易做出安全错误的判断。
动态计量经济理论要求在进⾏宏观经济实证的分析时,⾸先必须进⾏变量的平稳性检验,否则分析时会出现“伪回归”现象,以此作出的结论很可能是错误的。
对于⾮0阶单整的序列,则可⽤协整检验进⾏分析,因为对于不同时间序列变量,只有在协整的情况下,才可能存在⼀个长期稳定的⽐例关系。
(⼀)单位根检验(unit root test)检验变量是否稳定的过程称为单位根检验。
平稳序列将围绕⼀个均值波动,并有向其靠拢的趋势,⽽⾮平稳过程则不具有这个性质。
⽐较常⽤的单位根检验⽅法是ADF(Augented Dickey-Fuller Test)检验,这是⽬前普遍应⽤的单整检验⽅法。
该检验法的基本原理是通过n次差分的办法将⾮平稳序列转化为平稳序列。
(⼆)协整检验(cointegration test)变量序列之间的协整关系是由Engle和Granger⾸先提出的。
其基本思想在于,尽管两个或两个以上的变量序列为⾮平稳序列,但它们的某种线性组合却可能呈现稳定性,则这两个变量之间便存在长期稳定关系即协整关系。
单位根检验、协整检验和格兰杰因果关系检验三者之间的关系

实证检验步骤:先做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;若非平稳,进行差分,当进行到第i次差分时序列平稳,则服从i阶单整(注意趋势、截距不同情况选择,根据P值和原假设判定)。
若所有检验序列均服从同阶单整,可构造VAR模型,做协整检验(注意滞后期的选择),判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。
如果有,则可以构造VEC模型或者进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。
一、讨论一1、单位根检验是序列的平稳性检验,如果不检验序列的平稳性直接OLS容易导致伪回归。
2、当检验的数据是平稳的(即不存在单位根),要想进一步考察变量的因果联系,可以采用格兰杰因果检验,但要做格兰杰检验的前提是数据必须是平稳的,否则不能做。
3、当检验的数据是非平稳(即存在单位根),并且各个序列是同阶单整(协整检验的前提),想进一步确定变量之间是否存在协整关系,可以进行协整检验,协整检验主要有EG两步法和JJ检验A、EG两步法是基于回归残差的检验,可以通过建立OLS模型检验其残差平稳性B、JJ检验是基于回归系数的检验,前提是建立VAR模型(即模型符合ADL模式)4、当变量之间存在协整关系时,可以建立ECM进一步考察短期关系,Eviews这里还提供了一个Wald-Granger检验,但此时的格兰杰已经不是因果关系检验,而是变量外生性检验,请注意识别二、讨论二1、格兰杰检验只能用于平稳序列!这是格兰杰检验的前提,而其因果关系并非我们通常理解的因与果的关系,而是说x的前期变化能有效地解释y的变化,所以称其为“格兰杰原因”。
2、非平稳序列很可能出现伪回归,协整的意义就是检验它们的回归方程所描述的因果关系是否是伪回归,即检验变量之间是否存在稳定的关系。
所以,非平稳序列的因果关系检验就是协整检验。
3、平稳性检验有3个作用:1)检验平稳性,若平稳,做格兰杰检验,非平稳,作协正检验。
格兰杰因果关系检验

• 格兰杰因果关系检验概述 • 格兰杰因果关系检验的步骤 • 格兰杰因果关系检验的应用 • 格兰杰因果关系检验的局限性
• 格兰杰因果关系检验与其他方法的 比较
• 格兰杰因果关系检验的未来发展
01
格兰杰因果关系检验概述
定义与特点
定义
格兰杰因果关系检验是一种用于检验 两个时间序列变量之间是否存在一种 因果关系的统计方法。
自然科学领域的应用
1 2
气候变化与环境因素
研究气候变化与环境因素之间的因果关系,为环 境保护和可持续发展提供科学依据。
生物种群动态与环境因素
分析生物种群数量变化与环境因素之间的因果关 系,揭示生物种群动态的机制。
3
地之间的因果关系,为地 质灾害防治提供科学依据。
检验方法的改进与优化
非参数检验方法
针对参数检验方法的局限性,可以考虑使用非参数检验方法,如基于秩的检验或核密度 估计方法。
考虑非平稳性
对于非平稳时间序列数据,可以使用差分或协整技术来处理,以更准确地检测格兰杰因 果关系。
考虑其他相关因素
在解释格兰杰因果关系时,应综合考虑其他相关因素,如经济理论、市场环境等,以更 全面地理解因果关系的实际意义。
VS
相同点
格兰杰因果关系检验和其他因果关系检验 方法都是为了确定两个变量之间的因果关 系,为进一步的研究或决策提供依据。
与其他时间序列分析方法的比较
不同点
相同点
格兰杰因果关系检验专注于分析时间序列数 据中的因果关系,而其他时间序列分析方法, 如平稳性检验、季节性分解、趋势分析等, 则是针对时间序列数据的不同特征进行描述 和分析。
国际贸易与汇率
分析国际贸易流量和汇率变动之间的因果关系,揭示国际贸易对汇 率的影响机制。
计量、单位根、协整、格兰杰

一、向量自回归理论:对于简单的两变量的问题,这时解释变量与被解释变量之间的回归方程形式很容易确定,但是如果我们要处理多个变量之间的问题,对于哪个变量是被解释变量,哪些变量作为解释变量我们事先并不确定,对于这种相关变量交织在一起的,相互影响的问题,我们用一般的回归形式无法解决,这时我们就可以建立向量自回归模型,对系统中可能存在的关系作总体分析。
向量自回归模型是处理多个相关经济指标的分析与预测最容易操作的模型之一,常用于预测相关联系的时间序列系统及分析随机扰动对变量系统的动态冲击,从而解释各种经济冲击对经济变量形成的影响。
举例,用V AR模型研究货币政策股票市场的关系,货币政策选取货币供应量和利率两个变量,股票市场用股票价格的收益率来代表。
货币供应量课分别选取M0,M1,M2,利率变量用20天加权平均银行同业拆借利率表示,股票价格选取上证综指收益率。
在Eviews 下,打开Group组数据,Quick命令下选V AR,只需选择滞后阶数即可,一般月度数据p<12,季度数据p<4(这是在数据非常大时),若选取的数据不够多,p小于等于4即可。
这时eviews会给出我们选取的变量之间的所有关系方程中的系数,具有显著性的即为有影响的变量。
二、Granger因果检验这里的因果不是一般的因果关系,而是从预测的角度看变量x能否解释y的变动,主要看现在的y能够在多大程度上被过去的x解释,加入x的滞后值是否使解释程度提高。
进行Granger检验前必须对序列进行平稳性检验,只有平稳的数据序列才能进行Granger检验。
在eviews中,对于定义的组数据,view下选Granger Causality,输入相应的滞后阶数即可。
滞后阶数p应相对大一些,p的选择不同的得出的检验结果是不同的,滞后阶数越大越能完整反映所构造模型的动态特征,但是滞后阶数太大,又会使得估计的参数过多,模型的自由度就减少,一般不同的经济问题有不同的选择。
EG两步法单位根协整回归格兰杰
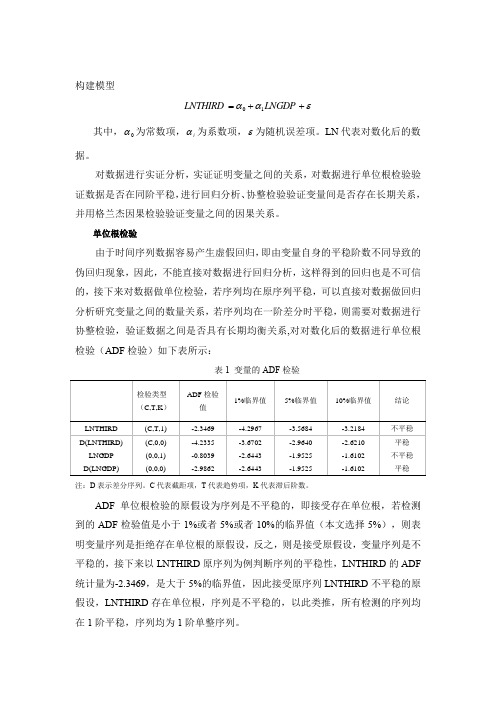
构建模型εαα++=LNGDP LNTHIRD 10其中,0α为常数项,i α为系数项,ε为随机误差项。
LN 代表对数化后的数据。
对数据进行实证分析,实证证明变量之间的关系,对数据进行单位根检验验证数据是否在同阶平稳,进行回归分析、协整检验验证变量间是否存在长期关系,并用格兰杰因果检验验证变量之间的因果关系。
单位根检验由于时间序列数据容易产生虚假回归,即由变量自身的平稳阶数不同导致的伪回归现象,因此,不能直接对数据进行回归分析,这样得到的回归也是不可信的,接下来对数据做单位检验,若序列均在原序列平稳,可以直接对数据做回归分析研究变量之间的数量关系,若序列均在一阶差分时平稳,则需要对数据进行协整检验,验证数据之间是否具有长期均衡关系,对对数化后的数据进行单位根检验(ADF 检验)如下表所示:表1 变量的ADF 检验注:D 表示差分序列。
C 代表截距项,T 代表趋势项,K 代表滞后阶数。
ADF 单位根检验的原假设为序列是不平稳的,即接受存在单位根,若检测到的ADF 检验值是小于1%或者5%或者10%的临界值(本文选择5%),则表明变量序列是拒绝存在单位根的原假设,反之,则是接受原假设,变量序列是不平稳的,接下来以LNTHIRD 原序列为例判断序列的平稳性,LNTHIRD 的ADF 统计量为-2.3469,是大于5%的临界值,因此接受原序列LNTHIRD 不平稳的原假设,LNTHIRD 存在单位根,序列是不平稳的,以此类推,所有检测的序列均在1阶平稳,序列均为1阶单整序列。
由于序列均为1阶单整序列,因此,变量序列之间的长期关系可能是具有协整关系,即具有均衡关系,为了进一步验证变量序列间的长期关系,对变量之间的关系进行协整检验,接下来对变量之间的关系用EG两步协整检验进行验证,对变量做回归,得到回归的残差,对残差进行单位根检验,若残差通过单位根检验,则表示变量之间的关系是长期均衡的,接下来对变量之间的关系进行协整检验。
什么是协整关系如何检验两个时间序列之间的协整关系

什么是协整关系如何检验两个时间序列之间的协整关系协整关系是指两个或多个时间序列之间的长期关系,当两个时间序列之间存在协整关系时,它们之间的差值序列是稳定的。
协整关系的发现对于金融、经济学和其他领域的研究具有重要意义。
本文将讨论协整关系的概念,并介绍如何进行协整关系的检验。
一、协整关系的概念协整关系是通过对两个或多个时间序列的统计分析而得出的。
它涉及到平稳性和长期关系两个概念。
1. 平稳性:平稳性是指序列的均值和方差不随时间的推移而发生显著变化。
在时间序列分析中,平稳性是一个重要的前提条件。
2. 长期关系:长期关系是指时间序列之间存在一个稳定的关系,即它们相对稳定地变动,而不是在短期内出现随机波动。
当两个时间序列同时是平稳的,并且它们之间存在长期关系时,就可以认为它们之间存在协整关系。
二、协整关系的检验方法为了检验两个时间序列之间是否存在协整关系,常用的方法有单位根检验和Engle-Granger检验。
1. 单位根检验:单位根检验用于判断一个时间序列是否为平稳序列。
常用的单位根检验方法有ADF检验和KPSS检验。
如果两个时间序列都是单位根非平稳序列,则它们之间可能不存在协整关系,需要进行后续检验;如果两个时间序列都是单位根平稳序列,则它们之间可能存在协整关系。
2. Engle-Granger检验:Engle-Granger检验用于判断两个时间序列之间是否存在协整关系。
该方法首先对两个时间序列进行回归分析,得到残差序列。
然后对残差序列进行单位根检验,如果残差序列是平稳的,则可以认为两个时间序列之间存在协整关系。
三、应用举例为了更好地理解协整关系,我们举一个实际的例子。
假设有两个股票价格的时间序列,分别是股票A和股票B。
我们想要检验股票A和股票B之间是否存在协整关系。
首先,我们对两个时间序列进行单位根检验。
假设经过ADF检验和KPSS检验后,股票A和股票B的价格序列均为平稳序列。
接下来,我们进行Engle-Granger检验,通过对股票A和股票B的价格序列进行回归分析得到残差序列。
格兰杰因果检验简要介绍

格兰杰(Granger)因果性检验目前在计量经济学中应用比较多,不过我们当初学习计量并没有学这个检验方法,经济学专业的学生应该会学到吧。
上次谭英平师姐给我们讲宏观经济统计分析课时曾经给我们介绍过,不过也只是很肤浅地说了说原理(这种教学有一定的危险性啊)。
要探讨因果关系,首先当然要定义什么是因果关系。
这里不再谈伽利略抑或休谟等人在哲学意义上所说的因果关系,只从统计意义上介绍其定义。
从统计的角度,因果关系是通过概率或者分布函数的角度体现出来的:在宇宙中所有其它事件的发生情况固定不变的条件下,如果一个事件A的发生与不发生对于另一个事件B的发生的概率(如果通过事件定义了随机变量那么也可以说分布函数)有影响,并且这两个事件在时间上又先后顺序(A前B后),那么我们便可以说A是B的原因。
早期因果性是简单通过概率来定义的,即如果P(B|A)>P(B)那么A就是B的原因(Suppes,1970);然而这种定义有两大缺陷:一、没有考虑时间先后顺序;二、从P(B|A)>P(B)由条件概率公式马上可以推出P(A|B)>P(A),显然上面的定义就自相矛盾了(并且定义中的“>”毫无道理,换成“<”照样讲得通,后来通过改进,把定义中的“>”改为了不等号“≠”,其实按照同样的推理,这样定义一样站不住脚)。
事实上,以上定义还有更大的缺陷,就是信息集的问题。
严格讲来,要真正确定因果关系,必须考虑到完整的信息集,也就是说,要得出“A是B的原因”这样的结论,必须全面考虑宇宙中所有的事件,否则往往就会发生误解。
最明显的例子就是若另有一个事件C,它是A和B的共同原因,考虑一个极端情况:若P(A|C)=1,P(B|C)=1,那么显然有P(B|AC)=P(B|C),此时可以看出A事件是否发生与B事件已经没有关系了。
因此,Granger(1980)提出了因果关系的定义,他的定义是建立在完整信息集以及发生时间先后顺序基础上的。
格兰杰因果检验解读

格兰杰因果检验解读格兰杰因果关系检验一、经济变量之间的因果性问题计量经济模型的建立过程,本质上是用回归分析工具处理一个经济变量对其他经济变量的依存性问题,但这并不是暗示这个经济变量与其他经济变量间必然存在着因果关系。
由于没有因果关系的变量之间常常有很好的回归拟合,把回归模型的解释变量与被解释变量倒过来也能够拟合得很好,因此回归分析本身不能检验因果关系的存在性,也无法识别因果关系的方向。
假设两个变量,比如国内生产总值GDP和广义货币供给量M,各自都有滞后的分量GDP(-1),GDP(-2)…,M(-1),M(-2),…,显然这两个变量都存在着相互影响的关系。
但现在的问题是:究竟是M引起GDP的变化,还是GDP引起M的变化,或者两者间相互影响都存在反馈,即M引起GDP的变化,同时GDP也引起M 的变化。
这些问题的实质是在两个变量间存在时间上的先后关系时,是否能够从统计意义上检验出因果性的方向,即在统计上确定GDP是M的因,还是M是GDP的因,或者M和GDP互为因果。
因果关系研究的有趣例子是回答“先有鸡还是先有蛋”的问题。
1988年有两位学者Walter N. Thurman和Mark E. Fisher用美国1930——1983年鸡蛋产量(EGGS)和鸡的产量(CHICKENS)的年度数据,对此问题进行了统计研究。
他们运用格兰杰的方法检验鸡和蛋之间的因果关系,结果发现,鸡生蛋的假设被拒绝,而蛋生鸡的假设成立,因此,蛋为因,鸡为果,也就是先有蛋。
他们并建议作其他诸如“谁笑在最后谁笑得最好”、“骄傲是失败之母”之类的格兰杰因果检验。
二、格兰杰因果关系检验经济学家开拓了一种可以用来分析变量之间的因果的办法,即格兰杰因果关系检验。
该检验方法为2003年诺贝尔经济学奖得主克莱夫·格兰杰(Clive W. J. Granger)所开创,用于分析经济变量之间的因果关系。
他给因果关系的定义为“依赖于使用过去某些时点上所有信息的最佳最小二乘预测的方差。
时间序列的平稳非平稳协整格兰杰因果关系

时间序列的平稳、非平稳、协整、格兰杰因果关系步骤:先做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;若非平稳,进行差分,当进行到第i次差分时序列平稳,则服从i阶单整(注意趋势、截距不同情况选择,根据P值和原假设判定)。
若所有检验序列均服从同阶单整,可构造VAR模型,做协整检验(注意滞后期的选择),判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。
如果有,则可以构造VEC模型或者进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。
1.单位根检验是序列的平稳性检验,如果不检验序列的平稳性直接OLS容易导致伪回归。
常用的ADF检验包括三个模型方程。
在李子奈的《高级计量经济学》上有该方法的全部步骤,即从含趋势项、截距项的方程开始,若接受原假设,则对模型中的趋势项参数进行t 检验,若接受则进行对只含截距项的方程进行检验,若接受,则对一阶滞后项的系数参数进行t检验,若接受,则进行差分后再ADF检验;若拒绝,则序列为平稳序列。
2.当检验的数据是平稳的(即不存在单位根),要想进一步考察变量的因果联系,可以采用格兰杰因果检验,但要做格兰杰检验的前提是数据必须是平稳的,否则不能做。
3.当检验的数据是非平稳(即存在单位根),并且各个序列是同阶单整(协整检验的前提),想进一步确定变量之间是否存在协整关系,可以进行协整检验,协整检验主要有EG两步法和JJ检验:(1)EG两步法是基于回归残差的检验,可以通过建立OLS模型检验其残差平稳性;(2)JJ检验是基于回归系数的检验,前提是建立VAR模型(即模型符合ADL模式)。
4.当变量之间存在协整关系时,可以建立ECM进一步考察短期关系,Eviews这里还提供了一个Wald-Granger检验,但此时的格兰杰已经不是因果关系检验,而是变量外生性检验,请注意识别。
5.格兰杰检验只能用于平稳序列!这是格兰杰检验的前提,而其因果关系并非我们通常理解的因与果的关系,而是说x的前期变化能有效地解释y的变化,所以称其为“格兰杰原因”。
格兰杰因果检验和协整检验的关系

格兰杰因果检验和协整检验是时间序列分析中常用的两种方法,它们在研究变量之间的关系和相互影响时起着重要的作用。
本文将从理论和实际应用两个方面探讨格兰杰因果检验和协整检验之间的关系。
一、格兰杰因果检验的概念和原理格兰杰因果检验是通过检验变量之间的因果关系来判断它们之间是否存在因果关系。
在进行格兰杰因果检验时,我们首先需要建立一个时间序列模型,然后对模型的误差项进行相关性分析,最终确定是否存在因果关系。
具体而言,格兰杰因果检验主要包括两个步骤:我们需要建立一个自回归模型(AR模型),然后对模型的残差序列进行检验。
如果检验结果表明残差序列存在因果关系,即序列中的一个变量的残差会对另一个变量产生影响,那么我们就可以认为这两个变量之间存在因果关系。
二、协整检验的概念和原理与格兰杰因果检验不同,协整检验主要用于判断时间序列变量之间是否存在长期均衡关系。
当两个变量之间存在长期均衡关系时,它们之间的波动会在一个相对稳定的范围内波动,而不会出现长时间的偏离,这就是协整关系的本质。
具体而言,协整检验是通过构建一个误差修正模型(Error Correction Model,ECM)来判断两个变量之间是否存在协整关系。
在协整检验中,我们首先需要对变量进行单位根检验,以确保它们是严格平稳的时间序列,然后建立误差修正模型,最终通过模型的残差序列来判断两个变量是否存在协整关系。
三、格兰杰因果检验和协整检验的关系格兰杰因果检验和协整检验虽然在理论和方法上有所不同,但它们之间存在着一定的关系。
具体而言,格兰杰因果检验可以帮助我们判断变量之间是否存在因果关系,而协整检验则可以帮助我们判断这种因果关系是否是长期的、稳定的。
在进行时间序列分析时,我们通常会先进行格兰杰因果检验,判断变量之间是否存在因果关系,然后再进行协整检验,判断这种因果关系是否是长期的、稳定的。
通过这两种方法的结合应用,我们可以更全面地了解变量之间的关系,为进一步的研究和分析提供有力的支持。
格兰杰因果关系检验

味着他们之间就一定存在着因果关系
例如,GDP和货币供应量M2通常是高度相关的,
但究竟是GDP的增长导致了M2的增加,还是M2增
加促进了GDP的增长,或者两者互为因果关系,从理
论和实践两方面来回答这个问题,就不是很简单的
问题 . 格兰杰首先提出了因果关系检验的思想:假定 X是Y的因,但Y不是X的因,则X的过去值能够帮助 预测Y的未来值,但Y的过去值不应该能够预测X的 未来值.
考虑检验模型的序列相关性以及赤池信息准则,发 现:滞后5阶的检验模型不具有1阶自相关性,而且 也拥有较小的AIC值,这时判断结果是:GDPP与 CONSP有双向的格兰杰因果关系,即相互影响。
表 5.2.3 中国 GDP 与消费支出(亿元) 年份 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 人均居民消费 CONSP 1759.1 2005.4 2317.1 2604.1 2867.9 3182.5 3674.5 4589 5175 5961.2 7633.1 8523.5 人均GDP GDPP 3605.6 4074.0 4551.3 4901.4 5489.2 6076.3 7164.4 8792.1 10132.8 11784.7 14704.0 16466.0 年份 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 人均居民消费 CONSP 9113.2 10315.9 12459.8 15682.4 20809.8 26944.5 32152.3 34854.6 36921.1 39334.4 42911.9 人均GDP GDPP 18319.5 21280.4 25863.7 34500.7 46690.7 58510.5 68330.4 74894.2 79003.3 82673.1 89112.5
单位根检验、协整检验和格兰杰因果关系检验三者之间的关

单位根检验、协整检验和格兰杰因果关系检验三者之间的关系
实证检验步骤:先做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;若非平稳,进行差分,当进行到第i次差分时序列平稳,则服从i阶单整(注意趋势、截距不同情况选择,根据P值和原假设判定)。若所有检验序列均服从同阶单整,可构造VAR模型,做协整检验(注意滞后期的选择),判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。如果有,则可以构造VEC模型或者进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。
二、讨论二 1、格兰杰检验只能用于平稳序列!这是格兰杰检验的前提,而其因果关系并非我们通常理解的因与果的关系,而是说x的前期变化能有效地解释y的变化,所以称其为“格兰杰原因”。 2、非平稳序列很可能出现伪回归,协整的意义就是检验它们的回归方程所描述的因果关系是否是伪回归,即检验变量之间是否存在稳定的关系。所以,非平稳序列的因果关系检验就是协整检验。 3、平稳性检验有3个作用:1)检验平稳性,若平稳,做格兰杰检验,非平稳,作协正检验。2)协整检验中要用到每个序列的单整阶数。3)判断时间学列的数据生成过程。
单位根检验和协整检验

单位根检验和协整检验单位根检验和协整检验是时间序列分析中常用的两种方法。
本文将分别介绍这两种检验方法的概念、原理和应用。
一、单位根检验1.概念单位根检验,又称为ADF(Augmented Dickey-Fuller)检验,是一种用于判断时间序列是否具有平稳性的方法。
它的基本原理是通过对时间序列进行一定程度的差分,使得序列变得平稳,从而判断序列是否具有单位根。
2.原理在时间序列中,如果一个变量具有单位根,则说明它在长期内存在趋势或者周期性波动。
而如果一个变量具有平稳性,则说明它在长期内不存在趋势或者周期性波动。
因此,通过对时间序列进行差分,可以消除其中的趋势或者周期性波动,使得序列变得平稳。
ADF检验的基本原理就是通过比较差分后的时间序列与原始时间序列之间的关系来判断是否存在单位根。
具体地说,在ADF检验中,我们需要假设一个线性回归模型:ΔYt = α + βt + γYt-1 + δ1ΔYt-1 + … + δpΔYt-p + εt其中,Δ表示差分符号;Yt表示时间序列;α、β、γ、δ1~δp和εt分别表示回归系数和误差项。
如果该模型中的γ等于0,则说明时间序列具有单位根,即存在趋势或者周期性波动;如果γ小于0,则说明时间序列具有平稳性,即不存在趋势或者周期性波动。
3.应用ADF检验通常用于判断时间序列是否具有平稳性。
在金融领域中,它常被用于股票价格的分析和预测。
例如,通过对股票价格进行ADF检验,可以判断该股票是否处于上涨或下跌趋势,并进一步预测未来的走势。
二、协整检验1.概念协整检验是一种用于判断两个或多个时间序列之间是否存在长期稳定的关系的方法。
它的基本原理是通过构建线性组合,使得两个或多个时间序列之间的关系变得平稳。
2.原理在协整检验中,我们需要假设一个线性组合模型:Yt = α + βXt + εt其中,Yt和Xt分别表示两个时间序列;α、β和εt分别表示回归系数和误差项。
如果该模型中的β等于0,则说明Yt和Xt之间不存在长期稳定的关系;如果β不等于0,则说明Yt和Xt之间存在长期稳定的关系,即它们是协整的。
单位根、协整检验、误差修正模型及因果关系检验
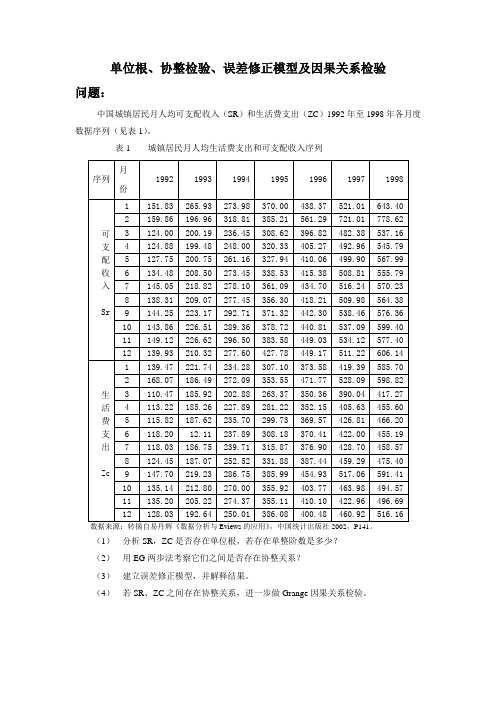
单位根、协整检验、误差修正模型及因果关系检验问题:中国城镇居民月人均可支配收入(SR)和生活费支出(ZC)1992年至1998年各月度数据序列(见表1)。
表1 城镇居民月人均生活费支出和可支配收入序列序列月份1992 1993 1994 1995 1996 1997 1998可支配收入Sr1 151.83 265.93 273.98 370.00 438.37 521.01 643.402 159.86 196.96 318.81 385.21 561.29 721.01 778.623 124.00 200.19 236.45 308.62 396.82 482.38 537.164 124.88 199.48 248.00 320.33 405.27 492.96 545.795 127.75 200.75 261.16 327.94 410.06 499.90 567.996 134.48 208.50 273.45 338.53 415.38 508.81 555.797 145.05 218.82 278.10 361.09 434.70 516.24 570.238 138.31 209.07 277.45 356.30 418.21 509.98 564.389 144.25 223.17 292.71 371.32 442.30 538.46 576.3610 143.86 226.51 289.36 378.72 440.81 537.09 599.4011 149.12 226.62 296.50 383.58 449.03 534.12 577.4012 139.93 210.32 277.60 427.78 449.17 511.22 606.14生活费支出 Zc1 139.47 221.74 234.28 307.10 373.58 419.39 585.702 168.07 186.49 272.09 353.55 471.77 528.09 598.823 110.47 185.92 202.88 263.37 350.36 390.04 417.274 113.22 185.26 227.89 281.22 352.15 405.63 455.605 115.82 187.62 235.70 299.73 369.57 426.81 466.206 118.20 12.11 237.89 308.18 370.41 422.00 455.197 118.03 186.75 239.71 315.87 376.90 428.70 458.578 124.45 187.07 252.52 331.88 387.44 459.29 475.409 147.70 219.23 286.75 385.99 454.93 517.06 591.4110 135.14 212.80 270.00 355.92 403.77 463.98 494.5711 135.20 205.22 274.37 355.11 410.10 422.96 496.6912 128.03 192.64 250.01 386.08 400.48 460.92 516.16数据来源:转摘自易丹辉《数据分析与Eviews的应用》,中国统计出版社2002,P141。
格兰杰因果分析及单位根检验解读

格兰杰因果分析及单位根检验一,首先我根据ADF检验结果,来说明这两组数据对数情况下是否是同阶单整的(同阶单整即说明二者是协整的,这是一种协整检验的方法),我对你的两组数据分别作了单位根检验,结果如下:1.LNFDI水平下的ADF结果:Null Hypothesis: LNFDI has a unit rootExogenous: ConstantLag Length: 2 (Automatic based on AIC, MAXLAG=3 Augmented Dickey-Fuller test statistict-Statistic Prob.*-1.45226403166189 0.526994561264069Test critical values:1% level -4.004424924017175% level -3.0988964053233710% level -2.69043949557234*MacKinnon (1996 one-sided p-values.Warning: Probabilities and critical values calculated for 20 observations and may not be accurate for a sample size of 14从上面的t-Statistic对应的值可以看到, -1.45226403166189大于下面所有的临界值,因此LNFDI在水平情况下是非平稳的。
然后我对该数据作了二阶,再进行ADF检验结果如下:t-Statistic Prob.*- 2.8606168858628 0.0770552989049772Test critical values:1% level -4.057909684396635% level -3.1199095651240810% level -2.70110325490427看到t-Statistic的值小于10% level下的-2.70110325490427,因此可以认为它在二阶时,有90%的可能性,是平稳的。
EVIEWS格兰杰检验解读

Eviews做单位根检验和格兰杰因果分析一,首先我根据ADF检验结果,来说明这两组数据对数情况下是否是同阶单整的(同阶单整即说明二者是协整的,这是一种协整检验的方法),我对你的两组数据分别作了单位根检验,结果如下:1.LNFDI水平下的ADF结果:Null Hypothesis: LNFDI has a unit rootExogenous: ConstantLag Length: 2 (Automatic based on AIC, MAXLAG=3 Augmented Dickey-Fuller test statistict-Statistic Prob.*-1.45226403166189 0.526994561264069Test critical values:1% level -4.004424924017175% level -3.0988964053233710% level -2.69043949557234*MacKinnon (1996 one-sided p-values.Warning: Probabilities and critical values calculated for 20observations and may not be accurate for a sample size of 14从上面的t-Statistic对应的值可以看到, -1.45226403166189大于下面所有的临界值,因此LNFDI在水平情况下是非平稳的。
然后我对该数据作了二阶,再进行ADF检验结果如下:t-Statistic Prob.*- 2.8606168858628 0.0770552989049772Test critical values:1% level -4.057909684396635% level -3.1199095651240810% level -2.70110325490427看到t-Statistic的值小于10% level下的-2.70110325490427,因此可以认为它在二阶时,有90%的可能性,是平稳的。
var格兰杰因果关系检验

var格兰杰因果关系检验【原创实用版】目录一、格兰杰因果关系检验的定义与背景二、格兰杰因果关系检验的方法三、格兰杰因果关系检验的应用领域四、格兰杰因果关系检验的局限性正文一、格兰杰因果关系检验的定义与背景格兰杰因果关系检验(Granger Causality Test)是一种用于分析经济变量之间因果关系的统计方法,该方法由 2003 年诺贝尔经济学奖得主克莱夫·格兰杰(Clive W.J.Granger)所开创。
格兰杰因果关系检验并不是检验逻辑上的因果关系,而是关注变量间的先后顺序,即一个变量的前期信息是否会影响到另一个变量的当期。
二、格兰杰因果关系检验的方法格兰杰因果关系检验主要包括以下几个步骤:1.单位根检验:检验变量序列是否稳定,若存在单位根,则需进行差分处理。
2.协整检验:检验变量间是否存在长期的均衡关系,若存在协整关系,则可以进行格兰杰因果关系检验。
3.格兰杰因果关系检验:根据协整关系,利用最小二乘法对变量进行预测,并计算预测误差的方差。
若某个变量的预测误差方差显著小于另一个变量的预测误差方差,则可以认为前者是后者的格兰杰原因。
三、格兰杰因果关系检验的应用领域格兰杰因果关系检验广泛应用于经济学、金融学、生物信息学、机器学习和数据挖掘等领域。
在经济学领域,格兰杰因果关系检验可用于分析不同经济变量之间的因果关系,如国内生产总值(GDP)与通货膨胀率(CPI)之间的关系等。
在生物信息学领域,格兰杰因果关系检验可用于分析基因与疾病之间的关联性。
四、格兰杰因果关系检验的局限性尽管格兰杰因果关系检验在分析变量间因果关系方面具有一定的优势,但该方法也存在一定的局限性:1.格兰杰因果关系检验只能检验变量间的先后关系,无法确认因果关系的具体方向。
2.该方法受到样本量和数据质量的影响较大,当样本量较小或数据质量较低时,检验结果可能存在偏误。
计量经济学中的因果关系

计量经济学中的因果关系
计量经济学中的因果关系是指经济变量之间的因果关系。
在计量经济学中,因果关系是研究经济变量之间的关系的重要方法之一。
因果关系的研究可以帮助我们了解经济现象的本质和发展趋势,为经济政策的制定和实施提供科学依据。
计量经济学中常用的因果关系研究方法包括协整分析、灰色关联分析、Granger因果关系检验等。
协整分析是利用时间序列的协整性来研究变量之间的长期因果关系;灰色关联分析是将数据集中的某些变量联系起来,寻找它们之间的相互关系;Granger因果关系检验是通过时间序列数据的因果关系检验来研究变量之间的因果关系。
在因果关系分析中,需注意变量之间的内因性问题。
内因性问题是指变量之间的因果关系可能被未观测到的其他变量影响而产生误差。
为了避免内因性问题对因果关系研究的影响,常采用工具变量法、自然实验法等方法来控制内因性问题。
总之,计量经济学中的因果关系研究是研究经济变量之间联系的重要方法,有助于我们了解经济现象的本质和发展趋势,为经济政策的制定和实施提供科学依据。
- 1 -。
常用的协整检验方法

常用的协整检验方法协整检验是一种用于检测时间序列数据之间是否存在长期关系的统计方法。
在金融经济学中,协整检验被广泛应用于价格和收益率之间的关系分析,以及股票市场和货币市场之间的关系研究。
以下是一些常用的协整检验方法:1. 奥格尔检验(Engle-Granger Test):奥格尔检验是最常见的协整检验方法之一。
它基于两个时间序列的单位根检验结果,通过构建误差修正模型(Error Correction Model,ECM)来检验它们之间的协整关系。
该方法的优点是简单易用,但对数据的要求较高,仅适用于两个时间序列的情况。
2. 约翰逊检验(Johansen Test):约翰逊检验是一种多元协整检验方法,可以同时检验多个时间序列之间的协整关系。
它基于向量自回归模型(Vector Autoregression Model,VAR)和特征根检验,通过判断特征根的数量和位置来确定协整关系的存在与否。
约翰逊检验适用于具有多个时间序列的复杂情况,但计算复杂度较高。
3. 格兰杰因果检验(Granger Causality Test):格兰杰因果检验是一种常用的时间序列分析方法,用于检验两个时间序列之间的因果关系。
如果两个时间序列之间存在协整关系,那么它们之间可能存在因果关系。
格兰杰因果检验通过引入滞后项来模拟时间序列之间的动态关系,并通过F统计量检验滞后项的显著性来判断因果关系的存在与否。
4. 面板数据协整检验(Panel Cointegration Test):面板数据协整检验是用于面板数据(Panel Data)的协整检验方法。
面板数据包含多个个体(Cross-section)和多个时间点(Time-series),可以用来分析不同时间点和不同个体之间的协整关系。
常用的面板数据协整检验方法包括西姆斯-休斯特(Seemingly Unrelated Regression,SUR)和极限法(Pedroni)等。
协整检验方法的选择应根据具体的研究目的和数据特点来确定。
(五)Granger因果关系检验

目录中文摘要··1英文摘要(Abstract)·1一、引言··1二、文献综述··2(一)早期的理论··2(二)现代实证经济学的理论··3三、模型结构··6(一)时间序列的平稳性··6(二)平稳性的单位根检验··6(三)协整关系的确立和检验··7(四)建立误差修正模型··7(五)Granger因果关系检验··8四、数据选取··8五、江苏省经济增长与对外贸易的实证分析··10 (一)图形分析··10(二)ADF检验··11(三)协整检验··11(四)误差修正模型··12(五)Granger因果关系检验·13六、总结和评价··13参考文献··16江苏省对外贸易与经济增长的关系研究统计051 马超2070405134摘要:本文通过用单位根检验、协整检验,并建立误差修正模型,分析对外贸易与经济增长之间的关系,并通过格兰杰因果检验分析之间的因果关系;进口增长对江苏省经济增长具有较大的促进作用,而出口增长对经济增长的影响不显著。
关键词:单位根检验,协整检验,误差修正模型,格兰杰因果Abstract: In this paper, unit root test, cointegration test and the building of error correct model are used for analysing the relation between the foreign trade and economic growth, furthermore, granger causality is used for examining and analysing the cause-effect relationship between the foreign trade and economic growth,and there comes to an conclusion that the growth in imports has significant promoting effect on the economic development of Jiangsu,but the growth in exports shows little influence on it.Keywords: unit root test , cointegration test , error correct model , granger causality一、引言自改革开放以来, 江苏省作为经济强省,其国民收入和对外贸易增长迅猛, 对外贸易在江苏省经济发展中的影响越来越显著, 国外要素已经渐渐成为一国或地区发展经济、增进居民福利的重要手段。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实证检验步骤:先做单位根检验,看变量序列是否平稳序列,若平稳,可构造回归模型等经典计量经济学模型;若非平稳,进行差分,当进行到第i次差分时序列平稳,则服从i阶单整(注意趋势、截距不同情况选择,根据P值和原假设判定)。
若所有检验序列均服从同阶单整,可构造VAR模型,做协整检验(注意滞后期的选择),判断模型内部变量间是否存在协整关系,即是否存在长期均衡关系。
如果有,则可以构造VEC模型或者进行Granger因果检验,检验变量之间“谁引起谁变化”,即因果关系。
一、讨论一
1、单位根检验是序列的平稳性检验,如果不检验序列的平稳性直接OLS容易导致伪回归。
2、当检验的数据是平稳的(即不存在单位根),要想进一步考察变量的因果联系,可以采用格兰杰因果检验,但要做格兰杰检验的前提是数据必须是平稳的,否则不能做。
3、当检验的数据是非平稳(即存在单位根),并且各个序列是同阶单整(协整检验的前提),想进一步确定变量之间是否存在协整关系,可以进行协整检验,协整检验主要有EG两步法和JJ检验
A、EG两步法是基于回归残差的检验,可以通过建立OLS模型检验其残差平稳性
B、JJ检验是基于回归系数的检验,前提是建立VAR模型(即模型符合ADL模式)
4、当变量之间存在协整关系时,可以建立ECM进一步考察短期关系,Eviews这里还提供了一个Wald-Granger检验,但此时的格兰杰已经不是因果关系检验,而是变量外生性检验,请注意识别
二、讨论二
1、格兰杰检验只能用于平稳序列!这是格兰杰检验的前提,而其因果关系并非我们通常理解的因与果的关系,而是说x的前期变化能有效地解释y的变化,所以称其为“格兰杰原因”。
2、非平稳序列很可能出现伪回归,协整的意义就是检验它们的回归方程所描述的因果关系是否是伪回归,即检验变量之间是否存在稳定的关系。
所以,非平稳序列的因果关系检验就是协整检验。
3、平稳性检验有3个作用:1)检验平稳性,若平稳,做格兰杰检验,非平稳,作协正检验。
2)协整检验中要用到每个序列的单整阶数。
3)判断时间学列的数据生成过程。
三、讨论三
其实很多人存在误解。
有如下几点,需要澄清:
第一,格兰杰因果检验是检验统计上的时间先后顺序,并不表示而这真正存在因果关系,是否呈因果关系需要根据理论、经验和模型来判定。
第二,格兰杰因果检验的变量应是平稳的,如果单位根检验发现两个变量是不稳定的,那么,不能直接进行格兰杰因果检验,所以,很多人对不平稳的变量进行格兰杰因果检验,这是错误的。
第三,协整结果仅表示变量间存在长期均衡关系,那么,到底是先做格兰杰还是先做协整呢?因为变量不平稳才需要协整,所以,首先因对变量进行差分,平稳后,可以用差分项进行格兰杰因果检验,来判定变量变化的先后时序,之后,进行协整,看变量是否存在长期均衡。
第四,长期均衡并不意味着分析的结束,还应考虑短期波动,要做误差修正检验。
