2008年高考数学试题分类汇编(数列)
2008年全国各地高考数学试题及解答分类汇编大全(14空间向量与立体几何)

2008年全国各地高考数学试题及解答分类汇编大全(14空间向量与立体几何)一、选择题:1.(2008全国Ⅰ卷理)已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( C )A .13B.3 C.3 D .231.解:C .由题意知三棱锥1A ABC -为正四面体,设棱长为a,则1AB =,棱柱的高13AO ===(即点1B 到底面ABC 的距离),故1AB 与底面ABC所成角的正弦值为11AO AB =另解:设1,,AB AC AA u u u r u u u r u u u r 为空间向量的一组基底,1,,AB AC AA u u u r u u u r u u u r 的两两间的夹角为060长度均为a ,平面ABC 的法向量为111133OA AA AB AC =--u u u r u u u r u u u r u u u r ,11AB AB AA =+u u u r u u ur u u u r211112,33OA AB a OA AB ⋅===u u u r u u u r u u u r u u u r则1AB 与底面ABC所成角的正弦值为11113OA AB AO AB ⋅=u u u u r u u u r u u u r u u u r .二、填空题:1.(2008全国Ⅰ卷理)等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C AB D --的余,M N ,分别是AC BC ,的中点,则EM AN ,所成角的余弦值等于 61. 1.答案:16.设2AB =,作CO ABDE ⊥面, OH,则CH AB ⊥,CHO ∠为二面角C AB D --cos 1CH OH CH CHO ==⋅∠=,结合等边三角形ABC 与正方形ABDE 可知此四棱锥为正四棱锥,则AN EM ==11(),22AN AC AB EM AC AE =+=-u u u r u u u r u u u r u u u u r u u u r u u u r,11()()22AN EM AB AC AC AE ⋅=+⋅-=u u u r u u u u r u u u r u u u r u u u r 12故EM AN ,所成角的余弦值16AN EM AN EM ⋅=u u u r u u u u r u u u r u u u u r另解:以O 为坐标原点,建立如图所示的直角坐标系, 则点(1,1,0),(1,1,0),(1,1,0),A B E C ----,1111(,(,2222M N ---, 则31131(,,),(,,,2222222AN EM AN EM AN ==-⋅=u u u r u u u u r u u u r u u u u r u u u r故EM AN ,所成角的余弦值16AN EM AN EM ⋅=u u u r u u u u r u u u r u u u u r .三、解答题:1.(2008安徽文)如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的 菱形,4ABC π∠=,OA ABCD ⊥底面, 2OA =,M 为OA 的中点。
2008年全国各地高考数学试题及解答分类汇编大全(02常用逻辑用语)

(02 常用逻辑用语)
一.选择题:
1.(2008 安徽文、理) a 0 是方程 ax2 2x 1 0 至少有一个负数根的( B )
A.必要不充分条件
B.充分不必要条件
C.充分必要条件
D.既不充分也不必要条件
2.(2008 北京理)“函数 f (x)(x R) 存在反函数”是“函数 f (x) 在 R 上为增函数”的
第 1 页 (共 3 页)
9.(2008 湖北理)若非空集合 A,B,C 满足 A∪B=C,且 B 不是 A 的子集,则(B )
A.“x∈C”是“x∈A”的充分条件但不是必要条件 B. “x∈C”是“x∈A”的必要条件但不是充分条件 C. “x∈C”是“x∈A”的充分条件 D. “x∈C”是“x∈A”的充分条件也不是“x∈A”必要条件
12.(2008 江西文) “ x y ”是“ x y ”的(B )
A.充分不必要条件 B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
13.(2008 山东文)给出命题:若函数 y f (x) 是幂函数,则函数 y f (x) 的图象不过第四
象限.在它的逆命题、否命题、逆否命题三个命题中,真命题的个数是( C )
A. a , b 方向相同
B. a , b 两向量中至少有一个为零向量
C. R , b a
D. 存在不全为零的实数 1 , 2 , 1a 2 b 0
8. (2008 湖北文)若集合 P {1, 2,3, 4},Q {x 0 x 5, x R},则 ( A ) A. “ x R ”是“ x Q ”的充分条件但不是必要条件 B. “ x R ”是“ x Q ”的必要条件但不是充分条件 C. “ x R ”是“ x Q ”的充要条件 D. “ x R ”既不是“ x Q ”的充分条件也不是“ x Q ”的必要条件
2008年全国各地高考数学试题及解答分类大全(统计、统计案例、算法初步、框图、推理与证明)

2008年全国各地高考数学试题及解答分类大全(统计、统计案例、算法初步、框图、推理与证明)一、选择题:1.(2008广东理)某校共有学生2000名,各年级男、女生人数如表1.已知在全校学生中随机抽取1名,抽到二年级女生的 概率是0.19 .现用分层抽样的方法在全校抽取64名 学生, 则应在三年级抽取的学生人数为( C ) A .24 B. 18 C. 16 D. 12解:由19.02000=x,得38019.02000=⨯=x , 三年级人数为500)370380377373(2000=+++-=+z y ,设应在三年级抽取m 人,则200064500=m ,解得m=16. 故答C.2、(2008海南、宁夏文、理)右面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( A ) A. c > x B. x > c C. c > b D. b > c3. (2008山东理)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图,图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( B )(A )304.6 (B )303.6 (C)302.6 (D)301.64.(2008山东文)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( B )A B .5C .3D .855.(2008陕西文) 某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为( C ) A .30 B .25 C .20 D .156.(2008陕西纹、理) 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为012i a a a a ,{01}∈,(012i =,,),传输信息为00121h a a a h ,其中001102h a a h h a =⊕=⊕,,⊕运算规则为:000⊕=,011⊕=,101⊕=,110⊕=,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( C )A .11010B .01100C .10111D .000117. (2008重庆文) 某校高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是 ( D )(A)简单随机抽样法 (B)抽签法 (C)随机数表法 (D)分层抽样法二、填空题:1.(2008广东文)为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量。
2008年高考数列题1

2008年高考数列题选(文)1.(北京7)已知等差数列{a n }中,a 2=6,a 5=15.若b n =a 2n ,则数列{b n }的前5项和等于( )A .30B .45C .90D .186 2.(北京20,总20))数列{a n }满足2111,()(1,2,),.n n a a n n a n λλ+==+-= 是常数 (Ⅰ)当a 2=-1时,求λ及a 3的值;(Ⅱ)数列{a n }是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由; (Ⅲ)求λ的取值范围,使得存在正整数m ,当n >m 时总有a n <0.3.(福建3)设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项和为( ) A.128B.80C.64D.564.(福建20)已知{}n a 是整数组成的数列,11a =,且点*1)()n a n N +∈在函数21y x =+的图像上:(1)求数列{}n a 的通项公式;(2)若数列{}n b 满足111,2n an n b b b +==+,求证:221n n n b b b ++⋅<5.(广东4)记等差数列的前n 项和为n S ,若244,20S S ==,则该数列的公差d =( )A 、2B 、3C 、6D 、76.(21广东21)设数列{}n a 满足11a =,22a =,121(2)3n n n a a a --=+ (3,4,)n = 。
数列{}n b 满足11,(2,3,)n b b n == 是非零整数,且对任意的正整数m 和自然数k ,都有111m m m k b b b ++-≤+++≤ 。
(1)求数列{}n a 和{}n b 的通项公式;(2)记(1,2,)n n n c na b n == ,求数列{}n c 的前n 项和n S 7.(21湖北21)已知数列12{}{},13n n x a b a an a λ=+=和满足:4,(1)(321)n n n n n b a n +-=--+,其中λ为实数,n 为正整数.(Ⅰ)证明:当18{}n b λ≠-时,数列是等比数列;(Ⅱ)设n S 为数列{}n b 的前n 项和,是否存在实数λ,使得对任意正整数n ,都有 12?n S >-若存在,求λ的取值范围;若不存在,说明理由 8.(21湖南21)数列{}n a 满足,2,021==a a ,,3,2,1,2sin 4)2cos1(222 =++=+n n a n a n n ππ(1)求43,a a ,并求数列{}n a 的通项公式;(2)设1231-+++=k k a a a S ,k k a a a T 242+++= ,)(22+∈+=N k T S W kkk ,求使1>k W 的所有k 的值,并说明理由。
2008年高考数学试题分类汇编—排列组合

2008年全国高考数学试题分类汇编排列与组合一、选择题:1. (全国II 文) 9.44)1()1(x x +-的展开式中x 的系数是( ) A .4- B .3-C .3D .4 2. (江西理)8.(1+3x )6(1+41x )10展开式中的常数项为A .1B .46C .4245D .42463. (陕西理)12.为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为012i a a a a ,{01}∈,(012i =,,),传输信息为00121h a a a h ,其中001102h a a h h a =⊕=⊕,,⊕运算规则为:000⊕=,011⊕=,101⊕=,110⊕=,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )A .11010B .01100C .10111D .000114. (安徽理)(12)12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是( )A .2283C AB .2686C A C .2286C AD .2285C A 5. (宁夏理)9、甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面。
不同的安排方法共有( )A. 20种B. 30种C. 40种D. 60种6. (浙江文)(6)在)5)(4)(3)(2)(1(-----x x x x x 的展开式中,含4x 的项的系数是(A )-15 (B )85 (C )-120 (D )2747. (上海理)12.组合数C rn (n >r ≥1,n 、r ∈Z )恒等于( )A .r +1n +1C r -1n -1B .(n +1)(r +1)C r -1n -1 C .nr C r -1n -1D .n r C r -1n -1 8. (全国I 文)3.512x ⎛⎫+ ⎪⎝⎭的展开式中2x 的系数为( ) A .10 B .5 C .52D .1 9. (全国I 文)12.将1,2,3填入33⨯的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填写方法共有( )A .6种B .12种C .24种D .48种10. (重庆文) (10)若(x +12x )n 的展开式中前三项的系数成等差数,则展开式中x 4项的系数为 (A)6(B)7 (C)8 (D)911. (天津理)(10)有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有(A) 1344种 (B) 1248种 (C) 1056种 (D) 960种12. (山东理)(9)(X -31x )12展开式中的常数项为(A )-1320 (B )1320 (C )-220 (D)22013. (全国II 理)12.如图,一环形花坛分成A 、B 、C 、D 四块,现有4种不同的花供选种,要求在每块里种一种花,且相邻的2块种不同的花,则不同的种法种数为(A)96 (B) 84(C) 60 (D) 4812.B.分三类:种两种花有24A 种种法;种三种花有342A 种种法;种四种花有44A 种种法.共有234444284A A A ++=. 14. (辽宁理) (9)一生产过程有4道工序,每道工序需要安排一人照看,现从甲、乙、丙等6名工人中安排4人分别照看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,则不同的安排方案共有A(A )24种 (B )36种 (C )48种 (D )72种15. (湖南理)10.设[x ]表示不超过x 的最大整数(如[2]=2, [54]=1),对于给定的n ∈N *,定义[][]2(1)(1)(1)(1)n n n n x C x x x x --+=--+,x ∈[)1,+∞,则当x ∈3,32⎡⎫⎪⎢⎣⎭时,函数2n C 的值域是 A.16,283⎡⎤⎢⎥⎣⎦ B.16,563⎡⎫⎪⎢⎣⎭C.284,3⎛⎫⋃ ⎪⎝⎭[)28,56 D.16284,,2833⎛⎤⎛⎤⋃ ⎥⎥⎝⎦⎝⎦(D) 12 3 31 2 2 3 116. (湖北文)2. 321(2)2x x -的展开式中常数项是 A.210 B.1052 C.14 D.-105 17. (湖北理)6.将5名志愿者分配到3个不同的奥运场馆参加接待工作,每个场馆至少分配一名志愿者的方案种数为A.540B.300C.180 D .15018. (湖北文)2. 321(2)2x x -的展开式中常数项是 A.210 B.1052 C.14 D.-105 19. (福建文) (9)某班级要从4名男士、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A .14 B.24 C.28 D.4820. (福建理) (7)某班级要从4名男生、2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为A .14 B.24 C.28 D.48二、填空题:21. (北京文)(12)若532)1(x x +展开式的各项数之和为 ; 各项系数之和为 .(用数字作答)(12)10 3222. (北京理)(11)若n xx )1(22+展开式的各项数之和为32,则n = ,其展开式中的常数项为 。
2008年全国各地高考数学试题及解答分类汇编大全(06数列)

2008年全国各地高考数学试题及解答分类汇编大全(06数列)一、选择题: 1.(2008北京文)已知等差数列{a n }中,a 2=6,a 5=15.若b n =a 2n ,则数列{b n }的前5项和等于(C ) (A)30 (B )45 (C)90 (D)1862.(2008北京理)已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于(C )A .165-B .33-C .30-D .21-3.(2008福建文)设{}n a 是等差数列,若273,13a a ==,则数列{}n a 前8项和为( C ) A.128 B.80 C.64 D.564.(2008福建理)设{a n }是公比为正数的等比数列,若n 1=7,a 5=16,则数列{a n }前7项的和为(C )A.63B.64 C .127 D.1285.(2008广东文)记等差数列{}n a 的前n 项和为n S ,若42=S ,204=S ,则该数列的公差d=( C )A .7 B. 6 C. 3 D. 26.(2008广东理)记等差数列{}n a 的前n 项和为n S ,若211=a ,204=S ,则=6S ( D ) A .16 B. 24 C. 36 D. 487、(2008海南、宁夏文、理)设等比数列{}n a 的公比2q =, 前n 项和为n S ,则42S a =( C ) A. 2 B. 4C.152 D. 1728.(2008江西文、理)在数列{}n a 中,1112,ln 1n n a a a n +⎛⎫==++⎪⎝⎭,则n a =( A ) A .2ln n + B .()21ln n n +- C .2ln n n + D .1ln n n ++9.(2008全国Ⅰ卷文)已知等比数列{}n a 满足122336a a a a +=+=,,则7a =( A )A .64B .81C .128D .24310.(2008全国Ⅰ卷理)已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( C )A .138B .135C .95D .2311.(2008陕西文、理)已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于(B )A .64B .100C .110D .12012.(2008上海文\理)若数列{}n a 是首项为l ,公比为32a -的无穷等比数列,且{}n a 各项的和为a ,则a 的值是( B ) A.1 B.2 C.12 D.5413.(2008四川理)已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是( D ) (A)(],1-∞- (B)()(),01,-∞+∞U (C)[)3,+∞ (D)(][),13,-∞-+∞U 13.【解1】:∵等比数列()n a 中21a = ∴当公比为1时,1231a a a ===,33S = ; 当公比为1-时,1231,1,1a a a =-==-,31S =- 从而淘汰(A)(B)(C)故选D ;【解2】:∵等比数列()n a 中21a = ∴312321111S a a a a q q q q⎛⎫=++=++=++ ⎪⎝⎭∴当公比0q >时,31113S q q =++≥+=;当公比0q <时,31111S q q ⎛⎫=---≤-=- ⎪⎝⎭ ∴(][)3,13,S ∈-∞-+∞U 故选D ;14.(2008天津文) 若等差数列{}n a 的前5项和525S =,且23a =,则7a =( B )A .12B .13C .14D .1515.(2008浙江文)已知{a n }是等比数列,a n =2,a 3=41,则公比q=( D ) (A)21-(B)-2 (C)2 (D)2116.(2008浙江理)已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a Λ= ( C )(A )16(n --41) (B )16(n --21) (C )332(n --41) (D )332(n --21)17. (2008重庆文)已知{a n }为等差数列,a 2+a 8=12,则a 5等于( C )(A)4 (B)5 (C)6 (D)7二、填空题:1.(2008安徽文)在数列{}n a 在中,542n a n =-,212n a a a an bn ++=+L ,*n N ∈,其中,a b 为常数,则ab = -12.(2008安徽理)在数列{}n a 在中,542n a n =-,212n a a a an bn ++=+L ,*n N ∈,其中,a b 为常数,则lim n nn nn a b a b →∞-+的值是 13.(2008海南、宁夏文)已知{a n }为等差数列,a 3 + a 8 = 22,a 6 = 7,则a 5 = ___15__4. (2008湖北理)已知函数f(x)=2x ,等差数列{a x }的公差为2.若f(a 2+a 4+a b +a 2+a 1)=4,则 Log 2[f(a 1)·f(a 2)·f(a)·…·f(a 10)]= -6 .5.(2008四川文) 设数列{}n a 中,112,1n n a a a n +==++,则通项n a =()112n n ++__。
2008年高考数学考试试题分类汇编——数列

2008年高考数学试题分类汇编数列一. 选择题:1.(全国一5)已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( C )A .138B .135C .95D .232.(上海卷14) 若数列{a n }是首项为1,公比为a -32的无穷等比数列,且{a n }各项的和为a ,则a 的值是(B )A .1B .2C .12D .543.(北京卷6)已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于( C )A .165-B .33-C .30-D .21-4.(四川卷7)已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是(D ) (A)(],1-∞- (B)()(),01,-∞+∞(C)[)3,+∞ (D)(][),13,-∞-+∞5.(天津卷4)若等差数列{}n a 的前5项和525S =,且23a =,则7a =B (A )12 (B )13 (C )14 (D )156.(江西卷5)在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a = AA .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++ 7.(陕西卷4)已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于( B )A .64B .100C .110D .1208.(福建卷3)设{a n }是公比为正数的等比数列,若n 1=7,a 5=16,则数列{a n}前7项的和为CA.63B.64C.127D.1289.(广东卷2)记等差数列{}n a 的前n 项和为n S ,若112a =,420S =,则6S =( D ) A .16B .24C .36D .4810.(浙江卷6)已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a =C (A )16(n --41) (B )16(n --21) (C )332(n --41) (D )332(n --21) 11.(海南卷4)设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( C ) A. 2B. 4C.152D.172二. 填空题:1.(四川卷16)设等差数列{}n a 的前n 项和为n S ,若4510,15S S ≥≤,则4a 的最大值为______4_____。
2008年高考试题分类(4)(数学-数列)

4 数列一、选择题1.(北京 7).已知等差数列a n 中, a 2 6 , a 5 15 ,若b n a 2n ,则数列 b n 的前 5 项和等于 ( C )A .30B . 45C . 90D . 1862.(广东 4)记等差数列 {a n }的前 n 项和为 S n ,若 S 1=4,S 4=20,则该数列的公差d= ( B )A.7B.6C.3D.23.(宁夏 8)设等比数列 a n 的公比 q=2,前 n 项和为 S n ,则S 4=(C)a 2A . 2B . 41517 C .D .221) ,则 a n4.(江西 5)在数列 { a n } 中, a 1 2 , a n1a n ln(1( A )nA . 2 ln nB . 2 (n 1)ln nC . 2 n ln nD . 1 n ln n5.(全国Ⅰ 7)已知等比数列 { a n } 知足 a 1 a 2 3, a 2 a 3 6 ,则 a 7 ( A)A .64B .81C . 128D . 2436.(福建 3)设 { a n } 是等差数列,若 a 2 3, a 7 13,则数列 { a n } 前 8 项和为( C)A. 128B. 80C. 64D. 567.(上海 14)若 a 是首项为 l ,公比为 a3各项的和为 a ,则 a 的值是( B )的无量等比数列, 且 an2nA. 1B. 2C.1D. 5248.(天津 4) 若等差数列 a n 的前 5项和 S 5 25 ,且 a 2 3 ,则 a 7(B )A .12B .13C . 14D . 159.(浙江 4)已知 a n a 2 2, a 51是等比数列,,则公比 q = ( D )4( A )1 (B ) 2(C )212( D )210.(重庆 1)已知{ a n }为等差数列, a 2+a 8=12,则 a 5 等于( C)(A)4(B)5(C)6(D)711.(陕西 4) 已知 { a n } 是等差数列, a 1 a 2 4 , a 7 a 8 28 ,则该数列前10 项和 S 10 等于( B )A .64B .100C . 110D . 120二、填空题1.(安徽 15) 在数列 { a n } 在中, a n 4n 5 , a 1 a 2a nan 2 bn , n N * ,此中 a, b 为常数,则2ab- 12.(宁夏)已知a n为, a1 a322 , a67 ,则 a5. 153.(江苏 10)将全体正整数排成一个三角形数阵:12 34 5 678910。
2008年高考数学试题及答案

2008年高考数学试题及答案一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 设集合A={x|0≤x≤3},B={x|x≤1或x≥2},则A∩B=()A.{x|0≤x≤1}B.{x|1≤x≤2}C.{x|0≤x≤3}D.{x|0≤x≤1或2≤x≤3}2. 函数y=(x-1)^2+2的最小值为()A.0B.1C.2D.33. 已知等差数列{an}的前n项和为Sn,若S4=16,S7=28,则该数列的通项公式为()A.an=2n-3B.an=2n-1C.an=3n-4D.an=3n-24. 已知函数f(x)=2x^3-3ax^2+bx+c,其中a、b、c是常数,且f(x)在x=1处取得极大值,则a、b的值分别为()A.2,-6B.2,6C.-2,-6D.-2,65. 若三角形ABC的三边长分别为a、b、c,且a^2+b^2+c^2=ab+bc+ac,则三角形ABC的形状为()A.等边三角形B.等腰三角形C.直角三角形D.钝角三角形6. 已知函数f(x)=x^3-3x+1,求不等式f(x)<0的解集。
A.{x|-1<x<1}B.{x|x<-1或x>1}C.{x|-1<x<2}D.{x|x<-2或x>2}7. 设函数g(x)=x^2+2ax+b(a<0)的图象上存在点P(t,m),使得该图象在点P处的切线斜率为2,则t的取值范围是()A.t<0B.t=0C.t>0D.t≥08. 若函数y=f(x)的定义域为(-∞,2),则函数y=f(x-1)的定义域为()A.(-∞,1)B.(-∞,3)C.(1,+∞)D.(3,+∞)9. 已知函数f(x)=x^3-3x^2+x+1,求证:方程f(x)=0在区间(0,2)内至少有一个实根。
10. 若函数y=(2x-1)/(x-2)在区间(1,3)上是减函数,则实数x的取值范围是()A.1<x<2B.2<x<3C.1<x<3D.x≥3二、填空题(本大题共5小题,每小题5分,共25分。
2008年全国各地高考数学试题及解答分类汇编大全(04导数及其应用)
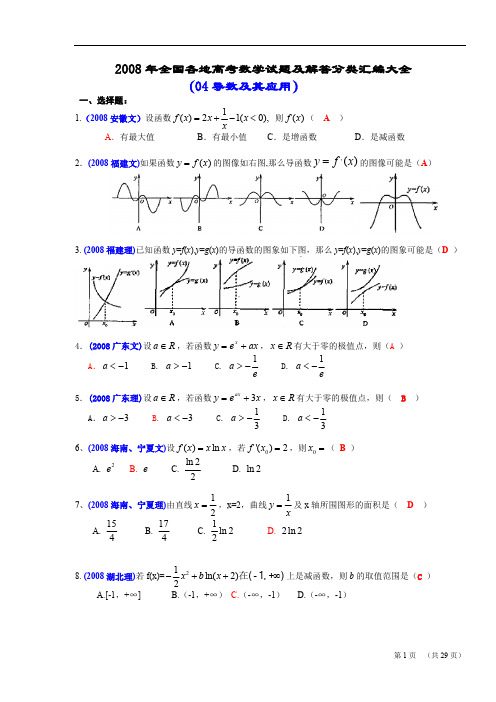
1.解: (1) f ' (x) ax2 3x (a 1) ,由于函数 f (x) 在 x 1 时取得极值,所以 f ' (1) 0 即 a 3 a 1 0,∴a 1
(2) 方法一:由题设知: ax2 3x (a 1) x2 x a 1 对任意 a (0, ) 都成立 即 a(x2 2) x2 2x 0 对任意 a (0, ) 都成立 设 g(a) a(x2 2) x2 2x(a R) , 则对任意 x R , g(a) 为单调递增函数 (a R) 所以对任意 a (0, ) , g(a) 0 恒成立的充分必要条件是 g(0) 0 即 x2 2x 0 ,∴2 x 0
(- b , b ) b
( b ,+∞)
f′(x)
+
0
-
0
+
所以,当 b<0 时,函数 f (x)在(-∞,- b )上单调递增,在(- b , b )上单调递减,在 ( b ,+∞)上单调递增.
当 b>0 时,f′(x)>0.所以函数 f (x)在(-∞,+∞)上单调递增.
4.(2008
(0,4),(2,0),(6,4) ,则 f ( f (0))
lim f (1 x) f (1) —2
x0
x
2; .(用数字作答)
y
4A
C
3
2
3.
(2008
湖南理)
lim
x1
x2
x 1 3x
4
______
.
1 5
1 B
O 1 234 5 6 x
第 2 页 (共 29 页)
4. (2008 江苏)直线 y 1 x b 是曲线 y ln x x 0 的一条切线,则实数 b= ln2-1 .
2008年全国各地高考数学试题及解答分类汇编大全

2008年全国各地高考数学试题及解答分类汇编大全(15统计、统计案例、算法初步、框图、推理与证明)一、选择题:1.(2008广东理)某校共有学生2000名,各年级男、女生人数如表1.已知在全校学生中随机抽取1名,抽到二年级女生的 概率是0.19 .现用分层抽样的方法在全校抽取64名 学生, 则应在三年级抽取的学生人数为( C ) A .24 B. 18 C. 16 D. 12解:由19.02000=x,得38019.02000=⨯=x , 三年级人数为500)370380377373(2000=+++-=+z y ,设应在三年级抽取m 人,则200064500=m ,解得m=16. 故答C.2、(2008海南、宁夏文、理)右面的程序框图,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( A ) A. c > x B. x > c C. c > b D. b > c3. (2008山东理)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图,图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( B )(A )304.6 (B )303.6 (C)302.6 (D)301.64.(2008山东文)从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为( B )A B C .3 D .855.(2008陕西文) 某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为( C ) A .30 B .25 C .20 D .156.(2008陕西纹、理) 为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为012i a a a a ,{01}∈,(012i =,,),传输信息为00121h a a a h ,其中001102h a a h h a =⊕=⊕,,⊕运算规则为:000⊕=,011⊕=,101⊕=,110⊕=,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( C )A .11010B .01100C .10111D .000117. (2008重庆文) 某交高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是 ( D )(A)简单随机抽样法 (B)抽签法 (C)随机数表法 (D)分层抽样法二、填空题:1.(2008广东文)为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量。
2008年普通高等学校招生全国统一考试数学试卷分类汇编3.4 数列综合应用

第三章 数列四 数列综合应用【考点阐述】 数列综合应用 【考试要求】(4)运用等差数列、等比数列及求和知识解决数列综合问题。
【考题分类】(一)解答题(共35题)1.(安徽卷理21)设数列{}n a 满足3*010,1,,n n a a ca c c N c +==+-∈其中为实数(Ⅰ)证明:[0,1]n a ∈对任意*n N ∈成立的充分必要条件是[0,1]c ∈;(Ⅱ)设103c <<,证明:1*1(3),n n a c n N -≥-∈; (Ⅲ)设103c <<,证明:222*1221,13n a a a n n N c++>+-∈- 解 (1) 必要性 :120,1a a c ==-∵∴ ,又 2[0,1],011a c ∈≤-≤∵∴ ,即[0,1]c ∈充分性 :设[0,1]c ∈,对*n N ∈用数学归纳法证明[0,1]n a ∈ 当1n =时,10[0,1]a =∈.假设[0,1](1)k a k ∈≥则31111k k a ca c c c +=+-≤+-=,且31110k k a ca c c +=+-≥-=≥1[0,1]k a +∈∴,由数学归纳法知[0,1]n a ∈对所有*n N ∈成立(2) 设 103c <<,当1n =时,10a =,结论成立 当2n ≥ 时,3211111,1(1)(1)n n n n n n a ca c a c a a a ----=+--=-++∵∴103C <<∵,由(1)知1[0,1]n a -∈,所以 21113n n a a --++≤ 且 110n a --≥ 113(1)n n a c a --≤-∴21112113(1)(3)(1)(3)(1)(3)n n n n n a c a c a c a c -----≤-≤-≤≤-= ∴1*1(3)()n n a c n N -≥-∈∴(3) 设 103c <<,当1n =时,2120213a c=>--,结论成立 当2n ≥时,由(2)知11(3)0n n a c -≥->21212(1)1(1(3))12(3)(3)12(3)n n n n n a c c c c ----≥-=-+>-∴ 222222112212[3(3)(3)]n n n a a a a a n c c c -+++=++>--+++ ∴2(1(3))2111313n c n n c c-=+->+---2.(安徽卷文21)设数列{}n a 满足*01,1,,n n a a a ca c c N +==+-∈其中,a c 为实数,且0c ≠(Ⅰ)求数列{}n a 的通项公式 (Ⅱ)设11,22a c ==,*(1),n n b n a n N =-∈,求数列{}n b 的前n 项和n S ; (Ⅲ)若01n a <<对任意*n N ∈成立,证明01c <≤ 解 (1) 方法一: 11(1)n n a c a +-=-∵∴当1a ≠时,{}1n a -是首项为1a -,公比为c 的等比数列。
2008年高考数学试题分类汇编数列2008年高考数学试题分类汇编数列

数列作业一. 选择题:1.已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( ) A .138B .135C .95D .23 2. 若数列{a n }是首项为1,公比为a -32的无穷等比数列,且{a n }各项的和为a ,则a的值是( )A .1 B .2 C .12 D .543.已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于( ) A .165-B .33-C .30-D .21-4.已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是( ) (A)(],1-∞- (B)()(),01,-∞+∞(C)[)3,+∞ (D)(][),13,-∞-+∞5.若等差数列{}n a 的前5项和525S =,且23a =,则7a =(A )12 (B )13 (C )14 (D )156.在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a =A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++ 7.已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于( ) A .64B .100C .110D .1208.(福建卷3)设{a n }是公比为正数的等比数列,若n 1=7,a 5=16,则数列{a n }前7项的和为A.63B.64C.127D.1289.记等差数列{}n a 的前n 项和为n S ,若112a =,420S =,则6S =( ) A .16B .24C .36D .4810.已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a = (A )16(n --41) (B )16(n --21) (C )332(n --41) (D )332(n --21) 11.设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( ) A. 2B. 4C.152D.172二. 填空题:1.设等差数列{}n a 的前n 项和为n S ,若4510,15S S ≥≤,则4a 的最大值为___________。
2008年普通高等学校招生全国统一考试数学试卷分类汇编1.1集合

第一章 集合与简易逻辑一 集合【考点阐述】集合.子集.补集.交集.并集. 【考试要求】(1)理解集合、子集、补集、交集、并集的概念.了解空集和全集的意义.了解属于、包含、相等关系的意义.掌握有关的术语和符号,并会用它们正确表示一些简单的集合. 【考题分类】(一)选择题(共20题)1、(安徽卷理2)集合{}|lg ,1A y R y x x =∈=>,}{2,1,1,2B =--则下列结论正确的是( )A .}{2,1A B =-- B . ()(,0)R C A B =-∞ C .(0,)A B =+∞D . }{()2,1R C A B =--解: }{0A y Ry =∈>,R (){|0}A y y =≤ð,又{2,1,1,2}B =--∴ }{()2,1R A B =-- ð,选D 。
2、(安徽卷文1)若A 为全体正实数的集合,{}2,1,1,2B =--则下列结论正确的是( )A .}{2,1A B =-- B . ()(,0)R C A B =-∞ C .(0,)A B =+∞D . }{()2,1R C A B =--解:R A ð是全体非正数的集合即负数和0,所以}{()2,1R A B =-- ð3、(北京卷理1)已知全集U =R ,集合{}|23A x x =-≤≤,{}|14B x x x =<->或,那么集合A ∩(C U B )等于( )A .{}|24x x -<≤ B .{}|34x x x 或≤≥ C .{}|21x x -<-≤ D .{}|13x x -≤≤【标准答案】: D【试题分析】: C U B=[-1, 4],()U A B ð={}|13x x -≤≤ 【高考考点】:集合【易错提醒】: 补集求错【备考提示】: 高考基本得分点4、(北京卷文1)若集合{|23}A x x =-≤≤,{|14}B x x x =<->或,则集合A B 等于( )A .{}|34x x x >或≤ B .{}|13x x -<≤ C .{}|34x x <≤D .{}|21x x --<≤【答案】D【解析】{}|21A B x x =-≤-<5、(福建卷文1)若集合A ={x |x 2-x <0},B={x |0<x <3},则A ∩B 等于( )A.{x |0<x <1}B.{x |0<x <3}C.{x |1<x <3}D. Φ 解:A ={x |0<x<1}∴A ∩B={x |0<x <1} 6、(广东卷文1)第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A ={参加北京奥运会比赛的运动员},集合B ={参加北京奥运会比赛的男运动员}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2008年高考数学试题分类汇编数列一. 选择题:1.(全国一5)已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( C )A .138B .135C .95D .232.(上海卷14) 若数列{a n }是首项为1,公比为a -32的无穷等比数列,且{a n }各项的和为a ,则a 的值是(B )A .1B .2C .12D .543.(北京卷6)已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于( C ) A .165-B .33-C .30-D .21-4.(四川卷7)已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是(D ) (A)(],1-∞- (B)()(),01,-∞+∞ (C)[)3,+∞ (D)(][),13,-∞-+∞5.(天津卷4)若等差数列{}n a 的前5项和525S =,且23a =,则7a =B (A )12 (B )13 (C )14 (D )156.(江西卷5)在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a = AA .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++ 7.(陕西卷4)已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于( B )A .64B .100C .110D .1208.(福建卷3)设{a n }是公比为正数的等比数列,若n 1=7,a 5=16,则数列{a n }前7项的和为CA.63B.64C.127D.1289.(广东卷2)记等差数列{}n a 的前n 项和为n S ,若112a =,420S =,则6S =( D ) A .16B .24C .36D .4810.(浙江卷6)已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a =C (A )16(n --41) (B )16(n --21) (C )332(n --41) (D )332(n --21) 11.(海南卷4)设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( C ) A. 2B. 4C.152D.172二. 填空题:1.(四川卷16)设等差数列{}n a 的前n 项和为n S ,若4510,15S S ≥≤,则4a 的最大值为______4_____。
安徽卷(14)在数列{}n a 在中,542n a n =-,212n a a a an bn ++=+ ,*n N ∈,其中,a b为常数,则lim n nn nn a b a b →∞-+的值是 12.(江苏卷10)将全体正整数排成一个三角形数阵:1 2 3 4 5 6 7 8 9 10. . . . . . .按照以上排列的规律,第n 行(n ≥3)从左向右的第3 个数为 .262n n -+3.(湖北卷14)已知函数()2x f x =,等差数列{}x a 的公差为2.若246810()4f a a a a a ++++=,则212310log [()()()()]f a f a f a f a ⋅⋅⋅= .-6 4.(湖北卷15)观察下列等式:2111,22ni i n n ==+∑2321111,326ni i n n n ==++∑ 34321111,424ni i n n n ==++∑ 454311111,52330n i i n n n n ==++-∑ 5654211151,621212n i i n n n n ==++-∑ 67653111111,722642n i i n n n n n ==++-+∑ ……………………………………212112101,nkk k k k k k k k i ia n a n a n a n a n a +--+--==++++⋅⋅⋅++∑可以推测,当x ≥2(*k N ∈)时,1111,,12k k k a a a k +-===+ 12k2k a -= .,05.(重庆卷14)设S n =是等差数列{a n }的前n 项和,a 12=-8,S 9=-9,则S 16= .-72三. 解答题:1.(全国一22).(本小题满分12分)(注意:在试题卷上作答无效.........) 设函数()ln f x x x x =-.数列{}n a 满足101a <<,1()n n a f a +=.(Ⅰ)证明:函数()f x 在区间(01),是增函数; (Ⅱ)证明:11n n a a +<<; (Ⅲ)设1(1)b a ∈,,整数11ln a bk a b-≥.证明:1k a b +>. 解析:(Ⅰ)证明:()ln f x x x x =-,()()()'ln ,0,1'ln 0f x x x f x x =-∈=->当时, 故函数()f x 在区间(0,1)上是增函数;(Ⅱ)证明:(用数学归纳法)(i )当n=1时,101a <<,11ln 0a a <,211111()ln a f a a a a a ==->由函数()f x 在区间(01),是增函数,且函数()f x 在1x =处连续,则()f x 在区间(01],是增函数,21111()ln 1a f a a a a ==-<,即121a a <<成立;(ⅱ)假设当(*)x k k N =∈时,11k k a a +<<成立,即1101k k a a a +<<<≤ 那么当1n k =+时,由()f x 在区间(01],是增函数,1101k k a a a +<<<≤得1()()(1)k k f a f a f +<<.而1()n n a f a +=,则121(),()k k k k a f a a f a +++==,121k k a a ++<<,也就是说当1n k =+时,11n n a a +<<也成立;根据(ⅰ)、(ⅱ)可得对任意的正整数n ,11n n a a +<<恒成立. (Ⅲ)证明:由()ln f x x x x =-.1()n n a f a +=可得kk k k a a b a b a ln 1--=-+11ln ki i i a b a a ==--∑ 1, 若存在某i k ≤满足i a b ≤,则由⑵知:1k i a b a b +-<-≥02, 若对任意i k ≤都有b a i >,则kk k k a a b a b a ln 1--=-+ 11ln k i i i a b a a ==--∑11ln k i i a b a b ==--∑11()ln ki i a b a b ==--∑b ka b a ln 11--> b ka b a ln 11--≥)(11b a b a --->0=,即1k a b +>成立. 2.(全国二20).(本小题满分12分)设数列{}n a 的前n 项和为n S .已知1a a =,13n n n a S +=+,*n ∈N .(Ⅰ)设3n n n b S =-,求数列{}n b 的通项公式; (Ⅱ)若1n n a a +≥,*n ∈N ,求a 的取值范围.解:(Ⅰ)依题意,113n n n n n S S a S ++-==+,即123nn n S S +=+, 由此得1132(3)n n n n S S ++-=-. ·························································································· 4分 因此,所求通项公式为13(3)2n n n n b S a -=-=-,*n ∈N .① ·············································································· 6分(Ⅱ)由①知13(3)2n n n S a -=+-,*n ∈N , 于是,当2n ≥时,1n n n a S S -=-1123(3)23(3)2n n n n a a ---=+-⨯---⨯ 1223(3)2n n a --=⨯+-,12143(3)2n n n n a a a --+-=⨯+-22321232n n a --⎡⎤⎛⎫=+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦, 当2n ≥时,21312302n n n a a a -+⎛⎫⇔+- ⎪⎝⎭≥≥9a ⇔-≥.又2113a a a =+>.综上,所求的a 的取值范围是[)9-+∞,. ········································································· 12分 3.(四川卷20).(本小题满分12分)设数列{}n a 的前n 项和为n S ,已知()21nn n ba b S -=-(Ⅰ)证明:当2b =时,{}12n n a n --⋅是等比数列;(Ⅱ)求{}n a 的通项公式 【解】:由题意知12a =,且()21n n n ba b S -=- ()11121n n n ba b S +++-=-两式相减得()()1121nn n n b a a b a ++--=-即12n n n a ba +=+ ①(Ⅰ)当2b =时,由①知122n n n a a +=+ 于是()()1122212nnnn n a n a n +-+⋅=+-+⋅()122n n a n -=-⋅又111210n a --⋅=≠,所以{}12n n a n --⋅是首项为1,公比为2的等比数列。
