光子晶体并行Matlab仿真研究与实现
基于Matlab的光学实验仿真

基于Matlab的光学实验仿真基于Matlab的光学实验仿真一、引言光学是研究光的传播、反射、折射和干涉等现象的学科,广泛应用于光学器件、光通信等领域。
在光学实验中,通过搭建实验装置来观察和研究光的行为,以验证光学理论并深入理解光的特性。
然而,传统的光学实验不仅设备复杂,成本高昂,而且需要大量的实验时间和实验设计。
因此,基于计算机仿真的方法成为了一种重要的补充和替代。
Matlab作为一种强大的数值计算和仿真工具,具有强大的数学运算能力和友好的图形界面,被广泛应用于科学研究和工程设计。
在光学实验中,Matlab可以模拟光的传播、折射、干涉等各种光学现象,使得研究人员可以在计算机上进行光学实验,加速实验过程并提高实验效率。
二、光的传播仿真在光学实验中,光的传播是一项重要的研究内容。
通过Matlab的计算能力,我们可以模拟光线在不同介质中的传播情况,并观察其光程差、折射等现象。
光的传播可以用波动光学的理论来描述,其中最经典的是亥姆霍兹方程。
在Matlab中,我们可以利用波动光学的相关工具箱,通过求解亥姆霍兹方程来模拟光的传播。
例如,我们可以模拟光在一特定系统中的衍射效应。
在Matlab中,衍射效应可以通过菲涅尔衍射和弗雷涅尔衍射来模拟。
我们可以设定特定的光源和障碍物,通过Matlab的计算能力计算光的传播、衍射和干涉等现象,得到不同条件下的衍射效应,并可视化展示。
三、光的折射仿真光的折射是光学领域中的另一个重要现象,研究光的折射对于理解光在不同介质中的传播行为至关重要。
通过Matlab的仿真,我们可以模拟光的折射行为,并研究不同介质对光的影响。
在Matlab中,我们可以利用光学工具箱中的折射相关函数,输入光线的入射角度、折射率等参数,模拟光线在不同介质中的折射行为。
通过改变不同介质的折射率、入射角度等参数,我们可以观察到光的全反射、折射偏折等现象,并进行定量分析和比较。
四、光的干涉仿真光的干涉是光学领域的重要研究课题之一,通过模拟光的干涉行为,可以深入理解光的相干性、波动性质等特性。
一维光子晶体 matlab程序

一维光子晶体 matlab程序编写一维光子晶体的Matlab程序涉及到许多方面,包括光子晶体的结构定义、光子晶体的色散关系、波导模式的计算等。
以下是一个简单的一维光子晶体Matlab程序的框架,供你参考:matlab.% 定义光子晶体的结构参数。
a = 1; % 光子晶格常数。
n1 = 3.5; % 光子晶体的折射率。
n2 = 1; % 外部介质的折射率。
% 计算光子晶体的色散关系。
k = linspace(0, 2pi/a, 100); % 波矢k的取值范围。
omega = 2pi3e8./a sqrt(n1^2 n2^2); % 光子晶体的色散关系。
% 绘制色散曲线。
figure;plot(k, omega);xlabel('波矢k');ylabel('频率omega');% 计算光子晶体中的波导模式。
beta = linspace(0, 2pi/a, 100); % 波导模式的波矢范围。
omega_waveguide = 2pi3e8./a sqrt(n1^2 n2^2); % 波导模式的色散关系。
% 绘制波导模式的色散曲线。
figure;plot(beta, omega_waveguide);xlabel('波导模式的波矢beta');ylabel('波导模式的频率omega_waveguide');以上代码是一个简单的一维光子晶体的Matlab程序框架,其中包括了光子晶体的结构定义、色散关系的计算以及波导模式的计算。
当然,实际编写光子晶体的Matlab程序涉及到更多的细节和复杂的算法,需要根据具体的研究目的和光子晶体的特性进行更详细的设计和编写。
希望这个简单的框架能够为你提供一些参考。
西安邮电大学光学实验matlab仿真结果分析与程序

光学实验实验报告课程名称:光学实验*名:***学院:电子工程学院系部:光电子技术系专业:电子科学与技术年级:科技1201学号:********指导教师:**2014年12 月24 日光波在介质中界面上的反射及透射特性一.实验目的:1.掌握反射系数及透射系数的概念;2.掌握反射光与透射光振幅和相位的变化规律; 3.掌握布儒斯特角和全反射临界角的概念。
二.实验原理:1 反射定律和折射定律光由一种介质入射到另一种介质时,在界面上将产生反射和折射。
现假设二介质为均匀、透明、各向同性介质,分界面为无穷大的平面,入射、反射和折射光均为平面光波,其电场表示式为)(0r k t i l l l l e E E ⋅--=ω l =i, r, t式中,脚标i 、r 、t 分别代表入射光、反射光和折射光;r 是界面上任意点的矢径,在图2-1所示的坐标情况下,有r=ix+jy图2-1 平面光波在界面上的反射和折射 图2-2 k i 、k r 、k t 三波矢关系根据电磁场的边界条件,可以得到如下关系)(0)(t i r i tr i =⋅-=⋅-==r k k r k k ωωω 这些关系表明:①入射光、反射光和折射光具有相同的频率;②入射光、反射光和折射光均在入射面内,k i 、k r 和k t 波矢关系如图2-2所示。
进一步可得tt i i r r i i sin sin sin sin θθθθk k k k == 或tt i i r r i i sin sin sin sin θθθθn n n n ==即介质界面上的反射定律和折射定律,它们给出了反射光、折射光的方向。
折射定律又称为斯涅耳(Snell)定律。
2 菲涅耳公式 s 分量和p 分量通常把垂直于入射面振动的分量称做s 分量,把平行于入射面振动的分量称做p 分量。
为讨论方便起见,规定s 分量和p 分量的正方向如图2-3所示。
图2-3 s 分量和p 分量的正方向反射系数和透射系数 假设介质中的电场矢量为)(i 0e r k t l l l E E ⋅--=ω l =i, r, t其s 分量和p 分量表示式为)(i 0e r k t lm lm l E E ⋅--=ω m =s,p则定义s 分量、p 分量的反射系数、透射系数分别为tmtm m im rmm E E t E E r 0000==菲涅耳公式假设界面上的入射光、反射光和折射光同相位,根据电磁场的边界条件及s 分量、p 分量的正方向规定,可得ts rs s E E E i =+和2tp 1rp 1ip cos cos cos θθθH H H =-利用E H εμ=,上式变为22ts 11rs is cos cos )(θθn E n E E =-再利用折射定律,消去E ts ,经整理可得)sin()sin(1212is rs θθθθ+-=E E 根据反射系数定义,得到)sin()sin(2121θθθθ+--=s r221111cos cos cos 2θθθn n n t s +=将所得到的表示式写成一个方程组,就是著名的菲涅耳公式:212122112*********tan tan tan tan cos cos cos cos )sin()sin(θθθθθθθθθθθθ+--=+-=+--==n n n n E E r is rs s 2121211221122121002sin 2sin 2sin 2sin cos cos cos cos )tan()tan(θθθθθθθθθθθθ+-=+-=+-==n n n n E E r iprp p 21121121112100221111212100cos cos cos 2)cos()sin(sin cos 2cos cos cos 2)sin(sin cos 2θθθθθθθθθθθθθθθθn n n E E t n n n E E t iptp p is ts s +=-+==+=+==这些系数首先是由菲涅耳用弹性波理论得到的,所以又叫做菲涅耳系数。
MATLAB仿真技术实验教案

MATLAB仿真技术实验教案第一篇:MATLAB仿真技术实验教案《MATLAB仿真技术》实验教案实验一实验名称:熟悉Matlab交互工作界面一、实验目的1、熟悉Matlab各种工作界面的操作要旨2、掌握Matlab的基本操作命令二、实验步骤1、命令窗口(1)体验命令窗口的菜单及各项功能(2)尝试命令窗口编辑特殊功能键和设置2、工作空间窗口与当前路径窗口(1)在工作空间窗口查看及修改变量(2)添加新的路径为Matlab路径3、图形窗口和文本编辑窗口(1)练习图形窗口中修改图形的方法(2)在文本编辑窗口调试程序4、体会Matlab的基本操作命令三、实验仪器PC机 MATLAB软件四、实验结果五、结论实验二实验名称:Matlab在符号计算方面的应用一、实验目的1、掌握标识符的生成和使用2、掌握矩阵及变量的赋值3、熟悉三类运算符及其功能二、实验内容1、标识符的生成和使用1)、计算y=x+(x-0.98)/(x+1.35)-5(x+1/x),当x=2和x=4时的值。
>>x=[2 4];y=x.^3+(x-0.98).^2./(x+1.35).^3-5*(x+1./x);y y = -4.4723 42.8096 32)、计算cos60-9-2。
ο323>> y=cos(pi/3)-(9-sqrt(2))^(1/3)y =-1.46492、矩阵及变量的赋值21)、已知a=3,A=4,b=a,B=b2-1,c=a+A-2B,C=a+2B+c,求C >> a=3;A=4;b=a^2;B=b^2-1;c=a+A-2*B;C=a+2*B+c;C C = 2)、创建3×4矩阵魔方阵和相应的随机矩阵,将两个矩阵并接起来,然后提取任意两个列向量。
>> A=magic(4);A(4,:)=[];B=rand(3,4);C=[A B];D=C(:,3);E=C(:,4);D,E D = 3 10 6E =8 12 3)、创建一个5×5随机阵并求其逆。
如何使用Matlab技术进行模拟仿真

如何使用Matlab技术进行模拟仿真引言在科学研究和工程设计中,模拟仿真是一种重要的工具。
它可以帮助研究人员和工程师预测和评估系统的性能、优化设计方案、解决问题等。
近年来,Matlab成为了广泛使用的科学计算软件,具有强大的数值计算和仿真功能。
本文将介绍如何使用Matlab技术进行模拟仿真,以及一些常见的应用案例。
一、Matlab的基本介绍Matlab是由美国MathWorks公司开发的一种科学计算软件。
它具有丰富的数学函数库和各种工具箱,可以进行数值计算、数据可视化、统计分析、信号处理、控制系统设计等。
Matlab是一种解释性的编程语言,用户可以通过编写脚本文件或使用命令行进行交互式计算。
二、Matlab的仿真建模工具Matlab提供了Simulink这一强大的仿真建模工具。
Simulink使用图形化界面,可以直观地构建系统模型。
可以将系统抽象成各种不同的模块,通过连接这些模块来描述系统的结构和行为。
Simulink支持常见的连续时间仿真、离散时间仿真和混合仿真,并提供了丰富的仿真调试工具。
三、Matlab的数值计算和优化在模拟仿真过程中,通常需要进行数值计算和参数优化。
Matlab提供了强大的数值计算功能,可以进行矩阵运算、数值积分、微分方程求解、优化等。
用户可以通过编写自定义函数和调用内置函数来实现数值计算和优化任务。
Matlab还提供了各种优化算法,如遗传算法、模拟退火算法、粒子群优化算法等,可以解决复杂的优化问题。
四、Matlab在控制系统设计中的应用控制系统是一种常见的工程系统,如何设计合适的控制策略是一个重要的问题。
Matlab提供了专门的控制系统工具箱,包括系统建模、控制器设计、仿真测试等功能。
用户可以使用Matlab进行控制系统建模,通过调整控制器参数来达到所需的性能指标,并使用Simulink进行仿真测试。
Matlab还提供了自适应控制、最优控制、模糊控制等高级控制方法,可以满足不同的控制需求。
利用平面波展开法在matlab中计算一维光子晶体的带隙结构

利用平面波展开法在matlab中计算一维光子晶体的带隙结构1. 引言1.1 研究背景光子晶体是近年来新型功能性材料的研究热点之一,其具有周期性结构对光子的传播性质具有重要影响,表现出许多独特的光学性质。
光子晶体的带隙结构是其中一个最基本的性质,也是许多光子晶体应用的关键。
通过调控光子晶体的结构参数,可以实现对光子带隙的调控,从而实现光子晶体的光学性能优化和设计。
利用平面波展开法在Matlab中计算一维光子晶体的带隙结构具有重要意义,可以为光子晶体的设计和性能优化提供有力支持。
本文将从理论基础出发,详细介绍平面波展开法的原理,光子晶体的带隙结构计算方法,以及在Matlab中实现算法的过程。
希望通过本研究对光子晶体的带隙结构有更深入的理解,为未来的光子晶体研究和应用提供新的思路和方法。
1.2 研究目的研究目的是利用平面波展开法在Matlab中计算一维光子晶体的带隙结构,通过研究光子晶体的带隙结构,可以深入了解光子晶体的光学特性和传输特性。
这对于设计和制造新型光子晶体材料具有重要意义。
目的在于探究光子晶体的带隙结构与其微结构之间的关系,为调控光子晶体的光学性质提供理论指导。
通过计算一维光子晶体的带隙结构,可以更好地理解光子晶体在光学通信、光子器件和传感器等领域的应用潜力,并为实际应用提供技术支持。
研究光子晶体的带隙结构还有助于拓展光学材料的设计思路,推动光子晶体材料在光电子领域的发展。
通过本研究,可以为光子晶体的应用研究和材料设计提供重要的理论基础和技术支持。
1.3 研究意义光子晶体的带隙结构计算是光子学研究的重要内容之一,能够揭示光子在晶格周期性结构中的行为规律。
利用平面波展开法在Matlab 中计算一维光子晶体的带隙结构,可以快速准确地获得光子晶体的能带结构,为进一步研究光子传输、光谱性质等提供重要依据。
通过本研究,可以深入了解光子晶体的光学性质,为光子学领域的发展和光子晶体材料的应用提供理论支持。
matlab仿真二维光子晶体最简程序

matlab仿真⼆维光⼦晶体最简程序本程序为初学者使⽤,只考虑MT⽅向下⾯的程序为matlab代码只考虑MT⽅向%This is a simple demo for Photonic Crystals simulation%This is a simple demo for Photonic Crystals simulation%This demo is for TE wave only, so only h wave is considered.%for TM direction only,10 points is considered.%---------------------------------------M%| / |%| / |%| / |%| --------------------|X%| T |%| |%| |%---------------------------------------%equation :sum_{G',k}(K+G)(K+G')f(G-G')hz(k+G')=(omega/c)^2*hz(k+G)%G' can considerd as the index of column, and G as index of rows%[(K+G1)(K+G1)f(G1-G1) (K+G1)(K+G2)f(G1-G2) ][hz(G1)]=(omega/c)^2[hz(G1)]%[(K+G2)(K+G1)f(G2-G1) (K+G2)(K+G2)f(G2-G2) ][hz(G2)] [hz(G2)]%or: THETA_TE*Hz=(omega/c)^2*Hz%by Gao Haikuo%date:20170411clear; clc; epssys=1.0e-6; %设定⼀个最⼩量,避免系统截断误差或除0错误%this is the lattice vector and the reciprocal lattice vectora=1; a1=a*[1 0]; a2=a*[0 1];b1=2*pi/a*[1 0];b2=2*pi/a*[0 1]; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%定义晶格的参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%epsa = 1; %介质柱的介电常数epsb = 13; %背景的介电常数Pf = 0.7; %Pf = Ac/Au 填充率,可根据需要⾃⾏设定Au =a^2; %⼆维格⼦原胞⾯积Rc = (Pf *Au/pi)^(1/2); %介质柱截⾯半径Ac = pi*(Rc)^2; %介质柱横截⾯积%construct the G listNrSquare = 10;NG =(2*NrSquare+1)^2; % NG is the number of the G valueG = zeros(NG,2);i = 1;for l = -NrSquare:NrSquarefor m = -NrSquare:NrSquareG(i,:)=l*b1+m*b2;i = i+1;endend%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%⽣成k空间中的f(Gi-Gj)的值,i,j 从1到NG。
matlab激光器仿真

Matlab激光器仿真简介激光器是一种能够产生激光光束的设备,广泛应用于通信、医疗、材料加工等领域。
在激光器设计和优化的过程中,进行仿真是非常重要的一步。
Matlab作为一款功能强大的数学软件,提供了丰富的工具和函数库,可以方便地进行激光器仿真。
本文将介绍如何使用Matlab进行激光器仿真,包括模型建立、参数设置、仿真结果分析等内容。
激光器模型建立激光器基本原理在进行激光器仿真之前,我们首先需要了解激光器的基本原理。
激光器的核心部件是激光介质,通常是由半导体材料或激光晶体构成。
在激光介质中,通过泵浦能量的输入,激发介质内部的原子或分子从低能级跃迁到高能级,形成电子激发态。
当这些激发态的粒子回到低能级时,会放出光子,这些光子受到激发态的粒子数目和能级之间的能量差的限制,具有相干性并具有特定的频率和相位。
模型建立步骤激光器仿真的第一步是建立激光器模型。
在Matlab中,我们可以通过使用光线追踪或波动光学等方法来建立激光器模型。
以下是建立激光器模型的一般步骤:1.定义激光介质的材料属性,包括吸收率、发射截面等。
2.设计激光器的几何结构,包括激光介质的形状、激光器的长度、腔内的镜子等。
3.设置激光器的泵浦方式和泵浦能量,这将决定激光器的输出功率。
4.定义激光器的初始状态,包括介质的初始粒子数目和能级分布等。
参数设置在进行激光器仿真之前,我们还需要设置一些重要的参数,以确保仿真结果的准确性和可靠性。
以下是一些常用的参数设置:1.激光器的波长:激光器的波长决定了输出光的频率,对于不同的应用需求可能有不同的要求。
2.激光器的腔长:激光器的腔长决定了激光器的工作模式,一般可以选择连续模式或脉冲模式。
3.激光器的输出功率:激光器的输出功率可以通过调整泵浦能量或改变激光介质的特性来控制。
4.激光器的损耗:激光器的损耗来自于各种因素,如腔内的镜子反射率、介质的吸收等,需要进行准确的估计和设置。
仿真结果分析通过进行激光器仿真,我们可以得到激光器的输出光强、波形、频谱等信息,并进行相应的分析。
西安邮电大学光学实验matlab仿真结果分析与程序

光学实验实验报告课程名称:光学实验姓名:伍金霄学院:电子工程学院系部:光电子技术系专业:电子科学与技术年级:科技1201学号:指导教师:刘娟2014年12 月24 日光波在介质中界面上的反射及透射特性一.实验目的:1.掌握反射系数及透射系数的概念;2.掌握反射光与透射光振幅和相位的变化规律; 3.掌握布儒斯特角和全反射临界角的概念。
二.实验原理:1 反射定律和折射定律光由一种介质入射到另一种介质时,在界面上将产生反射和折射。
现假设二介质为均匀、透明、各向同性介质,分界面为无穷大的平面,入射、反射和折射光均为平面光波,其电场表示式为)(0r k t i l l l l e E E ⋅--=ω l =i, r, t式中,脚标i 、r 、t 分别代表入射光、反射光和折射光;r 是界面上任意点的矢径,在图2-1所示的坐标情况下,有r=ix+jy图2-1 平面光波在界面上的反射和折射 图2-2 k i 、k r 、k t 三波矢关系根据电磁场的边界条件,可以得到如下关系)(0)(t i r i tr i =⋅-=⋅-==r k k r k k ωωω 这些关系表明:①入射光、反射光和折射光具有相同的频率;②入射光、反射光和折射光均在入射面内,k i 、k r 和k t 波矢关系如图2-2所示。
进一步可得tt i i r r i i sin sin sin sin θθθθk k k k == 或tt i i r r i i sin sin sin sin θθθθn n n n ==即介质界面上的反射定律和折射定律,它们给出了反射光、折射光的方向。
折射定律又称为斯涅耳(Snell)定律。
2 菲涅耳公式 s 分量和p 分量通常把垂直于入射面振动的分量称做s 分量,把平行于入射面振动的分量称做p 分量。
为讨论方便起见,规定s 分量和p 分量的正方向如图2-3所示。
图2-3 s 分量和p 分量的正方向反射系数和透射系数 假设介质中的电场矢量为)(i 0e r k t l l l E E ⋅--=ω l =i, r, t其s 分量和p 分量表示式为)(i 0e r k t lm lm l E E ⋅--=ω m =s,p则定义s 分量、p 分量的反射系数、透射系数分别为tmtm m im rmm E E t E E r 0000==菲涅耳公式假设界面上的入射光、反射光和折射光同相位,根据电磁场的边界条件及s 分量、p 分量的正方向规定,可得ts rs s E E E i =+和2tp 1rp 1ip cos cos cos θθθH H H =-利用E H εμ=,上式变为22ts 11rs is cos cos )(θθn E n E E =-再利用折射定律,消去E ts ,经整理可得)sin()sin(1212is rs θθθθ+-=E E 根据反射系数定义,得到)sin()sin(2121θθθθ+--=s r221111cos cos cos 2θθθn n n t s +=将所得到的表示式写成一个方程组,就是著名的菲涅耳公式:212122112*********tan tan tan tan cos cos cos cos )sin()sin(θθθθθθθθθθθθ+--=+-=+--==n n n n E E r is rs s 2121211221122121002sin 2sin 2sin 2sin cos cos cos cos )tan()tan(θθθθθθθθθθθθ+-=+-=+-==n n n n E E r iprp p 21121121112100221111212100cos cos cos 2)cos()sin(sin cos 2cos cos cos 2)sin(sin cos 2θθθθθθθθθθθθθθθθn n n E E t n n n E E t iptp p is ts s +=-+==+=+==这些系数首先是由菲涅耳用弹性波理论得到的,所以又叫做菲涅耳系数。
利用平面波展开法在matlab中计算一维光子晶体的带隙结构

利用平面波展开法在matlab中计算一维光子晶体的带隙结构【摘要】本文利用平面波展开法在Matlab中计算了一维光子晶体的带隙结构。
在理论基础部分,介绍了光子晶体的基本原理和相关知识。
平面波展开法原理详细解释了该方法在计算带隙结构中的应用。
通过建立合适的计算模型,使用Matlab编程进行计算,并对数值模拟结果进行了分析。
实验验证部分通过与已有实验结果的对比,证明了本文方法的有效性。
展望未来研究,在总结了本文研究意义的基础上,指出了对一维光子晶体带隙结构进一步研究的方向和价值。
通过本文的研究,可以更好地理解光子晶体的特性和应用,为相关领域的研究提供重要的理论指导和实验依据。
【关键词】平面波展开法、一维光子晶体、带隙结构、理论基础、计算模型、数值模拟、实验验证、研究展望、总结1. 引言1.1 研究背景光子晶体是一种具有周期性介质结构的材料,其具有优良的光学性能,被广泛应用于光学通信、传感器、光子集成电路等领域。
光子晶体的带隙结构是其独特光学性质的基础,通过调控光子晶体的结构参数可以实现对特定光波的传输、反射、折射等控制。
随着光子晶体在光学领域的应用日益增多,对光子晶体的带隙结构进行深入研究已成为当前光子晶体研究的热点之一。
利用平面波展开法在matlab中计算一维光子晶体的带隙结构是一种常见且有效的方法,可以快速准确地获取光子晶体的带隙特性。
本文旨在探讨利用平面波展开法在matlab中计算一维光子晶体的带隙结构,通过建立合适的计算模型和采用相应的计算方法,分析一维光子晶体在不同结构参数下的带隙特性。
通过数值模拟结果的分析,可以深入了解一维光子晶体的光学性能,为进一步优化光子晶体结构和拓展其应用领域提供参考。
1.2 研究目的本文旨在利用平面波展开法在matlab中计算一维光子晶体的带隙结构。
通过对一维光子晶体的带隙结构进行研究,我们可以更深入地了解光子晶体的特性及其在光学领域中的应用。
具体来说,我们的研究目的包括:探索平面波展开法在计算光子晶体带隙结构中的有效性和精度,建立一套完整的计算模型,为进一步研究光子晶体的光学性质奠定基础;分析不同参数对光子晶体带隙结构的影响,从而优化光子晶体的设计及应用;最终,利用数值模拟结果,得出关于一维光子晶体带隙结构的相关规律和特性,为实际应用提供理论指导和参考。
MATLAB仿真实例(计算机仿真研究的步骤)
(1.1)
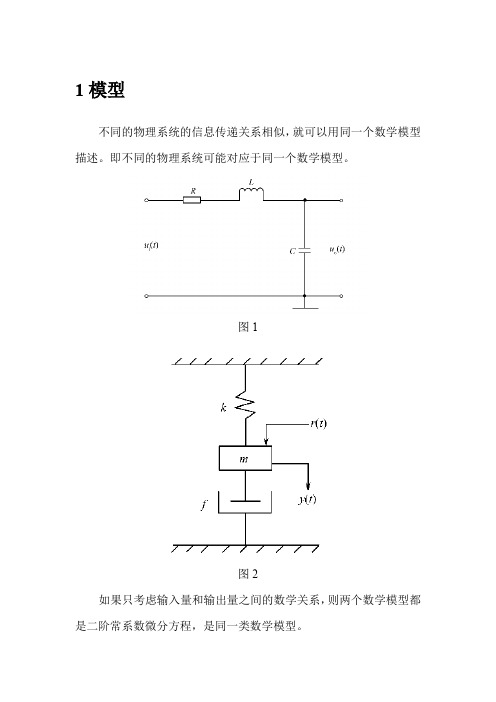
这是一个二阶常微分方程,为了后续步骤的需要,将它转换成状态方 程及输出方程
0 1 x k x 2 m 1 x1 0 f 1 r x m 2 m
当m1k4时分析系统在外力rt1t的作用下要使响应不发生振荡应在什么范围内取值其中f的取值约束为10建立系统的数学模型描述该系统输入输出关系的数学模型为11这是一个二阶常微分方程为了后续步骤的需要将它转换成状态方程及输出方程数学模型转换成仿真模型采用数值积分法中的欧拉公式可以得到离散状态方程及输出方编程和调试采用matlab语言进行编程文件名为exam20001m
【例 2.2】 利用 Simulink 对【例 2.1】中的质量-弹簧-阻尼器系统进 行仿真研究。 【解】 首先将描述该系统输入—输出关系的数学模型改写成传递 函数形式
G (s) Y (s) 1 2 R ( s ) ms fs k
(1.6)
从 Simulink 模块库的信号源子库(Sources)中,选择 Step 模块, 拖 入模型窗口,双击该模块,设置参数 Step time 为:0;从 Simulink 模 块库的连续模块子库(Continuous)中,选择 Tranfer Fcn 模块,拖入 模型窗口, 双击该模块,设置参数 Numerator 为:[1], Denominator [1 f 4] ; 为: 从 Simulink 模块库的接收器子库 (Sinks) 中, 选择 Scope 模块,拖入模型窗口。
% 置状态变量初值,其中 x(i)代表 xi(0) % Y 为 N×1 阵,记录输出 y,初始时为 1×1 阵,
% H 为 N×1 阵,记录时间 t,初始时为 1×1 阵 xs=x+(A*x+B)*T; % 计算离散状态方程
利用平面波展开法在matlab中计算一维光子晶体的带隙结构

利用平面波展开法在matlab中计算一维光子晶体的带隙结构作者:黄晓泽周琦饶黄云来源:《科技创新与应用》2019年第13期摘 ;要:利用平面波展开法,在王建东所研究的光在光子晶体(photonic crystal)中传输所满足的非线性薛定谔方程基础上,计算光子晶体间隙结构的本征方程,根据本征方程在matlab 中进行运算,得到光子晶体的带隙结构。
关键词:平面波展开;本征方程;光子晶体;matlab;带隙结构中图分类号:O734 ; ; ; ; 文献标志码:A ; ; ; ; 文章编号:2095-2945(2019)13-0029-03Abstract: Based on the nonlinear Schrodinger equation of light propagation in photonic crystal (photonic crystal) studied by Wang Jiandong, the intrinsic equation of photonic crystal gap structure is calculated by plane wave expansion method. According to the intrinsic equation, the operation is carried out in matlab, and the band gap structure of photonic crystal is obtained.Keywords: plane wave expansion; eigenequation; photonic crystal; matlab; band gap structure1 概述1987年,埃利·雅布羅诺维奇和萨耶夫·约翰提出了潜力材料光子晶体的概念,而在后来的二十多年里,通过科学家们的不断努力,光子晶体成为了一种超越半导体材料的新型材料,成为了新能源以及新材料领域之中的一颗璀璨新星,具有划时代的标志。
利用平面波展开法在matlab中计算一维光子晶体的带隙结构

利用平面波展开法在matlab中计算一维光子晶体的带隙结构1. 引言1.1 背景介绍随着光子晶体材料的制备技术不断提升,人们对其带隙结构的研究也变得更加深入。
而在计算光子晶体的带隙结构时,平面波展开法成为一种常用且有效的方法。
通过将光波场用一组基础函数(平面波)展开,可以得到光子晶体的频谱信息,进而确定其带隙结构。
在此基础上,借助matlab等数值计算工具,可以方便地模拟和计算一维光子晶体的带隙结构。
本文将介绍利用平面波展开法在matlab中计算一维光子晶体的带隙结构的方法及其原理,并对计算结果进行分析和讨论。
通过对一维光子晶体的带隙结构进行深入研究,有助于深化对光子晶体材料性质的理解,为其在光学器件和光子学应用中的设计与优化提供理论依据和技术支持。
1.2 光子晶体的基本概念光子晶体是一种具有周期性结构的材料,它的周期性结构能够产生光子带隙,从而实现光子的禁带传导和光子晶体的光学性质调控。
光子晶体的基本单位通常是由介电常数或折射率不同的材料构成的周期性排列的点阵结构。
通过调控点阵结构的周期、形状和材料的光学参数,可以实现对光子的传输、调制和控制。
光子晶体具有许多独特的物理性质,如光学带隙、负折射率、反射率增强和光子导波等。
这些性质被广泛应用于传感器、激光器、光学通信、光子计算和光伏等领域。
光子晶体的基本概念包括周期性结构、光子带隙、布里渊区等,对于理解光子晶体的性质和设计光子晶体器件至关重要。
在本文中,我们将介绍利用平面波展开法在matlab中计算一维光子晶体的带隙结构的方法和原理,以期为光子晶体的研究和应用提供参考和指导。
通过计算与分析一维光子晶体的带隙结构,可以深入了解光子晶体的光学性质,为设计新型光子晶体器件提供理论基础和指导。
这一部分的内容是对光子晶体的基本特性和重要性进行介绍和阐述,为后续章节的内容提供必要的背景知识。
1.3 研究现状虽然光子晶体的研究已经取得了一定的进展,但仍然存在一些问题和挑战,如光子晶体的制备技术、带隙结构的优化设计等方面仍需进一步深入研究。
光子晶体并行Matlab仿真研究与实现

( col f hs a Eet nc , nvrt o l t ncSineadT cnlg f hn , Sh o o yi l l r i U ie i f e r i c c n ehooyo ia P c co s sy E co e C
( 电子科技大学物理 电子学院 , 四川 成都 6 05 ) 10 4 摘要 : 由于 M t b a a 软件的网络通信局限 , l 使得在并行时域有限差分( D D 计 算仿真 中, 以实现子域 间的消息发送 与接收 FT ) 难 操作。针对这个问题 , 提出一种新 的基于磁盘 一 内存互逆 映射 的解决 方法 , 在简化并行 F T D D算法实现 的同时 , 显著提 高了 算法执行性能。作为算法实现的应用 , 对光子晶体光波导的电磁耦合 效应进行了数值 仿真研 究 , 结果证 实 : 波导耦合 区域 内
KEYW ORDS: a al l n t — i e e c i P l i r e f e— df r n e t i f me— d ma n a g rt m;Mu u l n e s p i g o h ik— me r ; — o i o h l i t al iv re ma p n f e ds — mo y t y P o o i r sa s lcr ma n t o p i g e e t h t nc c t ;E e to g ei c u l f c y l c n
不同半径 比介质柱所导致的结构变化将造成耦合长度的改变 , 且其耦合 关系曲线具有 平稳 区与迅变 区两类 不同特性 的变化
范 围 区间 。
关键 诵: 并行时域有限差分算法 ; 磁盘 一内存互逆映射 ; 光子晶体 ; 电磁耦合效应
1维光子晶体的能带结构分析

1维光子晶体的能带结构分析张志新;肖峻【摘要】为了分析研究1维光子晶体的结构参量对其能带结构的影响,并把这种影响作用应用到滤波器的设计中,采用传输矩阵法、利用MATLAB仿真软件,对不同结构参量的1维光子晶体的能带结构进行了计算仿真,分别得到了不同周期数、不同介质层厚度、不同介质折射率的1维光子晶体的能带分布图,进一步分析比较,得出了1维光子晶体的结构参量对其能带结构的影响。
结果表明,较大的周期数可以使1维光子晶体的禁带边缘更加陡峭,通带透射性增强,能带分布更加分明;介质层厚度可以调节光子晶体的能带分布情况及能带宽度;介质折射率比值可以改变禁带宽度,禁带宽度随介质折射率比值的增大而增大。
这些结果对宽带带阻滤波器的设计是有帮助的。
%In order to analyze effect of structure parameters of 1-D photonic crystal on energy band structure systematically and apply the result in filter design , transmission matrix method was used .Different energy band structures of photonic crystals of different structural parameters were calculated by MALTAB simulation software .Energy band distributions of 1-D photonic crystal with different cycles , different dielectric layer thickness and different media refractive indices were gotten .Through analysis and comparison , the effects of 1-D photonic crystal structure parameters on energy band structure were gotten .The results show that 1-D photonic crystal with larger cycle number has a steeper forbidden band-edge and higher transmission of pass band .In other word, the band distribution is more distinct .Energy distribution and energy width can be adjusted with dielectric layerthickness of photonic crystal .The width of band gap can be changed by the ratio of the refractive index of the medium .The width of band gap increases with the increase of the ratio of the refractive index of the medium .These results are helpful for the design of filters .【期刊名称】《激光技术》【年(卷),期】2015(000)004【总页数】3页(P525-527)【关键词】材料;光子晶体;传输矩阵法;能带结构;结构参量【作者】张志新;肖峻【作者单位】电子科技大学光电信息学院,成都610054;电子科技大学光电信息学院,成都610054【正文语种】中文【中图分类】O734引言1987年,YABLONOVITCH在讨论如何抑制自发辐射[1]与JOHN在讨论光子局域[2]时各自提出了光子晶体(photonic crystal,PC)的概念。
纳米级光子晶体调控与谐振效应仿真模型构建

纳米级光子晶体调控与谐振效应仿真模型构建光子晶体是一种具有周期性介电常数或折射率的材料。
它们可以通过调控光波的传播和耦合来实现光子的调制和控制。
在纳米级别上构建光子晶体有着重要的应用潜力,可以用于光学器件的设计、光子集成电路的实现以及光信息的处理。
为了准确地了解纳米级光子晶体的特性和调控机制,科学家们利用仿真模型来研究和预测其行为。
通过构建精确的仿真模型,可以模拟光子晶体中的谐振效应,探索其在不同频率、波长和角度下的光学响应。
本文将详细介绍纳米级光子晶体调控与谐振效应仿真模型的构建过程和应用。
首先,构建纳米级光子晶体调控与谐振效应仿真模型需要对光子晶体的基本结构和性质有深入的了解。
光子晶体可以分为一维、二维和三维结构,其周期性和排列方式对于其光学特性具有重要影响。
在仿真模型中,需要考虑光子晶体的结构参数,如周期性、单元单结构、填充率等。
同时,还需考虑光子晶体所用材料的光学特性,如折射率、透射率等。
其次,纳米级光子晶体调控仿真模型的构建需要选择合适的仿真软件和方法。
目前常用的基于有限元方法的光子晶体仿真软件有COMSOL Multiphysics、Lumerical FDTD、MEEP等。
这些软件可以模拟光在晶体中的传播、折射、反射和吸收等过程,能够准确地描述光子晶体的光学行为。
在构建仿真模型时,需要根据实际需求选择适合的仿真软件,并结合所研究的问题设定相应的模型边界条件和光源参数。
第三,纳米级光子晶体的调控与谐振效应仿真模型的构建需要考虑调控手段和光学效应。
光子晶体的调控通常通过改变晶体的结构参数、材料参数或通过外界的光场等手段实现。
研究不同调控方式对光子晶体的响应变化,可以进一步揭示光子晶体的调控机制。
在仿真模型中,可以通过改变晶体的周期性、填充率、材料的折射率等参数来模拟不同的调控方式,并分析其在不同波长、频率和角度下的光学效应。
最后,纳米级光子晶体调控仿真模型的构建不仅需要模拟和分析光子晶体的谐振效应,还需要与实际实验结果进行验证和比对。
基于光子晶体的matlab仿真

0.1
0.396 3.2
0.0995 3.2
3.25
3.3
3.35 3.4 介 质 d的 厚 度
3.45
3.5
3.55 x 10
-7
图 20 一维光子晶体群速度随介质 d的厚度的变化曲线
图21 一维光子晶体带宽随介质 d的厚度的变化曲线
由图20、图21可得出,随着介质d的厚度的增加,群速度和带宽都减小。由此可以 得到与a厚度变化相同的规律:宽的带宽和小的群速度是相互矛盾的,所以,要选择 合适的d的厚度,从而兼顾带宽和群速度的要求。
图14 一维光子晶体禁带宽 度随|Na|/|Nb|的变化曲线| 介质厚度对光子晶体性能的影响
图15 一维光子晶体群速 度随|Na|/|Nb|的变化曲线|
(1)介质a的厚度对群速度和带宽的影响 Na=1.81;Nb=1.41; NN=4
介 质 a的 厚 度 与 群 速 度 的 关 系 0.41 0.408 0.406 0.404
5 结论
5.1 本文介绍了特殊矩阵法,并利用特殊矩阵法对一维光子晶体的带隙特 性的影响因素进行了探究,得出了一系列因素对光子晶体特性影响的变化
曲线,为今后光子晶体带隙方面的实际应用提供一定的数据和基础。
5.2 光子晶体的研究、开发和应用将对现有的一些理论和工程基础产生变
革性的影响,对未来世界经济的发展提供一个新的生长点。
介 质 b的 厚 度 与 群 速 度 的 关 系 0.4105 0.41 0.4095 0.409
群 速 度 Vg
0.4085 0.408 0.4075 0.407 0.4065 0.406 2.75
2.8
2.85
2.9 2.95 介 质 b的 厚 度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基金项目:国家自然科学基金(60571020)收稿日期:2007-08-09 修回日期:2007-08-22第25卷 第9期计 算 机 仿 真2008年9月文章编号:1006-9348(2008)09-0312-04光子晶体并行M atl ab 仿真研究与实现刘 瑜,梁 正,杨梓强(电子科技大学物理电子学院,四川成都610054)摘要:由于M atl ab 软件的网络通信局限,使得在并行时域有限差分(FDTD)计算仿真中,难以实现子域间的消息发送与接收操作。
针对这个问题,提出一种新的基于磁盘-内存互逆映射的解决方法,在简化并行F DTD 算法实现的同时,显著提高了算法执行性能。
作为算法实现的应用,对光子晶体光波导的电磁耦合效应进行了数值仿真研究,结果证实:波导耦合区域内不同半径比介质柱所导致的结构变化将造成耦合长度的改变,且其耦合关系曲线具有平稳区与迅变区两类不同特性的变化范围区间。
关键词:并行时域有限差分算法;磁盘-内存互逆映射;光子晶体;电磁耦合效应中图分类号:TP391.9 文献标识码:AStudy and I mple m entati on of Parallel FDTD A l gorith m for Si m ul ati on of Photonic C rystals U si ng M atl abL I U Yu ,LI ANG Zheng ,YANG Z i-qiang(Schoo l of Phy si ca l E l ec tron i cs ,U nivers it y of E lectronic Sc ience and T echno l ogy of Chi na ,S i chuan Chengdu 610054,China)ABSTRACT :O n account o f the li m itati on of the communicati ons i n M a tlab soft w are ,it is d ifficult to carry out mes sage send i ng and rece iv i ng a m ong subdo m a i ns fo r the pa ra lle l fi n ite-diff e rence ti m e-doma i n (FDTD )a l gor it hm .T o reso l ve t h is proble m,a new m ethod based on m ut ua lly i nv erse m apping o f the d i sk-m e m ory is presented ,w hich can s i m p lify and i m prove obv i ousl y t he para llel FDTD a l go rith m.By usi ng this me t hod ,si m ulati on o f the e lectro m ag ne tic coupli ng effect of photon i c crystals w avegu i de i s co m pleted .N u m erical resu lts show that the structural changes caused by d ifferent rad i us rati o of die l ectric cy li ndersw ill a lter the coupli ng length o f the w aveguide ,and the coup li ng re l ationsh i p curve has t wo k i nds of d ifferent v ary i ng scope zone :stab l e zone and a ltering zone .KEY W ORDS :P ara ll e l fi n ite-difference ti m e-do m a i n a l go rith m;M utua ll y i nverse m appi ng o f the disk-m e m ory ;Photon i c crystals ;E lectro m agne tic coupli ng effect1 引言作为一种强有力的工程仿真工具,M a tlab 在光子晶体的FDTD (时域有限差分法)模拟中得到了广泛应用。
由于M at lab 具有数值计算与图形处理能力,可以很好的简化FDTD 算法的编程实现,使研究者将重点放在模拟算法本身上,而不必在编程细节上花费过多时间。
因此,对于光子晶体数值研究的一些原型问题,M atlab 平台是算法实现的一种很好选择。
M a tl ab 软件本身不具备网络通信的功能,限制了其在并行与协同仿真计算中的应用,但数值模拟问题规模的不断扩大,使单机的内存容量与计算能力都难以承担。
对此,文献[1]通过开发M a tlab 环境下的网络通信工具箱来扩展并行功能,而M atlab 软件本身也从7.0版本后增加了分布式计算工具箱[2],对并行计算提供一定的支持。
但是,这些工具箱存在种种使用上的限制,对FDTD 仿真缺乏通用性,计算性能也难以令人满意。
本文针对光子晶体并行FDTD 仿真的实际情况,利用操作系统提供的内存-网络-硬盘三者之间的映射与重定向功能,通过统一简洁的M atlab 文件I /O (输入/输出)方式来实现并行协同计算。
并以此为工具,对光子晶体光波导的电磁耦合效应进行了FDTD 仿真研究。
2 M atlab 并行FDTD 仿真原理FDTD 算法的基础是对M ax w e ll 方程组中两个旋度方程在时间和空间上进行差分离散[3],空间离散在计算机内存中的表示形式是多维数组,而时间离散则表现为紧耦合多维数组的步进迭代。
一个典型的FDTD迭代片段如下[4]:E n+1x (i,j,k)=CA(i,j,k)E nx(i,j,k)+CB(i,j,k)[H nz(i,j,k)-H nz(i,j-1,k)y][H ny(i,j,k)-H ny(i,j,k-1)z](1)其中,CA(i,j,k),CB(i,j,k)为媒质特性参数,n为时间步,(i,j,k)为网格点坐标。
可以看出,在FDTD计算域任一网格点上的电场分量只与其前一时间步的值及其四周环绕的网格点上的磁场分量有关,而与其他网格点上的场量没有直接关系。
这样的局域特征非常适于执行基于域分解的并行计算,每个子区域可单独由一台PC机进行计算,在迭代中只需在其边界处与相邻子域执行切向场分量的通信操作。
因此,通常的并行FDTD 实现,其关键过程可概括为以下三步:1)子域内部网格点的迭代计算;2)相邻子域间的场值传递;3)对各子域计算结果进行全局归并,输出最终结果。
在M atl ab编程中,由于网络/通信函数的欠缺,难以用常规方式完成子域间的数据传递。
对此,考虑利用M atl ab文件I/O作为各子域交换数据的中介。
但如前所述,FDTD模拟在计算机内部实质上表现为场值数组之间的传递与迭代操作,如果每一时间步均需在文件与数组之间进行转换,将严重影响并行算法的执行性能,需要寻求一种从系统底层将文件与数组进行高效统一处理的算法实现机制。
仔细分析M atl ab的I/O接口,可以发现在数据导入/导出功能中存在一种对文件进行读写的特殊方法:内存映射技术[5]。
其基本原理是把文件中的内容直接映射到程序的内存空间,然后可以在程序中以普通的动态数组方式存取数据,从而达到在计算中避免文件与数组数据进行转换的目的。
由于内存映射对象同时具有数组数据与磁盘文件两方面的属性,而操作系统利用其内核远程FSD(文件系统驱动)提供了完善的网络文件共享与操作支持[6],因此,作为一种文件,内存映射对象可以在算法中通过文件的UN C路径(通用命名规范)来调用操作系统的重定向FSD,实现M atl ab软件所不具备的网络/通信功能。
在具体的并行FDTD计算中,尽管利用内存映射技术有效避免了文件 数组格式转换,从一定程度上提高了算法性能。
但以文件I/O作为通信中介,是建立在磁盘存取的基础上,由于受限于磁盘固有的机械运动特性,其访问延迟与长时重载工作能力与内存相比差了几个数量级。
这也是基于文件的M atl ab并行计算性能难以进一步提高的主要原因。
因此,有必要将子域间数据通信由网络磁盘文件I/O重定向为网络内存文件I/O,其实现的基础仍然是操作系统的重定向FSD,通过调用设备驱动程序在内存中创建一个指定大小的虚拟磁盘分区,然后将子域间的场值交换文件均重定向到此内存盘中,从而实现并行计算的网络内存读写。
综上所述,在M a tlab并行FDTD仿真中,存在着一对关键的互逆映射:电/磁场值数组实现是由磁盘文件向内存映射,而子域间通信则是基于内存向磁盘文件(虚拟盘)逆向映射。
磁盘-内存互逆映射有力地保证了M atlab并行仿真的高效与简洁,同时,由于映射实现的基础均源于操作系统的固有功能,这实际上也保证了并行算法实现的通用性。
3 光子晶体并行FDTD仿真实现作为M atl ab并行FDTD仿真实现的一个应用,对耦合型光子晶体光波导进行了数值模拟研究。
考虑如下结构:空气中正方晶格排列的光子晶体光波导,耦合长度Lc=48a,介质柱折射率n=3.4,取r=0.2a,a=0.5 m,耦合区域内的介质柱为两层,由文献[7]可知,当入射光波长=1.42 m 时,此时光波会完全耦合而从端口3输出。
现将耦合区域内的圆柱改为椭圆柱,如图1所示,设其半径比s=r2/r1,s=1时,即为正常圆柱,s!1,则为椭圆柱,我们关注不同半径比s造成的耦合区域结构变化会对波导耦合长度Lc产生什么样的影响。
图1 椭圆柱耦合型光子晶体光波导并行FDTD仿真实施环境如图2所示,由3台PC机构成的一个小型局域网系统,其模拟平台为w i ndo w s XP与M at lab2006a。
计算节点承担FDTD算法中各子域的迭代计算任务,具有典型的并行特征;而服务节点完成结果分析、绘图以及一些必要的辅助计算功能(如傅立叶变换等),表现出显著的协同工作特点。
因此,服务与计算两类节点共同组成一个并行-协同仿真系统。
算法实现的关键过程如下:1)在服务节点上开放W indow s文件共享服务,建立对所有计算节点都拥有读写权限的共享文件夹,并在各计算节点将其映射为一个网络盘,然后使用C reateF ile()函数在其中创建数据文件,访问标志为可读写,大小等于FDTD计算域离散的电/磁场值数组占用内存大小。
