空间点的对称问题 PPT
合集下载
点直线的对称问题课件

详细描述
直线关于点的对称定义是几何学中的基本概念之一。如果一条直线上的任意一点关于某一定点对称的点都在该直 线上,则这条直线被称为关于该定点对称。这个定义是理解点、线、面对称关系的基础。
直线关于点的对称性质
总结词
根据对称的性质,直线关于点的对称具 有平移不变性、旋转不变性和反射不变 性。
VS
详细描述
详细描述
直线关于点的对称是几何学中的基本概念之一,它在解 析几何、光学、力学和机器人学等领域中都有广泛的应 用。例如,在光学中,光的反射和折射都涉及到对称的 概念;在力学中,物体运动轨迹的对称性可以用对称的 直线来表示;在机器人学中,机器人的运动路径规划和 姿态调整也需要用到对称的概念。因此,理解直线关于 点的对称性质和应用对于深入理解这些领域中的基本概 念和原理非常重要。
点关于直线的对称性质
总结词
点关于直线的对称具有一些重要的性质,如对称点的连线与 对称轴垂直,且被对称轴平分。
详细描述
如果点A关于直线l对称于点B,则线段AB与直线l垂直,且线 段AB的中点M位于直线l上。此外,对称轴上的任意一点到两 个对称点的距离相等。
点关于直线的对称应用
总结词
点关于直线的对称在几何学、物理学和工程学等领域有广泛的应用。
详细描述
在几何学中,点关于直线的对称可用于研究图形的性质和变换。在物理学中,点关于直线的对称可用 于描述粒子的运动轨迹和电磁场的分布。在工程学中,点关于直线的对称可用于设计、分析和优化各 种结构。
03
直线关于点的对称
直线关于点的对称定义
总结词
根据对称的定义,如果一个直线上的任意一点关于某一定点对称的点都在该直线上,则该直线被称为关于该定点 对称。
美丽的图案。
直线关于点的对称定义是几何学中的基本概念之一。如果一条直线上的任意一点关于某一定点对称的点都在该直 线上,则这条直线被称为关于该定点对称。这个定义是理解点、线、面对称关系的基础。
直线关于点的对称性质
总结词
根据对称的性质,直线关于点的对称具 有平移不变性、旋转不变性和反射不变 性。
VS
详细描述
详细描述
直线关于点的对称是几何学中的基本概念之一,它在解 析几何、光学、力学和机器人学等领域中都有广泛的应 用。例如,在光学中,光的反射和折射都涉及到对称的 概念;在力学中,物体运动轨迹的对称性可以用对称的 直线来表示;在机器人学中,机器人的运动路径规划和 姿态调整也需要用到对称的概念。因此,理解直线关于 点的对称性质和应用对于深入理解这些领域中的基本概 念和原理非常重要。
点关于直线的对称性质
总结词
点关于直线的对称具有一些重要的性质,如对称点的连线与 对称轴垂直,且被对称轴平分。
详细描述
如果点A关于直线l对称于点B,则线段AB与直线l垂直,且线 段AB的中点M位于直线l上。此外,对称轴上的任意一点到两 个对称点的距离相等。
点关于直线的对称应用
总结词
点关于直线的对称在几何学、物理学和工程学等领域有广泛的应用。
详细描述
在几何学中,点关于直线的对称可用于研究图形的性质和变换。在物理学中,点关于直线的对称可用 于描述粒子的运动轨迹和电磁场的分布。在工程学中,点关于直线的对称可用于设计、分析和优化各 种结构。
03
直线关于点的对称
直线关于点的对称定义
总结词
根据对称的定义,如果一个直线上的任意一点关于某一定点对称的点都在该直线上,则该直线被称为关于该定点 对称。
美丽的图案。
关于x轴、y轴对称的点 ppt课件

对称点.
思考:
Y 5
关于y轴
4
对称的点
· B (-4, 2) 3 2
·B’ (4, 2) 的坐标具 有怎样的
1
关系?
-4 -3 -2 -1-10 1 2 3 4 5 X
-2
-3
· -4
C’(-3, -4)
·C(3, -4)
ppt课件
8
归纳:关于y轴对称的点的坐标的特 点是: 横坐标互为相反数,纵坐标相等.
2、学习了在平面直角坐标系中如何画一个图形 关于x轴或y轴的对称图形
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的
坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
ppt课件
14
练习一
1、完成下表.
已知点
(9,-7) (-3,6) (-3,-5) (0,10) (4,0)
关于x轴的对称点 (9,7) (-3,-6) (-3, 5) (0,-10) (4,0) 关于y轴的对称点 (-9, -7) (3, -6) (3, -5) (0, 10) (-4,0)
ppt课件
6
探究2:如图,你能在平面直角坐标系中画出点A关 于 y轴的对称点吗?
你能说出 点A与点 A’坐标的 关系吗?
Y 5
· A’(-2,3) 4 3 2
·A (2,3)
1
-4 -3 -2 -1 0 1 2 3 4 5 X -1
-2 -3
-4ppt课件
7
在平面直角坐标系中画出下列各点关于y轴的
纵坐标相等.
点(x, y)关于x轴对称的点的坐标为_(x_,_-__y_).
点(x, y)关于y轴对称的点的坐标为_(-__x_,_y_).
《有关对称问题》课件

06 对称问题的哲学思考
CHAPTER
对称与美的关系
总结词
对称被广泛认为是美的,因为它能给 人带来一种平衡和和谐的感觉。
详细描述
在艺术、建筑和自然界中,对称的形 状和图案常常被认为是具有审美价值 的。这是因为对称能创造出一种平衡 和和谐的感觉,使观察者能够轻松地 理解和欣赏。
对称与平衡的关系
总结词
音乐作品的对称性
总结词
音乐作品中,对称性是一种重要的结构 原则,它能够使乐曲更加规整、平衡和 有节奏感。
VS
详细描述
在音乐作品中,对称性可以通过重复、倒 影、逆行等方式实现。对称的乐曲结构可 以使音乐作品更加有层次感、逻辑感和美 感。例如,贝多芬的《命运交响曲》就运 用了对称性的结构原则,使乐曲更加紧凑 、有力和动人。
对称性是普遍存在的特性,自然 界和人造物中都可以找到对称的
例子。
对称性在数学、物理学、工程学 等领域有广泛的应用,如建筑设
计、机械制造、电路设计等。
对称性也是美学中的一个重要概 念,被广泛应用于艺术创作和装
饰设计中。
02 对称问题在几何中的应用
CHAPTER
点对称
总结词
点对称是指两个点关于某一点位 置相对,保持距离不变。
晶体结构的对称性对于理解晶体的物理性质和化学性质非常 重要。例如,某些晶体在特定方向上具有更高的导电性或光 学性能,这与其对称性有关。
电磁波的对称性
电磁波的对称性是指电磁波在空间中的传播方式和分布特 征的对称性质。例如,电磁波可以具有偶极子对称、四极 子对称等。
电磁波的对称性对于理解电磁波的传播规律和散射特性非 常重要。例如,在雷达和通信领域中,电磁波的对称性对 于信号的传输和接收具有重要影响。
23.2.1 中心对称(共43张PPT)
15 8
2
OF
15 8
同理OE 15 ,即 OF OE OF 15
8
4
A
D
C′
D′
O 重合
B′
A′
B
C
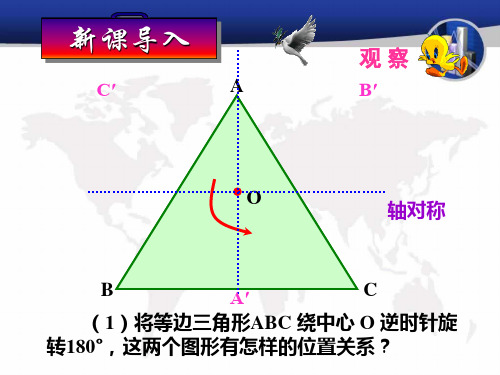
(4)将平行四边形ABCD绕中心O逆时针旋 转180°,这两个图形有怎样的位置关系?
有的轴对称, 有的重合。
绕中心旋转180°,旋转后的图 形与原图的位置关系有什么不同?
教学目标
【知识与能力】
了解中心对称、对称中心、关于中心的对称 点等概念。 通过具体实例认识两个图形关于某一点成中 心对称的本质:就是一个图形绕一点旋转180° 而成。 作出中心对称的图形。
它是轴对称图形吗? 不是轴对称图形。
这个图形是否能够通过某种图形运动与自 身重合?
探究
下列图形是否能够通过某种图形运动与自
身重合?图旋Biblioteka 形转绕后中与
线段绕中点旋转180°
心原 旋图
旋转后与原图重合
转重
180 合
°
知识要点
把一个图形绕着某一个点旋转180°, 如果它能够与另一个图形重合,那么就说 这两个图形关于这个点对称或中心对称 (central symmetry),这个点叫做对称中 心。这两个图形中的对应点叫做关于中心 的对称点。
经历对日常生活中与中心对称有关的图形进行 观察、分析、欣赏、动手操作、画图等过程,发 展审美能力,增强对图形的欣赏意识。
从图形变化过程中,树立正确的辩证唯物主义 观点。
认识几何图形的对称美,培养学生热爱数学, 热爱生活。
教学重难点
利用中心对称、对称中心、关于中心的 对称点的概念解决一些问题。 从一般旋转中导入中心对称。 中心对称的性质及初步应用。 中心对称与旋转之间的关系。
对称问题PPT完美课件

点M(或直线l)的对称点仍在C上 .
1.两点之间的中心对称
如果点P1(x1, y1), P2(x2, y2),关于点M(a, b)对称,
那么点M是线段P1P2的中点,
y
根据中点坐标公式有:
.P 1(x 1,y1)
x1 x2 2 a
y1
y2
2b
M(a,b)
.x . O
P 2(x 2,y 2)
|AB | 5
B
在 RA t B 中 |C B|C 1, ta nABC 2.C o
x
设所求直线斜率为 k
则
k ( 3) 4
1 ( 3) k
2 k1或k11
2
2
4
故所求直线 x2方 y4 程 0或 1 为 x 1: 2y16 0.
对称问题PPT完美课件
对称问题PPT完美课件
巩固1.光线沿着x直 2y线 50射入 ,遇到直线
则点P关于点A(1,2)的对称点为 Q(2x,4y)
由点Q在直线 x-y+2=0上得 (2 x ) (4 y) 2 0
即 x y 0 为所求对称直线方程.
. y
l
Q
l’
.. A P
②点A(1,2)关于直线x-y+2=0对称的点为 ;
解:设所求的对称点为 A(x, y), 则
1 x
2 y
2
x 1
1
2 y 2
1
2
0
x
y
0 3
A(0,3).
对称问题PPT完美课件
对称问题PPT完美课件
③直线x-y+2=0关于点A(1,2)对称的直线为
;
解:在直线 x-y+2=0上取两点P1(-2,0),P2(0, 2), 设它们关于点A(1,2)对称点Q1(x1, y1), Q2(x2, y2), 则中点公式得
1.两点之间的中心对称
如果点P1(x1, y1), P2(x2, y2),关于点M(a, b)对称,
那么点M是线段P1P2的中点,
y
根据中点坐标公式有:
.P 1(x 1,y1)
x1 x2 2 a
y1
y2
2b
M(a,b)
.x . O
P 2(x 2,y 2)
|AB | 5
B
在 RA t B 中 |C B|C 1, ta nABC 2.C o
x
设所求直线斜率为 k
则
k ( 3) 4
1 ( 3) k
2 k1或k11
2
2
4
故所求直线 x2方 y4 程 0或 1 为 x 1: 2y16 0.
对称问题PPT完美课件
对称问题PPT完美课件
巩固1.光线沿着x直 2y线 50射入 ,遇到直线
则点P关于点A(1,2)的对称点为 Q(2x,4y)
由点Q在直线 x-y+2=0上得 (2 x ) (4 y) 2 0
即 x y 0 为所求对称直线方程.
. y
l
Q
l’
.. A P
②点A(1,2)关于直线x-y+2=0对称的点为 ;
解:设所求的对称点为 A(x, y), 则
1 x
2 y
2
x 1
1
2 y 2
1
2
0
x
y
0 3
A(0,3).
对称问题PPT完美课件
对称问题PPT完美课件
③直线x-y+2=0关于点A(1,2)对称的直线为
;
解:在直线 x-y+2=0上取两点P1(-2,0),P2(0, 2), 设它们关于点A(1,2)对称点Q1(x1, y1), Q2(x2, y2), 则中点公式得
《对称性原理》课件

05 对称性原理的证明方法
代数证明方法
代数方法:通过代数运算和证明,得出对称性原理的结论 代数方程:建立代数方程,求解方程,得出对称性原理的结论 代数变换:通过代数变换,得出对称性原理的结论 代数结构:研究代数结构,得出对称性原理的结论
几何证明方法
利用几何图形的对称性,如轴对称、中心对称等 通过几何图形的变换,如旋转、反射等,来证明对称性原理 利用几何定理,如平行线、垂直线等,来证明对称性原理 通过几何图形的性质,如面积、周长等,来证明对称性原理
03 对称性原理的基本概念
轴对称
轴对称的定义: 如果一个图形沿 着一条直线折叠 后,两侧的图形 能够完全重合, 那么这个图形就 是轴对称图形。
轴对称的性质: 轴对称图形的对 称轴是图形的对 称中心,也是图 形的对称轴。
轴对称的应用: 在几何学、物理 学、化学等领域 都有广泛的应用。
轴对称的种类: 包括线对称、点 对称、面对称等。
了对称性
对称性在数学 中的地位不可 替代,它是数 学研究的重要
工具和方法
对称性在数学 中的地位不断 提升,越来越 多的数学家开 始关注对称性 在数学中的作
用和意义
对称性原理的提出
提出者:杨振宁 和李政道来自提出时间:1956 年
目的:解释弱相 互作用中的宇称 不守恒现象
影响:推动了物 理学的发展,改 变了人们对宇宙 的认识
对称性原理的未来发展
应用领域:物理、 化学、生物、数 学等学科
研究方法:理论 研究、实验验证、 数值模拟等
发展趋势:从微 观到宏观,从简 单到复杂,从静 态到动态
挑战与机遇:解 决实际问题,推 动学科发展,促 进技术创新
07 总结与展望
对称性原理的重要性和意义
高中数学平面几何对称问题(共25张PPT)

思考:若l1//l2, 如何求l1 关于l2的对称直线方程?
直线关于特殊直线的对称
Ax By C 0
x轴
Ax B( y) C 0
A( x) B( y) C 0
y轴
Ay Bx C 0
yx
A( y) B( x) C 0
练习
求直线m:2x+3y-1=0关于点P(1,4)对称的直线 n的方程.
二.轴对称(即关于直线的对称)
(一)点关于直线的对称:
例3.求点A(-7,1)关于直线l:2x-y-5=0的对称点B的坐标.
解(法一) 设B(m,n)由点关于直线对称的定义知: 线段AB⊥l 即;
n 1 2 m (7)
y x
几种特殊的对称(当堂口答):
点P(x,y)关于下列点或线的对称点分别为:
(-x,-y) 关于原点:__________; 关于y轴: __________; (-x,y) (-y,-x) 关于直线y=-x:______; (x,-y) 关于x轴:__________; (y,x) 关于直线y=x:______; 关于直线x=a:_______. (2a-x,y)
(1)|PA|+|PB|最小,并求出其最小值;
(2)||PA|-|PB||最大,并求出其最大值.
例:已知x,y满足x+y=0,求
( x 3) 2 ( y 1) 2 ( x 2) 2 ( y 3) 2 y 的最小值。 N(-2,3)
P O x M(3,-1)
M′(1,-3)
A( x) B( y) C 0 补:关于原点:____________ ;
应用一:解决物理光学方面的问题
直线关于特殊直线的对称
Ax By C 0
x轴
Ax B( y) C 0
A( x) B( y) C 0
y轴
Ay Bx C 0
yx
A( y) B( x) C 0
练习
求直线m:2x+3y-1=0关于点P(1,4)对称的直线 n的方程.
二.轴对称(即关于直线的对称)
(一)点关于直线的对称:
例3.求点A(-7,1)关于直线l:2x-y-5=0的对称点B的坐标.
解(法一) 设B(m,n)由点关于直线对称的定义知: 线段AB⊥l 即;
n 1 2 m (7)
y x
几种特殊的对称(当堂口答):
点P(x,y)关于下列点或线的对称点分别为:
(-x,-y) 关于原点:__________; 关于y轴: __________; (-x,y) (-y,-x) 关于直线y=-x:______; (x,-y) 关于x轴:__________; (y,x) 关于直线y=x:______; 关于直线x=a:_______. (2a-x,y)
(1)|PA|+|PB|最小,并求出其最小值;
(2)||PA|-|PB||最大,并求出其最大值.
例:已知x,y满足x+y=0,求
( x 3) 2 ( y 1) 2 ( x 2) 2 ( y 3) 2 y 的最小值。 N(-2,3)
P O x M(3,-1)
M′(1,-3)
A( x) B( y) C 0 补:关于原点:____________ ;
应用一:解决物理光学方面的问题
空间与轴对称问题有限元分析课件

02
CATALOGUE
有限元分析基础
有限元分析的基本概念
有限元分析是一种数值分析方法,通过将复杂 的物理系统离散化为有限个简单元(或称为元 素)的组合,以求解复杂系统的物理行为。
它基于变分原理和加权余量法,通过数学模型 将实际工程问题转化为数学问题,从而得到近 似的数值解。
有限元分析广泛应用于工程领域,如结构分析 、流体动力学、电磁场等。
求解线性方程组
通过求解线性方程组得到每个节 点的位移和应力等物理量。
有限元分析的常用软件
ANSYS
功能强大的有限元分析软件,适用于各种工 程领域。
COMSOL Multiphysics
多物理场有限元分析软件,适用于模拟复杂 的多物理场耦合问题。
ABAQUS
专业的有限元分析软件,广泛应用于结构分 析、流体动力学等领域。
空间与轴对称问题有限元分析的优缺点
01
数值误差
有限元分析依赖于离散化的网格 ,存在数值误差,可能影响结果 的精度。
建模难度
02
03
计算资源需求
对于复杂问题的建模,需要较高 的专业知识和技巧,建模难度较 大。
对于大规模问题,有限元分析需 要大量的计算资源,如内存和计 算时间。
未来发展方向与挑战
优化算法
建筑领域
建筑设计中的对称和均衡问题需要考虑空间对称 性,以提高建筑的美观性和稳定性。
机械工程领域
机械零件的形状和结构需要考虑轴对称性,以确 保零件的稳定性和可靠性。
空间与轴对称问题的解析方法
解析法
通过数学公式和定理推导出问题的解 ,适用于简单的问题和特定条件下的 求解。
有限元法
将问题分解为有限个小的单元,通过 求解每个单元的近似解来逼近原问题 的解,适用于复杂的问题和不规则区 域的处理。
关于原点对称的点的坐标(2)(共12张PPT)

点对称的图形.
23.2.3 关于原点对称的点的坐标
目标突破
例2 教材例2针对训练 如图23-2-7,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,4),B(-6,1),
3 关于原点对称的点的坐标
知识点二 知识点一
作关目关于于原标原点点对一对称称的的点图的会形坐标利特征用关于原点对称的点的坐标特征解决问题
两个点关于原点对称时,它们的坐标符号相反,即1点P(x,y)关于原点的对称2点为P′________.
∴a=4,b=-3,∴(a+b)2018=(4-3)2018=1.
23.2.3 关于原点对称的点的坐标
【归纳总结】直角坐标系中对称点的坐标特征:
设点 P 的坐标为(x,y),则有: (1) P(x,y) 关于原点对称 P′(-x,-y); (2) P(x,y) 关于x轴对称 P′(x,-y); (3)P(x,y) 关于y轴对称 P′(-x,y).
3 关于原点对称的点的坐标
关于原点对称的点的坐标特征
例2 教材例2针对训练 如图23-2-7,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,4),B(-6,1),
【归纳总结】作已知图形关于原点中心对称的图形时,可先运用两个点关于原点对称的规律得到关键点的坐标,然后根据坐标描点作图.
3 关于原点对称的点的坐标
3 关于原点对称的点的坐标
3 关于原点对称的点ቤተ መጻሕፍቲ ባይዱ坐标
3 关于原点对称的点的坐标
2.在理解两点关于原点对称的坐标特征的情况下,会作关于坐标原点对称的图形.
(点G,H,M分别是点A,B,C的对称点)
目标一 会利用关于原点对称的点的坐标特征解决问题
23.2.3 关于原点对称的点的坐标
23.2.3 关于原点对称的点的坐标
目标突破
例2 教材例2针对训练 如图23-2-7,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,4),B(-6,1),
3 关于原点对称的点的坐标
知识点二 知识点一
作关目关于于原标原点点对一对称称的的点图的会形坐标利特征用关于原点对称的点的坐标特征解决问题
两个点关于原点对称时,它们的坐标符号相反,即1点P(x,y)关于原点的对称2点为P′________.
∴a=4,b=-3,∴(a+b)2018=(4-3)2018=1.
23.2.3 关于原点对称的点的坐标
【归纳总结】直角坐标系中对称点的坐标特征:
设点 P 的坐标为(x,y),则有: (1) P(x,y) 关于原点对称 P′(-x,-y); (2) P(x,y) 关于x轴对称 P′(x,-y); (3)P(x,y) 关于y轴对称 P′(-x,y).
3 关于原点对称的点的坐标
关于原点对称的点的坐标特征
例2 教材例2针对训练 如图23-2-7,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,4),B(-6,1),
【归纳总结】作已知图形关于原点中心对称的图形时,可先运用两个点关于原点对称的规律得到关键点的坐标,然后根据坐标描点作图.
3 关于原点对称的点的坐标
3 关于原点对称的点的坐标
3 关于原点对称的点ቤተ መጻሕፍቲ ባይዱ坐标
3 关于原点对称的点的坐标
2.在理解两点关于原点对称的坐标特征的情况下,会作关于坐标原点对称的图形.
(点G,H,M分别是点A,B,C的对称点)
目标一 会利用关于原点对称的点的坐标特征解决问题
23.2.3 关于原点对称的点的坐标
大班科学活动《对称》PPT课件

THANK YOU
感谢聆听
根据对称元素的不同组合 ,将分子结构分为不同的 对称性类别。
化学反应中对称性变化
反应前后对称性比较
分析反应物和生成物的对称性,探讨反应过程中对称性的变化。
对称性破缺
某些化学反应可能导致对称性的破缺,如手性分子的生成。
对称性保持
在特定条件下,化学反应可能保持或恢复对称性,如环加成反应。
对称性在晶体结构中应用
80%
节日庆典中的对称
在节日庆典中,人们常用对称的 布置和装饰来表达喜庆和庄重, 如春节的对联、中秋的月饼等。
对称在建筑与艺术中的应用
建筑中的对称
许多著名建筑都采用了对称设 计,如故宫、天安门广场等, 彰显出庄重与和谐之美。
绘画和雕塑中的对称
艺术家在创作过程中也常运用 对称原则,使作品呈现出平衡 与和谐的美感,如达芬奇的《 最后的晚餐》、米开朗基罗的 雕塑等。
04
对称在物理学领域应用
镜像对称在光学中应用
01
02
03
平面镜成像
当光线照射到平面镜上时 ,遵循反射定律,形成与 物体关于镜面对称的虚像 。
光学仪器设计
利用镜像对称原理,设计 制造望远镜、显微镜等光 学仪器,提高成像质量和 观测效果。
干涉和衍射现象
在波动光学中,光的干涉 和衍射现象也表现出镜像 对称的特点,如双缝干涉 实验中的明暗条纹分布。
03
对称在数学领域应用
几何图形中对称性应用
对称轴
对称图形
在平面几何中,对称轴是一条直线,,即高所在 的直线。
具有对称性的图形称为对称图形。例 如,圆、正方形、等边三角形等都是 对称图形。
对称中心
在平面几何中,对称中心是一个点, 使得图形关于这个点对称。例如,正 方形有一个对称中心,即两条对角线 的交点。
人教A版高中数学必修二4.3.空间直角坐标系课件

所以点B′的坐标是(3,4,2).
【变式练习】 如图,在长方体OABC-D′A′B′C′中,|OA|
=3,|OC|=4,|OD′|=3,A′C′与B′D′相交于点P.
分别写出点C,B′,P的坐标. z
答案:ห้องสมุดไป่ตู้
D
A
P
C
B
AO x
Cy B
例2 结晶体的基本单位称为晶胞,如图(1)是食 盐晶胞的示意图(可看成是八个棱长为 1 的小正
z
在空间中,到定点的距离
等于定长的点的轨迹是 以原点为球心,
半径长为 r 的球面.
P
O y
x
2.如果是空间中任意一点P1(x1,y1,z1)到点P2 (x2,y2,z2)之间的距离公式会是怎样呢?
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)
是空间中任意两点,且点P1(x1,y1,z1)、
轴,这三个平面的唯一交点就是有序实数组 (x, y, z)
确定的点M. z
R
pO x
M y
Q
这样,空间一点M的坐标可以用有序实数组 (x, y, z)
来表示,有序实数组 (x, y, z) 叫做点M在空间直角坐标 系中的坐标,记作M (x, y, z).其中 x, y, z
分别叫做点M的横坐标、纵坐标、竖坐标.
关于谁对称谁 不变
在空间直角坐标系中,若 已知两个点的坐标,则这两点 之间的距离是惟一确定的,我 们希望有一个求两点间距离的 计算公式,对此,我们从理论 上进行探究.
y
y2
P2(x2, y2)
y1 P1(x1,y1) Q(x2,y1)
O x1
x2 x
长a,宽b,高c的长方体的对角线,怎么求?
【变式练习】 如图,在长方体OABC-D′A′B′C′中,|OA|
=3,|OC|=4,|OD′|=3,A′C′与B′D′相交于点P.
分别写出点C,B′,P的坐标. z
答案:ห้องสมุดไป่ตู้
D
A
P
C
B
AO x
Cy B
例2 结晶体的基本单位称为晶胞,如图(1)是食 盐晶胞的示意图(可看成是八个棱长为 1 的小正
z
在空间中,到定点的距离
等于定长的点的轨迹是 以原点为球心,
半径长为 r 的球面.
P
O y
x
2.如果是空间中任意一点P1(x1,y1,z1)到点P2 (x2,y2,z2)之间的距离公式会是怎样呢?
如图,设P1(x1,y1,z1)、P2(x2,y2,z2)
是空间中任意两点,且点P1(x1,y1,z1)、
轴,这三个平面的唯一交点就是有序实数组 (x, y, z)
确定的点M. z
R
pO x
M y
Q
这样,空间一点M的坐标可以用有序实数组 (x, y, z)
来表示,有序实数组 (x, y, z) 叫做点M在空间直角坐标 系中的坐标,记作M (x, y, z).其中 x, y, z
分别叫做点M的横坐标、纵坐标、竖坐标.
关于谁对称谁 不变
在空间直角坐标系中,若 已知两个点的坐标,则这两点 之间的距离是惟一确定的,我 们希望有一个求两点间距离的 计算公式,对此,我们从理论 上进行探究.
y
y2
P2(x2, y2)
y1 P1(x1,y1) Q(x2,y1)
O x1
x2 x
长a,宽b,高c的长方体的对角线,怎么求?
大班数学有趣的对称ppt课件

对称连连看游戏
设计一款以对称图形为主题的连连看游戏,让幼儿在游戏中加深对 对称图形的认识。
对称挑战任务
设置一系列与对称相关的挑战任务,如寻找教室中的对称物品、拍 摄具有对称美的照片等,激发幼儿探索对称奥秘的兴趣。
THANKS
感谢观看
艺术中的对称元素
绘画
在绘画中,艺术家常运用对称构图来营造平衡感,如达·芬奇的《最 后的晚餐》就采用了对称构图。
雕塑
雕塑作品中也常出现对称元素,如米开朗基罗的《大卫像》就展现 了完美的对称比例。
图案设计
对称在图案设计中应用广泛,如民族服饰、地毯、墙纸等,通过对称 图案创造出丰富多彩的视觉效果。
对称在建筑和艺术中的意义
对称轴或对称中心
对称图形有一个对称轴或 对称中心,使得两部分能 够完全重合。
对称轴和对称中心
对称轴
一条直线,使得图形关于这条直线对称,两部分能够完全重合。如长方形的长边或短边所在 直线就是其对称轴。
对称中心
一个点,使得图形关于这个点对称,两部分能够完全重合。如圆的圆心就是其对称中心。
旋转对称
图形绕一个点旋转一定角度后能够与自身重合,这个点称为旋转中心,旋转的角度称为旋转 角。如正三角形绕其重心旋转120度后能够与自身重合。
制作对称图形的手工活动
剪纸对称
提供纸张和剪刀,引导幼儿剪出对称的图形,如 蝴蝶、窗花等。
绘画对称
使用颜料和画笔,在纸张或画布上创作对称的图 案,培养幼儿的绘画技巧和审美能力。
拼贴对称
利用废旧杂志、彩纸等材料,让幼儿拼贴出具有 对称美的作品,锻炼其动手能力和创造力。
对称游戏和趣味挑战
对称拼图游戏
提供具有对称特点的拼图,让幼儿尝试拼凑出完整的图形,锻炼 其空间感知能力。
设计一款以对称图形为主题的连连看游戏,让幼儿在游戏中加深对 对称图形的认识。
对称挑战任务
设置一系列与对称相关的挑战任务,如寻找教室中的对称物品、拍 摄具有对称美的照片等,激发幼儿探索对称奥秘的兴趣。
THANKS
感谢观看
艺术中的对称元素
绘画
在绘画中,艺术家常运用对称构图来营造平衡感,如达·芬奇的《最 后的晚餐》就采用了对称构图。
雕塑
雕塑作品中也常出现对称元素,如米开朗基罗的《大卫像》就展现 了完美的对称比例。
图案设计
对称在图案设计中应用广泛,如民族服饰、地毯、墙纸等,通过对称 图案创造出丰富多彩的视觉效果。
对称在建筑和艺术中的意义
对称轴或对称中心
对称图形有一个对称轴或 对称中心,使得两部分能 够完全重合。
对称轴和对称中心
对称轴
一条直线,使得图形关于这条直线对称,两部分能够完全重合。如长方形的长边或短边所在 直线就是其对称轴。
对称中心
一个点,使得图形关于这个点对称,两部分能够完全重合。如圆的圆心就是其对称中心。
旋转对称
图形绕一个点旋转一定角度后能够与自身重合,这个点称为旋转中心,旋转的角度称为旋转 角。如正三角形绕其重心旋转120度后能够与自身重合。
制作对称图形的手工活动
剪纸对称
提供纸张和剪刀,引导幼儿剪出对称的图形,如 蝴蝶、窗花等。
绘画对称
使用颜料和画笔,在纸张或画布上创作对称的图 案,培养幼儿的绘画技巧和审美能力。
拼贴对称
利用废旧杂志、彩纸等材料,让幼儿拼贴出具有 对称美的作品,锻炼其动手能力和创造力。
对称游戏和趣味挑战
对称拼图游戏
提供具有对称特点的拼图,让幼儿尝试拼凑出完整的图形,锻炼 其空间感知能力。
人教A版高中数学必修2课件4.3.2空间中点的对称问题课件

2 B.(2,2, 3) 4 D.(2,2, ) 3
解析:∵|EB|=2|EB1|,
2 4 ∴|EB|= ,|BB1|= . 3 3
4 又E在B1B上,∴E的坐标为(2,2, ). 3
答案:D.
空间中点的对称问题
【典型例题】 4、已知A(x,5-x,2x-1),B(1,x+2,2-x)两点 ,当|AB|取最小值时,x的值为( ) 8 A.19 B. 7 8 19 C. D.
解析:关于谁对称,谁的坐标不变,其它是相反数, ∴A(-3,1,-4)关于x轴对称的点为(-3,-1,4). 答案:B
空间中点的对称问题
【典型例题】 3、如图,在正方体OABC-O1A1B1C1中,棱长 为2,E是B1B上的点,且|EB|=2|EB1|,则点E的 坐标为( )
A.(2,2,1)
1 C.(2,2, ) 3
知识点—— 空间中点的对称问题
空间中点的对称问题
【公式】 1、已知两点的中点坐标: 平面上的中点坐标公式可以推广到空间,即设
A( x1,y1, z1),B( x2,y2, z2),
x1 x2 y1 y2 z1 z2 , , ) 则AB中点的坐标为 ( 2 2 2
2、一个点关于坐标轴和坐标平面的对称点的坐标特点 点P(x,y,z)关于坐标原点的对称点为 P1(-x,-y,-z); 点P(x,y,z)关于坐标横轴(x轴)的对称点为 P2 (x,-y,-z); 点P(x,y,z)关于坐标纵轴(y轴)的对称点为 P3(-x,y,-z)
空间中点的对称问题
【变形训练】
解:设正方体的棱长为a.
a a a (1)当点P为对角线AB的中点时,点P的坐标是 , , . 2 2 2
∵点Q在线段CD上,设Q(0,a,z).
对称性原理PPT课件

x
右手坐
标
z′ y′··y z
反射面
反射面
(b)
(c)
只左右对称 坐标系反射
根据镜象反射的性质可将物理学中的矢量
分成两类: 极矢量 和 轴矢量 4 第4页/共24页
极矢量:镜象反射中垂直反射面的分量反向,
平行反射面的分量不变向。
如:r,v,a,E ,
…
v′
v′ v
v
v′ v
v′
v
v′ v
反射面
5
第5页/共24页
22
第22页/共24页
参考书目
▲ 新概念物理教程《力学》赵凯华、罗蔚茵 ▲《对称》 H. Weyl 商务印书馆 1986 ▲《大学物理学》(第一册) 张三慧 主编 ▲ “Lecture on Physics” R.Feynman.
Vol.1
—完—
23
第23页/共24页
感谢您的观看!
24
第24页/共24页
南山长生松生长山南 南山长生松生长山南 8 第8页/共24页
④空间反演:
r
r
的操作称为对原点O
的空间反演。
x x
直角坐标系中的空间反演 y y
z z
空间反演不变的系统具有对O的点对称性。
例如,立方体对其中心具有点对称性。
反映空间反演对称性的物理量叫宇称 (parity)。
y′
x
空
镜面反射
z′ ·o
I = I1 +(I I1)
节点 C → D 的电流为:
I1 (I I1)= 2 I1 I
17
第17页/共24页
A I
I1
RC
(1)
R
《解析几何》:对称问题

对称性与生物分子结构
生物分子如蛋白质和核酸等也具有对称性,通过对称性分析可以深入理解生物分子的结 构和功能。
对称性与生物演化
生物演化过程中,某些物种可能会因为环境压力而发生对称性的变化,通过对称性分析 可以深入理解生物演化的规律和机制。
THANKS FOR WATCHING
感谢您的观看
对称的性质
对称性质1
对称的图形是全等的。
对称性质2
对称的图形具有等长的对应边和等角。
对称性质3
对称的图形具有等面积的对应部分。
02 平面上的对称问题
点关于点的对称
总结词
若点A关于点B的对称,则线段AB的中点是两点的对称中心,且AB与对称中心连 线垂直。
详细描述
设点A和点B为平面上的两个点,如果存在另一点C,使得线段AC与线段BC的中点都 是B,并且线段AB与线段BC垂直,则称点A关于点B有对称点C。
详细描述
设直线l和点P为平面上的一个直线和一个点,如果存在另一直 线m,使得点P位于直线m上,并且直线l与过点P的垂线垂直, 则称直线l关于点P有对称直线m。
直线关于直线的对称
总结词
若直线l1关于直线l2的对称,则两直线的斜率互为相反数。
详细描述
设直线l1和直线l2为平面上的两条直线,如果存在另一直线l3,使得直线l1与直线l3平行且等距,并且直 线l2与直线l3垂直,则称直线l1关于直线l2有对称直线l3。
03
对称性与物理现象
对称性在物理现象中也有广泛应用,如晶体结构、电磁波的传播等。通
过对称性分析,可以深入理解这些物理现象的本质和规律。
对称与化学
分子的对称性
化学中的分子具有不同的对称性,如对称轴、对称面等。这些对称性对分子的性质和反应 活性有重要影响,可以通过对称性分析来预测和解释化学反应的规律。
生物分子如蛋白质和核酸等也具有对称性,通过对称性分析可以深入理解生物分子的结 构和功能。
对称性与生物演化
生物演化过程中,某些物种可能会因为环境压力而发生对称性的变化,通过对称性分析 可以深入理解生物演化的规律和机制。
THANKS FOR WATCHING
感谢您的观看
对称的性质
对称性质1
对称的图形是全等的。
对称性质2
对称的图形具有等长的对应边和等角。
对称性质3
对称的图形具有等面积的对应部分。
02 平面上的对称问题
点关于点的对称
总结词
若点A关于点B的对称,则线段AB的中点是两点的对称中心,且AB与对称中心连 线垂直。
详细描述
设点A和点B为平面上的两个点,如果存在另一点C,使得线段AC与线段BC的中点都 是B,并且线段AB与线段BC垂直,则称点A关于点B有对称点C。
详细描述
设直线l和点P为平面上的一个直线和一个点,如果存在另一直 线m,使得点P位于直线m上,并且直线l与过点P的垂线垂直, 则称直线l关于点P有对称直线m。
直线关于直线的对称
总结词
若直线l1关于直线l2的对称,则两直线的斜率互为相反数。
详细描述
设直线l1和直线l2为平面上的两条直线,如果存在另一直线l3,使得直线l1与直线l3平行且等距,并且直 线l2与直线l3垂直,则称直线l1关于直线l2有对称直线l3。
03
对称性与物理现象
对称性在物理现象中也有广泛应用,如晶体结构、电磁波的传播等。通
过对称性分析,可以深入理解这些物理现象的本质和规律。
对称与化学
分子的对称性
化学中的分子具有不同的对称性,如对称轴、对称面等。这些对称性对分子的性质和反应 活性有重要影响,可以通过对称性分析来预测和解释化学反应的规律。
