(完整)相交线与平行线考点及题型总结,推荐文档
2023年相交线与平行线知识点归纳总结

《相交线与平行线》知识点总结一: 相交线(1)相交线旳定义两条直线交于一点, 我们称这两条直线相交.相对旳, 我们称这两条直线为相交线.(2)两条相交线在形成旳角中有特殊旳数量关系和位置关系旳有对顶角和邻补角两类.(3)在同一平面内, 两条直线旳位置关系有两种: 平行和相交(4)对顶角: 有一种公共顶点, 并且一种角旳两边分别是另一种角旳两边旳反向延长线, 具有这种位置关系旳两个角, 互为对顶角.∠1和∠3, ∠2和∠4是对顶角.(5)邻补角:只有一条公共边,它们旳另一边互为反向延长线,具有这种关系旳两个角,互为邻补角.如图:∠1和∠2,∠2和∠3是邻补角.(6)对顶角旳性质:对顶角相等.(如图∠1=∠3, ∠2=∠4)(7)邻补角旳性质:邻补角互补, 即和为180°.(如图∠1+∠2=180°)(8)邻补角、对顶角成对出现, 在相交直线中, 一种角旳邻补角有两个. 邻补角、对顶角都是相对与两个角而言, 是指旳两个角旳一种位置关系. 它们都是在两直线相交旳前提下形成旳。
二、垂线(1)、垂线旳定义: 当两条直线相交所成旳四个角中, 有一种角是直角时, 就说这两条直线互相垂直, 其中一条直线叫做另一条直线旳垂线, 它们旳交点叫做垂足.如图, OD⊥AB, 垂足为O(2)、垂线旳性质过一点有且只有一条直线与已知直线垂直.注意: “有且只有”中, “有”指“存在”, “只有”指“唯一”“过一点”旳点在直线上或直线外都可以。
(3)、垂线段: 从直线外一点引一条直线旳垂线, 这点和垂足之间旳线段叫做垂线段.(4)垂线段旳性质: 垂线段最短.对旳理解此性质, 垂线段最短, 指旳是从直线外一点到这条直线所作旳垂线段最短. 它是相对于这点与直线上其他各点旳连线而言.(如图, PA,PB,PC等线段中, PO最短)(4)、点到直线旳距离(如图, PO旳长)(1)点到直线旳距离:直线外一点到直线旳垂线段旳长度, 叫做点到直线旳距离.(2)点到直线旳距离是一种长度, 而不是一种图形, 也就是垂线段旳长度, 而不是垂线段.它只能量出或求出, 而不能说画出, 画出旳是垂线段这个图形.三、平行线1.在同一平面内, 两条直线旳位置关系有两种: 平行和相交.(1)平行线旳定义:在同一平面内,不相交旳两条直线叫平行线.记作: a∥b;读作: 直线a平行于直线b.(2)同一平面内, 两条直线旳位置关系: 平行或相交, 对于这一知识旳理解过程中要注意:①前提是在同一平面内;②对于线段或射线来说, 指旳是它们所在旳直线.(3)平行公理:通过直线外一点, 有且只有一条直线与这条直线平行.如图, 过点P只有直线a 与直线b 平行(4)平行公理中要精确理解“有且只有”旳含义.从作图旳角度说, 它是“能但只能画出一条”旳意思.(5)平行公理旳推论:假如两条直线都与第三条直线平行, 那么这两条直线也互相平行.如图, 假如a∥c, b∥c, 那么a∥c2.同位角、内错角、同旁内角(1)同位角: 两条直线被第三条直线所截形成旳角中, 若两个角都在两直线旳同侧, 并且在第三条直线(截线)旳同旁, 则这样一对角叫做同位角.例如∠1和∠5,∠3和∠7,∠4和∠8,∠2和∠6.(2)内错角: 两条直线被第三条直线所截形成旳角中, 若两个角都在两直线旳之间, 并且在第三条直线(截线)旳两旁, 则这样一对角叫做内错角. 例如∠3和∠5, ∠4和∠6.(3)同旁内角: 两条直线被第三条直线所截形成旳角中, 若两个角都在两直线旳之间, 并且在第三条直线(截线)旳同旁, 则这样一对角叫做同旁内角。
相交线与平行线考点及题型总结

相交线与平行线考点及题型总结-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII相交线与平行线考点及题型总结第一节相交线一、知识要点:(一)当同一平面内的三条直线相交时,有三种情况:一种是只有一个交点;一种是有两个交点,即两条直线平行被第三条直线所截;还有一种是三个交点,即三条直线两两相交。
(二)余角、补角、对顶角1、余角:如果两个角的和是直角,那么称这两个角互为余角.2、补角:如果两个角的和是平角,那么称这两个角互为补角.3、对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.4、互为余角的有关性质:①∠1+∠2=90°,则∠1、∠2互余;反过来,若∠1,∠2互余,则∠1+∠2=90°;②同角或等角的余角相等,如果∠l十∠2=90°,∠1+∠ 3=90°,则∠2=∠3.5、互为补角的有关性质:①若∠A+∠B=180°,则∠A、∠B互补;反过来,若∠A、∠B互补,则∠A+∠B=180°.②同角或等角的补角相等.如果∠A+∠C=180°,∠A+∠B=180°,则∠B=∠C.6、对顶角的性质:对顶角相等.(三)垂直:相交的一种特殊情况是垂直,两条直线交角成90 。
1、经过直线外一点,作直线垂线,有且只有一条;2、点到直线上各点的距离中,垂线段最短。
(四)两条直线被第三条直线所截,产生两个交点,形成了八个角(不可分的):1、同位角:没有公共顶点的两个角,它们在直线AB,CD的同侧,在第三条直线EF的同旁(即位置相同),这样的一对角叫做同位角;2、内错角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的两旁(即位置交错),这样的一对角叫做内错角;3、同旁内角:没有公共顶点的两个角,它们在直线AB,CD之间,在第三条直线EF的同旁,这样的一对角叫做同旁内角;二、题型分析: 题型一:列方程求角例1:一个角的余角比它的补角的21少20°.则这个角为 ( ) A 、30° B 、40° C 、60° D 、75° 答案:B分析:若设这个角为x ,则这个角的余角是90°-x ,补角是180°-x ,于是构造出方程即可求解求解:设这个角为x ,则这个角的余角是90°-x ,补角是180°-x .则根据题意,得21(180°-x )-(90°-x )=20° ; 解得:x =40°. 故应选B . 说明:处理有关互为余角与互为补角的问题,除了要弄清楚它们的概念,通常情况下还要引进未知数,构造方程求解.习题演练:1、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30 ,那么这两个角是( )A 、42138 、B 、都是10C 、42138 、或4210 、D 、以上都不对 答案:A分析:两个条件可以确定两个角互补,列方程即可解得A 。
人教版数学七年级下册《相交线与平行线》的考点归纳

的一元二次方程或不等式,然后求其解.需要注意的是,求解后还得根据题目的实际情况确定适当的值.例3某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.现该商品要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?分析:此题只涉及盈利的涨价与否问题,可以设一个未知数(设每千克应涨价x元),涨价x元以后,每千克盈利为(10+x)(元),日销售减少量为x×20=20x(千克),每天可售出量为(500-20x)(千克).此时每天的盈利可表示为(10+x)×(500-20x).题目中指出使顾客得到实惠(即x尽量取较小值),又要保证每天盈利6000元,所以可以转化为求满足(10+x)×(500-20x)≥6000条件的x的最小值问题.解:设每千克应涨价x元,由题意可得每千克盈利:10+x(元),日销售量减少:x×20=20x(千克)日销售量为:500-20x(千克)据题意得(10+x)(500-20x)≥6000,解一元二次不等式得,5≤x≤10.因为题目中要求“使顾客得到实惠”,所以x应当尽量小,故而x=5.答:现该商品要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价5元.点评:该题是一元二次方程与不等式的结合问题,设一个未知数x即可,但用含有x 的式子表示其他量时容易出错,特别是涨价x元后每千克盈利是10+x元,而不是10x 元,一定要细心以避免出错.总之,列方程解应用题可以化逆向思维为正向思维,让解题更加容易.列方程解应用题的难点在于设未知数,以及如何用未知数表示其他量,再根据等量关系列出方程求解.最后还要重视方程解完后的检验环节,这样才能确保解题的准确率.相交线与平行线是平面几何的重点内容,是以后深入学习三角形、四边形等几何知识的基础.其中互余和互补的概念、平行线的性质与判定等都是考试中常考的重要内容.现对与相交线与平行线相关的常见考点进行归纳说明.考点一补角与余角的概念如果两个角的和是180°,那么称这两个角互为补角,其中一个角叫做另一个角的补角.类似地,如果两个角的和是90°,那么称这两个角互为余角,其中一个角叫做另一个角的余角.同角或等角的余角相等,同角或等角的补角相等.例1(1)如图1,已知:线段AB,延长线段AB到C,使AC=32AB,反向延长线段AB到D,使AD=2AB,①请画出图形;②若AB=4,计算CD的长度.(2)如图2,已知A、O、E三点在同一条直线上,∠1=∠2,且∠1和∠4互为余角.①∠2和∠3互余吗?为什么?②∠3和∠4有什么关系,为什么?《相交线与平行线》的考点归纳③∠3的补角是哪个角?若∠AOC:∠COE=2:7,请计算这个补角的度数.图1图2解:(1)①画出图形,如图3:D A B C图3②∵AC=32AB,AB=4,∴BC=12AB=2,又∵AD=2AB=8,∴CD=AD+AB+BC=8+4+2=14.(2)①∠2与∠3互余,∵∠1+∠4=90°,∴∠2+∠3=180°-(∠1+∠4)=90°,即∠2与∠3互余,②∠3=∠4,∵∠1+∠4=90°,∠1=∠2,由①∠2+∠3=90°,即∠3=∠4(等角的余角相等),③∠3的补角是∠AOD,若∠AOC:∠COE=2:7,又∵∠AOC+∠COE=180°,∴∠AOC=40°,∠COE=140°,又∵∠1=∠2=12∠AOC=20°,∴∠4=90°-∠1=70°(∠1与∠4互为余角),又∵∠AOD+∠4=180°,即∠AOD=180°-∠4=180°-70°=110°.评注:本题考查了余角、补角和两点间的距离以及角与角之间的关系.解答这类题目时,我们要熟悉线段和角的概念.考点二对顶角的定义及其性质若两个角有公共顶点,且它们的两边互为反向延长线,则这两个角互为对顶角.对顶角是两条直线相交所成的角,它们是成对出现的,若∠1和∠3为对顶角,则必有∠1=∠3;但反过来,若∠1=∠3,则∠1和∠3不一定是对顶角.例2如图4所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=4:1,则∠AOF等于().A.130°B.120°C.110°D.100°解:设∠BOE=α,∵∠AOD:∠BOE=4:1,∴∠AOD=4α,∵OE平分∠BOD,∴∠DOE=∠BOE=α,∴∠AOD+∠DOE+∠BOE=180°,∴4α+α+α=180°,∴α=30°,∴∠AOD=4α=120°,∴∠BOC=∠AOD=120°,∵OF平分∠COB,∴∠COF=12∠BOC=60°,∵∠AOC=∠BOD=2α=60°,∴∠AOF=∠AOC+∠COF=120°,故选B项.评注:解本题的关键是找到角与角之间的关系,然后运用方程思想解题.考点三垂线的性质两条直线相交所成的角中,若有一个为直角,则这两条直线互相垂直,其中一条叫做另一条的垂线,这两条直线互相垂直的交点叫垂足.垂线具有如下性质:①一条线段有无数条垂线;②连接直线外一点与直线上各点的所有线段中,垂线段最短;③经过直线或直线外一点,有且只有一条直线与已知直线垂直.例3在直线AB上任取一点O,过点O 作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是().A.60°B.120°C.60°或90°D.60°或120°分析:本题没有图形,OC、OD的位置不BAFEOCD图4确定,存在两种情况,画出图形,再分类讨论才能解题.O B AOBADDC C (1)(2)图5解:如图5(1)所示,∵OC ⊥OD ,∴∠COD =90°,∵∠AOC =30°,∴∠AOD =120°,∴∠BOD =60°;如图5(2),∵OC ⊥OD ,∴∠COD =90°,∵∠AOC =30°,∴∠AOD =90°-∠AOC =60°,∴∠BOD =120°.故答案选D 项.评注:正确画出示意图,灵活运用分类讨论思想及垂线的性质,才能顺利解答此题.考点四平行线的性质在同一平面内,两条直线若没有公共点,则这两条直线必为平行线.过直线外一点有且只有一条直线和已知直线平行.平行线具有如下性质:①两直线平行,同位角相等;②两直线平行,内错角相等;③两直线平行,同旁内角互补.例4如图6,AB ∥CD ,AE 平分∠CAB 交CD 于点E ,若∠C =50°,则∠AED =().A.65°B.115°C.125°D.130°解:∵AB ∥CD ,∴∠C +∠CAB =180°,∵∠C =50°,∴∠CAB =180°-50°=130°,∵AE 平分∠CAB ,∴∠EAB =65°,∵AB ∥CD ,∴∠EAB +∠AED =180°,∴∠AED =180°-65°=115°,故选B 项.评注:本题考查了平行线的性质,角平分线的定义,熟记性质并准确识图是解题的关键.考点五平行线的判定当两条直线被第三条直线所截,要判定这两条直线为平行线,可借助如下方法:①同一平面内,垂直于同一条直线的两条直线互相平行;②若同位角相等,则这两条直线平行;③若内错角相等,则这两条直线平行;④若同旁内角互补,则这两条直线平行.例5如图7所示,DE 、BE 分别为∠BDC ,∠DBA 的角平分线,且∠DEB =∠1+∠2.求证:(1)AB ∥CD ;(2)∠DEB =90°.D CABF E21图7证明:(1)以点E 为顶点,DE 为一边,在∠DEB 的内部作∠DEF =∠2.∵DE 为∠BDC 的平分线,∴∠2=∠EDC ,∴∠FED =∠EDC ,∴EF ∥CD ,∵∠FEB =∠DEB -∠DEF =∠DEB -∠2,∠1+∠2=∠DEB ,∴∠FEB =∠1,∵∠1=∠ABE ,∴∠FEB =∠ABE ,∴EF ∥AB ,又∵EF ∥CD ,∴∠CDF +∠DFE =180°,∴∠CDF +∠FBA =180°,∴AB ∥CD ;(2)∵AB ∥CD ,∴∠BDC +∠DBA =180°,又∵∠1=12∠DBA ,∠2=12∠BDC ,∴∠1+∠2=90°,∵∠1+∠2=∠DEB ,∴∠DEB =90°.评注:解答第(1)题时,平行线的性质和判定定理可以帮助我们转化角或找到角与角之间的关系,也有利于我们确定两条直线的位置关系;解答第(2)题时,我们要对条件进行综合分析,对结论进行转化.这是找寻思路、顺利解题的一般方法.6。
相交线与平行线(知识总结,试题和答案)

初中精品数学精选精讲学科:数学任课教师: 授课时间: 年月日姓名年级课时教学课题相交线与平行线教学目标(知识点、考点、能力、方法)知识点:两条直线相交,两条直线被第三条直线所截,平行线的判断及性质,命题定理证明,平移、考点:平行线的判断,平行线的性质能力:灵活运用角的关系,应用平行线的判断,平行线的性质解题方法:掌握角的计算,灵活运用角的关系难点重点平行线的判断,平行线的性质课堂教学过程课前检查作业完成情况:优□良□中□差□建议______________________________________________一、知识点大集锦相交线与平行线1、相交线假如两条直线只有一个公共点时,我们称这两条直线相交。
相对的,我们称这两条直线为相交线。
2、邻补角,对顶角ﻩ对顶角与邻补角是依照它们的位置命名的,因此它们各有不同的特点。
对顶角的特点:有公共顶点,角的两边互为反向延长线、图1中的∠1与∠2、∠3与∠4都是对顶角。
对顶角是两个角的位置关系,不是数量关系、图1邻补角的特点:有公共顶点和一条公共边,另一边互为反向延长线。
图1中的∠1与∠3、∠3与∠2、∠2与∠4、∠4与∠1都互为邻补角、邻补角即是两个角的位置关系,也是数量关系、对顶角与邻补角都是成对出现的,单独一个角不能称为对顶角或邻补角,这一点大伙儿要注意、例如我们不能说图1中的∠1是对顶角(或邻补角),能够说∠1与∠2是对顶角,∠1是∠3或∠的邻补角、注意:对顶角的性质:对顶角相等。
邻补角的性质:一个角与它的邻补角的和为180°、A 。
一个角的补角一定是钝角 B、互补的两个角不估计相等C 、若∠A+∠B+∠C=900,则∠A+∠B是∠C的余角 D 。
∠A 的补角与∠A 的余角的差一定等于直角 (二)平行线1、如图,下列判断正确的是:( )A 、若∠1=∠2,则AD ∥BCB 、若∠1=∠2,则AB ∥CDC 、若∠A =∠3,则AD ∥BC D 、若∠3+∠AD C=180° ,则A B∥CD2、下列说法正确的有〔 〕①不相交的两条直线是平行线; ②在同一平面内,不相交的两条线段平行③过一点有且只有一条直线与已知直线平行; ④若a∥b,b∥c,则a 与c 不相交、 A、1个 B 、2个 C、3 D、4个 3、在同一平面内,两条不重合直线的位置关系估计是〔 〕A 。
相交线与平行线知识点+考点+典型例题

第二章相交线与平行线【知识要点】1.两直线相交2.邻补角:有一条公共边,另一条边互为反向延长线的两个角互为邻补角。
3.对顶角(1)定义:有一个公共顶点,且一个角的两边分别是另一个角的两边的反向延长线,这样的两个角互为对顶角 (或两条直线相交形成的四个角中,不相邻的两个角叫对顶角) 。
(2)对顶角的性质:对顶角相等。
4.垂直定义:当两条直线相交所形成的四个角中,有一个角是90°那么这两条线互相垂直。
5.垂线性质:①过一点有且只有一条直线与已知直线垂直;②垂线段最短。
6.平行线的定义:在同一平面内,不相交的两条直线叫平行线,“平行”用符号“∥”表示,如直线a,b是平行线,可记作“a∥b”7.平行公理及推论(1)平行公理:过已知直线外一点有且只有一条直线与已知直线平行。
(2)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
注:(1)平行公理中的“有且只有”包含两层意思:一是存在性;二是唯一性。
(2)平行具有传递性,即如果a∥b,b∥c,则a∥c。
8.两条直线的位置关系:在同一平面内,两条直线的位置关系有相交和平行。
9.平行线的性质:(1)两直线平行,同位角相等(在同一平面内)(2)两直线平行,内错角相等(在同一平面内)(3)两直线平行,同旁内角互补(在同一平面内)10.平行线的判定(1)同位角相等,两直线平行;(在同一平面内)(2)内错角相等,两直线平行;(在同一平面内)(3)同旁内角互补,两直线平行;(在同一平面内)(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行;补充:(5)平行的定义;(在同一平面内)(6)在同一平面内......,垂直于同一直线的两直线平行。
【典型例题】考点一:对相关概念的理解对顶角的性质,垂直的定义,垂线的性质,点到直线的距离,垂线性质与平行公理的区别等例1:判断下列说法的正误。
(1)对顶角相等;(2)相等的角是对顶角;(3)邻补角互补;(4)互补的角是邻补角;(5)同位角相等;(6)内错角相等;(7)同旁内角互补;(8)两直线不相交就平行;(9)直线外一点到直线的垂线段的长度叫做点到直线的距离;(10)过一点有且只有一条直线与已知直线垂直;(11)过一点有且只有一条直线与已知直线平行;(12)互为邻补角的两个角的平分线互相垂直。
相交线与平行线篇(解析版)--中考数学必考考点总结+题型专训

知识回顾微专题相交线与平行线--中考数学必考考点总结+题型专训考点一:相交线与平行线之邻补角、对顶角1.邻补角:①定义:两条相交之间构成的四个角中,有公共顶点且有一条公共边,另一边互为反向延长线的两个角是邻补角。
②性质:邻补角互补。
2.对顶角:①定义:有公共顶点,两边均互为反向延长线的两个角是对顶角。
②性质:对顶角相等。
1.(2022•北京)如图,利用工具测量角,则∠1的大小为()A .30°B .60°C .120°D .150°【分析】根据对顶角的性质解答即可.【解答】解:根据对顶角相等的性质,可得:∠1=30°,故选:A .2.(2022•苏州)如图,直线AB 与CD 相交于点O ,∠AOC =75°,∠1=25°,则∠2的度数是()A .25°B .30°C .40°D .50°【分析】先求出∠BOD 的度数,再根据角的和差关系得结论.【解答】解:∵∠AOC=75°,∴∠AOC=∠BOD=75°.∵∠1=25°,∠1+∠2=∠BOD,∴∠2=∠BOD﹣∠1=75°﹣25°=50°.故选:D.3.(2022•自贡)如图,直线AB、CD相交于点O,若∠1=30°,则∠2的度数是()A.30°B.40°C.60°D.150°【分析】根据对顶角相等可得∠2=∠1=30°.【解答】解:∵∠1=30°,∠1与∠2是对顶角,∴∠2=∠1=30°.故选:A.4.(2022•桂林)如图,直线l1,l2相交于点O,∠1=70°,则∠2=°.【分析】根据对顶角的性质解答即可.【解答】解:∵∠1和∠2是一对顶角,∴∠2=∠1=70°.故答案为:70.考点二:相交线与平行线之垂直知识回顾微专题1.垂直的定义:两条直线相交形成的四个角中,若其中有一个角是90°,则此时我们说这两条直线垂直。
(完整word版)七年级数学相交线与平行线精选知识点及习题(人教版),推荐文档

七年级数学相交线与平行线精选知识点及习题(人教版)相交线与平行线精选知识点平行线的性质【平行线性质】①两条平行线被第三条直线所截,同位角相等;②两条平行线被第三条直线所截,内错角相等;③两条平行线被第三条直线所截,同旁内角互补.包含知识点平行线的性质,平行线之间的距离,同位角、内错角、同旁内角选择练习题1. 如图:(1)若∠1=∠2,则AB∥CD;(2)若AB∥CD,则∠3=∠4;(3)若∠ABC+∠BCD=180°,则AD∥BC;(4)若∠ABC=∠ADC,∠1=∠2,则AB∥CD上述推理正确的有()A.1个B.2个C.3个D.4个答案:B解析:结合图形分析两角的位置关系,根据平行线的判定和性质判断.解:(1)若∠1=∠2,则AD∥BC,故不对;(2)若AB∥CD,则∠3=∠4,故正确;(3)若∠ABC+∠BCD=180°,则AB∥DC,故不对;(4)若∠ABC=∠ADC,∠1=∠2,可推出∠3=∠4,则AB∥CD,故正确.所以有2个正确.故选B.2. 如图,若∠1=∠2,则下列结论一定成立的是()A.AB∥CDB.∠B=∠DC.AD∥BCD.∠3=∠4答案:C解析:根据平行线的判定定理(内错角相等,两直线平行)作出选择.解:∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行);故选C.3. 下列说法中,正确的有()(1)在同一平面内,两条直线被第三条直线所截,那么同位角相等;(2)两条平行线被第三条直线所截,同位角的平分线平行;(3)两条平行线被第三条直线所截,内错角的平分线平行;(4)两条平行线被第三条直线所截,同旁内角的平分线平行;(5)两条直线被第三条直线所截,形成4对同位角,2对内错角和2对同旁内角.A.2个B.3个C.4个D.5个答案:B解析:根据平行线的性质及平行线的判定定理进行逐一判断即可.解:(1)错误,因为不是两条平行线;(2)正确,因为两条平行线被第三条直线所截,同位角相等,其角平分线所形成的角也相等;(3)正确,因为两条平行线被第三条直线所截,内错角相等,其角平分线所形成的角也相等;(4)错误,因为两条平行线被第三条直线所截,同旁内角互补,其角的平分线必相交,且夹角等于90°;(5)正确,两条直线被第三条直线所截,形成4对同位角,2对内错角和2对同旁内角.故选B.4. 如图,直线a,b与直线c,d相交,若∠1=∠2,∠3=70°,则∠4的度数是()A.35°B.70°C.90°D.110°答案:D解析:解:∵∠1=∠2,∴a∥b,∴∠3=∠5,∵∠3=70°,∴∠5=70°,∴∠4=180°-70°=110°,故选:D.5. 如图,点D在直线AE上,量得∠CDE=∠A=∠C,有以下三个结论:①AB∥CD;②AD∥BC;③∠B=∠CDA.则正确的结论是()A.①②③B.①②C.①D.②③答案:A解析:根据平行线的判定推出AD∥BC,AB∥CD,根据平行线的性质得出∠B+∠A=180°,∠A+∠CDA=180°,即可得出答案.解:∵∠C=∠CDE,∴AD∥BC(内错角相等,两直线平行),(故①正确)∵∠A=∠CDE,∴AB∥CD(同位角相等,两直线平行),(故②正确)∴∠B+∠A=180°,∠A+∠CDA=180°,∴∠B=∠CDA(等量代换),(故③正确)即正确的结论有①②③,故选:A.解答练习题如图,已知AB∥CD,BE平分∠ABC,且交CD于D点,∠CDE=160°,求∠C的度数.答案:解:∵∠CDE=160°,∴∠CDB=180°-∠CDE=180°-160°=20°,∵AB∥CD,∴∠ABD=∠CDB=20°,∵BE平分∠ABC,∴∠ABC=2∠ABD=2×20°=40°,∴∠C=180°-∠ABC=180°-40°=140°.解析:先根据邻补角的定义求出∠CDB的度数,再根据平行线的性质及角平分线的定义得出∠ADB 及∠ABC的度数,由平行线的性质可得出∠C的度数.如图AE∥BD,∠CBD=57°,∠AEF=125°,求∠C的度数,并说明理由.答案:解:∵∠AEF=125,∴∠CEA=55°∵AE∥BD,∠CDB=∠CEA=55°,在△BCD中,∵∠CBD=57°,∴∠C=68°.解析:要求∠C的度数,在△BCD中,由三角形内角和定理可知,求出另外两角即可.3. 如图1,是大众汽车的图标,图2反映其中直线间的关系,并且AC∥BD,AE∥BF.∠A 与∠B的关系如何?解:∵AC∥BD,∴∠A=∠DOE,∵AE∥BF,∴∠DOE=∠B,∴∠A=∠B.解析:根据两直线平行同位角相等,可判断∠A=∠B.如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,(1)求证:∠EDC=90°.(2)若∠ABD的平分线与CD的延长线交于F(图2),且∠F=55°,求∠ABC.答案:(1)证明:在△BCD中,∠CBD+∠BDC+∠BCD=180°,∵∠BDC=∠BCD,∴∠CBD+2∠BDC=180°,∵AD∥BC,∴∠CBD=∠ADB,∵DE平分∠ADB,∴∠BDE=∠ADB,∴∠EDC=∠BDE+∠BDC=(∠CBD+2∠BDC)=×180°=90°,故:∠EDC=90°;(2)解:设BF、DE相交于点O,∵∠EDC=90°,∴∠FDO=90°,∴∠DOF=90°-∠F=90°-55°=35°,由三角形的外角性质,∠OBD+∠ODB=∠DOF=35°,∵DE平分∠ADB,BF平分∠ABD,∴∠ABD+∠ADB=2(∠OBD+∠ODB)=2×35°=70°,在△ABD中,∠A=180°-(∠ABD+∠ADB)=180°-70°=110°,∵AD∥BC,∴∠ABC=180°-∠A=180°-110°=70°.解析:(1)根据三角形的内角和定理列式求出∠CBD+2∠BDC=180°,根据两直线平行,内错角相等可得∠CBD=∠ADB,再根据角平分线的定义可得∠BDE=∠ADB,然后求出∠EDC=90°;(2)设BF、DE相交于点O,根据直角三角形两锐角互余求出∠DOF,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠OBD+∠ODB,然后根据角平分线的定义求出∠ABD+∠ADB,再根据三角形的内角和定理求出∠A,然后根据两直线平行,同旁内角互补解答.(1)如图(1),AB∥EF.求证:∠BCF=∠B+∠F.(2)当点C在直线BF的右侧时,如图(2),若AB∥EF,则∠BCF与∠B、∠F的关系如何?请说明理由.答案:(1)证明:过C作CD∥AB,∵AB∥EF,∴CD∥AB∥EF,∴∠B=∠BCD,∠F=∠FCD,∴∠B+∠F=∠BCF.(2)∠B+∠F+∠BCF=360°,理由是:过C作CD∥AB,则∠B+∠BCD=180°,又∵AB∥EF,AB∥CD,∴CD∥EF∥AB,∴∠F+∠FCD=180°,∴∠B+∠F+∠BCF=360°.解析:(1)过C作CD∥AB,推出AB∥CD∥EF,根据平行线性质得出∠B=∠BCD,∠F=∠FCD,即可得出答案;(2)过C作CD∥AB,推出AB∥CD∥EF,根据平行线性质得出∠B+∠BCD=180°,∠F+∠FCD=180°,即可得出答案.。
人教版七年级(下)相交线与平行线知识点及典型例题

相交线与平行线知识点整理及测试题一、相交线1、邻补角与对顶角两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:注意点:[1]顶角是成对出现的,对顶角是具有特殊位置关系的两个角;⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与 ∠β不一定是对顶角⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
[4]两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
练习:1.如图所示,∠1和∠2是对顶角的图形有( )A.1个B.2个C.3个D.4个 2.如图1-1,直线AB 、CD 、EF 都经过点O , 图中有几对对顶角?3.如图1-2,若∠AOB 与∠BOC 是一对邻补角,OD 平分∠AOB ,OE 在∠BOC 内部,并且∠BOE =12∠COE ,∠DOE =72°。
求∠COE 的度数。
12121221(图1-2)2、垂线⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:如图所示:AB ⊥CD ,垂足为O⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记) ⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简称:垂线段最短。
3、垂线的画法:⑴过直线上一点画已知直线的垂线; ⑵过直线外一点画已知直线的垂线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上。
画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象是线段的线。
4、点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离记得时候应该结合图形进行记忆。
(完整版)平行线与相交线知识点整理总复习.doc
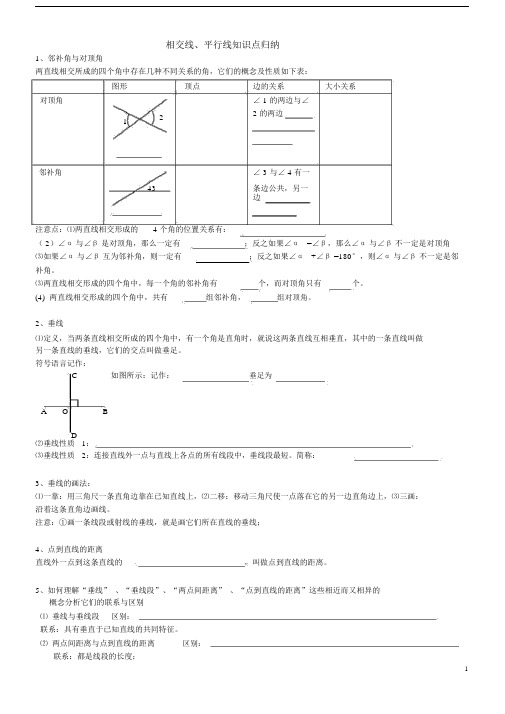
1、邻补角与对顶角两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:图形顶点边的关系大小关系对顶角∠ 1 的两边与∠2 的两边1 2邻补角∠ 3 与∠ 4 有一43 条边公共,另一边注意点:⑴两直线相交形成的 4 个角的位置关系有:( 2)∠α与∠β是对顶角,那么一定有;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角⑶如果∠α与∠β互为邻补角,则一定有;反之如果∠α+∠β =180°,则∠α与∠β不一定是邻补角。
⑶两直线相交形成的四个角中,每一个角的邻补角有个,而对顶角只有个。
(4) 两直线相交形成的四个角中,共有组邻补角,组对顶角。
2、垂线⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:C如图所示:记作:垂足为A O BD⑵垂线性质1:⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
简称:3、垂线的画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线。
注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;4、点到直线的距离直线外一点到这条直线的,叫做点到直线的距离。
5、如何理解“垂线” 、“垂线段”、“两点间距离” 、“点到直线的距离”这些相近而又相异的概念分析它们的联系与区别⑴ 垂线与垂线段区别:联系:具有垂直于已知直线的共同特征。
⑵ 两点间距离与点到直线的距离区别:⑶ 线段与距离区别6、平行线的概念:在同一平面内,不相交的两条直线叫做平行线,直线 a 与直线b互相平行,记作 a ∥b。
7、两条直线的位置关系,两条直线的位置关系只有两种:8、平行公理――平行线的存在性与惟一性经过一点,一条直线与这条直线平行9、平行公理的推论:如果那么这两条直线也互相平行a如左图所示,∵ b ∥a,c∥ab ∴ b ∥c注意符号语言书写,前提条件是两直线都平行于第三条直线,才会结论,这两条直线都平行。
(完整版)相交线与平行线最全知识点

一、本章共分4大节共14个课时;(2.16~3.7第1、4周)章节内容课时第五章 相交线与平行线145.1 相交线35.2 平行线及其判定 35.3 平行线的性质 45.4 平移2单元小结2二、本章有四个数学基本事实1.过直线外一点有且只有一条直线与这条直线平行;2.过一点有且只有一条直线与这条直线垂直;3.两条直线被第三条直线所截,如果同位角相等,那么两直线平行;4.两直线平行,同位角相等. 三、本章共有19个概念1.对顶角2.邻补角3.垂直4.垂线5.垂足6.垂线段7.点到直线的距离8.同位角9.内错角10.同旁内角11.平行12.数学基本事实13.平行公理14.命题15.真命题16.假命题17.定理18.证明19.平移四、转化的数学思想遇到新问题时,常常把它转化为已知(或已解决)的问题.P14五、平移1.找规律2.转化求面积3.作图(2009年安徽中考)学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加d cm ,如图所示.已知每个菱形图案的边长cm ,其一个内角为60°.(1)若d =26,则该纹饰要231个菱形图案,求纹饰的长度L ;【解】(2)当d =20时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?【解】第19题图相交线与平行线知识点5.1相交线1、邻补角与对顶角两直线相交所成的四个角中存在几种不同关系的角,它们的概念及性质如下表:图形顶点边的关系大小关系对顶角∠1与∠2有公共顶点∠1的两边与∠2的两边互为反向延长线对顶角相等即∠1=∠2邻补角∠3与∠4有公共顶点∠3与∠4有一条边公共,另一边互为反向延长线.∠3+∠4=180°注意点:⑴对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角.⑶两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.2、垂线⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.符号语言记作:如图所示:AB ⊥CD ,垂足为O⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短.简称:垂线段最短.3、垂线的画法:⑴过直线上一点画已知直线的垂线;⑵过直线外一点画已知直线的垂线.注意:①画一条线段或射线的垂线,就是画它们所在直线的垂线;②过一点作线段的垂线,垂足可在线段上,也可以在线段的延长线上.画法:⑴一靠:用三角尺一条直角边靠在已知直线上,⑵二移:移动三角尺使一点落在它的另一边直角边上,⑶三画:沿着这条直角边画线,不要画成给人的印象是线段的线.1243AB C DO4、点到直线的距离直线外一点到这条直线的垂线段的长度,叫做点到直线的距离记得时候应该结合图形进行记忆.如图,PO ⊥AB ,同P 到直线AB 的距离是PO 的长.PO 是垂线段.PO 是点P 到直线AB 所有线段中最短的一条.现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用.5、如何理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近而又相异的概念分析它们的联系与区别⑴垂线与垂线段 区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度. 联系:具有垂直于已知直线的共同特征.(垂直的性质)⑵两点间距离与点到直线的距离 区别:两点间的距离是点与点之间,点到直线的距离是点与直线之间. 联系:都是线段的长度;点到直线的距离是特殊的两点(即已知点与垂足)间距离.⑶线段与距离 距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同.5.2平行线1、平行线的概念:在同一平面内,不相交的两条直线叫做平行线,直线与直线互相平行,记作∥a b a .b 2、两条直线的位置关系在同一平面内,两条直线的位置关系只有两种:⑴相交;⑵平行.因此当我们得知在同一平面内两直线不相交时,就可以肯定它们平行;反过来也一样(这里,我们把重合的两直线看成一条直线)判断同一平面内两直线的位置关系时,可以根据它们的公共点的个数来确定:①有且只有一个公共点,两直线相交;②无公共点,则两直线平行;③两个或两个以上公共点,则两直线重合(因为两点确定一条直线)3、平行公理――平行线的存在性与惟一性经过直线外一点,有且只有一条直线与这条直线平行4、平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行 如左图所示,∵∥,∥b a c a ∴∥b cPA BOab 注意符号语言书写,前提条件是两直线都平行于第三条直线,才会结论,这两条直线都平行.5、三线八角 两条直线被第三条直线所截形成八个角,它们构成了同位角、内错角与同旁内角. 如图,直线被直线所截b a ,l ①∠1与∠5在截线的同侧,同在被截直线的上方,l b a ,叫做同位角(位置相同) ②∠5与∠3在截线的两旁(交错),在被截直线之间(内),叫做内错角(位置在l b a ,内且交错) ③∠5与∠4在截线的同侧,在被截直线之间(内),叫做同旁内角.l b a , ④三线八角也可以成模型中看出.同位角是“F ”型;内错角是“Z ”型;同旁内角是“U ”型.6、如何判别三线八角 判别同位角、内错角或同旁内角的关键是找到构成这两个角的“三线”,有时需要将有关的部分“抽出”或把无关的线略去不看,有时又需要把图形补全. 例如: 如图,判断下列各对角的位置关系:⑴∠1与∠2;⑵∠1与∠7;⑶∠1与∠BAD ;⑷∠2与∠6;⑸∠5与∠8. 我们将各对角从图形中抽出来(或者说略去与有关角无关的线),得到下列各图. 如图所示,不难看出∠1与∠2是同旁内角;∠1与∠7是同位角;∠1与∠BAD 是同旁内角;∠2与∠6是内错角;∠5与∠8对顶角.abl1234567816B A D 2345789FEC A BF 21ABC17ABCD26ADBF1AF58C注意:图中∠2与∠9,它们是同位角吗?不是,因为∠2与∠9的各边分别在四条不同直线上,不是两直线被第三条直线所截而成.7、两直线平行的判定方法方法一 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 简称:同位角相等,两直线平行方法二 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行 简称:内错角相等,两直线平行方法三 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行 简称:同旁内角互补,两直线平行 几何符号语言: ∵ ∠3=∠2 ∴ AB ∥CD (同位角相等,两直线平行) ∵ ∠1=∠2 ∴ AB ∥CD (内错角相等,两直线平行) ∵ ∠4+∠2=180° ∴ AB ∥CD (同旁内角互补,两直线平行)请同学们注意书写的顺序以及前因后果,平行线的判定是由角相等,然后得出平行.平行线的判定是写角相等,然后写平行.注意:⑴几何中,图形之间的“位置关系”一般都与某种“数量关系”有着内在的联系,常由“位置关系”决定其“数量关系”,反之也可从“数量关系”去确定“位置关系”.上述平行线的判定方法就是根据同位角或内错角“相等”或同旁内角“互补”这种“数量关系”,判定两直线“平行”这种“位置关系”.⑵根据平行线的定义和平行公理的推论,平行线的判定方法还有两种:①如果两条直线没有交点(不相交),那么两直线平行.②如果两条直线都平行于第三条直线,那么这两条直线平行.典型例题:判断下列说法是否正确,如果不正确,请给予改正: ⑴不相交的两条直线必定平行线. ⑵在同一平面内不相重合的两条直线,如果它们不平行,那么这两条直线一定相交. ⑶过一点可以且只可以画一条直线与已知直线平行解答:⑴错误,平行线是“在同一平面内不相交的两条直线”.“在同一平面内”是一项重要条件,不能遗漏. ⑵正确 ⑶不正确,正确的说法是“过直线外一点”而不是“过一点”.因为如果这一点不在已知直线上,是作不出这条直线的平行线的.典型例题:如图,根据下列条件,可以判定哪两条直线平行,并说明判定的根据是什么?解答:⑴由∠2=∠B 可判定AB ∥DE ,根据是同位角相等,两直线平行;A BC DEF 1234⑵由∠1=∠D 可判定AC ∥DF ,根据是内错角相等,两直线平行;⑶由∠ACF +∠F =180°可判定AC ∥DF ,根据同旁内角互补,两直线平行.5.3平行线的性质1、平行线的性质: 性质1:两直线平行,同位角相等; 性质2:两直线平行,内错角相等; 性质3:两直线平行,同旁内角互补. 几何符号语言: ∵AB ∥CD ∴∠1=∠2(两直线平行,内错角相等) ∵AB ∥CD ∴∠3=∠2(两直线平行,同位角相等) ∵AB ∥CD ∴∠4+∠2=180°(两直线平行,同旁内角互补)2、两条平行线的距离 如图,直线AB ∥CD ,EF ⊥AB 于E ,EF ⊥CD 于F ,则称线段EF 的长度为两平行线AB 与CD 间的距离.注意:直线AB ∥CD ,在直线AB 上任取一点G ,过点G 作CD 的垂线段GH ,则垂线段GH 的长度也就是直线AB 与CD 间的距离.3、命题:⑴命题的概念:判断一件事情的语句,叫做命题.⑵命题的组成每个命题都是题设、结论两部分组成.题设是已知事项;结论是由已知事项推出的事项.命题常写成“如果……,那么……”的形式.具有这种形式的命题中,用“如果”开始的部分是题设,用“那么”开始的部分是结论. 有些命题,没有写成“如果……,那么……”的形式,题设和结论不明显.对于这样的命题,要经过分析才能找出题设和结论,也可以将它们改写成“如果……,那么……”的形式.注意:命题的题设(条件)部分,有时也可用“已知……”或者“若……”等形式表述;命题的结论部分,有时也可用“求证……”或“则……”等形式表述.4、平行线的性质与判定①平行线的性质与判定是互逆的关系A BC DEF 1234A EGBC FHDn 两直线平行 内错角相等; 两直线平行 同旁内角互补.其中,由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.典型例题:已知∠1=∠B ,求证:∠2=∠C 证明:∵∠1=∠B (已知) ∴DE ∥BC (同位角相等, 两直线平行) ∴∠2=∠C (两直线平行 同位角相等)注意,在了DE ∥BC ,不需要再写一次了,得到了DE ∥BC ,这可以把它当作条件来用了.典型例题:如图,AB ∥DF ,DE ∥BC ,∠1=65° 求∠2、∠3的度数解答:∵DE ∥BC (已知) ∴∠2=∠1=65°(两直线平行,内错角相等) ∵AB ∥DF (已知) ∴AB∥DF (已知) ∴∠3+∠2=180°(两直线平行,同旁内角互补) ∴∠3=180°-∠2=180°-65°=115°5.4平移1、平移变换 ①把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同. ②新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点 ③连接各组对应点的线段平行且相等2、平移的特征: ①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化. ②经过平移后,对应点所连的线段平行(或在同一直线上)且相等.典型例题:如图,△ABC 经过平移之后成为△DEF ,那么:⑴点A 的对应点是点_________;⑵点B 的对应点是点______.⑶点_____的对应点是点F ;⑷线段AB的对应线段是线段_______;⑸线段BC 的对应线段是线段_______;⑹∠A 的对应角是______. ⑺____的对应角是∠F.AD FBE C123解答: ⑴D;⑵E;⑶C;⑷DE;⑸EF;⑹∠D;⑺∠ACB.思维方式:利用平移特征:平移前后对应线段相等,对应点的连线段平行或在同一直线上解答.考点一:对相关概念的理解对顶角的性质,垂直的定义,垂线的性质,点到直线的距离,垂线性质与平行公理的区别等例1:判断下列说法的正误。
相交线与平行线知识点总结及例题解析

相交线与平行线知识点总结、例题解析知识点1【相交线】在同一平面内,不重合的两条直线的位置关系有两种:平行和相交1、相交线相交线的定义:两条直线交于一点,我们称这两条直线相交.相对的,我们称这两条直线为相交线.知识点2【对顶角和邻补角】两条相交线在形成的角中有对顶角和邻补角两类,它们具有特殊的数量关系和位置关系。
1、邻补角(1)邻补角的概念:两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角叫做互为邻补角.如图,∠1与∠2有一条公共边OD,它们的另一条边OA、OB互为反向延长线,则∠1与∠2互为邻补角(2)邻补角的性质:邻补角互补,即和为180°。
例如:若∠1与∠2互为邻补角,则∠1+∠2=180°注意:①互为邻补角的两个角一定互补,但互补的两个角不一定互为邻补角;②相交的两条直线会产生4对邻补角。
2、对顶角(1)对顶角的概念:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.如图,∠3与∠4有一个公共顶点O,并且∠3的两边OB、OC分别是∠4的两边OA、OD的反向延长线,则∠1与∠2互为对顶角.(2)对顶角的性质:对顶角相等.注意:两条相交的直线,会产生2对对顶角。
3、邻补角、对顶角成对出现,在相交直线中,一个角对顶角只有一个,但邻补角有两个.邻补角、对顶角都是相对与两个角而言,是指的两个角的一种位置关系.它们都是在两直线相交的前提下形成的.注意:如果多条直线相交于同一点,那么产生的邻补角的数量是对顶角的2倍。
【例题1】如图所示,∠1的邻补角是( )A、∠BOCB、∠BOE和∠AOFC、∠AOFD、∠BOC和∠AOF【解析】】据相邻且互补的两个角互为邻补角进行判断,∠1是直线AB、EF相交于点O形成的角,所以它的邻补角与直线CD无关,即它的邻补角是∠BOE和∠AOF,故选B【答案】B【例题2】下面四个图形中,∠1与∠2是邻补角的是( )【答案】D【例题3】如图所示,∠1和∠2是对顶角的图形有( )A、1个B、2个C、3个D、4个【解析】考察对顶角的概念【答案】A【例题4】下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;④因为∠1与∠2不是邻补角,所以∠1+∠2≠180,其中正确的有________ (填序号)【解析】对顶角、邻补角【答案】①【例题5】如图1,直线AB、CD、EF都经过点O,图中有几对对顶角?几对邻补角?【解析】考察对顶角的概念。
相交线与平行线知识点归纳及练习

第一讲 相交线与平行线知识点1 相交与垂直(1)邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角。
(2)对顶角:一个角的两边分别是另一个叫的两边的反向延长线,像这样的两个角互为对顶角。
对顶角的性质:对顶角相等(3)垂线:两条直线相交成直角时,叫做互相垂直,其中一条叫做另一条的垂线。
垂线的性质:性质1:过一点有且只有一条直线与已知直线垂直。
性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
例题:如图所示,下列判断正确的是( )⑴ ⑵ ⑶ ⑷A 、图⑴中∠1和∠2是一组对顶角B 、图⑵中∠1和∠2是一组对顶角C 、图⑶中∠1和∠2是一对邻补角D 、图⑷中∠1和∠2互为邻补角知识点2 三线八角1、同位角、内错角、同旁内角:同位角:∠1与∠5像这样具有相同位置关系的一对角叫做同位角。
内错角:∠2与∠6像这样的一对角叫做内错角。
同旁内角:∠2与∠5像这样的一对角叫做同旁内角。
2、平行线:在同一平面内,不相交的两条直线叫做平行线。
(1)平行公理:经过直线外一点有且只有一条直线与已知直线平行。
推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
(2)平行线的性质:性质1:两直线平行,同位角相等。
性质2:两直线平行,内错角相等。
性质3:两直线平行,同旁内角互补。
(3)平行线的判定:判定1:同位角相等,两直线平行。
判定2:内错角相等,两直线平行。
判定3:同旁内角相等,两直线平行。
例题1、如图,AB ∥DE ,试问∠B 、∠E 、∠BCE 有什么关系.解:∠B +∠E =∠BCE过点C 作CF ∥AB ,则B ∠=∠____( )又∵AB ∥DE ,AB ∥CF ,∴____________( )∴∠E =∠____( )1 21 2 12 1 2∴∠B +∠E =∠1+∠2即∠B +∠E =∠BCE .,2,、设c b a ,,是三条不同的直线,则在下面四个命题中,正确的有( )①如果a 与b 相交,b 与c 相交,那么a 与c 相交;②如果a 与b 平行,b 与c 平行,那么a 与c 平行;③如果a 与b 垂直,b 与c 垂直,那么a 与c 垂直;④如果a 与b 平行,b 与c 相交,那么a 与c 相交。
相交线与平行线考点及题型总结

相交线与平行线考点及题型总结(总7页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--相交线与平行线考点及题型总结第一节相交线一、知识要点:(一)当同一平面内的三条直线相交时,有三种情况:一种是只有一个交点;一种是有两个交点,即两条直线平行被第三条直线所截;还有一种是三个交点,即三条直线两两相交。
(二)余角、补角、对顶角1、余角:如果两个角的和是直角,那么称这两个角互为余角.2、补角:如果两个角的和是平角,那么称这两个角互为补角.3、对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.4、互为余角的有关性质:①∠1+∠2=90°,则∠1、∠2互余;反过来,若∠1,∠2互余,则∠1+∠2=90°;②同角或等角的余角相等,如果∠l十∠2=90°,∠1+∠ 3=90°,则∠2=∠3.5、互为补角的有关性质:①若∠A+∠B=180°,则∠A、∠B互补;反过来,若∠A、∠B互补,则∠A+∠B=180°.②同角或等角的补角相等.如果∠A+∠C=180°,∠A+∠B=180°,则∠B=∠C.6、对顶角的性质:对顶角相等.(三)垂直:相交的一种特殊情况是垂直,两条直线交角成90 。
1、经过直线外一点,作直线垂线,有且只有一条;2、点到直线上各点的距离中,垂线段最短。
(四)两条直线被第三条直线所截,产生两个交点,形成了八个角(不可分的):1、同位角:没有公共顶点的两个角,它们在直线AB,CD 的同侧,在第三条直线EF 的同旁(即位置相同),这样的一对角叫做同位角;2、内错角:没有公共顶点的两个角,它们在直线AB,CD 之间,在第三条直线EF 的两旁(即位置交错),这样的一对角叫做内错角;3、同旁内角:没有公共顶点的两个角,它们在直线AB,CD 之间,在第三条直线EF 的同旁,这样的一对角叫做同旁内角;二、题型分析: 题型一:列方程求角例1:一个角的余角比它的补角的21少20°.则这个角为 ( ) A 、30° B 、40° C 、60° D 、75° 答案:B分析:若设这个角为x ,则这个角的余角是90°-x ,补角是180°-x ,于是构造出方程即可求解求解:设这个角为x ,则这个角的余角是90°-x ,补角是180°-x .则根据题意,得21(180°-x )-(90°-x )=20° ; 解得:x =40°. 故应选B . 说明:处理有关互为余角与互为补角的问题,除了要弄清楚它们的概念,通常情况下还要引进未知数,构造方程求解.习题演练:1、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30 ,那么这两个角是( )A 、42138 、B 、都是10C 、42138 、或4210 、D 、以上都不对 答案:A分析:两个条件可以确定两个角互补,列方程即可解得A 。
(完整)初一数学七下相交线与平行线所有知识点总结和常考题型练习题,推荐文档
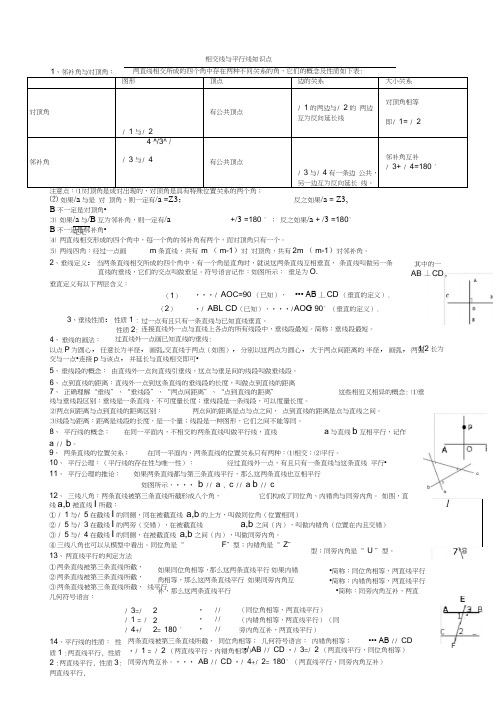
相交线与平行线知识点⑵ 如果/a 与是 对 顶角,则一定有/a =Z3; 反之如果/a = Z3,B 不一定是对顶角•⑶ 如果/a 与/B 互为邻补角,则一定有/a+/3 =180 ° ; 反之如果/a + /3 =180°B 不一定是邻补角• ⑷ 两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
⑸ 两线四角:经过一点画m 条直线,共有 m ( m-1)对 对顶角,共有2m ( m-1)对邻补角。
2、垂线定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直, 条直线叫做另一条直线的垂线,它们的交点叫做垂足。
符号语言记作:如图所示: 垂足为O.垂直定义有以下两层含义:心曰 疋疋•••/ AO C=90 (已知),••• AB 丄CD (垂直的定义).•/ ABL CD (已知),•••/AO G 90° (垂直的定义).3、垂线性质:性质1 : 性质2: (1) (2)过一点有且只有一条直线与已知直线垂直。
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简称:垂线段最短。
其中的一4、 垂线的画法:以点P 为圆心,任意长为半径,画弧,交直线于两点(如图),分别以这两点为圆心,大于两点间距离的 半径,画弧,两弧交与一点•连接p 与该点,并延长与直线相交即可• 5、 垂线段的概念: 由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段。
6、 点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离7、 正确理解“垂线”、“垂线段”、“两点间距离”、“点到直线的距离”这些相近又相异的概念: ⑴垂线与垂线段区别:垂线是一条直线,不可度量长度;垂线段是一条线段,可以度量长度。
⑵两点间距离与点到直线的距离区别: 两点间的距离是点与点之间, 点到直线的距离是点与直线之间。
⑶线段与距离:距离是线段的长度,是一个量;线段是一种图形,它们之间不能等同。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相交线与平行线考点及题型总结第一节 相交线一、知识要点:(一)当同一平面内的三条直线相交时,有三种情况:一种是只有一个交点;一种是有两个交点,即两条直线平行被第三条直线所截;还有一种是三个交点,即三条直线两两相交。
(二)余角、补角、对顶角1、余角:如果两个角的和是直角,那么称这两个角互为余角.2、补角:如果两个角的和是平角,那么称这两个角互为补角.3、对顶角:如果两个角有公共顶点,并且它们的两边互为反向延长线,这样的两个角叫做对顶角.4、互为余角的有关性质:①∠1+∠2=90°,则∠1、∠2互余;反过来,若∠1,∠2互余,则∠1+∠2=90°;②同角或等角的余角相等,如果∠l 十∠2=90°,∠1+∠ 3=90°,则∠2=∠3.5、互为补角的有关性质:①若∠A +∠B =180°,则∠A 、∠B 互补;反过来,若∠A 、∠B 互补,则∠A +∠B =180°.②同角或等角的补角相等.如果∠A +∠C =180°,∠A +∠B =180°,则∠B =∠C .6、对顶角的性质:对顶角相等.(三)垂直:相交的一种特殊情况是垂直,两条直线交角成90 。
1、经过直线外一点,作直线垂线,有且只有一条; 2、点到直线上各点的距离中,垂线段最短。
(四)两条直线被第三条直线所截,产生两个交点,形成了八个角(不可分的):1、同位角:没有公共顶点的两个角,它们在直线AB,CD 的同侧,在第三条直线EF 的同旁(即位置相同),这样的一对角叫做同位角;2、内错角:没有公共顶点的两个角,它们在直线AB,CD 之间,在第三条直线EF 的两旁(即位置交错),这样的一对角叫做内错角;3、同旁内角:没有公共顶点的两个角,它们在直线AB,CD 之间,在第三条直线EF 的同旁,这样的一对角叫做同旁内角;二、题型分析: 题型一:列方程求角例1:一个角的余角比它的补角的21少20°.则这个角为 ( ) A 、30° B 、40° C 、60° D 、75° 答案:B分析:若设这个角为x ,则这个角的余角是90°-x ,补角是180°-x ,于是构造出方程即可求解 求解:设这个角为x ,则这个角的余角是90°-x ,补角是180°-x .则根据题意,得21(180°-x )-(90°-x )=20° ; 解得:x =40°. 故应选B . 说明:处理有关互为余角与互为补角的问题,除了要弄清楚它们的概念,通常情况下还要引进未知数,构造方程求解.习题演练:1、如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30ο,那么这两个角是()A、42138οο、B、都是10οC、42138οο、或4210οο、D、以上都不对答案:A分析:两个条件可以确定两个角互补,列方程即可解得A。
2、如图1,∠1=21∠2,∠1+∠2=162°,求∠3与∠4的度数.答案:54°;72°题型二:三线八角判断例1:如图2,直线AB、CD、EF相交于点O,AOE∠的对顶角是,COF∠的邻补角是若AOC∠:AOE∠=2:3,ο130=∠EOD,则BOC∠=答案:BOF∠;COE∠或FOD∠;130°图2 图3图4例2:如图3,以下说法错误的是()A、1∠与2∠是内错角B、2∠与3∠是同位角C、1∠与3∠是内错角D、2∠与4∠是同旁内角答案:A例3:如图4,按各角的位置,下列判断错误的是()A、∠1与∠2是同旁内角B、∠3与∠4是内错角C、∠5与∠6是同旁内角D、∠5与∠8是同位角答案:C例4:直线AB、CD相交于点O,过点O作射线OE,则图中的邻补角一共有()A、3对B、4对C、5对D、6对答案:D习题演练:1、两条直线相交,有_____对对顶角,三条直线两两相交,有_____对对顶角.答案:2 ;62、下列所示的四个图形中,1∠和2∠是同位角...的是()2121112图1图1图5a M P12 3 B EA CFA 、②③B 、 ①②③C 、①②④D 、 ①④ 答案:C3、下面四个图形中,∠1与∠2是对顶角的图形的个数是( )12121212A 、0B 、1C 、2D 、3 答案:B4、三条直线相交于一点,构成的对顶角共有( ) A 、3对 B 、4对 C 、5对 D 、6对 答案:D题型三:做辅助线(平行线)求角例1:已知AB ∥CD ,∠1=30°,∠2=90°,则∠3等于( )A 、60°B 、50°C 、40°D 、30°答案:A分析:要求∠3的大小,为了能充分运用已知条件,可以过∠2的顶点作EF ∥AB ,由有∠1=∠AEF ,∠3=∠CEF ,再由∠1=30°,∠2=90°求解:过∠2的顶点作EF ∥AB .所以∠1=∠AEF ,又因为AB ∥CD ,所以EF ∥CD ,所以∠3=∠CEF ,而∠1=30°,∠2=90°,所以∠3=90°-30°=60°.故应选A . 说明:本题在求解时连续两次运用了两条直线平行,内错角相等求解. 例2:如图6,若AB ∥CD ,则∠A 、∠E 、∠D 之间的关系是 ( )A 、∠A +∠E +∠D =180°B 、∠A -∠E +∠D =180°C 、∠A +∠E -∠D =180° D 、∠A +∠E +∠D =270° 答案:C例3:如图7,已知AB ∥CD ,∠1=100°,∠2=120°,则∠α=_____. 答案: 40°习题演练:FE图6图7图8 图91、如图8,a b ∥,M N ,分别在a b ,上,P 为两平行线间一点,那么123∠+∠+∠=( ) A 、180oB 、270oC 、360oD 、540o答案:C2、如图9,AB DE ∥,65E ∠=o,则B C ∠+∠=( )A 、135oB 、115oC 、36oD 、65o答案:D题型四:求点到直线的距离例1:如图8,能表示点到直线的距离的线段共有( )A、2条 B、3条C、4条D、5条答案:D例2:已知线段AB 的长为10cm ,点A 、B 到直线L 的距离分别为6cm 和4cm ,•则符合条件的直线L 的条数为( )A 、1B 、2C 、3D 、4 答案:C 习题演练:1、平面内三条直线的交点个数可能有 ( ) A 、1个或3个 B 、2个或3个 C 、1个或2个或3个 D 、0个或1个或2个或3 答案:D第二节 平行线一、知识要点:(一)平行线的定义:在同一平面内,不相交的两条直线是平行线. (二)平行公理1、经过直线外一点,有且只有一条直线与这条直线平行2、如果两条直线都与第三条直线平行,那么这两条直线也互相平行 (三)平行线的判定1、平行线判定定理1:同位角相等,两直线平行2、平行线判定定理2:内错角相等,两直线平行3、平行线判定定理3:同旁内角互补,两直线平行4、平行线判定定理4:两条直线同时垂直于第三条直线,两条直线平行5、平行线判定定理5:两条直线同时平行于第三条直线,两条直线平行二、题型分析:题型一:概念判断例1:下列语句:①三条直线只有两个交点,则其中两条直线互相平行;②如果两条平行线被第三条直线相截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中()A、①②是正确的命题B、②③是正确命题C、①③是正确命题D、以上结论皆对答案:D例2:下列语句错误的是()A、连接两点的线段的长度叫做两点间的距离;B、两条直线平行,同旁内角互补C、若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角D、平移变换中,各组对应点连成两线段平行且相等答案:C习题演练:1、在同一平面内,两条直线可能的位置关系是.答案:相交或平行2、在同一平面内,三条直线的交点个数可能是.答案:0个或1个或2个或3个3、下列说法正确的是()A.经过一点有且只有一条直线与已知直线平行B.经过一点有无数条直线与已知直线平行C.经过一点有一条直线与已知直线平行D.经过直线外一点有且只有一条直线与已知直线平行答案:D题型二:平行线判定定理例1:如图10,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°。
其中能判断a∥b的条件是()A、①②B、②④C、①③④D、①②③④答案:D习题演练:1、如图(1),EF⊥GF,垂足为F,∠AEF=150°,∠DGF=60°.试判断AB和CD的位置关系,并说明理由.(1)(2)(3)(4)如图(2):AB∥DE,∠ABC=70°,∠CDE=147°,∠C= .(直接给出答案)如图(3):CD∥BE,则∠2+∠3-∠1=.(直接给出答案)如图(4):AB∥CD,∠ABE=∠DCF,求证:BE∥CF.答案:平行;37°;180°;略第三节平行线的性质一、知识要点:(一)平行线的性质1、平行线的性质:两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补.2、两条平行线之间的距离是指在一条直线上任意找一点向另一条直线作垂线,垂线段的长度就是两条平行线之间的距离.(二)常见的几种两条直线平行的结论:1、两条平行线被第三条直线所截,一组同位角的角平分线平行;2、两条平行线被第三条直线所截,一组内错角的角平分线互相平行.二、题型分析:题型一:根据平行线的性质求角例1:如图1,AB∥CD,且∠BAP=60°-α,∠APC=45°+α,∠PCD=30°-α,则α=( )A、10°B、15°C、20°D、30°答案:B图1 图2 图3 例2:如图2,CDAB//,且ο25=∠A,ο45=∠C,则E∠的度数是()A、ο60 B、ο70 C、ο110 D、ο80答案:B例3:如图3,已知AB∥CD,则角α、β、γ之间的关系为()EDCBAA BPC DA BC DEαβγA 、α+β+γ=1800B 、α—β+γ=1800C 、α+β—γ=1800D 、α+β+γ=3600答案:A习题演练:1、如图,AB ∥CD ,∠BEF =85°,求∠ABE +∠EFC+∠FCD 的度数。
