七年级上学期期末复习题
2022-2023年度部编版七年级期末复习试卷

2022—2023年度部编版七年级上学期期末测试卷(学生版)一、积累与运用(30分)1.下列加点的字注音无误的一项是(3分)A.红绫.(línɡ)庇.护(pì)赏赐.(cì)莽莽榛榛..(zhēn)B.虐.待(nuè)称.职(chèn)缥.缈(piāo)杞.人忧天(qǐ)C.较.量(jiào)掺.和(chān)温驯.(shun)骇.人听闻(hài)D.怅.然(chànɡ)怂.恿(sǒng)余晖.(huī)神采奕奕..(yì)2.下列书写全部正确....的一项是(3分)A.怂恿怅然笃志漠不关心力不暇供B.篷勃荫蔽派遣躇步呲蹈麻木不仁C.温驯暮色搓捻精益求精由然而生D.溉及晕炫坍塌呼朋引伴哄堂大笑3.下列各句中加点词语使用不恰当的一项是(3分)A.在众目睽睽....之下,这个本来从容自若的姑娘也不禁有点窘迫了。
B.小猴子总是担心月亮会掉下来,天天失眠,真是杞人忧天....。
C.大家认为他提出的这条建议很有价值,都随声附和....表示赞成。
D.谢老师的讲学,语言幽默、精彩、机智,常常引得学生哄堂大笑....。
4.下列标点符号使用不正确...的一项是(3分)A.她还在哼着德彪西的月光,那轻柔的旋律一直在我的梦中飘荡着。
B.6月23日,随着总指挥“点火!”一声令下,北斗三号最后一颗全球组网卫星发射升空。
C.《假如生活欺骗了你》作者是俄国诗人普希金,代表诗作有《自由颂》《致大海》等。
D.一个关键的操作——抛伞,即将开始。
5.下列句子中没有语病....的一项是(3分)A.网络不仅与我们每个人息息相关,更牵涉着国家安全。
B.这个医生表示,戒烟是治疗和预防糖尿病大血管并发症的有效手段之一。
C.这部电视剧,对我很熟悉,因为它反映了当代中学生的学习生活。
D.通过开展“校园书香节”,使同学们的阅读兴趣越来越浓。
6.下列说法完全正确的一项是(3分)A.《世说新语》是东晋时刘义庆编写的一部志人小说集。
2022-2023学年京改版七年级上期末复习数学试卷含答案解析

2022-2023学年北京课改新版七年级上册数学期末复习试卷一.选择题(共7小题,满分14分,每小题2分)1.计算﹣﹣(﹣)的结果为()A.﹣B.C.﹣D.2.通过严格实施低碳管理等措施,2022年北京冬奥会和冬残奥会全面实现了碳中和.根据测算,北京冬奥会三个赛区的场馆使用绿电4亿千瓦时,可以减少燃烧12.8万吨标准煤,减少排放二氧化碳32万吨,实现了“山林场馆、生态冬奥”的目标:其中的32万用科学记数法表示为()A.32×104B.3.2×104C.3.2×105D.3.2×1063.下列各组中的两个图形为全等形的是()A.两块三角尺B.两枚硬币C.两张A4纸D.两片枫树叶4.下面几何体中,由一个平面和一个曲面围成的是()A.圆锥B.正方体C.圆柱D.球5.下列运算中,正确的是()A.B.2a+3b=5abC.(﹣6)÷(﹣2)=﹣3D.﹣|﹣2|=﹣26.有理数a,b在数轴上的位置如图所示,下列各式正确的是()A.a+b<0B.|b|>2C.ab>0D.a﹣b>07.如图,点P是直线a外一点,过点P作PA⊥a于点A,在直线a上取一点B,连接PB,使PB=PA,C在线段AB上,连接PC.若PA=4,则线段PC的长不可能是()A.3.8B.4.9C.5.6D.5.9二.填空题(共8小题,满分24分,每小题3分)8.如果向东行走10m,记作10m,那么向西行走15m,应记作.9.已知x=2是关于x的方程3a=2(x+1)的解,则代数式﹣a2的值为.10.当时,﹣2x的值为正数;不等式3(x+1)≥5x﹣3的正整数解是.11.如图,直线AB、CD交于点O,CO⊥OE,OF是∠AOD的平分线,OG是∠EOB的平分线,∠AOC=44°,则∠FOG=.12.小明的存款是a元,小华的存款比小明存款的一半多2元,则小华的存款为元.13.小王同学在解方程4x﹣2=□x﹣5时,发现“□“处的数字模糊不清,但察看答案可知该方程的解为x =3,则□处的数字为.14.对任意有理数a,b,c,d,规定一种新运算:,已知,则x=.15.按一定规律排列的多项式:2x2﹣2y,4x3﹣3y,6x4﹣4y,8x5﹣5y,…,根据上述规律,则第n个多项式是.三.解答题(共11小题,满分60分)16.(5分)阅读下列材料:|x|=,即当x<0时,.用这个结论可以解决下面问题:(1)已知a、b是有理数,当ab≠0时,求的值;(2)已知a、b是有理数当abc≠0时,求+的值;(3)已知a、b、c是有理数,a+b+c=0,abc<0,求的值.17.(5分)计算(1)﹣17+(﹣6)+23﹣(﹣20);(2);(3);(4).18.(5分)解下列方程:(1)3x﹣2=4+5x;(2).19.(5分)解下列方程.(1)x+2(x+1)=8+x;(2)=﹣1.20.(5分)化简与求值:(1)化简;a2﹣2ab﹣3a2+6ab;(2)先化简,再求值:2(3x2y﹣xy2)﹣3(﹣xy2+3x2y),其中x=﹣2,y=3.21.(5分)按要求画图:(1)如图1,平面上有四个点A,B,C,D,按下列要求画出图形.①连接BD;②画直线AC交BD于点M;③画出线段CD的反向延长线;(2)有5个大小一样的正方形制成如图2所示的拼接图形(阴影部分),请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.(注意:添加所有符合要求的正方形,添加的正方形用阴影和序号表示).22.(6分)按要求画图,并回答问题:如图,平面内有三个点A,B,C.根据下列语句画图:(1)画直线AB;(2)射线BC;(3)延长线段AC到点D,使得CD=AC;(4)通过画图、测量,点B 到点D 的距离约为 cm (精确到0.1);(5)通过画图、测量,点D 到直线AB 的最短距离约为 cm (精确到0.1).23.(6分)中国银行的个人所得税自2011年9月1日起施行,其中规定个人所得税纳税办法如下:一、以个人每月工资收入额减去3500元后的余额作为其每月应纳税所得额;二、个人所得税纳税税率如下表:纳税级数个人每月应纳税所得额 纳税税率 1不超过1500元的部分 3% 2 超过1500元但不超过4500元的部分10%3 超过4500元但不超过9000元部分20% … … … (1)若甲、乙两人的每月工资收入额分别为4000元和6000元,请分别求出甲、乙两人每月应缴纳的个人所得税;(2)若丙每月缴纳的个人所得税为95元,则丙每月的工资收入额为多少?24.(6分)如图,O 为AB 上一点,∠BOC =40°,OD 平分∠AOC ,∠DOE =90°,求∠AOE 的度数.25.(6分)已知线段AB 上有若干个不重合的点,求出该线段上任意两点所决定的线段长度(包括线段AB ),并记所有这些线段的长度总和为αAB .例如:图1中,AB =12,C 为AB 的中点,则αAB =AB +AC +CB =12+6+6=24.(1)如图2,线段AB 上有C 、D 两点,其中AB =12,AC :CD :DB =1:2:3,求αAB ;(2)如图3,线段AB 上有C 、D 、E 三点,其中C 为AB 的中点,E 为DB 的中点,且CE =4,αAB =64,求AB 的长度;(3)线段AB 上有C 、D 两点,线段上任意两点所决定的线段长度是整数,若αAB =38,且CD 的长度为奇数,直接写出AB 的长度.26.(6分)如图1,点A、B分别在数轴原点O的左右两侧,且OA=OB,点B对应的数是10.(1)求A点对应的数.(2)如图2,动点M、N、P分别从原点O、A、B同时出发,其中M、N均向右运动,速度分别为4个单位长度/秒、2个单位长度/秒,点P向左运动,速度为5个单位长度/秒.设它们运动时间为t秒,当点P是MN的中点时,求t的值.参考答案解析一.选择题(共7小题,满分14分,每小题2分)1.解:﹣﹣(﹣)==﹣.故选:A.2.解:32万=320000=3.2×105.故选:C.3.解:A、两块三角尺不一定是全等形,故此选项不合题意;B、两枚硬币不一定是全等形,故此选项不合题意;C、两张A4纸是全等形,故此选项符合题意;D、两片枫树叶不一定是全等形,故此选项不合题意;故选:C.4.解:A.因为圆锥是由1个平面和1个曲面围成,故A选项符合题意;B.因为正方体是由6个平面围成,故B选项不符合题意;C.因为圆柱是由2个平面和1个曲面围成,故C选项不符合题意;D.因为球体是1个曲面围成,故D选项不符合题意.故选:A.5.解:A.()3=,故A不符合题意;B.2a与3b不能合并,故B不符合题意;C.(﹣6)÷(﹣2)=3,故C不符合题意;D.﹣|﹣2|=﹣2,故D符合题意;故选:D.6.解:由题意:a=﹣1<0,b=2.5>0,|b|>|a|,∴ab<0,a+b>0,a﹣b<0,|b|>2•,故选:B.7.解:∵过点P作PA⊥a于点A,在直线a上取一点B,连接PB,使PB=PA,C在线段AB上,连接PC.若PA=4,∴PB=6,∴4≤PC≤6,故PC不可能是3.8,故选:A.二.填空题(共8小题,满分24分,每小题3分)8.解:如果向东行走10m,记作10m,那么向西行走15m,应记作﹣15m.故答案为:﹣15m.9.解:将x=2代入3a=2(x+1),∴3a=2×3,∴a=2,∴原式=﹣4=,故答案为:10.解:﹣2x>0,x<0;3(x+1)≥5x﹣3,3x+3≥5x﹣3,3x﹣5x≥﹣3﹣3,﹣2x≥﹣6,x≤3;∴不等式3(x+1)≥5x﹣3的正整数解是1,2,3.故答案为:x<0;1,2,3.11.解:∵CO⊥OE,∴∠COE=90°.∴∠EOB=180°﹣∠AOC﹣∠COE=46°.又∵OG是∠EOB的平分线,∴∠BOG==23°.∵∠AOC=44°,∴∠AOD=180°﹣∠AOC=136°.又∵OF是∠AOD的平分线,∴∠AOF==68°.∴∠BOF=180°﹣∠AOF=112°.∴∠FOG=∠FOB+∠BOG=112°+23°=135°.12.解:依题意得,小华存款:a+2.故答案为:a+2.13.解:设“□”处的数字为a,把x=3代入方程,得4×3﹣2=3a﹣5,解得:a=5,则“□”处的数字为5.故答案为:5.14.解:∵,∴x•(﹣1)﹣2×3=2,∴﹣x﹣6=2,∴﹣x=2+6,∴﹣x=8,∴x=﹣8,故答案为:﹣8.15.解:∵2x2﹣2y,4x3﹣3y,6x4﹣4y,8x5﹣5y,…,∴第n个多项式为2n•x n+1﹣(n+1)y,故答案为:2n•x n+1﹣(n+1)y.三.解答题(共11小题,满分60分)16.解:(1)①当a>0,b>0时,==1+1=2;②当a<0,b<0时,==﹣1﹣1=﹣2;当a>,b<0时,==1﹣1=0;当a<0,b>0时,==﹣1+1=0;综上,当ab≠0时,的值为2或﹣2或0;(2)当a>0,b>0,c>0时,+==1+1+1=3;当a<0,b<0,c<0时,+==﹣1﹣1﹣1=﹣3;当a,b,c中两正一负时,+=1,当a,b,c中两负一正时,+=﹣1,综上,当abc≠0时,+的值为3或﹣3或1或﹣1;(3)∵a+b+c=0,∴b+c=﹣a,a+c=﹣b,a+b=﹣c,∴==﹣().∵abc<0,∴a,b,c中两正一负,当a,b,c中两正一负时,∵+=1,∴原式=﹣()=﹣1.∴的值为﹣1.17.解:(1)﹣17+(﹣6)+23﹣(﹣20)=﹣17﹣6+23+20=20;(2)=﹣60×﹣60×+60×+60×=﹣45﹣50+44+35=﹣16;(3)=(﹣50+)×(﹣8)=﹣50×(﹣8)+×(﹣8)=400﹣=399;(4)=(1.75﹣1.75)+(3+2)﹣6=0+6﹣6=﹣.18.解:(1)移项得:3x﹣5x=4+2,合并得:﹣2x=6,解得:x=﹣3;(2)去分母得:2(2x﹣1)﹣(10x+1)=12,去括号得:4x﹣2﹣10x﹣1=12,移项得:4x﹣10x=12+2+1,合并得:﹣6x=15,解得:x=﹣2.5.19.解:(1)x+2(x+1)=8+x,去括号,得,移项,得,合并同类项,得2x=6,系数化成1,得x=3;(2)=﹣1,去分母,得3(1﹣x)=2(4x﹣1)﹣6,去括号,得3﹣3x=8x﹣2﹣6,移项,得﹣3x﹣8x=﹣2﹣6﹣3,合并同类项,得﹣11x=﹣11,系数化成1,得x=1.20.解:(1)a2﹣2ab﹣3a2+6ab=(a2﹣3a2)+(﹣2ab+6ab)=﹣2a2+4ab;(2)2(3x2y﹣xy2)﹣3(﹣xy2+3x2y)=6x2y﹣2xy2+3xy2﹣9x2y=﹣3x2y+xy2,当x=﹣2,y=3时,原式=﹣3×(﹣2)2×3+(﹣2)×9=﹣36﹣18=﹣54.21.解:(1)如图1中,线段BD,直线AC,射线DC即为所求作.(2)如图2中,有四种情形.22.解:(1)如图,直线AB即为所求;(2)如图,射线BC即为所求;(3)如图,线段CD即为所求;(4)通过画图、测量,点B到点D的距离约为3.1cm;(5)通过画图、测量,点D到直线AB的最短距离约为3.1cm.23.解:(1)(4000﹣3500)×3%=500×3%=15(元),1500×3%+(6000﹣3500﹣1500)×10%=45+1000×10%=45+100=145(元).答:甲每月应缴纳的个人所得税为15元;乙每月应缴纳的个人所得税为145元.(2)若丙每月工资收入额为1500+3500=5000(元),则每月应缴税:1500×3%=45(元).45<95<145,则丙的纳税级数为2.设丙每月的工资收入额应为y元,则45+(y﹣3500﹣1500)×10%=95,解得y=5500.答:丙每月的工资收入额应为5500元.24.解:∵O为AB上一点,∠BOC=40°,∴∠AOC=180°﹣40°=140°∵OD平分∠AOC∴∠AOD=∠AOC=70°又∵∠DOE=90°∴∠AOE=20°25.解:(1)∵AB=12,AC:CD:DB=1:2:3,∴AC=2,CD=4,DB=6,∴AD=AC+CD=2+4=6,BC=CD+BD=4+6=10,∴αAB=AC+CD+DB+AD+CB+AB=2+4+6+6+10+12=40;(2)设BE=x,∵E是DB的中点,∴DE=EB=x,∴DB=2x,CD=CE﹣DE=4﹣x,∵C为AB的中点,∴AC=BC=CD+DE+EB=(4﹣x)+x+x=4+x,∴AB=2AC=8+2x,AD=AC+CD=(4+x)+(4﹣x)=8,∴AE=AD+DE=8+x,∵αAB=64,∴AC+CD+DE+EB+AD+AE+AB+CE+CB+DB=64,即(4+x)+(4﹣x)+x+x+8+(8+x)+(8+2x)+4+(4+x)+2x=64,解得x=3,∴AB=8+2x=14;(3)∵αAB=38,∴AC+CD+DB+AD+AB+CB=38,即3AB+CD=38,∴,∵CD是奇数,AB为正整数,∴CD=5,11,17,23,29,35,而CD<AB,∴满足条件的有CD=5,∴AB=11.26.解:(1)∵点B对应的数是10,∴OB=10,∵OA=OB,∴OA=12.又∵点A在原点的左侧,∴点A对应的数为﹣12.(2)当运动时间为t秒时,点M对应的数为4t,点N对应的数为2t﹣12,点P对应的数为﹣5t+10,依题意,得:4t+2t﹣12=2(﹣5t+10),解得:t=2.答:当点P是MN的中点时,t的值为2.。
七年级语文上册期末试卷附答案

七年级语文上册期末试卷附答案七年级语文上册期末试卷附答案七年级的学生在进行语文期末复习的时候,多做一些复习试卷能够帮助我们巩固知识点,有效应对考试,店铺为大家力荐了七年级语文上册期末试卷以及参考答案,给大家作为参考,欢迎阅读!七年级语文上册期末试卷一、积累与运用(23分)1.默写填空。
(5分)(1) , 若出其中; , 若出其里。
(2) ,风正一帆悬。
(3)小明学习成绩好,组织能力强,但他刚转到这个班,不为同学所了解,因此在班干部竞选中落选了。
李老师引述了《论语(十二章)》中的两句话:“ , ”帮他解开了心中的疙瘩。
2.下列加点字的读音全都正确的一项是( )(2分)A.静谧(bì) 枯涸(hé) 啜泣(zhuì)B.骸骨(hé) 玷污(diàn) 清洌(liè)C.梦寐(mèi) 泯灭(mǐn) 分歧(qí)D.禀告(bǐng) 厄运(è) 迸溅(bìng)3.下列词语中没有错别字的一项是( )(2分)A.留连忘返屈径通幽险象迭生恍然大悟B.瘦骨嶙峋黯然缥缈随声附合苦心孤诣C.小心翼翼精疲力尽各得其所嫦娥奔月D.一丝不苟得意忘形引人瑕思水波粼粼4.下面的连接不正确的一项是 ( ) (2分)A.《绿色蝈蝈》——散文——法布尔——德国B.《西游记》——小说——吴承恩——中国C.《皇帝的新装》——童话——安徒生——丹麦D.《济南的冬天》——散文——老舍——中国5.下列句子中加点的成语运用错误的项是( )(2分)A.语文老师每每讲到精彩处,会情不自禁地把衣袖越捋越高,连下课时间也忘了。
B.他知道最好的办法就是和大家保持一致,然而他不肯做一个随声附和的人。
C.《西游记》给人们提供了一个又一个神通广大、除恶灭邪、大快人心的英雄梦!D.2013年中国成功地发射了“神舟”十号,这是多么骇人听闻的消息!6.下列句子中修辞手法运用不恰当的一项是( )(2分)A.图书馆是书籍的宝库,那里贮藏着无数的人类智慧的结晶。
初中七年级数学上册期末专项复习4套含答案

A. 2.2 104
B. 22 103
C. 2.2 103
8.对于用四舍五入法得到的近似数4.609万,下列说法正确的是( )
D. 0.22 105
A.它精确到千分位
B.它精确到0.01
C.它精确到万位
D.它精确到十位
9. 1 3 5 2 013 2 015 2 4 6 2 014 2 016 = ( )
么位置时,他们两家相距最远,最远是多少?处在什么位置时,他们两家相距最近,最近是多少?
23.(6分)草履虫可以吞食细菌使污水得到净化.1个草履虫每小时大约能形成60个食物泡,每个食物泡大 约吞食30个细菌,那么1个草履虫每天(以24小时计算)大约能吞食多少个细菌?100个草履虫呢?(用科 学记数法表示)
【解析】1 3 5 2013 2015 2 4 6 2014 2016 1 2 3 4 2015 2016
1 1 1 1008 .故选D.
10.【答案】B
二、
11.【答案】 7 或 9 12.【答案】713.【答案】 2 , 4 2 , 0.83 3.7 , 2
(2)计算:①
1 1 2
2
1
3
1 3
4
2
019
1
2
020
;
② 1 1 1
1
;
13 35 5 7
2 017 2 019
期末专项复习—有理数
答案解析
一、
1.【答案】C 【解析】由题意,得 8℃ 表示下降 8℃ .故选C.
2.【答案】A【解析】 1 的相反数是 1 .故选A.
2020
2020
(3)若巡逻车每一百千米耗油12升,求该晚巡逻车共耗油多少升.
人教版初中数学七年级上期末复习专题卷(1-4及答案

第一学期七年级数学期末复习专题有理数姓名:_______________班级:_______________得分:_______________一选择题:1.如果+20%表示增加20%,那么﹣6%表示()A.增加14%B.增加6%C.减少6%D.减少26%2.一种零件的直径尺寸在图纸上是30±(单位:mm),它表示这种零件的标准尺寸是30mm,加工要求尺寸最大不超过()A.0.03mmB.0.02mmC.30.03mmD.29.98mm3.某项科学研究,以45分钟为1个时间单位,并记每天上午10时为0,10时以前记为负,10时以后记为正,例如:9:15记为-1,10:45记为1等等.依此类推,上午7:45应记为()A.3B.-3C.-2.5D.-7.452.010010001…中,有理数有()4.在-,3.1415,0,-0.333…,-,-,A.2个B.3个C.4个D.5个5.10月7日,铁路局“十一”黄金周运输收官,累计发送旅客640万人,640万用科学计数法表示为()A.6.4×102B.640×104C.6.4×106D.6.4×1056.若向北走27米记为-27米,则向南走34米记为()A.34米B.+7米C.61米D.+34米7.实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,相反数最大是()A.aB.bC.cD.d8.比较,,的大小,结果正确的是()A. B.C. D.9.如果,则x的取值范围是()A.x>0B.x≥0C.x≤0D.x<010.已知ab≠0,则+的值不可能的是()A.0B.1C.2D.﹣211.如图,M、N、P、R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1.数a对应的点在M与N之间,数b对应的点在P与R之间,若+=3,则原点是().A.M或NB.M或RC.N或PD.P或R12.一只蚂蚁从数轴上A点出发爬了4个单位长度到了表示-1的点B,则点A所表示的数是()A.-3或5B.-5或3C.-5D.313.已知=3,=4,且x>y,则2x-y的值为()A.+2B.±2C.+10D.-2或+1014.有理数a,b,c在数轴上的位置如图所示,则()A.-2bB.0C.2cD.2c-2b15.计算1﹣2+3﹣4+5﹣6+7﹣8+…+2009﹣2010的结果是()A.﹣1005B.﹣2010C.0D.﹣116.填在下面各正方形中的四个数之间都有一定的规律,按此规律得出a、b的值分别为()A.10、91B.12、91C.10、95D.12、9517.下列是用火柴棒拼成的一组图形,第①个图形中有3根火柴棒,第②个图形中有9根火柴棒,第②个图形中有18根火柴棒,…依此类推,则第6个图形中火柴棒根数是()A.60B.61C.62D.6318.a为有理数,定义运算符号“※”:当a>-2时,※a=-a;当a<-2时,※a=a;当a=-2时,※a=0.根据这种运算,则※[4+※(2-5)]的值为()A.1B.-1C.7D.-719.计算:31+1=4,32+1=10,33+1=28,34+1=82,35+1=244,…,归纳各计算结果中的个位数字的规律,猜测32017+1的个位数字是()A.0B.2C.4D.820.计算(﹣2)2016+(﹣2)2015的结果是()A.﹣1B.﹣22015C.22015D.﹣22016二填空题:21.把下面的有理数填在相应的大括号里:15,-,0,-30,0.15,-128,,+20,-2.6.(1)非负数集合:{,…};(2)负数集合:{,…};(3)正整数集合:{,…};(4)负分数集合:{,…}.22.近似数3.06亿精确到___________位.23.按照如图所示的操作步骤,若输入的值为3,则输出的值为________.24.已知(x﹣2)2+|y+4|=0,则2x+y=_______.25.绝对值不大于5的整数有个.26.小韦与同学一起玩“24点”扑克牌游戏,即从一幅扑克牌(去掉大、小王)中任意抽出4张,根据牌面上的数字进行有理数混合运算(每张牌只能用一次)使运算结果等于24或-24,小韦抽得四张牌如图,“哇!我得到24点了!”他的算法是__27.有理数在数轴上的对应点如图所示,化简:.28.观察下列各题:1+3=4=221+3+5=9=321+3+5+7=16=421+3+5+7+9=25=52…根据上面各式的规律,请直接写出1+3+5+7+9+…+99=________.29.观察下列等式:,,,…则=.(直接填结果,用含n的代数式表示,n是正整数,且n≥1)30.观察下列等式:解答下面的问题:21+22+23+24+25+26+…+22015的末位数字是三计算题:31.32.33.34.35.小丽有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题:(1)从中取出2张卡片,使这2张卡片上数字乘积最大,如何抽取?最大值是多少?(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?(3)从中取出2张卡片,利用这2张卡片上数字进行某种运算,得到一个最大的数,如何抽取?最大的数是多少?(4)从中取出4张卡片,用学过的运算方法,使结果为24,如何抽取?写出运算式子(一种即可).37.如图所示,一个点从数轴上的原点开始,先向右移动3单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照下列图象并思考,完成下列各题:(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_______,A,B两点间的距离是________;(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是_______,A,B两点间的距离为________;(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_________,A,B两点间的距离是________.(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么,请你求出终点B表示什么数?A,B两点间的距离为多少?38.同学们都知道,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离;同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索:(1)求|4﹣(﹣2)|=.(2)若|x﹣2|=5,则x=.(3)同理|x﹣4|+|x+2|=6表示数轴上有理数x所对应的点到4和﹣2所对应的两点距离之和,请你找出所有符合条件的整数x,使得|x﹣4|+|x+2|=6,这样的整数是.39.阅读材料:求1+2+22+23+24+…+2200的值.解:设S=1+2+22+23+24+…+2199+2200,将等式两边同时乘以2得2S=2+22+23+24+25+…+2200+2201,将下式减去上式得2S-S=2201-1,即S=2201-1,即1+2+22+23+24+…+2200=2201-1.请你仿照此法计算:(1)1+2+22+23+24+ (210)(2)1+3+32+33+34+…+3n.(其中n为正整数)40.已知数轴上有A、B、C三个点,分别表示有理数﹣24,﹣10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.(1)用含t的代数式表示P到点A和点C的距离:PA=,PC=;(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,运动到终点A.在点Q开始运动后,P、Q两点之间的距离能否为2个单位?如果能,请求出此时点P表示的数;如果不能,请说明理由.第一学期七年级数学期末复习专题有理数参考答案1、C2、C3、B4、D5、C6、D7、A8、D9、C10、B11、B12、B13、D14、B15、A16、A17、D18、B19、C20、C21、(1)15,0,0.15,,+20(2)-,-30,-128,-2.6(3)15,+20(4)-,-2.622、百万;23、5524、0.25、1126、23(1+2)__.27、-b+c+a;28、502.29、30、4.31、32、.33、;34、原式=-1×[-32-9+]-2.5=-1×(-32-9+2.5)-2.5=+32+9-2.5-2.5=36.35、(1)抽取;(2)抽取;(3)抽取;(4)答案不唯一;例如抽取-3,-5,3,4;36、37、(1)4_7__(2)1_2__(3)—92__88__(4)m+n-p_38、【解答】解:(1)∵4与﹣2两数在数轴上所对应的两点之间的距离是6,∴|4﹣(﹣2)|=6.(2)|x﹣2|=5表示x与2两数在数轴上所对应的两点之间的距离是5,∵﹣3或7与2两数在数轴上所对应的两点之间的距离是5,∴若|x﹣2|=5,则x=﹣3或7.(3)∵4与﹣2两数在数轴上所对应的两点之间的距离是6,∴使得|x﹣4|+|x+2|=6成立的整数是﹣2和4之间的所有整数(包括﹣2和4),∴这样的整数是﹣2、﹣1、0、1、2、3、4.故答案为:6;﹣3或7;﹣2、﹣1、0、1、2、3、4.39、解:(1)211-1(2)设S=1+3+32+33+34+…+3n ,将等式两边同乘以3得3S=3+32+33+34+35+…+3n+1,所以3S-S=3n+1-1,即2S=3n+1-1,所以S=2131-+n ,即1+3+32+33+34+ (3)=2131-+n 40、【解答】解:(1)∵动点P 从A 出发,以每秒1个单位的速度向终点C 移动,设移动时间为t 秒,∴P 到点A 的距离为:PA=t,P 到点C 的距离为:PC=(24+10)﹣t=34﹣t;故答案为:t,34﹣t;(2)当P 点在Q 点右侧,且Q 点还没有追上P 点时,3t+2=14+t 解得:t=6,∴此时点P 表示的数为﹣4,当P 点在Q 点左侧,且Q 点追上P 点后,相距2个单位,3t﹣2=14+t 解得:t=8,∴此时点P 表示的数为﹣2,当Q 点到达C 点后,当P 点在Q 点左侧时,14+t+2+3t﹣34=34解得:t=13,∴此时点P 表示的数为3,当Q 点到达C 点后,当P 点在Q 点右侧时,14+t﹣2+3t﹣34=34解得:t=14,∴此时点P 表示的数为4,综上所述:点P 表示的数为﹣4,﹣2,3,4.第一学期七年级数学期末复习专题整式的加减姓名:_______________班级:_______________得分:_______________一选择题:1.下列说法中错误的是()A.-x2y的系数是-B.0是单项式C.xy的次数是1D.-x是一次单项式2.下列说法:①最大的负整数是;②的倒数是;③若互为相反数,则;④=;⑤单项式的系数是-2;⑥多项式是关于x,y的三次多项式。
七年级(上)数学期末总复习

等于20分钟的人数占总人数的40% 大于20分钟的人数占总人数的20% (3)老师随机地问一个同学,最可能得到 的答案是20分钟.
课后练习 一、填空题 1.数一数,在图中,共有_2_2_条线段.
2.如图 ( 1 ) 如 果 AD//BC , 那 么 根 据两__直__线__平__行__同__位__角__相__等__ ,
例6.下面是某班30学生每天上学单程所到时间(分钟)
(1)在这个统计表中,单程花_______分钟这一数 据的频数最大.
(2)若把这些数据分成小于20分钟,等于20分钟, 和大于20分钟这三档,则各档人数各占总人数的多少.
(3)Байду номын сангаас如老师随机地问一个同学,你认为老师最可 能得到的答案是几分钟
答:
(2)线段、射线、直线等简单平面图形的有关概念,特 征和表示法,三者的区别和联系,及线段中点概念,和进 行有关的简单计算.
(3)角的有关概念.表示法,度、分、秒、间的 换算及简单的计算.会比较角的大小及分类.
(4)平行线,相交线,了解了有关平行线垂线 的特征及识别.
4.数据的收集 通过解决简单的实际问题,体会大千世界的 不确定性,熟悉收集,整理数据,学会根据 不同问题选择适当统计图描述数据得到较明 显的结论,理解频数、频率,不可能发生, 可能发生和必然发生的概念.
二、典型例题分析 例1.把下面各数填入表示它所在数集里.
-3,11, 2 ,0,2003,0.414,-0.618,-7% 5
解:
例2.有理数a、b、c在数轴上的位置如图所示: 化简|a+b|-|c-b|
解:由a、b、c在数轴上所处的 位置可知:a<0、b>0、c<0, 且|a|<|b|<|c|.a+b>0,c-b<0 所以|a+b|=a+b,|c-b|=b-c. |a+b|-|c-b|=a+b-(b-c)=a+c.
人教版七年级数学第一学期期末复习压轴训练(含答案)

1.武汉市居民用电电费目前实行梯度价格表(为计算方便,数据进行了处理)(1)若月用电150千瓦时,应交电费_______元;若月用电250千万时,应交电费____元(2)若居民王成家12月应交电费150元,请计算他们家12月的用电量(3)若居民王成家12月份交纳的电费,经过测算,平均每千万时0.55元,请计算他们家12月的用电量2.根据给出的数轴及已知条件,解答下面的问题:(1)已知点A,B,C表示的数分别为1,﹣,﹣3观察数轴,与点A的距离为3的点表示的数是__________,B,C两点之间的距离为__________;(2)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是__________;若此数轴上M,N两点之间的距离为2015(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则M,N两点表示的数分别是:M__________,N__________;(3)若数轴上P,Q两点间的距离为m(P在Q左侧),表示数n的点到P,Q两点的距离相等,则将数轴折叠,使得P点与Q点重合时,P,Q两点表示的数分别为:P__________,Q__________(用含m,n的式子表示这两个数).1.平价商场经销甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元(1) 甲种商品每件进价为_______元,每件乙种商品利润率为________(2) 若该商场同时购进甲、乙两种商品共50件,恰好总进价为2100元,求购进甲种商品多少件?(3) 在“元旦”期间,该商场只对甲乙两种商品进行如下的优惠促销活动:按上述优惠条件,若小聪第一天只购买乙种商品,实际付款360元,第二天只购买甲种商品实际付款432元,求小聪这两天在该商场购买甲、乙两种商品一共多少件?2.如图,在数轴上A 点表示数a ,B 点示数b ,C 点表示数c ,b 是最小的正整数,且a 、b 满足:|a+2|+(c ﹣7)2=0.(1)a = ,b= ,c= ;(2)若将数轴折叠,使得A 点与C 点重合,则点B 与数 表示的点重合;(3)点A .B 、C 开始在数轴上运动,若点A 以每秒1个单位长度的速度向左运动,同时,点B 和点C 分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t 秒钟过后,若点A 与点B 之间的距离表示为AB ,点A 与点C 之间的距离表示为AC ,点B 与点C 之间的距离表示为BC .则AB = ,AC = ,BC = .(用含t 的代数式表示)(4)请问:3BC ﹣2AB 的值是否随着时间t 的变化而改变?若变化,请说明理由;若不变,请求其值.1、七年级学习代数式求值时,遇到这样一类题“代数式6351ax y x y -++--的值与x 的取值无关,求a 的值”,通常的解题方法是:把x 、y 看作字母,a 看作系数合并同类项,因为代数式的值与x 的取值无关,所以含x 项的系数为0,即原式=(3)65a x y +-+,所以30a +=,则 3a =-.(1)若关于x 的多项式2(23)23x m m x -+-的值与x 的取值无关,求m 值;(2)已知A 22321x xy x =+--,B 21x xy =-+-;且3A +6B 的值与x 无关,求y 的值;(3)7张如图1的小长方形,长为a ,宽为b ,按照图2方式不重叠地放在大长方形ABCD 内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为1S ,左下角的面积为2S ,当AB 的长变化时,12S S -的值始终保持不变,求a 与b 的等量关系.2、如图,已知数轴上有A .B 、C 三点,分别表示有理数﹣26、﹣10、10,动点P 从点A 出发,以每秒1个单位的速度向终点C 移动,当点P 运动到B 点时,点Q 从A 点出发,以每秒3个单位的速度向C 点运动,问当点Q 从A 点出发几秒钟时,点P 和点Q 相距2个单位长度?直接写出此时点Q 在数轴上表示的有理数.1、现在有一种既隔热又耐老化的新型窗框材料——“断桥铝”,下图是这种材料做成的两种长方形窗框,已知窗框的长都是y米,宽都是x米.(1)(3分)若一用户需Ⅰ型的窗框2个,Ⅱ型的窗框3个,求共需这种材料多少米(接缝忽略不计)?(2)(4分)已知y>x,求一个Ⅰ型的窗框比一个Ⅱ型的窗框节约这种材料多少米?,4,P、M、N为数轴上的三个动点,点M从B点出发速度2、已知数轴上两点A,B对应的数分别是10为每秒2个单位,点N从A点出发速度为M点的2倍,点P从原点出发速度为每秒1个单位.(1)(1分)线段AB之间的距离为个单位长度.(2)(4分)若点M向左运动,同时点N向右运动,求多长时间点M与点N相遇?(3)(4分)若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?七上数学压轴1参考答案1.解答:解:(1)0.5×150=75(元),0.5×180+0.6×(250-180)=90+0.6×70=90+42=132(元).答:若月用电150千瓦时,应交电费75元,若月用电250千瓦时,应交电费132元.(2)设他们家12月的用电量是x千瓦时,依题意有0.5×180+0.6(x-180)=150,解得x=280.答:他们家12月的用电量是280千瓦时.(3)设他们家12月的用电量是y千瓦时,依题意有0.5×180+0.6(y-180)=0.55y,解得y=360.答:他们家12月的用电量是360千瓦时.故答案为:75,132.2.解:(1)点A的距离为3的点表示的数是1+3=4或1﹣3=﹣2;B,C两点之间的距离为﹣2.5﹣(﹣3)=0.5;(2)B点重合的点表示的数是:﹣1+[﹣1﹣(﹣0.5)]= 0.5;M=﹣1﹣=﹣1008.5,n=﹣1+=1006.5;(3)P=n﹣,Q=n+.故答案为:4或﹣2,0.5;0.5,﹣1008.5,1006.5;n﹣,n+.七上数学压轴2参考答案(2)(7+2)÷2=4.5,对称点为7-4.5=2.5,2.5+(2.5-1)=4;故答案为:4.(3)AB=t+2t+3=3t+3,AC=t+4t+9=5t+9,BC=2t+6;故答案为:3t+3,5t+9,2t+6.(4)不变. 3BC-2AB=3(2t+6)-2(3t+3)=12.压轴3答案1、【答案】(1)解:22(23)232323x m m x mx m m x -+-=-+-2(23)32m x m m =--+,关于x 的多项式2(23)23x m m x -+-的值与x 的取值无关,230m ∴-=, 解得32m =. (2)解:2223211A x xy x B x xy =+--=-+-,, 22363(2321)6(1)A B x xy x x xy ∴+=+--+-+-226963666x xy x x xy =+---+-1569xy x =--(156)9y x =--,36A B +的值与x 无关,1560y ∴-=, 解得25y =. (3)解:设AB x =,由图可知,1(3)3S a x b ax ab =-=-,22(2)24S b x a bx ab =-=-,则123(24)S S ax ab bx ab -=---324ax ab bx ab =--+(2)a b x ab =-+,当AB 的长变化时,12S S -的值始终保持不变,12S S ∴-的值与x 的值无关,20a b ∴-=,2a b ∴=.【思路引导】(1)由题可知代数式的值与x 的取值无关,所以含x 项的系数为0, 故将多项式进行整理,令x 的系数为0,即可求出m ;可;(3)设AB =x , 由图可知,1(3)3S a x b ax ab =-=-,22(2)24S b x a bx ab =-=- ,即可得S 1-S 2 的代数式,根据取值与x 无关可得a-2b=0,即a =2b.2、【答案】解:有两种情况:①点Q 追上点P 之前相距2个单位长度.设此时点Q 从A 点出发t 秒钟.依题意,得(16+t )﹣3t =2,解得,t =7.此时点Q 在数轴上表示的有理数为﹣5;②点Q 追上点P 之后相距2个单位长度.设此时点Q 从A 点出发m 秒钟.依题意,得3m ﹣(16+m )=2,解得,m =9.此时点Q 在数轴上表示的有理数为1.综上所述,当点Q 从A 点出发7秒和9秒时,点P 和点Q 相距2个单位长度,此时点Q 在数轴上表示的有理数分别为﹣5和1【思路引导】根据题意分两种情况进行分析:①点Q 追上点P 之前相距2个单位长度可得方程,解方程即可;②点Q 追上点P 之后相距2个单位长度可得方程,解法即可,最后总结可得结论.压轴4答案1、【答案】(1)解:根据图形,1个Ⅰ型窗框用料(32x y +)米;1个Ⅱ型窗框用料(23x y +)米;2个Ⅰ型窗框和3个Ⅱ型窗框共需这种材料(单位:米)2、【答案】(1)14(2)解:设运动时间为t 秒时,点M 与点N 相遇.2t+2 ⨯ 2t =146t =14t = 73; ∴ 当运动时间为73 秒时,点M 与点N 相遇. (3)解:点M 、N 、P 运动的时间为y 秒时,点P 到点M 、N 的距离相等,①(2y +4)-y =4y -10-yy =7②2y +4-y =y -(4y -10)y =1.5∴当点M 、N 、P 运动时间为7S 或1.5S 时,点P 到点M ,N 的距离相等.故答案为:14;【思路引导】(1)根据数轴上两点间的距离公式求解即可;(2)设运动时间为t秒时,根据点M移动的距离+点N移动的距离=AB=14,列出方程并解之即可;(3)分两种情况:①点P在AB之间,②点M、N在点P的右侧时,据此分别列出方程并解之即可.+++x y x y2(32)3(23)=+++x y x y6469=+;x y1213(2)解:1个Ⅱ型窗框和1个Ⅰ型窗框多用这种材料(单位:米)+-+(23)(32)x y x y=+--2332x y x y=-.y x【思路引导】(1)根据题意列出算式,去掉括号合并即可;(2)用1个Ⅱ型窗框用料-1个Ⅰ型窗框用料,列出算式,去掉括号合并即可。
人教版七年级上数学期末复习训练卷

人教版七年级上数学期末复习训练卷一.选择题(共12小题,满分36分,每小题3分)1.(3分)计算|﹣6|﹣1的最后结果是()A.﹣5B.5C.﹣7D.72.(3分)已知﹣7是关于x的方程2x﹣7=ax的解,则a的值是()A.﹣2B.﹣3C.3D.﹣143.(3分)如果x=y,那么根据等式的性质下列变形不正确的是()A.x+2=y+2B.3x=3y C.5﹣x=y﹣5D.=4.(3分)下列计算正确的是()A.2﹣3=1B.a2+2a2=3a4C.3×(﹣1)2=3D.﹣|﹣3|=3 5.(3分)一张桌子摆放着若干盘子,从三个方向上看,三种视图如下所示,则这张桌子上共有()个盘子A.10B.11C.12D.136.(3分)1﹣2x2+xy﹣y2=1﹣(),在括号里填上适当的项应该是()A.2x2+xy﹣y2B.﹣2x2﹣xy﹣y2C.2x2﹣xy+y2D.x2﹣xy+y2 7.(3分)如图,点C在线段AB上,若AB=10,BC=2,M是线段AB的中点,则MC的长为()A.2B.3C.4D.58.(3分)下列四个说法:①射线AB和射线BA是同一条射线;②若点B为线段AC的中点,则AB=BC;③锐角和钝角互补;④一个角的补角一定大于这个角.其中正确说法的个数是()A.0个B.1个C.2个D.3个9.(3分)三个连续奇数的和为81,则其中最小的一个奇数是()A.23B.25C.27D.2910.(3分)已知AB是圆锥(如图1)底面的直径,P是圆锥的顶点,此圆锥的侧面展开图如图2所示.一只蚂蚁从A点出发,沿着圆锥侧面经过PB上一点,最后回到A点.若此蚂蚁所走的路线最短,那么M,N,S,T(M,N,S,T均在PB上)四个点中,它最有可能经过的点是()A.M B.N C.S D.T11.(3分)一只笼子中装有若干只蜘蛛和3只甲虫,共42条腿,每只蜘蛛8条腿,每条甲虫6条腿,则笼子中蜘蛛有()A.1只B.2只C.3只D.4只12.(3分)点C为线段AB的延长线上的一点,则下列各式中成立的是()A.BC>AB B.AB>BC C.AB=BC D.AC>AB二.填空题(共4小题,满分12分,每小题3分)13.(3分)若∠α=42°,则∠α的余角为°,∠α的补角为°.14.(3分)已知x=3是关于x的方程x﹣1=a的一个解,则a=.15.(3分)如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,若将露出的表面都涂上颜色(底面不涂色),则第n个几何体中只有两个面涂色的小立方体共有个.16.(3分)铁路上的火车票价是根据两站距离的远近而定的,距离愈远,票价愈高.如果一段铁路上共有五个车站,每两站间的距离都不相等,则这段铁路上的火车票价共有种.三.解答题(共9小题,满分72分,每小题8分)17.(8分)某饮品店只出售甲、乙两种奶茶,每杯甲奶茶需用糖15克,每杯乙奶茶需用糖18克.在某半个小时内,售出的两种奶茶恰好用去了相同数量的糖,问:(1)这半个小时内,这两种奶茶分别至少用去了多少克糖?(2)如果这半个小时内,这两种奶茶一共售出的杯数在20至30之间,则这两种奶茶一共售出多少杯?18.(8分)解方程:(1)x=;(2)x÷=12.19.(6分)先化简,再求值:5x2y﹣7(x2y﹣xy2)﹣3xy2,其中x=2,y=﹣1.20.(6分)一只小虫从点A出发向北偏西30°方向爬行了3cm到点B,再从点B出发向北偏东60°方向爬行了3cm到点C,(1)试画图确定A、B、C的位置;(2)从图上量出点C到点A的距离.(精确到0.1cm)(3)指出点C在点A的什么方位?21.(6分)(1)已知:点C在线段AB上,线段AC=6厘米,BC=4厘米,点M、N分别是AC、BC的中点,求线段MN的长度.(2)根据上述计算过程和结果,设AC+BC=a,其他的条件不变,你能猜出MN的长度吗?请用一句简洁的语言表述你的发现.22.(8分)某城市按以下规定收取每月的水费:用水量如果不超过6吨,按每吨1.2元收费;如果超过6吨,未超过的部分仍按每吨1.2元收取,而超过部分则按每吨2元收费.如果某用户5月份水费平均为每吨1.4元,那么该用户5月份应交水费多少元?23.(8分)教育部数据显示,近五年共有创业大学生约55万人,国务院办公厅也出台了《关于进一步支持大学生创业的指导意见》来支持大学生创新创业.河南的小张也加入了创业大军,回到自己家乡,做茶叶加工,然后销售到全国各地,创业初期,小张从茶农那里采购甲,乙两种品种的茶叶共100千克.(1)如果小张购进甲,乙两种茶叶共用了9600元,已知每千克甲种茶叶进价80元,每千克乙种茶叶进价120元,求小张购进甲,乙两种茶叶各多少千克?(2)在(1)的条件下,经过加工,小张把甲种茶叶加价50%作为标价,乙种茶叶加价40%作为标价.由于乙种茶叶深受大众的喜爱,在按标价进行销售的情况下,乙种茶叶很快售完,接着甲种茶叶的最后10千克按标价打折处理全部售完.在这次销售中,小张获得的利润率为42.5%.求甲种茶叶打几折销售?24.(10分)已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA<OB.(1)若A、B的位置如图所示,试化简:|a|﹣|b|+|a+b|+|a﹣b|.(2)如图,若|a|+|b|=8.9,MN=3,求图中以A、N、O、M、B这5个点为端点的所有线段长度的和;(3)如图,M为AB中点,N为OA中点,且MN=2AB﹣15,a=﹣3,若点P为数轴上一点,且P A=AB,试求点P所对应的数为多少?25.(12分)如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.(1)如果∠AOB=50°,∠DOE=35°,那么∠BOD是多少度?(2)如果∠AOE=160°,∠COD=25°,那么∠AOB是多少度?。
辽宁省沈阳市2023-2024学年上学期人教版七年级生物期末复习试题(含解析)

2023-2024学年上学期人教版七年级生物期末复习试题(辽宁沈阳)一、选择题1.“桔生淮南则为桔,桔生于淮北则为枳”,这体现了影响桔生长的主要非生物因素是A.温度B.湿度C.酸碱度D.阳光2.下列不具有生物基本特征的是()A.运动出汗B.春暖花开C.铁钉生锈D.猫豹捕羊3.如图是植物根尖模式图,有关叙述不正确的是()A.①是吸收水分和无机盐的主要部位B.③处的细胞具有较强的分裂能力C.②处的细胞没有细胞核D.④具有保护作用4.下面为绿色开花植物不同结构层次的变化过程示意图,a过程指的是()A.细胞分裂B.细胞生长C.细胞分化D.染色体的复制5.下列哪项是植物生长需要量最多的无机盐()A.含钙、铁、磷的无机盐B.含硼、锌、钾的无机盐C.含氮、磷、钾的无机盐D.含氮、铜、铁的无机盐A.A B.B C.C D.D11.下列农业生产中的措施及原理,说法不正确的是( )A.新疆棉在种植过程中需要进行“打顶”,目的是保护顶端优势,促进多结棉桃B.小麦播种前通常要对土地进行深耕,是由于深耕后的土壤中含有较充足的空气C.枣树树皮环割一周后,结出的果实会更多更大,是由于阻断了筛管向下运输有机物D.葡萄扦插时要选择健壮且带芽的枝条,扦插成活率更高12.在研究响尾蛇追踪老鼠的实验中,能与被响尾蛇咬死的老鼠形成对照的是()A.用一只未被响尾蛇咬过的死老鼠按照相同的路线拖行相同的距离B.用一只未被响尾蛇咬过的死老鼠按照相同的路线拖行不同的距离C.用一只被响尾蛇咬过的死老鼠按照不同的路线拖行相同的距离D.用一只被响尾蛇咬过的死老鼠按照不同的路线拖行不同的距离二、综合题(1)该同学观察到的细胞结构与图1中的(填甲或乙)相同。
(2)本实验中用生理盐水而不用清水的原因是。
(3)图1甲中①所指示的结构是,具有支持和保护细胞的作用。
(4)图1中细胞的控制中心是④所指示的结构是。
(1)图甲中的①是细胞,无色透明有利于光线透入。
(2)枇杷植株进行光合作用的主要部位是图甲中的[ ],产生的有机物通过图甲参考答案:1.A【分析】环境中影响生物生活的各种因素叫生态因素,分为非生物因素和生物因素。
2022-2023学年人教版七年级数学上册期末综合复习训练题(附答案)

2022-2023学年人教版七年级数学上册期末综合复习训练题(附答案)一.选择题1.下列各组式子中,属于同类项的是()A.ab与a B.ab与ac C.xy与﹣2yx D.a与b2.已知关于x的方程2x+a﹣9=0的解是x=2,则a的值为()A.2B.3C.4D.53.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是()A.30°B.60°C.120°D.150°4.下列说法中正确的是()A.射线AB和射线BA是同一条射线B.延长线段AB和延长线段BA的含义是相同的C.延长直线ABD.经过两点可以画一条直线,并且只能画一条直线5.某正方体的每个面上都有一个汉字.它的一种平面展开图如图所示,那么在原正方体中,与“筑”字所在面相对的面上的汉字是()A.抗B.疫C.长D.城6.如图,小林利用圆规在线段CE上截取线段CD,使CD=AB.若点D恰好为CE的中点,则下列结论中错误的是()A.CD=DE B.AB=DE C.CE=CD D.CE=2AB7.如图,O是直线AB上一点,∠AOC=46°,OD是∠COB的角平分线,则∠DOB等于()A.46°B.60°C.67°D.76°8.如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=40°,∠BOC=50°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为()A.135°B.140°C.152°D.45°9.把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.若设这个班有x名学生,则依题意所列方程正确的是()A.3x﹣20=4x﹣25B.3x+20=4x+25C.3x﹣20=4x+25D.3x+20=4x﹣2510.如图,C,D是线段AB上的两点,E是AC的中点,F是BD的中点,若EF=m,CD =n,则AB=()A.m﹣n B.m+n C.2m﹣n D.2m+n二.填空题11.已知|a+2|=0,则a=.12.数轴上与原点的距离等于2个单位的点表示的数是.13.已知﹣5x m y3与4x3y n能合并,则m n=.14.若方程(m﹣1)x|m|+1+2mx﹣3=0是关于x的一元二次方程,则m=.15.已知∠A=100°,则∠A的补角等于°.16.已知∠A=30°45',∠B=30.45°,则∠A∠B.(填“>”、“<”或“=”)17.如图,射线OA的方向是北偏东27°35',那么∠α=.三.解答题18.计算:(1)6×(1﹣)﹣32÷(﹣9).(2)﹣22+|5﹣8|+24÷(﹣3)×.19.先化简再求值:2(3x2y﹣xy2)﹣3(x2y﹣2xy2),其中x=﹣1,y=﹣2.20.补全解题过程:如图,已知线段AB=6,延长AB至C,使BC=2AB,点P、Q分别是线段AC和AB的中点,求PQ的长.解:∵BC=2AB,AB=6∴BC=2×6=12∴AC=+=6+12=18∵点P、Q分别是线段AC和AB的中点∴AP==×18=9AQ==×6=3∴PQ=﹣=9﹣3=621.若a、b互为相反数,c、d互为倒数,m的绝对值为2.(1)直接写出:a+b=,cd=,m=;(2)求的值.22.某车间有62个工人,生产甲、乙两种零件,每人每天平均能生产甲种零件12个或乙种零件23个.已知每3个甲种零件和2个乙种零件配成一套,问应分配多少人生产甲种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?23.如图,已知线段a和线段AB,(1)延长线段AB到C,使BC=a(尺规作图,不写作法,保留作图痕迹);(2)在(1)的条件下,若AB=5,BC=3,点O是线段AC的中点,求线段OB的长.24.在数轴上点A表示数a,点B表示数b,点C表示数c,并且a是多项式﹣2x2﹣4x+1的一次项系数,b是数轴上最小的正整数,单项式的次数为c.(1)a=,b=,c=.(2)请你画出数轴,并把点A,B,C表示在数轴上;(3)请你通过计算说明线段AB与AC之间的数量关系.25.如图,已知点A,O,B在同一条直线上,OE平分∠BOC,∠DOE=90°.(1)填空:与∠COD互余的角有;(2)若∠COE=30°,求∠AOE的度数;(3)求证:OD是∠AOC的平分线.26.一架飞机在两城之间飞行,风速为24千米/小时,顺风飞行需2小时50分,逆风飞行需要3小时.(1)求无风时飞机的飞行速度;(2)求两城之间的距离.27.已知m,x,y满足:(1)(x﹣5)2+|m|=0;(2)﹣2ab y+1与4ab3是同类项.求代数式(2x2﹣3xy+6y2)﹣m(3x2﹣xy+9y2)的值.28.某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.优惠一:非会员购物所有商品价格可获九折优惠;优惠二:交纳200元会费成为该超市的一员,所有商品价格可优惠八折优惠.(1)若用x(元)表示商品价格,请你用含x的式子分别表示两种购物优惠后所花的钱数;(2)当商品价格是多少元时,两种优惠后所花钱数相同;(3)若某人计划在该超市购买价格为2700元的一台电脑,请分析选择哪种优惠更省钱?29.(1)如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点,求线段MN的长;(2)若C为线段上任一点,满足AC+CB=acm,点M、N分别是AC、BC的中点,你能猜想MN的长度吗?并说明理由;(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,点M、N分别是AC、BC的中点,你能猜想MN的长度吗?请画出图形,并说明理由.30.如图,A、B、C是数轴上的三点,O是原点,BO=3,AB=2BO,5AO=3CO.(1)写出数轴上点A、C表示的数;(2)点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒6个单位长度的速度沿数轴向左匀速运动,M为线段AP的中点,点N在线段CQ上,且CN=CQ.设运动的时间为t(t>0)秒.①数轴上点M、N表示的数分别是(用含t的式子表示);②t为何值时,M、N两点到原点的距离相等?参考答案一.选择题1.解:xy与﹣2yx属于同类项,故选:C.2.解;∵方程2x+a﹣9=0的解是x=2,∴2×2+a﹣9=0,解得a=5.故选:D.3.解:∵∠A=60°,∠A与∠B互余,∴∠B=90°﹣∠A=90°﹣60°=30°,∵∠B与∠C互补,∴∠C=180°﹣∠B=180°﹣30°=150°.故选:D.4.解:A、射线用两个大写字母表示时,端点字母写在第一个位置,所以射线AB和射线BA不是同一条射线,此选项错误;B、延长线段AB是按照从A到B的方向延长的,而延长线段BA是按照从B到A的方向延长的,意义不相同,故此选项错误;C、直线本身就是无限长的,不需要延长,故此选项错误;D、根据直线的公理可知:两点确定一条直线,故此选项正确.故选:D.5.解:这是一个正方体的平面展开图,共有六个面,其中与“筑”字所在面相对的面上的汉字是疫.故选:B.6.解:∵点D恰好为CE的中点,∴CD=DE,∵CD=AB,∴AB=DE=CE,即CE=2AB=2CD,故A,B,D选项正确,C选项错误,故选:C.7.解:∵∠AOC=46°,∴∠BOC=180°﹣46°=134°,∵OD是∠COB的角平分线,∴∠DOB=∠COB=×134°=67°,故选:C.8.解:易知:∠COD=180°﹣∠AOD﹣∠BOC=90°,∵OM、ON分别平分∠BOC和∠AOD,∴∠NOD=∠AOD=20°,∠COM=∠BOC=25°,∴∠MON=20°+25°+90°=135°故选:A.9.解:设这个班有学生x人,由题意得,3x+20=4x﹣25.故选:D.10.解:由题意得,EC+FD=m﹣n∵E是AC的中点,F是BD的中点,∴AE+FB=EC+FD=EF﹣CD=m﹣n又∵AB=AE+FB+EF∴AB=m﹣n+m=2m﹣n故选:C.二.填空题11.解:由绝对值的意义得:a+2=0,解得:a=﹣2;故答案为:﹣2.12.解:数轴上与原点的距离等于2的点所表示的数是x,则|x|=2,解得x=±2.故答案为:±2.13.解:∵﹣5x m y3与4x3y n能合并,∴﹣5x m y3与4x3y n是同类项,∴m=3,n=3,∴m n=27.故答案为:27.14.解:由题意得:,解得:m=﹣1.15.解:∵∠A=100°,∴∠A的补角=180°﹣100°=80°.故答案为:80.16.解:∵∠A=30°45'=30.75°,∠B=30.45°,30.75°>30.45°,∴∠A>∠B.故答案为:>.17.解:∵射线OA的方向是北偏东27°35',∴∠α=90°﹣27°35′=62°25′,故答案为:62°25°.三.解答题18.解:(1)6×(1﹣)﹣32÷(﹣9)=6×﹣9÷(﹣9)=4+1=5;(2)﹣22+|5﹣8|+24÷(﹣3)×=﹣4+3+(﹣8)×=﹣1﹣=﹣.19.解:原式=6x2y﹣2xy2﹣3x2y+6xy2=3x2y+4xy2,把x=﹣1,y=﹣2代入,原式=3×(﹣1)2×(﹣2)+4×(﹣1)×(﹣2)2=﹣6﹣16=﹣22.20.解:∵BC=2AB,AB=6∴BC=2×6=12∴AC=AB+BC=6+12=18∵点P、Q分别是线段AC和AB的中点∴AP=AC=×18=9AQ=AB=×6=3∴PQ=AP﹣AQ=9﹣3=6,故答案为:AB;BC;AC;AB;AP;AQ.21.解:(1)∵a、b互为相反数,c、d互为倒数,m的绝对值为2,∴a+b=0,cd=1,m=±2;故答案为:0,1,±2;(2)当m=2时,原式=2+1=3;当m=﹣2时,原式=﹣2+1+0=﹣1,则原式=3或﹣1.22.解:设应分配x人生产甲种零件,12x×2=23(62﹣x)×3,解得x=46,62﹣46=16(人).故应分配46人生产甲种零件,16人生产乙种零件才能使每天生产的甲种零件和乙种零件刚好配套.23.解:(1)如图:(2)∵AB=5,BC=3,∴AC=8,∵点O是线段AC的中点,∴AO=CO=4,∴BO=AB﹣AO=5﹣4=1,∴OB长为1.24.解:(1)多项式﹣2x2﹣4x+1的一次项系数是﹣4,则a=﹣4,数轴上最小的正整数是1,则b=1,单项式的次数为6,则c=6,故答案为:﹣4,1,6;(2)如图所示,,点A,B,C即为所求.;(3)AB=b﹣a=1﹣(﹣4)=5,AC=c﹣a=6﹣(﹣4)=10.∵10÷5=2,∴AC=2AB.25.解:(1)∵OE平分∠BOC,∴∠COE=∠BOE,∵∠COD+∠COE=∠DOE=90°,∴∠COD+∠BOE=90°,与∠COD互余的角有∠BOE、∠COE;故答案为:∠BOE、∠COE;(2)∵OE平分∠BOC,∴∠COE=∠BOE=30°,∴∠AOE=180°﹣30°=150°;(3)证明:∵OE是∠BOC的平分线,∴∠COE=∠BOE,∵∠DOE=90°,∴∠COD+∠COE=90°,且∠DOA+∠BOE=180°﹣∠DOE=90°,∴∠DOC+∠COE=∠DOA+∠BOE,所以∠DOC=∠DOA,所以OD是∠AOC的平分线.26.解:(1)设无风时飞机的速度为x千米每小时,两城之间的距离为S千米.则顺风飞行时的速度v1=x+24,逆风飞行的速度v2=x﹣24顺风飞行时:S=v1t1逆风飞行时:S=v2t2即S=(x+24)×=(x﹣24)×3解得x=840,答:无风时飞机的飞行速度为840千米每小时.(2)两城之间的距离S=(x﹣24)×3=2448千米答:两城之间的距离为2448千米.27.解:∵(x﹣5)2+|m|=0,∴(x﹣5)2≥0|m|≥0,∴x=5,m=0,∵﹣2ab y+1与4ab3是同类项,∴y+1=3,∴y=2,∴(2x2﹣3xy+6y2)﹣m(3x2﹣xy+9y2)=2x2﹣3xy+6y2=2×52﹣3×5×2+6×22=50﹣30+24=44.28.解:(1)由题意可得:优惠一:付费为:0.9x,优惠二:付费为:200+0.8x;(2)当两种优惠后所花钱数相同,则0.9x=200+0.8x,解得:x=2000,答:当商品价格是2000元时,两种优惠后所花钱数相同;(3)∵某人计划在该超市购买价格为2700元的一台电脑,∴优惠一:付费为:0.9x=2430,优惠二:付费为:200+0.8x=2360,答:优惠二更省钱.29.解:(1)∵AC=8cm,点M是AC的中点,∴CM=0.5AC=4cm,∵BC=6cm,点N是BC的中点,∴CN=0.5BC=3cm,∴MN=CM+CN=7cm,∴线段MN的长度为7cm,(2)MN=a,由M,N分别是AC,BC的中点,得MC=AC,NC=BC.MN=MC+NC=AC+BC=(AC+BC)=a,∴当C为线段AB上一点,且M,N分别是AC,BC的中点,则存在MN=a,(3)当点C在线段AB的延长线时,如图:,则AC>BC,∵M是AC的中点,∴CM=AC,∵点N是BC的中点,∴CN=BC,∴MN=CM﹣CN=(AC﹣BC)=b.30.解析(1)点A、C表示的数分别是﹣9、15.(2)①点M、N表示的数分别是t﹣9、15﹣4t,故答案为:t﹣9、15﹣4t.②当点M,点N分别在原点两侧时,由题意可知9﹣t=15﹣4t.解这个方程,得t=2.此时点M在原点左侧,点N在原点右侧.当点M、N在原点同侧时,由题意可知t﹣9=15﹣4t.解这个方程,得t=.此时点M、N同时在原点左侧.所以当t=2或 时,M、N两点到原点的距离相等.。
七年级上期数学期末总复习题
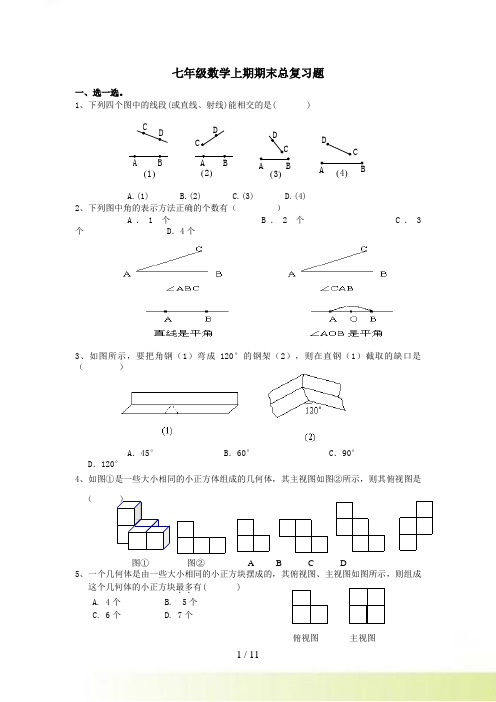
七年级数学上期期末总复习题一、选一选。
1、下列四个图中的线段(或直线、射线)能相交的是( )1()CDBA2()CD BA3()C D BA4()CDBAA.(1)B.(2)C.(3)D.(4) 2、下列图中角的表示方法正确的个数有( )A .1个B .2个C .3个 D .4个3、如图所示,要把角钢(1)弯成120°的钢架(2),则在直钢(1)截取的缺口是( )A .45°B .60°C .90°D .120°4、如图①是一些大小相同的小正方体组成的几何体,其主视图如图②所示,则其俯视图是( )5、一个几何体是由一些大小相同的小正方块摆成的,其俯视图、主视图如图所示,则组成这个几何体的小正方块最多..有( ) A. 4个 B. 5个 C. 6个 D. 7个图① 图② A B C D俯视图主视图6、已知线段AB=6厘米,在直线AB 上画线段AC=2厘米,则BC 的长是( ) A .8厘米 B .4厘米 C .8厘米或4厘米 D .不能确定7、如图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是( )8、下列说法中正确的是( )A.若AP=21AB ,则P 是AB 的中点 B.若AB =2PB ,则P 是AB 的中点 C .若AP =PB ,则P 为AB 的中点 D.若AP =PB=21AB ,则P 是AB 的中点9、甲看乙的方向为北偏东30°,那么乙看甲的方向是( )A .南偏东60°B .南偏西60°C .南偏东30°D .南偏西30° 10、如右图,AB 、CD 交于点O ,∠AOE=90°,若∠AOC :∠COE=5:4,则∠AOD 等于 ( ) A .120° B .130°C .140°D .150°11、下列各组数中,不相等...的一组是 ( ) A .()23-与23- B .-23-与23- C . -33-与 33- D .()33- 与33-12、《广东省重点建设项目计划(草案)》显示,港珠澳大桥工程估算总726亿元,用科学记数法表示正确的是( ) A .107.2610⨯ 元 B .972.610⨯ 元 C .110.72610⨯ 元 D .117.2610⨯元 13、国家体育场“鸟巢”建筑面积达25.8万平方米,将25.8万平方米用科学记数法(四舍五入保留2个有效数字)表示约为( )A .42610⨯平方米B .42.610⨯平方米 C .52.610⨯平方米D .62.610⨯平方米14、如果ab <0,那么下列判断正确的是( ).A .a <0,b <0B . a >0,b >0C . a ≥0,b ≤0D . a <0,b >0或a >0,b <0 15、实数a ,b 在数轴上的对应点如图所示,则下列不等式中错误的是( ) A .0ab > B .0a b +< C .ba<0 D .0a b -< 16、下列运算正确的是( )A .b a b a --=--2)(2B .b a b a +-=--2)(2C .b a b a 22)(2--=--D .b a b a 22)(2+-=--17、已知一个多项式与239x x +的和等于2341x x +-,则这个多项式是( )ab 0A B C DA .51x --B .51x +C .131x --D .131x +18、下列变形中,正确的是( )A 、若ac=bc ,那么a=b 。
新人教版七年级上册数学总复习知识点和练习题

新人教版七年级上册数学总复习知识点和练习题新人教版数学七年级上期末总复期末复一有理数的意义一、双基回顾1、前进8米的相反意义的量是;盈利50元的相反意义的量是。
2、向东走5m记作+5m,则向西走8记作,原地不动用表示。
正数{…};负数{…};分数{…};整数{…};非负整数{…};非正数{…}。
4、与表示-1的点距离为3个单位的点所表示的数是。
5、数轴上到原点的距离为2的点所表示的数是。
6、3的相反数的倒数是。
7、最小的自然数是;最小的正整数是;绝对值最小的数是;最大的负整数是。
8、相反数等于它本身的数是,绝对值等于它本身的数是,平方等于它本身的数是,,倒数即是它自己的数是。
9、如图,如果a<,b>0,那么a、b、-a、-b的大小关系是.10、已知︱a+2︱+(3- b)2=0,则a b =。
ab二、例题导引例1(1)大于-3且小于2.1的整数有哪些?(2)绝对值大于1小于4.3的整数的和是多少?例2已知a、b互为相反数,m、n互为倒数,︱x︱=3,求(a+b)2-3mn+2x的值。
例3(1)若a<,a2=4,b3=-8,求a+b的值。
(2)已知︱a︱= 2,︱b︱=5,求a-b的值;3、操演升华1、判断下列叙述是否正确:①零上6℃的相反意义的量是零下6℃,而不是零下8℃()②如果a是负数,那末-a就是正数()③正数与负数互为相反数()④一个数的相反数长短正数,那末这个数肯定长短负数()⑤若a=b,则︱a︱=︱b︱;若︱a︱=︱b︱,则a=b()2、一种零件标明的要求是Ф10(单位:mm)表示这种零件的标准尺寸是10mm,加工零件要求最大直径不超过mm,最小直径不小于mm.。
3、某天气温上升了-2℃的意义是。
5、12的相反数与-7的绝对值的和是。
6、若a<0,b<0,则下列各式正确的是( )A、a-b<0 B、a-b>0 C、a-b=0 D、(-a)+(-b)>07、两个非零有理数的和是,它们的商是()A、0B、-1C、1D、不能确定8、若|x|=-x,则x=_____;若︱x-2︱=3,则x= .9、古希腊科学家把数1,3,6,10,15,21,……叫做三角形数它有一定的规律性,第个三角形数为_______。
人教版七年级上册数学期末综合复习解答题专题训练(含答案)

人教版七年级上册数学期末综合复习解答题专题训练一、有理数的计算:1.计算:(1)(﹣5)+(﹣4)﹣(+101)﹣(﹣9).(2).(3).(4)﹣24+3×(﹣1)6﹣(﹣2)3.2.计算:(1)﹣20+(﹣14)﹣(﹣18)﹣13(2)4﹣8×(﹣)3(3)(4)3.计算(1);(2);(3);(4).4.为庆祝端午节,和平加油站开展了加油每满10L返现金5元(不足10L不返现金)的活动.出租车司机王师傅只在东西走向的路上开车接送乘客,他7:00从甲地出发(向东行驶的里程数记作正数),到8:00为止,他所行驶的里程记录如下(单位:公里)+4,﹣3,﹣6,+13,﹣10,﹣4,+5.(1)计算到8:00时,王司机在甲地的哪个方向,距甲地多远?(2)若王师傅当日工作10小时,每小时行驶的里程相同,该车每百公里耗油6L,每升油5元,则王师傅当日在该加油站加油共花费多少元?5.已知13=1=×12×22,13+23=9=×22×32,13+23+33=36=×32×42,…,按照这个规律完成下列问题:(1)13+23+33+43+53==×2×2.(2)猜想:13+23+33+…+n3=.(3)利用(2)中的结论计算:(写出计算过程)113+123+133+143+153+163+…+393+403.6.定义新运算“@”与“⊕”:a@b=,a⊕b=.(1)计算3@(﹣2)﹣(﹣2)⊕(﹣1)的值;(2)若A=3b@(﹣a)+a⊕(2﹣3b),B=a@(﹣3b)+(﹣a)⊕(﹣2﹣9b),比较A 和B的大小.二、解一元一次方程:7.解方程:(1)4x﹣3=7﹣x;(2)4x﹣2(3x﹣2)=2(x﹣1);(3);(4).8.解方程:(1)5x﹣4=2(2x﹣3);(2)﹣=1;(3)﹣=1+;(4)﹣=0.75.9.解方程(1)3x﹣5=8;(2)﹣2x+3=4x﹣9;(3)3(x+2)﹣2(x+2)=2x+4;(4).10.解下列方程.(1)2(x﹣2)﹣3(4x﹣1)=9(1﹣x);(2)﹣=﹣2;(3)﹣=1+(4)=0.75三、整式的加减11.若多项式2mx2﹣x2+5x+8﹣(7x2﹣3y+5x)的值与x无关,求m2﹣[2m2﹣(5m﹣4)+m]的值.12.先化简,再求值:(1)(5a2+2a+1)﹣4(3﹣8a+2a2)+(3a2﹣a),其中.(2),其中13.先化简再求值:3(x2﹣2xy)﹣[3x2﹣2y+2(xy+y)],其中.14.化简并求值.(1)2(2x﹣3y)﹣(3x+2y+1),其中x=2,y=﹣0.5(2)﹣(3a2﹣4ab)+[a2﹣2(2a+2ab)],其中a=﹣2.15.先化简,再求值:2(x2y+xy2)﹣2(x2y﹣x)﹣2xy2﹣2y,其中x=﹣2,y=2.16.先化简,再求值:4xy﹣[(x2+5xy﹣y2)﹣2(x2+3xy﹣)],其中x=﹣1,y=2.17.a、b、c三个数在数轴上位置如图所示,且|a|=|b|(1)求出a、b、c各数的绝对值;(2)比较a,﹣a、﹣c的大小;(3)化简|a+b|+|a﹣b|+|a+c|+|b﹣c|.18.有理数a、b、c在数轴上的位置如图.(1)判断正负,用“>”或“<”填空:c﹣b0,a+b0,﹣a+c0(2)化简:|c﹣b|+|a|.19.化简已知a,b,c在数轴上的位置如图所示:(1)化简:|a+b|﹣|c﹣b|+|b﹣a|(2)若a的绝对值的相反数是﹣2,﹣b的倒数是它本身,c2=4,求﹣a+2b+c﹣(a+b﹣c)的值.20.已知有理数a、b、c在数轴上的位置,(1)a+b0;a+c0;b﹣c0;(用“>,<,=”填空)(2)试化简|a+b|﹣|a+c|+|b﹣c|.四、几何图形初步:21.如图,C是线段AB上一点,M,N分别是AC,BC的中点.(1)若AC=6cm,BC=4cm,求线段MN的长;(2)若线段CM与线段CN的长度之比为2:1,且线段CN=2cm,求线段AB的长.22.如图,C、D是线段AB上的点,AD=7cm,CB=7cm.(1)线段AC与BD相等吗?请说明理由.(2)如果M是CD的中点,MD=2cm,求线段AB的长.23.如图,延长线段AB到点F,延长线段BA到点E,若点M、N分别是线段AE、BF的中点,若AE:AB:BF=1:2:3,且EF=24cm,求线段MN的长.24.如图,点C在线段AB上,点M、N分别是线段AC,BC的中点.线段AB=14cm.(1)求线段MN的长;(2)若点C在线段AB的延长线上,求线段MN的长;(3)若点C在直线AB上,求线段MN的长.25.如图,AB:BC:CD=2:3:4,AB的中点M与CD的中点N的距离是3cm,则线段BC的长度.26.如图,直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,若∠BOC比∠DOE大75o.求∠AOD和∠EOF的度数.27.如图,直线AB,CD相交于点O,EO⊥CD于点O,FO⊥AB于点O.若∠AOE=50°,求∠BOC和∠COF.28.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.(1)若∠EOC=35°,求∠AOD的度数;(2)若∠BOC=2∠AOC,求∠DOE的度数.参考答案1.解:(1)(﹣5)+(﹣4)﹣(+101)﹣(﹣9)=﹣5﹣4﹣101+9=﹣101.(2)=﹣18﹣1÷(﹣16)=﹣18﹣(﹣)=﹣17.(3)=(5﹣5×)×(﹣4)=(5﹣)×(﹣4)=×(﹣4)=﹣15.(4)﹣24+3×(﹣1)6﹣(﹣2)3=﹣16+3×1﹣(﹣8)=﹣16+3+8=﹣5.2.解:(1)原式=﹣20﹣14+18﹣13=﹣47+18=﹣29;(2)原式=4﹣8×(﹣)=4+1=5;(3)原式=(﹣﹣+)×36=﹣×36﹣×36+×36=﹣27﹣20+21=﹣26;(4)原式=÷﹣×16=×﹣=﹣=﹣.3.解:(1)=++﹣=﹣+=﹣=﹣;(2)=(﹣)×÷(﹣6)2﹣1=(﹣)×÷36﹣1=(﹣)××﹣1=﹣1=﹣;(3)=﹣1×(﹣9×﹣2)×(﹣)=﹣1×(﹣4﹣2)×(﹣)=﹣1×(﹣6)×(﹣)=﹣9;(4)=×(﹣25)﹣49×(﹣+)=(﹣1)﹣49×+49×﹣49×=(﹣1)﹣42+﹣1=﹣33.4.解:(1)4﹣3﹣6+13﹣10﹣4+5=﹣1(公里),∴王师傅在甲地的西1公里位置;(2)10×(4+3+6+13+10+4+5)=450(公里),450÷100×6=27(L),27×5﹣2×5=125(元).∴王师傅当日在该加油站加油共花费125元.5.解:(1)13+23+33+43+53=225=×52×62(2)猜想:13+23+33+…+n3=×n2×(n+1)2(3)利用(2)中的结论计算:113+123+133+143+153+163+…+393+403.解:原式=13+23+33+...+393+403﹣(13+23+33+ (103)=×402×412﹣×102×112=672400﹣3025=6693756.解:(1)3@(﹣2)﹣(﹣2)⊕(﹣1)=﹣=+=1;(2)A=3b@(﹣a)+a⊕(2﹣3b)=+=3b﹣1,B=a@(﹣3b)+(﹣a)⊕(﹣2﹣9b)=+=3b+1,则A<B.7.解:(1)∵4x﹣3=7﹣x,∴4x+x=7+3.∴5x=10.∴x=2.(2)∵4x﹣2(3x﹣2)=2(x﹣1),∴4x﹣6x+4=2x﹣2.∴4x﹣6x﹣2x=﹣2﹣4.∴﹣4x=﹣6.∴x=.(3)∵,∴6x﹣3(3x+2)=18﹣2(5x﹣2).∴6x﹣9x﹣6=18﹣10x+4.∴6x﹣9x+10x=18+4+6.∴7x=28.∴x=4.(4)∵,∴30(0.6x+0.5)﹣100(0.03x+0.2)=2(x﹣9).∴18x+15﹣3x﹣20=2x﹣18.∴18x﹣3x﹣2x=﹣18+20﹣15.∴13x=﹣13.∴x=﹣1.8.解:(1)5x﹣4=2(2x﹣3),5x﹣4=4x﹣6,x=﹣2.(2)﹣=1,5(x﹣3)﹣2(4x+1)=10,5x﹣15﹣8x﹣2=10,﹣3x=10+15+2,x=﹣9;(3)﹣=1+,6x﹣2(5x+11)=12+4(2x﹣4),6x﹣10x﹣22=12+8x﹣16,6x﹣10x﹣8x=12﹣16+22,﹣12x=18,x=﹣;(4)﹣=0.75,﹣=0.75,2(30+2x)﹣4(20+3x)=3,60+4x﹣80﹣12x=3,4x﹣12x=3﹣60+80,﹣8x=23,x=﹣.9.解:(1)3x﹣5=8移项,3x=8+5.合并同类项,3x=13.x的系数化为1,x=.∴这个方程的解为x=.(2)﹣2x+3=4x﹣9移项,﹣2x﹣4x=﹣9﹣3.合并同类项,﹣6x=﹣12.x的系数化为1,x=2.∴这个方程的解为x=2.(3)3(x+2)﹣2(x+2)=2x+4去括号,3x+6﹣2x﹣4=2x+4.移项,3x﹣2x﹣2x=4+4﹣6.合并同类项,﹣x=2.x的系数化为1,x=﹣2.∴这个方程的解为x=﹣2.(4)去分母,3(3y﹣1)﹣12=2(5y﹣7).去括号,9y﹣3﹣12=10y﹣14.移项,9y﹣10y=﹣14+12+3.合并同类项,﹣y=1.y的系数化为1,y=﹣1.∴这个方程的解为y=﹣1.10.解:(1)去括号得:2x﹣4﹣12x+3=9﹣9x,移项合并得:﹣x=10,解得:x=﹣10;(2)去分母得:4x﹣2﹣5x﹣2=3﹣6x﹣12,移项合并得:5x=﹣5,解得:x=﹣1;(3)去分母得:3x﹣5x﹣11=6+4x﹣8,移项合并得:﹣6x=9,解得:x=﹣1.5;(4)方程整理得:﹣=0.75,即15+x﹣20﹣3x=0.75,移项合并得:﹣2x=5.75,解得:x=﹣.11.解:原式=2mx2﹣x2+5x+8﹣7x2+3y﹣5x=(2m﹣8)x2+3y+8,因为此多项式的值与x无关,所以2m﹣8=0,解得:m=4.m2﹣[2m2﹣(5m﹣4)+m]=m2﹣(2m2﹣5m+4+m)=﹣m2+4m﹣4,当=4时,原式=﹣42+4×4﹣4=﹣4.12.解:(1)∵(5a2+2a+1)﹣4(3﹣8a+2a2)+(3a2﹣a)=5a2+2a+1﹣12+32a﹣8a2+3a2﹣a=33a﹣11,∴当a=时,原式=33a﹣11=33×﹣11=0;(2)∵=2x2﹣2x2﹣2+5x2﹣3=5x2﹣5,∴x=﹣时,原式=5x2﹣5=5×(﹣)2﹣5=﹣.13.解:原式=3x2﹣6xy﹣[3x2﹣2y+2xy+2y]=3x2﹣6xy﹣(3x2+2xy)=3x2﹣6xy﹣3x2﹣2xy=﹣8xy当时原式=﹣8×(﹣)×(﹣3)=﹣12.14.解:(1)原式=4x﹣6y﹣3x﹣2y﹣1=x﹣8y﹣1,将x=2,y=﹣0.5代入,得原式=x﹣8y﹣1=2﹣8×(﹣0.5)﹣1=2+4﹣1=5;(2)原式=﹣3a2+4ab+a2﹣4a﹣4ab=﹣2a2﹣4a,当a=﹣2时,原式=﹣8+8=0.15.解:原式=2x2y+2xy2﹣2x2y+2x﹣2xy2﹣2y=2x﹣2y,当x=﹣2,y=2时,原式=﹣4﹣4=﹣8.16.解:原式=4xy﹣(x2+5xy﹣y2﹣2x2﹣6xy+y2)=4xy﹣(﹣x2﹣xy)=5xy+x2,因为x=﹣1,y=2,所以原式=5×(﹣1)×2+(﹣1)2=﹣9.17.解:(1)∵从数轴可知:c<b<0<a,∴|a|=a,|b|=﹣b,|c|=﹣c;(2)∵从数轴可知:c<b<0<a,|c|>|a|,∴﹣a<a<﹣c;(3)根据题意得:a+b=0,a﹣b>0,a+c<0,b﹣c>0,则|a+b|+|a﹣b|+|a+c|+|b﹣c|=0+a﹣b﹣a﹣c+b﹣c=﹣2c.18.解:由图可知,a<0,b>0,c>0,且|b|<|a|<|c|,(1)c﹣b>0,a+b<0,﹣a+c>0;(2)原式=c﹣b﹣a.故答案为:>,<,>.19.解:(1)∵a+b>0,c﹣b<0,b﹣a<0,∴原式=a+b+c﹣b﹣b+a=2a﹣b+c;(2)由题意,得a=2,b=﹣1,c=﹣2,∴﹣a+2b+c﹣(a+b﹣c)=﹣a+2b+c﹣a﹣b+c=﹣2a+b+2c=﹣4﹣1﹣4=﹣9.20.解:(1)由数轴可得:c<a<0<b,∴a+b<0,a+c<0,b﹣c>0,(2)∵a+b<0,a+c<0,b﹣c>0,∴|a+b|﹣|a+c|+|b﹣c|=﹣a﹣b+a+c+b﹣c=0.故答案为:(1)<;<;>;(2)原式=0.21.解:(1)因为M,N分别是AC,BC的中点,所以,,所以MN=CM+CN=3+2=5(cm).(2)因为线段CM与线段CN的长度之比为2:1,CN=2cm,所以线段CM=4cm.因为M,N分别是AC,BC的中点,所以AC=2CM=8cm,BC=2CN=4cm,所以AB=AC+BC=8+4=12(cm).22.解:(1)相等,因为AD=7cm,CB=7cm.所以AD=CB,因为AC=AD﹣CD,BD=CB﹣CD,所以AC=BD;(2)因为M是CD的中点,所以CM=MD,由(1)得,AC=BD,所以AC+CM=BD+MD,所以AM=MB,因为AD=7cm,MD=2 cm,所以AM=7﹣2=5(cm),所以AB=2AM=10(cm).23.解:设EA=xcm,则AB=2xcm,BF=3xcm,EF=6xcm.∵点M,N分别是线段EA,BF的中点,∴EM=MA=xcm,BN=NF=xcm.∵AB=2xcm,∴MN=MA+AB+BN=4xcm.∵EF=24cm,∴6x=24,解得:x=4,∴MN=4x=16cm.24.解:(1)∵点M,N分别是线段AC,BC的中点.∴MC=AC,CN=BC.∴MN=MC+CN=AC+BC=AB=7cm.(2)当点C在线段AB的延长线上时,如下图:∵点M,N分别是线段AC,BC的中点.∴MC=AC,CN=BC.∴MN=MC﹣NC==AC﹣BC=AB=7cm.(3)由(1)、(2)小题知,当点C在线段AB上或点C在线段AB的延长线上时,MN=AB=7cm.当点C在线段AB的反向延长线上时,如下图:点M,N分别是线段AC,BC的中点.∴MC=AC,CN=BC.∴MN=NC﹣MC=BC﹣AC=AB=7cm.综上:当点C在直线AB上时MN=7cm.25.解:设AB=2xcm,BC=3xcm,CD=4xcm,∵M是AB的中点,N是CD的中点,∴MB=xcm,CN=2xcm,∴MB+BC+CN=x+3x+2x=3,∴x=0.5,∴3x=1.5,即BC=1.5cm.26.解:设∠BOD=2x,∵OE平分∠BOD,∴∠DOE=∠EOB==x,∵∠BOC=∠DOE+75°=x+75°.∴x+75°+2x=180°,解得:x=35°,∴∠BOD=2×35°=70°,∴∠AOD=180°﹣∠BOD=180°﹣70°=110°,∵FO⊥CD,∴∠BOF=90°﹣∠BOD=90°﹣70°=20°,∴∠EOF=∠FOB+∠BOE=20°+35°=55°.所以∠AOD和∠EOF的度数分别为:110°、55°.27.解:∵EO⊥CD于点O,∴∠DOE=90°,∴∠AOD=∠DOE﹣∠AOE=90°﹣50°=40°,∵∠BOC和∠AOD为对顶角,∴∠BOC=∠AOD=40°,∵FO⊥AB于点O,∴∠BOF=90°,∴∠COF=∠BOF+∠BOC=90°+40°=130°.28.解:(1)∵EO⊥AB,∴∠BOE=90°,∵∠EOC=35°,∴∠BOC=∠BOE+∠EOC=125°.∴∠AOD=∠BOC=125°,答:∠AOD的度数为125°;(2)∵∠AOC+∠BOC=180°,∠BOC=2∠AOC,∴∠AOC+2∠AOC=180°∴∠AOC=60°,∴∠BOD=∠AOC=60°,∴∠EOD=∠BOE+∠BOD=90°+60°=150°,答:∠DOE的度数为150°.。
精品 七年级数学上册 重点难点 期末复习题

3 5 7 , , , 4 9 16
-19x , 20x , …根据你发现的规律, 第 2015 个单项式是_______
8.如图,要使图中平面展开图按虚线折叠成正方体后,相对面上两个数之积为 12,则 x+y=
第 1 页 共 10 页
七年级数学上册 期末复习题
9.如图所示的运算程序中,若开始输入的 x 值为 48,我们发现第一次输出的结果为 24,第二次输出的 结果为 12,…,则第 2015 次输出的结果为
第 2 页 共 10 页
七年级数学上册 期末复习题
13.为节约能源,某单位按以下规定收取每月电费, 用电不超过 140 度,按每度 0.43 元收费, 如果超过 140 度,超过部分按每度 0.57 元收费.若某用户四月份的电费平均每度 0.5 元,问该用户四月份应交电费多 少元?
14.小刘和小周站在正方形的对角 A、 C 两点处,小刘以 2 米/秒的速度走向点 D 处, 途中位置记为 P,小周 以 3 米/秒的速度走向点 B 处,途中位置记为 Q,假设两人同时出发, 已知正方形的边长为 8 米,E 在 AB 上, AE=6 米,记三角形 AEP 的面积为 S1,三角形 BEQ 的面积为 S2,如图: (1)他们出发后几秒钟时 S1=S2。 (2)当 S1+S2=14 平方米时,小周距离点 B 处还有多远?
0
27.解方程: (1) 4 x 2 5 x 7 1 5 10
9.若 2a 1 2 b 3 0, 则a b =( A.
1 6
B.
1 2
)
D.
1 8
10.某种商品每件的进价为 190 元, 按标价的九折销售时,利润率为 15. 2%。 设这种商品的标价为每件 x 元,依题意列方程正确的是( A. 190 0.9 x 190 0.152 C. 0.9 x 190 190 0.152
人教版七年级上册数学期末复习典型试题(按题型总结)

数学期末复习典型试题A一.填空题1、-0.5的绝对值是 ,相反数是 ,倒数是 。
2、一个数的绝对值是4,则这个数是 ,数轴上与原点的距离为5的数是 。
3、—2x 与3x —1互为相反数,则=x 。
4、(1)设b a 、互为相反数,d c 、互为倒数,则2013(b a +)-cd 的值是_____________。
(2)已知a 、b 互为相反数,c 、d 互为倒数,且3=m ,则20052)(242cd b m a -+-=_________。
5、已知bbaa ab +≠,则0=___________。
已知0)1(32=-++b a ,则=+b a 3 。
6、(1)如果2|1|(2)0a b -++=,则的值是______。
(2)若()0522=++-y x ,则y x = 。
7、单项式 -22xy π的系数是 ,次数是 ;多项式 125323+--xy yx 的次数 。
8、(1)如果123304kxk 是关于x 的一元一次方程,则k ____。
(2)如果0m 21y 32m -9=+关于y 的一元一次方程,则m = 。
9、(1)已知x=3是方程ax-6=a+10的解,则a=_____________。
(2)若x =2是方程a xx -=-243的解,则201120111aa +的值是 。
10、将弯曲的河道改直,可以缩短航程,是因为:两点之间, 最短11、小明将一根木条固定在墙上只用了两个钉子,他这样做的依据是 ____.12、如图, ∠AOB 是平角, ∠AOC=300, ∠BOD=600, OM 、ON 分别是∠AOC、∠BOD的平分线, ∠MON 等于______.13、如图,图中共有 条线段,共有 个三角形。
14. 如图3,∠AOD=80°,∠AOB=30°,OB 是∠AOC 的平分线,则∠AOC 的度数为______,∠COD 的度数为________.15、计算51°36ˊ=____°25.14°= ___° ____′____″;下午1点24分,时针与分针所组成的____度。
七年级数学上册期末复习综合测试题(含答案)

七年级数学上册期末复习综合测试题(含答案)一.精心选择(本大题有12小题,每小题2分,共24分)1.12021-的倒数是( ) A .2021- B .12021- C .2021 D .120212.关于直线,下列说法正确的是( )A .可以量长度B .有两个端点C .可以用两个小写字母来表示D .没有端点 3.下列说法不正确的是( )A .2a 是2个数a 的和B .2a 是2和a 的积C .2a 是偶数D .2a 是单项式4.下列各组中的两项,是同类项的为( ) A .25x y 与xyB .25x y -与2yxC .25ax 与2yx D .38与3x5.在下列方程中:①0x =;②21x y -=;③20n n +=;④532yy =+;⑤221x x -=+.其中一元一次方程的个数是( ). A .1 B .2 C .3 D .46.钟表上的时间指示为两点半,这时时针和分针之间的夹角为( ) A .120° B .105° C .100° D .90° 7.计算2136⎛⎫--- ⎪⎝⎭的结果为( ) A .12-B .12C .56-D .568.图(1)是一个长为2a ,宽为2b (a b >)的长方形,用剪刀沿图中虚线剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的正方形的面积是( )A .abB .2()a b +C .22a b - D .2()a b -9.当1x =时,代数式31px qx ++的值为2021,则当1x =-时,31px qx ++的值为( ) A .2019- B .2021- C .2020 D .202110.如图,将一副三角板的直角顶点重合放置于点A 处(两块三角板看成在同一平面内),将其中一块三角板绕点A 旋转的过程中,下列结论一定成立的是( )A .BAD DAC ∠=∠B .BAD EAC ∠≠∠C .90BAE DAC ∠-∠=︒D .180BAE DAC ∠+∠=︒11.一件夹克衫先按成本价提高60%标价,再将标价打7折出售,结果获利36元,设这件夹克衫的成本价是x 元,那么根据题意,所列方程正确的是( ) A .0.7160%6()3x x +=- B .0.7160%6()3x x +=+ C .0.7160%6(3)x x +=-D .0.7160%6(3)x x +=+12.人行道用同样大小的灰、白两种不同颜色的小正方形地砖铺设而成,如图中的每一个小正方形表示一块地砖.如果按图①②③…的次序铺设地砖,把第n 个图形用图ⓝ表示,那么第50个图形中的白色小正方形地砖的块数是( )A .150B .200C .355D .505二.准确填空(本大题有6个小题,每小题3分,共18分)13.如果零上2℃记为2+℃,那么3-℃表示_______________. 14.3015︒'=__________°.15.一个长方形的宽为cm x ,长比宽的2倍多1 cm ,这个长方形的周长为__________cm .16.若27x a b 与3ya b -的和为单项式,则xy =_______.17.如图,线段AB 表示一根对折以后的绳子,现从P 处把绳子剪断,剪断后的各段绳子中最长的一段为32cm ,若12AP PB =,则这条绳子的原长为__________cm .18.做一个数字游戏:第一步:取一个自然数18n =,计算211n +得1a ; 第二步:算出1a 的各位数字之和得2n ,计算221n +得2a ; 第三步:算出2a 的各位数字之和得3n ,计算231n +得3a ;…,以此类推,则2021a =__________.三.细心解答(本大题有8个小题,共58分)19.(本小题满分6分)计算:()32142⎛⎫-⨯- ⎪⎝⎭20.(本小题满分6分)已知232A a ab b =-+-,22B a ab =-,化简2A B -.21.(本小题满分6分) 以下是小明解方程1323x x +--=1的解答过程. 解:去分母,得31231()()x x +--=.去括号,得31231x x +-+=.移项,合并同类项,得3x =-.小明的解答过程是否有错误?如果有错误,写出正确的解答过程. 22.(本小题满分6分)已知:如图,点D 、C 、E 是线段AB 上依次排列的三点,当点C 、D 分别是AB 和AE 的中点,且15AB =, 4.5CE =时,求线段CD 的长.23.(本小题满分8分)将连续偶数2,4,6,8,…排成如图数表.(1)十字框中的五个数的和与中间的数16有什么关系?(2)设中间的数为a ,用代数式表示十字框中的五个数的和.(3)若将十字框上下左右移动,可框住另外的五个数,所框五个数的和能等于2020吗?若能,写出这五个数;如不能,请说明理由. 24.(本小题满分8分)为了预防新冠肺炎的发生,学校免费为师生提供防疫物品.某校购进洗手液与84消毒液共400瓶.已知洗手液的价格是25元/瓶,84消毒液的价格是15元/瓶,总共消费了7200元.该校购进洗手液和84消毒液各多少瓶?25.(本小题满分9分)已知:点O 是直线AB 上的一点,90COD ∠=︒.OE 是BOD ∠的平分线. (1)当点C 、D 、E 在直线AB 的同侧(如图)时,①若35COE ∠=︒,求AOD ∠的度数. ②若COE α∠=,则AOD ∠=________.(用含α的式子表示) (2)当点C 与点D 、E 在直线AB 的两侧(如图)时,(1)中②的结论是否仍然成立?请给你的结论并说明理由.26.(本小题满分9分)如图,甲、乙两人(看成点)分别在数轴3-和5的位置上,沿数轴做移动游戏.每次的移动游戏规则如下:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位; ②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位; ③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.(1)若第一次移动游戏,甲、乙两人都猜对了,则甲、乙两人之间的距离是_______个单位; (2)若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n 次,且他最终停留的位置对应的数为m .请你用含n 的代数式表示m ; (3)经过_______次移动游戏,甲、乙两人相遇。
七年级语文上册期末综合复习测试题(含答案)

七年级语文上册期末综合复习测试题(含答案)一、积累与运用(20 分)1.根据语境,补写出古代诗文名句。
(10 分)⑴_______________,切问而近思。
(《<论语>十二章》)⑵晴空一鹤排云上,_______________。
(刘禹锡《秋词》)⑶_______________,山入潼关不解平。
(谭嗣同《潼关》)⑷知之者不如好之者,_______________。
(《<论语>十二章》)⑸《诫子书》中阐释过度享乐和急躁对人修身养性产生不利影响的句子是:_______________,_______________。
⑹《夜雨寄北》一诗“_______________,_______________”体现了诗人李商隐对未来团聚情景的想象。
⑺小明在游九龙江时,看到九龙江涨潮时水面宽阔,渔船顺风而行的情景,不禁吟诵起《次北固山下》“_______________,_______________。
”两句诗来。
2.阅读下面文字,按要求写出相应的汉字或选出正确的读音。
(4 分)⑴看着三轮车远去,也绝没有想到,那竟是永远的jué()别。
(《秋天的怀念》)⑵三妹便sǒng()恿着她去拿一只来。
(《猫》)⑶人类就世世代代绵yán()下来,并且一天比一天加多了。
(《女娲造人》)⑷凡是由人工孵卵器养出的小凫,总是极其羞怯() ( A.qiè B.què )难以接近,每次一出壳,就赶紧逃开,躲到附近的暗角里不肯出来。
(《动物笑谈》)3.下列句子中没有语病的一项是()(3 分)....A.学校能否形成良好的校园文化氛围,对教育活动的有效开展有重要作用。
B.文章中很多的事例都表现出莎莉文老师的耐心、爱心和高超的教育艺术。
C.这次诗歌朗诵比赛活动中的经验和教训都值得大家认真学习和积极发扬。
D.充沛的兴趣,真实的体验,积极的思考,是成功完成这一次实践活动的保障。
4.下列填入文中括号内的语句,衔接最恰当的一项是() (3 分)我需要清静……最好去处是到个庙宇前小河旁边大石头上坐坐,()。
人教版七年级上册数学期末总复习题

第一章 有理数第一课 有理数 数轴 相反数 绝对值 倒数知识构造图⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎪⎭⎪⎪⎬⎫数轴倒数绝对值大小比较相反数有理数的分类热身练习:1.如果+20%表示增加20%,那么-6%表示( ). A .增加14% B .增加6% C .减少6% D .减少26%2.如果2()13⨯-=,那么“〞内应填的实数是〔 〕 A .32B .23C .23-D .32-3.-213的相反数是___ ____,—2的倒数是,|—311|=。
4.假设||2,3,x y x y ==+=则。
典例分析:1.把以下各数填入表示它所在的数集中:16,0.618, 3.14,260,2008,,0.21,5%37-----。
整数有 分数有 负数有 有理数有2.如果a ,b 是互为相反数,c ,d 是互为倒数,x 的绝对值等于2,那么b a cdx x 24--+ 的值是;3.假设23(2)0m n -++=,那么2m n +的值为〔 〕 A .4- B .1-C .0D .4点评:一个数的绝对值是指数轴上表示这个数的点到的距离,所以某数的绝对值是非负数。
几个非负数的和等于零,那么这几个非负数同时为零。
4.实数a 、b 在数轴上的位置如图1所示,那么a 与b 的大小关系是〔 〕A .a > bB . a = bC . a < bD . 不能判断点评:有理数大小比拟:正数零负数,两个负数,大的反而小;数轴上表示的两个数边的数总比边的数大。
o图1ba5.某工厂在上一星期的星期日生产了100台彩电,下表是本星期的生产情况:比前一天的产量多的记为正数,比前一天产量少的记为负数。
请算出本星期最后一天星期日的产量是台,本星期的总产量是台,星期的产量最多,星期的产量最少。
反应练习:1.如果水位升高3m 时水位变化记作+3m ,那么水位下降5米时水位变化记作:2.大于–3且不大于2的所有整数写出来是3.将有理数0,722-,2.7,-4,0.14按从小到大的顺序排列,用“<〞号连接起来应为_____________ ______.4.有理数a 、b 在数轴上的位置如下图,以下结论正确的选项是〔〕 A 、b <a B 、ab <0 C 、b —a >0 D 、a +b >0 5.与a-b 互为相反数的是( )A .a+bB .a-bC .-a-bD .b-a6.假设0>a ,0<b ,且b a <,试用“<〞号连接a ,b ,-a ,-b 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级上学期期末复习题
七年级上学期期末复习题1
1.世界三大宗教为基督教、伊斯兰教和佛教。
2.聚落的主要形式包括城市和乡村。
3.气候关注的两个要素是气温和降水。
4.热带的气候类型主要有热带雨林气候、热带草原气候、热带季风气候和热带沙漠气候。
5.亚热带的气候类型主要有亚热带季风和亚热带湿润性气候、地中海气候。
地中海气候最显著的特征是夏季炎热干燥,冬季温和多雨。
6.温带的气候类型主要有温带季风气候、温带海洋性气候和温带大陆性气候。
温带季风气候的特征是夏季暖热多雨,冬季寒冷干燥。
7.寒带的气候类型主要有苔原气候和冰原气候。
8.根据经济发展水平的高低,通常可把世界上的国家划分为发达国家和发展中国家。
9.地图是我们日常生活和学习地理必不可少的工具。
10.地球上最大的大陆是亚欧大陆。
11.陆地地形分为平原、高原、山地、丘陵和盆地五种基本类型。
12.火山与地震主要位于两大地带:环太平洋火山地震带和阿尔卑斯—喜马拉雅火山地震带。
13.人口的增长应与资源、环境相协调,与社会经济发
展相适应。
14.天气的突出特点是多变,气候具有相对的稳定性。
15.一般情况下,海拔每增高100米,气温约下降0.6°C。
16.纬度相同的地方,在夏季陆地气温高于海洋,在冬季陆地气温低于海洋,北半球陆地月平均气温最高和最低的月份一般分别出现在7月、1月,而海洋则分别出现在8月、2月。
9.世界最大的平原是亚马孙平原,世界最高的高原是青藏高原,世界最长的山脉是安第斯山脉,世界最大的盆地是刚果盆地,世界最深的海沟是马里亚纳海沟。
9.地球自转和公转的特征相同的是运动的方向。
10.亮亮正驾驶汽艇在亚洲与非洲的分界线上航行,他现在的位置是苏伊士运河。
11.完全位于北半球的大洲是欧洲和北美洲。
12.既以白色人种为主,又通用英语的是欧洲和北美洲
13.一天当中,最高气温一般出现在午后2点。
14.地形崎岖不利于聚落的形成。
15.“明天北方会有一股冷空气南下,与暖空气交汇,在江淮流域形成降雨”,请你分析该天气预报所描绘的降雨类型是锋面雨。
16.太阳直射北回归线的日期约是6月22日。
17.形成“一山有四季,十里不同天”现象的主要因素是地形地势的影响。
18.热带草原分布面积最大的洲是非洲。
19.世界上面积最大的是俄罗斯,面积最小的是梵蒂冈。
世界上最大的发展中国家是中国。
20.世界大洲中,被三大洋包围,孤立存在于地球南端的是南极洲。
21.销售黑种人使用的化妆品请到非洲中部和南部。
22.巴拿马运河沟通的大洋是太平洋和大西洋。
23.联合国----纽约世界贸易组织-----日内瓦
亚太经济合作组织----上海
24.在温带大陆性分布区内,随着降水量的多少,依次呈现温带森林、温带森林草原、温带草原、温带半荒漠和温带荒漠景观。
复习题2
1.地球表面积约是5.1亿平方千米。
2.世界面积最大的大洋是太平洋,纬度最高的大洲是南极洲。
3.气温和降水对生活和生产影响最大,是我们最为关注的气候
要素。
4.教徒最多的宗教是基督教,在中国称为回教或清真教的宗教
是伊斯兰教。
5.世界上共有220多个国家和地区,其中面积最大的是俄罗斯。
6.对于一副既无指向标,又无经纬网的地图,辨别方向的方法
通常采用的是“上北下南,左西右东”来确定方向。
7.地图的三要素是方向、比例尺、图例和注记。
8.当前人口总数最多的国家是中国。
9.世界上使用最广泛的语言是英语。
10.乡村和城市的本质区别是产业类型不同。
11.划分南北半球的界线是0度纬线。
12.世界上规模最大、最有影响力的国际组织是联合国。
13.世界上唯一地跨两大洲和东西半球的国家是俄罗斯。
14.热带雨林地区分布最广的大洲是南美洲。
15.四季如春是气候现象。
16.降水的形式包括:雨、雪、冰雹。
17.亚洲和欧洲分界线的是土耳其海峡。
18.有关世界平均气温分布规律的,正确的是自赤道向两极依次
递减。
19.24岁的玛利亚在她的国家从没见过下雪,她最有可能来自印
度尼西亚。
1.
2.候要素。
3.世界上最大的大洋是太平洋,最大的大洲是亚洲。
4.世界上使用人数最多的语言是汉语。
5.地球的真实形状是不规则的球体。
6.经纬网中,经线和纬线的形状组合正确的是半圆、圆圈。
7.东西半球的分界线是20°W、160°E。
8.与地球自转有关的自然现象是昼夜更替。
9.规模最大与最有影响力的全球性国际组织是UN。
10.地球表面海洋和陆地的比例是三分陆地七分海洋。
11.目前,人类居住在世界上220多个国家和地区,这些国家和
地区分布在六大洲。
12.属于描写天气状况的是晴空万里。
13.某地有“早穿皮袄午穿纱”的说法,这说明当地气温日较差
比较大。
14.没有热带气候分布的大洲是欧洲。
15.在卫星云图中,能看到绿色的区域,则天气状况一般为晴朗。
16.世界使用最广的语言是英语。
17.区分人种的主要依据是体质特征。
18.世界人口稠密区往往分布于中低纬度临海地带。
19.澳大利亚所在的板块是大洋洲板块。
20.以苏伊士运河为分界线的两个大洲是非洲和亚洲。
21.以英语作为母语的发达国家是澳大利亚、英国、美国。
22.造成世界人口急剧膨胀的主要原因是医疗卫生事业不断进
步,死亡率下降。
23.能把地球平分为两个半球的纬线圈是0°纬线圈。
24.从南、北半球的位置看,发达国家大部分位于北半球。
