VaR计量模型分析案例
VAR模型分析

H : 0 0 1 2 p
显然,如果(4)式中 x t 的滞后变量的回归 系数估计值都不显著,则 H0 不能被拒绝,即 x t 对 y t 不 存在 格兰杰因果性。反之,如果 x t 的任何 一个滞后变量回归系数的估计值是显著的,则 x t 对 y t 存在格兰杰因果关系。
19
建立VAR模型
在工作文件窗口,在主菜单栏选 Quicp/Estimate VAR,OK,弹出VAR定义窗口, 见图5。
图5 VAR模型定义窗口
20
在VAR模型定义窗口中填毕(选择包括截距 )有关内容后,点击OK。输出结果包含三部分 ,分别示于表9、表10和表11。 表9 VAR模型参数估计结果
格兰杰因果性检验的EViews命令:
在工作文件窗口,选中全部欲检序列名后, 选择Quicp/Group Statistics/Granger Causality Test,在弹出的序列名窗口,点击OK即可。
18
表8 格兰杰因果性检验结果
由表8知,LGDPt、LCt 和LIt之间存在格兰 杰因果性,故LGDPt、LCt和LIt均可做为VAR模 型的应变量。
待估参数个数为2 × 2×2= P N 2 用线性方程组表示VAR(2)模型:
y y x y x u t 1 1 1 t 1 1 1 2 t 1 2 1 1 t 2 2 1 2 t 2 1 t x y x y x u t 1 2 1 t 1 1 2 2 t 1 2 2 1 t 2 2 2 2 t 2 2 t
8
( 2 ) VAR 模型对参数不施加零约束 (如 t 检 验); (3)VAR模型的解释变量中不含t期变量,所 有与联立方程组模型有关的问题均不存在; (4)VAR模型需估计的参数较多。如VAR模型 含3个变量(N=3),最大滞后期为p=2,则有 P N 2 =2×32=18个参数需要估计; (5)当样本容量较小时,多数参数估计的精 度较差,故需大样本,一般n>50。 注意: “VAR”需大写,以区别金融风险管理 中的VaR。
VAR案例分析范文

VAR案例分析范文
一、VAR案例分析
VAR,或“经济风险测量”,是用来度量经济实体暴露于金融风险的
一种常用方法。
它将交易风险和投资风险(由不确定的市场价格产生)组
合起来,以估计可能损失的潜在最大额度。
它并不是一种单独的工具,而
是一系列工具和系统,可以帮助金融机构识别和评估风险,以便做出准确
的商业决策。
本文将分析一个关于VAR的案例,以了解它的应用价值。
案例:银行希望使用VAR技术来改进其风险管理进程。
1.分析目标:银行希望改进其风险管理进程,以便尽量减少潜在损失。
2.分析方法:VAR技术可以帮助银行改进其风险管理过程,以便识别
和评估风险。
它通过分析历史行为和当前情况,以预测未来可能发生的交
易风险和投资风险,以识别可能损失的最大值,并制定相关的风险管理措施。
3.分析步骤:
(1)分析现有的交易风险和投资风险,包括市场风险、信用风险、
流动性风险等;
(2)根据历史行为和当前情况,利用VAR技术来估计可能发生的最
大损失;
(3)根据VAR估计值,进一步针对不同的类型风险制定具体的风险
管理措施,以减少风险;
(4)定期对金融市场进行预警和监测。
VaR模型

VaR模型在人民币英镑汇率收益率风险度量中的实证研究内容摘要汇率对一国的国内经济、对外经济和贸易以及国际间的经济联系都产生了重大影响。
汇率的变动直接影响进出口价格的变动,因而关系到以进出口贸易为主要收入的中国外贸企业生存,以及人均GDP和我国在国际贸易和国际金融环境中的地位等;间接影响一国资本流量,从而影响本国资本市场的稳定性等。
汇率波动性风险也日益得到人们的关注,目前国际流行的风险测量工具是VaR(Value at Risk),作为一种量化风险管理工具,其结果一目了然,能够提供管理者一个确定的量化了的汇率风险,并且计算方法简单,具有极强的操作性,VaR已发展成银行、非银行金融机构等各类组织风险度量的标准方法。
为提高基于VaR的汇率风险度量水平,本文首先从VaR模型的前提假设入手,对人民币汇率改革后的序列分别进行平稳性检验,自回归移动平均检验ARMA(p,q)模型和异方差检验ARCH(m)模型和广义的ARCH 模型(GARCH),综合验证了使用VaR模型度量人民币汇率风险具有适用性。
通过VaR体系可以完善银行风险绩效评价、优化银行信用风险资本配置和实现银行汇率风险的动态管理。
关键词:ARCH模型,波动性,VaR模型I目录摘要 (Ⅰ)一、引言 (1)1.1选题背景 (1)1.2文献综述 (2)二、波动率估计模型与VaR测度 (3)2.1平稳性检验 (3)2.2波动率估计模型 (4)2.2.1 ARMA(p,q)模型 (4)2.2.2ARCH模型 (8)2.2.3GARCH模型 (10)2.3VaR模型的测度 (12)三、结论 (14)3.1基础理论 (14)3.2结果分析 (14)3.3政策建议 (15)文献综述 (16)一、引言1.1选题背景随着现代经济活动国际化和国际经济一体化、国际贸易持续增长及资金调拨技术的迅速发展,汇率在国际经济中已具有越来越重要的地位。
自1973年布雷顿森林体系崩溃以后,国际货币体系进入了一个新的阶段——牙买加体系。
第六讲 VAR模型(高级计量经济学课件-对外经济贸易大学 潘红宇)

预测总结
预测有许多前提假设: 假设是平稳过程;假设正态分布;是VAR(1)过
程;并且参数是估计的不是已知的。 所以需要检验这些假设是否正确。一个方法是把
预测值与实际值比较。 如果预测值都包含在相应的置信区间内。从预测
角度不能否认模型的正确性。
结束语
谢谢大家聆听!!!
18
贸易大学 潘红宇)
向量自回归模型VAR
定义 稳定条件 预测
定义:p-阶向量自回归模型(p-阶向量 自回归过程)
对一个n维时间序列{ Yt },tT,T={1,2,…}来说,如果
Y t C 1 Y t 1 p Y t p t
其中E(t)=0
E(t ’t )= t 并且不同时刻t相互0独立t 同分 布,服从正态分布
判断下面的随机过程是否是平稳的解特征方程得z1961所以该模型是稳定的aicakaike赤池和scschwarz施瓦兹准则aicplndetn是向量维数t样本长度p滞后长度ln表示自然对数det表示对矩阵求行列式是当滞后长度为p时残差向量白噪声协方差阵的估计
第六讲 VAR模型(高级计 量经济学课件-对外经济
估计方法:每个方程用OLS法估计,可以得到的 一致估计量
预测
预测公式
Y T ( h ) C 1 Y T ( h 1 ) p Y T ( h p )
ih,Y T(hi)Y T h i
预测-VAR(1)
样本长度为T,对T+1,T+2,…进行预测
Yt C 1Yt1t
YT(1)C1YT YT(2)C1YT(1)C1C12YT YT(3)C1YT(2)(I112)C13YT
预测的均方差阵
(h) M1M1'Mh1Mh1'
VAR模型、Johansen协整检验在eviews中的具体操作步骤及结果解释

19
利用Genr命令可算得用于检验原假设是否 成立的伴随概率 P:
p=1-@cchisq(42.4250,18) =0.000964
故 P=0.000964< =0.05,应拒绝原假设
,建立VAR(3)模型。
20
三、约翰森(Jonhamson)协整检验
Jonhamson(1995)协整检验是基于VAR模 型的一种检验方法,但也可直接用于多变量间的协 整检验。
1.Johanson协整似然比(LR)检验 H0:有 0个协整关系; H1:有M个协整关系。 检验迹统计量:
N
LRM n
log(1 i )
i M 1
图11-1和图11-2,由图11-2可以看出,三个对数序列的
变化趋势基本一致,可能存在协整关系。
13
160000
120000
80000
40000
0 55 60 65 70 75 80 85 90 95 00
GDP
CT
IT
图11-1 GDPt、 Ct和 It
的时序图
12
11
10
9
8
7
6
5 55 60 65 70 75 80 85 90 95 00
LR 2(Lnl(1) Lnl(3)) 2(108.7551 129.9676) 42.4250
其中,Lnl(1)和Lnl(3)分别为P=1和P=3时VAR(P) 模型的对数似然函数值。在零假设下,该统计量 服从渐进的 2 ( f ) 分布,其自由度f为从VAR(3) 到VAR(1)对模型参数施加的零约束个数。对本 例:
这种方程组模型主要用于分析联合内生变量 间的动态关系。联合是指研究N个变量 y1t y2t yNt 间的相互影响关系,动态是指p期滞后。故称VAR 模型是分析联合内生变量间的动态关系的动态模 型,而不带有任何约束条件,故又称为无约束 VAR模型。建VAR模型的目的:
VaR计量模型分析案例

ln (ht ) = ω + ∑ α i g (z t −i ) + ∑ β ln (ht − j ), g (z t −i ) = θzt + γ [ zt −i − E z t ], z t =
q p i =1 j =1
εt
ht
在 TGARCH 模型中,条件方差 ht 表示为:
ht = ω + ∑ βht − j + γε t −1 d t −1 + ∑ α J ε 2 t −i 其中
这里的 Γ(• ) 是 GAMMA 函数,v 是自由度。似然函数可通过对偶牛顿算法或信赖域算 法极大化得到。 由于股市收益率的波动回随信息的变化而出现非对称性的特点, 利空消息引 起的波动一般更大,为了刻画波动的非对称性,Nelson 等人提出了非对称性(Asymmetric) GARCH 模型,包括 EGARCH 及 TGARCH 等模型。 在 EGARCH 模型中,条件方差 ht 为延迟扰乱 ε t −i 的反对称函数:
对于Normal和 t 分布,分别使用ML方法估计其中参数如下: 表2 GARCH模型估计结果
GARCH-M
C
ϕ
ρ
δ
ω
α
β
0.71726 (40.315) 0.70626 (39.327)
Nor14 0.04461 (-3.4319) (2.777) (2.507) -0.003298 0.056527 0.043925 (-3.363) (2.912) (2.491) v 的估计值为4.255 C
pt 是 t 日上证综合指数的收盘价格。以下模型中的参数估计均是用 SAS6.12 统计软件实现
的。 如图 1 所示,上证综合指数收益率集中在(-0.05,0.05)之间,在波动较大的几个时段 上收益率绝对值的峰值达到了 0.1,在到达顶峰后又迅速回落。在样本期间,平均收益率为 0.00284,偏度为-0.256529,峰度为 9.401051,数据分布向左偏移,有一个沉重的尾巴。这 说明从整体上看,收益率低于其均值的时候较多,波动性强,尾部和中间包含了大量的统计 信息。J-B 正态性检验得到的统计量值为 2558.392,也说明收益率序列显著异于正态分布。
VAR

3、VAR模型的建立
其次,我们要确定VAR模型的滞后阶。最 优时滞的选择,需要经过多次重复试验 比较得到。当我们选择一阶滞后时,输 出结果如下:
二阶滞后输出结果
3、VAR模型的建立
VAR模型的输出结果包括三个部分,第一 部分是模型的参数估计结果,第一个括 号内是估计系数标准差,第二个括号内 是t检验统计量;第二部分是各子方程的 相关检验结果,显示的是VAR模型的回归 统计量;输出结果的最后一部分也是最 值得关注的,因为它的结果是针对VAR系 统整体而言的。基于VAR模型的保障性来自房政策对房价的抑制功能分析
1、分析指标与数据描述 采用保障性住房供给面积与住宅商品房价格两 项指标验证住房保障政策是否具有房价抑制功 能。鉴于北京的高房价,这里选取北京作为分 析对象,用“经济适用房销售面积”这一指标 代表保障性住房供给面积,用J表示;采用 “住宅商品房平均销售价格”这一指标代表房 价,用P表示。对这两个指标取对数后分别命 名为LJ;LP
2、变量平稳性检验
对时间序列数据进行计量分析时,首先要对各 变量进行平稳性检验,以保证回归结果的无偏 性和有效性。采用ADF检验方法对各组变量数 据进行单位根检验,进而确定各变量的平稳性。 通过分析,确定了lj、lp在二阶差分序列时是序 列平稳的。
3、VAR模型的建立
首先,创建一个VAR对象,如图
Yt c A( L)Yt 1 t
其中,Yt ((LJ ), (LP))
A(L)是滞后算子, t 是残差向量 VAR模型估计结果显示,模型的R2>0.6,说 明模型能够很好解释变量之间的影响。
5、VAR模型的分析结果
在进行进一步分析之前,我 们有必要对VAR模型的平稳 性进行检验,因为一旦VAR 模型不平稳,模型分析结果 将不是有效的。这里,我们 对VAR模型的根表进行平稳 性检验,如果被估计的VAR 模型所有根的模的倒数小于1, 即位于单位圆内,则是平稳 的。经检验,本文的VAR模 型的分析过程是平稳的
VAR模型应用案例解析

VAR模型应用案例解析
摘要
VAR模型,即向量自回测模型,是一种时间序列技术,它可以用来证明一些财务和非财务变量之间的关联,从而让研究者更了解潜在的经济变量如何影响市场上的另一个变量。
本文将对VAR模型在实际经济和财务应用中的应用情况进行分析和讨论。
首先,将介绍VAR模型的概念和构成,然后分析它与传统经济学和金融学研究中的应用情况,最后介绍具体的案例(欧元区和美国)。
关键词:VAR模型,实际应用,时间序列技术,传统经济学和金融学一、VAR模型简介
VAR模型最早由Christopher Sims提出,他是1981年诺贝尔经济学奖得主,它在计量经济学中的发展非常迅速,并成为经济学家们最常用的时间序列分析方法之一、VAR模型的核心就是建模变量之间的动态关系,而这些变量可以是财务变量(如股价、收益率和利率),也可以是非财务变量(如汇率、消费者物价指数等)。
VAR模型PPT演示课件

E(t ) 0
E(
t
t
)
E(
t
s
)
0,
对于t
s
5
一个两变量(VAR)模型的例子
Yt C Yt1 t ,
y1t y2t
c1 c2
11 21
12 22
y1,t 1 y2,t 1
y1,t 2 y2,t 2
1t 2t
0 y1,t2
(2) 22
y2,t
2
26
LR 检验:
如果拒绝原假设,则称 y2t是y1t的格兰杰 因果关系。
与此不同,
y1t C1 1 y1,t1 2 y1,t2 L p y1,t p 1 y2,t1 2 y2,t2 L p y2,t- p 1t
y1t
Yt
y2t
,
t
1, 2,
,T
ynt
4
• 那么,一个p阶VAR模型,即VAR(p),定义为:
Yt C 1Yt1 2Yt2 pYt p t
• C系为数n矩×阵1维。常t 为数n向×量1,维向i 为量n白×噪n音维,自满回足归如
平稳序列仍然可以放在VAR模型中,通过估 计结果分析经济、金融含义。 • 但是,如果利用VAR模型分析实际问题时, 使用非平稳序列变量,却会带来统计推断 方面的麻烦,因为标准的统计检验和统计 推断要求分析的所有序列必须都是平稳序 列。
计量经济学第六部分VAR

如果所有变量是单整的,且非平稳变量之间存在着协 整关系时: 1、对一阶差分的方法来构造VAR模型; 2、建立VECM模型。
16
八、 VAR的应用:Granger因果关系检验
2024/10/15
13
七、 最大滞后阶数k的确定:AIC统计量
AIC
log
T t 1
et2
2k
T T
min{AIC} k
log
T
ek2t
t 1
T
e2 (k 1)t
t 1
2 T
滞后阶数分别为k和k+1的两个VAR模型,只要它们 的AIC统计量越接近,就表明滞后阶数越适度!
Yt 1 11Yt1 ... 1pYt p 11X t1 ... 1p X t p 11Zt1 ... 1pZt p e1t X t 1 21Yt1 ... 2 pYt p 21X t1 ... 2 p X t p 21Zt1 ... 2 pZt p e2t Zt 1 31Yt1 ... 3 pYt p 31X t1 ... 3 p X t p 31Zt1 ... 3 p Zt p e3t
假设
:
E
(u1t
)
E
(u2t
)
0,Var(u1t
)
2 1
,Var(u2t
)
2 2
;
E(u1tu2t ) 12
6
四、 同期自相关问题:方法一
X 2t
12
2 1
X 1t
0
* 21
X
1t
1
时间序列建模案例VAR模型分析与协整检验.doc

传统的经济计量方法是以经济理论为基础来描述变量关系的模型。
但是,经济理论通常并不足以对变量之间的动态联系提供一个严密的说明,而且内生变量既可以出现在方程的左端又可以出现在方程的右端使得估计和推断变得更加复杂。
为了解决这些问题而出现了一种用非结构性方法来建立各个变量之间关系的模型。
本章所要介绍的向量自回归模型(vector autoregression ,V AR)和向量误差修正模型(vector error correction model ,VEC)就是非结构化的多方程模型。
向量自回归(V AR)是基于数据的统计性质建立模型,V AR 模型把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型,从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。
V AR 模型是处理多个相关经济指标的分析与预测最容易操作的模型之一,并且在一定的条件下,多元MA 和ARMA 模型也可转化成V AR 模型,因此近年来V AR 模型受到越来越多的经济工作者的重视。
V AR(p ) 模型的数学表达式是t=1,2,…..,T其中:yt 是 k 维内生变量列向量,xt 是d 维外生变量列向量,p 是滞后阶数,T 是样本个数。
k ⨯k 维矩阵Φ1,…, Φp 和k ⨯d 维矩阵H 是待估计的系数矩阵。
εt 是 k 维扰动列向量,它们相互之间可以同期相关,但不与自己的滞后值相关且不与等式右边的变量相关,假设 ∑ 是εt 的协方差矩阵,是一个(k ⨯k )的正定矩阵。
注意,由于任何序列相关都可以通过增加更多的yt 的滞后而被11t t p t p t t --=+⋅⋅⋅+++y Φy Φy Hx ε消除,所以扰动项序列不相关的假设并不要求非常严格。
以1952一1991年对数的中国进、出口贸易总额序列为例介绍V AR模型分析,其中包括;①V AR模型估计;②V AR模型滞后期的选择;③V AR模型平隐性检验;④V AR模型预侧;⑤协整性检验V AR模型佑计数据Lni(进口贸易总额), ,Lne的时间序列见图。
VAR模型应用案例 (完成)
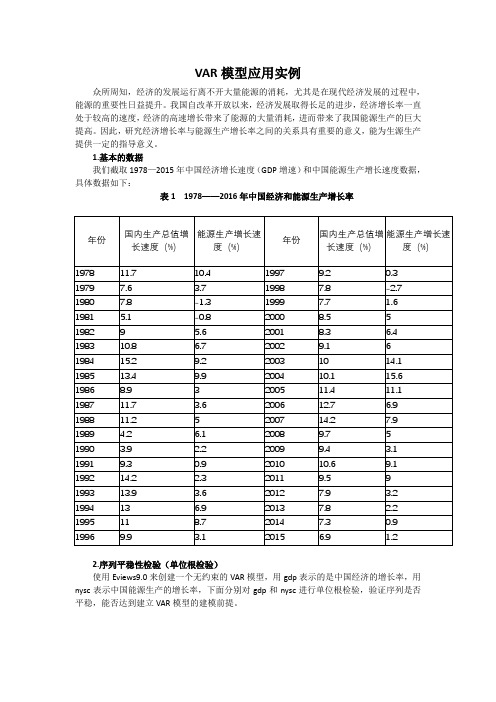
VAR模型应用实例众所周知,经济的发展运行离不开大量能源的消耗,尤其是在现代经济发展的过程中,能源的重要性日益提升。
我国自改革开放以来,经济发展取得长足的进步,经济增长率一直处于较高的速度,经济的高速增长带来了能源的大量消耗,进而带来了我国能源生产的巨大提高。
因此,研究经济增长率与能源生产增长率之间的关系具有重要的意义,能为生源生产提供一定的指导意义。
1.基本的数据我们截取1978—2015年中国经济增长速度(GDP增速)和中国能源生产增长速度数据,具体数据如下:表1 1978——2016年中国经济和能源生产增长率2.序列平稳性检验(单位根检验)使用Eviews9.0来创建一个无约束的VAR模型,用gdp表示的是中国经济的增长率,用nysc表示中国能源生产的增长率,下面分别对gdp和nysc进行单位根检验,验证序列是否平稳,能否达到建立VAR模型的建模前提。
图2.1 经济增速(GDP)的单位根检验图2.2 能源生产增速(nysc)的单位根检验经过检验,在1%的显著性水平上,gdp和nysc两个时间序列都是平稳的,符合建模的条件,我们建立一个无约束的VAR模型。
3.VAR模型的估计图3.1 模型的估计结果图3.2 模型的表达式4.模型的检验4.1模型的平稳性检验图4.1.1 AR根的表由图4.1.1知,AR所有单位根的模都是小于1的,因此估计的模型满足稳定性的条件。
图4.1.2 AR根的图通过对GDP增长率和能源生产增长率进进行了VAR模型估计,并采用AR根估计的方法对VAR模型估计的结果进行平稳性检验。
AR根估计是基于这样一种原理的:如果VAR模型所有根模的倒数都小于1,即都在单位圆内,则该模型是稳定的;如果VAR模型所有根模的倒数都大于1,即都在单位圆外,则该模型是不稳定的。
由图4.1.2可知,没有根是在单位圆之外的,估计的VAR模型满足稳定性的条件。
4.2 Granger因果检验图4.2.1 Granger因果检验结果图Granger因果检验的原假设是:H0:变量x不能Granger引起变量y备择假设是:H1:变量x能Granger引起变量y对VAR(2)进行Granger因果检验在1%的显著性水平之下,经济增速(GDP)能够Granger 引起能源生产增速(NYSC)的变化,即拒绝了原假设;同时,能源生产增速(NYSC)能够Granger经济增速(GDP)的变化,即拒绝了原假设,接受备择假设。
SPSSAU_计量经济研究_VAR模型

SPSS分析向量自回归V AR模型SPSSAUV AR模型Contents1背景 (2)2理论 (2)3操作 (4)4 SPSSAU输出结果 (5)5文字分析 (5)6剖析 (11)7疑难解惑 (12)在时间序列进行预测时,ARIMA可用于单一变量(比如GDP增长率)的预测,如果需要同时考虑几个变量的预测时(比如GDP增长率、失业率、储蓄率),此时可考虑分别针对研究变量进行,即多次重复进行。
通常情况下同一系统的几个研究变量之间均有着相互依旧关系,因而为更好的利用各变量的此类关系,此时可以使用V AR模型(Vector autoregressive model)进行多变量预测。
V AR模型的构建流程较为复杂,如下图所述:通常情况下,V AR模型需要满足单位根检验,如果没有单位根则直接构建V AR模型即可,如果研究变量有单位根,则说明不适合进行V AR模型构建,但是如果有单位根且满足同阶单整,此时说明V AR模型构建是适合的,与此同时研究变量满足协整关系也是一种常见的前提条件。
V AR模型构建时,通常包括定阶这一步骤,即选择适合的滞后阶数。
V AR模型构建完成后,接着还需要对模型的有效性进行分析,通常是针对AR特征根图进行分析。
另外,理论上V AR模型的残差还满足满足正态性,并且通过自相关检验等,但通常对此类检验的关注度相对较少。
V AR模型构建之后,通常需要进行比如格兰杰困果检验,脉冲响应和方差分析,用于进一步分析研究变量之间的相互作用依存关系情况。
最后,可得到模型的预测数据,满足模型预测目的。
特别提示:如果是使用V AR模型判断平稳性,其为直观图示法,带有一定的主观性,反之使用比如SPSSAU的ADF检验平稳性,二者有可能出现不同的结论。
V AR模型案例Contents1背景 (2)2理论 (2)3操作 (4)4 SPSSAU输出结果 (5)5文字分析 (5)6剖析 (11)7疑难解惑 (12)1背景当前有一项美国宏观联邦基金利率、通货膨胀率和失业率的数据,数据日期从1960年第1季度到2012年第1季度,单位为季度,共计209个数据。
金融计量var、vec模型讲义

收集相关经济指标的历史数据,如GDP、通货膨胀率、利率、汇率 等,并对数据进行清洗和整理,确保数据质量和一致性。
数据频率
选择适当的数据频率,如年度、季度或月度数据,以满足分析需求。
模型估计与结果解读
1 2
模型估计
采用适当的统计软件(如EViews、Stata等)对 VAR或VEC模型进行估计,确定模型的最佳滞后 阶数,并检验模型的稳定性。
模型检验与诊断
平稳性检验
残差检验
诊断检验
在建立VAR、VEC模型之前, 需要对数据进行平稳性检验, 如ADF检验、PP检验等。如果 数据不平稳,需要进行差分或 其他处理使其平稳。
在模型估计完成后,需要对残 差进行检验,以判断模型是否 拟合良好。常见的残差检验方 法有自相关检验、异方差检验 和正态性检验等。
结果解读
对模型估计结果进行解读,分析各经济变量之间 的动态关系和相互影响,以及模型的拟合优度。
3
检验与诊断
对模型进行各种诊断检验,如残差检验、自相关 检验等,以确保模型的有效性和可靠性。
模型预测与政策建议
模型预测
利用估计好的VAR或VEC模型对 未来经济走势进行预测,为政策 制定提供参考依据。
政策建议
根据模型结果和预测,提出针对 性的政策建议,如财政政策、货 币政策等,以促进经济稳定和增 长。
政策效果评估
通过VAR或VEC模型对政策效果 进行评估,分析政策对经济的长 期和短期影响,为政策调整提供 依据。
04
VAR、VEC模型的优缺 点与改进方向
VAR、VEC模型的优点
数据要求低
VAR、VEC模型对数据的要求相对较低,只需要时间序列数据即可 进行分析,不需要复杂的样本设计和实验过程。
基于VAR模型的三线城市商品房价格动态计量分析——以唐山市为例

金融计量学向量自回归(VAR)模型

第7章 向量自回归(VAR)模型
7.1 向量自回归模型介 7.2 VAR模型的估计与相关检验 7.3 格兰杰因果关系 7.4 向量自回归模型与脉冲相应分析 7.5 VAR模型与方差分解
2
7.1 向量自回归模型介绍
7.1.1 VAR模型的基本概念
考 虑 一 组 变 量 y 1 t,y 2 t, ,y n t,定 义
12 y2,t 1 22 y2,t 1
1t 2t
E ( t t)
E(12t ) E( 2t1t
)
E(1t 2t
E
(
2 2t
)
)
2121
12
2 2
1 (L) L 0
0 1
11L 21L
12 L
22
L
1 11L
21L
12 L
1
22
L
高阶VAR模型要使用很多的上标和
1 2 3
n
0
0
0
F
0
n 0
0 n
0 0 0
p 1 0 0 0
n
p
0
0
0
0
以 及 一 个 (np 1)的 矩 阵 Vt
t
Vt
0
0
Yt
F Yt 1
Vt , 其 中
并且:
0
npnp
0
0
0
0
E (VtVt )
E
(VtV
s
)
0,
t
s
0
0
0
7.1.4 向量自协方差和向量自相关函数
z1 1, z 2 1 0 / 7
7.1.3 VAR(p)模型与VAR(1)的转化
VAR模型应用案例

VAR模型应用案例
一、背景
随着现代经济的发展,多元化的外汇投资已经成为企业和金融机构寻求利润增长的重要方式。
有关外汇投资领域的研究越来越重视外汇市场经济环境变量和多元组合投资的影响。
其中,多元组合投资可以充分利用经济环境变量对外汇汇率的影响,以更好地实现风险控制的目的。
基于该概念,有很多研究开发出了基于前沿的时变多元组合投资模型,其中VAR模型是最重要的模型之一
二、VAR模型的概述
运动变量分析(VAR)模型是有关金融时间序列分析的一种经典方法。
它是通过线性回归分析,来探索多变量之间的线性关系,以及它们对于其他变量均衡状态的影响,从而有效地捕获金融市场的变换动态,更好地掌握金融风险暴露量,并针对其进行风险管理。
三、VAR模型在外汇投资领域的应用
众所周知,外汇市场是最具挑战性和复杂性的投资市场之一,因此利用VAR模型来实现外汇投资是可行的。
var计量模型

铜的日期货(qcu)和现货(xcu)价格的协整关系分析【案例file:6copper-dayly】上海金属网和上海期货交易所的铜的期货和现货价格的关系研究,选取2001:6-2007:3间1297个铜的期货和现货价格观测值。
qcu表示铜的期货价格(千元),xcu表示铜的现货价格(千元)。
对铜的日期货(qcu)和现货(xcu)价格取对数,做序列图和散点图如下:不存在异方差,可以直接用qcu和xcu建V AR。
V AR模型估计的EViews操作:打开工作文件,点击Quick键, 选Estimate VAR功能。
作相应选项后(k=2),即可得到V AR的表格式输出方式。
在VAR模型估计结果窗口点击View 选representation功能可得到V AR的代数式输出结果。
V AR模型的特点是:(1)不以严格的经济理论为依据。
在建模过程中只需明确两件事:①共有哪些变量是相互有关系的,把有关系的变量包括在V AR模型中;②确定滞后期k。
使模型能反映出变量间相互影响的绝大部分。
(2)V AR模型对参数不施加零约束。
(对无显着性的参数估计值并不从模型中剔除,不分析回归参数的经济意义。
)(3)V AR模型的解释变量中不包括任何当期变量,所有与联立方程模型有关的问题在V AR模型中都不存在(主要是参数估计量的非一致性问题)。
(4)V AR模型的另一个特点是有相当多的参数需要估计。
比如一个V AR模型含有三个变量,最大滞后期k = 3,则有k N2 = 3 × 32 = 27个参数需要估计。
当样本容量较小时,多数参数的估计量误差较大。
(5)无约束V AR模型的应用之一是预测。
由于在V AR模型中每个方程的右侧都不含有当期变量,这种模型用于样本外一期预测的优点是不必对解释变量在预测期内的取值做任何预测。
(6)用V AR模型做样本外近期预测非常准确。
做样本外长期预测时,则只能预测出变动的趋势,而对短期波动预测不理想。
VAR模型应用案例 (完成)
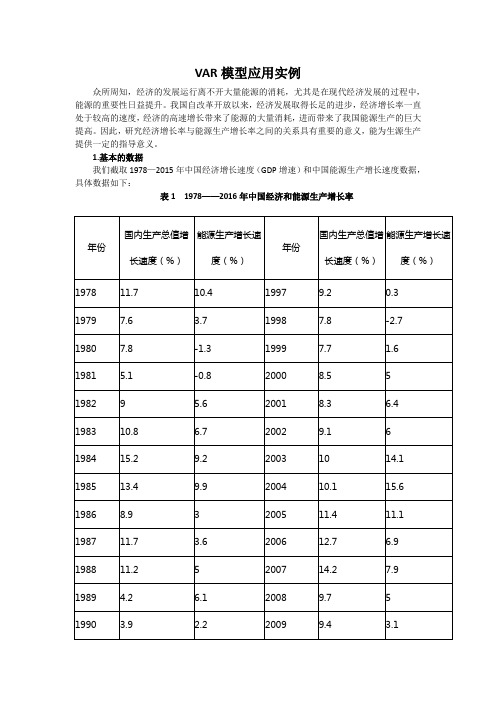
VAR模型应用实例众所周知,经济的发展运行离不开大量能源的消耗,尤其是在现代经济发展的过程中,能源的重要性日益提升。
我国自改革开放以来,经济发展取得长足的进步,经济增长率一直处于较高的速度,经济的高速增长带来了能源的大量消耗,进而带来了我国能源生产的巨大提高。
因此,研究经济增长率与能源生产增长率之间的关系具有重要的意义,能为生源生产提供一定的指导意义。
1.基本的数据我们截取1978—2015年中国经济增长速度(GDP增速)和中国能源生产增长速度数据,具体数据如下:表1 1978——2016年中国经济和能源生产增长率2.序列平稳性检验(单位根检验)使用Eviews9.0来创建一个无约束的VAR模型,用gdp表示的是中国经济的增长率,用nysc表示中国能源生产的增长率,下面分别对gdp和nysc进行单位根检验,验证序列是否平稳,能否达到建立VAR模型的建模前提。
图2.1 经济增速(GDP)的单位根检验图2.2 能源生产增速(nysc)的单位根检验经过检验,在1%的显著性水平上,gdp和nysc两个时间序列都是平稳的,符合建模的条件,我们建立一个无约束的VAR模型。
3.VAR模型的估计图3.1 模型的估计结果图3.2 模型的表达式4.模型的检验4.1模型的平稳性检验图4.1.1 AR根的表由图4.1.1知,AR所有单位根的模都是小于1的,因此估计的模型满足稳定性的条件。
图4.1.2 AR根的图通过对GDP增长率和能源生产增长率进进行了VAR模型估计,并采用AR根估计的方法对VAR模型估计的结果进行平稳性检验。
AR根估计是基于这样一种原理的:如果VAR模型所有根模的倒数都小于1,即都在单位圆内,则该模型是稳定的;如果VAR模型所有根模的倒数都大于1,即都在单位圆外,则该模型是不稳定的。
由图4.1.2可知,没有根是在单位圆之外的,估计的VAR模型满足稳定性的条件。
4.2 Granger因果检验图4.2.1 Granger因果检验结果图Granger因果检验的原假设是:H0:变量x不能Granger引起变量y备择假设是:H1:变量x能Granger引起变量y对VAR(2)进行Granger因果检验在1%的显著性水平之下,经济增速(GDP)能够Granger 引起能源生产增速(NYSC)的变化,即拒绝了原假设;同时,能源生产增速(NYSC)能够Granger经济增速(GDP)的变化,即拒绝了原假设,接受备择假设。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ln (ht ) = ω + ∑ α i g (z t −i ) + ∑ β ln (ht − j ), g (z t −i ) = θzt + γ [ zt −i − E z t ], z t =
q p i =1 j =1
εt
ht
在 TGARCH 模型中,条件方差 ht 表示为:
ht = ω + ∑ βht − j + γε t −1 d t −1 + ∑ α J ε 2 t −i 其中
ORDER 1 2 3 4 5 6 Q 73.8759 118.067 147.268 166.016 171.458 183.292 Prob>Q 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 LM 71.9199 94.3105 103.077 106.446 106.448 109.604 Prob>LM 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 ORDER 7 8 9 10 11 12 Q 189.701 192.070 194.180 200.472 207.641 208.600 Prob>Q 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 LM 110.049 110.074 110.101 112.086 114.006 114.455 Prob>LM 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
N ⎡ ⎛ ε 2 ⎞⎤ 1 ⎛ ⎛ v ⎞⎞ 1 ⎛ ⎛ v +1⎞⎞ ⎜ ( ( ) ) ( ) − − − + + L = ∑ ⎢log⎜ Γ⎜ v h v 1 log 1 log log 2 − Γ ⎜ ⎟ ⎟ ⎜ ⎟ ⎟ t ⎜ h (v − 2 ) ⎟ ⎟⎥ 2 t =1 ⎣ ⎝ ⎝ 2 ⎠⎠ 2 ⎝ ⎝ 2 ⎠⎠ t ⎝ ⎠⎦
2
j =1 i =1
p
q
d t −1 = 1, ε t −1 < 0; d t −1 = 0, ε t −1 > 0
2
另外,以上模型中
∑ β j + ∑ α i <1,蕴涵 GARCH 过程为宽平稳。如果将此限制放宽
j =1 i =1
p
q
即是积分型 GARCH 模型,即 IGARCH 模型。对于 IGARCH 模型而言,无条件方差并不存 在。 同时, 考虑到股票市场的风险溢价, 在均值方程中加入条件方差的函数, 得到 GARCH-M 模型。一般来说,有效的股票市场上股价与其风险是正向相关的。 GARCH 模型建模程序包括: (1) 用 Augunmented-Dikey Fuller 方法检验序列平稳性。 (2) 用 Q 统计量识别序列自相关或偏自相关的阶数。 (3) 用 Lagrange multiplier 方法检验序列残差项的异方差性以确定条件方差方程数。 (4) 用 Most—Likelihood 方法得到方程中参数的最大似然估计。 (5) 评价模型。 3、VaR 模型检验方法 对 VaR 模型可采用 Kupiec 检验。设 N 为检验样本中损失高于 VaR 的次数,T 为检验样 本总数,P=1-C,C 是即定的置信水平。则检验的假设为:
2
逼近,同样有较好的检验效果。
三、沪市动态 VaR 模型的实证分析
1、数据选取和统计描述 本案例以上海证券市场综合指数为例,说明 VaR 的计算。考虑到中国股市是从 1996 年 12 月 16 日起实行涨跌停板限价交易制度的,采用此后的数据可以减少异常值的干扰,提高 模型的精度。 因此收集的数据为 1996 年 12 月 16 日至 2002 年 10 月 22 日的上证综合指数收 盘价格,共计 1404 个。 数据来源于中国股票市场交易数据库和证券之星 () 网站。收益率是采用对数一阶差分形式,即设第 t 日的收益率为 rt ,则 rt = ln pt − ln pt −1 ,
pt 是 t 日上证综合指数的收盘价格。以下模型中的参数估计均是用 SAS6.12 统计软件实现
的。 如图 1 所示,上证综合指数收益率集中在(-0.05,0.05)之间,在波动较大的几个时段 上收益率绝对值的峰值达到了 0.1,在到达顶峰后又迅速回落。在样本期间,平均收益率为 0.00284,偏度为-0.256529,峰度为 9.401051,数据分布向左偏移,有一个沉重的尾巴。这 说明从整体上看,收益率低于其均值的时候较多,波动性强,尾部和中间包含了大量的统计 信息。J-B 正态性检验得到的统计量值为 2558.392,也说明收益率序列显著异于正态分布。
H0 :
N =P T
H1 :
N ≠P T
似然比统计量为:
⎡ ⎛ ⎛ N ⎞ N ⎛ N ⎞T −N ⎞ T −N lr = 2⎢log⎜ ⎜ ⎟ ⎜1 − ⎟ ⎟ − log p N (1 − P) ⎟ ⎜ ⎢ ⎣ ⎝⎝ T ⎠ ⎝ T ⎠ ⎠
(
)⎤ ⎥
⎥ ⎦
在原假设下, lr 服从于自由度为 1 的 χ 分布。在大样本条件下,也可以用正态分布来
3
0 .1 0 0 .0 5 0 .0 0 - 0 .0 5 - 0 .1 0 - 0 .1 5 2 0 0 4 0 0 6 0 0
图
8 0 0
1 上 证
1 0 0 0
综 合 指
1 2 0 0
数 收 益
1 4 0 0
2、 GARCH 模型族的建立 利用Q检验和LM检验识别序列的异方差性,结果见表1 。 表1 异方差性检验结果
这里的 Γ(• ) 是 GAMMA 函数,v 是自由度。似然函数可通过对偶牛顿算法或信赖域算 法极大化得到。 由于股市收益率的波动回随信息的变化而出现非对称性的特点, 利空消息引 起的波动一般更大,为了刻画波动的非对称性,Nelson 等人提出了非对称性(Asymmetric) GARCH 模型,包括 EGARCH 及 TGARCH 等模型。 在 EGARCH 模型中,条件方差 ht 为延迟扰乱 ε t −i 的反对称函数:
检验说明直到高阶收益率序列仍然存在着强烈的异方差性, 用ENGARCH模型族来拟合 数据是合理的。随后用Augument-Dikey Fuller方法对收益率进行单位根检验,得到的ADF值 拒绝了单位根的假设,序列是平稳的。 对序列 {rt }进行了自相关和偏自相关的检验后,我们选用的均值模型为:
rt = c + ϕrt −12 + ρ rt −15 + δ ht + ε t
1
二、GARCH
模型与 VaR 计算方法简介
1、VaR 计算模型 VaR(Value-at-Risk)是一定时期内,在一定的置信度下,投资组合可能出现的最大损 失,用公式表示为: VaR= − pt −1 e
(
μ +σF −1 ( p )
−1
)
(1)
其中, F (• ) 是收益序列的分布函数, p 为给定的显著性水平,即左尾概率。如果是静 态 VaR 只需利用极大似然法估计出参数 μ 和 σ ,将之代入计算公式即可。 2、基于 GARCH 模型的 VaR 计算方法 VaR 估计的条件方差方法属于动态 VaR 计算的分析方法,由于实际金融市场中收益率的 厚尾性会导致 VaR 对风险的低估,因此可以利用 GARCH 模型类中的条件方差来度量股票市 场 VaR。这样,VaR = pt −1 zα ht ,其中 ht 是由 GARCH 模型估计得到的条件方差, zα 根 据收益率分布决定。GARCH 模型的一般表达式可写成:
沪市动态 VaR 计量模型分析案例
西南财经大学统计学院 马 丹
一、案例背景
金融风险是指由于经济活动的不确定性而导致资金在筹措和运用中遭受损失的可能 性。在 20 世纪 80 年代以前,金融机构所面临的风险还主要是信用风险。然而,近 20 多年 来金融市场发生了重大变化,全球化的证券市场迅猛发展,资产证券化的趋势越来越强,外 汇交易和衍生品交易成了金融市场交易的重要组成部分。 这使得金融机构所面临的主要风险 已从信用风险转向了市场风险。 市场风险度量的方法有多种, VaR(Value-at-Risk)方法是目前金融市场风险测量的主 流方法。VaR 是一定的概率水平下,证券组合在未来特定一端时间内的最大可能损失。其优 点在于将不同的市场因子、 不同市场的风险集成为一个数, 较准确测量由不同风险来源及其 相互作用而产生的潜在损失,适应了金融市场发展的动态性、复杂性和全球整合性的趋势。 应该注意的是,VaR 本身的含义是风险价值,是一个数值,但是它是由一系列统计方法实现 的,因此在许多场合它又被称为风险度量方法。 VaR 方法是由 JP MORGAN 公司率先提出来的,并在实践中得到广泛应用。其在风险 测量合管理中的巨大优点已为国际金融监管当局认可和接受,1990 年以来的许多金融监管 法案和原则都充分强调了基于 VaR 的风险监管方法。巴塞尔委员会的巴塞尔银行业有效监 管核心原则、欧盟的资本充足法令等都要求金融机构用 VaR 技术确定内部风险资本要求、 风险控制等。 VaR 计算方法包括历史模拟法、方差——斜方差法和蒙特卡罗模拟法。历史模拟法和蒙 特卡罗模拟法由于在技术上较为复杂,较难实现,因此,在实践中常用的方法仍然是方差— —斜方差法。 方差——斜方差法中有两个需要注意的问题。 一是如何刻画金融数据的尖峰厚尾、 波动 簇集的时变特征。二是如何寻找金融数据的分布密度函数。 Risk MrtricsTM利用指数平滑技术来反映波动时变现象,并假定金融数据服从正态分布。 然而,大量文献资料证明,金融数据有强烈的ARCH效应,其尾部和中间部位集中了大量的 概率分布,比正态分布拥有“肥尾”特性。金融数据的集群性,异方差性等特征显然违背了 古典假设, 利用传统的基于古典假设的回归模型, OLS建模方法难以刻画出真实的数量规律, 所做出的统计推断也是不精确的。为了对金融数据做出有效的描述,Engle于 1982 提出了 ARCH 模型,模拟出数据的集群性特征,他的学生 Bollerslev 在 1986 年提出了 GARCH (Generalized Auto Regressive Conditional Heteroscedasiticity)模型[1],将高阶的ARCH模型 转化成为简洁的 GARCH 模型 , 描绘出金融数据方差项的某种自相关性。但实际应用中, GARCH模型虽然有助于模拟金融数据分布的宽尾特征,却不能解释金融市场上存在的杠杆 效应。针对这一问题,近年来Nelson等人提出了非对称性(Asymmetric)GARCH模型以刻 画出条件方差对正的价格变化反应弱而对负的价格变化反应强这一现象。这类模型包括 TARCH、EGARCH等,收益率序列残差往往假定为正态分布,但实际上正态GARCH模型不 能充分描述数据的尖峰厚尾性。对此,可以假定残差服从 t 分布、混合正态分布或一般误差 分布。本案例讨论了基于Normol-GARCH、t-GARCH的中国股市动态VaR测度方法,并比较 了两种假定下VaR的估计效果。
